小学数学奥数测试题-立体图形|2015人教版
小学数学立体图形模块考试卷+答案解析(人教版)

小学数学立体图形模块考试卷+答案解析(人教版)总分100分,考试时间90分钟,立体图形的表面积与体积一.选择题。
(9)(1)一个长9厘米,宽6厘米,高3厘米的长方体,切割成3个体积相等的长方体,表面积最大可增加()平方厘米。
A.72B.216C.108D.36(2)一个圆柱体侧面展开是正方形,这个圆柱体底面直径和高的比是()。
A.2π:1B.1:1C.1:πD.π:1(3)一个底面积为3.14平方分米,高3分米的圆柱体容器中装了一半的水,把一个底面积相等,高为12厘米的圆锥形容器装满水倒入圆柱体容器中,水面会上升()厘米。
A.12B.5C.4D.3二.填空题。
(15)(1)一个正方体的棱长总和是84厘米,它的表面积是(),体积是()。
(2)圆锥的底面直径是4米,高是3米,它的底面积是(),体积是()。
(3)一个圆柱体,侧面积是37.68平方分米,高是2分米,它的底面直径是()。
(4)等底等高的圆柱体与圆锥体的体积比是()(5)一台压路机滚筒长1.8米,直径1米,这台压路机转动10周,可以压路()平方米。
三.判断题。
(6)(1)圆柱体的体积是圆锥体体积的3倍。
()(2)长方体和圆柱体底面积相等,高也相等,它们的体积一定相等。
()四.解答题1.有一种无盖的玻璃鱼缸,长25厘米,宽20厘米,高15厘米,做这样一个鱼缸需要多少平方厘米的玻璃?(8分)2.把一块棱长6分米的正方体钢坯,熔铸成横截面是9平方分米的长方体的钢材。
铸成的钢材有多长?(6分)3.一个长方形硬纸,长18.84厘米,宽6.28厘米,把这样的长方形卷成一个圆柱的侧面,问:怎样卷成圆柱的体积最大?(6分)4.用一些棱长是1的小正方体搭成一个立体图形。
从上往下看这个立体图形,如图1所示;从前往后看这个立体图形,如图2所示。
这个立体图形最多有几个小正方体?最少有几个小正方体?请你画出小正方体最少时,从右往左看的平面示意图。
(6分)5.自来水管的内直径是3厘米,水管内水流速度是每秒8厘米。
小学奥数几何专题--立体图形(六年级)竞赛测试.doc

小学奥数几何专题--立体图形(六年级)竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)【题文】如图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?【答案】600【解析】我们从三个方向(前后、左右、上下)考虑,新几何体的表面积仍为原立方体的表面积:10106600.【题文】右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、上面挖去的正方体)【答案】120【解析】原正方体的表面积是44696(平方厘米).每一个面被挖去一个边长是1厘米的正方形,同时又增加了5个边长是1厘米的正方体作为玩具的表面积的组成部分.总的来看,每一个面都增加了4个边评卷人得分长是1厘米的正方形.从而,它的表面积是:9646120平方厘米.【题文】在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?【答案】15000【解析】对于和长方体相关的立体图形表面积,一般从上下、左右、前后3个方向考虑.变化前后的表面积不变:5050615000(平方厘米).【题文】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为厘米,那么最后得到的立体图形的表面积是多少平方厘米?【答案】【解析】我们仍然从3个方向考虑.平行于上下表面的各面面积之和:2228(平方厘米);左右方向、前后方向:22416(平方厘米),1144(平方厘米),41(平方厘米),4(平方厘米),这个立体图形的表面积为:41(平方厘米).【题文】一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?【答案】18【解析】锯一次增加两个面,锯的总次数转化为增加的面数的公式为:锯的总次数2增加的面数.原正方体表面积:1166(平方米),一共锯了(21)(31)(41)6次,6112618(平方米).【题文】一个表面积为的长方体如图切成27个小长方体,这27个小长方体表面积的和是多少平方厘米?【答案】168平方厘米【解析】每一刀增加两个切面,增加的表面积等于与切面平行的两个表面积,所以每个方向切两刀后,表面积增加到原来的3倍,即表面积的和为.【题文】如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?【答案】54【解析】当小积木互相重合的面最多时表面积最小.设想27块边长为1的正方形积木,当拼成一个的正方体时,表面积最小,现在要去掉2块小积木,只有在两个角上各去掉一块小积木,或在同一个角去掉两块相邻的积木时,表面积不会增加,该几何体表面积为54.【题文】要把12件同样的长a、宽b、高h的长方体物品拼装成一件大的长方体,使打包后表面积最小,该如何打包?⑴当 b2h时,如何打包?⑵当 b2h时,如何打包?⑶当 b2h时,如何打包?【答案】如解析图【解析】图2和图3正面的面积相同,侧面面积正面周长长方体长,所以正面的周长愈大表面积越大,图2的正面周长是8h6b,图3的周长是12h4b.两者的周长之差为2(b2h).当b2h时,图2和图3周长相等,可随意打包;当b2h时,按图2打包;当b2h时,按图3打包.【题文】要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体,表面积最小是多少?【答案】1034【解析】考虑所有的包装方法,因为6123,所以一共有两种拼接方式:第一种按长宽高116拼接,重叠面有三种选择,共3种包装方法.第二种按长宽高123拼接,有3个长方体并列方向的重叠面有三种选择,有2个长方体并列方向的重叠面剩下2种选择,一共有6种包装方法.其中表面积最小的包装方法如图所示,表面积为1034.【题文】如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.【答案】214【解析】我们把上面的小正方体想象成是可以向下“压缩”的,“压缩”后我们发现:小正方体的上面与大正方体上面中的阴影部分合在一起,正好是大正方体的上面.这样这个立体图形的表面积就可以分成这样两部分:上下方向:大正方体的两个底面;四周方向(左右、前后方向):小正方体的四个侧面,大正方体的四个侧面.上下方向:(平方分米);侧面:(平方分米),(平方分米).这个立体图形的表面积为:(平方分米).【题文】如图,棱长分别为厘米、厘米、厘米、厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是多少平方厘米?【答案】194平方厘米【解析】 (法1)四个正方体的表面积之和为:(平方厘米),重叠部分的面积为:(平方厘米),所以,所得到的多面体的表面积为:(平方厘米).(法2)三视图法.从前后面观察到的面积为平方厘米,从左右两个面观察到的面积为平方厘米,从上下能观察到的面积为平方厘米.表面积为(平方厘米).【题文】把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.,求这个立体图形的表面积.【答案】54【解析】从上下、左右、前后观察到的的平面图形如下面三图表示.因此,这个立体图形的表面积为:2个上面个左面个前面.上表面的面积为:9平方厘米,左表面的面积为:8平方厘米,前表面的面积为:10平方厘米.因此,这个立体图形的总表面积为:(平方厘米).上下面左右面前后面【题文】用棱长是1厘米的立方块拼成如图所示的立体图形,问该图形的表面积是多少平方厘米?【答案】46平方厘米【解析】该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成.该图形的表面积等于个小正方形的面积,所以该图形表面积为46平方厘米.【题文】有30个边长为1米的正方体,在地面上摆成右上图的形式,然后把露出的表面涂成红色.求被涂成红色的表面积.【答案】56【解析】(平方米).【题文】棱长是厘米(为整数)的正方体的若干面涂上红色,然后将其切割成棱长是1厘米的小正方体.至少有一面红色的小正方体个数和表面没有红色的小正方体个数的比为,此时的最小值是多少?【答案】5【解析】切割成棱长是1厘米的小正方体共有个,由于其中至少有一面是红色的小正方体与没有红色面的个数之比为,而,所以小正方体的总数是25的倍数,即是25的倍数,那么是5的倍数.当时,要使得至少有一面的小正方体有65个,可以将原正方体的正面、上面和下面涂色,此时至少一面涂红色的小正方体有个,表面没有红色的小正方体有个,个数比恰好是,符合题意.因此,的最小值是5.【题文】有64个边长为1厘米的同样大小的小正方体,其中34个为白色的,30个为黑色的.现将它们拼成一个的大正方体,在大正方体的表面上白色部分最多可以是多少平方厘米?【答案】74【解析】要使大正方体的表面上白色部分最多,相当于要使大正方体表面上黑色部分最少,那么就要使得黑色小正方体尽量不露出来.在整个大正方体中,没有露在表面的小正方体有(个),用黑色的;在面上但不在边上的小正方体有(个),其中个用黑色.这样,在表面的个的正方形中,有22个是黑色,(个)是白色,所以在大正方体的表面上白色部分最多可以是74平方厘米.【题文】三个完全一样的长方体,棱长总和是288厘米,每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数,给这三个长方体涂色,一个涂一面,一个涂两面,一个涂三面.涂色后把三个长方体都切成棱长为1厘米的小正方体,只有一个面涂色的小正方体最少有多少个?【答案】307【解析】每个长方体的棱长和是厘米,所以,每个长方体长、宽、高的和是厘米.因为,每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数,所以,每个长方体的长、宽、高分别是9厘米、8厘米、7厘米.要求切割后只有一个面涂色的小正方体最少有多少个,则需每一个长方体按题意涂色时,应让切割后只有一个面涂色的小正方体最少.所以,涂一面的长方体应涂一个面,有个;涂两面的长方体,若两面不相邻,应涂两个面,有个;若两面相邻,应涂一个面和一个面,此时有个,所以涂两面的最少有105个;涂三面的长方体,若三面不两两相邻,应涂两个面、一个面,有个;若三面两两相邻,有个,所以涂三面的最少有146个.那么切割后只有一个面涂色的小正方体最少有个.【题文】把一个大长方体木块表面上涂满红色后,分割成若干个同样大小的小正方体,其中恰好有两个面涂上红色的小正方体恰好是100块,那么至少要把这个大长方体分割成多少个小正方体?【答案】108【解析】设小正方体的棱长为1,考虑两种不同的情况,一种是长方体的长、宽、高中有一个是1的情况,另一种是长方体的长、宽、高都大于1的情况.当长方体的长、宽、高中有一个是1时,分割后只有一层小正方体,其中有两个面涂上红色的小正方体是去掉最外层一圈的小正方体后剩下的那些.因为有两个面涂上红色的小正方体恰好是100块,设,那么分成的小正方体个数为,为了使小正方体的个数尽量少,应使最小,而两数之积一定,差越小积越小,所以当时它们的和最小,此时共有个小正方体.当长方体的长、宽、高都大于1时,有两个面涂上红色的小正方体是去掉8个顶点所在的小正方体后12条棱上剩余的小正方体,因为有两个面涂上红色的小正方体恰好是100块,所以长方体的长、宽、高之和是.由于三个数的和一定,差越大积越小,为了使小正方体的个数尽量少,应该令,此时共有个小正方体.因为,所以至少要把这个大长方体分割成108个小正方体.【题文】把正方体的六个表面都划分成9个相等的正方形.用红、黄、蓝三种颜色去染这些小正方形,要求有公共边的正方形染不同的颜色,那么,用红色染的正方形最多有多少个?【答案】22【解析】一个面最多有5个方格可染成红色(见左下图).因为染有5个红色方格的面不能相邻,可以相对,所以至多有两个面可以染成5个红色方格.其余四个面中,每个面的四个角上的方格不能再染成红色,至多能染4个红色方格(见上中图).因为染有4个红色方格的面也不能相邻,可以相对,所以至多有两个面可以染成4个红色方格.最后剩下两个相对的面,每个面最多可以染2个红色方格(见右上图).所以,红色方格最多有(个).(另解)事实上上述的解法并不严密,“如果最初的假设并没有两个相对的有5个红色方格的面,是否其他的四个面上可以出现更多的红色方格呢?”这种解法回避了这个问题,如果我们从约束染色方格数的本质原因入手,可严格说明是红色方格数的最大值.对于同一个平面上的格网,如果按照国际象棋棋盘的方式染色,那么至少有一半的格子可以染成红色.但是现在需要染色的是一个正方体的表面,因此在分析问题时应该兼顾棱、角等面与面相交的地方:⑴⑵⑶⑴如图,每个角上三个方向的3个方格必须染成不同的三种颜色,所以8个角上最多只能有8个方格染成红色.⑵如图,阴影部分是首尾相接由个方格组成的环,这9个方格中只能有个方格能染成同一种颜色(如果有5个方格染同一种颜色,必然出现相邻,可以用抽屉原理反证之:先去掉一个白格,剩下的然后两两相邻的分成四个抽屉,必然有一个抽屉中有两个红色方格),像这样的环,在正方体表面最多能找到不重叠的两道(关于正方体中心对称的两道),涉及的个方格中最多能有个可染成红色.⑶剩下个方格,分布在条棱上,这个格子中只能有个能染成红色.综上所述,能被染成红色的方格最多能有个格子能染成红色,第一种解法中已经给出个红方格的染色方法,所以个格子染成红色是最多的情况.【题文】一个长、宽、高分别为厘米、厘米、厘米的长方形.现从它的上面尽可能大的切下一个正方体,然后从剩余的部分再尽可能大的切下一个正方体,最后再从第二次剩余的部分尽可能大的切下一个正方体,剩下的体积是多少立方厘米?【答案】1107【解析】本题的关键是确定三次切下的正方体的棱长.由于,为了方便起见.我们先考虑长、宽、高分别为厘米、厘米、厘米的长方体.因为,容易知道第一次切下的正方体棱长应该是厘米,第二次切时,切下棱长为厘米的正方体符合要求.第三次切时,切下棱长为厘米的正方体符合要求.那么对于原长方体来说,三次切下的正方体的棱长分别是12厘米、9厘米和6厘米,所以剩下的体积应是:(立方厘米).【题文】有黑白两种颜色的正方体积木,把它摆成右图所示的形状,已知相邻(有公共面)的积木颜色不同,标的为黑色,图中共有黑色积木多少块?【答案】17【解析】分层来看,如下图(切面平行于纸面)共有黑色积木17块.【题文】有许多相同的立方体,每个立方体的六个面上都写着同一个数字(不同的立方体可以写相同的数字)先将写着2的立方体与写着1的立方体的三个面相邻,再将写着3的立方体写着2的立方体相邻(见左下图).依这样构成右下图所示的立方体,它的六个面上的所有数字之和是多少?【答案】216【解析】第一层如下图,第二层、第三层依次比上面一层每格都多1(见下图).上面的9个数之和是27,由对称性知,上面、前面、右面的所有数之和都是27.同理,下面的9个数之和是45,下面、左面、后面的所有数之和都是45.所以六个面上所有数之和是.【题文】如图所示,一个的立方体,在一个方向上开有的孔,在另一个方向上开有的孔,在第三个方向上开有的孔,剩余部分的体积是多少?表面积为多少?【答案】100;204【解析】求体积:开了的孔,挖去,开了的孔,挖去;开了的孔,挖去,剩余部分的体积是:.(另解)将整个图形切片,如果切面平行于纸面,那么五个切片分别如图:得到总体积为:.求表面积:表面积可以看成外部和内部两部分.外部的表面积为,内部的面积可以分为前后、左右、上下三个方向,面积分别为、、,所以总的表面积为.(另解)运用类似于三视图的方法,记录每一方向上的不同位置上的裸露正方形个数:前后方向:上下方向:左右方向:总表面积为.总结:“切片法”:全面打洞(例如本题,五层一样),挖块成线(例如本题,在前一层的基础上,一条线一条线地挖),这里体现的思想方法是:化整为零,有序思考!【题文】如图,原来的大正方体是由个小正方体所构成的.其中有些小正方体已经被挖除,图中涂黑色的部分就是贯穿整个大正方体的挖除部分.请问剩下的部分共有多少个小正方体?【答案】72【解析】对于这一类从立体图形中间挖掉一部分后再求体积(或小正方体数l【题文】一个由125个同样的小正方体组成的大正方体,从这个大正方体中抽出若干个小正方体,把大正方体中相对的两面打通,右图就是抽空的状态.右图中剩下的小正方体有多少个?【答案】73【解析】解法一:(用“容斥原理”来解)由正面图形抽出的小正方体有个,由侧面图形抽出的小正方体有个,由底面图形抽出的小正方体有个,正面图形和侧面图形重合抽出的小正方体有个,正面图形和底面图形重合抽出的小正方体有个,底面图形和侧面图形重合抽出的小正方体有个,三个面的图形共同重合抽出的小正方体有4个.根据容斥原理,,所以共抽出了52个小正方体.,所以右图中剩下的小正方体有73个.注意这里的三者共同抽出的小正方体是4个,必须知道是哪4块,这是最让人头疼的事.但你可以先构造空的两个方向上共同部分的模型,再由第三个方向来穿过“花墙”.这里,化虚为实的思想方法很重要.解法二:(用“切片法”来解)可以从上到下切五层,得:⑴从上到下五层,如图:⑵或者,从右到左五片,如图:请注意这里的挖空的技巧是:先认一种方向.比如:从上到下的每一层,首先都应该有第一层的空四块的情况,即——如果挖第二层:第(1)步,把中间这些位置的四块挖走如图:第(2)步,把从右向左的两块成线地挖走.(请注意挖通的效果就是成线挖去),如图:第(3)步,把从前向后的一块(请注意跟第二层有关的只是一块!)挖成线!如图:【题文】右图中的⑴⑵⑶⑷是同样的小等边三角形,⑸⑹也是等边三角形且边长为⑴的2倍,⑺⑻⑼⑽是同样的等腰直角三角形,⑾是正方形.那么,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的多少倍.【答案】16【解析】本题中的两个图都是立体图形的平面展开图,将它们还原成立体图形,可得到如下两图:其中左图是以⑴⑵⑶⑷为平面展开图的立体图形,是一个四个面都是正三角形的正四面体,右图以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形,是一个不规则图形,底面是⑾,四个侧面是⑺⑻⑼⑽,两个斜面是⑸⑹.对于这两个立体图形的体积,可以采用套模法来求,也就是对于这种我们不熟悉的立体图形,用一些我们熟悉的基本立体图形来套,看看它们与基本立体图形相比,缺少了哪些部分.由于左图四个面都是正三角形,右图底面是正方形,侧面是等腰直角三角形,想到都用正方体来套.对于左图来说,相当于由一个正方体切去4个角后得到(如下左图,切去、、、);而对于右图来说,相当于由一个正方体切去2个角后得到(如下右图,切去、).假设左图中的立方体的棱长为,右图中的立方体的棱长为,则以⑴⑵⑶⑷为平面展开图的立体图形的体积为:,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积为.由于右图中的立方体的棱长即是题中正方形⑾的边长,而左图中的立方体的每一个面的对角线恰好是正三角形⑴的边长,通过将等腰直角三角形⑺分成4个相同的小等腰直角三角形可以得到右图中的立方体的棱长是左图中的立方体的棱长的2倍,即.那么以⑴⑵⑶⑷为平面展开图的立体图形的体积与以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积的比为:,也就是说以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的16倍.【题文】图⑴和图⑵是以正方形和等边三角形为面的立体图形的展开图,图中所有的边长都相同.请问:图⑴能围起来的立体图形的体积是图⑵能围起来的立体图形的体积的几倍?图⑴图⑵【答案】20【解析】首先,我们把展开图折成立体图形,见下列示意图:图⑴图⑵对于这类题目,一般采用“套模法”,即用一个我们熟悉的基本立体图形来套,这样做基于两点考虑,一是如果有类似的模型,可以直接应用其计算公式;二是如果可以补上一块或者放到某个模型里面,那么可以从这个模型入手.我们把图⑴中的立体图形切成两半,再转一转,正好放进去!我们看到图⑴与图⑶的图形位置的微妙关系:图⑶图⑷由图⑷可见,图⑴这个立体的体积与图⑶这个被切去了8个角后的立体图形的体积相等.假设立方体的1条边的长度是1,那么一个角的体积是,所以切掉8个角后的体积是.再看图⑵中的正四面体,这个正四面体的棱长与图⑶中的每一条实线线段相等,所以应该用边长为的立方体来套.如果把图⑵的立体图形放入边长为的立方体里的话是可以放进去的.这是切去了四个角后的图形,从上面的分析可知一个角的体积为,所以图⑵的体积是:,那么前者的体积是后者的倍.【题文】如图,用高都是米,底面半径分别为米、米和米的个圆柱组成一个物体.问这个物体的表面积是多少平方米?(取)【答案】32.97【解析】从上面看到图形是右上图,所以上下底面积和为(立方米),侧面积为(立方米),所以该物体的表面积是(立方米).【题文】有一个圆柱体的零件,高厘米,底面直径是厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是厘米,孔深厘米(见右图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?【答案】307.72【解析】涂漆的面积等于大圆柱表面积与小圆柱侧面积之和,为(平方厘米).【题文】圆柱体的侧面展开,放平,是边长分别为10厘米和12厘米的长方形,那么这个圆柱体的体积是多少立方厘米.(结果用表示)【答案】立方厘米或立方厘米【解析】当圆柱的高是12厘米时体积为(立方厘米)当圆柱的高是12厘米时体积为(立方厘米).所以圆柱体的体积为立方厘米或立方厘米.【题文】如右图,是一个长方形铁皮,利用图中的阴影部分,刚好能做成一个油桶(接头处忽略不计),求这个油桶的容积.()【答案】100.48【解析】圆的直径为:(米),而油桶的高为2个直径长,即为:,故体积为立方米.【题文】如图,有一张长方形铁皮,剪下图中两个圆及一块长方形,正好可以做成1个圆柱体,这个圆柱体的底面半径为10厘米,那么原来长方形铁皮的面积是多少平方厘米?()【答案】2056【解析】做成的圆柱体的侧面是由中间的长方形卷成的,可见这个长方形的长与旁边的圆的周长相等,则剪下的长方形的长,即圆柱体底面圆的周长为:(厘米),原来的长方形的面积为:(平方厘米).【题文】把一个高是8厘米的圆柱体,沿水平方向锯去2厘米后,剩下的圆柱体的表面积比原来的圆柱体表面积减少平方厘米.原来的圆柱体的体积是多少立方厘米?【答案】25.12【解析】沿水平方向锯去2厘米后,剩下的圆柱体的表面积比原来的圆柱体表面积减少的部分为减掉的2厘米圆柱体的侧面积,所以原来圆柱体的底面周长为厘米,底面半径为厘米,所以原来的圆柱体的体积是(立方厘米).【题文】一个圆柱体的体积是立方厘米,底面半径是2厘米.将它的底面平均分成若干个扇形后,再截开拼成一个和它等底等高的长方体,表面积增加了多少平方厘米? ()【答案】16【解析】从图中可以看出,拼成的长方体的底面积与原来圆柱体的底面积相同,长方体的前后两个侧面面积与原来圆柱体的侧面面积相等,所以增加的表面积就是长方体左右两个侧面的面积.(法1)这两个侧面都是长方形,且长等于原来圆柱体的高,宽等于圆柱体底面半径.可知,圆柱体的高为(厘米),所以增加的表面积为(平方厘米);(法2)根据长方体的体积公式推导.增加的两个面是长方体的侧面,侧面面积与长方体的长的乘积就是长方体的体积.由于长方体的体积与圆柱体的体积相等,为立方厘米,而拼成的长方体的长等于圆柱体底面周长的一半,为厘米,所以侧面长方形的面积为平方厘米,所以增加的表面积为平方厘米.【题文】一个拧紧瓶盖的瓶子里面装着一些水(如图),由图中的数据可推知瓶子的容积是多少立方厘米.(取)【答案】100.48【解析】由于瓶子倒立过来后其中水的体积不变,所以空气部分的体积也不变,从图中可以看出,瓶中的水构成高为厘米的圆柱,空气部分构成高为厘米的圆柱,瓶子的容积为这两部分之和,所以瓶。
小学立体图形认知练习题

小学立体图形认知练习题一、选择题1. 下列哪个图形是正方体?A. 长方体B. 正方形C. 球体D. 正方体2. 下列哪个图形的表面由三角形组成?A. 三棱锥B. 四棱锥C. 圆柱D. 球体3. 下列哪个图形没有曲面?A. 圆柱B. 立方体C. 球体D. 圆锥4. 下列哪个图形的底面是正方形?A. 圆柱B. 三棱柱C. 立方体D. 圆锥二、判断题1. 圆柱的侧面是曲面。
()2. 立方体的每个面都是正方形。
()3. 球体的表面是平面。
()4. 三棱锥的底面是三角形。
()三、填空题1. 立方体有________个面,________个顶点,________条棱。
2. 圆柱的底面是________,侧面是________。
3. 球体的表面是________。
4. 三棱锥有________个面,________个顶点,________条棱。
四、连线题请将下列立体图形与其对应的名称连线:1. 正方体 A. 圆锥2. 圆柱 B. 球体3. 球体 C. 正方体4. 圆锥 D. 圆柱五、简答题1. 请简要描述正方体的特征。
2. 请列举出三种常见的立体图形。
3. 请说出圆柱和圆锥的区别。
4. 请举例说明生活中哪些物体是球体。
六、作图题一个正方体一个圆柱一个圆锥一个三棱柱一个球体七、应用题1. 小明有一个长方体纸箱,长、宽、高分别是20厘米、15厘米和10厘米。
请计算纸箱的表面积。
2. 一个圆柱的底面直径是10厘米,高是20厘米。
请计算圆柱的体积。
3. 一个圆锥的底面半径是5厘米,高是12厘米。
请计算圆锥的体积。
4. 下列四个球体的半径分别是2厘米、4厘米、6厘米和8厘米,比较它们的体积大小。
八、分类题正方体、长方体、三棱锥、球体、圆柱、圆锥、圆台、四棱锥九、观察题1. 观察教室内的物体,找出三种不同的立体图形,并说出它们的特点。
2. 观察日常生活中使用的容器,判断它们分别属于哪种立体图形,并说明理由。
十、探究题1. 如何计算一个不规则立体图形的体积?请举例说明。
2022-2023学年小学六年级奥数典型题测评卷15《立体图形的表面积》(解析版)

【六年级奥数举一反三—全国通用】测评卷15《立体图形的表面积》试卷满分:100分考试时间:100分钟姓名:_________班级:_________得分:_________一.选择题(共7小题,满分21分,每小题3分)1.(2015•创新杯)如图,一个长8厘米、宽6厘米、高10厘米的长方体木块中,挖去一个棱长为3厘米的正方形的孔,木块现在的表面积是()平方厘米.A.367 B.376 C.412 D.430【分析】由题意可知:挖去一个棱长为3厘米的正方形的孔,木块的表面积减少了1个小3×3的面,增加了5个3×3的面,实际相当于只增加了4个面;所以木块现在的表面积为原来长方体的表面积再加上中间的正方体的4个面的面积即可.【解答】解:(8×6+8×10+10×6)+3×3×4=376+36=412(平方厘米)答:木块现在的表面积是412平方厘米.故选:C.2.(2007•创新杯)把10个相同的小正方体按如图所示的位置堆放,它的外表含有若干个小正方形,如图将图中标有字母A的一个小正方体搬去,这时外表含有的小正方形个数与搬动前相比()A.不增不减B.减少1个C.减少2个D.减少3个【分析】根据图形,搬动前小正方体A外表含有3个小正方形,搬动后A所在的位置有3个小正方形作为外表露出解答.【解答】解:由图可知,搬动前小正方体A外表含有3个小正方形,搬动后A所在的位置有3个小正方形作为外表露出,所以小正方形的个数与搬动前相比不增不减.故选:A.3.正方体的棱长扩大2倍,它的表面积就()A.扩大2倍B.扩大4倍C.扩大6倍【分析】正方体的表面积=棱长×棱长×6;由此利用积的变化规律:一个因数不变,另一个因数扩大几倍积就扩大几倍,即可解决问题.【解答】解:正方体的表面积=棱长×棱长×6;正方体的棱长扩大2倍,根据积的变化规律可得:表面积扩大了2×2=4倍;故选:B.4.(2012•其他杯赛)一个长方体,它的高和宽相等,若把长去掉2.5厘米,就成为表面积是150平方厘米的正方体,长方体的长是宽的()倍.A.1.5 B.2 C.2.5 D.3【分析】已知长方体的宽和高相等,把长去掉2.5cm,就成为表面积150平方厘米的正方体,根据正方体的表面积公式:S=6a2,据此可以求出正方体的一个面的面积,进而求出正方体的棱长(长方体的宽和高),用正方体的棱长加上2.5厘米就是长方体的长,然后根据求一个数是另一个数的几倍用除法解答.【解答】解:正方体的一个的面积是:150÷6=25(平方厘米),正方体的棱长是:因为5的平方是25,所以正方体的棱长是5厘米,长方体的长是:5+2.5=7.5(厘米),长是宽的:7.5÷5=1.5倍;故选:A.5.把三个棱长为1厘米的正方体拼成一个长方体,这个长方体的表面积比原来三个正方体的表面积的和减少()A.2平方厘米B.3平方厘米C.4平方厘米【分析】3个小正方体拼成一个长方体只有一种拼组方法:一字排列法,拼组后长方体的表面积比原来减少了4个小正方体的面的面积,据此即可解答.【解答】解:1×1×4=4(平方厘米)故选:C.6.正方体的棱长扩大2倍,表面积就扩大()倍.A.2 B.4 C.6 D.8【分析】设正方体的棱长为a,则扩大后的棱长为2a,利用正方体的表面积公式求出扩大前后的表面积,即可求得表面积扩大的倍数.根据正方体表面积扩大的倍数是棱长扩大倍数的平方求解即可.【解答】解:设正方体的棱长为a,则扩大后的棱长为2a,原正方体的表面积:a×a×6=6a2,现在的正方体的表面积:2a×2a×6=24a2,表面积扩大24a2÷6a2=4倍;故选:B.7.(2011•华罗庚金杯模拟)如图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长1厘米的正方体,做成一种玩具,它的表面积是x平方厘米,那么x等于()A.114 B.120 C.126 D.132【分析】这个玩具的表面积是大正方体的面积,加上6个边长为1厘米的小正方体的4个侧面的面积,据此解答即可.【解答】解:玩具的表面积:4×4×6+1×1×6×4=96+24=120(平方厘米).答:它的表面积是120平方厘米.故选:B.二.填空题(共11小题,满分33分,每小题3分)8.(2016•其他杯赛)如图是棱长10厘米的两个正方体果盒,用一张长4分米,宽3分米的长方形彩色纸包装(接头处忽略不计).这张彩色纸够吗?够.【分析】两个正方体拼成了一个长方体,表面积总和减少了两个正方形的面,即还剩下6×2﹣2=10个正方形的面,即需要包装的面,然后根据正方形和长方形的面积公式进一步解答即可.【解答】解:6×2﹣2=10(个)10厘米=1分米1×1×10=10(平方分米)4×3=12(平方分米)12>10所以,这张彩色纸够了.故答案为:够.9.(2016•学而思杯)如图,将一个棱长为4cm的正方体从中间切开,再拼成一个长方体,那么,表面积增加了16cm2.【分析】把正方体切成完全一样的两块长方体后,它的表面积比原来增加了2个正方体的面的面积;再拼成一个长方体,那么,表面积又减少了1个正方体的面的面积;综合上述,实际相当于只增加了1个正方体的面的面积;由此即可解答问题.【解答】解:根据分析可得,表面积增加了1个正方体的面的面积:4×4=16(平方厘米)答:表面积增加了16平方厘米.故答案为:16.10.(2015•小机灵杯)把一个正方体切成27个相等的小正方体.这些小正方体的表面积之和比大正方体的表面积大432平方厘米.那么,大正方体的体积是216立方厘米.【分析】能把一个正方体切成27个相等的小正方体,说明在上下、左右和前后各切2次,共切6次;每切一次就多出2个大正方形1个面的面积,共多出12个大正方形的一个面的面积.由432÷12=36平方厘米,得其边长是6厘米.再运用正方体的体积公式,即可求出此题.【解答】解:432÷12=36(平方厘米)正方体的边长:=6(厘米)6×6×6=216(立方厘米)故:答正方体的体积是216立方厘米.11.(2018•学而思杯)一个长为4厘米,宽和高均为2厘米的长方体,从中间切一刀分成两个完全相同的小正方体,那么这两个小正方体的表面积之和与原来的长方体表面积相比增加了8平方厘米.【分析】由题意,锯成的正方体的棱长是2厘米,会增加两个面,每个面的面积是2×2平方厘米,所以再乘以2就是增加的面积.【解答】解:2×2×2=8(平方厘米)故答案为:8.12.(2016•其他杯赛)如图,把一根长方体木料,锯成大小不等的三个小长方体,则表面积比原来增加160平方厘米.【分析】由题意可知:把该长方体木料沿虚线平均截成3段后,表面积比原来增加了4个长为8厘米、宽为5厘米的长方形的面积,由此解答即可.【解答】解:8×5×4=160(平方厘米)故答案为:160.13.(2016•迎春杯)如图是由9块相同的长方体摆放而成的大长方体,已知大长方体的表面积是360平方厘米,那么一个小长方体的表面积是88平方厘米.【分析】可以设小长方体的长为a,宽为b,高为c,根据表面积公式,可以列出关系式,2×(b+c)×(b+b+b)+2×(b+c)×a+2×a×(b+b+b)=360,又3b=2a,a=3c,即可求出a、b、c的值进而可以求得小正方体的表面积.【解答】解:根据分析,设小长方体的长为a,宽为b,高为c,如下图所示,则有:3b=2a,a=3c故大长方体的表面积=2×(b+c)×(b+b+b)+2×(b+c)×a+2×a×(b+b+b)=360⇒3b2+3bc+4ab+ac =180又3b=2a,a=3c,可解得:a=6,b=4,c=2,则一个小长方体的表面积是:2×6×4+2×6×2+2×4×2=88平方厘米.故答案是:88平方厘米.14.(2015•创新杯)如图,在一个棱长40厘米的正方体的上、下两个底面的正中间,各有一个直径为6厘米的圆孔,孔深15厘米,则这个几何体的表面积是10165.2平方厘米,体积是63152.5立方厘米.(π取3.14)【分析】表面积比原来正方体的表面积多了两个圆柱的侧面积,体积比原来的正方体少了两个圆柱的体积.【解答】解:正方体的表面积40×40×6=9600(平方厘米)一个圆柱的侧面积6×3.14×15=282.6(平方厘米)这个几何体的表面积9600+282.6×2=10165.2(平方厘米)正方体的体积40×40×40=64000(立方厘米)圆柱的半径6÷2=3(厘米)两个圆柱的体积3.14×3×3×15×2=847.8(立方厘米)几何体的体积64000﹣847.9=63152.2(立方厘米)故填10165.2和63152.515.(2016•其他杯赛)将表面积分别为150平方分米、54平方分米、96平方分米的三个正方体铁块熔铸成一个大正方体铁块,这个大正方体铁块的表面积是216平方分米.【分析】根据正方体的特征,它的12条棱的长度都相等,6个面的面积都相等;正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长;已知三个正方体的表面积分别是54平方分米、96平方分米、150平方分米,先分别求出三个正方体的棱长,把它们熔铸成一个大的正方体铁块,体积不变,由此再求三个正方体的体积之和即可.【解答】解:54÷6=9(平方分米),因为:3×3=9,所以:棱长是3分米;96÷6=16(平方分米),因为:4×4=16,所以:棱长是4分米;150÷6=25(平方分米),因为:5×5=25,所以:棱长是5分米;3×3×3+4×4×4+5×5×5=27+64+125=216(立方分米);因为:6×6×6=216,所以:大正方体的棱长是6分米;6×6×6=216(平方分米);故答案为:216.16.(2016•陈省身杯)如图,用6个完全相同的小正方体组成了一个长方体,如果每个小正方体的表面积均为48平方厘米,那么整个长方体的表面积为208平方厘米.【分析】每个小正方体的表面积均为48平方厘米,则每个面的面积是48÷6=8平方厘米;用6个完全相同的小正方体组成了一个长方体,减少了2×5=10面,所以还剩下6×6﹣10=26个面,然后再乘每个面的面积即可.【解答】解:48÷6=8(平方厘米)8×(6×6﹣5×2)=8×26=208(平方厘米)答:整个长方体的表面积为208平方厘米.故答案为:208.17.(2012•其他杯赛)一块正方体木块棱长为8厘米,从上面向下挖一个棱长为2厘米的小正方体(如图)后,余下部分的表面积是400平方厘米.【分析】根据题意,并结合正方体的切割特点可知:挖去一个棱长为2厘米的小正方体后,增加了4个侧面的面积,然后根据正方体的表面积=棱长×棱长×6,求出正方体的表面积,然后加上4个边长为2厘米的正方形的面积即可.【解答】解:8×8×6+2×2×4=384+16=400(平方厘米)故答案为:400.18.(2014•希望杯)如图,用若干个棱长为1的小正方体堆成一个大的几何体,这个几何体的表面积(含底面积)是90.【分析】求这个几何体的表面积,就要数出这个图形中小正方体露在外面的面数,从前、后、左、右、上、下方向上来数面的个数,然后用一个面的面积乘面的个数即可.【解答】解:从前、后、左、右、上、下方向,看到的面的个数分别为:14、14、16、16、15、15.表面积是:1×1×(14+14+16+16+15+15)=1×90=90.答:这个几何体的表面积(含底面积)是90.故答案为:90.三.解答题(共10小题,满分46分)19.(4分)从一个棱长为4厘米的正方形的每个面的中心位置分别挖去一个底面半径为1厘米、高为1.5厘米的圆柱.求挖去后的图形的表面积是多少平方厘米?【分析】每挖去一个圆柱,表面积就增加一个圆柱的侧面积,由题意可知,挖的四个圆柱没有接触.【解答】解:4×4×6+3.14×1×2×1.5×4=96+37.68=133.68(平方厘米)答:挖去后的图形的表面积是133.68平方厘米.20.(4分)从一个棱长10厘米的正方体木块上挖去一个长10厘米、宽2厘米、高2厘米的小长方体,剩下部分的表面积是多少?【分析】图1剩下部分的表面积比原来正方体的表面积减少了两个边长是2厘米的小正方形的面积;图2剩下部分的表面积比原来正方体的表面积增加了两个长是10厘米,宽是2厘米的长方形面积,同时又减少了两个边长是2厘米的小正方形的面积;图3剩下部分的表面积比原来正方体的表面积增加了四个长是10厘米,宽是2厘米的长方形的面积,再减去两个边长是2厘米的小正方形的面积,据此解答即可.【解答】解:图1:10×10×6﹣2×2×2=592(平方厘米)图2:10×10×6+10×2×2﹣2×2×2=632(平方厘米)图3:10×10×6+10×2×4﹣2×2×2=672(平方厘米)21.(4分)用棱长是1厘米的立方块拼成如图所示的立体图形,问该图形的表面积是多少平方厘米?【分析】这个图形的表面积等于露在外面的面的面积,只要求出分别从正面、侧面、上面看到的面的个数,据此解答即可.【解答】解:从正面可以看到:2+2+3=7(个)从左面可以看到:2+2+3=7(个)从上面可以看到:3+3+3=9(个)所以这个图形的表面积是:(7+7+9)×2×1×1=46(平方厘米)答:这个图形的表面积是46平方厘米.22.(4分)(2016•华罗庚金杯)如图,有30个棱长为1米的正方体堆成一个四层的立体图形.请问:这个立体图形的表面积等于多少?【分析】这个几何体的表面积就是露出小正方体的面的面积之和,从上面看有16个面;从下面看有16个面;从前面看有10个面;从后面看有10个面;从左面看有10个面;从右面看有10个面.由此即可解决问题.【解答】解:图中几何体露出的面有:10×4+16×2=72(个)所以这个几何体的表面积是:1×1×72=72(平方米)答:这个立体图形的表面积等于72平方米.23.(5分)有一个长方体的铁块,这个铁块正好可以锯成三个正方体的铁块,表面积会增加20平方厘米,那么,这个长方体铁块原来的表面积是多少?【分析】把一个长方体木块正好横锯成三个大小相等的小正方体,切了2次,增加了4个小正方形的面积,增加了20cm2,用“20÷4”求出一个小正方形的面积,可以把原来的长方体的表面积理解为是14个小正方形面的面积之和,进而求出14个小正方形的面积之和即可.【解答】解:(20÷4)×(6×3﹣4)=5×14=70(平方厘米)答:原来长方体的表面积是70平方厘米.24.(5分)一个长方体,如果长减少2cm,则体积减少80cm3;如果宽增加3cm,则体积增加150cm3;如果高增加4cm,则体积增加320cm3.原来这个长方体的表面积是多少?【分析】根据题意,长方体的体积=长×宽×高,一个长方体,如果长减少2cm,则体积减少80cm3,则宽×高即左右侧面的面积是80÷2=40cm2,如果宽增加3cm,则体积增加150cm3,则长×高即前后面的面积是150÷3=50cm2,如果高增加4cm,则体积增加320cm3,则长×宽即上下侧面的面积是320÷4=80cm2,所以根据长方体的表面积=(长×宽+宽×高+长×高)×2,据此回答.【解答】解:宽×高:80÷2=40(cm2)长×高:150÷3=50(cm2)长×宽:320÷4=80(cm2)表面积:(40+50+80)×2=340(cm2)答:这个长方体的表面积是340cm2.25.(5分)(2012•奥林匹克)如图所示,有一个长方体,先后沿不同方向切了三刀.切完第一刀后得到的两个小长方体的表面积之和是472平方厘米,切完第二刀后得到的四个小长方体的表面积之和是632平方厘米,切完第三刀后得到的八个小长方体的表面积之和是752平方厘米.那么在原来长方体的6个面中,面积最小的面是多少平方厘米?【分析】切完三刀之后,表面积之和是原来大长方体表面积的2倍,所以原来的大长方体的表面积是:752÷2=376,切完第一刀,增加的两个面的面积是472﹣376=96平方厘米,一个面的面积是96÷2=48平方厘米;切完第二刀,又增加的两个面的面积是632﹣472=160,一个面的面积是160÷2=80平方厘米;切完第三刀,又增加两个面的面积是752﹣632=120平方厘米,一个面的面积是120÷2=60平方厘米,然后比较即可.【解答】解:752÷2=376(平方厘米)(472﹣376)÷2=48(平方厘米)(632﹣472)÷2=80(平方厘米)(752﹣632)÷2=60(平方厘米)48<60<80答:在原来长方体的6个面中,面积最小的面是48平方厘米.26.(5分)(2012•奥林匹克)欧欧收到一个长方体礼物盒,如果礼物盒的长增加4厘米,则体积增加80立方厘米;如果宽增加6厘米,则体积增加180立方厘米;如果高增加8厘米,则体积增加192立方厘米.请问:这个长方体的表面积是多少平方厘米?【分析】根据题意,用增加的体积除以增加的长、宽、高可得对应的三种面的面积,然后再用三个面积和乘2就是表面积.【解答】解:80÷4=20(平方厘米)180÷6=30(平方厘米)192÷8=24(平方厘米)(20+30+24)×2=74×2=148(平方厘米)答:这个长方体的表面积是148平方厘米.27.(5分)(2016•希望杯)如图所示,图①由1个棱长为1的小正方体堆成,图②由5个棱长为1的小正方体堆成,图③由14个棱长为1的小正方体堆成,按照此规律,求:(1)图⑥由多少个棱长为1的小正方体堆成?(2)图⑩所示的立体图形的表面积.【分析】(1)先找到小正方体个数的规律,不难求出图⑥的正方体的个数;(2)先推测出图⑩所示的立体图形的小正方体的个数,再求表面积.【解答】解:(1)根据观察,图①中有12小正方体;图②有1+22个小正方体;图③有1+22+32个小正方体;图④有1+22+32+42个小正方体;图⑤有1+22+32+42+52个小正方体;图⑥有1+22+32+42+52+62=91个小正方体,故答案是:91.(2)堆积体的表面积包括:前后2面、左右2面和上下2面.图⑩中有12+22+32+42+52+62+72+82+92+102=385个小正方体,表面积为:2×(1+2+3+…+10)+2×(1+2+3+…+10)+2×10×10=420.故答案为:420.28.(5分)将一个表面积为30cm2的正方体等分成两个长方体,再将这两个长方体拼成一个大长方体,求大长方体的表面积.【分析】正方体的每个面面积为30÷6=5平方厘米,切开后增加了两个面,又拼成一个长方体后正好减少了一个面,所以最后相当于增加了一个面,表面积为30+5=35平方厘米.【解答】解:30÷6=5(平方厘米)30+5=35(平方厘米)答:这个大长方体的表面积是35平方厘米.。
小学数学奥数测试题立体图形_人教版

61.圆柱体的正面展开,放平,是边长区分为10厘米和12厘米的长方形,那么这个圆柱体的体积是多少立方厘米.(结果用 表示)
5.一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共失掉大大小小的长方体24块,那么这24块长方体的外表积之和是多少?
6.一个外表积为 的长方体如图切成27个小长方体,这27个小长方体外表积的和是多少平方厘米?
7.如图,25块边长为1的正方体积木拼成一个几何体,外表积最小是多少?
27.图⑴和图⑵是以正方形和等边三角形为面的平面图形的展开图,图中一切的边长都相反.请问:图⑴能围起来的平面图形的体积是图⑵能围起来的平面图形的体积的几倍?
图⑴ 图⑵
28.如图,用高都是 米,底面半径区分为 米、 米和 米的 个圆柱组成一个物体.问这个物体的外表积是多少平方米?( 取 )
29.有一个圆柱体的零件,高 厘米,底面直径是 厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是 厘米,孔深 厘米(见右图).假设将这个零件接触空气的局部涂上防锈漆,那么一共要涂多少平方厘米?
55.一个透明的封锁盛水容器,由一个圆柱体和一个圆锥体组成,圆柱体的底面直径和高都是12厘米.其内有一些水,正放时水面离容器顶 厘米,倒放时水面离顶部5厘米,那么这个容器的容积是多少立方厘米?( )
56.如图,有一个边长为20厘米的大正方体,区分在它的角上、棱上、面上各挖掉一个大小相反的小立方体后,外表积变为2454平方厘米,那么挖掉的小立方体的边长是多少厘米?
小学奥数:第5讲 立体图形(一)
第五讲立体图形(一)姓名:得分:我们学过的立体图形有长方体、正方体、圆柱体、圆锥体等。
这一讲将通过长方体、正方体及其组合图形,讲解有关的计数问题。
例1右下图中共有多少个面?多少条棱?例2右图是由18个边长为1厘米的小正方体拼成的,求它的表面积。
例3右图是由22个小正方体组成的立体图形,其中共有多少个大大小小的正方体?由两个小正方体组成的长方体有多少个?例4右图是由120块小立方体构成的4×5×6的立方体,如果将其表面涂成红色,那么其中一面、二面三面被涂成红色的小立方体各有多少块?例5 给一个立方体的每个面分别涂上红、黄、蓝三种颜色中的一种,每种颜色涂两个面,共有多少种不同涂法?(两种涂法,经过翻动能使各种颜色的位置相同,认为是相同的涂法。
)练习1.下左图中共有多少个面?多少条棱?2.有30个边长为1米的正方体,在地面上摆成右上图的形式,然后把露出的表面涂成红色。
求被涂成红色的表面积。
4.将一个表面涂有红色的长方体分割成若干个体积为1厘米3的小正方体,其中一点红色都没有的小立方体只有3块。
求原来长方体的体积。
5.将一个5×5×5的立方体表面全部涂上红色,再将其分割成1×1×1的小立方体,取出全部至少有一个面是红色的小立方体,组成表面全部是红色的长方体。
那么,可组成的长方体的体积最大是多少?6.在边长为3分米的立方体木块的每个面的中心打一个直穿木块的洞,洞口呈边长为1分米的正方形(见左下图)。
求挖洞后木块的体积及表面积。
7.把正方体的六个表面都划分成9个相等的正方形(右上图)。
用红、黄、蓝三种颜色去染这些小正方形,要求有公共边的正方形染不同的颜色,那么,用红色染的正方形最多有多少个?。
小学数学六年级奥数《立体图形(1)》练习题(含答案)

小学数学六年级奥数《立体图形(1)》练习题(含答案)一、填空题1.一个正方体的表面积是384平方分米,体积是512立方分米,这个正方体棱长的总和是 .2.如图,在一块平坦的水泥地上,用砖和水泥砌成一个长方体的水泥池,墙厚为10厘米(底面利用原有的水泥地).这个水泥池的体积是 .3.一个边长为4分米的正方形,以它的一条边为轴,把正方形旋转一周后,得到一个 ,这个形体的体积是 .4.把19个边长为2厘米的正方体重叠起来堆成如右图所示的立方体,这个立方体的表面积是 平方厘米.5.图中是一个圆柱和一个圆锥(尺寸如图).问:柱锥V V 等于 .6.一个长方体的表面积是67.92平方分米.底面的面积是19平方分米.底面周长是17.6分米,这个长方体的体积是 .2 单位:米7.一块长方体木块长2.7米,宽1.8分米,高1.5分米.要把它裁成大小相等的正方体小木块,不许有剩余,小正方体的棱长最大是 分米.8.王师傅将木方刨成横截面如右图(单位:厘米)那样高40厘米的一根棱柱.虚线把横截面分成大小两部分,较大的那部分的面积占整个底面的60%.这个棱柱的体积是 立方厘米.9.小玲有两种不同形状的纸板.一种是正方形的,一种是长方形的(如下图).正方形纸板的总数与长方形纸板的总数之比是1:2.她用这些纸板做成一些竖式和横式的无盖纸盒,正好将纸板用完.在小玲所做的纸盒中,坚式纸盒的总数与横式纸盒的总数之比是 .10.在桌面上摆有一些大小一样的正方体木块,从正南方向看如下图(1),从正东方向看如下图(2),要摆出这样的图形至多能用 块正方体木块,至少需要 块正方体木块.二、解答题11.一个长方形水箱,从里面量长40厘米,宽30厘米,深35厘米.原来水深10厘米,放进一个棱长20厘米的正方形铁块后,铁块的顶面仍然高于水面,这时水面高多少厘米?12.如图表示一个正方体,它的棱长为4厘米,在它的上下、前后、左右的正中位置各挖去一个棱长为1厘米的正方体,问此图的表面积是多少?8 28 2412(图1)(图2)13.下图是正方体,四边形APQC 是表示用平面截正方体的截面,截面的线表现在展开图的哪里呢?把大致的图形在右面展开图里画出来.14.雨哗哗地不停地下着,如在雨地里放一个如图1那样的长方形的容器,雨水将它下满要用1小时.有下列(A )-(E )不同的容器(图2),雨水下满各需多少时间(注面是朝上的敞口部分.)PF2cm 2cm (A ) (B ) (C ) (D ) (E ) 雨———————————————答 案——————————————————————1. 96分米.正方体的底面积为384÷6=64(平方分米).故它的棱长为512÷64=8(分米),棱长的总和为8×12=96(分米).2. 8.96立方米.(3-0.1×2)×(1.8-0.1×2)×2=8.96(立米米).3. 圆柱体,200.96立方分米.(3.14×42)×4=200.96(立方分米).4. 216.这个立方体的表面由3×3×2+8×2+10×2=54个小正方形组成,故表面积为4×54=216(平方厘米).5. 241. ππππ816828,3164243122⨯=⨯⎪⎭⎫ ⎝⎛⨯==⨯⎪⎭⎫ ⎝⎛⨯⨯=柱锥V V ,故241=柱锥V V .6. 32.3立方分米.长方体的侧面积是67.92-19×2=29.92(平方分米),长方体的高为29.92÷17.6=1.7(分米),故长方体的体积为19×1.7=32.3(立方分米).7. 0.3长、宽、高分别是270厘米、18厘米和15厘米,而270、18和15的最大公约数为3(厘米),这就是小正方体棱长的最大值.8. 17200.设较大部分梯形高为x 厘米,则较小部分高为(28- x )厘米.依题意有: 4:6)28()824(21:)2412(21=⎥⎦⎤⎢⎣⎡-⨯+⨯⎥⎦⎤⎢⎣⎡+⨯x x 解得x =16,故这棱柱的体积为 1920040)1628()824(2116)2412(21=⨯⎥⎦⎤⎢⎣⎡-⨯+⨯+⨯+⨯(立方厘米).9. 3:1.一个竖式的无盖纸盒要用一个正方形纸板和4个长方形纸板,一个横式的无盖纸盒要用2个正方形纸板和3个长方形纸板.设小玲做的纸盒中,有x 个竖式的, y 个横式的,则共用正方形纸板(x +2 y )个,用长方形纸板(4 x +3 y )个,依题意有: (x +2 y ):(4 x +3 y )=1:3.解得x : y =3:1.10. 20,6.至多要20块(左下图),至少需要6块(右下图).11. 若铁块完全浸入水中,则水面将提高326)3040(203=⨯÷(厘米).此时水面的高小于20厘米,与铁块完全浸入水中矛盾,所以铁块顶面仍然高于水面.设放入铁块后,水深为x 厘米.因水深与容器底面积的乘积应等于原有水体积与铁块浸入水中体积之和,故有:x x 20201030403040⨯+⨯⨯=⨯解得x =15,即放进铁块后,水深15厘米.12. 大正方体的表面还剩的面积为()9014622=-⨯(厘米2),六个小孔的表面积为()305162=⨯⨯(厘米2),因此所求的表面积为90+30=120(厘米2).13. 截面的线在展开图中如右图的A -C -Q -P -A .14. 在例图所示的容器中,容积:按水面积=(10×10×30):(10×30)=10:1,需1小时接满,所以容器(A):容积:接水面积=(10×10×10):(10×10)=10:1,需1小时接满; 容器(B):容积:接水面积=(10×10×30):(10×10)=30:1,需3小时接满; 容器(C):容积:接水面积=(20×20×10-10×10×10):(10×10)=30:1,需32 1 2 1 2 2 1 2 1 1 1 1 1 1 1 1 1 2 1 1A小时接满;容器(D):容积:接水面积=(20×20×10-10×10×10):(20×10)=15:1,需1.5小时接满;容器(E):容积:接水面积=20×S:S=20:1(S为底面积),接水时间为2小时.。
小升初数学复习专题《立体图形》练习及答案

小升初数学复习专题《立体图形》练习一、填空题1.圆锥是由两个面组成,其中一个面是平面,另一个面是。
2.正方体的棱长是2a厘米,它的表面积是平方厘米,体积是立方厘米。
3.小明家挖了一个长为6m、宽为5m、深为2m的长方体地窖,这个地窖占地m2。
4.一个圆锥的体积是4.2dm3,底面积是0.9 dm2,高是。
5.一个正方体木块的棱长是6cm,把它削成一个最大的圆柱体,圆柱体的体积是cm3,再把这个圆柱体削成一个最大的圆锥体,圆锥体的体积约是cm3.6.圆柱的侧面沿高展开后是形或形。
一个圆柱的侧面沿高展开是正方形,正方形的边长是12.56cm,圆柱的底面积是cm2。
7.圆柱有个面是大小相同的圆,有一个面是面,圆柱的两个底面是半径相等的两个圆,两个底面间的距离叫做,圆柱周围的曲面叫做面。
8.把一个底面半径6厘米、高8厘米的圆柱体,切拼成一个近似的长方体,表面积比原来增加了平方厘米。
9.如图,在直角三角形MON中,MO=2cm,NO=5cm,如果分别以MO、NO边为轴旋转一周形M成圆锥,那么以MO为轴和以NO为轴的圆锥体积之比是。
二、单选题10.下面的图形中,()是正方体的展开图。
A.B.C.D.11.把一个圆柱的侧面展开,不可能得到()。
A.长方形B.正方形C.平行四边形D.梯形12.下列图形由()组成。
A.圆锥和圆柱B.圆柱和球体C.圆锥和球体D.圆锥和圆台13.小强测量一个土豆的体积,在一个棱长1分米的正方体容器中装了一些水,水面距离杯口2厘米(如图)。
他把土豆浸没在水中,有部分水溢出,接着他又把土豆取出来,水面下降了3厘米,土豆的体积是()立方厘米。
A.200B.500C.100D.30014.如图(单位:厘米),酒瓶中装有一些酒,倒进一只酒杯中,酒杯的直径是酒瓶内直径的一半,共能倒满()杯。
A.10B.15C.20D.3015.将一个棱长是6分米的正方体木块削成一个最大的圆锥,圆锥的体积是()立方分米。
人教版小学数学六年级《立体图形》基础训练题

立体图形基础题一、选择题1.一个长方体的长、宽、高都扩大2倍,它的体积扩大()倍。
A、2B、6C、8【答案】C【解析】长方体的体积=长×宽×高,长、宽和高都扩大2倍,则体积就扩大了2×2×2=8倍,根据此选择即可。
2.我们在画长方体时一般只画出三个面,这是因为长方体()。
A.只有三个面 B.只能看到三个面 C.最多只能看到三个面【答案】C【解析】把长方体放在桌面上,最多可以看到3个面。
根据此选择。
3.沿着圆柱上下两个底面的直径把圆柱切开,可以得出()形。
A.长方形B.圆形C.梯形【答案】A。
【解析】沿着圆柱的上下两个底面的直径把圆柱切开,可以得出长方形。
根据此选择即可。
4.一个圆锥是由橡皮泥捏成的,要切一刀把它分成两块,()切割,截面会是圆;()切割,截面会是三角形。
A.垂直于底面B.平行于底面【答案】B;A。
【解析】一个圆锥是由橡皮泥捏成的,要切一刀把它分成两块,平行于底面切割,截面会是圆;垂直于底面切割,截面会是三角形,根据此选择即可。
5.沿着圆柱的高,把圆柱的侧面展开,得不到()。
A. 梯形B.长方形C.正方形【答案】A【解析】沿着圆柱的高把圆柱的侧面展开,可以得到长方形或正方形,根据此选择即可。
6.一个长方体的长是4厘米,宽是3.5厘米,高是1.5厘米,它的底面的面积是()平方厘米。
A.6B.14C.5.25D.21【答案】B【解析】长方体的底面的面积=长×宽7.一个长方体的棱长和是36厘米,它的长、宽、高的和是()厘米。
A.3 B.9 C.6 D.4【答案】B【解析】棱长总和除以4,得出长、宽、高的和:36÷4=9;据此选择即可。
8.下列说法错误的是()。
A.正方体是长、宽、高都相等的长方体。
B.长方体与正方体都有12条棱。
C.长方体的6个面中至少有4个面是长方形。
D.长方体的6个面中最多有4个面是长方形。
【答案】D【解析】长方体的6个面一般情况下都是长方形,特殊的情况下,至少有4个面是长方形,所以D的说法是错误的;据此选择即可。
五年级奥数学练习试卷思维培训资料立体图形(一)
第二讲 立体图形(一)卷Ⅰ本讲的知识点主要是求复杂立体图形的表面积,竞赛班要求学生掌握复杂立体图形的组合、复杂的面垂直的图形组合和立体图形的切、拼、挖.对表面积的极值问题也要掌握.本讲重在培养学生的空间想象能力,教师可以让学生多思考,多动手,多画图,注重“数形结合”的思想。
本讲的主线是培养学生的空间想象能力,亮点在于极值问题的体现、例3及展开图的应用。
(一)巧解复杂的组合图形表面积【例1】 用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?分析:该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成.该图形的表面积等于(9+7+7)×2=46个小正方形的面积,所以该图形表面积为46平方厘米.专题精讲教学目标在墙角处有若干个体积都等于1的正方体堆成如图的立体图形(每个正方体都可独立地搬走,但如果抽走下面的正方体,上面的正方体就会自动落下去),有人希望搬走其中部分正方体,但从上面和前面用平行光线照射时,在墙面及地面上的影子不变,则最多可以搬走多少个小正方体?答案:留下靠墙及地面上的正方体,其余均可搬走共1+3+6=10块.想挑战吗?长方体:6个面,8个顶点,12条棱,表面积=2×(长×宽+宽×高+长×高).正方体:6个面(每个面都是正方形),8个顶点,12条棱(棱长相等),表面积=6×边长×边长.圆柱体:2个底面圆,1个侧面(长方形或正方形),表面积=2×底面圆面积+侧面面积.【例2】边长为1厘米的正方体,如图这样层层重叠放置,那么当重叠到第5层时,这个立体图形的表面积是多少平方厘米?分析:这个图形的表面积是俯视面、左视面、上视面得到的图形面积的2倍. 该立体图形的上下、左右、前后方向的表面面积都是15平方厘米,该图形的总表面积为90立方厘米.[拓展] 如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?分析:当小积木互相重合的面最多时表面积最小.设想27块边长为1的正方形积木,当拼成一个3×3×3的正方体时,表面积最小,现在要去掉2块小积木,只有在两个角上各去掉一块小积木,或在同一个角去掉两块相邻的积木时,表面积不会增加,该几何体表面积为54.【例3】(奥数网原创题)按照上题的堆法一直堆到N层(N>3),要想使总表面积恰好是一个完全平方数,则N的最小值是多少?N N 个小面,总表面积是6个“大面”,所以就增加到分析:每增加一层,每一个“大面”就增加到(1)23N(N+1)个小面,几何题变成数论题,问题转化为“3N(N+1)是一个完全平方数,N的最小值是几(N>3)?”因为N和N+1互质,所以N和N+1必须有一个是完全平方数,一个是平方数的3倍,但N+1不能是平方数的3倍,因为此时N被3除余2,不可能是完全平方数,所以N是平方数的3倍,N+1是完全平方数,开始试验:当N=3×12=3,不符合题意;当N=3×22=12,N+1=13,不是完全平方数;当N=3×32=27,N+1=28,不是完全平方数;当N=3×42=48,N+1=49,是完全平方数,所以N的最小值是48,即堆到第48层时,总表面积是完全平方数,为3×48×49=842.(二)表面积的最值问题【例4】一个正方体木块,棱长是15.从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体.这个木块剩下部分的表面积最少是多少?分析:截去一个小正方体,表面积不变,只有在截去的小正方体的面相重合时,表面积才会减少,所以要使木块剩下部分的表面积尽可能小,应该在同一条棱的两端各截去棱长7与8的小正方体(如图所示),这时剩下部分的表面积比原正方体的表面积减少最多.剩下部分的表面积最小是:15×15×6-7×7×2=1252.【例5】边长分别是3、5、8的三个正方体拼在一起,在各种拼法中,表面积最小多少?分析:三个正方体两两拼接时,最多重合3个正方形面,其中边长为3的正方体与其它两个正方体重合的面积不超过边长为3的正方形,边长为5和边长为8的正方体的重合面面积不超过边长为5的正方形,三个正方形表面积和为6×3×3+6×5×5+6×8×8-2×2×3×3-2×5×5=502.【例6】用10块长7厘米,宽5厘米,高3厘米的长方体积木堆成一个长方体,这个长方体的表面积最小是多少?分析:教师可以先提问:这个长方体的表面积最大是多少?为使表面积最大,要尽量保证10×2个7×5的面成为表面,想要做到这点很容易,只需将7×5面做底面,而后将10个立方体连排,衔接的面选用3×5的面(衔接的面将不能成为表面积),这样得到的长方体表面积最大.同样要想最小,可把7×5面做衔接的面,可得到10个长方体的连排,但此时我们还可以再制造出衔接面,如图:此时增加了2个5×7的面,减少了10个3×7的面,总体来讲表面积减少了.表面积是:2×(7×15+15×10+10×7)=650(平方厘米),所以这就是最小的表面积.[前铺] 用6块右图所示(单位:cm)的长方体木块拼成一个大长方体,有许多种拼法,其中表面积最小的是多少平方厘米?最大是多少平方厘米?分析:最小:66cm2;最大:(1×2+1×3+2×3)×2×6-1×2×5×2=112.【例7】要把12件同样的长a、宽b、高h的长方体物品拼装成一件大的长方体,使打包后表面积最小,该如何打包?(1)当b=2h时,按图几打包?(2)当b<2h时,按图几打包?(3)当b>2h时,按图几打包?分析:图2和图3正面的面积相同,侧面面积=正面周长×长方体长,所以正面的周长愈大表面积越大,图2的正面周长是8h+6b,图3的周长是12h+4b.两者的周长之差为2(b-2h).当b=2h时,图2和图3周长相等,可随意打包;当b﹤2h时,按图2打包;当b﹥2h时,按图3打包.[前铺] 要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体,表面积最小是多少?分析:考虑所有的包装方法,因为6=1×2×3,所以一共有两种拼接方式:第一种按长宽高1×1×6拼接,重叠面有三种选择,共3种包装方法.第二种按长宽高1×2×3拼接,有3个长方体并列方向的重叠面有三种选择,有2个长方体并列方向的重叠面剩下2种选择,一共有6种包装方法.其中表面积最小的包装方法如图所示,表面积为1034.卷Ⅱ(三)立体图形的切、拼、挖【例8】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为1/2厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为1/4厘米,那么最后得到的立体图形的表面积是多少平方厘米?分析:我们仍然从3个方向考虑.平行于上下表面的各面面积之和:2×2×2=8(平方厘米);左右方向、前后方向:2×2×4=16(平方厘米),1×1×4=4(平方厘米),1/2×1/2×4=1(平方厘米),1/4×1/4×4=1/4 (平方厘米),这个立体图形的表面积为:8+16+4+1+1/4=29又1/4 (平方厘米).【例9】如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,那么挖掉的小立方体的边长是多少厘米?分析:大立方体的表面积是20×20×6=2400平方厘米.挖掉了三个小正方体,反而多出了6个面,可以计算出每个面的面积:(2454-2400)÷6=9平方厘米,说明小正方体的棱长是3.[拓展1] 图中是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?分析:原正方体的表面积是4×4×6=96(平方厘米).每一个面被挖去一个边长是1厘米的正方形,同时又增加了5个边长是1厘米的正方体作为玩具的表面积的组成部分.总的来看,每一个面都增加了4个边长是1厘米的正方形.从而,它的表面积是:96+4×6=120平方厘米.[拓展2] 如右图,一个边长为3a厘米的正方体,分别在它的前后、左右、上下各面的中心位置挖去一个截口是边长为a厘米的正方形的长方体(都和对面打通).如果这个镂空的物体的表面积为2592平方厘米,试求正方形截口的边长.分析:原来正方体的表面积为:6×3a×3a=6×9a2(平方厘米),六个边长为a的小正方形的面积为(减少部分):6×a×a=6a2(平方厘米);挖成的每个长方体空洞增加的侧面积为:a×a×4×2=8a2(平方厘米);根据题意可得:54a2-6a2+3×8a2=2592,解得a2=36(平方厘米),故a=6厘米.【例10】有一个棱长为 5 cm的正方体木块,从它的每个面看都有一个穿透的完全相同的孔(右上图),求这个立体图形的内、外表面的总面积.分析:将此带孔的正方体看做由八个8cm3的正方体(8个顶点)和12个1cm3的正方体(12条棱)粘成的.每个正方体有两个面粘接,减少表面积4cm2,所以总的表面积为:(4×6)×8+6×12-4×12=216(cm2).[拓展] 边长分别是3、5、8的三个正方体拼在一起,在各种拼法中,表面积最小多少?分析:三个正方体两两拼接时,最多重合3个正方形面,其中边长为3的正方体与其它两个正方体重合的面积不超过边长为3的正方形,边长为5和边长为8的正方体的重合面面积不超过边长为5的正方形,三个正方形表面积和为6×3×3+6×5×5+6×8×8-2×2×3×3-2×5×5=502.【例11】如图,在一个正方体的两对侧面的中心各打通一个长方体的洞,在上下侧面的中心打通一个圆柱形的洞.已知正方体边长为10厘米,侧面上的洞口是边长为4厘米的正方形,上下侧面的洞口是直径为4厘米的圆,求此立体图形的表面积.分析:外侧表面积为:6×10×10-4×4×4-π×22×2=536-8π.内侧表面积为:16×4×3+2× (4×4-π×2)+2×2π×2×3=192+32-8π+24π=224+16π.总表面积=224+16π+536-8π=760+8π=785.12(平方厘米).【例12】如图,用455个棱长为1 的小正方体粘成一个大的长方体,若拆下沿棱的小正方体,则余下371个小正方体,问:所堆成的大长方体的棱长各是多少?拆下沿棱的小正方体后的多面体的表面积是多少?分析:设长方体棱长为分别为y zx、、.,他们只能取正整数,则有:4554(222)8455371x y zx y z⨯⨯=⎧⎨-+-+-+=-⎩因为4555713=⨯⨯方程组的有序正整数解只有(5,7,13),拆下沿棱的的小正方体后的多面体如图所示,首先计算突出在外面的6个平面,面积是2(11511335)206⨯⨯+⨯+⨯=再计算24个宽都是1的长⨯++=,总面积为358. 条,面积是8(1135)152(三)展开图【例13】在小于16 的自然数中选出6个不同的数,分别写在正方体的6个面上,要求各组相对的两个面上的数的乘积都相等,下图是正方体的展开图,并填上了1,请将其它数填上。
一年级奥数有趣的立体图形

立体几何图形是数学中一个重要的组成部分。
这节课通过看一看、认一认、想一想等活动使大家认识最基础的立体几何图形,从而增加对图形的感性认识,培养初步的图形概念认识,为以后的学习打下良好的基础。
【例1】 这是( )。
有( )个面,( )条棱,其中( )条长,( )条宽,( )条高,( )个顶点。
并在括号里面填上相应的名称。
并在展开图上标出相同的面。
【例2】 这是( )。
有( )个面,( )条棱,( )个顶点。
并在括号里面填上相应的名称。
并在展开图上标出相对的面。
【例3】 这是( )。
它是由( )个圆和( )个长方形组成的。
( )( )( )( )( )( )( )( )( )( )( )例题精讲知识框架有趣的立体图形【例4】这是()。
它是由()个圆和()个扇形组成的。
【例5】这是()。
它是由()个三角形和()个长方形组成的。
【例6】这些是()。
【例7】这是()。
【例8】 这是( )。
【随练1】 认一认,请在下面的括号里填上正确的名称。
【随练2】 将下图中(1)、(2)号棱锥剪开铺平后,哪一个是它对应的展开图,请用线连起来。
( )( )( )( )( )( )( )( )( )( )( )( )课堂检测家庭作业【作业1】看看摸摸,并在自己周围寻找具有这些形状的物体。
1.长方体2.正方体3.圆柱4.圆锥5.棱锥6.球【作业2】下图有哪些图形组成?【作业3】下列图中的(1)(2)(3)号盒子剪开铺平后,展开图是哪一个,请你用线连起来。
【作业4】用一些立体图形画一幅画吧!【作业5】请你将能找到的包装盒如:月饼盒、冷饮盒、鞋盒等等,用剪刀剪开,平铺在桌面上观察并画出展开图。
小学奥数思维训练-几何(三)立体图形(拓展训练)(通用,含答案)
保密★启用前小学奥数思维训练几何(三)立体图形一、选择题1.如图给出了一个立体图形的正视图、左视图和俯视图,图中单位为厘米.立体图形的体积()立方厘米.A.2πB.2.5πC.3πD.3.5π二、解答题2.将NNN(N是正整数)正方体的一些面涂上颜色以后,再将它切割成111的小正方体.已知至少有一面涂色的小正方体恰好占总数的52%,N是多少?3.小红的生日舞会,做了一顶圆锥形帽子,要将帽子涂成红色和蓝色,O点为顶点,BC为底面圆直径30cm,A点是OB的下三分之一处,OB=30cm,从A点出发,CA 之间最短的距离之上涂成红色,下边涂成蓝色.那么小红的帽子有多大地方涂的是蓝色?(π=3)4.一个正方体纸盒中恰好能放入一个体积为628立方厘米的圆柱,纸盒的容积有多大?(π=3.14)5.图中的立体图形是由14个棱长为5cm的立方体组成的,求这个立体图形的表面积?6.圆柱形的售报亭的高和底面直径相等(如图),开一个边长等于底面半径的正方形售报窗口.问窗口处挖去的圆柱部分的面积占圆柱形侧面积的几分之几?7.一个正方体木块,棱长是15.从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体.这个木块剩下部分的表面积最少是多少?8.如图,一个正方体形状的木块,棱长1米,沿水平方向将它锯成3片,每片又锯成4长条,每条又锯成5小块,共得到大大小小的长方体60块.那么这60块长方体表面积的和是多少平方米?9.如图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为1/2厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同,棱长为1/4厘米,那么最后得到的立体图形的表面积是多少平方厘米?10.把一个棱长为2cm正方体在同一平面的边的中点用线段连接起来,如图.然后把正方体顶点上的三角锥锯掉,请问最后所得的立体图形的表面积的多少平方厘米?(1.732×1.732=3)参考答案:1.A【解析】【详解】首先确定此图形为“不完整的圆柱”,先求出圆柱体积,再求出缺失的半个小圆柱,最后作差.如图,从给定的正视图、左视图和俯视图可以看出,该立体图形由一个半径为1厘米、高为1厘米的圆柱和一个半径为1厘米、高为2厘米的半圆柱组成..π×1×1×(1+2)-12π×1×1×2=2π,选A【点睛】这里的要点在于还原,还原的技巧在于先补全,再细雕刻2.5【解析】【详解】一个正整数×52%=另一个正整数,那么这个正整数必须能被25整除1352%25⎛⎫=⎪⎝⎭因为.那么N必须能被5整除.当N取最小N=5 正方体有5×5×5=125个小正方体涂色的小正方体5×5×5×52%=65(个)不可能被涂色的小正方体3×3×3=27(个)27+65小于125成立当N=2×5=10时,正方体有10×10×10=1000个小正方体涂色的小正方体10×10×10×52%=520(个)不可能被涂色的小正方体 8×8×8=512(个) 512+520大于1000 不成立同理N 大于10都不成立所以 N=53.750平方厘米【解析】【详解】底面周长为圆锥展开后 扇形的弧长蓝色面积=圆锥侧面积-红色面积底面周长=30×π=30×3=90侧面展开后扇形所在圆的周长=2×π×30=1809011802= 所以侧面展开图为半圆 蓝色面积=π×30×30×12-12×(20+20) ×30 =1350-600=750(平方厘米)4.800cm 3【解析】【详解】设纸盒棱长为x圆柱体积=22x x x π⨯⨯⨯=628 整理上边式子得x 3=800(cm 3) 即为纸盒容积.5.1050平方厘米【解析】【详解】用透视法观察 上、下两个面的面积相等4个侧面的每个侧面面积为6个小正方形面积底面棱长5×3=15 上、下两个面的面积=15×15×2=4504个侧面面积=4×6×5×5=600总面积=450+600=1050(平方厘米)6.1 12【解析】【详解】窗口上下的弧长为底面圆周长的六分之一窗口的高为圆柱的高的二分之一挖去的圆柱部分的面积占圆柱形侧面积的16×12=1127.1252【解析】【详解】截去一个小正方体,表面积不变.只有在截去的小正方体的面相重合时,表面积才会减少.所以要使木块剩下部分的表面积尽可能小,应该在同一条棱的两端各截去棱长7与8的小正方体(如图所示),这时剩下部分的表面积比原正方体的表面积减少最多.剩下部分的表面积最小是:15×15×6-7×7×2=1252.想想为什么不是15×15×6-7×7-8×8.8.24平方米【解析】【详解】我们知道每切一刀,多出的表面积恰好是原正方体的2个面的面积.现在一共切了(3-1)+(4-1)+(5-1)=9刀,而原正方体一个面的面积1×1=1(平方米),所以表面积增加了9×2×1=18(平方米).原来正方体的表面积为6×1=6(平方米).所以现在的这些小长方体的表积之和为6+18=24(平方米).9.29.25平方厘米【解析】【详解】俯视图发现上表面积就是大正方体的一个面的面积表面积为大正方体表面积加上3个小正方体的侧面积2×2×6+1×1×4+12×12×4+14×14×4=24+4+1+1 4=29.25(平方厘米)10.18.928cm2【解析】【详解】所得立体图形表面为6个正方形和8个等边三角形勾股定理等边三角形的高的平方=底边的平方-半个底边的平方=34底边的平方6个正方形面积=6×(1×1+1×1)=6×2=12等边三角形的高的平方=34×2=32等边三角形的高的平方×底边的平方=32×2=3所以等边三角形的高×底边=1.732,等边三角形的面积=1/2×1.732=0.866立体图形的表面积=12+8×0.866=18.928(cm2)。
五年级奥数学练习试卷思维培训资料立体图形(一)

第二讲 立体图形(一)卷Ⅰ本讲的知识点主要是求复杂立体图形的表面积,竞赛班要求学生掌握复杂立体图形的组合、复杂的面垂直的图形组合和立体图形的切、拼、挖.对表面积的极值问题也要掌握.本讲重在培养学生的空间想象能力,教师可以让学生多思考,多动手,多画图,注重“数形结合”的思想。
本讲的主线是培养学生的空间想象能力,亮点在于极值问题的体现、例3及展开图的应用。
(一)巧解复杂的组合图形表面积【例1】 用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?分析:该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成.该图形的表面积等于(9+7+7)×2=46个小正方形的面积,所以该图形表面积为46平方厘米.专题精讲教学目标在墙角处有若干个体积都等于1的正方体堆成如图的立体图形(每个正方体都可独立地搬走,但如果抽走下面的正方体,上面的正方体就会自动落下去),有人希望搬走其中部分正方体,但从上面和前面用平行光线照射时,在墙面及地面上的影子不变,则最多可以搬走多少个小正方体?答案:留下靠墙及地面上的正方体,其余均可搬走共1+3+6=10块.想挑战吗?长方体:6个面,8个顶点,12条棱,表面积=2×(长×宽+宽×高+长×高).正方体:6个面(每个面都是正方形),8个顶点,12条棱(棱长相等),表面积=6×边长×边长.圆柱体:2个底面圆,1个侧面(长方形或正方形),表面积=2×底面圆面积+侧面面积.【例2】边长为1厘米的正方体,如图这样层层重叠放置,那么当重叠到第5层时,这个立体图形的表面积是多少平方厘米?分析:这个图形的表面积是俯视面、左视面、上视面得到的图形面积的2倍. 该立体图形的上下、左右、前后方向的表面面积都是15平方厘米,该图形的总表面积为90立方厘米.[拓展] 如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?分析:当小积木互相重合的面最多时表面积最小.设想27块边长为1的正方形积木,当拼成一个3×3×3的正方体时,表面积最小,现在要去掉2块小积木,只有在两个角上各去掉一块小积木,或在同一个角去掉两块相邻的积木时,表面积不会增加,该几何体表面积为54.【例3】(奥数网原创题)按照上题的堆法一直堆到N层(N>3),要想使总表面积恰好是一个完全平方数,则N的最小值是多少?N N 个小面,总表面积是6个“大面”,所以就增加到分析:每增加一层,每一个“大面”就增加到(1)23N(N+1)个小面,几何题变成数论题,问题转化为“3N(N+1)是一个完全平方数,N的最小值是几(N>3)?”因为N和N+1互质,所以N和N+1必须有一个是完全平方数,一个是平方数的3倍,但N+1不能是平方数的3倍,因为此时N被3除余2,不可能是完全平方数,所以N是平方数的3倍,N+1是完全平方数,开始试验:当N=3×12=3,不符合题意;当N=3×22=12,N+1=13,不是完全平方数;当N=3×32=27,N+1=28,不是完全平方数;当N=3×42=48,N+1=49,是完全平方数,所以N的最小值是48,即堆到第48层时,总表面积是完全平方数,为3×48×49=842.(二)表面积的最值问题【例4】一个正方体木块,棱长是15.从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体.这个木块剩下部分的表面积最少是多少?分析:截去一个小正方体,表面积不变,只有在截去的小正方体的面相重合时,表面积才会减少,所以要使木块剩下部分的表面积尽可能小,应该在同一条棱的两端各截去棱长7与8的小正方体(如图所示),这时剩下部分的表面积比原正方体的表面积减少最多.剩下部分的表面积最小是:15×15×6-7×7×2=1252.【例5】边长分别是3、5、8的三个正方体拼在一起,在各种拼法中,表面积最小多少?分析:三个正方体两两拼接时,最多重合3个正方形面,其中边长为3的正方体与其它两个正方体重合的面积不超过边长为3的正方形,边长为5和边长为8的正方体的重合面面积不超过边长为5的正方形,三个正方形表面积和为6×3×3+6×5×5+6×8×8-2×2×3×3-2×5×5=502.【例6】用10块长7厘米,宽5厘米,高3厘米的长方体积木堆成一个长方体,这个长方体的表面积最小是多少?分析:教师可以先提问:这个长方体的表面积最大是多少?为使表面积最大,要尽量保证10×2个7×5的面成为表面,想要做到这点很容易,只需将7×5面做底面,而后将10个立方体连排,衔接的面选用3×5的面(衔接的面将不能成为表面积),这样得到的长方体表面积最大.同样要想最小,可把7×5面做衔接的面,可得到10个长方体的连排,但此时我们还可以再制造出衔接面,如图:此时增加了2个5×7的面,减少了10个3×7的面,总体来讲表面积减少了.表面积是:2×(7×15+15×10+10×7)=650(平方厘米),所以这就是最小的表面积.[前铺] 用6块右图所示(单位:cm)的长方体木块拼成一个大长方体,有许多种拼法,其中表面积最小的是多少平方厘米?最大是多少平方厘米?分析:最小:66cm2;最大:(1×2+1×3+2×3)×2×6-1×2×5×2=112.【例7】要把12件同样的长a、宽b、高h的长方体物品拼装成一件大的长方体,使打包后表面积最小,该如何打包?(1)当b=2h时,按图几打包?(2)当b<2h时,按图几打包?(3)当b>2h时,按图几打包?分析:图2和图3正面的面积相同,侧面面积=正面周长×长方体长,所以正面的周长愈大表面积越大,图2的正面周长是8h+6b,图3的周长是12h+4b.两者的周长之差为2(b-2h).当b=2h时,图2和图3周长相等,可随意打包;当b﹤2h时,按图2打包;当b﹥2h时,按图3打包.[前铺] 要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体,表面积最小是多少?分析:考虑所有的包装方法,因为6=1×2×3,所以一共有两种拼接方式:第一种按长宽高1×1×6拼接,重叠面有三种选择,共3种包装方法.第二种按长宽高1×2×3拼接,有3个长方体并列方向的重叠面有三种选择,有2个长方体并列方向的重叠面剩下2种选择,一共有6种包装方法.其中表面积最小的包装方法如图所示,表面积为1034.卷Ⅱ(三)立体图形的切、拼、挖【例8】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为1/2厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为1/4厘米,那么最后得到的立体图形的表面积是多少平方厘米?分析:我们仍然从3个方向考虑.平行于上下表面的各面面积之和:2×2×2=8(平方厘米);左右方向、前后方向:2×2×4=16(平方厘米),1×1×4=4(平方厘米),1/2×1/2×4=1(平方厘米),1/4×1/4×4=1/4 (平方厘米),这个立体图形的表面积为:8+16+4+1+1/4=29又1/4 (平方厘米).【例9】如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,那么挖掉的小立方体的边长是多少厘米?分析:大立方体的表面积是20×20×6=2400平方厘米.挖掉了三个小正方体,反而多出了6个面,可以计算出每个面的面积:(2454-2400)÷6=9平方厘米,说明小正方体的棱长是3.[拓展1] 图中是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?分析:原正方体的表面积是4×4×6=96(平方厘米).每一个面被挖去一个边长是1厘米的正方形,同时又增加了5个边长是1厘米的正方体作为玩具的表面积的组成部分.总的来看,每一个面都增加了4个边长是1厘米的正方形.从而,它的表面积是:96+4×6=120平方厘米.[拓展2] 如右图,一个边长为3a厘米的正方体,分别在它的前后、左右、上下各面的中心位置挖去一个截口是边长为a厘米的正方形的长方体(都和对面打通).如果这个镂空的物体的表面积为2592平方厘米,试求正方形截口的边长.分析:原来正方体的表面积为:6×3a×3a=6×9a2(平方厘米),六个边长为a的小正方形的面积为(减少部分):6×a×a=6a2(平方厘米);挖成的每个长方体空洞增加的侧面积为:a×a×4×2=8a2(平方厘米);根据题意可得:54a2-6a2+3×8a2=2592,解得a2=36(平方厘米),故a=6厘米.【例10】有一个棱长为 5 cm的正方体木块,从它的每个面看都有一个穿透的完全相同的孔(右上图),求这个立体图形的内、外表面的总面积.分析:将此带孔的正方体看做由八个8cm3的正方体(8个顶点)和12个1cm3的正方体(12条棱)粘成的.每个正方体有两个面粘接,减少表面积4cm2,所以总的表面积为:(4×6)×8+6×12-4×12=216(cm2).[拓展] 边长分别是3、5、8的三个正方体拼在一起,在各种拼法中,表面积最小多少?分析:三个正方体两两拼接时,最多重合3个正方形面,其中边长为3的正方体与其它两个正方体重合的面积不超过边长为3的正方形,边长为5和边长为8的正方体的重合面面积不超过边长为5的正方形,三个正方形表面积和为6×3×3+6×5×5+6×8×8-2×2×3×3-2×5×5=502.【例11】如图,在一个正方体的两对侧面的中心各打通一个长方体的洞,在上下侧面的中心打通一个圆柱形的洞.已知正方体边长为10厘米,侧面上的洞口是边长为4厘米的正方形,上下侧面的洞口是直径为4厘米的圆,求此立体图形的表面积.分析:外侧表面积为:6×10×10-4×4×4-π×22×2=536-8π.内侧表面积为:16×4×3+2× (4×4-π×2)+2×2π×2×3=192+32-8π+24π=224+16π.总表面积=224+16π+536-8π=760+8π=785.12(平方厘米).【例12】如图,用455个棱长为1 的小正方体粘成一个大的长方体,若拆下沿棱的小正方体,则余下371个小正方体,问:所堆成的大长方体的棱长各是多少?拆下沿棱的小正方体后的多面体的表面积是多少?分析:设长方体棱长为分别为y zx、、.,他们只能取正整数,则有:4554(222)8455371x y zx y z⨯⨯=⎧⎨-+-+-+=-⎩因为4555713=⨯⨯方程组的有序正整数解只有(5,7,13),拆下沿棱的的小正方体后的多面体如图所示,首先计算突出在外面的6个平面,面积是2(11511335)206⨯⨯+⨯+⨯=再计算24个宽都是1的长⨯++=,总面积为358. 条,面积是8(1135)152(三)展开图【例13】在小于16 的自然数中选出6个不同的数,分别写在正方体的6个面上,要求各组相对的两个面上的数的乘积都相等,下图是正方体的展开图,并填上了1,请将其它数填上。
小学六年级奥数题:立体图形
十三、立体图形( 1)一、填空题1.一个正方体的表面积是 384 平方分米,体积是 512 立方分米,这个正方体棱长的总和是.2.如图 , 在一块平坦的水泥地上 , 用砖和水泥砌成一个长方体的水泥池 , 墙厚为 10 厘米 ( 底面利用原有的水泥地 ). 这个水泥池的体积是.21.83单位 :米3.一个边长为 4 分米的正方形 , 以它的一条边为轴 , 把正方形旋转一周后 , 得到一个,这个形体的体积是.4.把 19 个边长为 2 厘米的正方体重叠起来堆成如右图所示的立方体 , 这个立方体的表面积是平方厘米 .V锥5. 图中是一个圆柱和一个圆锥( 尺寸如图 ). 问 :等于.48486.一个长方体的表面积是 67.92 平方分米 . 底面的面积是 19 平方分米 . 底面周长是 17.6 分米 , 这个长方体的体积是.7.一块长方体木块长 2.7 米 , 宽 1.8 分米 , 高 1.5 分米 . 要把它裁成大小相等的正方体小木块 , 不许有剩余 , 小正方体的棱长最大是分米.8.王师傅将木方刨成横截面如右图 ( 单位 : 厘米 ) 那样高 40 厘米的一根棱柱 . 虚线把横截面分成大小两部分 , 较大的那部分的面积占整个底面的60%.这个棱柱的体积是立方厘米 .28812249.小玲有两种不同形状的纸板 . 一种是正方形的 , 一种是长方形的 ( 如下图 ). 正方形纸板的总数与长方形纸板的总数之比是1:2. 她用这些纸板做成一些竖式和横式的无盖纸盒 , 正好将纸板用完 . 在小玲所做的纸盒中 , 坚式纸盒的总数与横式纸盒的总数之比是.10.在桌面上摆有一些大小一样的正方体木块 , 从正南方向看如下图 (1), 从正东方向看如下图 (2), 要摆出这样的图形至多能用块正方体木块 , 至少需要块正方体木块 .(图 1)(图2)二、解答题11.一个长方形水箱 , 从里面量长 40 厘米 , 宽 30 厘米 , 深 35 厘米 . 原来水深10 厘米 , 放进一个棱长 20 厘米的正方形铁块后 , 铁块的顶面仍然高于水面 , 这时水面高多少厘米 ?12.如图表示一个正方体 , 它的棱长为 4 厘米 , 在它的上下、前后、左右的正中位置各挖去一个棱长为 1 厘米的正方体 , 问此图的表面积是多少 ?13.下图是正方体 , 四边形 APQC 是表示用平面截正方体的截面 , 截面的线表现在展开图的哪里呢 ?把大致的图形在右面展开图里画出来 .D CA D C G HBBHG A B F EQEP F14.雨哗哗地不停地下着 , 如在雨地里放一个如图 1 那样的长方形的容器 , 雨水将它下满要用 1 小时 . 有下列 ( A)-( E) 不同的容器 ( 图 2), 雨水下满各需多少时间 ? ( 注:面是朝上的敞口部分.)雨10cm10cm10cm10cm10cm10cm10cm30cm图 110cm10cm10cm20cm10cm30cm 20cm10cm10cm 20cm10cm20cm10cm10cm20cm 10cm2cm10cm10cm ( A)( B)( C)( D )( E)10cm10cm20cm20cm10cm10cm10cm10cm10cm10cm10cm10cm20cm2cm 10cm10cm10cm10cm———————————————答案——————————————————————1. 96 分米.正方体的底面积为 384÷6=64(平方分米 ). 故它的棱长为 512÷64=8( 分米 ), 棱长的总和为 8×12=96(分米 ).2. 8.96 立方米 .(3-0.1 ×2) ×(1.8-0.1 ×2) ×2=8.96( 立米米 ).3.圆柱体 ,200.96 立方分米 .(3.14 × 42) ×4=200.96( 立方分米 ).4. 216.这个立方体的表面由 3×3×2+8×2+10×2=54 个小正方形组成 , 故表面积为4×54=216(平方厘米 ).5.1. 241 4 21682V 锥 1 .V 锥4, V 柱8168,故3 23 2V 柱246. 32.3 立方分米 .长方体的侧面积是 67.92-19 × 2=29.92( 平方分米 ), 长方体的高为 29.92 ÷ 17.6=1.7( 分米 ), 故长方体的体积为 19× 1.7=32.3( 立方分米 ).7. 0.3长、宽、高分别是 270 厘米、 18 厘米和 15 厘米 , 而 270、18 和 15 的最大公约数为 3( 厘米 ), 这就是小正方体棱长的最大值 .8.17200.设较大部分梯形高为 x 厘米 , 则较小部分高为 ( 28- x) 厘米 . 依题意有 :1 (12 24) x :1(24 8) (28 x)6 : 422解得 x =16, 故这棱柱的体积为11 (12 24) 16( 24 8) (28 16) 40 19200 ( 立方厘米 ).229. 3:1.一个竖式的无盖纸盒要用一个正方形纸板和 4 个长方形纸板 , 一个横式的无盖纸盒要用 2 个正方形纸板和 3 个长方形纸板 . 设小玲做的纸盒中 , 有 x 个竖式的 , y 个横式的 , 则共用正方形纸板 ( x +2 y) 个, 用长方形纸板 (4 x +3 y) 个, 依题意有 : ( x +2 y):(4 x +3 y)=1:3. 解得 x: y =3:1.10. 20,6.至多要 20 块( 左下图 ), 至少需要 6 块( 右下图 ).2211211111111112211211.若铁块完全浸入水中 , 则水面将提高 203 (40 30) 6 2( 厘米 ). 此时水面3的高小于 20 厘米 , 与铁块完全浸入水中矛盾, 所以铁块顶面仍然高于水面.设放入铁块后 , 水深为 x 厘米 . 因水深与容器底面积的乘积应等于原有水体积与铁块浸入水中体积之和 , 故有 :40 30x 40 30 10 2020x解得 x =15, 即放进铁块后 , 水深 15 厘米 .12.大正方体的表面还剩的面积为 6 42 12 90 (厘米2),六个小孔的表面积为 6 12 5 30 (厘米2),因此所求的表面积为90+30=120( 厘米2).13.截面的线在展开图中如右图的 A- C- Q- P- A.C DD C GHD QPAA B F EB A14.在例图所示的容器中 , 容积 : 按水面积 =(10× 10×30):(10 ×30)=10:1, 需 1 小时接满 , 所以容器 (A): 容积 : 接水面积 =(10 ×10×10):(10 ×10)=10:1, 需 1 小时接满 ;容器 (B): 容积 : 接水面积 =(10 ×10×30):(10 ×10)=30:1, 需 3 小时接满 ;容器 (C): 容积 : 接水面积 =(20 ×20×10-10 × 10×10):(10 ×10)=30:1, 需 3 小时接满 ;容器 (D): 容积 : 接水面积 =(20 × 20× 10-10 × 10× 10):(20 × 10)=15:1, 需1.5 小时接满 ;容器 (E): 容积 : 接水面积 =20× S:S=20:1(S 为底面积 ), 接水时间为 2 小时 .。
一年级数学10道奥数练习题立体图形找规律计算解决问题附答案

一年级数学10道奥数练习题立体图形找规律计算解决问题附
答案
一直觉得奥数属于兴趣特长类的学习,比较适合数学方面有天赋和爱好的孩子。
如果孩子乐于钻研,奥数其实是很有趣的,而且特别锻炼孩子的思维。
答案解析——
2.用一个平底锅烙饼,每次最多只能烙2个,烙熟一个需要2分钟(正面反面各需用时1分钟),若烙熟3个至少需要用时几分钟?
答案解析——
3.图形认知——
答案解析——
4.立体图形——
答案解析——
5、立体图形认知——
答案解析——
6.一共多少人在一起玩游戏。
答案解析——
7.计算——
答案解析——
8.计算——
9.计算——
答案解析——
10.卡片组成数——
答案解析——
奥数题算是兴趣训练,如果孩子对数学感兴趣,并在这方面有特长,可以每天做一道奥数题活动活动脑子。
五年级上册奥数试题第9讲.立体图形的体积(含解析)人教版
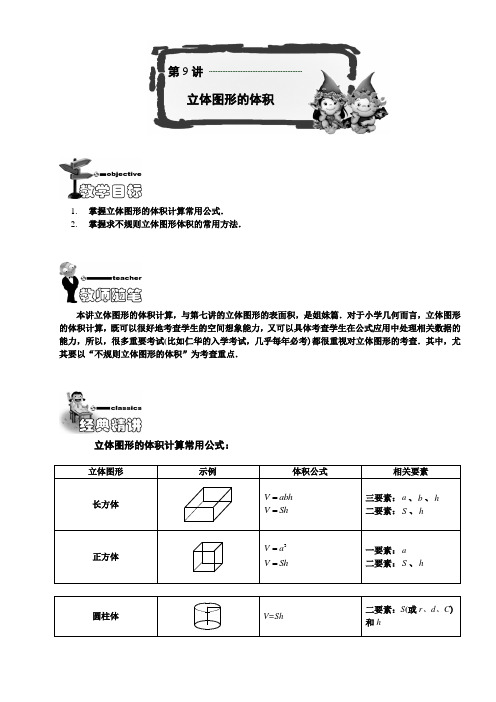
1.掌握立体图形的体积计算常用公式.2.掌握求不规则立体图形体积的常用方法.本讲立体图形的体积计算,与第七讲的立体图形的表面积,是姐妹篇.对于小学几何而言,立体图形的体积计算,既可以很好地考查学生的空间想象能力,又可以具体考查学生在公式应用中处理相关数据的能力,所以,很多重要考试(比如仁华的入学考试,几乎每年必考)都很重视对立体图形的考查.其中,尤其要以“不规则立体图形的体积”为考查重点.立体图形的体积计算常用公式:立体图形示例体积公式相关要素长方体V abh=V Sh=三要素:a、b、h二要素:S、h正方体3V a=V Sh=一要素:a二要素:S、h圆柱体V=Sh 二要素:S(或r、d、C)和h第9讲立体图形的体积圆锥体V=13Sh 二要素:S 、h不规则形体的体积常用方法:一、 化虚为实法 二、 切片转化法 三、 先补后去法 四、 实际操作法 五、 画图建模法【例 1】 (第五届《小数报》数学竞赛决赛)一个长方体的宽和高相等,并且都等于长的一半(如图).将这个长方体切成12个小长方体,这些小长方体的表面之和为600平方分米.求这个大长方体的体积.【分析】 设大长方体的宽(高)为a 分米,则长为2a ,右(左)面积为2a ,其余面的面积为22a ,根据题意, 22222862600a a a ⨯++⨯= 所以225a =,5a =. 大长方体的体积2555250=⨯⨯⨯=(立方分米).[铺垫] (第十五届“迎春杯”决赛)把一根长2.4米的长方体木料锯成5段(如图),表面积比原来增加了96平方厘米.这根木料原来的体积是_____立方厘米.2.4米[分析] 96812÷=(平方厘米),122402880⨯=(立方厘米).所以这根木料原来的体积为2880立方厘米.【例 2】 (第九届“祖冲之杯”数学邀请赛)有一个长方体的盒子,从里面量长40厘米,宽12厘米,高7厘米,在这个盒子里放长5厘米,宽4厘米,高3厘米的长方体木块.最多可放 块.【分析】 下图表明34⨯的长方形可以填满712⨯的长方形.于是534⨯⨯的长方体可以填满40712⨯⨯的长方体,即盒子中最多可放这种长方体40712(534)56⨯⨯÷⨯⨯=(个).[巩固] (第九届“迎春杯”数学竞赛决赛)把1个棱长是3厘米的正方体分割成若干个小的正方体,这些小正方体的棱长必须是整厘米数.如果这些小正方体的体积不要求都相等,那么最少可分割 成 个小正方体.[分析] 因为小正方体的棱长只可能是2厘米或1厘米.必须分割出棱长是2厘米的小正方体才能使数量规则立体图形体积的计算444433333减少.显然,棱长是3厘米的正方体只能切割出一个棱长为2厘米的小正方体,剩余部分再切割出33322227819+=(个)⨯⨯-⨯⨯=-=个棱长是1厘米的小正方体,这样总共可以分割成11920小正方体.现有一张长40厘米、宽20厘米的长方形铁皮,请你用它做一只深是5厘米的长方体无盖铁皮盒(焊接处及铁皮厚度不计,容积越大越好),你做出的铁皮盒容积是多少立方厘米?【分析】如图,在4020⨯的长方形铁皮的四角截去边长5厘米的正方形铁皮,然后焊接成长方形无盖铁皮盒.这个铁皮盒的长405530=--=(厘米).宽205510=--=(厘米),高5=(厘米).体积301051500=⨯⨯=(立方厘米).如图,在4020⨯长方形铁皮的左侧两角上割下 边长5厘米的正方形(二块),紧密焊接到右侧的中间部分,这样做成的无盖铁皮盒的长40535=-=(厘米),宽205510=--=(厘米), 高5=(厘米),体积351051750=⨯⨯=(立方厘米).如图,在4020⨯的长方形铁皮的左右两侧各割 下一条宽为5厘米的长方形铁皮(共二块),分 别焊到上、下的中间部分,这样做成的无盖铁 皮盒的长40555520=----=(厘米), 宽20=(厘米),高5=(厘米),体积202052000=⨯⨯=(立方厘米). 因此,最后一种容积最大.[铺垫] (第三届“华杯赛”复赛)如图从长为13厘米,宽为9厘米的长方形硬纸板的四角去掉边长2厘米的正方形,然后,沿虚线折叠成长方体容器.这个容器的体积是多少立方厘米?[分析] 容器的底面积是(134)(94)45-⨯-=(平方厘米),高为2厘米,所以容器的体积是,45290⨯=(立方厘米).【例 3】 (第七届“华杯赛”决赛)用大小相等的无色透明玻璃小正方体和红色玻璃小正方体拼成一个大正方体1111ABCD A B C D -(如图),大正方体内的对角线1AC ,1BD ,1CA ,1DB 所穿的小正方体都是红色玻璃小正方体,其它部分都是无色透明玻璃小正方体,小红正方体共用了401个,问:无色透明小正方体用了多少个?【分析】 1AC 、1BD ,1CA ,1DB ,四条对角线都穿过在正中央的那个小正方体.除此而外,每条对角线穿过相同的小正方体,所以每条对角线穿过401111014-+=个小正方体这就表明大正方体的每条边由101个小正方体组成.因此大正方体由3101个小正方体组成,其中无色透明的小正方体有310140110303014011029900-=-=. 即用了1029900个无色透明的小正方体.D 1C 1B 1A 1D C BA【例 4】 小明用若干个大小相同的正方体木块堆成一个几何体,这个几何体从正面看如下图左,从上面看如下图右.那么这个几何体至少用了 块木块.【分析】 这道题很多同学认为答案是26块.这是受思维定势的影响,认为右图中每一格都要至少放一块.其实,有些格不放,看起来也是这样的.如右图,带阴影的3块不放时,小正方体块数最少,为23块.[拓展] 右图是由22个小正方体组成的立体图形,其中共有多少个大大小小的正方体?由两个小正方体组成的长方体有多少个?[分析] 正方体只可能有两种:由1个小正方体构成的正方体,有22个;由8个小正方体构成的222⨯⨯的正方体,有4个. 所以共有正方体22426+=(个). 由两个小正方体组成的长方体,根据摆放的方向可分为下图所示的上下位、左右位、前后位三种,其中上下位有13个,左右位有13个,前后位有14个,共有13131440++=(个).【例 5】 有黑白两种颜色的正方体积木,把它摆成右图所示的形状,已知相邻(有公共面)的积木颜色不同,标A 的为黑色,图中共有黑色积木多少块?【分析】 分层来看,如下图(切面平行于纸面)共有黑色积木17块.[拓展] 这个图形,是否能够由112⨯⨯的长方体搭构而成? [分析] 每一个112⨯⨯的长方体无论怎么放,都包含了一个黑色正方体和一个白色正方体,而黑色积木有17块,白色积木有15块,所以该图形不能够由112⨯⨯的长方体搭构而成.A不规则立体图形体积的计算【例 6】 一个酒瓶里面深30cm ,底面内直径是10cm ,瓶里酒深15cm .把酒瓶塞紧后使其瓶口向下倒立这时酒深25cm .酒瓶的容积是多少?(π取3)253015【分析】 观察前后,酒瓶中酒的总量没变,即瓶中液体体积不变.当酒瓶倒过来时酒深25cm ,因为酒瓶深30cm ,这样所剩空间为高5cm 的圆柱,再加上原来15cm 高的酒即为酒瓶的容积.酒的体积:101015π375π22⨯⨯=瓶中剩余空间的体积1010(3025)π125π22-⨯⨯=酒瓶容积:375π125π500π1500(ml)+==[巩固] 输液100毫升,每分钟输2.5毫升.如图,请你观察第12分钟时图中的数据,问:整个吊瓶的容积是多少毫升?[分析] 100毫升的吊瓶在正放时,液体在100毫升线下方,上方是空的,容积是多少不好算.但倒过来后,变成圆柱体,根据标示的格子就可以算出来.由于每分钟输2.5毫升,12分钟已输液2.51230⨯=(毫升),因此开始输液时液面应与50毫升的格线平齐,上面空的部分是50毫升的容积.所以整个吊瓶的容积是 10050150+=(毫升).【例 7】 一只装有水的圆柱形玻璃杯,底面积是80平方厘米,高是15厘米,水深10厘米.现将一个底面积是16平方厘米,高为12厘米的长方体铁块竖放在水中后.现在水深多少厘米?【分析】 8010(8016)12.5⨯÷-=,因为12.512>,所以此时水已淹没过铁块,8010(8016)1232⨯--⨯=,32800.4÷=,所以现在水深为120.412.4+=厘米[铺垫] 一只装有水的圆柱形玻璃杯,底面积是80平方厘米,高是15厘米,水深8厘米.现将一个底面积是16平方厘米,高为12厘米的长方体铁块竖放在水中后.现在水深多少厘米?[分析] 根据等积变化原理:用水的体积除以水的底面积就是水的高度.(法1):808(8016)6406410⨯÷-=÷=(厘米);(法2):设水面上升了x 厘米.根据上升部分的体积=浸入水中铁块的体积列方程为:8016(8)x x =+,解得:2x =,8210+=(厘米). (提问“圆柱高是15厘米”,和“高为12厘米的长方体铁块”这两个条件给的是否多余?)[拓展] 一只装有水的圆柱形玻璃杯,底面积是80平方厘米,高是15厘米,水深13厘米.现将一个底面积是16平方厘米,高为12厘米的长方体铁块竖放在水中后.现在水深多少厘米?【分析】 玻璃杯剩余部分的体积为80(1513)160⨯-=立方厘米,铁块体积为1612192⨯=立方厘米,因为160192<,所以水会溢出玻璃杯,所以现在水深就为玻璃杯的高度15厘米总结铁块放入玻璃杯会出现三种情况①放入铁块后,水深不及铁块高.②放入铁块后,水深比铁块高但未溢出玻璃杯,③水有溢出玻璃杯.小故事 教师可以在此穿插一个关于阿基米德测量黄金头冠的体积的故事.一天国王让工匠做了一顶黄金的头冠,不知道工匠有没有掺假,必须知道黄金头冠的体积是多少,可是又没有办法来测量.(如果知道体积,就可以称一下纯黄金相应体积的重量,再称一下黄金头冠的重量,就能知道是否掺假的结果了)于是,国王就把测量头冠体积的任务交给他的大臣阿基米德.(小朋友们,你们能帮阿基米德解决难题吗?)阿基米德苦思冥想不得其解,就连晚上沐浴时还在思考这个问题.当他坐进水桶里,看到水在往外满溢时,突然灵感迸发,大叫一声:“我找到方法了……”,就急忙跑出去告诉别人,大家看到了一个还光着身子的阿基米德.他的方法是:把水桶装满水,当把黄金头冠放进水桶,浸没在水中时,所收集的溢出来的水的体积正是头冠的体积.【例 8】(武汉明心杯数学挑战赛)如图所示,一个555⨯⨯的立方体,在一个方向上开有115⨯⨯的孔,在另一个方向上开有215⨯⨯的孔,在第三个方向上开有315⨯⨯的孔,剩余部分的体积是多少?表面积为多少?【分析】求体积:开了315⨯⨯的孔,挖去31515⨯⨯=,开了115⨯⨯的孔,挖去11514⨯⨯-=;开了215⨯⨯的孔,挖去215(22)6⨯⨯-+=,剩余部分的体积是:555(1546)100⨯⨯-++=.(另解)将整个图形切片,如果切面平行于纸面,那么五个切片分别如图:得到总体积为:22412100⨯+=.求表面积:表面积可以看成外部和内部两部分.外部的表面积为55612138⨯⨯-=,内部的面积可以分为前后、左右、上下三个方向,面积分别为()22515121320⨯⨯+⨯-⨯-⨯=、()2153513132⨯⨯+⨯-⨯-=、()2151511214⨯⨯+⨯-⨯-=,所以总的表面积为138203214204+++=.(另解)运用类似于三视图的方法,记录每一方向上的不同位置上的裸露正方形个数:前后方向:32上下方向:30左右方向:40总表面积为()2323040204⨯++=.[巩固]一个由125个同样的小正方体组成的大正方体,从这个大正方体中抽出若干个小正方体,把大正方体中相对的两面打通,右图就是抽空的状态.右图中剩下的小正方体有多少个?[分析]解法一:(用“容斥原理”来解)由正面图形抽出的小正方体有5525⨯=个,由侧面图形抽出的小正方体有5525⨯=个,由底面图形抽出的小正方体有4520⨯=个,正面图形和侧面图形重合抽出的小正方体有1221228⨯+⨯+⨯=个,正面图形和底面图形重合抽出的小正方体有13227⨯+⨯=个,底面图形和侧面图形重合抽出的小正方体有1211227⨯+⨯+⨯=个,三个面的图形共同重合抽出的小正方体有4个.根据容斥原理,252520877452++---+=,所以共抽出了52个小正方体.1255273-=,所以右图中剩下的小正方体有73个.注意这里的三者共同抽出的小正方体是4个,必须知道是哪4块,这是最让人头疼的事.但你可以先构造空的两个方向上共同部分的模型,再由第三个方向来穿过“花墙”.这里,化虚为实的思想方法很重要. 解法二:(用“切片法”来解) 可以从上到下切五层,得: (1) 从上到下五层,如图:(2) 或者,从右到左五片,如图:请注意这里的挖空的技巧是:先认一种方向.比如:从上到下的每一层,首先都应该有第一层的空四块的情况,即——如果挖第二层:第(1)步,把中间这些位置的四块挖走如图:第(2)步,把从右向左的两块成线地挖走.(请注意挖通的效果就是成线挖去),如图:第(3)步,把从前向后的一块(请注意跟第二层有关的只是一块!)挖成线!如图:总结一下“切片法”: 全面打洞(例如本题,五层一样)挖块成线(例如本题,在前一次的基层上,一条线一条线地挖). 这里体现的思想方法是:化整为零,有序思考!【例10】 如图,已知A 、B 、C 分别是相邻的三条棱的中点.沿三个中点连成一个正三角形,把原来的立方体切掉一角.如果原来的立方体棱长为8,求: ⑴切掉的小部分的体积是多少? ⑵剩下的大部分的体积是多少?【分析】 本题应用相关体积公式.⑴2111244103323V Sh ==⨯⨯⨯=锥BCA⑵3185013V V =-=剩锥⑴教师可以沿三个不相邻的顶点再切一下,求小的图形与大的图形的体积各是多少?小的是:21118885323⨯⨯⨯=;大的是:24263.⑵教师可以提问:去掉一个角上的部分后,它的体积是原立方体体积的几分之几?【例11】 如图,是一个正方体,将正方体的A 、C 、B '、D '四个顶点两两连接就构成一个正四面体,已知正方体的边长为3,求正四面体的体积.D′C′B′A′DC BA【分析】 这个正四面体可以看作由正方体切掉A '、C '、B 、D 四个角后得到的,如图所示:D′D′D′C′B′B′B′B′A′DCC BAAA A所以正四面体的体积1133343332718932⎛⎫=⨯⨯-⨯⨯⨯⨯⨯=-= ⎪⎝⎭.【例12】 如图是一个四棱锥的展开图,该展开图由正三角形和正方形构成,其中正方形的面积为8平方厘米,那么该四棱锥的体积为多少?【分析】 知道四棱锥的底面面积,只要知道四棱锥的高就能求得四棱锥的体积.将四棱锥沿对角线和顶点构成的平面剖开,剖面是一个三角形.该三角形的斜边等于正方形的对角线,直角边等于正方形和等边三角形的边长,所以三角形是一个等腰直角三角形,它的高等于对角线的一半,根据对称性,这条高也等于四棱锥的高.本题,我们要想知道四棱锥的高,如果仅仅通过操作法,可能无法准确得知.我们隆重推出“画图建模法”,比如:请注意在一个正方体中如何作等边三角形,这一经验,会让我们“类比联想”到,如何让四个等边三角形围绕一个正方形,得到四棱锥.另外,这个四棱锥的高正好等于原正方体棱长的一半.根据小正方形面积是8推得,大正方形面积是小正方形的2倍, 所以大正方形面积是16,所以大正方体的边长是4. 所以小正方体的棱长为2. 即四棱锥的高度为2.四棱锥的体积为168233⨯÷=立方厘米.1.(第十一届“迎春杯”)有一个长方体,长是宽的2倍,宽是高的3倍;长的12与高的13之和比宽多1厘米.这个长方体的体积是 立方厘米.【分析】 长的12即宽,所以高的13就是1厘米,高是3厘米,宽是339⨯=厘米,长是9218⨯=厘米,体积是3918486⨯⨯=(立方厘米).2. (第六届“华杯赛”决赛口试)某工人用薄木板钉成一个长方体的邮件包装箱,并用尼龙编织条(如图所示)在三个方向上的加固.所用尼龙编织条分别为365厘米,405厘米,485厘米.若每个尼龙加固时接头重叠都是5厘米.问这个长方体包装箱的体积是多少立方米?【分析】 长方体中高+宽1(3655)1802=-=, ⑴高+长1(4055)2002=-=, ⑵长+宽1(4855)2402=-=, ⑶⑵-⑴:长-宽20=, ⑷ ⑷+⑶:长130=,从而宽110=, 代入⑴得高70=. 所以长方体体积为701101301001000⨯⨯=(立方厘米) 1.001=(立方米)3. 有三个大小一样的正方体,将接触的面用胶粘接在一起成图示的形状,表面积比原来减少了16平方厘米.求所成形体的体积.【分析】 三个小正方体拼接成图中的样子,减少了小正方体的4个侧面正方形的面积,表面积减少了16平方厘米,每个正方形侧面为1644÷=平方厘米,每个正方体棱长为2厘米,三个小正方体体积(即所成形体的体积)高宽长是33224⨯=立方厘米.4.一个盖着瓶盖的瓶子里面装着一些水,瓶底面积为10平方厘米,(如下图所示),请你根据图中标明的数据,计算瓶子的容积是______.【分析】 由已知条件知,第二个图上部空白部分的高为752cm -=,从而水与空着的部分的比为4:22:1=,由图1知水的体积为104⨯,所以总的容积为()4022160÷⨯+=立方厘米. 5.有许多相同的立方体,每个立方体的六个面上都写着同一个数字(不同的立方体可以写相同的数字)先将写着2的立方体与写着1的立方体的三个面相邻,再将写着3的立方体写着2的立方体相邻(见左下图).依这样构成右下图所示的立方体,它的六个面上的所有数字之和是多少?33223323322323111111【分析】 第一层如下图,第二层、第三层依次比上面一层每格都多1(见下图).765434565第三层654323454第二层第一层343212345上面的9个数之和是27,由对称性知,上面、前面、右面的所有数之和都是27.同理,下面的9个数之和是45,下面、左面、后面的所有数之和都是45.所以六个面上所有数之和是(2745)3216+⨯=.6.把一个长方体形状的木料分割成3小块,使这3小块的体积相等.已知这长方体的长为15厘米,宽为12厘米,高为9厘米.分割时要求只能锯两次,如图1就是一种分割线的图.除这种分割的方法外,还可有其他不同的分割方法,请把分割线分别画在图2的各图中.图1图2【分析】分割方法很多,如图3,给出以下9种分割方法:图3低地的价值加州海岸的一座城市中,所有适合建筑的土地在不断的开发中都已经被开发,并予以利用,城市的地皮不断飙升着。
小学数学六年级奥数《立体图形(2)》练习题(含答案)

小学数学六年级奥数《立体图形(2)》练习题(含答案)一、填空题1.右图表示的长方体(单位:米),长和宽都是3米,体积是24立方米.这个长方体的表面积是 平方米.2.把两个相同的正方体拼在一起成一个长方体,这个长方体的表面积是两个正方体表面积之和的 分之 .3.一个长6分米、宽4分米、高2分米的木箱.用三根铁丝捆起来(如右图),打结处要用1分米铁丝.这根铁丝总长至少为 分米.4.一个长方体的底面、侧面和前面的面积分别是12平方厘米、8平方厘米和6平方厘米.那么它的体积是 .5.如图,从长为13厘米,宽为9厘米的长方形硬纸板的四角去掉2厘米的正方形,然后,沿虚线折叠成长方体容器.这个容器的体积是 立方厘米.6.将高都是1米,底面半径分别为1.5米、1米和0.5米的三个圆柱组成一个物体.这个物体的表面积是 .(14.3=π)7.把一个长、宽、高分别是7,截成两个长方体,使这两个长方体的表面积之和最大.这时表面积之和是平方厘米.8.一个圆柱形玻璃杯中盛有水,水面高2.5厘米,玻璃内侧的底面积是72平方厘米,在这个杯中放进棱长6厘米的正方体的铁块后,水面没有淹没铁块,这时水面高厘米.9.正方体的每一条棱长是一个一位数;表面的每个正方形面积是一个两位数,整个表面积是一个三位数.而且若将正方形面积的两位数中两个数码调过来恰好是三位数的十位上与个位上的数码.这个正方形的体积是 .10.如图所示,剪一块硬纸片可以做成一个多面体的纸模型(沿虚线折,沿实线粘).这个多面体的面数、顶点数和棱数的总和是 .二、解答题11.在底面边长为60厘米的正方形的一个长方体的容器里,直立着一个长1米,底面为正方形,边长15厘米的四棱柱铁棍.这时容器里的水半米深,现在把铁棍轻轻地向正上方提起24厘米,露出水面的四棱柱铁棍浸湿部分长多少厘米?12.一个长、宽和高分别为21厘米、15厘米和12厘米的长方体,现从它的上面尽可能大地切下一个正方体,然后从剩余的部分再尽可能大地切下一个正方体,最后再从第二次剩余的部分尽可能大地切下一个正方体,剩下的体积是多少立方厘米?13.如图是一个立体图形的侧面展开图,求它的全面积和体积.14.现有一个长,宽,高都为1cm的正方体,一个长,宽,为1cm,高为2cm的长方体,三个长,宽为1cm,高为3cm的长方体.下列图是把这五个立体图形合并成某一立体图形时,从上面,前面,侧面所看到的图形.试利用下面三个图形把合并成的立体图形如(例)的样子画出来,并求出其表面积.———————————————答 案——————————————————————1. 50.长方体的底面积为3×3=9(米2),故其高为322924=÷(米),从而其表面积为5023223322333=⨯⎪⎭⎫ ⎝⎛⨯+⨯+⨯(米2)2. 六分之五.设一个正方体的一个面积为1,则两个正方体表面积为1×6×2=12.而将两个正方体拼成一个长方体之后,这个长方体的表面积是10,它是12的65.3. 43.铁丝总长等于长方体长的2倍,宽的4倍与高的6倍之和,再加上三个打结处所用铁丝长,即(6×2+2×6+4×4)+1×3=43(分米)4. 24平方厘米.设长方体的长宽高分别为x ,y ,z 厘米,体积为V 立方厘米,则xy =12, yz=8, xz=6,将上面三式相乘,有5766812222=⨯⨯=z y x ,故24=xyz ,即24=V .5. 90.长方体容器的长为13-2×2=9(厘米),宽为9-2×2=5(厘米),高为2厘米,故体积9×5×2=90(立方厘米).6. 32.97平方米.这个物体的表面积是大圆柱的表面积加上中、小圆柱的侧面积,故它的表面积为:前面所看到的图形97.325.1015.0211215.1225.12≈=⨯⨯+⨯⨯+⨯⨯+⨯⨯πππππ(平方米).7. 298.把一个长方体截成两个长方体,只截一次,增加两个横截面,由题意应增加面积为7×6=42(平方厘米)的横截面,其表面之和最大,最大面积为(7×6+7×5+6×5)×2+7×6×2=298(平方厘米).8. 5.水的体积为72×2.5=180(cm 2),放入铁块后可以将水看作是底面积为72-6×6=36(cm 2)的柱体,所以它的高为180÷36=5(cm )9. 343.根据“正方体的每一条棱长是一个一位数,表面积的每个正方形面积是一个两位数,整个表面积是一个三位数”的条件,可以判断正方体的棱长有5,6,7,8,9这五种可能性.由下表的数据及条件: “将正方形面积的两位数中两个数码调过来恰好是三位数的十位数上与个位数上的数码”可知这个正方体的棱长是7.因此,这个长方体的体积是7×7×7=343.10. 74.这个多面体的面数可以直接数出是20,而棱数为“实线条数÷2+虚线条数”,等于34÷2+19=36.顶点数=棱数-面数+2(欧拉定理)是36-20+2=18,所以这个多面体的面数、顶点数和棱数的总和是20+18+36=74.11. 水的体积为()16875050156022=⨯-立方厘米.当将铁棍提起后,铁棍下方水的体积为8640024602=⨯(立方厘米),所以浸湿部分长为 ()()4.2415608640016875022=-⨯-(厘米).12. 第一次切下的尽可能大的正方体的棱长是12厘米,体积为1728123=(立方厘米)这时剩余立体底面形状如图(1),其高是12厘315213639( 2 )米.这样第二次切下的尽可能大的正方体棱长为9厘米,其体积是92993=(立方厘米).第二次切割后,剩下的立体可以看作是由两部分组成的:一部分的底面形状如图(2),高为12厘米,另一部分底面形状如图3,高是3厘米.显然,第三次切下的尽可能大的正方体棱长为6厘米,其体积为21663=(立方厘米).所以,剩下的体积为21×15×12-1728-729-216=1107(立方厘米).13. 这个立体图形是一个圆柱的四分之一(如图),圆柱的底面半径为10厘米,高为8厘米. 它的全面积为:810281014.32411014.34122⨯⨯+⨯⨯⨯⨯+⨯⨯⨯6.4421606.125157=++=(平方厘米).它的体积为:62881014.3412=⨯⨯⨯(立方厘米).14. 立体图形的形状如右图所示.从上面和下面看到的形状面积都是9 cm 2,共cm 2; 从两个侧面看到的形状面积都为7 cm 2,共14 cm 2; 从前面和后面看到的形状面积都为6 cm 2,共12 cm 2隐藏着的面积有2 cm 2.一共有18+16+12+2=46(cm 2).9( 3 )9。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年小学奥数几何专题——立体图形1.如图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?2.右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、上面挖去的正方体)3.在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?4.下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为14厘米,那么最后得到的立体图形的表面积是多少平方厘米?5.一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?6.一个表面积为256cm的长方体如图切成27个小长方体,这27个小长方体表面积的和是多少平方厘米?7.如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?25块积木8.要把12件同样的长a、宽b、高h的长方体物品拼装成一件大的长方体,使打包后表面积最小,该如何打包?⑴当 b=2h时,如何打包?⑵当 b<2h时,如何打包?⑶当 b>2h时,如何打包?9.要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体,表面积最小是多少?10.如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.11.如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是多少平方厘米?12.把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.,求这个立体图形的表面积.13.用棱长是1厘米的立方块拼成如图所示的立体图形,问该图形的表面积是多少平方厘米?14.有30个边长为1米的正方体,在地面上摆成右上图的形式,然后把露出的表面涂成红色.求被涂成红色的表面积.15.棱长是m厘米(m为整数)的正方体的若干面涂上红色,然后将其切割成棱长是1厘米的小正方体.至少有一面红色的小正方体个数和表面没有红色的小正方体个数的比为13:12,此时m的最小值是多少?16.有64个边长为1厘米的同样大小的小正方体,其中34个为白色的,30个为黑色的.现将它们拼成一个444⨯⨯的大正方体,在大正方体的表面上白色部分最多可以是多少平方厘米?17.三个完全一样的长方体,棱长总和是288厘米,每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数,给这三个长方体涂色,一个涂一面,一个涂两面,一个涂三面.涂色后把三个长方体都切成棱长为1厘米的小正方体,只有一个面涂色的小正方体最少有多少个?18.把一个大长方体木块表面上涂满红色后,分割成若干个同样大小的小正方体,其中恰好有两个面涂上红色的小正方体恰好是100块,那么至少要把这个大长方体分割成多少个小正方体?19.把正方体的六个表面都划分成9个相等的正方形.用红、黄、蓝三种颜色去染这些小正方形,要求有公共边的正方形染不同的颜色,那么,用红色染的正方形最多有多少个?20.一个长、宽、高分别为21厘米、15厘米、12厘米的长方形.现从它的上面尽可能大的切下一个正方体,然后从剩余的部分再尽可能大的切下一个正方体,最后再从第二次剩余的部分尽可能大的切下一个正方体,剩下的体积是多少立方厘米?21.有黑白两种颜色的正方体积木,把它摆成右图所示的形状,已知相邻(有公共面)的积木颜色不同,标A 的为黑色,图中共有黑色积木多少块?A22.有许多相同的立方体,每个立方体的六个面上都写着同一个数字(不同的立方体可以写相同的数字)先将写着2的立方体与写着1的立方体的三个面相邻,再将写着3的立方体写着2的立方体相邻(见左下图).依这样构成右下图所示的立方体,它的六个面上的所有数字之和是多少?3322332332232311111123.如图所示,一个555⨯⨯的立方体,在一个方向上开有115⨯⨯的孔,在另一个方向上开有215⨯⨯的孔,在第三个方向上开有315⨯⨯的孔,剩余部分的体积是多少?表面积为多少?24.如图,原来的大正方体是由125个小正方体所构成的.其中有些小正方体已经被挖除,图中涂黑色的部分就是贯穿整个大正方体的挖除部分.请问剩下的部分共有多少个小正方体?第8题25.一个由125个同样的小正方体组成的大正方体,从这个大正方体中抽出若干个小正方体,把大正方体中相对的两面打通,右图就是抽空的状态.右图中剩下的小正方体有多少个?26.右图中的⑴⑵⑶⑷是同样的小等边三角形,⑸⑹也是等边三角形且边长为⑴的2倍,⑺⑻⑼⑽是同样的等腰直角三角形,⑾是正方形.那么,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的多少倍.⑷⑶⑵⑴⑾⑽⑼⑻⑺⑹⑸27.图⑴和图⑵是以正方形和等边三角形为面的立体图形的展开图,图中所有的边长都相同.请问:图⑴能围起来的立体图形的体积是图⑵能围起来的立体图形的体积的几倍?图⑴ 图⑵28.如图,用高都是1米,底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体.问这个物体的表面积是多少平方米?(π取3.14)1110.511.529.有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米(见右图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?30.圆柱体的侧面展开,放平,是边长分别为10厘米和12厘米的长方形,那么这个圆柱体的体积是多少立方厘米.(结果用π表示)31.如右图,是一个长方形铁皮,利用图中的阴影部分,刚好能做成一个油桶(接头处忽略不计),求这个油桶的容积.(π 3.14 )32.如图,有一张长方形铁皮,剪下图中两个圆及一块长方形,正好可以做成1个圆柱体,这个圆柱体的底面半径为10厘米,那么原来长方形铁皮的面积是多少平方厘米?(π 3.14=)33.把一个高是8厘米的圆柱体,沿水平方向锯去2厘米后,剩下的圆柱体的表面积比原来的圆柱体表面积减少12.56平方厘米.原来的圆柱体的体积是多少立方厘米?34.一个圆柱体的体积是50.24立方厘米,底面半径是2厘米.将它的底面平均分成若干个扇形后,再截开拼成一个和它等底等高的长方体,表面积增加了多少平方厘米?(π 3.14=)35.一个拧紧瓶盖的瓶子里面装着一些水(如图),由图中的数据可推知瓶子的容积是多少立方厘米.(π取3.14)(单位:厘米)36.一个酒精瓶,它的瓶身呈圆柱形(不包括瓶颈),如图.已知它的容积为26.4π立方厘米.当瓶子正放时,瓶内的酒精的液面高为6厘米;瓶子倒放时,空余部分的高为2厘米.问:瓶内酒精的体积是多少立方厘米?合多少升?37.一个盖着瓶盖的瓶子里面装着一些水,瓶底面积为10平方厘米,(如下图所示),请你根据图中标明的数据,计算瓶子的容积是多少立方厘米?38.一个盛有水的圆柱形容器,底面内半径为5厘米,深20厘米,水深15厘米.今将一个底面半径为2厘米,高为17厘米的铁圆柱垂直放入容器中.求这时容器的水深是多少厘米?39.有甲、乙两只圆柱形玻璃杯,其内直径依次是10厘米、20厘米,杯中盛有适量的水.甲杯中沉没着一铁块,当取出此铁块后,甲杯中的水位下降了2厘米;然后将铁块沉没于乙杯,且乙杯中的水未外溢.问:这时乙杯中的水位上升了多少厘米?40.如图,甲、乙两容器相同,甲容器中水的高度是锥高的13,乙容器中水的高度是锥高的23,比较甲、乙两容器,哪一只容器中盛的水多?多的是少的的几倍?甲乙41.如图,有一卷紧紧缠绕在一起的塑料薄膜,薄膜的直径为20厘米,中间有一直径为8厘米的卷轴,已知薄膜的厚度为0.04厘米,则薄膜展开后的面积是多少平方米?42.图为一卷紧绕成的牛皮纸,纸卷直径为20厘米,中间有一直径为6厘米的卷轴.已知纸的厚度为0.4毫米,问:这卷纸展开后大约有多长?43.如图,ABC是直角三角形,AB、AC的长分别是3和4.将ABC∆绕AC旋转一周,求ABC∆扫出的立体图形的体积.(π 3.14=)CB A 4344.已知直角三角形的三条边长分别为3cm ,4cm ,5cm ,分别以这三边轴,旋转一周,所形成的立体图形中,体积最小的是多少立方厘米?(π取3.14)45.如图,直角三角形如果以BC 边为轴旋转一周,那么所形成的圆锥的体积为16π,以AC 边为轴旋转一周,那么所形成的圆锥的体积为12π,那么如果以AB 为轴旋转一周,那么所形成的几何体的体积是多少?ABC46.如图,ABCD 是矩形,6cm BC =,10cm AB =,对角线AC 、BD 相交O .E 、F 分别是AD 与BC 的中点,图中的阴影部分以EF 为轴旋转一周,则白色部分扫出的立体图形的体积是多少立方厘米?(π取3)A BA B47.如图,ABCD 是矩形,6cm BC =,10cm AB =,对角线AC 、BD 相交O .图中的阴影部分以CD 为轴旋转一周,则阴影部分扫出的立体的体积是多少立方厘米?B A48.如图,在一个正方体的两对侧面的中心各打通一个长方体的洞,在上下底面的中心打通一个圆柱形的洞.已知正方体边长为10厘米,侧面上的洞口是边长为4厘米的正方形,上下底面的洞口是直径为4厘米的圆,求此立体图形的表面积和体积.49.从一个棱长为10厘米的正方形木块中挖去一个长10厘米、宽2厘米、高2厘米的小长方体,剩下部分的表面积是多少?(写出符合要求的全部答案)50. 一个酒瓶里面深30cm ,底面内直径是10cm ,瓶里酒深15cm .把酒瓶塞紧后使其瓶口向下倒立这时酒深25cm .酒瓶的容积是多少?(π取3)25301551.如右图所示,由三个正方体木块粘合而成的模型,它们的棱长分别为1米、2米、4米,要在表面涂刷油漆,如果大正方体的下面不涂油漆,则模型涂刷油漆的面积是多少平方米?52.一个圆柱体形状的木棒,沿着底面直径竖直切成两部分.已知这两部分的表面积之和比圆柱体的表面积大22008cm ,则这个圆柱体木棒的侧面积是多少2cm .(π取3.14)第2题53.如图,厚度为0.25毫米的铜版纸被卷成一个空心圆柱(纸卷得很紧,没有空隙),它的外直径是180厘米,内直径是50厘米.这卷铜版纸的总长是多少米?54.如右图,一个正方体形状的木块,棱长l米,沿水平方向将它锯成3片,每片又锯成4长条,每条又锯成5小块,共得到大大小小的长方体60块.那么,这60块长方体表面积的和是多少平方米?55.一个透明的封闭盛水容器,由一个圆柱体和一个圆锥体组成,圆柱体的底面直径和高都是12厘米.其内有一些水,正放时水面离容器顶11厘米,倒放时水面离顶部5厘米,那么这个容器的容积是多少立方厘米?(π3)5cm56.如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,那么挖掉的小立方体的边长是多少厘米?57.一个圆柱体底面周长和高相等.如果高缩短4厘米,表面积就减少50.24平方厘米.求这个圆柱体的表面积是多少?58.如图,圆锥形容器中装有水50升,水面高度是圆锥高度的一半,这个容器最多能装水多少升.59.如图,用高都是1米,底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体.问这个物体的表面积是多少平方米?(π取3.14)1110.511.560.有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米(见右图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?61.圆柱体的侧面展开,放平,是边长分别为10厘米和12厘米的长方形,那么这个圆柱体的体积是多少立方厘米.(结果用π表示)62.如右图,是一个长方形铁皮,利用图中的阴影部分,刚好能做成一个油桶(接头处忽略不计),求这个油桶的容积.(π 3.14 )63.如图,有一张长方形铁皮,剪下图中两个圆及一块长方形,正好可以做成1个圆柱体,这个圆柱体的底面半径为10厘米,那么原来长方形铁皮的面积是多少平方厘米?(π 3.14=)64.把一个高是8厘米的圆柱体,沿水平方向锯去2厘米后,剩下的圆柱体的表面积比原来的圆柱体表面积减少12.56平方厘米.原来的圆柱体的体积是多少立方厘米?65.一个圆柱体底面周长和高相等.如果高缩短4厘米,表面积就减少50.24平方厘米.求这个圆柱体的表面积是多少?66.一个圆柱体形状的木棒,沿着底面直径竖直切成两部分.已知这两部分的表面积之和比圆柱体的表面积大2cm?(π取3.14)2008cm,则这个圆柱体木棒的侧面积是多少2第2题67.已知圆柱体的高是10厘米,由底面圆心垂直切开,把圆柱分成相等的两半,表面积增加了40平方厘米,求圆柱体的体积.(π3=)68.一个圆柱体的体积是50.24立方厘米,底面半径是2厘米.将它的底面平均分成若干个扇形后,再截开拼成一个和它等底等高的长方体,表面积增加了多少平方厘米?(π 3.14=)69.右图是一个零件的直观图.下部是一个棱长为40cm的正方体,上部是圆柱体的一半.求这个零件的表面积和体积.70.输液100毫升,每分钟输2.5毫升.如图,请你观察第12分钟时图中的数据,问:整个吊瓶的容积是多少毫升?71.一个拧紧瓶盖的瓶子里面装着一些水(如图),由图中的数据可推知瓶子的容积是多少立方厘米.(π取3.14)(单位:厘米)72.一个酒精瓶,它的瓶身呈圆柱形(不包括瓶颈),如图.已知它的容积为26.4π立方厘米.当瓶子正放时,瓶内的酒精的液面高为6厘米;瓶子倒放时,空余部分的高为2厘米.问:瓶内酒精的体积是多少立方厘米?合多少升?73.一个酒瓶里面深30cm,底面内直径是10cm,瓶里酒深15cm.把酒瓶塞紧后使其瓶口向下倒立这时酒深25cm.酒瓶的容积是多少?(π取3)25301574.一个盖着瓶盖的瓶子里面装着一些水,瓶底面积为10平方厘米,(如下图所示),请你根据图中标明的数据,计算瓶子的容积是多少立方厘米?75.一个透明的封闭盛水容器,由一个圆柱体和一个圆锥体组成,圆柱体的底面直径和高都是12厘米.其内有一些水,正放时水面离容器顶11厘米,倒放时水面离顶部5厘米,那么这个容器的容积是多少立方厘米?(π3)5cm76.如图,底面积为50平方厘米的圆柱形容器中装有水,水面上漂浮着一块棱长为5厘米的正方体木块,木块浮出水面的高度是2厘米.若将木块从容器中取出,水面将下降多少厘米?77.有两个棱长为8厘米的正方体盒子,A盒中放入直径为8厘米、高为8厘米的圆柱体铁块一个,B盒中放入直径为4厘米、高为8厘米的圆柱体铁块4个,现在A盒注满水,把A盒的水倒入B盒,使B盒也注满水,问A盒余下的水是多少立方厘米?78.兰州来的马师傅擅长做拉面,拉出的面条很细很细,他每次做拉面的步骤是这样的:将一个面团先搓成圆柱形面棍,长1.6米.然后对折,拉长到1.6米;再对折,拉长到1.6米……照此继续进行下去,最后拉出的面条粗细(直径)仅有原先面棍的164.问:最后为粗细均匀的圆柱形,而且没有任何浪费)79.一个圆柱形容器内放有一个长方形铁块.现打开水龙头往容器中灌水.3分钟时水面恰好没过长方体的顶面.再过18分钟水灌满容器.已知容器的高为50厘米,长方体的高为20厘米,求长方体底面面积与容器底面面积之比.80.一只装有水的圆柱形玻璃杯,底面积是80平方厘米,高是15厘米,水深8厘米.现将一个底面积是16平方厘米,高为12厘米的长方体铁块竖放在水中后.现在水深多少厘米?81.一只装有水的圆柱形玻璃杯,底面积是80平方厘米,高是15厘米,水深10厘米.现将一个底面积是16平方厘米,高为12厘米的长方体铁块竖放在水中后.现在水深多少厘米?82.一只装有水的圆柱形玻璃杯,底面积是80平方厘米,高是15厘米,水深13厘米.现将一个底面积是16平方厘米,高为12厘米的长方体铁块竖放在水中后.现在水深多少厘米?83.一个圆柱形玻璃杯内盛有水,水面高2.5厘米,玻璃杯内侧的底面积是72平方厘米.在这个杯中放进棱长6厘米的正方体铁块后,水面没有淹没铁块.这时水面高多少厘米?84.一个盛有水的圆柱形容器,底面内半径为5厘米,深20厘米,水深15厘米.今将一个底面半径为2厘米,高为17厘米的铁圆柱垂直放入容器中.求这时容器的水深是多少厘米?85.有甲、乙两只圆柱形玻璃杯,其内直径依次是10厘米、20厘米,杯中盛有适量的水.甲杯中沉没着一铁块,当取出此铁块后,甲杯中的水位下降了2厘米;然后将铁块沉没于乙杯,且乙杯中的水未外溢.问:这时乙杯中的水位上升了多少厘米?86.有一只底面半径是20厘米的圆柱形水桶,里面有一段半径是5厘米的圆柱体钢材浸在水中.钢材从水桶里取出后,桶里的水下降了6厘米.这段钢材有多长?87.一个圆锥形容器高24厘米,其中装满水,如果把这些水倒入和圆锥底面直径相等的圆柱形容器中,水面高多少厘米?88.如图,圆锥形容器中装有水50升,水面高度是圆锥高度的一半,这个容器最多能装水多少升?参考答案1.600【解析】我们从三个方向(前后、左右、上下)考虑,新几何体的表面积仍为原立方体的表面积:10⨯10⨯6=600.2.120【解析】原正方体的表面积是4⨯4⨯6=96(平方厘米).每一个面被挖去一个边长是1厘米的正方形,同时又增加了5个边长是1厘米的正方体作为玩具的表面积的组成部分.总的来看,每一个面都增加了4个边长是1厘米的正方形.从而,它的表面积是:96+4⨯6=120平方厘米.3.15000【解析】对于和长方体相关的立体图形表面积,一般从上下、左右、前后3个方向考虑.变化前后的表面积不变:50⨯50⨯6=15000(平方厘米).4.1294【解析】我们仍然从3个方向考虑.平行于上下表面的各面面积之和:2⨯2⨯2=8(平方厘米);左右方向、前后方向:2⨯2⨯4=16(平方厘米),1⨯1⨯4=4(平方厘米),12⨯12⨯4=1(平方厘米),14⨯14⨯4=14(平方厘米),这个立体图形的表面积为:816++4+1+14=1294(平方厘米).5.18【解析】锯一次增加两个面,锯的总次数转化为增加的面数的公式为:锯的总次数⨯2=增加的面数.原正方体表面积:1⨯1⨯6=6(平方米),一共锯了(2-1)+(3-1)+(4-1)=6次, 6+1⨯1⨯2⨯6=18(平方米).6.168平方厘米【解析】每一刀增加两个切面,增加的表面积等于与切面平行的两个表面积,所以每个方向切两刀后,表面积增加到原来的3倍,即表面积的和为2563168(cm )⨯=.7.54【解析】当小积木互相重合的面最多时表面积最小.设想27块边长为1的正方形积木,当拼成一个333⨯⨯的正方体时,表面积最小,现在要去掉2块小积木,只有在两个角上各去掉一块小积木,或在同一个角去掉两块相邻的积木时,表面积不会增加,该几何体表面积为54.8.如解析图【解析】图2和图3正面的面积相同,侧面面积=正面周长⨯长方体长,所以正面的周长愈大表面积越大,图2的正面周长是8h +6b ,图3的周长是12h +4b.两者的周长之差为2(b -2h ).当b =2h 时,图2和图3周长相等,可随意打包;当b <2h 时,按图2打包;当b >2h 时,按图3打包.图3图2图1hba9.1034【解析】考虑所有的包装方法,因为6=1⨯2⨯3,所以一共有两种拼接方式:第一种按长宽高1⨯1⨯6拼接,重叠面有三种选择,共3种包装方法.第二种按长宽高1⨯2⨯3拼接,有3个长方体并列方向的重叠面有三种选择,有2个长方体并列方向的重叠面剩下2种选择,一共有6种包装方法.其中表面积最小的包装方法如图所示,表面积为1034.10.214【解析】我们把上面的小正方体想象成是可以向下“压缩”的,“压缩”后我们发现:小正方体的上面与大正方体上面中的阴影部分合在一起,正好是大正方体的上面.这样这个立体图形的表面积就可以分成这样两部分:上下方向:大正方体的两个底面;四周方向(左右、前后方向):小正方体的四个侧面,大正方体的四个侧面.上下方向:55250⨯⨯=(平方分米);侧面:554100⨯⨯=(平方分米),44464⨯⨯=(平方分米).这个立体图形的表面积为:5010064214++=(平方分米).11.194平方厘米【解析】 (法1)四个正方体的表面积之和为:2222(1235)6396234+++⨯=⨯=(平方厘米),重叠部分的面积为:22222222213(221)(321)(321)39141440⨯+⨯+++++++=+++=(平方厘米),所以,所得到的多面体的表面积为:23440194-=(平方厘米).(法2)三视图法.从前后面观察到的面积为22253238++=平方厘米,从左右两个面观察到的面积为225334+=平方厘米,从上下能观察到的面积为2525=平方厘米.表面积为()3834252194++⨯=(平方厘米).12.54【解析】从上下、左右、前后观察到的的平面图形如下面三图表示.因此,这个立体图形的表面积为:2个上面2+个左面2+个前面.上表面的面积为:9平方厘米,左表面的面积为:8平方厘米,前表面的面积为:10平方厘米.因此,这个立体图形的总表面积为:(9810)254++⨯=(平方厘米).上下面 左右面 前后面13.46平方厘米【解析】该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成.该图形的表面积等于(977)246++⨯=个小正方形的面积,所以该图形表面积为46平方厘米.14.56【解析】44(1234)456⨯++++⨯=(平方米).15.5【解析】切割成棱长是1厘米的小正方体共有3m 个,由于其中至少有一面是红色的小正方体与没有红色面的个数之比为13:12,而131225+=,所以小正方体的总数是25的倍数,即3m 是25的倍数,那么m 是5的倍数.当5m =时,要使得至少有一面的小正方体有65个,可以将原正方体的正面、上面和下面涂色,此时至少一面涂红色的小正方体有5554265⨯+⨯⨯=个,表面没有红色的小正方体有 1256560-=个,个数比恰好是13:12,符合题意.因此,m 的最小值是5.16.74【解析】要使大正方体的表面上白色部分最多,相当于要使大正方体表面上黑色部分最少,那么就要使得黑色小正方体尽量不露出来.在整个大正方体中,没有露在表面的小正方体有3(42)8-=(个),用黑色的;在面上但不在边上的小正方体有2(42)624-⨯=(个),其中30822-=个用黑色.这样,在表面的44696⨯⨯=个11⨯的正方形中,有22个是黑色,962274-=(个)是白色,所以在大正方体的表面上白色部分最多可以是74平方厘米.17.307【解析】每个长方体的棱长和是288396÷=厘米,所以,每个长方体长、宽、高的和是96424÷=厘米.因为,每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数,所以,每个长方体的长、宽、高分别是9厘米、8厘米、7厘米.要求切割后只有一个面涂色的小正方体最少有多少个,则需每一个长方体按题意涂色时,应让切割后只有一个面涂色的小正方体最少.所以,涂一面的长方体应涂一个87⨯面,有8756⨯=个;涂两面的长方体,若两面不相邻,应涂两个87⨯面,有872112⨯⨯=个;若两面相邻,应涂一个87⨯面和一个97⨯面,此时有()7892105⨯+-=个,所以涂两面的最少有105个; 涂三面的长方体,若三面不两两相邻,应涂两个87⨯面、一个97⨯面,有()78894147⨯++-=个;若三面两两相邻,有。
