空间模型曲面面积计算
高考数学一轮复习-81-空间几何体的三视图-直观图-表面积与体积课件-新人教A

=172a2.所以 S 球=4πR2=4π×172a2=73πa2.
(2)这个几何体是一个圆台被轴截面割出来的一半.
根据图中数据可知圆台的上底面半径为 1,下底面半径为 2,高为 3,母线长为 2,几何体的表面积是两个半圆的面 积、圆台侧面积的一半和轴截面的面积之和,故这个几何 体的表面积为 S=12π×12+12π×22+12π×(1+2)×2+12 ×(2+4)× 3=112π+3 3. 答案 (1)B (2)112π+3 3
可能是圆柱,排除选项C;又由俯视图可知,该几何体
不可能是棱柱或棱台,排除选项A,B,故选D.
(2)如图,在原图形OABC中, 应有 OD=2O′D′=2×2 2 =4 2(cm), CD=C′D′=2 cm. ∴OC= OD2+CD2 = (4 2)2+22=6(cm), ∴OA=OC, 故四边形 OABC 是菱形. 答案 (1)D (2)C
诊断自测
1.判断正误(在括号内打“√”或“×”) 精彩PPT展示
(1)有两个面平行,其余各面都是平行四边形的几何体是
棱柱.
(×)
(2)有一个面是多边形,其余各面都是三角形的几何体是
棱锥.
( ×)
(3)正方体、球、圆锥各自的三视图中,三视图均相同.
(×)
(4)圆柱的侧面展开图是矩形.
(√)
2.(2014·福建卷)某空间几何体的正视图是三角形,则该几
(2)画出坐标系 x′O′y′,作出△OAB 的 直观图 O′A′B′(如图).D′为 O′A′的中 点.易知 D′B′=12DB(D 为 OA 的中点), ∴S△O′A′B′=12× 22S△OAB= 42× 43a2= 166a2.
cad样条曲线围成的封闭区间的面积

cad样条曲线围成的封闭区间的面积【文章标题】:CAD样条曲线围成的封闭区域面积计算及应用探究【导言】:CAD(Computer Aided Design,计算机辅助设计)软件在现代设计领域发挥着重要作用。
其中,样条曲线是CAD设计中经常使用的一种曲线类型,具有较高的灵活性和平滑性。
当样条曲线围成一个封闭区域时,计算该区域的面积是一个关键问题,对于许多设计和计算任务具有重要意义。
本文将深入探讨CAD样条曲线围成的封闭区域面积的计算方法和应用。
【正文】:一、CAD样条曲线概述在CAD设计中,样条曲线是一种通过插值的方式生成的平滑曲线。
它通过经过一系列特定点的方法,产生可以平滑连接这些点的曲线。
样条曲线常用于曲面造型、路径规划、动画生成等领域,广泛应用于工程和设计行业。
二、封闭区域的概念与应用场景CAD样条曲线围成的封闭区域是由多个样条曲线连接而成的一个封闭形状。
这种封闭区域在许多设计和计算任务中具有广泛的应用场景,例如:1. 建筑设计中的室内空间规划;2. 车辆路径规划中的障碍物辨识;3. 产品设计中的曲面造型;4. 地理信息系统中的地块面积计算等。
三、CAD样条曲线围成的封闭区域面积的计算方法要计算CAD样条曲线围成的封闭区域的面积,可以采用以下方法:1. 数值积分法数值积分法是一种常用的计算封闭区域面积的方法。
该方法将封闭区域划分成多个小面积,并通过对每个小面积进行面积计算,最后求和得到封闭区域的总面积。
在CAD设计软件中,常用的数值积分法有辛普森法则和梯形法则等。
2. 数学模型拟合法数学模型拟合法是一种通过对样条曲线建立数学模型,并对模型进行曲面积分计算的方法。
该方法要求对样条曲线的方程进行建模,并应用曲面积分公式进行计算。
这种方法的优势在于可以精确地计算任意形状的封闭区域的面积。
四、CAD样条曲线围成的封闭区域面积的应用探究CAD样条曲线围成的封闭区域面积具有广泛的应用价值和实际意义。
在以下领域中,封闭区域面积的计算是非常重要的:1. 建筑设计和室内空间规划:计算房间平面图中各个房间的面积,以合理规划空间布局;2. 车辆路径规划和障碍物辨识:计算道路、交叉口和建筑物等封闭区域的面积,以准确规划车辆行驶路径;3. 产品设计和曲面造型:计算产品曲面的面积,以进行合理的造型设计;4. 地理信息系统和地块面积计算:计算地图上不规则地块的面积,以方便土地规划和土地评估。
3D模型的精确计算方法

3D模型的精确计算方法概述3D模型的精确计算方法是指通过数学和计算机科学技术,准确计算和表示三维模型的形状、颜色、纹理等属性的方法。
本文将介绍几种常用的精确计算方法。
1. 多边形网格计算方法多边形网格是3D模型中最常用的表示方法之一。
在多边形网格计算方法中,首先将三维模型表示为由许多小的多边形组成的网格,然后对每个多边形进行计算。
1.1 顶点计算对于每个多边形的顶点,可以通过计算其坐标来准确表示其位置。
常用的方法包括线性插值、加权平均等。
1.2 面积计算要计算多边形的面积,可以使用多边形的顶点坐标进行计算。
常用的方法包括向量叉积等。
1.3 法向量计算法向量表示多边形的朝向和表面的曲率。
通过计算多边形的顶点坐标,可以准确计算出法向量。
2. 体素网格计算方法体素网格是另一种常用的表示3D模型的方法。
在体素网格计算方法中,将三维空间划分为小的立方体单元,然后对每个立方体进行计算。
2.1 体素表示在体素网格计算方法中,需要将三维模型表示为由许多小的立方体单元组成的体素网格。
每个立方体单元可以表示为一个体素值,用于表示该区域的属性,如密度、颜色等。
2.2 体素计算对于每个立方体单元,可以进行各种计算,如密度计算、颜色计算等。
这些计算可以基于相邻立方体的属性进行推导。
3. 其他精确计算方法除了多边形网格和体素网格,还有其他一些精确计算方法,如参数化曲面计算、光线追踪等。
这些方法根据具体的3D模型和计算需求选择使用。
结论3D模型的精确计算方法是通过数学和计算机科学技术准确计算和表示三维模型的形状、颜色、纹理等属性的方法。
多边形网格和体素网格是常用的精确计算方法,但还有其他方法可供选择。
根据具体情况选择适当的计算方法,可以更好地表示和计算3D模型的属性。
proe如何计算零件中某一些表面的表面积之和

proe如何计算零件中某一些表面的总表面积
主要步骤是把要计算的曲面组在另一个模型空间生成,也就是把要计算的曲面组剥下来,作为新零件的特征存在。
1)先新建另一个零件,在新建的零件里点击插入—共享数据—复制几何
2)点击打开文件图标,在进程中找到我们需要计算表面的模型名称,点击打开,确定。
3)再点击“仅限发布几何”图标,会发现右上角出现我们要进行计算表面积的模型小窗口。
4)从菜单中找到参照,点击参照-曲面集-细节
5)默认单个曲面,可以按住CTRL,然后一个曲面一个曲面选择。
选择好按确定,以及对勾即可。
6)如果要计算的曲面多而杂,一个一个选太费劲,容易漏选,也可以不选单个曲面,直接点击“添加”,然后在要计算表面积的模型上点一下。
同时规则改为所有实体曲面,这样子先选中要计算模型的全部表面。
这是为下一步做减法做准备的(除去不需要的表面,就是我们要的表面集)
点选所有实体曲面下的“排除的曲面”,然后按住“ctrl”在模型中选择不需要计算的表面,点击确定,以及对勾。
7)完成步骤5)或6)之后,在新件模型空间上,就可以看到1个新特征,它就是剥下来的曲面组。
点选分析-测量-面积,然后在选择的下拉菜单上选择面组,选择图上的曲面,即可得面积。
双曲空间公式

双曲空间公式:双曲空间是一种非欧几何空间,它与欧几里得空间不同,具有负的曲率。
在双曲空间中,距离的计算方式也与欧几里得空间不同。
双曲空间的不同模型中,距离公式的表达方式各有特点。
以下是几种常见的双曲空间模型以及它们对应的距离公式:1. **Lorentz空间(双曲面模型)**:-在Lorentz空间中,双曲面模型通常用于描述具有相对论性质的情景。
-两点间的距离(测地线长度)公式为:\[ d(x, y) = \sqrt{-\sum_{i=1}^n (x_i - y_i)^2} \]其中,\( x, y \) 是双曲面上的点,\( n \) 是空间的维数,上述公式中求和是对所有维度上的差值求平方和,但因为双曲空间的性质,这些差值的平方前面要带上负号。
2. **Poincaré圆盘模型**:- Poincaré圆盘模型是双曲空间的一种直观模型,它将双曲空间映射到二维平面上的圆盘。
-在这个模型中,两点间的距离可以用极坐标来表示,公式为:\[ d(x, y) = \arccos\left(\frac{x_1 y_2 - x_2 y_1}{\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}}\right) \]其中,\( (x_1, y_1), (x_2, y_2) \) 是圆盘上的点,该公式适用于二维双曲空间。
3. **上半空间模型**:-上半空间模型是双曲空间的一种扩展,它包含了所有正的实数轴。
-两点距离公式可以表示为:\[ d(x, y) = \sqrt{-(\sum_{i=1}^n x_i y_i)^2} \]这里同样需要对维度上的乘积求和,并带上负号,以确保结果是正数。
这些公式在数学、物理学、计算机等领域有广泛的应用,例如在理论物理中的相对论、在几何学中的双曲几何研究、以及在信息科学和网络分析中的社区检测算法等。
积分方程中对空间立体角及曲面积分的计算方法

积分方程中对空间立体角及曲面积分的计算方法
空间立体角及曲面积分是解决空间积分方程常用的一种计算方法,用来确定相应物理参数的变化规律,是空间积分方程的关键。
空间立体角积分可以用来求解不同物理场中变量的变化情况,其中用到的几何图形象投影元法为三角形、一边三角形和四边形,与普通空间积分方法相比,该方法通过改变参考平面和平行投影来改变域的体积和形状,从而将复杂的问题分解成几个可以独立求解的简单问题。
其计算结果包括立体角内曲面积面积、外曲面积积分等。
曲面积分是求解复杂物理场中变量变化规律的方法之一,用来反映曲面表面总流量、周期性改变形状或时变形状等问题。
其计算方法主要由梯度模糊、路径积分和面积积分组成。
面积积分采用曲线面积分或多边形面积分等技术,而路径积分则可以利用特殊结构的空间图形,如网状、矩形网格等进行近似求解。
最后,梯度模糊就是反映曲面表面的梯度不要计算,而基于某种特定模型,把梯度模糊成若干个区域来表示不确定的流量。
以上就是关于空间立体角及曲面积分的计算方法,它们是解决空间积分方程常用的方法之一,有效地解决了复杂物理场中变量变化规律问题,是空间积分方程的关键。
3D建模:实体建模和曲面建模的比较

3D建模:实体建模和曲面建模的比较在计算机图形学领域中,3D建模是指在计算机中构建三维模型的过程。
随着科技的不断发展,越来越多的行业开始采用3D建模技术,如游戏、影视、医学等。
3D建模技术可以分为实体建模和曲面建模两种类型,本文将对二者进行比较,探讨它们各自的优缺点和适用场景。
1.实体建模实体建模又称为多面体建模,它主要通过将多个基本几何体(如立方体、球体、圆柱体等)组合而成。
实体建模更加注重物体的几何形状和几何属性,可以准确地刻画物体的体积、重量、密度等特征。
实体建模的主要优点是可以在工程设计、生产制造和数值仿真等领域中得到广泛应用。
实体建模的模型表现也更加稳定,容易进行后续操作和加工。
此外,实体建模的表面光滑,能够快速生成定向性纹理,更加适用于物理仿真等领域。
然而,实体建模也存在一些缺点,主要体现在以下两个方面。
首先,当需要细化模型细节时,实体建模需要添加更多的面片,会增加模型的复杂度,从而导致计算机处理速度变慢,消耗更多的计算资源。
其次,在建模过程中,实体建模需要对每个面进行逐一定义,因此比较耗时、复杂。
2.曲面建模曲面建模是按照各种曲线和曲面来构建物体模型,可以构建出比实体建模更加自然、真实的三维模型。
曲面建模更加注重物体表面的光滑度和曲度连续性,因此可以创造出更加真实、逼真的表面效果。
曲面建模的主要优点是可以更加容易地对物体的曲面进行调整和自定义,使得建模更加具有创造性和灵活性。
曲面建模主要适用于影视特效、游戏制作、产品设计等领域。
然而,曲面建模也存在一些缺点。
首先,在模型生成过程中,曲面建模需要多次周转,优胜缺陷也不易补救。
其次,在曲面建模的过程中,很难控制曲面的表现形式和细节效果。
最后,在处理较大场景时,曲面建模建模模型可能会变得更为复杂,从而也会影响计算机性能,降低建模速度。
3.实体建模和曲面建模的比较(1)使用场景:在一般的工程设计和生产中,为了准确描述物体的几何形状和属性,建议使用实体建模。
黎曼几何空间模型-概述说明以及解释

黎曼几何空间模型-概述说明以及解释1.引言1.1 概述黎曼几何是一门研究曲面和高维流形的几何学分支,它是由德国数学家黎曼在19世纪提出的,并被广泛应用于数学、物理学和工程学等领域。
黎曼几何的研究对象是具有度量的空间,它将几何中的度量概念引入了数学的领域,使得我们能够通过度量来描述空间的性质和变化。
黎曼几何的主要研究内容包括曲率、联络和度量等方面。
曲率是黎曼几何的核心概念之一,它描述了空间的弯曲性质。
在黎曼几何中,我们可以用曲率张量来度量空间的曲率,从而获得空间的几何信息。
联络则用来描述空间中点之间的连接方式,它在黎曼几何中起着举足轻重的作用。
而度量是黎曼几何中的基本概念,它定义了空间中点之间的距离和角度,使得我们能够进行几何量的计算和推导。
黎曼几何的空间模型是对空间的一种抽象和描述,它通过数学符号和公式来表示空间的性质和结构。
黎曼几何的空间模型包括欧氏空间、球面空间和超几何空间等。
欧氏空间是我们熟知的平面和三维空间,它的度量方式是直角坐标系。
球面空间则是由一个以一点为中心的球面构成,它的度量方式是球面坐标系。
超几何空间则是一类具有非欧几何性质的空间,它的度量方式是广义的。
黎曼几何空间模型不仅在纯数学领域有着重要的应用,还在物理学、工程学和计算机图形学等应用领域发挥着重要作用。
例如,在相对论理论中,黎曼几何被用来描述时空的弯曲性质。
在计算机图形学中,黎曼几何的概念被应用于曲面建模和形状分析等方面。
因此,深入理解和研究黎曼几何空间模型对于提高我们对空间性质的认识和应用具有重要意义。
本文将介绍黎曼几何的基本概念和空间模型,并对其在数学、物理学和工程学等领域的应用进行讨论。
通过对黎曼几何空间模型的探索和研究,我们能够更好地理解空间的本质和性质,为我们的学科研究和实际应用提供更多的工具和方法。
文章结构部分的内容可以是对整篇文章的章节和内容安排进行介绍和总结,以便读者能够更好地理解文章的组织和主要内容。
以下是文章1.2文章结构部分的一个可能的内容段落:文章结构本文将按照以下结构进行讨论黎曼几何空间模型的基本概念和应用。
探索数学中的空间曲线与曲面

探索数学中的空间曲线与曲面数学中的空间曲线与曲面是一门精彩纷呈的学科,通过对曲线与曲面的探索,我们可以深入了解空间的几何特征和数学规律。
本文将通过数学模型和实例来探讨数学中的空间曲线与曲面,分析它们的性质和应用。
一、空间曲线空间曲线是在三维空间中的曲线,是由一系列点组成的集合。
它可以用参数方程或者隐函数来表示。
常见的空间曲线有直线、曲线和螺旋线等。
下面以参数方程为例,介绍几个常见的空间曲线:1. 直线:直线是最简单的空间曲线,可以用参数方程表示为:```mathx = x_0 + aty = y_0 + btz = z_0 + ct```其中 `(x_0, y_0, z_0)` 是直线上的一个点,`(a, b, c)` 是直线的方向向量,`t` 是参数。
2. 曲线:曲线是具有一定弯曲的空间曲线,可以用参数方程表示为:```mathx = x(t)y = y(t)z = z(t)```其中 `x(t)`、`y(t)`、`z(t)` 分别是曲线在参数 `t` 下的坐标函数。
3. 螺旋线:螺旋线是一种具有环绕性质的空间曲线,它可以用参数方程表示为:```mathx = a * cos(t)y = a * sin(t)z = b * t```其中 `a` 和 `b` 分别是螺旋线的参数,`t` 是参数。
二、空间曲面空间曲面是三维空间中的曲面,是由一系列点组成的集合。
它可以用隐函数或者参数方程来表示。
常见的空间曲面有平面、球面和圆柱面等。
下面以隐函数为例,介绍几个常见的空间曲面:1. 平面:平面是最简单的空间曲面,可以用隐函数表示为:```mathAx+ By + Cz + D = 0```其中 `A`, `B`, `C` 和 `D` 是常数,且 `A`、`B`、`C` 不同时为零。
2. 球面:球面是由圆周绕着某个直径旋转而形成的曲面,可以用隐函数表示为:```math(x-a)^2 + (y-b)^2 + (z-c)^2 = r^2```其中 `(a, b, c)` 是球心的坐标,`r` 是球的半径。
三维模型体积算法

三维模型体积算法一、引言在计算机图形学和计算机辅助设计领域中,三维模型的体积计算是一个重要的问题。
准确计算三维模型的体积可以帮助我们理解物体的空间占用情况,对于工程设计、建筑规划、虚拟现实等应用具有重要意义。
本文将介绍几种常用的三维模型体积算法,并进行比较与分析。
二、多边形网格算法多边形网格算法是最常用的三维模型体积计算方法之一。
该算法将三维模型表示为由三角形组成的网格,通过计算网格中三角形的面积并求和得到模型的体积。
具体步骤如下:1. 将三维模型离散化为由三角形组成的网格;2. 遍历网格中的每个三角形,计算其面积;3. 将每个三角形的面积加总,得到模型的体积。
多边形网格算法的优点是简单易实现,适用于各种三维模型。
然而,该算法在处理复杂模型时可能会出现误差较大的情况,且计算量较大。
三、边界表示算法边界表示算法是另一种常用的三维模型体积计算方法。
该算法通过表示模型的边界曲面,计算曲面所包围的空间体积。
具体步骤如下:1. 将三维模型表示为边界曲面;2. 计算曲面的法向量,确定曲面的内外;3. 根据曲面的内外关系,计算模型的体积。
边界表示算法的优点是能够处理复杂的曲面模型,并且计算结果较为精确。
但是该算法的实现相对复杂,计算量也较大。
四、体素化算法体素化算法是一种基于体素(三维像素)的三维模型体积计算方法。
该算法将三维模型表示为由立方体组成的体素网格,通过统计网格中被模型所占据的体素数量来计算体积。
具体步骤如下:1. 将三维模型离散化为由立方体组成的体素网格;2. 统计网格中被模型所占据的体素数量;3. 根据体素的大小和数量计算模型的体积。
体素化算法的优点是适用于各种三维模型,且计算结果较为精确。
但是该算法的计算量较大,特别是在处理高分辨率的模型时。
五、对比与分析从上述三种算法可以看出,多边形网格算法是最简单的体积计算方法,但在处理复杂模型时可能会出现误差较大的情况。
边界表示算法能够处理复杂的曲面模型,但实现较为复杂。
高考专题练习: 空间几何体的表面积与体积
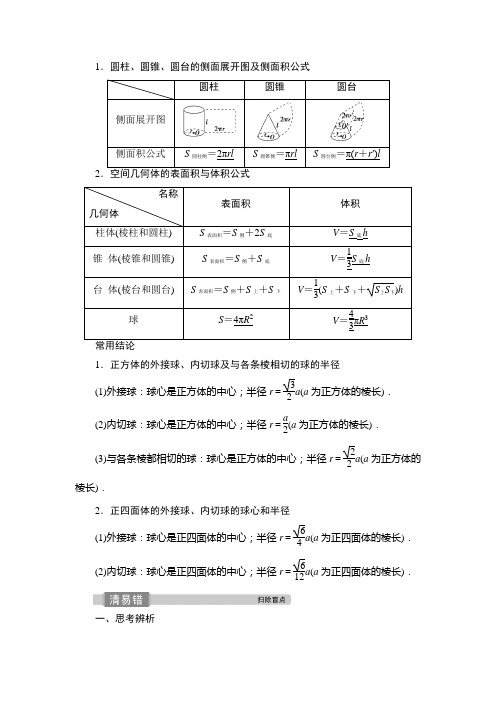
1.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S圆柱侧=2πrl S圆锥侧=πrl S圆台侧=π(r+r′)l2.空间几何体的表面积与体积公式名称几何体表面积体积柱体(棱柱和圆柱)S表面积=S侧+2S底V=S底h锥体(棱锥和圆锥)S表面积=S侧+S底V=13S底h台体(棱台和圆台)S表面积=S侧+S上+S下V=13(S上+S下+S上S下)h球S=4πR2V=43πR3常用结论1.正方体的外接球、内切球及与各条棱相切的球的半径(1)外接球:球心是正方体的中心;半径r=32a(a为正方体的棱长).(2)内切球:球心是正方体的中心;半径r=a2(a为正方体的棱长).(3)与各条棱都相切的球:球心是正方体的中心;半径r=22a(a为正方体的棱长).2.正四面体的外接球、内切球的球心和半径(1)外接球:球心是正四面体的中心;半径r=64a(a为正四面体的棱长).(2)内切球:球心是正四面体的中心;半径r=612a(a为正四面体的棱长).一、思考辨析判断正误(正确的打“√”,错误的打“×”) (1)多面体的表面积等于各个面的面积之和.( ) (2)锥体的体积等于底面积与高之积.( ) (3)球的体积之比等于半径比的平方.( )(4)简单组合体的体积等于组成它的简单几何体体积的和或差.( ) (5)长方体既有外接球又有内切球.( ) 答案:(1)√ (2)× (3)× (4)√ (5)× 二、易错纠偏常见误区| (1)考虑不周,忽视分类讨论; (2)锥体的底面及其对应高不清楚; (3)组合体的表面积没注意衔接部分.1.将一个相邻边长分别为4π,8π的矩形卷成一个圆柱,则这个圆柱的表面积是________.解析:当底面周长为4π时,底面圆的半径为2,两个底面的面积之和是8π;当底面周长为8π时,底面圆的半径为4,两个底面的面积之和为32π.无论哪种方式,侧面积都是矩形的面积32π2,故所求的表面积是32π2+8π或32π2+32π.答案:32π2+8π或32π2+32π2.已知三棱锥S -ABC 中,∠SAB =∠ABC =π2,SB =4,SC =213,AB =2,BC =6,则三棱锥S -ABC 的体积是________.解析:由∠ABC =π2,AB =2,BC =6,得AC =210.由∠SAB =π2,AB =2,SB =4,得SA =2 3.由SA 2+AC 2=SC 2,得SA ⊥AC ,又SA ⊥AB ,所以SA ⊥平面ABC .所以三棱锥S -ABC 的体积为13S △ABC ·SA =13×12×2×6×23=4 3.答案:4 33.已知一几何体的三视图如图所示,它的侧视图与正视图相同,则该几何体的表面积为________.解析:由三视图知,该几何体是一个正四棱柱与半球的组合体,且正四棱柱的高为2,底面对角线长为4,球的半径为2,所以该正四棱柱的底面正方形的边长为22,该几何体的表面积S=12×4π×22+π×22+22×2×4=12π+16.答案:12π+16空间几何体的表面积(师生共研)(1)在梯形ABCD中,∠ABC=π2,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的表面积为()A.(5+2)πB.(4+2)πC.(5+22)πD.(3+2)π(2)(2021·吉林梅河口五中模拟)阳马和鳖臑(biē nào)是《九章算术·商功》里对两种锥体的称谓.如图所示,取一个长方体,按下图斜割一分为二,得两个一模一样的三棱柱,称为堑堵.再沿其中一个堑堵的一个顶点与相对的棱剖开,得四棱锥和三棱锥各一个,有一棱与底面垂直的四棱锥称为阳马(四棱锥S-ABCD),余下三棱锥称为鳖臑(三棱锥S-ECD),若将某长方体沿上述切割方法得到一个阳马和一个鳖臑,且该阳马的正视图和鳖臑的侧视图如图所示,则该阳马和鳖臑的表面积之和为()A.12+13+3 5 B.11+13+3 5 C.12+313+ 5 D.11+313+ 5【解析】(1)因为在梯形ABCD中,∠ABC=π2,AD∥BC,BC=2AD=2AB=2,所以将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体是一个底面半径为AB=1,高为BC=2的圆柱挖去一个底面半径为AB=1,高为BC-AD=1的圆锥,所以该几何体的表面积S=π×12+2π×1×2+π×1×12+12=(5+2)π.故选A.(2)由三视图可知,在阳马中,AS=2,AD=3,CD=1,SD=13,SB=5,所以S阳马=S△SAD+S△SCD+S△SBC+S△SAB+S矩形ABCD=3×22+1×132+3×52+1×2 2+3=7+13+352.S鳖臑=S△SCD+S△CDE+S△SDE+S△SCE=132+1×22+2×32+3×52=4+13+352,所以所求表面积之和=11+13+35,故选B.【答案】(1)A(2)B空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量.(2)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.(3)旋转体的表面积问题注意其侧面展开图的应用.某几何体的三视图如图所示,其中正视图和侧视图均为直角梯形,俯视图为两个正方形,则该几何体的表面积为()A.992B.61C.62 D.73解析:选C.由三视图画出几何体的直观图如图所示,上、下底面分别为边长是1,4的正方形;图中朝里的两个侧面是上底为1,下底为4,高为4的梯形;图中朝外的两个侧面是上底为1,下底为4,高为5的梯形,其表面积为S=1×1+4×4+12×(1+4)×4×2+12×(1+4)×5×2=62.空间几何体的体积(多维探究)角度一求简单几何体的体积(1)(2020·石家庄质量检测)某几何体的三视图如图所示(图中小正方形网格的边长为1),则该几何体的体积是()A .8B .6C .4D .2(2)如图,在直四棱柱ABCD -A 1B 1C 1D 1中,底面ABCD 是平行四边形,点E 是棱BB 1的中点,点F 是棱CC 1上靠近C 1的三等分点,且三棱锥A 1AEF 的体积为2,则四棱柱ABCD -A 1B 1C 1D 1的体积为( )A .12B .8C .20D .18【解析】 (1)由三视图可得该几何体为底面是直角梯形的直四棱柱(如图所示),其中底面直角梯形的上、下底分别为1,2,高为2,直四棱柱的高为2,所以该几何体的体积为(1+2)×22×2=6,故选B .(2)设点F 到平面ABB 1A 1的距离为h ,由题意得V A 1AEF=VF A 1AE.又VF A 1AE=13S△A 1AE ·h =13×⎝ ⎛⎭⎪⎫12AA 1·AB ·h =16(AA 1·AB )·h =16S 四边形ABB 1A 1·h =16V ABCD A 1B 1C 1D1,所以VABCD A 1B 1C 1D 1=6VA 1AEF=6×2=12.所以四棱柱ABCD -A 1B 1C 1D 1的体积为12.故选A .【答案】 (1)B (2)A 角度二 求组合体的体积(1)(2020·高考浙江卷)某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是()A.73B.143C.3 D.6(2)(2021·贵阳市第一学期监测考试)某几何体的三视图如图所示,则该几何体的体积为(俯视图中弧线是14圆弧)()A.4-πB.π-2C.1-π2D.1-π4【解析】(1)由三视图可知,该几何体是三棱柱和三棱锥的组合体,结合图中数据可得该几何体的体积V=12×2×1×2+13×12×2×1×1=73(cm3),故选A.(2)由题设知,该几何体是棱长为1的正方体被截去底面半径为1的14圆柱后剩下的部分,直观图如图所示,该几何体的体积V=1×1×1-14×π×12×1=1-π4,故选D.【答案】(1)A (2)D(1)处理体积问题的思路(2)求体积的常用方法直接法对于规则的几何体,利用相关公式直接计算割补法把不规则的几何体分割成规则的几何体,然后进行体积计算;或者把不规则的几何体补成规则的几何体,不熟悉的几何体补成熟悉的几何体,便于计算等体积法选择合适的底面来求几何体体积,常用于求三棱锥的体积,即利用三棱锥的任一个面作为三棱锥的底面进行等体积变换1.《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何?刍甍:底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图,设网格纸上每个小正方形的边长为1),那么该刍甍的体积为()A.4 B.5C.6 D.12解析:选B.如图所示,由三视图可还原得到几何体ABCDEF,过E,F分别作垂直于底面的截面EGH和FMN,可将原几何体切割成三棱柱EHG-FNM,四棱锥EADHG和四棱锥F-MBCN,易知三棱柱的体积为12×3×1×2=3,两个四棱锥的体积相同,都为13×1×3×1=1,则原几何体的体积为3+1+1=5.故选B.2.学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm.3D打印所用原料密度为0.9 g/cm3.不考虑打印损耗,制作该模型所需原料的质量为________g.解析:由题易得长方体ABCD-A1B1C1D1的体积为6×6×4=144(cm3),四边形EFGH为平行四边形,如图所示,连接GE,HF,易知四边形EFGH的面积为矩形BCC1B1面积的一半,即12),所以V四棱锥O-EFGH=13×3×122×6×4=12(cm=12(cm3),所以该模型的体积为144-12=132(cm3),所以制作该模型所需原料的质量为132×0.9=118.8(g).答案:118.8球与空间几何体的接、切问题(多维探究) 角度一 外接球(1)已知三棱柱ABC -A 1B 1C 1的底面是边长为6的正三角形,侧棱垂直于底面,且该三棱柱的外接球的表面积为12π,则该三棱柱的体积为________.(2)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S -ABC 的体积为9,则球O 的表面积为________.【解析】 (1)设球的半径为R ,上,下底面中心设为M ,N ,由题意,外接球球心为MN 的中点,设为O ,则OA =R ,由4πR 2=12π,得R =OA = 3.又易得AN =2,由勾股定理可知ON =1,所以MN =2,即棱柱的高h =2,所以该三棱柱的体积为34×(6)2×2=3 3.(2)设球O 的半径为R ,因为SC 为球O 的直径,所以点O 为SC 的中点,连接AO ,OB ,因为SA =AC ,SB =BC ,所以AO ⊥SC ,BO ⊥SC ,因为平面SCA ⊥平面SCB ,平面SCA ∩平面SCB =SC ,所以AO ⊥平面SCB ,所以V S ABC =V A SBC =13×S △SBC ×AO =13×⎝ ⎛⎭⎪⎫12×SC ×OB ×AO ,即9=13×⎝ ⎛⎭⎪⎫12×2R ×R ×R ,解得R =3,所以球O 的表面积为S =4πR 2=4π×32=36π.【答案】 (1)33 (2)36π(1)求解多面体的外接球时,经常用到截面圆.如图所示,设球O的半径为R,截面圆O′的半径为r,M为截面圆上任意一点,球心O到截面圆O′的距离为d,则在Rt△OO′M中,OM2=OO′2+O′M2,即R2=d2+r2.(2)求解球的内接正方体、长方体等问题的关键是把握球的直径即是几何体的体对角线.(3)若球面上四点P,A,B,C的连线中P A,PB,PC两两垂直或三棱锥的三条侧棱两两垂直,则可构造长方体或正方体解决问题.角度二内切球(1)(2021·重庆七校联考)已知正三棱锥的高为6,内切球(与四个面都相切)的表面积为16π,则其底面边长为()A.18 B.12C.6 3 D.4 3(2)(2020·高考全国卷Ⅲ)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为________.【解析】(1)如图,由题意知,球心在三棱锥的高PE上,设内切球的半径为R,则S球=4πR2=16π,所以R=2.所以OE=OF=2,OP=4.在Rt△OPF中,PF=OP2-OF2=2 3.因为△OPF∽△DPE,所以OFDE=PFPE,得DE=23,AD=3DE=63,AB=23AD=12.故选B.(2)易知半径最大的球即为该圆锥的内切球.圆锥PE及其内切球O如图所示,设内切球的半径为R,则sin∠BPE=ROP =BEPB=13,所以OP=3R,所以PE=4R=PB2-BE2=32-12=22,所以R=22,所以内切球的体积V=43πR3=23π,即该圆锥内半径最大的球的体积为2 3π.【答案】(1)B(2)2 3π(1)在求四面体内切球的半径时,应重视分割的思想方法,即将该四面体分割为以球心为顶点,各面为底面的四个三棱锥,通过其体积关系求得半径.(2)与球有关的组合体问题,一种是内切,一种是外接.球与旋转体的组合通常作出它们的轴截面解题;球与多面体的组合,一般通过多面体的一条侧棱和球心,并结合“切点”或“接点”作出截面图,把空间问题化归为平面问题求解.1.已知正四棱锥P-ABCD内接于一个半径为R的球,则正四棱锥P-ABCD 体积的最大值是()A.16R381B.32R381C.64R381D.R3解析:选C.如图,记O为正四棱锥PABCD外接球的球心,O1为底面ABCD 的中心,则P,O,O1三点共线,连接PO1,OA,O1A.设OO 1=x ,则O 1A =R 2-x 2,AB =2·R 2-x 2,PO 1=R +x ,所以正四棱锥P -ABCD 的体积V =13AB 2·PO 1=13×2(R 2-x 2)(R +x )=23(-x 3-Rx 2+R 2x +R 3),求导得V ′=23(-3x 2-2Rx +R 2)=-23(x +R )·(3x -R ),当x =R3时,体积V 有最大值64R 381,故选C .2.设球O 内切于正三棱柱ABC -A 1B 1C 1,则球O 的体积与正三棱柱ABC -A 1B 1C 1的体积的比值为________.解析:设球O 的半径为R ,正三棱柱ABC -A 1B 1C 1的底面边长为a ,则R =33×a 2=36a ,即a =23R .又正三棱柱ABC -A 1B 1C 1的高为2R ,所以球O 的体积与正三棱柱ABC -A 1B 1C 1的体积的比值为43πR 334a 2×2R =43πR 334×12R 2×2R =23π27.答案:23π27核心素养系列14 直观想象——确定球心位置的三种方法决定球的几何要素是球心的位置和球的半径,在球与其他几何体的结合问题中,通过位置关系的分析,找出球心所在的位置是解题的关键,不妨称这个方法为球心位置分析法.方法一 由球的定义确定球心若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球.也就是说如果一个定点到一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体外接球的球心.(1)长方体或正方体的外接球的球心是其体对角线的中点; (2)正三棱柱的外接球的球心是上、下底面中心连线的中点;(3)直三棱柱的外接球的球心是上、下底面三角形外心连线的中点;(4)正棱锥的外接球球心在其高上,具体位置可通过建立直角三角形运用勾股定理计算得到;(5)若棱锥的顶点可构成共斜边的直角三角形,则公共斜边的中点就是其外接球的球心.已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是()A.16πB.20πC.24πD.32π【解析】已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,可求得底面边长为2,故球的直径为22+22+42=26,则半径为6,故球的表面积为24π,故选C.【答案】 C方法二构造长方体或正方体确定球心(1)正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥,可将三棱锥补形成长方体或正方体;(2)同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥,可将三棱锥补形成长方体或正方体;(3)若已知棱锥含有线面垂直关系,则可将棱锥补形成长方体或正方体;(4)若三棱锥的三个侧面两两垂直,则可将三棱锥补形成长方体或正方体.如图,边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△EBF,△FCD分别沿DE,EF,FD折起,使A,B,C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为()A. 2 B.6 2C.112D.52【解析】 易知四面体A ′EFD 的三条侧棱A ′E ,A ′F ,A ′D 两两垂直,且A ′E =1,A ′F =1,A ′D =2,把四面体A ′EFD 补成从顶点A ′出发的三条棱长分别为1,1,2的一个长方体,则长方体的外接球即为四面体A ′EFD 的外接球,球的半径为r =1212+12+22=62.故选B .【答案】 B方法三 由性质确定球心利用球心O 与截面圆圆心O ′的连线垂直于截面圆及球心O 与弦中点的连线垂直于弦的性质,确定球心.正三棱锥A -BCD 内接于球O ,且底面边长为3,侧棱长为2,则球O 的表面积为________.【解析】 如图,M 为底面△BCD 的中心,易知AM ⊥MD ,DM =1,AM = 3.在Rt △DOM 中,OD 2=OM 2+MD 2,即OD 2=(3-OD )2+1,解得OD =233,故球O 的表面积为4π×⎝ ⎛⎭⎪⎫2332=163π.【答案】 163π[A 级 基础练]1.(2020·高考全国卷Ⅲ)如图为某几何体的三视图,则该几何体的表面积是( )A .6+42B .4+4 2C .6+2 3D .4+2 3解析:选C .由三视图知该几何体为如图所示的三棱锥P -ABC ,其中P A ⊥平面ABC ,AB ⊥AC ,AB =AC =AP =2,故其表面积S =⎝ ⎛⎭⎪⎫12×2×2×3+12×(22)2×sin 60°=6+2 3.2.(2021·贵阳市适应性考试)某几何体的三视图如图所示,已知正视图和侧视图是全等的直角三角形,俯视图是圆心角为90°的扇形,则该几何体的体积是( )A .2πB .π2C .3π2D .3π解析:选D .依题意,题中的几何体是一个圆锥的14(其中该圆锥的底面半径为23,高为3),如图所示,因此该几何体的体积为14×⎣⎢⎡⎦⎥⎤13×π×(23)2×3=3π,选D .3.(2020·高考全国卷Ⅰ)已知A,B,C为球O的球面上的三个点,⊙O1为△ABC的外接圆.若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为()A.64πB.48πC.36πD.32π解析:选A.如图所示,设球O的半径为R,⊙O1的半径为r,因为⊙O1的面积为4π,所以4π=πr2,解得r=2,又AB=BC=AC=OO1,所以ABsin 60°=2r,解得AB=23,故OO1=23,所以R2=OO21+r2=(23)2+22=16,所以球O的表面积S=4πR2=64π.故选A.4.(2021·东北三校第一次联考)如图,四边形ABCD是边长为2的正方形,ED⊥平面ABCD,FC⊥平面ABCD,ED=2FC=2,则三棱锥A-BEF的体积为()A.13B.23C.1 D.4 3解析:选B.如图,分别取BC,ED,AD的中点G,P,Q,连接FG,FP,PQ,QG,因为ED⊥平面ABCD,FC⊥平面ABCD,ED=2FC=2,所以PD∥=FC,所以四边形FCDP为平行四边形,所以PF∥DC.又Q,G分别为DA,CB的中点,所以QG ∥DC ,且QG =DC ,所以QG ∥PF ,且QG =PF ,所以四边形QGFP 为平行四边形,所以PQ ∥FG .又P 为DE 的中点,所以PQ ∥EA ,所以FG ∥EA ,因为EA ⊂平面EAB ,FG ⊄平面EAB ,所以FG ∥平面EAB .连接EG ,AG ,则V 三棱锥A -BEF =V 三棱锥F -ABE =V 三棱锥G -ABE =V 三棱锥E -ABG =13·ED ·S △ABG=23,故选B .5.(2021·福建省质量检测)某学生到工厂实践,欲将一个底面半径为2,高为3的实心圆锥体工件切割成一个圆柱体,并使圆柱体的一个底面落在圆锥体的底面内.若不考虑损耗,则得到的圆柱体的最大体积是( )A .16π9 B .8π9 C .16π27D .8π27解析:选A .方法一:如图,OC =2,OA =3,由△AED ∽△AOC 可得EDOC =AEAO .设圆柱体的底面半径r =ED =2x (0<x <1),可得AE =3x ,则圆柱体的高h =OE =3-3x ,圆柱体的体积V =π(2x )2(3-3x )=12π(x 2-x 3),令V (x )=12π(x 2-x 3),则V ′(x )=12π(2x -3x 2),令V ′(x )=0,解得x =23或x =0(舍去),可得V (x )在⎝ ⎛⎭⎪⎫0,23上单调递增,在⎝ ⎛⎭⎪⎫23,1上单调递减,故当x =23时,V (x )取得最大值,V (x )max =16π9,即圆柱体的最大体积是16π9.方法二:同方法一,则圆柱体的体积V =12πx 2(1-x )=6π·x ·x (2-2x )≤6π·⎣⎢⎡⎦⎥⎤x +x +(2-2x )33=16π9,当且仅当x =2-2x ,即x =23时等号成立,故圆柱体的最大体积是16π9.6.已知圆柱的底面积为S ,侧面展开图是一个正方形,那么圆柱的侧面积是________.解析:由πr 2=S 得圆柱的底面半径是Sπ,故侧面展开图的边长为2π·S π=2πS ,所以圆柱的侧面积是4πS .答案:4πS7.(2020·高考浙江卷)已知圆锥的侧面积(单位:cm 2)为2π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:cm)是________.解析:方法一:设该圆锥的母线长为l ,因为圆锥的侧面展开图是一个半圆,其面积为2π,所以12πl 2 =2π,解得l =2,所以该半圆的弧长为2π.设该圆锥的底面半径为R ,则2πR =2π,解得R =1.方法二:设该圆锥的底面半径为R ,则该圆锥侧面展开图中的圆弧的弧长为2πR .因为侧面展开图是一个半圆,设该半圆的半径为r ,则πr = 2πR ,即r =2R ,所以侧面展开图的面积为12·2R ·2πR =2πR 2=2π,解得R =1.答案:18.(2021·长沙市统一模拟考试)在四面体P ABC 中,△ABC 为等边三角形,且边长为6,P A =6,PB =8,PC =10,则四面体P ABC 的体积为________.解析:如图,延长CA 到D ,使得AD =6,连接DB ,PD .因为AD =AB =6,所以△ADB 为等腰三角形,又∠DAB =180°-∠CAB =120°,所以∠ABD =12(180°-120°)=30°,所以∠ABD +∠CBA =90°,即∠DBC =90°,故CB ⊥DB .因为PB =8,PC =10,BC =6,所以PC 2=PB 2+BC 2,所以CB ⊥PB .因为DB ∩PB =B ,DB ⊂平面PBD ,PB ⊂平面PBD ,所以CB ⊥平面PBD ,所以V三棱锥C -PBD=13×CB ×S △PBD .因为DA =AC =AP =6,所以△PDC 为直角三角形,所以PD =CD 2-PC 2=144-100=211.又DB =3AD =63,PB =8,所以DB 2=PD 2+PB 2,故BP ⊥DP ,即△PBD 为直角三角形,所以S △PBD =12×8×211=811.因为A 为DC 的中点,所以V 四面体P ABC =12V 三棱锥P -CBD =12V 三棱锥C -PBD =12×13×6×811=811.答案:8119.已知一个几何体的三视图如图所示.(1)求此几何体的表面积;(2)如果点P ,Q 在正视图中所示位置,P 为所在线段的中点,Q 为顶点,求在几何体表面上,从P 点到Q 点的最短路径的长.解:(1)由三视图知该几何体是由一个圆锥与一个圆柱组成的组合体,其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.S 圆锥侧=12(2πa )·(2a )=2πa 2, S 圆柱侧=(2πa )·(2a )=4πa 2, S 圆柱底=πa 2,所以S 表=2πa 2+4πa 2+πa 2=(2+5)πa 2.(2)沿P点与Q点所在母线剪开圆柱侧面,如图.则PQ=AP2+AQ2=a2+(πa)2=a1+π2,所以从P点到Q点在侧面上的最短路径的长为a1+π2.10.如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.(1)证明:平面AEC⊥平面BED;(2)若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为63,求该三棱锥的侧面积.解:(1)证明:因为四边形ABCD为菱形,所以AC⊥BD.因为BE⊥平面ABCD,所以AC⊥BE.因为BD∩BE=B,BD⊂平面BED,BE⊂平面BED,所以AC⊥平面BED.又AC⊂平面AEC,所以平面AEC⊥平面BED.(2)设AB=x,在菱形ABCD中,由∠ABC=120°,可得AG=GC=32x,GB=GD=x 2.因为AE⊥EC,所以在Rt△AEC中,可得EG=32x.由BE⊥平面ABCD,知△EBG为直角三角形,可得BE=22x.由已知得,三棱锥E-ACD的体积V三棱锥E-ACD=13×12·AC·GD·BE=624x3=63,故x=2.从而可得AE=EC=ED= 6.所以△EAC的面积为3,△EAD的面积与△ECD的面积均为 5.故三棱锥E-ACD的侧面积为3+2 5.[B级综合练]11.(2021·安徽省部分重点学校联考)已知三棱锥D-ABC的体积为2,△ABC 是边长为2的等边三角形,且三棱锥D-ABC的外接球的球心O恰好是CD的中点,则球O的表面积为()A.52π3B.24πC.56π3D.20π3解析:选A.设球O的半径为R,球心O到平面ABC的距离为d,因为O是CD的中点,所以点D到平面ABC的距离为2d,则V DABC=13S△ABC2d=13×34×22×2d=2,解得d= 3.过点O向平面ABC作垂线,垂足为O′,则O′为等边三角形ABC的外心,连接O′A,则O′A=2×32×23=233,R2=d2+O′A2=3+43=133,所以球O的表面积S=4πR2=52π3.12.(2021·南充市第一次适应性考试)如图,在正三棱锥A-BCD中,AB=BC,E为棱AD的中点.若△BCE的面积为2,则三棱锥A-BCD的体积为()A.23B.33C.233D.223解析:选D.因为AB=BC,所以正三棱锥A-BCD为正四面体,因为E为AD 的中点,所以AD ⊥BE ,AD ⊥CE ,又CE ∩BE =E ,所以AD ⊥平面BCE .设AD =a ,则BE =CE =32a ,所以等腰三角形BCE 的面积S △BCE =12×BC × BE 2-⎝ ⎛⎭⎪⎫BC 22=12×a ×⎝ ⎛⎭⎪⎫32a 2-⎝ ⎛⎭⎪⎫a 22=12×22a 2=2,所以a =2,所以V 三棱锥A -BCD =V 三棱锥A -BCE +V 三棱锥D -BCE =2V 三棱锥A -BCE =2×13S △BCE ×AE =2×13×2×a 2=223.13.如图所示是一个几何体的三视图,根据图中所给的数据,这个几何体的表面积为________,体积为________.解析:如图所示是还原后的几何体的直观图,分别取BC ,AD 的中点E ,F ,连接SE ,EF ,SF ,由图中数据有AB =BC =CD =DA =SE =EF =2,BE =EC =1,因为△SBC 是等腰三角形,所以SB =SC = 5. 因为△SBA 为直角三角形,所以SA =3. 又因为△SAD 是等腰三角形,所以SF ⊥AD . 所以SF =2 2.所以S 正方形ABCD =4,S △SBC =2,S △SAB =S △SCD =5,S △SAD =2 2. 所以S S ABCD =6+2(2+5). 所以V S ABCD =13·S 正方形ABCD ·SE =83. 答案:6+2(2+5) 8314.(2020·河北九校第二次联考)如图,正方体ABCD -A 1B 1C 1D 1的棱长为a ,E ,F ,G 分别是DD 1,AB ,BC 的中点,过点E ,F ,G 的截面将正方体分割成两部分,则较大几何体的体积为________.解析:如图所示,延长GF ,DA 交于点M ,延长FG ,DC 交于点N ,连接EM ,EN 分别与A 1A ,C 1C 交于点P ,Q ,连接PF ,QG ,则五边形EPFGQ 即为过点E ,F ,G 的平面与正方体的截面图形.易得P A =QC =a6,连接EA ,EC ,截面下面部分可分割成三部分,分别是三棱锥E -P AF 、三棱锥E -CGQ 、五棱锥E -AFGCD ,则截面下面部分的体积V 1=V E P AF +V E CGQ +V E AFGCD =13×12×a 6×a2×a +13×12×a 6×a 2×a +13(a 2-12×a 2×a 2)×a 2=25144a 3,则较大几何体的体积V =a 3-25144a 3=119144a 3.答案:119144a 3[C级提升练]15.设A,B,C,D是同一个半径为4的球的球面上的四点,△ABC为等边三角形且其面积为93,则三棱锥D-ABC体积的最大值为() A.12 3 B.18 3C.24 3 D.54 3解析:选B.如图,E是AC的中点,M是△ABC的重心,O为球心,连接BE,OM,OD,BO.因为S△ABC=34AB2=93,所以AB=6,BM=23BE=23AB2-AE2=2 3.易知OM⊥平面ABC,所以在Rt△OBM中,OM=OB2-BM2=2,所以当D,O,M三点共线且DM=OD+OM时,三棱锥D-ABC的体积取得最大值,且最大值V max=13S△ABC×(4+OM)=13×93×6=18 3.故选B.16.如图,正方体ABCD-A1B1C1D1的棱长为3,线段B1D1上有两个动点E,F且EF=1,则当E,F移动时,下列结论正确的有________.(填序号)①AE∥平面C1BD;②四面体ACEF的体积为定值;③三棱锥A-BEF的体积为定值;④四面体ACDF 的体积为定值.解析:对于①,如图1,AB 1∥DC 1,易证AB 1∥平面C 1BD ,同理AD 1∥平面C 1BD ,且AB 1∩AD 1=A ,所以平面AB 1D 1∥平面C 1BD ,又AE ⊂平面AB 1D 1,所以AE ∥平面C 1BD ,①正确;对于②,如图2,S △AEF =12EF ·h 1=12×1×(32)2-⎝⎛⎭⎪⎫3222=364,点C 到平面AEF 的距离为点C 到平面AB 1D 1的距离d 为定值,所以V A CEF =V C AEF =13×364×d =64d 为定值,所以②正确;对于③,如图3,S △BEF =12×1×3=32,点A 到平面BEF 的距离为A 到平面BB 1D 1D 的距离d 为定值,所以V A BEF =13×32×d =12d 为定值,③正确;对于④,如图4,四面体ACDF 的体积为V A CDF =V F ACD =13×12×3×3×3=92为定值,④正确.答案:①②③④。
《地理信息系统》自考知识要点

《地理信息系统》复习题一、单项选择题1、地理信息系统应用普及时期: 90年代。
2、“3S”技术指的是: GIS、RS、GPS。
3、下列属于GIS输出设备的是:绘图机。
4、通过行列矩阵表示地理要素的离散化数值的数据结构是:栅格结构。
5、世界上建立的第一个地理信息系统是:加拿大地理信息系统。
6、在GIS数据中,把非空间数据称为:属性数据。
7、下列软件中,属于GIS软件的是:ARCGIS 。
8、将数据组织看成为一张二维表格,用二维结构来表示实体以及实体之间联系的数据模型,称为:关系模型。
9、下列数据源中属于地理信息系统的图形数据源的是:航空与遥感影像。
10、我国基本比例尺的地形图不包括:1:2500。
11、在确定建设项目环境评价影响区范围时,可应用的空间分析方法是:缓冲区分析。
12、利用数字高程模型(DEM)数据可以进行:洪水淹没损失估算。
13、与传统的基于桌面或局域网的GIS相比,WebGIS具有什么优点:更广泛的访问范围。
14、空间实体的坐标数据与实体真实位置的接近程度,常表现为空间三维坐标数据的精度。
它不包括:属性精度。
15、存在于空间图形的不同类元素之间的拓扑关系属于:拓扑关联。
16、地理信息系统形成于20世纪:60年代。
17、在GIS中组织属性数据,应用较多的数据库模型是:关系模型。
18、“3S”技术指的是:GIS、RS、GPS 。
19、下列属于GIS输入设备的是:扫描仪。
20、世界上第一个地理信息系统是:加拿大地理信息系统。
)21、存在于空间图形的同类元素之间的拓扑关系是:拓扑邻接。
22、存在于空间图形的不同类元素之间的拓扑关系属于:拓扑关联。
23、下列软件中,属于GIS软件的是:ARC/INFO。
24、下列数据源中属于地理信息系统的文字数据源的是:统计数据。
25、下列投影中不是根据正轴投影时经纬网形状的投影分类的是:等角投影。
26、我国基本比例尺的地形图不包括:1:1000 。
27、解决道路拓宽中拆迁指标的计算问题,可应用的空间分析方法是:缓冲区分析。
matlab曲面拟合并求面积

一、引言在工程和科学领域中,曲面拟合是一项重要的数学和计算技术,它可以帮助研究人员或工程师从实验或观测数据中找到最佳的曲面模型,以便进行进一步的分析和应用。
在众多的曲面拟合方法中,MATLAB 作为一种强大的数学建模和计算软件,具有丰富的曲面拟合工具箱,能够进行曲面拟合并求出面积,本文将介绍如何使用MATLAB进行曲面拟合并求面积的操作方法。
二、MATLAB曲面拟合的基本原理MATLAB中的曲面拟合通常通过拟合曲面上的数据点来实现。
曲面拟合的基本原理是在给定数据点的情况下,找到一个曲面模型来最好地拟合这些数据点。
常用的曲面拟合方法包括最小二乘法、样条插值、高阶多项式拟合等。
在MATLAB中,通过调用曲面拟合工具箱中的相应函数,可以很容易地实现曲面拟合操作。
三、MATLAB曲面拟合并求面积的步骤1. 数据准备在进行曲面拟合之前,首先需要准备好要拟合的数据。
这些数据可以是实验测量得到的点,也可以是由其他方法计算得出的点。
在MATLAB中,可以将这些数据点表示为一组(x, y, z)的坐标,其中x和y表示数据点的空间位置,z表示对应这些位置的数值。
2. 曲面拟合在准备好数据后,可以使用MATLAB中曲面拟合工具箱中的函数来进行曲面拟合。
可以使用“fit”函数来拟合一个曲面模型,比如二次曲面、三次曲面或其他自定义的曲面模型。
拟合的结果可以用于后续的分析和计算。
3. 计算面积在获得曲面拟合模型之后,可以利用该模型来计算曲面的面积。
MATLAB提供了丰富的数学计算函数,可以方便地进行曲面积分和面积计算。
通过调用这些函数,可以得到拟合曲面的面积,该面积反映了原始数据点所描述的曲面的实际面积。
四、MATLAB曲面拟合并求面积的实例下面以一个简单的实例来演示如何使用MATLAB进行曲面拟合并求面积。
假设有一组数据点如下所示:```x = [1, 2, 3, 4, 5];y = [1, 2, 3, 4, 5];z = [1, 4, 9, 16, 25];```我们可以利用这些数据点来进行曲面拟合,假设我们使用二次曲面模型来拟合这些数据点:```MATLABp = polyfitn([x', y'], z, 2); % 二次曲面拟合[X, Y] = meshgrid(1:0.1:5, 1:0.1:5);Zfit = polyvaln(p, [X(:), Y(:)]);Zfit = reshape(Zfit, size(X));```通过上述代码,我们可以得到拟合曲面Zfit。
第六章-三维数据的空间分析方法

观察坐标系中 的三维裁剪
三维坐标投影为 二维坐标
光照模型与纹理映射
视口变换
屏幕坐标系中的 三维图形图像
三维可视化的基本流程
• 观察坐标系中的三维裁剪:
– 人眼的观察范围是有一定角度和距离范围。在计算 机实现三维可视化的时候,也有一定的观察范围, 可用视景体(Frustum)来表示这个范围。
– 视景体(Frustum):由远、近、左、右、上、下6个平 面确定。包括: • 平行投影视景体 • 透视投影视景体
– 首先根据DEM数据计算坡度和坡向; – 将坡向数据与光源方向比较:
• 面向光源的斜坡得到浅色调灰度值; • 反方向得到深色调灰度值; • 两者之间得到中间灰值,中间灰值由坡度进
一步确定。
DEM在地图制图学与地学分析中的应用
地面晕渲图与航片、卫片的区别:
– 晕渲图不包括任何地面覆盖信息,仅仅是数字化 的地表起伏显示;
不规则三角网(TIN)
优点:
• 可根据地形的复杂程度确定采样点的密度和位置,能充 分表示地形特征点和线,减少了地形较平坦地区的数据 冗余。
• 在显示速度及表示精度方面优于规则格网 •TIN是一种变精度表示方法:平坦地区数据点较少,地形起伏 较大的地区数据点密度较大。这种机制使得TIN数据可用较小 的数据量实现较高的表达精度。
– 从数据结构占用的数据量来看,在顶点个数相同的情况 下,TIN的数据量要比规则格网的大(约3~10倍)。
图形法表示DEM的比较
规则格网
不规则三角网
数据结构
1、坐标原点
1、坐标点
2、坐标间隔和方向 2、坐标关系
主要数据源
原始数据插值
离散数据点
建模的难易度
难
微分几何第二章曲面论曲面的概念

VS
高斯曲率
设曲面$S$在点$P$处的两个主曲率分别为 $k_1, k_2$,则称$K = k_1k_2$为曲面在 点$P$处的高斯曲率。高斯曲率是曲面内蕴 几何量的重要代表,反映了曲面在一点处 的弯曲程度。
法截线和法截线族
法截线
设曲面$S$在点$P$处的法向量为 $mathbf{n}$,过点$P$且与法向量 $mathbf{n}$垂直的平面称为法截面。 法截面与曲面交于一条曲线,该曲线 称为法截线。
曲面性质
曲面具有连续性、光滑性、可定向性等性质。其中连续性指 曲面上任意两点都可以用一条连续曲线连接;光滑性指曲面 上任意一点都存在切线平面;可定向性指曲面存在连续的单 位法向量场。
曲面分类与举例
曲面分类
根据曲面的形状和性质,可以将曲面分为闭曲面、开曲面、紧致曲面、非紧致曲面等类 型。
举例
球面、环面、柱面、锥面等都是常见的曲面类型。例如,球面可以表示为 $mathbf{r}(theta, varphi) = (Rcosthetasinvarphi, Rsinthetasinvarphi,
法截线族
过曲面上一点的所有法截线构成的集 合称为该点的法截线族。法截线族在 微分几何中具有重要的研究价值,与 曲面的形状和性质密切相关。
04
曲面局部理论:可 展曲面与极小曲面
可展曲面定义及性质
定义
可展曲面是一类特殊的曲面,它可以在不改 变距离的情况下完全展开到一个平面上。也 就是说,它的高斯曲率为零。
02
第一基本形式与度 量性质
第一基本形式定义及性质
第一基本形式定义
第一基本形式是微分几何中曲面论的基本概念,用于描述曲面上的度量性质。它是一个二次微分形式,记作$I = Edu^2 + 2Fdudv + Gdv^2$,其中$E, F, G$是曲面上的系数函数。
曲面的参数方程面积

曲面的参数方程面积曲面是指空间中的一种几何体,它由无数个曲面元素构成。
曲面元素与平面元素相似,都可以用其参数方程来定义。
曲面的参数方程面积是指使用参数方程计算出的曲面的面积,下面将介绍参数方程的定义以及如何计算曲面的面积。
1. 参数方程的定义参数方程通常用于描述平面或空间中的曲线或曲面。
在平面坐标系中,一个点(x,y)可以由两个参数t1和t2来表示,即x=f(t1,t2)、y=g(t1,t2);在空间坐标系中,一个点(x,y,z)可以由三个参数t1、t2和t3来表示,即x=f(t1,t2,t3)、y=g(t1,t2,t3)、z=h(t1,t2,t3)。
这些参数的范围可以是任意的,这样就可以用参数方程来描述曲线或曲面。
2. 曲面参数方程的计算方法通过使用曲面参数方程,可以计算得出曲面的面积。
具体来讲,首先需要确定曲面所在的范围,然后在这个范围内对参数方程进行积分,通过这个积分来求解曲面的面积。
曲面的面积公式如下:S = ∫∫D √[f^2t1 + g^2t1 + h^2t1] dt1 dt2其中,D为曲面所在的范围,f(t1,t2)、g(t1,t2)和h(t1,t2)为曲面参数方程所表示的函数。
3. 曲面参数方程面积的应用曲面参数方程面积的计算方法不仅适用于数学中的曲面,还适用于物理学、工程学等领域的曲面。
例如在船舶设计中,需要计算船体表面的面积,参数方程面积的计算方法就可以派上用场。
在计算机图形学中,曲面参数方程面积的计算方法也广泛应用于三维模型的建立和计算中。
此外,在物理学中,曲面参数方程面积的计算方法也常常用来研究液滴、气泡等液体和气体的表面张力现象。
4. 总结通过以上介绍,我们了解到了曲面参数方程的含义以及曲面参数方程面积的计算方法。
曲面参数方程面积的计算方法广泛应用于各个领域中,是一种非常重要的计算方法。
通过对该方法的掌握,可以更好地应用于实际工作和学习中。
3D模型的精确计算方法

3D模型的精确计算方法介绍在计算机图形学和计算机辅助设计领域,3D模型的精确计算方法是一个重要的主题。
精确计算方法旨在提供准确的数学表示和计算技术,以便准确地描述和操作3D模型。
三维坐标系在进行3D模型的精确计算时,我们首先需要建立一个三维坐标系。
三维坐标系由三个相互垂直的坐标轴(x、y、z)组成。
通过在这个坐标系中定义点的位置,我们可以准确地描述3D模型的几何特征。
几何计算方法几何计算方法是3D模型精确计算的核心。
它包括了许多用于计算和操作3D模型的数学技术和算法。
一些常用的几何计算方法包括:- 点之间的距离计算:通过计算两个点之间的欧几里得距离,可以确定它们在空间中的相对位置。
- 直线和平面的交点计算:通过计算直线和平面的方程,可以确定它们在空间中的交点,从而实现模型的相交检测。
- 曲线和曲面的包围体计算:通过计算曲线和曲面的包围体,可以确定它们的边界和形状,进而实现模型的可视化和分析。
数值计算方法除了几何计算方法外,数值计算方法也是3D模型精确计算的重要组成部分。
它包括了在计算过程中使用数值计算技术来处理和近似复杂的数学运算。
一些常用的数值计算方法包括:- 数值积分:通过数值方法计算曲线或曲面的面积、体积等特征,从而实现对模型的量化分析。
- 近似算法:通过近似数学运算,例如多项式拟合和数值优化,可以实现对复杂几何形状和运算的近似计算。
应用领域3D模型的精确计算方法在许多应用领域中发挥着重要作用。
一些常见的应用领域包括:- 计算机辅助设计:精确计算方法为计算机辅助设计工具提供了准确的几何计算和模型编辑功能。
- 游戏开发:通过精确计算方法,游戏开发者可以创建逼真的3D场景和角色模型。
- 虚拟现实和增强现实:精确计算方法用于构建虚拟和增强现实系统中的3D模型和交互。
结论3D模型的精确计算方法是计算机图形学和计算机辅助设计领域的重要研究方向。
几何计算和数值计算方法为准确描述和操作3D模型提供了重要的技术基础。
空间曲线与曲面的曲率半径

空间曲线与曲面的曲率半径空间曲线和曲面的曲率半径是微分几何学中重要的概念,用于描述曲线和曲面的弯曲程度。
在本文中,我们将探讨空间曲线和曲面的曲率半径的定义、计算方法以及其在实际应用中的意义。
空间曲线的曲率半径是用来衡量曲线在给定点处的局部弯曲程度的。
曲线的曲率半径越小,曲线在该点处的弯曲程度越大。
曲线的曲率半径可以通过求曲线在该点的切线与切线上的一点之间的距离来计算。
设曲线在点P处的切线方程为t,过点P和曲线上一点Q的割线方程为l。
曲率半径r可以根据下面的公式计算:r = lim(d->0) (|PQ|/2sinθ)其中,|PQ|表示割线l的长度,θ表示割线l与切线t之间的夹角。
曲率半径的计算方法可以应用于各种类型的曲线,如直线、圆等。
不同类型的曲线在给定点处的曲率半径的计算方法略有不同,但基本原理是相同的。
与曲线相对应的是曲面的曲率半径。
曲面的曲率半径用于描述曲面在给定点处的局部弯曲程度。
与曲线类似,曲面的曲率半径越小,曲面在该点处的弯曲程度越大。
曲面的曲率半径可以通过曲面上的两条曲线的曲率半径来计算。
在某一点处,曲率半径的计算可以借助于曲面的法向量以及两个切向量之间的夹角。
对于曲面上的点P,曲面的法向量为N,通过该点的两个曲线的切向量分别为u和v。
曲面的曲率半径可以通过下面的公式计算:1/r = K = (N·u) × (N·v) / |N|^2= Euclidean Norm((N·u) × (N·v)) / |N|^2其中,×表示向量的叉积,·表示向量的点积。
曲率半径的计算对于曲面的分析和建模非常重要。
例如,在计算机图形学中,曲率半径用于生成逼真的曲面模型,使得渲染的结果更加真实。
在物理学中,曲率半径可以用于描述光线在曲面上的折射现象,从而帮助我们理解光的传播规律。
总结起来,空间曲线和曲面的曲率半径是微分几何学中的重要概念。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间模型曲面面积计算
空间模型曲面的面积计算通常依赖于具体的模型形状和参数。
以下是一些常见的空间模型曲面的面积计算方法:
1. 球体表面积:对于半径为 r 的球体,其表面积为4πr^2。
2. 圆柱体表面积:对于底面半径为 r、高为 h 的圆柱体,其表
面积为2πrh + 2πr^2。
3. 圆锥体表面积:对于底面半径为 r、高为 h 的圆锥体,其表
面积为πr(r + √(r^2 + h^2))。
4. 正多面体表面积:对于特定的正多面体,可以根据其形状和边长计算表面积。
例如,对于正立方体,其表面积为 6a^2,
其中 a 是边长。
以上只是一些常见模型的面积计算方法,对于更加复杂的模型,一般需要使用积分或数值方法进行求解。
具体的面积计算方法还需要考虑到模型的具体参数和方程。
