二面角8种求法专题
二面角求法总结

二面角求法总结一、定义法定义法是求二面角的基本方法,它通过定义二面角的平面角来求解。
具体来说,如果两个平面相交,那么它们会在交线上形成一个角,这个角就是二面角的平面角。
通过找到这个角的两边,我们可以使用三角函数来求解这个角的大小。
二、垂线法垂线法是一种常用的求二面角的方法,它通过找到一个垂直于两个平面的交线的直线,并将这个直线延长到一个已知点,然后使用三角函数来求解这个角的大小。
这个方法的关键在于找到正确的垂线,并且这个垂线应该是垂直于交线的。
三、射影面积法射影面积法是一种利用射影面积定理求解二面角的方法。
通过找到两个平面上的两条射线和它们之间的夹角,我们可以使用射影面积定理来求解这个角的大小。
这种方法需要先找到正确的射线和夹角,然后使用射影面积定理来计算结果。
四、三垂线定理法三垂线定理法是一种利用三垂线定理来求解二面角的方法。
如果一个平面内的直线与另一个平面垂直,那么这个直线与第一个平面的交点与第二个平面的交点的连线与原直线的夹角就是要求的二面角。
这种方法的关键在于找到正确的三垂线定理的应用条件,并且正确地应用三垂线定理来计算结果。
五、角平分线法角平分线法是一种利用角平分线定理来求解二面角的方法。
如果一个平面内的角平分线与另一个平面垂直,那么角平分线与原直线的夹角就是要求的二面角。
这种方法的关键在于找到正确的角平分线的应用条件,并且正确地应用角平分线定理来计算结果。
六、向量法向量法是一种利用向量的数量积和向量积来求解二面角的方法。
通过找到两个平面上的两个向量,我们可以使用向量的数量积和向量积来计算这两个向量的夹角,这个夹角就是要求的二面角。
这种方法的关键在于正确地找到两个向量,并且正确地应用向量的数量积和向量积来计算结果。
七、坐标法坐标法是一种利用坐标系来求解二面角的方法。
通过建立适当的坐标系,我们可以将二面角的问题转化为求解一个几何量的值的问题。
这种方法的关键在于建立正确的坐标系,并且正确地使用代数方法来计算结果。
二面角8种求法

二面角求法正方体是研究立体几何概念的一个重要模型,中学立体几何教学中,求平面与平面所成的二面角是转化为平面角来度量的,也可采用一些特殊的方法求二面角,而正方体也是探讨求二面角大小方法的典型几何体。
笔者通过探求正方体中有关二面角,分析求二面角大小的八种方法:(1)平面角定义法;(2)三垂线定理法;(3)线面垂直法;(4)判定垂面法;(5)异面直线上两点间距离公式法;(6)平行移动法;(7)投影面积法;(8)棱锥体积法。
一、平面角定义法此法是根据二面角的平面角定义,直接寻求二面角的大小。
以所求二面角棱上任意一点为端点,在二面角两个平面内分别作垂直于棱的两条射线所成角就是二面角的平面角,如图二面角α-l-β中,在棱l上取一点O,分别在α、β两个平面内作AO⊥l,BO⊥l,∠AOB即是所求二面角的平面角。
例题1:已知正方体ABCD-A1B1C1D1中,O、O1是上下底面正方形的中心,求二面角O1-BC-O的大小。
例题2:已知正方体ABCD-A1B1C1D1中,E、F为A1D1、C1D1的中点,求平面EFCA与底面ABCD所成的二面角。
二、 利用三垂线定理法此方法是在二面角的一个平面内过一点作另一个面的垂线,再由垂足(或仍是该点)作棱的垂线,连接该点和棱上的垂足(或连两垂足)两点线,即可得二面角的平面角。
如图二面角α-l-β中,在平面α内取一点A ,过A 作AB ⊥平面β,B 是垂足, 由B (或A )作BO (或AO )⊥l ,连接AO (或BO )即得AO 是平面β的斜线, BO 是AO 在平面β中的射影,根据三垂线定理(或逆定理)即得AO ⊥l ,BO ⊥l , 即∠AOB 是α-l-β的平面角。
例题3:已知正方体ABCD-A 1B 1C 1D 1中,求二面角B-AC-B 1的大小。
例题4:已知正方体ABCD-A 1B 1C 1D 1中,求平面ACD 1与平面BDC 1所成的二面角。
三、 线面垂直法此法利用直线垂直平面即该直线垂直平面内任何直线的性质来寻求二面角的平面角。
求二面角的六种方法

求二面角的六种方法一、引言二面角是几何学中的一个重要概念,它用于描述两个平面的夹角。
求解二面角的方法有多种,本文将介绍六种常用的方法,包括向量法、三角函数法、三边长法、内外法、旋转法和平行四边形法。
对于每种方法,我们将详细介绍其原理和具体步骤,并给出相关的实例来加深理解。
二、向量法向量法是最常用的求解二面角的方法之一,其基本原理是通过两个平面的法向量来计算二面角。
具体步骤如下:2.1 确定两个平面首先,我们需要确定需要求解的两个平面。
平面可以由三个不共线的点或者法向量和过点的方程来确定。
2.2 求解法向量找到两个平面的法向量,分别记作n1⃗⃗⃗⃗ 和n2⃗⃗⃗⃗ 。
2.3 计算二面角的余弦值通过法向量n1⃗⃗⃗⃗ 和n2⃗⃗⃗⃗ 的点积计算二面角的余弦值:cosθ=n1⃗⃗⃗⃗ ⋅n2⃗⃗⃗⃗ ∥n1⃗⃗⃗⃗ ∥∥n2⃗⃗⃗⃗ ∥2.4 计算二面角通过余弦值反函数(如反余弦函数)计算二面角的值:θ=arccos(cosθ)三、三角函数法三角函数法是另一种常用的求解二面角的方法,主要基于三角函数的关系来计算二面角。
具体步骤如下:3.1 确定两个平面同样,我们首先需要确定需要求解的两个平面。
3.2 求解法向量和对应边长求解两个平面的法向量n 1⃗⃗⃗⃗ 和n 2⃗⃗⃗⃗ ,以及两个平面上的边长。
3.3 计算三角函数的值根据边长和法向量的乘积,分别计算sinα=∥n 1⃗⃗⃗⃗⃗ ×n 2⃗⃗⃗⃗⃗ ∥∥n 1⃗⃗⃗⃗⃗ ∥∥n 2⃗⃗⃗⃗⃗ ∥和cosα=n1⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗⃗ ∥n 1⃗⃗⃗⃗⃗ ∥∥n 2⃗⃗⃗⃗⃗ ∥,其中α为两个边向量构成的夹角。
3.4 计算二面角通过三角函数的反函数(如反正弦函数、反余弦函数)计算夹角α的值,即得到二面角的值。
四、三边长法三边长法是一种适用于三角形的方法,其原理是利用给定的三边长计算三角形的角度,进而求得二面角。
具体步骤如下:4.1 确定三个边长根据具体情况,确定三个边长a 、b 和c 。
二面角的多种求法

二面角的多种求法1.概念法例1:如图所示,在四面体ABCD 中,1AC AB ==,2CD BD ==,3AD =。
求二面角A BC D --的大小。
分析:四面体ABCD 的各个棱长都已经给出来了,这是一个典型的根据长度求角度的问题。
解:设线段BC 的中点是E ,接AE 和DE 。
根据已知的条件1AC AB ==,2CD BD ==,可以知道AE BC ⊥且DE BC ⊥。
又BC 是平面ABC 和平面DBC 的交线。
根据定义,可以得出:AED ∠即为二面角A BC D --的平面角。
可以求出32AE =,3DE =3AD =。
根据余弦定理知:22222233)372cos 243232AE DE ADAED AE DE+-+-∠==-⨯⨯⨯即二面角A BC D --的大小为7arccos4π-。
例2:如图所示,ABCD 是正方形,PB ABCD ⊥平面,1PB AB ==,求二面角A PD C --的大小。
解:作辅助线CE PD ⊥于点E ,连接AC 、AE 。
由于AD CD =,PA PC =,所以PAD PCD ≅三角形三角形。
即AE PD ⊥。
由于CE PD ⊥,所以AEC ∠即为所求的二面角的大小。
通过计算可以得到:2PC =3PD =,又1CD =,在三角形PCD 中可以计算得到63CE =。
由此可以得到:63AE CE ==,又2AC =。
由余弦定理:222222133cos 22223AE CE AC AEC AE AC +-+-∠===-⋅⋅即:23AEC π∠=。
2.空间变换法空间变换法指的是基本的空间方法,包括三垂线法、补角法、垂面法、切平面法等方法。
下面用例3介绍三垂线法、补角法和垂面法。
例3:如图所示,现有平面α和平面β,它们的交线是直线DE ,点F 在平面α内,点C 在平面β内。
求二面角F DE C --的大小。
分析:过点C 作辅助线CA 垂直于DE ,作CB 垂直于平面β于点B 。
高中数学二面角求法

高中数学二面角求法
一、直接法
嘿,小伙伴们!直接法呢,就是直接根据二面角的平面角的定义去找角。
这就需要咱们有一双善于观察的眼睛啦。
比如说,看看题目中有没有给出垂直于棱的直线,或者有没有给出两个面内与棱垂直的直线,如果有的话,那这两条直线所成的角就是二面角啦。
二、三垂线法
这个方法有点小神奇哦!咱们得先找到一个面的垂线,然后通过垂足向棱作垂线,连接斜足和垂足,这样得到的角就是二面角。
是不是感觉有点绕?其实多做几道题就明白啦。
三、射影面积法
这个方法相对简单粗暴一些。
如果一个三角形在另一个平面上的射影面积是 S1,原三角形面积是 S2,那么二面角的余弦值就是
S1/S2 哟。
是不是感觉很神奇?
四、向量法
对于那些比较复杂的图形,向量法就派上用场啦!先建立空间直角坐标系,然后求出两个面的法向量,通过法向量的夹角来求二面角。
不过要注意哦,法向量夹角可能不是二面角,要根据图形判断是相等还是互补。
总之呢,二面角的求法多种多样,咱们要根据具体的题目灵活选择合适的方法,这样才能又快又准地求出答案。
加油吧,小伙伴们!。
二面角8种求法

平面角定义法例题2:已知正方体 ABCD-ABCD 中,E 、 所成的二面角二面角求法正方体是研究立体几何概念的一个重要模型,中学立体几何教学中,求平面与平面所成的二 面角是转化为平面角来度量的,也可采用一些特殊的方法求二面角,而正方体也是探讨求二面角 大小方法的典型几何体。
笔者通过探求正方体中有关二面角, 分析求二面角大小的八种方法:(1) 平面角定义法;(2)三垂线定理法;(3)线面垂直法;(4)判定垂面法;(5)异面直线上两点间 距离公式法;(6)平行移动法;(7)投影面积法;(8)棱锥体积法。
此法是根据二面角的平面角定义,直接寻求二面角的大小。
以所求二面角棱上任意一点为端点,在二面角两个平面内 分别作垂直于棱的两条射线所成角就是二面角的平面角, 如图二面角a -l- B 中,在棱I 上取一点O,分别在a 、B 两个平面内作AC L I ,BOLI ,/ AOB 即是所求二面角的平面角例题1:已知正方体ABCD-AB i CD 中,C O 是上下底面正方形的中心,求二面角 O-BC-O 的大小。
C iC利用三垂线定理法此方法是如图二面角a -l- B 中,在平面a 内取一点A, 过A 作AB 丄平面B ,B 是垂足,由B (或A )作B0(或AO 丄l ,连接A0(或B0即得A0是平面B 的斜线,B0是 A0在平面B 中的射影,根据三垂线定理(或逆定理)即得 A0LI , B0LI , 即/ A0B 是 a -I- B 的平面角。
例题3 :已知正方体 ABCD-A i C l D 中,求二面角 B-AC-B 的大小。
线面垂直法例题4:已知正方体ABCD-ABiGD 中,求平面 ACD 与平面BDC 所成的二面角。
此法利用直线垂直平面即该直线垂直平面内任何直线的性质来寻求二面角的平面角。
方法是 过所求二面角的棱上一点,作棱的垂面,与两个平面相交所得两条交线的所成角即是二面角的平 面角。
如图在二面角a -I- B 的棱上任取一点0过0作平面丫丄I , a G 丫 =A0 B G Y =B0得/ A0B 是平面角, v I 丄丫,I 丄 A0I 丄 B0•••/ A0B是二面角的平面角。
数学二面角的求法总结

数学二面角的求法总结数学二面角是指在三维空间中,两个平面的夹角。
它是一个重要的几何概念,在计算机图形学、物理学、化学等领域都有广泛的应用。
本文将总结数学二面角的求法,帮助读者更好地理解和应用这一概念。
一、定义数学二面角是指在三维空间中,两个平面的夹角。
具体来说,设平面P1和平面P2相交于一条直线L,将P1和P2分别沿着L旋转,直到它们重合为止。
此时,P1和P2的夹角就是它们的二面角。
二、求法1. 余弦定理法设P1和P2的法向量分别为n1和n2,它们的夹角为θ,则有:cosθ =(n1·n2) / (|n1|·|n2|)其中,·表示向量的点积,|n1|和|n2|分别表示n1和n2的模长。
由于n1和n2都是单位向量,所以|n1|=|n2|=1。
因此,上式可以简化为:cosθ = n1·n2这个式子就是余弦定理。
它告诉我们,两个向量的点积等于它们的模长乘以夹角的余弦值。
因此,我们可以通过求出n1和n2的点积来计算二面角的余弦值,然后再用反余弦函数求出夹角。
2. 向量叉积法设P1和P2的法向量分别为n1和n2,它们的夹角为θ,则有:sinθ = |n1×n2| / (|n1|·|n2|)其中,×表示向量的叉积。
由于n1和n2都是单位向量,所以|n1|=|n2|=1。
因此,上式可以简化为:sinθ = |n1×n2|这个式子就是向量叉积的模长公式。
它告诉我们,两个向量的叉积的模长等于它们的模长乘以夹角的正弦值。
因此,我们可以通过求出n1和n2的叉积的模长来计算二面角的正弦值,然后再用反正弦函数求出夹角。
3. 三角形面积法设P1和P2的法向量分别为n1和n2,它们的夹角为θ,则有:sinθ = 2·S / (|P1|·|P2|)其中,S表示P1和P2的交线段所在的平面的面积,|P1|和|P2|分别表示P1和P2的面积。
利用传统方法解决二面角问题(五大题型)(解析版)

利用传统方法解决二面角问题【题型归纳目录】题型一:定义法题型二:三垂线法题型三:射影面积法题型四:垂面法题型五:补棱法【方法技巧与总结】二面角的求法法一:定义法在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角,如图在二面角α-l -β的棱上任取一点O ,以O 为垂足,分别在半平面α和β内作垂直于棱的射线OA 和OB ,则射线OA 和OB 所成的角称为二面角的平面角(当然两条垂线的垂足点可以不相同,那求二面角就相当于求两条异面直线的夹角即可).法二:三垂线法在面α或面β内找一合适的点A ,作AO ⊥β于O ,过A 作AB ⊥c 于B ,则BO 为斜线AB 在面β内的射影,∠ABO 为二面角α-c -β的平面角.如图1,具体步骤:①找点做面的垂线;即过点A ,作AO ⊥β于O ;②过点(与①中是同一个点)做交线的垂线;即过A 作AB ⊥c 于B ,连接BO ;③计算:∠ABO 为二面角α-c -β的平面角,在Rt △ABO 中解三角形.图1图2图3法三:射影面积法凡二面角的图形中含有可求原图形面积和该图形在另一个半平面上的射影图形面积的都可利用射影面积公式(cos θ=S 射S 斜=S △A 'B 'C 'S △ABC,如图2)求出二面角的大小;法四:补棱法当构成二面角的两个半平面没有明确交线时,要将两平面的图形补充完整,使之有明确的交线(称为补棱),然后借助前述的定义法与三垂线法解题.当二平面没有明确的交线时,也可直接用法三的摄影面积法解题.法五:垂面法由二面角的平面角的定义可知两个面的公垂面与棱垂直,因此公垂面与两个面的交线所成的角,就是二面角的平面角.【典型例题】题型一:定义法1.(2024·高一·江西宜春·期末)如图(1),六边形ABCDEF 是由等腰梯形ADEF 和直角梯形ABCD 拼接而成,且∠BAD =∠ADC =90°,AB =AF =EF =ED =2,AD =CD =4,沿AD 进行翻折,得到的图形如图(2)所示,且∠AEC =90°.(1)求证:CD ⊥平面ADEF .(2)求二面角C -AE -D 的余弦值;【解析】(1)在等腰梯形ADEF 中,作EM ⊥AD 于M ,则DM =AD -EF 2=1,AM =3,EM =3,可得AE =3+9=23,连接AC ,则AC =42,因为∠AEC =90°,可得EC =25,由ED 2+DC 2=EC 2,可得CD ⊥ED ,且CD ⊥AD ,AD ∩ED =D ,AD ,ED ⊂平面ADEF ,所以CD ⊥平面ADEF .(2)由(1)可知CD ⊥平面ADEF ,且AE ⊂平面ADEF ,可得CD ⊥AE ,且CE ⊥AE ,CE ∩CD =C ,CE ,CD ⊂平面CDE ,可得AE ⊥平面CDE ,且DE ⊂平面CDE ,可得AE ⊥DE ,又AE ⊥CE ,可知∠CED 就是二面角C -AE -D 的平面角,在Rt △CDE ,可得cos ∠CDE =DE CE =225=55,所以二面角C -AE -D 的余弦值为55.2.(2024·高一·全国·随堂练习)如图,在圆锥PO 中,已知PO =2,⊙O 的直径AB =2,点C 在AB上,且∠CAB =30°,点D 为AC 的中点.(1)证明:AC ⊥平面POD(2)求二面角P -AC -O 的正弦值.【解析】(1)证明:连接PC ,则PC =PA ,因为点D 为AC 的中点,所以PD ⊥AC ,因为AB 为⊙O 的直径,所以∠ACB =90°,所以AC ⊥BC ,因为O 为AB 的中点,D 为AC 的中点,所以OD ‖BC ,OD =12BC ,所以OD ⊥AC ,因为PD ∩OD =D ,PD ,OD ⊂平面POD ,所以AC ⊥平面POD ,(2)由(1)知PD ⊥AC ,OD ⊥AC ,所以∠PDO 为二面角P -AC -O 的平面角,因为PO ⊥平面ABC ,OD ⊂平面ABC ,所以PO ⊥OD ,因为∠ACB =90°,∠CAB =30°,AB =2,所以BC =12AB =1,所以OD =12BC =12,所以在Rt △POD 中,sin ∠PDO =OP PD =22+14=223,所以二面角P -AC -O 的正弦值为2233.(2024·高一·河南商丘·阶段练习)如图,四边形ABCD 是正方形,PA ⊥平面ABCD ,且PA =AB =2 . 求:(1)求二面角B -PA -C 的大小.(2)求二面角A -PD -C 的大小.(3)求二面角B -PD -A 的大小的正弦值.【解析】(1)∵PA ⊥平面ABCD ,AB ,AC ⊂面ABCD ,∴PA ⊥AB ,PA ⊥AC ,∴∠BAC 为二面角B -PA -C 的平面角,又∵四边形ABCD 是正方形,∴∠BAC =45°,即二面角B -PA -C 的大小为45°;(2)作PD 的中点E ,PC 的中点F ,连接AE ,EF ,AF ,∵PA ⊥平面ABCD ,AD ⊂面ABCD ,∴PA ⊥AD ,∵PA =AB ,∴△PAD 为等腰直角三角形,∵E 为PD 的中点,∴AE ⊥PD ,又∵PA ⊥CD ,AD ⊥CD ,PA ,AD ⊂平面PAD ,且PA ∩AD =A ,∴CD ⊥平面PAD ,∴CD ⊥PD ,∵E ,F 分别为PD 和PC 的中点,∴EF ⊥PD ,∴∠AEF 为二面角A -PD -C 的平面角,∵EF ⎳CD ,∴EF ⊥平面PAD ,∴EF ⊥AE ,∴∠AEF =90°,即二面角A -PD -C 的大小为90°;(3)连接BE ,BD ,∵PB =AP 2+AB 2=22,BD =AB 2+AD 2=22,∴PB =BD ,∴BE ⊥PD ,∴∠AEB 二面角B -PD -A 的大小的平面角,又∵PA ⊥AB ,AB ⊥AD ,AP ,AD ⊂平面PAD ,且PA ∩AD =A ,∴AB ⊥平面PAD ,∴AB ⊥AE ,∵PD =2AP =22,∴ED =12PD =2,∴BE =BD 2-ED 2=6,∴sin ∠AEB =AB BE=63 ,即二面角B -PD -A 的大小的正弦值63.题型二:三垂线法1.(2024·高一·湖南长沙·阶段练习)如图,AB 是圆O 的直径,点C 是圆O 上异于A ,B 的点,直线PC ⊥平面ABC .(1)证明:平面PBC⊥平面PAC;(2)设AB=PC=2,AC=1,求二面角B-PA-C的余弦值.【解析】(1)证明:∵AB是圆O的直径,∴BC⊥AC,又∵PC⊥平面ABC,BC⊂平面ABC,∴PC⊥BC,∵PC∩AC=C,且PC,AC⊂平面PAC,∴BC⊥平面PAC,又BC⊂平面PBC,∴平面PBC⊥平面PAC.(2)过C作CM⊥PA于M,连结BM,∵BC⊥平面PAC,PA⊂平面PAC,∴PA⊥BC,∵BC∩CM=C,且BC,CM⊂平面BCM,∴PA⊥平面BCM,又BM⊂平面BCM,∴PA⊥BM,∴∠BMC为二面角B-PA-C的平面角,在Rt△BMC中,∵CM=25,BC=3,∴BM=45+3=195,则cos∠BMC=MCBM=25195=21919,∴二面角B-PA-C的余弦值为21919.2.(2024·高一·江苏南京·阶段练习)如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为菱形,且有AB=1,PA=2,∠ABC=60°,E为PC中点.(1)证明:AC⊥面BED;(2)求二面角E-AB-C的平面角的正弦值.【解析】(1)证明:设AC与BD交于点O,连接EO,因为E,O分别为PC,AC的中点,所以EO⎳PA,又因为PA⊥底面ABCD,且BD、AC⊂底面ABCD,所以PA⊥BD,PA⊥AC,又因为EO⎳PA,所以EO⊥BD,EO⊥AC,AC∩BD=O,所以EO⊥底面ABCD,又四边形ABCD为菱形,所以BD⊥AC,则EO⊥AC,BD⊥AC,且EO∩BD=O,EO,BD⊂平面BED,所以AC⊥平面BED;(2)过O作OF⊥AB于F,连接EF,由(1)知OE⊥底面ABCD,且FO、AB⊂底面ABCD,所以OE⊥AB,OE⊥FO,又EO∩FO=O,EO、FO⊂平面EOF,所以AB⊥平面EOF,又EF⊂平面EOF,所以AB⊥EF,即∠EFO为二面角E-AB-C的平面角,因为底面ABCD为菱形,AB=1,∠ABC=60°,所以△ABC是边长为1的等边三角形,则AO=12,FO=12sin60°=34,又PA=2,则EO=12PA=22,在直角三角形EOF中,EF=11 4,则cos∠EFO=FOEF=3311,所以sin∠EFO=22211,故所求二面角的正弦值为222 11.3.(2024·高二·江苏南京·阶段练习)如图,在四棱锥PABCD中,PA⊥平面ABCD,四边形ABCD为菱形,∠ADC=60°,PA=AD=4,E为AD的中点.(1)求证:平面PCE⊥平面PAD;(2)求二面角A-PD-C的平面角的正弦值.【解析】(1)由题意,因为四边形ABCD为菱形,所以DA=DC.连接AC.因为∠ADC=60°,所以△ADC为等边三角形,从而CA=CD.在△ADC中,E是AD的中点,所以CE⊥AD.因为PA⊥平面ABCD,CE⊂平面ABCD,所以CE⊥PA.∵PA∩AD=A,PA⊂面PAD,AD⊂平面PAD,CE⊄面PAD,∴EC⊥平面PAD.又CE⊂平面PCE,∴平面PCE⊥平面PAD(2)由题意及(1)得,在平面PAD中,过点E作EM⊥PD,垂足为M,连接CM.因为EC⊥平面PAD,PD⊂平面PAD,所以EC⊥PD.又EM∩CE=E, EM⊂平面EMC,CE⊂平面EMC,所以PD⊥平面EMC.又CM⊂平面EMC,所以PD⊥CM,从而∠EMC是二面角APDC的平面角.在Rt△EMD中,ED=2,∠ADP=45°,所以EM=MD= 2.在Rt△CMD中,MD=2,CD=4,所以CM=CD2-MD2=14.在Rt△CME中,CE=23,sin∠EMC=CECM =2314=427,所以二面角APDC的平面角的正弦值为42 7.题型三:射影面积法1.如图,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥平面ABCD,PA=AB=a,求平面PBA与平面PDC所成二面角的大小.【解析】因为PA⊥平面ABCD,AD⊂平面ABCD,所以PA⊥AD,又AD⊥AB,且PA∩AB=A,PA,AB⊂平面PAB,所以AD⊥平面PAB,同理BC⊥平面PAB,所以ΔPCD在平面PBA上的射影为ΔPAB.设平面PBA与平面PCD所成二面角为θ,所以cosθ=SΔPABSΔPCD=12a212a⋅2a=22,所以θ=45°.故平面PBA与平面PCD所成二面角的大小为45°.2.(2024·新疆和田·高一校考期末)在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,平面PAD⊥底面ABCD.(1)证明:AB⊥平面PAD;(2)求面PAD与面PDB所成的二面角的正切值.【解析】(1)证明:∵底面ABCD是正方形,∴AB ⊥AD ,∵平面PAD ⊥底面ABCD ,平面PAD ∩底面ABCD =AD ,∴由面面垂直的性质定理得,AB ⊥平面PAD ;(2)(法一)由题意,△PBD 在面PAD 上的射影为△PAD .设AD =a ,则S △PAD =34a 2,△PBD 中,PD =a ,BD =2a ,PB =2a ,∴S △PBD =12×a ×2a 2-a 24=74a 2,∴面PAD 与面PDB 所成的二面角的余弦值为37,∴面PAD 与面PDB 所成的二面角的正切值为23=233.(法二)如图所示:取PD 中点E ,连接AE ,BE .设AD =a ,则BD =PB =2a ,所以AE ⊥PD ,BE ⊥PD ,所以∠AEB 是平面PAD 与平面PDB 所成的二面角的平面角,在Rt △AEB 中,AE =32a ,AB =a ,∠BAE =π2,所以tan ∠AEB =AB AE =a 32a =23=233.3.(2024·高一课时练习)直角三角形ABC 的斜边在平面α内,两条直角边分别与平面α成30°和45°角,则这个直角三角形所在的平面与平面α所成的锐二面角的余弦值为.【答案】64【解析】过点C 作CD ⊥平面α,垂足为D ,连接AD ,BD ,∵AD ,BD ,AB ⊂平面α,则CD ⊥AD ,CD ⊥BD ,CD ⊥AB ,设CD =h >0,不妨设AC ,BC 分别与平面α成30°和45°角,则BC =2h ,AC =2h ,AD =3h ,BD =h ,过C 作CE ⊥AB ,垂足为E ,连接ED ,∵CD ⊥AB ,CE ∩CD =C ,CE ,CD ⊂平面CDE ,则AB ⊥平面CDE ,且DE ⊂平面CDE ,∴DE ⊥AB ,即所求二面角的平面角为∠CED ,由△ABC 的面积可得S △ABC =12AB ⋅CE =12AC ⋅BC ,由△ABD 的面积可得S △ABD =12AB ⋅DE =12AD ⋅BD ,∵cos ∠CED =DE CE =S △ABD S △ABC =12AD ⋅BD 12AC ⋅BC =3h ⋅h 2h ⋅2h =64,故所求锐二面角的余弦值为64.故答案为:64.题型四:垂面法1.(2024·高一·云南玉溪·期末)如图,三棱锥P -ABC 的底面△ABC 是等腰直角三角形,其中AB =AC =PA =PB =2,平面PAB ⊥平面ABC ,点E ,N 分别是AB ,BC 的中点.(1)证明:EN ⊥平面PAB ;(2)求二面角C -PB -A 的余弦值.【解析】(1)证明:因为三棱锥P -ABC 的底面是等腰直角三角形,且AB =AC =2,所以AB ⊥AC ,又点E ,N 分别是AB ,BC 的中点,故EN ∥AC ,故EN ⊥AB ,又平面PAB ⊥平面ABC ,平面PAB ∩平面ABC =AB ,EN ⊂平面ABC ,故EN ⊥平面PAB .(2)如图,取PB 的中点为F ,连接AF ,CF ,因为PA =PB =AB =2,所以AF ⊥PB ,AF =3.又平面PAB ⊥平面ABC ,平面PAB ∩平面ABC =AB ,AB ⊥AC ,AC ⊂平面ABC ,故AC ⊥平面ABP ,PB ⊂平面ABP ,故AC ⊥PB ,AC ∩AF =A ,AC ,AF ⊂平面ACF ,故PB ⊥平面ACF ,CF ⊂平面ACF ,故PB ⊥CF ,则∠CFA 即为所求的角,于是tan ∠CFA =CA AF =23,cos ∠CFA =217,所以二面角C -PB -A 的余弦值为217.2.(2024·高一·安徽芜湖·期末)如图,在三棱台ABC -DEF 中,∠ACB =90°,BF ⊥AD ,BC =2,BE =EF =FC =1.(1)求证:平面BCFE ⊥平面ABC ;(2)若直线AE 与平面BCFE 所成角为π3,求平面DEC 和平面ABC 所成角的正切值.【解析】(1)取BC 中点为O ,连接FO ,∵BE =EF =FC =1,BC =2,所以BO =OC =FC =1,故∠BFO =∠OBF ,∠CFO =∠COF =∠FCO ,由三角形内角和可得∠BFO +∠CFO =90°,故BF ⊥FC ,又∵BF ⊥AD ,AD ,FC ⊂平面ADFC ,AD ,FC 为相交直线,∴BF ⊥平面ADFC ,AC ⊂平面ADFC ,∴BF ⊥AC又∵∠ACB =90°,即BC ⊥AC ,BF ∩BC =B ,BF ,BC ⊂平面BCFE ,∴AC ⊥平面BCFE ,AC 在平面ABC 内,∴平面BCFE ⊥平面ABC(2)由(1)知直线AE 与平面BCFE 所成角为∠AEC ,∴AC EC=3,由于AE =AF =BC 2-FC 2=3,∴AC =3设平面DEC 和平面ABC 的交线为l ,由于AB ⎳平面DEC ,AB ⊂平面ABC ,所以l ∥AB ,过点E 作EG ⊥BC 于G ,又(1)知平面BCFE ⊥平面ABC ,且两平面的交线为BC ,EG ⊂平面BCFE ,∴EG ⊥平面ABC ,l ∈平面ABC ,所以EG ⊥l ,且EG =EB 2-BC -EF 2 2=32,再过点G 作GK ⊥l 于K ,连接EK ,GK ∩EG =G ,GK ,EG ⊂平面EGK ,所以l ⊥平面EGK ,EK ⊂平面EGK ,故l ⊥EK ,∵∠EKG 即为所求角,BG =12,GC =32,GK =GC ⋅sin ∠BCK =32sin ∠BCK =32sin ∠B =32×313=9213∵tan ∠EKG =EG EK =32×2139=399题型五:补棱法1.(2024·山东淄博·高一统考期末)如图,已知正方体ABCD -A 1B 1C 1D 1的棱长为2,M 、N 分别为棱BB 1、BC 的中点.(1)证明:直线DN ⎳平面AMD 1;(2)设平面AMD 1与平面ABCD 的交线为l ,求点M 到直线l 的距离及二面角D 1-l -C 的余弦值.【解析】(1)证明:取CC 1的中点E ,连接DE 、NE 、ME ,在正方体ABCD -A 1B 1C 1D 1中,BB 1⎳CC 1且BB 1=CC 1,∵M 、E 分别为BB 1、CC 1的中点,则BM ⎳CE 且BM =CE ,故四边形BCEM 为平行四边形,则ME ⎳BC 且ME =BC ,又因为AD ⎳BC 且AD =BC ,则ME ⎳AD 且ME =AD ,故四边形ADEM 为平行四边形,则DE ⎳AM ,∵DE ⊄平面AMD 1,AM ⊂平面AMD 1,∴DE ⎳平面AMD 1,因为AB ⎳C 1D 1且AB =C 1D 1,故四边形ABC 1D 1为平行四边形,则BC 1⎳AD 1,∵N 、E 分别为BC 、CC 1的中点,则NE ⎳BC 1,则NE ⎳AD 1,∵NE ⊄平面AMD 1,AD 1⊂平面AMD 1,∴NE ⎳平面AMD 1,∵DE ∩NE =E ,DE 、NE ⊂平面DEN ,所以,平面DEN ⎳平面AMD 1,∵DN ⊂平面DEN ,∴DN ⎳平面AMD 1.(2)延长D 1M 、DB 交与点P ,连接AP ,则直线AP 即为直线l ,因为BB 1⎳DD 1且BB 1=DD 1,M 为BB 1的中点,则PM PD 1=PB PD =BM DD 1=12,故点B 为PD 的中点,M 为PD 1的中点,在△ABP 中,AB =2,BP =BD =22,∠ABP =135°,由余弦定理可得AP2=AB2+BP2-2AB⋅BP cos135°=20,则AP=25,cos∠BAP=AB2+AP2-BP22AB⋅AP =255,则sin∠BAP=1-cos2∠BAP=55,过点D在平面ABCD内作DF⊥直线AP,垂足为点F,连接D1F,sin∠DAF=sin90°-∠BAP=cos∠BAP=255,所以,DF=AD sin∠DAF=455,∵DD1⊥平面ABCD,l⊂平面ABCD,∴DD1⊥l,∵DF⊥l,DF∩DD1=D,DF、DD1⊂平面DD1F,∴l⊥平面DD1F,∵D1F⊂平面DD1F,∴D1F⊥l,故二面角D1-l-C的平面角为∠D1FD,且D1F=DD21+DF2=655,故点M到直线l的距离为355,cos∠D1FD=DFD1F =23,因此,二面角D1-l-C的平面角的余弦值为23.2.(2024·湖南常德·高一临澧县第一中学校考期末)《九章算术》是中国古代的一部数学专著,是《算经十书》中最重要的一部,成于公元一世纪左右.它是一本综合性的历史著作,是当时世界上最简练有效的应用数学,它的出现标志着中国古代数学形成了完整的体系.《九章算术》中将由四个直角三角形组成的四面体称为“鳖臑”,已知在三棱锥P-ABC中,PA⊥平面ABC.(1)从三棱锥P-ABC中选择合适的两条棱填空:⊥,则三棱锥P-ABC为“鳖臑”;(2)如图,已知AD⊥PB,垂足为D,AE⊥PC,垂足为E,∠ABC=90°.(i)证明:平面ADE⊥平面PAC;(ii)设平面ADE与平面ABC交线为l,若PA=23,AC=2,求二面角E-l-C的大小.【解析】(1)因为“鳖臑”是由四个直角三角形组成的四面体,又PA⊥平面ABC,所以PA⊥AB,PA⊥AC,PA⊥BC;即△PAB,△PAC为直角三角形;若BC⊥AB,由AB∩PA=A,AB,PA⊂平面PAB,可得:BC⊥平面PAB;所以BC⊥PB,即△ABC,△PBC为直角三角形;满足四个面都是直角三角形;同理,可得BC⊥AC或BC⊥PB或BC⊥PC,都能满足四个面都是直角三角形;故可填:BC⊥AB或BC⊥AC或BC⊥PB或BC⊥PC;(2)(i)证明:∵PA⊥平面ABC,BC⊂平面ABC,∴PA⊥BC,又BC⊥AB,PA∩AB=A,PA,AB⊂平面PAB,∴BC⊥平面PAB,又AD⊂平面PAB,∴BC⊥AD,又AD⊥PB,PB∩BC=B,PB,BC⊂平面PBC,∴AD⊥平面PBC,又PC⊂平面PBC,∴PC⊥AD,又AE⊥PC,AE∩AD=A,AD,AE⊂平面ADE,∴PC⊥平面ADE,又PC⊂平面PAC,∴平面ADE⊥平面PAC.(ii)由题意知,在平面PBC中,直线DE与直线BC相交.如图所示,设DE∩BC=F,连结AF,则AF即为l.∵PC⊥平面AED,l⊂平面AED,∴PC⊥l,∵PA⊥平面ABC,l⊂平面ABC,∴PA⊥l,又PA∩PC=P,PA,PC⊂平面PAC,∴l⊥平面PAC,又AE,AC⊂平面PAC,∴AE⊥l,AC⊥l.∴∠EAC即为二面角E-l-C的一个平面角.在△PAC中,PA⊥AC,PA=23,AC=2,∴PC=4,又AE⊥PC,∴AE=AP×ACPC =23×24=3,∴cos∠EAC=AEAC =32,∴∠EAC=30°,∴二面角E-l-C的大小为30°.3.(2024·黑龙江牡丹江·高一牡丹江一中校考期末)如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.(1)记平面BEF 与平面ABC 的交线为l ,试判断直线l 与平面PAC 的位置关系,并加以证明;(2)设PC =2AB =4,求二面角E -l -C 大小的取值范围.【解析】(1)∵EF ⎳AC ,AC ⊂平面ABC ,EF ⊄平面ABC ,∴EF ⎳平面ABC ,又EF ⊂平面BEF ,平面BEF 与平面ABC 的交线为l ,所以EF ⎳l ,而l ⊄平面PAC ,EF ⊂平面PAC ,所以l ⎳平面PAC ;(2)设直线l 与圆O 的另一个交点为D ,连接DE ,FB ,如图:由(1)知,BD ⎳AC ,而AC ⊥BC ,所以BD ⊥BC ,所以PC ⊥平面ABC ,所以PC ⊥BD ,而PC ∩BC =C ,所以BD ⊥平面PBC ,又FB ⊂平面PBC ,所以BD ⊥BF ,所以∠FBC 就是二面角E -l -C 的平面角,因为PC =2AB =4,点F 是PC 的中点,所以FC =12PC =AB =2,故tan ∠FBC =FC BC =AB BC =1cos ∠ABC ,注意到0<∠ABC <π2,所以0<cos ∠ABC <1,所以tan ∠FBC >1,因为0<∠FBC <π2,所以∠FBC ∈π4,π2 ,所以二面角E -l -C 大小的取值范围为π4,π2.【过关测试】1.(2024·高一·广西玉林·阶段练习)如图,在直三棱柱ABC -A 1B 1C 1中,∠ABC =90°,2AB =2BC =CC 1=2,D 是棱CC 1的中点,(1)求证:B1D⊥平面ABD;(2)求平面AB1D与侧面BB1C1C所成锐角的正切值.【解析】(1)证明:因为直三棱柱ABC-A1B1C1中,2BC=CC1=2,D是棱CC1的中点,所以BC=CD=C1D=B1C1=1,BB1=2,∠BCD=∠B1C1D=90°,所以BD2=BC2+CD2=2,B1D2=C1D2+B1C21=2,所以BD2+B1D2=4=BB21,所以BD⊥B1D,因为BB1⊥平面ABC,AB⊂平面ABC,所以BB1⊥AB,因为∠ABC=90°,所以AB⊥BC,因为BB1∩BC=B,BB1,BC⊂平面BB1C1C,所以AB⊥平面BB1C1C,所以B1D⊂平面BB1C1C,所以AB⊥B1D,因为AB∩BD=B,AB,BD⊂平面ABD,所以B1D⊥平面ABD;(2)因为B1D⊥平面ABD,AD⊂平面ABD,所以B1D⊥AD,因为BD⊥B1D,平面AB1D∩平面BB1C1C=B1D,所以∠ADB就是平面AB1D与侧面BB1C1C所成的平面角,因为AB⊥平面BB1C1C,BD⊂平面BB1C1C,所以AB⊥BD,在Rt△ADB中,AB=1,BD=2,则tan∠ADB=ABBD=12=22,所以平面AB1D与侧面BB1C1C所成锐角的正切值为2 2 .2.(2024·高一·河南商丘·阶段练习)如图,在棱长为3的正方体ABCD-A1B1C1D1中,E,F为棱AA1的两个三等分点.(1)求证:CE∥平面BDF;(2)求二面角C1-BD-F的余弦值.【解析】(1)如图,连接AC交BD于点O,连接OF.在△ACE中,O为AC的中点,F为AE的中点,所以OF∥CE,又平面BDF,OF⊂平面BDF,所以CE∥平面BDF.(2)连接C1O,C1F,A1C1.在正方体中,BD⊥AC,AA1⊥BD,AC∩AA1=A,AC,AA1⊂平面A1AC 所以BD⊥平面A1AC,而OF,OC1均在平面A1AC内,所以BD⊥OF,BD⊥OC1,所以∠FOC1是二面角C1-BD-F的平面角.因为正方体的棱长为3,所以AC=32,AO=322,AF=1,由勾股定理得FO=3222+12=222,C1O=322 2+32=362,C1F=(32)2+22=22.在△FOC1中,由余弦定理得cos∠FOC1=FO2+C1O2-C1F22FO⋅C1O=-3333,所以二面角C1-BD-F的余弦值为-33 33.3.(2024·高一·山东淄博·阶段练习)在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,AB=2,AC∩BD=O,PO⊥底面ABCD,PO=2,点E在棱PD上,且CE⊥PD.(1)证明:平面PBD⊥平面ACE;(2)证明:OE⊥PD(3)求二面角D-AC-E的余弦值【解析】(1)∵PO⊥平面ABCD,AC⊂平面ABCD,∴PO⊥AC,∵在菱形ABCD中,AC⊥BD,且BD∩PO=O,BD,PO⊂平面PBD,∴AC⊥平面PBD,∵AC⊂平面ACE,∴平面ACE⊥平面PBD,即平面PBD⊥平面ACE;(2)连接OE,则平面ACE∩平面PBD=OE,由(1)知AC ⊥平面PBD ,PD ⊂平面PBD ,则AC ⊥PD ,又∵CE ⊥PD ,CE ∩AC =C ,CE ,AC ⊂平面ACE ,∴PD ⊥平面ACE ,OE ⊂平面ACE ,∴PD ⊥OE ,即OE ⊥PD .(3)由于AC ⊥平面PBD ,OE ⊂平面PBD ,则AC ⊥OE ,又AC ⊥OD ,且平面EAC ∩平面DAC =AC ,OE ⊂平面EAC ,OD ⊂平面DAC ,故∠DOE 为二面角D -AC -E 的平面角;在菱形ABCD 中,AB =2,∠ABC =60°,则△ABC 是等边三角形,而O 为AC ,BD 的中点,则OD =OB =3,又OP =2,∴PD =22+3 2=7,故OE =OP ⋅OD PD =237=2217,∴cos ∠DOE =OE OD =22173=277,即二面角D -AC -E 的余弦值为277.4.(2024·高一·陕西西安·阶段练习)如图,在三棱柱ABC -A 1B 1C 1中,AA 1⊥平面ABC ,E ,F 分别为A 1B ,A 1C 的中点,D 为B 1C 1上的点,且A 1D ⊥B 1C .(1)求证:平面A 1FD ⊥平面BCC 1B 1;(2)若三棱柱所有棱长都为a ,求二面角A 1-B 1C -C 1的平面角的正切值.【解析】(1)在三棱柱ABC -A 1B 1C 1中,AA 1⊥平面ABC ,则三棱柱ABC -A 1B 1C 1为直三棱柱,∴BB 1⊥平面A 1B 1C 1,A 1D ⊂平面A 1B 1C 1,∴BB 1⊥A 1D ,∵A 1D ⊥B 1C ,B 1C ∩BB 1=B 1,B 1C ,BB 1⊂平面BCC 1B 1,∴A 1D ⊥平面BCC 1B 1,又A 1D ⊂平面A 1FD ,∴平面A 1FD ⊥平面BCC 1B 1;(2)因为三棱柱所有棱长都为a,则△A1B1C1为等边三角形,A1D⊥平面BCC1B1,B1C1⊂平面BCC1B1,所以A1D⊥B1C1,所以D为B1C1的中点,过点D作B1C垂线,垂足为H,连接A1H,∵A1D⊥B1C,DH⊥B1C,A1D∩DH=D,A1D,DH⊂平面A1DH,∴B1C⊥平面A1DH,又A1H⊂平面A1DH,所以B1C⊥A1H,则∠A1HD是二面角A1-B1C-C1的平面角,A1D⊥平面BCC1B1,DH⊂平面BCC1B1,所以A1D⊥DH,∴A1D=32a,DH=22B1D=24a,tan∠A1HD=A1DDH=6,故二面角A1-B1C-C1的平面角的正切值为6.5.(2024·高一·广东云浮·阶段练习)如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为菱形,且有AB=1,PA=2,∠ABC=60°,E为PC中点.(1)证明:PA⎳平面BED;(2)求二面角E-AB-C的平面角的正弦值.【解析】(1)设AC与BD交于点O连接EO,因为E,O分别为PC,AC的中点,所以EO∥PA,又因为PA⊄平面BED,EO⊂平面BED,所以PA ⎳平面BED ;(2)过O 作OF ⊥AB 于F ,连接EF ,因为PA ⎳OE ,且PA ⊥平面ABCD所以OE ⊥平面ABCD ,AB ⊂平面ABCD ,所以OE ⊥AB ,又EO ∩FO =O ,EO ,OF ⊂平面EOF ,所以AB ⊥平面EOF ,又EF ⊂平面EOF ,所以AB ⊥EF ,即∠EFO 为二面角E -AB -C 的平面角,由EO =12PA =22,△ABC 是边长为1的等边三角形,即FO =12sin60°=34,在直角三角形EOF 中,EF =114,即cos ∠EFO =FO EF =3311,sin ∠EFO =1-cos 2∠EFO =22211.所以所求二面角的正弦值为22211.6.(2024·高一·山东枣庄·阶段练习)如图,E 是直角梯形ABCD 底边AB 的中点,AB =2DC =2BC ,将△ADE 沿DE 折起形成四棱锥A -BCDE .(1)求证:DE ⊥平面ABE ;(2)若二面角A -DE -B 为60°,求二面角A -DC -B 的余弦值.【解析】(1)在直角梯形ABCD 中,易知DC ⎳BE ,且DC =BE ,所以四边形BCDE 为平行四边形,又∠EBC =90°,AB =2DC =2BC ,E 是AB 的中点,所以四边形BCDE 是正方形,从而DE ⊥EB ,也即DE ⊥EA ,因此,在四棱锥A -BCDE 中,EB ∩EA =A ,EB ,EA ⊂平面ABE ,所以DE ⊥平面ABE ;(2)由(1)知,∠AEB 即二面角A -DE -B 的平面角,故∠AEB =60°,又AE =EB ,可得△AEB 为等边三角形;设BE 的中点为F ,CD 的中点为G ,连接AF ,FG ,AG ,从而AF ⊥BE ,FG ⎳DE ,于是AF ⊥CD ,FG ⊥CD ,AF ∩FG =F ,AF ,FG ⊂平面AFG ,从而CD ⊥平面AFG ,AG ⊂平面AFG ,因此CD ⊥AG ;所以∠AGF 即所求二面角A -DC -B 的平面角.由(1)中DE ⊥平面ABE ,且FG ⎳DE ,从而FG ⊥平面ABE ,AF ⊂平面ABE 所以FG ⊥AF ,设原直角梯形中,AB =2DC =2BC =2a ,则折叠后四棱锥中AF =32a ,FG =a ,从而AG =AF 2+FG 2=72a 于是在Rt △AFG 中,cos ∠AGF =FG AG=277;即二面角A -DC -B 的余弦值为277.7.(2024·高一·北京怀柔·期末)如图,正方体ABCD -A 1B 1C 1D 1的棱长为2.(1)证明:CD 1⎳平面A 1BD ;(2)证明:BD ⊥平面A 1AC ;(3)求二面角A 1-BD -A 的正弦值.【解析】(1)在正方体ABCD -A 1B 1C 1D 1,A 1D 1⎳BC 且A 1D 1=BC ,∴A 1BCD 1为平行四边形,∴A 1B ⎳CD 1,∵CD 1⊄平面A 1BD ,A 1B ⊂平面A 1BD ∴CD 1⎳平面A 1BD ;(2)∵正方体ABCD -A 1B 1C 1D 1,AA 1⊥底面ABCD ,BD ⊂底面ABCD ,∴AA 1⊥BD ,∵正方形ABCD 中,AC ⊥BD ,又∵AA 1⊂平面A 1AC ,AC ⊂平面A 1AC ,AA 1∩AC =A ,∴BD ⊥平面A 1AC ;(3)∵在正方形ABCD 中,设AC ∩BD =O ,连接A 1O ,∴AC ⊥BD ,AO ⊥BD ,∵△A 1BD 中,A 1B =A 1D =22,△A 1BD 为等腰三角形,∴A 1O ⊥BD ,∴∠A 1OA 即为二面角A 1-BD -A 的平面角,∵在Rt △A 1AO 中,AA 1=2,AO =2,∴A 1O =6,∴sin ∠A 1OA =A 1A A 1O=63,即二面角A 1-BD -A 的正弦值为63.8.(2024·高一·广西·期末)如图,四棱锥P -ABCD ,PA ⊥平面ABCD ,∠BAD =∠BCD =π2,AB =BC =2,PA =BD =4,过点C 作直线AB 的平行线交AD 于F ,G 为线段PD 上一点.(1)求证:平面PAD ⊥平面CFG ;(2)求平面PBC 与平面PDC 所成二面角的余弦值.【解析】(1)因为PA ⊥平面ABCD ,AB ⊂平面ABCD ,所以PA ⊥AB ,因为∠BAD =π2,所以AB ⊥AD ,因为PA ∩AD =A ,PA 、AD ⊂平面PAD ,所以AB ⊥平面PAD ,因为CF ⎳AB ,所以CF ⊥平面PAD ,因为CF ⊂平面CFG ,所以平面CFG ⊥平面PAD ;(2)连结AC ,过点B 作BE ⊥PC 于点E ,连接DE ,如图,PA ⊥平面ABCD ,AD 、AC ⊂平面ABCD ,所以PA ⊥AD ,PA ⊥AC ,因为∠BAD =∠BCD =π2,AB =BC =2,PA =BD =4,由勾股定理得:AD=BD2-AB2=23,则∠ADB=30°,同理可得CD=23,∠CDB=30°,故∠ADC=60°,所以三角形ACD为等边三角形,AC=CD=23,同理可得:PB=PA2+AB2=25,PC=PA2+AC2=27,PD=PA2+AD2=27,在△BCP中,由余弦定理得:cos∠BCP=BC2+CP2-PB22BC⋅CP=4+28-2087=327,则CE=BC cos∠BCP=627,BE=BC2-CE2=197,在△CDP中,由余弦定理得:cos∠PCD=PC2+CD2-DP22PC⋅CD=12+28-2823×47=327,在△CDE中,DE2=CE2+CD2-2CE⋅CD cos∠PCD=3628+12-2×627×23×327=757,因为CE2+DE2=12=CD2,所以DE⊥PC,所以∠BED是平面PBC与平面PDC所成二面角的平面角,由余弦定理得:cos∠BED=BE2+DE2-BD22BE⋅DE=197+757-162×197×757=-35795.9.(2024·高一·辽宁葫芦岛·期末)如图,在多面体ABCDEF中,菱形ABCD的边长为2,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3.(1)在线段FC上确定一点H,使得平面BDH⎳平面AEF;(2)设G是线段EC的中点,在(1)的条件下,求二面角A-HG-B的大小.【解析】(1)H为线段FC的中点.证明如下:在菱形ABCD中,连接AC与BD交于点O,于是O为AC中点,在△AFC中,OH为中位线,所以OH⎳AF,因为OH⊂平面BDH,AF⊄平面BDH,所以AF⎳平面BDH,又因为四边形BDEF是矩形,BD⎳EF,因为BD ⊂平面BDH ,EF ⊄平面BDH ,所以EF ⎳平面BDH ,又AF ,EF ⊂平面AEF ,且AF ∩EF =E ,所以平面AEF ⎳平面BDH .(2)分别取EF ,HG ,OC 中点M ,N ,P ,连接MO ,MA ,MC ,NP ,NO ,NA ,于是,N 为线段MC 中点,易知,在矩形BDEF 中MO ⊥BD ,菱形ABCD 中AC ⊥BD ,且MO ∩AC =O ,MO ,AC ⊂平面AMC ,所以BD ⊥平面AMC .又GH 为△CEF 的中位线,故GH ⎳EF ,且BD ⎳EF ,所以GH ⎳BD .所以GH ⊥平面AMC .又AN ,ON ⊂平面AMC ,所以GH ⊥AN ,GH ⊥ON .所以∠ANO 为二面角A -HG -B 的平面角.由已知,平面BDEF ⊥平面ABCD ,平面BDEF ∩平面ABCD =BD ,MO ⊂平面BDEF ,且MO ⊥BD ,可得MO ⊥ABCD .又NP 为△CMO 的中位线,所以NP ⎳MO ,且NP =12MO =32,所以NP ⊥平面ABCD ,进而NP ⊥AP .在菱形ABCD 中,AO =3,PO =32,AP =AO +PO =332.在直角△NPA 中,tan ∠NAP =NP AP=33,所以∠NAP =π6.在直角△NPO 中,tan ∠NOP =NP OP=3,所以∠NOP =π3,所以,∠ANO =∠NOP -∠NAP =π6.即二面角A -HG -B 的大小为π6.10.(2024·高一·贵州毕节·期末)如图,在四棱锥P -ABCD 中,底面ABCD 为矩形,且AB =3,AD =2,侧面PAD 是等腰三角形,且PA =PD =2,侧面PAD ⊥底面ABCD .(1)求证:AP ⊥平面PCD ;(2)求侧面PBC 与底面ABCD 所成二面角的正弦值.【解析】(1)证明:在△APD 中,AD =2,PA =PD =2∴AD 2=AP 2+DP 2∴AP ⊥DP又∵侧面PAD ⊥底面ABCD ,侧面PAD ∩底面ABCD =AD ,AD ⊥CD ,CD ⊂平面ABCD ,∴CD ⊥平面APD ,又AP ⊂平面APD ,∴CD ⊥AP ,又CD ∩DP =D ,CD ,DP ⊂平面PCD ,∴AP ⊥平面PCD .(2)取AD 的中点为M ,连接PM ,∵PA =PD ,所以PM ⊥AD又∵侧面PAD ⊥底面ABCD ,侧面PAD ∩底面ABCD =AD ,PM ⊂面PAD ,∴PM ⊥平面ABCD又BC ⊂平面ABCD ,∴PM ⊥BC ,过点M 作MG ⊥BC ,垂足为G ,连接PG ,又PM ∩MG =M ,PM ,MG ⊂平面PMG ,∴BC ⊥平面PMG ,又MG ⊂平面PMG ,PG ⊂平面PMG ,∴BC ⊥MG ,BC ⊥PG ,∴∠PGM 为侧面PBC 与底面ABCD 所成二面角的平面角,在直角△PMG 中,PM =12AD =1,MG =3,∴PG =10,∴sin ∠PGM =PM PG =110=1010,即侧面PBC 与底面ABCD 所成二面角的正弦值为1010.11.(2024·高一·内蒙古包头·期末)如图,已知AB 是圆的直径,且AB =4,PA 垂直圆所在的平面,且PA =3,M 是弧AB 的中点.(1)求点A 到平面PBM 的距离;(2)求二面角A -BM -P 的正弦值.【解析】(1)设点A 到平面PBM 的距离为d ,由题意知BM ⊥AM ,因为PA ⊥平面MAB ,BM ⊂平面MAB ,所以BM ⊥PA ,又AM ∩PA =A ,AM ,PA ⊂平面PAM ,则BM ⊥平面PAM ,又PM ⊂平面PAM ,所以BM ⊥PM ,由V A -PBM =V P -ABM ,得13S △PBM ⋅d =13S △ABM ⋅PA ,12PM ⋅BM ⋅d =12AM ⋅BM ⋅3,即17d =62,故d =63417,所以点A 到平面PBM 的距离为63417;(2)由(1)得BM ⊥AM ,BM ⊥PM ,所以∠PMA 即为二面角A -BM -P 的平面角,因为AB =4,M 是弧AB 的中点,所以MA =MB =22,因为PA ⊥平面MAB ,AM ⊂平面MAB ,所以AM ⊥PA ,则PM =9+8=17,则sin ∠PMA =PA PM =317=31717,所以二面角A -BM -P 的正弦值为31717.12.(2024·高一·辽宁·期末)如图1,在等腰直角△ABC 中,∠C =π2,D ,E 分别是AC ,AB 的中点,F 为线段CD 上一点(不含端点),将△ADE 沿DE 翻折到△A 1DE 的位置,连接A 1C ,A 1B ,得到四棱锥A 1-BCDE ,如图2所示,且A 1F ⊥CD .(1)证明:A 1F ⊥平面BCDE ;(2)若直线A 1E 与平面BCDE 所成角的正切值为155,求二面角A 1-BD -C 的平面角的正切值.【解析】(1)证明:因为∠C =π2,且DE ∥BC ,所以DE ⊥AD ,所以DE ⊥A 1D ,DE ⊥DC ,又因为A 1D ∩CD =D ,且A 1D ,CD ⊂平面A 1DC ,所以DE ⊥平面A 1DC ,因为A 1F ⊂平面A 1DC ,所以DE ⊥A 1F ,又因为A 1F ⊥CD ,CD ∩DE =D 且CD ,DE ⊂平面BCDE ,所以A 1F ⊥平面BCDE .(2)如图所示,连接EF ,因为D ,E 分别是AC 与AB 的中点,可得A 1D =CD =DE ,又因为A 1F ⊥平面BCDE ,所以直线A 1E 与平面BCDE 所成的角为∠A 1EF ,由直线A 1E 与平面BCDE 所成角的正切值为155,即tan ∠A 1EF =155,设DF=x,则A1F=A1D2-DF2=A1D2-x2,EF=DE2+DF2=A1D2+x2,所以tan∠A1EF=A1FEF=A1D2-x2A1D2+x2=155,解得A1D=2x,即F为CD的中点,过F作FO⊥BD,垂足为O,因为A1F⊥平面BCDE,BD⊂平面BCDE,所以A1F⊥BD,又因为A1F∩OF=F,且A1F,OF⊂平面A1OF,所以BD⊥平面A1OF,因为A1O⊂平面A1OF,所以A1O⊥BD,所以二面角A1-BD-C的平面角为∠A1OF,由BC=4x,CD=2x,则BD=BC2+CD2=25x,所以OF=12⋅CD⋅BCBD=255x,因为A1F=A1D2-x2=3x,所以tan∠A1OF=A1FOF=152.13.(2024·高一·安徽宣城·期末)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点,△OCD是边长为2的等边三角形.(1)若AB=22,求直线AB和CD所成角的余弦值;(2)若点E在棱AD上,AE=13AD且三棱锥A-BCD的体积为4,求二面角E-BC-D平面角大小的正弦值.【解析】(1)分别取BC、AC的中点M、N,连接OM,ON,MN,因为О为BD中点,所以MO∥CD,MN∥AB且MO=12CD,MN=12AB,所以异面直线AB和CD所成角(或为邻补角)即为∠OMN,因为AB=AD,O为BD中点,所以AO⊥BD,因为△OCD是边长为2的等边三角形,所以BO=DO=2,MN=12AB=2,MO=12CD=1,又因为平面ABD⊥平面BCD,AO⊥BD,平面ABD∩平面BCD=BD,AO⊂平面ABD,所以AO⊥平面BCD,因为OC⊂平面BCD,所以AO⊥OC,由OC=OD,得△AOC≌△AOD,得AC=AD=AB=22.在直角三角形△AOC中,则ON=12AC=2,在△MON中,根据余弦定理得,cos∠OMN=MN2+MO2-ON22MN⋅MO =(2)2+1-(2)22×2×1=24或cos∠OMN=122=24所以直线AB和CD所成角的余弦值为2 4.(2)过点E作EN∥AO交BD于N.过点N作NM∥CD交BC于点M,连接ME,因为EN∥AO且AO⊥BD,所以EN⊥BD,因为平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,EN⊂平面ABD,所以EN⊥平面BCD,因为BC⊂平面BCD,所以EN⊥BC,在△BCD中,因为OB=OD=OC,所以BC⊥CD,因为NM∥CD,所以MN⊥BC,因为MN∩EN=N,MN,EN⊂平面MNE,所以BC⊥平面MNE,因为ME⊂平面MNE,所以BC⊥ME,所以∠EMN为所求的二面角E-BC-D的平面角,因为S△BCD=12BD⋅CD⋅sin∠BDC=12×4×2×32=23,因为V A-BCD=13S△BCD⋅OA=13×23⋅OA=4,所以OA=23,又因为AE=13AD,EN∥AO,所以ENAO=DEDA=23,得EN=23OA=433,因为NM ∥CD ,所以MN CD=BN DB =46=23,因为CD =2,所以MN =43.又EN =433,所以3MN =EN .所以tan ∠EMN =EN MN =3,所以sin ∠EMN cos ∠EMN =3,得sin ∠EMN3=cos ∠EMN ,因为sin 2∠EMN +cos 2∠EMN =1,sin ∠EMN >0,所以解得sin ∠EMN =32.所以二面角E -BC -D 平面角大小的正弦值为32.14.(2024·高一·福建福州·期末)如图,四棱锥P -ABCD 的侧面PAD 是边长为2的正三角形,底面ABCD 为正方形,且平面PAD ⊥平面ABCD ,M ,N 分别为AB ,AD 的中点.(1)求证:DM ⊥PC ;(2)在线段PB 上是否存在一点Q 使得MQ ⎳平面PNC ,存在指出位置,不存在请说明理由.(3)求二面角B -PC -N 的正弦值.【解析】(1)∵△PAD 为正三角形,N 为AD 中点,∴PN ⊥AD ,又∵平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD ,PN ⊂平面PAD ,∴PN ⊥平面ABCD ,DM ⊂平面ABCD ,∴PN ⊥DM ,在正方形ABCD 中,易知△DAM ≌△CDN ,∴∠ADM =∠DCN ,而∠ADM +∠MDC =90°,∴∠DCN +∠MDC =90°,∴DM ⊥CN ,∵PN ∩CN =N ,PN ,CN ⊂平面PNC ,∴DM ⊥平面PNC ,∵PC ⊂平面PNC ,∴DM ⊥PC .(2)存在,当BQ =14BP时MQ ⎳平面PNC ,取BE 的四等分点E (靠近B ),取BP 的四等分点Q (靠近B ),连接ME 、EQ 、MQ ,则QE ⎳PC ,QE ⊄平面PNC ,PC ⊂平面PNC ,所以QE ⎳平面PNC ,由BM DC=BE DN =12,所以△MBE ∽△CDN ,所以∠EMB =∠DCN ,又∠EMB +∠MEB =90°,∠DCN +∠NCB =90°,所以∠NCB =∠MEB ,所以ME ⎳NC ,ME ⊄平面PNC ,NC ⊂平面PNC ,所以ME ⎳平面PNC ,又ME ∩QE =E ,ME ,QE ⊂平面MEQ ,所以平面MEQ ⎳平面PNC ,MQ ⊂平面MEQ ,所以MQ ⎳平面PNC ,即当BQ =14BP时MQ ⎳平面PNC .(3)取DC 的中点F ,连接BF 交NC 于点G ,过点G 作GH ⊥PC 交PC 于点H ,连接BH ,则DF ⎳BM 且DF =BM ,所以四边形DFBM 为平行四边形,所以BF ⎳DM ,又DM ⊥平面PNC ,所以BF ⊥平面PNC ,PC ⊂平面PNC ,所以BF ⊥PC ,又GH ∩BF =G ,GH ,BF ⊂平面GHB ,所以PC ⊥平面GHB ,BH ⊂平面GHB ,所以PC ⊥BH ,所以∠BHG 为二面角B -PC -N 的平面角,因为△BCF ∽△CGF ,所以BC CG =CF FG =BF CF,又CG =BC ⋅CF BF =255,所以FG =55,BG =455,又△CGH ∽△CPN ,所以CG CP =GHPN ,又CN =22+12=5,PN =22-12=3,PC =5 2+3 2=22,即25522=GH 3,所以GH =3010,所以BH =30102+4552=142,所以sin ∠BHG =BG BH =455142=47035,故二面角B -PC -N 的正弦值为47035.。
二面角求解方法

二面角的作与求求角是每年高考必考内容之一,可以做为选择题,也可作为填空题,时常作为解答题形式出现,重点把握好二面角,它一般出现在解答题中。
下面就对求二面角的方法总结如下:1、定义法:在棱上任取一点,过这点在两个面内分别引棱的垂线,这两条射线所成的角就是二面角的平面角。
2、三垂线定理及逆定理法:自二面角的一个面上的一点向另一个面引垂线,再由垂足向棱作垂线得到棱上的点。
斜足与面上一点连线,和斜足与垂足连线所夹的角即为二面角的平面角。
3、作棱的垂面法:自空间一点作与棱垂直的平面,截二面角的两条射线所成的角就是二面角的平面角。
4、投影法:利用s投影面=s被投影面θcos 这个公式对于斜面三角形,任意多边形都成立,是求二面角的好方法。
尤其对无棱问题5异面直线距离法: EF 2=m 2+n 2+d 2-2mn θcos例1:若p 是ABC ∆所在平面外一点,而PBC ∆和ABC ∆都是边长为2的正三角形,PA=6,求二面角P-BC-A 的大小。
分析:由于这两个三角形是全等的三角形, 故采用定义法解:取BC 的中点E ,连接AE 、PEAC=AB ,PB=PC ∴ AE ⊥ BC ,PE ⊥BC∴PEA ∠为二面角P-BC-A 的平面角在PAE ∆中AE=PE=3,PA=6PCBAE∴PEA ∠=90∴二面角P-BC-A 的平面角为900。
例2:已知ABC ∆是正三角形,⊥PA 平面ABC 且PA=AB=a,求二面角A-PC-B 的大小。
[思维]二面角的大小是由二面角的平面角 来度量的,本题可利用三垂线定理(逆)来作 平面角,还可以用射影面积公式或异面直线上两点 间距离公式求二面角的平面角。
解1:(三垂线定理法)取AC 的中点E ,连接BE ,过E 做EF ⊥PC,连接BF ⊥PA 平面ABC ,PA ⊂平面PAC∴平面PAC ⊥平面ABC, 平面PAC 平面ABC=AC ∴BE ⊥平面PAC由三垂线定理知BF ⊥PC∴BFE ∠为二面角A-PC-B 的平面角设PA=1,E 为AC 的中点,BE=23,EF=42 ∴tan BFE ∠=6=EFBE∴BFE ∠=arctan 6解2:(三垂线定理法)取BC 的中点E ,连接AE ,PE 过A 做AF ⊥PE, FM ⊥PC,连接FMAB=AC,PB=PC ∴ AE ⊥BC,PE ⊥BC∴ BC ⊥平面PAE,BC ⊂平面PBC∴平面PAE ⊥平面PBC, 平面PAE 平面PBC=PE由三垂线定理知AM ⊥PCPC BAEF MEPCBAF图1图2∴FMA ∠为二面角A-PC-B 的平面角设PA=1,AM=22,AF=721.=PE AE AP ∴sin FMA ∠=742=AM AF ∴FMA ∠=argsin742解3:(投影法)过B 作BE ⊥AC 于E,连结PE ⊥PA 平面ABC ,PA ⊂平面PAC∴平面PAC ⊥平面ABC, 平面PAC 平面ABC=AC ∴BE ⊥平面PAC∴PEC ∆是PBC ∆在平面PAC 上的射影设PA=1,则PB=PC=2,AB=141=∆PEC S ,47=∆PBC S由射影面积公式得,77cosarg ,77=∴==∆∆θθPBC PEC S S COS , 解4:(异面直线距离法)过A 作AD ⊥PC,BE ⊥PC 交PC 分别于D 、E 设PA=1,则AD=22,PB=PC=2 ∴BE=PC S PBC 21∆=414,CE=42,DE=42由异面直线两点间距离公式得 AB 2=AD 2+BE 2+DE 2-2ADBE θCOS ,θCOS =77cos arg ,77=∴θ [点评]本题给出了求平面角的几种方法,应很好掌握。
二面角求值方法八种

二面角求值方法八种摘要】在奥妙无穷的空间形式里,二面角的平面角总是以量的大小决定着某些图形的空间形式,使得立体几何研究中,求二面角的大小成为了一个“角量计算”的重要内容。
那么怎样去求二面角的大小呢?笔者通过自身的实践,总结出常见的八种求法。
【关键词】二面角;二面角求值;八种1定义法11定义:二面角求值的“定义法”就是依二面角的平面角的定义,通过对线线垂直关系的研究,首先将空间角转化为平面角,然后依据解三角形的相关知识或某些公理体系的保证求出这个平面角,从而达到求二面角大小的数学方法。
它体现了“回到定义中去”是数学解题的根本方法。
12用“定义法”求二面角大小的解题思路是:求作二面角的平面角→证明这个平面角是所求→解出这个二面角。
13求作二面角的平面角应把握的原则:先找后作。
常见的作法有两种:其一,根据定义或图形的特征作。
其二,根据三垂线定理(或逆定理)作。
此法难点在于找到平面的垂线,解决的办法:先找面面垂直,利用面面垂直的性质定理找到面的垂线,作棱的垂线,连接垂足与面的垂线的端点,利用线线垂直得出所求角是二面角的平面角。
14常见的线线垂直的判断方法有:①三垂线定理及逆定理。
②等腰三角形“中线是高线”的性质。
③勾股定理的逆定理。
④菱形对角线互相垂直的性质。
⑤线面垂直则线线垂直的性质。
⑥同一法(有公共边的全等三角形中,公共边上的垂足相同)例1(2005年全国卷Ⅰ.18):已知四棱锥P-ABCD的底面是直角梯形,AB//DC,∠DAB=90°,PA⊥底面ABCD且PA=AD=DC=12AB=1,M是PB的中点,求平面AMC与平面BMC所成二面角的大小。
解:过点A作AN⊥CM,垂足为N,连BN,过点M作MQ⊥AB,垂足为Q,连QN,QC,由三垂线的逆定理知:MC⊥NQ,由三垂线定理知:BN⊥MC,故∠ANB为所求二面角的平面角。
由勾股定理的逆定理知:BC⊥AC,再由三垂线定理知:BC⊥PC,由直角三角形中线的性质有:MA=MC,由等面积求高法知:AN=NB=305,在△ANB中,由余弦定理有:cos∠ANB=AN2+BN2-AB22AN·BN=-23,从而所求二面角的大小是:π-arccos23题评:本例也可以先证△AMC≌△BMC,再利用“同一法”得出BN⊥MC。
二面角及其求法总结
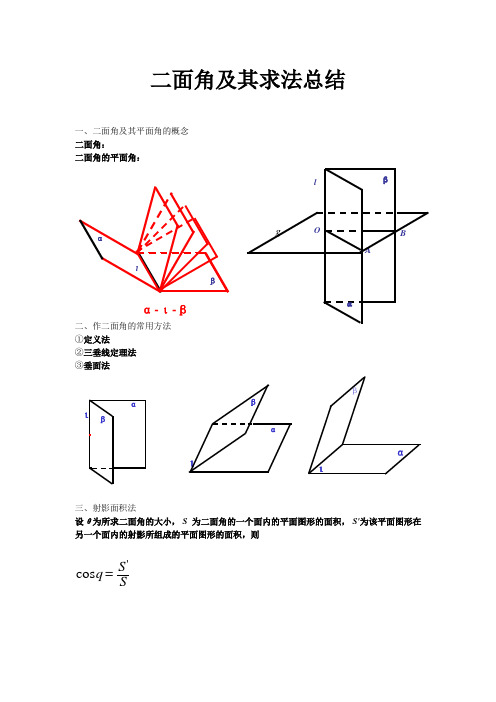
二面角及其求法总结一、二面角及其平面角的概念 二面角:二面角的平面角:二、作二面角的常用方法 ①定义法②三垂线定理法 ③垂面法三、射影面积法设θ为所求二面角的大小, S 为二面角的一个面内的平面图形的面积, S'为该平面图形在另一个面内的射影所组成的平面图形的面积,则'cos S Sq = α βια-ι-βABOβαlgια βα β ι α βι四、平面法向量法练 习:(1)如图,AB 是圆的直径,PA 垂直圆所在的平面,C 是圆上任一点,则二面角P-BC-A 的平面角为:A.∠ABPB.∠ACPC.∠APCD.都不是(2)在正方体ABCD-A 'B 'C 'D '中,求作二面角B-B 'C-A 的平面角. (3)在正四面体ABCD 中,求作二面角A-BC-D 的平面角.ABCPB A CD B A C D A 'AB 'C'C D 'D B经典例题:如图,PA ⊥平面ABC ,∠ACB=90°,PA=AC=1,BC=2.求(1)二面角A-PC-B 的大小;(2)求二面角A-PB-C 的大小.思路1:思路2:思路3:思路4: P B A C PBACPBAC练习:如图,正方体ABCD-A 1B 1C 1D 1中,E ,F ,M ,N 分别是A 1B 1,BC ,C 1D 1,B 1C 1的中点,求二面角M-EF-N 的大小.五、二面角大小求法总结:1、通过求平面角;2、向量法;3、射影面积法. 六、课后巩固1、四棱锥P-ABCD 中,底面ABCD 是正方形,PD ⊥面ABCD,PD=AD.求面PAD 和面PBC 所成二面角的大小.2、如图,长方体ABCD-A 1B 1C 1D 1中,底面ABCD 为正方形,AA 1=2AB=4,点E 在CC 1上且C 1E=3EC 。
(Ⅰ)证明:A 1C ⊥平面BED ;(Ⅱ)求二面角A 1-DE-B 的大小.MA C 1B 1A 1N FE D CB D 1 PADBCA 1 D 1 C 1B 1 ABCE D。
二面角的基本求法例题及练习
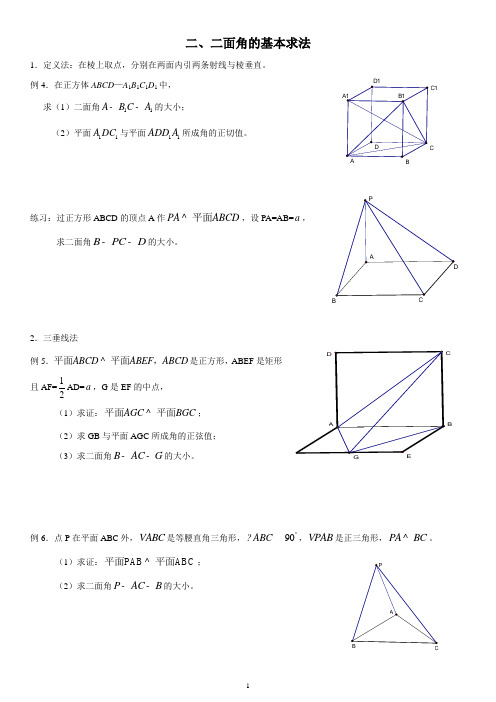
C1B二、二面角的基本求法1.定义法:在棱上取点,分别在两面内引两条射线与棱垂直。
例4.在正方体ABCD—A1B1C1D1中,求(1)二面角11A B C A--的大小;(2)平面11A DC与平面11ADD A所成角的正切值。
练习:过正方形ABCD的顶点A作PA ABCD^平面,设PA=AB=a,求二面角B PC D--的大小。
2.三垂线法例5.ABCD ABEF ABCD^平面平面,是正方形,ABEF是矩形且AF=12AD=a,G是EF的中点,(1)求证:AGC BGC^平面平面;(2)求GB与平面AGC所成角的正弦值;(3)求二面角B AC G--的大小。
例6.点P在平面ABC外,ABC是等腰直角三角形,90ABC°?,PAB是正三角形,PA BC^。
(1)求证:^平面PA B平面A BC;(2)求二面角P AC B--的大小。
练习:正方体ABCD —A 1B 1C 1D 1的棱长为1,P 是AD 的中点,求二面角1A BD P--的大小。
3.垂面法例7.SA ABC AB BC SA AB BC ^^==平面,,, (1)求证:SB BC ^;(2)求二面角C SA B --的大小; (3)求异面直线SC 与AB 所成角的余弦值。
4.无棱二面角的处理方法 (1)找棱例8.过正方形ABCD 的顶点A 作PA ABCD ^平面,设PA=AB=a , 求平面PAB 与平面PCD 所成二面角的大小。
(2)射影面积法(cos s Sq =射影)例9.正方体ABCD —A 1B 1C 1D 1的棱长为1,P 是棱1AA 的中点, 求平面11PB C 与平面ABCD 所成二面角的大小。
B1A。
五种方式求二面角及练习题

五种方式求二面角及练习题一、概念法:从一条直线起身的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,别离在两面内引两条射线与棱垂直,这两条垂线所成的角的大小确实是二面角的平面角。
1.如图,在棱长为a 的正方体ABCD —A 1B 1C 1D 1中,求: (1)二面角C 1—BD —C 的正切值(2)二面角11B BC D --2.如图,四棱锥中,底面为矩形,底面,,,点M 在侧棱上,=60,M 在侧棱的中点 (1)求二面角的余弦值。
S ABCD -ABCD SD ⊥ABCD 2AD =2DC SD ==SC ABM ∠SC S AM B --A B CDAD C B二、三垂线法:三垂线定理:在平面内的一条直线,若是和那个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.通常当点P 在一个半平面上那么通常常利用三垂线定理法求二面角的大小。
1. 如图,在直四棱柱ABCD -A B C D 中,底面ABCD 为等腰梯形,AB//CD ,AB=4, BC=CD=2, AA =2, E 、E 、F 别离是棱AD 、AA 、AB 的中点。
(1) 证明:直线EE //平面FCC ;(2)求二面角B -FC -C 的余弦值。
2.如图,在四棱锥ABCD P -中,底面ABCD 是矩形.已知60,22,2,2,3=∠====PAB PD PA AD AB .(Ⅰ)证明⊥AD 平面PAB ;(Ⅱ)求异面直线PC 与AD 所成的角的大小; (Ⅲ)求二面角A BD P --的大小.三.补棱法1111111111EABCF E A BCDD本法是针对在解组成二面角的两个半平面没有明确交线的求二面角题目时,要将两平面的图形补充完整,使之有明确的交线(称为补棱),然后借助前述的概念法与三垂线法解题。
即当二平面没有明确的交线时,一样用补棱法解决1.已知斜三棱柱ABC—A 1B 1C 1的棱长都是a ,侧棱与底面成600的角,侧面BCC 1B 1⊥底面ABC 。
二面角的多种求法(最新经典版)

六种方法求二面角从全国19份高考试卷中我们知道,立体几何题中命有求二面角大小的试题共有12份,并都为分值是12分的大题,足以说明这一知识点在高考中的位置,据有关专家分析,它仍然是2010年高考的重点,因此,我们每位考生必须注意,学会其解题方法,掌握其解题技巧,是十分重要的。
一、 定义法:从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。
本定义为解题提供了添辅助线的一种规律。
如例1中从二面角S —AM —B 中半平面ABM 上的一已知点(B )向棱AM 作垂线,得垂足(F );在另一半平面ASM 内过该垂足(F )作棱AM 的垂线(如GF ),这两条垂线(BF 、GF )便形成该二面角的一个平面角,再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理解题。
例1(2009全国卷Ⅰ理)如图,四棱锥S ABCD -中,底面ABCD 为矩形,SD ⊥底面ABCD,AD =2DC SD ==,点M 在侧棱SC 上,ABM ∠=60°(I )证明:M 在侧棱SC 的中点 (II )求二面角S AM B --的大小。
证(I )略解(II ):利用二面角的定义。
在等边三角形ABM 中过点B作BF AM ⊥交AM 于点F ,则点F 为AM 的中点,过F 点在平面ASM 内作GF AM ⊥,GF 交AS 于G ,连结AC ,∵△ADC ≌△ADS ,∴AS-AC ,且M 是SC 的中点, ∴AM ⊥SC , GF ⊥AM ,∴GF ∥AS ,又∵F 为AM 的中点,∴GF 是△AMS 的中位线,点G 是AS 的中点。
则GFB ∠即为所求二面角. ∵2=SM ,则22=GF ,又∵6==AC SA ,∴2=AM ∵2==AB AM ,060=∠ABM ∴△ABM 是等边三角形,∴3=BF在△GAB 中,26=AG ,2=AB ,090=∠GAB ,∴211423=+=BG FG366232222113212cos 222-=-=⨯⨯-+=⋅-+=∠FB GF BG FB GF BFG ∴二面角S AM B --的大小为)36arccos(-练习1(2008山东)如图,已知四棱锥P -ABCD ,底面ABCD 为菱形,P A ⊥平面ABCD ,60ABC ∠=︒,E ,F 分别是BC , PC 的中点. (Ⅰ)证明:AE ⊥PD ;(Ⅱ)若H 为PD 上的动点,EH 与平面P AD 所成最大角E —AF —C 的余弦值. 分析:第1题容易发现,可通过证AE ⊥AD 后推出AE ⊥平面APD ,使命题获证,而第2题,则首先必须在找到最大角正切值有关的线段计算出各线段的长度之后,考虑到运用在二面角的棱AF 上找到可计算二面角的平面角的顶点S ,和两边SE 与SC ,进而计算二面角的余弦值。
立体几何中二面角8个常用求法

⽴体⼏何中⼆⾯⾓8个常⽤求法
⼆⾯⾓定义的回顾:
⼆⾯⾓的通常求法
1、由定义作出⼆⾯⾓的平⾯⾓;
2、利⽤三垂线定理(逆定理)作出⼆⾯⾓的平⾯⾓;
3、作⼆⾯⾓棱的垂⾯,则垂⾯与⼆⾯⾓两个⾯的交线所成的⾓就是⼆⾯⾓的平⾯⾓。
4、空间坐标法求⼆⾯⾓的⼤⼩
5、平移或延长(展)线(⾯)法
6、射影公式S射影=S斜⾯cosθ
7、化归为分别垂直于⼆⾯⾓的两个⾯的两条直线所成的⾓
⼀、利⽤定义作出⼆⾯⾓的平⾯⾓,并设法求出其⼤⼩。
⼆、三垂线定理(逆定理)法
由⼆⾯⾓的⼀个⾯上的斜线(或它的射影)与⼆⾯⾓的棱垂直,推得它位于⼆⾯⾓的另⼀的⾯上的射影(或斜线)也与⼆⾯⾓的棱垂直,从⽽确定⼆⾯⾓的平⾯⾓。
四、找(作)公垂⾯法
由⼆⾯⾓的平⾯⾓的定义可知两个⾯的公垂⾯与棱垂直,因此公垂⾯与两个⾯的交线所成的⾓,就是⼆⾯⾓的平⾯⾓。
五、平移或延长(展)线(⾯)法
将图形中有关线段或平⾯进⾏平移或延长(展),以其得到⼆⾯⾓的两个平⾯的交线。
图⼆:
六、射影公式
由公式S射影=S斜⾯cosθ,作出⼆⾯⾓的平⾯⾓直接求出。
运⽤这⼀⽅法的关键是从图中找出斜⾯多边形和它在有关平⾯上的射影,⽽且它们的⾯积容易求得。
图⼆:
七、化归为分别垂直于⼆⾯⾓的两个⾯的两条直线所成的⾓
图⼆:
图三:
⼋、空间向量求解⼆⾯⾓
求解⼆⾯⾓⼤⼩的⽅法很多,诸如定义法、三垂线法、垂⾯法、射影法、向量法等若⼲种。
⽽这些⽅法中最简单易学的就是向量法。
图⼆:
图四:
图五:
图六:
图七:
图⼋:
图九:
图⼗:。
专题 立体几何中二面角的求法

专题立体几何中二面角的求法二面角的常见求法:(1)定义法(2)垂线法(3)垂面法(4)延伸法(5)射影法一、定义法:直接在二面角的棱上取一点(特殊点),分别在两个半平面内作棱的垂线,得出平面角,用定义法时,要认真观察图形的特性例1:如图1,设正方形ABCD-A1B1C1D!中,E为CC1中点,求截面A1BD和EBD所成二面角的度数。
练习在四棱锥P-ABCD中,ABCD是正方形,PA⊥平面ABCD,PA=AB=a,求二面角B-PC—-D的大小。
二、垂线法已知二面角其中一个面内一点到一个面的垂线,用三垂线定理或逆定理作出二面角的平面角;例2如图3,设三棱锥V-ABC中,V A⊥底面ABC,AB⊥BC,DE垂直平分VC,且分别交AC、VC于D、E,又V A=AB,VB=BC,求二面角E-BD-C的度数。
四、延伸法对于一类没有给出棱的二面角,应先延伸两个半平面,使之相交出现棱,然后再选用上述方法(尤其要考虑射影法)。
例4、在四棱锥P-ABCD中,ABCD为正方形,PA⊥平面ABCD,PA=AB=a,求平面PBA与平面PDC所成二面角的大小。
(补形化为定义法)练习如图10,设正三棱柱ABC-A'B'C'各棱长均为α,D为CC1中点,求平面A'BD与平面ABC所成二面角的度数。
五、射影法利用面积射影公式S射=S原cosθ,其中θ为平面角的大小,此方法不必在图形中画出平面角;例5 在四棱锥P-ABCD中,ABCD为正方形,PA⊥平面ABCD,PA=AB=a,求平面PBA与平面PDC所成二面角的大小。
练习如图12,设正方体ABCD-A1B1C1D1中,M为AA1上点,A1M:MA=3:1,求截面B1D1M 与底面ABCD所成二面角。
二面角问题求解方法大全

二面角问题求解方法大全(总6页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--五法求二面角一、 定义法:从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。
例1如图,四棱锥SABCD -中,底面ABCD 为矩形,SD ⊥底面ABCD ,2AD =2DC SD ==,点M 在侧棱SC 上,ABM∠=60°(I )证明:M 在侧棱SC 的中点 (II )求二面角S AM B --的大小。
练习1如图,已知四棱锥P -ABCD ,底面ABCD 为菱形,PA ⊥平面ABCD ,60ABC ∠=︒,E ,F 分别是BC , PC 的中点.(Ⅰ)证明:AE ⊥PD ; (Ⅱ)若H 为PD 上的动点,EH 与平面PAD 所成最大角的正切值为62,求二面角E —AF —C 的余弦值.二、三垂线法三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.通常当点P 在一个半平面上则通常用三垂线定理法求二面角的大小。
例2. 如图,在直四棱柱ABCD-A 1B 1C 1D 1中,底面ABCD 为等腰梯形,AB 111111ABCD P -ABCD60,22,2,2,3=∠====PAB PD PA AD AB ⊥AD PABPC AD A BD P -- (Ⅰ)证明:平面PBE ⊥平面PAB ;(Ⅱ)求平面PAD 和平面PBE 所成二面角(锐角)的大小.练习3已知斜三棱柱ABC —A 1B 1C 1的棱长都是a ,侧棱与底面成600的角,侧面BCC 1B 1⊥底面ABC 。
(1)求证:AC 1⊥BC ;(2)求平面AB 1C 1与平面 ABC 所成的二面角(锐角)的大小。
四、射影面积法(coss S射影)凡二面角的图形中含有可求原图形面积和该图形在另一个半平面上的射影图形面积的都可利用射影面积公式(cos 斜射S S =θ)求出二面角的大小。
二面角求法及经典题型归纳

二面角求法归纳18题,通常是立体几何(12-14分),本题考查空间线面平行、线面垂直、面面垂直的判断与证明,考查二面角的求法以及利用向量知识解决几何问题的能力,同时考查空间想象能力、推理论证能力和运算能力。
以下是求二面角的五种方法总结,及题形归纳。
定义法:从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。
本定义为解题提供了添辅助线的一种规律。
如例1中从二面角S —AM —B 中半平面ABM 上的一已知点(B )向棱AM 作垂线,得垂足(F );在另一半平面ASM 内过该垂足(F )作棱AM 的垂线(如GF ),这两条垂线(BF 、GF )便形成该二面角的一个平面角,再在该平面角内建立一个可解三角形,然后借助直角三角函数、正弦定理与余弦定理解题。
例1(2009全国卷Ⅰ理)如图,四棱锥S ABCD -中,底面ABCD 为矩形,SD ⊥底面ABCD ,2AD =2DC SD ==,点M 在侧棱SC 上,ABM ∠=60°(I )证明:M 在侧棱SC 的中点 (II )求二面角S AM B --的大小。
证(I )略解(II ):利用二面角的定义。
在等边三角形ABM 中过点B作BF AM ⊥交AM 于点F ,则点F 为AM 的中点,过F 点在平面ASM 内作GF AM ⊥,GF 交AS 于G ,连结AC ,∵△ADC ≌△ADS ,∴AS-AC ,且M 是SC 的中点, ∴AM ⊥SC , GF ⊥AM ,∴GF ∥AS ,又∵F 为AM 的中点,∴GF 是△AMS 的中位线,点G 是AS 的中点。
则GFB ∠即为所求二面角. ∵2=SM ,则22=GF ,又∵6==AC SA ,∴2=AM ∵2==AB AM ,060=∠ABM ∴△ABM 是等边三角形,∴3=BF在△GAB 中,26=AG ,2=AB ,090=∠GAB ,∴211423=+=BG 366232222113212cos 222-=-=⨯⨯-+=⋅-+=∠FB GF BG FB GF BFG FGFG∴二面角S AM B --的大小为)36arccos(-例2. (2010全国I 理,19题,12分)如图,四棱锥S-ABCD 中,SD ⊥底面ABCD ,AB//DC ,AD ⊥DC ,AB=AD=1,DC=SD=2,E 为棱SB 上的一点,平面EDC ⊥平面SBC . (Ⅰ)证明:SE=2EB ;(Ⅱ)求二面角A-DE-C 的大小 . (Ⅱ) 由225,1,2,,SA SD AD AB SE EB AB SA =+===⊥知22121,AD=133AE SA AB ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭又.故ADE ∆为等腰三角形.取ED 中点F,连接AF,则226,3AF DE AF AD DF ⊥=-=. 连接FG ,则//,FG EC FG DE ⊥.所以,AFG ∠是二面角A DE C --的平面角. 连接AG,A G=2,2263FG DG DF =-=, 2221cos 22AF FG AG AFG AF FG +-∠==-,所以,二面角A DE C --的大小为120°.例3(2010浙江省理,20题,15分)如图, 在矩形ABCD 中,点,E F 分别 在线段,AB AD 上,243AE EB AF FD ====.沿直线EF 将 AEF 翻折成'A EF ,使平面'A EF BEF ⊥平面.(Ⅰ)求二面角'A FD C --的余弦值;(Ⅱ)点,M N 分别在线段,FD BC 上,若沿直线MN 将四边形MNCD 向上翻折,使C 与'A 重合,求线段FM 的长.练习(2008山东)如图,已知四棱锥P-ABCD,底面ABCD为菱形,P A⊥平面ABCD,60ABC∠=︒,E,F分别是BC, PC的中点.(Ⅰ)证明:AE⊥PD;(Ⅱ)若H为PD上的动点,EH与平面P AD所成最大角的正切值为62,求二面角E—AF—C的余弦值.分析:第1题容易发现,可通过证AE⊥AD后推出AE⊥平面APD,使命题获证,而第2题,则首先必须在找到最大角正切值有关的线段计算出各线段的长度之后,考虑到运用在二面角的棱AF上找到可计算二面角的平面角的顶点S,和两边SE与SC,进而计算二面角的余弦值。
二面角求法专题

αβaOAB二面角求法专题一、知识准备1.二面角的概念:从一条直线出发的两个半平面所组成的图形叫做二面角, 这条直线叫做二面角的棱, 这两个半平面叫做二面角的面.2.二面角的平面角的概念:平面角是指以二面角的棱上一点为端点,在两个半平面内分别做垂直于棱的两条射线,这两条射线所成的角就叫做该二面角的平面角。
3.二面角的大小范围:[ 0°,180°]4.三垂线定理:平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它就和这条斜线垂直 5.二面角做法:做二面角的平面角主要有3种方法:(1)定义法:在棱上取一点,在两个半平面内作垂直于棱的2 条射线,这2条所夹 的角;(2)垂面法:做垂直于棱的一个平面,这个平面与2个半平面分别有一条交线,这2条交线所成的角; (3)三垂线法:过一个半平面内一点(记为A )做另一个半平面的一条垂线,过这个垂足(记为B )再做棱的垂线,记垂足为C ,连接AC ,则∠ACB 即为该二面角的平面角。
二、二面角的基本求法及练习1、定义法:从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面,在棱上取点,分别在两面内引两条射线与棱垂直,这两条垂线所成的角的大小就是二面角的平面角。
例1 在正方体ABCD —A 1B 1C 1D 1中,求:(1)二面角11AB C A 的大小;(2)平面11A DC 与平面11ADD A 所成角的正切值。
ABCDA 1B 1C 1D 1例2 如图1,设正方体ABCD —A 1B 1C 1D 1中,E 为CC 1中点,求截面A 1BD 和EBD 所成二面角的度数。
2、三垂线法三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.通常当点P 在一个半平面上则通常用三垂线定理法求二面角的大小。
例 3 平面⊥ABCD 平面ABEF ,ABCD 是正方形,ABEF 是矩形且AF=12AD=a ,G 是EF 的中点, (1)求证:平面AGC ⊥平面BGC ; (2)求GB 与平面AGC 所成角的正弦值; (3)求二面角B AC G 的大小。
二面角的求法
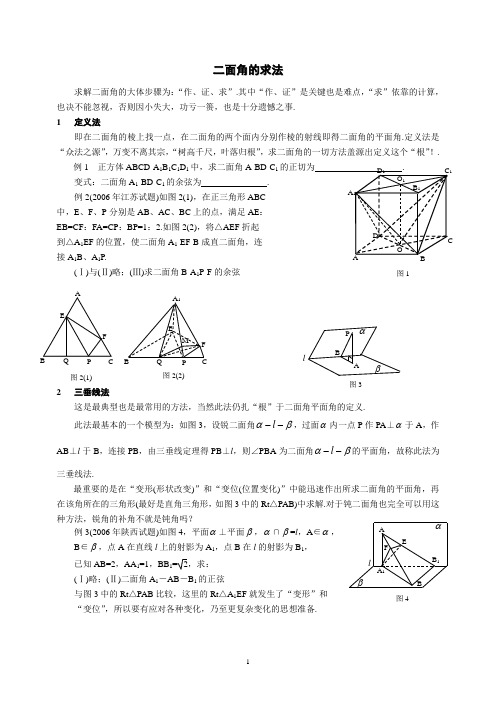
二面角的求法求解二面角的大体步骤为:“作、证、求”.其中“作、证”是关键也是难点,“求”依靠的计算,也决不能忽视,否则因小失大,功亏一篑,也是十分遗憾之事. 1 定义法即在二面角的棱上找一点,在二面角的两个面内分别作棱的射线即得二面角的平面角.定义法是“众法之源”,万变不离其宗,“树高千尺,叶落归根”,求二面角的一切方法盖源出定义这个“根”!.例1 正方体ABCD-A 1B 1C 1D 1中,求二面角A-BD-C 1的正切为 . 变式:二面角A 1-BD-C 1的余弦为 . 例2(2006年江苏试题)如图2(1),在正三角形ABC 中,E 、F 、P 分别是AB 、AC 、BC 上的点,满足AE : EB=CF :FA=CP :BP=1:2.如图2(2),将△AEF 折起 到△A 1EF 的位置,使二面角A 1-EF-B 成直二面角,连 接A 1B 、A 1P.(Ⅰ)与(Ⅱ)略;(Ⅲ)求二面角B-A 1P-F 的余弦2 三垂线法这是最典型也是最常用的方法,当然此法仍扎“根”于二面角平面角的定义.此法最基本的一个模型为:如图3,设锐二面角βα--l ,过面α内一点P 作PA ⊥α于A ,作AB ⊥l 于B ,连接PB ,由三垂线定理得PB ⊥l ,则∠PBA 为二面角βα--l 的平面角,故称此法为三垂线法.最重要的是在“变形(形状改变)”和“变位(位置变化)”中能迅速作出所求二面角的平面角,再在该角所在的三角形(最好是直角三角形,如图3中的Rt △PAB)中求解.对于钝二面角也完全可以用这种方法,锐角的补角不就是钝角吗?例3(2006年陕西试题)如图4,平面α⊥平面β,α∩β=l ,A ∈α, B ∈β,点A 在直线l 上的射影为A 1,点B 在l 的射影为B 1, 已知AB=2,AA 1=1,BB 1=2,求: (Ⅰ)略;(Ⅱ)二面角A 1-AB -B 1的正弦与图3中的Rt △PAB 比较,这里的Rt △A 1EF 就发生了“变形”和 “变位”,所以要有应对各种变化,乃至更复杂变化的思想准备.DB 1图1AOA 1CBD 1 C 1O 1M AFA 1QPECBPEF 图2(2)图2(1)Q A图3αβPBl图4B 1A αβA 1B lEF3 垂面法事实上,图1中的平面COC 1、图2(2)中的平面QMF 、图3中的平面PAB 、图4中的平面A 1FE 都是相关二面角棱的垂面,这种通过作二面角棱的垂面得平面角的方法就叫做垂面法.在某些情况下用这种方法可取得良好的效果.例4空间的点P 到二面角βα--l 的面α、β及棱l 的距离分别为4、3、3392,求二面角βα--l 的大小. 4 面积法(射影法)如图1,设二面角C-BD-C 1的大小为θ,则在Rt △COC 1中,cos BDC CBD S S BD O C BDCO O C CO1112121∆∆=⋅⋅==θ,在某些情况下用此法特别方便.例5 如图6,平面α外的△A 1B 1C 1在α内的射影是边长为1的 正三角形ABC ,且AA 1=2,BB 1=3,CC 1=4,求△A 1B 1C 1所在的平 面与平面α所成锐二面角的余弦. 5 变式二面角的求法以上列举了求解二面角的四种基本方法,但在现实中,问题往往不是那么简单与单纯,而是有诸多的变化,“源于基本方法,适应各种变化”就是我们总的策略. 5.1 “无棱”二面角的求法严格地说,任何二面角都是有棱的,“无棱”其实是指二面角的棱处于隐含的状态.对于这样的问题,有两种处理办法:(1)用面积法,见例5;(2)找出隐含的棱,此法可称为“找棱法”.在原图中,面A 1B 1C 1与α的公共点都不知道,所以必须找出它们的两个公共点,才能找到二面角的棱;而在另一些问题中,知道两个面的一个公共点,那么只须再找出另一个公共点就可以了.面积法比找棱法似乎要简单些,但看问题不能简单化,例5的第二种解法是非常重要的一种方法,其中蕴涵的知识和技能的“营养”对于滋补人大大脑是十分有价值的,所以决不要忽视找棱法. 5.2 平面图形折转后的二面角的求法例6(2005年湖南试题)如图7(1),已知ABCD 是上、下底边长分别为2和 6,高为3的等腰梯形,将它沿对称轴OO 1折成直二面角,如图7(2). (Ⅰ)求证:AC ⊥BO 1; (Ⅱ)求二面角O-AC-O 1的正弦Rt △O 1FE 被挤在一个十分狭窄的空间内,不容易分清谁是直角,谁是锐角,可单独将它画出来,以避免混淆.对于折转问题,将原来的平面图形与折转后的空间进行比照是很好的一种策略.P图5βαlCBAαD AM 图6E CB C 1A 1B 1H GCBAO 1OD图7(2)FEAO 1 O DCB图7(1) E5.3 求二面角转移法转化是重要的数学思想之一,当所求的二面角为钝角时,可先求其“补角”.转移也是一种转化,就是将待求的二面角转移到另一个简单的环境之中,从而得解.例7例2(2005年重庆高考试题)如图2,在三棱柱ABC-A 1B 1C 1中, AB ⊥侧面BB 1C 1C ,E 为棱CC 1上异于C 、C 1的一点,EA ⊥EB 1,已知AB=2,BB 1=2,BC=1,∠BCC 1=3π,求(Ⅰ)略;(Ⅱ)二面角A-EB 1-A 1的平面角的正切值. 5.4 有关二面角的最值问题求最值是代数、三角、解几的“热点”问题,殊不知立体几何中也有引人入胜的最值问题. 例8 二面角α-l -β的大小是变量)20(πθθ<<,点B 、C 在l上,A 、D 分别在面α、β内,且AD ⊥BC ,AD 与面β成6π角,若 △ABC 的面积为定值S ,求△BCD 面积Q 的最大值.ADB B 11A 1图8G 图9αEDCBA lβ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二面角求法专题
正方体是研究立体几何概念的一个重要模型,中学立体几何教学中,求平面与平面所成的二面角是转化为平面角来度量的,也可采用一些特殊的方法求二面角,而正方体也是探讨求二面角大小方法的典型几何体。
笔者通过探求正方体中有关二面角,分析求二面角大小的八种方法:(1)平面角定义法;(2)三垂线定理法;(3)线面垂直法;(4)判定垂面法;(5)异面直线上两点间距离公式法;(6)平行移动法;(7)投影面积法;(8)棱锥体积法。
一、平面角定义法
此法是根据二面角的平面角定义,直接寻求二面角的大小。
以所求二面角棱上任意一点为端点,在二面角两个平面内
分别作垂直于棱的两条射线所成角就是二面角的平面角,
如图二面角α-l-β中,在棱l上取一点O,分别在α、β
两个平面内作AO⊥l,BO⊥l,∠AOB即是所求二面角的平面角。
例题1:已知正方体ABCD-A
1B
1
C
1
D
1
中,O、O
1
是上下底面正方形的中心,求二面角O
1
-BC-O的
大小。
例题2:已知正方体ABCD-A
1B
1
C
1
D
1
中,E、F为A
1
D
1
、C
1
D
1
的中点,求平面EFCA与底面ABCD
所成的二面角。
二、 利用三垂线定理法
此方法是在二面角的一个平面内过一点作另一个面的垂线,再由垂足(或仍是该点)作棱的垂线,连接该点和棱上的垂足(或连两垂足)两点线,即可得二面角的平面角。
如图二面角α-l-β中,在平面α内取一点A ,
过A 作AB ⊥平面β,B 是垂足, 由B (或A )作BO (或AO )⊥l ,
连接AO (或BO )即得AO 是平面β的斜线, BO 是AO 在平面β中的射影,
根据三垂线定理(或逆定理)即得AO ⊥l ,BO ⊥l , 即∠AOB 是α-l-β的平面角。
例题3:已知正方体ABCD-A 1B 1C 1D 1中,求二面角B-AC-B 1的大小。
例题4:已知正方体ABCD-A 1B 1C 1D 1中,求平面ACD 1与平面BDC 1所成的二面角。
三、 线面垂直法
此法利用直线垂直平面即该直线垂直平面内任何直线的性质来寻求二面角的平面角。
方法是过所求二面角的棱上一点,作棱的垂面,与两个平面相交所得两条交线的所成角即是二面角的平面角。
如图在二面角α-l-β的棱上任取一点O ,过O 作 平面γ⊥l ,α∩γ=AO ,β∩γ=BO ,得∠AOB 是平面角,
∵l ⊥γ,l ⊥AO ,l ⊥BO 。
例题5:已知正方体ABCD-A
1B
1
C
1
D
1
中,求二面角B-A
1
C-D的大小。
例题6:已知正方体ABCD-A
1B
1
C
1
D
1
中,E、F分别是BB
1
、DD
1
的中点,求平面BC
1
D与平面EC
1
F
所成的二面角。
四、判定垂面法
此法根据平面垂直的定义:两个平面相交,如果所成的二面角是直二面角,那么这两个平面垂直,反之,若能判定两个平面垂直,则这两个平面所成的二面角是900,无须寻作二面角的平面角。
如图若已知或证得a α,a⊥β∴α⊥β。
则二面角α-l-β的大小即是900。
可见判定面面垂直是求二面角的
一种特殊情况。
例题7:已知正方体ABCD-A
1B
1
C
1
D
1
中,求平面BDC
1
与平面ACC
1
A
1
所成的二面角。
例题8:已知正方体ABCD-A
1B
1
C
1
D
1
中,O
1
、O是上下底面正方形的中心,
V是OO
1的中点,求平面AVB与平面CVD所成的二面角。
五、 异面直线上两点间距离公式法
此法按高中立体几何课本P45页例2证明的公式,求二面角大小,题意是已知两条异面直线a 、b 上分别取点E 、F ,设A ’E=m ,AF=n ,求EF 。
如图公式是:EF=θcos 2222mn n m d ±++(注意E 、F 在AA 1同侧时取“-”,EF 在AA 1异侧时取“+”号。
)应用该公式是求异面直线上两点间的距离,
若把所求二面角当作θ角,即是异面直线a 、b 和公垂线AA 1
确定的两个平面所成的二面角,用函数观念来理解公式中 五个量,已知其中四个量即可求第五个量,若已知或易求 知EF 、d 、m 、n 则求cos θ,θ即是所求二面角。
例题9:已知正方体ABCD-A 1B 1C 1D 1中,H 是BC 棱上一点 且BH :BC=1:3,求二面角H-AA 1-C 1的大小。
例题10:已知正方体ABCD-A 1B 1C 1D 1中,O 1、O 是上下底面正方形的中心,E 是AB 棱上一点,且AE :EB=1:2,求二面角A 1-O 1O-E 的大小。
六、 平行移动法
位置,作得新的二面角大小与所求二面角相等,并可求得新的二面角大小。
如图将所求平面α与平面β所成的二面角中α平面平行移动到平面γ位置处,即求γ与β所成的二面角即是所求二面角大小。
例题11:已知正方体ABCD-A 1B 1C 1D 1中,G 、E 、F 是所在棱的中点,求平面EFG 与平面ABCD 所成的二面角。
例题12:已知正方体ABCD-A 1B 1C 1D 1中,O 1是上底面正方形的中心,E 、F 是AB 、CD 的中点,求平面AO 1D 与平面EO 1F 所成的二面角。
七、 投影面积法
在二面角一个平面内若已知一个任意多边形的面积为S , 该多边形在另一个平面内投影面积为S 射,该二面角大 小θ可用S
S 射=
θcos
高中课本P68页习题八中11题就是类似证明习题。
此方法适合求二面角中易解得S 、S 射时用。
例题13:已知正方体ABCD-A 1B 1C 1D 1中,E 是BC 的中点,F 在AA 1上,且A 1F :FA=1:2,求平面
B 1EF 与底面A 1B 1
C 1
D 1所成的二面角。
例题14:已知正方体
ABCD-A 1B 1C 1D 1中,E 是CC 1的中点,求平面AED 1与平面ABCD 所成二面角。
八、 棱锥体积法
此方法把所求二面角看作为求棱锥的一个侧面与底面所成的二面角,在已知或易求棱锥底面面积、侧面一个面面积和体积前提下,即可用锥体体积公式V=h S ⋅底3
1,来探求二面角大小。
如图已知三棱锥V-ABC 中,VO 是高线,若已得底面面积是S ,AB=a , 一个侧面⊿ABV 面积是S 1,体积是V ,求二面角C-AB-V 大小。
现设所求C-AB-V 平面角是如图中的∠VDO ,
⊿ABV 面积S 1=VD a ⋅21,sin ∠VDO=VD
VO ,
∴VD=
a
S 12,VDO a
S VO ∠⋅=
sin 21
,利用棱锥体积公式,
VDO a
S S VDO a S S VO S V ∠⋅⋅=∠⋅⋅⋅=⋅⋅=
sin 32sin 231
3111,
∴sin ∠VDO=
1
23S S V
a ⋅⋅⋅,即求出了二面角C-AB-V 的大小。
例题15:已知正方体ABCD-A 1B 1C 1D 1中,求二面角A-A 1C-D 的大小。
例题16:已知正方体ABCD-A 1B 1C 1D 1中,M 、N 是所在棱的中点,。
