典型习题解析
欧姆定律知识练习题及详细解析

欧姆定律知识练习题及详细解析【典型例题】类型一、探究电流与电压、电阻的关系1.某小组在探究电流与电压关系时,得到的实验数据如下表:R=10Ω电压U/V 2 4 6电流I/A 0.2 0.4 0.6(1) 分析数据发现:在______时,______跟______成______(填“正”或“反”)比。
(2)在坐标纸上画出U-I关系图。
(3) 在本实验中,滑动变阻器的作用除了保护电路外,主要是__________________。
【思路点拨】本题是物理课上常用的控制变量法,注意不变量,也就是在一定的前提下,还要注意电压和电流的因果关系,所以在表达时需注意。
【答案】(1)电阻一定;导体中的电流;导体两端的电压;正;(2) 如图所示;(3)改变定值电阻两端的电压【解析】(1)注意:在回答结论时一定要说上前提条件即电阻不变。
由表格可知电流改变的倍数与电压改变的倍数相等,即正比例关系。
在结论中一定要说电流与电压成正比,而不能说反。
这是因为有电压才有电流,电压是因,电流是果,因此结论一定要说电阻一定时,电流和电压成正比。
(2)做图时,在坐标上描出对应的点连线即可以。
因为电压若为0,电流也为0,所以该图象过原点。
【总结升华】本题的主要意图是考查描点作图法、分析实验结论的能力以及滑动变阻器在电路中的作用.举一反三:【变式】(2014•大港区二模)某同学在探究“电阻上的电流跟两端电压的关系”时,利用如图所示电路,在a、b两点间分别接入定值电阻R1、R2,R1>R2,通过调节滑动变阻器测得了多组数据,并根据数据绘制了两个电阻的U-I 关系图象,图中能正确反映两个电阻大小关系的是()【答案】B2. 小明同学,探究保持电压不变时,电流跟电阻的关系,得到的数据如下表。
电阻 5 6 1120 3(1)分析表中的数据,可以得出的结论【答案】(1)电压一定时,通过导体的电流与导体的电阻成反比(2)调节R′的阻值,保持电阻R两端电压不变【解析】(1)从表中的数据知在电压不变时,电阻增大到原来的几倍,电流就减小到原来的几分之一。
物理作业 第二章 典型习题答案与解析

【第二章典型习题】1.教室门框的高度最接近于()A 1米B 2米C 5米D 8米2.小明同学用刻度尺测出一个物体的长度为,下面物体中最接近这个数值的是( )A、物理课本的厚度B、一根粉笔的长度C、黑板的长度D、饮水杯的高度3.章天同学用一把刻度尺4次测量物理课本的宽度,下列记录数据中错误的是()A.B.C.D.4.以相同速度同方向飞行的加油机和受油机,选地面为参照物,它们是的;选其中的任何一个为参照物,另一个是的。
5.小船在河里顺流而下,船上坐着一个人,河岸上有树,那么相对于船来说,人是_____的,树是_______的(填“运动”或“静止”)6.诗人曾写下这样的诗句:“人在桥上走,桥流水不流”。
其中“桥流水不流”,诗人选择的参照物是( )A、桥B、河岸C、水D、岸上的树7.小明骑自行车在沱江河堤上沿河岸向下游行驶,感觉无风,但堤上柳树的枝叶却在随风飘动,此时的风向是( )A、向下游B、向上游C、向河对岸D、从对岸吹过来8.坐在逆水驶向上游的船中的乘客,我们说他静止是以下列哪个物体为参照物的?( )A.河岸上的树B.船舱C.迎面驶来的船D.河水9.临沂是一座历史文化名城,今天的临沂更是美丽壮观。
位于临沂市中心处的某大酒店建有观光电梯,乘客在竖直上下的过程中便可欣赏到临沂城的美丽景色。
在这一过程中,下列说法正确的是 ( )A.以电梯内的某一乘客为参照物,其他乘客是运动的B.以电梯为参照物,所有乘客都是运动的C.以地面上的树为参照物,乘客是运动的D.以路面上行驶的汽车为参照物,乘客是静止的10.谁也没有我跑得快!我是()A.高速奔驰的磁悬浮列车B.高空翱翔的超音速战机C.让万物生长的阳光D.把“神六"送上天的“长征”运载火箭11.即将开工建设的京沪高速列车运行速度可达350㎞/h,这个速度相当于m/s,两地之间的铁路线长为1400㎞,那么列车从北京到上海至少需要h.12.飞机在10min内飞行了180km,它的速度是_________km/h,合_____m/s。
化学平衡典型习题和答案解析

化学平衡1.某温度下,在固定容积的密闭容器中,可逆反应A(g)+3B(g)→2C(g)达到平衡,测得平衡时A、B、C物质的量之比为n(A):n(B):n(C)=1:1:2,若保持温度不变,以1:1:2的物质的量之比再充入A、B和C,下列判断中正确的是()A.平衡不移动 B.平衡向逆反应方向移动C.新平衡时各物质的浓度都比原平衡时增大 D.C的质量分数减小2. 在一固定容积的密闭容器中充入2molA和1molB发生反应2A(g)+B(g) xC(g),达到平衡后 C体积分数为w% 若维持容器体积和温度不变按0.6mol A 0.3molB 1.4mol C为起始物质,达到平衡后 C体积分数仍为W% 则X的值为() A 1 B 2 C 3 D 43.对于密闭容器中的反应:N2(g) +3H2(g) 2NH3(g)△H<0,673K、30MPa下n(NH3)和n(H2)随时间变化的关系如下图所示。
下列叙述不正确的是A.点a的正反应速率比点b的大B.点c处的正反应速率比逆反应的大C.点d(t1时刻) 和点e(t2时刻) 处n(N2)一样多D.其他条件不变,773K下反应至t1时刻,n(H2)比上图中d点的值小4. 在4L密闭容器中充入6mol A气体和5mol B气体,在一定条件下发生反应:3A(g)+B(g)2C(g)+xD(g),10min达到化学平衡,生成了2mol C,经测定D的平均反应速率为0.05mol•L-1•min-1.下列判断正确的是()A.平衡时A的浓度为1.50mol•L- 1 B.x=1C.达到平衡时,在相同温度下容器内混合气体的压强是反应前的0.8倍 D.B的转化率为20%5. 体积相同的甲.乙两个容器中,分别都充有等物质的量的SO2和O2,在相同温度下发生反应:2SO2+O2⇌2SO3,并达到平衡.在这过程中,甲容器保持体积不变,乙容器保持压强不变,若甲容器中SO2的转化率为p%,则乙容器中SO2的转化率()A.等于p% B.大于p% C.小于p% D.无法6. 在相同温度下,有相同体积的甲、乙两容器,甲容器中充入1g N2和1g H2,乙容器中充入2g N2和2g H2。
值域的求法典型习题及解析

值域的求法习题一.解答题(共10小题)1.已知函数的定义域为集合A,函数的值域为集合B,求A∩B和(C R A)∩(C R B).2.已知函数f(x)=x2﹣bx+3,且f(0)=f(4).(1)求函数y=f(x)的零点,写出满足条件f(x)<0的x的集合;(2)求函数y=f(x)在区间(0,3]上的值域.3.求函数的值域:.4.求下列函数的值域:(1)y=3x2﹣x+2;(2);(3);(4);(5)(6);5.求下列函数的值域(1);(2);(3)x∈[0,3]且x≠1;(4).6.求函数的值域:y=|x﹣1|+|x+4|.7.求下列函数的值域.(1)y=﹣x2+x+2;(2)y=3﹣2x,x∈[﹣2,9];(3)y=x2﹣2x﹣3,x∈(﹣1,2];(4)y=.8.已知函数f(x)=22x+2x+1+3,求f(x)的值域.9.已知f(x)的值域为,求y=的值域.10.设的值域为[﹣1,4],求a、b的值.参考答案与试题解析一.解答题(共10小题)1.已知函数的定义域为集合A,函数的值域为集合B,求A∩B和(C R A)∩(C R B).考点:函数的值域;交、并、补集的混合运算;函数的定义域及其求法。
1457182专题:计算题。
分析:由可求A,由可求B可求解答:解:由题意可得∴A=[2,+∞),∵∴B=(1,+∞),C R A=(﹣∞,2),C R B=(﹣∞,1]﹣﹣﹣(4分)∴A∩B=[2,+∞)∴(C R A)∩(C R B)=(﹣∞,1]﹣﹣﹣﹣﹣(6分)点评:本题主要考查了函数的定义域及指数函数的值域的求解,集合的交集、补集的基本运算,属于基础试题2.已知函数f(x)=x2﹣bx+3,且f(0)=f(4).(1)求函数y=f(x)的零点,写出满足条件f(x)<0的x的集合;(2)求函数y=f(x)在区间(0,3]上的值域.考点:函数的值域;二次函数的性质;一元二次不等式的解法。
1457182专题:计算题。
材料力学典型例题与详解(经典题目)
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18,或 1.33∶1.09∶1。 讨论:计算结果表明,采用等强度石柱时最节省材料,这是因为这种设计使得各截面的正应 力均达到许用应力,使材料得到充分利用。 3 滑轮结构如图,AB 杆为钢材,截面为圆形,直径 d = 20 mm ,许用应力 [σ ] = 160 MPa ,BC 杆为木材,截面为方形,边长 a = 60 mm ,许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
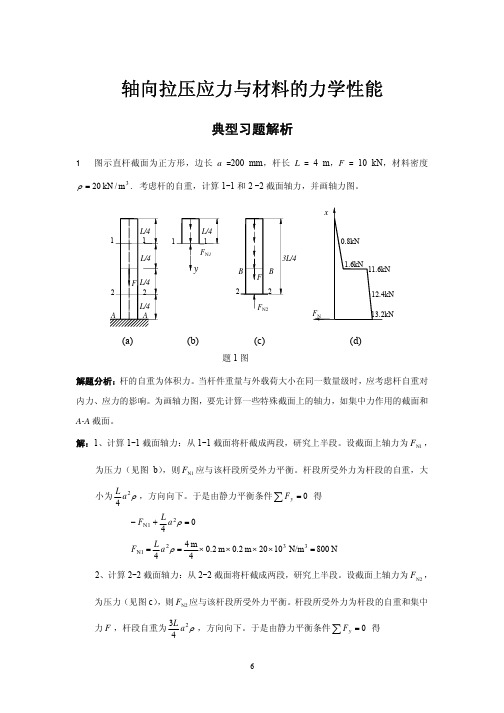
解:1、计算 1-1 截面轴力:从 1-1 截面将杆截成两段,研究上半段。设截面上轴力为 FN1 ,
为压力(见图 b),则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重,大
(完整版)溶液配制与稀释典型习题+详解

(完整版)溶液配制与稀释典型习题+详解溶液配制练习一、固—水例1:配制50 g质量分数为5%的氯化钠钠溶液,需要氯化钠多少克?水多少亳升?解析:这是溶液配制最基本、最典型的类型。
可由公式:溶质质量=溶液质量×溶质质量分数;溶剂质量=溶液质量—溶质质量和体积=质量/密度直接计算。
氯化钠质量=50 g×5%=2.5 g 水的质量=50 g—2.5 g =47.5 g水的体积=47.5 g/1 g/ ml=47.5 ml例2:配制500 ml质量分数为10%的氢氧化钠溶液(密度为1.1 g/cm3)需要氢氧化钠和水的质量各多少?解析:此题涉及溶液密度,要注意转化成质量来计算。
溶液中只有质量有加和关系,体积不能直接进行和差计算。
氢氧化钠溶质质=500 ml1.1 g/cm310%=55 g水的质量=500 ml1.1 g/cm3-55 g=495 g(不要计算成500—55=445)二、液—水例3:用25%的氯化钠溶液和水配制30kg10%的食盐溶液。
需要25%的氯化钠溶液和水各多少kg?解析:紧紧抓住配制前后的等量关系是关键。
可以利用配制前后溶质、溶剂的相对应相等来列方程解决。
设需要25%的氯化钠溶液和水质量为x和y25%x=30k g10%,解得x=12k g;Y=30k g—12k g=18k g例4:某工厂化验室配制5000 g20%的盐酸,需要38%的盐酸(密度为1.19 g/cm3)和水各多少毫升?解析:可以直接利用质量列方程计算。
设需要30%的盐酸体积为x,水的体积为y,5000 g×20%=x×1。
19 g/cm338% 解得x=2212 mlY=5000 g—2212 ml×1.19 g/cm338% =2453 ml三、液—液例5:要配制20%的食盐溶液100 g,需要10%和50%的食盐溶液各多少亳升?解析:此题可根据溶液配制前后的溶质、溶剂、溶液相等来列出议程组解决。
三视图习题加解析

三视图典型例题加解析一、选择题1如图,在下列四个几何体中,其三视图(正视图、侧视图、俯视图)中有且仅有两个相同的是( )A .②③④B .①②③C .①③④D .①②④解析:①的三个视图都是边长为1的正方形;②的俯视图是圆,正视图、侧视图都是边长为1的正方形;③的俯视图是一个圆及其圆心,正视图、侧视图是相同的等腰三角形;④的俯视图是边长为1的正方形,正视图、侧视图是相同的矩形.A2、平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( )A.6π B .43π C .46πD .63π解析:利用截面圆的性质先求得球的半径长. 如图,设截面圆的圆心为O ′,M 为截面圆上任一点, 则OO ′=2,O ′M =1,∴OM =(2)2+1=3,即球的半径为3, ∴V =43π(3)3=43π.3.若一个几何体的三视图如图所示,则此几何体的体积为( )A.112 B .5 C.92D .4解析:三视图还原为实物图,利用六棱柱体积公式求解.由三视图可知,此几何体为直六棱柱,且底面的面积为4,高为1,则体积V =Sh =4.D4.一个几何体的三视图如图所示,则这个几何体的表面积为( )A .6+ 5B .6+2 5C .8+ 5D .8+2 5解析:由三视图知,该几何体是一个底面为直角三角形的直棱柱,其表面积等于2×(12×1×2)+(2×12+22+1×2+2×2)=8+25,选D.5.如图,正方体ABCD -A ′B ′C ′D ′的棱长为4,动点E 、F 在棱AB 上,且EF =2,动点Q 在棱D ′C ′上,则三棱锥A ′EFQ 的体积( )A .与点E 、F 位置有关B .与点Q 位置有关C .与点E 、F 、Q 位置都有关D .与点E 、F 、Q 位置均无关,是定值解析:因为V A ′-EFQ =V Q -A ′EF =13×(12×2×4)×4=163,故三棱锥A ′-EFQ 的体积与点E 、F 、Q 的位置均无关,是定值.6.一个几何体的三视图如图所示,则该几何体的表面积为________.解析:将三视图还原为直观图后求解.根据三视图可知几何体是一个长方体挖去一个圆柱,所以S =2×(4+3+12)+2π-2π=38.7.某商店门口标识墩的直观图以及正视图和俯视图如图所示,墩的上半部分是正四棱锥P -EFGH ,下半部分是长方体ABCD -EFGH .(1)请画出该标识墩的侧视图; (2)求该标识墩的体积.解析:(1)由于墩的上半部分是正四棱锥P -EFGH ,下半部分是长方形ABCD -EFGH ,故其侧视图与正视图全等.该标识墩的侧视图如图所示.(2)由三视图易得,长方体与正四棱锥的底面均是边长为40 cm 的正方形,长方体的高为20 cm ,正四棱锥的高为60 cm.故该标识墩的体积V =V P -EFGH +V ABCD -EFGH =13×40×40×60+40×40×20=64 000(cm 3).8.已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.(1)若M 为CB 的中点,证明:MA ∥平面CNB 1; (2)求这个几何体的体积.解析:(1)证明:取CB 1的中点P ,连接MP ,NP .因为M 为CB 的中点,所以MP ∥BB 1,且MP =12BB 1.由三视图可知,四边形ABB 1N 为直角梯形,AN ∥BB 1且AN =12BB 1,则MP ∥AN 且MP =AN ,所以四边形ANPM 为平行四边形,所以AM ∥NP .又因为AM ⊄平面 CNB 1,NP ⊂平面CNB 1,所以AM ∥平面CNB 1. (2)因为该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,所以BC ⊥BA ,BC ⊥B 1B .又BB 1与BA 相交于点B ,连接BN ,所以BC ⊥平面ABB 1N ,所以BC 为三棱锥C -ABN 的高.取BB 1的中点Q ,连接QN ,因为四边形ABB 1N 是直角梯形且AN =12BB 1=4,所以四边形ABQN 为正方形,所以NQ ⊥BB 1,又BC ⊥平面ABB 1N ,NQ ⊂平面ABB 1N ,所以BC ⊥NQ ,又BC 与BB 1相交于点B ,所以NQ ⊥平面C 1B 1BC ,所以NQ 为四棱锥N -CBB 1C 1的高.所以该几何体的体积V =V C -ABN +VN -CBB 1C 1 =13CB ·S △ABN +13NQ ·S 四边形BCC 1B 1 =13×4×12×4×4+13×4×4×8=1603.9.给出如下四个命题:①棱柱的侧面都是平行四边形;②棱锥的侧面为三角形,且所有侧面都有一个共同的公共点;③多面体至少有四个面;④棱台的侧棱所在直线均相交于同一点.其中正确的命题个数有( ) A .1个 B .2个 C .3个 D .4个【解】D .10.圆锥底面半径为1cm,其中有一个内接正方体,求这个内接正方体的棱长.【解】分析:画出轴截面图,设正方体的棱长为x ,利用相似列关系求解. 过圆锥的顶点S 和正方体底面的一条对角线CD 作圆锥的截面,得圆锥的轴截面SEF ,正方体对角面CDD 1C 1,如图所示. 设正方体棱长为x ,则CC 1=x ,C 1D1=. 作SO ⊥EF 于O ,则SO =OE =1,1~ECC EOS ∆∆, ∴11CC EC SO EO ==.11∴ x =, cm 11.如图,正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上,点P 在球面上,如果163P ABCD V -=,则球O 的表面积是A. 4πB. 8πC. 12π D. 16π【解】如图,正四棱锥P ABCD -底面的四个顶点,,,A B C D在球O 的同一个大圆上,点P在球面上,PO 与平面ABCD 垂直,是棱锥的高,PO =R ,22ABCD S R =,163P ABCD V -=,所以2116233R R ⋅⋅=,解得R =2,则球O 的表面积是16π,选D. 12求球的表面积和体积.【解】分析:作出轴截面,利用勾股定理求解.作轴截面如图所示,CC '=AC == 设球半径为R ,则222R OC CC '=+229=+= ∴3R =,∴2436S R ππ==球,34363V R ππ==球.。
[全]管道工程--典型习题+解析[全考点]
![[全]管道工程--典型习题+解析[全考点]](https://img.taocdn.com/s3/m/84f777853c1ec5da51e270d5.png)
管道工程典型习题+解析一、单项选择题1、下列管道开槽的施工要求错误的是()。
A、在沟槽边坡稳固后设置供施工人员上下沟槽的安全梯B、采用机械挖槽时,沟槽分层的深度应按机械性能确定C、人工开挖沟槽的槽深超过2m时应分层开挖,每层的深度不超过2mD、槽底原状地基不得扰动,机械开挖时槽底预留200~300mm土层,由人工开挖、整平【本题1 分,建议1 分钟内完成本题】【正确答案】C【答案解析】本题考查的是开槽管道的地基处理与安管。
人工开挖沟槽的槽深超过3m时应分层开挖,每层的深度不超过2m。
2、下面关于顶管工作井设备施工安全表述错误的是()。
A、施工供电应设置双路电源,自动切换B、动力、照明应分路供电,作业面移动照明应采用低压供电C、起重作业前应试吊,吊离地面100mm左右时,检查重物捆扎情况和制动性能D、起吊时工作井内可以站人,但必须采取防护罩等保护措施【本题1 分,建议1 分钟内完成本题】【正确答案】D【答案解析】本题考查的是不开槽管道施工方法与设备施工安全的有关规定。
起吊时工作井内严禁站人,当吊运重物下井距作业面底部小于500mm时,操作人员方可近前工作。
3、给水管道水压试验中,管道内注水与浸泡的做法错误的是()。
A、应从上游缓慢注入B、球墨铸铁管、钢管、化学建材管不少于24hC、内径小于1000mm的现浇钢筋混凝土管渠不少于48hD、内径大于1000mm的预应力钢筒混凝土管不少于72h【本题1 分,建议1 分钟内完成本题】【正确答案】A【答案解析】本题考查的是压力管道的水压试验。
管道内注水应从下游缓慢注入,注入时在试验管段上游的管顶及管段中的高点应设置排气阀,将管道内的气体排除。
4、下列属于管道的更新方法是()。
A、破管外挤B、内衬法C、缠绕法D、喷涂法【本题1 分,建议1 分钟内完成本题】【正确答案】A【答案解析】本题考查的是管道修复与更新。
常见的管道更新方法有破管外挤和破管顶进两种,其余三项为修复管道的方法。
高中数学典型例题解析

任意角三角函数三、经典例题导讲[例1] 若A 、B 、C 是ABC ∆的三个内角,且)2(π≠<<C C B A ,则下列结论中正确的个数是( )①.C A sin sin < ②.C A cot cot < ③.C A tan tan < ④.C A cos cos < A .1 B.2 C.3 D.4错解:C A < ∴ C A sin sin <,C A tan tan <故选B错因:三角形中大角对大边定理不熟悉,对函数单调性理解不到位导致应用错误 正解:法1C A < 在ABC ∆中,在大角对大边,A C a c sin sin ,>∴>法2 考虑特殊情形,A 为锐角,C 为钝角,故排除B 、C 、D ,所以选A . [例2]已知βα,角的终边关于y 轴对称,则α与β的关系为 . 错解:∵βα,角的终边关于y 轴对称,∴22πβα=++πk 2,()z k ∈错因:把关于y 轴对称片认为关于y 轴的正半轴对称. 正解:∵βα,角的终边关于y 轴对称 ∴)(,22Z k k ∈+=+ππβα即)(,2z k k ∈+=+ππβα说明:(1)若βα,角的终边关于x 轴对称,则α与β的关系为)(,2Z k k ∈=+πβα(2)若βα,角的终边关于原点轴对称,则α与β的关系为)(,)12(Z k k ∈++=πβα (3)若βα,角的终边在同一条直线上,则α与β的关系为)(,Z k k ∈+=παβ[例3] 已知542cos ,532sin-==θθ,试确定θ的象限. 错解:∵0542cos ,0532sin <-=>=θθ,∴2θ是第二象限角,即.,222z k k k ∈+<<ππθπ从而.,244z k k k ∈+<<ππθπ故θ是第三象限角或第四象限角或是终边在y 轴负半轴上的角.错因:导出2θ是第二象限角是正确的,由0542cos ,0532sin <-=>=θθ即可确定, 而题中542cos ,532sin -==θθ不仅给出了符号,而且给出了具体的函数值,通过其值可进一步确定2θ的大小,即可进一步缩小2θ所在区间.正解:∵0542cos ,0532sin<-=>=θθ,∴2θ是第二象限角, 又由43sin 22532sinπθ=<=知z k k k ∈+<<+,22432ππθππ z k k k ∈+<<+,24234ππθππ,故θ是第四象限角. [例4]已知角α的终边经过)0)(3,4(≠-a a a P ,求ααααcot ,tan ,cos ,sin 的值. 错解:a y x r a y a x 5,3,422=+=∴=-=3434cot ,4343tan ,5454cos ,5353sin -=-=-=-=-=-===∴a a a a a a a a αααα错因:在求得r 的过程中误认为a >0正解:若0>a ,则a r 5=,且角α在第二象限3434cot ,4343tan ,5454cos ,5353sin -=-=-=-=-=-===∴a a a a a a a a αααα 若0<a ,则a r 5-=,且角α在第四象限3434cot ,4343tan ,5454cos ,5353sin -=-=-=-==--=-=-=∴a a a a a a a a αααα说明:(1)给出角的终边上一点的坐标,求角的某个三解函数值常用定义求解; (2)本题由于所给字母a 的符号不确定,故要对a 的正负进行讨论. [例5] (1)已知α为第三象限角,则2α是第 象限角,α2是第 象限角; (2)若4-=α,则α是第 象限角. 解:(1)α 是第三象限角,即Z k k k ∈+<<+,2322ππαππZ k k k ∈+<<+∴,4322ππαππ,Z k k k ∈+<<+,34224ππαππ当k 为偶数时,2α为第二象限角当k 为奇数时,2α为第四象限角而α2的终边落在第一、二象限或y 轴的非负半轴上.(2)因为ππ-<-<-423,所以α为第二象限角. 点评:α为第一、二象限角时,2α为第一、三象限角,α为第三、四象限角时,2α为第二、四象限角,但是它们在以象限角平分线为界的不同区域.[例6]一扇形的周长为20cm ,当扇形的圆心角α等于多少时,这个扇形的面积最大?最大面积是多少?解:设扇形的半径为rcm ,则扇形的弧长cm r l )220(-=扇形的面积25)5()220(212+--=⋅-=r r r S 所以当cm r 5=时,即2,10===rl cm l α时2max 25cm S =.点评:涉及到最大(小)值问题时,通常先建立函数关系,再应用函数求最值的方法确定最值的条件及相应的最值.[例7]已知α是第三象限角,化简ααααsin 1sin 1sin 1sin 1+---+。
摩擦力典型练习题两套含解析

摩擦力练习题一班级成绩一、选择题〔此题包括12小题,每题给出的四个选项中,只有一个选项是正确的,有的有两个选项正确,全部选对的得5分,选对但不全的得3分,有选错或不选的得0分,共60分〕1.关于摩擦力的方向,以下说确的是( )A.摩擦力的方向总是与运动方向相反B.滑动摩擦力的方向总是与运动方向相反C.滑动摩擦力一定是阻力D.摩擦力的方向一定与压力的方向垂直2.关于滑动摩擦力,以下说确的是〔〕A.两个运动的物体,压力大的,所受滑动摩擦力也大B.压力不变,动摩擦因数不变,接触面积越大,滑动摩擦力越大C.压力不变,动摩擦因数不变,速度越大,滑动摩擦力越大D.动摩擦因数不变,压力越大,滑动摩擦力越大3.置于水平面上的物体在沿水平方向的拉力作用下,仍处于静止,则物体所受静摩擦力大小〔〕A.与压力成正比B.等于水平拉力C.小于滑动摩擦力D.在物体上叠放另一物体,该物体受到的静摩擦力不变4.以下说法中正确的选项是( )A.两个相互接触的物体之间一定有弹力作用B.一个物体静止在另一个物体的外表上,它们之间一定不存在摩擦力的作用C.两个物体之间如果有弹力的作用,就一定有摩擦力的作用D.两个物体之间如果有摩擦力的作用,就一定有弹力的作用5.如图1,木块质量为m,跟水平桌面的动摩擦因数为μ,受水平向右的力F的作用匀速运动,从物体到边缘开场,到物体下落为止,在此过程中物体保持匀速运动,以下说确的是〔〕A.推力F因物体悬空局部越来越大而变小B.推力F在物体下落前会变为原来的1/2 C.推力F始终是μmgD.因接触面变小,动摩擦因数μ会变大6.关于由滑动摩擦力公式推出的μ=fF N,下面说确的是( ) A.动摩擦因数μ与摩擦力f成正比,f越大,μ越大B.动摩擦因数μ与正压力F N成反比,F N越大,μ越小C.动摩擦因数μ与摩擦力f成正比,与正压力F N成反比D.动摩擦因数μ的大小由两物体接触的情况及材料决定7.在奥运会上,体操运发动在上单杠之前,总要在手上抹些镁粉;而在单杠上做回环动作时,手握单杠又不能太紧。
典型习题解析

第二章组织、器官和系统一、选择题1.花生雌蕊柄之所以能将花生的花推入土中因为其基部有下列之故?A.顶端分生组织 B.侧生分生组织 C.居间分生组织 D.原分生组织2.被子植物中,具有功能的死细胞是。
A.导管分子和筛管分子 B.筛管分子和纤维 C.导管分子和纤维 D.纤维和伴胞3.裸子植物靠输导水分。
A.导管和管胞 B.管胞 C.筛管 D.筛胞4.筛管分子最明显的特征是其。
A.侧壁具筛域 B.为具核的生活细胞 C.端壁具筛板 D.为有筛域、筛板而无核的生活细胞5.次生分生组织可由直接转变而成。
A.原分生组织 B.初生分生组织 C.侧生分生组织 D.薄壁组织6.周皮上的通气结构是。
A.气孔 B.皮孔 C.穿孔 D.纹孔7.水稻和小麦等禾本科植物拔节、抽穗时,茎迅速长高,是借助的活动。
A.顶端分生组织 B.侧生分生组织 C.次生分生组织 D.居间分生组织8.厚角组织与厚壁组织的差别,在于厚壁组织是。
A.细胞,壁均匀地次生加厚 B.胞,壁均匀地次生加厚C.细胞,壁均匀地初生加厚 D.细胞,壁均匀地初生加厚9.下列哪种组织常常有叶绿体,能进行光合作用。
A.厚壁组织 B.厚角组织 C.输导组织 D.分泌组织10.草本植物体内数量最多,分布最广的组织是。
A.输导组织 B.薄壁组织 C.机械组织 D.厚壁组织11.韭菜叶切断后,能继续生长,是因为下列何种生长的结果。
A.顶端生长 B.侧生生长 C.居间生长 D.产生离层12.根的吸收作用主要在________。
A.根冠 B.分生区 C.根毛区 D.伸长区13.中柱鞘细胞可产生________。
A.部分维管形成层和木栓形成层 B.不定芽和不定根 C.侧根 D.A、B和C14.原表皮、基本分生组织和原形成层属于________。
A.居间分生组织 B.原分生组织 C.初生分生组织 D.伸长区15.根初生维管组织中,木质部与韧皮部的排列是________。
A.内外排列 B.散生 C.相间排列16.根毛区表皮细胞的主要作用是________。
水浒传中考真题及典型习题训练解析版

"水浒传"中考真题及典型习题训练答案解析一、"水浒传"历年中考真题精选1.【2019年潍坊市初中学业水平考试语文试题】阅读"水浒传"中的两个片段,答复以下问题。
①宋江听罢,吃了一惊,肚里寻思道:"晁盖是我心腹兄弟。
他如今犯了弥天大罪,我不救他时,捕获将去,性命便休了!〞……晁盖听罢,吃了一惊道:"贤弟大恩难报!〞宋江道:"哥哥,你休要多说,只顾安排走路,不要缠障。
我便回去了。
〞②宋江大醉,叫取纸笔来,一时乘着酒兴,作满江红一词:"……衷心愿平虏,保民安国。
日月常悬忠烈胆,风尘障却奸邪目。
望天王降诏,早招安,心方足。
〞……宋江道:"今皇上至圣至明,只被奸臣闭塞,暂时昏昧,有日云开见日,知我等替天行道,不扰良民,同心报国,青史留名,有何不美!〞〔1〕从上述两段选文中可以看出宋江、的性格特点。
〔2〕结合整部小说,简要分析宋江以上性格对小说情节开展的作用。
【答案】〔1〕义忠〔2〕义使宋江成为梁山义军的领袖,忠使宋江最终引导义军走向招安。
【解析】试题解析:此题考察学生对文学名著的阅读与识记能力。
解答文学名著题,必须建立在阅读原著的根底之上,不仅要"博闻强记〞,还要对容进展归纳整理。
要熟记其名称、作者、主要人物形象、精彩的故事情节、艺术特色等容,并反复阅读书中的精彩片段,以形成自己的阅读体验。
〔1〕选文①主要叙写了宋江"义〞救晁盖;选文②主要叙写了宋江大醉作"满江红"和其言论,从"衷心愿平虏,保民安国。
日月常悬忠烈胆,风尘障却奸邪目。
望天王降诏,早招安,心方足〞和"同心报国,青史留名,有何不美!〞可以看出宋江一心想招安,忠心报国,突出了其特点"忠〞。
据此可填写作答。
〔2〕从选文看,宋江有着"义〞和"忠〞的性格特点,这"义〞使他召集了众多的梁山好汉,最终成为梁山义军的首领。
高中数学典型例题解析立体几何

高中数学典型例题分析 第六章 立体几何初步§6.1 两条直线之间的位置关系一、知识导学1. 平面的基本性质.公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.公理2:如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线.公理3:经过不在同一条直线上的三点,有且只有一个平面.推论1:经过一条直线和这条直线外的一点,,有且只有一个平面.推论2:经过两条相交直线,有且只有一个平面.推论3:经过两条平行直线,有且只有一个平面. 2. 空间两条直线的位置关系,包括:相交、平行、异面.3. 公理4:平行于同一条直线的两条直线平行.定理4:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等.推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.4. 异面直线.异面直线所成的角;两条异面直线互相垂直的概念;异面直线的公垂线及距离.5. 反证法.会用反证法证明一些简单的问题. 二、疑难知识导析1.异面直线是指不同在任何一个平面内,没有公共点.强调任何一个平面.2.异面直线所成的角是指经过空间任意一点作两条分别和异面的两条直线平行的直线所成的锐角(或直角).一般通过平移后转化到三角形中求角,注意角的范围. 3.异面直线的公垂线要求和两条异面直线垂直并且相交,4.异面直线的距离是指夹在两异面直线之间公垂线段的长度.求两条异面直线的距离关键是找到它们的公垂线.5.异面直线的证明一般用反证法、异面直线的判定方法:如图,如果b α⊂,A α∈且A b ∉,a A =⋂α,则a 与b 异面. 三、经典例题导讲[例1]在正方体ABCD-A 1B 1C 1D 1中,O 是底面ABCD 的中心,M 、N 分别是棱DD 1、D 1C 1的中点,则直线OM( ).A .是AC 和MN 的公垂线.B .垂直于AC 但不垂直于MN. C .垂直于MN ,但不垂直于AC.D .与AC 、MN 都不垂直. 错解:B.错因:学生观察能力较差,找不出三垂线定理中的射影. 正解:A. [例2]如图,已知在空间四边形ABCD 中,E,F 分别是AB,AD 的中点,G,H 分别是BC,CD 上的点,且2==HCDH GCBG,求证:直线EG,FH,AC相交于一点.错解:证明:E 、F 分别是AB,AD 的中点,EF ∴∥BD,EF=21BD,又2==HCDH GCBG ,∴ GH ∥BD,GH=31BD,∴四边形EFGH 是梯形,设两腰EG,FH 相交于一点T,2=HCDH ,F 分别是AD.∴AC 与FH 交于一点.∴直线EG,FH,AC 相交于一点正解:证明:E 、F 分别是AB,AD 的中点,EF ∴ ∥BD,EF=21BD,又2==HCDH GCBG ,∴GH ∥BD,GH=31BD,∴四边形EFGH 是梯形,设两腰EG,FH 相交于一点T, ⊂EG 平面ABC,FH ⊂平面ACD,∴T ∈面ABC,且T ∈面ACD,又平面ABC 平面ACD=AC, AC T ∈∴,∴直线EG,FH,AC 相交于一点T.[例3]判断:若a,b 是两条异面直线,P 为空间任意一点,则过P 点有且仅有一个平面与a,b 都平行.错解:认为正确.错因:空间想像力不够.忽略P 在其中一条线上,或a 与P 确定平面恰好与b 平行,此时就不能过P 作平面与a 平行. 正解:假命题.[例4] 如图,在四边形ABCD 中,已知AB ∥CD ,直线AB ,BC ,AD ,DC 分别与平面α相交于点E ,G ,H ,F .求证:E ,F ,G ,H 四点必定共线(在同一条直线上). 分析:先确定一个平面,然后证明相关直线在这个平面内,最后证明四点共线. 证明 ∵ AB//CD , AB ,CD 确定一个平面β. 又∵AB ∩α=E ,AB β,∴ E ∈α,E ∈β, 即 E 为平面α与β的一个公共点. 同理可证F ,G ,H 均为平面α与β的公共点. ∵ 两个平面有公共点,它们有且只有一条通过公共点的公共直线, ∴ E,F ,G ,H 四点必定共线.点 评:在立体几何的问题中,证明若干点共线时,先证明这些点都是某两平面的公共点,而后得出这些点都在二平面的交线上的结论.[例5]如图,已知平面α,β,且α∩β=l.设梯形ABCD 中,AD∥BC,且AB α,CDβ,求证:AB ,CD ,l共点(相交于一点).分析:AB ,CD 是梯形ABCD 的两条腰,必定相交于一点M ,只要证明M 在l 上,而l 是两个平面α,β的交线,因此,只要证明M∈α,且M∈β即可.证明: ∵ 梯形ABCD 中,AD∥BC, ∴AB,CD 是梯形ABCD 的两条腰. ∴ AB,CD 必定相交于一点, 设 AB ∩CD=M .又∵ AB α,CD β,∴ M∈α,且M∈β. ∴ M∈α∩β. 又∵α∩β=l ,∴ M∈l ,即AB ,CD ,l 共点.点 评:证明多条直线共点时,与证明多点共线是一样的.[例6]已知:a ,b ,c ,d 是不共点且两两相交的四条直线,求证:a ,b ,c ,d 共面. 分析:弄清楚四条直线不共点且两两相交的含义:四条直线不共点,包括有三条直线共点的情况;两两相交是指任何两条直线都相交.在此基础上,根据平面的性质,确定一个平面,再证明所有的直线都在这个平面内.证明 1º若当四条直线中有三条相交于一点,不妨设a ,b ,c 相交于一点 A ∴ 直线d 和A 确定一个平面α.又设直线d 与a ,b ,c 分别相交于E ,F ,G , 则 A ,E ,F ,G∈α. ∵ A ,E∈α,A ,E∈a, ∴ a α. 同理可证 b α,c α. ∴ a,b ,c ,d 在同一平面α内. 2º当四条直线中任何三条都不共点时,如图. ∵ 这四条直线两两相交, 则设相交直线a ,b 确定一个平面α. 设直线c 与a ,b 分别交于点H ,K , 则 H ,K∈α.又∵ H,K∈c,∴ c α. 同理可证 d α.∴ a,b ,c ,d 四条直线在同一平面α内.点 评:证明若干条线(或若干个点)共面的一般步骤是:首先由题给条件中的部分线(或点)确定一个平面,然后再证明其余的线(或点)均在这个平面内.本题最容易忽视“三线共点”这一种情况.因此,在分析题意时,应仔细推敲问题中每一句话的含义. [例7] 在立方体ABCD -A 1B 1C 1D 1中,(1)找出平面AC 的斜线BD 1在平面AC 内的射影; (2)直线BD 1和直线AC 的位置关系如何?(3)直线BD 1和直线AC 所成的角是多少度?解:(1)连结BD, 交AC 于点O 上的射影在平面就是斜线平面AC BD BD AC DD 11,∴⊥ . (2)BD 1和AC 是异面直线.(3)过O 作BD 1的平行线交DD 1于点M ,连结MA 、MC ,则∠MOA 或其补角即为异面直线AC 和BD 1所成的角.不难得到MA =MC ,而O 为AC 的中点,因此MO ⊥AC ,即∠MOA =90°,∴异面直线BD 1与AC 所成的角为90°.[例8] 已知:在直角三角形ABC 中,∠A 为直角,PA⊥平面ABC ,BD⊥PC,垂足为D ,求证:AD⊥PC 证明:∵ PA ⊥平面ABC∴ PA⊥BA 又∵ BA⊥AC ∴ BA⊥平面PAC ∴ AD 是BD 在平面PAC 内的射影又∵ BD ⊥PC ∴ AD ⊥PC .(三垂线定理的逆定理) 四、典型习题导练1.如图, P 是△ABC 所在平面外一点,连结PA 、PB 、PC 后,在包括AB 、BC 、CA 的六条棱所在的直线中,异面直线的对数为( )A.2对B.3对C.4对D.6对2. 两个正方形ABCD 、ABEF 所在的平面互相垂直,则异面直线AC 和BF 所成角的大小为 .3. 在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,体对角线DB 1与面对角线BC 1所成的角是 ,它们的距离是 .4.长方体ABCD A B C D -1111中,BC CD DD ===2214251,,,则A C B D 111和所成角的大小为_ ___.5.关于直角AOB 在定平面α内的射影有如下判断:①可能是0°的角;②可能是锐角;③可能是直角;④可能是钝角;⑤可能是180°的角. 其中正确判断的序号是_____.(注:把你认为正确的序号都填上).6.在空间四边形ABCD 中,AB ⊥CD ,AH ⊥平面BCD ,求证:BH ⊥CD7.如图正四面体中,D 、E 是棱PC 上不重合的两点;F 、H 分别是棱PA 、PB 上的点,且与P 点不重合. 求证:EF 和DH 是异面直线.§6.2直线与平面之间的位置关系一、知识导学1.掌握空间直线与平面的三种位置关系(直线在平面内、相交、平行).2.直线和平面所成的角,当直线与平面平行或在平面内时所成的角是 0,当直线与平面垂直时所成的角是9 0,当直线与平面斜交时所成的角是直线与它在平面内的射影所成的锐角.3.掌握直线与平面平行判定定理(如果平面外的一条直线和平面内的一条直线平行,那么这条直线和平面平行)和性质定理(如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行).4.直线与平面垂直的定义是:如果一条直线和一个平面内所有直线垂直,那么这条直线和这个平面垂直;掌握直线与平面垂直的判定定理(如果一条直线和平面内的两条相交直线都垂直,那么这条直线垂直于这个平面)和性质定理(如果两条直线同垂直于一个平面,那么这两条直线平行).5.直线与平面的距离(一条直线和一个平面平行时,这条直线上任意一点到这个平面的距离,叫做这条直线和这个平面的距离).6.三垂线定理(在平面内的一条直线,如果和这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直)、逆定理(在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线在这个平面内的射影垂直).7.从平面外一点向这个平面所引的垂线段和斜线段中:①射影相等的两条斜线段相等,射影较长的斜线段也较长;②相等的斜线段的射影相等,较长的斜线段的射影也较长;③垂线段比任何一条斜线段都短.二、疑难知识导析1.斜线与平面所成的角关键在于找射影,斜线与平面所成的角,是这条斜线和这个平面内的直线所成的一切角中最小的角.2.在证明平行时注意线线平行、线面平行及面面平行判定定理和性质定理的反复运用.3.在证明垂直时注意线线垂直、线面垂直及面面垂直判定定理和性质定理的反复运用,同时还要注意三垂线定理及其逆定理的运用.要注意线面垂直的判定定理中的“两条相交直线”,如果用“无数”或“两条”都是错误的.4.直线与平面的距离一般是利用直线上某一点到平面的距离.“如果在平面的同一侧有两点到平面的距离(大于0)相等,则经过这两点的直线与这个平面平行.”要注意“同一侧”、“距离相等”.三、经典例题导讲l⊂平面α,点P∈直线l,平面α、β间的距离为8,则在β内[例1]已知平面α∥平面β,直线l的距离为9的点的轨迹是()到点P的距离为10,且到A.一个圆B.四个点C.两条直线 D .两个点错解:A.错因:学生对点线距离、线线距离、面面距离的关系掌握不牢.正解:B.[例2] a和b为异面直线,则过a与b垂直的平面( ).A .有且只有一个B .一个面或无数个C .可能不存在D .可能有无数个 错解:A.错因:过a 与b 垂直的平面条件不清. 正解:C.[例3]由平面α外一点P 引平面的三条相等的斜线段,斜足分别为A,B,C ,O 为⊿ABC 的外心,求证:OP α⊥.错解:因为O 为⊿ABC 的外心,所以OA =OB =OC ,又因为PA =PB =PC ,PO 公用,所以⊿POA ,⊿POB ,⊿POC 都全等,所以∠POA =∠POB=∠POC =2π,所以OP α⊥. 错因:上述解法中∠POA =∠POB =∠POC =RT ∠,是对的,但它们为什么是直角呢?这里缺少必要的证明.正解:取BC 的中点D ,连PD 、OD ,,,,,,,AB PO PO .PB PC OB OC BC PD BC OD BC POD BC PO α==∴⊥⊥∴⊥∴⊥⊥∴⊥面同理,[例4]如图,在正三棱柱ABC-A 1B 1C 1中,AB=3,AA 1=4,M 为AA 1的中点,P 是BC 上一点,且由P 沿棱柱侧面经过棱CC 1到M 点的最短路线长为29,设这条最短路线与C 1C 的交点为N,求: (1)该三棱柱的侧面展开图的对角线长;(2)PC 和NC 的长;(3)平面NMP 和平面ABC 所成二面角(锐角)的大小(用反三角函数表示)错因:(1)不知道利用侧面BCC 1 B 1展开图求解,不会找29 的线段在哪里;(2)不会找二面角的平面角.正解:(1)正三棱柱ABC-A 1B 1C 1的侧面展开图是一个长为9,宽为4的矩形,其对角线长为974922=+(2)如图,将侧面BC 1旋转120使其与侧面AC 1在同一平面上,点P 运动到点P 1的位置,连接MP 1 ,则MP 1就是由点P 沿棱柱侧面经过CC 1到点M 的最短路线. 设PC =x ,则P 1C =x ,在2,292)3221==+∆x x MAP Rt +中,(54,5211=∴==∴NC A P C P MA NC (3)连接PP 1(如图),则PP 1就是平面NMP 与平面ABC 的交线,作NH 1PP ⊥于H ,又CC 1⊥平面ABC ,连结CH ,由三垂线定理的逆定理得,1PP CH ⊥.所成二面角的平面角。
《结构力学》典型习题与解答-知识归纳整理

《结构力学》经典习题及详解一、判断题(将判断结果填入括弧内,以 √表示正确 ,以 × 表示错误。
)1.图示桁架结构中有3个杆件轴力为0 。
(×)2.图示悬臂梁截面A 的弯矩值是ql 2。
(×)l lqA3.静定多跨梁中基本部分、附属部分的划分与所承受的荷载无关。
(√ ) 4.普通来说静定多跨梁的计算是先计算基本部分后计算附属部分。
(× ) 5.用平衡条件能求出全部内力的结构是静定结构。
( √ )6.求桁架内力时截面法所截取的隔离体包含两个或两个以上的结点。
(√ ) 7.超静定结构的力法基本结构不是唯一的。
(√)8.在桁架结构中,杆件内力不是惟独轴力。
(×) 9.超静定结构由于支座位移可以产生内力。
(√ ) 10.超静定结构的内力与材料的性质无关。
(× ) 11.力法典型方程的等号右端项不一定为0。
(√ )12.计算超静定结构的位移时,虚设力状态可以在力法的基本结构上设。
(√)13.用力矩分配法计算结构时,汇交于每一结点各杆端分配系数总和为1,则表明分配系数的计算无错误。
(× )14.力矩分配法适用于所有超静定结构的计算。
(×) 15.当AB 杆件刚度系数i S AB3 时,杆件的B 端为定向支座。
(×)F P知识归纳整理二、单项挑选题(在每小题的四个备选答案中选出一具正确答案,并将其代号填在题干后面的括号内。
不选、错选或多选者,该题无分。
) 1.图示简支梁中间截面的弯矩为( A )qlA . 82qlB . 42ql C . 22ql D . 2ql2.超静定结构在荷载作用下产生的内力与刚度(B )A . 无关B . 相对值有关C . 绝对值有关D . 相对值绝对值都有关 3.超静定结构的超静定次数等于结构中(B )A .约束的数目B .多余约束的数目C .结点数D .杆件数4.力法典型方程是根据以下哪个条件得到的(C )。
积分练习题解析

积分练习题解析一、简介积分是微积分中的重要概念,用于求解曲线下面的面积、求解曲线的长度、求解曲线的平均值等问题。
本文将通过解析一些典型的积分练习题,帮助读者更好地理解和掌握积分的求解方法和技巧。
二、题目一解析题目描述:计算函数f(x)=2x的不定积分。
解析:根据不定积分的定义,可以直接求解该积分。
不定积分是求解原函数,因此我们需要找到一个函数F(x),使得F'(x)=f(x)=2x。
解题步骤如下:1. 找到F(x)的原函数,根据幂函数的求导法则,可知F(x)的原函数是x的平方。
2. 验证F'(x)=f(x),即验证(x^2)'=2x。
根据幂函数的求导法则,可知(x^2)'=2x,所以F'(x)=2x,符合要求。
3. 得出不定积分的结果为F(x)+C,其中C为常数。
因此,f(x)=2x 的不定积分为F(x)+C=x^2+C。
三、题目二解析题目描述:计算定积分∫[0, 1] (3x^2+2x+1)dx。
解析:定积分是求解函数在两个给定点之间区域的面积,可以看成是不定积分在两个给定点之间的差值。
解题步骤如下:1. 对被积函数进行不定积分,得到其原函数。
根据幂函数的积分法则,可以得到原函数F(x) = x^3 + x^2 + x。
2. 计算原函数在积分区间的值,即F(1)和F(0)。
代入得到F(1) = 3,F(0) = 0。
3. 计算定积分的结果,即F(1) - F(0) = 3 - 0 = 3。
因此,定积分∫[0, 1] (3x^2+2x+1)dx的结果为3。
四、题目三解析题目描述:计算定积分∫[-1, 1] (e^x - e^-x)dx。
解析:定积分的求解同样可以通过不定积分的方法来完成。
解题步骤如下:1. 对被积函数进行不定积分,得到其原函数。
根据指数函数的积分法则,可以得到原函数F(x) = e^x + e^-x。
2. 计算原函数在积分区间的值,即F(1)和F(-1)。
[全]轨道交通--典型习题+解析[全考点]
![[全]轨道交通--典型习题+解析[全考点]](https://img.taocdn.com/s3/m/ce1e79d8f78a6529657d53bd.png)
轨道交通--典型习题+解析一、单项选择题1、关于隧道浅埋暗挖法施工的说法,错误的是()。
A、施工时不允许带水作业B、要求开挖面具有一定的自立性和稳定性C、常采用预制装配式衬砌D、与新奥法相比,初期支护允许变形量较小【本题1 分,建议1 分钟内完成本题】【正确答案】C【答案解析】本题考查的是地铁车站施工方法(工艺)与选择条件。
喷锚暗挖法施工隧道通常采用复合式衬砌设计,衬砌结构由初期支护、防水层和二次衬砌所组成。
2、设有支护的基坑土方开挖过程中,能够反映坑底土体隆起的检测项目是()。
A、立柱变形B、冠梁变形C、土地变形D、支撑梁变形【本题1 分,建议1 分钟内完成本题】【正确答案】A【答案解析】本题考查的是基坑的变形控制。
由于基坑一直处于开挖过程中,直接监测坑底土体隆起较为困难,一般通过监测立柱变形来反映基坑底土体隆起情况。
3、水泥土搅拌法地基加固适用于()。
A、障碍物较多的杂填土B、欠固结的淤泥质土C、可塑的黏性土D、密实的砂类土【本题1 分,建议1 分钟内完成本题】【正确答案】C【答案解析】本题考查的是地基加固常用方法和技术要点。
水泥土搅拌法适用于加固淤泥、淤泥质土、素填土、黏性土(软塑和可塑)、粉土(稍密、中密)、粉细砂(稍密、中密)、中粗砂(松散、稍密)、饱和黄土等土层。
4、关于隧道全断面暗挖法施工的说法,错误的是()。
A、可减少开挖对围岩的扰动次数B、围岩必须有足够的自稳能力C、自上而下一次开挖成型并及时进行初期保护D、适用于地表沉降难于控制的隧道施工【本题1 分,建议1 分钟内完成本题】【正确答案】D【答案解析】本题考查的是浅埋暗挖法与掘进方式。
全断面开挖法的优点是可以减少开挖对围岩的扰动次数,有利于围岩天然承载拱的形成,工序简便;缺点是对地质条件要求严格,围岩必须有足够的自稳能力。
5、下列盾构类型中,属于密闭式盾构的是()。
A、泥土加压式盾构B、手掘式盾构C、半机械挖掘式盾构D、机械挖掘式盾构【本题1 分,建议1 分钟内完成本题】【正确答案】A【答案解析】本题考查的是盾构类型与适用条件。
空间向量典型习题含详解
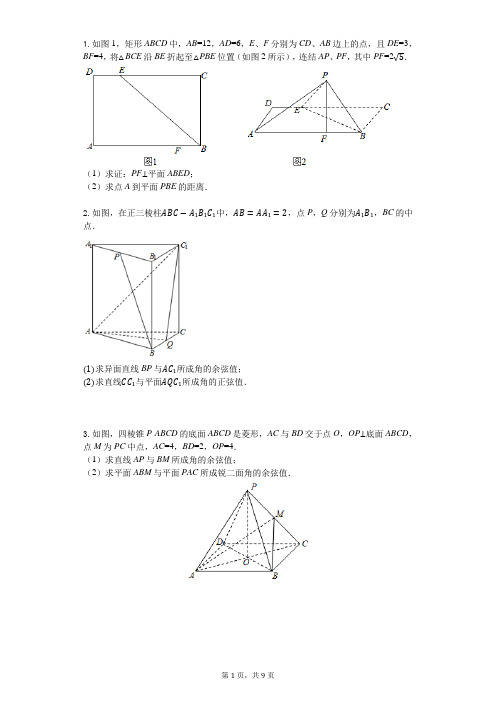
1.如图1,矩形ABCD中,AB=12,AD=6,E、F分别为CD、AB边上的点,且DE=3,BF=4,将△BCE沿BE折起至△PBE位置(如图2所示),连结AP、PF,其中PF=2.(1)求证:PF⊥平面ABED;(2)求点A到平面PBE的距离.2.如图,在正三棱柱中,,点P,Q分别为,BC的中点.求异面直线BP与所成角的余弦值;求直线与平面所成角的正弦值.3.如图,四棱锥P-ABCD的底面ABCD是菱形,AC与BD交于点O,OP⊥底面ABCD,点M为PC中点,AC=4,BD=2,OP=4.(1)求直线AP与BM所成角的余弦值;(2)求平面ABM与平面PAC所成锐二面角的余弦值.4.如图,在三棱柱ABC-A1B1C1中,平面A1B1C⊥平面AA1C1C,∠BAC=90°.(1)证明:AC⊥CA1;(2)若△A1B1C是正三角形,AB=2AC=2,求二面角A1-AB-C的大小.5.如图,四棱锥P-ABCD中,AB∥DC,DC⊥BC,AB=2,CD=DP=1,PA=PB=BC=3,侧棱PC上点E满足PE=2EC.(1)求证PA∥平面BED;(2)求二面角A-PB-C的余弦值.6.如图,在正方体ABCD-A1B1C1D1中,E,F分别为底面A1B1C1D1和侧面B1C1CB的中心.求证:(1)EF∥A1B;(2)EF∥平面A1BD;(3)平面B1EF∥平面A1BD.7.如图,四边形为正方形,分别为的中点,以为折痕把折起,使点到达点的位置,且.(1)证明:平面平面;(2)求与平面所成角的正弦值.答案和解析1.【答案】解:(1)连结EF,由翻折不变性可知,PB=BC=6,PE=CE=9,在△PBF中,PF2+BF2=20+16=36=PB2,所以PF⊥BF,在图1中,利用勾股定理,得EF==,在△PEF中,EF2+PF2=61+20=81=PE2,∴PF⊥EF,又∵BF∩EF=F,BF⊂平面ABED,EF⊂平面ABED,∴PF⊥平面ABED.(2)解:由(1)知PF⊥平面ABED,∴PF为三棱锥P-ABE的高.设点A到平面PBE的距离为h,由等体积法得V A-PBE=V P-ABE,即∴h=,即点A到平面PBE的距离为.【解析】本题考查直线与平面垂直的证明,考查点到平面距离的求法,解题时要注意空间思维能力的培养,要注意等积法的合理运用.(1)连结EF,由翻折不变性可知,PB=BC=6,PE=CE=9,由已知条件,利用勾股定理推导出PF⊥BF,PF⊥EF,由此能够证明PF⊥平面ABED.(2)由PF⊥平面ABED,知PF为三棱锥P-ABE的高,利用等积法能求出点A 到平面PBE的距离.2.【答案】解:如图,在正三棱柱ABC-A1B1C1中,设AC,A1C1的中点分别为O,O1,则,OB⊥OC,OO1⊥OC,OO1⊥OB,故以{,,}为基底,建立空间直角坐标系O-xyz,∵AB=AA1=2,A(0,-1,0),B(,0,0),C(0,1,0),A1(0,-1,2),B1(,0,2),C1(0,1,2).(1)点P为A1B1的中点.∴,,,∴,,,,,.|cos<,>|===.∴异面直线BP与AC1所成角的余弦值为:;(2)∵Q为BC的中点.∴Q(,,)∴,,,,,,,,,设平面AQC1的一个法向量为=(x,y,z),由,可取=(,-1,1),设直线CC1与平面AQC1所成角的正弦值为θ,sinθ=|cos<,>|==,∴直线CC1与平面AQC1所成角的正弦值为.【解析】本题考查了向量法求空间角,属于中档题.设AC,A1C1的中点分别为O,O1,以{}为基底,建立空间直角坐标系O-xyz,(1)由|cos|=可得异面直线BP与AC1所成角的余弦值;(2)求得平面AQC 1的一个法向量为,设直线CC1与平面AQC1所成角的正弦值为θ,可得sinθ=|cos|=,即可得直线CC1与平面AQC1所成角的正弦值.3.【答案】解:(1)因为ABCD是菱形,所以AC⊥BD.又OP⊥底面ABCD,以O为原点,直线OA,OB,OP分别为x轴,y轴,z轴,建立如图所示空间直角坐标系.则A(2,0,0),B(0,1,0),P(0,0,4),C(-2,0,0),M(-1,0,2).=(-2,0,4),=(01,-1,2),cos<,>===.故直线AP与BM所成角的余弦值为.(2)=(-2,1,0),=(-1,-1,2).设平面ABM的一个法向量为=(x,y,z),则,令x=2,得=(2,4,3).又平面PAC的一个法向量为=(0,1,0),∴cos<,>===.故平面ABM与平面PAC所成锐二面角的余弦值为.【解析】(1)以O为原点,直线OA,OB,OP分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出直线AP与BM所成角的余弦值.(2)求出平面ABM的一个法向量和平面PAC的一个法向量,利用向量法能求出平面ABM与平面PAC所成锐二面角的余弦值.本题考查异面直线所成角的余弦值的求法,考查二面角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想、函数与方程思想,是中档题.4.【答案】证明:(Ⅰ)过点B1作A1C的垂线,垂足为O,由平面A1B1C⊥平面AA1C1C,平面A1B1C∩平面AA1C1C=A1C,得B1O⊥平面AA1C1C,又AC⊂平面AA1C1C,得B1O⊥AC.由∠BAC=90°,AB∥A1B1,得A1B1⊥AC.又B1O∩A1B1=B1,得AC⊥平面A1B1C.又CA1⊂平面A1B1C,得AC⊥CA1.(Ⅱ)以C为坐标原点,的方向为x轴正方向,||为单位长,建立空间直角坐标系C-xyz.由已知可得A(1,0,0),A1(0,2,0),B1(0,1,).所以=(1,0,0),=(-1,2,0),==(0,-1,).设n=(x,y,z)是平面A1AB的法向量,则,即可取=(2,,1).设=(x,y,z)是平面ABC的法向量,则,即,可取=(0,,1).则cos⟨ ,>==.又因为二面角A1-AB-C为锐二面角,所以二面角A1-AB-C的大小为.【解析】(Ⅰ)过点B1作A1C的垂线,推导出B1O⊥平面AA1C1C,从而B1O⊥AC.由∠BAC=90°,AB∥A1B1,得A1B1⊥AC.从而AC⊥平面A1B1C.由此能证明AC⊥CA1.(Ⅱ)以C为坐标原点,的方向为x轴正方向,||为单位长,建立空间直角坐标系C-xyz.利用向量法能求出二面角A1-AB-C的大小.本题考查线线垂直的证明,考查二面角的求法,考查推理论证能力、运算求解能力,考查函数与方程思想,是中档题.5.【答案】(12分)(1)证明:连接AC,交BD于F,连接EF,因为AB∥DC,所以,即AF=2FC,又PE=2EC,所以AP∥FE,又FE⊆平面BDE,AP⊄平面BDE,所以PA∥平面BED.(4分)(2)解:取AB中点M,连接PM,DM,过点P作PN⊥MD,垂足为N.因为PA=PB,所以PM⊥AB,又MB=DC且MB=DC,则四边形BCDM是平行四边形,所以MD∥BC,所以MD⊥AB,又PM∩MD=M,所以AB⊥平面PMD,又AB⊂平面ABCD,所以平面PMD⊥平面ABCD,又平面PMD∩平面ABCD=MD及PN⊥MD,所以PN⊥平面ABCD.由MB=1,PB=3得,则有PM2+PD2=DM2,即PM⊥PD,所以,所以,(8分)如图建立空间直角坐标系C-xyz,则D(1,0,0),,,,B(0,3,0),A (2,3,0),,,,,,,,,设平面PAB法向量,,,由得,取,可得,,.设平面PBC法向量,,,由得,取,可得,,..所以<,>=.二面角A-PB-C的余弦值为:.(12分)【解析】(1)连接AC,交BD于F,连接EF,通过AB∥DC,证明AP∥FE,即可证明PA∥平面BED.(2)取AB中点M,连接PM,DM,过点P作PN⊥MD,垂足为N.建立空间直角坐标系C-xyz,求出平面PAB法向量,平面PBC法向量,利用空间向量的数量积求解二面角A-PB-C的余弦值即可.本题考查直线与平面平行的判断定理的应用,二面角的平面角的求法,考查空间想象力以及计算能力.6.【答案】证明:以点D为原点,DA,DC,DD1分别为x轴、y轴、z轴,建立空间直角坐标系,令正方体的棱长为2,则D(0,0,0),A1(2,0,2),B(2,2,0),B1(2,2,0),E(1,1,2),F(1,2,1),(1),因为,所以,所以EF//A1B;(2)设平面A1BD的一个法向量为,则,即2y-2z=0,2x+2y=0,令x=1,则,因为,所以EF∥平面A1BD;(3)由(2),同理求出平面EFB1的一个法向量,所以平面B1EF∥平面A1BD.【解析】本题主要考查利用空间向量判断线线、线面、面面之间的平行. 建立空间直角坐标系,求出线面的方向向量与法向量,(1)由两条直线的方向向量共线,即可判断出结论;(2)由直线的方向向量与平面的法向量垂直,即可得出结论;(3)由两个平面的法向量共线,即可得出结论.。
匀加速直线运动典型习题及答案

匀加速直线运动典型习题及答案1.一辆汽车以10 m/s的速度匀速行驶了10秒后,突然踩下刹车,以每秒2m/s的加速度减速。
求汽车停下来所需的时间和停下来时所走过的距离。
解析:首先,汽车匀速行驶10秒后的速度为10 m/s,刹车减速度为2m/s^2。
根据匀加速直线运动的公式v = u + at,其中v为末速度,u为初速度,a 为加速度,t为时间。
代入已知条件,可得 0 = 10 - 2t 解方程得到t = 5秒,即汽车停下来所需的时间为5秒。
接下来,根据匀加速直线运动的公式s = ut + (1/2)at^2,其中s为位移。
代入已知条件,可得 s = 10(5) + (1/2)(-2)(5)^2 解算得到s = 25米,即汽车停下来时所走过的距离为25米。
因此,汽车停下来所需的时间为5秒,停下来时所走过的距离为25米。
2.一个物体从静止开始,以每秒5 m/s^2的加速度匀加速运动,求物体在6秒内所走过的距离和速度。
解析:首先,物体从静止开始,加速度为5 m/s^2,时间为6秒。
根据匀加速直线运动的公式s = ut + (1/2)at^2,其中s为位移,u为初速度,a为加速度,t为时间。
代入已知条件,可得 s = 0(6) + (1/2)(5)(6)^2 解算得到s = 90米,即物体在6秒内所走过的距离为90米。
接下来,根据匀加速直线运动的公式v = u + at,其中v为末速度,u为初速度,a为加速度,t为时间。
代入已知条件,可得 v = 0 + (5)(6) 解算得到v = 30 m/s,即物体在6秒时的速度为30 m/s。
因此,物体在6秒内所走过的距离为90米,速度为30 m/s。
3.一个悬挂的重物以2 m/s^2的加速度向下运动,经过3秒后,它的速度为10 m/s。
求重物初始时的速度和位移。
解析:重物向下运动,加速度为2 m/s^2,时间为3秒,末速度为10 m/s。
根据匀加速直线运动的公式v = u + at,其中v为末速度,u为初速度,a为加速度,t为时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章生物与环境一、选择题1.绿色植物光合活性辐射带波长位于 。
A.380nm~700nm B.380nm~760nm C.150nm~4000nm D.490nm~620nm2.植物光合作用同化量与呼吸消耗量相等时的光合活性光照强度称为 。
A.饱和点 B.补偿点 C.平衡点 D.稳定点3.下图表表示北温带海洋的硅藻和一些非生物因子随季节而变化的数据,以下那一项对图的A.提高光强度破坏硅藻B.硅藻数量增加会降低磷和硝酸盐的含量C.光强度提高增强了分解者的活力,其结果是养分降低D.硅藻数量的下降导致养分的降低4.生物体对实验环境条件变化产生的适应性反应称为 。
A.气候驯化 B.调节C.驯化 D.适应5.有效积温法则公式中,T0为 。
A.平均温度 B.生物学零度 C.有效积温 D.天数6.阴性植物的特点是 。
A.光补偿点较高,生长在全光照条件下 B.光补偿点较高,生长在阴湿条件下C.光补偿点较低,生长在全光照条件下D.光补偿点较低,生长在阴湿条件下7.阳地植物光补偿点的位置较阴地植物 。
A.高 B.低 C.一样 D.不确定8.当光强度不足时,C02浓度的适当提高,则使植物光合作用强度不致于降低,这种作用称为 。
A.综合作用 B.阶段性作用 C.补偿作用 D.不可替代作用9.下列植物中,属于长日照植物的是 。
A.大豆 B.玉米C.冬小麦 D.水稻10.影响植物水平和垂直分布上限的主要因素是 。
A.温度 B.光照C.水分 D.土壤11.蚂蚁在自然界的分布型为 。
A.均匀分布 B.成群分布 C.随机分布 D.带状分布12.下列生物中属于种群的是 。
A.一个校园里生长着的各种各样高大的树B.生活在一片森林中的全部雄鸟和雌鸟C.一块菜地上生长着的大白菜、大蒜、大葱D.生活在青海湖鸟岛保护区内不同年龄的棕头鸥13.沿海地区出现的“赤潮”从种群数量变动角度看是属于 。
A.季节性消长B.不规则波动 C.周期性波动 D.种群的爆发14.按一对夫妇一两个孩子计算,人口学家统计和预测,墨西哥等发展中国家的人口翻一番大约20—40年,美国需要40—80年,瑞典人口将会相对稳定,德国人口将减少。
预测人口的这种增减动态主要决定于 。
A.种群数量和密度B.种群年龄结构C.种群性别比例D.出生率和死亡率15.我国的计划生育政策为“提倡一个夫妇只生一个孩子”,从种群特征看,这种措施直接调节 。
A.种群密度B.年龄组成C.性别比例D.出生率16.下列不属于种群的是 。
A.一个池塘中的全部鲤鱼B.一片森林中的全部山毛榉C.一块棉田中的全部蚜虫D.一片草原上的全部生物17.下面关于种群的叙述不正确的是 。
A.种群中的个体之间可相互交配繁殖B.一个种群由许多同种个体组成C.种群的个体数量是经常变动的D.种群内的个体间常因空间和食物发生竞争18.决定种群个体数量变动的因素,主要是 。
①种群密度和出生率、死亡率②年龄组成和性别比例③出生数量和死亡数量••• •④迁出和迁入数量A.①② B.②③ C.③④D.④①19.某种群中年轻的个体非常多,年老的个体很少,这样的种群密度会 。
A.越来越大 B.相对稳定 C.越来越小 D.绝对不变20.预测一个国家或地区的人口数量未来动态的信息主要来自于 。
A.现有人口数量和密度B.不同年龄组成的比例C.男女之间的性别比例 D.出生率、死亡率和迁移率21.有一位学者正在研究某种鸟的季节性迁徙行为,他研究的对象从生态学水平看属于。
A.生态系统 B.群落 C.个体 D.种群22.下图是一个种群的年龄分布图。
种群绝灭的机会最大。
A B C D23.有一块草原上,有8户牧民,每户牧民各养了一群羊,其中,有6户养的绵羊,有两户养的山羊,这8群羊是 。
A.一个群落B.一个种群C.两个种群D.八个种群24.利用人工合成的性引诱剂诱杀棉铃虫中的雄性个体,则该种群的密度会 。
A.明显增大B.明显减小C.相对稳定D.先增后减25.下列可以称为种群密度的是 。
A.一定地区内单位面积内的驴数量B.一口池塘中单位体积内鲢鱼的数量C.一片森林中单位面积内乔木的数量D.一条江河中单位体积内鱼的数量26.下列对种群密度无直接影响的是 。
A.出生率和死亡率B.迁入率和迁出率C.年龄组成和性别比例D.生态系统结构的复杂程度27.如果一个种群的密度愈来愈小,下列选项中与之无关的是 。
A.种群处于衰退期B.种群内雄性趋于不育C.种群死亡率超过出生率D.群落结构太复杂28.与调节雪兔的种群大小无关的是 。
A.以雪兔为食的猞猁的数量B.雪兔能随季节变化变换毛色C.栖息地青草的生长状况D.雪兔种群原来密度的大小29.原始森林遭到破坏后,形成森林的过程为 。
A.原生演替 B.次生演替 C.水生演替 D.旱生演替30.从裸岩开始的旱生演替又属于 。
A.次生演替 B.快速演替 C.内因性演替 D.外因性演替31.群落结构最复杂的是 。
A.苔原 B.荒漠 C.落叶阔叶林 D.常绿阔叶林32.在渔业生产上为获得持续最大捕捞量,海洋捕捞时,应使鱼类的种群数量保持在 。
A.K/2 B.K C.K/4 D.K/333.种群呈“S”型增长过程中,当种群数量超过环境容量一半时,种群的 。
A.密度增长越来越快 B.环境阻力越来越大C.环境阻力越来越小 D.密度增长越来越小34.所有生态系统都可以区分为四个组成成分,即生产者、消费者、分解者和()。
A.非生物环境B.温度C.空气D.矿质元素35.下列生物在生态系统中属于初级生产者的是()。
A.动物B.真菌C.酵母菌D.绿色植物36.下列几种生态系统中,自动调节能力最强的是()。
A.北方针叶林B.温带落叶林C.热带雨林D.温带草原37.下列产品中不属于是次级生产的为()。
A.肉B.毛皮C.毛栗D.鸡蛋38.中国现在的人口现状是()。
A.零增长型B.负增长型C.增长型D.不确定型39.可持续发展总体策略的内容包括()方面的多项政策和行动计划。
A.科学技术B.人口C.生产D.环境保护二、判断题1.植物的生长取决于那些处于最少量状态的营养成分。
()2.生物圈的范围包括大气圈的上层。
()3.生物的环境就是生物周围对其有影响的无机环境。
()4.环境中直接影响生物的生态分布的因素就是生态因素。
()5.内稳态机制只是为生物提供一种提高耐受性的一种方式。
()6.生态幅因植物的生长发育阶段、环境条件的不同而变化。
()7.直接对生物生长发育发生影响的是小环境,大环境对生物不起作用。
()8.森林生态系统在演替初期是开放的生态系统,演替后期是封闭的生态系统。
()9.种群呈“S”型增长过程中,当种群数量超过环境容量一半时,种群的环境容纳量越来越小。
()10.适应的相对性是遗传物质的稳定性与环境条件的变化相互作用的结果。
()11.种内互助对种的生存有利,种内斗争对种的生存不利。
()12.捕食动物有时变成了猎物不可缺少的生存条件。
()13.种群越小,遗传漂变越弱;种群越大,遗传漂变越强。
()14.生物的适应性不一定会创造“最好”或“最优”的表现型。
()15.社会生活对每一个社会性生物总是非常有利的。
()16.能量通过食物链中各个营养级由低向高流动时逐级增加,形成能量金字塔。
()17.食物网越复杂,生态系统就越稳定;食物网越简单,生态系统就越容易发生波动或遭受毁灭。
()18.从陆地上看,凡是水的循环越活跃的地方,生命的活动就越活跃。
()19.池塘污染造成鱼死亡,大量鱼死亡后造成池塘污染更严重,从而造成更多的鱼死亡,这种现象是负反馈。
()20.人工改造的农业生态系统是不稳定的。
()21.铁矿属于是可更新的自然资源。
()22.藕田养泥鳅不是一项行之有效的水产生产方式。
()三、名词解释生态系统;生物圈;食物链;食物网;生态金字塔;生态平衡;反馈;生物地化循环;环境;生境;生态幅;限制因子;生态因子;最小因子定律;有效积温;内稳态;生物的光周期;群落;种内竞争;演替;原生演替;次生演替;竞争;捕食;自然资源;可持续发展;生态农业四、问答题1.什么是环境?环境和生境有什么区别?2.什么是自然环境?自然环境有那些?3.什么是生态因子?生态因子有那些类型和特点?4.光对植物和动物有什么影响?5.温度对植物和动物有什么影响?6.水分对植物和动物有什么影响?7.什么叫最小因子定律和耐受性定律?8.试举一例说明作物对不良环境的耐受性?9.试举例说明大环境和小环境分别怎样影响作物的生长?10.什么是种群?种群有什么特征?11.种群的数量受到哪些参数的影响?这些参数是怎样影响种群数量的?12.种群的增长有哪些模型?13.种群的社会关系有哪些?14.什么是群落?群落有哪些特征?15.生物群落有哪些结构?16.什么是群落演替?群落演替有哪些类型?17.群落演替包括哪些过程?请举例进行说明。
18.地球上有哪些生物群落?19.随着群落的演替,群落的物种多样性和群落结构的变化趋势如何?20.论述单种群在有限环境中的连续增长规律,该规律有何实际意义?21.论述逻辑斯谛方程的存在条件及所描述的种群变化过程,该规律有何实际意义?22.试分生态系统的基本特征。
23.试分析生态系统的基本成分及其作用。
24.什么是正反馈和负反馈?请分别举一个正反馈和负反馈的例子,并分别说明其反馈机理。
25.试分析生态平衡的调节机制及对现实的指导意义。
26.中国现在的人口现状怎么样?如何应对现在面临的人口问题?27.什么是资源?资源的分类如何?28.什么是生态农业?生态农业有什么特点?生态农业有哪些主要类型?29.人类活动对地球环境有哪些重大影响?你对“可持续发展”的含义是怎样理解的?。
