习题解答第7章
第7章气体动理论习题解答

第7章 气体动理论7.1基本要求1.理解平衡态、物态参量、温度等概念,掌握理想气体物态方程的物理意义及应用。
2.了解气体分子热运动的统计规律性,理解理想气体的压强公式和温度公式的统计意义及微观本质,并能熟练应用。
3.理解自由度和内能的概念,掌握能量按自由度均分定理。
掌握理想气体的内能公式并能熟练应用。
4.理解麦克斯韦气体分子速率分布律、速率分布函数及分子速率分布曲线的物理意义,掌握气体分子热运动的平均速率、方均根速率和最概然速率的求法和意义。
5.了解气体分子平均碰撞频率及平均自由程的物理意义和计算公式。
7.2基本概念1 平衡态系统在不受外界的影响下,宏观性质不随时间变化的状态。
2 物态参量描述一定质量的理想气体在平衡态时的宏观性质的物理量,包括压强p 、体积V 和温度T 3 温度宏观上反映物体的冷热程度,微观上反映气体分子无规则热运动的剧烈程度。
4 自由度确定一个物体在空间的位置所需要的独立坐标数目,用字母i 表示。
5 内能理想气体的内能就是气体内所有分子的动能之和,即2iE RT ν= 6 最概然速率速率分布函数取极大值时所对应的速率,用p υ表示,p υ==≈其物理意义为在一定温度下,分布在速率p υ附近的单位速率区间内的分子在总分子数中所占的百分比最大。
7 平均速率各个分子速率的统计平均值,用υ表示,υ==≈8 方均根速率各个分子速率的平方平均值的算术平方根,用rms υ表示,rms υ==≈ 9 平均碰撞频率和平均自由程平均碰撞频率Z 是指单位时间内一个分子和其他分子平均碰撞的次数;平均自由程λ是每两次碰撞之间一个分子自由运动的平均路程,两者的关系式为:Zυλ==或λ=7.3基本规律1 理想气体的物态方程pV RT ν=或'm pV RT M=pV NkT =或p nkT =2 理想气体的压强公式23k p n ε=3 理想气体的温度公式21322k m kT ευ==4 能量按自由度均分定理在温度为T 的平衡态下,气体分子任何一个自由度的平均动能都相等,均为12kT 5 麦克斯韦气体分子速率分布律 (1)速率分布函数()dNf Nd υυ=表示在速率υ附近单位速率区间内的分子数占总分子数的百分比或任一单个分子在速率υ附近单位速率区间内出现的概率,又称为概率密度。
第7章习题解答

z 2 = z 1 + 130
2 z z ) 2 + 100 z ( z ) = 0 1 - ( 1 + 130 1 + 82 1 + 130
2 - 260 z z ´ 130 = 0 1 - 130 + 182 1 + 82
78 z ´ 130 - 130 2 = -48 ´ 130 = -6240 1 = 82 z 1 = -80 z 2 = z 1 + 130 = 130 - 80 = 50 f = 40cm
p 3 . 14 - 8 2 l 2 ´ 6328 ´ 10 - 3 ④ q= = = 2 . 315 ´ 10 rad pw0 3 . 14 ´ 0 . 0174
(5)有一个平凹腔,凹面镜曲率半径 R=5m,腔长 L=1m,光波长l=0.5mm,求①两镜 面上的基模光斑半径②基模高斯光束的远场发散角 解:①
2、双凹腔两反射镜面曲率半径分别为 R1=100cm、R2=82cm,腔长 L=130cm,求等价共焦 腔的焦参数。 解:
z1 +
f 2 = - R 1 z 1
z 1 +
f 2 = -100 z 1
2 2 z 100 z 1 + 1 + f = 0
w 0 =
f l
p
=
0 . 4 R l
p
(2)对称双凹腔长为 L,反射镜曲率半径 R=2.5L,光波长为l,求镜面上的基模光斑半 径。 解:
L L 2 f 2 = ( 2 R - L ) = (2 ´ 2 . 5 L - L ) = L 4 4 f = L
2 z 2
f
2
第7章 信号处理电路 习题解答

7.3简述电荷放大器有什么特点,应用于何种场合。
解:电荷放大器应用于压电式加速度传感器、压力传感器等的后端放大。
上述两种传感器属于电容性传感器,这类传感器的阻抗非常高,呈容性,输出电压很微弱;他们工作时,将产生正比于被测物理量的电荷量,积分运算电路可以将电荷量转换成电压量,电路如下图所示。
解:1)LBF;2)BPF;3)HPF;4)BEF。
二、判断下列说法是否正确,用 “√”(正)和“ ”(误)填入括号内。
1)高通滤波器的通频带是指电压的放大倍数不变的频率范围。()
2)低通滤波器的截止频率就是电压放大倍数下降1/2的频率点。()
3)带通滤波器的频带宽度是指电压放大倍数大于或等于通带内放大倍数0.707的频率范围。()
其中 ;
该滤波器为二阶低通滤波电路,幅频特性如下图:
7.7试说明图P7-8所示各电路属于哪种类型的滤波电路,是几阶滤波电路。
(1)
(2)
图P7-7
解:
图(1)所示电路二阶带通滤波器或者二阶带阻滤波器。
前一个运放为高通滤波器(截止频率f1),后一个运放为低通滤波器(截止频率f2),如果 ,则f1<f2,该滤波器为二阶带通滤波器;如果 ,则f1>f2,该滤波器为二阶带阻滤波器。
电容性传感器可等效为因存储电荷而产生的电动势Ut与一个输出电容Ct串联,如图中虚线框内所示。根据集成运放的特点,可得到输出电压为: 。
7.4简述隔离放大器有什么特点,应用于何种场合。
解:隔离放大器通常应用于远距离信号传输。
在远距离信号传输的过程中,常因强干扰的引入使放大电路的输出有很强的干扰背景,甚至将有用信号淹没,造成系统无法正常工作。隔离放大器将电路的输入侧和输出侧在电气上完全隔离,它既可切断输入侧和输出侧电路间的直接联系,避免干扰混入输出信号,又可使有用信号畅通无阻。目前集成隔离放大器有变压器耦合式、光电耦合式和电容耦合式三种。
第七章习题解答

计算图示各系统的动能:(1)偏心圆盘的质量为,偏心距OC m e =,对质心的回转半径为C ρ,绕轴O 以角速度0ω转动(图a )。
(2)长为l ,质量为的匀质杆,其端部固结半径为,质量为的匀质圆盘。
杆绕轴O 以角速度m r m 0ω转动(图b )。
(3)滑块A 沿水平面以速度移动,重块B 沿滑块以相对速度下滑,已知滑块A 的质量为,重块B 的质量为(图c )。
1v 2v 1m 2m (4)汽车以速度沿平直道路行驶,已知汽车的总质量为0v M ,轮子的质量为m ,半径为R ,轮子可近似视为匀质圆盘(共有4个轮子)(图d )。
解:(1) 222200111()222C C C T mv J m e 2ωρω=+=+(2) 2222111(83)326O J ml mr ml m l r =++=+2220011(83)212O T J m l r 22ωω==+(3) 22121122A B T m v m v =+2221121212221212221211(2cos150)2211()m v m v v v v m m v m v m v v °=+++=++(4) ()2222000211111(4)422222v T M m v mv mR M m v R ⎛⎞=−+⋅+⋅⋅=+⎜⎟⎝⎠20一常力矩M 作用在绞车的鼓轮上,轮的半径为r ,质量为。
缠在鼓轮上绳索的末端A 系一质量为的重物,沿着与水平倾斜角为1m 2m α的斜面上升,如图所示。
重物与斜面间的滑动摩擦系数为μ。
绳索的质量不计,鼓轮可看成为匀质圆柱体,开始时系统静止。
求鼓轮转过ϕ角时的角速度。
解:为一自由度理想约束系统。
取鼓轮、重物及绳索组成的系统为研究对象,受力图如下图所示。
鼓轮转过ϕ角时系统的动能为2222212111222T m r m r 2ωω=⋅⋅+ 重力、摩擦力和力矩M 在此有限路程上所做的功为122sin W M Fr m gr ϕϕϕ→α=−−根据动能定理,有()222212211sincos 42m r m r M m gr ωωαμ+=−+αϕ⎡⎤⎣⎦ ω=绞车提升一质量为m 的重物,如图所示。
第7章习题详细解答

第7章习题解答7—1判断题(对的打√,不对的打×)1。
数字电路分为门电路和时序逻辑电路两大类。
(× )2。
边沿触发器和基本RS触发器相比,解决了空翻的问题.(×)3. 边沿触发器的状态变化发生在CP上升沿或下降沿到来时刻,其他时间触发器状态均不变。
(√)4. 基本RS 触发器的输入端就是直接置0端和直接置1端。
(√)23 的计数器。
(×)5。
3位二进制计数器可以构成模为16。
十进制计数器最高位输出的周期是输入CP脉冲周期的10倍。
(√)7. 构成一个7进制计数器需要7个触发器。
(×)8.当时序电路存在无效循环时该电路不能自启动.( √)9。
寄存器要存放n位二进制数码时,需要n2个触发器。
(×)10.同步计数器的计数速度比异步计数器快。
(√)11。
在计数器电路中,同步置零与异步置零的区别在于置零信号有效时,同步置零还需要等到时钟信号到达时才能将触发器置零,而异步置零不受时钟的控制。
(√)12。
计数器的异步清零端或异步置数端在计数器正常计数时应置为无效状态。
(√)13。
自启动功能是任何一个时序电路都具有的。
(× )14。
无论是用置零法还是用置数法来构成任意N进制计数器时,只要置零或置数控制端是异步的,则在状态循环过程中一定包含一个过渡状态;只要是同步的,则不需要过渡状态。
(√)15。
用置零法或置位法可以设计任意进制的计数器.(×)7—2 由或非门组成的基本RS触发器如图7—38所示,已知R、S的电压波形,试画出与之对应的Q和Q的波形。
图7—38 题7-2图解:由或非门组成的基本RS触发器的特性表,可得该题的输出端波形如下图所示:或非门RS 触发器特性表 题7—2 波形图7—3由与非门组成的基本RS 触发器如图7-39所示,已知R 、S 的电压波形,试画出与之对应的Q 和Q 的波形。
图7-39 题7-3图解:由与非门组成的基本RS 触发器的特性表,可得该题的输出端波形如下图所示:与非门RS 触发器特性表 题7—3波形图7-4已知如图7-40所示的各触发器的初始状态均为0,试对应画出在时钟信号CP 的连续作用下各触发器输出端Q 的波形。
第7章 基本放大电路习题与解答

第7章放大电路基础题解答习题A 选择题7-1在固定式偏置电路中,若偏置电阻R B的值增大了,则静态工作点Q将()。
BA. 上移B. 下移C. 不动D.上下来回移动7-2在图7-5中,若将R B减小,则集电极电流I C、集电极电位U C分别是()。
D A.减小、增大 B. 减小、减小 C.增大、增大 D. 增大、减小7-3在图7-5中的晶体管原处于放大状态,若将R B调到零,则晶体管()。
CA.处于饱和状态B.仍处于放大状态C.被烧毁7-4图7-9中交流分量u o与u i、u o与i c、i b与i c的相位关系分别是是()。
CA同相、反相、反相 B.反相、同相、反相 C.反相、反相、同相 D.反相、同相、同相7-5在共发射极放大电路中,()是正确的。
BA.r be=U BE/i B B.r be=u be/i b C. r be=U BE/I B7-6在图7-17(a)所示的分压式偏置放大电路中,通常偏置电阻R B1( )R B2。
AA. >B. <C. =7-7图7-17(a)所示电路中,若只将交流旁路电容C E出去,则电压放大倍数| A u |()。
AA.减少B.增大C.不变7-8射极输出器()。
BA.有电流放大作用,也有电压放大作用B.有电流放大作用,没有电压放大作用C.没有电流放大作用,也没有电压放大作用7-9射极跟随器适合作多级放大电路的输出级,是因为它的()BA. 电压放大倍数近似为1B. r i很大C. r O很小7-10在甲类工作状态的功率放大电路中,在不失真的条件下增大输入信号,则电源供给的功率、管耗分别是()。
CA.增大、减小B.减小、不变C. 不变、减小D. 不变、增大7-11在共射放大电路中,若测得输入电压有效值U i=5mV时,当未带上负载时U=1V,负载电阻R L值与R C相等,则带上负载输出电压有输出电压有效值'o效值U o=()V。
BA.1B.0.5C.-1D.-0.57-12在NPN型构成CE放大器,在非线性失真中,饱和失真也称为()。
第7章输入输出习题参考解答

第7章思考题与习题参考答案1.计算机的I/O系统的功能是什么?它由哪几个部分组成?答:计算机的I/O系统,主要用于解决主机与外部设备间的信息通讯,提供信息通路,使外围设备与主机能够协调一致地工作。
计算机的I/O系统由I/O硬件和I/O软件两大部分组成。
其中I/O硬件包括:系统总线、I/O接口、I/O设备及设备控制器。
I/O软件包括:用户的I/O程序、设备驱动程序、设备控制程序。
2.I/O硬件包括哪几个部分?各部分的作用是什么?答:I/O硬件包括:系统总线、I/O接口、I/O设备及设备控制器。
系统总线的作用是为CPU、主存、I/O设备(通过I/O接口)各大部件之间的信息传输提供通路。
I/O接口通常是指主机与I/O设备之间设置的一个硬件电路及其相应的控制软件。
它用于在系统总线和外设之间传输信号,并起缓冲作用,以满足接口两边的时序要求。
I/O设备的作用是为主机与外部世界打交道提供一个工具。
设备控制器用来控制I/O设备的具体动作,不同的I/O设备需要完成的控制功能不同。
3.什么是用户I/O程序?什么是设备驱动程序?什么是设备控制程序?答:用户I/O程序是指用户利用操作系统提供的调用界面编写的具体I/O设备的输入输出程序。
例如用户编写的用打印机输出文本的程序。
设备驱动程序是一种可以使计算机和设备通信的特殊程序。
可以说相当于操作系统与硬件的接口,操作系统只有通过这个接口,才能控制硬件设备的工作,假如某设备的驱动程序未能正确安装,便不能正常工作。
设备控制程序就是驱动程序中具体对设备进行控制的程序。
设备控制程序通过接口控制逻辑电路,发出控制命令字。
命令字代码各位表达了要求I/O设备执行操作的控制代码,由硬件逻辑解释执行,发出控制外设的有关控制信号。
4.说明设计I/O系统的三个要素的具体内容。
答:设计I/O系统应该考虑如下三个要素:①数据定位: I/O系统必须能够根据主机提出的要求进行设备的选择,并按照数据在设备中的地址找到相应的数据。
第7章习题解答

第7章思考题及习题7参考答案一、填空1. AT89S52单片机任何一个端口要想获得较大的驱动能力,要采用电平输出。
答:低2.检测开关处于闭合状态还是打开状态,只需把开关一端接到I/O端口的引脚上,另一端接地,然后通过检测来实现。
答: I/O端口引脚的电平3. “8”字型的LED数码管如果不包括小数点段共计段,每一段对应一个发光二极管,有和两种。
答:7,共阳极,共阴极4. 对于共阴极带有小数点段的数码管,显示字符“6”(a段对应段码的最低位)的段码为,对于共阳极带有小数点段的数码管,显示字符“3”的段码为。
答:7DH,B0H5. 已知8段共阳极LED数码显示器要显示某字符的段码为A1H(a段为最低位),此时显示器显示的字符为。
答:d6. LED数码管静态显示方式的优点是:显示闪烁,亮度,比较容易,但是占用的线较多。
答:无,较高,软件控制,I/O口7. 当显示的LED数码管位数较多时,一般采用显示方式,这样可以降低,减少的数目。
答:动态,成本,I/O端口8. LCD 1602是型液晶显示模块,在其显示字符时,只需将待显示字符的由单片机写入LCD 1602的显示数据RAM(DDRAM),内部控制电路就可将字符在LCD上显示出来。
答:字符,ASCII码9. LCD 1602显示模块内除有字节的 RAM外,还有字节的自定义,用户可自行定义个5×7点阵字符。
答:80,显示数据,64,字符RAM,810.当按键数目少于8个时,应采用式键盘。
当按键数目为64个时,应采用式键盘。
答:独立,矩阵11.使用并行接口方式连接键盘,对独立式键盘而言,8根I/O口线可以接个按键,而对矩阵式键盘而言,8根I/O口线最多可以接个按键。
答:8,6412.LCD 1602显示一个字符的操作过程为:首先,然后,随后,最后。
答:读忙标志位BF,写命令,写显示字符,自动显示字符13.由于微型打印机TPµP-40A/16A是一种外设,因此单片机与微型打印机的的命令与数据传送,必须采用方式。
第7章 稳恒磁场习题解答

第7章 稳恒磁场7-1 如图,一个处在真空中的弓形平面载流线圈acba ,acb 为半径cm 2=R 的圆弧,ab 为圆弧对应的弦,圆心角090aob ∠=,A 40=I ,试求圆心O 点的磁感应强度的大小和方向。
解 由例7-1 线段ba 的磁感应强度 o o 40140(cos45-cos135) =410T4π0.02cos45B μ-=⨯⨯︒方向垂直纸面向外。
由例7-2 圆弧acb 的磁感应强度4002π1402 3.1410T 2π2420.02I μB R μ-==⨯=⨯方向垂直纸面向内。
4120.8610TB B B -=-=⨯方向垂直纸面向外。
7-2 将载流长直导线弯成如图所示的形状,求圆心O 点处磁感应强度。
解 如图,将导线分成1(左侧导线)、2(半圆导线)、3(右侧导线)三部分,设各部分在O 点处产生的磁感应强度分别为1B 、2B 、3B 。
根据叠加原理可知,O 点处磁感应强度321B B B B++=。
01=B024I B Rμ=,方向垂直于纸面向里034πI B Rμ=,方向垂直于纸面向里O 点处磁感应强度大小为习题7-1图0O 23(1π)4πIB B B Rμ=+=+ ,方向垂直于纸面向里。
7-3 一圆形载流导线圆心处的磁感应强度为1B ,若保持导线中的电流强度不变,而将导线变成正方形,此时回路中心处的磁感应强度为2B ,试求21:B B解 设导线长度为l ,为圆环时, 2πl R = 001π2I I B R l μμ==为正方形时,边长为4l,由例7-100024(cos 45cos135)4π8IB lμ=⨯-=⨯212 :πB B =7-4 如图所示,一宽为a 的薄长金属板,均匀地分布电流I ,试求在薄板所在平面、距板的一边为a 的点P 处的磁感应强度。
解 取解用图示电流元,其宽度为d r ,距板下边缘距离为r ,其在P 点处激发的磁感应强度大小为00d d d 2π22π(2)II r B (a r)a r aμμ==--,方向垂直于纸面向外。
无机及分析化学第7章 习题解答

第七章 水溶液中的解离平衡 习题解答1.写出下列物质的共轭酸。
S 2-、SO 42-、H 2PO 4-、HSO 4-、NH 3、NH 2OH 、55C H N 。
1.依次为:HS -、HSO 4-、H 3PO 4、H 2SO 4、NH 4+、NH 2OH ⋅H +、55C H N ⋅H +。
2.写出下列物质的共轭碱。
H 2S 、HSO 4-、H 2PO 4-、H 2SO 4、NH 3、NH 2OH 、3+26[Al(H O)]。
2.依次为:HS -、SO 42-、HPO 42-、HSO 4-、NH 2-、NH 2O -、2+25[Al(OH)(H O)]。
3.根据酸碱质子理论,按由强到弱的顺序排列下列各碱。
NO 2-、SO 42-、HCOO -、HSO 4-、Ac -、CO 32-、S 2-、ClO 4-。
3.下列碱由强到弱的顺序:S 2-> CO 32-> Ac-> HCOO-> NO 2-> SO 42-> HSO 4-> ClO 4-1414.151010-- 1410.251010-- 144.741010-- 143.741010-- 143.371010-- 141.991010--4.pH =7.00的水溶液一定是中性水溶液吗?请说明原因。
4.不一定。
K w 随温度的改变而改变,在常温下它的值为10-14,此时的中性溶液pH 为7.005.常温下水的离子积w K θ=1.0×10-14,是否意味着水的解离平衡常数K θ=1.0×10-14?5.不。
w K θ=[H +][OH -],而K θ=[H +][OH -]/c (H 2O);c (H 2O)=11000/18.0255.5mol L 1-=⋅ 6.判断下列过程溶液pH 的变化(假设溶液体积不变),说明原因。
(1)将NaNO 2加入到HNO 2溶液中; (2)将NaNO 3加入到HNO 3溶液中; (3)将NH 4Cl 加入到氨水中; (4)将NaCl 加入到HAc 溶液中;6. (1)pH 变大。
第7章习题解答

第7章思考题及习题71.如果采用的晶振的频率为24MHz,定时器/计数器工作在方式0、1、2下,其最大定时时间各为多少?答:晶振的频率为24MHz, 机器周期为0.5µs。
方式0最大定时时间=0.5µs×213=0.5µs×8192=4096µs方式1最大定时时间=0.5µs×216=0.5µs×65536=327686µs方式2最大定时时间=0.5µs×28=0.5µs×256=128µs2.定时器/计数器用作计数器模式时,对外界计数频率有何限制?答:外部输入的计数脉冲的最高频率为系统振荡器频率的1/24。
3.定时器/计数器的工作方式2有什么特点?适用于哪些应用场合?答:方式2为初值自动装入的8位定时器/计数器,克服了在循环定时或循环计数应用时就存在用指令反复装入计数初值影响定时精度的问题。
4.TH x与TL x(x= 0,1)是普通寄存器还是计数器?其内容可以随时用指令更改吗?更改后的新值是立即刷新还是等当前计数器计满后才能刷新?答:THx与TLx(x = 0,1)是计数器,其内容可以随时用指令更改,但是更改后的新值要等当前计数器计满后才能刷新。
5.Proteus虚拟仿真使用定时器T0,采用方式2定时,在P1.0脚输出周期为400µs,占空比为4:1的矩形脉冲,要求在P1.0脚接有虚拟示波器,观察P1.0脚输出的矩形脉冲波形。
答:略6.Proteus虚拟仿真利用定时器T1的中断来使P1.7控制蜂鸣器发出1kHz的音频信号,假设系统时钟频率为12MHz。
答:利用定时器T1的中断控制P1.7引脚输出频率为1kHz的方波音频信号,驱动蜂鸣器发声。
系统时钟为12MHz。
方波音频信号的周期为1ms,因此T1的定时中断时间为0.5 ms,进入中断服务程序后,对P1.7求反。
无机化学(周祖新)习题解答-第七章

第七章分子结构和晶体习题解答(7)思考题1.举例说明下列概念的区别:离子键与共价键、共价键与配位键、σ键和Л键、极性键和非极性键、极性分子与非极性分子、分子间力与氢键。
1.离子键是得到电子的阴离子与失去电子的阳离子的强烈静电吸引作用;共价键是原子间通过共用电子对(或电子云重叠)而形成的相互吸引作用,无阴、阳离子;配位键也是共价键中的一种,只不过共用的一对电子有一个原子提供。
σ键是各自电子云用密度最大的一头相互重叠,以使重叠体积最大,两原子间形成共价键时首先肯定以σ键成键,但两原子间只能形成σ键一次。
Л键是在原子间已形成一根σ键后,其余原子轨道以“肩并肩”在侧面重叠的成键方式,其重叠体积比σ键要小,但两原子间根据各自的单电子数可形成几个Л键。
极性键是两不同原子间形成共价键时,由于两原子的电负性不同,吸引公用电子对的作用不同,使某一端带有部分正电荷,另一端带有部分负电荷,这就是极性键;若两相同的原子间形成共价键,由于彼此电负性相同,吸引共用电子对的能力相同,公用电子对不偏向任何一个原子,两原子不带“净”电荷,没有“正”或“负”的一端,即非极性键。
极性分子是整个分子中正、负电荷重心不重合,使分子一端带部分正电荷,为正极,另一端带部分负电荷,为负极。
分子之间由于偶极间的相互作用力为分子间力。
氢键是氢原子与电负性大、半径小的原子形成共价键后,由于氢原子唯一的电子被其他原子吸引到离氢原子核较远的地方,氢原子几乎成了“裸露”的质子,有很强的正电场,吸引另一电负性大、半径小的原子的孤对电子,形成了一种作用力,这个作用力本质上还是分子间作用力,但比一般的分子间力强。
2.离子键是怎样形成的?离子键的特征和本质是什么?为什么离子键无饱和性和方向性?2.离子键是失电子的金属阳离子和德电子的非金属阴离子通过静电引力形成的。
离子键的特征是无方向性、无饱和性。
其本质是正、负点电荷间的静电引力。
点电荷产生的电场向空间各个方向均匀传播,每一个在其电场中的异号电荷都会受到它的吸引作用,在理论上它可吸引无数个异号电荷,所以离子键无饱和性;由于点电荷产生的电场向空间各个方向的传播是均匀的,只要距离相等,不管在哪个方向,受到的作用里是一样的,这就是离子键的无方向性。
经济应用文书写作习题解答-第七章经济筹划总结文书

第七章经济筹划总结文书参考答案【习题7-1】参考答案一、名词解释计划二、填空题1.计划具有和两个特点。
答案:预测性;具体可行性。
2.按写法分,计划可分为、和三种类型。
答案:条文式计划;图表式计划;条文图表结合式计划3.计划的标题,一般有、和三种写法。
答案:完整式;省略式;公文式三、简答题1.计划的导言部分通常可写哪些内容?答案:计划的导言部分通常可写以下四方面的内容:(1)说明制定计划的依据;(2)概述本单位的基本情况,分析完成计划的主、客观条件;(3)提出总的任务和要求,或完成计划指标的意义;(4)指出制定计划的目的。
2.计划的主体必须写清哪些内容?答案:计划的主体一般必须写清以下三方面的内容:(1)目标任务;(2)措施;(3)步骤程序。
3.在计划正文里不便表述的内容该如何处理?答案:另作“附件”。
4.制订计划有哪些注意事项?答案:注意事项有如下:(1)预测性和可行性很好地结合起来。
(2)计划的目标、任务、措施、步骤程序等都要写得明确具体,切忌含糊不清、模棱两可。
(3)要走群众路线,集思广益,把计划变成群体的共同意志,以保证计划的认同度和可行性。
(4)语言要准确、明晰。
四、病文析评下面是一篇病文,试指出其存在的毛病。
××县经委今后八个月工作计划为了完成县委、县政府下达3.1亿工业总产值 (力争3.5亿)的任务以及各项经济指标,我们计划在今后八个月主要抓好几方面工作:(一)进一步深化企业改革。
我们在全面推行厂长 (经理)任期目标责任制的基础上,从实际出发,有针对性地分别实行租赁、承包、百元工资税利制和工资总额与企业经济效益包干等经营方式,把权、责、利全面落实到企业及其经营者身上,使企业真正成为相对独立的经济实体,成为自主经营、自负盈亏的社会主义商品生产者和经营者,较好地调动企业厂长职工的积极性,增强企业活力,促进生产发展,并使这一改革能够健康发展,深入持久地坚持下去,采取有效措施加以保证。
第7章习题解答哈工大习题册
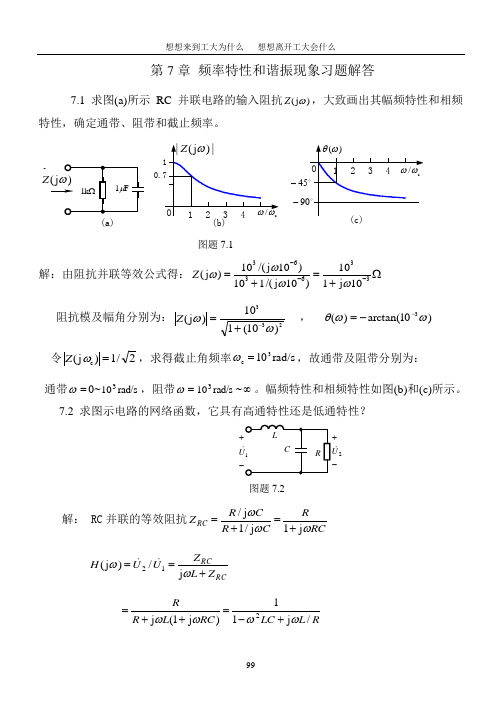
第7章 频率特性和谐振现象习题解答7.1 求图(a)所示RC 并联电路的输入阻抗)j (ωZ ,大致画出其幅频特性和相频特性,确定通带、阻带和截止频率。
(a)Z (b)--图题7.1解:由阻抗并联等效公式得:36336310/(j 10)10(j )101/(j 10)1j 10Z ωωωω---==Ω++ 阻抗模及幅角分别为:233)10(110)j (ωω-+=Z , )10arctan()(3ωωθ--=令2/1)j (c =ωZ ,求得截止角频率rad/s 103c =ω,故通带及阻带分别为: 通带=ω0~rad/s 103,阻带=ωrad/s 103~∞。
幅频特性和相频特性如图(b)和(c)所示。
7.2 求图示电路的网络函数,它具有高通特性还是低通特性?2图题7.2解: RC 并联的等效阻抗RCRC R C R Z RC ωωωj 1j /1j /+=+=RCRCZ L Z U U H +==ωωj /)j (12RL LC RC L R R /j 11)j 1(j 2ωωωω+-=++=幅频特性222)/()1(1)j (R L LC H ωωω+-=当0→ω时, 1)j (=ωH ;当∞→ω时,0)j (=ωH所以它具有低通特性。
7.3求图示电路的转移电压比21(j )/H U U ω=,当1122R C R C =时,此网络函数有何特性?2图 题7.3解:设1111111j j 1//C R R R C R Z ωω+==, 2222222j j 1//C R R R C R Z ωω+==由分压公式得:12122U Z Z Z U += )j 1()j 1()j 1()j (11222111212C R R C R R C R R U U H ωωωω++++== 当R 1C 1=R 2C 2时,得212)j (R R R H +=ω,此网络函数模及辐角均不与频率无关。
7.4设图示电路处于谐振状态,其中S 1A I =,150V U =,1100C R X ==Ω。
第七章习题解答

习 题 七1. 判断下面所定义的变换,哪些是线性的,哪些不是:(1) 在向量空间V 中,σ (ξ)=ξ+α,α是V 中一固定的向量;(2) 在向量空间R 3中,σ (x 1, x 2, x 3)=),,(233221x x x x +;(3) 在向量空间R 3中,σ (x 1, x 2, x 3)=),,2(13221x x x x x +-; (4) 把复数域看作复数域上的向量空间,σ (ξ)=ξ. 解 (1)当0=α时,σ是线性变换;当0≠α时,σ不是线性变换; (2)σ不是线性变换; (3)σ是线性变换; (4)σ不是线性变换;2. 设V 是数域F 上一维向量空间. 证明,σ是V 的一个线性变换的充要条件是:存在F 中的一个数a ,使得对任意ξ∈V ,都有σ (ξ)=a ξ .证明:充分性显然.必要性:令σ是ν的一个线性变换,设1ξ是ν的一个基.则νξσ∈)(1.那么)(1ξσ可由1ξ线性表示,不妨设11)(ξξσa =.对任意的νξ∈,有1ξξk =,则ξξξξσξσξσa k a a k k k =====)()()()()(1111.3. 设σ是向量空间V 的线性变换,如果σ k -1ξ≠0, 但σ k ξ=0,求证ξ, σξ, …, σk -1ξ (k >0)线性无关.证明: 令++σξξ10l l ┄ +011=--ξσk k l ┈┈┈┈(1)(1)式两端用1-k σ作用得:++-ξσξσkk l l 110+0221=--ξσk k l由已知得: ==+ξσξσ1k k=,022=-ξσk 01≠-ξσk ,所以有00=l .则(1)式变为: +σξ1l +011=--ξσk k l ┈┈┈┈(2)(2)式两端用2-k σ 作用得:ξσξσkk l l 211+-+0321=--ξσk k l同理01=l .重复上述过程有: ==10l l 01=-k l . 4. 在向量空间R [x ]中,σ (f (x ))=f '(x ), τ (f (x ))=xf (x ), 证明,στ -τσ=ι.证明:对任意][)(x R x f ∈,有))(())()((x f x f σττσστ=-=-+=-=-)()()()())((())(('''x xf x xf x f x f x f x x f τστσ)(x f .所以στ -τσ=ι.5. 在向量空间R 3中,线性变换σ, τ如下:σ (x 1, x 2, x 3)=(x 1, x 2, x 1+x 2)τ (x 1, x 2, x 3)=(x 1+x 2-x 3, 0, x 3-x 1-x 2)(1) 求στ, τσ, σ2;(2) 求σ+τ, σ -τ, 2σ.解: (1) =---+=),0,(),,(213321321x x x x x x x x x σστ,(321x x x -+0,),,()321321x x x x x x τ=-+,∴τστ=.)0,0,0(),,(),,(2121321=+=x x x x x x x ττσ,∴0=τσ ),,(),,(21213212x x x x x x x +=σσ=),,(2121x x x x +.∴σσ=2.(2) ),,)((321x x x τσ+=),,(321x x x σ+),,(321x x x τ ),,(2121x x x x +=+),0,(213321x x x x x x ---+),,2(32321x x x x x -+=.),,)((321x x x τσ-=),,(321x x x σ),,(321x x x τ-),,(2121x x x x +=),0,(213321x x x x x x ---+-=)22,,(321232x x x x x x -++-.2),,(2321=x x x σ),,(2121x x x x +=)22,2,2(2121x x x x +.6. 已知向量空间R 3的线性变换σ为σ (x 1, x 2, x 3)=(x 1+x 2+x 3, x 2+x 3,-x 3) 证明,σ是可逆变换,并求σ-1.证明:),0,0,1(),0,0,1(=σ, ),0,1,1(),0,1,0(=σ,),1,1,1(),1,0,0(-=σ.∴ σ关于3R 的一个基),0,0,1(, ),0,1,0(,),1,0,0(的矩阵为:⎪⎪⎪⎭⎫ ⎝⎛-=100110111A . 显然,A 可逆,所以σ是可逆变换,而且⎪⎪⎪⎭⎫ ⎝⎛--=-1001100111A所以-=⎪⎪⎪⎭⎫⎝⎛=--132113211(),,(x x x x A x x x σ,2x ,32x x +)3x -.7. 设σ, τ, ρ都是向量空间V 的线性变换,试证,(1)如果σ, τ都与ρ可交换,则στ, σ2也都与ρ可交换(若对任意α∈V ,都有στ (α)=τσ (α),就说σ与τ可交换);(2)如果σ+τ, σ-τ都与ρ可交换,则σ, τ也都与ρ可交换. 证:(1)由已知ρττρρσσρ==,.那么==)()(τρσρστ)(ρτσ =)()(στρτσρ=.22)()()(ρσσσρρσσσρσρσ====.(2)同理可证.8. 证明,数域F 上的有限维向量空间V 的线性变换σ是可逆变换的充分必要条件是σ把非零向量变为非零向量.证明:不妨设ν是n 维的. ,,21ξξ,n ξ是它的一个基.σ关于这个基的矩阵为A .显然,σ可逆当且仅当A 可逆. σ把非零向量变为非零向量当且仅当{}0=σKer ,而秩σ=秩A ,σ的零度=σker dim .且秩σ+σ的零度=n.所以秩σ=n 当且仅当σ的零度是0,即A 可逆当且仅当0=σKer .故σ可逆当且仅当σ把非零向量变为非零向量.9. 证明,可逆线性变换把线性无关的向量组变为线性无关的向量组. 证明:令σ是向量空间ν的可逆线性变换, ,,21αα,m α是ν的一组线性无关的向量,令++)()(2211ασασk k +0)(=m m k ασ.两端用1-σ作用得: +11αk +0=m m k α.由已知 ,,21αα,m α 线性无关,所以: ==21k k =0=m k .故 ),(),(21ασασ,)(m ασ 线性无关.10. 设{ε1, ε2, ε3}是F 上向量空间V 的一个基. 已知V 的线性变换σ在{ε1,ε2, ε3}下的矩阵为A =⎪⎪⎪⎭⎫⎝⎛333231232221131211a a aa a a a a a (1) 求σ在{ε1, ε3, ε2}下的矩阵;(2) 求σ在{ε1, k ε2, ε3}下的矩阵(k ≠0,k ∈F );(3) 求σ在{ε1, ε1+ε2, ε3}下的矩阵. 解:(1)⎪⎪⎪⎭⎫⎝⎛=222321323331121311231231),,(),,(a a a a a a a a a εεεεεεσ. (2)⎪⎪⎪⎪⎭⎫⎝⎛=33323123222113121132132111),,(),,(a ka a a k a a k a ka a k k εεεεεεσ. (3) =+),,(3211εεεεσ),,(3211εεεε+⎪⎪⎪⎭⎫⎝⎛++---+-⋅33323131232221212313222112112111a a a aa a a a a a a a a a a a11. 在R 3中定义线性变换σ如下σ (x 1, x 2, x 3)=(2x 2+x 3, x 1-4x 2, 3x 1),∀(x 1, x 2, x 3)∈R 3. (1) 求σ在基ε1=(1, 0, 0), ε2=(0, 1, 0), ε3=(0, 0, 1)下的矩阵;(2) 利用(1)中结论,求σ在基α1=(1, 1, 1),α2=(1, 1, 0),α3=(1, 0, 0)下的矩阵.解:(1) ⎪⎪⎪⎭⎫⎝⎛-=003041120),,(),,(321321εεεεεεσ (2)从基{}321,,εεε到基{}321,,ααα的过渡矩阵为⎪⎪⎪⎭⎫⎝⎛=001011111P .σ在{}321,,ααα下的矩阵为:⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--=⋅⎪⎪⎪⎭⎫ ⎝⎛-⋅-0010111110030411200111101000030411201P P =⎪⎪⎪⎭⎫ ⎝⎛---156266333. 12. 已知M 2(F )的两个线性变换σ,τ如下σ (X )=X ⎪⎪⎭⎫⎝⎛-1111, τ (X )=⎪⎪⎭⎫⎝⎛-0201X , ∀X ∈M 2(F ). 试求σ+τ, στ在基E 11, E 12, E 21, E 22下的矩阵. 又问σ和τ是否可逆?若可逆,求其逆变换在同一基下的矩阵. 证明:⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=+021202011111)(111111E E E τσ =12112E E +222102E E +-.⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=+200102011111)(121212E E E τσ =12110E E +222120E E -+.⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=+110002011111)(212121E E E τσ=121100E E +2221E E ++.⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=+10002011111)(222222E E E τσ =121100E E +2221E E -+.所以τσ+在基22211211,,,E E E E 下的矩阵为⎪⎪⎪⎪⎪⎭⎫⎝⎛---=1120110200010012A . 同理可证στ在基22211211,,,E E E E 下的矩阵.121111)(E E E +=σ,121112)(E E E -=σ,222112112100)(E E E E E +++=σ,=)(22E σ2221121100E E E E -++.所以σ在此基下的矩阵为:⎪⎪⎪⎪⎪⎭⎫⎝⎛--=110110000110011B . 显然,B 可逆.所以σ可逆. σ在同一基下的矩阵为:⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=-21210021*******1210021211B. 同理可讨论τ的可逆性及求τ的矩阵.13. 设σ是数域F 上n 维向量空间V 的一个线性变换. W 1, W 2是V 的子空间,并且V =W 1⊕W 2证明,σ是可逆变换的充要条件是V =σ ( W 1)⊕σ ( W 2)证明:令 ,1α,r α是1W 的一个基. 令 ,1+r α,n α是2W 的一个基. 由已知得: ,1α, n α是ν的一个基.必要性:设σ可逆,则 ),(1ασ,)(r ασ, )(1+r ασ,)(n ασ 也是ν的一个基.但=)(1W σ£( ),(1ασ,)(r ασ). =)(2W σ£( )(1+r ασ,)(n ασ)所以=ν+)(1W σ)(2W σ,⋂)(1W σ}0{)(2=W σ,故V =σ ( W 1)⊕ σ ( W 2).充分性:将必要性的过程倒过去即可.14. 设R 3的线性变换σ定义如下:σ (x 1, x 2, x 3)=(2x 1-x 2, x 2-x 3, x 2+x 3)求σ在基ε1=(1, 0, 0), ε2=(0, 1, 0), ε3=(0, 0, 1) 及基η1=(1, 1, 0), η2=(0, 1, 1),η3=(0, 0, 1)下的矩阵.解: σ在基{ε1, ε3, ε2}下的矩阵为:⎪⎪⎪⎭⎫⎝⎛--=110110012A . σ在基{321,,ηηη}下的矩阵为:⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛=-110110011101100121100110011B =⎪⎪⎪⎭⎫⎝⎛--211110011. 15. 在M 2(F )中定义线性变换σ为σ (X )=⎪⎪⎭⎫⎝⎛-3210X , ∀X ∈M 2(F ). 求σ在基{ E 11, E 12, E 21, E 22}下的矩阵,其中E 11=⎪⎪⎭⎫⎝⎛0001, E 12=⎪⎪⎭⎫ ⎝⎛0010, E 21=⎪⎪⎭⎫ ⎝⎛0100, E 22=⎪⎪⎭⎫⎝⎛1000. 解: σ在基{22211211,,,E E E E }下的矩阵为⎪⎪⎪⎪⎪⎭⎫⎝⎛--=30200302100001A . 16. 证明,与n 维向量空间V的全体线性变换可交换的线性变换是数量变换.证明:由105P 习题二及第10题的结论易得. 17. 给定R 3的两个基α1=(1, 0, 1), α2=(2, 1, 0), α3=(1, 1, 1);和 β1=(1, 2,-1), β2=(2, 2, -1), β3=(2, -1, -1). σ是R 3的线性变换,且σ(αi )=βi ,i =1, 2,3. 求(1) 由基{α1, α2 , α3}到基{β1, β2 , β3}的过渡矩阵; (2) σ关于基{α1, α2 , α3}的矩阵; (3) σ关于基{β1, β2 , β3}的矩阵.解: (1)令)0,0,1(1=ε,)0,1,0(2=ε,)1,0,0(3=ε.则由{α1, α2 , α3}到{ε1,ε3, ε2}的过渡矩阵为:1101110121-⎪⎪⎪⎭⎫⎝⎛. 由基{ε1, ε3, ε2}到基{β1, β2 , β3}的过渡矩阵为:⎪⎪⎪⎭⎫ ⎝⎛101110221. 所以由基{α1, α2 , α3}到基{β1, β2 , β3}的过渡矩阵为:⎪⎪⎪⎭⎫ ⎝⎛----⋅⎪⎪⎪⎭⎫ ⎝⎛---=-1111222211111101211P =⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---252112323123232 (2) σ ==),,(),,(321321βββαααP ),,(321ααα.所以σ在),,(321ααα下的矩阵为:⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---252112323123232. σ关于基{β1, β2 , β3}的矩阵为: ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---252112323123232 18. 设α1=(-1, 0, -2), α2=(0, 1, 2), α3=(1, 2, 5),β1=(-1, 1, 0), β2=(1, 0, 1), β3=(0, 1, 2),ξ=(0, 3, 5)是R 3中的向量,σ是R 3的线性变换,并且σ(α1)=(2, 0, -1), σ(α2)=(0, 0, 1),σ(α3)=(0, 1, 2).(1) 求σ关于基{β1, β2 , β3}的矩阵; (2) 求σ(ξ)关于基{α1, α2 , α3}的坐标; (3) 求σ(ξ)关于基{β1, β2 , β3}的坐标. 解:令⎪⎪⎪⎭⎫⎝⎛--=5222101011T ,⎪⎪⎪⎭⎫⎝⎛-=2101011112T .则从基{α1, α2 , α3}到基{β1, β2 , β3}的过渡矩阵为:⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛----=⋅=-0101210011222341212211T T T T . 又321135310311)1,0,2()(αααασ-+-=-=321203231)1,0,0()(αααασ+-==321300)2,1,0()(αααασ++==所以σ关于),,(321ααα的矩阵为:⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---03135132310031311.从而σ关于基{β1, β2 , β3}的矩阵为:⋅⎪⎪⎪⎭⎫ ⎝⎛-==-2111000011AT T B ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---03135132310031311⎪⎪⎪⎭⎫ ⎝⎛-⋅010121001= ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----31353103132343132310. (2)==)5,3,0(ξ321353135ααα+-.所以关于)(ξσ),,(321ααα的坐标为:⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-⋅926967956353135A 由(2)可知=)(ξσ⋅),,(321ααα⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--926967956=(β1, β2 , β3)⋅⋅-1T ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--926967956 所以关于)(ξσ{β1, β2 , β3}的坐标为:⋅-1T ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--926967956=⋅⎪⎪⎪⎭⎫ ⎝⎛-211100001⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--926967956=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--971926956. 19. 设R 3有一个线性变换σ定义如下:σ (x 1, x 2, x 3)=(x 1+x 2,x 2+x 3,x 3),∀(x 1, x 2, x 3)∈R 3.下列R 3的子空间哪些在σ之下不变?(1) {(0, 0, c )| c ∈R }; (2) {(0, b , c )| b , c ∈R };(3) {(a , 0, 0)| a ∈R }; (4) {(a , b , 0)| a , b ∈R }; (5) {(a , 0, c )| a , c ∈R }; (6) {(a , -a , 0)| a ∈R }.解:(3)与(4)在σ之下不变.20. 设σ是n 维向量空间V 的一个线性变换,证明下列条件等价: (1) σ (V )=V ; (2) ker σ={0}.证明:因为秩σ+σ的零度=n. 所以秩σ=n 当且仅当σ的零度是0,即n =)(dim νσ当且仅当0ker dim =σ,因此V V =)(σ当且仅当}0{=σK e r .21. 已知R 3的线性变换σ定义如下:σ (x 1, x 2, x 3)=(x 1+2x 2-x 3, x 2+x 3, x 1+x 2-2x 3),∀(x 1, x 2, x 3)∈R 3. 求σ的值域σ (V )与核Ker σ的维数和基.解: σ关于基)0,0,1(1=ε,)0,1,0(2=ε,)1,0,0(3=ε的矩阵为:⎪⎪⎪⎭⎫ ⎝⎛--=211110121A .)1,0,1()(1=εσ,)1,1,2()(2=εσ,)(νσ ))(),((21εσεσL =.),(ker ξσL =其中)1,1,3(-=ξ,1ker dim =σ.22. 设σ是向量空间V 的一个线性变换,W 是σ的一个不变子空间,证明,W 是σ 2的不变子空间.证明:由不变子空间的定义易证. 23. 设σ是数域F 上n (>0)维向量空间V 的一个线性变换,{α1, α2 ,…, αr , αr +1,…, αn }是V 的基. 证明,如果{α1, α2 ,…, αr }是Ker σ的基,那么{σ (αr +1),…,σ (αn )}是Im σ的基.证明:已知{α1, α2 ,…, αr }是Ker σ的基, 则σ (αi )=0, i =1,2, …, r . 令 l r +1σ (αr +1)+ l r +2σ (αr +2)+ …+ l n σ (αn )=0, 则σ ( l r +1αr +1+…+ l n αn )=0, l r +1αr +1+…+ l n αn ∈ Ker σ .所以 l r +1αr +1+…+ l n αn =l 1α 1+…+ l r αr但 α1, α2 ,…, αr , αr +1,…, αn 是V 的一个基, 故 l r +1=…= l n =0. 所以 σ (αr +1),…, σ (αn ) 线性无关.又 Im σ = £(σ (α1), σ (α2)…, σ (αn )) = (σ (αr +1),…, σ (αn )).从而结论成立.24. 对任意α∈R 4,令σ (α)=A α,其中A =⎪⎪⎪⎪⎪⎭⎫⎝⎛---2122552131211201 求线性变换σ的核与象. 解: α1 = ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--02232, α2 =⎪⎪⎪⎪⎪⎭⎫⎝⎛--1021, Ker σ =£(α1,α2). σ (ε1) = ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-2111, σ (ε2) = ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-2220. Im σ =£(σ (ε1), σ (ε2)).25. 设 σ,τ 是向量空间V 的线性变换,且σ+τ=ι,στ=τσ=θ. 这里ι是V 的恒等变换,θ 是V 的零变换. 证明:(1) V =σ(V )⊕τ (V ); (2) σ(V )=Ker τ.证明: (1) ∀ξ∈ V, ξ=ι (ξ)=(σ+τ)(ξ)=σ (ξ)+τ (ξ).所以V =σ (V )+τ (V ).对任意ξ∈σ (V )∩τ (V ). 则ξ=σ (ξ1)+ τ (ξ2).由已知条件可得ξ= ι (σ (ξ1)) = (σ+τ)(σ (ξ1)) = σ·(σ (ξ1) = σ·(τ (ξ2)= στ (ξ2) = 0 . 故结论成立.(2 ) 对任意σ (ξ)∈σ (V ), 则 τ(σ (ξ))= 0, 所以 σ (ξ)∈Ker τ .反之, 对任意ξ∈Ker τ , 则τ(ξ)= 0.由已知条件可得,ξ= (σ+τ)(ξ)=σ (ξ)+τ (ξ)=σ (ξ),所以ξ∈σ (V ).26. 在向量空间F n [x ]中,定义线性变换τ为:对任意f (x )∈F n [x ],τ(f (x )) =x f '(x )-f (x ). 这里f '(x )表示f (x )的导数. (1)求Ker τ及Im τ;(2)证明,V =Ker τ⊕Im τ. 解: (1) 令τ ( f (x )) = x f'(x )-f (x ) = 0其中 f (x ) = a 0 + a 1x + … + a n x n . 则(a 1x +2a 2x 2+ … +n a n x n )- f (x ) = 0(0- a 0) + ( a 1- a 1)x + (2a 2- a 2) x 2+ … + (n a n -a n )x n= 0 有 ⎪⎪⎩⎪⎪⎨⎧===00020na a a, 所以 f (x ) = a 1x ,Ker τ =£(x ), Im τ=£(1,x 2, … ,x n ).(2) 显然 .27. 已知向量空间V 的线性变换σ在基{ε1, ε2, ε3}下的矩阵为A =⎪⎪⎪⎭⎫⎝⎛--121101365 求σ的本征值及相应的本征向量. 问是否存在V 的一个基使得σ 关于这个基的矩阵是对角阵?解: 本征值λ=2 (三重), 属于λ=2的线性无关的本征向量为:ξ1=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛0131 , ξ2=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-1031, 故σ 不能对角化.28. 设σ是向量空间V 的可逆线性变换,证明 (1) σ的本征值一定不为0; (2) 如果λ是σ 的本征值,那么λ1是σ-1的本征值.证明: (1) 反设σ 有一本征值为0,则存在ξ≠0,ξ∈ V , 使得σ (ξ)=0·ξ= 0 . 因为σ 可逆, 所以 σ -1(σ (ξ))=0, 即ξ= 0.矛盾.(2) 设λ是σ 的本征值,由(1)得λ≠0,且有σ (ξ)=λξ,ξ≠0.σ -1(σ (ξ))=λσ -1 (ξ). 即 σ -1 (ξ)=λ1ξ, 所以结论成立.补 充 题1. 设σ是数域F 上n 维向量空间V 的一个线性变换. 证明 (1) Ker σ ⊆Ker σ2⊆ Ker σ3⊆…(2) Im σ ⊇Im σ2 ⊇Im σ3 ⊇…证明: (1)对任意正整数n ,下证Ker σ n ⊆ Ker σ n +1 对任意ξ∈ Ker σ n., σ n(ξ)=0, σ (σ n(ξ))=0 即σn +1(ξ)=0, 所以ξ∈ Ker σn +1.(2) 对任意正整数n ,下证Im σ n ⊇Im σ n +1.对任意ξ∈Im σ n +1, 则存在 η∈ V , 使得ξ=σn +1(η)=σ n (σ (η))∈Im σ n.2. 设A 是数域F 上的n 阶矩阵. 证明,存在F 上的一个非零多项式f (x ), 使得f (A )=0.[不用Cayley-Hamilton 定理证. ]证明: 由于dimM n (F) = n 2, 所以I, A, A 2, …, A 2n线性相关,故存在F 上的不全为零的一组数k 0,, k 1, … ,k 2n ,使得+++2210A k A k I k ┄+022=nn Ak .取=)(x f +++2210x k x k k ┄+ 022=nn xk ,结论得证.3. 设V 是n 维向量空间, σ是V 的一个可逆线性变换, W 是σ的一个不变子空间. 证明, W 也是σ-1的不变子空间.证明:令{α1, α2 ,…, αr }是W 的一个基,因为W 是σ的不变子空间,所以 ,1,)(=∈i i ωασ,r .又σ是可逆的,所以 ),(1ασ,)(r ασ线性无关,故),(1ασ,)(r ασ也是W 的一个基.因为r i i i ,,1,))((1=∈=-ωαασσ.所以W 关于1-σ不变.4. 设σ是数域F 上向量空间V 的一个线性变换, σ2=σ. 证明: (1) Ker σ ={ξ-σ (ξ)|ξ∈V }; (2) V =Ker σ ⊕Im σ ;(3) 若τ是V 的一个线性变换, 那么Ker σ 和Im σ 都在τ之下不变的充要条件是στ=τσ.[提示:证(3)的必要性,利用(2). ]证明:(1)对于任意的,ker σξ∈则.0)(=ξσ那么{}V ∈-∈-=-=ξξσξξσξξξ)()(0.反之,任意的{}V ∈-∈-ξξσξξσξ)()(,有-=-)())((ξσξσξσ0)()()(2=-=ξσξσξσ,故σξσξker )(∈-.(2)由(1)的解果可知:σσIm ker +=V ,对任意的σσξIm ker ⋂∈,则有:)()(211ησησηξ=-=,因此0)()()(121=-=ησησξσ. 同时还有:ξησησξσ===)()()(222所以0=ξ,结论成立.(3)充分性易证.必要性:设Ker σ 和Im σ 都在τ之下不变,由(2)的结论得:1,ξξξ=∈∀V ),(2ξσ+其中σξker 1∈.又因为+-=+-=-))(())(())()(())((1121ξστξτσξσξτσστξτσστ )()))(((222ξτσξστσ-.由已知,,Im ))((,ker )(21σξστσξτ∈∈不妨设)())((32ξσξστ=,所以)()())(())(())((2323=-=-=-ξτσξσξστξσσξτσστ.5. 设σ是数域F 上n 维向量空间V 的一个线性变换, σ2=ι. 证明, V =W 1⊕W 2, 这里W 1={ξ∈V |σ(ξ)=ξ},W 2={η∈V |σ(η)=-η}.[提示:∀α∈V ,α=21(α+σ(α))+21(α-σ(α)). ]证明:首先对2)(2)(,ασαασααα-++=∈∀V ,由于=+)2)((ασασ2)(2)()(2ασαασασ+=+,=-)2)((ασασ=-2)()(2ασασ 2)(ασα--所以12)(W ∈+ασα,22)(W ∈-ασα,故21W W V +=.其次对任意的21W W ⋂∈α,则αασ=)(,αασ-=)(.所以0,02==αα.那么V =W 1⊕W 2,结论成立.6. 设V 是复数域C 上一个n 维向量空间, σ, τ是V 的线性变换, 且στ=τσ . 证明(1) 对σ的每一本征值λ来说,V λ={ξ∈V |σ(ξ)=λξ}是τ的不变子空间; (2) σ与τ有一公共本征向量.[提示:证(2)时,考虑τ在V λ上的限制. ] 证明: (1)易证.(2).由(1)可知λV 是τ的不变子空间.则λτV 是λV 的一个线性变换.因此λτV 在复数域C 上一定有一个本征值,不妨设为μ.即存在λαV ∈≠0,使得μαατλ=))((V .而)())((ατατλ=V ,所以α是τ的属于μ的一个本征向量.由α的取法,结论得证.7. 设A 是秩为r 的n 阶半正定矩阵. 证明,W ={ξ∈R n |ξ T A ξ=0}是R n 的n -r 维子空间.[提示:利用习题三第33题的结论,可得W 是齐次线性方程组BX =0的解空间. ]证明:由习题三第33题的结论得:B B A T =,其中B 是秩为r 的n r ⨯矩阵.则)()(ξξξξξξB B B B A T T T T ==,那么0=ξξA T当且仅当0=ξB .=W{}0=∈ξξB Rn.因为秩r B =,所以齐次线性方程组0=Bx 的解空间是r n -维的.即r n W -=dim .8. 设σ,τ是F 上向量空间V 的线性变换,且σ2=σ,τ2=τ. 证明,(1) Im σ=Im τ 当且仅当 στ=τ, τσ=σ; (2) Ker σ=Ker τ 当且仅当 στ=σ, τσ=τ.证明:(1)必要性:设τσm m I I =,,V ∈∀ξ则σξτIm )(∈.令)()(1ξσξτ=,则)()())(()(11ξτξσξσσξστ===.所以τστ=.同理可证στσ=.充分性:设τστ=,στσ=.对任意的σξσIm )(∈,则τξστξτσξσIm ))(())(()(∈==所以τσIm Im ⊆,同理可证στIm Im ⊆. (2)必要性:设Ker σ=Ker τ.对任意的V ∈ξ,因为0)()())((2=-=-ξτξτξξττ所以τξξτker )(∈-,则0))((=-ξξτσ,即)())((ξσξτσ=,故σστ=.同理可证ττσ=.充分性:设ττσ=,σστ=.对任意的σξker ∈,则0)(=ξσ.且0)0())(())(()(====τξστξτσξτ所以τξker ∈,故τσker ker ⊆.同理可证στker ker ⊆.。
武大第7章习题解答(高频)

4 4
= 2 2 10 rad s 。
3
解: (1) o t 为单音调制的普通调幅信号。
o t 2 1 0.1cos4 103 t cos4 10 6 t
1 2 Pav P0 1 ma 2.01W , 2
D1=υ D2=υ c+υ
Ω
,υ c 正向地加到两个二极管两端,故 g1 t g 2 t
g D K c t , i i1 i2 g D K c t D1 gK c t D 2 0 。因此,题图( a)所示电路没
有输出,不能完成双边带调制功能。 (2)υ D1=υ c+υ Ω ,υ D2=-υ c-υ =-υ
i i1 i2 g D K c t D1 g D K c t D 2 g D K c t c g D K c t c g D K c t K c t c g D K c t K c t g D c g D K c t
D1,υ c 正向地加到
Ω
D1 两端,反向地加
到 D2 两端,故 g1 t g D K c t , g 2 t g D K c t ,i1 与 i 2 流向一致,在输出变压 器中产生的磁通相加,则输出电流 i 为
i i1 i2 g D K c t D1 g D K c t D 2 g D K c t D1 g D K c t D1 g D K c t K c t D1 g D K c t C
6 6 3 6 4
1.6 cos 2 10 6 103 t 0.4 cos 2 10 6 10 4 t V
第7章 习题解答
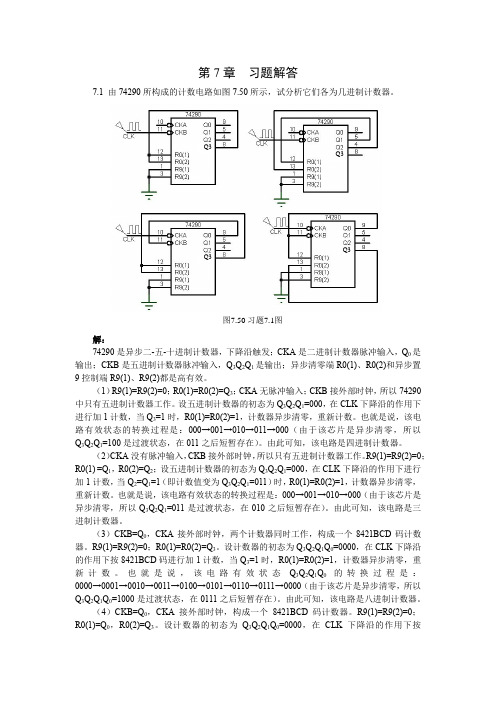
第7章 习题解答7.1 由74290所构成的计数电路如图7.50所示,试分析它们各为几进制计数器。
图7.50 习题7.1图Q3Q3Q3Q3解:74290是异步二-五-十进制计数器,下降沿触发;CKA 是二进制计数器脉冲输入,Q 0是输出;CKB 是五进制计数器脉冲输入,Q 3Q 2Q 1是输出;异步清零端R0(1)、R0(2)和异步置9控制端R9(1)、R9(2)都是高有效。
(1)R9(1)=R9(2)=0;R0(1)=R0(2)=Q 3;CKA 无脉冲输入;CKB 接外部时钟,所以74290中只有五进制计数器工作。
设五进制计数器的初态为Q 3Q 2Q 1=000,在CLK 下降沿的作用下进行加1计数,当Q 3=1时,R0(1)=R0(2)=1,计数器异步清零,重新计数。
也就是说,该电路有效状态的转换过程是:000→001→010→011→000(由于该芯片是异步清零,所以Q 3Q 2Q 1=100是过渡状态,在011之后短暂存在)。
由此可知,该电路是四进制计数器。
(2)CKA 没有脉冲输入,CKB 接外部时钟,所以只有五进制计数器工作。
R9(1)=R9(2)=0;R0(1) =Q 1,R0(2)=Q 2;设五进制计数器的初态为Q 3Q 2Q 1=000,在CLK 下降沿的作用下进行加1计数,当Q 2=Q 1=1(即计数值变为Q 3Q 2Q 1=011)时,R0(1)=R0(2)=1,计数器异步清零,重新计数。
也就是说,该电路有效状态的转换过程是:000→001→010→000(由于该芯片是异步清零,所以Q 3Q 2Q 1=011是过渡状态,在010之后短暂存在)。
由此可知,该电路是三进制计数器。
(3)CKB=Q 0,CKA 接外部时钟,两个计数器同时工作,构成一个8421BCD 码计数器。
R9(1)=R9(2)=0;R0(1)=R0(2)=Q 3。
设计数器的初态为Q 3Q 2Q 1Q 0=0000,在CLK 下降沿的作用下按8421BCD 码进行加1计数,当Q 3=1时,R0(1)=R0(2)=1,计数器异步清零,重新计数。
习题解答---大学物理第7章习题2

专业班级_____ 姓名________学号________ 第七章静电场中的导体和电介质一、选择题:1,在带电体A旁有一不带电的导体壳B,C为导体壳空腔内的一点,如下图所示。
则由静电屏蔽可知:[ B ](A)带电体A在C点产生的电场强度为零;(B)带电体A与导体壳B的外表面的感应电荷在C点所产生的合电场强度为零;(C)带电体A与导体壳B的内表面的感应电荷在C点所产生的合电场强度为零;(D)导体壳B的内、外表面的感应电荷在C点产生的合电场强度为零。
解答单一就带电体A来说,它在C点产生的电场强度是不为零的。
对于不带电的导体壳B,由于它在带电体A这次,所以有感应电荷且只分布在外表面上(因其内部没有带电体)此感应电荷也是要在C点产生电场强度的。
由导体的静电屏蔽现象,导体壳空腔内C点的合电场强度为零,故选(B)。
2,在一孤立导体球壳内,如果在偏离球心处放一点电荷+q,则在球壳内、外表面上将出现感应电荷,其分布情况为 [ B ](A)球壳内表面分布均匀,外表面也均匀;(B)球壳内表面分布不均匀,外表面均匀;(C)球壳内表面分布均匀,外表面不均匀;(D)球壳的内、外表面分布都不均匀。
解答 由于静电感应,球壳内表面感应-q ,而外表面感应+q ,由于静电屏蔽,球壳内部的点电荷+q 和内表面的感应电荷不影响球壳外的电场,外表面的是球面,因此外表面的感应电荷均匀分布,如图11-7所示。
故选(B )。
3. 当一个带电导体达到静电平衡时:[ D ](A) 表面上电荷密度较大处电势较高 (B) 表面曲率较大处电势较高。
(C)导体内部的电势比导体表面的电势高。
(D)导体内任一点与其表面上任一点的电势差等于零。
4. 如图示为一均匀带电球体,总电量为+Q ,其外部同心地罩一内、外半径分别为r 1、r 2的金属球壳、设无穷远处为电势零点,则在球壳内半径为r 的P 点处的场强和电势为: [ D ](A )E= (B )E=0,(C )E=0,(D )E=0,5. 关于高斯定理,下列说法中哪一个是正确的? [ C ](A )高斯面内不包围自由电荷,则面上各点电位移矢量为零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
哈尔滨理工大学电气学院理论电工教研室第七章(一阶电路)习题解答一、选择题1.由于线性电路具有叠加性,所以C。
A.电路的全响应与激励成正比;B.响应的暂态分量与激励成正比;C.电路的零状态响应与激励成正比;D.初始值与激励成正比2.动态电路在换路后出现过渡过程的原因是A。
A.储能元件中的能量不能跃变;B.电路的结构或参数发生变化;C.电路有独立电源存在;D.电路中有开关元件存在3.图7—1所示电路中的时间常数为C。
A.( CC 12R1R);B.2CC12CC12 R;2CC12C.R2(C1C2);D.(R1R2)(C1C2)解:图7—1中C1和C2并联的等效电容为C1C2,而将两个电容摘除后,余下一端口电路的戴维南等效电阻为R,所以此电路的时间常数为R2(C1C2)。
24.图7—2所示电路中,换路后时间常数最大的电路是A。
解:图7—2(A)、(B)、(C)、(D)所示四个电路中的等效电感L eq分别为L1L22M、哈尔滨理工大学电气学院理论电工教研室L 1L 、L 1L 22M 和L 1L 22M 。
t0时,将图6—2(A )、(B )、(C )、(D )中 2的电感摘除后所得一端口电路的戴维南等效电阻R 分别为R 、R 2、R 2和R 1R 2。
由于 eq2RL 电路的时间常数等于L eq R eq,所以图7—2(A )所示电路的时间常数最大。
10t5.RC 一阶电路的全响应u (106e)V ,若初始状态不变而输入增加一倍,则c 全响应u 变为D 。
cA .10t2012e ;B .10t 206e ; C . 10t 1012e ;D. 2016e10tt解:由求解一阶电路的三要素法u c u()[u (0)u()]e τ可知在原电路中cccu()10V ,u c (0)4V 。
当初始状态不变而输入增加一倍时,有 c10t10tu20[420]e(2016e)V c 二、填空题1.换路前电路已处于稳态,已知U s110V ,U s 21V ,C 10.6F ,C 20.4F 。
t0时,开关由a 掷向b ,则图7—3所示电路在换路后瞬间的电容电压u6.4V ,u c2(0)6.4V 。
(0)c1解:由t0时刻电路得:u c ,u c2(0)U s21V 1(0)U s110V换路后,电容 C ,C 2构成纯电容的回路(两电容并联),电容电压发生强迫跃变,此时应由1电荷守恒原理求解换路后瞬刻的电容电压。
由KVL 得:u c (0)u 2(0)⋯⋯① 1cC 1u c (0)C 2u c2(0)C 1u c1(0)C 2u c 2(0)⋯⋯②1由以上两式解得CUCU 1s12(0)(0) uu c1CCc212s2 6.4V2.图7—4所示电路的时间常数τ0.1s 。
解:将储能元件开路,独立电源置0后,可得求戴维南等效电阻的电路如图7—4(a)所示。
由于电路中含有受控源,因此需用外加电压法求戴维南等效电阻R。
由图7—4(a)得44(3)Ui1ii,U4i14i1即4U20i1L于是R5,0.1sτR3.某RC串联电路中,u c随时间的变化曲线如图6—5所示,则t0时tu c(t)[33e2]V。
解:由图7—5可得u(0)6V,u c()3Vctt而u c u()[u(0)u()]eτccc33e τ由图7—5可见ductdt064。
将u c的表达式代入此式得3 64,即2stt因此u(t)3(63)e[33e2]V(t0)τc4.换路后瞬间(t0),电容可用电压源等效替代,电感可用电流源等效替代。
若储能元件初值为零,则电容相当于短路,电感相当于开路。
5.图7—6所示电路,开关在t0时刻动作,开关动作前电路已处于稳态,则i(0)0.25A。
1解:t0时刻,电路处于直流稳态,电感相当于短路,电容相当于开路,等效电路如图7—6(a)所示。
由图7—6(a)解得(0)1Ai,u C(0)20V。
L如图7—6(b),由此图解得(0)0.25Ai。
1 t0 时刻的等效电路三、计算题1.图7—7所示电路,电容原未充电,U s100V,R500,C10F。
t0时开关S闭合,求:1).t0时的u和i;2).u c达到80V所需时间。
c解:1).由于电容的初始电压为0,所以tu c U(1e)s63将τ5001010510s,及U s100V代入上式得RC200tu100(1e)V(t0)ctduU200cSt而e0.2eA(0)RCiCtdtR2).设开关闭合后经过t秒uc充电至80V,则1ln(0.2)200t200t100(1e),即0.2180e1由此可得t8.045ms12002.图7—8所示电路,开关S在t0时刻闭合,开关动作前电路已处于稳态,求t0时的i(t)。
解:电流i为电感中的电流,适用换路定则,即i(0)i(0)4A10L3而i5A,s()τR222t2t于是()5(45)e[5e3]A(0)3itt3.图7—9所示电路,开关S在t0时刻从a掷向b,开关动作前电路已处于稳态。
求:1).i L(t)(t0);2).i1(t)(t0)。
32解:1).i1.2A,i L()1.2AL(0)i L(0)123112L3τ1.8s12R112tτ于是iL(t)i()[i(0)i()]eLLL5t1.22.4e9A(0)t2).注意到()i1t为电阻中的电流,不能直接应用换路定则。
画出t0时刻电路如图6 —9(a)所示,等效变换后的电路如图7—9(b)所示。
由图7—9(b)可得0.63i(0)0.2A,i()1.8A11123112τ1.8s5t5t因而()1.8[0.21.8]e[1.81.69]A(0)9i1tet4.图7—10所示电路,开关S在t0时刻打开,开关动作前电路已处于稳态。
求:t0时的u(t) c。
哈尔滨理工大学电气学院理论电工教研室解:u c(0)(0)0。
稳态时电容相当于开路,u c()(即电容的开路电压)uc和R可由图7—10(a)的电路计算。
由图7—10(a)得:4(1.5)2(1.51)uiu1iu⋯⋯(1)12(1.51)u1iu⋯⋯(2)1由(2)得0.5(1)u1i,将此带入(1)式,得u1.5i2.5由此可见()2.5Vu,R1.5c3而sτRC4 uc 44 t6.5[0(2.3[..e35)]e2525 t]V(t0) 1.3t5.图7—11中,C0.2F时零状态响应u20(1e)V。
若电容C改为0.05F,c 且(0)5Vu,其它条件不变,再求u c(t)。
c如图7 解:以储能元件为外电路,线性含源电阻网络可用相应的戴维南,代等效电路替—11(a)所示。
由题意可知1τRC2s,R100.7而()20Vu s uc当C改为0.05F,且(0)5Vu时,c哈尔滨理工大学电气学院理论电工教研室 τRC0.5s ,u c (0)u c (0)5Vt2t因而u c (t)20(520)e(2015e)V(t0)0.5t6.图7—12中,u s 8()V ,u 210e(t)1tsV ,全响应t 。
求:1).2ttu c (t)(5e3e2)()Vu 、u s2单独作用时的零状态响应u c 和u c ; s12).零输入响应u c 3。
解:图7—12的全响u c 应等于零状态响应加零输入响应,即u c uuu ⋯⋯①ccc3t而u c (t)u()u()e τ⋯⋯②cctu c 3u(0)e τ⋯⋯③ct将图7—12等效为图7—12(a ),设图中的u s A(t)Be(t)。
t 当Be(t)单独作用时,有d u cuBRCecdtt 其通解为 t t u c k 1ek 2e (其中τk B 2)1RC 将上式及②、③代入①得u c t u c ()u()e+τ ctt tk 1ek 2e+u(0)e ⋯⋯④ ττ c 考虑到u 是u s1激励时的零状态响应,并将④和题中给出的u c 的全响应的表达式对比,可得cu()2V,k25V,cu C V,k15V,0.5s(0)4 因此2tu c t2e()2(t0)2t(t0)tu5e5ec2tu c34e(t0)哈尔滨理工大学电气学院理论电工教研室7.图7—13所示电路中,激励u s的波形如图7—13(a)所示,求响应u c。
解:本题的激励可用三个阶跃函数之和表示,即:u s[20(t)30(t2)10(t6)]V电路的响应就是上述三个阶跃函数分别作用产生的零状态响应之和。
将图7—13等效为如图7—13(b)所示的电路。
20(t)作用时的响应为u ct 10(1e)(t)30(t2)作用时的响应为u c 15(1e (tt2))(2)10(t6)作用时的响应为u c 5(1e (t6)t)(6)总的零状态响应为uc t(t)[10(1e)(t)15(1e (ttt2)(t6))(2)5(1e)(6)] V8.图7—14所示电路中,激励为单位冲激函数δ(t)A,求零状态响应i L(t)。
解:设激励为(t)A,用三要素法求电路的单位阶跃响应。
5(0)(0)0i L i,i()0.5ALεLεε55(55)10LR5,0.1sτ5510R10tt电流的单位阶跃响应为()0.5(1e)ε()AitLε根据单位冲激响应和单位阶跃响应的关系,可得电路中的i(t)L:i(t) Lddti (t)Lε5e 10t10tttε()0.5(1e)()哈尔滨理工大学电气学院理论电工教研室5e 10ttε()A9.图7—15所示电路中,i s5(t)A,u s6(t)V,求t0时的响应u。
解:应用叠加原理求解此题。
i s5tA单独作用时,电路如图7—15(a)所示。
对于冲激响应,可先求其相应的阶跃响应。
设激励为i sε5ε(t)A,则uε(0)u cε(0)u cε(0)0uεi() sε6.63101.410 3 V3τRC510s200t3t因此()[2.52.5e]10ε()Vutε由冲激响应和阶跃响应的关系得u(t) du(t)200tt3200ttε[0.5e()2.510(1e)(εdt200tt0.8e()V)]u s6ε(t)V单独作用时,电路如图7—15(b)所示。
6 u(0)u c(0)u c(0)0,u()621.5V,122123τRC510s而u(t)1.5(1e200t)ε(t)V因此u(t)u(t)u(t)(1.5e200t)ε(t)V10.图7—16所示电路,开关动作前电路已处于稳态,t0时开关S打开,求t0时的i(t)。
哈尔滨理工大学电气理论电工教研室学院得解:由图示电路可求(0)5Ai,i L2(0)0开关动作后i(0)i L2(0)⋯⋯①电流发生强迫跃变。
