数值分析matlab代码

合集下载

MATLAB数值分析实验二(复合梯形、辛普森和龙贝格求积,以及二重积分计算等)

佛山科学技术学院实验报告课程名称_______________ 数值分析________________________实验项目_______________ 数值积分____________________专业班级机械工程姓名余红杰学号2111505010 指导教师陈剑成绩日期月日一、实验目的b1、理解如何在计算机上使用数值方法计算定积分 a f ""X的近似值；2、学会复合梯形、复合Simpson和龙贝格求积分公式的编程与应用。

3、探索二重积分.11 f （x, y）dxdy在矩形区域D = ｛（ x, y） | a _ x _ b, c _ y _ d｝的数值D积分方法。

二、实验要求（1）按照题目要求完成实验内容；（2）写出相应的Matlab程序；（3）给出实验结果（可以用表格展示实验结果）；（4）分析和讨论实验结果并提出可能的优化实验。

（5）写出实验报告。

三、实验步骤1、用不同数值方法计算积xln xdx =-- 0 9（1）取不同的步长h，分别用复合梯形及复合辛普森求积计算积分，给出误差中关于h的函数，并与积分精确值比较两公式的精度。

（2）用龙贝格求积计算完成问题（1 ）。

2、给出一种求矩形区域上二重积分的复化求积方法，然后计算二重积分..e"y dxdy，其中积分区域D二｛0乞x岂1,0岂y乞1｝。

1.%lnt_t.m复化梯形：function F = Int_t(x1,x2,n)%复化梯形求积公式% x1,x2为积分起点和中点%分为n个区间，没选用步长可以防止区间数为非整数。

%样点矩阵及其函数值：x = lin space(x1,x2 ,n+1);y = f(x);m = len gth(x);%本题中用Matlab计算端点位置函数值为NaN,故化为零: y(1) = 0;y(m) = 0;%算岀区间长度，步长h：h = (x2 -x1)/n;a = [1 2*o nes(1,m-2) 1];%计算估计的积分值：F = h/2*sum(a.*y);%f.mfun cti on y = f(x)y = sqrt(x).*log(x);%run 11.mclc,clear;%分为10个区间，步长0.1的积分值：F = In t_t(0,1,10);F10 = F%分为100个区间F = In t_t(0,1,100);F100 = F%误差计算W10 = abs((-4/9)-F10);W100 = abs((-4/9)-F100);W = [W10 W100]%复化辛普森：%l nt_s.mfun cti on F = In t_s(x1,x2 ,n)%复化梯形求积公式% x1,x2区间，分为n个区间。

#数值分析Matlab作业

数值分析编程作业2012年12月第二章14.考虑梯形电阻电路的设计，电路如下：电路中的各个电流{i1,i2,…,i8}须满足下列线性方程组：121232343454565676787822/252025202520252025202520250i i V R i i i i i i i i i i i i i i i i i i i i -=-+-=-+-=-+-=-+-=-+-=-+-=-+=这是一个三对角方程组。

设V=220V ，R=27Ω，运用追赶法，求各段电路的电流量。

Matlab 程序如下：function chase () %追赶法求梯形电路中各段的电流量 a=input('请输入下主对角线向量a='); b=input('请输入主对角线向量b='); c=input('请输入上主对角线向量c='); d=input('请输入右端向量d='); n=input('请输入系数矩阵维数n='); u(1)=b(1); for i=2:nl(i)=a(i)/u(i-1); u(i)=b(i)-c(i-1)*l(i); endy(1)=d(1); for i=2:ny(i)=d(i)-l(i)*y(i-1); endx(n)=y(n)/u(n); i=n-1; while i>0x(i)=(y(i)-c(i)*x(i+1))/u(i); i=i-1;end x输入如下: >> chase请输入下主对角线向量a=[0,-2,-2,-2,-2,-2,-2,-2]; 请输入主对角线向量b=[2,5,5,5,5,5,5,5];请输入上主对角线向量c=[-2,-2,-2,-2,-2,-2,-2,0]; 请输入方程组右端向量d=[220/27,0,0,0,0,0,0,0]; 请输入系数矩阵阶数n=8 运行结果如下：x = 8.1478 4.0737 2.0365 1.0175 0.5073 0.2506 0.1194 0.0477第三章14.试分别用(1)Jacobi 迭代法；(2)Gauss-Seidel 迭代法解线性方程组1234510123412191232721735143231211743511512x x x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦ 迭代初始向量(0)(0,0,0,0,0)T x =。

matlab编程实例100例

1-32是：图形应用篇33-66是：界面设计篇67-84是：图形处理篇85-100是：数值分析篇实例1：三角函数曲线（1）function shili01h0=figure('toolbar','none',...'position',[198 56 350 300],...'name','实例01');h1=axes('parent',h0,...'visible','off');x=-pi:0.05:pi;y=sin(x);plot(x,y);xlabel('自变量X');ylabel('函数值Y');title('SIN( )函数曲线');grid on实例2：三角函数曲线（2）function shili02h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例02');x=-pi:0.05:pi;y=sin(x)+cos(x);plot(x,y,'-*r','linewidth',1);grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例3：图形的叠加function shili03h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例03');x=-pi:0.05:pi;y1=sin(x);y2=cos(x);plot(x,y1,...'-*r',...x,y2,...'--og');grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例4：双y轴图形的绘制function shili04h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例04');x=0:900;a=1000;b=0.005;y1=2*x;y2=cos(b*x);[haxes,hline1,hline2]=plotyy(x,y1,x,y2,'semilogy','plot'); axes(haxes(1))ylabel('semilog plot');axes(haxes(2))ylabel('linear plot');实例5：单个轴窗口显示多个图形function shili05h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例05');t=0:pi/10:2*pi;[x,y]=meshgrid(t);subplot(2,2,1)plot(sin(t),cos(t))axis equalsubplot(2,2,2)z=sin(x)-cos(y);plot(t,z)axis([0 2*pi -2 2])subplot(2,2,3)h=sin(x)+cos(y);plot(t,h)axis([0 2*pi -2 2])subplot(2,2,4)g=(sin(x).^2)-(cos(y).^2);plot(t,g)axis([0 2*pi -1 1])实例6：图形标注function shili06h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例06');t=0:pi/10:2*pi;h=plot(t,sin(t));xlabel('t=0到2\pi','fontsize',16);ylabel('sin(t)','fontsize',16);title('\it{从0to2\pi 的正弦曲线}','fontsize',16) x=get(h,'xdata');y=get(h,'ydata');imin=find(min(y)==y);imax=find(max(y)==y);text(x(imin),y(imin),...['\leftarrow最小值=',num2str(y(imin))],...'fontsize',16)text(x(imax),y(imax),...['\leftarrow最大值=',num2str(y(imax))],...'fontsize',16)实例7：条形图形function shili07h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例07');tiao1=[562 548 224 545 41 445 745 512];tiao2=[47 48 57 58 54 52 65 48];t=0:7;bar(t,tiao1)xlabel('X轴');ylabel('TIAO1值');h1=gca;h2=axes('position',get(h1,'position'));plot(t,tiao2,'linewidth',3)set(h2,'yaxislocation','right','color','none','xticklabel',[]) 实例8：区域图形function shili08h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例08');x=91:95;profits1=[88 75 84 93 77];profits2=[51 64 54 56 68];profits3=[42 54 34 25 24];profits4=[26 38 18 15 4];area(x,profits1,'facecolor',[0.5 0.9 0.6],...'edgecolor','b',...'linewidth',3)hold onarea(x,profits2,'facecolor',[0.9 0.85 0.7],...'edgecolor','y',...'linewidth',3)hold onarea(x,profits3,'facecolor',[0.3 0.6 0.7],...'edgecolor','r',...'linewidth',3)hold onarea(x,profits4,'facecolor',[0.6 0.5 0.9],...'edgecolor','m',...'linewidth',3)hold offset(gca,'xtick',[91:95])set(gca,'layer','top')gtext('\leftarrow第一季度销量')gtext('\leftarrow第二季度销量')gtext('\leftarrow第三季度销量')gtext('\leftarrow第四季度销量')xlabel('年','fontsize',16);ylabel('销售量','fontsize',16);实例9：饼图的绘制function shili09h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例09');t=[54 21 35;68 54 35;45 25 12;48 68 45;68 54 69];x=sum(t);h=pie(x);textobjs=findobj(h,'type','text');str1=get(textobjs,{'string'});val1=get(textobjs,{'extent'});oldext=cat(1,val1{:});names={'商品一：';'商品二：';'商品三：'};str2=strcat(names,str1);set(textobjs,{'string'},str2)val2=get(textobjs,{'extent'});newext=cat(1,val2{:});offset=sign(oldext(:,1)).*(newext(:,3)-oldext(:,3))/2; pos=get(textobjs,{'position'});textpos=cat(1,pos{:});textpos(:,1)=textpos(:,1)+offset;set(textobjs,{'position'},num2cell(textpos,[3,2]))实例10：阶梯图function shili10h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例10');a=0.01;b=0.5;t=0:10;f=exp(-a*t).*sin(b*t);stairs(t,f)hold onplot(t,f,':*')hold offglabel='函数e^{-(\alpha*t)}sin\beta*t的阶梯图'; gtext(glabel,'fontsize',16)xlabel('t=0:10','fontsize',16)axis([0 10 -1.2 1.2])实例11：枝干图function shili11h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例11');x=0:pi/20:2*pi;y1=sin(x);y2=cos(x);h1=stem(x,y1+y2);hold onh2=plot(x,y1,'^r',x,y2,'*g');hold offh3=[h1(1);h2];legend(h3,'y1+y2','y1=sin(x)','y2=cos(x)') xlabel('自变量X');ylabel('函数值Y');title('正弦函数与余弦函数的线性组合');实例12：罗盘图function shili12h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例12');winddirection=[54 24 65 84256 12 235 62125 324 34 254];windpower=[2 5 5 36 8 12 76 14 10 8];rdirection=winddirection*pi/180;[x,y]=pol2cart(rdirection,windpower); compass(x,y);desc={'风向和风力','气象台','10月1日0：00到','10月1日12：00'};gtext(desc)实例13：轮廓图function shili13h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例13');[th,r]=meshgrid((0:10:360)*pi/180,0:0.05:1); [x,y]=pol2cart(th,r);z=x+i*y;f=(z.^4-1).^(0.25);contour(x,y,abs(f),20)axis equalxlabel('实部','fontsize',16);ylabel('虚部','fontsize',16);h=polar([0 2*pi],[0 1]);delete(h)hold oncontour(x,y,abs(f),20)实例14：交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点'); disp('单击鼠标右键点取最后一个点'); but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点');x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例14：交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点'); disp('单击鼠标右键点取最后一个点'); but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点');x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例15：变换的傅立叶函数曲线function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren') h=uicontrol('style','slider','position',...[100 10 500 20],'min',1,'max',20) for j=1:20plot(fft(eye(j+16)))set(h,'value',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例16：劳伦兹非线形方程的无序活动function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren') h=uicontrol('style','slider','position',...[100 10 500 20],'min',1,'max',20) for j=1:20plot(fft(eye(j+16)))set(h,'value',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例17：填充图function shili17h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例17');t=(1:2:15)*pi/8;x=sin(t);y=cos(t);fill(x,y,'r')axis square offtext(0,0,'STOP',...'color',[1 1 1],...'fontsize',50,...'horizontalalignment','center') 例18：条形图和阶梯形图function shili18h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例18');subplot(2,2,1)x=-3:0.2:3;y=exp(-x.*x);bar(x,y)title('2-D Bar Chart')subplot(2,2,2)x=-3:0.2:3;y=exp(-x.*x);bar3(x,y,'r')title('3-D Bar Chart')subplot(2,2,3)x=-3:0.2:3;y=exp(-x.*x);stairs(x,y)title('Stair Chart')subplot(2,2,4)x=-3:0.2:3;y=exp(-x.*x);barh(x,y)title('Horizontal Bar Chart')实例19：三维曲线图function shili19h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例19');subplot(2,1,1)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,y1,z1,x,y2,z2,x,y3,z3)grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:3-D Plot')subplot(2,1,2)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,z1,y1,x,z2,y2,x,z3,y3)grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:3-D Plot')实例20：图形的隐藏属性function shili20h0=figure('toolbar','none',...'position',[200 150 450 300],...'name','实例20');subplot(1,2,1)[x,y,z]=sphere(10);mesh(x,y,z)axis offtitle('Figure1:Opaque')hidden onsubplot(1,2,2)[x,y,z]=sphere(10);mesh(x,y,z)axis offtitle('Figure2:Transparent') hidden off实例21PEAKS函数曲线function shili21h0=figure('toolbar','none',...'position',[200 100 450 450],...'name','实例21');[x,y,z]=peaks(30);subplot(2,1,1)x=x(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(x>-0.6&x<0.5);z(i,j)=nan*z(i,j);surfc(x,y,z)xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:surfc函数形成的曲面') subplot(2,1,2)x=x(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(x>-0.6&x<0.5);z(i,j)=nan*z(i,j);surfl(x,y,z)xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:surfl函数形成的曲面')实例22：片状图function shili22h0=figure('toolbar','none',...'position',[200 150 550 350],...'name','实例22');subplot(1,2,1)x=rand(1,20);y=rand(1,20);z=peaks(x,y*pi);t=delaunay(x,y);trimesh(t,x,y,z)hidden offtitle('Figure1:Triangular Surface Plot'); subplot(1,2,2)x=rand(1,20);y=rand(1,20);z=peaks(x,y*pi);t=delaunay(x,y);trisurf(t,x,y,z)title('Figure1:Triangular Surface Plot'); 实例23：视角的调整function shili23h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例23');x=-5:0.5:5;[x,y]=meshgrid(x);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;subplot(2,2,1)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure1')view(-37.5,30)subplot(2,2,2)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure2')view(-37.5+90,30)subplot(2,2,3)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure3')view(-37.5,60)subplot(2,2,4)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure4')view(180,0)实例24：向量场的绘制function shili24h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例24');subplot(2,2,1)z=peaks;ribbon(z)title('Figure1')subplot(2,2,2)[x,y,z]=peaks(15);[dx,dy]=gradient(z,0.5,0.5); contour(x,y,z,10)hold onquiver(x,y,dx,dy)hold offtitle('Figure2')subplot(2,2,3)[x,y,z]=peaks(15);[nx,ny,nz]=surfnorm(x,y,z);surf(x,y,z)hold onquiver3(x,y,z,nx,ny,nz)hold offtitle('Figure3')subplot(2,2,4)x=rand(3,5);y=rand(3,5);z=rand(3,5);c=rand(3,5);fill3(x,y,z,c)grid ontitle('Figure4')实例25：灯光定位function shili25h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例25');vert=[1 1 1;1 2 1;2 2 1;2 1 1;1 1 2;12 2;2 2 2;2 1 2];fac=[1 2 3 4;2 6 7 3;4 3 7 8;15 8 4;1 2 6 5;5 6 7 8];grid offsphere(36)h=findobj('type','surface');set(h,'facelighting','phong',...'facecolor',...'interp',...'edgecolor',[0.4 0.4 0.4],...'backfacelighting',...'lit')hold onpatch('faces',fac,'vertices',vert,...'facecolor','y');light('position',[1 3 2]);light('position',[-3 -1 3]); material shinyaxis vis3d offhold off实例26：柱状图function shili26h0=figure('toolbar','none',...'position',[200 50 450 450],...'name','实例26');subplot(2,1,1)x=[5 2 18 7 39 8 65 5 54 3 2];bar(x)xlabel('X轴');ylabel('Y轴');title('第一子图');subplot(2,1,2)y=[5 2 18 7 39 8 65 5 54 3 2];barh(y)xlabel('X轴');ylabel('Y轴');title('第二子图');实例27：设置照明方式function shili27h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例27');subplot(2,2,1)sphereshading flatcamlight leftcamlight rightlighting flatcolorbaraxis offtitle('Figure1')subplot(2,2,2)sphereshading flatcamlight leftcamlight rightlighting gouraudcolorbaraxis offtitle('Figure2')subplot(2,2,3)sphereshading interpcamlight rightcamlight leftlighting phongcolorbaraxis offtitle('Figure3')subplot(2,2,4)sphereshading flatcamlight leftcamlight rightlighting nonecolorbaraxis offtitle('Figure4')实例28：羽状图function shili28h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例28');subplot(2,1,1)alpha=90:-10:0;r=ones(size(alpha));m=alpha*pi/180;n=r*10;[u,v]=pol2cart(m,n);feather(u,v)title('羽状图')axis([0 20 0 10])subplot(2,1,2)t=0:0.5:10;x=0.05+i;y=exp(-x*t);feather(y)title('复数矩阵的羽状图')实例29：立体透视（1）function shili29h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例29');[x,y,z]=meshgrid(-2:0.1:2,...-2:0.1:2,...-2:0.1:2);v=x.*exp(-x.^2-y.^2-z.^2);grid onfor i=-2:0.5:2;h1=surf(linspace(-2,2,20),...linspace(-2,2,20),...zeros(20)+i);rotate(h1,[1 -1 1],30)dx=get(h1,'xdata');dy=get(h1,'ydata');dz=get(h1,'zdata');delete(h1)slice(x,y,z,v,[-2 2],2,-2)hold onslice(x,y,z,v,dx,dy,dz)hold offaxis tightview(-5,10)drawnowend实例30：立体透视（2）function shili30h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例30');[x,y,z]=meshgrid(-2:0.1:2,...-2:0.1:2,...-2:0.1:2);v=x.*exp(-x.^2-y.^2-z.^2); [dx,dy,dz]=cylinder;slice(x,y,z,v,[-2 2],2,-2)for i=-2:0.2:2h=surface(dx+i,dy,dz);rotate(h,[1 0 0],90)xp=get(h,'xdata');yp=get(h,'ydata');zp=get(h,'zdata');delete(h)hold onhs=slice(x,y,z,v,xp,yp,zp);axis tightxlim([-3 3])view(-10,35)drawnowdelete(hs)hold offend实例31：表面图形function shili31h0=figure('toolbar','none',...'position',[200 150 550 250],...'name','实例31');subplot(1,2,1)x=rand(100,1)*16-8;y=rand(100,1)*16-8;r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;xlin=linspace(min(x),max(x),33); ylin=linspace(min(y),max(y),33); [X,Y]=meshgrid(xlin,ylin);Z=griddata(x,y,z,X,Y,'cubic'); mesh(X,Y,Z)axis tighthold onplot3(x,y,z,'.','Markersize',20)subplot(1,2,2)k=5;n=2^k-1;theta=pi*(-n:2:n)/n;phi=(pi/2)*(-n:2:n)'/n;X=cos(phi)*cos(theta);Y=cos(phi)*sin(theta);Z=sin(phi)*ones(size(theta));colormap([0 0 0;1 1 1])C=hadamard(2^k);surf(X,Y,Z,C)axis square实例32：沿曲线移动的小球h0=figure('toolbar','none',...'position',[198 56 408 468],...'name','实例32');h1=axes('parent',h0,...'position',[0.15 0.45 0.7 0.5],...'visible','on');t=0:pi/24:4*pi;y=sin(t);plot(t,y,'b')n=length(t);h=line('color',[0 0.5 0.5],...'linestyle','.',...'markersize',25,...'erasemode','xor');k1=uicontrol('parent',h0,...'style','pushbutton',...'position',[80 100 50 30],...'string','开始',...'callback',[...'i=1;',...'k=1;,',...'m=0;,',...'while 1,',...'if k==0,',...'break,',...'end,',...'if k~=0,',...'set(h,''xdata'',t(i),''ydata'',y(i)),',...'drawnow;,',...'i=i+1;,',...'if i>n,',...'m=m+1;,',...'i=1;,',...'end,',...'end,',...'end']);k2=uicontrol('parent',h0,...'style','pushbutton',...'position',[180 100 50 30],...'string','停止',...'callback',[...'k=0;,',...'set(e1,''string'',m),',...'p=get(h,''xdata'');,',...'q=get(h,''ydata'');,',...'set(e2,''string'',p);,',...'set(e3,''string'',q)']); k3=uicontrol('parent',h0,...'style','pushbutton',...'position',[280 100 50 30],...'string','关闭',...'callback','close');e1=uicontrol('parent',h0,...'style','edit',...'position',[60 30 60 20]);t1=uicontrol('parent',h0,...'style','text',...'string','循环次数',...'position',[60 50 60 20]);e2=uicontrol('parent',h0,...'style','edit',...'position',[180 30 50 20]); t2=uicontrol('parent',h0,...'style','text',...'string','终点的X坐标值',...'position',[155 50 100 20]); e3=uicontrol('parent',h0,...'style','edit',...'position',[300 30 50 20]); t3=uicontrol('parent',h0,...'style','text',...'string','终点的Y坐标值',...'position',[275 50 100 20]);实例33：曲线转换按钮h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例33');x=0:0.5:2*pi;y=sin(x);h=plot(x,y);grid onhuidiao=[...'if i==1,',...'i=0;,',...'y=cos(x);,',...'delete(h),',...'set(hm,''string'',''正弦函数''),',...'h=plot(x,y);,',...'grid on,',...'else if i==0,',...'i=1;,',...'y=sin(x);,',...'set(hm,''string'',''余弦函数''),',...'delete(h),',...'h=plot(x,y);,',...'grid on,',...'end,',...'end'];hm=uicontrol(gcf,'style','pushbutton',...'string','余弦函数',...'callback',huidiao);i=1;set(hm,'position',[250 20 60 20]);set(gca,'position',[0.2 0.2 0.6 0.6])title('按钮的使用')hold on实例34：栅格控制按钮h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例34');x=0:0.5:2*pi;y=sin(x);plot(x,y)huidiao1=[...'set(h_toggle2,''value'',0),',...'grid on,',...];huidiao2=[...'set(h_toggle1,''value'',0),',...'grid off,',...];h_toggle1=uicontrol(gcf,'style','togglebutton',...'string','grid on',...'value',0,...'position',[20 45 50 20],...'callback',huidiao1);h_toggle2=uicontrol(gcf,'style','togglebutton',...'string','grid off',...'value',0,...'position',[20 20 50 20],...'callback',huidiao2);set(gca,'position',[0.2 0.2 0.6 0.6])title('开关按钮的使用')实例35：编辑框的使用h0=figure('toolbar','none',...'position',[200 150 350 250],...'name','实例35');f='Please input the letter';huidiao1=[...'g=upper(f);,',...'set(h2_edit,''string'',g),',...];huidiao2=[...'g=lower(f);,',...'set(h2_edit,''string'',g),',...];h1_edit=uicontrol(gcf,'style','edit',...'position',[100 200 100 50],...'HorizontalAlignment','left',...'string','Please input the letter',...'callback','f=get(h1_edit,''string'');',...'background','w',...'max',5,...'min',1);h2_edit=uicontrol(gcf,'style','edit',...'HorizontalAlignment','left',...'position',[100 100 100 50],...'max',5,...'min',1);h1_button=uicontrol(gcf,'style','pushbutton',...'string','小写变大写',...'position',[100 45 100 20],...'callback',huidiao1);h2_button=uicontrol(gcf,'style','pushbutton',...'string','大写变小写',...'position',[100 20 100 20],...'callback',huidiao2);实例36：弹出式菜单h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例36');x=0:0.5:2*pi;y=sin(x);h=plot(x,y);grid onhm=uicontrol(gcf,'style','popupmenu',...'string',...'sin(x)|cos(x)|sin(x)+cos(x)|exp(-sin(x))',...'position',[250 20 50 20]);set(hm,'value',1)huidiao=[...'v=get(hm,''value'');,',...'switch v,',...'case 1,',...'delete(h),',...'y=sin(x);,',...'h=plot(x,y);,',...'grid on,',...'case 2,',...'delete(h),',...'y=cos(x);,',...'h=plot(x,y);,',...'grid on,',...'case 3,',...'delete(h),',...'y=sin(x)+cos(x);,',...'h=plot(x,y);,',...'grid on,',...'case 4,',...'y=exp(-sin(x));,',...'h=plot(x,y);,',...'grid on,',...'end'];set(hm,'callback',huidiao)set(gca,'position',[0.2 0.2 0.6 0.6])title('弹出式菜单的使用')实例37：滑标的使用h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例37');[x,y]=meshgrid(-8:0.5:8);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;h0=mesh(x,y,z);h1=axes('position',...[0.2 0.2 0.5 0.5],...'visible','off');htext=uicontrol(gcf,...'units','points',...'position',[20 30 45 15],...'string','brightness',...'style','text');hslider=uicontrol(gcf,...'units','points',...'position',[10 10 300 15],...'min',-1,...'max',1,...'style','slider',...'callback',...'brighten(get(hslider,''value''))');实例38：多选菜单h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例38');[x,y]=meshgrid(-8:0.5:8);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;h0=mesh(x,y,z);hlist=uicontrol(gcf,'style','listbox',...'string','default|spring|summer|autumn|winter',...'max',5,...'min',1,...'position',[20 20 80 100],...'callback',[...'k=get(hlist,''value'');,',...'switch k,',...'case 1,',...'colormap default,',...'case 2,',...'colormap spring,',...'case 3,',...'colormap summer,',...'case 4,',...'colormap autumn,',...'case 5,',...'colormap winter,',...'end']);实例39：菜单控制的使用h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例39');x=0:0.5:2*pi;y=cos(x);h=plot(x,y);grid onset(gcf,'toolbar','none')hm=uimenu('label','example');huidiao1=[...'set(hm_gridon,''checked'',''on''),',...'set(hm_gridoff,''checked'',''off''),',...'grid on'];huidiao2=[...'set(hm_gridoff,''checked'',''on''),',...'set(hm_gridon,''checked'',''off''),',...'grid off'];hm_gridon=uimenu(hm,'label','grid on',...'checked','on',...'callback',huidiao1);hm_gridoff=uimenu(hm,'label','grid off',...'checked','off',...'callback',huidiao2);实例40：UIMENU菜单的应用。

数值分析(hilbert矩阵)病态线性方程组的求解matlab程序

（Hilbert 矩阵）病态线性方程组的求解理论分析表明，数值求解病态线性方程组很困难。

考虑求解如下的线性方程组的求解Hx = b ，期中H 是Hilbert 矩阵，()ij n n Hh ，11ij h i j ，i ，j = 1,2，…，n 1.估计矩阵的2条件数和阶数的关系2.对不同的n ，取(1,1,,1)nx K ?，分别用Gauss 消去，Jacobi 迭代，Gauss-seidel 迭代，SOR 迭代和共轭梯度法求解，比较结果。

3.结合计算结果，试讨论病态线性方程组的求解。

第1小题：condition.m %第1小题程序t1=20;%阶数n=20x1=1:t1;y1=1:t1;for i=1:t1H=hilb(i);y1(i)=log(cond(H));endplot(x1,y1);xlabel('阶数n');ylabel('2-条件数的对数（log(cond(H)）');title('2-条件数的对数（log(cond(H)）与阶数n 的关系图');t2=200;%阶数n=200x2=1:t2;y2=1:t2;for i=1:t2H=hilb(i);y2(i)=log(cond(H));endplot(x2,y2);xlabel('阶数n');ylabel('2-条件数的对数（log(cond(H)）');title('2-条件数的对数（log(cond(H)）与阶数n 的关系图');画出Hilbert 矩阵2-条件数的对数和阶数的关系n=200时n=20时从图中可以看出，1）在n小于等于13之前，图像近似直线log（cond（H））~1.519n-1.8332）在n大于13之后，图像趋于平缓，并在一定范围内上下波动，同时随着n的增加稍有上升的趋势第2小题：solve.m%m第2小题主程序N=4000;xGauss=zeros(N,1);xJacobi=zeros(N,1);xnJ=zeros(N,1);xGS=zeros(N,1);xnGS=zeros(N,1);xSOR=zeros(N,1);xnSOR=zeros(N,1);xCG=zeros(N,1);xnCG=zeros(N,1);for n=1:N;x=ones(n,1);t=1.1;%初始值偏差x0=t*x;%迭代初始值e=1.0e-8;%给定的误差A=hilb(n);b=A*x;max=100000000000;%可能最大的迭代次数w=0.5;%SOR迭代的松弛因子G=Gauss(A,b);[J,nJ]=Jacobi(A,b,x0,e,max);[GS,nGS]=G_S(A,b,x0,e,max);[S_R,nS_R]=SOR(A,b,x0,e,max,w);[C_G,nC_G]=CG(A,b,x0,e,max);normG=norm(G'-x);xGauss(n)=normG;normJ=norm(J-x);nJ;xJacobi(n)=normJ;xnJ(n)=nJ;normGS=norm(GS-x);nGS;xGS(n)=normGS;xnGS(n)=nGS;normS_R=norm(S_R-x);nS_R;xSOR(n)=normS_R;xnSOR(n)=nS_R;normC_G=norm(C_G-x);nC_G;xCG(n)=normC_G;xnCG(n)=nC_G;endGauss.m%Gauss消去法function x=Gauss(A,b)n=length(b);l=zeros(n,n);x=zeros(1,n);%消去过程for i=1:n-1for j=i+1:nl(j,i)=A(j,i)/A(i,i);for k=i:nA(j,k)=A(j,k)-l(j,i)*A(i,k);endb(j)=b(j)-l(j,i)*b(i);endend%回代过程x(n)=b(n)/A(n,n);for i=n-1:-1:1c=A(i,:).*x;x(i)=(b(i)-sum(c(i+1:n)))/A(i,i);endJacobi.m%Jacobi迭代,x0表示迭代初值,e表示允许误差(迭代停止条件),n表示迭代次数,m 可能最大的迭代次数function [x,n]=Jacobi(A,b,x0,e,m)n=length(A);D=diag(diag(A));U=-triu(A,1);L=-tril(A,-1);B=D\(L+U);f=D\b;x=B*x0+f;n=1;while norm(x-x0)>ex0=x;x=B*x0+f;n=n+1;if n>mdisp('Jacobi迭代次数过多，迭代可能不收敛');break;endendG_S.m%Gauss-Seidel迭代,x0表示迭代初值,e表示允许误差(迭代停止条件),n表示迭代次数,m可能最大的迭代次数function [x,n]=G_S(A,b,x0,e,m)n=length(A);D=diag(diag(A));U=-triu(A,1);L=-tril(A,-1);B=(D-L)\U;f=(D-L)\b;x=B*x0+f;n=1;while norm(x-x0)>ex0=x;x=B*x0+f;n=n+1;if n>mdisp('Gauss-Seidel迭代次数过多，迭代可能不收敛');break;endendSOR.m%SOR超松弛迭代,x0表示迭代初值,e表示允许误差(迭代停止条件),n表示迭代次数,m可能最大的迭代次数,w松弛因子function [x,n]=SOR(A,b,x0,e,m,w)n=length(A);D=diag(diag(A));U=-triu(A,1);L=-tril(A,-1);B=(D-w*L)\((1-w)*D+w*U);f=(D-w*L)\b*w;x=B*x0+f;n=1;while norm(x-x0)>ex0=x;x=B*x0+f;n=n+1;if n>mdisp('SOR超松弛迭代次数过多，迭代可能不收敛');break;endendCG.m%CG共轭梯度法,x0表示迭代初值,e表示允许误差(迭代停止条件),n表示迭代次数,m可能最大的迭代次数function [x,n]=CG(A,b,x0,e,m)r=b-A*x0;p=r;alpha=(r'*r)/(p'*(A*p));x=x0+alpha*p;r1=b-A*x;n=1;while norm(r1)>ebelta=(r1'*r1)/(r'*r);p=r1+belta*p;r=r1;x0=x;alpha=(r'*r)/(p'*(A*p));x=x0+alpha*p;r1=b-A*x;n=n+1;if n>mdisp('CG共轭梯度法迭代次数过多，迭代可能不收敛');break;endend。

数值分析MATLAB编程——数值积分法

数值分析MATLAB编程——数值积分法1、调用函数--f.Mfunction y=f(x)%------------------------------------------------------------函数1 y=sqrt(4-sin(x)*sin(x));%------------------------------------------------------------函数2 %y=sin(x)/x;%if x==0% y=0;%end%------------------------------------------------------------函数3 %y=exp(x)/(4+x*x);%------------------------------------------------------------函数4 %y=(log(1+x))/(1+x*x);2、复合梯形公式--tixing.M%复合梯形公式clear alla=input('请输入积分下限:');b=input('请输入积分上限:');n=input('区间n等分：');h=(b-a)/n;x=a:h:b;T=0;for k=1:n;T=0.5*h*(f(x(k))+f(x(k+1)))+T;endT=vpa(T,8)3、复合Simpson公式--simpson.M%复合Simpson公式clear alla=input('请输入积分下限:');b=input('请输入积分上限:');n=input('区间n等分：');h=(b-a)/n;x=a:h:b;S=0;for k=1:n;xx=(x(k)+x(k+1))/2;S=(1/6)*h*(f(x(k))+4*f(xx)+f(x(k+1)))+S;endS=vpa(S,8)4、Romberg算法--romberg.M%Romberg算法clear alla=input('请输入积分下限:');b=input('请输入积分上限:');n=input('区间n等分：');num=0:n;R=[num'];h=b-a;T=h*(f(a)+f(b))/2;t(1)=T;for i=2:n+1;u=h/2;H=0;x=a+u;while x<b;H=H+f(x);x=x+h;endt(i)=(T+h*H)/2;T=t(i);h=u;endR=[R,t'];for i=2:n+1for j=n+1:-1:1if j>=it(j)=(4^(i-1)*t(j)-t(j-1))/(4^(i-1)-1);elset(j)=0;endendR=[R,t'];endR=vpa(R,8)R(n,n)5、变步长算法（以复化梯形公式为例）--tixing2.M%复合梯形公式，确定最佳步长format longclear alla=input('请输入积分下限:');b=input('请输入积分上限:');eps=input('请输入误差：');k=1;T1=(b-a)*(f(a)+f(b))/2;T2=(T1+(b-a)*(f((a+b)/2)))/2; while abs((T1-T2)/3)>=epsM=0;n=2^k;h=(b-a)/n;T1=T2;x=a:h:b;for i=1:n;xx=(x(i)+x(i+1))/2;M=M+f(xx);endT2=(T1+h*M)/2;k=k+1;endT=vpa(T2,8)n=2^k。

如何在Matlab中进行数值积分和数值解

如何在Matlab中进行数值积分和数值解在数学和工程领域，数值积分和数值解是常见的技术手段，可以帮助我们求解复杂的数学问题和实际工程中的模型。

本文将介绍如何使用Matlab进行数值积分和数值解，以及一些注意事项和常用的方法。

一、数值积分数值积分是计算定积分的近似值的方法，可以通过数值逼近或数值插值来实现。

在Matlab中，有几种常用的函数可以用于数值积分，比如trapz、quad等。

1. trapz函数trapz函数是用梯形法则计算积分的函数。

它的使用方法是将要积分的函数作为输入的第一个参数，x轴上的点作为输入的第二个参数。

例如，要计算函数f(x)在区间[a, b]上的积分，可以使用以下代码：result = trapz(x, f(x));2. quad函数quad函数是使用自适应数值积分算法计算积分的函数。

它的使用方法是将要积分的函数作为输入的第一个参数，积分区间的下限和上限作为输入的第二个和第三个参数。

例如，要计算函数f(x)在区间[a, b]上的积分，可以使用以下代码：result = quad(@(x) f(x), a, b);二、数值解数值解是使用数值方法求解复杂的数学问题或实际工程中的模型的近似解。

在Matlab中，有几种常用的函数可以用于数值解，比如fsolve、ode45等。

1. fsolve函数fsolve函数是用于求解非线性方程组的函数。

它的使用方法是将非线性方程组表示为一个函数，然后将该函数作为输入的第一个参数。

例如，要求解方程组f(x) = 0，可以使用以下代码：x = fsolve(@(x) f(x), x0);其中x0是方程的初始猜测值。

2. ode45函数ode45函数是求解常微分方程初值问题的函数。

它的使用方法是将微分方程表示为一个函数，然后将该函数作为输入的第一个参数。

例如，要求解常微分方程dy/dx = f(x, y)，可以使用以下代码：[t, y] = ode45(@(t, y) f(t, y), tspan, y0);其中tspan是时间区间，y0是初始条件。

东南大学《数值分析》上机题

数值分析上机题1设2211NN j S j ==-∑，其精确值为1311221N N ⎛⎫-- ⎪+⎝⎭。

（1）编制按从大到小的顺序22211121311N S N =+++---，计算N S 的通用程序。

（2）编制按从小到大的顺序2221111(1)121N S N N =+++----，计算NS 的通用程序。

（3）按两种顺序分别计算210S ，410S ，610S ，并指出有效位数。

（编制程序时用单精度）（4）通过本上机题，你明白了什么？程序代码（matlab 编程）：clc cleara=single(1./([2:10^7].^2-1)); S1(1)=single(0); S1(2)=1/(2^2-1); for N=3:10^2 S1(N)=a(1); for i=2:N-1S1(N)=S1(N)+a(i); end endS2(1)=single(0); S2(2)=1/(2^2-1); for N=3:10^2 S2(N)=a(N-1);for i=linspace(N-2,1,N-2) S2(N)=S2(N)+a(i); end endS1表示按从大到小的顺序的S N S2表示按从小到大的顺序的S N通过本上机题，看出按两种不同的顺序计算的结果是不相同的，按从大到小的顺序计算的值与精确值有较大的误差，而按从小到大的顺序计算的值与精确值吻合。

从大到小的顺序计算得到的结果的有效位数少。

计算机在进行数值计算时会出现“大数吃小数”的现象，导致计算结果的精度有所降低，我们在计算机中进行同号数的加法时，采用绝对值较小者先加的算法，其结果的相对误差较小。

数值分析上机题220．（上机题）Newton 迭代法（1）给定初值0x 及容许误差ε，编制Newton 法解方程()0f x =根的通用程序。

（2）给定方程3()/30f x x x =-=，易知其有三个根1x *=，20x *=，3x *=。

matlab_examples(数值分析)

方程求根数值实验
Experiments in Finding Root of Equation
计算方法课程组
华中科技大学数学与统计学院
1
方程求根 —二分法
一、实验目的
1) 熟悉Matlab编程 ; 2) 应用 Matlab实现二分法，牛顿迭代法等求根算法 ;
二、二分法
基本思想: 二分法通过不断搜索有根区间，最终收缩为一点。算法简单、容易且保证算法收敛。
答案: x=1.3247
f(x)=-7.6580e-005
5
作
业
参看范例代码(.m文件) 独立完成如下编程内容:
6
2
方程求根 —二分法
function [xvect,xdif,fx,nit]=bisect(fun,a,b,toll,nmax)
% % % % % % % % % % 求根算法:二分法 [xvect,xdif,fx,nit]=bisect(fun,a,b,toll,nmax) fun 求根函数名 [a,b] 最初的有根区间的范围 toll 精度,默认为10e-5 nmax 最大迭代次数 xvect 返回所得根 xdif 返回缩小的根区间的长度 fx 返回函数值 nit 返回满足要求的迭代次数
bisect _main.m
x=1:0.01:2;
y=x.^3-x-1; plot(xห้องสมุดไป่ตู้y);hold on;
运行结果:
plot(x,zeros(size(x)),'r-.');
fun=inline('x^3-x-1');
[xvect,xdif,fx,nit]=bisect(fun,1,2,0.005,100);
disp((['

数值分析在生活中的应用举例及Matlab实现

一、最小二乘法，用MATLAB实现1. 数值实例下面给定的是乌鲁木齐最近1个月早晨7：00左右（新疆时间）的天气预报所得到的温度，按照数据找出任意次曲线拟合方程和它的图像。

下面用MATLAB编程对上述数据进行最小二乘拟合。

下面用MATLAB编程对上述数据进行最小二乘拟合2、程序代码x=[1:1:30];y=[9,10,11,12,13,14,13,12,11,9,10,11,12,13,14,12,11,10,9,8,7,8,9,11,9,7,6,5,3,1];a1=polyfit(x,y,3) %三次多项式拟合%a2= polyfit(x,y,9) %九次多项式拟合%a3= polyfit(x,y,15) %十五次多项式拟合%b1=polyval(a1,x)b2=polyval(a2,x)b3=polyval(a3,x)r1= sum((y-b1).^2) %三次多项式误差平方和%r2= sum((y-b2).^2) %九次次多项式误差平方和%r3= sum((y-b3).^2) %十五次多项式误差平方和%plot(x,y,'*') %用*画出x,y图像%hold onplot(x,b1, 'r') %用红色线画出x,b1图像%hold onplot(x,b2, 'g') %用绿色线画出x,b2图像%hold onplot(x,b3, 'b:o') %用蓝色o线画出x,b3图像%3、数值结果不同次数多项式拟合误差平方和为：r1=67.6659r2=20.1060r3=3.7952r1、r2、r3分别表示三次、九次、十五次多项式误差平方和。

4、拟合曲线如下图二、线性方程组的求解（高斯-塞德尔迭代算法）1、实例：求解线性方程组（见书P233页）⎪⎪⎩⎪⎪⎨⎧=++=-+=+-3612363311420238321321321x x x x x x x x x 记A x=b, 其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=363320,,12361114238321b x A x x x任取初始值()()Tx0000=，进行迭代。

数值分析matlab数值试验

实验一：误差传播及算法稳定性实验1.21、试验程序：function charpt1_2% 误差传播及算法稳定性实验clc;clear all;promps={'请选择递推关系式，若选E1=1/e,En=1-nEn-1,请输入1，若选EN=0，En-1=(1-En)/n,请输入2：'};I=1;while Iresult=inputdlg(promps,'charpt1_2',1,{'1'});Nb=str2num(char(result));if ((Nb~=1)|(Nb~=2))I=0;endend%%%%%%%%%%%%%%%%%I=1;while Iresult=inputdlg('请输入递推步数 n>=1:','charpt1_2',1,{'10'});steps=str2num(char(result));if (steps>0)&(steps==fix(steps)) %% 如果steps大于0且为整数I=0;endend%%%%%%%%%%%%%%%%%result=inputdlg('请输入计算中所采用的有效数字位数n:','charpt1_2',1,{'5'});Sd=str2num(char(result));format long %% 设置显示精度result=zeros(1,steps); %% 存储计算结果err=result; %% 存储计算的绝对误差值func=result; %% 存储用quadl计算的近似值%%%%%%%%%%%%%%%%%%% 用quadl计算积分近似值for n=1:stepsfun=@(x) x.^n.*exp(x-1);func(n)= quadl(fun,0,1);end%%%%%%%%%%%%%%%%%%% 用自定义算法计算if(Nb==1)digits(Sd);result(1)=subs(vpa(1/exp(1)));for n=2:stepsresult(n)=subs(vpa(1-n*result(n-1)));enderr=abs(result-func);elseif(Nb==2)digits(Sd);result(steps)=0;for n=(steps-1):-1:1result(n)=subs(vpa((1-result(n+1))/(n+1)));enderr=abs(result-func);end%%%%%%%%%%%%%%%%%%% 输出结果数值及图像clf;disp('库函数计算值:');disp(sprintf('%e ',func));disp('递推值:');disp(sprintf('%e ',result));disp('误差值:');disp(sprintf('%e ',err));if(Nb==1)plot([1:steps],result,'-rs',[1:steps],func,':k*',[1:steps],err,'-.bo' );elseif(Nb==2)plot([steps:-1:1],result,'-rs',[steps:-1:1],func,':k*',[steps:-1:1],e rr,'-.bo');endxlabel('第n步');ylabel('计算值');legend('自定义算法结果','库函数计算结果','误差值');grid on2、试验结果：选择递推关系式1，递推步数为10，有效数字为5位，计算结果如下：库函数计算值:3.678794e-001 2.642411e-001 2.072766e-001 1.708934e-001 1.455329e-0011.268024e-001 1.123836e-001 1.009323e-001 9.161229e-002 8.387707e-002递推值:3.678800e-001 2.642400e-001 2.072800e-001 1.708800e-001 1.456000e-0011.264000e-001 1.152000e-001 7.840000e-0022.944000e-001 -1.944000e+000误差值:5.588280e-007 1.117662e-006 3.352927e-006 1.341222e-0056.705713e-005 4.023702e-004 2.816427e-003 2.253226e-002 2.027877e-001 2.027877e+00012345678910第n 步计算值选择递推关系式2，递推步数为10，有效数字为5位，计算结果如下：库函数计算值:3.678794e-001 2.642411e-001 2.072766e-001 1.708934e-001 1.455329e-001 1.268024e-001 1.123836e-001 1.009323e-001 9.161229e-002 8.387707e-002 递推值:3.678800e-001 2.642400e-001 2.072800e-001 1.708900e-001 1.455300e-001 1.267900e-001 1.125000e-001 1.000000e-001 1.000000e-001 0.000000e+000 误差值:5.588280e-007 1.117662e-006 3.352927e-006 3.412224e-006 2.942873e-006 1.237016e-005 1.164270e-004 9.322618e-004 8.387707e-003 8.387707e-002第n 步计算值选择递推关系式1，递推步数为10，有效数字为6位，计算结果如下：库函数计算值:3.678794e-001 2.642411e-001 2.072766e-001 1.708934e-001 1.455329e-001 1.268024e-001 1.123836e-001 1.009323e-001 9.161229e-002 8.387707e-002 递推值:3.678790e-001 2.642420e-001 2.072740e-001 1.709040e-001 1.454800e-001 1.271200e-001 1.101600e-001 1.187200e-001 -6.848000e-002 1.684800e+000 误差值:4.411720e-007 8.823378e-007 2.647073e-006 1.058778e-0055.294287e-005 3.176298e-004 2.223573e-003 1.778774e-002 1.600923e-001 1.600923e+00012345678910第n 步计算值选择递推关系式2，递推步数为10，有效数字为6位，计算结果如下：库函数计算值:3.678794e-001 2.642411e-001 2.072766e-001 1.708934e-001 1.455329e-001 1.268024e-001 1.123836e-001 1.009323e-001 9.161229e-002 8.387707e-002 递推值:3.678800e-001 2.642410e-001 2.072770e-001 1.708930e-001 1.455360e-001 1.267860e-001 1.125000e-001 1.000000e-001 1.000000e-001 0.000000e+000 误差值:5.588280e-007 1.176622e-007 3.529274e-007 4.122239e-007 3.057127e-006 1.637016e-005 1.164270e-004 9.322618e-004 8.387707e-003 8.387707e-002第n 步计算值3、结果分析：很明显第二种递推式结果要比第一种好，式1在第七步后有明显误差，而式2在第三步后基本与近似解一致。

三种迭代法matlab程序数值分析

•
end
• end
• err=abs(norm(X'-P));
• P=X'；
• if(err<delta)
•
break
• end
• end
• X=X';
• err,k
function X=jacobi(A,b,P,delta,max1) %A是n维非奇异阵。%b是n维向量。%P是初值。%delta是误差界。 %max1是给定的迭代最高次数。%X为所求的方程组AX=b的近似解。 N=length(b); for k=1:max1 for j=1:N
X(j)=(b(j)-A(j,[1:j-1,j+1:N])*P([1:j-1,j+1:N]))/A(j,j); end err=abs(norm(X'-P)); P=X'； if(err<delta)
break end end X=X';k,erction X=gseid(A,b,P,delta,max1)
• %A是n维非奇异阵。%b是n维向量。%P是初值。
• %delta是误差界。%max1是给定的迭代最高次数。%X为所求的方程组AX=b的近似解。
• N=length(b);
• for k=1:max1
• for j=1:N
•
if j==1
•
X(1)=(b(1)-A(1,2:N)*P(2:N))/A(1,1);
•
elseif j==N
•
X(N)=(b(N)-A(N,1:N-1)*(X(1:N-1))')/A(N,N);
•
else
•
X(j)=(b(j)-A(j,1:j-1)*X(1:j-1)-A(j,j+1:N)*P(j+1:N))/A(j,j);

哈工大-数值分析上机实验报告

Emax= 0.70770085900503，0 此时由 Emax 可以看出，不选主元的结果应该可以说是不正确了，这是由机器误差引起的。当 10 20 时，不选主元和选主元的计算结果如下 NaN NaN NaN Emax=NaN, 0 不选主元时，程序报错： Warning: Divide by zero. 。这是因为机器计算的最小精度为 10-15，所以此时的 10 20 就认为是 0，故出现了错误现象。而选主元时则没有这种现象，而且由 Emax 可以看出选主元时的结果应该是精确解。
x3 x 1 0
x0=1； x0=0.45, x0=0.65；
( x 1) 2 (2 x 1) 0
当 x0=0.45 时，计算结果为 x= 0.49999999999983； f(x)= -8.362754932994584e-014； k=4；由 f(x)知结果满足要求，而且又迭代次数只有 4 次看出收敛速度很快，实际上该方程确实有真解 x=0.5。当 x0=0.65 时，计算结果为 x= 0.50000000000000； f(x)=0； k=9；由 f(x)知结果满足要求，实际上该方程确实有真解 x=0.5，但迭代次数增多，实际上当取 x0〉0.68 时，x≈1，就变成了方程的另一个解，这说明 Newton 法收敛与初值很有关系，有的时候甚至可能不收敛。
实验报告
结果分析和讨论：例用最小二乘法处理下面的实验数据 . xi fi 3 2.01 4 2.98 5 3.50 6 5.02 7 5.47 8 6.02 9 7.05
Hale Waihona Puke 并作出 f ( x) 的近似分布图。分别采用一次，二次和五次多项式来拟合数据得到相应的拟合多项式为： y1=-0.38643+0.82750x ； y2=-1.03024+1.06893x-0.02012x2； y5=-50.75309+51.53527x-19.65947x2+3.66585x3-0.32886x4+0.01137x5；分别作出它们的曲线图，图中点划线为 y1 曲线，实线为 y2 曲线，虚线为 y5 曲线。’x’为给定的数据点。从图中可以看出并不是多项式次数越高越好，次数高了，曲线越能给定点处和实际吻合，但别的地方就很差了。因此，本例选用一次和两次的多项式拟合应该就可以了。

(完整word版)matlab数值分析例题

1、在MATLAB 中用Jacobi 迭代法讨论线性方程组,1231231234748212515x x x x x x x x x -+=⎧⎪-+=-⎨⎪-++=⎩（1）给出Jacobi 迭代法的迭代方程，并判定Jacobi 迭代法求解此方程组是否收敛。

（2）若收敛，编程求解该线性方程组.解（1）：A=[4 -1 1;4 —8 1;-2 1 5］ %线性方程组系数矩阵A =4 -1 1 4 -8 1 —2 1 5>> D=diag(diag(A)）D =4 0 0 0 —8 0 0 0 5〉〉 L=—tril （A,-1) ％ A 的下三角矩阵L =0 0 0 —4 0 0 2 —1 0〉〉U=-triu(A，1）% A的上三角矩阵U =0 1 —10 0 —10 0 0B=inv（D）*（L+U）% B为雅可比迭代矩阵B =0 0.2500 —0。

25000.5000 0 0.12500。

4000 —0.2000 0〉〉r=eigs(B,1）%B的谱半径r =0。

3347 〈1Jacobi迭代法收敛。

(2）在matlab上编写程序如下:A=[4 —1 1;4 -8 1;—2 1 5]；〉〉b=［7 —21 15］'；>〉x0=［0 0 0]’;〉〉［x,k］=jacobi（A,b，x0，1e—7)x =2。

00004.00003。

0000k =17附jacobi迭代法的matlab程序如下：function [x,k］=jacobi（A,b，x0，eps)% 采用Jacobi迭代法求Ax=b的解％A为系数矩阵％b为常数向量％x0为迭代初始向量％eps为解的精度控制max1= 300; %默认最多迭代300，超过300次给出警告D=diag（diag（A）)；％求A的对角矩阵L=-tril(A，—1); %求A的下三角阵U=—triu（A,1); %求A的上三角阵B=D\(L+U);f=D\b;x=B＊x0+f；k=1；%迭代次数while norm（x-x0）>=epsx0=x;x=B＊x0+f；k=k+1;if（k〉=max1)disp(’迭代超过300次，方程组可能不收敛’）；return；endend2、设有某实验数据如下：（1)在MATLAB中作图观察离散点的结构,用多项式拟合的方法拟合一个合适的多项式函数；（2）在MATLAB中作出离散点和拟合曲线图。

数值分析分段线性插值样条插值Runge函数Newton-Lagrange-Chebyshev插值多项式Runge现象matlab源程序代码

题目1：对Runge 函数R(x ) =1在区间[-1,1]作下列插值逼近，并和1 + 25x 2R(x)的图像进行比较，并对结果进行分析。

= -1 + ih,h= 0.1,0 ≤ i≤ 20 绘出它的20 次Newton 插值(1)用等距节点xi多项式的图像。

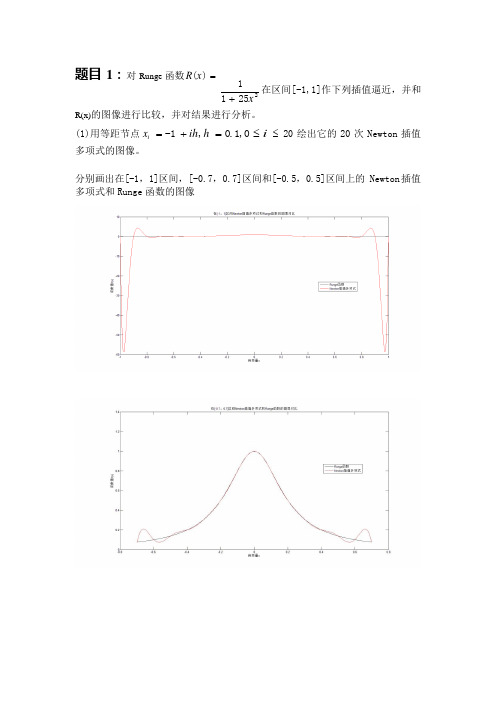
分别画出在[-1，1]区间，[-0.7，0.7]区间和[-0.5，0.5]区间上的 Newton 插值多项式和Runge 函数的图像从图中可以看出： 1）在[-0.5，0.5]区间 Newton 插值多项式和 Runge 函数的图像偏差较小，这说明 Newton 插值多项式在此区间上可以较好的逼近 Runge 函数； 2）在边界（自变量 x=-1 和 x=1）附近，Newton 插值多项式和 Runge 函数的图像偏差很大，Newton 插值多项式出现了剧烈的震荡。

（Runge 现象） (2)用节点 x = cos(2i + 1π）（, i = 0，1,2，⋅ ⋅ ⋅ ，20），绘出它的 20 次 Lagrangei 42 插值多项式的图像。

画出在[-1，1]区间上的 Lagrange 插值多项式和 Runge 函数的图像从图中可以看出：使用 Chebyshev 多项式零点构造的 Lagrange 插值多项式和 Runge 函数的图像偏差较小，没有出现 Runge 现象。

(3)用等距节点 x i 的图像。

= -1 + ih ,h = 0.1,0 ≤ i ≤ 20 绘出它的分段线性插值函数画出在[-1，1]区间上分段线性插值函数和 Runge 函数的图像从图中可以看出：使用分段线性插值函数和 Runge 函数的图像偏差较小，也没有出现 Runge 现象，只在自变量 x=0 处有稍许偏差。

(4)用等距节点 x i 函数的图像。

= -1 + ih ,h = 0.1,0 ≤ i ≤ 20 绘出它的三次自然样条插值画出在[-1，1]区间上三次自然样条插值函数和 Runge 函数的图像从图中可以看出：使用三次自然样条插值函数和 Runge 函数的图像偏差较小，也没有出现 Runge 现象。

同济大学数值分析matlab编程

同济⼤学数值分析matlab编程MATLAB 编程题库1.下⾯的数据表近似地满⾜函数21cx bax y ++=，请适当变换成为线性最⼩⼆乘问题，编程求最好的系数c b a ,,，并在同⼀个图上画出所有数据和函数图像.625.0718.0801.0823.0802.0687.0606.0356.0995.0628.0544.0008.0213.0362.0586.0931.0ii y x ----解：>> x=[-0.931 -0.586 -0.362 -0.213 0.008 0.544 0.628 0.995]'; >> y=[0.356 0.606 0.687 0.802 0.823 0.801 0.718 0.625]'; >> A= [x ones(8,1) -x.^2.*y]; >> z=A\y;>> a=z(1); b=z(2); c=z(3); >>xh=[-1:0.1:1]';>>yh=(a.*xh+b)./(1+c.*xh.^2); >>plot(x,y,'r+',xh,yh,'b*')2.若在Matlab ⼯作⽬录下已经有如下两个函数⽂件，写⼀个割线法程序，求出这两个函数精度为1010-的近似根，并写出调⽤⽅式：>> edit gexianfa.mfunction [x iter]=gexianfa(f,x0,x1,tol) iter=0;x=x1;while(abs(feval(f,x))>tol) iter=iter+1;x=x1-feval(f,x1).*(x1-x0)./(feval(f,x1)-feval(f,x0)); x0=x1;x1=x; end>> edit f.m function v=f(x) v=x.*log(x)-1;>> edit g.m function z=g(y) z=y.^5+y-1;>> [x1 iter1]=gexianfa('f',1,3,1e-10) x1 =1.7632 iter1 = 6>> [x2 iter2]=gexianfa('g',0,1,1e-10) x2 =0.7549 iter2 = 83.使⽤GS 迭代求解下述线性代数⽅程组：123123123521242103103x x x x x x x x x ì++=--++=í???-+=??解：>> edit gsdiedai.mfunction [x iter]=gsdiedai(A,x0,b,tol) D=diag(diag(A)); L=D-tril(A); U=D-triu(A); iter=0; x=x0;>> A=[5 2 1;-1 4 2;1 -3 10]; >> b=[-12 10 3]'; >>tol=1e-4; >>x0=[0 0 0]';>> [x iter]=gsdiedai(A,x0,b,tol); >>x x =-3.0910 1.2372 0.9802 >>iter iter = 64.⽤四阶Range-kutta ⽅法求解下述常微分⽅程初值问题（取步长h=0.01）,(1)2x dy y e xy dx y ì??=++?í??=??解：>> edit ksf2.mfunction v=ksf2(x,y)v=y+exp(x)+x.*y; >> a=1;b=2;h=0.01; >> n=(b-a)./h; >> x=[1:0.01:2]; >>y(1)=2;>>for i=2:(n+1)k1=h*ksf2(x(i-1),y(i-1));k2=h*ksf2(x(i-1)+0.5*h,y(i-1)+0.5*k1); k3=h*ksf2(x(i-1)+0.5*h,y(i-1)+0.5*k2); k4=h*ksf2(x(i-1)+h,y(i-1)+k3); y(i)=y(i-1)+(k1+2*k2+2*k3+k4)./6; end >>y调⽤函数⽅法>> edit Rangekutta.mfunction [x y]=Rangekutta(f,a,b,h,y0) x=[a:h:b]; n=(b-a)/h; y(1)=y0; for i=2:(n+1)k1=h*(feval(f,x(i-1),y(i-1)));k2=h*(feval(f,x(i-1)+0.5*h,y(i-1)+0.5*k1)); k3=h*(feval(f,x(i-1)+0.5*h,y(i-1)+0.5*k2)); k4=h*(feval(f,x(i-1)+h,y(i-1)+k3)); y(i)=y(i-1)+ (k1+2*k2+2*k3+k4)./6; end>> [x y]=Rangekutta('ksf2',1,2,0.01,2); >>y5.取0.2h =，请编写Matlab 程序，分别⽤欧拉⽅法、改进欧拉⽅法在12x ≤≤上求解初值问题。

同济大学数值分析matlab编程题汇编.doc

同济大学数值分析matlab编程题汇编.MATLAB编程题库1.下面的数据表近似地满足函数,请适当变换成为线性最小二乘问题,编程求最好的系数,并在同一个图上画出所有数据和函数图像。

解:x=[-x=[:文件一文件二函数v=f(x)v=x . * log(x)-1；函数z=g(y)z=y. y-1；解以下内容:编辑gex AFA。

m函数[x ITER]=gex AFA(f，x0，x1，tol)ITER=0；而(标准(x1-编辑gex AFA。

m函数[x ITER )=gex AFA(f，x0，x1，tol)ITER=0；同时（标准(x1:解以下内容:编辑gsdiedai。

m函数[x iter]=gsdiedai(A，x0，b，tol)D=diag(diag(A))；函数[x iter]=gsdiedai(A，x0，b，tol)D=diag(diag(A))；L=D:编辑ksf 2。

m函数v=ksf2(x，y)v=y exp(x)x . * y；a=1；b=2；h=0.01n=(b-a)./h .x=[1:0.01:2]；y(1)-省略部分-0.5000 1.0000 0.5000-1.0000 1.0000 UU=2.0000 3.0000 4.0000 0-0.5000 7.0000 0 0-1.0000 x=林空间(0，1，11)；x ' ans=0 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 0.90001.0000 x=[1 2 3 4]；y=[6 11 18 27]；p=polyfit(x，y，2)p=1.0000 2.0000 3.0000 diag(1(4，1)，1)ans=0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 012 .编程实现求解满足下列条件的区间[-1，2]上的三次样条函数S(x)，并画出此样条函数的图形: Xi-1 0 1 2 f(Xi)-1 0 1 0f(Xi)' 0-1函数splx=[-1 0 1 2]y=[0-1 0 1 0-1]PP=csape(x，y，'完整')[断点coefs、npolys、ncoefs、dim]=unmkpp(PP)xh=-1:0.133602 if-1=xh=0 yh=coefs(1，1)*(xh 1).3系数(1，2)*(xh 1).2系数(1，3)*(xh 1)系数(1，4)否则，如果0=xh=1 yh=系数(2，1)*(xh).3系数(2，2)*(xh).2系数(2，3)*(xh)系数(2，4)否则，如果1=xh=2 yh=系数(3，1)*(xh-1).3系数(3，2)*(xh-1).2系数(3，3)*(xh-1)系数(3，4)否则返回图(xh，yh，' r ')13 .二分法程序如果nargintol x=(a b)/2 fx=feval(f，x)如果符号(外汇)==符号(fa) a=x fa=fx elseif符号(外汇)==符号b=x FB=FX否则返回结束。

清华大学研究生高等数值分析计算实验奇异值分解SVD以及图像压缩matlab源程序代码

第1部分方法介绍奇异值分解（SVD ）定理：设m n A R ⨯∈，则存在正交矩阵m m V R ⨯∈和n n U R ⨯∈，使得TO A V U O O ∑⎡⎤=⎢⎥⎣⎦其中12(,,,)r diag σσσ∑= ，而且120r σσσ≥≥≥> ，(1,2,,)i i r σ= 称为A 的奇异值，V 的第i 列称为A 的左奇异向量，U 的第i 列称为A 的右奇异向量。

注：不失一般性，可以假设m n ≥，（对于m n <的情况，可以先对A 转置，然后进行SVD 分解，最后对所得的SVD 分解式进行转置，就可以得到原来的SVD 分解式）方法1：传统的SVD 算法主要思想：设()m n A R m n ⨯∈≥，先将A 二对角化，即构造正交矩阵1U 和1V 使得110T B n U AV m n⎡⎤=⎢⎥-⎣⎦其中1200n n B δγγδ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦然后，对三角矩阵T T B B =进行带Wilkinson 位移的对称QR 迭代得到:T B P BQ =。

当某个0i γ=时，B 具有形状12B O B O B ⎡⎤=⎢⎥⎣⎦，此时可以将B 的奇异值问题分解为两个低阶二对角阵的奇异值分解问题；而当某个0i δ=时，可以适当选取'Given s 变换，使得第i 行元素全为零的二对角阵，因此，此时也可以将B 约化为两个低阶二对角阵的奇异值分解问题。

在实际计算时，当i B δε∞≤或者()1j j j γεδδ-≤+（这里ε是一个略大于机器精度的正数）时，就将i δ或者i γ视作零，就可以将B 分解为两个低阶二对角阵的奇异值分解问题。

主要步骤：（1）输入()m n A R m n ⨯∈≥及允许误差ε（2）计算Householder 变换1,,,n P P ⋅⋅⋅，12,,n H H -⋅⋅⋅，使得112()()0Tn n B nP P A H H m n -⎡⎤⋅⋅⋅⋅⋅⋅=⎢⎥-⎣⎦其中1200n n B δγγδ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ 12:n U PP P =⋅⋅⋅，122:.n V H H H -=⋅⋅⋅ （3）收敛性检验：（i ）将所有满足()1j j j γεδδ-≤+的j γ置零；（ii ）如果0,2,,j j n γ== ，则输出有关信息结束；否则，1:0γ=，确定正整数p q <，使得10p q n γγγ+==⋅⋅⋅==，0j γ≠，p j q <≤；（iii ）如果存在i 满足1p i q ≤≤-使得i B δε∞≤，则:0i δ=，1:i x γ+=，1:i y δ+=，1:0i γ+=，:1l =，转步（iv ）；否则转步（4）（iv ）确定cos ,sin c s θθ==和σ使0c s x s c y σ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦这也相应于0Tc s y s c x σ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦所以可以直接调用'Given s 变换算法得到:i l δσ+=，:(,,)T U UG i i l θ=+这相当于(1:;,)(1:;,)(1:;,)Tc s c s U n i i l U n i i l U n i i l s c s c -⎡⎤⎡⎤+=+=+⎢⎥⎢⎥-⎣⎦⎣⎦（v ）如果l q i <-，则1:i l x s γ++=，11:i l i l c γγ++++=，1:i l y δ++=，:1l l =+转步（iv ），否则转步（i ）（4）构造正交阵P 和Q ，使12=T P B Q B 仍为上双对角阵，其中112100pp p p q q B δγδγγδ+++⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦，得121:=T B B P B Q =，:(,,)p n p q U Udiag I P I --=，:(,,)p n p q V Vdiag I Q I --=然后转步（3）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1、%用牛顿法求f(x)=x-sin x 的零点，e=10^(-6)disp('牛顿法');i=1;n0=180;p0=pi/3;tol=10^(-6);for i=1:n0p=p0-(p0-sin(p0))/(1-cos(p0));if abs(p-p0)<=10^(-6)disp('用牛顿法求得方程的根为')disp(p);disp('迭代次数为：')disp(i)break;endp0=p;endif i==n0&&~(abs(p-p0)<=10^(-6))disp(n0)disp('次牛顿迭代后无法求出方程的解')end2、disp('Steffensen加速');p0=pi/3;for i=1:n0p1=0.5*p0+0.5*cos(p0);p2=0.5*p1+0.5*cos(p1);p=p0-((p1-p0).^2)./(p2-2.*p1+p0);if abs(p-p0)<=10^(-6)disp('用Steffensen加速求得方程的根为')disp(p);disp('迭代次数为：')disp(i)break;endp0=p;endif i==n0&&~(abs(p-p0)<=10^(-6))disp(n0)disp('次Steffensen加速后无法求出方程的解')end1、%使用二分法找到方程 600 x^4 -550 x^3 +200 x^2 -20 x -1 =0 在区间[0.1,1]上的根，%误差限为 e=10^-4disp('二分法')a=0.2;b=0.26;tol=0.0001;n0=10;fa=600*(a.^4)-550*(a.^3)+200*(a.^2)-20*a-1;for i=1:n0p=(a+b)/2;fp=600*(p.^4)-550*(p.^3)+200*(p.^2)-20*p-1;if fp==0||(abs((b-a)/2)<tol)disp('用二分法求得方程的根p=')disp(p)disp('二分迭代次数为：')disp(i)break;endif fa*fp>0a=p;else b=p;endendif i==n0&&~(fp==0||(abs((b-a)/2)<tol))disp(n0)disp('次二分迭代后没有求出方程的根')end2、%使用牛顿法找到方程 600 x^4 -550 x^3 +200 x^2 -20 x -1 =0 在区间[0.1,1]上的根，%误差限为 e=10^-4disp('牛顿法')p0=0.3;for i=1:n0p=p0-(600*(p0.^4)-550*(p0.^3)+200*(p0.^2)-20*p0-1)./(2400*(p0.^3) -1650*p0.^2+400*p0-20);if(abs(p-p0)<tol)disp('用牛顿法求得方程的根p=')disp(p)disp('牛顿迭代次数为：')disp(i)break;endp0=p;endif i==n0&&~(abs(p-p0)<tol)disp(n0)disp('次牛顿迭代后没有求出方程的根')end3、%使用割线法找到方程 600 x^4 -550 x^3 +200 x^2 -20 x -1 =0 在区间[0.1,1]上的根，%误差限为 e=10^-4disp('割线法')p0=0.2;p1=0.25;q0=600*(p0.^4)-550*(p0.^3)+200*(p0.^2)-20*p0-1;q1=600*(p1.^4)-550*(p1.^3)+200*(p1.^2)-20*p1-1;for i=2:n0p=p1-q1*(p1-p0)/(q1-q0);if abs(p-p1)<toldisp('用割线法求得方程的根p=')disp(p)disp('割线法迭代次数为：')disp(i)break;endp0=p1;q0=q1;pp=p1;p1=p;q1=600*(p.^4)-550*(p.^3)+200*(p.^2)-20*p-1;endif i==n0&&~(abs(p-pp)<tol)disp(n0)disp('次割线法迭代后没有求出方程的根')end4、%使用试位法找到方程 600 x^4 -550 x^3 +200 x^2 -20 x -1 =0 在区间[0.1,1]上的根，%误差限为 e=10^-4disp('试位法')p0=0.2;p1=0.25;q0=600*(p0.^4)-550*(p0.^3)+200*(p0.^2)-20*p0-1;q1=600*(p1.^4)-550*(p1.^3)+200*(p1.^2)-20*p1-1;for i=2:n0p=p1-q1*(p1-p0)/(q1-q0);if abs(p-p1)<toldisp('用试位法求得方程的根p=')disp(p)disp('试位法迭代次数为：')disp(i)break;endq=600*(p.^4)-550*(p.^3)+200*(p.^2)-20*p-1;if q*q1<0p0=p1;q0=q1;endpp=p1;p1=p;q1=q;endif i==n0&&~(abs(p-pp)<tol)disp(n0)disp('次试位法迭代后没有求出方程的根')end5、%使用muller方法找到方程 600 x^4 -550 x^3 +200 x^2 -20 x -1 =0 在区间[0.1,1]上的根，%误差限为 e=10^-4disp('muller法')x0=0.1;x1=0.2;x2=0.25;h1=x1-x0;h2=x2-x1;d1=((600*(x1.^4)-550*(x1.^3)+200*(x1.^2)-20*x1-1)-(600*(x0.^4)-55 0*(x0.^3)+200*(x0.^2)-20*x0-1))/h1;d2=((600*(x2.^4)-550*(x2.^3)+200*(x2.^2)-20*x2-1)-(600*(x1.^4)-55 0*(x1.^3)+200*(x1.^2)-20*x1-1))/h2;d=(d2-d1)/(h2+h1);for i=3:n0b=d2+h2*d;D=(b*b-4*(600*(x2.^4)-550*(x2.^3)+200*(x2.^2)-20*x2-1)*d)^0.5;if(abs(d-D)<abs(d+D))E=b+D;else E=b-D;endh=-2*(600*(x2.^4)-550*(x2.^3)+200*(x2.^2)-20*x2-1)/E;p=x2+h;if abs(h)<toldisp('用muller方法求得方程的根p=')disp(p)disp('muller方法迭代次数为：')disp(i)break;endx0=x1;x1=x2;x2=p;h1=x1-x0;h2=x2-x1;d1=((600*(x1.^4)-550*(x1.^3)+200*(x1.^2)-20*x1-1)-(600*(x0.^4)-55 0*(x0.^3)+200*(x0.^2)-20*x0-1))/h1;d2=((600*(x2.^4)-550*(x2.^3)+200*(x2.^2)-20*x2-1)-(600*(x1.^4)-55 0*(x1.^3)+200*(x1.^2)-20*x1-1))/h2;d=(d2-d1)/(h2+h1);endif i==n0%条件有待商榷？！disp(n0)disp('次muller方法迭代后没有求出方程的根')end1、%观察Lagrange插值的Runge现象x=-1:0.05:1;y=1./(1+25.*x.*x);plot(x,y),grid on;n=5;x=-1:2/n:1;y=1./(1+25.*x.*x);for i=1:n+1q(1,i)=y(i);endh=0.05;z=-1:h:1;for k=1:2/h+1for i=2:n+1for j=2:iq(j,i)=((z(k)-x(i-j+1))*q(j-1,i)-(z(k)-x(i))*q(j-1,i-1))/(x(i)-x( i-j+1));endendw(k)=q(n+1,n+1);endhold on, plot(z,w,'r'),grid on;%**** n=10 ****n=10;x=-1:2/n:1;y=1./(1+25.*x.*x);for i=1:n+1q(1,i)=y(i);endh=0.05;z=-1:h:1;for k=1:2/h+1for i=2:n+1for j=2:iq(j,i)=((z(k)-x(i-j+1))*q(j-1,i)-(z(k)-x(i))*q(j-1,i-1))/(x(i)-x( i-j+1));endendw(k)=q(n+1,n+1);endhold on,plot(z,w,'k'),grid on;legend ('原始图','n=5','n=10');2、%固支样条插植%********第一段********x=[1,2,5,6,7,8,10,13,17];a=[3,3.7,3.9,4.2,5.7,6.6,7.1,6.7,4.5];n=numel(a);for i=1:n-1h(i)=x(i+1)-x(i);endA=[2*h(1),h(1),0,0,0,0,0,0,0;h(1),2*(h(1)+h(2)),h(2),0,0,0,0,0,0;0,h(2),2*(h(2)+h(3)),h(3),0,0,0,0,0;0,0,h(3),2*(h(3)+h(4)),h(4),0,0,0,0;0,0,0,h(4),2*(h(4)+h(5)),h(5),0,0,0;0,0,0,0,h(5),2*(h(5)+h(6)),h(6),0,0;0,0,0,0,0,h(6),2*(h(6)+h(7)),h(7),0;0,0,0,0,0,0,h(7),2*(h(7)+h(8)),h(8);0,0,0,0,0,0,0,h(8),2*h(8)];e=[3*(a(2)-a(1))/h(1)-3;3*(a(3)-a(2))/h(2)-3*(a(2)-a(1))/h(1);3*(a(4)-a(3))/h(3)-3*(a(3)-a(2))/h(2);3*(a(5)-a(4))/h(4)-3*(a(4)-a(3))/h(3);3*(a(6)-a(5))/h(5)-3*(a(5)-a(4))/h(4);3*(a(7)-a(6))/h(6)-3*(a(6)-a(5))/h(5);3*(a(8)-a(7))/h(7)-3*(a(7)-a(6))/h(6);3*(a(9)-a(8))/h(8)-3*(a(8)-a(7))/h(7);3*(-0.67)-3*(a(9)-a(8))/h(8)];c=inv(A)*e;for i=1:8b(i)=(a(i+1)-a(i))/h(i)-h(i)*(2*c(i)+c(i+1))/3;d(i)=(c(i+1)-c(i))/(3*h(i));endfor i=1:8z=x(i):0.05:x(i+1);w=a(i)+b(i).*(z-x(i))+c(i).*(z-x(i)).^2+d(i).*(z-x(i)).^3; grid on, plot(z,w),hold on;end%********第二段********x=[17,20,23,24,25,27,27.7];a=[4.5,7,6.1,5.6,5.8,5.2,4.1];for i=1:6h(i)=x(i+1)-x(i);endA=[2*h(1),h(1),0,0,0,0,0;h(1),2*(h(1)+h(2)),h(2),0,0,0,0;0,h(2),2*(h(2)+h(3)),h(3),0,0,0;0,0,h(3),2*(h(3)+h(4)),h(4),0,0;0,0,0,h(4),2*(h(4)+h(5)),h(5),0;0,0,0,0,h(5),2*(h(5)+h(6)),h(6)0,0,0,0,0,h(6),2*h(6)];e=[3*(a(2)-a(1))/h(1)-3*3;3*(a(3)-a(2))/h(2)-3*(a(2)-a(1))/h(1);3*(a(4)-a(3))/h(3)-3*(a(3)-a(2))/h(2);3*(a(5)-a(4))/h(4)-3*(a(4)-a(3))/h(3);3*(a(6)-a(5))/h(5)-3*(a(5)-a(4))/h(4);3*(a(7)-a(6))/h(6)-3*(a(6)-a(5))/h(5);3*(-4)-3*(a(7)-a(6))/h(6)];c=inv(A)*e;for i=1:6b(i)=(a(i+1)-a(i))/h(i)-h(i)*(2*c(i)+c(i+1))/3;d(i)=(c(i+1)-c(i))/(3*h(i));endfor i=1:6z=x(i):0.05:x(i+1);w=a(i)+b(i).*(z-x(i))+c(i).*(z-x(i)).^2+d(i).*(z-x(i)).^3; grid on, plot(z,w),hold on;end%********第三段********x=[27.7,28,29,30];a=[4.1,4.3,4.1,3];for i=1:3h(i)=x(i+1)-x(i);endA=[2*h(1),h(1),0,0;h(1),2*(h(1)+h(2)),h(2),0;0,h(2),2*(h(2)+h(3)),h(3);0,0,h(3),2*h(3)];e=[3*(a(2)-a(1))/h(1)-3*0.33;3*(a(3)-a(2))/h(2)-3*(a(2)-a(1))/h(1);3*(a(4)-a(3))/h(3)-3*(a(3)-a(2))/h(2);3*(-1.5)-3*(a(4)-a(3))/h(3)];c=inv(A)*e;for i=1:3b(i)=(a(i+1)-a(i))/h(i)-h(i)*(2*c(i)+c(i+1))/3;d(i)=(c(i+1)-c(i))/(3*h(i));endfor i=1:3z=x(i):0.05:x(i+1);w=a(i)+b(i).*(z-x(i))+c(i).*(z-x(i)).^2+d(i).*(z-x(i)).^3; grid on, plot(z,w),hold on;endgrid on,title('注：横纵坐标的比例不一样！！！');1、%用不动点迭代法求方程 x-e^x+4=0的正根与负根，误差限是10^-6%disp('不动点迭代法');n0=100;p0=-5;for i=1:n0p=exp(p0)-4;if abs(p-p0)<=10^(-6)if p<0disp('|p-p0|=')disp(abs(p-p0))disp('不动点迭代法求得方程的负根为:')disp(p);break;elsedisp('不动点迭代法无法求出方程的负根.')endelsep0=p;endendif i==n0disp(n0)disp('次不动点迭代后无法求出方程的负根')endp1=1.7;for i=1:n0pp=exp(p1)-4;if abs(pp-p1)<=10^(-6)if pp>0disp('|p-p1|=')disp(abs(pp-p1))disp('用不动点迭代法求得方程的正根为')disp(pp);elsedisp('用不动点迭代法无法求出方程的正根');endbreak;elsep1=pp;endendif i==n0disp(n0)disp('次不动点迭代后无法求出方程的正根')end2、%用牛顿法求方程 x-e^x+4=0的正根与负根，误差限是10^-6 disp('牛顿法')n0=80;p0=1;for i=1:n0p=p0-(p0-exp(p0)+4)/(1-exp(p0));if abs(p-p0)<=10^(-6)disp('|p-p0|=')disp(abs(p-p0))disp('用牛顿法求得方程的正根为')disp(p);break;elsep0=p;endendif i==n0disp(n0)disp('次牛顿迭代后无法求出方程的解')endp1=-3;for i=1:n0p=p1-(p1-exp(p1)+4)/(1-exp(p1));if abs(p-p1)<=10^(-6)disp('|p-p1|=')disp(abs(p-p1))disp('用牛顿法求得方程的负根为')disp(p);break;elsep1=p;endendif i==n0disp(n0)disp('次牛顿迭代后无法求出方程的解')end1、使用欧拉法、改进欧拉法和四阶R-K方法求下列微分方程的解。