初中数学锐角三角函数

合集下载

初中九年级数学中考锐角三角函数知识点总结

初中九年级数学中考锐角三角函数知识点总结1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。

2、如下图，在Rt △ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B)：3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。

4、任意锐角的正切值等于它的余角的余切值；任意锐角的余切值等于它的余角的正切值。

5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)A 90B 90∠-︒=∠︒=∠+∠得由B A 对边邻边 CA 90B 90∠-︒=∠︒=∠+∠得由B A6、正弦、余弦的增减性：当0°≤α≤90°时，sin α随α的增大而增大，cos α随α的增大而减小。

7、正切、余切的增减性：当0°<α<90°时，tan α随α的增大而增大，8、解直角三角形的定义：已知边和角（两个，其中必有一边）→所有未知的边和角。

依据：①边的关系：222c b a =+；②角的关系：A+B=90°；③边角关系：三角函数的定义。

(注意：尽量避免使用中间数据和除法)9、应用举例：(1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。

(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。

用字母i 表示，即hi l=。

坡度一般写成1:m 的形式，如1:5i =等。

把坡面与水平面的夹角记作α(叫做坡角)，那么tan hi lα==。

3、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。

如图3，OA 、OB 、OC 、OD 的方向角分别是：45°、135°、225°。

4、指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方向角。

如图4,OA 、OB 、OC 、OD 的方向角分别是：北偏东30°（东北方向），南偏东45°（东南方向），南偏西60°（西南方向），北偏西60°（西北方向）。

初三数学锐角三角函数

初三数学锐角三角函数中考要求中考要求模块一三角函数基础一、锐角三角函数的定义如图所示，在Rt ABC △中，a 、b 、c 分别为A ∠、B ∠、C ∠的对边．（1）正弦：Rt ABC ∆中，锐角A 的对边与斜边的比叫做A ∠的正弦，记作sin A ，即sin aA c=．（2）余弦：Rt ABC ∆中，锐角A 的邻边与斜边的比叫做A ∠的余弦，记作cos A ，即cos b A c =．（3）正切：Rt ABC ∆中，锐角A 的对边与邻边的比叫做A ∠的正切，记作tan A ，即tan a A b=．注意：①正弦、余弦、正切都是在直角三角形中给出的，要避免应用时对任意三角形随便套用定义． ② sin A 、cos A 、tan A 分别是正弦、余弦、正切的数学表达符号，是一个整体，不能理解为sin 与A 、cos 与A 、tan 与A 的乘积．③ 在直角三角形中，正弦、余弦、正切分别是某个锐角的对边与斜边、邻边与斜边、对边与邻边的比值，当这个锐角确定后，这些比值都是固定值．二、特殊角三角函数a A这些特殊角的三角函数值一定要牢牢记住！三、锐角三角函数的取值范围在Rt ABC ∆中，90C ∠=︒，000a b c a c b c >>><<，，，，，又sin a A c =，cos b A c =，tan aA b=，所以 0sin 10cos 1tan 0A A A <<<<>，，．四、三角函数关系 1．同角三角函数关系： 22sin cos 1A A +=，sin tan cos AA A= 2．互余角三角函数关系：(1) 任意锐角的正弦值等于它的余角的余弦值：()sin cos 90A A =︒-；(2) 任意锐角的余弦值等于它的余角的正弦值：()cos sin 90A A =︒-； (3) 任意锐角的正切值等于它的余角的余切值：()tan cot 90A A =︒-． 3．锐角三角函数值的变化规律：(1)A 、B 是锐角，若A >B ，则sin A >sin B ；若A <B ，则sin A <sin B(2) A 、B 是锐角，若A >B ，则cos A <cos B ；若A <B ，则cos A >cos B (3) A 、B 是锐角，若A >B ，则tan tan A B >；若A <B ，则tan tan A B <【例1】已知在ABC △中，A B ∠∠、是锐角，且5sin tan 22913A B AB cm ===，，，则ABC S =△ ．【巩固】如图，点A 在半径为R 的O 上，以A 为圆心，r 为半径作A ，设O 的弦PQ 与A 相切，求证PA QA ⋅为定值．【例2】求tan1tan2tan3tan89︒⋅︒⋅︒⋅⋅︒的值【巩固】化简：22sin cos sin 1tan sin cos αααααα++--【例3】已知tan α1）221cos sin cos 1sin cos sin a ααααα-+-+，（2090α︒<<︒）．【巩固】已知tan 2α=，求4sin 2cos 5cos 3sin αααα-+．【例4】已知α为锐角，且22sin 5cos 10αα-+=，求α的度数． OQPA【巩固】若α为锐角，且22cos 7sin 50αα+-=，求α的度数．【例5】已知sin cos αα+（α为锐角），求作以1sin α和1cos α为两根的一元二次方程．【巩固】若方程222210x ax a -+-=的一个根是sin α，则它的另一个根必是cos α或cos α-．【巩固】已知：ABC △中，方程2(sin sin )(sin sin )(sin sin )0B A x A C x C B -+-+-=的两根相等，求证60B <︒．【巩固】在ABC △中，60A =︒，最大边与最小边的边长分别是方程2327320x x -+=的两个根，求ABC △的外接圆半径和内切圆的面积．【例6】若0°<θ<30°，且1sin 3km θ=+(k 为常数，且k <0)，则m 的取值范是．模块二解直角三角形一、解直角三角形的概念根据直角三角形中已知的量（边、角）来求解未知的量（边、角）的过程就是解直角三角形．二、直角三角形的边角关系如图，直角三角形的边角关系可以从以下几个方面加以归纳：（1）三边之间的关系：222a b c += (勾股定理) （2）锐角之间的关系：90A B ∠+∠=︒（3）边角之间的关系：sin cos ,cos sin ,tan a b aA B A B A c c b=====三、解直角三角形的四种基本类型（1）已知斜边和一直角边(如斜边c ，直角边a )，由sin aA c=求出A ∠，则90B A ∠=︒-∠，b =；（2）已知斜边和一锐角(如斜边c ，锐角A )，求出90B A ∠=︒-∠，sin a c A =，cos b c A =；（3）已知一直角边和一锐角(如a 和锐角A )，求出90B A ∠=︒-∠，tan b a B =，sin ac A=；（4）已知两直角边(如a 和b )，求出c =tan aA b=，得90B A ∠=︒-∠．具体解题时要善于选用公式及其变式，如sin a A c =可写成sin a c A =，sin a c A=等．四、解直角三角形的方法解直角三角形的方法可概括为：“有斜(斜边)用弦(正弦，余弦)，无斜用切(正切，余切)，宁乘毋除，取原避中”．这几句话的意思是：当已知或求解中有斜边时，就用正弦或余弦；无斜边时，就用正切或余切；当所求的元素既可用乘法又可用除法时，则用乘法，不用除法；既可由已知数据又可用中间数据求得时，则用原始数据，尽量避免用中间数据．五、解直角三角形的技巧及注意点在Rt ABC ∆中，90A B ∠+∠=︒，故sin cos(90)cos A A B =︒-=，cos sin A B =．利用这些关系式，可在解题时进行等量代换，以方便解题．六、如何解直角三角形的非基本类型的题型对解直角三角形的非基本类型的题型，通常是已知一边长及一锐角三角函数值，可通过解方程(组)来cb aC BA（1）如果有些问题一时难以确定解答方式，可以依据题意画图帮助分析；（2）对有些比较复杂的问题，往往要通过作辅助线构造直角三角形，作辅助线的一般思路是：①作垂线构成直角三角形；②利用图形本身的性质，如等腰三角形顶角平分线垂直于底边等．七、直角三角形中其他重要概念（1）仰角与俯角：在视线与水平线所成的角中，视线在水平线上方的叫做仰角，在水平线下方的叫做俯角．如图⑴．（2）坡角与坡度：坡面的垂直高度h 和水平宽度l 的比叫做坡度（或叫做坡比），用字母表示为h i l=，坡面与水平面的夹角记作α，叫做坡角，则tan hi lα==．坡度越大，坡面就越陡．如图⑵．（3）方向角（或方位角）：方向角一般是指以观测者的位置为中心，将正北或正南方向作为起始方向旋转到目标的方向线所成的角（一般指锐角），通常表达为北（南）偏东（西）××度．如图⑶．八、解直角三角形应用题的解题步骤及应注意的问题：（1）分析题意，根据已知条件画出它的平面或截面示意图，分清仰角、俯角、坡角、坡度、水平距离、垂直距离等概念的意义；（2）找出要求解的直角三角形．有些图形虽然不是直角三角形，但可添加适当的辅助线，把它们分割成一些直角三角形和矩形（包括正方形）；（3）根据已知条件，选择合适的边角关系式解直角三角形；（4）按照题目中已知数据的精确度进行近似计算，检验是否符合实际，并按题目要求的精确度取近似值，注明单位．【例7】如图，某高层楼房与上海东方明珠电视塔隔江想望，甲、乙两学生分别在这楼房的A B ，两层，甲在A 层测得电视塔塔顶D 的仰角为α，塔底C 的俯角为β，乙在B 层测得塔顶D 的仰角为θ，由于塔底的视线被挡住，乙无法测得塔底的俯角，已知A B ，之间的高度差为a ，求电视塔高CD（用含a αβθ，，，的代数式表示）图(3)图(2)图(1)俯角仰角视线视线水平线铅垂线【例8】一座建于若干年前的水库大坝的横断面如图所示，其中背水面的整个坡面是长为90米、宽为5米的矩形．现需将其整修并进行美化，方案如下：①将背水坡AB的坡度由1:0.75改为；②用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域，依次相间地种草与栽花．（1）求整修后背水坡面的面积；（2）如果栽花的成本是每平方米25元，种草的成本是每平方米20元，那么种植花草至少需要多少元？【例9】如图，在某海域内有三个港口A、D、C．港口C在港口A北偏东60︒方向上，港口D在港口A 北偏西60︒方向上．一艘船以每小时25海里的速度沿北偏东30︒的方向驶离A港口3小时后到达B点位置处，此时发现船舱漏水，海水以每5分钟4吨的速度渗入船内．当船舱渗入的海水总量超过75吨时，船将沉入海中．同时在B处测得港口C在B处的南偏东75︒方向上．若船上的抽水机每小时可将8吨的海水排出船外，问此船在B处至少应以怎样的航行速度驶向最近的港口停靠，才能保证船在抵达港口前不会沉没（要求计算结果保留根号）？并指出此时船的航行方向．DC BA【巩固】海面上B 处有一货轮正在向正南方向航行，其航行路线是当它到达正南方C 时，在驶向正西方的目的地A 处，且200CA CB ==海里，在AB 中点O 处有一客轮，其速度为货轮的一半，现在客轮要截住货轮取一件货物，于是选择某一航向行驶去截住货轮，那么当客轮截住客轮时至少航行了多少海里，它所选择了怎样的方向角？（路程保留整数海里，角度精确到度）课堂检测1．（辽宁竞赛）如图，湖心岛上有一凉亭，现欲利用湖岸边的开阔平整地带，测量凉亭顶端到湖面所在平面的高度AB (见示意图)，可供使用的工具有测倾器、皮尺．（1）请你根据现有条件，设计一个测量凉亭顶端到湖面所在平面的高度AB 的方案，画出测量方案的平面示意图，并将测量的数据标注在图形上（所测的距离用m ，n 表示，角用α，β表示，测倾器高度忽略不计）；（2）根据你所测量的数据，计算凉亭到湖面的高度AB (用字母表示)．2．化简：222tan1tan 2....tan89sin 1sin 2...sin 89︒⋅︒︒︒+︒++︒3．如图1、图2，是一款家用的垃圾桶，踏板AB （与地面平行）或绕定点P （固定在垃圾桶底部的某一位置）上下转动（转动过程中始终保持''AP A P BP B P ==，）．通过向下踩踏点A 到'A （与地面接触点）使点B 上升到点'B ，与此同时传动杆BH 运动到''B H 的位置，点H 绕固定点D 旋转（DH 为旋转半径）至点'H ，从而使桶盖打开一个张角'HDH ∠．如图3，桶盖打开后，传动杆''H B 所在的直线分别与水平直线AB DH 、垂直，垂足为点M C 、，设''H C B M =．测得6cm 12cm '8cm AP PB DH ===，，．要使桶盖张开的角度'HDH ∠不小于60︒，那么踏板AB 离地面的高度至少等于多少cm ？（结果保留两位有效数字）课后作业1．化简求值：1sin 1sin 1cos 1cos 1sin 1sin 1cos 1cos αααααααα⎛⎫⎛⎫-+-+-- ⎪⎪ ⎪⎪+-+-⎝⎭⎝⎭（090α︒<<︒）2．若045α︒<<︒，且3sin cos 716αα=，求sin α的值．图3图2C MAA'P BB'HDH'H'DHB'BPA'A（图1）3．（2011甘肃兰州）通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad ）．如图①在ABC △中，AB AC =，顶角A 的正对记作sadA ，这时=BCsadA AB=底边腰．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题：（1）60sad ︒= ．（2）对于0180A ︒<<︒，∠A 的正对值sadA 的取值范围是．（3）如图②，已知3sin 5A =，其中A ∠为锐角，试求sadA 的值．图②图①C BAC B A。

九年级数学专题复习锐角三角函数

总复习锐角三角函数【考纲要求】1.理解锐角三角函数的定义、性质及应用，特殊角三角函数值的求法，运用锐角三角函数解决与直角三角形有关的实际问题.题型有选择题、填空题、解答题，多以中、低档题出现；2.命题的热点为根据题中给出的信息构建图形，建立数学模型，然后用解直角三角形的知识解决问题.【知识网络】【考点梳理】考点一、锐角三角函数的概念如图所示，在Rt△ABC中，∠C＝90°，∠A所对的边BC记为a，叫做∠A的对边，也叫做∠B的邻边，∠B所对的边AC记为b，叫做∠B的对边，也是∠A的邻边，直角C所对的边AB记为c，叫做斜边．锐角A的对边与斜边的比叫做∠A的正弦，记作sinA，即sinA aAc∠==的对边斜边；锐角A的邻边与斜边的比叫做∠A的余弦，记作cosA，即cosA bAc∠==的邻边斜边；锐角A的对边与邻边的比叫做∠A的正切，记作tanA，即tanA aAA b∠==∠的对边的邻边.同理sinB bBc∠==的对边斜边；cosB aBc∠==的邻边斜边；tanB bBB a∠==∠的对边的邻边．要点进阶：ABCabc(1)正弦、余弦、正切函数是在直角三角形中定义的，反映了直角三角形边与角的关系，是两条线段的比值．角的度数确定时，其比值不变，角的度数变化时，比值也随之变化．(2)sinA，cosA，tanA分别是一个完整的数学符号，是一个整体，不能写成，，，不能理解成sin与∠A，cos与∠A，tan与∠A的乘积．书写时习惯上省略∠A的角的记号“∠”，但对三个大写字母表示成的角(如∠AEF)，其正切应写成“tan∠AEF”，不能写成“tanAEF”；另外，、、常写成、、．(3)任何一个锐角都有相应的锐角三角函数值，不因这个角不在某个三角形中而不存在．(4)由锐角三角函数的定义知：当角度在0°＜∠A＜90°之间变化时，，，tanA＞0．考点二、特殊角的三角函数值利用三角函数的定义，可求出0°、30°、45°、60°、90°角的各三角函数值，归纳如下：要点进阶：(1)通过该表可以方便地知道0°、30°、45°、60°、90°角的各三角函数值，它的另一个应用就是：如果知道了一个锐角的三角函数值，就可以求出这个锐角的度数，例如：若，则锐角．(2)仔细研究表中数值的规律会发现：sin0︒、、、、sin90︒的值依次为0、、、、1，而cos0︒、、、、cos90︒的值的顺序正好相反，、、的值依次增大，其变化规律可以总结为：当角度在0°＜∠A＜90°之间变化时，①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)②余弦值随锐角度数的增大(或减小)而减小(或增大)．考点三、锐角三角函数之间的关系如图所示，在Rt△ABC中，∠C=90°．(1)互余关系：，；(2)平方关系：；(3)倒数关系：或；(4)商数关系：．要点进阶：锐角三角函数之间的关系式可由锐角三角函数的意义推导得出，常应用在三角函数的计算中，计算时巧用这些关系式可使运算简便．考点四、解直角三角形在直角三角形中，由已知元素(直角除外)求未知元素的过程，叫做解直角三角形.在直角三角形中，除直角外，一共有5个元素，即三条边和两个锐角.设在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，则有：①三边之间的关系：a2+b2=c2(勾股定理).②锐角之间的关系：∠A+∠B=90°.③边角之间的关系：，，，，，.④，h为斜边上的高.要点进阶：(1)直角三角形中有一个元素为定值(直角为90°)，是已知的值.(2)这里讲的直角三角形的边角关系指的是等式，没有包括其他关系(如不等关系).(3)对这些式子的理解和记忆要结合图形，可以更加清楚、直观地理解.考点五、解直角三角形的常见类型及解法已知条件解法步骤Rt△ABC两边两直角边(a，b)由求∠A，∠B=90°－∠A，斜边，一直角边(如c，a)由求∠A，∠B=90°－∠A，一边一直角边和一锐角锐角、邻边(如∠A，b)∠B=90°－∠A，一角，锐角、对边(如∠A，a)∠B=90°－∠A，，斜边、锐角(如c，∠A)∠B=90°－∠A，，要点进阶：1．在遇到解直角三角形的实际问题时，最好是先画出一个直角三角形的草图，按题意标明哪些元素是已知的，哪些元素是未知的，然后按先确定锐角、再确定它的对边和邻边的顺序进行计算.2．若题中无特殊说明，“解直角三角形”即要求出所有的未知元素，已知条件中至少有一个条件为边.考点六、解直角三角形的应用解直角三角形的知识应用很广泛，关键是把实际问题转化为数学模型，善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.解这类问题的一般过程是：(1)弄清题中名词、术语的意义，如仰角、俯角、坡度、坡角、方向角等概念，然后根据题意画出几何图形，建立数学模型.(2)将已知条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形的问题.(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.(4)得出数学问题的答案并检验答案是否符合实际意义，得出实际问题的解.拓展：在用直角三角形知识解决实际问题时，经常会用到以下概念：(1)坡角：坡面与水平面的夹角叫做坡角，用字母表示.坡度(坡比)：坡面的铅直高度h和水平距离的比叫做坡度，用字母表示，则，如图，坡度通常写成=∶的形式.(2)仰角、俯角：视线与水平线所成的角中，视线中水平线上方的叫做仰角，在水平线下方的叫做俯角，如图.(3)方位角：从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角，如图①中，目标方向PA，PB，PC的方位角分别为是40°，135°，245°.(4)方向角：指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方向角，如图②中的目标方向线OA，OB，OC，OD的方向角分别表示北偏东30°，南偏东45°，南偏西80°，北偏西60°.特别如：东南方向指的是南偏东45°，东北方向指的是北偏东45°，西南方向指的是南偏西45°，西北方向指的是北偏西45°.要点进阶：1．解直角三角形实际是用三角知识，通过数值计算，去求出图形中的某些边的长或角的大小，最好画出它的示意图.2．非直接解直角三角形的问题，要观察图形特点，恰当引辅助线，使其转化为直角三角形或矩形来解.例如：3．解直角三角形的应用题时，首先弄清题意(关键弄清其中名词术语的意义)，然后正确画出示意图，进而根据条件选择合适的方法求解.考点七、解直角三角形相关的知识如图所示，在Rt△ABC中，∠C＝90°，(1)三边之间的关系：222a b c +=； (2)两锐角之间的关系：∠A+∠B ＝90°； (3)边与角之间的关系：sin cos a A B c ==，cos cos a A B c==，cos sin b A B c ==，1tan tan a A b B==． (4) 如图，若直角三角形ABC 中，CD ⊥AB 于点D ，设CD ＝h ，AD ＝q ，DB ＝p ，则由△CBD ∽△ABC ，得a 2＝pc ；由△CAD ∽△BAC ，得b 2＝qc ；由△ACD ∽△CBD ，得h 2＝pq ；由△ACD ∽△ABC 或由△ABC 面积，得ab ＝ch ．(5)如图所示，若CD 是直角三角形ABC 中斜边上的中线，则①CD ＝AD ＝BD ＝12AB ； ②点D 是Rt △ABC 的外心，外接圆半径R ＝12AB ． (6)如图所示，若r 是直角三角形ABC 的内切圆半径，则2a b c abr a b c+-==++．直角三角形的面积： ①如图所示，111sin 222ABC S ab ch ac B ===△．（h 为斜边上的高）②如图所示，1()2ABC S r a b c =++△．【典型例题】类型一、锐角三角函数的概念与性质例1．(1)如图所示，在△ABC中，若∠C＝90°，∠B＝50°，AB＝10，则BC的长为( )．A．10·tan50° B．10·cos50° C．10·sin50° D．10 sin50°(2)如图所示，在△ABC中，∠C＝90°，sinA＝35，求cosA+tanB的值．(3)如图所示的半圆中，AD是直径，且AD＝3，AC＝2，则sinB的值等于________．举一反三：【变式】如图，已知△ABC的三个顶点均在格点上，则cosA的值为（）A ．B ．C ．D ．类型二、特殊角的三角函数值例2．解答下列各题： (1)化简求值：tan 60tan 45sin 45sin 30sin 60cos30cos 45--++°°°°°°°；(2)在△ABC 中，∠C ＝90°，化简12sin cos A A -．举一反三：【变式】若3sin 22α=，cos sin βα=，(2α，β为锐角)，求2tan()3β的值.例3．如图，在锐角△ABC 中，AB=15，BC=14，S △ABC =84，求：（1）tanC 的值；（2）sinA 的值．CBA举一反三：【变式】如图，AB 是江北岸滨江路一段，长为3千米，C 为南岸一渡口，为了解决两岸交通困难，拟在渡口C 处架桥.经测量得A 在C 北偏西30°方向，B 在C 的东北方向，从C 处连接两岸的最短的桥长为多少千米？(精确到0.1千米)类型三、解直角三角形及应用例4．如图所示，D 是AB 上一点，且CD ⊥AC 于C ，:2:3ACD CDB S S =△△，4cos 5DCB ∠=， AC+CD ＝18，求tanA 的值和AB 的长．例5．如图所示，山脚下有一棵树AB ，小华从点B 沿山坡向上走50 m 到达点D ，用高为1.5m 的测角仪CD 测得树顶的仰角为10°，已知山坡的坡角为15°，求树AB 的高(精确到0.1m)．(参考数据：sin10°≈0.17，cos10°≈0.98，tan10°≈0.18，sin15°≈0.26，cos15°≈0.97，tan15°≈0.27)．举一反三：【变式】如图所示，正三角形ABC的边长为2，点D在BC的延长线上，CD＝3．(1)动点P在AB上由A向B移动，设AP＝t，△PCD的面积为y，求y与t之间的函数关系式及自变量t的取值范围；(2)在(1)的条件下，设PC＝z，求z与t之间的函数关系式．例6．如图(1)所示，一架长4米的梯子AB斜靠在与地面OM垂直的墙ON上，梯子与地面的倾斜角α为60°．(1)求AO与BO的长．(2)若梯子顶端A沿NO下滑，同时底端B沿OM向右滑行．①如图(2)所示，设A点下滑到C点，B点向右滑行到D点，并且AC:BD＝2:3，试计算梯子顶端A 沿NO下滑了多少米；②如图(3)所示，当A点下滑到A′点，B点向右滑行到B′点时，梯子AB的中点P也随之运动到P′点，若∠POP′＝15°，试求AA′的长．【巩固练习】一、选择题1. 在△ABC 中，∠C ＝90°，cosA ＝35,则tan A 等于 ( )A ．35 B ．45 C ．34 D ．432．在Rt △ABC 中，∠C=90°，把∠A 的邻边与对边的比叫做∠A 的余切，记作cotA=ab．则下列关系式中不成立的是（）A ．tanA•cotA=1B ．sinA=tanA•cosAC ．cosA=cotA•sinAD ．tan 2A+cot 2A=1第2题第3题3．如图，在四边形ABCD 中，E 、F 分別是AB 、AD 的中点，若EF=2，BC=5，CD=3，则tanC 等于（） A ．34 B ．43 C ．35 D ．454．如图所示，直角三角形纸片的两直角边长分别为6、8，现将△ABC 如图那样折叠，使点A 与点B 重合，折痕为DE ，则tan ∠CBE 的值是( )A ．247B ．73C ．724D ．135．如图所示，已知∠α的终边OP ⊥AB ，直线AB 的方程为y ＝－33x ＋33，则cos α等于 ( ) A ．12B ．22C ．32D ．336．如图，一艘海轮位于灯塔P 的北偏东55°方向，距离灯塔2海里的点A 处，如果海轮沿正南方向航行到灯塔的正东方向，海轮航行的距离AB 长是（）A．2海里B．2sin55°海里C．2cos55°海里D．2tan55°海里二、填空题7．设θ为锐角，且x2＋3x＋2sinθ＝0的两根之差为5．则θ＝．8．如图，在矩形ABCD中，点E在AB边上，沿CE折叠矩形ABCD，使点B落在AD边上的点F处，若AB=4，BC=5，则tan∠AFE的值为 .9．已知△ABC的外接圆O的半径为3，AC=4，则sinB= .第8题第9题第11题10．当0°＜α＜90°时，求21sincosαα-的值为．11．如图，点E（0，4），O（0，0），C（5，0）在⊙A上，BE是⊙A上的一条弦．则t an∠OBE=．12．在△ABC中，AB=12，AC=13，cos∠B=，则BC边长为 .三、解答题13．如图，某仓储中心有一斜坡AB，其坡度为i=1：2，顶部A处的高AC为4m，B、C在同一水平地面上．（1）求斜坡AB的水平宽度BC；（2）矩形DEFG为长方体货柜的侧面图，其中DE=2.5m，EF=2m，将该货柜沿斜坡向上运送，当BF=3.5m 时，求点D离地面的高．（≈2.236，结果精确到0.1m）14. 为缓解“停车难”的问题，某单位拟建造地下停车库，建筑设计师提供了该地下停车库的设计示意图，如图所示．按规定，地下停车库坡道1:3上方要张贴限高标志，以便告知停车人车辆能否安全驶入，为标明限高，请你根据该图计算CE(精确到0.1 m)（sin18°≈0.3090，cos18°≈0.9511，tan18°≈0.3249）15．如图所示，某中学九年级一班数学课外活动小组利用周末开展课外实践活动，他们要在某公园人工湖旁的小山AB上，测量湖中两个小岛C、D间的距离．从山顶A处测得湖中小岛C的俯角为60°，测得湖中小岛D的俯角为45°．已知小山AB的高为180米，求小岛C、D间的距离．(计算过程和结果均不取近似值)16. 在△ABC中，AB＝AC，CG⊥BA，交BA的延长线于点G．一等腰直角三角尺按如图①所示的位置摆放，该三角尺的直角顶点为F，一条直角边与AC边在一条直线上，另一条直角边恰好经过点B．(1)在图①中请你通过观察、测量BF与CG的长度，猜想并写出BF与CG满足的数量关系，然后证明你的猜想；(2)当三角尺沿AC方向平移到图②所示的位置时，一条直角边仍与AC边在同一直线上，另一条直角边交BC边于点D，过点D作DE⊥BA于点E．此时请你通过观察、测量DE、DF与CG的长度，猜想并写出DE+DF与CG之间满足的数量关系；然后证明你的猜想；(3)当三角尺在②的基础上沿AC方向继续平移到图③所示的位置(点F在线段AC上，且点F与点C 不重合)时，(2)中的猜想是否仍然成立?(不用说明理由)。

中考数学-锐角三角函数(解析版)

专题 28 锐角三角函数
知识点一：锐角三角函数 1．三角函数定义在 Rt△ABC 中，若∠C=90°
sin A A的对边 a
斜边
c
A的邻边
b
cos A
斜边
c
A的对边
a
tan A A的邻边 b
A的邻边
b
cot A A的对边 a
2.同角三角函数的关系
（1）平方关系： sin2 Acos2 A1
（1）三边之间的关系为 a2 b2 c2 （勾股定理）
（2）锐角之间的关系为∠A+∠B=90°
（3）30°角所对直角边等于斜边的一半。
（4）直角三角形斜边上的中线等于斜边的一半。
（5）边角之间的关系为：（三角函数定义）
2.其他有关公式
（1）
S
1 2
ab sin C
=
1 2
bc sin
A
=
1 2
ac sin
B
（2）Rt△面积公式：
S
1 2
ab
1 2
ch
（3）直角三角形外接圆的半径
R c 2
，内切圆半径
r abc 2
结论：直角三角形斜边上的高 h ab c
3.实际问题中术语的含义
(1)仰角与俯角
在视线与水平线所成的角中，视线在水平线上方的角叫做仰角，在水平线下方的角叫做俯角。
(2)坡度：如图，我们通常把坡面的铅直高度和水平宽度的比叫做坡度（或坡比），用字母 i 表示，即 i h . l
见问题，这也是以后中考命题的趋势。 5.解决实际问题的关键在于建立数学模型，要善于把实际问题的数量关系转化为解直角三角形的问题．在解直角三角形的过程中，常会遇到近似计算，应根据题目要求的精确度定答案．

初中数学什么是锐角三角函数

初中数学什么是锐角三角函数锐角三角函数是指在单位圆上所定义的三角函数，其中包括正弦函数、余弦函数和正切函数。

这些函数在数学和几何中具有重要的应用和性质。

在本文中，我们将详细介绍锐角三角函数的定义、性质和应用。

1. 正弦函数（Sine Function）：正弦函数是在单位圆上定义的一个周期函数。

在锐角三角函数中，正弦函数表示三角形中对边与斜边的比例关系。

正弦函数的定义如下：sin(θ) = 对边/斜边2. 余弦函数（Cosine Function）：余弦函数也是在单位圆上定义的一个周期函数。

在锐角三角函数中，余弦函数表示三角形中邻边与斜边的比例关系。

余弦函数的定义如下：cos(θ) = 邻边/斜边3. 正切函数（Tangent Function）：正切函数是正弦函数和余弦函数的比值，也是在单位圆上定义的一个周期函数。

在锐角三角函数中，正切函数表示三角形中对边与邻边的比例关系。

正切函数的定义如下：tan(θ) = 对边/邻边4. 锐角三角函数的性质：-周期性：锐角三角函数是周期函数，其周期为360度或2π弧度。

-奇偶性：正弦函数是奇函数，余弦函数是偶函数，正切函数是奇函数。

-定义域和值域：正弦函数和余弦函数的定义域是实数集合R，值域是[-1, 1]；正切函数的定义域是除了其奇点（kπ+π/2，其中k为整数）的实数集合R，值域是全体实数集合R。

5. 锐角三角函数的应用：锐角三角函数在数学和几何中有广泛的应用，特别是在三角学和解析几何中。

-三角恒等式：锐角三角函数满足许多重要的三角恒等式，如正弦函数和余弦函数的平方和恒等于1，正切函数与正弦函数和余弦函数的关系等。

-角度的计算：通过锐角三角函数，可以计算给定三角形的角度大小。

-三角函数图像：通过绘制锐角三角函数的图像，可以帮助我们直观地理解三角函数的性质和变化规律。

通过以上介绍，我们了解了锐角三角函数的定义、性质和应用。

熟练掌握锐角三角函数的概念和性质，对于理解和解决与三角函数相关的数学问题至关重要。

初中锐角三角函数

初中锐角三角函数锐角三角函数是数学中重要的概念之一、在初中阶段，我们学习了正弦、余弦和正切三种锐角三角函数。

通过学习锐角三角函数，我们可以计算三角形的边长和角度，解决实际问题，提高数学思维能力。

本文将详细介绍锐角三角函数的定义、性质和应用。

一、正弦函数正弦函数是锐角三角函数中最基本的函数之一、我们用sin表示正弦函数。

设一个锐角的一条直角边的长度为a，斜边的长度为c，则正弦函数的定义如下：sinA = a / c其中A为角的度数，sinA为正弦值。

正弦函数的性质：1. 在0°至90°（不包括90°）的锐角范围内，正弦值的大小从0逐渐增大，最大值为1、所以sin0° = 0，sin90° = 12. 在90°至180°（不包括180°）的锐角范围内，正弦值的大小从1逐渐减小，最小值为0。

所以sin180° = 0。

正弦函数的应用：正弦函数可以用来计算三角形的边长和角度。

通过正弦函数，我们可以解决各种实际问题，例如航海中的船舶位置计算、建筑中的高度计算等。

二、余弦函数余弦函数是锐角三角函数中的另一种函数。

我们用cos表示余弦函数。

设一个锐角的一条直角边的长度为b，斜边的长度为c，则余弦函数的定义如下：cosA = b / c其中A为角的度数，cosA为余弦值。

余弦函数的性质：1. 在0°至90°（不包括90°）的锐角范围内，余弦值的大小从1逐渐减小，最大值为0。

所以cos0° = 1，cos90° = 0。

2. 在90°至180°（不包括180°）的锐角范围内，余弦值的大小从0逐渐增大，最小值为-1、所以cos180° = -1余弦函数的应用：余弦函数可以用来计算三角形的边长和角度。

通过余弦函数，我们可以解决各种实际问题，例如建筑物的倾斜角度计算、物体的投影计算等。

锐角三角函数

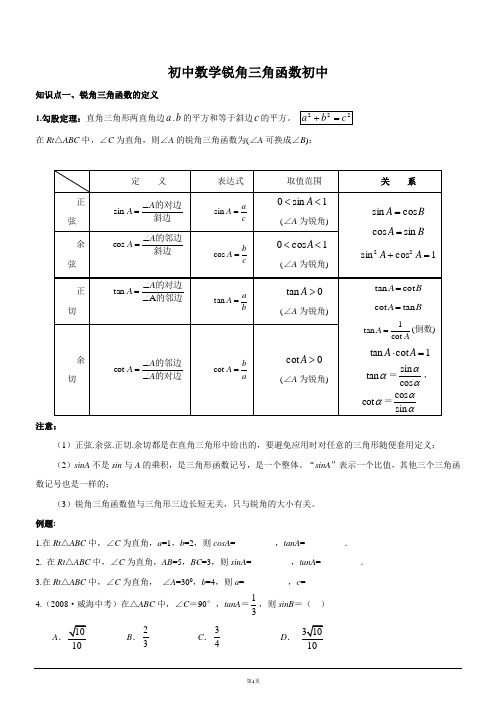
初中数学锐角三角函数初中知识点一、锐角三角函数的定义1.勾股定理：直角三角形两直角边a .b 的平方和等于斜边c 的平方。

222c b a =+ 在Rt △ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B )：定义表达式取值范围关系正弦斜边的对边A A ∠=sin c aA =sin1sin 0<<A(∠A 为锐角)B A cos sin = B A sin cos =1cos sin 22=+A A余弦斜边的邻边A A ∠=coscbA =cos1cos 0<<A(∠A 为锐角)正切的邻边的对边A tan ∠∠=A Aba A =tan 0tan >A(∠A 为锐角)B A cot tan = B A tan cot =AA cot 1tan =(倒数) 1cot tan =⋅A Atan α＝sin cos αα，cot α＝cos sin αα余切的对边的邻边A A A ∠∠=cotab A =cot 0cot >A(∠A 为锐角)注意：（1）正弦.余弦.正切.余切都是在直角三角形中给出的，要避免应用时对任意的三角形随便套用定义；（2）sinA 不是sin 与A 的乘积，是三角形函数记号，是一个整体。

“sinA ”表示一个比值，其他三个三角函数记号也是一样的；（3）锐角三角函数值与三角形三边长短无关，只与锐角的大小有关。

例题:1.在Rt △ABC 中，∠C 为直角，a =1，b =2，则cosA =________ ，tanA =_________．2. 在Rt △ABC 中，∠C 为直角，AB =5，BC =3，则sinA =________ ，tanA =_________．3.在Rt △ABC 中，∠C 为直角， ∠A =300，b =4，则a =__________，c =__________4.（2008·威海中考）在△ABC 中，∠C ＝90°，tanA ＝31，则sinB ＝（） A ．1010B ．23 C ．34D ．310105.在△ABC 中，∠C =90°，a, b, c 分别为∠A ，∠B ，∠C 的对边，下列各式错误的是（）A .a =c ·sinAB ．b =c ·cosBC ．b =a ·tanBD ．a =b ·tanA6.在△ABC 中，∠C ＝90°，(1)已知：c ＝ 83，∠A ＝60°，求∠B .a .b ． (2) 已知：a ＝36， ∠A ＝30°，求∠B .b .c .7.（2009·漳州中考）三角形在方格纸中的位置如图所示，则tan 的值是（）A ．35B ．43 C ．34D ．45练习:1.在Rt △ABC 中，∠C 为直角，若sinA =53，则cosB =_________． 2.已知cosA =23，且∠B =900-∠A ，则sinB =__________． 3.∠A 为锐角，已知sinA =135，那么cos (900-A)=___________ ． 4.在Rt △ABC 中，∠C 为直角，AC =4，BC =3，则sinA =（） A ．43 B ．34 C ． 53 D ．54 5.在Rt △ABC 中，∠C 为直角，sinA =22，则cosB 的值是( ) A ．21 B ．23 C ．1D ．22知识点二、特殊角所对的三角函数值1. 0°.30°.45°.60°.90°特殊角的三角函数值(重要)三角函数0° 30°45°60°90° αsin0 2122 231 αcos1 23 22210 αtan 0 331 3- αcot-3133注意：记忆特殊角的三角函数值，可用下述方法：0°.30°.45°.60°.90°的正弦值分别是02.12.22.32.42，而它们的余弦值分别是42.32.22.12.02；30°.45°.60°的正切值分别是13.22.31，而它们的余切值分别是31.22.13。

初中锐角三角函数及应用

初中锐角三角函数及应用锐角三角函数是指角度小于90度的三角函数，包括正弦、余弦和正切。

这些函数在数学和物理学中有着广泛的应用。

首先，我们来介绍一下锐角三角函数的定义和性质。

在一个直角坐标系中，对于一个锐角ABC（角A小于90度）, 我们可以定义正弦函数sinA 为点B的纵坐标除以斜边AC的长度，余弦函数cosA 为点B的横坐标除以斜边AC的长度，正切函数tanA 为点B的纵坐标除以横坐标。

其中，sinA、cosA和tanA都是角A的函数。

这些函数有许多重要的性质。

首先，它们的定义域都是锐角的正数集合，即(0,90)。

其次，它们的值域都是(-1,1)，即在定义域内，这些函数的值都在-1到1之间变化。

此外，正弦函数和余弦函数还具有周期性，周期为360度或2π弧度。

也就是说，对于一个锐角A，sin(A+360k) = sinA，cos(A+360k) = cosA，其中k 为整数。

在应用方面，锐角三角函数有着广泛的作用。

首先，它们被广泛应用于三角计算。

例如，我们可以利用正弦定理或余弦定理，通过已知边和角来求解三角形的其他未知边和角。

这在测量、建筑、工程等领域都有着重要的应用。

其次，锐角三角函数在物理学中也有着重要的应用。

例如，对于一个斜抛运动的物体，我们可以利用正弦函数和余弦函数来分析其垂直和水平方向上的运动。

它们可以帮助我们计算物体的落点、飞行时间、最大高度等。

另外，锐角三角函数还与周期函数和图像有着密切的关系。

它们的图像可以通过函数的周期性来得到。

例如，正弦函数的图像是一个周期为2π的曲线，具有对称性和单调性，而余弦函数的图像是一个周期为2π的曲线，也具有对称性和反单调性。

此外，锐角三角函数还与三角恒等式有着重要的联系。

三角恒等式是指对于锐角A和B，成立的恒等关系。

利用三角恒等式，我们可以化简复杂的三角函数表达式，简化计算过程。

总的来说，锐角三角函数是数学中一类重要的函数，具有广泛的应用。

它们不仅在三角计算和几何题目中有着重要作用，还与物理学、周期函数和三角恒等式等有着紧密的联系。

锐角三角函数(余弦、正切)

振动与波动
余弦函数在振动和波动的研究中有广泛应用。例如，简谐振动的位移、速度和加速度都可以表示为余弦函数的形式。
03
正切函数
正切函数的定义与性质
正切函数的定义
正切函数是锐角三角函数的一种，定义为直角三角形中锐角的对边与邻边的比值，记作tan(α)，其中α为锐角。
正切函数的性质
正切函数具有连续性、周期性、奇偶性等性质。在区间(0,π/2)和(π/2,π)内，正切函数是单调递增的，而在区间(-π/2,0)和(π/2,3π/2)内，正切函数是单调递减的。
01
余弦函数和正切函数的定义
余弦函数和正切函数是锐角三角函数的重要组成部分，它们分别描述了
直角三角形中锐角对应的邻边和斜边的比值，以及锐角对应的对边和邻
边的比值。
02
基本性质和应用
余弦函数和正切函数具有周期性、奇偶性等基本性质，这些性质在解决
几何、物理和工程问题中有着广泛的应用。例如，在计算角度、长度、
工程学中的应用
结构设计
在建筑和机械工程中，锐角三角函数用于设计各种结构，如桥梁、建筑和机器部件。
控制系统
在控制工程中，锐角三角函数用于设计和分析控制系统，以确保系统的稳定性和性能。
信号处理
在电子和通信工程中，锐角三角函数用于信号处理，如滤波、调制和解调等。
06
总结与展望
锐角三角函数的总结
正切函数的图像与周期性
正切函数的图像
正切函数的图像是一条周期函数，其周期为π，且在每一个周期内，图像呈现出先增后减的趋势。
正切函数的周期性
由于正切函数的周期为π，因此对于任意整数k，tan(x+kπ) = tan(x)，即正切函数在每个周期内具有相同的形状，但位置会随着k的变化而变化。

初中数学九年级锐角三角函数知识点总结

锐角三角函数是初中九年级数学中的一个重要内容，其中包括对正弦、余弦和正切函数的理解和应用。

下面是对锐角三角函数知识点的详细总结：1.三角函数的定义：- 正弦函数（sin）：对于单位圆上的一个角，其对边的长度与斜边的长度的比值。

- 余弦函数（cos）：对于单位圆上的一个角，其邻边的长度与斜边的长度的比值。

- 正切函数（tan）：对于单位圆上的一个角，其对边的长度与邻边的长度的比值。

2.锐角的定义：锐角是角度在0°到90°之间的角。

3.单位圆：单位圆指半径长度为1的圆，锐角三角函数可以通过单位圆来定义和理解。

4.三角函数的图像：正弦函数、余弦函数和正切函数的图像可以通过将单位圆绕过原点旋转得到。

5. 正弦函数（sin）的特点：-定义域：[0°,90°]或[0,π/2]-值域：[-1,1]-周期：360°或2π- 特殊值：sin0° = 0, sin30° = 1/2, sin45° = √2/2, sin60° = √3/2, sin90° = 1-图像特点：关于y轴对称6. 余弦函数（cos）的特点：-定义域：[0°,90°]或[0,π/2]-值域：[-1,1]-周期：360°或2π- 特殊值：cos0° = 1, cos30° = √3/2, cos45° = √2/2,cos60° = 1/2, cos90° = 0-图像特点：关于x轴对称7. 正切函数（tan）的特点：-定义域：(0°,90°)或(0,π/2)-值域：R（实数集）-周期：180°或π- 特殊值：tan30° = 1/√3, tan45° = 1, tan60° = √3, tan90° = 不存在（无限大）-图像特点：周期性递增8.三角函数之间的关系：- 正弦函数和余弦函数的关系：sinθ = cos(90° - θ)- 正切函数与正弦、余弦函数的关系：tanθ = sinθ / cosθ9.锐角三角函数的应用：-通过正弦函数、余弦函数和正切函数可以求解三角形的边长和角度大小。

初中数学锐角三角函数知识点

初中数学锐角三角函数知识点锐角三角函数是初中数学中的一个重要知识点。

本文将系统地介绍锐角三角函数的概念、性质和应用。

一、概念1.边长比在直角三角形中，我们可以定义三角函数。

对于锐角三角形，也可以把边长比看作三角函数的定义。

定义如下：- 正弦函数（sin）：指的是对边比斜边的比值，即sinA = 对边AB / 斜边AC。

- 余弦函数（cos）：指的是邻边比斜边的比值，即cosA = 邻边BC / 斜边AC。

- 正切函数（tan）：指的是对边比邻边的比值，即tanA = 对边AB / 邻边BC。

2.三角函数值的取值范围在锐角三角形中，三角函数的取值范围是(0,1)。

具体来说-正弦函数的值在0到1之间变化。

-余弦函数的值在0到1之间变化。

-正切函数的值在0到正无穷之间变化。

二、性质1.互余关系在锐角三角形中，对于同一个角的正弦和余弦函数，它们的数值互为倒数。

即sinA = 1 / cosA，cosA = 1 / sinA。

证明：由定义可知sinA = 对边AB / 斜边AC，cosA = 邻边BC / 斜边AC。

所以sinA / cosA = (对边AB / 斜边AC) / (邻边BC / 斜边AC) = 对边AB / 邻边BC = tanA。

又由于tanA = sinA / cosA，所以sinA = 1 / cosA。

同理可证cosA = 1 / sinA。

2.正切函数的性质在锐角三角形中，正切函数具有以下性质：-任何一个角的正切函数的值是唯一的。

- 对于锐角A和其补角（即90°-A），它们的正切值互为相反数。

（tanA = -tan(90°-A)）。

三、应用锐角三角函数在实际生活和学习中有着广泛的应用，以下是一些常见的应用：1.三角函数在测量中的应用例如，在建筑和工程中，我们经常需要测量高度、角度等，锐角三角函数可以帮助我们计算和测量。

2.角度的计算通过使用正弦函数、余弦函数和正切函数，我们可以根据已知的边长比计算出对应的角度。

中考总复习锐角三角函数综合复习--知识讲解

中考总复习锐角三角函数综合复习--知识讲解锐角三角函数是初中数学中的一个重要内容，也是中考数学考试中常考的内容之一、掌握了锐角三角函数的定义、性质和相关的计算方法，可以帮助我们解决与角度有关的各种问题，如计算角度的大小、求角的三角函数值等。

下面是锐角三角函数的综合复习知识讲解。

1.弧度制和角度制在介绍锐角三角函数之前，我们首先要了解弧度制和角度制。

在角度制中，一个圆的周长被定义为360度，而在弧度制中，一个圆的周长被定义为2π弧度。

所以可以得到以下关系：360度=2π弧度180度=π弧度90度=π/2弧度2.定义对于任意一个锐角A，我们可以在一个单位圆上面取点P，使得∠POA 的顶点为O，点O为圆心，点P在单位圆上。

这样，我们可以定义以下几个锐角三角函数：正弦函数sinA、余弦函数cosA、正切函数tanA、余切函数cotA。

3.性质(1) 正弦函数sinA：在单位圆上，点P的纵坐标就是正弦值sinA。

(2) 余弦函数cosA：在单位圆上，点P的横坐标就是余弦值cosA。

(3) 正切函数tanA：tanA的值等于sinA/cosA。

(4) 余切函数cotA：cotA的值等于cosA/sinA。

(5) 错位现象：sinA等于cos(90度-A)，cosA等于sin(90度-A)。

4.基本关系式(1) sin²A + cos²A = 1，即sin²A = 1 - cos²A，cos²A = 1 -sin²A。

(2) tanA = sinA/cosA，cotA = 1/tanA = cosA/sinA。

(3) sin(180度 - A) = sinA，cos(180度 - A) = -cosA。

(4) cos(360度 - A) = cosA，sin(360度 - A) = -sinA。

5.锐角三角函数的值(1)0度、30度、45度、60度、90度的正弦、余弦、正切值是特殊的，需要进行熟记。

初中数学锐角三角函数

初中数学锐角三角函数锐角三角函数是数学中的重要分支，用来描述角度和边长之间的关系。

在初中数学中，我们学习了正弦函数、余弦函数和正切函数，它们分别是三角形的对边比斜边、邻边比斜边，以及对边比邻边。

下面，让我们来详细了解一下这些锐角三角函数。

首先，让我们来了解正弦函数。

正弦函数给出了一个角度与其对边和斜边之间的关系。

我们可以通过以下公式来表示：sin(A) = a / c，其中A代表角度，a代表对边的长度，c代表斜边的长度。

通过正弦函数，我们可以求得一个锐角三角形中的对边和斜边之间的比例关系。

正弦函数的取值范围是-1到1之间。

接下来，我们来了解一下余弦函数。

余弦函数描述了一个角度与其邻边和斜边之间的关系。

余弦函数的表示形式为：cos(A) = b / c，其中A代表角度，b代表邻边的长度，c代表斜边的长度。

通过余弦函数，我们可以计算锐角三角形中邻边和斜边之间的比例关系。

余弦函数的取值范围也是-1到1之间。

最后，让我们来了解一下正切函数。

正切函数表示了一个角度与其对边和邻边之间的关系。

正切函数的表示形式为：tan(A) = a / b，其中A代表角度，a代表对边的长度，b代表邻边的长度。

通过正切函数，我们可以计算锐角三角形中对边和邻边之间的比例关系。

正切函数的取值范围可以是任意实数。

锐角三角函数在现实生活中有着广泛的应用。

例如，在建筑、工程、天文学和地理学等领域中，我们经常需要利用这些函数来计算各种三角形的边长和角度。

此外，在电视信号传输和音频处理中，正弦函数的应用也非常广泛。

通过学习锐角三角函数，我们不仅能够了解角度和边长之间的关系，还能够解决与三角形相关的实际问题。

因此，学习锐角三角函数对我们的数学学习和实际应用都具有重要的指导意义。

在学习锐角三角函数时，我们还需要注意一些常用的角度值。

例如，30度、45度和60度等特殊角度值，它们对应的三角函数值可以事先记住，以方便在计算中的应用。

此外，我们还可以利用三角函数的周期性，简化计算过程。

锐角三角函数

铅垂线仰角水平线俯角
如示意图：看图时，先要找水平线，再找视线，最后确定是仰角还是俯角。
若 ∠A+∠B=90°
a sinA= cosB= c b cosA= sinB= c
B
对边
A
邻边
C
tanA·tanB=1
同角三角函数关系：
（1） sin2a ＋ cos2 a ＝1
sinα （2） tan α = cos α
A D
∟
G
30°
C
E
B
F
(评价43页/例2 ）
∟
∟
P
30°
O
【例7】
已知：如图，在两面墙之间有一个底端在点A的梯子，（即AB=AD），已知 ∠BAC=60°， ∠DAE=45°， DE⊥AE于E， 2 BC. BC⊥AC，DE= m3 ，求 B D ？ C
60° 45°
∟
3 2
A
E
∟
评价 45页/8
运算结果一般保留根号。
1 2 1 2 解： (1) 原式= = ； 2 2 2
- 2 tan45 . (2) sin 60° + cos 60°
解：(2) 原式= ( 3 )2 + ( 1 )2 - 2×1 2 2
3 1 = 2 4 -1
练习:课本 47页/1
练习:课本 47页/2 已知：如图，在RtABC中，∠ACB=90°， CD⊥AB，垂足为D，BC=2，BD= 3 ，分别求出△ABC、△ACD、△BCD中各锐角。
【例8】一个小孩荡秋千, 秋千的链子的长度为2.5米, 当秋千向两边摆动时,摆角恰好为 60°, 且两边的摆动角度相同, 求它摆至最高位置与最低位置时的高度差.(结果精确到0.01米)

中考数学：锐角三角函数讲解

中考数学：锐角三角函数讲解锐角角A的正弦（sin）,余弦（cos）和正切（tan）,余切（cot）以及正割（sec），（余割csc）都叫做角A的锐角三角函数。

正弦等于对边比斜边余弦等于邻边比斜边正切等于对边比邻边余切等于邻边比对边正割等于斜边比邻边余割等于斜边比对边正切与余切互为倒数它的本质是任意角的集合与一个比值的集合的变量之间的映射。

通常的三角函数是在平面直角坐标系中定义的，其定义域为整个实数域。

另一种定义是在直角三角形中，但并不完全。

现代数学把它们描述成无穷数列的极限和微分方程的解，将其定义扩展到复数系。

由于三角函数的周期性，它并不具有单值函数意义上的反函数。

它有六种差不多函数(初等差不多表示)：函数名正弦余弦正切余切正割余割在平面直角坐标系xOy中，从点O引出一条射线OP,设旋转角为θ，设OP=r,P点的坐标为（x,y）有正弦函数sinθ=y/r余弦函数cosθ=x/r正切函数tanθ=y/x余切函数cotθ=x/y正割函数secθ=r/x余割函数cscθ=r/y（斜边为r,对边为y,邻边为x.）死记硬背是一种传统的教学方式,在我国有悠久的历史。

但随着素养教育的开展,死记硬背被作为一种僵化的、阻碍学生能力进展的教学方式,慢慢为人们所摒弃;而另一方面,老师们又为提高学生的语文素养煞费苦心。

事实上,只要应用得当,“死记硬背”与提高学生素养并不矛盾。

相反,它恰是提高学生语文水平的重要前提和基础。

以及两个不常用，已趋于被剔除的函数：那个工作可让学生分组负责收集整理,登在小黑板上,每周一换。

要求学生抽空抄录同时阅读成诵。

其目的在于扩大学生的知识面,引导学生关注社会,热爱生活,因此内容要尽量广泛一些,能够分为人一辈子、价值、理想、学习、成长、责任、友谊、爱心、探究、环保等多方面。

如此下去,除假期外,一年便能够积存40多则材料。

假如学生的脑海里有了众多的鲜活生动的材料,写起文章来还用乱翻参考书吗?正矢函数versinθ=1-cosθ“师”之概念，大体是从先秦时期的“师长、师傅、先生”而来。

初中九年级数学中考锐角三角函数知识点总结

九年级数学中，锐角三角函数是一个重要的知识点。

锐角三角函数是指对于锐角的正弦、余弦和正切函数。

下面我将对锐角三角函数的基本概念、性质和应用进行总结。

一、基本概念1.弧度和角度：角度是常用的角度度量单位，弧度是角度的另一种度量单位。

1个弧度对应360°/2π≈57.3°。

角度和弧度之间的关系式：弧度=角度×π/180°。

2.锐角：指角度小于90°的角。

3. 三角函数：对于一个锐角A，定义其正弦(sin A)为对边与斜边的比值，余弦(cos A)为邻边与斜边的比值，正切(tan A)为对边与邻边的比值。

二、性质1.正弦函数的性质：（1）对于锐角A，0 < A < 90°，sin A > 0；（2）sin A = sin (180° - A) = sin (A + 360°)；（3）sin (90° - A) = cos A；（4）sin A ≠ 0，当且仅当A是锐角。

2.余弦函数的性质：（1）对于锐角A，0 < A < 90°，cos A > 0；（2）cos A = cos (180° - A) = cos (360° + A)；（3）cos (90° - A) = sin A；（4）cos A ≠ 0，当且仅当A是锐角。

3.正切函数的性质：（1）对于锐角A，0 < A < 90°，tan A > 0；（2）tan A = tan (180° + A)；（3）tan (90° - A) = 1/tan A；（4）tan A ≠ 0，当且仅当A是锐角。

4.三角函数的关系：（1）sin^2 A + cos^2 A = 1；（2）tan A = sin A / cos A。

三、应用1.解三角形：利用已知角的正弦、余弦和正切的值，可以求解未知边长或角度的三角形问题。

初三锐角三角函数复习讲义

锐角三角函数：知识点一：锐角三角函数的定义：一、锐角三角函数定义：如图所示，在 Rt△ ABC 中，∠ C=90 0, ∠A 、∠ B 、∠ C 的对边分别为a、 b、 c，则∠ A 的正弦可表示为： sinA∠ A 的余弦可表示为： cosA∠ A 的正切可表示为： tanA，它们称为∠ A 的锐角三角函数① sin A ()＝______，斜边②cosA ()＝______，斜边③ tanA ( )＝______，A的邻边【特别提醒： 1、sinA、cosA、 tanA 表示的是一个整体，是两条线段的比，没有单位，这些比值只与有关，与直角三角形的无关。

2、取值范围<sinA< ，<cosA< ， tanA>例 1. 锐角三角函数求值：在Rt△ ABC 中，∠ C＝ 90°，若 a＝ 9， b＝ 12，则 c＝ ______，sinA＝ ______， cosA＝ ______， tanA＝______ ，sinB＝ ______， cosB＝ ______， tanB＝______ ．典型例题：类型一：利用直角三角形求值1．已知：如图，Rt△TNM 中，∠ TMN ＝90°， MR⊥ TN 于 R 点， TN＝ 4， MN＝ 3．求： sin∠TMR、 cos∠TMR 、 tan∠ TMR．2．已知：如图，⊙3 O 的半径 OA＝ 16cm， OC⊥AB 于 C 点， sinAOC4求： AB 及 OC 的长．类型二 . 利用角度转化求值：1．已知：如图， Rt △ABC 中，∠ C ＝ 90°． D 是 AC 边上一点， DE ⊥ AB 于 E 点．DE ∶ AE ＝1∶ 2．求： sinB 、 cosB 、tanB ．2．如图，直径为 10 的⊙ A 经过点 C (0，5) 和点 O (0，0) ，与 x 轴的正半轴交于点 D ，B 是 y轴右侧圆弧上一点，则 cos ∠ OBC 的值为（） A ．1B ．3 C ．3 4 2 2 D ．5 y 5C AOB D x第 8题图3， AC 5.如图， ⊙O 是 △ ABC 的外接圆， AD 是 ⊙O 的直径，若 ⊙O的半径为2 ，则 2sin B 的值是（）2 3 3 4 A ． B ． C ． D ． 3 2 4 36. 如图 4，沿 AE 折叠矩形纸片ABCD ，使点 D 落在 BC 边的点 F 处．已知AB 8 ， BC 10 ， AB=8,则 tan ∠ EFC 的值为 ( ) A DEＡ． 3 Ｂ． 4Ｃ． 3Ｄ．4 B FC43557. 如图 6，在等腰直角三角形 ABC 中， C90 ， AC6 ， D 为 AC 上一点，若tan DBA 1 ) ，则 AD 的长为 (5A ． 2B． 2C． 1 D ． 2 2类型三 . 化斜三角形为直角三角形1. 如图，在△ ABC 中，∠ A=30°，∠ B=45°， AC=2 3 ，求 AB 的长．2．如图，在 Rt△ ABC 中，∠ BAC=90°，点 D 在 BC 边上，且△ ABD 是等边三角形．若 AB=2 ，求△ ABC 的周长．（结果保留根号）3. ABC 中，∠ A=60°， AB=6 cm， AC=4cm ，则△ ABC 的面积是（）A.2 3 cm2B.4 3 cm2C.6 3 cm2D.12 cm2类型四：利用网格构造直角三角形1.如图所示，△ ABC 的顶点是正方形网格的格点，则sinA 的值为（）1B．5C．10 D ．2 5A ．2 5 10 5ACO BA B2．如图，△ ABC 的顶点都在方格纸的格点上，则sin A=_______.3．如图， A、 B、C 三点在正方形网络线的交点处，若将ABC 绕着点 A 逆时针旋转得到AC 'B' ，则 tan B' 的值为（）1B. 1 1D. 1A.3 C.4 24．正方形网格中，∠AOB如图放置，则tan∠ AOB 的值是（）5 2 5 1A ． 5 B. 5 C.2 D. 2知识点二：特殊角的三角函数值锐角 30° 45° 60°sin cos tan 当时，正弦和正切值随着角度的增大而余弦值随着角度的增大而例 1．求下列各式的值．1.计算： tan 60 sin 245 2 cos30－ 1+(2 π－ 1)0－ 3tan30－°tan45 ° 2.计算：3313tan30 0 tan 45 sin 303．计算： 2 cos60 sin 45 4．计算：221 cos60例 2．求适合下列条件的锐角．(1) cos 1 3(3) sin 2 2 (4) 6 cos(16 ) 3 3(2) tan 3 2 2（）已知为锐角，且tan(300 )3 ，求 tan的值（）在 ABC 中， cos A 1 (sin B2 )20 ， A ， B 都是锐角，求 C 的度数2 2例 3. 三角函数的增减性1 1．已知∠ A 为锐角，且 sinA < 2，那么∠ A 的取值范围是A. 0 °<A < 30 °B. 30 <°A ＜60°C. 60 <°A < 90 °D.30 <°A < 90 °2. 已知 A 为锐角，且cos A sin 300，则（）A. 0 °<A < 60 °B. 30 <°A < 60 °C. 60 <°A < 90 °D. 30 <°A <90 °类型五：三角函数在几何中的应用1．已知：如图，在菱形ABCD 中， DE ⊥AB 于 E， BE＝16cm， sin A求此菱形的周长．12132．已知：如图， Rt△ ABC 中，∠ C＝ 90°， AC BC 3 ，作∠ DAC ＝30°， AD 交 CB 于 D 点，求：(1) ∠ BAD；(2)sin∠ BAD 、 cos∠BAD 和 tan∠BAD ．3. 已知：如图△ ABC 中， D 为 BC 中点，且∠ BAD ＝90°， tan B 1，求： sin∠CAD 、cos 3∠CAD 、 tan∠ CAD ．4. 如图，在 Rt△ ABC 中，∠C=90°，sin B 3，点 D 在 BC 边上，DC= AC = 6 ，求 tan∠ BAD 5的值． AB CD5（.本小题 5 分）如图，△ ABC 中，∠A=30°，tan B3 ，2AC 4 3 ．求 AB 的长 . CA B知识点三：解直角三角形：1．在解直角三角形的过程中，一般要用的主要关系如下(如图所示 )：在Rt△ABC 中，∠ C＝ 90°， AC＝ b，BC＝a， AB＝c，①三边之间的等量关系：________________________________ ．②两锐角之间的关系：_________________________________ _ ．③边与角之间的关系：sinA cosB ______；cos A sin B _______；1_____；1tan A tan B ______．tan B tan A④直角三角形中成比例的线段(如图所示 )．在Rt△ ABC 中，∠ C＝ 90°， CD ⊥ AB 于 D．CD 2＝ _________； AC2＝ _________；BC 2＝ _________ ；AC· BC＝ _________．例 1．在 Rt△ ABC 中，∠ C＝ 90°．(1) 已知：a 2 3 ，b 2 ，求∠ A、∠ B，c；(2) 已知： sinA2 6 ，求 a、b；， c3（3）．已知：△ ABC 中，∠ A＝ 30°，∠ B＝ 60°， AC＝ 10cm．求 AB 及 BC 的长．类型六：解直角三角形的实际应用仰角与俯角1．如图，从热气球C 处测得地面 A 、 B 两点的俯角分别是30°、 45°，如果此时热气球C处的高度 CD 为 100 米，点 A 、D 、B 在同一直线上，则AB 两点的距离是（）A ．200 米B ．200 米C． 220 米D． 100（）米2．在一次数学活动课上，海桂学校初三数学老师带领学生去测万泉河河宽，如图13 所示，某学生在河东岸点 A 处观测到河对岸水边有一点 C ，测得 C 在 A 北偏西的方向上，沿31河岸向北前行 20 米到达 B 处，测得 C 在 B 北偏西 45 的方向上，请你根据以上数据，帮助该同学计算出这条河的宽度．（参考数值： tan31 °≈3， sin31 °≈1）5 2图133 .如图，小聪用一块有一个锐角为 30 的直角三角板测量树高，已知小聪和树都与地面垂直，且相距 3 3 米，小聪身高AB 为 1.7 米，求这棵树的高度.CA DBE4．一数学兴趣小组为测量河对岸树 AB 的高，在河岸边选择一点 C ，从 C 处测得树梢 A 的仰角为 45°，沿 BC 方向后退 10 米到点 D ，再次测得点 A 的仰角为 30°．求树高． (结果精确到 0.1 米．参考数据：2 1.414 ，3 1.732 )A30° 45°DC B5．超速行驶是引发交通事故的主要原因之一．上周末，小明和三位同学尝试用自己所学的知识检测车速．如图，观测点设在 A 处，离益阳大道的距离（ AC ）为 30 米．这时，一辆小轿车由西向东匀速行驶，测得此车从 B 处行驶到 C 处所用的时间为 8 秒，∠ BAC=75° ．（1）求 B 、 C 两点的距离；（2）请判断此车是否超过了益阳大道 60 千米 /小时的限制速度？（计算时距离精确到 1 米，参考数据： sin75 °≈ 0.9659，cos75°≈ 0.2588， tan75 °≈ 3.732，3 ≈ 1.732， 60 千米 /小时 ≈ 16.7米 /秒）坡度与坡角1.如图，某水库堤坝横断面迎水坡AB 的坡比是1：3 ，堤坝高BC=50m ，则应水坡面AB 的长度是（）A ． 100mB ．100 3 m C． 150m D ．50 3 m2.数学活动课上，老师和学生一起去测量学校升旗台上旗杆 AB 的高度 .如图，老师测得升旗台前斜坡 FC 的坡比为i=1:10 ，学生小明站在离升旗台水平距离为35m（即 CE=35m ）处的 C 点，测得旗杆顶端 B 的仰角为α，已知 tanα= 3，升旗台高AF=1m，小明身高7CD=1.6m ，请帮小明计算出旗杆AB 的高度 .BiFC =1:10ADα FCE3.如图，有两条公路 OM ，ON 相交成 30°角，沿公路 OM 方向离 O 点 80 米处有一所学校A ，当重型运输卡车P 沿道路 ON 方向行驶时，在以 P 为圆心、 50 米长为半径的圆形区域内部会受到卡车噪声的影响，且卡车P 与学校 A 的距离越近噪声影响越大，若已知重型运输卡车 P 沿道路 ON 方向行驶的速度为 18 千米 /时 .(1)求对学校 A 的噪声影响最大时 ,卡车 P 与学校 A 的距离 ;(2)求卡车 P 沿道路 ON 方向行驶一次给学校 A 带来噪影响的时间.NP30°O 80米 A M4.如图是某儿童乐园为小朋友设计的滑梯平面图．已知 BC=4 米， AB=6 米，中间平台宽度DE=1 米，EN、DM 、CB 为三根垂直于AB 的支柱，垂足分别为N、M、B，∠ EAB=31 °，DF ⊥ BC 于 F，∠ CDF =45 °．求 DM 和 BC 的水平距离 BM 的长度．（结果精确到 0.1 米，参考数据： sin31 °≈ 0.，52cos31°≈ 0.86，tan31 °≈ 0.）60CE D 45°F31°A N M B5.如图，某幼儿园为了加强安全管理，决定将园内的滑滑板的倾角由45o 降为 30o，已知原滑滑板AB 的长为 5 米，点 D 、B、C 在同一水平地面上．（1）改善后滑滑板会加长多少？（精确到0.01）（2）若滑滑板的正前方能有 3 米长的空地就能保证安全，原滑滑板的前方有 6 米长的空地，像这样改造是否可行？说明理由。

初中数学锐角三角函数知识点

初中数学锐角三角函数知识点锐角三角函数是高中数学的重要内容，它涉及到三角函数的定义、性质以及与三角函数相关的常见解题方法。

以下将详细介绍锐角三角函数的知识点。

一、锐角三角函数的定义1. 正弦函数（sine function）：在锐角ABC中，以角A为自变量，以对边AB与斜边AC的比值作为函数值。

记作sinA = AB/AC。

2. 余弦函数（cosine function）：在锐角ABC中，以角A为自变量，以邻边BC与斜边AC的比值作为函数值。

记作cosA = BC/AC。

3. 正切函数（tangent function）：在锐角ABC中，以角A为自变量，以对边AB与邻边BC的比值作为函数值。

记作tanA = AB/BC。

4. 余切函数（cotangent function）：在锐角ABC中，以角A为自变量，以邻边BC与对边AB的比值作为函数值。

记作cotA = BC/AB。

5. 正割函数（secant function）：在锐角ABC中，以角A为自变量，以斜边AC与邻边BC的比值作为函数值。

记作secA = AC/BC。

6. 余割函数（cosecant function）：在锐角ABC中，以角A为自变量，以斜边AC与对边AB的比值作为函数值。

记作cscA = AC/AB。

二、锐角三角函数的性质1. 正弦函数的定义域为[0, π/2]，值域为[0, 1]，是一个奇函数，即sin(π/2 - A) = cosA。

2. 余弦函数的定义域为[0, π/2]，值域为[0, 1]，是一个偶函数，即cos(π/2 - A) = sinA。

3.正割函数和余割函数的定义域为(0,π/2)∪(π/2,π)，值域为R^+∪R^-。

4.正弦函数和余弦函数的图像是一条周期为2π的曲线，对称于直线x=π/25.正切函数和余切函数的定义域为(0,π/2)∪(π/2,π)，值域为R^+∪R^-。

6.正切函数和余切函数的图像是一条周期为π的曲线，对称于直线x=π/2三、常用的锐角三角函数解题方法1. 利用定义求函数值：根据三角函数的定义，利用已知信息计算出函数值。

初中数学锐角三角函数有哪些主要函数

初中数学锐角三角函数有哪些主要函数在初中数学中，主要的锐角三角函数有正弦函数（sin）、余弦函数（cos）、正切函数（tan）和它们的倒数函数，即余割函数（csc）、正割函数（sec）和余切函数（cot）。

下面我将详细介绍这些函数及其性质。

1. 正弦函数（sin）：正弦函数是指锐角三角形中某一角的对边与斜边的比值。

在一个锐角三角形中，如果角A的对边为a，斜边为c，则正弦函数可以表示为sin(A) = a/c。

正弦函数的定义域是锐角，即0°到90°之间。

2. 余弦函数（cos）：余弦函数是指锐角三角形中某一角的邻边与斜边的比值。

在一个锐角三角形中，如果角A的邻边为b，斜边为c，则余弦函数可以表示为cos(A) = b/c。

余弦函数的定义域也是锐角，即0°到90°之间。

3. 正切函数（tan）：正切函数是指锐角三角形中某一角的对边与邻边的比值。

在一个锐角三角形中，如果角A的对边为a，邻边为b，则正切函数可以表示为tan(A) = a/b。

正切函数的定义域是所有不等于90°的角。

4. 余割函数（csc）：余割函数是正弦函数的倒数，即csc(A) = 1/sin(A)。

它表示锐角三角形中某一角的斜边与对边的比值的倒数。

5. 正割函数（sec）：正割函数是余弦函数的倒数，即sec(A) = 1/cos(A)。

它表示锐角三角形中某一角的斜边与邻边的比值的倒数。

6. 余切函数（cot）：余切函数是正切函数的倒数，即cot(A) = 1/tan(A)。

它表示锐角三角形中某一角的邻边与对边的比值的倒数。

这些锐角三角函数在数学中有广泛的应用。

通过它们，我们可以计算锐角三角形中的各个边长和角度，解决与三角形相关的问题。

此外，这些函数具有一些重要的性质，例如：-正弦函数和余弦函数的值都在-1到1的范围内。

-正切函数的值可以是任何实数，除了90°的整数倍角。

-正弦函数和余弦函数是周期函数，周期为360°或2π弧度。

初中数学tan sin cos公式

1.锐角三角函数锐角三角函数定义:锐角角A的正弦(s i n),余弦(c o s)和正切(t an),余切(c o t)以及正割(s e c)，余割(c s c)都叫做角A的锐角三角函数。

正弦(s i n)：对边比斜边，即s i n A=a/c余弦(c o s)：邻边比斜边，即c o s A=b/c正切(t a n)：对边比邻边，即t a n A=a/b余切(c o t)：邻边比对边，即c o t A=b/a正割(s e c)：斜边比邻边，即s e c A=c/b余割(c s c)：斜边比对边，即c s c A=c/a2.特殊角三角函数值3.互余角的关系s i n(π-α)=c o sα,c o s(π-α)=s i nα,t an(π-α)=c o tα,c o t(π-α)=t a nα.4.平方关系sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)5.积的关系s i nα=t a nα·c o sαc o sα=c o tα·s i nαt anα=s i nα·s e cαc o tα=c o sα·c s cαs e cα=t anα·c s cαc s cα=s e cα·c o tα6.倒数关系t anα·c o tα=1s i nα·c s cα=1c o sα·s e cα=17.诱导公式公式一：设α为任意角，终边相同的角的同一三角函数的值相等：s i n(2kπ+α)=s i nαk∈zc o s(2kπ+α)=c o sαk∈zt an(2kπ+α)=t a nαk∈zc o t(2kπ+α)=c o tαk∈z公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：s i n(π+α)=-s i nαc o s(π+α)=-c o sαt an(π+α)=t anα8.两角和差公式(1)s i n(A+B)=s i n A c o s B+c o s A s i n B(2)s i n(A-B)=s i n A c o s B-s i n B c o s A(3)c o s(A+B)=c o s A c o s B-s i n A s i n B(4)c o s(A-B)=c o s A c o s B+s i n A s i n B(5)t a n(A+B)=(t a n A+t a n B)/(1-t an A t an B)(6)t a n(A-B)=(t a n A-t a n B)/(1+t a n A t an B)(7)c o t(A+B)=(c o t A c o t B-1)/(c o t B+c o t A)(8)c o t(A-B)=(c o t A c o t B+1)/(c o t B-c o t A)除了以上常考的三角函数公式外，掌握下面半角公式，积化和差和万能公式有利于快速解决选择题，达到事半功倍的效果哦！1.半角公式注：正负由α/2所在的象限决定。

初中数学锐角三角函数

初中九年级数学中考锐角三角函数知识点总结

初三数学锐角三角函数

九年级数学专题复习锐角三角函数

中考数学-锐角三角函数(解析版)

初中数学 什么是锐角三角函数

初中锐角三角函数

锐角三角函数

初中锐角三角函数及应用

锐角三角函数(余弦、正切)

初中数学九年级锐角三角函数知识点总结

初中数学锐角三角函数知识点

中考总复习锐角三角函数综合复习--知识讲解

初中数学锐角三角函数

锐角三角函数

中考数学：锐角三角函数讲解

初中九年级数学中考锐角三角函数知识点总结

初三锐角三角函数复习讲义

初中数学锐角三角函数知识点

初中数学 锐角三角函数有哪些主要函数

初中数学tan sin cos公式

初中数学什么是锐角三角函数

初中数学锐角三角函数有哪些主要函数