第十六章分式知识点和典型例习题
新人教版八年级数学下册第十六章分式知识点总结

第十六章 分式知识点及典型例子一、分式的定义:如果A 、B 表示两个整式,并且B 中含有字母,那么式子BA 叫做分式。
例1.下列各式a π,11x +,15x+y ,22a b a b --,-3x 2,0•中,是分式的有( )个。
二、 分式有意义的条件是分母不为零;【B ≠0】分式没有意义的条件是分母等于零;【B=0】分式值为零的条件分子为零且分母不为零。
【B ≠0且A=0 即子零母不零】例2.下列分式,当x 取何值时有意义。
(1)2132x x ++; (2)2323x x +-。
例3.下列各式中,无论x 取何值,分式都有意义的是( )。
A .121x +B .21x x +C .231x x+ D .2221x x + 例4.当x______时,分式2134x x +-无意义。
当x_______时,分式2212x x x -+-的值为零。
例5.已知1x -1y=3,求5352x xy y x xy y +---的值。
三、分式的基本性质:分式的分子与分母同乘或除以一个不等于0的整式,分式的值不变。
(0≠C )四、分式的通分和约分:关键先是分解因式。
例6.不改变分式的值,使分式115101139x y x y -+的各项系数化为整数,分子、分母应乘以(• )。
例7.不改变分式2323523x x x x -+-+-的值,使分子、分母最高次项的系数为正数,则是(• )。
例8.分式434y x a +,2411x x --,22x xy y x y-++,2222a ab ab b +-中是最简分式的有( )。
例9.约分:(1)22699x x x ++-; (2)2232m m m m-+- 例10.通分:(1)26x ab ,29y a bc ; (2)2121a a a -++,261a - 例11.已知x 2+3x+1=0,求x 2+21x 的值. C B C A B A ⋅⋅=C B C A B A ÷÷=例12.已知x+1x=3,求2421x x x ++的值. 五、分式的运算:分式乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为分母。
华东师大版八年级下册第十六章分式知识点总结与典型例题讲义(无答案)

目录一、分式的概念1考向1:考查分式的定义2考向2:考查分式有意义的条件2 考向3:考查分式值为0的条件2 考向4:考查分式值为正、负的条件2 考向5:考查分式的值为1,-1的条件2 二、分式的基本性质2考向6:化分数系数、小数系数为整数系数3 考向7:分数的系数变号3 考向8:分式的约分3 考向9:分式的通分3 三、分式的运算3考向10:分式的混合运算4 考向11:化简求值4考向12:求待定字母的值5 四、解分式方程5考向13:用常规方法解分式方程5 考向14:用特殊方法解分式方程5 考向15:分式方程无解忘检验6 考向16:漏乘无分母的项6考向17:由分式方程无解或有增根求未知字母的值6 五、列分式方程应用题6考向18:行程中的应用性问题6 考向19:轮船顺逆水应用问题6 考向20:工程类应用性问题6 考向21:营销类应用性问题7 考向22:浓度应用性问题7 考向23:货物运输应用性问题7分式知识点总结与典型例题一、分式的概念1、定义:一般地,如果A ,B 表示两个整式,并且B 中含有字母,那么式子BA叫做分式,A 为分子,B 为分母。
2、与分式有关的条件:①分式有意义:分母不为0(0B ≠) ②分式无意义:分母为0(0B =) ③分式值为0:分子为0且分母不为0(⎩⎨⎧≠=0B A )④分式值为正或大于0:分子分母同号(⎩⎨⎧>>00B A 或⎩⎨⎧<<00B A )⑤分式值为负或小于0:分子分母异号(⎩⎨⎧<>00B A 或⎩⎨⎧><00B A ) ⑥分式值为1:分子分母值相等(A=B )⑦分式值为-1:分子分母值互为相反数(A+B=0) 典型例题:考向1:考查分式的定义1、下列代数式中:y x yx y x y x ba b a y x x -++-+--1,,,21,22π,是分式的有: 考向2:考查分式有意义的条件2、当有何值时,下列分式有意义(1)44+-x x (2)232+x x (3)122-x (4)3||6--x x(5)xx 11-考向3:考查分式值为0的条件 3、当取何值时,下列分式的值为0.(1)31+-x x (2)42||2--x x考向4:考查分式值为正、负的条件4、当为何值时,分式x-84为正; 5、当为何值时,分式2)1(35-+-x x 为负;6、当为何值时,分式32+-x x 为非负数 考向5:考查分式的值为1,-1的条件 7、若22||+-x x 的值为1,-1,则x 的取值分别为 二、分式的基本性质1、分式的基本性质:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变。
八年级下册数学第十六章《分式》知识点练习

八年级下册数学第十六章《分式》知识点练习一、分式定义及相关题型形如A(A 、B 是整式,且中含有字母,B≠0)的式子叫分式。
此中A 叫做分式的分子,BB叫做分式的分母。
【例题】以下代数式中:b ,x ,1x y , ab ,x 2y 2 ,25, y ,是分式的有:。
a2a b x y 3xx 5【练习】1、各式中,1x+1y, 1 , 5 1, —4xy,x 2,x分式的个数有( )3 2x yaxA 、1个B、2个C 、3个D 、4个2、在ab ,x 3,5 x ,ab,21中,是分式的有()2xa baA 、1个B、2个C、3个D 、4个3、以下各式:ab ,x3,5y , 3 x 21,ab,1(xy)中,是分式的共有()2x4a bmA 、1个B 、2个C、3个D、4个题型二:考察分式存心义的条件1、分式有无心义的条件取决于能否等于零,分式无心义。
2、分式值为零的条件:【例题】当x________时,分式x1 存心义;当x_______时,分式|x|2 无心义。
x 3x 24【练习】(1)当x________时,分式2x存心义;(2)当x_______时,分式4存心义;x2x21(3)当x________时,分式2x1无心义;(4)当x________时,分式x2无心义;2x x2(5)当x为随意实数时,以下分式必定存心义的是()A、2B、1C、2D、11x3x22x2x2(6)已知当x2时,分式x b 无心义,x4时,此分式的值为0,则ab的值等于()x aA、-6B、-2C、6D、2题型三:考察分式的值为0的条件【例题】当x 时,分式3x的值为;时,分式x29的值为0 x20当xx32x+2x21【练习】(1)当x时,分式x 2的值为0;(2)当x时,分式x1的值为(3)能使分式x2x的值为零的全部x的值是()x21A 、 x 0B 、x 1C 、x 0或x 1D 、x 0或x1二、分式的基天性质及相关题型题型一:化分数系数、小数系数为整数系数【例题】不改变分式的值,把分子、分母的系数化为整数.1 2x y=___________________(1)23=_________________________(2)1x 1y3 4【练习】1、不改变分式的值,把以下分式的分子、分母的系数化为整数.(1)=______________3b=_______________________ (2)51 a 1 b4 10题型二:分式的系数变号【例题】不改变分式的值,把以下分式的分子、分母的首项的符号变成正号.(1) x y=________(2) a=________()a=____________x y a b3b【练习】不改变分式的值,把以下分式的分子、分母的首项的符号变成正号(1)a b=________ (2)x y() na bx=________3=____________y m题型三:分式中的字母扩大、减小【例题】若将分式ab(a,b均为正数)中的字母a,b的值分别扩大为本来的2倍,则分式的值为ab()A、扩大为本来的2倍B、减小为本来的1C、不变D、减小为本来的1 24【练习】1.假如把2y中的x和y都扩大5倍,那么分式的值()2x3yA扩大5倍B不变C减小5倍D扩大4倍2、若x、y的值均扩大为本来的2倍,则以下分式的值保持不变的是()A、3x B、3x C、3x2D、3x32y2y22y2y25、以下各式中,正确的选项是()A.a m a B.a b=0C.ab1b1D.x y1b m b a b ac1c1x2y2xy三、分式的运算题型一:约分【例题】约分:(1)12xy(2)a2b2(3)x29(4)a2b29x2b a x26x9a2a b【练习】约分:(1)x 26x9=2x4x2;(2)2x28x8=;9m23m的结果是()(3)化简m29A 、mB、m、m、mC D3m3m3题型二:通分【例题】以下各题中,所求的最简公分母,错误的选项是()m3 m A、1与a最简公分母是6x2B1与1最简公分母是a2b3c3x6x2、3a2b3c3 3a2b3C、1与1的最简公分母是m2n2D、1与1是简公分母是ab(x y)(y x)mnmn a(xy)b(yx)【练习】1、1,1,1的最简公分母是() a2222a1a1a2a1A、a42a21B、(a21)(a21)C、a42a21D、(a1)42、分式1与x 的最简公分母是__________。
(完整版)初中数学分式方程典型例题讲解

第十六章分式知识点和典型例习题【知识网络】【思想方法】 1.转化思想转化是一种重要的数学思想方法,应用非常广泛,运用转化思想能把复杂的问题转化为简单问题,把生疏的问题转化为熟悉问题,本章很多地方都体现了转化思想,如,分式除法、分式乘法;分式加减运算的基本思想:异分母的分式加减法、同分母的分式加减法;解分式方程的基本思想:把分式方程转化为整式方程,从而得到分式方程的解等. 2.建模思想本章常用的数学方法有:分解因式、通分、约分、去分母等,在运用数学知识解决实际问题时,首先要构建一个简单的数学模型,通过数学模型去解决实际问题,经历“实际问题———分式方程模型———求解———解释解的合理性”的数学化过程,体会分式方程的模型思想,对培养通过数学建模思想解决实际问题具有重要意义. 3.类比法本章突出了类比的方法,从分数的基本性质、约分、通分及分数的运算法则类比引出了分式的基本性质、约分、通分及分式的运算法则,从分数的一些运算技巧类比引出了分式的一些运算技巧,无一不体现了类比思想的重要性,分式方程解法及应用也可以类比一元一次方程.第一讲 分式的运算【知识要点】1.分式的概念以及基本性质;2.与分式运算有关的运算法则3.分式的化简求值(通分与约分)4.幂的运算法则【主要公式】1.同分母加减法则:()0b c b ca a a a±±=≠2.异分母加减法则:()0,0b d bc da bc daa c a c ac ac ac±±=±=≠≠;3.分式的乘法与除法:b d bd ac ac •=,b c b d bda d a c ac÷=•= 4.同底数幂的加减运算法则:实际是合并同类项 5.同底数幂的乘法与除法;am●a n =a m+n ; a m ÷ a n =a m -n6.积的乘方与幂的乘方:(ab)m= a mb n, (a m)n= amn7.负指数幂: a-p=1pa a 0=18.乘法公式与因式分解:平方差与完全平方式(a+b)(a-b)= a2- b 2 ;(a ±b)2= a 2±2ab+b 2(一)、分式定义及有关题型题型一:考查分式的定义(一)分式的概念: 形如AB(A 、B 是整式,且B 中含有字母,B ≠0)的式子,叫做分式.其中 A 叫做分式的分子,B 叫做分式的分母.【例1】下列代数式中:yx yx y x y x b a b a y x x -++-+--1,,,21,22π,是分式的有: .题型二:考查分式有意义的条件:在分式中,分母的值不能是零.如果分母的值是零,则分式没有意义.【例2】当x 有何值时,下列分式有意义(1)44+-x x (2)232+x x (3)122-x (4)3||6--x x(5)xx 11-题型三:考查分式的值为0的条件:1、分母中字母的取值不能使分母值为零,否则分式无意义2、当分子为零且分母不为零时,分式值为零。
分式的知识点及典型例题分析

分式的知识点及典型例题分析1、分式的定义:例:下列式子中, 152 9a 、 5a b 、 3a 2b 2 2 、 1 、 5xy 1 、xy 、8a b 、-23 2x y 4 、2- m 6 x a1 、 x 221 、 3xy 、 3 、 a 1 中分式的个数为()2x y m(A ) 2 (B ) 3 (C ) 4(D) 5 练习题:(1)下列式子中,是分式的有.⑴ 2x 7 ; ⑵ x1 ;⑶ 5a 2;⑷ x 2x 2;⑸2 b 2;⑹xyy 2.x 5 2 3a b 2x 2⑵ 下列式子,哪些是分式?a ;x23; y 3; 7 x ; x xy ; 1 b .54y 8 x 2 y 4 52、分式有、无意义 :( 1)使分式有意义:令分母≠ 0 按解方程的方法去求解; ( 2)使分式无意义:令分母 =0 按解方程的方法去求解;例 1:当 x 时,分式 1 有意义;x 5例 2:分式 2x1中,当 x ____ 时,分式没有意义;2 x例 3:当 x 时,分式 1 有意义;2 1 x例 4:当 x 时,分式 x 有意义;2 1 x 例 5: x , y 满足关系时,分式 xy无意义;x y例 6:无论 x 取什么数时,总是有意义的分式是()A . 2x B. x C. 3xx 52 2x 13 1 D.x 2 x 1 x x 有意义的 x 的取值范围为() 例 7:使分式x 2 A . x 2 B . x2 C . x 2 D . x 2例 8:要是分式x 2没有意义,则 x 的值为()1)( x(x3)A. 2B.-1 或-3C. -1D.33、分式的值为零:使分式值为零:令分子 =0 且分母≠ 0,注意:当分子等于 0 使,看看是否使分母 =0 了,如果使分母 =0 了,那么要舍去。
例 1:当 x 时,分式1 2a的值为 0; a 12 x1例 2:当 x 时,分式的值为 0例 3:如果分式a2的值为为零 , 则 a 的值为 ( ) a 2A.2 B.2 C.2 D. 以上全不对例 4:能使分式 x2x 的值为零的所有 x 的值是() x 21A x 0 Bx 1 C x 0 或 x1 D x 0 或 x1例 5:要使分式x 29的值为 0,则 x 的值为()x 25x 6 A.3 或-3 B.3 C.-3 D 2 例 :若 a1 0 , 则 a 是 ( ) 6 aA. 正数B. 负数C. 零D. 任意有理数4、分式的基本性质的应用:分式的基本性质: 分式的分子与分母同乘或除以一个不等于 0 的整式,分式的值不变。
第16章--分式知识点总结与例题讲解

第16章 分式的学习及知识点清单一.本章介绍【本章重点】分式有意义的条件、分式的四则运算和解分式方程.【本章难点】分式的基本性质、分式方程的增根及列分式方程解决实际问题. 【本章考点】对分式的概念、分式有意义、分式的值为0及科学记数法的考查,常以选择题和填空题为主,难度较小;对零指数幂和负整指数幂的考查多与整式等知识综合考查;对分式的混合运算的考查多以计算题为主(如先化简,再求值),难度较小,但计算起来容易出错;对分式方程及其应用的考查,常以解答题的形式呈现,难度较高.【特别说明】根据近几年河南中考的命题规律,解答题的第16题为“先化简,再求值”题型,分值8分,其中化简的对象按计算的类型主要分为两种: ①整式的运算; ②分式的运算. 举例如下:(2013.河南)16. 先化简,再求值:()()()()14121222+--+++x x x x x ,其中2-=x .(2014.河南)16. 先化简,再求值:⎪⎪⎭⎫ ⎝⎛++÷--x x x x x 121222,其中12-=x .(2015.河南)16. 先化简,再求值:⎪⎭⎫⎝⎛-÷-+-a b b a b ab a 1122222,其中15,15-=+=b a .(2016.河南)16. 先化简,再求值:1211222++-÷⎪⎭⎫⎝⎛-+x x x x x x ,其中x 的值从不等式组⎩⎨⎧<-≤-4121x x 的整数解中选取.(2017.河南)16. 先化简,再求值:()()()()y x x y x y x y x --+-++522,其中12,12-=+=y x第16题作为河南中考解答题的第一个大题,难度是较小的,属于“送分题”,因此我们对本题的要求是必须做对. 【学法指导】1. 在学习的过程中要注意新旧知识的类比和衔接.例如在学习分式的基本性质、分式的运算时,可与分数的基本性质、分数的运算相比较,在类比中加深对知识的理解.2. 学习时要善于归纳总结,并注意知识的形成过程以及知识之间的相互联系.3. 体会转化的数学思想,如:分式的除法是转化为分式的乘法进行计算的;异分母分式的加减是转化为同分母分式的加减进行计算的;解分式方程的关键是把分式方程转化为整式方程进行求解的.(关注:转化化归思想) 【知识点清单】一、分式的概念形如BA(B A ,是整式,且B 中含有字母,0≠B )的式子,叫做分式. 其中A 叫做分式的分子,B 叫做分式的分母.注意:(1)BA可以写成B A ÷的形式,如:()()2222+÷-=+-x x x x ;(2)分式的识别 关键是看代数式的分母中是否含有字母,有字母的则为分式.特别指出的是π为常数不是字母. 如πba +2就不是分式,而是整式.1. 下列各式中,哪些是整式?哪些是分式?xx a b a a y x y x x 2,4,2,5,2,2,31---+π 整式:_________________________________________; 分式:_________________________________________.2. 下列各式中,是分式的是 【 】(A )32x (B )15-πx (C )x x 3 (D )6322+y x二、分式有、无意义的条件对于分式BA(B 中含有字母),当0≠B 时,分式有意义;当0=B 时,分式无意义. 注意:(1)根据分式有意义的条件,我们可以确定字母的取值范围. (2)根据分式无意义的条件,我们可以确定字母的值.(3)有些分式无论字母的取值如何,分式都有意义,即分母不等于0. 如分式222++x x ,因为x 无论取何值,2x ≥0,022>+x ,所以x 无论取任何实数,分式222++x x 都有意义. 类似的分式还有12++x x 等. 3. 下列分式中,当x 取何值时,分式有意义: (1)321+-x x ; (2)922-x x ; (3)22xx +.4. 当x 取何值时,下列分式无意义: (1)x x 312-; (2)273152-+x x .5. 要使分式38-x 有意义,则x 应满足的条件是 【 】(A )3>x (B )3=x (C )3<x (D )3≠x6. 当x 为任意实数时,下列分式一定有意义的是 【 】(A )21x x - (B )112-+x x (C )112+-x x (D )11+-x x三、分式的值为0的条件 对于分式B A (B 中含有字母),当0=A 且0≠B 时,0=B A(即分式的值等于0).反过来,若分式0=BA,则有0=A 且0≠B .注意:(1)分式的值为0是在分式有意义的前提下才有的,若使分子等于0的数也能使分母等于0,则必须舍去.(2)解题时容易出现只考虑分子为0,而忽略了分母不能为0的情况. 7. 当x 取何值时,下列分式的值为0: (1)x x -+532; (2)2232+-x x; (3)414+--x x x .8. 若分式11+-x x 的值为零,则x 的值是 【 】 (A )1 (B )1- (C )1± (D )2 9. 若代数式xx 2+有意义,则x 的取值范围是__________. 10. 若0112=--x x ,则x 的值是_________. 11. 当=x _________时,分式325+-x x 的值为零.四、有理式整式和分式统称为有理式,即有理式⎩⎨⎧分式整式.注意:(1)对于一个有理式,如果它不是整式,那么它一定是分式.(2)分式的分母必须含有字母,而整式有分母出现的,其分母中不能含有字母.这是区分整式和分式的基本方法.12. 下列各式中,哪些是分式?哪些是整式?哪些是有理式?12,2,,126,32,222+-+-+-x x b a b a x x x a b五、分式的基本性质分式的分子与分母都乘以(或都除以)同一个不等于零的整式,分式的值不变.用式子表示为:MB MA B A M B M A B A ÷÷=⋅⋅=,(M 为整式,且0≠M ). 注意:(1) 利用分式的基本性质时要正确理解分式的基本性质中的关键词“都”“同”“不等于零”的意义,“都”说明分子与分母要同时“乘以”或“除以”,“同”说明分子与分母同时乘以或除以的整式必须是相同的,“不等于零”是对分子、分母乘以或除以的整式的限制.(2)运用分式的基本性质时,要正确理解分式的“变”与“不变”:分式的分子、分母要改变,而分式的值不变.(3)如果分式的分子或分母是多项式,利用分式的基本性质时要把分子或分母用小括号括起来,再进行变形.(4)分式的基本性质中的“可乘不变性”用于分式的通分,“可除不变性”用于分式的约分,从而把原分式化为最简分式或整式.13. 不改变分式的值,把下列各式的分子、分母中的各项系数都化为整数:(1)yx yx 2.025.0315.0--; (2)y x y x 31433245-+.14. 已知0432=--x x ,则代数式42--x x x的值为 【 】 (A )3 (B )2 (C )31 (D )2115. 已知分式3312+-x x 的值等于零,那么x 的值为_________.六、分式的约分把分式的分子与分母的公因式约去叫做分式的约分.约分后,分式的分子与分母不再含有公因式,这样的分式叫做最简分式.注意:(1)如果分式的分子与分母是多项式时,应先将多项式分解因式,再确定公因式. (2)约分时,利用分式的基本性质将分式的分子与分母同时除以它的公因式. (3)分式的约分是等式的恒等变形,约分前后分式的值不变. (4)约分所得的结果必须是最简分式或整式. 16. 约分:(1)x b a bx a 25434827; (2)44422++-a a a .17. 计算:()=-ba ab 22_________.18. 约分:(1)b ab 262-; (2)22222bab a b a ++-.19. 下列各式中,最简分式是 【 】(A )1122+-x x (B )112-+x x(C )xyx y xy x -+-2222 (D )122362+-x x 20. 化简:()=--222x y y x __________.21. 将分式x x x +22化简得1+x x,则x 应满足的条件是__________.22. 化简:=+-12412a a __________. 23. 化简:=+--122222x x x __________. 24. 与分式11--+-x x 的值相等的是 【 】 (A )11--+x x (B )11-+-x x (C )11+-x x (D )11-+x x25. 分式x --11可化为 【 】(A )11--x (B )x +11 (C )x +-11 (D )11-x26. 约分:=--222b a aba __________. 七、与约分有关的新题型27. 已知311=-y x ,求代数式yxy x y xy x ---+232的值. 分析: 利用分式的基本性质,分式yxy x yxy x ---+232的分子、分母同时除以xy ,对式子稍作变形即可代入求值. 解: ∵311=-yx ∴431333211131121113112111232232=+-⨯=+⎪⎭⎫⎝⎛--⎪⎭⎫⎝⎛-=-⎪⎭⎫ ⎝⎛--+⎪⎭⎫ ⎝⎛--=---+=---+y x y x y x y x x y x y y xy x y xy x . 28. 若543zy x ==)0(≠xyz ,试求z y x z y x +-++23的值. 分析: 本题有两种解答方法:①可设连等式的值为k )0(≠k ,从而得到z y x ,,的值(当然是用含k 的代数式表示),再代入求值;②可直接利用其中一个未知数表示另外两个,然后再代入求值. 解:设k zy x ===543,则 k z k y k x 5,4,3===∴261258954323==+-++=+-++kkk k k k k k z y x z y x .或解:∵543zy x == ∴35,34x z x y == ∴22435383353423==+-++=+-++x x x x x xx x zy x z y x .29. 若0≠-b a ,且032=-b a ,则代数式ba ba --2的值是__________. 30. 已知31=+x x ,则=+221xx __________. 31. 若0132=+-a a ,则=+a a 1__________,=+221aa __________.32. 若c b a 432==,且0≠abc ,则b c ba 2-+的值是 【 】(A )2 (B )2- (C )3 (D )3- 33. 已知0643≠==zy x ,求z y x z y x +--+的值. 34. 已知511=+y x ,求yxy x yxy x +++-2232的值.八、分式的通分利用分式的基本性质把异分母分式转化为同分母分式的变形叫做通分. 通分的关键在于确定最简公分母,其方法是:①若各分母是单项式,则最小公分母的系数取各分母系数的最小公倍数,相同字母取最高次幂,单独出现的字母连同它的指数作为最简公分母的一个因式,这样取得的因式的积就是最简公分母;②若各分母都是多项式,则先分解因式,然后按单项式求最简公分母的方法,从系数、相同因式、不同因式三个方面确定最简公分母.注意:(1)通分时,分子或分母中有“﹣”时,可把“﹣”号提到分数线前面.(2)确定最简公分母后,要确定分子、分母要乘的因式,这个因式就是最简公分母除以原分母的商.(3)通分后不能再进行约分.35. 通分:(1)2291,32xy x ; (2)()332,123-+a a a a ; (3)()2211,1--x x x .36. 分式b a 31,21的最简公分母是【 】 (A )ab 6 (B )ab 5 (C )ab 61 (D )ab 5237. 分式m n n m +-1,1的最简公分母是【 】(A )n m - (B )n m +(C )m n - (D )22n m -38. 分式22225,103,54ac bb ac c b a -的最简公分母是__________.39. 分式x yx x x --23,42,12的最简公分母是__________.40. 通分:x x x x 261,91,3322----.41. 通分:11,122-+x x x .新题型42. 若2<x ,则22--x x 的值为 【 】 (A )1- (B )0 (C )1 (D )243. 若代数式4162--x x 的值为0,则=x __________. 44. 已知0544422=+--+y x y x ,则=-xy y x __________. 45. (全国初中数学竞赛黄冈市选拔赛)若12,10-<<-<<b a ,则ba b a b b a a +++++---2211的值是 【 】 (A )0 (B )1- (C )3- (D )4-46. 如果2=b a ,则=++-2222ba b ab a __________. 47. 若072,0634=-+=--z y x z y x ()0≠xyz ,则=---+222222103225zy x z y x __________. 48. 如果分式()()118-+-x x x 的值等于零,则=x __________.49. (整除问题)当a 是整数时,使分式1236-+a a 的值为整数的a 共有__________个. 50. 要使分式xx-24有意义,则x 的取值范围是 【 】 (A )0≠x (B )2≠x 或2-≠x(C )0≠x ,且1≠x ,且2≠x (D )0≠x ,且2±≠x51. 若分式622+-x x 的值为负,则x 的取值范围是____________. (本题为分式的值与不等式组的联系)九、分式的乘除运算分式相乘,用分子的积作积的分子,用分母的积作积的分母,结果要化为最简分式或整式.分式相除时,先把除法转化为乘法,再进行计算,结果要化为最简分式或整式. 注意:(1)无论是分式的乘法运算还是除法运算,结果都要化为最简分式或整式(即结果的分子和分母不再含有公因式).(2)为便于计算和约分,算式中的多项式要先进行因式分解再约分.(3)分式的分子、分母的系数是负数时,要先把负号提到分式的前面再进行计算.(4)分式的乘除法是同级运算,多个分式相乘除时应按照从左到右的顺序进行运算.(5)当除式是整式时,可以把其分母看作是1,然后按照除法法则进行运算.52. 计算:y x a xy 28512÷ 解:原式axy x a xy 103815122=⋅=. 53. 计算:xyx y x y xy x y x ++÷++-22222224 解:原式()()()()y x x y x y x y x y x ++÷+-+=2222 ()()()()()yx xy x y x y x x y x y x x y x y x y x +-=+-=++⋅+-+=222222254. 计算:xx x x x x x +-⋅-+÷+--111112122 解:原式()()()x x x x x x x +-⋅+-⋅--+=11111112xx +-=11.(对于同级运算,要按照从左到右的顺序进行计算) 十、分式的乘方分式的乘方法则: 分式的乘方,等于把分子、分母分别乘方.用公式表示: n n nb a b a =⎪⎭⎫ ⎝⎛(n b ,0≠为正整数) 注意: (1)分式的乘方法则中“把分子、分母分别乘方”,这里的分子、分母是指分子、分母的整体,而不是部分.(2)在进行分式的乘方运算时,要先确定结果的符号.(3)在进行分式的乘方、乘除混合运算时,要先算乘方,再算乘除.(4)系数不要漏掉乘方.(5)注意乘方运算中的符号问题.55. 计算:221⎪⎭⎫ ⎝⎛÷⎪⎭⎫ ⎝⎛-xy x y . 解:原式4222222221y y x xy y x x y =⋅=÷=. 56. 计算:=⋅ba x xb a 422489154__________. 57. 计算:=+-⋅++-442444222a a a a a a ____________. 58. 计算:=⎪⎭⎫ ⎝⎛-÷⎪⎪⎭⎫ ⎝⎛-⋅⎪⎪⎭⎫ ⎝⎛-43222x y x y y x __________. 59. 化简: ()=-+÷+-+22213123x x x x x x ____________. 60. 计算:(1)=÷⎪⎭⎫ ⎝⎛-⋅⎪⎭⎫ ⎝⎛-232ab a b b a __________; (2)=⎪⎭⎫ ⎝⎛⋅⋅⎪⎪⎭⎫ ⎝⎛3223x yz y xz z y x __________.61. 当1-=x 时,计算33212⎪⎭⎫ ⎝⎛⋅÷⎪⎭⎫ ⎝⎛x x x 的结果为__________. 62. 化简: =-÷-11122x x __________. 十一、分式有意义的条件与分式的化简求值分式有意义的条件是分母不等于零.在进行分式的运算时,分式有意义是前提:各分母都不等于零.对于除式的分子,由于在转化为乘法运算时成为分母,所以要求除式的分子也不等于零,这一点是容易忽视和出错的地方.我们不妨把除式的分子称为“隐分母”,在分式的除法运算中, “隐分母”不能为零.63. 先化简()()12121222+++-÷--x x x x x x ,然后选择一个你喜欢的x 值代入求值. 分析: ()()()()()()()11121112121212222-=+-+⋅-+-=+++-÷--x x x x x x x x x x x x x ,由于x 的取值应使各分式都有意义,所以1±≠x 且2≠x .2,1=±=x x 这三个值不能取.解: ()()12121222+++-÷--x x x x x x ()()()()()111211122-=+-+⋅-+-=x x x x x x x ∵2,1≠≠x x∴当3=x 时 原式21131=-=. 64. 化简1112+-÷⎪⎭⎫ ⎝⎛+-x x x x x ,再任取一个你喜欢的数代入求值. 解: 1112+-÷⎪⎭⎫ ⎝⎛+-x x x x x()1111111111111-=-+⋅+=-+⋅⎪⎭⎫ ⎝⎛+-=-+⋅⎪⎭⎫ ⎝⎛+-=x x x x x x x x x x x x x x 当2=x 时,原式2122=-=. 分析:考虑到分式有意义的条件,本题中0≠x 且1±≠x .65. 化简:aa a 214122-÷-,并任选一个你认为合适的正整数作为a 的值代入求值.66. 先化简,再求值:9612122+--⋅⎪⎭⎫ ⎝⎛--x x x x x ,其中x 是从1 , 2 , 3中选取的一个合适的数.67. 先化简14411122-+-÷⎪⎭⎫ ⎝⎛--x x x x ,再从不等式612<-x 的正整数解中选一个适当的数代入求值.68. 先化简,再求值:1221214322+-+÷⎪⎭⎫ ⎝⎛---+x x x x x x ,其中x 是不等式组⎩⎨⎧<+>+15204x x 的整数解.十二、分式的加减运算同分母的分式相加减,分母不变,分子相加减.用公式表示为:ac b a c a b ±=±(0≠a ). 注意: (1)分式加减运算的结果能约分的一定要约分,结果必须化为最简分式或整式. 异分母分式相加减的法则:异分母分式相加减,先通分,化为同分母分式,然后再加减.用公式表示为:acad bc ac ad ac bc c d a b ±=±=±(0,0≠≠c a ). 异分母分式相加减的一般步骤:①通分,将异分母分式化为同分母分式;②通分后的分母不变,分子相加减;③化简分子,如去括号、合并同类项等;④将结果化为最简分式或整式.注意:(1)异分母分式相加减,通分是关键.(2)若加减运算中含有整式,应视其为分母为1的分式,然后再进行加减.69. 计算:221515a aa ---.解:原式151522-+-=a aa()()()1511151552-=-++=-+=a a a a a a70. 计算:()()ab b a ab b a 22--+.71.计算:21422---a a a解:原式()()()()222222-++--+=a a aa a a()()()()212222222+=-+-=-+--=a a a a a a a a72. 计算:1624432---x x .73. 计算:x x x x ---231.解:原式()x x x x +--=231()()()()1111111111332333-=-+-=---=--+--=+--=x xx xx x x x x x x x x x x x x x x x74. 计算:224-++a a .75. 先化简,再求值:a a a a a 1122-÷⎪⎭⎫ ⎝⎛++,其中2=a .十三、分式的混合运算进行分式的混合运算时要特别注意运算法则和运算顺序,最终的结果还要化为最简分式或整式.76. 计算:2444222-÷⎪⎭⎫ ⎝⎛+-+-+x x x x x x . 解:原式()224222-÷⎥⎦⎤⎢⎣⎡-+-+=x x x x x ()()()()()()2222244224222222222-=-⋅-=-÷-+-=-÷⎥⎦⎤⎢⎣⎡-+--+=x x xx x x x x x x x x x x x x 注意: (1)注意运算顺序.(2)异分母分式相加减时,通分是关键,应正确确定最简公分母.(3)分式的除法运算要统一为乘法运算,除式的分子和分母要颠倒位置.(4)运算的最终结果应为最简分式或整式.(5)为正确确定最简公分母和约分,要对式子中出现的某些多项式进行因式分解.77. 计算:()x y y yx x y x -+-⋅+2222.78. 计算:222ba b b a a b a a -÷⎪⎭⎫ ⎝⎛+--.79. 计算:x y x y y x x y x y x x -÷⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-+⋅+-3232. 分析:如果先算小括号里面的,过程就比较麻烦,而用乘法分配律进行计算就简单多了.当然,这是由题目本身的特点决定的.解:原式y x x y y x y x x y x y x x -⋅⎪⎭⎫ ⎝⎛+⋅+++⋅+-=23232 ()y x y x yx x y y x x y x x -=-⋅=-⋅⎪⎭⎫ ⎝⎛+-=2223232 80. 计算:()()⎪⎭⎫ ⎝⎛--+÷⎥⎦⎤⎢⎣⎡--+b a b a b a b a 111122.十四、分式的值与非负性的综合81. 若()132+-=-y x ,求分式()212--y x 的值.分析:本题需要求出y x ,的值,然后代入求值.根据非负数的和为零的性质即可求出y x ,的值.解: ∵()132+-=-y x∴()0132=++-y x ∵()23-x ≥0,1+y ≥0 ∴01,03=+=-y x∴1,3-==y x∴原式()343421132-=-=---=. 82. 已知()0322=+-+-b a b a ,计算22222b a ab a b ab a --⋅+的值.83. 已知325102--=++b a a ,求代数式()2223223242bab a b b b a ab a b a b +-÷-+⋅-的值.84. 已知0544422=+--+y x y x ,则=-xy y x __________. 十五、分式的运算与方程(组)的综合 85. 已知()()212143-+-=---x B x A x x x ,求A 、B 的值. 分析:这是“部分分式”问题,有两种解法:一是待定系数法,二是采用特殊值法. 解法1: ()()212143-+-=---x B x A x x x ()()()()()()()()()()()212214*********----+=------+-=---x x B A x B A x x x x x x B x A x x x ∴⎩⎨⎧-=--=+423B A B A 解之得:⎩⎨⎧==21B A . 解法2: ()()212143-+-=---x B x A x x x 等式两边都乘以()()21--x x 得:()()1243-+-=-x B x A x由于多项式的恒等与x 的值无关,所以分别令2,1==x x .当1=x 时,1=A ;当2=x 时,2=B .∴2,1==B A .86. 已知()()122143+--=-++x B x A x x x ,其中A 、B 为常数,则=-B A 4__________.87. 已知22442-++=-x b x a x x ,则=a _________,=b _________. 88. 已知()()2222221+++=++x b x a x x ,则=+b a _________. 89. 若52107412-+-=+-+x b x a x x x ,则=ab _________. 90. 已知()()11311335-+-=---x b x a x x x ,其中b a ,是常数,求b a ,的值.91. 已知()11112222-++=--+x C x B x A x x x x ,其中A ,B ,C 为常数,求C B A ++的值.十五、分式的求值一般是对分式先化简,再求值.分式的化简求值是河南中考的重点.分式的求值方法主要有:(1)直接代入法(2)整体代入法(3)倒数法(4)设参数法直接代入法对所给的分式先化简,化为最简分式后把字母的值直接代入求值的方法.92. 先化简,再求值:⎪⎪⎭⎫ ⎝⎛++÷--a b ab a ab a b a 22222,其中5,2=-=b a .整体代入法首先介绍整体思想.整体思想就是考虑数学问题时,不着眼于它的局部特征,而是把着眼点放在问题的整体结构上,通过对其全面深刻的观察,从宏观整体上认识问题的本质,把一些看似彼此独立但实质上联系紧密的量当作整体来处理的思想方法.整体思想在处理和解决数学问题时,有着非常广泛的应用.93. 先化简,再求值:12212122++-÷⎪⎭⎫ ⎝⎛+---x x x x x x xx ,其中x 满足012=--x x . 分析:由已知条件012=--x x ,得12+=x x ,整体代入化简的结果求值,而不用解方程.解: 12212122++-÷⎪⎭⎫ ⎝⎛+---x x x x x x xx ()()()()()()()()()12112112112112222-+⋅++--=-+⋅+---+=x x x x x x x x x x x x x x x x x ()()()221121112x x x x x x x x +=-+⋅+-= ∵012=--x x∴12+=x x ∴原式111=++=x x . 94. 先化简,再求值:⎪⎭⎫ ⎝⎛++-÷⎪⎭⎫ ⎝⎛++23221a a a a ,其中a 满足022=--a a .95. 已知511=-yx ,求y xy x y xy x ---+3353的值. 解: ∵511=-yx ∴5,5=--=-xyy x xy x y∴xy y x 5-=- ∴()()45810355153533353=--=--+-=--+-=---+xy xy xy xy xy xy xy y x xy y x yxy x y xy x .96. 已知0142=+-x x ,求221x x +的值.97. 已知12,4-==+xy y x ,求y xx y+的值.98. 已知0142=+-x x ,求()x x x x 6412+---的值.99. 已知2016,2015,2014222=+=+=+x c x b x a ,且24=abc . 求cb a abc ac b bc a 111---++的值. 提示:()()()2222222a c c b b a ab ca bc c b a -+-+-=---++.100. 已知1=abc ,求111++++++++c ac c b bc b a ab a 的值. 分析:利用分式的基本性质对和项进行变形处理.倒数法101. 已知31=+x x ,求1242++x x x 的值. 分析:易求出22224111xx x x x ++=++的值,然后再取倒数即可.本题会用到的重要结论:211222-⎪⎭⎫ ⎝⎛+=+x x x x . 解: ∵31=+x x ∴7232112222=-=-⎪⎭⎫ ⎝⎛+=+x x x x ∴817111112222224=+=++=++=++xx x x x x x ∴811242=++x x x . 102. 已知51=+a a ,求1242++a a a 的值.103. 如果411242=++x x x ,求22435155xx x +-的值.104. 已知16,171,151=+=+=+ca a c c b bc b a ab ,则acbc ab abc ++的值是 【 】 (A )24 (B )48(C )241 (D )481 105. 已知三个数z y x ,,满足34,34,2-=+=+-=+x z zx z y yz y x xy ,求yz xz xy xyz ++的值. 提示: ∵2-=+yx xy ,∴2111,21-=+-=+x y xy y x .设参数法 106. 已知543z y x ==,求z y x y x 32+-+的值. 分析:前面在讲解分式的约分时已有所涉及,见第28题的解法.107. 已知cb a b ac a c b +=+=+,求()()()a c c b b a abc +++的值. 分析:本题难度较高,应分为两种情况:①0≠++c b a ;②0=++c b a .108. 已知0623,032=--=+-z y x z y x ,且0≠xyz ,求下列各式的值:(1)z y x ::;(2)2222222zy x z y x -+++.109. 已知zx z y y x +=+=+543,求()()()z x z y y x xyz +++的值. 分析:由条件可知:543z x z y y x +=+=+,设出参数k ,再分别用参数k 表示z y x ,,的值.巩固训练 110. 已知211=+ba (b a ≠),求()()b a a b b a b a ---的值.111. 已知311=-y x ,求322333yx y x y x xy +-的值.112. 若020162=--x x ,求分式x x x ---1201623的值.十六、从中考题,看分式的拆项113. 观察下列等式:第1个等式:⎪⎭⎫ ⎝⎛-⨯=⨯=311213111a ; 第2个等式:⎪⎭⎫ ⎝⎛-⨯=⨯=5131215312a ; 第3个等式:⎪⎭⎫ ⎝⎛-⨯=⨯=7151217513a ; 第4个等式:⎪⎭⎫ ⎝⎛-⨯=⨯=9171219714a . 请回答下列问题:(1)按以上规律列出第5个等式;(2)用含n 的代数式表示第n 个等式:=n a ____________________________;(3)求10004321a a a a a +++++ 的值.拆项技巧类型一:()11111+-=+x x x x (x 为正整数). 类型二:()⎪⎭⎫ ⎝⎛+-=+n x x n n x x 1111(n x ,均为正整数) 114. 观察下列等式:4131431,3121321,211211-=⨯-=⨯-=⨯. 将以上三个等式两边分别相加得:4341141313121211431321211=-=-+-+-=⨯+⨯+⨯. (1)猜想并写出:()=+11n n ____________; (2)直接写出下列各式的计算结果: ①=⨯++⨯+⨯+⨯201820171431321211 __________; ②()=+++⨯+⨯+⨯11431321211n n __________. (3)探究并计算:201820161861641421⨯+⨯+⨯+⨯ .十七、分式运算中的“温柔陷阱”违背运算顺序115. 计算:ab b a a b 34433⋅÷. 错解:原式a b a b 313=÷=. 分析:错解违背了运算顺序,乘除是同级运算,应按照从左到右的顺序进行计算.正解:原式33271634343ab a b a b a b =⋅⋅=. 忽视分数线的括号作用116. 计算:xx x x --+-11213. 错解:原式111112311213=--=---=----=x x x x x x x x x . 分析:在进行分式的减法运算时,如果减式的分子是一个多项式,则应给减式的分子加上小括号.正解:原式()111123112311213-+=-+-=---=----=x x x x x x x x x x x x . 误用分配律 117. 计算:⎪⎭⎫ ⎝⎛+÷b a ab 111. 错解:原式abb a a b b ab a ab b ab a ab +=+=⋅+⋅=÷+÷=11111111. 分析:除法没有分配律. 正解:原式b a b a ab ab ab b a ab +=+⋅=+÷=111. 结果不是最简分式118. 计算:bcc b ab b a +-+.错解:原式()abcab bc abc ac ab bc ac abc c b a bc ac -=--+=+-+=. 分析:计算的结果中分子和分母还含有公因式b ,所以其结果不是最简分式,应通过约分化为最简分式.正解:原式()aca c abc a cb abc ab bc abc ac ab bc ac -=-=-=--+=.因“喜欢”而出错 119. 已知:2-≤2<a ,化简:12211112+-÷⎪⎭⎫ ⎝⎛++-a a a a a ,再选一个你喜欢的整数a 代入求值.错解: 12211112+-÷⎪⎭⎫ ⎝⎛++-a a a a a ()()()()()()112111221111122+-=-⋅+-=-⋅+--++=a a aa a a a a a a a a a 由题意得012,01,012≠+-≠+≠-a a a a ,所以1±≠a∴当0=a 时 原式11010-=+-=. 分析:原代数式中,字母的取值忽略了除号变乘号后,a 2跑到分母上了,所以0≠a .正解:由题意得: 02,012,01,012≠≠+-≠+≠-a a a a a ,所以1±≠a 且0≠a . ∴当2-=a 时 原式31212=+---=. 十八、可化为一元一次方程的分式方程分母中含有未知数的方程叫做分式方程.注意:(1)理解分式方程要明确两点:①含有分母;②分母中含有未知数.(2)分式方程的解也叫作分式方程的根.(3)整式方程和分式方程统称为有理方程.(4)分式方程与整式方程的主要区别在于分母中是否含有未知数:分母中含有未知数的方程是分式方程,分母中不含有未知数的方程是整式方程.120. 下列方程中是分式方程的是 【 】(A )413142=+x x (B )513126=++-x x (C )3231=+xx (D )51=-x 121. 下列关于x 的方程是分式方程的是 【 】(A )63352x x +=-+ (B )x ax -=+-371 (C )bx a b b a a x -=- (D )()1112=--x x 122. 下列关于x 的方程:①531=-x ;②141-=x x ;③()111=+-⋅x x x ;④11-=b a x .其中是分式方程的有__________(填序号).十九、分式方程的解法分式方程的解法是数学思想中转化化归思想的又一体现:把分式方程转化为整式方程进行求解,转化的方法是利用等式的性质在分式方程的左右两边分别乘以各分母的最简公分母.解分式方程的一般步骤:(1)去分母: 在分式方程的左右两边分别乘以最简公分母,把分式方程转化为整式方程(目前只学习可转化为一元一次方程的分式方程);(2)解整式方程;(3)检验: 把整式方程的解代入最简公分母,结果不为0的是原分式方程的解(也叫根),否则就是增根,必须舍去.123. 解分式方程:1132-=+-x x x x . 解: ()1113-=+-x x x x (此步是为了正确确定分式方程的最简公分母)方程两边同时乘以()1-x x 得:()213x x x =-+解这个整式方程得:3=x检验:把3=x 代入()1-x x 得:()0133≠-⨯所以3=x 是原分式方程的解.124. 解方程:(1)x x 332=-; (2)275-=x x .125. 解方程:(1)1132-=+x x ; (2)01522=--+x x x x .126. 解方程:12112-=-x x . 解: ()()11211-+=-x x x 方程两边同时乘以()()11-+x x 得:21=+x解这个整式方程得:1=x检验:把1=x 代入()()11-+x x 得:()()01111=-⨯+所以1=x 是增根,原分式方程无解.注意: 解分式方程必须检验(即验根),增根表示原分式方程无解.二十、增根在第126题的解法中,1=x 虽是整式方程21=+x 的解,但却使分式方程左右两边的分式无意义,不适合原分式方程的解,1=x 就是增根.使分式方程的最简公分母等于0的解,不是原分式方程的解,是增根.一般地,解分式方程时,去分母后所得整式方程的解可能使最简公分母为0,即产生增根,因此一定要检验:将整式方程的解代入最简公分母,如果最简公分母不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,是增根,原分式方程无解.重要的事情说三遍:解分式方程要检验,解分式方程要检验,解分式方程要:检验注意:(1)增根使最简公分母等于0.(2)增根表示原分式方程无解.(3)增根是去分母后所得整式方程的解,但不是原分式方程的解.(4)解分式方程可能会产生增根,因此一定要检验.127. 解方程:()()21311+-=--x x x x .128. 解方程:(1)12422=---xx x ; (2)114112=-+-+x x x .二十一、解分式方程中的“温柔陷阱”去分母时,漏乘 129. 解方程:xx x --=+-21322. 错解:21322--=+-x x x 方程两边都乘以()2-x 得:132-=+x分析:在转化为整式方程时出错,常数3漏乘了最简公分母()2-x ,这是不符合等式的性质的,必然得到一个错解.正解:忽视分数线的小括号作用130. 解方程:013132=-+--x x x . 错解:()()011313=-++--x x x x 方程两边都乘以()()11-+x x 得:()0313=+-+x x分析:去分母后应对分子3+x 加小括号,正确的结果为()()0313=+-+x x .正解:解分式方程不检验(易忽略检验)131. 解方程:22121--=--xx x 错解:22121---=--x x x方程两边都乘以()2-x 得:()2211---=-x x解这个整式方程得:2=x分析: 2=x 并不是原分式方程的解,因为当2=x 时,原分式方程的最简公分母为0,分式无意义,2=x 是增根,所以解分式方程时必须检验,否则,不能作出结论. 正解:132. 解方程:14122=---x x x .133. 解方程:xxx --=+-21221.二十二、拆项法解分式方程 知识回顾 拆项技巧类型一:()11111+-=+x x x x (x 为正整数).类型二:()⎪⎭⎫⎝⎛+-=+n x x n n x x 1111(n x ,均为正整数)134. 解方程:()()()()()()()xx x x x x x x x 1120182017132121111+=+++++++++++ .135.解方程:411271651231222+=++++++++x x x x x x x .二十三、解分式方程新题型135. 如果分式方程xax x -=-+222的解为1=x ,则=a _________. 136. 如果关于x 的方程m m x x 22+=+有两个解mx m x 2,21==,那么关于x 的方程1212-+=-+m m x x 的两个解是 【 】 (A )mm 2, (B )12,1++m m(C )12,1--m m (D )11,-+m m m137. 如果z y x ,,满足方程组:32,22,12=+=+=+xz zxz y yz y x xy . 那么可以得到关系式 【 】 (A )032=++z y x (B )0257=++z y x (C )0369=++z y x (D )0710=++z y x 138. 对任意正整数n ,()=+21n n _________⎪⎭⎫ ⎝⎛+-211n n .139. 已知x z z z y y y xx 121,121,121222222=+=+=+,求z y x ,,的值. 分析:y xy x x y x x 211,21,12122222=+=+=+.二十四、利用分式方程“解的情况”,求字母的值或取值范围解分式方程时,时常会遇到分式方程中“有增根”、“无解”、“解为正数”、“解为负数”的情况,现逐一作出探讨.分式方程有增根140. 若关于x 的方程3312-+=-+x xm x x 有增根,求m 的值. 解:3312-+=-+x x m x x 方程两边同时乘以()3-x 得:x m x +=+12 ∴1+=x m ∵该方程有增根 ∴3,03==-x x ∴413=+=m .总结 当分式方程有增根时,先把分式方程转化为整式方程,令最简公分母等于0,求出方程的增根(可能不唯一),再代入整式方程即可求出字母的值. 特别地,当增根不唯一时,字母的值也不唯一. 141. 若关于x 的分式方程3212---=-xxx m 有增根,求m 的值.142. 当a 为何值时,关于x 的方程234222+=-+-x x ax x 会产生增根?分式方程无解143. 若关于x 的方程1242+-=-x x ax 无解,则a 的值是_________. 解:1242+-=-x x ax 方程两边同时乘以()2-x 得:24-+=x ax ∴()21=-x a 分为两种情况:(1)当01=-a ,即1=a 时,方程()21=-x a 无解,此时分式方程也无解;(2)当01≠-a ,即1≠a 时,令02=-x ,2=x ,分式方程无解.把2=x 代入()21=-x a 得:2=a .综上所述,1=a 或2=a .总结 注意分式方程有增根和分式方程无解是不一样的:分式方程有增根只是分式方程无解的一种情况,分式方程无解包括有增根时无解和转化为整式方程时整式方程无解导致分式方程无解两种情况.144. 若关于x 的分式方程1317-=+-x mxx 无解,求m 的值.145. 若关于x 的分式方程1131=-+-x x m 无解,则m 的值是_________. 146. 若关于x 的方程2222=-++-x mx x 有增根,则m 的值是_________.147. 若分式方程211=---x mx x 有增根,则这个增根是_________.分式方程的解为负数148. 已知关于x 的分式方程111=--++x kx k x 的解为负数,则k 的取值范围是____________.分析:本题为易错题,易忽视分式方程有解(如负数解)时,其最简公分母不能等于0,导致求得的k 的取值范围不完整. 解:111=--++x kx k x 方程两边同时乘以()()11-+x x 得:()()()()()1111-+=+--+x x x k x k x解之得:k x 21-=∵该分式方程的解为负数 ∴021<-k 解之得:21>k ∵01,01≠-≠+x x (为什么会有这样的要求?) ∴0121≠+-k ,0121≠--k ∴0,1≠≠k k∴k 的取值范围是21>k ,且1≠k . 149. 已知关于x 的方程323-=--x m x x 有一个正数解,求m 的取值范围.150. 若关于x 的分式方程211=+-x k 的解为负数,则k 的取值范围是__________. 151. 已知关于x 的分式方程112=++x a 的解是非正数,则a 的取值范围是 【 】(A )a ≤1- (B )a ≤1-且2-≠a (C )a ≤1且2-≠a (D )a ≤1 152. 已知关于x 的分式方程1131=-+-xx m 的解是非负数,则实数m 的取值范围是____________.二十五、分式方程的应用列分式方程解应用题可按以下步骤进行: (1)审清题意,弄清题目中的数量关系; (2)巧设未知数;(一般是求什么设什么) (3)列出分式方程;(找出等量关系很重要) (4)解分式方程;(要转化为整式方程) (5)检验;(看是否为增根,是否符合题意) (6)作答.可以简单概括为六个字:审、设、列、解、检、答.153. 用A 、B 两种机器人搬运大米,A 型机器人比B 型机器人每小时多搬运20袋大米,A 型机器人搬运700袋大米与B 型机器人搬运500袋大米所用时间相等.求A ,B 型机器人每小时分别搬运多少袋大米.二十六、零指数幂任何不等于零的数的零次幂都等于1,即10=a ()0≠a . 零的零次幂没有意义.注意:(1)10=a 的条件是0≠a .(2)根据“零的零次幂没有意义”可以确定字母的取值范围. 154. 计算:(1)()=÷-0053_________; (2)=⎪⎪⎭⎫ ⎝⎛+0232x _________;(3)()=-014.3π_________.155. 式子()0212++-x x x 有意义的条件是__________. 二十七、负整指数幂任何不等于零的数的n -(n 为正整数)次幂,等于这个数的n 次幂的倒数. 即注意:(1)负整指数幂成立的条件仍是底数不等于零.(2)以前学过的幂的运算:()()n n nmn nm n m n m b a ab a a a a a ===⋅+,,,以及同底数幂的除法n m n m a a a -=÷,对于零指数幂和负整指数幂仍然成立. (3)幂的运算结果的符号与指数的正负无关,只与指数的奇偶有关.如()()()()81212,412123322-=-=-=-=---. 156. 若()()0121-+--x x 有意义,则x 的取值范围是__________.157. 计算:()=-+⎪⎭⎫ ⎝⎛-+--0231318π_________.158. 若1512=-x ,则=x _________;若2713=x ,则=x _________. 159. 计算:=⋅-3022_________. 160. 计算:()=⎪⎭⎫ ⎝⎛---12018211_________.161. 计算:=⎪⎭⎫⎝⎛-+--+--031312829_________.162. 已知()()321,13,2-=-==-c b a ,则c b a ,,的大小关系是 【 】(A )c b a >> (B )c a b >> (C )b a c >> (D )a c b >>163. 已知y x m m ==5,2,则m 210-可表示为 【 】 (A )xy (B )22y x (C )xy 1(D )221yx 164. 若n m ,满足()0201832=-+-n m ,则=+-01n m _________. 165. 若a x =-23,b y =-23,则=-y x 3_________. 166. 已知0152=+-x x ,求下列各式的值: (1)1-+x x ; (2)22-+x x .。
(word完整版)新人教版八年级数学下册第十六章分式知识点总结,文档

一、分式的定义: 若是 A 、 B 表示两个整式,并且B 中含有字母,那么式子A叫做分式。
B例 1. 以下各式 a ,1, 1x+y ,a 2b 2 ,-3x 2,0?中,是分式的有〔 〕个。
x 15ab二、 分式有意义的条件是分母不为零; 【B ≠0】分式没有意义的条件是分母等于零; 【B=0】分式值为零的条件分子为零且分母不为零。
【B ≠0 且 A=0 即子零母不零】例 2. 以下分式,当 x 取何值时有意义。
〔 1〕2x1 ;〔 2〕 3 x2。
3x 22x 3例 3. 以下各式中,无论 x 取何值,分式都有意义的是〔 〕。
A .1 B . xC .3x 1D .x 212x 12x 1x 22x 2例 4.当 x______时,分式2x1没心义。
当 x_______时,分式x 21 的值为零。
3x 4x 2x 2例 5. 1 - 1 =3,求5x3xy 5 y的值。
x y x2xyy三、分式的根本性质: 分式的分子与分母同乘或除以一个不等于0 的整式,分式的值不变。
〔 CA A C A A C0 〕B C B B CB四、分式的通分和约分:要点先是分解因式。
1 x 1 y例 6. 不改变分式的值,使分式510的各项系数化为整数,分子、分母应乘以〔 ? 〕。
1 x 1 y3 9例 7. 不改变分式2 3x 2 x 的值,使分子、分母最高次项的系数为正数,那么是〔 ?〕。
5x 3 2x 3分式 4 y 3x , x2 1 , x2xy y 2, a22ab2中是最简分式的有〔例 8. 4x 〕。
4ax1 y ab 2b例 9. 约分:〔1〕x 26x9 ; 〔2〕 m 23m 2x29m2m例 10. 通分:〔 1〕x ,y;〔2〕a 1,66ab 29a 2bc22a 2a 1 a 1例 11. x 2 +3x+1=0,求 x 2+12 的值. x例 12. x+ 1=3,求x 4x 2 2 的值. xx 1五、分式的运算:分式乘法法那么:分式乘分式,用分子的积作为积的分子,分母的积作为分母。
第16章《分式》知识要点复习及典型练习

第16章《分式》知识要点复习一、本章主要内容本章主要内容是分式的概念;分式的基本性质;分式混合运算和可化为一元一次方程的分式方程及其应用,这些内容在今后进一步学习方程、函数等知识时占有重要地位和作用. ★(一)概念1、分式的概念:BA (注明:A 、B 都是整式,并且B 中都含有字母) 说明:分式比分数更具有一般性,如分式B A 可以表示为两个整式相除的商(除式不能为零),其中包括所有的分数。
2、分式的表示:B A (注明: B ≠0才有意义) 3、分式的值:⑴0=BA 时,A=0且B ≠0;⑵1=B A 时,A=B 且B ≠0。
4、最简分式: ★(二)分式的基本性质(类似分数的性质,运用类比数学思想)1.分式的基本性质是分式恒等变形的依据,•正确理解和熟练掌握这一性质是学好分式的关键,因此学习中要注意以下几点:(1)基本性质中的字母表示整数,(,A A M A A M B B M B B M⨯÷==⨯÷,M ≠0) (2)要特别强调M ≠0,且是一个整式,由于字母的取值可以是任意的,所以M•就有等于零的可能性,因此,应用基本性质时,重点要考查M 的值是否为零.2. 运用分式的基本性质进行约分、通分.值得注意的是:约分是要找准分子和分母的公因式,最后的结果要是最简分式;通分是要正确地确定各个分母的最简公分母,一般的取系数的最小公倍数,以及所有因式的最高次幂的积,作为最简公分母.(三)分式运算(最后的结果要是最简分式,转化数学思想)1、分式的乘除法 分式乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为分母。
分式除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
分式乘方法则: 分式乘方要把分子、分母分别乘方。
(1)约分,约分的目的是化简,关键是找分子和分母的最高公因式,•即系数的最大公约数、 相同因式的最低次幂. n n n ba b a =)(bcad c d b a d c b a bd ac d c b a =⋅=÷=⋅;(2)如何找分子和分母的最高公因式(3)分式的乘除法本质就是:①因式分解,②约分。
第十六章分式知识点和典型例习题

第十六章分式知识点和典型例习题【知识网络】【思想方法】 1.转化思想转化是一种重要的数学思想方法,应用非常广泛,运用转化思想能把复杂的问题转化为简单问题,把生疏的问题转化为熟悉问题,本章很多地方都体现了转化思想,如,分式除法、分式乘法;分式加减运算的基本思想:异分母的分式加减法、同分母的分式加减法;解分式方程的基本思想:把分式方程转化为整式方程,从而得到分式方程的解等. 2.建模思想本章常用的数学方法有:分解因式、通分、约分、去分母等,在运用数学知识解决实际问题时,首先要构建一个简单的数学模型,通过数学模型去解决实际问题,经历“实际问题———分式方程模型———求解———解释解的合理性”的数学化过程,体会分式方程的模型思想,对培养通过数学建模思想解决实际问题具有重要意义. 3.类比法本章突出了类比的方法,从分数的基本性质、约分、通分及分数的运算法则类比引出了分式的基本性质、约分、通分及分式的运算法则,从分数的一些运算技巧类比引出了分式的一些运算技巧,无一不体现了类比思想的重要性,分式方程解法及应用也可以类比一元一次方程.第一讲 分式的运算【知识要点】1.分式的概念以及基本性质; 2.与分式运算有关的运算法则3.分式的化简求值(通分与约分)4.幂的运算法则【主要公式】1.同分母加减法则:()0b c b ca a a a±±=≠2.异分母加减法则:()0,0b d bc da bc daa c a c ac ac ac±±=±=≠≠;3.分式的乘法与除法:b d bd a c ac ∙=,b c b d bda d a c ac÷=∙=4.同底数幂的加减运算法则:实际是合并同类项5.同底数幂的乘法与除法;am●a n =a m+n ; a m ÷ a n =a m -n6.积的乘方与幂的乘方:(ab)m= a mb n, (a m)n= amn7.负指数幂: a-p=1pa a 0=18.乘法公式与因式分解:平方差与完全平方式(a+b)(a-b)= a2- b 2 ;(a ±b)2= a 2±2ab+b 2(一)、分式定义及有关题型题型一:考查分式的定义【例1】下列代数式中:yx yx y x y x b a b a y x x -++-+--1,,,21,22π,是分式的有: .题型二:考查分式有意义的条件【例2】当x 有何值时,下列分式有意义(1)44+-x x (2)232+x x (3)122-x (4)3||6--x x(5)xx 11-题型三:考查分式的值为0的条件【例3】当x 取何值时,下列分式的值为0.(1)31+-x x(2)42||2--x x (3)653222----x x x x题型四:考查分式的值为正、负的条件【例4】(1)当x 为何值时,分式x-84为正; (2)当x 为何值时,分式2)1(35-+-x x 为负;(3)当x 为何值时,分式32+-x x 为非负数. 练习:1.当x 取何值时,下列分式有意义:(1)3||61-x(2)1)1(32++-x x (3)x111+2.当x 为何值时,下列分式的值为零: (1)4|1|5+--x x(2)562522+--x x x3.解下列不等式(1)012||≤+-x x(2)03252>+++x x x(二)分式的基本性质及有关题型1.分式的基本性质:M B MA MB M A B A ÷÷=⨯⨯= 2.分式的变号法则:bab a b a b a =--=+--=-- 题型一:化分数系数、小数系数为整数系数【例1】不改变分式的值,把分子、分母的系数化为整数.(1)y x yx 41313221+- (2)ba ba +-04.003.02.0题型二:分数的系数变号【例2】不改变分式的值,把下列分式的分子、分母的首项的符号变为正号.(1)y x yx --+- (2)b a a --- (3)b a ---题型三:化简求值题【例3】已知:511=+y x ,求yxy x yxy x +++-2232的值.提示:整体代入,①xy y x 3=+,②转化出yx 11+.【例4】已知:21=-x x ,求221xx +的值.【例5】若0)32(|1|2=-++-x y x ,求yx 241-的值.练习:1.不改变分式的值,把下列分式的分子、分母的系数化为整数.(1)yx yx 5.008.02.003.0+-(2)b a ba 10141534.0-+2.已知:31=+x x ,求1242++x x x 的值.3.已知:311=-b a ,求aab b bab a ---+232的值.4.若0106222=+-++b b a a ,求ba ba 532+-的值.5.如果21<<x ,试化简x x --2|2|xx x x |||1|1+---.(三)分式的运算1.确定最简公分母的方法: ①最简公分母的系数,取各分母系数的最小公倍数; ②最简公分母的字母因式取各分母所有字母的最高次幂. 2.确定最大公因式的方法:①最大公因式的系数取分子、分母系数的最大公约数;②取分子、分母相同的字母因式的最低次幂. 题型一:通分【例1】将下列各式分别通分. (1)cb ac a b ab c 225,3,2--; (2)a b b b a a 22,--; (3)22,21,1222--+--x x x x xx x ; (4)aa -+21,2题型二:约分【例2】约分: (1)322016xy y x -;(3)n m m n --22;(3)6222---+x x x x .题型三:分式的混合运算【例3】计算:(1)42232)()()(abc ab c c b a ÷-⋅-;(2)22233)()()3(x y x y y x y x a +-÷-⋅+; (3)mn mn m n m n n m ---+-+22;(4)112---a a a ; (5)874321814121111x x x x x x x x +-+-+-+--;(6))5)(3(1)3)(1(1)1)(1(1+++++++-x x x x x x ; (7))12()21444(222+-⋅--+--x x x x x x x题型四:化简求值题【例4】先化简后求值(1)已知:1-=x ,求分子)]121()144[(48122x x x x -÷-+--的值;(2)已知:432zy x ==,求22232z y x xz yz xy ++-+的值;(3)已知:0132=+-a a ,试求)1)(1(22a a aa --的值.题型五:求待定字母的值【例5】若111312-++=--x Nx M x x ,试求N M ,的值. 练习:1.计算(1))1(232)1(21)1(252+-++--++a a a a a a ;(2)ab abb b a a ----222; (3)b a c c b a c b c b a c b a c b a ---++-+---++-232;(4)ba b b a ++-22; (5))4)(4(b a ab b a b a ab b a +-+-+-; (6)2121111x x x ++++-; (7))2)(1(1)3)(1(2)3)(2(1--+-----x x x x x x .2.先化简后求值(1)1112421222-÷+--⋅+-a a a a a a ,其中a 满足02=-a a .(2)已知3:2:=y x ,求2322])()[()(yxx y x y x xy y x ÷-⋅+÷-的值.3.已知:121)12)(1(45---=---x Bx A x x x ,试求A 、B 的值.4.当a 为何整数时,代数式2805399++a a 的值是整数,并求出这个整数值.(四)、整数指数幂与科学记数法题型一:运用整数指数幂计算【例1】计算:(1)3132)()(---⋅bc a(2)2322123)5()3(z xy z y x ---⋅(3)24253])()()()([b a b a b a b a +--+--(4)6223)(])()[(--+⋅-⋅+y x y x y x题型二:化简求值题【例2】已知51=+-x x ,求(1)22-+x x 的值;(2)求44-+x x 的值.题型三:科学记数法的计算【例3】计算:(1)223)102.8()103(--⨯⨯⨯;(2)3223)102()104(--⨯÷⨯. 练习:1.计算:(1)20082007024)25.0()31(|31|)51()5131(⋅-+-+-÷⋅-- (2)322231)()3(-----⋅n m n m(3)23232222)()3()()2(--⋅⋅ab b a b a ab (4)21222)]()(2[])()(4[----++-y x y x y x y x2.已知0152=+-x x ,求(1)1-+x x ,(2)22-+x x 的值.第二讲 分式方程【知识要点】1.分式方程的概念以及解法;2.分式方程产生增根的原因3.分式方程的应用题【主要方法】1.分式方程主要是看分母是否有外未知数;2.解分式方程的关健是化分式方程为整式方程;方程两边同乘以最简公分母.3.解分式方程的应用题关健是准确地找出等量关系,恰当地设末知数.(一)分式方程题型分析题型一:用常规方法解分式方程【例1】解下列分式方程 (1)x x 311=-;(2)0132=--x x ;(3)114112=---+x x x ;(4)x x x x -+=++4535提示易出错的几个问题:①分子不添括号;②漏乘整数项;③约去相同因式至使漏根;④忘记验根. 题型二:特殊方法解分式方程【例2】解下列方程 (1)4441=+++x x x x ; (2)569108967+++++=+++++x x x x x x x x提示:(1)换元法,设y x x =+1;(2)裂项法,61167++=++x x x . 【例3】解下列方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=+)3(4111)2(3111)1(2111x z z y y x题型三:求待定字母的值【例4】若关于x 的分式方程3132--=-x mx 有增根,求m 的值.【例5】若分式方程122-=-+x ax 的解是正数,求a 的取值范围.提示:032>-=ax 且2≠x ,2<∴a 且4-≠a . 题型四:解含有字母系数的方程【例6】解关于x 的方程 )0(≠+=--d c dcx b a x提示:(1)d c b a ,,,是已知数;(2)0≠+d c . 题型五:列分式方程解应用题练习:1.解下列方程: (1)021211=-++-xx x x ;(2)3423-=--x x x ; (3)22322=--+x x x ;(4)171372222--+=--+x x x x x x(5)2123524245--+=--x x x x (6)41215111+++=+++x x x x (7)6811792--+-+=--+-x x x x x x x x2.解关于x 的方程: (1)b x a 211+=)2(a b ≠;(2))(11b a xbb x a a ≠+=+.3.如果解关于x 的方程222-=+-x xx k 会产生增根,求k 的值.4.当k 为何值时,关于x 的方程1)2)(1(23++-=++x x kx x 的解为非负数.5.已知关于x 的分式方程a x a =++112无解,试求a 的值.(二)分式方程的特殊解法解分式方程,主要是把分式方程转化为整式方程,通常的方法是去分母,并且要检验,但对一些特殊的分式方程,可根据其特征,采取灵活的方法求解,现举例如下:一、交叉相乘法例1.解方程:231+=x x二、化归法例2.解方程:012112=---x x三、左边通分法例3:解方程:87178=----xx x四、分子对等法例4.解方程:)(11b a xb b x a a ≠+=+五、观察比较法例5.解方程:417425254=-+-x x x x六、分离常数法例6.解方程:87329821+++++=+++++x x x x x x x x七、分组通分法例7.解方程:41315121+++=+++x x x x(三)分式方程求待定字母值的方法例1.若分式方程xmx x -=--221无解,求m 的值。
第十六章分式全章总结
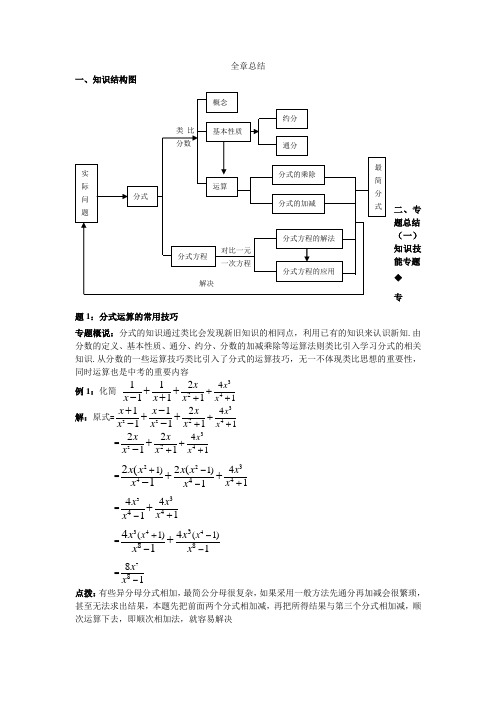
全章总结一、知识结构图二、专题总结 (一)知识技能专题 ◆专题1:分式运算的常用技巧专题概说:分式的知识通过类比会发现新旧知识的相同点,利用已有的知识来认识新知.由分数的定义、基本性质、通分、约分、分数的加减乘除等运算法则类比引入学习分式的相关知识.从分数的一些运算技巧类比引入了分式的运算技巧,无一不体现类比思想的重要性,同时运算也是中考的重要内容例1:化简 34241211111x x x x x x +++++-+解:原式=2234241211111x x x x x x x x ++++-++--=2342412121x x x x x x ++++- =2243441)1)412(12(1x x x x x x x x +--+++- =33444141x x x x -++ =344388(1)(1)4141x x x x x x +---+ =7881x x - 点拨:有些异分母分式相加,最简公分母很复杂,如果采用一般方法先通分再加减会很繁琐,甚至无法求出结果,本题先把前面两个分式相加减,再把所得结果与第三个分式相加减,顺次运算下去,即顺次相加法,就容易解决例2:计算:1111+(1)(1)(2)(2)(3)(2009)(2010)a a a a a a a a ++++++++++…解:原式=1111----12320101111+122009a a a a a a a a ++++++++++())))((…( =1111----12320101111+122009a a a a a a a a ++++++++++… =120101a a +—=2010(2010)a a +=220102010a a+ 点拨:对于分子相同,分母是相邻两个连续整数的积的分式相加减,这样的分式无法进行通分,因此,可以用公式:111(1)1n n n n =-++,这样可以抵消一些项,即巧用裂项法;要注意裂项法计算时可能会出现公式:1111(()n n k k n n k=-++)●专题1的即时练习1.计算:2411241-111x x x x ++++++ 2.计算:1271651231222++++++++x x x x x x◆专题2:与增根有关的问题专题概说:分式方程我们通常转化为已经学习过的整式方程来解决.在去分母时,方程两边同时乘以所有分母的最简公分母.这种转化可能是等价转化,也就是说转化前的分式方程的解与转化后的整式方程的解完全一致;也可能是非等价转化,即在将分式方程转化为整式方程的过程中,x 的的取值范围发生了变化,这时整式方程的解不一定是原分式方程的解,这种解题过程中增加的根称为分式方程的增根. 例3:a 为何值时,关于x 的方程223242ax x x x +=--+会产生增根? 解: 在方程两边同时乘以(2)(2)x x +-,得2(2)3(2)x ax x ++=-整理,得(1)10a x -=- 如果方程有增根,则x=2或-2当x=2时,(1)210a -⨯=-,解得4a =- 当x=-2时,(1)(2)10a -⨯-=-,解得6a = 所以,当46a =-或时,原方程会产生增根点拨:分式方程的增根是使最简公分母为零的根,但增根一定是由分式方程得到的整式方程的根。
新人教版八年级数学下册第十六章分式知识点总结

第十六章 分式知识点及典型例子一、分式的定义:如果A 、B 表示两个整式,并且B 中含有字母,那么式子B A 叫做分式。
例1.下列各式a π,11x +,15x+y ,22a b a b--,-3x 2,0•中,是分式的有( )个。
二、 分式有意义的条件是分母不为零;【B ≠0】分式没有意义的条件是分母等于零;【B=0】分式值为零的条件分子为零且分母不为零。
【B ≠0且A=0 即子零母不零】例2.下列分式,当x 取何值时有意义。
(1)2132x x ++; (2)2323x x +-。
例3.下列各式中,无论x 取何值,分式都有意义的是( )。
A .121x +B .21x x +C .231x x +D .2221x x + 例4.当x______时,分式2134x x +-无意义。
当x_______时,分式2212x x x -+-的值为零。
例5.已知1x -1y =3,求5352x xy y x xy y+---的值。
三、分式的基本性质:分式的分子与分母同乘或除以一个不等于0的整式,分式的值不变。
(0≠C )四、分式的通分和约分:关键先是分解因式。
例6.不改变分式的值,使分式115101139x y x y -+的各项系数化为整数,分子、分母应乘以(• )。
例7.不改变分式2323523x x x x -+-+-的值,使分子、分母最高次项的系数为正数,则是(• )。
例8.分式434y x a +,2411x x --,22x xy y x y-++,2222a ab ab b +-中是最简分式的有( )。
例9.约分:(1)22699x x x ++-; (2)2232m m m m-+- 例10.通分:(1)26x ab ,29y a bc ; (2)2121a a a -++,261a - 例11.已知x 2+3x+1=0,求x 2+21x 的值. C B C A B A ⋅⋅=C B C A B A ÷÷=例12.已知x+1x =3,求2421x x x ++的值. 五、分式的运算:分式乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为分母。
分式的知识点+典例

分式★学习目标1.知道分式的概念,会进行分式的约分与通分2.会分式的加减、乘除及分式的混合运算3、能根据分式的定义解决分式有无意义问题和分式的值为0问题 案例导学【题型一】分式的概念1、使分式4x 2x -有意义的x 的取值范围是( ) A. x=2 B. x ≠2C. x=-2D. x ≠-2 【题型二】分式的约分与通分1、 计算:1x xx 2--2、已知两个分式4x 4A 2-=,x 212x 1B -++=,其中x ≠±2,则A 与B 的关系是( ) A. 相等 B. 互为倒数 C. 互为相反数D. A 大于B 【题型三】分式的计算1、化简:b a b b a a 22--- 2、1x 2x 21x 1x 2x 22+-÷-+-3、)2a 42a a (a 2a a 222---⋅+ 4、化简1x x )1x 11(2-÷-+【题型四】分式有无意义问题1、使式子1|x |1-有意义的取值为( )A. x>0B. x ≠1C. x ≠-1D. 1x ±≠2、当x=_________时,分式3x 1-没有意义。
3、函数x 212y -=的自变量x 的取值范围是_________________。
【题型四】分式的值为0问题1、当m=_________时,分式2m 3m )3m )(1m (2+---的值为0。
2、若3x 2x 1|x |2-+-的值为0,则x 的值是( )A. ±1B. 1C. -1D. 不存在【题型五】条件求值问题1、若3x 1x =+,则1x x x 242++的值是( ) A. 81B. 101C. 21D. 412、已知12x +=,求x 1)1x 2x x x x 1x (22÷+---+的值。
3、若关于x 的方程ax=3x-5有负数解,则a 的取值范围是( )A.a<3B.a>3C.a ≥3D.a ≤3【题型六】分式方程问题1、解方程:x 312212x 61--=-2、若关于x 的方程01x x1x 1m =----有增根,则m 的值是( )A. 3B. 2C. 1D. -13、已知x=12+,求xx x x x x x 112122÷⎪⎭⎫ ⎝⎛+---+的值.4、当m=______时,方程233xmx x =---会产生增根.。
分式 知识点及典型例题

分式知识点及典型例题一、分式的定义如果 A、B 表示两个整式,并且 B 中含有字母,那么式子 A/B 就叫做分式。
其中 A 叫做分子,B 叫做分母。
需要注意的是,分式的分母不能为 0,因为分母为 0 时,分式没有意义。
例如:\(\frac{x}{y}\),\(\frac{a + b}{c}\)都是分式,而\(\frac{3}{5}\)(分母不含有字母)就不是分式。
二、分式有意义的条件分式有意义的条件是分母不为 0。
即:对于分式\(\frac{A}{B}\),当\(B ≠ 0\)时,分式有意义。
例如:对于分式\(\frac{x + 1}{x 2}\),要使其有意义,则\(x 2 ≠ 0\),即\(x ≠ 2\)。
三、分式的值为 0 的条件分式的值为 0 时,要同时满足两个条件:1、分子为 0,即\(A = 0\);2、分母不为 0,即\(B ≠ 0\)。
例如:若分式\(\frac{x 3}{x + 5}\)的值为 0,则\(x 3 = 0\)且\(x +5 ≠ 0\),解得\(x = 3\)。
四、分式的基本性质分式的分子与分母同时乘以(或除以)同一个不为 0 的整式,分式的值不变。
用式子表示为:\(\frac{A}{B} =\frac{A×C}{B×C}\),\(\frac{A}{B} =\frac{A÷C}{B÷C}\)(\(C ≠ 0\))例如:\(\frac{2}{3} =\frac{2×2}{3×2} =\frac{4}{6}\),\(\frac{6}{9} =\frac{6÷3}{9÷3} =\frac{2}{3}\)五、约分把一个分式的分子与分母的公因式约去,叫做分式的约分。
约分的关键是确定分子与分母的公因式。
例如:对分式\(\frac{6x}{9x^2}\)进行约分,分子分母的公因式为\(3x\),约分后为\(\frac{2}{3x}\)六、通分把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分。
(完整版)分式专题讲解(知识点+例题+练习+中考经典题)

分式专题讲解 知识点一、分式的概念: 一般地,如果A 、B 表示两个整式,并且除式B 中含有字母,那么式子叫分式。
解读:(1)分母中含有字母是分式的一个重要标志,它是分式与分数、整式的根本区别;分式A/B 有意义,则B =0(2)分式的分母的值不能等于零.若分母的值为零,则分式无意义;反之,若分式A/B 无意义,则B =0(3)当分子等于零而分母不等于零时,分式的值才是零.反之,若分式A/B=0,则A =0,且B ≠0例题1、下列各式中,哪些是整式?哪些是分式?a ab 2,x 1,3s ,b a a --,πy x +,)(21b a -,)(1z x y -,a-31练习:这些代数式中x -,π4,x a ,y x y x -+2,a 5-,71,2ba -,x -3中,是分式的有( )。
A.3个B.4个C.5个D.6个练习:已知的值。
,求x x x 011=--练习:的值是的值为零,则b 32122---b b b ( ) A.1 B.-1 C.1± D.2练习:写出一个含字母x 的分式,使得不论x 取何值,分式都有意义。
练习:若0y 3y 21,322是)为负数()为正数;()(为何值时,y x xx y -=探索题型:观察下列各等式:323112=+,434122=+,545132=+,656142=+,......,设n 为正整数,试用含n 的等式表示这个规律。
1、分式的基本性质分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.用式子表示是:MB MA MB M A B A ÷÷=⨯⨯=(其中M 是不等于0的整式).特别提示:(1)在解题过程中,分母不为0是作为隐含条件给出的.若是分式,则说明分母中的字母一定能满足使分母不为0;(2)在运用分式的基本性质时,一定要重点强调分母不为0这个条件,没有给出的,要讨论是否等于0.例题1:下列运算中,错误的是( ).A.2b ab b a =B.b ab ab =2 C.b a b a b a b a 321053.02.05.0-+=-+ D .bc acb a =2、分式的约分根据分式的基本性质,把一个分式的分子和分母分别除以它们的公因式叫做分式的约分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十六章分式知识点和典型例习题【知识网络】【思想方法】 1.转化思想转化是一种重要的数学思想方法,应用非常广泛,运用转化思想能把复杂的问题转化为简单问题,把生疏的问题转化为熟悉问题,本章很多地方都体现了转化思想,如,分式除法、分式乘法;分式加减运算的基本思想:异分母的分式加减法、同分母的分式加减法;解分式方程的基本思想:把分式方程转化为整式方程,从而得到分式方程的解等. 2.建模思想本章常用的数学方法有:分解因式、通分、约分、去分母等,在运用数学知识解决实际问题时,首先要构建一个简单的数学模型,通过数学模型去解决实际问题,经历“实际问题———分式方程模型———求解———解释解的合理性”的数学化过程,体会分式方程的模型思想,对培养通过数学建模思想解决实际问题具有重要意义. 3.类比法本章突出了类比的方法,从分数的基本性质、约分、通分及分数的运算法则类比引出了分式的基本性质、约分、通分及分式的运算法则,从分数的一些运算技巧类比引出了分式的一些运算技巧,无一不体现了类比思想的重要性,分式方程解法及应用也可以类比一元一次方程.第一讲 分式的运算【知识要点】1.分式的概念以及基本性质; 2.与分式运算有关的运算法则3.分式的化简求值(通分与约分)4.幂的运算法则【主要公式】1.同分母加减法则:()0b c b ca a a a±±=≠2.异分母加减法则:()0,0b d bc da bc daa c a c ac ac ac±±=±=≠≠;3.分式的乘法与除法:b d bd a c ac ∙=,b c b d bda d a c ac÷=∙=4.同底数幂的加减运算法则:实际是合并同类项5.同底数幂的乘法与除法;am●a n =a m+n ; a m ÷ a n =a m -n6.积的乘方与幂的乘方:(ab)m= a mb n, (a m)n= amn7.负指数幂: a-p=1pa a 0=18.乘法公式与因式分解:平方差与完全平方式(a+b)(a-b)= a2- b 2 ;(a ±b)2= a 2±2ab+b 2(一)、分式定义及有关题型题型一:考查分式的定义【例1】下列代数式中:y x yx y x y x ba b a y x x -++-+--1,,,21,22π,是分式的有: .题型二:考查分式有意义的条件【例2】当x 有何值时,下列分式有意义(1)44+-x x (2)232+x x (3)122-x (4)3||6--x x题型三:考查分式的值为0的条件【例3】当x 取何值时,下列分式的值为0.(1)31+-x x (2)42||2--x x题型四:考查分式的值为正、负的条件【例4】(1)当x 为何值时,分式x-84为正; (2)当x 为何值时,分式2)1(35-+-x x 为负;(3)当x 为何值时,分式32+-x x 为非负数.练习:1.当x 取何值时,下列分式有意义:(1)3||61-x (2)1)1(32++-x x2.当x 为何值时,下列分式的值为零: (1)4|1|5+--x x3.解下列不等式(1)012||≤+-x x (2)03252>+++x x x(二)分式的基本性质及有关题型1.分式的基本性质:M B MA MB M A B A ÷÷=⨯⨯= 2.分式的变号法则:bab a b a b a =--=+--=-- 题型一:化分数系数、小数系数为整数系数【例1】不改变分式的值,把分子、分母的系数化为整数.(1)y x yx 41313221+- (2)ba ba +-04.003.02.0题型二:分数的系数变号【例2】不改变分式的值,把下列分式的分子、分母的首项的符号变为正号.(1)y x yx --+- (2)b a a --- (3)b a ---题型三:化简求值题【例3】已知:511=+y x ,求y xy x yxy x +++-2232的值.提示:整体代入,①xy y x 3=+,②转化出yx 11+. 【例4】已知:21=-x x ,求221xx +的值.【例5】若0)32(|1|2=-++-x y x ,求yx 241-的值.练习:1.不改变分式的值,把下列分式的分子、分母的系数化为整数.(1)yx yx 5.008.02.003.0+-(2)b a ba 10141534.0-+2.已知:31=+x x ,求1242++x x x 的值.3.已知:311=-b a ,求aab b bab a ---+232的值.4.若0106222=+-++b b a a ,求ba ba 532+-的值.5.如果21<<x ,试化简x x --2|2|xx x x |||1|1+---.(三)分式的运算1.确定最简公分母的方法: ①最简公分母的系数,取各分母系数的最小公倍数; ②最简公分母的字母因式取各分母所有字母的最高次幂. 2.确定最大公因式的方法:①最大公因式的系数取分子、分母系数的最大公约数;②取分子、分母相同的字母因式的最低次幂.题型一:通分【例1】将下列各式分别通分.(1)cb ac a b ab c 225,3,2--; (2)a b b b a a 22,--; (3)22,21,1222--+--x x x x xx x ; (4)aa -+21,2题型二:约分【例2】约分:(1)322016xy y x -;(3)n m m n --22;(3)6222---+x x x x .题型三:分式的混合运算【例3】计算:(1)42232)()()(abc ab c c b a ÷-⋅-; (2)22233)()()3(x y x y y x y x a +-÷-⋅+; (3)m n m n m n m n n m ---+-+22;(4)112---a a a ; (5)874321814121111x x x x x x x x +-+-+-+--;(6))5)(3(1)3)(1(1)1)(1(1+++++++-x x x x x x ; (7))12()21444(222+-⋅--+--x x x x x x x题型四:化简求值题【例4】先化简后求值(1)已知:1-=x ,求分子)]121()144[(48122x x x x -÷-+--的值;(2)已知:432zy x ==,求22232z y x xz yz xy ++-+的值;(3)已知:0132=+-a a ,试求)1)(1(22a a a a --的值.题型五:求待定字母的值【例5】若111312-++=--x Nx M x x ,试求N M ,的值.练习1.计算(1))1(232)1(21)1(252+-++--++a a a a a a ; (2)ab abb b a a ----222; (3)b a c c b a c b c b a c b a c b a ---++-+---++-232;(4)ba b b a ++-22; (5))4)(4(b a ab b a b a ab b a +-+-+-;(6)2121111x x x ++++-; (7))2)(1(1)3)(1(2)3)(2(1--+-----x x x x x x .2.先化简后求值(1)1112421222-÷+--⋅+-a a a a a a ,其中a 满足02=-a a .(2)已知3:2:=y x ,求2322])()[()(yxx y x y x xy y x ÷-⋅+÷-的值.3.已知:121)12)(1(45---=---x Bx A x x x ,试求A 、B 的值.4.当a 为何整数时,代数式2805399++a a 的值是整数,并求出这个整数值.(四)、整数指数幂与科学记数法题型一:运用整数指数幂计算【例1】计算:(1)3132)()(---⋅bc a(2)2322123)5()3(z xy z y x ---⋅(3)24253])()()()([b a b a b a b a +--+--(4)6223)(])()[(--+⋅-⋅+y x y x y x题型二:化简求值题【例2】已知51=+-x x ,求(1)22-+x x 的值;(2)求44-+x x 的值.题型三:科学记数法的计算【例3】计算:(1)223)102.8()103(--⨯⨯⨯;(2)3223)102()104(--⨯÷⨯.练习:1.计算:(1)20082007024)25.0()31(|31|)51()5131(⋅-+-+-÷⋅-- (2)322231)()3(-----⋅n m n m(3)23232222)()3()()2(--⋅⋅ab b a b a ab (4)21222)]()(2[])()(4[----++-y x y x y x y x2.已知0152=+-x x ,求(1)1-+x x ,(2)22-+x x 的值.第二讲 分式方程【知识要点】1.分式方程的概念以及解法;2.分式方程产生增根的原因3.分式方程的应用题【主要方法】1.分式方程主要是看分母是否有外未知数;2.解分式方程的关健是化分式方程为整式方程;方程两边同乘以最简公分母.3.解分式方程的应用题关健是准确地找出等量关系,恰当地设末知数.(一)分式方程题型分析题型一:用常规方法解分式方程【例1】解下列分式方程(1)x x 311=-;(2)0132=--x x ;(3)114112=---+x x x ;(4)x x x x -+=++4535提示易出错的几个问题:①分子不添括号;②漏乘整数项;③约去相同因式至使漏根;④忘记验根. 题型二:特殊方法解分式方程【例2】解下列方程(1)4441=+++x x x x ; (2)569108967+++++=+++++x x x x x x x x提示:(1)换元法,设y x x =+1;(2)裂项法,61167++=++x x x . 【例3】解下列方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=+)3(4111)2(3111)1(2111x z z y y x题型三:求待定字母的值【例4】若关于x 的分式方程3132--=-x mx 有增根,求m 的值.【例5】若分式方程122-=-+x ax 的解是正数,求a 的取值范围.提示:032>-=ax 且2≠x ,2<∴a 且4-≠a . 题型四:解含有字母系数的方程【例6】解关于x 的方程)0(≠+=--d c dcx b a x 提示:(1)d c b a ,,,是已知数;(2)0≠+d c .题型五:列分式方程解应用题练习:1.解下列方程:(1)021211=-++-xxx x ; (2)3423-=--x x x ; (3)22322=--+x x x ;(4)171372222--+=--+x x x x xx (5)2123524245--+=--x x x x(6)41215111+++=+++x x x x (7)6811792--+-+=--+-x x x x x x x x2.解关于x 的方程:(1)b x a 211+=)2(a b ≠;(2))(11b a xbb x a a ≠+=+.3.如果解关于x 的方程222-=+-x xx k 会产生增根,求k 的值.4.当k 为何值时,关于x 的方程1)2)(1(23++-=++x x kx x 的解为非负数.5.已知关于x 的分式方程a x a =++112无解,试求a 的值.(二)分式方程的特殊解法解分式方程,主要是把分式方程转化为整式方程,通常的方法是去分母,并且要检验,但对一些特殊的分式方程,可根据其特征,采取灵活的方法求解,现举例如下:一、交叉相乘法例1.解方程:231+=x x11 二、化归法例2.解方程:012112=---x x三、左边通分法例3:解方程:87178=----x x x四、分子对等法例4.解方程:)(11b a x bb x a a ≠+=+五、观察比较法例5.解方程:417425254=-+-x x x x六、分离常数法例6.解方程:87329821+++++=+++++x xx x x x x x七、分组通分法例7.解方程:41315121+++=+++x x x x12 (三)分式方程求待定字母值的方法例1.若分式方程x mx x -=--221无解,求m 的值。
