奥数练习题[1]
六年级奥数练习(阴影面积)1

六年级奥数练习题(圆和组合图形)1、算出圆内正方形的面积为多少2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是多少平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是多少4.右图中三角形是等腰直角三角形,阴影部分的面积是(平方厘米).5.三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB长40厘米, BC长厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积为 .7.扇形的面积是平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是度.8.图中扇形的半径OA=OB=6厘米.45=∠AOB, AC垂直OB于C,那么图中阴影部分的面积是平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是平方厘米.12.如图,半圆S1的面积是平方厘米,圆S2的面积是平方厘米.那么长方形(阴影部分的面积)是多少平方厘米13.如图,已知圆心是O,半径r=9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米)14.3(≈π13、如图,求阴影部分的面积 .14、大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大平方厘米.212112215、在一个半径是厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取,结果精确到1平方厘米)16、如图所求,圆的周长是厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π17.下图中正方形部分是一个水池,其余部分是草坪,已知正方形的面积是300平方米,草坪的面积是多少平方米17、已知:ABCD 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .18、如图:阴影部分的面积是多少四分之一大圆的半径为r .(计算时圆周率取722)19、已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.20.如图{图在下面}两个连在一起的轮轴,已知小轮的半径是3分米,当这个小轮转3圈时,大轮正好转一圈,只蜜蜂分别沿着阴影部分的边缘飞1次,那只蜜蜂飞过的路线最长(3个正方形的边长都为4m )23.将半径分别是3厘米和2厘米的两个半圆如图放置,求阴影部分的周长24.求阴影部分的面积25.一个圆环外直径是内直径的二分之三倍,圆环面积150cm ,求外圆的面积26.一个长方形的面积是20平方厘米,如果在这个长方DCB AGF形里画一个最大的半圆形,这个半圆形是多少平方厘米因为这个半圆的直径是长方形的长,半径是宽,说明长方形的长是宽的2倍。
奥数题100道经典解题

奥数题100道经典解题(1)哥哥5年前的年龄和妹妹3年后的年龄相等,当哥哥()岁时,正好是妹妹年龄的3倍。
(2)从午夜零时到中午12时,时针和分针共重叠()次。
(3)一根木头长24分米,要锯成4分米长的木棍,每锯一次要3分,锯完一段休息2分,全部锯完需要()分。
(4)王冬有存款50元,张华有存款30元,张华想赶上王冬。
王冬每月存5元,张华每月存9元,()个月后才能赶上王冬。
(5)三年级有164名学生,参加美术兴趣小组的共有28人,参加音乐兴趣小组的人数是美术小组人数的2倍,参加体育兴趣小组的是音乐小组的2倍,如果每人至少参加一项兴趣小组,最多只能参加两项兴趣小组活动,那么参加两项至少有()人。
(6)张三、李四、王五三位同学中有一个人在别人不在时为集体做好事,事后老师问谁做的好事,张三说是李四,李四说不是他,王五说也不是他。
它们三人中有一个说了真话,做好事的是()。
(7)一本故事书,李明12天可以看完,而王芳要比李明多2天看完,李明每天比王芳多看4页。
这本故事书有()页。
(8)一个三位数,各位上的数之和是15,百位上的数比个位上的数小5;如果把个位和百位数对调,那么得到的新数比原数的3倍少39。
则原来的这个三位数是()。
(9)今年父子的年龄和是48岁,再过四年父亲比儿子大24岁,今年父子各多少岁?(10)4年前父子年龄和是40岁,今年父亲年龄是儿子的3倍,今年儿子多少岁?(11)4年前父亲年龄是儿子的3倍,今年父亲比儿子大24岁,今年父子各多少岁?(12)父亲今年50岁,儿子今年26岁.问几年前父亲年龄是儿子的2倍?(13)兄弟两今年的年龄和是60岁,当哥哥像弟弟现在这样大时,弟弟的年龄恰好是哥哥的一半,哥哥今年几岁?(14)10年前父亲比儿子大24岁,10年后父子的年龄和是50岁,今年父子各多少岁?(15)今年哥哥26岁,弟弟18岁.问:几年前,哥哥的年龄是弟弟的3倍?(16)一白头老翁有三个孙子,长孙22岁,次孙20岁,小孙15岁,25年后,这三个孙子的年龄之和比白头老翁那时的年龄的2倍还少60岁,老翁现在多少岁?(17)求从1~2000的自然数中,所有偶数之和与所有奇数之和的差。
小学生奥数练习题及答案六篇

小学生奥数练习题及答案六篇1.小学生奥数练习题及答案篇一1、晶晶用围棋子摆成一个三层空心方阵,最外一层每边有围棋子14个。
晶晶摆这个方阵共用围棋子多少个?分析:方阵每向里面一层,每边的个数就减少2个。
知道最外面一层每边放1 4个,就可以求第二层及第三层每边个数。
知道各层每边的个数,就可以求出各层总数。
解:最外边一层棋子个数:(14-1)×4=52(个)第二层棋子个数:(14-2-1)×4=44(个)第三层棋子个数:(14-2×2-1)×4=36(个)。
摆这个方阵共用棋子:52+44+36=132(个)还可以这样想:中空方阵总个数=(每边个数一层数)×层数×4进行计算。
解:(14-3)×3×4=132(个)答:摆这个方阵共需132个围棋子。
2、用个同样的杯子装水,水面高度分别是4厘米、5厘米、7厘米和8厘米,这4个杯子水面平均高度是多少厘米?解:分析求4个杯子水面的平均高度,就相当于把4个杯子里的水合在一起,再平均倒入4个杯子里,看每个杯子里水面的高度。
解:(4+5+7+8)÷4=6(厘米)答:这4个杯子水面平均高度是6厘米。
2.小学生奥数练习题及答案篇二1、计算:123+234+345-456+567-678+789-890123+234+345-456+567-678+789-890=123+234+345+(567-456)+(7*78)-890=123+234+345+111+111-890=234+(123+567)-890=234+690-890=34+890-890=342、569+384+147-328-167-529569+384+147-328-167-529=(569-529)+147-(147+20)+388-4-328=40-20+56=763、计算:6472-(4476-2480)+5319-(3323-1327)+9354-(7358-5362)+ 6839-(4843-2847)6472-(4476-2480)+5319-(3323-1327)+9354-(7358-5362)+6839-(48 43-2847)=(6480-8)+(5320-1)+(9360-6)+(6840-1)-(4476-2476-4)-(332 3-1323-4)-(7358-5358-4)-(4843-2843-4)=(6480+5320)+(9360+6840)-8-1-6-1-2000+4-2000+4-2000+4-2000+4=11800+16200-8000-16+16=28000-8000=200003.小学生奥数练习题及答案篇三1、甲、乙两位学生原计划每天自学的时间相同,若甲每天增加自学时间半小时,乙每天减少自学时间半小时,则乙自学6天的时间仅相等于甲自学一天的时间。
小升初奥数练习题【5篇】

小升初奥数练习题【5篇】1.小升初奥数练习题1、用一个小杯子向空瓶倒水,如果倒5杯水,连瓶共重50克;如果倒进7杯水(水没溢出来),连瓶共重66克,求一杯水和空瓶各重多少克?解答:杯子从加入5杯水,到加7杯水,多加入了2杯水,总重量就增加了66-50=16克,所以可以求出1杯水的重量是16÷2=8(克),由此可以算出5杯水重:5×8=40(克),那么空瓶重:50-40=10(克)2、四根长都是8厘米的绳子,把它们打结连在一起,成为一根长绳,打结处每根绳用去1厘米,绳结长度不计,现在这根长绳长多少厘米?解答:因为第一根和第四根只有一头打结,第二根和第三根有两头打结,所以一共要用去6个1厘米。
4×8-6=26(厘米)3、昨天是11月3日,今天是星期三,那么11月29日是星期几?解答:昨天是星期二,29-3=26(天)。
26÷7=3……5,星期二再过5天是星期日,所以11月29日是星期日。
2.小升初奥数练习题1、从9开始,把9的倍数依次写下去,一直写到999,成了一个很大的数:91827364554637281……990999,这个数一共有多少位?解答:999是9的111倍。
9的倍数中,一位数的只有一个,两位数从9×2=18到9×11=99,共10个,其它都是三位数,共111-1-10=100个。
1×1+2×10+3×100=321(位)2、两个四位数的差是2009,那么这两个四位数的和是多少?最小是多少?解答:就是9999-2009=7990,9999+7990=17989。
最小就是2009+1000=3009,3009+1000=4009。
3、甲、乙两地相距346千米,某车从早上7点出发,以每小时60千米的速度从甲地出发去乙地。
在中途丙地修车用了18分钟,修车以后用每小时80千米的速度行驶,结果在中午12点到达乙地。
经典小学1奥数题(带答案)

经典小学奥数题目1.一张圆形纸片的半径是3厘米,一张正方形纸片上的边长是4厘米。
两张纸片重叠一部分放在左面上,覆盖桌面的面积为38平方厘米。
问:两张纸片重合部分的面积是多少3*3*+4*4-38=平方厘米3.某班参加体育活动的学生有25人,参加音乐活动的有26人,参加美术活动的有24人,同时参加体、音活动的有16人,同时参加音、美活动的有15人同时参加体、美活动的有14人,三个组同时都参加的有5人。
这个班共有多少名学生参加活动?25+26+24-16-14-15+5=35人4.某校六年级举行语文和数学竞赛,参加人数占全年级总人数的百分之40.参加语文竞赛的占竞赛人数的五分之二,参加数学竞赛的占竞赛人数的四分之三,两项都参加的有12人。
这个学校六年级共有多少人40%*2/5*X+40%*3/4*X-40%X=12 X=2005.某班有52人,其中会下棋的有48人,会画画的有37人,会跳舞的有39人,这个班三项都会的至少有几人48+37+39-52*2=20人6.分母是385的最简真分数共有多少个这些真分数的和是多少385的最简真分数的个数240个,真分数的和是120牛吃草问题例1:一片青草地,每天都匀速长出青草,这片青草可供27头牛吃6周或23头牛吃9周,那么这片草地可供21头牛吃几周?这片草地上的草的数量每天都在变化,解题的关键应找到不变量——即原来的草的数量。
因为总草量可以分成两部分:原有的草与新长出的草。
新长出的草虽然在变,但应注意到是匀速生长,因而这片草地每天新长出的草的数量也是不变的。
假设1头牛一周吃的草的数量为1份,那么27头牛6周需要吃27×6=162(份),此时新草与原有的草均被吃完;23头牛9周需吃23×9=207(份),此时新草与原有的草也均被吃完。
而162份是原有的草的数量与6周新长出的草的数量的总和;207份是原有的草的数量与9周新长出的草的数量的总和,因此每周新长出的草的份数为:(207-162)÷(9-6)=15(份),所以,原有草的数量为:162-15×6=72(份)。
奥数题20道

奥数题20道【题-001】抽屉原理有5个小朋友,每人都从装有许多黑白围棋子的布袋中任意摸出3枚棋子.请你证明,这5个人中至少有两个小朋友摸出的棋子的颜色的配组是一样的。
【题-002】牛吃草:(中等难度)一只船发现漏水时,已经进了一些水,水匀速进入船内.如果10人淘水,3小时淘完;如5人淘水8小时淘完.如果要求2小时淘完,要安排多少人淘水?【题-003】奇偶性应用:(中等难度)桌上有9只杯子,全部口朝上,每次将其中6只同时“翻转”.请说明:无论经过多少次这样的“翻转”,都不能使9只杯子全部口朝下。
【题-004】整除问题:(中等难度)用一个自然数去除另一个整数,商40,余数是16.被除数、除数、商数与余数的和是933,求被除数和除数各是多少?【题-005】填数字:(中等难度)请在下图的每个空格内填入1至8中的一个数字,使每行、每列、每条对角线上8个数字都互不相同.【题-006】灌水问题:(中等难度)公园水池每周需换一次水.水池有甲、乙、丙三根进水管.第一周小李按甲、乙、丙、甲、乙、丙……的顺序轮流打开小1时,恰好在打开某根进水管1小时后灌满空水池.第二周他按乙、丙、甲、乙、丙、甲……的顺序轮流打开1小时,灌满一池水比第一周少用了15分钟;第三周他按丙、乙、甲、丙、乙、甲……的顺序轮流打开1小时,比第一周多用了15分钟.第四周他三个管同时打开,灌满一池水用了2小时20分,第五周他只打开甲管,那么灌满一池水需用________小时.【题-007】浓度问题:(中等难度)瓶中装有浓度为15%的酒精溶液1000克,现在又分别倒入100克和400克的A、B两种酒精溶液,瓶中的浓度变成了14%.已知A种酒精溶液浓度是B种酒精溶液浓度的2倍,那么A种酒精溶液的浓度是百分之几?【题-008】水和牛奶:(中等难度)一个卖牛奶的人告诉两个小学生:这儿的一个钢桶里盛着水,另一个钢桶里盛着牛奶,由于牛奶乳脂含量过高,必须用水稀释才能饮用.现在我把A桶里的液体倒入B桶,使其中液体的体积翻了一番,然后我又把B桶里的液体倒进A桶,使A桶内的液体体积翻番.最后,我又将A桶中的液体倒进B桶中,使B桶中液体的体积翻番.此时我发现两个桶里盛有同量的液体,而在B桶中,水比牛奶多出1升.现在要问你们,开始时有多少水和牛奶,而在结束时,每个桶里又有多少水和牛奶?【题-009】巧算:(中等难度)计算:【题-010】队形:(中等难度)做少年广播体操时,某年级的学生站成一个实心方阵时(正方形队列)时,还多10人,如果站成一个每边多1人的实心方阵,则还缺少15人.问:原有多少人?【题-011】计算:(中等难度)一个自然数,如果它的奇数位上各数字之和与偶数位上各数字之和的差是11的倍数,那么这个自然数是11的倍数,例如1001,因为1+0=0+1,所以它是11的倍数;又如1234,因为4+2-(3+1)=2不是11的倍数,所以1234不是11的倍数.问:用0、1、2、3、4、5这6个数字排成不含重复数字的六位数,其中有几个是11的倍数?【题-012】分数:(中等难度)某学校的若干学生在一次数学考试中所得分数之和是8250分.第一、二、三名的成绩是88、85、80分,得分最低的是30分,得同样分的学生不超过3人,每个学生的分数都是自然数.问:至少有几个学生的得分不低于60分?【题-013】四位数:(中等难度)某个四位数有如下特点:①这个数加1之后是15的倍数;②这个数减去3是38的倍数;③把这个数各数位上的数左右倒过来所得的数与原数之和能被10整除,求这个四位数.【题-014】行程:(中等难度)王强骑自行车上班,以均匀速度行驶.他观察来往的公共汽车,发现每隔12分钟有一辆汽车从后面超过他,每隔4分钟迎面开来一辆,如果所有汽车都以相同的匀速行驶,发车间隔时间也相同,那么调度员每隔几分钟发一辆车?【题-015】跑步:(中等难度)狗跑5步的时间马跑3步,马跑4步的距离狗跑7步,现在狗已跑出30米,马开始追它。
小学奥数练习题汇总1-18

小学奥数练习题,工程问题(一)1、一项工程,甲单独完成需12天,乙单独完成需要9天,若甲先做若干天后乙接着做,共用10天完成,问甲做了几天?2、一件工作,甲5小时完成了全部工作的1/4,乙6小时又完成剩下任务的一半,最后余下的部分由甲、乙合作,还需几小时?3、一项工程,甲独做需12小时,乙独做需18小时,若甲先做1小时,然后乙接替甲做1小时,再由甲接乙做1小时,……,两人如此交替工作,问完成任务时共用多少小时?4、一项工程甲队独做24天完成,乙队独做30天完成,甲乙两队合作8天后,余下的由丙队做,又做了6天才完成。
这个工程由丙队单独作需几天完成?5、一项工程,甲队独做20天完成,乙队独做30天完成,现在他们两队一起做,其间甲队休息了3天,乙队休息若干天,从开始到完工共用了16天,问乙队休息了多少天?6、修一段公路,甲队独做要用40天,乙队独做要用24天,现在两队同时从两端开工,结果在距中点750米处相遇。
这段公路长多少米?7、一项工程,甲乙两队合作需12天完成,乙丙两队合作需15天完成,甲丙两队合作需20天完成,问由甲乙丙三队合作需几天完成?8、加工一批零件,甲乙合作24天可以完成,现在由甲先做16天,然后乙再做12天,还剩这批零件的2/5没有完成,已知甲每天比乙多加工3个零件,这批零件共有多少个?9、一件工作甲先做6小时,乙接着做12小时可以完成;甲先做8小时,乙接着做6小时也可以完成。
如果甲先做3小时后由乙接着做,还需要多少小时完成?10、甲乙丙三人合作完成一件工程,共得报酬1800元。
三人完成这项工作的情况是:甲乙合作8天完成工程的1/3;接着乙丙又合作2天,完成余下的1/4;以后三人合作5天完成了这项工程。
按劳付酬,各人应得报酬多少元?11、制造一批零件,甲车间独做要10天完成,若甲车间与乙车间一起做则要6天完成,而乙车间与丙车间一起做需8天才能完成,现在三个车间一起做,完工时发现甲车间比乙车间多做2400个,问丙车间做了多少零件?12、一件工作,一个技工与3个学徒工完成需要4天,2个技工与1个学徒工完成需要3天,那么1个学徒工完成这件工作需要多少天?13、甲、乙两项工程分别由一、二队来完成。
小学二年级下册奥数练习题

小学二年级下册奥数练习题【#二年级# 导语】在解奥数题时,经常要提醒自己,遇到的新问题能否转化成旧问题解决,化新为旧,透过表面,抓住问题的实质,将问题转化成自己熟悉的问题去解答。
转化的类型有条件转化、问题转化、关系转化、图形转化等。
以下是整理的《小学二年级下册奥数练习题》相关资料,希望帮助到您。
小学二年级下册奥数练习题篇一1、一桶油连桶重19千克,吃了一半油后,连桶重12千克。
吃掉了多少油?油桶里原来有多少千克油?2、一条河堤长12米,每隔4米栽一棵树,从头到尾一共栽多少棵?3、书架上的故事书比连环画少15本,书架上有杂志8本,有故事书32本。
连环画有多少本?故事书和连环画一共有多少本?4、少年宫新购进小提琴52把,中提琴比小提琴少20把,两种琴一共有多少把?5、鱼缸里共有50条金鱼,其中红金鱼有15条,花金鱼20条,其余是黑金鱼。
黑金鱼有多少条?(用两种方法解答)6、科学宫里有一个奇妙的大盒子里装着4个中盒子,每个中盒子里又装4个小盒子,一共有多少个盒子?7、妈妈买一双皮鞋花52元,买一双布鞋花12元,付给售货员100元,应该找回多少元?(用两种方法解答)8、把一根木头锯断要4分钟,把这根木头锯成8段,要几分钟?9、一条路每隔40米埋设一根电线杆,现在包括这条路的两端一共埋设了10根电线杆,这条路长多少米?10、上体育课时,同学们站成方队做体操,从前、后、左、右数,小芳都是第3个,一共有多少个同学在做体操?(画图表示,并计算)小学二年级下册奥数练习题篇二1、山上有群猴子,摘了一篮桃子。
一只吃一个,刚好剩1个,一只吃两个,有只没吃着。
让你算一算,()只()桃子。
2、一条路长600米,在路的一边每隔20米放一个垃圾桶,起点和终点不放,一共需要准备多少个垃圾桶?3、一条河堤长350米,从头到尾要载71棵,每隔几米载一棵?4、一条路长100米,在路的一边从头到尾每隔10米插一面彩旗,一共要多少面彩旗?5、小红做一个两位数和一个三位数相加的计算题时,由于粗心大意,把一个加数个位上的8错误地当作了3,把十位上的6错当成了9,所得的和是438,正确的和是多少?6、刘杰做加法时,错把一个数个位上的2当作8,十位上的4当作7,结果和是95。
小学奥数精选100题 (1)

100道奥数题1、王家养了5头奶牛,7天产牛奶630千克,照这样计算,8头奶牛15天可产牛奶多少千克?2、小丽计划用35元买每支2元、3元、4元三种不同价格的圆珠笔,每种至少买1支.她最多能买( )支,最少能买()支.3、甲、乙、丙、丁4名同学排成一行。
从左到右数,如果甲不排在第一个位置上,乙不排在第二个位置上,丙不排在第三个位置上,丁不排在第四个位置上,那么不同的排法共有多少种?4、a b c d代表一个四位数,其中a,b,c,d均为1,2,3,4中的某个数字,但彼此不同,例如2134。
请写出所有满足关系a<b,b>c,c<d的四位数a bc d来。
5、小红在计算有余数除法时,把被除数113错写成131,这样商比原来多2,但余数恰好相同。
正确的除数和余数是多少?6、6、100与500之间能被9整除的所有自然数之和?7、两个数的和是2016,其中一个加数的个位是0,如果把这个0去掉,就正好等于另一个加数的两倍。
这两个加数各是多少?8、小华今年12岁,他妈妈今年48岁,多少年以前妈妈的年龄是小华的5倍?9、哥哥6年前的岁数等于弟弟8年后的岁数.哥哥5年后与弟弟3年前的年龄和是38岁.求兄弟二人今年各几岁?10、赵、田、钱、李、吴五位老师,赵老师比田老师大4岁,钱老师比赵老师大3岁,李老师比赵老师小3岁,吴老师比钱老师小2岁.这五位老师的年龄加在一起是122岁.问:五位老师各多少岁?11、母女的年龄和是64岁,女儿年龄的3倍比母亲大8岁,求母女二人的年龄各是多少岁?12、哥哥今年比小丽大12岁,8年前哥哥的年龄是小丽的4倍,今年二人各几岁?13、妈妈买回一筐苹果,按计划吃的天数算了一下,如果每天吃4个,要多出48个苹果;如果每天吃6个,则又少8个苹果.那么妈妈买回的苹果有多少个?计划吃多少天?14、学校为新生分配宿舍.每个房间住3人,则多出23人;每个房间住5人,则空出3个房间.问宿舍有多少间?新生有多少人?15、裁缝有一段16米长的呢子,每天剪去2米,第几天剪去最后一段?16、小明计划用若干天做一本习题集。
一年级奥数数学练习题[5篇]
![一年级奥数数学练习题[5篇]](https://img.taocdn.com/s3/m/76e0a9a20342a8956bec0975f46527d3250ca678.png)
一年级奥数数学练习题[5篇]1.一年级奥数数学练习题篇一1、黑兔、兔和白兔三只兔子在赛跑。
黑免说:“我跑得不是最快的,但比白兔快。
”请你说说,谁跑得最快?谁跑得最慢?()跑得最快,()跑得最慢。
2、三个小朋友比大小。
根据下面三句话,请你猜一猜,谁最大?谁最小?(1)芳芳比阳阳大3岁;(2)燕燕比芳芳小1岁;(3)燕燕比阳阳大2岁。
()最大,()最小。
3、根据下面三句话,猜一猜三位老师年纪的大小。
(1)王老师说:“我比武老师小。
”(2)张老师说:“我比王老师大。
”(3)武老师说:“我比张老师小。
”年纪最大的是(),最小的是()。
4、光明幼儿园有三个班。
根据下面三句括,请你猜一措,哪一班人数最少?哪一班人数最多?(1)中班比小班少;(2)中班比大班少;(3)大班比小班多。
()人数最少,()人数最多。
5、三个同学比身高。
甲说:我比乙高;乙说:我比丙矮;丙:说我比甲高。
()最高,()最矮。
2.一年级奥数数学练习题篇二1、哥哥4个苹果,姐姐有3个苹果,弟弟有8个苹果,哥哥给弟弟1个后,弟弟吃了3个,这时谁的苹果多?2、小明今年6岁,小强今年4岁,2年后,小明比小强大几岁?3、同学们排队做操,小明前面有4个人,后面有4个人,这一队一共有多少人?4、有一本书,小华第一天看了2页,以后每一天都比前一天多看2页,第4天看了多少页?5、同学们排队做操,从前面数,小明排第4,从后面数,小明排第5,这一队一共有多少人?6、有8个皮球,如果男生每人发一个,就多2个,如果女生每人发一个,就少2个,男生有多少人,女生有多少人?7、老师给9个三好生每人发一朵花,还多出1朵红花,老师共有多少朵红花?8、有5个同学投沙包,老师如果发给每人2个沙包就差1个,老师共有多少个沙包?9、刚刚有9本书,爸爸又给他买了5本,小明借去2本,刚刚还有几本书?10、一队小学生,李平前面有8个学生比他高竺嬗?个学生比他矮,这队小学生共有多少人?3.一年级奥数数学练习题篇三1、日落西山晚霞红,我把小鸡赶进笼。
五年级奥数练习题一

五年级奥数练习题一 work Information Technology Company.2020YEAR练习一1/牧场上有一片匀速生长的草地,可供27头牛吃6周,或供23头牛吃9周,那么它可供21头牛吃几周2.一只船发现漏水时,已经进了一些水,水继续不断均速进入船内,如果10人淘水,3小时淘完,如果5人淘水,8小时淘完,如果要求2小时淘完,要安排多少人淘水?3.有一牧场,若牧牛17头,30天牧场上的草全部吃完,若牧牛19头,则24天牧场上的草全部吃完.现在牧牛若干头,6天后4头牛死亡,余下的牛吃了2天将草吃完,问原来牧牛多少头?4.画展9时开门,但早有人来排队等候入场,从第一个观众来时起,每分钟来的观众人数一样多,如果开了3个入场口,9时9分就不再有有人排队,如果同时开5个入场口,9时5分就没人排队,那么第一个观众到达的时间是几时几分?5.由于天气逐渐寒冷起来,牧场上的草不仅不长出,反而以固定的速度在减少,照这样计算,某块草地上的草可供20头牛吃5天,或可供15头牛吃6天,那么可供多少头牛吃10天?6.一块草地,每天生长的速度相同,现在这片牧场可供16头牛吃20天,或者供80只吃12天,如果一头牛一天的吃草量等于4只羊一天的吃草量,那么12头牛与24只羊一起吃可以吃多少天?7.快中慢三辆车从同地出发,沿同一公路追赶前面的一个骑车人,这三辆车的速度分别是每小时25千米.15千米.10千米,已知慢中车分别用20小时,10小时追上汽车人,那么快车用多长时间追上骑车人?8牧场上有一片匀速生长的草地,可供10头牛吃20周,或供15头牛吃10周,那么它可供21头牛吃几周9.一个水果仓库,原来库存了一批水果,现在每天都运进相同数量的水果,如果用汽车把所有水果全部运走,用32辆汽车16天可以运完,或用48辆汽车8天可以运完,如果要4天运完,需要多少辆车?10/有一口井,井底连续不断涌出泉水,每分钟涌出的水量相等,如果使用5架抽水机来抽水,20分分钟可以抽完,如果使用3架抽水机,36分钟可以抽完,现在要求12分钟内抽完井水,需要抽水机多少架?11某车站检票前若干分钟就开始排队,每分钟来的旅客人数一样多,若同时开4个检票口,从开始检票到等候检票的队伍小时需要30分钟,同时开5个检票口只需20分钟,如果同时开7个检票口需要多少分钟?12.由于天气逐渐寒冷起来,牧场上的草不仅不长出,反而以固定的速度在减少,照这样计算,某块草地上的草可供20头牛吃5天,或可供12头牛吃7天,那么可供6头牛吃多少天?13. 一块草地,每天生长的速度相同,现在这片牧场可供16头牛吃15天,或者供100只吃6天,如果一头牛一天的吃草量等于4只羊一天的吃草量,那么8头牛与48只羊一起吃可以吃多少天?14有一个酒槽,每天漏出等量的酒,如果让6人饮,则4天喝完,如果让4人饮,则5天喝完(每人的饮酒量相同)如果要8天喝完,只能由几人来饮?15一片草地,可供6头牛i吃30天,或者供5头牛吃40天,如果4头牛吃了30天,又增加2头牛一起吃,还可以吃几天?16经测算,地球上的资源可以供100亿人生活100年,或者供80亿人生活300年,假设地球每年新生成的资源增长速度是一定的,为了使人类有不断发展的潜力,那么地球上最多生活多少亿人?17甲乙丙三个仓库个存放着同样多的大米,甲仓库用皮带输送机一台和12名工人5小时运完大米,乙仓库用皮带输送机一台和28名工人3小时运完,丙用2台皮带输送机,如果要把丙仓库的大米在2小时内搬完,还需要多少工人?练习二有6箱苹果,每箱的个数相等,现在从每箱中拿出12个送给幼儿园小朋友吃,剩下的苹果正好是原来4箱苹果的个数,原来每箱苹果有多少个?(1)张老师把一些笔记本奖给在数学竞赛中获奖的小红。
一年级小学生奥数数学练习题[5篇]
![一年级小学生奥数数学练习题[5篇]](https://img.taocdn.com/s3/m/3fd558377ed5360cba1aa8114431b90d6c8589ea.png)
一年级小学生奥数数学练习题[5篇]1.一年级小学生奥数数学练习题篇一1、小强、小清、小玲、小红四人中,小强不是最矮的,小红不是最高的,但比小强高,小玲不比大家高。
请按从高到矮的顺序,把名子写出来。
【解析】简单逻辑推理题,因为小强不是最矮的,小红不是最高的,但比小强高,所以小强只能是第三高的,小红是第二高的;而小玲不比大家高,说明小玲最矮,此外就是小清最高;即从高到矮的顺序为:小清、小红、小强、小玲。
2、用0、6、7、8、9这五个数字组成各个数位上数字不相同的两位数共有多少个?【解析】两位数由个位和十位组成,而十位上一定不能为0,所以可能有6、7、8、9中的4种情况;而个位上除掉十位上的数字以外,还有4种可能,所以根据乘法原理可得:组成各个数位上数字不相同的两位数共有4×4=16个。
3、五个同学参加乒乓球赛,每两人都要赛一场,一共要赛多少场?【解析】排列组合,一共需要赛的场次为1+2+3+4=10次4、2把小刀与3本笔记本的价钱相等,3本笔记本与6支铅笔的价钱相等,一把小刀1角8分,一支铅笔多少钱?【解析】因为2把小刀与3本笔记本的价钱相等,3本笔记本与6支铅笔的价钱相等;所以2把小刀与6支铅笔的价钱相等,即1把小刀与3支铅笔的价钱相等;因为一把小刀1角8分,所以一支铅笔3角24分,即5角4分5、两筐水果共重124千克,第一筐比第二筐多8千克,两筐水果各重多少千克?【解析】和差问题,第一筐重量为(124+8)÷2=66千克,第二筐重量为(124-8)÷2=58千克2.一年级小学生奥数数学练习题篇二1、8个小男孩在一起要比谁的力气大,各人都说自己力气。
这时过来一位老先生,说:"不要吵了,我们用淘汰制,两个人一组掰手腕,每场比赛淘汰一人,最后决出冠军,也就是力气的人。
"大家一致赞成。
老先生又说:"那这样一共要赛多少场呢?你们算一算,算好了,我来当裁判。
十道奥数题及答案

十道奥数题及答案1. 题目:一个数字问题,如果将数字1234567890的每一位数字都乘以2,得到的新数字是多少?答案:将每一位数字乘以2,得到的新数字是 2468135180。
2. 题目:一个数列问题,数列的前五项是1, 1, 2, 3, 5,求第六项。
答案:这是一个斐波那契数列,每一项都是前两项的和。
所以第六项是5+3=8。
3. 题目:一个几何问题,一个圆的半径是10厘米,求圆的面积。
答案:圆的面积公式是A = πr²,代入 r = 10 得到A = π *10² = 100π 平方厘米。
4. 题目:一个组合问题,有5个不同的球和3个不同的盒子,求将所有球放入盒子中的方法总数。
答案:每个球都有3种选择,所以总的方法数是 3^5 = 243种。
5. 题目:一个概率问题,抛掷一枚均匀的硬币两次,求至少出现一次正面的概率。
答案:至少一次正面的概率等于1减去两次都是反面的概率,即 1 - (1/2) * (1/2) = 3/4。
6. 题目:一个逻辑问题,有5个盒子,每个盒子里都有一个数字,分别是1, 2, 3, 4, 5。
如果将数字1放入数字2的盒子,数字2放入数字3的盒子,以此类推,问最后数字5会在哪里?答案:数字5会被放入数字4的盒子。
7. 题目:一个算术问题,求1到100所有整数的和。
答案:这是一个等差数列求和问题,公式为 (首项 + 末项) * 项数 / 2,即 (1 + 100) * 100 / 2 = 5050。
8. 题目:一个时间问题,如果现在是3点15分,那么45分钟后是几点?答案:45分钟后是3点60分,即4点。
9. 题目:一个速度问题,一辆车以每小时60公里的速度行驶,求它在2小时内行驶的距离。
答案:距离等于速度乘以时间,即 60 公里/小时 * 2 小时 = 120 公里。
10. 题目:一个体积问题,一个长方体的长、宽、高分别是10厘米、8厘米和6厘米,求它的体积。
五年级奥数题及答案[1]
![五年级奥数题及答案[1]](https://img.taocdn.com/s3/m/d9d1fa0103d8ce2f0066235e.png)
五年级奥数题问题1 如果一个四位数与一个三位数的和是1999,并且四位数和三位数是由7个不同的数字组成的。
那么,这样的四位数最多能有多少个?这是北京市小学生第十五届《迎春杯》数学竞赛决赛试卷的第三大题的第4小题,也是选手们丢分最多的一道题。
得到a=1,b+e=9,(e≠0),c+f=9,d+g=9。
为了计算这样的四位数最多有多少个,由题设条件a,b,c,d,e,f,g互不相同,可知,数字b有7种选法(b≠1,8,9),c有6种选法(c≠1,8,b,e),d有4种选法(d≠1,8,b,e,c,f)。
于是,依乘法原理,这样的四位数最多能有(7×6×4=)168个。
在解答完问题1以后,如果再进一步思考,不难使我们联想到下面一个问题。
问题2 有四张卡片,正反面各写有1个数字。
第一张上写的是0和1,其他三张上分别写有2和3,4和5,7和8。
现在任意取出其中的三张卡片,放成一排,那么一共可以组成多少个不同的三位数?此题为北京市小学生第十四届《迎春杯》数学竞赛初赛试题。
其解为:后,十位数字b可取其他三张卡片的六种数字;最后个位数c可取剩余两张卡片的四种数字。
综上所述,一共可以组成不同的三位数共(7×6×4=)168个。
如果从甲仓库搬67吨货物到乙仓库,那么甲仓库的货物正好是乙仓库的2倍;如果从甲仓库搬17吨货物到乙仓库,那么甲仓库的货物正好是乙仓库的5倍,原来两仓库各存货物多少吨?67×(2+1)-17×(5+1)=201-102=99(吨)99÷…(5+1)-(2+1)‟=99÷3=33(吨)答:原来的乙有33吨。
(33+67)×2+67=200+67=267(吨)答:原来的甲有267吨。
分析:1、如果从甲仓库搬67吨货物到乙仓库,那么甲仓库的货物正好是乙仓库的2倍;甲和乙总的数量没有变,总的数量包括2+1=3个现在的乙,现在的乙是原来的乙加上67得来。
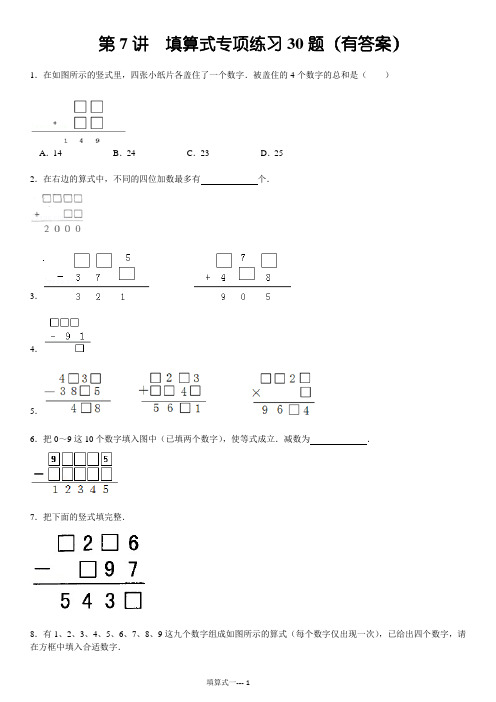
奥数(1)填算式(加减法)专项练习30题有答案
第7讲填算式专项练习30题(有答案)1.在如图所示的竖式里,四张小纸片各盖住了一个数字.被盖住的4个数字的总和是()A.14 B.24 C.23 D.252.在右边的算式中,不同的四位加数最多有_________个.3.4.5.6.把0~9这10个数字填入图中(已填两个数字),使等式成立.减数为_________.7.把下面的竖式填完整.8.有1、2、3、4、5、6、7、8、9这九个数字组成如图所示的算式(每个数字仅出现一次),已给出四个数字,请在方框中填入合适数字.9.在下面几道题中填上适当的数字:(1)(2)(3)10.在括号里填上合适的数.11.是三个数的加法算式,每个“□”内有一个数字,则三个加数中最大的是_________.12.13.算式里,每个方框代表一个数字.问:这6个方框中的数字的总和是_________.14.请你把图中算式补完整.15.如图,方格内的数字分别为1,2,3,4,5,6,7,8中的一个,那么四个加数中最大的一个数最小是_________.16.在右边的算式中,被加数的数字和是和数的数字和的三倍.问:被加数至少是_________.17.如图所示的算式中,如果七个方格中的数字互不相同,那么和的最大值是_________.18.将1﹣9这9个数字分别填入如图所示的方框内,使算式成立.(给出一种填法即可)19.用0、1、2、3、…、9这十个数字分别填到各个□中,使下面的式子成为两个三位数,之和是一个四位数的竖式.20.请完成如图的竖式.21.在图中所示的方格中适当地填上1、2、3、4、5、6、7、8,使它的和为153.此时所有“个位数字”之和与所有“十位数字”之和相差_________.22.将数字1至9分别填入右边竖式的方格内使算式成立(每个数字恰好使用一次),那么加数中的四位数最小是_________.23.在括号里填上合适的数.24.在下面的算式里,空格里的四个数字的和是_________.25.用0﹣9 填写.26.下面有一个加法竖式,其中每个□盖着一个数码,则被盖住的九个数码之和等于_________.27.在下面的□里填上适当的数.28.29.30.在下面的□里填上合适的数.参考答案:1.个位上,两个数字的和是9,可以得出其中一个2+7=9;十位上,两个数字和是14,可以得出其中一个8+6=14;由以上分析可得其中一个竖式是:那么,被盖住的4个数字的总和就是:8+2+6+7=23.故答案为:C2.四位加数千位上只能是1,百位上必须向千位进一,这样和的千位才能得到2,由于另一个加数最高位是十位,所以,四位加数的百位数字是9,这样可得到四位加数是:19□□;因为和是2000,所以,十位上必须向百位进一;根据竖式可知,个位上,□+□=0,可得这两个加数的个位都是0或它们相加的和是10;当这两个加数的个位都是0,十位上相加必须是10,才能进一,由1+9=10,2+8=10,3+7=10,4+6=10,5+5=10,6+4=10,7+3=10,8+2=10,9+1=10,可得共有9种组合方式;当这两个加数的个位相加的和是10,有9种方式,即:1+9=10,2+8=10,3+7=10,4+6=10,5+5=10,6+4=10,7+3=10,8+2=10,9+1=10,,向十位进一,十位上加上进位一是10,可得十位上相加是10﹣1=9即可,这时由0+9=9,1+8=9,2+7=9,3+6=9,4+5=9,5+4=9,6+3=9,7+2=9,8+1=9,有10种方式,根据乘法原理可得:9×10=90(种);两位加数十位上不能是0,所以要去掉十位上是0的,共9种.总共有:9+90﹣9=90(种).答:不同的四位加数最多有90个.故填:903.4.当差是9时这个算式才成立,被减数就是91+9=100,那么这个算式就是:100﹣91=9.5.6.根据题干分析可得:,答:减数是81420.故答案为:814207.根据题干分析可得:故答案为:6;3;7;98.9.(1)个位上:4+□=7,□=7﹣4=3,所以,个位上的□填3;十位上:3+□=9,□=9﹣3=6,所以,十位上的□填6;百位上:□+2=3,□=3﹣2=1,所以,百位上的□填1;千位上:□+5=6,□=6﹣5=1,所以,千位上的□填1;由以上推算可得竖式是:(2)个位上:6+□=6,□=6﹣6=0,所以,个位上的□填0;十位上:□+7=7,□=7﹣7=0,所以,十位上的□填0;百位上:5+□=8,□=8﹣5=3,所以,百位上的□填3;千位上:□+3=9,□=9﹣3=6,所以,千位上的□填6;由以上推算可得竖式是:(3)个位上:8+□=7,因为8+9=17,所以,个位上的□填9.向十位进1;十位上:□+6+1=5,因为8+6+1=15,所以,十位上的□填8,向百位进1;百位上:□+5+1=8,□=8﹣5﹣1=2,所以,百位上的□填2;千位上:□+1=5,□=5﹣1=4,所以,千位上的□填4;由以上推算可得竖式是:10.(1)个位上:8+8=16,向十位上进1;十位上:2+7+1=10,向百位上进1;百位上:3+1+1=5.由以上推算可得:;(2)个位上:6﹣8不够减,十位上退1,16﹣8=8;十位上:百位退1,16﹣1﹣7=8,所以,十位上是6;百位上退1后,与减数相同,只要比减数大1即可;由以上推算可得:;(3)个位上:4+2=6;十位上:6+3=9;百位上:2+5=7.由以上推算可得:.11.根据题意可知,个位上,1+□+1=11,□=11﹣1﹣1=9,向十位进一;十位上,□+1□+1=11,这两个□的和是11﹣1﹣1=9,向百位进一;百位上,1+□+1+1=11,□=11﹣1﹣1﹣1=8;那么中间的一个加数是819,根据整数的大小比较,最高位百位上是:8>1>1,所以最大的数是:819.故答案为:81912..13.根据题干分析可得:所以9×5+8=53,答:这六个数的和是53.故答案为:5314.根据竖式可得:十位上数字相加一定有进位,即□+□=19,而9+9=18,比19小1,可以得出,个位上数字相加必定大于等于10.2+8=10,向十位进1,9+9+1=19;2+9=11,向十位进1,9+9+1=19.由以上分析可得竖式是:15.根据题意,由竖式可得:个位上,1~8中,四个数相加的和的末尾是5,当这四个数的和是5明显不行;那么这四个数的和只能是15或25;当这四个数的和是25时,只有4+6+7+8=25,向十位上进2,还剩下1、2、3、5,而十位上1+2+3+5+2=13,不符合题意,因此个位上的四个数的和是15;这时有1+3+4+7=15,1+2+4+8=15,2+3+4+6=15,都要向十位进1;当1+3+4+7=15,也就是个位上分别填入1、3、4、7时,还剩下2、5、6、8,2+5+6+8+1=22,符合题意,那么所组成的两位数中,最大的一个数最小是81;当1+2+4+8=15,也就是个位上分别填入1、2、4、8时,还剩下3、5、6、7,3+5+6+7+1=22,符合题意,那么所组成的两位数中,最大的一个数最小是71;当2+3+4+6=15,也就是个位上分别填入2、3、4、6时,还剩下1、5、7、8,1+5+7+8+1=22,符合题意,那么所组成的两位数中,最大的一个数最小是82;由以上可得:四个加数中最大的一个数最小是71.故答案为:7116.根据题干分析可得:这个算式是:18+3=21,所以被加数最小是18.故答案为:1817.要使和最大,那么两个加数的十位要尽量大,即分别为8和9,那么和的前两位是17或18,数字不能重复,所以只能是17,个位不能有进位,那么和的个位最大是6,这时加数的个位分别是2和4,符合题意,所以和的最大值是176.故答案为:17618.首先确定个位数字和为19(2+8+9,4+7+8,3+7+9,5+6+8),十位数字和为18(5+6+7,3+6+9,4+6+8,2+7+9),个位数字和为8(1+3+4,1+2+5,1+2+51+3+4 ),符合题意的算式不唯一(在本数位的数字可以任意调换),举例如下:19.,,,;其它的可类似写出:对两个加数交换个位,交换十位,交换百位,即可得出另一组能成立的算式20.据以上分析知:三位数的加数是998时,它对应的另一个两位数加数就是90,三位数的加数是997时,它对应的另一个两位数加数就是91,三位数的加数是996时,它对应的另一个两位数加数就是92,三位数的加数是995时,它对应的另一个两位数加数就是93,三位数的加数是994时,它对应的另一个两位数加数就是94,三位数的加数是993时,它对应的另一个两位数加数就是95,三位数的加数是992时,它对应的另一个两位数加数就是96,三位数的加数是991时,它对应的另一个两位数加数就是97,三位数的加数是990时,它对应的另一个两位数加数就是98,三位数的加数是989时,它对应的另一个两位数加数就是99,三位数的加数是999时,它对应的另一个两位数加数就是8921.所有“个位数字”之和=23,所有“十位数字”之和=13,所以23﹣13=10.故答案为:1022.:首先从1﹣﹣﹣9中选三个数相加得8或18,确定各位上的数字:(1)1+3+4=8,(2)1+2+5=8,(3)1+8+9=18,(4)3+7+8=18,(5)4+6+8=18,(6)5+6+7=18.假如(1)成立,则各位上的三个数字确定是:1,3,4.则十位上的三个数字应该从2,5,6,7,8,9中确定,并且需要满足三个数相加是10或20.成立的有:A:5+6+9=20;B:5+7+8=20.假如A成立,那么十位上的三个数字确定是:5,6,9.那么百位上的数字只能是2,7,8.但是,2+7+8=17,再加上十位上的相加进的2.17+2=19,不是整十的数.不满足题目要求.同样的方法验证B也不符合题目要求.用同样的方法验证(2),(3)都不满足题目要求.而(4)个位上的三个数是:3,7,8.十位上的三个数是:4,6,9,百位上的三个数是:1,2,5.要求最小的四位数是:1143.而(5)个位上的三个数是:4,6,8,十位上的三个数是:3,7,9,百位上的三个数是:1,2,5.要求最小的四位数是:1134.而(6)个位上的三个数是:5,6,7,十位上的三个数是:2,8,9,百位上的三个数是:1,3,4.要求最小的四位数是:1125.很明显这三个四位数最小的是一个1125.故答案为:112523.根据分析可得:24.根据竖式可得:个位上:□+□=8,如果没有进位,那么十位上不会有两个一位数相加的和是19,因此,个位上相加必须向十位进1,由9+9=18,可得个位上都填9,向十位进1;十位上:□+□+1=19,由9+9+1=19,所以,十位上的也都填9.由以上推算可得竖式是:空格里的四个数字的和是:9×4=36.故答案为:3625. 根据分析,算式如下:246+789=1035,249+786=1035,264+789=1053,269+784=1053,284+769=1053286+749=1035,289+746=1035,289+764=1053,324+765=1089,325+764=1089342+756=1098,346+752=1098,347+859=1206,349+857=1206,352+746=1098356+742=1098,357+849=1206,359+847=1206,364+725=1089,365+724=1089423+675=1098,425+673=1098,426+879=1305,429+876=1305,432+657=1089437+589=1026,437+652=1089,439+587=1026,452+637=1089,457+632=1089473+589=1062,473+625=1098,475+623=1098,476+829=1305,479+583=1062479+826=1305,483+579=1062,487+539=1026,489+537=1026,489+573=1062537+489=1026,539+487=1026,573+489=1062,579+483=1062,583+479=1062587+439=1026,589+437=1026,589+473=1062,623+475=1098,624+879=1503625+473=1098,629+874=1503,632+457=1089,637+452=1089,652+437=1089657+432=1089,673+425=1098,674+829=1503,675+423=1098,679+824=1503724+365=1089,725+364=1089,742+356=1098,743+859=1602,746+289=1035746+352=1098,749+286=1035,749+853=1602,752+346=1098,753+849=1602756+342=1098,759+843=1602,764+289=1053,764+325=1089,765+324=1089769+284=1053,784+269=1053,786+249=1035,789+246=1035,789+264=1053824+679=1503,826+479=1305,829+476=1305,829+674=1503,843+759=1602847+359=1206,849+357=1206,849+753=1602,853+749=1602,857+349=1206859+347=1206,859+743=1602,874+629=1503,876+429=1305,879+426=1305879+624=150326.根据以上分析可知这两个加数分别是9999和9998,和的最高位是1.所以被盖住的九个数码之和是:9+9+9+9+9+9+9+8+1=72.故答案为:7227.根据题意与分析,这两个竖式的答案有很多种,答案不唯一,在这里只是解出一种答案.加法竖式注意百位上两个数相加是10,其余根据给出的数就可以得出答案,加法竖式是:7 8 3 7+3 2 7 3﹣﹣﹣﹣﹣﹣﹣﹣1 1 1 1 0减法竖式注意百位上不够减是关键,个位上8﹣8=0,十位上8﹣2=6,百位上用0﹣8不够减,减法竖式是:5 0 8 8﹣8 2 8﹣﹣﹣﹣﹣﹣﹣﹣﹣4 2 6 028.答案不唯一,如:29.(1)个位上,3+7=10,所以个位上的□填7,向十位进1;十位上:□+5+1=7,□=7﹣1﹣5=1;由以上可得竖式是:;(2)根据竖式可得:被减数是82,差是45,那么减数=被减数﹣差=82﹣45=37;由以上可得竖式是:30.由以上分析得如下算式:填算式一------ 11。
奥数题及答案(合集15篇)

奥数题及答案(合集15篇)奥数题及答案1加工零件:(中等难度)甲、乙、丙3名工人准备在同样效率的3个车床上车出7个零件,加工各零件所需要的'时间分别为4,5,6,6,8,9,9分钟。
3人同时开始工作,问最少经过多少分钟可车完全部零件?加工零件答案:加工所有的零件供需:4+5+6+6+8+9+9=47分钟,平均到三台车床上加工,平均每台加工时间为分钟。
由于加工各零部件需要整数分钟,因此最快需16分钟完成,但是无论怎么分组,都做不到。
因此延长1分钟,即17分钟,有(6,9),(6,9),(4,5,8),满足题意。
所以,最少经过17分钟可完成全部零件。
奥数题及答案2一大块金帝牌巧克力可以分成若干大小一样的正方形小块。
小明和小强各有一大块金帝巧克力,他们同时开始吃第一小块巧克力。
小明每隔20分钟吃1小块,14时40分吃最后1小方块;小强每隔30分钟吃1小块,18时吃最后1小方块。
那么他们开始吃第1小块的'时间是几时几分?分析:小明每隔20分钟吃1小块,小强每隔30分钟吃1小块,小强比小明多间隔10分钟,小明14时40分吃最后1小方块,小强18时吃最后1小方块,小强比小明晚3小时20分,说明在吃最后一块前面共有(3*60+20)/10=20个间隔,即已经吃了20块。
那么,20*20=400分钟=6小时40 分钟,14时40分-6小时40分=8时。
解:18时-14时40分=3小时20分=3*60+20=200分钟,已经吃的块数=200/(30-20)=20块,小明吃20块用时20*20=400分钟=6小时40分钟,开始吃第一块的时间为14时40分-6小时40分=8时。
奥数题及答案31、难度:一块长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?2、难度:甲乙两座城市相距530千米,货车和客车从两城同时出发,相向而行.货车每小时行50千米,客车每小时行70千米.客车在行驶中因故耽误1小时,然后继续向前行驶与货车相遇.问相遇时客车、货车各行驶多少千米?1、难度:一块长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?2、难度:甲乙两座城市相距530千米,货车和客车从两城同时出发,相向而行.货车每小时行50千米,客车每小时行70千米.客车在行驶中因故耽误1小时,然后继续向前行驶与货车相遇.问相遇时客车、货车各行驶多少千米?因为客车在行驶中耽误1小时,而货车没有停止继续前行,也就是说,货车比客车多走1小时.如果从总路程中把货车单独行驶小时的`路程减去,然后根据余下的就是客车和货车共同走过的.再求出货车和客车每小时所走的速度和,就可以求出相遇时间.然后根据路程=速度×时间,可以分别求出客车和货车在相遇时各自行驶的路程.相遇时间:奥数题及答案4一、按规律填数.1)64,48,40,36,34,( ) 2)8,15,10,13,12,11,( )3)1、4、5、8、9、()、13、()、()4)2、4、5、10、11、()、()5)5,9,13,17,21,( ),( )二、等差数列1.在等差数列3,12,21,30,39,48,…中912是第几个数?2.求1至100内所有不能被5或9整除的整数和3.把210拆成7个自然数的和,使这7个数从小到大排成一行后,相邻两个数的差都是5,那么,第1个数与第6个数分别是多少?4.把从1开始的所有奇数进行分组,其中每组的第一个数都等于此组中所有数的个数,如(1),(3、5、7),(9、11、13、15、17、19、21、23、25),(27、29、……79),(81、……),求第5组中所有数的和三、平均数问题1.已知9个数的平均数是72,去掉一个数后,余下的数平均数为78,去掉的数是______ .2.某班有40名学生,期中数学考试,有两名同学因故缺考,这时班级平均分为89分,缺考的同学补考各得99分,这个班级中考平均分是_______ .3.今年前5个月,小明每月平均存钱4.2元,从6月起他每月储蓄6元,那么从哪个月起小明的平均储蓄超过5元?4.A、B、C、D四个数,每次去掉一个数,将其余下的三个数求平均数,这样计算了4次,得到下面4个数.23,26,30,33A、B、C、D 4个数的平均数是多少?5 A、B、C、D4个数,每次去掉一个数,将其余3个数求平均数,这样计算了4次得到下面4个数23、26、30、33,A、B、C、D4个数的和是 .四、加减乘除的简便运算1)100-98+96-94+92-90+……+8-6+4-2=()2)1976+1977+……20xx-1975-1976-……-1999=()3)26×99 =()4)67×12+67×35+67×52+67=()5)(14+28+39)×(28+39+15)-(14+28+39+15)×(28+39)五、数阵图1、△、□、〇分别代表三个不同的数,并且;△+△+△=〇+〇;〇+〇+〇+〇=□+□+□;△+〇+〇+□=60 求:△= 〇= □=2.将九个连续自然数填入3行3列的九个空格中,使每一横行及每一竖列的三个数之和都等于60.3.将从1开始的九个连续奇数填入3行3列的九个空格中,使每一横行、每一竖列及两条对角线上的三个数之和都相等.4 用1至9这9个数编制一个三阶幻方,写出所有可能的结果.所谓幻方是指在正方形的方格表的每个方格内填入不同的数,使得每行、每列和两条对角线上的各数之和相等;而阶数是指每行、每列所包含的方格的数.六、和差倍问题1.果园里一共种340棵桃树和杏树,其中桃树的棵数比杏树的3倍多20棵,两种树各种了多少棵?2.一个长方形,周长是30厘米,长是宽的.2倍,求这个长方形的面积.3.甲、乙两个数,如果甲数加上320就等于乙数了.如果乙数加上460就等于甲数的3倍,两个数各是多少?4.有两块同样长的布,第一块卖出25米,第二块卖出14米,剩下的布第二块是第一块的2倍,求每块布原有多少米?5.果园里有桃树和梨树共150棵,桃树比梨树多20棵,两种果树各有多少棵?6.甲、乙两桶油共重30千克,如果把甲桶中6千克油倒入乙桶,那么两桶油重量相等,问甲、乙两桶原有多少油?七、年龄问题1.兄弟俩今年的年龄和是30岁,当哥哥像弟弟现在这样大时,弟弟的年龄恰好是哥哥年龄的一半,哥哥今年几岁?2.母女的年龄和是64岁,女儿年龄的3倍比母亲大8岁,求母女二人的年龄各是多少岁?3.哥哥今年比小丽大12岁,8年前哥哥的年龄是小丽的4倍,今年二人各几岁?4.爷爷今年72岁,孙子今年12岁,几年后爷爷的年龄是孙子的5倍?几年前爷爷的年龄是孙子的13倍?八、假设问题1、有42个同学参加植树,男生平均每人种3棵,女生平均每人种2棵,男生比女生多种56棵.男、女生各多少人?2.某小学举行一次数学竞赛,共15道题,每做对一题得8分,每做错一题倒扣4分,小明共得了72分,他做对了多少道题?3.一张试卷有25道题,答对一题得4分,答错或不答均倒扣1分,某同学共得60分,他答对了多少道题?4.小华解答数学判断题,答对一题给4分,答错一题要倒扣4分,她答了20个判断题,结果只得了56分,她答错了多少道题?5.育才小学五年级举行数学竞赛,共10道题,每做对一道题得8分,错一题倒扣5分,张小灵最终得分为41分,她做对了多少道题?奥数题及答案5请你从01、02、03、…、98、99中选取一些数,使得对于任何由0~9当中的某些数字组成的无穷长的一串数当中,都有某两个相邻的数字,是你所选出的那些数中当中的'一个。
奥数试题1

一个奇怪的动物庄园里住着猫和狗, 狗比猫多180只. 有20% 的狗错认为自己是猫;有20% 的猫错认为自己是狗. 在所有的猫和狗中, 有32% 认为自己是猫, 那么狗有()只.(A)240 (B)248 (C)420 (D)842详细解析:方法1:方程法设猫有a只,其中认为自己猫的有80%a只,狗有b%只,其中认为自己是猫的有20%b只。
根据题意可得:b-a=180(80%a+20%b)÷(a+b)=32%解方程可得:b=240所以:狗有240只。
方法2:浓度法狗中认为自己是猫的有20%,猫中认为自己是猫的有80%,此两种混合后共有32%的认为自己是猫,用十字交叉所以狗和猫的比是48%:12%=4:1,而狗比猫多180只,所以狗一共有180÷(4-1)×4=240只答案揭晓有四个自然数A、B、C、D,它们的和不超过400,A除以B的商是5余5,A除以C商是6余6,A除以D商7余7,这四个数的和是多少?答案揭晓解析:A除以B商是5余5所以A=5B+5所以A是5的倍数同理,A除以C商是6余6,A除以D商是7除7则A是6和7的倍数5,6,7的最小公倍数是5×6×7=210和不超过400则A<400而210的2倍大于400所以A=210B=(210-5)÷5=41C=(210-6)÷6=34D=(210-7)÷7=29所以A+B+C+D=314平面上,一个圆把平面分为2部分,一个圆和一条直线最多把平面分为4部分,一个圆和两条直线最多把平面分为8部分,一个圆和5条直线最多把平面分为几部分?答案揭晓解析:本题运用递推计数:1个线:1+3=4部分;2个线:1+3+4=8部分;3个线:1+3+4+5=13部分;4个线:1+3+4+5+6=19部分;5个线:1+3+4+5+6+7=26部分;……红光小学每周星期一、三、五、六各举办一种课外活动,问:至少要有多少名学生报名参加,才能保证其中至少有3位学生所参加的课外活动完全一样?答案揭晓答案:31解析:一共4种活动.可能的情况有:参加一种的:4种参加二种的:6种参加三种的:4种参加四种的:1种一共有:4+6+4+1=15种,不同的情况.至少有3位同学相同,那么至少要有:15×2+1=31名。
小学经典奥数题 (1)

小学经典奥数题1.已知一张桌子的价钱是一把椅子的10倍,又知一张桌子比一把椅子多288元,一张桌子和一把椅子各多少元?解题思路:由已知条件可知,一张桌子比一把椅子多的288元,正好是一把椅子价钱的(10-1)倍,由此可求得一把椅子的价钱。
再根据椅子的价钱,就可求得一张桌子的价钱。
答题:解:一把椅子的价钱:288÷(10-1)=32(元)一张桌子的价钱:32×10=320(元)答:一张桌子320元,一把椅子32元。
2. 3箱苹果重45千克。
一箱梨比一箱苹果多5千克,3箱梨重多少千克?解题思路:可先求出3箱梨比3箱苹果多的重量,再加上3箱苹果的重量,就是3箱梨的重量。
答题:解:45+5×3=45+15=60(千克)答:3箱梨重60千克。
3. 甲乙二人从两地同时相对而行,经过4小时,在距离中点4千米处相遇。
甲比乙速度快,甲每小时比乙快多少千米?解题思路:根据在距离中点4千米处相遇和甲比乙速度快,可知甲比乙多走4×2千米,又知经过4小时相遇。
即可求甲比乙每小时快多少千米。
答题:解:4×2÷4=8÷4=2(千米)答:甲每小时比乙快2千米。
4. 李军和张强付同样多的钱买了同一种铅笔,李军要了13支,张强要了7支,李军又给张强0.6元钱。
每支铅笔多少钱?解题思路:根据两人付同样多的钱买同一种铅笔和李军要了13支,张强要了7支,可知每人应该得(13+7)÷2支,而李军要了13支比应得的多了3支,因此又给张强0.6元钱,即可求每支铅笔的价钱。
答题:解:0.6÷[13-(13+7)÷2]=0.6÷[13—20÷2]=0.6÷3=0.2(元)答:每支铅笔0.2元。
5.甲乙两辆客车上午8时同时从两个车站出发,相向而行,经过一段时间,两车同时到达一条河的两岸。
由于河上的桥正在维修,车辆禁止通行,两车需交换乘客,然后按原路返回各自出发的车站,到站时已是下午2点。
一年级下册奥数练习题

读书破万卷下笔如有神奥数练习题一姓名:班级:1、小虎学写毛笔字,第一天写6个,以后每天比前一天多写3个,四天一共写了多少个?(想一想每天比前一天多写3个是什么意思。
)第一天()个、第二天()个、第三天()个、第四天()个2、妈妈从家里到工厂要走3千米,一次,她上班走到工厂,又回家取一很重要工具,再到工厂。
这次妈妈上班一共走了多少千米?想一想:从工厂到家一条路妈妈走了几趟,再画出家工厂路线图。
你就知道妈妈走了几千米了3、一只猫吃一只老鼠用5分钟吃完,5只猫同时吃5只同样大小的老鼠,需要几分钟才能吃完?(同时吃)4、有两篮苹果,第一篮13个,第二篮7,从第一篮中拿几个放入第二篮,两篮的苹果数相等?(能找到东西就试一试,没东西就画图)5、哥哥4个苹果,姐姐有3个苹果,弟弟有8个苹果,哥哥给弟弟1个后,弟弟吃了3个,这时谁的苹果多?原来:哥哥()个姐姐()个弟弟()个现在:哥哥()个姐姐()个弟弟()个6、同学们排队做操,小明前面有4个人,后面有4个人,这一队一共有多少人?(必须得画图,还是先画小明吧)7、3个男同学借走6本书,4个女同学借走7本书,他们一共借走多少本书?(一定要看清问题是问一共借走了多少本书,与人无关)8、2个白气球可以换1个红气球,10个白气球可以换几个红气球?(可以用东西摆一摆也可以画图帮助理解)9、小军跟爸爸到外地旅游,爸爸买一张火车票是12元,小军买半票,他们两人要付多少钱?(爸爸一张票多少元?小军半票要多少元?他俩呢))道)道,在爸妈的帮助下完成(这份题你独立完成(.读书破万卷下笔如有神奥数练习题二班级:姓名:1、8名女同学站成一排,每隔2名女同学插进3名男同学,共插进()名男同学。
(先画出8名女生,再给女生的中间插入男生。
)2、车站的钟表几时就敲几下,请问从3时到5时车站的钟表一共敲了多少下?(先想想经过了哪几个时间,再想想每个时间各几下,一共敲了几下)3、把3、4、5、6、7、8、9、10 这八个数分别填入下面的括号里(每个数只能用一次),()+ ()—()=()()+ ()—()=()4、小明今年6 岁,姐姐今年13 岁,5 年后,姐姐比小明大几岁?(5年后小明几岁,姐姐几岁。
三年级奥数题 (1)

三年级奥数题1、.一条路长100米,从头到尾每隔10米栽1棵梧桐树,共栽多少棵树?2、12棵柳树排成一排,在每两棵柳树中间种3棵桃树,共种多少棵桃树?3、一根200厘米长的木条,要锯成10厘米长的小段,需要锯几次?4、蚂蚁爬树枝,每上一节需要10秒钟,从第一节爬到第13节需要多少分钟?5.在花圃的周围方式菊花,每隔1米放1盆花。
花圃周围共20米长。
需放多少盆菊花?6.从发电厂到闹市区一共有250根电线杆,每相邻两根电线杆之间是30米。
从发电厂到闹市区有多远?7.王老师把月收入的一半又20元留做生活费,又把剩余钱的一半又50元储蓄起来,这时还剩40元给孩子交学费书本费。
他这个月收入多少元?8.一个人沿着大提走了全长的一半后,又走了剩下的一半,还剩下1千米,问:大提全长多少千米?9.甲在加工一批零件,第一天加工了这堆零件的一半又10个,第二天又加工了剩下的一半又10个,还剩下25个没有加工。
问:这批零件有多少个?10.一条毛毛虫由幼虫长到成虫,每天长一倍,16天能长到16厘米。
问它几天可以长到4厘米?11.一桶水,第一次倒出一半,然后倒回桶里30千克,第二次倒出桶中剩下水的一半,第三次倒出180千克,桶中还剩下80千克。
桶里原来有水多少千克?12.甲、乙两书架共有图书200本,甲书架的图书数比乙书架的3倍少16本。
甲、乙两书架上各有图书多少本?13.小燕买一套衣服用去185元,问上衣和裤子各多少元?14.甲、乙、丙三人年龄之和是94岁,且甲的2倍比丙多5岁,乙2倍比丙多19岁,问:甲、乙、丙三人各多大?15.小明、小华捉完鱼。
小明说:“如果你把你捉的鱼给我1条,我的鱼就是你的2倍。
如果我给你1条,咱们就一样多了。
“请算出两个各捉了多少条鱼。
16.小芳去文具店买了13本语文书,8本算术书,共用去10元。
已知6本语文本的价钱与4本算术本的价钱相等。
问:1本语文本、1本算术本各多少钱?17、.A、B、C、D四人在一场比赛中得了前4名。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小数乘法的简便计算小数乘除法的计算中,正确运用“等积变形”、“商不变的性质”等,可将小数乘除法转化成整数乘除进行计算。
等积变形:一个因数扩大若干倍(0除外),另一个因数同时缩小相同地倍数,积不变。
商不变的性质:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变。
实题与求解1、 12.5×0.76×0.4×8×2.52、 9.81×0.1+0.5×98.1+0.049×9813、 172.4×6.2+2724×0.384、 7.2×4.5×8.1÷(1.8×1.5×2.7)5、 327×2.8+17.3×286、 75×4.67+17.9×2.57、 1.25×5.6+2.25×4.4 8、 99.99×0.8+11.11×2.89、 3.75×4.23×36-125×0.423×2.8 10、 2424.2424÷242.411、 3.9÷(1.3÷1.5) 12、 1.3×1.3×1.3-1.3×1.3-0.3速算与巧算实题与求解1、2005×200420042004-2004×2005200520052、1997×20002000÷2000×199719971998个19983、1998+19981998+…+19981998……199819984、99999999×88888888÷666666661999+19991999+...+19991999 (19991999)199819995、 98989898×99999999÷1010101÷111111116、 5795.5795÷5.795×579.59、 1+3+5+7+……+23 10、 498×381+3822+5+8+11+……+35 382×498-11611、 363+411×362 12、 1999+1998×2000 363×411-48 1999×2000-1 13、 (9619+96961919+969696191919)÷969696961919191913、(100+621+739+458)×(621+739+458+378)-(100+621+739+458+378)×(621+739+458)圆的周长和面积1、如图,扇形的半径AO=OB=6厘米,角AOB 等于450,AC 垂直于OB ,那 么途中阴影部分的面积是多少平方厘米?2、三角形ABC 为等腰直角三角形,AB 是半圆的直径,C 是扇形的圆心,已 知AB=10厘米,求阴影部分的面积。
3、如图,大小两圆相交部分(阴影区域)面积是大圆面积的154,是小圆面积的53,量得小圆的半径是5厘米,那么大圆的半径是多少厘米?4、右图中,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等,图 中阴影部分的周长是多少厘米?5、如图,长方形ABCD 中,AB=6厘米,BC=4厘米,AED 和FCD 是扇形,求阴 影部分面积。
6、右图等腰直角三角形的直角边长10厘米,求它的阴影部分的面积。
7、右图中,ABC 是等腰直角三角形,D 是半圆周的中点,BC 是半圆的直径, 已知AB=BC=10厘米,那么阴影部分的面积是多少平方厘米?第五讲:行程问题一、环形跑道的行程问题、常用公式: S÷V和=T相遇, S差÷V差=T相遇实题与求解1、小明与小华分别以不同速度,在周长为500米的环形跑道上跑步,小华的速度为180米/分,(1) 他们同时从同一地点出发,反向跑步,75秒后两人第一次相遇,小明的速度是多少米/分?(2)若他们以上述速度同时从同一地点出发,同一方向跑步,那么小明要跑多少圈才能第一次追上小华?2、甲乙两人在周长是1200米的环形跑道上同时,同向而行。
甲的速度100米/分,乙的速度是甲的2倍,经过多少分钟,乙能追上甲?3、甲乙两人沿着400米跑道跑步,甲每分钟跑280米,乙每分钟跑260米。
两人同时由同一地点同向而行,甲跑多少分钟后能超过乙一圈?4、在300米的跑道上,甲乙两人同时并排起跑。
甲的速度是每秒5米,乙的速度是每秒3米,等甲超过乙一圈时在起跑线前多少米?5、甲用40秒可绕600米的跑道跑一圈,乙反方向跑,每隔15秒与甲相遇一次,乙跑一圈要多少秒?6、有一条80米的圆形走廊,兄弟二人同时,同向沿走廊出发,弟弟以每秒1米的速度步行,哥哥以每秒5米的速度奔跑,哥哥在第二次追上弟弟时,所用的是时间是多少?7.小明在360米长的环形跑道上跑了一圈,已知他前一半时间每秒跑5米,后一半时间每秒跑4米,那么小明后一半用了多少秒?8、甲乙二人在400米环形跑道上练习竞走,两人同时出发,出发时甲在乙后面,出发后6分钟甲第一次超过乙,26分钟后甲第二次超过乙。
假设两人的速度不变,问出发时甲在乙后面多少米?9、两人骑自行车沿着900米长的环形跑道行驶,他们从同一地点反向而行,经过18分钟后相遇。
如果他们从同一地点同向而行,那么经过180分钟后快车追上慢车一次。
求两人骑自行车的速度。
10、两名运动员在环形跑到上练习长跑。
甲每分钟比乙多跑50米。
如果两人同时同地同向出发,经过45分钟甲追上乙,如果两人同时同地反向出发,经过5分钟相遇,求甲乙两人的速度。
11、两辆汽车同时从东西两站相对开出,第一次在离东站60千米的地方相遇之后,两车继续以原速前进,各车到站后立即返回,又在离中点30千米处相遇,两站相距多少千米?12、柳山茶园是一个近似的圆,周长180千米,两辆骑车同时从同地背向出发绕茶园行驶了2.5小时相遇。
如果其中一辆车先出发了72千米,那么在另一辆车出发几小时后,两车相遇?二、其他相遇情况的行程问题1、甲乙两辆汽车同时从东西两地相向开出,甲车每小时行56千米,乙车每小时行48千米,两车在离中点32千米处相遇,求东西两地的距离是多少千米?画图:2、甲乙两辆汽车同时从东站开往西站。
甲车每小时比乙车多行12千米,甲车行驶四个半小时到达西站后,没有停留,立即从原路返回,在距离西站31.5千米的地方和乙车相遇,甲车每小时行多少千米?画图:3、两辆汽车同时从东西两站相对开出,第一次在离东站60千米的地方相遇之后,两车继续以原速前进,各车到站后立即返回,又在离中点30千米处相遇,两站相距多少千米?画图:4、甲乙两人同时从A地出发到B地,甲到B后立即按原路返回,在距B地32千米处与乙相遇。
已知甲每小时行20千米,乙每小时行12千米,那么A、B两地的距离是多少千米?画图:5、甲乙两辆车的速度分别是每小时55千米好每小时43千米,它们同时从A地到B地去。
出发后15小时,甲车遇到一辆迎面开来的摩托车。
2小时后,乙车也遇到这辆摩托车,这辆摩托车每小时行多少千米?画图:6、甲乙丙三人,速度分别是每分钟100米、80米、75米。
甲从东村,乙丙从西村同时出发相向而行,途中甲与乙相遇后3分钟又与丙相遇,求东西两村的距离。
画图:7、甲乙两人同时从A地到B地去。
甲每分钟走43米,乙每分钟走58米,出发后40分钟,乙遇到迎面骑车而来的丙,再经过2分钟后甲也遇到丙,求丙骑车的速度。
画图:8、甲乙两车同时从相距315千米的两地相向而行。
甲车每小时行40千米,乙车每小时行50千米,行了几小时后两车相距45千米?再行几小时两车又相距45千米?画图:9、甲和乙两人骑车同时从A地出发,向同一方向行进。
甲的速度比乙的速度每小时快4千米,甲比乙早20分钟通过途中B地时,甲又前进了8千米,那么AB两地相距多少千米?画图:10、两辆汽车上午8点整分别从相距210千米的甲乙两地相向而行。
第一辆汽车在途中修车停了45分钟,第二辆车因加油停了半小时,结果在当天上午11点整相遇。
如果第一辆骑车每小时行40千米,那么第二辆汽车每小时行多少千米?画图:11、在一条笔直的公路上,甲乙两人骑车从相距900米的AB两地同时出发,甲每分钟200米,乙每分钟250米,经过多少时间两人相距2700米?(分析各种情况)画图:12、甲乙两地相距84千米,汽车和自行车同时从甲乙两地相向开出,相遇时,汽车距甲地48千米。
汽车每小时比自行车多行8千米,那么汽车还要多少小时才能到底乙地?画图:13、甲乙丙三人行路。
速度分别是每分钟60米、50米、40米,甲从A地,乙和丙从B地同时出发,相向而行,甲和乙相遇后,过了15分钟后又与丙相遇,求AB两地的距离。
画图:14、小明步行45分从A地到B地,小华乘车15分可从B地到A地。
当小明和小华在路上相遇时,小明已经走了30分,小华接小明乘车返回B地,还需要多少分钟?画图:15、王明回家,距家门300米的时候,妹妹好小狗一齐向他跑来,王明和妹妹的速度都是每分钟50米,小狗的速度是每分钟200米,小狗遇到王明后用同样的速度不停往返于王明和妹妹之间,当王明于妹妹相距10米时,小狗一共跑了多少米?画图:16、甲乙两车同时从A地出发到B地,甲到B地后立即按原路返回,在距B地24千米处与乙相遇。
已知甲每小时行55千米,乙每小时行47千米,求AB相距多少千米?画图:17、甲乙两人分别从AB两地同时相向出发,往返与AB之间。
第一次相遇在距A地20千米处,第二次相遇在距A地40千米处,求AB两地之间的距离。
画图:18、甲乙两地相距4.5千米。
小强和小军分别从甲乙两地同时出发相向而行,当他们分别到达对方的出发地后,立即沿原路返回。
已知小强每分钟行85米,小军每分行65米。
求他们第二次相遇的地方距甲地有多远?画图:19、从甲地到乙地的公路只有上坡和下坡路,没有平路。
乙辆汽车上坡每小时行20千米,下坡每小时行35千米。
车从甲地开往乙地要9小时,从乙地开往甲地要7.5小时。
那么,甲乙两地间的公路有多长?从甲地到乙地须行驶多少千米的上坡路?行程问题——行船问题常用公式:顺水速度= 逆水速度=船速= 水速=实题与求解1、甲、乙两港间的水路长270千米,一只船从甲港开往乙港,顺水9小时到达,从乙港返回甲港,逆水15小时到达,求船在静水中的速度和水流的速度。
2、一只小船在静水中每小时行16千米,逆水航行5小时行了50千米,现在它从A地到B地顺水的路程是110千米,求它从A地到B地所用的时间。
