大物实验数据处理方法
大学物理实验 常用的数据处理方法范文
1.7 常用的数据处理方法实验数据及其处理方法是分析和讨论实验结果的依据。
在物理实验中常用的数据处理方法有列表法、作图法、逐差法和最小二乘法(直线拟合)等。
1.7.1 列表法在记录和处理数据时,常常将所得数据列成表。
数据列表后,可以简单明确、形式紧凑地表示出有关物理量之间的对应关系;便于随时检查结果是否合理,及时发现问题,减少和避免错误;有助于找出有关物理量之间规律性的联系,进而求出经验公式等。
列表的要求是:(1)要写出所列表的名称,列表要简单明了,便于看出有关量之间的关系,便于处理数据。
(2)列表要标明符号所代表物理量的意义(特别是自定的符号),并写明单位。
单位及量值的数量级写在该符号的标题栏中,不要重复记在各个数值上。
(3)列表的形式不限,根据具体情况,决定列出哪些项目。
有些个别的或与其他项目联系不大的数据可以不列入表内。
列入表中的除原始数据外,计算过程中的一些中间结果和最后结果也可以列入表中。
(4)表中所列数据要正确反映测量结果的有效数字。
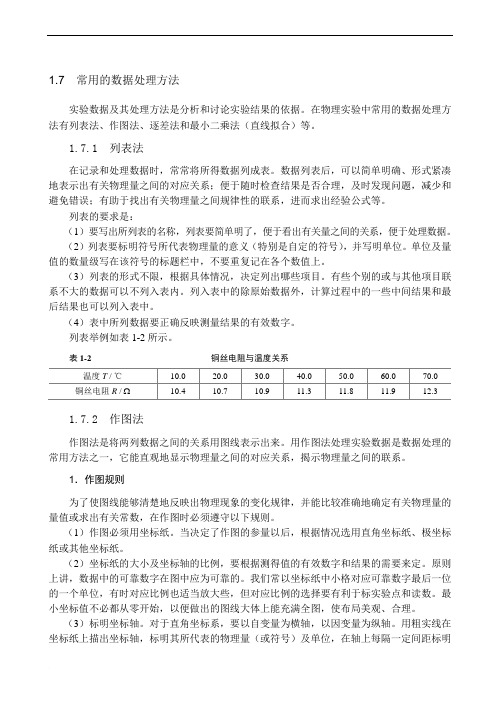
列表举例如表1-2所示。
表1-2铜丝电阻与温度关系1.7.2 作图法作图法是将两列数据之间的关系用图线表示出来。
用作图法处理实验数据是数据处理的常用方法之一,它能直观地显示物理量之间的对应关系,揭示物理量之间的联系。
1.作图规则为了使图线能够清楚地反映出物理现象的变化规律,并能比较准确地确定有关物理量的量值或求出有关常数,在作图时必须遵守以下规则。
(1)作图必须用坐标纸。
当决定了作图的参量以后,根据情况选用直角坐标纸、极坐标纸或其他坐标纸。
(2)坐标纸的大小及坐标轴的比例,要根据测得值的有效数字和结果的需要来定。
原则上讲,数据中的可靠数字在图中应为可靠的。
我们常以坐标纸中小格对应可靠数字最后一位的一个单位,有时对应比例也适当放大些,但对应比例的选择要有利于标实验点和读数。
最小坐标值不必都从零开始,以便做出的图线大体上能充满全图,使布局美观、合理。
(3)标明坐标轴。
满分大物实验迈克尔逊数据处理
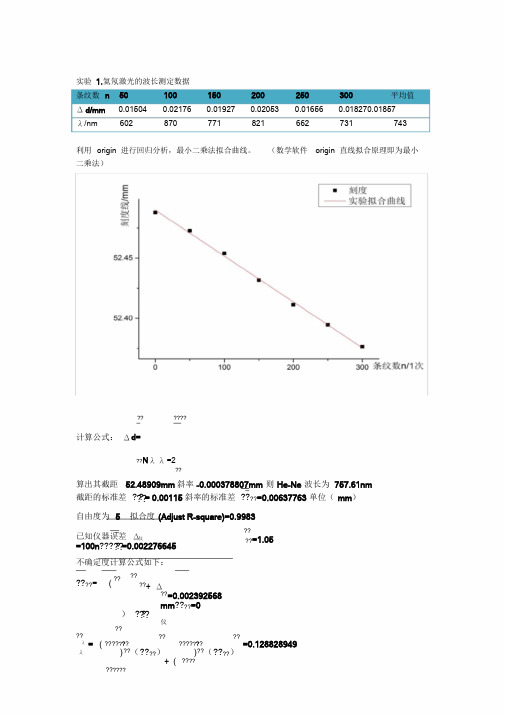
λ/nm602870771821662731743
利用origin进行回归分析,最小二乘法拟合曲线。(数学软件origin直线拟合原理即为最小
二乘法)
??????
计算公式:Δd=
??Nλλ=2
实验过程虽然比较简单但是波长的测量等级达到了纳米级仪器的误差达到了100nm在测量过程中目测条纹变化数目有一定的观测误差特别是在第二个实验中通过一块反射镜来观测条纹会产生较大误差对记录人员也有一定的伤害可以采用一块放大镜方便读数
实验1.氦氖激光的波长测定数据
条纹数n50100150200250300平均值
??
算出其截距52.48909mm斜率-0.000378807mm则He-Ne波长为757.61nm截距的标准差????= 0.00115斜率的标准差????=0.00637763单位(mm)
自由度为5拟合度(Adjust R-square)=0.9983
已知仪器误差Δ仪=100n??????=0.002276645
已知仪器误差Δ仪=100n??????=0.000530346
??
=1.59
??
??Nλλ=2
??
通过对matlab绘图程序,对实验测得的六个点进行最小二乘法数据分析:
经过分析,发现有一组数据发生明显错误,故舍去该组数据进行分析。
算出其截距53.54667mm斜率-0.00030188mm则He-Ne波长为603.8nm
截距的标准差????= 0.000365斜率的标准差????=0.0000078059单位(mm)自由度为2拟合度(Adjust R-square)=0.998
大物实验数据处理的基本流程

大物实验数据处理的基本流程English Answer:1. Data Curation.Data curation involves collecting, cleaning, and organizing the raw experimental data. This step ensures that the data is accurate, consistent, and suitable for further analysis. Common data curation tasks include:Data cleaning: Removing errors, outliers, and missing values from the data.Data standardization: Converting data into a common format or units for easier comparison.Data integration: Combining data from multiple sources or experiments into a single dataset.2. Exploratory Data Analysis.Exploratory data analysis (EDA) is used to gain insights into the data and identify potential patterns or trends. EDA techniques include:Visualization: Creating graphs, charts, and histograms to visualize the data distribution.Descriptive statistics: Calculating summary statistics (e.g., mean, median, standard deviation) to describe the data's central tendency and variability.Hypothesis generation: Formulating hypotheses based on the observed patterns in the data.3. Data Transformation.Data transformation involves modifying the data to improve its suitability for analysis. Common data transformation techniques include:Normalization: Scaling the data to a common range tofacilitate comparison.Logarithm transformation: Applying a logarithmic function to the data to reduce skewness.Feature engineering: Creating new features or variables from the original data to enhance its predictive power.4. Modeling.Modeling involves using statistical or machine learning algorithms to analyze the transformed data and identify relationships between variables. Common modeling techniques include:Regression models: Used to predict continuous outcomes based on independent variables.Classification models: Used to classify data pointsinto different categories.Clustering algorithms: Used to group data points basedon their similarities.5. Model Evaluation.Model evaluation assesses the performance of the fitted model and identifies areas for improvement. Evaluation techniques include:Cross-validation: Splitting the data into multiple subsets and iteratively training and evaluating the model on different combinations of these subsets.Metrics calculation: Using metrics (e.g., accuracy, precision, recall) to quantify the model's performance.Model tuning: Adjusting model parameters to optimizeits performance.6. Reporting and Interpretation.The final step involves reporting the results of the data analysis and interpreting them in the context of theresearch question. The report should include:Summary of findings: A clear and concise summary of the key insights and conclusions drawn from the data analysis.Discussion of limitations: Acknowledging anylimitations or assumptions associated with the data or methodology.Recommendations for future work: Suggesting future directions for research based on the findings.Chinese Answer:1. 数据整理。
物理实验中数据处理方法总结

物理实验中数据处理方法总结在物理实验中,数据处理是一个关键的环节,它涉及到对实验数据的整理、分析和解释。
下面将总结一些常用的物理实验数据处理方法,以帮助实验者更好地处理和利用实验数据。
一、基本数据处理方法1. 数据整理在实验中,通常会得到一系列的实验数据。
首先,需要将这些数据整理成表格或图表的形式。
表格可以清晰地显示各个实验数据的数值,而图表则可以更直观地反映数据的变化趋势。
2. 均值计算均值是一组数据的平均数,常用于表示实验测量结果的集中趋势。
计算均值的方法是将所有数据相加,然后除以数据的个数。
3. 不确定度处理在实验测量中,由于各种误差和误差源的存在,测量结果是有一定误差的。
为了对实验结果的可靠性进行评估,需要计算实验数据的不确定度。
常用的处理方法有“直接法”和“间接法”。
二、不确定度处理方法1. 直接法直接法适用于直接测量得到的数据。
在实验中,通常会进行多次测量,得到一系列的实验数据。
直接法的不确定度计算可以根据测量值的散布程度来确定。
常用的方法有平均差法、标准差法和绝对误差法。
2. 间接法间接法适用于通过一些物理关系来计算得到的数据。
在实验中,有时候需要通过已知数据和物理公式来计算其他物理量。
在进行间接测量时,不仅需要考虑直接测量的不确定度,还需要考虑间接测量的不确定度。
常用的方法有误差传递法和线性法则法。
三、图像处理方法1. 绘制拟合曲线在实验中,有时候需要绘制实验数据的曲线以展示数据的变化趋势。
拟合曲线可以用来更准确地描述实验数据的变化规律。
拟合曲线有线性拟合、多项式拟合等方法,可以根据实际情况选择合适的拟合方法。
2. 提取实验参数通过拟合曲线,可以提取出一些与实验参数相关的信息。
例如,可以通过拟合得到的直线斜率来计算物理量的大小,或者通过拟合曲线和已知的物理模型来研究物理现象的规律性。
四、误差分析方法1. 系统误差分析系统误差是在实验过程中存在的、对测量结果产生一致影响的误差。
在处理实验数据时,需要对系统误差进行分析和估计,并给出相应的修正方法。
满分大物实验迈克尔逊数据处理-V1

满分大物实验迈克尔逊数据处理-V1
本文将为大家整理介绍一下满分大物实验——迈克尔逊干涉仪实验中的数据处理。
该实验是物理学中非常重要的实验之一,因为它可以验证相对论的基本概念,并且数据处理过程也相对较为复杂。
以下将对实验步骤和数据处理进行详细说明。
一、实验步骤
1.调整干涉仪:首先,需要调整干涉仪的镜子,让光线以等长的时间通过两条路线,且两条光路的光程差小于光波长的一半。
2.测量光程差:用红光光源照射干涉仪,使用微调节固定平台调节平台距离,测量光程差。
3.取样数据:每测一组数据,需将光源位置改变一个可测量的角度,共取多组数据。
4.测量环形条纹:最后,使用目镜对干涉图形进行观察,记录下环形条纹的条数。
二、数据处理
1.计算光程差:通过所测得的干涉仪两条光线达到的光程差ΔL,可以根据下面的公式来计算出干涉仪镜子间的距离L:
L=ΔL/2
2.计算平均光程差:将多组数据的光程差求平均,可以得到平均光程
差。
3.计算光速:根据光速公式:v=c/f(波长λ=c/f),来计算光的速度。
4.计算狭缝间距:通过所测得的环形条纹数n,可以计算得到狭缝间距d:
d=λ/(2n)
5.计算误差:根据多组数据的光程差和平均光程差的差值,可以计算
得到误差值,进一步验证实验的准确性。
以上就是整个实验过程以及数据处理过程的详细介绍。
通过实验和数
据处理,我们可以更加深入地了解迈克尔逊干涉仪的基本原理和物理
学理论的应用。
大物实验逐差法处理数据

大物实验逐差法处理数据大物实验是物理学实验的重要组成部分,而逐差法则是处理实验数据的重要方法之一。
逐差法是通过对实验数据的差值进行统计分析,并得到误差估计值,以评估实验数据的可靠性和准确性。
下面将介绍逐差法在实验数据处理中的应用。
首先,我们需要明确实验所涉及的物理量,如光强、电压、电流等。
在进行实验时,我们需要记录每次实验所得的数据,比如用光强计测量实验光源的光强时所得的光强值、用万用表测量电路中电流的电压值等。
这些数据通常会有一些随机误差和系统误差,因此需要进行处理和分析,以获取相对准确的物理量值和误差估计值。
其次,我们需要进行数据处理,使用逐差法则。
逐差法在处理数据时,通常采取两个数据之间的差值来计算误差,即每次测量所得的数据与第一次测量所得的数据之差。
将每次测量所得的数据与第一次测量所得的数据之差加起来,并除以测量次数,即可得到所求物理量的平均值。
然后,根据数据的分布情况计算误差,通常采用标准差公式或残差平方和公式计算误差。
最后,我们需要对处理后的数据进行分析,以评估实验数据的可靠性和准确性。
对于误差的估计,我们需要比较其与测量值的大小关系,通常采用相对误差衡量。
若误差较小,则证明实验数据较为可靠。
根据实验的目的和要求,我们可以进行多组实验数据的比较和分析,进一步验证实验结果的可靠性和准确性。
综上所述,逐差法在实验数据处理中具有重要的应用价值,能够有效地评估实验数据的可靠性和准确性。
在进行实验过程中,我们应注意数据的记录和分析,并结合实验的目的和要求,合理地使用逐差法,让实验结果更加准确可靠。
大学物理实验数据处理方法

5.标出图线特征:
在图上空白位置标明实 验条件或从图上得出的某些 参数。如利用所绘直线可给 出被测电阻R即直线斜率的 大小:从所绘直线上读取两 点 A、B 的坐标就可求出 R 值。要注意的是,A,B两点 不能是实验测得的数据点。
I (mA)
20.00 18.00 16.00 14.00
电阻伏安特性曲线 作者:xx
电学元件伏安特性曲线
20.00
18.00 16.00 14.00 12.00 10.00 8.00 6.00 4.00 2.00
横轴坐标分度选取不当 。横轴以3 cm 代表1 V,使作
图和读图都很困难。实际在选 择坐标分度值时,应既满足有 效数字的要求又便于作图和读 图,一般以1 mm 代表的量
值是10的整数次幂,或是 其2倍、5倍等。
55
1 1 1 42.746 15 11.668 xy x y 6 6 6 A 0.7758 2 2 1 1 x x 55 ( 15) 2 6 6
1 1 B y Ax 11.668 0.7758 15 0.0052 6 6
△ B (7.00, 18.58)
12.00
10.00 8.00 6.00
6.标出图名:
在图线下方或空白位置 写出图线的名称及某些必要 的说明。
由图上A、B两点可得被测电阻R为: U U A 7.00 1.00 R B 0.379( k) I B I A 18.58 2.76
中间测量值没起作用,为了发挥多次测量的优势,
应采用以下逐差法。
逐差法: • 连续测偶数个测量值; • 将实验数据前后对分为两组;
• 取对应项的差值(逐差);
• 再求平均值。
大物实验~~核磁共振实验数据处理

大物实验~~核磁共振实验数据处理核磁共振(NMR)实验是物理学和化学领域中常用的一种实验方法,其数据处理过程包括多个步骤,包括数据采集、数据预处理、数据分析和数据可视化等。
以下是对这些步骤的详细描述。
一、数据采集在核磁共振实验中,数据采集是实验的核心部分。
实验人员需要设置适当的实验条件,如磁场强度、射频脉冲频率和脉冲宽度等,以获取清晰的核磁共振信号。
在实验过程中,通常使用核磁共振谱仪来收集数据。
核磁共振谱仪可以产生高精度的射频脉冲,并测量它们与原子核之间的相互作用。
二、数据预处理数据预处理是去除噪声和干扰,提高数据质量的过程。
在核磁共振实验中,数据预处理包括对数据进行平滑处理、基线校正、相位调整等操作。
这些操作可以改善数据的信噪比,并使后续的数据分析和可视化更加准确。
三、数据分析数据分析是通过对预处理后的数据进行处理和分析,提取有关样品中原子核分布的信息。
在核磁共振实验中,数据分析包括对谱峰的识别、峰面积的测量、化学位移的计算等操作。
这些操作可以得出原子核在不同磁场下的分布情况,从而了解样品的分子结构和化学性质。
四、数据可视化数据可视化是将数据分析得到的结果以图表的形式呈现出来。
在核磁共振实验中,数据可视化包括绘制核磁共振谱图、制作三维图像等操作。
这些图像可以直观地展示样品中原子核的分布情况,帮助实验人员更好地理解实验结果。
除了以上四个步骤外,核磁共振实验的数据处理还包括其他一些步骤,如实验设计、实验操作、数据处理和结果解释等。
这些步骤需要实验人员具备一定的物理学和化学知识,以及对数据处理方法的了解和应用能力。
在核磁共振实验中,数据处理是一个非常重要的环节。
通过对数据的采集、预处理、分析和可视化,实验人员可以得出有关样品中原子核分布的信息,并了解样品的分子结构和化学性质。
这些信息对于科学研究、化学分析、材料开发等领域都具有重要的意义。
需要注意的是,核磁共振实验的数据处理过程具有一定的复杂性和专业性,需要实验人员具备一定的技能和经验。
大物实验数据处理方法

按照实验设计进行操作,记录实验过程中的原始数据,包括测量 值、环境条件等。
数据整理与初步分析
数据整理
对原始数据进行分类、筛选和整 理,去除异常值和无效数据,保 证数据的准确性和可靠性。
初步分析
对整理后的数据进行初步分析, 计算平均值、标准差等统计量, 了解数据的分布规律和特点。
数据可视化方法
法,如Mann-Whitney U检验、Kruskal-Wallis H检验等。
显著性检验与置信区间估计
显著性水平
在假设检验中,用于判断假设是否成立的临界值,通常取 0.05或0.01。当p值小于显著性水平时,拒绝原假设。
置信区间估计
根据样本数据对总体参数进行区间估计,表示参数的真实 值有一定概率落在该区间内。置信水平通常取95%或99%。
数据驱动的科学发现
随着大数据时代的到来,未来 的实验数据处理将更加注重数 据驱动的科学发现,通过对海 量数据的挖掘和分析,揭示新 的科学规律和现象。
THANK YOU
感谢聆听
多项式拟合方法
多项式拟合原理
多项式拟合是一种通过多项式函数对实验数据进行拟合的方 法。它利用多项式函数的灵活性,可以逼近各种复杂的函数 关系。在大物实验中,多项式拟合常用于描述非线性关系的 实验数据。
多项式拟合应用
应用多项式拟合进行数据处理时,需根据实验数据的分布特 点选择合适的多项式次数。通过多项式拟合,可以得到与实 验数据相符合的多项式函数表达式,用于描述物理量之间的 非线性关系或进行实验结果预测。
效应量与效应大小
除了显著性检验外,还应关注效应量(如均值差、相关系 数等)和效应大小(如效应量占总体标准差的比例),以 更全面地评价实验结果。
06
大物实验数据处理

x Y ax c e f x3 x 4
b 1
总不确定度
d 2
Y YE(Y )
间接测量量的不确定度的计算过程分三步
1、先估计个直接测量量 X i 的不确定度 X i 2、写出不确定度的传递公式; 3、结果
Y Y Y Y 1 E (Y ) (单位)
M 例: V
(Y1 Y2 Y3 ) Y n
M V
Y的计算:
1、和差形式的函数
2
(如Y ax1 bx2 )
2
f f 2 2 Y x1 x2 x1 x2
2、乘积商形式的函数
测量结果x=
x
Δ (单位)
不确定度Δ值可以通过一定的方法估算。
2、测量结果的表达(报告)方法 测量结果的科学表达方法:
X X
(单位)
表达式的物理意义( X , X )
恒为正,不确定度与误差是完全不同的概念。
相对不确定度: E 100%
x
置信度
不确定度包括两方面:
仪器误差(限)举例
a:游标卡尺,仪器示值误差一律取卡尺分度值。
b:螺旋测微计,量程在0—25mm及25—50mm的一 级千分尺的仪器示值误差均为仪 0.004mm。 c:天平的示值误差,本书约定天平标尺分度值的 一半为仪器的示值误差。 d:电表的示值误差, m 量程 准确度等级%。
(0 8)
(6)求总不确定度
A B
2
2
(7)写出最终结果表示: x x
S 2 B n
E 100% x
(单位)
大物实验----误差理论与数据处理

随机误差具有以下的性质: (1)单峰性 绝对值小的误差出现的机会(概率) 大,绝对值大的误差出现的机会(概率)小。 (2)对称性 大小相等、 符号相反的误差出现的概 率相等。 (3)有界性 非常大的正 负误差出现的概率趋于零。 (4)抵偿性 当测量次数 非常多时,由于正负误差 相互抵消,各误差的代数 随机误差的正态分布曲线 和趋于零。
(1)理论分析法 观测者凭借有关某项实验的物理理论、实验 方法和实验经验等对实验理论公式的近似性、所 采用的实验方法的完善性等进行研究与分析。 (2)对比法 (3)数据分析法
4.系统误差的减小或消除
(1)利用标准器具减消系统误差; (2)修正已经确定的定值系统误差; (3)采用合理、规范的测量步骤减消系统误差; (4)选择或改进测量方法减消系统误差。
根据统计理论可得:
f ( ) 1 e 2
2 2 2
式中σ是一个取决于具体测量条件的常数称为标 准误差(或称均方误差)。 σ反映的是一组测量数据的离散程度,常称 它为测量列的标准误差;它的数学表达式为:
( xi a ) 2 lim n n
可以证明
f ( )d 0.683 68.3%
称为绝对误差。 相对误差是误差与真值之比;通常用标准偏 差和平均值之比作为相对误差的估计值。相对误 差常他用符号 E 来表示,并表示成百分数。
三.过失误差(异常值)的剔除 1.拉依达准则:适用于测量次数n较大的测 量。 2.肖维涅准则: x cn S (x) (16页) 3.格拉布斯准则:x g( n, P ) S ( x)
(3)人的因素 由于观测者本人的生理或心理特 点所造成的误差。 (4)环境 由于环境条件如温度、气压、湿度的 变化等所引起的误差。
大学物理实验常用的数据处理方法

⼤学物理实验常⽤的数据处理⽅法1.7 常⽤的数据处理⽅法实验数据及其处理⽅法是分析和讨论实验结果的依据。
在物理实验中常⽤的数据处理⽅法有列表法、作图法、逐差法和最⼩⼆乘法(直线拟合)等。
1.7.1 列表法在记录和处理数据时,常常将所得数据列成表。
数据列表后,可以简单明确、形式紧凑地表⽰出有关物理量之间的对应关系;便于随时检查结果是否合理,及时发现问题,减少和避免错误;有助于找出有关物理量之间规律性的联系,进⽽求出经验公式等。
列表的要求是:(1)要写出所列表的名称,列表要简单明了,便于看出有关量之间的关系,便于处理数据。
(2)列表要标明符号所代表物理量的意义(特别是⾃定的符号),并写明单位。
单位及量值的数量级写在该符号的标题栏中,不要重复记在各个数值上。
(3)列表的形式不限,根据具体情况,决定列出哪些项⽬。
有些个别的或与其他项⽬联系不⼤的数据可以不列⼊表内。
列⼊表中的除原始数据外,计算过程中的⼀些中间结果和最后结果也可以列⼊表中。
(4)表中所列数据要正确反映测量结果的有效数字。
列表举例如表1-2所⽰。
表1-2铜丝电阻与温度关系1.7.2 作图法作图法是将两列数据之间的关系⽤图线表⽰出来。
⽤作图法处理实验数据是数据处理的常⽤⽅法之⼀,它能直观地显⽰物理量之间的对应关系,揭⽰物理量之间的联系。
1.作图规则为了使图线能够清楚地反映出物理现象的变化规律,并能⽐较准确地确定有关物理量的量值或求出有关常数,在作图时必须遵守以下规则。
(1)作图必须⽤坐标纸。
当决定了作图的参量以后,根据情况选⽤直⾓坐标纸、极坐标纸或其他坐标纸。
(2)坐标纸的⼤⼩及坐标轴的⽐例,要根据测得值的有效数字和结果的需要来定。
原则上讲,数据中的可靠数字在图中应为可靠的。
我们常以坐标纸中⼩格对应可靠数字最后⼀位的⼀个单位,有时对应⽐例也适当放⼤些,但对应⽐例的选择要有利于标实验点和读数。
最⼩坐标值不必都从零开始,以便做出的图线⼤体上能充满全图,使布局美观、合理。
物理实验数据处理的基本方法

物理实验数据处理的基本方法1.数据收集:在物理实验中,首先需要收集实验数据。
可以使用各种仪器和设备进行测量、记录和采集实验数据。
确保数据的准确性和可靠性。
2.数据整理:在数据收集后,需要对数据进行整理和整合。
这可以包括删除无效数据、排除异常值、对数据进行分类等。
确保数据的整洁和一致性。
3.数据可视化:将数据可视化是一个有力的方法,可以帮助研究人员更好地理解数据和发现隐藏在数据中的模式和趋势。
常用的数据可视化方法包括绘制直方图、散点图、线图等。
4.数据分析:对数据进行分析是了解数据背后规律的重要手段。
常用的数据分析方法包括统计分析、查找关联性、回归分析、频谱分析等。
这些方法可以帮助确定数据之间的相互关系,提取重要的特征和信息。
5.误差分析:误差是物理实验中不可避免的部分,对实验数据的误差进行分析是确保实验结果可靠性的重要环节。
常用的误差分析方法包括确定绝对误差、相对误差、平均误差、标准差等。
通过误差分析,可以评估实验的准确性和精确性。
6.结果解释:在完成数据处理和分析后,需要对结果进行解释和讨论。
这包括总结数据的主要趋势和规律,解释与已有理论和模型的一致性,讨论实验结果的物理意义等。
7.结论和讨论:在数据分析和结果解释的基础上,得出结论和讨论物理实验的目标和研究问题。
这可以包括总结实验结果的重要发现和贡献,提出对未来研究的建议和思考。
总之,物理实验数据处理是一个复杂的过程,需要科学的方法和技巧。
通过合理地应用数据收集、整理、可视化、分析和解释的方法,可以更好地理解实验数据和揭示实验中的物理规律。
物理实验中的数据处理方法

物理实验中的数据处理方法实验室中的物理实验是科学研究中不可或缺的一环,通过实验可以获得数据和观测结果来验证理论,从而深入了解自然规律。
然而,仅仅获得数据还不足以得出结论,需要采取一定的数据处理方法来提取有用的信息并进行分析。
本文将介绍几种常见的物理实验数据处理方法。
一、数据整理与校正在实验中,我们通常会得到原始实验数据,这些数据可能存在误差。
在处理之前,我们首先要进行数据整理和校正。
1. 数据整理数据整理是指对原始数据进行排序、分类和归档的过程,以便后续处理。
可以使用电子表格软件,如Excel,来整理数据。
将数据按照不同的实验条件和观测参数进行分类,并加上相应的标签和单位。
2. 数据校正数据校正是指对原始数据进行误差校正,消除因仪器误差、环境因素等引起的系统误差。
常见的校正方法包括零位校正、仪器响应校正等。
二、数据处理与分析在数据整理和校正之后,我们需要进行数据处理和分析来得出实验结论。
1. 统计分析统计分析是最常见也是最基本的数据处理方法之一。
通过对数据进行平均、中值、标准差、方差等统计计算,可以得到一些重要的统计指标,如数据的集中趋势和离散程度。
2. 图表绘制图表是展示实验数据和结果的重要工具。
可以根据实验数据的特点选择合适的图表类型,如折线图、柱状图、散点图等,使用数据处理软件(如Origin)进行图表绘制和美化。
3. 曲线拟合曲线拟合是通过数学函数对实验数据进行拟合,以获得一条最佳拟合曲线。
常用的拟合方法有线性拟合、多项式拟合、指数拟合等。
曲线拟合可以揭示实验数据的规律和趋势,方便后续分析和预测。
4. 参数求解实验数据通常与理论模型相关联,我们可以通过对数据进行计算和优化,求解出理论模型中的参数。
例如,根据牛顿第二定律推导的公式F=ma,可以通过实验数据求解出物体的质量和加速度。
5. 不确定度评定在进行数据处理和分析时,我们需要评估结果的不确定度,以判断实验结果的可靠性。
不确定度主要包括随机误差和系统误差。
大物实验之实验数据的处理

05
实验数据处理实例分析
实验数据处理实例分析 实例一:用平均值法处理数据
总结词
简单易行,适用于数据量较小、误差较小的 实验。
详细描述
将多次测量的数据求平均值,以减小随机误 差,得到更接近真实值的结果。
总结词
适用于处理具有线性关系的实验数据。
实验数据处理实例分析 实例一:用平均值法处理数据
详细描述
详细描述
曲线拟合法是一种通过数学模型来描述实验数据的方法。通过选择合适的数学函 数(如线性、二次、指数等)来拟合实验数据,可以揭示变量之间的内在关系和 变化规律。这种方法能够更好地处理非线性关系和复杂数据。
最小二乘法
总结词
通过最小化误差的平方和来拟合数据,以得到最佳的数学描 述。
详细描述
最小二乘法是一种数学优化技术,通过最小化数据点与拟合 曲线之间的误差平方和,来找到最佳的数学描述。这种方法 在回归分析、曲线拟合等领域广泛应用,能够得到更精确的 数学模型和预测结果。
异常值检验
03
在处理异常值后,应进行检验,确保处理后的数据仍然符合预
期分布和规律。
数据误差的分析
误差来源分析
分析实验过程中可能产生的误差来源,如测量设备误差、环境因 素误差等。
误差传播分析
根据误差来源和性质,分析误差对实验结果的影响程度和传播方式。
减小误差的措施
针对不同的误差来源和性质,采取相应的措施减小误差对实验结果 的影响,如采用更精确的测量设备、改进实验方法等。
04
实验数据处理中的注意事项
数据的有效性判断
判断数据是否符合预期
在处理实验数据时,首先要判断所获得的数据是否符合实 验预期,如不符合,则可能存在误差或错误,需要重新测 量或检查实验过程。
大学物理实验数据处理基本方法

能小。个别偏离曲线较远的点,应检查标点是否错误,若无误表明该点可能是错误数据,
在连线时不予考虑。对于仪器仪表的校准曲线和定标曲线,连接时应将相邻的两点连成直
线,整个曲线呈折线形状。
6. 注解与说明 在图纸上要写明图线的名称、坐标比例及必要的说明 件 ) ,并在恰当地方注明作者姓名、日期等。
( 主要指实验条
为线性关系, b 为斜率, lg a 为截距。 ( 4) y aebx ( a 和 b 为常数 ) 。等式两边取自然对数得, ln y ln a bx 。于是, ln y 与
x 为线性关系, b 为斜率, ln a 为截距。
—1—
3. 确定坐标比例与标度 合理选择坐标比例是作图法的关键所在。作图时通常以自变
12. 300
△+ B(83.5,12.600) +
12. 100
11. 900
+
11. 700
+
11. 500
11. 300
+
11. 100
10. 900
+
10. 700
0101101 班 陈建军 2001 年 3 月 15 日
10. 500 △+A(13.0,10.500)
10. 300 10. 0
i t (℃ )
R( )
1 10.5 10.423
2 26.0 10.892
3 38.3 11.201
4 51.0 11.586
5 62.8 12.025
6 75.5 12.344
7 85.7 12.679
R( )
12. 700 12. 500
R~t 图
坐标比例: 5.0℃/cm,0.100Ω / cm
大学物理中的实验数据处理与分析方法

大学物理中的实验数据处理与分析方法在大学物理课程中,实验数据处理与分析是非常关键的部分,能帮助学生深入理解物理原理和提高实验操作和数据分析能力。
本文将介绍一些常见的实验数据处理与分析方法,以帮助大家更好地应对物理实验。
一、误差分析与处理在物理实验中,由于种种因素的干扰,我们得到的实验数据往往会存在误差。
为了准确地反映实验现象,我们需要对这些误差进行分析和处理。
1. 系统误差:系统误差是由于实验仪器或装置的固有缺陷导致的误差,它存在于所有实验数据中,并且通常是固定的。
我们可以通过对仪器进行校准或者进行适当的修正来减小系统误差。
2. 随机误差:随机误差是由于实验条件的不确定性或人为操作的随机性导致的误差,它在重复实验中会发生变化。
为了减小随机误差,我们可以多次重复实验并取平均值,以提高数据的可靠性。
3. 最小可区分误差:最小可区分误差是指实验数据中能够明显区分的最小单位误差。
在数据处理过程中,我们需要注意到最小可区分误差,以避免在数据分析过程中忽略这些细微的差别。
二、数据处理方法在获得实验数据后,我们需要对其进行处理,以得到更有意义和可靠的结果。
1. 平均值:将多次实验获得的数据进行求和,并除以实验次数,即可得到平均值。
通过求平均值,可以减小随机误差对结果的影响。
2. 不确定度:不确定度是用于表示测量结果的范围。
通常,我们可以通过标准差、相对误差等方式来计算不确定度。
3. 误差传递:在进行多个量的计算时,不同量之间的误差会相互影响。
我们可以利用误差传递法则来计算复合量的误差。
该法则包括加减法、乘除法和函数的误差传递规则。
三、数据分析方法在获得实验数据后,我们还需要对其进行分析,以得到对实验现象的深入理解。
1. 图表分析:将实验数据绘制成图表,可以直观地展示数据规律和趋势。
在进行图表分析时,需要注意选择适当的坐标轴、标记数据点和合理选择曲线拟合等。
2. 直线拟合:对于线性关系的实验数据,我们可以利用最小二乘法进行直线拟合,以获得直线的斜率和截距。
大物实验之实验数据的处理 ppt
前一页 休息
-
7
系统误差与随机误差
系统误差 由于某种原因所产生,并遵循一定的规 律进行变化. 例如,随样品或试剂用量的大小按比 例进行变化.
系统误差有一定的指向,例如称量一种吸湿性物质, 其误差总是正值. 它属于方法和技术问题,知道了 产生的原因,便可消除或修正,所以此种误差也称 可定误差.
随机误差 在相同条件下重复多次测定同一物理 量时,误差大小或正负变化纯属偶然而毫无规律, 这种误差称为随机误差,也叫偶然误差.
前一页 休息
-
17
拉依达( Ρайта)准则
拉依达准则又被简称为3σ准则。由于随 机误差服从正态分布规律,因此 P{|ε|≤ 3σ}=99.7%
有限次测量误差超过3σ的几率很小,可 以剔除
由于实际上σ未知,如果 xi x 3S 可以剔除,弃真几率很小
前一页 休息
-
18
例
某合金导线的电阻值
• 例如,某仪表正确度等级为R级(引
用误差R%),满量程的刻度为X,实
际使用时的测量值为 x (x ≤ X),则
测 测量 量值 值的 的相 绝对 对 XX误 误 xRR% % 差 差
前一页 休息
-
13
通过上面的分析,可知为了减少 仪表测量的误差,提高正确度, 应该使仪表尽可能在靠近满量程 刻度的2/3以上的区域内使用的原 则。
真值往往很难得到,因而误差的绝对 值也是无法知道的。但是根据测量工 具或计算情况可以估计误差值上限或 估计值的精确程度。
前一页 休息
-
6
相对误差
误差限的大小还不能完全表示近似值 的好坏,如10±1与1000±5两个量, 虽然前者绝对误差较小,但是显然后 者更精确。
大物实验数据处理示例(大字版)
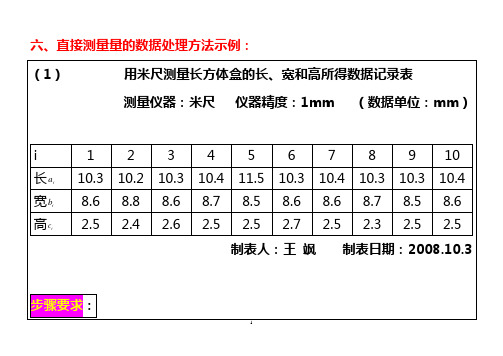
六、直接测量量的数据处理方法示例:12345678七、间接测量结果的计算,误差的传递与合成例 2 测得一小球的质量m=(10.06土 0.02)g ,直径d=(1.3471土 0.0006)cm ,求小球的密度ρ及其测量误差。
解:小球的体积361dV π=,小球的密度36dmVm πρ==9则密度ρ的算术平均值:333860.73471.114.306.1066cmg dmV m =⨯⨯===πρ密度ρ的相对误差:)(ln )(ln )(ˆ2222d s d m s m E ⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂==ρρρρσ22)(9)(⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛=d d s m m s223471.10006.0906.1002.0⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛==0.002436密度ρ的标准偏差3019.0cmg E s ==ρρ)(10则,小球密度ρ的实验结果表达式为302.086.7cmg)(±=ρ%25.0=E八、逐差法的运用及结果表达式写法以及与作图法的比较任何测量结果都有偶然误差。
做等精度测量时,如用螺旋测微器测量一个金属圆球的直径,其测量结果的特点是从理论上讲各次得到的数据应当相等,但实际上不会相等,这是由于存在着偶然误差的缘故。
根据偶然误差分布的特点,采用多次测量取平均值的方法,可以有效地减小最终测量结果的偶然误差。
因此通常认为多次测量结果的算术平均值是最可信值。
用逐差法处理数据是上述思想的推广。
我们以测定弹簧劲度系数的实验为例来说明这一点。
实验装置如图所示。
我们在弹簧的下端悬挂钩码,并依次增加钩码的个数,得到弹簧指针的位置坐标,如表一所列。
表一、弹簧所受的外力与指针的位置坐标从上面处理实验数据的过程中我们得知,采用逐差法处理实验实据的思想,就是通过隔项求差,使偶然误差含在了(理论上应该)相等的量(即Xn+4-Xn)中,隔项求差客观上是将非等精度测量的结果转变成“类等精度测量” 的结果,以便可以用求算术平均值的方法来减小偶然误差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一 位
直接 :仪器最小分度
不确定度未知
间接 :位数+运算方式
加减运算:最大不确定度分量决定: 432.3+0.1263-2=430 乘除运算:最少有效数字分量决定: 48X3.2345/1.732=52
运算结果第一位是1,2时,多保留一位: 6.3X4.3=27.1
例:测量圆柱体合金的密度,求标准不确定度
10.495 20.00
10.470 20.02
D 10.4918
mm
中间结果可多保留一位
uAD 0.007
uBD
mm
mm
D 0.004 0.0013 3 3
uD
1.11u AD
2
uBD 2
2
1.11 0.007
mm
0.00132
mm
=0.008
mm
2
H H uH (20.003 0.016)
P 68.3%
uBm
0.04 0.013 3
g
2 2 um u Am uBm
0.04 3 0.01
g
g ( P 0.68)
m (14.00 0.01)
4m 4 14.00 3 3 8.094 10 g / mm 8.094 2 2 D H 10.492 20.003
D D uD (10.492 0.008)
P 68.3%
H 20.003
mm
中间结果可多保留一位
uAH 0.006mm源自uBH0.02 0.0115 0.012 3
mm
2
uH
1.11u AH 1.183uBH
2 2
= 1.11 0.006 1.183 0.012 0.016 mm
0.675 0.877 0.717
0.577
0.650
0.683
1.000
0.900
1.650 1.559 1.675
0.950
1.960 1.645 1.901
0.955
2.000 1.654 1.929
0.990
2.580 1.715 2.204
0.997
3.000 1.727 2.315
正态分布 均匀分布 三角分布
谢 谢!
1.000 0.862 1.000
1.183 1.064
几种常见仪器的误差分布与置信系数 仪器 误差分布
置信系数C
米尺 正态 3
游标卡尺 均匀 √3
千分尺 正态 3
物理天平 正态 3
秒表 正态 3
D/mm H/mm
10.502 20.00
10.488 20.02
10.516 19.98
10.480 20.00
Y a0 X a1 X …
2
• 最小二乘法:
s yi f xi
i 2
最小
yi (b1 xi b0 )
i 1
k
2
y
xy xy b1 2 x ( x )2 b0 y b1 x
1 n x xi n i 1 1 n y yi n i 1
∆V/V
V V0e
ad
1.9
1.6
1.3
1.1
0.9
0.8
0.6
V-d: 2∆V
lnV-d: 2∆V/V
作图软件介绍:Origin
• • • • 自己摸索 教学平台课件:Origin8简易使用教程 图书馆有教程 图书馆的课件
图书馆→服务指南→课件天地→文献管理与信息分析→第十一讲 /2012/plus/view.php?aid=1013
2 2 2
g / cm3
常数多取一位3.1416
u
um 2ud uh m D H
2 2
0.02 2 0.008 0.016 14.00 10.492 20.003 0.0022
1 x ( x 2 x1 ) ( x 3 x 2 ) ( x8 x7 ) 7 1 ( x8 x1 ) 错误!! 7
1 x [( x5 x1 ) ( x6 x2 ) 44 ( x7 x3 ) ( x8 x4 )]
4、最小二乘法
2
u 8.1 0.0020 0.016 g / cm3 0.02 g / cm3
8.09 0.02 g / cm3
P 68.3%
实验结果的表示
测量结果的有效数字的位数取决于测量结果的不确定度。 1、不确定度通常只取一位有效数字,首位数字小于3时,可 取两位有效数字 2、不确定度的取舍也采用四舍六入五凑偶 3、测量结果的有效位数要向不确定度看齐 4、实验结果一般用绝对不确定度表示,也可用相对不确定 度表示。
X X X X X
X
X
X
X
O
x
1 n xy xi yi n i 1 n 1 x 2 xi 2 n i 1
xy xy r x 2 x 2 y 2 y 2 1 r 1
相关系数r:定量描述x、y变量之间线性相关程度的好坏。
测量圆柱体的直径D(千分尺)和高H(游标卡尺)
D/mm H/mm 10.502 20.00 10.488 20.02 10.516 19.98 10.480 20.00 10.495 20.00 10.470 20.02
或者
测量圆柱体的直径D(千分尺)和高H(游标卡尺) D/mm 10.502 10.488 10.516 10.480 10.495 10.470 H/mm 20.00 20.02 19.98 20.00 20.00 20.02
大学物理一级实验绪论
数据处理
物理教学实验中心 2014-3
有效数字
测量结果中可靠的几位数加上不确定的一位数
测量只写到开始有误差的那一位,该位数后:四舍六入五凑偶
有效数字的位数与小数点无关:1.23 同123
0.0123, 0.01230, 1.35 和1.3500
已知不确定度
有效数字 取 齐
8.03 0.02
x, y 之间线性相 r 值在中 0 r 1, r 越接近于1, 关越好; r 为正,称为正相关;r 为负,称为负相 xi , yi为非线性。 关; r 接近于0,
相关系数阈值r0:
r0是与测量次数n有关的量,一般可以通过查表得到。 r>r0:x,y之间是线性,可以用最小二乘法进行回归; r<r0:x,y之间是非线性,不可以用最小二乘法进行回归。
用作图法把实验数据表示成曲线,固然可 以看出事物之间的规律,但毕竟不如方程来得确 切。如何从实验数据出发求出方程,这也是数据 处理中常常遇到的问题。
方程的回归,首先要确定函数的形式
• 线性的函数关系,则可写成Y=aX+b;
• 指数函数关系,则可写成: Y
ae c
bx
• 函数关系不明确,则常用多项式来表示:
拟合数据:
l/m
实验数据:
160 140 120 100 80 60 40 20 0 0 5 10 温度 15 20 25 30
experimental data liner fit
l 4.35 + 4.98t
d/um 25 V/V 50 75 100
t/s
125
150
175
44.26 37.71 31.19 25.79 20.90 18.36 15.00
优点:
(1)数据易于参考比较,便于检查数据的合理性、 发现问题,指导实验 (2)一个表可同时记录多个变量间的变化而不紊乱 (3)便于以后随时处理数据,分析问题
2、作图法
• 坐标纸 直角、半对数、对数坐标纸等
• 应用软件 origin、matlab、mathematica
常用数据处理方法
(1)列表法 (2)作图法 (3) 逐差法 (4)最小二乘法
1、列表法
• 记录原始数据的最好方法
• 格式要求: (1)应注明测量数据的名称、单位等信息 (2)要正确反映测量数据的有效数字 (3)用钢笔/圆珠笔,如实记录数据 (4)表格力求简单明了,一目了然
图上曲线的拟合
• 在多数情况下,两个物理量直接的关系在 一定的范围内应是渐变的.因此,曲线拟 合的原则是使各数据点(沿纵轴方向)到 所拟合的曲线的距离平方之和为最小.在 数学上这叫最小二乘法.根据这个原则, 各数据点要均匀分布在曲线的两侧.
B
4.6 4.4 4.2 4.0 3.8 3.6 3.4 3.2 3.0 30 40 50 60 70 80 90
图的格式
• 坐标轴、方向,物理量名称和单位,分度。
• 图号和图的名称。
• 可靠数字在图中应可靠,估读位在图中应是估计的, 即图纸中的一小格对应数值中可靠数字的最后一位。 • 适当选取x轴和y轴的比例和坐标的起点,使图线比 较对称的充满整个图纸,不要缩在一边或一角。除 特殊需要以外,坐标轴的起点一般不一定取为零值。
Y Axis Title
×
X Axis Title
望远镜读数 /mm
温度 /℃
图1
光杠杆法测铜棒的长度与温度的关系
误差杆:不确定度的图示
• 以数据点为基点,误差杆长度的一半表示 相应不确定度的大小。
l 4+5t+2 sin (t)
已知:m=14.00 g 允差0.04g
直径D用千分尺,高H用游标卡尺
D/mm H/mm 10.502 20.00 10.488 20.02 10.516 19.98 10.480 20.00 10.495 20.00 10.470 20.02
