(完整版)中考数学圆-经典压轴题(带答案)

合集下载

九年级中考数学压轴题《圆》专题练习

九年级中考数学压轴题《圆》专题练习1、如图，BD为△ABC外接圆⊙O的直径，且∠BAE=∠C．（1）求证：AE与⊙O相切于点A；（2）若AE∥BC，BC=2，AC=2，求AD的长．2、如图，在△ABC中，BA=BC，以AB为直径作半圆⊙O，交AC于点D.连结DB，过点D作DE⊥BC，垂足为点E.（1）求证：DE为⊙O的切线；（2）求证：DB2=AB·BE.3、如图，△ABC为等腰三角形，O是底边BC的中点，腰AB与⊙O相切于点D，OB与⊙O相交于点E．（1）求证：AC是⊙O的切线；（2）若BD=，BE=1．求阴影部分的面积．4、如图，在Rt△ABC中，点O在斜边AB上，以O为圆心，OB为半径作圆，分别与BC，AB相交于点D，E，连结AD．已知∠CAD=∠B．（1）求证：AD是⊙O的切线．（2）若BC=8，tanB=，求⊙O的半径．5、如图，△ABC 中，以BC 为直径的圆交AB 于点D ，∠ACD =∠ABC ．（1）求证：CA 是圆的切线；（2）若点E 是BC 上一点，已知BE =6，tan ∠ABC =32，tan ∠AEC =35，求圆的直径．6、如图，AB 为⊙O 的直径，点E 在⊙O 上，C 为弧BE 的中点，过点C 作直线CD ⊥AE 于D ，连接AC ，BC 。

（1）试判断直线CD 与⊙O 的位置关系，并说明理由；（2）若AD=2，AC=6，求AB 的长。

7、如图，AB是⊙O的直径，AF是⊙O切线，CD是垂直于AB的弦，垂足为E，过点C作DA的平行线与AF相交于点F，CD=，BE=2．求证：（1）四边形F ADC是菱形；（2）FC是⊙O的切线．8、如图，A，P，B，C是半径为8的⊙O上的四点，且满足∠BAC=∠APC=60°，（1）求证：△ABC是等边三角形；（2）求圆心O到BC的距离OD．9、如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，点O在AB 上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC，AB于点E，F.（1）试判断直线BC与⊙O的位置关系，并说明理由；（2）若BD=23，BF=2，求阴影部分的面积（结果保留π）10、如图，在Rt△ABC中，∠ABC=900,点M是AC的中点，以AB为直径作⊙O分别交AC、BM于点D、E（1）求证：MD=ME（2）填空：①若AB=6，当AD=2DM时，DE= ；②连接OD，OE，当∠A的度数为时，四边形ODME是菱形。

2020年九年级数学典型中考压轴题：圆专项训练题(含答案)

2020年九年级数学典型中考压轴题：圆专项训练题1、如图，△ABC是⊙O的内接三角形，AB为直径，过点B的切线与AC的延长线交于点D，E是BD中点，连接CE．（1）求证：CE是⊙O的切线；（2）若AC=4，BC=2，求BD和CE的长．2、如图，在⊙O中，AB为直径，D、E为圆上两点，C为圆外一点，且∠E+∠C=90°．（1）求证：BC为⊙O的切线．（2）若sinA=，BC=6，求⊙O的半径．3、如图，AB是⊙O的直径，点P在BA的延长线上，弦CD⊥AB，垂足为E，且PC2=PE•PO．（1）求证：PC是⊙O的切线．（2）若OE：EA=1：2，PA=6，求⊙O的半径．4、如图，AB是⊙O的直径，点D是上一点，且∠BDE=∠CBE，BD与AE交于点F．（1）求证：BC是⊙O的切线；（2）若BD平分∠ABE，求证：DE2=DF•DB；（3）在（2）的条件下，延长ED、BA交于点P，若PA=AO，DE=2，求PD的长．5、如图，点A是⊙O直径BD延长线上的一点，C在⊙O上，AC=BC，AD=CD （1）求证：AC是⊙O的切线；（2）若⊙O的半径为2，求△ABC的面积．6、已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED=EC．（1）求证：AB=AC；（2）若AB=4，BC=2，求CD的长．7、如图，O是△AB C内一点，与BC相交于F、G两点，且与AB、AC分别相切于点D、E，DE∥BC。

连接DF、EG。

(1) 求证：AB=AC(2) 已知AB=10，BC=12，求四边形DFGE是矩形时的半径.8、如图，过⊙O上的两点A、B分别作切线，并交BO、AO的延长线于点C、D，连接CD，交⊙O于点E、F，过圆心O作OM⊥CD，垂足为M点．求证：（1）△ACO≌△BDO；（2）CE=DF．9、如图，AB是⊙O的直径，点C、D在圆上，且四边形AOCD是平行四边形，过点D作⊙O的切线，分别交OA延长线与OC延长线于点E、F，连接BF．（1）求证：BF是⊙O的切线；（2）已知圆的半径为1，求EF的长．10、如图，在△ABC中，E是AC边上的一点，且AE=AB，∠BAC=2∠CBE，以AB 为直径作⊙O交AC于点D，交BE于点F．（1）求证：BC是⊙O的切线；（2）若AB=8，BC=6，求DE的长．11、在图“书香八桂，阅读圆梦”读数活动中，某中学设置了书法、国学、诵读、演讲、征文四个比赛项目如图，在Rt△ABC中，∠C=90°，BD是角平分线，点O在AB上，以点O为圆心，OB为半径的圆经过点D，交BC于点E．（1）求证：AC是⊙O的切线；（2）若OB=10，CD=8，求BE的长．12、如图，在⊙O中，半径OA⊥OB，过点OA的中点C作FD∥OB交⊙O于D、F 两点，且CD=，以O为圆心，OC为半径作，交OB于E点．（1）求⊙O的半径OA的长；（2）计算阴影部分的面积．13、如图，△ABC中，∠ACB=90°，D为AB上一点，以CD为直径的⊙O交BC于点E，连接AE交CD于点P，交⊙O于点F，连接DF，∠CAE=∠ADF．（1）判断AB与⊙O的位置关系，并说明理由；（2）若PF：PC=1：2，AF=5，求CP的长．14、如图所示，在Rt△ABC与Rt△OCD中，∠ACB=∠DCO=90°，O为AB的中点．（1）求证：∠B=∠ACD．（2）已知点E在AB上，且BC2=AB•BE．（i）若tan∠ACD=，BC=10，求CE的长；（ii）试判定CD与以A为圆心、AE为半径的⊙A的位置关系，并请说明理由．15、如图，AB为⊙O的直径，直线CD切⊙O于点M，BE⊥CD于点E．（1）求证：∠BME=∠MAB；（2）求证：BM2=BE•AB；（3）若BE=，sin∠BAM=，求线段AM的长．16、如图，在Rt△ABC中，∠BAC=90°，O是AB边上的一点，以OA为半径的⊙O与边BC相切于点E．（1）若AC=5，BC=13，求⊙O的半径；（2）过点E作弦EF⊥AB于M，连接AF，若∠F=2∠B，求证：四边形ACEF是菱形．17、如图，AB为⊙O的直径，C是⊙O上一点，过点C的直线交AB的延长线于点D，AE⊥DC，垂足为E，F是AE与⊙O的交点，AC平分∠BAE．（1）求证：DE是⊙O的切线；（2）若AE=6，∠D=30°，求图中阴影部分的面积．18、如图，在Rt△ABC中，∠C=90°，点O在AB上，经过点A的⊙O与BC相切于点D，与AC，AB分别相交于点E，F，连接AD与EF相交于点G．（1）求证：AD平分∠CAB；（2）若OH⊥AD于点H，FH平分∠AFE，DG=1．①试判断DF与DH的数量关系，并说明理由；②求⊙O的半径．参考答案：1、【解答】（1）证明：连接OC，如图所示：∵BD是⊙O的切线，∴∠CBE=∠A，∠ABD=90°，∵AB是⊙O的直径，∴∠ACB=90°，∴∠ACO+∠BCO=90°，∠BCD=90°，∵E是BD中点，∴CE=BD=BE，∴∠BCE=∠CBE=∠A，∵OA=OC，∴∠ACO=∠A，∴∠ACO=∠BCE，∴∠BCE+∠BCO=90°，即∠OCE=90°，CE⊥OC，∴CE是⊙O的切线；（2）解：∵∠ACB=90°，∴AB===2，∵tanA====，∴BD=AB=，∴CE=BD=．2、【解答】（1）证明：∵∠A与∠E所对的弧都是，∴∠A=∠E，又∵∠E+∠C=90°，∴∠A+∠C=90°，在△ABC中，∠ABC=180°﹣90°=90°，∵AB为直径，∴BC为⊙O的切线；（2）解：∵sinA=，BC=6，∴=，即=，解得AC=10，由勾股定理得，AB===8，∵AB为直径，∴⊙O的半径是×8=4．3、【解答】（1）证明：连结OC，如图，∵CD⊥AB，∴∠PEC=90°，∵PC2=PE•PO，∴PC：PO=PE：PC，而∠CPE=∠OPC，∴△PCE∽△POC，∴∠PEC=∠PCO=90°，∴OC⊥PC，∴PC是⊙O的切线；（2）解：设OE=x，则EA=2x，OA=OC=3x，∵∠COE=∠POC，∠OEC=∠OCP，∴△OCE∽△OPC，∴OC：OP=OE：OC，即3x：OP=x：3x，解得OP=9x，∴3x+6=9x，解得x=1，∴OC=3，即⊙O的半径为3．4、【解答】（1）证明：∵AB是⊙O的直径，∴∠AEB=90°，∴∠EAB+∠ABE=90°，∵∠EAB=∠BDE，∠BDE=∠CBE，∴∠CBE+∠ABE=90°，即∠ABC=90°，∴AB⊥BC，∴BC是⊙O的切线；（2）证明：∵BD平分∠ABE，∴∠1=∠2，而∠2=∠AED，∴∠AED=∠1，∵∠FDE=∠EDB，∴△DFE∽△DEB，∴DE：DF=DB：DE，∴DE2=DF•DB；（3）连结DE，如图，∵OD=OB，∴∠2=∠ODB，而∠1=∠2，∴∠ODB=∠1，∴OD∥BE，∴△POD∽△PBE，∴=，∵PA=AO，∴PA=AO=BO，∴=，即=，∴PD=4．5、【解答】解：（1）连接OC．∵AC=BC，AD=CD，OB=OC，∴∠A=∠B=∠1=∠2．∵∠ACO=∠DCO+∠2，∴∠ACO=∠DCO+∠1=∠BCD，又∵BD是直径，∴∠BCD=90°，∴∠ACO=90°，又C在⊙O上，∴AC是⊙O的切线；（2）由题意可得△DCO是等腰三角形，∵∠CDO=∠A+∠2，∠DOC=∠B+∠1，∴∠CDO=∠DOC，即△DCO是等边三角形．∴∠A=∠B=∠1=∠2=30°，CD=AD=2，在直角△BCD中，BC===2．又AC=BC，∴AC=2．作CE⊥AB于点E．在直角△BEC中，∠B=30°，∴CE=BC=，=AB•CE=×6×=3．∴S△ABC6、【解答】（1）证明：∵ED=EC，∴∠EDC=∠C，∵∠EDC=∠B，∴∠B=∠C，∴AB=AC；（2）解：连接AE，∵AB为直径，∴AE⊥BC，由（1）知AB=AC，∴BE=CE=BC=，∵CE•CB=CD•CA，AC=AB=4，∴•2=4CD，∴CD=．7、解析：（1）证明：∵⊙O 与AB、AC 分别相切于点D、E，∴AD＝AE．∴∠ADE＝∠AED．∵DE∥BC，∴∠B＝∠ADE，∠C＝∠AED．∴∠B＝∠C．∴AB＝AC．（2）解：如图，连接AO，交DE 于点M，延长AO 交BC 于点N，连接OE、DG．设⊙O 的半径为r．∵四边形DFGE 是矩形，[来源:学科网]∴∠DFG＝90°．∴DG 是⊙O 的直径．∵⊙O 与AB、AC 分别相切于点D、E，∴OD⊥AB，OE⊥AC．又OD＝OE，∴AN 平分∠BAC．又AB＝AC，∴AN⊥BC，BN＝12BC＝6．在Rt△ABN 中，AN＝＝8．∵OD⊥AB，AN⊥BC，∴∠ADO＝∠ANB＝90°．又∠OAD＝∠BAN，∴△AOD∽△ABN．．∵OD⊥AB，∴∠GDB＝∠ANB＝90°．又∠B＝∠B，∴△GBD∽△ABN．∴四边形DFGE 是矩形时⊙O 的半径为60 17·8、【解答】证明：（1）∵过⊙O上的两点A、B分别作切线，∴∠CAO=∠DBO=90°，在△ACO和△BDO中∵，∴△ACO≌△BDO（ASA）；（2）∵△ACO≌△BDO，∴CO=DO，∵OM⊥CD，∴MC=DM，EM=MF，∴CE=DF．9、【解答】（1）证明：连结OD，如图，∵四边形AOCD是平行四边形，而OA=OC，∴四边形AOCD是菱形，∴△OAD和△OCD都是等边三角形，∴∠AOD=∠COD=60°，∴∠FOB=60°，∵EF为切线，∴OD⊥EF，∴∠FDO=90°，在△FDO和△FBO中，∴△FDO≌△FBO，∴∠ODF=∠OBF=90°，∴OB⊥BF，∴BF是⊙O的切线；（2）解：在Rt△OBF中，∵∠FOB=60°，而tan∠FOB=，∴BF=1×tan60°=．∵∠E=30°，∴EF=2BF=2．10、【解答】（1）证明：∵AE=AB，∴△ABE是等腰三角形，∴∠ABE=（180°﹣∠BAC=）=90°﹣∠BAC，∵∠BAC=2∠CBE，∴∠CBE=∠BAC，∴∠ABC=∠ABE+∠CBE=（90°﹣∠BAC）+∠BAC=90°，即AB⊥BC，∴BC是⊙O的切线；（2）解：连接BD，∵AB是⊙O的直径，∴∠ADB=90°，∵∠ABC=90°，∴∠ADB=∠ABC，∵∠A=∠A，∴△ABD∽△ACB，∴=，∵在Rt△ABC中，AB=8，BC=6，∴AC==10，∴，解得：AD=6.4，∴DE=AE﹣AD=8﹣6.4=1.6．11、【解答】（1）证明：连接OD，∵BD为∠ABC平分线，∴∠1=∠2，∵OB=OD，∴∠1=∠3，∴∠2=∠3，∴OD∥BC，∵∠C=90°，∴∠ODA=90°，则AC为圆O的切线；（2）解：过O作OG⊥BC，∴四边形ODCG为矩形，∴GC=OD=OB=10，OG=CD=8，在Rt△OBG中，利用勾股定理得：BG=6，∴BC=BG+GC=6+10=16，∴△AOD∽△ABC，∴=，即=，解得：OA=，∴AB=+10=，连接EF，∵BF为圆的直径，∴∠BEF=90°，∴∠BEF=∠C=90°，∴EF∥AC，∴=，即=，解得：BE=12．12、【解答】解；（1）连接OD，∴∠AOB=90°，∵CD∥OB，∴∠OCD=90°，在RT△OCD中，∵C是AO中点，CD=，∴OD=2CO，设OC=x，∴x2+（）2=（2x）2，∴x=1，∴OD=2，[来源:Z|xx|]∴⊙O的半径为2．（2）∵sin∠CDO==，∴∠CDO=30°，∵FD∥OB，∴∠DOB=∠ODC=30°，∴S圆=S△CDO+S扇形OBD﹣S扇形OCE=×+﹣=+．13、【解答】解：（1）AB是⊙O切线．理由：连接DE、CF．∵CD是直径，∴∠DEC=∠DFC=90°，∵∠ACB=90°，∴∠DEC+∠ACE=180°，∴DE∥AC，∴∠DEA=∠EAC=∠DCF，∵∠DFC=90°，∴∠FCD+∠CDF=90°，∵∠ADF=∠EAC=∠DCF，∴∠ADF+∠CDF=90°，∴∠ADC=90°，∴CD⊥AD，∴AB是⊙O切线．（2）∵∠CPF=∠CPA，PCF=∠PA C，∴△PCF∽△PAC，∴=，∴PC2=PF•PA，设PF=a．则PC=2a，∴4a2=a（a+5），∴a=，∴PC=2a=．14、【解答】解：（1）∵∠ACB=∠DCO=90°，∴∠ACB﹣∠ACO=∠DCO﹣∠ACO，即∠ACD=∠OCB，又∵点O是AB的中点，∴OC=OB，∴∠OCB=∠B，∴∠ACD=∠B，（2）（i）∵B C2=AB•BE，∴=，∵∠B=∠B，∴△ABC∽△CBE，∴∠ACB=∠CEB=90°，∵∠ACD=∠B，∴tan∠ACD=tan∠B=，设BE=4x，CE=3x，由勾股定理可知：BE2+CE2=BC2，∴（4x）2+（3x）2=100，∴解得x=2，∴CE=6；（ii）过点A作AF⊥CD于点F，∵∠CEB=90°，∴∠B+∠ECB=90°，∵∠ACE+∠ECB=90°，∴∠B=∠ACE，∵∠ACD=∠B，∴∠ACD=∠ACE，∴CA平分∠DCE，∵AF⊥CE，AE⊥CE，∴AF=AE，∴直线CD与⊙A相切．15、【解答】解：（1）如图，连接OM，∵直线CD切⊙O于点M，∴∠OMD=90°，∴∠BME+∠OMB=90°，∵AB为⊙O的直径，∴∠AMB=90°．∴∠AMO+∠OMB=90°，∴∠BME=∠AMO，∵OA=OM，∴∠MAB=∠AMO，∴∠BME=∠MAB；（2）由（1）有，∠BME=∠MAB，∵BE⊥CD，∴∠BEM=∠AMB=90°，∴△BME∽△BAM，∴，[来源:学科网]∴BM2=BE•AB；（3）由（1）有，∠BME=∠MAB，∵sin∠BAM=，∴sin∠BME=，在Rt△BEM中，BE=，∴sin∠BME==，∴BM=6，在Rt△ABM中，sin∠BAM=，∴sin∠BAM==，∴AB=BM=10，根据勾股定理得，AM=8．16、【解答】（1）解：连接OE，设圆O半径为人，在Rt△ABC中，BC=13，AC=5，根据勾股定理得：AB==12，∵BC与圆O相切，∴OE⊥BC，∴∠OEB=∠BAC=90°，∵∠B=∠B，∴△BOE∽△BCA，∴=，即=，解得：r=；（2）∵=，∠F=2∠B，∴∠AOE=2∠F=4∠B，∵∠AOE=∠OEB+∠B，∴∠B=30°，∠F=60°，∵EF⊥AD，∴∠EMB=∠CAB=90°，∴∠MEB=∠F=60°，CA∥EF，∴CB∥AF，∴四边形ACEF为平行四边形，∵∠CAB=90°，OA为半径，∴CA为圆O的切线，∵BC为圆O的切线，∴CA=CE，∴平行四边形ACEF为菱形．[来源:学|科|网]17、【解答】解：（1）连接OC，∵OA=OC，∴∠OAC=∠OCA，∵AC平分∠BAE，∴∠OAC=∠CAE，∴∠OCA=∠CAE，∴OC∥AE，∴∠OCD=∠E，∵AE⊥DE，∴∠E=90°，∴∠OCD=90°，∴OC⊥CD，∵点C在圆O上，OC为圆O的半径，∴CD是圆O的切线；（2）在Rt△AED中，∵∠D=30°，AE=6，∴AD=2AE=12，在Rt△OCD中，∵∠D=30°，∴DO=2OC=DB+OB=DB+OC，∴DB=OB=OC=AD=4，DO=8，∴CD===4，∴S△OCD===8，∵∠D=30°，∠OCD=90°，∴∠DOC=60°，∴S扇形OBC=×π×OC2=，∵S阴影=S△COD﹣S扇形OBC∴S阴影=8﹣，∴阴影部分的面积为8﹣．18、【解答】解：（1）如图，连接OD，∵⊙O与BC相切于点D，∴OD⊥BC，∵∠C=90°，∴OD∥AC，∴∠CAD=∠ODA，∵OA=OD，∴∠OAD=∠ODA，∴∠CAD=∠BAD，∴AD平分∠CAB．（2）①DF=DH，理由如下：∵FH平分∠AFE，∴∠AFH=∠EFH，又∠DFG=∠EAD=∠HAF，∴∠DFG=∠EAD=∠HAF，∴∠DFG+∠GFH=∠HAF+∠HFA，即∠DFH=∠DHF，∴DF=DH．②设HG=x，则DH=DF=1+x，∵OH⊥AD，∴AD=2DH=2（1+x），∵∠DFG=∠DAF，∠FDG=∠FDG，∴△DFG∽△DAF，∴，∴，∴x=1，∵DF=2，AD=4，∵AF为直径，∴∠ADF=90°，∴AF=∴⊙O的半径为．。

中考数学压轴题专题圆的综合的经典综合题附详细答案

中考数学压轴题专题圆的综合的经典综合题附详细答案中考数学压轴题专题：圆的综合一、圆的综合1.如图，⊙O的半径为6cm，经过⊙O上一点C作⊙O的切线交半径OA的延长于点B，作∠ACO的平分线交⊙O于点D，交OA于点F，延长DA交BC于点E。

1) 求证：AC∥OD；2) 如果DE⊥BC，求AC的长度。

答案】(1) 证明见解析；(2) 2π。

解析】试题分析：(1) 由OC=OD，CD平分∠ACO，易证得∠ACD=∠ODC，即可证得AC∥OD；(2) BC切⊙O于点C，DE⊥BC，易证得平行四边形ADOC是菱形，继而可证得△AOC是等边三角形，则可得：∠AOC=60°，继而求得弧AC的长度。

试题解析：1) 证明：因为OC=OD，所以∠OCD=∠XXX。

因为CD平分∠ACO，所以∠XXX∠ACD。

因此，∠ACD=∠ODC，即可证得AC∥OD。

2) 因为BC切⊙XXXC，所以XXX。

因为DE⊥BC，所以OC∥DE。

因为AC∥OD，所以四边形ADOC是平行四边形。

因为OC=OD，所以平行四边形ADOC是菱形，所以OC=AC=OA。

因为△AOC是等边三角形，所以∠AOC=60°，因此弧AC的长度为2π。

点睛：本题考查了切线的性质、等腰三角形的判定与性质、菱形的判定与性质以及弧长公式。

此题难度适中，注意掌握数形结合思想的应用。

2.(类比概念) 三角形的内切圆是以三个内角的平分线的交点为圆心，以这点到三边的距离为半径的圆，则三角形可以称为圆的外切三角形，可以得出三角形的三边与该圆相切。

以此类推，如图1，各边都和圆相切的四边形称为圆外切四边形。

性质探究) 如图1，试探究圆外切四边形的ABCD两组对边AB，CD与BC，AD之间的数量关系。

猜想结论：(要求用文字语言叙述)写出证明过程（利用图1，写出已知、求证、证明）性质应用)①初中学过的下列四边形中哪些是圆外切四边形(填序号)：A：平行四边形；B：菱形；C：矩形；D：正方形。

2023年九年级数学中考复习圆综合压轴题解答题专题训练(含解析)

2022-2023学年九年级数学中考复习《圆综合压轴题》解答题专题训练（附答案）1．如图．在Rt△ABC中，∠ACB＝90°，D为AB边的中点，连接CD．以CD为直径作⊙O，分别与AC，BC相交于点M，N．过点N作⊙O的切线交AB于点E．（1）求证：∠BEN＝90°．（2）若AB＝10，请填空：①迮接OE，ON，当NE＝时，四边形OEBN是平行四边形；②连接DM，DN，当AC＝时，四边形CMDN为正方形．2．如图，以AB为直径的半圆中，点O为圆心，点C在圆上，过点C作CD∥AB，且CD ＝OB．连接AD，分别交OC，BC于点E，F，与⊙O交于点G，若∠ABC＝45°．（1）求证：①△ABF∽△DCF；②CD是⊙O的切线．（2）求的值．3．如图，△ABC内接于⊙O，AB为直径，点D为半径OA上一点，过点D作AB的垂线交AC于点E，交BC的延长线于点P，点F在线段PE上，且PF＝CF．（1）求证：CF是⊙O的切线；（2）连接AP与⊙O相交于点G，若∠ABC＝2∠P AC，求证：AB＝BP；（3）在（2）的条件下，若AC＝4，BC＝3，求CF的长．4．如图，△ABC内接于⊙O，AB是⊙O的直径，⊙O的切线PC交BA的延长线于点P，OF∥BC交AC于点E，交PC于点F，连接AF．（1）判断直线AF与⊙O的位置关系并说明理由；（2）若⊙O的半径为6，AF＝2，求AC的长；（3）在（2）的条件下，求阴影部分的面积．5．如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC于点E，交AB的延长线于点F，连接AD．（1）求证：EF是⊙O的切线．（2）求证：△FBD∽△FDA．（3）若DF＝4，BF＝2，求⊙O的半径长．6．如图1，已知AB是⊙O的直径，AC是⊙O的弦，过O点作OF⊥AB交⊙O于点D，交AC于点E，交BC的延长线于点F，点G是EF的中点，连接CG．（1）判断CG与⊙O的位置关系，并说明理由；（2）求证：2OB2＝BC•BF；（3）如图2，当∠DCE＝2∠F，DG＝2.5时，求DE的长．7．已知：△ABC内接于⊙O，连接AO并延长交BC于点D，且AD⊥BC于点D．（1）如图1，求证：∠B＝∠C；（2）如图2，点E在上，连接AE，CE，∠ACE＝∠ACB，求证：∠CAE＝2∠ACE；（3）如图3，在（2）的条件下，过点A作AF⊥CE交CE的延长线于点F，若AE＝5，AB＝13，求AF的长．8．在Rt△ABC中，∠ACB＝90°，AC＝6，∠B＝30°，点M是AB上的动点，以M为圆心，MB为半径作圆交BC于点D，（1）若圆M与AC相切，如图1，求圆的半径；（2）若AM＝2MB，连接AD，如图2．①求证：AD与圆M相切；②求阴影部分的面积．9．如图，已知AB是⊙O的直径，C是⊙O上的一点，D是AB上的一点，DE⊥AB于D，DE交BC于F，且EF＝EC．（1）求证：EC是⊙O的切线；（2）求证：△OAC∽△ECF；（3）若BD＝4，BC＝8，圆的半径OB＝5，求EC的长．10．如图，已知以BC为斜边的Rt△ABC内接于⊙O，∠BAC的平分线交⊙O于点D，过点D作DE∥BC交AB的延长线于点E，连接DB，DC．（1）求证：ED为⊙O的切线；（2）求证：BC2＝2ED•FC；（3）若tan∠ABC＝2，AD＝，求BC的长．11．已知△ABC内接于⊙O，D是弧AC上一点，连接BD、AD，BD交AC于点M，∠BMC ＝∠BAD．（1）如图1，求证：BD平分∠ABC；（2）如图2，过点D作⊙O的切线，交BA的延长线于点F，求证：DF∥AC；（3）如图3，在（2）的条件下，BC是⊙O的直径，连接DC，AM＝1，DC＝，求四边形BFDC的面积．12．如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，P为弧AD上一点．（1）如图1，连接AC、PC、P A，求证：∠APC＝∠ACD；（2）如图2，连接PB，PB交CD于E，过点P作⊙O的切线交CD的延长线于点F，求证：FE＝PF；（3）如图3，在（2）的条件下，连接AE，且∠P AE＝∠F，过点A作AG⊥PF，垂足为G，若PG＝6，，求BH的长．13．如图，⊙O的半径为1，点A是⊙O的直径BD延长线上的一点，C为⊙O上的一点，AD＝CD，∠A＝30°．（1）求证：直线AC是⊙O的切线；（2）求△ABC的面积；（3）点E在上运动（不与B、D重合），过点C作CE的垂线，与EB的延长线交于点F．①当点E运动到与点C关于直径BD对称时，求CF的长；②当点E运动到什么位置时，CF取到最大值，并求出此时CF的长．14．如图所示，AB是⊙O的直径，点E为线段OB上一点（不与O，B重合），作CE⊥OB，交⊙O于点C，垂足为点E，作直径CD，过点C的切线交DB的延长线于点P，作AF ⊥PC于点F，连接CB．（1）求证：AC平分∠F AB．（2）求证：BC2＝CE•CP．（3）当AB＝4时，求劣弧BC长度（结果保留π）．15．已知：如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O于点E，AE与BC交于点H，连接CE，BD是⊙O的切线与OE的延长线相交于点D．（1）求证：∠D＝∠AEC；（2）求证：CE2＝EH•EA；（3）若⊙O的半径为5，，求FH的长．16．如图，在平面直角坐标系xOy中，已知点A（0，8），点B是x轴正半轴上一点，连接AB，过点A作AC⊥AB，交x轴于点C，点D是点C关于点A的对称点，连接BD，以AD为直径作⊙Q交BD于点E，连接并延长AE交x轴于点F，连接DF．（1）求线段AE的长；（2）若∠ABE＝∠FDE，求EF的值．（3）若AB﹣BO＝4，求tan∠AFC的值．17．如图，在Rt△ABC中，∠B＝90°，AE平分∠BAC，交BC于点E，点D在AC上，以AD为直径的⊙O经过点E，点F在⊙O上，且EF平分∠AED，交AC于点G，连接DF．（1）求证：△DEF∽GDF；（2）求证：BC是⊙O的切线；（3）若cos∠CAE＝，DF＝10，求线段GF的长．18．如图，⊙O是△ABC的外接圆，AC是⊙O的直径，过圆心O的直线PF⊥AB于D，交⊙O于E，F，PB是⊙O的切线，B为切点，连接AP，AF．（1）求证：直线P A为⊙O的切线；（2）求证：AC2＝4OD•OP；（3）若BC＝6，，求AC的长．19．如图，AB是半圆O的直径，AB＝10．C是弧AB上一点，连接AC，BC，∠ACB的平分线交AB于点P，过点P分别作PE⊥AC，PF⊥BC，垂足分别为E、F．（1）求证：四边形CEPF是正方形；（2）当sin A＝时，求CP的长；（3）设AP的长为x，图中阴影部分的面积为y，求y与x之间的函数关系式，并写出y 的最大值．20．问题提出（1）如图①，△ABC为等边三角形，若AB＝2，则△ABC的面积为．问题探究（2）如图②，在Rt△ABC中，∠ABC＝90°，AC＝3，BD是△ABC的角平分线，过点D作DE⊥BD交BC边于点E．若AD＝1，求图中阴影部分的面积．问题解决（3）如图③，是某公园的一个圆形施工区示意图，其中⊙O的半径是4米，公园开发部门计划在该施工区内设计一个四边形绿化区域ABCD，连接AC、BD，现准备在△ADC 区域种植花卉供游人欣赏．按设计要求，A、B、C、D四个点都在圆上，∠ADB＝∠BDC ＝60°．设BD的长为x米，△ADC的面积为y平方米．①求y与x之间的函数关系式；②按照设计要求，为让游人有更好的观赏体验，△ADC花卉区域的面积越大越好，那么请求出花卉区域△ADC面积的最大值．参考答案1．（1）证明：如图，连接ON，DN，∵CD是⊙O的直径，∴∠CND＝∠DNB＝90°，∵NE是⊙O的切线，∴∠ONE＝90°，∴∠BNE＝∠OND，∵ON＝OD，∴∠ODN＝∠OND，∴∠ODN＝∠BNE，∵D是斜边AB的中点，∴CD＝AD＝BD，∴∠B＝∠BCD，∵∠BCD+∠ODN＝90°，∴∠B+∠BNE＝90°，∴∠NEB＝90°；（2）解：①∵四边形OEBN是平行四边形，∴BE＝ON＝，∵E为BD的中点，∴N为BC的中点，∴NE为△BCD的中位线，∴NE∥CD，且NE＝CD＝．故答案为：；②∵四边形CMDN为正方形，∴∠MCD＝∠MDC＝45°，∠CMD＝90°，∴MC＝MD＝CD，∵AD＝DC，∴M是AC的中点，AC＝2MC＝CD，∴CD＝AB＝5，∴AC＝5．故答案为：5．2．（1）证明：①∵CD∥AB，∴∠F AB＝∠D，∵∠AFB＝∠DFC，∴△ABF∽△DCF；②∵∠ABC＝45°，∴∠AOC＝2∠ABC＝90°，∵CD∥AB，∴∠DCO＝∠AOC＝90°，∵OC是半圆的半径，∴CD是⊙O的切线；（2）解：过点F作FH∥AB交OC于H，设圆的半径为2a，∵CD＝OB＝OA，CD∥AB，∴CE＝OE＝a，AE＝DE，由勾股定理得：AE＝＝a，∴AD＝2a，∵△ABF∽△DCF，∴＝＝，∵FH∥AB，∴＝＝，∵FH∥AB，∴＝＝，∴EF＝，∵CD是⊙O的切线，∴DC2＝DG•DA，即（2a）2＝DG•2a，解得：DG＝，∴FG＝a﹣﹣＝，∴＝＝．3．（1）证明：连接OC，∵PF＝FC，OC＝OB，∴∠PCF＝∠CPF，∠OCB＝∠OBC，∵PD⊥AB，∴∠PDB＝90°，∴∠CPF+∠OBC＝90°，∴∠PCF+∠OCB＝90°，∴∠FCO＝90°，∴OC⊥CF，∴CF是⊙O的切线．（2）证明：连接BG，∵，∴∠P AC＝∠PBG，∵∠PBA＝2∠P AC，∴∠PBA＝2∠PBG，∵AB为⊙O的直径，∴∠AGB＝∠PGB＝90°，∴∠APB＝∠P AB，∴AB＝BP；（3）解：∵AB为⊙O的直径，∴∠ACB＝90°，∵AC＝4，BC＝3，∴AB＝＝＝5，∴AB＝BP＝5，∴PC＝2，∵∠PDA＝∠PCA＝90°，P A＝P A，∠APB＝∠P AB，∴△APC≌△APD（AAS），∴AD＝PC＝2，PD＝AC＝4，∠P AC＝∠APD，∴AE＝PE，设DE＝x，AE＝PE＝4﹣x，在Rt△AED中，AD2+DE2＝AE2，即22+x2＝（4﹣x）2，解得x＝，∴EP＝4﹣x＝，∵∠PEC＝90°﹣∠EPC，∠FCE＝90°﹣∠PCF，即∠PEC＝∠FCE，∴EF＝CF＝PF，∴CF＝．4．解：（1）直线AF与⊙O相切．理由如下：连接OC，∵PC为圆O切线，∴CP⊥OC，∴∠OCP＝90°，∵OF∥BC，∴∠AOF＝∠B，∠COF＝∠OCB，∵OC＝OB，∴∠OCB＝∠B，∴∠AOF＝∠COF，∵在△AOF和△COF中，，∴△AOF≌△COF（SAS），∴∠OAF＝∠OCF＝90°，∴AF⊥OA，又∵OA为圆O的半径，∴AF为圆O的切线；（2）∵∠AOF＝∠COF，OA＝OC，∴E为AC中点，即AE＝CE＝AC，OE⊥AC，∵∠OAF＝90°，OA＝6，AF＝2，∴tan∠AOF＝，∴∠AOF＝30°，∴AE＝OA＝3，∴AC＝2AE＝6；（3）∵AC＝OA＝6，OC＝OA，∴△AOC是等边三角形，∴∠AOC＝60°，OC＝6，∵∠OCP＝90°，∴CP＝OC＝6，∴S△OCP＝OC•CP＝＝18，S扇形AOC＝＝6π，∴阴影部分的面积为S△OCP﹣S扇形AOC＝18﹣6π．5．（1）证明：连接OD，如图所示：∵AB为⊙O的直径，∴∠ADB＝90°．∴AD⊥BC．∵AB＝AC，∴CD＝BD＝BC．∵OA＝OB，∴OD是△ABC的中位线，∴OD∥AC．∵EF⊥AC，∴EF⊥OD．∵OD是半径，∴EF与⊙O相切．（2）证明：∵AB为直径，∴∠ADB＝90°，∴∠BAD+∠ABD＝90°，∵OD⊥DE，∴∠FDB+∠ODB＝90°，∵OB＝OD，∴∠OBD＝∠ODB，∴∠BAD＝∠FDB，∵∠F＝∠F，∴△FBD∽△FDA；（3）解：设⊙O的半径为r，则AB＝2r，∵△FBD∽△FDA，∴，∵DF＝4，BF＝2，∴，∴r＝3．6．解：（1）CG与⊙O相切，理由如下：如图1，连接CO，∵AB是⊙O的直径，∴∠ACB＝∠ACF＝90°，∵点G是EF的中点，∴GF＝GE＝GC，∴∠AEO＝∠GEC＝∠GCE，∵OA＝OC，∴∠OCA＝∠OAC，∵OF⊥AB，∴∠OAC+∠AEO＝90°，∴∠OCA+∠GCE＝90°，即OC⊥GC，∵OC是圆的半径，∴CG与⊙O相切；（2）证明：∵∠AOE＝∠FCE＝90°，∠AEO＝∠FEC，∴∠OAE＝∠F，又∵∠B＝∠B，∴△ABC∽△FBO，∴，即BO•AB＝BC•BF，∵AB＝2BO，∴2OB2＝BC•BF；（3）由（1）知GC＝GE＝GF，∴∠F＝∠GCF，∴∠EGC＝2∠F，又∵∠DCE＝2∠F，∴∠EGC＝∠DCE，∵∠DCE＝∠AOD＝45°，∴∠EGC＝45°，又∵∠OCG＝90°，∴△OCG为等腰直角三角形，∴GC＝OC，OG＝OC，∴OD+DG＝OC，即OC+2.5＝OC，解得OC＝，∵GF＝GE＝GC＝OC，∴DE＝GE﹣DG＝OC﹣DG＝．7．（1）证明：∵AD⊥BC，AD过圆心O，∴BD＝CD，且AD⊥BC，∴AB＝AC，∴∠B＝∠C；（2）证明：连接BE，设∠ACE＝α，则∠ACB＝3α，∴∠ABC＝∠ACB＝3α，∵∠ABE＝∠ACE＝α，∴∠CBE＝∠ABC﹣∠ABE＝3α﹣α＝2α，∴∠CAE＝∠CBE＝2α＝2∠ACE；（3）解：过点E作EG⊥AC于点G，在CG上截取GH＝AG，连接EH，∴EH＝AE＝5，∴∠AHE＝∠EAH＝2α，∴∠CEH＝∠AHE﹣∠ECH＝2α﹣α＝α＝∠ECH，∴CH＝EH＝5，∵AC＝AB＝13，∴AH＝AC﹣CH＝13﹣5＝8，∴AG＝GH＝4，∴CG＝4+5＝9，在Rt△AEG中，EG＝＝＝3，在Rt△CEG中，CE＝＝＝3，∵，∴，∴．8．解：（1）过点M作MN⊥AC于点N，∵圆M与AC相切，∴MN＝MB，∵∠ACB＝90°，AC＝6，∠B＝30°，∴AB＝12，设MN＝MB＝R．∴AM＝12﹣R，∵∠ACB＝90°，MN⊥AC，∴MN∥BC，∴∠B＝∠AMB＝30°，∴，∴，解得R＝24﹣36．（2）①连接DM，由题意可知MB＝MD，∴∠B＝∠MDB＝30°，∴∠AMD＝60°，∵AM＝2MB，∴AM＝2MD，∵∠ACB＝90°，∠B＝30°，∴AB＝2AC，∠BAC＝60°，∴△AMD∽△ABC，∴∠ADM＝∠ACB＝90°，∴AD与圆M相切；②∵AB＝12，AM＝2MB，∴BM＝4，AM＝8，∵∠ADM＝90°，∴AD＝＝4，∴S阴影部分＝4．9．（1）证明：∵OC＝OB，∴∠OBC＝∠OCB，∵DE⊥AB，∴∠OBC+∠DFB＝90°，∵EF＝EC，∴∠ECF＝∠EFC＝∠DFB，∴∠OCB+∠ECF＝90°，∴OC⊥CE，∴EC是⊙O的切线；（2）证明：∵AB是⊙O的直径，∴∠ACB＝90°，∴∠ABC+∠A＝90°，∠ABC+∠BFD＝90°，∴∠BFD＝∠A，∴∠A＝∠BFD＝∠ECF＝∠EFC，∵OA＝OC，∴∠OCA＝∠A＝∠BFD＝∠ECF＝∠EFC，∴△OAC∽△ECF；（3）解：∵AB是⊙O的直径，∴∠ACB＝90°，∵OB＝5，∴AB＝10，∴AC＝＝＝6，∵cos∠ABC＝，∴，∴BF＝5，∴CF＝BC﹣BF＝3，∵△OAC∽△ECF，∴，∴EC＝＝．10．（1）证明：如图1，连接OD．∵BC为⊙O的直径，∴∠BAC＝90°．∵AD平分∠BAC，∴．∴OD⊥BC，∵DE∥BC，∴OD⊥ED，又∵OD为半径，∴ED为⊙O的切线；（2）证明：由（1）可得△BCD为等腰直角三角形．∵DE∥BC，∴∠E＝∠ABC＝∠ADC，∠BDE＝∠DBC＝∠DCB＝45°．∴△BED∽△FDC，∴，即BD2＝DE•FC，又，∴BC2＝2ED•FC；（3）解：如图2，过点D作DG⊥AD，交AC的延长线于点G．∴∠CDG+∠ADC＝90°，∠DGC＝∠DAG＝45°．又∵∠ADB+∠ADC＝90°，∴∠ADB＝∠GDC，∵DB＝DC，∠BAD＝∠DGC＝45°，∴△ABD≌△GCD（AAS），∴AB＝CG．∵∠DAG＝45°，∠ADG＝90°，∴△ADG为等腰直角三角形，∴AB+AC＝AG＝AD＝＝3，∵tan∠ABC＝2，∴设AB＝x，则AC＝2x．∴3x＝3，∴x＝1．即AB＝1，AC＝2．∴BC＝＝＝．11．（1）证明：∵∠BMC＝∠BAD，又∵∠BMC＝∠BAC+∠ABD，∠BAD＝∠BAC+∠DAM，∴∠ABD＝∠DAC，又∵弧DC＝弧DC，∴∠DAC＝∠DBC，∴∠ABD＝∠CBD，∴BD平分∠ABC；（2）证明：连接OA、OB、OD，OD交AC于点N，∵FD是⊙O的切线，D为切点，OD是⊙O的半径，∴OD⊥FD，∴∠FDO＝90°，又∵∠AOD＝2∠ABD，∠DOC＝2∠DBC，∠ABD＝∠CBD，∴∠AOD＝∠COD，又∵AO＝CO，∴ON⊥AC，∴∠ANO＝90°，∴∠ANO＝∠FDO，∴AC∥FD；（3）解：连接OD，交AC于N，∵BC是⊙O的直径，∴∠BAC＝∠BDC＝90°，∴∠F AC＝180°﹣∠BAC＝90°，又∵∠ANO＝∠FDN＝90°，∴四边形ANDF是矩形，∴AF＝DN，∠F＝90°，又∵ON⊥AC，∴AN＝CN，∴设MN＝a，则AN＝CN＝MN+AM＝a+1，∴CM＝MN+CN＝2a+1，在Rt△MDC中，cos∠ACD＝，在Rt△NDC中，cos∠ACD＝，∴，解得a1＝﹣（舍去），a2＝1，∴MN＝1，CN＝a+1＝2，∴DN＝AF＝＝，又∵MN＝AM＝1，∠AMB＝∠NMD，∠BAM＝∠MND＝90°，∴△BAM≌△DNM（AAS），∴BA＝ND＝，∴BF＝AB+AF＝2，∴AN＝FD＝a+1＝2，∴BD＝＝2，∴S△BFD＝，S△DBC＝BD•CD＝＝3，∴S四边形BFDC＝S△BFD+S△BDC＝2．12．（1）证明：连接AD，∵AB是⊙O的直径，弦CD⊥AB，∴，∴∠ACD＝∠DC，∵，∴∠APC＝∠ADC，∴∠APC＝∠ACD；（2）证明：连接OP，∵PF是⊙O的切线，∴OP⊥PF，即∠EPF+∠OPE＝90°，∵OP＝OB，∴∠OPB＝∠OBP，∵CD⊥AB，∴∠HEB+∠HBE＝90°，∵∠PEF＝∠HEB，∴∠PEF＝∠FPE，∴FE＝PF；（3）解：过E作EM⊥PF，垂足为M，∵AG⊥PF，∴∠GAP+∠GP A＝90°，∵∠APE＝90°，∴∠GP A+∠EPM＝90°，∵∠AGP＝∠EMP＝90°，∴△GP A∽△MEP，∴，∵∠P AE＝∠F，∴tan∠P AE＝tan∠F，则，∵，∴，∴MF＝PG＝6，设PM＝x，∵PE2﹣PM2＝EF2﹣FM2，∴，解得：x1＝﹣10，x2＝4，即PM＝4，∴EM＝＝8，∵，即，∴P A＝3，∵CD⊥AB，AB是直径，∴∠BHE＝∠APB＝90°，∴∠HEB＝∠BAP，∵∠MPE＝∠HEB，∴tan∠P AB＝，即，∴PB＝6，∴BE＝PB﹣PE＝2，∵sin∠HEB＝，即，∴BH＝4．13．（1）证明：连接OC，如图1，∵AD＝CD，∠A＝30°，∴∠ACD＝30°，∴∠CDB＝60°，∵OD＝OC，∴∠OCD＝60°，∴∠ACO＝∠ACD+∠OCD＝90°，∵OC是半径，∴直线AC是⊙O的切线；（2）解：∵∠OCD＝60°，OC＝OD，∴△DCO是等边三角形，∴CD＝AD＝OD＝1，作CH⊥BD于点H，则DH＝，如图2，∴CH＝＝＝，∵AB＝AD+BD＝3，∴S△ABC＝＝．（3）①当点E运动到与点C关于直径AB对称时，CE⊥AB于点K，如图3，∵BD为⊙O的直径，CK＝，∴CE＝2CK＝，∵CF⊥CE，∴∠ECF＝90°，∵∠CDB＝∠CEB＝60°，∴CF＝CE•tan60°＝＝3，②∵点E在上运动过程中，∠CDB＝∠CEB＝60°，在Rt△ECF中，tan60°＝，∴CF＝CE，∴当CE最大时，CF取得最大值，∴当CE为直径，即CE＝2时，CF最大，最大值为2．14．（1）证明：连接AC，BC，∵OC＝OA，∴∠OCA＝∠OAC，∵PF是⊙O的切线，CE⊥AB，∴∠OCP＝∠F＝90°，∴AF∥OC，∴∠F AC＝∠OCA，∴∠F AC＝∠OAC，∴CA平分∠F AB．（2）证明：∵CD是直径，∴∠CBD＝90°，∴∠CBP＝90°，∵CE⊥OB，∴∠CEB＝∠CBP＝90°，∵PC切⊙O于点C，∴∠PCB＝∠CAB，∵AB是直径，∴∠ACB＝90°，∴∠ABC+∠CAB＝90°，∠BCE+∠ABC＝90°，∵∠CAB＝∠BCE，∴∠PCB＝∠BCE，∴△BCE∽△PCB，∴，∴BC2＝CE•CP；（3）解：，设CF＝3a，CP＝4a，∵BC2＝CE•CP＝3a•4a＝12a2，∴BC＝2a，在Rt△BCE中，sin∠CBE＝，∴∠CBE＝60°，∴∠BCE＝30°，∴△COB是等边三角形，∵AB＝4，∴OB＝BC＝2，∴劣弧BC的长＝＝π．15．（1）证明：∵BD是⊙O的切线，∴∠OBD＝90°，∠ABC+∠DBC＝90°，∵BC⊥OD，∴∠D+∠DBC＝90°，∴∠ABC＝∠D，∵∠AEC＝∠ABC，∴∠D＝∠AEC；（2）证明：连接AC，如图所示：∵OF⊥BC，∴，∴∠CAE＝∠ECB，∵∠CEA＝∠HEC，∴△CEH∽△AEC，∴，∴CE2＝EH•EA；（3）解：连接BE，过O作OG⊥BE于G，如图所示：∵AB是⊙O的直径，∴∠AEB＝90°，∵⊙O的半径为5，∴AB＝10，∵cos∠BCE＝，∴cos∠BAE＝＝，∴AE＝8，∴BE＝＝＝6，∵，∴BE＝CE＝6，∵CE2＝EH•EA，∴EH＝，在Rt△BEH中，BH＝．∵OG⊥BE，OB＝OE，∴BG＝3，∴OG＝＝＝4，∴BF•OE，∴BF＝，∴HF＝BH﹣BF＝．16．解：（1）∵点A（0，8），∴AO＝8，∵AD是⊙Q的直径，∴∠AEB＝∠AED＝90°，∴∠AEB＝∠AOB＝90°，∵BA垂直平分CD，∴BC＝BD，∴∠ABO＝∠ABE在△ABE和△ABO中，，∴△ABE≌△ABO（AAS），∴AE＝AO＝8；（2）∵∠ABE＝∠FDE，∴AB∥DF，∴△CAB∽△CDF，∴，又∵∠ABE＝∠FDE，∠AEB＝∠FED∴△DEF∽△BEA，∴，∴EF＝2AE＝16；（3）设BO＝x，则AB＝x+4，在Rt△ABO中，由AO2+OB2＝AB2得：82+x2＝（x+4）2，解得：x＝6，∴OB＝BE＝6，AB＝10，∵∠EAB+∠ABE＝90°，∠ACB+∠ABC＝90°，∴∠EAB＝∠ACB，∵∠BF A＝∠AFC，∴△BF A∽△AFC，∴；设EF＝m，则AF＝8+m，BF＝（8+m），∵在Rt△BEF中，BE2+EF2＝BF2，∴62+m2＝[（8+m）]2，解得：m＝，即EF＝，∴tan∠AFC＝．17．（1）证明：如图1，∵EF平分∠AED，∴∠AEF＝∠FED，∵∠AEF＝∠ADF，∴∠FED＝∠ADF，∵∠GFD＝∠DFE，∴△GFD∽△DFE；（2）证明：如图2，∵AE平分∠BAC，∴∠BAE＝∠EAO，∵OA＝OE，∴∠EAO＝∠OEA，∴∠BAE＝∠OEA，∴AB∥OE，∴∠OEC＝∠B，∵∠B＝90°，∴∠OEC＝90°，∵OE为半径，∴BC是⊙O的切线；（3）解：如图3，连接OF、AF，∵AD为直径，∴∠AFD＝∠AED＝90°，∵EF平分∠AED，∴∠AEF＝∠FED＝45°，∴∠AFD＝∠AEF＝45°，∴△AFD为等腰直角三角形，∵DF＝10，OA＝OD∴AD＝DF＝×10＝20，OF⊥AD，OA＝OD＝OF＝10，∵cos∠CAE＝，∴AE＝AD•cos∠CAE＝20×＝10，∵∠AEF＝∠ADF，∠AGE＝∠FGD，∴△AGE∽△FGD，∴，∴AG＝GF，∵AG＝AO+OG＝10+OG，∴10+OG＝GF，∴OG＝GF﹣10，在Rt△FOG中，GF2＝OF2+OG2，∴GF2＝102+（GF﹣10）2，解得：GF＝或（不符合题意，舍去），∴线段GF的长为．18．（1）证明：连接OB，∵PB是⊙O的切线，∴∠PBO＝90°，∵OA＝OB，BA⊥PO于D，∴AD＝BD，∠POA＝∠POB，又∵PO＝PO，∴△P AO≌△PBO（SAS），∴∠P AO＝∠PBO＝90°，∵OA为圆的半径，∴直线P A为⊙O的切线；（2）证明：∵∠P AO＝∠PDA＝90°，∴∠OAD+∠AOD＝90°，∠OP A+∠AOP＝90°，∴∠OAD＝∠OP A，∴△OAD∽△OP A，∴，∴OA2＝OD•OP，又∵AC＝2OA，∴AC2＝4OD•OP；（3）解：∵OA＝OC，AD＝BD，BC＝6，∴OD＝BC＝3，设AD＝x，∵tan∠F＝，∴FD＝2x，OA＝OF＝2x﹣3，在Rt△AOD中，由勾股定理，得，（2x﹣3）2＝x2+32，解之得，x1＝4，x2＝0（不合题意，舍去），∴AD＝4，OA＝2x﹣3＝5，∵AC是⊙O的直径，∴AC＝2OA＝10．∴AC的长为10．19．（1）证明：∵∠ACB＝90°，PE⊥AC，PF⊥BC，∴四边形PECF是矩形，∵CP平分∠ACB，PE⊥AC，PF⊥BC，∴PE＝PF，∴四边形CEPF是正方形；（2）解：∵sin A＝，AB＝10，∴，∴BC＝8，∴AC＝＝＝6，∴tan A＝，设PE＝CE＝m，则AE＝6﹣m，∴tan A＝，∴m＝，∴PC＝PE＝；（3）解：∵四边形CEPF是正方形，∴PE＝PF，∠APE+∠BPF＝90°，∠PEA＝∠PFB＝90°，∴将△APE绕点P顺时针旋转90°，得到△A′PF，P A′＝P A，如图所示：则A′、F、B三点共线，∠APE＝∠A′PF，∴∠A′PF+∠BPF＝90°，即∠A′PB＝90°，∴S△P AE+S△PBF＝S△P A′B＝P A′•PB＝x（10﹣x），∴y与x之间的函数关系式为y＝﹣+5x，∵y＝﹣+5x＝﹣，∴x＝5时，y有最大值为．20．解：（1）如图①，AD⊥BC，∵△ABC为等边三角形，AB＝2，∴∠B＝60°，BC＝AB＝2，∵AD⊥BC，∴∠ADB＝90°，在Rt△ABD中，＝sin B＝sin60°，∴＝，∴AD＝，∴△ABC的面积＝AB•AD＝×2×＝，故答案为：；（2）如图②，过点D作DH⊥BC于点H，∵∠ABC＝90°，BD是△ABC的角平分线，∴∠DBC＝∠ABD＝45°，∵DE⊥BD，∴∠BDE＝90°，∴∠DEB+∠DBE＝90°，∴∠DEB＝90°﹣∠DBE＝90°﹣45°＝45°，∴BD＝ED，∵DH⊥BC，∴BH＝EH，∴DH＝BE＝BH＝EH，设DH＝BH＝EH＝a，∵∠ABC＝90°，∴AB⊥BC，∵DH⊥BC，∴AB∥DH，∴△CDH∽△CAB，∴＝＝，∵AD＝1，AC＝3，∴CD＝3﹣1＝2，∴＝＝，∴AB＝a，CE＝a，∴BC＝CE+BE＝a+2a＝3a，∵AB2+BC2＝AC2，∴a2+9a2＝9，∴a2＝1，∴S阴影＝S△ABC﹣S△BDE＝AB•BC﹣BE•DH＝×a•3a﹣×2a•a＝a2﹣a2＝a2＝1；（3）①设AC与BD相交于点E，连接OB，OA，OC，过点O作OH⊥AB于点H，∵∠ADB＝∠BDC＝60°，∴AB＝BC，∠BAC＝∠BDC＝60°，∴△ABC是等边三角形，∴∠ACB＝60°，AB＝AC＝BC，在△ABO和△ACO中，，∴△ABO≌△ACO（SSS），同理△ABO≌△CBO（SSS），∴S△ABO＝S△ACO＝S△CBO，∴S△ABC＝3S△ABO，∵∠AOB＝2∠ACB，∴∠AOB＝120°，在Rt△OAH和Rt△OBH中，，∴Rt△OAH≌Rt△OBH（HL），∴∠AOH＝∠BOH，AH＝BH，在Rt△OAH中，OA＝4，∠AOH＝∠AOB＝60°，∴cos∠AOH＝cos60°＝＝，sin∠AOH＝sin60°＝＝，∴OH＝OA＝2，AH＝OA＝2，∴AB＝2AH＝4，∴S△ABC＝3S△ABO＝3××4×2＝12，∵∠ABE＝∠DBA，∠BAE＝∠BDA＝60°，∴△ABE∽△DBA，∴＝＝＝，即S△DBA＝S△ABE，∵∠CBE＝∠DBC，∠BCE＝∠BDC＝60°，∴△CBE∽△DBC，∴＝＝＝，即S△DBC＝S△CBE，∴S四边形ABCD＝S△DBA+S△DBC＝S△ABE+S△CBE，＝（S△ABE+S△CBE）＝S△ABC＝×12＝x2，∴S△ADC＝S四边形ABCD﹣S△ABC＝x2﹣12，即y＝x2﹣12；∵BD的长度大于AB，小于等于直径，∴4＜x≤8，∴y与x之间的函数关系式为y＝x2﹣12（4＜x≤8）；②由①知，y与x之间的函数关系式为y＝x2﹣12，则对称轴为y轴，∵＞0，∴x＞0时，y随x的增大而增大，∵4＜x＜8，∴当x＝8时，y有最大值，即当BD为⊙O的直径时，y取最大值，即y＝×82﹣12＝4，∴花卉区域△ADC面积的最大值是4．。

压轴题圆的五种考法(解析版)--九年级数学常考压轴题

压轴题圆的五种考法目录解题知识必备压轴题型讲练类型一、四点共圆类型二、圆中最值问题类型三、定点定长构造辅助圆类型四、定弦定角构造辅助圆类型五、对角互补构造辅助圆压轴能力测评(10题)类型一、四点共圆一．填空题1.(2022秋•大丰区期中)如图，ΔABC中，AD⊥BC，∠B=45°，∠C=30°．以AD为弦的圆分别交AB、AC于E、F两点．点G在AC边上，且满足∠EDG=120°．若CD=4+22，则ΔDEG的面积的最小值是．【分析】连接EF，利用四点共圆和同弧所对的圆周角相等证明EF⎳DG，从而得到SΔEDG=S△EDG，当FG最小时，ΔDFG的面积就最小，作ΔDFG的外接圆O，过O点作OH⊥FG交于点H，连接OF、OG，DO+OH=12+22FG，当DO+OH最小时，FG就最小，当D、O、H三点共线时，DO+OH最小，此时DH⊥FG，在RtΔFHO中，(2FH)2=FH2+(2+2-2FH)2，求出FH=2，可得FG的最小值为22，再求SΔDFG =22+2，即ΔDEG的面积的最小值为22+2．【解答】解：连接EF，AD⊥BC，∠B=45°，∠C=30°，∴∠B=45°，∠DAC=60°，∵∠BAC=105°，∵A、E、F、D四点共圆，∴∠EDF=75°，∵∠EDG=120°，∴∠FDG=45°，∵ED =ED ，∴∠EFD =∠FDG ，∴EF ⎳DG ，∴S ΔEDG =S △EDG ，∵CD =4+22，∠C =30°，∴AC =833+463，AD =433+263，∴AC 边上的高=AD ⋅DC AC=2+2，∴当FG 最小时，ΔDFG 的面积就最小，作ΔDFG 的外接圆O ，过O 点作OH ⊥FG 交于点H ，连接OF 、OG ，∵∠FDG =45°，∴∠FOG =90°，∵OF =GO ，∴ΔFOG 是等腰直角三角形，∵∠FOH =12∠FOG =45°，∴ΔFOH 是等腰直角三角形，∴FH =OH =12FG ，FO =2FH ，∴DO +OH =22FG +12FG =12+22FG ，∴当DO +OH 最小时，FG 就最小，∵DO +OH ≥DH ，∴当D 、O 、H 三点共线时，DO +OH 最小，此时DH ⊥FG ，∴DH =2+2，在Rt ΔFHO 中，(2FH )2=FH 2+(2+2-2FH )2，解得FH =2或FH =4+32，∵OH =2+2=FH +FO ，∴FH =2，∴FG 的最小值为22，∴S ΔDFG =12×22×(2+2)=22+2，∴ΔDEG 的面积的最小值为22+2，故答案为：22+2．【点评】本题考查圆的综合应用，熟练掌握圆心角与圆周角的关系，四点共圆的性质，三角形外接圆的性质是解题的关键．二．解答题2.(2022秋•建湖县期中)如图，在⊙O 的内接四边形ABCD 中，DB =DC ，∠DAE 是四边形ABCD 的一个外角．(1)若∠DAE =75°，则∠DAC =°；(2)过点D 作DE ⊥AB 于E ，判断AB 、AE 、AC 之间的数量关系并证明；(3)若AB =6、AE =2，求BD 2-AD 2的值．【分析】(1)根据四边形外接圆的性质，同弧所对的圆周角相等，可得∠DCB=∠DBC=∠DAC=75°；(2)过点D作DF⊥AC于点F，可证明ΔBDE≅ΔCDF(AAS)，ΔADE≅ΔADF(AAS)，则AC=AF+FC= AE+BE=AE+AE+AB=2AE+AB；(3)在RtΔBDE中，BD2=64+DE2，在RtΔAED中，AD2=4+ED2，再求解即可．【解答】解：(1)∵四边形ABCD是圆O的内接四边形，∴∠BCD+∠BAD=180°，∵∠DAE是四边形ABCD的一个外角，∴∠DAE=∠BCD，∵BD=CD，∴∠CBD=∠DCB，∵弧CD所对的圆周角分别为∠CAD、∠CBD，∴∠CBD=∠CAD，∵∠DAE=75°，∴∠DCB=∠DBC=∠DAC=75°，故答案为：75；(2)过点D作DF⊥AC于点F，∵DE⊥AB，∴∠DEA=90°，∵∠ABD=∠ACD，BD=CD，∠E=∠DFC=90°，∴ΔBDE≅ΔCDF(AAS)，∴DE=DF，AE=CF，∴∠ADE=∠ADF，又∵∠E=∠AFD，AD=AD，∴ΔADE≅ΔADF(AAS)，∴AE=AF，∴AC=AF+FC=AE+BE=AE+AE+AB=2AE+AB，即AC=2AE+AB；(3)在RtΔBDE中，BD2=BE2+DE2，在RtΔAED中，AD2=AE2+ED2，∵AB=6，AE=2，∴BE=8，∴BD2=64+DE2，AD2=4+ED2，∴BD2-AD2=60．【点评】本题考查圆的综合应用，熟练掌握同弧所对的圆周角相等，四点共圆的性质，直角三角形勾股定理，三角形全等的判定及性质是解题的关键．3.(2023秋•鄞州区期中)如图，在△ABC 中，点D ，E 为AB ，AC 上的点，BE =CD ，DC ，BE 交于F ，△BDF 与△CEF 的外接圆相交于点G (异于F )，H 1，H 2分别为△ABC 和△ADE 的垂心．证明：(1)GF 平分∠BFC ；(2)H 1，H 2，G 三点共线．(注：利用坐标系、复数解题者不给分)【分析】(1)通过证明△BGE ≅△DGC 得出DG =BG ，然后由BG =DG 推导出∠BFG +∠DFG =180°，再由邻补角的性质得出∠BFG =∠GFC ，即可证明结论；(2)根据题意构造B 、E 、B ′、E ′四点共⊙P ，以及D 、C 、D ′、C ′四点共⊙Q ，然后由相似三角形推导出点H 1、H 2对于⊙P 和⊙Q 等幂，再由根轴的性质得出H 1H 2是PQ 的垂直平分线，最后根据GP =GQ 得到GM ⊥PQ ，进而证得三点共线．【解答】(1)证明：在△BGE 和△DGC 中，∠GBE =∠GDC ，BE =CD ，∠GEB =∠GCD ，∴△BGE ≅△DGC (ASA )．∴DG =BG ，∴BG =DG ，∵DBG +DG =2πR (R 为△BDF 的外接圆半径)．∴∠BFG +∠DFG =180°．又∵∠GFC +∠DFG =180°，∴∠BFG =∠GFC ，∴GF 平分∠BFC ．(2)证明：连接BH 1、DH 2并延长分别交AC 于B ′、D ′，连接CH 1、EH 2并延长交AB 于C ′、E ′．BE 中点为P ，CD 中点为Q .∵BB ′⊥AC ，EE ′⊥AB ，∴B 、E 、B ′、E ′四点共⊙P ．∵DD ′⊥AC ，CC ′⊥AB ，∴D 、C 、D ′、C ′四点共⊙Q ．∵∠DE ′H 2=∠ED ′H 2，∠DH 2E ′∽△EH 2D ′，∴△DE ′H2∽△ED ′H 2，∴DH 2:EH 2=E ′H 2:D ′H 2，∴DH 2⋅D ′H 2=EH 2⋅E ′H 2．同理得CH 1⋅C ′H 1=BH 1⋅B ′H 1．∴H 1，H 2在⊙P 和⊙Q 的根轴上．∵⊙P 和⊙Q 的根轴是过两圆的交点的直线．∴H 1，H 2在⊙P 和⊙Q 的公共弦JK 上．又∵BE =CD ，即⊙P 和⊙Q 是等圆，∴四边形PJQK 为菱形．∴H 1H 2是PQ 的垂直平分线，M 为PQ 中点．由(1)知△BGE ≅△DGC ，∵GP 、GQ 分别为△BGE 和△DGC 的对应边上的中线，∴GP =GQ ，∴点G 在PQ 的垂直平分线上．∴H 1，H 2，G 三点共线．【点评】本题考查了全等三角形的判定和性质，圆周角定理，圆幂定理，菱形的性质，等腰三角形的性质等．本题辅助线繁多，综合性强，通过四点共圆判断出H 1、H 2两点对于⊙P 和⊙Q 等幂是解答本题的关键．4.(2022秋•沙坪坝区校级期中)在ΔABC 中，已知AB =AC ，作AM ⊥BC ，D 是AM 上一点，∠DBC =30°，连接BD 、CD ，在BD 上截取DE =AD ，连接AE ．(1)如图1所示，若∠BAC =90°，AD =3，求ΔABE 的周长；(2)如图2所示，若分别取AE 、AC 的中点N 、H ，连接MN 、MH ，求证：MN =MH ；(3)如图3所示，∠BAC =90°，BC =2，将AC 沿着直线AP 翻折得到AQ ，连接BQ ，直线BQ 交AP 于点P ，N 为AE 中点，当PN 取得最小值时，请直接写出ΔAPN 的面积．【分析】(1)过点D 作DL ⊥AE 于L ，则∠ALD =∠ELD =90°，由∠DBC =30°，可得BD =2DM ，设DM =x ，则BD =2x ，由勾股定理可得BM =3x ，AM =x +3，可得BM =CM =AM =33+32，AB =2BM =2×33+32=36+322，利用勾股定理可得AL =AD 2-DL 2=(3)2-32 2=32，进而可得AE =2AL =2×32=3，即可求得答案；(2)延长AM 至F ，使MF =AM ，在DF 上截取DT =DE ，连接EF ，ET ，设∠ABM =α，则∠BAM =90°-α，可证得ΔDET 是等边三角形，得出：DT =ET =DE =AD ，∠DTE =60°，再证得ΔABD ≅ΔEFT (SAS )，可得AB =EF =AC ，利用三角形中位线定理可得MN =12EF ，再由直角三角形性质可得MH =12AC ，即可证得结论；(3)连接CP ，先证得点P 在ΔABC 的外接圆⊙M 上，当且仅当点P 为半径MP 经过点N 时，PN 取得最小值，连接DN ，过点N 作NG ⊥AM 于G ，利用解直角三角形可得DM =BM ⋅tan30°=33，AD =DE =1-33，AN =EN =32AD =321-33 ，NG =12AN =12×321-33 =3-14，AG =3NG =3-34，GM =AM -AG =1-3-34=1+34，由勾股定理可得MN =GM 2+NG 2=1+34 2+3-14 2=22，PN =MP -MN =1-22，再利用S ΔAPN S ΔAMN =PN MN=2-1，即可求得答案．【解答】(1)解：过点D 作DL ⊥AE 于L ，则∠ALD =∠ELD =90°，∵∠BAC =90°，AB =AC ，AM ⊥BC ，∴AM =BM =CM ，∠BMD =90°，∠ABM =∠BAM =45°，∵∠DBC =30°，∴BD =2DM ，设DM =x ，则BD =2x ，∴BM =BD 2-DM 2=(2x )2-x 2=3x ，AM =x +3，∴3x =x +3，∴x =3+32，∴BM =CM =AM =33+32，∴AB =2BM =2×33+32=36+322，∵DE =AD ，∴∠DAE =∠DEA ，∵∠DAE +∠DEA =∠BDM =90°-30°=60°，∴∠DAE =∠DEA =30°，∴∠BAE =∠BAM -∠DAE =45°-30°=15°，∵∠ABD =∠ABM -∠DBC =45°-30°=15°，∴∠BAE =∠ABD ，∴AE =BE ，在Rt ΔADL 中，DL =12AD =32，∴AL =AD 2-DL 2=(3)2-322=32，∵DE =AD ，DL ⊥AE ，∴AE =2AL =2×32=3，∴ΔABE 的周长=AB +AE +BE =36+322+3+3=36+32+122；(2)证明：延长AM 至F ，使MF =AM ，在DF 上截取DT =DE ，连接EF ，ET ，设∠ABM =α，则∠BAM =90°-α，∵∠DBC =30°，∴∠BDT =60°，∠ABD =α-30°，BD =2DM ，∵DE =AD ，∴∠AED =∠DAE =30°，∴ΔDET 是等边三角形，∴DT =ET =DE =AD ，∠DTE=60°，∵AF =2(AD +DM )=AT +FT ，∴FT =2DM =BD ，∵∠EDT =∠ETD =60°，∴∠ADB =180°-60°=120°=∠ETF ，在ΔABD 和ΔEFT 中，AD =ET∠ADB =∠ETF BD =FT，∴ΔABD ≅ΔEFT (SAS )，∴AB =EF ，∵AB =AC ，∴EF =AC ，∵N 、M 分别是AE 、AF 的中点，∴MN =12EF ，∵点H 是Rt ΔACM 斜边AC 的中点，∴MH =12AC ，∴MN =MH ；(3)解：如图，连接CP ，由翻折得：∠ACP =∠AQP ，AC =AQ ，∵AB =AC ，∠BAC =90°，BC =2，AM ⊥BC ，∴AB =AQ ，AM =BM =CM =1，∴∠ABP =∠AQB ，∵∠AQB +∠AQP =180°，∴∠ABP +∠ACP =180°，∴点P 在ΔABC 的外接圆⊙M 上，当且仅当点P 为半径MP 经过点N 时，PN 取得最小值，如图，连接DN ，过点N 作NG ⊥AM 于G ，∵∠DBC =30°，∴DM =BM ⋅tan30°=33，∴AD =DE =1-33，∴AN =EN =32AD =321-33，∵∠AGN =90°，∠NAG =30°，∴NG =12AN =12×321-33 =3-14，∴AG =3NG =3-34，∴GM =AM -AG =1-3-34=1+34，在Rt ΔMNG 中，MN =GM 2+NG 2=1+342+3-14 2=22，∴PN =MP -MN =1-22，∴SΔAPNSΔAMN=PNMN=1-2222=2-1，∵SΔAMN=12AM⋅NG=12×1×3-14=3-18，∴SΔAPN=(2-1)SΔAMN=(2-1)×3-18=6-3-2+18．【点评】本题是几何综合题，考查了等腰三角形性质，等腰直角三角形性质，直角三角形性质，等边三角形性质，全等三角形的判定和性质，勾股定理，圆内接四边形的判定，三角形面积等，涉及知识点多，难度大，添加适当的辅助线是解题的关键与难点．5.(2022秋•鼓楼区期中)以下是“四点共圆”的几个结论，你能证明并运用它们吗？Ⅰ．若两个直角三角形有公共斜边，则这两个三角形的4个顶点共圆(图1、2)；Ⅱ．若四边形的一组对角互补，则这个四边形的4个顶点共圆(图3)；Ⅲ．若线段同侧两点与线段两端点连线的夹角相等，则这两点和线段两端点共圆(图4)．(1)在图1、2中，取AC的中点O，根据得OA=OB=OC=OD，即A，B，C，D共圆；(2)在图3中，画⊙O经过点A，B，D(图5)．假设点C落在⊙O外，BC交⊙O于点E，连接DE，可得=180°，所以∠BED=，得出矛盾；同理点C也不会落在⊙O内，即A，B，C，D共圆．结论Ⅲ同理可证．(3)利用四点共圆证明锐角三角形的三条高交于一点．已知：如图6，锐角三角形ABC的高BD，CE相交于点H，射线AH交BC于点F．求证：AF是ΔABC的高．(补全以下证明框图，并在图上作必要标注)(4)如图7，点P是ΔABC外部一点，过P作直线AB，BC，CA的垂线，垂足分别为E，F，D，且点D，E，F在同一条直线上．求证：点P在ΔABC的外接圆上．【分析】(1)根据直角三角形斜边中线的性质可得结论；(2)由圆周角的性质可得∠BED+∠A=180°，再结合题干条件，得出矛盾，由此可得出结论；(3)如图，连接DE，由点B、C、D、E四点共圆得∠BDE=∠ECB，由点A、D、H、E四点共圆得∠BDE=∠BAF，从而证明∠BAF+∠ABF=90°即可；(4)连接BP和CP，由点A，E，P，F四点共圆可得，∠BEF=∠BPF，由点C，P，D，F四点共圆可得∠CDF =∠CPF，再由外角的性质及角的和差可得∠BAC=∠BPC，由此可得点A，B，C，P四点共圆，即点P在ΔABC的外接圆上．【解答】解：(1)在图1、2中，取AC的中点O，根据直角三角形斜边上的中线等于斜边的一半，得OA=OB= OC=OD，即A，B，C，D共圆；故答案为：直角三角形斜边上的中线等于斜边的一半；(2)在图3中，画⊙O经过点A，B，D(图5)．假设点C落在⊙O外，BC交⊙O于点E，连接DE，可得∠BED+∠A=180°，∴∠BED=180°-∠A，得出矛盾；同理点C也不会落在⊙O内，即A，B，C，D共圆．结论Ⅲ同理可证．故答案为：∠BED+∠A；180°-∠A；(3)如图6，连接DE，由点B、C、D、E四点共圆得∠BDE=∠ECB，由点A、D、H、E四点共圆得∠BDE=∠BAF，∴∠ECB=∠BAF，∵∠BEC=90°，∴∠ECB+∠ABF=90°，∴∠BAF+∠ABF=90°，∴∠BFA=90°，∴AF为ΔABC的边BC上的高．(4)如图7，连接BP和CP，由点A，E，P，F四点共圆可得∠BEF=∠BPF，由点C，P，D，F四点共圆可得∠CDF=∠CPF，∵∠ADE=∠CDF，∴∠ADE=∠CPF，∵∠BAC=∠BEF+∠ADE，∠BPC=∠BPF+∠CPF，∴∠BAC=∠BPC，∴点A，B，C，P四点共圆，即点P在ΔABC的外接圆上．【点评】本题考查了圆的定义，直角三角形斜边上的中线等于斜边一半，圆内接四边形对角互补，圆周角定理，内心的定义．第(3)(4)题解题关键是选取适当的四点证明共圆，再利用圆周角定理证明角相等．类型二、圆中最值问题一．填空题6.(2022秋•长沙期中)如图，⊙O 的半径为1，P A ，PB 为⊙O 的切线，切点为A ，B ，∠APB =60°，点M 为劣弧AB 上一动点，过点M 作⊙O 的切线，分别交P A ，PB 于点E ，F ，EF 的最小值是．【分析】由切线的性质定理，全等三角形的判定和性质，三角形外心的性质，可以求解．【解答】解：连接OA ，OE ，OM ，OF ，OB ，∵P A ，PB 为⊙O 的切线，EF 切⊙O 于M ，∴OA ⊥P A ，OB ⊥PB ，OM ⊥EF ，∵四边形PBOA 内角和是360°，∴∠P +∠AOB =360°-∠P AB -∠PBA =180°，∴∠AOB =180°-∠P =120°，∵OE =OE ，OA =OM ，∴Rt ΔOAE ≅Rt ΔOME (HL )，∴∠AOE =∠MOE ，同理：∠MOF =∠BOF ，∴∠EOF =∠EOM +∠FOM =12∠AOB =60°，设ΔOEF 的外心是点C ，作CH ⊥EF 于H ，连接CO ，CE ，CF ，OM ，∵点C 是ΔOEF 的外心，∴OC =EC =FC ，∴∠CEF =∠CFE ，EH =FH ，∵∠ECF =2∠EOF =120°，∴∠CEF =30°，∴CH =12CE =12OC ，∵OC +CH ≥OM ，∴3CH ≥1，∴CH ≥13，∵tan ∠CEH =CH EH，∴EH =3CH ，∴EF =2EH =23CH ，∴EF ≥233，∴EF 的最小值是233，故答案为：233．【点评】本题考查有关圆的最值问题，关键是掌握切线的性质定理，全等三角形的判定和性质，三角形外心的性二．解答题7.(2022秋•东城区校级期中)对于平面直角坐标系xOy中的图形G和点P给出如下定义；Q为图形G上任意一点，若P，Q两点间距离的最大值和最小值都存在，且最大值是最小值的k倍，则称点P为图形G 的“k分点”．已知点N(3,0)，A(1,0)，B(0,3)，C(1,-1)．(1)①在点A，B，C中，线段ON的“2分点”是；②点D(a,0)，若点C为线段OD的“二分点”，求a的值；(2)以点O为圆心，r为半径画图，若线段AN上存在⊙O的“二分点”，直接写出r的取值范围．【分析】(1)①分别求出点A、B、C到线段ON的最小值和最大值，看是否满足“2分点”定义即可，②对a的取值分情况讨论：0<a≤1，1<a≤2，a>2和a<0，根据“二分点”的定义可求解，(2)设线段AN上存在⊙O的“二分点”为M(m，0)(1≤m≤3)．对r的取值分情况讨论0<r≤1，1<r<3且m<r，1<r<3且m>r，r≥3，根据二分点的定义可求解．【解答】(1)解：①如图，∵点A在ON上，故最小值为0，不符合题意，点B到ON的最小值为OB=3，最大值为BN=32+32=32，∴点B是线段ON的“2分点”，点C到ON的最小值为1，最大值为CN=22+12=5∴点C不是线段ON的“2分点”，故答案为：点B；②当0<a≤1时，点C到OD的最小值为CD=(1-a)2+(-1)2=2-2a+a2，点C到OD的最大值为CO=12+(-1)2=2，∴2=22-2a+a2，即2a2-4a+3=0，∵△<0，故无解，舍去；当1<a≤2时，点C到OD的最小值为1，点C到OD的最大值为CO=12+(-1)2=2，最大值不是最小值的2倍，所以舍去，当a>2时，点C到OD的最小值为1，点C到OD的最大值为CD=(a-1)2+(0-1)2=a2-2a+2，∵点C为线段OD的“二分点”，∴a2-2a+2=2×1，a1=1+3,a2=1-3(舍去)，当a<0时，点C到OD的最小值为CO=12+(-1)2=2，点C到OD的最大值为CD=(1-a)2+(-1-0)2=a2-2a+2，∵点C为线段OD的“二分点”，同0<a≤1时，无解，舍去；综上，a=1+3．(2)如图所示，设线段AN上存在⊙O的“二分点”为M(m，0)(1≤m≤3)，当0<r≤1时，最小值为：m-r，最大值为：m+r，m，∴2(m-r)=m+r，即r=13∵1≤m≤3，≤r≤1，∴13当1<r<3且m<r时，最小值为：r-m，最大值为r+m，∴2(r-m)=r+m，即r=3m，∵1≤m≤3，∴3≤r≤9，∵1<r<3，∴r不存在，当1<r<3且m>r时，最小值为：m-r，最大值为：m+r，m，∴2(m-r)=r+m，即r=13≤r≤1，∴13∵1<r<3，∴r 不存在．当r ≥3时，最小值为：r -m ，最大值为：m +r ，∴2(r -m )=r +m ，即r =3m ，∴3≤r ≤9．综上所述，r 的取值范围为13≤r ≤1或3≤r ≤9．【点评】本题考查坐标上的两点距离，勾股定理，点到圆的距离．根据题目所给条件，掌握“k 分点”的定义是解题的关键．8.(2022秋•江阴市期中)如图，在平面直角坐标系中，点A 的坐标为(-3，0)，点B 在y 轴的正半轴上，且∠ABO =30°，以点B 为圆心，1为半径画⊙B ，与y 轴交于点C (点C 在点B 的下方)，点Q 是AB 的中点，点P 是⊙B 上的一个动点，从点C 开始以5度/秒的速度沿圆周逆时针运动一周，设运动时间为t 秒．(1)如图1，连接OQ ，当OQ ⎳BP 时，求t 的值；(2)如图2，点P 在运动过程中，连接AP ，以AP 为边在左侧作等边ΔAPD ，①当t =12秒时，求点D 的坐标；②连接DQ ，当DQ 最大时，求此时t 的值和这个最大值．【分析】(1)如图，过点B 作BP ⎳OQ ，交⊙B 于点P 1，P 2，由平行得出点P 的旋转角，进而可得出时间t ；(2)①将线段AB 绕点A 逆时针旋转60°到线段AB ′，连接B ′D ，易证△AB ′D ≅ΔABP (SAS )，所以B ′D =BP =1，∠AB ′D =∠ABP =90°；过点B ′作B ′N ⊥x 轴于点N ，过点D 作DM ⊥B ′N 于点M ，所以∠M =∠ANB ′=90°，由互余可知，∠MBD ′=∠B ′AN ，所以∠B ′AB =60°，∠BAO =60°，所以∠B ′AN =60°，AN =3，B ′N =3，则MB ′=12，MD =32，进而可得点D 的坐标；②由旋转可知，点D 在以点B ′为圆心，1长为半径的圆上运动，当DQ 最大时，点D ，B ′，Q 三点共线，设⊙B与y 轴的另一个交点为C ′，则C ′(0,4)，OC ′=4，由点Q 是AB 的中点可知，Q -32，32，B ′(-23，3)，进而可得B ′Q =3，所以DQ =4，易证△AB ′Q ≅ΔABO (SSS )，进而可得ΔADQ ≅△AC ′O (SAS )，所以AD =AC ′，即此时点P 与点C ′重合，所以t =180°5°=36．【解答】解：(1)如图：∵ΔABO 是直角三角形，Q 是AB 中点，∴OQ =QA =QB ，∴∠BOQ =∠ABO =30°，又∵OQ ⎳BP 1，∴∠OBP 1=∠BOQ =30°，∴点P 的轨迹是⊙B 中30°圆心角所对的弧，∴t =30°5°=6，∵当点P 运动到P 1B 延长线与⊙B 的交点P 2时，点P 的轨迹是⊙B 中180°+30°=210°圆心角所对的弧，∴t =210°5°=42．故t 的值为6或42；(2)①如图，∵∠ABO =30°，OA =3，∴OB =3，AB =23，当t =12时，∠CBP =60°，∴∠ABP =90°，将线段AB 绕点A 逆时针旋转60°到线段AB ′，连接B ′D ，由旋转可知，∠BAB ′=60°，AB =AB ′=23，∵ΔADP 是等边三角形，∴∠DAP =60°，AD =AP ，∴∠B ′AD =∠BAP ，∴△AB ′D ≅ΔABP (SAS )，∴B ′D =BP =1，∠AB ′D =∠ABP =90°，过点B ′作B ′N ⊥x 轴于点N ，过点D 作DM ⊥B ′N 于点M ，∴∠M =∠ANB ′=90°，∴∠AB ′N +∠B ′AN =90°，∠MB ′D +∠AB ′N =90°，∴∠MB ′D =∠B ′AN ，∵∠B ′AB =60°，∠BAO =60°，∴∠B ′AN =60°，AN =3，B ′N =3，∴∠MB ′D =60°，∴MB ′=12，MD =32，∴MN =72．∴D -332，72；②由旋转可知，点D 在以点B ′为圆心，1长为半径的圆上运动，∴当DQ 最大时，点D ，B ′，Q 三点共线，如图所示，设⊙B 与y 轴的另一个交点为C ′，∴C ′(0,4)，∴OC ′=4，∵点Q 为AB 的中点，∴AQ =BQ =3，AB ′=AB =23，由①可知，B (0,3)，∴Q -32，32，B ′(-23，3)，∴DQ =4，∴B ′Q =BO ，AQ =BQ =3，AB ′=AB =23，∴△AB ′Q ≅ΔABO (SSS )，∴∠AQB ′=∠AOB =90°，∵DQ =OC ′，AQ =AO ，∴ΔADQ ≅△AC ′O (SAS )，∴AD =AC ′，即此时点P 与点C ′重合，∴t =180°5°=36．综上，t =36，DQ 最大值是4．【点评】本题属于圆的综合题，涉及考查旋转的性质，等边三角形的性质，全等三角形的性质与判定，相似三角形的相似与判定，含30°的直角三角形的三边关系，根据题意得出点D 的轨迹是解题关键．类型三、定点定长构造辅助圆一．填空题9.(2023秋•常州期中)如图，点A ，B 的坐标分别为A (4,0)，B (0,4)，C 为坐标平面内一点，BC =2，点M 为线段AC 的中点，连接OM ，OM 的最大值为．【分析】先判断出点C 的运动轨迹是在半径为2的⊙B 上，再取OD =OA =4，连接OD ，则OM 是ΔACD 的中位线，OM =12CD ，进而可得OM 最大值时，CD 取最大值，此时D 、B 、C 三点共线，计算即可求出结果．【解答】解：∵C 为坐标平面内一点，BC =2，∴点C 的运动轨迹是在半径为2的⊙B 上，如图，取OD =OA =4，连接OD ，∵点M 为线段AC 的中点，∴OM 是ΔACD 的中位线，∴OM =12CD ，∴OM 最大值时，CD 取最大值，此时D 、B 、C 三点共线，此时在Rt ΔOBD 中，BD =42+42=42，∴CD =2+42，∴OM 的最大值是1+22．故答案为：1+22．【点评】本题考查了坐标和三角形的中位线，定点定长构造辅助圆等，解题关键是确定点C 的运动轨迹．二．解答题10.(2022秋•秀洲区期中)如图，ΔABC 中，AC =BC =4，∠ACB =90°，过点C 任作一条直线CD ，将线段BC 沿直线CD 翻折得线段CE ，直线AE 交直线CD 于点F ．(1)小智同学通过思考推得当点E 在AB 上方时，∠AEB 的角度是不变的，请按小智的思路帮助小智完成以下推理过程：∵AC =BC =EC ，∴A 、B 、E 三点在以C 为圆心以AC 为半径的圆上．∴∠AEB =∠ACB =°．(2)若BE =2，求CF 的长．(3)线段AE 最大值为；若取BC 的中点M ，则线段MF 的最小值为．【分析】(1)根据AC =BC =EC ，得A 、B 、E 三点在以C 为圆心以AC 为半径的圆上，根据圆周角定理可知∠AEB 的度数；(2)由ΔEFG 是等腰三角形可求出FG =1，利用勾股定理求出CG 的长，从而得出答案；(3)根据直径是圆中最大的弦知当AE 经过圆心C 时，线段AE 的最大值为2AC =8，取AB 的中点O ，连接OF ，可证∠AFB =90°，则点F 在以AB 为直径的圆O 上，当OF 经过点M 时，MF 最短，此时OF ⊥BC ，从而解决问题．【解答】解：(1)∵AC =BC =EC ，∴A 、B 、E 三点在以C 为圆心以AC 为半径的圆上，∴∠AEB =12∠ACB =45°，故答案为：12，45；(2)由折叠可知，CD 垂直平分BE ，∴BE ⊥CD ，设CD 、BE 交于点G ，则GE =BG =12BE =1，∴∠FGE =90°，∵∠AEB =45°，∴FG =GE =1，在Rt ΔCEG 中，由勾股定理得，CG =CE 2-DE 2=15，∴CF =CG -FG =15-1；当点E 在AB 的下方时，如图，∵AC =BC =EC ，∴A 、B 、E 三点在以C 为圆心以AC 为半径的圆上，∴∠EAB +∠EBA =12∠ACB =45°，即∠BEF =45°，由翻折可知，∠EGF=90°，EG=GB 12BE=1，∴ΔEGF是等腰直角三角形，∴GF=EG=1，在RtΔCEG中，CG=CE2-EG2=42-12=15，∴CF=15+1，综上所述，CF的长为15-1或15+1；(3)∵A，B，E，三点在以C为圆心，以AC为半径的圆上，∴当AE经过圆心C时，线段AE的最大值为2AC=8，在RtΔABC中，AC=BC=4，∠ACB=90°，∴AB=AC2+BC2=42，BM=CM=12BC=2，∠ABC=∠BAC=45°，连接BF，取AB的中点O，连接OF，如图，∵CD垂直平分BE，∠AEB=45°，∴BF=EF，∴∠EBF=∠AEB=45°，∴∠EFB=90°，∴∠AFB=90°，∴OF=12AB=OA=OB=22，∴点F在以点O为圆心，AB为直径的圆上，∵∠ACB=90°，∴点C在⊙O上，∴当OF经过点M时，MF最短，此时OF⊥BC，∴OM=BM⋅tan∠ABC=2×1=2，∴MF=OF-OM=22-2，即线段MF的最小值为22-2，故答案为：8；22-2．【点评】本题是圆的综合题，主要考查了等腰直角三角形的性质，线段垂直平分线的性质，圆周角定理，利用定点定长构造辅助圆是解题的关键．类型四、定弦定角构造辅助圆一．填空题11.(2023春•梁子湖区期中)如图，矩形ABCD的边AB=8，AD=6，M为BC的中点，P是矩形内部一动点，且满足∠ADP=∠P AB，N为边CD上的一个动点，连接PN，MN，则PN+MN的最小值为．【分析】先找出点P 的运动路线为以AD 为直径的圆，设圆心为O ，作点M 关于直线DC 的对称点M ′，连接OM ′交⊙O 于点P ′，可推出M ′P ′的长即为PN +MN 的最小值，再求出M ′P ′的长即可．【解答】解：∵四边形ABCD 是矩形，∴∠BAD =90°，∵∠ADP =∠P AB ，∴∠ADP +∠P AD =∠P AB +∠P AD =∠BAD =90°，∴点P 的运动路线为以AD 为直径的圆，作以AD 为直径的⊙O ，作点M 关于直线DC 的对称点M ′，连接OM ′交⊙O 于点P ′，连接M ′N ，OP ，则OP =OP ′=3，M ′N =MN ，∴PN +MN =PN +M ′N =PN +M ′N +OP -OP ′≥OM ′-OP ′=OM ′-3，∴PN +MN 的最小值为OM ′-3；连接OM ，∵四边形ABCD 是矩形，点O 是AD 的中点，点M 为BC 的中点，∴OD =12AD =12BC =CM =3，OD ⎳CM ，∠ODC =90°，∴四边形OMCD 是矩形，∴OM =DC =AB =8，∵点M 关于直线DC 的对称点M ′，∴M ′M =2MC =6，在Rt △M ′OM 中，由勾股定理，得OM ′=OM 2+M ′M 2=82+62=10，∴PN +MN 的最小值为OM ′-3=10-3=7，故答案为：7．【点评】本题考查轴对称-最短路线问题，矩形的性质，勾股定理，能利用一条线段的长表示两线段的和的最小值是解题的关键．二．解答题小赵同学在学习完“圆”这一章内容后，感觉到一些几何问题，如果添加辅助圆，运用圆的知识解决，可以使问题变得非常容易．我们把这个过程称为“化隐圆为显圆”．①已知：如图1，OA =OB =OC ，若∠AOB =50°，求∠ACB 的度数．解：若以点O 为圆心，OA 为半径作辅助圆，∠AOB 是⊙O 的圆心角，而∠ACB 是圆周角，从而可容易得到∠ACB = °．②如图2，点P 为正方形ABCD 内一点，且∠BPC =90°，若AB =4，求AP 的最小值．解：∵BC =4，∠BPC =90°，∴点P 在以BC 为直径的圆上，设圆心为点O ，则O 、P 、A 三点共线时AP 最小，最小值为．(2)【问题解决】①如图3，在平行四边形ABCD 中，已知AB =4，BC =6，∠ABC =60°，点P 是BC 边上一动点(点P 不与B ，C 重合)，连接AP ，作点B 关于直线AP 的对称点Q ，则线段QC 的最小值为．②如图4，△ABC 中，∠BAC =90°，AB =4，AC =3，D 为AC 上一动点，以AD 为直径的⊙O 交BD 于E ，求线段CE 的最小值．(3)【问题拓展】如图5，在平面直角坐标系中，已知两点A (2,3)，B (6,7)，x 轴上有一动点P ，当∠APB 最大时，直接写出点P 的坐标．【分析】(1)①利用圆周角定理即可求得答案；②由正方形性质可得：∠ABC =90°，BC =AB =4，OB =12BC =2，由勾股定理得：AO =25，推出点P 在以BC 为直径的⊙O 上，则O 、P 、A 三点共线时AP 最小，即可求得答案；(2)①过点A 作AH ⊥BC 于H ，利用解直角三角形得AH =AB ⋅sin ∠ABC =23，BH =AB ⋅cos ∠ABC =2，CH =BC -BH =4，由勾股定理得AC =27，再由AQ =AB =4，可得点Q 在以A 为圆心AB 为半径的⊙A 上，即当C 、Q 、A 三点共线时QC 最小，QC 的最小值=AC -AQ =27-4；②连接AE ，由AD 是⊙O 的直径，可得∠AED =90°，推出∠AEB =90°，即点E 在以AB 为直径的圆上，进而可得当C 、E 、Q 三点共线时，CE 最小，运用勾股定理即可求得答案；(3)当∠APB 最大时，过A 、B 两点的⊙O ′与x 轴相切，利用待定系数法可得直线AB 的解析式为y =x +1，线段AB 的垂直平分线为y =-x +9，设O ′(m ,-m +9)，根据O ′A =O ′B =O ′P ，建立方程求解即可得出答【解答】解：(1)①如图1，以点O为圆心，OA为半径作辅助圆⊙O，∵AB =AB ，∠AOB=50°，∠AOB=25°，∴∠ACB=12故答案为：25．②点P为正方形ABCD内一点，且∠BPC=90°，若AB=4，求AP的最小值．如图②，以BC为直径作⊙O，∵四边形ABCD是正方形，∴∠ABC=90°，BC=AB=4，BC=2，∴OB=12在Rt△ABO中，AO=AB2+OB2=42+22=25，∵BC=4，∠BPC=90°，∴点P在以BC为直径的⊙O上，则O、P、A三点共线时AP最小，∴AP的最小值=AO-OP=25-2，故答案为：25-2．(2)①如图3，过点A作AH⊥BC于H，∵AB=4，BC=6，∠ABC=60°，则AH=AB⋅sin∠ABC=4sin60°=23，BH=AB⋅cos∠ABC=4cos60°=2，∴CH=BC-BH=6-2=4，在Rt△ACH中，AC=AH2+CH2=(23)2+42=27，∵点B与点Q关于直线AP对称，∴AQ=AB=4，∴点Q在以A为圆心AB为半径的⊙A上，∴当C、Q、A三点共线时QC最小，QC的最小值=AC-AQ=27-4，故答案为：27-4．②如图4，连接AE，∵AD是⊙O的直径，∴∠AED=90°，∴∠AEB=180°-∠AED=90°，以AB 为直径作⊙Q ，交⊙O 于E ，当C 、E 、Q 三点共线时，CE 最小，∵△ABC 中，∠BAC =90°，AB =4，AC =3，∴QE =AQ =12AB =2，∴CQ =AC 2+AQ 2=32+22=13，∴CE =CQ -QE =13-2，故线段CE 的最小值为13-2．(3)当∠APB 最大时，过A 、B 两点的⊙O ′与x 轴相切，设直线AB 的解析式为y =kx +b ，把A (2,3)，B (6,7)代入，得：2k +b =36k +b =7 ，解得：k =1b =1 ，∴直线AB 的解析式为y =x +1，∵线段AB 的中点坐标为(4,5)，圆心O ′在AB 的垂直平分线上，∴线段AB 的垂直平分线为y =-x +9，设O ′(m ,-m +9)，∵O ′A =O ′B =O ′P ，∴(m -2)2+(-m +9-3)2=(-m +9)2，解得：m =42-1或m =-42-1(舍去)，∴点P 的坐标为(42-1，0)，故答案为：42-1．【点评】本题是圆的综合题，考查了圆的有关知识，正方形的性质，平行四边形的性质，解直角三角形等知识，灵活运用这些性质解决问题是解题的关键．13.(2022秋•泗洪县期中)已知：⊙O 和⊙O 外一点P ．(1)如图甲，P A 和PB 是⊙O 的两条切线，A 、B 分别为切点，求证：P A =PB ．(2)尺规作图：在图乙中，过P 点画⊙O 的两条切线PE 、PF ，E 、F 为切点(要求：保留作图痕迹，不写作法)．【分析】(1)如图，连接OP、OA、OB．只要证明RtΔP AO≅RtΔPBO(HL)，可得P A=PB．(2)以OP为直径作⊙O′，两圆交于点E、F，直线PE、PF即为所求；【解答】解：(1)如图，连接OP、OA、OB．∵P A、PB是切线，∴P A⊥OA，PB⊥OB，∴∠P AO=∠PBO=90°，在RtΔP AO和RtΔPBO中，OP=OP，OA=OB∴RtΔP AO≅RtΔPBO，∴P A=PB．(2)以OP为直径作⊙O′，两圆交于点E、F，直线PE、PF即为所求；【点评】本题考查切线的性质、全等三角形的判定和性质，直径的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用辅助圆解决问题，属于中考常考题型．类型五、对角互补构造辅助圆14.(2021秋•越秀区校级期中)如图1，在ΔABC中，∠ACB=90°，CD平分∠ACB，且AD⊥BD于点D．(1)判断ΔABD的形状；(2)如图2，在(1)的结论下，若BQ=22，DQ=3，∠BQD=75°，求AQ的长；(3)如图3，在(1)的结论下，若将DB绕着点D顺时针旋转α(0°<α<90°)得到DP，连接BP，作DE⊥BP交AP于点F．试探究AF与DE的数量关系，并说明理由．【分析】(1)由∠ACB+∠ADB=90°+90°=180°，知点A、C、B、D上四点共圆，则∠ACD=∠ABD=45°，即可得出结论；(2)将ΔADQ绕点D顺时针旋转90°得ΔBDE，连接EQ，过点B作EQ的垂线，交EQ的延长线于H，得ΔQDE是等腰直角三角形，从而可解直角三角形BQH，在RtΔBEH中，利用勾股定理得可求出BE的长度，从而解决问题；(3)在AF上截取AM=PF，利用SAS证明ΔADM≅ΔPDF，得∠ADM=∠PDE，DM=DF，可证明ΔMDF、ΔPEF是等腰直角三角形，从而解决问题．【解答】解：(1)∵∠ACB=90°，CD平分∠ACB，∴∠ACD=45°，∵∠ACB+∠ADB=90°+90°=180°，∴点A、C、B、D上四点共圆，∴∠ACD=∠ABD=45°，∴∠BAD=∠ABD=45°，∴ΔABD是等腰直角三角形；(2)将ΔADQ绕点D顺时针旋转90°得ΔBDE，连接EQ，过点B作EQ的垂线，交EQ的延长线于H，∴DQ=DE，∠QDE=90°，AQ=BE，∴ΔQDE是等腰直角三角形，∴∠DQE=45°，∴QE=2DQ=32，∵∠BQD=75°，∴∠BQE=∠BQD+∠DQE=120°，∴∠BQH=60°，BQ=2，BH=6，∴QH=12在RtΔBEH中，由勾股定理得BE=BH2+EH2=(42)2+(6)2=38，∴AQ=BE=38；(3)AF=2DE．，理由如下：如图，在AF上截取AM=PF，∵DA=DP，∴∠DAM=∠DPF，∴ΔADM≅ΔPDF(SAS)，∴∠ADM=∠PDE，DM=DF，∵BD=DP，DE⊥BP，∴∠BDE=∠PDE，∴∠ADM=∠BDE，∴ΔMDF是等腰直角三角形，∴∠MFD=45°，MF=2DF，∴∠EFP=45°，∴ΔPEF是等腰直角三角形，∴PF=2EF，∴AF=2DE．【点评】本题主要考查了等腰直角三角形的判定与性质，全等三角形的判定与性质，等腰三角形的性质，含30°角的直角三角形的性质，勾股定理，四点共圆等知识，作辅助线构造全等三角形是解题的关键．15.(2021秋•西城区校级期中)如图，ΔABC为等边三角形，点P是线段AC上一动点(点P不与A，C重合)，连接BP，过点A作直线BP的垂线段，垂足为点D，将线段AD绕点A逆时针旋转60°得到线段AE，连接DE，CE．(1)求证：BD=CE；(2)延长ED交BC于点F，求证：F为BC的中点；(3)若ΔABC的边长为1，直接写出EF的最大值．【分析】(1)利用SAS证明ΔBAD≅ΔCAE，即可得出结论；(2)过点C作CG⎳BP交DF的延长线于点G，利用等角对等边可得CG=CE，由(1)ΔBAD≅ΔCAE，得BD=CE，再利用AAS证明ΔBDF≅ΔCGF，从而解决问题；(3)由(2)知∠AFC=∠AEC=90°，则点A，F，C，E四点在以AC为直径的圆上，故EF的最大值为直径．【解答】(1)证明：∵线段AD绕点A逆时针旋转60°得到线段AE，∴ΔADE是等边三角形，∴AD=AE，∠DAE=60°，∵ΔABC是等边三角形，∴AB=AC，∠BAC=60°，∴∠BAC=∠DAE，∴∠BAD=∠CAE，在ΔBAD和ΔCAE中，AB=AC∠BAD=∠CAE AD=AE，∴ΔBAD≅ΔCAE(SAS)，∴BD=CE；(2)证明：如图，过点C作CG⎳BP交DF的延长线于点G，∴∠G=∠BDF，∴∠G =30°，由(1)可知，BD =CE ，∠CEA =∠BDA ，∵AD ⊥BP ，∴∠BDA =90°，∴∠CEA =90°，∵∠AED =60°，∴∠CED =30°=∠G ，∴CE =CG ，∴BD =CG ，在ΔBDF 和ΔCGF 中，∠BDF =∠G∠BFD =∠CFG BD =CG，∴ΔBDF ≅ΔCGF (AAS )，∴BF =FC ，即F 为BC 的中点；(3)解：如图，连接AF ，∵ΔABC 是等边三角形，BF =FC ，∴AF ⊥BC ，∴∠AFC =90°，∴∠AFC =∠AEC =90°，∴点A ，F ，C ，E 四点在以AC 为直径的圆上，∴EF 的最大值为直径，即最大值为1．【点评】本题主要考查了等边三角形的性质，全等三角形的判定与性质，四点共圆等知识，作辅助线构造全等三角形是解题的关键．16.(2023秋•东城区校级期中)如图1，在Rt ΔABC 中，∠ABC =90°，BA =BC ，直线MN 是过点A 的直线CD ⊥MN 于点D ，连接BD ．(1)观察猜想张老师在课堂上提出问题：线段DC ，AD ，BD 之间有什么数量关系．经过观察思考，小明出一种思路：如图1，过点B 作BE ⊥BD ，交MN 于点E ，进而得出：DC +AD =BD ．(2)探究证明将直线MN 绕点A 顺时针旋转到图2的位置写出此时线段DC ，AD ，BD之间的数量关系，并证明(3)拓展延伸在直线MN 绕点A 旋转的过程中，当ΔABD 面积取得最大值时，若CD 长为1，请直接写BD 的长．【分析】(1)由题意：ΔBAE≅ΔBCD，推出AE=CD，BE=BD，推出CD+AD=AD+AE=DE，ΔBDE是等腰直角三角形，推出DE=2BD，可得DC+AD=2BD；(2)结论：AD-DC=2BD．过点B作BE⊥BD，交MN于点E．AD交BC于O．只要证明ΔCDB≅ΔAEB，即可解决问题；(3)如图3中，当点D在线段AB的垂直平分线上且在AB的右侧时，ΔABD的面积最大．【解答】解：(1)如图1中，由题意：ΔBAE≅ΔBCD，∴AE=CD，BE=BD，∴CD+AD=AD+AE=DE，∵ΔBDE是等腰直角三角形，∴DE=2BD，∴DC+AD=2BD，故答案为2．(2)AD-DC=2BD．证明：如图，过点B作BE⊥BD，交MN于点E．AD交BC于O．∵∠ABC=∠DBE=90°，∴∠ABE+∠EBC=∠CBD+∠EBC，∴∠ABE=∠CBD．∵∠BAE+∠AOB=90°，∠BCD+∠COD=90°，∠AOB=∠COD，∴∠BAE=∠BCD，∴∠ABE=∠DBC．又∵AB=CB，∴ΔCDB≅ΔAEB，∴CD=AE，EB=BD，∴△BD为等腰直角三角形，DE=2BD．∵DE=AD-AE=AD-CD，∴AD-CD=2BD．(3)如图3中，易知A、B、C、D四点共圆，当点D在线段AB的垂直平分线上且在AB的右侧时，ΔABD的面积最大．。

2020-2021中考数学圆的综合-经典压轴题含答案

2020-2021中考数学圆的综合-经典压轴题含答案一、圆的综合1．如图1，直角梯形OABC中，BC∥OA，OA=6，BC=2，∠BAO=45°．（1）OC的长为；（2）D是OA上一点，以BD为直径作⊙M，⊙M交AB于点Q．当⊙M与y轴相切时，sin∠BOQ=；（3）如图2，动点P以每秒1个单位长度的速度，从点O沿线段OA向点A运动；同时动点D以相同的速度，从点B沿折线B﹣C﹣O向点O运动．当点P到达点A时，两点同时停止运动．过点P作直线PE∥OC，与折线O﹣B﹣A交于点E．设点P运动的时间为t （秒）．求当以B、D、E为顶点的三角形是直角三角形时点E的坐标．【答案】（1）4；（2）35；（3）点E的坐标为（1，2）、（53，103）、（4，2）．【解析】分析：（1）过点B作BH⊥OA于H，如图1（1），易证四边形OCBH是矩形，从而有OC=BH，只需在△AHB中运用三角函数求出BH即可．（2）过点B作BH⊥OA于H，过点G作GF⊥OA于F，过点B作BR⊥OG于R，连接MN、DG，如图1（2），则有OH=2，BH=4，MN⊥OC．设圆的半径为r，则MN=MB=MD=r．在Rt△BHD中运用勾股定理可求出r=2，从而得到点D与点H重合．易证△AFG∽△ADB，从而可求出AF、GF、OF、OG、OB、AB、BG．设OR=x，利用BR2=OB2﹣OR2=BG2﹣RG2可求出x，进而可求出BR．在Rt△ORB中运用三角函数就可解决问题．（3）由于△BDE的直角不确定，故需分情况讨论，可分三种情况（①∠BDE=90°，②∠BED=90°，③∠DBE=90°）讨论，然后运用相似三角形的性质及三角函数等知识建立关于t的方程就可解决问题．详解：（1）过点B作BH⊥OA于H，如图1（1），则有∠BHA=90°=∠COA，∴OC∥BH．∵BC∥OA，∴四边形OCBH是矩形，∴OC=BH，BC=OH．∵OA=6，BC=2，∴AH=0A﹣OH=OA﹣BC=6﹣2=4．∵∠BHA=90°，∠BAO=45°，∴tan∠BAH=BHHA=1，∴BH=HA=4，∴OC=BH=4．故答案为4．（2）过点B作BH⊥OA于H，过点G作GF⊥OA于F，过点B作BR⊥OG于R，连接MN、DG，如图1（2）．由（1）得：OH =2，BH =4．∵OC 与⊙M 相切于N ，∴MN ⊥OC ．设圆的半径为r ，则MN =MB =MD =r ．∵BC ⊥OC ，OA ⊥OC ，∴BC ∥MN ∥OA ．∵BM =DM ，∴CN =ON ，∴MN =12（BC +OD ），∴OD =2r ﹣2，∴DH =OD OH -=24r -．在Rt △BHD 中，∵∠BHD =90°，∴BD 2=BH 2+DH 2，∴（2r ）2=42+（2r ﹣4）2．解得：r =2，∴DH =0，即点D 与点H 重合，∴BD ⊥0A ，BD =AD ．∵BD 是⊙M 的直径，∴∠BGD =90°，即DG ⊥AB ，∴BG =AG ．∵GF ⊥OA ，BD ⊥OA ，∴GF ∥BD ，∴△AFG ∽△ADB ， ∴AF AD =GF BD =AG AB =12，∴AF =12AD =2，GF =12BD =2，∴OF =4，∴OG同理可得：OB AB ，∴BG =12AB ．设OR =x ，则RG x ．∵BR ⊥OG ，∴∠BRO =∠BRG =90°，∴BR 2=OB 2﹣OR 2=BG 2﹣RG 2，∴（2﹣x 2=（）2﹣（x ）2．解得：x =5，∴BR 2=OB 2﹣OR 2=（2﹣（5）2=365，∴BR =5．在Rt △ORB 中，sin ∠BOR =BR OB35．故答案为35．（3）①当∠BDE =90°时，点D 在直线PE 上，如图2．此时DP =OC =4，BD +OP =BD +CD =BC =2，BD =t ，OP =t ．则有2t =2．解得：t =1．则OP =CD =DB =1．∵DE ∥OC ，∴△BDE ∽△BCO ，∴DE OC =BD BC =12，∴DE =2，∴EP =2， ∴点E 的坐标为（1，2）．②当∠BED =90°时，如图3．∵∠DBE =OBC ，∠DEB =∠BCO =90°，∴△DBE ∽△OBC ，∴BEBC =2DB BE OB ∴，∴BE =5t ． ∵PE ∥OC ，∴∠OEP =∠BOC ．∵∠OPE =∠BCO =90°，∴△OPE ∽△BCO ，∴OEOB =25OPBC∴，=2t，∴OE=5t．∵OE+BE=OB=255，∴t+5t=25．解得：t=53，∴OP=53，OE=55，∴PE=22OE OP-=103，∴点E的坐标为（51033，）．③当∠DBE=90°时，如图4．此时PE=PA=6﹣t，OD=OC+BC﹣t=6﹣t．则有OD=PE，EA=22PE PA+=2（6﹣t）=62﹣2?t，∴BE=BA﹣EA=42﹣（62﹣2t）=2t﹣22．∵PE∥OD，OD=PE，∠DOP=90°，∴四边形ODEP是矩形，∴DE=OP=t，DE∥OP，∴∠BED=∠BAO=45°．在Rt△DBE中，cos∠BED=BEDE=2，∴DE=2BE，∴t=22（t﹣22）=2t﹣4．解得：t=4，∴OP=4，PE=6﹣4=2，∴点E的坐标为（4，2）．综上所述：当以B、D、E为顶点的三角形是直角三角形时点E的坐标为（1，2）、（51033，）、（4，2）．点睛：本题考查了圆周角定理、切线的性质、相似三角形的判定与性质、三角函数的定义、平行线分线段成比例、矩形的判定与性质、勾股定理等知识，还考查了分类讨论的数学思想，有一定的综合性．2．如图，在直角坐标系中，已知点A(－8，0)，B(0，6)，点M在线段AB上。

中考数学《圆》真题压轴题总汇【附解析】

中考数学《圆》真题压轴题总汇【附解析】1．（2019•阿坝州）如图，AB为⊙O的直径，C为⊙O上的一点，∠BCH＝∠A，∠H＝90°，HB的延长线交⊙O于点D，连接CD．（1）求证：CH是⊙O的切线；（2）若B为DH的中点，求tan D的值．2．（2019•德阳）如图，AB是⊙O的直径，点C为⊙O上一点，OE⊥BC于点H，交⊙O于点E，点D为OE的延长线上一点，DC的延长线与BA的延长线交于点F，且∠BOD＝∠BCD，连结BD、AC、CE．（1）求证：DF为⊙O的切线；（2）过E作EG⊥FD于点G，求证：△CHE≌△CGE；（3）如果AF＝1，sin∠FCA＝，求EG的长．3．（2019•雅安）如图，已知AB是⊙O的直径，AC，BC是⊙O的弦，OE∥AC交BC于E，过点B作⊙O的切线交OE的延长线于点D，连接DC并延长交BA的延长线于点F．（1）求证：DC是⊙O的切线；（2）若∠ABC＝30°，AB＝8，求线段CF的长．4．（2019•内江）AB与⊙O相切于点A，直线l与⊙O相离，OB⊥l于点B，且OB＝5，OB 与⊙O交于点P，AP的延长线交直线l于点C．（1）求证：AB＝BC；（2）若⊙O的半径为3，求线段AP的长；（3）若在⊙O上存在点G，使△GBC是以BC为底边的等腰三角形，求⊙O的半径r的取值范围．5．（2019•广元）如图，AB是⊙O的直径，点P是BA延长线上一点，过点P作⊙O的切线PC，切点是C，过点C作弦CD⊥AB于E，连接CO，CB．（1）求证：PD是⊙O的切线；（2）若AB＝10，tan B＝，求PA的长；（3）试探究线段AB，OE，OP之间的数量关系，并说明理由．6．（2019•成都）如图，AB为⊙O的直径，C，D为圆上的两点，OC∥BD，弦AD，BC相交于点E．（1）求证：＝；（2）若CE＝1，EB＝3，求⊙O的半径；（3）在（2）的条件下，过点C作⊙O的切线，交BA的延长线于点P，过点P作PQ∥CB 交⊙O于F，Q两点（点F在线段PQ上），求PQ的长．7．（2019•资阳）如图，AC是⊙O的直径，PA切⊙O于点A，PB切⊙O于点B，且∠APB＝60°．（1）求∠BAC的度数；（2）若PA＝1，求点O到弦AB的距离．8．（2019•绵阳）如图，AB是⊙O的直径，点C为的中点，CF为⊙O的弦，且CF⊥AB，垂足为E，连接BD交CF于点G，连接CD，AD，BF．（1）求证：△BFG≌△CDG；（2）若AD＝BE＝2，求BF的长．9．（2019•乐山）如图，直线l与⊙O相离，OA⊥l于点A，与⊙O相交于点P，OA＝5．C 是直线l上一点，连结CP并延长交⊙O于另一点B，且AB＝AC．（1）求证：AB是⊙O的切线；（2）若⊙O的半径为3，求线段BP的长．10．（2019•泰州）如图，四边形ABCD内接于⊙O，AC为⊙O的直径，D为的中点，过点D作DE∥AC，交BC的延长线于点E．（1）判断DE与⊙O的位置关系，并说明理由；（2）若⊙O的半径为5，AB＝8，求CE的长．11．（2019•乐山）已知关于x的一元二次方程x2﹣（k+4）x+4k＝0．（1）求证：无论k为任何实数，此方程总有两个实数根；（2）若方程的两个实数根为x1、x2，满足+＝，求k的值；（3）若Rt△ABC的斜边为5，另外两条边的长恰好是方程的两个根x1、x2，求Rt△ABC的内切圆半径．12．（2019•株洲）四边形ABCD是⊙O的圆内接四边形，线段AB是⊙O的直径，连结AC、BD．点H是线段BD上的一点，连结AH、CH，且∠ACH＝∠CBD，AD＝CH，BA的延长线与CD的延长线相交于点P．（1）求证：四边形ADCH是平行四边形；（2）若AC＝BC，PB＝PD，AB+CD＝2（+1）①求证：△DHC为等腰直角三角形；②求CH的长度．13．（2019•巴中）如图，在菱形ABCD中，连结BD、AC交于点O，过点O作OH⊥BC于点H，以点O为圆心，OH为半径的半圆交AC于点M．①求证：DC是⊙O的切线．②若AC＝4MC且AC＝8，求图中阴影部分的面积．③在②的条件下，P是线段BD上的一动点，当PD为何值时，PH+PM的值最小，并求出最小值．14．（2019•广安）如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，AD平分∠BAC，AD 交BC于点D，ED⊥AD交AB于点E，△ADE的外接圆⊙O交AC于点F，连接EF．（1）求证：BC是⊙O的切线；（2）求⊙O的半径r及∠3的正切值．15．（2019•达州）如图，⊙O是△ABC的外接圆，∠BAC的平分线交⊙O于点D，交BC于点E，过点D作直线DF∥BC．（1）判断直线DF与⊙O的位置关系，并说明理由；（2）若AB＝6，AE＝，CE＝，求BD的长．16．（2019•凉山州）如图，点D是以AB为直径的⊙O上一点，过点B作⊙O的切线，交AD的延长线于点C，E是BC的中点，连接DE并延长与AB的延长线交于点F．（1）求证：DF是⊙O的切线；（2）若OB＝BF，EF＝4，求AD的长．17．（2019•遂宁）如图，△ABC内接于⊙O，直径AD交BC于点E，延长AD至点F，使DF ＝2OD，连接FC并延长交过点A的切线于点G，且满足AG∥BC，连接OC，若cos∠BAC＝，BC＝6．（1）求证：∠COD＝∠BAC；（2）求⊙O的半径OC；（3）求证：CF是⊙O的切线．18．（2019•宜宾）如图，线段AB经过⊙O的圆心O，交⊙O于A、C两点，BC＝1，AD为⊙O 的弦，连结BD，∠BAD＝∠ABD＝30°，连结DO并延长交⊙O于点E，连结BE交⊙O于点M．（1）求证：直线BD是⊙O的切线；（2）求⊙O的半径OD的长；（3）求线段BM的长．19．（2019•南充）如图，在△ABC中，以AC为直径的⊙O交AB于点D，连接CD，∠BCD＝∠A．（1）求证：BC是⊙O的切线；（2）若BC＝5，BD＝3，求点O到CD的距离．20．（2019•自贡）如图，⊙O中，弦AB与CD相交于点E，AB＝CD，连接AD、BC．求证：（1）＝；（2）AE＝CE．参考答案1．（1）证明：连接OC，∵AB为⊙O的直径，∴∠ACB＝90°，∴∠ACO+∠BCO＝90°，∵OA＝OC，∠A＝∠ACO，∴∠A+∠BCO＝90°，∵∠A＝∠BCH，∴∠BCH+∠BCO＝90°，∴∠HCO＝90°，∴CH是⊙O的切线；（2）解：∵B为DH的中点，∴设BD＝BH＝x，∴DH＝2x，∵∠A＝∠D，∠A＝∠BCH，∴∠D＝∠BCH，∵∠H＝∠H，∴△DCH∽△CBH，∴＝，∴CH＝＝，∵∠H＝90°，∴tan D＝＝＝．2．（1）证明：如图，连结OC，∵OE⊥BC，∴∠OHB＝90°，∴∠OBH+∠BOD＝90°，∵OB＝OC，∴∠OBH＝∠OCB，∵∠BOD＝∠BCD，∴∠BCD+∠OCB＝90°，∴OC⊥CD，∵点C为⊙O上一点，∴DF为⊙O的切线；（2）解：∵∠OCD＝90°，∴∠ECG+∠OCE＝90°，∵OC＝OE，∴∠OCE＝∠OEC，∴∠ECG+∠OEC＝90°，∵∠OEC+∠HCE＝90°，∴∠ECG＝∠HCE，在△CHE和△CGE中，，∴△CHE≌△CGE（AAS）；（3）解：∵AB是⊙O的直径，∴∠ACB＝90°，∴∠ABC+∠BAC＝90°，∵DF为⊙O的切线，∴∠OCA+∠FCA＝90°，∵OA＝OC，∴∠OAC＝∠OCA，∴∠FCA＝∠ABC，∴sin∠ABC＝sin∠FCA＝，设AC＝a，则AB＝3a，∴BC＝＝＝a，∵∠FCA＝∠ABC，∠AFC＝∠CFB，∴△ACF∽△CFB，∴＝＝＝，∵AF＝1，∴CF＝，∴BF＝＝2，∴BF﹣AF＝AB＝1，∴OC＝，BC＝，∵OE⊥BC，∴CH＝BC＝，∴OH＝＝＝，∴HE＝OE﹣OH＝﹣，∵△CHE≌△CGE，∴EG＝HE＝﹣．3．（1）证明：连接OC，∵OE∥AC，∴∠1＝∠ACB，∵AB是⊙O的直径，∴∠1＝∠ACB＝90°，∴OD⊥BC，由垂径定理得OD垂直平分BC，∴DB＝DC，∴∠DBE＝∠DCE，又∵OC＝OB，∴∠OBE＝∠OCE，即∠DBO＝∠OCD，∵DB为⊙O的切线，OB是半径，∴∠DBO＝90°，∴∠OCD＝∠DBO＝90°，即OC⊥DC，∵OC是⊙O的半径，∴DC是⊙O的切线；（2）解：在Rt△ABC中，∠ABC＝30°，∴∠3＝60°，又OA＝OC，∴△AOC是等边三角形，∴∠COF＝60°，在Rt△COF中，tan∠COF＝，∴CF＝4．4．（1）证明：如图1，连接OA，∵AB与⊙O相切，∴∠OAB＝90°，∴∠OAP+∠BAC＝90°，∵OB⊥l，∴∠BCA+∠BPC＝90°，∵OA＝OP，∴∠OAP＝∠OPA＝∠BPC，∴∠BAC＝∠BCA，∴AB＝BC；（2）解：如图1，连接AO并延长交⊙O于D，连接PD，则∠APD＝90°，∵OB＝5，OP＝3，∴PB＝2，∴BC＝AB＝＝4，在Rt△PBC中，PC＝＝2，∵∠DAP＝∠CPB，∠APD＝∠PBC＝90°，∴△DAP∽△PBC，∴＝，即＝，解得，AP＝；（3）解：如图2，作BC的垂直平分线MN，作OE⊥MN于E，则OE＝BC＝AB＝×，由题意得，⊙O于MN有交点，∴OE≤r，即×≤r，解得，r≥，∵直线l与⊙O相离，∴r＜5，则使△GBC是以BC为底边的等腰三角形，⊙O的半径r的取值范围为：≤r＜5．。

中考数学压轴题-圆的压轴题含解析

圆的压轴题（1）1、如图，BF 为⊙O 的直径，直线AC 交⊙O 于A ，B 两点，点D 在⊙O 上，BD 平分∠OBC ，DE ⊥AC 于点E 。

（1）求证：直线DE 是⊙O 的切线；（2）若 BF=10，sin ∠BDE=，求DE 的长。

2、如图，AN 是M ⊙的直径，NB x ∥轴，AB 交M ⊙于点C .(1)若点()0,6A ，()0,2N ，30ABN =∠°，求点B 的坐标；(2)若D 为线段NB 的中点，求证：直线CD 是M ⊙的切线.x y C D M O B NA3、如图，△ABD是⊙O的内接三角形，E是弦BD的中点，点C是⊙O外一点且∠DBC=∠A，连接OE延长与圆相交于点F，与BC相交于点C．（1）求证：BC是⊙O的切线；（2）若⊙O的半径为6，BC=8，求弦BD的长．4、已知△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F，若=，如图1，．（1）判断△ABC的形状，并证明你的结论；（2）设AE与DF相交于点M，如图2，AF=2FC=4，求AM的长．5、如图，AB是⊙O的直径，AC是上半圆的弦，过点C作⊙O的切线DE交AB的延长线于点E，过点A作切线DE的垂线，垂足为D，且与⊙O交于点F，设∠DAC，∠CEA的度数分别是α，β．（1）用含α的代数式表示β，并直接写出α的取值范围；（2）连接OF与AC交于点O′，当点O′是AC的中点时，求α，β的值．6、如图，在菱形ABCD中，点P在对角线AC上，且PA=PD，⊙O是△PAD的外接圆．（1）求证：AB是⊙O的切线；（2）若AC=8，tan∠BAC=，求⊙O的半径．7、如图，AB为⊙O的直径，CB，CD分别切⊙O于点B，D，CD交BA的延长线于点E，CO的延长线交⊙O于点G，EF⊥OG于点F．（1）求证：∠FEB=∠ECF；（2）若BC=6，DE=4，求EF的长．8、如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O的切线，交OD的延长线于点E，连接BE．（1）求证：BE与⊙O相切；（2）设OE交⊙O于点F，若DF=1，BC=2 ，求阴影部分的面积．9、如图，已知⊙O的直径CD=6，A，B为圆周上两点，且四边形OABC是平行四边形，过A点作直线EF∥BD，分别交CD，CB的延长线于点E，F，AO与BD交于G点．（1）求证：EF是⊙O的切线；（2）求AE的长．10、如图，C、D是半圆O上的三等分点，直径AB=4，连接AD、AC，DE⊥AB，垂足为E，DE交AC于点F．（1）求∠AFE的度数；（2）求阴影部分的面积（结果保留π和根号）．11、如图，MN是⊙O的直径，MN=4，点A在⊙O上，∠AMN=30°，B为的中点，P是直径MN上一动点．（1）利用尺规作图，确定当PA+PB最小时P点的位置（不写作法，但要保留作图痕迹）．（2）求PA+PB的最小值．12、如图，已知直线PT与⊙O相切于点T，直线PO与⊙O相交于A，B两点．（1）求证：PT2=PA•PB；（2）若PT=TB=，求图中阴影部分的面积．13、如图，PA、PB是⊙O的切线，A、B为切点，∠APB=60°，连接PO并延长与⊙O交于C点，连接AC，BC．（1）求证：四边形ACBP是菱形；（2）若⊙O半径为1，求菱形ACBP的面积．14、如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC边于点D，过点C作CF ∥AB，与过点B的切线交于点F，连接BD．（1）求证：BD=BF；（2）若AB=10，CD=4，求BC的长．15、如图，梯形ABCD中，AD∥BC，AE⊥BC于E，∠ADC的平分线交AE于点O，以点O为圆心，OA为半径的圆经过点B，交BC于另一点F．（1）求证：CD与⊙O相切；（2）若BF=24，OE=5，求tan∠ABC的值．16、已知：如图，MN为⊙O的直径，ME是⊙O的弦，MD垂直于过点E的直线DE，垂足为点D，且ME平分∠DMN．求证：（1）DE是⊙O的切线；（2）ME2=MD•MN．参考答案1、【解答】解：（1）如图所示，连接OD，∵OD=OB，∴∠ODB=∠OBD，∵BD平分∠OBC，∴∠OBD=∠DBE，∴∠ODB=∠DBE，∴OD∥AC，∵DE⊥AC，∴OD⊥DE，∵OD是⊙O的半径，∴直线DE是⊙O的切线；（2）如图，连接DF，∵BF是⊙O的直径，∴∠FDB=90°，∴∠F+∠OBD=90°，∵∠OBD=∠DBE，∠BDE+∠DBE=90°，∴∠F=∠BDE，在Rt△BDF中，=sinF=sin∠BDE=，∴BD=10×=2，∴在Rt△BDE中，sin∠BDE==，∴BE=2×=2，∴在Rt△BDE中，DE===4。

2024数学中考压轴题-圆(九大题型和解题方法)

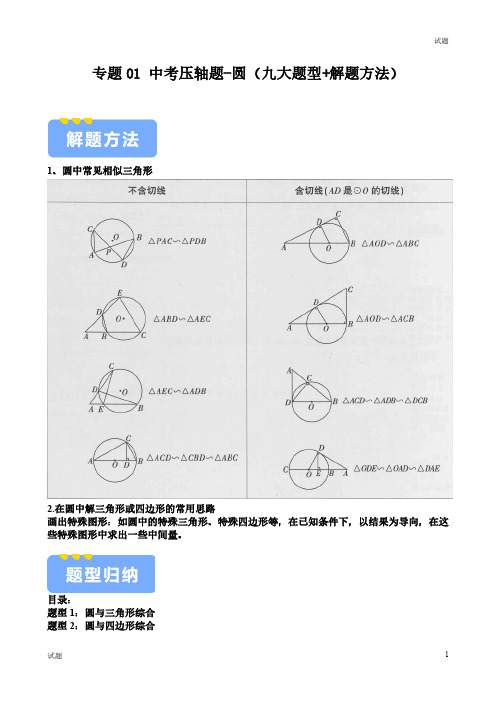
专题01 中考压轴题-圆（九大题型+解题方法）1、圆中常见相似三角形2.在圆中解三角形或四边形的常用思路画出特殊图形：如圆中的特殊三角形、特殊四边形等，在已知条件下，以结果为导向，在这些特殊图形中求出一些中间量。

目录：题型1：圆与三角形综合题型2：圆与四边形综合题型3：圆有关的动态问题题型4：圆与坐标系或函数题型5：以实际问题为背景，求圆与三角形、四边形综合问题题型6：最值问题题型7：在解三角形、四边形中作辅助圆题型8：定值问题题型9：在圆综合中求解三角函数值题型1：圆与三角形综合1．（2024·黑龙江哈尔滨·一模）已知，AD 、BC 为O 两条弦，AD BC ⊥于点E ，连接OE ，AE CE =．(1)如图1，连接OE ，求AEO ∠的度数；(2)如图2，连接AC ，延长EO 交AC 于点N ，点F 为AC 上一点，连接EF ，在EF 上方作等腰直角三角形EFG ，且90EGF ∠=︒，连接NG ，求证：NG BC ∥；(3)在（2）的条件下，连接AB ，CD ，当点G 落在线段AB 上时，过点O 做OL OE ⊥，交CD 于点L ，交CE于点T ，若2OE EG CL ==，求O 半径的长．2．（2024·黑龙江哈尔滨·一模）已知：AB 为O 的直径，点C 为 AB 上一点，连接AC ，点D 为 BC上一点，连接AD ，过点D 作AB 的垂线，垂足为点F ，交O 于点E ，连接CE ，分别交AD 和AB 于点H 和点K ，且90AHE =︒∠．(1)如图1，求证：CAD BAD ∠=∠；(2)如图2，连接HF ，过点H 作HF 的垂线交AB 于点T ，求证：2AB FT =；(3)如图3，在（2）的条件下，连接BC 交AD 于点G ，延长CD 交AB 的延长线于点M ，若CM AG =，5FT =，求CG 的长．3．（2024·黑龙江哈尔滨·一模）如图1，在O 中，直径AB 垂直弦CD 于点G ，连接AD ，过点C 作CF AD ⊥于F ，交AB 于点H ，交O 于点E ，连接DE ．(1)如图1，求证：2E C ∠=∠；(2)如图2，求证：DE CH =；(3)如图3，连接BE ，分别交AD CD 、于点M N 、，当2OH OG =，HF =EN 的长．4．（2024·浙江·模拟预测）如图1，ABC 内接于O ，作AD BC ⊥于点D ．(1)连结AO ，BO ．求证：2180AOB DAC ∠+∠=︒；(2)如图2，若点E 为弧AC 上一点，连结BE 交AD 于点F ，若2BAD CAD ∠∠＝，490DBF CAD ∠+∠=︒，连结OF ，求证：OF 平分AFB ∠；(3)在（2）的条件下，如图3，点G 为BC 上一点，连结EG ，2BGE C ∠=∠．若AD =3BD EG +=，求DF 的长．题型2：圆与四边形综合5．（2024·浙江杭州·模拟预测）如图，四边形ABCD 内接于O ，AC 为O 的直径，DE AC ⊥于点F 交BC 于点E ．(1)设DBC α∠=，试用含α的代数式表示ADE ∠；(2)如图2，若3BE CE =，求BDDE的值；(3)在（2）的条件下，若,AC BD 交于点G ，设FGx CF=，cos BDE y ∠=．①求y 关于x 的函数表达式．②若BC BD =，求y 的值．6．（2024·广东珠海·一模）如图1，F 为正方形ABCD 边BC 上一点，连接AF ，在AF 上取一点O ，以OA 为半径作圆，恰好使得O 经过点B 且与CD 相切于点E ．(1)若正方形的边长为4时，求O 的半径；(2)如图2，将AF 绕点A 逆时针旋转45︒后，其所在直线与O 交于点G ，与边CD 交于点H ，连接DG BG ，．①求ADG ∠的度数；②求证：··²AB BF AG FG BG +=．题型3：圆有关的动态问题7．（2024·广东·一模）综合探究：如图，已知10AB =，以AB 为直径作半圆O ，半径OA 绕点O 顺时针旋转得到OC ，点A 的对应点为C ，当点C 与点B 重合时停止．连接BC 并延长到点D ，使得CD BC =，过点D 作DE AB ⊥于点E ，连接AD ，AC ．(1)如图1，当点E 与点O 重合时，判断ABD △的形状，并说明理由；(2)如图2，当1OE =时，求BC 的长；(3)如图3，若点P 是线段AD 上一点，连接PC ，当PC 与半圆O 相切时，判断直线PC 与AD 的位置关系，并说明理由．8．（2024·浙江湖州·一模）如图，在ABCD Y 中，∠B 是锐角，AB =10BC =，在射线BA 上取一点P ，过P 作PE BC ⊥于点E ，过P ，E ，C 三点作O ．(1)当3cos 5B =时，①如图1，若AB 与O 相切于点P ，连结CP ，求CP 的长；②如图2，若O 经过点D ，求O 的半径长．(2)如图3，已知O 与射线BA 交于另一点F ，将BEF △沿EF 所在的直线翻折，点B 的对应点记为B '，且B '恰好同时落在O 和边AD 上，求此时PA 的长．9．（2024·云南昭通·模拟预测）如图，在O 中，AB 是O 的直径，点M 是直径AB 上的一个动点，过点M 的弦CD AB ⊥，交O 于点C 、D ，连接BC ，点F 为BC 的中点，连接DF 并延长，交AB 于点E ，交O 于点G ．图1 图2 备用图(1)如图1，连接CG ，过点G 的直线交DC 的延长线于点P ．当点M 与圆心O 重合时，若PGC MDE ∠=∠，求证：PG 是O 的切线；(2)在点M 运动的过程中，DE kDF =（k 为常数），求k 的值；(3)如图2，连接BG OF MF 、、，当MOF △是等腰三角形时，求BGD ∠的正切值．题型4：圆与坐标系或函数10．（2024·福建龙岩·一模）如图，抛物线234y x x =-++与x 轴分别交于A 、B 两点(点A 在点B 的左侧)与y 轴交于点C ．(1)直接写出A 、B 、C 三点的坐标；(2)如图(1)，P 是抛物线上异于A ，B 的一点，将点B 绕点P 顺时针旋转45︒得到点Q ，若点Q 恰好在直线AP 上，求点P 的坐标；(3)如图(2)，MN 是抛物线上异于B ，C 的两个动点，直线BN 与直线CM 交于点T ，若直线MN 经过定点()1,3，求证：点T 的运动轨迹是一条定直线．11．（2024·江苏常州·模拟预测）定义：在平面直角坐标系xOy 中，P 、Q 为平面内不重合的两个点，其中1122(,),(,)P x y Q x y ．若：1122x y x y +=+，则称点Q 为点P 的“等和点”．(1)如图1，已知点()21P ，，求点P 在直线1y x =+上“等和点”的坐标；(2)如图2，A 的半径为1，圆心A 坐标为()20，．若点()0P m ，在A 上有且只有一个“等和点”，求m 的值；(3)若函数()22y x x m =-+≤的图像记为1W ，将其沿直线x m =翻折后的图像记为2W ．当1W ，2W 两部分组成的图像上恰有点()0P m ，的两个“等和点”，请直接写出m 的取值范围．12．（2024·江苏宿迁·一模）如图1，在平面直角坐标系xOy 中，抛物线23y ax bx =++与x 轴分别相交于A 、B 两点，与y 轴相交于点C ，已知点A 的坐标为(10)-，，点B 的坐标为(30)，．(1)求出这条抛物线的函数表达式；(2)如图2，点D 是第一象限内该抛物线上一动点，过点D 作直线l y 轴，直线l 与ABD △的外接圆相交于点E ．①仅用无刻度直尺找出图2中ABD △外接圆的圆心P ．②连接BC 、CE ，BC 与直线DE 的交点记为Q ，如图3，设CQE △的面积为S ，在点D 运动的过程中，S是否存在最大值？如果存在，请求出S 的最大值；如果不存在，请说明理由．13．（2024·江苏宿迁·二模）中国象棋棋盘上双方的分界处称为“楚河汉界”，以“楚河汉界”比喻双方对垒的分界线．在平面直角坐标系中，为了对两个图形进行分界，对“楚河汉界线”给出如下定义：点()11,P x y 是图形1G 上的任意一点，点()22,Q x y 是图形2G 上的任意一点，若存在直线()0l y kx b k =+≠∶满足11y kx b ≤+且22y kx b ≥+，则直线(0)y k b k =+≠就是图形1G 与2G 的“楚河汉界线”．例如：如图1，直线4l y x =--∶是函数6(0)y x x=<的图像与正方形OABC 的一条“楚河汉界线”．(1)在直线①2y x =-，②41y x =-，③23y x =-+，④31y x =--中，是图1函数6(0)y x x=<的图像与正方形OABC 的“楚河汉界线”的有______；（填序号）(2)如图2，第一象限的等腰直角EDF 的两腰分别与坐标轴平行，直角顶点D 的坐标是()2,1，EDF 与O 的“楚河汉界线”有且只有一条，求出此“楚河汉界线”的表达式；(3)正方形1111D C B A 的一边在y 轴上，其他三边都在y 轴的右侧，点(2,)M t 是此正方形的中心，若存在直线2y x b =-+是函数2)304(2y x x x =-++≤≤的图像与正方形1111D C B A 的“楚河汉界线”，求t 的取值范围．题型5：以实际问题为背景，求圆与三角形、四边形综合问题14．（2024·陕西西安·一模）【问题提出】（1）如图1，已知在边长为5的等边ABC 中，点D 在边BC 上，3BD =，连接AD ，则ACD 的面积为；【问题探究】（2）如图2，已知在边长为6的正方形ABCD 中，点E 在边BC 上，点F 在边CD 上，且45EAF ∠=︒，若5EF =，求AEF △的面积；【问题解决】（3）如图3是某座城市廷康大道的一部分，因自来水抢修在4AB =米，AD =ABCD 区域内开挖一个AEF △的工作面，其中B 、F 分别在BC CD 、边上（不与B 、C 、D 重合），且60EAF ∠=︒，为了减少对该路段的拥堵影响，要求AEF △面积最小，那么是否存在一个面积最小的AEF △？若存在，请求出AEF △面积的最小值；若不存在，请说明理由．15．（2024·陕西西安·一模）【问题提出】（1）如图1，点D 为ABC 的边BC 上一点，连接2,,3BD AD BDA BAC AB ∠=∠=，若ABD △的面积为4，则ACD 的面积为______；【问题探究】（2）如图2，在矩形ABCD 中，6,5AB BC ==，在射线BC 和射线CD 上分别取点E F 、，使得65BE CF =，连接AE BF 、相交于点P ，连接CP ，求CP 的最小值；【问题解决】（3）如图3，菱形ABCD 是某社区的一块空地，经测量，120AB =米，60ABC ∠=︒．社区管委会计划对该空地进行重新规划利用，在射线AD 上取一点E ，沿BE CE 、修两条小路，并在小路BE 上取点H ，将CH 段铺设成某种具有较高观赏价值的休闲通道（通道宽度忽略不计），根据设计要求，BHC BCE ∠=∠，为了节省铺设成本，要求休闲通道CH 的长度尽可能小，问CH 的长度是否存在最小值？若存在，求出CH 长度的最小值；若不存在，请说明理由．题型6：最值问题16．（2024·湖南长沙·三模）如图1，,,A B C 为O 上不重合的三点，GC 为O 的切线，1902G A ∠+∠=︒．(1)求证：GB 为O 的切线；(2)若ABC 为等腰三角形，345,tan 4BAC BAC ∠<︒∠=，求BC AG的值；(3)如图2，若AB 为直径，M 为线段AC 上一点且GM GB ⊥，2223880AM OB GB GB +-+-=，02GB <<，求MGBA S 四边形的最大值．17．（2024·重庆·模拟预测）如图，在直角ABC 中，90BAC ∠=︒．点D 为ABC 内一点，且60ADB ∠=︒，E 为线段BD 的中点，连接AE ．(1)如图1，若AB AC ==，2AD =，求BE 的长；(2)如图2，连接CD ，若AB AC =，BAE ACD ∠=∠，过点E 作EF AD ⊥交于F ，求证：AE =；(3)如图3，过点D 作DM AC ⊥于点M ，DN BC ⊥于点N ，连接MN ，若AB =4AC =，求MN 的最小值．题型7：在解三角形、四边形中作辅助圆18．（2024·福建泉州·一模）如图1，在ABCD Y 中，BE 平分ABC ∠交AD 于点E ，F 是CD 上一点，且DF DE =．(1)求证：BE EF ⊥；(2)如图2，若120A ∠=︒，FG BC ⊥于点G ，H 是BF 的中点，连接DG ，EH ，EG ，且EG 与BF 相交于点K ．①求证：DG EH =；②若2CF DF =，求KFGK的值．题型8：定值问题19．（2024·浙江·模拟预测）如图1，E 点为x 轴正半轴上一点，E 交x 轴于A 、B 两点，P 点为劣弧 BC上一个动点，且(1,0)A -、(1,0)E ．(1) BC的度数为 °；(2)如图2，连结PC ，取PC 中点G ，则OG 的最大值为；(3)如图3，连接AC 、AP 、CP 、CB ．若CQ 平分PCD ∠交PA 于Q 点，求AQ 的长；(4)如图4，连接PA 、PD ，当P 点运动时（不与B 、C 两点重合），求证：PC PDPA+为定值，并求出这个定值．题型9：在圆综合中求解三角函数值20．（2024·湖南长沙·一模）如图1，在Rt ABC △中，90ABC ∠=︒，30C ∠=︒，B C =，D 是BC 的中点．经过A ，B ，D 三点的O 交AC 于点E ，连接BE ．(1)求AE 和BE 的长；(2)如图2，两动点P 、Q 分别同时从点A 和点C 出发匀速运动，当点P 运动到点E 时，点Q 恰好运动到点B ，P 、Q 停止运动，连接PQ ．①记AP x =，当PQC △的面积最大时，求x 的值；②如图3，连接BP 并延长交O 于点F ，连接AF 、FE ．当BE 平分FBC ∠时，求sin ABF ∠的值．21．（2024·上海杨浦·一模）已知以AB 为直径的半圆O 上有一点C ，CD OA ⊥，垂足为点D ，点E 是半径OC 上一点（不与点O 、C 重合），作EF OC ⊥交弧BC 于点F ，连接OF ．(1)如图1，当FE 的延长线经过点A 时，求CDAF的值；(2)如图2，作FG AB ⊥，垂足为点G ，连接EG ．①试判断EG 与CD 的大小关系，并证明你的结论；②当EFG 是等腰三角形，且4sin 5COD ∠=，求OE OD的值．专题01 中考压轴题-圆（九大题型+解题方法）1、圆中常见相似三角形2.在圆中解三角形或四边形的常用思路画出特殊图形：如圆中的特殊三角形、特殊四边形等，在已知条件下，以结果为导向，在这些特殊图形中求出一些中间量。

中考压轴题专题：与圆有关的最值问题(附答案)

与圆有关的最值（取值范围）问题引例1：在坐标系中，点A的坐标为(3，0)，点B为y轴正半轴上的一点，点C是第一象限内一点，且AC=2．设tan∠BOC=m，则m的取值范围是_________．引例2：如图，在边长为1的等边△OAB中，以边AB为直径作⊙D，以O为圆心OA长为半径作⊙O，C为半圆弧上的一个动点（不与A、B两点重合），射线AC交⊙O于点E，»ABBC=，AC=，求的最大值.a b a b引例3：如图，∠BAC=60°，半径长为1的圆O与∠BAC的两边相切，P为圆O上一动点，以P为圆心，PA长为半径的圆P交射线AB、AC于D、E两点，连接DE，则线段DE长度的最大值为( ).A．3 B．6 CD．一、题目分析：此题是一个圆中的动点问题，也是圆中的最值问题，主要考察了圆内的基础知识、基本技能和基本思维方法，注重了初、高中知识的衔接1．引例1：通过隐藏圆（高中轨迹的定义），寻找动点C与两个定点O、A构成夹角的变化规律，转化为特殊位置（相切）进行线段、角度有关计算，同时对三角函数值的变化（增减性）进行了延伸考查，其实质是高中“直线斜率”的直接运用；2．引例2：通过圆的基本性质，寻找动点C与两个定点A、B构成三角形的不变条件，结合不等式的性质进行转化，其实质是高中“柯西不等式”的直接运用；3．引例3：本例动点的个数由引例1、引例2中的一个动点，增加为三个动点，从性质运用、构图形式、动点关联上增加了题目的难度，解答中还是注意动点D、E与一个定点A 构成三角形的不变条件（∠DAE=60°），构造弦DE、直径所在的直角三角形，从而转化为弦DE与半径AP之间的数量关系，其实质是高中“正弦定理”的直接运用；综合比较、回顾这三个问题，知识本身的难度并不大，但其难点在于学生不知道转化的套路，只能凭直观感觉去寻找、猜想关键位置来求解，但对其真正的几何原理却无法通透.二、解题策略1．直观感觉，画出图形；2．特殊位置，比较结果；3．理性分析动点过程中所维系的不变条件，通过几何构建，寻找动量与定量（常量）之间的关系，建立等式，进行转化.A 三、中考展望与题型训练例一、斜率运用1.如图，A 点的坐标为（﹣2，1），以A 为圆心的⊙A 切x 轴于点B ，P （m ，n）为⊙A 上的一个动点，请探索n+m 的最大值．例二、圆外一点与圆的最近点、最远点1．如图，在Rt △ABC 中，∠ACB=90°，AC=4，BC=3，点D 是平面内的一个动点，且AD=2，M 为BD 的中点，在D 点运动过程中，线段CM 长度的取值范围是 .2．如图，⊙O 的直径为4，C 为⊙O 上一个定点，∠ABC=30°，动点P 从A 点出发沿半圆弧»AB 向B 点运动（点P 与点C 在直径AB 的异侧)，当P 点到达B 点时运动停止，在运动过程中，过点C 作CP 的垂线CD 交PB 的延长线于D 点．（1）在点P 的运动过程中，线段CD 长度的取值范围为；（2）在点P 的运动过程中，线段AD 长度的最大值为 .例三、正弦定理 1．如图，△ABC 中，∠BAC=60°，∠ABC=45°，AB=D 是线段BC 上的一个动点，以AD 为直径作⊙O 分别交AB ，AC 于E ，F 两点，连接EF ，则线段EF 长度的最小值为．2. 如图，定长弦CD 在以AB 为直径的⊙O 上滑动（点C 、D 与点A 、B 不重合），M 是CD 的中点，过点C 作CP ⊥AB 于点P ，若CD=3，AB=8，则PM 长度的最大值是．A例四、柯西不等式、配方法1．如图，已知半径为2的⊙O 与直线l 相切于点A ，点P 是直径AB 左侧半圆上的动点，过点P 作直线l 的垂线，垂足为C ，PC 与⊙O 交于点D ，连接PA 、PB ，设PC 的长为x （2＜x ＜4），则当x= 时，PD•CD 的值最大，且最大值是为 .2．如图，线段AB=4，C 为线段AB 上的一个动点，以AC 、BC 为边作等边△ACD 和等边△BCE ，⊙O 外接于△CDE ，则⊙O 半径的最小值为( ).D. 23．在平面直角坐标系中，以坐标原点O 为圆心，2为半径画⊙O ，P 是⊙O 上一动点，且P 在第一象限内，过点P 作⊙O 的切线与轴相交于点A ，与轴相交于点B ，线段AB 长度的x y 最小值是 .例四、相切的应用（有公共点、最大或最小夹角）1．如图，在Rt △ABC 中，∠C=90°，AC=6，BC=8，D 为AB 边上一点，过点D 作CD 的垂线交直线BC 于点E ，则线段CE 长度的最小值是 .2．如图，Rt△ABC 中，∠C=90°，∠A=30°，AB=4，以AC 上的一点O 为圆心OA 为半径作⊙O ，若⊙O 与边BC 始终有交点（包括B 、C 两点），则线段AO 的取值范围是 .3．如图，⊙O的半径为2，点O到直线l的距离为3，点P是直线l上的一个动点，PQ切⊙O 于点Q，则PQ的最小值为（）A．B．C．3 D．2例五、其他知识的综合运用1.（2015•济南）抛物线y=ax2+bx+4（a≠0）过点A（1，﹣1），B（5，﹣1），与y轴交于点C．（1）求抛物线的函数表达式；（2）如图1，连接CB，以CB为边作▱CBPQ，若点P在直线BC上方的抛物线上，Q为坐标平面内的一点，且▱CBPQ的面积为30，求点P的坐标；（3）如图2，⊙O1过点A、B、C三点，AE为直径，点M为上的一动点（不与点A，E 重合），∠MBN为直角，边BN与ME的延长线交于N，求线段BN长度的最大值．2.（2013秋•相城区校级期末）如图，已知A、B是⊙O与x轴的两个交点，⊙O的半径为1，P是该圆上第一象限内的一个动点，直线PA、PB分别交直线x=2于C、D两点，E为线段CD的中点．（1）判断直线PE与⊙O的位置关系并说明理由；（2）求线段CD长的最小值；（3）若E点的纵坐标为m，则m的范围为．B【题型训练】1．如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5，OA与⊙O相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C，若在⊙O上存在点Q，使△QAC是以AC为底边的等腰三角形，则⊙O的半径r的取值范围为 .2．已知：如图，RtΔABC中，∠B=90º，∠A=30º，BC=6cm，点O从A点出发，沿AB以每秒cm的速度向B点方向运动，当点O运动了t秒(t＞0)时，以O点为圆心的圆与边AC相切于点D，与边AB相交于E、F两点，过E作EG⊥DE交射线BC于G.（1）若点G在线段BC上，则t的取值范围是；（2）若点G在线段BC的延长线上，则t的取值范围是 .3．如图，⊙M，⊙N的半径分别为2cm，4cm，圆心距MN=10cm．P为⊙M上的任意一点，Q为⊙N上的任意一点，直线PQ与连心线所夹的锐角度数为，当P、Q在两圆上任意运动时，lα的最大值为； (B)；； (D) tanα∠43344．如图，在矩形ABCD中，AB=3，BC=4，O 为矩形ABCD的中心，以D为圆心1为半径作⊙D，P为⊙D上的一个动点，连接AP、OP，则△AOP面积的最大值为( ).(A)4 (B) (C) (D)215358174 5．如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，经过点C且与边AB相切的动圆与CA、CB 分别相交于点P、Q，则线段PQ长度的最小值是( ).A． B． C．5 D．1942456．如图，在等腰Rt△ABC中，∠C=90°，AC=BC=4，D是AB的中点，点E在AB边上运动（点E不与点A重合），过A、D、E三点作⊙O，⊙O交AC于另一点F，在此运动变化的过程中，线段EF长度的最小值为．7．如图，A、B两点的坐标分别为(2，0)、(0，2)，⊙C的圆心的坐标为(-1，0)，半径为1，若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积的最小值是( ).A．2 B．1 C. D.22-8．如图，已知A、B两点的坐标分别为(-2，0)、(0，1)，⊙C的圆心坐标为(0，-1)，半径为1，D是⊙C上的一个动点，射线AD与y轴交于点E，则△ABE面积的最大值是( ).A．3 B． C．103D．41139．如图，等腰Rt△ABC中，∠ACB=90°，AC=BC=4，⊙C的半径为1，点P在斜边AB上，PQ 切⊙O于点Q，则切线长PQ长度的最小值为( ).B.10．如图∠BAC＝60°，半径长1的⊙O与∠BAC的两边相切，P为⊙O上一动点，以P为圆心，PA长为半径的⊙P交射线AB、AC于D、E两点，连接DE，则线段DE长度的范围为 .11．在直角坐标系中，点A的坐标为（3，0），点P（）是第一象限内一点，且AB=2，m n，则的范围为 .m n-12．在坐标系中，点A的坐标为（3，0），点P是y轴右侧一点，且AP=2，点B上直线y=x+1上一动点，且PB⊥AP于点P，则，则的取值范围是 .tan ABP m∠=m13．在平面直角坐标系中，M（3，4），P是以M为圆心，2为半径的⊙M上一动点，A（-1，0）、B（1，0），连接PA、PB，则PA2+PB2最大值是 .蔡老师点评：与圆有关的最值问题，看着无从下手，但只要仔细观察，分析图形，寻找动点与定点之间不变的维系条件，构建关系，将研究的问题转化为变量与常量之间的关系，就能找到解决问题的突破口！几何中的定值问题，是指变动的图形中某些几何元素的几何量保持不变，或几何元素间的某些几何性质或位置关系不变的一类问题，解几何定值问题的基本方法是：分清问题的定量及变量，运用特殊位置、极端位置，直接计算等方法，先探求出定值，再给出证明．几何中的最值问题是指在一定的条件下，求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值，求几何最值问题的基本方法有：1．特殊位置与极端位置法；2．几何定理(公理)法；3．数形结合法等．注：几何中的定值与最值近年广泛出现于中考试题中，由冷点变为热点．这是由于这类问题具有很强的探索性(目标不明确)，解题时需要运用动态思维、数形结合、特殊与一般相结合、逻辑推理与合情想象相结合等思想方法．参考答案：引例1.解：C在以A为圆心，以2为半径作圆周上，只有当OC与圆A相切（即到C点）时，∠BOC最小，AC=2，OA=3，由勾股定理得：OC=，∵∠BOA=∠ACO=90°，∴∠BOC+∠AOC=90°，∠CAO+∠AOC=90°，∴∠BOC=∠OAC，tan∠BOC=tan∠OAC= =，随着C的移动，∠BOC越来越大，∵C在第一象限，∴C不到x轴点，即∠BOC＜90°，∴tan∠BOC≥，故答案为：m≥．引例1图引例2图+≤引例2.a b原题：（2013•武汉模拟）如图，在边长为1的等边△OAB中，以边AB为直径作⊙D，以O为圆心OA长为半径作圆O，C为半圆AB上不与A、B重合的一动点，射线AC交⊙O 于点E，BC=a，AC=b．（1）求证：AE=b+a；（2）求a+b的最大值；（3）若m是关于x的方程：x2+ax=b2+ab的一个根，求m的取值范围．【考点】圆的综合题．【分析】（1）首先连接BE，由△OAB为等边三角形，可得∠AOB=60°，又由圆周角定理，可求得∠E的度数，又由AB为⊙D的直径，可求得CE的长，继而求得AE=b+a；（2）首先过点C作CH⊥AB于H，在Rt△ABC中，BC=a，AC=b，AB=1，可得（a+b）2=a2+b2+2ab=1+2ab=1+2CH•AB=1+2CH≤1+2AD=1+AB=2，即可求得答案；（3）由x2+ax=b2+ab，可得（x﹣b）（x+b+a）=0，则可求得x的值，继而可求得m 的取值范围．【解答】解：（1）连接BE，∵△OAB为等边三角形，∴∠AOB=60°，∴∠AEB=30°，∵AB为直径，∴∠ACB=∠BCE=90°，∵BC=a，∴BE=2a，CE=a，∵AC=b，∴AE=b+a；（2）过点C作CH⊥AB于H，在Rt△ABC中，BC=a，AC=b，AB=1，∴a2+b2=1，∵S△ABC=AC•BC=AB•CH，∴AC•BC=AB•CH，∴（a+b）2=a2+b2+2ab=1+2ab=1+2CH•AB=1+2CH≤1+2AD=1+AB=2，∴a+b≤，故a+b的最大值为，（3）∵x2+ax=b2+ab，∴x2﹣b2+ax﹣ab=0，∴（x+b）（x﹣b）+a（x﹣b）=0，∴（x﹣b）（x+b+a）=0，∴x=b或x=﹣（b+a），当m=b时，m=b=AC＜AB=1，∴0＜m＜1，当m=﹣（b+a）时，由（1）知AE=﹣m，又∵AB＜AE≤2AO=2，∴1＜﹣m≤2，∴﹣2≤m＜﹣1，∴m的取值范围为0＜m＜1或﹣2≤m＜﹣1．【点评】此题考查了圆周角定理、等边三角形的性质、完全平方公式的应用以及一元二次方程的解法．此题难度较大，注意掌握数形结合思想与分类讨论思想的应用．引例3.解：连接EP，DP，过P点作PM垂直DE于点M，过O做OF⊥AC与F，连接AO，如图，∵∠BAC=60°，∴∠DPE=120°．∵PE=PD，PM⊥DE，∴∠EPM=60°，∴ED=2EM=2EP•sin60°=EP=PA．当P与A、O共线时，且在O点右侧时，⊙P直径最大．∵⊙O与∠BAC两边均相切，且∠BAC=60°，∴∠OAF=30°，OF=1，∴AO==2，AP=2+1=3，∴DE=PA=3．故答案为：D。

人教中考数学圆的综合-经典压轴题附详细答案

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，在⊙O 中，直径AB ⊥弦CD 于点E ，连接AC ，BC ，点F 是BA 延长线上的一点，且∠FCA ＝∠B .(1)求证：CF 是⊙O 的切线； (2)若AE ＝4，tan ∠ACD ＝ 12，求AB 和FC 的长．【答案】(1)见解析;(2) ⑵AB=20 ， 403CF =【解析】分析：（1）连接OC ，根据圆周角定理证明OC ⊥CF 即可；（2）通过正切值和圆周角定理，以及∠FCA ＝∠B 求出CE 、BE 的长，即可得到AB 长，然后根据直径和半径的关系求出OE 的长，再根据两角对应相等的两三角形相似（或射影定理）证明△OCE ∽△CFE ，即可根据相似三角形的对应线段成比例求解.详解：⑴证明：连结OC∵AB 是⊙O 的直径∴∠ACB=90°∴∠B+∠BAC=90°∵OA=OC∴∠BAC=∠OCA∵∠B=∠FCA∴∠FCA+∠OCA=90°即∠OCF=90°∵C 在⊙O 上∴CF 是⊙O 的切线⑵∵AE=4，tan ∠ACD12AE EC = ∴CE=8∵直径AB ⊥弦CD 于点E∴AD AC =∵∠FCA ＝∠B∴∠B=∠ACD=∠FCA∴∠EOC=∠ECA∴tan ∠B=tan ∠ACD=1=2CE BE ∴BE=16∴AB=20∴OE=AB÷2-AE=6∵CE ⊥AB ∴∠CEO=∠FCE=90°∴△OCE ∽△CFE ∴OC OE CF CE= 即106=8CF ∴40CF 3= 点睛：此题主要考查了圆的综合知识，关键是熟知圆周角定理和切线的判定与性质，结合相似三角形的判定与性质和解直角三角形的知识求解，利用数形结合和方程思想是解题的突破点，有一定的难度，是一道综合性的题目.2．函数是描述客观世界运动变化的重要模型，理解函数的本质是重要的任务。

（1）如图1，在平面直角坐标系中，已知点A 、B 的坐标分别为A （6，0）、B （0，2），点C （x ，y ）在线段AB 上，计算（x+y ）的最大值。

(完整)中考数学圆-经典压轴题(带答案)

1。

如图,四边形ABCD内接于⊙O，AB是⊙O的直径，AC和BD相交于点E，且DC2=CE•CA．（1）求证:BC=CD;（2）分别延长AB，DC交于点P,过点A作AF⊥CD交CD的延长线于点F，若PB=OB，CD =，求DF的长．2。

如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F．切点为G，连接AG交CD于K．（1）求证：KE=GE；（2）若=KD·GE，试判断AC与EF的位置关系,并说明理由;(3）在（2）的条件下，若sinE=，AK=，求FG的长．3.如图，AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE．（1)求证：AC 平分∠DAB ；(2）求证：△PCF 是等腰三角形；（3）若tan ∠ABC=34，BE=72，求线段PC 的长．4.5。

已知:如图，在半径为4的⊙O 中，AB ，CD 是两条直径，M 为OB 的中点，CM 的延长线交⊙O 于点E，且EM＞MC，连结DE，DE=。

（1）求证：AM·MB=EM·MC；（2）求EM的长；(3）求sin∠EOB的值。

6。

如图，AE切⊙O于点E，AT交⊙O于点M,N,线段OE交AT于点C,OB⊥AT于点B，已知∠EAT=30°,AE=3，MN=2．(1）求∠COB的度数;（2）求⊙O的半径R；（3)点F在⊙O上（是劣弧）,且EF=5,把△OBC经过平移、旋转和相似变换后，使它的两个顶点分别与点E,F重合．在EF的同一侧，这样的三角形共有多少个？你能在其中找出另一个顶点在⊙O上的三角形吗？请在图中画出这个三角形，并求出这个三角形与△OBC的周长之比．7.如图，AB是半径O的直径，AB=2．射线AM、BN为半圆O的切线．在AM上取一点D,连接BD交半圆于点C，连接AC．过O点作BC的垂线OE，垂足为点E，与BN相交于点F．过D点作半圆O的切线DP，切点为P,与BN相交于点Q．（1）求证：△ABC∽△OFB；（2）当△ABD与△BFO的面枳相等时，求BQ的长；（3）求证：当D在AM上移动时（A点除外）,点Q始终是线段BF的中点8.如图，在⊙O的内接△ABC中,∠ACB=90°，AC=2BC，过C作AB的垂线l交⊙O于另一点D，垂足为E.设P是上异于A,C的一个动点，射线AP交l于点F，连接PC与PD，PD交AB于点G.（1）求证：△PAC∽△PDF；（2）若AB=5，，求PD的长；（3）在点P运动过程中，设，求与之间的函数关系式。

人教中考数学(圆的综合提高练习题)压轴题训练附答案

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，⊙O是△ABC的外接圆，点E为△ABC内切圆的圆心，连接AE的延长线交BC于点F，交⊙O于点D；连接BD，过点D作直线DM，使∠BDM=∠DAC．（1）求证：直线DM是⊙O的切线；（2）若DF=2，且AF=4，求BD和DE的长．【答案】（1）证明见解析（2）23【解析】【分析】（1）根据垂径定理的推论即可得到OD⊥BC，再根据∠BDM=∠DBC，即可判定BC∥DM，进而得到OD⊥DM，据此可得直线DM是⊙O的切线；（2）根据三角形内心的定义以及圆周角定理，得到∠BED=∠EBD，即可得出DB=DE，再判定△DBF∽△DAB，即可得到DB2=DF•DA，据此解答即可．【详解】（1）如图所示，连接OD．∵点E是△ABC的内心，∴∠BAD=∠CAD，∴BD CD=，∴OD⊥BC．又∵∠BDM=∠DAC，∠DAC=∠DBC，∴∠BDM=∠DBC，∴BC∥DM，∴OD⊥DM．又∵OD为⊙O半径，∴直线DM是⊙O的切线．（2）连接BE．∵E为内心，∴∠ABE=∠CBE．∵∠BAD=∠CAD，∠DBC=∠CAD，∴∠BAD=∠DBC，∴∠BAE+∠ABE=∠CBE+∠DBC，即∠BED=∠DBE，∴BD=DE．又∵∠BDF=∠ADB（公共角），∴△DBF∽△DAB，∴DF DBDB DA=，即DB2=DF•DA．∵DF=2，AF=4，∴DA=DF+AF=6，∴DB2=DF•DA=12，∴DB=DE=23．【点睛】本题主要考查了三角形的内心与外心，圆周角定理以及垂径定理的综合应用，解题时注意：平分弦所对一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧；三角形的内心到三角形三边的距离相等；三角形的内心与三角形顶点的连线平分这个内角．2．已知：如图，在矩形ABCD 中，点O 在对角线BD 上，以OD 的长为半径的⊙O 与AD ，BD 分别交于点E 、点F ，且∠ABE=∠DBC ．（1）判断直线BE 与⊙O 的位置关系，并证明你的结论；（2）若sin ∠ABE=33，CD=2，求⊙O 的半径．【答案】（1）直线BE 与⊙O 相切，证明见解析；（2）⊙O 的半径为3．【解析】分析：（1）连接OE ，根据矩形的性质，可证∠BEO =90°，即可得出直线BE 与⊙O 相切；（2）连接EF ，先根据已知条件得出BD 的值，再在△BEO 中，利用勾股定理推知BE 的长，设出⊙O 的半径为r ，利用切线的性质，用勾股定理列出等式解之即可得出r 的值．详解：（1）直线BE 与⊙O 相切．理由如下：连接OE ，在矩形ABCD 中，AD ∥BC ，∴∠ADB =∠DBC ． ∵OD =OE ，∴∠OED =∠ODE ．又∵∠ABE =∠DBC ，∴∠ABE =∠OED ， ∵矩形ABDC ，∠A =90°，∴∠ABE +∠AEB =90°，∴∠OED +∠AEB =90°，∴∠BEO =90°，∴直线BE 与⊙O 相切；（2）连接EF ，方法1：∵四边形ABCD 是矩形，CD =2，∴∠A =∠C =90°，AB =CD =2． ∵∠ABE =∠DBC ，∴sin ∠CBD =3sin ABE ∠= ∴23DCBD sin CBD∠==在Rt △AEB 中，∵CD =2，∴22BC =．∵tan ∠CBD =tan ∠ABE ，∴2222DC AE AEAE BC AB ，，=∴=∴=，由勾股定理求得6BE =．在Rt △BEO 中，∠BEO =90°，EO 2+EB 2=OB 2．设⊙O 的半径为r ，则222623r r +=-（）（），∴r =3，方法2：∵DF 是⊙O 的直径，∴∠DEF =90°． ∵四边形ABCD 是矩形，∴∠A =∠C =90°，AB =CD =2． ∵∠ABE =∠DBC ，∴sin ∠CBD =33sin ABE ∠=．设3DC x BD x ==，，则2BC x =．∵CD =2，∴22BC =． ∵tan ∠CBD =tan ∠ABE ，∴2222DC AE AEAE BC AB ，，=∴=∴=， ∴E 为AD 中点．∵DF 为直径，∠FED =90°，∴EF ∥AB ，∴132DF BD ==，∴⊙O 的半径为3．点睛：本题综合考查了切线的性质、勾股定理以及三角函数的应用等知识点，具有较强的综合性，有一定的难度．3．已知：如图，△ABC 中，AC=3，∠ABC=30°．（1）尺规作图：求作△ABC 的外接圆，保留作图痕迹，不写作法；（2）求（1）中所求作的圆的面积．【答案】（1）作图见解析；（2）圆的面积是9π．【解析】试题分析：（1）按如下步骤作图：①作线段AB 的垂直平分线；②作线段BC 的垂直平分线；③以两条垂直平分线的交点O 为圆心，OA 长为半圆画圆，则圆O 即为所求作的圆．如图所示（2）要求外接圆的面积，需求出圆的半径，已知AC ＝3，如图弦AC 所对的圆周角是∠ABC=30°，所以圆心角∠AOC=60°，所以∆AOC是等边三角形，所以外接圆的半径是3故可求得外接圆的面积．（2）连接OA，OB．∵AC=3，∠ABC=30°，∴∠AOC=60°，∴△AOC是等边三角形，∴圆的半径是3，∴圆的面积是S=πr2=9π．4．如图，△ABC中，∠A=45°，D是AC边上一点，⊙O经过D、A、B三点，OD∥BC．（1）求证：BC与⊙O相切；（2）若OD=15，AE=7，求BE的长．【答案】(1)见解析;(2)18.【解析】分析：（1）连接OB，求出∠DOB度数，根据平行线性质求出∠CBO=90°，根据切线判定得出即可；（2）延长BO交⊙O于点F，连接AF，求出∠ABF，解直角三角形求出BE．详解：（1）证明：连接OB．∵∠A=45°，∴∠DOB=90°．∵OD∥BC，∴∠DOB+∠CBO=180°．∴∠CBO=90°．∴直线BC是⊙O的切线．（2）解：连接BD．则△ODB是等腰直角三角形，∴∠ODB=45°，BD=OD=15，∵∠ODB=∠A，∠DBE=∠DBA，∴△DBE∽△ABD，∴BD2=BE•BA，∴（15）2=（7+BE）BE，∴BE=18或﹣25（舍弃），∴BE=18．点睛：本题考查了切线的判定，圆周角定理，解直角三角形等知识点，能综合运用定理进行推理和计算是解此题的关键，题目综合性比较强，难度偏大．5．如图，已知AB为⊙O直径，D是BC的中点，DE⊥AC交AC的延长线于E，⊙O的切线交AD的延长线于F．（1）求证：直线DE与⊙O相切；（2）已知DG⊥AB且DE=4，⊙O的半径为5，求tan∠F的值．【答案】（1）证明见解析；（2）2．【解析】试题分析：（1）连接BC、OD，由D是弧BC的中点，可知：OD⊥BC；由OB为⊙O的直径，可得：BC⊥AC，根据DE⊥AC，可证OD⊥DE，从而可证DE是⊙O的切线；（2）直接利用勾股定理得出GO的长，再利用锐角三角函数关系得出tan∠F的值．试题解析：解：（1）证明：连接OD，BC，∵D是弧BC的中点，∴OD垂直平分BC，∵AB 为⊙O的直径，∴AC⊥BC，∴OD∥AE．∵DE⊥AC，∴OD⊥DE，∵OD为⊙O的半径，∴DE 是⊙O的切线；（2）解：∵D是弧BC的中点，∴DC DB，∴∠EAD=∠BAD，∵DE⊥AC，DG⊥AB且DE=4，∴DE=DG=4，∵DO=5，∴GO=3，∴AG=8，∴tan∠ADG=84=2，∵BF是⊙O的切线，∴∠ABF=90°，∴DG∥BF，∴tan∠F=tan∠ADG=2．点睛：此题主要考查了切线的判定与性质以及勾股定理等知识，正确得出AG，DG的长是解题关键．6．阅读：圆是最完美的图形，它具有一些特殊的性质：同弧或等弧所对的圆周角相等，一条弧所对的圆周角等于这条弧所对的圆心角的一半……先构造“辅助圆”，再利用圆的性质将问题进行转化，往往能化隐为显、化难为易。

2020年中考数学复习：《圆》解答题压轴专题训练(解析版)

2020年中考数学复习：《圆》解答题压轴专题训练1．如图，AB是⊙O的直径，AC是⊙O的切线，连接OC交⊙O于E，过点A作AF⊥AC于F 交⊙O于D，连接DE，BE，BD（1）求证：∠C＝∠BED；（2）若AB＝12，tan∠BED＝，求CF的长．（1）证明：∵AB是⊙O的直径，CA切⊙O于A，∴∠C+∠AOC＝90°；又∵OC⊥AD，∴∠OFA＝90°，∴∠AOC+∠BAD＝90°，∴∠C＝∠BAD．又∵∠BED＝∠BAD，∴∠C＝∠BED．（2）解：由（1）知∠C＝∠BAD，tan∠BED＝，∴tan∠C＝，∴tan∠C＝＝，且OA＝AB＝6，∴，解得AC＝8，∴＝10，∵OC•AF＝OA•AC，∴．∴＝＝．2．如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D 为弧BE的中点，连接AD交BC于F，AC＝FC，连接BD．（1）求证：AC是⊙O的切线；（2）已知⊙O的半径R＝5cm，AB＝8cm，求△ABD的面积．（1）证明：连接OA，OD．∵点D是弧BE的中点，∴∠BOD＝∠EOD＝90°，∴∠ODF+∠OFD＝90°又∵∠OFD＝∠AFC，∴∠ODF+∠AFC＝90°又∵AC＝FC，∴∠AFC＝∠CAF，∵OA＝OD，∴∠ODF＝∠OAF，∴∠OAF+∠CAF＝90°，即∠OAC＝90°，故AC是⊙O的切线；（2）解：过点B作BG⊥AD于G，∵∠BOD＝90°，OB＝OD＝R＝5，∴，∵点D是弧BE的中点，∴∠BAD＝45°，∵∠AGB＝90°，∴∠ABG＝∠BAD＝45°，即BG＝AG．∴又∵，∴＝AD•BG＝＝28（cm2）．故S△ABD3．如图所示，以△ABC的边AB为直径作⊙O，点C在⊙O上，BD是⊙O的弦，∠A＝∠CBD，过点C作CF⊥AB于点F，交BD于点G过C作CE∥BD交AB的延长线于点E．（1）求证：CE是⊙O的切线；（2）求证：CG＝BG；（3）若∠DBA＝30°，CG＝8，求BE的长．（1）证明：连接OC，∵∠A＝∠CBD，∴＝，∴OC⊥BD，∵CE∥BD，∴OC⊥CE，∴CE是⊙O的切线；（2）证明：∵AB为直径，∵CF⊥AB，∴∠ACB＝∠CFB＝90°，∵∠ABC＝∠CBF，∴∠A＝∠BCF，∵∠A＝∠CBD，∴∠BCF＝∠CBD，∴CG＝BG；（3）解：连接AD，∵AB为直径，∴∠ADB＝90°，∵∠DBA＝30°，∴∠BAD＝60°，∵＝，∴∠DAC＝∠BAC＝∠BAD＝30°，∴＝tan30°＝，∵CE∥BD，∴∠E＝∠DBA＝30°，∴AC＝CE，∴＝，∵∠A＝∠BCF＝∠CBD＝30°，∴∠BCE＝30°，∴BE＝BC，∴△CGB∽△CBE，∴＝＝，∵CG＝8，∴BC＝8，∴BE＝8．4．如图，B，E是⊙O上的两个定点，A为优弧BE上的动点，过点B作BC⊥AB交射线AE于点C，过点C作CF⊥BC，点D在CF上，且∠EBD＝∠A．（1）求证：BD与⊙O相切；（2）已知∠A＝30°．①若BE＝3，求BD的长；②当O，C两点间的距离最短时，判断A，B，C，D四点所组成的四边形的形状，并说明理由．（1）证明：如图1，作直径BG，连接GE，则∠GEB＝90°，∴∠G+∠GBE＝90°，∵∠A＝∠EBD，∠A＝∠G，∴∠EBD＝∠G，∴∠EBD+∠GBE＝90°，∴∠GBD＝90°，∴BD⊥OB，∴BD与⊙O相切；（2）解：如图2，连接AG，∵BC⊥AB，∴∠ABC＝90°，由（1）知∠GBD＝90°，∴∠GBD＝∠ABC，∴∠GBA＝∠CBD，又∵∠GAB＝∠DCB＝90°，∴△BCD∽△BAG，∴＝＝tan30°＝，又∵Rt△BGE中，∠BGE＝30°，BE＝3，∴BG＝2BE＝6，∴BD＝6×＝2；（3）解：四边形ABCD是平行四边形，理由如下，由（2）知＝，＝，∴＝，∵B，E为定点，BE为定值，∴BD为定值，D为定点，∵∠BCD＝90°，∴点C在以BD为直径的⊙M上运动，∴当点C在线段OM上时，OC最小，此时在Rt△OBM中，＝＝，∴∠OMB＝60°，∴MC＝MB，∴∠MDC＝∠MCD＝30°＝∠A，∵AB⊥BC，CD⊥BC，∴∠ABC＝∠DCB＝90°，∴AB∥CD，∴∠A+∠ACD＝180°，∴∠BDC+∠ACD＝180°，∴AC∥BD，∴四边形ABCD为平行四边形．5．如图，在△ABC中，A B＝AC，⊙O是△ABC的外接圆，连结OA、OB、OC，延长BO与AC 交于点D，与⊙O交于点F，延长BA到点G，使得∠BGF＝∠GBC，连接FG．（1）求证：FG是⊙O的切线；（2）若⊙O的径为4．①当OD＝3，求AD的长度；②当△OCD是直角三角形时，求△ABC的面积．（1）证明：连接AF，∵BF为⊙O的直径，∴∠BAF＝90°，∠FAG＝90°，∴∠BGF+∠AFG＝90°，∵AB＝AC，∴∠ABC＝∠ACB，∵∠ACB＝∠AFB，∠BGF＝∠ABC，∴∠BGF＝∠AFB，∴∠AFB+∠AFG＝90°，即∠OFG＝90°，又∵OF为半径，∴FG是⊙O的切线；（2）解：①连接CF，则∠ACF＝∠ABF，∵AB＝AC，AO＝AO，BO＝CO，∴△ABO≌△ACO（SSS），∴∠ABO＝∠BAO＝∠CAO＝∠ACO，∴∠CAO＝∠ACF，∴AO∥CF，∴＝，∵半径是4，OD＝3，∴DF＝1，BD＝7，∴＝＝3，即CD＝AD，∵∠ABD＝∠FCD，∠ADB＝∠FDC，∴△ADB∽△FDC，∴＝，∴AD•CD＝BD•DF，∴AD•CD＝7，即AD2＝7，∴AD＝（取正值）；②∵△ODC为直角三角形，∠DCO不可能等于90°，∴存在∠ODC＝90°或∠COD＝90°，当∠ODC＝90°时，∵∠ACO＝∠ACF，∴OD＝DF＝2，BD＝6，∴AD＝CD，∴AD•CD＝AD2＝12，∴AD＝2，AC＝4，＝×4×6＝12；∴S△ABC当∠COD＝90°时，∵OB＝OC＝4，∴△OBC是等腰直角三角形，∴BC＝4，延长AO交BC于点M，则AM⊥BC，∴MO＝2，∴AM＝4+2，＝×4×（4+2）＝8+8，∴S△ABC∴△ABC的面积为12或8+8．6．如图⊙O的直径AB＝10cm，弦BC＝6cm，∠ACB的平分线交⊙O于D，交AB于E，P是AB 延长线上一点，且PC＝PE．（l）求证：PC是⊙O的切线；（2）求AC、AD的长．（1）证明：连结OC，如图所示：∵PC＝PE，∴∠PCE＝∠PEC，∵∠PEC＝∠EAC+∠ACE＝∠EAC+45°，而∠CAB＝90°﹣∠ABC，∠ABC＝∠OCB，∴∠PCE＝90°﹣∠OCB+45°＝90°﹣（∠OCE+45°）+45°，∴∠OCE+∠PCE＝90°，即∠PCO＝90°，∴OC⊥PC，∴PC为⊙O的切线；（2）连结BD，如图所示，∵AB为直径，∴∠ACB＝90°，在Rt△ACB中，AB＝10cm，BC＝6cm，∴AC＝＝8（cm）；∵DC平分∠ACB，∴∠ACD＝∠BCD＝45°，∴∠DAB＝∠DBA＝45°∴△ADB为等腰直角三角形，∴AD＝AB＝5（cm）．7．如图，在Rt△ABC中，∠BAC＝90°，CD平分∠ACB，交AB于点D，以点D为圆心，DA 为半径的圆与AB相交于点E，与CD交于点F．（1）求证：BC是⊙D的切线；（2）若EF∥BC，且BC＝6，求图中阴影部分的面积．（1）证明：过D作DG⊥BC于G，∵DA⊥AC，∠ACD＝∠BCD，∴DG＝DA，∴BC是⊙D的切线；（2）解：连接EF，∵EF∥BC，由（1）DG⊥BC，∴DG⊥EF，∴＝．∴∠EDG＝∠CDG．由（1）∠ACD＝∠BCD，∠ACD+∠ADC＝∠BCD+∠CDG＝90°，∴∠CDG＝∠ADC，∴∠CDG＝∠ADC＝∠BDG＝60°．∵EF∥BC，∴∠DEF＝∠B，∠DFE＝∠DCB，在⊙D中，DE＝DF，∴∠DFE＝∠DEF．∴∠B＝∠DCB，∴DB＝DC．∵DG⊥BC，∴CG＝BC＝3．在Rt△DCG中，D G＝CG/＝．∴S＝×3×﹣π（）2＝﹣．阴影8．请阅读下列材料，并完成相应的任务．人类会作圆并且真正了解圆的性质是在2000多年前，由我国的墨子给出圆的概念：“一中同长也．”．意思说，圆有一个圆心，圆心到圆周的长都相等．这个定义比希腊数学家欧几里得给圆下的定义要早100年．与圆有关的定理有很多，弦切角定理就是其中之一．我们把顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角．弦切角定理：弦切角的度数等于它所夹弧所对的圆周角度数．下面是弦切角定理的部分证明过程：证明：如图①，AB与⊙O相切于点A．当圆心O在弦AC上时，容易得到∠CAB＝90°，所以弦切角∠BAC的度数等于它所夹半圆所对的圆周角度数．如图②，AB与⊙O相切于点A，当圆心O在∠BAC的内部时，过点A作直径AD交⊙O于点D，在上任取一点E，连接EC，ED，EA，则∠CED＝∠CAD．任务：（1）请按照上面的证明思路，写出该证明的剩余部分；（2）如图③，AB与⊙O相切于点A．当圆心O在∠BAC的外部时，请写出弦切角定理的证明过程．解：（1）如图②，∵AD是⊙O直径，∴∠DEA＝90°．∵AB与⊙O相切于点A，∴∠DAB＝90°．∴∠CED+∠DEA＝∠CAD+∠DAB，即∠CEA＝∠CAB，∴弦切角的度数等于它所夹弧所对的圆周角度数；（2）证明：如图③，过点A作直径AF交⊙O于点F，连接FC，∵AF是直径，∴∠ACF＝90°，∴∠CFA+∠FAC＝90°，∵AB与⊙O相切于点A，∴∠FAB＝90°，∴∠CAB+∠FAC＝90°，∴∠CAB＝∠CFA，即弦切角的度数等于它所夹弧所对的圆周角度数．9．【问题背景】（1）如图1，⊙O与∠P的两边分别切与A，B两点．求证：PA＝PB．【深入探究】（2）在（1）的条件下，若∠APB＝60°，连接PO，以PO为一条边向上作等边三角形POQ，连接AO，AQ．求证：AO＝AQ．（3）若在（1）的条件下，以OP为斜边向上作等腰直角三角形POQ，取OP中点M，连接MB，MQ，BQ，求证：∠MQB＝∠MBQ．【拓展延伸】在（3）的条件下，连接AO，AQ，探索AO，AQ，AP之间的数量关系．解：【问题背景】（1）连接OA，OB，OP，∵PA、PB是切线，∴PA⊥OA，PB⊥OB，∴∠PAO＝∠PBO＝90°，在Rt△PAO和Rt△PBO中，，∴Rt△PAO≌Rt△PBO（HL），∴PA＝PB；【深入探究】（2）∵Rt△PAO≌Rt△PBO，∴∠APO＝∠BPO，∵∠APB＝60°，∴∠APO＝∠BPO＝30°，∵△POQ是等边三角形，∴∠OPQ＝60°，PO＝PQ，∴∠APQ＝∠APO＝30°，且PO＝PQ，∴PA垂直平分OQ，∴AO＝AQ；（3）如图3，连接OB，∵PB是⊙O是切线，∴PB⊥OB，且点M是OP的中点，∴BM＝PO，∵△OPQ是等腰直角三角形，且点M是OP的中点，∴QM＝OP，∴QM＝BM，∴∠MQB＝∠MBQ；拓展延伸】AO+AQ＝AP，理由如下：过点Q作QH⊥AQ交AP于点H，∴∠AQH＝∠PQO＝90°，∴∠AQO＝∠PQH，∵∠QPO+∠QOP＝90°，∠AOP+∠APO＝90°，∴∠APQ+∠APO＝∠APO+∠AOQ，∴∠APQ＝∠AOP，且∠AQO＝∠PQH，QP＝OQ，∴△AOQ≌△HPQ（ASA）∴QH＝AQ，AO＝PH，∴AH＝AQ，∵AP＝PH+AH，∴AO+AQ＝AP．10．如图，AB、CE是⊙O的直径，过点C的切线与AB的延长线交于点P，AD⊥PC于D，连接AC、OD、PE．（1）求证：AC是∠DAP的角平分线；（2）求证：PC2＝PA•PB；（3）若AD＝3，PE＝2DO，求⊙O的半径．证明：（1）∵PC是圆的切线，AD⊥PD，∴AD∥OC，∴∠DAC＝∠ACO，∵AO＝CO，∴∠CAO＝∠ACO，∴∠DAC＝∠CAO，∴AC是∠DAP的平分线；（2）如右图，连接BC，∵OC＝OB，∴∠OCB＝∠OBC，∵AB为⊙O的直径，∴∠ACB＝90°，∴∠CAB+∠OBC＝90°，∵PC是⊙O的切线，∴∠OCB+∠BCP＝90°，∴∠CAB＝∠BCP，又∵∠CPB＝∠APC，∴△CPB∽△APC，∴＝，∴PC2＝PA•PB；（3）设半径为r，在Rt△PCE中，PE2＝（2r）2+PC2＝4r2+PC2，∵PE＝2DO，∴4DO2＝4r2+PC2，∴4（DO2﹣r2）＝PC2，∴4DC2＝PC2，∴PC＝2CD，∵AD∥OC，∴△PCO∽△PDA，∴＝，∴＝，∴r＝2．11．如图，AB是直经，D是的中点，DE⊥AC交AC的延长线于E，⊙O的切线BF交AD的延长线于点F．（1）求证：DE是⊙O的切线．（2）试探究AE，AD，AB三者之间的等量关系．（3）若DE＝3，⊙O的半径为5，求BF的长．（1）证明：如图1，连接OC，OD，BC，∵AB是直径，∵DE⊥AC于E，∴∠E＝90°，∴∠ACB＝∠E，∴BC∥DE，∵点D是的中点，∴，∴∠COD＝∠BOD，又∵OC＝OB，∴OD垂直平分BC，∵BC∥DE，∴OD⊥DE，∴DE是⊙O的切线；（2）AD2＝AE•AB，理由如下：如图2，连接BD，由（1）知，，∴∠EAD＝∠DAB，∵AB为直径，∴∠ADB＝∠E＝90°，∴△AED∽△ADB，∴＝，即AD2＝AE•AB；（3）由（1）知，∠E＝∠ECH＝∠CHD＝90°，∴四边形CHDE为矩形，∴ED＝CH＝BH＝3，∴OH＝＝＝4，∴CE＝HD＝OD﹣OH＝5﹣4＝1，AC＝＝＝8，∵BF是⊙O的切线，∴∠FBA＝∠E＝90°，又∵∠EAD＝∠DAB，∴△EAD∽△BAF，∴＝，即＝，∴BF＝．12．如图1，在直角坐标系中，直线l与x、y轴分别交于点A（2，0）、B（0，）两点，∠BAO的角平分线交y轴于点D．点C为直线l上一点，以AC为直径的⊙G经过点D，且与x轴交于另一点E．（1）求出⊙G的半径r，并直接写出点C的坐标；（2）如图2，若点F为⊙G上的一点，连接AF，且满足∠FEA＝45°，请求出EF的长？解：（1）连接GD，EC．∵∠OAB的角平分线交y轴于点D，∴∠GAD＝∠DAO，∵GD＝GA，∴∠GDA＝∠GAD，∴∠GDA＝∠DAO，∴GD∥OA，∴∠BDG＝∠BOA＝90°，∵GD为半径，∴y轴是⊙G的切线；∵A（2，0），B（0，），∴OA＝2，OB＝，在Rt△AOB中，由勾股定理可得：AB＝＝＝设半径GD＝r，则BG＝﹣r，∵GD∥OA，∴△BDG∽△BOA，∴＝，∴r＝2（﹣r），∴r＝，∵AC是直径，∴∠AEC＝∠AOB＝90°，∴EC∥OB，∴＝＝，∴＝＝，∴EC＝2，AE＝，∴OE＝2﹣＝，∴C的坐标为（，2）；（2）过点A作AH⊥EF于H，连接CE、CF，∵AC是直径，∴AC＝2×＝∴∠AEC＝∠AFC＝90°∵∠FEA＝45°∴∠FCA＝45°∴在Rt△AEH中，由勾股定理可知：AF＝CF＝，设OE＝a∴AE＝2﹣a∵CE∥OB∴△ACE∽△ABO∴＝，∴CE＝，∵CE2+AE2＝AC2，∴（2﹣a）2+（2﹣a）2＝∴a＝或a＝（不合题意，舍去）∴AE＝∴在Rt△AEH中，由勾股定理可得，AH＝EH＝，∴在Rt△AEH中，由勾股定理可知：FH2＝AF2﹣AH2＝（）2﹣（）2＝2，∴FH＝，∴EF＝EH+FH＝．13．如图I，四边形ADBC内接于⊙O，E为BD延长线上一点，AD平分∠EDC，（1）求证：AB＝AC；（2）如图2，若CD为直径，过A点的圆的切线交BD延长线于E，若DE＝1，AE＝2．求⊙O的半径．（1）证明：∵四边形ADBC内接于⊙O，∴∠EDA＝∠ACB，由圆周角定理得，∠CDA＝∠ABC，∵AD平分∠EDC，∴∠EDA＝∠CDA，∴∠ABC＝∠ACB，∴AB＝AC；（2）解：连接AO并延长交BC于H，AM⊥CD于M，∵AB＝AC，∴AH⊥BC，又AH⊥AE，∴AE∥BC，∵CD为⊙O的直径，∴∠DBC＝90°，∴∠E＝∠DBC＝90°，∴四边形AEBH为矩形，∴BH＝AE＝2，∴BC＝4，∵AD平分∠EDC，∠E＝90°，AM⊥CD，∴DE＝DM＝1，AE＝AM＝2，在Rt△ABE和Rt△ACM中，∴Rt△ABE≌Rt△ACM（HL），∴BE＝CM，设BE＝x，CD＝x+2，在Rt△BDC中，x2+42＝（x+2）2，解得，x＝3，∴CD＝5，∴⊙O的半径为2.5．14．如图，AB为⊙O的直径，弦CD⊥AB，垂足为F，CG⊥AE，交弦AE的延长线于点G，且CG＝CF．（1）求证：CG是⊙O的切线；（2）若AE＝2，EG＝1，求由弦BC和所围成的弓形的面积．解：（1）证明：连接OC．∵CD⊥AB，CG⊥AE，CG＝CF，∴∠CAG＝∠BAC，∠AFC＝∠G＝90°，∵OA＝OC，∴∠ACO＝∠BAC．∴∠CAG＝∠ACO，∴OC∥AG，∴∠OCG＝180°﹣∠G＝90°，∴CG是⊙O的切线；（2）过点O作OM⊥AE，垂足为M，则AM＝ME＝AE＝1，∠OMG＝∠OCG＝∠G＝90°．∴四边形OCGM为矩形，∴OC＝MG＝ME+EG＝2．在Rt△AGC和Rt△AFC中∴Rt△AGC≌Rt△AFC（HL），∴AF＝AG＝AE+EG＝3，∴OF＝AF﹣OA＝1，在Rt△COF中，∵cos∠COF＝＝．∴∠COF＝60°，CF＝OC•sin∠COF＝2×＝，＝﹣×2×＝π﹣．∴S弓形BC15．如图，AB、AC是⊙O的两条弦，M是的中点，N是的中点，弦MN分别交AB、AC 于点P、D．（1）求证：AP＝AD；（2）连接PO，当AP＝3，OP＝，⊙O的半径为5，求MP的长．（1）证明：连AM，AN，∵＝，＝，∴∠BAM＝∠ANM，∠AMN＝∠CAN，∵∠APD＝∠AMN+∠BAM，∠ADP＝∠CAN+∠ANM，∴∠APD＝∠ADP，∴AP＝AD．（2 ）解：连AO，OM交AB于E，设PE＝x，∵＝，∴OM⊥AB，∴∠AEO＝90°，∵OE2＝OA2﹣AE2＝OP2﹣PE2∴52﹣（x+3）2＝（）2﹣x2，∴x＝1，∴AE＝4，OE＝3，ME＝2，∴MP＝＝＝．16．如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（0，4），点B的坐标为（4，0），点C的坐标为（﹣4，0），点P在AB上，连结CP与y轴交于点D，连结BD．过P，D，B三点作⊙Q与y轴的另一个交点为E，延长DQ交⊙Q于点F，连结EF，BF．（1）求直线AB的函数解析式；（2）求证：∠BDE＝∠ADP；（3）设DE＝x，DF＝y．请求出y关于x的函数解析式．解：（1）设直线AB的函数解析式为y＝kx+4，将点B（4，0）代入y＝kx+4，得：4k+4＝0，解得：k＝﹣1，则直线AB的函数解析式为y＝﹣x+4；（2）由已知得：OB＝OC，∠BOD＝∠COD＝90°，又∵OD＝OD，∴△BOD≌△COD（SAS），∴∠BDO＝∠CDO，∵∠CDO＝∠ADP，∴∠BDE＝∠ADP；（3）如图2，连结PE，∵∠ADP是△DPE的一个外角，∴∠ADP＝∠DEP+∠DPE，∵∠BDE是△ABD的一个外角，∴∠BDE＝∠ABD+∠OAB，∵∠ADP＝∠BDE，∠DEP＝∠ABD，∴∠DPE＝∠OAB，∵OA＝OB＝4，∠AOB＝90°，∴∠OAB＝45°，∴∠DPE＝45°，∴∠DFE＝∠DPE＝45°，∵DF是⊙Q的直径，∴∠DEF＝90°，∴△DEF是等腰直角三角形，∴DF＝DE，即y＝x．17．如图1，AB为⊙O的弦，弧AC＝弧BC，G为弧BC上一点，连接AG交BC于点D，连接CG、BG．（1）求证：∠GCB+∠GBC＝∠CBA；（2）如图2，若AB为⊙O的直径，求证：AG＝CG+BG；（3）如图3，在（2）的条件下，F为圆上一点，连接CF交AB于点E，若CD：DB＝5：7，∠ACF＝∠CAG，AE＝，求线段CG的长．证明：（1）∵＝，∴∠CAB＝∠CBA，∵∠GCB＝∠GAB，∠CBG＝∠CAG，∴∠GCB+∠GBC＝∠GAB+∠CAG＝∠CAB＝∠CBA；（2）如图2，过点C作CH⊥CG交AG于点H，∵AB为⊙O的直径，∴∠AGB＝∠ACB＝90°，且AC＝BC，∴∠ABC＝∠BAC＝45°．∵∠AGC＝∠ABC，∴∠AGC＝45°，且CH⊥CG，∴∠CHG＝∠AGC＝45°，∴CH＝CG，∠AHC＝135°∴GH＝CG．∵∠CGB＝∠CGA+∠AGB＝135°，∴∠AHC＝∠CGB，CH＝CG，∠CAH＝∠CBG，∴△ACH≌△BCG（AAS）∴AH＝BG，∴AG＝CG+BG；（3）∵CD：DB＝5：7，∴设CD＝5a，DB＝7a，∴BC＝AC＝12a，∴AD＝＝＝13a．如图3，过点E作EH⊥AC于H，作AP平分∠GAC，交BC于P，作PQ⊥AD于Q，∴∠CAP＝∠DAP＝∠CAG，∠PQA＝90°＝∠ACB，且AP＝AP，∴△CAP≌△QAP（AAS）∴AC＝AQ＝12a，CP＝PQ，∴QD＝AD﹣AQ＝a．∵PD2＝PQ2+QD2，∴（5﹣PQ）2＝PQ2+a2，∴PQ＝a，∴CP＝a，∵HE⊥AC，∠CAB＝45°，∴∠HEA＝∠CAB＝45°，∴AH＝HE，∵AE2＝AH2+HE2＝（3）2，∴AH＝HE＝3，∵∠ACF＝∠CAG，∠CAP＝∠DAP＝∠CAG，∴∠ACF＝∠CAP，∴tan∠CAP＝tan∠ACF＝，∴∴CH＝15，∴AC＝3+15＝18＝12a，∴a＝，∴CD＝，BD＝，AD＝．∵∠ACD＝∠AGB＝90°，∠CAD＝∠DBG，∴△ACD∽△BGD，∴，∴，∴BG＝，DG＝，∴AG＝AD+DG＝+＝，∵AG＝CG+BG，∴＝＝CG，∴CG＝．18．如图1，在△ABC中，∠ACB＝90°，∠ABC的角平分线交AC上点E，过点E作BE的垂线交AB于点F，△BEF的外接圆⊙O与CB交于点D．（1）求证：AC是⊙O的切线；（2）若BC＝9，EH＝3，求⊙O的半径长；（3）如图2，在（2）的条件下，过C作CP⊥AB于P，求CP的长．（1）证明：连接OE．如图1所示：∵BE⊥EF，∴∠BEF＝90°，∴BF是圆O的直径，∴OB＝OE，∴∠OBE＝∠OEB，∵BE平分∠ABC，∴∠CBE＝∠OBE，∴∠OEB＝∠CBE，∴OE∥BC，∴∠AEO＝∠C＝90°，∴AC⊥OE，∴AC是⊙O的切线；（2）解：∵∠ACB＝90°，∴EC⊥BC，∵BE平分∠ABC，EH⊥AB，∴EH＝EC，∠BHE＝90°，在Rt△BHE和Rt△BCE中，，∴Rt△BHE≌Rt△BCE（HL），∴BH＝BC＝9，∵BE⊥EF，∴∠BEF＝90°＝∠BHE，BF是圆O的直径，∴BE＝＝＝3，∵∠EBH＝∠FBE，∴△BEH∽△BFE，∴＝，即＝，解得：BF＝10，∴⊙O的半径长＝BF＝5；（3）解：连接OE，如图2所示：由（2）得：OE＝OF＝5，EC＝EH＝3，∵EH⊥AB，∴OH＝＝＝4，在Rt△OHE中，cos∠EOA＝＝，在Rt△EOA中，cos∠EOA＝＝，∴OA＝OE＝，∴AE＝＝＝，∴AC＝AE+EC＝+3＝，，∵AB＝OB+OA＝5+＝，∠ACB＝90°，∴△ABC的面积＝AB×CP＝BC×AC，∴CP＝＝＝．19．△ABC内接于⊙O，弦BD与AC相交于点E，连接BO，且AC⊥BD．（1）如图1，求证：∠OBC＝∠ABD；（2）如图2，作CG⊥AB于G，交BD于F，若∠BAC＝∠ABO+30°，求证：BO＝BF；（3）如图3，在（2）的条件下，直线OF与AB相交于点M，与BC相交于点N，若NC：MA＝5：3，且S＝16，求线段AE的长．△BMN解：（1）延长BO交⊙O于点K，连接CK，则BK为⊙O的直径，∴∠BCK＝90°，∴∠OBC+∠K＝90°，∵AC⊥BD，∴∠AEB＝90°，∴∠ABE+∠A＝90°，∵，∴∠A＝∠K∴∠OBC＝∠ABD；（2）作OH⊥BC于H，则BC＝2BH，∵∠K+∠KBC＝90°，∴∠BAC+∠KBC＝90°，∴∠ABO+30°+∠KBC＝90°，∴∠ABC＝60°∴BC＝2BG，∴BG＝BH，且∠ABD＝∠OBC，∠BGF＝∠BHO＝90°，∴△BFG≌△BOH（AAS）∴BO＝BF；（3）作OH⊥BC于H，∵△BFG≌△BOH，∴BF＝BO，∴∠MFB＝∠BON，且BF＝BO，∠ABD＝∠OBN，∴△BFM≌△BON（ASA）∴BM＝BN，且∠ABC＝60°，∴△MBN为等边三角形，∴S＝BM2＝16，△BMN∴BM＝BN＝8，∵NC：MA＝5：3，∴设NC＝5x，AM＝3x，∴BC＝8+5x，BH＝＝BG，CG＝BG＝•（）∴GM＝HN＝8﹣＝，∵∠MNB＝60°，∴OH＝HN＝•（），∵∠OBC＝∠ABD＝∠ACG，∴tan∠OBC＝tan∠ACG，∴，∴＝，∴x＝1，∴AM＝3，CN＝5，HN＝GM＝，OH＝，BH＝∴OB＝＝＝7，∵sin∠OBH＝sin∠ABD，∴∴AE＝＝．20．如图1，AB为⊙O的直径，BC为⊙O的切线，过点B作OC的垂线与⊙O的另一交点为点E，连接CE．（1）求证：CE为⊙O的切线；（2）如图2，过点C作BC的垂线交AE的延长线于点F，若BC＝AB，求的值．解：（1）证明：如图，连接OE，设OC与BE的交点为M∵OB＝OE∠OBM＝∠OEM∵BE⊥OC∴∠BMO＝∠EMO∴∠BOC＝∠EOC∴在△OBC和△OEC中∴△OBC≌△OEC（SAS）∴∠OEC＝∠OBC∵BC为⊙O的切线∴OB⊥BC∴∠OBC＝90°∴∠OEC＝90°∴CE为⊙O的切线；（2）∵AB为⊙O的直径，∴∠BEA＝90°∵OB⊥BC∴AF∥OC∵AB⊥BC，CF⊥BC∴AO∥CF∴四边形AOCF为平行四边形∴AF＝OC∵BC＝AB∴设BC＝AB＝2k，则OB＝OA＝k在Rt△OBC中，由勾股定理得：OC＝＝k∴AF＝k∵∠ABE+∠CBE＝90°，∠CBE+∠BCO＝90°∴∠ABE＝∠BCO∴sin∠ABE＝sin∠BCO∵＝sin∠BCO＝＝∴＝sin∠ABE＝∴AE＝×2k＝∴EF＝AF﹣AE＝∴＝．。

备战中考数学圆的综合-经典压轴题含答案解析

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，已知AB 是⊙O 的直径，点C ，D 在⊙O 上，BC=6cm,AC=8cm,∠BAD=45°．点E 在⊙O 外，做直线AE ，且∠EAC=∠D ．（1）求证：直线AE 是⊙O 的切线．（2）求图中阴影部分的面积.【答案】(1)见解析;(2)25-504π. 【解析】分析：（1）根据圆周角定理及推论证得∠BAE=90°，即可得到AE 是⊙O 的切线；（2）连接OD ，用扇形ODA 的面积减去△AOD 的面积即可.详解：证明：（1） ∵AB 是⊙O 的直径，∴∠ACB=90°，即∠BAC+∠ABC=90°，∵∠EAC=∠ADC ，∠ADC=∠ABC ，∴∠EAC=∠ABC∴∠BAC+∠EAC =90°，即∠BAE= 90°∴直线AE 是⊙O 的切线；（2）连接OD∵ BC=6 AC=8∴ 226810AB =+=∴ OA = 5又∵ OD = OA∴∠ADO =∠BAD = 45°∴∠AOD = 90°∴AOD ODA S S S ∆-阴影扇形＝ =90155553602π⨯⨯-⨯⨯ 25504π-= （2cm ）点睛：此题主要考查了圆周角定理和圆的切线的判定与性质，关键是利用圆周角定理和切线的判定与性质，结合勾股定理的和弓形的面积的求法求解，注意数形结合思想的应用.2．已知，如图：O1为x轴上一点，以O1为圆心作⊙O1交x轴于C、D两点，交y轴于M、N两点，∠CMD的外角平分线交⊙O1于点E，AB是弦，且AB∥CD，直线DM的解析式为y=3x+3．（1）如图1，求⊙O1半径及点E的坐标．（2）如图2，过E作EF⊥BC于F，若A、B为弧CND上两动点且弦AB∥CD，试问：BF+CF 与AC之间是否存在某种等量关系？请写出你的结论，并证明．（3）在（2）的条件下，EF交⊙O1于点G，问弦BG的长度是否变化？若不变直接写出BG 的长（不写过程），若变化自画图说明理由．【答案】（1）r=5 E（4，5）（2）BF+CF=AC （3）弦BG的长度不变，等于2【解析】分析：（1）连接ED、EC、EO1、MO1，如图1，可以证到∠ECD=∠SME=∠EMC=∠EDC，从而可以证到∠EO1D=∠EO1C=90°．由直线DM的解析式为y=3x+3可得OD=1，OM=3．设⊙O1的半径为r．在Rt△MOO1中利用勾股定理就可解决问题．（2）过点O1作O1P⊥EG于P，过点O1作O1Q⊥BC于Q，连接EO1、DB，如图2．由AB∥DC可证到BD=AC，易证四边形O1PFQ是矩形，从而有O1P=FQ，∠PO1Q=90°，进而有∠EO1P=∠CO1Q，从而可以证到△EPO1≌△CQO1，则有PO1=QO1．根据三角形中位线定理可得FQ=12BD．从而可以得到BF+CF=2FQ=AC．（3）连接EO1，ED，EB，BG，如图3．易证EF∥BD，则有∠GEB=∠EBD，从而有BG=ED，也就有BG=DE．在Rt△EO1D中运用勾股定理求出ED，就可解决问题．详解：（1）连接ED、EC、EO1、MO1，如图1．∵ME平分∠SMC，∴∠SME=∠EMC．∵∠SME=∠ECD，∠EMC=∠EDC，∴∠ECD=∠EDC，∴∠EO1D=∠EO1C．∵∠EO1D+∠EO1C=180°，∴∠EO1D=∠EO1C=90°．∵直线DM的解析式为y=3x+3，∴点M的坐标为（0，3），点D的坐标为（﹣1，0），∴OD=1，OM=3．设⊙O1的半径为r，则MO1=DO1=r．在Rt△MOO1中，（r﹣1）2+32=r2．解得：r=5，∴OO1=4，EO1=5，∴⊙O1半径为5，点E的坐标为（4，5）．（2）BF+CF=AC．理由如下：过点O1作O1P⊥EG于P，过点O1作O1Q⊥BC于Q，连接EO1、DB，如图2．∵AB∥DC，∴∠DCA=∠BAC，∴AD=BC BD∴，=AC，∴BD=AC．∵O1P⊥EG，O1Q⊥BC，EF⊥BF，∴∠O1PF=∠PFQ=∠O1QF=90°，∴四边形O1PFQ是矩形，∴O1P=FQ，∠PO1Q=90°，∴∠EO1P=90°﹣∠PO1C=∠CO1Q．在△EPO1和△CQO1中，111111EO P CO QEPO CQOO E O C∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△EPO1≌△CQO1，∴PO1=QO1，∴FQ=QO1．∵QO1⊥BC，∴BQ=CQ．∵CO1=DO1，∴O1Q=12 BD，∴FQ=12BD．∵BF+CF=FQ+BQ+CF=FQ+CQ+CF=2FQ，∴BF+CF=BD=AC．（3）连接EO1，ED，EB，BG，如图3．∵DC是⊙O1的直径，∴∠DBC=90°，∴∠DBC+∠EFB=180°，∴EF∥BD，∴∠GEB=∠EBD，∴BG=ED，∴BG=DE．∵DO1=EO1=5，EO1⊥DO1，∴DE=52，∴BG=52，∴弦BG的长度不变，等于52．点睛：本题考查了圆周角定理、圆内接四边形的性质、弧与弦的关系、垂径定理、全等三角形的判定与性质、矩形的判定与性质、三角形中位线定理、平行线的判定与性质、勾股定理等知识，综合性比较强，有一定的难度．而由AB∥DC证到AC=BD是解决第（2）小题的关键，由EG ∥DB 证到BG =DE 是解决第（3）小题的关键．3．如图，⊙M 与菱形ABCD 在平面直角坐标系中，点M 的坐标为（3，﹣1），点A 的坐标为（﹣2，3），点B 的坐标为（﹣3，0），点C 在x 轴上，且点D 在点A 的左侧．（1）求菱形ABCD 的周长；（2）若⊙M 沿x 轴向右以每秒2个单位长度的速度平移，同时菱形ABCD 沿x 轴向右以每秒3个单位长度的速度平移，设菱形移动的时间为t （秒），当⊙M 与BC 相切，且切点为BC 的中点时，连接BD ，求：①t 的值；②∠MBD 的度数；（3）在（2）的条件下，当点M 与BD 所在的直线的距离为1时，求t 的值．【答案】（1）8；（2）①7；②105°；（3）t=633 【解析】分析：（1）根据勾股定理求菱形的边长为2，所以可得周长为8；（2）①如图2，先根据坐标求EF 的长，由EE '﹣FE '=EF =7，列式得：3t ﹣2t =7，可得t 的值；②先求∠EBA =60°，则∠FBA =120°，再得∠MBF =45°，相加可得：∠MBD =∠MBF +∠FBD =45°+60°=105°；（3）分两种情况讨论：作出距离MN 和ME ，第一种情况：如图5由距离为1可知：BD 为⊙M 的切线，由BC 是⊙M 的切线，得∠MBE =30°，列式为3t 3=2t +6，解出即可；第二种情况：如图6，同理可得t 的值．详解：（1）如图1，过A 作AE ⊥BC 于E ．∵点A 的坐标为（﹣23），点B 的坐标为（﹣3，0），∴AE 3，BE =3﹣2=1，∴AB 22AE BE +2231+（）=2． ∵四边形ABCD 是菱形，∴AB =BC =CD =AD =2，∴菱形ABCD 的周长=2×4=8；（2）①如图2，⊙M 与x 轴的切点为F ，BC 的中点为E ．∵M （3，﹣1），∴F （3，0）．∵BC =2，且E 为BC 的中点，∴E （﹣4，0），∴EF =7，即EE '﹣FE '=EF ，∴3t ﹣2t =7，t =7；②由（1）可知：BE =1，AE 3∴tan∠EBA=AEBE =31=3，∴∠EBA=60°，如图4，∴∠FBA=120°．∵四边形ABCD是菱形，∴∠FBD=12∠FBA=11202⨯︒=60°．∵BC是⊙M的切线，∴MF⊥BC．∵F是BC的中点，∴BF=MF=1，∴△BFM是等腰直角三角形，∴∠MBF=45°，∴∠MBD=∠MBF+∠FBD=45°+60°=105°；（3）连接BM，过M作MN⊥BD，垂足为N，作ME⊥BC于E，分两种情况：第一种情况：如图5．∵四边形ABCD是菱形，∠ABC=120°，∴∠CBD=60°，∴∠NBE=60°．∵点M与BD所在的直线的距离为1，∴MN=1，∴BD为⊙M的切线．∵BC是⊙M的切线，∴∠MBE=30°．∵ME=1，∴EB=3，∴3t+3=2t+6，t=6﹣3；第二种情况：如图6．∵四边形ABCD是菱形，∠ABC=120°，∴∠DBC=60°，∴∠NBE=120°．∵点M与BD所在的直线的距离为1，∴MN=1，∴BD为⊙M的切线．∵BC是⊙M的切线，∴∠MBE=60°．∵ME=MN=1，∴Rt△BEM中，tan60°=MEBE，EB=160tan︒=3，∴3t=2t+6+3，t=6+3；综上所述：当点M与BD所在的直线的距离为1时，t=6﹣3或6+33．点睛：本题是四边形和圆的综合题，考查了菱形的性质、圆的切线的性质和判定、特殊的三角函数值、等腰直角三角形的性质、动点运动问题，此类问题比较复杂，弄清动点运动方向、速度、时间和路程的关系，并与方程相结合，找等量关系，求出时间t的值．4．在平面直角坐标系xOy中，点M的坐标为（x1，y1），点N的坐标为（x2，y2），且x1≠x2，y1≠y2，以MN为边构造菱形，若该菱形的两条对角线分别平行于x轴，y轴，则称该菱形为边的“坐标菱形”．（1）已知点A（2，0），B（0，23），则以AB为边的“坐标菱形”的最小内角为；（2）若点C（1，2），点D在直线y=5上，以CD为边的“坐标菱形”为正方形，求直线CD 表达式；（3）⊙O的半径为2，点P的坐标为（3，m）．若在⊙O上存在一点Q，使得以QP为边的“坐标菱形”为正方形，求m的取值范围．【答案】（1）60°；（2）y=x+1或y=﹣x+3；（3）1≤m≤5或﹣5≤m≤﹣1【解析】分析：（1）根据定义建立以AB为边的“坐标菱形”，由勾股定理求边长AB=4，可得30度角，从而得最小内角为60°；（2）先确定直线CD与直线y=5的夹角是45°，得D（4，5）或（﹣2，5），易得直线CD的表达式为：y=x+1或y=﹣x+3；（3）分两种情况：①先作直线y=x，再作圆的两条切线，且平行于直线y=x，如图3，根据等腰直角三角形的性质分别求P'B=BD=1，PB=5，写出对应P的坐标；②先作直线y=﹣x，再作圆的两条切线，且平行于直线y=﹣x，如图4，同理可得结论．详解：（1）∵点A（2，0），B（0，23），∴OA=2，OB=23．在Rt△AOB中，由勾股定理得：AB=22（）=4，∴∠ABO=30°．223∵四边形ABCD是菱形，∴∠ABC=2∠ABO=60°．∵AB∥CD，∴∠DCB=180°﹣60°=120°，∴以AB为边的“坐标菱形”的最小内角为60°．故答案为：60°；（2）如图2．∵以CD为边的“坐标菱形”为正方形，∴直线CD与直线y=5的夹角是45°．过点C作CE⊥DE于E，∴D（4，5）或（﹣2，5），∴直线CD的表达式为：y=x+1或y=﹣x+3；（3）分两种情况：①先作直线y=x，再作圆的两条切线，且平行于直线y=x，如图3．∵⊙O的半径为2，且△OQ'D是等腰直角三角形，∴OD=2OQ'=2，∴P'D=3﹣2=1．∵△P'DB是等腰直角三角形，∴P'B=BD=1，∴P'（0，1），同理可得：OA=2，∴AB=3+2=5．∵△ABP是等腰直角三角形，∴PB=5，∴P（0，5），∴当1≤m≤5时，以QP为边的“坐标菱形”为正方形；②先作直线y=﹣x，再作圆的两条切线，且平行于直线y=﹣x，如图4．∵⊙O的半径为2，且△OQ'D是等腰直角三角形，∴OD=2OQ'=2，∴BD=3﹣2=1．∵△P'DB是等腰直角三角形，∴P'B=BD=1，∴P'（0，﹣1），同理可得：OA=2，∴AB=3+2=5．∵△ABP是等腰直角三角形，∴PB=5，∴P（0，﹣5），∴当﹣5≤m≤﹣1时，以QP为边的“坐标菱形”为正方形；综上所述：m的取值范围是1≤m≤5或﹣5≤m≤﹣1．点睛：本题是一次函数和圆的综合题，考查了菱形的性质、正方形的性质、点P，Q的“坐标菱形”的定义等知识，解题的关键是理解题意，学会利用图象解决问题，学会用分类讨论的思想思考问题，注意一题多解，属于中考创新题目．5．如图，AB是⊙O的直径，D、D为⊙O上两点，CF⊥AB于点F，CE⊥AD交AD的延长线于点E，且CE=CF.（1）求证：CE是⊙O的切线；（2）连接CD、CB，若AD=CD=a，求四边形ABCD面积.【答案】（1）证明见解析；（2）【解析】【分析】（1）连接OC，AC，可先证明AC平分∠BAE，结合圆的性质可证明OC∥AE，可得∠OCB＝90°，可证得结论；（2）可先证得四边形AOCD为平行四边形，再证明△OCB为等边三角形，可求得CF、AB，利用梯形的面积公式可求得答案．【详解】（1）证明：连接OC，AC．∵CF⊥AB，CE⊥AD，且CE＝CF．∴∠CAE＝∠CAB．∵OC＝OA，∴∠CAB＝∠OCA．∴∠CAE＝∠OCA．∴OC∥AE．∴∠OCE＋∠AEC＝180°，∵∠AEC＝90°，∴∠OCE＝90°即OC⊥CE，∵OC是⊙O的半径，点C为半径外端，∴CE是⊙O的切线．（2）解：∵AD＝CD，∴∠DAC＝∠DCA＝∠CAB，∴DC∥AB，∵∠CAE＝∠OCA，∴OC∥AD，∴四边形AOCD是平行四边形，∴OC＝AD＝a，AB＝2a，∵∠CAE＝∠CAB，∴CD＝CB＝a，∴CB＝OC＝OB，∴△OCB是等边三角形，在Rt△CFB中，CF＝，∴S四边形ABCD＝（DC＋AB）•CF＝【点睛】本题主要考查切线的判定，掌握切线的两种判定方法是解题的关键，即有切点时连接圆心和切点，然后证明垂直，没有切点时，过圆心作垂直，证明圆心到直线的距离等于半径．6．如图，在直角坐标系中，⊙M经过原点O(0，0)，点A(6，0)与点B(0，－2)，点D 在劣弧OA上，连结BD交x轴于点C，且∠COD＝∠CBO.(1)求⊙M的半径；(2)求证：BD平分∠ABO；(3)在线段BD的延长线上找一点E，使得直线AE恰为⊙M的切线，求此时点E的坐标．【答案】（1）M的半径r2；（2）证明见解析；（3）点E的坐标为262)．【解析】试题分析：根据点A 和点B 的坐标得出OA 和OB 的长度，根据Rt △AOB 的勾股定理得出AB 的长度，然后得出半径；根据同弧所对的圆周角得出∠ABD=∠COD ，然后结合已知条件得出角平分线；根据角平分线得出△ABE ≌△HBE ，从而得出BH=BA=22，从而求出OH 的长度，即点E 的纵坐标，根据Rt △AOB 的三角函数得出∠ABO 的度数，从而得出∠CBO 的度数，然后根据Rt △HBE 得出HE 的长度，即点E 的横坐标.试题解析：（1）∵点A 为（6，0），点B 为（0，－2） ∴OA=6OB=2 ∴根据Rt △AOB 的勾股定理可得：AB=22∴M 的半径r=12AB=2. （2）根据同弧所对的圆周角相等可得：∠ABD=∠COD ∵∠COD=∠CBO ∴∠ABD=∠CBO ∴BD 平分∠ABO（3）如图，由（2）中的角平分线可得△ABE ≌△HBE ∴BH=BA=22∴OH=22－2=2在Rt △AOB 中，3OA OB=∴∠ABO=60° ∴∠CBO=30° 在Rt △HBE 中，HE=2633BH =∴点E 的坐标为（263，2）考点：勾股定理、角平分线的性质、圆的基本性质、三角函数.7．如图, Rt △ABC 中，∠B=90°，它的内切圆分别与边BC 、CA 、AB 相切于点D 、E 、F ， (1)设AB=c, BC=a, AC=b, 求证: 内切圆半径r ＝12(a+b-c). (2) 若AD 交圆于P , PC 交圆于H, FH//BC, 求∠CPD; (3)若r=310, PD ＝18, PC=272. 求△ABC 各边长.【答案】（1）证明见解析（2）45°（3）1010,1510，12【解析】【分析】（1）根据切线长定理，有AE=AF，BD=BF，CD=CE．易证四边形BDOF为正方形，BD=BF=r，用r表示AF、AE、CD、CE，利用AE+CE=AC为等量关系列式．（2）∠CPD为弧DH所对的圆周角，连接OD，易得弧DH所对的圆心角∠DOH=90°，所以∠CPD=45°．（3）由PD=18和r=310,联想到垂径定理基本图形，故过圆心O作PD的垂线OM，求得弦心距OM=3，进而得到∠MOD的正切值．延长DO得直径DG，易证PG∥OM，得到同位角∠G=∠MOD．又利用圆周角定理可证∠ADB=∠G，即得到∠ADB的正切值，进而求得AB．再设CE=CD=x，用x表示BC、AC，利用勾股定理列方程即求出x．【详解】解：（1）证明：设圆心为O，连接OD、OE、OF，∵⊙O分别与BC、CA、AB相切于点D、E、F∴OD⊥BC，OE⊥AC，OF⊥AB，AE=AF，BD=BF，CD=CE∴∠B=∠ODB=∠OFB=90°∴四边形BDOF是矩形∵OD=OF=r∴矩形BDOF是正方形∴BD=BF=r∴AE=AF=AB-BF=c-r，CE=CD=BC-BD=a-r∵AE+CE=AC∴c-r+a-r=b整理得：r=12（a+b-c）（2）取FH中点O，连接OD ∵FH∥BC∴∠AFH=∠B=90°∵AB与圆相切于点F，∴FH为圆的直径，即O为圆心∵FH∥BC∴∠DOH=∠ODB=90°∴∠CPD=12∠DOH=45°（3）设圆心为O ，连接DO 并延长交⊙O 于点G ，连接PG ，过O 作OM ⊥PD 于M ∴∠OMD=90°∵PD=18∴DM=12PD=9 ∵10∴22OD DM -22(310)9-9081-3∴tan ∠MOD=DM OM ＝3 ∵DG 为直径∴∠DPG=90°∴OM ∥PG ，∠G+∠ODM=90°∴∠G=∠MOD∵∠ODB=∠ADB+∠ODM=90°∴∠ADB=∠G∴∠ADB=∠MOD∴tan ∠ADB=AB BD=tan ∠MOD=3 ∴10∴10−10＝10设CE=CD=x ，则10+x ，10+x∵AB 2+BC 2=AC 2∴10)2．10+x)2＝10+x)2解得：10∴10，10∴△ABC 各边长10，10，10【点睛】本题考查切线的性质，切线长定理，正方形的判定，圆周角定理，垂径定理，勾股定理．切线长定理的运用是解决本题的关键，而在不能直接求得线段长的情况下，利用勾股定理作为等量关系列方程解决是常用做法．8．已知：如图，四边形ABCD为菱形，△ABD的外接圆⊙O与CD相切于点D，交AC于点E．（1）判断⊙O与BC的位置关系，并说明理由；（2）若CE=2，求⊙O的半径r．【答案】（1）相切，理由见解析；（2）2.【解析】试题分析：（1）根据切线的性质，可得∠ODC的度数，根据菱形的性质，可得CD与BC 的关系，根据SSS，可得三角形全等，根据全等三角形的性质，可得∠OBC的度数，根据切线的判定，可得答案；（2）根据等腰三角形的性质，可得∠ACD=∠CAD，根据三角形外角的性质，∠COD=∠OAD+∠AOD，根据直角三角形的性质，可得OC与OD的关系，根据等量代换，可得答案．（1）⊙O与BC相切，理由如下连接OD、OB，如图所示：∵⊙O与CD相切于点D，∴OD⊥CD，∠ODC=90°．∵四边形ABCD为菱形，∴AC垂直平分BD，AD=CD=CB．∴△ABD的外接圆⊙O的圆心O在AC上，∵OD=OB，OC=OC，CB=CD，∴△OBC≌△ODC．∴∠OBC=∠ODC=90°，又∵OB为半径，∴⊙O与BC相切；（2）∵AD=CD，∴∠ACD=∠CAD．∵AO=OD，∴∠OAD=∠ODA．∵∠COD=∠OAD+∠AOD，∠COD=2∠CAD．∴∠COD=2∠ACD又∵∠COD+∠ACD=90°，∴∠ACD=30°．∴OD=12OC，即r=12（r+2）．∴r=2．【点睛】运用了切线的判定与性质，利用了切线的判定与性质，菱形的性质，直角三角形的性质．9．如图，AB是⊙O的直径，∠ACB的平分线交AB于点D，交⊙O于点E，过点C作⊙O 的切线CP交BA的延长线于点P，连接AE．（1）求证：PC=PD；（2）若AC=5cm，BC=12cm，求线段AE，CE的长．【答案】(1)见解析172132【解析】试题分析：（1）如图1中，连接OC 、OE ．利用等角的余角相等，证明∠PCD =∠PDC 即可；（2）如图2中．作EH ⊥BC 于H ，EF ⊥CA 于F ．首先证明Rt △AEF ≌Rt △BEH ，推出AF =BH ，设AF =BH =x ，再证明四边形CFEH 是正方形，推出CF =CH ，可得5+x =12﹣x ，推出x =72，延长即可解决问题；试题解析：（1）证明：如图1中，连接OC 、OE ．∵AB 直径，∴∠ACB =90°，∴CE 平分∠ACB ，∴∠ECA =∠ECB =45°，∴AE =BE ，∴OE ⊥AB ，∴∠DOE =90°．∵PC 是切线，∴OC ⊥PC ，∴∠PCO =90°．∵OC =OE ，∴∠OCE =∠OEC ．∵∠PCD +∠OCE =90°，∠ODE +∠OEC =90°，∠PDC =∠ODE ，∴∠PCD =∠PDC ，∴PC =PD ．（2）如图2中．作EH ⊥BC 于H ，EF ⊥CA 于F ．∵CE 平分∠ACB ，EH ⊥BC 于H ，EF ⊥CA 于F ，∴EH =EF ，∠EFA =∠EHB =90°．∵AE =BE ，∴AE =BE ，∴Rt △AEF ≌Rt △BEH ，∴AF =BH ，设AF =BH =x ．∵∠F =∠FCH =∠CHE =90°，∴四边形CFEH 是矩形．∵EH =EF ，∴四边形CFEH 是正方形，∴CF =CH ，∴5+x =12﹣x ，∴x =72，∴CF =FE =172，∴EC 2CF 172，AE 22EF AF +2217722（）（）+132 点睛：本题考查了切线的性质、圆周角定理、勾股定理、垂径定理、正方形的判定和性质、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．10．如图，AB 为⊙O 的直径，DA 、DC 分别切⊙O 于点A ，C ，且AB =AD ．（1）求tan ∠AOD 的值．（2）AC，OD交于点E，连结BE．①求∠AEB的度数；②连结BD交⊙O于点H，若BC=1，求CH的长．【答案】（1）2；（2）①∠AEB＝135°；②2 CH=【解析】【分析】（1）根据切线的性质可得∠BAD=90°，由题意可得AD=2AO，即可求tan∠AOD的值；（2）①根据切线长定理可得AD=CD，OD平分∠ADC，根据等腰三角形的性质可得DO⊥AC，AE=CE，根据圆周角定理可求∠ACB=90°，即可证∠ABC=∠CAD，根据“AAS”可证△ABC≌△DAE，可得AE=BC=EC，可求∠BEC=45°，即可求∠AEB的度数；②由BC=1，可求AE=EC=1，BE2=，根据等腰直角三角形的性质可求∠ABE=∠HBC，可证△ABE∽△HBC，可求CH的长．【详解】（1）∵DA是⊙O切线，∴∠BAD=90°．∵AB=AD，AB=2AO，∴AD=2AO，∴tan∠AODADAO==2；（2）①∵DA、DC分别切⊙O于点A，C，∴AD=CD，OD平分∠ADC，∴DO⊥AC，AE=CE．∵AB是直径，∴∠ACB=90°，∴∠BAC+∠ABC=90°，且∠BAC+∠CAD=90°，∴∠ABC=∠CAD，且AB=AD，∠ACB=∠AED=90°，∴△ABC≌△DAE（AAS），∴CB=AE，∴CE=CB，且∠ACB=90°，∴∠BEC=45°=∠EBC，∴∠AEB=135°．②如图，∵BC=1，且BC=AE=CE，∴AE=EC=BC=1，∴BE2=．∵AD=AB，∠BAD=90°，∴∠ABD=45°，且∠EBC=45°，∴∠ABE=∠HBC，且∠BAC=∠CHB，∴△ABE∽△HBC，∴BC CHEB AE=，即12CH=，∴CH22=．【点睛】本题考查了切线的性质，圆周角定理，锐角三角函数，全等三角形的判定和性质，相似三角形的判定和性质，等腰三角形的性质等知识，灵活运用相关的性质定理、综合运用知识是解题的关键．。

2020年九年级中考数学考前专项练习：圆的压轴综合题(含答案)

圆的压轴综合题1．如图，已知AB是⊙O的直径，弦CD⊥AB于点E．点P是劣弧上任一点（不与点A，D重合），CP交AB于点M，AP与CD的延长相交于点F．（1）设∠CPF＝α，∠BDC＝β，求证：α＝β+90°；（2）若OE＝BE，设tan∠AFC＝x，．①求∠APC的度数；②求y关于x的函数表达式及自变量x的取值范围．2．如图，P A、PB是⊙O的切线，A、B为切点，连接AO并延长，交PB的延长线于点C，连接PO，交⊙O于点D．（1）求证：∠APO＝∠CPO；（2）若⊙O的半径为3，OP＝6，∠C＝30°，求PC的长．3．如图所示AB是⊙O的直径，圆心为点O，点C为⊙O上一点，OM⊥AB于点O交AC 于点D，MC＝MD,求证：MC为⊙O的切线．4．如图1，以BC为直径的半圆O上有一动点F，点E为弧CF的中点，连接BE、FC相交于点M，延长CF到A点，使得AB＝AM，连接AB、CE．（1）求证：AB是⊙O的切线；（2）如图2，连接BF，若AF＝FM，求的值；（3）如图3．若tan∠ACB＝，BM＝10．求EC的长．5．如图，在△ABC中，以AC为直径的⊙O与边AB交于点D，点E为⊙O上一点，连接CE并延长交AB于点F，连接ED．（1）若BC是⊙O的切线，求证：∠B+∠FED＝90°；（2）若FC＝6，DE＝3，FD＝2．求⊙O的直径．6．如图，矩形ABCD中，AB＝4，BC＝3，点E是线段AB上的一个动点，经过A，D，E 三点的⊙O交线段AC于点K，交线段CD于点H，连接DE交线段AC于点F．（1）求证：AE＝DH；（2）连结DK，当DE平分∠ADK时，求线段DE的长；（3）连结HK，KE，在点E的运动过程中，①当线段DH，HK，KE中满足某两条线段相等，求所有满足条件的AE的长．②当DA＝AE时，连结OA，记△AOF的面积为S1，△EFK的面积为S2，求的值．（请直接写出答案）7．如图，OA、OB是⊙O的两条半径，OA⊥OB，C是半径OB上一动点，连接AC并延长交⊙O于D，过点D作圆的切线交OB的延长线于E，已知OA＝6．（1）求证：∠ECD＝∠EDC；（2）若BC＝2OC，求DE长；（3）当∠A从15°增大到30°的过程中，求弦AD在圆内扫过的面积．8．如图，AB是半⊙O的直径，点C，D在半圆上，CD＝BD，过点D作EF⊥AC于E，交AB的延长线于F．（1）求证：EF是⊙O的切线．（2）当BF＝4，sin F＝时，求AE的长．9．已知：如图，AB是⊙O的直径，直线DC，DA分别切⊙O于点C，点A，连结BC，OD．（1）求证：BC∥OD．（2）若∠ODC＝36°，AB＝6，求出的长．10．如图，在△ABC中，以AB为直径的⊙O分别与BC，AC相交于点D，E，BD＝CD，过点D作⊙O的切线交边AC于点F．（1）求证：DF⊥AC；（2）若⊙O的半径为2，CF＝1，求的长（结果保留π）．11．如图，AB，CD是圆O的直径，AE是圆O的弦，且AE∥CD，过点C的圆O切线与EA的延长线交于点P，连接AC．（1）求证：AC平分∠BAP；（2）求证：PC2＝P A•PE；（3）若AE﹣AP＝PC＝4，求圆O的半径．12．如图，AB是⊙O的直径，BE是弦，点D是弦BE上一点，连接OD并延长交⊙O于点C，连接BC，在过点D垂直于OC的直线上取点F．使∠DFE＝2∠CBE．（1）请说明EF是⊙O的切线；（2）若⊙O的半径是6，点D是OC的中点，∠CBE＝15°，求线段EF的长．13．如图，四边形ABCD内接于⊙O，∠BAD＝90°，AD、BC的延长线交于点F，点E在CF上，且∠DEC＝∠BAC．（1）求证：DE是⊙O的切线；（2）当AB＝AC时，若CE＝4，EF＝6，求⊙O的半径．14．如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC，交AC于点E，AC的反向延长线交⊙O于点F．（1）求证：DE是⊙O的切线；（2）若DE+EA＝8，AF＝16，求⊙O的半径．15．如图，在⊙O的内接三角形ABC中，∠ACB＝90°，AC＝2BC，过C作AB的垂线l交⊙O于另一点D，垂足为E．设P是上异于A，C的一个动点，射线AP交l于点F，连接PC与PD，PD交AB于点G．（1）求证：△P AC≌△PDF；（2）若AB＝5，＝，求PD的长．16．如图，AB是⊙O的直径，点E是劣弧AD上一点，∠PBD＝∠BED，且DE＝，BE 平分∠ABD，BE与AD交于点F．（1）求证：BP是⊙O的切线；（2）若tan∠DBE＝，求EF的长；（3）延长DE，BA交于点C，若CA＝AO，求⊙O的半径．17．如图，在△ABC中，AB＝AC＝10，以AB为直径的OO与BC相交于点D，与AC相交于点E，DF⊥AC，垂足为F，连接DE，过点A作AG⊥DE，垂足为G，AG与⊙O交于点H．（1）求证：DF是⊙O的切线；（2）若∠CAG＝25°，求弧AH的长；（3）若tan∠CDF＝，求AE的长；18．如图，在Rt△ABC中，∠ACB＝90°，点O为△ABC外接圆的圆心，将△ABC沿AB翻折后得到△ABD．（1）求证：点D在⊙O上；（2）在直径AB的延长线上取一点E，使DE2＝BE•AE．①求证：直线DE为⊙O的切线；②过点O作OF∥BD交AD于点H，交ED的延长线于点F．若⊙O的半径为5，cos∠DBA＝，求FH的长．参考答案1．解：（1）∵CD⊥AB，∴∠+∠＝90°，即：180°﹣α+β＝90°，∴α＝β+90°；（2）如图1，连接OD，①OE＝BE，OB⊥BE，设圆的半径为r，∴∠BOD＝∠OBD＝∠ODB＝60°，即：△BOD为等边三角形，∴BC＝r，∴∠CDB＝30°，∴∠APC＝90°﹣30°＝60°；②连接BC，过点M组MH⊥BC于点H，则∠MCB＝∠F AB，∴∠CMH＝∠F，在△CBM中，设BC＝r，∠CBA＝60°，∴MH＝BM sin∠CBA＝MB，BH＝MB，CH＝MH tan∠CMH＝MH•x，CH+HB＝BC，即，，而AM+BM＝2r，即：，∴1x＝1+y，即：y＝x．2．（1）证明：∵P A、PB是⊙O的切线，∴∠APO＝∠CPO；（2）解：∵P A是⊙O的切线，∴∠P AC＝90°，∴AP＝＝3，在Rt△CAP中，∠C＝30°，∴PC＝2AP＝3．3．证明：连接OC，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠A+∠B＝90°，∵OM⊥AB，∴∠AOD＝90°，∴∠A+∠ADO＝90°，∴∠ADO＝∠B，∵∠ADO＝∠CDM，∴∠CDM＝∠B，∵MC＝MD，∴∠MDC＝∠MCD，∴∠MCD＝∠B，∵OA＝OC，∴∠A＝∠ACO，∴∠MCD+∠ACO＝90°，∴∠MCO＝90°，∴MC为⊙O的切线．4．解：（1）如图1，AB＝AM，∴∠ABM＝∠AMB＝∠EMC，点E为弧CF的中点，则∠EBC＝∠ECM，∵BC为直径，∴∠BEC＝90°，∠BFC＝90°，∴∠EMC+∠ECM＝90°，∴∠ABM+∠MBC＝90°，∴AB是⊙O的切线；（2）如图2，∵AF＝FM，∠BFC＝90°，∴∠ABF＝∠MBF＝α＝∠MCE，而∠ABF＝∠ACB＝α，∴∠ABF+∠MBF+∠EBC＝∠ABC＝90°＝3α，∴α＝30°，则BF＝BC＝r，同理BE＝r，而BC＝2r，∴求＝＝；（3）如图3，tan∠ACB＝＝设：AB＝5m，BC＝12m，则AC＝13m，CM＝AC﹣AM＝8m，∵∠EBC＝∠ECM，∴Rt△CEM∽Rt△BEC，∴，即：，解得：EC＝12．5．（1）证明：∵∠A+∠DEC＝180°，∠FED+∠DEC＝180°，∴∠FED＝∠A，∵BC是⊙O的切线，∴∠BCA＝90°，∴∠B+∠A＝90°，∴∠B+∠FED＝90°；（2）解：∵∠CF A＝∠DFE，∠FED＝∠A，∴△FED∽△F AC，∴＝，∴＝，解得：AC＝9，即⊙O的直径为9．6．（1）证明：连接HE，如图1所示：∵矩形ABCD，∴∠DAB＝∠ADC＝90°，∴DE为⊙O直径，∴∠DHE＝90°，∴四边形ADHE是矩形，∴DH＝AE；（2）解：如图2所示：∵四边形ABD是矩形，∴∠B＝∠ADC＝90°，AD＝BC＝3，AB∥CD，∴AC＝＝5，∵DE平分∠ADK，∴∠DAE＝∠EDK，，∵DE为⊙O直径，∴DE⊥AC，∴∠ADE＝∠CAB，∴cos∠ADE＝cos∠CAB＝，即＝，∴DE＝；（3）解：①若HK＝KE时，过K作MN⊥CD，交CD于M，交AB于N，如图3所示：则，MN＝BC＝3，∴∠EDK＝∠MDK＝∠CAB＝∠DCA，∵∠ADC＝90°，∴DK＝AK＝CK，∵AB∥CD，∴KM＝KN＝，AN＝CM＝DM＝2，∵DE为⊙O直径，∴∠DKE＝90°，∴tan∠EKN＝tan∠MDK＝，∴NE＝，∴AE＝AN﹣NE＝2﹣＝；若DH＝KE时，∴，∴tan∠ADE＝tan∠CAB＝，即＝，∴AE＝；若DH＝HK时，∵∠ADC＝90°，∴∠AKH＝90°，设：DH＝HK＝3x，∵sin∠ACD＝＝，∴CH＝5x，∵DH+CH＝CD，∴5x+3x＝4，∴x＝∴DH＝AE＝；②如图4所示：当DA＝AE＝3时，△ADE是等腰直角三角形，∴OA⊥DE，DE＝AD＝3，∴OA＝OD＝OE＝DE＝，∵AB∥CD，∴△CDF∽△AEF，∴＝＝＝，∴DF＝×3＝，EF＝DE＝，AF＝AC＝，∴OF＝DF﹣OD＝﹣＝，∴△AOF的面积为S1＝OF×O A＝××＝，∵∠ADF＝∠EKF，∠AFD＝∠EFK，∴△ADF∽△EKF，∴＝（）2＝，∴S2＝S△EFK＝＝＝，∴＝＝．7．（1）证明：连接OD，如图1所示：∵DE是⊙O的切线，∴∠EDC+∠ODA＝90°，∵OA⊥OB，∴∠ACO+∠OAC＝90°，∵OA、OB是⊙O的两条半径，∴OA＝OB，∴∠ODA＝∠OAC，∴∠EDC＝∠ACO，∵∠ECD＝∠ACO，∴∠ECD＝∠EDC；（2）解：∵BC＝2OC，OB＝OA＝6，∴OC＝2，设DE＝x，∵∠ECD ＝∠EDC ，∴CE ＝DE ＝x ，∴OE ＝2+x ，∵∠ODE ＝90°，∴OD 2+DE 2＝OE 2，即：62+x 2＝（2+x ）2，解得：x ＝8，∴DE ＝8；（3）解：过点D 作DF ⊥AO 交AO 的延长线于F ，如图2所示：当∠A ＝15°时，∠DOF ＝30°，∴DF ＝OD ＝OA ＝3，∠DOA ＝150°，S 弓形ABD ＝S 扇形ODA ﹣S △AOD ＝﹣OA •DF ＝15π﹣×6×3＝15π﹣9，当∠A ＝30°时，∠DOF ＝60°，∴DF ＝OD ＝OA ＝3，∠DOA ＝120°，S 弓形ABD ＝S 扇形ODA ﹣S △AOD ＝﹣OA •DF ＝12π﹣×6×3＝12π﹣9，∴当∠A 从15°增大到30°的过程中，AD 在圆内扫过的面积＝（15π﹣9）﹣（12π﹣9）＝3π+9﹣9．8．（1）证明：连接AD ，OD ，∵CD ＝BD ， ∴＝，∴∠1＝∠2，∵OA ＝OD ，∴∠2＝∠3，∴∠1＝∠3，∴AE∥OD，∵EF⊥AC，∴EF⊥OD，∴EF是⊙O的切线；（2）解：设⊙O的半径为r，在Rt△ODF中，sin F＝，∴＝，∴r＝6，∵AE∥OD，∴，∴＝，∴AE＝．9．解：（1）连接OC，∵直线DC，DA分别切⊙O于点C，∴CD＝AD，在△ADO与△CDO中，，∴△ADO≌△CDO（SSS），∴∠AOD＝∠COD，∴∠AOD＝AOC，∵∠B＝AOC，∴∠B＝∠AOD，∴BC∥OD；（2）∵∠ODC＝36°，直线DC，DA分别切⊙O于点C，点A，∴∠ADC＝2∠CDO＝72°，∴∠AOC＝180°﹣∠ADC＝108°，∴∠BOC＝72°，∵AB＝6，∴OB＝3，∴的长＝＝．10．（1）证明：连接OD，如图所示．∵DF是⊙O的切线，D为切点，∴OD⊥DF，∴∠ODF＝90°．∵BD＝CD，OA＝OB，∴OD是△ABC的中位线，∴OD∥AC，∴∠CFD＝∠ODF＝90°，∴DF⊥AC．（2）解：连接BE，∵AB是直径，∴BE⊥AC，∵DF⊥AC，∴＝＝，∵FC＝1，∴EC＝2，∵OD＝AC＝2，∴A C＝4，∴AE＝EC＝2，∴AB＝BC，∵AB＝AC＝4，∴AB＝BC＝AC，∴△ABC是等边三角形，∴∠BAC＝60°，∵OD∥AC，∴∠BOD＝∠BAC＝60°，∴的长：＝．11．解：（1）∵OA＝OC，∴∠OCA＝∠OAC，∵CD∥AP，∴∠OCA＝∠P AC，∴∠OAC＝∠P AC，∴AC平分∠BAP；（2）连接AD，∵CD为圆的直径，∴∠CAD＝90°，∴∠DCA+∠D＝90°，∵CD∥P A，∴∠DCA＝∠P AC，又∠P AC+∠PCA＝90°，∴∠P AC＝∠D＝∠E，∴△P AC∽△PCE，∴，∴PC2＝P A•PE；（3）AE＝AP+PC＝AP+4，由（2）得16＝P A（P A+P A+4），P A2+2P A﹣8＝0，解得，P A＝2，连接BC，∵CP是切线，则∠PCA＝∠CBA，Rt△P AC∽Rt△CAB，，而PC2＝AC2﹣P A2，AC2＝AB2﹣BC2，其中P A＝2，解得：AB＝10，则圆O的半径为5．12．（1）证明：连接OE交DF于点H，∵DF⊥OC，∴∠FDO＝90°，∵∠COE＝2∠CBE，∠DFE＝2∠CBE．∴∠F＝∠DOE，∵∠EHF＝∠OHD，∴∠FEH＝∠ODH＝90°，∴EF是⊙O的切线；（2）解：∵∠CBE＝15°，∴∠F＝∠COE＝2∠CBE＝30°．∵⊙O的半径是6，点D是OC中点，∴OD＝3，在Rt△ODH中，cos∠DOH＝，∴OH＝2．∴HE＝6﹣2．在Rt△FEH中，tan F＝＝6﹣2＝．∴EF＝6﹣6．13．解：（1）如图，连接BD，∵∠BAD＝90°，∴点O必在BD上，即：BD是直径，∴∠BCD＝90°，∴∠DEC+∠CDE＝90°，∵∠DEC＝∠BAC，∴∠BAC+∠CDE＝90°，∵∠BAC＝∠BDC，∴∠BDC+∠CDE＝90°，∴∠BDE＝90°，即：BD⊥DE，∵点D在⊙O上，∴DE是⊙O的切线；（2）∵∠BAF＝∠BDE＝90°，∴∠F+∠ABC＝∠FDE+∠ADB＝90°，∵AB＝AC，∴∠ABC＝∠ACB，∵∠ADB＝∠ACB，∴∠F＝∠EDF，∴DE＝EF＝6，∵CE＝4，∠BCD＝90°，∴∠DCE＝90°，∴CD＝＝2，∵∠BDE＝90°，CD⊥BE，∴△CDE∽△CBD，∴＝，∴BD＝＝3，∴⊙O的半径＝．14．（1）证明：∵OB＝OD，∴∠ABC＝∠ODB，∵AB＝AC，∴∠ABC＝∠ACB，∴∠ODB＝∠ACB，∴OD∥AC．∵D E⊥AC，OD是半径，∴DE⊥OD，∴DE是⊙O的切线；（2）解：如图，过点O作OH⊥AF于点H，则∠ODE＝∠DEH＝∠OHE＝90°，∴四边形ODEH是矩形，∴OD＝EH，OH＝DE．∴AH＝AF＝8，设AE＝x．∵DE+AE＝8，∴OH＝DE＝8﹣x，OA＝OD＝HE＝AH+AE＝8+x，在Rt△AOH中，由勾股定理知：AH2+OH2＝OA2，即82+（8﹣x）2＝（8+x）2，解得：x＝2，∴OA＝8+2＝10．∴⊙O的半径为10．15．（1）证明：连接AD，∵AB⊥CD，AB是⊙O的直径，∴＝，∴∠ACD＝∠B＝∠ADC，∵∠FPC＝∠B，∴∠ACD＝∠FPC，∴∠APC＝∠ACF，∵∠F AC＝∠CAF，∴△P AC∽△CAF；（2）连接OP，则OA＝OB＝OP＝AB＝，∵＝，∴OP⊥AB，∠OPG＝∠PDC，∵AB是⊙O的直径，∵AC＝2BC，∴tan∠CAB＝tan∠DCB＝，∴＝＝，∴AE＝4BE，∵AE+BE＝AB＝5，∴AE＝4，BE＝1，CE＝2，∴OE＝OB﹣BE＝2.5﹣1＝1.5，∵∠OPG＝∠PDC，∠OGP＝∠DGE，∴△OPG∽△EDG，∴＝，∴＝＝，∴GE＝，OG＝，∴PG＝＝，GD＝＝，∴PD＝PG+GD＝．16．（1）证明：∵AB是⊙O的直径，∴∠ADB＝90°，∴∠DAB+∠ABD＝90°，∵∠BED＝∠DAB，∠PBD＝∠BED，∴∠DAB＝∠PBD，∴∠PBD+∠ABD＝90°，∴AB⊥PB，∴BP是⊙O的切线；（2）解：连接AE，∴∠AEB＝90°，∵BE平分∠ABD，∴∠ABE＝∠DBE，∴＝，∴AE＝DE＝，∴∠ABE＝∠DBE＝∠DAE，∴tan∠DBE＝tan∠ABE＝tan∠DAE＝＝，∴＝，∴EF＝；（3）解：连接OE，∵OE＝OB，∴∠ABE＝∠OEB，∵∠ABE＝∠DBE，∴∠DBE＝∠OEB，∴△CEO∽△CDB，∴，∵CA＝AO，设CA＝AO＝BO＝R，∴＝，即＝2，∴CE＝2，∴DC＝3，∵∠ADC＝∠ABE，∠C＝∠C，∴△CAD∽△CEB，∴＝，∴＝，∴R＝，∴⊙O的半径为．17．（1）证明：连接OD、AD，AB是⊙O的半径，∴∠ADB＝90°，∵AB＝AC，∵点D是BC的中点，O是AB的中点，∴OD∥AC，∵DF⊥AC，∴OD⊥DF，∵OD是⊙O的半径，DF是⊙O的切线；（2）解：连接OH，∵AG⊥DG，∴∠G＝90°，∵∠CAG＝25°，∴∠AEG＝65°，∴∠B＝∠AEG＝65°，∴∠BAC＝180°﹣65°﹣65°＝50°，∴∠OAH＝75°，∴∠AOH＝30°，∴l＝＝；弧AH（3）解：∵∠CAD+∠C＝90°，∠CDF+∠C＝90°，∴∠CAD＝∠CDF，∴tan∠CAD＝tan∠CDF＝，∴AD＝2CD，∴DC2+（2CD）2＝102，∴CD＝2，∵△CDF∽△CAD，∴DC2＝CF•AC，∴CF＝2，∴CD＝DE，∵OF⊥AC，∴EF＝CF＝2，∴AE＝10﹣2﹣2＝6．18．（1）证明：连接OD，如图所示：∵∠ACB＝90°，∴AB为直径，由翻折可知△ADB≌△ACB，∴∠ADB＝90°，∵O为AB中点，∴OD＝AB，∴D在⊙O上；（2）①证明：∵DE2＝BE•AE，∴，∠E＝∠E，∴△EBD∽△EDA，∴∠EDB＝∠DAE，∵OD＝OB，∴∠ABD＝∠ODB，∵∠ADB＝90°，∴∠DAB+∠DBA＝90°，∴∠EDB+∠ODB＝90°，∴∠EDO＝90°，∴DE为⊙O切线；②解：在Rt△ADB中，∵cos∠DBA＝，AB＝10，∴BD＝6，∴AD＝＝＝8，∵∠ADB＝90°，OF∥BD，∴∠FHD＝∠ADB＝90°，∵OH⊥AD，∴HD＝AD＝4，又∵OA＝OB，∴OH＝BD＝3，∵∠HOD＝∠ODB＝∠ABD，∴cos∠HOD＝，即，∴FO＝，∴FH＝FO﹣HO＝﹣3＝．。

中考数学压轴题100题(附答案)

中考数学压轴题100题（附答案）一、中考压轴题1．如图，△ABC内接于⊙O，AB＝6，AC＝4，D是AB边上一点，P是优弧BAC的中点，连接P A、PB、PC、PD．（1）当BD的长度为多少时，△P AD是以AD为底边的等腰三角形？并证明；（2）在（1）的条件下，若cos∠PCB＝，求P A的长．【分析】（1）根据等弧对等弦以及全等三角形的判定和性质进行求解；（2）过点P作PE⊥AD于E．根据锐角三角函数的知识和垂径定理进行求解．【解答】解：（1）当BD＝AC＝4时，△P AD是以AD为底边的等腰三角形．∵P是优弧BAC的中点，∴＝．∴PB＝PC．又∵∠PBD＝∠PCA（圆周角定理），∴当BD＝AC＝4，△PBD≌△PCA．∴P A＝PD，即△P AD是以AD为底边的等腰三角形．（2）过点P作PE⊥AD于E，由（1）可知，当BD＝4时，PD＝P A，AD＝AB﹣BD＝6﹣4＝2，则AE＝AD＝1．∵∠PCB＝∠P AD（在同圆或等圆中，同弧所对的圆周角相等），∴cos∠P AD＝cos∠PCB＝，∴P A＝．【点评】综合运用了等弧对等弦的性质、全等三角形的判定和性质、锐角三角函数的知识以及垂径定理．2．如图，一次函数y＝﹣x﹣2的图象分别交x轴、y轴于A、B两点，P为AB的中点，PC⊥x轴于点C，延长PC交反比例函数y＝（x＜0）的图象于点Q，且tan∠AOQ＝．（1）求k的值；（2）连接OP、AQ，求证：四边形APOQ是菱形．【分析】（1）由一次函数解析式确定A点坐标，进而确定C，Q的坐标，将Q的坐标代入反比例函数关系式可求出k的值．（2）由（1）可分别确定QC＝CP，AC＝OC，且QP垂直平分AO，故可证明四边形APOQ是菱形．【解答】（1）解：∵y＝﹣x﹣2令y＝0，得x＝﹣4，即A（﹣4，0）由P为AB的中点，PC⊥x轴可知C点坐标为（﹣2，0）又∵tan∠AOQ＝可知QC＝1∴Q点坐标为（﹣2，1）将Q点坐标代入反比例函数得：1＝，∴可得k＝﹣2；（2）证明：由（1）可知QC＝PC＝1，AC＝CO＝2，且A0⊥PQ∴四边形APOQ是菱形．【点评】本题考查了待定系数法求函数解析式，又结合了几何图形进行考查，属于综合性比较强的题目，有一定难度．3．某公司经营杨梅业务，以3万元/吨的价格向农户收购杨梅后，分拣成A、B两类，A类杨梅包装后直接销售；B类杨梅深加工后再销售．A类杨梅的包装成本为1万元/吨，根据市场调查，它的平均销售价格y（单位：万元/吨）与销售数量x（x≥2）之间的函数关系如图；B类杨梅深加工总费用s（单位：万元）与加工数量t（单位：吨）之间的函数关系是s＝12+3t，平均销售价格为9万元/吨．（1）直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式；（2）第一次，该公司收购了20吨杨梅，其中A类杨梅有x吨，经营这批杨梅所获得的毛利润为w万元（毛利润＝销售总收入﹣经营总成本）．①求w关于x的函数关系式；②若该公司获得了30万元毛利润，问：用于直销的A类杨梅有多少吨？（3）第二次，该公司准备投入132万元资金，请设计一种经营方案，使公司获得最大毛利润，并求出最大毛利润．【分析】（1）这是一个分段函数，分别求出其函数关系式；（2）①当2≤x＜8时及当x≥8时，分别求出w关于x的表达式．注意w＝销售总收入﹣经营总成本＝w A+w B﹣3×20；②若该公司获得了30万元毛利润，将30万元代入①中求得的表达式，求出A类杨梅的数量；（3）本问是方案设计问题，总投入为132万元，这笔132万元包括购买杨梅的费用+A类杨梅加工成本+B类杨梅加工成本．共购买了m吨杨梅，其中A类杨梅为x吨，B类杨梅为（m﹣x）吨，分别求出当2≤x＜8时及当x≥8时w关于x的表达式，并分别求出其最大值．【解答】解：（1）①当2≤x＜8时，如图，设直线AB解析式为：y＝kx+b，将A（2，12）、B（8，6）代入得：，解得，∴y＝﹣x+14；②当x≥8时，y＝6．所以A类杨梅平均销售价格y与销售量x之间的函数关系式为：y＝；（2）设销售A类杨梅x吨，则销售B类杨梅（20﹣x）吨．①当2≤x＜8时，w A＝x（﹣x+14）﹣x＝﹣x2+13x；w B＝9（20﹣x）﹣[12+3（20﹣x）]＝108﹣6x∴w＝w A+w B﹣3×20＝（﹣x2+13x）+（108﹣6x）﹣60＝﹣x2+7x+48；当x≥8时，w A＝6x﹣x＝5x；w B＝9（20﹣x）﹣[12+3（20﹣x）]＝108﹣6x∴w＝w A+w B﹣3×20＝（5x）+（108﹣6x）﹣60＝﹣x+48．∴w关于x的函数关系式为：w＝．②当2≤x＜8时，﹣x2+7x+48＝30，解得x1＝9，x2＝﹣2，均不合题意；当x≥8时，﹣x+48＝30，解得x＝18．∴当毛利润达到30万元时，直接销售的A类杨梅有18吨．（3）设该公司用132万元共购买了m吨杨梅，其中A类杨梅为x吨，B类杨梅为（m﹣x）吨，则购买费用为3m万元，A类杨梅加工成本为x万元，B类杨梅加工成本为[12+3（m﹣x）]万元，∴3m+x+[12+3（m﹣x）]＝132，化简得：x＝3m﹣60．①当2≤x＜8时，w A＝x（﹣x+14）﹣x＝﹣x2+13x；w B＝9（m﹣x）﹣[12+3（m﹣x）]＝6m﹣6x﹣12∴w＝w A+w B﹣3×m＝（﹣x2+13x）+（6m﹣6x﹣12）﹣3m＝﹣x2+7x+3m﹣12．将3m＝x+60代入得：w＝﹣x2+8x+48＝﹣（x﹣4）2+64∴当x＝4时，有最大毛利润64万元，此时m＝，m﹣x＝；②当x≥8时，w A＝6x﹣x＝5x；w B＝9（m﹣x）﹣[12+3（m﹣x）]＝6m﹣6x﹣12∴w＝w A+w B﹣3×m＝（5x）+（6m﹣6x﹣12）﹣3m＝﹣x+3m﹣12．将3m＝x+60代入得：w＝48∴当x＞8时，有最大毛利润48万元．综上所述，购买杨梅共吨，其中A类杨梅4吨，B类吨，公司能够获得最大毛利润，最大毛利润为64万元．【点评】本题是二次函数、一次函数的综合应用题，难度较大．解题关键是理清售价、成本、利润三者之间的关系．涉及到分段函数时，注意要分类讨论．4．已知：y关于x的函数y＝（k﹣1）x2﹣2kx+k+2的图象与x轴有交点．（1）求k的取值范围；（2）若x1，x2是函数图象与x轴两个交点的横坐标，且满足（k﹣1）x12+2kx2+k+2＝4x1x2．①求k的值；②当k≤x≤k+2时，请结合函数图象确定y的最大值和最小值．【分析】（1）分两种情况讨论，当k＝1时，可求出函数为一次函数，必与x轴有一交点；当k≠1时，函数为二次函数，若与x轴有交点，则△≥0．（2）①根据（k﹣1）x12+2kx2+k+2＝4x1x2及根与系数的关系，建立关于k的方程，求出k 的值；②充分利用图象，直接得出y的最大值和最小值．【解答】解：（1）当k＝1时，函数为一次函数y＝﹣2x+3，其图象与x轴有一个交点．当k≠1时，函数为二次函数，其图象与x轴有一个或两个交点，令y＝0得（k﹣1）x2﹣2kx+k+2＝0．△＝（﹣2k）2﹣4（k﹣1）（k+2）≥0，解得k≤2．即k≤2且k≠1．综上所述，k的取值范围是k≤2．（2）①∵x1≠x2，由（1）知k＜2且k≠1，函数图象与x轴两个交点，∴k＜2，且k≠1．由题意得（k﹣1）x12+（k+2）＝2kx1①，将①代入（k﹣1）x12+2kx2+k+2＝4x1x2中得：2k（x1+x2）＝4x1x2．又∵x1+x2＝，x1x2＝，∴2k•＝4•．解得：k1＝﹣1，k2＝2（不合题意，舍去）．∴所求k值为﹣1．②如图，∵k1＝﹣1，y＝﹣2x2+2x+1＝﹣2（x﹣）2+．且﹣1≤x≤1．由图象知：当x＝﹣1时，y最小＝﹣3；当x＝时，y最大＝．∴y的最大值为，最小值为﹣3．【点评】本题考查了抛物线与x轴的交点、一次函数的定义、二次函数的最值，充分利用图象是解题的关键．5．广安市某楼盘准备以每平方米6000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4860元的均价开盘销售．（1）求平均每次下调的百分率．（2）某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？【分析】（1）根据题意设平均每次下调的百分率为x，列出一元二次方程，解方程即可得出答案；（2）分别计算两种方案的优惠价格，比较后发现方案①更优惠．【解答】解：（1）设平均每次下调的百分率为x，则6000（1﹣x）2＝4860，解得：x1＝0.1＝10%，x2＝1.9（舍去），故平均每次下调的百分率为10%；（2）方案①购房优惠：4860×100×（1﹣0.98）＝9720（元）；方案②可优惠：80×100＝8000（元）．故选择方案①更优惠．【点评】本题主要考查一元二次方程的实际应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解，属于中档题．6．我们学习了利用函数图象求方程的近似解，例如：把方程2x﹣1＝3﹣x的解看成函数y ＝2x﹣1的图象与函数y＝3﹣x的图象交点的横坐标．如图，已画出反比例函数y＝在第一象限内的图象，请你按照上述方法，利用此图象求方程x2﹣x﹣1＝0的正数解．（要求画出相应函数的图象；求出的解精确到0.1）【分析】根据题意可知，方程x2﹣x﹣1＝0的解可看做是函数y＝和y＝x﹣1的交点坐标，所以根据图象可知方程x2﹣x﹣1＝0的正数解约为1.1．【解答】解：∵x≠0，∴将x2﹣x﹣1＝0两边同时除以x，得x﹣1﹣＝0，即＝x﹣1，把x2﹣x﹣1＝0的正根视为由函数y＝与函数y＝x﹣1的图象在第一象限交点的横坐标．如图：∴正数解约为1.1．【点评】主要考查了反比例函数和一元二次方程之间的关系．一元二次方程的解都可化为一个反比例函数和一次函数的交点问题求解．7．用两种方法解答：已知m、n是关于x的方程x2+（p﹣2）x+1＝0两个实数根，求代数式（m2+mp+1）（n2+np+1）的值．【分析】本题主要是利用韦达定理来计算．已知m、n是关于x的方程x2+（p﹣2）x+1＝0两个实数根，有四个等式可供使用：m+n＝2﹣p①，mn＝1②，m2+（p﹣2）m+1＝0③，n2+（p﹣2）n+1＝0④．通过变形方法，合理地选择解题方法．【解答】解：∵m、n是x2+（p﹣2）x+1＝0的根，∴m+n＝2﹣p，mn＝1．方法一：m2+（p﹣2）m+1＝0，n2+（p﹣2）n+1＝0．即m2+pm+1＝2m，n2+pn+1＝2n．原式＝2m×2n＝4mn＝4．方法二：（m2+mp+1）（n2+np+1）＝（m2+mp）（n2+np）+m2+mp+n2+np+1＝m2n2+m2np+mpn2+mnp2+m2+mp+n2+np+1＝1+mp+np+p2+m2+n2+mp+np+1＝2+p2+m2+n2+2（m+n）p＝2+p2+m2+n2+2（2﹣p）p＝2+p2+m2+n2+4p﹣2p2＝2+（m+n）2﹣2mn+4p﹣2p2+p2＝2+（2﹣p）2﹣2+4p﹣2p2+p2＝4﹣4p+p2+4p﹣p2＝4．【点评】本题主要是通过根与系数的关系来求值．注意把所求的代数式转化成m+n＝2﹣p，mn＝1的形式，正确对所求式子进行变形是解题的关键．8．九年级（1）班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度CD＝3m，标杆与旗杆的水平距离BD＝15m，人的眼睛与地面的高度EF＝1.6m，人与标杆CD的水平距离DF＝2m，求旗杆AB的高度．【分析】利用三角形相似中的比例关系，首先由题目和图形可看出，求AB的长度分成了2个部分，AH和HB部分，其中HB＝EF＝1.6m，剩下的问题就是求AH的长度，利用△CGE∽△AHE，得出，把相关条件代入即可求得AH＝11.9，所以AB＝AH+HB＝AH+EF＝13.5m．【解答】解：∵CD⊥FB，AB⊥FB，∴CD∥AB∴△CGE∽△AHE∴即：∴∴AH＝11.9∴AB＝AH+HB＝AH+EF＝11.9+1.6＝13.5（m）．【点评】主要用到的解题思想是把梯形问题转化成三角形问题，利用三角形相似比列方程来求未知线段的长度．9．在△ABC中，AB＝BC，将△ABC绕点A沿顺时针方向旋转得△A1B1C1，使点C1落在直线BC上（点C1与点C不重合），（1）如图，当∠C＞60°时，写出边AB1与边CB的位置关系，并加以证明；（2）当∠C＝60°时，写出边AB1与边CB的位置关系（不要求证明）；（3）当∠C＜60°时，请你在如图中用尺规作图法作出△AB1C1（保留作图痕迹，不写作法），再猜想你在（1）、（2）中得出的结论是否还成立并说明理由．【分析】（1）AB1∥BC．因为等腰三角形，两底角相等，再根据平行线的判定，内错角相等两直线平行，可证明两直线平行．（2）当∠C＝60°时，写出边AB1与边CB的位置关系也是平行，证明方法同（1）题．（3）成立，根据旋转变换的性质画出图形．利用三角形全等即可证明．【解答】解：（1）AB1∥BC．证明：由已知得△ABC≌△AB1C1，∴∠BAC＝∠B1AC1，∠B1AB＝∠C1AC，∵AC1＝AC，∴∠AC1C＝∠ACC1，∵∠C1AC+∠AC1C+∠ACC1＝180°，∴∠C1AC＝180°﹣2∠ACC1，同理，在△ABC中，∵BA＝BC，∴∠ABC＝180°﹣2∠ACC1，∴∠ABC＝∠C1AC＝∠B1AB，∴AB1∥BC．（5分）（2）如图1，∠C＝60°时，AB1∥BC．（7分）（3）如图，当∠C＜60°时，（1）、（2）中的结论还成立．证明：显然△ABC≌△AB1C1，∴∠BAC＝∠B1AC1，∴∠B1AB＝∠C1AC，∵AC1＝AC，∴∠AC1C＝∠ACC1，∵∠C1AC+∠AC1C+∠ACC1＝180°，∴∠C1AC＝180°﹣2∠ACC1，同理，在△ABC中，∵BA＝BC，∴∠ABC＝180°﹣2∠ACC1，∴∠ABC＝∠C1AC＝∠B1AB，∴AB1∥BC．（13分）【点评】考查图形的旋转，等腰三角形的性质，平行线的判定．本题实质是考查对图形旋转特征的理解，旋转前后的图形是全等的．10．汽车产业的发展，有效促进我国现代化建设．某汽车销售公司2005年盈利1500万元，到2007年盈利2160万元，且从2005年到2007年，每年盈利的年增长率相同．（1）该公司2006年盈利多少万元？（2）若该公司盈利的年增长率继续保持不变，预计2008年盈利多少万元？【分析】（1）需先算出从2005年到2007年，每年盈利的年增长率，然后根据2005年的盈利，算出2006年的利润；（2）相等关系是：2008年盈利＝2007年盈利×每年盈利的年增长率．【解答】解：（1）设每年盈利的年增长率为x，根据题意得1500（1+x）2＝2160解得x1＝0.2，x2＝﹣2.2（不合题意，舍去）∴1500（1+x）＝1500（1+0.2）＝1800答：2006年该公司盈利1800万元．（2）2160（1+0.2）＝2592答：预计2008年该公司盈利2592万元．【点评】本题的关键是需求出从2005年到2007年，每年盈利的年增长率．等量关系为：2005年盈利×（1+年增长率）2＝2160．11．如图，在△ABC中，∠BAC＝30°，以AB为直径的⊙O经过点C．过点C作⊙O的切线交AB的延长线于点P．点D为圆上一点，且＝，弦AD的延长线交切线PC于点E，连接BC．（1）判断OB和BP的数量关系，并说明理由；（2）若⊙O的半径为2，求AE的长．【分析】（1）首先连接OC，由PC切⊙O于点C，可得∠OCP＝90°，又由∠BAC＝30°，即可求得∠COP＝60°，∠P＝30°，然后根据直角三角形中30°角所对的直角边等于斜边的一半，证得OB＝BP；（2）由（1）可得OB＝OP，即可求得AP的长，又由＝，即可得∠CAD＝∠BAC＝30°，继而求得∠E＝90°，继而在Rt△AEP中求得答案．【解答】解：（1）OB＝BP．理由：连接OC，∵PC切⊙O于点C，∴∠OCP＝90°，∵OA＝OC，∠OAC＝30°，∴∠OAC＝∠OCA＝30°，∴∠COP＝60°，∴∠P＝30°，在Rt△OCP中，OC＝OP＝OB＝BP；（2）由（1）得OB＝OP，∵⊙O的半径是2，∴AP＝3OB＝3×2＝6，∵＝，∴∠CAD＝∠BAC＝30°，∴∠BAD＝60°，∵∠P＝30°，∴∠E＝90°，在Rt△AEP中，AE＝AP＝×6＝3．【点评】此题考查了切线的性质、直角三角形的性质以及圆周角定理．此题难度适中，注意掌握数形结合思想的应用，注意掌握辅助线的作法．12．已知⊙O1与⊙O2相交于A、B两点，点O1在⊙O2上，C为⊙O2上一点（不与A，B，O1重合），直线CB与⊙O1交于另一点D．（1）如图（1），若AD是⊙O1的直径，AC是⊙O2的直径，求证：AC＝CD；（2）如图（2），若C是⊙O1外一点，求证：O1C丄AD；（3）如图（3），若C是⊙O1内的一点，判断（2）中的结论是否成立？【分析】（1）连接C01，利用直径所对圆周角等于90度，以及垂直平分线的性质得出即可；（2）根据已知得出四边形AEDB内接于⊙O1，得出∠ABC＝∠E，再利用＝，得出∠E＝∠AO1C，进而得出CO1∥ED即可求出；（3）根据已知得出∠B＝∠EO1C，又∠E＝∠B，即可得出∠EO1C＝∠E，得出CO1∥ED，即可求出．【解答】（1）证明：连接C01∵AC为⊙O2直径∴∠AO1C＝90°即CO1⊥AD，∵AO1＝DO1∴DC＝AC（垂直平分线的性质）；（2）证明：连接AO1，连接AB，延长AO1交⊙O1于点E，连接ED，∵四边形AEDB内接于⊙O1，∴∠E+∠ABD＝180°，∵∠ABC+∠ABD＝180°，∴∠ABC＝∠E，又∵＝，∴∠ABC＝∠AO1C，∴∠E＝∠AO1C，∴CO1∥ED，又AE为⊙O1的直径，∴ED⊥AD，∴O1C⊥AD，（3）（2）中的结论仍然成立．证明：连接AO1，连接AB，延长AO1交⊙O1于点E，连接ED，∵∠B+∠AO1C＝180°，∠EO1C+∠AO1C═180°，∴∠B＝∠EO1C，又∵∠E＝∠B，∴∠EO1C＝∠E，∴CO1∥ED，又ED⊥AD，∴CO1⊥AD．【点评】此题主要考查了圆周角定理以及相交两圆的性质和圆内接四边形的性质，根据圆内接四边形的性质得出对应角之间的关系是解决问题的关键．13．⊙O1与⊙O2相交于A、B两点，如图（1），连接O2O1并延长交⊙O1于P点，连接P A、PB并分别延长交⊙O2于C、D两点，连接CO2并延长交⊙O2于E点．已知⊙O2的半径为R，设∠CAD＝α．（1）求CD的长（用含R、α的式子表示）；（2）试判断CD与PO1的位置关系，并说明理由；（3）设点P’为⊙O1上（⊙O2外）的动点，连接P’A、P’B并分别延长交⊙O2于C’、D’，请你探究∠C’AD’是否等于α？C’D’与P’O1的位置关系如何？并说明理由．（注：图（2）与图（3）中⊙O1和⊙O2的大小及位置关系与图（1）完全相同，若你感到继续在图（1）中探究问题（3），图形太复杂，不便于观察，可以选择图（2）或图（3）中的一图说明理由）．【分析】（1）作⊙O2的直径CE，连接DE．根据圆周角定理的推论，得∠E＝∠CAD＝α，再利用解直角三角形的知识求解；（2）连接AB，延长PO1与⊙O1相交于点E，连接AE．根据圆内接四边形的性质，得∠ABP′＝∠C′，根据圆周角定理的推论，得∠ABP′＝∠E，∠EAP′＝90°，从而证明∠AP′E+∠C′＝90°，则CD与PO1的位置关系是互相垂直；（3）根据同弧所对的圆周角相等，则说明∠C’AD’等于α；根据（2）中的证明过程，则可以证明C’D’与P’O1的位置关系是互相垂直．【解答】解：（1）连接DE．根据圆周角定理的推论，得∠E＝∠CAD＝α．∵CE是直径，∴∠CDE＝90°．∴CD＝CE•sin E＝2R sinα；（2）CD与PO1的位置关系是互相垂直．理由如下：连接AB，延长PO1与⊙O1相交于点E，连接AE．∵四边形BAC′D′是圆内接四边形，∴∠ABP′＝∠C′．∵P′E是直径，∴∠EAP′＝90°，∴∠AP′E+∠E＝90°．又∠ABP′＝∠E，∴∠AP′E+∠C′＝90°，即CD与PO1的位置关系是互相垂直；（3）根据同弧所对的圆周角相等，则说明∠C’AD’等于α；根据（2）中的证明过程，则可以证明C’D’与P’O1的位置关系是互相垂直．【点评】此题综合运用了圆周角定理及其推论、直角三角形的性质、圆内接四边形的性质．注意：连接两圆的公共弦、构造直径所对的圆周角都是圆中常见的辅助线．14．一个不透明的口袋里有红、黄、绿三种颜色的球（除颜色外其余都相同），其中红球有2个，黄球有1个，任意摸出一个黄球的概率为．（1）试求口袋里绿球的个数；（2）若第一次从口袋中任意摸出一球（不放回），第二次任意摸出一球，请你用树状图或列表法，求出两次都摸到红球的概率．【分析】（1）根据概率的求解方法，利用方程求得绿球个数；（2）此题需要两步完成，所以采用树状图法或者列表法都比较简单，解题时要注意是放回实验还是不放回实验，此题为不放回实验．【解答】解：（1）设口袋里绿球有x个，则，解得x＝1．故口袋里绿球有1个．（2）红一红二黄绿红一红二，红一黄，红一绿，红一红二红一，红二黄，红一绿，红二黄红一，黄红二，黄绿，黄绿红一，绿红二，绿黄，绿故，P（两次都摸到红球）＝．【点评】（1）解题时要注意应用方程思想；（2）列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．用到的知识点为：概率＝所求情况数与总情况数之比．15．经统计分析，某市跨河大桥上的车流速度v（千米/小时）是车流密度x（辆/千米）的函数，当桥上的车流密度达到220辆/千米时，造成堵塞，此时车流速度为0千米/小时；当车流密度不超过20辆/千米时，车流速度为80千米/小时，研究表明：当20≤x≤220时，车流速度v是车流密度x的一次函数．（1）求大桥上车流密度为100辆/千米时的车流速度；（2）在交通高峰时段，为使大桥上的车流速度大于40千米/小时且小于60千米/小时，应控制大桥上的车流密度在什么范围内？（3）车流量（辆/小时）是单位时间内通过桥上某观测点的车辆数，即：车流量＝车流速度×车流密度．求大桥上车流量y的最大值．【分析】（1）当20≤x≤220时，设车流速度v与车流密度x的函数关系式为v＝kx+b，根据题意的数量关系建立方程组求出其解即可；（2）由（1）的解析式建立不等式组求出其解即可；（3）设车流量y与x之间的关系式为y＝vx，当x＜20和20≤x≤220时分别表示出函数关系由函数的性质就可以求出结论．【解答】解：（1）设车流速度v与车流密度x的函数关系式为v＝kx+b，由题意，得，解得：，∴当20≤x≤220时，v＝﹣x+88，当x＝100时，v＝﹣×100+88＝48（千米/小时）；（2）由题意，得，解得：70＜x＜120．∴应控制大桥上的车流密度在70＜x＜120范围内；（3）设车流量y与x之间的关系式为y＝vx，当0≤x≤20时y＝80x，∴k＝80＞0，∴y随x的增大而增大，∴x＝20时，y最大＝1600；当20≤x≤220时y＝（﹣x+88）x＝﹣（x﹣110）2+4840，∴当x＝110时，y最大＝4840．∵4840＞1600，∴当车流密度是110辆/千米，车流量y取得最大值是每小时4840辆．【点评】本题考查了车流量＝车流速度×车流密度的运用，一次函数的解析式的运用，一元一次不等式组的运用，二次函数的性质的运用，解答时求出函数的解析式是关键．16．（1）已知一元二次方程x2+px+q＝0（p2﹣4q≥0）的两根为x1、x2；求证：x1+x2＝﹣p，x1•x2＝q．（2）已知抛物线y＝x2+px+q与x轴交于A、B两点，且过点（﹣1，﹣1），设线段AB的长为d，当p为何值时，d2取得最小值，并求出最小值．【分析】（1）先根据求根公式得出x1、x2的值，再求出两根的和与积即可；（2）把点（﹣1，﹣1）代入抛物线的解析式，再由d＝|x1﹣x2|可知d2＝（x1﹣x2）2＝（x1+x2）2﹣4 x1•x2＝p2，再由（1）中x1+x2＝﹣p，x1•x2＝q即可得出结论．【解答】证明：（1）∵a＝1，b＝p，c＝q∴△＝p2﹣4q∴x＝即x1＝，x2＝∴x1+x2＝+＝﹣p，x1•x2＝•＝q；（2）把（﹣1，﹣1）代入y＝x2+px+q得1﹣p+q＝﹣1，所以，q＝p﹣2，设抛物线y＝x2+px+q与x轴交于A、B的坐标分别为（x1，0）、（x2，0）∵d＝|x1﹣x2|，∴d2＝（x1﹣x2）2＝（x1+x2）2﹣4x1•x2＝p2﹣4q＝p2﹣4p+8＝（p﹣2）2+4当p＝2时，d2的最小值是4．【点评】本题考查的是抛物线与x轴的交点及根与系数的关系，熟知x1，x2是方程x2+px+q ＝0的两根时，x1+x2＝﹣p，x1x2＝q是解答此题的关键．17．如图，菱形、矩形与正方形的形状有差异，我们将菱形、矩形与正方形的接近程度称为“接近度”．在研究“接近度”时，应保证相似图形的“接近度”相等．（1）设菱形相邻两个内角的度数分别为m°和n°，将菱形的“接近度”定义为|m﹣n|，于是|m﹣n|越小，菱形越接近于正方形．①若菱形的一个内角为70°，则该菱形的“接近度”等于40；②当菱形的“接近度”等于0时，菱形是正方形．（2）设矩形相邻两条边长分别是a和b（a≤b），将矩形的“接近度”定义为|a﹣b|，于是|a﹣b|越小，矩形越接近于正方形．你认为这种说法是否合理？若不合理，给出矩形的“接近度”一个合理定义．【分析】（1）根据相似图形的定义知，相似图形的形状相同，但大小不一定相同，相似图形的“接近度”相等．所以若菱形的一个内角为70°，则该菱形的“接近度”等于|m﹣n|；当菱形的“接近度”等于0时，菱形是正方形；（2）不合理，举例进行说明．【解答】解：（1）①∵内角为70°，∴与它相邻内角的度数为110°．∴菱形的“接近度”＝|m﹣n|＝|110﹣70|＝40．②当菱形的“接近度”等于0时，菱形是正方形．（2）不合理．例如，对两个相似而不全等的矩形来说，它们接近正方形的程度是相同的，但|a﹣b|却不相等．合理定义方法不唯一．如定义为，越接近1，矩形越接近于正方形；越大，矩形与正方形的形状差异越大；当时，矩形就变成了正方形，即只有矩形的越接近1，矩形才越接近正方形．【点评】正确理解“接近度”的意思，矩形的“接近度”|a﹣b|越小，矩形越接近于正方形．这是解决问题的关键．18．如图所示，AB＝AC，AB为⊙O的直径，AC、BC分别交⊙O于E、D，连接ED、BE．（1）试判断DE与BD是否相等，并说明理由；（2）如果BC＝6，AB＝5，求BE的长．【分析】（1）可通过连接AD，AD就是等腰三角形ABC底边上的高，根据等腰三角形三线合一的特点，可得出∠CAD＝∠BAD，根据圆周角定理即可得出∠DEB＝∠DBE，便可证得DE＝DB．（2）本题中由于BE⊥AC，那么BE就是三角形ABC中AC边上的高，可用面积的不同表示方法得出AC•BE＝CB•AD．进而求出BE的长．【解答】解：（1）DE＝BD证明：连接AD，则AD⊥BC，在等腰三角形ABC中，AD⊥BC，∴∠CAD＝∠BAD（等腰三角形三线合一），∴＝，∴DE＝BD；（2）∵AB＝5，BD＝BC＝3，∴AD＝4，∵AB＝AC＝5，∴S△ABC＝•AC•BE＝•CB•AD，∴BE＝4.8．【点评】本题主要考查了等腰三角形的性质，圆周角定理等知识点的运用，用等腰三角形三线合一的特点得出圆周角相等是解题的关键．19．下框中是小明对一道题目的解答以及老师的批改．题目：某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为2：1，在温室内，沿前侧内墙保留3m的空地，其他三侧内墙各保留1m的通道，当温室的长与宽各为多少时，矩形蔬菜种植区域的面积是288m2？解：设矩形蔬菜种植区域的宽为xm，则长为2xm，根据题意，得x•2x＝288．解这个方程，得x1＝﹣12（不合题意，舍去），x2＝12所以温室的长为2×12+3+1＝28（m），宽为12+1+1＝14（m）答：当温室的长为28m，宽为14m时，矩形蔬菜种植区域的面积是288m2．我的结果也正确！小明发现他解答的结果是正确的，但是老师却在他的解答中画了一条横线，并打了一个？．结果为何正确呢？（1）请指出小明解答中存在的问题，并补充缺少的过程：变化一下会怎样…（2）如图，矩形A′B′C′D′在矩形ABCD的内部，AB∥A′B′，AD∥A′D′，且AD：AB＝2：1，设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d，要使矩形A′B′C′D′∽矩形ABCD，a、b、c、d应满足什么条件？请说明理由．【分析】（1）根据题意可得小明没有说明矩形蔬菜种植区域的长与宽之比为2：1的理由，所以应设矩形蔬菜种植区域的宽为xm，则长为2xm，然后由题意得，矩形蔬菜种植区域的长与宽之比为2：1，再利用小明的解法求解即可；（2）由使矩形A′B′C′D′∽矩形ABCD，利用相似多边形的性质，可得，即，然后利用比例的性质，即可求得答案．【解答】解：（1）小明没有说明矩形蔬菜种植区域的长与宽之比为2：1的理由．在“设矩形蔬菜种植区域的宽为xm，则长为2xm．”前补充以下过程：设温室的宽为xm，则长为2xm．则矩形蔬菜种植区域的宽为（x﹣1﹣1）m，长为（2x﹣3﹣1）m．∵，∴矩形蔬菜种植区域的长与宽之比为2：1；（2）要使矩形A′B′C′D′∽矩形ABCD，就要，即，即，即2AB﹣2（b+d）＝2AB﹣（a+c），∴a+c＝2（b+d），即．【点评】此题考查了相似多边形的性质．此题属于阅读性题目，注意理解题意，读懂题目是解此题的关键．20．二次函数y＝ax2+bx+c图象的一部分如图所示，则a的取值范围是﹣1＜a＜0．【分析】由抛物线的开口方向判断a的符号，由抛物线与y轴的交点得出c的值，然后根据图象经过的点的情况进行推理，进而推出所得结论．【解答】解：抛物线开口向下，a＜0，图象过点（0，1），c＝1，图象过点（1，0），a+b+c＝0，∴b＝﹣（a+c）＝﹣（a+1）．由题意知，当x＝﹣1时，应有y＞0，∴a﹣b+c＞0，∴a+（a+1）+1＞0，∴a＞﹣1，∴实数a的取值范围是﹣1＜a＜0．【点评】根据开口判断a的符号，根据与x轴，y轴的交点判断c的值以及b用a表示出的代数式．难点是推断出当x＝﹣1时，应有y＞0．21．今年，我国政府为减轻农民负担，决定在5年内免去农业税．某乡今年人均上缴农业税25元，若两年后人均上缴农业税为16元，假设这两年降低的百分率相同．（1）求降低的百分率；（2）若小红家有4人，明年小红家减少多少农业税？（3）小红所在的乡约有16000农民，问该乡农民明年减少多少农业税？【分析】（1）设降低的百分率为x，则降低一次后的数额是25（1﹣x），再在这个数的基础上降低x，则变成25（1﹣x）（1﹣x）即25（1﹣x）2，据此即可列方程求解；（2）每人减少的税额是25x，则4个人的就是4×25x，代入（1）中求得的x的值，即可求解；（3）每个人减少的税额是25x，乘以总人数16000即可求解．【解答】解：（1）设降低的百分率为x，依题意有，25（1﹣x）2＝16，解得，x1＝0.2＝20%，x2＝1.8（舍去）；（2）小红全家少上缴税25×20%×4＝20（元）；（3）全乡少上缴税16000×25×20%＝80 000（元）．答：降低的增长率是20%，明年小红家减少的农业税是20元，该乡农民明年减少的农业税是80 000元．【点评】本题考查求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2＝b．22．如图，在矩形ABCD中，AB＝m（m是大于0的常数），BC＝8，E为线段BC上的动点（不与B、C重合）．连接DE，作EF⊥DE，EF与射线BA交于点F，设CE＝x，BF＝y．（1）求y关于x的函数关系式；（2）若m＝8，求x为何值时，y的值最大，最大值是多少？（3）若y＝，要使△DEF为等腰三角形，m的值应为多少？【分析】（1）利用互余关系找角相等，证明△BEF∽△CDE，根据对应边的比相等求函数关系式；（2）把m的值代入函数关系式，再求二次函数的最大值；（3）∵∠DEF＝90°，只有当DE＝EF时，△DEF为等腰三角形，把条件代入即可．【解答】解：（1）∵EF⊥DE，∴∠BEF＝90°﹣∠CED＝∠CDE，又∠B＝∠C＝90°，∴△BEF∽△CDE，∴＝，即＝，解得y＝；（2）由（1）得y＝，将m＝8代入，得y＝﹣x2+x＝﹣（x2﹣8x）＝﹣（x﹣4）2+2，所以当x＝4时，y取得最大值为2；（3）∵∠DEF＝90°，∴只有当DE＝EF时，△DEF为等腰三角形，∴△BEF≌△CDE，∴BE＝CD＝m，此时m＝8﹣x，解方程＝，得x＝6，或x＝2，当x＝2时，m＝6，当x＝6时，m＝2．【点评】本题把相似三角形与求二次函数解析式联系起来，在解题过程中，充分运用相似三角形对应边的比相等，建立函数关系式．23．某市城建部门经过长期市场调查发现，该市年新建商品房面积P（万平方米）与市场新房均价x（千元/平方米）存在函数关系P＝25x；年新房销售面积Q（万平方米）与市场新房均价x（千元/平方米）的函数关系为Q＝﹣10；（1）如果年新建商品房的面积与年新房销售面积相等，求市场新房均价和年新房销售总额；（2）在（1）的基础上，如果市场新房均价上涨1千元，那么该市年新房销售总额是增加还是减少？变化了多少？结合年新房销售总额和积压面积的变化情况，请你提出一条合理化的建议．（字数不超过50）【分析】（1）根据“新建商品房的面积与年新房销售面积相等”作为相等关系求x的值即可；（2）分别求算出市场新房均价上涨1千元后的新建商品房面积P，年新房销售面积Q再来求算其变化的量和积压的情况．【解答】解：（1）根据题意得：25x＝﹣10，解得x1＝2，x2＝﹣（舍去），则Q＝﹣10＝50万平方米，所以市场新房均价为2千元．则年新房销售总额为2000×500000＝10亿元．（2）因为Q＝﹣10＝30万平方米，P＝25x＝75万平方米，所以市场新房均价上涨1千元则该市年新房销售总额减少了100000﹣30×（2000+1000）＝10000万元，年新房积压面积增加了45万平方米．建议：对于新房的销售应订一个合理的价格，不能过高，只有考虑成本与人们的购买力才能使利润最大．【点评】主要考查了函数在实际问题中的应用．解题的关键是理解题意能准确的找到函数中对应的变量的值，根据题意求解．24．已知：如图，在平面直角坐标系中，点P（m，m）（m＞0），过点P的直线AB 与x轴正半轴交于点A，与直线y＝x交于点B．（1）当m＝3且∠OAB＝90°时，求BP的长度；（2）若点A的坐标是（6，0），且AP＝2PB，求经过点P且以点B为顶点的抛物线的函数表达式．。

2024年中考数学高频压轴题训练——圆-动点问题及参考答案

2024年中考数学高频压轴题训练——圆-动点问题1．“同弧或等弧所对的圆周角相等”，利用这个推论可以解决很多数学问题．（1）【知识理解】如图1，圆O 的内接四边形ACBD 中，60ABC ∠=︒，BC AC =，①BDC ∠=；DAB ∠DCB ∠（填“>”，“=”，“<”）②将D 点绕点B 顺时针旋转60︒得到点E ，则线段DB DC DA ，，的数量关系为．（2）【知识应用】如图2，AB 是圆O 的直径，1tan 2ABC ∠=，猜想DA DB DC ，，的数量关系，并证明；（3）【知识拓展】如图3，已知2AB =，A B ，分别是射线DA DB ，上的两个动点，以AB 为边往外构造等边ABC ，点C 在MDN ∠内部，若120D ∠=︒，直接写出四边形ADBC 面积S 的取值范围．2．如图1，对于PMN 的顶点P 及其对边MN 上的一点Q ，给出如下定义：以P 为圆心，PQ 为半径的圆与直线MN 的公共点都在线段MN 上，则称点Q 为PMN 关于点P 的内联点．在平面直角坐标系xOy 中：（1）如图2，已知点(70)A ，，点B 在直线1y x =+上．①若点(34)B ，，点(30)C ，，则在点O ，C ，A 中，点是AOB 关于点B 的内联点；②若AOB 关于点B 的内联点存在，求点B 纵坐标n 的取值范围；（2）已知点(20)D ，，点(42)E ，，将点D 绕原点O 旋转得到点F ．若EOF 关于点E 的内联点存在，直接写出点F 横坐标m 的取值范围．3．在平面直角坐标系xOy 中，O 的半径为1，对于点A 和线段BC ，给出如下定义：若将线段BC 绕点A 旋转可以得到O 的弦B C ''（B C ''，分别是B C ，的对应点），则称线段BC 是O 的以点A 为中心的“关联线段”．（1）如图，点112233A B C B C B C ，，，，，，的横､纵坐标都是整数．在线段112233B C B C B C ，，中，O 的以点A 为中心的“关联线段”是；（2）ABC 是边长为1的等边三角形，点()0A t ，，其中0t ≠．若BC 是O 的以点A 为中心的“关联线段”，求t 的值；（3）在ABC 中，12AB AC ==，．若BC 是O 的以点A 为中心的“关联线段”，直接写出OA 的最小值和最大值，以及相应的BC 长．4．已知：点C 为⊙O 的直径AB 上一动点，过点C 作CD ⊥AB ，交⊙O 于点D 和点E ，连接AD 、BD ，∠DBA 的角平分线交⊙O 于点F ．（1）若DF ＝BD ，求证：GD ＝GB ；（2）若AB ＝2cm ，在（1）的条件下，求DG 的值；（3）若∠ADB 的角平分线DM 交⊙O 于点M ，交AB 于点N ．当点C 与点O 重合时，AD BD DM+＝；据此猜想，当点C 在AB （不含端点）运动过程中，AD BD DM +的值是否发生改变？若不变，请求其值；若改变，请说明理由．5．在平面直角坐标系xOy 中，O 的半径为1，对于ABC 和直线l 给出如下定义：若ABC 的一条边关于直线l 的对称线段PQ 是O 的弦，则称ABC 是O 的关于直线l 的“关联三角形”，直线l 是“关联轴”．（1）如图1，若ABC 是O 的关于直线l 的“关联三角形”，请画出ABC 与O 的“关联轴”（至少画两条）；（2）若ABC 中，点A 坐标为(23)，，点B 坐标为(41)，，点C 在直线3y x =-+的图像上，存在“关联轴l ”使ABC 是O 的关联三角形，求点C 横坐标的取值范围；（3）已知A ，将点A 向上平移2个单位得到点M ，以M 为圆心MA 为半径画圆，B ，C 为M 上的两点，且2AB =（点B 在点A 右侧），若ABC 与O 的关联轴至少有两条，直接写出OC 的最小值和最大值，以及OC 最大时AC 的长．6．如图，在⊙O 中，AB 为弦，CD 为直径，且AB ⊥CD ，垂足为E ，P 为 AC 上的动点（不与端点重合），连接PD ．（1）求证：∠APD ＝∠BPD ；（2）利用尺规在PD 上找到点I ，使得I 到AB 、AP 的距离相等，连接AD （保留作图痕迹，不写作法）．求证：∠AIP+∠DAI ＝180°；（3）在（2）的条件下，连接IC 、IE ，若∠APB ＝60°，试问：在P 点的移动过程中，IC IE 是否为定值？若是，请求出这个值；若不是，请说明理由．7．在平面直角坐标系xOy 中，已知线段AB 和点P ，给出如下定义：若PA PB =且点P 不在线段AB 上，则称点P 是线段AB 的等腰顶点．特别地，当90APB ∠≥︒时，则称点P 是线段AB 的非锐角等腰顶点．（1）已知点(20)A ，，(42)B ，．①在点(40)C ，，(31)D ，，(15)E -，，(05)F ，中，是线段AB 的等腰顶点的是▲；②若点P 在直线3(0)y kx k =+≠上，且点P 是线段AB 的非锐角等腰顶点，求k 的取值范围；（2）直线33y x =-+与x 轴交于点M ，与y 轴交于点N ．⊙P 的圆心为(0)P t ，，半径为，若⊙P 上存在线段MN 的等腰顶点，请直接写出t 的取值范围．8．在平面直角坐标系xOy中，⊙O的半径为1，T（0，t）为y轴上一点，P为平面上一点．给出如下定义：若在⊙O上存在一点Q，使得△TQP是等腰直角三角形，且∠TQP＝90°，则称点P为⊙O的“等直点”，△TQP为⊙O的“等直三角形”．如图，点A，B，C，D的横、纵坐标都是整数．（1）当t＝2时，在点A，B，C，D中，⊙O的“等直点”是；（2）当t＝3时，若△TQP是⊙O“等直三角形”，且点P，Q都在第一象限，求CPOQ的值．9．综合与实践动手操作利用正方形纸片的折叠开展数学活动．探究体会在正方形折叠过程中，图形与线段的变化及其蕴含的数学思想方法．如图1，点E 为正方形ABCD 的AB 边上的一个动点，3AB =，将正方形ABCD 对折，使点A 与点B 重合，点C 与点D 重合，折痕为MN ．思考探索（1）将正方形ABCD 展平后沿过点C 的直线CE 折叠，使点B 的对应点B '落在MN 上，折痕为EC ，连接DB '，如图2．①点B '在以点E 为圆心，的长为半径的圆上；②B M '=；③DB C ' 为三角形，请证明你的结论．（2）拓展延伸当3AB AE =时，正方形ABCD 沿过点E 的直线l （不过点B ）折叠后，点B 的对应点B '落在正方形ABCD 内部或边上．①ABB ' 面积的最大值为；②连接AB '，点P 为AE 的中点，点Q 在AB '上，连接PQ AQP AB E ∠=∠'，，则2B C PQ '+的最小值为．10．在平面直角坐标系xOy 中，过⊙T （半径为r ）外一点P 引它的一条切线，切点为Q ，若0＜PQ≤2r ，则称点P 为⊙T 的伴随点．（1）当⊙O 的半径为1时，①在点A(4，0)，B(0，)，C(1，)中，⊙O 的伴随点是▲；②点D 在直线y ＝x+3上，且点D 是⊙O 的伴随点，求点D 的横坐标d 的取值范围；（2）⊙M 的圆心为M(m ，0)，半径为2，直线y ＝2x ﹣2与x 轴，y 轴分别交于点E ，F ．若线段EF 上的所有点都是⊙M 的伴随点，直接写出m 的取值范围．11．定义：在平面直角坐标系xOy 中，点P 为图形M 上一点，点Q 为图形N 上一点．若存在OP OQ =，则称图形M 与图形N 关于原点O “平衡”．（1）如图，已知⊙A 是以()1,0为圆心，2为半径的圆，点()1,0C -，()2,1D -，()3,2E ．①在点C ，D ，E 中，与⊙A 关于原点O “平衡”的点是；②点H 为直线y x =-上一点，若点H 与⊙A 关于原点O “平衡”，点H 的横坐标的取值范围为：；（2）如图，已知图形G 是以原点O 为中心，边长为2的正方形．⊙K 的圆心在x 轴上，半径为2．若⊙K 与图形G 关于原点O “平衡”，请直接写出圆心K 的横坐标的取值范围．12．阅读下列材料，并按要求解答相关问题：【思考发现】根据直径所对的圆周角是直角，我们可以推出“如果一条定边所对的角始终为直角，那么所有满足条件的直角顶点组成的图形是以定边为直径的圆或圆弧（直径的两个端点除外）”这一正确的结论．如图1，若AB 是一条定线段，且90APB ∠=︒，则所有满足条件的直角顶点P 组成的图形是定边AB 为直径的O （直径两端点A 、B 除外）（1）已知：如图2，四边形ABCD 是边长为8的正方形，点E 从点B 出发向点C 运动，同时点F 从点C 出发以相同的速度向点D 运动，连接AE ，BF 相交于点P ．①当点E 从点B 运动到点C 的过程中，APB ∠的大小是否发生变化？若发生变化，请说明理由；若不发生变化，请直接写出APB ∠的度数．②当点E 从点B 运动到点C 的过程中，点P 运动的路径是（）A ．线段；B ．弧；C ．半圆；D ．圆③点P 运动的路经长是▲．（2）已知：如图3，在图2的条件下，连接CP ，请直接写出E 、F 运动过程中，CP 的最小值．13．对于平面内的图形1G 和图形2G ，记平面内一点P 到图形1G 上各点的最短距离为1d ，点P 到图形2G 上各点的最短距离为2d ，若12d d =，就称点P 是图形1G 和图形2G 的一个“等距点”．在平面直角坐标系xOy 中，已知点()60A ，，(0B ．（1）在()30R ，，()20S ，，(1T 三点中，点A 和点B 的等距点是；（2）已知直线2y =-．①若点A 和直线2y =-的等距点在x 轴上，则该等距点的坐标为▲；②若直线y a =上存在点A 直线2y =-的等距点，求实数a 的取值范围；（3）记直线AB 为直线1l ，直线2l ：33y x =-，以原点O 为圆心作半径为r 的O ．若O 上有m 个直线1l 和直线2l 的等距点，以及n 个直线1l 和y 轴的等距点（0m ≠，0n ≠），求m n ≠时，求r 的取值范围．14．如图，平面上存在点P 、点M 与线段AB ．若线段AB 上存在一点Q ，使得点M 在以PQ 为直径的圆上，则称点M 为点P 与线段AB 的共圆点．已知点P （0，1），点A （﹣2，﹣1），点B （2，﹣1）．（1）在点O （0，0），C （﹣2，1），D （3，0）中，可以成为点P 与线段AB 的共圆点的是；（2）点K 为x 轴上一点，若点K 为点P 与线段AB 的共圆点，请求出点K 横坐标x K 的取值范围；（3）已知点M （m ，﹣1），若直线y ＝12x +3上存在点P 与线段AM 的共圆点，请直接写出m 的取值范围．15．如图，在ABC 中，AB BC =，30CAB ∠=︒，8AC =，半径为2的O 从点A 开始（如图1）沿直线AB 向右滚动，滚动时始终与直线AB 相切（切点为D ），当O 与ABC 只有一个公共点时滚动停止，作OG AC ⊥于点G ．（1）图1中，O 在AC 边上截得的弦长AE =；（2）当圆心落在AC 上时，如图2，判断BC 与O 的位置关系，并说明理由．（3）在O 滚动过程中，线段OG 的长度随之变化，设AD x =，OG y =，求出y 与x 的函数关系式，并直接写出x 的取值范围．16．在平面直角坐标系xOy 中，给出如下定义：若点P 在图形M 上，点Q 在图形N 上，称线段PQ 长度的最小值为图形M ，N 的“近距离”，记为d(M ，N)，特别地，若图形M ，N 有公共点，规定d(M ，N)＝0．已知：如图，点A(2-，0)，B(0，．（1）如果⊙O 的半径为2，那么d(A ，⊙O)＝，d(B ，⊙O)＝．（2）如果⊙O 的半径为r ，且d （⊙O ，线段AB ）=0，求r 的取值范围；（3）如果C(m ，0)是x 轴上的动点，⊙C 的半径为1，使d （⊙C ，线段AB ）<1，直接写出m 的取值范围．17．在平面直角坐标系xOy 中，对于点()P m n ，，我们称直线y mx n =+为点P 的关联直线.例如，点()24P ，的关联直线为24y x =+．（1）已知点()12A ，．①点A 的关联直线为；②若O 与点A 的关联直线相切，则O 的半径为；（2）已知点()02C ，，点()0.D d ，点M 为直线CD 上的动点．①当2d =时，求点O 到点M 的关联直线的距离的最大值；②以()11T -，为圆心，3为半径作.T 在点M 运动过程中，当点M 的关联直线与T 交于E ，F 两点时，EF 的最小值为4，请直接写出d 的值．18．在平面直角坐标系xOy 中，给定圆C 和点P ，若过点P 最多可以作出k 条不同的直线，且这些直线被圆C 所截得的线段长度为正整数，则称点P 关于圆C 的特征值为.k 已知圆O 的半径为2，（1）若点M 的坐标为()11，，则经过点M 的直线被圆O 截得的弦长的最小值为，点M 关于圆O 的特征值为；（2）直线y x b =+分别与x ，y 轴交于点A ，B ，若线段AB 上总存在关于圆O 的特征值为4的点，求b 的取值范围；（3）点T 是x 轴正半轴上一点，圆T 的半径为1，点R ，S 分别在圆O 与圆T 上，点R 关于圆T 的特征值记为r ，点S 关于圆O 的特征值记为.s 当点T 在x 轴正轴上运动时，若存在点R ，S ，使得3r s +=，直接写出点T 的横坐标t 的取值范围．答案解析部分1．【答案】（1）60︒；=；DC DB DA=+（2）解：在AB 上取一点E ，使ADE BDC ∠=∠，如图所示：∵AB 是圆O 的直径，1tan 2ABC ∠=，∴1tan 2AC ABC BC BC =∠⋅=，∴在Rt ACB 中，52AB BC ==，∵ BD BD =，∴DAB DCB ∠=∠，∵ADE BDC ∠=∠，∴ADE CDB ∽，∴ADAECD CB =，∴AD CB CD AE ⋅=⋅，∵ AD AD =，∴DBA DCA ∠=∠，∵ADE CDE CDB CDE ∠-∠=∠-∠，即ADC BDE ∠=∠，∴BDE CDA ∽，∴BDBECD AC =，∴BD AC CD BE ⋅=⋅，∴()AD CB AC BD CD AE CD BE CD AE BE CD AB⋅+⋅=⋅+⋅=⋅+=⋅，∴AB CD AC DB AD BC ⋅=⋅+⋅，∴122BC CD BC DB AD BC ⋅=⋅+⋅，∴5122CD DB AD ⋅=⋅+，∴5122CD DB AD =+，即2DB AD =+，故答案为：2DB AD =+．（3）解：∵A B ，分别是射线DA DB ，上的两个动点，120D ∠=︒，ABC 是等边三角形，∴四边形ADBC 的两个对角180ADB ACB ∠+∠=︒，∴构造四边形ADBC 的外接圆，∴根据四边形外接圆的性质可得：当点A 和点D 重合时，四边形ADBC 面积S 最小；当CD AB ⊥时，四边形ADBC 面积S 最大，①当点A 和点D 重合时，四边形ADBC 面积S 最小，∵CBD 时等边三角形，且2AB =，∴60CBD ∠=︒，2AB BD BC ===∴1sin 602CBD S BC BD =⋅⋅⋅= ，②当CD AB ⊥时，四边形ADBC 面积S 最大，∵CBD 时等边三角形，且2AB =，∴30ACD ∠=︒，2AC =，∴tan 233AD ACD AC =∠⋅==，∴11232322233ADC S AD DC =⋅⋅=⨯= ，∴23ADC ADBC S S == 四边形；433S <≤．2．【答案】（1）解：①O ，C ②当点B 的坐标为（0，1）时，如图，此时以BO 为半径的B 与线段OA 相切于点O ，∴点O 是OAB 关于点B 的内联点；当点B 移动到在y 轴左侧时，作图发现B 与x 轴有相交，且有一个交点不在线段OA 上，∴不再有OAB 关于点B 的内联点；当点B 的坐标为（7，8）时，以BA 为半径的B 与x 轴相切于点A ，∴点A 是OAB 关于点B 的内联点；当点B 直线x=7的右侧时，以BA 为半径的B 与x 轴相交，且有一个交点不在线段OA 上∴不再有OAB 关于点B 的内联点；综上所述，若AOB 关于点B 的内联点存在，求点B 纵坐标n 的取值范围为18n ≤≤；（2）80m 555m -≤≤≤≤或3．【答案】（1）22B C （2）解：由题意可得：当BC 是O 的以点A 为中心的“关联线段”时，则有AB C '' 是等边三角形，且边长也为1，当点A 在y 轴的正半轴上时，如图所示：设B C ''与y 轴的交点为D ，连接OB '，易得B C y ''⊥轴，∴12B D DC ''==，∴32OD ==，32==，∴OA =，∴t =；当点A 在y 轴的正半轴上时，如图所示：同理可得此时的OA =，∴t =；（3）当1min OA =时，此时BC =；当2max OA =时，此时2BC =．4．【答案】（1）证明：∵CD ⊥直径AB ，∴ BDBE =，∵DF ＝BD ，∴ DFBD =，∴ BEDF =，∴∠1＝∠2，∴DG ＝BG（2）解：∠DBA 的角平分线交⊙O 于点F ，∴∠2＝∠3，由（1）知，∠1＝∠2，∴∠1＝∠2＝∠3，∵∠BCD ＝90°，∴∠1+∠2+∠3＝90°，∴∠1＝∠2＝∠3＝30°，∵AB 是⊙O 的直径，∴∠ADB ＝90°，∴∠4＝90°﹣∠2﹣∠3＝30°，∵AB ＝2，∴BD ＝1，在Rt △BCD 中，∠1＝30°，∴BC ＝12BD ＝12，在Rt △BCG 中，∠3＝30°，∴CG ＝＝6，∴BG ＝2CG ＝33，由（1）知，DG ＝BG ＝33（3）5．【答案】（1）解：如图1，作BM ⊥x 轴，垂足为M ，根据题意AB=AE=EF=BF=，且∠EFO=∠BFM=45°，∴∠EFB=90°，∴四边形ABFE 是正方形，∴边AE ，BF 的中点所在直线就是ABC 与O 的一条“关联轴”；∵O 的半径为1，∴，且∠EFG=90°，∴四边形EFGH 是正方形，∵∠EFG+∠EFB=180°，∴B 、F 、G 三点共线，∴直线EF 是ABC 与O 的一条“关联轴”．（2）解：如图2，根据A （2，3），B （4，1），C （4，1），计算2=，故AB 不能落在圆的内部；过点A 作AN ⊥y 轴，垂足为N ，则AN=2，等于圆的直径，存在“关联轴l ”使ABC 是O 的关联三角形，此时0C x =；作点B 关于x 轴的对称点P ，此时BP=2，等于圆的直径，存在“关联轴l ”使ABC 是O 的关联三角形，此时4C x =，综上所述，点C 横坐标的范围是04C x ≤≤．（3）解：OC 的最小值为2-；OC 最大，根据勾股定理，AC=4.6．【答案】（1）证明：∵直径CD ⊥弦AB ，∴ AD BD=，∴∠APD=∠BPD ；（2）解：如图，作∠BAP 的平分线，交PD 于I ，证：∵AI 平分∠BAP ，∴∠PAI=∠BAI ，∴∠AID=∠APD+∠PAI=∠APD+BAI ，∵ AD BD=，∴∠DAB=∠APD ，∴∠DAI=∠DAB+∠BAI=∠APD+∠BAI ，∴∠AID=∠DAI ，∵∠AIP+∠DAI=180°，∴∠AIP+∠DAI=180°；（3）解：如图2，连接BI ，AC ，OA ，OB ，∵AI 平分∠BAP ，PD 平分∠APB ，∴BI 平分∠ABP ，∠BAI=12∠BAP ，∴∠ABI=12∠ABP ，∵∠APB=60°，∴∠PAB+∠PBA=120°，∴∠BAI+∠ABI=12（∠BAP+∠ABP ）=60°，∴∠AIB=120°，∴点I 的运动轨迹是 AB ，∴DI=DA ，∵∠AOB=2∠APB=120°，∵AD ⊥AB ，∴ AD BD=，∴∠AOB=∠BOD=60°，∵OA=OD ，∴△AOD 是等边三角形，∴AD=AO ，∵CD 是⊙O 的直径，∴∠DAC=90°，∵CD ⊥AB ，∴∠AED=90°，∴∠AED=∠CAD ，∵∠ADC=∠ADE ，∴△ADE ∽△CDA ，∴AD DE CD AD=，∴AD 2=DE•CD ，∵DI′=DI=AD ，∴DI 2=DE•CD ，∵∠I′DE 是公共角，∴△DIE ∽△DCI ，∴2IC CD IE DI==．7．【答案】（1）解：①C(4，0)，E(-1，5)；②（Ⅰ）当点(40)，在直线3y kx =+上时，430k +=，34k =-；（Ⅱ）当点(31)，在直线3y kx =+上时，331k +=，23k =-；（Ⅲ）当点(22)，在直线3y kx =+上时，232k +=，12k =-；结合图象可得3142k -≤≤-且23k ≠-；（2）解：直线333y x =-+与x 轴的交点M 坐标为()30，，与y 轴交点N 的坐标为(03，，∴tan 3NMO ∠=，∴30NMO ∠=︒，如图，作出线段MN 的垂直平分线，如图为两个临界情况：，利用待定系数法求得MN 垂直平分线解析式为y =，∴(0R -，，12230ORQ P RQ ∠=∠=︒，∴1112PR PQ ==，2222P R P Q ==，∴(10P ，(20P -，，∴t -≤<．8．【答案】（1）A 、B 、D（2）解：如图，依题意作⊙O 的“等直三角形”△TQP∴TQ=PQ ，∠TQP=90°过Q 点作MH //x 轴，交y 轴于M 点，过点P 作PH ⊥MH 于H 点∴∠TMQ=∠QHP=90°∴∠TQM+∠MTQ=∠TQM+∠HQP=90°∴∠MTQ=∠HQP∴△TMQ ≌△QHP （AAS ）∴TM=QH ，MQ=HP设Q （x ，y ）∴HM=MQ+QH=MQ+TM=x+3-y ，PH=MQ=x∴P （x-y+3，x+y ）∵C （3，0）∴∵∴CP OQ ．9．【答案】（1）BE ；3332-；等边；证明：B′D=BC CD ==，∴△DB'C 为等边三角形（2）310．【答案】（1）B ，C ；解：②如图2中，设点D 的坐标为(3)d d +，当过点D 的切线长为22r =时，OD ==由两点之间的距离公式得：OD =解得1221d d =-=-，结合图象可知，点D 的横坐标d 的取值范围是21d -≤≤-；（2）解：对于22y x =-当0y =时，220x -=，解得1x =，则点E 的坐标为(10)E ，当0x =时，2y =-，则点F 的坐标为(02)F -，⊙M 的半径为2，⊙M 的圆心为(0)M m ，24r ∴=，OM m=由题意，由以下两种情况：如图3-1中，点M 在点E 的右侧设FT 是⊙M 的切线则有两个临界位置：4FT =和点E 对应的切线长为0当4FT =时，则4OM m FT ===当点E 对应的切线长为0，即2EM =12EM m ∴=-=解得3m =结合图象得，当34m <≤时，线段EF 上的所有点都是⊙M 的伴随点②如图3-2和3-3中，点M 在点E 的左侧则有如下两个临界位置：如图3-2，设ET 是⊙M 的切线，连接MT ，则90MTE ∠=︒当4ET =时，2222245EM MT ET =+=+此时15m -=解得15m =-如图3-3，当⊙M 在直线EF 的左侧与EF 相切时，设切点为T ，连接MT∵(10)(02)E F -，，，∴12OE OF ==，∴22125EF =+=∵EF 是切线∴EF MT⊥∴90MTE FOE ∠=∠=︒∵MET FEO∠=∠∴MTE FOE~ ∴EM MTEF OF =，即22=解得EM =，即1m -=解得1m =-结合图象得，当11m -≤<-时，线段EF 上的所有点都是⊙M 的伴随点综上，m 的取值范围是11m -≤<-或34m <≤．11．【答案】（1）点C 、D ；22H x -≤≤-或22H x ≤≤（2）解：图形G 是以原点O 为中心，边长为2的正方形，∴原点O 到正方形的最短距离是1d =，最长距离是d =，⊙K 与图形G 关于原点O “平衡”，∴原点O 到⊙K 上一点的距离1d ≤≤，⊙K 的圆心在x 轴上，半径为2，∴当⊙K 在x 轴正半轴时，圆心K 的横坐标的取值范围为：22x -≤≤+，当⊙K 在x 轴负半轴时，圆心K 的横坐标的取值范围为：22x --≤≤，综上所述，圆心K 的横坐标的取值范围22x -≤≤+或22x --≤≤．12．【答案】（1）解：①90°；②B ；③2π（2）解：413．【答案】（1）S(2，0)（2）解：①（4，0）或（8，0）；②如图，设直线y a =上的点Q 为点A 和直线2y =-的等距点，连接QA ，过点Q 作直线2y =-的垂线，垂足为点C ．点Q 为点A 和直线2y =-的等距点，QA QC ∴=．22QA QC ∴=．点Q 在直线y a =上，∴可设点Q 的坐标为()Q x a ，．()()22262x a a ∴-+=--⎡⎤⎣⎦．整理得2123240x x a -+-=．由题意得关于x 的方程2123240x x a -+-=有实数根．()()()212413241610a a ∴∆=--⨯⨯-=+≥．解得1a ≥-．（3）解：如图．直线l 1和直线l 2的等距点在直线l 3：33y x =-+上，直线l 1和y 轴的等距点在直线4l y =+：或33y x =+上，点O 与l 4的距离为32，点O 与l 3的距离为，点O 与l 5的距离为3，当r ＜时，n=0不符合题意，当r=时，m=2，n=0，符合题意，当＜r ＜3时，m=n=2，不符合题意，当r≥3时，m=2，n=3或4，符合题意，综上所述，r=或r≥3.14．【答案】（1）C（2）解：∵P （0，1），点A （﹣2，﹣1），点B （2，﹣1）．∴AP ＝BP ＝＝2，如图2，分别以PA 、PB 为直径作圆，交x 轴于点K 1、K 2、K 3、K 4，∵OP＝OG＝1，OE∥AB，∴PE＝AE＝，∴OE＝12AG＝1，∴K1（﹣1﹣，0），k2（1﹣，0），k3（﹣1，0），k4（1+，0），∵点K为点P与线段AB的共圆点，∴﹣1﹣≤x k≤1﹣或﹣1≤x k≤1+（3）解：分两种情况：①如图3，当M在点A的左侧时，Q为线段AM上一动点，以PQ为直径的圆E与直线y＝12x+3相切于点F，连接EF，则EF⊥FH，当x＝0时，y＝3，当y＝0时，y＝12x+3＝0，x＝﹣6，∴ON＝3，OH＝6，∵tan∠EHF＝ON EFOH FH＝36＝12，设EF＝a，则FH＝2a，EH＝a，∴OE＝6﹣a，Rt △OEP 中，OP ＝1，EP ＝a ，由勾股定理得：EP 2＝OP 2+OE 2，∴2221(6)a =+-，解得：a ＝2+（舍去）或2，∴QG ＝2OE ＝2（6﹣a ）＝﹣3+2，∴m≤3﹣2；②如图4，当M 在点A 的右侧时，Q 为线段AM 上一动点，以PQ 为直径的圆E 与直线y ＝12x+3相切于点F ，连接EF ，则EF ⊥FH ，同理得QG ＝3+2，∴m≥3+2，综上，m 的取值范围是m≤3﹣2或m≥3+215．【答案】（1）2（2）解：BC 与O 相切；理由：如图2，过点O 作OH BC ⊥于H ，连接OD ，∵O 与AB 相切于D ，∴OD AB ⊥，在Rt AOD 中，30BAC ∠=︒，∴24OA OD ==，∵8AC =，∴4OC =，在ABC 中，AB BC =，∴30C BAC ∠=∠=︒，在Rt OHC 中，30C ∠=︒，∴122OH OC OD ===，∴BC 与O 相切，（3）解：①当点O 在AC 的左侧时，连接OD 交AC 于F ，如备用图1，∵O 与AB 相切于D ，∴OD AB ⊥，∵OG AC ⊥，∴30FOG BAC ∠=∠=︒，在Rt FDA 中，tan FD BAC AD ∠=，∴tan 3FD AD BAC x =⋅∠=，∴23OF x =-，在Rt FOG 中，331cos 2322y OG OF FOG ⎛⎫==⋅∠=-⨯-+ ⎪ ⎪⎝⎭，即12y x =-+，此时x 的取值范围为0x ≤≤；②当点O 在AC 的右侧时，连接DO 并延长交AC 于F ，如备用图2，同①的方法得，33FD x =，∴23OF x =-，∵FD AB ⊥，∴90BAC AFD ∠+∠=︒，∴30FOG BAC ∠=∠=︒，在Rt FOG 中，331cos 2322y OG OF FOG x x ⎛⎫==⋅∠=-⨯- ⎪⎪⎝⎭，即12y x =-，此时x 的取值范围为1433x ≤≤．16．【答案】（1）0；2-（2）解：过点O 作OD ⊥AB 于点D ，∵点A(2-，0)，B(0，．∴2OA OB ==，，∴4AB ==，∵1122OA OB AB OD ⋅=⋅，∴112422OD ⨯⨯=⨯⨯∴DO =，∵d （⊙O ，线段AB ）=0，∴当⊙O 的半径等于OD 时最小，当⊙O 的半径等于OB 时最大，∴r r ≤≤（3）43423m -<<-17．【答案】（1）2y x =+（2）解：①当2d =时，()20D ，，设直线CD 的解析式为：y kx b =+，()02C ，，202k b b +=⎧∴⎨=⎩，解得：12k b =-⎧⎨=⎩，∴直线CD 的解析式为：y x =-+，设点M 的坐标为()2m m -+，，∴点M 的关联直线为：()212y mx m m x =-+=-+，∴点M 的关联直线经过定点()12N ，，如图2，过点O 作直线2y mx m =--+的垂线，垂足为H ，连接ON ，ON OH ∴≥，∴当点H与点N重合时，OH最大，即点O到点M的关联直线的距离最大，∴点O到点M=；2 d=②或2 3-18．【答案】（1）；3（2）解：设点G是O的特征值为4的点，∴经过一点G且弦长为4(最长弦)的直线有1条，弦长为3的直线有2条，弦长为2的直线有且只有1条，经过点G的直线被O截得的弦长的最小值为2，=，∴关于O的特征值为4的所有点都在以O为半径的圆周上，直线y x b=+分别与x，y轴交于点A、B，()0A b∴-，，()B b，，OA OB b∴==，45OBH∴∠=︒，当0b>时，线段AB与以O为半径的圆相切时，点G特征值为4，设切点为为H，连接OH，则OH=，OB∴==，b∴=，设以O 为半径的圆与y 轴正半轴的交点记为1B ，则1OB =，当线段AB 与以O 1B 时，可得b =，b ≤≤同理可求当0b <时，b ≤≤，综上，b b b ≤≤-≤（3）当372122t -≤≤+时，存在点R ，S ，使得3r s +=。

中考数学圆的综合-经典压轴题附答案

中考数学圆的综合-经典压轴题附答案一、圆的综合1．如图1，已知扇形MON 的半径为2，∠MON=90°，点B 在弧MN 上移动，联结BM ，作OD ⊥BM ，垂足为点D ，C 为线段OD 上一点，且OC=BM ，联结BC 并延长交半径OM 于点A ，设OA=x ，∠COM 的正切值为y.（1）如图2，当AB ⊥OM 时，求证：AM=AC ；（2）求y 关于x 的函数关系式，并写出定义域；（3）当△OAC 为等腰三角形时，求x 的值.【答案】 (1)证明见解析;(2) 2=+y x 02<≤x 1422=x . 【解析】分析：（1）先判断出∠ABM =∠DOM ，进而判断出△OAC ≌△BAM ，即可得出结论；（2）先判断出BD =DM ，进而得出DM ME BD AE =，进而得出AE =122x （），再判断出2OA OC DM OE OD OD==，即可得出结论；（3）分三种情况利用勾股定理或判断出不存在，即可得出结论．详解：（1）∵OD ⊥BM ，AB ⊥OM ，∴∠ODM =∠BAM =90°．∵∠ABM +∠M =∠DOM +∠M ，∴∠ABM =∠DOM ．∵∠OAC =∠BAM ，OC =BM ，∴△OAC ≌△BAM ， ∴AC =AM ．（2）如图2，过点D 作DE ∥AB ，交OM 于点E ． ∵OB =OM ，OD ⊥BM ，∴BD =DM ． ∵DE ∥AB ，∴DM ME BD AE =，∴AE =EM ．∵OM 2，∴AE =122x （）． ∵DE ∥AB ，∴2OA OC DM OE OD OD ==， ∴22DM OA y OD OE x =∴=+，02x ≤＜（3）（i ）当OA =OC 时．∵111222DM BM OC x ===．在Rt △ODM 中，222124OD OM DM x =-=-． ∵2121224x DM x y OD x x =∴=+-，．解得1422x -=，或1422x --=（舍）．（ii ）当AO =AC 时，则∠AOC =∠ACO ．∵∠ACO ＞∠COB ，∠COB =∠AOC ，∴∠ACO ＞∠AOC ，∴此种情况不存在．（ⅲ）当CO =CA 时，则∠COA =∠CAO =α．∵∠CAO ＞∠M ，∠M =90°﹣α，∴α＞90°﹣α，∴α＞45°，∴∠BOA =2α＞90°．∵∠BOA ≤90°，∴此种情况不存在．即：当△OAC 为等腰三角形时，x 的值为1422-．点睛：本题是圆的综合题，主要考查了相似三角形的判定和性质，圆的有关性质，勾股定理，等腰三角形的性质，建立y 关于x 的函数关系式是解答本题的关键．2．如图，已知在△ABC 中，AB=15，AC=20，tanA=12，点P 在AB 边上，⊙P 的半径为定长.当点P 与点B 重合时，⊙P 恰好与AC 边相切；当点P 与点B 不重合时，⊙P 与AC 边相交于点M 和点N ．（1）求⊙P 的半径；（2）当AP=5△APM 与△PCN 是否相似，并说明理由．【答案】（1）半径为52）相似，理由见解析.【解析】【分析】（1）如图，作BD ⊥AC ，垂足为点D ，⊙P 与边AC 相切，则BD 就是⊙P 的半径，利用解直角三角形得出BD 与AD 的关系，再利用勾股定理可求得BD 的长；（2）如图，过点P 作PH ⊥AC 于点H ，作BD ⊥AC ，垂足为点D ，根据垂径定理得出MN=2MH ，PM=PN ，再利用勾股定理求出PH 、AH 、MH 、MN 的长，从而求出AM 、NC 的长，然后求出AM MP 、PN NC 的值，得出AM MP =PN NC，利用两边对应成比例且夹角相等的两三角形相似即可证明.【详解】（1）如图，作BD ⊥AC ，垂足为点D ，∵⊙P 与边AC 相切，∴BD 就是⊙P 的半径，在Rt △ABD 中，tanA= 1BD 2AD =，设BD=x ，则AD=2x ，∴x 2+(2x)2=152，解得：5∴半径为5（2）相似，理由见解析，如图，过点P 作PH ⊥AC 于点H ，作BD ⊥AC ，垂足为点D ，∴PH 垂直平分MN ，∴PM=PN ，在Rt △AHP 中，tanA=12PH AH =，设PH=y ，AH=2y ，y 2+（2y ）2=（52解得：y=6（取正数），∴PH=6，AH=12，在Rt △MPH 中， ()22356-，∴MN=2MH=6，∴AM=AH-MH=12-3=9，NC=AC-MN-AM=20-6-9=5， ∴3535AM MP ==，35PN NC =，∴AMMP =PN NC，又∵PM=PN，∴∠PMN=∠PNM，∴∠AMP=∠PNC，∴△AMP∽△PNC.【点睛】本题考查了解直角三角形、垂径定理、相似三角形的判定与性质等，综合性较强，有一定的难度，正确添加辅助线、灵活应用相关的性质与定理是解题的关键.3．在⊙O 中，点C是AB上的一个动点(不与点A，B重合)，∠ACB=120°，点I是∠ABC的内心，CI的延长线交⊙O于点D，连结AD,BD．（1）求证：AD=BD．（2）猜想线段AB与DI的数量关系，并说明理由．（3）若⊙O的半径为2，点E，F是AB的三等分点，当点C从点E运动到点F时，求点I 随之运动形成的路径长．【答案】（1）证明见解析；（2）AB=DI，理由见解析（323【解析】分析：（1）根据内心的定义可得CI平分∠ACB，可得出角相等，再根据圆周角定理，可证得结论；（2）根据∠ACB=120°，∠ACD=∠BCD，可求出∠BAD的度数，再根据AD=BD，可证得△ABD是等边三角形，再根据内心的定义及三角形的外角性质，证明∠BID=∠IBD，得出ID=BD，再根据AB=BD，即可证得结论；（3）连接DO，延长DO根据题意可知点I随之运动形成的图形式以D为圆心，DI1为半径的弧，根据已知及圆周角定理、解直角三角形，可求出AD的长，再根据点E，F是弧AB ⌢的三等分点，△ABD是等边三角形，可证得∠DAI1=∠AI1D，然后利用弧长的公式可求出点I随之运动形成的路径长.详解：（1）证明：∵点I是∠ABC的内心∴CI平分∠ACB∴∠ACD=∠BCD∴弧AD=弧BD∴AD=BD（2）AB=DI理由：∵∠ACB=120°，∠ACD=∠BCD∴∠BCD=×120°=60°∵弧BD=弧BD∴∠DAB=∠BCD=60°∵AD=BD∴△ABD是等边三角形，∴AB=BD，∠ABD=∠C∵I是△ABC的内心∴BI平分∠ABC∴∠CBI=∠ABI∵∠BID=∠C+∠CBI，∠IBD=∠ABI+∠ABD∴∠BID=∠IBD∴ID=BD∵AB=BD∴AB=DI（3）解：如图，连接DO，延长DO根据题意可知点I随之运动形成的图形式以D为圆心，DI1为半径的弧∵∠ACB=120°，弧AD=弧BD∴∠AED=∠ACB=×120°=60°∵圆的半径为2，DE是直径∴DE=4，∠EAD=90°∴AD=sin∠AED×DE=×4=2∵点E，F是弧AB ⌢的三等分点，△ABD是等边三角形，∴∠ADB=60°∴弧AB的度数为120°，∴弧AM、弧BF的度数都为为40°∴∠ADM=20°=∠FAB∴∠DAI1=∠FAB+∠DAB=80°∴∠AI1D=180°-∠ADM-∠DAI1=180°-20°-80°=80°∴∠DAI1=∠AI1D∴AD=I1D=2∴弧I1I2的长为：点睛：此题是一道圆的综合题，有一定的难度，熟记圆的相关性质与定理，并对圆中的弦、弧、圆心角、圆周角等进行灵活转化是解题关键，注意数形结合思想的渗透.4．如图，⊙M与菱形ABCD在平面直角坐标系中，点M的坐标为（3，﹣1），点A的坐标为（﹣23B的坐标为（﹣3，0），点C在x轴上，且点D在点A的左侧．（1）求菱形ABCD的周长；（2）若⊙M沿x轴向右以每秒2个单位长度的速度平移，同时菱形ABCD沿x轴向右以每秒3个单位长度的速度平移，设菱形移动的时间为t（秒），当⊙M与BC相切，且切点为BC的中点时，连接BD，求：①t的值；②∠MBD的度数；（3）在（2）的条件下，当点M 与BD 所在的直线的距离为1时，求t 的值．【答案】（1）8；（2）①7；②105°；（3）t=636+33．【解析】分析：（1）根据勾股定理求菱形的边长为2，所以可得周长为8；（2）①如图2，先根据坐标求EF 的长，由EE '﹣FE '=EF =7，列式得：3t ﹣2t =7，可得t 的值；②先求∠EBA =60°，则∠FBA =120°，再得∠MBF =45°，相加可得：∠MBD =∠MBF +∠FBD =45°+60°=105°；（3）分两种情况讨论：作出距离MN 和ME ，第一种情况：如图5由距离为1可知：BD 为⊙M 的切线，由BC 是⊙M 的切线，得∠MBE =30°，列式为3t 3=2t +6，解出即可；第二种情况：如图6，同理可得t 的值．详解：（1）如图1，过A 作AE ⊥BC 于E ．∵点A 的坐标为（﹣23），点B 的坐标为（﹣3，0），∴AE 3，BE =3﹣2=1，∴AB 22AE BE +2231+（）=2． ∵四边形ABCD 是菱形，∴AB =BC =CD =AD =2，∴菱形ABCD 的周长=2×4=8；（2）①如图2，⊙M 与x 轴的切点为F ，BC 的中点为E ．∵M （3，﹣1），∴F （3，0）．∵BC =2，且E 为BC 的中点，∴E （﹣4，0），∴EF =7，即EE '﹣FE '=EF ，∴3t ﹣2t =7，t =7；②由（1）可知：BE =1，AE 3∴tan ∠EBA =AE BE =33，∴∠EBA =60°，如图4，∴∠FBA =120°． ∵四边形ABCD 是菱形，∴∠FBD =12∠FBA =11202⨯︒=60°． ∵BC 是⊙M 的切线，∴MF ⊥BC ．∵F 是BC 的中点，∴BF =MF =1，∴△BFM 是等腰直角三角形，∴∠MBF =45°，∴∠MBD =∠MBF +∠FBD =45°+60°=105°；（3）连接BM ，过M 作MN ⊥BD ，垂足为N ，作ME ⊥BC 于E ，分两种情况：第一种情况：如图5．∵四边形ABCD 是菱形，∠ABC =120°，∴∠CBD =60°，∴∠NBE =60°．∵点M 与BD 所在的直线的距离为1，∴MN =1，∴BD 为⊙M 的切线．∵BC 是⊙M 的切线，∴∠MBE =30°．∵ME=1，∴EB=3，∴3t+3=2t+6，t=6﹣3；第二种情况：如图6．∵四边形ABCD是菱形，∠ABC=120°，∴∠DBC=60°，∴∠NBE=120°．∵点M与BD所在的直线的距离为1，∴MN=1，∴BD为⊙M的切线．∵BC是⊙M的切线，∴∠MBE=60°．∵ME=MN=1，∴Rt△BEM中，tan60°=MEBE，EB=160tan=33，∴3t=2t+6+33，t=6+33；综上所述：当点M与BD所在的直线的距离为1时，t=6﹣3或6+33．点睛：本题是四边形和圆的综合题，考查了菱形的性质、圆的切线的性质和判定、特殊的三角函数值、等腰直角三角形的性质、动点运动问题，此类问题比较复杂，弄清动点运动方向、速度、时间和路程的关系，并与方程相结合，找等量关系，求出时间t的值．5．函数是描述客观世界运动变化的重要模型，理解函数的本质是重要的任务。