第九讲——卷积码的维特比译码和卷积码的性能分析
卷积码+交织+维特比译码+解交织
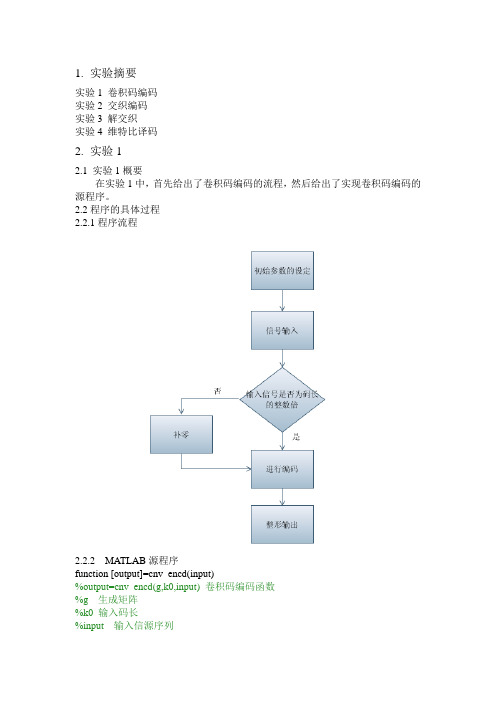
1.实验摘要实验1 卷积码编码实验2 交织编码实验3 解交织实验4 维特比译码2.实验12.1 实验1概要在实验1中,首先给出了卷积码编码的流程,然后给出了实现卷积码编码的源程序。
2.2程序的具体过程2.2.1程序流程2.2.2MATLAB源程序function [output]=cnv_encd(input)%output=cnv_encd(g,k0,input) 卷积码编码函数%g 生成矩阵%k0 输入码长%input 输入信源序列%output 输出卷积编码序列g=[1 1 1;1 0 1];%编码矩阵k0=1;input=[1 1 0 1];if rem(length(input),k0)>0input=[input,zeros(size(1:k0-rem(length(input),k0)))];endn=length(input)/k0;if rem(size(g,2),k0)>0error('Error,g is not of the right size.')endli=size(g,2)/k0;n0=size(g,1);u=[zeros(size(1:(li-1)*k0)),input,zeros(size(1:(li-1)*k0))];u1=u(li*k0:-1:1);for i=1:n+li-2u1=[u1,u((i+li)*k0:-1:i*k0+1)];enduu=reshape(u1,li*k0,n+li-1);output=reshape(rem(g*uu,2),1,n0*(n+li-1));3.实验23.1 实验2概要在实验2中,给出了两种交织编码的过程—卷积交织和循环等差交织,然后给出了实现这两种交织编码的源程序。
3.2程序的具体过程3.2.1程序流程3.2.2MATLAB源程序(1)卷积交织function [aa]=jiaozhi(bb,n)%jiaozhi.m 卷积交织函数n=28; %分组长度%bb 卷积交织前原分组序列%aa 卷积交织后分组序列%序号重排方式:cc=[123171151721;82241812628;159****9137;22161042620 14 ];%交织矩阵bb=[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28]; for i=1:naa(i)=bb(cc(i));end(2)循环等差交织function [aa]=jiaozhi_nocnv(bb,n)%jiaozhi_nocnv.m 循环等差交织函数n=28; %分组长度%bb 循环等差交织前原分组序列%aa 循环等差交织后还原分组序列%序号重排方式:bb=[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 ];j=1;for i=1:nj=rem(j+5-1,n)+1; %序号重排方式迭代算法aa(n+1-i)=bb(j);end3.2.3程序说明交织码通常表示为(M,N),分组长度L=MN,交织方式用M行N列的交织矩阵表示。
DSP卷积码的维特比译码的分析与实现要点

编号:《DSP技术与应用》课程论文卷积码的维特比译码的分析与实现论文作者姓名:______ ______作者学号:___ ______所在学院:所学专业:_____ ___导师姓名职称:__ _论文完成时间: _目录摘要: (1)0 前言 (2)1 理论基础 (2)1.1信道理论基础 (2)1.2差错控制技术 (3)1.3纠错编码 (4)1.4线性分组码 (5)2 卷积码编码 (7)2.1 卷积码概要 (7)2.2 卷积码编码器 (8)2.3卷积码的图解表示 (8)2.4 卷积码的解析表示 (11)3 卷积码的译码 (14)3.1 维特比译码 (15)3.2 代数译码 (17)3.3 门限译码 (18)4 维特比译码器实现 (18)4.1 TMS320C54 系列DSP概述 (18)4.2 Viterbi译码器的DSP实现 (19)4.3 实现结果 (21)5 结论 (21)参考文献 (22)II卷积码的维特比译码的分析与实现摘要:针对数据传输过程中的误码问题,本文论述了提高数据传输质量的一些编码及译码的实现问题。
自P.Elias 首次提出卷积码编码以来,这一编码技术至今仍显示出强大的生命力。
在与分组码同样的码率R 和设备复杂性的条件下,无论从理论上还是从实际上均己证明卷积码的性能至少不比分组码差,且实现最佳和准最佳译码也较分组码容易。
目前,卷积码已广泛应用在无线通信标准中,其维特比译码则利用码树的重复性结构,对最大似然译码算法进行了简化。
本文所做的主要工作:首先对信道编码技术进行了研究,根据信道中可能出现的噪声等问题对卷积码编码方法进行了主要阐释。
其次,对卷积码维特比译码器的实现算法进行了研究,完成了译码器的软件设计。
最后,结合实例,采用DSP芯片实现卷积码的维特比译码算法的仿真和运行。
关键词:卷积码维特比译码DSPConvolutional codes and Viterbi decoding analysis andrealizationZhang Yi-Fei(School of Physics and Electronics, Henan University, Henan Kaifeng 475004, China)Abstract:Considering the error bit problem during data transmission,this thesis discussed some codings and decoders,aiming at enhancing transmission performance. From P.Elias first gave the concept of convolutional code, it has show its’ great advantage. Under the same condition and the same rate of block code, the performance of convolutional code is better than block code, and it’s easier to implement the best decoding.Convolutional codes have been widely used in wireless communication standards, the Viterbi decoding using the repetitive structure of the code tree, the maximum likelihood decoding algorithm has been simplified. Major work done in this article: First, the channel coding techniques have been studied, the main interpretation of the convolutional code encoding method according to the channel may be noise and other issues.Secondly, the convolutional code Viterbi decoder algorithm has been studied, the software design of the decoder.Finally, with examples, simulation and operation of the DSP chip convolutional codes, Viterbi decoding algorithm.1Key words:convolutional code Vltebri decoder DSP0 前言随着数据处理、计算机通信、卫星通信以及高速数据通信网的飞速发展,用户对数据传输的可靠性提出了越来越高的要求,因此如何在保证数据传输速率的前提下,提高传输数据的可靠性,就成为一个迫切需要解决的问题。
卷积码及维特比译码 notes
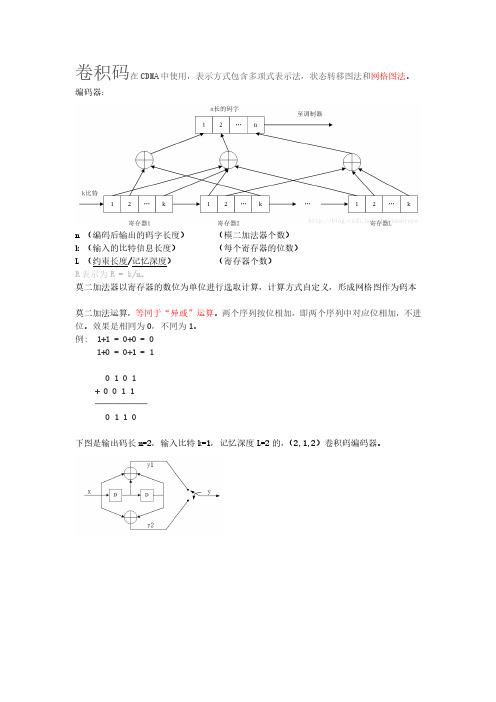
卷积码在CDMA中使用,表示方式包含多项式表示法,状态转移图法和网格图法。
编码器:n (编码后输出的码字长度)(模二加法器个数)k (输入的比特信息长度)(每个寄存器的位数)L (约束长度/记忆深度)(寄存器个数)R表示为R = k/n。
莫二加法器以寄存器的数位为单位进行选取计算,计算方式自定义,形成网格图作为码本莫二加法运算,等同于“异或”运算。
两个序列按位相加,即两个序列中对应位相加,不进位。
效果是相同为0,不同为1。
例: 1+1 = 0+0 = 01+0 = 0+1 = 10 1 0 1+ 0 0 1 1──────0 1 1 0下图是输出码长n=2,输入比特k=1,记忆深度L=2的,(2,1,2)卷积码编码器。
如编码序列“0 1 1 0 0”在图中的序列如下:汉明距离两个二进制数之间进行逐位对比,得到不同的个数如1000,与1100为1,与1110为2,与1111为3维特比算法综合状态之间的转移概率和前一层各状态的概率情况计算出概率最大的状态转换路径,从而推断出隐含状态的序列的情况。
的分支度量(汉明距离)。
其中有两条路径的分支量度为0。
3.寻找最大似然路径 - 译码过程维特比算法的关键点在于,接收机可以使用分支度量和先前计算的路径度量递推地计算当前状态的路径度量。
初始时,状态00代价为0,其它状态代价为正无穷(∞)。
算法的主循环由两个主要步骤组成:首先计算下一时刻监督比特序列的分支度量,然后计算该时刻各状态的路径度量。
路径度量的计算可以认为是一个“加-比-选”的过程1)将分支度量与上一时刻状态的路径度量相加。
2)每一状态比较来自前一时刻状态可达到的所有路径(只有两条这样的路径进行比较)3)每一状态删除其余到达路径,选择最小度量的路径保留(称为幸存路径/存活路径)若进入某个状态的部分路径中,有两条路径的度量值相等,则可以任选其一作为幸存路径。
下图显示了维特比译码的过程。
此例接收到的位序列为11 10 11 00 01 10(偷偷告诉你:这是有误码的信息)此时,产生了具有相同路径度量的四个不同路径,通向这四个状态的任一路径都是可能发送的比特序列(它们都具有度量为2的汉明距离)。
卷积码

译码主要确定译码规则,使其差错率最小
1 2 – 译码器根据接收序列来产生信息序列M的一个估值M’,如果两者不同,
则表示译码出错 – 如信道传输的码字是X,当且只有当接收序列Y不等于X时,出现译码错 误
最大似然译码
译码主要确定译码规则,使其差错率最小
– 译码器必须根据接受序列y来产生信息序列M的一个估计
§12.1.1 卷积码的图解表示
树状图- tree
– 一个(2,1,3)卷积码编码器。 假设初始状态为全0 第一个比特输入为 0->00 ,1->11 第二个比特输入时,第一个比特右移一位,这时输出比特同时受前输入比 特和前一位比特决定 ...... 第四个比特输入时,第一个比特移出移位寄存器而消失
编码后序列。由于卷积码的线性性质,所有码序列之间的最 小汉明距应等于非零码序列的最小汉明重量,即非零码序列 中1码的个数。由此可见,要求最小距或自由距,只要考虑码 树中下半部的码序列就可以了 – 例: abca abcb abdc abdd 5 3 4 4 因而:dmin = 3
§12.2 卷积码的距离特性
维特比译码
进入第四级网格时,4条幸存支路又延伸为8条, 经计算路径量度并比较后又丢弃其中4条。在 比较是如果出现量度相同的情况,可以任意选 取其中一条。继续下去,到第10步时,会发现, 所有幸存路径已经合并称为一条全0路径,纠 错完毕。 译码结束的判断:可以在网格图的终结出加上 (N-1)*K个已知信息(即N-1条支路),发送固定 码,如全零,作为结束信息。
– 应用最多也是性能最接近最佳的是维特比译码,但
是硬件复杂。门限译码性能最差,但硬件简单。维 特比译码和序列译码都是建立在最大似然译码的基 础之上的
卷积编码和Viterbi译码

卷积编码和Viterbi译码摘要本文的目的是向读者介绍了前向纠错技术的卷积编码和Viterbi译码。
前向纠错的目的(FEC)的是改善增加了一些精心设计的冗余信息,正在通过信道传输数据的通道容量。
在添加这种冗余信息的过程称为信道编码。
卷积编码和分组编码是两个主要的渠道形式编码。
简介前向纠错的目的(FEC)的是改善增加了一些精心设计的冗余信息,正在通过信道传输数据的通道容量。
在添加这种冗余信息的过程称为信道编码。
卷积编码和分组编码是两个主要的渠道形式编码。
卷积码串行数据操作,一次一个或数位。
分组码操作比较大(通常,多达几百个字节的情侣)消息块。
有很多有用的分组码和卷积多种,以及接收解码算法编码信息的DNA序列来恢复原来的各种数据。
卷积编码和Viterbi译码前向纠错技术,是一种特别适合于在其中一个已损坏的发射信号加性高斯白噪声(AWGN)的主要通道。
你能想到的AWGN信道的噪声,其电压分布也随着时间的推移,可以说是用高斯,或正常,统计分布特征,即一钟形曲线。
这个电压分布具有零均值和标准差这是一个信号与噪声比接收信号的信噪比(SNR)函数。
让我们承担起接收到的信号电平是固定的时刻。
这时如果信噪比高,噪声标准偏差小,反之亦然。
在数字通信,信噪比通常是衡量Eb /N的它代表噪声密度双面能源每比特除以之一。
卷积码通常是描述使用两个参数:码率和约束长度。
码率k/n,是表示为比特数为卷积编码器(十一)信道符号卷积编码器输出的编码器在给定的周期(N)的数量之比。
约束长度参数,钾,表示该卷积编码器的“长度”,即有多少K位阶段提供饲料的组合逻辑,产生输出符号。
K是密切相关的参数米,这表明有多少位的输入编码器周期被保留,用于编码后第一次在卷积编码器输入的出现。
的m参数可以被认为是编码器的记忆长度。
在本教程中,并在此示例的源代码,我集中精力率1 / 2卷积码。
Viterbi译码是一种两个卷积编码与解码,其他类型的算法类型的顺序解码。
卷积码编码和维特比译码的原理、性能与仿真分析

卷积码编码和维特比译码的原理、性能与仿真分析1.引言卷积码的编码器是由一个有k位输入、n位输出,且具有m位移位寄存器构成的有限状态的有记忆系统,通常称它为时序网络。
编码器的整体约束长度为v,是所有k个移位寄存器的长度之和。
具有这样的编码器的卷积码称作[n,k,v]卷积码。
对于一个(n,1,v)编码器,约束长度v等于存储级数m.卷积码是由k个信息比特编码成n(n>k)比特的码组,编码出的n比特码组值不仅与当前码字中的k个信息比特值有关,而且与其前面v个码组中的v*k个信息比特值有关。
卷积码有三种译码方式:序列译码、门限译码和概率译码。
其中,概率译码根据最大似然译码原理在所有可能路径中求取与接收路径最相似的一条路径,具有最佳的纠错性能,维特比译码是概率译码中极重要的一种方式。
序列译码和门限译码则不一定能找出与接收路径最相似的一条路径。
不同于维特比译码,门限译码与序列译码所需的计算量是可变的且对于给定信息分组的最终判决仅仅基于(m+1)个接收分组,而不是基于整个接收序列。
与维特比译码所使用的对数似然量度不同,序列译码所使用的量度为Fano量度。
在接收序列受扰严重的情况下,序列译码的计算量大于维特比译码所需的固定计算量,虽然序列译码要求的平均计算次数通常小于维特比译码。
在采用并行处理的情况下,维特比译码的速度会优于序列译码。
在同样码率和存储级数的条件下,门限译码的性能比维特比译码低大约3dB.维特比译码的数据输出方式有硬判决及软判决两种方式,本文选取生成多项式为561,753的(2,1,8)卷积码对硬判决的性能进行分析,并依据维特比译码的原理以及卷积码的特性,对卷积码编码和维特比译码过程在加性高斯白噪声(AWGN)信道下进行仿真,并且根据仿真结果对维特比译码(硬判决)的结果进行分析。
由于卷积码的生成可以看做一个马尔科夫过程,因此,不同状态间的转移概率对描述这个过程有极关键的作用。
本文则基于MATLAB对不同状态间的转移概率进行求解,从而更准确地分析维特比译码的性能。
卷积码的维特比译码

卷积码的维特比译码卷积编码器自身具有网格结构,基于此结构我们给出两种译码算法:Viterbi 译码算法和BCJR 译码算法。
基于某种准则,这两种算法都是最优的。
1967 年,Viterbi 提出了卷积码的Viterbi 译码算法,后来Omura 证明Viterbi 译码算法等效于在加权图中寻找最优路径问题的一个动态规划(Dynamic Programming)解决方案,随后,Forney 证明它实际上是最大似然(ML,Maximum Likelihood)译码算法,即译码器选择输出的码字通常使接收序列的条件概率最大化。
BCJR 算法是1974 年提出的,它实际上是最大后验概率(MAP,Maximum A Posteriori probability)译码算法。
这两种算法的最优化目标略有不同:在MAP 译码算法中,信息比特错误概率是最小的,而在ML 译码算法中,码字错误概率是最小的,但两种译码算法的性能在本质上是相同的。
由于Viterbi 算法实现更简单,因此在实际应用比较广泛,但在迭代译码应用中,例如逼近Shannon 限的Turbo 码,常使用BCJR 算法。
另外,在迭代译码应用中,还有一种Viterbi 算法的变种:软输出Viterbi 算法(SOV A,Soft-Output Viterbi Algorithm),它是Hagenauer 和Hoeher 在1989 年提出的。
为了理解Viterbi 译码算法,我们需要将编码器状态图按时间展开(因为状态图不能反映出时间变化情况),即在每个时间单元用一个分隔开的状态图来表示。
例如(3,1,2)非系统前馈编码器,其生成矩阵为:G(D)=[1+D1+D21+D+D2](1)图1 (a)(3,1,2)编码器(b)网格图(h=5)假定信息序列长度为h=5,则网格图包含有h+m+1=8 个时间单元,用0 到h+m=7 来标识,如图1(b)所示。
假设编码器总是从全0 态S0 开始,又回到全0 态,前m=2 个时间单元对应于编码器开始从S0“启程”,最后m=2 个时间单元对应于向S0“返航”。
第9讲 信道编码:维特比译码

假设在信道上发送时,产生了2个突发错误,如下红色部分所示:
x1x6 x11x16 x21x2 x7 x12 x17 x22 x3 x8 x13 x18 x23 x4 x9 x14 x19 x24 x5 x10 x15 x20 x25
接收端收到这长度为25的序列先进行去交织处理,同样将序列写入 到一个55的存储阵列中,写入和读出顺序与发送端相反,即按行 写入,按列读出。写入之后的情况如下:
x1 x2 x3 x4 x5
x6 x7 x8 x9 x10
x11 x12 x13 x14 x15
x16 x17 x18 x19 x20
x21 x22 x23 x24 x25
按列读出的序列:
x1x2 x3 x4 x5 x6 x7 x8 x9 x10 x11x12 x13 x14 x15 x16 x17 x18 x19 x20 x21x22 x23 x24 x25
交织过程:
1)发送端将序列按列的顺序写入,然后按行的顺序输出;
2)接收端将接收到的序列按行写入,然后按列的顺序输出 周期性交织特性: 1)l ≤M的突发错误 → 至少被N – 1个位隔开的独立随机错误 2)l > M的突发错误 → 变成 l1 = [l / M]短突发错误
3)交织和去交织的处理会造成2MN个符号的延迟
随机过程的基本概念
初等概率论研究的主要对象是一个或有限个随机变量
但在一些科学技术中需要对一些随机现象的变化过程进 行研究,必须考虑无穷多个随机变量 用一族随机变量才能刻划这种随机现象的全部统计规律 性
可以把这样的一族随机变量称为随机过程
随机过程的数学定义:
设随机试验的样本空间 S {ei },如果对于空间的每一个样本 t T 总有一个时间函数 X (t, ei ) 与之对应。对于样本空间S 的所有样 本 ei S,有一族时间函数 e S与其对应,这族时间函数 X (t , e) 定义为随机过程
卷积码

2.7.卷积码分组码是把k个信息比特的序列编成n个比特的码组,每个码组的n-k个校验位仅与本码组的k个信息位有关,而与其他码组无关。
为了达到一定的纠错能力和编码效率,分组码的码组长度一般都比较大。
编译码时必须把整个信息码组存储起来,由此产生的译码时延随n的增加而增加。
卷积码是另外一种编码方法,它也是将k个信息比特编成n个比特,但k和n通常很小,特别适合以串行形式进行传输,时延小。
与分组码不同,卷积码编码后的n个码元不仅与当前段的k个信息有关,还与前面的N-1段信息有关,编码过程中互相关联的码元个数为nN。
卷积码的纠错性能随N的增加而增大,而差错率随N的增加而指数下降。
在编码器复杂性相同的情况下,卷积码的性能优于分组码。
但卷积码没有分组码那样严密的数学分析手段,目前大多是通过计算机进行好码的搜索。
2.7.1.卷积码的结构和描述一、卷积码的一般结构卷积码编码器的形式如图所示,它包括:一个由N段组成的输入移位寄存器,每段有k个,共Nk个寄存器;一组n个模2和相加器,一个由n级组成的输出移位寄存器。
对应于每段k个比特的输入序列,输出n个比特。
由上图可以看到,n个输出比特不仅与当前的k个输入信息有关,还与前(N-1)k个信息有关。
通常将N称为约束长度,(有的书的约束长度为Nn)。
常把卷积码记为:(n,k,N),当k=1时,N-1就是寄存器的个数。
二、卷积码的描述描述卷积码的方法有两类:图解法和解析表示。
图解法包括:树图、状态图、网格图解析法包括:矩阵形式、生成多项式形式。
以如下的结构说明各种描述方法。
1、树图根据上图,我们可以得到下表:我们可以画出如下的树状图:2、 状态图3、 网格图例1, 输入为1 1 0 1 1 1 0,输出为: 11 01 01 00 01 10 014、 生成多项式表示 定义],,[1211101g g g g=,],,[2221202g g g g=则上述结构为71=g,52=g,这里用8进制表示21,g gabcd⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2101211101],,[m m m g g g c ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2102221202],,[m m m g g g c定义2212111011)(DD Dg D g g D g ++=++=2222212021)(DDg D g g D g +=++=则输入信息,...,,210b b b 的多项式为....)(332210++++=b D b D b b D M那么我们可以得到输出)()()(11D g D M D C = )()()(22D g D M D C =最终输出是)(),(21D C D C的相同次数项的排列。
卷积码的维特比译码

卷积码的维特比译码卷积编码器自身具有网格构造,基于此构造我们给出两种译码算法:Viterbi 译码算法和BCJR 译码算法。
基于某种准那么,这两种算法都是最优的。
1967 年,Viterbi 提出了卷积码的Viterbi 译码算法,后来Omura 证明Viterbi 译码算法等效于在加权图中寻找最优途径问题的一个动态规划〔Dynamic Programming〕解决方案,随后,Forney 证明它实际上是最大似然〔ML,Maximum Likelihood〕译码算法,即译码器选择输出的码字通常使接收序列的条件概率最大化。
BCJR 算法是1974 年提出的,它实际上是最大后验概率〔MAP,Maximum A Posteriori probability〕译码算法。
这两种算法的最优化目的略有不同:在MAP 译码算法中,信息比特错误概率是最小的,而在ML 译码算法中,码字错误概率是最小的,但两种译码算法的性能在本质上是一样的。
由于Viterbi 算法实现更简单,因此在实际应用比较广泛,但在迭代译码应用中,例如逼近Shannon 限的Turbo 码,常使用BCJR 算法。
另外,在迭代译码应用中,还有一种Viterbi 算法的变种:软输出Viterbi 算法〔SOV A,Soft-Output Viterbi Algorithm〕,它是Hagenauer 和Hoeher 在1989 年提出的。
为了理解Viterbi 译码算法,我们需要将编码器状态图按时间展开〔因为状态图不能反映出时间变化情况〕,即在每个时间单元用一个分隔开的状态图来表示。
例如〔3,1,2〕非系统前馈编码器,其生成矩阵为:G(D)=[1+D1+D21+D+D2]〔1〕图1 〔a〕〔3,1,2〕编码器〔b〕网格图〔h=5〕假定信息序列长度为h=5,那么网格图包含有h+m+1=8 个时间单元,用0 到h+m=7 来标识,如图1〔b〕所示。
假设编码器总是从全0 态S0 开始,又回到全0 态,前m=2 个时间单元对应于编码器开始从S0“启程〞,最后m=2 个时间单元对应于向S0“返航〞。
卷积码编码和维特比译码

卷积码编码维特比译码实验设计报告SUN一、实验目的掌握卷积码编码和维特比译码的基本原理,利用了卷积码的特性, 运用网格图和回溯以得到译码输出。
二、实验原理1.卷积码是由连续输入的信息序列得到连续输出的已编码序列。
其编码器将k个信息码元编为n个码元时,这n个码元不仅与当前段的k个信息有关,而且与前面的(m-1)段信息有关(m为编码的约束长度)。
2.一般地,最小距离d表明了卷积码在连续m段以内的距离特性,该码可以在m个连续码流内纠正(d-1)/2个错误。
卷积码的纠错能力不仅与约束长度有关,还与采用的译码方式有关。
3. 维特比译码算法基本原理是将接收到的信号序列和所有可能的发送信号序列比较,选择其中汉明距离最小的序列认为是当前发送序列。
卷积码的Viterbi 译码是根据接收码字序列寻找编码时通过网格图最佳路径的过程,找到最佳路径即完成了译码过程,并可以纠正接收码字中的错误比特。
4.所谓“最佳”, 是指最大后验条件概率:P( C/ R) = max [ P ( Cj/ R) ] , 一般来说, 信道模型并不使用后验条件概率,因此利用Beyes 公式、根据信道特性出结论:max[ P ( Cj/ R) ]与max[ P ( R/ Cj) ]等价。
考虑到在系统实现中往往采用对数形式的运算,以求降低运算量,并且为求运算值为整数加入了修正因子a1 、a2 。
令M ( R/ Cj) = log[ P ( R/ Cj) ] =Σa1 (log[ P( Rm/ Cmj ) ] + a2) 。
其中, M 是组成序列的码字的个数。
因此寻找最佳路径, 就变成寻找最大M( R/ Cj) , M( R/ Cj) 称为Cj 的分支路径量度,含义为发送Cj 而接收码元为R的似然度。
5.卷积码的viterbi译码是根据接收码字序列寻找编码时通过网格图最佳路径的过程,找到最佳路径即完成了译码过程并可以纠正接收码字中的错误比特。
三、实验代码#include<stdio.h>#include "Conio.h"#define N 7#include "math.h"#include <stdlib.h>#include<time.h>#define randomize() srand((unsigned)time(NULL))encode(unsigned int *symbols, /*编码输出*/unsigned int *data, /*编码输入*/unsigned int nbytes, /*nbytes=n/16,n为实际输入码字的数目*/unsigned int startstate /*定义初始化状态*/)////////////////////////////////////////////////////////////////////////////卷积码编码///////////////////////////////////////////////////////////////////////////////{unsigned int j;unsigned int input,a1=0,a2=0,a3=0,a4=0,a5=0,a6=0;for(j=0;j<nbytes;j++){input=*data;data++;*symbols = input^a1^a2^a3^a6; //c1(171)symbols++;*symbols = input^a2^a3^a5^a6; //c2(133)symbols++;a2=a1;a1=input;}return 0;}int trandistance(int m, int state1, int state2)/*符号m与从state1到state2时输出符号的汉明距离,如果state1无法到state2则输出度量值为100*/{int c;int sym,sym1,sym2;sym1=((state2>>1)&1)^(state2&1)^(state1&1);sym2=((state2>>1)&1)^(state1&1);sym=(sym1<<1) | sym2;if ( ((state1&2)>>1)==(state2&1))c=((m&1)^(sym&1))+(((m>> 1)&1)^((sym >> 1)&1));elsec=10000;return(c);}int traninput(int a,int b) /*状态从a到b时输入卷积码的符号*/{int c;c=((b&2)>>1);return(c);}int tranoutput(int a,int b) /*状态从a到b时卷积码输出的符号*/{int c,s1,s2;s1=(a&1)^((a&2)>>1)^((b&2)>>1);s2=(a&1)^((b&2)>>1);c=(s1<<1)|s2;return(c);}////////////////////////////////////////////////////////////////////////////维特比译码///////////////////////////////////////////////////////////////////////////////void viterbi(int initialstate, /*定义解码器初始状态*/int *viterbiinput, /*解码器输入码字序列*/int *viterbioutput /*解码器输出码字序列*/){struct sta /*定义网格图中每一点为一个结构体,其元素包括*/ {int met; /*转移到此状态累计的度量值*/int value; /*输入符号*/struct sta *last; /*及指向前一个状态的指针*/};struct sta state[4][N];struct sta *g,*head;int i,j,p,q,t,r,u,l;for(i=0;i<4;i++) /* 初始化每个状态的度量值*/for(j=0;j<N;j++)state[i][j].met=0;for(l=0;l<4;l++){state[l][0].met=trandistance(*viterbiinput,initialstate,l);state[l][0].value=traninput(initialstate,l);state[l][0].last=NULL;}viterbiinput++; /*扩展第一步幸存路径*/for(t=1;t<N;t++){for(p=0;p<4;p++){state[p][t].met=state[0][t-1].met+trandistance(*viterbiinput,0,p);state[p][t].value=traninput(0,p);state[p][t].last=&state[0][t-1];for(q=0;q<4;q++){if(state[q][t-1].met+trandistance(*viterbiinput,q,p)<state[p][t].met){state[p][t].met=state[q][t-1].met+trandistance(*viterbiinput,q,p);state[p][t].value=traninput(q,p);state[p][t].last=&state[q][t-1];}}}viterbiinput++;} /*计算出剩余的幸存路径*/r=state[0][N-1].met; /*找出n步后度量值最小的状态准备回溯路由*/g=&state[0][N-1];for(u=N;u>0;u--) /*向前递归的找出最大似然路径*/{*(viterbioutput+(u-1))=g->value;g=g->last;}/* for(u=0;u<8;u++)*(viterbioutput+u)=state[u][2].met; */ /*此行程序可用于检测第n列的度量值*/}void decode(unsigned int *input, int *output,int n){int viterbiinput[100];int j;for(j=0;j<n+2;j++){viterbiinput[j]=(input[j*2]<<1)|input[j*2+1];}viterbi(0,viterbiinput,output);}void main(){unsigned intencodeinput[100],wrong[10]={0,0,0,0,0,0,0,0,0,0},encodeoutput[100];int n=5,i,m,j=0,decodeinput[100],decodeoutput[100];randomize();for(i=0; i<n; i++)encodeinput[i]=rand()%2;encodeinput[n]= encodeinput[n+1]=0;encode(encodeoutput,encodeinput,n+2,0);printf("the input of encoder is :\n"); //信息源输入的信息码(随机产生)for(i=0;i<n; i++)printf("%2d",encodeinput[i]);printf("\n");printf("the output of encoder is :\n"); //编码之后产生的卷积码for(i=0;i<(n+2)*2;i++){printf("%2d",encodeoutput[i]);if(i%20==19)printf("\n");}printf("\n");printf("please input the number of the wrong bit\n"); //信道传输收到干扰而产生的错误码scanf("%d",&m);printf("please input the positions of the wrong bit(0-9)\n");for(i=0;i<m;i++){scanf("%d",&wrong[m]);if(encodeoutput[wrong[m]]==0)encodeoutput[wrong[m]]=1;elseencodeoutput[wrong[m]]=0;}printf("the input of decoder is :\n");for(i=0;i<(n+2)*2;i++){printf("%2d",encodeoutput[i]);if(i%20==19)printf("\n");}printf("\n");decode(encodeoutput,decodeoutput,n+2);printf("the output of decoder is :\n");for(i=0;i<n;i++)printf("%2d",decodeoutput[i]);printf("\n");for(i=0;i<n;i++){if(encodeinput[i]!=decodeoutput[i])j++;}printf("the number of incorrect bit is:%d\n",j);}四、实验总结(1)了解实验原理,分析实验所占数组变量很重要,也是相对考虑较多的;(2)对于读写文件,通过本实验更加熟悉;(3)记录实验程序最佳路径是本实验的难点;。
卷积码编码与译码

例: (n, k, N) = (3, 1, 3)卷积码编码器方框图设输入信息比特序列是bi-2 bi-1 bi bi+1,则当输入bi时,此编码器输出3比特ci di ei,输入和输出的关系如下:
实际应用时常用的卷积码是(2,1,7)卷积码例如:IEEE 802.11a、DVB-T的内码;(2,1,7)卷积码的编码器,如图:
(3, 1, 3)卷积码 设现在的发送信息位为1101,为了使图中移存器的信息位全部移出,在信息位后面加入3个“0”,故编码后的发送序列为111 110 010 100 001 011 000。并且假设接收序列为111 010 010 110 001 011 000,其中第4和第11个码元为错码。 由于这是一个(n, k, N) = (3, 1, 3)卷积码,发送序列的约束度N = 3,所以首先需考察nN = 9比特。第1步考察接收序列前9位“111 010 010”。由此码的网格图可见,沿路径每一级有4种状态a, b, c和d。每种状态只有两条路径可以到达。故4种状态共有8条到达路径。 现在比较网格图中的这8条路径和接收序列之间的汉明距离。
4
是
现在将到达每个状态的两条路径的汉明距离作比较,将距离小的一条路径保留,称为幸存路径。若两条路径的汉明距离相同,则可以任意保存一条。这样就剩下4条路径了,即表中第2, 4, 6和8条路径。
第2步继续考察接收序列的后继3个比特“110”。计算4条幸存路径上增加1级后的8条可能路径的汉明距离。结果如下表。 表中最小的总距离等于2,其路径是abdc+b,相应序列为111 110 010 100。它和发送序列相同,故对应发送信息位1101。 按照表中的幸存路径画出的网格图示于下图中。
序号
路径
对应序列
卷积编码和维特比译码的研究及其TMS320c54x上的实现

1.1研究背景
卷积编码和维特比译码是现代通信中普遍应用的技术,由于在现代通信中,大量应用DSP及FPGA等大规模、高速率、可编程芯片,给采用卷积编码和维特比译码带来了实现的可能,卷积编码和维特比译码的方法可以获得比其他编译码额外的编码增益,其应用会更普遍家知道,在实际信道传输数字信号过程中,由于信道传输特性不理想会导致信号波形失真,接收端会不可避免地产生错误判决而产生误码。由信道乘性干扰引起的码间串扰通常可以采用均衡的技术纠正。而对于由信道加性噪声产生的影响,人们研究出了许多差错控制编码技术来解决。而由P.Elias于1955年提出的卷积码就是其中一种性能很好的编码。这种编码是深度空间通信系统和无线通信系统中常用的一种差错控制编码。在编码过程中,卷积码充分利用了各码字间的相关性。在与分组码同样的码率和设备复杂性的条件下,无论从理论上还是从实践上都证明,卷积码的性能都比分组码具有优势。而且卷积码在实现最佳译码方面也较分组码容易。因此卷积码广泛应用于卫星通信,CDMA数字移动通信等通信系统,是很有前途的一种编码方式,对其性能进行研究有很大的现实意义。
第三章是研究在TMS320C54X上实现卷积码编译码的算法。
第四章用matlab语言编程和仿真,对卷积码的性能进了研究,分析了在不同码率、不同约束长度、不同回溯长度以及不同译码判决方式下viterbi译码的性能。
第五部分主要是对本课题的研究进行全文总结。
第二章 相关理论/技术研究
本章主要介绍卷积编码和维特比译码的原理以及其算法,并在文中对其性能就行了分析阐述
1.4本文工作安排
第一章讲述了卷积编码和维特比译码的研究内容和背景。
第二章论述卷积码的编码译码原理,生成矩阵法(输入信息序列与子生成元卷积运算,再将得到的编码按顺序排列得到)、状态图、网格图、树图。译码部分主要论述了viterbi译码基本原理,即以接收码流为基础,逐个计算它与其他所有可能出现的、连续的网格图路径的距离,选出其中量度最小的一条路径作为译码估值输出。
基于FPGA的卷积码Viterbi译码器性能研究

基于FPGA的卷积码Viterbi译码器性能研究卷积码是一种前向纠错控制(Forward Error Control,FEC)编码方式,其特点是接收端根据接收码字自动检测和纠正信道传输引入的错误。
由于FEC方式不需要反馈信道,译码实时性比较好,控制电路比较简单,因此,卷积码在卫星通信、数字话音通信等实时性要求较高的场合有着重要的应用。
卷积码的编译码器的实现可以利用EDA技术,采用硬件描述语言VerilogHDL或VHDL等进行FPGA 编程设计,这种实现方式在集成度、可靠性和灵活性方面可达到比较满意的效果。
在设计卷积码FPGA 译码器时,需要考虑所用芯片规格、成本、系统计算量以及时延等因素。
目前现有文献多对卷积码的实现进行研究,而对译码算法中参数设置情况研究较少。
本文采用VHDL语言,在设计实现卷积码FPGA编译码器的基础上,通过仿真对Viterbi译码算法中的参数进行了讨论。
1 Viterbi译码算法Viterbi译码算法由维特比在1967年提出。
Viterbi译码算法实质上是最大似然译码,他巧妙利用编码网格图的特殊结构,从而降低计算的复杂性。
例如图1即为(2,1,2)卷积码的网格图。
这里(n,k,m)分别指码组宽度n,信息元个数k和编码存储度m,称m+1=N为编码约束度。
该算法思想是:计算网格图上在时刻L到达各个状态的路径和接收序列之间的相似度;在形成的多条路径中,去除不可能成为最大似然选择对象的网格图上的路径,即,如果有两条路径到达同一状态,则具有最佳量度的路径被选中,称为幸存路径。
对所有状态都将进行这样的路径选择操作,译码器不断在网格图上深入,通过去除可能性最小的路径实现判决。
Viterbi译码算法步骤如下:(1)用数组p(i,j),c(i,j)描述网格图结构。
p(i,j)表示到达状态i的第j个前状态,其对应的码字是(i,j)。
(2)计算第L时刻接收码RL相对于各码字睁相似度,亦称作分支量度BM(Branch Metric)。
卷积码2019PPT课件

(g0 , g1, g2 , g3, 0,...)
成矩阵 14
14
从卷积码编码器的框图可以看出有3个存储单元,g 完全由 m+1=4段值 g0 , g1, g2 , g3 决定,从m+2=5段起均为0
g(1) (g0 g1 g2 g3) (111 001 010 011)
完全可以决定 g ,从而确定G
27
27
101 000 001
用矩阵表示为
011 001 001
101 000 001
C mG (11 11 11 00 )
011 001 001
101 000 001 011 001 001
101 000
011 001
101 000 001
G
011 001 001 101 000
任一时刻t送至编码器的信息组记为:
mt
m (1) t
,
mt(
2
)
,
mt(
k
0
)
相应的编码输出码段为:
ct
c (1) t
,
ct(
2
)
,
ct(
n0
)
ct 不仅与前面m个时刻的m段输入信息组有关,
还参与此时刻之后m个时刻的输出码段的计 算,其中m为编码器中移位寄存器的个数。
6
6
• 定义:如果在n0位长的子码中,前k0位是原 输入的信息元,则称该卷积码为系统码,
g(1) (g0 g1 g2 g3) (111 001 010 011)
完全可以决定 g ,从而确定G
g(1) 称为该(3, 1, 3)卷积码的生成元。
c (1) l
卷积码编码和维特比译码的性能对比

卷积码编码和维特比译码的性能对比1.引言卷积码的编码器是由一个有k位输入、n位输出,且具有m位移位寄存器构成的有限状态的有记忆系统,通常称它为时序网络。
编码器的整体约束长度为v,是全部k个移位寄存器的长度之和。
具有这样的编码器的卷积码称作[n,k,v]卷积码。
对于一个(n,1,v)编码器,约束长度v等于存储级数m.卷积码是由k个信息比特编码成n(nk)比特的码组,编码出的n比特码组值不仅与当前码字中的k个信息比特值有关,而且与其前面v个码组中的v*k个信息比特值有关。
卷积码有三种译码方式:序列译码、门限译码和概率译码。
其中,概率译码依据最大似然译码原理在全部可能路径中求取与接收路径最相像的一条路径,具有最佳的纠错性能,维特比译码是概率译码中极重要的一种方式。
序列译码和门限译码则不肯定能找出与接收路径最相像的一条路径。
不同于维特比译码,门限译码与序列译码所需的计算量是可变的且对于给定信息分组的最终判决仅仅基于(m+1)个接收分组,而不是基于整个接收序列。
与维特比译码所使用的对数似然量度不同,序列译码所使用的量度为Fano量度。
在接收序列受扰严峻的状况下,序列译码的计算量大于维特比译码所需的固定计算量,虽然序列译码要求的平均计算次数通常小于维特比译码。
在采纳并行处理的状况下,维特比译码的速度会优于序列译码。
在同样码率和存储级数的条件下,门限译码的性能比维特比译码低大约3dB.维特比译码的数据输出方式有硬判决及软判决两种方式,本文选取生成多项式为561,753的(2,1,8)卷积码对硬判决的性能进行分析,并依据维特比译码的原理以及卷积码的特性,对卷积码编码和维特比译码过程在加性高斯白噪声(AWGN)信道下进行仿真,并且依据仿真结果对维特比译码(硬判决)的结果进行分析。
由于卷积码的生成可以看做一个马尔科夫过程,因此,不同状态间的转移概率对描述这个过程有极关键的作用。
本文则基于MATLAB对不同状态间的转移概率进行求解,从而更精确地分析维特比译码的性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
卷积码收尾的实现
• 非递归卷积码:约束长度为m+1的卷积 码,只要在信息序列输入完成后连续送 入m个0,即可使任一路径都到达最终的 状态0。 • 递归卷积码:也可通过将输入值置成反 馈值的负值,而使m个时钟后的状态到达 0。
卷积码收尾
非系统非递归码
D D
D
D
递归系统码
维特比译码的复杂度
• 对信息序列长度为L,信息符号取自 GF(p),R=k/n,约束长度为m+1的卷积码。 状态数为pkm,因此对每个时刻要做pkm次 加比选得到pkm个状态的残留路径,每次 加比选包括pk次加法和pk-1次比较。因此 总运算量约为Lpkm次加比选。同时要能 保存pkm条残留路径,因此需要Lpkm个存 贮单元。
• 显然,两条路径分离后一般并不会立即合并, 而是要经过一段时间后才可能合并,这段时 间可长可短,是随机的。因此卷积码中出现 的误码一般也有较强的突发性,一般突发长 度不小于约束长度。 • 对半无限的卷积码而言,总是开始于状态0, 我们要研究的就是什么时候会发生第一次错 误事件?这一次错误事件的长度是多少?它 引起了多少比特错误?错误概率如何?等等。
第九讲
卷积码的维特比译码及卷积码性能分析
回顾
• • • • 卷积码的编码:有记忆的信道编码 卷积码的概率译码 序列译码:费诺算法和堆栈算法 最大似然译码:维特比算法
维特比译码的描述
• 从第1时刻的全零状态开始(零状态初始度量为0,其 它状态初始度量为负无穷) • 在任一时刻t,对每一个状态只记录到达路径中度量最 大的一个(残留路径)及其度量(状态度量) • 在向t+1时刻前进过程中,对t时刻的每个状态作延伸, 即在状态度量基础上加上分支度量,得到M*2k条路径 • 对所得到的t+1时刻到达每一个状态的2k条路径进行比 较,找到一个度量最大的作为残留路径 • 直到码的终点,如果确定终点是一个确定状态,则最 终保留的路径就是译码结果
01
10 0/10 11
0/10 1/01
0/10 1/01
0/10 1/01
维特比译码——收尾
• 最大似然序列译码要求序列有限,因此 对卷积码来说,要求能收尾。 • 收尾的原则:在信息序列输入完成后, 利用输入一些特定的比态 (一般是全零状态)。这样就变成只有 一条残留路径,这就是最大似然序列。
F(N,S,D)的含义
• 它表示,在所有可能路径中,长度是i个 时刻,输入重量为j,输出重量为k的路径 共有A(i,j,k)条。 • 这个式子包含了有关卷积码性能的大量 信息,可以从它得到误比特率、误事件 率及误帧率的性能界。
如何计算F(N,S,D)
• 为了得到F(N,S,D),我们可以借助流图的 方法,即将各分支的乘积增量做为该分 支的转移函数或增益,而计算从0状态注 入到0’状态输出的总增益,这个总增益 就是F(N,S,D)。
维特比译码的特点
• • • • • • 维特比算法是最大似然的序列译码算法 译码复杂度与信道质量无关 运算量与码长呈线性关系 存贮量与码长呈线性关系 运算量和存贮量都与状态数呈线性关系 状态数随分组大小k及编码深度m呈指数 关系
吞吐量与存储量
• 运算量与码长呈线性关系意味着平均吞 吐量与码长无关 • 存贮量与码长呈线性关系意味着对无限 码长(流的情况)要求有无限的存贮量。
状态数对维特比译码的影响
• 由于运算量与k和m呈指数关系,因此维 特比译码算法一般只适合于k和m较小的 场合。大多数情况下k=1,m<10。 • 对状态数很大的卷积码,维特比算法要 经一定的修正后才可能实用,常用的算 法是缩减状态的维特比译码,即在每一 时刻,只处理部分的状态。
序列译码与维特比译码的比较
图解维特比译码
00 0/00 1/11 0/01 0/11 1/00 1/10 1/10 0/01 0/00 1/11 0/11 1/00 1/10 1/10 0/00 1/11 0/11 0/01 1/00 1/10 1/10 0/10 1/01 1/01 0/01 0/00 1/11 0/11 1/00 1/10 1/10 0/01 0/00 1/11 0/11 1/00 1/10 1/10
• 信道质量对前者运算量影响较大,而对 后者运算量没有影响 • 前者是次优的,后者是最优的 • 前者运算量与约束长度无关,而后者运 算量与约束长度呈指数关系 • 前者会有译码失败,而后者只有译码错 误 • 在不同场合有不同用途
卷积码的性能分析
• 误码分析 • 重量或距离谱 • 首次差错率
两个序列间差异的扩大
对于线性卷积码
• 对线性卷积码而言,输入全0时输出也是 全0,构成一条全0序列,这是一个合法 的编码序列。因此研究误码可以假设发 的是全0序列,而研究译成非0序列的概 率。为此我们要研究卷积码的距离谱或 重量谱。
线性卷积码的首次错误事件
• 在研究首次错误事件概率时,要研究的是第一次与 全0序列分离并再次回到全0序列的事件。它等价于 在网格图上第一次离开状态0并再次回到状态0的路 径。 • 由于这些事件要离开状态0,而再次回到状态0后就 不允许离开状态0,因此状态0要分解成两个状态:0 和0’,其中0为注入态,而0’为吸收态。我们要研究 的就是从注入到吸收所有可能的路径,及它们的各 种特性,如长度、输入重量、输出重量等等。
• 对于有限状态的流编码传输而言,如果 两个序列不起始于同一状态且终于同一 状态,则可以通过网格图的继续延伸而 呈现出更大的差别。而只有有限的差别 才有可能造成误判。 • 因此对卷积码而言,我们关心的是某一 时刻两条路径分离,而在有限时间内又 再次合并的情形。这就是流编码中的一 次错误事件。
首次错误事件
重量表示
• 由于路径每走一步,长度、输入重量、输出重 量等参数都要随各自的分支而进行累加,因此 如果将这些参数在每个分支上的值用指数标注, 则可以用乘积的方式表示一条路径的各项值。 例如,一条路径的乘积项为NiSjDk,表示该路径 长度是i个时刻,输入重量为j,输出重量为k。 当将所有可能路径的乘积项加起来,合并同类 项,就可以得到下面的式子: • F(N,S,D)=i,j,kA(i,j,k) NiSjDk
滑动窗维特比译码算法
• 基本思想:当状态数有限时,给定时刻 的各状态残留路径在一定时间(L)之前 来自于同一状态的可能性随L的增加而迅 速趋近于1。因此当前时刻各残留路径很 可能来自于L时刻前的同一路径。
滑动窗维特比译码算法实现
• 在第k时刻,可以将t-L时刻前的路径结果直接 输出,而在存贮空间中不再保存t-L时刻前的内 容。因此存贮量控制在Lpkm。这里的L就被称 做译码深度。不再随码长的增加而增加。因而 特别适合信息流的卷积码编译码。在这种情况 下甚至不需要对流分段加尾比特。这里的L就 被称做译码深度。 • 显然,滑动窗算法是一种准最优算法。但通常 译码深度只要有编码约束长度的5到10倍,其 性能损失就可以忽略不计了。
