信息学 校内选拔赛试题
信息学竞赛初赛试题及答案

信息学竞赛初赛试题及答案一、选择题(每题2分,共10题)1. 在计算机科学中,以下哪个选项不是数据结构?A. 数组B. 链表C. 函数D. 栈答案:C2. 以下哪种排序算法的时间复杂度为O(n^2)?A. 快速排序B. 归并排序C. 插入排序D. 冒泡排序答案:D3. 在计算机网络中,TCP/IP协议栈的第四层是什么?A. 应用层B. 传输层C. 网络层D. 数据链路层答案:B4. 下列哪种编程语言不是面向对象的?A. JavaB. C++C. PythonD. C答案:D5. 在关系型数据库中,用于创建新表的SQL语句是?A. SELECTB. INSERTC. CREATED. DROP答案:C6. 在HTML中,用于定义文档标题的标签是?A. <h1>B. <title>C. <header>D. <head>答案:B7. 在Python中,以下哪个关键字用于定义一个函数?A. defB. ifC. forD. while答案:A8. 在操作系统中,用于管理内存的机制是?A. 进程B. 线程C. 分页D. 虚拟内存答案:D9. 在计算机系统中,以下哪个选项不是操作系统的功能?A. 进程管理B. 设备驱动C. 网络通信D. 数据加密答案:D10. 在计算机视觉中,用于识别图像中物体的算法是?A. 卷积神经网络B. 决策树C. 支持向量机D. 随机森林答案:A二、填空题(每题2分,共5题)1. 在计算机科学中,算法的时间复杂度是指算法执行时间与输入数据量之间的关系,通常用大O符号表示,例如O(1)表示______。
答案:常数时间复杂度2. 在编程中,______是一种将数据结构和操作这些数据的方法封装在一起的编程范式。
答案:面向对象编程3. 在网络协议中,HTTP协议默认使用的端口号是______。
答案:804. 在数据库设计中,______是一种用于确保数据完整性和避免数据冗余的策略。
信息学选拔试题及答案

信息学兴趣小组选拔试题班级: 姓名: 学号: 成绩1、有红、黄、黑、白四色球各一个,放置在一个内存编号为1、2、3、4四个格子的盒中,每个格子放置一只球,它们的顺序不知。
甲、乙、丙三人猜测放置顺序如下: 甲:黑编号1,黄编号2; 乙:黑编号2,白编号3; 丙:红编号2,白编号4 。
结果证明甲乙丙三人各猜中了一半。
写出四色球在盒子中放置情况及推理过程。
2、 列举一个算法,使算法的解能对应相应的问题。
例如,设问题为:学生答题,答对一题可得10分,答错一题则要扣去5分,输入答对的题数(M )与答错的题数(N ),求最后得分(S )是多少? 列举出相应算法为:X :=10; Y :=5;READ (M ,N ); S :=X*M-Y*N ;现有以下问题:用五角钱换成5分、2分与1分的硬币,可有多少种换法? 请列出该问题的算法。
3、下图中用点表示城市,点与点之间的联系表示城市间的道路:D CA B试问:① 能否找出一条从A 城市出发,经过图中所有道路一次后又回到出发点的通路来?② 能否从A 出发,找出去每个城市且只去一次的通路来? 若能,则写出通路,否则说明理由。
4、一个将角编了号的正三角形可以绕着外心O (中心)逆时针旋转1200,如下图所示: 1 30 02 3 1 2 如果将这一旋转用字母a 来表示,看作运算对象,同时用aa 或a 2 表示旋转1200EFa后再旋转1200,也就是说将连续运动看作乘法运算,那么三角形状态(可简称为元素)即可与运动表达式关联起来,请回答:①如果将图一的原始三角形连续旋转1200N次,简单地表示为a n(N为任意自然数),试求a n的值(指三角形旋转后的结果状态);②如果将下面的旋转看作是a的逆元素,记为a-1,则有a-1= a2试求:a-n3 10 0aa1 2 2 3图三5、已知一个数列U1,U2,U3,…,U N,…往往可以找到一个最小的K值和K个数a1,a2,…,a k使得数列从某项开始都满足:U N+K=a1U N+K-1+a2U N+K-2+……+a k U N(A) 例如对斐波拉契数列1,1,2,3,5,…可以发现:当K=2,a1 =1,a2 =1时,从第3项起(即N>=1)都满足U n+2 =U n+1+U n 。
衢州市青少年信息学竞赛选拔赛试题

var i,j,k,top:integer;
q:link;
begin
top:=0;
for i:=1 to n do
if ali.vex=0 then
begin
ali.vex:=top;
top:=i;
end;
i:=0;
1.选择排序的算法是:首先找出关键字值最小的记录,然后把这个记录与第一个位置上的记录对换;这样,就使关键字值最小的记录取得了应占的位置;接着,再在余下的记录中找关键字值最小的记录,并把它与第二个位置上的记录对换,使关键字值第二小的记录取得了应占的位置;依次类推,一直到所有的记录都处在它应占的位置上,便得到了按关键字值非减次序排序的有序文件;如果有n个数据,按上述方法排序,总的比较次数为;
代号 课程名称 先行课程
C1 英语基础 无
C2 数学基础 无
C3 离散数学 C2
C4 计算机基础知识 C1,C2
C5 程序设计基础 C1,C2
C6 Pascal语言程序设计 C1,C2,C4,C5
C7 数据结构 C2,C6
C8 算法设计 C2,C6,C7
C9 人工智能 C2,C5,C8
C10 运筹学 C2,C8
else fi,j:=22;
end;
end;
procedure print;
var get:tlist;
i,j:byte;
begin
fillcharget,sizeofget,0;
i:=n;23;
while i>0 do
if fi,j=fi-1,j
then deci
信息学奥赛选拔试题

信息学奥赛选拔试题
信息学奥赛选拔试题一般会包括基础题、提高题和综合题。
以下是一些可能的信息学奥赛选拔试题:
基础题:
1. 什么是信息学?请简要解释。
2. 什么是算法?请简要解释。
3. 什么是数据结构?请简要解释。
4. 请解释以下信息学术语:数组、链表、栈、队列。
5. 请写出一个简单的计算器程序,可以执行加、减、乘、除四个基本运算。
提高题:
1. 请设计一个程序,实现将一个整数列表按照升序排序。
2. 请设计一个程序,实现将一个字符串列表按照字典序排序。
3. 请写出一个程序,可以判断一个数是否为素数。
4. 请设计一个程序,实现将一个字符串转换为整数。
5. 请设计一个程序,实现将两个有序整数列表合并为一个有序整数列表。
综合题:
1. 请设计一个程序,实现求解以下数学表达式:max(a, b, c) + min(a, b, c) + avg(a, b,
c)。
其中,a、b、c为整数,函数avg计算a、b、c的平均值。
2. 请写出一个程序,可以判断一个字符串是否为回文串。
3. 请设计一个程序,实现求解以下数学表达式:sqrt(a^2 + b^2) + log(c * d)。
其中,
a、b、c、d为实数,函数sqrt计算平方根,函数log计算自然对数。
NOIP信息学初赛模拟试题C++(1)

NOIP信息学初赛模拟试题C++(1)信息学初赛模拟试题(四)一、选择题:(选出每题正确的答案代码,填在括号里,1—10题为单选题,每小题只有一个正确答案,11—20题为不定项选择题,每小题有一个或一个以上的正确答案,共20题,每题1.5,共30分)1、二进制数01100100转换成十六进制数是()。
A.32 B.64 C.128 D.100 E.2562、操作系统是一类重要的系统软件,下面几个软件中,不属于系统软件的是()。
A.Java B.MS-DOS C.Linux D.Windows7 E.Unix3、计算机病毒的传染是以计算机运行和()为基础的,没有这两个条件,病毒是不会传染的。
A.编辑文稿 B.读写磁盘 C.编程序 D.扫描图画 E.打印4、因特网不属于任何个人,也不属于任何组织。
其中在网络知识这一块中有一个英文简写ISP,它的中文意思是()。
A.因特网连接 B.因特网使用 C.因特网设计 D.因特网服务提供者 E.信息传输5、Internet给我们提供了资源共享、浏览、检索信息和远程登录等多种服务,下面几个选项中用于远程登录的是()。
A.WWW B.TCP/IP C.Telnet D.E-mail E.FTP6、IE是目前流行的浏览器软件,它的工作基础是解释执行用()语言书写的文件。
A.VC B.HTML C.BASIC D.HTTP E.VB7、给出3种排序:插入排序、冒泡排序、选择排序。
这3种排序的时间代价分别是()。
A.O(n)、O(n2)、O(logn) B.O(logn) 、O(n)、O(n2) C.O(n2)、O(n)、O(logn) D.O(n2)、O(n)、O(n) E.O(n2)、O(n2)、O(n2)8、一棵完全二叉树的结点总数为18,其叶结点数为()。
A.7个 B.8个 C.9个 D.10个 E.11个9、在流程图的符号中,菱形框一般作为()。
A.起始框 B.判断框 C.输入输出框 D.处理工作框 E.结速框10、在解决计算机主机与打印机之间速度不匹配时通常设置一个打印数据缓冲区,主要将要输出打印的数据依次写入该缓冲区,而打印机从该缓冲区中取出数据打印。
2023年海淀区信息学竞赛初赛试题

2023年海淀区信息学竞赛初赛试题近年来,信息学竞赛在海淀区的中小学生中越来越受欢迎。
信息学竞赛作为一项考察学生计算机科学知识和解决问题能力的比赛,对培养学生的创新思维和实践能力具有重要意义。
以下是2023年海淀区信息学竞赛初赛试题的相关内容。
题目1:二进制计数请编写一个程序,要求输入一个十进制数n,将其转换为二进制表示,并输出二进制数。
解题思路:1. 接收输入的十进制数n。
2. 将n逐步除以2,将余数记录下来,直到商为0为止。
3. 将记录下来的余数倒序输出,即得到n的二进制表示。
题目2:寻找最大值给定一个包含n个整数的数组,编写一个程序,找到数组中的最大值并输出。
解题思路:1. 创建一个变量max,用于保存最大值。
初始值为数组的第一个元素。
2. 遍历数组,将每个元素与max进行比较,如果大于max,则将其赋值给max。
3. 遍历结束后,max即为数组中的最大值,将其输出。
题目3:图形打印请编写一个程序,输入一个正整数n,输出一个n行n列的图形,如下所示:示例输入:4示例输出:****************解题思路:1. 接收输入的正整数n。
2. 使用嵌套循环,外层循环控制行数,内层循环控制列数。
3. 在内层循环中,输出一个"*",并重复n次,即为一行的内容。
4. 外层循环结束后,即可得到n行n列的图形。
题目4:字符串处理请编写一个程序,输入一个字符串,将字符串中的小写字母转换为大写字母,并输出结果。
解题思路:1. 接收输入的字符串。
2. 使用循环遍历字符串的每个字符。
3. 对于每个小写字母,将其转换为大写字母,并输出。
4. 遍历结束后,即可得到转换后的字符串。
通过以上题目的解答,可以看出信息学竞赛注重学生的编程能力、问题解决能力和逻辑思维能力。
参加竞赛的学生需要具备一定的计算机基础知识,并且能够将知识运用到实际问题中。
信息学竞赛的题目涵盖了编程、算法、数据结构、数学等多个领域,对学生的综合能力提出了挑战。
(信息学奥赛)选拔考试试题A卷

(信息学奥赛)选拔考试试题A卷编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((信息学奥赛)选拔考试试题A卷)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(信息学奥赛)选拔考试试题A卷的全部内容。
信息学奥赛选拔考试试题(A卷)班级________ 姓名________ 自己手机_________ 家庭电话_________考试说明:(1)时量:40分钟;(2)每道题简要写出关键过程,写出答案.1、猴子吃枣问题。
猴子摘了一堆枣,第一天吃了一半,还嫌不过瘾又吃了一个;第二天又吃了剩下的一半零一个;以后每天如此。
到第十天,猴子一看只剩下一个了.问最初有多少个枣?2、警察局抓了A、B、C、D四名偷窃嫌疑犯,其中有一个人是小偷。
审问中A说:“我不是小偷。
"B说:“C是小偷."C说:“小偷肯定是D。
"D说:“C在冤枉人。
”现在已经知道四个人中三个人的是真话,一人说的是假话,问到底谁是小偷?3、任何一个整数的立方都可以写成一串连续奇数之和,这就是著名的尼科梅彻斯定理。
13=1;23=3+5;33=7+9+11;43=13+15+17+19……,给出n,求n3是哪些奇数之和?4、桌上放了8张扑克牌,都是背面向上,牌放置的位置如右图所示.已知:(1)每张牌都是A、K、Q、J中的一张;(3)8张牌中只有一张A;(4)每一张Q都夹在两张K之间;(5)至少有一张K夹在两张J之间;(6)J与Q互不相邻,A与K也互不相邻;(7)至少有两张K彼此相邻。
注意:这里所说的“相邻”,只指横着相邻。
求出符合条件的任意一种解,并添涂在图中。
信息学奥赛考试题型及答案

信息学奥赛考试题型及答案一、选择题1. 在计算机科学中,以下哪个选项不是数据结构的基本类型?A. 线性结构B. 树形结构C. 图形结构D. 量子结构答案:D2. 以下哪种算法不是排序算法?A. 快速排序B. 归并排序C. 深度优先搜索D. 堆排序答案:C二、填空题1. 在信息学奥赛中,常用的图遍历算法有深度优先搜索(DFS)和______。
答案:广度优先搜索(BFS)2. 哈希表是一种通过______来访问数据的数据结构。
答案:键值对三、简答题1. 描述二分查找算法的基本步骤。
答案:二分查找算法的基本步骤包括:首先确定要查找的元素所在的区间,然后取区间的中间值与目标值进行比较。
如果中间值等于目标值,则查找成功;如果中间值小于目标值,则在区间的右半部分继续查找;如果中间值大于目标值,则在区间的左半部分继续查找。
重复以上步骤,直到找到目标值或区间为空。
2. 解释什么是递归,并给出一个递归算法的例子。
答案:递归是一种在函数中调用自身的编程技巧,用于解决可以分解为相似子问题的问题。
一个递归算法的例子是计算阶乘,即n的阶乘(n!)可以通过递归函数实现:n! = n * (n-1)!,其中基本情况是0! = 1。
四、编程题1. 给定一个整数数组,请编写一个函数,找出数组中第二大的数。
答案:以下是一个可能的解决方案的伪代码:```function findSecondLargest(nums):if length of nums < 2:return nullmax1 = max2 = -∞for num in nums:if num > max1:max2 = max1max1 = numelse if num > max2 and num != max1:max2 = numreturn max2```2. 实现一个函数,判断一个链表是否为回文结构。
答案:以下是一个可能的解决方案的伪代码:```function isPalindrome(head):if head is null or next of head is null:return truefast = slow = headwhile fast and next of fast:fast = next of next of fastslow = next of slowsecondHalf = reverse(slow)while secondHalf:if head.value != secondHalf.value:return falsehead = next of headsecondHalf = next of secondHalfreturn true```注意:以上编程题答案中的伪代码仅供解题思路参考,实际编程语言实现可能有所不同。
信息学奥赛入门级选手选拔试题

信息学奥赛入门级选手选拔试题1. 下列不属于信息学奥赛编程语言的是:C语言C++语言Pascal语言英语(正确答案)2. 计算机中存储进制是以0、1表示的二进制存储单元。
二进制的意思是逢二进一,十进制是逢十进一,例如十进制数字中的2在二进制中就是10,十进制3就是二进制中的11,请问在十进制中的11在二进制中的数为()。
1011(正确答案)1111111213. 下列不属于文本编辑软件的是word记事本wpsphotoshop(正确答案)4. 我们在用计算机录入文本内容时,要双手放在键盘上打字,食指要放在键盘的基准键位上,拇指自然搭在空格上,请问键盘的基准键位是哪两个键位?A和BF和J(正确答案)x和Y回车键5. 下列不属于计算机的输入设备的是()键盘鼠标显示器(正确答案)手写输入板6. 某个车站呈狭长形,宽度只能容下一台车,并且只有一个出入口。
已知某时刻该车站状态为空,从这一时刻开始的出入记录为:“进,出,进,进,进,出,出,进,进,进,出,出”。
假设车辆入站的顺序为 1,2,3,……,则车辆出站的顺序为()。
1, 2, 3, 4, 51, 2, 4, 5, 71, 4, 3, 7, 6(正确答案)1, 4, 3, 7, 27. 根据你的理解你认为下列不属于计算机的特点的是计算机能在程序控制下自动连续地高速运算。
计算机能以极快的速度进行计算计算机能自动判断人们的错误指令并修正,很智能(正确答案)计算机运算精度高8. 中国的国家顶级域名是().cn(正确答案).ch.china.chn9. 下列软件中不是计算机操作系统的是:WindowsLinux苹果操作系统OSWPS(正确答案)10. —副纸牌除掉大小王有52张牌,四种花色,每种花色13张。
假设从这52张牌中随机抽取13张纸牌,则至少()张牌的花色一致。
4(正确答案)52311. 素数就是质数,素数有无限个。
一个大于1的自然数,且除了1和它本身外,不能被其他自然数整除的数叫素数。
第十二届“新道杯”信息化大赛校内选拔赛试题
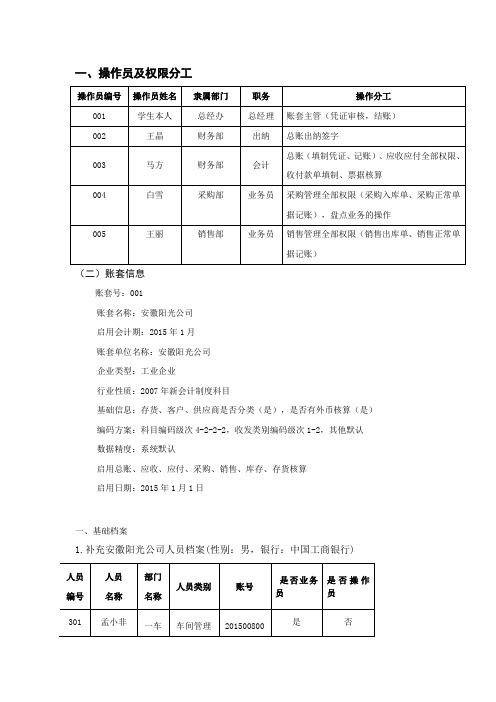
3、1 月 02 日,从金融证券市场购买 5000 股股票,每股 10 元,另支付手续费 150 元,短期 持有。
4、1 月 4 日,销售部王丽购买了 200 元的办公用品,以现金支付,附单据一张。
5、2015 年 1 月 5 日,销售部王丽向昌新贸易公司采购计算机 11 台,(不含税单价)为 6500 元/台(订单号:XS01),当日收到专用发票(发票号:2015010531)并当日收到转账支票(支 票号:010525)。(使用现结)
9、1 月 11 日,财务部王晶从工行提取现金 10 000 元,作为备用金,现金支票号 XJ001。
10、2015 年 1 月 12 日,业务员白雪与兴华公司签订一笔采购合同(cg002),购买 500GB 硬 盘,数量 150 盒,单价为 820 元。(15 日到货)
11、2015 年 1 月 15 日,收到兴华公司 500GB 硬盘,于当日收到发票(AS42356),货已全部 验收入原料库,款尚未支付。
二、业务题 1、安徽阳光公司 2015 年 1 月 1 日向兴华公司签发并承兑的商业承兑汇票一张(NO.12345), 面值为 276850.00 元,到期日为 2015 年 1 月 10 日。(应付款管理系统处理)、
2、2015 年 1 月 01 日,业务员白雪与建昌公司签订一笔采购合同(合同号:CG02),提供的 23 英寸液晶屏,数量 200 套,单价为 1150 元。验收入原料库。同日,收到建昌公司开具的 专用发票一张,其发票号为 AS4408。进行采购结算。
参数设置 0.5% 10000
坏账准备科目 对方科目
1231 6701
8、指定现金和银行科目。 9、应付账款期初余额设置。
应付账款/应付货款期初余额
信息学 校内选拔赛试题

信息学竞赛选拔赛试题(满分100分,时间120分钟)一、选择题(15分):1.十进制数2003等值于二进制数( )。
A . 010******* B. 10000011 C. 110000111 D. 11111010011 E. 11110100112.已知数组中A 中,每个元素A (I ,J )在存贮时要占3个字节,设I 从1变化到8,J 从1变化到10,分配内存时是从地址SA 开始连续按行存贮分配的。
试问:A (5,8)的起始地址为( )A.SA+141B. SA+180C. SA+222D. SA+2253.将 5 个数的序列排序,不论原先的顺序如何,最少都可以通过( )次比较,完成从小到大的排序。
A. 6B. 7C. 8D. 9E. 104.在 Pascal 语言中,表达式 (21 xor 2)的值是( )A. 441B. 42C.23D.24E.255.在顺序表(2,5,7,10,14,15,18,23,35,41,52)中,用二分法查找12,所需的关键码比较的次数为( )A.2B.3C.4D.5 二、数学问题及算法分析:1.(5分)一棵二叉树的前序遍历和中序遍历分别如下,画出该二叉树。
前序遍历:ABCDEFGHIJ 中序遍历:CBEDAGHFJI 2. (5分)在印度,有这么一个古老的传说:在世界中心贝拿勒斯(在印度北部)的圣庙里,一块黄铜板上插着三根宝石针。
印度教的主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的64片金片,这就是所谓的汉诺塔。
不论白天黑夜,总有一个僧侣在按照下面的法则移动这些金片:一次只移动一片,不管在哪根针上,小片必须在大片上面。
僧侣们预言,当所有的金片都从梵天穿好的那根针上移到另外一根针上时,世界就将在一声霹雳中消灭,而梵塔、庙宇和众生也都将同归于尽。
不管这个传说的可信度有多大,我们先来做题! 给定A 、B 、C 三根足够长的细柱,在A 柱上放有2n 个中间有孔的圆盘,共有n 个不同的尺寸,每个尺寸都有两个相同的圆盘,注意这两个圆盘是不加区分的(下图为n=3的情形)。
信息学选拔试题及答案

信息学兴趣小组选拔试题班级: 姓名: 学号: 成绩1、有红、黄、黑、白四色球各一个,放置在一个内存编号为1、2、3、4四个格子的盒中,每个格子放置一只球,它们的顺序不知。
甲、乙、丙三人猜测放置顺序如下: 甲:黑编号1,黄编号2; 乙:黑编号2,白编号3; 丙:红编号2,白编号4 。
结果证明甲乙丙三人各猜中了一半。
写出四色球在盒子中放置情况及推理过程。
2、 列举一个算法,使算法的解能对应相应的问题。
例如,设问题为:学生答题,答对一题可得10分,答错一题则要扣去5分,输入答对的题数(M )与答错的题数(N ),求最后得分(S )是多少? 列举出相应算法为:X :=10; Y :=5;READ (M ,N ); S :=X*M-Y*N ;现有以下问题:用五角钱换成5分、2分与1分的硬币,可有多少种换法? 请列出该问题的算法。
3、下图中用点表示城市,点与点之间的联系表示城市间的道路:D CA B试问:① 能否找出一条从A 城市出发,经过图中所有道路一次后又回到出发点的通路来?② 能否从A 出发,找出去每个城市且只去一次的通路来? 若能,则写出通路,否则说明理由。
4、一个将角编了号的正三角形可以绕着外心O (中心)逆时针旋转1200,如下图所示: 1 30 02 3 1 2 如果将这一旋转用字母a 来表示,看作运算对象,同时用aa 或a 2 表示旋转1200EFa后再旋转1200,也就是说将连续运动看作乘法运算,那么三角形状态(可简称为元素)即可与运动表达式关联起来,请回答:①如果将图一的原始三角形连续旋转1200N次,简单地表示为a n(N为任意自然数),试求a n的值(指三角形旋转后的结果状态);②如果将下面的旋转看作是a的逆元素,记为a-1,则有a-1= a2试求:a-n3 10 0aa1 2 2 3图三5、已知一个数列U1,U2,U3,…,U N,…往往可以找到一个最小的K值和K个数a1,a2,…,a k使得数列从某项开始都满足:U N+K=a1U N+K-1+a2U N+K-2+……+a k U N(A) 例如对斐波拉契数列1,1,2,3,5,…可以发现:当K=2,a1 =1,a2 =1时,从第3项起(即N>=1)都满足U n+2 =U n+1+U n 。
信息学奥林匹克联赛辅导组选拔赛试题及答案.doc

6、 Menu ( )7、 Microsoft Windows XP ( )8、 Media Player ( )9、 Hardware ( ) 10、 Keyboard ( ) 信息学奥林匹克联赛辅导组选拔赛试题 考试时间:45分钟 卷面总分:100分 班级________ 姓名 分数第Ⅰ卷( 共55分)一、 按要求把每小题的最佳答案,填在题目中的相应括号中。
(共40分) 1、微型计算机的问世是由于( ) 的出现。
A 、小规模集成电路B 、晶体管电路C 、(超)大规模集成电路D 、电子管电路 2、在计算机内部,一切信息存取、处理和传递的形式是( )A 、 ascii 码B 、 bcd 码C 、 二进制D 、 十六进制 3、下列存储器中,存取速度最快的是( )。
A 、硬盘B 、光盘C 、软盘D 、内存 4、多媒体计算机是指( ) 计算机。
A 、专供家庭使用的 B 、装有光驱的 C 、连接在网络上的高级D 、具有处理文字、图形、声音、影像等信息的5、E-mail 地址中用户名和邮件所在服务器名之间的分隔符号是( ) 。
A 、# B 、@ C 、& D 、$6、下列设备中,(1___)不是微型计算机的输出设备,(2____)不是微型计算机的输入设备,计算机能同外部环境进行信息交换的设备是(3____)。
(1):A 、打印机 B 、显示器 C 、绘图仪 D 、键盘 (2):A 、显示器 B 、鼠标 C 、键盘 D 、手写板 (3):A 、输入、输出设备 B 、磁盘 C 、显示器 D 、打印机7、下列类型的文件中,不是图片文件的是( ) A 、*.bmp B 、*.jpg C 、*.ttf D 、*.wmv8、(多选题)下列不是计算机的存储设备的是( )。
A 、文件管理器B 、内存C 、显卡D 、硬盘E 、U 盘9、在树形目录结构中,不允许两个文件名相同主要是指( )。
A 、同一个磁盘的不同目录下 B 、不同磁盘的同一个目录下 C 、不同磁盘的不同目录下 D 、同一个磁盘的同一个目录下10、资源管理器的目录前图标中增加“+”号,这个符号的意思是( )。
信息学初赛模拟试题.doc

信息学初赛模拟试题一、选择一个正确答案代码(A/B/C/D ),填入每题的揺号内1、 M AN 英文缩写的含义是()A. 局域网B.城域网C.广域网D.增值网2、 小张用十六进制,八进制和十进制写了如下一个等式:64-13=33式中三个数是各不相同进位制的数,试问64, 13, 33,分别为 ________ oA.八进制,十进制,十六进制 B.十进制,十六进制,八进制 C.八进制,十六进制,十进制 D •十进制,八进制,十六进制3、 操作系统是一类重要的系统软件,下面几个软件中,不属于系统软件的是()。
A. Java B. MS-DOS C. Linux D. Windows2000 E. Unix4、 计算机病毒的传染是以计算机运行和( )为基础的,没有这两个条件,病毒是不会传染的。
A.编辑文稿B.读写磁盘C.编程序D.扔描图画E.打印5、 因特网不属于任何个人,也不属于任何组织。
其屮在网络知识这一块中有一个英文简写TSP,它的屮文 意思是( )。
A.因特网连接B.因特网使用C.因特网设计D.因特网服务提供者E.信息传输6、 I nternet 给我们提供了资源共享、浏览、检索信息和远程登录等多种服务,下面儿个选项中用于远程 登录的是( )。
A. WWWB. TCP/TPC. TelnetD. E-mailE. FTP 7、 T E 是冃前流行的浏览器软件,它的工作基础是解释执行用()语言书写的文件。
A. VC B. HTML C. BASIC D. HTTP E. VB8、 试指岀:下列if 语句中,当x=80吋,运行的结果为 _____ obeginy :=0;readln (x );if x<10 then beginy:=10;if x<100 then y:=100;endelse y:二200; writey 二',y); end.9、ASCII 码是( )oA.国标码B.二进制编码C.十进制编码D.美国标准信息交换码 10、一台计算机的字长是4个字节,这意味着( )。
信息学奥赛选拔考试

信息学奥赛选拔考试第一题(基础题,10分)题目描述:给定一个整数N(1 <= N <= 1000),计算并输出从1到N(包括N)之间所有整数的和。
输入:一行,包含一个整数N。
输出:一行,输出从1到N的和。
第二题(简单应用题,20分)题目描述:给定一个字符串S,只包含小写字母,请统计并输出每个字母出现的次数,按字母顺序排列。
输入:一行,包含一个字符串S(长度不超过1000)。
输出:多行,每行包含一个字母及其出现次数,按字母顺序排列。
第三题(中等题,30分)题目描述:给定一个整数数组A,数组中的元素两两不同。
现在要求你进行一系列操作,每次操作可以选择数组中的任意两个元素进行交换。
问至少需要多少次操作,才能使得数组A变为非递减序列(即对于任意i < j,都有A[i] <= A[j])。
输入:第一行包含一个整数N(1 <= N <= 1000),表示数组A的长度。
第二行包含N个整数,表示数组A的元素。
输出:一行,输出至少需要多少次操作才能将数组A变为非递减序列。
第四题(难题,40分)题目描述:给定一个无向图G,顶点集为V,边集为E。
图G中可能存在重边和自环。
现在要求你找出图G中所有简单环(即环中不重复经过任何顶点,但允许重复经过边)的长度,并按升序输出。
输入:第一行包含两个整数N和M(1 <= N <= 100, 1 <= M <= 1000),分别表示顶点数和边数。
接下来M行,每行包含两个整数u和v(1 <= u, v <= N),表示顶点u和v之间有一条边。
输出:多行,按升序输出图G中所有简单环的长度。
如果图中没有环,则输出一行"No cycles found."。
注意:本题可能需要使用深度优先搜索(DFS)结合回溯或并查集等高级算法技巧来解决。
2020 年第一届大湾区信息学竞赛 U12 组预赛真题及参考答案

一、选择1 下列不属于人工智能的应用实例是()A 车库门口的车牌自动识别系统B 商场卫生间的自动感应出水龙头C 苹果IOS里的Siri语音助手D 车站的人脸识别检测进站2 学校的电脑室里所有电脑都在同一网段,这些电脑都没装还原系统,信息课上淘气的小明将自己用的A电脑的IP地址改成了和同桌的B电脑一样的IP,下节课老师重启了全班的电脑后,会出现()A. A电脑可以上网,B电脑上不了网B. B电脑可以上网,A电脑上不了网C. 先联入网者可以上网,另一台则无法上网D. 两台电脑都无法上网3 for(int i = 0; i = 1; i++); for循环执行次数是()A. 0次B. 1次C. 2次D. 无限次4 黄女士买了一些点心去看一个老朋友,但这些点心被他的4个儿子偷吃了。
她问四个儿子是谁偷吃的,老大说“是老二吃的”,老二说“是老四吃的”,老三说“反正我没吃”,老四说“老二在说谎”,四个儿子中只有一人说了真话。
那么()偷吃了点心。
A. 老大B. 老二C. 老三D. 老四5 下列能控制和管理计算机系统的各种硬件和软件资源使用的软件是()A. 操作系统B. 中央处理器C. 数据库管理系统D. DevC++6 “大湾区青少年信息学编程竞赛”缩写为“BBCC”,请问字符串“BBCC”含有()个非空子串A. 10B. 9C. 7D. 47 不同类型的存储器组成了多层次结构的存储器体系,按存取速度由快排列的是()A. 快存>辅存>主存B. 外存>主存>辅存C. 快存>主存>辅存D. 主存>辅存>外存8 世界上有10种人,一种懂二进制,一种不懂。
这里的“10”是二进制表示法,若换成十进制则为()A. 0B. 1C. 2D. 39 实验小学原来体育成绩达标的人数与未达标的人数比是3:5,后来又有24名同学达标,这时达标人数与未达标人数的比是9/11,实验小学共有学生多少名?A. 300B. 320C. 500D. 80010 计算机最早的应用领域是A. 人工智能B. 文字处理C. 图形图像处理D. 数值计算二、填空1 执行C++语句int x = ‘y’- ‘a’后,变量x的值为()。
信息学奥赛学生选拔试题

信息学奥赛选拔学生试题班级:_________ 姓名:____________ 分数:____________一、警察局抓了ABCD四个偷窃嫌疑犯,其中只有一人是小偷。
审问中:A说:“我不是小偷”。
B说:“C 是小偷"。
C说:“小偷肯定是D”。
D说:“C冤枉人"。
现在知道四人中,只有一人说的假话,请你帮助警察叔叔说出谁是小偷。
二、这里有一系列数字,可是不全,你能把它们补充完整嘛?在横线上填写.0 1 1 2 3 5 8 13 21 ()55 ()144三、有一只猴子摘了一堆枣,第一天吃了一半,还嫌不过瘾,又吃了一个;第二天又吃了剩余的一半零一个,以后每天如此,到第五天,猴子一看只剩余一个了。
问最初有多少枣子?四、张明小朋友想把一张一元的钞票兑换成一分,二分和五分的硬币,要求每种至少一枚,三种硬币的总和为40枚。
你能不能帮助张明想一下,各种硬币应该各有多少呢?(写出一种即可).五、俗话说的好“一山不容二虎”,可是有一个山头却来了10只老虎,这可怎么办啊?谁来当大王呢?他们想到一个办法,就是10只老虎站成一排,先从左边开始数,1,2,3,1,2,3这样来数,数到头以后,数3的老虎退出大王竞选,剩余的老虎再从右面开始数,1,2,3,1,2,3,也是数3的老虎退出竞选;依次类推,直到剩下两只老虎时,数2的老虎为大王。
请问,第几只老虎是大王呢(以最初10只老虎站队时为标准,从左向右数.)六、某医院有A,B,C,D,E,F,G七位大夫。
他们在一星期内每天要值班一次。
排班的要求为(1)A大夫值班日比C大夫晚一天;(2)D大夫值班日比E大夫晚两天;(3)B大夫值班日比G大夫早三天;(4)F大夫值班日在B,C大夫值班日中间,且在星期四.你能否帮助医院给这七位大夫排出值班日呢?七、有一天张晓同学在做数学题时发现一个好玩的游戏。
游戏是这样的:他把一个数,比如123,然后在数的中间填上两个运算符号,如1X2X3,当然也可以1+2X3,他奇怪的发现1+2X3竟然比1X2X3还要大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信息学竞赛选拔赛试题(满分100分,时间120分钟)一、选择题(15分):1.十进制数2003等值于二进制数( )。
A . 010******* B. 10000011 C. 110000111 D. 11111010011 E. 11110100112.已知数组中A 中,每个元素A (I ,J )在存贮时要占3个字节,设I 从1变化到8,J 从1变化到10,分配内存时是从地址SA 开始连续按行存贮分配的。
试问:A (5,8)的起始地址为( )A.SA+141B. SA+180C. SA+222D. SA+2253.将 5 个数的序列排序,不论原先的顺序如何,最少都可以通过( )次比较,完成从小到大的排序。
A. 6B. 7C. 8D. 9E. 104.在 Pascal 语言中,表达式 (21 xor 2)的值是( )A. 441B. 42C.23D.24E.255.在顺序表(2,5,7,10,14,15,18,23,35,41,52)中,用二分法查找12,所需的关键码比较的次数为( )A.2B.3C.4D.5 二、数学问题及算法分析:1.(5分)一棵二叉树的前序遍历和中序遍历分别如下,画出该二叉树。
前序遍历:ABCDEFGHIJ 中序遍历:CBEDAGHFJI 2. (5分)在印度,有这么一个古老的传说:在世界中心贝拿勒斯(在印度北部)的圣庙里,一块黄铜板上插着三根宝石针。
印度教的主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的64片金片,这就是所谓的汉诺塔。
不论白天黑夜,总有一个僧侣在按照下面的法则移动这些金片:一次只移动一片,不管在哪根针上,小片必须在大片上面。
僧侣们预言,当所有的金片都从梵天穿好的那根针上移到另外一根针上时,世界就将在一声霹雳中消灭,而梵塔、庙宇和众生也都将同归于尽。
不管这个传说的可信度有多大,我们先来做题! 给定A 、B 、C 三根足够长的细柱,在A 柱上放有2n 个中间有孔的圆盘,共有n 个不同的尺寸,每个尺寸都有两个相同的圆盘,注意这两个圆盘是不加区分的(下图为n=3的情形)。
现要将这些圆盘移到C 柱上,在移动过程中可放在B 柱上暂存。
要求:(1)每次只能移动一个圆盘;(2)A 、B 、C 三根细柱上的圆盘都要保持上小下大的顺序; 任务:设An 为2n 个圆盘完成上述任务所需的最少移动次数,对于输入的N ,写出An 的解析式。
3. (10分)打水问题有N 个人在一个水龙头前排队接水,每个人接水的时间Ti 是互不相等的。
找到一种这N 个人排队接水的顺序,使他们平均等待的时间达到最小。
请写出这道题的解题思路。
4. (10分)合并果子在一个果园里,多多已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。
多多决定把所有的果子合成一堆。
每一次合并,多多可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。
可以看出,所有的果子经过n-1次合并之后,就只剩下一堆了。
多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家,所以多多在合并果子时要尽可能地节省体力。
假定每个果子重量都为1,并且已知果子的种类数和每种果子的数目,你的任务是设计出合并的次序方案,使多多耗费的体力最少,并输出这个最小的体力耗费值。
例如有3种果子,数目依次为1,2,9。
可以先将 1、2堆合并,新堆数目为3,耗费体力为3。
接着,将新堆与原先的第三堆合并,又得到新的堆,数目为12,耗费体力为 12。
所以多多总共耗费体力=3+12=15。
可以证明15为最小的体力耗费值。
对给定的果子的堆数和每堆果子的果子数目,请写出该题的解题思路。
.三、程序阅读(30分):1. program ex2;var i,j,n:longint;b:array [0..31] of 0..1; begin n=1999; i:=0;while n<>0 do beginb[i]:=n mod 2; i:=i+1; n:=n div 2 end;for j:=i-1 downto 0 do write(b[j]); end.输出: 2. program primenumber; varflag :boolean; n,sum,i,j,p :integer;rec :array[1..25] of integer; begin n:=100;sum:=0;for i:=1 to n do beginflag:=true;if i=1 thenbeginflag:=false;endelsebeginp:=trunc(sqrt(i));for j:=2 to p do if i mod j =0 then flag:=false; end;if flag then begin inc(sum); rec[sum]:=i; end;end;for i:=1 to sum dobeginif (i mod 5=1)and(i<>1) then writeln;write(rec[i],' ');end;end.程序运行结果:3.program pascaltriangle;varf :array[0..20,0..20] of integer;i,j,n :integer;beginn:=9;for i:=0 to 20 dofor j:=0 to 20 do f[i,j]:=0;f[1,1]:=1;for i:=2 to n dofor j:=1 to j dof[i,j]:=f[i-1,j-1]+f[i-1,j];for i:=1 to n dobeginfor j:= 1 to i do write(f[i,j],' ');writeln;end;end.程序运行结果: 四、程序填空(25分):1.每一趟从待排序的数据元素中选出最小(或最大)的一个元素用变量K记录该元素的位置,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。
在该程序中用数组a记录待排序列。
program selectsort;var i,j,k,temp:integer;a:array[0..100] of integer;beginfor i:=n downto 2 dobegink:=1;for j:=1 to i do ①___________;temp:=a[k];②________________;a[j]:=temp;end;for i:=1 to n do write(a[i],' ');end.2.高精度算法,属于处理大数字的数学计算方法。
在一般的科学计算中,会经常算到小数点后几百位或者更多,当然也可能是几千亿几百亿的大数字。
一般这类数字我们统称为高精度数,高精度算法是用计算机对于超大数据的一种模拟加,减,乘,除,乘方,阶乘,开方等运算。
对于非常庞大的数字无法在计算机中正常存储,于是,将这个数字拆开,拆成一位一位的,或者是四位四位的存储到一个数组中,用一个数组去表示一个数字,这样这个数字就被称谓是高精度数。
高精度算法就是能处理高精度数各种运算的算法。
在该题中,用数组A记录加数,B记录小数字加数,用数组C记录A与B的和,A[0]和c[0]存放该数字的位数。
program add;typedata =array[0..1000] of integer;vara,c :data;b :integer;procedure inputdata;vari,j,len :integer;s :string;beginreadln(s);①_______len:=length(s);for i:=1 to len do val(s[len+1-i],a[i]);a[0]:=len;end;procedure work(a:data; b:Integer; var c:data); vari,k :integer;beginfillchar(c,sizeof(c),0);for i:=1 to a[0] dobegin②_______c[i]:=k mod 10;c[i+1]:=k div 10;end;i:=i+1;while c[i] div 10 > 0 dobegink:=c[i];c[i]:=k mod 10;c[i+1]:=k div 10;i:=i+1;end;while (c[i]=0)and(i>1) do ③_______c[0]:=i;end;procedure outputdata(a:data);vari :integer;beginfor i:=a[0] downto 1 do write(a[i]);end;begininputdata;work(a,b,c);outputdata(c);end. 请将答案写在下面:一、选择题(15分):1-5:二、数学问题与算法分析:1.(5分)2.(5分)3.(10分)4.(10分)三、程序阅读(30分)1.2.3.四、程序填空(25分)1. ①_______________________②_______________________2. ①_______________________②_______________________③_______________________。
