2016年4月自考高等数学工本(00023)试题及答案
00023高等数学(工本)201504【答案在试卷后】

2015年4月高等教育自学考试全国统一命题考试高等数学(工本) 试卷(课程代码 00023)第一部分选择题一、单项选择题[更多科目真题及答案请访问/zikao.htm](本大题共5小题,每小题3分,共15分)1.向量a={2,1,-l}与b={1,2,1}的夹角为2.已知函数,3. 已知二重积分,则积分区域D为4. 微分方程笔是A.可分离变量的微分方程 B.齐次微分方程C.一阶线性齐次微分方程 D.一阶线性非齐次微分方程5.无穷级数的敛散性为A.条件收敛 B. 绝对收敛 C发散 D.敛散性无法确定第二部分非选择题二、填空题(本大题共5小题,每小题2分,共10分)请在答题卡上作答。
6.点P(-5,-3,2)到oyz坐标面的距离为________。
7.函数z=z2 y+y2在点(2,1)处的全微分=_________。
8. 设积分区域D:x2+y2≤a2(a﹥0),且二重积分,则常数a=_______。
9.微分方程y〞+3y=e2x的特解y*=_________。
10.已知无穷级数。
三、计算题(本大题共l2小题,每小题5分,共60分)请在答题卡上作答。
11.求过点M l(3,-l,5)及点M2(-1,2,-3)的直线方程.12.求曲面z=2xy在点处的切平面方程.13.已知方程2xy2—3y2+5z2一z=1确定函数z=z(x,y),求14.求函数f(x,y)=2xy2--3x2y在点P(1,--1)处沿P(1,-1)到Q(2,0)方向的方向导数.15.计算二重积分,其中D是由y=x2,y=z所围成的区域.16.计算三重积分,其中积分区域Ω:|x|≤1,|y|≤1,|z|≤1.17.计算对弧长的曲线积分,其中C为从点A(2,0)到B(4,0)的直线段.18.计算对坐标的曲线积分,其中C是抛物线z—y2从点0(0,0)到点P(4,2)的一段弧.19.求微分方程的通解.20.求微分方程y〞+yˊ-30y=0的通解.21. 判断无穷级数的敛散性.22.已知f(x)是周期为的周期函数,它在上的表达式为,求f(x)傅里叶级数中系数a6四、综合题(本大题共3小题,每小题5分,共15分)请在答题卡上作答。
四川省高等教育自学考试2016年4月(16·1次)
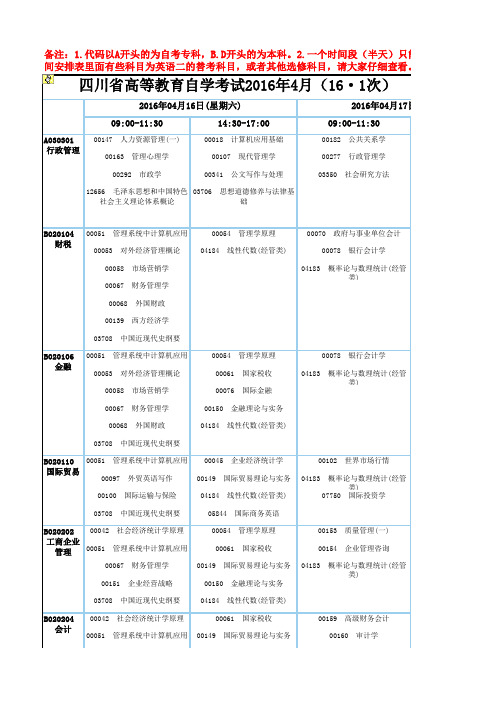
09:00-11:3014:30-17:0009:00-11:3000147 人力资源管理(一)00018 计算机应用基础00182 公共关系学00163 管理心理学00107 现代管理学00277 行政管理学00292 市政学00341 公文写作与处理03350 社会研究方法12656 毛泽东思想和中国特色社会主义理论体系概论03706 思想道德修养与法律基础00051 管理系统中计算机应用00054 管理学原理00070 政府与事业单位会计00053 对外经济管理概论04184 线性代数(经管类)00078 银行会计学00058 市场营销学04183 概率论与数理统计(经管类)00067 财务管理学00068 外国财政00139 西方经济学03708 中国近现代史纲要00051 管理系统中计算机应用00054 管理学原理00078 银行会计学00053 对外经济管理概论00061 国家税收04183 概率论与数理统计(经管类)00058 市场营销学00076 国际金融00067 财务管理学00150 金融理论与实务00068 外国财政04184 线性代数(经管类)03708 中国近现代史纲要00051 管理系统中计算机应用00045 企业经济统计学00102 世界市场行情00097 外贸英语写作00149 国际贸易理论与实务04183 概率论与数理统计(经管类)00100 国际运输与保险04184 线性代数(经管类)07750 国际投资学03708 中国近现代史纲要05844 国际商务英语00042 社会经济统计学原理00054 管理学原理00153 质量管理(一)00051 管理系统中计算机应用00061 国家税收00154 企业管理咨询00067 财务管理学00149 国际贸易理论与实务04183 概率论与数理统计(经管类)00151 企业经营战略00150 金融理论与实务03708 中国近现代史纲要04184 线性代数(经管类)00042 社会经济统计学原理00061 国家税收00159 高级财务会计00051 管理系统中计算机应用00149 国际贸易理论与实务00160 审计学备注:1.代码以A开头的为自考专科,B.D开头的为本科。
自学考试 《高等数学(工本)》历年真题全套试题

自考00023《高等数学(工本)》历年真题集电子书目录1. 目录 (2)2. 历年真题 (5)2.1 00023高等数学(工本)200404 (5)2.2 00023高等数学(工本)200410 (7)2.3 00023高等数学(工本)200504 (9)2.4 00023高等数学(工本)200507 (11)2.5 00023高等数学(工本)200510 (14)2.6 00023高等数学(工本)200604 (15)2.7 00023高等数学(工本)200607 (18)2.8 00023高等数学(工本)200610 (21)2.9 00023高等数学(工本)200701 (24)2.10 00023高等数学(工本)200704 (26)2.11 00023高等数学(工本)200707 (28)2.12 00023高等数学(工本)200710 (29)2.13 00023高等数学(工本)200801 (34)2.14 00023高等数学(工本)200804 (35)2.15 00023高等数学(工本)200807 (36)2.16 00023高等数学(工本)200810 (38)2.17 00023高等数学(工本)200901 (39)2.18 00023高等数学(工本)200904 (40)2.19 00023高等数学(工本)200907 (42)2.20 00023高等数学(工本)200910 (43)2.21 00023高等数学(工本)201001 (45)2.22 00023高等数学(工本)201004 (46)2.23 00023高等数学(工本)201007 (47)2.24 00023高等数学(工本)201010 (49)2.25 00023高等数学(工本)201101 (50)2.26 00023高等数学(工本)201104 (52)2.27 00023高等数学(工本)201107 (54)2.28 00023高等数学(工本)201110 (55)2.29 00023高等数学(工本)201204 (57)3. 相关课程 (59)1. 目录历年真题()00023高等数学(工本)200404()00023高等数学(工本)200410()00023高等数学(工本)200504()00023高等数学(工本)200507()00023高等数学(工本)200510()00023高等数学(工本)200604()00023高等数学(工本)200607()00023高等数学(工本)200610()00023高等数学(工本)200701()00023高等数学(工本)200704() 00023高等数学(工本)200707() 00023高等数学(工本)200710() 00023高等数学(工本)200801() 00023高等数学(工本)200804() 00023高等数学(工本)200807() 00023高等数学(工本)200810() 00023高等数学(工本)200901() 00023高等数学(工本)200904() 00023高等数学(工本)200907()00023高等数学(工本)200910()00023高等数学(工本)201001()00023高等数学(工本)201004()00023高等数学(工本)201007()00023高等数学(工本)201010()00023高等数学(工本)201101()00023高等数学(工本)201104()00023高等数学(工本)201107()00023高等数学(工本)201110()00023高等数学(工本)201204() 相关课程()2. 历年真题2.1 00023高等数学(工本)200404高等数学(工本)试题(课程代码0023)一、单项选择题(本大题共20小题,每小题2分,共40分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
2010-2014年高等数学(工本)00023历年精彩试题及参考问题详解

2010-2014年高等数学(工本)00023历年试题及参考答案 全国2010年10月自学考试高等数学(工本)试题一、单项选择题(本大题共5小题,每小题3分,共15分) 1.在空间直角坐标系下,方程2x 2+3y 2=6表示的图形为( ) A .椭圆 B .柱面 C .旋转抛物面D .球面2.极限021lim →→y x arcsin(x +y 2)=( )A .6πB .3π C .2π D .π3.设积分区域22:y x Ω+≤R 2,0≤z ≤1,则三重积分⎰⎰⎰=+Ωdxdydz y xf )(22( )A .⎰⎰⎰π200102)(Rdz r f drd θ B .⎰⎰⎰π20012)(Rdz r f rdrd θC .⎰⎰⎰+π201022)(Rrdz y x f dr d θD .⎰⎰⎰π102)(Rdz r f rdrd θ4.以y =sin 3x 为特解的微分方程为( ) A .0=+''y y B .0=-''y y C .09=+''y y D .09=-''y y5.设正项级数∑∞=1n nu收敛,则下列无穷级数中一定发散的是( )A .∑∞=+1100n nuB .∑∞=++11)(n n n u uC .∑∞=1)3(n nuD .∑∞=+1)1(n nu二、填空题(本大题共5小题,每小题2分,共10分)请在每小题的空格中填上正确答案。
错填、不填均无分。
6.向量a ={1,1,2}与x 轴的夹角=α__________. 7.设函数22),(y x xy y x f -=,则=)1,(x yf __________.8.设∑是上半球面z =221y x --的上侧,则对坐标的曲面积分⎰⎰∑=dxdy y 3__________.9.微分方程x y y sin 3='+'''的阶数是__________.10.设)(x f 是周期为2π的函数,)(x f 在[)ππ,-上的表达式为[)[)⎪⎩⎪⎨⎧∈-∈=.π,0,23sin .0,π,0)(x x x x f )(x S 是)(x f 的傅里叶级数的和函数,则S (0) =__________.三、计算题(本大题共12小题,每小题5分,共60分)11.设平面π过点P 1(1,2,-1)和点P 2(-5,2,7),且平行于y 轴,求平面π的方程. 12.设函数22ln y x z +=,求yx z∂∂∂2.13.设函数232y x e z -=,求全微分dz .14.设函数)2,(22xy y x f z -=,其中f (u , v )具有一阶连续偏导数,求xz ∂∂和y z ∂∂. 15.求曲面x 2+y 2+2z 2=23在点(1,2,3)处的切平面方程. 16.计算二重积分⎰⎰+D dxdy y x )sin(22,其中积分区域D :x 2+y 2≤a 2.17.计算三重积分⎰⎰⎰Ωzdxdydz ,其中Ω是由曲面z =x 2+y 2,z =0及x 2+y 2=1所围区域.18.计算对弧长的曲线积分⎰Cds x 2,其中C 是圆周x 2+y 2=4的上半圆.19.计算对坐标的曲线积分⎰+-+-Cdy y x dx y )21()31(,其中C 为区域D :| x |≤1,| y |≤1 的正向边界曲线.20.求微分方程02=-+-dy e dx e y x y x 的通解. 21.判断无穷级数∑∞=--+1212)1(1n n n 的敛散性. 22.将函数51)(+=x x f 展开为x +1的幂级数. 四、综合题(本大题共3小题,每小题5分,共15分)23.设函数)(x yz ϕ=,其中)(u ϕ为可微函数.证明:0=∂∂+∂∂y zy x z x24.设曲线y =y (x )在其上点(x , y )处的切线斜率为xyx -24,且曲线过点(1,1),求该曲线的方程. 25.证明:无穷级数∑∞=-=++-+121)122(n n n n .全国2011年1月自学考试高等数学(工本)试题一、单项选择题(本大题共5小题。
全国2016年10月高等教育(工本)自学考试试题、详细答案及考点分析

一、单项选择题(本大题共 5 小题,每小题 3 分,共 15 分) 在每小题列出的四个备选项中只有一个是最符合题目要求的,请将其选出并将“答题卡” 的相应代码涂黑。错涂、多涂或未涂均无分。
1. 在空间直角坐标系中,点 14,3,24 在
A.第二卦限
0
0
0
2 d 2 d 1 r 2 1 r 2 sin dr
0
0
0
2 d 2 sin d 1 r 4 r 2 dr
0
0
0
2
1
1 5
r
5
1 3
r
3
1 0
4 . 15
考核知识点:三重积分的计算(简单应用); 考核要求:掌握计算三重积分的柱面坐标、球面坐标变换法.
考核要求:熟练掌握偏导数求法.
3. 设积分区域 D: x2 y2 1,则二重积分 x d D
A. 4
2 d
1 r cosdr
0
0
B. 2 d 1 r sindr
0
0
C. 2 d 1 r 2 sindr
0
0
D. 2 d 1 r 2 cosdr
0
0
解答:根据极坐标下二重积分的计算方法进行求解。由于积分区域 D: x2 y2 1 ,因此积
dy dx
ex
ey
dy ey
e x dx
故该微分方程为可分离变量的微分方程,选 A.
考核知识点:三类一阶微分方程(简单应用); 考核要求:会求可.分.离.变.量.的.微.分.方.程.、齐次方程、一阶线性微分方程这三种类型方程的通
解和特解.
5.
设无穷级数
1
2016年4月全国自考高等数学(工本)真题试卷(题后含答案及解析)

2016年4月全国自考高等数学(工本)真题试卷(题后含答案及解析) 题型有:1. 单项选择题 2. 填空题 3. 计算题 4. 综合题单项选择题在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.直线z=1+2t,y=一1一t,z=2t的方向向量是( )A.{2,一1,2}B.{2,1,2}C.{一1,1,0}D.{1,一1,0}正确答案:A解析:直线x=1+2t,y=-1-t,z=2t可以转化为对称式方程,故直线的方向向量为{2,一1,2}.2.设函数f(x,y)=h(x)g(y)在点(x0,y0)的某邻域内有定义,且存在一阶偏导数,则fy(x0,y0)= ( )A.B.C.D.正确答案:C3.设积分区域D:x2+y2≤1,则二重积分f()dxdy= ( ) A.4πf(r)drB.2πrf(r)drC.2πf(r2)drD.2πF(r)dr正确答案:B4.微分方程+x2y=cosx是( )A.可分离变量的微分方程B.齐次微分方程C.一阶线性齐次微分方程D.一阶线性非齐次微分方程正确答案:D5.设无穷级数收敛,则在下列数值中p的取值为( ) A.B.C.1D.2正确答案:D解析:收敛,故||1,故本题选D.填空题请在每小题的空格中填上正确答案。
错填、不填均无分。
6.点P(3,2,0)到平面3x-2y+z+7=0的距离为________.正确答案:3解析:点P到平面3x-2y+z+7=0的距离d==3.7.已知函数f(x,y)=,则f()=_____________.正确答案:解析:8.设积分区域D:|x|≤a,|y|≤a,且二重积分=4,则常数a=__________.正确答案:19.微分方程y”一y=e-3x的特解y*=___________.正确答案:.解析:已知微分方程y”一y=e-3x为二阶常系数线性非齐次微分方程,m=0,λ=一3,而对应齐次方程的特征方程为r2—1=0,解得r=±1,故λ不是该齐次方程的特征根,故可设原微分方程的特解为y*=a0e-3x,则y*’=一3a0e-3x,y*”=9a0e-3x,代入原微分方程可得9a0e-3x一a0e-3x=e-3x,得a0=,故原微分方程的特解为y*=e-3x.10.已知无穷级数,则un=___________.正确答案:计算题11.求过点C(一1,2,一4)并且垂直于平面2x-3y+z-6=0的直线方程.正确答案:因为直线方向向量S={2,一3,1},所以,所求直线方程为.12.求曲线x=2t,y=t2,z=1+t3在对应于t=1的点处的法平面方程.正确答案:对应于t=1的点为(2,1,2),因为x’=2,y’=2t,z’=3t2,所以,对应于t=1的点处的法向量n={2,2,3},从而所求法平面方程为2(x 一2)+2(y一1)+3(z一2)=0,即2x+2y+3z一12=0.13.求函数z=e2x+3y的全微分dz.正确答案:因为2e2x+3y,=3e2x+3y,所以dz=2e2x+3ydx+3e2x+3ydy=e2x+3y(2dx+3dy)14.求函数f(x,y,z)=x2+2y2+3z2+xy一3x+2y一6z在点P(1,1,1)处的梯度gradf(1,1,1).正确答案:因为=2x+y--3,=4y+x+2,=6z一6,所以从而gradf(1,1,1)={0,7,0}.15.计算二重积分,其中D是由y=x,x=1及y=0所围成的区域.正确答案:16.计算三重积分(1一x)dv,其中Ω是由曲面z=x2+y2和z=1所围成的区域.正确答案:由对称性得xdv=0,所以17.计算对弧长的曲线积分(2-2x2y+x)ds,其中C是从点A(一1,一1)到B(-1,2)的直线段.正确答案:直线段C的方程为x=一1(一1≤y≤2),ds=dy=dy,所以(2—2x2y+x)ds=(1—2y)dy=(y-y2)=018.计算对坐标的曲线积分(x—y)dx+xydy,其中C为直线y=x从点O(0,0)到点A(1,1)的线段.正确答案:C的方程y=x,x从0变到1,所以19.求微分方程的通解.正确答案:分离变量后得e2ydy=exdx,两边积分得,从而通解为e2y=ex+C.20.求微分方程y”+y’一6y=0的通解.正确答案:特征方程为r2+r一6=0,特征根为r1=2,r2=一3,所以通解为y=C1e2x+C2e-3x.21.判断无穷级数的敛散性.正确答案:令,则,并且收敛.22.已知f(x)是周期为2π的周期函数,它在[一π,π)上的表达式为求f(x)傅里叶级数(ancosnx+bnsinnx)中系数a4.正确答案:综合题23.某工厂生产的两种商品的产量x和y的利润函数为L(x,y)=64x+32y+4xy 一2x2一4y2+36求获得最大利润时两种商品的产量,并求最大利润.正确答案:令解得x=40,y=24,驻点唯一.并且L(40,24)=1700,故两种商品的产量分别为40和24时,获得最大利润为1700.24.证明对坐标的曲线积分(20sin3x+2y)dx+(2x一14cosy)dy在整个xOy 面内与路径无关.正确答案:令P(x,y)=20sin3x+2y,Q(x,y)=2x一14cosy,因为=2,=2,且,所以,在整个xOy面内曲线积分与路径无关.25.将函数f(x)=展开为x的幂级数.正确答案:。
4月全国自考高等数学(工本)试题及答案解析

1全国2018年4月自学考试高等数学(工本)试题课程代码:00023一、单项选择题(本大题共5小题,每小题3分,共15分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.在空间直角坐标系中,方程1222222=++cz b y a x 表示的图形是( )A.椭圆抛物面B.圆柱面C.单叶双曲面D.椭球面2.设函数z =x 2y ,则=∂∂xz( ) A.212-y yxB.x xyln 2C.x x yln 22 D.()12-y yx3.设Ω是由平面01=-+-z y x 及坐标面所围成的区域,则三重积分=⎰⎰⎰Ωdxdydz ( ) A.81 B.61 C.31 D.21 4.已知微分方程)()(x Q y x P y =+'的两个特解为y 1=2x 和y 2=cos x ,则该微分方程的通解是y =( ) A.2C 1x +C 2cos x B.2Cx +cos x C.cos x +C (2x -cos x ) D.C (2x -cos x )5.设幂级数∑∞--1)3(n n nx a在x =1处收敛,则在x =4处该幂级数( )A.绝对收敛B.条件收敛2C.发散D.敛散性不定二、填空题(本大题共5小题,每小题2分,共10分)请在每小题的空格中填上正确答案。
错填、不填均无分。
6.设函数y x y z cos sin =,则=∂∂xz. 7.已知dy e dx e y x yx +++是某函数()y x u ,的全微分,则()=y x u , .8.设∑是上半球面()01222≥=++z z y x ,则对面积的曲面积分⎰⎰∑=dS .9.微分方程x y 2sin =''的通解为y= .10.无穷级数∑∞=0!2n nn 的和为 .三、计算题(本大题共12小题,每小题5分,共60分) 11.求过点P (3,-1,0)并且与直线321-=-=z y x 垂直的平面方程. 12.设函数()y x x f z -=,3,其中f 是可微函数,求x z ∂∂,yz∂∂. 13.设方程xyx ln=确定函数()y x z z ,=,求全微分dz. 14.求函数()22,xy y x y x f +=在点(1,-1)沿与x 轴正向成30°角的方向l 的方向导数.15.求空间曲线t z t y t x ===,sin ,cos 在点⎪⎪⎭⎫⎝⎛4,22,22π处的切线方程.16.计算二重积分()dxdy e I Dy x⎰⎰+-=22,其中区域D :.0,422≥≤+y y x17.计算二次积分⎰⎰=22sin ππydx xxdy I . 18.计算对弧长的曲线积分()⎰+-L ds y x 132,其中L 是直线2-=x y 上从点(-1,-3)到点(1,-1)的直线段. 19.计算对坐标的曲线积分⎰+Lydx xdy 其中L 是抛物线2x y =上从点(-2,4)到点(2,4)的一段3弧.20.求微分方程034=+'-''y y y 满足初始条件()8)0(,40='=y y 的特解. 21.判断级数()∑∞=-+-131321n n nn 是否收敛,如果收敛,是条件收敛还是绝对收敛?22.设函数()⎩⎨⎧<≤<≤-=ππx x x x f 0,0,0的傅里叶级数展开式为()∑∞=++10sin cos 2n n n nx b nx a a ,求系数b 7.四、综合题(本大题共3小题,每小题5分,共15分) 23.求函数()y x xy y x y x f 311381021,22-----=的极值.24.设曲线()x y y =在其上点(x ,y )处的切线斜率为x +y ,且过点(-1,e -1),求该曲线方程. 25.将函数()2312+-=x x x f 展开为(x +1)的幂级数.。
4月全国高等数学(工本)自考试题及答案解析

全国2019年4月高等数学(工本)试题课程代码:00023第一部分 选择题 (共40分)一、单项选择题(本大题共20小题,每小题2分,共40分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.下列各对函数中,表示同一个函数的是( ) A.f(x)=1x 1x 2+-与g(x)=x-1B.f(x)=lgx 2与g(x)=2lgxC.f(x)=x cos 12-与g(x)=sinxD.f(x)=|x|与g(x)=2x 2.函数f(x)=sine x 是( ) A.奇函数B.偶函数C.单调函数D.非奇非偶函数3.x=2是函数f(x)=2)2x (1-的( )A.可去间断点B.跳跃间断点C.无穷间断点D.振荡间断点4.f(x)在x 0处左、右极限存在并相等是f(x)在x 0处连续的( ) A.充分条件 B.必要条件 C.充分必要条件 D.前三者均不对5.=+++∞→3n n )3n )(2n )(1n (lim ( )A.0B.1C.3D.66.设函数f(x)=xx 1x232-,则=')1(f ( )A.67B.67-C.61D. 61-7.设y=x+lnx,则=dy dx( ) A.x1x + B. y 1y + C1x x+D.1y y+ 8.=)x log x1(d 3( )A.3ln x 12B.xdx log x 132-C. 3ln x 1D.dx xxlog 3ln 123-9.若a,b 是方程f(x)=0的两个不同的根,函数f(x)在[a,b]上满足罗尔定理条件,那么方程0)x (f ='在(a,b)内( ) A.仅有一个根B.至少有一个根C.没有根D.以上结论均不对 10.函数f(x)=x-ln(1+x 2)的极值( ) A.是1-ln2 B.是-1-ln2 C.不存在D.是011.若⎰⎰=++=dx )1x 2(f ,C )x (F dx )x (f 则( ) A.2F(2x+1)+C B.C )1x 2(F 21++ C.C )x (F 21+D.2F(x)+C12.设I=⎰-22,dx )x 2x (则I 满足( )A.0I 2≤≤-B.2I 0≤≤C.1I 1≤≤-D.4I 1≤≤13.曲线y=22x 5y x 41-=和所围图形面积为( ) A.⎰---2222dx )x 41x 5(B.⎰---2222dx )x 5x 41( C.⎰---1122dx )x 41x 5( D. ⎰---1122dx )x 5x 41(14.二个平面14z3y 2x =++和2x+3y-4z=1位置关系是( )A.相交但不垂直B.重合C.平行但不重合D.垂直15.函数z=22y x 1--的定义域是( ) A. D={(x,y)|x 2+y 2=1} B. D={(x,y)|x 2+y 2≥1} C. D={(x,y)|x 2+y 2<1}D. D={(x,y)|x 2+y 2≤1}16.交换积分次序后,⎰⎰=xln 0e1dy )y ,x (f dx ( ) A. ⎰⎰ye e10dx )y ,x (f dyB. ⎰⎰eedx )y ,x (f dyC.⎰⎰ee10ydx )y ,x (f dyD.⎰⎰eee 0ydx )y ,x (f dy17.设C 是以O(0,0),A(1,0),B(0,1)为顶点的三角形边界,则曲线积分⎰=+C ds )y x (( )A.2B.2+2C.1+2D.1+22 18.微分方程0y 3y 4y =+'-''的通解y=( ) A.C 1C 2e 3x +e x B.Ce 3x +Ce x C.e 3x +C 1e x +C 2e xD.C 1e 3x +C 2e x19.若0u lim n n =∞→,则无穷级数∑∞=1n n u ( )A.条件收敛B.绝对收敛C.发散D.不能确定是否收敛或发散20.幂级数∑∞=⋅-1n nn 3n )3x (的收敛域是( ) A.(-3,3)B.(-3,3]C.[-3,3]D.[0,6)第二部分 非选择题 (共60分)二、填空题(本大题共10小题,每小题2分,共20分) 21.已知f(x)=x11-,则f[f(x)]=____________. 22.已知42x x 20ax x lim222x =---+→,则a=___________.23.设函数f(x)为可导的偶函数,则=')0(f ___________. 24.若c )x (f lim x =+∞→,则曲线y=f(x)有渐近线___________.25.⎰=+_________dx )x1x (.26.⎰-=+aa43dx x1x 2cos x ____________.27.点M (-1,2,3)关于坐标面xoy 的对称点为_____________. 28.设B 是由x=1,x=0,y=1和y=0所围成的区域,则⎰⎰+Bdxdy )x 1(=_________.29.函数f(x)=2xe 在x=0处的泰勒级数为_________.30.微分方程0y dxdy=-的通解为___________. 三、计算题(本大题共5小题,每小题5分,共25分)31.求极限xx )x1x 1(lim -+∞→32.计算不定积分⎰+dx )tgx 1(x cos 12 33.求过点(1,0,0),(0,2,0)和(0,0,3)的平面方程。
高等数学(工本)00023历年试题及参考答案

高等数学(工本)历年试题及参考答案 自学考试高等数学(工本)试题一、单项选择题(本大题共5小题,每小题3分,共15分) 1.在空间直角坐标系下,方程2x 2+3y 2=6表示的图形为( ) A .椭圆 B .柱面 C .旋转抛物面D .球面2.极限021lim →→y x arcsin(x +y 2)=( )A .6πB .3π C .2π D .π3.设积分区域22:y x Ω+≤R 2,0≤z ≤1,则三重积分⎰⎰⎰=+Ωdxdydz y xf )(22( )A .⎰⎰⎰π200102)(Rdz r f drd θ B .⎰⎰⎰π20012)(Rdz r f rdrd θC .⎰⎰⎰+π20122)(Rrdz y x f dr d θD .⎰⎰⎰π102)(Rdz r f rdrd θ4.以y =sin 3x 为特解的微分方程为( ) A .0=+''y y B .0=-''y y C .09=+''y y D .09=-''y y5.设正项级数∑∞=1n nu收敛,则下列无穷级数中一定发散的是( )A .∑∞=+1100n nuB .∑∞=++11)(n n n u uC .∑∞=1)3(n nuD .∑∞=+1)1(n nu二、填空题(本大题共5小题,每小题2分,共10分)请在每小题的空格中填上正确答案。
错填、不填均无分。
6.向量a ={1,1,2}与x 轴的夹角=α__________. 7.设函数22),(y x xy y x f -=,则=)1,(x yf __________.8.设∑是上半球面z =221y x --的上侧,则对坐标的曲面积分⎰⎰∑=dxdy y 3__________.9.微分方程x y y sin 3='+'''的阶数是__________.10.设)(x f 是周期为2π的函数,)(x f 在[)ππ,-上的表达式为[)[)⎪⎩⎪⎨⎧∈-∈=.π,0,23sin .0,π,0)(x x x x f )(x S 是)(x f 的傅里叶级数的和函数,则S (0) =__________.三、计算题(本大题共12小题,每小题5分,共60分)11.设平面π过点P 1(1,2,-1)和点P 2(-5,2,7),且平行于y 轴,求平面π的方程. 12.设函数22ln y x z +=,求yx z∂∂∂2.13.设函数232y x e z -=,求全微分dz .14.设函数)2,(22xy y x f z -=,其中f (u , v )具有一阶连续偏导数,求xz ∂∂和y z ∂∂. 15.求曲面x 2+y 2+2z 2=23在点(1,2,3)处的切平面方程. 16.计算二重积分⎰⎰+D dxdy y x )sin(22,其中积分区域D :x 2+y 2≤a 2.17.计算三重积分⎰⎰⎰Ωzdxdydz ,其中Ω是由曲面z =x 2+y 2,z =0及x 2+y 2=1所围区域.18.计算对弧长的曲线积分⎰Cds x 2,其中C 是圆周x 2+y 2=4的上半圆.19.计算对坐标的曲线积分⎰+-+-Cdy y x dx y )21()31(,其中C 为区域D :| x |≤1,| y |≤1 的正向边界曲线.20.求微分方程02=-+-dy e dx e y x y x 的通解. 21.判断无穷级数∑∞=--+1212)1(1n n n 的敛散性. 22.将函数51)(+=x x f 展开为x +1的幂级数. 四、综合题(本大题共3小题,每小题5分,共15分)23.设函数)(x yz ϕ=,其中)(u ϕ为可微函数.证明:0=∂∂+∂∂y zy x z x24.设曲线y =y (x )在其上点(x , y )处的切线斜率为xyx -24,且曲线过点(1,1),求该曲线的方程. 25.证明:无穷级数∑∞=-=++-+121)122(n n n n .全国2011年1月自学考试高等数学(工本)试题一、单项选择题(本大题共5小题。
学历类《自考》自考公共课《高等数学(工本)》考试试题及答案解析

学历类《自考》自考公共课《高等数学(工本)》考试试题及答案解析姓名:_____________ 年级:____________ 学号:______________题型选择题填空题解答题判断题计算题附加题总分得分评卷人得分1、将函数展开为2的幂级数.正确答案:答案解析:暂无解析2、证明对坐标的曲线积分曲在整个xoy面内与路径无关.正确答案:答案解析:暂无解析3、求函数f(x,y)(x0,y0)的极值正确答案:答案解析:暂无解析4、已知f(x)是周期为2π的周期函数,它在[-π,π)上的表达式为f(x)=x+1,求f(x)傅里叶级数中系数b正确答案:答案解析:暂无解析5、判断无穷级数的敛散性正确答案:答案解析:暂无解析6、求微分方程的通解正确答案:答案解析:暂无解析7、求微分方程的通解正确答案:答案解析:暂无解析8、计算对坐标的曲线积分,其中N抛物线y=x2上从点A(一1,1)到点B(1,1)的一段弧。
正确答案:答案解析:暂无解析9、计算对弧长的曲线积分,其中C是从点A(3,0)到点B(3,1)的直线段·正确答案:答案解析:暂无解析10、计算三重积分,其中积分区域正确答案:答案解析:暂无解析11、计算二重积分,其中D是由y2=x和y=x2所围成的区域.正确答案:答案解析:暂无解析12、已知方程x2+y2-z2+2z=5确定函数z=z(x,y),求正确答案:答案解析:暂无解析13、求曲线x=4cost,y=4sint,z=3t在对应于的点处的法平面方程正确答案:答案解析:暂无解析14、求过点A(2,10,4),并且与直线x=-1+2t,y=1-3t,z=4-t平行的直线方程正确答案:答案解析:暂无解析15、已知向量a={-1,3,2),b={-3,0,1),则a×b=A、{3,5,9}B、{-3,5,9)C、(3,-5,9)D、{-3,-5,-9)正确答案:C答案解析:暂无解析16、已知函数,则全微分dz=A、B、C、D、正确答案:D答案解析:暂无解析17、设积分区域D:x²+y²≤4,则二重积分A、B、C、D、正确答案:A答案解析:暂无解析18、微分方程是A、可分离变量的微分方程B、齐次微分方程C、一阶线性齐次微分方程D、一阶线性非齐次微分方程正确答案:A答案解析:暂无解析19、无穷级数的敛散性为A、条件收敛B、绝对收敛C、发散D、敛散性无法确定正确答案:B答案解析:暂无解析20、已知无穷级数,则u1=正确答案:答案解析:暂无解析21、已知点p(-4,2+√3,2-√3)和点Q(-1,√3,2),则向量的模=正确答案:6.4答案解析:暂无解析22、已知函数f(x,y)=,则=正确答案:答案解析:暂无解析23、设积分区域D:|x|≤1,0≤y≤a,且二重积分,则常数a=正确答案:8.4答案解析:暂无解析24、微分方程的特解y*=正确答案:答案解析:暂无解析25、求过点A(2,10,4),并且与直线x=-1+2t,y=1-3t,z=4-t平行的直线方程正确答案:答案解析:暂无解析26、求曲线x=4cost,y=4sint,z=3t在对应于的点处的法平面方程正确答案:答案解析:暂无解析27、已知方程x2+y2-z2+2z=5确定函数z=z(x,y),求正确答案:答案解析:暂无解析28、计算二重积分,其中D是由y2=x和y=x2所围成的区域.正确答案:答案解析:暂无解析29、计算三重积分,其中积分区域正确答案:答案解析:暂无解析30、计算对弧长的曲线积分,其中C是从点A(3,0)到点B(3,1)的直线段·正确答案:答案解析:暂无解析。
2016年4月自学考试00023高等数学(工本)真题试卷及参考答案

wª:«¬¨©¤¥¦§A£Dyw«¬¨©0
!'(¶G- ( ! "0 #&!·¸m !A¹e-0
!" !"#$ # % $%&'()*+,%&-* ./ ,0 6
!" !"#$ # % $%&'()*+,
!"#$%&'()*
0&1
2
3
4
5
6&7
0&7
#'
#"
$"
#'
879
:&7
;<9
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
!"#
:&7
=>9 !"#$%& '(&) # *&+*& $ ,) "# ,-+*&./ & 0123$#456!2789&:;<0=>?@ABC-&
?}~{ $@# AIACD @%!$!$0&
ºwopBCm& !! !&!" #!! %&#" #0! '&!" ""
【全国自考历年真题10套】00023高等数学(工本)2012月10月至2019年10月试题

∫∫∫ 8.设积分区域 Ω : x2 + y2 + z2 ≤ 9 ,三重积分 f (x2 + y2 + z2 )dv 在球面坐标下三次积分为 Ω
__________.
9.微分方程 y′′ + y =2ex 的一个特解 y*=__________.
∑ 10.已知无穷级数
∞
un
n =1
=1 +
2 3
h→0
h
D. lim f (x0 + h, y0 ) − f (x0 , y0 )
h→0
h
∫ 3.设积分曲线 L : x2 + y2 = 1 ,则对弧长的曲线积分 (x + y)ds = L
A.0 C. π 4.微分方程 xy′ + y=
x2 + y2 是
B.1 D.2 π
A.可分离变量的微分方程
B.齐次微分方程
24.求由平面 z= 0, x + y= 1 及曲 z = xy 面所围立体的体积. 25.将函数 f (x) = sin 2x 展开为 x 的幂级数.
00023# 高等数学(工本)试题 第3页(共3页)
绝密 ★ 考试结束前
全国 2013 年 10 月高等教育自学考试
高等数学(工本)试题
课程代码:00023
00023# 高等数学(工本)试题 第1页(共3页)
C.一阶线性齐次微分方程
D.一阶线性非齐次微分方程
5.已知函数 f (x) 是周期为 2π 的周期函数,它在 [-π,π) 上的表达式为
f
(x)
=
0, −π ≤ x 1, 0 ≤ x <
< π
0
2016年4月全国自考高等数学(工专)真题试卷(题后含答案及解析)

2016年4月全国自考高等数学(工专)真题试卷(题后含答案及解析) 题型有:1. 单项选择题 2. 填空题 3. 计算题 4. 综合题单项选择题在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.设f(x)的定义域为[0,1],则g(x)=的定义域为【】A.B.C.D.正确答案:A2.设函数f(x)=3x+a3-x是偶函数,则a= 【】A.一2B.一1C.0D.1正确答案:D解析:因为f(x)为偶函数,故f(一x)=3-x+a3x=f(x)=3x+a3-x,故a=1.3.级数【】A.收敛B.发散C.部分和有极限D.不一定发散正确答案:B解析:由于所以,级数收敛的必要条件不满足,该级数发散.4.微分方程(y′)2+y′(y″)3+xy4=0的阶数是【】A.1B.2C.3D.4正确答案:B5.设矩阵A=,则A的逆矩阵A-1= 【】A.B.C.D.正确答案:C填空题请在每小题的空格中填上正确答案。
错填、不填均无分。
6.函数y=lnx+1的反函数是______.正确答案:y=ex-17.若则a=______.正确答案:08.设函数f(e)=,则x=0是f(x)的第______类间断点.正确答案:二9.设函数y=x2+3x,则dy=______.正确答案:(2x+3xln3)dx解析:y′=2x+3xln3,故dy(2x+3xln3)dx.10.曲线y=6x的凹区间(下凸区间)为______.正确答案:(一∞,+∞)11.______.正确答案:012.行列式______.正确答案:一27解析:13.曲线的水平渐近线方程为______.正确答案:y=0解析:故y=0为曲线y的水平渐近线.14.无穷限反常积分______·正确答案:π解析:15.设矩阵则2A一3B=______.正确答案:解析:2A-3B计算题16.求极限正确答案:17.求微分方程y′+xy=0的通解.正确答案:分离变量得=(一x)dx,两端积分∫=∫(一x)dx,lny=—+lnC,所给微分方程的通解为(其中C为任意常数)18.设y=y(x)是由方程xy=ex+y确定的隐函数,求dy.正确答案:方程两边同时对x求导得y+xy′=ex+y+y(1+y′),解得从而19.求曲线y=xex+1在点(0,1)处的切线方程和法线方程.正确答案:y′=ex +xex ,所求切线的斜率k= y′|x=0=1.所求切线的方程为y一1=x,即x—y+1=0.所求法线的方程为y一1=一x,即x+y一1=0.20.求不定积分∫cosx(tanx+secx)dx.正确答案:∫cosx(tanx+secx)dx=∫(sinx+1)dx=—cosx+C.21.确定函数y=3x4一4x3+1的单调区间.正确答案:函数y=3x4一4x3+1的定义域为(一∞,+∞),y′=12x3一12x2=12x2(x一1),令y′=0,得x1=0,x2=1,列表:所以y=3x4一4x3+1在(一∞,1)内单调减少;在(1,+∞)内单调增加.22.计算定积分∫01ln(1+x2)dx.正确答案:∫01ln(1+x2)dx=xln(1+x2)|01—∫01x[ln(1+x2)] ′dx23.a,b取何值时,齐次方程组有非零解?正确答案:当方程组的系数行列式|A|=0时,齐次方程组有非零解,而=(a—1)(b—2b)=(a—1)(—b)由|A|=0,得a=1或b=0,因此当a=1或b=0时,所给齐次方程组有非零解.综合题24.求由抛物线y=x2与y=2一x2所围成图形的面积.正确答案:由得交点(—1,1)D和(1,1).所求图形的面积为A=∫—11(2一x2一x2)dx=4—2∫—11x2dx=4—4∫01x2dx25.求函数在[0,2]上的最大值和最小值.正确答案:令y′=0得y在[0,2]内的驻点x=1.而y(0)=0,所以函数在区间[0,2]上的最大值为y(1)=,最小值为y(0)=0.。
(完整)自考《高等数学(工专)》课后习题答案详解

自考《高等数学(工专)》课后习题答案详解《高等数学(工专)》真题:积分的性质单选题正确答案:A答案解析:本题考查积分的性质。
由于在[0,1]上,根号x大于x,所以I1>I2。
《高等数学(工专)》真题:微分概念单选题《高等数学(工专)》真题:驻点的概念单选题1.函数f(x,y)=x2+xy+y2+x-y+1的驻点为()。
A.(1,-1)B.(-1,-1)C.(-1,1)D.(1,1)正确答案:C答案解析:本题考查驻点的概念。
对x的偏导数为2x+y+1,对y的偏导数为x+2y-1,由于求驻点,也就是偏导数为0的点,所以2x+y+1=0,x+2y-1=0,得到x=-1,y=1。
《高等数学(工专)》真题:矩阵逆的求法单选题1.如果A2=10E,则(A+3E)-1=()。
A.A-2EB.A+2EC.A+3ED.A-3E正确答案:D答案解析:本题考查矩阵逆的求法。
A2-9E=E,(A+3E)(A-3E)=E,(A+3E)-1=A-3E《高等数学(工专)》真题:连续的概念单选题A.f(x)在(-∞,1)上连续B.f(x)在(-1,+∞)上连续C.f(x)在(-∞,0)∪(0,+∞)上连续D.f(x)在(-∞,+∞)上连续正确答案:C答案解析:本题考查连续的概念。
《高等数学(工专)》真题:矩阵的计算性质单选题1.设A是k×l阶矩阵,B是m×n阶矩阵,如果A·CT·B有意义,则C是()矩阵。
A.k×nB.k×mC.l×mD.m×l正确答案:D答案解析:本题考查矩阵的计算性质。
首先我们判断CT是l×m阶矩阵,所以C是m×l阶矩阵。
《高等数学(工专)》真题:连续的定义单选题1.试确定k的值,使f(x)在x=1处连续,其中()A.k=-2B.k=-1C.k=0D.k=2正确答案:D答案解析:本题考查连续的定义。
《高等数学(工专)》真题:矩阵的性质单选题1.关于矩阵的乘法的说法,正确的是()。
