逻辑学的符号大全
数理逻辑符号

数理逻辑符号引言数理逻辑是逻辑学的一个重要分支,研究符号和符号之间的关系、命题的真值和推理的有效性等。
在数理逻辑中,符号是一种用来代表逻辑概念和关系的抽象表示,它能够将复杂的逻辑思维用简洁的方式表达出来。
本文将介绍数理逻辑中常见的符号及其运用。
命题逻辑符号1. 命题变量在命题逻辑中,命题变量是表示命题的未知量,一般用英文字母小写来表示,如p、q、r等。
2. 逻辑联结词逻辑联结词是用来描述命题间关系的符号,包括合取、析取、否定、蕴含和等值等常见的逻辑操作。
它们分别用∧、∨、¬、→和≡等符号来表示。
3. 真值表真值表是用来表示逻辑表达式真假的一种表格形式。
在真值表中,可以用0和1来表示命题的真值,其中0表示假,1表示真。
通过列举逻辑表达式中各命题变量的所有可能取值,可以得出逻辑表达式的真值。
4. 全真和全假全真和全假分别指命题逻辑中的最简单的逻辑表达式,全真用1来表示,全假用0来表示。
例如,p∨¬p为全真,p∧¬p为全假。
5. 优先级在命题逻辑中,存在运算符的优先级。
一般来说,否定运算¬的优先级最高,然后是合取运算∧,接着是析取运算∨,最后是蕴含运算→和等值运算≡。
如果有多个运算符出现在一个逻辑表达式中,应先计算优先级高的运算符。
谓词逻辑符号1. 谓词变量在谓词逻辑中,谓词变量是表示命题中的个体和关系的未知量,一般用英文字母大写来表示,如X、Y、Z等。
2. 量词量词用于描述命题的范围,包括全称量词∀和存在量词∃。
全称量词表示“对于所有的”,存在量词表示“存在一个”。
3. 函数符号函数符号用于表示带有参数的谓词,它可以将个体映射到个体。
例如,f(x)表示将x映射到f的函数。
4. 等词等词用于表示两个个体是相等的。
一般用“=”来表示。
5. 多层量词在谓词逻辑中,可以存在多层量词。
例如,∀x∃y(R(x,y))表示“对于所有的x存在一个y,使得R(x,y)成立”。
结论数理逻辑符号是数理逻辑研究中不可或缺的工具,它们能够将复杂的逻辑关系用简洁的方式表达出来。
表示逻辑关系的数学符号

表示逻辑关系的数学符号在数学的广袤天地中,存在着一系列用于表示逻辑关系的符号,它们就像是精确表达思维和推理的工具,为我们解决问题和推导结论提供了清晰而有力的手段。
首先,让我们来认识一下“等于”符号“=”。
这是我们最早接触也是最基础的逻辑关系符号之一。
它表示两个量或者表达式在数值上是完全相同的。
例如,当我们说 2 + 3 = 5 时,“=”清晰地传达了左边的运算结果和右边的数字具有相等的价值。
与“等于”密切相关的是“不等于”符号“≠”。
它表示两个量或者表达式不相等。
比如,若说x ≠ 5 ,那就意味着 x 的取值不是 5 。
“大于”符号“>”和“小于”符号“<”在比较两个数的大小时发挥着重要作用。
例如 7 > 5 ,表示 7 比 5 大;而 3 < 8 ,则表明 3 比 8 小。
还有“大于等于”符号“≥”和“小于等于”符号“≤”。
当我们说x ≥ 5 时,意思是 x 大于或者等于 5 ;若说y ≤ 10 ,则是指 y 小于或者等于 10 。
接下来是“且”(“∧”)和“或”(“∨”)这两个逻辑关系符号。
“且”表示两个条件必须同时成立。
例如,“x > 3 且 x <7 ”,意味着 x 的取值要同时满足大于 3 并且小于 7 。
而“或”则表示两个条件中至少有一个成立即可。
比如“x = 2 或 x =5 ”,说明 x 的值要么是 2 ,要么是 5 ,或者两者皆可。
再说说“蕴含”符号“→”。
“如果 p ,那么q ”可以表示为“p → q ”。
这意味着如果前提 p 成立,那么结论 q 一定成立。
例如,“如果今天下雨,那么街道会湿”,可以写成“今天下雨→ 街道会湿”。
“等价”符号“↔”表示两个命题在逻辑上是完全等价的。
例如“p ↔q ”,意味着 p 成立当且仅当 q 成立。
在集合论中,也有一些表示逻辑关系的符号。
“属于”符号“∈”用于表示一个元素属于某个集合。
比如“x ∈ A ”,表示元素 x 属于集合 A 。
“不属于”符号“∉”则表示相反的意思。
常用符号表

普通逻辑符号1.⇒实质蕴涵读作“如果..那么”, A⇒B意味着如果A为真,则B也为真;如果A为假,则对B没有任何影响。
例子:x= 2⇒x2= 4为真,但x2= 4⇒x= 2一般为假(因为x可以是−2)2.→ 可能意味着同⇒一样的意思(这个符号也可以指示函数的域和陪域;参见数学符号表)。
范畴为命题逻辑3.⊃蕴涵,可能意味着同⇒一样的意思(这个符号也可以指示超集)。
范畴为命题逻辑,例子:A⊃B⇔A→B4.⇔,↔实质等价,当且仅当。
A⇔B意味着A为真如果B为真,和A为假如果B为假。
5.¬逻辑否定非,陈述¬A 为真,当且仅当A为假。
穿过其他算符的斜线同于在它,例子:¬(¬A)⇔A,x≠y⇔¬(x=y) ,6.˜逻辑否定,非,穿过其他算符的斜线同于在它前面放置的"¬"。
例子:~A⇔Ā⇔-A⇔¬A7.∧逻辑合取“与”如果A与B二者都为真,则陈述A∧B为真;否则为假。
例子:n< 4∧n>2⇔n= 3当n是自然数的时候。
A·B⇔A&B⇔A∧B⇔A和B8.∨逻辑析取“或”如果A或B或二者均为真陈述,则A∨B为真;如果二者都为假,则陈述为假。
例子:n≥ 4∨n≤ 2⇔n≠ 3当n是自然数的时候。
9.⊕、⊻,范畴为命题逻辑、布尔代数、“异或”陈述A⊕B为真,在要么A要么B但不是二者为真的时候为真。
A⊻B 意思相同。
例子:(¬A) ⊕A总是真,A⊕A总是假。
10.∀全称量词“对于所有;对于任何;对于每个”谓词逻辑,∀x:P(x)意味着所有的x都使P(x)都为真。
例子:∀n∈N:n2≥n.(x)F(x)⇔∀xF(x),∧xF(x)11.∃存在量词“存在着”谓词逻辑,∃x:P(x)意味着有至少一个x使P(x)为真。
例子:∃n∈N:n 是偶数。
(∃x)F(x)⇔∃xF(x),∨xF(x)12.∃!唯一量词“精确的存在一个”谓词逻辑,∃!x:P(x)意味着精确的有一个x使P(x)为真。
常用符号及基本规律
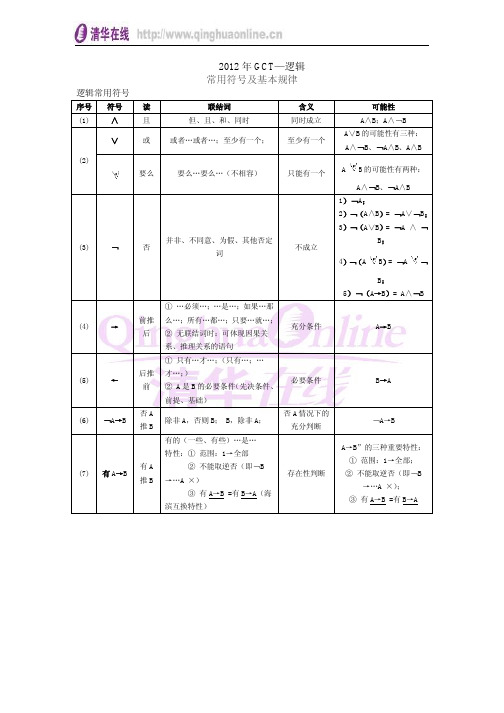
2012年GCT—逻辑常用符号及基本规律逻辑常用符号序号符号读联结词含义可能性(1) ∧且但、且、和、同时同时成立A∧B;A∧﹁B(2) ∨或或者…或者…;至少有一个;至少有一个A∨B的可能性有三种:A∧﹁B、﹁A∧B、A∧B 要么要么…要么…(不相容)只能有一个A B的可能性有两种:A∧﹁B、﹁A∧B(3) ﹁否并非、不同意、为假、其他否定词不成立1)﹁A;2)﹁(A∧B)= ﹁A∨﹁B;3)﹁(A∨B)= ﹁A ∧﹁B;4)﹁(A B)= ﹁A﹁B;5)﹁(A→B)= A∧﹁B(4) →前推后①…必须…;…是…;如果…那么…;所有…都…;只要…就…;②无联结词时:可体现因果关系、推理关系的语句充分条件A→B(5) ←后推前①只有…才…;(只有…;…才…;)② A是B的必要条件(先决条件、前提、基础)必要条件B→A(6) ﹁A→B 否A推B除非A,否则B; B,除非A;否A情况下的充分判断﹁A→B(7) 有A→B 有A推B有的(一些、有些)…是…特性:①范围:1→全部②不能取逆否(即﹁B→…A ×)③有A→B =有B→A(海滨互换特性)存在性判断A→B”的三种重要特性:①范围:1→全部;②不能取逆否(即﹁B→…A ×);③有A→B =有B→A逻辑常用基本规律名称内容公式逻辑要求常犯错误同一律就是在同一思维过程中,必须在同一意义上使用概念和判断,不能混淆不相同的概念和判断A是A保持概念的同一性保持判断的同一性保持论题的同一性偷换概念混淆概念偷换论题转移论题矛盾律,又称不矛盾律在同一思维过程中,对同一对象不能同时作出两个矛盾的判断,即不能既肯定它,又否定它。
A不是非A,或A不能既是B又不是B。
思想前后一贯,不能自相矛盾自相矛盾排中律在同一思维过程中,两个相互反对或矛盾的命题不能同时是真的。
要么A,要么非A保持思维和表达的明确性“两不可”的错误“未置可否”的错误充足理由律要确定某个判断为真,就必须有(充足)理由A真是因为B真,并且由B可以推出A保持思维有论证性有论无据理由虚假推导不出。
基本逻辑符号

⊃
⊃ 可能意味着同 ⇒ 一样的意 思(这个符号也可以指示超集)。
⇔ 实质等价 当且仅当;
iff
A ⇔B 为真,和
意味着 A 为真如果 B A 为假如果 B 为假。
x
+5
=y
+2
↔ 命题逻辑
⇔ x +3 =y
¬ 逻辑否定 陈述 ¬A 为真,当且仅当 A 为
非
假。
¬(¬A) ⇔ A
nቤተ መጻሕፍቲ ባይዱ
∈ N: n2
≥ n.
都使 P(x) 都为真。
对于每个
谓词逻辑
存在量词
∃ 存在着
∃ x: P(x) 意味着有至少一个 ∃ n ∈ N: n 是偶数。
x 使 P(x) 为真。
谓词逻辑
唯一量词
∃! 精 确 的 存 ∃! x: P(x) 意味着精确的有 ∃! n ∈ N: n + 5 = 2n. 在一个 一个 x 使 P(x) 为真。
n n
≥4 ∨ n 是自然数的时候。
≤
2
命题逻辑 都为假,则陈述为假。
⇔n ≠3当
异或
⊕ xor
陈述 A ⊕ B 为真,在要么 A 要 么 B 但不是二者为真的时候为 (¬A) ⊕ A 总是真,A ⊕ A 总是假。
命题逻辑, 真。A ⊻ B 意思相同。
布尔代数
⊻
全称量词
对于所有;
∀∀ 对于任何;
x: P(x) 意味着所有的 x ∀
x≠y
命题逻辑 穿过其他算符的斜线同于在它前
˜
面放置的 "¬"。
⇔ ¬(x = y)
逻辑合取
∧与
钩针符号知识点总结大全

钩针符号知识点总结大全一、逻辑运算符号1. 逻辑与逻辑与运算表示为“∧”,也可以用“&&”进行表示。
当p和q均为真时,p∧q为真;否则为假。
2. 逻辑或逻辑或运算表示为“∨”,也可以用“||”进行表示。
当p和q至少有一个为真时,p∨q为真;否则为假。
3. 逻辑非逻辑非运算表示为“¬”,也可以用“!”进行表示。
当p为真时,¬p为假;当p为假时,¬p 为真。
4. 逻辑蕴含逻辑蕴含运算表示为“→”。
p→q表示“如果p,则q”,当p为真、q为假时,p→q为假;否则为真。
5. 逻辑等价逻辑等价运算表示为“↔”。
p↔q表示“p当且仅当q”,当p和q等价时,p↔q为真;否则为假。
二、数学运算符号1. 加法加法运算表示为“+”,如3+5=8。
2. 减法减法运算表示为“-”,如7-4=3。
3. 乘法乘法运算表示为“×”或“*”,如2×6=12。
4. 除法除法运算表示为“÷”或“/”,如8÷2=4。
5. 等于等于运算表示为“=”,如5+3=8。
6. 不等于不等于运算表示为“≠”,如4+2≠7。
7. 小于小于运算表示为“<”,如3<7。
8. 大于大于运算表示为“>”,如9>4。
9. 小于等于小于等于运算表示为“≤”,如5≤5。
10. 大于等于大于等于运算表示为“≥”,如6≥4。
三、逻辑符号的应用1. 命题逻辑命题逻辑是逻辑学中的一个基本分支,它研究命题之间的关系和逻辑推理。
在命题逻辑中,钩针符号可以帮助人们表达和理解各种逻辑关系,比如真值表、逻辑等价、逻辑蕴含等。
2. 数理逻辑数理逻辑是逻辑学的一个重要分支,它运用数学方法来研究命题的形式和结构。
在数理逻辑中,钩针符号被广泛应用于命题的符号化、形式化证明、逻辑推理等方面。
3. 哲学逻辑哲学逻辑是哲学研究的重要内容,它探讨思维的规律和辨析真理的方法。
在哲学逻辑中,钩针符号被用来分析和解释命题、推理、认知等问题。
逻辑学符号的含义

逻辑学符号的含义1. 亲,你知道“∧”这个逻辑学符号吗?它表示“且”的意思哟!就好比你说“我要吃蛋糕∧我要喝奶茶”,那意思就是你既想吃蛋糕又想喝奶茶,是不是很神奇?2. 嘿!“∨”这个符号也很有趣呢,它代表“或”。
比如说“我今天选择跑步∨游泳”,这就意味着你要么跑步,要么游泳,难道你不觉得这很简单明了?3. 朋友们,“→”这个符号可重要啦,意思是“如果……那么……”。
就像“如果明天天晴→我们去公园”,要是明天天晴,咱们就去公园玩,多期待啊!4. 来看看“↔”这个符号,它表示“当且仅当”。
好比“我喜欢你↔你也喜欢我”,这得多难得呀!5. 亲,“¬”符号了解一下,这表示“否定”。
比如“¬我今天没迟到”,那意思就是我今天没有迟到,是不是一下子就清楚啦?6. 哟呵,“∀”这个符号可厉害啦,它是“全称量词”。
像“∀动物都需要水”,这不就是说所有动物都离不开水嘛!7. 嗨呀,“∃”符号代表“存在量词”哟。
比如说“∃一个人爱我”,是不是意味着有那么一个人是爱你的呢?8. 大家注意啦,“⇒”符号意味着“蕴含”。
就好像“努力学习⇒取得好成绩”,努力学习就有可能取得好成绩,你说对不对?9. 哇塞,“⇔”符号表示“等价”。
好比“我爱你⇔你爱我”,这要是成立,得多幸福啊!10. 嘿,“⊕”符号代表“异或”。
比如说“今天是晴天⊕今天是阴天”,只能是晴天或者阴天,是不是很直接?11. 亲,“⊂”符号表示“包含于”。
就像“集合 A⊂集合B”,集合 A 就在集合 B 里面呢!12. 哟,“⊃”符号是“包含”。
比如说“集合 B⊃集合A”,集合 B 把集合 A 包含住啦!13. 朋友们,“≡”符号代表“恒等于”。
比如“x + 1 ≡ y - 1”,这就表示一直相等,多奇妙!14. 哇,“≈”符号表示“约等于”。
像“3.14 ≈ π”,是不是很形象?15. 嗨呀,“≠”符号表示“不等于”。
比如说“5 ≠ 6”,这太明显啦!16. 哟呵,“>”符号是“大于”。
布尔逻辑符号及含义

布尔逻辑符号及含义1. 嘿,朋友!你知道布尔逻辑中的“与”符号(&&)吗?它就像两只手紧紧相握,只有两边条件都满足时才成立。
比如说,找工作时要求“会编程 && 有相关经验”,少了哪一样都不行,是不是很严格呀?2. 亲,布尔逻辑里的“或”符号(||)可有意思啦!它就像岔路口,走这边或者走那边都行。
就像你去超市买东西,“买苹果 || 买香蕉”,只要买到其中一种就满足啦,多灵活!3. 哇塞!布尔逻辑的“非”符号(!)简直太神奇了!它就像一个反转按钮。
比如说“成绩优秀(!成绩差)”,一用它,意思完全反过来啦,是不是很奇妙?4. 小伙伴们,想想看,布尔逻辑中的“异或”符号(^)是不是像一个特立独行的家伙?只有两边条件不同时才为真。
就像“选红色 ^ 选蓝色”,不能两个都选,也不能都不选,是不是有点烧脑但又很有趣?5. 朋友呀,“与”符号(&&)在程序里的作用可大了!好比你做饭,“有食材&& 有工具”才能做出美味佳肴,缺一样都不行,难道不是吗?6. 亲,“或”符号(||)在判断条件时可好用啦!就像你决定周末出去玩,“去公园 || 去电影院”,总有一个能让你开心,对吧?7. 哎呀!“非”符号(!)有时候真能让人恍然大悟呢!比如说“不喜欢雨天(!喜欢雨天)”,一下就把态度变了,像变魔术一样,你说神奇不神奇?8. 小伙伴,“异或”符号(^)就像一场独特的竞赛,只有双方不一样才能赢。
比如“奇数 ^ 偶数”,是不是很独特?9. 朋友,你能想象没有“与”符号(&&)的逻辑世界会多混乱吗?就像搭积木没有胶水,根本不稳定,对吧?10. 亲,要是没有“或”符号(||),那做选择得多难呀!就像只有一条路可走,太可怕啦,不是吗?11. 哇哦!“非”符号(!)能带来意想不到的反转。
好比你原本以为会成功,结果“!成功”,这种落差感,是不是很惊人?12. 小伙伴们,“异或”符号(^)就像一场刺激的拔河比赛,双方力量不同才有结果,是不是很刺激?13. 朋友呀,“与”符号(&&)在筛选数据时特别重要!比如“年龄大于 18 && 学历本科”,一下子就能找到合适的,厉害吧?14. 亲,“或”符号(||)在设置选项时可自由啦!像“坐火车 || 坐飞机”,随你怎么选,多爽!15. 哎呀!“非”符号(!)常常能打破常规思维。
逻辑学常用图表和公式3篇

逻辑学常用图表和公式第一篇:逻辑学常用图表和公式(上)逻辑学是哲学中非常重要的一个分支,它主要研究思维、推理和证明等方面的问题。
在逻辑学研究过程中,人们经常会使用一些图表和公式,以便更加清晰地表达和解决问题。
本文将介绍一些在逻辑学中常用的图表和公式。
一、命题逻辑符号在命题逻辑中,人们使用一些符号来表示不同的关系。
这些符号包括:1. 非(¬):表示否定,例如¬p 表示“不是p”。
2. 与(∧):表示合取,例如p ∧ q 表示“既有 p,又有q”。
3. 或(∨):表示析取,例如p ∨ q 表示“有 p 或q”。
4. 蕴含(→):表示蕴含,例如p → q 表示“如果 p,那么q”。
5. 等价(↔):表示等价,例如 p ↔ q 表示“p 和 q 是等价的”。
这些符号可以组成复合命题,例如(p ∧ q) → r 表示“如果既有 p 又有 q,那么就有r ”。
这些符号还可以用于逻辑推理的推导过程中。
二、真值表真值表是一种逻辑学中常用的图表,用于展示命题逻辑中的真值情况。
在真值表中,每个命题变量都有两种可能的取值:真(T)或假(F)。
真值表中的每一行表示一组取值,而每个命题逻辑符号则可能根据每个命题变量的取值而有不同的结果。
例如,对于以下逻辑命题:p ∧ q根据真值表的规则,p 与 q 只有在同时为真时,才会使得整个命题为真。
在真值表中,p 和 q 的所有可能取值情况如下:p q p ∧ q---------------T T TT F FF T FF F F根据上表可以看出,只有 p 和 q 同时为真时,p ∧ q 才会为真。
三、全称量词和存在量词在第一阶段逻辑中,全称量词和存在量词是很常见的概念。
全称量词通常用符号 (∀) 表示,表示“对于所有的x ”;存在量词通常用符号 (∃) 表示,表示“存在一个x ”。
在以下命题中:∀xP(x)表示命题 P(x) 对于 x 的所有取值都为真。
另一个例子:∃xP(x)表示命题 P(x) 对于至少一个 x 的取值为真,即存在一个 x 使命题 P(x) 为真。
数学-逻辑符号

数学-逻辑符号关系符号符号(Symbol) 意义(Meaning)=等于is equal to≠不等于is not equal to≈大约等于≒≡恒等于或同余∽相似is similar to≌全等is equal to(especially for triangle )>大于is greater than<小于is less than≥大于等于(或作≯)is greater than or equal to ≤小于等于(或写作≮)is less than or equal to >>远远大于号<<远远小于号∈属于∉不属于⊆真包含于⊇真包含⊂包含于⊃包含∪并集∩交集||平行is parallel to∥⊥垂直├断定符(公式在L中可证)╞满足符(公式在E上有效,公式在E上可满足)┐命题的“非”运算∧命题的“合取”(“与”)运算∨命题的“析取”(“或”,“可兼或”)运算→命题的“条件”运算↔命题的“双条件”运算的A<=>B命题A与B等价关系A=>B命题A与B的蕴涵关系A*公式A的对偶公式wff合式公式iff当且仅当↑命题的“与非”运算(“与非门”)↓命题的“或非”运算(“或非门”)□模态词“必然”◇模态词“可能”R关系r相容关系运算符号+加号-减号×乘号(或·)÷除号(或/,含分数):比∪两个集合的并集∩交集П连乘(集合论中的相乘)Σ连加√根号log对数(或lg,ln)dx微分∫积分∮曲线积分性质符号+正号-负号±正负号| |绝对值(|x|绝对值absolute value of X)结合符号()小括号[]中括号{}大括号省略符号△三角形Rt△直角三角形∠角⊙圆º度||平行is parallel to∥⊥垂直Sin正弦Cos余弦f(x)x的函数lim极限∵因为∴所以∑总和∏连乘C(r)(n)从n个元素中每次取出r个元素所有不同的组合数幂(A,Ac,Aq,x^n)等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
逻辑学使用一系列符号来表示不同的逻辑关系和操作。
以下是逻辑学中常用的符号大全:命题逻辑符号:
逻辑连接词:¬(非)、∧(合取)、∨(析取)、→(蕴含)、↔(等价)
括号:( )
真值:T(真)、F(假)
等同符号:≡
谓词逻辑符号:
量词:∀(全称量词)、∃(存在量词)
唯一性量词:∃!(存在唯一)
谓词:P, Q, R, ...
关系运算符:=(相等)、≠(不等)、<(小于)、>(大于)、≤(小于等于)、≥(大于等于)
集合论符号:
集合:A, B, C, ...
元素关系:∈(属于)、∉(不属于)、⊆(包含于)、⊇(包含)
推理规则和符号:
蕴含关系:⊢(可推导)、⊨(语义蕴含)
推理规则:Modus Ponens(分离规则)、Modus Tollens(否定规则)、Hypothetical Syllogism (假言三段论)等
这些符号用于描述和表示命题逻辑、谓词逻辑、集合论和推理规则等不同领域的逻辑关系。
需要注意的是,不同的逻辑学派和教材可能会稍有差异,因此符号的具体用法和解释可能会有所不同。
