八年级全等三角形简单证明题及答案15道[1]
八年级数学上册第12章全等三角形证明经典50题(含答案)

3. 已知:∠ 1=∠2,CD=DE,EF//AB ,求证: EF=AC
A 12
F
C D E B
过 C 作 CG∥EF 交 AD 的延长线于点 G
CG∥EF,可得,∠ EFD=CGD
DE= DC
第 3 页 共 46 页
∠FDE=∠ GDC(对顶角) ∴△EFD≌△ CGD EF=CG ∠CGD=∠ EFD 又, EF∥AB ∴,∠ EFD=∠ 1 ∠1= ∠2 ∴∠ CGD=∠2 ∴△AGC 为等腰三角形, AC= CG 又 EF=CG ∴EF= AC
∵∠ EAB= ∠ BDE,
∴∠ AED= ∠ABD ,
∴四边形 ABDE 是平行四边形。
∴得: AE=BD ,
∵AF=CD,EF=BC ,
∴三角形 AEF 全等于三角形 DBC,
∴∠ F=∠C。
14.已知: AB=CD ,∠ A= ∠D,求证:∠ B=∠C
第 14 页 共 46 页
A
D
B
C
证明:设线段 AB,CD 所在的直线交于 E,(当 AD<BC 时,E 点是射 线 BA,CD 的交点, 当 AD>BC 时,E 点是射线 AB,DC 的交点) 。则: △AED 是等腰三角形。 ∴ AE=DE 而 AB=CD ∴BE=CE (等量加等量,或等量减等量) ∴△ BEC 是等腰三角形 ∴∠ B=∠C.
AE=AD+BE
第 11 页 共 46 页
在 AE 上取 F,使 EF=EB,连接 CF ∵ CE⊥AB ∴∠ CEB=∠CEF=90° ∵ EB=EF, CE=CE, ∴△ CEB≌△CEF ∴∠ B=∠ CFE ∵∠ B+∠ D=180°,∠ CFE+∠ CFA=180° ∴∠ D=∠ CFA ∵AC 平分∠ BAD ∴∠ DAC =∠ FAC 又∵ AC=AC ∴△ ADC ≌△ AFC(SAS) ∴AD =AF ∴AE=AF+FE=AD +BE
人教版数学八年级上册第12章全等三角形证明经典题练习(含答案)

⼈教版数学⼋年级上册第12章全等三⾓形证明经典题练习(含答案)全等三⾓形证明经典题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC 在△ACD 和△BDE 中AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4 即4-2<2AD <4+2 1<AD <3 ∴AD=2 2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP ,BP∵DP=DC,DA=DB ∴ACBP 为平⾏四边形⼜∠ACB=90 ∴平⾏四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF ∴三⾓形BCF 全等于三⾓形EDF(边⾓边) ∴ BF=EF,∠CBF=∠DEF 连接BE 在三⾓形BEF 中,BF=EF ∴∠EBF=∠BEF 。
∵∠ABC=∠AED 。
∴∠ABE=∠AEB 。
∴ AB=AE 。
在三⾓形ABF 和三⾓形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴三⾓形ABF 和三⾓形AEF 全等。
∴∠BAF=∠EAF(∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=ACBC ADBC过C 作CG ∥EF 交AD 的延长线于点G CG ∥EF ,可得,∠EFD =CGD DE =DC ∠FDE =∠GDC (对顶⾓)∴△EFD≌△CGDEF =CG ∠CGD =∠EFD ⼜EF ∥AB ∴∠EFD =∠1 ∠1=∠2 ∴∠CGD =∠2∴△AGC 为等腰三⾓形,AC =CG ⼜ EF =CG∴EF =AC 5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠ C证明:延长AB 取点E ,使AE =AC ,连接DE∵AD 平分∠BAC ∴∠EAD =∠CAD ∵AE =AC ,AD =AD ∴△AED ≌△ACD (SAS )∴∠E =∠C ∵AC =AB+BD ∴AE =AB+BD ∵AE =AB+BE ∴BD =BE ∴∠BDE =∠E ∵∠ABC =∠E+∠BDE ∴∠ABC =2∠E ∴∠ABC =2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE 证明:在AE 上取F ,使EF =EB ,连接CF ∵CE ⊥AB ∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE ∵∠B +∠D =180°,∠CFE +∠CFA =180° ∴∠D =∠CFA ∵AC 平分∠BAD ∴∠DAC =∠FAC ∵AC =AC ∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
人教版 八年级上册 12.2 三角形全等的判定证明题-(含答案)
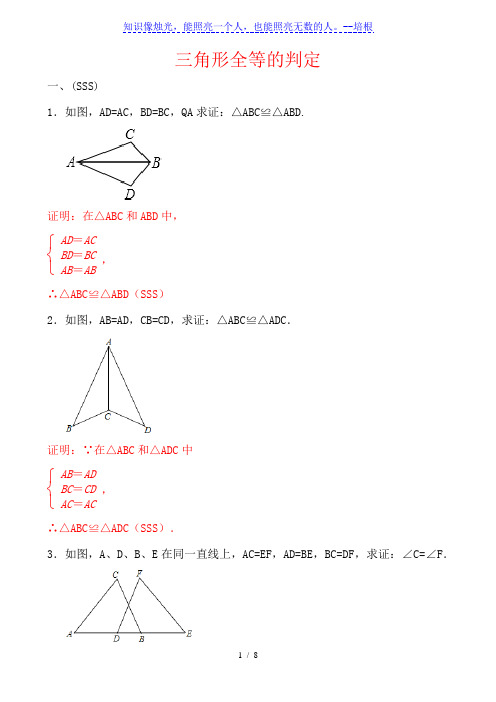
三角形全等的判定一、(SSS)1.如图,AD=AC ,BD=BC ,QA 求证:△ABC≌△ABD .证明:在△ABC 和ABD 中,⎩⎨⎧ AD =ACBD =BCAB =AB ,∴△ABC≌△ABD(SSS )2.如图,AB=AD ,CB=CD ,求证:△ABC≌△AD C .证明:∵在△ABC 和△ADC 中⎩⎨⎧ AB =ADBC =CDAC =AC,∴△ABC≌△ADC(SSS ).3.如图,A 、D 、B 、E 在同一直线上,AC=EF ,AD=BE ,BC=DF ,求证:∠C=∠F.证明:∵AD=BE∴AD+DB=BE+DB,即:AB=DE,在△ABC和△DEF中,⎩⎨⎧AC=EFAB=DEBC=DF,∴△ABC≌△DEF(SSS),∴∠C=∠F.4.如图,已知线段AB、CD相交于点O,AD、CB的延长线交于点E,OA=OC,EA=EC,请说明∠A=∠C.解:连结OE在△EAC和△EBC中OA OCEA ECOE OE⎧⎪⎨⎪⎩===(已知)(已知)(公共边)∴△EAC≌△EBC(SSS)∴∠A=∠C(全等三角形的对应角相等)二、(SAS)5.已知:如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.求证:∠ACE =∠DBF .证明:∵AB =DC∴AC =DB∵EA ⊥AD ,FD ⊥AD∴∠A =∠D =90°在△EAC 与△FDB 中⎪⎩⎪⎨⎧=∠=∠=DBAC D A FDEA∴△EAC ≌△FDB (SAS )∴∠ACE =∠DBF .6.如图CE=CB ,CD=CA ,∠DCA=∠ECB ,求证:DE=AB .证明:∵∠DCA=∠ECB ,∴∠DCA+∠ACE=∠BCE+∠ACE ,∴∠DCE=∠ACB ,∵在△DCE 和△ACB 中,∴△DCE ≌△ACB (SAS )∴DE=AB .7. 已知:如图,点A 、B 、C 、D 在同一条直线上,EA ⊥AD ,FD ⊥AD ,AE =DF ,AB =DC .求证:∠ACE =∠DBF .证明:∵AB =DC∴AC =DB∵EA ⊥AD ,FD ⊥AD∴∠A =∠D =90°在△EAC 与△FDB 中⎪⎩⎪⎨⎧=∠=∠=DBAC D A FDEA∴△EAC ≌△FDB (SAS )∴∠ACE =∠DBF .8. 如图CE=CB ,CD=CA ,∠DCA=∠ECB ,求证:DE=AB .证明:∵∠DCA=∠ECB,∴∠DCA+∠ACE=∠BCE+∠ACE,∴∠DCE=∠ACB,∵在△DCE和△ACB中,∴△DCE≌△ACB(SAS)∴DE=AB.三、(ASA)(AAS)9.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD.求证:AC=DF.证明:∵FB=CE,∴BC=EF.∵AB∥ED,∴∠B=∠E∵AC∥EF,∴∠ACB=∠DFE.在△ABC和△DEF中{∠B=∠EBC=EF∠ACB=∠DFE∴△ABC≌△DEF(ASA).∴AC=DF.10. 如图,在△AEC 和△DFB 中,∠E=∠F,点A ,B ,C ,D 在同一直线上, AE∥DF,AB=CD ,求证:CE=BF 。
八年级全等三角形证明经典50题(含答案)

1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGB ACDF21E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+2 1<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
人教版数学八年级上册 第十二章《全等三角形》证明练习题(含答案)

人教版数学八年级上《全等三角形》经典习题集锦1.如图所示,△ABC≌△ADE,BC的延长线过点E,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,求∠DEF的度数。
2.如图,△AOB中,∠B=30°,将△AOB绕点O顺时针旋转52°,得到△A′OB′,边A′B′与边OB交于点C(A′不在OB上),则∠A′CO的度数为多少?3.如图所示,在△ABC中,∠A=90°,D、E分别是AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数是多少?4.如图所示,把△ABC绕点C顺时针旋转35°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A= .5.已知,如图所示,AB=AC,AD⊥BC于D,且AB+AC+BC=50cm,而AB+BD+AD=40cm,则AD是多少?6.如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的垂线BC、CE,垂足分别为D、E,若BD=3,CE=2,则DE= .7.如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,连接EF,交AD于G,AD与EF垂直吗?证明你的结论。
8.如图所示,在△ABC中,AD为∠BAC的角平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是28cm2,AB=20cm,AC=8cm,求DE的长。
9.已知,如图:AB=AE,∠B=∠E,∠BAC=∠EAD,∠CAF=∠DAF,求证:AF⊥CD10.如图,AD=BD,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点H,则BH与AC相等吗?为什么?11.如图所示,已知,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,求证:BE⊥AC12.△DAC、△EBC均是等边三角形,AF、BD分别与CD、CE交于点M、N,求证:(1)AE=BD (2)CM=CN (3)△CMN为等边三角形(4)MN∥BC13.已知:如图1,点C为线段AB上一点,△ACM、△CBN都是等边三角形,AN交MC于点E,BM交CN于点F(1)求证:AN=BM(2)求证:△CEF为等边三角形14.如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD,其中正确的有()A.3个 B. 4个 C. 5个 D. 6个15.已知:BD、CE是△ABC的高,点F在BD上,BF=AC,点G在CE的延长线上,CG=AB,求证:AG⊥AF16.如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG求证:(1)AD=AG(2)AD与AG的位置关系如何17.如图,已知E是正方形ABCD的边CD的中点,点F在BC上,且∠DAE=∠FAE求证:AF=AD-CF18.如图所示,已知△ABC中,AB=AC,D是CB延长线上一点,∠ADB=60°,E是AD上一点,且DE=DB,求证:AE=BE+BC19.如图所示,已知在△AEC中,∠E=90°,AD平分∠EAC,DF⊥AC,垂足为F,DB=DC,求证:BE=CF20.已知如图:AB=DE,直线AE、BD相交于C,∠B+∠D=180°,AF∥DE,交BD于F,求证:CF=CD21.如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于D,PE⊥OB于E,F是OC上一点,连接DF和EF,求证:DF=EF22.已知:如图,BF⊥AC于点F,CE⊥AB于点E,且BD=CD,求证:(1)△BDE≌△CDF (2)点D在∠A的平分线上23.如图,已知AB∥CD,O是∠ACD与∠BAC的平分线的交点,OE⊥AC于E,且OE=2,则AB与CD之间的距离是多少?24.如图,过线段AB的两个端点作射线AM、BN,使AM∥BN,按下列要求画图并回答:画∠MAB、∠NBA的平分线交于E(1)∠AEB是什么角?(2)过点E作一直线交AM于D,交BN于C,观察线段DE、CE,你有何发现?(3)无论DC的两端点在AM、BN如何移动,只要DC经过点E,①AD+BC=AB;②AD+BC=CD谁成立?并说明理由。
八年级全等三角形简单证明题及答案(15道)

∴BC=ED.
全等三角形的判定与性 质.
01
如图,在△ABC中, ∠C=90°,点D是AB边上的 一点,DM⊥AB,且 DM=AC,过点M作 ME∥BC交AB于点E.求证: △ABC≌△MED。
02
证明:∵MD⊥AB,
∴∠MDE=∠C=90°,
∵ME∥BC,
∴∠B=∠MED,
在△ABC与△MED中, ∠B=∠MED ∠C=∠EDM DM=AC ,
∠D=∠B , ∴△ADF≌△CBE(ASA), ∴AF=CE, ∴AF+EF=CE+EF,即
AE=CF.
全等三角形的判定与性 质.
11.在△ABC中,AB=CB,∠ABC=90°,F为AB延 长线上一点,点E在BC上,且AE=CF.求证: Rt△ABE≌Rt△CBF;
证明:∵∠ABC=90°,
角平分线的性质;全等三角形的判定与性质.
全等三角形的判定.
如图,在△ABC中, AB=AC,AD平分 ∠BAC.求证: ∠DBC=∠DCB.
解:∵AD平分∠BAC, ∴∠BAD=∠CAD. ∴在△ACD和△ABD中 AB=AC ∠BAD=∠CAD
AD=AD , ∴△ACD≌△ABD, ∴BD=CD, ∴∠DBC=∠DCB.
:∵AC平分∠BAD,
∴∠BAC=∠DAC,
在△ABC和△ADC中, AB=AD ∠BAC=∠DAC AC=AC ,
∴△ABC≌△ADC.
全等三角形的判定.
9.如图,已知 点E,C在线段
BF上, BE=CF, AB∥DE, ∠ACB=∠F.
求证: △ABC≌△DEF
.
证明:∵AB∥DE,
∴∠B=∠DEF.
全等三角形的判定与性质.
人教版八年级数学上册《第12章全等三角形证明》经典题(含答案)
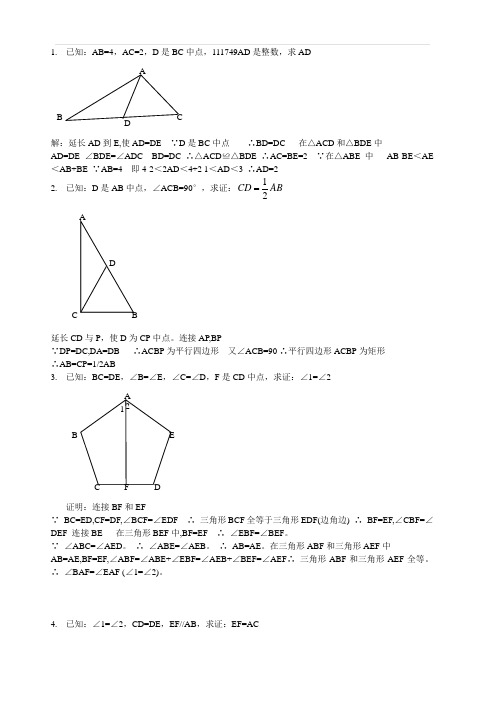
1. 已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4 即4-2<2AD <4+2 1<AD <3 ∴AD=2 2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB ∴ACBP 为平行四边形 又∠ACB=90 ∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF ∴ 三角形BCF 全等于三角形EDF(边角边) ∴ BF=EF,∠CBF=∠DEF 连接BE 在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=ACA C DEF 21 DABADBC过C 作CG ∥EF 交AD 的延长线于点G CG ∥EF ,可得,∠EFD =CGD DE =DC ∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CG ∠CGD =∠EFD 又EF ∥AB ∴∠EFD =∠1 ∠1=∠2 ∴∠CGD =∠2∴△AGC 为等腰三角形,AC =CG 又 EF =CG ∴EF =AC 5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠ C证明:延长AB 取点E ,使AE =AC ,连接DE∵AD 平分∠BAC ∴∠EAD =∠CAD ∵AE =AC ,AD =AD ∴△AED ≌△ACD (SAS ) ∴∠E =∠C ∵AC =AB+BD ∴AE =AB+BD ∵AE =AB+BE ∴BD =BE ∴∠BDE =∠E ∵∠ABC =∠E+∠BDE ∴∠ABC =2∠E ∴∠ABC =2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE 证明:在AE 上取F ,使EF =EB ,连接CF ∵CE ⊥AB ∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE , ∴△CEB ≌△CEF∴∠B =∠CFE ∵∠B +∠D =180°,∠CFE +∠CFA =180° ∴∠D =∠CFA ∵AC 平分∠BAD ∴∠DAC =∠FAC ∵AC =AC ∴△ADC ≌△AFC (SAS ) ∴AD =AF∴AE =AF +FE =AD +BE7. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
人教版八年级数学上册 第12章 全等三角形证明50题(含答案)
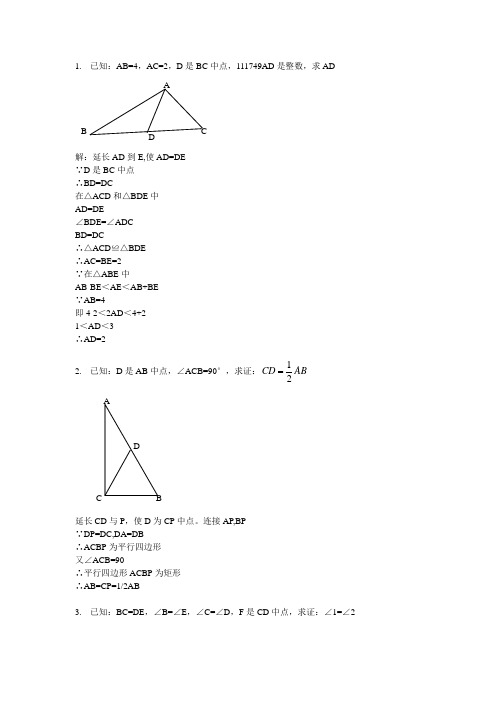
1. 已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴三角形BCF全等于三角形EDF(边角边)∴BF=EF,∠CBF=∠DEF连接BE在三角形BEF中,BF=EF∴∠EBF=∠BEF。
∵∠ABC=∠AED。
∴∠ABE=∠AEB。
∴AB=AE。
在三角形ABF和三角形AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴三角形ABF和三角形AEF全等。
∴∠BAF=∠EAF (∠1=∠2)。
4.已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC过C作CG∥EF交AD的延长线于点GCG∥EF,可得,∠EFD=CGDDE=DC∠FDE=∠GDC(对顶角)∴△EFD≌△CGDEF=CG∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+21<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
(完整word版)八年级全等三角形证明经典50题(含答案).doc

1.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求ADA 解:延长AD 至IJE,使AD=DE・・・D 是BC 中点BD=DC在厶ACD 和厶BDE 中AD=DEZBDE= ZADC BD=DCAA ACD A BDE•*. AC=BE=2・・•在△ ABE 中AB-BE < AE<AB+BE・・・AB=4即 4・2 <2AD < 4+21 < AD < 3・・・AD=2延长CD 与P,使D 为CP 中点。
连接VDP=DC,DA=DBA AC BP 为平行四边形又 Z ACB=90・・・平行四边形ACBP 为矩形AAB=CP=1/2AB 2.已知:D 是AB 中点,Z ACB=90 0,求证:CD [AB 2AAP,BP3.已知:BC=DE , Z B= ZE, Z C= ZD , F 是CD 中点,求证:Z 1= Z2证明:连接BF和EF・・・ BC=ED,CF=DF, Z BCF= Z EDF・・・三角形BCF全等于三角形EDF(边角边)・・・ BF=EF, ZCBF=Z DEF连接BE在三角形BEF中,BF=EF/. Z EBF=Z BEFo・・・ Z ABC= Z AED o・・・ Z ABE= Z AEBo/. AB=AE o在三角形ABF和三角形AEF屮AB=AE,BF=EF,ZABF= Z ABE+ Z EBF= ZAEB+ Z BEF= Z AEF・・・三角形ABF和三角形AEF全等。
・・・ Z BAF= Z EAF(Z 1= Z 2)o4. 己知:Z 1= Z 2 , CD=DE , EF//AB ,求证:EF=AC过C作CG〃EF交AD的延长线于点GCG// EF,可得,Z EFD= CGDDE= DCZFDE= Z GDC (对顶角)AA EFD^A CGDEF= CGZCGD = Z EFD又,EF// AB・・・,Z EFD= Z 1Z1= Z 2・・・Z CGD= Z 2・・・△ AGC为等腰三角形,AC= CG又EF=CG・・・EF= AC5.已知:AD 平分Z BAC, AC=AB+BD ,求证:Z B=2 Z C证明:延长AB取点E,使AE=AC,连接DEVAD 平分Z BACAZ EAD=Z CAD・・・AE=AC, AD = ADA A AED^A ACD ( SAS)AZ E=Z CVAC = AB+BD・・・AE= AB+BD・・・AE= AB+BEABD = BE・・・Z BDE=Z EVZ ABC=Z E+ Z BDEAZ ABC = 2 ZEAZ ABC = 2 ZC6.己知:AC 平分Z BAD , CE丄AB , Z B+ Z D=180 ° ,求证:AE=AD+BE・・・CE丄AB ・・・Z CEB=Z CEF= 90° ・・・EB=EF, CE = CE, AACEB^ACEF ・・・Z B=Z CFEVZ B+Z D= 180 ° , ZCFE+Z CFA= 180 0AZ D = Z CFAVAC 平分Z BAD・・・Z DAC = Z FACVAC = AC・・・△ ADC 竺△ AFC ( SAS)/.AD = AF ・・・AE= AF+ FE= AD + BE解:延长AD至IJE,使AD=DE・・・D是BC中点・・・BD=DC在厶ACD和厶BDE中AD=DEZBDE= Z ADCBD=DC7.已知:AB=4 , AC=2 , D是BC屮点, AD是整数,求ADA 证明:在AE上取F,使EF= EB,连接CFAAACD^ABDE•*. AC=BE=2・・•在△ ABE中AB-BE < AE<AB+BE・・・AB=4即4・2 < 2AD < 4+21 < AD < 3・・・AD=218.已知:D 是AB 中点,Z ACB=90 0,求证:CD -AB2解:延长AD到E,使AD=DE・・・D是BC屮点・・・BD=DC在厶ACD和厶BDE中AD=DEZBDE= Z ADCBD=DCAA ACD A BDE•*. AC=BE=2•・•在A ABE中9.已知:BC=DE , Z B= ZE, Z C= ZD , F 是CD 中点,求证:Z 1= Z2A证明:连接BF和EF。
八年级数学上册《三角形全等的判定》练习题及答案

八年级数学上册《三角形全等的判定》练习题及答案学校:___________姓名:___________班级:___________一、单选题1.如图,//BC EF ,BC EF =,要使得ABC DEF △≌△,需要补充的条件不能是( )A .B E ∠=∠ B .AB DE =C .AD CF = D .//AB DE2.如图,已知ABC ,用直尺和圆规按以下步骤作出DEF .(1)画射线DM ,以点D 为圆心,AB 长为半径画弧,与DM 交于点E ;(2)分别以D ,E 为圆心,线段AC ,BC 长为半径画弧,两弧相交于点F ;(3)连接DF ,EF .则能用于证明ABC DEF ≌△△的依据是( )A .SSSB .SASC .ASAD .AAS3.如图,由AB =AC ,∠B =∠C ,便可证得BAD ∠CAE ,其全等的理由是( )A .SSSB .SASC .ASAD .AAS4.如图,在矩形ABCD 中,DE 平分ADC ∠交BC 于点E ,点F 是CD 边上一点(不与点D 重合).点P 为DE 上一动点,PE PD <,将DPF ∠绕点P 逆时针旋转90°后,角的两边交射线DA 于H ,G 两点,有下列结论:∠DH DE =;∠DP DG =;∠DG DF +;∠DP DE DH DC ⋅=⋅,其中一定正确的是( )A .∠∠B .∠∠C .∠∠D .∠∠5.已知:如图AB //EF ,BC ∠CD ,则∠α,∠β,∠γ之间的关系是( )A .βαγ∠=∠+∠B .180αβγ∠+∠+∠=C .90αβγ∠+∠-∠=D .90βγα∠+∠-∠=6.如图所示,E 是正方形ABCD 的对角线BD 上一点,EF ∠BC ,EG ∠CD ,垂足分别是F 、G .若CG =3,CF =4,则AE 的长是( )A .3B .4C .5D .7二、填空题7.如图,在Rt ABC 中,90C ∠=︒,10AC =,5BC =,线段PQ AB =,P ,Q 两点分别在AC 和过点A 且垂直于AC 的射线AO 上运动,当AP =__________时,ABC 和PQA △全等.8.如图,AB 是∠O 的直径,AC 是∠O 的切线,A 为切点,连接BC ,与∠O 交于点D ,连接OD .若82AOD ∠=︒,则C ∠=_________︒.9.正方形ABCD 在平面直角坐标系中的位置如图所示,点A 的坐标为(2,0),点B 的坐标为(0,4).若反比例函数y =k x(k ≠0)的图象经过点C ,则k 的值为 _____.10.如图,已知l 1∠l 2,MN 分别和直线1l 、2l 交于点A 、B ,ME 分别和直线1l 、2l 交于点C 、D ,点P 在MN 上(P 点与A 、B 、M 三点不重合)如果点P 在直线AB 运动时,α∠、β∠、γ∠之间有何数量关系______.11.如图,EFG 和HIJ 都是等边三角形,连接HG ,EI 交于点P ,则EPH ∠=_________度.12.如图,ABC 中,AB AC =,AD BD ⊥于点D ,20BAD ∠=︒,若2BC BD =,则BAC ∠的度数为 _____.三、解答题13.如图,已知ABC(1)用直尺和圆规按下列要求作图:(保留作图痕迹)在BC 上作点D ,使点D 到AB 和AC 的距离相等;过点B 作//BE AD 交CA 的延长线于E ;(2)若AF BE ⊥,垂足为F ,证明BF EF =.14.在∠ABC 中,D 是BC 的中点,DE ∠AB ,DF ∠AC ,垂足分别是E ,F .(1)若BE =CF ,求证:AD 是∠ABC 的角平分线.(2)若AD 是∠ABC 的角平分线,求证:BE =CF .15.如图,AB CD ,AD 与BC 交于点O ,40C ∠=︒,80AOB ∠=︒,求A ∠的度数.16.在ABC 中,AB AC =,D 是BC 边的中点,E 、F 分别是AD 、AC 边上的点.(1)如图∠,连接BE 、EF ,若ABE EFC ∠=∠,求证:BE EF =;(2)如图∠,若B 、E 、F 在一条直线上,且45ABE BAC ∠=∠=︒,探究BD 与AE 的数量之间有何等量关系,并说明理由;17.如图,在Rt DEF △和Rt ABC 中,90D A ∠=∠=︒,30E ∠=︒,45C ∠=︒,AC 与DF 相交于点G ,若105FGC ∠=︒,请判断EF 与BC 是否平行?并说明理由.18.如图,点D ,E 分别在OA ,OB 上,点P 在OC 上,且PD PE =.若180ODP OEP ∠+∠=︒,求证:OC 平分AOB ∠.参考答案:1.B【分析】根据全等三角形的判定定理判断解答即可.【详解】解:A 、∠BC ∠EF ,∠∠ACB =∠DFE ,又∠B =∠E ,BC =EF ,∠∠ABC ∠∠DEF (ASA ),正确,不符合题意;B 、根据全等三角形的判定定理,不能证明∠ABC ∠∠DEF ,错误,符合题意;C 、∠BC ∠EF ,∠∠ACB =∠DFE ,∠AD=CF ,∠AD+DC=CF+DC ,∠AC=DF ,∠BC=EF ,∠ACB =∠DFE ,AC=DF ,∠∠ABC ∠∠DEF (SAS ),正确,不符合题意;D 、∠BC ∠EF ,AB ∠DE ,∠∠ACB =∠DFE ,∠BAC =∠EDF ,又BC=EF ,∠∠ABC ∠∠DEF (AAS ),正确,不符合题意,故选:B .【点睛】本题考查全等三角形的判定、平行线的性质,熟练掌握全等三角形的判定是解答的关键.2.A【分析】根据作图方法可知,DE AB =,DF AC =,EF BC =,由此可解.【详解】解:根据作图的步骤(1)知DE AB =,由步骤(2)知DF AC =,EF BC =,根据三组边对应相等(SSS ),可证ABC DEF ≌△△. 故答案为:A .【点睛】本题考查尺规作图和全等三角形的判定,根据作图的方法判断出两个三角形的三条边对应相等是解题的关键.3.C【分析】根据全等三角形的判定定理解答即可.【详解】解:在BAD 和CAE 中,A A AB AC B C ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∠BAD ∠CAE ()ASA ,故选:C .【点睛】本题考查了全等三角形的判定,熟练掌握全等三角形的判定定理是解本题的关键.4.D【分析】根据旋转的性质判断得()GPH DPF ASA ∆≅∆,可判断∠正确,证PDHCDE ∆∆可判断∠正确,从而得出结果.【详解】解:根据旋转的性质可知,90DPH GPF ∠=∠=︒,∠DE 平分ADC ∠,∠45HDP ∠=︒,∠45DHP PDH PDF ∠=∠=∠=︒,∠PH =PD ,∠90DPH GPF ∠=∠=︒∠GPH DPF ∠=∠在GPH ∆和DPF ∆中, ∠GHP FDP PH PD GPH DPF ∠=∠⎧⎪=⎨⎪∠=∠⎩∠()GPH DPF ASA ∆≅∆∠HG DF =∠45PDH ∠=︒∠DH =∠DF DG GH DG DH +=+==故∠正确;∠45PDH PDF ∠=∠=︒,90DPH DCE ∠=∠=︒∠PDHCDE ∆∆ ∠DH DP DE CD= 即DP DE DH DC ⋅=⋅,故∠正确;根据已知条件无法证明∠DH =DE ,∠DP =DG .故选:D .【点睛】本题主要考查矩形的性质、三角形的全等、三角形的相似,掌握相关知识并灵活应用是解题的关键.5.C【分析】分别过C 、D 作AB 的平行线CM 和DN ,由平行线的性质可得到最终结果.【详解】如图,分别过C 、D 作AB 的平行线CM 和DN ,,,,,,,90,90,AB EF AB CM DN EF BCM MCD NDC NDE BC CD BCD BCM MCD NDCNDE αγααβαβγ∴∴∠=∠∠=∠∠=∠⊥∴∠=∠+∠=∠+∠=∠+∠-∠=︒∴∠+∠-∠=︒故选:C .【点睛】本题主要考查平行线的性质,掌握平行线的性质是解题的关键,即∠两直线平行,同位角相等;∠两直线平行,内错角相等;∠两直线平行,同旁内角互补.6.C【分析】由“SAS”可证△ABE ∠∠CBE ,可得AE =CE ,可证四边形CFEG 是矩形,可得GC =EF =3,∠EFC =90°,由勾股定理可求解.【详解】解:如图,连接CE ,∠四边形ABCD 是正方形,∠AB =BC ,∠ABD =∠CBD =45°,在△ABE 和△CBE 中,AB BC ABE CBE BE BE =⎧⎪∠=∠⎨⎪=⎩,∠∠ABE ∠∠CBE (SAS ),∠AE =CE ,∠EF ∠BC ,EG ∠CD ,∠BCD =90°,∠四边形CFEG 是矩形,∠GC =EF =3,∠EFC =90°,∠CE5,∠AE =5,故选:C .【点睛】本题考查了正方形的性质,全等三角形的判定和性质,勾股定理,灵活运用这些性质解决问题是解题的关键.7.5或10【分析】当AP =5或10时,∠ABC 和∠PQA 全等,根据HL 定理推出即可.【详解】解:∠∠C =90°,AO ∠AC ,∠∠C =∠QAP =90°,∠当AP =5=BC 时,在Rt ∠ACB 和Rt ∠QAP 中∠AB PQ BC AP =⎧⎨=⎩, ∠Rt ∠ACB ∠Rt ∠QAP (HL ),∠当AP =10=AC 时,在Rt ∠ACB 和Rt ∠P AQ 中AB PQ AC AP =⎧⎨=⎩, ∠Rt ∠ACB ∠Rt ∠P AQ (HL ),故答案为:5或10.【点睛】本题考查了全等三角形的判定定理的应用,注意:判定两直角三角形全等的方法有ASA ,AAS ,SAS ,SSS ,HL .8.49【分析】利用同弧所对的圆周角等于圆心角的一半求得∠B =12∠AOD =41°,根据AC 是∠O 的切线得到∠BAC =90°,即可求出答案.【详解】解:∠∠AOD =82°,∠∠B =12∠AOD =41°,∠AC 为圆的切线,A 为切点,∠∠BAC =90°,∠∠C =90°-41°=49°故答案为49.【点睛】此题考查圆周角定理,圆的切线的性质定理,直角三角形两锐角互余,正确理解圆周角定理及切线的性质定理是解题的关键.9.24【分析】过点C 作CE ∠y 轴,由正方形的性质得出∠CBA =90°,AB =BC ,再利用各角之间的关系得出∠CBE =∠BAO ,根据全等三角形的判定和性质得出OA =BE =2,OB =CE =4,确定点C 的坐标,然后代入函数解析式求解即可.【详解】解:如图所示,过点C 作CE ∠y 轴,∠点B(0,4),A(2,0),∠OB=4,OA=2,∠四边形ABCD为正方形,∠∠CBA=90°,AB=BC,∠∠CBE+∠ABO=90°,∠∠BAO+∠ABO=90°,∠∠CBE=∠BAO,∠∠CEB=∠BOA=90°,,∠ABO BCE∠OA=BE=2,OB=CE=4,∠OE=OB+BE=6,∠C(4,6),将点C代入反比例函数解析式可得:k=24,故答案为:24.【点睛】题目主要考查正方形的性质,全等三角形的判定和性质,反比例函数解析式的确定等,理解题意,综合运用这些知识点是解题关键.10.∠α+∠β=∠γ【分析】根据平行线的性质可求出它们的关系,从点P作平行线,平行于AC,根据两直线平行内错角相等可得出.【详解】解:如图,过点P作AC的平行线PO,∠AC∠PO,∠∠β=∠CPO,又∠AC∠BD,∠PO∠BD,∠∠α=∠DPO ,∠∠α+∠β=∠γ,故答案为:∠α+∠β=∠γ.【点睛】本题主要考查了两直线平行,内错角相等,正确作出辅助线是解题的关键.11.60【分析】根据等边三角形的性质可证∠FIH ∠∠GJI ,再证明∠FGH ∠∠GEI ,根据全等三角形的性质可得∠FGH =∠GEI ,从而可得∠GEI +∠HGE =60°,根据外角的性质可得∠EPH 的度数.【详解】解:在等边∠EFG 中,∠F =∠FGE =60°,FG =GE ,∠∠FHI +∠FIH =120°,在等边∠HIJ 中,∠HIJ =60°,HI =JI ,∠∠FIH +∠JIG =120°,∠∠FHI =∠JIG ,在∠FIH 和∠GJI 中,F G FHI GIJ HI JI ∠=∠⎧⎪∠=∠⎨⎪=⎩,∠∠FIH ∠∠GJI (AAS ),∠FH =GI ,在∠FGH 和∠GEI 中,FH GI F G FG GE =⎧⎪∠=∠⎨⎪=⎩,∠∠FGH ∠∠GEI (SAS ),∠∠FGH =∠GEI ,∠∠FGH +∠HGE =60°,∠∠GEI +∠HGE =60°,∠∠EPH =60°,故答案为:60【点睛】本题考查了全等三角形的判定和性质,等边三角形的性质等,熟练掌握全等三角形的判定和性质是解题的关键.12.40︒【分析】如图(见详解),根据等腰三角形的三线合一性质,过点A 作AE BC ⊥于点E ,可证RT ABE RT ABD △≌△,即可求出BAC ∠的度数.【详解】解:如图,过点A 作AE BC ⊥于点E ,∠AB =AC ,∠E 是BC 的中点,且AE 平分BAC ∠.∠2BC BD =,∠BD =BE .在RT ABE 和RT ABD 中,()AB AB RT ABE RT ABD HL BD BE =⎧⇒⎨=⎩△≌△, ∠20BAD BAE CAE ∠=∠=∠=︒.∠40BAC ∠=︒.故答案为:40︒.【点睛】本题考查等腰三角形的三线合一性质以及直角三角形全等的判定定理,正确运用定理进行判定是解题的关键.13.(1)见解析;(2)见解析【分析】(1)作∠BAC 的平分线,交BC 于D ,作∠ABE =∠BAD ,交CA 延长线于E 即可;(2)根据已知条件,利用ASA 证明∠AFE ∠∠AFB ,可得结果.【详解】解:(1)如图所示,AD 和BE 即为所作;(2)∠BE ∠AD ,AF ∠BE ,∠∠DAF =180°-90°=90°,∠EAF +∠CAD =90°,即∠BAF +∠BAD =90°,由(1)可知:∠BAD =∠CAD ,∠∠CAD +∠BAF =90°,∠∠BAF =∠EAF ,∠∠AFE =∠AFB =90°,AF =AF ,∠∠AFE ∠∠AFB (ASA ),∠EF =BF .【点睛】本题考查了尺规作图,平行线的性质,角平分线的判定,全等三角形的判定和性质,正确的作出图形是解题的关键.14.(1)证明见解析;(2)证明见解析【分析】(1)根据D 是BC 的中点可得BD DC =,根据 DE ∠AB 可得90DEB DFC ∠=∠=︒,利用直角三角形全等的判定和性质可得Rt Rt BDE CDF ≌,DE =DF ,再用角平分线得判定定理即可证明;(2)根据角平分线的性质得到DE =DF ,根据D 是BC 的中点可得BD DC =,再用HL 证明Rt Rt BDE CDF ≌,最后用全等三角形对应边相等证明.(1)证明:∠DE ∠AB ,DF ∠AC ,∠∠BDE 与∠DCF 是直角三角形.在Rt∠BDE 与Rt∠CDF 中,BD CD BE CF=⎧⎨=⎩, ∠Rt∠BDE ∠Rt∠CDF (HL ),∠DE =DF .又∠DE ∠AB ,DF ∠AC ,∠AD 是∠ABC 的角平分线;(2)∠AD 是∠ABC 的角平分线,DE ∠AB 于E ,DF ∠AC 于F ,∠DE =DF ,∠AD 是BC 边的中线,∠BD =CD .在Rt∠BDE 和Rt∠CDF 中,BD CD DE DF =⎧⎨⎩=, ∠Rt∠BDE ∠Rt∠CDF (HL ),∠BE =CF .【点睛】本题考查直角三角形全等的判定(HL ),角平分线的性质定理和判定定理,用HL 证明Rt∠BDE ∠Rt∠CDF 是解题的关键.15.60︒【分析】由AB 与CD 平行,利用两直线平行内错角相等求出B 的度数,在AOB 中,利用三角形内角和定理即可求出A ∠的度数.【详解】解:∠AB CD ,40C ∠=︒,∠40B C ∠=∠=︒,∠180A B AOB ∠+∠+∠=︒,∠18060∠=︒-∠-∠=︒A AOB B .【点睛】此题考查了平行线的性质以及三角形内角和定理,熟练掌握平行线的性质及三角形内角和定理是解本题的关键.16.(1)证明见解析;(2)2AE BD =,理由见解析【分析】(1)AD 为线段BC 的垂直平分线,垂直平分线的性质可得∠ABC =∠ACB ,BE =CE ,通过角的等量替换可得∠ACE =∠EFC ,再证边长相等即可.(2)由(1)可得∠ABE =∠ACE ,直角三角形证明全等即可得出.(1)连接CE ,AB AC =,D 是BC 边的中点,AD ∴为线段BC 的垂直平分线,A ABC CB =∠∠,BE CE ∴=,EBC ECB ∴∠=∠,ABC EBC ACB ECB ∴∠-∠=∠-∠,即ABE ACE =∠∠,ABE EFC ∠=∠,ACE EFC ∴∠=∠,EF CE ∴=,BE EF ∴=;(2)连接CE ,由(1)可得ABE ACE =∠∠,45ABE BAC ∠=∠=︒,ABF ∴和CEF △都是等腰直角三角形,AF BF CF EF ∴==,,CBF EAF ∴≌△△,BC AE ∴=,2AE BD ∴=;(注:辅助线连接CE 不要求)17.EF BC ∥,理由见解析【分析】过G 点作GH BC ∥,根据平行线的性质,角的和差关系,三角形内角和定理可得∠F =∠FGH ,再根据平行线的判定即可求解.【详解】解:EF BC ∥.理由如下:过G 点作GH BC ∥,∠∠C =45°,90A ∠=︒,∠∠CGH =45°,∠∠FGC =105°,∠∠FGH =105°−45°=60°,在Rt ∠DEF 中,∠D =90°,∠E =30°,∠∠F =60°,∠∠F =∠FGH ,∠EF GH ∥,∠EF BC ∥.【点睛】本题考查了平行线的判定与性质,三角形内角和定理,关键是熟悉两条直线都和第三条直线平行,那么这两条直线平行.18.见解析【分析】过点P 作PF OA ⊥,PH OB ⊥,证明∠PDF ∠∠PEH ,得出PF PH =,根据角平分线的判定定理得出OC 平分AOB ∠.【详解】证明:过点P 作PF OA ⊥,PH OB ⊥,∠90PFD PHE ∠=∠=︒∠180ODP OEP ∠+∠=︒,180PEB OEP ∠+∠=︒∠ODP PEB ∠=∠在∠PDF 和∠PEH 中PFD PHE PDF PEH PF PH ∠=∠⎧⎪∠=∠⎨⎪=⎩∠∠PDF ∠∠PEHPF PH ∴=,∠OC 平分AOB ∠.【点睛】本题考查了角平分线的判定定理,全等三角形的性质与判定,掌握角平分线的判定定理是解题的关键.。
人教版八年级数学上册《全等三角形证明》专项练习题-附含答案

人教版八年级数学上册《全等三角形证明》专项练习题-附含答案 专题简介:本份资料包含《全等三角形》这一章的六种主流中档证明题 所选题目源自各名校期中、期末 试题中的典型考题 具体包含的题型有:重叠边技巧、重叠角技巧、等角的余角相等技巧、证两次全等的证明题、手拉手模型、角平分线的性质与判定的中档题。
适合于公立学校老师和培训机构的老师给学生作全等三角形证明题专项复习时使用或者学生考前刷题时使用。
题型1:重叠边技巧①短边相等+重叠边=长边相等②长边相等-重叠边=短边相等1.(2019·广东)如图 点A 、C 、F 、D 在同一直线上 AF=DC AB=DE BC=EF 求证:AB ∥DE .【详解】∵AF=DC ∴AF ﹣FC=DC ﹣CF 即AC=DF .在△ACB 和△DFE 中AC DF AB DE BC EF =⎧⎪=⎨⎪=⎩∴△ACB ≌△DFE (SSS ) ∴∠A=∠D ∴AB ∥DE .2.(2021·重庆)已知点A 、E 、F 、C 在同一直线上 已知AD BC ∥ AD BC = AE CF = 试说明BE 与DF 的关系.【详解】解:数量关系BE DF = 位置关系BE DF ∥.理由:∵AD BC ∥ ∴∠A =∠C又AE CF = ∴AE +EF =CF +EF 即AF =CE 在ADF 和CBE △中 AD BC A C AF CE =⎧⎪∠=∠⎨⎪=⎩ ADF ∴≌()CBE SAS △∴BE =DF ∠BEF =∠DFE ∴BE DF ∥.3.(2021·湖北荆门)如图点E、F在BC上BE=CF AB=DC∠B=∠C.求证:∠A=∠D.【详解】解∵BE=CF∴BE+EF=CF+EF即BF=CE.在△ABF和△DCE中AB DCB C BF CE=⎧⎪∠=∠⎨⎪=⎩∴△ABF≌△DCE∴∠A=∠D.4.(2021·甘肃)如图AB∥CD BN∥MD点M、N在AC上且AM=CN求证:BN=DM.【详解】解:∵AB∥CD BN∥MD ∴∠A=∠C∠CMD=∠ANB ∵AM=CN∴AM+MN=MN+CN即AN=MC 在△ANB和△CMD中∠A=∠C AN=MC∠ANB=∠CMF ∴△ANB≌△CMD(ASA)∴BN=MD.5.(2021·新疆)如图点A、F、C、D在同一直线上点B和点E分别在直线AD的两侧且AB=DE∠A =∠D AF=DC.求证:(1)△ABC≌△DEF;(2)BC∥EF.【详解】(1)证明:∵AF=DC∴AF+CF=DC+CF∴AC=DF∵在△ABC和△DEF中AB DEA DAC DF=⎧⎪∠=∠⎨⎪=⎩∴△ABC≌△DEF(SAS);(2)证明:由(1)知△ABC≌△DEF∴∠BCA=∠EFD∴BC∥EF.题型2:重叠角技巧重叠角技巧:①小角相等+重叠角=大角相等②大角相等-重叠角=小角相等6.(2022·福建·福州)如图AC=AE∠1=∠2 AB=AD.求证:△ABC≌△ADE.【详解】证明:∵∠1=∠2 12EAB EAB∴∠+∠=∠+∠即CAB EAD∠=∠在ABC和ADE中{AC AECAB EAD AB AD=∠=∠=() ABC ADE SAS∴≅.7.(2022·四川资阳)如图在△ABC和△ADE中AB=AD∠B=∠D∠1=∠2.求证:BC=DE.【详解】证明:∵∠1=∠2 ∵∠DAC+∠1=∠2+∠DAC∴∠BAC=∠DAE在△ABC和△ADE中B DAB ADBAC DAE∠∠⎧⎪⎨⎪∠∠⎩===∴△ADE≌△ABC(ASA)∴BC=DE8.如图AB=AD∠C=∠E∠1=∠2 求证:△ABC≌△ADE.【解答】证明:∵∠1=∠2 ∴∠1+∠EAC=∠2+∠EAC即∠BAC=∠DAE在△ABC和△ADE中BAC DAE C E AB AD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADE (AAS ). 9.(雅礼)如图 △ABC 和△ADE 都是等腰三角形 且∠BAC =90° ∠DAE =90° B C D 在同一条直线上.求证:BD =CE .【解答】证明:∵△ABC 和△ADE 都是等腰直角三角形 ∴AD =AE AB =AC 又∵∠EAC =90°+∠CAD ∠DAB =90°+∠CAD ∴∠DAB =∠EAC∵在△ADB 和△AEC 中 ∴△ADB ≌△AEC (SAS ) ∴BD =CE .10.(2020·四川达州)已知△ABN 和△ACM 位置如图所示 AB =AC AD =AE ∠1=∠2.(1)求证:BD =CE ;(2)求证:∠M=∠N .【详解】(1)证明:在△ABD 和△ACE 中 12AB AC AD AE =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△ACE (SAS ) ∴BD =CE ; (2)证明:∵∠1=∠2 ∴∠1+∠DAE =∠2+∠DAE 即∠BAN =∠CAM 由(1)知:△ABD ≌△ACE∴∠B =∠C 在△ACM 和△ABN 中 C B AC AB CAM BAN ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ACM ≌△ABN (ASA ) ∴∠M =∠N . 题型3:等角的余角相等技巧:∠1+∠2=90 ∠2+∠3=90 ∴∠1=∠3技巧:把全等三角形中一个三角形的两个锐角分别随意标上∠1、∠2 再从第二个三角形的两个锐角中挑一个和∠1或∠2互余的角标上∠3。
(完整版)全等三角形证明经典50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CDAB B A CDF2 1 EAC D E F 21 A D BC A6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
13.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C14. P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB15. 已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BED C B A FE PD A CB16. 已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC18.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .19.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA20.(5分)如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .21.如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B22.(6分)如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .(1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.F AEDCB P E D CB A DC B A23.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC . (2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):24.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .证明:25、如图:DF=CE ,AD=BC ,∠D=∠C 。
(完整版)全等三角形证明经典50题(含答案)
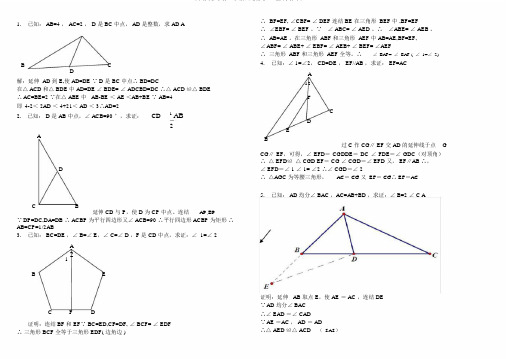
1.已知: AB=4 , AC=2 , D 是 BC 中点, AD 是整数,求 AD AB CD解:延伸 AD 到 E,使 AD=DE ∵ D 是 BC 中点∴ BD=DC在△ ACD 和△ BDE 中 AD=DE ∠ BDE= ∠ ADCBD=DC ∴△ ACD ≌△ BDE∴AC=BE=2 ∵在△ ABE 中 AB-BE < AE <AB+BE ∵ AB=4即4-2< 2AD < 4+21< AD < 3∴AD=22. 已知: D 是 AB 中点,∠ ACB=90 °,求证:CD 1 AB2ADC B延伸 CD 与 P,使 D 为 CP 中点。
连结AP,BP∵DP=DC,DA=DB ∴ ACBP 为平行四边形又∠ ACB=90 ∴平行四边形 ACBP 为矩形∴AB=CP=1/2AB3.已知: BC=DE ,∠ B=∠ E,∠ C=∠ D ,F 是 CD 中点,求证:∠ 1=∠ 2A12B EC F D证明:连结 BF 和 EF∵ BC=ED,CF=DF, ∠ BCF= ∠ EDF∴三角形 BCF 全等于三角形 EDF( 边角边 )∴BF=EF, ∠CBF= ∠ DEF 连结 BE 在三角形 BEF 中 ,BF=EF∴∠EBF= ∠ BEF 。
∵ ∠ ABC= ∠ AED 。
∴ ∠ABE= ∠ AEB 。
∴AB=AE 。
在三角形 ABF 和三角形 AEF 中 AB=AE,BF=EF,∠ABF= ∠ ABE+ ∠ EBF= ∠ AEB+ ∠ BEF= ∠AEF∴三角形 ABF 和三角形 AEF 全等。
∴∠ BAF=∠ EAF (∠ 1=∠ 2) 4.已知:∠ 1=∠2, CD=DE , EF//AB ,求证: EF=ACA12FCDEB过 C 作 CG∥ EF 交 AD 的延伸线于点G CG∥ EF,可得,∠ EFD= CGDDE= DC ∠ FDE=∠ GDC(对顶角)∴ △ EFD≌ △ CGD EF= CG ∠ CGD=∠ EFD 又, EF∥AB ∴,∠ EFD=∠ 1 ∠ 1= ∠2 ∴∠ CGD=∠ 2∴ △AGC 为等腰三角形,AC= CG 又 EF= CG∴ EF=AC5.已知: AD 均分∠ BAC ,AC=AB+BD ,求证:∠ B=2 ∠ C A证明:延伸AB 取点 E,使 AE = AC ,连结 DE∵AD 均分∠ BAC∴∠ EAD =∠ CAD∵AE =AC , AD = AD∴△ AED ≌△ ACD(SAS)∴∠ E=∠ C∵AC =AB+BD∴AE = AB+BD∵AE = AB+BE∴ BD =BE∴∠ BDE =∠ E∵∠ ABC =∠ E+ ∠ BDE∴∠ ABC = 2∠E∴∠ ABC = 2∠C6.已知: AC 均分∠ BAD ,CE⊥AB ,∠ B+ ∠ D=180 °,求证: AE=AD+BE证明:在AE 上取 F,使 EF=EB ,连结 CF∵ CE⊥ AB∴∠ CEB =∠ CEF= 90°∵ EB= EF, CE= CE,∴△ CEB ≌△ CEF∴∠ B =∠ CFE∵∠ B +∠ D= 180°,∠ CFE+∠ CFA = 180°∴∠ D =∠ CFA∵AC 均分∠ BAD∴∠ DAC =∠ FAC∵AC =AC∴△ ADC ≌△ AFC ( SAS)∴AD =AF ∴AE =AF + FE=AD + BE12.如图,四边形 ABCD 中, AB ∥ DC ,BE、CE 分别均分∠ ABC 、∠ BCD ,且点 E在AD 上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形的判定与性质 八年级全等三角形简单证明题及答案15道
.
2Hale Waihona Puke 2.如图,在△ABC中,∠C=90°,点D是AB边上的一点,DM⊥AB,
且DM=AC,过点M作ME∥BC交AB于点E.求证:△ABC≌△MED。
证明:∵MD⊥AB, ∴∠MDE=∠C=90°, ∵ME∥BC, ∴∠B=∠MED, 在△ABC与△MED中, ∠B=∠MED ∠C=∠EDM DM=AC ,
全等三角形的判定与性质.
八年级全等三角形简单证明题及答案15道
6
7.如图,D、E分别是AB、AC上的点,且 AB=AC,AD=AE.求证:∠B=∠C.
在△ABE和△ACD中, ∵ AB=AC ∠A=∠A AE=AD , ∴△ABE≌△ACD(SAS), ∴∠B=∠C.
全等三角形的判定与性质. 八年级全等三角形简单证明题及答案15道
证明:∵AD∥CB, ∴∠A=∠C, 在△ADF和△CBE中, ∠A=∠C AD=CB ∠D=∠B , ∴△ADF≌△CBE(ASA), ∴AF=CE, ∴AF+EF=CE+EF,即AE=CF.
全等三角形的判定与性质.
八年级全等三角形简单证明题及答案15道
10
11.在△ABC中,AB=CB,∠ABC=90°,F为AB延 长线上一点,点E在BC上,且AE=CF.求证: Rt△ABE≌Rt△CBF;
∵∠ABC=∠BAC=45° ∴∠ACB=90°,AC=BC ∵∠DAC+∠ACD=90°,∠BCE+∠ACD=90° ∴∠DAC=∠BCE 又∵∠ADC=∠CEB ∴△ACD≌△CEB ∴BE=CD=2.
直角三角形全等的判定;八年级全全等等三角三形简单角证明形题及的答案性15道质.
12
如图,△ABC中,AB=AC,∠1=∠2,求 证:AD平分∠BAC.
∴∠BCF=∠CBD,
∴ ∠BCF=∠CBD BC=BC八年∠级全A等三B角C形=简单∠证明A题C及B答案15道
14
∴△BCF≌△CBD(ASA).
全等三角形的判定.
解:∵AB=AC, ∴∠ABC=∠ACB. ∵∠1=∠2, ∴∠ABD=∠ACD,BD=CD. ∵AB=AC,BD=CD, ∴△ABD≌△ACD. ∴∠BAD=∠CAD. 即AD平分∠BAC.
全等三角形的判定与性质.
八年级全等三角形简单证明题及答案15道
13
如图,△ABC中,AB=AC,过点A作GE∥BC,角平
分线BD、CF相交于点H,它们的延长线分别交GE于
点E、G.试在图中找出3对全等三角形,并对其中
:△BCF≌△CBD.
一对全等三角形给出证明.
△BHF≌△CHD.
△BDA≌△CFA.
证明:在△BCF与△CBD中,
∵AB=AC.
∴∠ABC=∠ACB
∵BD、CF是角平分线.
∴∠BCF=1 2 ∠ACB,∠CBD=1 2 ∠ABC.
(1)证明:∵∠ABC=90°, ∴∠CBF=∠ABE=90°, 在Rt△ABE和Rt△CBF中, AE=CF AB=BC , ∴Rt△ABE≌Rt△CBF(HL);
直角三角形全等的判定
八年级全等三角形简单证明题及答案15道
11
如图,△ABC中,∠ABC=∠BAC=45°,点P 在AB上,AD⊥CP,BE⊥CP,垂足分别为D, E,已知DC=2,求BE的长.
八年级全等三角形简单证明题及答案15道
1
1.已知:如图,AB=AE,∠1=∠2,∠B=∠E.求证: BC=ED.
证明:∵∠1=∠2, ∴∠1+∠BAD=∠2+∠BAD, 即:∠EAD=∠BAC,
在△EAD和△BAC中
∠B=∠E AB=AE ∠BAC=∠EAD , ∴△ABC≌△AED(ASA), ∴BC=ED.
全等三角形的判定与性质. 八年级全等三角形简单证明题及答案15道
5
6.已知:如图,点E,A,C在同一直线上,AB∥CD ,AB=CE,AC=CD.求证:BC=ED.
证明:∵AB∥CD, ∴∠BAC=∠ECD, 在△BAC和△ECD中 AB=EC ∠BAC=∠ECD AC=CD , ∴△BAC≌△ECD(SAS), ∴CB=ED.
∴△ABC≌△MED(AAS).
全等三角形的判定. 八年级全等三角形简单证明题及答案15道
3
如图,E、F是四边形ABCD的对角线BD上的两点,AE∥CF, AE=CF,BE=DF.求证:△ADE≌△CBF.
证明:∵AE∥CF ∴∠AED=∠CFB, ∵DF=BE, ∴DF+EF=BE+EF, 即DE=BF, 在△ADE和△CBF中,
证明:∵AB∥DE, ∴∠B=∠DEF. ∵BE=CF, ∴BC=EF. ∵∠ACB=∠F, ∴ ∠B=∠DEF BC=EF∠ACB=∠F , ∴△ABC≌△DEF.
全八等年级三全等角三角形形简单的证明判题及定答案;15道 平行线的性质. 9
10.已知:如图,E、F在AC上,AD∥CB且 AD=CB,∠D=∠B.求证:AE=CF.
AE=CF ∠AED=∠CFB DE=BF , ∴△ADE≌△CBF(SAS).
全等三角形的判定.
八年级全等三角形简单证明题及答案15道
4
5.如图,在△ABC中,AB=AC,AD平分∠BAC.求 证:∠DBC=∠DCB.
解:∵AD平分∠BAC, ∴∠BAD=∠CAD. ∴在△ACD和△ABD中 AB=AC ∠BAD=∠CAD AD=AD , ∴△ACD≌△ABD, ∴BD=CD, ∴∠DBC=∠DCB.
7
8.已知AC平分∠BAD,AB=AD.求证: △ABC≌△ADC.
:∵AC平分∠BAD, ∴∠BAC=∠DAC, 在△ABC和△ADC中,
AB=AD ∠BAC=∠DAC AC=AC , ∴△ABC≌△ADC.
全等三角形的判定.
八年级全等三角形简单证明题及答案15道
8
9.如图,已知点E,C在线段BF上,BE=CF, AB∥DE,∠ACB=∠F.求证: △ABC≌△DEF.
