三角函数近似计算
三角函数的泰勒展开式

三角函数的泰勒展开式泰勒展开式是将一个函数在其中一点附近用多项式近似表示的方法。
对于三角函数来说,它们也可以用泰勒展开式来表示。
首先,我们从最基本的三角函数开始,即正弦函数sin(x)和余弦函数cos(x)。
它们的常用的泰勒展开式如下:对于正弦函数sin(x),其泰勒展开式为:sin(x) = x - (x^3)/3! + (x^5)/5! - (x^7)/7! + ...对于余弦函数cos(x),其泰勒展开式为:cos(x) = 1 - (x^2)/2! + (x^4)/4! - (x^6)/6! + ...这两个展开式可以无限地继续下去,每一项都是x的幂次是奇数时的负倒数阶乘乘上x的幂次是该奇数的项。
我们可以通过增加展开式的项数来获得更高精度的近似。
此外,正切函数tan(x)也可以用泰勒展开式来表示。
对于tan(x),其泰勒展开式为:tan(x) = x + (x^3)/3 + (2*x^5)/15 + (17*x^7)/315 + ...这里,tan(x)的泰勒展开式的每一项的系数是Fibonacci数列(1, 1, 2, 5, 14, 42, ...)的一部分。
同样地,我们可以通过增加展开式的项数来获得更高精度的近似。
此外,其他的三角函数如sec(x)、csc(x)、cot(x)等也都可以用泰勒展开式来表示。
它们分别对应cos(x)的倒数、sin(x)的倒数、tan(x)的倒数。
需要注意的是,泰勒展开式只在展开点附近有效,越远离展开点,近似程度越低。
因此,在实际计算中,我们需要根据具体的问题来确定展开点和展开式的项数,以获得所需的精度。
此外,值得一提的是,泰勒展开式是一种数学工具,可以用于近似计算三角函数的值。
但在计算机中,通常会使用一些更高效的算法来计算三角函数,如Cordic算法、查表法等。
这些方法能够在保证较高精度的同时,提高计算速度。
总之,泰勒展开式是一种用多项式来近似表示三角函数的方法。
三角函数的近似计算

三角函数的近似计算三角函数是数学中非常重要的概念,广泛应用于各个领域。
然而,计算机在处理三角函数时通常需要进行近似计算。
本文将介绍三角函数的近似计算方法。
首先,我们来了解一下三角函数的定义。
在一个直角三角形中,正弦(sin)、余弦(cos)和正切(tan)分别定义为三角形的一条边和斜边之比。
弧度制下的正弦、余弦和正切函数可以通过三角形的边长比例计算得到。
然而,在计算机中,我们通常使用近似计算方法来计算三角函数的值。
最常用的方法之一是泰勒级数展开。
泰勒级数是一种逼近函数的方法,通过迭代无穷次求和来逼近函数的真实值。
以正弦函数为例,其泰勒级数展开式为:sin(x) = x - (x^3 / 3!) + (x^5 / 5!) - (x^7 / 7!) + ...可以看到,随着求和次数的增加,越来越多的项被纳入计算中,从而得到更精确的近似值。
然而,需要注意的是,泰勒级数的收敛速度并不是很快,因此需要考虑迭代次数的选择。
另一种经典的方法是查表法。
通过事先计算和存储三角函数在一组离散的输入值下的输出值,可以通过查表的方式快速获得三角函数的近似值。
对于计算机来说,查表法是一种高效的近似计算方法。
当然,近似计算方法还有很多其他的形式,如拉格朗日插值法、牛顿法等。
它们的原理都是通过一定的数学模型来逼近三角函数的值。
这些方法的选择主要取决于所需精度和计算效率的权衡。
除了以上方法,还有一些辅助近似计算的技巧可以提高计算速度和精度。
例如,通过对输入值进行范围限制,可以将三角函数的计算范围缩小到一个有限的区间内,从而提高计算速度。
另外,在一些特定的应用场景中,可以利用三角函数的周期性质,使用简单的等效变换来近似计算,以提高运算效率。
综上所述,三角函数的近似计算在计算机科学中是十分重要的。
各种近似计算方法可以根据需求灵活选择,以求得合适的精度和计算效率。
对于需要大量三角函数计算的应用,选择适当的近似计算方法可以有效降低计算复杂度,提高处理速度。
三角函数计算,Cordic 算法入门

三角函数计算,Cordic 算法入门三角函数的计算是个复杂的主题,有计算机之前,人们通常通过查找三角函数表来计算任意角度的三角函数的值。
这种表格在人们刚刚产生三角函数的概念的时候就已经有了,它们通常是通过从已知值(比如sin(π/2)=1)开始并重复应用半角和和差公式而生成。
现在有了计算机,三角函数表便推出了历史的舞台。
但是像我这样的喜欢刨根问底的人,不禁要问计算机又是如何计算三角函数值的呢。
最容易想到的办法就是利用级数展开,比如泰勒级数来逼近三角函数,只要项数取得足够多就能以任意的精度来逼近函数值。
除了泰勒级数逼近之外,还有其他许多的逼近方法,比如切比雪夫逼近、最佳一致逼近和Padé逼近等。
所有这些逼近方法本质上都是用多项式函数来近似我们要计算的三角函数,计算过程中必然要涉及到大量的浮点运算。
在缺乏硬件乘法器的简单设备上(比如没有浮点运算单元的单片机),用这些方法来计算三角函数会非常的费时。
为了解决这个问题,J. Volder于1959年提出了一种快速算法,称之为CORDIC(COordinate Rotation DIgital Computer) 算法,这个算法只利用移位和加减运算,就能计算常用三角函数值,如Sin,Cos,Sinh,Cosh等函数。
J. Walther在1974年在这种算法的基础上进一步改进,使其可以计算出多种超越函数,更大的扩展了Cordic 算法的应用。
因为Cordic 算法只用了移位和加法,很容易用纯硬件来实现,因此我们常能在FPGA运算平台上见到它的身影。
不过,大多数的软件程序员们都没有听说过这种算法,也更不会主动的去用这种算法。
其实,在嵌入式软件开发,尤其是在没有浮点运算指令的嵌入式平台(比如定点型DSP)上做开发时,还是会遇上可以用到Cordic 算法的情况的,所以掌握基本的Cordic算法还是有用的。
从二分查找法说起先从一个例子说起,知道平面上一点在直角坐标系下的坐标(X,Y)=(100,200),如何求的在极坐标系下的坐标(ρ,θ)。
三角函数公式大全(同名11461)

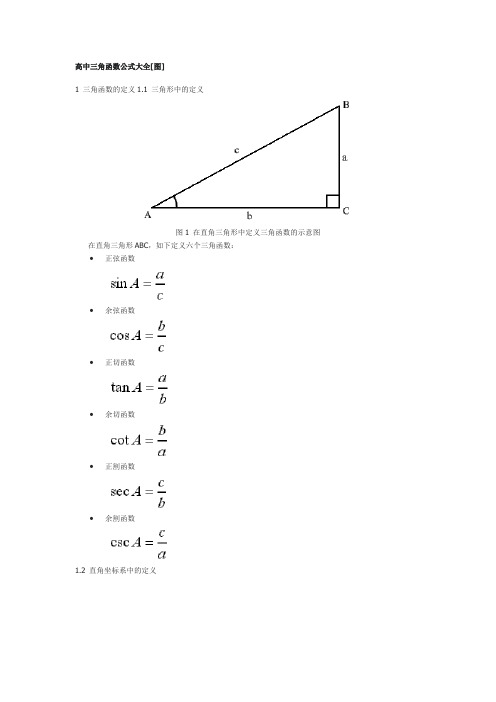
高中三角函数公式大全[图]1 三角函数的定义1.1 三角形中的定义图1 在直角三角形中定义三角函数的示意图在直角三角形ABC,如下定义六个三角函数:•正弦函数•余弦函数•正切函数•余切函数•正割函数•余割函数1.2 直角坐标系中的定义图2 在直角坐标系中定义三角函数示意图在直角坐标系中,如下定义六个三角函数:•正弦函数•余弦函数•正切函数•余切函数•正割函数•余割函数2 转化关系2.1 倒数关系2.2 平方关系2 和角公式3 倍角公式、半角公式3.1 倍角公式3.2 半角公式3.3 万能公式4 积化和差、和差化积4.1 积化和差公式4.2 和差化积公式诱导公式•sin(-a)=-sin(a)•cos(-a)=cos(a)•sin(pi/2-a)=cos(a)•cos(pi/2-a)=sin(a)•sin(pi/2+a)=cos(a)•cos(pi/2+a)=-sin(a)•sin(pi-a)=sin(a)•cos(pi-a)=-cos(a)•sin(pi+a)=-sin(a)•cos(pi+a)=-cos(a)•tgA=tanA=sinA/cosA两角和与差的三角函数•sin(a+b)=sin(a)cos(b)+cos(α)sin(b)•cos(a+b)=cos(a)cos(b)-sin(a)sin(b)•sin(a-b)=sin(a)cos(b)-cos(a)sin(b)•cos(a-b)=cos(a)cos(b)+sin(a)sin(b)•tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))•tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))三角函数和差化积公式•sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)•sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)•cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)•cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)积化和差公式•sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]•cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]•sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]二倍角公式•sin(2a)=2sin(a)cos(a)•cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a) 半角公式•sin^2(a/2)=(1-cos(a))/2•cos^2(a/2)=(1+cos(a))/2•tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))万能公式•sin(a)= (2tan(a/2))/(1+tan^2(a/2))•cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))•tan(a)= (2tan(a/2))/(1-tan^2(a/2))其它公式•a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c) [其中,tan(c)=b/a]•a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c) [其中,tan(c)=a/b]• 1+sin(a)=(sin(a/2)+cos(a/2))^2 • 1-sin(a)=(sin(a/2)-cos(a/2))^2 其他非重点三角函数• csc(a)=1/sin(a) •sec(a)=1/cos(a)双曲函数• sinh(a)=(e^a-e^(-a))/2 • cosh(a)=(e^a+e^(-a))/2 •tgh(a)=sinh(a)/cosh(a)常用公式表(一)1。
反正切函数的定义及其求解方法

反正切函数的定义及其求解方法反正切函数是一种常见的三角函数,通常表示为tan^(-1)(x),也可以写作arctan(x)。
反正切函数的定义是:对于任何实数x,tan^(-1)(x)的值是使得-tan^(-1)(x)≤y≤tan^(-1)(x)成立的唯一实数y。
反正切函数可以用来解决许多实际问题,尤其在几何和物理学中经常用到。
它通常用于求解角度,特别是在计算机图形学和信号处理中。
下面将介绍两种常见的求解反正切函数的方法:近似法和数值法。
一、近似法近似法是使用数学公式或表格来求解反正切函数的方法。
其中,最常用的近似公式是泰勒级数展开,可以通过不断增加级数的项数来提高计算的精确度。
以下是泰勒级数展开的反正切函数的表达式:arctan(x) = x - x^3/3 + x^5/5 - x^7/7 + ...使用泰勒级数展开求解反正切函数需要对表达式进行截断,保留一定的项数来达到所需的精确度。
截断的级数项数越多,计算的结果越精确,但计算的时间也越长。
另外,还可以使用预先计算好的表格来进行反正切函数的近似计算。
这种方法适用于只需要有限精度的情况。
二、数值法数值法是通过迭代计算来逼近反正切函数的方法。
其中,最常用的数值方法是牛顿法。
牛顿法的基本思想是从一个初始点开始,通过无限逼近来找到函数的根。
对于反正切函数而言,我们可以通过不断逼近反正切函数在某一点的导数为零的点,来找到函数的根。
具体而言,我们可以通过以下迭代公式来逼近反正切函数的根:x_(n+1) = x_n - (tan^(-1)(x_n) - a)/(1 + x_n^2)其中,x_n表示第n次迭代的近似值,a表示待求解的反正切函数的值。
通过不断迭代计算,当计算结果与所需精度足够接近时,可以得到反正切函数的近似解。
总结:反正切函数的定义是:tan^(-1)(x)的值是使得-tan^(-1)(x)≤y≤tan^(-1)(x)成立的唯一实数y。
求解反正切函数可以通过近似法和数值法两种方法进行。
三角函数公式

第一部分三角函数公式tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·积化和差公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·倍角公式:sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=(cosα)^2-(sinα)^2=2(cosα)^2-1=1-2(sinα)^2tan(2α)=2tanα/(1-tan^2α)cot(2α)=(cot^2α-1)/(2cotα)sec(2α)=sec^2α/(1-tan^2α)csc(2α)=1/2*secα·cscα·三倍角公式:sin(3α) = 3sinα-4sin^3α= 4sinα·sin(60°+α)sin(60°-α) cos(3α) = 4cos^3α-3cosα= 4cosα·cos(60°+α)cos(60°-α)tan(3α) = (3tanα-tan^3α)/(1-3tan^2α) = tanαtan(π/3+α)tan(π/3-α)cot(3α)=(cot^3α-3cotα)/(3cot^2α-1)·n倍角公式:sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n, 5)cos^(n-5)α·sin^5α-…cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n -4)α·sin^4α-…·半角公式:sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cos α)/sinαcot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinα=sinα/(1 -cosα)sec(α/2)=±√((2secα/(secα+1))csc(α/2)=±√((2secα/(secα-1))·辅助角公式:Asinα+Bcosα=√(A^2+B^2)sin(α+φ)(tanφ=B/A)Asinα+Bcosα=√(A^2+B^2)cos(α-φ)(tanφ=A/B)·万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2))cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))·降幂公式sin^2α=(1-cos(2α))/2=versin(2α)/2cos^2α=(1+cos(2α))/2=covers(2α)/2tan^2α=(1-cos(2α))/(1+cos(2α))·三角和的三角函数:sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cos β·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·s inγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tan α·tanβ-tanβ·tanγ-tanγ·tanα)·其它公式1+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a /2))^2csc(a)=1/sin(a) sec(a)=1/cos(a)cos30=sin60sin30=cos60·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=[sin(α/2)+cos(α/2)]^21+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/ 2))^2csc(a)=1/sin(a) sec(a)=1/cos(a)cos30=sin60sin30=cos60·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=[sin(α/2)+cos(α/2)]^2[转]洛必达公式+泰勒公式+柯西中值定理+罗尔定理来源:王艺璇的日志洛必达法则洛必达法则(L'Hospital法则),是在一定条件下通过分子分母分别求导再求极限来确定未定式值的方法。
三角函数的泰勒展开

三角函数的泰勒展开三角函数是数学中常见的函数类型之一,它在科学和工程领域中具有广泛的应用。
其中,泰勒展开是一种重要的数学工具,它能够将任何光滑函数表示为无穷级数的形式,从而简化计算和分析过程。
本文将介绍三角函数的泰勒展开,并探讨其应用。
泰勒展开是将函数在某一点附近进行多项式逼近的方法。
对于任意函数f(x),可以利用泰勒展开将其表示为一个无穷级数的形式:f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2! + f'''(a)(x-a)^3/3! + ...,其中f'(a)表示函数在点a处的一阶导数,f''(a)表示函数在点a处的二阶导数,以此类推。
这种展开方式可以方便地对函数进行近似计算。
对于三角函数,我们可以将其进行泰勒展开来得到近似表示。
以sin(x)为例,我们将其在x=0附近展开:sin(x) = sin(0) + cos(0)x - sin(0)x^2/2! - cos(0)x^3/3! + ...,其中sin(0)=0,cos(0)=1。
根据三角函数的性质,我们可以得知,sin(x)在x=0处的导数是cos(x),cos(x)在x=0处的导数是-sin(x)。
因此,对于sin(x)的泰勒展开式,我们可以得到:sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ...。
类似地,对于cos(x)的泰勒展开,我们可以得到:cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ...。
通过截取这些级数的部分项,我们可以得到三角函数的近似值。
当我们计算的精度要求不高时,只需要截取前几项级数的和即可得到一个较为准确的结果。
三角函数的泰勒展开在科学和工程中具有广泛的应用。
例如,在物理学中,当我们需要对复杂的运动进行数值模拟时,可以利用三角函数的泰勒展开来近似描述物体的运动规律。
三角函数的泰勒级数展开与应用

三角函数的泰勒级数展开与应用三角函数是高中数学中经常出现的一类函数,它们在数学和物理等学科中有着广泛的应用。
在三角函数的研究中,泰勒级数展开是一种重要的方法,可以用来近似计算三角函数的值,并且在数学和工程领域中有许多实际的应用案例。
泰勒级数是一种用多项式逼近函数的方法,它将函数表示为一系列的幂函数相加,形式上是f(x) = a0 + a1x + a2x^2 + a3x^3 + ...,其中a0, a1, a2, a3, ...是待定系数。
当我们选取适当的系数时,可以使得级数展开后的多项式逼近原函数,在某个范围内具有较高的精度。
对于三角函数而言,我们可以使用泰勒级数展开来近似计算它们的值。
例如,我们可以使用泰勒级数展开来计算正弦函数sin(x)在x=0附近的近似值。
正弦函数的泰勒级数展开的公式可以表示为: sin(x) = x - (x^3 / 3!) + (x^5 / 5!) - (x^7 / 7!) + ...在这个级数展开中,我们可以看到x的每一次幂的系数都是交替出现的,并且系数的值随着次数的增加而递减。
因此,我们可以通过截取级数展开中的有限项来逼近计算正弦函数的值。
通常情况下,我们可以选择合适的项数来平衡计算的精度和计算的速度。
同样的,我们也可以使用泰勒级数展开来计算余弦函数cos(x)的值。
余弦函数的泰勒级数展开的公式可以表示为:cos(x) = 1 - (x^2 / 2!) + (x^4 / 4!) - (x^6 / 6!) + ...通过选取合适的项数,我们可以使用级数展开来近似计算余弦函数的值。
这种方法在数学计算和工程计算中都有广泛的应用,特别是在没有计算器或计算机的情况下,可以通过手算来估计三角函数的值。
泰勒级数展开不仅仅可以用于计算三角函数的值,还可以应用到其他的数学和物理问题中。
例如,在微积分中,通过对函数进行泰勒级数展开,可以推导出一些重要的公式和定理,如复合函数的导数、多项式函数的积分等。
三角函数求值的几种方法

三角函数求值的几种方法三角函数是数学中重要的一部分,它与圆的关系密切。
三角函数的求值是在给定一个角度时,计算其正弦、余弦、正切等函数值的过程。
本文将介绍三角函数求值的几种常见方法。
一、定义法三角函数的定义法是最基本的方法,它直接使用三角函数的定义公式进行计算。
例如,正弦函数的定义为sin(x) = b/c,其中b和c分别为角x所对应直角三角形的对边和斜边的长度。
通过观察角度对应的三角形特点,可以求出函数值。
二、图表法三角函数图表法是通过查阅三角函数表格,根据给定的角度,在表格中查找对应的函数值。
例如,可以查阅三角函数表格得到30°的正弦函数值为0.5三、计算器法计算器法是利用现代科技设备来进行三角函数求值的方法。
几乎所有的计算器都内置了三角函数求值功能,只需输入角度值,即可得到相应的函数值。
四、迭代法迭代法是一种数值计算方法,通过连续迭代计算来逼近精确解。
使用迭代法计算三角函数值时,可以使用泰勒级数展开式或欧拉公式来逼近函数值。
例如,sin(x)可以展开为无穷级数:sin(x) = x - x^3/3! +x^5/5! - x^7/7! + ...,通过截取有限项和进行计算,可以得到近似的函数值。
五、差值法差值法是一种数值逼近方法,通过已知点的函数值来估计其它点的函数值。
三角函数的差值法是利用已知的函数值,通过插值公式逼近所求函数值。
例如,当已知sin(30°) = 0.5,sin(45°) = 0.7071时,可以使用线性插值的方法来估计sin(40°)的值。
六、三角恒等式法三角函数有很多恒等式,可以用于简化三角函数的计算。
例如,利用和差角公式sin(x + y) = sin(x)cos(y) + cos(x)sin(y),可以将复杂角度的三角函数值转化为已知角度的三角函数值来计算。
总结:本文介绍了三角函数求值的几种常见方法,包括定义法、图表法、计算器法、迭代法、差值法和三角恒等式法。
解决三角函数的种方法

解决三角函数的种方法方法一:代入法将给定的三角函数表达式代入三角恒等式,化简得到新的三角函数表达式。
这种方法适用于简单的恒等式,例如将sin^2x和cos^2x代入1−cot^2x=0,得到1−(cos^2x/sin^2x)=0,然后通过化简解方程得到解x的值。
方法二:化简法将给定的复杂三角函数表达式化简为简单形式。
例如将sin(x+a)−sin(x−a)的差化积公式应用,并使用和差化积公式,最后化简为2sin(a)cos(x)。
方法三:换元法通过引入新的变量或替换三角函数表达式,将原问题化简为更简单的形式。
例如可以通过令t=tan(x/2)将tan^2x转化为t^2,然后解方程t^2+1=0。
方法四:反函数法使用正弦、余弦、正切的反函数,将已知的值代入反函数的表达式,解方程找到相应的角度值。
例如通过arcsin函数,可以求解sin(x)=0.5的解x=π/6方法五:复数法将三角函数表达式转化为复数形式,利用复数的运算性质来解决问题。
例如欧拉公式e^ix=cos(x)+isin(x)可以将三角函数问题转化为复数的运算问题。
方法六:图像法根据三角函数的周期性和图像特点,结合图像的性质去解决问题。
例如可以通过观察sin函数的图像,得知sin(x)=0的解为x=nπ,其中n 为整数。
方法七:恒等式法利用三角函数的恒等式解决问题。
例如通过化简sin2x−cos^2x−1=0的表达式为−cos^2x+(1−cos^2x)−1=0,然后使用三角恒等式cos^2x=1−sin^2x,最终化简得到sin^4x=0。
方法八:半角公式通过半角公式将复杂的三角函数表达式化简为简单的形式。
例如将sin(2θ)化简为2sinθcosθ的形式,然后代入原方程得到更简单的表达式。
方法九:三倍角公式通过三倍角公式将复杂的三角函数表达式化简为简单的形式。
例如将sin(3θ)化简为3sinθ−4sin^3θ的形式,然后代入原方程得到更简单的表达式。
三角函数的近似计算

三角函数的近似计算
简介
三角函数是数学中的重要概念,主要指正弦函数、余弦函数、
正切函数和余切函数。
在实际问题中,常常需要进行三角函数运算,但计算精确的三角函数值并不容易。
因此,我们需要使用一些近似
的方法来计算三角函数值。
常用近似方法
泰勒级数展开法
泰勒级数展开法是一种常见的计算三角函数值的方法。
该方法
通过对三角函数的泰勒级数进行截断来近似计算三角函数值。
例如,对于正弦函数,它的泰勒级数展开式为:
$$\sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-
\frac{x^7}{7!}+\cdots$$
在实际计算中,我们可以选择一定的级数截断,即只考虑前几项,来近似计算正弦函数值。
插值法
插值法是另一种常见的计算三角函数值的方法。
该方法通过构造一个多项式函数来近似三角函数。
例如,我们可以选择拉格朗日插值多项式来近似计算正弦函数值。
拉格朗日插值多项式的表达式为:
$$f(x)=\sum_{i=0}^{n}y_i\prod_{j=0,j\neq i}^{n}\frac{x-
x_j}{x_i-x_j}$$
其中,$y_i$表示已知函数值,$x_i$为对应的自变量取值。
在实际计算中,我们可以选择若干个离目标点较近的点,来构造拉格朗日插值多项式来近似计算正弦函数值。
结语
以上是三角函数的近似计算方法的简单介绍。
在实际问题中,我们需要根据具体情况选择合适的计算方法,以求得尽可能精确的计算结果。
计算余弦近似值c语言

计算余弦近似值c语言余弦函数是高中数学中常见的三角函数之一,其定义域为实数集,其值域为[-1,1]。
余弦函数在计算机领域有着广泛的应用,特别是在图形绘制中,通过余弦函数可以快速计算出物体的位置及形状。
本文将介绍如何用C语言计算余弦近似值。
计算余弦近似值的方法有很多种,其中一个常见的方法是泰勒展开式。
泰勒展开式指的是将一个函数在某一点展开成一个无穷级数的形式。
对于余弦函数而言,其泰勒展开式为:cos(x) = 1 - (x^2)/2! + (x^4)/4! - (x^6)/6! + ...在计算余弦函数时,我们只需要选取展开式中前几项进行求和即可得到余弦近似值。
由于无穷级数无法计算到无限项,我们需要设定一个精度误差限度,计算到满足误差限度的项数即可。
以下是一个用C 语言实现余弦近似值计算的程序示例:include <stdio.h>include <math.h>double cosine(double x, double precision) {double result = 1, term = 1;int n = 2;do {term = term * (-1) * x * x / ((n - 1) * n);result += term;n += 2;} while (fabs(term) > precision);return result;}int main() {double x = 1.2; // 求cos(1.2)的近似值double precision = 1e-6; // 精度误差限度为10^-6 printf("cos(%.2f) ≈ %.6f\n", x, cosine(x, precision));return 0;}上述程序中,cosine函数中的do-while循环会不断计算出展开式中的每一项,当当前项的绝对值小于精度误差限度时,停止计算并返回结果。
三角函数公式大全(很详细)
高中三角函数公式大全[图]1 三角函数的定义1.1 三角形中的定义图1 在直角三角形中定义三角函数的示意图在直角三角形ABC,如下定义六个三角函数:•正弦函数•余弦函数•正切函数•余切函数•正割函数•余割函数1.2 直角坐标系中的定义图2 在直角坐标系中定义三角函数示意图在直角坐标系中,如下定义六个三角函数:•正弦函数r•余弦函数•正切函数•余切函数•正割函数•余割函数2 转化关系2.1 倒数关系2.2 平方关系2 和角公式3 倍角公式、半角公式3.1 倍角公式3.2 半角公式3.3 万能公式4 积化和差、和差化积4.1 积化和差公式证明过程首先,sin(α+β)=sinαcosβ+sinβcosα(已证。
证明过程见《和角公式与差角公式的证明》)因为sin(α+β)=sinαcosβ+sinβcosα(正弦和角公式)则sin(α-β)=sin[α+(-β)]=sinαcos(-β)+sin(-β)cosα=sinαcosβ-sinβcosα于是sin(α-β)=sinαcosβ-sinβcosα(正弦差角公式)将正弦的和角、差角公式相加,得到sin(α+β)+sin(α-β)=2sinαcosβ则sinαcosβ=sin(α+β)/2+sin(α-β)/2(“积化和差公式”之一)同样地,运用诱导公式cosα=sin(π/2-α),有cos(α+β)=sin[π/2-(α+β)]=sin(π/2-α-β)=sin[(π/2-α)+(-β)]=sin(π/2-α)cos(-β)+sin(-β)cos(π/2-α)=cosαcosβ-sinαsinβ于是cos(α+β)=cosαcosβ-sinαsinβ(余弦和角公式)那么cos(α-β)=cos[α+(-β)]=cosαcos(-β)-sinαsin(-β)=cosαcosβ+sinαsinβcos(α-β)=cosαcosβ+sinαsinβ(余弦差角公式)将余弦的和角、差角公式相减,得到cos(α+β)-cos(α-β)=-2sinαsinβ则sinαsinβ=cos(α-β)/2-cos(α+β)/2(“积化和差公式”之二)将余弦的和角、差角公式相加,得到cos(α+β)+cos(α-β)=2cosαcosβ则cosαcosβ=cos(α+β)/2+cos(α-β)/2(“积化和差公式”之三)这就是积化和差公式:sinαcosβ=sin(α+β)/2+sin(α-β)/2sinαsinβ=cos(α-β)/2-cos(α+β)/2cosαcosβ=cos(α+β)/2+cos(α-β)/24.2 和差化积公式部分证明过程:sin(α-β)=sin[α+(-β)]=sinαcos(-β)+sin(-β)cosα=sinαcosβ-sinβcosαcos(α+β)=sin[90-(α+β)]=sin[(90-α)-β]=sin(90-α)cosβ-sinβcos(90-α)=cosαcosβ-sinαs inβcos(α-β)=cos[α+(-β)]=cosαcos(-β)-sinαsin(-β)=cosαcosβ+sinαsinβtan(α+β)=sin(α+β)/cos(α+β)=(sinαcosβ+sinβcosα)/(cosαcosβ-sinαsinβ)=(cosαtanαcosβ+cosβtanβcosα)/(cosαcosβ-cosαtanαcosβtanβ)=(tanα+tanβ)/(1-tanαtanβ)tan(α-β)=tan[α+(-β)]=[tanα+tan(-β)]/[1-tanαtan(-β)]=(tanα-tanβ)/(1+tanαtanβ)诱导公式•sin(-a)=-sin(a)•cos(-a)=cos(a)•sin(pi/2-a)=cos(a)•cos(pi/2-a)=sin(a)•sin(pi/2+a)=cos(a)•cos(pi/2+a)=-sin(a)•sin(pi-a)=sin(a)•cos(pi-a)=-cos(a)•sin(pi+a)=-sin(a)•cos(pi+a)=-cos(a)•tgA=tanA=sinA/cosA两角和与差的三角函数•sin(a+b)=sin(a)cos(b)+cos(α)sin(b)•cos(a+b)=cos(a)cos(b)-sin(a)sin(b)•sin(a-b)=sin(a)cos(b)-cos(a)sin(b)•cos(a-b)=cos(a)cos(b)+sin(a)sin(b)•tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))•tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))三角函数和差化积公式•sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)•sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)•cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)•cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)积化和差公式•sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]•cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]•sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]二倍角公式•sin(2a)=2sin(a)cos(a)•cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)半角公式•sin^2(a/2)=(1-cos(a))/2•cos^2(a/2)=(1+cos(a))/2•tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))万能公式•sin(a)= (2tan(a/2))/(1+tan^2(a/2))•cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))•tan(a)= (2tan(a/2))/(1-tan^2(a/2))其它公式•a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c) [其中,tan(c)=b/a]•a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c) [其中,tan(c)=a/b]•1+sin(a)=(sin(a/2)+cos(a/2))^2•1-sin(a)=(sin(a/2)-cos(a/2))^2其他非重点三角函数•csc(a)=1/sin(a)•sec(a)=1/cos(a)双曲函数•sinh(a)=(e^a-e^(-a))/2•cosh(a)=(e^a+e^(-a))/2•tgh(a)=sinh(a)/cosh(a)常用公式表(一)1。
余弦函数在x趋于0的计算公式

余弦函数在x趋于0的计算公式余弦函数在数学中是一种常见的三角函数,用于计算一个角的余弦值。
当角度趋近于0时,余弦函数的计算公式可以用泰勒级数展开来近似计算。
本文将介绍余弦函数在x趋于0时的计算公式,并探讨其应用和性质。
余弦函数的计算公式如下所示:cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ...这个公式是通过泰勒级数展开得到的,其中x表示角度,阶乘符号“!”表示连乘,^表示乘方。
根据这个公式,我们可以通过不断增加级数中的项数来逼近余弦函数在任意角度的值。
当角度趋近于0时,我们只需要保留前几项即可得到较为精确的结果。
在实际计算中,我们通常只保留前几项来近似计算余弦函数在x趋于0时的值。
例如,如果我们只保留前4项来计算cos(x),则有:cos(x) ≈ 1 - x^2/2! + x^4/4!通过这个公式,我们可以计算出余弦函数在任意角度x趋近于0时的近似值。
这在数学、物理、工程等领域中都有广泛的应用。
余弦函数在x趋于0时的计算公式有一些重要的性质。
首先,根据泰勒级数展开的特性,我们知道只有当x趋近于0时,级数中的每一项才会趋近于0,从而使得余弦函数的值趋近于1。
当x不等于0时,余弦函数的计算公式无法使用泰勒级数展开来近似计算,而需要使用其他方法来计算。
根据公式的形式,我们可以看出余弦函数在x趋于0时是偶函数,即cos(-x) = cos(x)。
这是因为在计算公式中,x的所有奇次幂的系数都为0,只有偶次幂的系数不为0。
这个性质在实际应用中也是非常有用的。
余弦函数在x趋于0时的计算公式还与其他三角函数的计算公式有密切的关系。
例如,正弦函数在x趋于0时的计算公式可以通过余弦函数的计算公式推导得出。
具体推导过程是通过将sin(x)展开为其泰勒级数形式,然后将其中的奇次幂的系数变换为cos(x)的系数,从而得到sin(x)的计算公式。
余弦函数在x趋于0时的计算公式是通过泰勒级数展开得到的。
三角函数公式大全很详细

高中三角函数公式大全图1 三角函数的定义三角形中的定义图1 在直角三角形中定义三角函数的示意图在直角三角形ABC,如下定义六个三角函数:•正弦函数•余弦函数•正切函数•余切函数•正割函数•余割函数直角坐标系中的定义图2 在直角坐标系中定义三角函数示意图在直角坐标系中,如下定义六个三角函数:•正弦函数r •余弦函数•正切函数•余切函数•正割函数•余割函数2 转化关系倒数关系平方关系2 和角公式3 倍角公式、半角公式倍角公式半角公式万能公式4 积化和差、和差化积积化和差公式证明过程首先,sinα+β=sinαcosβ+sinβcosα已证;证明过程见因为sinα+β=sinαcosβ+sinβcosα正弦和角公式则sinα-β=sinα+-β=sinαcos-β+sin-βcosα=sinαcosβ-sinβcosα于是sinα-β=sinαcosβ-sinβcosα正弦差角公式将正弦的和角、差角公式相加,得到sinα+β+sinα-β=2sinαcosβ则sinαcosβ=sinα+β/2+sinα-β/2“积化和差公式”之一同样地,运用诱导公式cosα=sinπ/2-α,有cosα+β=sinπ/2-α+β=sinπ/2-α-β=sinπ/2-α+-β=sinπ/2-αcos-β+sin-βcosπ/2-α=cosαcosβ-sinαsinβ于是cosα+β=cosαcosβ-sinαsinβ余弦和角公式那么cosα-β=cosα+-β=cosαcos-β-sinαsin-β=cosαcosβ+sinαsinβcosα-β=cosαcosβ+sinαsinβ余弦差角公式将余弦的和角、差角公式相减,得到cosα+β-cosα-β=-2sinαsinβ则sinαsinβ=cosα-β/2-cosα+β/2“积化和差公式”之二将余弦的和角、差角公式相加,得到cosα+β+cosα-β=2cosαcosβ则cosαcosβ=cosα+β/2+cosα-β/2“积化和差公式”之三这就是积化和差公式:sinαcosβ=sinα+β/2+sinα-β/2sinαsinβ=cosα-β/2-cosα+β/2cosαcosβ=cosα+β/2+cosα-β/2和差化积公式部分证明过程:sinα-β=sinα+-β=sinαcos-β+sin-βcosα=sinαcosβ-sinβcosαcosα+β=sin90-α+β=sin90-α-β=sin90-αcosβ-sinβcos90-α=cosαcosβ-sinαsinβcosα-β=cosα+-β=cosαcos-β-sinαsin-β=cosαcosβ+sinαsinβtanα+β=sinα+β/cosα+β=sinαcosβ+sinβcosα/cosαcosβ-sinαsinβ=cosαtanαcosβ+cosβtanβcosα/cosαcosβ-cosαtanαcosβtanβ=tanα+tanβ/1-tanαtanβtanα-β=tanα+-β=tanα+tan-β/1-tanαtan-β=tanα-tanβ/1+tanαtanβ•sin-a=-sina•cos-a=cosa•sinpi/2-a=cosa•cospi/2-a=sina•sinpi/2+a=cosa•cospi/2+a=-sina•sinpi-a=sina•cospi-a=-cosa•sinpi+a=-sina•cospi+a=-cosa•tgA=tanA=sinA/cosA两角和与差的三角函数•sina+b=sinacosb+cosαsinb•cosa+b=cosacosb-sinasinb•sina-b=sinacosb-cosasinb•cosa-b=cosacosb+sinasinb•tana+b=tana+tanb/1-tanatanb•tana-b=tana-tanb/1+tanatanb 三角函数和差化积公式•sina+sinb=2sina+b/2cosa-b/2•sina−sinb=2cosa+b/2sina-b/2•cosa+cosb=2cosa+b/2cosa-b/2•cosa-cosb=-2sina+b/2sina-b/2 积化和差公式•sinasinb=-1/2cosa+b-cosa-b•cosacosb=1/2cosa+b+cosa-b•sinacosb=1/2sina+b+sina-b•sin2a=2sinacosa•cos2a=cos^2a-sin^2a=2cos^2a-1=1-2sin^2a半角公式•sin^2a/2=1-cosa/2•cos^2a/2=1+cosa/2•tana/2=1-cosa/sina=sina/1+cosa万能公式•sina= 2tana/2/1+tan^2a/2•cosa= 1-tan^2a/2/1+tan^2a/2•tana= 2tana/2/1-tan^2a/2其它公式•asina+bcosa=sqrta^2+b^2sina+c 其中,tanc=b/a•asina-bcosa=sqrta^2+b^2cosa-c 其中,tanc=a/b•1+sina=sina/2+cosa/2^2•1-sina=sina/2-cosa/2^2其他非重点三角函数•csca=1/sina•seca=1/cosa双曲函数•sinha=e^a-e^-a/2•cosha=e^a+e^-a/2•tgha=sinha/cosha常用公式表一1;乘法公式1a+b ²=a 2+2ab+b 22a-b ²=a ²-2ab+b ² 3a+ba-b=a ²-b ²4a ³+b ³=a+ba ²-ab+b ² 5a ³-b ³=a-ba ²+ab+b ²2、指数公式:1a 0=1 a ≠0 2a P -=P a 1a ≠0 3a mn=m n a 4a m a n =a n m + 5a m ÷a n =n ma a =a n m - 6a m n =a mn7ab n =a n b n8b an =n nb a 9a 2=a102a =|a| 3、指数与对数关系:1若a b =N,则N b a log = 2若10b=N,则b=lgN3若b e =N,则b=㏑N 4、对数公式:1b a b a =log , ㏑e b=b 2N a aN =log ,e Nln =N3aNN a ln ln log =4a b b e a ln = 5N M MN ln ln ln += 6N M N M ln ln ln -= 7M n M nln ln = 8㏑n M =M nln 15、三角恒等式:1Sin α²+Cos α²=1 21+tan α²=sec α²31+cot α²=csc α² 4αααtan cos sin = 5αααcot sin cos =6ααtan 1cot = 7ααcos 1csc = 8ααcos 1sec =1αααcos sin 22sin = 2ααα2tan 1tan 22tan -=3ααααα2222sin 211cos 2sin cos 2cos -=-=-=8.半角公式降幂公式:12sin α2=2cos 1a - 22cos α2=2cos 1a +32tan α=a a sin cos 1+=a a cos 1sin +9、三角函数与反三角函数关系:1若x=siny,则y=arcsinx 2若x=cosy,则y=arccosx 3若x=tany,则y=arctanx 4若x=coty,则y=arccotx10、函数定义域求法:1分式中的分母不能为0, a 1α≠02负数不能开偶次方, a α≥0 3对数中的真数必须大于0, N a log N>0 4反三角函数中arcsinx,arccosx 的x 满足:--1≤x ≤1 5上面数种情况同时在某函数出现时,此时应取其交集;11、直线形式及直线位置关系:1直线形式:点斜式:()00x x k y y -=-斜截式:y=kx+b两点式:121121x x x x y y y y --=--2直线关系:111:b x k y l += 222:b x k y l +=平行:若21//l l ,则21k k = 垂直:若21l l ⊥,则121-=⋅k k常用公式表二1、求导法则:1u+v /=u /+v / 2u-v /=u /-v /3cu /=cu /4uv /=uv /+u /v 52v v u v u v u '-'='⎪⎭⎫ ⎝⎛ 2、基本求导公式:1c /=0 2xa /=ax1-a 3ax /=a xlna4e x /=e x 5㏒a x /=a x ln 1 6lnx /=x 17sinx /=cosx 8cosx /=-sinx9tanx /=2)(cos 1x =secx 210cotx /=-2)(sin 1x =-cscx 211secx /=secxtanx 12cscx /=-cscxcotx13arcsinx /=211x - 14arccosx /=-211x -15arctanx /=211x + 16()211cot x x arc +-='3、微分1函数的微分:dy=y /dx2近似计算:|Δx|很小时,f ()x x ∆+0=fx 0+f/x 0x ∆4、基本积分公式1kdx=kx+c 2C x a dx x a a ++=+⎰111 3c x dx x +=⎰ln 14C aa dx a x x+=⎰ln 5⎰+=c e dx e xx 6⎰+-=C x xdx cos sin7⎰+=C x xdx sin cos 8C x dx xxdx +==⎰⎰tan cos 1sec 22 9c x dx x xdx +-==⎰⎰cot sin 1csc 2210⎰+=-cx dx x arcsin 11211c x dx x +=+⎰arctan 1125、定积分公式:1⎰⎰=babadtt f dx x f )()( 2⎰=aadx x f 0)(3()()dx x f dx x f abb a⎰⎰-= 4⎰⎰⎰+=bacabcdxx f dx x f dx x f )()()(5若fx 是-a,a 的连续奇函数,则⎰-=aadx x f 0)(6若fx 是-a,a 的连续偶函数,则:6、积分定理:1()()x f dt t f x a ='⎥⎦⎤⎢⎣⎡⎰ ⎰⎰- = aa a dx x f dx x f 02()()()()()[]()()[]()x a x a f x b x b f dt t f x b x a '-'='⎥⎦⎤⎢⎣⎡⎰2 3若Fx 是fx 的一个原函数,则)()()()(a F b F x F dx x f bab a -==⎰7.积分表()C x x xdx ++=⎰tan sec ln sec 1 ()C x x xdx +-=⎰cot csc ln csc 2 ()C a xa dx x a +=+⎰arctan 11322 ()C a x dx xa +=-⎰arcsin 1422 ()C a x ax a dx a x ++-=-⎰ln 2115228.积分方法()()b ax x f +=1;设:t b ax =+()()222x a x f -=;设:t a x sin =()22a x x f -=;设:t a x sec = ()22x a x f +=;设:t a x tan =()3分部积分法:⎰⎰-=vdu uv udv。
三角函数公式大全(很详细)

三角函数公式大全(很详细)在三角函数的定义方面,可以通过在直角三角形和直角坐标系中定义六个三角函数来理解。
其中包括正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数。
转化关系方面,倒数关系和平方关系都是常见的转化方式。
此外,还有和角公式、倍角公式、半角公式和万能公式等。
在积化和差、和差化积方面,可以利用正弦和余弦的和角、差角公式来得到“积化和差公式”。
同样地,余弦的和角、差角公式也可以用来得到相应的公式。
需要注意的是,在文章中有明显的格式错误和段落缺失,需要进行删除和修改。
Cosine of the sum and difference of two angles can be expressed as follows using the product-to-sum identities:cos(α + β) = cosα cosβ - sinα sinβcos(α - β) = cosα cosβ + sinα sinβSimilarly。
sine of the sum and difference of two angles can be expressed as follows:sin(α + β) = sinα cosβ + cosα sinβsin(α - β) = sinα cosβ - cosα sinβThese are known as the sum-to-product identities.Another set of identities that relate the sum and difference of two angles to their sines and cosines are the difference-to-product identities:sinα - sinβ = 2 cos((α + β)/2) sin((α - β)/2)sinα + sinβ = 2 sin((α + β)/2) cos((α - β)/2)cosα - cosβ = -2 sin((α + β)/2) sin((α - β)/2)cosα + cosβ = 2 cos((α + β)/2) cos((α - β)/2)These can be derived using the sum-to-product identities and some algebraic n.There are also several trigonometric identities that involve negative angles or angles that differ by π/2.For example:sin(-a) = -sin(a)cos(-a) = cos(a)sin(π/2 - a) = cos(a)cos(π/2 - a) = sin(a)sin(π/2 + a) = cos(a)cos(π/2 + a) = -sin(a)sin(π - a) = sin(a)cos(π - a) = -cos(a)sin(π + a) = -sin(a)cos(π + a) = -cos(a)Finally。
三角函数简便算法

三角函数简便算法三角函数是数学中非常重要的概念,广泛应用于物理、工程和计算机图形学等领域。
在计算三角函数时,有一些简便算法可以帮助我们快速且准确地计算出三角函数的值。
本文将介绍一些三角函数的简便计算算法。
一、正弦函数的简便计算算法1.查表法:正弦函数的值可以通过查表法来计算。
事先将一些特定角度的正弦值计算出来并存储在一个表格中,当需要计算正弦函数的值时,只需要查表即可。
这种方法可以快速计算出正弦函数的值,但是需要事先计算并存储大量的数值,当需要计算其他角度的正弦函数值时,就需要进行插值计算。
2. 三角恒等式法:利用三角函数的恒等式,可以将复杂的三角函数计算转化为简单的三角函数计算。
例如,sin(x) = cos(π/2 - x),所以当角度在0到π/2之间时,可以使用余弦函数来计算正弦函数的值。
二、余弦函数的简便计算算法1.查表法:与正弦函数类似,余弦函数的值也可以通过查表法来计算。
事先将一些特定角度的余弦值计算出来并存储在一个表格中,当需要计算余弦函数的值时,只需要查表即可。
2. 泰勒级数法:余弦函数可以用泰勒级数展开来计算,即cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ...,通过截断级数的方式可以得到余弦函数的近似值。
截断级数的次数越高,计算结果越精确,但计算量也越大。
三、正切函数的简便计算算法1. 利用正弦和余弦函数:正切函数可以通过正弦和余弦函数来计算,即tan(x) = sin(x)/cos(x),利用正弦和余弦函数的简便计算算法,可以得到正切函数的值。
2.牛顿迭代法:利用牛顿迭代法可以快速计算正切函数的值。
首先选择一个近似值作为初始值,然后通过迭代的方式逐步逼近真实值。
牛顿迭代法的优点是收敛速度较快,但需要事先选择一个近似值。
四、反三角函数的简便计算算法1.查表法:反三角函数的值也可以通过查表法来计算。
根据反三角函数的定义,当知道三角函数的值时,可以通过查表的方式计算出角度的近似值。
arccosx泰勒展开式常用公式

arccosx泰勒展开式常用公式一、研究背景在数学中,泰勒展开式是一种将一个函数表示为无穷级数的方法。
其中,ar cc os函数是反余弦函数,常用于解决三角函数方程和概率统计等问题。
鉴于a rc co s函数的复杂性,使用泰勒展开式对ar cc os函数进行近似求值是一种常用公式,本文将重点介绍ar cc osx泰勒展开式的应用。
二、arccos x泰勒展开式介绍对于给定的实数x,我们希望计算其对应的a rc co s值。
泰勒展开式可以将其近似表示为一个无穷级数:```a r cc os(x)=π/2-x-(x^3)/6-(3x^5)/40-(5x^7)/112-...```三、泰勒展开式的推导为了推导ar cc os x的泰勒展开式,我们首先需要了解反余弦函数的性质。
考虑单位圆上的点P(x,y),其中x代表点P在x轴上的投影坐标,y代表点P在y轴上的投影坐标。
假设点P与单位圆原点O的连线与单位圆的交点为A。
那么反余弦函数可以定义为:```a r cc os(x)=∠B OA```其中B为单位圆上与A关于x轴对称的点。
根据三角函数的定义,我们可以得到:```c o s(∠B OA)=x```结合单位圆上的三角关系,我们有:```O A=r=1O B=xA B=√(O A^2-OB^2)=√(1-x^2)```根据三角函数中的余弦值定义,我们可以得到:```c o s(∠B OA)=√(1-x^2)```于是,我们可以得到a rc co sx的泰勒展开式。
四、使用泰勒展开式进行近似计算使用泰勒展开式对ar c co sx进行近似计算可以得到精度可控的结果。
根据泰勒展开式的定义,我们可以通过将前n项相加来获得近似值,其中n代表展开式中的项数。
更重要的是,随着n的增加,近似值的精度将不断提高。
以下是一个示例代码,用于计算a rc co sx的近似值,其中n为展开式的项数,x为待计算的值:```p yt ho ni m po rt ma thd e fa rc co s_ta yl or(x,n):初始化结果为π/2符号初始为负号幂初始为1f o ri in ra ng e(1,n+1):符号取反计算幂计算每一项并相加r e tu rn re su lt```五、应用实例a r cc os x泰勒展开式在实际应用中具有广泛的用途。
tan25°三角函数

tan25°三角函数在三角学中,tan(tangent)是一个重要的三角函数,表示角的正切值。
我们今天要探讨的是tan 25°这个特定角度下的三角函数。
1. tan 25°的定义tan 25°可以表示为直角三角形中对边与邻边之比。
具体而言,tan 25°的定义可以表示为:\tan 25° = \frac{{\text{对边}}}}{{\text{邻边}}}2. tan 25°的计算我们可以使用计算器或数学表,通过输入25°来获取tan 25°的数值。
在计算时,确保角度的单位是度。
计算结果是tan 25°的近似值。
3. tan 25°的性质正切函数的定义域是所有实数,但在某些特定角度下,tan的值可能是有限的。
tan 25°是一个正值,因为在第一象限,tan值是正的。
通过tan 25°可以推导出其他相关角的tan值,如tan(180°+25°)=tan205°tan(180°+25°)=tan205°,因为它们共享相同的正切值。
4. tan 25°的应用tan 25°的数值常常用于解决实际问题,特别是涉及角度为25°的直角三角形或其他几何情境。
例如,测量物体的高度、建筑物的倾斜度等。
5. tan 25°的图示在直角坐标系中,角度为25°的直角三角形可以画出来。
对应角度的tan值可以通过在单位圆上寻找相应的点得到。
结束语:总之,在三角函数中,tan 25°是一个具体而特殊的角度,它有其独特的数值和性质。
通过深入理解tan 25°,我们能够更好地应用三角函数解决实际问题,并在数学世界中展开更为丰富的探索。
sinx与cosx的泰勒公式

sinx与cosx的泰勒公式sinx与cosx是数学中常见的三角函数,它们在泰勒公式中起到了重要的作用。
泰勒公式是一种将一个函数表示为无穷级数的方法,可以用来近似计算复杂函数的值。
下面我们来详细介绍一下sinx与cosx的泰勒公式。
我们来看sinx的泰勒公式。
根据泰勒公式,sinx可以展开为一个无穷级数:sinx = x - (x^3)/3! + (x^5)/5! - (x^7)/7! + ...其中x为实数。
这个级数可以无限地进行下去,但我们通常在计算中只使用其中的有限项来进行近似计算。
接下来,我们来看cosx的泰勒公式。
根据泰勒公式,cosx可以展开为一个无穷级数:cosx = 1 - (x^2)/2! + (x^4)/4! - (x^6)/6! + ...同样地,在实际计算中我们只使用有限项来进行近似计算。
泰勒公式的应用非常广泛。
它可以用来计算各种函数的近似值,特别是当函数无法直接计算时,可以通过泰勒公式将其转化为一个无穷级数,然后利用级数的性质进行计算。
泰勒公式的应用领域包括物理、工程、计算机科学等等。
泰勒公式的近似性质取决于级数的收敛性。
对于sinx与cosx的泰勒级数,当x的取值较小时,级数的收敛性较好,可以得到较为准确的近似值。
但当x的取值较大时,级数的收敛性会变差,近似值的准确性也会下降。
除了泰勒公式,sinx与cosx还有其他的近似公式。
例如,对于较小的x,可以使用简化的近似公式sinx ≈ x,cosx ≈ 1。
这些近似公式在一些简单计算中非常实用,可以节省计算的时间与精力。
在实际应用中,我们经常会遇到需要计算sinx与cosx的值的情况。
这时,我们可以利用泰勒公式进行近似计算。
通过取级数的前几项,我们可以得到一个较为准确的近似值。
当我们需要更高精度的结果时,可以增加级数的项数,但这样会增加计算的复杂度。
因此,在实际应用中,我们需要根据具体情况来选择合适的级数项数。
总结起来,sinx与cosx的泰勒公式是一种将函数表示为无穷级数的方法,可以用来近似计算复杂函数的值。
