RSA生成公私钥及加密解密过程演示
rsa算法过程

rsa算法过程RSA算法是一种非对称加密算法,其过程主要包括密钥生成、加密和解密三个步骤。
在RSA算法中,使用了两个不同的密钥,一个是公钥,用于加密数据;另一个是私钥,用于解密数据。
下面将详细介绍RSA算法的过程。
一、密钥生成1.1 选择两个不同的质数p和q,计算它们的乘积n=p*q。
这个n 将作为RSA算法的模数。
1.2 计算欧拉函数φ(n)=(p-1)*(q-1)。
欧拉函数表示小于n且与n 互质的正整数的个数。
1.3 选择一个小于φ(n)且与φ(n)互质的整数e,作为公钥的指数。
这个e将与n一起作为公钥对外公开。
1.4 计算e关于模φ(n)的模反元素d,即满足(e*d)%φ(n)=1的d。
这个d将作为私钥的指数。
二、加密2.1 将需要加密的数据转换为一个整数m,使得0≤m<n。
2.2 使用公钥(e, n)对整数m进行加密,加密后的密文c=m^e mod n。
三、解密3.1 使用私钥(d, n)对密文c进行解密,解密后的明文m=c^d modn。
3.2 将得到的明文m转换回原始的数据。
需要注意的是,RSA算法中的加密和解密操作都是使用指数模幂运算来实现的。
在加密过程中,明文m通过公钥的指数e进行幂运算,再取模n得到密文c。
而在解密过程中,密文c通过私钥的指数d 进行幂运算,再取模n得到明文m。
RSA算法的安全性基于大数分解的困难性,即通过已知的n很难分解出p和q。
因此,要确保RSA算法的安全性,需要选择足够大的质数p和q,并且保证私钥d的安全性,避免私钥泄露。
总结起来,RSA算法是一种非对称加密算法,通过公钥加密,私钥解密的方式来实现数据的保密性。
其过程包括密钥生成、加密和解密三个步骤,通过指数模幂运算实现加密和解密操作。
RSA算法的安全性基于大数分解的困难性,而选择足够大的质数和保护私钥的安全性则是确保RSA算法安全性的关键。
RSA加密、解密原理及秘钥生成
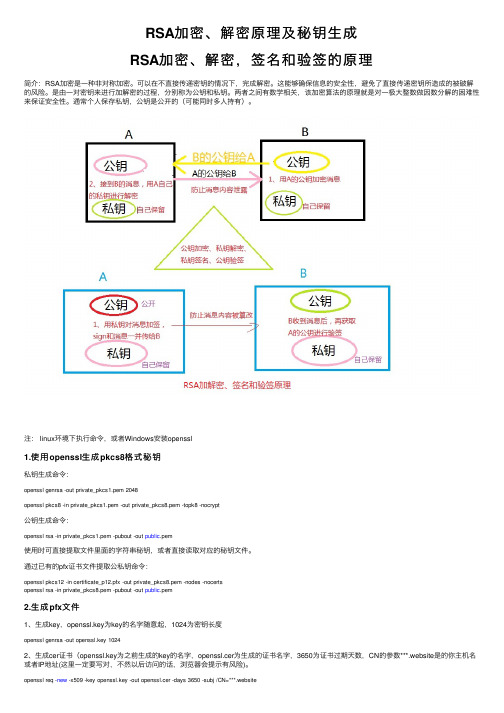
RSA加密、解密原理及秘钥⽣成RSA加密、解密,签名和验签的原理简介:RSA加密是⼀种⾮对称加密。
可以在不直接传递密钥的情况下,完成解密。
这能够确保信息的安全性,避免了直接传递密钥所造成的被破解的风险。
是由⼀对密钥来进⾏加解密的过程,分别称为公钥和私钥。
两者之间有数学相关,该加密算法的原理就是对⼀极⼤整数做因数分解的困难性来保证安全性。
通常个⼈保存私钥,公钥是公开的(可能同时多⼈持有)。
注: linux环境下执⾏命令,或者Windows安装openssl1.使⽤openssl⽣成pkcs8格式秘钥私钥⽣成命令:openssl genrsa -out private_pkcs1.pem 2048openssl pkcs8 -in private_pkcs1.pem -out private_pkcs8.pem -topk8 -nocrypt公钥⽣成命令:openssl rsa -in private_pkcs1.pem -pubout -out public.pem使⽤时可直接提取⽂件⾥⾯的字符串秘钥,或者直接读取对应的秘钥⽂件。
通过已有的pfx证书⽂件提取公私钥命令:openssl pkcs12 -in certificate_p12.pfx -out private_pkcs8.pem -nodes -nocertsopenssl rsa -in private_pkcs8.pem -pubout -out public.pem2.⽣成pfx⽂件1、⽣成key,openssl.key为key的名字随意起,1024为密钥长度openssl genrsa -out openssl.key 10242、⽣成cer证书(openssl.key为之前⽣成的key的名字,openssl.cer为⽣成的证书名字,3650为证书过期天数,CN的参数***.website是的你主机名或者IP地址(这⾥⼀定要写对,不然以后访问的话,浏览器会提⽰有风险)。
在C#中使用RSA进行加密和解密

在C#中使⽤RSA进⾏加密和解密这篇⽂章向您展⽰了如何在c#.net Windows窗体应⽤程序中使⽤RSA算法对字符串进⾏加密和解密。
RSA是由Ron Rivest,Adi Shamir和Leonard Adleman开发的⾮对称编码系统(其名称也是这三位作者的缩写)。
它被⼴泛⽤于加密和电⼦签名技术。
它通过使⽤公共密钥与所有⼈共享来⼯作。
RSA操作基于四个主要步骤:密钥⽣成,密钥共享,加密和解密。
本⽂将介绍有关c#rsa⽣成公共和私有密钥的算法,密钥如何在c#中进⾏加密和解密。
拖动⽂本框,标签和按钮从Visual Studio⼯具箱到您的WinForm设计,那么你可以设计⼀个简单的⽤户界⾯,使您可以加密和使⽤C#代码RSA算法解密字符串,如下图所⽰。
在C#中使⽤RSA算法进⾏加密和解密通过本c#密码学教程,我将创建⼀个Encrypt⽅法来使⽤RSA算法加密您的数据。
byte[] Encrypt(byte[] data, RSAParameters RSAKey, bool fOAEP){byte[] encryptedData;using (RSACryptoServiceProvider rSACryptoServiceProvider = new RSACryptoServiceProvider()){rSACryptoServiceProvider.ImportParameters(RSAKey);encryptedData = rSACryptoServiceProvider.Encrypt(data, fOAEP);}return encryptedData;}同样,创建Decrypt⽅法以使⽤RSA算法解密数据。
byte[] Decrypt(byte[] data, RSAParameters RSAKey, bool fOAEP){byte[] decryptedData;using (RSACryptoServiceProvider rSACryptoServiceProvider = new RSACryptoServiceProvider()){rSACryptoServiceProvider.ImportParameters(RSAKey);decryptedData = rSACryptoServiceProvider.Decrypt(data, fOAEP);}return decryptedData;}C#RSA⽤公钥加密接下来,声明 unicodeEncoding, rSACryptoServiceProvider, data 和 cryptoData变量,如下所⽰。
rsa加密算法详解及例题

RSA加密算法详解及例题
RSA加密算法是一种非对称加密算法,其安全性基于对极大整数做因数分解的困难性。
以下是RSA加密算法的详解及例题:
1. 密钥生成:
* 随机选择两个质数P和Q,越大越安全。
* 计算它们的乘积N=P*Q。
* 计算欧拉函数φ(N)=(P-1)*(Q-1)。
* 随机选择一个整数E,条件是1<E<φ(N),且E与φ(N)互质。
* 计算E对于φ(N)的模反元素D,使得EDmodφ(N)=1,即D=E-1modφ(N)。
* 公钥为(E, N),私钥为(D, N)。
2. 加解密过程:
* 加密:明文M进行加密后得到密文C,计算公式为C=MemodN。
* 解密:将密文C进行解密后得到明文M,计算公式为M=CdmodN。
例题:在RSA加密体制中,已知素数P=7,Q=11,公钥E=13,试计算私钥D并给出对明文M=5的加密,求其密文。
解:首先,根据上述算法进行密钥生成。
根据素数P和Q得到N=77。
计算φ(N)=60。
因为E小于φ(N)且与φ(N)互质,选择E=13作为公钥。
根据公式计算D模反元素得到D=7。
现在有公钥(E, N)=(13, 77)和私钥(D, N)=(7, 77)。
接下来,用公钥加密明文M=5得到密文C=5^13mod77=15。
所以,密文为15。
此例题仅展示了RSA加密算法的基本原理和步骤,实际应用中需要考虑更多安全因素和操作细节。
RSA加解密私钥加密公钥解密私加公解C++调用openssl库的代码实例

RSA加解密私钥加密公钥解密私加公解C++调⽤openssl库的代码实例前提:秘钥长度=1024============================================== 对⼀⽚(117字节)明⽂加密私加==============================================// 私钥加密std::string rsa_pri_encrypt(const std::string &clearText, std::string &pubKey){std::string strRet;BIO *keybio = BIO_new_mem_buf((unsigned char *)pubKey.c_str(), -1);// 此处有三种⽅法// 1, 读取内存⾥⽣成的密钥对,再从内存⽣成rsa// 2, 读取磁盘⾥⽣成的密钥对⽂本⽂件,在从内存⽣成rsa// 3,直接从读取⽂件指针⽣成rsa//RSA* pRSAPublicKey = RSA_new();RSA* rsa = RSA_new();rsa = PEM_read_bio_RSAPrivateKey(keybio, &rsa, NULL, NULL);if (!rsa){BIO_free_all(keybio);return std::string("");}int len = RSA_size(rsa);//int len = 1028;char *encryptedText = (char *)malloc(len + 1);memset(encryptedText, 0, len + 1);// 加密int ret = RSA_private_encrypt(clearText.length(), (const unsigned char*)clearText.c_str(), (unsigned char*)encryptedText, rsa, RSA_PKCS1_PADDING);if (ret >= 0)strRet = std::string(encryptedText, ret);// 释放内存free(encryptedText);BIO_free_all(keybio);RSA_free(rsa);return strRet;}============================================== 对⼀⽚(128字节)密⽂解密公解==============================================// 公钥解密std::string rsa_pub_decrypt(const std::string &clearText, std::string &pubKey){std::string strRet;BIO *keybio = BIO_new_mem_buf((unsigned char *)pubKey.c_str(), -1);//keybio = BIO_new_mem_buf((unsigned char *)strPublicKey.c_str(), -1);// 此处有三种⽅法// 1, 读取内存⾥⽣成的密钥对,再从内存⽣成rsa// 2, 读取磁盘⾥⽣成的密钥对⽂本⽂件,在从内存⽣成rsa// 3,直接从读取⽂件指针⽣成rsa//RSA* pRSAPublicKey = RSA_new();RSA* rsa = RSA_new();rsa = PEM_read_bio_RSAPublicKey(keybio, &rsa, NULL, NULL);if (!rsa){BIO_free_all(keybio);return std::string("");}int len = RSA_size(rsa);//int len = 1028;char *encryptedText = (char *)malloc(len + 1);memset(encryptedText, 0, len + 1);//解密int ret = RSA_public_decrypt(clearText.length(), (const unsigned char*)clearText.c_str(), (unsigned char*)encryptedText, rsa, RSA_PKCS1_PADDING);if (ret >= 0)strRet = std::string(encryptedText, ret);// 释放内存free(encryptedText);BIO_free_all(keybio);RSA_free(rsa);return strRet;}============================================== 对整体明⽂加密私加==============================================//私钥加密 + 分⽚std::string rsa_pri_split117_encrypt(const std::string &clearText, std::string &pubKey) {std::string result;std::string input;result.clear();for(int i = 0 ; i < clearText.length()/117; i++){input.clear();input.assign(clearText.begin() + i*117, clearText.begin() + i*117 + 117);result = result + rsa_pri_encrypt(input, pubKey);}if( clearText.length()%117 != 0){int tem1 = clearText.length()/117*117;int tem2 = clearText.length() - tem1;input.clear();input.assign(clearText.begin()+ tem1, clearText.end());result = result + rsa_pri_encrypt(input, pubKey);}return result;}============================================== 对整体密⽂解密公解==============================================//公钥解密 + 分⽚std::string rsa_pub_split128_decrypt(const std::string &clearText, std::string &pubKey) {//Base64 *base = new Base64();std::string result;std::string input;result.clear();for(int i = 0 ; i< clearText.length()/128; i++){input.clear();input.assign(clearText.begin() + i*128, clearText.begin() + i*128 + 128);result = result + rsa_pub_decrypt(input, pubKey);}if(clearText.length()%128 != 0){int tem1 = clearText.length()/128 * 128;int tem2 = clearText.length() - tem1;input.clear();input.assign(clearText.begin()+ tem1, clearText.end());result = result + rsa_pri_encrypt(input, pubKey);}return result;}附1:附2:。
实验三--RSA算法和SHA1算法

实验三 RSA算法和SHA1哈希算法古典密码算法曾经被广泛应用,大都比较简单,使用手工和机械操作来实现加密和解密。
它的主要对象是文字信息,利用密码算法实现文字信息的加密和解密。
古典密码学可以分为代替密码(也叫做移位密码)和置换密码(也叫做换位密码)两种,其中代替密码典型的有Caesar密码,数乘密码和仿射变换等,置换密码有单表置换和多表置换等。
一、实验目的1.理解代替密码学加密过程2.理解置换密码学加密过程二、实验环境Windows,交换网络结构,每组2人,,密码工具三、实验原理1.非对称密钥加密也称为公开密钥加密,或者叫做公钥加密算法。
使用公开密钥密码的每一个用户都分别拥有两个密钥:加密密钥和解密密钥,它们两者并不相同,并且由加密密钥得到解密密钥在计算机上是不可行的。
每一个用户的加密密钥都是公开的。
因此,加密密钥也称为公开密钥。
所有用户的公开密钥都将记录在作用类似于电话号码薄的密钥本上,而它可以被所有用户访问,这样每一个用户都可以得到其他所有用户的公开密钥。
同时,每一个用户的解密密钥将由用户保存并严格保密。
因此,解密密钥也称为私有密钥。
RSA加密算法利用了数论领域的一个事实,那就是虽然把两个大质数相乘生成一个合数是件十分容易的事情,但要把一个合数分解为两个质数的乘积却十分困难。
合数分解问题目前仍然是数学领域尚未解决的一大难题,至今没有任何高效的分解方法。
它无须收发双方同时参与加密过程,既可以用于保密也可以用于签名,因而非常适合于电子邮件系统的加密,互连网和信用卡安全系统。
RSA算法的加密和解密过程在RSA算法中,每个实体有自己的公钥(e,n)及私钥(d,n),其中n = p*q,p,q是两个大素数,e*d = 1 mod ф(n),显然e应该满足gcd(e,ф(n))= 1。
实体B加密消息m,将密文在公开信道上传送给实体A。
实体A接到密文后对其解密。
具体算法如下。
●公钥的生成算法RSA的公钥生成算法十分简单,可以分为四步:a)选择两个素数,p和q;b)计算n = p×q和z = (p-1)×(q-1);c)选择一个与z互质的数d;d)找出一个e,使得e×d = 1 mod z。
简单的rsa加密解密计算

简单的rsa加密解密计算
RSA加密算法是一种非对称加密算法,它使用一对密钥(公钥
和私钥)来加密和解密数据。
下面我将简单介绍RSA加密和解密的
计算过程。
1. 生成密钥对,首先,选择两个不同的大质数p和q,并计算
它们的乘积n=pq。
然后选择一个整数e,使得e与(p-1)(q-1)互质,并计算出e的模反元素d。
公钥是(n, e),私钥是(n, d)。
2. 加密,假设要加密的消息为M,首先将消息M转换为整数m,满足0≤m<n。
然后使用公钥(n, e)进行加密,加密后的密文C等于
m的e次方再对n取模,即C≡m^e (mod n)。
3. 解密,接收到密文C后,使用私钥(n, d)进行解密,解密后
的明文M等于C的d次方再对n取模,即M≡C^d (mod n)。
下面我举一个简单的例子来说明RSA加密和解密的计算过程:
假设我们选择两个质数p=11和q=3,计算n=pq=33,然后选择
e=3,并计算d=7。
这样我们得到公钥(n, e)=(33, 3)和私钥(n,
d)=(33, 7)。
现在假设要加密的消息为M=5,将其转换为整数m=5。
使用公钥进行加密,计算C≡5^3 (mod 33),得到C=5。
接收到密文C=5后,使用私钥进行解密,计算M≡5^7 (mod 33),得到M=5。
因此,我们成功地将消息M=5加密为密文C=5,然后再解密回到原始消息M=5。
这就是RSA加密和解密的简单计算过程。
RSA公钥密码算法的加密和解密

RSA的安全性
对RSA的攻击方法主要有以下三种: 1. 强力攻击(穷举法):尝试所有可能的私有密 钥 2. 数学分析攻击:有多种数学攻击方法,其本质 等价于试图分解两个素数的乘积 3. 计时攻击:记录计算机解密消息所用的时间。
谢谢!
a a
m
(
bi 0
2i )
a
bi 0
( 2i )
a modn ( a
m bi 0
( 2i )
) modn ( [a
bi 0
( 2i )
modn]) modn
密钥产生
确定两个素数p和q 选择e或d计算另外一个
素数选取
为了避免攻击者用穷举法求出p和q,应该从足够 大的集合中选取p和q。即p和q必须是大素数。 没有产生任意的大素数的有效技术,通常的作法 是随机选取一个需要的数量级的奇数并检验这个 数是否是素数。若不是则挑选下一个随机数直至 检测到素数为止。
公钥:(e, n) =(7, 33) 密钥:(d, n) =(3, 33) 加密算法: 密文c=m7mod33 解密算法: 明文m=c3mod33 对m=8加密 密文 c=87mod33= 2097152 mod33=2 对c=2解密 明文m=23mod33=8
RSA算法中的计算问题
1. RSA的加密与解密过程 RSA的加密、解密过程都为求一个整数的整数次 幂,再取模。如果按其含义直接计算,则中间结 果非常大,有可能超出计算机所允许的整数取值 范围。 而用模运算的性质: (a×b) mod n=[(a mod n)×(b mod n)] mod n 就可减小中间结果
假设m为要传送的报文。
(1)选取两个大素数 p, q (2) 计算n=pq, (n)=(p-1)(q-1) (3) 随机选取e: 1<e<(n),与(n)互素 (4) 使用扩展欧几里德算法计算 即ed = 1 mod (n) (5)以(e,n)为公钥,(d,n)为密钥
javaRSA实现私钥签名、公钥验签、私钥加密数据、公钥解密数据

javaRSA实现私钥签名、公钥验签、私钥加密数据、公钥解密数据通过OpenSSL⽣成公私钥⽂件(如果没有OpenSSL⼯具建议下载Cmder⼯具⾃带OpenSSL指令)1、⽣成RSA密钥的⽅法genrsa -out private-rsa.key 20482、获取客户端公钥⽂件openssl req -new -x509 -key private-rsa.key -days 750 -out public-rsa.cer3、获取服务器私钥⽂件openssl pkcs12 -export -name zhangsan -in public-rsa.cer -inkey private-rsa.key -out user-rsa.pfx4、获取密钥⽂件的5元组数据openssl rsa -in private-rsa.key -noout -textJava实现私钥签名、公钥验签、私钥加密数据、公钥解密数据import javax.crypto.Cipher;import java.io.File;import java.io.FileInputStream;import java.io.IOException;import java.io.InputStream;import java.security.KeyStore;import java.security.PrivateKey;import java.security.PublicKey;import java.security.Signature;import java.security.cert.Certificate;import java.security.cert.CertificateFactory;public class Sha1withRSAUtil {private static final String publicKeyFileName = System.getProperty("user.dir") + File.separator + "pubkey.cer";private static final String privateKeyFileName = System.getProperty("user.dir") + File.separator + "private.pfx";private static final String pfxPassword = "123";//私钥⽂件获取时设置的密钥private static String aliasName = "003";//alias名称/*** 签名** @return签名后经过base64处理的字符串* @throws Exception*/public static String sign(String str) {String base64Sign = "";InputStream fis = null;try {fis = new FileInputStream(privateKeyFileName);KeyStore keyStore = KeyStore.getInstance("PKCS12");char[] pscs = pfxPassword.toCharArray();keyStore.load(fis, pscs);PrivateKey priKey = (PrivateKey) (keyStore.getKey(aliasName, pscs));// 签名Signature sign = Signature.getInstance("SHA1withRSA");sign.initSign(priKey);byte[] bysData = str.getBytes("UTF-8");sign.update(bysData);byte[] signByte = sign.sign();BASE64Encoder encoder = new BASE64Encoder();base64Sign = encoder.encode(signByte);} catch (Exception e) {e.printStackTrace();} finally {if (fis != null) {try {fis.close();} catch (IOException e) {e.printStackTrace();}}}return base64Sign;}/*** 数据验证** @param signStr 加密后的数据* @param verStr 原始字符* @return*/public static boolean verify(String signStr, String verStr)throws Exception {boolean verfy = false;InputStream fis = null;try {fis = new FileInputStream(publicKeyFileName);CertificateFactory cf = CertificateFactory.getInstance("x509");Certificate cerCert = cf.generateCertificate(fis);PublicKey pubKey = cerCert.getPublicKey();BASE64Decoder decoder = new BASE64Decoder();byte[] signed = decoder.decodeBuffer(signStr);Signature sign = Signature.getInstance("SHA1withRSA");sign.initVerify(pubKey);sign.update(verStr.getBytes("UTF-8"));verfy = sign.verify(signed);} catch (Exception e) {e.printStackTrace();} finally {if (fis != null) {try {fis.close();} catch (IOException e) {e.printStackTrace();}}}return verfy;}/*** 通过公钥⽂件进⾏加密数据** @return加密后经过base64处理的字符串*/public static String encrypt(String source) throws Exception {InputStream fis = null;try {fis = new FileInputStream(publicKeyFileName);CertificateFactory cf = CertificateFactory.getInstance("x509");Certificate cerCert = cf.generateCertificate(fis);PublicKey pubKey = cerCert.getPublicKey();Cipher cipher = Cipher.getInstance("RSA");cipher.init(Cipher.ENCRYPT_MODE, pubKey);byte[] sbt = source.getBytes();byte[] epByte = cipher.doFinal(sbt);BASE64Encoder encoder = new BASE64Encoder();String epStr = encoder.encode(epByte);return epStr;} finally {if (fis != null) {try {fis.close();} catch (IOException e) {e.printStackTrace();}}}}/*** 通过私钥⽂件进⾏解密数据** @return解密后的明⽂字符串*/public static String decode(String source) throws Exception {BASE64Decoder b64d = new BASE64Decoder();byte[] keyByte = b64d.decodeBuffer(source);InputStream fis = null;try {fis = new FileInputStream(privateKeyFileName);KeyStore keyStore = KeyStore.getInstance("PKCS12");char[] pscs = pfxPassword.toCharArray();keyStore.load(fis, pscs);PrivateKey priKey = (PrivateKey) (keyStore.getKey(aliasName, pscs)); Cipher cipher = Cipher.getInstance("RSA");cipher.init(Cipher.DECRYPT_MODE, priKey);byte[] epByte = cipher.doFinal(keyByte);return new String(epByte, "UTF-8");} finally {if (fis != null) {try {fis.close();} catch (IOException e) {e.printStackTrace();}}}}}使⽤⽅法import com.util.rsa.Sha1withRSAUtil;public class Main {public static void main(String[] args) {String data = "name123456789";String signData = Sha1withRSAUtil.sign(data);System.out.println(signData);try {boolean flag = Sha1withRSAUtil.verify(signData, data); System.out.println(flag);String eData = Sha1withRSAUtil.encrypt(data);System.out.println(eData);String dData = Sha1withRSAUtil.decode(eData);System.out.println(dData);} catch (Exception e) {e.printStackTrace();}}}。
rsa公钥加密私钥解密原理

rsa公钥加密私钥解密原理RSA公钥加密私钥解密原理RSA是一种非对称加密算法,其安全性基于大数分解的困难性。
在RSA算法中,公钥和私钥是成对生成的,公钥可以公开给任何人使用,而私钥只有拥有者可以使用。
公钥加密的过程如下:首先,选择两个不同的质数p和q,并计算它们的乘积n。
然后,选择一个整数e,使得e与(p-1)(q-1)互质。
这样,n和e就组成了公钥。
要加密一条消息m,使用公钥(n, e),将消息m转换为整数M,然后计算密文C = M^e mod n。
这样,密文C就可以被发送给接收方,而只有拥有私钥的人才能解密它。
私钥解密的过程如下:首先,使用私钥(d)和模数n,计算明文M = C^d mod n。
然后,将明文M转换回消息m。
RSA算法的安全性基于两个数学问题的困难性:大数分解和模数取离散对数。
大数分解是指将一个大整数分解成两个或多个质数的乘积,这个问题在当前计算机技术下是非常困难的。
而模数取离散对数是指已知一个数的幂和模数,求解这个数的幂的问题,这个问题也是非常困难的。
在公钥加密的过程中,由于只有拥有私钥的人才能解密密文,所以即使中间人截获了密文,也无法获取原始消息。
而在私钥解密的过程中,由于只有拥有私钥的人才能计算出明文,所以即使有人截获了密文,也无法获取原始消息。
RSA算法还具有数字签名的功能。
数字签名可以用于验证消息的真实性和完整性。
发送方可以使用私钥对消息进行签名,接收方可以使用公钥验证签名的有效性。
这样,接收方可以确保消息是由发送方发送的,并且在传输过程中没有被篡改。
总结起来,RSA公钥加密私钥解密的原理是基于大数分解和模数取离散对数的困难性。
公钥加密过程中,使用公钥对消息进行加密,只有拥有私钥的人才能解密密文。
私钥解密过程中,使用私钥对密文进行解密,只有拥有私钥的人才能获取明文。
RSA算法还可以用于数字签名,用于验证消息的真实性和完整性。
通过使用RSA算法,可以实现安全的通信和数据传输。
rsa公钥和私钥产生加密解密
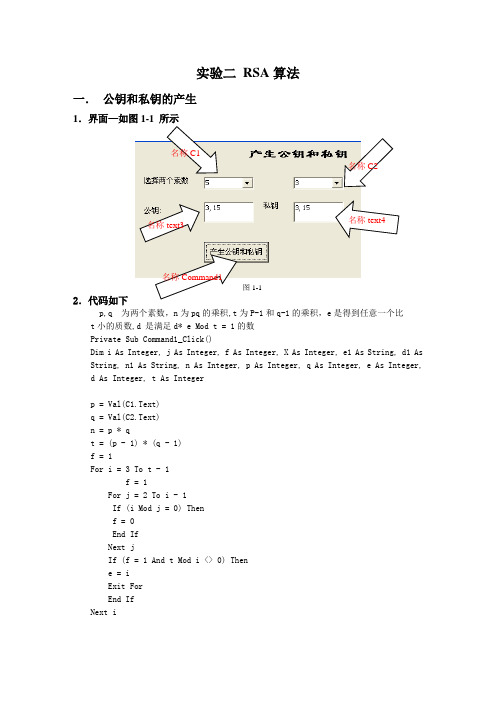
实验二RSA算法一.公钥和私钥的产生1.界面—如图1-1 所示名称text3图1-12.代码如下p,q 为两个素数,n为pq的乘积,t为P-1和q-1的乘积,e是得到任意一个比t小的质数,d 是满足d* e Mod t = 1的数Private Sub Command1_Click()Dim i As Integer, j As Integer, f As Integer, X As Integer, e1 As String, d1 As String, n1 As String, n As Integer, p As Integer, q As Integer, e As Integer,d As Integer, t As Integerp = Val(C1.Text)q = Val(C2.Text)n = p * qt = (p - 1) * (q - 1)f = 1For i = 3 To t - 1f = 1For j = 2 To i - 1If (i Mod j = 0) Thenf = 0End IfNext jIf (f = 1 And t Mod i <> 0) Thene = iExit ForEnd IfNext iFor X = 1 To tIf (X * e Mod t = 1) Thend = XExit ForEnd IfNext Xn1 = ne1 = ed1 = dText3.Text = e1 + "," + n1Text4.Text = d1 + "," + n1n1 = nEnd Sub二. Rsa1.界面—如图1-2图1-22.代码如下e,n 是一组公钥对其加密mw 是c3的text ,c 由mw ^ e Mod n 得到Private Sub Command2_Click()Dim mw As Long, c As Long, e As Long, n As Long e = Val(Text1.Text)n = Val(Text5.Text)mw = Asc(c3.Text) - 64c = mw ^ e Mod nText2.Text = cEnd Sub三. Rsa 对单个字母解密1.界面—如图1-3 所示图1-32.代码如下d,n 是一组私钥对其解密,c 是密文得到明文chr((c ^ d Mod n )+64)Private Sub Command3_Click()Dim jm As Long, c As Long, d As Long, n As Long d = Val(Text7.Text)n = Val(Text8.Text)c = Val(Text6.Text)jm = c ^ d Mod nText9.Text = Chr(jm + 64)End Sub名称 text9。
RSA算法私钥公钥生成和导入秘钥库步骤,加签名和验签Java代码

RSA算法私钥公钥⽣成和导⼊秘钥库步骤,加签名和验签Java代码1)RSA私钥和公钥⽣成步骤步骤⼀,⽣成JKS⽂件ecouponNotificationRsa.jks,别名为:ecoupon_notification_key,期限20年,jks证书密码123456,算法是RSAkeytool -genkeypair -keyalg RSA -keysize 2048 -validity 7300 -dname "CN=disney, OU=disney, O=disney, L=shanghai, ST=shanghai, C=CN" -alias ecoupon_notification_key -keystore myRsa.jks -storepass 123456步骤⼆,查看JKS证书信息keytool -list -v -keystore ecouponNotificationRsa.jks -storepass 123456步骤三,根据 jks 私钥⽣成cer证书, cer证书密码设置为 555666keytool -export -alias my_service_key -keystore myRsa.jks -storepass 555666 -file myRsaPublicKey.cer步骤四,根据 cer 证书⽣成公钥,并将公钥导⼊到客户端秘钥库中(这⼀步是调⽤此service的对⽅app操作,需要借助第三步⽣成的cer证书)keytool -import -alias ecoupon_notification_rsa_public_key -file myRsaPublicKey.cer -keystore ecoupon_notification_rsa_public_key.jks -storepass 555666步骤五,将第⼀步⽣成好的jks证书的绝对路径地址配置到配置中⼼,例⼦如下rsa.private.key.jks.path=/key/library/myRsa.jksrsa.private.key.jks.password=123456rsa.public.key.certificate.alias=my_service_keyrsa.public.key.certificate.password=5556662)⽣成私钥 bean 和公钥 bean,注⼊到 spring 容器import java.io.FileInputStream;import java.io.IOException;import java.security.KeyStore;import java.security.KeyStoreException;import java.security.NoSuchAlgorithmException;import java.security.PrivateKey;import java.security.PublicKey;import java.security.UnrecoverableKeyException;import java.security.cert.CertificateException;@Slf4j@Configurationpublic class ConfigRsa {@Bean("keyStore")public KeyStore getKeyStore(@Value("${rsa.private.key.jks.path}") String privateKeyJksPath,@Value("${rsa.private.key.jks.password}") String privateKeyJksPassword) throws KeyStoreException, IOException, CertificateException, NoSuchAlgorithmException {try (FileInputStream fis = new FileInputStream(privateKeyJksPath)) {KeyStore keyStore = KeyStore.getInstance("JKS");keyStore.load(fis, privateKeyJksPassword.toCharArray());return keyStore;}}@Bean("privateKey")public PrivateKey getPrivateKey(@Qualifier("keyStore") KeyStore keyStore,@Value("${rsa.public.key.certificate.alias}") String publicKeyCertificateAlias,@Value("${rsa.public.key.certificate.password}") String publicKeyCertificatePassword) throws UnrecoverableKeyException, NoSuchAlgorithmException, KeyStoreException {return (PrivateKey) keyStore.getKey(publicKeyCertificateAlias, publicKeyCertificatePassword.toCharArray());}@Bean("publicKey")public PublicKey getPublicKey(@Qualifier("keyStore") KeyStore keyStore,@Value("${rsa.public.key.certificate.alias}") String publicKeyCertificateAlias) throws KeyStoreException {return keyStore.getCertificate(publicKeyCertificateAlias).getPublicKey();}}3)⾃定义 RsaUtil 类去签名和验签import lombok.extern.slf4j.Slf4j;import org.springframework.beans.factory.annotation.Autowired;import org.springframework.beans.factory.annotation.Qualifier;import ponent;import java.security.InvalidKeyException;import java.security.NoSuchAlgorithmException;import java.security.PrivateKey;import java.security.PublicKey;import java.security.Signature;import java.security.SignatureException;import java.util.Base64;@Slf4j@Component("rsaUtil")public class RsaUtil {private static final String ALGORITHM = "SHA256withRSA"; // sign type: RSA2, refer doc: https:///open/291/106115@Autowired@Qualifier("privateKey")private PrivateKey privateKey;@Autowired@Qualifier("publicKey")private PublicKey publicKey;public String sign(String originalData) throws NoSuchAlgorithmException, InvalidKeyException, SignatureException {Signature signature = Signature.getInstance(ALGORITHM);signature.initSign(privateKey);signature.update(originalData.getBytes());String signedData = java.util.Base64.getEncoder().encodeToString(signature.sign()).replace("\r\n","").replace("\n","");return signedData;}public boolean verify(String originalData, String signedData) throws NoSuchAlgorithmException, InvalidKeyException, SignatureException { Signature signature = Signature.getInstance(ALGORITHM);signature.initVerify(publicKey);signature.update(originalData.getBytes());boolean isVerify = signature.verify(Base64.getDecoder().decode(signedData));return isVerify;}}end.。
用RSA算法进行加密和解密

21.BigInteger d=prk.getPrivateExponent();
22.BigInteger n=prk.getModulus();
23.System.out.println("d= "+d);
24.System.out.println("n= "+n);
16.//获取私钥
17.FileInputStream f=new FileInputStream("Skey_RSA_priv.dat");
18.ObjectInputStream b=new ObjectInputStream(f);
19.RSAPrivateKey prk=(RSAPrivateKey)b.readObject( );
31.for(int i=0;i<mt.length;i++){
32.System.out.print((char) mt[i]);
33.}
34.}
35.}
36.
9.KeyPairGenerator kpg=KeyPairGenerator.getInstance("RSA");
10.//指定密钥的长度,初始化密钥对生成器
11.kpg.initialize(1024);
12.//生成密钥对
13.KeyPair kp=kpg.genKeyPair();
14.//获取公钥
11.//读取密文
12.BufferedReader in=
13.new BufferedReader(new InputStreamReader(new FileInputStream("Enc_RSA.dat")));
RSA加密解密算法

RSA加密解密算法RSA(Rivest-Shamir-Adleman)是一种非对称加密算法,由三位密码学家发明。
RSA加密算法能够实现数据的加密、解密和数字签名的功能,广泛应用于信息安全领域。
RSA算法的基本原理是利用大数分解的困难性来保证数据的安全性。
它采用了一对公钥和私钥来进行加密和解密操作。
公钥可以公开给他人,而私钥必须由加密方保密。
具体步骤如下:1. 密钥生成:选择两个大素数p和q,计算n = p * q,计算欧拉函数ϕ(n) = (p-1) * (q-1),选择一个与ϕ(n)互质的整数e作为公钥,计算私钥d使得(e * d) mod ϕ(n) = 12. 加密:加密方使用公钥(e,n)对明文进行加密。
明文m需小于n,计算密文c = m^e mod n。
3. 解密:解密方使用私钥(d,n)对密文进行解密。
计算明文m = c^d mod n。
RSA算法的安全性基于大数分解问题的困难性。
大数分解是指将一个大素数分解成两个素数的乘积。
目前最快的分解算法是基于数域筛选的RSA整数分解算法,其时间复杂度为O(exp((64/9)^(1/3) * (ln N)^(1/3) * (ln ln N)^(2/3))),其中N为待分解的大数。
根据目前的计算能力,RSA算法在合适的密钥长度下是足够安全的。
除了加密和解密,RSA算法还可以用于数字签名。
数字签名可以实现身份认证和数据完整性验证。
签名方使用私钥对消息进行签名,验证方使用公钥进行验证。
签名的过程如下:1. 签名:签名方使用私钥(d,n)对消息进行签名。
计算签名值s = m^d mod n。
2. 验证:验证方使用公钥(e,n)对签名值进行验证。
计算摘要v = s^e mod n,将v与原消息进行比较。
RSA算法的应用非常广泛。
在网络通信中,RSA算法可用于保护数据的机密性;在数字货币领域,RSA算法可用于数字签名和加密;在电子商务中,RSA算法可用于保护用户的隐私信息等。
rsa公钥密码算法的公私钥

rsa公钥密码算法的公私钥
RSA(Rivest-Shamir-Adleman)公钥密码算法是一种常用的非
对称加密算法,它使用了一对密钥,即公钥和私钥。
公钥是用于加密数据的密钥,可以公开给任何人使用。
私钥是
用于解密数据的密钥,应该保密不被他人获取。
RSA算法的公私钥生成过程如下:
1. 选择两个不同的大素数p和q。
2. 计算n = p q,其中n是公钥和私钥的一部分。
3. 计算欧拉函数φ(n) = (p-1) (q-1)。
4. 选择一个整数e,满足1 < e < φ(n),且e与φ(n)互质。
e是公钥的一部分。
5. 计算整数d,满足d e ≡ 1 (mod φ(n))。
d是私钥的一
部分。
最终生成的公钥是(n, e),私钥是(n, d)。
公钥(n, e)可以用于加密数据,加密过程如下:
1. 将待加密的数据转换为整数m,满足0 ≤ m < n。
2. 计算密文c = m^e (mod n)。
私钥(n, d)用于解密数据,解密过程如下:
1. 将密文c转换为整数。
2. 计算明文m = c^d (mod n)。
需要注意的是,RSA算法的安全性依赖于大素数的难以分解性。
因此,在实际应用中,选择足够大的素数和密钥长度是必要的,以
确保安全性。
总结起来,RSA公钥密码算法的公私钥是通过选择大素数和进
行一系列计算生成的,公钥用于加密数据,私钥用于解密数据。
RSA加密与解密

RSA加密与解密数据信息安全对我们每个⼈都有很重要的意义,特别是⼀些敏感信息,可能⼀些类似于收货地址、⼿机号还没引起⼤家的注意。
但是最直⽩的,银⾏卡、姓名、⼿机号、⾝份证号,如果这些信息被⿊客拦截到,他就可以伪装成你,把你的钱都取⾛。
那我们该怎么防⽌这样的事情发⽣?报⽂加密解密,加签验签。
我害怕什么我害怕卡⾥的钱被别⼈取⾛我害怕转账的时候,报⽂被⿊客拦截到,篡改信息转到别⼈的账户。
我害怕我的敏感信息被有⼼⼈获取做⼀笔游戏充值,半个⼩时就收到各种游戏⼴告,我并不能抵挡诱惑我要做什么1. 交易报⽂不被篡改防⽌报⽂被篡改,需要对报⽂进⾏验签操作。
2. 敏感信息不被读取防⽌报⽂被读取,则需要将敏感信息加密。
公钥和私钥公钥和私钥,加密解密和加签验签。
加解密⽤来保证数据安全,加签验签⽤来证明⾝份。
商户⽣成⼀对公私钥(商公,商私),商户会把公钥给银⾏;银⾏也会⽣成⼀对公私钥(银公,银私),银⾏会把公钥给商户。
也就是说:商户有银⾏的公钥,⾃⼰的公钥和私钥。
银⾏有商户的公钥,⾃⼰的公钥和私钥加密解密保证数据安全:商户使⽤⾃⼰公钥加密,银⾏没有商户私钥解不开报⽂,排除商户使⽤⾃⼰的私钥加密,银⾏使⽤商户公钥解密。
理论上可⾏,然⽽会出现这种情况,商户和银⾏1,2,3都使⽤相同的公私钥,那么⾃⼰私钥加密后发送给银⾏1的报⽂,被银⾏2截取到也可以被解密开,违背了我们加密的⽬的--保证数据安全,排除。
商户使⽤银⾏的公钥加密,让银⾏⽤⾃⼰的私钥解密。
理论上可⾏,然⽽会出现这种情况,银⾏会和商户A,B,C都使⽤相同的公私钥,那么商户A和商户B发送过去的报⽂,银⾏都能解开,⽽且只有此银⾏的私钥可以解开,达成了我们的⽬的。
但是新的问题出现了,这种情况假如商户A模拟商户B的报⽂把商户B的钱转移⾛该怎么办?所以除了加密解密,还需要加签验签。
加签验签证明⾝份:加密已经完成,现在的问题只有怎么让银⾏区分这笔请求是商户A发的,还是商户B发的。
tp5 rsa公钥私钥方法 -回复

tp5 rsa公钥私钥方法-回复RSA公钥私钥方法(TP5)RSA(Rivest-Shamir-Adleman)是一种非对称加密算法,广泛应用于信息安全领域。
它通过生成一对公钥和私钥,实现安全的加密和解密过程。
本文将详细介绍RSA公钥私钥方法在TP5框架中的应用,包括生成密钥对、加密与解密的过程,并提供示例代码。
一、生成RSA密钥对1.1 安装openssl扩展在开始之前,我们需要确保在TP5框架中安装了openssl扩展。
我们可以通过在php.ini文件中取消以下行的注释来实现:extension=openssl1.2 生成RSA密钥对要生成RSA密钥对,可以使用openssl扩展提供的openssl_pkey_new 函数。
该函数将返回一个包含公钥和私钥的资源标识符。
下面是生成密钥对的示例代码:php生成新的RSA密钥对resource = openssl_pkey_new(['private_key_bits' => 2048, 指定密钥长度'private_key_type' => OPENSSL_KEYTYPE_RSA 指定密钥算法]);提取私钥openssl_pkey_export(resource, privateKey);提取公钥publicKey = openssl_pkey_get_details(resource)['key'];保存密钥对file_put_contents('private.key', privateKey);file_put_contents('public.key', publicKey);在这个示例中,我们使用openssl_pkey_new函数生成了一个新的RSA 密钥对,指定了2048位的密钥长度和RSA密钥算法。
然后,我们使用openssl_pkey_export和openssl_pkey_get_details函数提取了私钥和公钥,并将它们保存到了文件中。
java rsa 加密解密流程

java rsa 加密解密流程RSA是一种非对称加密算法,用于数据的加密和解密。
它涉及到公钥和私钥的使用,其中公钥用于加密数据,私钥用于解密数据。
下面是Java中使用RSA 加密和解密的基本流程:1. 生成密钥对:首先需要生成一对RSA密钥,包括公钥和私钥。
可以使用Java提供的`KeyPairGenerator`类来生成密钥对。
```javaKeyPairGenerator keyPairGenerator = KeyPairGenerator.getInstance("RSA");keyPairGenerator.initialize(2048); // 指定密钥长度KeyPair keyPair = keyPairGenerator.generateKeyPair();PublicKey publicKey = keyPair.getPublic();PrivateKey privateKey = keyPair.getPrivate();```2. 加密数据:使用公钥对需要加密的数据进行加密。
可以使用`Cipher`类来进行加密操作。
```javaString data = "Hello, World!";Cipher cipher = Cipher.getInstance("RSA");cipher.init(Cipher.ENCRYPT_MODE, publicKey);byte[] encryptedData = cipher.doFinal(data.getBytes());```3. 解密数据:使用私钥对加密后的数据进行解密,还原为原始数据。
```javacipher.init(Cipher.DECRYPT_MODE, privateKey);byte[] decryptedData = cipher.doFinal(encryptedData);String decryptedText = new String(decryptedData);```请注意,以上示例代码只是一个简单的RSA加密和解密流程的示例。
C#Rsa加密(私钥加密、公钥解密、密钥格式转换、支持超大长度分段加密)

C#Rsa加密(私钥加密、公钥解密、密钥格式转换、⽀持超⼤长度分段加密)此为⼯具类,这个和java版本的加密对⽐过了,结果是⼀样的,代码赋值黏贴直接⽤,不多⽐⽐,直接上代码(需要在nuget上寻找"Portable.BouncyCastle"包安装):using Org.BouncyCastle.Asn1.Pkcs;using Org.BouncyCastle.Asn1.X509;using Org.BouncyCastle.Crypto;using Org.BouncyCastle.Crypto.Parameters;using Org.BouncyCastle.Math;using Org.BouncyCastle.Pkcs;using Org.BouncyCastle.Security;using Org.BouncyCastle.X509;using System;using System.IO;using System.Security.Cryptography;using System.Text;using System.Xml;public class RSAUtil{///<summary>///⽣成公钥与私钥⽅法///</summary>///<returns></returns>public static string[] CreateKey(KeyType keyType, KeySize keySize){try{string[] sKeys = new string[2];RSACryptoServiceProvider rsa = new RSACryptoServiceProvider((int)keySize);switch (keyType){case KeyType.XML:{//私钥sKeys[0] = rsa.ToXmlString(true);//公钥sKeys[1] = rsa.ToXmlString(false);}break;case KeyType.PKS8:{sKeys[0] = rsa.ToXmlString(true);//公钥sKeys[1] = rsa.ToXmlString(false);//JAVA私钥sKeys[0] = RSAPrivateKeyDotNet2Java(sKeys[0]);//JAVA公钥sKeys[1] = RSAPublicKeyDotNet2Java(sKeys[1]);}break;default:break;}return sKeys;}catch (Exception ex){return null;}}///<summary>///密钥类型///</summary>public enum KeyType{///<summary>/// xml类型///</summary>XML,///<summary>/// pks8类型///</summary>PKS8}///<summary>///密钥尺⼨(⼀般都是1024位的)///</summary>public enum KeySize{SMALL = 1024,BIG = 2048}///<summary>/// RSA私钥格式转换,.net->java///</summary>///<param name="privateKey">.net⽣成的私钥</param>///<returns></returns>public static string RSAPrivateKeyDotNet2Java(string privateKey){XmlDocument doc = new XmlDocument();doc.LoadXml(privateKey);BigInteger m = new BigInteger(1, Convert.FromBase64String(doc.DocumentElement.GetElementsByTagName("Modulus")[0].InnerText));BigInteger exp = new BigInteger(1, Convert.FromBase64String(doc.DocumentElement.GetElementsByTagName("Exponent")[0].InnerText));BigInteger d = new BigInteger(1, Convert.FromBase64String(doc.DocumentElement.GetElementsByTagName("D")[0].InnerText));BigInteger p = new BigInteger(1, Convert.FromBase64String(doc.DocumentElement.GetElementsByTagName("P")[0].InnerText));BigInteger q = new BigInteger(1, Convert.FromBase64String(doc.DocumentElement.GetElementsByTagName("Q")[0].InnerText));BigInteger dp = new BigInteger(1, Convert.FromBase64String(doc.DocumentElement.GetElementsByTagName("DP")[0].InnerText));BigInteger dq = new BigInteger(1, Convert.FromBase64String(doc.DocumentElement.GetElementsByTagName("DQ")[0].InnerText));BigInteger qinv = new BigInteger(1, Convert.FromBase64String(doc.DocumentElement.GetElementsByTagName("InverseQ")[0].InnerText));RsaPrivateCrtKeyParameters privateKeyParam = new RsaPrivateCrtKeyParameters(m, exp, d, p, q, dp, dq, qinv);PrivateKeyInfo privateKeyInfo = PrivateKeyInfoFactory.CreatePrivateKeyInfo(privateKeyParam);byte[] serializedPrivateBytes = privateKeyInfo.ToAsn1Object().GetEncoded();return Convert.ToBase64String(serializedPrivateBytes);}///<summary>/// RSA公钥格式转换,.net->java///</summary>///<param name="publicKey">.net⽣成的公钥</param>///<returns></returns>public static string RSAPublicKeyDotNet2Java(string publicKey){XmlDocument doc = new XmlDocument();doc.LoadXml(publicKey);BigInteger m = new BigInteger(1, Convert.FromBase64String(doc.DocumentElement.GetElementsByTagName("Modulus")[0].InnerText));BigInteger p = new BigInteger(1, Convert.FromBase64String(doc.DocumentElement.GetElementsByTagName("Exponent")[0].InnerText));RsaKeyParameters pub = new RsaKeyParameters(false, m, p);SubjectPublicKeyInfo publicKeyInfo = SubjectPublicKeyInfoFactory.CreateSubjectPublicKeyInfo(pub);byte[] serializedPublicBytes = publicKeyInfo.ToAsn1Object().GetDerEncoded();return Convert.ToBase64String(serializedPublicBytes);}///<summary>/// RSA私钥格式转换,java->.net///</summary>///<param name="privateKey">java⽣成的RSA私钥</param>///<returns></returns>public static string RSAPrivateKeyJavaToDotNet(string privateKey){RsaPrivateCrtKeyParameters privateKeyParam = (RsaPrivateCrtKeyParameters)PrivateKeyFactory.CreateKey(Convert.FromBase64String(privateKey));return string.Format("<RSAKeyValue><Modulus>{0}</Modulus><Exponent>{1}</Exponent><P>{2}</P><Q>{3}</Q><DP>{4}</DP><DQ>{5}</DQ><InverseQ>{6}</InverseQ><D>{7}</D></RSAKeyValue>", Convert.ToBase64String(privateKeyParam.Modulus.ToByteArrayUnsigned()),Convert.ToBase64String(privateKeyParam.PublicExponent.ToByteArrayUnsigned()),Convert.ToBase64String(privateKeyParam.P.ToByteArrayUnsigned()),Convert.ToBase64String(privateKeyParam.Q.ToByteArrayUnsigned()),Convert.ToBase64String(privateKeyParam.DP.ToByteArrayUnsigned()),Convert.ToBase64String(privateKeyParam.DQ.ToByteArrayUnsigned()),Convert.ToBase64String(privateKeyParam.QInv.ToByteArrayUnsigned()),Convert.ToBase64String(privateKeyParam.Exponent.ToByteArrayUnsigned()));}///<summary>/// RSA公钥格式转换,java->.net///</summary>///<param name="publicKey">java⽣成的公钥</param>///<returns></returns>public static string RSAPublicKeyJavaToDotNet(string publicKey){RsaKeyParameters publicKeyParam = (RsaKeyParameters)PublicKeyFactory.CreateKey(Convert.FromBase64String(publicKey));return string.Format("<RSAKeyValue><Modulus>{0}</Modulus><Exponent>{1}</Exponent></RSAKeyValue>",Convert.ToBase64String(publicKeyParam.Modulus.ToByteArrayUnsigned()),Convert.ToBase64String(publicKeyParam.Exponent.ToByteArrayUnsigned()));}///<summary>///最⼤加密长度///</summary>private const int MAX_ENCRYPT_BLOCK = 245;///<summary>///最⼤解密长度///</summary>private const int MAX_DECRYPT_BLOCK = 256;///<summary>///⽤私钥给数据进⾏RSA加密///</summary>///<param name="xmlPrivateKey"></param>///<param name="strEncryptString"></param>///<returns></returns>public static string PrivateKeyEncrypt(string xmlPrivateKey, string strEncryptString){//加载私钥RSACryptoServiceProvider privateRsa = new RSACryptoServiceProvider();privateRsa.FromXmlString(xmlPrivateKey);//转换密钥AsymmetricCipherKeyPair keyPair = DotNetUtilities.GetKeyPair(privateRsa);IBufferedCipher c = CipherUtilities.GetCipher("RSA/ECB/PKCS1Padding"); //使⽤RSA/ECB/PKCS1Padding格式c.Init(true, keyPair.Private);//第⼀个参数为true表⽰加密,为false表⽰解密;第⼆个参数表⽰密钥byte[] dataToEncrypt = Encoding.UTF8.GetBytes(strEncryptString);//获取字节byte[] cache;int time = 0;//次数int inputLen = dataToEncrypt.Length;int offSet = 0;MemoryStream outStream = new MemoryStream();while (inputLen - offSet > 0){if (inputLen - offSet > MAX_ENCRYPT_BLOCK){cache = c.DoFinal(dataToEncrypt, offSet, MAX_ENCRYPT_BLOCK);}else{cache = c.DoFinal(dataToEncrypt, offSet, inputLen - offSet);}//写⼊outStream.Write(cache, 0, cache.Length);time++;offSet = time * MAX_ENCRYPT_BLOCK;}byte[] resData = outStream.ToArray();string strBase64 = Convert.ToBase64String(resData);outStream.Close();return strBase64;}///<summary>///⽤公钥给数据进⾏RSA解密///</summary>///<param name="xmlPublicKey">公钥(XML格式字符串) </param>///<param name="strDecryptString">要解密数据</param>///<returns>解密后的数据</returns>public static string PublicKeyDecrypt(string xmlPublicKey, string strDecryptString){//加载公钥RSACryptoServiceProvider publicRsa = new RSACryptoServiceProvider();publicRsa.FromXmlString(xmlPublicKey);RSAParameters rp = publicRsa.ExportParameters(false);//转换密钥AsymmetricKeyParameter pbk = DotNetUtilities.GetRsaPublicKey(rp);IBufferedCipher c = CipherUtilities.GetCipher("RSA/ECB/PKCS1Padding");//第⼀个参数为true表⽰加密,为false表⽰解密;第⼆个参数表⽰密钥c.Init(false, pbk);byte[] DataToDecrypt = Convert.FromBase64String(strDecryptString);byte[] cache;int time = 0;//次数int inputLen = DataToDecrypt.Length;int offSet = 0;MemoryStream outStream = new MemoryStream();while (inputLen - offSet > 0){if (inputLen - offSet > MAX_DECRYPT_BLOCK){cache = c.DoFinal(DataToDecrypt, offSet, MAX_DECRYPT_BLOCK);}else{cache = c.DoFinal(DataToDecrypt, offSet, inputLen - offSet);}//写⼊outStream.Write(cache, 0, cache.Length);time++;offSet = time * MAX_DECRYPT_BLOCK;}byte[] resData = outStream.ToArray();string strDec = Encoding.UTF8.GetString(resData);return strDec;}///<summary>///签名///</summary>///<param name="str">需签名的数据</param>///<returns>签名后的值</returns>public static string Sign(string str, string privateKey, SignAlgType signAlgType){//根据需要加签时的哈希算法转化成对应的hash字符节byte[] bt = Encoding.GetEncoding("utf-8").GetBytes(str);byte[] rgbHash = null;switch (signAlgType){case SignAlgType.SHA256:{SHA256CryptoServiceProvider csp = new SHA256CryptoServiceProvider(); rgbHash = puteHash(bt);}break;case SignAlgType.MD5:{MD5CryptoServiceProvider csp = new MD5CryptoServiceProvider();rgbHash = puteHash(bt);}break;case SignAlgType.SHA1:{SHA1 csp = new SHA1CryptoServiceProvider();rgbHash = puteHash(bt);}break;default:break;}RSACryptoServiceProvider key = new RSACryptoServiceProvider();key.FromXmlString(privateKey);RSAPKCS1SignatureFormatter formatter = new RSAPKCS1SignatureFormatter(key);formatter.SetHashAlgorithm(signAlgType.ToString());//此处是你需要加签的hash算法,需要和上边你计算的hash值的算法⼀致,不然会报错。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本练习主机A、B为一组,C、D为一组,E、F为一组。
首先使用“快照X”恢复Windows系统环境。
一.RSA生成公私钥及加密解密过程演示
(1)本机进入“密码工具”|“加密解密”|“RSA加密算法”|“公私钥”页签,在生成公私钥区输入素数p和素数q,这里要求p和q不能相等(因为很容易开平方求出p与q的值)并且p与q的乘积也不能小于127(因为小于127不能包括所有的ASCII码,导致加密失败),你选用的素数p与q分别是:p=11;q=13。
(2)单击“随机选取正整数e”下拉按钮,随机选取e,e= 103 。
(3)单击“生成公私钥”按钮生成公私钥,记录下公钥(e,n)=(103,143),私钥
(d,n)=(7,143)。
(4)在公私钥生成演示区中输入素数p=11 和素数q=13,还有正整数e=103。
单击“开始演示”按钮查看结果,填写表7-1-1。
表7-1-1 公私钥生成演示结果
(5)在加/解密演示区中输入明文m=45,公钥n=143(m<n),公钥e=103。
单击“加密演示”按钮,查看RSA加密过程,然后记录得到的密文c=111。
(6)在密文c编辑框输入刚刚得到的密文,分别输入私钥n= 143 ,私钥d= 7 ,点击“解密演示”按钮,查看RSA解密过程,然后记录得到的明文m= 45 。
(7)比较解密后的明文与原来的明文是否一致。
根据实验原理中对RSA加密算法的介绍,当素数p=13,素数q=17,正整数e=143时,写出RSA私钥的生成过程: n=p*q=13*17=221, φ(n)=(p-1)*(q-1) =12*16=192 ,
e*d=1 mod φ(n),d=47。
(d,n)=(47,221)。
当公钥e=143时,写出对明文m=40的加密过程(加密过程计算量比较大,请使用密码工具
的RSA工具进行计算): c=m e
mod n40
143
(mod 221)= 密文c: 105 。
利用生成的私钥d,对生成的密文进行解密:m=c d
mod n105
47
(mod 221)= 明文
m:40 。
二.RSA加密解密
(1)本机在生成公私钥区输入素数p和素数q,这里要求p和q不能相等,并且p与q的乘积也不能小于127,记录你输入的素数,p=13,q=17。
(2)点击“随机选取正整数e:”下拉按钮,选择正整数e,e=143。
(3)点击“生成公私钥”按钮生成公私钥,记录下公钥e= 143 , n= 221 ;私钥d= 47 ,n= 221 。
将自己的公钥通告给同组主机。
(4)本机进入“加密/解密”页签,在“公钥e部分”和“公钥n部分”输入同组主机的公钥,在明文输入区输入明文:计算机网络安全。
单击“加密”按钮对明文进行加密,单击“导出”按钮将密文导出到RSA共享文件夹
(D:\Work\Encryption\RSA\)中,通告同组主机获取密文。
得到密文
-204,-141,-196,-61,-205,-37,-51,-83,-82,-168,-163,-182,-75,-119
(5)进入“加密/解密”页签,单击“导入”按钮,从同组主机的RSA共享文件夹中将密文导入,点击“解密”按钮,切换到解密模式,在“私钥d部分47”和“私钥n部分221”输入自己的私钥,再次点击“解密”按钮进行RSA解密。
得到明文:计算机网络安全(6)将破解后的明文与同组主机记录的明文比较。
