SPSS中两因素完全随机方差分析交互作用及简单效应Synta
用spss20进行二因素设计的简单效应分析

用SPSS20进行二因素设计的简单效应分析两因素试验要检验互作效应,如果互作显著则应进一步做简单效应分析。
SPSS20图形界面无法简单效应分析,其实SPSS大多数功能均无法利用图形界面实现。
所以SPSS的优点并不是其易用性,而重点在于输出结果丰富、编排合理。
比较SAS、和R软件均能利用图形界面进行简单的统计分析,但其输出结果简单,无法直接发布。
我们用一个两因素裂区试验的产量数据进行简单的说明。
这个试验是一个品种密度试验,品种为主区,种植密度为副区,三次重复,籽粒产量为每公顷公斤产量。
其分析语法为:UNIANOVA 单产BY a b r/RANDOM=r/METHOD=SSTYPE(3)/INTERCEPT=INCLUDE/CRITERIA=ALPHA(0.05)/POSTHOC=a b(DUNCAN LSD)/DESIGN=a b r r(a) a*b/EMMEANS = TABLES(a*b) COMPARE (b) ADJ(LSD)/EMMEANS = TABLES(a*b) COMPARE (a) ADJ(LSD).注意最后两句,采用EMMEANS进行简单效应分析,其选项ADJ表示均值检验方法,有3种方法可供选择,常用的是LSD。
运行该语句(Ctrl+r)的下列结果。
注意,该语句前面还有数据集设置(DATASET ACTIVATE 数据集1.),不能写错数据集的名称。
表1 主体间效应的检验因变量: 单产源III 型平方和df 均方 F Sig.截距假设1524883353.546 1 1524883353.546 41177.914 .000误差74063.167 2 37031.584aa假设5090978.401 2 2545489.201 257.340 .000误差39566.096 4 9891.524bb假设2253126.736 2 1126563.368 79.838 .000误差169326.808 12 14110.567cr假设74063.167 2 37031.584 3.744 .121误差39566.096 4 9891.524br(a)假设39566.096 4 9891.524 .701 .606误差169326.808 12 14110.567ca * b假设836244.524 4 209061.131 14.816 .000误差169326.808 12 14110.567ca. MS(r)b. MS(r(a))c. MS(错误) 主区a 副区b 重复r 籽粒产量xm26 10万 1 6942 xm26 10万 2 6725.3 xm26 10万 3 6692 xm26 15万 1 7658.7 xm26 15万 2 7467 xm26 15万 3 7375.4xm26 20万1 7642 xm26 20万 2 7683.7 xm26 20万3 7467 9398 10万 1 6775.3 9398 10万 2 6900.3 9398 10万 3 6748.7 9398 15万 1 6950.3 9398 15万 2 6825.3 9398 15万 3 6775.3 9398 20万 1 7725.4 9398 20万 2 7575.4 9398 20万 3 7883.7 ts28 10万 1 8167.1 ts28 10万 2 8033.7 ts28 10万 3 7858.7 ts28 15万 1 7975.4 ts28 15万 2 8025.4 ts28 15万 3 7908.7 ts28 20万 1 8450.4 ts28 20万 2 8200.4 ts28 20万 3 8475.4表1显示互作显著,因此有必要进行简单效应分析。
SPSS统计简单效应分析语法语句

在SPSS里实现被试间设计简单效应分析的方法作者: Highway 发布时间: 2008-7-7简单效应(simple effect)分析通常是在作方差分析时存在交互效应的情况下的进一步分析。
需要在SPSS中编写syntax实现。
比如:MANO y BY x1(1 2) x2(1 3)/DESI/DESI=x1 WITHIN x2(1)x1 WITHIN x2(2)x1 WITHIN x2(3)上述只是一个简单的完全随机设计,若x1与x2存在交互作用而进行的进一步分析(即简单效应分析)。
同时你可以再加一个design:/DESI=x2 WITHIN x1(1)x2 WITHIN x1(2).===========说明=============因变量为Y,自变量1为X1,(两水平),自变量2为X2(三水平),DESI即是DESIGN,表示实验设计效应类型计算,/DESI=X1 WITHIN X2(1)表示在自变量X2水平1层面上考察X1的两个水平之间是否存在显著性差异.余类推.下面那句/DESI=X2 WITHIN X1(1)表示在自变量X1水平1的层面上考察自变量X2的三个水平之间是否存在显著性差异.被试内、被试间、混合实验设计简单效应分析作者: Highway 发布时间: 2008-7-7简单效应(simple effect)分析简单效应(simple effect)分析通常是在作方差分析时存在交互效应的情况下的进一步分析。
你需要在SPSS中编写syntax实现。
一、完全随机因素实验中简单效应得分析程序假如一个两因素随机实验中,A因素有两个水平、B因素有三个水平,因变量是Y,检验B因素在A因素的两个水平上的简单效应分析。
TWO-FACTOR RANDOMIZED EXPERIMENTSIMPLE EFFECTS.DA TA LIST FREE /A B Y.BEGIN DATA1 3 41 1 21 1 32 2 52 1 61 2 82 1 91 2 82 3 102 3 112 3 92 3 8END DATA.MANOV A y BY A(1,2) B(1,3)/DESIGN/DESIGN=A WITHIN B(1)A WITHIN B(2)A WITHIN B(3).若A与B存在交互作用而进行的进一步分析(即简单效应分析)。
两因素实验设计SPSS操作技巧

两因素重复测量实验设计SPSS操作
简单效应检验
GLM 无标记短句 无标记中句 无标记长句 有标记短句 有标记中句 有标记长句 /WSFACTOR=标记类型 2 Polynomial 句长类型 3 Polynomial /METHOD=SSTYPE(3) /PLOT=PROFILE(标记类型*句长类型) /EMMEANS=TABLES(标记类型*句长类型) COMPARE(标记类型) ADJ(LSD) /EMMEANS=TABLES(标记类型*句长类型) COMPARE(句长类型) ADJ(LSD) /PRINT=DESCRIPTIVE /CRITERIA=ALPHA(.05) /WSDESIGN=标记类型 句长类型 标记类型*句长类型.
短句与长句的差异不显著(P=.107) 中句与长句的差异是显著的(P=.002)
两因素完全随机实验设计SPSS操作
输出结果
(5)均值显示图
代表中句和长句的两 条直线大体平行,而代表 短句的直线与两条直线交 叉。因此,大致可以判断 两个因素之间存在交互效 应。
两因素完全随机实验设计SPSS操作
简单效应检验
交互作用显著时,通常需要进行简单效应分析,如果某因素在另一因素的某一个水 平内简单效应显著,还需要进行多重比较,以发现具体的差异所在。
SPSS双因素方差分析

SPSS双因素方差分析例1 对小白鼠喂以三种不同的营养素,目的是了解不同营养素增重的效果。
采用随机区组设计方法,以窝别作为划分区组的特征,以消除遗传因素对体重增长的影响。
现将同品系同体重的24只小白鼠分为8个区组,每个区组3只小白鼠。
三周后体重增量结果(克)列于下表,问小白鼠经三种不同营养素喂养后所增体重有无差别?区组号营养素1 营养素2 营养素31 50.10 58.20 64.502 47.80 48.50 62.403 53.10 53.80 58.604 63.50 64.20 72.505 71.20 68.40 79.306 41.40 45.70 38.407 61.90 53.00 51.208 42.20 39.80 46.20这可以认为是无重复实验的双因素方差分析,SPSS软件版本:18.0中文版。
1、建立数据文件变量视图:建立3个变量,如下图1数据视图:如下图:区组号用1-8表示,营养素号用1-3表示。
数据文件见“小白鼠喂3种不同的营养素增重数量.sav”,可以直接使用。
2、统计分析菜单选择:分析-> 一般线性模型-> 单变量1点击进入“单变量”对话框1旗开得胜将“体重”选入“因变量”框,“区组”、“营养素”选入固定因子框点击右边“模型”按钮,进入“单变量:模型对话框”1点击“设定”单选按钮(无重复双因素方差分析不能选全因子!),在“构建项”下拉菜单中选择“主效应”(只能选主效应)1把左边的因子与协变量框中区组和营养素均选入右边的模型框中其余选项取默认值就行,点击“继续”按钮,回到“单变量”界面1点击“两两比较”按钮,进入下面对话框1将左边框中“区组”、“营养素”均选入右边框中再选择两两比较的方法,LSD、S-N-K,Duncan为常用的三种方法,点击“继续”按钮回到“单变量”主界面。
1点击“选项”按钮1勾选“统计描述”及“方差齐性检验”,设置显著性水平,点击“继续”按钮,回到“单变量”主界面1点击下方“确定”按钮,开始分析。
双因素方差分析spss步骤

双因素方差分析spss步骤双因素方差分析SPSS步骤导言:双因素方差分析是一种常用的统计分析方法,用于分析两个或两个以上因素对于研究对象的影响是否存在差异。
在实际研究中,我们通常使用SPSS软件来进行双因素方差分析的计算和结果呈现。
本文将介绍使用SPSS软件进行双因素方差分析的步骤和注意事项。
一、准备数据在进行双因素方差分析之前,我们首先需要准备好所需的数据。
数据应该是一个二维矩阵,其中行代表不同的观测对象,列代表不同的变量。
变量可以分为两个因素,分别是因素A和因素B。
确保数据的格式正确,并且每一列都应该有对应的变量名称。
二、导入数据到SPSS打开SPSS软件,选择“文件”-“打开”-“数据”,然后选择包含你准备好的数据的文件。
在打开数据之后,你将看到数据被加载到SPSS软件的数据编辑器中。
三、设置变量属性在SPSS软件的数据编辑器中,右键点击每个变量的列,然后选择“变量视图”。
在变量视图中,你可以设置每个变量的属性,包括变量的名称、标签、测量尺度等。
对于因素A和因素B,你可以将它们设为分类变量。
四、进行双因素方差分析在SPSS软件中,选择“分析”-“一般线性模型”-“单因素”。
在对话框中,将因变量添加到“因变量”框中,将因素A和因素B 添加到“因子”框中。
确保选择双因素方差分析选项,并点击“确定”按钮。
五、检查假设条件在进行双因素方差分析之前,我们需要确保满足一些假设条件。
首先,各个观测值是彼此独立的,且满足正态分布假设。
其次,各个因子水平的方差相等。
可以使用一些统计方法,如Shapiro-Wilk 检验和Levene检验,来验证这些假设条件。
六、解读结果SPSS软件将为我们提供双因素方差分析的结果。
主要包括因素A 和因素B的主效应、交互效应以及误差项。
对于主效应,我们可以通过检查P值来决定该因素是否对因变量有显著影响。
对于交互效应,我们可以通过检查因素A和因素B的交互作用项的P值来判断是否存在显著交互效应。
在SPSS里实现被试间设计简单效应分析的方法

被试内、被试间、混合实验设计简单效应分析作者: Highway 发布时间: 2008-7-7简单效应(simple effect)分析简单效应(simple effect)分析通常是在作方差分析时存在交互效应的情况下的进一步分析。
你需要在SPSS中编写syntax实现。
一、完全随机因素实验中简单效应得分析程序假如一个两因素随机实验中,A因素有两个水平、B因素有三个水平,因变量是Y,检验B因素在A因素的两个水平上的简单效应分析。
TWO-FACTOR RANDOMIZED EXPERIMENTaaaSIMPLE EFFECTS.DATA LIST FREE /A B Y.BEGIN DATA1 3 41 1 21 1 32 2 52 1 61 2 82 1 91 2 82 3 102 3 112 3 92 3 8END DATA.MANOVA y BY A(1,2) B(1,3)/DESIGN/DESIGN=A WITHIN B(1)A WITHIN B(2)A WITHIN B(3).若A与B存在交互作用而进行的进一步分析(即简单效应分析)。
同时你可以再加一个design: /DESIGN=B WITHIN A(1)B WITHIN A(2).自编数据试试y A B4.00 1.00 3.002.00 1.00 1.003.00 1.00 1.005.00 2.00 2.006.00 2.00 1.008.00 1.00 2.009.00 2.00 1.008.00 1.00 2.0010.00 2.00 3.0011.00 2.00 3.009.00 2.00 3.008.00 1.00 2.00当然,你可也直接贴下述语句至syntax编辑框:应会输出下述结果:The default error term in MANOVA has been changed from WITHIN CELLS toWITHIN+RESIDUAL. Note that these are the same for all full factorialdesigns.* * * * * * A n a l y s i s o f V a r i a n c e * * * * * *12 cases accepted.0 cases rejected because of out-of-range factor values.0 cases rejected because of missing data.6 non-empty cells.3 designs will be processed.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -* * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * *Tests of Significance for Y using UNIQUE sums of squaresSource of Variation SS DF MS F Sig of FWITHIN CELLS 10.00 6 1.67X1 15.00 1 15.00 9.00 .024X2 6.46 2 3.23 1.94 .224X1 BY X2 33.00 2 16.50 9.90 .013(Model) 80.92 5 16.18 9.71 .008 (Total) 90.92 11 8.27R-Squared = .890Adjusted R-Squared = .798- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -* * * * * * A n a l y s i s o f V a r i a n c e -- design 2 * * * * * *Tests of Significance for Y using UNIQUE sums of squaresSource of Variation SS DF MS F Sig of FWITHIN+RESIDUAL 16.46 8 2.06X1 WITHIN X2(1) 25.00 1 25.00 12.15 .008X1 WITHIN X2(2) 8.15 1 8.15 3.96 .082 X1 WITHIN X2(3) 43.74 1 43.74 21.26 .002(Model) 74.46 3 24.82 12.06 .002 (Total) 90.92 11 8.27R-Squared = .819Adjusted R-Squared = .751- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -* * * * * * A n a l y s i s o f V a r i a n c e -- design 3 * * * * * * Tests of Significance for Y using UNIQUE sums of squaresSource of Variation SS DF MS F Sig of F WITHIN+RESIDUAL 25.00 7 3.57X2 WITHIN X1(1) 30.30 2 15.15 4.24 .062 X2 WITHIN X1(2) 35.58 2 17.79 4.98 .045 (Model) 65.92 4 16.48 4.61 .039 (Total) 90.92 11 8.27R-Squared = .725Adjusted R-Squared = .568另外,三因素完全随机实验中的简单效应和简单简单效应的分析。
双因素方差分析spss

双因素方差分析spss双因素方差分析(Two-WayFactorialVarianceAnalysis)是一种重要的统计分析方法,用于研究实验设计的影响。
它可以帮助研究人员了解变量之间的关系,从而更好地理解研究结果。
本文将介绍双因素方差分析的概念,以及如何使用SPSS软件进行此类分析。
双因素方差分析是一种常见的实验设计,它将实验变量分成两个因素,并利用这两个因素研究变量之间的关系。
例如,研究人员可以研究学习水平和参与班级活动的关系。
学习水平和参与班级活动可以作为两个因素,而学习成果就可以作为评估的变量。
以SPSS为例,双因素方差分析可以使用General Linear Model 中的2x2 Factorial模型完成。
首先,研究人员需要了解实验变量之间的关系。
然后,在SPSS中,需要将所有这些变量输入数据集中。
最后,在General Linear Model选择2x2 Factorial模型,并设定两个因素。
一旦设定好模型,SPSS可以对变量进行多重比较。
这种比较可以帮助研究人员了解变量之间的关系,并确定哪些变量具有统计学意义。
此外,结果可以用于检查实验设计的有效性,以及较低的水平是否具有统计学意义。
另外,双因素方差分析还可以完成变量之间的交互分析。
一个典型的交互分析是学习水平,班活的量的相互作用。
在SPSS中,用户可以按照以上流程操作,并且最终获得完整的结果。
总之,双因素方差分析是一个重要的统计分析方法,可以帮助研究人员了解变量之间的关系。
使用SPSS软件可以轻松完成双因素方差分析,而且可以做出复杂的统计模型,更好地理解实验结果。
同时,使用SPSS,用户不仅可以轻松完成双因素方差分析,而且可以将分析结果转换为图表,更容易理解结果。
简单效应.

简单效应(simple effect分析通常是在作方差分析时存在交互效应的情况下的进一步分析。
你需要在SPSS 中编写syntax实现一、完全随机因素实验中简单效应得分析程序假如一个两因素随机实验中,A因素有两个水平、B因素有三个水平,因变量是Y,检验B因素在A因素的两个水平上的简单效应分析。
TWO-FACTOR RANDOMIZED EXPERIMENTSIMPLE EFFECTSDATA LIST FREE /A B Y.BEGIN DATA1 3 41 1 21 1 32 2 52 1 61 2 82 1 91 2 82 3 102 3 112 3 92 3 8END DATA.MANOVA y BY A(1,2 B(1,3/DESIGN/DESIGN=A WITHIN B(1A WITHIN B(2A WITHIN B(3.若A与B存在交互作用而进行的进一步分析(即简单效应分析。
同时你可以再加一个design:/DESIGN=B WITHIN A(1B WITHIN A(2.另外,三因素完全随机实验中的简单效应和简单简单效应的分析。
当实验设计中的因素多于两个时,做简单效应检验的前提仍然是,方差分析中发现了显著的两次交互作用。
而当三因素完全随机实验中发现了显著的三次交互作用时,可以进一步作简单简单效应检验。
也是DESIGN。
/DESIGN=A WITHIN B(1WITHIN C(1A WITHIN B(2WITHIN C(2.例如:THREE-FACTOR RANDOMIZED EXPERIMENTSIMPLE EFFECTS.SIMPLE SIMPLE EFFECTS. DATA LIST FREE /A B C Y. BEGIN DATA1 3 1 41 1 1 21 1 1 32 2 1 52 1 1 61 2 2 82 1 2 91 2 2 82 3 2 102 3 2 11……2 3 2 92 3 2 8END DATA.MANOVA y BY A(1,2 B(1,3 C(1,2./DESIGN/DESIGN=A WITHIN B(1A WITHIN B(2A WITHIN B(3A WITHIN C(1A WITHIN C(2/DESIGN=A WITHIN B(1 WITHIN C(1A WITHIN B(2 WITHIN C(2.二、被试内因素实验的简单效应分析程序与完全随机实验的不同之处:需要加一个WITHIN关键词说明的WSDESIGN 分命令。
基于SPSS的两因素完全随机实验的方差分析

6 4.80 0
1 8.6 47
.0 01
5 1.20 0
1 4.7 34
.0 01
3 9.20 0
1 1.2 81
.0 04
3.4 75
4 22
文化视野
变异来源
平方和 (ss) 自由度 (df) 均方 (MS) F 值 显著 (Sig)
A( 人员 )
6 4.8 00
1
64.800 18.647
.0 01
B(棋局 )
5 1.2 00
1
51.200 14.734
.0 01
A×B
3 9.2 00
1
39.200 11.281
.0 04
A(在 B1 水平 )
1.6 0
1
1.60
.25
.6 20
A(在 B2 水平 ) 102.40
1
102.40 16.30
.0 01
单元内误差
55 .6
16
3.48
3. 交互作用图
表 3 中是 A 因素在 B 的两个水平上的简单效应,可以看出,A 因素在 B2 水平上的简单效应显著,F(1,16)=16.30,P=.001(<.05), 表明,专家和新手对比赛中盘的棋子位置的记忆成绩差异显著,可 以解释为:对于比赛中盘的棋子位置,专家的记忆成绩远远高于 新手 的。A 因素 在 B1 水 平上 的简 单效 应 不显 著,F(1,16)=.25, P=.620( > .05),表明,专家和新手对随机摆放的棋子位置的记忆成 绩的差异不显著,可以解释为:对于随机摆放的棋子位置,专家和 新手的记忆成绩都比较差,并没有什么差别。
5 83 .20 0
16 7.82 7
【简单效应分析】使用SPSS完成两变量交互项显著时的简单效应分析——【杏花开医学统计】

【简单效应分析】使用SPSS完成两变量交互项显著时的简单效应分析——【杏花开医学统计】医务工作者的医学统计词典品质源于专注服务源于真心【简单效应分析】使用SPSS完成两变量交互项显著时的简单效应分析关键词:SPSS、简单效应导读我们在医学方差分析研究时,可能会遇到变量与变量的交互项存在显著的交互效应的情况,此时,仅仅只知道两个或多个变量间存在一个因素在另一个因素的不同水平上存在差异,但想进一步了解这种差异具体表现在哪些因素和哪些水平上时,还需要进行简单效应分析。
本期,我们来具体介绍两个变量交互项简单效应分析的基本原理、适用范围及其在SPSS软件中。
下方为视频版和音频版,含软件操作步骤两变量交互项显著简单效应分析来自杏花开医学统计00:00 17:50一、基本原理简单效应(simple effect),可以认为是方差分析时出现因素间交互效应显著时的下一个分析步骤,它是指一个因素的不同水平在另一个因素的某个水平上的效应。
详见:《用SPSS进行两因素两水平的医学析因设计资料的方差分析》即A1情况下B1在因变量上的变化,A2情况下B1在因变量上的变化,A1情况下B2在因变量上的变化,A2情况下B2在因变量上的变化。
二、适用范围简单效应是基于方差分析交互项显著情况下的进一步分析,因此,简单效应分析的样本应符合方差分析对样本数据的要求,即数据不明显偏态,组间方差轻微不齐也可以接受。
三、案例解读我们收集了一份儿童流感持续的天数的数据,欲研究儿童流感症状(发热、咳嗽、鼻塞)和用药情况是否会对儿童流感持续的天数产生影响。
采用多因素方差分析进行研究。
详见:《用SPSS进行两因素两水平的医学析因设计资料的方差分析》若症状与用药情况交互效应显著时,再进行简单效应分析。
具体操作如下:(1)在SPSS中的具体操作①进行多因素方差分析:以持续天数为研究变量,症状和是否用药为因子。
依次点击“分析——一般线性模型——单变量”,出现“单变量”窗口,在“对比”对话框中将“症状”和“是否用药”均选择为“简单”,在“选项”对话框中,勾选“描述统计”,即得到分析结果如下:(点击图片查看大图)由结果可知,症状和是否用药在流感持续天数上交互效应显著,因此,需要进一步做简单效应分析。
怎样使用SPSS进行双因素方差分析

熟练使用SPSS进行双因素方差分析试验内容:[试验][例] 某厂医务室测定了10 名氟作业工人工前、工中及工后4 个小时的尿氟浓度(μ mol/L), 结果如下表,问氟作业工人在这三个不同时间的尿氟浓度有无差别。
表1 尿氟浓度测试结果编号工前工中工后1 90.53 142.12 87.382 88.43 163.17 65.273 47.37 63.16 68.434 175.80 166.33 210.545 100.01 144.75 194.756 46.32 126.33 65.277 73.69 138.96 200.028 105.27 126.33 100.019 86.32 121.06 105.2710 60.01 73.69 58.951. 数据录入。
以变量x 表示尿氟浓度,变量g 表示时间(工前、工中或工后),可设1 为工前,2 为工中,3 为工后。
变量id表示工人(以编号代表不同工人),如编号为1 的工人工前尿氟浓度为90.53,则录入数据时x为90.53,g 为1,id 为1,数据录入格式如下图。
图1 数据输入界面2. 统计分析。
依次选取“Analyze”、“General Linear Model”、“Univariate” 。
图2 选择分析工具展开对话框如下图,将x选入Dependent Variable(因变量框),g、id 选入Fixed Factors(固定因素框)。
图3 选择变量进入右侧的分析列表对话框右边有一排按钮Mode、 Contrasts 、Plots、 Post Hoc、 Save 和Options,下面分别对其子对话框选项作一简单介绍:Model:指定不同的模型,除方差分析外General Linear Model可作其他统计分析;Contrasts:指定一种要用t 检验来检验的priori 对比;Plots:指定作某种图;Post Hoc:指定两两比较的方法;Save:指定将产生的一些指标保存为新的变量;Options:指定要输出的一些选项,如数据的描述方差齐性检等单击Model 展开其子对话框如下图,最上方Specify Model 定义模型,有两个选项:Full factorial(全因子)和Custom,选取Custom(自定义),Build Terms (选取模型中各项)下方有一选项,单击下拉箭头将其展开,选择Main Effects(主效应因)(本例不考虑交互作用),再将Factors 框中的g、 id 选入Model:框,按Continue返回主对话框,单击Post Hoc 按钮展开其子对话框,将g 选入Post Hoc Test for,即要做两两比较的因素框,选取SNK 即q检验,返回主对话框,单击OK 键提交执行。
SPSS中两因素完全随机方差分析交互作用及简单效应Syntax
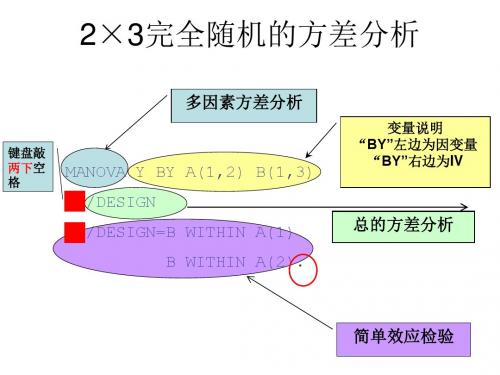
多因素方差分析
键盘敲 两下空 格
MANOVA Y BY A(1,2) B(1,3) /DESIGN /DESIGN=B WITHIN A(1) B WITHIN A(2).
ቤተ መጻሕፍቲ ባይዱ
变量说明 “BY”左边为因变量 “BY”右边为IV
总的方差分析
简单效应检验
2×3完全随机的方差分析
Y表示因变量 A.B分别表示自变量
均可替换为其他字母
键盘敲 两下空 格
Data View 与 Syntax 中的 “name” 务必保持一致 A因素各个水平的最小值与最大值 B因素同理 MANOVA Y BY A(1,2) B(1,3) /DESIGN /DESIGN=B WITHIN A(1) B WITHIN A(2).
实 心 点
请问:3×4完全随机的方差分析,C因素3个水平,D因素4 个水平,因变量为F,应如何改写以上语句?
MANOVA F BY C(1,3) D(1,4) /DESIGN /DESIGN=D WITHIN C(1) D WITHIN C(2)
D WITHIN C(3).
23完全随机的方差分析manovaa12b13designdesignbwithin键盘敲两下空多因素方差分析变量说明by左边为因变量by右边为iv总的方差分析简单效应检验23完全随机的方差分析manovaa12b13designdesignbwithindataview与syntax中的name务必保持一致y表示因变量ab分别表示自变量a因素各个水平的最小值与最大值b因素同理键盘敲两下空
单因素、交互作用、简单效应分析

4
2
5:1
10:1
生字密度
文章类型
不熟悉的 熟悉的 15:1
结果5:对简单效应的综合分析
阅读理解成绩
14
a2 对于熟悉的文章,被试的阅读理解成绩无显
12
著差异(F(2,19)=0.12,P=0.883)
10
8
对于不熟悉的文章,被试的阅读理解成绩存
本例没有交互作用 可分析,所以要改
即 【custom 】
【Buil Term】【main effcts】 左边变量的全选入右边
单击后出现一个对话框,用于设置在模型中包含哪些 主效应和交互因子,默认情况为Full factorial,即分 析所有的主效应和交互作用。
本例没有交互作用 可分析,所以要改
Corrected Total
251. 833
23
a. R Squared = .867 (Adjusted R Squared = . 830)
F 23.463 477. 224 43.343 21.784 15.201
Sig. .000 .000 .000 .000 .000
A因素的 主效应
B因素的 主效应
单因素、交互作用、 简单效,应分析
方差分析的适用条件
变异的可加性 总体正态分布 方差齐性(总体方差相等)
实际应用中,对方差齐性要求较高,因此需要单独检验。
SPSS中的4个方差分析菜单
Compare Means
One-Way ANOVA
单因素方差分析
General Linear Model
AB的交 互效应
A因素主效应显著 不同主题熟悉性的成绩存在显著差异。
B因素主效应显著 不同生字密度的成绩存在显著差异。
在SPSS里实现被试间设计简单效应分析的方法

被试内、被试间、混合实验设计简单效应分析作者: Highway 发布时间: 2008-7-7简单效应(simple effect)分析简单效应(simple effect)分析通常是在作方差分析时存在交互效应的情况下的进一步分析。
你需要在SPSS中编写syntax实现。
一、完全随机因素实验中简单效应得分析程序假如一个两因素随机实验中,A因素有两个水平、B因素有三个水平,因变量是Y,检验B因素在A因素的两个水平上的简单效应分析。
TWO-FACTOR RANDOMIZED EXPERIMENTaaaSIMPLE EFFECTS.DA TA LIST FREE /A B Y.BEGIN DATA1 3 41 1 21 1 32 2 52 1 61 2 82 1 91 2 82 3 102 3 112 3 92 3 8END DATA.MANOV A y BY A(1,2) B(1,3)/DESIGN/DESIGN=A WITHIN B(1)A WITHIN B(2)A WITHIN B(3).若A与B存在交互作用而进行的进一步分析(即简单效应分析)。
同时你可以再加一个design: /DESIGN=B WITHIN A(1)B WITHIN A(2).自编数据试试y A B4.00 1.00 3.002.00 1.00 1.003.00 1.00 1.005.00 2.00 2.006.00 2.00 1.008.00 1.00 2.009.00 2.00 1.008.00 1.00 2.0010.00 2.00 3.0011.00 2.00 3.009.00 2.00 3.008.00 1.00 2.00当然,你可也直接贴下述语句至syntax编辑框:应会输出下述结果:The default error term in MANOV A has been changed from WITHIN CELLS toWITHIN+RESIDUAL. Note that these are the same for all full factorialdesigns.* * * * * * A n a l y s i s o f V a r i a n c e * * * * * *12 cases accepted.0 cases rejected because of out-of-range factor values.0 cases rejected because of missing data.6 non-empty cells.3 designs will be processed.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -* * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * *Tests of Significance for Y using UNIQUE sums of squaresSource of Variation SS DF MS F Sig of FWITHIN CELLS 10.00 6 1.67X1 15.00 1 15.00 9.00 .024X2 6.46 2 3.23 1.94 .224X1 BY X2 33.00 2 16.50 9.90 .013(Model) 80.92 5 16.18 9.71 .008 (Total) 90.92 11 8.27R-Squared = .890Adjusted R-Squared = .798- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -* * * * * * A n a l y s i s o f V a r i a n c e -- design 2 * * * * * *Tests of Significance for Y using UNIQUE sums of squaresSource of Variation SS DF MS F Sig of FWITHIN+RESIDUAL 16.46 8 2.06X1 WITHIN X2(1) 25.00 1 25.00 12.15 .008X1 WITHIN X2(2) 8.15 1 8.15 3.96 .082 X1 WITHIN X2(3) 43.74 1 43.74 21.26 .002(Model) 74.46 3 24.82 12.06 .002 (Total) 90.92 11 8.27R-Squared = .819Adjusted R-Squared = .751- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -* * * * * * A n a l y s i s o f V a r i a n c e -- design 3 * * * * * * Tests of Significance for Y using UNIQUE sums of squaresSource of Variation SS DF MS F Sig of F WITHIN+RESIDUAL 25.00 7 3.57X2 WITHIN X1(1) 30.30 2 15.15 4.24 .062 X2 WITHIN X1(2) 35.58 2 17.79 4.98 .045 (Model) 65.92 4 16.48 4.61 .039 (Total) 90.92 11 8.27R-Squared = .725Adjusted R-Squared = .568另外,三因素完全随机实验中的简单效应和简单简单效应的分析。
