中考数学专题复习(四)压轴题北师大版

合集下载

中考数学复习专题四几何变换压轴题试题(2)

中考数学复习专题四几何变换压轴题试题(2)类型一图形的旋转变换几何图形的旋转变换是近年来中考中的常考点，多与三角形、四边形相结合．解决旋转变换问题，首先要明确旋转中心、旋转方向和旋转角，关键是找出旋转前后的对应点，利用旋转前后两图形全等等性质解题．如图，在菱形ABCD中，AB＝2，∠BAD＝60°，过点D作DE⊥AB于点E，DF⊥BC于点F.(1)如图1，连接AC分别交DE，DF于点M，N，求证：MN＝AC；(2)如图2，将∠EDF以点D为旋转中心旋转，其两边DE′，DF′分别与直线AB，BC相交于点G，P.连接GP，当△DGP的面积等于3时，求旋转角的大小并指明旋转方向．【分析】 (1)连接BD，由∠BAD＝60°，得到△ABD为等边三角形，进而证明点E是AB的中点，再根据相似三角形的性质解答；(2)分∠EDF顺时针旋转和逆时针旋转两种情况，然后根据旋转的性质解题．1．(20__·潍坊)边长为6的等边△ABC中，点D，E分别在AC，BC边上，DE∥AB，EC＝2.(1)如图1，将△DEC沿射线EC方向平移，得到△D′E′C′，边D′E′与AC的交点为M，边C′D′与∠ACC′的角平分线交于点N.当CC′多大时，四边形MCND′为菱形？并说明理由．(2)如图2，将△DEC绕点C旋转∠α(0°<α<360°)，得到△D′E′C，连接AD′，BE′.边D′E′的中点为P.①在旋转过程中，AD′和BE′有怎样的数量关系？并说明理由；②连接AP，当AP最大时，求AD′的值．(结果保留根号)图1 图22．(20__·成都)如图1，△ABC中，∠ABC＝45°，AH⊥BC于点H，点D在AH上，且DH＝CH，连接BD.(1)求证：BD＝AC；(2)将△BHD绕点H旋转，得到△EHF(点B，D分别与点E，F对应)，连接AE.①如图2，当点F落在AC上时(F不与C重合)，若BC＝4，tan C＝3，求AE的长；②如图3，当△EHF是由△BHD绕点H逆时针旋转30°得到时，设射线CF与AE相交于点G，连接GH，试探究线段GH与EF之间满足的等量关系，并说明理由．类型二图形的翻折变换几何图形的翻折变换也是近年来中考中的常考点，多与三角形、四边形相结合．翻折变换的实质是对称，翻折部分的两图形全等，找出对应边、对应角，再结合勾股定理、相似的性质与判定解题．(20__·苏州)如图，在△ABC中，AB＝10，∠B＝60°，点D，E分别在AB，BC上，且BD＝BE＝4，将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内)，连接AB′，则AB′的长为____．【分析】作DF⊥B′E于点F，B′G⊥AD于点G，由∠B＝60°，BD＝BE，得到△BDE是等边三角形，由对称的性质得到△B′DE也是等边三角形，从而GD＝B′F，然后利用勾股定理求解．、3．(20__·安徽)在三角形纸片ABC中，∠A＝90°，∠C＝30°，AC＝30 cm，将该纸片沿过点B的直线折叠，使点A落在斜边BC上的一点E处，折痕记为BD(如图1)，剪去△CDE后得到双层△BDE(如图2)，再沿着过△BDE某顶点的直线将双层三角形剪开，使得展开后的平面图形中有一个是平行四边形，则所得平行四边形的周长为40或cm.图1 图24．如图，在矩形ABCD中，点E在边CD上，将矩形沿AE折叠，使点D落在边BC上的点F处，过点F作FG∥CD，交AE于点G，连接DG.(1)求证：四边形DEFG为菱形；(2)若CD＝8，CF＝4，求的值．类型三图形的相似图形的相似常以三角形、四边形为背景，与旋转、翻折、动点相结合，考查三角形相似的性质及判定，难度较大，是中考中常考的几何压轴题．与动点相关的相似三角形，要根据动点的运动情况讨论相似三角形的对应边、对应角，进而判定相似三角形，再利用相似三角形的性质解题．(20__·青岛)如图，在矩形ABCD中，AB＝6 cm，BC＝8 cm，对角线AC，BD交于点O.点P从点A出发，沿AD方向匀速运动，速度为1 cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为1 cm/s；当一个点停止运动时，另一个点也停止运动．连接PO并延长，交BC于点E，过点Q作QF∥AC，交BD于点F.设运动时间为t(s)(0＜t＜6) ，解答下列问题：(1)当t为何值时，△AOP是等腰三角形；(2)设五边形OECQF的面积为S(cm2)，试确定S与t的函数关系式．【分析】 (1)根据勾股定理求出AC的值，然后分类讨论：当AP＝PO时，求出t的值；当AP＝AO时，求出t的值；(2)过点E作EH⊥AC于点H，过点Q作QM⊥AC于点M，过点D作DN⊥AC于点N，交QF于点G，分别用t表示出EH，DN，DG，再利用面积的和差计算即可．5．(20__·常德)如图，Rt△ABC中，∠BAC＝90°，D在BC上，连接AD，作BF⊥AD分别交AD于E，AC于F.(1)如图1，若BD＝BA，求证：△ABE≌△DBE；(2)如图2，若BD＝4DC，取AB的中点G，连接CG交AD于点M.求证：①GM＝2MC；②AG2＝AF·AC.图1 图2参考答案【例1】 (1)如图，连接BD，设BD交AC于点O，∵在菱形ABCD中，∠D AB＝60°，AD＝AB，∴△ABD为等边三角形．∵DE⊥AB，∴点E为AB的中点．∵AE∥CD，∴＝＝.同理＝.∴M，N是线段AC的三等分点，∴MN＝AC.(2)∵AB∥CD，∠BAD＝60°，∴∠ADC＝120°.∵∠ADE＝∠CDF＝30°，∴∠EDF＝60°.当∠EDF顺时针旋转时，由旋转的性质知，∠EDG＝∠FDP，∠GDP＝∠EDF＝60°.∵DE＝DF＝，∠DEG＝∠DFP＝90°，∴△DEG≌△DFP，∴DG＝DP，∴△DGP是等边三角形．则S△DGP＝DG2.由DG2＝3，又∵DG＞0，解得DG＝2.∴cos∠EDG＝＝＝，∴∠EDG＝60°.∴当顺时针旋转60°时，△DGP的面积是3.同理，当逆时针旋转60°时，△DGP的面积也是3.综上所述，当∠EDF以点D为旋转中心，顺时针或逆时针旋转60°时，△DGP的面积是3.【变式训练】1．解：(1)当CC′＝时，四边形MCND′为菱形．理由：由平移的性质得CD∥C′D′，DE∥D′E′.∵△ABC为等边三角形，∴∠B＝∠ACB＝60°，∴∠ACC′＝180°－60°＝120°.∵CN是∠ACC′的角平分线，∴∠NCC′＝60°.∵AB∥DE，DE∥D′E′，∴AB∥D′E′，∴∠D′E′C′＝∠B＝60°，∴∠D′E′C′＝∠NCC′，∴D′E′∥CN.∴四边形MCND′为平行四边形．∵∠ME′C′＝∠MCE′＝60°，∠NCC′＝∠NC′C＝60°，∴△MCE′和△NCC′为等边三角形，故MC＝CE′，NC＝CC′.又E′C′＝2，CC′＝，∴CE′＝CC′＝，∴MC＝CN，∴四边形MCND′为菱形．(2)①AD′＝BE′.理由：当α≠180°时，由旋转的性质得∠ACD′＝∠BCE′.由(1)知AC＝BC，CD′＝CE′，∴△ACD′≌△BCE′，∴AD′＝BE′.当α＝180°时，AD′＝AC＋CD′，BE′＝BC＋CE′，即AD′＝BE′.综上可知，AD′＝BE′.②连接CP，在△ACP中，由三角形三边关系得，AP<AC＋CP，∴当A，C，P三点共线时AP最大，如图所示．此时，AP＝AC＋CP.在△D′CE′中，由P为D′E′中点，得AP⊥D′E′，PD′＝，∴CP＝3，∴AP＝6＋3＝9.在Rt△APD′中，由勾股定理得AD′＝＝＝2.2．解：(1)在Rt△AHB中，∠ABC＝45°，∴AH＝BH.∵∠BHD＝∠AHC＝90°，DH＝CH，∴△BHD≌△AHC，∴BD＝AC.(2)①在Rt△AHC中，∵tan C＝3，∴＝3.设CH＝_，则BH＝AH＝3_，∴BC＝BH＋CH＝4_＝4，∴_＝1，∴AH＝3，CH＝1.由旋转的性质知，∠EHF＝∠BHD＝∠AHC＝90°，EH＝AH＝3，CH＝DH＝FH，∴∠EHA＝∠FHC，＝＝1，∴△EHA∽△FHC，∴∠EAH＝∠C，∴tan∠EAH＝tan C＝3.如图，过点H作HP⊥AE于点P，则HP＝3AP，AE＝2AP.在Rt△AHP中，AP2＋HP2＝AH2，即AP2＋(3AP)2＝9.∴AP＝，∴AE＝.②由①知，△AEH和△FHC都为等腰三角形，设AH交CG于点Q，∴∠GAH＝∠HCG，∴△AGQ∽△CHQ，∴＝，∴＝，∠AGQ＝∠CHQ＝90°.∵∠AQC＝∠GQH，∴△AQC∽△GQH.又∵旋转角为30°，∴∠EHA＝∠FHC＝120°，∴∠QAG＝30°，∴＝＝＝＝2.【例2】如图，作DF⊥B′E于点F，B′G⊥AD于点G，∵∠B＝60°，BD＝BE＝4，∴△BDE是边长为4的等边三角形．∵将△BDE沿DE所在的直线折叠得到△B′DE，∴△B′DE也是边长为4的等边三角形，∴GD＝B′F＝2.∵B′D＝4，∴B′G＝＝2.∵AB＝10，∴AG＝10－6＝4，∴AB′＝＝2.故答案为2.【变式训练】3．40或4．(1)证明：由折叠的性质知，DG＝FG，ED＝EF，∠AED＝∠AEF，∵FG∥CD，∴∠FGE＝∠AED，∴∠FGE＝∠AEF，∴FG＝FE，∴DG＝GF＝EF＝DE，∴四边形DEFG为菱形．(2)解：设DE＝_，根据折叠的性质，EF＝DE＝_，EC＝8－_，在Rt△EFC中，FC2＋EC2＝EF2，即42＋(8－_)2＝_2.解得_＝5，CE＝8－_＝3.∴＝.【例3】(1)∵在矩形ABCD中，AB＝6 cm，BC＝8 cm，∴AC＝10 cm.①当AP＝PO时，如图，过点P作PM⊥AO，∴AM＝AO＝.∵∠PMA＝∠ADC＝90°，∠PAM＝∠CAD，∴△APM∽△ACD，∴＝，∴AP＝t＝.②当AP＝AO时，t＝5.∵0＜t＜6，∴t＝或t＝5均符合题意，∴当t＝或t＝5时，△AOP是等腰三角形．(2)如图，过点E作EH⊥AC于点H，过点Q作QM⊥AC于点M，过点D作DN⊥AC于点N，交QF于点G，∵四边形ABCD是矩形，∴AD∥BC，∴∠PAO＝∠ECO.∵点O是对角线AC的中点，∴AO＝CO.又∵∠AOP＝∠COE，∴△AOP≌△COE，∴CE＝AP＝t.∵△CEH∽△CAB，∴＝，∴EH＝.∵S△ADC＝AD·DC＝DN·AC，∴DN＝＝.∵QM∥DN，∴△CQM∽△CDN，∴＝，即＝.∴QM＝，∴DG＝－＝.∵FQ∥AC，∴△DFQ∽△DOC，∴＝＝，∴FQ＝，∴S＝S△OEC＋S△OCD－S△DFQ＝OC·EH＋OC·DN－DG·FQ＝－t2＋t＋12，即S与t的函数关系式为S＝－t2＋t＋12.【变式训练】5．证明：(1)在Rt△ABE和Rt△DBE中，∴△ABE≌△DBE.(2)①如图，过点G作GH∥AD交BC于H，∵AG＝BG，∴BH＝DH.∵BD＝4DC，设DC＝1，则BD＝4，∴BH＝DH＝2.∵GH∥AD，∴＝＝，∴GM＝2MC.②如图，过点C作CN⊥AC交AD的延长线于N，则CN∥AG，∴△AGM∽△NCM，∴＝.由①知GM＝2MC，∴AG＝2NC.∵∠BAC＝∠AEB＝90°，∴∠ABF＝∠CAN＝90°－∠BAE，∴△ACN∽△BAF，∴＝.∵AB＝2AG，∴＝，∴2CN·AG＝AF·AC，∴AG2＝AF·AC.。

北师大版初中中考数学压轴题及答案精编WORD版

北师大版初中中考数学压轴题及答案精编W O R D版IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】中考数学专题复习(压轴题)1.已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A （-1，0）、B （0，3）两点，其顶点为D.（1）求该抛物线的解析式；（2）若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积；（3） △AOB 与△BDE 是否相似？如果相似，请予以证明；如果不相似，请说明理由.（注：抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫⎝⎛--a b ac a b 44,22）2. 如图，在Rt ABC △中，90A ∠=，6AB =，8AC =，D E ，分别是边AB AC ，的中点，点P 从点D 出发沿DE 方向运动，过点P 作PQ BC ⊥于Q ，过点Q 作QR BA ∥交AC 于R ，当点Q 与点C 重合时，点P 停止运动．设BQ x =，QR y =．（1）求点D 到BC 的距离DH 的长；（2）求y 关于x 的函数关系式（不要求写出自变量的取值范围）；（3）是否存在点P ，使PQR △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由．3在△ABC 中，∠A ＝90°，AB ＝4，AC ＝3，M 是AB 上的动点（不与A ，B 重合），过M 点作MN ∥BC 交AC 于点N ．以MN 为直径作⊙O ，并在⊙O 内作内接矩形AMPN ．令AM ＝x ．（1）用含x 的代数式表示△ＭNP 的面积S ；（2）当x 为何值时，⊙O 与直线BC 相切？A BC D ER P H Q（3）在动点M 的运动过程中，记△ＭNP 与梯形BCNM 重合的面积为y ，试求y 关于x 的函数表达式，并求x 为何值时，y 的值最大，最大值是多少？4.如图1，在平面直角坐标系中，己知ΔAOB 是等边三角形，点A 的坐标是(0，4)，点B 在第一象限，点P 是x 轴上的一个动点，连结AP ，并把ΔAOP 绕着点A 按逆时针方向旋转.使边AO 与AB 重合.得到ΔABD.（1）求直线AB 的解析式；（2）当点P 运动到点（3，0）时，求此时DP 的长及点D 的坐标；（3）是否存在点P ，使ΔOPD 的面积等于43，若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由.5如图，菱形ABCD 的边长为2，BD=2，E 、F 分别是边AD ，CD 上的两个动点，且满足AE+CF=2.（1）求证：△BDE ≌△BCF ；（2）判断△BEF 的形状，并说明理由；（3）设△BEF 的面积为S ，求S 的取值范围.6如图，抛物线21:23L y x x =--+交x 轴于A 、B 两点，交y 轴于M 点.抛物线1L 向右平移2个单位后得到抛物线2L ，2L 交x 轴于C 、D 两点. （1）求抛物线2L 对应的函数表达式；（2）抛物线1L 或2L 在x 轴上方的部分是否存在点N ，使以A ，C ，M ，N 为顶点的四边形是平行四边形.若存在，求出点N 的坐标；若不存在，请说明理由；（3）若点P 是抛物线1L 上的一个动点（P 不与点A 、B 重合），那么点P 关于原点的对称点Q 是否在抛物线2L 上，请说明理由.B图 1BD 图 2图 37.如图，在梯形ABCD 中，AB ∥CD ，AB ＝7，CD ＝1，AD ＝BC ＝5．点M ，N 分别在边AD ，BC 上运动，并保持MN ∥AB ，ME ⊥AB ，NF ⊥AB ，垂足分别为E ，F ．（1）求梯形ABCD 的面积；（2）求四边形MEFN 面积的最大值．（3）试判断四边形MEFN 能否为正方形，若能，求出正方形MEFN 的面积；若不能，请说明理由．8.如图，点A （m ，m ＋1），B （m ＋3，m －1）都在反比例函数xk y =的图象上．（1）求m ，k 的值；（2）如果M 为x 轴上一点，N 为y以点A ，B ，M ，N 试求直线MN 的函数表达式．（3）选做题：在平面直角坐标系中，点P 的坐标为（5，0），点Q 的坐标为（0，3），把线段PQ移4个单位，然后再向上平移2个单位，得到线段则点P 1的坐标为，点Q 1的坐标为．9.如图16，在平面直角坐标系中，直线y =-x 轴交于点A ，与y 轴交于点C ，抛物线2(0)3y ax x c a =-+≠经过A B C ，，三点．（1）求过A B C ，，三点抛物线的解析式并求出顶点F 的坐标；（2）在抛物线上是否存在点P ，使ABP △为直角三角形，若存在，直接写出P 点坐标；若不存在，请说明理由；C D A BE F NM友情提示：本大题第（1）小题4分，第（2）小题7分．对完成第（2）小题有困难的同学可以做下面的（3）选做题．选做题2分，所得分数计入总分．但第（2）、（3）小题都做的，第（3）小题的得分不重复计入总分．（3）试探究在直线AC 上是否存在一点M ，使得MBF △的周长最小，若存在，求出M 点的坐标；若不存在，请说明理由．10.如图所示，在平面直角坐标系中，矩形ABOC 的边BO 在x 轴的负半轴上，边OC 在y 轴的正半轴上，且1AB =，OB =ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD ．点A 的对应点为点E ，点B 的对应点为点F ，点C 的对应点为点D ，抛物线2y ax bx c =++过点A E D ，，．（1）判断点E 是否在y 轴上，并说明理由；（2）求抛物线的函数表达式；（3）在x 轴的上方是否存在点P ，点Q ，使以点O B P Q ，，，为顶点的平行四边形的面积是矩形ABOC 面积的2倍，且点P 在抛物线上，若存在，请求出点P ，点Q 的坐标；若不存在，请说明理由．压轴题答案1. 解：（ 1）由已知得：310c b c =⎧⎨--+=⎩解得c=3,b =2图∴抛物线的线的解析式为223y x x =-++(2)由顶点坐标公式得顶点坐标为（1，4所以对称轴为x=1,A,E 关于x=1E(3,0)设对称轴与x 轴的交点为F 所以四边形ABDE 的面积=ABO DFE BOFD S S S ∆∆++梯形=111()222AO BO BO DF OF EF DF ⋅++⋅+⋅=11113(34)124222⨯⨯++⨯+⨯⨯ =9 （3）相似如图，====所以2220BD BE +=, 220DE =即： 222BD BE DE +=,所以BDE ∆是直角三角形所以90AOB DBE ∠=∠=︒,且AO BO BD BE == 所以AOB DBE ∆∆. 2 解：（1）Rt A ∠=∠，6AB =，8AC =，10BC ∴=．点D 为AB 中点，132BD AB ∴==． 90DHB A ∠=∠=，B B ∠=∠．BHD BAC ∴△∽△， DH BD AC BC ∴=，3128105BD DH AC BC ∴==⨯=．（2）QR AB ∥，90QRC A ∴∠=∠=．C C ∠=∠，RQC ABC ∴△∽△，RQ QC AB BC ∴=，10610y x-∴=，即y 关于x 的函数关系式为：365y x =-+．（3）存在，分三种情况：①当PQ PR =时，过点P 作PM QR ⊥于M ，则QM RM =．1290∠+∠=，290C ∠+∠=，1C ∴∠=∠．84cos 1cos 105C ∴∠===，45QM QP ∴=， 1364251255x ⎛⎫-+ ⎪⎝⎭∴=，185x ∴=． ②当PQ RQ =时，312655x -+=，6x ∴=．③当PR QR =时，则R 为PQ 中垂线上的点，于是点R 为EC 的中点，11224CR CE AC ∴===．tan QR BAC CR CA ==， 366528x -+∴=，152x ∴=．综上所述，当x 为185或6或152时，PQR △3解：（1）∵MN ∥BC ，∴∠AMN =∠B ，∠ANM ＝∠ ∴ △AMN ∽ △ABC ．∴ AM AN AB AC=，即43x AN=．∴ AN ＝43x ． ……………2分ABCD ERPH QM 2 1 A BCD E R PHQB图 1∴ S =2133248MNP AMN S S x x x ∆∆==⋅⋅=．（0＜x ＜4） ……………3分（2）如图2，设直线BC 与⊙O 相切于点D ，连结AO ，OD ，则AO =OD =21MN ．在Rt △ABC 中，BC．由（1）知 △AMN ∽ △ABC ．∴ AM MN ABBC=，即45x MN=． ∴ 54MN x =， ∴ 58OD x =． …………………5分过M 点作MQ ⊥BC 于Q ，则58MQ OD x ==．在Rt △BMQ 与Rt △BCA 中，∠B 是公共角， ∴ △BMQ ∽△BCA ． ∴ BM QM BCAC=．∴ 55258324xBM x ⨯==，25424AB BM MA x x =+=+=． ∴ x ＝4996． ∴ 当x ＝4996时，⊙O 与直线B C 相切．…………………………………7分（3）随点M 的运动，当P 点落在直线BC 上时，连结AP ，则O 点为AP 的中点． ∵ MN ∥BC ，∴ ∠AMN =∠B ，∠AOM ＝∴ △AMO ∽ △ABP ．∴ 12AM AO ABAP==． AM ＝MB ＝2．故以下分两种情况讨论：① 当0＜x ≤2时，2Δ83x S y PMN ==．∴ 当x ＝2时，2332.82y =⨯=最大 ……………………………………8分 ② 当2＜x ＜4时，设PM ，PN 分别交BC 于E ，F ．∵ 四边形AMPN 是矩形，BD 图 2P图 3∴ PN ∥AM ，PN ＝AM ＝x ．又∵ MN ∥BC ，∴ 四边形MBFN 是平行四边形． ∴ FN ＝BM ＝4－x ． ∴ ()424PF x x x =--=-．又△PEF ∽ △ACB ．∴ 2PEF ABC S PF AB S ∆∆⎛⎫= ⎪⎝⎭． ∴ ()2322PEF S x ∆=-． ……………………………………………… 9分 MNP PEF y S S ∆∆=-＝()222339266828x x x x --=-+-．……………………10分当2＜x ＜4时，29668y x x =-+-298283x ⎛⎫=--+ ⎪⎝⎭．∴ 当83x =时，满足2＜x ＜4，2y =最大． ……………………11分综上所述，当83x =时，y 值最大，最大值是2． …………………………12分4 解：（1）作BE ⊥OA ，∴ΔAOB 是等边三角形∴BE=OB ·sin60o=B(∵A(0,4),设AB 的解析式为4y kx =+,所以42+=,解得3k =-, 以直线AB的解析式为43y x =-+ （2）由旋转知，AP=AD, ∠PAD=60o ,∴ΔAPD 是等边三角形，=如图，作B E ⊥AO,DH ⊥OA,GB ⊥DH,显然ΔGBD 中∠GBD=30°∴GD=12BD=,∴GB=2BD=32,OH=OE+HE=OE+BG=37222+=∴,7 2)(3)设OP=x,则由（2）可得D(,22x x+)若ΔOPD的面积为：13(2)224x x+=解得：3x-=所以P(3-,0)567解：（1）分别过D，C两点作DG⊥AB于点G，CH⊥AB于点H．……………1分∵AB∥CD，∴DG＝CH，DG∥CH．∴四边形DGHC为矩形，GH＝CD＝1．∵DG＝CH，AD＝BC，∠AGD＝∠BHC＝90∴△AGD≌△BHC（HL）．∴AG＝BH＝2172-=-GHAB＝3．………2分∵在Rt△AGD中，AG＝3，AD＝5，∴DG＝4．∴()174162ABCDS+⨯==梯形．………………………………………………3分（2）∵MN∥AB，ME⊥AB，NF⊥AB，∴ME＝NF，ME∥NF．∴四边形MEFN为矩形．∵AB∥CD，AD＝BC，∴∠A＝∠B．∵ME＝NF，∠MEA＝∠NFB＝90°，∴△MEA≌△NFB（AAS）．∴AE＝BF．……………………4分设AE＝x，则EF＝7－2x．……………5分A BE FG HA BE FG H∵ ∠A ＝∠A ，∠MEA ＝∠DGA ＝90°， ∴ △MEA ∽△DGA ．∴DGMEAG AE =． ∴ ME ＝x 34． …………………………………………………………6分∴ 6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN矩形． ……………………8分当x ＝47时，ME ＝37＜4，∴四边形MEFN 面积的最大值为649．……………9分（3）能． ……………………………………………………………………10分由（2）可知，设AE ＝x ，则EF ＝7－2x ，ME ＝x 34．若四边形MEFN 为正方形，则ME ＝EF ．即=34x 7－2x ．解，得 1021=x ． ……………………………………………11分 ∴ EF ＝21147272105x -=-⨯=＜4．∴ 四边形MEFN 能为正方形，其面积为251965142=⎪⎭⎫⎝⎛=MEFNS 正方形．8解：（1）由题意可知，()()()131-+=+m m m m ．解，得 m ＝3． ………………………………3分∴ A （3，4），B （6，2）；∴ k ＝4×3=12． ……………………………4分（2）存在两种情况，如图：①当M 点在x 轴的正半轴上，N 点在y 轴的正半轴上时，设M 1点坐标为（x 1，0），N 1点坐标为（0，y 1）．∵ 四边形AN 1M 1B 为平行四边形，∴ 线段N 1M 1可看作由线段AB 向左平移3个单位，再向下平移2个单位得到的（也可看作向下平移2个单位，再向左平移3个单位得到的）．由（1）知A 点坐标为（3，4），B 点坐标为（6，2），∴ N 1点坐标为（0，4－2），即N 1（0，2）； ………………………………5分 M 1点坐标为（6－3，0），即M 1（3，0）． ………………………………6分设直线M 1N 1的函数表达式为21+=x k y ，把x ＝3，y ＝0代入，解得321-=k ． ∴ 直线M 1N 1的函数表达式为232+-=x y ． ……………………………………8分②当M 点在x 轴的负半轴上，N 点在y 轴的负半轴上时，设M 2点坐标为（x 2，0），N 2点坐标为（0，y 2）．∵ AB ∥N 1M 1，AB ∥M 2N 2，AB ＝N 1M 1，AB ＝M 2N 2， ∴ N 1M 1∥M 2N 2，N 1M 1＝M 2N 2．∴ 线段M 2N 2与线段N 1M 1关于原点O 成中心对称．∴ M 2点坐标为（-3，0），N 2点坐标为（0，-2）． ………………………9分设直线M 2N 2的函数表达式为22-=x k y ，把x ＝-3，y ＝0代入，解得322-=k ， ∴ 直线M 2N 2的函数表达式为232--=x y ．所以，直线MN 的函数表达式为232+-=x y 或232--=x y ． ………………11分（3）选做题：（9，2），（4，5）． ………………………………………………2分9解：（1）直线y =x 轴交于点A ，与y 轴交于点C ．(10)A ∴-，，(0C ，······································································· 1分点A C ，都在抛物线上，∴抛物线的解析式为233y x x =-·········································· 3分∴顶点1F ⎛ ⎝⎭，··········································································· 4分（2）存在 ······················································································ 5分1(0P ······················································································ 7分2(2P ······················································································ 9分（3）存在 ····················································································· 10分理由：解法一：延长BC到点B'，使B C BC'=，连接B F'交直线AC于点M，则点M就是所求的点． ·················································································11分过点B'作B H AB'⊥于点H．B点在抛物线233y x x=-(30)B∴，在Rt BOC△中，tan OBC∠=，30OBC∴∠=，BC=在Rt BB H'△中，12B H BB''==6BH H'==，3OH∴=，(3B'∴--， ·······································12分设直线B F'的解析式为y kx b=+3k bk b⎧-=-+⎪∴⎨=+⎪⎩解得6kb⎧=⎪⎪⎨⎪=⎪⎩y x∴=·············································································13分yy x⎧=⎪∴⎨=⎪⎩解得377xy⎧=⎪⎪⎨⎪=-⎪⎩37M⎛∴⎝⎭，∴在直线AC上存在点M，使得MBF△的周长最小，此时377M⎛⎫-⎪⎪⎝⎭，．14分解法二：过点F作AC的垂线交y轴于点H，则点H为点F关于直线AC的对称点．连接BH交AC于点M，则点M即为所求． ···································11分过点F作FG y⊥轴于点G，则OB FG∥，BC FH∥．90BOC FGH∴∠=∠=，BCO FHG∠=∠图9同方法一可求得(30)B ，．在Rt BOC △中，tan OBC ∠=，30OBC ∴∠=，可求得GH GC ==， GF ∴为线段CH 的垂直平分线，可证得CFH △为等边三角形， AC ∴垂直平分FH ．即点H 为点F 关于AC的对称点．0H ⎛∴ ⎝⎭， ·································· 12分设直线BH 的解析式为y kx b =+，由题意得03k b b =+⎧⎪⎨=⎪⎩解得k b ⎧=⎪⎪⎨⎪=⎪⎩y ∴=············································································ 13分y y ⎧=⎪∴⎨⎪=⎩解得377x y ⎧=⎪⎪⎨⎪=-⎪⎩37M ⎛∴ ⎝⎭ ∴在直线AC 上存在点M ，使得MBF △的周长最小，此时37M ⎛ ⎝⎭，．110解：（1）点E 在y 轴上 ································································· 1分理由如下：连接AO ，如图所示，在Rt ABO △中，1AB =，BO =，2AO ∴=1sin 2AOB ∴∠=，30AOB ∴∠= 由题意可知：60AOE ∠=点B 在x 轴上，∴点E 在y 轴上． ····················································· 3分（2）过点D 作DM x ⊥轴于点M1OD =，30DOM ∠=∴在Rt DOM △中，12DM =，OM =点D 在第一象限，∴点D的坐标为122⎛⎫⎪ ⎪⎝⎭， ··································································· 5分由（1）知2EO AO ==，点E 在y 轴的正半轴上∴点E 的坐标为(02)，∴点A的坐标为( ····································································· 6分抛物线2y ax bx c =++经过点E ，由题意，将(A ，12D ⎫⎪⎪⎝⎭，代入22y ax bx =++中得321312422a a ⎧+=⎪⎨++=⎪⎩解得899a b ⎧=-⎪⎪⎨⎪=-⎪⎩∴所求抛物线表达式为：2829y x x =--+ ······································· 9分（3）存在符合条件的点P ，点Q ． ···················································· 10分理由如下：矩形ABOC 的面积3AB BO ==∴以O B P Q ，，，为顶点的平行四边形面积为由题意可知OB 为此平行四边形一边，又3OB =OB ∴边上的高为2 ·········································································· 11分依题意设点P 的坐标为(2)m ，点P在抛物线28299y x x =--+上解得，10m =，2m =1(02)P ∴，，228P ⎛⎫- ⎪ ⎪⎝⎭以O B P Q ，，，为顶点的四边形是平行四边形，PQ OB ∴∥，PQ OB == ∴当点1P 的坐标为(02)，时，点Q的坐标分别为1(Q，22)Q ；当点2P的坐标为2⎛⎫⎪ ⎪⎝⎭时，点Q的坐标分别为32Q ⎛⎫ ⎪ ⎪⎝⎭，42Q ⎫⎪⎪⎝⎭． ·································· 14分（以上答案仅供参考，如有其它做法，可参照给分）。

2020年中考数学压轴题专题4 几何最值存在性问题学案(原版+解析)

专题四几何最值的存在性问题【考题研究】在平面几何的动态问题中，当某几何元素在给定条件变动时，求某几何量（如线段的长度、图形的周长或面积、角的度数以及它们的和与差）的最大值或最小值问题，称为最值问题。

从历年的中考数学压轴题型分析来看，经常会考查到距离或者两条线段和差最值得问题，并且这部分题目在中考中失分率很高，应该引起我们的重视。

几何最值问题再教材中虽然没有进行专题讲解，到却给了我们很多解题模型，因此在专题复习时进行压轴训练是必要的。

【解题攻略】最值问题是一类综合性较强的问题，而线段和（差）问题，要归归于几何模型：（1）归于“两点之间的连线中，线段最短”凡属于求“变动的两线段之和的最小值”时，大都应用这一模型．（2）归于“三角形两边之差小于第三边”凡属于求“变动的两线段之差的最大值”时，大都应用这一模型．两条动线段的和的最小值问题，常见的是典型的“牛喝水”问题，关键是指出一条对称轴“河流”（如图1）．三条动线段的和的最小值问题，常见的是典型的“台球两次碰壁”或“光的两次反射”问题，关键是指出两条对称轴“反射镜面”（如图2）．两条线段差的最大值问题，一般根据三角形的两边之差小于第三边，当三点共线时，两条线段差的最大值就是第三边的长．如图3，PA与PB的差的最大值就是AB，此时点P在AB 的延长线上，即P′．解决线段和差的最值问题，有时候求函数的最值更方便，建立一次函数或者二次函数求解最值问题．【解题类型及其思路】解决平面几何最值问题的常用的方法有：（1）应用两点间线段最短的公理（含应用三角形的三边关系）求最值；（2）应用垂线段最短的性质求最值；（3）应用轴对称的性质求最值；（4）应用二次函数求最值；（5）应用其它知识求最值。

【典例指引】类型一【确定线段（或线段的和，差）的最值或确定点的坐标】【典例指引1】（2018·天津中考模拟）如图，在平面直角坐标系中，长方形OABC的顶点A、C分别在x轴、y轴的正半轴上．点B的坐标为（8，4），将该长方形沿OB翻折，点A的对应点为点D，OD与BC交于点E．（I）证明：EO=EB；（Ⅱ）点P是直线OB上的任意一点，且△OPC是等腰三角形，求满足条件的点P的坐标；（Ⅲ）点M是OB上任意一点，点N是OA上任意一点，若存在这样的点M、N，使得AM+MN 最小，请直接写出这个最小值．【举一反三】（2020·云南初三）如图，抛物线y=ax2+bx+3经过点B（﹣1，0），C（2，3），抛物线与y轴的焦点A，与x轴的另一个焦点为D，点M为线段AD上的一动点，设点M的横坐标为t．（1）求抛物线的表达式；（2）过点M作y轴的平行线，交抛物线于点P，设线段PM的长为1，当t为何值时，1的长最大，并求最大值；（先根据题目画图，再计算）（3）在（2）的条件下，当t为何值时，△PAD的面积最大？并求最大值；（4）在（2）的条件下，是否存在点P，使△PAD为直角三角形？若存在，直接写出t的值；若不存在，说明理由．类型二【确定三角形、四边形的周长的最值或符合条件的点的坐标】【典例指引2】（2020·重庆初三期末）如图，抛物线2y ax bx =+（0a >）与双曲线k y x=相交于点A 、B ，已知点A 坐标()1,4，点B 在第三象限内，且AOB ∆的面积为3（O 为坐标原点）.（1）求实数a 、b 、k 的值；（2）在该抛物线的对称轴上是否存在点P 使得POB ∆为等腰三角形？若存在请求出所有的P 点的坐标，若不存在请说明理由.（3）在坐标系内有一个点M ，恰使得MA MB MO ==，现要求在y 轴上找出点Q 使得BQM ∆的周长最小，请求出M 的坐标和BQM ∆周长的最小值.【举一反三】（2019·重庆实验外国语学校初三）如图1，已知抛物线y ＝﹣23384x +x +3与x 轴交于A 和B 两点，（点A 在点B 的左侧），与y 轴交于点C ．（1）求出直线BC 的解析式．（2）M 为线段BC 上方抛物线上一动点，过M 作x 轴的垂线交BC 于H ，过M 作MQ ⊥BC 于Q ，求出△MHQ 周长最大值并求出此时M 的坐标；当△MHQ 的周长最大时在对称轴上找一点R ，使|AR ﹣MR |最大，求出此时R 的坐标．（3）T 为线段BC 上一动点，将△OCT 沿边OT 翻折得到△OC ′T ，是否存在点T 使△OC ′T 与△OBC 的重叠部分为直角三角形，若存在请求出BT 的长，若不存在，请说明理由．类型三【确定三角形、四边形的面积最值或符合条件的点的坐标】【典例指引3】（2019·甘肃中考真题）如图，已知二次函数y ＝x 2+bx +c 的图象与x 轴交于点A （1，0）、B （3，0），与y 轴交于点C ．（1）求二次函数的解析式；（2）若点P 为抛物线上的一点，点F 为对称轴上的一点，且以点A 、B 、P 、F 为顶点的四边形为平行四边形，求点P 的坐标；（3）点E 是二次函数第四象限图象上一点，过点E 作x 轴的垂线，交直线BC 于点D ，求四边形AEBD 面积的最大值及此时点E 的坐标．【举一反三】（2019·内蒙古中考真题）如图，在平面直角坐标系中，已知抛物线22(0)y ax bx a =++≠与x 轴交于()1,0A -），()3,0B 两点，与y 轴交于点C ，连接BC ．（1）求该抛物线的解析式，并写出它的对称轴；（2）点D 为抛物线对称轴上一点，连接CD BD 、，若DCB CBD ∠=∠，求点D 的坐标；（3）已知()1,1F ，若(),E x y 是抛物线上一个动点（其中12x <<），连接CE CF EF 、、，求CEF ∆面积的最大值及此时点E 的坐标．B C M N为顶点（4）若点N为抛物线对称轴上一点，抛物线上是否存在点M，使得以,,,的四边形是平行四边形？若存在，请直接写出所有满足条件的点M的坐标；若不存在，请说明理由．【新题训练】1．如图，直线y＝5x＋5交x轴于点A，交y轴于点C，过A，C两点的二次函数y＝ax2＋4x ＋c的图象交x轴于另一点B.(1)求二次函数的表达式；(2)连接BC，点N是线段BC上的动点，作ND⊥x轴交二次函数的图象于点D，求线段ND 长度的最大值；(3)若点H为二次函数y＝ax2＋4x＋c图象的顶点，点M(4，m)是该二次函数图象上一点，在x轴，y轴上分别找点F，E，使四边形HEFM的周长最小，求出点F、E的坐标．2．（2019·江苏中考真题）如图，已知等边△ABC的边长为8，点P是AB边上的一个动点（与点A、B不重合），直线l是经过点P的一条直线，把△ABC沿直线l折叠，点B的对应点是点B’.（1）如图1，当PB=4时，若点B’恰好在AC边上，则AB’的长度为_____；（2）如图2，当PB=5时，若直线l//AC，则BB’的长度为；（3）如图3，点P在AB边上运动过程中，若直线l始终垂直于AC，△ACB’的面积是否变化？若变化，说明理由；若不变化，求出面积；（4）当PB=6时，在直线l变化过程中，求△ACB’面积的最大值.3．（2019·湖南中考真题）如图，在平面直角坐标系xOy中，矩形ABCD的边AB＝4，BC＝6．若不改变矩形ABCD的形状和大小，当矩形顶点A在x轴的正半轴上左右移动时，矩形的另一个顶点D始终在y轴的正半轴上随之上下移动．(1)当∠OAD＝30°时，求点C的坐标；(2)设AD的中点为M，连接OM、MC，当四边形OMCD的面积为212时，求OA的长；(3)当点A移动到某一位置时，点C到点O的距离有最大值，请直接写出最大值，并求此时cos∠OAD的值．4.（2018·江苏中考真题）如图，在平面直角坐标系中，一次函数y=﹣23x+4的图象与x轴和y轴分别相交于A、B两点．动点P从点A出发，在线段AO上以每秒3个单位长度的速度向点O作匀速运动，到达点O停止运动，点A关于点P的对称点为点Q，以线段PQ为边向上作正方形PQMN．设运动时间为t秒．（1）当t=13秒时，点Q的坐标是；（2）在运动过程中，设正方形PQMN与△AOB重叠部分的面积为S，求S与t的函数表达式；（3）若正方形PQMN对角线的交点为T，请直接写出在运动过程中OT+PT的最小值．5.（2020·江苏初三期末）已知二次函数223y x x =--+的图象和x 轴交于点A 、B ，与y轴交于点C ，点P 是直线AC 上方的抛物线上的动点.(1)求直线AC 的解析式.(2)当P 是抛物线顶点时，求APC ∆面积.(3)在P 点运动过程中，求APC ∆面积的最大值.6．（2020·江苏初三期末）如图，抛物线265y ax x =+-交x 轴于A 、B 两点，交y 轴于点C ，点B 的坐标为()5,0，直线5y x =-经过点B 、C .（1）求抛物线的函数表达式；（2）点P 是直线BC 上方抛物线上的一动点，求BCP ∆面积S 的最大值并求出此时点P 的坐标；（3）过点A 的直线交直线BC 于点M ，连接AC ，当直线AM 与直线BC 的一个夹角等于ACB ∠的3倍时，请直接写出点M 的坐标.7.（2019·石家庄市第四十一中学初三）如图，在平面直角坐标系中，抛物线y ＝x （x ﹣b ）﹣与y轴相交于A点，与x轴相交于B、C两点，且点C在点B的右侧，设抛物线的顶点为P．（1）若点B与点C关于直线x＝1对称，求b的值；（2）若OB＝OA，求△BCP的面积；（3）当﹣1≤x≤1时，该抛物线上最高点与最低点纵坐标的差为h，求出h与b的关系；若h 有最大值或最小值，直接写出这个最大值或最小值．8.（2020·江西初三期中）如图①，已知抛物线y=ax2+bx+3（a≠0）与x轴交于点A（1，0）和点B（-3，0），与y轴交于点C．（1）求抛物线的解析式；（2）设抛物线的对称轴与x轴交于点M，问在对称轴上是否存在点P，使△CMP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由；（3）如图②，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．9．（2020·山东初三期末）如图，抛物线y=ax2+bx+c（a≠0）的图象过点C（0，1），顶点为Q （2，3），点D在x轴正半轴上，且OD=OC．（1）求直线CD的解析式；（2）求抛物线的解析式；（3）将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E，求证：△CEQ ∽△CDO；（4）在（3）的条件下，若点P是线段QE上的动点，点F是线段OD上的动点，问：在P 点和F点移动过程中，△PCF的周长是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．10．（2020·盘锦市双台子区第一中学初三月考）如图①,已知抛物线y=ax2+bx+c的图像经过点A（0，3)、B（1，0），其对称轴为直线l：x=2，过点A作AC∥x轴交抛物线于点C，∠AOB 的平分线交线段AC于点E，点P是抛物线上的一个动点，设其横坐标为m.（1）求抛物线的解析式；（2）若动点P在直线OE下方的抛物线上，连结PE、PO，当m为何值时，四边形AOPE面积最大，并求出其最大值；（3）如图②，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由.11．（2020·四川初三）如图，一次函数122y x=-+的图像与坐标轴交于A、B两点，点C 的坐标为(1,0)-，二次函数2y ax bx c =++的图像经过A 、B 、C 三点．（1）求二次函数的解析式（2）如图1，已知点(1,)D n 在抛物线上，作射线BD ，点Q 为线段AB 上一点，过点Q 作QM y ⊥轴于点M ，作QN BD ⊥于点N ，过Q 作//QP y 轴交抛物线于点P ，当QM 与QN 的积最大时，求点P 的坐标；（3）在（2）的条件下，连接AP ，若点E 为抛物线上一点，且满足APE ABO ∠=∠，求点E 的坐标．12．（2019·广东初三）如图，已知抛物线y ＝﹣3x 2+bx +c 与x 轴交于原点O 和点A （6，0），抛物线的顶点为B ．（1）求该抛物线的解析式和顶点B 的坐标；（2）若动点P 从原点O 出发，以每秒1个长度单位的速度沿线段OB 运动，设点P 运动的时间为t （s ）．问当t 为何值时，△OPA 是直角三角形？（3）若同时有一动点M 从点A 出发，以2个长度单位的速度沿线段AO 运动，当P 、M 其中一个点停止运动时另一个点也随之停止运动．设它们的运动时间为t （s ），连接MP ，当t 为何值时，四边形ABPM 的面积最小？并求此最小值．13．（2019·山东初三期中）如图，已知抛物线经过两点A （﹣3，0），B （0，3），且其对称轴为直线x ＝﹣1．（1）求此抛物线的解析式．（2）若点Q 是对称轴上一动点，当OQ +BQ 最小时，求点Q 的坐标．（3）若点P 是抛物线上点A 与点B 之间的动点（不包括点A ，点B ），求△PAB 面积的最大值，并求出此时点P 的坐标．14.（2019·四川中考真题）如图，抛物线212y x bx c =-++过点(3,2)A ，且与直线72y x =-+交于B 、C 两点，点B 的坐标为(4,)m ．（1）求抛物线的解析式；（2）点D 为抛物线上位于直线BC 上方的一点，过点D 作DE x ⊥轴交直线BC 于点E ，点P 为对称轴上一动点，当线段DE 的长度最大时，求PD PA +的最小值；（3）设点M 为抛物线的顶点，在y 轴上是否存在点Q ，使45AQM ︒∠=？若存在，求点Q的坐标；若不存在，请说明理由．15.（2019·天津中考真题）已知抛物线2y x bx c =-+（b c ，为常数，0b >）经过点(1,0)A -，点(,0)M m 是x 轴正半轴上的动点．（Ⅰ）当2b =时，求抛物线的顶点坐标；（Ⅱ）点(,)D D b y 在抛物线上，当AM AD =，5m =时，求b 的值；（Ⅲ）点1(,)2Q Q b y +在抛物线上，当22AM QM +的最小值为332时，求b 的值． 16.（2019·湖南中考真题）如图，抛物线y ＝ax 2+bx （a ＞0）过点E （8，0），矩形ABCD 的边AB 在线段OE 上（点A 在点B 的左侧），点C 、D 在抛物线上，∠BAD 的平分线AM 交BC 于点M ，点N 是CD 的中点，已知OA ＝2，且OA ：AD ＝1：3.（1）求抛物线的解析式；（2）F 、G 分别为x 轴，y 轴上的动点，顺次连接M 、N 、G 、F 构成四边形MNGF ，求四边形MNGF 周长的最小值；（3）在x 轴下方且在抛物线上是否存在点P ，使△ODP 中OD 610求出点P 的坐标；若不存在，请说明理由；（4）矩形ABCD 不动，将抛物线向右平移，当平移后的抛物线与矩形的边有两个交点K 、L ，且直线KL 平分矩形的面积时，求抛物线平移的距离.17.（2019·辽宁中考真题）如图，在平面直角坐标系中，抛物线y ＝ax 2+bx +2（a ≠0）与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C ，抛物线经过点D （﹣2，﹣3）和点E （3，2），点P 是第一象限抛物线上的一个动点．（1）求直线DE 和抛物线的表达式；（2）在y 轴上取点F （0，1），连接PF ，PB ，当四边形OBPF 的面积是7时，求点P 的坐标；（3）在（2）的条件下，当点P 在抛物线对称轴的右侧时，直线DE 上存在两点M ，N （点M 在点N 的上方），且MN ＝22，动点Q 从点P 出发，沿P →M →N →A 的路线运动到终点A ，当点Q 的运动路程最短时，请直接写出此时点N 的坐标．18.（2019·湖南中考真题）已知抛物线2(0)y ax bx c a =++≠过点(1,0)A ，(3,0)B 两点，与y 轴交于点C ，=3OC ．(1)求抛物线的解析式及顶点D 的坐标；(2)过点A 作AM BC ⊥，垂足为M ，求证：四边形ADBM 为正方形；(3)点P 为抛物线在直线BC 下方图形上的一动点，当PBC ∆面积最大时，求点P 的坐标； (4)若点Q 为线段OC 上的一动点，问：12AQ QC +是否存在最小值？若存在，求岀这个最小值；若不存在，请说明理由．专题四几何最值的存在性问题【考题研究】在平面几何的动态问题中，当某几何元素在给定条件变动时，求某几何量（如线段的长度、图形的周长或面积、角的度数以及它们的和与差）的最大值或最小值问题，称为最值问题。

2023年中考数学压轴题培优教案专题04 一线三等角模型(含答案解析)

【压轴必刷】2023年中考数学压轴大题之经典模型培优案专题4一线三等角模型在直线AB 上有一点P,以A,B,P 为顶点的∠1,∠2,∠3相等,∠1,∠2的一条边在直线AB 上,另一条边在AB 同侧,∠3两边所在的直线分别交∠1,∠2非公共边所在的直线于点C,D ． 1．当点P 在线段AB 上,且∠3两边在AB 同侧时．（1）如图,若∠1为直角,则有△ACP ∽△BPD ．（2）如图,若∠1为锐角,则有△ACP ∽△BPD ．2．当点P 在AB 或BA 的延长线上,且∠3两边在AB 同侧时．如图,则有△ACP ∽△BPD ．3．当点P 在AB 或BA 的延长线上,且∠3两边在AB 异侧时．如图,则有△ACP ∽△BPD ．【例1】．（2022·全国·八年级课时练习）（1）某学习小组在探究三角形全等时,发现了下面这种典型的基本图形．如图1,已知：在△ABC 中,∠BAC =90°,AB =AC ,直线l 经过点A ,BD ⊥直线l ,CE ⊥直线l ,垂足分别为点D ,E ．求证：DE =BD +CE ．321DBPAC 3CDBP A321CPDBA321CDBAP（2）组员小明想,如果三个角不是直角,那结论是否会成立呢？如图2,将（1）中的条件改为：在△ABC 中,AB=AC,D,A,E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？若成立,请你给出证明；若不成立,请说明理由．（3）数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题：如图3,过△ABC的边AB,AC 向外作正方形ABDE和正方形ACFG,AH是BC边上的高．延长HA交EG于点I．若S△AEG=7,则S△AEI=______．【例2】．（2022·全国·八年级专题练习）在直线m上依次取互不重合的三个点D,A,E,在直线m上方有AB= AC,且满足∠BDA=∠AEC=∠BAC=α．(1)如图1,当α=90°时,猜想线段DE,CE之间的数量关系是____________；(2)如图2,当0<α<180°时,问题（1）中结论是否仍然成立？如成立,请你给出证明；若不成立,请说明理由；(3)应用：如图3,在△ABC中,∠BAC是钝角,AB=AC,∠BAD<∠CAE,∠BDA=∠AEC=∠BAC,直线m与CB的延长线交于点F,若BC=3FB,△ABC的面积是12,求△FBD与△ACE的面积之和．【例3】．（2022·浙江绍兴·模拟预测）如图,△ABC中∠B=∠C=30°,∠DEF=30°,且点E为边BC的中点．将∠DEF绕点E旋转,在旋转过程中,射线DE与线段AB相交于点P,射线EF与射线CA相交于点Q,连结PQ．(1)如图1,当点Q在线段CA上时,①求证：△BPE∽△CEQ；②线段BE,BP,CQ之间存在怎样的数量关系？请说明理由；(2)当△APQ为等腰三角形时,求CQBP 的值．一、解答题1．（2022·全国·八年级课时练习）在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E．(1)当直线MN绕点C旋转到图1的位置时．①请说明△ADC≌△CEB的理由；②请说明DE=AD+BE的理由；(2)当直线MN绕点C旋转到图2的位置时,DE、AD、BE具有怎样的等量关系?请写出等量关系,并予以证明．(3)当直线MN绕点C旋转到图3的位置时,DE、AD、BE具有怎样的等量关系?请直接在横线上写出这个等量关系：________．2．（2022·江苏·八年级课时练习）（1）如图1,在△ABC中,∠BAC＝90°,AB＝AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E．求证：△ABD≌△CAE；（2）如图2,将（1）中的条件改为：在△ABC中,AB＝AC,D、A、E三点都在直线m上,并且有∠BDA＝∠AEC＝∠BAC＝α,其中α为任意锐角或钝角．请问结论△ABD≌△CAE是否成立？如成立,请给出证明；若不成立,请说明理由．（3）拓展应用：如图3,D,E是D,A,E三点所在直线m上的两动点（D,A,E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE,若∠BDA＝∠AEC＝∠BAC,求证：△DEF是等边三角形．3．（2022·全国·九年级专题练习）感知：（1）数学课上,老师给出了一个模型：如图1,∠BAD=∠ACB=∠AED=90°,由∠1+∠2+∠BAD=180°,∠2+∠D+∠AED=180°,可得∠1==______．我们把这个模型称为“一线三∠D；又因为ACB=∠AED=90°,可得△ABC∽△DAE,进而得到BCAC等角”模型．应用：（2）实战组受此模型的启发,将三等角变为非直角,如图2,在△ABC中,AB=AC=10,BC=12,点P是BC边上的一个动点（不与B、C,点D是AC边上的一个动点,且∠APD=∠B．①求证：△ABP∽△PCD；②当点P为BC中点时,求CD的长；拓展：（3）在（2）的条件下如图2,当△APD为等腰三角形时,请直接写出BP的长．4．（2022·山东烟台·七年级期末）问题背景：（1）如图①,已知△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E,易证：DE=______+______．（2）拓展延伸：如图②,将（1）中的条件改为：在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,请求出DE,BD,CE三条线段的数量关系,并证明．（3）实际应用：如图③,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(−2,0),点A的坐标为(−6,3),请直接写出B点的坐标．5．（2021·浙江·义乌市绣湖中学教育集团八年级阶段练习）（1）模型建立,如图1,等腰直角三角形ABC中,∠ACB＝90°,CB＝CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E．求证：△BEC≌△CDA；（2）模型应用：x+3与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过①已知直线y＝34点A,C作直线,求直线AC的解析式；②如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A,C分别在坐标轴上,P是线段BC上动点,已知点D在第一象限,且是直线y＝2x﹣5上的一点,若△APD是不以A为直角顶点的等腰直角三角形,请直接写出所有符合条件的点D的坐标．6．（2022·江苏·八年级专题练习）（1）课本习题回放：“如图①,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,DE=1.7cm．求BE的长”,请直接写出此题答案：BE的长为________．（2）探索证明：如图②,点B,C在∠MAN的边AM、AN上,AB=AC,点E,F在∠MAN内部的射线AD上,且∠BED=∠CFD=∠BAC．求证：ΔABE≌ΔCAF．（3）拓展应用：如图③,在ΔABC中,AB=AC,AB>BC．点D在边BC上,CD=2BD,点E、F在线段AD上,∠BED=∠CFD=∠BAC．若ΔABC的面积为15,则ΔACF与ΔBDE的面积之和为________．（直接填写结果,不需要写解答过程）7．（2022·全国·八年级课时练习）通过对下面数学模型的研究学习,解决下列问题：（1）如图1,∠BAD＝90°,AB＝AD,过点B作BC⊥AC于点C,过点D作DE⊥AC于点E．由∠1+∠2＝∠2+∠D＝90°,得∠1＝∠D．又∠ACB＝∠AED＝90°,可以推理得到△ABC≌△DAE．进而得到AC＝,BC ＝AE．我们把这个数学模型称为“K字”模型或“一线三等角”模型；（2）如图2,∠BAD＝∠CAE＝90°,AB＝AD,AC＝AE,连接BC,DE,且BC⊥AF于点F,DE与直线AF交于点G．求证：点G是DE的中点；（深入探究）（3）如图,已知四边形ABCD和DEGF为正方形,△AFD的面积为S1,△DCE的面积为S2,则有S1S2（填“＞、＝、＜”）8．（2021·北京·东北师范大学附属中学朝阳学校八年级期中）如图,在△ABC中,∠ACB＝90°,AC＝BC,直线l 经过顶点C,过A、B两点分别作l的垂线AE、BF,E、F为垂足．（1）当直线l不与底边AB相交时,①求证：∠EAC＝∠BCF．②猜想EF、AE、BF的数量关系并证明．（2）将直线l绕点C顺时针旋转,使l与底边AB交于点D（D不与AB点重合）,请你探究直线l,EF、AE、BF之间的关系．（直接写出）9．（2021·四川达州·九年级期中）模型探究：（1）如图1,在等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E．求证：BE=CD；模型应用：（2）已知直线l1:y=2x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转90°至直线l2,如图2,求直线l2的函数表达式；x+4上,且AB=4√2．若直线与y轴的交点为M,M为AB中点．试判断（3）如图3,已知点A、B在直线y=12在x轴上是否存在一点C,使得△ABC是以AB为斜边的等腰直角三角形．10．（2022·全国·八年级课时练习）如图,线段AB=6,射线BG⊥AB,P为射线BG上一点,以AP为边做正方形APCD,且点C、D与点B在AP两侧,在线段DP上取一点E,使得∠EAP=∠BAP,直线CE与线段AB相交于点F（点F与点A、B不重合）,（1）求证：△AEP≌△CEP；（2）判断CF与AB的位置关系,并说明理由；（3）△AEF的周长是否为定值,若是,请求出这个定值,若不是,请说明理由．11．（2022·全国·八年级课时练习）如图,在△ABC中,AB＝AC＝2,∠B＝40°,点D在线段BC上运动（D不与B,C重合）,连接AD,作∠ADE＝40°,DE交线段AC于E．（1）当∠BDE＝115°时,∠BAD＝°,点D从B向C运动时,∠BAD逐渐变（填“大”或“小”）；（2）当DC等于多少时,△ABD≌△DCE,请说明理由；（3）在点D的运动过程中,△ADE的形状也在改变,判断当∠BAD等于多少时,△ADE是等腰三角形．12．（2022·重庆江北·,在平面直角坐标系中,已知A(a,0)、B(0,b)分别在坐标轴的正半轴上．（1）如图1,若a、b满足(a−4)2+√b−3=0,以B为直角顶点,AB为直角边在第一象限内作等腰直角△ABC,则点C的坐标是（________）；（2）如图2,若a=b,点D是OA的延长线上一点,以D为直角顶点,BD为直角边在第一象限作等腰直角△BDE,连接AE,求证：∠ABD=∠AED；（3）如图3,设AB=c,∠ABO的平分线过点D(2,−2),直接写出a−b+c的值．13．（2021·湖北·咸宁市第三初级中学八年级期中）如图,在等腰Rt△ABC中,∠ABC=90°,点A、B分别在x 轴、y轴上．（1）如图①,若点C的横坐标为5,求点B的坐标；的值；（2）如图②,若x轴恰好平分∠BAC,BC交x轴于点M,过点C作CD⊥x轴于点D,求CDAM（3）如图③,若点A的坐标为(−4,0),点B在y轴的正半轴上运动时,分别以OB、AB为边在第一、第二象限中作等腰Rt△OBF,等腰Rt△ABE,连接EF交y轴于点P,当点B在y轴上移动时,PB的长度是否发生改变？若不变求PB的值；若变化,求PB的取值范围．14．（2022·江西·丰城九中七年级期末）综合与探究：在平面直角坐标系中,已知A（0,a）,B（b,0）且a,b满足（a﹣3）2+|a﹣2b﹣1|＝0（1）求A,B两点的坐标（2）已知△ABC中AB=CB,∠ABC＝90°,求C点的坐标（3）已知AB＝√10,试探究在x轴上是否存在点P,使△ABP是以AB为腰的等腰三角形？若存在,请直接写出点P的坐标；若不存在,请说明理由．15．（2022·全国·八年级课时练习）如图,在△ABC中,AB＝AC＝2,∠B＝∠C＝40°,点D在线段BC上运动（点D不与点B、C重合）,连接AD,作∠ADE＝40°,DE交线段AC于点E．（1）当∠BDA＝105°时,∠EDC＝°,∠DEC＝°；点D从点B向点C运动时,∠BDA逐渐变．（填“大”或“小”）（2）当DC等于多少时,△ABD≌△DCE？请说明理由．（3）在点D的运动过程中,△ADE的形状可以是等腰三角形吗？若可以,请直接写出∠BDA的度数；若不可以,请说明理由．16．（2021·北京·北师大实验中学九年级开学考试）在正方形ABCD中,点E在射线CB上（不与点B,C重合）,连接DB,DE,过点E作EF⊥DE,并截取EF=DE（点D,F在BC同侧）,连接BF．（1）如图1,点E在BC边上．①依题意补全图1；②用等式表示线段BD,BE,BF之间的数量关系,并证明；（2）如图2,点E在CB边的延长线上,其他条件均不变,直接写出线段BD,BE,BF之间的数量关系．17．（2022·全国·八年级课时练习）在综合实践课上,李老师以“含30°的三角板和等腰三角形纸片”为模具与同学们开展数学活动．已知,在等腰△ABC纸片中,CA=CB=5,∠ACB=120°,将一块含30°角的足够大的直角三角尺PMN（∠M=90°,∠MPN=30°）按如图所示放置,顶点P在线段BA上滑动（点P不与A,B重合）,三角尺的直角边PM始终经过点C,并与CB的夹角∠PCB=α,斜边PN交AC于点D．（1）当∠BPC=100°时,α=______°；（2）当AP等于何值时,△APD≌△BCP？请说明理由；（3）在点P的滑动过程中,存在△PCD是等腰三角形吗？若存在,请求出夹角α的大小；若不存在,请说明理由．18．（2021·河南·舞阳县教研室八年级期中）如图,等腰直角△ABC中,BC＝AC,∠ACB＝90°,现将该三角形放置在平面直角坐标系中,点B坐标为（0,2）,点C坐标为（6,0）．（1）过点A作AD⊥x轴,求OD的长及点A的坐标；（2）连接OA,若Р为坐标平面内不同于点A的点,且以O、P、C为顶点的三角形与△OAC全等,请直接写出满足条件的点P的坐标；（3）已知OA＝10,试探究在x轴上是否存在点Q,使△OAQ是以OA为腰的等腰三角形？若存在,请求出点Q的坐标；若不存在,请说明理由．19．（2021·山东·肥城市汶阳镇初级中学七年级阶段练习）已知：CD是经过∠BCA的顶点C的一条直线,CA=CB．E、F是直线CD上两点,∠BEC=∠CFA=∠α．（1）若直线CD经过∠BCA的内部,∠BCD>∠ACD．①如图1,∠BCA=90°,∠α=90°,直接写出BE,EF,AF间的等量关系：__________．②如图2,∠α与∠BCA具有怎样的数量关系,能使①中的结论仍然成立？写出∠α与∠BCA的数量关系,并对结论进行证明；（2）如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,①中的结论是否成立？若成立,进行证明；若不成立,写出新结论并进行证明．20．（2022·全国·八年级课时练习）（1）如图（1）在△ABC中,∠BAC＝90°,AB＝AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E．求证：DE＝BD+CE；（2）如图（2）将（1）中的条件改为：在△ABC中,AB＝AC,D、A、E三点都在直线m上,并且有∠BDA＝∠AEC＝∠BAC＝α,其中α为任意锐角或钝角．请问结论DE＝BD+CE是否成立？如成立,请给出证明；若不成立,请说明理由．【例1】．（2022·全国·八年级课时练习）（1）某学习小组在探究三角形全等时,发现了下面这种典型的基本图形．如图1,已知：在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D,E．求证：DE=BD+CE．（2）组员小明想,如果三个角不是直角,那结论是否会成立呢？如图2,将（1）中的条件改为：在△ABC 中,AB=AC,D,A,E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？若成立,请你给出证明；若不成立,请说明理由．（3）数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题：如图3,过△ABC的边AB,AC 向外作正方形ABDE和正方形ACFG,AH是BC边上的高．延长HA交EG于点I．若S△AEG=7,则S△AEI=______．{∠ABD=∠CAE ∠BDA=∠CEAAB=AC,∴△ADB≌△CEA（AAS）,∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE．（2）解：成立．理由：如图2中,∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,∴∠DBA=∠CAE,在△ADB和△CEA中,{∠BDA=∠AEC ∠DBA=∠CAEAB=AC,∴△ADB≌△CEA（AAS）,∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE．（3）如图3,过E作EM⊥HI于M,GN⊥HI的延长线于N．∴∠EMI=∠GNI=90°由（1）和（2）的结论可知EM=AH=GN∴EM=GN在△EMI和△GNI中,{∠GIN=∠EIM EM=GN∠GNI=∠EMI,∴△EMI≌△GNI（AAS）,∴EI=GI,∴I是EG的中点．S△AEG=3.5．∴S△AEI=12故答案为：3.5．【点睛】本题是四边形综合题,考查了全等三角形的判定和性质,正方形的性质,直角三角形的性质,熟练掌握全等三角形的判定与性质是解题的关键．【例2】．（2022·全国·八年级专题练习）在直线m上依次取互不重合的三个点D,A,E,在直线m上方有AB= AC,且满足∠BDA=∠AEC=∠BAC=α．(1)如图1,当α=90°时,猜想线段DE,BD,CE之间的数量关系是____________；(2)如图2,当0<α<180°时,问题（1）中结论是否仍然成立？如成立,请你给出证明；若不成立,请说明理由；(3)应用：如图3,在△ABC中,∠BAC是钝角,AB=AC,∠BAD<∠CAE,∠BDA=∠AEC=∠BAC,直线m与CB的延长线交于点F,若BC=3FB,△12,求△FBD与△ACE的面积之和．【答案】(1)DE＝BD+CE(2)DE＝BD+CE仍然成立,理由见解析(3)△FBD与△ACE的面积之和为4【分析】（1）由∠BDA＝∠BAC＝∠AEC＝90°得到∠BAD+∠EAC＝∠BAD+∠DBA＝90°,进而得到∠DBA＝∠EAC,然后结合AB＝AC得证△DBA≌△EAC,最后得到DE＝BD+CE；（2）由∠BDA＝∠BAC＝∠AEC＝α得到∠BAD+∠EAC＝∠BAD+∠DBA＝180°﹣α,进而得到∠DBA＝∠EAC,然后结合AB＝AC得证△DBA≌△EAC,最后得到DE＝BD+CE；（3）由∠BAD＞∠CAE,∠BDA＝∠AEC＝∠BAC,得出∠CAE＝∠ABD,由AAS证得△ADB≌△CAE,得出S△ABD＝S△CEA,再由不同底等高的两个三角形的面积之比等于底的比,得出S△ABF即可得出结果．（1）解：DE＝BD+CE,理由如下,∵∠BDA＝∠BAC＝∠AEC＝90°,∴∠BAD +∠EAC ＝∠BAD +∠DBA ＝90°,∴∠DBA ＝∠EAC ,∵AB ＝AC ,∴△DBA ≌△EAC （AAS ）,∴AD ＝CE ,BD ＝AE ,∴DE ＝AD +AE ＝BD +CE ,故答案为：DE ＝BD +CE ．（2）DE ＝BD +CE 仍然成立,理由如下,∵∠BDA ＝∠BAC ＝∠AEC ＝α,∴∠BAD +∠EAC ＝∠BAD +∠DBA ＝180°﹣α,∴∠DBA ＝∠EAC ,∵AB ＝AC ,∴△DBA ≌△EAC （AAS ）,∴BD ＝AE ,AD ＝CE ,∴DE ＝AD +AE ＝BD +CE ；（3）解：∵∠BAD ＜∠CAE ,∠BDA ＝∠AEC ＝∠BAC ,∴∠CAE ＝∠ABD ,在△ABD 和△CAE 中,{∠ABD =∠CAE ∠BDA =∠CEA AB =AC,∴△ABD ≌△CAE （AAS ）,∴S △ABD ＝S △CAE ,设△ABC 的底边BC 上的高为h ,则△ABF 的底边BF 上的高为h ,∴S △ABC ＝12BC •h ＝12,S △ABF ＝12BF •h ,∵BC ＝3BF ,∴S △ABF ＝4,∵S △ABF ＝S △BDF +S △ABD ＝S △FBD +S △ACE ＝4,∴△FBD与△ACE的面积之和为4．【点睛】本题考查了全等三角形的判定与性质、直角三角形的性质,三角形的面积,解题的关键是熟练掌握全等三角形的判定与性质．【例3】．（2022·浙江绍兴·模拟预测）如图,△ABC中∠B=∠C=30°,∠DEF=30°,且点E为边BC的中点．将∠DEF绕点E旋转,在旋转过程中,射线DE与线段AB相交于点P,射线EF与射线CA相交于点Q,连结PQ．(1)如图1,当点Q在线段CA上时,①求证：△BPE∽△CEQ；②线段BE,BP,CQ之间存在怎样的数量关系？请说明理由；(2)当△APQ为等腰三角形时,求CQ的值．BP②BE²=BP·CQ,理由如下∶∵△BPE∽△CEQ∴BE CQ=BPCE∴BE·CE=BP·CQ∵点E为边BC的中点,∴BE=CE,∴BE²=BP·CQ；(2)解：①当点Q在线段AC上时,∵∠A=180°-∠B-∠C=120°,为钝角,∴△APQ为等腰三角形时有AP=AQ,∵∠B=∠C,∴AB=AC,∴BP=CQ,∴CQBP=1②当点Q在线段CA的延长线上时,如图：连接PQ∵∠BAC=120°,∴∠BAQ=60°,当△APQ为等腰三角形时,有△APQ为等边三角形设AB=AC=2a,则BC=2√3a,BE=CE=√3a,设AQ=AP=x,则CQ=2a+x,BP=2a-x,由（1）得∶BE²=BP·CQ∴(√3a)²=(2a+x)(2a-x),解得∶x=a,∴BP=a,CQ=3a,∴CQBP=3综上CQBP的值为1或3．【点睛】本题考查三角形相似综合问题,熟练掌握一线三等角的相似三角形模型是解题关键．一、解答题1．（2022·全国·八年级课时练习）在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E．(1)当直线MN绕点C旋转到图1的位置时．①请说明△ADC≌△CEB的理由；②请说明DE=AD+BE的理由；(2)当直线MN绕点C旋转到图2的位置时,DE、AD、BE具有怎样的等量关系?请写出等量关系,并予以证明．(3)当直线MN绕点C旋转到图3的位置时,DE、AD、BE具有怎样的等量关系?请直接在横线上写出这个等量关系：________．【答案】(1)①理由见解析；②理由见解析(2)DE=AD−BE,证明见解析(3)DE=BE−AD【分析】本题“一线三垂直”模型即可证明全等,根据全等三角形的性质即可分别在三个图形中证明AD、EB、DE之间的关系．(1)解：①∵AD⊥MN于D,BE⊥MN于E,∴∠ADC=∠BEC=90°,∵∠ACB=90°,∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,∴∠DAC=∠BCE,在△ADC和△CEB中{∠ADC=∠BEC ∠DAC=∠BCEAC=BC,∴△ADC≌△CEB,②∵△ADC≌△CEB,∴AD=EC,CD=BE,∵DC+CE=DE,∴AD+EB=DE,(2)结论：DE=AD−BE,∵BE⊥EC,AD⊥CE,∴∠ADC=∠BEC=90°,∴∠EBC+∠BCE=90°,∵∠ACB=90°,∴∠ACE+∠BCE=90°,∴∠ACD=∠EBC,∴△ADC≌△CEB,∴AD=EC,CD=BE,∴DE=EC−CD=AD−EB, (3)结论：DE=BE−AD,∵∠ACB=90°,∴∠ACD+∠BCE=90°,∵BE⊥MN,AD⊥MN,∴∠ADC=∠DEC=90°,∴∠ACD+∠DAC=90°,∴∠DAC=∠BCE,在△ADC和△CEB中{∠ADC=∠BEC ∠DAC=∠BCE AC=BC∴△ADC≌△CEB,∴AD=EC,CD=BE,∴DE=CD−EC=EB−AD．【点睛】本题考查全等三角形的判断和性质,灵活运用“一线三垂直”模型是解题的关键．2．（2022·江苏·八年级课时练习）（1）如图1,在△ABC中,∠BAC＝90°,AB＝AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E．求证：△ABD≌△CAE；（2）如图2,将（1）中的条件改为：在△ABC中,AB＝AC,D、A、E三点都在直线m上,并且有∠BDA＝∠AEC＝∠BAC＝α,其中αABD≌△CAE是否成立？如成立,请给出证明；若不成立,请说明理由．（3）拓展应用：如图3,D,E是D,A,E三点所在直线m上的两动点（D,A,E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE,若∠BDA＝∠AEC＝∠BAC,求证：△DEF是等边三角形．【答案】（1）见详解；（2）成立,理由见详解；（3）见详解【分析】（1）根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断ΔADB≌ΔCEA；（2）利用∠BDA=∠BAC=α,则∠DBA+∠BAD=∠BAD+∠CAE=180°−α,得出∠CAE=∠ABD,然后问题可求证；（3）由题意易得BF=AF=AB=AC,∠ABF=∠BAF=∠FAC=60°,由（1）（2）易证ΔADB≌ΔCEA,则有AE=BD,然后可得∠FBD=∠FAE,进而可证ΔDBF≌ΔEAF,最后问题可得证．【详解】（1）证明：∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=90°,∵∠BAC=90°,∴∠BAD+∠CAE=90°,∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD,∵在ΔADB和ΔCEA中,{∠ABD=∠CAE ∠BDA=∠CEAAB=AC,∴ΔADB≌ΔCEA(AAS)；解：（2）成立,理由如下：∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°−α, ∴∠CAE=∠ABD,∵在ΔADB和ΔCEA中,{∠ABD=∠CAE ∠BDA=∠CEAAB=AC,∴ΔADB≌ΔCEA(AAS)；（3）证明：∵△ABF和△ACF均为等边三角形,∴BF=AF=AB=AC,∠ABF=∠BAF=∠FAC=60°,∴∠BDA＝∠AEC＝∠BAC=120°,∴∠DBA+∠BAD=∠BAD+∠CAE=180°−120°,∴∠CAE=∠ABD,∴ΔADB≌ΔCEA(AAS),∴AE=BD,∵∠FBD=∠FBA+∠ABD,∠FAE=∠FAC+∠CAE,∴∠FBD=∠FAE,∴ΔDBF≌ΔEAF（SAS）,∴FD=FE,∠BFD=∠AFE,∴∠BFA=∠BFD+∠DFA=∠AFE+∠DFA=∠DFE=60°,∴△DFE是等边三角形．【点睛】本题主要考查全等三角形的判定与性质及等边三角形的性质与判定,熟练掌握全等三角形的判定与性质及等边三角形的性质与判定是解题的关键．3．（2022·全国·九年级专题练习）感知：（1）数学课上,老师给出了一个模型：如图1,∠BAD=∠ACB=∠AED=90°,由∠1+∠2+∠BAD=180°,∠2+∠D+∠AED=180°,可得∠1=∠D；又因为ACB=∠AED=90°,可得△ABC∽△DAE,进而得到BCAC=______．我们把这个模型称为“一线三等角”模型．应用：（2）实战组受此模型的启发,将三等角变为非直角,如图2,在△ABC中,AB=AC=10,BC=12,点P是BC边上的一个动点（不与B、C重合）,点D是AC边上的一个动点,且∠APD=∠B．①求证：△ABP∽△PCD；②当点P为BC中点时,求CD拓展：（3）在（2）的条件下如图2,当△APD为等腰三角形时,请直接写出BP的长．【答案】感知：（1）AEDE ；应用：（2）①见解析；②3.6；拓展：（3）2或113【分析】（1）根据相似三角形的性质,即可求解；（2）①根据等腰三角形的性质得到∠B=∠C,根据三角形的外角性质得到∠BAP=∠CPD,即可求证；②根据相似三角形的性质计算,即可求解；（3）分P A=PD、AP=AD、DA=DP三种情况,根据等腰三角形的性质、相似三角形的性质,即可求解．．综上所述,当△APD为等腰三角形时, BP的长为2或113【点睛】本题考查的是三角形相似的判定定理和性质定理、全等三角形的判定定理和性质定理以及三角形的外角性质,掌握相似三角形的判定定理和性质定理是解题的关键．4．（2022·山东烟台·七年级期末）问题背景：（1）如图①,已知△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E,易证：DE=______+______．（2）拓展延伸：如图②,将（1）中的条件改为：在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,请求出DE,BD,CE三条线段的数量关系,并证明．（3）实际应用：如图③,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(−2,0),点A的坐标为(−6,3),请直接写出B点的坐标．∴△ADB≌△CEA,∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE,即：DE=BD+CE,故答案为：BD；CE；（2）解：数量关系：DE=BD+CE,证明：在△ABD中,∠ABD=180°−∠ADB−∠BAD,∵∠CAE=180°−∠BAC−∠BAD,∠BDA=∠AEC,∴∠ABD=∠CAE,在△ABD和△CAE中,{∠ABD＝∠CAE∠BDA＝∠AECAB＝CA∴△ABD≌△CAE,∴AE=BD,AD=CE,∴DE=AD+AE=BD+CE；（3）解：如图,作AE⊥x轴于E,BF⊥x轴于F,由（1）可知,△AEC≌△CFB,∴CF=AE=3,BF=CE=OE−OC=4,∴OF=CF−OC=1,∴点B的坐标为B(1,4)．【点睛】本题考查的是全等三角形的判定和性质、坐标与图形性质,掌握全等三角形的判定定理和性质定理是解题的关键．5．（2021·浙江·义乌市绣湖中学教育集团八年级阶段练习）（1）模型建立,如图1,等腰直角三角形ABC中,∠ACB＝90°,CB＝CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E．求证：△BEC≌△CDA；（2）模型应用：x+3与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过①已知直线y＝34点A,C作直线,求直线AC的解析式；②如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A,C分别在坐标轴上,P是线段BC上动点,已知点D在第一象限,且是直线y＝2x﹣5上的一点,若△APD是不以A为直角顶点的等腰直角三角形,请直接写出所有符合条件的点D的坐标．综上可知满足条件的点D的坐标分别为(3,1)或(9，13)或(193，233)．【点睛】本题为一次函数的综合应用,涉及全等三角形的判定与性质、等腰直角三角形的性质、旋转的性质、分类讨论及数形结合的思想,解题的关键是熟练掌握并灵活运用相关性质进行求解．6．（2022·江苏·八年级专题练习）（1）课本习题回放：“如图①,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,DE=1.7cm．求BE的长”,请直接写出此题答案：BE的长为________．（2）探索证明：如图②,点B,C在∠MAN的边AM、AN上,AB=AC,点E,F在∠MAN内部的射线AD上,且∠BED=∠CFD=∠BAC．求证：ΔABE≌ΔCAF．（3）拓展应用：如图③,在ΔABC中,AB=AC,AB>BC．点D在边BC上,CD=2BD,点E、F在线段AD上,∠BED=∠CFD=∠BAC．若的面积为15,则ΔACF与ΔBDE的面积之和为________．（直接填写结果,不需要写解答过程）【答案】（1）0.8cm；（2）见解析（3）5【分析】（1）利用AAS定理证明△CEB≌△ADC,根据全等三角形的性质解答即可；（2）由条件可得∠BEA＝∠AFC,∠4＝∠ABE,根据AAS可证明△ABE≌△CAF；（3）先证明△ABE≌△CAF,得到ΔACF与ΔBDE的面积之和为△ABD的面积,再根据CD=2BD故可求解．【详解】解：（1）∵BE⊥CE,AD⊥CE,∴∠E＝∠ADC＝90°,∴∠EBC＋∠BCE＝90°．∵∠BCE＋∠ACD＝90°,∴∠EBC＝∠DCA．在△CEB和△ADC中,{∠E=∠ADC∠EBC=∠DCABC=AC∴△CEB≌△ADC（AAS）,∴BE＝DC,CE＝AD＝2.5cm．∵DC＝CE−DE,DE＝1.7cm,∴DC＝2.5−1.7＝0.8cm,∴BE＝0.8cm故答案为：0.8cm；（2）证明：∵∠1＝∠2,∴∠BEA＝∠AFC．∵∠1＝∠ABE＋∠3,∠3＋∠4＝∠BAC,∠1＝∠BAC,∴∠BAC＝∠ABE＋∠3,∴∠4＝∠ABE．∵∠AEB＝∠AFC,∠ABE＝∠4,AB＝AC,∴△ABE≌△CAF（AAS）．（3）∵∠BED=∠CFD=∠BAC7．（2022·全国·八年级课时练习）通过对下面数学模型的研究学习,解决下列问题：（1）如图1,∠BAD＝90°,AB＝AD,过点B作BC⊥AC于点C,过点D作DE⊥AC于点E．由∠1+∠2＝∠2+∠D＝90°,得∠1＝∠D．又∠ACB＝∠AED＝90°,可以推理得到△ABC≌△DAE．进而得到AC＝,BC ＝AE．我们把这个数学模型称为“K字”模型或“一线三等角”模型；（2）如图2,∠BAD＝∠CAE＝90°,AB＝AD,AC＝AE,连接BC,DE,且BC⊥AF于点F,DE与直线AF交于点G．求证：点G是DE的中点；（深入探究）（3）如图,已知四边形ABCD和DEGF为正方形,△AFD的面积为S1,△DCE的面积为S2,则有S1S2（填“＞、＝、＜”）【答案】（1）DE；（2）见解析；（3）=【分析】（1）根据全等三角形的性质可直接进行求解；（2）分别过点D和点E作DH⊥FG于点H,EQ⊥FG于点Q,进而可得∠BAF=∠ADH,然后可证△ABF≌△DAH,则有AF=DH,进而可得DH=EQ,通过证明△DHG≌△EQG可求解问题；（3）过点D作DO⊥AF交AF于O,过点E作EN⊥OD交OD延长线于N,过点C作CM⊥OD交OD延长线于M,由题意易得∠ADC=∠90°,AD=DC,DF=DE,然后可得∠ADO=∠DCM,则有△AOD≌△DMC,△FOD≌△DNE,进而可得OD=NE,通过证明△ENP≌△CMP及等积法可进行求解问题．【详解】解：（1）∵△ABC≌△DAE,∴AC=DE；（2）分别过点D和点E作DH⊥FG于点H,EQ⊥FG于点Q,如图所示：∴∠DAH+∠ADH=90°,∵∠BAD=90°,∴∠BAF+∠DAH=90°,∴∠BAF=∠ADH,∵BC⊥AF,∴∠BFA=∠AHD=90°,∵AB=DA,∴△ABF≌△DAH,∴AF=DH,同理可知AF=EQ,∴DH=EQ,∵DH⊥FG,EQ⊥FG,∴∠DHG=∠EQG=90°,∵∠DGH=∠EGQ∴△DHG≌△EQG,∴DG=EG,即点G是DE的中点；（3）S1=S2,理由如下：如图所示,过点D作DO⊥AF交AF于O,过点E作EN⊥OD交OD延长线于N,过点C作CM⊥OD交OD延长线于M∵四边形ABCD与四边形DEGF都是正方形∴∠ADC=∠90°,AD=DC,DF=DE∵DO⊥AF,CM⊥OD,∴∠AOD=∠CMD=90°,∠OAD+∠ODA=90°,∠CDM+∠DCM=90°,又∵∠ODA+∠CDM=90°,∴∠ADO=∠DCM,∴△AOD≌△DMC,∴S△AOD=S△DMC,OD=MC,同理可以证明△FOD≌△DNE,∴S△FOD=S△DNE,OD=NE,∴MC =NE,∵EN⊥OD,CM⊥OD,∠EPN=∠CMP,∴△ENP≌△CMP,∴S△ENP=S△CMP,∵S△ADF=S△AOD+S△FOD,S△DCE=S△DCM−S△CMP+S△DEN+S△ENP,∴S△DCE=S△DCM+S△DEN=S△AOD+S△FOD,∴S△DCE=S△ADF即S1=S2．【点睛】本题主要考查全等三角形的性质与判定、直角三角形的两个锐角互余及等积法,熟练掌握全等三角形的判定条件是解题的关键．8．（2021·北京·东北师范大学附属中学朝阳学校八年级期中）如图,在△ABC中,∠ACB＝90°,AC＝BC,直线l 经过顶点C,过A、B两点分别作l的垂线AE、BF,E、F为垂足．（1）当直线l不与底边AB相交时,①求证：∠EAC＝∠BCF．②猜想EF、AE、BF的数量关系并证明．（2）将直线l绕点C顺时针旋转,使l与底边AB交于点D（D不与AB点重合）,请你探究直线l,EF、AE、BF之间的关系．（直接写出）【答案】（1）①证明见解析,②EF＝AE+BF；证明见解析；（2）AE＝BF+EF或BF＝AE+EF．【分析】（1）①根据∠AEC＝∠BFC＝90°,利用同角的余角相等证明∠EAC＝∠FCB即可；②根据AAS证△EAC≌△FCB,推出CE＝BF,AE＝CF即可；（2）类比（1）证得对应的两个三角形全等,求出线段之间的关系即可．【详解】（1）证明：①∵AE⊥EF,BF⊥EF,∠ACB＝90°,∴∠AEC＝∠BFC＝∠ACB＝90°,∴∠EAC+∠ECA＝90°,∠ECA+∠FCB＝90°,∴∠EAC＝∠FCB,②EF＝AE+BF；证明：在△EAC和△FCB中,{∠AEC =∠CFB ∠EAC =∠FCB AC =BC,∴△EAC ≌△FCB （AAS ）,∴CE ＝BF ,AE ＝CF ,∴EF ＝CE +CF ＝AE +BF ,即EF ＝AE +BF ；（2）①当AD ＞BD 时,如图①,∵∠ACB ＝90°,AE ⊥l 直线,同理可证∠BCF ＝∠CAE （同为∠ACD 的余角）,又∵AC ＝BC ,BF ⊥l 直线即∠BFC ＝∠AEC ＝90°,∴△ACE ≌△CBF （AAS ）,∴CF ＝AE ,CE ＝BF ,∵CF ＝CE +EF ＝BF +EF ,∴AE ＝BF +EF ；②当AD ＜BD 时,如图②,∵∠ACB ＝90°,BF ⊥l 直线,同理可证∠CBF ＝∠ACE （同为∠BCD 的余角）,又∵AC ＝BC ,BE ⊥l 直线,即∠AEC ＝∠BFC ＝90°．∴△ACE ≌△CBF （AAS ）,∴CF ＝AE ,BF ＝CE ,∵CE ＝CF +EF ＝AE +EF ,∴BF ＝AE +EF ．【点睛】本题考查了三角形综合题,主要涉及到了全等三角形的判定与性质,解题关键是证明△ACE≌△CBF（AAS）,利用全等三角形的性质得出线段之间的关系．9．（2021·四川达州·九年级期中）模型探究：（1）如图1,在等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E．求证：BE=CD；模型应用：（2）已知直线l1:y=2x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转90°至直线l2,如图2,求直线l2的函数表达式；x+4上,且AB=4√2．若直线与y轴的交点为M,M为AB中点．试判断（3）如图3,已知点A、B在直线y=12在x轴上是否存在一点C,使得△ABC是以AB为斜边的等腰直角三角形．。

2021年中考数学复习《中考压轴题：二次函数应用题》经典题型靶向提升练习(四)

2021年中考数学复习《中考压轴题：二次函数应用题》经典题型靶向提升练习（四）1．某工厂计划投资生产A、B两种产品，根据市场调查与预测，产品A的利润y1（万元）与投资量x（万元）成正比例关系，如图①所示：产品B的利润y2（万元）与投资量x（万元）成顶点在原点的二次函数关系，如图②所示．（1）请直接写出利润y1与y2关于投资量x的函数关系式y1＝，y2＝；（2）如果工厂以9万元资金投入生产A、B两种产品，要求A产品的投资金额不超过B 的2倍，且不少于3万元，则如何投资该工厂能获得最大利润？最大利润是多少？（3）在（2）问的情况下，工厂要获得不低于18万的利润，工厂要如何投资？2．如图，一座拱桥的轮廓呈抛物线形，拱高6m，跨度为20m，相邻两立柱间的距离均为5m．（1）建立适当的直角坐标系，求这条抛物线的表达式．（2）求立柱EF的长．（3）拱桥下面拟铺设行车道，要保证高3m的汽车能够通过（车顶与桥拱的距离不小于0.3m），行车道最宽可铺设多少米？3．某电器公司推出一款智能空调扇，经市场调研发现，该产品的月销售量y（台）与销售单价x（元）之间满足如图所示的一次函数关系，已知该产品的成本是每台1500元．（1）求出y关于x的函数解析式．（2）设月销售利润为ω（元），求ω关于x的函数解析式，并求出当销售单价定为多少时，月销售利润最大，最大月销售利润是多少，（3）公司开展了技术创新，以降低成本，预计在今后的销售中，月销售量与销售单价仍存在（1）中的函数关系，若想实现当销售单价为1900元时，月销售利润不低于114000元的销售目标，则该产品的成本单价应不超过多少元？4．在长、宽均为45米的十字路口，现遇到红灯，有10辆车依次呈一直线停在路口的交通白线后，每两辆车间隔为2.5米，每辆车长5米，每辆车的速度v（米/秒）关于时间t （秒）的函数（如图1）所示，当绿灯亮起，第一辆车的车头与交通白线的距离s（米）关于时间t（秒）的函数解析式为s＝a（t﹣1）2（1≤t≤4），如图2所示当前车启动后，后面一辆车在1秒后也启动．（1）求a的值；（2）当t＞4时，求第一辆车的车头与交通白线的距离s（米）关于时间（秒）的函数解析式；（3）当t＞4时，求第一辆车和第二辆车在这个十字路口中的最大间距；（第一辆车的车尾和第二辆车的车头哦）（4）绿灯持续时间至少要设置多长才能保证在绿灯期间这十辆车都能通过交通白线．5．【问题实验】如图①，在地面BD上有两根等长立柱AB，CD之间悬挂一根近似成抛物线y＝x2﹣x+3的绳子．（1）求绳子最低点到地面的距离；（2）如图②，因实际需要，需用一根立柱MN撑起绳子．①若在离AB为4米的位置处用立柱MN撑起，使立柱左侧的抛物线的最低点距MN为1米，离地面1.8米，求MN的长；②将立柱MN来回移动，移动过程中，在一定范围内，总保持立柱MN左侧抛物线的形状不变，其函数表达式为y＝x2﹣mx+3，当抛物线最低点到地面距离为0.5米时，求m的值．【问题抽象】如图③，在平面直角坐标系中，函数y ＝﹣mx +3（x ＜0）的图象记为M 1，函数y ＝﹣mx +3（x ≥0）的图象记为M 2，其中m 是常数，图象M 1、M 2合起来得到的图象记为M ．设M 在﹣3≤x ≤2上的最低点纵坐标为y 0，当﹣6≤y 0≤2时，直接写出m 的取值范围．6．一场篮球赛中，小明跳起投篮，已知球出手时离地面高米，与篮圈中心的水平距离为8米，当球出手后水平距离为4米时到达最大高度4米，设篮球运行的轨迹为抛物线，篮圈中心距离地面3米．（1）按如图所示建立的平面直角坐标系，求抛物线的解析式；（2）小明的这次投篮未能命中篮圈中心，请说明理由；（3）假设出手的角度和力度都不变，请直接回答：小明应该向前走或向后退多少米才能命中篮圈中心？7．某单位不断美化环境，拟在一块矩形空地上修建绿色植物园，其中一边靠墙，可利用的墙长不超过18m，另外三边由36m长的栅栏围成．设矩形ABCD空地中，垂直于墙的边AB ＝xm，面积为ym2（如图）．（1）求y与x之间的函数关系式，并写出自变量x的取值范围；（2）若矩形空地的面积为160m2，求x的值；（3）矩形空地的面积能否为164m2，若能，求x的值；不能，请说明理由．8．某商店购进一批成本为每件30元的商品，经调查发现，该商品每天的销售量y（件）与销售单价x（元）之间满足一次函数关系，其图象如图所示．（1）求该商品每天的销售量y与销售单价x之间的函数关系式；（2）销售单价定为多少，才能使销售该商品每天获得的利润w（元）最大？最大利润是多少？（3）若商店要使销售该商品每天获得的利润不低于800元，直接写出此时销售单价的取值范围．9．如图1，用长为60m的篱笆围成一个一边靠墙的矩形菜园，墙长为28m，设垂直于墙的一边长为xm，平行于墙的一边长为ym．（1）直接写出y与x满足的函数关系式及x的取值范围；（2）求菜园面积S的最大值；（3）如图2，在菜园内修建两横一竖且宽均为am的小路，其余部分种菜，若种菜部分的面积随x的增大而减小，则a的取值范围为．10．为做好扶贫帮扶工作，某地市政府规定，企业按成本价提供产品给被帮扶对象，成本价与出厂价之间的差价由政府承担，李师傅按照政策投资销售本市生产的一品牌牛奶．已知这种品牌牛奶的成本价为每箱12元，出厂价为每箱16元，每天销售y（箱）与销售单价x（元）之间满足如图所示函数的关系．（1）求y与x之间的一次函数关系式（2）如果李师傅想要每天获得的利润是216元，那么政府每天为他承担的总差价最少为多少元？（3）设李师傅每天获得的利润为w（元），当销售单价为多少元时，每天可获得最大利润？最大利润是多少？参考答案＝kx，1．解：（1）由题意设y1∵点P（2，4）在该函数的图象上，∴4＝2k，∴k＝2，＝2x；∴y1＝ax2，设y2∵点Q（2，3），∴3＝4a，∴a＝，∴y 2＝x 2．故答案为：2x ；x 2；（2）设投资A 产品x 万元，则投资B 产品（9﹣x ）万元，由题意得：，∴3≤x ≤6，∴该工厂能获得的利润为：y 1+y 2＝2x +（9﹣x ）2＝x 2﹣x +＝+，∴当x ＝3时，y 1+y 2取得最大值，最大值是+＝33（万元）．∴投资A 产品3万元，投资B 产品6万元时，该工厂能获得最大利润，最大利润是33万元；（3）由（2）知，3≤x ≤6，y 1+y 2＝+≥18，∴≥18﹣＝，∴≥，∴x ﹣≥或x ﹣≤﹣，∴x ≥9或x ≤，∵3≤x≤6，∴当投资A产品不少于3万元且不超过6万元时，工厂获得的利润不低于18万元．2．解：（1）建立直角坐标系，如图所示：设所求抛物线解析式为y＝ax2+bx+c，由图可知抛物线过点（﹣10，0）、（10，0）和（0，6），∴解得：．∴所求抛物线的解析式为y＝﹣x2+6．（2）根据题意，可知点F在抛物线上，且F的横坐标为5，将x＝5代入抛物线解析式，得y＝﹣×52+6＝4.5．∴EF＝8﹣4.5＝3.5．∴立柱EF的长为3.5m．（3）设行车道宽为2xm，则车顶与桥拱的距离为（﹣x2+6﹣3）m．根据题意可得﹣x2+6﹣3≥0.3解得﹣3≤x≤3，结合实际，可知0＜x≤3，3×2＝6，∴行车道最宽可铺设6米．3．解：（1）设y关于x的函数解析式为y＝kx+b，将（1800，200）、（2000，180）分别代入，可得：，解得：，∴y关于x的函数解析式为y＝﹣0.1x+380（1500＜x≤3800）；（2）由题意得：ω＝（x﹣1500）y＝（x﹣1500）（﹣0.1x+380）＝﹣0.1x2+530x﹣570000＝﹣0.1（x﹣2650）2+132250，∵﹣0.1＜0，∴当x＝2650时，ω有最大值132250，∴ω关于x的函数解析式为ω＝﹣0.1x2+530x﹣570000（1500＜x≤3800），当销售单价定为2650元时，月销售利润最大，最大月销售利润是132250元；（3）当x＝1900时，y ＝﹣0.1x +380＝﹣0.1×1900+380＝190，设该产品的成本单价为m 元，由题意得：（1900﹣m ）×190≥114000，解得：m ≤1300．∴该产品的成本单价应不超过1300元．4．解：（1）∵s ＝a （t ﹣1）2（1≤t ≤4）过（4，22.5），∴9a ＝22.5，解得：a ＝；（2）由图1可知，当t ＝4时，v ＝15，t ＞4时，s ＝22.5+（t ﹣4）×15＝15t ﹣37.5， ∴当t ＞4时，第一辆车的车头与交通白线的距离s （米）关于时间（秒）的函数解析式为s ＝15t ﹣37.5；（3）当t ＞4时，v 1＝v 2＝15，45﹣22.5＝22.5，∴t ＝4++＝4++＝（秒），∴s 2＝15×（﹣1）﹣37.5﹣（2.5+5）＝27.5（米），∴最大间距是45﹣27.5＝17.5（米）．∴当t ＞4时，第一辆车和第二辆车在这个十字路口中的最大间距是17.5米；（4）间隔为10×5+9×2.5+s ，由题意得：s +9×2.5+15（t ﹣13）≥10×5+9×2.5+s ，解得：t ≥．∴绿灯持续时间至少要设置秒才能保证在绿灯期间这十辆车都能通过交通白线．5．解：【问题实验】（1）∵y ＝x 2﹣x +3＝（x ﹣5）2+，∴抛物线的顶点坐标为（5，），∴绳子最低点到地面的距离为米；（2）①由题意可知，立柱左侧的抛物线的顶点坐标为（3，1.8），∴设y ＝a （x ﹣3）2+1.8∵抛物线y ＝x 2﹣x +3与y 轴的交点A 的坐标为（0，3），∴把（0，3）代入，得3＝a （0﹣3）2+1.8，∴，∴，∴当x ＝4时，．∴．②∵抛物线y ＝x 2﹣mx +3对称轴为x ＝m ，∴把（m ，0.5）代入中，得：，∴，（舍）．【问题抽象】由题意知：抛物线M 1、M 2均过定点（0，3），当m ≥0时，M 1的最低点为（0，3），此时，抛物线M 的最低点在M 2上．当x ≥0时，M 2：y ＝﹣mx +3的对称轴是x ＝2m ，①当2m≥2时，即m≥1时，∵当0≤x≤2时，y随x的增大而减小，＝×22﹣2m+3＝4﹣2m，∴当x＝2时，y最小，此时y≤2，∵﹣6≤y∴﹣6≤4﹣2m≤2，解得1≤m≤5；②当0≤2m＜2时，即0≤m＜1时，∵x的范围是0≤x≤2，＝×（2m）2﹣m×2m+3＝﹣m2+3，∴当x＝2m时y最小，此时y≤2，∵﹣6≤y∴﹣6≤﹣m2+3≤2，解得：1≤m≤3，∵0≤m＜1∴此种情况的m的值不存在；当m＜0时，M2的最低点为（0，3），此时，抛物线M的最低点在M上，当x＜0时，对1：y＝﹣mx+3，其对称轴是直线x＝m．于M1③当m≤﹣3时，∵当﹣3≤x＜0时，y随x的增大而增大，＝×（﹣3）2+3m+3＝3m+，∴当x＝﹣3时，y最小，此时y≤2，∵﹣6≤y∴﹣6≤3m+≤2时，解得：﹣≤m≤﹣，∵m≤﹣3，∴m的范围是：﹣≤m≤﹣3；④当﹣3＜m＜0时，∵x的范围是﹣3≤x＜0，＝m2﹣m2+3＝﹣m2+3，∴当x＝m时，y最小，此时，y≤2，∵﹣6≤y∴﹣6≤﹣m2+3，≤2时，解得：﹣3≤m≤﹣，∵﹣3＜m＜0，∴﹣3＜m≤﹣，综上所述，m的取值范围是：﹣≤m≤﹣或1≤m≤5．6．解：（1）由题意可知，抛物线的顶点坐标为（4，4），球出手时的坐标为（0，），设抛物线的解析式为y＝a（x﹣4）2+4，将（0，）代入得：16a+4＝，解得：a＝﹣，∴y＝﹣（x﹣4）2+4；（2）∵y＝﹣（x﹣4）2+4，∴当x＝8时，y＝﹣（8﹣4）2+4＝≠3，∴小明的这次投篮未能命中篮圈中心；（3）∵出手的角度和力度都不变，∴设抛物线的解析式为y＝﹣（x﹣4+m）2+4，将（8，3）代入得：3＝﹣（8﹣4+m）2+4，∴（4+m）2＝9，解得：m1＝﹣1，m2＝﹣7，∵向前走7米，位于篮圈正下方，故舍去．∴小明应该向前走1米才能命中篮圈中心．7．解：（1）AB＝xm，则BC＝（36﹣2x）m，由题意：y＝x（36﹣2x）＝﹣2x2+36，∵0＜BC≤18，即0＜36﹣2x≤18，解得9≤x＜18，即y＝﹣2x2+36（9≤x＜18）；（2）由题意：﹣2x2+36x＝160，解得x＝10或8．∵9≤x＜18，故x＝10；（3）不能，理由：由题意：﹣2x2+36x＝164，即x2﹣18x+82＝0，即（x﹣9）2＝﹣1＜0，故此方程无解，故矩形空地的面积不能为164m2．8．解：（1）设y与销售单价x之间的函数关系式为：y＝kx+b，将点（30，100）、（45，70）代入一次函数表达式得：，解得：，故函数的表达式为：y＝﹣2x+160；（2）由题意得：w＝（x﹣30）（﹣2x+160）＝﹣2（x﹣55）2+1250，∵﹣2＜0，故函数有最大值，∴当x＝55时，w有最大值，此时，w＝1250，故销售单价定为55元时，该超市每天的利润最大，最大利润1250元；（3）由题意得：（x﹣30）（﹣2x+160）≥800，解得：40≤x≤70，故销售单价x的取值范围为40≤x≤70．9．解：（1）由题意得：y＝60﹣2x，∵墙长为28m，篱笆长为60m，∴0＜y≤28，∴0＜60﹣2x≤28，∴﹣60＜﹣2x≤﹣32，∴16≤x＜30，∴y＝60﹣2x（16≤x＜30）；（2）∵y＝60﹣2x，∴S＝xy＝x（60﹣2x）＝﹣2x2+60x＝﹣2（x﹣15）2+450，∵a＝﹣2＜0∴开口向下，∵对称轴为x＝15，∴当16≤x＜30时，S随x增大而减小．∴当x＝16时，S有最大值，最大值为448m2；（3）由题意得：S路＝2ay+ax﹣2a2，∴S种＝S﹣S路＝﹣2x2+60x﹣[2a（60﹣2x）+ax﹣2a2]＝﹣2x2+60x﹣120a+4ax﹣ax+2a2＝﹣2x2+（3a+60）x+2a2﹣120a，∵种菜部分的面积随x的增大而减小，且16≤x＜30，∴﹣≤16，∴3a+60≤64，∴3a≤4，∴a≤，又∵a＞0，∴0＜a≤．10．解：（1）设y＝kx+b，根据题意，得：，解得，∴y＝﹣3x+90；（2）根据题意，得：（x﹣12）（﹣3x+90）＝216，解得：x1＝24，x2＝18，当x＝24时，y＝﹣3×24+90＝18，此时政府承担的总差价为18×（16﹣12）＝72（元）；当x＝18时，y＝﹣3×18+90＝36，此时政府承担的总差价为36×（16﹣12）＝144（元）；答：政府每天为他承担的总差价最少为72元；（3）w＝（x﹣12）（﹣3x+90）＝﹣3x2+126x﹣1080＝﹣3（x﹣21）2+243，∴当x＝21时，w取得最大值243，答：当销售单价为21元时，每天可获得最大利润，最大利润是243元．。

2021年~2021年北师大版山东济南“九年级中考”数学解答题“二次函数压轴题”练习试题以及答案

九年级中考数学压轴题二次函数练习题一、解答题。

1、（2011年济南中考）如图，矩形OABC中，点O为原点，点A的坐标为（0，8），点C的x2+bx+c经过A、C两点，与AB边交于点D。

坐标为（6，0），抛物线y=﹣49（1）求抛物线的函数表达式；（2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ=CP，连接PQ，设CP=m，△CPQ的面积为S。

①求S关于m的函数表达式，并求出m为何值时，S取得最大值；x2+bx+c的对称轴l上若存在点F，使△FDQ为直角三角形，②当S最大时，在抛物线y=﹣49请直接写出所有符合条件的F的坐标；若不存在，请说明理由．备用图2、（2012年济南中考）如图1，抛物线y=ax2+bx+3与x轴相交于点A（﹣3，0），B（﹣1，0），与y轴相交于点C，⊙O1为△ABC的外接圆，交抛物线于另一点D。

（1）求抛物线的解析式；（2）求cos∠CAB的值和⊙O1的半径；（3）如图2，抛物线的顶点为P，连接BP，CP，BD，M为弦BD中点，若点N在坐标平面内，满足△BMN∽△BPC，请直接写出所有符合条件的点N的坐标．3、（2013年济南中考）如图，在平面直角坐标系中，有一个直角△AOB，O是坐标原点，OA=1，tan∠BAO=3，将此三角形绕原点O逆时针旋转90°，得到△D0C，抛物线y=ax2+bx+c经过点A、B、C。

（1）求抛物线的表达式；（2）若点P是第二象限内抛物线上的动点，其坐标为t；①设抛物线对称轴l与x轴交于一点E，连接PE，交CD于F，求当△CEF与△COD相似时，点P的坐标；②是否存在一点P，使△PCD得面积最大，若存在，求出△PCD的面积的最大值；若不存在，说明理由；4、（2014年济南中考）如图1，抛物线y=﹣3x2平移后过点A（8，0）和原点，顶点为B，16对称轴与x轴相交于点C，与原抛物线相交于点D．；（1）、求平移后抛物线的解析式并直接写出阴影部分的面积S阴影（2）、如图2，直线AB与y轴相交于点P，点M为线段OA上一动点，∠PMN为直角，边MN与AP相交于点N，设OM=t，试探究：①、t为何值时，△MAN为等腰三角形；②、t为何值时，线段PN的长度最小，最小长度是多少；5、（2015年济南中考）抛物线y=ax2+bx+4经过A（1，﹣1）、B（5，﹣1）与y轴交于点C。

2014中考数学压轴题练习(四)四边形与函数

压轴题周周练之4：四边形与函数1，已知平面直角坐标系xOy （如图1），一次函数334y x =+的图像与y 轴交于点A ，点M 在正比例函数32y x =的图像上，且MO ＝MA ．二次函数 y ＝x 2＋bx ＋c 的图像经过点A 、M ．（1）求线段AM 的长；（2）求这个二次函数的解析式；（3）如果点B 在y 轴上，且位于点A 下方，点C 在上述二次函数的图像上，点D 在一次函数334y x =+的图像上，且四边形ABCD 是菱形，求点C 的坐标．2 将抛物线c 1：2y =x 轴翻折，得到抛物线c 2，如图1所示．（1）请直接写出抛物线c 2的表达式；（2）现将抛物线c 1向左平移m 个单位长度，平移后得到新抛物线的顶点为M ，与x 轴的交点从左到右依次为A 、B ；将抛物线c 2向右也平移m 个单位长度，平移后得到新抛物线的顶点为N ，与x 轴的交点从左到右依次为D 、E ．①当B 、D 是线段AE 的三等分点时，求m 的值；②在平移过程中，是否存在以点A 、N 、E 、M 为顶点的四边形是矩形的情形？若存在，请求出此时m 的值；若不存在，请说明理由．图13.已知平面直角坐标系xOy 中，抛物线y ＝ax 2－(a ＋1)x 与直线y ＝kx 的一个公共点为A(4，8)．（1）求此抛物线和直线的解析式；（2）若点P 在线段OA 上，过点P 作y 轴的平行线交（1）中抛物线于点Q ，求线段PQ 长度的最大值；（3）记（1）中抛物线的顶点为M ，点N 在此抛物线上，若四边形AOMN 恰好是梯形，求点N 的坐标及梯形AOMN 的面积．4. 已知二次函数的图象经过A （2，0）、C (0，12) 两点，且对称轴为直线x ＝4，设顶点为点P ，与x 轴的另一交点为点B ．（1）求二次函数的解析式及顶点P 的坐标；（2）如图1，在直线 y ＝2x 上是否存在点D ，使四边形OPBD为等腰梯形？若存在，求出点D 的坐标；若不存在，请说明理由；（3）如图2，点M 是线段OP 上的一个动点（O 、P 两点除外），以每秒2个单位长度的速度由点P 向点O 运动，过点M 作直线MN //x 轴，交PB 于点N ．将△PMN 沿直线MN 对折，得到△P 1MN ．在动点M 的运动过程中，设△P 1MN 与梯形OMNB 的重叠部分的面积为S ，运动时间为t 秒，求S 关于t 的函数关系式．。

(完整版)北师大版初中中考数学压轴题及答案

中考数学专题复习（压轴题）1.已知:如图,抛物线 y=-x 2+bx+c 与x 轴、 y轴分别相交于点 A（-1，0）、B（0，3）两点，其顶点为 D. （ 1）求该抛物线的解析式；（ 2）若该抛物线与 x 轴的另一个交点为 E. 求四边形 ABDE 的面积；（3）△AOB 与△ BDE 是否相似？如果相似，请予以证明；如果不相似，请说明理由 .注：抛物线 y=ax 2+bx+c（a ≠0）的顶点坐b ,4ac b2标为2a 4a2. 如图，在Rt△ABC 中，A 90o，AB 6，AC 8 ，D，E分别是边AB，AC的中点，点P从点D出发沿DE方向运动，过点P作PQ BC 于Q，过点Q作QR∥ BA 交AC 于R，当点Q与点C重合时，点P停止运动．设BQ x，QR y．1）求点D到BC的距离DH 的长；2）求y关于x 的函数关系式（不要求写出自变量的取值3）是否存在点P，使△PQR 为等腰三角形？若存在，请求出所有满足要求的x的值；若不存在，请说明理由．3在△ABC中，∠A＝90°，AB＝4，AC＝3，M是 AB上的动点（不与 A，B重合），过M点作 MN∥BC交AC于点 N．以MN 为直径作⊙ O，并在⊙ O内作内接矩形 AMPN ．令 AM＝x．（1）用含 x的代数式表示△ＭNP 的面积 S；（2）当 x为何值时，⊙ O与直线 BC 相切？（3）在动点 M的运动过程中，记△ＭNP与梯形 BCNM重合的面积为 y，试求 y关于 x的函数表达式，并求 x为何值时， y的值最大，最大值是多少？AC图2图1 图5如图，菱形 ABCD 的边长为 2，BD=2，E 、F 分别是边 AD ，CD 上的两个动点，且满足 AE+CF=2.（1）求证：△ BDE ≌△ BCF ；（ 2）判断△ BEF 的形状，并说明理由；4. 如图 1 ，在平面直角坐标系中，己知ΔAOB 是等边三角形，点 A 的坐标是（0 ，4），点 B 在第一象限，点 P 是x 轴上的一个动点，连结 AP ，并把Δ AOP 绕着点 A按逆时针方向旋转 .使边 AO 与AB 重合 . 得到Δ ABD. （ 1 ）求直线 AB 的解析式； 2）当点 P 运动到点（ 3 ， 0）时，求此时 DP 的长及点 D 的坐标；（ 3）是否存 43 ，若存在，请求出符合条件的点 P 的坐标；若不存在，请说明理由在点 P ，使Δ OPD 的面积等于3）设△ BEF 的面积为 S，求 S 的取值范围26如图，抛物线L1:y x22x 3交x轴于 A、B两点，交y轴于 M 点.抛物线L1向右平移 2个单位后得到抛物线L2 ，L2交x轴于 C、D两点.（1）求抛物线L2对应的函数表达式；（2）抛物线L1或L2在x轴上方的部分是否存在点 N，使以 A ， C， M ， N为顶点的四边形是平行四边形 .若存在，求出点 N的坐标；若不存在，请说明理由；（3）若点 P是抛物线L1上的一个动点（ P不与点 A、B 重合），那么点 P关于原点的对称点 Q是否在抛物线L2上，请说明理由 .7.如图，在梯形 ABCD 中，AB∥CD，AB＝7，CD＝1，AD＝BC＝5．点 M， N分别在边 AD，BC 上运动，并保持 MN∥AB，ME⊥AB，NF⊥AB，垂足分别为E，F．（ 1）求梯形 ABCD 的面积；（ 2）求四边形 MEFN 面积的最大值．（ 3）试判断四边形 MEFN 能否为正方形，若能，求出正方形 MEFN 的面积；若不能，请说明理由．E F8.如图，点 A（m，m＋1）， B（m＋3，m－1）都在反比例函数 y（ 1）求 m，k 的值；（ 2）如果 M 为 x 轴上一点， N 为 y 轴上一点，以点 A，B，M，N 为顶点的四边形是平行四边形，试求直线 MN 的函数表达式．友情提示：本大题第（1）小题4分，第（2）小题7分．对完成第（2）小题有困难的同学可以做下面的（3）选做题．选做题2 分，所得分数计入总分．但第（2）、（3）小题都做的，第（3）小题的得分不重复计入总分．（3）选做题：在平面直角坐标系中，点 P 的坐标为（ 5，0），点 Q的坐标为（ 0，3），把线段 PQ 向右平移 4 个单位，然后再向上平移 2 个单位，得到线段P1Q1，则点 P1 的坐标为，点 Q1 的坐标为．yO yOQ21239.如图 16，在平面直角坐标系中，直线y 3x 3 与x 轴交于点A ，与y 轴交于点C ，抛物线y ax2 2 3x c（a 0）经过A，B，C 三点．31）求过A，B，C三点抛物线的解析式并求出顶点F 的坐标；2）在抛物线上是否存在点P ，使△ABP为直角三角形，若存在，直接写出P点坐标；若不存在，请说明理由；3）试探究在直线AC上是否存在一点M ，使得△MBF 的周长最小，若存在，求出M 点的坐标；若不存在，请说明理由．60o后得到矩形EFOD ．点A的对应点为点E，点B的对应点为点F ，点C的对应点为点D，抛物线y1）判断点E是否在y 轴上，并说明理由；2）求抛物线的函数表达式；3）在x轴的上方是否存在点P，点Q，使以点O，B，P，Q为顶点的平行四边形的面积是矩形ABOC面积的 2 倍，且点P在抛物线上，若存在，请求出点P，点Q10.如图所示，在平面直角坐标系中，矩形ABOC 的边BO在x轴的负半轴上，边OC在y轴的正半轴上，且AB 1，OB3 ，矩形ABOC 绕点O 按顺时针方向旋转ax2bx c 过点A，E，D ．的坐标；若不存在，请说明理由．压轴题答案所以四边形 ABDE 的面积 =S ABO S 梯形 BOFD S DFE1 1 1= AO BO (BO DF) OF EF DF 2 2 21 1 1= 1 3 (3 4) 1 2 4 2 2 2=9(3)相似如图， BD= BG 2 DG 2 12 12 2 c 31. 解：( 1)由已知得：解1 bc0 c=3,b=2∴抛物线的线的解析式为 y 2x 2x 3 (2) 由顶点坐标公式得顶点坐标为 ( 1，4)所以对称轴为 x=1,A,E 关于 x=1 对称，所以 E(3,0) 设对称轴与 x 轴的交点为 FBE= BO2 OE232 32 3 2DE= DF 2 EF 2 22 42 2 5所以 BD 2 BE 2 20, DE 2 20即： BD 2 BE 2 DE 2,所以 BDE 是直角三角形3）存在，分三种情况：Q 1 2 90o ， C 2 90o ， 1 C ．所以 AOB DBE 90 , 且 AO BO 2,BD BE 2所以 AOB: DBE .2 解：（ 1） Q A Rt ， AB 6 ， AC 8 ， BC 10Q 点D 为 AB 中点， 1 BD AB 3．2Q DHB A 90o ， B B ．△BHD ∽△BAC ，DH BD BD312 ， DH gAC 8AC BC BC 10 5．（2）Q QR∥ AB ， QRC A 90o ．QC C ， △ RQC ∽△ ABC ， ①当 PQ PR 时，过点 P 作 PM QR 于M ，则 QMRM RQ AB QC y 10 x BC ， 6 10即 y 关于 x 的函数关系式为： 3x 6．5Acos 1 cosC 84 10 5 QM 4QP 51218 x ．5 3 12 ②当PQ RQ 时， 3x 6 12， 55x 6 ． C ③当 PR QR 时，则 R 为 PQ 中垂线上的点，于是点 R 为 EC 的中点，1AC 4BA，CA ， 1 CR CE 2 QR CR 2．Q tanC 15，x综上所述，当 3 解：（ 1） ∴ △ AMN 8 x 为18或 6或15时， △ PQR 为等腰三角形． 2∴∠AM N = ∠ B ，∠ AN M ＝∠C ．5∵ MN ∥ BC ， ∽ △ ABC ． AM AN ，即 x ANAB AC 4 3AN ＝ 3 x ．2分4S =S S1 3 3x 2．（0<x <4）MNP AMN xx2 4 8图1 3分2）如图 2，设直线 BC 与⊙O 相切于点 D，连结 AO，OD，则 AO=OD = 1MN．在 Rt△ABC 中， BC ＝AB2AC2=5．由（ 1）知△AMN AMAB ∴MN ∴ OD MN，BC 5 x，45 x．8过 M 点作△ABC．MN5分MQ⊥BC 于Q，则MQ OD在 Rt△BMQ 与 Rt△BCA 中，∠ B 是公共角，∴ △BMQ ∽△ BCA．∴BMBC QM AC∴BM 55x8325x，AB BM2496 ∴ x ＝49（ 3）随点M ∵ MN∥ BC，∴ △ AMO ∽96时，49 的运动，当 P 点落在直线∴∠AMN=∠B，∠ AOM △ABP ．∴ AM AO 1． AM ＝MB＝2．AB AP 2故以下分两种情况讨论：① 当 0< x≤2时， y SΔPMN 3x28图25x．8MA25x24⊙O 7分AP，则 O 点为 AP 的中点．BC 上时，连结图333∴ 当x＝2时，y最大83 22 32. ⋯⋯⋯⋯⋯⋯⋯② 当 2< x<4时，设 PM，PN 分别交 BC于 E，F．∵ 四边形 AMPN 是矩形，∴ PN∥AM，PN＝AM ＝x．又∵ MN∥ BC，∴ 四边形 MBFN 是平行四边形．∴ FN＝BM＝4－ x．∴ PF x 4 x 2x 4．又△ PEF ∽ △ ACB．∴PF2SS PEF AB S ABCS PEF 2x 2y S MNP S PEF ＝32 3 2 92x x 2 x8 2 89 826x 6 x 2．8 392当 2< x < 4 时，y x28 6x 69分1 0 分8当x 83时，满足 2< x<4，y最大2．11 分8综上所述，当x 38时，y值最大，最大值是2．1分24 解：( 1)作 BE⊥OA，∴ΔAOB 是等边三角形∴BE=OB·sin60o= 2 3，∴B(2 3,2) ∵A(0,4), 设 AB的解析式为y kx 4,所以2 3k 4 2 ,解得k以直线 AB的解析式为y2）由旋转知，AP=AD, ∠PAD=60o ,∴Δ APD是等边三角形，PD=PA= AO2 OP219如图，作 BE⊥AO,DH⊥OA,GB⊥DH,显然Δ GBD中∠GBD=30°∴GD=1 BD= 3 ,DH=GH+GD= 3 +2 3 =5 32 2 23 3 3 ∴ GB=BD= ,OH=OE+HE=OE+BG2= 22∴D(5 3 ,272)(3) 设 OP=x,则由( 2)可得 D( 2 3 x,2 23x)若ΔOPD的面积为：21xg(2 23x) 43解得：x2 3 21所以 P( 2 3 21,0)(2)解：△ MEF 为正三角形.理由；VΔBDE^ΔBCF,Λ ZDBE= Z CBF.BE=BF tV Z DEe ■ SBF+Z CBF=6『TΛ -Z DKF÷ DBE= 60\ 即ZfλBF=6<Λ ΛΔBΓΓ为正三角形.(3)解：设 BE=BF=EF=Jr,则 S =-I- * z * X * sin60°= -^-X t +当 Br LAD 时心M -2 XSinCO ft -√J 1当IiE 与AB ⅛⅛时,工仆・2, *--s *x≡^^×23-√3.給⑴令 J y^O,⅛-√-2JC ÷3=□, .∖jr 1≡"-3,-τ3 = l∙ΛΛ<-3.0) *B( 1 >□λT 拗物绒L L 向右平移2个単位得嫌物线匸“ΛCC t-1∙0)»DC3,0) ,α≡-L化施物线厶为y ■—(JE 十J(J :一3),卸 y≡ — 1z 4+2κT 3*AB∥ CD ，DG＝CH，DG∥CH．四边形 DGHC 为矩形，GH ＝CD＝1． DG＝CH，AD＝BC，∠AGD ＝∠ BHC ＝ 90°，△AGD ≌△ BHC （HL）．E G H FAB7 解：1）分别过 D，C 两点作 DG ⊥AB 于点 G，CH ⊥AB 于点 H．1分AG ＝BH ＝ AB GH 7 1＝3． ⋯⋯⋯ 2分 22在 Rt △ AGD 中， AG ＝3，AD ＝5，DG ＝4．∴ 1 7 4 ． ⋯∴ S 梯形 ABCD 2 16 ． ⋯（2）∵ MN ∥AB ，ME ⊥ AB ，NF ⊥AB ， ∴ ME ＝NF ，ME ∥NF ．∴ 四边形 MEFN 为矩形．∵ AB ∥CD ，AD ＝BC ，∴ ∠ A ＝∠ B ．∵ ME ＝NF ，∠MEA ＝∠ NFB ＝90°，∴ △ MEA ≌△ NFB （ AAS ）．∴ AE ＝ BF ． ⋯⋯⋯⋯⋯⋯⋯⋯ 4 分设 AE ＝ x ，则 EF ＝ 7－ 2x ． ⋯⋯⋯⋯⋯ 5 分∠A ＝∠ A ，∠ MEA ＝∠ DGA ＝90°， ∴ △ MEA ∽△ DGA ．∴ AE ME ．AG DG ． 4∴ ME ＝ x ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分 3 24 8 7 49∴ S 矩形 MEFN ME EF x （7 2x ） x ． ⋯⋯⋯⋯⋯⋯⋯⋯ 8 分3 34 6当 x ＝ 7 时，ME ＝ 7 <4，∴四边形 MEFN 面积的最大值为 49 ． ⋯⋯⋯⋯⋯ 9 分由（ 2）可知，设 AE ＝x ，则 EF ＝7－2x ，ME ＝ 4 x ． 3 若四边MEF 为正方则 ME ＝EF ． 4x 4x 7－2x ．解，得 x 21 ． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 11 分 3 10 ∴ EF ＝21 14 7 2x 72 <4． 10 53分4 3 63）能． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 10 分8 解：（ 1 ）由题意可知， m m 1 m 3 m 1 解，得 m ＝3． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分∴ A （3，4）， B （6，2）；∴ k ＝4× 3=12． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分（2）存在两种情况，如图：①当 M 点在 x 轴的正半轴上， N 点在 y 轴的正半轴上时，设 M 1点坐标为（ x 1， 0）， N 1点坐标为（ 0，y 1）∵ 四边形 AN 1M 1B 为平行四边形，∴ 线段 N 1M 1可看作由线段 AB 向左平移 3 个单位，再向下平移 2个单位得到的（也可看作向下平移 2个单位，再向左平移 3 个单位得到的）由（1）知 A 点坐标为（ 3，4），B 点坐标为（ 6，2），∴ N 1点坐标为（ 0，4－2），即 N 1（0，2）； ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分 M 1点坐标为（ 6－3， 0），即 M 1（3，0）． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分2设直线 M 1 N 1的函数表达式为 y k 1x 2 ，把 x ＝3，y ＝0 代入，解得 k 12 ． 32 ∴ 直线 M 1N 1 的函数表达式为 y x 2 ． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 8 分3②当 M 点在 x 轴的负半轴上， N 点在 y 轴的负半轴上时，设 M 2点坐标为（ x 2，0），N 2点坐标为（ 0，y 2） ∵ AB ∥N 1M 1， AB ∥ M 2N 2， AB ＝N 1M 1，AB ＝M 2N 2， ∴ N 1M 1∥M 2N 2， N 1M 1＝M 2N 2．∴ 线段 M 2N 2与线段 N 1M 1关于原点 O 成中心对称．∴ M 2点坐标为（ - 3， 0）， N 2点坐标为（ 0，-2）． ⋯⋯⋯⋯⋯⋯⋯⋯⋯ 9 分2设直线 M 2 N 2的函数表达式为 y k 2x 2，把 x ＝-3，y ＝0代入，解得 k 22 ， 32 四边形 MEFN 能为正方形，其面积为 S正方形 MEFN 14 5 19 6 253所以，直线 MN 的函数表达式为 y 2x 2 或 y 2x 2 ．⋯⋯⋯⋯⋯⋯ 11 分33（3）选做题：（ 9，2），（ 4，5）．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2分∴ 直线 M2N2的函数表达式为 y 2x 2 ．9解：（ 1）Q 直线 y 3x 3与 x 轴交于点 A ，与 y 轴交于点 C ．x抛物线的解析式为x 23分顶点 F 1， 4 334分 2）存在5分 P 1（0， 3） 7分 P 2（2， 3）9分（ 3）存在 · 理由：解法一：延长 BC 到点 B 10 分，使 BC BC ，连接 BF 交直线 AC 于点 M ，则点 M 就是所求的点．·· ······· · ···· · ····· · ······ · ···11 分过点 B 作 BH AB 于点 H ．Q B 点在抛物线y 3x2 2 3x 3上， B （3，0）33在Rt △BOC 中， tan OBC 3，3A （ 1，0）， C （0， 3） Q 点 A ，C 都在抛物线上， 23 c 31分0ax过点 F 作 FG y 轴于点 G ，则 OB ∥FG ， BC ∥FH ．BOC FGH 90o ， BCO FHGOBC 30o ， BC 2 3 ，1 在 Rt△BBH 中， BH BB 2 3，2BH 3BH 6， OH 3， B （ 3，2 3） ·· ······ · ······ ····12分23 3k b k343kb解得633 3 b233 3 ·y 6x 2·13 分y 3x 33 3 3 yx 62x解得y10 33，10 377在直线 AC 上存在点 M ，使得 △ MBF 的周长最小，此时10 314 分解法过点 F 作 AC 的垂线交 y 轴于点 H ，则点H 为点 F 关于直线 AC 的对称点．连接 BH 交 AC 于点 M ，则点 M 即为所求． 11分设直线 BF 的解析式为 y kx b3HFG CBO 同方法一可求得 B （3，0）．在 Rt △BOC 中， tan OBC3，OBC 30o ，可求得 GHGC 3 ，33GF 为线段 CH 的垂直平分线， AC 垂直平分 FH ．可证得 △CFH 为等边三角形，0， 5 3 · ······ ·3即点 H 为点 F 关于 AC 的对称点．H ······ ····12 分设直线 BH 的解析式为 y kx b ，由题意得59 3 53 310 解：（ 1）点 E 在 y 轴上理由如下：0 3k b b 53 3k 解得 b59 353 3 13 分59 3x 53 3y 3x 3x解得y 3 7 10 3 73 ， 10 377在直线 AC 上存在点 M ，使得 △ MBF 的周长最小，此时10 31分连接 AO ，如图所示，在 Rt △ ABO 中， Q AB 1，BO 3， AO 21，osin AOBAOB 30o2由题意可知：AOE60oQ 点 D 在第一象限， 3，122c2BOEAOB AOE 30o 60o 90o Q 点 B在 x 轴上，点 E 在 y 轴上．3分2）过点 D 作DM x 轴于点M Q OD 1，DOMo30o在 Rt △ DOM 中，DM1 ，OM2点 D 的坐标为5分由（ 1）知 EO AO 2 ，点 E 在 y 轴的正半轴上点 E 的坐标为（0，2）点 A 的坐标为（ 3，1） 6分Q 抛物线 y2ax bx c 经过点 E ，953 83）存在符合条件的点 P ，点 Q ．理由如下： Q 矩形 ABOC 的面积 ABgBO 3 以O ，B ，P ，Q 为顶点的平行四边形面积为 23 ．由题意可知 OB 为此平行四边形一边，又 Q OB 3OB 边上的高为 2依题意设点 P 的坐标为（m ，2）53m由题意，将 A （ 3，1）， D 3，1 代入 y ax 2 22bx 2 中得3a 3b 2 1 3 3 1 a b 2 4 22a解得b8 9 53 9所求抛物线表达式为：y82 x 953x9分 10 分11 分Q 点 P 在抛物线 y82 x 9 53 x9 2上229解得，m1 0 ，m295388P 1 （0，2）， P253 8Q 以 O ，B ，P ，Q为顶点的四边形是平行四边形， PQ∥OB ，PQ OB 3，当点 P1 的坐标为（0，2）时，点 Q的坐标分别为 Q 1（ 3，2）， Q 2（ 3，2）；53当点 P 2 的坐标为，2 时，8 点 Q 的坐标分别为Q 313 3 8Q 43 3，2 ．以上答案仅供参考，如有其它做法，可参照给分）8。

2019年中考数学专题4四边形证明及计算压轴题

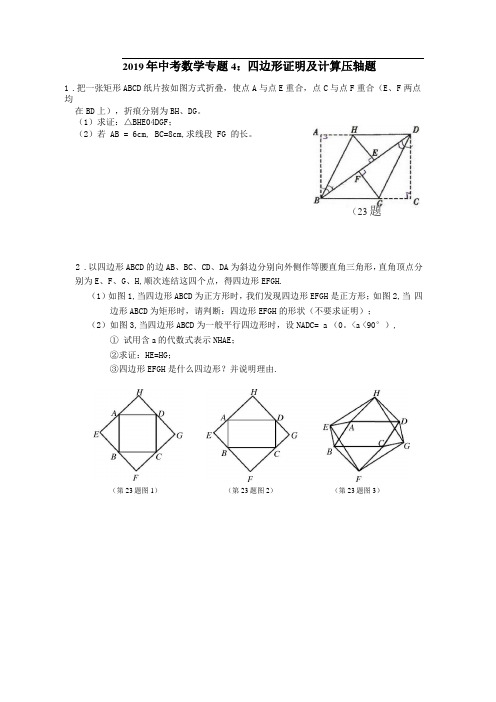
2019年中考数学专题4：四边形证明及计算压轴题1.把一张矩形ABCD纸片按如图方式折叠，使点A与点E重合，点C与点F重合（E、F两点均在BD上），折痕分别为BH、DG。

（1）求证：△BHE04DGF；（2）若 AB = 6cm, BC=8cm,求线段 FG 的长。

（23题2.以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形，直角顶点分别为E、F、G、H,顺次连结这四个点，得四边形EFGH.（1）如图1,当四边形ABCD为正方形时，我们发现四边形EFGH是正方形；如图2,当四边形ABCD为矩形时，请判断：四边形EFGH的形状（不要求证明）；（2）如图3,当四边形ABCD为一般平行四边形时，设NADC= a （0。

<a <90°）,① 试用含a的代数式表示NHAE；②求证：HE=HG；③四边形EFGH是什么四边形？并说明理由.（第23题图1）（第23题图2）（第23题图3）3.如图7,在一方形ABCD中.E为对角线AC上一点，连接EB、ED,(1)求证：△BEC04DEC：(2)延长BE交AD于点F,若NDEB=140°.求NAFE的度数.... 一厘＞一、_ .4.直角梯形 ABCD 中，AD〃BC,NA=90。

，AB = AD = 6 , DE± DC交 AB 于 E, DF 平分ZEDC交BC于F,连结EF.(1)证明：EF = CF；(2)当tan Z ADE = 3 时，求 EF 的长.5.两个大小相同且含30。

角的三角板ABC和DEC如图①摆放，使直角顶点重合.将图①中△DEC绕点C逆时针旋转30。

得到图②，点F、G分别是CD、DE与AB的交点，点H是DE与AC的交点.(1)不添加辅助线，写出图②中所有与4BCF全等的三角形;(2)将图②中的4DEC绕点C逆时针旋转45。

得△0旦。

点F、G、H的对应点分别为F1、G1、H1 ,如图③.探究线段D1F1与AH1之间的数量关系，并写出推理过程；(3)在(2)的条件下，若D1E1与CE交于点I,求证：G1I图②=CI.D6.如图，在平行四边形ABCD中，E为BC中点，AE的延长线与DC的延长线相交于点F. (1)证明：NDFA=NFAB； (2)证明：△ABE04FCE.7、如图，在口ABCD中，E,F分别是BC，AD中点。

中考数学复习类比归纳专题：圆中利用转化思想求角度压轴题四种模型全攻略(原卷+答案解析)

类比归纳专题：圆中利用转化思想求角度压轴题四种模型全攻略【考点导航】目录【典型例题】1【类型一利用同弧或等弧转化圆周角与圆心角】1【类型二构造圆内接四边形转化角】5【类型三利用直径构造直角三角形转化角】9【类型四利用特殊数量关系构造特殊角转化角】15【典型例题】【类型一利用同弧或等弧转化圆周角与圆心角】1(2023·北京·九年级专题练习)如图，AB 为⊙O 的直径，C ，D 为⊙O 上的点，BC=DC．若∠CBD =35°，则∠ABD 的度数为()A.20°B.35°C.40°D.70°【变式训练】1(2022秋·浙江温州·九年级校考阶段练习)如图，在⊙O 中，点A 是BC的中点，若∠ADC =24°，则∠AOB 的度数为()A.12°B.24°C.36°D.48°2(2023秋·江苏镇江·九年级统考期末)如图，点A ，B ，C 都在⊙O 上，B 是AC的中点，∠OBC =50°，则∠AOB 等于°．3(2023·湖北随州·统考中考真题)如图，在⊙O 中，OA ⊥BC ，∠AOB =60°，则∠ADC 的度数为．4(2023春·北京西城·九年级北师大实验中学校考开学考试)如图，四边形ABCD 内接于⊙O ，AB 为直径，BC=CD，∠A =50°，则∠B =．【类型二构造圆内接四边形转化角】1(2022秋·山西临汾·九年级统考期末)⊙O 是△ABC 的外接圆，连接OA 、OB ，若∠OBA =50°，则∠C 的度数为()A.150°B.140°C.130°D.100°【变式训练】1(2023·浙江·九年级假期作业)如图，点A ，B ，C ，D ，E 均在⊙O 上，且BD 经过圆心O ，连接AB ，AE ，CE ，若∠B +∠E =150°，则弧CD 所对的圆心角的度数为()A.30°B.40°C.50°D.60°2(2023·江苏盐城·统考一模)如图，点A 、B 、C 都在⊙O 上，如果∠AOC =∠ABC ，那么∠ABC 的度数为°．3(2023·江苏·九年级假期作业)如图，在⊙O 中，C 为AB 上的点，BC =2AC．若∠ACB =120°，则∠OBC =．4(2023·吉林松原·校联考三模)如图，点A ，B ，C ，D ，E 都是⊙O 上的点，AC=AE，∠D =128°，则∠B =°．【类型三利用直径构造直角三角形转化角】1(2023·湖北襄阳·统考一模)如图，AB 为⊙O 的直径，点C ，点D 是⊙O 上的两点，连接CA ，CD ，AD ．若∠CAB =40°，则∠ADC 的度数是°．【变式训练】1(2023·安徽宣城·校考三模)如图，AE 是直径，点B 、C 、D 在半圆上，若∠B =125°，则∠D =．2(2023·辽宁营口·校联考一模)如图，AB 是⊙O 的直径，弦CD 交AB 于点E ，连接AC ，AD ．若∠BAC =29°，则∠D =．3(2022秋·安徽阜阳·九年级校考期中)如图，AB 是⊙O 的直径，C ，D 两点在圆上，且BC=CD，连接AD ,AC ,∠CAB =25°，P 为ABC一动点(点P 不与点A ，C 重合)，连接DP ，在运动过程中，DP 与AC 相交于点M ，连接DC ．(1)∠BAD 的度数为．(2)当DM =DC 时，∠PDC 的度数为．4(2022秋·浙江杭州·九年级统考期末)如图，以△ABC 的边BC 为直径的⊙O 分别交AB ，AC 于点D ，E ，且点E 是CD的中点，连接DE ．(1)求证：△ABC是等腰三角形．(2)若BC=10，CE=6，求线段AD的长．【类型四利用特殊数量关系构造特殊角转化角】1(2023·江苏连云港·校联考三模)如图，已知：四个边长为1的小正方形拼成一个大正方形，A、B、O是小正方形顶点，⊙O的半径为1，P是⊙O上的点，且位于右上方的小正方形内，则∠APB等于()A.30°B.45°C.60°D.90°【变式训练】1(2023·辽宁朝阳·校联考三模)如图，点A、B、C、D在⊙O上，四边形OBCD是平行四边形，则∠A 的大小为()A.30°B.45°C.60°D.无法确定2(2023·广西防城港·统考一模)如图，点A，B，C，D都在⊙O上，OA⊥BC，∠ADC=30°，则∠AOB的度数为()A.15°B.30°C.45°D.60°3(2023·广东佛山·校考三模)如图，四边形ABCD内接于⊙O,AB=BC，连接OA，OB，若∠BAO= 70°，则∠D=()A.40°B.60°C.45°D.30°4(2023春·陕西西安·九年级高新一中校考期中)如图，四边形ABCD是⊙O的内接四边形，BE是⊙O的直径，连接AE，若∠BCD=2∠BAD，若连接OD，则∠DOE的度数是()A.30°B.35°C.45°D.60°类比归纳专题：圆中利用转化思想求角度压轴题四种模型全攻略【考点导航】目录【典型例题】1【类型一利用同弧或等弧转化圆周角与圆心角】1【类型二构造圆内接四边形转化角】5【类型三利用直径构造直角三角形转化角】9【类型四利用特殊数量关系构造特殊角转化角】15【典型例题】【类型一利用同弧或等弧转化圆周角与圆心角】1(2023·北京·九年级专题练习)如图，AB 为⊙O 的直径，C ，D 为⊙O 上的点，BC=DC．若∠CBD =35°，则∠ABD 的度数为()A.20°B.35°C.40°D.70°【答案】A【分析】根据等弧所对的圆周角相等可得∠CAB =∠CBD =35°，根据直径所对的圆周角为90度可得∠ADB =90°，进而可得∠CBA =90°-∠CAB =55°，∠ABD =∠CBA -∠CBD =20°．【详解】解：如图，连接AD ，AC ，∵BC=DC，∠CBD =35°，∴∠CAB =∠CBD =35°，∵AB 为⊙O 的直径，∴∠ADB =90°，∴∠CBA =90°-∠CAB =55°，∴∠ABD =∠CBA -∠CBD =55°-35°=20°，故选A ．【点睛】本题考查圆周角定理，解题的关键是掌握：在同圆或等圆中，同弧或等弧所对的圆周角相等，半圆(或直径)所对的圆周角是直角．【变式训练】1(2022秋·浙江温州·九年级校考阶段练习)如图，在⊙O 中，点A 是BC的中点，若∠ADC =24°，则∠AOB 的度数为()A.12°B.24°C.36°D.48°【答案】D【分析】直接利用圆周角定理求解．【详解】解：∵点A 是BC的中点，∴AC=AB，∴∠AOB =2∠ADC =2×24°=48°．故选：D ．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．2(2023秋·江苏镇江·九年级统考期末)如图，点A ，B ，C 都在⊙O 上，B 是AC的中点，∠OBC =50°，则∠AOB 等于°．【答案】80°/80度【分析】利用等腰三角形的性质和三角形内角和计算出∠BOC =80°，然后根据圆心角、弧的关系即可求出答案．【详解】解：∵∠OBC =50°，OB =OC ，∴∠OCB =50°，∴∠BOC =180°-∠OBC -∠OCB =80°，∵B 是AC的中点，∴AB=BC ，∴∠AOB =∠BOC =80°，故答案为：80°．【点睛】本题考查了圆心角、弧的的关系，熟练掌握知识点是解题的关键．3(2023·湖北随州·统考中考真题)如图，在⊙O 中，OA ⊥BC ，∠AOB =60°，则∠ADC 的度数为．【答案】30°/30度【分析】根据垂径定理得到AB =AC，根据圆周角定理解答即可．【详解】解：∵OA ⊥BC ，∴AB=AC，∴∠ADC =12∠AOB =30°，故答案为：30°．【点睛】本题考查的是垂径定理和圆周角定理，掌握同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解题的关键．4(2023春·北京西城·九年级北师大实验中学校考开学考试)如图，四边形ABCD 内接于⊙O ，AB 为直径，BC=CD，∠A =50°，则∠B =．【答案】65°/65度【分析】连接AC ．利用等弧所对圆周角相等，得出∠DAC =∠BAC ，从而得出∠BAC =12∠DAB =25°，再利用直径所对圆周角是直角，最后由直角三角形两锐角互余求解即可．【详解】解：如图所示，连接AC ．∵BC=CD，∴∠DAC =∠BAC ．∵∠DAB =50°，∴∠BAC =12∠DAB =25°．∵AB 为直径，∴∠ACB =90°．∴∠B =90°-∠BAC =65°，故答案为：65°．【点睛】本题主要考查了圆周角定理的推论，直角三角形的性质，熟练掌握圆周角定理的推论是解题的关键．【类型二构造圆内接四边形转化角】1(2022秋·山西临汾·九年级统考期末)⊙O 是△ABC 的外接圆，连接OA 、OB ，若∠OBA =50°，则∠C 的度数为()A.150°B.140°C.130°D.100°【答案】B【分析】在优弧AB 上取一点E ，连接AE 、BE ，由⊙O 是△ABC 的外接圆，∠AOB =80°，利用在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得∠AEB 的度数，最后由圆内接四边形的性质可得答案．【详解】解：如图，在优弧AB 上取一点E ，连接AE 、BE ，∵∠OBA =50°，OA =OB ，∴∠AOB =80°，∴∠AEB =12∠AOB =12×80°=40°．∵四边形ACBE 是圆内接四边形，∴∠AEB +∠C =180°，∴∠C =180°-∠AEC =140°，故选：B ．【点睛】本题考查了圆周角定理及圆内接四边形的性质．此题比较简单，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用．【变式训练】1(2023·浙江·九年级假期作业)如图，点A ，B ，C ，D ，E 均在⊙O 上，且BD 经过圆心O ，连接AB ，AE ，CE ，若∠B +∠E =150°，则弧CD 所对的圆心角的度数为()A.30°B.40°C.50°D.60°【答案】D【分析】连接DE ，OC ，根据圆内接四边形的性质可得∠B +∠AED =180°，从而得到∠CED =30°，进而得到∠COD =2∠CED =50°，即可求解．【详解】解：如图，连接DE ，OC ，∵四边形ABDE 是⊙O 的内接四边形，∴∠B +∠AED =180°，∵∠B +∠AEC =150°，∴∠CED =30°，∴∠COD =2∠CED =60°，∴弧CD 所对的圆心角的度数为60°．故选：D ．【点睛】本题主要考查了圆内接四边形的性质，圆周角定理，熟练掌握圆内接四边形的性质，圆周角定理是解题的关键．2(2023·江苏盐城·统考一模)如图，点A 、B 、C 都在⊙O 上，如果∠AOC =∠ABC ，那么∠ABC 的度数为°．【答案】120【分析】如图：在优弧AC 上取一点D ，连接AD 、CD ，由圆周角定理和圆的内接四边形可得∠ADC =12∠AOC ，∠ADC +∠ABC =180°，再结合∠AOC =∠ABC 求得∠ABC =120°．【详解】解：如图所示，在优弧AC 上取一点D ，连接AD 、CD ，∴∠ADC =12∠AOC ，∠ADC +∠ABC =180°，∵∠AOC =∠ABC ，∴∠ADC =12∠ABC ∴12∠ABC +∠ABC =180°，∴∠ABC =120°故答案为：120．【点睛】本题主要考查了圆周角定理、圆的内接四边形的性质，掌握圆的内接四边形对角互补是解答本题的关键．3(2023·江苏·九年级假期作业)如图，在⊙O 中，C 为AB 上的点，BC =2AC．若∠ACB =120°，则∠OBC =．【答案】50°【分析】在优弧AB 上取一点D ，连接AD ，BD ，OC ，根据圆周角定理即可得到结论．【详解】解：在优弧AB 上取一点D ，连接AD ，BD ，OC ，∵∠ACB =120°，∴∠D =180°-∠ACB =60°，∴∠AOB =2∠D =120°，∵BC =2AC，∴∠BOC =2∠AOC ，∴∠BOC =80°，∵OC =OB ，∴∠OCB =∠OBC =50°，故答案为：50°．【点睛】本题考查了圆周角定理，添加辅助线构造圆心角和圆周角是解题的关键．4(2023·吉林松原·校联考三模)如图，点A ，B ，C ，D ，E 都是⊙O 上的点，AC =AE ，∠D =128°，则∠B =°．【答案】116【分析】连接AC 、CE ，根据圆内接四边形的性质求出∠CAE ，根据圆心角、弧、弦之间的关系定理求出∠ACE ，根据圆内接四边形的性质计算，得到答案．【详解】解：连接AC 、CE ，∵点A 、C 、D 、E 都是⊙O 上的点，∴∠CAE +∠D =180°，∴∠CAE =180°-128°=52°，∵AC =AE，∴∠ACE =∠AEC =12180°-52° =64°，∵点A 、B 、C 、E 都是⊙O 上的点，∴∠AEC +∠B =180°，∴∠B =180°-64°=116°，故答案为：116．【点睛】本题考查的是圆内接四边形的性质、等腰三角形的性质、掌握圆内接四边形的对角互补是解题的关键．【类型三利用直径构造直角三角形转化角】1(2023·湖北襄阳·统考一模)如图，AB 为⊙O 的直径，点C ，点D 是⊙O 上的两点，连接CA ，CD ，AD ．若∠CAB =40°，则∠ADC 的度数是°．【答案】130【分析】连接BC，如图，利用圆周角定理得到∠ACB=90°，则∠B=50°，然后利用圆的内接四边形的性质求∠ADC的度数．【详解】解：如图，连接BC，∵AB为⊙O的直径，∴∠ACB=90°，∴∠B=90°-∠CAB=90°-40°=50°，∵∠B+∠ADC=180°，∴∠ADC=180°-50°=130°．故答案为：130．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．半圆(或直径)所对的圆周角是直角，90°的圆周角所对的弦是直径．【变式训练】1(2023·安徽宣城·校考三模)如图，AE是直径，点B、C、D在半圆上，若∠B=125°，则∠D=．【答案】145°/145度【分析】连接BE，根据直径所对的圆周角为90度可得∠ABE=90°，进而可得∠CBE=35°，再根据圆内接四边形对角互补即可求解．【详解】解：如图，连接BE，∵AE是直径，点B在半圆上，∴∠ABE=90°，∴∠CBE=∠ABC-∠ABE=125°-90°=35°，∵四边形BCDE是⊙O的内接四边形，∴∠D+∠CBE=180°，∴∠D=180°-∠CBE=145°，故答案为：145°．【点睛】本题考查圆周角定理、圆内接四边形的性质等，解题的关键是掌握圆内接四边形的对角互补．2(2023·辽宁营口·校联考一模)如图，AB是⊙O的直径，弦CD交AB于点E，连接AC，AD．若∠BAC=29°，则∠D=．【答案】61°/61度【分析】如图，连接BC ，证明∠ACB =90°，求出∠ABC ，可得结论．【详解】解：如图，连接BC ．∵AB 是直径，∴∠ACB =90°，∴∠ABC =90°-∠CAB =61°，∴∠D =∠ABC =61°，故答案为：61°．【点睛】本题考查圆周角定理，解题的关键是熟练掌握圆周角定理，属于中考常考题型．3(2022秋·安徽阜阳·九年级校考期中)如图，AB 是⊙O 的直径，C ，D 两点在圆上，且BC =CD，连接AD ,AC ,∠CAB =25°，P 为ABC 一动点(点P 不与点A ，C 重合)，连接DP ，在运动过程中，DP 与AC 相交于点M ，连接DC ．(1)∠BAD 的度数为．(2)当DM =DC 时，∠PDC 的度数为．【答案】 50°100°【分析】(1)根据BC =CD ，可得∠CAD =∠CAB =25°，进而可求∠BAD 的度数；(2)由AB 是⊙O 的直径得∠ACB =90°，再根据圆内接四边形的性质求出∠BCD ，然后可求∠PDC 的度数．【详解】(1)∵BC =CD，∠CAB =25°，∴∠CAD =∠CAB =25°，∴∠BAD =50°；(2)连接BC ．∵AB 是⊙O 的直径，∴∠ACB =90°，∵∠BAD +∠BCD =180°，∴∠ACD =180-50°-90°=40°∵DM =DC ，∴∠DMC =∠ACD =40°，∴∠PDC =180°-40°-40°=100°．故答案为：(1)50°；(2)100°．【点睛】本题考查了圆周角定理，圆内接四边形的性质，等腰三角形的性质等知识，关键是熟练掌握圆的性质．4(2022秋·浙江杭州·九年级统考期末)如图，以△ABC 的边BC 为直径的⊙O 分别交AB ，AC 于点D ，E ，且点E 是CD的中点，连接DE ．(1)求证：△ABC 是等腰三角形．(2)若BC =10，CE =6，求线段AD 的长．【答案】(1)证明见解析(2)AD =365【分析】(1)连接BE ，根据直径所对的圆周角为直角，得出BE ⊥AC ，再根据同弧或等弧所对的圆周角相等，得出BE 是∠ABC 的角平分线，然后再根据等腰三角形的判定定理，即可得出结论；(2)连接CD ，根据勾股定理，得出BE =8，再根据三角形的面积公式，结合等腰三角形的性质，得出S △ABC =2S △BCE =48，再根据三角形的面积公式，得出S △ABC =12AB ⋅CD =12×10×CD =48，解得CD =485，再根据勾股定理，得出BD =145，然后根据线段之间的数量关系，即可得出答案．【详解】(1)证明：如图，连接BE ，∵BC 是⊙O 的直径，∴∠BEC =90°，∴BE ⊥AC ，∵点E 是CD的中点，∴DE =CE ，∴∠DBE =∠CBE ，∴BE 是∠ABC 的角平分线，∴△ABC 是等腰三角形；(2)解：如图，连接CD ，在Rt △BCE 中，∵BC =10，CE =6，∴BE =BC 2-CE 2=8，∴S △BCE =12CE ⋅BE =12×6×8=24，又∵BE ⊥AC ，△ABC 是等腰三角形，∴BE 是△ABC 的中线，AB =BC =10，∴S △ABC =2S △BCE =48，∵BC 是⊙O 的直径，∴∠BDC =90°，∴CD ⊥AB ，∴S △ABC =12AB ⋅CD =12×10×CD =48，解得：CD =485，∴BD =BC 2-CD 2=145，∴AD =AB -BD =10-145=365．【点睛】本题考查了直径所对的圆周角为直角、同弧或等弧所对的圆周角相等、等腰三角形的判定与性质、勾股定理，解本题的关键在熟练掌握相关的性质定理和等面积法．【类型四利用特殊数量关系构造特殊角转化角】1(2023·江苏连云港·校联考三模)如图，已知：四个边长为1的小正方形拼成一个大正方形，A 、B 、O 是小正方形顶点，⊙O 的半径为1，P 是⊙O 上的点，且位于右上方的小正方形内，则∠APB 等于()A.30°B.45°C.60°D.90°【答案】B【分析】根据圆周角定理求解即可．【详解】∠APB =12∠AOB =45°，故选：B ．【点睛】本题考查圆周角定理，熟记同圆中一条弧所对的圆周角等于所对圆心角的一半是解题的关键．【变式训练】1(2023·辽宁朝阳·校联考三模)如图，点A 、B 、C 、D 在⊙O 上，四边形OBCD 是平行四边形，则∠A 的大小为()A.30°B.45°C.60°D.无法确定【答案】A【分析】连接OC ，证明△OBC 为等边三角形，得出∠BOC =60°，根据圆周角定理得出∠A =12∠BOC =30°即可．【详解】解：连接OC ，如图所示：∵四边形OBCD 是平行四边形，∴BC =OD ，∴BC =OB =OC ，∴△OBC 为等边三角形，∴∠BOC =60°，∴∠A =12∠BOC =30°，故A 正确．故选：A ．【点睛】本题主要考查了圆周角定理，平行四边形的性质，等边三角形的判定和性质，解题的关键是证明△OBC 为等边三角形，求出∠BOC =60°．2(2023·广西防城港·统考一模)如图，点A ，B ，C ，D 都在⊙O 上，OA ⊥BC ，∠ADC =30°，则∠AOB 的度数为()A.15°B.30°C.45°D.60°【答案】D【分析】由OA ⊥BC ，根据垂径定理的即可求得：AC =AB ，然后由圆周角定理，即可求得∠AOB 的度数．【详解】解：∵OA ⊥BC ，∴AC =AB ，∵∠ADC =30°，∴∠AOB =2∠ADC =2×30°=60°．故选：D ．【点睛】此题考查了圆周角定理以及垂径定理，解题的关键是掌握数形结合思想的应用．3(2023·广东佛山·校考三模)如图，四边形ABCD 内接于⊙O ,AB =BC ，连接OA ，OB ，若∠BAO =70°，则∠D =()A.40°B.60°C.45°D.30°【答案】A【分析】连接OC ，证明△OAB ≌△OCB SSS ，得出∠OBA =∠OBC =∠OCB =∠BAO =70°，则∠ABC =140°，再根据圆内接四边形对角互补，即可求解．【详解】解：连接OC ，在△OAB 和△OBC 中，AB =BCOB =OB OA =OC，∴△OAB ≌△OCB SSS ，∵∠BAO =70°，OA =OB =OC ，∴∠OBA =∠OBC =∠OCB =∠BAO =70°，∴∠ABC =140°，∵四边形ABCD 内接于⊙O ，∴∠D =180°-∠ABC =40°，故选：A ．【点睛】本题主要考查了圆内接四边形，解题的关键是掌握圆的内接四边形对角互补．4(2023春·陕西西安·九年级高新一中校考期中)如图，四边形ABCD 是⊙O 的内接四边形，BE 是⊙O 的直径，连接AE ，若∠BCD =2∠BAD ，若连接OD ，则∠DOE 的度数是()A.30°B.35°C.45°D.60°【答案】D 【分析】根据内接四边形的性质，得到∠BCD +∠BAD =180°，进而得到∠BAD =60°，再根据圆周角定理得到∠BOD =120°，即可求出∠DOE 的度数．【详解】解：∵四边形ABCD 是⊙O 的内接四边形，∴∠BCD +∠BAD =180°，∵∠BCD =2∠BAD ，∴∠BAD =60°，∴∠BOD =120°，∴∠DOE =180°-∠BOD =60°，故选D ．【点睛】本题考查了圆内接四边形的性质，圆周角定理，熟练掌握内接四边形的对角互补，以及一条弧所对的圆周角等于它所对的圆心角的一半是解题关键．。

2021-2022学年北师大版九年级数学中考复习压轴题专题提升训练(附答案)

2021-2022学年北师大版九年级数学中考复习压轴题专题提升训练（附答案）1．如图，在平面直角坐标系中，菱形ABCD的顶点D在第二象限，其余顶点都在第一象限，AB∥x轴，AO⊥AD，AO＝AD．过点A作AE⊥CD，垂足为E，DE＝4CE．反比例函数y＝（x＞0）的图象经过点E，与边AB交于点F，连接OE，OF，EF．若S△EOF＝，则k的值为（）A．B．C．7D．2．在△ABC中，AB＝AC，D是边BC上一动点，连接AD，将AD绕点A逆时针旋转至AE 的位置，使得∠DAE+∠BAC＝180°．（1）如图1，当∠BAC＝90°时，连接BE，交AC于点F．若BE平分∠ABC，BD＝2，求AF的长；（2）如图2，连接BE，取BE的中点G，连接AG．猜想AG与CD存在的数量关系，并证明你的猜想；（3）如图3，在（2）的条件下，连接DG，CE．若∠BAC＝120°，当BD＞CD，∠AEC ＝150°时，请直接写出的值．3．有公共顶点A的正方形ABCD与正方形AEGF按如图1所示放置，点E，F分别在边AB 和AD上，连接BF，DE，M是BF的中点，连接AM交DE于点N．【观察猜想】（1）线段DE与AM之间的数量关系是，位置关系是；【探究证明】（2）将图1中的正方形AEGF绕点A顺时针旋转45°，点G恰好落在边AB上，如图2，其他条件不变，线段DE与AM之间的关系是否仍然成立？并说明理由．4．在▱ABCD中，∠BAD＝α，DE平分∠ADC，交对角线AC于点G，交射线AB于点E，将线段EB绕点E顺时针旋转α得线段EP．（1）如图1，当α＝120°时，连接AP，请直接写出线段AP和线段AC的数量关系；（2）如图2，当α＝90°时，过点B作BF⊥EP于点F，连接AF，请写出线段AF，AB，AD之间的数量关系，并说明理由；（3）当α＝120°时，连接AP，若BE＝AB，请直接写出△APE与△CDG面积的比值．5．已知点O是线段AB的中点，点P是直线l上的任意一点，分别过点A和点B作直线l 的垂线，垂足分别为点C和点D．我们定义垂足与中点之间的距离为“足中距”．（1）[猜想验证]如图1，当点P与点O重合时，请你猜想、验证后直接写出“足中距”OC和OD的数量关系是．（2）[探究证明]如图2，当点P是线段AB上的任意一点时，“足中距”OC和OD的数量关系是否依然成立，若成立，请给出证明；若不成立，请说明理由．（3）[拓展延伸]如图3，①当点P是线段BA延长线上的任意一点时，“足中距”OC和OD的数量关系是否依然成立，若成立，请给出证明；若不成立，请说明理由；②若∠COD＝60°，请直接写出线段AC、BD、OC之间的数量关系．6．如图，在矩形ABCD中，AB＝3cm，AD＝cm．动点P从点A出发沿折线AB﹣BC向终点C运动，在边AB上以1cm/s的速度运动；在边BC上以cm/s的速度运动，过点P作线段PQ与射线DC相交于点Q，且∠PQD＝60°，连接PD，BD．设点P的运动时间为x（s），△DPQ与△DBC重合部分图形的面积为y（cm2）．（1）当点P与点A重合时，直接写出DQ的长；（2）当点P在边BC上运动时，直接写出BP的长（用含x的代数式表示）；（3）求y关于x的函数解析式，并写出自变量x的取值范围．7．在等腰△ADE中，AE＝DE，△ABC是直角三角形，∠CAB＝90°，∠ABC＝∠AED，连接CD、BD，点F是BD的中点，连接EF．（1）当∠EAD＝45°，点B在边AE上时，如图①所示，求证：EF＝CD；（2）当∠EAD＝45°，把△ABC绕点A逆时针旋转，顶点B落在边AD上时，如图②所示，当∠EAD＝60°，点B在边AE上时，如图③所示，猜想图②、图③中线段EF和CD又有怎样的数量关系？请直接写出你的猜想，不需证明．8．如图，已知△ABC是等边三角形，P是△ABC内部的一点，连接BP，CP．（1）如图1，以BC为直径的半圆O交AB于点Q，交AC于点R，当点P在上时，连接AP，在BC边的下方作∠BCD＝∠BAP，CD＝AP，连接DP，求∠CPD的度数；（2）如图2，E是BC边上一点，且EC＝3BE，当BP＝CP时，连接EP并延长，交AC 于点F，若AB＝4BP，求证：4EF＝3AB；（3）如图3，M是AC边上一点，当AM＝2MC时，连接MP．若∠CMP＝150°，AB ＝6a，MP＝a，△ABC的面积为S1，△BCP的面积为S2，求S1﹣S2的值（用含a的代数式表示）．9．（1）已知△ABC，△ADE如图①摆放，点B，C，D在同一条直线上，∠BAC＝∠DAE ＝90°，∠ABC＝∠ADE＝45°．连接BE，过点A作AF⊥BD，垂足为点F，直线AF 交BE于点G．求证：BG＝EG．（2）已知△ABC，△ADE如图②摆放，∠BAC＝∠DAE＝90°，∠ACB＝∠ADE＝30°．连接BE，CD，过点A作AF⊥BE，垂足为点F，直线AF交CD于点G．求的值．10．已知△ABC和△DEC都为等腰三角形，AB＝AC，DE＝DC，∠BAC＝∠EDC＝n°．（1）当n＝60时，①如图1，当点D在AC上时，请直接写出BE与AD的数量关系：；②如图2，当点D不在AC上时，判断线段BE与AD的数量关系，并说明理由；（2）当n＝90时，①如图3，探究线段BE与AD的数量关系，并说明理由；②当BE∥AC，AB＝3，AD＝1时，请直接写出DC的长．11．如图1，对角线互相垂直的四边形叫做垂美四边形．（1）概念理解：如图2，在四边形ABCD中，AB＝AD，CB＝CD，问四边形ABCD是垂美四边形吗？请说明理由；（2）性质探究：如图1，垂美四边形ABCD的对角线AC，BD交于点O．猜想：AB2+CD2与AD2+BC2有什么关系？并证明你的猜想．（3）解决问题：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE，连结CE，BG，GE．已知AC＝4，AB＝5，求GE的长．12．如图1，在正方形ABCD中，点E是边BC上一点，且点E不与点B、C重合，点F是BA的延长线上一点，且AF＝CE．（1）求证：△DCE≌△DAF；（2）如图2，连接EF，交AD于点K，过点D作DH⊥EF，垂足为H，延长DH交BF 于点G，连接HB，HC．①求证：HD＝HB；②若DK•HC＝，求HE的长．13．综合与实践数学实践活动，是一种非常有效的学习方式，通过活动可以激发我们的学习兴趣，提高动手动脑能力，拓展思维空间，丰富数学体验，让我们一起动手来折一折、转一转、剪一剪，体会活动带给我们的乐趣．折一折：将正方形纸片ABCD折叠，使边AB、AD都落在对角线AC上，展开得折痕AE、AF，连接EF，如图1．（1）∠EAF＝°，写出图中两个等腰三角形：（不需要添加字母）；转一转：将图1中的∠EAF绕点A旋转，使它的两边分别交边BC、CD于点P、Q，连接PQ，如图2．（2）线段BP、PQ、DQ之间的数量关系为；（3）连接正方形对角线BD，若图2中的∠P AQ的边AP、AQ分别交对角线BD于点M、点N，如图3，则＝；剪一剪：将图3中的正方形纸片沿对角线BD剪开，如图4．（4）求证：BM2+DN2＝MN2．14．实践与探究操作一：如图①，已知正方形纸片ABCD，将正方形纸片沿过点A的直线折叠，使点B 落在正方形ABCD的内部，点B的对应点为点M，折痕为AE，再将纸片沿过点A的直线折叠，使AD与AM重合，折痕为AF，则∠EAF＝度．操作二：如图②，将正方形纸片沿EF继续折叠，点C的对应点为点N．我们发现，当点E的位置不同时，点N的位置也不同．当点E在BC边的某一位置时，点N恰好落在折痕AE上，则∠AEF＝度．在图②中，运用以上操作所得结论，解答下列问题：（1）设AM与NF的交点为点P．求证：△ANP≌△FNE；（2）若AB＝，则线段AP的长为．15．【阅读理解】如图①，l1∥l2，△ABC的面积与△DBC的面积相等吗？为什么？解：相等．在△ABC和△DBC中，分别作AE⊥l2，DF⊥l2，垂足分别为E，F．∴∠AEF＝∠DFC＝90°，∴AE∥DF．∵l1∥l2，∴四边形AEFD是平行四边形，∴AE＝DF．又S△ABC＝BC•AE，S△DBC＝BC•DF．∴S△ABC＝S△DBC．【类比探究】如图②，在正方形ABCD的右侧作等腰△CDE，CE＝DE，AD＝4，连接AE，求△ADE的面积．解：过点E作EF⊥CD于点F，连接AF．请将余下的求解步骤补充完整．【拓展应用】如图③，在正方形ABCD的右侧作正方形CEFG，点B，C，E在同一直线上，AD＝4，连接BD，BF，DF，直接写出△BDF的面积．16．如图①，在△ABC中，AD⊥BC于点D，BC＝14，AD＝8，BD＝6，点E是AD上一动点（不与点A，D重合），在△ADC内作矩形EFGH，点F在DC上，点G，H在AC上，设DE＝x，连接BE．（1）当矩形EFGH是正方形时，直接写出EF的长；（2）设△ABE的面积为S1，矩形EFGH的面积为S2，令y＝，求y关于x的函数解析式（不要求写出自变量x的取值范围）；（3）如图②，点P（a，b）是（2）中得到的函数图象上的任意一点，过点P的直线l 分别与x轴正半轴，y轴正半轴交于M，N两点，求△OMN面积的最小值，并说明理由．17．下面是某数学兴趣小组探究用不同方法作一个角的平分线的讨论片段，请仔细阅读，并完成相应的任务．小明：如图1，（1）分别在射线OA，OB上截取OC＝OD，OE＝OF（点C，E不重合）；（2）分别作线段CE，DF的垂直平分线l1，l2，交点为P，垂足分别为点G，H；（3）作射线OP，射线OP即为∠AOB的平分线．简述理由如下：由作图知，∠PGO＝∠PHO＝90°，OG＝OH，OP＝OP，所以Rt△PGO≌Rt△PHO，则∠POG＝∠POH，即射线OP是∠AOB的平分线．小军：我认为小明的作图方法很有创意，但是太麻烦了，可以改进如下，如图2，（1）分别在射线OA，OB上截取OC＝OD，OE＝OF（点C，E不重合）；（2）连接DE，CF，交点为P；（3）作射线OP．射线OP即为∠AOB的平分线．……任务：（1）小明得出Rt△PGO≌Rt△PHO的依据是（填序号）．①SSS②SAS③AAS④ASA⑤HL（2）小军作图得到的射线OP是∠AOB的平分线吗？请判断并说明理由．（3）如图3，已知∠AOB＝60°，点E，F分别在射线OA，OB上，且OE＝OF＝+1．点C，D分别为射线OA，OB上的动点，且OC＝OD，连接DE，CF，交点为P，当∠CPE ＝30°时，直接写出线段OC的长．18．如图，在四边形ABCD中，AB∥CD，AB≠CD，∠ABC＝90°，点E、F分别在线段BC、AD上，且EF∥CD，AB＝AF，CD＝DF．（1）求证：CF⊥FB；（2）求证：以AD为直径的圆与BC相切；（3）若EF＝2，∠DFE＝120°，求△ADE的面积．19．已知四边形ABCD是边长为1的正方形，点E是射线BC上的动点，以AE为直角边在直线BC的上方作等腰直角三角形AEF，∠AEF＝90°，设BE＝m．（1）如图，若点E在线段BC上运动，EF交CD于点P，AF交CD于点Q，连接CF，①当m＝时，求线段CF的长；②在△PQE中，设边QE上的高为h，请用含m的代数式表示h，并求h的最大值；（2）设过BC的中点且垂直于BC的直线被等腰直角三角形AEF截得的线段长为y，请直接写出y与m的关系式．20．【推理】如图1，在正方形ABCD中，点E是CD上一动点，将正方形沿着BE折叠，点C落在点F处，连结BE，CF，延长CF交AD于点G．（1）求证：△BCE≌△CDG．【运用】（2）如图2，在【推理】条件下，延长BF交AD于点H．若，CE＝9，求线段DE的长．【拓展】（3）将正方形改成矩形，同样沿着BE折叠，连结CF，延长CF，BF交直线AD于G，H两点，若＝k，＝，求的值（用含k的代数式表示）．21．如图，在△ABC中，AB＝AC，∠BAC＝α，M为BC的中点，点D在MC上，以点A 为中心，将线段AD顺时针旋转α得到线段AE，连接BE，DE．（1）比较∠BAE与∠CAD的大小；用等式表示线段BE，BM，MD之间的数量关系，并证明；（2）过点M作AB的垂线，交DE于点N，用等式表示线段NE与ND的数量关系，并证明．22．如图1，在△ABC中，∠ACB＝90°，AC＝BC，点D是AB边上一点（含端点A、B），过点B作BE垂直于射线CD，垂足为E，点F在射线CD上，且EF＝BE，连接AF、BF．（1）求证：△ABF∽△CBE；（2）如图2，连接AE，点P、M、N分别为线段AC、AE、EF的中点，连接PM、MN、PN．求∠PMN的度数及的值；（3）在（2）的条件下，若BC＝，直接写出△PMN面积的最大值．23．某数学兴趣小组在数学课外活动中，对多边形内两条互相垂直的线段做了如下探究：【观察与猜想】（1）如图1，在正方形ABCD中，点E，F分别是AB，AD上的两点，连接DE，CF，DE⊥CF，则的值为；（2）如图2，在矩形ABCD中，AD＝7，CD＝4，点E是AD上的一点，连接CE，BD，且CE⊥BD，则的值为；【类比探究】（3）如图3，在四边形ABCD中，∠A＝∠B＝90°，点E为AB上一点，连接DE，过点C作DE的垂线交ED的延长线于点G，交AD的延长线于点F，求证：DE•AB＝CF•AD；【拓展延伸】（4）如图4，在Rt△ABD中，∠BAD＝90°，AD＝9，tan∠ADB＝，将△ABD沿BD 翻折，点A落在点C处得△CBD，点E，F分别在边AB，AD上，连接DE，CF，DE⊥CF．①求的值；②连接BF，若AE＝1，直接写出BF的长度．24．在平面直角坐标系中，O为原点，△OAB是等腰直角三角形，∠OBA＝90°，BO＝BA，顶点A（4，0），点B在第一象限，矩形OCDE的顶点E（﹣，0），点C在y轴的正半轴上，点D在第二象限，射线DC经过点B．（Ⅰ）如图①，求点B的坐标；（Ⅱ）将矩形OCDE沿x轴向右平移，得到矩形O′C′D′E′，点O，C，D，E的对应点分别为O′，C′，D′，E′．设OO′＝t，矩形O′C′D′E′与△OAB重叠部分的面积为S．①如图②，当点E′在x轴正半轴上，且矩形O′C′D′E′与△OAB重叠部分为四边形时，D′E′与OB相交于点F，试用含有t的式子表示S，并直接写出t的取值范围；②当≤t≤时，求S的取值范围（直接写出结果即可）25．如图1，在△ABC中，AB＝AC，N是BC边上的一点，D为AN的中点，过点A作BC 的平行线交CD的延长线于T，且AT＝BN，连接BT．（1）求证：BN＝CN；（2）在图1中AN上取一点O，使AO＝OC，作N关于边AC的对称点M，连接MT、MO、OC、OT、CM得图2．①求证：△TOM∽△AOC；②设TM与AC相交于点P，连接PD，求证：PD∥CM，PD＝CM．26．问题提出如图（1），在△ABC和△DEC中，∠ACB＝∠DCE＝90°，BC＝AC，EC＝DC，点E在△ABC内部，直线AD与BE交于点F．线段AF，BF，CF之间存在怎样的数量关系？问题探究（1）先将问题特殊化如图（2），当点D，F重合时，直接写出一个等式，表示AF，BF，CF之间的数量关系；（2）再探究一般情形如图（1），当点D，F不重合时，证明（1）中的结论仍然成立．问题拓展如图（3），在△ABC和△DEC中，∠ACB＝∠DCE＝90°，BC＝kAC，EC＝kDC（k是常数），点E在△ABC内部，直线AD与BE交于点F．直接写出一个等式，表示线段AF，BF，CF之间的数量关系．27．【证明体验】（1）如图1，AD为△ABC的角平分线，∠ADC＝60°，点E在AB上，AE＝AC．求证：DE平分∠ADB．【思考探究】（2）如图2，在（1）的条件下，F为AB上一点，连结FC交AD于点G．若FB＝FC，DG＝2，CD＝3，求BD的长．【拓展延伸】（3）如图3，在四边形ABCD中，对角线AC平分∠BAD，∠BCA＝2∠DCA，点E在AC上，∠EDC＝∠ABC．若BC＝5，CD＝2，AD＝2AE，求AC的长．28．已知，在△ABC中，∠BAC＝90°，AB＝AC．（1）如图1，已知点D在BC边上，∠DAE＝90°，AD＝AE，连结CE．试探究BD与CE的关系；（2）如图2，已知点D在BC下方，∠DAE＝90°，AD＝AE，连结CE．若BD⊥AD，AB＝2，CE＝2，AD交BC于点F，求AF的长；（3）如图3，已知点D在BC下方，连结AD、BD、CD．若∠CBD＝30°，∠BAD＞15°，AB2＝6，AD2＝4+，求sin∠BCD的值．29．在平面直角坐标系中，点A的坐标为（﹣，0），点B在直线l：y＝x上，过点B 作AB的垂线，过原点O作直线l的垂线，两垂线相交于点C．（1）如图，点B，C分别在第三、二象限内，BC与AO相交于点D．①若BA＝BO，求证：CD＝CO．②若∠CBO＝45°，求四边形ABOC的面积．（2）是否存在点B，使得以A，B，C为顶点的三角形与△BCO相似？若存在，求OB 的长；若不存在，请说明理由．30．如图，△OAB的顶点坐标分别为O（0，0），A（3，4），B（6，0），动点P、Q同时从点O出发，分别沿x轴正方向和y轴正方向运动，速度分别为每秒3个单位和每秒2个单位，点P到达点B时点P、Q同时停止运动．过点Q作MN∥OB分别交AO、AB于点M、N，连接PM、PN．设运动时间为t（秒）．（1）求点M的坐标（用含t的式子表示）；（2）求四边形MNBP面积的最大值或最小值；（3）是否存在这样的直线l，总能平分四边形MNBP的面积？如果存在，请求出直线l 的解析式；如果不存在，请说明理由；（4）连接AP，当∠OAP＝∠BPN时，求点N到OA的距离．参考答案1．解：延长EA交x轴于点G，过点F作FH⊥x轴于点H，如图，∵AB∥x轴，AE⊥CD，AB∥CD，∴AG⊥x轴．∵AO⊥AD，∴∠DAE+∠OAG＝90°．∵AE⊥CD，∴∠DAE+∠D＝90°．∴∠D＝∠OAG．在△DAE和△AOG中，．∴△DAE≌△AOG（AAS）．∴DE＝AG，AE＝OG．∵四边形ABCD是菱形，DE＝4CE，∴AD＝CD＝DE．设DE＝4a，则AD＝OA＝5a．∴OG＝AE＝．∴EG＝AE+AG＝7a．∴E（3a，7a）．∵反比例函数y＝（x＞0）的图象经过点E，∴k＝21a2．∵AG⊥GH，FH⊥GH，AF⊥AG，∴四边形AGHF为矩形．∴HF＝AG＝4a．∵点F在反比例函数y＝（x＞0）的图象上，∴x＝．∴F（）．∴OH＝a，FH＝4a．∴GH＝OH﹣OG＝．∵S△OEF＝S△OEG+S梯形EGHF﹣S△OFH，S△EOF＝，∴．××﹣＝．解得：a2＝．∴k＝21a2＝21×＝．故选：A．2．解：（1）连接CE，过点F作FQ⊥BC于Q，∵BE平分∠ABC，∠BAC＝90°，∴F A＝FQ，∵AB＝AC，∴∠ABC＝∠ACB＝45°，∴FQ＝CF，∵∠BAC+∠DAE＝180°，∴∠DAE＝∠BAC＝90°，∴∠BAD＝∠CAE，由旋转知，AD＝AE，∴△ABD≌△ACE（SAS），∴BD＝CE＝2，∠ABD＝∠ACE＝45°，∴∠BCE＝90°，∴∠CBF+∠BEC＝90°，∵BE平分∠ABC，∴∠ABF＝∠CBF，∴∠ABF+∠BEC＝90°，∵∠BAC＝90°，∴∠ABF+∠AFB＝90°，∴∠AFB＝∠BEC，∵∠AFB＝∠CFE，∴∠BEC＝∠CFE，∴CF＝CE＝2，∴AF＝FQ＝CF＝；（2）AG＝CD，理由：延长BA至点M，使AM＝AB，连接EM，∵G是BE的中点，∴AG＝ME，∵∠BAC+∠DAE＝∠BAC+∠CAM＝180°，∴∠DAE＝∠CAM，∴∠DAC＝∠EAM，∵AB＝AM，AB＝AC，∴AC＝AM，∵AD＝AE，∴△ADC≌△AEM（SAS），∴CD＝EM，∴AG＝CD；（3）如图3，连接DE，AD与BE的交点记作点N，∵∠BAC+∠DAE＝180°，∠BAC＝120°，∴∠DAE＝60°，∵AD＝AE，∴△ADE是等边三角形，∴AE＝DE，∠ADE＝∠AED＝60°，∵∠AEC＝150°，∴∠DEC＝∠AEC﹣∠AED＝90°，在△ABC中，AB＝AC，∠BAC＝120°，∴∠ACB＝∠ABC＝30°，∵∠AEC＝150°，∴∠ABC+∠AEC＝180°，∴点A，B，C，E四点共圆，∴∠BEC＝∠BAC＝120°，∴∠BED＝∠BEC﹣∠DEC＝30°，∴∠DNE＝180°﹣∠BED﹣∠ADE＝90°，∵AE＝DE，∴AN＝DN，∴BE是AD的垂直平分线，∴AG＝DG，BA＝BD＝AC，∴∠ABE＝∠DBE＝∠ABC＝15°，∴∠ACE＝∠ABE＝15°，∴∠DCE＝45°，∵∠DEC＝90°，∴∠EDC＝45°＝∠DCE，∴DE＝CE，∴AD＝DE，设AG＝a，则DG＝a，由（2）知，AG＝CD，∴CD＝2AG＝2a，∴CE＝DE＝CD＝a，∴AD＝a，∴DN＝AD＝a，过点D作DH⊥AC于H，在Rt△DHC中，∠ACB＝30°，CD＝2a，∴DH＝a，根据勾股定理得，CH＝a，在Rt△AHD中，根据勾股定理得，AH＝＝a，∴AC＝AH+CH＝a+a，∴BD＝a+a，∴＝＝．3．解：（1）∵四边形ABCD和四边形AEGF都是正方形，∴AD＝AB，AF＝AE，∠DAE＝∠BAF＝90°，∴△DAE≌△BAF（SAS），∴DE＝BF，∠ADE＝∠ABF，∵∠ABF+∠AFB＝90°，∴∠ADE+∠AFB＝90°，在Rt△BAF中，M是BF的中点，∴AM＝FM＝BM＝BF，∴DE＝2AM．∵AM＝FM，∴∠AFB＝∠MAF，又∵∠ADE+∠AFB＝90°，∴∠ADE+∠MAF＝90°，∴∠AND＝180°﹣（∠ADE+∠MAF）＝90°，即AN⊥DN；故答案为DE＝2AM，DE⊥AM．（2）仍然成立，证明如下：延长AM至点H，使得AM＝MH，连接FH，∵M是BF的中点，∴BM＝FM，又∵∠AMB＝∠HMF，∴△AMB≌△HMF（SAS），∴AB＝HF，∠ABM＝∠HFM，∴AB∥HF，∴∠HFG＝∠AGF，∵四边形ABCD和四边形AEGF是正方形，∴∠DAB＝∠AFG＝90°，AE＝AF，AD＝AB＝FH，∠EAG＝∠AGF，∴∠EAD＝∠EAG+∠DAB＝∠AFG+∠AGF＝∠AFG+∠HFG＝∠AFH，∴△EAD≌△AFH（SAS），∴DE＝AH，又∵AM＝MH，∴DE＝AM+MH＝2AM，∵△EAD≌△AFH，∴∠ADE＝∠FHA，∵△AMB≌△HMF，∴∠FHA＝∠BAM，∴∠ADE＝∠BAM，又∵∠BAM+∠DAM＝∠DAB＝90°，∴∠ADE+∠DAM＝90°，∴∠AND＝180°﹣（∠ADE+∠DAM）＝90°，即AN⊥DN．故线段DE与AM之间的数量关系是DE＝2AM．线段DE与AM之间的位置关系是DE ⊥AM．4．解：（1）方法一：如图1，连接PB，PC，∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，AD＝BC，∵α＝120°，即∠BAD＝120°，∴∠B＝∠ADC＝60°，∴∠BEP＝60°＝∠B，由旋转知：EP＝EB，∴△BPE是等边三角形，∴BP＝EP，∠EBP＝∠BPE＝60°，∴∠CBP＝∠ABC+∠EBP＝120°，∵∠AEP＝180°﹣∠BEP＝120°，∴∠AEP＝∠CBP，∵DE平分∠ADC，∴∠ADE＝∠CDE＝30°，∴∠AED＝∠CDE＝30°＝∠ADE，∴AD＝AE，∴AE＝BC，∴△APE≌△CPB（SAS），∴AP＝CP，∠APE＝∠CPB，∴∠APE+∠CPE＝∠CPB+∠CPE，即∠APC＝∠BPE＝60°，∴△APC是等边三角形，方法二：如图1，延长PE交CD于点Q，连接AQ，∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，∵α＝120°，即∠BAD＝120°，∴∠B＝∠ADC＝60°，∴∠BEP＝60°＝∠B，∴PE∥BC∥AD，∴四边形ADQE和四边形BCQE是平行四边形，∵DE平分∠ADC，∴∠ADE＝∠CDE＝30°，∴∠AED＝∠CDE＝30°＝∠ADE，∴AD＝AE，∴四边形ADQE是菱形，∴∠EAQ＝∠AEQ＝60°，∴△AEQ是等边三角形，∴AE＝AQ，∠AQE＝60°，∵四边形BCQE是平行四边形，∴PE＝BE＝CQ，∠B＝∠CQE＝60°，∵∠AEP＝120°，∠AQC＝∠AQE+∠CQE＝120°，∴∠AEP＝∠AQC，∴△AEP≌△AQC（SAS），∴AP＝AC；（2）AB2+AD2＝2AF2，理由：如图2，连接CF，在▱ABCD中，∠BAD＝90°，∴∠ADC＝∠ABC＝∠BAD＝90°，AD＝BC，∵DE平分∠ADC，∴∠ADE＝∠CDE＝45°，∴∠AED＝∠ADE＝45°，∴AE＝BC，∵BF⊥EP，∴∠BFE＝90°，∵∠BEF＝α＝∠BAD＝×90°＝45°，∴∠EBF＝∠BEF＝45°，∴BF＝EF，∵∠FBC＝∠FBE+∠ABC＝45°+90°＝135°，∠AEF＝180°﹣∠FEB＝135°，∴∠CBF＝∠AEF，∴△BCF≌△EAF（SAS），∴CF＝AF，∠CFB＝∠AFE，∴∠AFC＝∠AFE+∠CFE＝∠CFB+∠CFE＝∠BFE＝90°，∴∠ACF＝∠CAF＝45°，∵sin∠ACF＝，∴AC＝＝＝＝AF，在Rt△ABC中，AB2+BC2＝AC2，∴AB2+AD2＝2AF2；（3）方法一：由（1）知，BC＝AD＝AE＝AB﹣BE，∵BE＝AB，AB＝CD，∴AB＝CD＝2BE，设BE＝a，则PE＝AD＝AE＝a，AB＝CD＝2a，①当点E在AB上时，如图3，过点G作GM⊥AD于点M，作GN⊥CD于点N，过点C作CK⊥AD于点K，过点A作AH⊥PE的延长线于点H，当α＝120°时，∠B＝∠ADC＝60°，∵DE平分∠ADC，GM⊥AD，GN⊥CD，∴GM＝GN，∵S△ACD＝AD•CK＝a•2a•sin60°＝a2，＝＝＝＝2，∴S△CDG＝2S△ADG，∴S△CDG＝S△ACD＝a2，由（1）知PE∥BC，∴∠AEH＝∠B＝60°，∵∠H＝90°，∴AH＝AE•sin60°＝a，∴S△APE＝PE•AH＝a•a＝a2，∴＝＝．②如图4，当点E在AB延长线上时，由①同理可得：S△CDG＝S△ACD＝××2a××3a＝a2，S△APE＝PH•AE＝×a×3a＝a2，∴＝＝，综上所述，△APE与△CDG面积的比值为或．方法二：如图3，∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，AB＝CD，∴△AEG∽△CDG，∴＝（）2，＝，①当点E在AB上时，∵BE＝AB，∴AE＝BE＝AB＝CD，∴＝（）2＝，又∵＝＝，∴＝，即＝3，∴＝＝3，当α＝120°时，∠B＝∠ADC＝60°，∵DE平分∠ADC，∴∠ADE＝30°，∴∠AED＝180°﹣∠BAD﹣∠ADE＝30°＝∠ADE，∴AE＝AD，∵EP＝EB＝AE，EP∥AD，∴EP＝AD＝AE，∠AEP＝∠DAE＝120°，∴△AED≌△EAP（SAS），∴S△AED＝S△EAP，∴＝•＝•＝3×＝；②如图4，当点E在AB延长线上时，∵BE＝AB，∴AE＝AB＝CD，由①知，AD＝AE＝CD，∵EP＝BE＝AE＝AD，EP∥AD，∴＝＝，∵＝＝，∴＝，∴＝＝，∵＝（）2＝（）2＝，∴＝••＝××＝；综上所述，△APE与△CDG面积的比值为或．5．解：（1）猜想：OC＝OD．理由：如图1中，∵AC⊥CD，BD⊥CD，∴∠ACO＝∠BDO＝90°在△AOC与△BOD中，，∴△AOC≌△BOD（AAS），∴OC＝OD，故答案为：OC＝OD；（2）数量关系依然成立．理由：过点O作直线EF∥CD，交AC的延长线于点E，∵EF∥CD，∴∠DCE＝∠E＝∠CDF＝90°，∴四边形CEFD为矩形，∴∠OFD＝90°，CE＝DF，由（1）知，OE＝OF，在△COE与△DOF中，，∴△COE≌DOF（SAS），∴OC＝OD；（3）①结论成立．理由：如图3中，延长CO交BD的延长线于点E，∵AC⊥CD，BD⊥CD，∴AC∥BD，∴∠ACO＝∠E，∵点O为AB的中点，∴AO＝BO，又∵∠AOC＝∠BOE，∴△AOC≌△BOE（AAS），∴CO＝OE，∵∠CDE＝90°，∴OD＝OC＝OE，∴OC＝OD．②结论：AC+BD＝OC．理由：如图3中，∵∠COD＝60°，OD＝OC，∴△COD是等边三角形，∴CD＝OC，∠OCD＝60°，∵∠CDE＝90°，∴tan60°＝，∴DE＝CD，∵△AOC≌△BOE，∴AC＝BE，∴AC+BD＝BD+BE＝DE＝CD，∴AC+BD＝OC．6．解：（1）如图，在Rt△PDQ中，AD＝cm，∠PQD＝60°，∴tan60°＝＝，∴DQ＝AD＝1cm．（2）点P在AB上运动时间为3÷1＝3（s），∴点P在BC上时PB＝（x﹣3）．（3）当0≤x≤3时，点P在AB上，作PM⊥CD于点M，PQ交AB于点E，作EN⊥CD 于点N，同（1）可得MQ＝AD＝1cm．∴DQ＝DM+MQ＝AP+MQ＝（x+1）cm，当x+1＝3时x＝2，∴0≤x≤2时，点Q在DC上，∵tan∠BDC＝＝，∴∠DBC＝30°，∵∠PQD＝60°，∴∠DEQ＝90°．∵sin30°＝＝，∴EQ＝DQ＝，∵sin60°＝＝，∴EN＝EQ＝（x+1）cm，∴y＝DQ•EN＝（x+1）×（x+1）＝（x+1）2＝x2+x+（0≤x≤2）．当2＜x≤3时，点Q在DC延长线上，PQ交BC于点F，如图，∵CQ＝DQ﹣DC＝x+1﹣3＝x﹣2，tan60°＝，∴CF＝CQ•tan60°＝（x﹣2）cm，∴S△CQF＝CQ•CF＝（x﹣2）×（x﹣2）＝（x2﹣2x+2）cm2，∴y＝S△DEQ﹣S△CQF＝x2+x+﹣（x2﹣2x+2）＝（﹣x2+x﹣）cm2（2＜x≤3）．当3＜x≤4时，点P在BC上，如图，∵CP＝CB﹣BP＝﹣（x﹣3）＝（4﹣x）cm，∴y＝DC•CP＝×3（4﹣x）＝6﹣x（3＜x≤4）．综上所述，y＝7．（1）证明：如图①中，∵EA＝ED，∠EAD＝45°，∴∠EAD＝∠EDA＝45°，∴∠AED＝90°，∵BF＝FD，∴EF＝DB，∵∠CAB＝90°，∴∠CAD＝∠BAD＝45°，∵∠ABC＝∠AED＝45°，∴∠ACB＝∠ABC＝45°，∴AD垂直平分线段BC，∴DC＝DB，∴EF＝CD．（2）解：如图②中，结论：EF＝CD．理由：取CD的中点T，连接AT，TF，ET，TE交AD于点O．∵∠CAD＝90°，CT＝DT，∴AT＝CT＝DT，∵EA＝ED，∴ET垂直平分线段AD，∴AO＝OD，∵∠AED＝90°，∴OE＝OA＝OD，∵CT＝TD，BF＝DF，∴BC∥FT，∴∠ABC＝∠OFT＝45°，∵∠TOF＝90°，∴∠OTF＝∠OFT＝45°，∴OT＝OF，∴AF＝ET，∵FT＝TF，∠AFT＝∠ETF，F A＝TE，∴△AFT≌△ETF（SAS），∴EF＝CD．如图③中，结论：EF＝CD．理由：取AD的中点O，连接OF，OE．∵EA＝ED，∠AED＝60°，∴△ADE是等边三角形，∵AO＝OD，∴OE⊥AD，∠AEO＝∠OED＝30°，∴tan∠AEO＝＝，∴＝，∵∠ABC＝∠AED＝30°，∠BAC＝90°，∴AB＝AC，∵AO＝OD，BF＝FD，∴OF＝AB，∴＝，∴＝，∵OF∥AB，∴∠DOF＝∠DAB，∵∠DOF+∠EOF＝90°，∠DAB+∠DAC＝90°，∴∠EOF＝∠DAC，∴△EOF∽△DAC，∴＝＝，∴EF＝CD．8．解：（1）如图1，连接BD，∵△ABC是等边三角形，∴AB＝BC，∠ABC＝60°，在△BAP和△BCD中，，∴△BAP≌△BCD（SAS），∴BP＝BD，∠ABP＝∠CBD，∵∠ABP+∠PBC＝60°，∴∠CBD+∠PBC＝60°，即∠PBD＝60°，∴△BDP是等边三角形，∴∠BPD＝60°，∵BC是⊙O的直径，∴∠BPC＝90°，∴∠CPD＝∠BPC﹣∠BPD＝90°﹣60°＝30°；（2）如图2，连接AP交BC于D，∵△ABC是等边三角形，∴AB＝AC＝BC，∠ABC＝∠ACB＝60°，∵BP＝CP，∴AD⊥BC，BD＝CD＝BC＝AB，∴AD＝AB•sin∠ABC＝AB•sin60°＝AB，∵AB＝4BP，∴BP＝AB，∴PD＝＝＝AB，∴PD＝AD，即点P是AD的中点，∵EC＝3BE，∴BE＝BC，BC＝4BE，∵BD＝BC，∴BE＝BD，即点E是BD的中点，∴EP是△ABD的中位线，∴EF∥AB，∴△CEF∽△CBA，∴＝＝＝，∴4EF＝3AB；（3）如图3，过点A作AD⊥BC于点D，过点P作PE⊥BC于点E，交AC于点F，作PH⊥AC于点H，由（2）得：AD＝AB＝3a，∠ACB＝60°，BC＝AC＝AB＝6a，∵∠CMP＝150°，∴∠PMF＝180°﹣∠CMP＝180°﹣150°＝30°，∵∠CHP＝90°，∴PH＝PM•sin∠PMF＝a•sin30°＝a，MH＝PM•cos∠PMF＝a•cos30°＝a，∵EF⊥BC，∴∠CEF＝90°，∴∠CFE＝90°﹣∠ACB＝90°﹣60°＝30°，∴∠CFE＝∠PMF，∴PF＝PM＝a，∴FH＝PF•cos∠PFH＝a•cos30°＝a，∵AM＝2MC，∴CM＝AC＝×6a＝2a，∴CF＝CM++MH+HF＝5a，∴EF＝CF•sin∠ACB＝5a•sin60°＝a，∴PE＝EF﹣PF＝a﹣a＝a，∴S1﹣S2＝S△ABC﹣S△BCP＝BC•AD﹣BC•PE＝BC•（AD﹣PE）＝×6a×（3a ﹣a）＝a2．9．（1）证明：如图，连接EC，∵∠BAC＝∠DAE＝90°，∠ABC＝∠ADE＝45°，∴△ABC和△ADE为等腰直角三角形，∴AB＝AC，AD＝AE，∠BAC+∠CAD＝∠DAE+∠CAD，即∠BAD＝∠CAE，在△BAD与△CAE中，，∴△BAD≌△CAE（SAS），∴∠ABD＝∠ACE＝45°，∴∠ACB+∠ACE＝90°，则CE⊥BD，∵AF⊥BD，∴AF∥CE，BF＝FC，∴＝＝1，∴BG＝EG．（2）解：如图，过点D作DM⊥AG，垂足为点M，过点C作CN⊥AG，交AG的延长线于点N，在△ABC和△AED中，∠BAC＝∠DAE＝90°，∠ACB＝∠ADE＝30°，设AE＝a，AB＝b，则AD＝a，AC＝b，∵∠1+∠EAF＝90°，∠2+∠EAF＝90°，∴∠1＝∠2，∴sin∠1＝sin∠2，∴＝，即＝＝＝，同理可证∠3＝∠4，＝＝，∴＝，∴DM＝CN，在△DGM和△CGN中，有：，∴△DGM≌△CGN（AAS），∴DG＝CG，∴＝1．10．解：（1）①当n＝60时，△ABC和△DEC均为等边三角形，∴BC＝AC，EC＝DC，又∵BE＝BC﹣EC，AD＝AC﹣DC，∴BE＝AD，故答案为：BE＝AD；②BE＝AD，理由如下：当点D不在AC上时，∵∠ACB＝∠ACD+∠DCB＝60°，∠DCE＝∠BCE+∠DCB＝60°，∴∠ACD＝∠BCE，在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴AD＝BE；（2）①BE＝AD，理由如下：当n＝90时，在等腰直角三角形DEC中：＝sin45，在等腰直角三角形ABC中：＝，∵∠ACB＝∠ACE+∠ECB＝45°，∠DCE＝∠ACE+∠DCA＝45°，∴∠ECB＝∠DCA在△DCA和△ECB中，，∴△DCA∽△ECB，∴，∴BE＝，②DC＝5或，理由如下：当点D在△ABC外部时，设EC与AB交于点F，如图所示：∵AB＝3，AD＝1由上可知：AC＝AB＝3，BE＝＝，又∵BE∥AC，∴∠EBF＝∠CAF＝90°，而∠EFB＝∠CF A，∴△EFB∽△CF A，∴＝＝，∴AF＝3BF，而AB＝BF+AF＝3，∴BF＝＝，在Rt△EBF中：EF＝＝＝，又∵CF＝3EF＝3×＝，∴EC＝EF+CF＝＝5（或EC＝4EF＝5），在等腰直角三角形DEC中，DC＝EC•cos45°＝5×＝5．当点D在△ABC内部时，过点D作DH⊥AC于H∵AC＝3，AD＝1，∠DAC＝45°∴AH＝DH＝，CH＝AC﹣AH＝，∴CD＝＝＝，综上所述，满足条件的CD的值为5或．11．解：（1）四边形ABCD是垂美四边形．理由如下：如图2，连接AC、BD，∵AB＝AD，∴点A在线段BD的垂直平分线上，∵CB＝CD，∴点C在线段BD的垂直平分线上，∴直线AC是线段BD的垂直平分线，∴AC⊥BD，即四边形ABCD是垂美四边形；（2）AB2+CD2＝AD2+BC2，理由如下：如图1中，∵AC⊥BD，∴∠AOD＝∠AOB＝∠BOC＝∠COD＝90°，由勾股定理得，AD2+BC2＝AO2+DO2+BO2+CO2，AB2+CD2＝AO2+BO2+CO2+DO2，∴AD2+BC2＝AB2+CD2；（3）如图3，连接CG、BE，∵正方形ACFG和正方形ABDE，∴AG＝AC，AB＝AE，∠CAG＝∠BAE＝90°，∴∠CAG+∠BAC＝∠BAE+∠BAC，即∠GAB＝∠CAE，在△GAB和△CAE中，，∴△GAB≌△CAE（SAS），∴∠ABG＝∠AEC，∵∠AEC+∠AME＝90°，∴∠ABG+∠AME＝90°，∵∠AME＝∠BMN，∴∠ABG+∠BMN＝90°，即CE⊥BG，∴四边形CGEB是垂美四边形，由（2）得，CG2+BE2＝CB2+GE2，∵AC＝4，AB＝5，∴BC＝＝＝3，∵CG＝＝＝4，BE＝＝＝5，∴GE2＝CG2+BE2﹣CB2＝（4）2+（5）2﹣32＝73，∴GE＝．12．解：（1）∵四边形ABCD为正方形，∴CD＝AD，∠DCE＝∠DAF＝90°，∵CE＝AF，∴△DCE≌△DAF（SAS）；（2）①∵△DCE≌△DAF，∴DE＝DF，∠CDE＝∠ADF，∴∠FDE＝∠ADF+∠ADE＝∠CDE+∠ADE＝∠ADC＝90°，∴△DFE为等腰直角三角形，∵DH⊥EF，∴点H是EF的中点，∴DH＝EF，同理，由HB是Rt△EBF的中线得：HB＝EF，∴HD＝HB；②∵四边形ABCD为正方形，故CD＝CB，∵HD＝HB，CH＝CH，∴△DCH≌△BCH（SSS），∴∠DCH＝∠BCH＝45°，∵△DEF为等腰直角三角形，∴∠DFE＝45°，∴∠HCE＝∠DFK，∵四边形ABCD为正方形，∴AD∥BC，∴∠DKF＝∠HEC，∴△DKF∽△HEC，∴，∴DK•HC＝DF•HE，在等腰直角三角形DFH中，DF＝HF＝HE，∴DK•HC＝DF•HE＝HE2＝，∴HE＝1．13．（1）解：如图1中，∵四边形ABCD是正方形，∴AB＝AD＝BC＝CD，∠BAD＝90°，∴ABC，△ADC都是等腰三角形，∵∠BAE＝∠CAE，∠DAF＝∠CAF，∴∠EAF＝（∠BAC+∠DAC）＝45°，∵∠BAE＝∠DAF＝22.5°，∠B＝∠D＝90°，AB＝AD，∴△BAE≌△DAF（ASA），∴BE＝DF，AE＝AF，∵CB＝CD，∴CE＝CF，∴△AEF，△CEF都是等腰三角形，故答案为：45，△AEF，△EFC，△ABC，△ADC．（2）解：结论：PQ＝BP+DQ．理由：如图2中，延长CB到T，使得BT＝DQ．∵AD＝AB，∠ADQ＝∠ABT＝90°，DQ＝BT，∴△ADQ≌△ABT（SAS），∴AT＝AQ，∠DAQ＝∠BAT，∵∠P AQ＝45°，∴∠P AT＝∠BAP+∠BAT＝∠BAP+∠DAQ＝45°，∴∠P AT＝∠P AQ＝45°，∵AP＝AP，∴△P AT≌△P AQ（SAS），∴PQ＝PT，∵PT＝PB+BT＝PB+DQ，∴PQ＝BP+DQ．故答案为：PQ＝BP+DQ．（3）解：如图3中，∵四边形ABCD是正方形，∴∠ABM＝∠ACQ＝∠BAC＝45°，AC＝AB，∵∠BAC＝∠P AQ＝45°，∴∠BAM＝∠CAQ，∴△CAQ∽△BAM，∴＝＝，故答案为：．（4）证明：如图4中，将△ADN绕点A顺时针旋转90°得到△ABR，连接RM．∵∠BAD＝90°，∠MAN＝45°，∴∠DAN+∠BAM＝45°，∵∠DAN＝∠BAR，∴∠BAM+∠BAR＝45°，∴∠MAR＝∠MAN＝45°，∵AR＝AN，AM＝AM，∴△AMR≌△AMN（SAS），∴RM＝MN，∵∠D＝∠ABR＝∠ABD＝45°，∴∠RBM＝90°，∴RM2＝BR2+BM2，∵DN＝BR，MN＝RM，∴BM2+DN2＝MN2．14．操作一：解：∵四边形ABCD是正方形，∴∠C＝∠BAD＝90°，由折叠的性质得：∠BAE＝∠MAE，∠DAF＝∠MAF，∴∠MAE+∠MAF＝∠BAE+∠DAF＝∠BAD＝45°，即∠EAF＝45°，故答案为：45；操作二：解：∵四边形ABCD是正方形，∴∠B＝∠C＝90°，由折叠的性质得：∠NFE＝∠CFE，∠ENF＝∠C＝90°，∠AFD＝∠AFM，∴∠ANF＝180°﹣90°＝90°，由操作一得：∠EAF＝45°，∴△ANF是等腰直角三角形，∴∠AFN＝45°，∴∠AFD＝∠AFM＝45°+∠NFE，∴2（45°+∠NFE）+∠CFE＝180°，∴∠NFE＝∠CFE＝30°，∴∠AEF＝90°﹣30°＝60°，故答案为：60；（1）证明：∵△ANF是等腰直角三角形，∴AN＝FN，∵∠AMF＝∠ANF＝90°，∠APN＝∠FPM，∴∠NAP＝∠NFE＝30°，在△ANP和△FNE中，，∴△ANP≌△FNE（ASA）；（2）由（1）得：△ANP≌△FNE，∴AP＝FE，PN＝EN，∵∠NFE＝∠CFE＝30°，∠ENF＝∠C＝90°，∴∠NEF＝∠CEF＝60°，∴∠AEB＝60°，∵∠B＝90°，∴∠BAE＝30°，∴BE＝AB＝1，∴AE＝2BE＝2，设PN＝EN＝a，∵∠ANP＝90°，∠NAP＝30°，∴AN＝PN＝a，AP＝2PN＝2a，∵AN+EN＝AE，∴a+a＝2，解得：a＝﹣1，∴AP＝2a＝2﹣2，故答案为：2﹣2．15．解：【类比探究】过点E作EF⊥CD于点F，连接AF，∵四边形ABCD是正方形，∴AD＝CD＝4，∠ADC＝90°，∵DE＝CE，EF⊥CD，∴DF＝CF＝CD＝2，∠ADC＝∠EFD＝90°，∴AD∥EF，∴S△ADE＝S△ADF，∴S△ADE＝×AD×DF＝×4×2＝4；【拓展应用】如图③，连接CF，∵四边形ABCD和四边形CGFE都是正方形，∴∠BDC＝45°，∠GCF＝45°，∴∠BDC＝∠GCF，∴BD∥CF，∴S△BDF＝S△BCD，∴S△BDF＝BC×BC＝8．16．解：（1）设EF＝m．∵BC＝14，BD＝6，∴CD＝BC﹣BD＝14﹣6＝8，∵AD＝8，∴AD＝DC＝8，∵AD⊥BC，∴∠ADC＝90°，∴AC＝AD＝8，∵四边形EFGH是正方形，∴EH＝FG＝GH＝EF＝m，∠EHG＝∠FGH＝90°，∴∠AHE＝∠FGC＝90°，∵∠DAC＝∠C＝45°，∴∠AEH＝∠EAH＝45°，∠GFC＝∠C＝45°，∴AH＝EH＝m，CG＝FG＝m，∴3m＝8，∴m＝，∴EF＝．（2）∵四边形EFGH是矩形，∴EF∥AC，∴∠DEF＝∠DAC，∠DFE＝∠C，∵∠DAC＝∠C，∴∠DEF＝∠DFE，∴DE＝DF＝x，DA＝DC＝8，∴AE＝CF＝8﹣x，∴EH＝AE＝（8﹣x），EF＝DE＝x，∴y＝＝＝，∴y＝（0＜x＜8）．（3）如图②中，由（2）可知点P在y＝上，设直线MN的解析式为y＝kx+b，把P（a，）代入得到，＝ka+b，∴b＝﹣ka，∴y＝kx+﹣ka，∴N（0，﹣ka），M（a﹣，0），∴ON＝﹣ka，OM＝a﹣∴△MON的面积＝•ON•OM＝×（6﹣a2k﹣）≥×（6+2）•＝6，∴△MON的面积的最小值＝6．解法二：过点P作PR⊥OM于M，PQ⊥ON于Q．设P（a，b），由△NQP∽△NOM，∴＝，设＝＝k，∴MO＝，NQ＝kON，ON＝，∴S△MON＝•OM•ON＝•＝•，∴k＝时，△OMN的面积的最小值为×＝6．17．解：（1）如图1，由作图得，OC＝OD，OE＝OF，PG垂直平分CE，PH垂直平分DF，∴∠PGO＝∠PHO＝90°，∵OE﹣OC＝OF﹣OD，。

专题04 有关全等三角形的常见压轴题(原卷版)-【聚焦压轴】2022届中考数学压轴大题专项训练

专题4 有关全等三角形的常见压轴题1．（2021·杏花岭·山西实验中学九年级月考）如图，平面直角坐标系中()2,0A ，()0,1D ，过O 作OB AD ⊥于点E ，B 为第一象限的点，过点B 作BC y ⊥轴于点C ，连接BC 、BA ．（1）求直线AD 的解析式；（2）若CD BC =，求证：OBC ADO ≌△△；（3）在第（2）问条件下，若点M 是直线AD 上的一个动点，在x 轴上存在另一个点N ，且以O 、B 、M 、N 为顶点的四边形是平行四边形，请直接写出点N 的坐标． 2．（2021·甘肃兰州十一中九年级月考）如图1，在△ABC 中，AB ＝AC ，AD 是△ABC 的一条角平分线，AN 为△ABC 的外角∠BAM 的平分线，BE ⊥AN ，垂足为E ．已知AD ＝4，BD ＝3．（1）求证：四边形ADBE 是矩形；（2）如图2，延长AD 至点F ，使AF ＝AB ，连接BF ，G 为BF 的中点，连接EG ，DG ．求EG 的长．（3）如图3，在（2）问的条件下，P 为BE 边上的一个动点，连接PG 并延长交AD 延长线于点Q ，连接CQ ，H 为CQ 的中点，求点P 从E 点运动到B 点时，点H 所经过的路径长．3．（2021·合肥市第四十八中学九年级开学考试）如图1，A ，B 分别在射线OM ，ON 上，且MON ∠为钝角，现以线段OA ，OB 为斜边向MON ∠的外侧作等腰直角三角形，分别是OAP △，OBQ △，点C ，D ，E 分别是OA ，OB ，AB 的中点．（1）求证：PCE EDQ ≌△△．（2）延长PC ，QD 交于点R ．①如图2，若150MON ∠=︒，求证：ABR △为等边三角形．②如图3，若ARB PEQ ∽△△，求MON ∠大小和AB PQ的值．4．（2021·辽宁建昌·九年级期末）已知在矩形ABCD 中，∠ADC 的平分线DE 与BC 交于点E ，点P 是线段DE 上一定点（其中EP ＜PD ）（1）如图1，若点F 在CD 边上（不与C ，D 重合），将∠DPF 绕点P 逆时针旋转90°后，角的两边PD ，PF 分别交射线DA 于点H ，G ．①直接写出PG 与PF 之间的数量关系；②猜想DF ，DG ，DP 的数量关系，并证明你的结论．（2）如图2，若点F 在CD 的延长线上（不与D 重合），将PF 绕点P 逆时针旋转90°，交射线DA 于点G ，判断（1）②中DF ，DG ，DP 之间的数量关系是否仍然成立？若成立，给出证明；若不成立，请直接写出它们所满足的数量关系式．5．（2021·佛山市华英学校九年级期末）已知正方形ABCD ，45MAN ∠=︒，MAN ∠绕点A 顺时针旋转，它的两边分别交CB 、DC 于点M 、N ，AH MN ⊥于点H ．（1）如图①，当BM DN =时，可以通过证明≌ADN ABM ，得到AH 与AB 的数量关系，这个数量关系是___________；（2）如图②，当BM DN ≠时，（1）中发现的AH 与AB 的数量关系还成立吗？说明理由；（3）如图③，已知AMN 中，45MAN ∠=︒，AH MN ⊥于点H ，3MH =，7=NH ，求AH 的长．6．（2021·沭阳县怀文中学九年级月考）已知：AOB ∆和COD △均为等腰直角三角形，90AOB COD ∠=∠=︒，连接AD ，BC ，点H 为BC 中点，连接OH ．（1）如图1所示，点C 、D 分别在边OA 、OB 上，求证：12OH AD =且OH AD ⊥；（2）将COD △绕点O 旋转到图2所示位置时，线段OH 与AD 又有怎样的关系，证明你的结论．（3）如图3所示，当8AB =，2CD =时，求OH 长的取值范围．7．（2021·青海西宁·中考真题）如图，在平面直角坐标系xOy 中，一次函数132y x =-+的图象与x 轴交于点A ，与y 轴交于点B ，点C 的坐标为()2,0-，抛物线经过A ，B ，C 三点．（1）求抛物线的解析式；（2）直线AD 与y 轴负半轴交于点D ，且BAO DAO ∠=∠，求证：OB OD =；（3）在（2）的条件下，若直线AD 与抛物线的对称轴l 交于点E ，连接BE ，在第一象限内的抛物线上是否存在一点P ，使四边形BEAP 的面积最大？若存在，请求出点P 的坐标及四边形BEAP 面积的最大值；若不存在，请说明理由．8．（2021·广州市黄埔华南师范大学附属初级中学九年级期中）在正方形ABCD 中，M 是BC 边上一点，且点M 不与B 、C 重合，点P 在射线AM 上，将线段AP 绕点A 顺时针旋转90°得到线段AQ ，连接BP ，DQ ．（1）依题意补全图1，并求证：ABP ADQ ≌△△．（2）连接DP ，若点P ，Q ，D 恰好在同一条直线上，求证：2222DP DQ AB +=． 9．（2021·哈尔滨市第十七中学校九年级二模）已知AB 、AC 是⊙O 的两条弦，OA 为半径，∠OAB ＝∠OAC ．（1）如图（1），求证：AB ＝AC ；（2）如图（2），延长AO 交⊙O 于点D ，点E 是BC 延长线上的一点，EF 切⊙O 于点F ，连DF 交BC 于点G ，求证：EF ＝EG ；（3）如图（3），在（2）的条件下，设DF 交AC 于点H ，若DF ∥AB ，tan E ＝43，CH 352求DG 长．10．（2021·河南平顶山·九年级期中）（1）阅读理解如图1，在正方形ABCD中，若E，F分别是CD，BC边上的点，∠EAF＝45°，则我们常常会想到：把∆ADE绕点A顺时针旋转90°，得到∆ABG．易证∆AEF≌，得出线段BF，DE，EF之间的关系为；（2）类比探究如图2，在等边∆ABC中，D，E为BC边上的点，∠DAE＝30°，BD＝1，EC＝2．求线段DE的长；（3）拓展应用如图3，在∆ABC中，AB＝AC＝62+，∠BAC＝150°，点D，E在BC边上，∠DAE＝75°，若DE是等腰ADE的腰，请直接写出线段BD的长．11．（2021·辽宁立山·九年级期中）已知：∠AOB＝∠COD＝90°，OA＝OB，OC＝OD．（OC22>OA）（1）如图1：连AC、BD，判断：AC与BD之间的关系；并说明理由．（2）若将△COD绕点O逆时针旋转，①如图2，当点C恰好在AB边上时，请写出AC、BC、OC之间数量关系；并说明理由．②当点B 、D 、C 在同一条直线上时，若OB ＝6，OC ＝5，求AC 的长．12．（2021·广西河池·中考真题）如图，在Rt ABC △中，90A ∠=︒，4AB =，3AC =，D ，E 分别是AB ，BC 边上的动点，以BD 为直径的圆O 交BC 于点F ．（1）当AD DF =时，求证：CFD CAD ∆≅∆；（2）当CED ∆是等腰三角形且DEB ∆是直角三角形时，求AD 的长．13．（2021·辽宁锦州·中考真题）在△ABC 中，AC ＝AB ，∠BAC ＝α，D 为线段AB 上的动点，连接DC ，将DC 绕点D 顺时针旋转α得到DE ，连接CE ，BE ．（1）如图1，当α＝60°时，求证：△CAD ≌△CBE ；（2）如图2，当tan α＝34时， ①探究AD 和BE 之间的数量关系，并说明理由；②若AC ＝5，H 是BC 上一点，在点D 移动过程中，CE ＋EH 是否存在最小值？若存在，请直接写出CE ＋EH 的最小值；若不存在，请说明理由．14．（2021·辽宁丹东·中考真题）已知,在正方形ABCD 中,点M ､N 为对角线AC 上的两个动点,且45MBN ∠=︒,过点M 、N 分别作AB ､BC 的垂线相交于点E ,垂足分别为F ､G ,设AFM △的面积为1S ,NGC ∆的面积为2S ,MEN ∆的面积为3S ．（1）如图（1）,当四边形EFBG 为正方形时,①求证:CGN AFM ∆≅∆;②求证:312S S S =+;（2）如图（2）,当四边形EFBG 为矩形时,写出1S ,2S ,3S 三者之间的数量关系,并说明理由; （3）在（2）的条件下,若()::BG GC m n m n =>,请直接写出:AF FB 的值．15．（2021·山东潍坊·中考真题）如图1，在△ABC 中，∠C =90°，∠ABC =30°，AC =1，D 为△ABC 内部的一动点（不在边上），连接BD ，将线段BD 绕点D 逆时针旋转60°，使点B 到达点F 的位置；将线段AB 绕点B 顺时针旋转60°，使点A 到达点E 的位置，连接AD ，CD ，AE ，AF ，BF ，EF ．（1）求证：△BDA ≌△BFE ；（2）①CD +DF +FE 的最小值为；②当CD +DF +FE 取得最小值时，求证：AD ∥BF ．（3）如图2，M ，N ，P 分别是DF ，AF ，AE 的中点，连接MP ，NP ，在点D 运动的过程中，请判断∠MPN 的大小是否为定值．若是，求出其度数；若不是，请说明理由．。

中考数学：以四边形为载体的几何压轴问题真题+模拟(原卷版北京专用)

中考数学以四边形为载体的几何压轴问题【方法归纳】北京市中考数学倒数第二道压轴题会以四边形为载体的几何压轴题出现，要求学生理解和掌握平行四边形、矩形、菱形、正方形的性质定理和判定定理，会画出四边形全等变换后的图形，并会结合其他知识解答一些有探索性、开放性的问题，提高解决问题的能力.解决此类问题的关键是要牢牢把握四边形的性质与特征，挖掘相关图形之间的联系，利用所给图形及图形之间形状、大小、位置关系，进行观察、实验、比较、联想、类比、分析、综合等.常用到的矩形、菱形、正方形的解题策略有：（1）对于矩形：①判定四边形是矩形，一般先判定是平行四边形，然后再判定是矩形；②矩形的内角是直角和对角线相等，相对于平行四边形来说是矩形特殊的性质；③利用矩形的性质计算或证明时，常常运用勾股定理，锐角三角函数或相似三角形求解．（2）对于菱形：①判定四边形是菱形，一般先判定是平行四边形，然后再判定是菱形；②菱形的邻边相等和对角线垂直，相对于平行四边形来说是菱形特殊的性质；③利用菱形的性质计算或证明时，常常运用勾股定理，锐角三角函数或相似三角形求解；④求线段和的最小值时，往往运用菱形的轴对称的性质转化为求线段的长度．（3）对于正方形：①判定四边形是正方形，一般先判定是平行四边形，然后再判定是矩形或菱形，最后判定这个四边形是正方形；②正方形是最特殊的四边形，在正方形的计算或证明时，要特别注意线段或角的等量转化．【典例剖析】【例1】（2018·北京·中考真题）如图，在正方形ABCD中，E是边AB上的一动点（不与点A、B重合），连接DE，点A关于直线DE的对称点为F，连接EF并延长交BC于点G，连接DG，过点E作EH⊥DE交DG的延长线于点H，连接BH．（1）求证：GF=GC；（2）用等式表示线段BH与AE的数量关系，并证明．【真题再现】1．（2014·北京·中考真题）在正方形ABCD外侧作直线AP，点B关于直线AP的对称点为E，连接BE，DE，其中DE交直线AP于点F．（1）依题意补全图1．（2）若∠PAB=20°，求∠ADF的度数．（3）如图2，若45°<∠PAB<∠90°，用等式表示线段AB，FE，FD之间的数量关系，并证明．2．（2015·北京·中考真题）在正方形ABCD中，BD是一条对角线.点P在射线CD上（与点C，D不重合），连接AP，平移△ADP，使点D移动到点C，得到△BCQ，过点Q作QH⊥BD于点H，连接AH、PH.（1）若点P在线CD上，如图1，①依题意补全图1；②判断AH与PH的数量关系与位置关系并加以证明；（2）若点P在线CD的延长线上，且∠AHQ＝152°，正方形ABCD的边长为1，请写出求DP长的思路.（可以不写出计算结果）3．（2013·北京·中考真题）请阅读下列材料：小明遇到这样一个问题：如图1，在边长为a(a＞2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1，当∠AFQ=∠BGM=∠CHN=∠DEP=45°时，求正方形MNPQ的面积．小明发现，分别延长QE，MF，NG，PH交F A，GB，HC，ED的延长线于点R，S，T，W，可得△RQF，△SMG，△TNH，△WPE是四个全等的等腰直角三角形(如图2) ．请回答：(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙不重叠)，则这个新正方形的边长为_________；(2)求正方形MNPQ的面积；(3)参考小明思考问题的方法，解决问题：如图3，在等边△ABC各边上分别截取AD=BE=CF，，求AD的再分别过点D，E，F作BC，AC，AB的垂线，得到等边△RPQ．若S△RPQ=√33长．4．（2016·北京·中考真题）如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN．（1）求证：BM=MN；（2）∠BAD=60°，AC平分∠BAD，AC=2，求BN的长．【模拟精练】1．（2022·北京昌平·模拟预测）两张宽度均为4的矩形纸片按如图所示方式放置(1)如图①，求证：四边形ABCD是菱形．(2)如图②，点P在BC上，PF⊥AD于F，若S四边形ABCD＝16√2，PB＝2，①求∠BAD的度数；②求DF的长．2．（2021·北京四中模拟预测）如图所示，四边形ABCD为菱形，AB＝2，∠ABC＝60°，点E为边BC上动点（不含端点），点B关于直线AE的对称点为点F，点G为DF中点，连接AG．（1）依题意，补全图形；（2）点E运动过程中，是否可能EF∥AG？若可能，求BE长；若不可能，请说明理由；（3）连接CG，点E运动过程中，直接写出CG的最小值．3．（2021·北京门头沟·一模）在正方形ABCD中，将边AD绕点A逆时针旋转a(0°<a<90°)得到线段AE，AE与CD延长线相交于点F，过B作BG//AF交CF于点G，连接BE．（1）如图1，求证：∠BGC=2∠AEB；（2）当（45°<a<90°）时，依题意补全图2，用等式表示线段AH，EF，DG之间的数量关系，并证明．4．（2020·北京亦庄实验中学二模）如图，在正方形ABCD中，E是边BC上一动点（不与点B，C重合），连接DE，点C关于直线DE的对称点为C′，连接AC′并延长交直线DE于点P，过点D作DF AP于F．（1）求∠FDP的度数；（2）连接BP，请用等式表示线段BP与线段AF之间的数量关系，并证明．（3）连接PC，若正方形的边长为√2，直接写出△BCP面积的最大值．5．（2020·北京四中模拟预测）在△ABC中，点D在AB边上（不与点B重合），DE⊥BC，垂足为点E，如果以DE为对角线的正方形上的所有点都在△ABC的内部或边上，则称该正方形为△ABC的内正方形．（1）如图，在△ABC中，AB=4，∠B=30°，点D是AB的中点，画出△ABC的内正方形，直接写出此时内正方形的面积；t,0)．（2）在平面直角坐标系xOy中，点A(t,2)，B(0,0)，C(32①若t=2，求△ABC的内正方形的顶点E的横坐标的取值范围；②若对于任意的点D，△ABC的内正方形总是存在，直接写出t的取值范围．6．（2020·北京延庆·一模）四边形ABCD 中，∠A＝∠B= 90°，点E在边AB上，点F在AD的延长线上，且点E与点F关于直线CD对称，过点E作EG∥AF交CD于点G，连接FG，DE．（1）求证：四边形DEGF 是菱形；（2）若AB＝10，AF＝BC=8，求四边形DEGF 的面积．7．（2019·北京·一模）如图1，正方形ABCD中，AB＝5，点E为BC边上一动点，连接AE，以AE为边，在线段AE右侧作正方形AEFG，连接CF、DF．设BE=x．(当点E与点B重合时，x的值为0)，DF=y，CF=y2．小明根据学习函数的经验，对函数y1、y2随自变量1x的变化而变化的规律进行了探究．下面是小明的探究过程，请补充完整：(1)通过取点、画图、测量、观察、计算，得到了x与y1、y2的几组对应值；(2)在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点(x ， y1) ， (x ， y2)，并画出函数y1，y2的图象；(3)结合函数图象2，解决问题：当△CDF为等腰三角形时，BE的长度约为cm．8．（2017·北京顺义·一模）在正方形ABCD和正方形DEFG中，顶点B、D、F在同一直线上，H是BF的中点．（1）如图1，若AB=1，DG=2，求BH的长；（2）如图2，连接AH，GH．小宇观察图2，提出猜想：AH=GH，AH⊥GH．小宇把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：想法1：延长AH交EF于点M，连接AG，GM，要证明结论成立只需证△GAM是等腰直角三角形；想法2：连接AC，GE分别交BF于点M，N，要证明结论成立只需证△AMH≌△HNG．…请你参考上面的想法，帮助小宇证明AH=GH，AH⊥GH．（一种方法即可）9．（2018·北京顺义·一模）如图1，在长方形ABCD中，AB=12cm，BC=10cm，点P从A出发，沿A→B→C→D的路线运动，到D停止；点Q从D点出发，沿D→C→B→A路线运动，到A点停止．若P、Q两点同时出发，速度分别为每秒1cm、2cm，a秒时P、Qcm(P、Q两点速度改变后一直保持此速度，直到两点同时改变速度，分别变为每秒2cm、54停止)，如图2是ΔAPD的面积s(cm2)和运动时间x(秒)的图象．(1)求出a值；(2)设点P已行的路程为y1(cm)，点Q还剩的路程为y2(cm)，请分别求出改变速度后，y1,y2和运动时间x(秒)的关系式；(3)求P、Q两点都在BC边上，x为何值时P，Q两点相距3cm？10．（2021·北京四中模拟预测）在平面直角坐标系xOy中，如果点A，点C为某个菱形的一组对角的顶点，且点A，C在直线y＝x上，那么称该菱形为点A，C的“极好菱形”．如图为点A，C的“极好菱形”的一个示意图．已知点M的坐标为（1，1），点P的坐标为（3，3）．（1）点E（2，1），F（1，3），G（4，0）中，能够成为点M，P的“极好菱形”的顶点的是；（2）如果四边形MNPQ是点M，P的“极好菱形”．①当点N的坐标为（3，1）时，求四边形MNPQ的面积；②当四边形MNPQ的面积为8，且与直线y＝x+b有公共点时，写出b的取值范围．11．（2021·北京四中九年级开学考试）定义：如果一条直线把一个平面图形的面积分成相等的两部分，我们把这条直线称为平面图形的一条面积等分线．（1）如图1，已知△ABC，请用尺规作出△ABC的一条面积等分线．（2）已知：如图2，在平面直角坐标系xOy中，矩形OABC的边OA在x轴的正半轴上、OC在y轴的正半轴上，OA=6,OC=4．①请判断直线y=43x−83是否为矩形OABC的面积等分线，并说明理由；②若矩形OABC的面积等分线与坐标轴所围成的三角形面积为4，请直接写出此面积等分线的函数表达式．（3）如图3，在△ABC中，点A的坐标为(−2,0)，点B的坐标为(4,3)，点C的坐标为(2,0)，点D的坐标(0,−2)，求过点D的一条△ABC的面积等分线的解析式．（4）在△ABC中点A的坐标为(−1,0)，点B的坐标为(1,0)，点C的坐标为(0,1)，直线y= ax+b(a>0)是△ABC的一条面积等分线，请直接写出b的取值范围．12．（2021·北京·九年级专题练习）如图，在四边形ABCD中，∠ACB=∠CAD=90°，点E在BC上，AE//DC,EF⊥AB，垂足为F．（1）求证：四边形AECD是平行四边形；（2）若AE平分∠BAC,BE=5,cosB=45，求BF和AD的长．13．（2021·北京·九年级专题练习）如图，在正方形ABCD中，AB=3，M是CD边上一动点（不与D点重合），点D与点E关于AM所在的直线对称，连接AE，ME，延长CB到点F，使得BF=DM，连接EF，AF．（1）依题意补全图1；（2）若DM=1，求线段EF的长；（3）当点M在CD边上运动时，能使△AEF为等腰三角形，直接写出此时tan∠DAM的值．14．（2021·北京石景山·九年级期末）已知矩形MBCD的顶点M是线段AB上一动点，AB=BC，矩形MBCD的对角线交于点O，连接MO，BO．点P为射线OB上一动点（与点B不重合），连接PM，作PN⊥PM交射线CB于点N．（1）如图1，当点M与点A重合时，且点P在线段OB上．①依题意补全图1；②写出线段PM与PN的数量关系并证明．（2）如图2，若∠OMB=α，当点P在OB的延长线上时，请补全图形并直接写出PM与PN的数量关系．15．（2020·北京·北师大实验中学九年级开学考试）如图，在正方形ABCD中，AB=6，M是CD边上一动点（不与D点重合），点D与点E关于AM所在的直线对称，连接AE，ME，延长CB 到点F，使得BF=DM，连接EF，AF．（1）当DM=2时，依题意补全图1；（2）在（1）的条件下，求线段EF的长；（3）当点M在CD边上运动时，能使△AEF为等腰三角形，请直接写出此时DM与AD的数量关系________．16．（2017·全国·九年级专题练习）猜想与证明：如图①摆放矩形纸片ABCD与矩形纸片ECGF，使B，C，G三点在一条直线上，CE在边CD上．连结AF，若M为AF的中点，连结DM，ME，试猜想DM与ME的数量关系，并证明你的结论．拓展与延伸：(1)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF，其他条件不变，则DM和ME的关系为__________________；(2)如图②摆放正方形纸片ABCD与正方形纸片ECGF，使点F在边CD上，点M仍为AF的中点，试证明(1)中的结论仍然成立．[提示：直角三角形斜边上的中线等于斜边的一半]①②17．（2020·北京通州·一模）已知线段AB，过点A的射线l⊥AB．在射线l上截取线段AC=AB，连接BC，点M为BC的中点，点P为AB边上一动点，点N为线段BM上一动点．以点P为旋转中心，将△BPN逆时针旋转90°得到△DPE,B的对应点为D,N的对应点为E．(1)当点N与点M重合，且点P不是AB中点时，①据题意在图中补全图形；②证明：以A,M,E,D为顶点的四边形是矩形．(2)连接EM，若AB=4，从下列3个条件中选择1个：①BP=1，②PN=1，③BN=√2，当条件______(填入序号)满足时，一定有EM=EA，并证明这个结论．18．（2020·北京一七一中九年级阶段练习）在四边形ABCD中，∠B+∠D=180°，对角线AC 平分∠BAD．（1）如图1，若∠DAB=120°，且∠B=90°，直接写出线段AD、AB、AC的数量关系．（2）如图2，若将（1）中的条件“∠B=90°”去掉，求边AD、AB与对角线AC的数量关系．请证明．（3）如图3，若∠DAB=2αAD、AB与对角线AC的数量关系（用α来表示）19．（2020·北京四中九年级阶段练习）在菱形ABCD中，∠BAD=60°．（1）如图1，点E为线段AB的中点，连接DE，CE．若AB=4，求线段EC的长．（2）如图2，M为线段AC上一点（不与A，C重合），以AM为边向上构造等边三角形△AMN，线段AN与AD交于点G，连接NC，DM，Q为线段NC的中点．连接DQ，MQ，判断DM与DQ的数量关系，并证明你的结论．（3）在（2）的条件下，若AC=√3，请你直接写出DM+CN的最小值．20．（2020·北京顺义·九年级期末）已知：如图，在正方形ABCD中，点E在AD边上运动，从点A出发向点D运动，到达D点停止运动．作射线CE，并将射线CE绕着点C逆时针旋转45°，旋转后的射线与AB边交于点F，连接EF（1）依题意补全图形；（2）猜想线段DE，EF，BF的数量关系并证明；（3）过点C作CG⊥EF，垂足为点G，若正方形ABCD的边长是4，请直接写出点G运动的路线长．21．（2022·北京·九年级单元测试）图1，菱形ABCD的顶点A，D在直线上，∠BAD＝60°，以点A为旋转中心将菱形ABCD顺时针旋转α（0°＜α＜30°），得到菱形AB′C′D′，B′C′交对角线AC于点M，C′D′交直线l于点N，连接MN．（1）当MN∥B′D′时，求α的大小．（2）如图2，对角线B′D′交AC于点H，交直线l与点G，延长C′B′交AB于点E，连接EH．当△HEB′的周长为2时，求菱形ABCD的周长．22．（2022·北京·九年级单元测试）综合与实践动手操作：第一步：如图1，正方形纸片ABCD沿对角线AC所在直线折叠，展开铺平.在沿过点C的直线折叠，使点B，点D都落在对角线AC上.此时，点B与点D重合，记为点N，且点E，点N，点F三点在同一直线上，折痕分别为CE，CF.如图2.第二步：再沿AC所在的直线折叠，△ACE与△ACF重合，得到图3第三步：在图3的基础上继续折叠，使点C与点F重合，如图4，展开铺平，连接EF，FG，GM，ME，如图5，图中的虚线为折痕.问题解决：(1)在图5中，∠BEC的度数是，AE的值是；BE(2)在图5中，请判断四边形EMGF的形状，并说明理由；(3)在不增加字母的条件下，请你以图中5中的字母表示的点为顶点，动手画出一个菱形(正方形除外)，并写出这个菱形：.23．（2019·北京·101中学九年级阶段练习）在平行四边形ABCD中，E是AD上一点，AE=AB，过点E作射线EF，(1)若∠DAB=60°，EF∥AB交BC于点H，请在图1中补全图形，并直接写出四边形ABHE 的形状；(2)如图2，若∠DAB=90°，EF与AB相交，在EF上取一点G，使得∠EGB=∠EAB，连接AG.请在图2中补全图形，并证明点A，E，B，G在同一个圆上；(3)如图3，若∠DAB=α(0°<α<90°)，EF与AB相交，在EF上取一点G，使得∠EGB=∠EAB，连接AG.请在图3中补全图形(要求：尺规作图，保留作图痕迹)，并求出线段EG、AG、BG 之间的数量关系(用含α的式子表示)；24．（2022·北京朝阳·二模）在正方形ABCD中，E为BC上一点，点M在AB上，点N在DC上，且MN⊥DE，垂足为点F．(1)如图1，当点N与点C重合时，求证：MN=DE；(2)将图1中的MN向上平移，使得F为DE的中点，此时MN与AC相交于点H，①依题意补全图2；②用等式表示线段MH、HF，FN之间的数量关系，并证明．25．（2022·北京四中模拟预测）已知，点B是射线AP上一动点，以AB为边作△ABC，∠BCA= 90°，∠A=60°，将射线BC绕点B顺时针旋转120°，得到射线BD，点E在射线BD上，BE+BC= m．(1)如图1，若BE=BC，求CE的长（用含m的式子表示）；(2)如图2，点F在线段AB上，连接CF、EF．添加一个条件：AF、BC、BE满足的等量关系为______，使得EF=CF成立，补全图形并证明．。

2021年中考数学压轴题题型组合卷(四)【含答案】

2021年中考数学压轴题题型组合卷（四）（满分：30分）一、选择、填空题（共2小题，每小题3分，共6分）1.在平面直角坐标系中，将抛物线y＝x2+2x+3绕着它与y轴的交点旋转180°，所得抛物线的解析式是（）A．y＝﹣（x+1）2+2B．y＝﹣（x﹣1）2+4C．y＝﹣（x﹣1）2+2D．y＝﹣（x+1）2+42.如图所示，在菱形ABCD中，AB＝4，∠BAD＝120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．当点E、F在BC、CD上滑动时，则△CEF的面积最大值是．二、解答题（共2小题，每小题12分，共24分）3.如图，在平面直角坐标系xOy中，将抛物线y＝x2平移，使平移后的抛物线经过点A（﹣3，0）、B（1，0）．（1）求平移后的抛物线的表达式．（2）设平移后的抛物线交y轴与点C，在平移后的抛物线的对称轴上有一动点P，当BP与CP之和最小时，P 点坐标又是多少？（3）若y＝x2与平移后的抛物线对称轴交于D点，那么，在平移后的抛物线的对称轴上，是否存在一点M，使得以M、O、D为顶点的三角形△BOD相似？若存在，求点M坐标；若不存在，说明理由．4.如图，在△ABC中，已知AB＝AC＝5，BC＝6，且△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE始终经过点A，EF与AC交于M点．（1）求证：△ABE∽△ECM；（2）探究：在△DEF运动过程中，重叠部分能否构成等腰三角形？若能，求出BE的长；若不能，请说明理由；（3）当线段AM最短时，求重叠部分的面积．参考答案一、选择、填空题（共2小题，每小题3分，共6分）1.在平面直角坐标系中，将抛物线y＝x2+2x+3绕着它与y轴的交点旋转180°，所得抛物线的解析式是（）A．y＝﹣（x+1）2+2B．y＝﹣（x﹣1）2+4C．y＝﹣（x﹣1）2+2D．y＝﹣（x+1）2+4【分析】先将原抛物线化为顶点式，易得出与y轴交点，绕与y轴交点旋转180°，那么根据中心对称的性质，可得旋转后的抛物线的顶点坐标，即可求得解析式．【解答】解：由原抛物线解析式可变为：y＝（x+1）2+2，∴顶点坐标为（﹣1，2），与y轴交点的坐标为（0，3），又由抛物线绕着它与y轴的交点旋转180°，∴新的抛物线的顶点坐标与原抛物线的顶点坐标关于点（0，3）中心对称，∴新的抛物线的顶点坐标为（1，4），∴新的抛物线解析式为：y＝﹣（x﹣1）2+4．故选：B．【点评】本题主要考查了抛物线一般形式及于y轴交点，同时考查了旋转180°后二次项的系数将互为相反数，难度适中．2.如图所示，在菱形ABCD中，AB＝4，∠BAD＝120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．当点E、F在BC、CD上滑动时，则△CEF的面积最大值是．【分析】先求证AB＝AC，进而求证△ABC、△ACD为等边三角形，得∠4＝60°，AC＝AB进而求证△ABE≌△ACF，可得S△ABE＝S△ACF，故根据S四边形AECF＝S△AEC+S△ACF＝S△AEC+S△ABE＝S△ABC即可解题；当正三角形AEF的边AE与BC垂直时，边AE最短．△AEF的面积会随着AE的变化而变化，且当AE最短时，正三角形AEF 的面积会最小，又根据S△CEF＝S四边形AECF﹣S△AEF，则△CEF的面积就会最大．【解答】解：如图，连接AC，∵四边形ABCD为菱形，∠BAD＝120°，∠1+∠EAC＝60°，∠3+∠EAC＝60°，∴∠1＝∠3，∵∠BAD＝120°，∴∠ABC＝60°，∴△ABC和△ACD为等边三角形，∴∠4＝60°，AC＝AB，∴在△ABE和△ACF中，，∴△ABE≌△ACF（ASA），∴S△ABE＝S△ACF，∴S四边形AECF＝S△AEC+S△ACF＝S△AEC+S△ABE＝S△ABC，是定值，作AH⊥BC于H点，则BH＝2，∴S四边形AECF＝S△ABC＝BC•AH＝BC•＝4，由“垂线段最短”可知：当正三角形AEF的边AE与BC垂直时，边AE最短，∴△AEF的面积会随着AE的变化而变化，且当AE最短时，正三角形AEF的面积会最小，又∵S△CEF＝S四边形AECF﹣S△AEF，则此时△CEF的面积就会最大，∴S△CEF＝S四边形AECF﹣S△AEF＝4﹣×2×＝．故答案为：【点评】本题主要考查了菱形的性质、全等三角形判定与性质及三角形面积的计算，根据△ABE≌△ACF，得出四边形AECF的面积是定值是解题的关键．二、解答题（共2小题，每小题12分，共24分）3.如图，在平面直角坐标系xOy中，将抛物线y＝x2平移，使平移后的抛物线经过点A（﹣3，0）、B（1，0）．（1）求平移后的抛物线的表达式．（2）设平移后的抛物线交y轴与点C，在平移后的抛物线的对称轴上有一动点P，当BP与CP之和最小时，P点坐标又是多少？（3）若y＝x2与平移后的抛物线对称轴交于D点，那么，在平移后的抛物线的对称轴上，是否存在一点M，使得以M、O、D为顶点的三角形△BOD相似？若存在，求点M坐标；若不存在，说明理由．【分析】（1）设平移后抛物线的表达式为y＝a（x+3）（x﹣1）．由题意可知平后抛物线的二次项系数与原抛物线的二次项系数相同，从而可求得a的值，于是可求得平移后抛物线的表达式；（2）先根据平移后抛物线解析式求得其对称轴，从而得出点C关于对称轴的对称点C′坐标，连接BC′，与对称轴交点即为所求点P，再求得直线BC′解析式，联立方程组求解可得；（3）先求得点D的坐标，由点O、B、E、D的坐标可求得OB、OE、DE、BD的长，从而可得到△EDO为等腰三角直角三角形，从而可得到∠MDO＝∠BOD＝135°，故此当＝或＝时，以M、O、D为顶点的三角形与△BOD相似．由比例式可求得MD的长，于是可求得点M的坐标．【解答】解：（1）设平移后抛物线的表达式为y＝a（x+3）（x﹣1）．∵由平移的性质可知原抛物线与平移后抛物线的开口大小与方向都相同，∴平移后抛物线的二次项系数与原抛物线的二次项系数相同．∴平移后抛物线的二次项系数为1，即a＝1．∴平移后抛物线的表达式为y＝（x+3）（x﹣1），整理得：y＝x2+2x﹣3．（2）∵y＝x2+2x﹣3＝（x+1）2﹣4，∴抛物线对称轴为直线x＝﹣1，与y轴的交点C（0，﹣3），则点C关于直线x＝﹣1的对称点C′（﹣2，﹣3），如图1，连接B，C′，与直线x＝﹣1的交点即为所求点P，由B（1，0），C′（﹣2，﹣3）可得直线BC′解析式为y＝x﹣1，则，解得，所以点P坐标为（﹣1，﹣2）；（3）如图2，由得，即D（﹣1，1），则DE＝OE＝1，∴△DOE为等腰直角三角形，∴∠DOE＝∠ODE＝45°，∠BOD＝135°，OD＝，∵BO＝1，∴BD＝，∵∠BOD＝135°，∴点M只能在点D上方，∵∠BOD＝∠ODM＝135°，∴当＝或＝时，以M、O、D为顶点的三角形△BOD相似，①若＝，则＝，解得DM＝2，此时点M坐标为（﹣1，3）；②若＝，则＝，解得DM＝1，此时点M坐标为（﹣1，2）；综上，点M坐标为（﹣1，3）或（﹣1，2）．【点评】本题主要考查的是二次函数的综合应用，解答本题主要应用了平移的性质、翻折的性质、二次函数的图象和性质、待定系数法求二次函数的解析式、等腰直角三角形的性质、相似三角形的判定，证得∠ODM＝∠BOD ＝135°是解题的关键．4.如图，在△ABC中，已知AB＝AC＝5，BC＝6，且△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE始终经过点A，EF与AC交于M点．（1）求证：△ABE∽△ECM；（2）探究：在△DEF运动过程中，重叠部分能否构成等腰三角形？若能，求出BE的长；若不能，请说明理由；（3）当线段AM最短时，求重叠部分的面积．【分析】（1）由AB＝AC，根据等边对等角，可得∠B＝∠C，又由△ABC≌△DEF与三角形外角的性质，易证得∠CEM＝∠BAE，则可证得：△ABE∽△ECM；（2）首先由∠AEF＝∠B＝∠C，且∠AME＞∠C，可得AE≠AM，然后分别从AE＝EM与AM＝EM去分析，注意利用全等三角形与相似三角形的性质求解即可求得答案；（3）首先设BE＝x，由△ABE∽△ECM，根据相似三角形的对应边成比例，易得CM＝﹣+x＝﹣（x﹣3）2+，继而求得AM的值，利用二次函数的性质，即可求得线段AM的最小值，继而求得重叠部分的面积．【解答】（1）证明：∵AB＝AC，∴∠B＝∠C，∵△ABC≌△DEF，∴∠AEF＝∠B，又∵∠AEF+∠CEM＝∠AEC＝∠B+∠BAE，∴∠CEM＝∠BAE，∴△ABE∽△ECM；（2）能．解：∵∠AEF＝∠B＝∠C，且∠AME＞∠C，∴∠AME＞∠AEF，∴AE≠AM；当AE＝EM时，则△ABE≌△ECM，∴CE＝AB＝5，∴BE＝BC﹣EC＝6﹣5＝1，当AM＝EM时，则∠MAE＝∠MEA，∴∠MAE+∠BAE＝∠MEA+∠CEM，即∠CAB＝∠CEA，又∵∠C＝∠C，∴△CAE∽△CBA，∴，∴CE＝，∴BE＝6﹣＝；∴BE＝1或．（3）解：设BE＝x，又∵△ABE∽△ECM，∴，即：，∴CM＝﹣+x＝﹣（x﹣3）2+，∴AM＝5﹣CM═（x﹣3）2+，∴当x＝3时，AM最短为，又∵当BE＝x＝3＝BC时，∴点E为BC的中点，∴AE⊥BC，∴AE＝＝4，此时，EF⊥AC，∴EM＝＝，S△AEM＝．【点评】此题考查了相似三角形的判定与性质、全等三角形的判定与性质以及二次函数的最值问题．此题难度较大，注意数形结合思想、分类讨论思想与函数思想的应用是解此题的关键．。

【北师大版2020中考数学专项复习】：四边形综合复习

【2020中考数学专项复习】：四边形综合复习【考纲要求】1.探索并了解多边形的内角和与外角和公式，了解正多边形的概念.2.掌握平行四边形、矩形、菱形、正方形、梯形、直角梯形、等腰梯形的概念和性质，了解它们之间的关系；了解四边形的不稳定性.3.探索并掌握平行四边形的有关性质和四边形是平行四边形的条件.4.探索并掌握矩形、菱形、正方形的有关性质和四边形是矩形、菱形、正方形的条件.5.探索并了解等腰梯形的有关性质和四边形是等腰梯形的条件.6.通过探索平面图形的镶嵌，知道任意一个三角形、四边形或正六边形可以镶嵌平面，并能运用这几种图形进行简单的镶嵌设计.【知识网络】【考点梳理】考点一、四边形的相关概念1.多边形的定义：在平面内，由不在同一直线上的一些线段首尾顺次相接组成的封闭图形叫做多边形.2.多边形的性质：(1)多边形的内角和定理：n边形的内角和等于(n-2)·180°；(2)推论：多边形的外角和是360°；(3)对角线条数公式：n边形的对角线有条；(4)正多边形定义：各边相等，各角也相等的多边形是正多边形.3.四边形的定义：同一平面内，由不在同一条直线上的四条线段首尾顺次相接组成的图形叫做四边形.4.四边形的性质：(1)定理：四边形的内角和是360°； (2)推论：四边形的外角和是360°. 考点二、特殊的四边形1.平行四边形及特殊的平行四边形的性质2. 平行四边形及特殊的平行四边形的判定【要点诠释】面积公式：S 菱形 =21ab=ch.（a 、b 为菱形的对角线 ,c 为菱形的边长，h 为c 边上的高） S 平行四边形 =ah. a 为平行四边形的边，h 为a 上的高）考点三、梯形1.梯形的定义：一组对边平行而另一组对边不平行的四边形叫做梯形.(1)互相平行的两边叫做梯形的底；较短的底叫做上底，较长的底叫做下底.(2)不平行的两边叫做梯形的腰.(3)梯形的四个角都叫做底角.2.直角梯形：一腰垂直于底的梯形叫做直角梯形.3.等腰梯形：两腰相等的梯形叫做等腰梯形.4.等腰梯形的性质：(1)等腰梯形的两腰相等； (2)等腰梯形同一底上的两个底角相等. (3)等腰梯形的对角线相等.5.等腰梯形的判定方法：(1)两腰相等的梯形是等腰梯形(定义)；(2)同一底上的两个角相等的梯形是等腰梯形；(3)对角线相等的梯形是等腰梯形.6.梯形中位线：连接梯形两腰中点的线段叫梯形的中位线.7.面积公式： S=(a+b)h(a、b是梯形的上、下底，h是梯形的高).【要点诠释】解决四边形问题常用的方法（1）有些四边形问题可以转化为三角形问题来解决．（2）有些梯形的问题可以转化为三角形、平行四边形问题来解决．（3）有时也可以运用平移、轴对称来构造图形，解决四边形问题.考点四、平面图形1.平面图形的镶嵌的定义：用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙，不重叠地铺成一片，这就是平面图形的镶嵌，又称做平面图形的密铺.2.平面图形镶嵌的条件：(1)同种正多边形镶嵌成一个平面的条件：周角是否是这种正多边形的一个内角的整倍数.在正多边形里只有正三角形、正四边形、正六边形可以镶嵌.(2)n种正多边形组合起来镶嵌成一个平面的条件：①n个正多边形中的一个内角的和的倍数是360°；②n个正多边形的边长相等，或其中一个或n个正多边形的边长是另一个或n个正多边形的边长的整数倍.【典型例题】类型一、特殊的四边形1.如图所示，已知P 、R 分别是矩形ABCD 的边BC 、CD 上的点，E 、F 分别是PA 、PR 的中点，点P 在BC 上从B 向C 移动，点R 不动，那么下列结论成立的是（）A ．线段EF 的长逐渐增大B ．线段EF 的长逐渐变小C ．线段EF 的长不变D ．无法确定AB CD EFP R【思路点拨】此题的考点是矩形的性质；三角形中位线定理．【答案】C.2.过正方形ABCD 的顶点A 作线段AE 使DC=DE ，交DC 于G ，作DF ⊥AE ，连接CE.（1）若∠CDE=60°，AB=1，求DF 的长；（2）作∠CDE 平分线，交AE 于P ，交CE 与Q ，连接BP ，求证：；（3）若AD=2，DF=1，求PQ 的长.【思路点拨】（1）根据等边三角形三线合一，相似，勾股定理可求得；（2）巧妙运用旋转和四点共圆的知识即可.【答案与解析】(1)作EH⊥DC于H, (2)连PC,BD,AC,易证△PDE≌△PDC(SAS)【总结升华】考查了正方形的性质，勾股定理以及四点共圆，是一道综合性很强的运算证明相结合的中档题.举一反三：【变式】如图，E是正方形ABCD外的一点，连接AE、BE、DE，且∠EBA=∠ADE，点F在DE上，连接AF，BE=DF．（1）求证：△ADF≌△ABE；【答案】证明：（1）∵四边形正ABCD是正方形，∴AB=AD，∵在△ADF和△ABE中，AD ABADF EBADF BE=⎧⎪∠=∠⎨⎪=⎩，∴△ADF≌△ABE；（2）理由如下：由（1）有△ADF ≌△ABE，∴AF=AE ，∠1=∠2，在正方形ABCD 中，∠BAD=90°，∴∠BAF+∠3=90°，∴∠BAF+∠4=90°，∴∠EAF=90°，∴△EAF 是等腰直角三角形，∴EF 2=AE 2+AF 2，∴EF 2=2AE 2，∴EF=2AE ，即DE-DF=2AE ，∴DE-BE=2AE ．【高清课堂：四边形综合复习例2】 3．如图，在直角梯形ABCD 中，AD ∥BC ，∠B=90°，AB=8，，CA=CD ，E 、F 分别是线段AD 、AC 上的动点（点E 与点A 、D 不重合），且∠FEC=∠ACB ，设DE=x ，CF=y.（1）求AC 和AD 的长；（2）求y 与x 的函数关系式；（3）当△EFC 为等腰三角形时，求x 的值.【思路点拨】本题涉及到的考点有相似三角形的判定与性质；等腰三角形的判定；直角梯形；锐角三角34tan =∠CAD函数的定义．【答案与解析】（1）∵AD∥BC，∠B=90°，过点C作CH⊥AD于点H，∴CH=AB=8，则AH=6．∵CA=CD，∴AD=2AH=12．（2）∵CA=CD，∴∠CAD=∠D．∵∠FEC=∠ACB，∠ACB=∠CAD，∴∠FEC=∠D．∵∠AEC=∠1+∠FEC=∠2+∠D，∴∠1=∠2．∴△AEF∽△DCE．（3）若△EFC为等腰三角形．①当EC=EF时，此时△AEF≌△DCE，∴AE=CD．∵12-x=10，∴x=2．②当FC=FE时，有∠FCE=∠FEC=∠CAE，③当CE=CF时，有∠CFE=∠CEF=∠CAE，【总结升华】本题考查了相似三角形的判定和性质、等腰三角形的判定、直角梯形及锐角三角形函数的定义等知识；应用相似的性质，得到比例式，借助比例式解题是很重要的方法，做题时注意应用，对于等腰三角形问题要注意分类讨论也是比较重要的，注意掌握．举一反三：【变式】在直角梯形ABCD中，AB∥DC，AB⊥BC，∠A＝60°，AB＝2CD，E、F分别为AB、AD的中点，连结EF、EC、BF、CF.⑴判断四边形AECD的形状（不证明）；⑵在不添加其它条件下，写出图中一对全等的三角形，用符号“≌”表示，并证明.⑶若CD＝2，求四边形BCFE的面积.【答案】（1）平行四边形；（2）△BEF≌△CDF或（△AFB≌△EBC≌△EFC）证明：连接DE，∵AB=2CD，E为AB中点，∴DC=EB，又∵DC∥EB，∴四边形BCDE 是平行四边形，∵AB ⊥BC ，∴四边形BCDE 为矩形，∴∠AED=90°，∠CDE=∠BED=90°，BE=CD ，∴∠DFE=180°-60°=120°，∵EF=DF ，∴∠FDE=∠FED=30°．∴∠CDF=∠BEF=120°，在△BEF 和△FDC 中， 120DF EF CDF BEF DC BE =⎧⎪∠=∠=︒⎨⎪=⎩，∴△BEF ≌△CDF （SAS ）．（3）若CD=2，则AD=4，∵∠A=60°，∵四边形AECD 为平行四边形，类型二、四边形与其他知识的综合运用4. 有矩形纸片ABCD ，AB=2，AD=1，将纸片折叠，使顶点A 与边CD 上的点E 重合.（1）如果折痕FG分别与AD、AB交于点F、G，AF=23，求DE的长；（2）如果折痕FG分别与CD、DA交于点F、G，△AED的外接圆与直线BC相切，求折痕FG的长.【思路点拨】（1）根据AF，AD的长可以求得DF的长，根据折叠知EF=AF，再根据勾股定理即可计算得到DE的长；FOE相似于直角三角形ADE，求得OF的长，从而根据轴对称的性质得到FG=2OF．【高清课堂：四边形综合复习例3】5．已知如图，在Rt△ABC中，∠C=90°，AC=3，AB=5．点P从点C出发沿CA以每秒1个单位的速度向点A匀速运动；点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动，点P、Q同时出发，当点P到达点A时停止运动，点Q也随之停止．伴随着P、Q的运动，DE保持垂直平分PQ，且交PQ于点D，交折线QB-BC-CP于点E．设点P、Q运动的时间是t秒（t＞0）．在点E运动的过程中，四边形QBED 成为直角梯形时，t的值为 .t．【答案与解析】①如图，当DE∥QB时．∵DE⊥PQ，∴PQ⊥QB，四边形QBED是直角梯形，．此时∠APQ=90°．由△AQP∽△ABC，得AQAB=APAC，即353t t-=．解得t=158．【总结升华】本题考查了相似三角形的判定和性质、勾股定理等知识，是中考压轴题．6 .如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（－8，0），直线BC经过点B（－8，6），C（0，6），将四边形OABC绕点O按顺时针方向旋转а度得到四边形OAB'C'，此时直线OA’、直线B’C’分别与直线BC相交于点P、Q.（1）四边形OABC的现状是，当а=90°时，BP：BQ的值是；（2）①如图，当四边形OA’B’C’的顶点B’落在y轴正半轴时，求BP：BQ的值；②如图，当四边形OA’B’C’的顶点B’落在直线BC上时，求△OPB'的面积；（3）在四边形OA’B’C’旋转过程中，当0＜а°≤180°时，是否存在这样的点P和点Q，使BP=0.5BQ？若存在，请直接写出点P的坐标；若不存在，请说明理由.【思路点拨】（1）根据有一个角是直角的平行四边形进行判断当α=90°时，就是长与宽的比；（2）①利用相似三角形求得CP的比，就可求得BP，PQ的值；②根据勾股定理求得PB′的长，再根据三角形的面积公式进行计算．∴CQ=3，BQ=BC+CQ=11．②在△OCP 和△B ′A ′P 中，90OPC B PA OCP A OC B A ''∠=∠⎧⎪'∠=∠=︒⎨⎪''=⎩， ∴△OCP ≌△B ′A ′P （AAS ）．（3）如图1，当点P 在点B 左侧时，OP=PQ=BQ+BP=3x ，在Rt △PCO 中，（8+x ）2+62=（3x ）2，解得 x 1=1+362，x 2=1-362（不符实际，舍去）．∴PC=BC+BP=9+362，∴P 1（-9-362，6）．如图2，当点P 在点B 右侧时，举一反三：【变式】如图，直角梯形ABCD 中，BC AD ∥，90BCD ∠=°，且2tan 2CD AD ABC =∠=，，过点D 作AB DE ∥，交BCD ∠的平分线于点E ，连接BE ．（1）求证：BCCD =；（2）将BCE △绕点C ，顺时针旋转90°得到DCG △，连接EG.．求证：CD 垂直平分EG. （3）延长BE 交CD 于点P ．求证：P 是CD 的中点．【答案】（1）延长DE 交BC 于F ， ∵AD ∥BC ，AB ∥DF ， ∴AD=BF ，∠ABC=∠DFC ．在Rt △DCF 中，∵CD=2AD=2BF ，ADGECB∴BF=CF，∴BC=BF+CF=12CD+12CD=CD．即BC=CD．（2）∵CE平分∠BCD，∴∠BCE=∠DCE，由（1）知BC=CD，∵CE=CE，∴△BCE≌△DCE，∴BE=DE，由图形旋转的性质知CE=CG，BE=DG，∴DE=DG，∴C，D都在EG的垂直平分线上，∴CD垂直平分EG．（3）连接BD，由（2）知BE=DE，∴∠1=∠2．∵AB∥DE，∴∠3=∠2．∴∠1=∠3．∵AD∥BC，∴∠4=∠DBC．由（1）知BC=CD，∴∠DBC=∠BDC，∴∠4=∠BDP．又∵BD=BD，∴△BAD≌△BPD，中考总复习：四边形综合复习--巩固练习（提高）【巩固练习】一、选择题1．如图，在中，，是上异于、的一点，则的值是（）．A．16 B．20 C．25 D．302. 如图1，在矩形中，动点从点出发，沿→→→方向运动至点处停止．设点运动的路程为，的面积为，如果关于的函数图象如图2所示，则当时，点应运动到（）. A．处B．处C．处D．处3．（2019•孝感）如图，在菱形ABCD中，∠A=60°，E、F分别是AB，AD的中点，DE、BF相交于点G，连接BD，CG．有下列结论：①∠BGD=120°；②BG+DG=CG；③△BDF≌△CGB；④S△ABD=AB2其中正确的结论有（）. A．1个 B．2个 C．3个 D．4个4.一个正方形纸片，用剪刀沿一条不过任何顶点的直线将其剪成两部分；拿出其中一部分，再沿一条不过任何顶点的直线将其剪成两部分；又从得到的三部分中拿出其中之一，还是沿一条不过任何顶点的直线将其剪成两部分……如此下去，最后得到了34个六十二边形和一些多边形纸片，则至少要剪的刀数是（）.A. 2004 B. 2005 C. 2006 D. 20075．如图所示，已知菱形OABC ，点C 在x 轴上，直线y =x 经过点A ，菱形OABC 的面积是.若反比例函数的图象经过点B ，则此反比例函数表达式为（）. A ．B ．C ．D ．第5题第6题6. 如图,正方形ABCD 的边长为2，将长为2的线段QR 的两端放在正方形的相邻的两边上同时滑动．如果Q 点从A 点出发，沿图中所示方向按A→B→C→D→A 滑动到A 止，同时点R 从B 点出发，沿图中所示方向按B→C→D→A→B 滑动到B 止，在这个过程中，线段QR 的中点M 所经过的路线围成的图形的面积为（）．A ．2B ．C ．D ．二、填空题7. 如图，将两张长为8，宽为2的矩形纸条交叉，使重叠部分是一个菱形，容易知道当两张纸条垂直时，菱形的周长有最小值8，那么菱形周长的最大值是_________．第7题第8题4π-ππ1-A BCQRM D8. 如图，在等腰梯形中，，= 4=，=45°．直角三角板含45°角的顶点在边上移动，一直角边始终经过点，斜边与交于点．若为等腰三角形，则的长等于____________．9.（2019•锦州）如图，正方形A1B1B2C1，A2B2B3C2，A3B3B4C3，…，A n B n B n+1C n，按如图所示放置，使点A1、A2、A3、A4、…、A n在射线OA上，点B1、B2、B3、B4、…、B n在射线OB上．若∠AOB=45°，OB1=1，图中阴影部分三角形的面积由小到大依次记作S1，S2，S3，…，S n，则S n=________________-．第9题第10题10.（2019•深圳）如图，Rt△ABC中，∠C=90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC=5，OC=6，则另一直角边BC的长为．11.（2019•天津）如图，已知正方形ABCD的边长为1，以顶点A、B为圆心，1为半径的两弧交于点E，以顶点C、D为圆心，1为半径的两弧交于点F，则EF的长为．第11题第12题点E ，在射线DC 上取点F ，使得∠DEF=120°．（1）当点E 是AB 的中点时，线段DF 的长度是______；（2）若射线EF 经过点C ，则AE 的长是_______.三、解答题13.如图，在边长为4cm 的正方形ABCD 中，点E ，F ，G ，H 分别按A ⇒B ，B ⇒C ，C ⇒D ，D ⇒A 的方向同时出发，以1cm/s 的速度匀速运动．在运动过程中，设四边形EFGH 的面积为S （cm 2），运动时间为t （s ）．（1）试证明四边形EFGH 是正方形；（2）写出S 关于t 的函数关系式，并求运动几秒钟时，面积最小，最小值是多少？（3）是否存在某一时刻t ，使四边形EFGH 的面积与正方形ABCD 的面积比是5：8？若存在，求出t 的值；若不存在，请说明理由．14.如图,在矩形ABCD 中，AB=3，AD=1，点P 在线段AB 上运动，设AP=x ，现将纸片还原，使点D 与P 重合，得折痕EF （点E 、F 为折痕与矩形边的交点，再将纸片还原。

2021年九年级中考数学复习《中考压轴题：圆的综合应用》经典题型提升练习(四)

2021年中考数学复习《中考压轴题：圆的综合应用》经典题型提升练习（四）1．如图，在平面直角坐标系中，Rt△ABC的斜边AB在y轴上，边AC与x轴交于点D，AE 平分∠BAC交边BC与点E，经过A、D、E三点的即的圆心F恰好在y轴上，⊙F与y轴交于另一点G．（1）求证：BC是⊙F的切线；（2）试探究线段AG、AD、CD之间的关系，并证明；（3）若点A（O，﹣1）、D（2，0），求AB的长．2．如图，在Rt△ABC中，∠ABC＝90°，⊙O（圆心O在△ABC内部）经过B，C两点，交线段AC于点D，直径BH交AC于点E，点A关于直线BD的对称点F落在⊙O上．连结BF．（1）求证：∠C＝45°；（2）在圆心O的运动过程中；①若tan∠EDF＝，AB＝6，求CE的长；②若点F关于AC的对称点落在△BFE边上时，求点的值．（直接写出答案）；（3）令⊙O与边AB的另一个交点为P，连结PC，交BD于点Q，若PC⊥BF，垂足为点G，求证：BD＝AD+CE．3．如图①，△ABC和△CDE都是等腰直角三角形，∠ACB＝∠DCE＝90°，且点A在ED的延长线上，以DE为直径的⊙O与AB交于G、H两点，连接BE．（1）求证：BE是⊙O的切线；（2）如图②，连接OB、OC，若tan∠CAD＝，试判断四边形BECO的形状，请说明理由；（3）在（2）的条件下，若BF＝，请你求出HG的长．4．如图1，AB为半圆O的直径，半径OP⊥AB，过劣弧AP上一点D作DC⊥AB于点C．连接DB，交OP于点E，∠DBA＝22.5°．（1）若OC＝2，则AC的长为；（2）试写出AC与PE之间的数量关系，并说明理由；（3）连接AD并延长，交OP的延长线于点G，设DC＝x，GP＝y，请求出x与y之间的等量关系式．（请先补全图形，再解答）．5．如图，在△ABC中，AB＝AC＝4，以AB为直径的⊙O交BC于点D，交AC于点E，点P是AB的延长线上一点，且∠PDB＝∠A，连接DE、OE．（1）求证：PD是⊙O的切线；（2）填空：①当∠P的度数为时，四边形OBDE是菱形；②当∠BAC＝45°时，△CDE的面积为．6．如图，△OAB中，OA＝OB＝5cm，AB长为8cm，以点O为圆心6cm为直径的⊙O交线段OA 于点C，交直线OB于点E、D，连接CD，EC．（1）求证：△OCD∽△OAB；（2）求证：AB为⊙O的切线；（3）在（2）的结论下，连接点E和切点，交OA于点F求证：OF•CE＝OD•CF．7．已知：在Rt△ABC中，∠ACB＝90°，AC＝1，D是AB的中点，以CD为直径的⊙Q分别交BC、BA于点F、E，点E位于点D下方，连接EF交CD于点G．（1）如图1，如果BC＝2，求DE的长；（2）如图2，设BC＝x，＝y，求y关于x的函数关系式及其定义域；（3）如图3，连接CE，如果CG＝CE，求BC的长．8．已知：在矩形ABCD中，AB＝a（a为定值），连接AC，点O是AC上的一个动点，以AO 为半径的⊙O与AD交于点P．（1）如图（a），当∠DCP＝∠DAC时，求证：PC是⊙O的切线；（2）在（1）的条件下，若△APC是等腰三角形，①请你判断⊙O与BC的位置关系，并说明理由；②求⊙O的半径（用含a的代数式表示）；（3）如图（b），若BC＝AB＝a，且点O运动到AC与BD的交点处，在弧CD上任取一点Q，连接AQ、BQ分别交BD、AC于M，N．求证：四边形ABNM的面积为定值．9．如图，△ABC内接于⊙O，AB＝BC，AO⊥BC于D．（1）求证：△ABC是等边三角形；（2）若AB＝1，P是劣弧上一个动点，∠APC＝60°（点P与B、C不重合），PA交BC于点E，设AE＝x，EP＝y，求y与x之间的函数关系式，并写出自变量x的取值范围；（3）在（2）的前提下，令∠PAC＝α，∠APC＝β，当y取何值时，sin2α+sin2β＝1．10．如图①，已知A、B是⊙O1上的两点，直线l与⊙O1相交于B、C两点，过A点作⊙O1的切线AO，AO⊥l交于点O，已知BC＝8，⊙O1的半径为5．（1）证明：∠ABO1＝∠ABO．（2）求AB的长．（3）如图②，以AO所在直线为x轴，以直线l为y轴，建立如图所示的直角坐标系，过A、B两点作⊙O2与y轴的正半轴交于点M，与O1B的延长线交于点N，当⊙O2的大小变化时，BM﹣BN的值是否改变？若改变，请说明理由．若不变，请求出该值．参考答案1．（1）证明：连接EF，如图1所示：∵AE平分∠BAC，∴∠FAE＝∠CAE，∵FA＝FE，∴∠FAE＝∠FEA，∴∠FEA＝∠EAC，∴FE∥AC，∴∠FEB＝∠C＝90°，即BC是⊙F的切线；（2）解：AG＝AD+2CD；理由如下：作FR⊥AD于R，连接DF，如图2所示：则∠FRC＝90°，又∠FEC＝∠C＝90°，∴四边形RCEF是矩形，∴EF＝RC＝RD+CD，∠EFR＝90°，∵FR⊥AD，∴AR＝RD＝AD，∴EF＝RD+CD＝AD+CD，∵AF＝EF，∴AF＝AD+CD，∴AG＝2AF＝AD+2CD；（3）解：设⊙F的半径为r，则r2＝（r﹣1）2+22，解得，r＝，∴FA＝FG＝FE＝，∵点A（O，﹣1）、D（2，0），∴AD＝＝，∴AR＝，∵∠EFR＝90°，∴∠BFE+∠AFR＝90°，∵∠BFE+∠EBF＝90°，∴∠EBF＝∠AFR，∵∠BEF＝∠FRA＝90°，∴△BEF∽△FRA，∴＝，即＝，解得：BF＝，∴AB＝AF+BF＝+＝．2．（1）证明：∵点A，F关于直线BD对称，∵∠BFD＝∠C，∴∠A＝∠C，∵∠ABC＝90°，∴∠C＝45°；（2）①解：∵点A，F关于直线BD对称，∴AD＝DF，AB＝FB，∵∠A＝∠C＝45°，∴AB＝BC＝FB＝6，∴，∵BH是直径，∴由圆的对称性可知，△BFE≌△BCE，∴∠BFE＝∠C＝∠BFD＝45°，FE＝CE，∴∠DFE＝90°，∵tan∠EDF＝，AB＝6，∴设DF＝AD＝3a，则EF＝CE＝4a，DE＝5a，∵AC＝＝6，∴AC＝3a+4a+5a＝6，解得，a＝，∴CE＝4a＝2；②如图1，当点F关于AC的对称点落在BF边上时，连接DO，设FF'交AC于点M，则AC垂直平分FF'，由（1）知，∠A＝∠C＝45°，∠ABC＝90°，∴BA＝BC，∠ABM＝∠CBM＝×90°＝45°，∵点A，F关于直线BD对称，∴AD＝DF，AB＝FB，∴△ABD≌△FBD（SSS），∴∠ABD＝∠FBD，由（2）知，△BFE≌△BCE，∴∠FBE＝∠CBE，∴∠ABD＝∠FBD＝∠FBE＝∠CBE＝22.5°，∴∠DBE＝∠DBF+∠EBF＝45°，∵OD＝OB，∴∠OBD＝∠ODB＝45°，∴∠DOB＝90°，在△BDM与△BEM中，∠BDM＝∠BEM＝90°﹣22.5°＝67.5°，∴BD＝BE，在等腰Rt△BOD中，设OB＝OD＝r，则BD＝r，∴BE＝r，OE＝（﹣1）r，∴＝＝﹣1；如图2，当点F关于AC的对称点落在BE边上时，∵∠DF'E＝∠DOE＝90°，∴点F'与点O重合，连接OF，则OD＝OF＝DF，∴△DOF为等边三角形，∴∠ODF＝60°，由对称性知，∠ODE＝∠FDE＝30°，在Rt△DOE中，tan∠ODE＝＝tan30°＝，∴＝；综上所述，的值为﹣1或；（3）如图3，连接PD，FC，FC交BH于点M，∵∠ABC＝90°，∴PC⊥BF，∴CF＝BC＝BF，∴△FBC是等边三角形，∴BG＝CM＝BF，∠QGB＝∠CME＝90°，∠DBF＝∠DCF，∴△QBG≌△ECM（ASA），∴BQ＝CE，∵∠PDA＝90°，∠A＝45°，∴DP＝DA＝DF，∴，∵∠DPC＝（），∠DQP＝∠QDC+∠QCP＝（），∴∠DPC＝∠DQP，∴DQ＝DP＝AD，∴BD＝AD+CE．3．（1）证明：∵△ABC和△CDE都是等腰直角三角形，∴BC＝AC，EC＝DC，∴∠DCE＝∠ACB＝90°，∴∠DCE﹣∠FCD＝∠ACB﹣∠FCD，∴∠BCE＝∠ACD，∴△BCE≌△ACD（SAS），∴∠CBE＝∠CAD，∴∠ABE+∠BAE＝90°，∴∠AEB＝90°，∴BE⊥OE，又∵OE是⊙O的半径，∴BE是⊙O的切线；（2）四边形BECO是平行四边形，理由如下：∵点O是ED的中点，∴CO是DE边上的中线，∵△CDE是等腰三角形，∴CO是DE边上的高线，∴CO⊥DE，∴∠COE＝∠AOC＝90°，∵∠AEB＝90°，∴∠AEB＝COE，∴CO∥BE，∵在Rt△AOC中，tan∠CAD＝，∴＝，∴AO＝2CO，∴DO＝CO，∴AD＝CO，∵△BCE≌△ACD，∴BE＝AD，∴BE＝CO，∴四边形BECO是平行四边形；（3）∵四边形BECO是平行四边形，∴CF＝BF＝，∴BC＝2，∴AC＝BC＝2，∴AB＝＝2，设OC＝x，则AO＝2x，∵在Rt△AOC中，OC2+AO2＝AC2，∴x2+（2x）2＝（2）2，解得，x＝2（取正值），∴OC＝BE＝2，AO＝4，如图3，过点O作OM⊥AB于点M，连接OG，∴∠AMO＝90°，HG＝2MG，∴∠AMO＝∠AEB＝90°，∵∠MAO＝∠BAE，∴△MAO∽△BAE，∴＝，∴＝，∴OM＝，在Rt△MOG中，OM2+MG2＝OG2，∴（）2+MG2＝22，∴MG＝（取正值），∴HG＝2MG＝．4．解：（1）．∵∠DBA＝22.5°∴∠DOC＝45°∵OC＝2∴OD＝∴AC＝OA﹣OC＝（2）连接AD，DP，OD，过点D作DF⊥OP，垂足为点F．∵∠DCA＝∠DFP＝90°，AD＝DP，CD＝DF∴Rt△ACD≌Rt△DFP（HL）∴AC＝PF∵∠A＝∠CDB＝∠OEB＝∠DEF，∠ACD＝∠DFE＝90°，CD＝DF ∴Rt△ACD≌Rt△DEF（HL）∴AC＝EF∴PE＝2AC（3）如图所示，由∠DCO＝90°，∠DOC＝45°得OD＝＝∵∠ADB＝90°，点O是AB中点∴AB＝2OD＝∵∠A＝∠GED，∠GDE＝∠ADB，AD＝DE∴△DGE≌△DBA（ASA）∴GE＝AB＝x∵PE＝2AC∴PE＝2（）∴GP＝GE﹣PE＝即：y＝2x5．解：（1）如图，连接OD∵OB＝OD，∠PDB＝∠A∴∠ODB＝∠ABD＝90°﹣∠A＝90°﹣∠PDB ∴∠ODB+∠PDB＝90°∴∠ODP＝90°又∵OD是⊙O的半径∴PD是⊙O的切线（2）①30°若四边形OBDE为菱形，则OB＝BD＝DE＝EO＝OD ∴△OBD为等边三角形∴∠ABD＝∠A＝60°∴∠PDB＝30°∴∠P＝30°即当∠P为30°时，四边形OBDE为菱形②如图所示∵AO＝OE＝2，∠AOE＝90°∴AE＝∴EC＝4﹣∵∠BAC＝45°∴∠EDB＝135°∴∠EDC＝45°设DF＝EF＝b，FC＝a∵△EFC∽△ADC∴∴∵a2+b2＝（4﹣）2解得a＝（）b，b2＝4﹣2S＝＝＝b2＝△CDE6．证明：（1）∵OC＝OD，OA＝OB，∴＝，又∵∠COD＝∠AOB，∴△OCD∽△OAB；（2）过点O作OG⊥AB，垂足为G，∴∠OGA＝∠OGB＝90，∵OA＝OB，∴AG＝BG＝4，在Rt△AOG中，OA＝5，AG＝4，∴OG＝＝3，∵⊙O的直径为6，∴半径r为3，∴OG＝r＝3，又OG⊥AB，∴AB为⊙O的切线；（3）∵OA＝OB，AG＝BG，∴∠AOG＝∠BOG，∵OE＝OC，∴∠OEC＝∠OCE，∵∠AOB＝∠OEC+∠OCE，∴∠AOG＝∠OCE，∴OG∥EC，∴△FOG∽△FCE，∴＝，∴OF•CE＝OD•CF，∵OG＝OD，∴OF•CE＝OD•CF．7．解：（1）如图1中，连接CE．在Rt△ACB中，∵∠ACB＝90°，AC＝1，BC＝2，∴AB＝＝，∵CD是⊙Q的直径，∴∠CED＝90°，∴CE⊥AB，∵BD＝AD，∴CD＝AB＝，∵•AB•CE＝•BC•AC，∴CE＝，在Rt△CDE中，DE＝＝＝．（2）如图2中，连接CE，设AC交⊙Q于K，连接FK，DF，DK．∵∠FCK＝90°，∴FK是⊙Q的直径，∴直线FK经过点Q，∵CD是⊙Q的直径，∴∠CFD＝∠CKD＝90°，∴DF⊥BC，DK⊥AC，∵DC＝DB＝DA，∴BF＝CF，CK＝AK，∴FK∥AB，∴＝，∵BC＝x，AC＝1，∴AB＝，∴DC＝DB＝DA＝，∵△ACE∽△ABC，∴可得AE＝，∴DE＝AD﹣AE＝﹣，∴＝，∴＝，∴y＝（x＞1）．（3）如图3中，连接FK．∵CE＝CG，∴∠CEG＝∠CGE，∵∠FKC＝∠CEG，∵FK∥AB，∴∠FKC＝∠A，∵DC＝DA，∴∠A＝∠DCA，∴∠A＝∠DCA＝∠CEG＝∠CGE，∴∠CDA＝∠ECG，∴EC＝DE，由（2）可知：＝﹣，整理得：x2﹣2x﹣1＝0，∴x＝1+或1﹣（舍弃），∴BC＝1+．8．解：（1）证明：连接OP，如图a，∵OA＝OP，∴∠DAC＝∠APO，∵∠DCP＝∠DAC，∴∠DCP＝∠APO，∵四边形ABCD是矩形，∴∠D＝90°，CD＝AB＝a，∴∠DCP+∠DPC＝90°，∴∠OPC＝180°﹣∠DPC﹣∠APO＝180°﹣∠DPC﹣∠DCP＝90°，∴OP⊥PC，∴PC是⊙O的切线；（2）①BC是⊙O的切线，理由如下：如图a﹣1，过点O作OE⊥BC于E，∵△APC是等腰三角形，∴AP＝PC，∴∠PAC＝∠PCA，∵AD∥BC，∴∠PAC＝∠ACE＝∠PCA，又∵∠OPC＝∠OEC＝90°，OC＝OC，∴△OPC≌△OEC（AAS），∴OP＝OE，又∵OE⊥BC，∴BC是⊙O的切线；②∵AP＝PC，∴∠DAC＝∠ACP，∵∠DAC+∠ACD＝∠DAC+∠ACP+∠DCP＝90°，∴∠DAC＝∠DCP＝∠ACP＝30°，∵在Rt△CDP中，cos∠DCP＝＝，∴PC＝＝a，∵Rt△OPC中，tan∠OCP＝＝，∴OP＝PC＝，∴⊙O半径为；（3）连接DQ、CQ，如图b，∵矩形ABCD中，BC＝AB＝a，∴矩形ABCD是正方形，∴AB＝AD＝BC＝a，∠AOB＝∠AOM＝∠BON＝90°，∠ADM＝∠BCN＝45°，∴AC＝BD＝a，OA＝OB＝a，AC、BD为⊙O直径，∵Q在弧CD上运动，∴∠AQB＝∠AOB＝45°，∵∠ADM＝∠AQB＝45°，∠DAM＝∠QBM，∴△ADM∽△BQM，∴，∴BM＝，∵∠BCN＝∠AQB＝45°，∠CBN＝∠QAN，∴△BCN∽△AQN，∴，∴AN＝，∵AC、BD为⊙O直径，∴∠AQC＝∠BQD＝90°，∵∠AOM＝∠AQC＝90°，∠OAM＝∠QAC，∴△AOM∽△AQC，∴，∴AM•AQ＝AO•AC＝a2，∵∠BON＝∠BQD＝90°，∠OBN＝∠QBD，∴△BON∽△BQD，∴，∴BN•BQ＝BO•BD＝a2，∴S四边形AMNB ＝S△AMB+S△NMB＝MB•OA+MB•ON＝MB（OA+ON）＝MB•AN＝••＝•＝•＝a2，∴四边形AMNB的面积为定值．9．（1）证明：∵△ABC内接于⊙O，AO⊥BC，∴BD＝CD＝BC，∴AB＝AC，∵AB＝BC，∴AB＝BC＝AC，∴△ABC是等边三角形；（2）解：由（1）得：△ABC是等边三角形，∴AC＝AB＝BC＝1，∠ABC＝∠ACB＝60°，∴BD＝CD＝，AD＝BD＝，∵∠APC＝∠ABC，∴∠ACB＝∠APC，又∵∠CAE＝∠PAC，∴△ACE∽△APC，∴＝，∴AE×AP＝AC2＝1，即x（x+y）＝1，∴y＝又∵AD＜AE＜AB，∴＜x＜1；（3）解：∵∠APC＝∠B＝60°，∠PAC＝α，∠APC＝β，∴sin2α＝sin2∠APC＝（）2＝，∵sin2α+sin2β＝1．∴sin2β＝1﹣＝，∴sinβ＝，∴∠PAC＝30°，∴点E与D重合，如图所示：连接OB，则OB平分∠ABC，∴∠OBD＝30°，∵AD⊥BC，∴OD＝BD＝，OP＝OA＝OB＝2OD＝，∴PD＝PE＝OP﹣OD＝﹣＝；即y取时，sin2α+sin2β＝1．10．解：（1）连接O1A，过O1作EO1⊥BC于E，∵EO1⊥BC，∴BE＝BC＝4，∵O1B＝5，∴O1E＝＝＝3，∵过A点作⊙O1的切线AO，∴AO1⊥AO，且AO⊥l，EO1⊥BC，∴四边形OEO1A是矩形，∴AO＝O1E＝3，AO1∥OE，AO1＝EO＝5，∴∠O1AB＝∠ABO，∵O1A＝O1B，∴∠O1AB＝∠O1BA，∴∠ABO1＝∠ABO；（2）∵OB＝OE﹣BE＝5﹣4＝1，∴AB＝＝＝；（3）在MB上截取MG＝NB，连接AM，AN，AG，MN，∵四边形ABNM是圆内接四边形，＝∠NMA，∴∠ABO1＝∠ABO，∠ABO＝∠ANM∵∠ABO1∴∠AMN＝∠ANM，∴AM＝AN，∵＝，∴∠AMG＝∠ANB，且AM＝AN，MG＝NB，∴△AMG≌△ANB（SAS）∴AG＝AB，且AO⊥BC，∴BO＝GO＝1，∴BG＝2，∴BM﹣BN＝BM﹣MG＝BG＝2，∴BM﹣BN的值不变．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

中考专题复习（四）压轴题（学生卷）1、(2007宜宾)已知：如图，二次函数y=x2+(2k–1)x+k+1的图象与x轴相交于O、A两点.(1)求这个二次函数的解析式；(2)在这条抛物线的对称轴右边的图象上有一点B，使锐角△AOB的面积等于3.求点B的坐标；(3)对于(2)中的点B，在抛物线上是否存在点P，使∠POB=90°？若存在，求出点P的坐标，并求出△POB的面积；若不存在，请说明理由.2、（2007 广安）如图，已知抛物线y=－x2+2x+3交x轴于A、B两点（点A在点B的左侧），与y轴交于点C。

（1）求点A、B、C的坐标。

（2）若点M为抛物线的顶点，连接BC、CM、BM，求△BCM的面积。

（3）连接AC，在x轴上是否存在点P使△ACP为等腰三角形，若存在，请求出点P的坐标；若不存在，请说明理由。

3、（07泸洲）如图9，已知直线3:2l y x =及抛物线2:(0)C y ax bx c a =++≠，且抛物x…-2-11234…y … -5 0 3 4 3 0 -5 … (1) 求抛物线C 对应的函数解析式；(2) 求直线l 与抛物线C 的交点A 、B 的坐标；(3) 若动点M 在直线l 上方的抛物线C 上移动，求△ABM 的边AB 上的高h 的最大值。

4、（07成都）在平面直角坐标系xOy 中，已知二次函数2(0)y ax bx c a =++≠的图象与x 轴交于A B ，两点（点A 在点B 的左边），与y 轴交于点C ，其顶点的横坐标为1，且过点(23)，和(312)--，．（1）求此二次函数的表达式；（2）若直线:(0)l y kx k =≠与线段BC 交于点D （不与点B C ，重合），则是否存在这样的直线l ，使得以B O D ，，为顶点的三角形与BAC △相似？若存在，求出该直线的函数表达式及点D 的坐标；若不存在，请说明理由；（3）若点P 是位于该二次函数对称轴右边图象上不与顶点重合的任意一点，试比较锐角PCO ∠与ACO ∠的大小（不必证明），并写出此时点P 的横坐标p x 的取值范围．yx1 1O5、（07德阳）．如图，已知与x 轴交于点(10)A ，和(50)B ，的抛物线1l 的顶点为(34)C ，，抛物线2l 与1l 关于x 轴对称，顶点为C '．（1）求抛物线2l 的函数关系式；（2）已知原点O ，定点(04)D ，，2l 上的点P 与1l 上的点P '始终关于x 轴对称，则当点P 运动到何处时，以点D O P P '，，，为顶点的四边形是平行四边形？（3）在2l 上是否存在点M ，使ABM △是以AB 为斜边且一个角为30的直角三角形？若存，求出点M6、（07巴中）如图12线建立平面直角坐标系，抛物线2y x bx =+有一个公共点．（1）求直线AB 的解析式．（3分）（2）求抛物线2y x bx c =++（3）若点P 为（2）中抛物线上一点，过点是否存在这样的点P ，使PMC ADC △△？若存在，求出点P 的坐标；若不存在，请说明理由．（5分）x图127、（07自贡）△ABC中，∠A，∠B，∠C的对边分别为a，b，c，抛物线y＝x2－2ax＋b2交x轴于两点M，N，交y轴于点P，其中M的坐标是(a＋c，0)．（1）求证：△ABC是直角三角形．（2）若S△MNP＝3S△NOP，①求cos C的值；②判断△ABC的三边长能否取一组适当的值，使三角形MND（D为抛物线的顶点）是等腰直角三角形？如能，请求出这组值；如不能，请说明理由．8、（07资阳）如图10，已知抛物线P：y=ax2+bx+c(a≠0) 与x轴交于A、B两点(点A在x 轴的正半轴上)，与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线P上部分点的横坐标对应的纵坐标如下：x …-3 -2 1 2 …y …-52-4 -520 …(1) 求A、B、C三点的坐标；(2) 若点D的坐标为(m，0)，矩形DEFG的面积为S，求S与m的函数关系，并指出m的取值范围；(3) 当矩形DEFG的面积S取最大值时，连接DF并延长至点M，使FM=k·DF，若点M不在抛物线P上，求k的取值范围.9图109、（07绵阳）如图，已知抛物线y= ax2 + bx－3与x轴交于A、B两点，与y轴交于C点，经过A、B、C三点的圆的圆心M（1，m）恰好在此抛物线的对称轴上，⊙M的半径为5．设⊙M与y轴交于D，抛物线的顶点为E．（1）求m的值及抛物线的解析式；（2）设∠DBC = α，∠CBE = β，求sin（α－β）的值；（3）探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCE相似？若存在，请指出点P的位置，并直接写出点P的坐标；若不存在，请说明理由．“数形结合”练习1．已知∠AOB＝30︒，C是射线OB上的一点，且OC＝4．若以C为圆心，r为半径的圆与射线OA有两个不同的交点，则r的取值范围是______________．2．对于任意的有理数a，满足a≤x≤a＋10的整数x的个数为_________．3．用同样规格的黑白两种颜色的正方形瓷砖按下面方式铺地板，则第（3）个图形中有黑色瓷砖_______块，第n个图形中需要黑色瓷砖_______块（用含n的代数式表示）.4．在直角坐标系中，纵、横坐标都是整数的点，称为整点．设k为整数，当一次函数y＝x＋2与y＝kx－4的图象的交点为整点时，k的值可以取（） A．6个 B．7个 C．8个 D．9个5．在一直线型航道上，某人乘船由A地顺流而下到B地，然后又逆流而上到C地，共乘船4小时．已知船在静水中的速度为每小时7.5千米，水流速度为每小时2.5千米，若A、C 两地的距离为10千米，则A、B两地间的距离为（）A．20km B．203km C．20km或203km D．以上都不正确6．福娃们在一起探讨研究下面的题目：（1）（2）（3）……函数y ＝x 2－x ＋m （m 为常数）的图象如左图，如果 x ＝a 时，y ＜0；那么x ＝a －1时，函数值（）A ．y ＜0B ．0＜y ＜mC ．y ＞mD ．y ＝myxOx 1x 2参考下面福娃们的讨论，请你解该题，你选择的答案是（）贝贝：我注意到当x ＝0时，y ＝m ＞0．晶晶：我发现图象的对称轴为x ＝12．欢欢：我判断出x 1＜a ＜x 2．迎迎：我认为关键要判断a －1的符号．妮妮：m 可以取一个特殊的值．7．在数学活动中，小明为了求12＋122＋123＋124＋…＋12n ，的值（结果用n 表示），设计如图1所示的几何图形．（1）请你利用这个几何图形求12＋122＋123＋124＋…＋12n 的值为_______．12＋122＋（2）请你利用图2，再设计一个能求123＋124＋…＋12n 的值的几何图形．8．如图，在正△ABC 中，AF ＝CE ＝BD ＝13AB ，求证：BD 2＋DF 2＝FC 2．9．探索研究：如图，在直角坐标系xOy 中，点P 为函数y ＝14x 2在第一象限内的图象上的任一点，点A的坐标为（0，1），直线l 过B （0，－1）且与x 轴平行，过P 作y 轴的平行线分别交x 轴，l 于C ，Q ，连结AQ 交x 轴于H ，直线PH 交y 轴于R ．（1）求证：H 点为线段AQ 的中点；（2）求证：①四边形APQR 为平行四边形；②平行四边形APQR 为菱形；（3）除P 点外，直线PH 与抛物线y ＝14x 2有无其它公共点？并说明理由．x l Q C P A O B H Ry DCFB A12122 123 124…（图1）（图2）10．小明早晨从家里出发匀速步行去上学．小明的妈妈在小明出发后10分钟，发现小明的数学课本没带，于是她带上课本立即匀速骑车按小明上学的路线追赶小明，结果与小明同时到达学校．已知小明在整个上学途中，他出发后t 分钟时，他所在的位置与家的距离为s 千米，且s 与t 之间函数关系的图像如图中的折线段OA —AB 所示．（1）试求折线段OA —AB 所对应的函数关系式；（2）请解释图中线段AB 的实际意义；（3）请在所给的图中画出小明的妈妈在追赶小明的过程中，她所在的位置与家的距离s （千米）与小明出发后的时间t （分钟）之间函数关系的图像．（友情提醒：请对画出的图像用数据作适当的标注）参考答案：1．2＜r ≤4 2．10或11 3．10，3n ＋4 4．B 5．C 6．C7．（1）1－12n ；（2）答案不唯一，只要符合题意即可，略．8．提示：由结论中的等式特征联想到勾股定理，于是证明△BDE 为直角三角形．9．（1）、（2）略；（3）要判断直线PH 与抛物线y ＝14x 2有无其它公共点，只要研究由直线PH 的解析式与抛物线的解析式组成的方程组是否有两组不同的解．10．（1）线段OA 对应的函数关系式为：s ＝112t （0≤t ≤12）；线段AB 对应的函数关系式为：s＝1（12＜t ≤20）．（2）图中线段AB 的实际意义是：小明出发12分钟后，沿着以他家为圆心，1千米为半径的圆弧形道路上匀速步行了8分钟．（3）如图中折线段CD —DB ．2011年中考数学经典几何证明题（三）1.（1）如图1所示，在四边形ABCD 中，AC =BD ，AC 与BD 相交于点O ，E F 、分别是AD BC 、的中点，联结EF ，分别交AC 、BD 于点M N 、，试判断OMN △的形状，并加以证明；（2）如图2，在四边形ABCD 中，若AB CD =，E F 、分别是AD BC 、的中点，联结FE 并延长，分别与BA CD 、的延长线交于点M N 、，请在图2中画图并观察，图中是否有相等的角，若有，请直接写出结论：；（3）如图3，在ABC △中，AC AB >，点D 在AC 上，AB CD =，E F 、分别是AD BC 、的中点，联结FE 并延长，与BA 的延长线交于点M ，若45FEC ∠=︒，判断点M 与以AD 为直径的圆的位置关系，并简要说明理由．2．（1）如图1，已知矩形ABCD 中，点E 是BC 上的一动点，过点E 作EF ⊥BD 于点F ，EG ⊥A C于点G ，CH ⊥BD 于点H ，试证明CH=EF+EG;图 1 图2 图3BFB ACD EFM NODD(2) 若点E在ＢＣ的延长线上，如图2，过点E作EF⊥BD于点F，EG⊥A C的延长线于点G，CH⊥BD于点H，则EF、EG、ＣH三者之间具有怎样的数量关系，直接写出你的猜想；(3) 如图3，BD是正方形ABCD的对角线,L在BD上，且BL=BC, 连结CL，点E是CL上任一点, EF⊥BD于点F，EG⊥BC于点G，猜想EF、EG、BD之间具有怎样的数量关系，直接写出你的猜想；(4) 观察图1、图2、图3的特性，请你根据这一特性构造一个图形，使它仍然具有EF、EG、ＣH这样的线段，并满足（1）或（2）的结论，写出相关题设的条件和结论.3. 如图，△ABC是等边三角形，F是AC的中点，D在线段BC上，连接DF，以DF为边在DF的右侧作等边△DFE，ED的延长线交AB于H，连接EC，则以下结论：①∠AHE+∠AFD=180°；B GAF D E C H ②AF=21BC ；③当D 在线段BC 上（不与B ，C 重合）运动，其他条件不变时BDBH 是定值；④当D 在线段BC 上（不与B ，C 重合）运动，其他条件不变时DCEC BC +21是定值；（1）其中正确的是-------------------；（2）对于（1）中的结论加以说明；4. 在ABC △中，AC=BC ，90ACB ∠=︒，点D 为AC 的中点．（1）如图1，E 为线段DC 上任意一点，将线段DE 绕点D 逆时针旋转90°得到线段DF ，连结CF ，过点F 作FH FC ⊥，交直线AB 于点H ．判断FH 与FC 的数量关系并加以证明．（2）如图2，若E 为线段DC 的延长线上任意一点，（1）中的其他条件不变，你在（1）中得出的结论是否发生改变，直接写出你的结论，不必证明．5. 如图12，在△ABC 中，D 为BC 的中点，点E 、F 分别在边AC 、AB 上，并且∠ABE =∠ACF ，BE 、CF 交于点O ．过点O 作OP ⊥AC ，OQ ⊥AB ，P 、Q 为垂足．求证：DP=DQ ．6. 如图。