数字信号处理实验三 卷积
数字信号处理实验报告 3

数字信号处理实验报告姓名:班级:通信学号:实验名称:频域抽样定理验证实验类型:验证试验指导教师:实习日期:2013.频域采样定理验证实验一. 实验目的:1. 加深对离散序列频域抽样定理的理解2.了解由频谱通过IFFT 计算连续时间信号的方法3.掌握用MATLAB 语言进行频域抽样与恢复时程序的编写方法 4、用MATLAB 语言将X(k)恢复为X(z)及X(e jw )。
二. 实验原理:1、1、频域采样定理: 如果序列x(n)的长度为M ,频域抽样点数为N ,则只有当频域采样点数N ≥M 时,才有x N (n)=IDFT[X(k)]=x(n),即可由频域采样X(k)无失真的恢复原序列 x(n)。
2、用X(k)表示X(z)的内插公式:∑-=-----=10111)(1)(N k kNNzWz k X Nz X内插函数: zWzkNNN z 1k111)(-----=ϕ频域内插公式:∑-=-=10)2()()(N K j k Nk X e X πωϕω频域内插函数:e N j N N )21()2sin()2sin(1)(--=ωωωωϕ三. 实验任务与步骤:实验一:长度为26的三角形序列x(n)如图(b)所示,编写MATLAB 程序验证频域抽样定理。
实验二:已知一个时间序列的频谱为X(e jw )=2+4e -jw +6e -j2w +4e -j3w +2e -j4w分别取频域抽样点数N为3、5和10,用IPPT计算并求出其时间序列x(n),用图形显示各时间序列。
由此讨论原时域信号不失真地由频域抽样恢复的条件。
实验三:由X32(k)恢复X(z)和X(e jw)。
四.实验结论与分析:实验一:源程序:M=26;N=32;n=0:M; %产生M长三角波序列x(n)xa=0:floor(M/2);xb= ceil(M/2)-1:-1:0; xn=[xa,xb];Xk=fft(xn,512); %1024点FFT[x(n)], 用于近似序列x(n)的TFX32k=fft(xn,32); %32点FFT[x(n)]x32n=ifft(X32k); %32点IFFT[X32(k)]得到x32(n)X16k=X32k(1:2:N); %隔点抽取X32k得到X16(K)x16n=ifft(X16k,N/2); %16点IFFT[X16(k)]得到x16(n)subplot(3,2,2);stem(n,xn,'.');box ontitle('(b) 三角波序列x(n)');xlabel('n');ylabel('x(n)');axis([0,32,0,20])k=0:511;wk=2*k/512;subplot(3,2,1);plot(wk,abs(Xk));title('(a)FT[x(n)]');xlabel('\omega/\pi');ylabel('|X(e^j^\omega)|');axis([0,1,0,200])k=0:N/2-1;subplot(3,2,3);stem(k,abs(X16k),'.');box ontitle('(c) 16点频域');xlabel('k');ylabel('|X_1_6(k)|');axis([0,8,0,200])n1=0:N/2-1;subplot(3,2,4);stem(n1,x16n,'.');box ontitle('(d) 16点IDFT[X_1_6(k)]');xlabel('n');ylabel('x_1_6(n)');axis([0,32,0,20])k=0:N-1;subplot(3,2,5);stem(k,abs(X32k),'.');box ontitle('(e) 32点频域采样');xlabel('k');ylabel('|X_3_2(k)|');axis([0,16,0,200])n1=0:N-1;subplot(3,2,6);stem(n1,x32n,'.');box ontitle('(f) 32点IDFT[X_3_2(k)]');xlabel('n');ylabel('x_3_2(n)');axis([0,32,0,20])结果如下所示:实验一分析:序列x(n)的长度M=26,由图中可以看出,当采样点数N=16<M时,x16(n)确实等于原三角序列x(n)以16为周期的周期延拓序列的主值序列。
数字信号处理实验报告

实验一 信号、系统及系统响应一、实验目的1、熟悉理想采样的性质,了解信号采样前后的频谱变化,加深对时域采样定理的理解。
2、熟悉离散信号和系统的时域特性。
3、熟悉线性卷积的计算编程方法:利用卷积的方法,观察、分析系统响应的时域特性。
4、掌握序列傅里叶变换的计算机实现方法,利用序列的傅里叶变换对离散信号、系统及其系统响应进行频域分析。
二、 实验原理1.理想采样序列:对信号x a (t)=A e −αt sin(Ω0t )u(t)进行理想采样,可以得到一个理想的采样信号序列x a (t)=A e −αt sin(Ω0nT ),0≤n ≤50,其中A 为幅度因子,α是衰减因子,Ω0是频率,T 是采样周期。
2.对一个连续时间信号x a (t)进行理想采样可以表示为该信号与一个周期冲激脉冲的乘积,即x ̂a (t)= x a (t)M(t),其中x ̂a (t)是连续信号x a (t)的理想采样;M(t)是周期冲激M(t)=∑δ+∞−∞(t-nT)=1T ∑e jm Ωs t +∞−∞,其中T 为采样周期,Ωs =2π/T 是采样角频率。
信号理想采样的傅里叶变换为X ̂a (j Ω)=1T ∑X a +∞−∞[j(Ω−k Ωs )],由此式可知:信号理想采样后的频谱是原信号频谱的周期延拓,其延拓周期为Ωs =2π/T 。
根据时域采样定理,如果原信号是带限信号,且采样频率高于原信号最高频率分量的2倍,则采样以后不会发生频率混叠现象。
三、简明步骤产生理想采样信号序列x a (n),使A=444.128,α=50√2π,Ω0=50√2π。
(1) 首先选用采样频率为1000HZ ,T=1/1000,观察所得理想采样信号的幅频特性,在折叠频率以内和给定的理想幅频特性无明显差异,并做记录;(2) 改变采样频率为300HZ ,T=1/300,观察所得到的频谱特性曲线的变化,并做记录;(3) 进一步减小采样频率为200HZ ,T=1/200,观察频谱混淆现象是否明显存在,说明原因,并记录这时候的幅频特性曲线。
实验报告信号卷积实验

一、实验目的1. 理解卷积的概念及其物理意义。
2. 掌握卷积运算的原理和方法。
3. 通过实验加深对卷积运算在实际应用中的理解。
二、实验原理1. 卷积的定义:卷积是一种线性运算,它描述了两个信号在时域上的相互作用。
对于两个连续时间信号f(t)和g(t),它们的卷积定义为:F(t) = ∫f(τ)g(t-τ)dτ其中,F(t)是卷积结果,f(τ)是信号f(t)的任意时刻的值,g(t-τ)是信号g(t)在时刻t-τ的值。
2. 卷积的性质:卷积具有交换律、结合律和分配律等性质。
其中,交换律是指f(t)和g(t)的卷积与g(t)和f(t)的卷积相等;结合律是指三个信号f(t)、g(t)和h(t)的卷积可以分别进行两两卷积后再进行一次卷积;分配律是指一个信号与两个信号的卷积等于该信号分别与两个信号卷积后的和。
三、实验内容1. 实验一:连续时间信号卷积实验(1)选用信号:选取两个连续时间信号f(t)和g(t),其中f(t)为矩形脉冲信号,g(t)为指数衰减信号。
(2)卷积计算:根据卷积的定义,计算f(t)和g(t)的卷积F(t)。
(3)结果分析:观察F(t)的波形,分析卷积结果的物理意义。
2. 实验二:离散时间信号卷积实验(1)选用信号:选取两个离散时间信号f[n]和g[n],其中f[n]为单位阶跃信号,g[n]为矩形脉冲信号。
(2)卷积计算:根据离散时间信号卷积的定义,计算f[n]和g[n]的卷积F[n]。
(3)结果分析:观察F[n]的波形,分析卷积结果的物理意义。
3. 实验三:MATLAB仿真实验(1)选用信号:选取两个连续时间信号f(t)和g(t),其中f(t)为正弦信号,g(t)为余弦信号。
(2)MATLAB编程:利用MATLAB的信号处理工具箱,编写程序实现f(t)和g(t)的卷积运算。
(3)结果分析:观察MATLAB仿真得到的卷积结果,分析其物理意义。
四、实验结果与分析1. 实验一:连续时间信号卷积实验(1)实验结果:通过计算得到f(t)和g(t)的卷积F(t)的波形。
《数字信号处理》序列的基本运算和时域变换与离散信号的卷积和实验

《数字信号处理》序列的基本运算和时域变换与离散信号的卷积和实验一、实验目的1、掌握两个离散信号卷积和的计算方法和编程技术。
2、进一步熟悉用MATLAB 描绘二维图像的方法。
3、熟悉用MA TLAB 描绘二维图像的方法。
4、掌握用MA TLAB 对序列进行基本的运算和时域变换的方法。
二、实验器材 MATLAB 软件2019三、实验原理离散信号的卷积和原理:两个离散序列x (n )与y (n )的卷积和f (n )定义为∑∞-∞=-=*=m m n y m x n y n x n f )()()()()(由于通常信号处理中所碰到的都是有始信号或有限时间信号,因此在实际计算卷积和时,求和是在有限范围内进行的。
计算过程中上下限的选取和所得结果的分布区间取决于参与卷积的两个序列,下面将分别进行讨论:1、两个从n = 0开始的序列)()()(n u n x n x =和)()()(n u n y n y =的卷积和∑∑=∞-∞=-=--=nm m n u m n y m x m n u m n y m u m x n f 0)()]()([)()()()()( (1)上式右边因子u (n )表示卷积和的结果也是一个从n = 0开始的序列。
2、从n = n 1开始的序列)()()(1n n u n x n x -=和从n = n 2开始的序列)()()(2n n u n y n y -=的卷积和,其中n 1和n 2为任意整数。
∑∑-=∞-∞=---=----=21)()]()([)()()()()(2121n n n m m n nn u m n y m x n m n u m n y n m u m x n f (2)上式右边因子u (n -n 1-n 2)表示卷积和是一个从n = n 1+n 2开始的序列。
上机:conv.m 用来实现两个离散序列的线性卷积。
其调用格式是:y=conv(x,h)若x 的长度为N ,h 的长度为M ,则y 的长度L=N+M -1。
(完整版)数字信号处理实验三

3.41;3.42 由教材可知: ,即序列的偶部分的傅立叶变换是序列的傅立叶变换的实部。
5、实验步骤
1、进行本实验,首先必须熟悉matlab的运用,所以第一步是学会使用matlab。
2、学习相关基础知识,根据《数字信号处理》课程的学习理解实验内容和目的。
plot(w/pi,angle(h1));grid
xlabel('\omega/\pi');ylabel('以弧度为单位的相位');
title('原序列的相位谱')
subplot(2,2,4)
plot(w/pi,angle(h2));grid
xlabel('\omega/\pi');ylabel('以弧度为单位的相位');
grid;
title('相位谱arg[H(e^{j\omega})]');
xlabel('\omega/\pi');
ylabel('以弧度为单位的相位');
3.4
clf;
w=-4*pi:8*pi/511:4*pi;
num1=[1 3 5 7 9 11 13 15 17];
h=freqz(num,1,w);
Q3.32 通过加入合适的注释语句和程序语句,修改程序P3.8,对程序生成的图形中的两个轴加标记。时移量是多少?
Q3.33 运行修改后的程序并验证离散傅里叶变换的圆周时移性质。
Q3.36 运行程序P3.9并验证离散傅里叶变换的圆周卷积性质。
Q3.38 运行程序P3.10并验证线性卷积可通过圆周卷积得到。
实验三 线性卷积与循环卷积

实验三 线性卷积与循环卷积1、实验目的(1)掌握线性卷积的计算机编程方法,利用卷积的方法观察系统响应的时域特性。
(2)掌握循环卷积的计算机编程方法,并比较与线性卷积的差别,验证二者之间的关系。
利用循环卷积的方法观察、分析系统响应的时域特性。
2、实验原理(1)线性卷积:线性时不变系统(Linear Time-Invariant System, or LTI 系统)输入、输出间的关系为:当系统输入序列为)(n x ,系统的单位脉冲响应为)(n h ,输出序列为)(n y ,则系统输出为:∑∞-∞=-=*=m m n h m x n h n x n y )()()()()( 上式称为线性卷积。
(2)循环卷积设两个有限长序列)(1n x 和)(2n x ,长度分别为1N 和2N ,)()(11k X n x D FT N −−−→←点 )()(22k X n x D F T N −−−→←点如果)()()(21k X k X k X ⋅=则∑---==1021)())(()()]([)(N m N N n R m n x m x k X IDFT n x上式称为)(1n x 和)(2n x 的循环卷积。
(3)两个有限长序列的线性卷积序列)(1n x 和)(2n x ,长度分别为L 点和M 点,)(3n x 为这两个序列的线性卷积,则)(3n x 为∑∞-∞=-=*=m m n x m x n x n x n x )()()()()(21213且线性卷积)(3n x 的非零值长度为L +M -1点。
(4)循环卷积与线性卷积的关系 序列)(1n x 为L 点长,序列)(2n x 为M 点长,若序列)(1n x 和)(2n x 进行N 点的循环卷积)(n x c ,其结果是否等于该两序列的线性卷积)(n x l ,完全取决于循环卷积的长度。
由教材相关推导,得∑∞-∞=+=q N l c n R qN n x n x )()()(,也就是说,循环卷积是线性卷积的周期延拓序列再取主值区间。
信号卷积实验报告

信号卷积实验报告文档编制序号:[KKIDT-LLE0828-LLETD298-POI08]信号与系统实验报告学院:电子信息与电气工程学院班级: 13级电信<1>班学号:姓名:李重阳实验三 信号卷积实验一、实验目的1、理解卷积的概念及物理意义;2、通过实验的方法加深对卷积运算的图解方法及结果的理解。
二、实验原理说明卷积积分的物理意义是将信号分解为冲激信号之和,借助系统的冲激响应,求解系统对任意激励信号的零状态响应。
设系统的激励信号为x (t ),冲激响应为h (t ),则系统的零状态响应为()()()*y t x t h t ==()()x t h t d ττ∞-∞-⎰。
1、两个矩形脉冲信号的卷积过程两信号x (t )与h (t )都为矩形脉冲信号,如图3-1所示。
下面由图解的方法(图3-1)给出两个信号的卷积过程和结果,以便与实验结果进行比较。
图3-1 两矩形脉冲的卷积积分的运算过程与结果2、矩形脉冲信号与锯齿波信号的卷积信号f1(t )为矩形脉冲信号, f2(t )为锯齿波信号,如图3-2所示。
根据卷积积分的运算方法得到f1(t )和f2(t )的卷积积分结果f (t ),如图3-2(c )所示。
图3-2 矩形脉冲信号与锯齿脉冲信号的卷积积分的结果3、本实验进行的卷积运算的实现方法在本实验装置中采用了DSP 数字信号处理芯片,因此在处理模拟信号的卷积积分运算时,是先通过A/D 转换器把模拟信号转换为数字信号,利用所编写的相应程序控制DSP 芯片实现数字信号的卷积运算,再把运算结果通过D/A 转换为模拟信号输出。
结果与模拟信号的直接运算结果是一致的。
数字信号处理系统逐步和完全取代模拟信号处理系统是科学技术发展的必然趋势。
图3-3为信号卷积的流程图。
图3-3 信号卷积的流程图三、实验内容1、检测矩形脉冲信号的自卷积结果。
用双踪示波器同时观察输入信号和卷积后的输出信号,把输入信号的幅度峰峰值调节为4V,再调节输入信号的频率或占空比使输入信号的时间宽度满足表中的要求,观察输出信号有何变化,判断卷积的结果是否正确,并记录表3-1。
数字信号处理实验报告1-5

实验一时域离散信号的产生及时域处理实验目的:了解Matlab软件数字信号处理工具箱的初步使用方法。
掌握其简单的Matlab语言进行简单的时域信号分析。
实验内容:[1.1]已知两序列x1=[0,1,2,3,4,3,2,1,0];n1=[-2:6];x2=[2,2,0,0,0,-2,-2],n2=[2:8].求他们的和ya及乘积yp. 程序如下:x1=[0,1,2,3,4,3,2,1,0];ns1=-2;x2=[2,2,0,0,0,-2,-2];ns2=2;nf1=ns1+length(x1)-1;nf2=ns2+length(x2)-1;ny=min(ns1,ns2):max(nf1,nf2);xa1=zeros(1,length(ny));xa2=xa1;xa1(find((ny>=ns1)&(ny<=nf1)==1))=x1;xa2(find((ny>=ns2)&(ny<=nf2)==1))=x2;ya=xa1+xa2yp=xa1.*xa2subplot(4,4,1),stem(ny,xa1,'.')subplot(4,1,2),stem(ny,xa2,'.')line([ny(1),ny(end)],[0,0])subplot(4,1,3),stem(ny,ya,'.')line([ny(1),ny(end)],[0,0])subplot(4,1,4),stem(ny,yp,'.')line([ny(1),ny(end)],[0,0])[1.2]编写产生矩形序列的程序。
并用它截取一个复正弦序列,最后画出波形。
程序如下:clear;close alln0=input('输入序列起点:n0=');N=input('输入序列长度:N=');n1=input('输入位移:n1=');n=n0:n1+N+5;u=[(n-n1)>=0];x1=[(n-n1)>=0]-[(n-n1-N)>=0];x2=[(n>=n1)&(n<(N+n1))];x3=exp(j*n*pi/8).*x2;subplot(2,2,1);stem(n,x1,'.');xlabel('n');ylabel('x1(n)');axis([n0,max(n),0,1]);subplot(2,2,3);stem(n,x2,'.');xlabel('n');ylabel('x2(n)');axis([n0,max(n),0,1]);subplot(2,2,2);stem(n,real(x3),'.'); xlabel('n');ylabel('x3(n)的实部');line([n0,max(n)],[0,0]);axis([n0,max(n),-1,1]);subplot(2,2,4);stem(n,imag(x3),'.'); xlabel('n');ylabel('x3(n)的虚部');line([n0,max(n)],[0,0]);axis([n0,max(n),-1,1]);[1.3]利用已知条件,利用MATLAB生成图形。
数字信号处理卷积定理

数字信号处理实验报告实验二:卷积定理班级:10051041姓名:学号:10051041一、实验目的通过本实验,验证卷积定理,掌握利用DFT和FFT计算线性卷积的方法。
二、实验原理时域圆周卷积在频域上相当于两序列DFT的相乘,因而可以采用FFT的算法来计算圆周卷积,当满足121L N N≥+-时,线性卷积等于圆周卷积,因此可利用FFT计算线性卷积。
三、实验内容和步骤1.给定离散信号()x n和()h n,用图解法求出两者的线性卷积和圆周卷积;2.编写程序计算线性卷积和圆周卷积;3.比较不同列长时的圆周卷积与线性卷积的结果,分析原因。
四、实验设备计算机、Matlab软件五、实验报告要求1.整理好经过运行并证明是正确的程序,并且加上详细的注释。
2.给出笔算和机算结果对照表,比较不同列长时的圆周卷积与线性卷积的结果对照,作出原因分析报告。
3.给出用DFT计算线性卷积的方法。
六、实验结果与分析X=[0 0.5 1 1.5]Y=[1 1 1]笔算结果线性卷积:[0 0.5 1.5 3 2.5 1.5 0]圆周卷积:N=10 时[0 0.5 1.5 3 2.5 1.5 0 0 0 0 ]N=5 [1.5 0.5 1.5 3 2.5]机算结果线性卷积:[0 0.5 1.5 3 2.5 1.5 0]圆周卷积:N=10 时[0 0.5 1.5 3 2.5 1.5 0 0 0 0 ]N=5 [1.5 0.5 1.5 3 2.5]原因分析:循环卷积是线性卷积以L为周期的周期延拓序列的主值序列。
由于线性卷积的长度是N1+N2-1,所以只有当121L N N≥+-时,线性卷积以L为周期进行周期延拓时才不会发生混叠,周期序列的主值序列才等于线性卷积,即L点循环卷积代替线性卷积的条件是121L N N≥+-。
具体计算结果图示如下程序:用DFT 计算线性卷积的方法:七、实验体会通过本次实验,验证了卷积定理,熟悉了线性卷积与圆周卷积的计算方法,并验证了两者之间的关系。
华南理工大学数字信号处理实验报告3(曹老师)

华南理⼯⼤学数字信号处理实验报告3(曹⽼师)⼀、实验⽬的加深对LTI 系统的理解以及分析。
⼆、实验原理系统输⼊、输出关系可⽤以下差分⽅程描述:∑∑==-=-Mk k Nk kk n x p k n y d][][系统响应为如下的卷积计算式:∑∞-∞=-=*=m m n h m x n h n x n y ][][][][][当Nk d k ,...2,1,0==时,h[n]是有限长度的(n :[0,M]),称系统为FIR 系统;反之,称系统为IIR 系统。
系统的转移函数为 NN M M z d z d d z p z p p z D z p z H ----++++++==......)()()(110110三、实验内容1、⽤函数y=filter(p,d,x)实现差分⽅程的仿真,也可以⽤函数 y=conv(x,h)计算卷积,⽤y=impz(p,d,N)求系统的冲激响应,再⽤卷积来计算任意信号作⽤于系统的响应。
求两个系统]1[][]2[125.0]1[75.0][--=-+-+n x n x n y n y n y]}4[]3[]2[]1[{25.0][-+-+-+-=n x n x n x n x n y 各⾃的冲激响应,并且⽐较filter和conv 函数的区别实验代码如下:clear%离散时间序列x[n] n = 0:9; x = 5*exp(-n); subplot(4,2,1); stem(n,x)title('离散时间序列x[n]');%⽤filter函数滤波a1 = [1 , 0.75 , 0.125];b1 = [1 , -1];y1 = filter(b1,a1,x);subplot(4,2,3);stem(n,y1)title('filter滤波1');a2 = [1];b2 = [0 , 0.25 , 0.25 , 0.25 , 0.25]; y2 = filter(b2,a2,x);subplot(4,2,4);stem(n,y2)title('filter滤波2');%求系统的冲激响应h1 = impz(b1,a1,10);subplot(4,2,5);stem(n,h1)title('冲激响应1');h2 = impz(b2,a2,10);subplot(4,2,6);stem(n,h2)title('冲激响应2');%⽤conv函数计算卷积y3 = conv(x,h1);subplot(4,2,7);stem(y3)title('卷积1');y4 = conv(x,h2);subplot(4,2,8);stem(y4)title('卷积2');实验结果如下:离散时间序列x[n]filter 滤波2冲激响应1冲激响应22468101214161820卷积22、⽤函数[z ,p ,K]=tf2zp (num ,den )求得有理分式形式的系统转移函数的零、极点,⽤函数zplane (z ,p )绘出零、极点分布图;也可以⽤函数zplane (num ,den )直接绘出有理分式形式的系统转移函数的零、极点分布图。
实验3报告_信号的卷积实验

e
其输入输出符合卷积运算: y (t ) x (t ) h (t ) 。
实验内容: 1、测量信号的卷积运算并与理论计算值比较。
实验仪器: 1、信号与系统实验箱一台(主板) 。 2、系统时域与频域分析模块一块。 3、20MHz 示波器一台。
实验步骤: 1、把系统时域与频域分析模块插在主板上,用导线接通此模块“电源接入”和主 板上的电源(看清标识,防止接错,。 ) 2、接通主板上的电源,同时按下本模块的电源开关 S1,将“函数信号发生器”模 块中的输出通过导线引入到“零输入零状态响应”的输入端。 (将“波形选择”拨到方 波 “频率调节”用于在频段内的频率调节, “占空比”用于脉冲宽度的调节,可改变以 上的参数进行相关的操作) 。 3、 用示波器的两个探头,一个接函数信号发生器输出作同步,一个用于观察输出 信号的波形,观察在输入信号的高电平时段对应的输出信号。 4、改变函数信号发生器的“频率调节”“幅度调节”电位器,观察相应的输出信号。 、 5、将输入信号分别设置为正弦波和三角波,观察输出信号。 6、改变本实验的开关 K1 的位置,观察到的是不同系统下的输出信号,比较输入信 号分别是方波、正弦波和三角波时两个系统的输出信号。
数据处理分析方波信号的卷积三角波信号的卷积正弦波信号的卷积深圳大学学生实验报告用纸实验结论该试验主要为信号的卷积验证试验对输入的信号进行卷积后通过通过示波器将输出信号显示出来然后再通过与理论计算出的结果进行对比
深 圳 大 学 实 验 报 告
课程名称:
信号与系统
实验项目名称:
信号的卷积实验
学院:
信息工程
专业:
电子 信息
指导教师:
报告人: 学号: 班级:
实验时间:
实验报告提交时间:
数字信号处理第二版(吴镇扬)实验三

5
10
15
0
5
10
15 20
n
k
时域
(3)、观察三角波和反三角波序列的时域和幅频特性,用 N=8 点 FFT 分析信号序 列 xc(n)和 xd(n)的幅频特性,观察两者的序列形状和频谱曲线有什么异同?绘出 两序列及其幅频特性曲线。
在 xc(n)和 xd(n)末尾补零,用 N=16 点 FFT 分析这两个信号的幅频特性,观
时域
时域
1
4
a=0.1,f=0.0625
频域
0
2
a=0.1,f=0.0625
-1
0
0
5
10
15
0
5
10
15 20
n
k
1
4
a=0.1,f=0.4375
频域
0
2
a=0.1,f=0.4375
-1
0
0
5
10
15
0
5
10
15 20
n
k
1
4
a=0.1,f=0.5625
频域
0
2
a=0.1,f=0.5625
-1
0
0
figure(2) [x4,F4]=gauss(8,8); n=0:15; subplot(3,2,1); plot(n,x4);text(6,0.2,'p=8,q=8'); grid on; xlabel('n'); ylabel('时域'); subplot(3,2,2); plot(abs(F4));text(7.5,2,'p=8,q=8'); grid on; xlabel('k'); ylabel('频域');
实验三:信号卷积实验

信号与系统实验报告学院:物理与信息科学学院班级: 12级电信<2>班学号: 20121060241姓名:马路路实验三.信号卷积实验一.实验目的1.理解卷积的概念及物理意义2.通过实验的方法加深对卷积运算的图解方法及结果的理解二.实验内容1.检测矩形脉冲信号的自卷积结果用示波器观察输入信号和卷积后的输出信号,把输入信号的幅度峰峰值调节为4V;再调节输入信号的频率或占空比;使输入信号的时间宽度满足表中的要求,观察输出信号有何变化。
判断卷积的结果是否正确,并记录表3-1。
实验步骤如下:①将跳线开关J701至于“方波”上。
②连接P201与P501,在TP501上可观测到输入波形。
将示波器接在TP501上,并调节信号源模块上的旋钮W701与W705,使信号频率为1kHz,幅度为4V。
③将红色波动开关SW102调整为“0001”。
④按下复位键SW101 。
⑤将示波器接于TP911,观察到输入信号的波形,接于P913观察到卷积后的输出波形。
表3-1 输入信号卷积后的输出波形说明:本实验中采用矩形脉冲信号的自卷积。
因此,TP911与TP912上的波形一致。
在TP913上可观测到三角波。
2.信号与系统卷积原理与步骤:①将跳线开关J701至于“方波”上。
②连接P201与P501,在TP501上可观测到输入波形。
将示波器接在TP501上,并调节信号源模块上的旋钮W701与W705,使信号频率为1kHz,幅度为4V。
③将红色波动开关SW102调整为“0010”。
④按下复位键SW101。
⑤将示波器接于TP911或TP912,首先观测两个卷积信号。
TP911上的测得的是激励信号,TP912上测得的是系统信号(本实验中系统信号用的是锯齿波形),再用示波器测TP913可测到卷积后的输出信号的波形。
表3-2 输入信号和卷积后的信号3.思考题用图解的方法给出下图两个信号的卷积过程。
《数字信号处理》课程设计报告-卷积运算及算法实现

《数字信号处理》课程设计报告卷积运算及算法实现专业:通信工程班级:通信08-2BF组次:第10组姓名:学号:卷积运算及算法实现一、 设计目的卷积运算是一种有别于其他运算的新型运算,是信号处理中一种常用的工具。
随着信号与系统理论的研究的深入及计算机技术发展,卷积运算被广泛地运用到现代地震勘测,超声诊断,光学诊断,光学成像,系统辨识及其他诸多新处理领域中。
了解并灵活运卷积运算用去解决问题,提高理论知识水平和动手能力,才是学习卷积运算的真正目的。
通过这次课程设计,一方面加强对《数字信号处理》这门课程的理解和应用,另一方面体会到学校开这些大学课程的意义。
二、设计任务探寻一种运算量更少,算法步骤更简单的算法来实现卷积运算,文中主要通过阶梯函数卷积计算方法和斜体函数卷积计算方法对比来得出最终结论。
三、设计原理1,什么是卷积?卷积是数字信号处理中经常用到的运算。
其基本的表达式为:()()()∑=-=nm m n x m h n y 0换而言之,假设两个信号f 1(t)和f 2(t),两者做卷积运算定义为 f(t)d做一变量代换不难得出: f(t)d =f 1(t)*f 2(t)=f 2(t)*f 1(t)在教材上,我们知道用图解法很容易理解卷积运算的过程,在此不在赘述。
2,什么是阶梯函数所谓阶梯函数,即是可以用阶梯函数u(t) 和u(t-1)的线性组合来表示的函数,可以看做是一些矩形脉冲的集合,图1-1给除了两个阶梯函数的例子。
1—1其中f(t)=2u(t)+u(t-1)-2u(t-2)-u(t-3),h(t)= 2u(t)-u(t-1)+2u(t-2)-3u(t-3).以图1—1中两个阶梯函数为例介绍本文提出的阶梯函数卷积算法。
根据卷积的性质(又称为杜阿美尔积分),上述f(t)与h(t)的卷积等于f(t)的导数与h(t)的积分的卷积,即:f(t)*h(t)=*由于f(t)为阶梯函数,因此其导数也为冲击函数及其延时的线性组合,如图1—2(a)所示。
数字信号处理实验三报告 数字信号处理上机实验报告.doc

数字信号处理实验三报告数字信号处理上机实验报告实验一系统响应及系统稳定性一、实验目的(1)掌握求系统响应的方法。
(2)掌握时域离散系统的时域特性。
(3)分析、观察及检验系统的稳定性。
二、实验内容(1)给定一个低通滤波器的差分方程为y(n)=0.05x(n)+0.05x(n-1)+0.9y(n-1)输入信号x1(n)=R8(n)x2(n)=u(n)(a) 分别求出系统对x1(n)=R8(n) 和x2(n)=u(n)的响应序列,并画出其波形。
(b) 求出系统的单位冲响应,画出其波形。
实验程序:A=[1,-0.9];B=[0.05,0.05]; %%系统差分方程系数向量 B 和 Ax1n=[1 1 1 1 1 1 1 1 zeros(1,50)]; %产生信号 x1(n)=R8(n)x2n=ones(1,8); %产生信号 x2(n)=u(n)y1n=filter(B,A,x1n); %求系统对 x1(n)的响应 y1(n)n=0:length(y1n)-1;subplot(2,2,1);stem(n,y1n,".");title("(a) 系统对 R_8(n)的响应y_1(n)");xlabel("n");ylabel("y_1(n)");y2n=filter(B,A,x2n); %求系统对 x2(n)的响应 y2(n) n=0:length(y2n)-1;subplot(2,2,2);stem(n,y2n,".");title("(b) 系统对 u(n)的响应y_2(n)");xlabel("n");ylabel("y_2(n)");hn=impz(B,A,58); %求系统单位脉冲响应 h(n)n=0:length(hn)-1;subplot(2,2,3);y=hn;stem(n,hn,".");title("(c) 系统单位脉冲响应h(n)");xlabel("n");ylabel("h(n)");运行结果图:(2)给定系统的单位脉冲响应为h1(n)=R10(n)h2(n)= δ(n)+2.5δ(n-1)+2.5δ(n-2)+δ(n-3)用线性卷积法分别求系统h1(n)和h2(n)对x1(n)=R8(n)的输出响应,波形。
《数字信号处理》圆周卷积和与线性卷积和实验

《数字信号处理》圆周卷积和与线性卷积和实验一、实验目的1. 掌握用MTALAB软件实现有限长序列的圆周移位和圆周翻褶的方法;2. 掌握在MATLAB中圆周卷积和的时域和频域计算方法;3. 理解圆周卷积和与线性卷积和的关系,掌握用FFT计算线性卷积和的方法。
二、实验原理和实验内容1. 圆周移位和圆周翻褶(1)求余数(模运算)函数mod(n,N)调用方法:n1=mod(n,N)功能:n1=n + KN,0≤ n1≤ N-1,K为整数,余数n1在0至N-1之间将模运算用到位置向量上,可实现有限长序列的周期延拓,即1(mod)(())Nn n N n==。
设x的起始位置为0,长度为N,坐标为:n=0:K*N-1 % N为延拓周期,K为周期数延拓后序列的值为:x=x(mod(n, N)+1)由于MATLAB中数组x的下标是为nx=[1:N],而mod(n, N)的值在0到N-1之间,因此要将mod( )函数的结果加1。
➢练习调用该函数mod( )将序列()[1,2,3,4,5]x n=延拓5个周期得到序列y(n)。
程序x=[1,2,3,4,5]nx=[0:1:4];n=[0:1:24];N=5;y=x(mod(n,N)+1)subplot(121),stem(nx,x);title('原序列');subplot(122),stem(n,y);title('延拓后序列');结果x =1 2 3 4 5y =Columns 1 through 151 2 3 4 5 1 2 3 4 5 1 2 3 4 5 Columns 16 through 251 2 3 4 5 1 2 3 4 5(2)圆周移位N 点有限长序列的m 点移位可以看成将()x n 以N 为周期,延拓成周期序列()(())N x n x n =,将(())N x n 做m 点线性移位后,再取主值区间中的序列,即可得到()x n 的m 点圆周移位序列()m x n ,即()(())()m N N x n x n m R n =+注意:只能计算有限长序列的DTFT ,对于无限长序列,要进行截取。
实验三 信号卷积的MATLAB实现

实验三信号卷积的MATLAB实现一、实验名称:信号卷积的MATLAB实现二、实验目的:1.增加学生对卷积的认识2.了解MATLAB这个软件的一些基础知识3.利用MATLAB计算信号卷积4.验证卷积的一些性质三、实验原理:用MATLAB实现卷积我们先必须从信号下手,先把信号用MATLAB语句描述出来,然后再将这些信号带入到我们写好的求卷积的函数当中来计算卷积。
在本章中我们将信号分为连续信号和离散序列两种来实现卷积并验证卷积的一些性质。
MATLAB强大的图形处理功能及符号运算功能,为我们实现信号的可视化提供了强有力的工具。
在MATLAB中通常有两种方法来表示信号,一种是用向量来表示信号,另一种则是用符号运算的方法来表示信号。
用适当的MATLAB 语句表示出信号后,我们就可以利用MATLAB的绘图命令绘制出直观的信号波形。
连续时间信号,是指自变量的取值范围是连续的,且对于一切自变量的取值,除了有若干不连续点以外,信号都有确定的值与之对应的信号。
从严格意义上来讲,MATLAB并不能处理连续信号,在MATLAB中,是用连续信号在等时间间隔点的样值来近似地表示连续信号的,当取样时间间隔足够小时,这些离散的样值就能较好地近似出连续信号。
在MATLAB中连续信号可用向量或符号运算功能来表示。
1.向量表示法对于连续时间信号f(t),我们可以用两个行向量f和t来表示,其中向量t是行如t=t1:p:t2的MATLAB命令定义的时间范围向量,t1为信号起始时间,t2为中止时间,p为时间间隔。
向量f为连续信号f(t)在向量t所定义的时间点上的样值。
例如对于连续信号f(t)=sin(t),我们可以用如下两个向量来表示:t=-10:1.5:10;f=sin(t)用上述向量对连续信号表示后,就可以用plot命令来绘出该信号的时域波形。
Plot命令可将点与点间用直线连接,当点与点间的距离很小时,绘出的图形就成了光滑的曲线。
命令如下:plot(t,f)title(‘f(t)=sint’)xlabel(‘t’)axis([-10,10,-1.1,1.1])绘制的信号波形如图3.1所示,当把时间间隔p取得更小(如0.01)时,就可得到sint较好的近似波形,如图3.2所示。
2014数字信号处理第三章作业 (1)
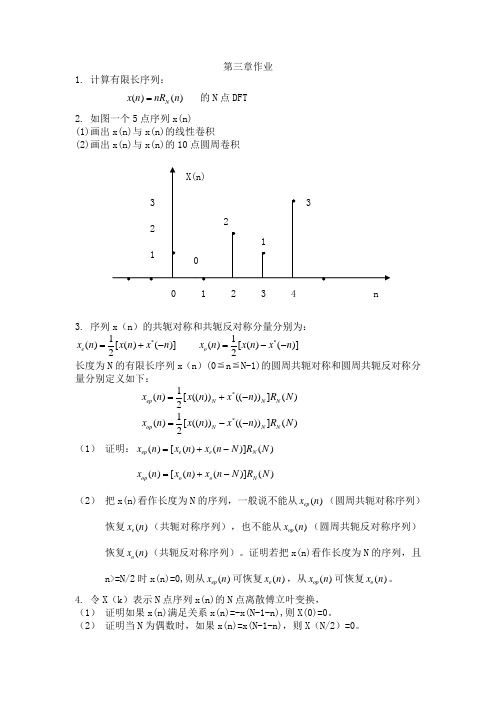
第三章作业1. 计算有限长序列:()()N x n nR n = 的N 点DFT2. 如图一个5点序列x(n)(1)画出x(n)与x(n)的线性卷积(2)画出x(n)与x(n)的10点圆周卷积3. 序列x (n )的共轭对称和共轭反对称分量分别为:*1()[()()]2e x n x n x n =+- *1()[()()]2o x n x n x n =-- 长度为N 的有限长序列x (n )(0≦n ≦N-1)的圆周共轭对称和圆周共轭反对称分量分别定义如下: *1()[(())(())]()2ep N N N x n x n x n R N =+- *1()[(())(())]()2op N N N x n x n x n R N =-- (1) 证明:()[()()]()ep e e N x n x n x n N R N =+-()[()()]()op o o N x n x n x n N R N =+-(2) 把x(n)看作长度为N 的序列,一般说不能从()ep x n (圆周共轭对称序列)恢复()e x n (共轭对称序列),也不能从()op x n (圆周共轭反对称序列)恢复()o x n (共轭反对称序列)。
证明若把x(n)看作长度为N 的序列,且n>=N/2时x(n)=0,则从()ep x n 可恢复()e x n ,从()op x n 可恢复()o x n 。
4. 令X (k )表示N 点序列x(n)的N 点离散傅立叶变换,(1) 证明如果x(n)满足关系x(n)=-x(N-1-n),则X(0)=0。
(2) 证明当N 为偶数时,如果x(n)=x(N-1-n),则X (N/2)=0。
0 1 2 3 4n5.频谱分析的模拟信号以8kHz被抽样,计算了512个抽样的DFT,试确定频谱抽样的频率间隔,并证明之。
6.已知x(n)是2N点的实序列(0≦n≦2N-1),其DFT为X(k)=DFT[x(n)],请用一个N点DFT运算来计算此X(k).。
数字信号处理卷积公式

数字信号处理卷积公式一、离散序列的卷积公式。
1. 定义。
- 设离散序列x(n)和h(n),它们的卷积y(n)定义为:y(n)=∑_m =-∞^∞x(m)h(n - m)- 这里m是求和变量,n表示卷积结果y(n)的序列序号。
2. 计算步骤示例。
- 例如,已知x(n)={1,2,3}(n = 0,1,2时的值,其他n时x(n)=0),h(n)={2,1}(n = 0,1时的值,其他n时h(n)=0)。
- 当n = 0时:- y(0)=∑_m =-∞^∞x(m)h(0 - m)=x(0)h(0)=1×2 = 2- 当n = 1时:- y(1)=∑_m =-∞^∞x(m)h(1 - m)=x(0)h(1)+x(1)h(0)=1×1+2×2=1 + 4=5- 当n = 2时:- y(2)=∑_m =-∞^∞x(m)h(2 - m)=x(0)h(2)+x(1)h(1)+x(2)h(0)=1×0+2×1+3×2=0 + 2+6 = 8- 当n = 3时:- y(3)=∑_m =-∞^∞x(m)h(3 - m)=x(1)h(2)+x(2)h(1)=2×0+3×1 = 3- 当n>3时,y(n)=0。
所以y(n)={2,5,8,3}。
3. 卷积的性质。
- 交换律:x(n)*h(n)=h(n)*x(n),即∑_m =-∞^∞x(m)h(n - m)=∑_m =-∞^∞h(m)x(n - m)。
- 结合律:(x(n)*h_1(n))*h_2(n)=x(n)*(h_1(n)*h_2(n))。
- 分配律:x(n)*(h_1(n)+h_2(n))=x(n)*h_1(n)+x(n)*h_2(n)。
二、连续信号的卷积公式。
1. 定义。
- 设连续时间信号x(t)和h(t),它们的卷积y(t)定义为:y(t)=∫_-∞^∞x(τ)h(t-τ)dτ- 这里τ是积分变量,t表示卷积结果y(t)的时间变量。
(完整版)数字信号处理实验三

实验三 离散时间信号的频域分析实验室名称:信息学院2204 实验时间:2015年10月15日姓 名:蒋逸恒 学号:20131120038 专业:通信工程 指导教师:陶大鹏成绩教师签名:一、实验目的1、 对前面试验中用到的信号和系统在频域中进行分析,进一步研究它们的性质。
2、 学习离散时间序列的离散时间傅立叶变换(DTFT 、离散傅立叶变换(DFT 和z 变换。
二、实验内容Q3.1在程序P3.1中,计算离散时间傅里叶变换的原始序列是什么?Matlab 命令pause的作用是什么?Q3.2运行程序P3.1,求离散时间傅里叶变换得的实部、虚部以及幅度和香相位谱。
离散时间傅里叶变换是 w 的周期函数吗?若是,周期是多少?描述这四个图形表示的 对称性。
Q3.2修改程序P3.1,在范围0W w Wn 内计算如下序列的离散时间傅里叶变换:0.7 0.5e jw 0.3e j2w e j3w1 0.3e jw 0.5e j2w 0.7e j3w并重做习题P3.2,讨论你的结果。
你能解释相位谱中的跳变吗? 可以移除变化。
试求跳变被移除后的相位谱。
Q3.6通过加入合适的注释语句和程序语句,修改程序 两个轴加标记。
哪个参数控制时移量?Q3.10通过加入合适的注释语句和程序语句,修改程序 两个轴加标记。
哪个参数控制频移量?Q3.14通过加入合适的注释语句和程序语句,修改程序 两个轴加标记。
Q3.15运行修改后的程序并讨论你的结果。
Q3.17通过加入合适的注释语句和程序语句,修改程序 两个轴加标记。
Q3.20通过加入合适的注释语句和程序语句,修改程序 两个轴加标记。
试解释程序怎样进行时间反转运算。
Q3.23编写一个MATLAB?序,计算并画出长度为为值,其中L > N,然后计算并画出L 点离散傅里叶逆变换X[k]。
对不同长度N 和不同的 离散傅里叶变换长度L ,运行程序。
讨论你的结果。
U(e jw )MATLAE 命P3.2,对程序生成的图形中的 P3.3,对程序生成的图形中的 P3.4,对程序生成的图形中的P3.5,对程序生成的图形中的 P3.6,对程序生成的图形中的 N 的L 点离散傅里叶变换X[k]的Q3.26在函数circshift 中,命令rem 的作用是什么? Q3.27解释函数circshift 怎样实现圆周移位运算。
