2020年初中几何模型大全
初中数学几何模型

全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型:说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是°、°、°、°及有一个角是°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇度旋度,造等边三角形遇度旋度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋度,造中心对称说明:IS 8模型变形BEFcEB说明:说明:nnnnnnnnnnnnnnnnnnnnnnn nnnnn口叩皿皿皿皿皿中点模型 边构诗中{fflt 逢阳点闵iS 中幽城 几何最值模型 VH *h 轴对称模型 对称最值 线mi 差模型 fflftffw 同侧"异侧两蜒段之利罐短视它 同侧、异删芮线投之羞媪小槐型 四边形周怏垠小根地 三角形眉长 必小檢哩三线穀之和 她知爬制过桥模取旋转最值说明:找到与所要求最值相关成三角形的两个定长线段,定长线段的和为最大值,定长线段的差为最小值。
简拼模型三角形j四边形E 面积等分说明:说明:3045602说明:ACOCOAA 模型一:手拉手模型-旋转型全等<2)等濮的AA Mfr=血°拟述°均为等媵直甬M 册A 结险(DA (UCtAO^l>j 超乙他»③。
E 平分£忖了儿(1)―况> Sfr :LDW 牛底皿力能转至右囲检置A 皓论:> 右图中①bOCWMe\QAC AOSD 』 >⑨延氏M 交购于点G 必肖5氏-LBOA⑵特燥惜况>条件m 3MB ,厶伽■剜,将AXD 龍讳至右團位蛊a gife :右gcp fflAfJCD^iOJ^AC?JCiM£33②延长M 交加于点瓦愁有3EC -LUGA f BD 000B (5)-—--——=—-=tan ZlfX D®ACOCOA 3f^SDLAC.灘接也JC >临加*†g ・a+o>s ⑥矢"訐c&J 冊哒相垂直的四嬷)<3)任翦腰三角晤†辭,。
初中数学几何模型大全

初中数学几何模型大全全等变换平移:平行等线段〔平行四边形〕对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型角分线模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等.两边进行边或者角的等量代换,产生联系.垂直也可以做为轴进行对称全等.对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称〔翻折〕,翻折成正方形或者等腰直角三角形、等边三角形、对称全等.旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等.自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角逼等腰旋顶点,造旋转全等遇中点旋180度,造中央对称说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容.通过“8〞字模型可以证实.模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用.当遇到复杂图形找不到旋转全等时,先找两个正多边组相邻等线段,分组组成三角形证全等.点,证实另外两个顶点与中点所成图形为翻腰直角三 角形.证实方法是倍长所要证等腰直角三角形的一直 角边,转化成要证实的等腰直角三角形和的等腰 直角三角形〔或者正方形〕公旋转顶点,通过证实旋形或者等腰三角形的公共顶点,围绕公共顶点找到两 一匚■中点旋转:方形一个等腰直角三角形及两个图形顶点连线的中转全等三角形证实倍长后的大三角形为等腰直角三角形从而得证.几何最值侬对称最值〔两点间线段最短〕二线段之和量短模型过桥模型四边脑周KM小模型三俗形用长最小模型同侧.异侧两线段之和最短就型轴对称模型同侧,异恻两线段之W最小段T;线段和差模型HIM对称最值〔点到直线垂线段最短〕说明:通过对称进行等量代换,转换成两点间距离及点到直线距离.旋转最值〔共线有最值〕说明:找到与所要求最值相关成三角形的两个定长线段,定长线段的和为最大值,定长线段的差为最小值.剪拼侬三角形—四边形边形.四边形说明:剪拼主要是通过中点的180度旋转及平移改变形的形状.矩形一正方形说明:通过射影定理找到正方形的边长,通过平移与旋转完成形状改变正方形+等腰直角三角形一正方形面积等分旋转相似侬说明:两个等腰直角三角形成旋转全等,两个有一个角是300角的直角三角形成旋转相似.推广:两个任意相似三角形旋转成一定角度,趣转相似.第三边所成夹角符合旋转〃8〞字的规律.相似模型说明:注意边和角的对应,相等线段或者相等比值在证实相似中起到通过等量代稣构造相帕角形的作用.说明:(1)三垂直到一线三等角的演变,三等角以30良45原60度形式出现的居多.(2 )内外角平分线定理到射影定理的演变,注意之间的相同与不同之处.另外,相似射影定理.相交弦定理〔可以推广到圆幂定理〕之间的比值可以转换口乘积,通过等线鼠等比值、等乘积进行代换,进行证实得到需要的结论.说明:相似证实中最常用的辅助线是做平行,根据题的条件或者结论的比值来做相应的平行线.A 模型一:手拉手模型-旋转型全等<1>融笈给a 条件:Q 均为等边三角形» 结论:① A 〔〃C ♦ M 〕BD ,② LAEB = 601 ③ OE 平分 LAED.<2〕等腰A 条件:A .4优均为等腰直用三角形a 结论,①△〔,〔 ■ N 〕BD J ② L.lEti - 9.\ A ③.E 平分乙IED .<3>任意等腰三角形A 轴:wcw 〞均为等股三龟形a 牯论二① A .,.・ &OBD ;② LAEB • LAOQ .»③0E 平分乙l£O .A 模型二:手拉手模型-旋转型相似〔DT^况A 条件:〔力〃,出,将△〃口〕旅转至右囹位贸 A 给论:> 右图中① A 〃C 〜AOMeMMC' M 〕BD ; a ②延长"交BD 于点E,必有UEC • LBOA⑵特殊情况 >条件,CD//AB ,乙〞财■佻产,将ACC 及旋转至右图 位置>牯论:右图中①AOC&SAOJ A O AOIC ROBD 3②⑤连接/D. BC,必有;6〞.二』炉,8;⑥=…・/.卬〕〔对角线互相垂直的四边形〕5 @RDLAC .延长/C 交加于点&必有tan LOCDA模型三;对角互补模型⑴全等型30a①乙北加•乙DCE - 9.° j②oc平分&CB JJA 结论:① CD=CE:② 0D + °E ■ 6oc J ③,SoDt'E - $!110cB + §皿LA证!搬示:的乍垂直,如图,证实"DM •&CEN]■<②过点C作b 1 0C,如上图(右),证实AODC- AFEC ;, a当乙DCE的一边交/O的延长线于点Q时:〞以上三个结论:(DCD=C£(不变)3厂心“-$的」"‘@OE-OI〉・GOC, @" 211愉论那么方法第IT摊况T,可自HiS.K'S C>t£X H~ X'Mu<2>全等型-1200»霜:044OB・2乙XE・I2O03a ®oc 平分20%1y/a 结论:①C〞・CEj②./) +.£・优3(X T/—SflDCT " ^AGCD + SwKT " 7 0°A③4.,\A证骊I示:①可参考〃全等型-知,,证法一;②如却在05上取一点尸,使.尸=0C,证实AO"^IT为等边三角形.a(3)全领任意角a> 新:(Q- 2a, LDCE - 18() - 2(c . ©CD-C£;A 结论;①0('平分乙IO% ②,OE -2PC*cosa ,a @s(m - 5^CD- OC^sina -cosaa当〃的一边交乂.的延长线于点口时(如右上图〉;原结论变成:①②③I可参考上述第②种万法西亍证实.语思考初始条件的变化对模型幡oK a—35晌.>对角研触克结:①常见初始条件:四边形芯角互扑;注意两点:四点共圆及直通三通形斜②初始条件「角平分线〞与“两边相等〞的区别;③两种富见硒图域轴法3④注意00平分乙时,LCDE - LCED - LCOA・WCQ相等如何边中线;47f 推导?A模型四:角含半角模型M<1〕角含半角模型90° -1»①正方形9C?,45\>牯论,①EF - BE ;②KEF的周长为正方形一出CO周长的一半;也可以哪:a W=①正方形dBC?②EF = DF・BEa 结论: Z£//:45.<2〕角含半角模型式.,a条件:①正方形/出8; © LEAF - 450a 结论二EF -DF-BE> '岫线如下列图所示:〔3〕角含半鱼模型90° -3A条件二①吟② a 结论;RD2 + CE1 = DE2假设UM 曲到&版外部时,结论5+3 =.「仍然成立.设明>遵履AC?方公不唯一〕V Z/JW«・・S〞・,4F •,4Ml・/CMAV Zl/W-Z(C £ - 45 \ .*. XIDIMXUT---A〞/s&sc Ai! X£a条件:①正方形/"CD;②LEAF - 45Q>结论:A"比为等艘直角三用形°A模型五:倍长中线类模型⑴倍长中物飕里-1A 条件二①矩形ABCD;②〃"■"心③.尸,£7、»结论一"\LC广模型拄取,①有平行线TQI山E:②平行线|胡戋段有中点.尸,EF砌屣"8"字第ZU/A:・ A/他射.〔25借长中绳械型-2> 条件:.¥行四边形RRCD ;②"C ■ 2AB;③AM - DM;@CELAD.a结论:乙EMD・3乙AIEA情助〞:有个什AB/fCD .市中版.d V - /AV/达长EM•利造/“I〃心,八〃',4M C.V杓连号・vj.ur T vvcA通过构迨8字先等八段也量庆C1JL美系.用的欠小小化A 模型六:相似三角形360°旋转模型⑴相似三角形?等JO 角)酬.旋转模型斗检法a 条件:①NDE 、A4 AC 均为等腰直角三角形m ②EF ・CF, a 结论:①DF ・BF ;②DF1 B 尸Ml 财观,尚迨哥腰JLMAJEG 、M 〞C技劝独弓咕;将/V 句仲化到与EU ⑵ 任鄢时三角形360'旋转模3H 除法a (D M)ABsz2c ,② LOAH - Z ODC -巩尸;③BE ・CE .» 结论:① AE= l)E j ② LAEly - 2 LABO,③就的画个〉件“化仇」叫3〃,MHO . it为收晟.#NM8A.4取,雄靖傅化由江那么\ ।外匕小j m.传网色以*比M 4商* 此处.•机a 施叫 乙区H ・N 〃M )H 削l:增长/)/: £ V .便\肥7出.杵修(O 形360°值 MM DF HAG.盘 FG ・DF . 4.li(Xi . B(i . Klf Um .MifKi京k 点;\加必“机;e A: U . 41)■ ZflC G横财姬:地太AJ «AG .使.0・AB .过长 < /> 财 A H 佗 DH = Cl> .林 t WB 〞OC7fHit J£ DE iiCG A KH .比 NJEDa 条件:① NXB SAODC :②乙.4B ・£(〞)( ■ 9() BE ・CE.A 结论二① 4月■ DE 3 ② LAEiy - 2 LAHOa 条件:①&〃兄・、MBC 均 为等腰直角三角形,② EF -CF a 结论:①DF =BF ;② DF1 BFA 模型七:最短程模型景后基幡化到:•两昆之昉,怪我累触2例二 财点一①4点AH 惕上:⑵依・心怨力国大垂线段另短 <2>最短路程彳 械劝愎」将作.美中0C H 俾九•豺比 傕•=,堂, -tA \1 作 MHKM,1俨.小・ A 俨-,Q2 M" 〔•0戊量收〕>条件,①OC 平分"O%②?为〔M 上一定点,@ 〃为OJtf 点;@°为OH 上一动点: A 求」“O+PO最小时,几°的位置?(3> 题雌(^JM^2)条件:*014〕.8〔-20〕J 〔0,〃〕PB +此 PAi 够:〃为何值时,5 最小c A .sin ^OA,C 0 ——求解方法:①工轴上取 〔口0〕,使5 ,②过码乍A/〕L4g 交〕'轴于点%艮防所求>tan LEiiO = tan LOAC ③>忤!®ttft ai-4. <w-2 <ufl>(Mr) 6«M «A<) &*专内360 **««; .S〞着幺OL乩亳:“A."■〜. <“牙导越力・・^^**. «HaHR,*-X»Oflil4.4*tMXa・,直£・•卜十n五调.A^(*;•・称:< |-«; 〃彳一,胸>fta①—■九〔瞰・1⑵"启〞.剧,.明r<F +小停/®A 〃〔金曲IM -AH«3 K/H>JH /,小僖.1. 〞,H •:3 J〞W/,卜低方2.妁八的以廿也向工OcAfiZCD «rWW . £GWC-3(rXrx -2;0:rH-| ; 4 %.刖・£yq③ U址也人9**M»ft:把I ・ Jl<A〞eH"班・1,,4PI a«i>u. *,・外•川•eai<4〕最短路程稳型三〔旋转类最值锲型〕H小值而A 模型九:相似三角形模型I 千(J).腿三角形蜩-根本型 (2)才械三的阳模蛰第交举44与二*“冷;片A 鹏如护外作的认化 । \」,兴5"了":3 加区旧•凤 r nft ~?而慢牛且小客」l frU -牙明 k 用tt <以上水论地可力d it 忻做三.就Hit 行或明平行号.汇川ST4 " 4J' DF 时是二 _ = —=_ ( jAB HC £「上Ft ;如仃面凸表画 r re 上・,i 印一耳e 伊司电4也 lii^t -M. .it'M “ e W - H L < J 1-JW - J/*忤r i:阍t 、_ 冰=l Hj.iT 廿=", Wl用ZAB 「,上 if £ -^< iiK- s JA ffl;一⑷「・_l£K ■-f¥比= J5 :中】Il./N 为图的hj 峰:在阍:P A rm = ft rn中酹! P I <xw-7v > mA 字:—生西/勺⑶4 f 〞»金产产・5Frtfti U - 4/?-,ir - . lfi A 字母。
2020年九年级初中必会几何模型-三垂直模型

三垂直模型【模型概述】出现3个直角,且3个直角的顶点共线时,角的边相交会形成相似(含全等)三角形。
【基本模型】图1 图2【解读】⑴图1和图2中,三个直角顶点B,C,D共线;⑵当△ABC和△CDE三组对应边均不相等时,有△ABC∽△CDE;⑶当△ABC和△CDE任意一组对应边相等时(如AC=CE),有△ABC≌△CDE;⑷证明思路:同角的余角相等⑸解题时往往只含有两个甚至一个垂直关系,需通过作垂线构造出三垂直模型,从而构造出全等或相似三角形,利用全等和相似的性质求解角度和线段长等问题。
典型例题1-1已知:∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E。
⑴如图1,①线段CD和BE的数量关系是②请写出线段AD,BE,DE之间的数量关系并证明。
⑵如图2,结论②还成立吗?如不成立,写出并证明AD,BE,DE之间的数量关系。
【小结】典型例题1-2如图,已知矩形ABCD的顶点A,D分别落在x轴,y轴上,OD=2OA=6,AD:AB=3:1,则点C的坐标是()典型例题1-3经过点A(-1,0),B(4,0),交y轴于点C。
⑴求抛物线的解析式;⑵点D为y轴右侧抛物线上一点,是否存在点D请直接写出点D的坐标;若不存在,请说明理由。
⑶将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长。
【小结】变式训练1-1如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα=( )变式训练1-2如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC,(1)求C点的坐标;扩展模型:共线三等角模型:当三垂直模型中3个直角变为相等的锐角或钝角时,仍会产生全等或相似三角形。
解读:⑴图1和图2中,大小均为的三个锐角(或钝角)顶点在同一直线你上。
⑵当三组对应边均不相等时,图1中有△ABC∽△ECD,图2中有△ABC∽△CDE(注意对应关系)⑶当△ABC和△CDE的任意一组对应边相等时,有两三角形全等。
2020年中考复习 初中几何模型总结
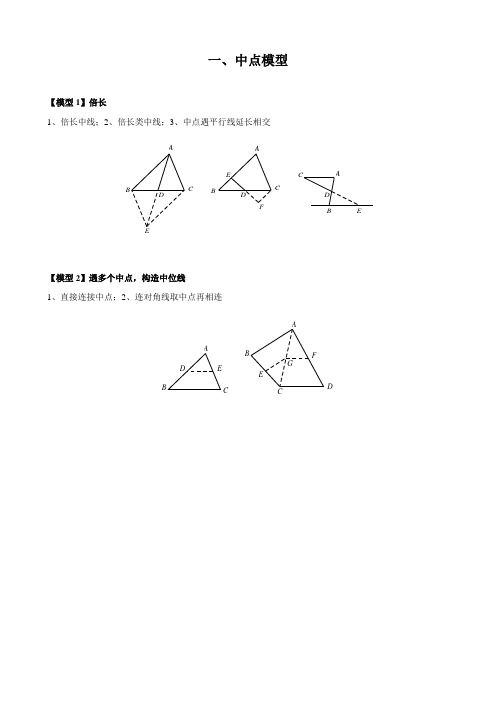
【解答】
【练习2】
问题1:如图1,在等腰梯形ABCD中,AD∥BC,AB=BC=CD,点M,N分别在AD,CD上,∠MBN ∠ABC,试探究线段MN,AM,CN有怎样的数量关系?请直接写出你的猜想;
【答案】
【例10】如图,正方形ABCD的面积为64,△BCE是等边三角形,F是CE的中点,AE、BF交于点G,则DG的长为___________.
【答案】4 +4
五、半角模型
【模型1】
【条件】如图,四边形ABCD中,AB=AD,∠BAD+∠BCD=∠ABC+∠ADC=180°,∠EAF= ∠BAD,点E在直线BC上,点F在直线CD上
则BC=BF+CF=HF-BH+FI-CI=GI-BH+HE-CI=
七、弦图模型
【条件】正方形内或外互相垂直的四条线段
【结论】新构成了同心的正方形
【例14】如图,点E为正方形ABCD边AB上一点,点F在DE的延长线上,AF=AB,AC与FD交于点G,∠FAB的平分线交FG于点H,过点D作HA的垂线交HA的延长线于点I.若AH=3AI,FH=2 ,则DG=__________.
【例5】(2014重庆市A卷)如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且 ,连接BE.过点C作CF⊥BE,垂足是F,连接OF,则OF的长为________.
【答案】
【例6】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,点E在AC边上,连接BE,AG⊥BE于F,交BC于点G,求∠DFG.
【结论】BE+EF=DF
2020年九年级初中必会几何模型-共点旋转模型

共点旋转模型模型概述:两个具有公共顶点的相似多边形,在绕着公共顶点旋转的过程中,产生伴随的全等或相似三角形,这样的图形称作共点旋转模型;为了更加直观,我们形象的称其为“手拉手”模型。
基本模型:一、等边三角形手拉手-出全等图1 图2图3 图41.解读:⑴图1中,等边△CDE和等边△CBA构成“A”字型相似;⑵将△CDE绕点C顺时针旋转一定角度,分别至图2、图3、和图4(B、C、E共线)⑶两三角形的“头部”C始终重合,“大手”A对应于“小手”E,“大手”B对应于“小手”D,旋转过程中,“大手”始终拉着(连接)“小手”;⑷“大手臂”CB、“小手臂”CD及其连线BD构成的△CBD与“大手臂”CA、“小手臂”CE及其连线AE构成的△CAE始终全等;⑸两连线BD和AE所在直线的夹角始终为60°。
2.结论:⑴图2、图3和图4中都有:①△CBD≌△CAE;②直线BD和直线AE的夹角为60°。
⑵图3中的其他结论:①FC平分∠BFE;②FB=FA+FC;③FE=FD+FC;⑶图3中结论在图4中成立,此外,在图4中还有:①△BCM≌△CAN;②△DCM≌△ECM;③MN∥BE;④△CMN为等边三角形;典型例题1-1如图,△ABC和△CDE均为等边三角形,连接BD、AE。
⑴求证:BD=AE;⑵直线BD和直线AE的夹角是多少?说明理由。
典型例题1-2如图,△ABC和△CDE均为等边三角形,连接BD,AE交于点F,连接FC。
求证:⑴FC平分∠BFE;⑵FB=FA+FC;⑶FE=FD+FC;典型例题1-3如图,△ABC和△CDE均为等边三角形,且B、C、E在同一直线上,连接BD交AC于M,连接AE交CD于N,连接MN,点F为AE与BD的交点。
求证:⑴△BCM≌△ACN;⑵△DCM≌△ECN;⑶MN∥BE;⑷△CMN为等边三角形。
变式训练1-1如图,△ABC和△CDE均为等边三角形,连接BD,AE交于点F,连接FC,则有以下结论:①BD=AE;②∠AFC=∠DFC③∠BFC=60°④变式训练1-2如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EB,GD.(1)求证:EB=GD;(2)若∠DAB=60∘,AB=2,AG=,求GD的长。
初中数学几何模型大全

初中数学几何模型大全初中数学几何模型大全全等变换:平移:平移是指将平行等线段(平行四边形)沿着相同的方向平移相同的距离。
这种变换可以用来构造平行四边形。
对称:对称变换可以通过角平分线、垂直线或半角来进行。
这种变换可以用来构造对称全等的图形。
旋转:旋转变换是指将相邻等线段绕公共顶点进行旋转。
这种变换可以用来构造旋转全等的图形。
对称全等模型:这种模型是以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型:这种模型是通过翻折构造对称全等的图形。
可以通过上图中的45°、30°、22.5°、15°及有一个角是30°直角三角形的对称来实现。
翻折后可以得到正方形或者等腰直角三角形、等边三角形、对称全等的图形。
旋转全等模型:半角:这种模型是指相邻等线段所成角含1/2角及相邻线段。
通过旋转将另外两个和为二分之一的角拼接在一起,形成对称全等的图形。
自旋转:这种模型是指有一对相邻等线段,需要构造旋转全等。
可以通过遇到60度旋60度,造等边三角形;遇到90度旋90度,造等腰直角;遇到等腰旋顶点,造旋转全等;遇中点旋180度,造中心对称的方法来实现。
共旋转:这种模型是指有两对相邻等线段,直接寻找旋转全等中点。
通过旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
可以通过“8”字模型来证明。
模型变形:这种变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,可以先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:这种模型是指通过两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
初中数学必背几何模型
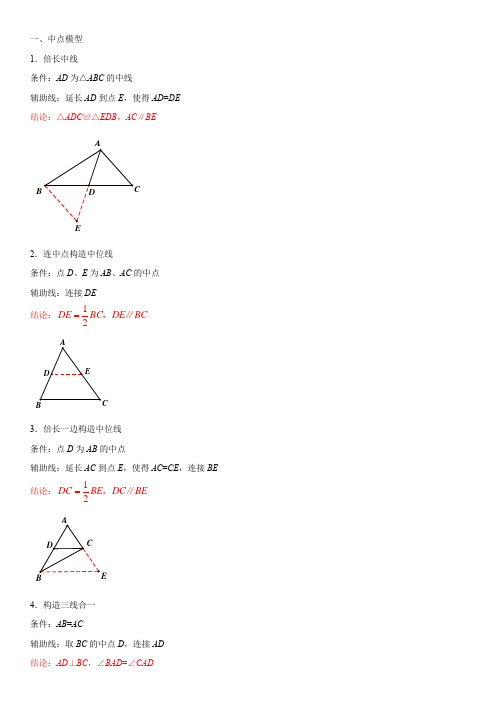
一、中点模型1.倍长中线条件:AD 为△ABC 的中线辅助线:延长AD 到点E ,使得AD =DE结论:△ADC ≌△EDB ,AC ∥BE2.连中点构造中位线条件:点D 、E 为AB 、AC 的中点辅助线:连接DE 结论:12DE BC DE BC =,∥3.倍长一边构造中位线条件:点D 为AB 的中点辅助线:延长AC 到点E ,使得AC =CE ,连接BE 结论:12DC BE DC BE =,∥4.构造三线合一条件:AB =AC辅助线:取BC 的中点D ,连接AD结论:AD ⊥BC ,∠BAD =∠CADB5.构造斜边中线条件:∠ABC =90°辅助线:取AC 的中点D ,连接BD 结论:12BD AC AD CD ===二、角平分线模型6.往角两边作垂线条件:AD 平分∠BAC辅助线:过点D 作AB 、AC 的垂线,垂足分别为E 、F结论:△ADE ≌△ADF7.在角的两边截取等长线段条件:AD 平分∠BAC辅助线:在AB 、AC 上取点E 、F ,满足AE =AF ,连接DE 、DF 结论:△ADE ≌△ADF8.过角平分线上一点作垂线条件:AD 平分∠BAC辅助线:过点D 作EF ⊥AD ,交AB 、AC 于点E 、FD CBB CCC结论:△ADE ≌△ADF三、双角平分线模型9.内内模型条件:BD 、CD 平分∠ABC 、∠ACB 结论:1902D A ∠=︒+∠10.内外模型条件:BD 、CD 平分∠ABC 、∠ACE 结论:12D A ∠=∠11.外外模型条件:BD 、CD 平分∠CBE 、∠BCF 结论:1902D A ∠=︒-∠四、平行线模型12.猪蹄模型CA BCC ED条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠B +∠D =∠BED13.铅笔头模型条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠B +∠D +∠BED =360°14.鸟头模型条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠D +∠BED =∠B15.平行线+角平分线模型条件:AB ∥CD ,CE 平分∠ACD结论:AC =AE五、等积模型16.等底等高条件:AD ∥BCFAFBC结论:ABC DBC S S =,ADB ADC S S =17.等高模型条件:B 、C 、D 共线结论:::ABD ADC S S BD CD =18.等底模型条件:AE 、DE 为△ABC 、△DBC 边BC 上的高结论:::ABC DBC S S AE DE =六、对称半角模型19.对称半角模型-含45°角的三角形条件:∠BAC =45°,AD ⊥BC辅助线:作点D 关于AB 的对称点E ,关于AC 的对称点F , 连接AE 、AF 、BE 、CF 、EF结论:△AEF 是等腰直角三角形20.对称半角模型-含30°角的三角形B CB C DED条件:∠BAC =30°,AD ⊥BC辅助线:作点D 关于AB 的对称点E ,关于AC 的对称点F , 连接AE 、AF 、BE 、CF 、EF结论:△AEF 是等边三角形七、旋转半角模型21.旋转半角模型-等腰直角三角形条件:AB =AC ,∠BAC =90°,∠MAN =45°辅助线:将△ABM 绕点A 逆时针旋转90°,得到△ACM ' 结论:ANM ANM '≌,222BM CN MN +=22.旋转半角模型-等边三角形条件:△ABC 是等边三角形,BD =CD ,∠BDC =120°, ∠MDN =60°辅助线:将△BDM 绕点D 顺时针旋转120°,得到△DCM ' 结论:NDM NDM '≌,BM CN MN +=23.旋转半角模型-正方形条件:正方形ABCD ,∠MAN =45°,FEAM'M CAB辅助线:将△ABM 绕点A 逆时针旋转90°,得到△ADM ' 结论:NAM NAM '≌,BM DN MN +=八、自旋转模型24.自旋转模型-等边三角形条件:△ABC 是等边三角形,点P 为其内任意一点辅助线:将△BAP 绕点B 顺时针旋转60°,得到△BCP ' 结论:△BPP '是等边三角形25.自旋转模型-等腰直角三角形条件:△ABC 中,∠BAC =90°,AB =AC ,点P 为△ABC 内任 意一点辅助线:将△BAP 绕点A 逆时针旋转90°,得到△ACP ' 结论:△APP '是等腰直角三角形26.自旋转模型-等腰三角形条件:△ABC 中,AB =AC ,点P 为△ABC 内任意一点,∠BAC =α 辅助线:将△BAP 绕点A 逆时针旋转α,得到△ACP ' 结论:△APP '是等腰三角形M'DNCBAB九、手拉手模型29.手拉手模型-等边三角形条件:△ABC和△CDE都是等边三角形结论:△ACE≌△BCD27.手拉手模型-等腰直角三角形条件:△ABC和△CDE都是等腰直角三角形结论:△ACE≌△BCD,AE⊥BDEE28.手拉手模型-等腰三角形条件:△ABC 和△CDE 都是等腰三角形,CA =CB , CD =CE ,且∠ACB =∠DCE结论:△ACE ≌△BCD30.手拉手模型-正方形条件:四边形ABCD 和AEFH 都是正方形结论:△ABE ≌△ADH ,BE ⊥DH十、最短路程模型31.直线同侧两线段之和最小(将军饮马)条件:点A 、B 在直线l 同侧,点P 为l 上一点辅助线:作点A 关于直线l 的对称点A ',连接A 'B 结论:点P 为A 'B 和l 交点时,AP +BP 最小C32.直线异侧两线段之差最小条件:点A 、B 在直线l 异侧,点P 为l 上一点辅助线:作线段AB 的垂直平分线m结论:点P 为m 和l 交点时,|AP -BP |最小33.直线同侧两线段之差最小条件:点A 、B 在直线l 同侧,点P 为l 上一点辅助线:作线段AB 的垂直平分线m结论:点P 为m 和l 交点时,|AP -BP |最小34.过桥模型(将军饮马)条件:A 、B 为定点,l 1∥l 2,MN 为定长线段且MN ⊥l 1 辅助线:将点A 向上平移MN 的长度得到A ',连接A 'B 结论:点N 为A 'B 与l 1交点时,AM +MN +BN 最小35.四边形周长最小(将军饮马)条件:A 、B 为定点,M 、N 为角两边上的动点辅助线:作点A 、B 关于角两边的对称点A '、B ',连接 lAlAll 1l 2A'B'结论:M、N为A'B'与角两边交点时,四边形ABMN的周长最小B'36.三角形周长最小(将军饮马)条件:A为定点,B、C为角两边上的动点辅助线:作点A关于角两边的对称点A'、A",连接A'A"结论:B、C为A'A"与角两边交点时,△ABC的周长最小37.旋转类最短路程模型条件:线段OA=a,OB=b(a>b),OB绕点O在平面内旋转结论:点B与点N重合时,AB最小;点B与点M重合时,AB最大十一、基本相似模型38.A字型条件:BC∥DE结论:△ABC∽△ADE条件:∠ABC =∠ADE结论:△ABC ∽△ADE39.8字型条件:AB ∥CD结论:△AOB ∽△DOC条件:∠BAO =∠DCO结论:△AOB ∽△COD40.母子型条件:△ABC 中,∠ACB =90°,CD ⊥AB结论:△ABC ∽△ACD ∽△CBD41.一线三等角模型条件:∠B =∠D =∠ACE结论:△ABC ∽△CDECBCC A42.手拉手相似模型条件:△ABC ∽△ADE结论:△ACE ∽△ABD十二、对角互补模型43.对角互补模型-90°全等型条件:∠AOB =∠DCE =90°,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,OD +OEOC ,212OECD S OC 四边形CB ACE AB D CDD44.对角互补模型-120°全等型条件:∠AOB =120°,∠DCE =60°,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,OD +OE =OC ,24OECD S =四边形45.对角互补模型-任意角全等型条件:∠AOB =2α,∠DCE =180°-2α,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,2cos OD OE OC α+=⋅, 2sin cos OEC OCD S S OC αα+=⋅46.邻边相等的对角互补模型条件:四边形ABCD 中,AB =AD ,∠ABC +∠ADC =180°D BAN E OB辅助线:延长CD 到E ,使得DE =BC ,连接AE结论:△ABC ≌△ADE ,CA 平分∠BCD十三、隐圆模型47.动点定长模型条件:AB =AC =AP ,点P 为动点结论:点B 、C 、P 三点共圆,点A 为圆心,AB 为半径48.直角圆周角模型条件:点C 为动点,∠ACB =90°结论:点A 、B 、C 三点共圆,线段AB 的中点为圆心,线段 AB 为直径49.定弦定长模型条件:点P 为动点,固定线段AB 所对的动角∠APB 为定值 结论:点A 、B 、P 三点共圆,线段AB 和BP 的中垂线的交点 为圆心BA50.四点共圆模型①条件:点A 、C 为动点,∠BAD +∠BCD =180°结论:点A 、B 、C 、D 四点共圆,线段AB 和BC 的中垂线的 交点为圆心当∠BAD =∠BCD =90°,BD 为直径51.四点共圆模型②条件:线段AB 为固定长度,点D 为动点,∠C =∠D结论:点A 、B 、C 、D 四点共圆,线段AB 和BC 的中垂线的 交点为圆心CCA当∠C=∠D=90°,AB为直径。
2020年山西中考重点专题讲解——几何“中点问题”六大模型(教师版)
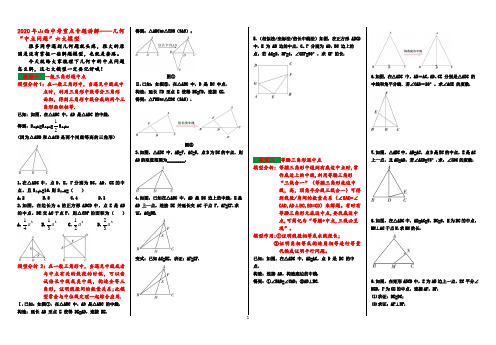
2020年山西中考重点专题讲解——几何“中点问题”六大模型很多同学遇到几何题就头疼,很大的原因是没有掌握一些解题模型,也就是套路。
今天就给大家梳理下几何中的中点问题怎么解,这七大模型一定要记好哦! 模型一 一般三角形遇中点模型分析1:在一般三角形中,当遇见中线或中点时,利用三角形中线等分三角形面积,得到三角形中线分成的两个三角形面积相等.已知:如图,在△ABC 中,AD 是△ABC 的中线.1.在△ABC 中,点D ,E ,F 分别为BC ,AD ,CE 的中点,且S △ABC =16.则S △DEF =( )A.2B.8C.4D.1 2.如图,在边长为a 的正方形ABCD 中,点E 是AB 432模型分析2:在一般三角形中,当遇见中线或者与中点有关的线段的时候,可以尝试倍长中线或类中线,构造全等三Ⅰ.已知:如图①,在△ABC 中,AD 是△ABC 的中线. 构造:延长 AD 至点 E 使得 DE=AD ,连接 BE. 得到:△ADC≌△EDB (SAS );图①Ⅱ.已知:如图②,在△ABC 中,D 是 BC 中点. 构造:延长 FD 至点 E 使得DE=FD ,连接 CE. 得到:△FDB ≌△EDC(SAS ).图②3.如图,△ABC 中,AB=7,AC=5,点D 为BC 的中点,则AD 的取值范围为________.4.如图,已知在△ABC 中,AD 是 BC 边上的中线,E 是 AD 上一点,连接 BE 并延长交 AC 于点F ,AF=EF.求证:AC=BE.变式:已知AC=BE ,求证:AF=EF.5.(相似法/坐标法/倍长中线法)如图,在正方形 ABCD 中,E 为 AB 边的中点,G 、F 分别为 AD ,BC 边上的点,若 AG=2,BF=4,∠GEF=90°,求 GF 的长.模型二 等腰三角形遇中点模型分析:等腰三角形中遇到有底边中点时,常作底边上的中线,利用等腰三角形“三线合一”(等腰三角形底边中线,高,顶角平分线三线合一)可得到线段/角间的数量关系(∠BAD=∠CAD,AD ⊥BC,BD=CD )来解题。
初中几何46种模型大全

初中几何46种模型大全篇一:初中几何46种模型大全引言几何是初中数学的重要分支,其知识点涵盖了平面几何、立体几何、向量等多个方面。
在学习几何时,掌握各种几何模型是非常重要的,这些模型可以帮助我们理解和解决几何问题,提高解题能力。
本文将介绍初中几何中的46种常见的模型,包括它们的名称、定义、性质和应用。
正文1. 正方形模型正方形模型是几何中最基本的模型之一,它是一种边长相等的矩形。
正方形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方。
正方形模型的性质有:- 正方形的四条边相等;- 正方形的对角线相等;- 正方形的面积等于其边长的平方。
2. 长方形模型长方形模型是有两个相等的长和两个不相等的宽的英雄。
长方形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和小于斜边的平方。
长方形模型的性质有:- 长方形的两条对角线相等;- 长方形的宽比长大,长比宽大;- 长方形的长和宽相等。
3. 平行线模型平行线模型是相互平行的直线。
平行线模型的定义如下:- 两直线平行,当且仅当它们的对应角相等且且它们的方向相同。
平行线模型的性质有:- 平行线之间有且仅有一个交点;- 平行线上的点的横坐标相等;- 平行线的方向相同。
4. 菱形模型菱形模型是具有四个相等的直角边的矩形。
菱形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方,且任意两条边的长度小于第三条边的长度。
菱形模型的性质有:- 菱形的四条边相等;- 菱形的对角线相等;- 菱形的面积等于其四条边长度的平方和。
5. 等腰三角形模型等腰三角形模型是有一个相等的腰部的两个三角形。
等腰三角形模型的定义如下:- 在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方。
等腰三角形模型的性质有:- 等腰三角形的两条直角边相等;- 等腰三角形的底角相等;- 等腰三角形的顶角平分线相等。
6. 等边三角形模型等边三角形模型是具有三个相等的边长的三角形。
初中数学30种模型汇总(最全几何知识点)

10.等面积模型:D是BC的中点
20.平移构造全等
30.二次函数中平行四边形存在性模型
01.三线八角
同位角:找F型
内错角:找Z型
同旁内角:找U型
02.拐角模型
一.锯齿型
1
1
3
2
2
3
4
∠1+∠3=∠2
∠1+∠2=∠3 +∠4
左和=右和
二.鹰嘴型
1
1
2
3
3
2
∠1+∠3=∠2
∠1+∠3=∠2
鹰嘴+小=大
一.大小等边三角形
虚线相等,且夹角为60°
(全等,八字形)
四.大小等腰三角形(顶角为α)
结论:虚线相等,且夹角为α
(全等,八字形)
三. 大小等腰直角三角形
结论:虚线相等,且夹角为90°
(全等,八字形)
二.大小正方形
结论:虚线相等,且夹角为90°
(全等,八字形)
15.半角模型
条件:正方形ABCD
∠EDF=45°
证:EF=AE+CF
条件:CD=AD,∠ADC=90°
∠EDF=45°
∠A+∠C=180°
证明:EF=AE+CF
条件:AB=AD
∠B+∠D=180°
∠EAF=1 ∠BAD
2
证明:EF=BE+DF
条件:AB=AC,∠BAC=90°
∠DAE=45°
证明:DE2=BD2+CE2
△CEF为直角三角形
初中数学30种模型汇总
(最全几何知识点)
01.三线八角
02.拐角模型
03.等积变换模型
(完整版)初中数学九大几何模型

初中数学九大几何模型一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OABCDE图 2OABC DEOABCD E图 1图 2二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90°将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-OB CO ACDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
初中数学几何模型大全

几何模型大全---第一部分一、全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转模型一:对称全等模型以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
模型二:对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
模型三:旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题(一)旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
(二)自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称(三)共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
(三)中点旋转模型说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
初中几何常考模型汇总(完整版)

第Ol讲8字模型与飞镖模型模型1角的“8”字模型如图所示,AB、CD相交于点O,连接AD、BC O 结论:ZA+ZD=ZB+ZCo模型分析8字模型往往在几何综合题目中推导角度时用到O模型实例观察下列图形,计算角度:(1)如图①,ZA+ZB+ZC+ZD+ZE= ________________ :(2)如图②,ZA+ZB+ZC+ZD+ZE+ZF= _________________热搜梢练1.(1)如图①,求ZCAD+ZB+ZC+ZD+ZE= _________________ :(2)如图②,求Z C A D+ Z B + Z AC E+ Z D+ Z E= ___2. ________________________________________________ 如图,求ZA+ZB+ZC+ZD+ZE+ZF+ZG+ZH= _______________________________图②模型2角的飞镖模型如图所示,有结论:ZD=ZA+ZB+ZCo模型分析飞镖模型往往在几何综合题目中推导角度时用到a模型实例如图,在四边形ABCD中,AM、CM分别平分ZDAB和ZDCB, AM与CM交于W 探究ZAMC与ZB、ZD间的数量关系。
热搜精练1._________________________________________如图,ΛRZA+ZB+ZC+ZD+ZE+ZF=2.__________________________________ 如图,求ZA+ZB+ZC+ZD=C F模型3边的“8”字模型如图所示,AC、BD相交于点O,连接AD、BC O 结论:AC+BD>AD+BCoD模型实例如图,四边形ABCD的对角线AC、BD相交于点0。
求证:(1) AB+BC+CD+AD>AC+BD:(2) AB+BC+CD+AD<2AC+2BD.模型4边的飞镖模型如图所示有结论:AB+AC>BD+CD.模型实例如图,点O为三角形内部一点。
初中数学几何模型大全(精心整理)
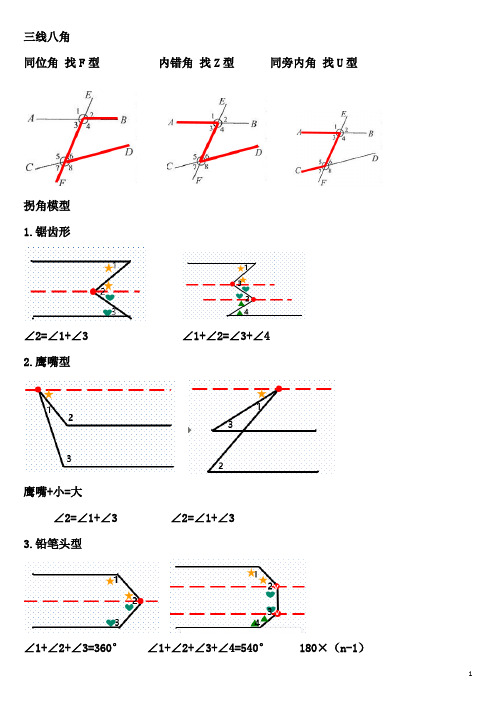
三线八角同位角找F型内错角找Z型同旁内角找U型拐角模型1.锯齿形∠2=∠1+∠3 ∠1+∠2=∠3+∠42.鹰嘴型鹰嘴+小=大∠2=∠1+∠3 ∠2=∠1+∠33.铅笔头型∠1+∠2+∠3=360° ∠1+∠2+∠3+∠4=540°180×(n-1)等积变换模型S△ACD=S△BCD 八字模型∠A+∠B=∠C+∠DAD+BC>AB+CD飞镖模型∠D=∠B+∠C+∠AAB+AC>BD+CD内内角平分线模型∠A∠D=90°+12内外角平分线模型∠D=1∠A2外外角平分线模型∠D=90°-1∠A2平行平分出等腰模型HG=HM等面积模型 D是BC的中点S△ABD= S△ACD 倍长中线模型:D是BC的中点S△FBD= S△ECD角平分线构造全等模型角平分线垂直两边角平分线垂直中间角平分线构造轴对称以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,垂直也可以做为轴进行对称全等。
三垂模型拉手模型大小等边三角形虚线相等且夹角为60°大小等腰三角形顶角为a,虚线相等,且夹角为a大小等腰直角三角形虚线相等且夹角为90°大小正方形虚线相等,且夹角为90°半角模型正方形ABCD ∠EDF=45°得:EF=AE+CFCD=AD,∠ADC=90°,∠EDF=45°,∠A+∠C=180°得:EF=AE+CF∠BADAB=AD,∠B+∠D=180°,∠EAF=12得:EF=BE+DFAB=AC,∠BAC=90°,∠DAE=45°得:DE2=BD2+CE2△CEF为直角三角形上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
2020-2021学年人教版八年级上册常考几何模型汇总

人教版八年级上常考几何模型汇总序号基本图形条件结论解题思路及作用1模型1 角的“8”字模型如图所示,AB、CD相交于点O,连接AD、BC。
结论:∠A+∠D=∠B+∠C8字模型往往在几何综合题目中推导角度时用到。
2模型角的双“8”字模型CP平分∠DCA,BP平分∠ABO,求∠P结论:∠P=12(∠A+∠D)设∠DCO=2α,∠DCO=2β,由8字形得∠P+α=∠D+β,∠P+β=∠A+α则∠P=12(∠A+∠D)3模型角的飞镖模型如图如图所示,有结论:∠D=∠A+∠B+∠C。
飞镖模型往往在几何综合题目中推导角度时用到。
4模型角的双飞镖模型CP平分∠DCA,BP平分∠ABD,求∠P∠P=12(∠A+∠D)设∠ABD=2α,∠ACD=2β由飞镖型得∠P=∠A+α+β∠P+α+β=∠D得∠P=12(∠A+∠D)5模型A字型及其变式如图∠ADE+∠AED=∠ABC+∠C在几何综合题目中推导角度时用到。
6模型4.内角平分线夹角在△ABC中,∠ABC与∠ACB的平分线相交于点D∠D=90°+12∠A思路;利用角平分线的性质及三角形内角和定理即可证明。
7模型5 内角和外角的平分线的夹角在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E∠E=12∠A∠E=∠ECM-∠EBC=12(∠ACM-∠ABC)=12∠A序号基本图形条件结论解题思路及作用8模型6 外角的平分线的夹角点P是△ABC的两个外角∠EBC,∠FCB的平分线的交点∠P=90°-12∠A.∠P=180°-(∠PBC+∠PCB)=180°-(90°+12∠A)=90°-12∠A.9类型7 线段(角)的和差(1)BE=CF(2)∠BAD=∠EAC(1)BC=EF(2)∠BAC=∠EAD1.∵BE=CF∴BE+EC=CF+EC即BC=EF2证法同110模型三垂直全等模型(K型)∠D=∠BCA=∠E=90°,BC=ACRt△BCD≌Rt△CAE图1中DE=BD+AE图2中DE=AD-BE利用互余证∠B=∠ACE,再AAS证全等。
【收藏】初中数学经典几何模型大全

【收藏】初中数学经典几何模型大全
中点模型
【模型1】倍长
1、倍长中线;
2、倍长类中线;
3、中点遇平行延长相交
【模型2】遇多个中点,构造中位线
1、直接连接中点;
2、连对角线取中点再相连
【例】在菱形ABCD和正三角形BEF中,∠ABC=60°,G是DF 的中点,连接GC、GE.
(1)如图1,当点E在BC边上时,若AB=10,BF=4,求GE的长;(2)如图2,当点F在AB的延长线上时,线段GC、GE有怎样的数量和位置关系,写出你的猜想;并给予证明;(3)如图3,当点F在CB的延长线上时,(2)问中关系还成立吗?写出你的猜想,并给予证明.
角平分线模型
【模型1】构造轴对称【模型2】角平分线遇平行构造等腰三角形
【例】如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,交AD边于H,延长BA到点G,使AG=CF,连接GF.若BC=7,DF=3,EH=3AE,则GF的长为 .
手拉手模型
【例】如图,正方形ABCD的边长为6,点O是对角线AC、BD 的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为 .
邻边相等的对角互补模型
【例】如图,矩形ABCD中,AB=6,AD=5,G为CD中点,DE=DG,FG⊥BE于F,则DF 为 .
半角模型
一线三角模型
弦图模型
最短路径模型
【两点之间线段最短】1、将军饮马
2、费马点【垂线段最短】
【两边之差小于第三边】。
