六年级下册数学试题-15讲 圆和扇形(含答案)全国通用
北师大版数学六年级下册提升卷 巧求半圆、圆环、扇形的周长和面积(含答案)

北师大版数学六年级下册提升卷巧求半圆、圆环、扇形的周长和面积一、我会辨。
(对的在括号里画“√”,错的画“×”)(每题2分,共6分) 1.半圆的面积是整圆面积的一半,则半圆的周长也是整圆周长的一半。
() 2.用4个半径相等的圆心角都是45°的扇形一定可以拼成一个圆。
() 3.圆的周长是直径的3.14倍。
()二、我会填。
(每空2分,共24分)1.一个扇形的圆心角是90°,它的面积是所在圆面积的();一个扇形的圆心角是45°,它的面积是所在圆面积的()。
2.一个圆的直径是10 cm,它的周长是()cm,圆周长的一半是()cm;一个半圆形的半径是 5 cm,这个半圆形的周长是()cm,面积是()cm2。
3.下图中,大半圆的半径是()cm,小半圆的半径是()cm。
4.一个圆环,内圆周长是 6.28 cm,环宽是1 cm,内圆半径是()cm,外圆半径是()cm。
5.钟面上的时针长5 cm,时针从6时走到9时,时针的针尖扫过的轨迹长()cm,时针扫过的面积是()cm2。
三、我会选。
(把正确答案前的字母填在括号里)(每题2分,共6分) 1.一个半圆形,半径是r,它的周长是()。
A.2πr B.πr C.πr+2r D.πr+r2.下面两幅图中阴影部分的面积相比,()。
A.A大B.B大C.一样大D.无法比较3.如图,沿半圆形草坪外围铺一条5 m宽的小路,小路的面积是多少平方米?列式正确的是()。
A.3.14×52÷2B.3.14×202÷2C.3.14×252÷2-3.14×202÷2四、按要求计算。
(共32分)1.计算下面各图形的周长。
(每题5分,共10分)2.计算下面阴影部分的面积。
(单位:cm)(每题5分,共10分)3.计算下面各图形的周长和面积。
(每题6分,共12分)五、我会应用。
(每题8分,共32分)1.在一个边长为16 cm的正方形铁片中,截去如图所示的2个半圆,求剩余铁片的面积。
六年级数学专题思维训练—圆与扇形(含答案及解析)

六年级数学专题思维训练—圆与扇形1、分别以一个边长为2厘米的等边三角形的三个顶点为圆心,以2厘米为半径画弧,得到下图.那么,阴影图形的周长是厘米.(取3. 14)2、有7根直径都是5分米的圆柱形木头,现用绳子分别在两处把它们捆绑在一起,其切面如下图所示,至少需要绳子分米.(取3.14)3、把同一段铁丝围成一个正方形后,又改围成一个圆形,发现按照面积公式得出的二者面积之比为4:5,那么在计算圆面积时,圆周率丌的取值为。
4、如下图所示,已知圆环的面积是141.3平方厘米,那么阴影部分的面积是平方厘米.(取3. 14)5、如下图所示,弧IFD与JED是分别以A、B为圆心、以AD、BD为半径的圆弧,已知AD1=DB=DC=4厘米,且AGDHB、AFC与BEC分别是三条直线段.线段IA、FG、CD、EH、JB都分别垂直于AB.请问图中阴影部分的面积是多少?(取)6、如下图所示的半圆的直径BC=8厘米,AB=AC,D是AC的中点,则阴影部分的面积是.(取3. 14)7、如下图所示,ABCD是边长为10厘米的正方形,且AB是半圆的直径,则阴影部分的面积是平方厘米.(取3. 14)8、下图中正方形ABCD及DCEG的面积均为64平方厘米,EFG则为一半圆,F是弧EFG的中点.请问阴影部分的面积为多少平方厘米?(3.14)9、半径为10、20、30的三个扇形如下图放置,是的倍,10、如下图所示,图中的曲线是用半径长度的比为2:1.5:o.5的6条半圆曲线连成的,问:涂有阴影的部分与未涂阴影的部分的面积比是多少?11、有三个同心圆,它们的半径之比是3:4:5,如果大圆的面积是100平方厘米,那么中圆与小圆所构成的圆环的面积是A.20平方厘米 B.28平方厘米 C.36平方厘米 D.60平方厘米12、下图是两个圆,它们的面积之和为1991平方厘米,小圆的周长是大圆周长的90%.问:大圆的面积是多少?13、下图中五个相同的圆的圆心连线构成一个边长为10厘米的正五边形.求五边形内阴影部分的面积. =3. 14)14、如下图所示,已知圆心是O,半径r=9厘米,∠1 =∠2=15°,那么阴影部分的面积是平方厘米。
人教版六年级下册数学第五单元《圆的周长计算及应用》专项练习(含答案)

人教版六年级下册数学第五单元《圆的周长计算及应用》专项练习(含答案)一、认真审题,填一填。
(每小题3分,共18分)1.战国时期《墨经》一书中记载:“圆,一中同长也。
”表示圆心到圆上各点的距离都相等,即( )都相等。
2.如图,圆向前滚动了一周,圆滚动了( )cm,这个圆的周长是( )cm。
3.要画一个周长是25.12 cm的圆,圆规的两脚叉开的距离应是( )cm。
4.一块正方形铁皮,周长是40分米,要剪下一个最大的圆,这个圆的直径是( )分米。
5.武汉长江公铁隧道是武汉市一条公路、地铁两用过江通道。
圆形隧道管片直径约15 m,是目前国内直径最大的江底隧道。
圆形隧道管片的周长约是( )m。
(π取3)6.一个半圆形鱼池的周长是51.4 m,它的半径是( )m。
二、火眼金睛,辨对错。
(每小题4分,共12分)1.大小不同的两个圆,若两个圆的周长都增加1米,各自半径增加的长度相同。
( )2.小圆和大圆的半径之比是2:3,它们的直径之比是3:2。
( )3.一个圆的半径扩大到原来的2倍,它的周长也扩大到原来的2倍。
( ) 三、仔细推敲,选一选。
(每小题3分,共15分)1.大小不同的两个圆,它们的半径各增加2 cm,和原来的圆相比较,哪个圆的周长增加得多?( )。
A.大圆B.小圆C.同样多2.下图中的阴影部分是扇形的是( )。
3.如图,图形的周长是( )m。
A.18.71B.15.71C.20.42D.23.424.圆周率是圆的周长与直径的比值。
如果下图中线段AE代表一个圆的周长,那么这个圆的直径可能是( )。
A.AB B.AC C.CD5.下面关于半圆形的周长,说法不正确的是( )。
A.是这个圆周长的一半B.是这个圆周长的一半再加上一条直径C.是这个圆周长的一半再加上两条半径四、细心的你,算一算。
(共18分)1.求阴影部分的周长。
(每小题6分,共12分)(1) (2)2.长方形的周长是36 cm,求一个圆的周长。
小学数学六年级几何练习册(附详细答案)

【练习1】【练习2】【练习3】【练习4】【练习5】【练习6】【练习7】【练习8】【练习9】【练习10】、相交于点;已知三角形与三角平方厘米,那么梯形的面积是平方厘【练习11】【练习12】,问阴影部分面积为多少?【练习13】【练习14】,三角形的面积为,那么三【练习15】【练习16】【练习17】【练习18】【练习19】【练习20】【练习21】【练习22】,则三角形的面积是.【练习23】【练习24】【练习25】【练习26】(取).【练习27】【练习28】【练习29】【练习30】平方厘米.【练习31】【练习32】【练习33】cm2,体积是cm【练习34】计算下面各圆锥体积(单位:厘米)(取)【练习35】【练习36】【练习1】【练习2】几何四边形一半模型等积变形【练习3】【练习4】,所以【练习5】【练习6】【练习7】【练习8】【练习9】:,所以【练习10】根据梯形中的蝴蝶模型(平方厘米),方厘米),故总面积为(平方厘米).蝴蝶模型【练习11】,根据蝴蝶模型和一半模型求出每一块的面积如图上标几何四边形蝴蝶模型基本梯形蝴蝶模型【练习12】如图,梯形面积为,四边形连接,在梯形中,;在梯形中,,并且四边形面积为,所以梯形空白部分的面积是,所以阴影的面积是【练习13】【练习14】.【练习15】【练习16】.【练习17】【练习18】平方厘米.【练习19】【练习20】【练习21】【练习22】,则三角形的面积是.可以看成三角形的“假高”(都是从顶点到底边连线,且两条“高”共线),【练习23】【练习24】【练习25】,【练习26】(取).【练习27】【练习28】【练习29】【练习30】平方厘米.【练习31】【练习32】【练习33】cm2,体积是cm(3)(4)【练习34】【练习35】【练习36】圆柱与圆锥圆柱与圆锥基本概念运用。
六年级下册数学试题-奥数专练:平面几何之圆与扇形(上)(含答案)全国通用

1.⑴圆:平面上到定点的距离等于定长的所有点所组成的图形叫做圆。
定点称为圆形,定长称为半径。
⑵半径:连接圆心和圆上任意一点的线段叫做半径;通常用字母r 表示;同圆或等圆的半径相等 。
⑶弦:连接圆上任意两点的线段叫做弦。
⑷直径:通过圆心并且两端都在圆上的线段叫做直径;直径常用字母d 表示;圆中最长的弦为直径⑸弧:圆上任意两点间的部分叫做圆弧,简称弧;大于半圆的弧为优弧,小于半圆的弧为劣弧。
⑹扇形:在圆上,由两条半径和一段弧围成的图形叫做扇形。
扇形由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形,扇形是圆的一部分,我们经常说的12圆、14圆、16圆等等其实都是扇形,而这个几分之几表示的其实是这个扇形的圆心角占这个圆周的几分之几。
⑺圆心角:顶点在圆心的角叫做圆心角。
⑻圆周角:顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角。
2.圆的性质:圆既是轴对称图形又是中心对称图形,经过圆心的每一条直线都是它的对称轴,圆心是的对称中心,围绕圆心旋转任何一个角度,都能和它原来的图形重合3.⑴圆的周长:L =2πr ;扇形的弧长:l =2πr ×360n(n 表示扇形圆心角的度数); ⑵圆的面积:S =πr 2; 扇形的面积:S =πr 2×13602n lr (n 表示扇形圆心角的度数)。
4.弓形:弓形一般不要求周长,主要求面积。
一般来说,弓形面积=扇形面积-三角形面积。
(除了半圆)5.常用的思想方法:⑴转化思想(复杂转化为简单,不熟悉的转化为熟悉的); ⑵等积变形(割补、平移、旋转等); ⑶借来还去(加减法);⑷外围入手(从会求的图形或者能求的图形入手,看与要求的部分之间的关系)。
平面几何之圆与扇形(上)板块一、圆与扇形的面积与周长1.圆的半径是6厘米,它的周长是()厘米,面积是( )平方厘米。
2.一个半圆形,半径是3厘米,周长是( )厘米,面积是( )平方厘米。
3.一张圆桌面的周长是376.8厘米,要在它上面配一块圆形玻璃,这块圆形玻璃的面积是( )平方厘米。
六年级数学圆扇形圆环试题答案及解析

六年级数学圆扇形圆环试题答案及解析1.(3分)半径是2米的圆的周长与圆的面积相等..(判断对错)【答案】错误【解析】首先理解圆的周长和面积的意义,圆的周长是圆一周的长度.圆的面积是指圆围成的平面的大小.它们不是同类量无法进行比较.由此解答.解:圆周长是:2×3.14×2=12.56(米);圆面积是:3.14×22=3.14×4=12.56(平方米);这个圆的周长与面积在数值上是相等的,但是单位不同,所以圆的周长和面积它们不是同类量无法进行比较.故答案为:错误.点评:此题考查的目的是理解圆的周长和面积的意义,明确:圆的周长和面积不是同类量无法进行比较,只有同类量才能比较大小.2.(2分)一个圆的周长是L的半圆,它的半径是()A.L÷2πB.L÷πC.L÷(π+2 )D.L÷(π+1)【答案】C【解析】半圆的周长=πd÷2+d=πr+2r=(π+2)r,由此即可解答.解:根据题干分析可得:它的半径r=,故选:C.点评:此题考查了半圆的周长公式的灵活应用.3.如图,在时钟的表盘上任意作个的扇形,使得每一个扇形都恰好覆盖个数,且每两个扇形覆盖的数不全相同,求证:一定可以找到个扇形,恰好覆盖整个表盘上的数.并举一个反例说明,作个扇形将不能保证上述结论成立.【答案】见解析【解析】要在表盘上共可作出12个不同的扇形,且1~12中的每个数恰好被4个扇形覆盖.将这12个扇形分为4组,使得每一组的3个扇形恰好盖住整个表盘.那么,根据抽屉原理,从中选择9个扇形,必有个扇形属于同一组,那么这一组的3个扇形可以覆盖整个表盘.另一方面,作8个扇形相当于从全部的12个扇形中去掉4个,则可以去掉盖住同一个数的4个扇形,这样这个数就没有被剩下的8个扇形盖住,那么这8个扇形不能盖住整个表盘.4.如图,长方形的长是,则阴影部分的面积是多少.()【答案】3.44【解析】阴影部分的面积实际上是右上图阴影部分面积的一半,所以求出右上图中阴影部分面积再除以2即可.长方形的长等于两个圆直径,宽等于1个圆直径,所以右图的阴影部分的面积等于:所以左图阴影部分的面积等于平方厘米.5.用一块面积为36平方厘米的圆形铝板下料,从中裁出了7个同样大小的圆铝板.问:所余下的边角料的总面积是多少平方厘米?【答案】8【解析】大圆直径是小圆的3倍,半径也是3倍,小圆面积∶大圆面积,小圆面积,个小圆总面积,边角料面积(平方厘米).6.如图,若图中的圆和半圆都两两相切,两个小圆和三个半圆的半径都是1.求阴影部分的面积.【答案】2.5【解析】由于直接求阴影部分面积太麻烦,所以考虑采用增加面积的方法来构造新图形.由右图可见,阴影部分面积等于大圆面积减去一个小圆面积,再加上的小扇形面积(即小圆面积),所以相当于大圆面积减去小圆面积.而大圆的半径为小圆的3倍,所以其面积为小圆的倍,那么阴影部分面积为.7.如图所示,求阴影面积,图中是一个正六边形,面积为1040平方厘米,空白部分是6个半径为10厘米的小扇形.(圆周率取)【答案】412【解析】所要求的阴影面积是用正六边形的面积减去六个小扇形面积、正六边形的面积已知,现在关键是小扇形面积如何求,有扇形面积公式.可求得,需要知道半径和扇形弧的度数,由已知正六边形每边所对圆心角为60°,那么,又知四边形是平行四边形,所以,这样就可求出扇形的面积和为(平方厘米),阴影部分的面积(平方厘米).8.在桌面上放置个两两重叠、形状相同的圆形纸片.它们的面积都是平方厘米,盖住桌面的总面积是平方厘米,张纸片共同重叠的面积是平方厘米.那么图中个阴影部分的面积的和多少是平方厘米?【答案】72【解析】根据容斥原理得,所以(平方厘米)9.一个长方形的长为9,宽为6,一个半径为l的圆在这个长方形内任意运动,在长方形内这圆无法运动到的部分,面积的和是多少.(取3)【答案】1【解析】方法一:圆在长方形内部无法运动到的地方就是长方形的四个角,而圆在角处运动时的情况如左下图,圆无法运动到的部分是图中阴影部分,那么我们可以先求出阴影部分面积,四个角的情况都相似,我们就可以求出总的面积是阴影部分面积的四倍.阴影部分面积是小正方形面积减去扇形面积,所以我们可以得到:每个角阴影部分面积为;那么圆无法运动到的部分面积为方法二:如果把四个角拼起来,则阴影如右上图所示,则阴影面积为10.如图中,正方形的边长是,两个顶点正好在圆心上,求图形的总面积是多少?(圆周率取)【答案】142.75【解析】.11.如图所示,直角三角形的斜边长为10厘米,,此时长5厘米.以点为中心,将顺时针旋转,点、分别到达点、的位置.求边扫过的图形即图中阴影部分的面积.(取3)【答案】0.6775【解析】如图,顺时针旋转后,A点沿弧转到点,B点沿弧转到点,D点沿弧转到点.因为CD是C点到AB的最短线段,所以AB扫过的面积就是图中的弧与之间的阴影图形.(平方米),(平方米),所以,(平方米),我们推知(平方米).12.半径为25厘米的小铁环沿着半径为50厘米的大铁环的内侧作无滑动的滚动,当小铁环沿大铁环滚动一周回到原位时,问小铁环自身转了几圈?【答案】1【解析】对于这类问题,可以在初始时在小环上取一点,观察半径,如图⑴,当小环沿大环内壁滚动到与初始相对的位置,即滚动半个大圆周时,如图⑵,半径也运动到了与初始时相对的位置.这时沿大环内壁才滚动了半圈.继续进行下半圈,直到与初始位置重合,这时自身转了1圈,因此小铁环自身也转了1圈.(1)(2)对于转动的圆来说,当圆心转动的距离为一个圆周长时,这个圆也恰好转了一圈.所以本题也可以考虑小铁环的圆心轨迹,发现是一个半径与小铁环相等的圆,所以小铁环的圆心转过的距离等于自己的圆周长,那么小铁环转动了1圈.13.如图,枚相同的硬币排成一个长方形,一个同样大小的硬币沿着外圈滚动一周,回到起始位置.问:这枚硬币自身转动了多少圈?【答案】6【解析】当硬币在长方形的一条边之内滚动一次时,由于三个硬币的圆心构成一个等边三角形,所以这枚硬币的圆心相当于沿着半径为硬币2倍的圆旋转了.而硬币上的每一点都是半径等于硬币的圆旋转,所以硬币自身旋转了120°.当硬币从长方形的一条边滚动到另一条边时,这枚硬币的圆心相当于沿着半径为硬币2倍的圆旋转了.而硬币上的每一点都是半径等于硬币的圆旋转,所以硬币自身旋转了300º.长方形的外圈有12个硬币,其中有4个在角上,其余8个在边上,所以这枚硬币滚动一圈有8次是在长方形的一条边之内滚动,4次是从长方形的一条边滚动到另一条边.,所以这枚硬币转动了2160º,即自身转动了6圈.另解:通过计算圆心轨迹的长度,每走一个即滚动了一周.14.图中阴影部分的面积是,求圆环的面积.【答案】157【解析】设大圆半径为,小圆半径为,依题有,即.则圆环面积为:.15.如果半径为25厘米的小铁环沿着半径为50厘米的大铁环的外侧作无滑动的滚动,当小铁环沿大铁环滚动一周回到原位时,问小铁环自身转了几圈?【答案】3【解析】如图,同样考虑小圆的一条半径,当小圆在大圆的外侧滚动一周,即滚动了大圆的半周时,半径滚动了,滚动了一圈半,所以当小圆沿大圆外侧滚动一周时,小圆自身转了3圈.也可以考虑小圆圆心转过的距离.小圆圆心转过的是一个圆周,半径是小圆的3倍,所以这个圆的周长也是小圆的3倍,由于小圆的圆心每转动一个自身的周长时,小圆也恰好转了一圈,所以本题中小圆自身转了3圈.16.一共圆形花坛,直径是10米,在它的周围有一条宽2米的环形小路。
六年级下册数学试题-奥数:几何之圆与扇形(解析版)全国通用

第二讲 几何之圆与扇形教学目标组合图形的面积计算,除了直线型面积计算“五大模型”,跟圆有关的曲线型面积也是得别重要的组成部分。
其中,尤以结合情境的曲线形面积计算为最常见考点。
教师版答案提示:纸的厚度为:(206)27-÷=(厘米),那么有70.04175÷=圈纸,中心的卷轴到纸用完时大约会转175圈;圆环的面积为:2210391ππ⨯(-)=,因为纸的厚度为0.4毫米,即0.04厘米,所以纸展开后的长度约为:910.0422757143.5ππ÷=≈厘米.利用“加、减”思想解答问题【例1】 如图,一个“月牙”形屏幕在屏幕上随意平行移动(不许发生转动也不越过屏幕边界),已知线段AB 是月牙外半圆弧的直径,长为2厘米。
初始时,A 、B 两点在矩形屏幕的一条边上。
屏幕的长和宽分别为30厘米和20厘米。
问:屏幕上“月牙”擦不到的部分的面积是多少平方厘米?(π取3)分析:由于“月牙”形屏幕在屏幕上只能平行移动(不许发生转动也不越过屏幕边界),所以它擦不到的地方只是屏幕的右上角和右下角两部分,如右下图中斜线所示区域,其面积为0.5平方厘米。
想 挑 战 吗 ?卷筒软纸中的数学右图为一圈“心相印”圈纸的截面图,纸卷直径 为20厘米,中间有一直径为6厘米的卷轴,若纸的 厚度为0.4毫米,问:中心的卷轴到纸用完时大约会转多少圈?这卷纸展开后大约有多长?(π取3.14)[前铺]如右图所示,等腰直角三角形ABC 的高AD=4厘米,以AD 为直径作圆分别交AB 、AC 与E 、F ,求阴影部分的面积。
(π取3) 分析:连接EF ,那么有BED ABD EOD S S S =-阴影三角形扇形,计算可得阴影部分面积为6平方厘米。
[巩固]一个长方形的长为9,宽为6,一个半径为l 的圆在这个长方形内任意运动,在长方形内这圆无法运动到的部分,面积的和是多少?(π取3)分析:圆无法运动到的部分是右下图中角处的阴影部分面积的4倍, 114111π⨯⨯-⨯⨯=[拓展]如右图所示,用一块面积为36平方厘米铝板下料,可裁出七个同样大小的圆铝板。
六年级下册数学试题-奥数专题12:圆和组合图形(二)(含解析)全国通用

212十二、圆和组合图形(2)年级班姓名得分一、填空题1.如图,阴影部分的面积是.2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大平方厘米.3.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是平方厘米.(π取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是(平方厘米).5.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.)14.3(=π6.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是.E D C B A GF O D CA B7.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是 平方厘米.8.已知:ABCD 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .9.图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是 度.10.右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是 平方厘米.(π取3.14)二、解答题11.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率取722)2 甲乙12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值.14.如图所示,一块半径为2厘米的圆板,从平面上1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、CD 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?120 ABCD 1 2A B Ca1 OC B A ED———————————————答 案——————————————————————1. 6.两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位.2. 188.4.小圆的半径为2)14(6=-÷(厘米),大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大4.18814.3)28(22=⨯-(平方厘米).3. 57.305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米).4. 10.26.从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即26.10621)26(14.322=⨯-÷⨯(平方厘米).5. 20.5.设圆的半径为r ,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++=5.204.1645=⨯=(厘米).6. 6548(平方厘米).如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD 的面积为502100=÷(平方厘米).又圆半径为10)214.3(28.6=⨯÷(厘米),因为151=∠, 又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为61261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为654861150=-(平方厘米).7. 19.1416.⌒E D C B AG F① ②花瓣图形的结构是正方形的面积,加上四个43圆面积后,再割去四个半圆的面积.圆的半径为1厘米,正方形边长为4厘米.故花瓣图形的面积是1416.1916421144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米).8. 2.43平方厘米. 如图,将①移到②得:阴影部分面积等于梯形CEFB 的 面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即 43.236045214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘米).9. 60.设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有2221311)2(360r r x ⨯⨯⨯=⨯⨯ππ,解得x=60.10. 0.14.扇形面积为14.341214.32=⨯⨯(平方厘米),甲部分面积为43.0214.32122=÷-⨯(平方厘米),乙部分面积为57.04122214.3=⨯⨯-÷(平方厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米).11. 如图,小正方形的边长为2r,则①的面积为:72227224122r r r r =⨯-⎪⎭⎫ ⎝⎛⨯⨯,②的面积为222417272221r r r =-⎪⎭⎫ ⎝⎛⨯⨯,①和②的面积和为2227224172241r r r =⨯⨯-⨯⨯.即阴影部分面积为272r .12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘米).13. 设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S (1)又9232=-x S ,于是有23184+-=S x ,解得S=6.③① ②14. 圆板的正面滚过的部分如右图阴影部分所求, 它的面积为:)420(4614)220(22122-+⨯⨯+⨯-+⨯⨯ππ07.228323204221)24(414)220(4222≈+=⨯⨯+⨯-⨯-⨯-+⨯πππ(平方厘米).ABD12。
六年级圆与扇形练习题

六年级圆与扇形练习题圆与扇形是初中数学中的重要概念,也是六年级学生需要掌握的知识点之一。
本篇文章将为你介绍一些六年级圆与扇形的练习题,帮助你巩固相关知识。
第一题:已知一个圆的半径为5cm,求其周长和面积。
解析:圆的周长可以通过公式C = 2πr 来计算,其中 r 表示圆的半径,π 的值可以取近似值3.14。
将半径 r 替换为5cm,即可得到圆的周长。
C = 2πr = 2 × 3.14 × 5 = 31.4cm圆的面积可以通过公式A = πr^2 来计算。
将半径 r 替换为5cm,即可得到圆的面积。
A = πr^2 = 3.14 × 5^2 = 78.5cm^2所以,该圆的周长为31.4cm,面积为78.5cm^2。
第二题:已知一个扇形的弧长为8cm,圆心角为30°,求扇形的面积。
解析:扇形的面积可以通过公式A = (θ/360°) × πr^2 来计算,其中θ 表示圆心角的度数,r 表示扇形所在圆的半径。
首先,我们需要将圆心角的度数转换为弧度。
由于180°等于π弧度,所以将30°转换为弧度的方法是:θ(弧度)= 30° × (π/180°) = π/6弧度然后,我们已知扇形的弧长为8cm,可以通过公式L = rθ 来计算弧长 L。
将已知数据代入公式,可以求得半径 r。
8 = r × (π/6)r = (8 × 6)/(π)r ≈ 3.818cm最后,将半径 r 和圆心角的弧度θ 代入扇形面积的公式,可以得到扇形的面积。
A = (π/6)/(2π) × (3.818)^2 ≈ 3.711cm^2所以,该扇形的面积约为3.711cm^2。
通过以上两个题目的练习,我们可以巩固圆与扇形的计算方法。
希望你能够理解并熟练运用这些知识,进一步提高数学水平。
祝你学业进步!。
六年级下册数学试题-小升初分班考试数学之几何 人教版(含答案)

一、几何图形的相关概念及基本公式1、点、线、面、体;直线、射线、线段、角;长方形(体)、正方形(体)、平行四边形、三角形、题型、多边形、圆与扇形、圆柱、圆锥、轴对称图形2、平面图形的周长、面积公式,立体图形的侧面积、表面积、体积公式3、定理、结论:三角形内角和、三角形三边关系、勾股定理、一笔画、格点图形面积公式(毕克定理)4、几何计数二、巧求周长和面积1、通过平移、旋转、翻折(对称)、割补等手段将图形转化成比较好求的形状2、利用差不变原理将图形转化3、利用面积之比与边长之比的关系解题三、几何五大模型1、等高模型及变型(如一半模型、鸟头模型等)2、风筝模型(也叫蝴蝶模型)3、相似三角形(金字塔模型、沙漏模型)4、题型比例关系(题型蝴蝶模型)5、燕尾模型四、长方体正方体及侧面展开图、圆柱圆锥【例 1】如图,阴影部分是正方形,则最大长方形的周长是_ _____厘米.知识框架例题精讲3 几何10答案: 30【练习】 如图7-20,在直角梯形ABCD 中,三角形ABE 和三角形CDE 都是等腰直角三角形,且BC=20厘米,那么直角梯形ABCD 的面积是多少?答案: 200平方厘米【例 2】 如图,有一块长方形的草坪,长20米,宽10米,现要在草坪上铺设两条宽1米的小路,则剩下草坪的面积是________平方米.答案: 171【练习】 一块矩形场地被一条路隔成甲、乙两块,甲乙的面积之比为3:8,尺寸如图,甲的面积是____。
21122乙甲答案: 60【例 3】 如图,一个梯形,面积为45,AB=10,高为6,则△AOB 的面积是___________.OCDA答案: 20【练习】如图,梯形ABCD的上底AD长5厘米,下底BC长12厘米,腰CD的长为8厘米,过B点向CD作出的垂线BE的长为9厘米,那么梯形ABCD的面积是多少?答案: 51平方厘米【例 4】已知如图,求阴影部分的面积(π取3.14)44答案: 4.56【练习】求图中阴影部分的面积。
六年级数学割补法求圆与扇形的面积(含答案)

圆与扇形———割补法课前预习彩虹的传说一个圆的故事(又名:彩虹的传说)从前,有一个非常完美的圆,没有任何缺口和毛刺,甚至连一点点划痕在它身上都找不到。
圆长得非常可爱,胖鼓隆冬的,从小就特别招人喜欢,时间久了,就自然觉得自己是世界上最完美的。
圆有很多好朋友:三角(快速灵活)、方块(稳重平和)、平行四边形(勇敢自信)、五角星(理性谦卑)、六边形(经验丰富)、心形(牺牲成全)。
它们每天在一起玩儿得很开心。
有一天,圆遇上了月亮姐姐,它对月亮姐姐说:“姐姐、姐姐,你挂在天空上可真漂亮啊!不过,为什么一定要有时圆有时缺呢?嘿嘿!如果我能像你一样挂在天空上,也放出光芒那该多好啊!”月亮姐姐淡淡地笑了,对圆说:“我告诉你一个地方,到了那里你就找到了智慧。
”圆迟疑地问道:“智慧是什么?我为什么要找它?”月亮姐姐说:“因为只有找到了智慧才能够回答你提出的这些问题,帮你实现愿望啊!”圆似懂非懂地点了点头,把这个消息告诉了它的好朋友们。
突然,三角大声地号召:“不如我们一起去月亮姐姐说的那个地方吧,人多力量大,我们这么多人一定能找到那个叫智慧的东西。
”于是大家都纷纷响应,收拾起行囊浩浩荡荡地上路了。
它们经历了千辛万苦,淌过了虚荣河,越过了贪婪海,走过了嗔恨桥,翻过了愚痴山。
有一天,终于来到了智慧门前。
这是一扇看起来很普通的门,长方形的门框没有任何修饰。
不同的是,这道门很矮小,也很窄。
几个小伙伴只能调整好最佳的位置,否则很难钻进去。
圆有些失望地对大家说:“我们经历了这么多坎坷,就是为了进这么一个门啊!”三角、方块、平行四边形、五角星、六边形、心形纷纷点头,觉得不可思议。
三角总是最有主意,行动最快的一个。
它放下所有行李跟大家说:“无论如何,我们费了这么大劲儿才找到这扇门,我的身体最小,我先进去。
”话音刚落,它哧溜一下,钻进了门里。
方块的为人正像它的体形,正直稳重。
它沉着冷静地紧跟其后,也顺利进入门内。
平行四边形的棱角比较尖锐,它自信地说了一句:“不成功就成仁!”,稍微一侧身,勇敢地冲进门里。
六年级下册数学试题-15讲 圆和扇形(含答案)全国通用

第十五讲 圆和扇形研究圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,通过变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形来计算它们的面积.圆的面积;扇形的面积;2πr =2π360nr =⨯圆的周长;扇形的弧长.2πr =2π360nr =⨯一、跟曲线有关的图形元素:①扇形:扇形由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形,扇形是圆的一部分.我们经常说的圆、圆、圆等等其实都是扇形,而这个几分之几表示的其实是这个扇形的圆心角占这121416个圆周角的几分之几.那么一般的求法是什么呢?关键是.360n比如:扇形的面积所在圆的面积;=360n⨯扇形中的弧长部分所在圆的周长=360n⨯扇形的周长所在圆的周长2半径(易错点是把扇形的周长等同于扇形的弧长)=360n⨯+⨯②弓形:弓形一般不要求周长,主要求面积.一般来说,弓形面积扇形面积-三角形面积.(除了半圆)=③”弯角”:如图: 弯角的面积正方形-扇形=④”谷子”:如图: “谷子”的面积弓形面积=2⨯一、常用的思想方法:①转化思想(复杂转化为简单,不熟悉的转化为熟悉的)②等积变形(割补、平移、旋转等)③借来还去(加减法)④外围入手(从会求的图形或者能求的图形入手,看与要求的部分之间的”关系”)板块一 平移、旋转、割补、对称在曲线型面积中的应用【例 1】下图中每一个小正方形的面积是1平方厘米,那么格线部分的面积是多少平方厘米?【解析】割补法.如右图,格线部分的面积是36平方厘米.【例 2】(2007年西城实验考题)在一个边长为2厘米的正方形内,分别以它的三条边为直径向内作三个半圆,则图中阴影部分的面积为 平方厘米.【解析】采用割补法.如果将阴影半圆中的2个弓形移到下面的等腰直角三角形中,那么就形成两个相同的等腰直角三角形,所以阴影部分的面积等于两个等腰直角三角形的面积和,即正方形面积的一半,所以阴影部分的面积等于平方厘米.21222⨯=【例 3】计算图中阴影部分的面积(单位:分米).A A【解析】将右边的扇形向左平移,如图所示.两个阴影部分拼成—个直角梯形. (平方分米).()5105275237.5+⨯÷=÷=【例 4】求图中阴影部分的面积.【解析】如图,连接,可知阴影部分的面积与三角形的面积相等,即为.BD BCD 1112123622⨯⨯⨯=【例 5】求如图中阴影部分的面积.(圆周率取)3.14【解析】,则阴影部分转化为四分之一圆90︒.211π444 4.5642⨯⨯-⨯⨯=【例 6】求下列各图中阴影部分的面积.10(2)ba【解析】在图10,高为5的三角形,利用三角形面积公式可以求得;110102522S =⨯⨯=阴影在图(2)中,阴影部分经过切割平移变成了一个长为b ,宽为a 的长方形,利用长方形面积公式可以求得.S a b ab =⨯=阴影【例 7】如图,长方形的长是,则阴影部分的面积是 .()ABCD 8cm 2cm π 3.14=【解析】阴影部分的面积实际上是右上图阴影部分面积的一半,所以求出右上图中阴影部分面积再除以2即可.长方形的长等于两个圆直径,宽等于1个圆直径,所以右图的阴影部分的面积等于:()2882822π2 6.88⨯÷-÷÷⨯⨯=所以左图阴影部分的面积等于平方厘米.6.882 3.44÷=【例 8】求右图中阴影部分的面积.(取3)π【解析】看到这道题,一下就会知道解决方法就是求出空白部分的面积,再通过作差来求出阴影部分面积,因为阴影部分非常不规则,无法入手.这样,平移和旋转就成了我们首选的方法.(法1)我们只用将两个半径为10厘米的四分之一圆减去空白的①、②部分面积之和即可,其中①、②面积相等.易知①、②部分均是等腰直角三角形,但是①部分的直角边AB 的长度未知.单独求①部分面积不易,于是我们将①、②部分平移至一起,如右下图所示,则①、②部分变为一个以AC 为直角边的等腰直角三角形,而AC 为四分之一圆的半径,所以有AC 10.两个四分之一圆的面积和为150,而①、②部分的面积和为,所以阴=11010502⨯⨯=影部分的面积为(平方厘米).15050100-=(法2)欲求图①中阴影部分的面积,可将左半图形绕B 点逆时针方向旋转180°,使A 与C 重合,从而构成如右图②的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.所以阴影部分面积为(平方厘米).21110101010022π⨯⨯-⨯⨯=A板块二 曲线型面积计算【例 9】如图,已知扇形的面积是半圆面积的34倍,则角的度数是________.BAC ADB CAB DCBA 【解析】设半圆的半径为1,则半圆面积为,扇形的面积为.因为扇ADB 21ππ122⨯=BAC π42π233⨯=形的面积为,所以,,得到,即角的度数是60BAC 2π360n r ⨯22ππ23603n ⨯⨯=60n =CAB 度.【例 10】如下图,直角三角形的两条直角边分别长和,分别以为圆心,为半径画ABC 67,B C 2圆,已知图中阴影部分的面积是,那么角是多少度()17A π3=【解析】,167212ABC S =⨯⨯=△三角形内两扇形面积和为,ABC 21174-=根据扇形面积公式两扇形面积和为,2π24360B C∠+∠⨯⨯=°所以,.120B C ∠+∠=°60A ∠=°【例 11】如图,大小两圆的相交部分(即阴影区域)的面积是大圆面积的,是小圆面积的.如41535果量得小圆的半径是5厘米,那么大圆半径是多少厘米?【解析】小圆的面积为,则大小圆相交部分面积为,那么大圆的面积为2π525π⨯=325π15π5⨯=,而,所以大圆半径为厘米.422515ππ154÷=2251515422=⨯7.5【例 12】有七根直径5厘米的塑料管,用一根橡皮筋把它们勒紧成一捆(如图),此时橡皮筋的长度是多少厘米?(取3)πCBA 【解析】由右图知,绳长等于6个线段与6个弧长之和.AB BC 将图中与弧相似的6个弧所对的圆心角平移拼补,可得到6个角的和是,BC 360︒所以弧所对的圆心角是,6个弧合起来等于直径5厘米的圆的周长.BC 60︒BC 而线段等于塑料管的直径,AB 由此知绳长为:(厘米).565π45⨯+=【例 13】用一块面积为36平方厘米的圆形铝板下料,从中裁出了7个同样大小的圆铝板.问:所余下的边角料的总面积是多少平方厘米?【解析】大圆直径是小圆的3倍,半径也是3倍,小圆面积∶大圆面积,22π:π1:9r R ==小圆面积,个小圆总面积,13649=⨯=74728=⨯=边角料面积(平方厘米).36288=-=【例 14】如图,两个正方形摆放在一起,其中大正方形边长为12,那么阴影部分面积是多少?(圆周率取)3.14AFEAFE【解析】方法一:设小正方形的边长为,则三角形与梯形 的面积均a ABF ABCD 为.阴影部分为:大正方形梯形三角形右上角不规则部分大正方()122a a +⨯÷+-ABF -=形右上角不规则部分圆.因此阴影部分面积为:.-=143.1412124113.04⨯⨯÷=方法二:连接、,设与的交点为,由于四边形是梯形,根据梯形AC DF AF CD M ACDF 蝴蝶定理有,所以ADM CMF S S =△△DCF S S =阴影扇形 3.1412124113.04=⨯⨯÷=【巩固】如右图,两个正方形边长分别是10和6,求阴影部分的面积.(取3)π【解析】(法1)观察可知阴影部分面积等于三角形的面积减去月牙的面积,那么求出月牙ACD BCD 的面积就成了解题的关键.BCD 月牙的面积为正方形的面积减去四分之一圆:;BCD BCDE 166π6694⨯-⨯⨯⨯=则阴影部分的面积为三角形的面积减去月牙的面积,为:ACD BCD .()110669392S =⨯+⨯-=阴影(法2)观察可知和是平行的,于是连接、、.AF BD AF BD DF 则与面积相等,那么阴影部分面积等于与小弓形的面积之和,也就等于ABD ∆BDF ∆BDF ∆与扇形的面积之和,为:.DEF ∆BED 211(106)6π63924-⨯⨯+⨯⨯=【例 15】如图,是等腰直角三角形,是半圆周的中点,是半圆的直径.已知ABC D BC ,那么阴影部分的面积是多少?(圆周率取)10AB BC == 3.14DD【解析】连接、、,如图,平行于,则在梯形中,对角线交于点,那么PD AP BD PD AB ABDP M 与面积相等,则阴影部分的面积转化为与圆内的小弓形的面积和.ABD ∆ABP ∆ABP ∆的面积为:;ABP ∆()10102225⨯÷÷=弓形面积: ;3.145545527.125⨯⨯÷-⨯÷=阴影部分面积为:.257.12532.125+=【例 16】CBC【解析】这道题目是很常见的面积计算问题.阴影部分是一个花瓣状的不规则图形,不能直接通过面积公式求解,观察发现阴影部分是一个对称图形,我们只需要在阴影部分的对称轴上作两条辅助线就明了了.如图,这样阴影部分就划分成了4个半圆减去三角形,我们可以求得,()4S S S =⨯-阴影半圆三角形 21142222a a a π⎡⎤⎛⎫=⨯⨯⨯-⨯⨯⎢⎥⎪⎝⎭⎢⎥⎣⎦ 212a =【巩固】如图,正方形ABCD 的边长为4厘米,分别以B 、D 为圆心以4厘米为半径在正方形内画圆.求阴影部分面积.(取3)πD BA DB【解析】由题可知,图中阴影部分是两个扇形重叠的部分,我们可以利用容斥原理从图形整体上考虑来求阴影部分面积;同样,我们也可以通过作辅助线直接求阴影部分的面积.解法一:把两个扇形放在一起得到1个正方形的同时还重叠了一块阴影部分.则阴影部分的面积为;=21π44482⋅⋅-⨯=解法二:连接AC ,我们发现阴影部分面积的一半就是扇形减去三角形的面积,所以阴影部分面积.=212π444284⨯⋅⋅-⨯÷=()【巩固】在图中,两个四分之一圆弧的半径分别是2和4,求两个阴影部分的面积差.(圆周率取)3.14【解析】我们只要看清楚阴影部分如何构成则不难求解.左边的阴影是大扇形减去小扇形,再扣除一个长方形中的不规则白色部分,而右边的阴影是长方形扣除这块不规则白色部分,那么它们的差应为大扇形减去小扇形,再减去长方形.则为:.ππ4422423 3.148 1.4244⨯⨯-⨯⨯-⨯=⨯-=【例 17】如图,矩形ABCD 中,AB 6厘米,BC 4厘米,扇形ABE 半径AE 6厘米,扇形CBF 的===半径CB 4厘米,求阴影部分的面积.(取3)=πA【解析】方法一:观察发现,阴影部分属于一个大的扇形,而这个扇形除了阴影部分之外,还有一个不规则的空白部分ABFD 在左上,求出这个不规则部分的面积就成了解决这个问题的关键.我们先确定ABFD 的面积,因为不规则部分ABFD 与扇形BCF 共同构成长方形ABCD ,所以不规则部分ABFD 的面积为(平方厘米),2164π4124⨯-⨯⨯=再从扇形ABE 中考虑,让扇形ABE 减去ABFD 的面积,则有阴影部分面积为(平方厘米).21π612154⨯⨯-=方法二:利用容斥原理(平方2211π6π4461544EAB BCF ABCD S S S S =+-=⨯+⨯-⨯=阴影扇形扇形长方形厘米)【例 18】如图,等腰直角三角形ABC 的腰为10;以A 为圆心,EF 为圆弧,组成扇形AEF ;两个阴影部分的面积相等.求扇形所在的圆面积.【解析】题目已经明确告诉我们ABC 是等腰直角三角形,AEF 是扇形,所以看似没有关系的两个阴影部分通过空白部分联系起来.等腰直角三角形的角A 为45度,则扇形所在圆的面积为扇形面积的8倍.而扇形面积与等腰直角三角形面积相等,即,11010502S =⨯⨯=扇形则圆的面积为508400⨯=【例 19】如图,直角三角形ABC 中,AB 是圆的直径,且,阴影甲的面积比阴影乙的面积20AB =大7,求BC 长.()π 3.14=【解析】因为两块阴影部分都是不规则图形,单独对待它们无法运用面积公式进行处理,而解题的关键就是如何把它们联系起来,我们发现把两块阴影加上中间的一块,则变成1个半圆和1个直角三角形,这个时候我们就可以利用面积公式来求解了.因为阴影甲比阴影乙面积大7,也就是半圆面积比直角三角形面积大7.半圆面积为:,则直角三角形的面积为1577150,可得BC 21502021π101572⨯⨯=-==⨯÷15.=【巩固】 如图,三角形是直角三角形,阴影部分①比阴影部分②的面积小28平方厘米,长ABC AB40厘米.求的长度?(取)BC π 3.14【解析】图中半圆的直径为,所以其面积为.AB 2120π200 3.146282⨯⨯≈⨯= 有空白部分③与①的面积和为628,又②-①,所以②、③部分的面积28=和.62828656+=有直角三角形的面积为.所以厘米.ABC 12AB BC ⨯⨯=1406562BC ⨯⨯=32.8BC =【例 20】(2009年十三分入学测试题)图中的长方形的长与宽的比为,求阴影部分的面积.8:3【解析】,连接.O OC ,,根据勾股定理可得.20=20416OB =-=12BC =阴影部分面积等于半圆的面积减去长方形的面积,为:.21π20(162)12200π3842442⨯⨯-⨯⨯=-=【例 21】如图,求阴影部分的面积.(取3)π【解析】求出 它们的面积,那么我们应该怎么来解决呢?首先,我们分析下月牙儿状是怎么产生的,观察发现月牙儿形是两条圆弧所夹部分,再分析可以知道,两条圆弧分别是不同圆的圆周的一部分,那么我们就找到了解决问题的方法了.阴影部分面积小圆面积中圆面积三角形面积大圆面积=12+12+-12=2221111π3π434π52222⋅⋅+⋅⋅+⨯⨯-⋅⋅6=【例 22】如图,直角三角形的三条边长度为,它的内部放了一个半圆,图中阴影部分的面6,8,10积为多少?6【解析】S 设半圆半径为,直角三角形面积用表示为:r r 610822r rr ⨯⨯+=又因为三角形直角边都已知,所以它的面积为,168242⨯⨯=所以,824r =3r =所以1249π=24 4.5π2S =-⨯-阴影 家庭作业【作业1】如图,在一个边长为4的正方形内,以正方形的三条边为直径向内作三个半圆.求阴影部分的面积.【解析】阴影部分经过切割平移变成了一个面积为正方形一半的长方形,则阴影部分面积为.4428⨯÷=【作业2】如图,阴影部分的面积是多少?24【解析】首先观察阴影部分,我们发现阴影部分形如一个号角,但是我们并没有学习过如何求号角的面积,那么我们要怎么办呢?阴影部分我们找不到出路,那么我们不妨考虑下除了阴影部分之外的部分吧!观察发现,阴影部分左侧是一个扇形,而阴影部分右边的空白部分恰好与左边的扇形构成一个边长为4的正方形,那么阴影部分的面积就等于大的矩形面积减去正方形面积.则阴影部分面积(222)4(22)48++⨯-+⨯=【作业3】如图,四分之一大圆的半径为7,求阴影部分的面积,其中圆周率取近似值.π227【解析】原题图中的左边部分可以割补至如右上图位置,这样只用先求出四分之一大圆的面积,再减去其内的等腰直角三角形面积即为所求.因为四分之一大圆的半径为7,所以其面积为:.2211227π738.5447⨯⨯≈⨯⨯=四分之一大圆内的等腰直角三角形的面积为,所以阴影部分的面积为ABC 17724.52⨯⨯=.38.524.514-=【作业4】求下列各图中阴影部分的面积(图中长度单位为,圆周率按3计算):cm⑴3⑵4⑶111⑷⑸2⑹【解析】⑴ ⑵ ⑶ ⑷ ⑸ ⑹4.5412 1.5 4.5【作业5】求图中阴影部分的面积(单位:).cm 【解析】从图中可以看出,两部分阴影的面积之和恰好是梯形的面积,所以阴影部分面积为.21(24)39cm 2⨯+⨯=【作业6】如图,若图中的圆和半圆都两两相切,两个小圆和三个半圆的半径都是1.求阴影部分的面积.【解析】的小扇形面积120︒3倍,所以其面积为小圆的倍,那么阴影部分面积为.239=21259π1π 2.5636⎛⎫⨯-⨯⨯== ⎪⎝⎭【作业7】如图是一个直径为的半圆,让这个半圆以点为轴沿逆时针方向旋转,此时点3cm A 60︒B 移动到点,求阴影部分的面积.(图中长度单位为,圆周率按计算).'B cm 3【解析】半圆空白部分面积(也是半圆)圆心角为的扇形面积+-=60︒.2)【作业8】三角形是直角三角形,阴影的面积比阴影的面积小,,求的ABC I II 225cm 8cm AB =BC 长度.IIAB CI【解析】由于阴影的面积比阴影的面积小,根据差不变原理,直角三角形面积减去半I II 225cm ABC 圆面积为,则直角三角形面积为(),225cm ABC 218π258π2522⎛⎫⨯+=+ ⎪⎝⎭2cm 的长度为().BC ()8π25282π 6.2512.53+⨯÷=+=cm 【作业9】下图中每一个小正方形的面积是1平方厘米,那么格线部分的面积是多少平方厘米?【解析】割补法.如右图,格线部分的面积是36平方厘米.【作业10】求图中阴影部分的面积.【解析】阴影部分面积半圆面积扇形面积三角形面积.=+-22211211π(π121241.042282=⨯+⨯-⨯=。
苏教版六年级下册数学《第1章 扇形统计图 》测试卷(附知识点归纳)

2020苏教版小学六年级数学下册单元知识点总结(后附单元试卷及答案)第1章扇形统计图【知识点归纳总结】扇形统计图1.扇形统计图的特点:扇形统计图是用整个圆的面积表示总数,用圆内的扇形面积表示各部分数量占总数的百分比.2.读懂扇形统计图:(1)获取信息的方法:运用综合、对比等多种观察方法,可以从扇形统计图中获取信息,还可以利用这些信息提出相应的问题.(2)扇形统计图的优点:它可以清楚地表示出部分数量与总数、部分数量与部分数量之间的关系.3.利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数应用题的解题思路和解题方法进行解答.【经典例题】例1:如图是某小学六年级学生视力情况统计图.①视力正常的有76人,视力近视的有60人;②假性近视的同学比视力正常的人少15.8%;(百分号前保留一位小数)③视力正常的学生与视力非正常学生人数的比是19:31.分析:由图可知:把总人数看成单位“1”,视力正常的人数占总人数的38%,近视的人数占总人数的30%,假性近视的人数占总人数的32%;①视力正常的有76人,它对应的百分数是38%,由此用除法求出总人数,再求出总人数的30%就是近似的人数;②用视力正常占的百分数减去假性近视人数占的百分数,然后用求得的差除以视力正常占的百分数即可;③先求出视力非正常学生人数占总人数的百分数,然后作比.解:①76÷38%×30%,=200×30%,=60(人);答:视力近视的有60人.②(38%-32%)÷38%,=6%÷38%,≈15.8%;答:假性近视的同学比视力正常的人少15.8%.③38%:(32%+30%),=38%:62%,=38:62,=19:31;答:视力正常的学生与视力非正常学生人数的比是19:31.故答案为:60,15.8%,19:31.点评:解决本题关键是从图中读出数据,找出单位“1”,再根据基本的数量关系求解.【同步测试】单元同步测试题一.选择题(共8小题)1.某村共种蔬菜40公顷,其中种西红柿8公顷若制成扇形统计图,则表示西红柿的扇形占整个圆的()A.8%B.20%C.40%2.一个花园里种了三种花,每种的占地面积如图所示,如果用条形统计图表示各种花的占地面积,应该是()A.B.C.D.3.画统计图时,要根据信息的特点来画.在下面的信息中,适合用扇形统计图的是()A.六年级一班女同学的身高B.芳芳6﹣12岁的身高变化C.大豆的营养成分4.下列用图()表示如图各部分所占长方形的比最准确.A.B.C.D.5.小贩设计了一个转盘游戏,2元钱玩一次,学生自由转动转盘,指针停止后所指向的物品即为学生所获物品,那么学生获得什么物品的可能性最大?()A.橡皮B.三角板C.圆珠笔D.文具盒6.小冬爸爸5月份的工资总收入约是8000元,按照如图进行支配,那么用于教育费用约是()A.4000元B.1200元C.2000元D.900元7.某市九月份的天气情况如图,本月的雨天有()天.A.21B.6C.38.如图是某小学六(1)班50名同学喜欢的体育运动统计图.下面说法不正确的是()A.喜欢篮球的人数占全班人数的40%.B.喜欢打乒乓球的有40人C.喜欢打乒乓球的人数是踢足球人数的2倍二.填空题(共6小题)9.如图是六年一班期中数学成绩统计图,请根据下列信息解答相关问题.(1)不合格率为%.(2)已知得优的有12人,全班有人.(3)得良的比得合格的多人.10.李红调查全班同学“你最喜欢哪一项球类活动?”,根据同学们的回答她制成了如图的扇形统计图,请看图填空.(1)活动最受欢迎.(2)和活动受欢迎程度差不多.(3)喜欢活动的同学大约占总人数的.11.如图是一件毛线衣中各种材质占总质量的统计图,根据右图回答问题.(1)棉的含量占这件衣服的%.(2)的含量最多,的含量最少.(3)兔毛含量比涤纶少占总数的%.(4)这件毛衣重200克,羊毛有克,兔毛有克.如果羊毛含量120克,那么棉含量是克.12.如图的扇形统计图清楚地表示参加与之间的关系.13.如图是某校六年级全体学生某次数学竞赛成绩的统计图.“不及格”部分的扇形圆心角是度.14.(1)妙想家其他支出占家庭总支出的?(2)如果伙食水电支出2700元,那么文化支出元.三.判断题(共5小题)15.扇形统计图能形象直观地展示数据间的关系,但不能明确表示具体的数量.(判断对错)16.扇形统计图和其他统计图一样也要有标题和图例..(判断对错)17.扇形统计图用圆柱表示就变成条形统计图.(判断对错)18.扇形统计图中,一个圆代表100%.(判断对错)19.在扇形统计图中是用整个圆来表示总数.(判断对错)四.应用题(共6小题)20.下面是某小学六年级学生参加社团人数的统计图,每人只能参加一项.六年级参加社团的学生共有多少人?21.六年(1 )班全体同学投票选班长,毎位同学投且只能投一票,得票数最高者当选.下面是全部候选人得票情况統汁图.(1)当选班长的同学姓名是.(2)王倩得票数占总票数的%.(3)如果张力得4票,那么吴佳得多少票?22.第三小学购买一批新书,数量如图所示.算一算,这个学校一共购进多少图书?23.一块菜地四种蔬菜的种植面积分布情况如下:①你获得哪些信息请逐条写下来.②如果种植黄瓜的面积有90平方米,你能提出哪些用百分数解决的问题?并解答.24.某脱贫村大力发展养殖业,如下图是该村2018年饲养家禽的统计图,其中养鸭7000只.该村养鸡、养鹅各多少只?25.小军家三月份的总支出情况如图:(1)小军家这个月的总开支是多少元?(2)根据扇形统计图把下表填写完整.项目购物生活开支水电费亲情开支其他费用/元400参考答案与试题解析一.选择题(共8小题)1.【分析】求西红柿的扇形占整个圆的百分之几,就相当于求8是40的百分之几,用8除以40即可.【解答】解:8÷40=20%答:西红柿的扇形占整个圆的20%.答:表示西红柿的扇形占整个圆的20%.故选:B.【点评】利用扇形统计图解决问题,就是解决有关不同类型的百分数应用题,按照百分数应用题的解题思路和解题方法进行解答.2.【分析】观察扇形统计图可知:迎春花的占地面积大约是总面积的50%,而菊花和月季花大约各占25%,也就是迎春花的占地面积大约是菊花、月季花占地面积的2倍,由此进行求解.【解答】解:迎春花的占地面积大约是总面积的50%,而菊花和月季花大约各占25%,50%÷25%=2即迎春花的占地面积大约是菊花、月季花占地面积的2倍,所以:是正确的.故选:A.【点评】解决本题关键是根据扇形统计图得出得出三种花的数量关系,从而解决问题.3.【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.【解答】解:根据统计图的特点可知:画统计图时,要根据信息的特点画.A、六年级一班女同学的身高,适合用条形统计图表示;B、芳芳6﹣12岁的身高变化,适合用折线统计图表示;C、大豆的营养成分,适合用扇形统计图表示;故选:C.【点评】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答.4.【分析】把整个长方形的面积看作单位“1”,把它平均分成15份,每份是它的,其中深色阴影部分占4份,表示,浅色阴影部分占9份,表示、白色部分占2份,表示.用360°分别乘、、就是表示各部分的扇形圆心角度数,根据计算结果即可进行选择.【解答】解:深色阴影部分占整个长方形的,浅色阴影部分占、白色部分占360°×=96°360°×=216°360°×=48°与图形相符.故选:B.【点评】此题也可分别求出各图中阴影扇形所占的百分率,再求出长方形中阴影部分所占的百分率,看哪个扇形所占的百分率与长方形中阴影部分所占的百分率相对应.5.【分析】根据事件发生的可能性,由于表示橡皮的扇形面积最大,也就是指针停在橡皮的可能性最大,所以学生获得橡皮的可能性最大.据此解答.【解答】解:因为表示橡皮的扇形面积最大,也就是指针停在橡皮的可能性最大,所以学生获得橡皮的可能性最大.故选:A.【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.6.【分析】根据这幅扇形统计图中各扇形的大小,储蓄占50%,生活费占25%,教育费用是15%,其它费用是10%,根据百分数乘法的意义,用小林家上月工资总收入乘教育费用所占的百分率;即可得解.【解答】解:如图,教育可以用占15%8000×15%=1200(元).故选:B.【点评】此题是考查如何从扇形统计图获取信息,并根据所获取的信息进行有关计算.7.【分析】把九月份的总天数看作1,即100%,根据扇形统计图所提供的信息,用九月份的天数乘雨天所占的百分率就是九月份的雨天数.【解答】解:30×10%=30×0.1=3(天)答:本月的雨天有3天.故选:C.【点评】本题是考查如何从扇形统计图中获取信息,并对所获取的信息进行分析或计算.扇形统计图的有关计算主要是百分数应用方面的.8.【分析】A.把六(1)班学生人数看作单位“1”,已知喜欢足球的人数占全班人数的20%,喜欢乒乓球的人数占全班人数的40%,根据减法的意义,用减法可以求出喜欢篮球的人数占全班人数的百分之几.B.把全班人数看作单位“1”,根据一个数乘百分数的意义,用乘法求出喜欢打乒乓球的人数与40人进行比较.C.根据求一个数是另一个数的几倍,用除法求出喜欢打乒乓球的人数是踢足球人数的几倍,然后与2倍进行比较.据此解答.【解答】解:A.1﹣20%﹣40%=40%,答:喜欢篮球的人数占全班人数的40%.因此,喜欢篮球的人数占全班人数的40%.说法正确.B.50×40%=20(人),答:喜欢打乒乓球的有20人.因此,喜欢打乒乓球的有40人.这种说法是错误的.C.40%÷20%=2,答:喜欢打乒乓球的人数是踢足球人数的2倍.因此,喜欢打乒乓球的人数是踢足球人数的2倍.这种说法是正确的.故选:B.【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.二.填空题(共6小题)9.【分析】(1)把全班的总人数看成单位“1”,用1减去合格、优、良占的分率和,即可求出不合格率是多少;(2)优的人数占总人数的30%,它对应的数量是12人,由此用除法求出全班的总人数;(3)得良的比得合格的多占总人数的(40%﹣25%),用总人数乘这个分率即可求解.【解答】解:(1)1﹣(25%+30%+40%)=1﹣95%=5%答:不合格率为5%.(2)12÷30%=40(人)答:已知得优的有12人,全班有40人.(3)40×(40%﹣25%)=40×15%=6(人)答:得良的比得合格的多6人.故答案为:5,40,6.【点评】此题主要考查的是如何观察扇形统计图并且从统计图中获取信息,然后再进行计算、解答即可.10.【分析】(1)通过观察扇形统计图可知:乒乓球活动最受欢迎.(2)通过观察扇形统计图可知:喜欢篮球的人数占总人数的19%,喜欢足球的人数占总人数的18%,所以篮球和足球活动受欢迎的程度差不多.(3)通过观察扇形统计图可知:喜欢羽毛球的人数占总人数的26%,因为25%=,所以喜欢羽毛球活动的同学大约占总人数的.据此解答.【解答】解:(1)答:乒乓球活动最受欢迎.(2)喜欢篮球的人数占总人数的19%,喜欢足球的人数占总人数的18%,所以篮球和足球活动受欢迎的程度差不多.(3)喜欢羽毛球的人数占总人数的26%,因为25%=,所以喜欢羽毛球活动的同学大约占总人数的.故答案为:乒乓球;足球、篮球;羽毛球.【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.11.【分析】(1)棉的含量占这件衣服的百分率,从扇形统计图中可以看出.(2)由扇形统计图即可看出哪种材质含量最多,哪种材质含量最少.(3)用涤纶所含的百分率减兔毛所含的百分率.(4)根据百分数乘法的意义,用这件毛衣的质量分别乘羊毛、兔毛所占的百分率即可分别求出羊毛、兔毛的克数.根据百分数除法的意义,用羊毛含量120克除以60%就是这件毛衣的质量,再根据百分数乘法的意义,用这件毛衣的质量乘棉花含量所占的百分率就是棉花的克数.【解答】解:(1)答:棉的含量占这件衣服的7%.(2)答:羊毛的含量最多,棉的含量最少.(3)25%﹣8%=17%答:兔毛含量比涤纶少占总数的17%.(3)200×60%=120(克)200×8%=16(克)120÷60%×7%=200×7%=14(克)答:羊毛有120克,兔毛有16克.棉含量是14克.故答案为:7,羊毛,棉,17,120,16,14.【点评】此题是考查如何从扇形统计图中获取信息,并根据所获取的信息解决实际问题.12.【分析】根据扇形的特点,扇形统计图可以比较清楚地反映出部分与整体之间的数量关系.在这时各社团人数,总人数是整体.【解答】解:如图如图的扇形统计图清楚地表示参加各社团人数与总人数之间的关系.故答案为:各社团人数,总人数.【点评】此题是考查扇形统计图的特征.扇形统计图、条形统计图、折线统计图各有特征,要记住:条形统计图可以清楚地表明各种数量的多少;折线统计图不仅可以表示数量的多少,而且可以反映同一事物在不同时间里的发展变化的情况;扇形统计图可以比较清楚地反映出部分与部分、部分与整体之间的数量关系.13.【分析】把六年级学生人数看作单位“1”,根据减法的意义,用减法求出不及格的占六年级学生人数的百分之几,也就是不及格人数的扇形圆心角度数占周角的百分之几,根据一个数乘百分数的意义,用乘法解答.【解答】解:360×(1﹣30%﹣40%﹣25%)=360×5%=360×0.05=18(度),答:.“不及格”部分的扇形圆心角是18度.故答案为:18.【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.14.【分析】(1)通过观察扇形统计图可知:妙想家其他支出占家庭总支出的12%.(2)把总支出看作单位“1”,伙食水电支出2700元,占总支出的45%,根据已知一个数的百分之几是多少,求这个数,用除法求出总支出,文化支出占总支出的22%,根据一个数乘百分数的意义,用乘法解答即可.【解答】解:(1)答:妙想家其他支出占家庭总支出的12%.(2)2700÷45%×22%=2700÷0.45×0.22=6000×0.22=1320(元),答:文化支出1320元.故答案为:12%;1320.【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.三.判断题(共5小题)15.【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.【解答】解:根据统计图的特点可知:条形统计图能直观的看出数量的多少;故答案为:×.【点评】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答.16.【分析】扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数.用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.扇形统计图和其他统计图一样也要有标题,但可以没有图例,由此判断.【解答】解:扇形统计图和其他统计图一样也要有标题,但可以没有图例,所以上在的说法是错误.故答案为:×.【点评】考查扇形统计图的意义.扇形统计图和其他统计图一样也要有标题,但可以没有图例.17.【分析】根据扇形统计图的特点,扇形统计图是用整个圆的面积表示总数,用圆中各扇形的面积表示各部分占总数的百分比,通过扇形统计图很容易看各部分与整个之间的关系.据此判断.【解答】解:扇形统计图是用整个圆的面积表示总数,用圆中各扇形的面积表示各部分占总数的百分比.扇形统计图用圆柱表示仍然是扇形统计图.因此,扇形统计图用圆柱表示就变成条形统计图,这种说法是错误的.故答案为:×.【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据扇形统计图提供的信息,解决有关的实际问题.18.【分析】根据扇形统计图的特点,扇形统计图是用整个圆的面积表示总数,用圆中各扇形的面积表示各部分占总数的百分比,通过扇形统计图很容易看各部分与整个之间的关系.据此判断.【解答】解:扇形统计图是用整个圆的面积表示总数(即100%),用圆中各扇形的面积表示各部分占总数的百分比.所以,扇形统计图中,一个圆代表100%.这种说法是正确的.故答案为:√.【点评】此题考查的目的是理解掌握扇形统计图的特点及作用.19.【分析】根据扇形统计图的意义,用整个圆表示整体或总数,即单位“1”,用圆内各扇形的大小表示各部分.【解答】解:扇形统计图是用整个圆表示整体(或总数),用圆内各个扇形的大小表示各部分.所以原题说法正确.故答案为:√.【点评】此题是考查扇形统计图的意义.扇形统计图是用整个圆表示整体(或总数),用圆内各个扇形的大小表示各部分,很容易看出各部分占整体的分率.四.应用题(共6小题)20.【分析】由图可知:把总人数看成单位“1”,体育社团的人数占总人数的(1﹣30%﹣20%﹣18%),求总人数用除法计算即可.【解答】解:96÷(1﹣30%﹣20%﹣18%)=96÷32%=300(人)答:六年级参加社团的学生共有300人.【点评】本题考查了百分数除法应用题,关键是确定单位“1”,找到具体数量对应的分率;解答依据是:已知一个数的百分之几是多少,求这个数用除法计算.21.【分析】(1)通过观察扇形统计图可知:当选班长的同学是吴佳.(2)把六年级(1)班的学生人数看作单位“1”,根据减法的意义,用减法求出王倩得票数占总票数的百分之几.(3)把六年级(1)班的学生人数看作单位“1”,其中张力得了4票,占总票数的10%,根据已知一个数的百分之几是多少,求这个数,用除法求出总票数,再根据一个数乘百分数的意义,用乘法解答.【解答】解:(1)当选班长的同学是吴佳.(1)1﹣55%﹣10%﹣12.5%=22.5%;答:王倩得票数占总票数的22.5%.(3)4÷10%×55%=4÷0.1×0.55=40×0.55=22(票)答:吴佳得了22票.故答案为:吴佳、22.5.【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.22.【分析】把第三小学购买新书的总数看作单位“1”,已知购买故事书占50%,购买科技书占30%,那么购买文艺书占(1﹣50%﹣30%),已知购买文艺书320本,根据已知一个数的百分之几是多少,求这个数,用除法解答.【解答】解:320÷(1﹣50%﹣30%)=320÷20%=320÷0.2=1600(本)答:这个学校一共购进1600本图书.【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.23.【分析】①根据统计图可知,种植的总面积看成单位“1”,其中每一项的面积就是总面积的百分之几,由此逐条写出即可;②种植黄瓜的面积有90平方米,则根据分数除法的意义可以求出种植的总面积;再根据种植的总面积利用分数乘法的意义可以求出其它蔬菜的种植面积,由此进行提问、解答即可.【解答】解:①可以获得的信息有:黄瓜的种植面积占总面积的30%;油菜的种植面积占总面积的20%;芹菜的种植面积占总面积的15%;西红柿的种植面积占总面积的35%.②可以选择下面其中的一、两个问题:问题一:种植的总面积是多少平方米?90÷30%=300(平方米)答:种植的总面积是300平方米.问题二:油菜的种植面积是多少平方米?300×20%=60(平方米)答:油菜的种植面积是60平方米.问题三:芹菜的种植面积是多少平方米?300×15%=45(平方米)答:芹菜的种植面积是45平方米.问题四:西红柿的种植面积是多少平方米?300×35%=105(平方米)答:西红柿的种植面积是105平方米.【点评】此题主要考查的是如何观察扇形统计图并且从统计图中获取信息,然后再进行计算、解答即可.24.【分析】把该村养殖鸡、鸭、鹅的总数看作单位“1”,其中养鸭7000只.占总数35%,根据已知一个数的百分之几是多少,求这个数,用除法求出总数,再根据一个数乘百分数的意义,用乘法解答.【解答】解:7000÷35%=7000÷0.35=20000(只);20000×40%=8000(只);20000×25%=5000(只);答:养鸡8000只,养鹅5000只.【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.25.【分析】(1)把小军家这个月的总开支看作单位“1”,其中生活可开支占总可知的40%,亲情开支占总可知的20%,水电费开支占总开支的15%,其他开支占总开支的5%,根据减法的意义,用减法求出购物开支(400元)占总开支的百分之几,根据已知一个数的百分之几是多少,求这个数,用除法求出总开支.然后根据一个数乘百分数的意义,用乘法分别求出生活开支、亲情开支、水电费开支、其他开支各是多少元.进而完成统计表.(2)根据购物开支占总开支的百分比,完成统计图即可.【解答】解:(1)400÷(1﹣40%﹣20%﹣15%﹣5%)=400÷20%=400÷0.2=2000(元),2000×40%=800(元),2000×20%=400(元),2000×15%=300(元),2000×5%=100(元),填表如下:项目购物生活开支水电费亲情开支其他费用/元400800300400100(2)作图如下:【点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.。
六年级下册数学试题--小升初专题复习 圆的认识与圆周率 人教版(含解析)
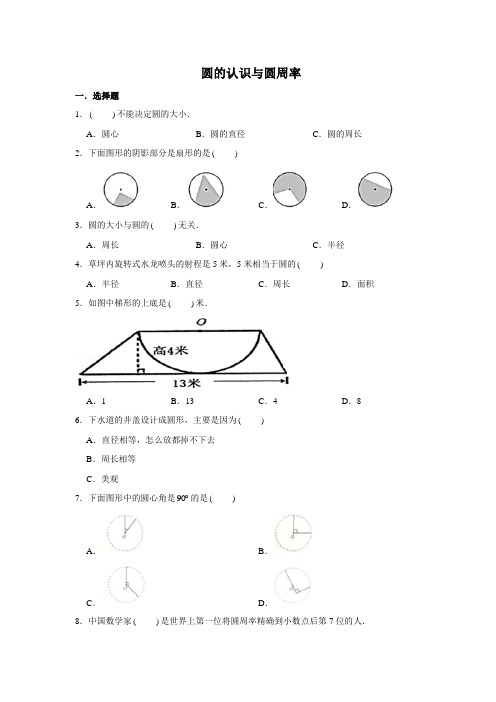
圆的认识与圆周率一.选择题1.()不能决定圆的大小.A.圆心B.圆的直径C.圆的周长2.下面图形的阴影部分是扇形的是()A.B.C.D.3.圆的大小与圆的()无关.A.周长B.圆心C.半径4.草坪内旋转式水龙喷头的射程是5米,5米相当于圆的() A.半径B.直径C.周长D.面积5.如图中梯形的上底是()米.A.1B.13C.4D.8 6.下水道的井盖设计成圆形,主要是因为()A.直径相等,怎么放都掉不下去B.周长相等C.美观7.下面图形中的圆心角是90 的是()A.B.C.D.8.中国数学家()是世界上第一位将圆周率精确到小数点后第7位的人.A.祖冲之B.杨辉C.刘徽D.张衡二.填空题9.圆周长:直径=,比值是,比值叫作.10.圆的位置由决定;圆的半径决定圆的.11.(1)半圆的直径是,半径是.(2)大圆的直径是,小圆的半径是.12.一个圆有条半径,有条直径.13.画圆时圆规两脚间的距离是圆的,圆内最长的线段是.14.1500多年前,我国南北时期著名的数学家算出π的值。
15.圆周率是和的比值.16.在边长为10厘米的正方形内画一个最大的圆,它的直径是厘米.在长10厘米.宽7厘米的长方形内画一个最大的圆,它的半径是厘米.三.判断题17.无论圆的大小如何,圆的周长与各自的直径的比值均为π.()18.南北朝时期著名数学家祖冲之进一步得出精确到小数点后7位的π值(约5世纪下半叶),给出不足近似值3.1415926和过剩近似值3.1415927,还得到两个近似分数值,密率355 113和约率227.他的辉煌成就比欧洲至少早了1000年.我们在计算有关圆柱表面积和体积是用到的π一般取3.()19.大圆的圆周率大于小圆的圆周率.()20.车轮滚动一周的距离是车轮的直径.()21.通过圆心的线段是半径.()22.在同一个圆中,圆心角越小,扇形也越小.()23.两个圆的半径相等,它们的直径也相等.()24.圆心决定圆的大小.()四.应用题25.在一个圆内有一个三角形,三个顶点都在圆上,且其中一条边是圆的直径.请你在圆上任取一点C,并连接AC,BC,得到一个三角形.量一量,ACB∠是多少度呢?一定是这个度数吗?再找几个点C试试.26.在边长为2cm的正方形内画一个最大的圆.想一想,圆的半径是多少?圆的直径是多少?27.一张圆形纸片,圆内画有一条线段AB,请你想办法判断这条线段是不是该圆半径.28.如图,直径为5米的圆形水池外有一条宽1.5米的小路,外圆的半径和直径各是多少米?29.小华在一个直径10厘米的圆中画了一个圆心角是120︒的扇形.这个扇形的大小是圆的() ().要使扇形的大小正好是圈的16,它的圆心角应是︒.30.已知线段AB的长度是45cm.(1)小的半径是多少厘米?(2)大圆的直径是多少厘米?31.如图,在长方形中有两个大小相等的圆,已知这个长方形的宽是10cm,圆半径是多少厘米?长方形的周长是多少厘米?五.操作题32.指出下列物体中的扇形.33.用彩色笔描出下面各圆的直径和半径,并量出长度.34.八名同学玩套圈游戏,圆圈处是这八名同学所处的位置,点P是目标的位置,哪种方式最公平?为什么?35.找出下列纸片上的圆心,标上字母,说一说你的方法.小升初复习34圆的认识与圆周率(等级四)参考答案与试题解析一.选择题(共8小题)1.解:A、圆心决定圆的位置,不能决定圆的大小;B、圆的直径越大,周长越大,面积越大;C、因为圆的周长越大,则圆的半径越大,则圆的面积越大;故选:A.2.解:图形的阴影部分是扇形的是;故选:C.3.解:半径决定圆的大小,圆心决定圆的位置在A,B,C三个答案中都与半径r的大小有关选项B,圆心的位置只能确定圆的位置,与圆的面积无关,圆的大小与半径有关,也就是周长有关;故选:B.4.解:旋转式水龙喷头的射程是5米,5米就是指圆的半径.故选:A.5.解:428⨯=(米)答:梯形的上底是8米;故选:D.6.解:下水道的井盖设计成圆形,主要是因为直径相等,怎么放都掉不下去.故选:A.7.解:由分析知,这些图形中圆心角是90︒的是B.故选:B.8.解:中国数学家祖冲之是世界上第一位将圆周率精确到小数点后第7位的人.故选:A.二.填空题(共8小题)9.解:圆周长:直径π=,比值是3.1415926⋯⋯,比值叫作圆周率.故答案为:π,3.1415926⋯⋯,圆周率.10.解:圆的位置由圆心决定;圆的半径决定圆的大小;故答案为:圆心,大小.11.解:(1)5210⨯=(厘米)半圆的直径是10厘米,半径是5厘米.(2)1064÷=(厘米)-=(厘米),422大圆的直径是6厘米,小圆的半径是2厘米.故答案为:10厘米,5厘米;6厘米,2厘米.12.解:从定义上看:一个圆有无数条半径,有无数条直径;故答案为:无数,无数.13.解:圆规两脚间的距离为圆的半径,圆内最长的线段是直径,故答案为:半径,直径.14.解:1500多年前,我国南北时期著名的数学家祖冲之算出π的值。
六年级圆的面积计算与扇形的认识练习题及答案解析

圆——面积计算与扇形的认识一、知识装备1、圆的面积公式推导过程:把圆平均分成若干份,可以拼成一个近似( ),这个近似长方形的长相当于( )(r π),宽相当于( )(r ),因为长方形的面积等于圆的面积,所以圆的面积是( )。
2、已知周长求面积:先求出半径()2r C π=÷÷,再根据半径求面积。
3、圆中特殊的比:(1)半径比=直径比=周长比;(2)面积比=半径的平方比(或直径的平方比,或周长的平方比); 4、圆环的面积:圆环的面积=大圆的面积-小圆的面积 (1)22S R r ππ=-环 (2)()22S R r π=-环 *(3)()()S R r R r π=+-环 5、记住结论:(1)周长相等的长方形、正方形、三角形和圆,圆的面积最大,三角形的面积最小。
(2)面积相等的长方形、正方形、三角形和圆,三角形的周长最长,圆的周长最短。
(3)如下图,在一个正方形中画一个最大的圆形,再在圆形中画一个最大的正方形。
S 大正∶S 圆∶S 小正= 4∶π∶2r πr6、扇形一条弧和经过这条弧两端的两条半径所围成的图形叫做()。
圆上A、B两点之间的部分叫做(),读作()。
顶点在圆心的()叫做圆心角。
二、经典例题例1、一个圆的周长是25.12厘米,它的面积是多少平方厘米?举一反三1:在距离地面2.5米的地方,用长31.4米的绳子去绕某一棵树的树干,正好可以绕10圈,这棵树的树干横截面的面积是多少平方米?例2、在直径8米的圆形花坛周围,铺一条2米宽的小路,这条小路的面积是多少平方米?举一反三2:一个圆形花坛,周长62.8米,如果在这个花坛周围铺上一条宽1米的环形小路。
这条小路的面积有多大?例3、若两个圆的半径比是2︰3,则它们的直径比是(),周长比是(),面积比是()。
举一反三3:(1)一个圆的半径扩大到原来的4倍,直径扩大到原来的()倍,周长扩大到原来的()倍,面积扩大原来的()倍。
(2)一个圆的半径缩小到原来的51,直径缩小到原来的( ),周长缩小到原来的( ),面积缩小到原来的( )。
六年级数学扇形的测试卷

一、选择题(每题2分,共10分)1. 下列图形中,不是扇形的是()A. 圆形B. 半圆C. 椭圆形D. 梯形2. 一个圆的半径为10cm,那么这个圆的周长是()A. 20πcmB. 30πcmC. 40πcmD. 50πcm3. 一个圆的直径是12cm,那么这个圆的面积是()A. 36πcm²B. 72πcm²C. 144πcm²D. 216πcm²4. 一个扇形的圆心角是90°,那么这个扇形的面积是()A. πr²/4B. πr²/2C. πr²D. 2πr²5. 一个圆的半径为5cm,那么这个圆的周长与面积之比是()A. 1:2B. 1:4C. 2:1D. 4:1二、填空题(每题2分,共10分)6. 一个圆的半径是r,那么这个圆的周长是______,面积是______。
7. 一个扇形的圆心角是θ,半径是r,那么这个扇形的面积是______。
8. 一个圆的直径是d,那么这个圆的周长是______,面积是______。
9. 一个扇形的圆心角是90°,半径是r,那么这个扇形的面积是______。
10. 一个圆的半径是5cm,那么这个圆的周长与面积之比是______。
三、计算题(每题5分,共15分)11. 一个圆的半径是8cm,求这个圆的周长和面积。
12. 一个扇形的圆心角是120°,半径是10cm,求这个扇形的面积。
13. 一个圆的直径是14cm,求这个圆的周长与面积之比。
四、应用题(每题10分,共20分)14. 一个圆形的面积是50πcm²,求这个圆的半径。
15. 一个扇形的圆心角是60°,半径是12cm,求这个扇形的面积。
答案:一、选择题1. C2. C3. C4. A5. B二、填空题6. 2πr πr²7. πr²θ/3608. πd π(d/2)²9. πr²/4 10. 2:1三、计算题11. 周长:16πcm,面积:64πcm²12. 面积:20πcm²13. 周长:14πcm,面积:49πcm²,周长与面积之比:2:1四、应用题14. 半径:5cm15. 面积:36πcm²。
六年级下册扇形测试卷数学

一、选择题(每题2分,共20分)1. 一个圆的半径是5cm,那么这个圆的周长是多少厘米?A. 15πB. 25πC. 10πD. 20π2. 一个圆的面积是78.5平方厘米,那么这个圆的半径是多少厘米?A. 5B. 10C. 15D. 203. 下列哪个图形不是轴对称图形?A. 正方形B. 圆C. 等边三角形D. 长方形4. 一个圆的直径是12cm,那么这个圆的周长是:A. 24cmB. 36cmC. 48cmD. 60cm5. 一个圆的半径增加了50%,那么这个圆的面积增加了:A. 25%B. 50%C. 100%D. 200%6. 一个圆的周长是31.4cm,那么这个圆的半径是:A. 5cmB. 10cmC. 15cmD. 20cm7. 一个扇形的圆心角是90°,如果圆的半径是10cm,那么这个扇形的面积是:A. 50πcm²B. 100πcm²C. 25πcm²D. 50cm²8. 一个圆的半径是6cm,那么这个圆的周长与面积的比是:A. 2:1B. 3:1C. 4:1D. 6:19. 下列哪个不是圆的性质?A. 圆是轴对称图形B. 圆的直径等于半径的两倍C. 圆的周长是直径的π倍D. 圆的面积是半径的平方乘以π10. 一个圆的半径是8cm,那么这个圆的面积是多少平方厘米?A. 64πB. 128πC. 256πD. 512π二、填空题(每题2分,共20分)11. 一个圆的半径是r,那么这个圆的周长是______cm。
12. 一个圆的直径是d,那么这个圆的面积是______cm²。
13. 一个圆的半径增加了a%,那么这个圆的面积增加了______%。
14. 一个扇形的圆心角是θ,圆的半径是r,那么这个扇形的面积是______cm²。
15. 一个圆的周长与面积的比是______。
16. 一个圆的半径是5cm,那么这个圆的直径是______cm。
六年级下册数学专项练习圆及扇形全国通用

圆与扇形——公式与割补内容概要本讲主要解说与圆和扇形相关的观点,及周长、面积公式等.下边我们来谈谈这方面的基础知识.圆是我们在生活中常常有到的图形,它也是最完满的平面图形:有无数条经过圆心的对称轴,绕圆心旋转任何角度还保持原状.并且,全部的平面图形在周长相同的状况下,圆的面积是最大的.我们知道,圆的周长和直径的比值是一个固定不变的数,这正是圆周率,用π表示.此外,一般把直径记作d,半径记作r,如图1所示.rd图1因此,圆的周长 C d 2 r,圆的面积 S r2.如图3,由构成圆心角的两条半径和圆心角所对的弧所围成的图形叫扇形.它是圆的一部分,因此对于扇形的各样计算能够应用圆里面的结论.n°r图3扇形的圆心角为n°时,它的弧长和面积应当分别是圆周长和圆面积的n.360因此,扇形弧长=n2r,面积=n r2.360360我们先来熟习一下这些公式.练习:1. 半径是2的圆的面积和周长分别是多少?第1页直径是5的圆的面积和周长分别是多少?周长是10π的圆的面积是多少?面积是9π的圆的周长是多少?例题一、基本公式运用例题1.已知扇形的圆心角为120°,半径为2,则这个扇形的面积和周长各是多少?(圆周率按计算)例题2.已知扇形面积为平方厘米,圆心角为60°,则这个扇形的半径和周长各是多少?(圆周率按计算)60°随堂练习:3.已知一个扇形的弧长为厘米,圆心角为45,这个扇形的半径和周长各是多少?4.5.6.7.8.2.扇形的面积是平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是多少?9.10.11.如图,直角三角形ABC的面积是45,分别以B,C为圆心,3为半径画圆.已知图中暗影部分的面积是.请问:角A是多少度?(π取)第2页ABC二、圆中方,方中圆如图,左以下图和右以下图中的正方形边长都是2,那么大圆、小圆的面积分别为________、________.随堂练习:1. 已知外面大圆的半径是4,里面小圆的面积是多少?(答案用π表示)二、割补法5.求以下各图中暗影部分的面积(图中长度单位为厘米,圆周率按计算):(1)(2)随堂练习:求以下图中暗影部分2的面积(图中长度单位为厘米,3圆周率按计算):2(1)(2)求以下各图中暗影部分的面积(图中长度单位为厘米,圆周率按7第3页4计算):(1)(2)22已知图中正方形的边长为2,分别以其四个极点为圆心的直角扇形恰巧交于正方形中心,那么图中暗影部分的面积为________.(答案用表示)7.依据图中所给数值,求下边图形的外周长和总面积分别是多少?(π取)4作业:半径为4厘米的圆的周长是________厘米,面积是________平方厘米;2. 半径为4厘米,圆心角为90的扇形周长是________厘米,面积是________平方厘米.(取)3.家里来客人了,调皮到商场买了4瓶啤酒,售货员阿姨将4瓶啤酒捆扎在一同(以以下图所示),捆4圈起码要用绳索________厘米.(取,接头处忽视7厘米O 不计)4.求以下各图中暗影部分的面积(图中长度单位为厘米,圆周率按计算):(1)(2)第4页1111010以下图形中的正方形的边长为2,则以下图中各个暗影部分面积的大小分别为______、______.(取)6. 用一块面积为36平方厘米的圆形铝板下料,从中裁出了7个相同大小圆与扇形O的圆铝板.问:所余下的边角料的总面积是多少平方厘米?旋转与重叠知识总结:学习怎样利用割补法和包括清除的思想计算图形中特定部分的面积;学会剖析几何图形的运动过程,并由此得出点的轨迹和图形扫过的地区.例题:一、重叠问题例题1.以下图中甲地区比乙地区的面积大57平方厘米,且半圆的半径是10厘米,那么此中直角三角形的另一条直角边的长度是多少?(圆周率取)乙甲第5页例题2.以下图中有一个等腰直角三角形ABC,一个以AB为直径的半圆,和一个以BC为半径的扇形.已知AB BC 10厘米.图中暗影部分的面积为多少平方厘米?(π取)AEDC B随堂练习1.如图17-13,以AB为直径做半圆,三角形ABC是直角三角形,暗影部分①比暗影部分②的面积小28平方厘米,AB长40厘米.求BC的长度.(取.)C②①B A例题3.如图,直角三角形的两条直角边分别为3和5,分别以三条边做了3个半圆(直角极点在以斜边为直径的半圆上),那么暗影部分的面积为______.435例题4.图1是一个直径是3厘米的半圆,AB是直径.如图2所示,让A点不动,把整个半圆逆时针转60°,此时B点挪动到C点.请问:图中暗影部分的面积是多少平方厘米?(π取)C图160A B图2第6页二、动向扫面积问题例题5.如图,正方形ABCD边长为1厘米,挨次以A、B、C、D为圆心,以AD、BE、CF、DG为半径画出四个直角扇形,那么暗影部分的面积为________平方厘米.(取)EA D HF CBG例题6.以下图,以等边三角形的B、C、A三点分别为圆心,分别以AB、CD、AE为半径画弧,这样形成的曲线ADEF被称为正三角形ABC的渐开线,假如正三角形ABC的边长为3厘米,那么此渐开线的长度为多少厘米,图中I、II、III三部分的面积之和是多少平方厘米?AIIIIC DBIIE三、运动圆扫面积例题7.图中正方形的边长是4厘米,而圆环的半径是1厘米.当圆围绕正方形无滑动地转动一周又回到原来地点时,其扫过的面积有多大?(π取)第7页随堂练习1. 图中长方形的长是10厘米,宽是4厘米,而圆环的半径是1厘米.当圆围绕正方形无滑动地转动一周又回到本来地点时,其扫过的面积有多大?(π取)例题8.图中等边三角形的边长是3厘米,而圆环的半径是1厘米.当圆围绕等边三角形无滑动地转动一周又回到本来地点时,其扫过的面积有多大?(π取)思虑题以下图,一只小狗被拴在一个边长为4米的正五边形的建筑物的一个极点处,周围都是空地.绳长恰巧够小狗走到建筑物外墙边的任一地点.小狗的活动范围是多少平方米?(建筑外墙不行超越,小狗身长忽视不计,π取3)狗第8页作业:1. 图17-14由一个长方形与两个90角的扇形构成,此中暗影部分的面积是_______平方厘米.(取.)25图17-14图中有一个矩形和两个半径分别为5和2的直角扇形,那么两个暗影部分的面积相差为_______.(π取)如图,直角三角形的两条直角边长分别是10cm和6cm,分别以直角边为直径作出两个半圆,这两个半圆的交点恰巧落在斜边上,那么暗影部分的面积是_______cm2.(取)1730)6cm10cm4. 图1是一个直径是3厘米的半圆,AB是直径.如图2所示,让A点不动,把整个半圆逆时针转60°,此时B点挪动到C点.请问:图中暗影部分的面积是_______平方厘米(π取)CC图140A B图25.图中正方形的边长是6厘米,而圆环的半径是1厘米.当圆围绕正方形无滑动地转动一周又回到本来地点时,其扫过的面积有______.(π取)第9页6. 图中等边三角形的边长是5厘米,圆形的半径是1厘米.当圆形绕等边三角形转动一周又回到原来地点时,扫过的面积有________.(π取)7.11 / 1211第10页12 / 1212。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十五讲 圆和扇形研究圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,通过变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形来计算它们的面积.圆的面积2πr =;扇形的面积2π360nr =⨯;圆的周长2πr =;扇形的弧长2π360nr =⨯.一、 跟曲线有关的图形元素:①扇形:扇形由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形,扇形是圆的一部分.我们经常说的12圆、14圆、16圆等等其实都是扇形,而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几分之几.那么一般的求法是什么呢?关键是360n.比如:扇形的面积=所在圆的面积360n⨯;扇形中的弧长部分=所在圆的周长360n⨯扇形的周长=所在圆的周长360n⨯+2⨯半径(易错点是把扇形的周长等同于扇形的弧长) ②弓形:弓形一般不要求周长,主要求面积.一般来说,弓形面积=扇形面积-三角形面积.(除了半圆)③”弯角”:如图: 弯角的面积=正方形-扇形④”谷子”:如图: “谷子”的面积=弓形面积2⨯一、常用的思想方法:①转化思想(复杂转化为简单,不熟悉的转化为熟悉的) ②等积变形(割补、平移、旋转等) ③借来还去(加减法)④外围入手(从会求的图形或者能求的图形入手,看与要求的部分之间的”关系”)板块一 平移、旋转、割补、对称在曲线型面积中的应用【例 1】 下图中每一个小正方形的面积是1平方厘米,那么格线部分的面积是多少平方厘米?【解析】 割补法.如右图,格线部分的面积是36平方厘米.【例 2】 (2007年西城实验考题)在一个边长为2厘米的正方形内,分别以它的三条边为直径向内作三个半圆,则图中阴影部分的面积为 平方厘米.【解析】 采用割补法.如果将阴影半圆中的2个弓形移到下面的等腰直角三角形中,那么就形成两个相同的等腰直角三角形,所以阴影部分的面积等于两个等腰直角三角形的面积和,即正方形面积的一半,所以阴影部分的面积等于21222⨯=平方厘米.【例 3】 计算图中阴影部分的面积(单位:分米).A A【解析】 将右边的扇形向左平移,如图所示.两个阴影部分拼成—个直角梯形. ()5105275237.5+⨯÷=÷=(平方分米).【例 4】 求图中阴影部分的面积.【解析】 如图,连接BD ,可知阴影部分的面积与三角形BCD 的面积相等,即为1112123622⨯⨯⨯=.【例 5】 求如图中阴影部分的面积.(圆周率取3.14)【解析】 可将左下橄榄型的阴影部分剖开,两部分分别顺逆时针90︒,则阴影部分转化为四分之一圆减去一个等腰直角三角形,所以阴影部分的面积为211π444 4.5642⨯⨯-⨯⨯=.【例 6】 求下列各图中阴影部分的面积.(1)1010(2)ba【解析】 在图(1)中,阴影部分经过切割平移变成了一个底为10,高为5的三角形,利用三角形面积公式可以求得110102522S =⨯⨯=阴影;在图(2)中,阴影部分经过切割平移变成了一个长为b ,宽为a 的长方形,利用长方形面积公式可以求得S a b ab =⨯=阴影.【例 7】 如图,长方形ABCD 的长是8cm ,则阴影部分的面积是 2cm .(π 3.14=)【解析】 阴影部分的面积实际上是右上图阴影部分面积的一半,所以求出右上图中阴影部分面积再除以2即可.长方形的长等于两个圆直径,宽等于1个圆直径,所以右图的阴影部分的面积等于:()2882822π2 6.88⨯÷-÷÷⨯⨯=所以左图阴影部分的面积等于6.882 3.44÷=平方厘米.【例 8】 求右图中阴影部分的面积.(π取3)45︒45︒20cm【解析】 看到这道题,一下就会知道解决方法就是求出空白部分的面积,再通过作差来求出阴影部分面积,因为阴影部分非常不规则,无法入手. 这样,平移和旋转就成了我们首选的方法.(法1)我们只用将两个半径为10厘米的四分之一圆减去空白的①、②部分面积之和即可,其中①、②面积相等.易知①、②部分均是等腰直角三角形,但是①部分的直角边AB 的长度未知.单独求①部分面积不易,于是我们将①、②部分平移至一起,如右下图所示,则①、②部分变为一个以AC 为直角边的等腰直角三角形,而AC 为四分之一圆的半径,所以有AC =10.两个四分之一圆的面积和为150,而①、②部分的面积和为11010502⨯⨯=,所以阴影部分的面积为15050100-=(平方厘米).(法2)欲求图①中阴影部分的面积,可将左半图形绕B 点逆时针方向旋转180°,使A 与C 重合,从而构成如右图②的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.所以阴影部分面积为21110101010022π⨯⨯-⨯⨯=(平方厘米).A板块二 曲线型面积计算【例 9】 如图,已知扇形BAC 的面积是半圆ADB 面积的34倍,则角CAB 的度数是________. DCBA【解析】 设半圆ADB 的半径为1,则半圆面积为21ππ122⨯=,扇形BAC 的面积为π42π233⨯=.因为扇形BAC 的面积为2π360n r ⨯,所以,22ππ23603n ⨯⨯=,得到60n =,即角CAB 的度数是60度.【例 10】 如下图,直角三角形ABC 的两条直角边分别长6和7,分别以,B C 为圆心,2为半径画圆,已知图中阴影部分的面积是17,那么角A 是多少度(π3=)【解析】 167212ABC S =⨯⨯=△, 三角形ABC 内两扇形面积和为21174-=,根据扇形面积公式两扇形面积和为2π24360B C∠+∠⨯⨯=°,所以120B C ∠+∠=°,60A ∠=°.【例 11】 如图,大小两圆的相交部分(即阴影区域)的面积是大圆面积的415,是小圆面积的35.如果量得小圆的半径是5厘米,那么大圆半径是多少厘米?【解析】 小圆的面积为2π525π⨯=,则大小圆相交部分面积为325π15π5⨯=,那么大圆的面积为422515ππ154÷=,而2251515422=⨯,所以大圆半径为7.5厘米.【例 12】 有七根直径5厘米的塑料管,用一根橡皮筋把它们勒紧成一捆(如图),此时橡皮筋的长度是多少厘米?(π取3)CBA【解析】 由右图知,绳长等于6个线段AB 与6个BC 弧长之和.将图中与BC 弧相似的6个弧所对的圆心角平移拼补,可得到6个角的和是360︒, 所以BC 弧所对的圆心角是60︒,6个BC 弧合起来等于直径5厘米的圆的周长. 而线段AB 等于塑料管的直径,由此知绳长为:565π45⨯+=(厘米).【例 13】 用一块面积为36平方厘米的圆形铝板下料,从中裁出了7个同样大小的圆铝板.问:所余下的边角料的总面积是多少平方厘米?【解析】 大圆直径是小圆的3倍,半径也是3倍,小圆面积∶大圆面积22π:π1:9r R ==,小圆面积13649=⨯=,7个小圆总面积4728=⨯=,边角料面积36288=-=(平方厘米).【例 14】 如图,两个正方形摆放在一起,其中大正方形边长为12,那么阴影部分面积是多少?(圆周率取3.14)AFEAFE【解析】 方法一:设小正方形的边长为a ,则三角形ABF 与梯形ABCD 的面积均为()122a a +⨯÷.阴影部分为:大正方形+梯形-三角形ABF -右上角不规则部分=大正方形-右上角不规则部分=14圆.因此阴影部分面积为:3.1412124113.04⨯⨯÷=.方法二:连接AC 、DF ,设AF 与CD 的交点为M ,由于四边形ACDF 是梯形,根据梯形蝴蝶定理有ADM CMF S S =△△,所以DCF S S =阴影扇形 3.1412124113.04=⨯⨯÷=【巩固】如右图,两个正方形边长分别是10和6,求阴影部分的面积.(π取3)【解析】 (法1)观察可知阴影部分面积等于三角形ACD 的面积减去月牙BCD 的面积,那么求出月牙BCD 的面积就成了解题的关键.月牙BCD 的面积为正方形BCDE 的面积减去四分之一圆:166π6694⨯-⨯⨯⨯=;则阴影部分的面积为三角形ACD 的面积减去月牙BCD 的面积,为:()110669392S =⨯+⨯-=阴影.(法2)观察可知AF 和BD 是平行的,于是连接AF 、BD 、DF .则ABD ∆与BDF ∆面积相等,那么阴影部分面积等于BDF ∆与小弓形的面积之和,也就等于DEF ∆与扇形BED 的面积之和,为:211(106)6π63924-⨯⨯+⨯⨯=.【例 15】 如图,ABC 是等腰直角三角形,D 是半圆周的中点,BC 是半圆的直径.已知10AB BC ==,那么阴影部分的面积是多少?(圆周率取3.14)D【解析】 连接PD 、AP 、BD ,如图,PD 平行于AB ,则在梯形ABDP 中,对角线交于M 点,那么ABD∆与ABP ∆面积相等,则阴影部分的面积转化为ABP ∆与圆内的小弓形的面积和. ABP ∆的面积为:()10102225⨯÷÷=;弓形面积: 3.145545527.125⨯⨯÷-⨯÷=; 阴影部分面积为:257.12532.125+=.【例 16】 如图,ABCD 是边长为a 的正方形,以AB 、BC 、CD 、DA 分别为直径画半圆,求这四个半圆弧所围成的阴影部分的面积.(π取3)DCBAaDCBAa【解析】 这道题目是很常见的面积计算问题.阴影部分是一个花瓣状的不规则图形,不能直接通过面积公式求解,观察发现阴影部分是一个对称图形,我们只需要在阴影部分的对称轴上作两条辅助线就明了了.如图,这样阴影部分就划分成了4个半圆减去三角形,我们可以求得,()4S S S =⨯-阴影半圆三角形 21142222a a a π⎡⎤⎛⎫=⨯⨯⨯-⨯⨯⎢⎥ ⎪⎝⎭⎢⎥⎣⎦212a =【巩固】如图,正方形ABCD 的边长为4厘米,分别以B 、D 为圆心以4厘米为半径在正方形内画圆.求阴影部分面积.(π取3) D BA DB【解析】 由题可知,图中阴影部分是两个扇形重叠的部分,我们可以利用容斥原理从图形整体上考虑来求阴影部分面积;同样,我们也可以通过作辅助线直接求阴影部分的面积. 解法一:把两个扇形放在一起得到1个正方形的同时还重叠了一块阴影部分.则阴影部分的面积为=21π44482⋅⋅-⨯=;解法二:连接AC ,我们发现阴影部分面积的一半就是扇形减去三角形的面积,所以阴影部分面积=212π444284⨯⋅⋅-⨯÷=().【巩固】在图中,两个四分之一圆弧的半径分别是2和4,求两个阴影部分的面积差.(圆周率取3.14)【解析】 我们只要看清楚阴影部分如何构成则不难求解.左边的阴影是大扇形减去小扇形,再扣除一个长方形中的不规则白色部分,而右边的阴影是长方形扣除这块不规则白色部分,那么它们的差应为大扇形减去小扇形,再减去长方形.则为:ππ4422423 3.148 1.4244⨯⨯-⨯⨯-⨯=⨯-=.【例 17】 如图,矩形ABCD 中,AB =6厘米,BC =4厘米,扇形ABE 半径AE =6厘米,扇形CBF 的半径CB =4厘米,求阴影部分的面积.(π取3)CB A【解析】 方法一:观察发现,阴影部分属于一个大的扇形,而这个扇形除了阴影部分之外,还有一个不规则的空白部分ABFD 在左上,求出这个不规则部分的面积就成了解决这个问题的关键. 我们先确定ABFD 的面积,因为不规则部分ABFD 与扇形BCF 共同构成长方形ABCD ,所以不规则部分ABFD 的面积为2164π4124⨯-⨯⨯=(平方厘米),再从扇形ABE 中考虑,让扇形ABE 减去ABFD 的面积,则有阴影部分面积为21π612154⨯⨯-=(平方厘米).方法二:利用容斥原理2211π6π4461544EAB BCF ABCD S S S S =+-=⨯+⨯-⨯=阴影扇形扇形长方形(平方厘米)【例 18】 如图,等腰直角三角形ABC 的腰为10;以A 为圆心,EF 为圆弧,组成扇形AEF ;两个阴影部分的面积相等.求扇形所在的圆面积.【解析】 题目已经明确告诉我们ABC 是等腰直角三角形,AEF 是扇形,所以看似没有关系的两个阴影部分通过空白部分联系起来.等腰直角三角形的角A 为45度,则扇形所在圆的面积为扇形面积的8倍.而扇形面积与等腰直角三角形面积相等,即11010502S =⨯⨯=扇形,则圆的面积为508400⨯=【例 19】 如图,直角三角形ABC 中,AB 是圆的直径,且20AB =,阴影甲的面积比阴影乙的面积大7,求BC 长.(π 3.14=)乙甲A【解析】 因为两块阴影部分都是不规则图形,单独对待它们无法运用面积公式进行处理,而解题的关键就是如何把它们联系起来,我们发现把两块阴影加上中间的一块,则变成1个半圆和1个直角三角形,这个时候我们就可以利用面积公式来求解了.因为阴影甲比阴影乙面积大7,也就是半圆面积比直角三角形面积大7.半圆面积为:21π101572⨯⨯=,则直角三角形的面积为157-7=150,可得BC =2⨯150÷20=15.【巩固】 如图,三角形ABC 是直角三角形,阴影部分①比阴影部分②的面积小28平方厘米,AB 长40厘米.求BC 的长度?(π取3.14)【解析】 图中半圆的直径为AB ,所以其面积为2120π200 3.146282⨯⨯≈⨯=.有空白部分③与①的面积和为628,又②-①28=,所以②、③部分的面积和62828656+=.有直角三角形ABC 的面积为12AB BC ⨯⨯=1406562BC ⨯⨯=.所以32.8BC =厘米.【例 20】 (2009年十三分入学测试题)图中的长方形的长与宽的比为8:3,求阴影部分的面积.204【解析】 如下图,设半圆的圆心为O ,连接OC .从图中可以看出,20OC =,20416OB =-=,根据勾股定理可得12BC =. 阴影部分面积等于半圆的面积减去长方形的面积,为:21π20(162)12200π3842442⨯⨯-⨯⨯=-=.CD【例 21】如图,求阴影部分的面积.(π取3)【解析】 如图,图中阴影部分为月牙儿状,月牙儿形状与扇形和弓形都不相同,目前我们还不能直接求出 它们的面积,那么我们应该怎么来解决呢?首先,我们分析下月牙儿状是怎么产生的,观察发现月牙儿形是两条圆弧所夹部分,再分析可以知道,两条圆弧分别是不同圆的圆周的一部分,那么我们就找到了解决问题的方法了.阴影部分面积=12小圆面积+12中圆面积+三角形面积-12大圆面积=2221111π3π434π52222⋅⋅+⋅⋅+⨯⨯-⋅⋅=6【例 22】 如图,直角三角形的三条边长度为6,8,10,它的内部放了一个半圆,图中阴影部分的面积为多少?68O【解析】S S S =-阴影直角三角形半圆, 设半圆半径为r ,直角三角形面积用r 表示为:610822r rr ⨯⨯+= 又因为三角形直角边都已知,所以它的面积为168242⨯⨯=,所以824r =,3r =所以1249π=24 4.5π2S =-⨯-阴影家庭作业【作业1】如图,在一个边长为4的正方形内,以正方形的三条边为直径向内作三个半圆.求阴影部分的面积.【解析】阴影部分经过切割平移变成了一个面积为正方形一半的长方形,则阴影部分面积为4428⨯÷=.【作业2】如图,阴影部分的面积是多少?24【解析】首先观察阴影部分,我们发现阴影部分形如一个号角,但是我们并没有学习过如何求号角的面积,那么我们要怎么办呢?阴影部分我们找不到出路,那么我们不妨考虑下除了阴影部分之外的部分吧!观察发现,阴影部分左侧是一个扇形,而阴影部分右边的空白部分恰好与左边的扇形构成一个边长为4的正方形,那么阴影部分的面积就等于大的矩形面积减去正方形面积.则阴影部分面积(222)4(22)48++⨯-+⨯=【作业3】如图,四分之一大圆的半径为7,求阴影部分的面积,其中圆周率π取近似值227.【解析】原题图中的左边部分可以割补至如右上图位置,这样只用先求出四分之一大圆的面积,再减去其内的等腰直角三角形面积即为所求.因为四分之一大圆的半径为7,所以其面积为:2211227π738.5447⨯⨯≈⨯⨯=.四分之一大圆内的等腰直角三角形ABC的面积为17724.52⨯⨯=,所以阴影部分的面积为38.524.514-=.【作业4】求下列各图中阴影部分的面积(图中长度单位为cm,圆周率按3计算):⑴3⑵4⑶111⑷2⑸2⑹【解析】 ⑴4.5 ⑵4 ⑶1 ⑷2 ⑸1.5 ⑹4.5【作业5】求图中阴影部分的面积(单位:cm ).2【解析】 从图中可以看出,两部分阴影的面积之和恰好是梯形的面积,所以阴影部分面积为21(24)39cm 2⨯+⨯=.【作业6】如图,若图中的圆和半圆都两两相切,两个小圆和三个半圆的半径都是1.求阴影部分的面积.【解析】 由于直接求阴影部分面积太麻烦,所以考虑采用增加面积的方法来构造新图形.由右图可见,阴影部分面积等于16大圆面积减去一个小圆面积,再加上120︒的小扇形面积(即13小圆面积),所以相当于16大圆面积减去23小圆面积.而大圆的半径为小圆的3倍,所以其面积为小圆的239=倍,那么阴影部分面积为21259π1π 2.5636⎛⎫⨯-⨯⨯== ⎪⎝⎭.【作业7】如图是一个直径为3cm 的半圆,让这个半圆以A 点为轴沿逆时针方向旋转60︒,此时B 点移动到'B 点,求阴影部分的面积.(图中长度单位为cm ,圆周率按3计算).【解析】 面积=圆心角为60︒的扇形面积+半圆-空白部分面积(也是半圆)=圆心角为60︒的扇形面积22603π3π 4.5(cm )3602=⨯⨯==.【作业8】三角形ABC 是直角三角形,阴影I 的面积比阴影II 的面积小225cm ,8cm AB =,求BC 的长度.I IABCI【解析】 由于阴影I 的面积比阴影II 的面积小225cm ,根据差不变原理,直角三角形ABC 面积减去半圆面积为225cm ,则直角三角形ABC 面积为218π258π2522⎛⎫⨯+=+ ⎪⎝⎭(2cm ),BC 的长度为()8π25282π 6.2512.53+⨯÷=+=(cm ).【作业9】下图中每一个小正方形的面积是1平方厘米,那么格线部分的面积是多少平方厘米?【解析】 割补法.如右图,格线部分的面积是36平方厘米.【作业10】求图中阴影部分的面积.【解析】 阴影部分面积=半圆面积+扇形面积-三角形面积22211211π()π121241.042282=⨯+⨯-⨯=.。
