第5讲假设检验1北京大学医学部,统计学基础,统计学课件
假设检验基础知识讲义PPT课件( 72页)

量,现代检验中人们直接使用由统计量 算出的犯第Ⅰ类错误的概率,即所tatistic)
1. 根据样本观测结果计算出对原假设和备择假 设做出决策某个样本统计量
2. 对样本估计量的标准化结果
H0 : 10cm H1 : 10cm
2011年
提出假设
(例题分析)
【例6.2】某品牌洗涤剂在它的产品说明书中声称: 平均净含量不少于500克。从消费者的利益出发, 有关研究人员要通过抽检其中的一批产品来验 证该产品制造商的说明是否属实。试陈述用于 检验的原假设与备择假设
解:研究者抽检的意图是倾向于证 绿叶
2. 先确定备择假设,再确定原假设 3. 等号“=”总是放在原假设上 4. 因研究目的不同,对同一问题可能提出不同
的假设(也可能得出不同的结论)
2011年
双侧检验与单侧检验
1. 备择假设没有特定的方向性,并含有符号 “”的假设检验,称为双侧检验或双尾 检验(two-tailed test)
2. 备择假设具有特定的方向性,并含有符号 “>”或“<”的假设检验,称为单侧检验或 单尾检验(one-tailed test)
可能犯错误
2. 原假设和备择假设不能同时成立,决策的结果要么拒绝 H0,要么不拒绝H0。决策时总是希望当原假设正确时没 有拒绝它,当原假设不正确时拒绝它,但实际上很难保 证不犯错误
3. 第Ⅰ类错误(错误)
原假设为正确时拒绝原假设
第Ⅰ类错误的概率记为,被称为显著性水平
2. 第Ⅱ类错误(错误)
3. 值越小,你拒绝原假设的理由就越充分
2011年
多大的P 值合适?
假设检验课件

假设检验课件假设检验课件假设检验是统计学中一种常用的推断方法,用于验证关于总体参数的假设。
在实际应用中,假设检验被广泛用于医学、经济、社会科学等领域。
本文将对假设检验的基本概念、步骤和常见方法进行介绍,并探讨其在实际问题中的应用。
一、假设检验的基本概念1.1 假设在假设检验中,我们需要对总体参数提出一个假设,并通过收集样本数据来判断这个假设是否成立。
一般来说,我们会提出一个原假设(H0)和一个备择假设(H1)。
原假设是我们需要进行检验的假设,备择假设则是对原假设的否定。
1.2 检验统计量检验统计量是用来衡量样本数据与原假设之间的差异程度的统计量。
常见的检验统计量有t值、F值、卡方值等。
通过计算检验统计量,我们可以得到一个观察到的差异程度,并据此进行假设检验。
1.3 显著性水平显著性水平是在假设检验中设定的一个临界值,用于判断原假设是否成立。
一般来说,我们将显著性水平设定为0.05或0.01。
如果计算得到的p值小于显著性水平,则拒绝原假设,否则接受原假设。
二、假设检验的步骤2.1 确定假设在进行假设检验之前,我们需要明确原假设和备择假设。
原假设通常是我们希望进行检验的假设,备择假设则是对原假设的否定。
2.2 选择适当的检验统计量根据问题的具体情况,选择适当的检验统计量进行计算。
不同的问题可能需要使用不同的统计量,例如,对两个总体均值的比较可以使用t检验,对多个总体均值的比较可以使用方差分析等。
2.3 计算检验统计量的值根据样本数据计算出检验统计量的值。
这一步需要根据具体的统计方法进行计算,例如,对于t检验,需要计算出样本均值、标准差和样本容量等。
2.4 计算p值根据检验统计量的值,计算出p值。
p值表示在原假设成立的情况下,观察到与之相差程度或更极端程度的结果出现的概率。
p值越小,说明观察到的差异越显著。
2.5 判断是否拒绝原假设根据显著性水平和计算得到的p值,判断是否拒绝原假设。
如果p值小于显著性水平,我们可以拒绝原假设,认为观察到的差异是显著的;如果p值大于显著性水平,我们则接受原假设,认为观察到的差异不是显著的。
医学统计学课件:假设检验

数据展示
不同职业人群的身高和体重数据。
统计方法
方差分析,推断不同职业人群的身 高和体重是否具有统计学差异。
06
总结与展望
医学统计学在假设检验中的重要性
数据驱动决策
医学统计学在假设检验中扮演着核心角色,其原理和方法为数 据驱动的决策提供了基础框架。
提高诊断准确性
通过假设检验,医学统计学可以帮助医生做出更准确的诊断, 从而更好地制定治疗方案。
详细描述
方差分析的步骤包括提出假设、计算统计 量F值、确定临界值和作出结论。该方法可 以分析多个样本数据之间的差异,推断出 各样本所代表的总体的平均值之间是否存 在显著差异。
04
假设检验的注意事项
假设检验的前提条件
ห้องสมุดไป่ตู้样本与总体
样本是总体的代表,总体是样本的来源。在进行假设检验时,必须清楚定义总体和样本, 并考虑样本的代表性、样本大小和效应大小等因素。
研究目的
探讨该地区高血压与年龄的关系。
研究设计
收集该地区各年龄组人群的高血压患病率 数据,进行分析。
数据展示
各年龄组高血压患病率数据。
统计方法
卡方检验,探索不同年龄组之间高血压患 病率是否存在差异。
实例三
研究目的
探讨该地区不同职业人群的身高与 体重是否存在差异。
研究设计
收集不同职业人群的身高和体重数 据,进行对比分析。
02
假设检验的统计学原理
概率论与统计学关系
1
概率论是数学的一个分支,主要研究随机事件 发生的可能性。
2
统计学是利用概率论研究随机数据的方法和原 理的一门学科。
3
假设检验是统计学中利用概率论原理对未知的 总体参数进行推断的方法。
第五章假设检验01精品PPT课件

1. 与原假设对立的假设, 也称“备择假设”
2. 表示为 H1 3. 总是有符号 , 或
H1 : <某一数值 或 某一数值
例如, H1 : < 10cm, 或 10cm
提出假设
1. 原假设和对立假设是一个完备事件组,而且相互 对立 在一项假设检验中,原假设和对立假设必有一 个成立,而且只有一个成立
然后利用样本信息来判断假设是否成立
2. 类型
总体分布已知,
参数假设检验
检验关于未知参数
非参数假设检验
的某个假设
总体分布未知时的 假设检验问题
假设检验的过程
(提出假设→抽取样本→作出决策)
总体
提出假设
X的均值
作出决策
???
☺☺ ☺
☺☺ ☺☺
☺☺
抽取随机样本
☺
样本 均值
☺
假设检验的思想
假设检验的基本思想:通过提出假设,利用“小 概率原理”和“概率反证法”,论证假设的真伪 的一种统计分析方法。
解:研究者想收集证据予以支持的假设是“该城市中 家庭拥有汽车的比例超过30%”。建立的原假设和对 立假设为
H0 :p 30% H1 : p 30%
双侧检验与单侧检验
1、对立假设没有特定的方向性,并含有符号 “”的假设检验,称为双侧检验或双尾检 验(two-tailed test)
2、对立假设具有特定的方向性,并含有符号 “>”或“<”的假设检验,称为单侧检验或单 尾检验(one-tailed test) 对立假设的方向为“<”,称为左侧检验 对立假设的方向为“>”,称为右侧检验
拒绝H0
拒绝H0
/2
1 -
/2
0 临界值
医学统计学课件:假设检验

统计推断基础
参数估计
用样本数据估计总体参数的方法。
显著性检验
理解显著性检验的基本原理和方法。
假设检验
根据样本数据对总体参数进行检验的方法。
置信区间
掌握置信区间的概念和计算方法。
03
参数假设检验
单参数假设检验
定义
单参数假设检验是当我们只有一个总 体参数需要检验时的假设检验。例如 ,我们可能需要确定一个药物是否对 一组患者的平均血压有降低作用。
应用场景:例如,检验某种新药的疗效是否显著优于安 慰剂。
案例二:两样本t检验
总结词:两样本t检验是一种常用的假设检验方 法,适用于比较两个独立样本的平均数是否存在 显著差异。
详细描述
1. 定义假设:通常包括零假设(H0,即两个样本的 平均数无差异)和对立假设(H1,即两个样本的平 均数存在差异)。
02
假设检验的数学基础
概率基础
概率定义
表示随机事件发生的可能性程度。
概率运算
掌握加法、乘法和条件概率等运算方法。
独立性和互斥性
理解事件之间的独立性和互斥性。
分布基础
分布定义
描述随机变量取值的概率规律。
连续型和离散型分布
理解连续型和离散型分布的概念和特点。
常用分布
掌握常用的分布及其性质,如正态分布、二项分布等。
假设检验步骤
根据符号分布,计算临界值和p值,判断假设是 否成立。
05
假设检验的注意事项与误用
假设检验的注意事项
明确研究目的和背 景
在假设检验前,需要明确研究目 的和背景,以便确定合适的假设 和检验方法。
合理选择样本量和 样本类型
样本量和样本类型的选择对假设 检验的结果具有重要影响。在确 定样本量时,需要考虑研究目的 、研究设计、误差概率等因素。
《假设检验》课件

方差分析
总结词
适用于多组数据比较的检验方法
详细描述
方差分析是一种适用于多组数据比较的假设检验方法。它通过比较不同组之间的变异和 误差来源,计算F值和对应的P值,以判断原假设是否成立。方差分析在很多领域都有
应用,如农业、生物统计学和心理学等。
秩和检验
总结词
适用于等级数据或非参数数据的检验方法
详细描述
秩和检验是一种适用于等级数据或非参数数 据的假设检验方法。它通过将数据排序后进 行比较,计算秩和值和对应的P值,以判断 原假设是否成立。秩和检验在很多领域都有 应用,如医学、生物学和环境科学等。
04 假设检验的实例分析
单样本Z检验实例
总结词
用于检验一个样本的平均值与已知的 某一总体均值之间是否存在显著差异 。
如果样本量过小,可能无 法得出可靠的结论,因为 小样本可能无法代表总体 。
样本量过大
如果样本量过大,可能会 导致统计效率降低,增加 计算复杂度和成本。
样本代表性
在选择样本时,需要确保 样本具有代表性,能
假设检验的结果只能给出拒绝或接受 假设的结论,但无法给出假设正确与 否的确凿证据。
置信区间有助于判断假设的正确性
02
通过比较置信区间和假设值的位置关系,可以判断假设是否成
立。
置信区间与假设检验的互补关系
03
置信区间和假设检验各有优缺点,可以结合使用以更全面地评
估数据的统计性质。
THANKS 感谢观看
提出假设
根据研究问题和目的,提出原 假设和备择假设。
确定临界值
根据统计量的性质和显著性水 平,确定临界值。
做出决策
根据计算出的样本统计量和临 界值,做出接受或拒绝原假设 的决策。
统计学课件假设检验.105页PPT

51、没有哪个社会可以制订一部永远 适用的 宪法, 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现,法律就是这样 一种的 网,触 犯法律 的人, 小的可 以穿网 而过, 大的可 以破网 而出, 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏,庇 护着我 们大家 ;它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
xiexie! 38、我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯
39、勿问成ቤተ መጻሕፍቲ ባይዱ的秘诀为何,且尽全力做你应该做的事吧。——美华纳
40、学而不思则罔,思而不学则殆。——孔子
谢谢!
36、自己的鞋子,自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
《假设检验的概念》PPT课件

假设检验实例及解读
• 生物统计学实例:比较两个药物治疗组的患者生存率是否存在显著差异。 • 社会调查实例:通过问卷调查数据,研究两个群体之间的收入差异是否显著。
总结与回顾
假设检验是一种重要的统计方法,帮助我们进行数据分析和科学决策。通过清晰的步骤和方法,我们可以对总体参 数进行有效推断。
3 方差分析
4 非参数检验
用于比较多个样本均值之间是否存在显著差异。
当数据不满足正态分布假设时,使用的一类假设 检验方法。
注意事项
1 假设检验的局限性
假设检验是概率性推断,结果并不能绝对确定总体参数,仅供参考。
2 防范与排除偏差
在实际研究中,要注意样本选择的随机性和可比性,以排除偏差对推断结果的影响。
p值判定
4
参数估计和假设检验。
根据计算出的统计量,计算p值,并与显著性
水平比较,判断是否拒绝原假设。
5
结论推断
根据p值的判定结果,得出对总体参数的推断 结论,并解释研究的统计显著性和实际意义。
常见假设检验方法
1 单样本t检验
2 双样本t检验
用于比较一个样本的均值与总体均值是否存在显 著差异。
用于比较两个独立样本的均值是否存在显著差异。
应用领域
假设检验广泛应用于医学、社会科学、经济学等领 域,帮助我们进行数据分析和做出科学决策。
假设检验的步骤
1
假设设立
首先,根据研究问题,明确原假设和备择假
ห้องสมุดไป่ตู้
显著性水平确定
2
设,以便进行后续统计推断。
确定假设检验的显著性水平,通常为0.05或
0.01,用于判断统计显著性。
3
统计量计算
计算适应研究问题的合适统计量,以便进行
《假设检验检验》课件

数据分析中的假设检验
什么是假设检验
假设检验是一种统计方法,用于通过样本数据来推断总体参数的性质。它可以帮助我们判断一个观察结 果是由偶然因素引起的,还是真实存在的差异。
假设检验的步骤
1
2. 选择检验统计量
2
选择适合问题的检验统计量,如t值、
z值等。
3
4. 计算统计量
4
利用样本数据计算检验统计量的值。
5
6. 得出结论
6
根据决策,得出关于总体参数的结论。
1. 建立假设
确定原始假设和备择假设,描述总体 参数的状态。
3. 设定显著性水平
选择显著性水平,决定拒绝原始假设 的界限。
5. 做出决策
根据检验统计量的值和显著性水平, 决定是否拒绝原始假设。
常用的假设检验方法
单样本t检验
结论的解释
根据结果的解释,得出关于总体参数的结论,并提供相应的推论。
实例演示及应用场景
通过具体的实例演示,展示假设检验在各个领域的应用,如医学、市场研究、环境保护等。
总结与展望
假设检验是数据分析中重要的工具之一,它可以帮助我们做出科学的决策, 并推动各个领域的发展。未来,我们可以进一步研究和改进假设检验方法, 提高其效能和适用性。
用于比较一个样本的平均值 与已知值或者另一个样本的 平均值。
独立样本t检验
用于比较两个独立样本的平 均值是否存在显著差异。
相关样本t检验
用于比较两个相关样本的平 均值是否存在显著差异。
如何解读假设检验结果
拒绝原始假设
如
接受原始假设
如果检验结果的p值大于等于显著性水平,我们接受原始假设。
假设检验《统计学原理》课件

X=X1>X0
H0为伪
从上图可以看出,如果临界值沿水平方向右移,α将变小而β变大,即若减小 α错误,就会增大犯β错误的机会;如果临界值沿水平方向左移,α将变大而 β变小,即若减小β错误,也会增大犯α错误的机会,
a 错误和 错误的关系
在样本容量n一定的情况下,假设检验不能同时做到犯α和 β两类错误的概率都很小,若减小α错误,就会增大犯β错误 的机会;若减小β错误,也会增大犯α错误的机会,要使α和 β同时变小只有增大样本容量,但样本容量增加要受人力、 经费、时间等很多因素的限制,无限制增加样本容量就会 使抽样调查失去意义,因此假设检验需要慎重考虑对两类 错误进行控制的问题,
参数假设检验举例
例2:某公司进口一批钢筋,根据要求,钢筋的 平均拉力强度不能低于2000克,而供货商强 调其产品的平均拉力强度已达到了这一要 求,这时需要进口商对供货商的说法是否真 实作出判断,进口商可以先假设该批钢筋的 平均拉力强度不低于2000克,然后用样本的 平均拉力强度来检验假设是否正确,这也是 一个关于总体均值的假设检验问题,
假设检验的两类错误
正确决策和犯错误的概率可以归纳为下表:
假设检验中各种可能结果的概率
H0 为真
接受H0
1-α 正确决策
拒绝H0,接受H1
α 弃真错误
H0 为伪
β 取伪错误
1-β 正确决策
•假设检验两类错误关系的图示
以单侧上限检验为例,设H0 :X≤X0 , H1:X>X0
图a X≤X0 H0为真
a
H0值
样本统计量 临界值
观察到 的样本 统计量
5、假设检验的两类错误
根据假设检验做出判断无非下述四种情况:
1、原假设真实, 并接受原假设,判断正确; 2、原假设不真实,且拒绝原假设,判断正确; 3、原假设真实, 但拒绝原假设,判断错误; 4、原假设不真实,却接受原假设,判断错误, 假设检验是依据样本提供的信息进行判断,有犯错误的可 能,所犯错误有两种类型: 第一类错误是原假设H0为真时,检验结果把它当成不真而 拒绝了,犯这种错误的概率用α表示,也称作α错误 αerror 或弃真错误, 第二类错误是原假设H0不为真时,检验结果把它当成真而 接受了,犯这种错误的概率用β表示,也称作β错误 βerror 或取伪错误,
5讲 假设检验基础ppt课件

假设检验的基本原理
• 已知健康成年男子的脉搏均数为72次/分。某医生在某山区随机调查25 名健康男子,求得脉搏均数为74.2次/分,标准差6.5次/分。能否认为该 山区的成年男子的脉搏均数高于一般成年男子的脉搏均数?
• 样本均数和总体均数的差异有两种可能: • 抽样误差所致, • 有本质差异
0 72
2
假设检验的原因
由于个体差异的存在,即使从同一总体中严格的随机抽样,X1、X2、X3、 X4、、、,不同。 因此,X1、X2 不同有两种(而且只有两种)可能: (1)分别所代表的总体均数相同,由于抽样误差造成了样本均数的差别。差别 无统计学意义 。 (2)分别所代表的总体均数不同。差别有统计学意义。
• (2)备择假设:拒绝双H侧0时检而验被H接0:受的假设0 ,与H0对立。有三种情况:
单侧检验 单侧检验
2.单、双侧的H选1 :择:由0专业知。通常取0.05。
H1:0
6
▲选定检验方法,计算检验统计量
• 根据资料类型和推断目的选用不同的检验方法。不同的检验方法有相应 不同的检验统计量及计算公式。
2.两大样本的u检验
u X 0 sn
u X 0 n
u x1 x2 s12 s2 2 n1 n2
11
例题7-1 • 根据1983年大量调查结果,已知某地成年男子的脉搏均数为72次/分,某医
生2003年在该地随机调查了75名成年男子,求其脉搏均数为74.2次/分,标 准差为6.5次/分,能否据此认为该地成年男子的脉搏不同于1983年?
• 所大有小检,验并统且计服量从都已是知在的分H0布成。立的条件下计算出来的,反映了抽样误差的
• 例:
成立条件下 ,
则
用s代替σ,检验统计量为
第五章参数估计和假设检验PPT课件
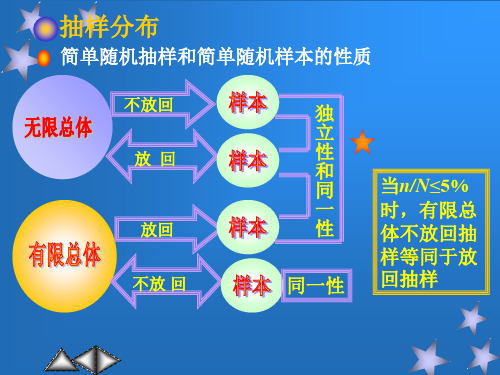
抽样
X ~ N(, 2)
n,S2
则 (n 1)S 2 / 2 ~ 2 (n 1)
当 n 30, 2分布趋近于正态分布
若X ~ x2 (n 1) 则 Z 2 2 2(n 1)
两个样本方差之比的抽样分布
从两个正态总体中分别独立抽样所得到的两个样本方 差之比的抽样分布。
抽样
X1
~
N
(
1
,
2 1
极大似然估计是根据样本的似然函数对总体参数进行 估计的一种方法 。
其实质就是根据样本观测值发生的可能性达到最大这 一原则来选取未知参数的估计量θ,其理论依据就是 概率最大的事件最可能出现。
区间估计
估计未知参数所在的可能的区间。 P(ˆL<<ˆU ) 1
评价准则
一般形式
置信度 精确度
(ˆ △)<<(ˆ △) 或 ˆ △
2
2
2
n
Z
2
2
Pq
△
2 pˆ
Z
2
PqN
n
2
N
△
2 pˆ
Z
2
Pq
2
假设检验
基本思想 检验规则 检验步骤 常见的假设检验 方差分析
基本思想
•小概率原理:如果对总体的某种假设是真实的,那么不利于 或不能支持这一假设的事件A(小概率事件) 在一次试验中几乎不可能发生的;要是在一次 试验中A竟然发生了,就有理由怀疑该假设的 真实性,拒绝这一假设。
参数的区间估计
待估计参数
已知条件
置信区间 ˆ △
总体均值 (μ)
正态总体,σ2已知 正态总体,σ2未知
非正态总体,n≥30
X Z / n
2
医学统计学(假设检验) ppt课件

了解:
置信区间与假设检验的关系
ppt课件 2
教学内容提要
重点讲解:
假设检验原理
单样本正态资料的假设检验 两样本正态资料的假设检验 Z检验 假设检验应注意的问题
介绍:
置信区间与假设检验的关系
ppt课件 3
假设检验的基本任务:事先对总体分布或总体 参数作出假设,利用样本信息判断原假设是否 合理,从而决定是否拒绝或接受原假设。 参数检验(parametric test):若总体分布类型已 知,需要对总体的未知参数进行假设检验。 非参数检验:若总体分布类型未知,需要对未 知分布函数的总体的分布类型或其中的某些未 知参数进行假设检验。
ppt课件 17
(3) 计算P值
P值:是在H0成立时,取得大于或等 于现有检验统计量值的概率。
ppt课件
18
(3)计算概率值(P) 将计算得到的Z值或 t值与查表得到Z或 t,ν ,比较,得到 P值的大小。根据u分布和 t分布我们知道,如果|Z|> Z或| t |> t , 则 P< ;如果|Z|< Z或| t | < t ,则P> 。
ppt课件 5
“小概率原理”
例如在2000粒中药丸中只有一粒是虫蛀过的,现从中随机取 一粒,则取得“虫蛀过的药丸”的概率是1/2000,这个概率 是很小的,因此也可以将这一事件看作在一次抽样中是不会 发生的。若从中随机抽取一粒,恰好是虫蛀过的,这种情况 发生了,我们自然可以认为“假设”有问题,即虫蛀率p不是 1/2000,从而否定了假设。否定假设的依据就是小概率事件 原理。由此我们得到一个推理方法:如果在某假设(记为H0) 成立的条件下,事件A是一个小概率事件,现在只进行一次 试验,事件A就发生了,我们就认为原来的假设(H0)是不 成立的。
《医学假设检验》课件

医学假设检验是一种科学的方法,用于验证一些关于人体健康和疾病的理论。 在这个PPT课件中,我们将会介绍医学假设检验的定义、重要性、步骤、常用 方法、实际案例、局限性以及应用前景。
医学假设检验的定义
1 什么是假设
假设是根据过去的经验或现有的知识推测,用来解释某些现象的一种猜测。
某种化合物的危害性
某种诊断工具的有效性
观察了长期接触某种化合物的工 人和没有接触该化合物的工人的 病情,证明了该化合物的危害性。
比较了一种新型的诊断工具和传 统的诊断工具在临床上的效果, 证明该新型诊断工具的有效性。
医学假设检验的局限性
1 人为因素
实验过程中人为因素的干 扰可能会影响实验结果。
2 样本不具代表性
2 医学假设
医学假设是一种关于人类健康和疾病的理论,用来预测治疗方法的有效性或疾病的发生 机制。
3 医学假设检验
医学假设检验是一种用科学方法来验证医学假设的过程,通过实验证明或推翻医学假设。
医学假设检验的重要性
科学依据
医学假设检验提供了科学的方法 来验证医学假设,使得我们能够 更加准确地了解人类的健康和疾 病。
促进医学科研
医学假设检验为医学科研提供 了科学化的方法,推动医疗科 学的发展。
实验中的样本如果不代表 整个人群,会影响实验结 果的可靠性。
3 实验过程可能不可重
复
无法保证实验过程的可重 复性,因此实验结果的可 药物研发的过程更加科学 化,降低新药研究的失败率。
提高临床治疗的效率
通过医学假设检验,提高临床 诊断和治疗的准确性和效率。
卡方检验
用于统计两个分类变量的概率,例如:男性和 女性吸烟的数量对肺癌发生率的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)
假设μ=0.5
(2)确定不利于假设μ=0.5 的范围
| X 0.5| c
| X 0.5 |
大
大
小
μ=0.5
0.5
(3)定义小概率事件 概率小于α=0.05的事件为小概率事件。
确定“界”的规则:
P(|X | c)
P{ X n
u } 2
(4)计算“界c”
0.012 X ~ N(0.5, )
第五讲 参数假设检验
第一节 假设检验的基本思想 一、小概率原理 二、假设检验的一些基本概念
问题讨论
某种药物有强烈作用,按规定每片有效成分含量均值为0.5mg,标准差为0.01mg。假定药片有效 成分含量服从正态分布。问怎样判断这个厂家的产品是否符合要求?
要解决的问题:是否合格?
有效成分含量为随机变量
第 5 讲 参 数 假 设 检 验
假设检验是统计推断的另一种方式,它与区间 估计的差别主要在于:区间估计是用给定的大 概率推断出总体参数的范围,而假设检验是以 小概率为标准,对总体的状况所做出的假设进 行判断。假设检验与区间估计结合起来,构成 完整的统计推断内容。假设检验分为两类:一 类是参数假设检验,另一类是非参数假设检验。 本章讨论参数检验方法。
事件 X不是0小.5概率事件c 0.0057
结论:
假设μ=0.5不成立,μ≠0.5。
二、假设检验的一些基本概念 •总体的均数是否等于一个特定的值: •两个总体分布的均数是否相等: •随机变量X是否服从二项分布:
关于总体的种种假设称为统计假设(statistical hypothesis)
0
1
2
X~B(n, p)
诊断结果 可疑 11 13 20 44
冠心病 6 6 19 31
合计
357 92 139 588
2.假设检验 利用样本提供的信息判断假设是否成立的统计方法,称为假设检验(hypothesis testing). •总体的均数是否等于一个特定的值:
(1)标准差为0.01mg
(2)随机抽取
(3) 0.5
— 随机误差 — 抽样误差
讨论
| X 0.5 |
大
小
大
μ=0.5
|X | c
0.5 寻找界值c
P(|X | c)
|X | c
一、小概率原理
例5.1 某种药物有强烈作用,按规定有效成分含量为0.5mg/片。今随机抽取某厂生产的这种药品 12片,测得平均有效含量为0.4938mg。假定药片有效成分含量服从标准差为0.01mg的正态分布。 问这个厂家的产品是否符合要求?
?
0 .5
?
0.01
讨论 判断方法:抽样
问题1 抽样方法? 问题2 样本容量?
估计
ˆ x
ˆ s
问题3: 时,能否说明产品不合格?
x 0.5
随机抽样模拟1 假设:药品符合要求μ=μ0=0.5;
随机抽样模拟1
data a1; n=12;sigma=0.01;mu=0.5;seed=1325; k=20; do j=1 to k; do i=1 to n; x=sigma*rannor(seed)+mu;/*x~N(mu,sigma^2)*/ output; end;end; proc means mean; var x; class j; output out=b1 mean=xmean; run;
随机抽样模拟2 假设:药品不符合要求μ≠μ0=0.5;
随机抽样模拟2
data a2; n=12;sigma=0.01;mu=0.49; seed=1325; k=20; do j=1 to k; do i=1 to n; x=sigma*rannor(seed)+mu;/*x~N(mu,sigma^2)*/ output; end;end; proc means mean; var x; class j; output out=b2 mean=xmean; run;
12 P{|X 0.5| c} 0.05
~ N(0,1)
P{|X 0.5|
c } 0.05
0.01 12 0.01 12
c 0.01 12
u0.052
1.96
c 1 .9 60 .0 11 2 0 .0 0 5 7
(5)根据当前样本数据作推断
|x 0 . 5 ||0 . 4 9 3 8 0 . 5 |0 . 0 0 6 2 c0 . 0 0 5 7
x0 .5 0 .4 9 3 80 .5
|
||
| 2 .1 4 7 7u 0 .0 5 1 .9 6
0 .0 1n 0 .0 11 2
2
判定μ=0.5不成立,即认为μ≠0.5.
“反证法” +小概率原理 理论上: 若假设μ=0.5成立
矛盾!!!
事件
X为小0概.5 率事件 c 0.0057
事实上:
|x 0 . 5 ||0 . 4 9 3 8 0 . 5 |0 . 0 0 6 2 c0 . 0 0 5 7
例5.1 某种药物有强烈作用,按规定有效成分含量为0.5mg/片。今随机抽取某厂生产的这种药品 12片,测得平均有效含量为0.4938mg。假定药片有效成分含量服从标准差为0.01mg的正态分布。 问这个厂家的产品是否符合要求?
例5.1
解 该药厂此药品的有效成分含量为X.
考虑两个假设: (a)该药厂的此药品符合要求μ=μ0=0.5; (b)该药厂的此药品不符合要求μ≠μ0=0.5.
有效病例 36 54
无效病例 24 6
总病例数 60(60%) 60(90%)
p1 p2
p 1 p 2(p 1 p 2 o rp 1 p 2 )
•统计假设 例 在冠心病普查中,研究冠心病与眼底动脉硬化两者之间是否存在一定的关系?
眼底动脉 硬化级别
0 I II及以上 合计
正常 340 73 100 513
1.统计假设 例
测得140例30岁以上的冠心病病人血清胆固醇为220.7±42.2,另有487名同龄非冠心病者血清胆固 醇为175.4±30.6,想了解冠心病病人的血清胆固醇是否较高?
1
2
1
2
•统计假设 例 某医师研究洛赛克治疗消化性溃疡的疗效,以泰胃美作为对照,观察结果如下:
药物 泰胃美 洛赛克
例5.1
140
120
样本均值
100
x0.4938 与0.5有差异,差异产
80
生的两种情形:
60
40
20
(1) 0.5
抽(样2X )误差~+N 抽(样0误.5 差,0.012/12)
140
120
100
0.5
80
60
40
20
0.45
0.50
0.55
讨论
x 样本均值 与0.5有差异,差异产生的原因:
