梁弯曲常用计算表格
各类梁反力、剪力弯矩、和挠度计算公式一览表

各类梁反力、剪力弯矩、和挠度计算公式一览表下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor.I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!各类梁反力、剪力弯矩及挠度计算公式一览在结构工程中,梁的力学性能分析是至关重要的。
各种梁的弯矩剪力计算(大全)表

表1 简单载荷下基本梁的剪力图与弯矩图注:外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件常用截面几何与力学特征表表2-5 .......资料.注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
2)三跨等跨梁的内力和挠度系数 表2-12注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
弯曲要素表

175
附 录
附录A 单跨梁的弯曲要素表
说明:
1.在弯曲要素表中采用下列符号: l ——梁的长度;
x ——沿梁长方向的坐标,向右为正; E ——材料的弹性模数; I ——梁的断面惯性矩: υ——梁的挠度,向下为正
θ——梁断面的转角,顺时钟方向为;2θθ、1分别为梁左、右支座断面的转角;
M ——梁断面的弯矩,在左断面逆时钟方向为正,在右断面顺时钟方向为正;
2M M 、1 分别为梁左、右支座断面的弯矩。
N ——梁断面的剪力,在左断面向下为正,在右断面向上为正;
12R R 、——梁左、右支座的支座反力,向上为正,
q ——梁上单位长度的分布荷重; Q ——梁上分布荷重的总值; P ——梁上的集中力; M ——梁上的集中外弯矩。
2.梁的坐标原点在左支座。
3.弯曲要素表的公式中,符号
后的项仅用于x c >的断面。
表A-l 悬臂梁的弯曲要素表
176
177
178
179
180
181
182
183
表A-5 一端弹性固定,另一端刚性支座的梁的固定断面弯矩
符号:
3,aEI AEI
a A l l
=
=; a ——弹性固定端的柔性系数; A ——弹性支座的柔性系数;
13
A K a A =++
031K a =+。
弯矩挠度表格new
4.39 5.83 7.33 10.44 10.79 15.4 8.78 14.67
26.13 31.62
I--惯性矩 (cm*4)
I--惯性矩 (cm*4)
0.869468442 mm 5 mm
槽钢类型 Iy(cm*4) Iz (cm*4) E=2.1×10e5MPa
公式: fc=p*l^3/(48*E*I)( 注意单位换算) 公式:允许扰度 =l/200
简支梁(承受 满布均布荷 载)
l--梁长(m) q--均布荷载(KN/m)
q
A
请输入: q= l= E I 计算结果
lC
fc--中点C处的挠度(mm)
E--弹性模量 (N/mm*2)
B
1 KN/m 1m 210000 N/mm*2 7.33 cm*4
fc= 允许挠度=
0.845893155 mm 5 mm
公式: fc=5*q*l^4/(384*E* I)(注意单位换算) 公式:允许扰度 =l/200
悬臂梁(承受 集中荷载) l--梁长(m) p--集中荷载值(KN) a--集中荷载 离左端点A的 距离(m)
公式: fb=q*l^4/(8*E*I)( 注意单位换算) 公式:允许扰度 =l/150
I--惯性矩 (cm*4)
MQ-21
MQ-31 MQ-41 MQ-41/3 MQ-52 MQ-72 MQ-21D MQ-41D MQ-52-72D MQ-124XD
0.2 2.6 5.37 7.02 11.41 28.7 4.98 30.69 115.41 118.04 (常用)
Байду номын сангаас
悬臂梁(承受 满布均布荷 载) l--梁长(m) q--均布荷载(KN/m)
矩形截面混凝土梁受弯计算表格
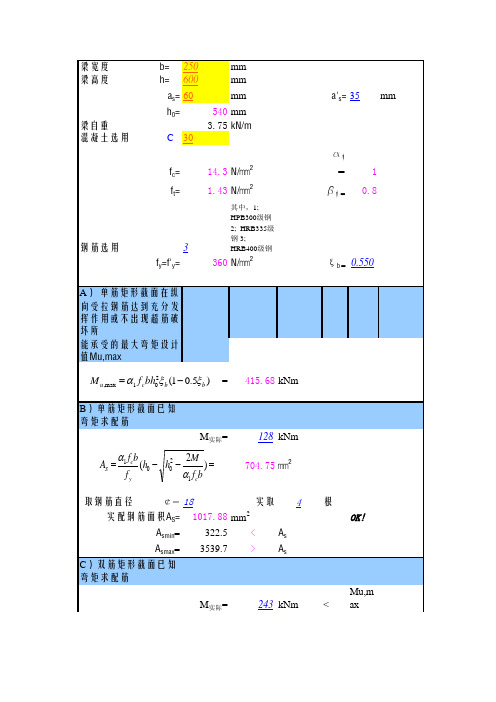
㎜2
20
¢=
8
mm >
根
2513.27 mm2 70 x
OK! NO!!!
验算受压区高度x=fyAs1/(α1fcb)=
360 N/㎜2
A) 单筋矩形截面在纵向受拉钢筋达到充分发挥作用或不出现超筋破坏所 能承受的最大弯矩设计值Mu,max
2 M u ,max = a1 f c bh0 x b (1 - 0.5x b )
=
415.68 kNm
B)单筋矩形截面已知弯矩求配筋 M实际= 128 kNm 704.75 ㎜2
AS =
纵向受拉钢筋总截面面积 As=As1+As2= 1999.51 ㎜2 受拉钢筋取钢筋直径
20¢=Biblioteka 2实取9 2
mm ≤
根
实配钢筋面积AS= 2827.43 mm 受压钢筋取钢筋直径 12 ¢= 实取 实配钢筋面积AS= 2α 's= 226.19 mm 70.00 mm
2
OK!
根
OK!
x
验算受压区高度x=fyAs1/(α1fcb)=
3
为充分发挥受压钢筋A's的作用,取As2=A's=
942.48 mm2
AS1 =
a1 fcb
fy
2 (h0 - h0 -
2M )= a1 fcb
-450.91 ㎜2
纵向受拉钢筋总截面面积 As=As1+As2= 受拉钢筋取钢筋直径 实配钢筋面积AS= 2α 's=
491.57 实取 -45.41 mm
a1 fcb 2M (h0 - h02 )= fy a1 fcb
¢=
取钢筋直径
18
1017.88 mm2 322.5
钢材理论计算表、钢筋弯曲调整值与弯钩计算计算表
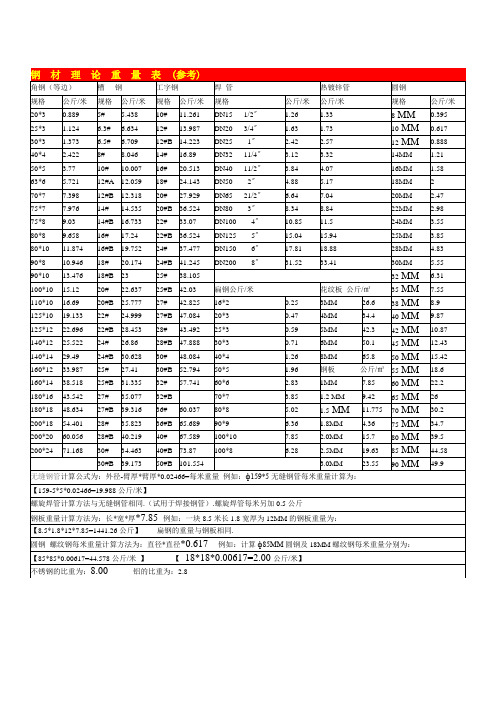
常用金属材料重量计算公式(每千只重量)园钢重量(公斤)=0.00617×直径×直径×长度方钢重量(公斤)=0.00785×边宽×边宽×长度六角钢重量(公斤)=0.0068×对边宽×对边宽×长度八角钢重量(公斤)=0.0065×对边宽×对边宽×长度螺纹钢重量(公斤)=0.00617×计算直径×计算直径×长度角钢重量(公斤)=0.00785×(边宽+边宽-边厚)×边厚×长度扁钢重量(公斤)=0.00785×厚度×边宽×长度钢管重量(公斤)=0.02466×壁厚×(外径-壁厚)×长度钢板重量(公斤)=7.85×厚度×面积钢材理论重量表钢筋弯曲调整值与弯钩计算一、弯曲调整值的概念对于单根预算长度和下料长度是不同的,预算长度是按照钢筋的外皮计算,下料长度是按照钢筋的中轴线计算。
例如一根预算长度为1米长的钢筋,其下料长度不需要1米,是小于1米的,因为钢筋在弯曲的过程中会变长,如果按照1米下料,肯定会长出一些。
预算长度和下料长度的差值也就是钢筋的弯曲调整值,也称为量度差值。
它实际上由两方面造成的,一是由于量度的不同,例如下面这根钢筋,预算的长度是100+300=400mm,而实际上在下料时只需要截取100-d/2+300-d/2长的一段钢筋即可弯制成下面的形式。
二是由于钢筋在弯曲的过程中长度会变化:外皮伸长、内皮缩短、中轴线不变。
二、弯曲调整值的计算在这里用到一个弧度和角度的换算公式:1rad=3.14*r*2/360,即一度角对应的弧长是0.01745r。
另外《钢筋混凝土施工及验收规范》(GB500204-2002)规定180度弯钩的弯曲直径不得小于2.5d,在下面的推导中D取2.5d。
各类梁的弯矩力计算汇总表

表1 简单载荷下基本梁的剪力图与弯矩图梁的简图剪力Fs 图弯矩M 图1laFsF F l a F l al -+-F la l a )(-+M2l eMsF lM e +MeM +3laeMsF lM e +Me M lal -e M la +-4lqsF +-2ql 2qlM82ql +2l5lqasF +-la l qa 2)2(-lqa 22M2228)2(l a l qa -+la l qa 2)(2-la l a 2)2(-6lqsF +-30l q 60l qM3920l q +3)33(l7aFlsF F+Fa-M8aleMsF+eM M9lqs F ql+M22ql -10lqsF 2l q +M620l q -注:外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·mV B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
钢梁受扭计算表格

工字 形
钢梁受扭计算
1.钢梁截面特征计算: 剪心b=距上翼40缘0中心:t= Ax=b*t + h*s +B*T =
主扇性 惯性 矩:
主扇性 静面 矩:
最大扇 性面 积: 2.简单梁受扭计算:
最大双 力矩:
最大扭 矩:
计算弯 扭正应 力:
计算最 大剪应 力:
20 h= 600 s=
it=
k=
0.0007
2291200
B=
300
T=
20
178.021978
1.13934E+13
71208791.21
35604.3956
1.65E+01 KN*M2 5.49E+07 N*mm
5.16E+01 Mpa
17.15625 Mpa
300 2.16E+12
主扇性 惯性 矩:
主扇性 静面 矩:
最大扇 性面 积: 2.简单梁受扭计算:
最大双 力矩:
最大扭 矩:
计算弯 扭正应 力:
计算最 大剪应 力:
300 t= 16 ax= d1/2 Jw= d12d22(d1-d2)2t/(24(d1+d2)) Sw= ax*tb2/8= w= d1d2(d1-d2)/(4(d1+d2)) Bmax= Mw= stress=Bmax*Wmax/Jw= shear=Mw*Sw/(Jw*t)
12
ax= TB3h/(tb3+TB3)=
Jw= ax2*tb3/12+(h-ax)2*TB3/12=
Sw= ax*tb2/8=
w= ax*b/2
Bmax= Mw=
以表格的形式列出框架梁跨中弯矩的计算结果。

框架梁跨中弯矩计算结果1. 背景介绍1.1 框架梁是结构工程中常见的构件,承担着承载结构荷载并传递到支座的重要作用。
1.2 框架梁的设计需要对其内部受力情况进行准确计算,其中跨中弯矩是其中关键的参数之一。
1.3 本文将针对框架梁跨中弯矩的计算方法进行介绍,并列出具体计算结果。
2. 跨中弯矩计算方法2.1 按照《建筑抗震设计规范》等相关标准,框架梁的跨中弯矩可以采用简支梁的计算方法进行估算。
2.2 在一般情况下,框架梁跨中弯矩可以通过梁的受力原理和力学公式进行计算。
2.3 具体计算中需要考虑梁的截面尺寸、荷载大小和作用点位置等多个因素。
3. 跨中弯矩计算实例3.1 以某框架梁为例,其跨度为10m,截面尺寸为0.3m*0.6m,工作荷载为20kN/m。
3.2 首先根据梁的受力原理和力学公式,可以计算出荷载作用下的弯矩大小。
3.3 然后考虑梁的自重和混凝土强度等因素,进一步修正跨中弯矩的计算结果。
4. 跨中弯矩计算结果4.1 经过具体计算,得出该框架梁跨中的弯矩为XXX。
4.2 该弯矩满足设计要求,并可以作为后续结构设计和施工的依据。
4.3 还可以根据不同框架梁的具体情况,进行类似的计算并得出相应的跨中弯矩结果。
5. 结论与展望5.1 跨中弯矩作为框架梁设计中重要的参数之一,需要通过严格的计算和验证来得出准确的结果。
5.2 本文介绍了跨中弯矩的计算方法,并给出了具体的计算实例和结果。
5.3 未来可以进一步研究不同类型框架梁的跨中弯矩计算方法,并结合实际工程进行验证和应用,以提高结构设计的准确性和可靠性。
为了更全面地了解框架梁的跨中弯矩计算结果,我们可以进一步讨论具体的计算步骤和公式,并深入探讨框架梁的设计原则和影响因素。
我们也可以分析不同类型框架梁的跨中弯矩计算方法,并结合实际案例进行说明。
我们将针对框架梁跨中弯矩的计算方法进行更详细的介绍。
在框架梁内部受力分析中,跨中弯矩是指梁在跨中位置所受的弯曲作用力,通常用M表示。
各类梁的弯矩剪力计算汇总表-剪力计算公式一览表
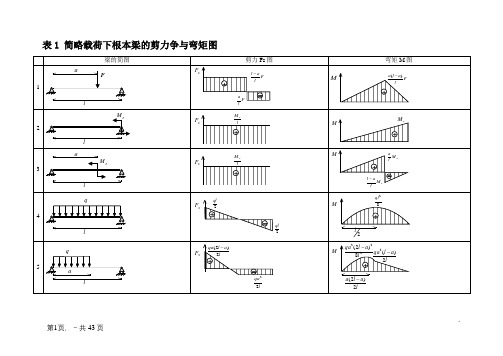
表1 简略载荷下根本梁的剪力争与弯矩图注:外伸梁= 悬臂梁+ 端部感化分散力偶的简支梁2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力.剪力.弯矩.挠度表2-6第3页,-共43页第4页,-共43页第5页,-共43页(2)悬臂梁的反力.剪力.弯矩和挠度表2-7 第6页,-共43页第7页,-共43页(3)一端简支另一端固定梁的反力.剪力.弯矩和挠度表2-8 第8页,-共43页第9页,-共43页(4)两头固定梁的反力.剪力.弯矩和挠度表2-9 第10页,-共43页第11页,-共43页(5)外伸梁的反力.剪力.弯矩和挠度表2-10 第12页,-共43页第13页,-共43页第14页,-共43页第15页,-共43页3.等截面持续梁的内力及变形表(1)等跨持续梁的弯矩.剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11第16页,-共43页第17页,-共43页注:1.在均布荷载感化下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=. 2.在分散荷载感化下:M =表中系数×Fl ;V =表中系数×F ;EI w 100Fl 表中系数3⨯=. [例1] 已知二跨等跨梁l =5m,均布荷载q =11.76kN/m,每跨各有一分散荷载F =29.4kN,求中央支座的最大弯矩和剪力.[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·m V B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m,均布荷载q =11.76kN/m,求边跨最大跨中弯矩. [解] M1=0.080×11.76×62=33.87kN ·m.2)三跨等跨梁的内力和挠度系数 表2-12第18页,-共43页第19页,-共43页注:1.在均布荷载感化下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=. 2.在分散荷载感化下:M =表中系数×Fl ;V =表中系数×F ;EI w 100Fl 表中系数3⨯=.3)四跨等跨持续梁内力和挠度系数表2-13 注:同三跨等跨持续梁.第20页,-共43页4)五跨等跨持续梁内力和挠度系数表2-14注:同三跨等跨持续梁.第21页,-共43页22第22页,-共43页 (2)不等跨持续梁的内力系数(表2-15.表2-16)1)二不等跨梁的内力系数 表2-15注:1.M=表中系数×ql21;V=表中系数×ql1;2.(M max).(V max)表示它为响应跨内的最大内力.23 第23页,-共43页2)三不等跨梁内力系数表2-1624 第24页,-共43页注:1.M=表中系数×ql21;V=表中系数×ql1;2.(M max).(V max)为荷载在最不利布置时的最大内力.25 第25页,-共43页第26页,-共43页 4.双向板在均布荷载感化下的内力及变形系数表(表2-17~表2-22)符号解释如下:刚度 )1(1223υ-=Eh K式中 E ——弹性模量;h ——板厚;ν——泊松比;ω.ωmax ——分离为板中间点的挠度和最大挠度;M x ——为平行于l x 偏向板中间点的弯矩;M y ——为平行于l y 偏向板中间点的弯矩;M x 0——固定边中点沿l x 偏向的弯矩;M y 0——固定边中点沿l y 偏向的弯矩.正负号的划定:弯矩——使板的受荷面受压者为正;挠度——变位偏向与荷载偏向雷同者为正.四边简支 表2-17三边简支,一边固定表2-18第27页,-共43页双方简支,双方固定表2-19一边简支,三边固定表2-20 第28页,-共43页四边固定表2-21 第29页,-共43页双方简支,双方固定表2-225.拱的内力盘算表(表2-23)各类荷载感化下双铰抛物线拱盘算公式表2-23 第30页,-共43页第31页,-共43页第32页,-共43页第33页,-共43页第34页,-共43页注:表中的K为轴向力变形影响的修改系数.(1)无拉杆双铰拱1)在竖向荷载感化下的轴向力变形修改系数式中 I c——拱顶截面惯性矩;A c——拱顶截面面积;A——拱上随意率性点截面面积.当为矩形等宽度实腹式变截面拱时,公式I=I c/cosθ所代表的截面惯性矩变化纪律相当于下列的截面面积变化公式:此时,上式中的n可表达成如下情势:下表中列出了矩形等宽度实腹式变截面拱的n值.f/l 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 n 1.67 1.59 1.51 1.43 1.36 1.29 1.23 1.17 1.12 2)在程度荷载感化下的轴向力变形修改系数,近似取K=1(2)带拉杆双铰拱1)在竖向荷载感化下的轴向力变形修改系数第35页,-共43页式中 E——拱圈材料的弹性模量;E1——拉杆材料的弹性模量;A1——拉杆的截面积.2)在程度荷载感化下的轴向力变形修改系数(略去拱圈轴向力变形影响)式中 f——为矢高;l——为拱的跨度.6.刚架内力盘算表内力的正负号划定如下:V——向上者为正;H——向内者为正;M——刚架中虚线的一面受拉为正.(1)“┌┐”形刚架内力盘算(表2-24.表2-25)“┌┐”形刚架内力盘算表(一)表2-34 第36页,-共43页第37页,-共43页第38页,-共43页“┌┐”形刚架内力盘算表(二)表2-35第39页,-共43页第40页,-共43页(2)“”形刚架的内力盘算(表2-26)“”形刚架的内力盘算表表2-26 第41页,-共43页第42页,-共43页第43页,-共43页。
各类梁支反力剪力弯矩挠度计算公式一览表

各类梁支反力剪力弯矩挠度计算公式一览表一、简支梁1、支反力对于均布荷载 q 作用下的简支梁,两端支反力大小相等,均为 R = qL / 2 ,其中 L 为梁的跨度。
2、剪力距离左端为 x 处的剪力 V = qx qL / 2 (0 < x < L )3、弯矩距离左端为 x 处的弯矩 M = qx^2 / 2 qLx / 2 (0 < x < L )最大弯矩发生在跨中,Mmax = qL^2 / 84、挠度均布荷载下的挠度ω = 5qL^4 / 384EI ,其中 E 为材料的弹性模量,I 为梁截面的惯性矩。
二、悬臂梁1、支反力固定端支反力 R = qL ,支反力矩 M = qL^2 / 22、剪力距离固定端为 x 处的剪力 V = qL + qx (0 < x < L )3、弯矩距离固定端为 x 处的弯矩 M = qLx + qx^2 / 2 (0 < x < L )最大弯矩发生在固定端,Mmax = qL^2 / 24、挠度均布荷载下的挠度ω = qL^4 / 8EI三、外伸梁外伸梁的计算较为复杂,需要根据具体的荷载分布和外伸长度进行分析。
1、支反力一般通过对梁的整体受力平衡和力矩平衡方程求解得出。
2、剪力分别计算各段的剪力表达式。
3、弯矩同样分段计算弯矩表达式。
4、挠度利用叠加原理,将各段的挠度贡献相加。
四、连续梁连续梁由多个跨度组成,各跨之间通过中间支座相连。
1、支反力通过结构力学的方法,如力法、位移法等求解。
2、剪力和弯矩根据求得的支反力,计算各跨的剪力和弯矩。
3、挠度通常采用结构力学的方法或有限元分析软件进行计算。
五、变截面梁对于变截面梁,其截面特性(惯性矩I 等)沿梁长度方向发生变化。
1、支反力计算方法与等截面梁类似,但需考虑截面变化的影响。
2、剪力和弯矩采用积分的方法求解。
3、挠度计算过程较为复杂,可能需要借助数值方法或专业软件。
在实际工程中,梁的受力情况往往较为复杂,可能同时受到多种荷载的作用,如集中力、集中力偶、分布荷载等。
excel计算大全-钢结构计算表格-简支钢梁计算

excel计算大全-钢结构计算表格-简支钢梁计算简支钢梁计算基本数据输入:梁跨度: l=9000mm梁间距a=2400mm钢材:Q 345f =315N/mm 2fv =185N/mm 2 上翼缘:b 1=400mm t 1=14mm 下翼缘:b 2=300mm t 2=12mm 腹板:h w =574mm t w =8mm即: 断面BH 600x8x400x14x300x12截面特性计算:钢梁截面:A 0=13792mm 2 重量108.3kg/m 钢梁中和轴的位置:y 0=342mm钢梁对X轴截面惯性矩:I z =8.94E+08mm 4 钢梁上翼缘的弹性抵抗矩:W 1x = 3.46E+06mm 3 钢梁下翼缘的弹性抵抗矩:W 2x = 2.61E+06mm 3钢梁对Y轴截面惯性矩:I y = 1.02E+08mm 4i y =85.9 mm y =104.8上翼缘对Y 轴的惯性矩:I 1=7.47E+07mm 4 下翼缘对Y 轴的惯性矩:I 2= 2.70E+07mm 40.73 截面不对称影响系数:0.380.53 工字形截面简支梁的系数0.76 梁的整体稳定系数:0.74 修正后:0.672.截面验算:(1)弯矩及剪力的计算:=+=211I I I b α=-=)12(8.0b b αη=bβ==hb t l 111ξ=bφ='bφλ钢梁自重: 1.30KN/m恒载: 4.00KN/m2=10.90KN/mg1k活载:q c= 3.0KN/m2p k=18.10KN/m p=23.16KN/m 弯矩:M=234.49KN·m 剪力:V=104.22KN(2)钢梁的强度、稳定和挠度的验算:梁的整体稳定应力:σ=101.01N/mm2钢梁上翼缘应力:σ1=67.70N/mm2钢梁下翼缘应力:σ2=89.68N/mm2钢梁剪应力:τ=22.70N/mm2挠度:w=8.4mmw/l=1/1072。
各类梁支反力剪力弯矩挠度计算公式一览表

各类梁支反力剪力弯矩挠度计算公式一览表在工程结构中,梁是一种常见的受力构件,为了确保梁的设计安全和合理,需要准确计算其支反力、剪力、弯矩和挠度。
下面为大家详细介绍各类梁的相关计算公式。
一、简支梁1、支反力对于承受集中荷载 P 作用于跨中的简支梁,其两端的支反力均为P/2 。
若梁上作用有均布荷载q ,跨度为L ,则两端的支反力均为qL/2 。
2、剪力在集中荷载作用下,若荷载作用点距离梁左端为 a ,则在梁左端至荷载作用点之间,剪力为 P/2 ,在荷载作用点至梁右端之间,剪力为P/2 。
对于均布荷载 q ,从梁左端至任意位置 x 处的剪力为 qx/2 ,从梁右端至任意位置 x 处的剪力为 q(L x)/2 。
3、弯矩集中荷载作用在跨中时,梁跨中弯矩为 PL/4 。
均布荷载作用下,梁跨中弯矩为 qL²/8 。
在均布荷载作用下,简支梁的挠度计算公式为 5qL^4/(384EI) ,其中 E 为材料的弹性模量, I 为梁截面的惯性矩。
二、悬臂梁1、支反力悬臂梁固定端的支反力包括水平支反力和垂直支反力。
若梁端承受集中力 P ,水平支反力为 0 ,垂直支反力为 P ,弯矩为 PL 。
若梁端承受均布荷载 q ,垂直支反力为 qL ,弯矩为 qL²/2 。
2、剪力在集中荷载作用下,从固定端至自由端,剪力始终为 P 。
在均布荷载作用下,从固定端至自由端,剪力从qL 线性减小至0 。
3、弯矩集中荷载作用下,悬臂梁固定端弯矩为 PL 。
均布荷载作用下,悬臂梁固定端弯矩为 qL²/2 。
4、挠度在集中荷载作用下,悬臂梁自由端的挠度为 PL³/(3EI) 。
在均布荷载作用下,悬臂梁自由端的挠度为 qL^4/(8EI) 。
三、外伸梁外伸梁的支反力计算较为复杂,需要根据具体的荷载情况,通过静力平衡方程求解。
2、剪力在计算外伸梁的剪力时,需要分别考虑梁的外伸部分和内部部分,根据荷载分布情况分段计算。
excel计算大全钢结构计算表格简支钢梁计算.xls

简 支基本数据输入:梁跨度: l=9000mm梁间距a=2400mm钢材:Q 345f =315N/mm 2fv =185N/mm 2 上翼缘:b 1=400mm t 1=14mm 下翼缘:b 2=300mm t 2=12mm 腹 板:h w =574mm t w =8mm即: 断面BH 600x8x400x 14x300x12截面特性钢梁截面:A 0=13792mm 2 重量108.3kg/m 钢梁中和轴的位置:y 0=342mm钢梁对X轴截面惯性矩:I z =8.94E+08mm 4钢梁上翼缘的弹性抵抗矩:W 1x =3.46E+06mm 3钢梁下翼缘的弹性抵抗矩:W 2x =2.61E+06mm 3 钢梁对Y轴截面惯性矩:I y =1.02E+08mm 4i y = 85.9mm y = 104.8上翼缘对Y 轴的惯性矩:I 1=7.47E+07mm 4下翼缘对Y 轴的惯性矩:I 2=2.70E+07mm 40.73截面不对称影响系数:0.380.53工字形截面简支梁的系数 0.76梁的整体稳定系数: 0.74修正后: 0.672.截面验算:(1)弯矩及剪力的计算:钢梁自重: 1.30KN/m恒载: 4.00KN/m2=10.90KN/mg1k活载:q c= 3.0KN/m2p k=18.10KN/m p=23.16KN/m 弯矩:M=234.49KN·m剪力:V=104.22KN(2)钢梁的强度、稳定和挠度的验算:梁的整体稳定应力:σ= 101.01N/mm2钢梁上翼缘应力:σ1= 67.70N/mm2钢梁下翼缘应力:σ2= 89.68N/mm2钢梁剪应力:τ= 22.70N/mm2挠度:w= 8.4mmw/l=1/1072。
静载荷梁的受力,力矩,变形计算公式整理总结
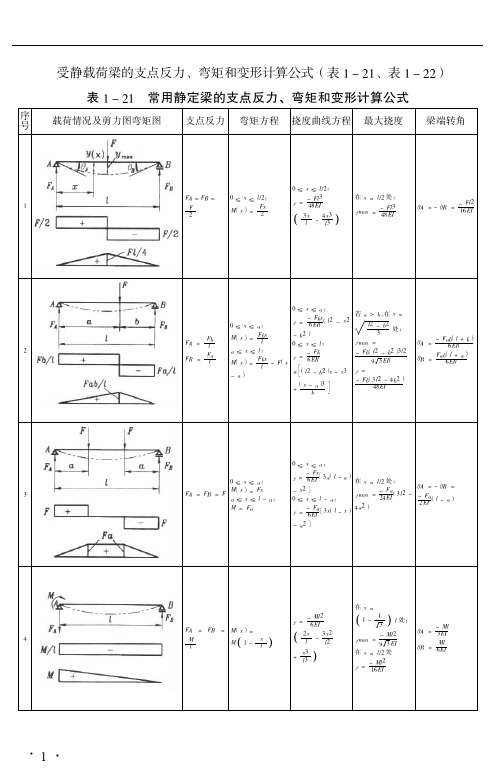
&
$# ,
即得 +’()
!’
"
#$ + ,-%
( ) $ $)*
#
*’() "
#$ %
} $ ,-$( ( & )),
[ ( ) %# &
)$
$ #
#
( ) $ #
$&
*
[ )$
$ #%
) $ $! (!+ " +&,#-$(% ) $ $)( % & ()*
] &
$# ,
(
$ #
$ &) ]
[ ( ) %# &
’" ! ’& ! &
# +
!$
’! !
# +
!$
() ()!
& !$% (+ *+
[ %(
) ( (
$
" &(
-" $"
’! ! ’)’"0+ -" $"
在 (’ ! ’)((1 $
() ()!
[ ( ) & -" $(
#"’ *+
( $
&"
("
$
$
(
( $
)*]
在 ( ! ’)((1 $ 处:
)-./
!
& -" $( (#0 *+
!"
!
-" $% #"’ *+
!" ! !& !
