完全主元素消去法
高斯列主元素消去法算法C++

#include<iostream>#include<fstream>#include<stdlib.h>#include<math.h>#define eps 0.0000000005using namespace std;void exchange(double A[3][3],double b[],int p,int q); void xiaoyuan(double A[3][3],double b[],int p,int n); void gauss(double A[3][3],double b[],int n);int main(int argv,char argc[]){double A[3][3];A[0][0]=0.00000001;A[0][1]=2;A[0][2]=3;A[1][0]=-1;A[1][1]=3.712;A[1][2]=4.623;A[2][0]=-2;A[2][1]=1.072;A[2][2]=5.643;double b[3]={1,2,3};gauss(A,b,3);return 0;}void exchange(double A[3][3],double b[],int p,int q,int n) {for(int i=0;i!=n;i++){double temp=0;temp=A[p][i];A[p][i]=A[q][i];A[q][i]=temp;}double temp=0;temp=b[p];b[p]=b[q];b[q]=temp;//cout<<"b[]"<<b[p]<<" "<<b[q]<<endl;}void xiaoyuan(double A[3][3],double b[],int p,int n) {cout<<"消元"<<endl;for(int i=p;i!=n-1;i++){cout<<"i="<<i<<endl;double temp=(0-A[i+1][p])/A[p][p];for(int j=p;j!=n;j++){A[i+1][j]=A[i+1][j]+A[p][j]*temp;cout<<A[i+1][j]<<" ";}b[i+1]=b[i+1]+b[i]*temp;cout<<b[i+1];}}void gauss(double A[3][3],double b[],int n){for(int k=0;k!=n-1;k++){double max=0;int index=k;cout<<A[k][k];max=A[k][k];for(int i=k+1;i!=n;i++){if(fabs(A[i][k])-fabs(max)>0){max=A[i][k];index=i;}}cout<<endl<<max<<endl;if(fabs(max)<eps){cout<<"无解"<<endl;exit(1);}if(k!=index){exchange(A,b,k,index,n);}xiaoyuan(A,b,k,n);system("PAUSE");}if(fabs(A[n-1][n-1])<eps){cout<<"无解"<<endl;exit(1);}//cout<<"b="<<endl;for(k=n-1;k!=-1;k--){cout<<b[k]<<" ";}cout<<endl;for(int i=n-1;i!=-1;i--){double sum=0;for(int j=i;j!=n-1;j++){double temp=0;temp=A[i][j+1]*b[j+1];sum=sum+temp;}b[i]=(b[i]-sum)/A[i][i];cout<<b[i]<<endl;}}。
列主元消去法与全主元消去法

山东省成人高等教育品牌专业网络课程
计算方法
x3
x1
x2
b
x3
x1 0 1 0
x2 0 0 1
b 1.4 消元 1.2 2
4 10 5 0 2.5 0.5 0 0 0.7
0 1 回代 2 0 0 1.4
因此,原方程组的计算解为x1 1.2,x2 2,x3 1.4. 把这些数值代入原方程组可以验证这是准确解。
Taishan University
山东省成人高等教育品牌专业网络课程
计算方法
例 4.5 用全主元法求解线性方程组
x1 2 x2 3 x3 1 5 x1 4 x2 10x3 0 3 x 0.1x x 2 2 3 1
4.2
Taishan University
消元
0.960 0.020 6.010
0.960 0.364 5.90
5.00 0.960 6.50 0 4.12 2.24 0 1.00 2.45
Taishan University
山东省成人高等教育品牌专业网络课程
计算方法
5.00 0.960 6.50 消元 0 4.12 2.24 0 0 2.99
1 1
不变,此即交换增广矩阵 A b 的第一与第l行,得新矩阵
主元比起第一列中其他元素有较大的绝对值。这时,消去 x1系数所用的乘数因子 ai1 al1 的绝对值不超过1,因而在消 元过程第一步中,舍入误差的影响得以减弱。
Taishan University
山东省成人高等教育品牌专业网络课程
Taishan University
高斯选主元消去法.ppt

1 0 r3 2 r20
2/3 0
1 1/2
0 1
1 1/2
2 / 3 3 0 2 r2
0 1 0 0
3/2 1/2
0 3/2 1 1/2
2 1 0
5
r1 3 r2
1 5/ 3 2 0 0 1/ 3
1 0 1/ 2 0 5/ 2 2
1 0 2/ 3 1 0 1 2/ 3 3 0 1 3/ 2 0 3/ 2 1
0 1
r1
r3
2 1
4 2
5 3
0 1
1 1 5/ 3 2 0
1 0 0
0 0
1/3
m31
1 3
1
m32 2
2 r2 3 r1
1 r3 3 r1
0 0
1
2/3 1/3 5/3
101 110
2/3
2 / 3 1 0 1 2/ 3 1/ 3 1 1 0 1/ 3
yn yi
bn (bi
/ ann
n
aij y j ) / aii
j i 1
(i n 1,,2,1)
优点 该方法数值稳定( mi k 1). 缺点 工作量大. 改进方法 列主元消去法,且此时mi k 1.
4.2 列主元素消去法
设已完成第1步~第k-1步计算,得到与原方程组等价的方程组
)第k列与第jk列元素;
1,, n)
bi bi mik bk (i k 1,, n)
二、 回代求解
a11 a12 a1n y1 b1
经过上述过程,方程组约化为
a22
a2n
y2
b2
ann
yn
方程组的解的三种情况

方程组的解的三种情况线性方程组的解的三种情况如下:第一种是无解。
也就是说,方程之间出现有矛盾的情况。
第二种情况是解为零。
这也是其次线性方程组唯一解的情况。
第三种是齐次线性方程组系数矩阵线性相关。
这种情况下有无数个解。
线性方程组是各个方程关于未知量均为一次的方程组(例如2元1次方程组)。
对线性方程组的研究,中国比欧洲至少早1500年,记载在公元初《九章算术》方程章中。
1、解线性方程组的方法大致可以分为两类:直接方法和迭代法。
直接方法是指假设计算过程中不产生舍入误差,经过有限次运算可求得方程组的精确解的方法;迭代法是从解的某个近似值出发,通过构造一个无穷序列去逼近精确解的方法。
2、消去法:Gauss(高斯)消去法——是最基本的和最简单的直接方法,它由消元过程和回代过程构成,基本思想是:将方程组逐列逐行消去变量,转化为等价的上三角形方程组(消元过程);然后按照方程组的相反顺序求解上三角形方程组,得到原方程组的解(回代过程)。
优缺点:简单易行,但是要求主元均不为0,适用范围小,数值稳定性差。
列主元素消去法——基本思想是在每次消元前,在要消去未知数的系数中找到绝对值大的系数作为主元,通过方程对换将其换到主对角线上,然后进行消元。
优点:计算简单,工作量大为减少,数值稳定性良好,是求解中小型稠密线性方程组的最好方法之一。
全主元素消去法——基本思想是在全体待选系数a(ij)(k)中选取主元,并通过行与列的互换把它换到a(kk)(k)的位置,进行消元。
优缺点:这种方法的精度优于列主元素法,它对控制舍入误差十分有效,但是需要同时作行列变换,因而程序比较复杂,计算时间较长。
3、直接三角分解法:消元过程实际上是把系数矩阵A分解成单位下三角形矩阵与上三角形矩阵乘积的过程,其中L为单位下三角形矩阵,U为上三角形矩阵。
这种分解过程称为杜利特尔(Doolittle分解),也称为LU 分解。
当系数矩阵进行三角分解后,求解方程组Ax = b的问题就等价于求解两个三角形方程组Ly=b和Ux=y。
数值分析4 高斯主元素消去法

§2高斯主元素消去法⎪⎩⎪⎨⎧=++-=++=++00.357.404.100.200.224.563.200.100.100.200.10120.0321321321x x x x x x x x x 解:clear alla=[0.0120 1.00 2.00;1.00 2.63 5.24;-2.00 1.04 4.57]; b=[1.00;2.00;3.00];x=a\b方程组的三位有效数字的解:Tx )266.0,476.0,645.0(*-=Gauss 消去法求解(取三位有效数字):[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---−−→−⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------−−−→−⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==-==00.300.5003.811627.80000.100.200.10120.016432916603.811627.80000.100.200.10120.000.357.404.100.200.224.563.200.100.100.200.10120.006.21673.83323121l l l b A 解出Tx )60.0,197.0,25.0(--≈。
【注】1)设Ax=b,其中A 为n 阶非奇异矩阵,可以应用高斯消元法。
2)消元过程中,即使0)(≠k kk a ,用其作除数)/()()(k kk k ik ik a a l =会导致计算中间结果数量级严重增长和舍入误差的累积、扩大,最后使得计算结果不可靠。
3)应避免采用绝对值很小的主元素)(k kk a ;对一般的系数矩阵,最好保持乘数1≤ik l ,因此,在高斯消去法中应引进选主元技巧,以便减少计算过程中舍入误差对求解的影响。
clear alla=[0.0120 1.00 2.00;1.00 2.63 5.24;-2.00 1.04 4.57]; b=[1.00;2.00;3.00];x_value=vpa(a\b,15)%10位有效数字的近似解a=[a,b];eps=1e-6;[n,m]=size(a);Gauss,x=vpa(x,15) %对比高斯消去法的结果一、列主元素消去法基本思想:在每轮消元之前,选列主元素(绝对值最大的元素),使乘数(即消元因子)1≤ik l步骤:设已进行k-1轮消元,得矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=)()()()()2(2)2(2)2(22)1(1)1(1)1(12)1(11)(k nn k nkk kn k kkn kn kk a a a a a a a a a a a A一落千丈 1 23S1:选列主元素: )()(0max k ik ni k k k i a a ≤≤= (1)S2:换行:如果)(0k k i a →0,则方程组解不唯一,停止运算; 否则,如果i0=k , 则可进行下一轮消元;如果k i ≠0,则r i0 r k ,然后进行下一轮消元。
mathematica典型例子(非常实用)

printf("\n");
}
puts("The solve is:\n");
for(i=1;i<=n;i++)
//输出方程的解
printf("x[%2d] = %lf\n",i,a[i][n+1]);
}
//======== gauss.txt 中的数据 ==========================
1、 利用Lagrange插值公式
Ln (x)
n k 0
n j0 jk
x xi xk xi
yk
编写出插值多项式程序;
2、 给出插值多项式或分段线性插值多项式的表达式;
3、 对此插值问题用Newton插值多项式其结果如何。Newton插值多项式如下:
Nn (x) f (x0) f [x0, x1](x x0) f [x0, x1, x2 ](x x0 )(x x1) ... f [x0, x1,..., xn](x x0 )(x x1)...(x xn 1),
求五次Lagrange多项式 L5 (x) ,和分段线性插值多项式,计算 f (5.96), f (5.99)
(2)
xi 1
2
3
4
5
6
7
yi 0.368 0.135 0.050 0.018 0.007 0.002 0.001
试构造Lagrange多项式 L6 (x) ,计算 f (1.8) 的值。
二、要求
}
printf("The variable x is not in the region [x0, xn]"); return 0; }
23.02 高斯选主元素消去法(1)
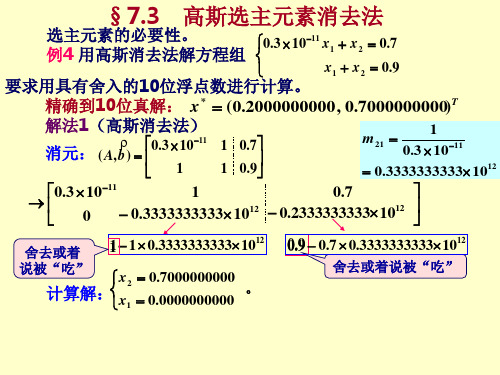
4.3 列主元高斯 约当(Gauss –Jordan)消去法 3 列主元高斯—约当 约当( 假设G--J消去法已完成第1步~第k-1步,得到与原方程组等价 消去法已完成第1 假设 消去法已完成第 步 的方程组 A( k ) x = b ( k ) ,其中
(k 1 a 1k ) M O ( 1 a kk )1, n − = (k a kk ) M (k a nk ) (k a1n ) ( L a kk )1, n − , (k ) L a kn M (k ) L a nn
x1 + x2 = 0.9
m 21 = r 0.3 × 10−11 1 0.7 0.3 × 10 −11 消元: 消元: ( A, b) = 1 1 0.9 = 0.3333333333 × 10 12 0.3 × 10 −11 1 0. 7 → 12 − 0.2333333333× 1012 − 0.3333333333× 10 0
0.3 ×10−11 x1 + x2 = 0.7 x1 + x2 = 0.9 ⇔ 0.3 × 10−11 x1 + x2 = 0.7 x1 + x2 = 0.9 r 0.3 × 10−11 1 0.7 r ↔ r 1 1 0 .9 消元: 消元:( A, b ) = → 0.3 × 10 −11 1 0.7 1 1 0.9 1 1 0.9 0.3 × 10−11 → (m21 = = 0.3 × 10−11 ) 1 0 1 0.7 x 2 = 0.7000000000 。 计算解: 计算解: x1 = 0.2000000000
k
bk ←bk ⋅ mkk 上述过程完成后 , 即 k = 1, 2 , L , n , 均已完成 , 则 有
(完整版)2.3高斯列主元消去法

2.3高斯列主元消去法解线性方程组一:问题的提出我们都知道,高斯列主元素消去法是计算机上常用来求解线性方程组的一种直接的方法。
就是在不考虑舍入误差的情况下,经过有限步的四则运算可以得到线性方程组的准确解的一类方法。
实际运算的时候因为只能有限小数去计算,因此只能得到近似值。
在实际运算的时候,我们很多时候也常用高斯消去法。
但是高斯消去法在计算机中运算的时候常会碰到两个问题。
1.一旦遇到某个主元等于0,消元过程便无法进行下去。
2.在长期使用中还发现,即使消元过程能进行下去,但是当某个主元的绝对值很小时,求解出的结果与真实结果相差甚远。
为了避免高斯消去法消元过程中出现的上述两个问题,一般采用所谓的选择主元法。
其中又可以分为列选主元和全面选主元两种方法。
目前计算机上常用的按列选主元的方法。
因此我在这里做的也是列选主元高斯消去法。
二、算法的基本思想大家知道,如果一个线性方程组的系数矩阵是上三角矩阵时,即这种方程组我们称之为上三角方程组,它是很容易求解的。
我们只要把方程组的最下面的一个方程求解出来,在把求得的解带入倒数第二个方程,求出第二个解,依次往上回代求解。
然而,现实中大多数线性方程组都不是上面所说的上三角方程组,所以我们有可以把不是上三角的方程通过一定的算法化成上三角方程组,由此我们可以很方便地求出方程组的解。
高斯消元法的目的就是把一般线性方程组简化成上三角方程组。
于是高斯消元法的基本思想是:通过逐次消元将所给的线性方程组化为上三角形方程组,继而通过回代过程求解线性方程组。
三、算法的描述1、设有n 元线性方程组如下:1111n n nn a a a a ⎛⎫ ⎪ ⎪ ⎪⎝⎭K M OM L1n x x ⎛⎫ ⎪ ⎪ ⎪⎝⎭M =1n b b ⎛⎫ ⎪ ⎪ ⎪⎝⎭M 2、 第一步:如果a 11!=0, 令l i1= ai1/a11, I= 2,3,……,n用(-li1)乘第一个方程加到第i 个方程上,得同解方程组:a (1)11 a (1)12 . . . a (1)1nx 1 b (1)1a (1)21 a (1)22 . . . a (1)2n x 2b (1)2. . . . . . . = .a (1)n-11 a (1)n-12 . . a (1)n-1n x n-1b (1)n-1a (1)n1 a (1)n2 . . . a (1)nn x nb (1)n简记为:A (2) x = b (2)其中a (2)ij = a (1)ij – l i1 * a (1)1j , I ,j = 2,3,..,nb(2)I = b(1)I– l i1 * b(1)1 , I = 2,3,...,n第二步:如果a(2)22 != 0,令l i2= a(2)i2/a(2)22, I= 3,……,n依据同样的原理,对矩阵进行化间(省略),依次下去,直到完成!最后,得到上三角方程组:a(1)11a(1)12 . . . a(1)1n x1b(1)10 a(1)22 . . . a(1)2n x2b(1)2. . . . . . . = .0 0 . . a(n-1)n-1n x n-1b(n-1)n-10 0 . . . a(n)nn x n b(n)n简记为:A(n) x = b(n)最后从方程组的最后一个方程进行回代求解为:X n = b(n) / a(n)nnX i = ( b(k)k - a(k)kj x j ) / a(k)kk以上为高斯消去法的基本过程。
全主元消去法例题详解

全主元消去法例题详解全主元消去法(Gaussian elimination with complete pivoting)是一种用于解线性方程组的数值方法,它通过矩阵的行变换将线性方程组转化为上三角矩阵,从而求解方程组的解。
下面我将从几个方面详细解释全主元消去法的步骤和原理。
1. 原理:全主元消去法的原理是通过消元过程将线性方程组转化为上三角矩阵,从而求解方程组的解。
在每一步消元过程中,选择主元元素(绝对值最大的元素)来进行行交换和列交换,以避免数值不稳定性问题。
2. 步骤:全主元消去法的步骤如下:a. 构造增广矩阵,将线性方程组的系数矩阵和常数向量合并为增广矩阵。
b. 选择主元素,在当前消元列中选择主元素,即绝对值最大的元素。
c. 行交换,将含有主元素的行与当前行交换,确保主元素位于当前行的对角线位置。
d. 列交换,将含有主元素的列与当前列交换,确保主元素位于当前列的对角线位置。
e. 消元,使用主元素对当前行以下的所有行进行消元,将当前列的下方元素置零。
f. 重复,重复步骤b-e,直到所有的行都被处理完毕。
g. 回代求解,从最后一行开始,依次回代求解方程组的解。
3. 数值稳定性:全主元消去法通过选择主元素来避免数值不稳定性问题。
选择绝对值最大的主元素可以减小误差的传播,提高数值计算的精度和稳定性。
4. 复杂度分析:全主元消去法的时间复杂度为O(n^3),其中n为方程组的未知数个数。
由于每一步都需要选择主元素并进行行列交换,因此全主元消去法的计算量较大。
5. 优缺点:全主元消去法的优点是可以避免数值不稳定性问题,提高计算的精度和稳定性。
然而,全主元消去法的缺点是计算量较大,对大规模方程组的求解效率较低。
总结,全主元消去法是一种用于解线性方程组的数值方法,通过选择绝对值最大的主元素,并进行行列交换和消元操作,将线性方程组转化为上三角矩阵,进而求解方程组的解。
它的优点是提高了计算的精度和稳定性,但缺点是计算量较大。
数值计算方法实验报告(含所有)

本科实验报告课程名称:计算机数值方法实验项目:计算机数值方法实验实验地点:虎峪校区致远楼B401专业班级:软件学院1217班学号:******xxxx 学生姓名:xxx指导教师:xxx2014 年 5 月21 日太原理工大学学生实验报告五、实验结果与分析二分法割线法分析:由程序知,使用二分法和割线法均能计算出方程的根,但利用割线法要比二分法计算的次数少,并且能够较早的达到精度要求。
相比之下,割线法程序代码量较少,精简明了。
六、讨论、心得本次数值计算方法程序设计实验从习题练习中跳脱出来,直接面对实用性较强的程序代码编写。
效果很好,不仅加深对二分法、割线法的理解,还加强了实际用运能力。
将理论知识成功地转化成实践结果。
实验地点虎峪校区致远楼B401指导教师xx太原理工大学学生实验报告l[i][k]=a[i][k];for(r=1;r<k;++r){l[i][k]-=l[i][r]*u[r][k];}l[i][k]/= u[k][k];}l[k][k]=1.0;}for(i=1;i<=n;++i){y[i] = b[i];for(j=1;j<i;++j){y[i]-=l[i][j]*y[j];}}for(i=n;i>0;--i){x[i] = y[i];for(j=i+1;j<=n;++j){x[i]-=u[i][j]*x[j];}x[i]/= u[i][i];}for(i=1;i<=n;++i){printf("%0.2lf\n",x[i]);}return 0;}五、实验结果与分析完全主元素消元法:列主元素消元法:LU分解法:分析:对于两种高斯解方程,完全主元素跟列主元素都是先消元、再回代,由程序段可以发现,始终消去对角线下方的元素。
即,为了节约内存及时效,可以不必计算出主元素下方数据。
列主元素消元法的算法设计上优于完全主元素消元法,它只需依次按列选主元素然后换行使之变到主元素位置,再进行消元即可。
§7.3 Gauss主元素消去法

1 1 2 0 1 1
109 9 10
9 9 1 10 10 例: 2 1 1
1 0
109 109
注意:这两个方程组 在数学上严格等价。
x2 1 , x1 0
© 2009, Henan Polytechnic University §3 Gauss主元素消去法
1 2 1
1 2 0 1 1 1
© 2009, Henan Polytechnic University §3 Gauss主元素消去法
1515
第七章 解线性方程组的直接方法
1 0 0 . 8 0. 4 1 0 .5 0 .5 0 .5 0 1 0.6 0.2 0 2.5 1.5 0.5 1.2 0 0 0. 4 0 1 .5 0 .5 1 .5
用顺序Gauss消去法计算:
8个 a 22 1 l 21 1 0.0 ...01 10 9 10 9 10 9
l21 a21 / a11 109
10 9 1
b2 2 l21 1 109
1 1
1 1 1 10 9 9 9 2 0 10 10 小主元 可能导致计 算失败。 x2 1, x1 0
1919
4 4
© 2009, Henan Polytechnic University §3 Gauss主元素消去法
第七章 解线性方程组的直接方法
7.3.1 列主元消去法
第一步:从第一列中选出绝对值最大的元素作为
主元素:
a11 max ai 1
2-2主元素法

回代得
x2 0.6667 , x1 0.3333
准确解为
1 2 x1 , x2 3 3
启示:可以通过交换方程的次序使对角元 素尽可能大,从而避免“小”数分 母 提高计算精度。===〉主元素法
全主元素消去法
基本思想:第k次消元前,在系数a 主元位置akk , 然后消元。 (实质:每次消元之前交换方程的位置及变量 的次序, 使对角线上的元素尽可能的大)。
回代得
x2 0.6667 , x1 0.0000
方法二: 若先交换两个方程的位置,将方程组变形为
1.0000 x1 1.0000 x2 1.0000 0.0003 x1 3.0000 x2 2.0001
消元得
1.0000 x1 1.0000 x2 1.0000 2.9997 x2 1.9998
x1 0.3333 x 2 0.6667
列主元素消去法 基本思想:在每次消元前,在要消去未知数的 系数中找到绝对值最大的系数作为主元,通过 对换行将其换到对角线上,然后进行消元.
省去换列的步骤,每次仅选一列中最大的元.
| a ik , k | max | a ik | 0
每一步选绝对值最大的元素为主元素,保证 | mik | 1。 Step k: ① 选取 | a i
k
(k ) ij
(i, j k ,...n)
中选绝对值最大元素,通过换行和换列将此元素换到
jk
| max | a ij | 0 ;
k i , jn
② If ik k then 交换第 k 行与第 ik 行; If jk k then 交换第 k 列与第 jk 列;
§2.2 主元素法
高斯列主元消去法

问题提出:采用高斯列主元消去法解线性方程组。
算法(公式)推导:高斯顺序消去法有一个最大的缺点就是一旦对角元素为0,就进行不下去了,为了解决这个问题就有了高斯主元消去法。
如果在高斯顺序消去法消去过程进行到第i 步时,先选取a ri ()n r i ≤≤中(即第i 列)绝对值最大的元素,设为第j 行的元素aji ,然后将第i+1行至第n 行中的每一行减去第i 行乘以ii kj a a (k 代表行号),依次进行消元,这样得到的算法叫高斯按列主元消去法。
高斯按列主元消去法的算法步骤介绍如下:1. 将方程组写成以下的增广矩阵的形式: 432144434241343332312423222114131211b b b b a a a a a a a a a a a a a a a a 2. 对k=1,2,3,…..,n-1,令∑==nk s sk pk a a max ,交换增广矩阵的第k 行与第p 行;对j=k+1,K+2,……..,n,计算*km jkjm jm kk a a a a a =-(m=k,k+1,....n)kk jk k j j a a b b b *-=算法结束。
3. 在MATLABE 中编程实现的高斯按列主元消去法函数为:GaussXQLineMain功能:高斯按列主元消去法求线性方程组Ax=b 的解调用格式:[x,XA]=GaussXQLineMain(A,b)其中,A :线性方程组的系数矩阵;B:线性方程组中的常数向量;x:线性方程组的解:XA:消元后的系数矩阵(可选的输出参数)。
高斯列主元消去法用MATLAB实现如下所示:4.其中用到上三角矩阵求解函数:在MATLABE中编程实现的上三角系数矩阵求解函数为:SolveUPTriangle 功能:求上三角系数矩阵的线性方程组Ax=b的解调用格式:x=SolveUpTriangel(A,b)其中,A :线性方程组的系数矩阵;b :线性方程组中的常数向量; X :线性方程组的解;上三角系数矩阵求解函数用MATLAB 实现如下所示:高斯按列主元消去法解线性方程组应用实例:用高斯按列主元消去法求解下列线性方程组的解。
计算方法_3

L L M L
( a11) n
(1 2 a2n) 2n
M
(2 an1)) 2
M
(1 2 ann))
(1) ( b11) 若 a11 ≠ 0 则: (2 b21) 第二行: a21) a11)×第一行 (1 (1 M ( (1 (1) 2 bn 第n行: an1) a11) ×第一行 1
第三章 线性代数方程组的解法
3-9
消元过程中的误差实例
0.001 2.000 3.000 1.000 3.712 4.623 2.000 1.072 5.643 x1 1.000 x = 2.000 2 x3 3.000
x1 = -0.4907 x2 = -0.05095 x3 = 0.3674
L L
M M
O O
M M
(k (k L akk) L akn)
(k (k L ank) L ann)
子块 A k n
~
第三章 线性代数方程组的解法
3-14
完全主元素消去法编程方法概要
k = 1, 2, L, n-1,进行以下 (2) ~ (6) 的循环计算 ~ (k ) ax (k ) (2) 在子块 A k 中选绝对值最大的元素(主元素) amax = m ai j n k≤i ≤n
迭代法 (雅可比迭代法、高斯-赛德尔迭代法、超松弛迭代法)
将线性方程组改写为: n 1 xi = bi ∑aij x j (i = 1,2,L, n) aii j =1 j ≠i 给出一组原始估计值,依次迭代逼近。 第三章 线性代数方程组的解法
3-17
关于三角分解法和迭代法
三角分解法 计算精度高于高斯消去法 计算量少、储存量小 需根据不同的系数矩阵类型选择不同的方法 迭代法 原理简单、编程方便、占用计算机内存少 尤其适用于大型方程组 (150个方程以上) 需根据具体情况选择迭代方程组以实现收敛
列主元素消去法求解方程组

列主元素消去法求解方程组[摘 要]在自然科学和工程中有很多问题的解决归结为求解线性方程组或者非线性方程组的数学问题。
例如,电学中的网络问题,用最小二乘法求实验数据的曲线拟合问题,三次样条的插值问题等等。
求解线性方程组的直接法主要有选主元高斯消去法、平方根法、追赶法等。
列主元素消去法既是选主元高斯消去法的一种,也是实际计算中常用的部分选主元消去法。
本文即是讨论利用列主元素消去法求解线性方程组问题。
[关键词]按列选主元 交换 消元 回代一 列主元素消去法背景在科学研究和工程技术中有许多问题可归结为求解线性代数方程组,其中所产生的线性方程组,其系数矩阵大致可分为两种:一种是低阶稠密矩阵;另一类是大型稀疏矩阵(此类矩阵阶数高,但零元素较多)。
对于这两种矩阵,我们可以把线性代数方程组的数值解法大致的分为两类:直接法和迭代法。
迭代法一般用来求解大型稀疏矩阵方程组(本文不予讨论);直接法是目前计算机上解低阶稠密矩阵的有效方法,如果计算过程中没有舍入误差,则此种方法通过有限步四则运算可求的方程组的精确解,但实际计算中由于舍入误差的存在和影响,这种方法也只能求得方程组的近似解。
直接法主要有选主元素高斯消去法、平方根法、追赶法等。
本文所要讨论的列主元素消去法就是选主元素高斯消去法中的一种。
高斯消去法是一个古老的求解线性方程组的方法,也是解线性方程组问题中较为常见的一种数值方法。
但在采取高斯消去法解方程组时,当采用绝对值很小的主元素时,可能导致计算结果的失败,故在消去法中应避免采用绝对值很小的主元素。
对于一般的线性方程组,需要引进选主元的技巧,即在高斯消去法的每一步应该在系数矩阵或消元后的低价矩阵中选取绝对值最大的元素作为主元素,保持乘数1 ik m ,以便减少计算过程中舍入误差对计算解的影响。
选主元素消元法则是对高斯消去法的改进,是解低价稠密矩阵方程组的有效方法。
选主元素消元法则避免了采用绝对值很小的主元素。
选主元素消去法主要有完全主元素消去法与列主元素消去法两种。
mathematica典型例子(非常实用)

a[label][j]=temp;
}
}
//==========================================
for (j=k+1;j<=n+1;j++) a[k][j]=a[k][j]/a[k][k]; a[k][k]=1.0; i=1; for(i=k+1;i<=n;i++) {
puts("The final matrix!\n"); for (i=1; i<=n; i++) // 输出消元之后的增广矩阵 {
for(j=1; j<=n+1; j++) printf("%6.3f ", a[i][j]);
printf("\n"); }
x[n] = a[n][n+1] ; for(i=n-1;i>=1;i--) {
(2)
xi 1
2
3
4
5
6
7
yi 0.368 0.135 0.050 0.018 0.007 0.002 0.001
试构造Lagrange多项式 L6 (x) ,计算 f (1.8) 的值。
二、要求
1、 利用Lagrange插值公式
Ln (x)
n k 0
n j0 jk
x xi xk xi
}
printf("The variable x is not in the region [x0, xn]"); return 0; }
void main(void) {
printf( "f(0.596)=%lf\n", line(0.596) ); printf( "f(0.99)=%lf\n", line(0.99) ); }
计算方法的课后答案
《计算方法》习题答案第一章 数值计算中的误差1.什么是计算方法?(狭义解释)答:计算方法就是将所求的的数学问题简化为一系列的算术运算和逻辑运算,以便在计算机上编程上机,求出问题的数值解,并对算法的收敛性、稳定性和误差进行分析、计算。
2.一个实际问题利用计算机解决所采取的五个步骤是什么?答:一个实际问题当利用计算机来解决时,应采取以下五个步骤: 实际问题→建立数学模型→构造数值算法→编程上机→获得近似结果 4.利用秦九韶算法计算多项式4)(53-+-=x x x x P 在3-=x 处的值,并编程获得解。
解:400)(2345-+⋅+-⋅+=x x x x x x P ,从而所以,多项式4)(53-+-=x x x x P 在3-=x 处的值223)3(-=-P 。
5.叙述误差的种类及来源。
答:误差的种类及来源有如下四个方面:(1)模型误差:数学模型是对实际问题进行抽象,忽略一些次要因素简化得到的,它是原始问题的近似,即使数学模型能求出准确解,也与实际问题的真解不同,我们把数学模型与实际问题之间存在的误差称为模型误差。
(2)观测误差:在建模和具体运算过程中所用的一些原始数据往往都是通过观测、实验得来的,由于仪器的精密性,实验手段的局限性,周围环境的变化以及人们的工作态度和能力等因素,而使数据必然带有误差,这种误差称为观测误差。
(3)截断误差:理论上的精确值往往要求用无限次的运算才能得到,而实际运算时只能用有限次运算的结果来近似,这样引起的误差称为截断误差(或方法误差)。
(4)舍入误差:在数值计算过程中还会用到一些无穷小数,而计算机受机器字长的限制,它所能表示的数据只能是一定的有限数位,需要把数据按四舍五入成一定位数的近似的有理数来代替。
这样引起的误差称为舍入误差。
6.掌握绝对误差(限)和相对误差(限)的定义公式。
答:设*x 是某个量的精确值,x 是其近似值,则称差x x e -=*为近似值x 的绝对误差(简称误差)。
全主元消去法

全主元消去法1. 通过编制全主元消去法的MATLAB 程序(见文件),并用12312312310x 19x 2x =320x 40x x =4x 4x 5x =5--⎧⎪-++⎨⎪++⎩ 验证,程序给出的结果为x = 4.4164 2.3523 -1.7651,这与原方程的解相同,说明程序是有效的。
2. 全主元消去法的运算保证是能稳定收敛的,并不会出现分母为零的现象,其误差来源于数据的舍入误差,而这个误差与采用普通高斯消去法和列主元消去法相比大大减小。
3. 当主元素选定后,要对选择出的第一个主元素变为1,这就需要将第一行元素都除以主元素,共需要1n -次乘除法运算,而要使第二行至最后一行的第一列元素都为零,则需要进行(1)*(1)n n -+次乘除法运算,所以第一步共需要22n n +-次乘除法运算,同理可算得进行第二步到最后一步所进行的乘除法运算为22112112n n -+--+-()()、……()可得消元过程中乘除法总和为*(1)*(21)(1)262n n n n n n ++++-次乘除法运算,回带过程中则产生n*(1)1234n=2n +++++……次乘除法运算,所以运用全主元消去法共会产生*(1)*(21)(1)26n n n n n n ++++-次乘除法运算,这也就是方程组的规模与计算量的关系。
4. 矩阵高度稀疏的情况下可以考虑对矩阵进行重新排列,使非零元素聚集在主对角线附近,可以减少运算量。
function [x]=gaussq(a,b)%%x为解,qa为全主元变换后的矩阵a d=[a b];RA=rank(a);RD=rank(d);L=length(b);n=size(a);pos=1:n(1)if RA~=RD %%根据增广矩阵判断有解条件fprintf('无解')elseif RA~=Lfprintf('无穷多解')elsefprintf('有唯一解')for q=1:nbig=max(max(abs(a(q:n,q:n))));for r=q:n %%在右下角矩阵中找到绝对值最大的值for t=q:nif big==abs(a(r,t))zhuh=r; %%记录最大值所在的行列zhul=t;endendendp=a(q,:);%%换主行a(q,:)=a(zhuh,:)%%a矩阵中换行a(zhuh,:)=p;bb=b(q);%%b矩阵中也进行换行b(q)=b(zhuh)b(zhuh)=bb;p=a(:,q);%%换主列a(:,q)=a(:,zhul);a(:,zhul)=p;p=pos(q);%%记录位置变化,调换列后对求解x的影响pos(q)=pos(zhul);pos(zhul)=p;endc=[a b]for j=1:L-1%%变换后将所在矩阵的下面行的第一个元素变为0for i=(j+1):Lm=c(i,j)/c(j,j)c(i,:)=c(i,:)-c(j,:)*mendendx(L,1)=c(L,L+1)/c(L,L);for k=L-1:-1:1x(k,1)=(c(k,L+1)-c(k,k+1:L)*x(k+1:L))/c(k,k);endy=[1:n(1)];%%交换被列调换打乱的位置for w=1:nfor v=1:nif (pos(v)==w)y(w)=x(v)endendendx=y;endend。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012-2013(1)专业课程实践论文
完全主元素消去法
董健0818180101,R数学08-1班
陈泊宇0818180116,R数学08-1班
一、算法理论
设方程组的增广矩阵为
⎥⎥⎥⎥⎥⎥⎥⎥⎦
⎤
⎢⎢⎢⎢⎢
⎢⎢⎢⎣⎡=n nn
nj n n i n i j i i i n j n
j b a a a a b a a a a b a a a a b a a a a B i
1
111111121
2122222211111211 首先在A 中选取绝对值最大的元素作为主元素,例如0max 1111≠=≤≤≤≤ij n
j n
i j i a a ,然后交
换B 的第一行与第1i 行,第1列于第1j 列,经第一次消元计算得 ()().,,)2()2(b A b A →
重复上述过程,设已完成第k-1步的选主元素,交换两行及交换两列,消元计算,(A ,b )约化为
()
⎥⎥⎥⎥⎥⎥⎥⎥⎦
⎤
⎢⎢
⎢⎢⎢
⎢⎢⎢⎣
⎡=n nn nk k kn
kk n n
k k b a a b a a b a a b a a a b A 2222111211)()(,, 其中)(k A 元素仍记作ij a ,)(k b 元素仍记作().1,.2,1-=n k b i 第K 步选主元素(在)(k A 右下角方框内选),即确定k k j i ,使 .0max ≠=≤≤≤≤ij n
j k n
i k j i a a k k
交换())()(,k k b A 第k 行与k i 行元素交换())(k A 第k 列与k j 列元素,将k k j i a 调到(k,k )位置,在进行消元计算,最后将原方程组化为
,212122211211⎥
⎥⎥⎥⎦
⎤
⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n n nn n n b b b y y y a a a a a a 其中n y y y ,,,21 的次序为未知数n x x x ,,21调换后的次序。
回代求解得
().1,2,,1/,/1 -=⎪⎩⎪⎨⎧⎪⎪⎭⎫ ⎝⎛-==∑+=n i a y a b y a b y ii
n i j j ij i i nn n n
二、算法框图
三、算法程序
#include<stdio.h>
#include<iostream.h>
#include"math.h"
float a[100][101];
float x[10];
int N; //阶数
void shuchu()
{
for(int i=1;i<=N;i++)
{
for(int j=1;j<=N+1;j++)
{
cout<<a[i][j];
cout<<" "<<" ";
}
cout<<endl;
}
}
void initdata()
{
cout<<"请输入阶数N:";
cin>>N;
cout<<endl;
cout<<"请输入N*(N+1)个数"<<endl; //输入矩阵中的数for(int i=1;i<=N;i++)
for(int j=1;j<=N+1;j++)
{
cin>>a[i][j];
}
cout<<endl;
cout<<"建立的矩阵为:"<<endl; //打印出矩阵
shuchu();
}
void main()
{
int z[10];
int maxi,maxj;
initdata();
for(int i=1;i<=N;i++)
z[i]=i;
for(int k=1;k<N;k++)
{
maxi=k;maxj=k;float maxv=abs(a[k][k]);
for(i=k;i<=N;i++)
for(int j=k;j<=N;j++)
if(abs(a[i][j])>maxv)
{
maxv=abs(a[i][j]);maxi=i;maxj=j;
}
if(maxi!=k) //换行
{
for(int j=1;j<=N+1;j++)
{
float t=a[k][j];a[k][j]=a[maxi][j];a[maxi][j]=t;
}
}
if(maxj!=k) //换列
{
for(i=1;i<=N;i++)
{
float t=a[i][k];a[i][k]=a[i][maxj];a[i][maxj]=t;
}
int t=z[k]; z[k]=z[maxj];z[maxj]=t;
}
for(int i=k+1;i<=N;i++) //消元
{
float l=a[i][k]/a[k][k];
for(int j=k;j<=N+1;j++)
{
a[i][j]+=-l*a[k][j];
}
}
}
//回代
for(i=N;i>0;i--)
{
float s=0;
for(int j=i+1;j<=N;j++)
{
s+=a[i][j]*x[z[j]];
}
x[z[i]]=(a[i][N+1]-s)/a[i][i];
}
cout<<"用完全主元素消去法后的矩阵为:" <<endl; shuchu();
for(i=1;i<=N;i++) // 打印出x[i]
cout<<"x["<<i<<"]="<<x[i]<<endl;
}
四、算法实现
例1. 利用完全主元素消去法求解三阶线性方程组
⎥⎥
⎥⎦
⎤
⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--000.3000.2000.1643.5072.1000.2623.4712.3000.1000.3000.2001.0321x x x 解:运行程序
(1)显示出 请输出阶数N: 输入N 的值为3,回车。
(2)显示出 请输入N*<N+1>个数:输入a[1][1]到a[n][n+1]的值
0.001 2.000 3.000 1.000 -1.000 3.712 4.623 2.000 -2.000 1.072 5.643 3.000,回车。
(3)显示结果:x[1]=-0.490396 x[2]=-0.0510352 x[3]=0.36752
例2. 利用全选主元素消去法求解四阶方程组
⎥
⎥
⎥⎥⎦
⎤
⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢
⎢⎢
⎢⎣⎡2557.04240.01550.04043.03927.02786.04002.01784.00643.03781.01920.03645.01129.04015.03872.02246
.02943.03678.01234.04096
.04321x x x x
解:运行程序
(1)显示出请输出阶数N: 输入N的值为4,回车。
(2)显示出请输入N*<N+1>个数:输入a[1][1]到a[n][n+1]的值
0.4096 0.1234 0.3678 0.2943 0.4043 0.2246 0.3872 0.4015 0.1129 0.1550 0.3645 0.1920 0.3781 0.0643 0.4200 0.1784 0.4002 0.2786 0.3927 -0.2557,回车。
(3)显示结果:x[1]=-0.181916
x[2]=-1.66303
x[3]=2.21723
x[4]=-0.446704。
