高一立体几何证明专题练习一

高一数学常考立体几何证明题及答案

1、如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。

求证：（1）⊥AB 平面CDE; （2）平面CDE ⊥平面ABC 。

2、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点，求证： 1//A C 平面BDE 。

3、已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证：AD ⊥面SBC ．4、已知正方体1111ABCD A B C D -，O 是底ABCD 对角线的交点.求证：(１) C 1O ∥面11AB D ；(2)1AC ⊥面11AB D ．5、正方体''''ABCD A B C D -中，求证：（1）''AC B D DB ⊥平面；（2）''BD ACB ⊥平面.6、正方体ABCD —A 1B 1C 1D 1中． (1)求证：平面A 1BD ∥平面B 1D 1C ；(2)若E 、F 分别是AA 1，CC 1的中点，求证：平面EB 1D 1∥平面FBD ．7、四面体ABCD 中，,,AC BD E F =分别为,AD BC 的中点，且22EF AC =，90BDC ∠=，求证：BD ⊥平面ACDAED BCAED 1CB 1DCBASDCB AD 1ODB AC 1B 1A 1CA 1 AB 1B C 1 CD 1DGEF8、如图，在正方体1111ABCD A B C D -中，E 、F 、G 分别是AB 、AD 、11C D 的中点.求证：平面1D EF ∥平面BDG .9、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点. （1）求证：1//A C 平面BDE ；（2）求证：平面1A AC ⊥平面BDE .10、已知ABCD 是矩形，PA ⊥平面ABCD ，2AB =，4PA AD ==，E 为BC 的中点．（1）求证：DE ⊥平面PAE ；（2）求直线DP 与平面PAE 所成的角．11、如图，在四棱锥P ABCD -中，底面ABCD 是060DAB ∠=且边长为a 的菱形，侧面PAD 是等边三角形，且平面PAD 垂直于底面ABCD ．（1）若G 为AD 的中点，求证：BG ⊥平面PAD ；（2）求证：AD PB ⊥．12、如图1,在正方体1111ABCD A B C D -中，M 为1CC 的中点，AC 交BD 于点O ，求证：1AO ⊥平面MBD ．13、如图２，在三棱锥Ａ－BCD 中，BC ＝AC ，AD ＝BD ，作BE ⊥CD ，Ｅ为垂足，作AH ⊥BE 于Ｈ．求证：AH ⊥平面BCD ．14．(12分)求证平行于三棱锥的两条相对棱的平面截三棱锥所得的截面是平行四边形．已知：如图，三棱锥S —ABC ，SC ∥截面EFGH ，AB ∥截面EFGH.求证：截面EFGH是平行四边形．15．(12分)已知正方体ABCD—A1B1C1D1的棱长为a，M、N分别为A1B和AC上的点，A1M＝AN＝23a，如图．(1)求证：MN∥面BB1C1C；(2)求MN的长．16．(12分)(2009·浙江高考)如图，DC⊥平面ABC，EB∥DC，AC＝BC＝EB＝2DC＝2，∠ACB＝120°，P，Q分别为AE，AB的中点．(1)证明：PQ∥平面ACD；(2)求AD与平面ABE所成角的正弦值．17．(12分)如图，在四面体ABCD中，CB＝CD，AD⊥BD，点E、F分别是AB、BD的中点．求证：(1)直线EF∥面ACD.（2）平面EFC⊥平面BCD.1、如图，已知空间四边形ABCD 中，,BC AC AD BD ==，E 是AB 的中点。

高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)

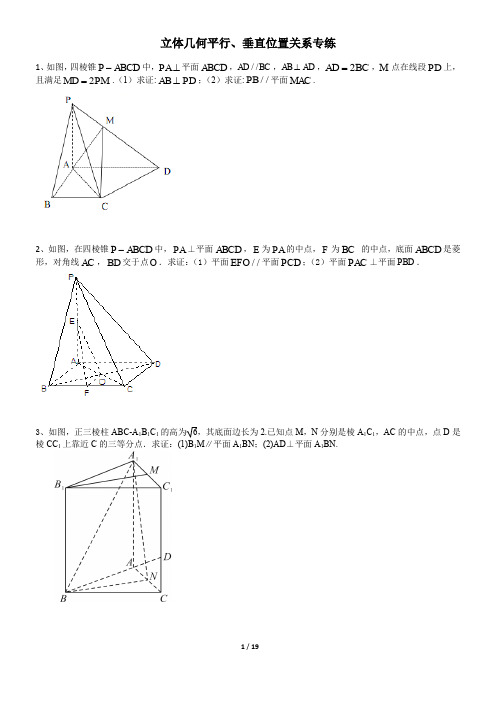
立体几何平行、垂直位置关系专练1、如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .2、如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ．3、如图，正三棱柱ABC-A 1B 1C 1的高为6，其底面边长为2.已知点M ，N 分别是棱A 1C 1，AC 的中点，点D 是棱CC 1上靠近C 的三等分点．求证：(1)B 1M ∥平面A 1BN ；(2)AD ⊥平面A 1BN.4、如图，等边三角形ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD＝2AE，AE⊥AB，M为AB的中点．(1)证明：CM⊥DE；(2)在边AC上找一点N，使CD∥平面BEN.5、如图，矩形ABCD所在平面与三角形ABE所在平面互相垂直，AE＝AB，M，N，H分别为DE，AB，BE 的中点．求证：(1)MN∥平面BEC；(2)AH⊥CE.6、如图，在三棱台ABCDEF中，CF⊥平面DEF，AB⊥BC.(1)设平面ACE∩平面DEF＝a，求证：DF∥a；(2)若EF＝CF＝2BC，试问在线段BE上是否存在点G，使得平面DFG⊥平面CDE？若存在请确定点G的位置；若不存在，请说明理由．7、在三棱锥S ABC -中，平面SAB ⊥平面SBC ，AB BC ⊥，AS AB =，过A 作AF SB ⊥，垂足为F ，点E ，G 分别是棱SA ，SC 的中点．（1）求证：平面EFG ∥平面ABC ．（2）求证：BC SA ⊥．8、如图，在直三棱柱111ABC A B C -中，AB BC ⊥，点D 为棱1C C 的中点，1AC 与1A D 交于点E ，1BC 与1B D 交于点F ，连结EF .求证：（1）//AB EF ；（2）平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A 1B 1∥平面DEC 1；（2）BE ⊥C 1E ．点，平面PAB ⊥底面ABCD ，90PAB ∠= ．求证：（1）//PB 平面AEC ；（2）平面PAC ⊥平面ABCD ．11、2.（2020·江苏省镇江高三二模）如图，三棱锥P ABC -中，点D ，E 分别为AB ，BC 的中点，且平面PDE ⊥平面ABC ．()1求证：//AC 平面PDE ；()2若2PD AC ==，PE =PBC ⊥平面ABC .12、（2020·江苏省建湖高级中学高三月考）如图，在四面体ABCD 中，,90AD BD ABC =∠= ，点,E F 分别为棱,AB AC 上的点，点G 为棱AD 的中点，且平面//EFG 平面BCD ．（1）求证：12EF BC =；（2）求证：平面EFD ⊥平面ABC ．点，PA ⊥平面ABCD .（1）求证：//PB 平面AEC ；（2）若四边形ABCD 是矩形且PA AD =，求证：AE ⊥平面PCD .14、（2020·江苏省高三二模）如图，在三棱柱111ABC A B C -中，侧面11ABB A ⊥底面ABC ，AB AC ⊥，E ，F 分别是棱AB ，BC 的中点.求证：（1）11AC ∥平面1B EF ；（2）1AC B E ⊥.15、（2020·江苏省连云港高三）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，E 、F 分别为AD 、PB 的中点.（Ⅰ）求证：PE BC ⊥；（Ⅱ）求证：平面PAB ⊥平面PCD ；（Ⅲ）求证：//EF 平面PCD .16、（2020·江苏省苏州高三）如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A1B 1∥平面DEC 1；（2）BE ⊥C 1E ．17、（2020·江苏省通州高三）如图，在三棱柱111ABC A B C -中，侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点．（1）求证: 平面ABE ⊥平面11B BCC ；（2）求证:1C F ∥平面ABE ；18、（2020·江苏省高三三模）如图，三棱柱111ABC A B C -中，1BC B C =，O 为四边形11ACC A 对角线交点，F 为棱1BB 的中点，且AF ⊥平面11BCC B .（1）证明：//OF 平面ABC ；（2）证明：四边形11ACC A 为矩形.参考答案1．如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .【解析】（1）∵四棱锥P ABCD -中，PA ⊥平面ABCD ，AB 平面ABCD ， ∴AB PA ⊥，又AB AD ⊥，,PA AD ⊂平面PAD ，PA AD A ⋂=， ∴AB ⊥面PAD .PD ⊂面PAD ，∴AB PD ⊥. （2）连结BD AC O ⋂=，连结MO ， ∵//AD BC ，2AD BC =，2DO BO ∴=,∵在PBD ∆中，2DM MP =，2DO BO =∴//PB MO ，又PB ⊄面MAC ，MO ⊂面MAC ，∴//PB 面MAC .2．如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ．【详解】（1）因为在ΔPAC 中，E 为PA 的中点，O 为AC 的中点，所以//EO PC又EO ⊄平面PCD ，PC ⊂平面PCD ，所以//EO 平面PCD同理可证，//FO 平面PCD ，又EO FO O = ，EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD ．（2）因为PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以PA BD ⊥因为底面ABCD 是菱形，所以AC BD ⊥，又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。

高中数学立体几何证明题汇总

高中数学立体几何证明题汇总立体几何常考证明题1.已知四边形ABCD是空间四边形，E,F,G,H分别是边AB,BC,CD,DA的中点。

1）证明EFGH是平行四边形。

2）已知BD=23，AC=2，EG=2，求异面直线AC、BD所成的角和EG、BD所成的角。

2.如图，已知空间四边形ABCD中，BC=AC,AD=BD，E 是AB的中点。

1）证明AB垂直于平面CDE。

2）证明平面CDE垂直于平面ABC。

3.如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点。

证明A1C平行于平面BDE。

4.已知三角形ABC中∠ACB=90，SA垂直于面ABC，AD垂直于SC。

证明AD垂直于面SBC。

5.已知正方体ABCD-A1B1C1D1，O是底面ABCD对角线的交点。

1）证明C1O平行于面AB1D1.2）证明AC1垂直于面AB1D1.6.正方体ABCD-A1B1C1D1中。

1）证明AC垂直于平面B1D1D。

2）证明BD1垂直于平面ACB1.7.正方体ABCD-A1B1C1D1中。

1）证明平面A1BD平行于平面B1DC。

2）已知E、F分别是AA1、CC1的中点，证明平面EB1D1平行于平面FBD。

8.四面体ABCD中，AC=BD，E、F分别为AD、BC的中点，且EF=AC/2，∠XXX。

证明BD垂直于平面ACD。

9.如图P是△ABC所在平面外一点，PA=PB，CB垂直于平面PAB，M是PC的中点，N是AB上的点，AN=3NB。

1）证明XXX垂直于AB。

2）当∠APB=90，AB=2BC=4时，求MN的长度。

10.如图，在正方体ABCD-A1B1C1D1中，E、F、G分别是AB、AD、C1D1的中点。

证明平面D1EF平行于平面BDG。

11.如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点。

1）证明A1C平行于平面BDE。

2）证明平面A1AC垂直于平面BDE。

12、已知矩形ABCD，PA垂直于平面ABCD，AB=2，PA=AD=4，E为BC的中点。

高一立体几何证明专题练习一精编版

高一立体几何证明专题练习一1.如图，在三棱柱ABC－A1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点，求证：(1)B，C，H，G四点共面；(2)平面EFA1∥平面BCHG.2.如图，在直三棱柱ABC－A1B1C1中，AB＝AC＝5，BB1＝BC＝6，D，E分别是AA1和B1C 的中点．(1)求证：DE∥平面ABC；(2)求三棱锥E－BCD的体积．3.如图，多面体ABFEDC的直观图及三视图如图所示，M，N分别为AF，BC的中点．(1)求证：MN∥平面CDEF；(2)求多面体A－CDEF的体积．4.如图所示，已知PA⊥矩形ABCD所在平面，M，N分别是AB，PC的中点．(1)求证：MN⊥CD；(2)若∠PDA＝45°，求证：MN⊥平面PCD.5.如图，在四棱锥P－ABCD中，平面PAD⊥平面ABCD，AB∥DC，△PAD是等边三角形，已知BD＝2AD＝4，AB＝2DC＝2 5.(1)求证：BD⊥平面PAD；(2)求三棱锥A－PCD的体积．6.已知正方体ABCD－A1B1C1D1中，E为棱CC1上的动点．(1)求证：A1E⊥BD；(2)当E恰为棱CC1的中点时，求证：平面A1BD⊥平面EBD.7.如图，直角梯形ACDE与等腰直角△ABC所在平面互相垂直，F为BC的中点，∠BAC ＝∠ACD＝90°，AE∥CD，DC＝AC＝2AE＝2.(1)求证：AF∥平面BDE；(2)求四面体B－CDE的体积．8. 如图所示，已知ABCD－A1B1C1D1是棱长为3的正方体，点E在AA1上，点F在CC1上，G在BB1上，且AE＝FC1＝B1G＝1，H是B1C1的中点．(1)求证：E、B、F、D1四点共面；(2)求证：平面A1GH∥平面BED1F.9.如图，直三棱柱ABC－A1B1C1中，D，E分别是AB，BB1的中点．(1)证明：BC1∥平面A1CD；(2)若AA1＝AC＝CB＝2，AB＝22，求三棱锥C－A1DE的体积．10.在如图所示的多面体中，四边形ABB1A1和ACC1A1都为矩形．(1)若AC⊥BC，证明：直线BC⊥平面ACC1A1；(2)设D，E分别是线段BC，CC1的中点，在线段AB上是否存在一点M，使直线DE∥平面A1MC？请证明你的结论．11.如图所示，在直三棱柱ABC－A1B1C1中(侧棱垂直于底面的三棱柱叫直三棱柱)，AB＝BB1，AC1⊥平面A1BD，D为AC的中点．求证：(1)B1C∥平面A1BD；(2)B1C1⊥平面ABB1A1.12. 如图所示，在正方体ABCD－A1B1C1D1中，E、F分别是CD、A1D1的中点．(1)求证：AB1⊥BF；(2)求证：AE⊥BF；(3)棱CC1上是否存在点P，使BF⊥平面AEP，若存在，确定点P的位置，若不存在，说明理由．13.如图，四棱锥P－ABCD的底面是边长为8的正方形，四条侧棱长均为217.点G，E，F，H分别是棱PB，AB，CD，PC上共面的四点，平面GEFH⊥平面ABCD，BC∥平面GEFH.(1)证明：GH∥EF；(2)若EB＝2，求四边形GEFH的面积．14.如图，在三棱柱ABC－A1B1C1中，侧棱垂直于底面，AB⊥BC，AA1＝AC＝2，BC＝1，E，F分别是A1C1，BC的中点．(1)求证：平面ABE⊥平面B1BCC1；(2)求证：C1F∥平面ABE；(3)求三棱锥E－ABC的体积．。

高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)

立体几何平行、垂直位置关系专练1、如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .2、如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ．3、如图，正三棱柱ABC-A 1B 1C 1的高为6，其底面边长为2.已知点M ，N 分别是棱A 1C 1，AC 的中点，点D 是棱CC 1上靠近C 的三等分点．求证：(1)B 1M ∥平面A 1BN ；(2)AD ⊥平面A 1BN.4、如图，等边三角形ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD＝2AE，AE⊥AB，M为AB的中点．(1)证明：CM⊥DE；(2)在边AC上找一点N，使CD∥平面BEN.5、如图，矩形ABCD所在平面与三角形ABE所在平面互相垂直，AE＝AB，M，N，H分别为DE，AB，BE 的中点．求证：(1)MN∥平面BEC；(2)AH⊥CE.6、如图，在三棱台ABCDEF中，CF⊥平面DEF，AB⊥BC.(1)设平面ACE∩平面DEF＝a，求证：DF∥a；(2)若EF＝CF＝2BC，试问在线段BE上是否存在点G，使得平面DFG⊥平面CDE？若存在请确定点G的位置；若不存在，请说明理由．7、在三棱锥S ABC -中，平面SAB ⊥平面SBC ，AB BC ⊥，AS AB =，过A 作AF SB ⊥，垂足为F ，点E ，G 分别是棱SA ，SC 的中点．（1）求证：平面EFG ∥平面ABC ．（2）求证：BC SA ⊥．8、如图，在直三棱柱111ABC A B C -中，AB BC ⊥，点D 为棱1C C 的中点，1AC 与1A D 交于点E ，1BC 与1B D 交于点F ，连结EF .求证：（1）//AB EF ；（2）平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A 1B 1∥平面DEC 1；（2）BE ⊥C 1E ．点，平面PAB ⊥底面ABCD ，90PAB ∠= ．求证：（1）//PB 平面AEC ；（2）平面PAC ⊥平面ABCD ．11、2.（2020·江苏省镇江高三二模）如图，三棱锥P ABC -中，点D ，E 分别为AB ，BC 的中点，且平面PDE ⊥平面ABC ．()1求证：//AC 平面PDE ；()2若2PD AC ==，PE =PBC ⊥平面ABC .12、（2020·江苏省建湖高级中学高三月考）如图，在四面体ABCD 中，,90AD BD ABC =∠= ，点,E F 分别为棱,AB AC 上的点，点G 为棱AD 的中点，且平面//EFG 平面BCD ．（1）求证：12EF BC =；（2）求证：平面EFD ⊥平面ABC ．点，PA ⊥平面ABCD .（1）求证：//PB 平面AEC ；（2）若四边形ABCD 是矩形且PA AD =，求证：AE ⊥平面PCD .14、（2020·江苏省高三二模）如图，在三棱柱111ABC A B C -中，侧面11ABB A ⊥底面ABC ，AB AC ⊥，E ，F 分别是棱AB ，BC 的中点.求证：（1）11AC ∥平面1B EF ；（2）1AC B E ⊥.15、（2020·江苏省连云港高三）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，E 、F 分别为AD 、PB 的中点.（Ⅰ）求证：PE BC ⊥；（Ⅱ）求证：平面PAB ⊥平面PCD ；（Ⅲ）求证：//EF 平面PCD .16、（2020·江苏省苏州高三）如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A1B 1∥平面DEC 1；（2）BE ⊥C 1E ．17、（2020·江苏省通州高三）如图，在三棱柱111ABC A B C -中，侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点．（1）求证: 平面ABE ⊥平面11B BCC ；（2）求证:1C F ∥平面ABE ；18、（2020·江苏省高三三模）如图，三棱柱111ABC A B C -中，1BC B C =，O 为四边形11ACC A 对角线交点，F 为棱1BB 的中点，且AF ⊥平面11BCC B .（1）证明：//OF 平面ABC ；（2）证明：四边形11ACC A 为矩形.参考答案1．如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .【解析】（1）∵四棱锥P ABCD -中，PA ⊥平面ABCD ，AB 平面ABCD ， ∴AB PA ⊥，又AB AD ⊥，,PA AD ⊂平面PAD ，PA AD A ⋂=， ∴AB ⊥面PAD .PD ⊂面PAD ，∴AB PD ⊥. （2）连结BD AC O ⋂=，连结MO ， ∵//AD BC ，2AD BC =，2DO BO ∴=,∵在PBD ∆中，2DM MP =，2DO BO =∴//PB MO ，又PB ⊄面MAC ，MO ⊂面MAC ，∴//PB 面MAC .2．如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ．【详解】（1）因为在ΔPAC 中，E 为PA 的中点，O 为AC 的中点，所以//EO PC又EO ⊄平面PCD ，PC ⊂平面PCD ，所以//EO 平面PCD同理可证，//FO 平面PCD ，又EO FO O = ，EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD ．（2）因为PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以PA BD ⊥因为底面ABCD 是菱形，所以AC BD ⊥，又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。

高中立体几何证明题

高中立体几何证明题一、线面平行的证明题1已知正方体ABCD - A_{1}B_{1}C_{1}D_{1}，E，F分别是AB，BC的中点，求证：EF∥平面A_{1}C_{1}D。

解析1. 连接AC。

- 在 ABC中，因为E，F分别是AB，BC的中点，所以EF∥ AC。

2. 正方体ABCD - A_{1}B_{1}C_{1}D_{1}中：- AC∥ A_{1}C_{1}。

- 由EF∥ AC和AC∥ A_{1}C_{1}可得EF∥ A_{1}C_{1}。

- 又A_{1}C_{1}⊂平面A_{1}C_{1}D，EFnot⊂平面A_{1}C_{1}D。

- 根据线面平行的判定定理，所以EF∥平面A_{1}C_{1}D。

题2在三棱柱ABC - A_{1}B_{1}C_{1}中，D是AB的中点，求证：AC_{1}∥平面CDB_{1}。

解析1. 连接BC_{1}，交B_{1}C于点E。

- 在三棱柱ABC - A_{1}B_{1}C_{1}中，E为BC_{1}的中点。

2. 因为D是AB的中点：- 所以在 ABC_{1}中，DE∥ AC_{1}。

- 又DE⊂平面CDB_{1}，AC_{1}not⊂平面CDB_{1}。

- 根据线面平行的判定定理，可得AC_{1}∥平面CDB_{1}。

二、线面垂直的证明题3在四棱锥P - ABCD中，底面ABCD是正方形，PA = PB = PC = PD，求证：PA⊥平面ABCD。

解析1. 连接AC，BD交于点O，连接PO。

- 因为底面ABCD是正方形，所以O为AC，BD中点。

- 又PA = PC，PB = PD，根据等腰三角形三线合一的性质：- 可得PO⊥ AC，PO⊥ BD。

- 而AC∩ BD = O，AC⊂平面ABCD，BD⊂平面ABCD。

- 根据直线与平面垂直的判定定理，所以PO⊥平面ABCD。

- 又PA = PB = PC = PD，AO = BO = CO = DO，所以 PAO≅ PBO≅ PCO ≅ PDO。

高中数学立体几何证明题练习卷

高中数学立体几何证明题练习卷立体几何作为高中数学的重要组成部分，其中的证明题对于同学们的空间想象能力、逻辑推理能力以及数学语言的运用能力都有着较高的要求。

为了帮助同学们更好地掌握这部分知识，提高解题能力，特编制此练习卷。

一、选择题1、已知直线\（a\），＼（b\）和平面\（＼alpha\），若\（a\perp b\），＼（a\perp\alpha\），则（）A ＼（b\parallel\alpha\）B ＼（b\subset\alpha\）C ＼（b\perp\alpha\）D ＼（b\）与\（＼alpha\）相交或\（b\subset\alpha\）2、设\（＼alpha\），＼（＼beta\）是两个不同的平面，＼（l\），＼（m\）是两条不同的直线，且\（l\subset\alpha\），＼（m\subset\beta\），则下列命题中正确的是（）A 若\（l\parallel\beta\），则\（＼alpha\parallel\beta\）B 若\（＼alpha\perp\beta\），则\（l\perp m\）C 若\（l\perp m\），则\（＼alpha\perp\beta\）D 若\（＼alpha\parallel\beta\），则\（l\parallel m\）3、在正方体\（ABCD A_{1}B_{1}C_{1}D_{1}＼）中，＼（E\）为\（A_{1}C_{1}＼）的中点，则异面直线\（AE\）与\（CD_{1}＼）所成角的余弦值为（）A ＼（＼dfrac{＼sqrt{2}｝｛6}＼）B ＼（＼dfrac{＼sqrt{3}｝｛6}＼）C ＼（＼dfrac{＼sqrt{6}｝｛6}＼）D ＼（＼dfrac{＼sqrt{10}｝｛6}＼）二、填空题1、已知正三棱柱\（ABC A_{1}B_{1}C_{1}＼）的各棱长都为\（2\），＼（E\），＼（F\）分别是\（AB\），＼（A_{1}C_{1}＼）的中点，则\（EF\）的长为________。

(完整版)高中立体几何证明题精选

1、已知正方体1111ABCD A B C D-，O是底ABCD对角线的交点.求证：(１) C1O∥面11AB D；(2)1AC⊥面11AB D．2、正方体''''ABCD A B C D-中，求证：（1）''AC B D DB⊥平面；（2）''BD ACB⊥平面.3、正方体ABCD—A1B1C1D1中．(1)求证：平面A1BD∥平面B1D1C；(2)若E、F分别是AA1，CC1的中点，求证：平面EB1D1∥平面FBD．D1ODBAC1B1A1CA1AB1C1D1DGEFN MPC BA4、四面体ABCD 中，,,AC BD E F =分别为,AD BC 的中点，且22EF AC =， 90BDC ∠=o ，求证：BD ⊥平面ACD5、如图P 是ABC ∆所在平面外一点，,PA PB CB =⊥平面PAB ，M 是PC 的中点，N 是AB 上的点，3AN NB =（1）求证：MN AB ⊥；6、如图，在正方体1111ABCD A B C D -中，E 、F 、G 分别是AB 、AD 、11C D 的中点.求证：平面1D EF ∥平面BDG .7、如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点. （1）求证：1//A C 平面BDE ；（2）求证：平面1A AC ⊥平面BDE .8、已知ABCD 是矩形，PA ⊥平面ABCD ，2AB =，4PA AD ==，E 为BC 的中点．求证：DE ⊥平面PAE ；9、如图，在四棱锥P ABCD -中，底面ABCD 是060DAB ∠=且边长为a 的菱形，侧面PAD 是等边三角形，且平面PAD 垂直于底面ABCD ．（1）若G 为AD 的中点，求证：BG ⊥平面PAD ；（2）求证：AD PB ⊥；。

立体几何证明题练习

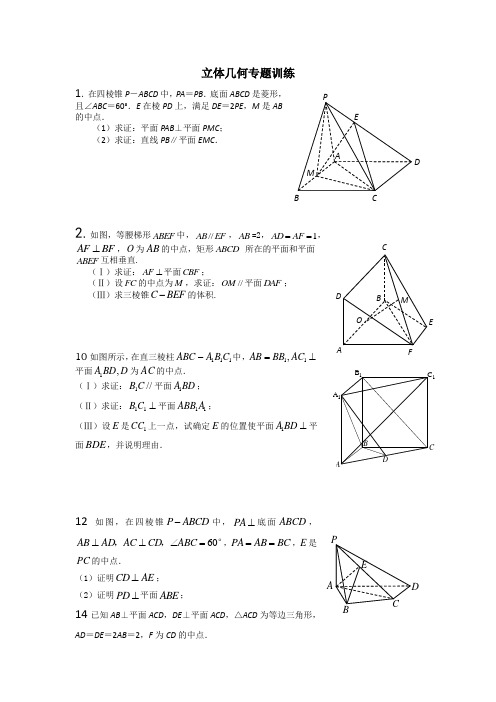
立体几何专题训练1．在四棱锥P －ABCD 中，PA ＝PB ．底面ABCD 是菱形，且∠ABC ＝60°．E 在棱PD 上，满足DE ＝2PE ，M 是AB 的中点．（1）求证：平面PAB ⊥平面PMC ；（2）求证：直线PB ∥平面EMC ．2.如图，等腰梯形ABEF 中，//AB EF ，AB =2，1AD AF ==，AF BF ⊥，O 为AB 的中点，矩形ABCD 所在的平面和平面ABEF 互相垂直.（Ⅰ）求证：AF ⊥平面CBF ；（Ⅱ）设FC 的中点为M ，求证：//OM 平面DAF ；（Ⅲ）求三棱锥C BEF -的体积.10如图所示，在直三棱柱111C B A ABC -中，⊥=11,AC BB AB 平面D BD A ,1为AC 的中点．（Ⅰ）求证：//1C B 平面BD A 1；（Ⅱ）求证：⊥11C B 平面11A ABB ；（Ⅲ）设E 是1CC 上一点，试确定E 的位置使平面⊥BD A 1平面BDE ，并说明理由．12如图，在四棱锥P ABCD -中，PA ⊥底面A B C D ，60AB AD AC CD ABC ⊥⊥∠=，，°，PA AB BC ==，E 是PC 的中点．（1）证明CD AE ⊥；（2）证明PD ⊥平面ABE ；14已知AB ⊥平面ACD ，DE ⊥平面ACD ，△ACD 为等边三角形，AD ＝DE ＝2AB ＝2，F 为CD 的中点．DAB CPEMBCDE FMO C 1B 1A 1DCBAACDPE(1)求证：AF ⊥平面CDE ； (2)求证：AF ∥平面BCE ；(3)求四棱锥C －ABED 的体积．15如图，菱形ABCD 所在平面与矩形ACEF 所在平面互相垂直，已知BD=2AF ，且点M 是线段EF 的中点.(1)求证：AM ∥平面BDE ； (2)求证：平面DEF ⊥平面BEF.18在直三棱柱ABC －A 1B 1C 1中，AC ＝3，BC ＝4，AB =5，AA 1＝4，点D 是AB 的中点，（1）求证：AC ⊥BC 1；（2）求证：AC 1//平面CDB 1；（3）求异面直线 AC 1与 B 1C 所成角的余弦值．BCDEFM19、如图所示，正方形与直角梯形所在平面互相垂直，，，.(1)求证：平面；（2）求四面体的体积.29、如图，平面平面，点E、F、O分别为线段PA、PB、AC的中点，点G是线段CO的中点，，．求证：（1）平面；（2）∥平面．33、已知在四棱锥P一ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=1，AB=2，E、F分别是AB、PD的中点。

高中立体几何证明平行的专题

FGG A B CD ECA BDE F DE B 1A 1C 1CM 立体几何——平行的证明【例1】如图，四棱锥P －ABCD 的底面是平行四边形，点E 、F 分别为棱AB 、 PD 的中点．求证：AF ∥平面PCE ；分析：取PC 的中点G ，连EG.，FG ，则易证AEGF 是平行四边形'【例2】如图，已知直角梯形ABCD 中，AB ∥CD ，AB ⊥BC ，AB ＝1，BC ＝2，CD ＝1＋3，过A 作AE ⊥CD ，垂足为E ，G 、F 分别为AD 、CE 的中点，现将△ADE 沿AE 折叠，使得DE ⊥EC 。

（Ⅰ）求证：BC ⊥面CDE ；（Ⅱ）求证：FG ∥面BCD ； &分析：取DB 的中点H ，连GH,HC 则易证FGHC 是平行四边形；【例3】已知直三棱柱ABC －A 1B 1C 1中，D, E, F 分别为AA 1, CC 1, AB 的中点， M 为BE 的中点, AC ⊥BE. 求证：（Ⅰ）C 1D ⊥BC ；（Ⅱ）C 1D ∥平面B 1FM. 分析：连EA ，易证C 1EAD 是平行四边形，于是MF -,,AD CD AD BA ⊥⊥//EB PAD 平面E F GM AD CD BD BC AM EFG 求证：E F BACDP （第1题图）AE;PEDCBAAB 1ABEF ⊥ABCD ABEF ABCD 090,BAD FAB BC ∠=∠=//=12AD BE //=12AF,G H ,FA FD BCHG ,,,C D F E ）利用平行四边形的性质【例9】正方体ABCD —A 1B 1C 1D 1中O 为正方形ABCD 的中心，M 为BB 1的中点，求证： D 1O21中点为PD E 求证：AE ∥平面PBC ； ~分析：取PC 的中点F ，连EF 则易证ABFE 是平行四边形【例11】在如图所示的几何体中，四边形ABCD 为平行四边形，∠ ACB=90︒，ＥＡ⊥平面ＡＢＣＤ，EF ∥ＡＢ，ＦＧ∥ＢＣ，ＥＧ∥ＡＣ.ＡＢ=２ＥＦ。

高中数学立体几何专题练习题1（含答案）

⾼中数学⽴体⼏何专题练习题1（含答案）⾼中数学⽴体⼏何专题练习题姓名班级学号得分说明：１、本试卷包括第Ⅰ卷（选择题）和第Ⅱ卷（⾮选择题）两部分。

满分100分。

考试时间90分钟。

２、考⽣请将第Ⅰ卷选择题的正确选项填在答题框内，第Ⅱ卷直接答在试卷上。

考试结束后，只收第Ⅱ卷第Ⅰ卷（选择题）⼀、选择题（每题2分，共40分）1、⼀个正⽅体的展开图如图所⽰，A、B、C、D为原正⽅体的顶点，则在原来的正⽅体中A.AB∥ CDB. AB与 CD相交C. AB⊥CDD. AB与CD所成的⾓为60°2、（多选）如果⼀个棱锥的底⾯是正⽅形，且顶点在底⾯内的射影是底⾯的中⼼，那么这样的棱锥叫正四棱锥．若⼀正四棱锥的体积为18，则该正四棱锥的侧⾯积最⼩时，以下结论正确的是（）．A．棱的⾼与底边长的⽐为 22B．侧棱与底⾯所成的⾓为π4C．棱锥的⾼与底⾯边长的⽐为 2 D．侧棱与底⾯所成的⾓为π33、某⼏何体的三视图如图所⽰，则该⼏何体的体积为（）A ．43B ．4C ．2D ．234、某⼏何体的三视图如图所⽰，则此⼏何体的体积为（）A.23 B. 1C.43D.135、已知圆锥的轴截⾯为正三⾓形，且边长为2，则圆锥的表⾯积为（） A ．3π3B ．πC ．2πD ．3π6、如图，在正⽅体中， E 为线段A 1C 1的中点，则异⾯直线与所成⾓的⼤⼩为（）度.A. 60B. 45C. 30D. 157、已知⼀个⽔平放置的平⾯四边形ABCD 的直观图是⾯积为2的正⽅形，则原四边形ABCD 的⾯积为（）A ．2B ．22C ．2 2D ．4 28、下列说法正确的是（）A ．通过圆台侧⾯上⼀点可以做出⽆数条母线B ．直⾓三⾓形绕其⼀边所在直线旋转⼀周得到的⼏何体是圆锥C ．圆柱的上底⾯下底⾯互相平⾏D ．五棱锥只有五条棱9、如图，是⼀个⼏何体的三视图，主视图和侧视图是全等的半圆，俯视图是⼀个圆，则该⼏何体的体积是（）A 、32π3．B ．26π3C ．16π3D ．64π310、某⼏何体的三视图如图所⽰，则该⼏何体的体积为（）A. 56B. 23C. 43D. 4511、⼀个⼏何体的三视图如图，则该⼏何体的体积为（）A.263 B .283C. 10D.32312、某⼏何体的三视图如图所⽰，则该⼏何体中的最长棱长为（）A ．3 2B ．2 5C ．2 6D ．2 713、(多选题）如图，在棱长为1的正⽅体中，下列结论正确的是A ．异⾯直线AC 与BC1所成的⾓为60°B ．直线AB 1与平⾯ABC 1D 1所成⾓为45° C ．⼆⾯⾓A-B 1C-B 的正切值为 2D ．四⾯体D 1-AB 1C 的的体积为1214、下列命题错误的是A ．不在同⼀直线上的三点确定⼀个平⾯B ．两两相交且不共点的三条直线确定⼀个平⾯C ．如果两个平⾯垂直，那么其中⼀个平⾯内的直线⼀定垂直于另⼀个平⾯D ．如果两个平⾯平⾏，那么其中⼀个平⾯内的直线⼀定平⾏于另⼀个平⾯15、某四棱锥的三视图如图所⽰，俯视图是⼀个等腰直⾓三⾓形，则该四棱锥的体积为（）A ．2B ．C. D ．16、如图所⽰，O 是正⽅体ABCD-A 1B 1C 1D 1对⾓线A 1C 与AC 1的交点，E 为棱BB 1的中点，则⼏何体OEC 1D 1 在正⽅体各⾯上的正投影不可能是（）A． B． C． D．17、如图，在正⽅体ABCD -A1B l C1D1中，已知E，F，G分别是线段A1C1上的点，且A1E=EF=FG =GC1．则下列直线与平⾯A1BD平⾏的是(A) CE (B) CF (C) CG (D) CC118、⼏何体的三视图如图所⽰，则它的体积是A． B．C． D．19、如图，三棱P-ABC中，PC⊥平⾯ABC，PC=3，∠ACB=90°D、E．分别为线段AB、BC上的点，且CD=DE= 2,CE=2EB=2,则⼆⾯⾓A-PD-C的余弦值是（）．A、 24B、62C、33D、3620、下图为某⼏何体的三视图，则该⼏何体的表⾯积是（）A. 6+4B. 4+4C. 6+2D. 4+2⼆、填空题（15分）21、如图，点P在长⽅体ABCD－A1B1C1D1的⾯对⾓线BC1（线段BC1）上运动，给出下列四个说法：①直线AD与直线B1P为异⾯直线；②恒有A1P∥⾯ACD1；③三棱锥A－D1PC的体积为定值；④当长⽅体各棱长都相等时，⾯PDB1⊥⾯ACD1．其中所有正确说法的序号是．22、已知⼀个⼏何体是由上下两部分构成的组合体，其三视图如下，若图中圆的半径为，等腰三⾓形的腰长为，则该⼏何体的体积是。