相似三角形中考题题型类
2024中考备考重难点重难点 相似三角形模型及其综合题综合训练(11大题型+满分技巧+限时分层检测)

重难点02 相似三角形模型及其综合题综合训练中考数学中《相似三角形模型及其综合题综合训练》部分主要考向分为五类:一、K型相似二、8字图相似三、A字图相似四、母子型相似五、手拉手相似相似三角形的综合题中各种相似模型的掌握是解决对应压轴题的便捷方法,所以本专题是专门针对相似三角形模型压轴题的,对提高类型的学生可以自主训练。
考向一:K型相似1.(2023•锡山区校级四模)如图,矩形ABCD中,AB=10,BC=8.点P在AD上运动(点P不与点A、D重合)将△ABP沿直线翻折,使得点A落在矩形内的点M处(包括矩形边界),则AP的取值范围是0<AP≤5,连接DM并延长交矩形ABCD的AB边于点G,当∠ABM=2∠ADG时,AP的长是25﹣5.【分析】根据矩形的性质得到AB=CD=5,BC=AD=4,∠A=∠C=∠D=90°,根据折叠的性质得到∠PMB=∠A=90°,BM=AB=5,根据勾股定理得到CM=3,DM=5﹣3=2,根据相似三角形的判定和性质定理即可得到结论;根据折叠的性质得到∠ABP=∠MBP,求得∠ABM=2∠ABP,根据相似三角形的性质得到==,设AP=5x,AG=4x,过M作MH⊥AD于H,根据折叠的性质得到AP=MP=5x,AM⊥BP,根据三角形中位线定理得到MN=AG=2x,根据勾股定理即可得到结论.【解答】解:当M落在CD上时,AP的长度达到最大,∵四边形ABCD是矩形,∴AB=CD=10,BC=AD=8,∠A=∠C=∠D=90°,∵△ABP沿直线翻折,∴∠PMB=∠A=90°,BM=AB=10,∴CM===6,∴DM=10﹣6=4,∴∠PMD+∠BMC=90°,∠PMD+∠MPD=90°,∴∠BMC=∠MPD,∴△PDM∽△MCB,∴=,∴=,∴PD=3,∴AP=8﹣3=5,∴AP的取值范围是0<AP≤5;如图,∵将△ABP沿直线翻折,使得点A落在矩形内的点M处,∴∠ABP=∠MBP,∴∠ABM=2∠ABP,∵∠ABM=2∠ADG,∴∠ABP=∠ADG,∵∠DAG=∠BAP,∴△ADG∽△ABP,∴==,设AP=5x,AG=4x,过M作MH⊥AD于H,∵将△ABP沿直线翻折,使得点A落在矩形内的点M处,∴AP=MP=5x,AM⊥BP,∴∠DAM=90°﹣∠BAM=∠ABP=∠ADG,∴AM=DM,∴DH=AH=4,HP=4﹣5x,∵∠BAD=∠MHA=90°,∴MH∥AG,∴MH为△ADG的中位线,∴MH=AG=2x,在Rt△PHM中,PM2=PH2+HM2,∴(5x)2=(2x)2+(4﹣5x)2,解得x1=5﹣,x2=5+(不合题意舍去),∴AP=5x=25﹣5.故答案为:0<AP≤5;25﹣5.2.(2023•福田区模拟)综合与探究在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使点C恰好落在AD边上的点F处.(1)如图①,若BC=2BA,求∠CBE的度数;(2)如图②,当AB=5,且AF•FD=10时,求EF的长;(3)如图③,延长EF,与∠ABF的角平分线交于点M,BM交AD于点N,当NF=AN+FD时,请直接写出的值.【分析】(1)由折叠的性质得出BC=BF,∠FBE=∠EBC,根据直角三角形的性质得出∠AFB=30°,可求出答案;(2)证明△F AB∽△EDF,由相似三角形的性质得出,可求出DE=2,求出EF=3,由勾股定理求出DF=,则可求出AF,即可求出BC的长;(3)过点N作NG⊥BF于点G,证明△NFG∽△BF A,,设AN=x,设FG=y,则AF =2y,由勾股定理得出(2x)2+(2y)2=(2x+y)2,解出y=x,则可求出答案.【解答】解:(1)∵四边形ABCD是矩形,∴∠C=90°,∵将△BCE沿BE翻折,使点C恰好落在AD边上点F处,∴BC=BF,∠FBE=∠EBC,∠C=∠BFE=90°,∵BC=2AB,∴BF=2AB,∴∠AFB=30°,∵四边形ABCD是矩形,∴AD∥BC,∴∠AFB=∠CBF=30°,∴∠CBE=∠FBC=15°;(2)∵将△BCE沿BE翻折,使点C恰好落在AD边上点F处,∴∠BFE=∠C=90°,CE=EF,又∵矩形ABCD中,∠A=∠D=90°,∴∠AFB+∠DFE=90°,∠DEF+∠DFE=90°,∴∠AFB=∠DEF,∴△F AB∽△EDF,∴,∴AF•DF=AB•DE,∵AF•DF=10,AB=5,∴DE=2,∴CE=DC﹣DE=5﹣2=3,∴EF=3;(3)过点N作NG⊥BF于点G,∵NF=AN+FD,∴NF=AD=BC,∵BC=BF,∴NF=BF,∵∠NFG=∠AFB,∠NGF=∠BAF=90°,∴△NFG∽△BF A,∴,设AN=x,∵BN平分∠ABF,AN⊥AB,NG⊥BF,∴AN=NG=x,AB=BG=2x,设FG=y,则AF=2y,∵AB2+AF2=BF2,∴(2x)2+(2y)2=(2x+y)2,解得y=x.∴BF=BG+GF=2x+x=x.∴=.3.(2023•桐柏县一模)【初步探究】(1)把矩形纸片ABCD如图①折叠,当点B的对应点B'在MN的中点时,填空:△EB'M∽△B'AN (“≌”或“∽”).【类比探究】(2)如图②,当点B的对应点B'为MN上的任意一点时,请判断(1)中结论是否成立?如果成立,请写出证明过程;如果不成立,请说明理由.【问题解决】(3)在矩形ABCD中,AB=4,BC=6,点E为BC中点,点P为线段AB上一个动点,连接EP,将△BPE沿PE折叠得到△B'PE,连接DE,DB',当△EB'D为直角三角形时,BP的长为或1.【分析】(1)由矩形纸片ABCD如图①折叠,可证△EB'M∽△B'AN;(2)同(1)由四边形ABCD是矩形,如图②折叠,可得∠EB'M=90°﹣∠AB'N=∠B'AN,即可得△EB'M ∽△B'AN,(3)分两种情况:当∠DB'E=90°时,证明Rt△CDE≌Rt△B'DE(HL),得B'D=CD=AB=4,设BP =x=B'P,在Rt△APD中,有(4﹣x)2+62=(x+4)2,可解得BP=;当∠B'ED=90°时,过B'作B'H⊥AB于H,作B'Q⊥BC于Q,则∠B'QE=∠C=90°,证明△B'EQ∽△EDC,可得==,设BP=y=B'P,在Rt△B'PH中,(﹣y)2+()2=y2,可解得BP=1.【解答】解:(1)∵四边形ABCD是矩形,∴∠B=90°,∵矩形纸片ABCD如图①折叠,∴∠EB'A=∠B=90°,∴∠EB'M=90°﹣∠AB'N=∠B'AN,∵∠EMB'=90°=∠B'NA,∴△EB'M∽△B'AN,故答案为:∽;(2)(1)中结论成立,理由如下:∵四边形ABCD是矩形,∴∠B=90°,∵矩形纸片ABCD如图①折叠,∴∠EB'A=∠B=90°,∴∠EB'M=90°﹣∠AB'N=∠B'AN,∵∠EMB'=90°=∠B'NA,∴△EB'M∽△B'AN;(3)如图所示,当∠DB'E=90°时,△EB'D是直角三角形,由折叠可得,∠PB'E=∠B=90°,BE=B'E=CE,∴∠DB'P=180°,即点P,B',D在一条直线上,在Rt△CDE和Rt△B'DE中,,∴Rt△CDE≌Rt△B'DE(HL),∴B'D=CD=AB=4,设BP=x=B'P,则AP=4﹣x,PD=x+4,在Rt△APD中,AP2+AD2=PD2,∴(4﹣x)2+62=(x+4)2,解得x=,∴BP=;如图所示,当∠B'ED=90°时,△EB'D是直角三角形,过B'作B'H⊥AB于H,作B'Q⊥BC于Q,则∠B'QE=∠C=90°,又∵∠B'ED=90°,∴∠B'EQ+∠CED=90°=∠EDC+∠CED,∴∠B'EQ=∠EDC,∴△B'EQ∽△EDC,∴==,∵CE=BE=BC=3,CD=4,∴DE==5,∵△BPE沿PE折叠得到△B'PE,∴B'E=BE=3,∴==,解得B'Q=,EQ=,∴BQ=BE﹣EQ==B'H,BH=B'Q=,设BP=y=B'P,则HP=BH﹣BP=﹣y,在Rt△B'PH中,HP2+B'H2=B'P2,∴(﹣y)2+()2=y2,解得y=1,∴BP=1.综上所述,BP的长为或1.考向二:8字图相似1.(2023•海州区校级二模)“关联”是解决数学问题的重要思维方式.角平分线的有关联想就有很多……【问题提出】(1)如图①,PC是△P AB的角平分线,求证:.小明思路:关联“平行线、等腰三角形”,过点B作BD∥P A,交PC的延长线于点D,利用“三角形相似”.小红思路:关联“角平分线上的点到角的两边的距离相等”,过点C分别作CD⊥P A交P A于点D,作CE⊥PB交PB于点E,利用“等面积法”.请根据小明或小红的思路,选择一种并完成证明.【理解应用】(2)如图②,在Rt△ABC中,∠BAC=90°,D是边BC上一点.连接AD,将△ACD沿AD所在直线折叠,使点C恰好落在边AB上的E点处,落AC=1,AB=2,则DE的长为.【深度思考】(3)如图③,△ABC中,AB=6,AC=4,AD为∠BAC的角平分线.AD的垂直平分线EF交BC延长线于点F,连接AF,当BD=3时,AF的长为6.【拓展升华】(4)如图④,PC是△P AB的角平分线,若AC=3,BC=1,则△P AB的面积最大值是3.【分析】(1)选择小明的思路,过点BD∥AP交PC的延长线于点D,易证△ACP∽△BCD,得到,由角平分线的性质和平行线的性质得∠BPC=∠D,可得PB=BD,等量代换即可证明;选择小红的思路,根据角平分线的性质得到CD=CE,再利用等面积;(2)利用(1)中的结论得到,再利用勾股定理即可解答;(3)利用(1)中的结论得到,再利用垂直平分线的性质得到∠B=∠F AC,再根据相似三角形得到AF的值;(4)作△APB的外角平分线PD,交AB的延长线于D,在AP的延长线上截取PE=PB,易得△BPD≌△EPD(SAS),由(1)结论可得,由等量代换可得,利用(1)中的结论得到,求得⊙O的半径为,当P运动到点P′,P′O⊥AD时,△APB的面积最大,计算即可.【解答】(1)证明:选择小明的思路,如图,过点BD∥AP交PC的延长线于点D,∵BD∥AP,∴∠APC=∠D,又∵∠ACP=∠BCD,∴△ACP∽△BCD,∴,∵PC是△P AB的角平分线,∴∠APC=∠BPC,∴∠BPC=∠D,∴PB=BD,∴;选择小红的思路,如图,过点C分别作CD⊥P A交P A于点D,作CE⊥PB交PB于点E,作PF⊥BC于点F,∵PC是△P AB的角平分线,∴CD=CE,∴,,,,∴BC•PF=PB•CE,P A•CD=AC•PF,∴,∴,∴.(2)解:∵将△ACD沿AD所在直线折叠点C恰好落在边AB上的E点处,∴AD平分∠BAC,∴,∵AC=1,AB=2,∴,∴BD=2CD,∵∠BAC=90°,∴,∴,∴,∴,∴;故答案为:;(3)解:∵AD为∠BAC的角平分线,∴,∠BAD=∠DAC,∵△ABC中,AB=6,AC=4,BD=3,∴,∴CD=2,∵AD的垂直平分线EF交BC延长线于F,∴AF=DF,∴∠F AD=∠FDA,∵∠F AD=∠F AC+∠DAC,∠FDA=∠B+∠BAD,∴∠B=∠F AC,∵∠AFB=∠CF A,∴△FBA∽△F AC,∴,∴,∴AF=6,故答案为:6.(4)解:如图,在AP的延长线上截取PE=PB,作△APB的外角平分线PD,交AB的延长线于D,∵PD是△APB的外角平分线,∴∠BPD=∠EPD,又∵PD=PD,∴△BPD≌△EPD(SAS),∴DB=DE,∠BDP=∠EDP,∴,∵PE=PB,DB=DE,∴,∵PC是△APB的角平分线,∴,∴,∴,∴,∴BD=2,∴CD=3,∵,∴点P在以半径为的⊙O上,如图,当P运动到点P′,P′O⊥AD时,△APB的面积最大,最大值为,故答案为:3.2.(2023•衢州二模)如图1,在正方形ABCD中,点E在线段BC上,连接AE,将△ABE沿着AE折叠得到△AFE,延长EF交CD于点G.(1)求证:DG=FG;(2)如图2,当点E是BC中点时,求tan∠CGE的值;(3)如图3,当时,连接CF并延长交AB于点H,求的值.【分析】(1)由“HL”可证Rt△AFG≌Rt△ADG,可得DG=FG;(2)由勾股定理可求GF的长,即可求解;(3)由勾股定理可求BC=CD=6x,由面积法可求FN的长,即可求FM的长,通过证明△MFH∽△NFC,可得=,即可求解.【解答】(1)证明:∵四边形ABCD是正方形,∴AB=AD,∠B=∠D=90°,∵将△ABE沿着AE折叠得到△AFE,∴AB=AF,∠B=∠AFE=90°,∴AD=AF,又∵AF=AD,∴Rt△AFG≌Rt△ADG(HL),∴DG=FG;(2)解:设BC=CD=2a,∵点E是BC的中点,∴BE=CE=a,∵将△ABE沿着AE折叠得到△AFE,∴BE=EF=a,∵EG2=EC2+CG2,∴(a+DG)2=a2+(2a﹣DG)2,∴DG=a,∴tan∠CGE===;(3)如图3,过点F作MN⊥AB于M,交CD于N,∵MN⊥AB,∠ABC=∠BCD=90°,∴四边形BCNM是矩形,∴BC=MN,∵,∴设BE=2x,DG=3x,则EG=5x,∵EG2=EC2+CG2,∴25x2=(CD﹣2x)2+(CD﹣3x)2,∴CD=6x(负值舍去),∴BC=6x,∴EC=4x,CG=3x,∵S△CFG=S△ECG,∴CG•FN=EC•CG,∴FN=x,∴MF=x,∵AB∥CD,∴△MFH∽△NFC,∴=,∴==,∴=.考向三:A字图相似1.(2023•宿城区一模)如图,在矩形ABCD中,AB=5,AD=3,先将△ABC沿AC翻折到△AB′C处,再将△AB'C沿翻折到△AB'C'处,延长CD交AC′于点M,则DM的长为.【分析】过点C′作C′E⊥AD的延长线于点E,设CD与AB′交于点G,根据矩形性质和翻折性质,设B′G=DG=x,CG=CD﹣DG=5﹣x,利用勾股定理求出x的值,证明△ADG∽△AB′F,求出B′F=,然后证明△CDF≌△AB′F(AAS),得DF=B′F=,再由△C′EF∽△CDF,得==,求出C′E=,EF=,证明△ADM∽△AEC′,对应边成比例即可求出DM的长.【解答】解:如图,过点C′作C′E⊥AD的延长线于点E,设CD与AB′交于点G,∵四边形ABCD是矩形,∴AB=CD=5,AD=BC=3,AB∥CD,∴∠BAC=∠DCA,由翻折可知:∠BAC=∠B′AC,∴∠B′AC=∠DCA,∴GA=GC,由翻折可知:B′A=BA=5,B′C=BC=B′C′=3,∴B′A=CD=5,∴B′G=DG,设B′G=DG=x,∴CG=CD﹣DG=5﹣x,在Rt△B′CG中,根据勾股定理得:B′G2+B′C2=CG2,∴x2+32=(5﹣x)2,∴x=,∴B′G=DG=x=,∴AG=CG=5﹣x=,∵∠DAG=∠B′AF,∠ADG=∠AB′F=90°,∴△ADG∽△AB′F,∴=,∴=,∴B′F=,∴C′F=C′B′﹣B′F=3﹣=,CF=CB′+B′F=3+=,∵∠CFD=∠AFB′,∠CDF=∠AB′F=90°,CD=AB′,∴△CDF≌△AB′F(AAS),∴DF=B′F=,∵C′E⊥AD,CD⊥AD,∴C′E∥CD,∴△C′EF∽△CDF,∴==,∴==,∴C′E=,EF=,∴DE=DF+EF=+=,∴AE=AD+DE=3+=,∵C′E∥DM,∴△ADM∽△AEC′,∴=,∴=,∴DM=.故答案为:.2.(2023•沙坪坝区校级模拟)如图,△ABC中,D在AB上,E在BC上,∠AED=∠ABC,F在AE上,EF=DE.(1)如图1,若CE=BD,求证:BE=CF;(2)如图2,若CE=AD,G在DE上,∠EFG=∠EFC,求证:CF=2GF;(3)如图3,若CE=AD,EF=2,∠ABC=30°,当△CEF周长最小时,请直接写出△BCF的面积.【分析】(1)先说明∠FEC=∠EDB,然后用SAS证明△FEC≌△EDB,得到BE=CF;(2)仿照(1)得△FEC≌△EDH,出现中点倍长中线,利用相似得CF=2GF;(3)先说明∠CJE=30°,即点C的轨迹是条直线,然后考虑将军饮马,最后求△BCF的面积.【解答】(1)证明:∵∠DEC=∠AED+∠FEC,∠DEC=∠ABC+∠EDB,∠AED=∠ABC,∴∠FEC=∠EDB,∵EF=DE,CE=BD,∴△FEC≌△EDB(SAS),∴BE=CF;(2)证明:延长AB至H使DH=AD,由(1)得△FEC≌△EDH,∴FC=HE,∠CFE=∠HED,延长ED至I使DI=ED,连接AI,则EF=DE=IE,∵DH=AD,∠ADI=∠HDE,∴△ADI≌△HDE(SAS),∴AI=HE,∠HED=∠AID,∴AI=FC,∠AID=∠CFE,∵∠EFG=∠EFC,∴∠EFG=∠AID,∵∠FEG=∠IEA,∴△FEG∽△IEA,∴=,∴=,∴CF=2GF;(3)解:延长FE至J使EJ=EF,∵EF=DE∴EJ=DE∵∠FEC=∠EDB,∴∠CEJ=∠ADE,∵CE=AD,∴△CEJ≌△ADE(SAS),∴∠CJE=∠AED,∵∠AED=∠ABC,∠ABC=30°,∴∠CJE=30°,过E作JC的对称点E',连接CE'、FE'、CE'、JE',C△CEF=EF+CF+CE=2+CF+CE'≥2+FE',∴当F、C、E'三点共线时周长最小,当周长最小时如图所示:∵∠CJE=30°,∴∠EJE'=60°,∵JE=JE',∴△EJE'是正三角形,∴∠JEE'=60°,EE'=EJ=EF,∴∠EFE'=∠EE'F=30°,∵CE=CE',∴∠CEE'=∠EE'F=30°,∴∠CEJ=90°,∴∠FEC=90°,∴EC===,∵∠AED=30°,∴∠BED=60°,∴∠BDE=90°,∴BE=2DE=4,∴S△BCF=×BC×EF=BC=BE+EC=4+.3.(2023•中山区模拟)如图,在平面直角坐标系中,直线y=﹣x+4与x轴,y轴分别交于点A、B,点P 为射线AO上的一个动点,过点P作PQ⊥AB于点Q,将沿PQ翻折得到R.设△PQR与△AOB重合部分的面积为S,点P的坐标为(m,0).(1)求AR的长.(用含m的代数式表示)(2)求S关于m的函数解析式,并直接写出自变量m的取值范围.【分析】(1)求出直线y=﹣x+4与x轴,y轴分别交于点A、B的坐标,得到OA,OB的长,利用勾股定理求AB得长.证出△PQA∽△BOA,利用对应线段成比例,求出AR.(2)点P为射线AO上的一个动点,在移动过程中,△PQR与△AOB重合部分有三种形状,①直角三角形②四边形③直角三角形.分类讨论,利用三角形相似对应边成比例,找边之间的转换关系,解决问题.【解答】解:(1)直线y=﹣x+4与x轴,y轴分别交于点A、B,当x=0时,y=4,∴点B坐标(0,4),∴OB=4.当y=0时,x=3,∴点A坐标(3,0),∴OA=3.Rt△AOB中,AB2=OA2+OB2,∴AB=5.∵∠P AQ=∠BAC,∠AQP=∠AOB,∴△PQA∽△BOA,∴,AQ=,AR=2AQ=.(2)在移动过程中,△PQR与△AOB重合部分有三种形状.①点P在线段OA上,△PQR与△AOB重合部分是△PQR.当0≤m<3时,∵∠P AQ=∠BAC,∠AQP=∠AOB,∴△PQA∽△BOA,∴S△APQ:S△ABO=AP2:AB2=(3﹣m)2:25,∵S△ABO==6,又∵△PQR≌△PQA,∴S=(3﹣m)2.②△PQR与△AOB重合部分是四边形CDRQ.作RE⊥OA于E,QF⊥OA于F.当R和B重合时,Q为AB中点,AQ=2.5,∵△PQA∽△BOA,∴,∴AP===,∴OP=AP﹣AO=﹣3=,∴m=.∴当<m<0时,△PQR与△AOB重合部分是四边形CDRQ.∵△PQA∽△BOA,∴∠APQ=∠ABO,∵∠AOB=∠OFQ,∴△AOB∽△QFP,∴,∴=,同理,∴,∴,∵AP=3﹣m,∴F A=.∴QF=AF×=(3﹣m).∴RE=2QF=(3﹣m),∴PE=P A﹣2AF=,∵OD∥RE,∴,∴OD===﹣,∵,∴OC=﹣m,∴CD=OD﹣OC=﹣=﹣m.∵S=S△PQR﹣S△PCD∴S=×P A×QF﹣×OP×CD=.,③△PQR与△AOB重合部分是△BQC,当Q、B重合时,AQ=5,∴AP=,OP==,m=,当时,△PQR与△AOB重合部分是△BQC.∵OC=OP=﹣,∴BC=4﹣OC=,∵CQ=,BQ=,∴S===,∴S=.考向四:母子型相似1.(2023•樊城区模拟)【基础巩固】(1)如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=AD•AB.【尝试应用】(2)如图2,在▱ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF =6,AD=9,求CE的长.【拓展提高】(3)如图3,在菱形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,AC=2EF,连接DE、DF分别交AC于M,N,∠EDF=∠BAD,DF=AE,若MN=18,求EF的值.【分析】(1)证△ADC∽△ACB,得=,即可得出结论;(2)证△BFE∽△BCF,得=,则BF2=BE•BC,求出BC=4,即可得出结论;(3)延长EF与DC相交于点G,证四边形AEGC为平行四边形,得EG=AC=2EF,CG=AE,∠EAC =∠G,设EF=x,则EG=2x,再证△EDF∽△EGD,得==,则ED=x,==,设CG=AE=k,则DF=2k,DG=CD+k,求出CD=3k,然后证△AEM∽△CDM,得==,进而证△DEF∽△DMN,得==,即可得出结论.【解答】(1)证明:∵∠ACD=∠B,∠A=∠A,∴△ADC∽△ACB.∴=,∴AC2=AD•AB;(2)解:∵四边形ABCD是平行四边形,∴BC=AD=9,∠A=∠C,又∵∠BFE=∠A,∴∠BFE=∠C.又∵∠FBE=∠CBF,∴△BFE∽△BCF.∴=,∴BF2=BE•BC,即62=9BE,∴BE=4,∴CE=BC﹣BE=9﹣4=5,即CE的长为5;(3)解:如图,延长EF与DC相交于点G,∵四边形ABCD是菱形,∴AB∥CD,AD=CD,∠DAC=∠BAD,∴∠DAC=∠DCA=∠BAD,∵EF∥AC,∴四边形AEGC为平行四边形,∠DCA=∠G,∴EG=AC=2EF,CG=AE,∠EAC=∠G,设EF=x,则EG=2x,∵∠EDF=∠BAD,∴∠DAC=∠DCA=∠EDF,∴∠EDF=∠G,又∵∠DEF=∠GED,∴△EDF∽△EGD,∴==,∴ED2=EF•EG=x•2x=2x2,∴ED=x(负值已舍去),∴==,设CG=AE=k,则DF=2k,DG=CD+k,∴=,解得:CD=3k,∵AB∥CD,∴△AEM∽△CDM,∴===,∴=,∵EF∥AC,∴△DEF∽△DMN,∴==,∴EF=MN=×18=24,即EF的值为24.2.(2023•润州区二模)如图1,在△ABC中,点D在边AB上,点P在边AC上,若满足∠BPD=∠BAC,则称点P是点D的“和谐点”.(1)如图2,∠BDP+∠BPC=180°.①求证:点P是点D的“和谐点”;②在边AC上还存在某一点Q(不与点P重合),使得点Q也是点D的“和谐点”,请在图2中仅用圆规作图,找出点Q的位置,并写出证明过程.(保留作图痕迹)(2)如图3,以点A为原点,AB为x轴正方向建立平面直角坐标系,已知点B(6,0),C(2,4),点P在线段AC上,且点P是点D的“和谐点”.①若AD=1,求出点P的坐标;②若满足条件的点P恰有2个,直接写出AD长的取值范围是≤AD<.【分析】(1)①由∠BDP+∠BPC=180°考虑平角APC,只要证明∠BPD=∠BAC即可;②分别做线段DB、BP的中垂线,两条中垂线交于点O,则O为△PDB的外心,以O为圆心,OP为半径作圆交AC于点Q,点Q即为所求.用同弧所对的圆周角相等证明;(2)①通过△PBD∽△ABP求出BP的长度,然后求出直线AC的表达式为:y=2x,设点P的坐标为(x,2x),利用B、P两点间的距离公式解方程求出点P;②求出两个临界状态时的AD:一是当点P与点C重合时;二是△BDP的外接圆与线段AC恰有一个交点时.【解答】(1)①证明:∵∠BDP+∠BPC=180°,∠BDP=∠BAC+∠APD,∴∠BAC+∠APD+∠BPC=180°,∵∠APD+∠BPD+∠BPC=180°,∴∠BPD=∠BAC,∴点P是点D的“和谐点”;②解:以B为圆心,BP为半径作弧交AC于点Q,点Q即为所求,如图:连接BQ,∵∠BDP=∠BAC+∠APD,∠BPD=∠BAC,∴∠BDP=∠BPD+∠APD,∵∠APD+∠BPD+∠BPC=180°,∴∠BDP+∠BPC=180°,∵BP=BQ,∴∠BPC=∠BQP,∴∠BDP+∠BQP=180°,∴B、Q、P、D四点共圆,∴∠BPD=∠DQB,∵∠BPD=∠BAC,∴∠DQB=∠BAC,∴Q也是点D的“和谐点”;(2)解:①∵∠BPD=∠BAP,∠PBD=∠ABP,∴△PBD∽△ABP,∴=,=,∴BP=,∵C(2,4),∴直线AC的表达式为:y=2x,设点P的坐标为(x,2x),∵点B(6,0),∴(x﹣6)2+(2x)2=30,∴5x2﹣12x+6=0,∴x1=,x2=,∴P(,)或(,);②当点P与点C重合时,△BDP的外接圆与线段AC恰有两个交点,恰有两个“和谐点”,如图:∵点B(6,0),C(2,4),∴BC==4,由①知△PBD∽△ABP,∴=,即=,∴BD=,∴AD=AB﹣BD=6﹣=;当△BDP的外接圆与线段AC恰有一个交点时,如图:此时△BDP的外接圆与线段AC相切,则AP⊥PB,且PB为直径,∴∠PDB=90°,∵点P的坐标为(x,2x),∴AD=x,PD=2x,BD=AB﹣AD=6﹣x,∵∠P AD+∠PBD=90°,∠P AD+∠APD=90°,∴∠APD=∠PBD,∵∠ADP=∠PDB=90°,∴△ADP∽△PDB,∴=,∴PD2=AD•DB,即(2x)2=x(6﹣x),∴x=,∴AD=;综上,若满足条件的点P恰有2个,AD长的取值范围是≤AD<,故答案为:≤AD<.考向五:手拉手相似1.(2023•宝安区校级三模)【问题背景】已知D、E分别是△ABC的AB边和AC边上的点,且DE∥BC,则△ABC∽△ADE,把△ADE绕着A逆时针方向旋转,连接BD和CE.①如图2,找出图中的另外一组相似三角形△BAD∽△CAE;②若AB=4,AC=3,BD=2,则CE=;【迁移应用】在Rt△ACB中,∠BAC=90°,∠C=60°,D、E,M分别是AB、AC、BC中点,连接DE和CM.①如图3,写出CE和BD的数量关系BD=EC;②如图4,把Rt△ADE绕着点A逆时针方向旋转,当D落在AM上时,连接CD和CE,取CD中点N,连接MN,若,求MN的长.【创新应用】如图5:,BC=4,△ADE是直角三角形,∠DAE=90°,tan∠ADE=2,将△ADE绕着点A旋转,连接BE,F是BE上一点,,连接CF,请直接写出CF的取值范围.【分析】【问题背景】①结论:△BAD∽△CAE.利用两边成比例夹角相等两三角形相似证明;②利用相似三角形的性质求解;【迁移应用】①结论:BD=CE,证明AB=AC,可得结论;②连接BD,利用相似三角形的性质,求出BD,再利用三角形的中位线定理求解即可;【创新应用】如图5中,过点A作AK⊥BC于点K,过点C作CJ⊥AB于点J,连接FJ.通过计算证明FJ∥AE,求出JF,JC,可得结论.【解答】解:【问题背景】①如图2中,∵△ABC∽△ADE,∴=,∴=,∵∠BAC=∠DAE,∴∠BAD=∠CAE,∴△BAD∽△CAE.故答案为:△BAD∽△CAE;②∵△BAD∽△CAE,∴=,∴=,∴CE=.故答案为:;【迁移应用】①如图3中,在Rt△ABC中,∠BAC=90°,∠C=60°,∴tan60°=,∴AB=AC,∵BD=AB,EC=AC,∴BD=EC.故答案为:BD=EC;②如图4中,连接BD,MN.∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∵==,∴△BAD∽△CAE,∴==,∵EC=2,∴BD=6,∵BM=CM,DN=CN,∴MN=BD=3;【创新应用】如图5中,过点A作AK⊥BC于点K,过点C作CJ⊥AB于点J,连接FJ.∵AB=AC=2,AK⊥BC,∴BK=CK=2,∴AK===4,∵•BC•AK=•AB•CJ,∴CJ=,∴AJ===,∴BJ=AJ=2﹣=,∴BJ:AB=2:5,∵BF:BE=2:5,∴==,∴FJ∥AE,∴△BJF∽△BAE,∴==,∴JF=AE=,∴CJ﹣JF≤CF≤FJ+CJ,∴≤CF≤.2.(2023•东港市二模)(1)问题发现:如图1,已知正方形ABCD,点E为对角线AC上一动点,将BE绕点B顺时针旋转90°到BF处,得到△BEF,连接CF.填空:①=1;②∠ACF的度数为90°;(2)类比探究:如图2,在矩形ABCD和Rt△BEF中,∠EBF=90°,∠ACB=∠EFB=60°,连接CF,请分别求出的值及∠ACF的度数;(3)拓展延伸:如图3,在(2)的条件下,将点E改为直线AC上一动点,其余条件不变,取线段EF 的中点M,连接BM,CM,若,则当△CBM是直角三角形时,请直接写出线段CF的长.【分析】(1)①由旋转的性质得出BE=BF,∠EBF=90°,由正方形的性质得出∠ABC=90°,AB=BC,证明△ABE≌△CBF(SAS),由全等三角形的性质得出AE=CF,则可得出答案;②由全等三角形的性质及等腰直角三角形的性质得出答案;(2)证明△ABE∽△CBF,由相似三角形的性质可得出,则可得出结论;(3)求出EF=2CM=2,设CF=x,则AE=x,分两种情况解答,由勾股定理可求出答案.【解答】解:(1)①∵将BE绕点B顺时针旋转90°到BF处,∴BE=BF,∠EBF=90°,∵四边形ABCD是正方形,∴∠ABC=90°,AB=BC,∴∠ABE=∠CBF,∴△ABE≌△CBF(SAS),∴AE=CF,∴=1,故答案为:1;②∵四边形ABCD是正方形,∴∠BAC=∠ACB=45°,∵△ABE≌△CBF,∴∠BAE=∠BCF=45°,∴∠ACF=∠ACB+∠BCF=45°+45°=90°.故答案为:90°;(2),∠ACF=90°.理由如下:∵四边形ABCD是矩形,∴∠ABC=90°,∵∠ACB=60°,∴,同理在Rt△EBF中,∠EFB=60°,∴,∴,∵∠ABC=∠EBF,∴∠ABC﹣∠EBC=∠EBF﹣∠EBC,即∠ABE=∠CBF,∴△ABE∽△CBF,∴,∴∠BCF=∠BAE=30°,∴∠ACF=∠ACB+∠BCF=60°+30°=90°.(3)由(2)知,∵AB=2,∴CB=2,∵△ABE∽△CBF,∴∠ABE=∠CBF,∴∠EBF=∠EBC+∠CBF=∠EBC+∠ABE=∠ABC=90°,∵M为EF的中点,∴BM=EF,由(2)知∠ACF=90°,∴CM=EF,∴BM=CM,又∵△CBM是直角三角形,∴CM=BC=,∴EF=2CM=2,设CF=x,则AE=x,∵∠CAB=30°,BC=2,∴AC=2BC=4,∴CE=AC﹣AE=4﹣x,∵∠ECF=90°,∴CE2+CF2=EF2,∴,∴x=﹣1或x=+1(不合题意,舍去),当∠MBC=90°或∠MCB=90°时,点M不存在,当E在AC延长线上时,设CF=x,则AE=x,∵∠CAB=30°,BC=2,∴AC=2BC=4,∴CE=AE﹣AC=x﹣4,∵∠ECF=90°,∴CE2+CF2=EF2,∴,∴x=﹣1(不合题意,舍去)或x=+1,综上所述,CF的长为﹣1或+1.3.(2023•晋中模拟)综合与实践问题情境:(1)如图1,在△ABC和△ADE中,AB=AC,AD=AE.如图2,将△ABC绕顶点A按逆时针方向旋转15°得到△AB'C',连接B′D,C′E,求证:B′D=C′E.深入研究:(2)①如图3,在正方形ABCD和正方形CEFG中,已知点B,C,E在同一直线上,连接DE,AF,交于点P,求AF:DE的值;②如图4,若将正方形CEFG绕点C按顺时针方向旋转一定角度,AF:DE的值变化吗?请说明理由.拓展应用:(3)如图5,若把正方形ABCD和正方形CEFG分别换成矩形ABCD和矩形CEFG,且AD:AB=CG:CE=k,请直接写出此时AF:DE的值.【分析】(1)根据旋转的性质得到∠DAB'=∠EAC',然后用SAS判定△DAB'=△EAC'即可得证;(2)①连接AC、CF,根据正方形的性质得到对应边成比例,对应角相等,判定△ACF∽△DCE后即可求出AF:DE的值;②根据正方形的性质和旋转的性质判定△ACF∽△DCE后求出AF:DE的值即可证明AF:DE的值没有变化;(3)连接AC、CF,根据矩形的性质得到对应边成比例,对应角相等,判定△ACF∽△DCE后即可求出AF:DE的值.【解答】(1)证明:由旋转得:∠DAB'=∠EAC',又∵AB'=AC',AD=AE,∴△DAB'≌△EAC',∴B′D=C′E;(2)解:①如图1,连接AC、CF,∵四边形ABCD,CEFG是正方形,∴∠ACF=∠DCE=90°,AC=CD,CF=CE,∴,∴△ACF∽△DCE,∴,即AF:DE=:1;②成立.证明如下:如图2,连接AC、CF,∵四边形ABCD,CEFG是正方形,∴∠ACD=∠FCE,∴∠ACF=∠DCE,∵AC=CD,CF=CE,∴,∴△ACF∽△DCE,∴AF:DE=AC:CD=:1,∴不变;(3)解:如图3,连接AC、CF,∵四边形ABCD,CEFG是矩形,且AD:AB=CG:CE=k,∴∠ACD=∠FCE,AC=CD,CF=CE,∴∠ACF=∠DCE,,∴△ACF∽△DCE,∴.(建议用时:150分钟)1.(2023•菏泽)(1)如图1,在矩形ABCD中,点E,F分别在边DC,BC上,AE⊥DF,垂足为点G.求证:△ADE∽△DCF.【问题解决】(2)如图2,在正方形ABCD中,点E,F分别在边DC,BC上,AE=DF,延长BC到点H,使CH=DE,连接DH.求证:∠ADF=∠H.【类比迁移】(3)如图3,在菱形ABCD中,点E,F分别在边DC,BC上,AE=DF=11,DE=8,∠AED=60°,求CF的长.【分析】(1)由矩形的性质得∠C=∠ADE=90°,再证∠AED=∠DFC,即可得出结论;(2)证Rt△ADE≌Rt△DCF(HL),得DE=CF,再证△DCF≌△DCH(SAS),得∠DFC=∠H,然后由平行线的性质得∠ADF=∠DFC,即可得出结论;(3)延长BC至点G,使CG=DE=8,连接DG,△ADE≌△DCG(SAS),得∠DGC=∠AED=60°,AE=DG,再证△DFG是等边三角形,得FG=DF=11,即可解决问题.【解答】(1)证明:∵四边形ABCD是矩形,∴∠C=∠ADE=90°,∴∠CDF+∠DFC=90°,∵AE⊥DF,∴∠DGE=90°,∴∠CDF+∠AED=90°,∴∠AED=∠DFC,∴△ADE∽△DCF;(2)证明:∵四边形ABCD是正方形,∴AD=DC,AD∥BC,∠ADE=∠DCF=90°,∵AE=DF,∴Rt△ADE≌Rt△DCF(HL),∴DE=CF,∵CH=DE,∴CF=CH,∵点H在BC的延长线上,∴∠DCH=∠DCF=90°,又∵DC=DC,∴△DCF≌△DCH(SAS),∴∠DFC=∠H,∵AD∥BC,∴∠ADF=∠DFC,∴∠ADF=∠H;(3)解:如图3,延长BC至点G,使CG=DE=8,连接DG,∵四边形ABCD是菱形,∴AD=DC,AD∥BC,∴∠ADE=∠DCG,∴△ADE≌△DCG(SAS),∴∠DGC=∠AED=60°,AE=DG,∵AE=DF,∴DG=DF,∴△DFG是等边三角形,∴FG=DF=11,∵CF+CG=FG,∴CF=FG﹣CG=11﹣8=3,即CF的长为3.2.(2023•济南)在矩形ABCD中,AB=2,AD=2,点E在边BC上,将射线AE绕点A逆时针旋转90°,交CD延长线于点G,以线段AE,AG为邻边作矩形AEFG.(1)如图1,连接BD,求∠BDC的度数和的值;(2)如图2,当点F在射线BD上时,求线段BE的长;(3)如图3,当EA=EC时,在平面内有一动点P,满足PE=EF,连接P A,PC,求P A+PC的最小值.【分析】(1)由锐角三角函数可求∠BDC=60°,通过证明△ADG∽△ABE,可得;(2)由“AAS”可证△ABE≌△GMF,可得BE=MF,AB=GM=2,由锐角三角函数可求MF=BE=x,DG=2+x,利用(1)的结论可求解;(3)通过证明△AGC是等边三角形,可得PE=EF=AG=4,由旋转的性质可得P A=P'C,∠PEP'=120°,EP=EP'=4,则当点P,C,P′三点共线时,P A+PC的值最小,即可求解.【解答】解:(1)∵矩形ABCD中,AB=2,,∴∠C=90°,CD=AB=2,,∴,∴∠BDC=60°,∵∠ABE=∠BAD=∠EAG=∠ADG=90°,∴∠EAG﹣∠EAD=∠BAD﹣∠EAD,即∠DAG=∠BAE,∴△ADG∽△ABE,∴;(2)如图2,过点F作FM⊥CG于点M,∵∠ABE=∠AGF=∠ADG=90°,AE=GF,∴∠BAE=∠DAG=∠CGF,∠ABE=∠GMF=90°,∴△ABE≌△GMF(AAS),∴BE=MF,AB=GM=2,∴∠MDF=∠BDC=60°,FM⊥CG,∴,∴,设DM=x,则,∴DG=GM+MD=2+x,由(1)可知:,∴,解得x=1,∴;(3)如图3,连接AC,将△AEP绕点E顺时针旋转120°,EA与EC重合,得到△CEP',连接PP',矩形ABCD中,AD=BC=,AB=2,∴tan∠ACB==,∴∠ACB=30°,∴AC=2AB=4,∵EA=EC,∴∠EAC=∠ACE=30°,∠AEC=120°,∴∠ACG=∠GAC=90°﹣30°=60°,∴△AGC是等边三角形,AG=AC=4,∴PE=EF=AG=4,∵将△AEP绕点E顺时针旋转120°,EA与EC重合,得到△CEP',∴P A=P'C,∠PEP'=120°,EP=EP'=4,∴,∴当点P,C,P′三点共线时,P A+PC的值最小,此时为.3.(2023•武汉)问题提出如图(1),E是菱形ABCD边BC上一点,△AEF是等腰三角形,AE=EF,∠AEF=∠ABC=α(α≥90°),AF交CD于点G,探究∠GCF与α的数量关系.问题探究(1)先将问题特殊化,如图(2),当α=90°时,直接写出∠GCF的大小;(2)再探究一般情形,如图(1),求∠GCF与α的数量关系.问题拓展将图(1)特殊化,如图(3),当α=120°时,若,求的值.【分析】问题探究(1)如图(2)中,在BA上截取BJ,使得BJ=BE.证明△EAJ≌△FEC(SAS),推出∠AJE=∠ECF,可得结论;(2)结论:∠GCF=α﹣90°;在AB上截取AN,使AN=EC,连接NE.证明方法类似;问题拓展解:过点A作CD的垂线交CD的延长线于点P,设菱形的边长为3m.用m表示出BE,CE,可得结论.【解答】解:问题探究(1)如图(2)中,在BA上截取BJ,使得BJ=BE.∵四边形ABCD是正方形,∴∠B=∠BCD=90°,BA=BC,∵BJ=BE,∴AJ=EC,∵∠AEC=∠AEF+∠CEF=∠BAE+∠B,∠AEF=∠B=90°,∴∠CEF=∠EAJ,∵EA=EF,∴△EAJ≌△FEC(SAS),∴∠AJE=∠ECF,∵∠BJE=45°,∴∠AJE=180°﹣45°=135°,∴∠ECF=135°,∴∠GCF=∠ECF﹣∠ECD=135°﹣90°=45°;(2)结论:∠GCF=α﹣90°;理由:在AB上截取AN,使AN=EC,连接NE.∵∠ABC+∠BAE+∠AEB=∠AEF+∠FEC+∠AEB=180°,∠ABC=∠AEF,∴∠EAN=∠FEC.∵AE=EF,∴△ANE≌△ECF(SAS).∴∠ANE=∠ECF.∵AB=BC,∴BN=BE.∵∠EBN=α,∴,∴∠GCF=∠ECF﹣∠BCD=∠ANE﹣∠BCD=;问题拓展:过点A作CD的垂线交CD的延长线于点P,设菱形的边长为3m.,∴DG=m,CG=2m.在Rt△ADP中,∠ADC=∠ABC=120°,∴∠ADP=60°,∴m,,∴α=120°,由(2)知,,∵∠AGP=∠FGC,∴△APG∽△FCG.∴,∴=,∴,由(2)知,,∴.∴.4.(2023•内蒙古)已知正方形ABCD,E是对角线AC上一点.(1)如图1,连接BE,DE.求证:△ABE≌△ADE;(2)如图2,F是DE延长线上一点,DF交AB于点G,BF⊥BE.判断△FBG的形状并说明理由;(3)在第(2)题的条件下,BE=BF=2.求的值.【分析】(1)由正方形的性质得AB=AD=CB=CD,∠ABC=∠ADC=90°,则∠BAC=∠BCA=∠DAC =∠DCA=45°,即可根据全等三角形的判定定理“SAS”证明△ABE≌△ADE;(2)由△ABE≌△ADE,得∠ABE=∠ADE,可推导出∠EBC=∠EDC,因为AB∥CD,所以∠FGB=∠EDC,则∠FGB=∠EBC,而∠FBE=90°,则∠FBG=∠EBC=90°﹣∠ABE,所以∠FGB=∠FBG,即可证明△FBG是等腰三角形;(3)由BE=BF=2,∠FBE=90°,得∠F=∠BEF=45°,则∠BAC=∠F,可证明∠AEG=∠FBG,进而证明∠AGE=∠AEG,则AE=AG,由勾股定理得EF==2,而BF=GF=2,所以GE=2﹣2,由全等三角形的性质得BE=DE=2,再证明△AGE∽△CDE,则==﹣1,所以=﹣1.【解答】(1)证明:∵四边形ABCD是正方形,∴AB=AD=CB=CD,∠ABC=∠ADC=90°,∴∠BAC=∠BCA=∠DAC=∠DCA=45°,在△ABE和△ADE中,,∴△ABE≌△ADE(SAS).(2)解:△FBG是等腰三角形,理由如下:∵△ABE≌△ADE,∴∠ABE=∠ADE,∴∠ABC﹣∠ABE=∠ADC﹣∠ADE,∴∠EBC=∠EDC,∵AB∥CD,∴∠FGB=∠EDC,∴∠FGB=∠EBC,∵BF⊥BE,∴∠FBE=90°,∴∠FBG=∠EBC=90°﹣∠ABE,∴∠FGB=∠FBG,∴BF=GF,∴△FBG是等腰三角形.(3)解:∵BE=BF=2,∠FBE=90°,∴∠F=∠BEF=45°,∴∠BAC=∠F,∴∠AEG=∠AGF﹣∠BAC=∠AGF﹣∠F=∠FBG,∵∠AGE=∠FGB,且∠FGB=∠FBG,∴∠AGE=∠AEG,∴AE=AG,∵EF===2,BF=GF=2,∴GE=EF﹣GF=2﹣2,∵△ABE≌△ADE,∴BE=DE=2,∵AG∥CD,∴△AGE∽△CDE,∴===﹣1,∴=﹣1,∴的值为﹣1.5.(2023•湖州)【特例感知】(1)如图1,在正方形ABCD中,点P在边AB的延长线上,连结PD,过点D作DM⊥PD,交BC的延长线于点M.求证:△DAP≌△DCM.【变式求异】(2)如图2,在Rt△ABC中,∠ABC=90°,点D在边AB上,过点D作DQ⊥AB,交AC于点Q,点P在边AB的延长线上,连结PQ,过点Q作QM⊥PQ,交射线BC于点M.已知BC=8,AC=10,AD =2DB,求的值.【拓展应用】(3)如图3,在Rt△ABC中,∠BAC=90°,点P在边AB的延长线上,点Q在边AC上(不与点A,C重合),连结PQ,以Q为顶点作∠PQM=∠PBC,∠PQM的边QM交射线BC于点M.若AC=mAB,CQ=nAC(m,n是常数),求的值(用含m,n的代数式表示).【分析】(1)根据正方形的性质及角的和差推出∠A=∠DCM,AD=DC,∠ADP=∠CDM,利用ASA 即可证明△DAP≌△DCM;(2)作QN⊥BC于点N,则四边形DBNQ是矩形,根据矩形的性质推出∠DQN=90°,QN=DB,根据角的和差推出∠DQP=∠MQN,结合∠QDP=∠QNM=90°,推出△DQP∽△NQM,根据相似三角形的性质得到,根据勾股定理求出AB=6,则DB=2,根据矩形的性质推出DQ∥BC,进而推出△ADQ∽△ABC,根据相似三角形的性质求解即可;(3)根据题意推出CQ=mnAB,AQ=(m﹣mn)AB,根据勾股定理求出BC=AB,根据四边形内角和定理及邻补角定义推出∠AQP=∠NQM,结合∠A=∠QNM=90°,推出△QAP∽△QNM,根据相似三角形的性质得出,根据题意推出△QCN∽△BCA,根据相似三角形的性质求出,据此求解即可.【解答】(1)证明:在正方形ABCD中,∠A=∠ADC=∠BCD=90°,AD=DC,∴∠DCM=180°﹣∠BCD=90°,∴∠A=∠DCM,∵DM⊥PD,∴∠ADP+∠PDC=∠CDM+∠PDC=90°,∴∠ADP=∠CDM,在△DAP和△DCM中,,∴△DAP≌△DCM(ASA);(2)解:如图2,作QN⊥BC于点N,∵∠ABC=90°,DQ⊥AB,QN⊥BC,∴四边形DBNQ是矩形,∴∠DQN=90°,QN=DB,∵QM⊥PQ,∴∠DQP+∠PQN=∠MQN+∠PQN=90°,∴∠DQP=∠MQN,∵∠QDP=∠QNM=90°,∴△DQP∽△NQM,∴,∵BC=8,AC=10,∠ABC=90°,∴,∵AD=2DB,∴DB=2,∵∠ADQ=∠ABC=90°,∴DQ∥BC,∴△ADQ∽△ABC,∴,∴,∴;(3)解:∵AC=mAB,CQ=nAC,∴CQ=mnAB,∴AQ=AC﹣CQ=(m﹣mn)AB,∵∠BAC=90°,∴,如图3,作QN⊥BC于点N,∵∠BAC+∠ABN+∠BNQ+∠AQN=360°,∠BAC=90°,∴∠ABN+∠AQN=180°,∵∠ABN+∠PBN=180°,∴∠AQN=∠PBN,∵∠PQM=∠PBC,∴∠PQM=∠AQN,∴∠AQP=∠NQM,∵∠A=∠QNM=90°,∴△QAP∽△QNM,∴,∵∠A=∠QNC=90°,∠QCN=∠BCA,∴△QCN∽△BCA,∴,∴,∴.6.(2023•鞍山)如图,在△ABC中,AB=AC,∠BAC=α,点D是射线BC上的动点(不与点B,C重合),连接AD,过点D在AD左侧作DE⊥AD,使AD=kDE,连接AE,点F,G分别是AE,BD的中点,连接DF,FG,BE.(1)如图1,点D在线段BC上,且点D不是BC的中点,当α=90°,k=1时,AB与BE的位置关系是垂直,=.(2)如图2,点D在线段BC上,当α=60°,k=时,求证:BC+CD=2FG.(3)当α=60°,k=时,直线CE与直线AB交于点N,若BC=6,CD=5,请直接写出线段CN的长.。
相似三角形中考题大全

中考数学专题练习:相似三角形一、选择题1.如图,将图形用放大镜放大,应该属于()A .平移变换B .相似变换C .旋转变换D .对称变换2.如图,在△ABC 中,点D ,E 分别在边AB ,AC 上,DE ∥BC .若BD =2AD ,则()A.AD AB =12B.AE EC =12C.AD EC =12D.DE BC =123.(2019•雅安)若34a b =∶∶,且14a b +=,则2a b -的值是A .4B .2C .20D .144.(2020·河南)如图,在△ABC 中,∠ACB=90°,边BC 在x 轴上,顶点A ,B 的坐标分别为(-2,6)和(7,0).将正方形OCDE 沿x 轴向右平移,当点E 落在AB 边上时,点D 的坐标为()A.(32,2) B.(2,2) C.(114,2) D.(4,2)5.(2019•重庆)下列命题是真命题的是A .如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为2∶3B .如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9C .如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为2∶3D .如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为4∶96.(2019•巴中)如图 ABCD ,F 为BC 中点,延长AD 至E ,使13DE AD =∶∶,连接EF 交DC 于点G ,则:DEG CFG S S △△=A .2∶3B .3∶2C .9∶4D .4∶97.(2020·威海)如图,矩形ABCD 的四个顶点分别在直线l 3,l 4,l 2,l 1上.若直线l 1∥l 2∥l 3∥l 4且间距相等,AB =4,BC =3,则tan α的值为()A .B .C .D .8.(2020·昆明)在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC 是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE ∽△ABC(同一位置的格点三角形△ADE 只算一个),这样的格点三角形一共有()个 D.7个B二、填空题9.(2020·盐城)如图,//,BC DE 且,4,10BCDE AD BC AB DE <==+=,则AEAC的值为.10.(2020·吉林)如图,在ABC 中,D ,E 分别是边AB ,AC 的中点.若ADE的面积为12.则四边形DBCE 的面积为_______.11.(2019•大庆)如图,在△ABC 中,D 、E 分别是BC ,AC 的中点,AD 与BE相交于点G ,若DG=1,则AD=__________.12.(2020·临沂)如图,在ABC ∆中,D ,E 为边AB 的三等分点,////EF DG AC ,H 为AF 与DG 的交点.若6AC =,则DH =_________.13.(2020·绥化)在平面直角坐标系中,△ABC和△A 1B 1C 1的相似比等于12,并且是关于原点O 的位似图形,若点A 的坐标为(2,4),则其对应点A 1的坐标是______.14.如图,在Rt △ABC 中,∠BAC =90°,AB =15,AC =20,点D 在边AC 上,AD =5,DE ⊥BC 于点E ,连接AE ,则△ABE 的面积等于________.15.(2019•辽阳)如图,平面直角坐标系中,矩形ABOC 的边BO CO ,分别在x 轴,y 轴上,A 点的坐标为(86)-,,点P 在矩形ABOC 的内部,点E 在BO 边上,满足PBE △∽CBO △,当APC △是等腰三角形时,P 点坐标为__________.16.(2019•伊春)一张直角三角形纸片ABC ,90ACB ∠=︒,10AB =,6AC =,点D 为BC 边上的任一点,沿过点D 的直线折叠,使直角顶点C 落在斜边AB 上的点E 处,当BDE △是直角三角形时,则CD 的长为__________.三、解答题17.如图,过☉O 外一点P 作☉O 的切线PA ,切☉O 于点A ,连接PO 并延长,与☉O 交于C ,D 两点,M 是半圆CD 的中点,连接AM 交CD 于点N ,连接AC ,CM.(1)求证:CM 2=MN ·MA ;(2)若∠P=30°,PC=2,求CM 的长.18.如图,M 为线段AB 的中点,AE 与BD 交于点C ,∠DME =∠A =∠B =α,且DM 交AC 于F ,ME 交BC 于G.(1)写出图中两对相似三角形,并证明其中的一对;(2)请连接FG ,如果α=45°,AB =42,AF =3,求FG 的长.19.(2020·杭州)如图,在正方形ABCD 中,点E 在BC 边上,连接AE ,DAE ∠的平分线AG 与CD 边交于点G ,与BC 的延长线交于点F .设()0CEEBλλ=>.(1)若2AB =,λ=1,求线段CF 的长.(2)连接EG ,若EG AF ⊥,①求证:点G 为CD 边的中点.②求λ的值.20.(2020·攀枝花)三角形三条边上的中线交于一点,这个点叫三角形的重心.如图G 是ABC ∆的重心.求证:3AD GD =.21.(2020·江苏徐州)我们知道:如图①,点B 把线段AC 分成两部分,如果BC ABAB AC=,那么称点B为线段AC的黄金分割点..(1)在图①中,若AC=20cm,则AB的长为cm;(2)如图②,用边长为20cm的正方形纸片进行如下操作:对折正方形ABCD得折痕EF,连接CE,将CB折叠到CE上,点B的对应点H,得折痕CG.试说明:G是AB的黄金分割点;(3)如图③,小明进一步探究:在边长为a的正方形ABCD的边AD上任取点E (AE>DE),连接BE,作CF⊥BE,交AB于点F,延长EF、CB交于点P.他发现当PB与BC满足某种关系时,E、F恰好分别是AD、AB的黄金分割点.请猜想小明的发现,并说明理由.图①图②图③22.(2020•丽水)如图,在△ABC中,AB=4,∠B=45°,∠C=60°.(1)求BC边上的高线长.(2)点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.①如图2,当点P落在BC上时,求∠AEP的度数.②如图3,连结AP,当PF⊥AC时,求AP的长.23.如图,AB是⊙O的直径,点E为线段OB上一点(不与O、B重合),作EC⊥OB 交⊙O于点C,作直径CD过点C的切线交DB的延长线于点P,作AF⊥PC于点F,连接CB.(1)求证:AC平分∠FAB;(2)求证:BC2=CE·CP;(3)当AB=43且CFCP=34时,求劣弧BD︵的长度.24.在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根.比如对于方程x2-5x+2=0,操作步骤是:第一步:根据方程的系数特征,确定一对固定点A(0,1),B(5,2);第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C的横坐标m即为该方程的一个实数根(如图①);第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D的横坐标n既为该方程的另一个实数根.(1)在图②中,按照“第四步”的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹);(2)结合图①,请证明“第三步”操作得到的m就是方程x2-5x+2=0的一个实数根;(3)上述操作的关键是确定两个固定点的位置.若要以此方法找到一元二次方程ax2+bx+c=0(a≠0,b2-4ac≥0)的实数根,请你直接写出一对固定点的坐标;(4)实际上,(3)中的固定点有无数对,一般地,当m1,n1,m2,n2与a,b,c之间满足怎样的关系时,点P(m1,n1).Q(m2,n2)就是符合要求的一对固定点?答案一、选择题1.【答案】B2.【答案】B【解析】∵DE ∥BC ,∴△ADE ∽△ABC ,∵BD =2AD ,∴AD AB =AEAC=13,∴AE EC =12,故选B .3.【答案】A【解析】由a ∶b =3∶4知34b a =,所以43a b =.所以由14a b +=得到:4143aa +=,解得6a =.所以8b =.所以22684a b -=⨯-=.故选A .4.【答案】B【解析】∵点A ,B 的坐标分别为(-2,6)和(7,0),∴OC=2,AC=6,OB=7,∴BC=9,正方形的边长为2.将正方形OCDE 沿x 轴向右平移,当点E 落在AB 边上时,设正方形与x 轴的两个交点分别为G 、F ,∵EF ⊥x 轴,EF=GF=DG=2,∴EF ∥AC ,D ,E 两点的纵坐标均为2,∴EF BF AC BC =,即269BF=,解得BF=3.∴OG=OB-BF-GF=7-3-2=2,∴D 点的横坐标为2,∴点D 的坐标为(2,2).5.【答案】B【解析】A 、如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9,是假命题;B 、如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9,是真命题;C 、如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为16∶81,是假命题;D 、如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为16∶81,是假命题,故选B .6.【答案】D【解析】设DE x =,∵13DE AD =∶∶,∴3AD x =,∵四边形ABCD 是平行四边形,∴AD BC ∥,3BC AD x ==,∵点F 是BC 的中点,∴1322CF BC x ==,∵AD BC ∥,∴DEG CFG △∽△,∴224()()392DEG CFG S DE x S CF x ===△△,故选D .7.【答案】:作CF ⊥l 4于点F ,交l 3于点E ,设CB 交l 3于点G ,由已知可得,GE∥BF ,CE =EF ,∴△CEG ∽△CFB ,∴,∵,∴,∵BC =3,∴GB,∵l 3∥l 4,∴∠α=∠GAB ,∵四边形ABCD 是矩形,AB =4,∴∠ABG =90°,∴tan ∠BAG ,∴tan α的值为,故选:A.8.【答案】A【解析】本题考查了相似三角形的判定.符合条件的三角形有四个,如图所示:B因此本题选A .二、填空题9.【答案】2【解析】∵BC ∥DE ,∴△ADE ∽△ABC ,∴AE AD DEAC AB BC ==,设DE =x ,则AB =10-x ∵AD =BC =4,∴4104AE x AC x ==-,∴x 1=8,x 2=2(舍去),824AE AC ==,此本题答案为2.10.【答案】32【解析】 点D ,E 分别是边AB ,AC 的中点,1//,2DE BC DE BC ∴=ADE ABC∴ 21()4ADE ABC S DE S BC ∴==△△,即4ABC ADES S =△△又12ADE S =,1422ABC S ∴=⨯= 则四边形DBCE 的面积为13222ABC ADE S S -=-= .故答案为:32.11.【答案】3【解析】∵D 、E 分别是BC ,AC 的中点,∴点G 为△ABC 的重心,∴AG=2DG=2,∴AD=AG+DG=2+1=3.故答案为:3.12.【答案】1【解析】∵D 、E 为边AB 的三等分点,∴BE=ED=AD=13AB.∵////EF DG AC ,∴123EF AC ==∴112DH EF ==.13.【答案】(-4,-8)或(4,8)【解析】∵△ABC 和△A1B1C1的相似比等于12,∴△A1B1C1和△ABC 的相似比等于2.因此将点A(2,4)的横、纵坐标乘以±2即得点A1的坐标,∴点A1的坐标是(-4,-8)或(4,8).14.【答案】78【解析】如解图,过A 作AH ⊥BC ,∵AB =15,AC =20,∠BAC=90°,∴由勾股定理得,BC =152+202=25,∵AD =5,∴DC =20-5=15,∵DE ⊥BC ,∠BAC =90°,∴△CDE ∽△CBA ,∴CE CA =CD CB ,∴CE =1525×20=12.法一:BC·AH =AB·AC ,AH =AB·AC BC =15×2025=12,S △ABE =12×12×13=78.法二:DE =152-122=9,由△CDE ∽△CAH 可得,CD CA =ED HA ,∴AH =9×2015=12,S △ABE =12×12×13=78.15.【答案】326()55-,或(43)-,【解析】∵点P 在矩形ABOC 的内部,且APC △是等腰三角形,∴P 点在AC 的垂直平分线上或在以点C 为圆心AC 为半径的圆弧上;①当P 点在AC 的垂直平分线上时,点P 同时在BC 上,AC 的垂直平分线与BO 的交点即是E ,如图1所示,∵PE BO ⊥,CO BO ⊥,∴PE CO ∥,∴PBE △∽CBO △,∵四边形ABOC 是矩形,A 点的坐标为(86)-,,∴点P 横坐标为﹣4,6OC =,8BO =,4BE =,∵PBE △∽CBO △,∴PE BE CO BO =,即468PE =,解得:3PE =,∴点(43)P -,.②P 点在以点C 为圆心AC 为半径的圆弧上,圆弧与BC 的交点为P ,过点P 作PE BO ⊥于E ,如图2所示,∵CO BO ⊥,∴PE CO ∥,∴PBE △∽CBO △,∵四边形ABOC 是矩形,A 点的坐标为(86)-,,∴8AC BO ==,8CP =,6AB OC ==,∴22228610BC BO OC =+=+=,∴2BP =,∵PBE △∽CBO △,∴PE BE BP CO BO BC ==,即:26810PE BE ==,解得:65PE =,85BE =,∴832855OE =-=,∴点326(55P -,,综上所述:点P 的坐标为:326(55-,或(43)-,,故答案为:326()55-,或(43)-,.16.【答案】3或247【解析】分两种情况:①若90DEB ∠=︒,则90AED C ∠=︒=∠,CD ED =,连接AD ,则Rt Rt ACD EAD △≌△,∴6AE AC ==,1064BE =-=,设CD DE x ==,则8BD x =-,∵Rt BDE △中,222DE BE BD +=,∴2224(8)x x +=-,解得3x =,∴3CD =;②若90BDE ∠=︒,则90CDE DEF C ∠=∠=∠=︒,CD DE =,∴四边形CDEF 是正方形,∴90AFE EDB ∠=∠=︒,AEF B ∠=∠,∴AEF EBD △∽△,∴AF EFED BD=,设CD x =,则EF DF x ==,6AF x =-,8BD x =-,∴68x x x x -=-,解得247x =,∴247CD =,综上所述,CD 的长为3或247,故答案为:3或247.三、解答题17.【答案】解:(1)证明:∵在☉O 中,点M 是半圆CD 的中点,∴∠CAM=∠DCM ,又∵∠CMA 是△CMN 和△AMC 的公共角,∴△CMN ∽△AMC ,∴=,∴CM 2=MN ·M A .(2)连接OA ,DM ,∵PA 是☉O 的切线,∴∠PAO=90°,又∵∠P=30°,∴OA=PO=(PC +CO ).设☉O 的半径为r ,∵PC=2,∴r=(2+r ),解得r=2.又∵CD 是直径,∴∠CMD=90°,∵点M 是半圆CD 的中点,∴CM=DM ,∴△CMD 是等腰直角三角形,∴在Rt △CMD 中,由勾股定理得CM 2+DM 2=CD 2,∴2CM 2=(2r )2=16,∴CM 2=8,∴CM=2.18.【答案】解:(1)△AMF ∽△BGM ,△DMG ∽△DBM ,△EMF ∽△EAM 等.(写出两对即可)以下证明△AMF ∽△BGM.由题知∠A =∠B =∠DME =α,而∠AFM =∠DME +∠E ,∠BMG =∠A +∠E ,∴∠AFM =∠BMG ,∴△AMF ∽△BGM.(2)当α=45°时,可得AC ⊥BC 且AC =BC ,∵M 为AB 中点,∴AM =BM =2 2.由△AMF ∽△BGM 得,AF·BG =AM·BM ,∴BG =83.又AC =BC =42cos 45°=4,∴CG =4-83=43,CF =4-3=1,∴FG =(43)2+12=53.19.【答案】解:(1)∵四边形ABCD 是正方形,∴AD ∥BC ,AB =BC =2,∴∠DAF =∠F .∵AG 平分∠DAE ,∴∠DAF =∠EAF ,∴∠EAF =∠F ,∴EA =EF .∵λ=1,∴BE =EC =1.在Rt △ABE 中,由勾股定理得EA ,∴CF =EF -EC -1.(2)①∵EA =EF ,EG ⊥AF ,∴AG =GF .又∵∠AGD =∠FGC ,∠DAG =∠F ,所以△DAG ≌△CFG ,∴DG =CG ,∴点G 为CD 边的中点.②不妨设CD =2,则CG =1.由①知CF =AD =2.∵EG ⊥AF ,∴∠EGF =90°.∵四边形ABCD 是正方形,∴∠BCD =90°,∴∠BCD =∠FCG ,∠EGC +∠CGF=90°,∠EGC +∠GEC =90°,∴∠CGF =∠GEC ,∴△EGC ∽△GFC ,∴ECCG =CG CF =12,∴EC =12,∴BE =32,∴λ=13.20.【答案】证明:连接DE ,∵点G 是△ABC 的重心,∴点E 和点D 分别是AB 和BC 的中点,∴DE 是△ABC 的中位线,∴DE ∥AC 且DE=12AC ,∴△DEG ∽△ACG ,∴2AG AC DG ED ==,∴2AG GD =∴AD=3DG ,即AD=3GD .21.【答案】解:(1)10-.解:∵ABAC=,AC=20,∴AB=10-.(2)延长CG 交DA 的延长线于点J ,由折叠可知:∠BCG=∠ECG ,∵AD ∥BC ,∴∠J=∠BCG=∠ECG ,∴JE=CE.由折叠可知:E 、F 为AD 、BC 的中点,∴DE=AE=10,由勾股定理可得:==,∴EJ=AJ=JE-AE=-10,∵AJ ∥BC ,∴△AGJ ∽△BGC,∴AG AJ BG BC ===,∴G 是AB 的黄金分割点.(3)PB=BC ,理由如下:∵E 为AD 的黄金分割点,且AE>DE ,∴AE=12 a.∵CF ⊥BE ,∴∠ABE+∠CBE=∠CBE+∠BCF=90˚,∴∠ABE=∠FCB,在△BEA 和△CFB 中,∵90ABE FCB AB BCA FBC ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩,∴△BEA ≌△CFB ,∴a.∴12AF BF BF AB ==,∵AE ∥BP ,∴△AEF ∽△BPF,∴AE AF BF PB BF AB==,∵AE=BF,∴PB=AB ,∴PB=BC.22.【答案】解:(1)如图1中,过点A 作AD ⊥BC 于D.在Rt △ABD 中,AD =AB•sin45°=44.(2)①如图2中,∵△AEF ≌△PEF ,∴AE =EP ,∵AE =EB ,∴BE =EP ,∴∠EPB =∠B =45°,∴∠PEB =90°,∴∠AEP =180°﹣90°=90°.②如图3中,由(1)可知:AC,∵PF ⊥AC ,∴∠PFA =90°,∵△AEF ≌△PEF ,∴∠AFE =∠PFE =45°,∴∠AFE=∠B,∵∠EAF=∠CAB,∴△AEF∽△ACB,∴,即,∴AF=2,在Rt△AFP,AF=FP,∴AP AF=2.23.【答案】(1)证明:∵PF切⊙O于点C,CD是⊙O的直径,∴CD⊥PF,又∵AF⊥PC,∴AF∥CD,∴∠OCA=∠CAF,∵OA=OC,∴∠OAC=∠OCA,∴∠CAF=∠OAC,∴AC平分∠FAB;(2)证明:∵AB是⊙O的直径,∴∠ACB=90°,∵∠DCP=90°,∴∠ACB=∠DCP=90°,又∵∠BAC=∠D,∴△ACB∽△DCP,∴∠EBC=∠P,∵CE⊥AB,∴∠BEC=90°,∵CD是⊙O的直径,∴∠DBC=90°,∴∠CBP=90°,∴∠BEC=∠CBP,∴△CBE∽△CPB,∴BCPC=CECB,∴BC2=CE·CP;(3)解:∵AC平分∠FAB,CF⊥AF,CE⊥AB,∴CF=CE,∵CFCP=34,∴CECP=34,设CE=3k,则CP=4k,∴BC2=3k·4k=12k2,∴BC=23k,在Rt△BEC中,∵sin∠EBC=CEBC=3k23k=32,∴∠EBC =60°,∴△OBC 是等边三角形,∴∠DOB =120°,∴BD ︵=120π·23180=43π3.24.【答案】【思路分析】(1)因为点C 是x 轴上的一动点,且∠ACB =90°保持不变,所以由圆周角的性质得,点C 必在以AB 为直径的圆上,所以以AB 为直径画圆,与x 轴相交于两点,除点C 的另一点就是所求;(2)因为∠ACB =90°,∠AOC =90°,所以过点B 作BE ⊥x 轴,垂足为E ,则构造了一个“K”字型的基本图形,再由相似三角的性质得出比例式,化简后得m 2-5m +2=0,问题得证;(3)由(2)中的证明过程可知,一个二次项系数为1的一元二次方程,一次项系数是点A 的横坐标与点B 的横坐标的和的相反数;常数项是点A 的纵坐标与点B 的纵坐标的积,先把方程ax 2+bx +c =0,化为x 2+b a x +ca=0,再根据上述关系写出一对固定点的坐标;(4)由(2)的证明中知,本题的关键点在“K”字型的构造,所以本小题解题的关键是要抓住图②中的“K”字型,只要P 、Q 两点分别在AD 、BD 上,过P 、Q 分别作x 轴垂线,垂足为M 、N ,这样就构造出满足条件的基本图形,再应用相似三角形的性质,可得相应的关系式.图①图②(1)解:如解图①,先作出AB 的中点O 1,以O 1为圆心,12AB 为半径画圆.x 轴上另外一个交点即为D 点;(4分)(2)证明:如解图①,过点B 作x 轴的垂线交x 轴于点E ,∵∠ADB =90°,∴∠ADO +∠BDE =90°,∵∠OAD +∠ADO =90°,∴∠OAD =∠BDE ,∵∠AOD =∠DEB =90°,∴△AOD ∽△DEB ,(6分)∴AO DE =OD EB ,即15-m =m2,∴m 2-5m +2=0,∴m 是x 2-5x +2=0的一个实根;(8分)(3)解:(0,1),(-b a,c a )或(0,1a ),(-ba ,c );(10分)(4)解:在解图②中,P 在AD 上,Q 在BD 上,过P ,Q 分别作x 轴的垂线交x轴于M ,N.由(2)知△PMD ∽△DNQ ,∴n 1m 2-x =x -m 1n 2,(12分)∴x 2-(m 1+m 2)x +m 1m 2+n 1n 2=0与ax 2+bx +c =0同解,∴-b a =m 1+m 2;ca=m 1m 2+n 1n 2.(14分)【难点突破】本题是一道考查数形结合思想的题.本题解题的突破口要抓住∠ACB =90°保持不变的特征,构造相似三角形中的基本图形,通过数形结合的方法,以相似三角形的比例式为桥梁,以此获得关于m 的等量关系,从而使问题得以解决.。
中考三角形相似压轴题

选择题在△ABC和△DEF中,若△A = △D,AB/DE = AC/DF,则下列结论正确的是:A. △ABC △ △DEFB. △ABC和△DEF不一定相似C. △ABC和△DEF仅在一种情况下相似D. △ABC △ △DEF(正确答案)已知△PQR中,PQ = 6,QR = 8,RP = 10,且△STU中,ST/PQ = SU/QR = 3/4,则:A. △PQR与△STU的周长比为4:3B. △PQR与△STU的面积比为3:4C. △PQR与△STU是等腰三角形D. △PQR △ △STU且相似比为4:3(正确答案)下列哪组条件不能判定两个三角形相似?A. 两角分别相等B. 三边对应成比例C. 两边对应成比例且夹角相等D. 两边对应成比例且一边的对角相等(正确答案)在△ABC和△A'B'C'中,若AB/A'B' = BC/B'C'且△B = △B',则:A. △A = △A'且△C = △C'(正确答案)B. △A = △C'且△C = △A'C. △A与△A'、△C与△C'均不相等D. 无法确定△A、△C与△A'、△C'的关系已知△MNO与△XYZ相似,且MN = 2,NO = 3,MO = 4,XY = 6,则YZ的长度为:A. 8B. 9(正确答案)C. 10D. 12下列关于相似三角形的性质,错误的是:A. 相似三角形的对应角相等B. 相似三角形的对应边成比例C. 相似三角形的面积比等于对应边长的平方比D. 相似三角形的周长比等于对应边长的立方比(正确答案)在△GHK和△LMN中,若GH/LM = HK/MN,且△G = △L,△H = △M,则:A. △GHK与△LMN仅面积相等B. △GHK与△LMN仅周长相等C. △GHK与△LMN全等D. △GHK △ △LMN且全等方面也成立(正确答案,但更严谨的表述应为“△GHK △ △LMN”)已知△ABC中,AB = 5,BC = 6,AC = 7,△DEF中,DE = 10,EF = 12,且△A = △D,则:A. DF = 15且△ABC △ △DEFB. DF = 14且△ABC与△DEF不全等C. DF = 16且△ABC △ △DEFD. DF = 14且△ABC △ △DEF(正确答案)下列哪组条件足以证明△PQR与△STU相似,但不需要额外条件即可直接判定?A. △P = △S,△Q = △TB. PQ/ST = QR/TU,且QR = 2PTC. PQ/ST = QR/TU = RP/SU(正确答案)D. △P = △S,PQ/ST = RP/SU且QR ≠ TU。
初三数学13 相似三角形-2024年中考数学真题分项汇编(全国通用)(解析版)

专题13 相似三角形一.选择题1.(2022·黑龙江哈尔滨)如图,,,AB CD AC BD ∥相交于点E ,1,2,3AE EC DE ===,则BD 的长为( )A .32B .4C .92D .6【答案】C【分析】根据相似三角形对应边长成比例可求得BE 的长,即可求得BD 的长.【详解】∵//AB CD ∴ABE CDE ∽ ∴AE BE EC DE= ∵1,2,3AE EC DE ===,∴32BE =∵BD BE ED =+ ∴92BD = 故选:C .【点睛】本题考查了相似三角形的对应边长成比例,解题的关键在于找到对应边长.2.(2022·广西贺州)如图,在ABC 中,25DE BC DE BC ==∥,,,则:ADE ABC S S 的值是( )A .325B .425C .25D .35【答案】B【分析】根据相似三角形的判定定理得到ADE ABC ,根据相似三角形的面积比等于相似比的平方计算,得到答案.【详解】解:25DE BC DE BC ==∥,,∴ADE ABC ,∴2224525ADE ABC S DE S BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ ,故选:B .【点睛】此题考查相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.3.(2022·广西梧州)如图,以点O 为位似中心,作四边形ABCD 的位似图形''''A B C D ﹐已知'13OA OA =,若四边形ABCD 的面积是2,则四边形''''A B C D 的面积是( )A .4B .6C .16D .18【答案】D 【分析】两图形位似必相似,再由相似的图形面积比等于相似比的平方即可求解.【详解】解:由题意可知,四边形ABCD 与四边形''''A B C D 相似,由两图形相似面积比等于相似比的平方可知:''''22'1139ABCD A B C D S OA S OA ⎛⎫⎛⎫= ⎪= ⎪= ⎪ ⎪⎝⎭⎝⎭,又四边形ABCD 的面积是2,∴四边形''''A B C D 的面积为18,故选:D .【点睛】本题考察相似多边形的性质,属于基础题,熟练掌握相似图形的性质是解决本题的关键.4.(2022·四川雅安)如图,在△ABC 中,D ,E 分别是AB 和AC 上的点,DE ∥BC ,若AD BD =21,那么DE BC =( )A .49B .12C .13D .23【答案】D【分析】先求解2,3AD AB =再证明,ADE ABC ∽可得2.3DE AD BC AB ==【详解】解: AD BD =21,2,3AD AB ∴= DE ∥BC ,,ADE ABC ∴ ∽ 2,3DE AD BC AB ∴== 故选D 【点睛】本题考查的是相似三角形的判定与性质,证明ADE ABC △△∽是解本题的关键.5.(2022·内蒙古包头)如图,在边长为1的小正方形组成的网格中,A ,B ,C ,D 四个点均在格点上,AC 与BD 相交于点E ,连接,AB CD ,则ABE △与CDE △的周长比为( )A .1:4B .4:1C .1:2D .2:1【答案】D 【分析】运用网格图中隐藏的条件证明四边形DCBM 为平行四边形,接着证明ABE CDE ∽,最后利相似三角形周长的比等于相似比即可求出.【详解】如图:由题意可知,3DM =,3BC =, ∴DM BC =,而DM BC ∥,∴四边形DCBM 为平行四边形,∴AB DC ∥,∴BAE DCE ∠=∠,ABE CDE ∠=∠,∴ABE CDE ∽,∴21ABE CDE C AB C CD ===△△.故选:D .【点睛】本题考查了平行四边形的判定与性质、相似三角形的判定与性质及勾股定理,熟练掌握相关知识并正确计算是解题关键.6.(2022·黑龙江绥化)如图,在矩形ABCD 中,P 是边AD 上的一个动点,连接BP ,CP ,过点B 作射线,交线段CP 的延长线于点E ,交边AD 于点M ,且使得ABE CBP =∠∠,如果2AB =,5BC =,AP x =,PM y =,其中25x < .则下列结论中,正确的个数为( )(1)y 与x 的关系式为4y x x =-;(2)当4AP =时,ABP DPC ∽;(3)当4AP =时,3tan 5EBP ∠=.A .0个B .1个C .2个D .3个【答案】C 【分析】(1)证明ABM APB ∽,得AB AM AP AB=,将2AB =,AP x =,PM y =代入,即可得y 与x 的关系式;(2)利用两组对应边成比例且夹角相等,判定ABP DPC ∽;(3)过点M 作MF BP ⊥垂足为F ,在Rt APB △中,由勾股定理得BP 的长,证明FPM APB ∽,求出MF ,PF ,BF 的长,在Rt BMF △中,求出tan EBP ∠的值即可.【详解】解:(1)∵在矩形ABCD 中,∴AD BC ∥,90A D ∠=∠=︒,5BC AD ==,2AB DC ==,∴APB CBP ∠=∠,∵ABE CBP =∠∠,∴ABE APB ∠=∠,∴ABM APB ∽,∴AB AM AP AB=,∵2AB =,AP x =,PM y =,∴22x y x -=,解得:4y x x=-,故(1)正确;(2)当4AP =时,541DP AD AP =-=-=,∴12DC DP AP AB ==,又∵90A D ∠=∠=︒,∴ABP DPC ∽,故(2)正确;(3)过点M 作MF BP ⊥垂足为F ,∴90A MFP MFB ∠=∠=∠=︒,∵当4AP =时,此时4x =,4413y x x =-=-=,∴3PM =,在Rt APB 中,由勾股定理得:222BP AP AB =+,∴BP ===,∵FPM APB ∠=∠,∴FPM APB ∽,∴MF PF PM AB AP PB ==,∴24MF PF ==∴MF =PF =∴BF BP PF =-=∴3tan 4MF EBP BF ∠===故(3)不正确;故选:C .【点睛】本题主要考查相似三角形的判定和性质,勾股定理的应用,矩形的性质,正确找出相似三角形是解答本题的关键.7.(2022·湖北鄂州)如图,定直线MN ∥PQ ,点B 、C 分别为MN 、PQ 上的动点,且BC =12,BC 在两直线间运动过程中始终有∠BCQ =60°.点A 是MN 上方一定点,点D 是PQ 下方一定点,且AE ∥BC ∥DF ,AE =4,DF =8,ADBC 在平移过程中,AB +CD 的最小值为()A .B .C .D .【答案】C 【分析】如图所示,过点F 作FH CD ∥交BC 于H ,连接EH ,可证明四边形CDFH 是平行四边形,得到CH =DF =8,CD =FH ,则BH =4,从而可证四边形ABHE 是平行四边形,得到AB =HE ,即可推出当E 、F 、H 三点共线时,EH +HF 有最小值EF 即AB +CD 有最小值EF ,延长AE 交PQ 于G ,过点E 作ET ⊥PQ 于T ,过点A 作AL ⊥PQ 于L ,过点D 作DK ⊥PQ 于K ,证明四边形BEGC 是平行四边形,∠EGT =∠BCQ =60°,得到EG =BC =12,然后通过勾股定理和解直角三角形求出ET 和TF 的长即可得到答案.【详解】解:如图所示,过点F 作FH CD ∥交BC 于H ,连接EH ,∵BC DF FH CD ∥∥,,∴四边形CDFH 是平行四边形,∴CH =DF =8,CD =FH ,∴BH =4,∴BH =AE =4,又∵AE BC ∥,∴四边形ABHE 是平行四边形,∴AB =HE ,∵EH FH EF +≥,∴当E 、F 、H 三点共线时,EH +HF 有最小值EF 即AB +CD 有最小值EF ,延长AE 交PQ 于G ,过点E 作ET ⊥PQ 于T ,过点A 作AL ⊥PQ 于L ,过点D 作DK ⊥PQ 于K ,∵MN PQ BC AE ∥∥,,∴四边形BEGC 是平行四边形,∠EGT =∠BCQ =60°,∴EG =BC =12,∴=cos =6=sin GT GE EGT ET GE EGT ⋅⋅∠,∠,同理可求得8GL AL ==,,4KF DK ==,,∴2TL =,∵AL ⊥PQ ,DK ⊥PQ ,∴AL DK ∥,∴△ALO ∽△DKO ,∴2AL AO DK DO==,∴2133AO AD DO AD ====∴24OL OK ===,,∴42TF TL OL OK KF =+++=,∴EF ==故选C .【点睛】本题主要考查了平行四边形的性质与判定,相似三角形的性质与判定,勾股定理,解直角三角形,正确作出辅助线推出当E 、F 、H 三点共线时,EH +HF 有最小值EF 即AB +CD 有最小值EF 是解题的关键.8.(2022·广西贵港)如图,在边长为1的菱形ABCD 中,60ABC ∠=︒,动点E 在AB 边上(与点A 、B 均不重合),点F 在对角线AC 上,CE 与BF 相交于点G ,连接,AG DF ,若AF BE =,则下列结论错误的是( )A .DF CE =B .120BGC ∠=︒C .2AF EG EC =⋅D .AG【答案】D【分析】先证明△BAF ≌△DAF ≌CBE ,△ABC 是等边三角形,得DF =CE ,判断A 项答案正确,由∠GCB +∠GBC =60゜,得∠BGC =120゜,判断B 项答案正确,证△BEG ∽△CEB 得BE CE GE BE= ,即可判断C 项答案正确,由120BGC ∠=︒,BC =1,得点G 在以线段BC 为弦的弧BC 上,易得当点G 在等边△ABC 的内心处时,AG 取最小值,由勾股定理求得AG D 项错误.【详解】解:∵四边形ABCD 是菱形,60ABC ∠=︒,∴AB =AD =BC =CD ,∠BAC =∠DAC =12∠BAD =12(180)ABC ⨯︒-∠=60ABC ︒=∠,∴△BAF ≌△DAF ≌CBE ,△ABC 是等边三角形,∴DF =CE ,故A 项答案正确,∠ABF =∠BCE ,∵∠ABC =∠ABF +∠CBF =60゜,∴∠GCB +∠GBC =60゜,∴∠BGC =180゜-60゜=180゜-(∠GCB +∠GBC )=120゜,故B 项答案正确,∵∠ABF =∠BCE ,∠BEG =∠CEB ,∴△BEG ∽△CEB ,∴BE CE GE BE = ,∴2BE GE CE = ,∵AF BE =,∴2AF GE CE = ,故C 项答案正确,∵120BGC ∠=︒,BC =1,点G 在以线段BC 为弦的弧BC 上,∴当点G 在等边△ABC 的内心处时,AG 取最小值,如下图,∵△ABC 是等边三角形,BC =1,∴BF AC ⊥,AF =12AC =12,∠GAF =30゜,∴AG =2GF ,AG 2=GF 2+AF 2,∴2221122AG AG ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭, 解得AG D 项错误,故应选:D【点睛】本题主要考查了菱形的基本性质、等边三角形的判定及性质、圆周角定理,熟练掌握菱形的性质是解题的关键.9.(2022·贵州贵阳)如图,在ABC 中,D 是AB 边上的点,B ACD ∠=∠,:1:2AC AB =,则ADC 与ACB △的周长比是( )A .B .1:2C .1:3D .1:4【答案】B 【分析】先证明△ACD ∽△ABC ,即有12AC AD CD AB AC BC ===,则可得12AC AD CD AB AC BC ++=++,问题得解.【详解】∵∠B =∠ACD ,∠A =∠A ,∴△ACD ∽△ABC ,∴AC AD CD AB AC BC ==,∵12AC AB =,∴12AC AD CD AB AC BC ===,∴12AC AD CD AC AD CD AB AC BC AB AC BC ++====++,∴△ADC 与△ACB 的周长比1:2,故选:B .【点睛】本题主要考查了相似三角形的判定与性质,证明△ACD ∽△ABC 是解答本题的关键.10.(2022·广西)已知△ABC 与△A 1B 1C 1是位似图形,位似比是1:3,则△ABC 与△A 1B 1C 1的面积比( )A .1 :3B .1:6C .1:9D .3:1【答案】C【分析】根据位似图形的面积比等于位似比的平方,即可得到答案.【详解】∵△ABC 与△A 1B 1C 1是位似图形,位似比是1:3,∴△ABC 与△A 1B 1C 1的面积比为1:9,故选:C .【点睛】本题考查位似图形的性质,熟练掌握位似图形的面积比等于位似比的平方是解题的关键.11.(2022·山东临沂)如图,在ABC 中,∥DE BC ,23AD DB =,若6AC =,则EC =( )A .65B .125C .185D .245【答案】C【分析】由∥DE BC ,23AD DB =,可得2,3AD AE DB EC ==再建立方程即可.【详解】解: ∥DE BC ,23AD DB =,2,3AD AE DB EC ∴== 6AC =,62,3CE CE -∴= 解得:18.5CE =经检验符合题意故选C 【点睛】本题考查的是平行线分线段成比例,证明“23AD AE DB EC ==”是解本题的关键.12.(2022·山东威海)由12个有公共顶点O 的直角三角形拼成如图所示的图形,∠AOB =∠BOC =∠COD =…=∠LOM =30°.若S △AOB =1,则图中与△AOB 位似的三角形的面积为( )A .(43)3B .(43)7C .(43)6D .(34)6【答案】C【分析】根据题意得出A 、O 、G 在同一直线上,B 、O 、H 在同一直线上,确定与△AOB 位似的三角形为△GOH ,利用锐角三角函数找出相应规律得出OG=6x ,再由相似三角形的性质求解即可.【详解】解:∵∠AOB =∠BOC =∠COD =…=∠LOM =30°∴∠AOG =180°,∠BOH =180°,∴A 、O 、G 在同一直线上,B 、O 、H 在同一直线上,∴与△AOB 位似的三角形为△GOH ,设OA =x ,则OB=1cos30OA x ==︒,∴OC=24cos303OB x x ==︒,∴OD=3cos30OC x ==︒,…∴OG=6x ,∴6OG OA =,∴12643GOH AOB S S ⎛⎫== ⎪⎝⎭ ,∵1AOB S = ,∴643GOH S ⎛⎫= ⎪⎝⎭ ,故选:C .【点睛】题目主要考查利用锐角三角函数解三角形,找规律问题,相似三角形的性质等,理解题意,找出相应边的比值规律是解题关键.二.填空题13.(2022·贵州黔东南)如图,折叠边长为4cm 的正方形纸片ABCD ,折痕是DM ,点C 落在点E 处,分别延长ME 、DE 交AB 于点F 、G ,若点M 是BC 边的中点,则FG =______cm.【答案】53【分析】根据折叠的性质可得DE =DC =4,EM =CM =2,连接DF ,设FE =x ,由勾股定理得BF ,DF ,从而求出x 的值,得出FB ,再证明FEG FBM ∆∆ ,利用相似三角形对应边成比例可求出FG .【详解】解:连接,DF 如图,∵四边形ABCD 是正方形,∴4,90.AB BC CD DA A B C CDA ︒====∠=∠=∠=∠=∵点M 为BC 的中点,∴114222BM CM BC ===⨯=由折叠得,2,4,ME CM DE DC ====∠90,DEM C ︒=∠=∴∠90DEF ︒=,90,FEG ∠=︒设,FE x =则有222DF DE EF =+∴2224DF x =+又在Rt FMB ∆中,2,2FM x BM =+=,∵222FM FB BM =+∴FB ==∴4AF AB FB =-=在Rt DAF ∆中,222,DA AF DF +=∴2224(44,x +=+解得,124,83x x ==-(舍去)∴4,3FE =∴410233FM FE ME =+=+=∴83FB ==∵∠90DEM ︒=∴∠90FEG ︒=∴∠,FEG B =∠又∠.GFE MFB =∠∴△FEG FBM∆ ∴,FG FE FM FB=即4310833FG =∴5,3FG =故答案为:53【点睛】本题主要考查了正方形的性质,折叠的性质,勾股定理,相似三角形的判定与性质,正确作出辅助线是解答本题的关键.14.(2022·上海)如图,在△ABC 中,∠A =30°,∠B =90°,D 为AB 中点,E 在线段AC 上,AD DE AB BC=,则AE AC =_____.【答案】12或14【分析】由题意可求出12DE BC =,取AC 中点E 1,连接DE 1,则DE 1是△ABC 的中位线,满足112DE BC =,进而可求此时112AE AC =,然后在AC 上取一点E 2,使得DE 1=DE 2,则212DE BC =,证明△DE1E2是等边三角形,求出E1E2=14AC ,即可得到214AE AC =,问题得解.【详解】解:∵D 为AB中点,∴12AD DE AB BC ==,即12DE BC =,取AC 中点E 1,连接DE 1,则DE 1是△ABC 的中位线,此时DE 1∥BC ,112DE BC =,∴112AE AD AC AB ==,在AC 上取一点E 2,使得DE 1=DE 2,则212DE BC =,∵∠A =30°,∠B =90°,∴∠C =60°,BC =12AC ,∵DE 1∥BC ,∴∠DE1E2=60°,∴△DE1E2是等边三角形,∴DE 1=DE 2=E1E2=12BC ,∴E1E2=14AC ,∵112AE AC =,∴214AE AC =,即214AE AC =,综上,AE AC 的值为:12或14,故答案为:12或14.【点睛】本题考查了三角形中位线的性质,平行线分线段成比例,等边三角形的判定和性质以及含30°角的直角三角形的性质等,根据12DE BC =进行分情况求解是解题的关键.15.(2022·北京)如图,在矩形ABCD 中,若13,5,4AF AB AC FC ===,则AE 的长为_______.【答案】1【分析】根据勾股定理求出BC ,以及平行线分线段成比例进行解答即可.【详解】解:在矩形ABCD 中:AD BC ∥,90ABC ∠=︒,∴14AE AF BC FC ==,4BC =,∴144AE =,∴1AE =,故答案为:1.【点睛】此题考查了勾股定理以及平行线分线段成比例,掌握平行线分线段成比例是解题的关键.16.(2022·江苏常州)如图,在Rt ABC △中,90C ∠=︒,9AC =,12BC =.在Rt DEF 中,90F ∠=︒,3DF =,4EF =.用一条始终绷直的弹性染色线连接CF ,Rt DEF 从起始位置(点D 与点B 重合)平移至终止位置(点E 与点A 重合),且斜边DE 始终在线段AB 上,则Rt ABC △的外部被染色的区域面积是______.【答案】28【分析】过点F 作AB 的垂线交于G ,同时在图上标出,,M N F '如图,需要知道的是Rt ABC 的被染色的区域面积是MNF F S '梯形,所以需要利用勾股定理,相似三角形、平行四边形的判定及性质,求出相应边长,即可求解.【详解】解:过点F 作AB 的垂线交于G ,同时在图上标出,,M N F '如下图:90C ∠=︒ ,9AC =,12BC =,15AB ∴==,在Rt DEF 中,90F ∠=︒,3DF =,4EF =.5DE ∴==,15510AE AB DE =-=-= ,//,EF AF EF AF ''= ,∴四边形AEFF '为平行四边形,10AE FF '∴==,11622DEF S DF EF DE GF =⋅=⋅= ,解得:125GF =, //DF AC ,,DFM ACM FDM CAM ∴∠=∠∠=∠,DFM ACM ∴ ∽,13DM DF AM AC ∴==,1115344DM AM AB ∴===,//BC AF ' ,同理可证:ANF DNC ' ∽,13AF AN BC DN '∴==,345344DN AN AB ∴===,451530444MN DN DM ∴=-=-=,Rt ABC 的外部被染色的区域面积为130121028245MNF F S '⎛⎫=⨯+⨯= ⎪⎝⎭梯形,故答案为:28.【点睛】本题考查了直角三角形,相似三角形的判定及性质、勾股定理、平行四边形的判定及性质,解题的关键是把问题转化为求梯形的面积.17.(2022·广西)数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2米的标杆影长为1.2米,此时旗杆影长为7.2米,则旗杆的高度为______米.【答案】12【分析】根据同时、同地物高和影长的比不变,构造相似三角形,然后根据相似三角形的性质解答.【详解】解:设旗杆为AB ,如图所示:根据题意得:ABC DEF ∆∆ ,∴DE EF AB BC= ∵2DE =米, 1.2EF =米,7.2BC =米,∴2 1.2=7.2AB 解得:AB =12米.故答案为:12.【点睛】本题考查了中心投影、相似三角形性质的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.18.(2022·广东深圳)已知ABC 是直角三角形,90,3,5,B AB BC AE ∠=︒===连接CE 以CE 为底作直角三角形CDE 且,CD DE =F 是AE 边上的一点,连接BD 和,BF BD 且45,FBD ∠=︒则AF 长为______.【分析】将线段BD 绕点D 顺时针旋转90︒,得到线段HD ,连接BH ,HE ,利用SAS 证明EDH CDB ∆≅∆,得5EH CB ==,90HED BCD ∠=∠=︒,从而得出////HE DC AB ,则ABF EHF ∆∆∽,即可解决问题.【详解】解:将线段BD 绕点D 顺时针旋转90︒,得到线段HD ,连接BH ,HE ,BDH ∴∆是等腰直角三角形,又EDC ∆ 是等腰直角三角形,HD BD ∴=,EDH CDB ∠=∠,ED CD =,()EDH CDB SAS ∴∆≅∆,5EH CB ∴==,90HED BCD ∠=∠=︒,90EDC ∠=︒ ,90ABC ∠=︒,////HE DC AB ∴,,ABF EHF BAF HEF ∴∠=∠∠=∠,ABF EHF ∴∆∆∽,∴==-AB AF AF EH EF AE AF ,AE =∴35=AF ∴=,【点睛】本题主要考查了等腰直角三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质等知识,解题的关键是作辅助线构造全等三角形.19.(2022·广西河池)如图,把边长为1:2的矩形ABCD 沿长边BC ,AD 的中点E ,F 对折,得到四边形ABEF ,点G ,H 分别在BE ,EF 上,且BG =EH =25BE =2,AG 与BH 交于点O ,N 为AF 的中点,连接ON ,作OM ⊥ON 交AB 于点M ,连接MN ,则tan ∠AMN =_____.【答案】58##0.625【分析】先判断出四边形ABEF 是正方形,进而判断出△ABG ≌△BEH ,得出∠BAG =∠EBH ,进而求出∠AOB =90°,再判断出△AOB ~△ABG ,求出OA OB ==△OBM ~△OAN ,求出BM =1,即可求出答案.【详解】解:∵点E ,F 分别是BC ,AD 的中点,∴11,22AF AD BE BC ==,∵四边形ABCD 是矩形,∴∠A =90°,AD ∥BC ,AD =BC ,∴12AF BE AD ==,∴四边形ABEF 是矩形,由题意知,AD =2AB ,∴AF =AB ,∴矩形ABEF 是正方形,∴AB =BE ,∠ABE =∠BEF =90°,∵BG =EH ,∴△ABG≌△BEH(SAS),∴∠BAG=∠EBH,∴∠BAG+∠ABO=∠EBH+∠ABO=∠ABG=90°,∴∠AOB=90°,∵BG=EH=25BE=2,∴BE=5,∴AF=5,∴AG==∵∠OAB=∠BAG,∠AOB=∠ABG,∴△AOB∽△ABG,∴OA OB ABAB BG AG==,即52OA OB==∴OA OB==∵OM⊥ON,∴∠MON=90°=∠AOB,∴∠BOM=∠AON,∵∠BAG+∠FAG=90°,∠ABO+∠EBH=90°,∠BAG=∠EBH,∴∠OBM=∠OAN,∴△OBM~△OAN,∴OB BM OA AN=,∵点N是AF的中点,∴1522AN AF==,52BM=,解得:BM=1,∴AM=AB-BM=4,∴552tan48ANAMNAM∠===.故答案为:5 8【点睛】此题主要考查了矩形性质,正方形性质和判定,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,求出BM 是解本题的关键.20.(2022·内蒙古赤峰)如图,为了测量校园内旗杆AB 的高度,九年级数学应用实践小组,根据光的反射定律,利用镜子、皮尺和测角仪等工具,按以下方式进行测量:把镜子放在点O 处,然后观测者沿着水平直线BO 后退到点D ,这时恰好能在镜子里看到旗杆顶点A ,此时测得观测者观看镜子的俯角α=60°,观测者眼睛与地面距离CD =1.7m ,BD =11m ,则旗杆AB 的高度约为_________m . 1.7≈)【答案】17【分析】如图容易知道CD ⊥BD ,AB ⊥BD ,即∠CDO =∠ABO =90°.由光的反射原理可知∠COD =∠AOB =60°,这样可以得到△COD ∽△AOB ,然后利用对应边成比例就可以求出AB .【详解】解:由题意知∠COD =∠AOB =60°,∠CDE =∠ABE =90°,∵CD =1.7m ,∴OD =60CD tan =︒≈1(m),∴OB =11-1=10(m),∴△COD ∽△AOB .∴CD OD AB OB =,即1.7110AB =,∴AB =17(m),答:旗杆AB 的高度约为17m .故答案为:17.【点睛】本题考查了解直角三角形的应用,相似三角形的应用,本题只要是把实际问题抽象到相似三角形中,利用相似三角形的性质就可以求出结果.21.(2022·湖北鄂州)如图,在边长为6的等边△ABC 中,D 、E 分别为边BC 、AC 上的点,AD 与BE 相交于点P ,若BD =CE =2,则△ABP 的周长为 _____.【答案】6+【分析】如图所示,过点E 作EF ⊥AB 于F ,先解直角三角形求出AF ,EF ,从而求出BF ,利用勾股定理求出BE 的长,证明△ABD ≌△BCE 得到∠BAD =∠CBE ,AD =BE ,再证明△BDP ∽△ADB ,得到62BP PD==,即可求出BP ,PD ,从而求出AP ,由此即可得到答案.【详解】解:如图所示,过点E 作EF ⊥AB 于F ,∵△ABC 是等边三角形,∴AB =BC ,∠ABD =∠BAC =∠BCE =60°,∵CE =BD =2,AB =AC =6,∴AE =4,∴cos 2sin AF AE EAF EF AE EAF =⋅∠==⋅∠=,,∴BF =4,∴BE =又∵BD =CE ,∴△ABD ≌△BCE (SAS ),∴∠BAD =∠CBE ,AD =BE ,又∵∠BDP =∠ADB ,∴△BDP ∽△ADB ,∴BD BP DP AD AB BD==,62BP PD==,∴BP PD =∴AP AD AP =-=,∴△ABP 的周长=6AB BP AP ++=故答案为:6+【点睛】本题主要考查了等边三角形的性质,解直角三角形,勾股定理,相似三角形的性质与判定,全等三角形的性质与判定,正确作出辅助线是解题的关键.22.(2022·山东潍坊)《墨子·天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD 的面积为4,以它的对角线的交点为位似中心,作它的位似图形A B C D '''',若:2:1A B AB ='',则四边形A B C D ''''的外接圆的周长为___________.【答案】【分析】根据正方形ABCD 的面积为4,求出2AB =,根据位似比求出4A B ''=,周长即可得出;【详解】解: 正方形ABCD 的面积为4,∴2AB =,:2:1A B AB ''=,∴4A B ''=,∴A C ''==所求周长=;故答案为:.【点睛】本题考查位似图形,涉及知识点:正方形的面积,正方形的对角线,圆的周长,解题关键求出正方形ABCD 的边长.23.(2022·内蒙古包头)如图,在Rt ABC 中,90ACB ∠=︒,3AC BC ==,D 为AB 边上一点,且BD BC =,连接CD ,以点D 为圆心,DC 的长为半径作弧,交BC 于点E (异于点C ),连接DE ,则BE的长为___________.【答案】3##3-+【分析】过点D 作DF ⊥BC 于点F ,根据题意得出DC DE =,根据等腰三角形性质得出CF EF =,根据90ACB ∠=︒,3AC BC ==,得出AB =CF x =,则3BF x =-,证明DF AC ,得出BF BDCF AD=,列出关于x 的方程,解方程得出x 的值,即可得出3BE =.【详解】解:过点D 作DF ⊥BC 于点F ,如图所示:根据作图可知,DC DE =,∵DF ⊥BC ,∴CF EF =,∵90ACB ∠=︒,3AC BC ==,∴AB ===∵3BD BC ==,∴3AD =,设CF x =,则3BF x =-,∵90ACB ∠=︒,∴AC BC ⊥,∵DF BC ⊥,∴DF AC ,∴BF BDCF AD =,即3x x -=,解得:x =,∴226CE x ===-,∴3363BE CE =-=-+=.故答案为:3.【点睛】本题主要考查了等腰三角形的性质和判定,勾股定理,平行线分线段成比例定理,平行线的判定,作出辅助线,根据题意求出CF 的长,是解题的关键.24.(2022·江苏泰州)如图上,Δ,90,8,6,ABC C AC BC ∠=== 中O 为内心,过点O 的直线分别与AC 、AB 相交于D 、E ,若DE=CD+BE ,则线段CD 的长为__________.【答案】2或12##12或2【分析】分析判断出符合题意的DE 的情况,并求解即可;【详解】解:①如图,作//DE BC ,OF BC OG AB ⊥⊥,,连接OB ,则OD ⊥AC ,∵//DE BC ,∴OBF BOE ∠=∠∵O 为ABC ∆的内心,∴OBF OBE ∠=∠,∴BOE OBE ∠=∠∴BE OE =,同理,CD OD =,∴DE=CD+BE ,10AB ===∵O 为ABC ∆的内心,∴OF OD OG CD ===,∴BF BG AD AG==,∴6810AB BG AG BC CD AC CD CD CD =+=-+-=-+-=∴2CD =②如图,作DE AB ⊥,由①知,4BE =,6AE =,∵ACB AED CAB EAD ∠=∠∠=∠,∴ABC ADE ∆∆ ∴AB ADAC AE=∴1061582AB AE AD AC ⋅⨯===∴151822CD AC AD =-=-=∵92DE ===∴19422DE BE CD =+=+=∴12CD =故答案为:2或12.【点睛】本题主要考查三角形内心的性质、勾股定理、三角形的相似,根据题意正确分析出符合题意的情况并应用性质定理进行求解是解题的关键.25.(2022·黑龙江绥化)如图,60AOB ∠=︒,点1P 在射线OA 上,且11OP =,过点1P 作11PK OA ⊥交射线OB 于1K ,在射线OA 上截取12PP ,使1211PPPK =;过点2P 作22P K OA ⊥交射线OB 于2K ,在射线OA 上截取23P P ,使2322P P P K =.按照此规律,线段20232023P K 的长为________.20221【分析】解直角三角形分别求得11PK ,22P K ,33P K ,……,探究出规律,利用规律即可解决问题.【详解】解:11PK OA ⊥ ,11OPK ∴△是直角三角形,在11Rt OPK 中,60AOB ∠=︒,11OP =,12111tan 60PP PK OP ∴==⋅︒=11PK OA ⊥ ,22P K OA ⊥,1122PK P K ∴∥,2211OP K OPK ∴△∽△,222111P K OP PK OP ∴=,=221P K ∴,同理可得:2331P K =+,3441P K =,……,11n n n P K -∴=,2022202320231P K ∴=,20221.【点睛】本题考查了图形的规律,解直角三角形,平行线的判定,相似三角形的判定与性质,解题的关键是学会探究规律的方法.26.(2022·黑龙江)如图,在平面直角坐标系中,点1A ,2A ,3A ,4A ……在x 轴上且11OA =,212OA OA =,322OA OA =,432OA OA =……按此规律,过点1A ,2A ,3A ,4A ……作x轴的垂线分别与直线y =交于点1B ,2B ,3B ,4B ……记11OA B ,22OA B △,33 OA B ,44 OA B ……的面积分别为1S ,2S ,3S ,4S ……,则2022S =______.【答案】2【分析】先求出11A B =,可得11OA B S =112233n n A B A B A B A B ⋯⋯∥∥∥∥,从而得到11OA B ∽22OA B △∽33 OA B ∽44 OA B ∽……∽n n OA B △,再利用相似三角形的性质,可得11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ∶……∶n n OA B S =()()()2222231:2:2:2::2n ,即可求解.【详解】解:当x =1时,y =,∴点(1B ,∴11A B =∴11112OA B S =⨯= ,∵根据题意得:112233n n A B A B A B A B ⋯⋯∥∥∥∥,∴11OA B ∽22OA B △∽33 OA B ∽44 OA B ∽……∽n n OA B △,∴11OA B S ∶22OA B S ∶33OA B S ∶44OA B S :……∶n n OA B S = OA 12∶OA 22∶OA 32∶……∶OAn 2,∵11OA =,212OA OA =,322OA OA =,432OA OA =,……,∴22OA =,2342OA ==,3482OA ==,……,12n n OA -=,∴11OA B S ∶22OA B S ∶33OA B S ∶44OA B S ∶……∶n n OA B S =()()()2222231246221:2:2:2::21:2:2:2::2n n --= ,∴11222n n n OA B OA B S S -= ,∴220222202222S ⨯-==故答案为:2【点睛】本题主要考查了图形与坐标的规律题,相似三角形的判定和性质,明确题意,准确得到规律,是解题的关键.27.(2022·广西)如图,在正方形ABCD 中,AB =,对角线,AC BD 相交于点O .点E 是对角线AC 上一点,连接BE ,过点E 作EF BE ⊥,分别交,CD BD 于点F 、G ,连接BF ,交AC 于点H ,将EFH △沿EF 翻折,点H 的对应点H '恰好落在BD 上,得到EFH '△若点F 为CD 的中点,则EGH '△的周长是_________.【答案】5+【分析】过点E 作PQ //AD 交AB 于点P ,交DC 于点Q ,得到BP =CQ ,从而证得BPE ≌EQF △,得到BE =EF ,再利用BC =F 为中点,求得BF ==BE EF ===,再求出2EO ==,再利用AB //FC ,求出ABH CFH △∽△21AH CH ==,求得216833AH =⨯=,18833CH =⨯=,从而得到EH =AH -AE =1610233-=,再求得EOB GOE △∽△得到21242OG ===,求得EG OG =1, 过点F 作FM ⊥AC 于点M ,作FN ⊥OD 于点N ,求得FM =2,MH =23,FN =2,证得Rt FH N '△≌Rt FMH 得到23H N MH '==,从而得到ON =2,NG =1,25133GH '=+=,从而得到答案.【详解】解:过点E 作PQ //AD 交AB 于点P ,交DC 于点Q ,∵AD //PQ ,∴AP =DQ ,BPQ CQE ∠=∠,∴BP =CQ ,∵45ACD ∠=︒,∴BP =CQ =EQ ,∵EF ⊥BE ,∴90PEB FEQ ∠+∠=︒∵90PBE PEB ∠+∠=︒∴PBE FEQ ∠=∠,在BPE 与EQF △中BPQ FQE PB EQPBE FEQ ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BPE ≌EQF △,∴BE =EF ,又∵BC AB ==F 为中点,∴CF =∴BF ==∴BE EF ===,又∵4BO ==,∴2EO ==,∴AE =AO -EO =4-2=2,∵AB //FC ,∴ABH CFH △∽△,∴AB AH CF CH=,21AH CH ==,∵8AC ==, ∴216833AH =⨯=,18833CH =⨯=,∴EH =AH -AE =1610233-=,∵90BEO FEO ∠+∠=︒,+90BEO EBO ∠∠=︒,∴FEO EBO ∠=∠,又∵90EOB EOG ∠=∠=︒,∴EOB GOE△∽△∴EG OG OE BE OE OB==,21242OG ===,∴EG OG =1,过点F 作FM ⊥AC 于点M ,∴FM=MC 2=,∴MH =CH -MC =82233-=, 作FN ⊥OD 于点N ,2,FN ==,在Rt FH N '△与Rt FMH 中FH FH FN FM'=⎧⎨=⎩∴Rt FH N '△≌Rt FHM∴23H N MH '==,∴ON =2,NG =1,∴25133GH '=+=,∴10533EGH C EH EG GH EH EG GH '''=++=++=△,故答案为:【点睛】本题考查了正方形的性质应用,重点是与三角形相似和三角形全等的结合,熟练掌握做辅助线是解题的关键.28.(2022·辽宁)如图,在正方形ABCD 中,E 为AD 的中点,连接BE 交AC 于点F .若6AB =,则AEF 的面积为___________.【答案】3【分析】由正方形的性质可知1113222AE AD AB BC ====,//AD BC ,则有AEF CBF ∽△△,然后可得12EF AE BF BC ==,进而问题可求解.【详解】解:∵四边形ABCD 是正方形,6AB =,∴6AD BC AB ===,//AD BC ,∴AEF CBF ∽△△,∴EF AE BF BC=,∵E 为AD 的中点,∴1113222AE AD AB BC ====,∴12EF AE BF BC ==,192ABE S AE AB =⋅= ,∴13EF BE =,∴133AEF ABE S S == ;故答案为3.【点睛】本题主要考查正方形的性质及相似三角形的性质与判定,熟练掌握正方形的性质及相似三角形的性质与判定是解题的关键.29.(2022·贵州贵阳)如图,在四边形ABCD 中,对角线AC ,BD 相交于点E ,6cm AC BC ==,90ACB ADB ∠=∠=︒.若2BE AD =,则ABE △的面积是_______2cm ,AEB ∠=_______度.【答案】 36-36- 112.5【分析】通过证明ADE BCE ,利用相似三角形的性质求出23m AE =,263m CE =-,再利用勾股定理求出其长度,即可求三角形ABE 的面积,过点E 作EF ⊥AB ,垂足为F ,证明AEF 是等腰直角三角形,再求出AE CE =,继而证明()Rt BCE Rt BFE HL ≅ ,可知122.52EBF EBC ABC ∠=∠=∠=︒,利用外角的性质即可求解.【详解】90,ACB ADB AED BEC ∠=∠=︒∠=∠ ,ADE BCE ∴ ,AD AE BC BE∴=,6,2BC AC BE AD === ,设,2AD m BE m ==,62m AE m∴=,23m AE ∴=,263m CE ∴=-,在Rt BCE 中,由勾股定理得222BC CE BE +=,22226(6)(2)2m m ∴+-=,解得236m =-或236m =+ 对角线AC ,BD 相交于点E ,236m ∴=-,12AE ∴=-,6CE ∴=,∴(2111263622ABE S AE BC =⋅⋅=⨯-⨯=- ,过点E 作EF ⊥AB ,垂足为F ,90,ACB AC BC ∠=︒= ,45BAC ABC AEF ∴∠=∠=︒=∠,6AE AF AE CE ∴====,BE BE = ,()Rt BCE Rt BFE HL ∴≅ ,122.52EBF EBC ABC ∴∠=∠=∠=︒,112.5AEB ACB EBC ∴∠=∠+∠=︒,故答案为:36-,112.5.【点睛】本题考查了相似三角形的判定和性质,勾股定理,等腰直角三角形的判定和性质,全等三角形的判定和性质及三角形外角的性质,熟练掌握知识点是解题的关键.三.解答题30.(2022·河北)如图,某水渠的横断面是以AB 为直径的半圆O ,其中水面截线MN AB ∥.嘉琪在A 处测得垂直站立于B 处的爸爸头顶C 的仰角为14°,点M 的俯角为7°.已知爸爸的身高为1.7m .(1)求∠C 的大小及AB 的长;(2)请在图中画出线段DH ,用其长度表示最大水深(不说理由),并求最大水深约为多少米(结果保留小数点后一位).(参考数据:tan 76︒取4 4.1)【答案】(1)=76C ∠︒, 6.8(m)AB =(2)见详解,约6.0米【分析】(1)由水面截线MN AB ∥可得BC AB ⊥,从而可求得76C ∠=︒,利用锐角三角形的正切值即可求解.(2)过点O 作O H M N ⊥,交MN 于D 点,交半圆于H 点,连接OM ,过点M 作MG ⊥OB 于G ,水面截线MN AB ∥,即可得DH 即为所求,由圆周角定理可得14BOM ∠=︒,进而可得ABC OGM ,利用相似三角形的性质可得4OG GM =,利用勾股定理即可求得GM 的值,从而可求解.(1)解:∵水面截线MN AB∥BC AB ∴⊥,90ABC ∴∠=︒,90=76C CAB ∴∠=︒-∠︒,在t R ABC 中,90ABC ∠=︒, 1.7BC =,tan 76 1.7AB AB BC ∴︒==,解得 6.8(m)AB ≈.(2)过点O 作O H M N ⊥,交MN 于D 点,交半圆于H 点,连接OM ,过点M 作MG ⊥OB 于G ,如图所示:水面截线MN AB ∥,OH AB ⊥,DH MN ∴⊥,GM OD =,DH ∴为最大水深,7BAM ∠=︒ ,214BOM BAM ∴∠=∠=︒,90ABC OGM ∠=∠=︒ ,且14BAC ∠=︒,ABC OGM ∴ ,OG MG AB CB ∴=,即6.8 1.7OG MG =,即4OG GM =,在Rt OGM △中,90OGM ∠=︒, 3.42AB OM =≈,222OG GM OM ∴+=,即2224(3.4)GM GM +=(),解得0.8GM ≈,= 6.80.86DH OH OD ∴-=-≈,∴最大水深约为6.0米.【点睛】本题考查了解直角三角形,主要考查了锐角三角函数的正切值、圆周角定理、相似三角形的判定及性质、平行线的性质和勾股定理,熟练掌握解直角三角形的相关知识是解题的关键.31.(2022·吉林)下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.【作业】如图①,直线12l l ∥,ABC 与DBC △的面积相等吗?为什么?解:相等.理由如下:设1l 与2l 之间的距离为h ,则12ABC S BC h =⋅ ,12DBC S BC h =⋅△.∴ABC DBC S S = .【探究】(1)如图②,当点D 在1l ,2l 之间时,设点A ,D 到直线2l 的距离分别为h ,h ',则ABC DBC S h S h ='△△.证明:∵ABC S(2)如图③,当点D 在1l ,2l 之间时,连接AD 并延长交2l 于点M ,则ABC DBC S AM S DM =△△.证明:过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,则90AEM DFM ∠=∠=︒,∴AE ∥ .∴AEM △∽ .∴AE AM DF DM =.由【探究】(1)可知ABC DBC S S =△△ ,∴ABC DBC S AM S DM =△△.(3)如图④,当点D 在2l 下方时,连接AD 交2l 于点E .若点A ,E ,D 所对应的刻度值分别为5,1.5,0,ABC DBC S S △△的值为 .【答案】(1)证明见解析(2)证明见解析(3)73【分析】(1)根据三角形的面积公式可得11,22ABC DBC S S BC h BC h '=⋅=⋅ ,由此即可得证;(2)过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,先根据平行线的判定可得AE DF ,再根据相似三角形的判定可证AEM DFM ~ ,根据相似三角形的性质可得AE AM DF DM=,然后结合【探究】(1)的结论即可得证;(3)过点A 作AM BC ⊥于点M ,过点D 作DN BC ⊥于点N ,先根据相似三角形的判定证出AME DNE ~ ,再根据相似三角形的性质可得73AM AE DN DE ==,然后根据三角形的面积公式可得12ABC S BC AM =⋅ ,12DBC S BC DN =⋅ ,由此即可得出答案.(1)证明:12ABC S BC h =⋅ ,12DBC BC h S '=⋅ ,ABC DBC S h S h ∴='.(2)证明:过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,则90AEM DFM ∠=∠=︒,AE DF ∴∥.AEM DFM ~∴ .AE AM DF DM∴=.由【探究】(1)可知ABC DBC S AE S DF= ,ABC DBC S AM S DM ∴= .(3)解:过点A 作AM BC ⊥于点M ,过点D 作DN BC ⊥于点N ,则90AME DNE ∠=∠=︒,AM DN ∴ ,AME DNE ∴~ ,AM AE DN DE∴=, 点,,A E D 所对应的刻度值分别为5,1.5,0,5 1.5 3.5AE ∴=-=, 1.5DE =,3.571.53AM DN ∴==,又12ABC S BC AM =⋅ ,12DBC S BC DN =⋅ ,73ABCDBC S AM S DN =∴= ,故答案为:73.【点睛】本题考查了相似三角形的判定与性质、平行线的判定、三角形的面积等知识点,熟练掌握相似三角形的判定与性质是解题关键.32.(2022·山东青岛)如图,在Rt ABC △中,90,5cm,3cm ACB AB BC ∠=︒==,将ABC 绕点A 按逆时针方向旋转90︒得到ADE ,连接CD .点P 从点B 出发,沿BA 方向匀速运动,速度为1cm/s ;同时,点Q 从点A 出发,沿AD 方向匀速运动,速度为1cm/s .PQ 交AC 于点F ,连接,CP EQ .设运动时间为(s)(05)t t <<.解答下列问题:(1)当EQ AD ⊥时,求t 的值;(2)设四边形PCDQ 的面积为()2cm S ,求S 与t 之间的函数关系式;(3)是否存在某一时刻t ,使PQ CD ∥?若存在,求出t 的值;若不存在,请说明理由.【答案】(1)16s 5(2)213714210S t t =-+(3)存在,65s 29t =【分析】(1)利用AQE AED △∽△得AQ AE AE AD =,即445t =,进而求解;(2)分别过点C ,P 作,CM AD PN BC ⊥⊥,垂足分别为M ,N ,证ABC CAM △∽△得,AB BC AC CA AM CM ==,求得121655AM CM ==,再证BPN BAC △∽△得BP PN BA AC=,得出45PN t =,根据ABC ACD APQ BPC PCDQ S S S S S S ==+-- 四边形即可求出表达式;(3)当PQ CD ∥时AQP ADC ∠=∠,易证APQ MCD △∽△,得出AP AQ MC MD =,则5161355t t -=,进而求出t 值.(1)解:在Rt ABC △中,由勾股定理得,4AC ===∵ABC 绕点A 按逆时针方向旋转90︒得到ADE。
中考专题-相似三角形

中考数学专题相似形(共40题)1.如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.(1)求证:BD=CE;(2)若AB=2,AD=1,把△ADE绕点A旋转,当∠EAC=90°时,求PB的长;2.如图,直角△ABC中,∠BAC=90°,D在BC上,连接AD,作BF⊥AD分别交AD于E,AC于F.(1)如图1,若BD=BA,求证:△ABE≌△DBE;(2)如图2,若BD=4DC,取AB的中点G,连接CG交AD于M,求证:①GM=2MC;②AG2=AF•AC.3.如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.(1)求证:△ADE∽△ABC;(2)若AD=3,AB=5,求的值.4.如图,点E是正方形ABCD的边BC延长线上一点,连结DE,过顶点B作BF ⊥DE,垂足为F,BF分别交AC于H,交CD于G.(1)求证:BG=DE;(2)若点G为CD的中点,求的值.5.(1)如图1,在正方形ABCD中,点E,F分别在BC,CD上,AE⊥BF于点M,求证:AE=BF;(2)如图2,将(1)中的正方形ABCD改为矩形ABCD,AB=2,BC=3,AE⊥BF 于点M,探究AE与BF的数量关系,并证明你的结论.6.如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.(1)证明:∠BDC=∠PDC;(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长.7.△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.8.如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH∥BC分别交AF,CD于G,H两点.(1)求证:DE=DC;(2)求证:AF⊥BF;(3)当AF•GF=28时,请直接写出CE的长.9.在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.(1)如图1,当∠ABC=45°时,求证:AD=DE;(2)如图2,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由.10.如图1,边长为2的正方形ABCD中,E是BA延长线上一点,且AE=AB,点P从点D出发,以每秒1个单位长度沿D→C→B向终点B运动,直线EP交AD 于点F,过点F作直线FG⊥DE于点G,交AB于点R.(1)求证:AF=AR;(2)设点P运动的时间为t,①求当t为何值时,四边形PRBC是矩形?②如图2,连接PB.请直接写出使△PRB是等腰三角形时t的值.11.如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.(1)已知BD=,求正方形ABCD的边长;(2)猜想线段EM与CN的数量关系并加以证明.12.将两块全等的三角板如图1摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.(1)将图1中△A1B1C绕点C顺时针旋转45°得图2,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;(2)在图2中,若AP1=a,则CQ等于多少?(3)将图2中△A1B1C绕点C顺时针旋转到△A2B2C(如图3),点P2是A2C与AP1的交点.当旋转角为多少度时,有△AP1C∽△CP1P2?这时线段CP1与P1P2之间存在一个怎样的数量关系?.13.把Rt△ABC和Rt△DEF按如图(1)摆放(点C与E重合),点B、C(E)、F 在同一条直线上.已知:∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=10cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点A出发,以2cm/s的速度沿AB向点B匀速移动;当点P移动到点B时,点P停止移动,△DEF也随之停止移动.DE与AC交于点Q,连接PQ,设移动时间为t(s).(1)用含t的代数式表示线段AP和AQ的长,并写出t的取值范围;(2)连接PE,设四边形APEQ的面积为y(cm2),试探究y的最大值;(3)当t为何值时,△APQ是等腰三角形.14.△ABC,∠A、∠B、∠C的对边分别是a、b、c,一条直线DE与边AC相交于点D,与边AB相交于点E.(1)如图①,若DE将△ABC分成周长相等的两部分,则AD+AE等于多少;(用a、b、c表示)(2)如图②,若AC=3,AB=5,BC=4.DE将△ABC分成周长、面积相等的两部分,求AD;(3)如图③,若DE将△ABC分成周长、面积相等的两部分,且DE∥BC,则a、b、c满足什么关系?15.已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.(1)求证:△ABM∽△NDA;(2)连接BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.16.如图,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.(1)点G在BE上,且∠BDG=∠C,求证:DG•CF=DM•EG;(2)在图中,取CE上一点H,使∠CFH=∠B,若BG=1,求EH的长.17.△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.(1)如图1,求证:DE•CD=DF•BE(2)D为BC中点如图2,连接EF.①求证:ED平分∠BEF;②若四边形AEDF为菱形,求∠BAC的度数及的值.18.如图,在△ABC 中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在线段BC上,联接AD交线段PQ于点E,且=,点G 在BC延长线上,∠ACG的平分线交直线PQ于点F.(1)求证:PC=PE;(2)当P是边AC的中点时,求证:四边形AECF是矩形.19.如图,已知△ABC中,AC=BC,点D、E、F分别是线段AC、BC、AD的中点,BF、ED的延长线交于点G,连接GC.(1)求证:AB=GD;(2)如图2,当CG=EG时,求的值.20.如图,在△ABC中,D、E分别为AB、AC上的点,线段BE、CD相交于点O,且∠DCB=∠EBC=∠A.(1)求证:△BOD∽△BAE;(2)求证:BD=CE;(3)若M、N分别是BE、CE的中点,过MN的直线交AB于P,交AC于Q,线段AP、AQ相等吗?为什么?21.如图,在矩形ABCD和矩形PEFG中,AB=8,BC=6,PE=2,PG=4.PE与AC 交于点M,EF与AC交于点N,动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,伴随点P的运动,矩形PEFG在射线AB上滑动;动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动.点P、K同时开始运动,当点K到达点F时停止运动,点P也随之停止.设点P、K运动的时间是t秒(t>0).(1)当t=1时,KE=,EN=;(2)当t为何值时,△APM的面积与△MNE的面积相等?(3)当点K到达点N时,求出t的值;(4)当t为何值时,△PKB是直角三角形?22.如图(1),在△ABC中,AD是BC边的中线,过A点作AE∥BC与过D点作DE∥AB交于点E,连接CE.(1)求证:四边形ADCE是平行四边形.(2)连接BE,AC分别与BE、DE交于点F、G,如图(2),若AC=6,求FG的长.23.已知:在正方形ABCD中,点E、F分别是CB、CD延长线上的点,且BE=DF,联结AE、AF、DE、DE交AB于点M.(1)如图1,当E、A、F在一直线上时,求证:点M为ED中点;(2)如图2,当AF∥ED,求证:AM2=AB•BM.24.已知,如图1,点D、E分别在AB,AC上,且=.(1)求证:DE∥BC.(2)已知,如图2,在△ABC中,点D为边AC上任意一点,连结BD,取BD中点E,连结CE并延长CE交边AB于点F,求证:=.(3)在(2)的条件下,若AB=AC,AF=CD,求的值.25.已知△ABC,AC=BC,点E,F在直线AB上,∠ECF=∠A.(1)如图1,点E,F在AB上时,求证:AC2=AF•BE;(2)如图2,点E,F在AB及其延长线上,∠A=60°,AB=4,BE=3,求BF的长.26.如图,正方形ABCD,∠EAF=45°.交BC、CD于E、F,交BD于H、G.(1)求证:AD2=BG•DH;(2)求证:CE=DG;(3)求证:EF=HG.27.如图,C为线段BD上一动点,过B、D分别作BD的垂线,使AB=BC,DE=DB,连接AD、AC、BE,过B作AD的垂线,垂足为F,连接CE、EF.(1)求证:AC•DF=BF•BD;(2)点C运动的过程中,∠CFE的度数保持不变,求出这个度数;(3)当点C运动到什么位置时,CE∥BF?并说明理由.28.如图,在△ABC中,点D在边AB上(不与A,B重合),DE∥BC交AC于点E,将△ADE沿直线DE翻折,得到△A′DE,直线DA′,EA′分别交直线BC于点M,N.(1)求证:DB=DM.(2)若=2,DE=6,求线段MN的长.(3)若=n(n≠1),DE=a,则线段MN的长为(用含n的代数式表示).29.如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A、D、G在同一直线上,且AD=3,DE=1,连接AC、CG、AE,并延长AE交OG于点H.(1)求证:∠DAE=∠DCG.(2)求线段HE的长.30.如图,△ABC中,点E、F分别在边AB,AC上,BF与CE相交于点P,且∠1=∠2=∠A.(1)如图1,若AB=AC,求证:BE=CF;(2)若图2,若AB≠AC,①(1)中的结论是否成立?请给出你的判断并说明理由;②求证:=.31.如图1,在锐角△ABC中,D、E分别是AB、BC的中点,点F在AC上,且满足∠AFE=∠A,DM∥EF交AC于点M.(1)证明:DM=DA;(2)点G在BE上,且∠BDG=∠C,如图2,求证:△DEG∽△ECF;(3)在图2中,取CE上一点H,使得∠CFH=∠B,若BG=5,求EH的长.32.如图,正方形ABCD中,边长为12,DE⊥DC交AB于点E,DF平分∠EDC 交BC于点F,连接EF.(1)求证:EF=CF;(2)当=时,求EF的长.33.如图,已知在△ABC中,P为边AB上一点,连接CP,M为CP的中点,连接BM并延长,交AC于点D,N为AP的中点,连接MN.若∠ACP=∠ABD.(1)求证:AC•MN=BN•AP;(2)若AB=3,AC=2,求AP的长.34.如图,已知AC、EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90°,当四边形ABCD和EFCG均为正方形时,连接BF.(1)求证:△CAE∽△CBF;(2)若BE=1,AE=2,求CE的长.35.如图①,矩形ABCD中,AB=2,BC=5,BP=1,∠MPN=90°,将∠MPN绕点P 从PB处开始按顺时针方向旋转,PM交边AB(或AD)于点E,PN交边AD(或CD)于点F,当PN旋转至PC处时,∠MPN的旋转随即停止.(1)特殊情形:如图②,发现当PM过点A时,PN也恰巧过点D,此时,△ABP △PCD(填“≌”或“~”);(2)类比探究:如图③,在旋转过程中,的值是否为定值?若是,请求出该定值;若不是,请说明理由.36.如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是.37.如图,△ABC中,∠ACB=90°,AC=5,BC=12,CO⊥AB于点O,D是线段OB 上一点,DE=2,ED∥AC(∠ADE<90°),连接BE、CD.设BE、CD的中点分别为P、Q.(1)求AO的长;(2)求PQ的长;(3)设PQ与AB的交点为M,请直接写出|PM﹣MQ|的值.38.尤秀同学遇到了这样一个问题:如图1所示,已知AF,BE是△ABC的中线,且AF⊥BE,垂足为P,设BC=a,AC=b,AB=c.求证:a2+b2=5c2该同学仔细分析后,得到如下解题思路:先连接EF,利用EF为△ABC的中位线得到△EPF∽△BPA,故,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证(1)请你根据以上解题思路帮尤秀同学写出证明过程.(2)利用题中的结论,解答下列问题:在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图2所示,求MG2+MH2的值.39.如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且.(1)求证:△ADF∽△ACG;(2)若,求的值.40.如图,四边形中ABCD中,E,F分别是AB,CD的中点,P为对角线AC延长线上的任意一点,PF交AD于M,PE交BC于N,EF交MN于K.求证:K是线段MN的中点.参考答案与试题解析(共40题)1.如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.(1)求证:BD=CE;(2)若AB=2,AD=1,把△ADE绕点A旋转,当∠EAC=90°时,求PB的长;【解答】解:(1)∵△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,∴AB=AC,AD=AE,∠DAB=∠CAE.∴△ADB≌△AEC.∴BD=CE.(2)解:①当点E在AB上时,BE=AB﹣AE=1.∵∠EAC=90°,∴CE==.同(1)可证△ADB≌△AEC.∴∠DBA=∠ECA.∵∠PEB=∠AEC,∴△PEB∽△AEC.∴=.∴=.∴PB=.②当点E在BA延长线上时,BE=3.∵∠EAC=90°,∴CE==.同(1)可证△ADB≌△AEC.∴∠DBA=∠ECA.∵∠BEP=∠CEA,∴△PEB∽△AEC.∴=.∴=.∴PB=.综上所述,PB的长为或.2.如图,直角△ABC中,∠BAC=90°,D在BC上,连接AD,作BF⊥AD分别交AD于E,AC于F.(1)如图1,若BD=BA,求证:△ABE≌△DBE;(2)如图2,若BD=4DC,取AB的中点G,连接CG交AD于M,求证:①GM=2MC;②AG2=AF•AC.【解答】证明:(1)在Rt△ABE和Rt△DBE中,,∴△ABE≌△DBE;(2)①过G作GH∥AD交BC于H,∵AG=BG,∴BH=DH,∵BD=4DC,设DC=1,BD=4,∴BH=DH=2,∵GH∥AD,∴==,∴GM=2MC;②过C作CN⊥AC交AD的延长线于N,则CN∥AG,∴△AGM∽△NCM,∴=,由①知GM=2MC,∴2NC=AG,∵∠BAC=∠AEB=90°,∴∠ABF=∠CAN=90°﹣∠BAE,∴△ACN∽△BAF,∴=,∵AB=2AG,∴=,∴2CN•AG=AF•AC,∴AG2=AF•AC.3.如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.(1)求证:△ADE∽△ABC;(2)若AD=3,AB=5,求的值.【解答】解:(1)∵AG⊥BC,AF⊥DE,∴∠AFE=∠AGC=90°,∵∠EAF=∠GAC,∴∠AED=∠ACB,∵∠EAD=∠BAC,∴△ADE∽△ABC,(2)由(1)可知:△ADE∽△ABC,∴=由(1)可知:∠AFE=∠AGC=90°,∴∠EAF=∠GAC,∴△EAF∽△CAG,∴,∴=4.如图,点E是正方形ABCD的边BC延长线上一点,连结DE,过顶点B作BF ⊥DE,垂足为F,BF分别交AC于H,交CD于G.(1)求证:BG=DE;(2)若点G为CD的中点,求的值.【解答】解:(1)∵BF⊥DE,∴∠GFD=90°,∵∠BCG=90°,∠BGC=∠DGF,∴∠CBG=∠CDE,在△BCG与△DCE中,∴△BCG≌△DCE(ASA),∴BG=DE,(2)设CG=1,∵G为CD的中点,∴GD=CG=1,由(1)可知:△BCG≌△DCE(ASA),∴CG=CE=1,∴由勾股定理可知:DE=BG=,∵sin∠CDE==,∴GF=,∵AB∥CG,∴△ABH∽△CGH,∴=,∴BH=,GH=,∴=5.(1)如图1,在正方形ABCD中,点E,F分别在BC,CD上,AE⊥BF于点M,求证:AE=BF;(2)如图2,将(1)中的正方形ABCD改为矩形ABCD,AB=2,BC=3,AE⊥BF 于点M,探究AE与BF的数量关系,并证明你的结论.【解答】(1)证明:∵四边形ABCD是正方形,∴∠ABC=∠C,AB=BC.∵AE⊥BF,∴∠AMB=∠BAM+∠ABM=90°,∵∠ABM+∠CBF=90°,∴∠BAM=∠CBF.在△ABE和△BCF中,,∴△ABE≌△BCF(ASA),∴AE=BF;(2)解:AE=BF,理由:∵四边形ABCD是矩形,∴∠ABC=∠C,∵AE⊥BF,∴∠AMB=∠BAM+∠ABM=90°,∵∠ABM+∠CBF=90°,∴∠BAM=∠CBF,∴△ABE∽△BCF,∴=,∴AE=BF.6.如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.(1)证明:∠BDC=∠PDC;(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长.【解答】(1)证明:∵AB=AD,AC平分∠BAD,∴AC⊥BD,∴∠ACD+∠BDC=90°,∵AC=AD,∴∠ACD=∠ADC,∴∠ADC+∠BDC=90°,∵PD⊥AD,∴∠ADC+∠PDC=90°,∴∠BDC=∠PDC;(2)解:过点C作CM⊥PD于点M,∵∠BDC=∠PDC,∴CE=CM,∵∠CMP=∠ADP=90°,∠P=∠P,∴△CPM∽△APD,∴=,设CM=CE=x,∵CE:CP=2:3,∴PC=x,∵AB=AD=AC=1,∴=,解得:x=,故AE=1﹣=.7.△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.【解答】(1)证明:∵△ABC是等腰直角三角形,∴∠B=∠C=45°,AB=AC,∵AP=AQ,∴BP=CQ,∵E是BC的中点,∴BE=CE,在△BPE和△CQE中,∵,∴△BPE≌△CQE(SAS);(2)解:∵△ABC和△DEF是两个全等的等腰直角三角形,∴∠B=∠C=∠DEF=45°,∵∠BEQ=∠EQC+∠C,即∠BEP+∠DEF=∠EQC+∠C,∴∠BEP+45°=∠EQC+45°,∴∠BEP=∠EQC,∴△BPE∽△CEQ,∴=,∵BP=2,CQ=9,BE=CE,∴BE2=18,∴BE=CE=3,∴BC=6.8.如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH∥BC分别交AF,CD于G,H两点.(1)求证:DE=DC;(2)求证:AF⊥BF;(3)当AF•GF=28时,请直接写出CE的长.【解答】解:(1)∵四边形ABCD是矩形,∴AB∥CD,∴∠DCE=∠CEB,∵EC平分∠DEB,∴∠DEC=∠CEB,∴∠DCE=∠DEC,∴DE=DC;(2)如图,连接DF,∵DE=DC,F为CE的中点,∴DF⊥EC,∴∠DFC=90°,在矩形ABCD中,AB=DC,∠ABC=90°,∴BF=CF=EF=EC,∴∠ABF=∠CEB,∵∠DCE=∠CEB,∴∠ABF=∠DCF,在△ABF和△DCF中,,∴△ABF≌△DCF(SAS),∴∠AFB=∠DFC=90°,∴AF⊥BF;(3)CE=4.理由如下:∵AF⊥BF,∴∠BAF+∠ABF=90°,∵EH∥BC,∠ABC=90°,∴∠BEH=90°,∴∠FEH+∠CEB=90°,∵∠ABF=∠CEB,∴∠BAF=∠FEH,∵∠EFG=∠AFE,∴△EFG∽△AFE,∴=,即EF2=AF•GF,∵AF•GF=28,∴EF=2,∴CE=2EF=4.9.在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.(1)如图1,当∠ABC=45°时,求证:AD=DE;(2)如图2,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由.【解答】(1)证明:如图1,过点D作DF⊥BC,交AB于点F,则∠BDE+∠FDE=90°,∵DE⊥AD,∴∠FDE+∠ADF=90°,∴∠BDE=∠ADF,∵∠BAC=90°,∠ABC=45°,∴∠C=45°,∵MN∥AC,∴∠EBD=180°﹣∠C=135°,∵∠BFD=45°,DF⊥BC,∴∠BFD=45°,BD=DF,∴∠AFD=135°,∴∠EBD=∠AFD,在△BDE和△FDA中,∴△BDE≌△FDA(ASA),∴AD=DE;(2)解:DE=AD,理由:如图2,过点D作DG⊥BC,交AB于点G,则∠BDE+∠GDE=90°,∵DE⊥AD,∴∠GDE+∠ADG=90°,∴∠BDE=∠ADG,∵∠BAC=90°,∠ABC=30°,∴∠C=60°,∵MN∥AC,∴∠EBD=180°﹣∠C=120°,∵∠ABC=30°,DG⊥BC,∴∠BGD=60°,∴∠AGD=120°,∴∠EBD=∠AGD,∴△BDE∽△GDA,∴=,在Rt△BDG中,=tan30°=,∴DE=AD.10.如图1,边长为2的正方形ABCD中,E是BA延长线上一点,且AE=AB,点P从点D出发,以每秒1个单位长度沿D→C→B向终点B运动,直线EP交AD 于点F,过点F作直线FG⊥DE于点G,交AB于点R.(1)求证:AF=AR;(2)设点P运动的时间为t,①求当t为何值时,四边形PRBC是矩形?②如图2,连接PB.请直接写出使△PRB是等腰三角形时t的值.【解答】(1)证明:如图,在正方形ABCD中,AD=AB=2,∵AE=AB,∴AD=AE,∴∠AED=∠ADE=45°,又∵FG⊥DE,∴在Rt△EGR中,∠GER=∠GRE=45°,∴在Rt△ARF中,∠FRA=∠AFR=45°,∴∠FRA=∠RFA=45°,∴AF=AR;(2)解:①如图,当四边形PRBC是矩形时,则有PR∥BC,∴AF∥PR,∴△EAF∽△ERP,∴,即:由(1)得AF=AR,∴,解得:或(不合题意,舍去),∴,∵点P从点D出发,以每秒1个单位长度沿D→C→B向终点B运动,∴(秒);②若PR=PB,过点P作PK⊥AB于K,设FA=x,则RK=BR=(2﹣x),∵△EFA∽△EPK,∴,即:=,解得:x=±﹣3(舍去负值);∴t=(秒);若PB=RB,则△EFA∽△EPB,∴=,∴,∴BP=AB=×2=∴CP=BC﹣BP=2﹣=,∴(秒).综上所述,当PR=PB时,t=;当PB=RB时,秒.11.如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.(1)已知BD=,求正方形ABCD的边长;(2)猜想线段EM与CN的数量关系并加以证明.【解答】解:(1)∵四边形ABCD是正方形,∴△ABD是等腰直角三角形,∴2AB2=BD2,∵BD=,∴AB=1,∴正方形ABCD的边长为1;(2)CN=2EM证明方法一、理由:∵四边形ABCD是正方形,∴AC⊥BD,OA=OC∵CF=CA,CE是∠ACF的平分线,∴CE⊥AF,AE=FE∴EO为△AFC的中位线∴EO∥BC∴∴在Rt△AEN中,OA=OC∴EO=OC=AC,∴CM=EM∵CE平分∠ACF,∴∠OCM=∠BCN,∵∠NBC=∠COM=90°,∴△CBN∽△COM,∴,∴CN=CM,即CN=2EM.证明方法二、∵四边形ABCD是正方形,∴∠BAC=45°=∠DBC,由(1)知,在Rt△ACE中,EO=AC=CO,∴∠OEC=∠OCE,∵CE平分∠ACF,∴∠OCE=∠ECB=∠OEC,∴EO∥BC,∴∠EOM=∠DBC=45°,∵∠OEM=∠OCE∴△EOM∽△CAN,∴,∴CN=2CM.12.将两块全等的三角板如图1摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.(1)将图1中△A1B1C绕点C顺时针旋转45°得图2,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;(2)在图2中,若AP1=a,则CQ等于多少?(3)将图2中△A1B1C绕点C顺时针旋转到△A2B2C(如图3),点P2是A2C与AP1的交点.当旋转角为多少度时,有△AP1C∽△CP1P2?这时线段CP1与P1P2之间存在一个怎样的数量关系?.【解答】(1)证明:∵∠B1CB=45°,∠B1CA1=90°,∴∠B1CQ=∠BCP1=45°;又B1C=BC,∠B1=∠B,∴△B1CQ≌△BCP1(ASA)∴CQ=CP1;(2)解:如图:作P1D⊥AC于D,∵∠A=30°,∴P1D=AP1;∵∠P1CD=45°,∴=sin45°=,∴CP1=P1D=AP1;又AP1=a,CQ=CP1,∴CQ=a;(3)解:当∠P1CP2=∠P1AC=30°时,由于∠CP1P2=∠AP1C,则△AP1C∽△CP1P2,所以将图2中△A1B1C绕点C顺时针旋转30°到△A2B2C时,有△AP1C∽△CP1P2.这时==,∴P1P2=CP1.13.把Rt△ABC和Rt△DEF按如图(1)摆放(点C与E重合),点B、C(E)、F 在同一条直线上.已知:∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=10cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点A出发,以2cm/s的速度沿AB向点B匀速移动;当点P移动到点B时,点P停止移动,△DEF也随之停止移动.DE与AC交于点Q,连接PQ,设移动时间为t(s).(1)用含t的代数式表示线段AP和AQ的长,并写出t的取值范围;(2)连接PE,设四边形APEQ的面积为y(cm2),试探究y的最大值;(3)当t为何值时,△APQ是等腰三角形.【解答】(1)解:AP=2t∵∠EDF=90°,∠DEF=45°,∴∠CQE=45°=∠DEF,∴CQ=CE=t,∴AQ=8﹣t,t的取值范围是:0≤t≤5;(2)过点P作PG⊥x轴于G,可求得AB=10,SinB=,PB=10﹣2t,EB=6﹣t,∴PG=PBSinB=(10﹣2t)∴y=S△ABC ﹣S△PBE﹣S△QCE==∴当(在0≤t≤5内),y有最大值,y最大值=(cm2)(3)若AP=AQ,则有2t=8﹣t解得:(s)若AP=PQ,如图①:过点P作PH⊥AC,则AH=QH=,PH∥BC ∴△APH∽△ABC,∴,即,解得:(s)若AQ=PQ,如图②:过点Q作QI⊥AB,则AI=PI=AP=t∵∠AIQ=∠ACB=90°∠A=∠A,∴△AQI∽△ABC∴即,解得:(s)综上所述,当或或时,△APQ是等腰三角形.14.△ABC,∠A、∠B、∠C的对边分别是a、b、c,一条直线DE与边AC相交于点D,与边AB相交于点E.(1)如图①,若DE将△ABC分成周长相等的两部分,则AD+AE等于多少;(用a、b、c表示)(2)如图②,若AC=3,AB=5,BC=4.DE将△ABC分成周长、面积相等的两部分,求AD;(3)如图③,若DE将△ABC分成周长、面积相等的两部分,且DE∥BC,则a、b、c满足什么关系?【解答】解:(1)∵DE将△ABC分成周长相等的两部分,∴AD+AE=CD+BC+BE=(AB+AC+BC)=(a+b+c);(2)设AD=x,AE=6﹣x,=AD•AE•sinA=3,∵S△ADE即:x(6﹣x)•=3,解得:x1=(舍去),x2=,∴AD=;(3)∵DE∥BC,∴△ADE∽△ABC,∴,∵=,∴AD=b,AE=c,∴b c=(a+b+c),∴=﹣1.15.已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.(1)求证:△ABM∽△NDA;(2)连接BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.【解答】(1)证明:∵四边形ABCD是正方形,∴∠ABC=∠ADC=∠BAD=90°,∵BM、DN分别是正方形的两个外角平分线,∴∠ABM=∠ADN=135°,∵∠MAN=45°,∴∠BAM=∠AND=45°﹣∠DAN,∴△ABM∽△NDA;(2)解:当∠BAM=22.5°时,四边形BMND为矩形;理由如下:∵∠BAM=22.5°,∠EBM=45°,∴∠AMB=22.5°,∴∠BAM=∠AMB,∴AB=BM,同理AD=DN,∵AB=AD,∴BM=DN,∵四边形ABCD是正方形∴∠ABD=∠ADB=45°,∴∠BDN=∠DBM=90°∴∠BDN+∠DBM=180°,∴BM∥DN∴四边形BMND为平行四边形,∵∠BDN=90°,∴四边形BMND为矩形.16.如图,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.(1)点G在BE上,且∠BDG=∠C,求证:DG•CF=DM•EG;(2)在图中,取CE上一点H,使∠CFH=∠B,若BG=1,求EH的长.【解答】(1)证明:如图1所示,∴D,E分别为AB,BC中点,∴DE∥AC∵DM∥EF,∴四边形DEFM是平行四边形,∴DM=EF,如图2所示,∵D、E分别是AB、BC的中点,∴DE∥AC,∴∠BDE=∠A,∠DEG=∠C,∵∠AFE=∠A,∴∠BDE=∠AFE,∴∠BDG+∠GDE=∠C+∠FEC,∵∠BDG=∠C,∴∠GDE=∠FEC,∴△DEG∽△ECF;∴,∴,∴,∴DG•CF=DM•EG;(2)解:如图3所示,∵∠BDG=∠C=∠DEB,∠B=∠B,∴△BDG∽△BED,∴,∴BD2=BG•BE,∵∠AFE=∠A,∠CFH=∠B,∴∠C=180°﹣∠A﹣∠B=180°﹣∠AFE﹣∠CFH=∠EFH,又∵∠FEH=∠CEF,∴△EFH∽△ECF,∴=,∴EF2=EH•EC,∵DE∥AC,DM∥EF,∴四边形DEFM是平行四边形,∴EF=DM=DA=BD,∴BG•BE=EH•EC,∵BE=EC,∴EH=BG=1.17.△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.(1)如图1,求证:DE•CD=DF•BE(2)D为BC中点如图2,连接EF.①求证:ED平分∠BEF;②若四边形AEDF为菱形,求∠BAC的度数及的值.【解答】(1)证明:∵△ABC中,AB=AC,∴∠B=∠C.∵∠B+∠BDE+∠DEB=180°,∠BDE+∠EDF+∠FDC=180°,∠EDF=∠B,∴∠FDC=∠DEB,∴△BDE∽△CFD,∴,即D E•CD=DF•BE;(2)解:①由(1)证得△BDE∽△CFD,∴,∵D为BC中点,∴BD=CD,∴=,∵∠B=∠EDF,∴△BDE~△DFE,∴∠BED=∠DEF,∴ED平分∠BEF;②∵四边形AEDF为菱形,∴∠AEF=∠DEF,∵∠BED=∠DEF,∴∠AEF=60°,∵AE=AF,∴∠BAC=60°,∵∠BAC=60°,∴△ABC是等边三角形,∴∠B=60°,∴△BED是等边三角形,∴BE=DE,∵AE=DE,∴AE=AB,∴=.18.如图,在△ABC 中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在线段BC上,联接AD交线段PQ于点E,且=,点G 在BC延长线上,∠ACG的平分线交直线PQ于点F.(1)求证:PC=PE;(2)当P是边AC的中点时,求证:四边形AECF是矩形.【解答】(1)证明:∵PQ∥BC,∴△AQE∽△ABD,△AEP∽△ADC,∴=,,∴=,∵=,∴=,∴PC=PE;(2)∵PF∥DG,∴∠PFC=∠FCG,∵CF平分∠PCG,∴∠PCF=∠FCG,∴∠PFC=∠FCG,∴PF=PC,∴PF=PE,∵P是边AC的中点,∴AP=CP,∴四边形AECF是平行四边形,∵PQ∥CD,∴∠PEC=∠DCE,∴∠PCE=∠DCE,∴∠PCE+∠PCF=(∠PCD+∠PCG)=90°,∴∠ECF=90°,∴平行四边形AECF是矩形.19.如图,已知△ABC中,AC=BC,点D、E、F分别是线段AC、BC、AD的中点,BF、ED的延长线交于点G,连接GC.(1)求证:AB=GD;(2)如图2,当CG=EG时,求的值.【解答】解:(1)∵D、E分别是线段AC、BC的中点,∴DE为△ABC的中位线,∴DE∥AB,即EG∥AB,∴∠FDG=∠A,∵点F为线段AD的中点,∴AF=DF,在△ABF与△DGF中,∴△ABF≌△DGF(ASA)∴AB=GD(2)∵DE为△ABC的中位线,∴DE=AB,CE=BC=AC∵DG=AB,∴EG=DE+DG∴EG=AB∵DE∥AB,∴∠GEC=∠CBA,∵AC=BC,CG=EG∴△GEC∽△CBA∴,即,∴20.如图,在△ABC中,D、E分别为AB、AC上的点,线段BE、CD相交于点O,且∠DCB=∠EBC=∠A.(1)求证:△BOD∽△BAE;(2)求证:BD=CE;(3)若M、N分别是BE、CE的中点,过MN的直线交AB于P,交AC于Q,线段AP、AQ相等吗?为什么?【解答】(1)证明:∵∠BCO=∠CBO,∴∠DOB=∠BCO+CBO=2∠BCO,∵∠A=2∠BCO,∴∠DOB=∠A,∵∠ABE=∠ABE,∴△BOD∽△BAE;(2)解:延长CD,在CD延长线上取一点F,使BF=BD,∴∠BDF=∠BFD,∵∠BDF=∠ABO+∠DOB,∠BEC=∠ABO+∠A,由(1)得∠BOD=∠A,∴∠BDF=∠BEC,∴∠BFD=∠BEC,在△BFC与△CEB中,,∴△BFC≌△CEB,∴BD=BF,∴BD=CE;(3)解:AP=AQ,理由:取BC的中点G,连接GM,GN,∵M,N分别是BE,CD的中点,∴GM,GN是中位线,∴GM∥CE,GM=CE,GN∥BD,GN=BD,∵BD=CE,∴GM=GN,∴∠3=∠4,∵GM∥CE,∴∠2=∠4,∵GN∥BD,∴∠3=∠1,∴∠1=∠2,∴AP=AQ.21.如图,在矩形ABCD和矩形PEFG中,AB=8,BC=6,PE=2,PG=4.PE与AC 交于点M,EF与AC交于点N,动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,伴随点P的运动,矩形PEFG在射线AB上滑动;动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动.点P、K同时开始运动,当点K到达点F时停止运动,点P也随之停止.设点P、K运动的时间是t秒(t>0).(1)当t=1时,KE=1,EN=;(2)当t为何值时,△APM的面积与△MNE的面积相等?(3)当点K到达点N时,求出t的值;(4)当t为何值时,△PKB是直角三角形?【解答】解:(1)当t=1时,根据题意得,AP=1,PK=1,∵PE=2,∴KE=2﹣1=1,∵四边形ABCD和PEFG都是矩形,∴△APM∽△ABC,△APM∽△NEM,∴=,=,∴MP=,ME=,∴NE=;故答案为:1;;(2)由(1)并结合题意可得,AP=t,PM=t,ME=2﹣t,NE=﹣t,∴t×t=(2﹣t)×(﹣t),解得,t=;(3)当点K到达点N时,则PE+NE=AP,由(2)得,﹣t+2=t,解得,t=;(4)①当K在PE边上任意一点时△PKB是直角三角形,即,0<t≤2;②当点k在EF上时,则KE=t﹣2,BP=8﹣t,∵△BPK∽△PKE,∴PK2=BP×KE,PK2=PE2+KE2,∴4+(t﹣2)2=(8﹣t)(t﹣2),解得t=3,t=4;③当t=5时,点K在BC边上,∠KBP=90°.综上,当0<t≤2或t=3或t=4或5时,△PKB是直角三角形.22.如图(1),在△ABC中,AD是BC边的中线,过A点作AE∥BC与过D点作DE∥AB交于点E,连接CE.(1)求证:四边形ADCE是平行四边形.(2)连接BE,AC分别与BE、DE交于点F、G,如图(2),若AC=6,求FG的长.【解答】(1)证明:∵AE∥BC,DE∥AB.∴四边形ABDE是平行四边形,∴AE=BD,又∵BD=DC,∴AE=DC,又∵AE∥DC,∴四边形ADCE是平行四边形.(2)解:∵四边形ADCE是平行四边形,AC=6,∴AG=GC=3,又∵AE∥BC,∴△AEF∽△CBF,∴==,∴AF=2,∴FG=AG﹣AF=1.23.已知:在正方形ABCD中,点E、F分别是CB、CD延长线上的点,且BE=DF,联结AE、AF、DE、DE交AB于点M.。
相似三角形中考复习(知识点+题型分类练习)

相似三角形一、知识概述1.平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其它直线上截得的线段也相等。
2.平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例。
3.相似三角形的定义对应边成比例、对应角相等的两个三角形叫做相似三角形.4.相似三角形的基本性质①相似三角形的对应边成比例、对应角相等.②相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。
③相似三角形的周长比等于相似比④面积比等于相似比的平方温馨提示:①全等三角形一定是相似三角形,其相似比k=1.所以全等三角形是相似三角形的特例.其区别在于全等要求对应边相等,而相似要求对应边成比例.②相似比具有顺序性.例如△ABC∽△A′B′C′的对应边的比,即相似比为k,则△A′B′C′∽△ABC的相似比,当且仅当它们全等时,才有k=k′=1.③相似比是一个重要概念,后继学习时出现的频率较高,其实质它是将一个图形放大或缩小的倍数,这一点借助相似三角形可观察得出.5. 相似三角形的判定定理①平行于三角形一边的直线和其他两边或其延长线相交,所得的三角形与原三角形相似;②三边对应成比例的两个三角形相似;③两角对应相等的两个三角形相似;④两边对应成比例且夹角相等的两个三角形相似。
温馨提示:(1)判定三角形相似的几条思路:①条件中若有平行,可采用判定定理1;②条件中若有一对角相等(包括隐含的公共角或对顶角),可再找一对角相等或找夹边对应成比例;③条件中若有两边对应成比例,可找夹角相等;但是,在选择利用判定定理2时,一对对应角相等必须是成比例两边的夹角对应相等.④条件中若有等腰关系,可找顶角相等或底角相等,也可找腰和底对应成比例。
(2)在综合题中,注意相似知识的灵活运用,并熟练掌握线段代换、等比代换、等量代换技巧的应用,培养综合运用知识的能力。
(3)运用相似的知识解决一些实际问题,要能够在理解题意的基础上,把它转化为纯数学知识的问题,要注意培养当数学建模的思想。
专题27 图形的相似(46题)(解析版)--2024年中考数学真题分类汇编

专题27图形的相似(46题)一、单选题1.(2024·重庆·中考真题)若两个相似三角形的相似比是1:3,则这两个相似三角形的面积比是()A .1:3B .1:4C .1:6D .1:9【答案】D【分析】此题考查了相似三角形的性质,根据“相似三角形的面积比等于相似比的平方”解答即可.【详解】解:两个相似三角形的相似比是1:3,则这两个相似三角形的面积比是1:9,故选:D .2.(2024·四川凉山·中考真题)如图,一块面积为260cm 的三角形硬纸板(记为ABC )平行于投影面时,在点光源O 的照射下形成的投影是111A B C △,若123OB BB =::,则111A B C △的面积是()A .290cmB .2135cmC .2150cmD .2375cm 【答案】D【详解】解:∵一块面积为260cm 的三角形硬纸板(记为ABC )平行于投影面时,在点光源O 的照射下形成的投影是111A B C △,123OB BB =::,∴125OB OB =,∴位似图形由三角形硬纸板与其灯光照射下的中心投影组成,相似比为2:5,∵三角形硬纸板的面积为260cm ,∴111224525ABC A B C S S ⎛⎫== ⎪⎝⎭ ,∴111A B C △的面积为2375cm .故选:D .3.(2024·陕西·中考真题)如图,正方形CEFG 的顶点G 在正方形ABCD 的边CD 上,AF 与DC 交于点H ,若6AB =,2CE =,则DH 的长为()A .2B .3C .52D .834.(2024·湖南·中考真题)如图,在ABC 中,点D E ,分别为边AB AC ,的中点.下列结论中,错误的是()A .DE BC ∥B .ADE ABC △△∽C .2BC DE=D .12ADE ABC S S =【答案】D【分析】本题考查了三角形中位线的性质,相似三角形的判定和性质,由三角形中位线性质可判断A C 、;由相似三角形的判定和性质可判断B D 、,掌握三角形中位线的性质及相似三角形的判定和性质是解题的关键.【详解】解:∵点D E ,分别为边AB AC ,的中点,∴DE BC ∥,2BC DE =,故A C 、正确;∵DE BC ∥,∴ADE ABC △△∽,故B 正确;∵ADE ABC △△∽,∴221124ADE ABC S DE S BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭△△,∴14ADE ABC S S =,故D 错误;故选:D .5.(2024·江苏连云港·中考真题)下列网格中各个小正方形的边长均为1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似形的为()A .甲和乙B .乙和丁C .甲和丙D .甲和丁【答案】D【分析】本题考查相似图形,根据对应角相等,对应边对应成比例的图形是相似图形结合正方形的性质,进行判断即可.【详解】解:由图可知,只有选项甲和丁中的对应角相等,且对应边对应成比例,它们的形状相同,大小不同,是相似形.故选D .6.(2024·浙江·中考真题)如图,在平面直角坐标系中,ABC 与A B C ''' 是位似图形,位似中心为点O .若点(3,1)A -的对应点为(6,2)A '-,则点(2,4)B -的对应点B '的坐标为()A .(4,8)-B .(8,4)-C .(8,4)-D .(4,8)-【答案】A【分析】本题考查了位似变换,根据点'A A 、的坐标可得到位似比,再根据位似比即可求解,掌握位似变换的性质是解题的关键.【详解】解:∵ABC 与A B C ''' 是位似图形,点(3,1)A -的对应点为(6,2)A '-,∴A B C ''' 与ABC 的位似比为2,∴点(2,4)B -的对应点B '的坐标为()22,42-⨯⨯,即()4,8-,故选:A .7.(2024·黑龙江绥化·中考真题)如图,矩形OABC 各顶点的坐标分别为()0,0O ,()3,0A ,()3,2B ,()0,2C ,以原点O 为位似中心,将这个矩形按相似比13缩小,则顶点B 在第一象限对应点的坐标是()A .()9,4B .()4,9C .31,2⎛⎫ ⎪D .21,3⎛⎫ ⎪8.(2024·四川成都·中考真题)如图,在ABCD Y 中,按以下步骤作图:①以点B 为圆心,以适当长为半径作弧,分别交BA ,BC 于点M ,N ;②分别以M ,N 为圆心,以大于12MN 的长为半径作弧,两弧在ABC ∠内交于点O ;③作射线BO ,交AD 于点E ,交CD 延长线于点F .若3CD =,2DE =,下列结论错误的是()A .ABE CBE ∠=∠B .5BC =C .DE DF =D .53BE EF =【答案】D【分析】本题考查角平分线的尺规作图、平行四边形的性质、等腰三角形的判定以及相似性质与判定的综合.先由作图得到BF 为ABC ∠的角平分,利用平行线证明AEB ABE ∠=∠,从而得到3AE AB CD ===,再利用平行四边形的性质得到325BC AD AE ED ==+=+=,再证明AEB DEF △∽△,分别求出32BE EF =,2DF =,则各选项可以判定.【详解】解:由作图可知,BF 为ABC ∠的角平分,∴ABE CBE ∠=∠,故A 正确;∵四边形ABCD 为平行四边形,∴,,AD BC AB CD AD BC == ,∵AD BC∥∴AEB CBE ∠=∠,∴AEB ABE ∠=∠,∴3AE AB CD ===,∴325BC AD AE ED ==+=+=,故B 正确;∵AB CD =,∴ABE F ∠=∠,∵AEB DEF ∠=∠,∴AEB DEF △∽△,∴BE AB AEEF DF ED ==,∴332BE EF DF ==,∴32BE EF =,2DF =,故D 错误;∵2DE =,∴DE DF =,故C 正确,故选:D .9.(2024·山东烟台·中考真题)如图,在正方形ABCD 中,点E ,F 分别为对角线BD AC ,的三等分点,连接AE 并延长交CD 于点G ,连接EF FG ,,若AGF α∠=,则FAG ∠用含α的代数式表示为()A .452α︒-B .902α︒-C .452α︒+D .2α【答案】B【分析】本题考查了正方形的性质,相似三角形的判定和性质,全等三角形的判定和性质,三角形的外角性质.证明EOF DOC ∽△△,求得45OFE ∠=︒,证明ABE GDE ∽,证得12DG CD CG ==,推出()SAS DEG CFG ≌,得到GE GF =,据此求解即可.【详解】解:∵正方形ABCD 中,点E ,F 分别为对角线BD AC ,的三等分点,∴OD OC =,45ODC OCD ∠=∠=︒,DE CF =,∴OE OF =,∵EOF DOC ∠=∠,OE OFOD OC=,∴EOF DOC ∽△△,∴45OFE OCD ∠=∠=︒,∵点E ,F 分别为对角线BD AC ,的三等分点,∴12DE BE =,∵正方形ABCD ,∴AB CD ∥,∴ABE GDE ∽,∴12DG DE AB BE ==,∴12DG CD CG ==,∴()SAS DEG CFG ≌,∴GE GF =,∴()111809022GEF AGF α∠=︒-∠=︒-,∴1190904545222FAG GEF AFE ααα∠=︒-︒--︒=︒-=∠-∠=,故选:B .10.(2024·江苏苏州·中考真题)如图,点A 为反比例函数()0y x x=-<图象上的一点,连接AO ,过点O 作OA 的垂线与反比例()40y x x =>的图象交于点B ,则AOBO的值为()A .12B .14C .33D .13【答案】A【分析】本题考查了反比例函数图象上点的坐标特征,反比例函数系数k 的几何意义,三角形相似的判定和性质,数形结合是解题的关键.过A 作AC x ⊥轴于C ,过B 作BD x ⊥轴于D ,证明AOC OBD △∽△,利用相似三角形的面积比等于相似比的平方求解即可.【详解】解:过A 作AC x ⊥轴于C ,过B 作BD x ⊥轴于D ,∴11122ACO S =⨯-= ,1422BDO S =⨯= ,90ACO ODB ∠=∠=︒,∵OA OB ⊥,∴90AOC OBD BOD ∠=∠=︒-∠,∴AOC OBD △∽△,∴2ACO BDO S OA S OB ⎛⎫= ⎪⎝⎭ ,即2122OA OB ⎛⎫= ⎪⎝⎭,∴12OA OB =(负值舍去),故选:A .11.(2024·山东威海·中考真题)如图,在ABCD Y 中,对角线AC ,BD 交于点O ,点E 在BC 上,点F 在CD 上,连接AE ,AF ,EF ,EF 交AC 于点G .下列结论错误的是()A .若CE ADCF AB=,则EF BD ∥B .若AE BC ⊥,AF CD ⊥,AE AF =,则EF BD ∥C .若EF BD ∥,CE CF =,则EAC FAC ∠=∠D .若AB AD =,AE AF =,则EF BD ∥∴AC BD⊥在Rt ,Rt ACE AFC 中,AE AF AC AC=⎧⎨=⎩∴Rt Rt ACE AFC ≌∴CE CF =又∵AE AF =∴AC EF⊥∴EF BD ∥,故B 选项正确,C.∵CE CF =,∴CFE CEF ∠=∠∵EF BD ∥,∴,CBD CEF CDB CFE ∠=∠∠=∠∴CBD CDB ∠=∠∴CB CD=∴四边形ABCD 是菱形,∴AC BD ⊥,又∵EF BD ∥∴AC EF ⊥,∵CE CF =,∴AC 垂直平分EF ,∴AE AF=∴EAC FAC ∠=∠,故C 选项正确;D.若AB AD =,则四边形ABCD 是菱形,由AE AF =,且BE DF =时,可得AC 垂直平分EF ,∵AC BD⊥∴EF BD ∥,故D 选项不正确故选:D .12.(2024·河南·中考真题)如图,在ABCD 中,对角线AC ,BD 相交于点O ,点E 为OC 的中点,EF AB ∥交BC 于点F .若4AB =,则EF 的长为()A .12B .1C .43D .213.(2024·安徽·中考真题)如图,在Rt ABC △中,90ABC ∠=︒,4AB =,2BC =,BD 是边AC 上的高.点E ,F 分别在边AB ,BC 上(不与端点重合),且DE DF ⊥.设AE x =,四边形DEBF 的面积为y ,则y 关于x 的函数图象为()A .B .C.D.【答案】A【分析】本题主要考查了函数图象的识别,相似三角形的判定以及性质,勾股定理的应用,过点E 作EH AC ⊥于点H ,由勾股定理求出AC ,根据等面积法求出BD ,先证明ABC ADB ∽,由相似三角形的性质可得出AB AC AD AB =,即可求出AD ,再证明AED BFD ∽,由相似三角形的性质可得出2AED BFD S AD S BD ⎛⎫= ⎪⎝⎭ ,即可得出4AED BFD S S = ,根据()ABC AED BDC BDF DEBF S S S S S =--- 四边形,代入可得出一次函数的解析式,最后根据自变量的大小求出对应的函数值.【详解】解:过点E 作EH AC ⊥于点H ,如下图:∵90ABC ∠=︒,4AB =,2BC =,∴2225AC AB BC =+=,∵BD 是边AC 上的高.∴1122AB BC AC BD ⋅=⋅,∴455BD =,∵BAC CAB ∠=∠,90ABC ADB ∠=∠=︒,∴ABC ADB ∽△△,∴AB AC AD AB=,解得:855AD =,∴85252555DC AC AD =-=-=,∵90BDF BDE BDE EDA ∠+∠=∠+∠=︒,90CBD DBA DBA A ∠+∠=∠+∠=︒,∴DBC A ∠=∠,BDF EDA ∠=∠,∴AED BFD ∽,14.(2024·山东·中考真题)如图,点E 为ABCD Y 的对角线AC 上一点,5AC =,1CE =,连接DE 并延长至点F ,使得EF DE =,连接BF ,则BF 为()A .52B .3C .72D .4【答案】B【分析】本题考查了平行四边形的性质,平行线分线段成比例定理,平行证明相似等知识点,正确作辅助线是解题关键.作辅助线如图,由平行正相似先证DEC GAE ∽,再证BGF AGE ∽,即可求得结果.【详解】解:延长DF 和AB ,交于G 点,∵四边形ABCD 是平行四边形,∴DC AB ∥,DC AB =即DC AG ∥,∴DEC GAE∽∴CE DE DC AE GE AG==,∵5AC =,1CE =,∴514AE AC CE =-=-=,∴14CE DE DC AE GE AG ===,又∵EF DE =,14DE DE GE EF FG ==+,∴13EF FG =,∵14DC DC AG AB BG ==+,DC AB =,∴13DC BG =,∴13EF DC FG BG ==,∴34BG FG AG EG ==∴AE BF ∥,∴BGF AGE ∽,∴34BF FG AE EG ==∵4AE =,∴3BF =.故选:B .二、填空题15.(2024·江苏盐城·中考真题)两个相似多边形的相似比为12∶,则它们的周长的比为.【答案】12∶/12【分析】本题考查了相似多边形的性质,根据相似多边形周长之比等于相似比即可求解,掌握相似多边形的性质是解题的关键.【详解】解:∵两个相似多边形的相似比为12∶,∴它们的周长的比为12∶,故答案为:12∶.16.(2024·云南·中考真题)如图,AB 与CD 交于点O ,且AC BD ∥.若12OA OC AC OB OD BD ++=++,则AC BD =.17.(2024·江苏扬州·中考真题)物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图像投影的方法.如图,燃烧的蜡烛(竖直放置)AB 经小孔O 在屏幕(竖直放置)上成像A B ''.设36cm AB =,24cm A B ''=.小孔O 到AB 的距离为30cm ,则小孔O 到A B ''的距离为cm .【答案】20【分析】此题主要考查了相似三角形的应用,由题意得AB A B ''∥,AOB A OB ''∽△△,过O 作OC AB ⊥于点C ,CO 交A B ''于点C ',利用已知得出''AOB A OB △∽△,进而利用相似三角形的性质求出即可,熟练掌握相似三角形的性质是解题关键.【详解】由题意得:AB A B ''∥,∴AOB A OB ''∽△△,如图,过O 作OC AB ⊥于点C ,CO 交A B ''于点C ',∴OC A B '''⊥,30cm OC =,∴A B OC AB OC '''=,即243630OC '=,∴20OC '=(cm ),即小孔O 到A B ''的距离为20cm ,故答案为:20.18.(2024·吉林·中考真题)如图,正方形ABCD 的对角线AC BD ,相交于点O ,点E 是OA 的中点,点F 是OD 上一点.连接EF .若45FEO ∠=︒,则EF BC 的值为.【答案】12【分析】本题主要考查了相似三角形的性质与判定,正方形的性质,先由正方形的性质得到45OAD ∠=︒,AD BC =,再证明EF AD ∥,进而可证明OEF OAD △∽△,由相似三角形的性质可得12EF OE AD OA ==,即12EF BC =.【详解】解:∵正方形ABCD 的对角线AC BD ,相交于点O ,∴45OAD ∠=︒,AD BC =,19.(2024·四川眉山·中考真题)如图,ABC 内接于O ,点O 在AB 上,AD 平分BAC ∠交O 于D ,连接BD .若10AB =,BD =BC 的长为.10AB = ,25BD =,()22102545AD ∴=-=,DAC CBD ∠=∠ ,又∵BAD DAE ∠=∠,∴BAD CBD ∠=∠,90ADB BCE ∠=∠=︒ ,ABD BEC ∴ ∽,BE BC AB AD∴=,451045BC ∴=,8BC ∴=,故答案为:8.20.(2024·湖北·中考真题)DEF 为等边三角形,分别延长FD DE EF ,,,到点A B C ,,,使DA EB FC ==,连接AB AC ,,BC ,连接BF 并延长交AC 于点G .若2AD DF ==,则DBF ∠=,FG =.【答案】30︒/30度435/435【分析】本题考查了相似三角形的判定和性质,等边三角形的性质,勾股定理.利用三角形的外角性质结合EB EF =可求得30DBF ∠=︒;作CH BG ⊥交BG 的延长线于点H ,利用直角三角形的性质求得1CH =,3FH =,证明AGF CGH ∽,利用相似三角形的性质列式计算即可求解.【详解】解:∵DEF 为等边三角形,DA EB FC ==,∴112CH CF ==,FH =∵90AFB H ∠=∠=︒,∴AF CH ∥,∴AGF CGH ∽,21.(2024·四川眉山·中考真题)如图,菱形ABCD 的边长为6,120BAD ∠=︒,过点D 作DE BC ⊥,交BC 的延长线于点E ,连结AE 分别交BD ,CD 于点F ,G ,则FG 的长为.【详解】解: 菱形ABCD 的边长为6,120BAD ∠=︒,6AD BC CD ∴===,AD BC ∥,120BCD ∠=︒,60DCE ∴∠=︒,DE BC ⊥ ,90DEC ∴∠=︒,在Rt DCE V 中,9030CDE DCE ∠=-︒∠=︒ ,132CE CD ∴==,2233DE CD CE ∴=-=,9BE BC CE ∴=+=,AD BE ,18090ADE DEC ︒︒∴∠=-∠=,在Rt ADE △中,()222233637AE DE AD =+=+=,AD BE ,AFD EFB ∴ ∽,6293AF AD FE BE ∴===,226737555AF AE ∴==⨯=,AD CE ∥,AGD EGC ∴△∽△,623AG AD EG CE ∴===,22372733AG AE ∴==⨯=,67472755FG AG AF ∴=-=-=.故答案为:475.22.(2024·四川乐山·中考真题)如图,在梯形ABCD 中,AD BC ∥,对角线AC 和BD 交于点O ,若13ABD BCD S S =△△,则AOD BOC S S =△△.【答案】19【分析】本题考查了平行线间的距离,相似三角形的判定与性质等知识.熟练掌握平行线间的距离,相似三角形的判定与性质是解题的关键.设AD BC ,的距离为d ,则112132ABD BCD AD d S S BC d ⋅==⋅△△,即13AD BC =,证明AOD COB ∽,则2AOD BOC S AD S BC ⎛⎫= ⎪⎝⎭△△,计算求解即可.【详解】解:设AD BC ,的距离为d ,∴112132ABD BCD AD d S S BC d ⋅==⋅△△,即13AD BC =,∵AD BC ∥,∴ADO CBO ∠=∠,DAO BCO ∠=∠,∴AOD COB ∽,∴221139AOD BOC S S AD BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭V V ,故答案为:19.23.(2024·黑龙江绥化·中考真题)如图,已知点()7,0A -,(),10B x ,()17,C y -,在平行四边形ABCO 中,它的对角线OB 与反比例函数()0k y k x =≠的图象相交于点D ,且:1:4OD OB =,则k =.【答案】15-【分析】本题考查了反比例函数与平行四边形综合,相似三角形的性质与判定,分别过点,B D ,作x 轴的垂线,垂足分别为,F E ,根据平行四边形的性质得出()2410B -,,证明ODE OBF △∽△得出6OE =,2.5DE =,进而可得()6,2.5D -,即可求解.【详解】如图所示,分别过点,B D ,作x 轴的垂线,垂足分别为,F E ,∵四边形AOCB 是平行四边形,点()7,0A -,(),10B x ,()17,C y -,∴7OA BC ==,∴24x =-,即()2410B -,,则24OF =,10BF =∵DE x ⊥轴,BF x ⊥轴,∴DE BF∥∴ODE OBF△∽△∴14OE OD DE OF OB BF ===∴6OE =, 2.5DE =∴()6,2.5D -∴6 2.515k =-⨯=-故答案为:15-.24.(2024·四川成都·中考真题)如图,在Rt ABC △中,90C ∠=︒,AD 是ABC 的一条角平分线,E 为AD 中点,连接BE .若BE BC =,2CD =,则BD =.【答案】1712+【分析】连接CE ,过E 作EF CD ⊥于F ,设BD x =,EF m =,根据直角三角形斜边上的中线性质和等腰三角形的性质证得112CF DF CD ===,EAC ECA =∠∠,ECD EDC BEC ∠=∠=∠,进而利用三角形的外角性质和三角形的中位线性质得到2CED CAE ∠=∠,22AC EF m ==,证明CBE CED ∽,利用相似三角形的性质和勾股定理得到232m x =+;根据角平分线的定义和相似三角形的判定与性质证明CAB FBE ∽∵90ACB ∠=︒,E 为AD 中点,∴CE AE DE ==,又2CD =∴112CF DF CD ===,EAC ∠25.(2024·江苏苏州·中考真题)如图,ABC ,90ACB ∠=︒,5CB =,10CA =,点D ,E 分别在AC AB ,边上,5AE =,连接DE ,将ADE V 沿DE 翻折,得到FDE V ,连接CE ,CF .若CEF △的面积是BEC 面积的2倍,则AD =.【答案】103/133【分析】本题考查了相似三角形的判定与性质、折叠性质、等腰直角三角形的判定与性质、全等三角形的判定与性质、三角形的面积公式等知识,是综合性强的填空压轴题,熟练掌握相关知识的联系与运用是解答的关键.设AD x =,5AE x =,根据折叠性质得DF AD x ==,ADE FDE ∠=∠,过E 作EH AC ⊥于H ,设EF 与AC 相交于M ,证明AHE ACB ∽得到EH AH AE BC AC AB==,进而得到EH x =,2AH x =,证明Rt EHD 是等腰直角三角形得到45HDE HED ∠=∠=︒,可得90FDM ∠=︒,证明()AAS FDM EHM ≌得到12DM MH x ==,则3102CM AC AD DM x =--=-,根据三角形的面积公式结合已知可得()31022552x x x ⎛⎫-⋅=- ⎪⎝⎭,然后解一元二次方程求解x 值即可.【详解】解:∵5AE AD =,∴设AD x =,5AE x =,∵ADE V 沿DE 翻折,得到FDE V ,∴DF AD x ==,ADE FDE ∠=∠,过E 作EH AC ⊥于H ,设EF 与AC 相交于M ,则90AHE ACB ︒∠=∠=,又A A ∠=∠,三、解答题26.(2024·四川眉山·中考真题)如图,BE 是O 的直径,点A 在O 上,点C 在BE 的延长线上,EAC ABC ∠=∠,AD 平分BAE ∠交O 于点D ,连结DE .(1)求证:CA 是O 的切线;(2)当8,4AC CE ==时,求DE 的长.【答案】(1)见解析(2)62【分析】本题考查了切线的判定和性质,等腰三角形的性质,勾股定理,圆周角定理,熟练掌握切线的判定是解题的关键.(1)连接OA ,根据圆周角定理得到90BAE ∠=︒,根据等腰三角形的性质得到ABC BAO ∠=∠,求得90OAC ∠=︒,根据切线的判定定理得到结论;(2)根据相似三角形的判定和性质定理得到16BC =,求得12BE BC CE =-=,连接BD ,根据角平分线的定义得到BAD EAD ∠=∠,求得 BDDE =,得到BD DE =,根据等腰直角三角形的性质即可得到结论.【详解】(1)证明:连接OA ,BE 是O 的直径,90BAE ∴∠=︒,90BAO OAE ∴∠+∠=︒,OA OB = ,ABC BAO ∴∠=∠,EAC ABC ∠=∠ ,CAE BAO ∴∠=∠,90CAE OAE ∴∠+∠=︒,90OAC ∴∠=︒,OA 是O 的半径,27.(2024·四川凉山·中考真题)如图,AB 是O 的直径,点C 在O 上,AD 平分BAC ∠交O 于点D ,过点D 的直线DE AC ⊥,交AC 的延长线于点E ,交AB 的延长线于点F .(1)求证:EF 是O 的切线;(2)连接EO 并延长,分别交O 于,M N 两点,交AD 于点G ,若O 的半径为230F ∠=, ,求GM GN ⋅的值.【答案】(1)见详解(2)7225【分析】(1)连接OD ,根据等腰三角形的性质及角平分线得到OD AC ∥,根据平行线的性质得90ODF ∠=︒即可证明;(2)连接,MD AN ,先解Rt ODF △,求得4OF =,23DF =,则6AF =,3AE =,可证明23AD DF ==,由DGO AGE ∽,得23DG OD AG AE ==,故23,55DG AD AG AD ==,证明MGD AGN △∽△,即可得到7225GM GN GD GA ⋅=⋅=.【详解】(1)解:连接OD ,∵OA OD =,∴23∠=∠,∵AD 平分BAC ∠,∴12∠=∠,∴13∠=∠,∴OD AC ∥,∴ODF AED∠=∠∵DE AC ⊥,∴90AED ∠=︒,∴90ODF ∠=︒,即OD EF ⊥,∵OD 是O 的半径∴EF 是O 的切线;∵30F ∠=︒,∴在Rt ODF △中,24OF OD ==,由勾股定理得:22DF OF OD =-∴246AF =+=,∵在Rt AEF 中,30F ∠=︒,∴132AE AF ==,【点睛】本题考查了圆的切线的判定,相似三角形的判定与性质,勾股定理,30︒的直角三角形的性质,等腰三角形的性质,正确添加辅助线是解题的关键.28.(2024·江苏盐城·中考真题)如图,点C 在以AB 为直径的O 上,过点C 作O 的切线l ,过点A 作AD l ⊥,垂足为D ,连接AC BC 、.(1)求证:ABC ACD △△∽;(2)若5AC =,4CD =,求O 的半径.【答案】(1)见解析(2)256【分析】题目主要考查切线的性质,相似三角形的判定和性质及勾股定理解三角形,作出辅助线,综合运用这些知识点是解题关键.(1)连接OC ,根据题意得90OCD OCA ACD ∠∠∠=+=︒,90ACB ACO OCB ∠∠∠=+=︒,利用等量代换确定ACD ABC ∠∠=,再由相似三角形的判定即可证明;(2)先由勾股定理确定3AD =,然后利用相似三角形的性质求解即可.【详解】(1)证明:连接OC ,如图所示:∵CD 是O 的切线,点C 在以AB 为直径的O 上,∴90OCD OCA ACD ∠∠∠=+=︒,90ACB ACO OCB ∠∠∠=+=︒,∴ACD OCB ∠∠=,∵OC OB =,∴OBC OCB ∠∠=,∴ACD ABC ∠∠=,∵AD l ⊥,29.(2024·陕西·中考真题)如图,直线l 与O 相切于点A ,AB 是O 的直径,点C ,D 在l 上,且位于点A 两侧,连接BC BD ,,分别与O 交于点E ,F ,连接EF AF ,.(1)求证:BAF CDB ∠=∠;(2)若O 的半径6r =,9AD =,12AC =,求EF 的长.∴90BAF ABD ∠+∠=︒,∴BAF CDB ∠=∠;(2)解:∵6r =,∴212AB r AC ===,222212915BD AB AD =+=+=,∵直线l 与O 相切于点A ,∴90BAC ∠=︒,∴ABC 是等腰直角三角形,∴45ABC ACB ∠=∠=︒,∵AB 是O 的直径,∴90BEA ∠=︒,∴ABE 也是等腰直角三角形,∴cos 4562AE BE AB ==⋅︒=,∵ BFBF =,∴BEF BAF ∠=∠,∵BAF CDB ∠=∠,∴BEF BDC ∠=∠,∴BEF BDC ∽,∴BE EF BD CD =,即6215129EF =+,∴4225EF =.【点睛】本题考查的是等腰三角形的性质和判定,相似三角形的性质和判定,切线的性质,勾股定理等知识点的应用,掌握切线的性质定理、相似三角形的判定定理和性质定理是解题的关键.30.(2024·上海·中考真题)如图所示,在矩形ABCD 中,E 为边CD 上一点,且AE BD ⊥.(1)求证:2AD DE DC =⋅;(2)F 为线段AE 延长线上一点,且满足12EF CF BD ==,求证:CE AD =.∠在矩形ABCD中,ADE ⊥,AE BD∴90∠+∠=︒DAE ADBADB AED∴∠=∠,FEC AED∠=∠,在矩形ABCD 中,12OA OD BD ==, 12EF CF BD ==,OA OD EF CF ∴===,ADO OAD ∴∠=∠,FEC FCE ∠=∠,ADO FEC ∠=∠,FEC E AD F O OAD C ∴∠∠=∠∠==,在ODA V 和FEC 中,ODA FEC OAD FCE OD FE ∠=∠⎧⎪∠=∠⎨⎪=⎩()AAS ODA FEC ∴ ≌,CE AD ∴=.【点睛】本题考查矩形综合,涉及矩形性质、相似三角形的判定与性质、等腰三角形的判定与性质、全等三角形的判定与性质等知识,熟练掌握相关几何性质与判定是解决问题第的关键.31.(2024·内蒙古赤峰·中考真题)如图,ABC 中,90ACB ∠=︒,AC BC =,O 经过B ,C 两点,与斜边AB 交于点E ,连接CO 并延长交AB 于点M ,交O 于点D ,过点E 作EF CD ∥,交AC 于点F .(1)求证:EF 是O 的切线;(2)若42BM =,1tan 2BCD ∠=,求OM 的长.【答案】(1)见解析(2)5OM =【分析】(1)连接OE ,延长EO ,交O 于点P ,连接,,PD BD 根据直径所对的圆周角是直角求出45DBE ∠=︒得45DPE ∠=︒,90DOE ∠=︒,由EF CD ∥可得90FED DOE ∠=∠=︒,从而可证明EF 是O 的切线;(2)由1tan 2BCD ∠=得12DB BC =,即12DB AC =,证明DBM ACM ∽ ,得12BM DM DB AM CM AC ===,由42BM =∵,AB BC ACB =∠∴ABC 是等腰直角三角形,∴45,ABC ∠=︒∵CD 是O 的直径,∴8242122AB AM BM =+=+=,在等腰直角三角形ABC 中,222AC BC AB +=,∴()2222122AC AC AB +==,解得,12AC =,∴12AC BC ==,∴16,2DB BC ==在t R BDC 中,222212665,CD BC DB =+=+=∴35CO DO ==,又12DM CM =,∴2,CM DM =∴265,DM DM CD +==∴25DM =∴35255OM OD DM =-=-=【点睛】本题主要考查平行线的性质,等腰直角三角形的判定与性质,切线的判定,圆周角定理,勾股定理以及相似三角形的判定与性质,正确作出辅助线构造圆周角是解答本题的关键.32.(2024·四川甘孜·中考真题)如图,在四边形ABCD 中,90A ∠=︒,连接BD ,过点C 作CE AB ⊥,垂足为E ,CE 交BD 于点F ,1ABC ∠=∠.(1)求证:23∠∠=;(2)若445∠=︒.①请判断线段BC ,BD 的数量关系,并证明你的结论;②若13BC =,5AD =,求EF 的长.【答案】(1)见解析∴EF BE AD AB =,∴5512EF =,2512EF ∴=.33.(2024·内蒙古赤峰·中考真题)数学课上,老师给出以下条件,请同学们经过小组讨论,提出探究问题.如图1,在ABC 中,AB AC =,点D 是AC 上的一个动点,过点D 作DE BC ⊥于点E ,延长ED 交BA 延长线于点F .请你解决下面各组提出的问题:(1)求证:AD AF =;(2)探究DF DE与AD DC 的关系;某小组探究发现,当13AD DC =时,23DF DE =;当45AD DC =时,85DF DE =.请你继续探究:①当76AD DC =时,直接写出DF DE 的值;②当AD m DC n =时,猜想DF DE的值(用含m ,n 的式子表示),并证明;(3)拓展应用:在图1中,过点F 作FP AC ⊥,垂足为点P ,连接CF ,得到图2,当点D 运动到使ACF ACB ∠=∠时,若AD m DC n =,直接写出AP AD的值(用含m ,n 的式子表示).【答案】(1)见解析(2)①73DF DE =②2DF DE m n =,证明见解析(3)2AP n AD m=【分析】(1)等边对等角,得到B C ∠=∠,等角的余角的相等,结合对顶角相等,得到F ADF ∠=∠,即可得出结论;∵DE BC ⊥,∴AG CE ∥,∴AGD CED ∽△△,∵AD m DC n =,∴GD AD m ==,由(1)知AD AF =,又AG EF ⊥,∴DG FG =,即2DF DG =,∴22GD m DE nDF DE ==;(3)2AP n AD m =,理由如下:过点D 作DG CF ⊥,∵ACF ACB ∠=∠,DE CE ⊥,∴DG DE =,由(2)知,当AD m DC n =时,2DF DE m n=,∴2DE n DF m =,∴2DG n DF m =,∵PF AC ⊥,∴90ACF CFP ∠+∠=︒,∵FE BC ⊥,∴90B AFD ∠+∠=︒,∵AB AC =,∴ACB B =∠∠,∴B ACF ∠=∠,∴AFD CFP ∠=∠,∴AFD PFD CFP PFD ∠-∠=∠-∠,∴AFP DFG ∠=∠,∴sin sin AFP DFG ∠=∠,∴2AP DG n AF DF m==,由(1)知AD AF =,34.(2024·福建·中考真题)如图,在ABC 中,90,BAC AB AC ∠=︒=,以AB 为直径的O 交BC 于点D ,AE OC ⊥,垂足为,E BE 的延长线交 AD 于点F .(1)求OE AE的值;(2)求证:AEB BEC △∽△;(3)求证:AD 与EF 互相平分.∴在Rt AOC 中,tan 2AC AOC AO∠==.AE OC ⊥ ,∴在Rt AOE △中,tan AE AOC OE∠=.2AE OE ∴=,12OE AE ∴=;(2)过点B 作BM AE ∥,交EO 延长线于点M .,90BAE ABM AEO BMO ∴∠=∠∠=∠=︒.AO BO = ,AOE BOM ∴△≌△,,AE BM OE OM ∴==.12OE AE = ,2BM OE EM ∴==,45MEB MBE ∴∠=∠=︒,135AEB AEO MEB ∴∠=∠+∠=︒,180135BEC MEB ∠=︒-∠=︒,AEB BEC ∴∠=∠.,90AB AC BAC =∠=︒ ,45ABC ∴∠=︒,ABM CBE ∴∠=∠,BAE CBE ∴∠=∠,AEB BEC ∴△∽△.(3)如图,连接,DE DF .90ADB AFB ∴∠=∠=,90AB AC BAC ∠== 2,BC BD DAB ∴=∠=由(2)知,AEB △∽△22AE AB AO BE BC BD ∴===35.(2024·北京·中考真题)如图,AB 是O 的直径,点C ,D 在O 上,OD 平分AOC ∠.(1)求证:OD BC ∥;(2)延长DO 交O 于点E ,连接CE 交OB 于点F ,过点B 作O 的切线交DE 的延长线于点P .若56OF BF =,1PE =,求O 半径的长.【答案】(1)见解析(2)32【分析】(1)根据题意,得AOC B C ∠=∠+∠,结合OB OC =,得到B C ∠=∠,继而得到2AOC B ∠=∠,根据OD 平分AOC ∠,得到2AOC AOD ∠=∠,继而得到B AOD ∠=∠,可证OD BC ∥;(2)不妨设5,6OF x BF x ==,则11OB OF BF x OC OE =+===,求得111OP OE PE x =+=+,证明OFE BFC ∽,OBM POB ∠=∠,求得665x BC =,取BC 的中点M ,连接OM ,则335x BM =,求得3cos 5OBM ∠=,3cos 5POB ∠=,结合切线性质,得到3cos 51OB OB OB POB OP OE PE OB ∠====++,解答即可.【详解】(1)根据题意,得AOC B C ∠=∠+∠,∵OB OC =,∴B C ∠=∠,∴2AOC B ∠=∠,∵OD 平分AOC ∠,∴2AOC AOD ∠=∠,∴B AOD ∠=∠,∴OD BC ∥;(2)∵56OF BF =,1PE =,不妨设5,6OF x BF x ==,则11OB OF BF x OC OE =+===,∴111OP OE PE x =+=+,∵OD BC ∥,2【点睛】本题考查了圆的性质,等腰三角形的性质,平行线的判定,三角形相似的判定和性质,切线的性质,解直角三角形的相关计算,等量代换思想,熟练掌握三角形相似的判定和性质,切线的性质,解直角三角形的相关计算是解题的关键36.(2024·四川广元·中考真题)数学实验,能增加学习数学的乐趣,还能经历知识“再创造”的过程,更是培养动手能力,创新能力的一种手段.小强在学习《相似》一章中对“直角三角形斜边上作高”这一基本图形(如图1)产生了如下问题,请同学们帮他解决.在ABC 中,点D 为边AB 上一点,连接CD .(1)初步探究如图2,若ACD B ∠=∠,求证:2AC AD AB =⋅;(2)尝试应用如图3,在(1)的条件下,若点D 为AB 中点,4BC =,求CD 的长;(3)创新提升如图4,点E 为CD 中点,连接BE ,若30CDB CBD ∠=∠=︒,ACD EBD ∠=∠,27AC =BE 的长.【答案】(1)证明见解析(2)22CD =(3)21【分析】(1)根据题意,由ACD B ∠=∠,A A ∠=∠,利用两个三角形相似的判定定理即可得到ACD ABC △△∽,再由相似性质即可得证;(2)设AD BD m ==,由(1)中相似,代值求解得到2AC m =,从而根据ACD 与ABC 的相似比为12AD AC =求解即可得到答案;(3)过点C 作EB 的平行线交AB 的延长线于点H ,如图1所示,设CE DE a ==,过点B 作BF EC ⊥于点F ,如图2所示,利用含30︒的直角三角形性质及勾股定理即可得到相关角度与线段长,再由三角形相似的判定与性质得到21277AD AC CD a AC AH CH a ====,代值求解即可得到答案.【详解】(1)证明:∵ACD B ∠=∠,A A ∠=∠,∴ACD ABC △△∽,∵点E 为CD 中点,∴设CE DE a ==,∵30CDB CBD ∠=∠=︒,∴2CB CD a ==,120DCB ∠=︒,∴60FCB ∠=︒,∴30CBF ∠=︒,∴12CF BC =,∴CF a =,3BF a =,∴2EF a =,∴7BE a =,∵CH BE ∥,点E 为CD 中点,∴227CH BE a ==,243DH DB a ==,EBD H ∠=∠,又∵ACD EBD ∠=∠,∴ACD H ∠=∠,ACD AHC ∽△△,∴21277AD AC CD a AC AH CH a ====,又∵27AC =,∴2AD =,14AH =,∴12DH =,即4312a =,∴3a =,∴721BE a ==.【点睛】本题考查几何综合,涉及相似三角形的判定与性质、含30︒的直角三角形性质、勾股定理等知识,熟练掌握三角形相似的判定与性质是解决问题的关键.37.(2024·安徽·中考真题)如图1,ABCD Y 的对角线AC 与BD 交于点O ,点M ,N 分别在边AD ,BC 上,且AM CN =.点E ,F 分别是BD 与AN ,CM 的交点.(1)求证:OE OF =;(2)连接BM 交AC 于点H ,连接HE ,HF .(ⅰ)如图2,若HE AB ∥,求证:HF AD ∥;(ⅱ)如图3,若ABCD Y 为菱形,且2MD AM =,60EHF ∠=︒,求AC BD 的值.∴OHF OAD ∠=∠,∴HF AD∥(ⅱ)∵ABCD 是菱形,∴AC BD ⊥,又OE OF =,60EHF ∠=︒,∴30EHO FHO ∠=∠=︒,∴3OH OE =,∵AM BC ∥.2MD AM =,∴AHM CHB ∽,∴13AH AM HC BC ==,即3HC AH =,∴()3OA AH OA OH +=-,∴2OA OH =,∵BN AD ∥,2MD AM =,AM CN =,∴BNE DAE ∽,∴23BE BN ED AD ==,即32BE ED =,∴()()32OB OE OB OE -=+∴5OB OE =,故22323555AC OA OH OE BD OB OE OE ⨯====.【点睛】本题主要考查了平行四边形的判定以及性质,全等三角形判定以及性质,相似三角形的判定以及性质,平行线截线段成比例以及菱形的性质,掌握这些判定方法以及性质是解题的关键.38.(2024·内蒙古包头·中考真题)如图,在ABCD Y 中,ABC ∠为锐角,点E 在边AD 上,连接,BE CE ,且ABE DCE S S = .(1)如图1,若F 是边BC 的中点,连接EF ,对角线AC 分别与,BE EF 相交于点,G H .①求证:H 是AC 的中点;②求::AG GH HC ;(2)如图2,BE 的延长线与CD 的延长线相交于点M ,连接,AM CE 的延长线与AM 相交于点N .试探究线段AM 与线段AN 之间的数量关系,并证明你的结论.【答案】(1)①见解析;②::2:1:3AG GH HC =(2)3AM AN =,理由见解析【分析】(1)①根据ABE DCE S S = ,得出E 为AD 的中点,证明出AHE CHF ≌即可;②先证明出AGB HGE ∽得到2AB AG EH GH==,然后再根据平行四边形的性质找到线段的数量关系求解;(2)连接BD 交CN 于点F ,证明()AAS AEB DEM ≌,进一步证明出四边形ABDM 为平行四边形,得出DF 为CMN 的中位线,得到12DF MN =,再证明出AEN DEF ≌得到DF AN =,再通过等量代换即可求解.【详解】(1)解:①ABE DCE S S = ,E ∴为AD 的中点,AE DE ∴=,F 是边BC 的中点,BF CF ∴=,AE CF ∴=,在ABCD Y 中,AD BC∴EAH FCH ∠=∠,又∵AHE CHF ∠=∠,()AAS AHE CHF ∴ ≌,。
中考中相似三角形的常见模型及典型例题

(1)A字、8字; (3)角平分线; (5)一线三等角; (7)内接矩形;
2.基本辅助线:
(2)反A、反8; (4)旋转型; (6)线束模型; (8)相似比与面积比。
(1)作平行线构造A字、8字; (2)作垂线构造直角三角形相似
3.基本问题类型:
(1)证明相似;
(2)求线段长;
(1)若点P在线段CB上,且BP=6,求线段CQ的长; (2)若BP=x,CQ=y,求y与x的关系式,并求出自变量x的取值范围。
例 9 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CD,
AD与BE相交于点F. (1)求证:△ABD≌△BCE; (2)求证:△ABE∽△FAE;
(3)当AF=7,DF=1时,求BD的长。
(量得BN=70cm)
C
C
DME
DME
A PN F
B
A PN F
B
1.如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80 毫米,要把它加工成正方形零件,使正方形的一边在BC上,其 余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
A
A
M
EN
H
KG
∟
B Q DPC
B
E
DF C
E
AB AC BC
B
C (2)公共边平方=共线边之积:AC 2 AE • AB
反A字 型 【模型2】反“A”字型&反“8”字型
(Ⅱ)DE拉下来经过点C,又称之为母子型,为相似常考模型:
A
A
E
B
C
AC2 AED • BC
AC2 CD • CB
AD2 BD • CD
中考数学几何专项——相似模型(相似三角形)
相似模型【相似模型一: A 字型】 特征 模型 结论DE ∥BCCBCBBC D E ADA E DA AD:AB=AE:AC=DE:BC 顺着比∠B=∠AEDCB C BDA EDAAD:AC=AE:AB=DE:BC 反着比AD×AB=AE×AC 顺着乘∠B =∠ACDCBED AAD:AC=AC:AB=CD:BC AC²=AD×AB当∠ BAC=90°AD B CB①△ABD ∽△CBA AB ²=BD×BC ②△ACD ∽△BCAAC²=CD×BC③△ADB ∽△CDA AD²=BD×CD【相似模型二: X 型】 特征 模型 结论AC ∥BDAD B CO DB A CC A OD BAD B CODBACCAO D B① △BD0∽△ACO ② DO:0C=BO:0A=BD:AC 交叉比③ △AOD 与△C0B 不相似∠B=∠C(也叫蝴蝶型相似)A D BC ODBACCAD B CODBACC① △AOC ∽△DOB② AO:OD=0C:0B=AC:BDAO×OB=OC×0D ③ 顺着比, 交叉乘 ④ △BOC∽△DOA【相似模型三: 旋转相似】 特征 模型结论成比例线段共端点① △ABC ∽△ADE ② △ABD∽△ACE【相似模型四: 三平行模型】 特征 模型结论AB ∥EF ∥CDFEBCD AF EDCBA图2① 有两对A 字型相似△BEF ∽△BCD △DEF∽△DAB ② 有一对X 型相似△AEB ∽△DEC ③111AB CD EF+=【相似模型五: 半角模型】 特征模型 结论ECD BAA BDC EEDCBA90度, 45度; 120度, 60度 120度,60度60°45°图2图1旋转N M 60°120°E D CB A 45°ED C B A ①△ABN ∽△MAN ∽△MCA ②△ABD ∽△CAE ∽△CBA【相似模型六: 三角形内接矩形模型】 特征模型 结论矩形EFGH 或正方形EFGH 内接与三角形H GFED C BA【相似模型七: 十字模型】 特征 模型结论正方形①若AF=BE,则AF ⊥BE ②若AF ⊥BE, 则AF=BE,②若AF ⊥BE ,则AF=BE,长方形PEAB CD矩形ABCD 中, CE ⊥BD, 则△CDE ∽△BCD,平行四边形△GME ∽△HNF△MED ≌△BFA三角形MED CAB在△ABC 中, AB =AC,AB ⊥AC, ①D 为中点, ②AE ⊥BD, ③BE :EC =2:1, ④∠ADB =∠CDE, ⑤∠AEB =∠CED,⑥∠BMC =135°, ⑦ , 这七个结论中, “知二得五”【A 型, X 型, 三平行模型】1.如图, 在△ABC 中, EF ∥DC, ∠AFE=∠B, AE=6, ED=3, AF=8, 则AC=_________, _________.F E DCBABCDE FA2. 如图, AB ∥CD, 线段BC, AD 相交于点F, 点E 是线段AF 上一点且满足∠BEF=∠C, 其中AF=6, DF=3, CF=2, 则AE=_________.3.如图, 在Rt △ABD 中, 过点D 作CD ⊥BD, 垂足为D, 连接BC 交AD 于点E, 过点E 作EF ⊥BD 于点F, 若AB=15, CD=10, 则BF:FD=_____________.FEBCD AN MEDCBA4.如图, 在□ABCD中, E为BC的中点, 连接AE, AC, 分别交BD于M, N, 则BM:DN=_____________.5.如图所示, AB∥CD, AD, BC相交于点E, 过E作EF∥AB交BD于点F.则下列结论:①△EFD∽△ABD;②;③;④.其中正确的有___________.F EDCBA图26.在△ABC中, AB=9, AC=6, 点M在边AB上, 且AM=3, 点N在AC边上.当AN= 时, △AMN与原三角形相似.7.如图, 在△ABC中, ∠C=90°, AC=8, BC=6, D是边AB的中点, 现有一点P位于边AC上, 使得△ADP与△ABC相似, 则线段AP的长为.8.如图, 已知O是坐标原点, 点A.B分别在轴上, OA=1, OB=2, 若点D在轴下方, 且使得△AOB与△OAD相似, 则这样的点D有个.9.如图, 在Rt△ACB中, ∠C=90°, AC=16cm, BC=8cm, 动点P从点C出发, 沿CA方向运动;动点Q同时从点B出发, 沿BC方向运动,如果点P的运动速度均为4cm/s, Q点的运动速度均为2cm/s, 那么运动几秒时, △ABC与△PCQ相似.10.将△ABC的纸片按如图所示的方式折叠, 使点B落地边AC上, 记为点B', 折叠痕为EF, 已知AB=AC=8, BC=10,若以点B'.F.C为顶点的三角形与△ABC相似, 那么BF的长度是.11.如图,在中,,,是角平分线.求证:(1)(2)12.如图, 四边形中, 平分, , , 为的中点.(1)求证: ;(2)与有怎样的位置关系?试说明理由;(3)若, , 求的值.13.如图, 在中, 为上一点, , , , 于, 连接.(1)求证:;(2)找出图中一对相似三角形, 并证明.14.如图, 在中, , 分别是, 上的点, , 的平分线交于点, 交于点.(1)试写出图中所有的相似三角形, 并说明理由(2)若, 求的值.15.如图, 在平行四边形ABCD中, 对角线AC.BD交于点O. M为AD中点, 连接CM交BD于点N, 且ON=1.(1)求BD的长;(2)若△DCN的面积为2, 求四边形ABNM的面积.16.如图,在中,于点,于点,连接,求证: ..17.如图,在△ABC中,DE∥FG∥BC,AD∶DF∶FB=1∶2∶3,若EG=3,则AC=________.图1 图218..如图,平行于BC的直线DE把△ABC分成的两部分面积相等.则ADAB = _________.19.如图所示, AD=DF=FB, DE∥FG∥BC,则=__________.20.如图, 在矩形ABCD中, 对角线AC, BD相交于点O, OE⊥BC于点E, 连接DE交OC于点F, 作FG⊥BC于点G, 则线段BG与GC的数量关系是___.21.如图, 已知点C为线段AB的中点, CD⊥AB且CD=AB=4, 连接AD, BE⊥AB, AE是∠DAB的平分线, 与DC相交于点F, EH⊥DC于点G, 交AD 于点H, 则HG的长为 .22.如图1, 在△ABC 中, 点D.E 、Q 分别在边AB.AC.BC 上, 且DE ∥BC, AQ 交DE 于点P. (1)求证: ;(2)如图, 在△ABC 中, ∠BAC=90°, 正方形DEFG 的四个顶点在△ABC 的边上, 连接AG 、AF, 分别交DE 于M 、N 两点. 如图2, 若AB=AC=1, 直接写出MN 的长;如图3, 求证MN2=DM【母子型】1.已知: 如图, △ABC 中, ∠ACB=90°, CD ⊥AB 于D, S △ABC=20, AB=10。
2023年中考九年级数学高频考点拔高训练--相似三角形(含答案)

2023年中考九年级数学高频考点拔高训练--相似三角形1.如图所示,在矩形MBCN中,点A是边MN的中点,MB=6cm,BC=16cm.点D由点A出发沿AB方向向点B匀速运动,同时点E由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接DE,设运动时间为t(s)(0<t< 10),解答下列问题:(1)求证:△AMB≌△ANC;(2)当t为何值时,△BDE的面积为7.5cm2;(3)在点D,E的运动中,是否存在时间t,使得△BDE与△ABC相似?若存在,请求出对应的时间t;若不存在,请说明理由.2.如图是由边长为1的小正方形组成的网格,A、B、C、D四点均在正方形网格的格点上,线段AB、CD相交于点O.(1)请在网格图中画出两条线段(不添加另外的字母),构成一对相似三角形,并用“∽”符号写出这对相似三角形:(2)线段AO的长为.3.如图,在∽ABCD中,点E在BC边上,点F在DC的延长线上,且∽DAE=∽F.(1)求证:∽ABE∽∽ECF;(2)若AB=3,AD=7,BE=2,求FC的长.4.如图,已知:AD为∽ABC的中线,过B、C两点分别作AD所在直线的垂线段BE 和CF,E、F为垂足,过点E作EG∽AB交BC于点H,连结HF并延长交AB于点P。
(1)求证:DE=DF(2)若BH:HC=11:5;①求:DF:DA的值;②求证:四边形HGAP为平行四边形。
5.如图,在ΔABC中,点D、E分别在边AB、AC上,且AD=3,AC=6,AE=4,AB=8.(1)如果BC=7,求线段DE的长;(2)设ΔDEC的面积为a,求ΔBDC的面积(用a的代数式表示).6.如图,∽ABC内接于∽O且AB=AC,延长BC至点D,使CD=CA,连接AD交∽O于点E,连接BE、CE.(1)求证:∽ABE∽∽CDE;(2)填空:①当∽ABC的度数为时,四边形AOCE是菱形;②若AE =6,EF=4,DE的长为.7.如图,在直角坐标系中,直线y=−2x+4分别交x轴,y轴于点E,F,交直线y=x于点P,过线段OP上点A作x轴,y轴的平行线分别交y轴于点C,直线EF 于点B.(1)求点P的坐标.(2)当AC=AB时,求点P到线段AB的距离.8.如图,Rt∽ABC中,∽ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA 边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.(1)若∽BPQ与∽ABC相似,求t的值;(2)连接AQ,CP,若AQ∽CP,求t的值.9.已知:四边形ABCD内接于⊙O,对角线AC平分∽BAD.(1)如图1,求证:BC=CD;(2)如图1,若AD+AB= √2AC,四边形ABCD的面积为8,求AC的值;(3)如图2,连接BD,把∽ABD沿着BD翻折得到∽FBD,延长CF、AD交于点G, 若CG//BD, AD=2,求CG的长.10.如图,(1)某学校“智慧方园”数学社团遇到这样一个题目:如图1,在∽ABC 中,点O 在线段BC 上,∽BAO =20°,∽OAC =80°,AO = 6√3 ,BO :CO =1:3,求AB 的长.经过社团成员讨论发现,过点B 作BD∽AC ,交AO 的延长线于点D ,通过构造∽ABD 就可以解决问题(如图2),请回答:∽ADB = °,AB = . (2)请参考以上思路解决问题:如图3,在四边形ABCD 中,对角线AC 、BD 相交于点O ,AC∽AD ,AO =6 √3 ,∽ABC =∽ACB =75°,BO :OD =1:3,求DC 的长.11.如图1,已知点O 在四边形ABCD 的边AB 上,且OA =OB =OC =OD =2,OC 平分∽BOD ,与BD 交于点G ,AC 分别与BD 、OD 交于点E 、F .(1)求证:OC∽AD ;(2)如图2,若DE =DF ,求AE AF的值; (3)当四边形ABCD 的周长取最大值时,求DE DF的值. 12.如图,在Rt∽ACB 中,∽C =90°,AC =4cm ,BC =3cm ,点P 由B 出发沿BA 方向向点A 匀速运动速度为1cm/s ;点Q 由A 出发沿AC 方向向点C 匀速运动,速度为2cm/s ;连接PQ .若设运动的时间为t(s)(0<t <2),解答下列问题:(1)当t 为何值时,点A 在PQ 垂直平分线上?(2)当t为何值时,∽APQ为直角三角形?(3)是否存在某一时刻t,使线段PQ恰好把Rt∽ACB的面积平分?若存在,求出此时t的值;若不存在,说明理由.13.如图,在直角坐标系中,直线AB分别与x轴、y轴交于B、A两点,OA、OB的长是关于x的一元二次方程x2﹣12x+32=0的两个实数根,且OB>OA,以OA为一边作如图所示的正方形AOCD,CD交AB于点P.(1)求直线AB的解析式;(2)在x轴上是否存在一点Q,使以P、C、Q为顶点的三角形与∽ADP相似?若存在,求点Q坐标;否则,说明理由;(3)设N是平面内一动点,在y轴上是否存在点M,使得以A、C、M、N为顶点的四边形是菱形?若存在,请直接写出点M的坐标;否则,请说明理由.14.如图,AC、BD为∽O的直径,且AC∽BD,P、Q分别为半径OB、OA(不与端点重合)上的动点,直线PQ交∽O于M、N.(1)比较大小:cos∽OPQ sin∽OQP;(2)请你判断MP−NP与OP·cos∽OPQ之间的数量关系,并给出证明;(3)当∽APO=60°时,设MQ=m·MP,NQ=n·NP.①求m+n的值;②以OD为边在OD上方构造矩形ODKS,已知OD=1,OS=√3−1,在Q点的移动过程中,1+√m+nMPMK−cMK恒为非负数,请直接写出实数c的最大值.15.如图,AB是∽O的直径,点C在∽O上,CD与∽O相切,AD∽BC,连结OD,AC.(1)求证:∽B=∽DCA;,OD= 3√6,求∽O的半径长.(2)若tanB= √5216.如图,∽O的弦AC与BD互相垂直于点E,OA交ED于点F.(1)如图(1),求证:∽BAC=∽OAD;(2)如图(2),当AC=CD时,求证:AB=BF;(3)如图(3),在(2)的条件下,点P,Q在CD上,点P为CQ中点,∽POQ=∽OFD,DF=EC,DQ=6,求AB的长.答案解析部分1.【答案】(1)证明:∵四边形MBCN是矩形,∴∠M=∠N=90°,MB=NC又∵点A是边MN的中点,∴AM=AN∴△AMB≌△ANC(2)解:分别过点D、A作DF⊥BC、AG⊥BC,垂足为F、G,如图:∴DF//AG,DFAG=BDAB∵△AMB≌△ANC∴AB=AC,∵MB=6 ,BC=16∴BG=8 , ∴AG=6∴∴AB=AC=10∵AD=BE=t ,∴BD=10−t ,∴DF6=10−t10解得DF=35(10−t)∵S△BDE=12BE⋅DF=7.5∴35(10−t)⋅t=15解得t=5.答:t为5秒时,△BDE的面积为7.5cm2.(3)解:存在.理由如下:①当BE=DE时,△BDE∽△BCA,BE AB=BDBC即t10=10−t16,解得t=5013,②当BD=DE时,△BDE∽△BAC,BE BC=BDAB即t16=10−t10,解得 t =8013. 答:存在时间t 为 5013或 8013 秒时,使得 △BDE 与 △ABC 相似. 2.【答案】(1)解:如图,连接AC ,BD ,由格点图可得BD∽AC ,∴△AOC ∽△BOD ,(2)3√223.【答案】(1)证明:如图.∵四边形ABCD 是平行四边形,∴AB∽CD ,AD∽BC.∴∽B=∽ECF ,∽DAE=∽AEB.又∵∽DAE=∽F ,∴∽AEB=∽F.∴∽ABE∽∽ECF.(2)解:∵∽ABE∽∽ECF ,∴AB EC =BE CF∵四边形ABCD 是平行四边形,∴BC=AD=8.∴EC=BC − BE=8 − 2="6."∴56=2CF. ∴CF =125. 4.【答案】(1)证明:∵AD 是∽ABC 的中线,∴BD =CD , ∵∽FDC 和∽EDB 是对顶角,∴∽FDC =∽EDB ,又∵BE∽AE ,CF∽AE ,∴∽DFC =∽DEB =90°, ∴∽BDE∽∽CDF (AAS ),∴DE=DF(2)解:设 BH =11x,HC =5x 则 BD =CD =12BC =8x DH =3x,HC =5x①∵EH∽AB∴∽EDH∽∽ADB ∴DE DA =DH DB =38∵DE =DF ∴DF DA =38②∵DF DA =38∴DF FA =35∵DH HC =35∴FH∽AC ∴PH∽AC ∵EG∽AB ∴四边形HGAP 为平行四边形 5.【答案】(1)解:∵AD =3,AC =6,AE =4,AB =8 , ∴AD AC =AE AB =12, ∵∽A=∽A,∴∽ADE∽ACB,∴DE BC =12, ∵BC =7∴DE= 72(2)解:∵AE EC =46−4=2 ∴S △ADE S △EDC=AE EC =2 , ∵S △DEC =a ,∴S △ADE =2a∵∽ADE∽ACB∴S △ADE S △ACB =(12)2 , ∴2a S △BDC +a+2a=14 , ∴S △BDE =5a .6.【答案】(1)证明:∵AB=AC ,CD=CA , ∴∽ABC=∽ACB ,AB=CD ,∵四边形ABCE 是圆内接四边形,∴∽ECD=∽BAE ,∽CED=∽ABC ,∵∽ABC=∽ACB=∽AEB ,∴∽CED=∽AEB ,∴∽ABE∽∽CDE (AAS );(2)60°;97.【答案】(1)解:解 {y =−2x +4y =x 得, {x =43y =43,∴ 点P 的坐标为 (43,43) ; (2)解: ∵ 直线 y =−2x +4 分别交x 轴,y 轴于点E ,F , ∴E(2,0) , F(0, 4),∴OE =2 , OF =4 , 延长BA 交x 轴于D ,设 A(a,a) ,∴AC =AB =a ,∵ 点A 在直线OP 上,∴AC =AD =a ,∴BD =2a ,∵BD//OF ,∴△EDB ∽ △EFO ,∴DE OE =BD OF, ∴2−a 2=2a 4 , ∴a =1 ,∴ 点P 到线段AB 的距离 =43−1=13 . 8.【答案】(1)解:根据勾股定理得:BA= √62+82 分两种情况讨论:①当∽BPQ∽∽BAC 时, BP BA =BQ BC , ∵BP=5t ,QC=4t ,AB=10,BC=8,∴5t 10=8−4t 8,解得,t=1, ②当∽BPQ∽∽BCA 时, BP BC =BQ BA, ∴5t 8=8−4t 10,解得,t= 3241 ; ∴t=1或 3241时,∽BPQ∽∽BCA (2)解:过P 作PM∽BC 于点M ,AQ ,CP 交于点N ,如图所示:则PB=5t ,PM=3t ,MC=8﹣4t ,∵∽NAC+∽NCA=90°,∽PCM+∽NCA=90°,∴∽NAC=∽PCM ,∵∽ACQ=∽PMC ,∴∽ACQ∽∽CMP ,∴AC CM =CQ MP, ∴68−4t =4t 3t ,解得t= 78.9.【答案】(1)证明:如图1,∵AC 平分∽BAD ,∴∽BAC =∽DAC ,∴BD =CD∴BC =CD .(2)解:如图所示,延长AB 至点E ,使BE =AD ,连接EC ,∵四边形BACD 为圆的内接四边形,∴∽ABC+∽ADC =180°,∴∽EBC =∽ADC ,∵BC =CD ,∴∽ACD∽∽ECB (SAS ),∴EC =AC ,∵AD+AB = √2 AC ,∴AE = √2 AC = √2 EC ,∴AC 2+EC 2=AE 2,∴∽ECA =90°,∴S ⊿ACE = 12AC 2 =8, ∴AC=4.(3)解:∵∽ADB =∽FDB ,CF∽BD ,∴∽DFG =∽BDF ,∽G =∽BDA ,∴∽DFG =∽G ,∴AD =DF =DG ,∵AD =2,∴DF =DG =2,∴D 为AG 的中点,∵∽DCG =∽BDC ,∽BDC =∽BAC =∽CAG ,∴∽DCG =∽CAG ,又∵∽G =∽CGA ,∴∽DCG∽∽ACG ,∴DG CG =CG AG ,即 2CG =CG 4, ∴CG =2 √2 .10.【答案】(1)80;8 √3(2)解:过点B 作BE∽AD 交AC 于点E ,如图3所示:∵AC∽AD ,BE∽AD ,∴∽DAC =∽BEA =90°,∵∽AOD =∽EOB ,∴∽AOD∽∽EOB ,∴BO OD =EO AO =BE DA∵BO :OD =1:3,∴EO AO =BE DA =13∵AO =6 √3 ,∴EO = 13AO =2 √3 , ∴AE =AO+EO =6 √3 +2 √3 =8 √3 ,∵∽ABC =∽ACB =75°,∴∽BAC =30°,AB =AC ,∴AB =2BE ,在Rt∽AEB 中,BE 2+AE 2=AB 2,即(8 √3 )2+BE 2=(2BE )2,解得:BE =8,∴AB =AC =16,AD =3BE =24,在Rt∽CAD 中,AC 2+AD 2=DC 2,即162+242=DC 2,解得:DC =8 √13 .11.【答案】(1)证明:∵AO =OD ,∴∽OAD =∽ADO ,∵OC 平分∽BOD ,∴∽DOC =∽COB ,又∵∽DOC+∽COB∽=∽OAD+∽ADO ,∴∽ADO =∽DOC ,∴CO∽AD ;(2)解: ∵OA=OB=OC ,∴∽ADB=90°,∴∽AOD 和∽ABD 是等腰直角三角形,∴AD= √2AO ,∴AD AO =√2,∵DE=DF ,∴∽DFE=∽AED ,∵∽DFE=∽AFO ,∴∽AFO=∽AED ,∵∽AOF=∽ADE=90°,∴∽ADE∽∽AOF ,∴AE AF =AD AO = √2;(3)解:如图2,∵OD =OB ,∽BOC =∽DOC ,∴∽BOC∽∽DOC (SAS ),∴BC =CD ,设BC =CD =x ,CG =m ,则OG =2﹣m ,∵OB 2﹣OG 2=BC 2﹣CG 2,∴4﹣(2﹣m )2=x 2﹣m 2,解得:m =14x 2 ,∴OG =2 −14x 2 ,∵OD =OB ,∽DOG =∽BOG ,∴G 为BD 的中点,又∵O 为AB 的中点,∴AD =2OG =4 −12x 2 ,∴四边形ABCD 的周长为2BC+AD+AB =2x+4 −12x 2+ 4 =−12x 2+ 2x+8=−12(x −2)2+ 10,∵−12< 0,∴x =2时,四边形ABCD 的周长有最大值为10.∴BC =2,∴∽BCO 为等边三角形,∴∽BOC =60°,∵OC∽AD ,∴∽DAC =∽COB =60°, ∴∽ADF =∽DOC =60°,∽DAE =30°,∴∽AFD =90°,∴DE DA =√33 ,DF =12DA ,∴DE DF =2√33 .12.【答案】(1)解: ∵ 在 Rt △ACB 中,∽C=90°,AC =4cm ,BC =3cm ,∴AB =√AC 2+BC 2=√42+32=5(cm),由题意得:BP =tcm ,AQ =2tcm ,∴AP =AB −BP =(5−t)cm ,当点A 在PQ 垂直平分线上时,则AP =AQ ,即 5−t =2t ,解得t =53, ∴当t =53时,点A 在PQ 垂直平分线上. (2)解:①当∠AQP =90°时,∠A =∠A ,∠AQP =∠C =90°,∴△AQP ∼△ACB ,∴AQ AC =AP AB ,即2t 4=5−t 5,解得t =107; ②当∠APQ =90°时,∠A =∠A ,∠APQ =∠C =90°,∴△APQ ∼△ACB ,∴AP AC =AQ AB ,即5−t 4=2t 5,解得t =2513, ∴综上所述,当t 为107或2513时,△APQ 为直角三角形. (3)解:如图,过点P 作PH ⊥AC 于H ,∴PH ∥BC ,∴△APH ∼△ABC ,∴PH BC =AP AB,即PH 3=5−t 5, 解得PH =3−35t , ∴y =12AQ ⋅PH =12×2t ⋅(3−35t),即y =−35t 2+3t(0<t <2), 若PQ 把△ABC 面积平分,则S ΔAPQ =12S ΔABC , ∴−35t 2+3t =12×12×3×4, 解得 t =5±√52,∵0<t <2,∴t=5−√52, ∴存在某一时刻t ,使线段PQ 恰好把Rt △ACB 的面积平分,此时t 的值为5−√52. 13.【答案】(1)解:解方程 x 2−12x +32=0 可得x=4或x=8, ∵OA 、OB 的长是关于x 的一元二次方程 x 2−12x +32=0 的两个实数根,且OB>OA , ∴OA=4,OB=8, ∴A(0,4),B(−8,0), 设直线AB 解析式为y=kx+b , ∴{−8k +b =0b =4,,解得 {k =12b =4,,∴直线AB 解析式为 y =12x +4; (2)解:∵四边形AOCD 为正方形, ∴AD=CD=OC=OA=4, ∴C(−4,0), 在y =12x +4 中,令x=−4,可得y=2, ∴PC=PD=2, 设Q(x ,0),则CQ=|x+4|, ∵以P 、C 、Q 为顶点的三角形与∽ADP 相似, ∴有∽PCQ∽∽PDA 和∽PCQ∽∽ADP 两种情况, ①当∽PCQ∽∽PDA 时,则有 PC PD =CQ AD ,即 22=|x+4|4,解得x=0或x=−8,此时Q 点坐标为(−8,0)或(0,0); ②当∽PCQ∽∽ADP 时,则有 PC AD =CQ PD , 即 24=|x+4|2,解得x=−3或x=−5,此时Q 点坐标为(−3,0)或(−5,0); 综上可知存在满足条件的点Q ,其坐标为(−8,0)或(0,0)或(−3,0)或(−5,0);(3)解:由题意可设M(0,y), ∵A(0,4),C(−4,0), ∴AC =4√2, 当AC 为菱形的一边时,则有AC=AM ,即|y−4|= 4√2 ,解得y=4± 4√2 ,此时M 点坐标为 (0,4+4√2) 或 (0,4−4√2); 当AC 为菱形的对角线时,则有MA=MC ,由题意可知此时M 点即为O 点,此时M 点坐标为(0,0); 综上可知存在满足条件的M 点,其坐标为 (0,4+4√2) 或 (0,4−4√2) 或(0,0).14.【答案】(1)=(2)解:过点O 作OG ⊥MN ,交MN 于点G∴GM =GN∴MP −NP =(GM +GP)−(GN −GP)=2GP∵OG ⊥MN∴OP ⋅cos∠OPQ =OP ×GP OP=GP ∴MP −NP =2OP ⋅cos∠OPQ ;(3)解:点O 作OG ⊥MN ,交MN 于点G ,连接BN 、MD ,AP∵MQ =m·MP ,NQ=n·NP∴m +n=MQ MP +NQ NP=MP −PQ MP +NP −PQ NP=2+PQ(1NP −1MP) =2+PQ ×MP −NP NP ×MP根据(2)的结论,得MP −NP =2GP∴m +n =2+2PQ×GP NP×MP∵∠GPO =∠OPQ ,∠PGO =∠POQ =90°∴△PGO ∽△POQ∴GP OP =OP PQ ,即GP ×PQ =OP 2∵∠BNM =∠BDM ,∠BPN =∠MPD∴△BNP ∽△MDP∴NP DP =BP MP∵OB =OD =OA∴NP ×MP =BP ×DP =(OB −OP)(OD +OP)=OB 2−OP 2∵∽APO=60°∴tan∠APO=OAOP=√3∴OA=√3OP∴OB=√3OP∴NP×MP=OB2−OP2=2OP2∴m+n=2+2×PQ×GPNP×MP=2+2×OP22OP2=3;②实数c的最大值为2√2.15.【答案】(1)证明:连结OC.∵CD与∽O相切,OC为半径,∴∽2+∽3=90°,∵AB是∽O的直径,∴∽ACB=90°,∴∽1+∽B=90°,又∵OA=OC,∴∽1=∽2,∴∽3=∽B,即∽B=∽DCA.(2)解:∵AD∽BC,AB是∽O的直径,∴∽DAC=∽ACB=90°,∵∽1+∽B=90°,∽2+∽3=90°,∽1=∽2,∴∽B=∽3,∴∽ABC∽∽DCA,∴ACDC=BC AB,∵∽B的正切值为√52,设AC= √5k,BC=2k,则AB=3k,∴√5k DC=23,∴DC=3√5k2,在∽ODC 中,OD= 3√6 ,OC= 12 AB= 32k , ∴(3√5k 2)2+(32k)2=(3√6)2 , ∴解得:k=2,∴∽O 的半径长为3.16.【答案】(1)证明:如图1,延长AO 交∽O 于M ,连接DM ,则AM 是∽O 直径,∴∽ADM =90°,∴∽AMD+∽MAD =90°∵AC∽BD ,∴∽AEB =90°,∴∽BAC+∽ABD =90°,∵∽ABD =∽AMD ,∽AMD+∽MAD =90°,∴∽BAC =∽MAD ,即∽BAC =∽OAD ;(2)证明:如图2,由(1)可得,∽BAC =∽OAD ,∴∽BAC+∽CAO =∽OAD+∽CAO ,∴∽BAF =∽CAD ,∵∽ABD =∽ACD ,∴∽ABF∽∽ACD ,∴AB AC =BF CD, ∵AC =CD ,∴AB =BF ;(3)解:连接OC 、OD ,在线CA 上取Q 1,使得CQ 1=DQ =6,连接QQ 1,OQ 1,线段QQ 1和线段O 交于点P 1,再过圆心O 作OO 1∽AC 于点O 1,如图:由(2)知:∽ABF∽∽ACD ,∴∽EFA =∽CDA ,∵∽CDA =∽EAD∴∽EAD =∽EFA ,又∵∽AEF =∽DEA =90°,∴∽EFA∽∽EAD ,∴EF AE =AE DE, ∵AC =CD ,EC =DF ,∴AE =AC ﹣EC =CD ﹣EC =CD ﹣DF ,∵DE =EF+DF ,∴EF CD−DF =CD−DF EF+DF, ∴(CD ﹣DF )2=EF (EF+DF )①,∵∽CED =90°,∴CD 2=EC 2+DE 2=DF 2+(EF+DF )2,∴(CD ﹣DF )(CD+DF )=(EF+DF )2②, 将②式除以①式得CD+DF CD−DF =EF+DF EF, ∵CD−DF+2DF CD−DF =1+2DF CD−DF ,EF+DF EF =1+DF EF , ∴2DF CD−DF =DF EF ,∴2EF=CD﹣DF,∴EF=CD−DF2,∴DE=EF+DF=CD−DF2+DF=CD+DF2,∴CD2=CE2+DE2=DF2+(CD+DF2)2∴5DF2+2CD⋅DF﹣3CD2=0,∴(5DF﹣3CD)•(DF+CD)=0,∵DF+CD>0,∴5DF﹣3CD=0,∴DF=35CD,∴EF=CD−DF2=CD−35CD2=15CD,∴AE=AC−CE=CD−DF=CD−35CD=25CD,在Rt∽AEF中AF=√AE2+EF2=√(25CD)2+(15CD)2=√55CD,∵OO1∽AC,∴∽OO1A=∽FEA=90°,O1是AC的中点,∴EF∽OO1,O1A=12AC=12CD,∴AFOA=AEO1A,即√5OA CD=25CD12CD=45,∴OA=√54CD,∴OC=OD=OA=√54CD,∵∽POQ=∽OFD,∽OFD=∽EFA,∴∽POQ=∽EFA,∵∽EAF+∽EFA=90°,∽EAF=∽CAO,∴∽CAO+∽POQ=90°,∵AC=CD,∴∽CAO=∽OCA=∽CDO=∽OCD,∴∽OCD+∽POQ=90°,∴∽COP+∽DOQ+∽CDO=90°,∵OC=OD,∽OCA=∽CDO,CQ1=DQ=6,∴∽OCQ 1∽∽ODQ (SAS ),∴OQ 1=OQ ,∽DOQ =∽COQ 1,∴∽COP+∽COQ 1+∽CDO =90°,∴∽POQ 1+∽OCD =90°,而∽OCD+∽POQ =90°,∴∽POQ =∽POQ 1,∴P 1Q 1=P 1Q ,∵P 为CQ 中点,∴P 1P 是∽CQ 1Q 的中位线,∴P 1P∽CQ 1,∴∽POC =∽OCQ 1,∴∽POC =∽CAO =∽OCA =∽CDO =∽OCD , ∴∽OPC∽∽DOC ,∴CP OC =OC CD, ∵CD =CQ+DQ =2CP+6,∴CP =CD−62, 又OC =√54CD , ∴CD−62√54CD =√54CD CD , 解得CD =16, ∴AE =25CD =325,DE =DF +EF =35CD +15CD =645 ∵∽BAC =∽BDC ,∽AEB =∽DEC , ∴∽ABE∽∽DCE ,∴AB CD =AE DE ,即AB 16=325645, ∴AB =8.。
中考数学《图形的相似》真题汇编含解析

图形的相似(29题)一、单选题1(2023·重庆·统考中考真题)如图,已知△ABC ∽△EDC ,AC :EC =2:3,若AB 的长度为6,则DE 的长度为()A.4B.9C.12D.13.5【答案】B【分析】根据相似三角形的性质即可求出.【详解】解:∵△ABC ∽△EDC ,∴AC :EC =AB :DE ,∵AC :EC =2:3,AB =6,∴2:3=6:DE ,∴DE =9,故选:B .【点睛】此题考查的是相似三角形的性质,掌握相似三角形的边长比等于相似比是解决此题的关键.2(2023·四川遂宁·统考中考真题)在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点△ABC 、△DEF 成位似关系,则位似中心的坐标为()A.-1,0B.0,0C.0,1D.1,0【答案】A【分析】根据题意确定直线AD 的解析式为:y =x +1,由位似图形的性质得出AD 所在直线与BE 所在直线x 轴的交点坐标即为位似中心,即可求解.【详解】解:由图得:A 1,2 ,D 3,4 ,设直线AD 的解析式为:y =kx +b ,将点代入得:2=k +b 4=3k +b ,解得:k =1b =1 ,∴直线AD 的解析式为:y =x +1,AD 所在直线与BE 所在直线x 轴的交点坐标即为位似中心,∴当y =0时,x =-1,∴位似中心的坐标为-1,0 ,故选:A .【点睛】题目主要考查位似图形的性质,求一次函数的解析式,理解题意,掌握位似图形的特点是解题关键.3(2023·浙江嘉兴·统考中考真题)如图,在直角坐标系中,△ABC 的三个顶点分别为A 1,2 ,B 2,1 ,C 3,2 ,现以原点O 为位似中心,在第一象限内作与△ABC 的位似比为2的位似图形△A B C ,则顶点C 的坐标是()A.2,4B.4,2C.6,4D.5,4【答案】C【分析】直接根据位似图形的性质即可得.【详解】解:∵△ABC 的位似比为2的位似图形是△A B C ,且C 3,2 ,∴C 2×3,2×2 ,即C 6,4 ,故选:C .【点睛】本题考查了坐标与位似图形,熟练掌握位似图形的性质是解题关键.4(2023·四川南充·统考中考真题)如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为1.6m ,同时量得小菲与镜子的水平距离为2m ,镜子与旗杆的水平距离为10m ,则旗杆高度为()A.6.4mB.8mC.9.6mD.12.5m【答案】B【分析】根据镜面反射性质,可求出∠ACB =∠ECD ,再利用垂直求△ABC ∽△EDC ,最后根据三角形相似的性质,即可求出答案.【详解】解:如图所示,由图可知,AB ⊥BD ,CD ⊥DE ,CF ⊥BD∴∠ABC =∠CDE =90°.∵根据镜面的反射性质,∴∠ACF =∠ECF ,∴90°-∠ACF =90°-∠ECF ,∴∠ACB =∠ECD ,∴△ABC ∽△EDC ,∴AB DE =BC CD.∵小菲的眼睛离地面高度为1.6m ,同时量得小菲与镜子的水平距离为2m ,镜子与旗杆的水平距离为10m ,∴AB =1.6m ,BC =2m ,CD =10m .∴1.6DE =210.∴DE =8m .故选:B .【点睛】本题考查了相似三角形的应用,解题的关键在于熟练掌握镜面反射的基本性质和相似三角形的性质.5(2023·安徽·统考中考真题)如图,点E 在正方形ABCD 的对角线AC 上,EF ⊥AB 于点F ,连接DE 并延长,交边BC 于点M ,交边AB 的延长线于点G .若AF =2,FB =1,则MG =()A.23B.352C.5+1D.10【答案】B 【分析】根据平行线分线段成比例得出DE EM =AF FB =2,根据△ADE ∽△CME ,得出AD CM =DE EM =2,则CM =12AD =32,进而可得MB =32,根据BC ∥AD ,得出△GMB ∽△GDA ,根据相似三角形的性质得出BG =3,进而在Rt △BGM 中,勾股定理即可求解.【详解】解:∵四边形ABCD 是正方形,AF =2,FB =1,∴AD =BC =AB =AF +FG =2+1=3,AD ∥CB ,AD ⊥AB ,CB ⊥AB ,∵EF ⊥AB ,∴AD ∥EF ∥BC∴DE EM =AFFB=2,△ADE∽△CME,∴AD CM =DEEM=2,则CM=12AD=32,∴MB=3-CM=32,∵BC∥AD,∴△GMB∽△GDA,∴BG AG =MBDA=323=12∴BG=AB=3,在Rt△BGM中,MG=MB2+BG2=322+32=352,故选:B.【点睛】本题考查了正方形的性质,平行线分线段成比例,相似三角形的性质与判定,勾股定理,熟练掌握以上知识是解题的关键.6(2023·湖北黄冈·统考中考真题)如图,矩形ABCD中,AB=3,BC=4,以点B为圆心,适当长为半径画弧,分别交BC,BD于点E,F,再分别以点E,F为圆心,大于12EF长为半径画弧交于点P,作射线BP,过点C作BP的垂线分别交BD,AD于点M,N,则CN的长为()A.10B.11C.23D.4【答案】A【分析】由作图可知BP平分∠CBD,设BP与CN交于点O,与CD交于点R,作RQ⊥BD于点Q,根据角平分线的性质可知RQ=RC,进而证明Rt△BCR≌Rt△BQR,推出BC=BQ=4,设RQ=RC=x,则DR=CD-CR=3-x,解Rt△DQR求出QR=CR=43.利用三角形面积法求出OC,再证△OCR∽△DCN,根据相似三角形对应边成比例即可求出CN.【详解】解:如图,设BP与CN交于点O,与CD交于点R,作RQ⊥BD于点Q,∵矩形ABCD中,AB=3,BC=4,∴CD =AB =3,∴BD =BC 2+CD 2=5.由作图过程可知,BP 平分∠CBD ,∵四边形ABCD 是矩形,∴CD ⊥BC ,又∵RQ ⊥BD ,∴RQ =RC ,在Rt △BCR 和Rt △BQR 中,RQ =RC BR =BR ,∴Rt △BCR ≌Rt △BQR HL ,∴BC =BQ =4,∴QD =BD -BQ =5-4=1,设RQ =RC =x ,则DR =CD -CR =3-x ,在Rt △DQR 中,由勾股定理得DR 2=DQ 2+RQ 2,即3-x 2=12+x 2,解得x =43,∴CR =43.∴BR =BC 2+CR 2=4310.∵S △BCR =12CR ⋅BC =12BR ⋅OC ,∴OC =CR ⋅BC BR =43×44310=2510.∵∠COR =∠CDN =90°,∠OCR =∠DCN ,∴△OCR ∽△DCN ,∴OC DC =CR CN ,即25103=43CN,解得CN =10.故选:A .【点睛】本题考查角平分线的作图方法,矩形的性质,角平分线的性质,全等三角形的判定与性质,勾股定理,相似三角形的判定与性质等,涉及知识点较多,有一定难度,解题的关键是根据作图过程判断出BP 平分∠CBD ,通过勾股定理解直角三角形求出CR .7(2023·四川内江·统考中考真题)如图,在△ABC 中,点D 、E 为边AB 的三等分点,点F 、G 在边BC 上,AC ∥DG ∥EF ,点H 为AF 与DG 的交点.若AC =12,则DH 的长为()A.1B.32C.2D.3【答案】C 【分析】由三等分点的定义与平行线的性质得出BE =DE =AD ,BF =GF =CG ,AH =HF ,DH 是△AEF 的中位线,易证△BEF ∽△BAC ,得EF AC =BE AB,解得EF =4,则DH =12EF =2.【详解】解:∵D 、E 为边AB 的三等分点,EF ∥DG ∥AC ,∴BE =DE =AD ,BF =GF =CG ,AH =HF ,∴AB =3BE ,DH 是△AEF 的中位线,∴DH =12EF ,∵EF ∥AC ,∴∠BEF =∠BAC ,∠BFE =∠BCA ,∴△BEF ∽△BAC ,∴EF AC =BE AB,即EF 12=BE 3BE ,解得:EF =4,∴DH =12EF =12×4=2,故选:C .【点睛】本题考查了三等分点的定义、平行线的性质、相似三角形的判定与性质、三角形中位线定理等知识;熟练掌握相似三角形的判定与性质是解题的关键.8(2023·湖北鄂州·统考中考真题)如图,在平面直角坐标系中,O 为原点,OA =OB =35,点C 为平面内一动点,BC =32,连接AC ,点M 是线段AC 上的一点,且满足CM :MA =1:2.当线段OM 取最大值时,点M 的坐标是()A.35,65B.355,655C.65,125D.655,1255 【答案】D【分析】由题意可得点C 在以点B 为圆心,32为半径的OB 上,在x 轴的负半轴上取点D -352,0 ,连接BD ,分别过C 、M 作CF ⊥OA ,ME ⊥OA ,垂足为F 、E ,先证△OAM ∽△DAC ,得OM CD =OA AD =23,从而当CD 取得最大值时,OM 取得最大值,结合图形可知当D ,B ,C 三点共线,且点B 在线段DC 上时,CD 取得最大值,然后分别证△BDO ∽△CDF ,△AEM ∽△AFC ,利用相似三角形的性质即可求解.【详解】解:∵点C 为平面内一动点,BC =32,∴点C 在以点B 为圆心,32为半径的OB 上,在x 轴的负半轴上取点D -352,0 ,连接BD ,分别过C 、M 作CF ⊥OA ,ME ⊥OA ,垂足为F 、E ,∵OA =OB =35,∴AD =OD +OA =952,∴OA AD=23,∵CM :MA =1:2,∴OA AD =23=CM AC,∵∠OAM =∠DAC ,∴△OAM ∽△DAC ,∴OM CD =OA AD=23,∴当CD 取得最大值时,OM 取得最大值,结合图形可知当D ,B ,C 三点共线,且点B 在线段DC 上时,CD 取得最大值,∵OA =OB =35,OD =352,∴BD =OB 2+OD 2=35 2+352 2=152,∴CD =BC +BD =9,∵OM CD=23,∴OM =6,∵y 轴⊥x 轴,CF ⊥OA ,∴∠DOB =∠DFC =90°,∵∠BDO =∠CDF ,∴△BDO ∽△CDF ,∴OB CF =BD CD 即35CF=1529,解得CF =1855,同理可得,△AEM ∽△AFC ,∴ME CF =AM AC =23即ME 1855=23,解得ME =1255,∴OE =OM 2-ME 2=62-1255 2=655,∴当线段OM 取最大值时,点M 的坐标是655,1255,故选:D .【点睛】本题主要考查了勾股定理、相似三角形的判定及性质、圆的一般概念以及坐标与图形,熟练掌握相似三角形的判定及性质是解题的关键.9(2023·山东东营·统考中考真题)如图,正方形ABCD 的边长为4,点E ,F 分别在边DC ,BC 上,且BF =CE ,AE 平分∠CAD ,连接DF ,分别交AE ,AC 于点G ,M ,P 是线段AG 上的一个动点,过点P 作PN ⊥AC 垂足为N ,连接PM ,有下列四个结论:①AE 垂直平分DM ;②PM +PN 的最小值为32;③CF 2=GE ⋅AE ;④S ΔADM =62.其中正确的是()A.①②B.②③④C.①③④D.①③【答案】D【分析】根据正方形的性质和三角形全等即可证明∠DAE =∠FDC ,通过等量转化即可求证AG ⊥DM ,利用角平分线的性质和公共边即可证明△ADG ≌△AMG ASA ,从而推出①的结论;利用①中的部分结果可证明△ADE ∽△DGE 推出DE 2=GE ⋅AE ,通过等量代换可推出③的结论;利用①中的部分结果和勾股定理推出AM 和CM 长度,最后通过面积法即可求证④的结论不对;结合①中的结论和③的结论可求出PM +PN 的最小值,从而证明②不对.【详解】解:∵ABCD 为正方形,∴BC =CD =AD ,∠ADE =∠DCF =90°,∵BF =CE ,∴DE =FC ,∴△ADE ≌△DCF SAS .∴∠DAE =∠FDC ,∵∠ADE =90°,∴∠ADG +∠FDC =90°,∴∠ADG +∠DAE =90°,∴∠AGD =∠AGM =90°.∵AE 平分∠CAD ,∴∠DAG =∠MAG .∵AG =AG ,∴△ADG ≌△AMG ASA .∴DG =GM ,∵∠AGD =∠AGM =90°,∴AE 垂直平分DM ,故①正确.由①可知,∠ADE =∠DGE =90°,∠DAE =∠GDE ,∴△ADE ∽△DGE ,∴DE GE=AE DE ,∴DE 2=GE ⋅AE ,由①可知DE =CF ,∴CF 2=GE ⋅AE .故③正确.∵ABCD 为正方形,且边长为4,∴AB =BC =AD =4,∴在Rt △ABC 中,AC =2AB =4 2.由①可知,△ADG ≌△AMG ASA ,∴AM =AD =4,∴CM =AC -AM =42-4.由图可知,△DMC 和△ADM 等高,设高为h ,∴S △ADM =S △ADC -S △DMC ,∴4×h 2=4×42-42-4 ⋅h 2,∴h =22,∴S △ADM =12⋅AM ⋅h =12×4×22=4 2.故④不正确.由①可知,△ADG ≌△AMG ASA ,∴DG =GM ,∴M 关于线段AG 的对称点为D ,过点D 作DN ⊥AC ,交AC 于N ,交AE 于P ,∴PM +PN 最小即为DN ,如图所示,由④可知△ADM 的高h =22即为图中的DN ,∴DN =2 2.故②不正确.综上所述,正确的是①③.故选:D .【点睛】本题考查的是正方形的综合题,涉及到三角形相似,最短路径,三角形全等,三角形面积法,解题的关键在于是否能正确找出最短路径以及运用相关知识点.10(2023·内蒙古赤峰·统考中考真题)如图,把一个边长为5的菱形ABCD 沿着直线DE 折叠,使点C 与AB 延长线上的点Q 重合.DE 交BC 于点F ,交AB 延长线于点E .DQ 交BC 于点P ,DM ⊥AB于点M ,AM =4,则下列结论,①DQ =EQ ,②BQ =3,③BP =158,④BD ∥FQ .正确的是()A.①②③B.②④C.①③④D.①②③④【答案】A【分析】由折叠性质和平行线的性质可得∠QDF =∠CDF =∠QEF ,根据等角对等边即可判断①正确;根据等腰三角形三线合一的性质求出MQ =AM =4,再求出BQ 即可判断②正确;由△CDP ∽△BQP 得CP BP =CD BQ=53,求出BP 即可判断③正确;根据EF DE ≠QE BE 即可判断④错误.【详解】由折叠性质可知:∠CDF =∠QDF ,CD =DQ =5,∵CD ∥AB ,∴∠CDF =∠QEF .∴∠QDF =∠QEF .∴DQ =EQ =5.故①正确;∵DQ =CD =AD =5,DM ⊥AB ,∴MQ =AM =4.∵MB =AB -AM =5-4=1,∴BQ =MQ -MB =4-1=3.故②正确;∵CD ∥AB ,∴△CDP ∽△BQP .∴CP BP =CD BQ=53.∵CP +BP =BC =5,∴BP =38BC =158.故③正确;∵CD ∥AB ,∴△CDF ∽△BEF .∴DF EF =CD BE =CD BQ +QE=53+5=58.∴EF DE =813.∵QE BE =58,∴EF DE ≠QE BE.∴△EFQ 与△EDB 不相似.∴∠EQF ≠∠EBD .∴BD 与FQ 不平行.故④错误;故选:A .【点睛】本题主要考查了折叠的性质,平行线的性质,等腰三角形的性质,相似三角形的判定和性质,菱形的性质等知识,属于选择压轴题,有一定难度,熟练掌握相关性质是解题的关键.11(2023·黑龙江·统考中考真题)如图,在正方形ABCD中,点E,F分别是AB,BC上的动点,且AF ⊥DE,垂足为G,将△ABF沿AF翻折,得到△AMF,AM交DE于点P,对角线BD交AF于点H,连接HM,CM,DM,BM,下列结论正确的是:①AF=DE;②BM∥DE;③若CM⊥FM,则四边形BHMF是菱形;④当点E运动到AB的中点,tan∠BHF=22;⑤EP⋅DH=2AG⋅BH.()A.①②③④⑤B.①②③⑤C.①②③D.①②⑤【答案】B【分析】利用正方形的性质和翻折的性质,逐一判断,即可解答.【详解】解:∵四边形ABCD是正方形,∴∠DAE=∠ABF=90°,DA=AB,∵AF⊥DE,∴∠BAF+∠AED=90°,∵∠BAF+∠AFB=90°,∴∠AED=∠BFA,∴△ABF≌△AED AAS,∴AF=DE,故①正确,∵将△ABF沿AF翻折,得到△AMF,∴BM⊥AF,∵AF⊥DE,∴BM∥DE,故②正确,当CM⊥FM时,∠CMF=90°,∵∠AMF=∠ABF=90°,∴∠AMF+∠CMF=180°,即A,M,C在同一直线上,∴∠MCF=45°,∴∠MFC=90°-∠MCF=45°,通过翻折的性质可得∠HBF=∠HMF=45°,BF=MF,∴∠HMF=∠MFC,∠HBC=∠MFC,∴BC∥MH,HB∥MF,∴四边形BHMF是平行四边形,∵BF=MF,∴平行四边形BHMF是菱形,故③正确,当点E运动到AB的中点,如图,设正方形ABCD的边长为2a,则AE=BF=a,在Rt △AED 中,DE =AD 2+AE 2=5a =AF ,∵∠AHD =∠FHB ,∠ADH =∠FBH =45°,∴△AHD ∽△FHB ,∴FH AH =BF AD=a 2a =12,∴AH =23AF =253a ,∵∠AGE =∠ABF =90°,∴△AGF ∽△ABF ,∴AE AF =EG BF =AG AB =a 5a=55,∴EG =55BF =55a ,AG =55AB =255a ,∴DG =ED -EG =455a ,GH =AH -AG =4515a ,∵∠BHF =∠DHA ,在Rt △DGH 中,tan ∠BHF =tan ∠DHA =DG GH=3,故④错误,∵△AHD ∽△FHB ,∴BH DH=12,∴BH =13BD =13×22a =223a ,DH =23BD =23×22a =423a ,∵AF ⊥EP ,根据翻折的性质可得EP =2EG =255a ,∴EP ⋅DH =255a ⋅423a =81015a 2,2AG ⋅BH =2⋅255a ⋅223a =81015a 2,∴EP ⋅DH =2AG ⋅BH =81015a 2,故⑤正确;综上分析可知,正确的是①②③⑤.故选:B .【点睛】本题考查了正方形的性质,翻折的性质,相似三角形的判定和性质,正切的概念,熟练按照要求做出图形,利用寻找相似三角形是解题的关键.二、填空题12(2023·湖北鄂州·统考中考真题)如图,在平面直角坐标系中,△ABC 与△A 1B 1C 1位似,原点O 是位似中心,且AB A 1B 1=3.若A 9,3 ,则A 1点的坐标是.【答案】3,1【分析】直接利用位似图形的性质得出相似比进而得出对应线段的长.【详解】解∶设A1m,n∵△ABC与△A1B1C1位似,原点O是位似中心,且ABA1B1=3.若A9,3,∴位似比为31,∴9 m =31,3n=31,解得m=3,n=1,∴A13,1故答案为:3,1.【点睛】此题主要考查了位似变换,正确得出相似比是解题关键.13(2023·吉林长春·统考中考真题)如图,△ABC和△A B C 是以点O为位似中心的位似图形,点A 在线段OA 上.若OA:AA =1:2,则△ABC和△A B C 的周长之比为.【答案】1:3【分析】根据位似图形的性质即可求出答案.【详解】解:∵OA:AA =1:2,∴OA:OA =1:3,设△ABC周长为l1,设△A B C 周长为l2,∵△ABC和△A B C 是以点O为位似中心的位似图形,∴l1l2=OAOA=13.∴l1:l2=1:3.∴△ABC和△A B C 的周长之比为1:3.故答案为:1:3.【点睛】本题考查了位似图形的性质,解题的关键在于熟练掌握位似图形性质.14(2023·四川乐山·统考中考真题)如图,在平行四边形ABCD中,E是线段AB上一点,连结AC、DE 交于点F .若AE EB =23,则S △ADF S △AEF =.【答案】52【分析】四边形ABCD 是平行四边形,则AB =CD ,AB ∥CD ,可证明△EAF ∽△DCF ,得到DF EF =CD AE =AB AE,由AE EB =23进一步即可得到答案.【详解】解:∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD ,∴∠AEF =∠CDF ,∠EAF =∠DCF ,∴△EAF ∽△DCF ,∴DF EF =CD AE =AB AE ,∵AE EB =23,∴AB AE =52,∴S △ADF S △AEF =DF EF =AB AE=52.故答案为:52【点睛】此题考查了平行四边形的性质、相似三角形的判定和性质等知识,证明△EAF ∽△DCF 是解题的关键.15(2023·江西·统考中考真题)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的ABC ).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度如图,点A ,B ,Q 在同一水平线上,∠ABC 和∠AQP 均为直角,AP 与BC 相交于点D .测得AB =40cm ,BD =20cm ,AQ =12m ,则树高PQ =m .【答案】6【分析】根据题意可得△ABD ∽△AQP ,然后相似三角形的性质,即可求解.【详解】解:∵∠ABC 和∠AQP 均为直角∴BD ∥PQ ,∴△ABD ∽△AQP ,∴BD PQ =AB AQ∵AB =40cm ,BD =20cm ,AQ =12m ,∴PQ =AQ ×BD AB=12×2040=6m ,故答案为:6.【点睛】本题考查了相似三角形的应用,熟练掌握相似三角形的性质与判定是解题的关键.16(2023·四川成都·统考中考真题)如图,在△ABC 中,D 是边AB 上一点,按以下步骤作图:①以点A 为圆心,以适当长为半径作弧,分别交AB ,AC 于点M ,N ;②以点D 为圆心,以AM 长为半径作弧,交DB 于点M ;③以点M 为圆心,以MN 长为半径作弧,在∠BAC 内部交前面的弧于点N :④过点N 作射线DN 交BC 于点E .若△BDE 与四边形ACED 的面积比为4:21,则BE CE的值为.【答案】23【分析】根据作图可得∠BDE =∠A ,然后得出DE ∥AC ,可证明△BDE ∽△BAC ,进而根据相似三角形的性质即可求解.【详解】解:根据作图可得∠BDE =∠A ,∴DE ∥AC ,∴△BDE ∽△BAC ,∵△BDE 与四边形ACED 的面积比为4:21,∴S △BDC S △BAC =421+4=BE BC2∴BE BC =25∴BE CE =23,故答案为:23.【点睛】本题考查了作一个角等于已知角,相似三角形的性质与判定,熟练掌握基本作图与相似三角形的性质与判定是解题的关键.17(2023·内蒙古·统考中考真题)如图,在Rt △ABC 中,∠ACB =90°,AC =3,BC =1,将△ABC 绕点A 逆时针方向旋转90°,得到△AB C .连接BB ,交AC 于点D ,则AD DC的值为.【答案】5【分析】过点D 作DF ⊥AB 于点F ,利用勾股定理求得AB =10,根据旋转的性质可证△ABB 、△DFB是等腰直角三角形,可得DF =BF ,再由S △ADB =12×BC ×AD =12×DF ×AB ,得AD =10DF ,证明△AFD ∼△ACB ,可得DF BC =AF AC ,即AF =3DF ,再由AF =10-DF ,求得DF =104,从而求得AD =52,CD =12,即可求解.【详解】解:过点D 作DF ⊥AB 于点F ,∵∠ACB =90°,AC =3,BC =1,∴AB =32+12=10,∵将△ABC 绕点A 逆时针方向旋转90°得到△AB C ,∴AB =AB =10,∠BAB =90°,∴△ABB 是等腰直角三角形,∴∠ABB =45°,又∵DF ⊥AB ,∴∠FDB =45°,∴△DFB 是等腰直角三角形,∴DF =BF ,∵S △ADB =12×BC ×AD =12×DF ×AB ,即AD =10DF ,∵∠C =∠AFD =90°,∠CAB =∠FAD ,∴△AFD ∼△ACB ,∴DF BC =AF AC,即AF =3DF ,又∵AF =10-DF ,∴DF =104,∴AD =10×104=52,CD =3-52=12,∴AD CD =5212=5,故答案为:5.【点睛】本题考查旋转的性质、等腰三角形的判定与性质、相似三角形的判定与性质、三角形的面积,熟练掌握相关知识是解题的关键.18(2023·河南·统考中考真题)矩形ABCD 中,M 为对角线BD 的中点,点N 在边AD 上,且AN =AB =1.当以点D ,M ,N 为顶点的三角形是直角三角形时,AD 的长为.【答案】2或2+1【分析】分两种情况:当∠MND =90°时和当∠NMD =90°时,分别进行讨论求解即可.【详解】解:当∠MND =90°时,∵四边形ABCD 矩形,∴∠A =90°,则MN ∥AB ,由平行线分线段成比例可得:AN ND =BM MD,又∵M 为对角线BD 的中点,∴BM =MD ,∴AN ND =BM MD=1,即:ND =AN =1,∴AD =AN +ND =2,当∠NMD =90°时,∵M 为对角线BD 的中点,∠NMD =90°∴MN 为BD 的垂直平分线,∴BN =ND ,∵四边形ABCD 矩形,AN =AB =1∴∠A =90°,则BN =AB 2+AN 2=2,∴BN =ND =2∴AD =AN +ND =2+1,综上,AD 的长为2或2+1,故答案为:2或2+1.【点睛】本题考查矩形的性质,平行线分线段成比例,垂直平分线的判定及性质等,画出草图进行分类讨论是解决问题的关键.19(2023·辽宁大连·统考中考真题)如图,在正方形ABCD 中,AB =3,延长BC 至E ,使CE =2,连接AE ,CF 平分∠DCE 交AE 于F ,连接DF ,则DF 的长为.【答案】3104【分析】如图,过F 作FM ⊥BE 于M ,FN ⊥CD 于N ,由CF 平分∠DCE ,可知∠FCM =∠FCN =45°,可得四边形CMFN 是正方形,FM ∥AB ,设FM =CM =NF =CN =a ,则ME =2-a ,证明△EFM ∽△EAB ,则FM AB=ME BE ,即a 3=2-a 3+2,解得a =34,DN =CD -CN =94,由勾股定理得DF =DN 2+NF 2,计算求解即可.【详解】解:如图,过F 作FM ⊥BE 于M ,FN ⊥CD 于N ,则四边形CMFN 是矩形,FM ∥AB ,∵CF 平分∠DCE ,∴∠FCM =∠FCN =45°,∴CM =FM ,∴四边形CMFN 是正方形,设FM =CM =NF =CN =a ,则ME =2-a ,∵FM ∥AB ,∴△EFM ∽△EAB ,∴FM AB =ME BE ,即a 3=2-a 3+2,解得a =34,∴DN =CD -CN =94,由勾股定理得DF =DN 2+NF 2=3104,故答案为:3104.【点睛】本题考查了正方形的判定与性质,勾股定理,相似三角形的判定与性质.解题的关键在于对知识的熟练掌握与灵活运用.20(2023·广东·统考中考真题)边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为.【答案】15【分析】根据正方形的性质及相似三角形的性质可进行求解.【详解】解:如图,由题意可知AD =DC =10,CG =CE =GF =6,∠CEF =∠EFG =90°,GH =4,∴CH =10=AD ,∵∠D =∠DCH =90°,∠AJD =∠HJC ,∴△ADJ ≌△HCJ AAS ,∴CJ =DJ =5,∴EJ =1,∵GI ∥CJ ,∴△HGI ∽△HCJ ,∴GI CJ =GH CH=25,∴GI =2,∴FI =4,∴S 梯形EJIF =12EJ +FI ⋅EF =15;故答案为:15.【点睛】本题主要考查正方形的性质及相似三角形的性质与判定,熟练掌握正方形的性质及相似三角形的性质与判定是解题的关键.21(2023·天津·统考中考真题)如图,在边长为3的正方形ABCD 的外侧,作等腰三角形ADE ,EA =ED =52.(1)△ADE 的面积为;(2)若F 为BE 的中点,连接AF 并延长,与CD 相交于点G ,则AG 的长为.【答案】3;13【分析】(1)过点E 作EH ⊥AD ,根据正方形和等腰三角形的性质,得到AH 的长,再利用勾股定理,求出EH 的长,即可得到△ADE 的面积;(2)延长EH 交AG 于点K ,利用正方形和平行线的性质,证明△ABF ≌△KEF ASA ,得到EK 的长,进而得到KH 的长,再证明△AHK ∽△ADG ,得到KH GD =AH AD ,进而求出GD 的长,最后利用勾股定理,即可求出AG的长.【详解】解:(1)过点E作EH⊥AD,∵正方形ABCD的边长为3,∴AD=3,∵△ADE是等腰三角形,EA=ED=52,EH⊥AD,∴AH=DH=12AD=32,在Rt△AHE中,EH=AE2-AH2=522-32 2=2,∴S△ADE=12AD⋅EH=12×3×2=3,故答案为:3;(2)延长EH交AG于点K,∵正方形ABCD的边长为3,∴∠BAD=∠ADC=90°,AB=3,∴AB⊥AD,CD⊥AD,∵EK⊥AD,∴AB∥EK∥CD,∴∠ABF=∠KEF,∵F为BE的中点,∴BF=EF,在△ABF和△KEF中,∠ABF=∠KEF BF=EF∠AFB=∠KFE,∴△ABF≌△KEF ASA,∴EK=AB=3,由(1)可知,AH=12AD,EH=2,∴KH=1,∵KH∥CD,∴△AHK∽△ADG,∴KH GD =AH AD,∴GD=2,在Rt△ADG中,AG=AD2+GD2=32+22=13,故答案为:13.【点睛】本题考查了正方形的性质,等腰三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理等知识,作辅助线构造全等三角形和相似三角形是解题关键.22(2023·四川泸州·统考中考真题)如图,E,F是正方形ABCD的边AB的三等分点,P是对角线AC上的动点,当PE+PF取得最小值时,APPC的值是.【答案】27【分析】作点F 关于AC 的对称点F ,连接EF 交AC 于点P ,此时PE +PF 取得最小值,过点F 作AD 的垂线段,交AC 于点K ,根据题意可知点F 落在AD 上,设正方形的边长为a ,求得AK 的边长,证明△AEP ∽△KF P ,可得KP AP=2,即可解答.【详解】解:作点F 关于AC 的对称点F ,连接EF 交AC 于点P ,过点F 作AD 的垂线段,交AC 于点K ,由题意得:此时F 落在AD 上,且根据对称的性质,当P 点与P 重合时PE +PF 取得最小值,设正方形ABCD 的边长为a ,则AF =AF =23a ,∵四边形ABCD 是正方形,∴∠F AK =45°,∠P AE =45°,AC =2a∵F K ⊥AF ,∴∠F AK =∠F KA =45°,∴AK =223a ,∵∠F P K =∠EP A ,∴△E KP ∽△EAP ,∴F K AE =KP AP=2,∴AP =13AK =292a ,∴CP =AC -AP =792a , ∴AP CP=27,∴当PE +PF 取得最小值时,AP PC 的值是为27,故答案为:27.【点睛】本题考查了四边形的最值问题,轴对称的性质,相似三角形的证明与性质,正方形的性质,正确画出辅助线是解题的关键.23(2023·山西·统考中考真题)如图,在四边形ABCD 中,∠BCD =90°,对角线AC ,BD 相交于点O .若AB =AC =5,BC =6,∠ADB =2∠CBD ,则AD 的长为.【答案】973【分析】过点A 作AH ⊥BC 于点H ,延长AD ,BC 交于点E ,根据等腰三角形性质得出BH =HC =12BC =3,根据勾股定理求出AH =AC 2-CH 2=4,证明∠CBD =∠CED ,得出DB =DE ,根据等腰三角形性质得出CE =BC =6,证明CD ∥AH ,得出CD AH=CE HE ,求出CD =83,根据勾股定理求出DE =CE 2+CD 2=62+83 2=2973,根据CD ∥AH ,得出DE AD =CE CH ,即2973AD=63,求出结果即可.【详解】解:过点A 作AH ⊥BC 于点H ,延长AD ,BC 交于点E ,如图所示:则∠AHC =∠AHB =90°,∵AB =AC =5,BC =6,∴BH =HC =12BC =3,∴AH =AC 2-CH 2=4,∵∠ADB =∠CBD +∠CED ,∠ADB =2∠CBD ,∴∠CBD =∠CED ,∴DB =DE ,∵∠BCD =90°,∴DC ⊥BE ,∴CE =BC =6,∴EH =CE +CH =9,∵DC ⊥BE ,AH ⊥BC ,∴CD ∥AH ,∴△ECD ~△EHA ,∴CD AH =CE HE ,即CD 4=69,解得:CD =83,∴DE =CE 2+CD 2=62+83 2=2973,∵CD ∥AH ,∴DE AD=CE CH ,即2973AD =63,解得:AD =973.故答案为:973.【点睛】本题主要考查了三角形外角的性质,等腰三角形的判定和性质,勾股定理,平行线分线段成比例,相似三角形的判定与性质,平行线的判定,解题的关键是作出辅助线,熟练掌握平行线分线段成比例定理及相似三角形的判定与性质.三、解答题24(2023·湖南·统考中考真题)在Rt △ABC 中,∠BAC =90°,AD 是斜边BC 上的高.(1)证明:△ABD ∽△CBA ;(2)若AB =6,BC =10,求BD 的长.【答案】(1)见解析(2)BD =185【分析】(1)根据三角形高的定义得出∠ADB =90°,根据等角的余角相等,得出∠BAD =∠C ,结合公共角∠B =∠B ,即可得证;(2)根据(1)的结论,利用相似三角形的性质即可求解.【详解】(1)证明:∵∠BAC =90°,AD 是斜边BC 上的高.∴∠ADB =90°,∠B +∠C =90°∴∠B +∠BAD =90°,∴∠BAD =∠C又∵∠B =∠B∴△ABD ∽△CBA ,(2)∵△ABD ∽△CBA∴AB CB =BD AB,又AB =6,BC =10∴BD =AB 2CB=3610=185.【点睛】本题考查了相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.25(2023·湖南·统考中考真题)如图,CA ⊥AD ,ED ⊥AD ,点B 是线段AD 上的一点,且CB ⊥BE .已知AB =8,AC =6,DE =4.(1)证明:△ABC∽△DEB.(2)求线段BD的长.【答案】(1)见解析(2)BD=3【分析】(1)根据题意得出∠A=∠D=90°,∠C+∠ABC=90°,∠ABC+∠EBD=90°,则∠C=∠EBD,即可得证;(2)根据(1)的结论,利用相似三角形的性质列出比例式,代入数据即可求解.【详解】(1)证明:∵AC⊥AD,ED⊥AD,∴∠A=∠D=90°,∠C+∠ABC=90°,∵CE⊥BE,∴∠ABC+∠EBD=90°,∴∠C=∠EBD,∴△ABC∽△DEB;(2)∵△ABC∽△DEB,∴AB DE =AC BD,∵AB=8,AC=6,DE=4,∴8 4=6 BD,解得:BD=3.【点睛】本题考查了相似三角形的性质与判定,熟练掌握相似三角形的性质与判定是解题的关键.26(2023·四川眉山·统考中考真题)如图,▱ABCD中,点E是AD的中点,连接CE并延长交BA的延长线于点F.(1)求证:AF=AB;(2)点G是线段AF上一点,满足∠FCG=∠FCD,CG交AD于点H,若AG=2,FG=6,求GH的长.【答案】(1)见解析(2)65【分析】(1)根据平行四边形的性质可得AB∥CD,AB=CD,证明△AEF≅△DEC ASA,推出AF= CD,即可解答;(2)通过平行四边形的性质证明GC=GF=6,再通过(1)中的结论得到DC=AB=AF=8,最后证明△AGH∽△DCH,利用对应线段比相等,列方程即可解答.【详解】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠EAF=∠D,∵E是AD的中点,∴AE=DE,∵∠AEF =∠CED ,∴△AEF ≅△DEC ASA ,∴AF =CD ,∴AF =AB ;(2)解:∵四边形ABCD 是平行四边形,∴DC =AB =AF =FG +GA =8,DC ∥FA ,∴∠DCF =∠F ,∠DCG =∠CGB ,∵∠FCG =∠FCD ,∴∠F =∠FCG ,∴GC =GF =6,∵∠DHC =∠AHG ,∴△AGH ∽△DCH ,∴GH CH =AG DC,设HG =x ,则CH =CG -GH =6-x ,可得方程x 6-x =28,解得x =65,即GH 的长为65.【点睛】本题考查了平行四边形的性质,等腰三角形的判定和性质,相似三角形的判定和性质,熟练运用上述性质证明三角形相似是解题的关键.27(2023·四川凉山·统考中考真题)如图,在▱ABCD 中,对角线AC 与BD 相交于点O ,∠CAB =∠ACB ,过点B 作BE ⊥AB 交AC 于点E .(1)求证:AC ⊥BD ;(2)若AB =10,AC =16,求OE 的长.【答案】(1)见详解(2)92【分析】(1)可证AB =CB ,从而可证四边形ABCD 是菱形,即可得证;(2)可求OB =6,再证△EBO ∽△BAO ,可得EO BO =BO AO,即可求解.【详解】(1)证明:∵∠CAB =∠ACB ,∴AB =CB ,∵四边形ABCD 是平行四边形,∴四边形ABCD 是菱形,∴AC ⊥BD .(2)解:∵四边形ABCD 是平行四边形,∴OA =12AC =8,∵AC ⊥BD ,BE ⊥AB ,∴∠AOB =∠BOE =∠ABE =90°,∴OB =AB 2-OB 2=102-82=6,∵∠EBO +∠BEO =90°,∠ABO +∠EBO =90°,∴∠BEO =∠ABO ,∴△EBO ∽△BAO ,∴EO BO =BO AO ,∴EO 6=68解得:OE =92.【点睛】本题考查了平行四边形的性质,菱形的判定及性质,勾股定理,三角形相似的判定及性质,掌握相关的判定方法及性质是解题的关键.28(2023·江苏扬州·统考中考真题)如图,点E 、F 、G 、H 分别是▱ABCD 各边的中点,连接AF 、CE 相交于点M ,连接AG 、CH 相交于点N .(1)求证:四边形AMCN 是平行四边形;(2)若▱AMCN 的面积为4,求▱ABCD 的面积.【答案】(1)见解析(2)12【分析】(1)根据平行四边形的性质,线段的中点平分线段,推出四边形AECG ,四边形AFCH 均为平行四边形,进而得到:AM ∥CN ,AN ∥CM ,即可得证;(2)连接HG ,AC ,EF ,推出S △ANH S △ANC =HN CN=12,S △FMC S △AMC =12,进而得到S △ANH +S △FMC =12S △ANC +S △AMC =12S ▱AMCN =2,求出S ▱AFCH =S △ANH +S △FMC +S ▱AMCN =2+4=6,再根据S ▱ABCD =2S ▱AFCH ,即可得解.【详解】(1)证明:∵▱ABCD ,∴AB ∥CD ,AD ∥BC ,AB =CD ,AD =BC ,∵点E 、F 、G 、H 分别是▱ABCD 各边的中点,∴AE =12AB =12CD =CG ,AE ∥CG ,∴四边形AECG 为平行四边形,同理可得:四边形AFCH 为平行四边形,∴AM ∥CN ,AN ∥CM ,∴四边形AMCN 是平行四边形;(2)解:连接HG ,AC ,EF ,∵H ,G 为AD ,CD 的中点,∴HG ∥AC ,HG =12AC ,∴△HNG ∽△CNA ,∴HN CN =HG AC =12,∴S △ANH S △ANC =HN CN=12,同理可得:S △FMC S △AMC =12∴S △ANH +S △FMC =12S △ANC +S △AMC =12S ▱AMCN =2,∴S ▱AFCH =S △ANH +S △FMC +S ▱AMCN =2+4=6,∵AH =12AD ,∴S ▱ABCD =2S ▱AFCH =12.【点睛】本题考查平行四边形的判定和性质,三角形的中位线定理,相似三角形的判定和性质,熟练掌握平行四边形的性质,以及三角形的中位线定理,证明三角形相似,是解题的关键.29(2023·上海·统考中考真题)如图,在梯形ABCD 中AD ∥BC ,点F ,E 分别在线段BC ,AC 上,且∠FAC =∠ADE ,AC =AD(1)求证:DE =AF(2)若∠ABC =∠CDE ,求证:AF 2=BF ⋅CE【答案】见解析【分析】(1)先根据平行线的性质可得∠DAE =∠ACF ,再根据三角形的全等的判定可得△DAE ≅△ACF ,然后根据全等的三角形的性质即可得证;(2)先根据全等三角形的性质可得∠AFC =∠DEA ,从而可得∠AFB =∠CED ,再根据相似三角形的判定可得△ABF ∼△CDE ,然后根据相似三角形的性质即可得证.【详解】(1)证明:∵AD ∥BC ,∴∠DAE =∠ACF ,在△DAE和△ACF中,∠DAE=∠ACF AD=CA∠ADE=∠CAF,∴△DAE≅△ACF ASA,∴DE=AF.(2)证明:∵△DAE≅△ACF,∴∠AFC=∠DEA,∴180°-∠AFC=180°-∠DEA,即∠AFB=∠CED,在△ABF和△CDE中,∠AFB=∠CED ∠ABF=∠CDE,∴△ABF∼△CDE,∴AF CE =BF DE,由(1)已证:DE=AF,∴AF CE =BF AF,∴AF2=BF⋅CE.【点睛】本题考查了三角形全等的判定与性质、相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题关键.。
中考相似三角形经典练习题及答案

相似三角形分类练习题(1)一、填空题1、如图,DE是△ABC的中位线,那么△ADE面积与△ABC面积之比是________。
2、如图,△ABC中,DE∥BC,,且,那么=________。
3、如图,△ABC中,∠ACB=90°,CD⊥AB,D为垂足,AD=8cm,DB=2cm,则CD=________cm。
4、如图,△ABC中,D、E分别在AC、AB上,且AD:AB=AE:AC=1:2,BC=5cm,则DE=________ cm。
5、如图,AD、BC相交于点O,AB∥CD,OB=2cm,OC=4cm,△AOB面积为4.5cm2,则△DOC面积为___cm2。
6、如图,△ABC中,AB=7,AD=4,∠B=∠ACD,则AC=_______。
7、如果两个相似三角形对应高之比为4:5,那么它们的面积比为_____。
8、如果两个相似三角形面积之比为1:9,那么它们对应高之比为_____。
9、两个相似三角形周长之比为2:3,面积之差为10cm2,则它们的面积之和为_____cm2。
10、如图,△ABC中,DE∥BC,AD:DB=2:3,则=______。
二、选择题1、两个相似三角形对应边之比是1:5,那么它们的周长比是()。
(A);(B)1:25;(C)1:5;(D)。
2、如果两个相似三角形的相似比为1:4,那么它们的面积比为()。
(A)1:16;(B)1:8;(C)1:4;(D)1:2。
3、如图,锐角三角形ABC的高CD和高BE相交于O,则与△DOB相似的三角形个数是()。
(A)1;(B)2;(C)3;(D)4。
4、如图,梯形ABCD,AD∥BC,AC和BD相交于O点,=1:9,则=()。
(A)1:9;(B)1:81;(C)3:1;(D)l:3。
三、如图,△ABC中,DE∥BC,BC=6,梯形DBCE面积是△ADE面积的2倍,求DE长。
四、如图,△ABE中,AD:DB=5:2,AC:CE=4:3,求BF:FC的值。
中考相似三角形经典题集锦

中考相似三角形经典题集锦1、如图,Rt三角形ABC中,∠BAC=90度,AB=AC=2,点D在BC上运动(不能经过B、C),过D作∠ADE=45度,DE交AC于E。
1)三角形ABD与三角形ABC一定相似,因为∠BAC=∠BAD=90度,∠ABD=∠ACB,且AB=AC;2)设BD=x,则AD=2-x,DE=x/2,由三角形ADE的余弦定理可得y=(2-x)²/2-x/2;定义域为0<x<2;3)当三角形ADE为等腰三角形时,有x=2/√3,代入公式得AE=2-√3.2、已知:∠A=90°,矩形DGFE的D、E分别在AB、AC上,G、F在BC上1)由勾股定理可得DG²+GF²=DF²,代入BG=22,FC=2可得DG=4,GF=5,因此DGFE为3×4的正方形,边长为12;2)由矩形面积公式可得y=xy/2,即y=x²/2;当y=10时,代入公式得AD=4/√5.3、如图,矩形EFGD的边EF在三角形ABC的BC边上,顶点D、G分别在边AB、AC上.已知AB=AC=5,BC=6,设BE=x,矩形EFGD的面积为y。
1)由相似三角形可得EF=5x/6,DG=5-5x/6,因此y=x(5x/6-5)/2;定义域为0<x<6/5;2)当三角形GEC为等腰三角形时,有x=3/5,代入公式得y=9/4.4、在Rt三角形ABC中,∠ACB=90°,CD⊥AB,垂足为D,E、F分别是AC、BC边上一点,且CE=AC,BF=BC。
1)由相似三角形可得CD=AB×BC/AC,BD=AB×AC/BC,因此XXX;2)由角平分线定理可得∠EDF=∠ADB=45°。
5、已知:在四边形ABCD中,∠B=90°,AD//BC,AB=2,AD=4,M是边CD中点,设BC=x,△ABM的面积为y。
相似三角形(8大题型)(48道压轴题专练)(原卷版)—2024-2025学年九年级数学上册单元速记巧
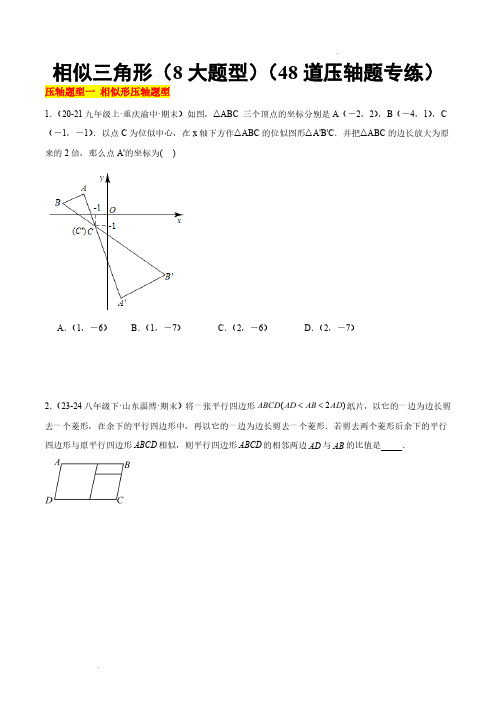
相似三角形(8大题型)(48道压轴题专练) 压轴题型一 相似形压轴题型1.(20-21九年级上·重庆渝中·期末)如图,△ABC 三个顶点的坐标分别是A (-2,2),B (-4,1),C (-1,-1).以点C 为位似中心,在x 轴下方作△ABC 的位似图形△A'B'C .并把△ABC 的边长放大为原来的2倍,那么点A'的坐标为( )A .(1,-6)B .(1,-7)C .(2,-6)D .(2,-7)2.(23-24八年级下·山东淄博·(2)ABCD AD AB AD <<纸片,以它的一边为边长剪去一个菱形,在余下的平行四边形中,再以它的一边为边长剪去一个菱形.若剪去两个菱形后余下的平行四边形与原平行四边形ABCD 相似,则平行四边形ABCD 的相邻两边AD 与AB 的比值是 .3.(2024·湖北武汉·一模)如图是由小正方形组成的网格,四边形ABCD的顶点都在格点上,仅用无刻度的直尺在所给定的网格中按要求完成下列画图,画图过程用虚线表示,画图结果用实线表示.(1)在图1中,先以点A为位似中心,将四边形ABCD缩小为原来的12,画出缩小后的四边形111AB C D,再在AB上画点E,使得DE平分四边形ABCD的周长;(2)在图2中,先在AB上画点F,使得CF BC=,再分别在AD,AB上画点M,N,使得四边形BCMN 是平行四边形.4.(23-24九年级上·江苏南京·阶段练习)形状相同(即长与宽之比相等)的矩形是相似矩形,已知一个矩形长为()1a a³,宽为1.一分为二(1)如图1,将矩形分割为一个正方形(阴影部分)和小矩形,小矩形恰与原矩形相似,则a的值为______.(2)如图2,将矩形分割为两个矩形,使每个小矩形均与原矩形相似,则a的值为______.一分为多(3)有同学说“无论a为何值,该矩形总可以分割为几个小矩形,这几个小矩形都与原矩形相似”,你同意这个说法吗?若同意,在图3中画出一种可行的分割方案;若不同意,举出反例.一分为三(4)将矩形分割为三个矩形,使每个小矩形均与原矩形相似.画出所有可能的分割方案的示意图,并在每个示意图下方直接写出对应的a 的值.5.(20-21八年级下·山东淄博·期末)如图,四边形ABCD ∽四边形A B C D ¢¢¢¢,且62A Ð=°,75B Ð=°,140D Т=°,9AD =,11A B ¢¢=,6A D ¢¢=,8B C ¢¢=.(1)请直接写出:C Ð= 度;(2)求边AB 和BC 的长.6.(23-24九年级上·广西南宁·阶段练习)如图,在平面直角坐标系中,ABC V 的三个顶点坐标分别为()1,1A ,()3,2B ,()2,3C (每个方格的边长均为1个单位长度),请按下列要求画图:(1)111A B C △与ABC V 关于原点O 成中心对称,画出111A B C △并写出点1A 的坐标;(2)以原点O 为位似中心,相似比为2,在第一象限内将ABC V 放大,画出放大后的222A B C △并写出点2B 的坐标;(3)根据信息回答问题:已知ABC V 的面积为32,AB ,请直接写出222A B C △的面积和22A B 边上的高的值.压轴题型二 比例线段压轴题型1.(2020古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底0.618≈,称为黄金分割比例),如图,著名的“断臂维纳斯”便是如此.此外,.若某人满足上述两个黄金分割比例,且腿长为105cm ,头顶至脖子下端的长度为26cm ,则其身高可能是( )A .165cmB .175cmC .185cmD .190cm2.(2024·四川乐山·一模)古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G 将线段MN 分为两线段MG ,GN ,使得其中较长的一段MG 是全长MN 与较短的一段GN 的比例中项,即满足MG GN MN MG ==这个数称为“黄金分割”数,把点G 称为线段MN 的“黄金分割”点.如图,在ABC V 中,已知3AB AC ==,4BC =,若D ,E 是边BC 的两个“黄金分割”点,则ADE V 的面积为 .3.(23-24八年级下·贵州六盘水·期末)已知a ,b ,c ,d ,e ,f 六个数,如果()0a c e k b d f b d f ===++¹,那么a c e k b d f++=++.理由如下:∵()0a c e k b d f b d f===++¹∴a bk =,c dk =,e fk =(第一步)∴()k b d f a c e bk dk fk k b d f b d f b d f++++++===++++++(第二步)(1)解题过程中第一步应用了______的基本性质;在第二步解题过程中,()k b d f k b d f ++=++应用了______的基本性质;(2)应用此解题过程中的思路和方法解决问题:①如果22567a b c ===,则218a b c ++=______;②已知0345x y z ==¹,求23x y z x y z -++-的值.4.(23-24九年级上··的矩形叫黄金矩形.如图①,已知黄金矩形ABCD 的宽1AB =.(1)黄金矩形ABCD 的长BC = ;(2)如图②,将图①中的黄金矩形裁剪掉一个以AB 为边的正方形ABEF ,得到新的矩形DCEF ,猜想矩形DCEF 是否为黄金矩形,并证明你的结论;(3)在图②中,连接AE ,求点D 到线段AE 的距离.5.(22-23九年级上·浙江·周测)若实数a b c ,,满足a b c b c a a c b c a b +-+-+-==,求()()()a b b c a c abc+×+×+的值.6.(23-24九年级下·山东淄博·期末)已知a ,b ,c ,d 为四个不为0的数.(1)如果3a b =,求a b b +与a b a b -+的值;(2)如果(),a c a b c d b d =¹¹,求证a c b a d c =--;(3)如果a c a b d b +=+,求证a c b d=.压轴题型三 相似三角形的判定压轴题型1.(21-22九年级上·陕西咸阳·期中)如图,在矩形ABCD 中,E 是AD 边的中点,BE ^F ,连接DF ,分析下列四个结论,①AEF CAB △∽△,②CF 2AF =;③DF DC =;④CD AC =.其中正确的结论有( )A .4个B .3个C .2个D .1个2.(2024·广东深圳·二模)如图,在等腰直角ABC V 中,4AB BC ==,D 为BC 上一点,E 为BC 延长线上一点,且45DAE =°∠,2AE AD =,则BD = .3.(2024·广东梅州·模拟预测)(1)如图1,在矩形ABCD 中,点C ,D 分别在边DC ,BC 上,AB AB ^,垂足为点G .求证:ADE DCF ∽V V .【问题解决】(2)如图2,在正方形ABCD 中,点E ,F 分别在边DC ,BC 上,AE DF =,延长BC 到点H ,使CH DE =,连接DH .求证:ADF H Ð=Ð.【类比迁移】(3)如图3,在菱形ABCD 中,E F 分别在边DC ,BC 上,10AE DF ==,7DE =,60AED Ð=°,求CF 的长.4.(2024·山西晋中·二模)综合与实践问题情境:数学活动课上,老师要求同学们以正方形为背景探索几何图形运动变化中的数学结论.如图1,正方形ABCD 中,4AB =,点E ,F 分别是边AB ,AD 的中点,连接EF ,点G 是线段EF 上的一个动点,连接AG ,将线段AG 绕点A 逆时针方向旋转90°,得到AH ,连接HD ,GB .猜想证明:(1)针对老师给出的问题背景,“智慧小组”发现GB HD =,请你证明这一结论;操作探究:(2)“善思小组”提出问题:如图2,当点G 为线段EF 的中点时,连接FH ,试判断四边形AGFH 的形状,并说明理由;深入探究:(3)“创新小组”BG 与直线DH 交于点M ,当AHD V 为直角三角形时,请直接写出四边形AGMH 的面积.5.(2024·安徽蚌埠·一模)如图1,在四边形ABCD 中,120ABC Ð=°,60ADC Ð=°,对角线AC ,BD 相交于点O ,且AC AD =,BD 平分ABC Ð.(1)求证:DB AB CB =+;(2)如图2,过点D 作DE AB ∥,使DE BC =,连接AE ,取AE 中点 F ,连接DF ,求证:22AC DF OD =×.6.(23-24九年级上·湖南常德·期中)(1)如图1,在四边形ABCD 中,90BAD BCD Ð=Ð=°,连接AC BD ,,过点A 作AE AC ^交CB 的延长线于点E ,求证:E ACD Ð=Ð.(2)如图2,在四边形ABCD 中,AB AD =,(1)中的其它条件不变,点M ,N 分别是BD EC ,的中点,连接AN AM ,,MN .①求证:AE AC =﹔②求证:N ABE AM ∽△△.压轴题型四 相似三角形的性质压轴题型1.(22-23九年级上·上海长宁·期中)已知点D 在ABC V 的边BC 上,联结AD ,如果ABD △与ACD V 相似,那么下列四个说法:①BAD C Ð=Ð;②AD BC ^;③2AD BD CD =×;④22AB BD AC CD =.一定成立的是( ).A .②④B .①③C .①②③D .②③④2.(2024·上海浦东新·三模)如图,在ABC V 中,3AC BC ==,90C Ð=°,点D 在边BC 上(不与点B ,点C 重合),连接AD ,点E 在边AB 上,EDB ADC Ð=Ð.已知点H 在射线AC 上,连接EH 交线段AD 于点G ,当1CH =,且AEH BED Ð=Ð时,则BE AB = .3.(23-24八年级下·山东威海·期末)如图1,矩形ABCD ,点E ,点F 分别为AD ,BC 上的点,将矩形沿EF 折叠,使点B 的对应点B ¢落在CD 上,连接BB ¢.(1)如图2,当点B ¢与点D 重合时,连接BE ,试判断四边形BEB F ¢的形状,并说明理由;(2)若6AB =,8BC =,求折痕EF 的最大值.4.(23-24八年级下·山东东营·期末)综合与探究(1)如图1,在正方形ABCD 中,点E ,F 分别在边BC CD ,上,且AE BF ^,则线段AE 与BF 的之间的数量关系为_____________;(2)【类比探究】如图2,在矩形ABCD 中,35AB AD ==,,点E ,F 分别在边BC ,CD 上,且AE BF ^,请写出线段AE 与BF 的数量关系,并证明你的结论.(3)【拓展延伸】如图3,在Rt ABC V 中,9046ABC AB BC Ð=°==,,,D 为BC 上一点,且2BD =,连接AD ,过点B 作BE AD ^于点F ,交AC 于点E ,求BE 的长.5.(23-24九年级下·广西南宁·阶段练习)已知等边ABC V ,以AC 为斜边向外作Rt ACD △,定义Rt ACD △为等边ABC V 的“关联直角三角形”,连接BD 交AC 于点E ,下面我们来研究与DE BE的值有关的问题.(1)如图①,当“关联直角三角形”是等腰直角三角形时,DE BE的值为______;(2)如图②,当“关联直角三角形”是含30°的直角三角形时,求DE BE的值;(3)如图③,当“关联直角三角形”是一般的直角三角形时,若16,3DE AB BE ==,求BD 的值.6.(2024·安徽·中考真题)如图1,ABCD Y 的对角线AC 与BD 交于点O ,点M ,N 分别在边AD ,BC 上,且AM CN =.点E ,F 分别是BD 与AN ,CM 的交点.(1)求证:OE OF =;(2)连接BM 交AC 于点H ,连接HE ,HF .(ⅰ)如图2,若HE AB ∥,求证:HF AD ∥;(ⅱ)如图3,若ABCD Y 为菱形,且2MD AM =,60EHF Ð=°,求AC BD 的值.压轴题型五 相似三角形的应用压轴题型1.(2024·浙江温州·三模)图1是《九章算术》中记载的“测井深”示意图,译文指出:“如图2,今有井直径CD 为5尺,不知其深AD .立5尺长的木CE 于井上,从木的末梢E 点观察井水水岸A 处,测得“入径CF ”为4寸,问井深AD 是多少?(其中1尺10=寸)”根据译文信息,则井深AD 为( )A .500寸B .525寸C .550寸D .575寸2.(2022·浙江金华·一模)将一本高为17cm (即17cm EF =)的词典放入高(AB )为16cm 的收纳盒中(如图1).恰好能盖上盒盖时,测得底部F 离收纳盒最左端B 处8cm ,若此时将词典无滑动向右倒,书角H 的对应点H ¢恰为CD 中点.(1)收纳盒的长BC = ;(2)现将若干本同样的词典放入此有盖的收纳盒中,如图2放置,则最多有本书可与边BC 有公共点.3.(2024·江苏南京·一模)在光学中,由实际光线会聚成的像,称为实像,而光线能会聚的是因为折射.图中,凸透镜EF 的焦距为f ,主光轴l EF ^,A ,B ,C ,D 都在l 上,其中O 是光心,2OB OD f ==,蜡烛PQ l ^(蜡烛可移动,且OQ f >),光线PG l ∥,其折射光线GC 与另一条经过光心的光线PP ¢相交于点P ¢(P Q l ¢¢^)即为蜡烛在光屏上所成的实像.图中所有点都在同一平面内.记物高()PQ 为h ,像高()P Q ¢¢为h ¢,物距()OQ ,像距()OQ ¢为v .(1)若10cm f =,10cm h =,15cm u =,=v cm .(2)求证111u v f+=.(3)当f 一定时,画出v 与u 之间的函数图象()u f >,并结合图象描述v 是怎么随着u 的变化而变化的?4.(23-24九年级上·河北邢台·1,小红家的阳台上放置了一个晒衣架,图2是晒衣架的侧面示意图,立杆AB 、CD 相交于点O ,B 、D 两点在地面上,经测量得到136cm AB CD ==,51cm OA OC ==,34cm OE OF ==,现将晒衣架完全稳固张开,扣链EF 成一条线段.发现:连接AC .则AC 与EF 有何位置关系?并说明理由;探究:若32cm EF =,求利用夹子垂挂在晒衣架上的连衣裙总长度小于多少时,连衣裙才不会拖在地面上?5.(22-23九年级上·浙江·单元测试)如图,Rt ABC V 为一块铁板余料,90B Ð=°,6cm BC =,8cm AB =,要把它加工成正方形小铁板,有如图所示的两种加工方案,请你分别计算这两种加工方案的正方形的边长.6.(2022九年级·全国·专题练习)阅读理解:如图1,AD 是△ABC 的高,点E 、F 分别在AB 和AC 边上,且EF //BC ,可以得到以下结论:AH EF AD BC=.拓展应用:(1)如图2,在△ABC 中,BC =3,BC 边上的高为4,在△ABC 内放一个正方形EFGM ,使其一边GM 在BC 上,点E 、F 分别在AB 、AC 上,则正方形EFGM 的边长是多少?(2)某葡萄酒庄欲在展厅的一面墙上,布置一个腰长为100cm ,底边长为160cm 的等腰三角形展台.现需将展台用隔板沿平行于底边,每间隔10cm 分隔出一排,再将每一排尽可能多的分隔成若干个无盖正方体格子,要求每个正方体格子内放置一瓶葡萄酒.平面设计图如图3所示,将底边BC 的长度看作是0排隔板的长度.①在分隔的过程中发现,当正方体间的隔板厚度忽略不计时,每排的隔板长度(单位:厘米)随着排数(单位:排)的变化而变化.请完成下表:排数/排0123…隔板长度/厘米160__________________…若用n 表示排数,y 表示每排的隔板长度,试求出y 与n 的关系式;②在①的条件下,请直接写出该展台最多可以摆放多少瓶葡萄酒?压轴题型六 重心的性质压轴题型1.(23-24九年级上·浙江宁波·期末)如图,点G 是ABC V 的重心,过点G 作MN BC ∥分别交AB AC ,于点M ,N ,过点N 作ND AB ∥交BC 于点D ,则四边形BDNM 与ABC V 的面积之比是( )A .1:2B .2:3C .4:9D .7:92.(2023·上海·一模)在Rt ABC △中,9030B BAC BC Ð=°Ð=°=,,1,以AC 为边在ABC V 外作等边ACD V ,设点E 、F 分别是ABC V 和ACD V 的重心,则两重心E 与F 之间的距离是 .3.(2024·江苏盐城·中考真题)如图1,E 、F 、G 、H 分别是平行四边形ABCD 各边的中点,连接AF CE 、交于点M ,连接AG 、CH 交于点N ,将四边形AMCN 称为平行四边形ABCD 的“中顶点四边形”.(1)求证:中顶点四边形AMCN 为平行四边形;(2)①如图2,连接AC BD 、交于点O ,可得M 、N 两点都在BD 上,当平行四边形ABCD 满足________时,中顶点四边形AMCN 是菱形;②如图3,已知矩形AMCN 为某平行四边形的中顶点四边形,请用无刻度的直尺和圆规作出该平行四边形.(保留作图痕迹,不写作法)4.(23-24七年级下·江苏扬州·阶段练习)作图.(1)直尺作图:如图1,已知D 、E 分别为AB 、AC 中点,过点A 作AF 平分ABC V 面积;(2)直尺作图:如图2,已知AD BC ∥,在四边形ABCD 中作一点O ,使AOB COD S S =△△;(3)尺规作图:如图3,已知D 为AC 中点,点M 在BC ,在AC 上作点N 使MN 平分ABC V 面积.5.(2024·辽宁丹东·二模)阅读与思考:三角形的重心定义:三角形三条中线相交于一点,这个交点叫做三角形的重心.三角形重心的一个重要性质:重心与一边中点的连线的长是对应中线长的13.下面是小明证明性质的过程.如图,在ABC V 中,D 、E 分别是边BC 、AC 的中点,AD 、BE 相交于点G ,求证:13GE GD BE AD ==证明:连接ED ,∵D ,E 是边BC ,AC 的中点,∴DE AB ∥,12DE AB =(依据1)∴ABG DEGV V ∽∴12GE GD DE GB GA AB ===(依据2)∴13GE GD BE AD ==(1)任务一,在小明的证明过程中,依据1和依据2的内容分别是:依据1:______________________依据2:______________________(2)应用①如图,在ABC V 中,点G 是ABC V 中的重心,连接AG 并延长交BC 与点E ,若 3.5GE =,求AG 长.②在ABC V 中,中线AD 、BE 相交于点O ,若ABC V 的面积等于30,求BOD V 的面积.6.(2024·河南周口·三模)(1)古往今来,人们在生产和生活中对三角形的应用层出不穷,三角形也是我们平时研究的重点,如图1,已知ABC V 是等边三角形. P 是ABC V 的重心,连接BP CP ,并延长分别交边AC AB ,于点E ,D .试判断:①BPD Ð的度数为 ;②线段PB PD PE ,,之间的数量关系:PB PD PE +;(填写“>”“<”或“=”)(2)如图2,若在等边ABC V 中,点E 是射线AC 上一动点(其中点E 不与点A 重合,且12CE AC <),连接BE ,作边BA 关于直线 BE 的对称线段 BD ,直线CD ,BE 相交于点 P ,试探究线段PB PC PD ,,的数量关系,并说明理由.压轴题型七 平面向量的线性运算压轴题型1.(23-24九年级上·上海·期中)下列判断不正确的是( )A .()222a b a b +=+r r r r ;B .如果向量a r 与b r 均为单位向量,那么a b =r r 或a b =-r r ;C .如果a b =r r ,那么a b =r r ;D .对于非零向量b r ,如果()0a k b k =×¹r r ,那么a b r r P .2.(2024·上海普陀·二模)如图,梯形ABCD 中,AD BC ∥,过点A 作AE DC ∥分别交BD 、BC 于点F 、E ,23BE BC =,设AD a =uuu r r ,AB b =uuu r r ,那么向量FE uuu r 用向量a r 、b r 表示为 .3.(23-24八年级下·上海崇明·期末)如图,点E 在平行四边形ABCD 的对角线BD 的延长线上.(1)填空:BA AB +uuu r uuu r = ,BA AE ED DC +++uuu r uuu r uuu r uuu r = ;(2)图中与AB uuu r 相等的向量是 ,与AD uuu r 相反的向量是 ;(3)求作:DC DE +uuu r uuu r (不写作法,保留作图痕迹,写出结论).4.(23-24八年级下·上海·期末)如图,在四边形ABCD 中,AD BC ∥,点O 是对角线AC 的中点,DO 的延长线与BC 相交于点E ,设AB a uuu r r =,AD b =uuu r r ,BE c =uuu r r .(1)试用向量a r 、b r 、c r 表示向量:ED =uuu r ______;(2)写出图中所有与AD uuu r 互为相反向量的向量:______;(3)求作:AD OC +uuu r uuu r.(画出所求向量,并直接写出结论)5.(23-24八年级下·上海闵行·期末)如图,已知梯形ABCD 中,AB DC P ,点E 在AB 上,ED BC ∥.(1)填空:BE ED DC CB +++=uuu r uuu r uuu r uuu r ,(2)填空:BA AD DC EA ++-=uuu r uuu r uuu r uuu r ;(3)在图中直接作出AE ED AB +-uuu r uuu r uuu r .(不写作法,写结论)6.(2022八年级下·上海·专题练习)如图,已知点M 是△ABC 边BC 上一点,设AB uuu r =a r ,AC uuu r =b r .(1)当BM MC=2时,AM uuuu r =______;(用a r 与b r 表示)(2)当AM uuuu r =4377a b +r r 时,BM MC =______;(3)在原图上作出AM uuuu r 在AB uuu r 、AC uuu r 上的分向量.压轴题型八 相似三角形的动点问题1.(2020·山西·一模)如图,在ABC V 中,8AB AC ==,6BC =,点P 从点B 出发以1个单位长度/秒的速度向点A 运动,同时点Q 从点C 出发以2个单位长度/秒的速度向点B 运动,其中一点到达另一点即停.当以B ,P ,Q 为顶点的三角形与ABC V 相似时,运动时间为( )A .2411秒B .95秒C .2411秒或95秒D .以上均不对2.(2023八年级上·江苏·专题练习)如图,在ABC V 中,90C Ð=°,3AC =,4BC =,动点P 从点B 出发以每秒1个单位长度的速度沿B A ®匀速运动;同时点Q 从点A 出发同样的速度沿A C B ®®匀速运动.当点P 到达点A 时,P 、Q 同时停止运动,设运动时间为t 秒,当t 为 时,以B 、P 、Q 为顶点的三角形是等腰三角形.3.(2024·吉林长春·三模)如图,在Rt ABC △中,90ABC Ð=°,8AB =,6BC =,点D 为AC 中点,动点P 从点A 出发,沿边AB 以每秒5个单位长度的速度向终点B 运动,连结DP ,将线段DP 绕点D 逆时针旋转90°得线段DE ,连结PE .设点P 运动的时间为t 秒.(1)用含t 的代数式表示点P 到AC 的距离为________;(2)当点E 落在ABC V 内部(不包括边界)时,求t 的取值范围;(3)当PE 与ABC V 的一边平行时,求线段PE 的长度;(4)当经过点E 与ABC V 的一个顶点的直线平分ABC V 面积时,直接写出t 的值.4.(2024·江苏苏州·二模)如图,矩形ABCD 中,4AB =厘米,3BC =厘米,点E 从A 出发沿AB BC -匀速运动,速度为1厘米/秒;同时,点F 从C 出发沿对角线CA 向A 匀速运动,速度为1厘米/秒,连接DE DF EF 、、,设运动时间为t 秒.请解答以下问题:(1)当0 2.5t <<时①t 为何值时,EF AD ∥;②设DEF V 的面积为y ,求y 关于t 的函数;5.(2023·吉林松原·模拟预测)已知ABC V 中,90C Ð=°,3cm AC =,4cm CD =,BD AD =.点F 从点A 出发,沿AC CD -运动,速度为1cm/s ,同时点E 从点B 出发,沿BD DA -运动,运动速度为1cm/s ,一个点到达终点,另一点也停止运动.设AEF △ 的面积为S 2cm ,点E ,F 运动时间为t s .(1)求BD 的长;(2)用含t 的代数式表示DE ;(3)求S 与t 的函数关系式,并写出t 的取值范围.6.(23-24九年级下·河北邯郸·阶段练习)如图1和2,在矩形ABCD 中,6,8AB BC ==,点K 在CD 边上.且73CK =.点M N ,分别在,AB BC 边上,且2AM CN ==.点P 从点M 出发沿折线MB BN -匀速运动,点E 在CD 边上随P 移动,且始终保持^PE AP ;点Q 从点D 出发沿DC 匀速运动,点P Q ,同时出发,点Q 的速度是点P 的一半,点P 到达点N 时停止,点Q 随之停止.设点P 移动的路程为x .(1)当点Q 与点K 重合时,通过计算确定点P 的位置;(2)若点P 在BN 上,当BP CE =时,如图2,求x 的值;(3)在点P 沿折线MB BN -运动过程中,求点Q ,E 的距离(用含x 的式子表示);(4)已知点P 从点M 到点B 再到点N 共用时20秒,请直接写出点K 在线段QE 上(包含端点)的总时长.。
2024年中考数学复习(全国版)第四讲 全等、相似三角形(原卷版)

→➌题型突破←→➍专题训练←题型一全等三角形1.如图,等腰△ABC 中,点D,E 分别在腰AB,AC 上,添加下列条件,不能判定△ABE≌△ACD 的是()A.AD=AE B.BE=CD C.∠ADC=∠AEB D.∠DCB=∠EBC2.如图,在△AOB 和△COD 中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连接AC,BD 交于点M,连接OM.下列结论:①∠AMB=36°,②AC=BD,③OM 平分∠AOD,④MO 平分∠AMD.其中正确的结论个数有()个.A.4B.3C.2D.13.如图所示,,ABC ECD 均为等边三角形,边长分别为5cm,3cm ,B、C、D 三点在同一条直线上,则下列结论正确的________________.(填序号)①AD BE ②7cm BE ③CFG △为等边三角形④13cm 7CM ⑤CM 平分BMD4.如图,在矩形ABCD 中,AD=4,将∠A 向内翻析,点A 落在BC 上,记为A 1,折痕为DE.若将∠B 沿EA 1向内翻折,点B 恰好落在DE 上,记为B 1,则AB=_____.5.如图,在平面直角坐标系中,点C 的坐标为 1,0 ,点A 的坐标为 3,3 ,将点A 绕点C 顺时针旋转90 得到点B ,则点B 的坐标为_____________.6.已知,如图1,若AD 是ABC 中BAC 的内角平分线,通过证明可得=AB BD AC CD,同理,若AE 是ABC 中BAC 的外角平分线,通过探究也有类似的性质.请你根据上述信息,求解如下问题:如图2,在ABC 中,2,3,BD CD AD 是ABC 的内角平分线,则ABC 的BC边上的中线长l 的取值范围是________7.如图,在Rt△ABC 中,∠ACB=90°,且AC=AD.(1)作∠BAC 的平分线,交BC 于点E;(要求尺规作图,不写作法,保留作图痕迹)(2)在(1)的条件下,连接DE,证明AB DE .8.如图,ABC 中,AB AC ,点,D E 在边BC 上,BD CE .求证ADE AED .9.如图,点D、E 分别是AB、AC 的中点,BE、CD 相交于点O,∠B=∠C,BD=CE.求证:(1)OD=OE;(2)△ABE≌△ACD.10.如图,点E、F 在线段BC 上,//AB CD ,A D ,BE CF ,证明:AE DF .11.如图,矩形ABCD 中为边BC 上一点,将ABE △沿AE 翻折后,点B 恰好落在对角线AC 的中点F 上.(1)证明:AEF CEF ≌;(2)若3AB AE 的长度12.如图,点A,D,B,E 在一条直线上AD BE ,AC DF ,//AC DF .求证:BC EF .13.如图,在矩形ABCD 中,点M 在DC 上,AM AB ,且BN AM ,垂足为N .(1)求证:ABN MAD ≌;(2)若2,4AD AN ,求四边形BCMN 的面积.14.如图,在ABC 中,点D 在AB 边上,CB CD ,将边CA 绕点C 旋转到CE 的位置,使得ECA DCB ,连接DE 与AC 交于点F ,且70B ,10A .(1)求证:AB ED ;(2)求AFE的度数.15.在四边形ABCD中,对角线AC平分∠BAD.(探究发现)(1)如图①,若∠BAD=120 ,∠ABC=∠ADC=90 .求证:AD+AB=AC;(拓展迁移)(2)如图②,若∠BAD=120 ,∠ABC+∠ADC=180 .①猜想AB、AD、AC三条线段的数量关系,并说明理由;②若AC=10,求四边形ABCD的面积.16.已知等边三角形ABC,过A点作AC的垂线l,点P为l上一动点(不与点A重合),连接CP,把线段CP绕点C逆时针方向旋转60 得到CQ,连QB.(1)如图1,直接写出线段AP 与BQ 的数量关系;(2)如图2,当点P、B 在AC 同侧且AP AC 时,求证:直线PB 垂直平分线段CQ ;(3)如图3,若等边三角形ABC 的边长为4,点P、B 分别位于直线AC 异侧,且APQ 的34AP 的长度.17.如图①,E F 、是等腰Rt ABC 的斜边BC 上的两动点,45,EAF CD BC 且CD BE .(1)求证:ABE ACD △≌△;(2)求证:222EF BE CF ;(3)如图②,作AH BC ,垂足为H,设,EAH FAH ,不妨设2AB 利用(2)的结论证明:当45 时,tan tan tan()1tan tan成立.题型二相似三角形18.如图,ABC 与111A B C △位似,位似中心是点O,若1:1:2OA OA ,则ABC 与111A B C △的周长比是()A.1:2B.1:3C.1:4D.219.如图, ABC 中,点D、E 分别在AB、AC 上,且12AD AE DB EC ==,下列结论正确的是()A.DE:BC=1:2B. ADE 与 ABC 的面积比为1:3C. ADE 与 ABC 的周长比为1:2D.DE //BC20.如图,在ACD △中,6AD ,5BC , 2AC AB AB BC ,且DAB DCA ,若3AD AP ,点Q 是线段AB 上的动点,则PQ 的最小值是()A.72B.6252D.8521.如图,△ABC 中,AB=AC,∠B=72°,∠ACB 的平分线CD 交AB 于点D,则点D 是线段AB 的黄金分割点.若AC=2,则BD=______.22.如图,矩形ABCD 中,6AB ,8BC ,对角线BD 的垂直平分线EF 交AD 于点E 、交BC 于点F ,则线段EF 的长为__.23.如图,在菱形ABCD 中,点M,N 分别是边BC ,DC 上的点,34BM BC ,34DN DC .连接AM ,AN ,延长AN 交线段BC 延长线于点E.(1)求证:ABM AND △≌△;(2)若4 AD ,则ME 的长是__________.24.已知AB BD ,AE EF , ABD AEF .(1)找出与DBF 相等的角并证明;(2)求证:BFD AFB ;(3)AF kDF ,180EDF MDF ,求AE MF .25.已知在 ABC 中,O 为BC 边的中点,连接AO,将 AOC 绕点O 顺时针方向旋转(旋转角为钝角),得到 EOF,连接AE,CF.(1)如图1,当∠BAC=90°且AB=AC 时,则AE 与CF 满足的数量关系是;(2)如图2,当∠BAC=90°且AB≠AC 时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)如图3,延长AO 到点D,使OD=OA,连接DE,当AO=CF=5,BC=6时,求DE 的长.26.在△ABC 中,AC=AB,∠BAC= ,D 为线段AB 上的动点,连接DC,将DC 绕点D 顺时针旋转 得到DE,连接CE,BE.(1)如图1,当 =60°时,求证:△CAD≌△CBE;(2)如图2,当tanα=34时,①探究AD和BE之间的数量关系,并说明理由;②若AC=5,H是BC上一点,在点D移动过程中,CE+EH是否存在最小值?若存在,请直接写出CE+EH的最小值;若不存在,请说明理由.。
中考数学专题训练:相似三角形(附参考答案)

中考数学专题训练:相似三角形(附参考答案)1.若a3=b2,则a+bb的值为( )A.32B.53C.52D.232.如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为( )A.3 B.4C.5 D.63.如图,AD∥BE∥FC,直线l1,l2分别与三条平行线交于点A,B,C和点D,E,F.若AB=3,BC=5,DF=12,则EF的长为( )A.4.5 B.6C.7.5 D.84.如图,小雅同学在利用标杆BE测量建筑物的高度时,测得标杆BE高1.2 m,又知AB∶BC=1∶8,则建筑物CD的高是( )A.9.6 m B.10.8 mC.12 m D.14 m5.如图,在平面直角坐标系中,△ABC的三个顶点分别为A(1,2),B(2,1),C(3,2).现以原点O为位似中心,在第一象限内作与△ABC的相似比为2的位似图形△A′B′C′,则顶点C′的坐标是( )A.(2,4) B.(4,2)C.(6,4) D.(5,4)6.如图(单位:mm),小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5 m时,标准视力表中最大的“E”字高度为72.7 mm,当测试距离为3 m时,最大的“E”字高度为( )A.121.17 mm B.43.62 mmC.29.08 mm D.4.36 mm7.如图,AC是□ABCD的对角线,点E在CD的延长线上,连接BE分别交AC,AD 于点F,G,则下列式子一定正确的是( )A.AFCF =AGDGB.ABCE=CFAFC.BFFG =EFBFD.ADDG=ABDE8.如图,在△ABC中,D,E分别为边AB,AC上的点,试添加一个条件:________________________,使得△ADE与△ABC相似.(任意写出一个满足的条件即可)9.如图,已知在梯形ABCD中,AD∥BC,S△ABDS△BCD =12,则S△BOCS△BCD=______.10.如图,在矩形ABCD中,若AB=3,AC=5,AFFC =14,则AE的长为_____.11.如图,为了测量山坡的护坡石坝高,把一根长为4.5 m 的竹竿AC斜靠在石坝旁,量出竿上AD长为1 m时,它离地面的高度DE为0.6 m,则坝高CF为________m.12.已知在平面直12角坐标系中,△AOB的顶点分别为A(2,1),B(2,0),O(0,0).若以原点O为位似中心,相似比为2,将△AOB放大,则点A的对应点的坐标为__________________________.13.如图,在△ABC中,点D,E分别是AB,AC的中点.若S△ADE=2,则S△ABC=_____.14.如图,在平面直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐标是____________.15.如图,在△ABC和△DEC中,∠A=∠D,∠BCE=∠ACD.(1)求证:△ABC∽△DEC;(2)若S△ABC∶S△DEC=4∶9,BC=6,求EC的长.16.如图,在△ABC中,AB=4,BC=5,点D,E分别在BC,AC上,CD=2BD,CE =2AE,BE交AD于点F,则△AFE面积的最大值是______.17.小孔成像的示意图如图所示,光线经过小孔O,物体AB在幕布前形成倒立的实像CD(点A,B的对应点分别是C,D).若物体AB的高为6 cm,小孔O到物体和实像的水平距离BE,CE分别为8 cm,6 cm,则实像CD的高度为________cm.18.如图,在正方形ABCD中,点E是边CD上一点,连接BE,以BE为对角线作正方形BGEF,边EF与正方形ABCD的对角线BD相交于点H,连接AF,有以下五个结论:①∠ABF=∠DBE;②△ABF∽△DBE;③AF⊥BD;④2BG2=BH·BD;⑤若CE∶DE=1∶3,则BH∶DH=17∶16.你认为其中正确的是____________.(填写序号)19.已知,如图1,若AD是△ABC中∠BAC的内角平分线,通过证明可得ABAC =BDCD,同理,若AE是△ABC中∠BAC的外角平分线,通过探究也有类似的性质.请你根据上述信息,求解如下问题:如图2,在△ABC中,BD=2,CD=3,AD是△ABC的内角平分线,则△ABC的BC边上的中线长l的取值范围是_____________.20.如图,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB 上,且CF=BE,AE2=AQ·AB.求证:(1)∠CAE=∠BAF;(2)CF·FQ=AF·BQ.21.在等腰三角形ABC中,AB=AC,点D是边BC上一点(不与点B,C重合),连接AD.(1)如图1,若∠C=60°,点D关于直线AB的对称点为点E,连接AE,DE,则∠BDE=________.(2)若∠C=60°,将线段AD绕点A顺时针旋转60°得到线段AE,连接BE.①在图2中补全图形;②探究CD与BE的数量关系,并证明.(3)如图3,若ABBC =ADDE=k,且∠ADE=∠C,试探究BE,BD,AC之间满足的数量关系,并证明.参考答案1.C 2.B 3.C 4.B 5.C 6.B 7.C8.ADAB =AEAC(答案不唯一) 9.2310.1 11.2.712.(4,2)或(-4,-2)13.8 14.(4,2) 15.(1)证明略(2)EC=916.43 17.4.5 18.①②③④ 19.12<l<25220.(1)证明略(2)证明略21.(1)30°(2)①图略②CD与BE的数量关系为CD=BE,证明略(3)AC=k(BD+BE),证明略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形1.如图,已知AB CD EF ∥∥,那么下列结论正确的是( )A .AD BCDF CE=B .BC DFCE AD=C .CD BCEF BE=D .CD ADEF AF=2.如图所示,给出下列条件:①B ACD ∠=∠; ②ADC ACB ∠=∠;③AC ABCD BC=; ④2AC AD AB = 其中单独能够判定ABC ACD △∽△的个数为( )A .1B .2C .3D .43.已知△ABC∽△DEF ,且AB :DE=1:2,则△ABC 的面积与△DEF 的面积之比为( )A .1:2B .1:4C .2:1D .4:14.如图,已知等边三角形ABC 的边长为2,DE 是它的中位线,则下面四个结论: (1)DE=1,(2)△CDE∽△CAB,(3)△CDE 的面积与△CAB 的面积之比为1:4. 其中正确的有:( )A .0个B .1个C .2个D .3个A B D C EF1题ACD B(第2题图)【参考答案】1.A2.C3.B4.D◆考点聚焦1.了解线段的比、成比例线段、黄金分割、相似图形有关概念及性质.2.探索并掌握三角形相似的性质及条件,•并能利用相似三角形的性质解决简单的实际问题.3.掌握图形位似的概念,能用位似的性质将一个图形放大或缩小.4.掌握用坐标表示图形的位置与变换,在给定的坐标系中,•会根据坐标描出点的位置或由点的位置写出它的坐标,灵活运用不同方式确定物体的位置.◆备考兵法1.证明三角形相似的方法常用的有三个,到底用哪个要根据具体情况而定,要注意基本图形的应用,如“A型”“X型”“母子型”等.2.用相似三角形的知识解决现实生活中实际问题,关键是要先把实际问题转化为数学问题,识别或作出相似三角形,再利用相似三角形的性质求解,并回答实际问题,注意题目的解一定要符合题意.3.用直角坐标系中的点描述物体的位置,用坐标的方法来研究图形的运动变换,是较为常见的考法,要注意训练.◆考点链接一、相似三角形的定义三边对应成_________,三个角对应________的两个三角形叫做相似三角形.二、相似三角形的判定方法1. 若DE∥BC(A型和X型)则______________.2. 射影定理:若CD为Rt△ABC斜边上的高(双直角图形)则Rt△ABC∽Rt△ACD∽Rt△CBD且AC2=________,CD2=_______,BC2=__ ____.3. 两个角对应相等的两个三角形__________.4. 两边对应成_________且夹角相等的两个三角形相似.5. 三边对应成比例的两个三角形___________.三、相似三角形的性质1. 相似三角形的对应边_________,对应角________.2. 相似三角形的对应边的比叫做________,一般用k表示.3. 相似三角形的对应角平分线,对应边的________线,对应边上的_______•线的比等于_______比,周长之比也等于________比,面积比等于_________.◆典例精析例1(2009山西太原)甲、乙两盏路灯底部间的距离是30米,一天晚上,当小华走到距路灯乙底部5米处时,发现自己的身影顶部正好接触路灯乙的底部.已知小华的身高为米,那么路灯甲的高为米.【答案】9.【解析】本题考查相似的有关知识,相似三角形的应用.设路灯高为x米,由相似得1.5530x=,解得9x=,所以路灯甲的高为9米,故填9.例2(2008年浙江丽水)如图,在已建立直角坐标系的4×4正方形方格纸中,△划格点三角形(三角形的三个顶点都是小正方形的顶点),若以格点P,A,B为顶点的三角形与△ABC相似(全等除外),则格点P的坐标是_______.【答案】 P1(1,4),P2(3,4).点拨:这种题常见的错误是漏解,平时要多加强这方面的训练,以培养思维的严密性.拓展变式在Rt△ABC中,斜边AC上有一动点D(不与点A,C重合),过D点作直线截△ABC,使截得的三角形与△ABC相似,则满足这样条件的直线共有______条.【答案】 3例3 如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC,DE把平行四边形A BCD分成的四部分的面积分别为S1,S2,S3,S4.下面结论:①只有一对相似三角形;②EF:ED=1:2;③S1:S2:S3:S4=1:2:4:5.其中正确的结论是()小华乙A.①③ B.③ C.① D.①②【答案】 B【解析】∵AB∥DC,∴△AEF•∽△CDF,•但本题还有一对相似三角形是△ABC•≌△CDA(全等是相似的特例).∴①是错的.∵12AE EFCD DF==,∴②EF:ED=1:2是错的.∴S△AEF:S△CDF =1:4,S△AEF:S△ADF =1:2.∴S1:S2:S3:S4=1:2:4:5,③正确.点拨①利用相似三角形的特征和等高三角形的面积比等于底边之比;(共底三角形的面积之比等于高之比)②和全等三角形一样,中考试题往往把需要证明的两个相似三角形置于其他图形(如等边三角形、等腰直角三角形、平行四边形、矩形、菱形、正方形和梯形)中,在解题时要充分挖掘其中隐含的相等角、成比例的线段和平行线,注意从复杂的图形中分离出基本的相似三角形.拓展变式点E是ABCD的边BC延长线上的一点,AE与CD相交于点G,则图中相似三角形共有()A.2对 B.3对 C.4对 D.5对【答案】 C◆迎考精练一、选择题1.(2009年江苏省)如图,在55⨯方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么,下面的平移方法中,正确的是()A.先向下平移3格,再向右平移1格B.先向下平移2格,再向右平移1格C.先向下平移2格,再向右平移2格D.先向下平移3格,再向右平移2格2.(2009年浙江杭州)如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值()A.只有1个 B.可以有2个C.有2个以上但有限 D.有无数个3.(2009年浙江宁波)如图,菱形ABCD中,对角线AC、BD相交于点O,M、N分别是边AB、AD的中点,连接OM、ON、MN,则下列叙述正确的是()A.△AOM和△AON都是等边三角形B.四边形MBON和四边形MODN都是菱形C.四边形AMON与四边形ABCD是位似图形D.四边形MBCO和四边形NDCO都是等腰梯形4.(2009年浙江义乌)在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比。
已知这本书的长为20cm,则它的宽约为()A.(2009年湖南娄底)小明在一次军事夏令营活动中,进行打靶训练,在用枪瞄准目标点B时,要使眼睛O、准星A、目标B在同一条直线上,如图所示,在射击时,小明有轻微的抖动,致使准星A偏离到A′,若OA=米,OB=40米,AA′=米,则小明射击到的点B′偏离目标点B的长度BB ′为()A.3米 B .米 C .米 D .米6.(2009年甘肃白银)如图,小东用长为的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m、与旗杆相距22m,则旗杆的高为()A.12m B.10m C.8m D.7mDBAN MO7.(2009年天津市)在ABC △和DEF △中,22AB DE AC DF A D ==∠=∠,,,如果ABC △的周长是16,面积是12,那么DEF △的周长、面积依次为( )A .8,3B .8,6C .4,3D .4,6 二、填空题1. (2009年山东滨州)在平面直角坐标系中,ABC △顶点A 的坐标为(23),,若以原点O 为位似中心,画ABC △的位似图形A B C '''△,使ABC △与A B C '''△的相似比等于12,则点A '的坐标为 .2.(2009年黑龙江牡丹江)如图,Rt ABC △中,90ACB ∠=°,直线EF BD ∥,交AB 于点E ,交AC 于点G ,交AD 于点F ,若13AEG EBCG S S =△四边形,则CFAD= .3.(2009年湖北孝感)如图,点M 是△ABC 内一点,过点M 分别作直线平行于△ABC 的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是4,9和49.则△ABC 的面积是 .4.(2009年山东日照)将三角形纸片(△ABC )按如图所示的方式折叠,使点B 落在边AC 上,记为点B ′,折痕为EF .已知AB =AC =3,BC =4,若以点B ′,F ,C 为顶点的三角形与△ABC 相似,那么BF 的长度是 .5.(2009年福建莆田)如图,A B 、两处被池塘隔开,为了测量A B 、两处的距离,在AB 外选一适当的点C ,连接AC BC 、,并分别取线段AC BC 、的中点E F 、,测得EF =20m ,则AB =__________m .E(第4题图)AB ′CFB AE F DG CB第2题三、解答题1.(2009年湖南郴州)如图,在ABC 中,已知DE ∥BC ,AD =4,DB =8,DE =3,(1)求ADAB的值,(2)求BC 的长2.(2009年湖南常德)如图,△ABC 内接于⊙O ,AD 是△ABC 的边BC 上的高,AE 是⊙O 的直径,连接BE ,△ABE 与△ADC 相似吗请证明你的结论.3.(2009年湖北武汉)如图1,在Rt ABC △中,90BAC ∠=°,AD BC ⊥于点D ,点O 是AC 边上一点,连接BO 交AD 于F ,OE OB ⊥交BC 边于点E .(1)求证:ABF COE △∽△;(2)当O 为AC 边中点,2ACAB=时,如图2,求OF OE 的值;(3)当O 为AC 边中点,ACn AB=时,请直接写出OF OE 的值.BBAACOE D DE COF图1图2F A E CF B 第5题图A CBDE4.(2009年安徽)如图,M 为线段AB 的中点,AE 与BD 交于点C ,∠DME =∠A =∠B =α,且DM 交AC 于F ,ME 交BC 于G .(1)写出图中三对相似三角形,并证明其中的一对;(2)连结FG ,如果α=45°,AB=AF =3,求FG 的长.5.(2009年吉林省)如图,⊙O 中,弦AB CD 、相交于AB 的中点E ,连接AD 并延长至点F ,使DF AD =,连接BC 、BF .(1)求证:CBE AFB △∽△; (2)当58BE FB =时,求CBAD 的值第5题图FBABMF G DEC 第4题图6.(2009年广东梅州)如图,梯形ABCD 中,AB CD ∥,点F 在BC 上,连DF 与AB 的延长线交于点G . (1)求证:CDF BGF △∽△;(2)当点F 是BC 的中点时,过F 作EF CD ∥交AD 于点E ,若6cm 4cm AB EF ==,,求CD 的长.【参考答案】 选择题 1. D 2. B 3. C 4. A 5. B 6. A 7. A 填空题 1. (4,6) 2.123. 144D C FE AG6题4.712或2; 5. 40 解答题1. 解:(1)∵48AD DB ,∴4812AB ADDB∴41123AD AB (2)∵DE BC ∥,所以ADE ABC △∽△∴DE ADBCAB∵3DE∴313BC∴9BC2. △ABE 与△ADC 相似.理由如下: 在△ABE 与△ADC 中∵AE 是⊙O 的直径, ∴∠ABE =90o, ∵AD 是△ABC 的边BC 上的高, ∴∠ADC =90o, ∴∠ABE =∠ADC . 又∵同弧所对的圆周角相等, ∴∠BEA =∠DCA . ∴△ABE ~△ADC .3. 解:(1)AD BC ⊥,90DAC C ∴∠+∠=°.90BAC BAF C ∠=∴∠=∠°,. 90OE OB BOA COE ∴∠+∠=⊥,°, 90BOA ABF ∠+∠=°,ABF COE ∴∠=∠. ABF COE ∴△∽△;BADE CF G(2)解法一:作OG AC ⊥,交AD 的延长线于G .2AC AB =,O 是AC 边的中点,AB OC OA ∴==.由(1)有ABF COE △∽△,ABF COE ∴△≌△,BF OE ∴=.90BAD DAC ∠+∠=°,90DAB ABD DAC ABD ∠+∠=∴∠=∠°,,又90BAC AOG ∠=∠=°,AB OA =.ABC OAG ∴△≌△,2OG AC AB ∴==.OG OA ⊥,AB OG ∴∥,ABF GOF ∴△∽△,OF OG BF AB ∴=,2OF OF OG OE BF AB ===.解法二:902BAC AC AB AD BC ∠==°,,⊥于D ,Rt Rt BAD BCA ∴△∽△.2AD AC BD AB∴==. 设1AB =,则2AC BC BO ===,12AD BD AD ∴=== 90BDF BOE BDF BOE ∠=∠=∴°,△∽△,BD BO DF OE∴=. 由(1)知BF OE =,设OE BF x ==,5DF ∴=x ∴=. 在DFB △中2211510x x =+,3x ∴=.OF OB BF ∴=-==322OF OE ∴==. (3)OF n OE=. 4. (1)证:△AMF ∽△BGM ,△DMG ∽△DBM ,△EMF ∽△EAM (写出两对即可)以下证明△AMF ∽△BGM .∵∠AFM =∠DME +∠E =∠A +∠E =∠BMG ,∠A =∠BBA D E CO F∴△AMF ∽△BGM .(2)解:当α=45°时,可得AC ⊥BC 且AC =BC∵M 为AB 的中点,∴AM =BM=又∵AMF ∽△BGM ,∴AF BM AM BG=∴283AM BM BG AF === 又4AC BC ===,∴84433CG =-=,431CF =-= ∴53FG == 5. (1)证明:,,AE EB AD DF ==ED ∴是ABF △的中位线,ED ∴,BF ∥ ,CEB ABF ∴∠=∠又,C A ∠=∠,CBE AFB ∴△∽△ (2)解:由(1)知,CBE AFB △∽△,5.8CB BE AF FB ∴== 又2,AF AD =54CB AD ∴=. 6. (1)证明:∵梯形ABCD ,AB CD ∥,∴CDF FGB DCF GBF ∠=∠∠=∠,,∴CDF BGF △∽△.(2) 由(1)CDF BGF △∽△,又F 是BC 的中点,BF FC =∴CDF BGF △≌△,∴DF FG CD BG ==,,又∵EF CD ∥,AB CD ∥ D C F E A B G 6题图∴EF AG ∥,得2EF BG AB BG ==+. ∴22462BG EF AB =-=⨯-=, ∴2cm CD BG ==.。
