[历年真题]2014年四川省高考数学试卷(文科)

合集下载

2014年四川省高考数学试题(卷)(文科)答案与解析

2014年四川省高考数学试卷（文科）参考答案与试题解析一、选择题（共10小题，每小题5分，共50分）1．（5分）（2014•四川）已知集合A={x|（x+1）（x﹣2）≤0}，集合B为整数集，则A∩B=（）A．{﹣1，0} B．{0，1} C．{﹣2，﹣1，0，1} D．{﹣1，0，1，2}考点：交集及其运算．专题：集合．分析：由题意，可先化简集合A，再求两集合的交集．解答：解：A={x|（x+1）（x﹣2）≤0}={x|﹣1≤x≤2}，又集合B为整数集，故A∩B={﹣1，0，1，2}故选D．点评：本题考查求交，掌握理解交的运算的意义是解答的关键．2．（5分）（2014•四川）在“世界读书日”前夕，为了了解某地5000名居民某天的阅读时间，从中抽取了200名居民的阅读时间进行统计分析，在这个问题中，5000名居民的阅读时间的全体是（）A．总体B．个体C．样本的容量D．从总体中抽取的一个样本考点：用样本的频率分布估计总体分布．专题：概率与统计．分析：根据题意，结合总体、个体、样本、样本容量的定义可得结论．解答：解：根据题意，结合总体、个体、样本、样本容量的定义可得，5000名居民的阅读时间的全体是总体，故选：A．点评：本题主要考查总体、个体、样本、样本容量的定义，属于基础题．3．（5分）（2014•四川）为了得到函数y=sin（x+1）的图象，只需把函数y=sinx的图象上所有的点（）A．向左平行移动1个单位长度B．向右平行移动1个单位长度C．向左平行移动π个单位长度D．向右平行移动π个单位长度考点：函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质．分析：直接利用函数图象的平移法则逐一核对四个选项得答案．解答：解：∵由y=sinx到y=sin（x+1），只是横坐标由x变为x+1，∴要得到函数y=sin（x+1）的图象，只需把函数y=sinx的图象上所有的点向左平行移动1个单位长度．故选：A．点评：本题主要考查三角函数的平移．三角函数的平移原则为左加右减上加下减．是基础题．4．（5分）（2014•四川）某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积为（）（锥体体积公式：V=Sh，其中S为底面面积，h为高）A．3B．2C．D．1考点：由三视图求面积、体积．专题：计算题；空间位置关系与距离．分析：根据三棱锥的俯视图与侧视图判定三棱锥的一个侧面与底面垂直，判断三棱锥的高与底面三角形的形状及边长，把数据代入棱锥的体积公式计算．解答：解：由三棱锥的俯视图与侧视图知：三棱锥的一个侧面与底面垂直，高为，底面为等边三角形，边长为2，∴三棱锥的体积V=××2××=1．故选：D．点评：本题考查了由三棱锥的侧视图与俯视图求体积，判断三棱锥的结构特征及相关几何量的数据是解题的关键．5．（5分）（2014•四川）若a＞b＞0，c＜d＜0，则一定有（）A．＞B．＜C．＞D．＜考点：不等关系与不等式．专题：不等式的解法及应用．分析：利用特例法，判断选项即可．解答：解：不妨令a=3，b=1，c=﹣3，d=﹣1，则，∴C、D不正确；=﹣3，=﹣∴A不正确，B正确．解法二：∵c＜d＜0，∴﹣c＞﹣d＞0，∵a＞b＞0，∴﹣ac＞﹣bd，∴，∴．故选：B．点评：本题考查不等式比较大小，特值法有效，带数计算正确即可．6．（5分）（2014•四川）执行如图所示的程序框图，若输入的x，y∈R，那么输出的S的最大值为（）A．0B．1C．2D．3考点：程序框图的三种基本逻辑结构的应用；简单线性规划．专题：算法和程序框图．分析：算法的功能是求可行域内，目标还是S=2x+y的最大值，画出可行域，求得取得最大值的点的坐标，得出最大值．解答：解：由程序框图知：算法的功能是求可行域内，目标还是S=2x+y的最大值，画出可行域如图：当时，S=2x+y的值最大，且最大值为2．故选：C．点评：本题借助选择结构的程序框图考查了线性规划问题的解法，根据框图的流程判断算法的功能是解题的关键．7．（5分）（2014•四川）已知b＞0，log5b=a，lgb=c，5d=10，则下列等式一定成立的是（）A．d=ac B．a=cd C．c=ad D．d=a+c考点：对数值大小的比较．专题：函数的性质及应用．分析：利用指数式与对数式的互化、对数的运算性质和换底公式即可得出．解答：解：由5d=10，可得，∴cd=lgb=log5b=a．故选：B．点评：本题考查了指数式与对数式的互化、对数的运算性质和换底公式，属于基础题．8．（5分）（2014•四川）如图，从气球A上测得正前方的河流的两岸B、C的俯角分别为75°、30°，此时气球的高是60m，则河流的宽度BC等于（）A．240（﹣1）m B．180（﹣1）m C．120（﹣1）m D．30（+1）m考点：解三角形的实际应用；余弦定理的应用．专题：解三角形．分析：由题意画出图形，由两角差的正切求出15°的正切值，然后通过求解两个直角三角形得到DC和DB的长度，作差后可得答案．解答：解：如图，由图可知，∠DAB=15°，∵tan15°=tan（45°﹣30°）==．在Rt△ADB中，又AD=60，∴DB=AD•tan15°=60×（2﹣）=120﹣60．在Rt△ADC中，∠DAC=60°，AD=60，∴DC=AD•tan60°=60．∴BC=DC﹣DB=60﹣（120﹣60）=120（）（m）．∴河流的宽度BC等于120（）m．故选：C．点评：本题考查了解三角形的实际应用，考查了两角差的正切，训练了直角三角形的解法，是中档题．9．（5分）（2014•四川）设m∈R，过定点A的动直线x+my=0和过定点B的直线mx﹣y﹣m+3=0交于点P（x，y），则|PA|+|PB|的取值范围是（）A．[，2] B．[，2] C．[，4] D．[2，4]考点：两条直线的交点坐标；函数最值的应用．专题：直线与圆．分析：可得直线分别过定点（0，0）和（1，3）且垂直，可得|PA|2+|PB|2=10．三角换元后，由三角函数的知识可得．解答：解：由题意可知，动直线x+my=0经过定点A（0，0），动直线mx﹣y﹣m+3=0即 m（x﹣1）﹣y+3=0，经过点定点B（1，3），∵动直线x+my=0和动直线mx﹣y﹣m+3=0的斜率之积为﹣1，始终垂直，P又是两条直线的交点，∴PA⊥PB，∴|PA|2+|PB|2=|AB|2=10．设∠ABP=θ，则|PA|=sinθ，|PB|=cosθ，由|PA|≥0且|PB|≥0，可得θ∈[0，]∴|PA|+|PB|=（sinθ+cosθ）=2sin（θ+），∵θ∈[0，]，∴θ+∈[，]，∴sin（θ+）∈[，1]，∴2sin（θ+）∈[，2]，故选：B．点评：本题考查直线过定点问题，涉及直线的垂直关系和三角函数的应用，属中档题．10．（5分）（2014•四川）已知F为抛物线y2=x的焦点，点A，B在该抛物线上且位于x轴的两侧，•=2（其中O为坐标原点），则△ABO与△AFO面积之和的最小值是（）A．2B．3C．D．考点：直线与圆锥曲线的关系．专题：圆锥曲线中的最值与范围问题．分析：可先设直线方程和点的坐标，联立直线与抛物线的方程得到一个一元二次方程，再利用韦达定理及•=2消元，最后将面积之和表示出来，探求最值问题．解答：解：设直线AB的方程为：x=ty+m，点A（x，y1），B（x2，y2），直线AB与x轴的交1点为M（m，0），由⇒y2﹣ty﹣m=0，根据韦达定理有y1•y2=﹣m，∵•=2，∴x1•x2+y1•y2=2，结合及，得，∵点A，B位于x轴的两侧，∴y1•y2=﹣2，故m=2．不妨令点A在x轴上方，则y1＞0，又，∴S△ABO+S△AFO==．当且仅当，即时，取“=”号，∴△ABO与△AFO面积之和的最小值是3，故选B．点评：求解本题时，应考虑以下几个要点：1、联立直线与抛物线的方程，消x或y后建立一元二次方程，利用韦达定理与已知条件消元，这是处理此类问题的常见模式．2、求三角形面积时，为使面积的表达式简单，常根据图形的特征选择适当的底与高．3、利用基本不等式时，应注意“一正，二定，三相等”．二、填空题（本大题共5小题，每小题5分，共25分）11．（5分）（2014•四川）双曲线﹣y2=1的离心率等于．考点：双曲线的简单性质．专题：圆锥曲线的定义、性质与方程．分析：根据双曲线的方程，求出a，b，c，即可求出双曲线的离心率．解答：解：由双曲线的方程可知a2=4，b2=1，则c2=a2+b2=4+1=5，则a=2，c=，即双曲线的离心率e==，故答案为：点评：本题主要考查双曲线的离心率的计算，求出a，c是解决本题的关键，比较基础．12．（5分）（2014•四川）复数= ﹣2i ．考点：复数代数形式的乘除运算．专题：数系的扩充和复数．分析：利用两个复数代数形式的乘除法法则化简所给的复数，可得结果．解答：解：复数===﹣2i，故答案为：﹣2i．点评：本题主要考查两个复数代数形式的乘除法法则的应用，属于基础题．13．（5分）（2014•四川）设f（x）是定义在R上的周期为2的函数，当x∈[﹣1，1）时，f（x）=，则f（）= 1 ．考点：函数的值．专题：计算题．分析：由函数的周期性f（x+2）=f（x），将求f（）的值转化成求f（）的值．解答：解：∵f（x）是定义在R上的周期为2的函数，∴=1．故答案为：1．点评：本题属于容易题，是考查函数周期性的简单考查，学生在计算时只要计算正确，往往都能把握住，在高考中，属于“送分题”．14．（5分）（2014•四川）平面向量=（1，2），=（4，2），=m+（m∈R），且与的夹角等于与的夹角，则m= 2 ．考点：数量积表示两个向量的夹角．专题：平面向量及应用．分析：利用向量的坐标运算、数量积运算、向量的夹角公式即可得出．解答：解：∵向量=（1，2），=（4，2），=m+（m∈R），∴=m（1，2）+（4，2）=（m+4，2m+2）．∴=m+4+2（2m+2）=5m+8，=4（m+4）+2（2m+2）=8m+20．，=2．∵与的夹角等于与的夹角，∴=，∴，化为5m+8=4m+10，解得m=2．故答案为：2．点评：本题考查了向量的坐标运算、数量积运算、向量的夹角公式，属于基础题．15．（5分）（2014•四川）以A表示值域为R的函数组成的集合，B表示具有如下性质的函数φ（x）组成的集合：对于函数φ（x），存在一个正数M，使得函数φ（x）的值域包含于区间[﹣M，M]．例如，当φ1（x）=x3，φ2（x）=sinx时，φ1（x）∈A，φ2（x）∈B．现有如下命题：①设函数f（x）的定义域为D，则“f（x）∈A”的充要条件是“∀b∈R，∃a∈D，f（a）=b”；②函数f（x）∈B的充要条件是f（x）有最大值和最小值；③若函数f（x），g（x）的定义域相同，且f（x）∈A，g（x）∈B，则f（x）+g（x）∉B．④若函数f（x）=aln（x+2）+（x＞﹣2，a∈R）有最大值，则f（x）∈B．其中的真命题有①③④．（写出所有真命题的序号）考点：命题的真假判断与应用；充要条件；全称命题；特称命题；函数的值域．专题：新定义；极限思想；函数的性质及应用；不等式的解法及应用；简易逻辑．分析：根据题中的新定义，结合函数值域的概念，可判断出命题①②③是否正确，再利用导数研究命题④中函数的值域，可得到其真假情况，从而得到本题的结论．解答：解：（1）对于命题①，若对任意的b∈R，都∃a∈D使得f（a）=b，则f（x）的值域必为R．反之，f（x）的值域为R，则对任意的b∈R，都∃a∈D使得f（a）=b，故①是真命题；（2）对于命题②，若函数f（x）∈B，即存在一个正数M，使得函数f（x）的值域包含于区间[﹣M，M]．∴﹣M≤f（x）≤M．例如：函数f（x）满足﹣2＜f（x）＜5，则有﹣5≤f（x）≤5，此时，f（x）无最大值，无最小值，故②是假命题；（3）对于命题③，若函数f（x），g（x）的定义域相同，且f（x）∈A，g（x）∈B，则f（x）值域为R，f（x）∈（﹣∞，+∞），并且存在一个正数M，使得﹣M≤g （x）≤M．故f（x）+g（x）∈（﹣∞，+∞）．则f（x）+g（x）∉B，故③是真命题；（4）对于命题④，∵﹣≤≤，当a＞0或a＜0时，alnx∈（﹣∞，+∞），f（x）均无最大值，若要使f（x）有最大值，则a=0，此时f（x）=，f（x）∈B，故④是真命题．故答案为①③④．点评：本题考查了函数值域的概念、基本不等式、充要条件，还考查了新定义概念的应用和极限思想．本题计算量较大，也有一定的思维难度，属于难题．三、解答题（共6小题，共75分）16．（12分）（2014•四川）一个盒子里装有三张卡片，分别标记有1，2，3，这三张卡片除标记的数字外完全相同，随机有放回地抽取3次，每次抽取1张，将抽取的卡片上的数字依次记为a，b，c．（Ⅰ）求“抽取的卡片上的数字满足a+b=c”的概率；（Ⅱ）求“抽取的卡片上的数字a，b，c不完全相同”的概率．考点：相互独立事件的概率乘法公式．专题：概率与统计．分析：（Ⅰ）所有的可能结果（a，b，c）共有3×3×3=27种，而满足a+b=c的（a，b，c 有计3个，由此求得“抽取的卡片上的数字满足a+b=c”的概率．（Ⅱ）所有的可能结果（a，b，c）共有3×3×3种，用列举法求得满足“抽取的卡片上的数字a，b，c完全相同”的（a，b，c）共计三个，由此求得“抽取的卡片上的数字a，b，c完全相同”的概率，再用1减去此概率，即得所求．解答：解：（Ⅰ）所有的可能结果（a，b，c）共有3×3×3=27种，而满足a+b=c的（a，b，c）有（1，1，2）、（1，2，3）、（2，1，3），共计3个，故“抽取的卡片上的数字满足a+b=c”的概率为=．（Ⅱ）满足“抽取的卡片上的数字a，b，c完全相同”的（a，b，c）有：（1，1，1）、（2，2，2）、（3，3，3），共计三个，故“抽取的卡片上的数字a，b，c完全相同”的概率为=，∴“抽取的卡片上的数字a，b，c不完全相同”的概率为1﹣=．点评：本题主要考查相互独立事件的概率乘法公式的应用，属于中档题．17．（12分）（2014•四川）已知函数f（x）=sin（3x+）．（1）求f（x）的单调递增区间；（2）若α是第二象限角，f（）=cos（α+）cos2α，求cosα﹣sinα的值．考点：两角和与差的余弦函数；正弦函数的单调性．专题：三角函数的求值．分析：（1）令2kπ﹣≤3x+≤2kπ+，k∈z，求得x的范围，可得函数的增区间．（2）由函数的解析式可得 f（）=sin（α+），又f（）=cos（α+）cos2α，可得sin（α+）=cos（α+）cos2α，化简可得（cosα﹣sinα）2=．再由α是第二象限角，cosα﹣sinα＜0，从而求得cosα﹣sinα 的值．解答：解：（1）∵函数f（x）=sin（3x+），令2kπ﹣≤3x+≤2kπ+，k∈Z，求得﹣≤x≤+，故函数的增区间为[﹣，+]，k∈Z．（2）由函数的解析式可得 f（）=sin（α+），又f（）=cos（α+）cos2α，∴sin（α+）=cos（α+）cos2α，即sin（α+）=cos（α+）（cos2α﹣sin2α），∴sinαcos+cosαsin=（cosαcos﹣sinαsin）（cosα﹣sinα）（cosα+sinα）即（sinα+cosα）=•（cosα﹣sinα）2（cosα+sinα），又∵α是第二象限角，∴cosα﹣sinα＜0，当sinα+cosα=0时，此时cosα﹣sinα=﹣．当sinα+cosα≠0时，此时cosα﹣sinα=﹣．综上所述：cosα﹣sinα=﹣或﹣．点评：本题主要考查正弦函数的单调性，三角函数的恒等变换，体现了分类讨论的数学思想，属于中档题．18．（12分）（2014•四川）在如图所示的多面体中，四边形ABB1A1和ACC1A1都为矩形（Ⅰ）若AC⊥BC，证明：直线BC⊥平面ACC1A1；（Ⅱ）设D、E分别是线段BC、CC1的中点，在线段AB上是否存在一点M，使直线DE∥平面A1MC？请证明你的结论．考点：直线与平面垂直的判定；直线与平面平行的判定．专题：综合题；空间位置关系与距离．分析：（Ⅰ）先证明AA⊥平面ABC，可得AA1⊥BC，利用AC⊥BC，可以证明直线BC⊥平面1ACC1A1；（Ⅱ）取AB的中点M，连接A1M，MC，A1C，AC1，证明四边形MDEO为平行四边形即可．解答：（Ⅰ）证明：∵四边形ABBA1和ACC1A1都为矩形，1∴AA1⊥AB，AA1⊥AC，∵AB∩AC=A，∴AA1⊥平面ABC，∵BC⊂平面ABC，∴AA1⊥BC，∵AC⊥BC，AA1∩AC=A，∴直线BC⊥平面ACC1A1；（Ⅱ）解：取AB的中点M，连接A1M，MC，A1C，AC1，设O为A1C，AC1的交点，则O 为AC1的中点．连接MD，OE，则MD∥AC，MD=AC，OE∥AC，OE=AC，∴MD∥OE，MD=OE，连接OM，则四边形MDEO为平行四边形，∴DE∥MO，∵DE⊄平面A1MC，MO⊂平面A1MC，∴DE∥平面A1MC，∴线段AB上存在一点M（线段AB的中点），使直线DE∥平面A1MC．点评：本题考查线面垂直的判定与性质的运用，考查存在性问题，考查学生分析解决问题的能力，属于中档题．19．（12分）（2014•四川）设等差数列{a n}的公差为d，点（a n，b n）在函数f（x）=2x的图象上（n∈N*）（Ⅰ）证明：数列{b n}为等比数列；（Ⅱ）若a1=1，函数f（x）的图象在点（a2，b2）处的切线在x轴上的截距为2﹣，求数列{a n b n2}的前n项和S n．考点：等差数列与等比数列的综合．专题：等差数列与等比数列．分析：（Ⅰ）利用等比数列的定义证明即可；（Ⅱ）先由（Ⅰ）求得a n，b n，再利用错位相减求数列{a n b n2}的前n项和S n．解答：（Ⅰ）证明：由已知得，b n=＞0，当n≥1时，===2d，∴数列{b n}为首项是，公比为2d的等比数列；（Ⅱ）解：f′（x）=2x ln2∴函数f（x）的图象在点（a2，b2）处的切线方程为y﹣=ln2（x﹣a2），∵在x轴上的截距为2﹣，∴a2﹣=2﹣，∴a2=2，∴d=a2﹣a1=1，a n=n，b n=2n，a n b n2=n4n，∴T n=1•4+2•42+3•43+…+（n﹣1）•4n﹣1+n•4n，4T n=1•42+2•43+…+（n﹣1）•4n+n•4n+1，∴T n﹣4T n=4+42+…+4n﹣n•4n+1=﹣n•4n+1=，∴T n=．点评：本题考查等差数列与等比数列的概念，等差数列与等比数列的通项公式及前n项和公式，导数的几何意义等知识；考查学生的运算求解能力、推理论证能力，属中档题．20．（13分）（2014•四川）已知椭圆C：+=1（a＞b＞0）的左焦点为F（﹣2，0），离心率为．（Ⅰ）求椭圆C的标准方程；（Ⅱ）设O为坐标原点，T为直线x=﹣3上一点，过F作TF的垂线交椭圆于P、Q，当四边形OPTQ是平行四边形时，求四边形OPTQ的面积．考点：直线与圆锥曲线的综合问题．专题：圆锥曲线的定义、性质与方程．分析：（Ⅰ）由题意可得，解出即可；（Ⅱ）由（Ⅰ）可得F（﹣2，0），设T（﹣3，m），可得直线TF的斜率k TF=﹣m，由于TF⊥PQ，可得直线PQ的方程为x=my﹣2．设P（x1，y1），Q（x2，y2）．直线方程与椭圆方程可得根与系数的关系．由于四边形OPTQ是平行四边形，可得，即可解得m．此时四边形OPTQ的面积S=．解答：解：（Ⅰ）由题意可得，解得c=2，a=，b=．∴椭圆C的标准方程为；（Ⅱ）由（Ⅰ）可得F（﹣2，0），设T（﹣3，m），则直线TF的斜率，∵TF⊥PQ，可得直线PQ的方程为x=my﹣2．设P（x1，y1），Q（x2，y2）．联立，化为（m2+3）y2﹣4my﹣2=0，△＞0，∴y1+y2=，y1y2=．∴x1+x2=m（y1+y2）﹣4=．∵四边形OPTQ是平行四边形，∴，∴（x1，y1）=（﹣3﹣x2，m﹣y2），∴，解得m=±1．此时四边形OPTQ的面积S=═=．点评：本题中考查了椭圆与圆的标准方程及其性质、直线与椭圆及圆相交可得根与系数的关系及弦长问题、向量相等问题、平行四边形的面积计算公式等基础知识与基本技能方法，考查了推理能力和计算能力，考查了数形结合和转化能力，属于难题．21．（14分）（2014•四川）已知函数f（x）=e x﹣ax2﹣bx﹣1，其中a，b∈R，e=2.71828…为自然对数的底数．（1）设g（x）是函数f（x）的导函数，求函数g（x）在区间[0，1]上的最小值；（2）若f（1）=0，函数f（x）在区间（0，1）内有零点，求a的取值范围．考点：导数在最大值、最小值问题中的应用；函数的零点．专题：导数的综合应用．分析：（1）求出f（x）的导数得g（x），再求出g（x）的导数，对它进行讨论，从而判断g（x）的单调性，求出g（x）的最小值；（2）利用等价转换，若函数f（x）在区间（0，1）内有零点，则函数f（x）在区间（0，1）内至少有三个单调区间，所以g（x）在（0，1）上应有两个不同的零点．解答：解：∵f（x）=e x﹣ax2﹣bx﹣1，∴g（x）=f′（x）=e x﹣2ax﹣b，又g′（x）=e x﹣2a，x∈[0，1]，∴1≤e x≤e，∴①当时，则2a≤1，g′（x）=e x﹣2a≥0，∴函数g（x）在区间[0，1]上单调递增，g（x）min=g（0）=1﹣b；②当，则1＜2a＜e，∴当0＜x＜ln（2a）时，g′（x）=e x﹣2a＜0，当ln（2a）＜x＜1时，g′（x）=e x ﹣2a＞0，∴函数g（x）在区间[0，ln（2a）]上单调递减，在区间[ln（2a），1]上单调递增，g（x）min=g[ln（2a）]=2a﹣2aln（2a）﹣b；③当时，则2a≥e，g′（x）=e x﹣2a≤0，∴函数g（x）在区间[0，1]上单调递减，g（x）min=g（1）=e﹣2a﹣b，综上：函数g（x）在区间[0，1]上的最小值为；（2）由f（1）=0，⇒e﹣a﹣b﹣1=0⇒b=e﹣a﹣1，又f（0）=0，若函数f（x）在区间（0，1）内有零点，则函数f（x）在区间（0，1）内至少有三个单调区间，由（1）知当a≤或a≥时，函数g（x）在区间[0，1]上单调，不可能满足“函数f（x）在区间（0，1）内至少有三个单调区间”这一要求．若，则g min（x）=2a﹣2aln（2a）﹣b=3a﹣2aln（2a）﹣e+1令h（x）=（1＜x＜e）则=，∴．由＞0⇒x＜∴h（x）在区间（1，）上单调递增，在区间（，e）上单调递减，==＜0，即g min（x）＜0 恒成立，∴函数f（x）在区间（0，1）内至少有三个单调区间⇔⇒，又，所以e﹣2＜a＜1，综上得：e﹣2＜a＜1．点评：本题考查了，利用导数求函数的单调区间，分类讨论思想，等价转换思想，函数的零点等知识点．是一道导数的综合题，难度较大．。

2014年高考数学四川卷(文科)word版

2014年普通高等学校招生全国统一考试（四川卷）数学（文史类）本试题卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）。

第Ⅰ卷1至2页，第Ⅱ卷3至4页，共4页.满分150分.考试时间120分钟.考生作答时，须将答案答在答题卡上，在本试题卷、草稿纸上答题无效.考试结束后，将本试题卷和答题卡一并交回.第Ⅰ卷（选择题共50分）注意事项：必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑. 第Ⅰ卷共10小题.一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一个是符合题目要求的.1.已知集合()(){}120A x x x =+-…，集合B 为整数集，则AB =（）.A.{}1,0-B.{}0,1C.{}2,1,0,1--D.{}1,0,1,2- 2.在“世界读书日”前夕，为了了解某地5000名居民某天的阅读时间，从中抽取了200名居民的阅读时间进行统计分析.在这个问题中，5000名居民的阅读时间的全体是（） . A.总体 B.个体C.样本的容量D.从总体中抽取的一个样本3.（2014四川文3）为了得到函数()sin 1y x =+的图像，只需把函数sin y x =的图像上所有的点（）.A.向左平行移动1个单位长度B.向右平行移动1个单位长度C.向左平行移动π个单位长度D.向右平行移动π个单位长度 4.某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积是（）. （锥体体积公式：13V Sh =，其中S 为底面面积，h 为高）A.3B.2D.1 5.若0a b >>，0c d <<，则一定有（）.侧视图俯视图11222211A.a b d c > B.a b d c < C.a b c d > D.a b c d< 6.（2014四川文6）执行如图所示的程序框图，如果输入的,x y ∈R ，那么输出的S 的最大值为（）.A.0B.1C.2D.37.（2014四川文7）已知0b >，5log b a =，lg b c =，510d=，则下列等式一定成立的是（）.A.d ac =B.a cd =C.c ad =D.d a c =+8.（2014四川文8）如图所示，从气球A 上测得正前方的河流的两岸B ，C 的俯角分别为75，30，此时气球的高是60m ，则河流的宽度BC 等于（）.A.)2401mB.)1801mC.)1201mD.)301m9.（2014四川文9）设m ∈R ，过定点A 的动直线0x my +=和过定点B的动直线否输出S S开始30mx y m --+=交于点(),P x y ，则PA PB +的取值范围是（）.A.B.C.D.⎡⎣10.（2014四川文10）已知F 为抛物线2y x =的焦点，点A ，B 在该抛物线上且位于x 轴的两侧，2OA OB ⋅=（其中O 为坐标原点），则ABO △与AFO △面积之和的最小值是（）.A.2B.3C.8第Ⅱ卷（非选择题共100分）注意事项：必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所示的答题区域内作答.作图题可先用铅笔绘出，确认后再用0.5毫米黑色墨迹签字笔描清楚.答在试题卷、草稿纸上无效.第Ⅱ卷共11小题.二、填空题：本大题共5小题，每小题5分，共25分.11.双曲线2214x y -=的离心率等于____________. 12.复数22i1i-=+____________. 13.设()f x 是定义在R 上的周期为2的函数，当[)1,1x ∈-时，()242,10,,01,x x f x x x ⎧-+-<=⎨<⎩……，则32f ⎛⎫= ⎪⎝⎭____________. 14.向量()1,2=a ，()4,2=b ，m =+c a b ()m ∈R ，且c 与a 的夹角等于c 与b 的夹角，则m =____________.15.（2014四川文15）以A 表示值域为R 的函数组成的集合，B 表示具有如下性质的函数()x ϕ组成的集合：对于函数()x ϕ，存在一个正数M ，使得函数()x ϕ的值域包含于区间[],M M -.例如，当()31x x ϕ=，()2sin x x ϕ=时，()1x A ϕ∈，()2x B ϕ∈.现有如下命题： ①设函数()f x 的定义域为D ，则“()f x A ∈”的充要条件是“b ∀∈R ，a D ∃∈，()f a b =”； ②若函数()f x B ∈，则()f x 有最大值和最小值；③若函数()f x ，()g x 的定义域相同，且()f x A ∈，()g x B ∈，则()()f x g x B +∉； ④若函数()()2ln 21xf x a x x =+++()2,x a >-∈R 有最大值，则()f x B ∈. 其中的真命题有____________（写出所有真命题的序号）.三、解答题：本大题共6小题，共75分。

2014年高考四川文科数学试题及答案(word解析版)

2014年高考四川文科数学试题及答案(word解析版)D于（）（A ）240(31)m （B ）180(21)m （C ）120(31)m（D ）30(31)m 【答案】C【解析】如图，30ACD ∠=，75ABD ∠=，60AD =m ，在Rt ACD △中，60603tan tan30AD CD=ACD ==∠m ，在Rt ABD △中，()606023tan tan 7523AD BD =ABD ===∠+m，所以()603602312031BC CD BD =-==m，故选C ．（9）【2014年四川卷，文9，5分】设m R ∈，过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+= 交于点(,)P x y ，则||||PA PB +的取值范围是（）（A ）[5,25] （B ）[10,25] （C ）[10,45] （D ）[25,45] 【答案】B【解析】直线0x my +=过定点()0,0A ，直线30mx y m --+=过定点()1,3B ．①当0m =时，过定点A 的直线方程为0x =，过定点B 的直线方程为3y =，两条直线互相垂直，此时()0,3P ，所以4PA PB +=．②当0m ≠时，直线0x my +=的斜率为1m -，直线30mx y m --+=的斜率为m ，因为11m m -⨯=-，所以两条直线互相垂直，即点P 可视为以AB 为直径的圆上的点．当点P 与点A 或点B 重合时，PA PB +有最小10P 不与点A ，点B 重合时，PAB △为直角CA 75°30°60 mmx-y-m+3=0x+my=0yx 213-1-2-1321PBA三角形，且22210PA PB AB +==．由不等式性质知222252PA PBPA PB++=，所以10,25PA PB ⎡⎤+∈⎣⎦．综合①②得10,25PA PB ⎡⎤+∈⎣⎦，故选B ．（10）【2014年四川卷，文10，5分】已知F 为抛物线2y x =的焦点，点A ，B 在该抛物线上且位于x 轴的两侧，2OA OB ⋅=（其中O 为坐标原点），则ABO ∆与AFO ∆面积之和的最小值是（）（A ）2 （B ）3 （C ）1728（D ）10 【答案】B【解析】如图所示，设()11,A x y ，()22,B x y ，则12122x x y y +=（*）．不妨设A 点在第一象限，则10y >，20y <．设直线AB ：x my n =+，代入2y x =中，得20y my n --=，则12y y n =-，代入（*）式，有220n n --=，解得2n =或1n =-（舍），故直线AB 过定点()2,0，所以ABO AFO S S +=△△1211112224y y y ⨯⨯-+⨯⨯1298y y =-()12923382ny y -==≥，故选B ．第II 卷（共100分）二、填空题：本大题共5小题，每小题5分（11）【2014年四川卷，文11，5分】双曲线2214x y-=的离心率等于．【答案】5【解析】由双曲线方程2214x y -=知24a=，21b=，2225ca b =+=，所以5c e a ==．（12）【2014年四川卷，文12，5分】复数22i1i-=+ ．【答案】2i -【解析】()()()()()2222i 1i 22i 1i 12i i 2i1i 1i 1i ---==-=-+=-++-．（13）【2014年四川卷，文13，5分】设()f x 是定义在R 上的周期为2的函数，当[1,1)x ∈-时，242,10,(),01,x x f x x x ⎧-+-≤<=⎨≤<⎩，则3()2f =________．【答案】1【解析】()f x 是定义域在R 上的圆周期为2的函数，且()2421001x x f x x x ⎧-+-<=⎨<⎩，所以231142121222f f ⎛⎫⎛⎫⎛⎫=-=-⨯-+=-+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．（14）【2014年四川卷，文14，5分】平面向量(1,2)a =，(4,2)b =，c ma b =+（m R ∈），且c 与a 的夹角等于c 与b 的夹角，则m =_______．【答案】2【解析】()1,2=a ，()4,2=b ，则()4,22m m m +=++c =a b ，5a =，25b =58m ⋅=+a c ，820m ⋅=+b c ．因为c 与a 的夹角等于c 与b 的夹角，所以⋅⋅=⋅⋅a c b c a c b c 525，解得2m =．（15）【2014年四川卷，文15，5分】以A 表示值域为R 的函数组成的集合，B 表示具有如下性质的函数()x ϕ组成的集合：对于函数()x ϕ，存在一个正数M ，使得函数()x ϕ的值域包含于区间[,]M M -．例如，当31()x x ϕ=，2()sin x x ϕ=时，1()x A ϕ∈，2()x B ϕ∈．现有如下命题：①设函数()f x 的定义域为D ，则“()f x A ∈”的充要条件是“b R ∀∈，x R ∃∈，()f a b =”；②若函数()f x B ∈，则()f x 有最大值和最小值；③若函数()f x ，()g x 的定义域相同，且()f x A ∈，()g x B ∈，则()()f x g x B +∉；④若函数2()ln(2)1x f x a x x =+++（2x >-，a R ∈）有最大值，则()f x B ∈．其中的真命题有____________．（写出所有真命题的序号）．【答案】①③④【解析】对于①，()f x A ∈⇔()f x 的值域为R ⇔b ∀∈R ，a D ∃∈，()f a b =，故①正确；对于②，当()1f x x =，1x >时，()1f x <，即()()[]1,00,11,1-⊆-，但()f x 无最值，故②不正确；对于③，因为x D ∀∈，()g x M ≤，所以总存在0x D ∈，使得()()0f xg x +趋近于无穷大，即()()f x g x B +∉，故③正确；对于④，令2()1x g x x =+，则()()()2222222121'11x x x g x xx+--==++()()()22111x x x+-=+，令()'0g x >，解得11x -<<，故()g x 在()1,1-上单调递增，且()112g =，()112g -=-，又()g x 在()1,+∞上单调递减，1x >时，()0g x >，又()g x 为奇函数，故()12g x ≤．而()ln(2)h x a x =+，当2x >-时，若0a ≠，则()h x A ∈由③知，()()h x g x B +∉，即()f x 无最大值，所以0a =时，()f x 有最大值，此时()2()1x f x g x B x ==∈+，故④正确．综上：真命题的有①③④．三、解答题：本大题共6题，共75分．（16）【2014年四川卷，文16，12分】一个盒子里装有三张卡片，分别标记有数字1，2，3，这三张卡片除标记的数字外完全相同．随机有放回地抽取3次，每次抽取1张，将抽取的卡片上的数字依次记为a ，b ，c ．（1）求“抽取的卡片上的数字满足a b c +=”的概率；（2）求“抽取的卡片上的数字a ，b ，c 不完全相同”的概率．解：（1）由题意知，(),,a b c 所有可能的结果为()1,1,1，()1,1,2，()1,1,3，()1,2,1，()1,2,2，()1,2,3，()1,3,1，()1,3,2，()1,3,3，()2,1,1，()2,1,2，()2,1,3，()2,2,1，()2,2,2，()2,2,3，()2,3,1，()2,3,2，()2,3,3，()3,1,1，()3,1,2，()3,1,3，()3,2,1，()3,2,2，()3,2,3，()3,3,1，()3,3,2，()3,3,3，共27种．设“抽取的卡片上的数字满足a b c +=”为事件A ，则事件A 包括()1,1,2，()1,2,3，()2,1,3，共3种．所以()31279P A ==．因此，“抽取的卡片上的数字满足a b c +=”的概率为19．（2）设“抽取的卡片上的数字a ，b ，c 不完全相同”为事件B ，则事件B 包括()1,1,1，()2,2,2，()3,3,3，共3种．所以()()3811279P B P B =-=-=．因此“抽取的卡片上的数字a ，b ，c 不完全相同”的概率为89．（17）【2014年四川卷，文17，12分】已知函数()sin(3)4f x x π=+．（1）求()f x 的单调递增区间；（2）若α是第二象限角，4()cos()cos2354f απαα=+，求cos sin αα-的值．解：（1）因为函数sin y x =的单调递增区间为ππ2π,2π22k k ⎡⎤-++⎢⎥⎣⎦，k ∈Z ．由πππ2π32π242k x k -+++，k ∈Z ，得π2ππ2π43123k k x -++，k ∈Z ．所以函数()f x 的单调递增区间为π2ππ2π,43123k k ⎡⎤-++⎢⎥⎣⎦，k ∈Z ．（2）由已知，有()22π4πsin cos cos sin 454αααα⎛⎫⎛⎫+=+- ⎪ ⎪⎝⎭⎝⎭，所以()22ππ4ππsin cos cos sin cos cos sin sin cos sin 44544αααααα⎛⎫+=-- ⎪⎝⎭，即()()2ππ4sin cos cos sin cos sin sin cos 445αααααα+=-+．当sin cos 0αα+=时，由α是第二象限角，知3π2π4k α=+，k ∈Z ．此时cos sin 2αα-=-当sin cos 0αα+≠时，有()25cos sin 4αα-=．由α是第二象限角，知cos sin 0αα-<，此时5cos sin αα-=．综上所述，cos sin 2αα-=-5．（18）【2014年四川卷，文18，12分】在如图所示的多面体中，四边形11ABB A 和11ACC A 都为矩形．（1）若AC BC ⊥，证明：直线BC ⊥平面11ACC A ；（2）设D ，E 分别是线段BC ，1CC 的中点，在线段AB 上是否存在一点M ，使直线//DE平面1A MC ？请证明你的结论．解：（1）因为四边形11ABB A 和11ACC A 都是矩形，所以1AA AB ⊥，1AA AC ⊥．因为AB ，AC 为平面ABC 内两条相交直线，所以1AA ⊥平面ABC ．因为直线BC ⊂平面ABC ，所以1AA BC ⊥．又AC BC ⊥，1AA ， AC 为平面11ACC A 内两条相交直线，所以BC ⊥平面11ACC A ．（2）取线段AB 的中点M ，连接1A M ，MC ，1A C ，1AC ，设O 为1A C ，1AC 的交点．由已知可知O 为1AC 的中点．连接MD ，OE ，则MD ，OE 分别为ABC ∆，1ACC ∆的中位线，所以=1//2MD AC ，=1//2OE AC ，因此=//MD OE ．连接OM ，从而四边形MDEO 为平行四边形，则//DE MO ．因为直线DE ⊄平面1A MC ，所以直线//DE 平面1A MC ，即线段AB 上存在一点M （线段AB 的中点），使直线//DE DB11AB A M E OC 1A 1B 1DC BA平面1A MC ．（19）【2014年四川卷，文19，12分】设等差数列{}na 的公差为d ，点(,)n na b 在函数()2x f x =的图象上（n N *∈）．（1）证明：数列{}nb 为等差数列；（2）若11a =，函数()f x 的图象在点22(,)a b 处的切线在x 轴上的截距为12ln 2-，求数列2{}n na b 的前n 项和nS ．解：（1）证明：由已知可知，20na nb=>，当1n 时，1122n naa dn nb b+-+==，所以数列{}nb 是首项为12a ，公比为2d等比数列．（2）函数()2xf x =在()22,a b 处的切线方程为()()22222ln 2a a y x a -=-，它在x 轴上的截距为21ln 2a -．由题意知，2112ln 2ln 2a -=-，解得22a=．所以211d aa =-=，na n=，2nn b =，24nn na bn =⋅．于是，()231142434144n nn T n n -=⨯+⨯+⨯++-⨯+⨯，()23141424144nn n T n n +=⨯+⨯++-⨯+⨯，因此()1121113444444444439n n n n n nnn T T n n ++++-+--=+++-⨯=-⨯=．所以()113449n n n T +-+=．（20）【2014年四川卷，文20，13分】已知椭圆C ：22221x y a b +=（0a b >>）的左焦点为(2,0)F -6．（1）求椭圆C 的标准方程；（2）设O 为坐标原点，T 为直线3x =-上一点，过F 作TF 的垂线交椭圆于P ，Q ．当四边形OPTQ 是平行四边形时，求四边形OPTQ 的面积．解：（1）因为(2,0)F -，所以2c =，又6e =，所以6a =，2222b a c =-=，即椭圆C 的方程为22162x y +=．（2）如图所示，由题意可设直线PQ 的方程为2x my =-．当0m =时，2x =-，此时()3,0T -，P ，Q 关于点F 对称，但DF TF ≠，故四边形OPTQ 不是平行四边形，与题意不符，故0m ≠．直线TF ：()2y m x =-+，令3x =-，得y m =，即()3,T m -，连接OT ，设OT PQ E =，则3,22m E ⎛⎫-⎪⎝⎭，联立方程222162x my x y =-⎧⎪⎨+=⎪⎩，消去x 整理得()22236my y -+=，即()223420m y my +--=，显然()2216830m m ∆=++>，令()11,P x y ，()22,Q x y ．则12243m y y m +=+，12223y y m -=+，则1222232E y y m my m +===+，解得21m=．此时()()221212PQ x x y y =-+-()22121214m y y y y=++-2126=+=，112TF =+=．所以四边形OPTQ 的面积1262232S PQ TF =⨯⨯⨯=⨯=．（21）【2014年四川卷，文21，14分】已知函数2()1xf x e ax bx =---，其中,a b R ∈， 2.71828e =⋅⋅⋅ 为自然对数的底数．（1）设()g x 是函数()f x 的导函数，求函数()g x 在区间[0,1]上的最小值；（2）若(1)0f =，函数()f x 在区间(0,1)内有零点，证明：21e a -<<．解：（1）()2e 1xf x ax bx =---，()()e 2xg x f x ax b '==--． ()e 2xg x a '=-．当[]0,1x ∈时，()[]12,e 2g x a a '∈--．当12a 时，()0g x '，所以()g x 在[]0,1上单调递增．因此()g x 在[]0,1上的最小值是()01gb =-；当e2a 时，()0g x '，所以()g x 在[]0,1上单调递减．因此()g x 在[]0,1上的最小值是()1e 2g a b =--；当1e22a <<时，令()0g x '=，得()()ln 20,1x a =∈．所以函数()g x 在区间()0,ln 2a ⎡⎤⎣⎦上单调递减，在区间()(ln 2,1a ⎤⎦上单调递增．于是，()g x 在[]0,1上的最小值是()()()ln 222ln 2g a a a a b =--．综上所述，当12a 时，()g x 在[]0,1上的最小值是()01gb =-；当1e22a <<时，()g x 在[]0,1上的最小值是()()()ln 222ln 2g a a a ab =--；当e2a 时，()g x 在[]0,1上的最小值是()1e 2g a b =--．（2）设0x 为()f x 在区间()0,1内的一个零点，则由()()000f f x ==可知，()f x 在区间()00,x 上不可能单调递增，也不可能单调递减．则()g x 不可能恒为正，也不可能恒为负．故()g x 在区间()00,x 内存在零点 1x ．同理()g x 在()0,1x 区间内存在零点2x ．所以()g x 在区间()0,1内至少有两个零点．由（1）知，当12a 时，()g x 在[]0,1上单调递增，故()g x 在()0,1内至多有一个零点．当e 2a 时，()g x 在[]0,1上单调递减，故()g x 在()0,1内至多有一个零点．所以1e22a <<．此时()g x 在区间()0,ln 2a ⎡⎤⎣⎦上单调递减，在区间()(ln 2,1a ⎤⎦上单调递增．因此()(10,ln 2x a ∈⎤⎦，()()2ln 2,1x a ∈，必有()010g b =->，()1e 20g a b =-->．由()10f =，有e 12a b +=-<，有()01e 20g b a =-=-+>，()1e 210g a b a =--=->，得e 21a -<<．所以函数()f x在区间()0,1内有零点时，e21-<<．a。

2014年四川省高考数学试卷(文科)学生版

2014 年四川省高考数学试卷（文科）一、选择题（共10 小题，每题 5 分，共 50 分）1．（ 5 分）（2014?四川）已知会合 A={ x| （x+1）（ x﹣ 2）≤0} ，会合 B 为整数集，则 A∩B=（）A．{ ﹣1，0}B．{ 0，1}C．{ ﹣2，﹣ 1，0，1} D．{ ﹣1，0，1，2}2．（5 分）（2014?四川）在“世界念书日”前夜，为了认识某地5000 名居民某天的阅读时间，从中抽取了200 名居民的阅读时间进行统计剖析，在这个问题中， 5000 名居民的阅读时间的全体是（）A．整体B．个体C．样本的容量D．从整体中抽取的一个样本3．（5 分）（2014?四川）为了获得函数y=sin（x+1）的图象，只要把函数y=sinx 的图象上全部的点（）A．向左平行挪动 1 个单位长度B．向右平行挪动 1 个单位长度C．向左平行挪动π个单位长度D．向右平行挪动π个单位长度4．（5 分）（2014?四川）某三棱锥的侧视图、俯视图以下图，则该三棱锥的体积为（）（锥体体积公式： V= Sh，此中 S 为底面面积， h 为高）A．3B．2C．D．15．（5 分）（2014?四川）若 a＞b＞0，c＜d＜0，则必定有（）A．＞B．＜C．＞D．＜6．（5 分）（2014?四川）履行以下图的程序框图，若输入的x，y∈ R，那么输出的 S 的最大值为（）A．0B．1C．2D．37．（5 分）（2014?四川）已知 b＞0，log5b=a， lgb=c， 5d =10，则以下等式必定成立的是（）A．d=ac B．a=cd C．c=ad D．d=a+c8．（5 分）（2014?四川）如图，从气球 A 上测得正前面的河流的两岸B，C的俯角分别为75°， 30°，此时气球的高是60m，则河流的宽度BC等于（）A．m B．m C．m D．m 9．（5 分）（2014?四川）设 m∈ R，过定点 A 的动直线 x+my=0 和过定点 B 的直线 mx﹣ y﹣m+3=0 交于点P（ x， y），则 | PA|+| PB| 的取值范围是（）A．[， 2]B．[，2]C．[，4]D．[ 2，4] 10．（5 分）（ 2014?四川）已知 F 为抛物线 y2=x 的焦点，点 A，B 在该抛物线上且位于 x 轴的双侧，? =2（此中 O 为坐标原点），则△ ABO 与△ AFO 面积之和的最小值是（）A ．2B ．3C ．D ．二、填空题（本大题共 5 小题，每题 5 分，共 25 分）11．（ 5 分）（2014?四川）双曲线 ﹣ y 2=1 的离心率等于．12．（ 5 分）（2014?四川）复数=．13．（5 分）（2014?四川）设 f （x ）是定义在 R 上的周期为 2 的函数，当 x ∈ [ ﹣ 1，）时，（），＜，则 f （）= ．1 f x = ，＜14．（ 5 分）（2014?四川）平面向量 =（1，2）， =（ 4， 2）， =m + （m ∈ R ），且与的夹角等于与的夹角，则 m=．15．（ 5 分）（2014?四川）以 A 表示值域为 R 的函数构成的会合， B 表示拥有以下性质的函数 φ（x ）构成的会合：关于函数 φ（x ），存在一个正数 M ，使得函数 φ（x ）的值域包括于区间 [ ﹣M ，M ] ．比如，当 φ1（x ）=x 3，φ2（x ）=sinx 时， φ1（x ）∈ A ，φ2（x ）∈ B ．现有以下命题：①设函数 f （ x ）的定义域为 D ，则 “f（x ）∈ A ”的充要条件是 “? b ∈R ，? a ∈D ，f（a ）=b ”；②函数 f （x ）∈ B 的充要条件是 f （x ）有最大值和最小值；③若函数 f （ x ），g （x ）的定义域同样，且 f （ x ）∈ A ，g （x ）∈ B ，则 f （x ）+g（ x ）?B ．④若函数 f （ x ）=aln （x+2）+（x ＞﹣ 2，a ∈R ）有最大值，则 f （x ）∈ B ．此中的真命题有．（写出全部真命题的序）三、解答题（共 6 小题，共 75 分）16．（12 分）（2014?四川）一个盒子里装有三张卡片，分别标志有数字1、2、3，这三张卡片除标志的数字外完整同样．随机有放回地抽取 3 次，每次抽取 1，将抽取的卡片上的数字挨次 a、b、c．（Ⅰ）求“抽取的卡片上的数字足 a+b=c”的概率；（Ⅱ）求“抽取的卡片上的数字a、b、c 不完整同样”的概率．17．（ 12 分）（ 2014?四川）已知函数 f （x）=sin（3x+ ）．（1）求 f （x）的增区；（2）若α是第二象限角， f（）= cos（α+ ）cos2α，求 cosα sin α的．18．（ 12 分）（ 2014?四川）在如所示的多面体中，四形1 1和 ACC1 1都ABB A A矩形（Ⅰ）若 AC⊥ BC，明：直 BC⊥平面 ACC；1A1（Ⅱ） D、E 分是段 BC、CC1的中点，在段AB 上能否存在一点 M，使直 DE∥平面A1 MC？明你的．19．（12 分）（2014?四川）等差数列 { a n} 的公差 d，点（ a n，b n）在函数 f（ x）=2x的象上（ n∈N*）（Ⅰ）明：数列 { b n} 等比数列；（Ⅱ）若 a1=1，函数 f（x）的象在点（ a2，b2）的切在 x 上的截距 2，求数列 { a n b n2} 的前 n 和 S n．20．（13 分）（2014?四川）已知 C：+ =1（a＞b＞0）的左焦点 F（ 2，0），离心率．（Ⅰ）求 C 的准方程；（Ⅱ） O 坐原点， T 直 x= 3 上一点， F 作 TF 的垂交于 P、Q，当四形 OPTQ是平行四形，求四形OPTQ的面．21．（14 分）（2014?四川）已知函数（fx）=e x ax2 bx 1，此中 a，b∈ R，e=2.71828⋯自然数的底数．（1）设 g（ x）是函数 f（x）的导函数，求函数 g（x）在区间 [ 0，1] 上的最小值；（2）若 f （1）=0，函数 f （x）在区间（ 0，1）内有零点，求 a 的取值范围．。

2014年高考文科数学四川卷有答案

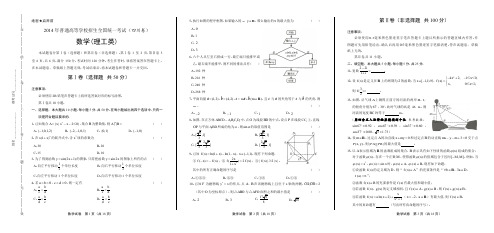
数学试卷第1页（共18页）数学试卷第2页（共18页）数学试卷第3页（共18页）绝密★启用前2014年普通高等学校招生全国统一考试（四川卷）数学(理工类)本试题卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）.第Ⅰ卷1至2页,第Ⅱ卷3至6页,共6页.满分150分.考试时间120分钟.考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效.考试结束后,将本试题卷和答题卡一并交回.第Ⅰ卷（选择题共50分）注意事项：必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑. 第Ⅰ卷共10小题.一、选择题：本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合2{|20}A x x x =--≤,集合B 为整数集,则A B = ( )A .{1,0,1,2}-B .{2,1,0,1}--C .{0,1}D .{1,0}- 2.在6(1)x x +的展开式中,含3x 项的系数为( )A .30B .20C .15D .103.为了得到函数sin(21)y x =+的图象,只需把函数sin 2y x =的图象上所有的点( )A .向左平行移动12个单位长度B .向右平行移动12个单位长度C .向左平行移动1个单位长度D .向右平行移动1个单位长度 4.若0a b >>,0c d <<,则一定有( )A .a bc d > B .a b c d < C .a b d c> D .a b d c<5.执行如图的程序框图,如果输入的x ,y ∈R ,那么输出的S 的最大值为( )A .0B .1C .2D .36.六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有( ) A .192 种B .216 种C .240 种D .288 种7.平面向量a (1,2)=,b (4,2)=,c m =a +b ()m ∈R ,且c 与a 的夹角等于c 与b 的夹角,则m =( )A .2-B .1-C .1D .28.如图,在正方体1111ABCD A B C D -中,点O 为线段BD 的中点.设点P 在线段1CC 上,直线OP 与平面1A BD 所成的角为α,则sin α的取值范围是 ( )A.B .C .[]33D .[39.已知()ln(1)ln(1)f x x x =+--,(1,1)x ∈-.现有下列命题：①()()f x f x -=-；②22()2()1xf f x x =+；③|()|2||f x x ≥.其中的所有正确命题的序号是( )A .①②③B .②③C .①③D .①②10.已知F 为抛物线2y x =的焦点,点A ,B 在该抛物线上且位于x 轴的两侧,2OA OB =（其中O 为坐标原点）,则ABO △与AFO △面积之和的最小值是( )A .2B .3CD 第Ⅱ卷（非选择题共100分）注意事项：必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答.作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚.答在试题卷、草稿纸上无效.第Ⅱ卷共11小题.二、填空题：本大题共5小题,每小题5分,共25分. 11.复数22i1i-=+ . 12.设()f x 是定义在R 上的周期为2的函数,当[1,1)x ∈-时,242,10,(),01,x x f x x x ⎧-+-=⎨⎩≤＜≤＜则3()2f = .13.如图,从气球A 上测得正前方的河流的两岸B ,C 的俯角分别为67,30,此时气球的高是46 m ,则河流的宽度BC 约等于m .（用四舍五入法将结果精确到个位.参考数据：sin670.92≈,cos670.39≈,sin370.60≈,cos370.80≈ 1.73≈）14.设m ∈R ,过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(,)P x y ,则||||PA PB 的最大值是 .15.以A 表示值域为R 的函数组成的集合,B 表示具有如下性质的函数()x ϕ组成的集合：对于函数()x ϕ,存在一个正数M ,使得函数()x ϕ的值域包含于区间[,]M M -.例如,当31()x x ϕ=,2()sin x x ϕ=时,1()x A ϕ∈,2()x B ϕ∈.现有如下命题：①设函数()f x 的定义域为D ,则“()f x A ∈”的充要条件是“b ∀∈R ,a D ∃∈,()f a b =”； ②函数()f x B ∈的充要条件是()f x 有最大值和最小值；③若函数()f x ,()g x 的定义域相同,且()f x A ∈,()g x B ∈,则()()f x g x B +∉； ④若函数2()ln(2)1xf x a x x =+++（2x >-,a ∈R ）有最大值,则()f xB ∈. 其中的真命题有（写出所有真命题的序号）.-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________三、解答题：本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.（本小题满分12分）已知函数π()sin(3)4f x x=+.（Ⅰ）求()f x的单调递增区间；（Ⅱ）若α是第二象限角,4π()cos()cos2354fααα=+,求cos sinαα-的值.17.（本小题满分12分）一款击鼓小游戏的规则如下：每盘游戏都需击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐；每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分（即获得-200分）.设每次击鼓出现音乐的概率为12,且各次击鼓出现音乐相互独立.（Ⅰ）设每盘游戏获得的分数为X,求X的分布列；（Ⅱ）玩三盘游戏,至少有一盘出现音乐的概率是多少？（Ⅲ）玩过这款游戏的许多人都发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因. 18.（本小题满分12分）三棱锥A BCD-及其侧视图、俯视图如图所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN NP⊥.（Ⅰ）证明：P为线段BC的中点；（Ⅱ）求二面角A NP M--的余弦值.19.（本小题满分12分）设等差数列{}na的公差为d,点(,)n na b在函数()2xf x=的图象上（n*∈N）.（Ⅰ）若12a=-,点87(,4)a b在函数()f x的图象上,求数列{}na的前n项和nS；（Ⅱ）若11a=,函数()f x的图象在点22(,)a b处的切线在x轴上的截距为12ln2-,求数列{}nnab的前n项和nT.20.（本小题满分13分）已知椭圆C：22221x ya b+=(0)a b>>的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.（Ⅰ）求椭圆C的标准方程；（Ⅱ）设F为椭圆C的左焦点,T为直线3x=-上任意一点,过F作TF的垂线交椭圆C于点P,Q.（ⅰ）证明：OT平分线段PQ（其中O为坐标原点）；（ⅱ）当||||TFPQ最小时,求点T的坐标.21.（本小题满分14分）已知函数2()e1xf x ax bx=---,其中,a b∈R,e 2.71828=⋅⋅⋅为自然对数的底数.（Ⅰ）设()g x是函数()f x的导函数,求函数()g x在区间[0,1]上的最小值；（Ⅱ）若(1)0f=,函数()f x在区间(0,1)内有零点,求a的取值范围.数学试卷第4页（共18页）数学试卷第5页（共18页）数学试卷第6页（共18页）101{A B-＝,【提示】由题意，可先化简集合【考点】交集及其运算32最大值，画出可行域如图：1x=⎧【解析】解：如图：31tan45tan30-︒-︒tan1560AD︒=，∴tan6060DC AD=︒=120(31)(m)-.数学试卷第7页（共18页）数学试卷第8页（共18页）数学试卷第9页（共18页）数学试卷第10页（共18页）数学试卷第11页（共18页）数学试卷第12页（共18页）2OA OB =，∴12122x x y y +=，结合，B 位于x 轴的两侧，∴122y y =-，故不妨令点A 在轴上方，则0y >，又1123y y =. 面积之和的最小值是【提示】可先设直线方程和点的坐标，联立直线与抛物线的方程得到一个一元二次方程，再利用韦达定理及2OA OB =消元，最后将面积之和表示出来，探求最值问题【考点】直线与圆锥曲线的关系【答案】2【解析】(,2)c a b m m m =+=||||||||a c b ca cbc =，即2252051620525m m m =+++，即584m +=解得2m =.【提示】利用向量的坐标运算、数量积运算、向量的夹角公式即可得出.数学试卷第13页（共18页）数学试卷第14页（共18页）数学试卷第15页（共18页）4cos sin 5α（﹣是第二象限角，∴cos α-ABAC A =1BC AA AC A =，，11BC ACC A ⊥平面AB 的中点M 1DEA MC 平面1DE A MC 平面231142434(1)44n nn n -++++-+2341142434(1)44n n n n +++++-+114(13)4443n n n n ++----⋅=，∴1(31)449n n n T +-+=. 是平行四边形，∴OP QT =，∴(1=±.2122242|||242333m y y m m -⎛⎫-=-= ⎪++⎝⎭. 22(,)Q x y .直线方程与椭圆方程可得根与系可得OP QT =，即可解得21|||y y -. 【考点】直线与圆锥曲线的综合问题数学试卷第16页（共18页）数学试卷第17页（共18页）数学试卷第18页（共18页）11ln 2x x ⎫=-⎪⎭上单调递增，在区间。

2014年高考文科数学四川卷-答案

设 ABP ，则 PA
10 sin ， PB
10cos
，由 |
PA |
0且|
PB
|
0
，可得
0,
π 2
∴ | PA | | PB |
10(sin cos ) 2
5 sin

4

，∵

0,
π 2

，∴

π 4
m

0
，根据韦达定理有
y1 y2
m ，∵ OA OB 2 ，∴ x1
x2 y1
y2
2 ，结合
y12 x1 及 y22 x2 ，得 ( y1 y2 )2 y1 y2 2 0 ，∵点 A，B 位于 x 轴的两侧，∴ y1 y2 2 ，故 m 2 .
不妨令点
2 / 10
【解析】解：如图：
由图可知， DAB 15 ，∵ tan15 tan（45-30）= tan 45 tan 30
1
3 3
2
3.
1 tan 45 tan 30
11
3 3
在 Rt△ADB 中，又 AD 60 ，∴ DB AD tan15 60 (2 3) 120 60 3 .

π 4

x

2kπ 3

π 12
，故函数的增区间为

2kπ 3

π 4
，2kπ 3

π 12
，k

Z
.
（2）由函数的解析式可得
f

a 3

sin

π 4

2014年四川高考文科数学试题含答案(Word版).

2014年普通高等学校招生全国统一考试(四川卷数学(文史类本试题卷分第Ⅰ卷(选择题和第Ⅱ卷(非选择题。

第Ⅰ卷1至2页,第Ⅱ卷3至4页,共4页。

满分150分。

考试时间120分钟。

考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效。

考试结束后,将本试题卷和答题卡一并交回。

第Ⅰ卷 (选择题共50分注意事项:必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑。

第Ⅰ卷共10小题。

一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一个是符合题目要求的。

1、已知集合{|(1(20}A x x x =+-≤,集合B 为整数集,则AB =(A 、{1,0}-B 、{0,1}C 、{2,1,0,1}--D 、{1,0,1,2}-2、在“世界读书日”前夕,为了了解某地5000名居民某天的阅读时间,从中抽取了200名居民的阅读时间进行统计分析。

在这个问题中,5000名居民的阅读时间的全体是( A 、总体 B 、个体C 、样本的容量D 、从总体中抽取的一个样本3、为了得到函数sin(1y x =+的图象,只需把函数sin y x =的图象上所有的点(A 、向左平行移动1个单位长度B 、向右平行移动1个单位长度C 、向左平行移动π个单位长度D 、向右平行移动π个单位长度 4、某三棱锥的侧视图、俯视图如图所示,则该三棱锥的体积是( (锥体体积公式:13V Sh =,其中S 为底面面积,h 为高 A 、3 B 、2 CD 、1 5、若0a b >>,0c d <<,则一定有(A 、a b d c > B 、a b d c < C 、a b c d > D 、a b c d<6、执行如图的程序框图,如果输入的,x y R ∈,那么输出的S 的最大值为(A 、0B 、1C 、2D 、3 7、已知0b >,5log b a =,lg b c =,510d=,则下列等式一定成立的是( A 、d ac = B 、a cd = C 、c ad = D 、d a c =+ 侧视图俯视图112222118、如图,从气球A 上测得正前方的河流的两岸B ,C 的俯角分别为75,30,此时气球的高是60m ,则河流的宽度BC 等于(A、1m B、1mC、1m D、1m9、设m R ∈,过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(,P x y ,则||||PA PB +的取值范围是(A、 B、 C、 D、10、已知F 为抛物线2y x =的焦点,点A ,B 在该抛物线上且位于x 轴的两侧,2OA OB ⋅=(其中O 为坐标原点,则ABO ∆与AFO ∆面积之和的最小值是( A 、2 B 、3 C、8D第Ⅱ卷 (非选择题共100分注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所示的答题区域内作答。

2014四川高考文科数学试题及答案(word)

2014年普通高等学校招生全国统一考试（四川卷）数学（文史类）第Ⅰ卷（选择题共50分）一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一个是符合题目要求的。

1、已知集合{|(1)(2)0}A x x x =+-≤，集合B 为整数集，则AB =（）A 、{1,0}-B 、{0,1}C 、{2,1,0,1}--D 、{1,0,1,2}-2、在“世界读书日”前夕，为了了解某地5000名居民某天的阅读时间，从中抽取了200名居民的阅读时间进行统计分析。

在这个问题中，5000名居民的阅读时间的全体是（）A 、总体B 、个体C 、样本的容量D 、从总体中抽取的一个样本3、为了得到函数sin(1)y x =+的图象，只需把函数sin y x =的图象上所有的点（） A 、向左平行移动1个单位长度 B 、向右平行移动1个单位长度 C 、向左平行移动π个单位长度 D 、向右平行移动π个单位长度4、某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积是（）（锥体体积公式：13V Sh =，其中S 为底面面积，h 为高）A 、3B 、2 CD 、15、若0a b >>，0c d <<，则一定有（）A 、a b d c > B 、a b d c < C 、a b c d > D 、a b c d<6、执行如图的程序框图，如果输入的,x y R ∈，那么输出的S 的最大值为（）A 、0B 、1C 、2D 、37、已知0b >，5log b a =，lg b c =，510d=，则下列等式一定成立的是（）侧视图俯视图112222118、如图，从气球A 上测得正前方的河流的两岸B ，C 的俯角分别为75，30，此时气球的高是60cm ，则河流的宽度BC 等于（）A、1)m B、1)m C、1)m D、1)m9、设m R ∈，过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(,)P x y ，则||||PA PB +的取值范围是（）A、 B、 C、 D、10、已知F 为抛物线2y x =的焦点，点A ，B 在该抛物线上且位于x 轴的两侧，2OA OB ⋅=（其中O 为坐标原点），则ABO ∆与AFO ∆面积之和的最小值是（） A 、2 B 、3 C、8D第Ⅱ卷（非选择题共100分）二、填空题：本大题共5小题，每小题5分，共25分。

2014年四川高考数学文史类试卷及答案

2014年四川高考数学文史类试卷及答案D10.已知F 为抛物线x =2y的焦点，点A ,B 在该抛物线上且位于x 轴的两侧，2=⋅（其中O 为坐标原点），则ABO ∆与AFO ∆面积之和的最小值是（A ）2 （B ）3（C ）8217 （D ）10第Ⅱ卷（非选择题共100分）注意事项：必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答案区域内作答。

作图题可先用铅笔绘出，确认后再用0.5毫米黑色墨迹签字笔描清楚。

答在试题卷，草稿纸上无效。

第Ⅱ卷共11小题。

二、填空题：本大题共5小题，每小题5分，共25分。

11.双曲线1422=-y x 的离心率等于_____________.12.复数ii +-122=____________. 13.设)(x f 是定义在R 上的周期为2的函数，当）1,1[-∈x 时，,,24{)(2x x x f +-=,10,01<≤<≤-x x 则)23(f =____________.14. 平面向量）（2,1=a ，）（2,4=b ，)(R m m ∈+=b a c ，且c 与a 的夹角等于c 与b 的夹角，则=m _____________.15.以A 表示值域为R 的函数组成的集合，B 表示具有如下性质的函数)(x ϕ组成的集合：对于函数)(x ϕ，存在一个正数M ，使得函数)(x ϕ的值域包含于区间],[M M -.例如，当31)(x x =ϕ，x x sin )(2=ϕ时，A x ∈)(1ϕ,B x ∈)(2ϕ. 现在如下命题：①设函数)(x f 的定义域为D ,则“A x f ∈)(”的充要条件是“b a f D a R b =∈∃∈∀)(,,”；②若函数B x f ∈)(,则)(x f 有最大值和最小值；③若函数)(x f ，)(x g 的定义域相同，且B x g A x f ∈∈)(,)(,则B x g x f ∉+)()(； ④若函数),2(1)2ln()(2R a x x x x a x f ∈->+++=有最大值，则B x f ∈)(.其中的真命题有________________.（写出所有真命题的序号）三、解答题：本大题共6小题，共75分。

2014年全国高考文科数学试题及答案-四川卷

2014年普通高等学校招生全国统一考试（四川卷）数学（文史类）本试题卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）。

第Ⅰ卷1至2页，第Ⅱ卷3至4页，共4页。

满分150分。

考试时间120分钟。

考生作答时，须将答案答在答题卡上，在本试题卷、草稿纸上答题无效。

考试结束后，将本试题卷和答题卡一并交回。

第Ⅰ卷（选择题共50分）注意事项：必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑。

第Ⅰ卷共10小题。

一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一个是符合题目要求的。

1、已知集合{|(1)(2)0}A x x x =+-≤，集合B 为整数集，则AB =（）A 、{1,0}-B 、{0,1}C 、{2,1,0,1}--D 、{1,0,1,2}- 2、在“世界读书日”前夕，为了了解某地5000名居民某天的阅读时间，从中抽取了200名居民的阅读时间进行统计分析。

在这个问题中，5000名居民的阅读时间的全体是（）A 、总体B 、个体C 、样本的容量D 、从总体中抽取的一个样本3、为了得到函数sin(1)y x =+的图象，只需把函数sin y x =的图象上所有的点（）A 、向左平行移动1个单位长度B 、向右平行移动1个单位长度C 、向左平行移动π个单位长度D 、向右平行移动π个单位长度4、某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积是（）（锥体体积公式：13V Sh =，其中S 为底面面积，h 为高）A 、3B 、2 C、1 5、若0a b >>，0c d <<，则一定有（）A 、a b d c >B 、a b d c<侧视图俯视图11222211C 、a b c d > D 、a b c d< 6、执行如图的程序框图，如果输入的,x y R ∈，那么输出的S的最大值为（） A 、0 B 、1 C 、2 D 、37、已知0b >，5log b a =，lg b c =，510d=，则下列等式一定成立的是（）A 、d ac =B 、a cd =C 、c ad =D 、d a c =+ 8、如图，从气球A 上测得正前方的河流的两岸B ，C 的俯角分别为75，30，此时气球的高是60m ，则河流的宽度BC 等于（）A、1)m B、1)m C、1)m D、1)m9、设m R ∈，过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(,)P x y ，则||||PA PB +的取值范围是（）A、 B、 C、 D、 10、已知F 为抛物线2y x =的焦点，点A ，B 在该抛物线上且位于x 轴的两侧，2OA OB ⋅=（其中O 为坐标原点），则ABO ∆与AFO ∆面积之和的最小值是（） A 、2 B 、3 CD第Ⅱ卷（非选择题共100分）注意事项：必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所示的答题区域内作答。

2014年四川高考数学文史类试卷及答案

绝密★启用前2014年普通高等学校招生全国统一考试(四川卷)数学(文史类)本试题卷分第I 卷(选择题)和n 卷(非选择题) 。

第I 卷1至2页，第n 卷3至4页。

满分150分。

考试时间120分钟。

考生作答时，须将答案答在答题卡上，在本试卷上答题无效。

考试结束后，将本试题卷和答题卡一并交回。

第I 卷(选择题共50分)注意事项：必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑。

第I 卷共10小题。

一、选择题：本大题共 10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一个是符合题目要求的。

1•已知集合A {x |(x 1)(x 2) 0}，集合B 为整数集，则 A B(A ) { 1,0} (B ) {0,1} (C ) { 2, 1,0,1}( D ) { 1,0,2}2•在“世界读书日”前夕，为了了解某地 5000名居民某天的阅读时间，从中抽取了 200名居民的阅读时间进行统计分析•在这个问题中，5000名居民的阅读时间的全体是 (A )总体 (B )个体(D )从总体中抽取的一个样本sin(x 1)的图象，只需把函数 y sinx 的图象上所有的点(A )向左平行移动1个单位长度 (B) 向右平行移动1个单位长度 (C) 向左平行移动个单位长度(D)向右平行移动个单位长度 4•某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积是1(椎体体积公式： V -Sh ，其中S 为底面面积，h 为高)3(A ) 3( B ) 2(C ) 3 ( D ) 1(C )样本的容量3•为了得到函数y5•若a b 0 , c d 0 ,则一定有(C) c ad (D) d a c8•如图，从气球A上测得正前方的河流的两岸 B , C的俯角分别为75，30，此时气球的高是60m，则河流的宽度BC等于（A）240（ 3 1）m （B）180（.2 1）m（C）120（ . 3 1）m （D）30（ . 3 1）my m 3 0交于点P(x, y)，则9.设m R，过定点A的动直线x my 0和过定点B的动直线mx| PA | |PB |的取值范围是（A）[ .5,2.5] （B）[ •一10,2.、5]（C）[ 10,4 5] （D）[2,5,4.5]10.已知F为抛物线y2 x的焦点，点A,B在该抛物线上且位于x轴的两侧，OA OB 2 （其中0为坐标原点），贝U ABO与AFO面积之和的最小值是（A）2 （B）3（C）17 2（D）. 108第n卷(非选择题共100分) 注意事项：必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答案区域内作答。

2014年四川省高考数学试卷(文科)(含解析版)

2014年四川省高考数学试卷（文科）一、选择题（共10小题，每小题5分，共50分）1．（5分）已知集合A={x|（x+1）（x﹣2）≤0}，集合B为整数集，则A ∩B=（）A ．{﹣1，0}B．{0，1}C．{﹣2，﹣1，0，1}D．{﹣1，0，1，2}2．（5分）在“世界读书日”前夕，为了了解某地5000名居民某天的阅读时间，从中抽取了200名居民的阅读时间进行统计分析，在这个问题中，5000名居民的阅读时间的全体是（）A．总体B．个体C．样本的容量D．从总体中抽取的一个样本3．（5分）为了得到函数y=sin（x+1）的图象，只需把函数y=sinx的图象上所有的点（）A．向左平行移动1个单位长度B．向右平行移动1个单位长度C．向左平行移动π个单位长度D．向右平行移动π个单位长度4．（5分）某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积为（）（锥体体积公式：V=Sh，其中S为底面面积，h为高）A．3B．2C．D．15．（5分）若a＞b＞0，c＜d＜0，则一定有（）A．＞B．＜C．＞D．＜6．（5分）执行如图所示的程序框图，若输入的x，y∈R，那么输出的S的最大值为（）第 1 页共 27 页 1A．0B．1C．2D．37．（5分）已知b＞0，log5b=a，lgb=c，5d=10，则下列等式一定成立的是（）A．d=ac B．a=cd C．c=ad D．d=a+c8．（5分）如图，从气球A上测得正前方的河流的两岸B ，C的俯角分别为75°，30°，此时气球的高是60m，则河流的宽度BC 等于（）A．m B．m C．m D．m 9．（5分）设m∈R，过定点A的动直线x+my=0和过定点B的直线mx﹣y﹣m+3=0交于点P（x，y ），则|PA |+|PB|的取值范围是（）A ．[，2]B ．[，2]C．[，4]D．[2，4] 10．（5分）已知F为抛物线y2=x的焦点，点A，B在该抛物线上且位于x轴的两侧，•=2（其中O为坐标原点），则△ABO与△AFO面积之和的最小值是（）2第 2 页共 27 页A．2B．3C．D．二、填空题（本大题共5小题，每小题5分，共25分）11．（5分）双曲线﹣y2=1的离心率等于．12．（5分）复数=．13．（5分）设f（x）是定义在R上的周期为2的函数，当x∈[﹣1，1）时，f （x）=，则f（）=．14．（5分）平面向量=（1，2），=（4，2），=m+（m∈R），且与的夹角等于与的夹角，则m=．15．（5分）以A表示值域为R的函数组成的集合，B表示具有如下性质的函数φ（x）组成的集合：对于函数φ（x），存在一个正数M，使得函数φ（x）的值域包含于区间[﹣M，M]．例如，当φ1（x）=x3，φ2（x）=sinx时，φ1（x）∈A，φ2（x）∈B．现有如下命题：①设函数f（x）的定义域为D，则“f（x）∈A”的充要条件是“∀b∈R，∃a∈D，f（a）=b”；②函数f（x）∈B的充要条件是f（x）有最大值和最小值；③若函数f（x），g（x）的定义域相同，且f（x）∈A，g（x）∈B，则f（x）+g（x）∉B．④若函数f（x）=aln（x+2）+（x＞﹣2，a∈R）有最大值，则f（x）∈B．其中的真命题有．（写出所有真命题的序号）三、解答题（共6小题，共75分）16．（12分）一个盒子里装有三张卡片，分别标记有数字1、2、3，这三张卡片除标记的数字外完全相同．随机有放回地抽取3次，每次抽取1张，将抽取的卡片上的数字依次记为a、b、c．（Ⅰ）求“抽取的卡片上的数字满足a+b=c”的概率；第 3 页共 27 页 3（Ⅱ）求“抽取的卡片上的数字a、b 、c 不完全相同”的概率．17．（12分）已知函数f（x）=sin（3x+）．（1）求f（x）的单调递增区间；（2）若α是第二象限角，f（）=cos（α+）cos2α，求cosα﹣sinα的值．18．（12分）在如图所示的多面体中，四边形ABB1A1和ACC1A1都为矩形（Ⅰ）若AC⊥BC，证明：直线BC⊥平面ACC1A1；（Ⅱ）设D、E分别是线段BC、CC1的中点，在线段AB上是否存在一点M，使直线DE∥平面A1MC？请证明你的结论．4第 4 页共 27 页19．（12分）设等差数列{a n}的公差为d，点（a n ，b n）在函数f（x）=2x的图象上（n∈N*）（Ⅰ）证明：数列{b n}为等比数列；（Ⅱ）若a1=1，函数f（x）的图象在点（a2，b2）处的切线在x轴上的截距为2﹣，求数列{a n b n2}的前n项和S n．20．（13分）已知椭圆C：+=1（a＞b＞0）的左焦点为F（﹣2，0），离心率为．（Ⅰ）求椭圆C的标准方程；（Ⅱ）设O为坐标原点，T为直线x=﹣3上一点，过F作TF的垂线交椭圆于P、Q，当四边形OPTQ是平行四边形时，求四边形OPTQ的面积．第 5 页共 27 页 521．（14分）已知函数f（x）=e x﹣ax2﹣bx﹣1，其中a，b∈R，e=2.71828…为自然对数的底数．（1）设g（x）是函数f（x）的导函数，求函数g（x）在区间[0，1]上的最小值；（2）若f（1）=0，函数f（x）在区间（0，1）内有零点，求a的取值范围．6第 6 页共 27 页2014年四川省高考数学试卷（文科）参考答案与试题解析一、选择题（共10小题，每小题5分，共50分）1．（5分）已知集合A={x|（x+1）（x﹣2）≤0}，集合B为整数集，则A∩B=（）A．{﹣1，0}B．{0，1}C．{﹣2，﹣1，0，1}D．{﹣1，0，1，2}【考点】1E：交集及其运算．【专题】5J：集合．【分析】由题意，可先化简集合A，再求两集合的交集．【解答】解：A={x|（x+1）（x﹣2）≤0}={x|﹣1≤x≤2}，又集合B为整数集，故A∩B={﹣1，0，1，2}故选：D．【点评】本题考查求交，掌握理解交的运算的意义是解答的关键．2．（5分）在“世界读书日”前夕，为了了解某地5000名居民某天的阅读时间，从中抽取了200名居民的阅读时间进行统计分析，在这个问题中，5000名居民的阅读时间的全体是（）A．总体B．个体C．样本的容量D．从总体中抽取的一个样本【考点】BE：用样本的数字特征估计总体的数字特征．【专题】5I：概率与统计．【分析】根据题意，结合总体、个体、样本、样本容量的定义可得结论．第 7 页共 27 页7【解答】解：根据题意，结合总体、个体、样本、样本容量的定义可得，5000名居民的阅读时间的全体是总体，故选：A ．【点评】本题主要考查总体、个体、样本、样本容量的定义，属于基础题．3．（5分）为了得到函数y=sin（x+1）的图象，只需把函数y=sinx的图象上所有的点（）A．向左平行移动1个单位长度B．向右平行移动1个单位长度C．向左平行移动π个单位长度D．向右平行移动π个单位长度【考点】HJ：函数y=Asin（ωx+φ）的图象变换．【专题】57：三角函数的图像与性质．【分析】直接利用函数图象的平移法则逐一核对四个选项得答案．【解答】解：∵由y=sinx到y=sin（x+1），只是横坐标由x变为x+1，∴要得到函数y=sin（x+1）的图象，只需把函数y=sinx的图象上所有的点向左平行移动1个单位长度．故选：A．【点评】本题主要考查三角函数的平移．三角函数的平移原则为左加右减上加下减．是基础题．4．（5分）某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积为（）（锥体体积公式：V=Sh，其中S为底面面积，h为高）A．3B．2C．D．18第 8 页共 27 页【考点】L!：由三视图求面积、体积．【专题】11：计算题；5F：空间位置关系与距离．【分析】根据三棱锥的俯视图与侧视图判定三棱锥的一个侧面与底面垂直，判断三棱锥的高与底面三角形的形状及边长，把数据代入棱锥的体积公式计算．【解答】解：由三棱锥的俯视图与侧视图知：三棱锥的一个侧面与底面垂直，高为，底面为等边三角形，边长为2，∴三棱锥的体积V=××2××=1．故选：D．【点评】本题考查了由三棱锥的侧视图与俯视图求体积，判断三棱锥的结构特征及相关几何量的数据是解题的关键．5．（5分）若a＞b ＞0，c＜d＜0，则一定有（）A．＞B．＜C．＞D ．＜【考点】R3：不等式的基本性质．【专题】59：不等式的解法及应用．【分析】利用特例法，判断选项即可．【解答】解：不妨令a=3，b=1，c=﹣3，d=﹣1，则，∴C、D不正确；=﹣3，=﹣∴A不正确，B正确．第 9 页共 27 页9解法二：∵c＜d＜0，∴﹣c＞﹣d＞0，∵a ＞b＞0，∴﹣ac＞﹣bd，∴，∴．故选：B．【点评】本题考查不等式比较大小，特值法有效，带数计算正确即可．6．（5分）执行如图所示的程序框图，若输入的x，y∈R，那么输出的S的最大值为（）A．0B．1C．2D．3【考点】7C：简单线性规划；E9：程序框图的三种基本逻辑结构的应用．10第 10 页共 27 页【专题】5K：算法和程序框图．【分析】算法的功能是求可行域内，目标函数S=2x+y的最大值，画出可行域，求得取得最大值的点的坐标，得出最大值．【解答】解：由程序框图知：算法的功能是求可行域内，目标还是S=2x+y的最大值，画出可行域如图：当时，S=2x+y的值最大，且最大值为2．故选：C．【点评】本题借助选择结构的程序框图考查了线性规划问题的解法，根据框图的流程判断算法的功能是解题的关键．7．（5分）已知b＞0，log5b=a，lgb=c，5d=10，则下列等式一定成立的是（）A．d=ac B．a=cd C．c=ad D．d=a+c【考点】4M：对数值大小的比较．【专题】51：函数的性质及应用．【分析】利用指数式与对数式的互化、对数的运算性质和换底公式即可得出．第 11 页共 27 页11【解答】解：由5d=10，可得，∴cd=lgb=log5b=a．故选：B．【点评】本题考查了指数式与对数式的互化、对数的运算性质和换底公式，属于基础题．8．（5分）如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为75°，30°，此时气球的高是60m，则河流的宽度BC等于（）A．m B．m C．m D．m【考点】HU：解三角形．【专题】12：应用题；58：解三角形．【分析】由题意画出图形，由两角差的正切求出15°的正切值，然后通过求解两个直角三角形得到DC和DB的长度，作差后可得答案．【解答】解：如图，∠DAB=15°，∵tan15°=tan（45°﹣30°）==2﹣．在Rt△ADB中，又AD=60，∴DB=AD•tan15°=60×（2﹣）=120﹣60．在Rt△ADC 中，∠DAC=60°，AD=60，∴DC=AD•tan60°=60．∴BC=DC﹣DB=60﹣（120﹣60）=120（﹣1）（m）．∴河流的宽度BC等于120（﹣1）m．12第 12 页共 27 页故选：B．【点评】本题给出实际应用问题，求河流在B、C两地的宽度，着重考查了三角函数的定义、正余弦定理解三角形的知识，属于中档题．9．（5分）设m∈R，过定点A的动直线x+my=0和过定点B的直线mx﹣y﹣m+3=0交于点P（x，y），则|PA|+|PB |的取值范围是（）A．[，2]B．[，2]C．[，4]D．[2，4]【考点】5A：函数最值的应用；IM：两条直线的交点坐标．【专题】5B：直线与圆．【分析】可得直线分别过定点（0，0）和（1，3）且垂直，可得|PA|2+|PB|2=10．三角换元后，由三角函数的知识可得．【解答】解：由题意可知，动直线x+my=0经过定点A（0，0），动直线mx﹣y﹣m+3=0即m（x﹣1）﹣y+3=0，经过点定点B（1，3），∵动直线x+my=0和动直线mx﹣y﹣m+3=0的斜率之积为﹣1，始终垂直，P又是两条直线的交点，∴PA⊥PB，∴|PA|2+|PB|2=|AB|2=10．设∠ABP=θ，则|PA|=sinθ，|PB|=cosθ，由|PA|≥0且|PB|≥0，可得θ∈[0，]∴|PA|+|PB|=（sinθ+cosθ）=2sin（θ+），∵θ∈[0，]，∴θ+∈[，]，∴sin（θ+）∈[，1]，第 13 页共 27 页13第 14 页共 27 页14 ∴2sin （θ+）∈[，2]，故选：B ．【点评】本题考查直线过定点问题，涉及直线的垂直关系和三角函数的应用，属中档题．10．（5分）已知F 为抛物线y 2=x 的焦点，点A ，B 在该抛物线上且位于x 轴的两侧，•=2（其中O 为坐标原点），则△ABO 与△AFO 面积之和的最小值是（）A ．2B ．3C ．D ．【考点】K8：抛物线的性质．【专题】5E ：圆锥曲线中的最值与范围问题．【分析】可先设直线方程和点的坐标，联立直线与抛物线的方程得到一个一元二次方程，再利用韦达定理及•=2消元，最后将面积之和表示出来，探求最值问题．【解答】解：设直线AB 的方程为：x=ty +m ，点A （x 1，y 1），B （x 2，y 2），直线AB 与x 轴的交点为M （m ，0），由⇒y 2﹣ty ﹣m=0，根据韦达定理有y 1•y 2=﹣m ， ∵•=2，∴x 1•x 2+y 1•y 2=2，结合及，得， ∵点A ，B 位于x 轴的两侧，∴y 1•y 2=﹣2，故m=2．不妨令点A 在x 轴上方，则y 1＞0，又，∴S △ABO +S △AFO ═×2×（y 1﹣y 2）+×y 1，=．当且仅当，即时，取“=”号，∴△ABO与△AFO面积之和的最小值是3，故选：B．【点评】求解本题时，应考虑以下几个要点：1、联立直线与抛物线的方程，消x或y后建立一元二次方程，利用韦达定理与已知条件消元，这是处理此类问题的常见模式．2、求三角形面积时，为使面积的表达式简单，常根据图形的特征选择适当的底与高．3、利用基本不等式时，应注意“一正，二定，三相等”．二、填空题（本大题共5小题，每小题5分，共25分）11．（5分）双曲线﹣y2=1的离心率等于．【考点】KC：双曲线的性质．【专题】5D：圆锥曲线的定义、性质与方程．【分析】根据双曲线的方程，求出a，b，c，即可求出双曲线的离心率．【解答】解：由双曲线的方程可知a2=4，b2=1，则c2=a2+b2=4+1=5，第 15 页共 27 页15则a=2，c=，即双曲线的离心率e==，故答案为：【点评】本题主要考查双曲线的离心率的计算，求出a，c是解决本题的关键，比较基础．12．（5分）复数=﹣2i．【考点】A5：复数的运算．【专题】5N：数系的扩充和复数．【分析】利用两个复数代数形式的乘除法法则化简所给的复数，可得结果．【解答】解：复数===﹣2i，故答案为：﹣2i．【点评】本题主要考查两个复数代数形式的乘除法法则的应用，属于基础题．13．（5分）设f（x）是定义在R上的周期为2的函数，当x∈[﹣1，1）时，f （x）=，则f（）=1．【考点】3Q：函数的周期性．【专题】11：计算题．【分析】由函数的周期性f（x+2）=f（x），将求f（）的值转化成求f（）的值．【解答】解：∵f（x）是定义在R上的周期为2的函数，∴=1．故答案为：1．16第 16 页共 27 页【点评】本题属于容易题，是考查函数周期性的简单考查，学生在计算时只要计算正确，往往都能把握住，在高考中，属于“送分题”．14．（5分）平面向量=（1，2），=（4，2），=m+（m∈R ），且与的夹角等于与的夹角，则m=2．【考点】9S：数量积表示两个向量的夹角．【专题】5A：平面向量及应用．【分析】利用向量的坐标运算、数量积运算、向量的夹角公式即可得出．【解答】解：∵向量=（1，2），=（4，2），=m+（m ∈R），∴=m（1，2）+（4，2）=（m+4，2m+2）．∴=m+4+2（2m+2）=5m+8，=4（m+4）+2（2m+2）=8m+20．，=2．∵与的夹角等于与的夹角，∴=，∴，化为5m+8=4m+10，解得m=2．故答案为：2．【点评】本题考查了向量的坐标运算、数量积运算、向量的夹角公式，属于基础题．15．（5分）以A表示值域为R的函数组成的集合，B表示具有如下性质的函数φ（x）组成的集合：对于函数φ（x），存在一个正数M，使得函数φ（x）的第 17 页共 27 页17值域包含于区间[﹣M，M]．例如，当φ1（x）=x3，φ2（x）=sinx时，φ1（x）∈A，φ2（x）∈B．现有如下命题：①设函数f（x）的定义域为D，则“f（x）∈A”的充要条件是“∀b∈R，∃a∈D，f（a）=b”；②函数f（x）∈B的充要条件是f（x）有最大值和最小值；③若函数f（x），g（x）的定义域相同，且f（x）∈A，g（x）∈B，则f（x）+g（x）∉B．④若函数f（x）=aln（x+2）+（x＞﹣2，a∈R）有最大值，则f（x）∈B．其中的真命题有①③④．（写出所有真命题的序号）【考点】29：充分条件、必要条件、充要条件；2H：全称量词和全称命题；2I：存在量词和特称命题；2K：命题的真假判断与应用；34：函数的值域．【专题】23：新定义；3A：极限思想；51：函数的性质及应用；59：不等式的解法及应用；5L：简易逻辑．【分析】根据题中的新定义，结合函数值域的概念，可判断出命题①②③是否正确，再利用导数研究命题④中函数的值域，可得到其真假情况，从而得到本题的结论．【解答】解：（1）对于命题①，若对任意的b∈R，都∃a∈D使得f（a）=b，则f（x）的值域必为R．反之，f（x）的值域为R，则对任意的b∈R，都∃a∈D使得f（a）=b，故①是真命题；（2）对于命题②，若函数f（x）∈B，即存在一个正数M，使得函数f（x）的值域包含于区间[﹣M，M]．∴﹣M≤f（x）≤M．例如：函数f（x）满足﹣2＜f（x）＜5，则有﹣5≤f（x）≤5，此时，f（x）无最大值，无最小值，故②是假命题；（3）对于命题③，若函数f（x），g（x）的定义域相同，且f（x）∈A，g （x）∈B，则f（x）值域为R，f（x）∈（﹣∞，+∞），并且存在一个正数M，使得﹣M≤g（x）≤M．故f（x）+g（x）∈（﹣∞，+∞）．18第 18 页共 27 页则f（x）+g（x）∉B，故③是真命题；（4）对于命题④，∵﹣≤≤，当a＞0或a＜0时，aln（x+2）∈（﹣∞，+∞），f（x）均无最大值，若要使f （x）有最大值，则a=0，此时f（x）=，f（x）∈B，故④是真命题．故答案为①③④．【点评】本题考查了函数值域的概念、基本不等式、充要条件，还考查了新定义概念的应用和极限思想．本题计算量较大，也有一定的思维难度，属于难题．三、解答题（共6小题，共75分）16．（12分）一个盒子里装有三张卡片，分别标记有数字1、2、3，这三张卡片除标记的数字外完全相同．随机有放回地抽取3次，每次抽取1张，将抽取的卡片上的数字依次记为a、b、c．（Ⅰ）求“抽取的卡片上的数字满足a+b=c”的概率；（Ⅱ）求“抽取的卡片上的数字a、b、c不完全相同”的概率．【考点】C8：相互独立事件和相互独立事件的概率乘法公式．【专题】5I：概率与统计．【分析】（Ⅰ）所有的可能结果（a，b，c）共有3×3×3=27种，而满足a+b=c 的（a，b，c有计3个，由此求得“抽取的卡片上的数字满足a+b=c”的概率．（Ⅱ）所有的可能结果（a，b，c）共有3×3×3种，用列举法求得满足“抽取的卡片上的数字a，b，c完全相同”的（a，b，c）共计三个，由此求得“抽取的卡片上的数字a，b，c完全相同”的概率，再用1减去此概率，即得所求．【解答】解：（Ⅰ）所有的可能结果（a，b，c）共有3×3×3=27种，而满足a+b=c的（a，b，c）有（1，1，2）、（1，2，3）、（2，1，3），共计3个，故“抽取的卡片上的数字满足a+b=c”的概率为=．（Ⅱ）满足“抽取的卡片上的数字a，b，c完全相同”的（a，b，c）有：（1，1，1）、（2，2，2）、（3，3，3），共计三个，第 19 页共 27 页19故“抽取的卡片上的数字a，b ，c完全相同”的概率为=，∴“抽取的卡片上的数字a，b，c不完全相同”的概率为1﹣=．【点评】本题主要考查相互独立事件的概率乘法公式的应用，属于中档题．17．（12分）已知函数f（x）=sin（3x+）．（1）求f（x）的单调递增区间；（2）若α是第二象限角，f（）=cos（α+）cos2α，求cosα﹣sinα的值．【考点】GP：两角和与差的三角函数；H5：正弦函数的单调性．【专题】56：三角函数的求值．【分析】（1）令2kπ﹣≤3x+≤2kπ+，k∈z ，求得x的范围，可得函数的增区间．（2）由函数的解析式可得f（）=sin （α+），又f （）=cos（α+）cos2α，可得sin（α+）=cos（α+）cos2α，化简可得（cosα﹣sinα）2=．再由α是第二象限角，cosα﹣sinα＜0，从而求得cosα﹣sinα 的值．【解答】解：（1）∵函数f（x）=sin （3x +），令2kπ﹣≤3x +≤2kπ+，k∈Z，求得﹣≤x≤+，故函数的增区间为[﹣，+]，k ∈Z．（2）由函数的解析式可得f（）=sin（α+），又f（）=cos（α+）cos2α，∴sin（α+）=cos（α+）cos2α，即sin（α+）=cos（α+）（cos2α﹣sin2α），∴sinαcos+cosαsin=（cosαcos﹣sinαsin）（cosα﹣sinα）（cosα+sinα）20第 20 页共 27 页即（sinα+cosα）=•（cosα﹣sinα）2（cosα+sinα），又∵α是第二象限角，∴cosα﹣sinα＜0，当sinα+cosα=0时，tanα=﹣1，sinα=，cosα=﹣，此时cosα﹣sinα=﹣．当sinα+cosα≠0时，此时cosα﹣sinα=﹣．综上所述：cosα﹣sinα=﹣或﹣．【点评】本题主要考查正弦函数的单调性，三角函数的恒等变换，体现了分类讨论的数学思想，属于中档题．18．（12分）在如图所示的多面体中，四边形ABB1A1和ACC1A1都为矩形（Ⅰ）若AC⊥BC，证明：直线BC⊥平面ACC1A1；（Ⅱ）设D、E分别是线段BC、CC1的中点，在线段AB上是否存在一点M，使直线DE∥平面A1MC？请证明你的结论．【考点】LS：直线与平面平行；LW：直线与平面垂直．【专题】15：综合题；5F：空间位置关系与距离．【分析】（Ⅰ）先证明AA1⊥平面ABC，可得AA1⊥BC，利用AC⊥BC，可以证明直线BC⊥平面ACC1A1；（Ⅱ）取AB的中点M，连接A1M，MC，A1C，AC1，证明四边形MDEO为平行四边形即可．【解答】（Ⅰ）证明：∵四边形ABB1A1和ACC1A1都为矩形，∴AA1⊥AB，AA1⊥AC，∵AB∩AC=A，第 21 页共 27 页21∴AA1⊥平面ABC，∵BC⊂平面ABC，∴AA1⊥BC，∵AC⊥BC，AA1∩AC=A，∴直线BC⊥平面ACC1A1；（Ⅱ）解：取AB的中点M，连接A1M，MC，A1C，AC 1，设O为A1C，AC1的交点，则O为AC1的中点．连接MD，OE，则MD∥AC，MD=AC，OE∥AC，OE=AC，∴MD∥OE，MD=OE，连接OM，则四边形MDEO为平行四边形，∴DE∥MO，∵DE⊄平面A1MC，MO⊂平面A1MC，∴DE∥平面A1MC，∴线段AB上存在一点M（线段AB的中点），使直线DE∥平面A1MC．【点评】本题考查线面垂直的判定与性质的运用，考查存在性问题，考查学生分析解决问题的能力，属于中档题．19．（12分）设等差数列{a n}的公差为d，点（a n，b n）在函数f（x）=2x的图象上（n∈N*）（Ⅰ）证明：数列{b n}为等比数列；（Ⅱ）若a1=1，函数f（x）的图象在点（a2，b2）处的切线在x轴上的截距为2﹣，求数列{a n b n2}的前n项和S n．22第 22 页共 27 页【考点】8M：等差数列与等比数列的综合．【专题】54：等差数列与等比数列．【分析】（Ⅰ）利用等比数列的定义证明即可；（Ⅱ）先由（Ⅰ）求得a n，b n，再利用错位相减求数列{a n b n2}的前n项和S n．【解答】（Ⅰ）证明：由已知得，b n =＞0，当n≥1时，===2d，∴数列{b n }为首项是，公比为2d的等比数列；（Ⅱ）解：f′（x）=2x ln2∴函数f（x）的图象在点（a2，b2）处的切线方程为y﹣=ln2（x﹣a2），∵在x轴上的截距为2﹣，∴a2﹣=2﹣，∴a2=2，∴d=a2﹣a1=1，a n=n，b n=2n，a n b n2=n4n，∴T n=1•4+2•42+3•43+…+（n﹣1）•4n﹣1+n•4n ，4T n=1•42+2•43+…+（n﹣1）•4n+n•4n+1，∴T n﹣4T n=4+42+…+4n﹣n•4n+1=﹣n•4n+1=，∴T n=．【点评】本题考查等差数列与等比数列的概念，等差数列与等比数列的通项公式及前n项和公式，导数的几何意义等知识；考查学生的运算求解能力、推理论证能力，属中档题．20．（13分）已知椭圆C：+=1（a＞b＞0）的左焦点为F（﹣2，0），离心率为．（Ⅰ）求椭圆C的标准方程；第 23 页共 27 页23（Ⅱ）设O为坐标原点，T为直线x=﹣3上一点，过F作TF的垂线交椭圆于P、Q，当四边形OPTQ是平行四边形时，求四边形OPTQ的面积．【考点】KH：直线与圆锥曲线的综合．【专题】5D：圆锥曲线的定义、性质与方程．【分析】（Ⅰ）由题意可得，解出即可；（Ⅱ）由（Ⅰ）可得F（﹣2，0），设T（﹣3，m），可得直线TF的斜率k TF=﹣m，由于TF⊥PQ ，可得直线PQ的方程为x=my﹣2．设P（x1，y 1），Q（x2，y2）．直线方程与椭圆方程可得根与系数的关系．由于四边形OPTQ是平行四边形，可得，即可解得m．此时四边形OPTQ的面积S=．【解答】解：（Ⅰ）由题意可得，解得c=2，a=，b=．∴椭圆C的标准方程为；（Ⅱ）由（Ⅰ）可得F（﹣2，0），设T（﹣3，m），则直线TF的斜率，∵TF⊥PQ，可得直线PQ的方程为x=my﹣2．设P （x1，y1），Q（x2，y2）．联立，化为（m2+3）y2﹣4my﹣2=0，△＞0，∴y1+y2=，y1y2=．24第 24 页共 27 页∴x1+x2=m（y1+y2）﹣4=．∵四边形OPTQ是平行四边形，∴，∴（x1，y1）=（﹣3﹣x2，m﹣y2），∴，解得m=±1．此时四边形OPTQ的面积S=═=．【点评】本题中考查了椭圆与圆的标准方程及其性质、直线与椭圆及圆相交可得根与系数的关系及弦长问题、向量相等问题、平行四边形的面积计算公式等基础知识与基本技能方法，考查了推理能力和计算能力，考查了数形结合和转化能力，属于难题．21．（14分）已知函数f（x）=e x﹣ax2﹣bx﹣1，其中a，b∈R，e=2.71828…为自然对数的底数．（1）设g（x）是函数f（x）的导函数，求函数g（x）在区间[0，1]上的最小值；（2）若f（1）=0，函数f（x）在区间（0，1）内有零点，求a的取值范围．【考点】51：函数的零点；6E：利用导数研究函数的最值．【专题】53：导数的综合应用．【分析】（1）求出f（x）的导数得g（x），再求出g（x）的导数，对它进行讨论，从而判断g（x）的单调性，求出g（x）的最小值；（2）利用等价转换，若函数f（x）在区间（0，1）内有零点，则函数f（x）在区间（0，1）内至少有三个单调区间，所以g（x）在（0，1）上应有两个不同的零点．第 25 页共 27 页25【解答】解：∵f（x）=e x﹣ax2﹣bx﹣1，∴g（x）=f′（x）=e x﹣2ax﹣b ，又g′（x）=e x﹣2a，x∈[0，1]，∴1≤e x≤e，∴①当时，则2a≤1，g′（x）=e x﹣2a≥0，∴函数g（x）在区间[0，1]上单调递增，g（x）min=g（0）=1﹣b；②当，则1＜2a＜e，∴当0＜x＜ln（2a）时，g′（x）=e x﹣2a＜0，当ln（2a）＜x＜1时，g′（x）=e x ﹣2a＞0，∴函数g（x）在区间[0，ln（2a）]上单调递减，在区间[ln（2a），1]上单调递增，g（x）min=g[ln（2a）]=2a﹣2aln（2a）﹣b；③当时，则2a≥e，g′（x）=e x﹣2a≤0，∴函数g（x）在区间[0，1]上单调递减，g（x）min=g（1）=e﹣2a﹣b，综上：函数g（x ）在区间[0，1]上的最小值为；（2）由f（1）=0，⇒e﹣a﹣b﹣1=0⇒b=e﹣a﹣1，又f（0）=0，若函数f（x）在区间（0，1）内有零点，则函数f（x）在区间（0，1）内至少有三个单调区间，由（1）知当a ≤或a≥时，函数g（x）在区间[0，1]上单调，不可能满足“函数f（x）在区间（0，1）内至少有三个单调区间”这一要求．若，则g min（x）=2a﹣2aln（2a）﹣b=3a﹣2aln（2a）﹣e+1令h（x）=（1＜x＜e）则=，∴．由＞0⇒x 26第 26 页共 27 页＜∴h （x）在区间（1，）上单调递增，在区间（，e）上单调递减，==＜0，即g min（x）＜0 恒成立，∴函数f（x）在区间（0，1）内至少有三个单调区间⇔⇒，又，所以e﹣2＜a＜1，综上得：e﹣2＜a＜1．另解：由g（0）＞0，g（1）＞0 解出e﹣2＜a＜1，再证明此时f（x）min＜0 由于f（x）最小时，f'（x）=g（x）=e x﹣2ax﹣b=0，故有e x=2ax+b且f（1）=0知e﹣1=a+b，则f（x）min=2ax+b﹣ax2﹣（e﹣1﹣a）x﹣1=﹣ax2+（3a +1﹣e）x+e﹣a﹣2，开口向下，最大值（5a2﹣（2e+2）a+e2﹣2e），分母为正，只需看分子正负，分子＜5﹣（2e+2）+e2﹣2e（a=1时取最大）=e2﹣4e+3＜0，故f（x）min＜0，故e﹣2＜a＜1．【点评】本题考查了，利用导数求函数的单调区间，分类讨论思想，等价转换思想，函数的零点等知识点．是一道导数的综合题，难度较大．第 27 页共 27 页27。

2014年普通高等学校招生全国统一考试数学(四川卷)文

2014年普通高等学校招生全国统一考试(四川卷)数学(文科)第Ⅰ卷(选择题共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.(2014四川,文1)已知集合A={x|(x+1)(x-2)≤0},集合B为整数集,则A∩B=()A.{-1,0}B.{0,1}C.{-2,-1,0,1}D.{-1,0,1,2}答案:D解析:∵A={x|(x+1)(x-2)≤0}={x|-1≤x≤2},A∩B=A∩Z={x|-1≤x≤2}∩Z={-1,0,1,2},故选D.2.(2014四川,文2)在“世界读书日”前夕,为了了解某地5000名居民某天的阅读时间,从中抽取了200名居民的阅读时间进行统计分析.在这个问题中,5000名居民的阅读时间的全体是()A.总体B.个体C.样本的容量D.从总体中抽取的一个样本答案:A解析:由题意知,5000名居民的阅读时间是总体,200名居民的阅读时间为一个样本;每个居民的阅读时间为个体;200为样本容量;故选A.3.(2014四川,文3)为了得到函数y=sin(x+1)的图象,只需把函数y=sin x的图象上所有的点()A.向左平行移动1个单位长度B.向右平行移动1个单位长度C.向左平行移动π个单位长度D.向右平行移动π个单位长度答案:A解析:根据图象的变换规律“左加右减”知,选A.4.(2014四川,文4)某三棱锥的侧视图、俯视图如图所示,则该三棱锥的体积是(锥体体积公式:V=13Sh,其中S为底面面积,h为高)()A.3B.2C.√3D.1答案:D解析:由俯视图知该三棱锥的底面积S底=12×2×√3=√3,由侧视图知该三棱锥的高h=√3.所以V三棱锥=13S底×h=13×√3×√3=1,故选D.5.(2014四川,文5)若a>b>0,c<d<0,则一定有()A.ad >bcB.ad<bcC.ac >bdD.ac<bd答案:B解析:∵a>b>0,c<d<0,∴-c>-d>0,∴-ac>-bd,即ac<bd.又∵dc>0,∴acdc <bddc,即ad <bc,故选B.6.(2014四川,文6)执行如图的程序框图,如果输入的x,y∈R,那么输出的S的最大值为()A.0B.1C.2D.3 答案:C解析:记M={(x,y)|{x≥0,y≥0,x+y≤1}.由程序框图知,当(x,y)∈M时,S=2x+y;当(x,y)∉M时,S=1.如图,画出集合M表示的可行域(阴影部分).移动直线l0:y=-2x.由图可知,当直线l0过点A(1,0)时,目标函数S=2x+y取得最大值,此时S max=2×1+0=2.所以,当(x,y)∈M时,S的最大值为2>1,所以输出的S的最大值为2.故选C.7.(2014四川,文7)已知b>0,log5b=a,lg b=c,5d=10,则下列等式一定成立的是()A.d=acB.a=cdC.c=adD.d=a+c答案:B解析:由log5b=a,得lgblg5=a;由5d=10,得d=log510=lg10lg5=1lg5,又lg b=c,所以cd=a.故选B.8.(2014四川,文8)如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是60m,则河流的宽度BC等于()A.240(√3-1)mB.180(√2-1)mC.120(√3-1)mD.30(√3+1)m答案:C解析:如图,作AD⊥BC,垂足为D.由题意,得DC=60×tan60°=60√3(m),DB=60×tan15°=60×tan(45°-30°)=60×tan45°-tan30°1+tan45°tan30°=60×-√331+√33=(120-60√3)m .所以BC=DC-DB=60√3-(120-60√3)=120√3-120=120(√3-1)(m),故选C .9.(2014四川,文9)设m ∈R ,过定点A 的动直线x+my=0和过定点B 的动直线mx-y-m+3=0交于点P (x ,y ),则|PA|+|PB|的取值范围是( ) A.[√5,2√5] B.[√10,2√5] C.[√10,4√5] D.[2√5,4√5]答案:B解析:由题意,得A (0,0),B (1,3),因为1×m+m×(-1)=0,所以两直线垂直,所以点P 在以AB 为直径的圆上,所以PA ⊥PB. 所以|PA|2+|PB|2=|AB|2=10, 设∠ABP=θ,则|PA|+|PB|=√10sin θ+√10cos θ =2√5sin (θ+π4). 因为|PA|≥0,|PB|≥0,所以0≤θ≤π2.所以√10≤|PA|+|PB|≤2√5,故选B .10.(2014四川,文10)已知F 为抛物线y 2=x 的焦点,点A ,B 在该抛物线上且位于x 轴的两侧,OA ⃗⃗⃗⃗⃗ ·OB ⃗⃗⃗⃗⃗ =2(其中O 为坐标原点),则△ABO 与△AFO 面积之和的最小值是( ) A.2 B.3 C.17√28D.√10答案:B解析:设AB 所在直线方程为x=my+t.由{x =my +t ,y 2=x ,消去x ,得y 2-my-t=0.设A (y 12,y 1),B (y 22,y 2)(不妨令y 1>0,y 2<0),故y 12+y 22=m ,y 1y 2=-t.而OA ⃗⃗⃗⃗⃗ ·OB ⃗⃗⃗⃗⃗ =y 12y 22+y 1y 2=2.解得y 1y 2=-2或y 1y 2=1(舍去). 所以-t=-2,即t=2.所以直线AB 过定点M (2,0). 而S △ABO =S △AMO +S △BMO =12|OM||y 1-y 2|=y 1-y 2, S △AFO =12|OF|×y 1=12×14y 1=18y 1,故S △ABO +S △AFO =y 1-y 2+18y 1=98y 1-y 2.由98y 1-y 2=98y 1+(-y 2)≥2√98y 1×(-y 2)=2√98×2=3, 得S △ABO +S △AFO 的最小值为3,故选B .第Ⅱ卷(非选择题共100分)二、填空题:本大题共5小题,每小题5分,共25分.11.(2014四川,文11)双曲线x 24-y 2=1的离心率等于 . 答案:√52解析:∵x 24-y 2=1,∴a 2=4,b 2=1,∴c 2=a 2+b 2=5,∴a=2,c=√5, ∴e=c a=√52.12.(2014四川,文12)复数2-2i1+i= .答案:-2i解析:2-2i 1+i=(2-2i )(1-i )(1+i )(1-i )=2(1-i )22=-2i.13.(2014四川,文13)设f (x )是定义在R 上的周期为2的函数,当x ∈[-1,1)时,f (x )={-4x 2+2,-1≤x <0,x ,0≤x <1,则f (32)= .答案:1解析:∵f (x )的周期为2,∴f (32)=f (32-2)=f (-12).又∵当x ∈[-1,0)时,f (x )=-4x 2+2, ∴f (-12)=-4×(-12)2+2=1.14.(2014四川,文14)平面向量a =(1,2),b =(4,2),c =m a +b (m ∈R ),且c 与a 的夹角等于c 与b 的夹角,则m= . 答案:2解析:∵a=(1,2),b=(4,2),∴c=m a+b =(m+4,2m+2).又∵c 与a 的夹角等于c 与b 的夹角, ∴cos <c ,a >=cos <c ,b >,∴c ·a |c ||a |=c ·b |c ||b |,即c ·a |a |=c ·b|b |, ∴√5|c |=√20|c |, ∴√5=√20,∴10m+16=8m+20,∴m=2.15.(2014四川,文15)以A 表示值域为R 的函数组成的集合,B 表示具有如下性质的函数φ(x )组成的集合:对于函数φ(x ),存在一个正数M ,使得函数φ(x )的值域包含于区间[-M ,M ].例如,当φ1(x )=x 3,φ2(x )=sin x 时,φ1(x )∈A ,φ2(x )∈B.现有如下命题:①设函数f (x )的定义域为D ,则“f (x )∈A”的充要条件是“∀b ∈R ,∃a ∈D ,f (a )=b”; ②若函数f (x )∈B ,则f (x )有最大值和最小值;③若函数f (x ),g (x )的定义域相同,且f (x )∈A ,g (x )∈B ,则f (x )+g (x )∉B ;④若函数f (x )=a ln(x+2)+xx 2+1(x>-2,a ∈R )有最大值,则f (x )∈B.其中的真命题有 .(写出所有真命题的序号) 答案:①③④解析:对于①,若对任意的b ∈R ,都∃a ∈D 使得f (a )=b ,则f (x )的值域必为R .反之,f (x )的值域为R ,则对任意的b ∈R ,都∃a ∈D 使得f (a )=b ,故正确.对于②,比如对f (x )=sin x (x ∈(-π2,π2))∈B ,但它无最大值也无最小值. 对于③,∵f (x )∈A ,∴f (x )∈(-∞,+∞). ∵g (x )∈B ,∴存在正数M 使得-M ≤g (x )≤M , 故f (x )+g (x )∈(-∞,+∞), ∴f (x )+g (x )∉B ,正确. 对于④,-12≤x x 2+1≤12,当a>0或a<0时,a ln x ∈(-∞,+∞),f (x )均无最大值,若f (x )有最大值,则a=0,此时f (x )=xx 2+1,f (x )∈B ,故正确. 三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.(本小题满分12分)(2014四川,文16)一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a ,b ,c. (1)求“抽取的卡片上的数字满足a+b=c”的概率; (2)求“抽取的卡片上的数字a ,b ,c 不完全相同”的概率.分析:(1)利用列举法分别求出基本事件空间和所求事件包含的基本事件,然后代入古典概型公式求解;注意该题抽取方式为有放回地抽取,故a ,b ,c 可取相同的数字;(2)因为a ,b ,c 不完全相同包含的基本事件较多,故可转化为其对立事件“a ,b ,c 相同”的概率求解. 解:(1)由题意,(a ,b ,c )所有的可能为(1,1,1),(1,1,2),(1,1,3),(1,2,1),(1,2,2),(1,2,3),(1,3,1),(1,3,2),(1,3,3),(2,1,1),(2,1,2),(2,1,3),(2,2,1),(2,2,2),(2,2,3),(2,3,1),(2,3,2),(2,3,3),(3,1,1),(3,1,2),(3,1,3),(3,2,1),(3,2,2),(3,2,3),(3,3,1),(3,3,2),(3,3,3),共27种.设“抽取的卡片上的数字满足a+b=c”为事件A, 则事件A包括(1,1,2),(1,2,3),(2,1,3),共3种.所以P(A)=327=19.因此,“抽取的卡片上的数字满足a+b=c”的概率为19. (2)设“抽取的卡片上的数字a,b,c不完全相同”为事件B, 则事件B包括(1,1,1),(2,2,2),(3,3,3),共3种.所以P(B)=1-P(B)=1-327=89.因此,“抽取的卡片上的数字a,b,c不完全相同”的概率为89.17.(本小题满分12分)(2014四川,文17)已知函数f(x)=sin(3x+π4).(1)求f(x)的单调递增区间;(2)若α是第二象限角,f(α3)=45cos(α+π4)cos2α,求cosα-sinα的值.分析:(1)利用换元法,将3x+π4视为整体t,即可将其转化为y=sin t的单调增区间,然后解不等式即得;(2)首先代入f(α3),然后化简等式,根据sinα+cosα是否为0进行分类讨论,即可求得cosα-sinα的值.解:(1)因为函数y=sin x的单调递增区间为[-π2+2kπ,π2+2kπ],k∈Z,由-π2+2kπ≤3x+π4≤π2+2kπ,k∈Z,得-π4+2kπ3≤x≤π12+2kπ3,k∈Z,所以,函数f(x)的单调递增区间为[-π4+2kπ3,π12+2kπ3],k∈Z.(2)由已知,有sin(α+π4)=45cos(α+π4)(cos2α-sin2α),所以,sinαcosπ4+cosαsinπ4=45(cosαcosπ4−sinαsinπ4)(cos2α-sin2α),即sinα+cosα=45(cosα-sinα)2(sinα+cosα).当sinα+cosα=0时,由α是第二象限角,知α=3π4+2kπ,k∈Z.此时,cosα-sinα=-√2.当sinα+cosα≠0时,有(cosα-sinα)2=54.由α是第二象限角,知cosα-sinα<0,此时cosα-sinα=-√52.综上所述,cosα-sinα=-√2或-√52.18.(本小题满分12分)(2014四川,文18)在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.(1)若AC⊥BC,证明:直线BC⊥平面ACC1A1;(2)设D,E分别是线段BC,CC1的中点,在线段AB上是否存在一点M,使直线DE∥平面A1MC?请证明你的结论.分析:(1)首先利用两个矩形中的垂直关系证明AA1⊥平面ABC,进而得到AA1⊥BC,然后结合已知AC⊥BC即可证得结论;(2)当M为线段AB中点时,取平行四边形ACC1A1的对角线交点O,即可利用中位线的性质构造平行关系证明DE∥平面A1MC.解:(1)因为四边形ABB1A1和ACC1A1都是矩形,所以AA1⊥AB,AA1⊥AC.因为AB,AC为平面ABC内两条相交直线,所以AA1⊥平面ABC.因为直线BC⊂平面ABC,所以AA1⊥BC.又由已知,AC⊥BC,AA1,AC为平面ACC1A1内两条相交直线,所以BC⊥平面ACC1A1.(2)取线段AB的中点M,连接A1M,MC,A1C,AC1,设O为A1C,AC1的交点.由已知,O为AC1的中点.连接MD,OE,则MD,OE分别为△ABC,△ACC1的中位线.所以,MD 12AC ,OE 12AC ,因此MD OE.连接OM ,从而四边形MDEO 为平行四边形, 则DE ∥MO.因为直线DE ⊄平面A 1MC ,MO ⊂平面A 1MC , 所以直线DE ∥平面A 1MC.即线段AB 上存在一点M (线段AB 的中点),使直线DE ∥平面A 1MC.19.(本小题满分12分)(2014四川,文19)设等差数列{a n }的公差为d ,点(a n ,b n )在函数f (x )=2x 的图象上(n ∈N *). (1)证明:数列{b n }为等比数列;(2)若a 1=1,函数f (x )的图象在点(a 2,b 2)处的切线在x 轴上的截距为2-1ln2,求数列{a n b n 2}的前n 项和S n .分析:(1)利用点(a n ,b n )在函数图象上建立a n 与b n 的关系式,然后利用等差数列和等比数列的定义证明结论;(2)先利用导数几何意义求出函数f (x )的图象在点(a 2,b 2)处的切线方程,根据已知截距求出a 2的值,从而求出数列{a n b n 2}的通项公式,然后根据通项的结构特征利用错位相减法求和. (1)证明:由已知,b n =2a n >0.当n ≥1时,b n+1b n=2a n+1-a n =2d .所以,数列{b n }是首项为2a 1,公比为2d 的等比数列.(2)解:函数f (x )=2x 在(a 2,b 2)处的切线方程为y-2a 2=(2a 2ln 2)(x-a 2),它在x 轴上的截距为a 2-1ln2. 由题意,a 2-1ln2=2-1ln2. 解得a 2=2.所以,d=a 2-a 1=1,a n =n ,b n =2n ,a n b n 2=n ·4n .于是,T n =1×4+2×42+3×43+…+(n-1)·4n-1+n ·4n ,4T n =1×42+2×43+…+(n-1)×4n +n ·4n+1. 因此,T n -4T n =4+42+…+4n -n ·4n+1=4n+1-43-n ·4n+1=(1-3n )4n+1-43. 所以,T n =(3n -1)4n+1+49.20.(本小题满分13分)(2014四川,文20)已知椭圆C :x 2a 2+y 2b2=1(a>b>0)的左焦点为F (-2,0),离心率为√63.(1)求椭圆C 的标准方程;(2)设O 为坐标原点,T 为直线x=-3上一点,过F 作TF 的垂线交椭圆于P ,Q.当四边形OPTQ 是平行四边形时,求四边形OPTQ 的面积.分析:(1)由焦点可求c ,然后利用离心率即可求a ,再求b ,即可求得方程;(2)由题意设T (-3,m ),然后利用TF ⊥PQ 求出PQ 的斜率,从而设出直线PQ 方程,与椭圆C 方程联立后,根据平行四边形OPTQ 的性质:对边平行且相等,即可求出m 的值,最后将四边形OPTQ 的面积转化为△OPQ 面积的两倍求解. 解:(1)由已知可得,c a=√63,c=2,所以a=√6.又由a 2=b 2+c 2,解得b=√2, 所以椭圆C 的标准方程是x 26+y 22=1. (2)设T 点的坐标为(-3,m ),则直线TF 的斜率k TF =m -0-3-(-2)=-m. 当m ≠0时,直线PQ 的斜率k PQ =1m,直线PQ 的方程是x=my-2.当m=0时,直线PQ 的方程是x=-2,也符合x=my-2的形式. 设P (x 1,y 1),Q (x 2,y 2),将直线PQ 的方程与椭圆C 的方程联立,得{x =my -2,x 26+y 22=1.消去x ,得(m 2+3)y 2-4my-2=0, 其判别式Δ=16m 2+8(m 2+3)>0.所以y 1+y 2=4m m 2+3,y 1y 2=-2m 2+3, x 1+x 2=m (y 1+y 2)-4=-12m 2+3.因为四边形OPTQ 是平行四边形, 所以OP ⃗⃗⃗⃗⃗ =QT ⃗⃗⃗⃗⃗ ,即(x 1,y 1)=(-3-x 2,m-y 2). 所以{x 1+x 2=-12m 2+3=-3,y 1+y 2=4mm 2+3=m .解得m=±1.此时,四边形OPTQ 的面积S OPTQ =2S OPQ =2×12·|OF|·|y 1-y 2|=2√(4m m 2+3)2-4·-2m 2+3=2√3. 21.(本小题满分14分)(2014四川,文21)已知函数f (x )=e x -ax 2-bx-1,其中a ,b ∈R ,e =2.718 28…为自然对数的底数.(1)设g (x )是函数f (x )的导函数,求函数g (x )在区间[0,1]上的最小值; (2)若f (1)=0,函数f (x )在区间(0,1)内有零点,证明:e -2<a<1.分析:(1)先利用求导求出g (x )的解析式,再求出其导函数g'(x ),根据a 的不同取值分类讨论g'(x )的符号变化,判断其单调性,从而求其最值;(2)先根据已知分析f (x )在(0,1)上的单调性与零点个数,将其转化为g (x )的零点个数,进而利用(1)中的结论判断a 的范围及其零点所在区间,结合函数g (x )在区间端点处的函数值及f (1)=0即可证得结论. 解:(1)由f (x )=e x -ax 2-bx-1,有g (x )=f'(x )=e x -2ax-b.所以g'(x )=e x -2a.当x ∈[0,1]时,g'(x )∈[1-2a ,e -2a ]. 当a ≤12时,g'(x )≥0,所以g (x )在[0,1]上单调递增,因此g (x )在[0,1]上的最小值是g (0)=1-b ;当a ≥e2时,g'(x )≤0,所以g (x )在[0,1]上单调递减,因此g (x )在[0,1]上的最小值是g (1)=e -2a-b ; 当12<a<e 2时,令g'(x )=0,得x=ln(2a )∈(0,1).所以函数g (x )在区间[0,ln(2a )]上单调递减,在区间(ln(2a ),1]上单调递增. 于是,g (x )在[0,1]上的最小值是g (ln(2a ))=2a-2a ln(2a )-b. 综上所述,当a ≤12时,g (x )在[0,1]上的最小值是g (0)=1-b ; 当12<a<e 2时,g (x )在[0,1]上的最小值是g (ln(2a ))=2a-2a ln(2a )-b ; 当a ≥e 2时,g (x )在[0,1]上的最小值是g (1)=e -2a-b. (2)设x 0为f (x )在区间(0,1)内的一个零点,则由f (0)=f (x 0)=0可知f (x )在区间(0,x 0)上不可能单调递增,也不可能单调递减. 则g (x )不可能恒为正,也不可能恒为负. 故g (x )在区间(0,x 0)内存在零点x 1, 同理g (x )在区间(x 0,1)内存在零点x 2. 所以g (x )在区间(0,1)内至少有两个零点. 由(1)知,当a ≤12时,g (x )在[0,1]上单调递增, 故g (x )在(0,1)内至多有一个零点.当a ≥e2时,g (x )在[0,1]上单调递减,故g (x )在(0,1)内至多有一个零点. 所以12<a<e 2.此时g (x )在区间[0,ln(2a )]上单调递减,在区间(ln(2a ),1]上单调递增. 因此x 1∈(0,ln(2a )],x 2∈(ln(2a ),1),必有g (0)=1-b>0,g (1)=e -2a-b>0. 由f (1)=0有a+b=e -1<2, 有g (0)=a-e +2>0,g (1)=1-a>0. 解得e -2<a<1.所以,函数f (x )在区间(0,1)内有零点时,e -2<a<1.。

2014年全国普通高等学校招生统一考试文科数学(四川卷带解析)试题

2014年全国普通高等学校招生统一考试文科（四川卷）数学试题1、【题文】已知集合，集合为整数集，则（）A．B．C．D．2、【题文】在“世界读书日”前夕，为了了解某地名居民某天的阅读时间，从中抽取了名居民的阅读时间进行统计分析。

在这个问题中，名居民的阅读时间的全体是（）A．总体B．个体C．样本的容量D．从总体中抽取的一个样本3、【题文】为了得到函数的图象，只需把函数的图象上所有的点（）A．向左平行移动1个单位长度B．向右平行移动1个单位长度C．向左平行移动个单位长度D．向右平行移动个单位长度4、【题文】某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积是（）（锥体体积公式：，其中为底面面积，为高）A．B．C．D．5、【题文】若，，则一定有（）A．B．C．D．6、【题文】执行如图1所示的程序框图，如果输入的，则输出的的最大值为（）A．B．C．D．7、【题文】已知，，，，则下列等式一定成立的是（）A．B．C．D．8、【题文】如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为，，此时气球的高是，则河流的宽度BC等于（）A．B．C．D．9、【题文】设，过定点的动直线和过定点的动直线交于点，则的取值范围是（）A．B．C．D．10、【题文】已知是抛物线的焦点，点，在该抛物线上且位于轴的两侧，（其中为坐标原点），则与面积之和的最小值是（）A．B．D．C．11、【题文】双曲线的离心率等于____________.12、【题文】复数 .13、【题文】设是定义在R上的周期为2的函数，当时，，则 .14、【题文】平面向量，，（），且与的夹角等于与的夹角，则 .15、【题文】以表示值域为R的函数组成的集合，表示具有如下性质的函数组成的集合：对于函数，存在一个正数，使得函数的值域包含于区间。

例如，当，时，，.现有如下命题：①设函数的定义域为，则“”的充要条件是“，，”；②若学科网函数，则有最大值和最小值；③若函数，的定义域相同，且，，则；④若函数（，）有最大值，则.其中的真命题有 .（写出所有真命题的序号）16、【题文】（本小题满分12分）一个盒子里装有三张卡片，分别标记有数字，，，这三张卡片除标记的数字外完全相同。

2014四川高考试题及答案(文科数学)

更多2014届高考试题答案及分数线信息及2015届复习信息奇速英语微信公众号qisuen,QQ757722345，每
更多2014届高考试题答案及分数线信息及2015届复习信息奇速英语微信公众号qisuen,QQ757722345，每
更多2014届高考试题答案及分数线信息及2015届复习信息奇速英语微信公众号qisuen,QQ757722345，每
更多2014届高考试题答案及分数线信息及2015届复习信息奇速英语微信公众号qisuen,QQ757722345，每
更多2014届高考试题答案及分数线信息及2015届复习信息奇速英语微信公众号qisuen,QQ757722345，每
更多2014届高考试题答案及分数线信息及2015届复习信息奇速英语微信公众号qisuen,QQ757722345，每
更多2014届高考试题答案及分数线信息及2015届复习信息奇速英语微信公众号qisuen,QQ757722345，每
更多2014届高考试题答案及分数线信息及2015届复习信息奇速英语微信公众号qisuen,QQ757722345，每。