黑龙江省哈尔滨三中2014_2015学年高二数学上学期期末试卷试卷理(含解析)

合集下载

黑龙江省哈师大附中2014-2015学年高二上学期期中考试数学理试卷Word版含答案

EA D CBPF哈师大附中2014-2015学年度高二上学期期中考试数学试题（理科）考试时间：120分钟满分：150分第Ⅰ卷（选择题共60分）一、选择题（本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的）1．中心在原点，焦点在坐标轴上，且过两点的椭圆的标准方程是（） A ． B ． C ． D ． 2．椭圆的一个焦点是，那么（）A ．B ．C ．D ． 3．在空间中，下列命题正确的个数是（） ①平行于同一直线的两直线平行 ②垂直于同一直线的两直线平行 ③平行于同一平面的两直线平行 ④垂直于同一平面的两直线平行 A ．1 B ．2 C ．3 D ．44．一个锥体的正视图和侧视图如图所示，下面选项中，不可能是该锥体的俯视图的是( )5．设抛物线上一点到轴距离是6，则点到该抛物线焦点的距离是（） A ．8 B ．6 C ．4 D ． 26．正方体AC1中，点P 、Q 分别为棱A1B1、DD1的中点，则PQ 与AC1所成的角为( )A ．30oB ．45oC ．60oD ．90o7．在三棱锥P －ABC 中，PA ⊥平面ABC ，∠BAC ＝90°，D 、E 、F 分别是棱AB 、 BC 、CP 的中点，AB ＝AC ＝1，PA ＝2，则直线PA 与平面DEF 所成角的正弦值为( )A ．15B ．25C ．55D ．2558．若点的坐标为，是抛物线的焦点，点在抛物线上移动时，使取得最小值的的坐标为（） A ． B ． C ． D ． 9．过双曲线的一个焦点作垂直于实轴的弦，是另一焦点，若∠，则双曲线的离心率等于（） A ． B ． C ． D ． 10．为椭圆上的一点，分别为左、右焦点，且则（）A ．B ．C ．D ．11．已知是直线被椭圆所截得的线段的中点，则直线的方程是（） A ． B ． C ． D ． 12．从双曲线的左焦点引圆的切线，切点为，延长交双曲线右支于点，若为线段的中点，为坐标原点，则与的大小关系为（） A ． B. C ． D.不确定第Ⅱ卷（非选择题共90分）侧视图正视图DC 1B 1A 1CBA二、填空题（本大题共4小题，每小题5分，共20分）13．已知过抛物线焦点的弦长为12，则此弦所在直线的倾斜角是 . 14．已知椭圆和双曲线有公共的焦点，则双曲线的渐近线方程为 .15．在四面体中，则二面角的大小为 .16．若抛物线的焦点是，准线是，则经过两点、且与相切的圆共有个.三、解答题（本大题共6小题，共70分. 解答应写出文字说明、证明过程或演算步骤） 17. （本题满分10分）已知抛物线，直线与抛物线交于两点（Ⅰ）求的值；（Ⅱ）求的面积.18. （本题满分12分）如图，在三棱柱中，侧棱底面，，是棱的中点，且. （Ⅰ）求证： //平面；（Ⅱ）求异面直线与所成的角.19. （本题满分12分）如图，在四棱锥中， //，，，平面，. （Ⅰ）求证：平面；（Ⅱ）点为线段的中点，求直线与平面所成角的正弦值.20. （本题满分12分）已知椭圆：的右焦点为，且椭圆过点. （Ⅰ）求椭圆的方程；（Ⅱ）设过点的直线与椭圆交于两点，与直线交于点，若直线的斜率成等差数列，求的值.zyx DC1B1A1C BAABCA1B1C1DO21. （本题满分12分）如图所示的几何体中，四边形是菱形，是矩形，平面⊥平面，，，，是的中点．（Ⅰ）求证：；（Ⅱ）在线段上是否存在点，使二面角的大小为？若存在，求出的长；若不存在，请说明理由.22. （本题满分12分）已知，直线：，椭圆：的左、右焦点分别为，（Ⅰ）当直线过时，求的值；（Ⅱ）设直线与椭圆交于两点，△、△的重心分别为、，若原点在以线段为直径的圆内，求实数的取值范围.哈师大附中2014-2015学年度高二上学期期中考试数学答案（理科）一、选择题：DCBCA DCDCB AB二、填空题：13．45o或135o 14．15．60o 16．2三、解答题：17．解：（Ⅰ）设，显然成立，……2分……4分……5分（Ⅱ）原点到直线的距离，……7分，……9分……10分18．解：（法一）（Ⅰ）连结交于点，侧棱底面侧面是矩形，为的中点，且是棱的中点，，……4分∵平面，平面平面……6分（Ⅱ），为异面直线与所成的角或其补角．……8分，为等边三角形，，异面直线与所成的角为. ……12分（法二）（Ⅰ）以为原点，所在直线分别为轴，轴，轴建立空间直角坐标系，，设为平面的一个法向量，令则……3分，又平面平面……6分（Ⅱ），……8分OHEAD CBQ P异面直线与所成的角为. ……12分 19．（法一）（Ⅰ）证明：以A 为原点，建立空间直角坐标系，如图，则…3分又，平面 ……6分（Ⅱ）由（Ⅰ）知，平面的一个法向量为， ……8分设直线与平面所成的角为，则，所以直线与平面所成的角的正弦值为． ……12分（法二）（Ⅰ）证明：设AC∩BD=O ，∵CD ∥AB ，∴OB:OD=OA:OC=AB:CD=2 Rt △DAB 中，DA=，AB=4，∴DB=，∴DO=DB=同理，OA=CA=，∴DO2+OA2=AD2，即∠AOD=90o ，∴BD ⊥AC ……3分又PA ⊥平面ABCD ，∴PA ⊥BD ……5分由AC∩PA=A ，∴BD ⊥平面PAC ……6分（Ⅱ）解：连PO ，取PO 中点H ，连QH ，则QH ∥BO ，由（Ⅰ）知，QH ⊥平面PAC∴∠QCH 是直线QC 与平面PAC 所成的角． ……8分由（Ⅰ）知，QH=BO=，取OA 中点E ，则HE=PA=2，又EC=OA+OC=Rt △HEC 中，HC2=HE2+EC2= ∴Rt △QHC 中，QC=，∴sin ∠QCH=∴直线与平面所成的角的正弦值为． ……12分20．解：（Ⅰ）由已知，因为椭圆过，所以解得，椭圆方程是 ……4分（Ⅱ）由已知直线的斜率存在，设其为，设直线方程为，易得由，所以……6分，， ……8分而+……10分因为、、成等差数列，故，解得 ……12分 21．（Ⅰ）证明：菱形ABCD 中，AD=2，AE=1，∠DAB=60o ，∴DE=．∴AD2=AE2+DE2，即∠AED=90o ，∵AB ∥DC ，∴DE ⊥DC …① ……1分∵平面ADNM ⊥平面ABCD ，交线AD ，ND ⊥AD ，ND 平面ADNM ，∴ND ⊥平面ABCD ， ∵DE 平面ABCD ，∴ND ⊥DE …② ……2分由①②及ND∩DC=D ，∴DE ⊥平面NDC∴DE ⊥NC ……4分（Ⅱ）解：设存在P 符合题意．由(Ⅰ)知，DE 、DC 、DN 两两垂直，以D 为原点，建立空间直角坐标系D-xyz （如图），则D,A,E,C,P ．∴，设平面PEC 的法向量为，则，令，则平面PEC 的一个法向量为……7分取平面ECD 的法向量， ……9分n∴，解得，即存在点P，使二面角P-EC-D的大小为，此时AP=．……12分22．解：（Ⅰ）由已知，交轴于为，，得…3分（Ⅱ）设，因为的重心分别为，所以因为原点在以线段为直径的圆内，所以……5分，∴①…6分∴……7分∵，∴，即…②…10分由及①②，得实数的取值范围是. ……12分。

黑龙江省哈尔滨师范大学附属中学2014-2015学年高二上

（考试时间：90分钟；满分：100分）一、选择题：本题共12小题，每小题4分，总计48分。

在每小题给出的四个选项中，有的只有一个选项正确，有的有多个选项正确，全部选对的得4分，选对但不全的得2分，有选错的得0分。

题目前方已注明该题为单选题还是多选题。

1．【单选】如图所示的四个电场中，均有相互对称分布的、两点，其中电势和电场强度都相同的是2．【单选】在“描绘小灯泡的伏安特性曲线”实验中，下列图象能正确反映小灯泡的伏安特性曲线的是3．【多选】如图所示是粒子速度选择器的原理图，如果粒子所具有的速率v ＝E /B ，那么 A ．带正电粒子沿ab 方向从左侧进入场区，能沿直线通过 B ．带负电粒子沿ba 方向从右侧进入场区，能沿直线通过C ．不论粒子电性如何，沿ab 方向从左侧进入场区，都能沿直线通过D ．不论粒子电性如何，沿ba 方向从右侧进入场区，都能沿直线通过 4．【单选】通有电流的导线L 1、L 2处在同一平面(纸面)内，L 1是固定的，L 2可绕垂直纸面的光滑固定转轴O 转动(O 为L 2的中心)，各自的电流方向如图所示。

下列哪种情况将会发生A ．因L 2不受磁场力的作用，故L 2不动B ．因L 2上、下两部分所受的磁场力平衡，故L 2不动C ．L 2绕轴O 按顺时针方向转动D ．L 2绕轴O 按逆时针方向转动5．【单选】如图所示，A 是一边长为 l 的正方形线框，电阻为 R 。

用力保持线框以恒定速度 v 沿 x 轴运动，并穿过图中所示的匀强磁场 B 区域，若以顺时针方向电流为正方向，从图示位置开始计时，则线框中产生的电流I 随时间 t 的变化图线为下图中的DA B C +Q +Q6．【多选】1930年劳伦斯制成了世界上第一台回旋加速器，其原理如图所示。

这台加速器由两个铜质D 形盒构成，其间留有空隙。

下列说法正确的是 A . 离子由加速器的边缘进入加速器 B . 离子由加速器的中心附近进入加速器 C . 离子从电场中获得能量 D . 离子从磁场中获得能量7．【多选】如图所示电路，电键K 原来是闭合的，悬在平行板电容器C 两水平极板间的带电尘埃P 恰好处于静止状态。

黑龙江哈尔滨三十二中2014-2015学年高二下学期期末考试数学(理)试卷

哈32中2014～2015学年度下学期期末考试数学（理）试题一、选择题（每小题只有1个选项符合题意，每小题5分，共60分）1.如果（2x- y)+(x+3)i=0(x ，y ∈R)则x+y 的值是（）A 18BC 3D 9．．．．12-2.从1,2,3,4,5中任取2个不同的数，事件A=“取到2个数之和为偶数” ，事件B=“取到2个数均为偶数”，则P （B|A ）=( ) A ．81B ．41 C ．52 D ．213．13()i i --的虚部为( )A ．8iB ．8i -C ．8D ．8- 4．函数xx y 142+=单调递增区间是（） A ．),0(+∞ B ．)1,(-∞ C ．),21(+∞ D ．),1(+∞ 5．函数xxy ln =的最大值为（） A ．1-e B ．e C ．2e D ．310 6．从4台甲型和5台乙型电视机中任意取出3台，其中至少有甲型与乙型电视机各1台，则不同的取法共有（） A ．140种 B.84种 C.70种 D.35种7．5个人排成一排,其中甲、乙两人至少有一人在两端的排法种数有（）A ．33AB ．334AC ．523533A A A -D ．2311323233A A A A A +8．在82x ⎛- ⎝的展开式中的常数项是（） A.7 B ．7- C ．28 D ．28- 9．5(12)(2)x x -+的展开式中3x 的项的系数是（）A.120 B ．120- C ．100 D ．100-10．设 ()()()()=<<=>=<10,2211~ξξξσμξP p P P 则，，且，( ) A ．p 21 B ． p -1 C ．p 21- D ．p -2111 已知()()()()的值为则dx x f x x x x f ⎰⎩⎨⎧<<≤≤-=11-2,10101（） A ．34 B ．32- C ．23 D ．34-12. 若()016677713a x a x a x a x ++⋅⋅⋅++=-，则7531a a a a +++=（）A ．1362-2B ．13622+C ．1472-2D ．14722+二、填空题（每空5分，共20分）13.如果35a <<,复数22(815)(514)z a a a a i =-++--在复平面上的对应点z 在象限.14. 观察下列等式：,,1043216321321233332333233⋅⋅⋅=+++=++=+，，根据上述规律，第五个等式为__________________________.15.设()()=≤<-3121~2X P X ，则， ()=≤<53X P(参考数据：()()9544.0226826.0=+≤<-=+≤<-σμσμσμσμX P X P ，,()9974.033=+≤<-σμσμX P )16.P 是抛物线2x y =上的点，若过点P 的切线方程与直线121+-=x y 垂直，则过P 点处的切线方程是____________.哈32中2014～2015学年度下学期末考试数学（理）试题答题卡一、选择题：(本大题共12小题，每小题5分，共60分。

2014-2015学年上学期期中考试高二数学试卷

2014-2015学年上学期期中考试高二数学试卷一．选择题（共12小题，每题5分，共60分.答案必须填涂在答题卡上）1．为了了解1200名学生对学校某项教改实验的意见，打算从中抽取一个容量为40的样本，考虑用系统抽样，则分段的间隔k为( )．A．40 B．30C．20 D．122．计算机执行下面的程序段后，输出的结果是()．A．4，－2 B．4,1C．1,4 D．－2,43. 线性回归方程ˆy bx a=+表示的直线必经过的一个定点是().A．(,y)x B．(,0)xC．(0,y)D．(0,0)4．如图所示的程序框图输出的结果为()．A．1 B．2C．4 D．85．设,x y满足约束条件12x yy xy+≤⎧⎪≤⎨⎪≥-⎩,则3z x y=+的最大值为（）A．5 B. 3C. 7D. -86．对一个样本容量为100的数据分组，各组的频数如下：估计小于29的数据大约占总体的 ( )． A ．42% B ．58% C ．40% D ．16% 7．下列各数中，最小的数是（） A ．75 B ．(6)210 C ．(2)111111 D ．(9)85 8． 10名工人某天生产同一零件，生产的件数是15,17,14,10,15,17,17,16,14,12，设其平均数为a ，中位数为b ，众数为c ，则有 ( )． A ．a>b>c B ．b>c>a C ．c>a>b D ．c>b>a 9．4张卡片上分别写有数字1,2,3,4，从这4张卡片中随机抽取2张，则取出的2张卡片上的数字之和为奇数的概率为 ( )． A.13 B.12 C.23 D.34 10．用秦九韶算法计算当x ＝0.4时，多项式f(x)＝3x6＋4x5＋6x3＋7x2＋1的值时，需要做乘法运算的次数是( ) A ．6 B ．5 C ．4 D ．3 11．一个游戏转盘上有四种颜色：红、黄、蓝、黑，并且它们所占面积的比为6∶2∶1∶4，则指针停在红色或蓝色的区域的概率为 ( )． A.613 B.713 C.413 D.1013 12．命题:“∀x ∈R,220x x -+≥”的否定是( ) A.∃x ∈R,220x x -+≥ B.∀x ∈R,220x x -+≥ C.∃x ∈R,220x x -+< D.∀x ∈R,220x x -+< 座位号：_________ 二、填空题(本大题共4小题，每小题4分，共16分．把答案填在题中横线上) 13．有324,243,270三个数，则它们的最大公约数是________． 14.则年降水量在[200,300](mm)范围内的概率是 15.某中学高三年级从甲、乙两个班级中各选出7名学生参加数学竞赛，他们取得的成绩(满分100分)的茎叶图如图，其中甲班学生的平均分是85，乙班学生成绩的中位数是83，则x ＋y 的值为答题座位16.已知命题:p:(3)(1)0x x-+>,命题q:22210(0)x x m m-+->>,若命题p是命题q的充分不必要条件,则实数m的范围是____________.三.解答题：（本题共6个小题，共70分，每题均要求写出解答过程）17. (10分)分别用辗转相除法和更相减损术求282与470的最大公约数．18．(12分)写出下列命题的否定,并判断其真假:(1)p:不论m取何实数,方程x2+mx-1=0必有实数根;(2)p:有些三角形的三条边相等;(3)p:菱形的对角线互相垂直;(4)p:存在一个实数x,使得3x <0.19．（12分）某校从高二年级学生中随机抽取60名学生，将其会考的政治成绩（均为整数）分成六段：[40，50），[50，60），…，[90，100]后得到如下频率分布直方图．（Ⅰ）求图中a的值（Ⅱ）根据频率分布直方图，估计该校高二年级学生政治成绩的平均分；20．(12分)某次运动会甲、乙两名射击运动员的成绩如下：甲：9.48.77.58.410.110.510.77.27．810.8乙：9.18.77.19.89.78.510.19.210.1 9．1(1)用茎叶图表示甲、乙两人的成绩；(2)根据茎叶图分析甲、乙两人的成绩；(3)分别计算两个样本的平均数x和标准差s，并根据计算结果估计哪位运动员的成绩比较稳定．21．设变量,x y满足约束条件25020x yx yx+-≤⎧⎪--≤⎨⎪≥⎩，求目标函数231z x y=++的最大值。

2014-2015年黑龙江省哈尔滨一中高二上学期期中数学试卷及参考答案

2014-2015学年黑龙江省哈尔滨一中高二（上）期中数学试卷一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的.1．（5分）命题“若a＞b，则a+c＞b+c”的逆否命题为（）A．若a＜b，则a+c＜b+c B．若a≤b，则a+c≤b+cC．若a+c＜b+c，则a＜b D．若a+c≤b+c，则a≤b2．（5分）与曲线共焦点，而与双曲线共渐近线的双曲线方程为（）A．B．C．D．3．（5分）已知双曲线=1（a＞0）的实轴长、虚轴长、焦距长成等差数列，则双曲线的渐近线方程为（）A．y=±x B．y=±x C．y=±x D．y=±x4．（5分）函数f（x）=x2﹣2ax+1在（﹣∞，2]上是单调递减函数的必要不充分条件是（）A．a≥2 B．a=6 C．a≥3 D．a≥05．（5分）过抛物线y2=﹣x的焦点F的直线交抛物线于A、B两点，且A、B在直线x=上的射影分别M，N，则∠MFN等于（）A．45°B．60°C．90°D．以上都不对6．（5分）有下列四个命题：①命题“若xy=1，则x，y互为倒数”的逆命题；②命题“面积相等的三角形全等”的否命题；③命题“若m＞1，则x2﹣2x+m=0有实根”的逆否命题；④命题“若A∩B=B，则A⊆B”的逆否命题．其中是真命题的个数是（）A．1 B．2 C．3 D．47．（5分）方程mx+ny2=0与mx2+ny2=1（|m|＞|n|＞0）的曲线在同一坐标系中的示意图应是（）A． B．C．D．8．（5分）已知动点P（x，y）满足=，则点P的轨迹是（）A．两条相交直线B．抛物线C．双曲线D．椭圆9．（5分）一个圆的圆心为椭圆的右焦点，且该圆过椭圆的中心交椭圆于P，直线PF1（F1为椭圆的左焦点）是该圆的切线，则椭圆的离心率为（）A．B．C．D．10．（5分）已知P为抛物线上的动点，点P在x轴上的射影为M，点A 的坐标是，则|PA|+|PM|的最小值是（）A．8 B．C．10 D．11．（5分）若椭圆=1与双曲线=1有相同的焦点F1、F2，P是这两条曲线的一个交点，则△F1PF2的面积是（）A．4 B．2 C．1 D．12．（5分）已知A，B是椭圆长轴的两个端点，M，N是椭圆上关于x轴对称的两点，直线AM，BN的斜率分别为k1，k2（k1k2≠0），若椭圆的离心率为，则|k1|+|k2|的最小值为（）A．1 B．C．D．2二、填空题：本大题共4小题，每小题5分，共20分．13．（5分）过椭圆=1的焦点F的弦中最短弦长是．14．（5分）过抛物线y2=﹣12x的焦点作直线l，直线l交抛物线于，A，B两点，若线段AB中点的横坐标为﹣9，则|AB|=．15．（5分）已知圆C过双曲线﹣=1的一个顶点和一个焦点，且圆心在此双曲线上，则圆心到双曲线中心的距离是．16．（5分）设点P是椭圆=1（a＞b＞0）与圆x2+y2=3b2的一个交点，F1，F2分别是椭圆的左、右焦点，且|PF1|=3|PF2|，则椭圆的离心率为．三、解答题：本大题共6小题，共70分，解答应有证明或演算步骤17．（10分）已知半径为5的圆C的圆心在x轴上，圆心的横坐标是整数，且与直线4x+3y﹣29=0相切．（1）求圆C的方程；（2）设直线ax﹣y+5=0与圆C相交于A、B两点，求实数a的取值范围．18．（12分）在平面直角坐标系xOy中，直线l与抛物线y2=4x相交于不同的两点A，B．（Ⅰ）如果直线l过抛物线的焦点，求•的值；（Ⅱ）在此抛物线上求一点P，使得P到Q（5，0）的距离最小，并求最小值．19．（12分）已知椭圆的一个顶点为A（0，﹣1），焦点在x轴上，若右焦点到直线x﹣y+2=0的距离为3．（Ⅰ）求椭圆的方程；（Ⅱ）设椭圆与直线y=x+m相交于不同的两点M、N，问是否存在实数m使|AM|=|AN|；若存在求出m的值；若不存在说明理由．20．（12分）如图，已知四棱锥S﹣ABCD中，△SAD是边长为a的正三角形，平面SAD⊥平面ABCD，四边形ABCD为菱形，∠DAB=60°，P为AD的中点，Q为SB的中点．（Ⅰ）求证：PQ∥平面SCD；（Ⅱ）求二面角B﹣PC﹣Q的大小．21．（12分）设过点P（x，y）的直线分别与x轴和y轴交于A，B两点，点Q 与点P关于y轴对称，O为坐标原点，若且．（1）求点P的轨迹M的方程；（2）过F（2，0）的直线与轨迹M交于C，D两点，求•的取值范围．22．（12分）如图，椭圆=1（a＞b＞0）的一个焦点是F（1，0），O为坐标原点．（Ⅰ）已知椭圆短轴的两个三等分点与一个焦点构成正三角形，求椭圆的方程；（Ⅱ）设过点F的直线l交椭圆于A、B两点．若直线l绕点F任意转动，值有|OA|2+|OB|2＜|AB|2，求a的取值范围．2014-2015学年黑龙江省哈尔滨一中高二（上）期中数学试卷参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的.1．（5分）命题“若a＞b，则a+c＞b+c”的逆否命题为（）A．若a＜b，则a+c＜b+c B．若a≤b，则a+c≤b+cC．若a+c＜b+c，则a＜b D．若a+c≤b+c，则a≤b【解答】解：把“若a＞b，则a+c＞b+c”看做原命题，它的逆否命题是题设和结论否定并且要交换位置，∴它的逆否命题是：“若a+c≤b+c，则a≤b”，故选：D．2．（5分）与曲线共焦点，而与双曲线共渐近线的双曲线方程为（）A．B．C．D．【解答】解：由题意知椭圆焦点在y轴上，且c==5，双曲线的渐近线方程为y=±x，设欲求双曲线方程为，则，解得a=4，b=3，所以欲求双曲线方程为．故选：D．3．（5分）已知双曲线=1（a＞0）的实轴长、虚轴长、焦距长成等差数列，则双曲线的渐近线方程为（）A．y=±x B．y=±x C．y=±x D．y=±x【解答】解：双曲线=1（a＞0）的实轴长2a、虚轴长：2、焦距长2，成等差数列，所以：4=2a+2，解得a=．双曲线=1的渐近线方程为：y=±x．故选：D．4．（5分）函数f（x）=x2﹣2ax+1在（﹣∞，2]上是单调递减函数的必要不充分条件是（）A．a≥2 B．a=6 C．a≥3 D．a≥0【解答】解：∵函数f（x）=x2﹣2ax+1在（﹣∞，2]上是单调递减函数，对称轴x=a∴a≥2，根据充分必要条件的定义可判断：a≥0是必要不充分条件，故选：D．5．（5分）过抛物线y2=﹣x的焦点F的直线交抛物线于A、B两点，且A、B在直线x=上的射影分别M，N，则∠MFN等于（）A．45°B．60°C．90°D．以上都不对【解答】解：根据抛物线的方程可知准线方程为x=，由抛物线的性质有|FA|=|MA|，∴∠AMF=∠AFM，同理∠BFN=∠BNF，∵AM∥x轴∥BN，∴∠MFO=∠AMF∴∠AFO=∠MFO，同理可知∠BFN=∠NFO∴∠MFN=∠MFO+∠NF0=90°故选：C．6．（5分）有下列四个命题：①命题“若xy=1，则x，y互为倒数”的逆命题；②命题“面积相等的三角形全等”的否命题；③命题“若m＞1，则x2﹣2x+m=0有实根”的逆否命题；④命题“若A∩B=B，则A⊆B”的逆否命题．其中是真命题的个数是（）A．1 B．2 C．3 D．4【解答】解：根据倒数的定义，可得“若xy=1，则x、y互为倒数”的逆命题：“若x、y互为倒数，则xy=1”是真命题，①正确；“面积相等的三角形全等”的否命题：“面积不相等的三角形不全等”是真命题，②正确；原命题与逆否命题有相同的真假性，∵方程x2﹣2x+m=0有实根⇔△=4﹣4m≥0⇔m≤1，∴原命题“若m＞1，则x2﹣2x+m=0有实根”是假命题，∴③错误；原命题与逆否命题有相同的真假性，∵命题“若A∩B=B，则A⊆B”为假命题，∴④错误．∴真命题的个数是2，故选：B．7．（5分）方程mx+ny2=0与mx2+ny2=1（|m|＞|n|＞0）的曲线在同一坐标系中的示意图应是（）A． B．C．D．【解答】解：方程mx+ny2=0 即y2=﹣，表示抛物线，方程mx2+ny2=1（|m|＞|n|＞0）表示椭圆或双曲线．当m和n同号时，抛物线开口向左，方程mx2+ny2=1（|m|＞|n|＞0）表示焦点在y轴上的椭圆，无符合条件的选项．当m和n异号时，抛物线y2=﹣开口向右，方程mx2+ny2=1（|m|＞|n|＞0）表示双曲线，故选：A．8．（5分）已知动点P（x，y）满足=，则点P的轨迹是（）A．两条相交直线B．抛物线C．双曲线D．椭圆【解答】解：令f（x）=，则其几何意义为点（x，y）到（1，2）的距离，令g（x）=，其几何意义为（x，y）点到直线y=3x+4y+12的距离，依题意二者相等，即点到点（1，2）的距离与到定直线的距离相等，进而可推断出P的轨迹为抛物线．故选：B．9．（5分）一个圆的圆心为椭圆的右焦点，且该圆过椭圆的中心交椭圆于P，直线PF1（F1为椭圆的左焦点）是该圆的切线，则椭圆的离心率为（）A．B．C．D．【解答】解：设F2为椭圆的右焦点由题意可得：圆与椭圆交于P，并且直线PF1（F1为椭圆的左焦点）是该圆的切线，所以点P是切点，所以PF2=c并且PF1⊥PF2．又因为F 1F2=2c，所以∠PF1F2=30°，所以．根据椭圆的定义可得|PF1|+|PF2|=2a，所以|PF2|=2a﹣c．所以2a﹣c=，所以e=．故选：D．10．（5分）已知P为抛物线上的动点，点P在x轴上的射影为M，点A 的坐标是，则|PA|+|PM|的最小值是（）A．8 B．C．10 D．【解答】解：依题意可知焦点F（0，），准线y=﹣，延长PM交准线于H点．则|PF|=|PH||PM|=|PH|﹣=|PF|﹣|PM|+|PA|=|PF|+|PA|﹣，我们只有求出|PF|+|PA|最小值即可．由三角形两边长大于第三边可知，|PF|+|PA|≥|FA|，①设直线FA与抛物线交于P0点，可计算得P0（3，），另一交点（﹣，舍去．当P重合于P0时，①可取得最小值，可得|FA|=10．则所求为|PM|+|PA|=故选：B．11．（5分）若椭圆=1与双曲线=1有相同的焦点F1、F2，P是这两条曲线的一个交点，则△F1PF2的面积是（）A．4 B．2 C．1 D．【解答】解：不妨设P为双曲线右支上的点，由椭圆的定义可得，PF1+PF2=4，由双曲线的定义，可得，PF1﹣PF2=2，解得PF1=2+，PF2=2﹣，F1F2=2，由于（2）2+（2﹣）2=（2）2，则三角形PF1F2为直角三角形，则面积为：=1，故选：C．12．（5分）已知A，B是椭圆长轴的两个端点，M，N是椭圆上关于x轴对称的两点，直线AM，BN的斜率分别为k1，k2（k1k2≠0），若椭圆的离心率为，则|k1|+|k2|的最小值为（）A．1 B．C．D．2【解答】解：设M（t，s），N（t，﹣s），t∈[0，a]，s∈[0，b]，A（﹣a，0），B（a，0），k1=，k2=﹣|k1|+|k2|=||+|﹣|≥2=2当且仅当=﹣，即t=0时等号成立．因为A，B是椭圆长轴的两个端点，M，N是椭圆上关于x轴对称的两点，M（t，s），N（t，﹣s），即s=b∴|k1|+|k2|的最小值为，∵椭圆的离心率为，∴，∴a=2b∴|k1|+|k2|的最小值为1故选：A．二、填空题：本大题共4小题，每小题5分，共20分．13．（5分）过椭圆=1的焦点F的弦中最短弦长是．【解答】解：由题意设F（），过F的弦中垂直于x轴的弦最短；∴x=时，y=；∴最短弦长为．故答案为：．14．（5分）过抛物线y2=﹣12x的焦点作直线l，直线l交抛物线于，A，B两点，若线段AB中点的横坐标为﹣9，则|AB|=24．【解答】解：∵抛物线的方程为y2=﹣12x，∵2p=12，p=6，∵|AB|=x A+x B+p=x A+x B+6，∵若线段AB的中点M的横坐标为﹣9，∴（x A+x B）=﹣9，∴x A+x B=﹣18，∴|AB|=18+6=24．故答案为：2415．（5分）已知圆C过双曲线﹣=1的一个顶点和一个焦点，且圆心在此双曲线上，则圆心到双曲线中心的距离是．【解答】解：由双曲线的几何性质易知圆C过双曲线同一支上的顶点和焦点，所以圆C的圆心的横坐标为4．故圆心坐标为（4，±）．∴它到中心（0，0）的距离为d==．故答案为：．16．（5分）设点P是椭圆=1（a＞b＞0）与圆x2+y2=3b2的一个交点，F1，F2分别是椭圆的左、右焦点，且|PF1|=3|PF2|，则椭圆的离心率为．【解答】解：根据已知条件知P点在y轴右侧；由得，；∵|PF1|+|PF2|=2a，∴由|PF1|=3|PF2|得，；∴，F2（c，0）；∴，整理得：a=2，或a=（舍去）；∴a2=8b2=8a2﹣8c2；∴7a2=8c2；∴．故答案为：．三、解答题：本大题共6小题，共70分，解答应有证明或演算步骤17．（10分）已知半径为5的圆C的圆心在x轴上，圆心的横坐标是整数，且与直线4x+3y﹣29=0相切．（1）求圆C的方程；（2）设直线ax﹣y+5=0与圆C相交于A、B两点，求实数a的取值范围．【解答】解：（1）设圆心为M（m，0）（m∈Z），∵圆C与直线4x+3y﹣29=0相切，且半径为5，∴圆心，到直线4x+3y﹣29=0的距离d=r，即=5，即|4m﹣29|=25，∵m为整数，∴m=1，则所求圆的方程为（x﹣1）2+y2=25；（2）直线ax﹣y+5=0即y=ax+5，代入圆的方程，消去y整理得：（a2+1）x2+2（5a﹣1）x+1=0，∵直线ax﹣y+5=0交圆于A，B两点，∴△=4（5a﹣1）2﹣4（a2+1）＞0，即12a2﹣5a＞0，解得：a＜0或a＞，则实数a的取值范围是（﹣∞，0）∪（，+∞）．18．（12分）在平面直角坐标系xOy中，直线l与抛物线y2=4x相交于不同的两点A，B．（Ⅰ）如果直线l过抛物线的焦点，求•的值；（Ⅱ）在此抛物线上求一点P，使得P到Q（5，0）的距离最小，并求最小值．【解答】解：（Ⅰ）由题意：抛物线焦点为（1，0）设l：x=ty+1代入y2=4x消去x得y2﹣4ty﹣4=0，设A（x1，y1），B（x2，y2）则y1+y2=4t，y1y2=﹣4∴•=x1x2+y1y2=（ty1+1）（ty2+1）+y1y2=t2y1y2+t（y1+y2）+1+y1y2=﹣4t2+4t2+1﹣4=﹣3．（Ⅱ）设P（x，y），则|PQ|===，∴x=3时，P到Q（5，0）的距离最小，此时，，|PQ|min=4．19．（12分）已知椭圆的一个顶点为A（0，﹣1），焦点在x轴上，若右焦点到直线x﹣y+2=0的距离为3．（Ⅰ）求椭圆的方程；（Ⅱ）设椭圆与直线y=x+m相交于不同的两点M、N，问是否存在实数m使|AM|=|AN|；若存在求出m的值；若不存在说明理由．【解答】解：（Ⅰ）依题意可设椭圆方程为，则右焦点F（）由题设，解得a2=3．故所求椭圆的方程为．（Ⅱ）设P为弦MN的中点，由得4x2+6mx+3m2﹣3=0由于直线与椭圆有两个交点，∴△＞0，解得：﹣2＜m＜2．由韦达定理可知：，从而．∴，又|AM|=|AN|，∴AP⊥MN，则，即m=2，因为：﹣2＜m＜2．所以不存在实数m使|AM|=|AN|．20．（12分）如图，已知四棱锥S﹣ABCD中，△SAD是边长为a的正三角形，平面SAD⊥平面ABCD，四边形ABCD为菱形，∠DAB=60°，P为AD的中点，Q为SB的中点．（Ⅰ）求证：PQ∥平面SCD；（Ⅱ）求二面角B﹣PC﹣Q的大小．【解答】证明：（1）证明取SC的中点R，连QR，DR．由题意知：PD∥BC且PD=BC；QR∥BC且QP=BC，∴QR∥PD且QR=PD．∴PQ∥DR，又PQ⊄面SCD，∴PQ∥面SCD．（6分）（2）解：以P为坐标原点，PA为x轴，PB为y轴，PS为z轴建立空间直角坐标系，则S（0，0，a），B（0，a，0），C（﹣a，a，0），Q（0，a）．面PBC的法向量为=（0，0，a），设为面PQC的一个法向量，由，cos＜，∴二面角B﹣PC﹣Q的大小为arccos．（12分）21．（12分）设过点P（x，y）的直线分别与x轴和y轴交于A，B两点，点Q 与点P关于y轴对称，O为坐标原点，若且．（1）求点P的轨迹M的方程；（2）过F（2，0）的直线与轨迹M交于C，D两点，求•的取值范围．【解答】解：（1）∵过点P（x，y）的直线分别与x轴和y轴交于A，B两点，点Q与点P关于y轴对称，∴Q（﹣x，y），设A（a，0），B（0，b），∵O为坐标原点，∴=（x，y﹣b），=（a﹣x，﹣y），=（﹣x，y），，∵且，∴，解得点P的轨迹M的方程为．（2）设过F（2，0）的直线方程为y=kx﹣2k，联立，得（3k2+1）x2﹣12k2x+12k2﹣3=0，设C（x1，y1），D（x2，y2），则x1+x2=，x1x2=，=（x1﹣2，y1），=（x2﹣2，y2），∴=（x1﹣2）（x2﹣2）+y1y2=（1+k2）（x1﹣2）（x2﹣2）=（1+k2）[x1x2﹣2（x1+x2）+4]=（1+k2）（﹣+4）==+，∴当k2→∞，•的最小值→；当k=0时，•的最大值为1．∴•的取值范围是（，1]．22．（12分）如图，椭圆=1（a＞b＞0）的一个焦点是F（1，0），O为坐标原点．（Ⅰ）已知椭圆短轴的两个三等分点与一个焦点构成正三角形，求椭圆的方程；（Ⅱ）设过点F的直线l交椭圆于A、B两点．若直线l绕点F任意转动，值有|OA|2+|OB|2＜|AB|2，求a的取值范围．【解答】解：（Ⅰ）设M，N为短轴的两个三等分点，因为△MNF为正三角形，所以，即1=，解得．a2=b2+1=4，因此，椭圆方程为．（Ⅱ）设A（x1，y1），B（x2，y2）．（ⅰ）当直线AB与x轴重合时，|OA|2+|OB|2=2a2，|AB|2=4a2（a2＞1），因此，恒有|OA|2+|OB|2＜|AB|2．（ⅱ）当直线AB不与x轴重合时，设直线AB的方程为：，整理得（a2+b2m2）y2+2b2my+b2﹣a2b2=0，所以因为恒有|OA|2+|OB|2＜|AB|2，所以∠AOB恒为钝角．即恒成立．x1x2+y1y2=（my1+1）（my2+1）+y1y2=（m2+1）y1y2+m（y1+y2）+1==．又a2+b2m2＞0，所以﹣m2a2b2+b2﹣a2b2+a2＜0对m∈R恒成立，即a2b2m2＞a2﹣a2b2+b2对m∈R恒成立．当m∈R时，a2b2m2最小值为0，所以a2﹣a2b2+b2＜0．a2＜a2b2﹣b2，a2＜（a2﹣1）b2=b4，因为a＞0，b＞0，所以a＜b2，即a2﹣a﹣1＞0，解得a＞或a＜（舍去），即a＞，综合（i）（ii），a的取值范围为（，+∞）．赠送初中数学几何模型【模型五】垂直弦模型：图形特征：运用举例：1.已知A、B、C、D是⊙O上的四个点.(1)如图1，若∠ADC＝∠BCD＝90°，AD＝CD，求证AC⊥BD；(2)如图2，若AC⊥BD，垂足为E，AB＝2，DC＝4，求⊙O的半径.O DAB CEAOD CB2.如图，已知四边形ABCD 内接于⊙O ，对角线AC ⊥BD 于P ，设⊙O 的半径是2。

2014-2015学年黑龙江省哈尔滨六中高二(上)期末数学试卷(理科)

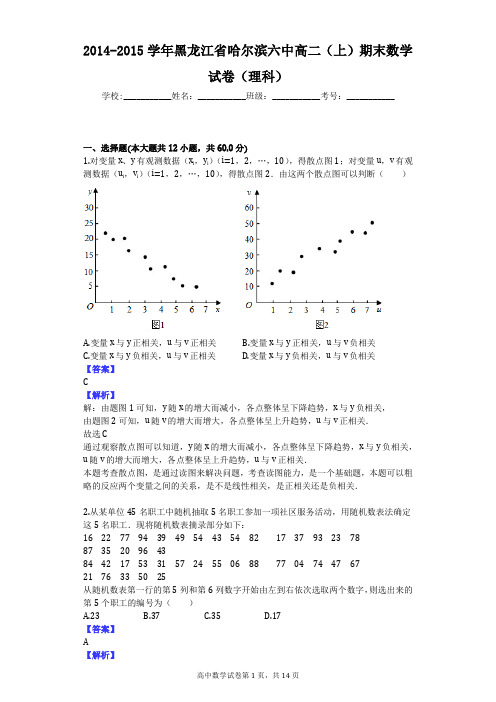
2014-2015学年黑龙江省哈尔滨六中高二（上）期末数学试卷（理科）学校:___________姓名：___________班级：___________考号：___________一、选择题(本大题共12小题，共60.0分)1.对变量x、y有观测数据（x i，y i）（i=1，2，…，10），得散点图1；对变量u，v有观测数据（u i，v i）（i=1，2，…，10），得散点图2．由这两个散点图可以判断（）A.变量x与y正相关，u与v正相关B.变量x与y正相关，u与v负相关C.变量x与y负相关，u与v正相关D.变量x与y负相关，u与v负相关【答案】C【解析】解：由题图1可知，y随x的增大而减小，各点整体呈下降趋势，x与y负相关，由题图2可知，u随v的增大而增大，各点整体呈上升趋势，u与v正相关．故选C通过观察散点图可以知道，y随x的增大而减小，各点整体呈下降趋势，x与y负相关，u随v的增大而增大，各点整体呈上升趋势，u与v正相关．本题考查散点图，是通过读图来解决问题，考查读图能力，是一个基础题，本题可以粗略的反应两个变量之间的关系，是不是线性相关，是正相关还是负相关．2.从某单位45名职工中随机抽取5名职工参加一项社区服务活动，用随机数表法确定这5名职工．现将随机数表摘录部分如下：162277943949544354821737932378 8735209643844217533157245506887704744767 2176335025从随机数表第一行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个职工的编号为（）A.23B.37C.35D.17【答案】A【解析】解：随机数表第一行的第5列和第6列数字开始由左到右依次选取两个数字，第一个数为39，然后是43，17，37，23，故选出来的第5个职工的编号是23，故选：A随机数表法也是简单随机抽样的一种方法，采用随机数表法读数时可以从左向右，也可以从右向左或者从上向下等等．应该注意的是，在读数中出现的相同数据只取一次，超过编号的数据要剔除．本题主要考查抽样方法，随机数表的使用，考生不要忽略．在随机数表中每个数出现在每个位置的概率是一样的，所以每个数被抽到的概率是一样的．3.已知向量=（1，1，0），=（-1，0，2），且与互相垂直，则k的值是（）A.1B.C.D.【答案】D【解析】解：根据题意，易得k+=k（1，1，0）+（-1，0，2）=（k-1，k，2），2-=2（1，1，0）-（-1，0，2）=（3，2，-2）．∵两向量垂直，∴3（k-1）+2k-2×2=0．∴k=，故选D．根据题意，易得k+，2-的坐标，结合向量垂直的性质，可得3（k-1）+2k-2×2=0，解可得k的值，即可得答案．本题考查向量数量积的应用，判断向量的垂直，解题时，注意向量的正确表示方法．4.已知正四棱柱ABCD-A1B1C1D1中，AA1=2AB=2，E为AA1中点，则异面直线BE与CD1所成角的余弦值为（）A. B. C. D.【答案】C【解析】解：如图连接A1B，则有A1B∥CD1，∠A1BE就是异面直线BE与CD1所成角，设AB=1，则A1E=AE=1，∴BE=，A1B=．由余弦定理可知：cos∠A1BE=．故选C．求异面直线所成的角，一般有两种方法，一种是几何法，其基本解题思路是“异面化共面，认定再计算”，即利用平移法和补形法将两条异面直线转化到同一个三角形中，结合余弦定理来求．还有一种方法是向量法，即建立空间直角坐标系，利用向量的代数法和几何法求解．本题采用几何法较为简单：连接A1B，则有A1B∥CD1，则∠A1BE就是异面直线BE与CD1所成角，由余弦定理可知cos∠A1BE的大小．本题主要考查了异面直线所成的角，考查空间想象能力和思维能力．5.设x∈Z，集合A是奇数集，集合B是偶数集．若命题p：∀x∈A，2x∈B，则（）A.￢p：∀x∈A，2x∉BB.￢p：∀x∉A，2x∉BC.￢p：∃x∉A，2x∈BD.￢p：∃x∈A，2x∉B【答案】D【解析】解：因为全称命题的否定是特称命题，所以设x∈Z，集合A是奇数集，集合B是偶数集．若命题p：∀x∈A，2x∈B，则￢p：∃x∈A，2x∉B．故选D．直接利用全称命题的否定是特称命题，写出命题的否定命题即可．本题考查命题的否定，全称命题与特称命题的否定关系，基本知识的考查．6.若P是以F1，F2为焦点的椭圆=1（a＞b＞0）上的一点，且=0，tan∠PF1F2=，则此椭圆的离心率为（）A. B. C. D.【答案】A【解析】解：∵∴，即△PF1F2是P为直角顶点的直角三角形．∵R t△PF1F2中，∠，∴=，设PF2=t，则PF1=2t∴=2c，又∵根据椭圆的定义，得2a=PF1+PF2=3t∴此椭圆的离心率为e====故选A根据向量、的数量积为零，可得△PF1F2是P为直角顶点的直角三角形．R t△PF1F2中，根据正切的定义及∠，可设PF2=t，PF1=2t，由勾股定理，得出．利用椭圆的定义得到2a=PF1+PF2=3t，最后由椭圆离心率的定义可得此椭圆的离心率．本题给出椭圆的一个焦点三角形为直角三角形，根据一个内角的正切值，求椭圆的离心率，着重考查了椭圆的基本概念和简单几何性质，属于基础题．7.甲、乙两名运动员的5次测试成绩如下图所示设s1，s2分别表示甲、乙两名运动员测试成绩的标准差，，分别表示甲、乙两名运动员测试成绩的平均数，则有（）A.，s1＜s2B.，s1＞s2C.＞，s1＞s2 D.，s1=s2【答案】B【解析】解：根据茎叶图可得，s1==，，s2==．所以，s1＞s2．故选B．根据均值与标准差的计算公式可得所以，s1＞s2．进而得到答案．解决此类问题的关键是熟练记忆均值与标准差的公式以及正确理解茎叶图的特征．8.设l，m，n表示三条不同的直线，α，β，γ表示三个不同的平面，给出下列四个命题：①若l⊥α，m⊥l，m⊥β，则α⊥β；②若m⊂β，n是l在β内的射影，m⊥n，则m⊥l；③若m是平面α的一条斜线，A∉α，l为过A的一条动直线，则可能有l⊥m，l⊥α；④若α⊥β，α⊥γ，则α∥β其中真命题的个数为（）A.1B.2C.3D.4【答案】B【解析】解：①由空间向量知m⊥l，则α⊥β正确；②由三垂线定理知正确；③若m是平面α的一条斜线，l⊥α，则l和m不可能垂直，故命题错误；④正方体从同一个顶点出发的三个平面知命题错误故选B①由空间向量知识可知正确；②由三垂线定理可证；③④可举反例说明错误．本题考查空间的线面位置关系，考查空间想象能力和逻辑推理能力．9.某四面体的三视图如图所示，三个三角形均为直角三角形，则该四面体的表面积是（）A.8B.22+2C.18+6D.24+6【答案】D【解析】解：根据几何体的三视图知，该几何体是三棱锥，如图所示；且底面△ABC为俯视图中的直角三角形，∠ABC=90°，其中AB=4，BC=3，∴AC=5，PA⊥底面ABC，且PA=4，∴∠PAB=∠PAC=90°，CB⊥PB；∴S△ABC=AB•BC=×4×3=6，S△PAB=PA•AB=×4×4=8，S△PAC=PA•AC=×4×5=10，S△PBC=PB•BC=××3=6；∴三棱锥P-ABC的表面积为S=S△ABC+S△PAB+S△PAC+S△PBC=6+8+10+6=24+6．故选：D．根据几何体的三视图，得出该几何体是三棱锥，并根据三棱锥的各棱之间的关系，求出它的表面积．本题考查了空间几何体的三视图的应用问题，解题时应根据三视图得出该几何体的结构特征，是基础题．10.已知两点A（1，0），B（b，0），若抛物线y2=4x上存在点C使△ABC为等边三角形，则b=（）A.5B.5或-C.4D.4或-2【答案】B【解析】解：过点C做x轴垂线，垂足为D，根据正三角形性质可知D为A，B的中点，坐标为（，0），则DC=•，∴C点坐标为（，±•），代入抛物线方程得，×4=×3，整理得3b2-14b-5=0，求得b=5或-，故选：B．过点C做x轴垂线，垂足为D，根据正三角形性质可知D为A，B的中点，坐标为（，0）求得DC的长，从而得到C点的坐标代入抛物线方程即可求得b．本题主要考查了抛物线的应用．解题的关键是充分利用正三角形的性质，求出C点的坐标．11.设F1、F2是双曲线C：=1（a＞0，b＞0）的两个焦点，P是C上一点，若|PF1|+|PF2|=6a，且△PF1F2最小内角的大小为30°，则双曲线C的渐近线方程是（）A.x±y=0 B.x±y=0 C.x±2y=0 D.2x±y=0【答案】B【解析】解：设|PF1|＞|PF2|，则|PF1|-|PF2|=2a，又|PF1|+|PF2|=6a，解得|PF1|=4a，|PF2|=2a．则∠PF1F2是△PF1F2的最小内角为30°，∴|PF2|2=|PF1|2+|F1F2|2-2|PF1|•|F1F2|cos30°，∴（2a）2=（4a）2+（2c）2-2×4a×2c×，同时除以a2，化简e2-2e+3=0，解得e=，∴c=，∴b==，∴双曲线C：=1的渐近线方程为y==±，即=0．故选：B．设|PF1|＞|PF2|，由已知条件求出|PF1|=4a，|PF2|=2a，e=，进而求出b=，由此能求出双曲线C：=1的渐近线方程．本题考查双曲线的渐近线方程的求法，是中档题，解题时要认真审题，要熟练掌握双曲线的简单性质．12.在球O表面上有A、B、C三个点，若∠AOB=∠BOC=∠COA=，且O到平面的距离为2，则此球的表面积为（）A.48πB.36πC.24πD.12π【答案】A【解析】解：由题意，∵∠AOB=∠BOC=∠COA=，OA=OB=OC∴四面体O-ABC为正四面体设球的半径为R∵O到平面的距离为2，∴R2=8+R2，∴R2=12，∴球的表面积为4π×12=48π，故选A．根据∠AOB=∠BOC=∠COA=，OA=OB=OC，可得四面体O-ABC为正四面体，利用O 到平面的距离为2，确定球的半径，进而可求球的表面积．本题考查球的表面积，考查正四面体的性质，解题的关键是确定球的半径．二、填空题(本大题共4小题，共20.0分)13.袋中有大小相同的红色、白色球各一个，每次任取一个，有放回地摸3次，3次摸到的红球比白球多1次的概率为______ ．【答案】【解析】解：列举可得总的基本事件为（红，红，红），（红，红，白）（红，白，红）（白，红，红），（红，白，白），（白，红，白）（白，白，红）（白，白，白）共8个，其中红球比白球多1次的有（红，红，白）（红，白，红）（白，红，红）共3个，∴所求概率为P=故答案为：列举可得总的基本事件共8个，满足题意的有3个，由概率公式可得．本题考查古典概型及其概率公式，列举是解决问题的关键，属基础题．14.如图，在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5，点D是线段AB上的一点，且∠CDB1=90°，AA1=CD，则点A1到平面B1CD的距离为______ ．【答案】 3【解析】解：∵在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5，∴AC⊥BC，以C为原点，CA为x轴，CB为y轴，CC1为z轴，建立空间直角坐标系，设AA1=CD=t，C（0，0，0），D（a，b，0），B1（0，4，t），A（3，0，0），B（0，4，0），，，设，则（a-3，b，0）=（-3λ，4λ，0），∴a=3-3λ，b=4λ，即D（3-3λ，4λ，0），∴=（3-3λ，4λ，0），=（3-3λ，4λ-4，-t），∵∠CDB1=90°，∴=25λ2-34λ+9=0，解得λ=1或，当λ=1时，D与B重合，点A到面B1CD的距离为3；当λ=时，=（，，0），t==，=（0，4，），设平面B1CD的法向量=（x，y，z），则，取x=3，得=（3，-4，），=（3，0，），∴点A1到平面B1CD的距离为：d===3．综上所述，点A1到平面B1CD的距离为3．故答案为：3．以C为原点，CA为x轴，CB为y轴，CC1为z轴，建立空间直角坐标系，利用向量法能求出点A1到平面B1CD的距离．本题主要考查了线面垂直的性质，以及线面平行的判定和二面角的度量，同时考查了转化与划归的思想，属于中档题．15.已知双曲线（a＞0，b＞0）的两条渐近线与抛物线y2=2px（p＞0）的准线分别交于A，B两点，O为坐标原点．若双曲线的离心率为2，△AOB的面积为，则p= ______ ．【答案】2【解析】解：∵双曲线（a＞0，b＞0），∴双曲线的渐近线方程是y=±x又抛物线y2=2px（p＞0）的准线方程是x=-，故A，B两点的纵坐标分别是y=±，又由双曲线的离心率为2，所以，则，A，B两点的纵坐标分别是y=±=±，又△AOB的面积为，x轴是角AOB的角平分线∴××=，得p=2．故答案为：2．求出双曲线（a＞0，b＞0）的渐近线方程与抛物线y2=2px（p＞0）的准线方程，进而求出A，B两点的坐标，再由双曲线的离心率为2，△AOB的面积为，列出方程，由此方程求出p的值．本题考查圆锥曲线的共同特征，解题的关键是求出双曲线的渐近线方程，解出A，B两点的坐标，列出三角形的面积与离心率的关系也是本题的解题关键，有一定的运算量，做题时要严谨，防运算出错．16.从双曲线x2-y2=1上一点Q引直线x+y=2的垂线，垂足为N，则线段QN的中点P 的轨迹方程为______ ．【答案】2x2-2y2-2x+2y-1=0【解析】解：设P（x，y），Q（x1，y1），则N（2x-x1，2y-y1），∵N在直线x+y=2上，∴2x-x1+2y-y1=2①又∵PQ垂直于直线x+y=2，∴=1，即x-y+y1-x1=0．②由①②得，又∵Q在双曲线x2-y2=1上，∴x12-y12=1．∴（x+y-1）2-（x+y-1）2=1．整理，得2x2-2y2-2x+2y-1=0即为中点P的轨迹方程．故答案为：2x2-2y2-2x+2y-1=0．设P（x，y），欲求其轨迹方程，即寻找其坐标间的关系，根据垂线的关系及点Q在双曲线上，代入其方程即可得到．本题主要考查了轨迹方程的问题．求曲线的轨迹方程是解析几何的基本问题．代入法：动点所满足的条件不易表述或求出，但形成轨迹的动点P（x，y）却随另一动点Q（x’，y’）的运动而有规律的运动，且动点Q的轨迹为给定或容易求得，则可先将x’，y’表示为x，y的式子，再代入Q的轨迹方程，然而整理得P的轨迹方程，代入法也称相关点法．三、解答题(本大题共6小题，共70.0分)17.（选做题）直角坐标系x O y和极坐标系O x的原点与极点重合，x轴正半轴与极轴重合，单位长度相同，在直角坐标系下，曲线C的参数方程为，为参数）．（1）在极坐标系下，曲线C与射线和射线分别交于A，B两点，求△AOB 的面积；（2）在直角坐标系下，直线l的参数方程为（t为参数），求曲线C与直线l的交点坐标．【答案】解：（1）曲线C的参数方程为，为参数）．消去参数得它的普通方程为：，将其化成极坐标方程为：，分别代入和得|OA|2=|OB|2=，因∠AOB=，故△AOB的面积S=|OA||OB|=．（2）将l的参数方程代入曲线C的普通方程，得（t-2）2=0，∴t=2，代入l的参数方程，得x=2，y=，∴曲线C与直线l的交点坐标为（2，）．【解析】（1）先消去参数方程中的参数得普通方程，再利用直角坐标与极坐标间的关系，即利用ρcosθ=x，ρsinθ=y，ρ2=x2+y2，进行代换将直角坐标方程化成极坐标方程，通过极坐标方程求出三角形的边长后求面积即可．（2）将l的参数方程代入曲线C的普通方程，得t的值，再代入l的参数方程，得曲线C与直线l的交点坐标．本题考查点的极坐标和直角坐标的互化，能在极坐标系中用极坐标刻画点的位置，体会在极坐标系和平面直角坐标系中刻画点的位置的区别，能进行极坐标和直角坐标的互化．18.三棱锥A-BCD中，面ACD与面BCD均为正三角形，点E，F，G，H分别为BD，BC，AC，AD中点（1）证明：四边形EFGH为矩形；（2）若二面角A-DC-B大小为60°，求直线EH与面BCD所成角的正弦值．【答案】（1）证明：∵三棱锥A-BCD中，面ACD与面BCD均为正三角形，点E，F，G，H分别为BD，BC，AC，AD中点，∴EF∥DC∥HG，且EF=，∴EFGH是平行四边形，取CD中点O，连结AO，BO，∴DC⊥平面AOB，∴CD⊥AB，EH⊥EF，∴四边形EFGH为矩形．（2）解：由（1）知∠AOB为二面角A-DC-B的平面角，∴∠AOB=60°，∵AB∥EH，∴EH与平面BCD所成角为AB与面BCD所成角，∵DC⊥平面AOB．∴AB在面BCD射影为BO，∵AO=BO，∴∠ABO=60°，∴EH与面BCD所成角的正弦为sin60°=．【解析】（1）由已知得EFGH是平行四边形，取CD中点O，连结AO，BO，则CD⊥AB，EH⊥EF，由此能证明四边形EFGH为矩形．（2）由已知得∠AOB=60°，EH与平面BCD所成角为AB与面BCD所成角，由此能求出EH与面BCD所成角的正弦．本题考查四边形为矩形的证明，考查直线与平面所成角的正弦值的求法，解题时要认真审题，注意空间思维能力的培养．19.从某学校高三年级共800名男生中随机抽取50人测量身高．据测量被测学生身高全部介于155cm到195cm之间，将测量结果按如下方式分成八组：第一组[155，160）；第二组[160，165）；…；第八组[190，195]．如图所示是按上述分组方法得到的频率分布直方图的一部分．已知第一组与第八组人数相同，第六组、第七组、第八组人数依次构成等差数列．（I）估计这所学校高三年级全体男生身高在180cm以上（含180cm）的人数；（II）求第六组、第七组的频率，并补充完整频率分布直方图；（III）试求被抽取50人的中位数的近似值．（精确到0.1cm）【答案】解：（I）前五组频率为（0.008+0.016+0.04+0.04+0.06）×5=0.82∴后三组频率为1-0.82=0.18，人数为0.18×50=9∴这所学校高三年级全体男生身高180cm以上（含180cm）人数800×0.18=144人（II）第八组频率为0.008×5=0.04，人数为0.04×50=2设第六组人数m，∴m+2=2（7-m）解得m=4∴六七组频率分别为0.08、0.06，纵坐标分别为0.016、0.012（III）该中位数为x，∴（0.008+0.016+0.04）×5+（x-170）×0.04=0.5解得：x=174.5 【解析】（I）根据已知中的频率分布直方图，我们分别求出180cm以上各组矩形的高度和，乘以组距即可得到高在180cm以上（含180cm）的频率，再乘以样本容量即可得到高在180cm以上（含180cm）的人数；（II）根据第一组与第八组人数相同，第六组、第七组、第八组人数依次构成等差数列我们可以求出第六组、第七组、第八组的频率也成等差数列，进而即可同答案．（III）根据中位数两边的频率相等，既左边和右边的频率和均为0.5，构造出关于中位数x的方程，即可得到答案．本题考查的知识点是频率分布直方图，用样本的频率分布估计总体分布，其中频率=矩形的高×组距=频数÷样本容量，是解答本题的关键．20.如图，已知椭圆=1（a＞b＞0），F1、F2分别为椭圆的左、右焦点，A为椭圆的上顶点，直线AF2交椭圆于另一点B、（1）若∠F1AB=90°，求椭圆的离心率；（2）若=2，•=，求椭圆的方程．【答案】解：（1）若∠F1AB=90°，则△AOF2为等腰直角三角形，所以有OA=OF2，即b=C、所以a=c，e==．（2）由题知A（0，b），F1（-c，0），F2（c，0），其中，c=，设B（x，y）．由=2⇔（c，-b）=2（x-c，y），解得x=，y=-，即B（，-）．将B点坐标代入=1，得+=1，即+=1，解得a2=3c2．①又由•=（-c，-b）•（，-）=⇒b2-c2=1，即有a2-2c2=1．②由①，②解得c2=1，a2=3，从而有b2=2．所以椭圆方程为+=1．【解析】（1）根据∠F1AB=90°推断出△AOF2为等腰直角三角形，进而可知OA=OF2，求得b 和c的关系，进而可求得a和c的关系，即椭圆的离心率．（2）根据题意可推断出A，和两个焦点的坐标，设出B的坐标，利用已知条件中向量的关系，求得x和y关于c的表达式，代入椭圆方程求得a和c的关系，利用•=求得a和c的关系，最后联立求得a和b，则椭圆方程可得．本题主要考查了椭圆的应用和椭圆的简单性质，向量的基本性质．注意挖掘题意中隐含的条件，充分利用．21.四棱锥P-ABCD中，棱长PD=a，底面ABCD是边长为a的菱形，点M为PB中点（1）若∠BCP=90°，证明：MD⊥PC；（2）若∠BCD=90°，∠PDA=PDC=60°，求二面角B-PD-A的余弦值．【答案】（1）证明：取PC中点N，连接MN，DN，则MN∥BC，∵∠BCP=90°，∴MN⊥PC，∵DP=DC，∴DN⊥PC，∵MN∩DN=N，∴PC⊥平面MND，∵MD⊂平面MND，∴MD⊥PC；（2）解：由题意，底面ABCD为正方形，△PAD与△PCD为正三角形，令AC∩BD=O，则PO⊥平面ABCD，作OQ⊥PD，连接AQ，则∠AQO为二面角B-PD-A的平面角，由题意，AO=a，AQ=，OQ=，∴cos∠AQO==．【解析】（1）取PC中点N，连接MN，DN，则MN∥BC，证明PC⊥平面MND，即可得出结论；（2）令AC∩BD=O，则PO⊥平面ABCD，作OQ⊥PD，连接AQ，则∠AQO为二面角B-PD-A的平面角，利用余弦定理，即可得出结论．本题考查线面垂直的判定与性质，考查二面角的平面角，考查学生分析解决问题的能力，属于中档题．22.椭圆G：+=1（a＞b＞0）的左、右焦点为F1F2，离心率为，连接椭圆的四个顶点得到的四边形的面积为2，直线l1过点F1且垂直于椭圆的长轴，动直线l2垂直l1于点P，线段PF2的垂直平分线交l2于点M．（1）求椭圆G的方程；（2）求点M的轨迹E的曲线方程；（3）点A，B为曲线E上异于原点O的两点，OA⊥OB，+=，求四边形AOBC的面积最小值．【答案】解：（1）由题意可得：，解得a2=3，c=1，b2=2．∴椭圆G的方程为．（2）点M满足：|MP|=|MF2|，∴点M是以F2为焦点，l1为准线的抛物线，其轨迹E的方程为：y2=4x．（3）设直线OA，OB的方程分别为：y=kx，．（k≠0）联立，解得A，，同理可得B（4k2，-4k）．∴S=|OA||OB|==≥32，当且仅当k=±1时取等号．∴四边形AOBC的面积最小值为32．【解析】（1）由题意可得：，解得即可得出；（2）点M满足：|MP|=|MF2|，由抛物线的定义可得：点M是以F2为焦点，l1为准线的抛物线，即可得出其轨迹E的方程．（3）设直线OA，OB的方程分别为：y=kx，．与抛物线方程联立解得A，，同理可得B（4k2，-4k）．可得S=|OA||OB|==，利用基本不等式的性质即可得出．本题考查了椭圆与抛物线的定义标准方程及其性质、直线与抛物线交转化为方程联立、四边形的面积计算公式、基本不等式的性质，考查了推理能力与计算能力，属于中档题．。

黑龙江省哈尔滨市第三十二中学2014-2015学年高二上学期期中考试数学(理)试题

黑龙江省哈尔滨市第三十二中学2014-2015学年高二上学期期中考试数学（理）试题一、选择题（每小题只有1个选项符合题意，每小题4分，共48分）1．已知椭圆1162522=+y x 上一点P 到椭圆一个焦点的距离为3，则P 到另一个焦点的距离为（） A ．2B ．3C ．5D ．72．抛物线y =-x 2 的焦点坐标为（）A ．(0,41) B ． (0, -41) C ．(41, 0) D ． (-41, 0) 3．过抛物线x y 42=的焦点F 作倾斜角为3π的弦AB ，则|AB|的值（） A ．738 B ．316 C ．38 D ．73164．以原点为圆心，且截直线01543=++y x 所得弦长为8的圆的方程是（）A ．522=+y xB ．2522=+y xC ．422=+y xD ．1622=+y x5．若过原点的直线与圆2x +2y +x 4+3=0相切，若切点在第三象限，则该直线的方程是（）A ．x y 3=B ．x y 3-=C ．x y 33=D ．x y 33-= 6．双曲线12222=-ay b x 的两条渐近线互相垂直，那么该双曲线的离心率是（）A ．2B ．3C ．2D ．237．设k>1，则关于x ，y 的方程(1-k) x 2+ y 2=k 2-1所表示的曲线是（）A ．长轴在y 轴上的椭圆B ．长轴在x 轴上的椭圆C ．实轴在y 轴上的双曲线D ．实轴在x 轴上的双曲线 8 231y x -=所表示的曲线是（）A ．双曲线B ．椭圆C ．双曲线的一部分D ．椭圆的一部分9椭圆12222=+b y a x (a >b>0)离心率为23,则双曲线12222=-by a x 的离心率为（）A ．45B ．25C ．32D ．4510 抛物线顶点在原点，焦点在y 轴上，其上一点P(m ，1)到焦点距离为5，则抛物线方程为（）A ．y x 82=B ．y x 82-=C ．y x 162=D ．y x 162-=11 如果实数x 、y 满足等式3)2(22=+-y x ，则xy最大值（） A ．21 B ．33 C ．23D ．312. 已知圆C 的半径为2，圆心在x 轴的正半轴上，直线0443=++y x 与圆C 相切，则圆C 的方程为（） A 03222=--+x y xB 0422=++x y xC 03222=-++x y xD 0422=-+x y x二、填空题（每空4分，共16分）13. 椭圆1422=+y m x 的一个焦点坐标是（0，1），则m= ． 14. 椭圆的焦点是F 1（－3，0）F 2（3，0），P 为椭圆上一点，且|F 1F 2|是|PF 1|与|PF 2|的等差中项，则椭圆的方程为_____________________________．15. 双曲线x 2-42y =1截直线y =x +1所得弦长是． 16．若经过点(1,0)P -的直线与圆032422=+-++y x y x 相切，则此直线在y 轴上的截距是 __________________ ．哈32中2014～2015学年度上学期中考试数学（理）试题答题卡一、选择题：(本大题共12小题，每小题4分，共48分。

黑龙江省哈三中2014-2015学年度高二上学期期末考试物理试卷扫描版含答案

哈三中2014—2015学年度上学期高二学年模块考试物理试卷答案1、C2、C3、C4、C5、B6、B7、D8、BC 9、 BD 10、ABD 11、BD 12、BC13、A ；5.25mm 14、短接（对接）（接触）；中央；3200 15、3.0；0.50；小于16、(1)根据库仑定律，A 、B 两点电荷间的库仑力大小为：F ＝k q 2L 2① 代入数据得： F ＝9.0×10－3 N ②(2)A 、B 两点电荷在C 点产生的场强大小相等，则A 、B 两点电荷形成的电场在C 点的合场强大小为：E ＝2k q L 2cos30°③ 代入数据得：E ＝7.8×103 N/C ④场强E 的方向沿y 轴正方向（或竖直向上）．⑤评分细则：①-⑤各2分，共10分。

17、（1）静止时：IL B mg 1030sin =-------2分R EI 2=--------2分得：EL mgRB =1----1分（2）静止且无压力时：IL B mg 2=-------2分EL mgRB 22=--------2分方向水平向左-------1分18、（1）（8分）设粒子经PT 直线上的点R 由E 2电场进入E 1电场，由Q 到R 及R 到M 点的时间分别为t 2与t 1，到达R 时竖直速度为v y ，则：在E 2中：22221t a L = -------- 2分 22ma qE =------2分得：22221t m qE L ⋅=-----1分在E 1中，同理可得：211212t m qE L ⋅=-----1分 1122t m qE t m qE v y ⋅=⋅=-------1分综上可得：221=E E ------1分（2）（8分）欲使粒子仍能从S 孔处射出，粒子的运动轨迹可能是如图甲、乙所示的两种情况。

对图甲所示的情形，粒子运动的半径为R 1，则⋯⋯=+=210,)12(21、、n n d R （1分）又12010R mv B qv = （1分）解得：⋯⋯=+=210,)12(201、、n qdmv n B （2分）对图乙所示的情形，粒子运动的半径为R 2，则⋯⋯==321,42、、n nd R （1分）又22020R mv B qv = （1分） ⋯⋯==321,402、、n qdnmv B （2分）综合B 1、B 2得：⋯⋯==32120、、N ,qa Nmv B乙。

2014-2015学年度高二上学期期末试卷

2014-2015学年度高二上学期期末试卷高二化学注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题（题型注释）1．2010年上海世博会主题“城市．让生活更美好”；2011年“国际化学年”的主题是“化学，我们的生活，我们的未来”；2013年1月全国大部分地区出现雾霾天气，北京PM2.5浓度达993，系中国有该监测数据以来最高的一次。

“拯救人类的最后机会”只有节能减排,下列属最有希望的新能源是 ( )①天然气 ②煤 ③石油 ④水能 ⑤太阳能 ⑥地热能 ⑦风能 ⑧氢能A.①②③④B.⑤⑥⑦⑧C.③④⑤⑥D.除①②外2．分子式为C 2H 6O 的有机物，有两种同分异构体，乙醇(CH 3CH 2OH)、甲醚(CH 3OCH 3)，则通过下列方法，不可能将二者区别开来的是 ( )A ．红外光谱B ．1H 核磁共振谱C ．质谱法D ．与钠反应3．下列有机物不是同一种物质的是（）A ．C ClCl H H 和C Cl Cl H H B ．CH 2=CH —CH=CH 2和 CH CH CH 2CH 2C．C(CH3)3C(CH3)3和CH3(CH2)3C(CH3)3 D．CH CHCH3CH3CH3CH3和CHCHCH3CH3CH3CH34．化学家们合成了如图所示的一系列的星烷，如三星烷、四星烷、五星烷等。

下列说法不正确的是 ( )A．它们之间互为同系物 B.三星烷的化学式为C9H12C．三星烷与丙苯互为同分异构体 D.它们的一氯代物均只有两种5．A、B两种有机物组成的混合物，当其质量相等时，无论A、B以何种比例混合，完全燃烧时产生H2O的量均相等，符合这一条件的组合是 ( )①同分异构体②同系物③最简式相同④含氢质量分数相同⑤分子中氢原子数相同⑥分子中氢、氧原子数分别相同A．①③④ B．①②③ C．①⑤⑥ D．②④⑥6．某有机物链状分子中含a个甲基，n个亚甲基（—CH2—），m个次甲基（），其余为氯原子。

黑龙江省哈三中2014-2015学年度高二上学期期末考试英语试卷扫描版含答案

2014年黑龙江省学业水平考试英语答案第一部分：听力1－5 BABCC 6－10 BAACB 11－15 ACABC 16－20 BBAAB第二部分：阅读理解21－25 BBADB 26－30 ACDCD 31－35 BCCDC 36－40 BDGFA第三部分：英语知识运用41~45 CABBD 46~50 ACBDA 51~55 CCCAB 56~60 BACBD单句改错61. Mr. Smith rose to his foot, cheering appreciatively when the concert ended.feet62. Thank to your great help, I managed to overcome many learning difficulties.Thanks63. A heated debate was held in front of a live audience which was consisted mainly of students from Grade 2.64. As we all know, the pressure from study is in the increase among young people.on65. I was on the point of enjoying the tasty Durian Cake while someone knocked at the door.when66. We’d like to know the reason that you lied to our company when applying for the position at that time.why67. I’m curious about what happened before the party started.加had68. Forcing to get up early in the morning, I am not in the mood for breakfast.Forced69. The little girl strongly suggested play a trick on her cousin at the party.playing70. That is essential to read any agreement carefully before you sign it.It单句填空71.turned 72. relaxing 73. performances 74. have caught 75. to be 76. Unless77. for 78. an 79. since 80. that语篇填空81. who/that 82. dangerous 83. in 84. However 85. climbs86. other 87. directions 88. much 89. Actually 90. taking第四部分：书面表达One possible version:Dear Mr. Dean,It is nice to learn that 10 students from America will come to our school for a Study Abroad program. After I consulted with my parents, my family would like to be a host family to one of them. We have the following advantages.First of all, my dad is a university teacher, and my mom is a saleswoman in a shop. We all can speak English, so it will be easy for us to communicate with our guest. Second, we have a spare room with a washroom and shower for our guest’s convenience. Third, my home is within easy reach of the school, and it normally takes about 10 minutes by subway or 25 minutes by bus. What is more, my mom is good at cookng. I believe my guest will have a pleasant stay with my family.I’m looking forward to your reply.Yours,Li Hua。

黑龙江省哈尔滨三中2014-2015学年高二上学期期末试卷试卷(理科)

黑龙江省哈尔滨三中2014-2015学年高二上学期期末试卷试卷（理科）一、选择题：每小题5分，共60分，在四个选项中，只有一项是符合题目要求的．1．（5分）集合M={1，2，3}的真子集个数为（）A．6B．7C．8D．92．（5分）过点（2，﹣2）且与双曲线﹣y2=1有公共渐近线的双曲线方程是（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=13．（5分）从装有4个红球、2个白球的袋中任取3个球，则所取的3个球中至少有1个白球的概率为（）A．B．C．D．4．（5分）（x2﹣）3的展开式中常数项是（）A．9B．﹣9 C．27 D．﹣275．（5分）已知两点M（﹣2，0），N（2，0），点P满足•=12，则点P的轨迹方程为（）A．+y2=1 B．x2+y2=16 C．y2﹣x2=8 D．x2+y2=86．（5分）已知椭圆的离心率，则实数k的值为（）A．3B．3或C．D．或7．（5分）已知直线mx+ny+1=0与圆x2+y2=1相切，则2m+n的最大值为（）A．2B．C．D．38．（5分）在长为12cm的线段AB上任取一点C．现做一矩形，邻边长分别等于线段AC，CB的长，则该矩形面积小于32cm2的概率为（）A．B．C．D．9．（5分）两个实习生每人加工一个零件．加工为一等品的概率分别为和，两个零件是否加工为一等品相互独立，则这两个零件中恰有一个一等品的概率为（）A．B．C．D．10．（5分）抛物线y=﹣x2上的点到直线4x+3y﹣8=0距离的最小值是（）A．B．C．D．311．（5分）已知随机变量X和Y，其中Y=12X+7，且EY=34，若X的分布列如表所示，则m的值为（）X 1 2 3 4P m nA．B．C．D．12．（5分）已知中心在原点的椭圆与双曲线有公共焦点，且左右焦点分别为F1F2，且两条曲线在第一象限的交点为P，△PF1F2是以PF1为底边的等腰三角形．若|PF1|=10，椭圆与双曲线的离心率分别为e1，e2，则e1•e2的取值范围是（）A．（0，）B．C．D．二、填空题：每小题5分，共20分．13．（5分）已知两点A（﹣2，﹣2）、B（3，7），则线段AB的垂直平分线的方程为．14．（5分）已知小明投10次篮，每次投篮的命中率均为0.7，记10次投篮命中的次数为X，则DX=．15．（5分）三位同学参加跳高、跳远、铅球项目的比赛，若每人都选择其中两个项目，则有且仅有两人选择的项目完全相同的概率是（结果用最简分数表示）．16．（5分）现要将编号为1，2，3，4的四个小球全部放入甲、乙、丙三个盒中，每个至少放一个球，且甲盒不能放入1号球，乙盒不能放入2号球，则所有不同的放法种数为（用数字作答）．三、解答题：共70分．解答应写出必要的文字说明、证明过程或演算步骤．17．（10分）（2x+）n展开式中所有的项的系数为243．（Ⅰ）求n的值；（Ⅱ）求展开式中x2项的系数．18．（12分）将一枚骰子先后抛掷两次，记第一次的点数为x，第二次的点数为y．（Ⅰ）求点P（x，y）在直线y=x+1上的概率；（Ⅱ）求y2＜4x的概率．19．（12分）某袋中有10个乒乓球，其中有7个新、3个旧球，从袋中任取3个来用，用后放回袋中（新球用后变为旧球），记此时袋中旧球个数为X，求X的数学期望．20．（12分）过抛物线y2=x的顶点O作两条相互垂直的弦OA，OB，求△AOB面积的最小值．21．（12分）小强参加一次测试，共有三道必答题，他是否答对每题互不影响．已知他只答对第一题的概率为0.08，只答对第一题和第二题的概率为0.1，至少答对一题的概率为0.88，用X表示小强答对题的数目．（Ⅰ）求小强答对第一题的概率；（Ⅱ）求X的分布列和数学期望．22．（12分）设椭圆C：过点（1，），F1，F2分别为椭圆C的左右焦点，且离心率（1）求椭圆C的方程．（2）已知A为椭圆C的左顶点，直线l过右焦点F2与椭圆C交于M，N两点，若AM、AN 的斜率k1，k2满足，求直线l的方程．黑龙江省哈尔滨三中2014-2015学年高二上学期期末试卷试卷（理科）参考答案与试题解析一、选择题：每小题5分，共60分，在四个选项中，只有一项是符合题目要求的．1．（5分）集合M={1，2，3}的真子集个数为（）A．6B．7C．8D．9考点：子集与真子集．专题：集合．分析：根据题意，集合M中有3个元素，由集合的子集与元素数目的关系，计算可得答案．解答：解：集合M中有3个元素，有23=8个子集，有23﹣1=7个真子集；故选B．点评：本题考查集合的元素数目与子集数目的关系，若集合中有n个元素，则其有2n个子集．2．（5分）过点（2，﹣2）且与双曲线﹣y2=1有公共渐近线的双曲线方程是（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=1考点：双曲线的标准方程．分析：设所求双曲线方程为﹣y2=λ，把（2，﹣2）代入方程﹣y2=λ，求出λ，可得到所求的双曲线方程．解答：解：设所求双曲线方程为﹣y2=λ，把（2，﹣2）代入方程﹣y2=λ，解得λ=﹣2．由此可求得所求双曲线的方程为．故选A．点评：本题考查双曲线的渐近线方程，解题时要注意公式的灵活运用．3．（5分）从装有4个红球、2个白球的袋中任取3个球，则所取的3个球中至少有1个白球的概率为（）A．B．C．D．考点：相互独立事件的概率乘法公式．专题：概率与统计．分析：用间接法，首先分析从6个球中任取3个球的情况数目，再求出所取的3个球中没有白球即全部红球的情况数目，计算可得没有白球的概率，而“没有白球”与“3个球中至少有1个白球”为对立事件，由对立事件的概率公式，计算可得答案．解答：解：根据题意，首先分析从6个球中任取3个球，共C63=20种取法，所取的3个球中没有白球即全部红球的情况有C43=4种，则没有白球的概率为=；则所取的3个球中至少有1个白球的概率是1﹣=；故选：B．点评：本题考查古典概型的计算，注意至多、至少一类的问题，可以选用间接法，即借助对立事件的概率的性质，先求其对立事件的概率，进而求出其本身的概率．4．（5分）（x2﹣）3的展开式中常数项是（）A．9B．﹣9 C．27 D．﹣27考点：二项式定理的应用．专题：二项式定理．分析：利用展开式的通项公式求出展开式的通项，令x的指数为0，求出r的值，求出答案．解答：解：展开式的通项为T r+1=×x2（3﹣r）×（﹣1）r×3r×x﹣r=×（﹣3）r×x6﹣3r，令6﹣3r=0⇒r=2，∴（x2﹣）3的展开式中常数项是T3=×9=27．故选：C．点评：本题考查利用二项展开式的通项公式解决二项展开式的特定项问题．5．（5分）已知两点M（﹣2，0），N（2，0），点P满足•=12，则点P的轨迹方程为（）A．+y2=1 B．x2+y2=16 C．y2﹣x2=8 D．x2+y2=8考点：轨迹方程．专题：计算题．分析：设P点坐标为（x，y），由•=12进而可得到x和y的关系式．解答：解：设P（x，y），则=（﹣2﹣x，﹣y），=（2﹣x，﹣y）∴•=（2﹣x）（﹣2﹣x）+y2=12整理可得x2+y2=16．故选B点评：本题主要考查了轨迹方程．解题的关键是设出所求点的坐标为（x，y）进而找到x和y的关系式．6．（5分）已知椭圆的离心率，则实数k的值为（）A．3B．3或C．D．或考点：椭圆的简单性质．专题：计算题．分析：当K＞5时，由e===求得K值，当0＜K＜5时，由e===，求得K值．解答：解：当K＞5时，e===，K=．当0＜K＜5时，e===，K=3．综上，K=3，或．故选B．点评：本题考查椭圆的标准方程，以及简单性质的应用，体现了分类讨论的数学思想，分类讨论是解题的关键．7．（5分）已知直线mx+ny+1=0与圆x2+y2=1相切，则2m+n的最大值为（）A．2B．C．D．3考点：圆的切线方程．专题：计算题；直线与圆．分析：利用直线mx+ny+1=0与圆x2+y2=1相切，可得=1，即m2+n2=1，设m=cosα，n=sinα，则2m+n=2cosα+sinα=sin（α+θ）≤，即可求出2m+n的最大值．解答：解：∵直线mx+ny+1=0与圆x2+y2=1相切，∴=1，∴m2+n2=1，设m=cosα，n=sinα，则2m+n=2cosα+sinα=sin（α+θ）≤，∴2m+n的最大值为，故选：C．点评：本题考查直线与圆的位置关系，考查三角函数知识，正确运用直线mx+ny+1=0与圆x2+y2=1相切是关键．8．（5分）在长为12cm的线段AB上任取一点C．现做一矩形，邻边长分别等于线段AC，CB的长，则该矩形面积小于32cm2的概率为（）A．B．C．D．考点：几何概型．专题：计算题．分析：设AC=x，则0＜x＜12，若矩形面积为小于32，则x＞8或x＜4，从而利用几何概型概率计算公式，所求概率为长度之比解答：解：设AC=x，则BC=12﹣x，0＜x＜12若矩形面积S=x（12﹣x）＜32，则x＞8或x＜4即将线段AB三等分，当C位于首段和尾段时，矩形面积小于32，故该矩形面积小于32cm2的概率为P==故选C点评：本题主要考查了几何概型概率的意义及其计算方法，将此概率转化为长度之比是解决本题的关键，属基础题9．（5分）两个实习生每人加工一个零件．加工为一等品的概率分别为和，两个零件是否加工为一等品相互独立，则这两个零件中恰有一个一等品的概率为（）A．B．C．D．考点：相互独立事件的概率乘法公式；互斥事件的概率加法公式．专题：计算题．分析：根据题意，分析可得，这两个零件中恰有一个一等品包含仅第一个实习生加工一等品与仅第二个实习生加工一等品两种互斥的事件，而两个零件是否加工为一等品相互独立，进而由互斥事件与独立事件的概率计算可得答案．解答：解：记两个零件中恰好有一个一等品的事件为A，即仅第一个实习生加工一等品（A1）与仅第二个实习生加工一等品（A2）两种情况，则P（A）=P（A1）+P（A2）=，故选B．点评：本题考查了相互独立事件同时发生的概率与互斥事件的概率加法公式，解题前，注意区分事件之间的相互关系（对立，互斥，相互独立）．10．（5分）抛物线y=﹣x2上的点到直线4x+3y﹣8=0距离的最小值是（）A．B．C．D．3考点：直线与圆锥曲线的关系．专题：圆锥曲线中的最值与范围问题．分析：首先判断出直线和抛物线无交点，然后设出与直线平行的直线方程，可抛物线方程联立后由判别式等于0求出切线方程，然后由两条平行线间的距离求出抛物线y=﹣x2上的一点到直线4x+3y﹣8=0的距离的最小值．解答：解：由，得3x2﹣4x+8=0．△=（﹣4）2﹣4×3×8=﹣80＜0．所以直线4x+3y﹣8=0与抛物线y=﹣x2无交点．设与直线4x+3y﹣8=0平行的直线为4x+3y+m=0联立，得3x2﹣4x﹣m=0．由△=（﹣4）2﹣4×3（﹣m）=16+12m=0，得m=﹣．所以与直线4x+3y﹣8=0平行且与抛物线y=﹣x2相切的直线方程为4x+3y﹣=0．所以抛物线y=﹣x2上的一点到直线4x+3y﹣8=0的距离的最小值是=．故选：A．点评：本题考查了直线与圆锥曲线的关系，考查了数学转化思想方法，训练了两条平行线间的距离公式，是中档题．11．（5分）已知随机变量X和Y，其中Y=12X+7，且EY=34，若X的分布列如表所示，则m的值为（）X 1 2 3 4P m nA．B．C．D．考点：离散型随机变量及其分布列．专题：计算题．分析：根据随机变量X分布的概率和为1，建立m、n的等式，根据数学期望公式再建立另一等式，联立方程组解之即可求出所求．解答：解：根据随机变量X分布的概率和为1，则+m+n+=1即m+n=①EX=1×+2m+3n+4×=2m+3n+∵Y=12X+7，且EY=34∴EY=12EX+7=24m+36n+14=34 ②联立①②得m=故选C．点评：本题主要考查了离散型随机变量及其分布列，以及随机变量的数学期望和二元一次方程组的解法，属于中档题．12．（5分）已知中心在原点的椭圆与双曲线有公共焦点，且左右焦点分别为F1F2，且两条曲线在第一象限的交点为P，△PF1F2是以PF1为底边的等腰三角形．若|PF1|=10，椭圆与双曲线的离心率分别为e1，e2，则e1•e2的取值范围是（）A．（0，）B．C．D．考点：双曲线的简单性质；椭圆的简单性质．专题：计算题．分析：设椭圆与双曲线的半焦距为c，PF1=r1，PF2=r2．利用三角形中边之间的关系得出c 的取值范围，再根据椭圆或双曲线的性质求出各自的离心率，最后依据c的范围即可求出e1•e2的取值范围，即可得答案．解答：解：设椭圆与双曲线的半焦距为c，PF1=r1，PF2=r2．由题意知r1=10，r2=2c，且r1＞r2，2r2＞r1，∴2c＜10，2c+2c＞10，⇒＜c＜5．⇒，∴=；=．∴，故选C．点评：本小题主要考查函数单调性的应用、椭圆的简单性质、双曲线的简单性质、不等式的性质等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．二、填空题：每小题5分，共20分．13．（5分）已知两点A（﹣2，﹣2）、B（3，7），则线段AB的垂直平分线的方程为5x+9y﹣25=0．考点：直线的一般式方程与直线的垂直关系．专题：直线与圆．分析：求出A，B的中点和斜率，根据点斜式方程即可求出直线方程．解答：解：∵两点A（﹣2，﹣2）、B（3，7），∴两点A，B的中点为（，），AB的斜率k==，则线段AB的垂直平分线的斜率k=﹣，则对于的直线方程为y﹣=﹣（x﹣），即5x+9y﹣25=0，故答案为：5x+9y﹣25=0．点评：本题主要考查直线方程的求解，根据条件求出中点坐标和斜率是解决本题的关键．14．（5分）已知小明投10次篮，每次投篮的命中率均为0.7，记10次投篮命中的次数为X，则DX=2.1．考点：离散型随机变量的期望与方差．专题：概率与统计．分析：由题意知ξ～B（10，0.7），由此能求出Dξ．解答：解：由题意知ξ～B（10，0.7），Dξ=10×0.7×0.3=2.1．故答案为：2.1．点评：本题考查离散型随机变量的分布列和数学方差的求法，是基础题，解题时要认真审题，注意二项分布的合理运用．15．（5分）三位同学参加跳高、跳远、铅球项目的比赛，若每人都选择其中两个项目，则有且仅有两人选择的项目完全相同的概率是（结果用最简分数表示）．考点：古典概型及其概率计算公式．专题：概率与统计．分析：先求出三个同学选择的所求种数，然后求出有且仅有两人选择的项目完全相同的种数，最后利用古典概型及其概率计算公式进行求解即可．解答：解：每个同学都有三种选择：跳高与跳远；跳高与铅球；跳远与铅球三个同学共有3×3×3=27种有且仅有两人选择的项目完全相同有××=18种其中表示3个同学中选2个同学选择的项目，表示从三种组合中选一个，表示剩下的一个同学有2中选择故有且仅有两人选择的项目完全相同的概率是=故答案为：点评：本题主要考查了古典概型及其概率计算公式，解题的关键求出有且仅有两人选择的项目完全相同的个数，属于基础题．16．（5分）现要将编号为1，2，3，4的四个小球全部放入甲、乙、丙三个盒中，每个至少放一个球，且甲盒不能放入1号球，乙盒不能放入2号球，则所有不同的放法种数为17（用数字作答）．考点：排列、组合及简单计数问题．专题：排列组合．分析：由题意知元素的限制条件比较多，可以利用间接法，先不考虑甲乙两盒的，再排除甲盒有1号，乙盒有2号球球，还要加上盒有1号球同时乙盒有2号球，问题得以解决．解答：解：不考虑甲盒不能放1号球，乙盒不能放入2号球，一共有=36种，甲盒为1号球有=12种，乙盒有2号球也有12种，甲盒有1号球同时乙盒有2号球1+2×2=5，所以不同的放法为36﹣12﹣12+5=17种，故答案为：17点评：本题考查排列组合及简单的计数原理，综合利用两个原理解决是关键，属中档题．三、解答题：共70分．解答应写出必要的文字说明、证明过程或演算步骤．17．（10分）（2x+）n展开式中所有的项的系数为243．（Ⅰ）求n的值；（Ⅱ）求展开式中x2项的系数．考点：二项式定理的应用．专题：二项式定理．分析：（I）依题意，得3n=243，可得n=5；（Ⅱ）由（2x+）5的二项展开式的通项公式T r+1=•（2x）5﹣r•=25﹣r••，知5﹣r=2，可求得r=2，从而可得展开式中x2项的系数．解答：解：（I）∵（2x+）n展开式中所有的项的系数为243，∴当x=1时，有3n=243，∴n=5；（Ⅱ）设（2x+）5展开式中的通项T r+1=•（2x）5﹣r•=25﹣r••，令5﹣r=2，得r=2，∴展开式中x2项的系数为：23•=80．点评：本题考查二项式定理的应用，着重考查二项式系数的性质及二项展开式的通项公式的应用，属于中档题．18．（12分）将一枚骰子先后抛掷两次，记第一次的点数为x，第二次的点数为y．（Ⅰ）求点P（x，y）在直线y=x+1上的概率；（Ⅱ）求y2＜4x的概率．考点：几何概型；古典概型及其概率计算公式．专题：应用题；概率与统计．分析：本题是一个古典概型，（Ⅰ）试验发生包含的事件是先后掷两次骰子，共有6×6种结果，满足条件的事件是（x，y）为坐标的点落在直线y=x+1上，列举共有5种结果，得到概率；（Ⅱ）满足条件的事件是（x，y）为坐标的点落在y2＜4x上，列举共有17种结果，得到概率．解答：解：（Ⅰ）由题意知本题是一个古典概型，∵试验发生包含的事件是先后掷两次骰子，共有6×6=36种结果，满足条件的事件是（x，y）为坐标的点落在直线y=x+1上，当x=1，y=2；x=2，y=3；x=3，y=4；x=4，y=5；x=5，y=6，共有5种结果，∴根据古典概型的概率公式得到P=；（II）满足条件的事件是（x，y）为坐标的点落在y2＜4x上，当x=1，y=1；x=2，y=1，2；x=3，y=1，2，3；x=4，y=1，2，3；x=5，y=1，2，3，4；x=6，y=1，2，3，4，共有17种结果，∴根据古典概型的概率公式得到P=．点评：本题考查古典概型的概率公式，考查满足直线方程的点，考查利用列举法得到事件数，本题是一个基础题，适合文科学生做，列举时注意要以x为主来讨论．19．（12分）某袋中有10个乒乓球，其中有7个新、3个旧球，从袋中任取3个来用，用后放回袋中（新球用后变为旧球），记此时袋中旧球个数为X，求X的数学期望．考点：离散型随机变量的期望与方差．专题：概率与统计．分析：由题意知，X的可能取值为3，4，5，6，分别求出相应的概率，由此能求出X的数学期望．解答：解：由题意知，X的可能取值为3，4，5，6，P（X=3）==，P（X=4）==，P（X=5）==，P（X=6）==，∴EX==5.1．故答案为：5.1．点评：本题考查离散型随机变量的数学期望的求法，是中档题，解题时要认真审题，在历年2015届高考中都是必考题型之一．20．（12分）过抛物线y2=x的顶点O作两条相互垂直的弦OA，OB，求△AOB面积的最小值．考点：直线与圆锥曲线的关系．专题：圆锥曲线的定义、性质与方程．分析：设A（x1，y1），B（x2，y2）与x轴的交点M点的坐标为（x0，0），直线l方程为x=my+x0，代入y2=x，根据OA⊥OB．求出m的值，然后表示出△AOB的面积，求解三角形面积的最小值即可．解答：解：设A（x1，y1），B（x2，y2）与x轴的交点M点的坐标为（x0，0），直线l方程为x=my+x0，代入y2=x得y2﹣my﹣x0=0 ①，y1、y2是此方程的两根，∴x0=﹣y1y2，∵x1x2+y1y2=y12y22+y1y2=y1y2（y1y2+1）=0，∴y1y2=﹣1∴x0=1．由方程①，y1+y2=m，y1y2=﹣1，且|OM|=x0=1，于是S△AOB=|OM||y1﹣y2|==≥1，∴当m=0时，△AOB的面积取最小值1．点评：本题考查抛物线的简单性质，考查三角形面积的最小值的求法，解题时要认真审题，仔细解答，注意抛物线性质的合理运用．21．（12分）小强参加一次测试，共有三道必答题，他是否答对每题互不影响．已知他只答对第一题的概率为0.08，只答对第一题和第二题的概率为0.1，至少答对一题的概率为0.88，用X表示小强答对题的数目．（Ⅰ）求小强答对第一题的概率；（Ⅱ）求X的分布列和数学期望．考点：离散型随机变量及其分布列；离散型随机变量的期望与方差．专题：概率与统计．分析：（I）设事件A表示“答对第一题”，事件B表示“答对第二题”，事件C表示“答对第三题”，由已知得，由此能求出小强答对第一题的概率．（Ⅱ）由已知得，X=0，1，3，分别求出相应的概率，由此能求出X的分布列和数学期望．解答：解：（I）设事件A表示“答对第一题”，事件B表示“答对第二题”，事件C表示“答对第三题”，由已知得，解得P（A）=，P（B）=，P（C）=，∴小强答对第一题的概率为．（Ⅱ）由已知得，X=0，1，3，P（X=0）=[1﹣P（A）][1﹣P（B）][1﹣P（C）]=1﹣0.88=，P（X=1）=P（A）[1﹣P（B）][1﹣P（C）]+P（B）[1﹣P（A）][1﹣P（C）]+P（C）[1﹣P （A）][1﹣P（B）]=，P（X=2）=P（A）P（B）[1﹣P（C）]+P（A）[1﹣P（B）]P（C）+[1﹣P（A）]P（B）P（C）=，P（X=3）=P（A）P（B）P（C）=，X 0 1 2 3PEX==．点评：本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，是中档题．22．（12分）设椭圆C：过点（1，），F1，F2分别为椭圆C的左右焦点，且离心率（1）求椭圆C的方程．（2）已知A为椭圆C的左顶点，直线l过右焦点F2与椭圆C交于M，N两点，若AM、AN 的斜率k1，k2满足，求直线l的方程．考点：直线与圆锥曲线的关系；椭圆的标准方程．专题：圆锥曲线的定义、性质与方程．分析：（1）由椭圆C过点（1，），且离心率，可得，解出即可；（2）由（1）可得：左顶点A（﹣2，0），右焦点（1，0）．由题意可知直线l不存在时不满足条件，可设直线l的方程为y=k（x﹣1），M（x1，y1），N（x2，y2）．与椭圆的方程联立可得根与系数的关系，再利用斜率计算公式可得，即，代入化简整理即可得出．解答：解：（1）∵椭圆C：过点（1，），且离心率，∴，解得，∴椭圆C的方程为．（2）由（1）可得：左顶点A（﹣2，0），右焦点（1，0）．由题意可知直线l不存在时不满足条件，可设直线l的方程为y=k（x﹣1），M（x1，y1），N（x2，y2）．联立，化为（3+4k2）x2﹣8k2x+4k2﹣12=0．由题意可得△＞0．∴，．∵，∴，化为2k（x1﹣1）（x2+2）+2k（x2﹣1）（x1+2）+（x1+2）（x2+2）=0，整理为（4k+1）x1x2+（2k+2）（x1+x2）+4﹣8k=0．代入得+4﹣8k=0，整理为k2﹣2k=0，解得k=0或2．k=0不满足题意，应舍去．故k=2，此时直线l的方程为y=2（x﹣1），即2x﹣y﹣2=0．点评：本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、斜率计算公式等基础知识与基本技能方法，属于难题．。

黑龙江省哈尔滨市第三中学2014届高三上学期第四次月考数学理答案.docx

哈三中2013－2014学年度高三学年第四次验收考试数学试卷（理）答案一选择题1.D2.A3.B4.C5.D6.A7.C8.B9.B10.C11.B12.C二填空题13.1 14.(0,1) 三解答题17.解：（Ⅰ）()2sin(2)6f x x π=+，2[0,],[,]63πππ单调递增，2[,]63ππ单调递减;（Ⅱ）cos α=18.解：;（Ⅱ）1CE =u u u r u u u u r ． 19.解：（Ⅰ）2214x y += （Ⅱ）由相切知：221m k =+，22440x y y kx m⎧+-=⎨=+⎩，代入得：()222148440k x kmx m +++-=，由于：2480k ∆=>恒成立，设()11,A x y 、()22,B x y ，则：1222212228144441414km x x k m kx x k k -⎧+=⎪⎪+⎨-⎪⋅==⎪++⎩，zxxkAB ==112S =⨯=1≤=当且仅当2231k k =+即212k =时取等;此时,直线斜率22k =±. 20.解：（Ⅰ）设),1,(),,(),,(002211-x x P y x B y x A 由121|'.',2x y x y y x x x ====因此得抛物线C 在点A 处的切线方程为.),(11111y x x y x x x y y -=-=-即……4分而A 点处的切线过点,1),1,(101000y x x x x x P -=--所以即.01)1(101=-+-y x x 同理，.01)1(202=-+-y x x可见，点A 、B 在直线01)1(0=-+-y x x 上．令1,01,01===-=-y x y x 解得，所以，直线AB 过定点()1,1Q ；（Ⅱ）设003344(,1),(,),(,)P x x M x y N x y -，直线PQ 的方程为.1112,1)1(11)1(00000-+--=+----=x x x x y x x x y 即由000221112,x y x x x x y -⎧=+⎪--⎨⎪=⎩，消去y ，得.0121)2(20002=-----x x x x x 由韦达定理，.12,1)2(20430043--=--=+x x x x x x x 而||||||||||||||||QN QM PN PM PN QM QN PM =⇔⋅=⋅ 303304403404343403401()(1)()(1)12()()20()x x x x x x x x x x x x x x x x x x x x --⇔=⇔--=----⇔-+-++=*将12,1)2(20430043--=--=+x x x x x x x 代入方程（*）的左边，得（*）的左边000000021)2(21)2(214x x x x x x x +--------=22000000424242201x x x x x x --+-++-==- 因而有PM QN QM PN ⋅=⋅.21.解：（Ⅰ）(0,2)单调递减,(2,)+∞单调递增；（Ⅱ）24ln 2-；（Ⅲ）]13,(--∞e . 22.解：（Ⅰ）曲线C的直角坐标方程220x y x +-=,zxxk直线l的普通方程20y -+=；（Ⅱ）6+.23. 解：（Ⅰ）10[2,]3-．zxxk （Ⅱ）实数a 的取值范围[)6,+∞．。

黑龙江省哈尔滨三中届高三数学上学期第二次检测试卷理(含解析)【含答案】

2015-2016学年黑龙江省哈尔滨三中高三（上）第二次检测数学试卷（理科）一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知全集U=R，集合P={x|x2≤1}，那么∁U P=（）A．（﹣∞，﹣1] B．[1，+∞）C．[﹣1，1] D．（﹣∞，﹣1）∪（1，+∞）2．已知向量=（1，m+2），=（m，﹣1），且∥，则||等于（）A．B．2 C．D．3．等比数列{a n}中，a1+a2+a3=1，a4+a5+a6=8，则该等比数列的公比为（）A．﹣2 B．2 C．﹣2或1 D．2或﹣14．sin182°cos28°﹣cos2°sin28°的值为（）A．B． C．D．5．使函数是奇函数，且在上是减函数的θ的一个值是（）A．B． C． D．6．在△ABC中，“A＞30°”是“sinA＞”的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也必要条件7．△ABC中，角A，B，C所对的边长分别为a，b，c， =， =（sinB，cosA），⊥，b=2，，则△ABC的面积为（）A．B．C．D．8．在等差数列{a n}中，对任意n∈N+，都有a n＞a n+1，且a2，a8是方程x2﹣12x+m=0的两根，且前15项的和S15=m，则数列{a n}的公差是（）A．﹣2或﹣3 B．2或3 C．﹣2 D．﹣39．已知数列{a n}中，a2=102，a n+1﹣a n=4n，则数列的最小项是（）A．第6项B．第7项C．第8项D．第9项10．函数f（x）=1+log2（﹣x）与g（x）=2x﹣1在同一直角坐标系下的图象大致是（）A．B． C．D．11．在正方形ABCD中，AB=AD=2，M，N分别为边BC，CD上的两个动点且MN=，则•的取值范围为（）A．[4，8﹣2] B．[4﹣2，8] C．[4，8+2] D．[4﹣2，8﹣2]12．若两个函数的图象有一个公共点，并在该点处的切线相同，就说明这两个函数有why 点，已知函数f（x）=lnx和g（x）=e x+m有why点，则m所在的区间为（）A．（﹣3，﹣e）B．（﹣e，﹣）C．（﹣，﹣）D．（﹣，﹣2）二、填空题（本大题共4小题，每小题5分.将答案填在答题卡相应的位置上）13．已知数列{x n}为等差数列，且x1+x2+x3=5，x18+x19+x20=25，则数列{x n}的前20项的和为．14．设2a+1，a，2a﹣1为钝角三角形的三边，则a范围为．15．设a＞0，b＞0，若是3a与3b的等比中项，则+的最小值是．16．△ABC中，AB=，cosB=，点D在边AC上，BD=，且=λ（+）（λ＞0）则sinA的值为．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤）17．（12分）（2015秋•哈尔滨校级月考）已知函数．（Ⅰ）求f（x）的最小正周期；（Ⅱ）求f（x）在区间上函数值的集合．18．（12分）（2015秋•黔东南州校级月考）设{a n}是公比大于1的等比数列，S n为数列{a n}的前n项和．已知S3=7且a1+3，3a2，a3+4构成等差数列．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）令b n=lna n，n=1，2，…，求数列{b n}的前n项和T n．19．（12分）（2015秋•哈尔滨校级月考）在△ABC中，角A，B，C所对的边长分别为a，b，c．已知sinA+sinC=psinB（p∈R），且b2=3ac．（Ⅰ）当时，求a，c的值；（Ⅱ）若角B为钝角，求p的取值范围．20．（12分）（2015秋•哈尔滨校级月考）已知数列{a n}中，．（Ⅰ）记b n=a n﹣2n，求数列{b n}的通项公式；（Ⅱ）设数列{a n}的前n项的和为S n，数列{c n}满足，若对任意的正整数n，当m∈[﹣2，4]时，不等式6t2﹣12mt+1＞6c n恒成立，求实数t的取值范围．21．（12分）（2015秋•哈尔滨校级月考）己知函数h（x）=lnx﹣x﹣有两个极值点x1，x2，且x1＜x2．（1）写出函数h（x）的单调区间（用x1，x2表示，不需要说明理由）（2）如果函数F（x）=h（x）+x在（1，b）上为增函数．求b的取值范围（3）当h（x1）+ln3+＜﹣+x2时．求h（x2）﹣x1的取值范围．请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分. 22．（10分）（2015秋•哈尔滨校级月考）如图，D是△ABC外接圆上的一点，弦AD与BC交于点E，且AB=AC=6，AE=4．（Ⅰ）求线段DE的长；（Ⅱ）若∠BAC=120°，求△BCD内切圆的面积．（2015秋•哈尔滨校级月考）在直角坐标系xoy中，直角l的参数方程为，23．（t为参数）．在极坐标系（与直角坐标系xoy取相同的长度单位，且以原点O为极点，以x 轴正半轴为极轴）中，圆C的方程为ρ=2sinθ．（Ⅰ）求圆C的直角坐标方程；（Ⅱ）设圆C与直线l交于点A、B，若点P的坐标为（3，），当≤α≤时，求|PA|﹣|PB|的取值范围．24．（2015秋•哈尔滨校级月考）己知a，b，c为正实数，且a+b+c=2．（1）求证：ab+bc+ac≤；（2）若a，b，c都小于1，求a2+b2+c2的取值范围．2015-2016学年黑龙江省哈尔滨三中高三（上）第二次检测数学试卷（理科）参考答案与试题解析一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知全集U=R，集合P={x|x2≤1}，那么∁U P=（）A．（﹣∞，﹣1] B．[1，+∞）C．[﹣1，1] D．（﹣∞，﹣1）∪（1，+∞）【考点】补集及其运算．【专题】集合．【分析】先求出集合P中的不等式的解集，然后由全集U=R，根据补集的定义可知，在全集R中不属于集合P的元素构成的集合为集合A的补集，求出集合P的补集即可．【解答】解：由集合P中的不等式x2≤1，解得﹣1≤x≤1，所以集合P=[﹣1，1]，由全集U=R，得到C U P=（﹣∞，1）∪（1，+∞）．故选D【点评】此题属于以不等式的解集为平台，考查了补集的运算，是一道基础题．2．已知向量=（1，m+2），=（m，﹣1），且∥，则||等于（）A．B．2 C．D．【考点】平行向量与共线向量；平面向量的坐标运算．【专题】计算题．【分析】根据题意，由结合向量平行的坐标表示方法，解可得m的值，即可得的坐标，然后求出向量的模．【解答】解：根据题意，若∥，，则有﹣1×1=（m+2）×m，解可得m=﹣1，则=（﹣1，﹣1），则||=故选A．【点评】本题考查向量平行的坐标表示与向量的坐标计算，关键是求出的坐标．3．等比数列{a n}中，a1+a2+a3=1，a4+a5+a6=8，则该等比数列的公比为（）A．﹣2 B．2 C．﹣2或1 D．2或﹣1【考点】等比数列的通项公式．【专题】计算题；方程思想；数学模型法；等差数列与等比数列．【分析】设出等比数列的公比，由已知列式求得q3，则公比可求．【解答】解：设等比数列{a n}的公比为q，由a1+a2+a3=1 ①，a4+a5+a6=q3（a1+a2+a3）=8 ②，②÷①得：q3=8，∴q=2．故选：B．【点评】本题考查等比数列的通项公式，是基础的计算题．4．sin182°cos28°﹣cos2°sin28°的值为（）A．B． C．D．【考点】两角和与差的正弦函数；两角和与差的余弦函数．【专题】计算题；函数思想；三角函数的求值．【分析】直接利用诱导公式以及两角和的正弦函数化简求解即可．【解答】解：sin182°cos28°﹣cos2°sin28°=﹣sin2°cos28°﹣cos2°sin28°=﹣sin30°=﹣．故选：B．【点评】本题考查两角和与差的三角函数，诱导公式的应用，考查计算能力．5．使函数是奇函数，且在上是减函数的θ的一个值是（）A．B． C． D．【考点】正弦函数的奇偶性；正弦函数的单调性．【专题】计算题．【分析】利用两角和正弦公式化简函数的解析式为2sin（2x+θ+），由于它是奇函数，故θ+=kπ，k∈z，当k为奇数时，f（x）=﹣2sin2x，满足在上是减函数，此时，θ=2nπ﹣，n∈z，当k为偶数时，经检验不满足条件．【解答】解：∵函数=2sin（2x+θ+）是奇函数，故θ+=kπ，k∈Z，θ=kπ﹣．当k为奇数时，令k=2n﹣1，f（x）=﹣2sin2x，满足在上是减函数，此时，θ=2nπ﹣，n∈Z，选项B满足条件．当k为偶数时，令k=2n，f（x）=2sin2x，不满足在上是减函数．综上，只有选项B满足条件．故选 B．【点评】本题考查两角和正弦公式，正弦函数的单调性，奇偶性，体现了分类讨论的数学思想，化简函数的解析式是解题的突破口．6．在△ABC中，“A＞30°”是“sinA＞”的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也必要条件【考点】必要条件、充分条件与充要条件的判断．【专题】常规题型．【分析】要注意三角形内角和是180度，不要丢掉这个大前提．【解答】解：∵在△ABC中，∠A+∠B+∠C=180°∵A＞30°∴30°＜A＜180°∴0＜sin A＜1∴可判读它是sinA＞的必要而不充分条件故选B．【点评】此题要注意思维的全面性，不能因为细节大意失分．7．△ABC中，角A，B，C所对的边长分别为a，b，c， =， =（sinB，cosA），⊥，b=2，，则△ABC的面积为（）A．B．C．D．【考点】数量积判断两个平面向量的垂直关系．【专题】计算题；转化思想；综合法；解三角形；平面向量及应用．【分析】由⊥，得sinB=﹣，由正弦定理得得sinA=﹣，再由同角三角函数关系式得到cosA=﹣，sinA=，从而sinB=，cosB=，从而求出sinC，由此利用△ABC的面积S=，能求出结果．【解答】解：∵△ABC中，角A，B，C所对的边长分别为a，b，c，=， =（sinB，cosA），⊥，b=2，，∴===0，∴sinB=﹣，由正弦定理得，整理，得sinA=﹣，∴sin2A+cos2A=4cos2A=1，∵0＜A＜π，∴cosA=﹣，sinA=，A=，∴sinB=，cosB==，∴sinC=sin[π﹣（A+B）]=sin（A+B）=sinAcosB+cosAsinB==，∴△ABC的面积S===．故选：C．【点评】本题考查三角形面积的求法，是中档题，解题时要认真审题，注意向量垂直、正弦定理、同角三角函数关系式等知识点的合理运用．8．在等差数列{a n}中，对任意n∈N+，都有a n＞a n+1，且a2，a8是方程x2﹣12x+m=0的两根，且前15项的和S15=m，则数列{a n}的公差是（）A．﹣2或﹣3 B．2或3 C．﹣2 D．﹣3【考点】等差数列的通项公式；等差数列的前n项和．【专题】方程思想；消元法；等差数列与等比数列．【分析】由根与系数的关系得出a2+a8=12，a2a8=m；再由{a n}的前15项的和为m，列出方程，求出a2、a8与m的值，即可求出公差．【解答】解：等差数列{a n}中，a n＞a n+1，且a2，a8是方程x2﹣12x+m=0的两根，∴a2+a8=12①，a2a8=m②；又{a n}的前15项和为m，∴=m，即15a8=m③；由①②③组成方程组，解得a2=15，a8=﹣3，m=﹣45；或a2=12，a8=0，m=0；当a2=15，a8=﹣3时，d=﹣3，当a2=12，a8=0时，d=﹣2；∴数列{a n}的公差是﹣3或﹣2．故选：A．【点评】本题考查了等差数列的通项公式与前n项和公式、一元二次方程的根与系数的关系的应用问题，是综合性题目．9．已知数列{a n}中，a2=102，a n+1﹣a n=4n，则数列的最小项是（）A．第6项B．第7项C．第8项D．第9项【考点】数列递推式．【专题】综合题；函数思想；综合法；等差数列与等比数列．【分析】由已知条件利用累加法求出a n=2n2﹣2n+98，得到，然后利用基本不等式求得数列的最小项．【解答】解：∵数列{a n}中，a2=102，a n+1﹣a n=4n，∴a n﹣a n﹣1=4（n﹣1），…a4﹣a3=4×3，a3﹣a2=4×2，以上等式相加，得a n﹣a2=4×2+4×3+…+4×（n﹣1）=4（2+3+…+n﹣1）=2（n+1）（n﹣2）．∴a n=2n2﹣2n+98．∴=2n+﹣2≥2﹣2=26，当且仅当=2n，即n=7时，等式成立．∴数列{}的最小项是第7项．故选：B．【点评】本题考查数列的最小项的求法，是中档题，解题时要认真审题，注意累加法和均值不等式的合理运用．10．函数f（x）=1+log2（﹣x）与g（x）=2x﹣1在同一直角坐标系下的图象大致是（）A．B． C．D．【考点】函数的图象．【专题】数形结合；数形结合法；函数的性质及应用．【分析】由条件利用函数的定义域和单调性，结合函数的图象特征，得出结论．【解答】解：函数f（x）=1+log2（﹣x）的定义域为（﹣∞，0），且单调递减；g（x）=2x﹣1 的定义域为R，且单调递增，故选：A．【点评】本题主要考查函数的定义域和单调性，函数的图象特征，属于基础题．11．在正方形ABCD中，AB=AD=2，M，N分别为边BC，CD上的两个动点且MN=，则•的取值范围为（）A．[4，8﹣2] B．[4﹣2，8] C．[4，8+2] D．[4﹣2，8﹣2]【考点】平面向量数量积的运算．【专题】数形结合；方程思想；平面向量及应用．【分析】如图所示，设M（2，y），N（x，2），．由于MN=，可得（x﹣2）2+（y﹣2）2=2．则•=2x+2y=t，数形结合即可得出．【解答】解：如图所示，设M（2，y），N（x，2），．∵MN=，∴=，化为（x﹣2）2+（y﹣2）2=2．则•=2x+2y=t，由=，解得t=4或12（舍去）．把x=2，y=2代入可得t=8﹣2．综上可得：t∈．故选：A．【点评】本题考查了数量积运算性质、两点之间的距离公式、直线与圆相切相交性质、点到直线的距离公式，考查了推理能力与计算能力，属于中档题．12．若两个函数的图象有一个公共点，并在该点处的切线相同，就说明这两个函数有why 点，已知函数f（x）=lnx和g（x）=e x+m有why点，则m所在的区间为（）A．（﹣3，﹣e）B．（﹣e，﹣）C．（﹣，﹣）D．（﹣，﹣2）【考点】利用导数研究曲线上某点切线方程．【专题】新定义；函数的性质及应用；导数的概念及应用．【分析】设f（x）和g（x）的公共点为（a，b），（a＞0），求导数，建立方程组，求得alna=1，确定a的范围，再由m=﹣lna﹣a=﹣（a+）确定单调递增，即可得到m的范围．【解答】解：设f（x）和g（x）的公共点为（a，b），（a＞0），函数f（x）=lnx的导数为f′（x）=，g（x）=e x+m有的导数为g′（x）=e x+m，即有=e a+m，lna=e a+m，即为alna=1，令h（a）=alna﹣1，可得h（）=ln﹣1＜0，h（2）=2ln2﹣1＞0，即有＜a＜2，则m=﹣lna﹣a=﹣（a+）∈（﹣，﹣），而﹣＞﹣，故选C．【点评】本题考查导数知识的运用，考查导数的几何意义，解题的关键是分离参数，确定函数的单调性，属于中档题．二、填空题（本大题共4小题，每小题5分.将答案填在答题卡相应的位置上）13．已知数列{x n}为等差数列，且x1+x2+x3=5，x18+x19+x20=25，则数列{x n}的前20项的和为100 ．【考点】数列的求和．【专题】计算题；整体思想；综合法；等差数列与等比数列．【分析】通过等差中项可知x2=，x19=，利用数列{x n}的前20项的和为，进而计算可得结论．【解答】解：∵数列{x n}为等差数列，∴2x n+1=x n+x n+2，又∵x1+x2+x3=5，x18+x19+x20=25，∴x2=，x19=，∴x2+x19=+=10，∴数列{x n}的前20项的和为=100，故答案为：100．【点评】本题考查数列的前n项和，考查运算求解能力，注意解题方法的积累，属于基础题．14．设2a+1，a，2a﹣1为钝角三角形的三边，则a范围为（2，8）．【考点】余弦定理．【专题】计算题．【分析】由三边长得到最大边为2a+1，所对的角为钝角，设为α，利用余弦定理表示出cosα，将三边长代入，根据cosα的值小于0，列出关于a的不等式，同时根据两边之和大于第三边列出不等式，求出两不等式解集的公共部分即可得到a的范围．【解答】解：由题意得：2a+1为最大边，所对的角为钝角，设为α，∴cosα==＜0，∵2a（2a﹣1）＞0，∴a2﹣8a＜0，解得：0＜a＜8，又a+2a﹣1＞2a+1，∴a＞2，则a的范围为（2，8）．故答案为：（2，8）【点评】此题考查了余弦定理，以及三角形的边角关系，熟练掌握余弦定理是解本题的关键．15．设a＞0，b＞0，若是3a与3b的等比中项，则+的最小值是 4 ．【考点】基本不等式在最值问题中的应用．【专题】计算题；压轴题．【分析】先根据等比中项的性质求得a+b的值，进而利用基本不等式取得ab的最大值，把+化简整理，根据ab的范围，求得答案．【解答】解：∵是3a与3b的等比中项∴3a•3b=3a+b=3∴a+b=1∴ab≤=（当a=b时等号成立）∴+==≥4．故答案为：4【点评】本题主要考查了基本不等式在最值问题中的应用．使用基本不等式时要注意等号成立的条件．16．△ABC中，AB=，cosB=，点D在边AC上，BD=，且=λ（+）（λ＞0）则sinA的值为．【考点】平面向量数量积的运算．【专题】数形结合；向量法；平面向量及应用．【分析】根据=λ（+），容易判断点D为AC的中点，由三角形的中线长定理和余弦定理，可得AC，BC的长，再由正弦定理，可得sinA．【解答】解：如图，过B作BE⊥AC，垂足为E，取AC中点F，连接BF，则=λ（+）（λ＞0）=λ（+）=；∴和共线，∴D点和F点重合，∴D是AC的中点，由中线长定理可得，BD===，又AC2=AB2+BC2﹣2AB•BC•cosB，即为AC2=+BC2﹣•BC•，解方程可得BC=2，AC=，由正弦定理可得=，可得sinA===．故答案为：．【点评】本题考查向量加法的平行四边形法则，共线向量基本定理，余弦定理的运用，考查运算能力，属于中档题．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤）17．（12分）（2015秋•哈尔滨校级月考）已知函数．（Ⅰ）求f（x）的最小正周期；（Ⅱ）求f（x）在区间上函数值的集合．【考点】三角函数的周期性及其求法．【专题】转化思想；综合法；三角函数的图像与性质．【分析】（Ⅰ）由调价利用三角函数的恒等变换化简函数的解析式，再利用正弦函数的周期性得出结论．（Ⅱ）由 x∈区间，利用正弦函数的定义域和值域，求得函数的值域．【解答】解：（Ⅰ）由于函数=4cosx（sinx+cosx）﹣1=sin2x+2cos2x﹣1=sin2x+cos2x=2sin（2x+），故函数的最小正周期为=π．（Ⅱ）∵x∈区间，∴2x+∈[﹣，]，∴sin（2x+）∈[﹣，1]，函数的值域为[﹣1 2]．【点评】本题主要考查三角函数的恒等变换及化简求值，正弦函数的周期性、定义域和值域，属于基础题．18．（12分）（2015秋•黔东南州校级月考）设{a n}是公比大于1的等比数列，S n为数列{a n}的前n项和．已知S3=7且a1+3，3a2，a3+4构成等差数列．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）令b n=lna n，n=1，2，…，求数列{b n}的前n项和T n．【考点】数列的求和．【专题】方程思想；转化思想；等差数列与等比数列．【分析】（I）设{a n}是公比q大于1的等比数列，由于a1+3，3a2，a3+4构成等差数列，可得6a2=a3+4+a1+3，即6a1q=+7+a1，又S3=a1（1+q+q2）=7，联立解出即可得出．（II）b n=lna n=（n﹣1）ln2，再利用等差数列的前n项和公式即可得出数列{b n}的前n项和．【解答】解：（I）设{a n}是公比q大于1的等比数列，∵a1+3，3a2，a3+4构成等差数列，∴6a2=a3+4+a1+3，化为6a1q=+7+a1，又S3=a1（1+q+q2）=7，联立解得a1=1，q=2．∴a n=2n﹣1．（II）b n=lna n=（n﹣1）ln2，∴数列{b n}的前n项和T n=ln2．【点评】本题考查了等差数列与等比数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．19．（12分）（2015秋•哈尔滨校级月考）在△ABC中，角A，B，C所对的边长分别为a，b，c．已知sinA+sinC=psinB（p∈R），且b2=3ac．（Ⅰ）当时，求a，c的值；（Ⅱ）若角B为钝角，求p的取值范围．【考点】余弦定理；正弦定理．【专题】转化思想；综合法；解三角形．【分析】（Ⅰ）由条件利用正弦定理可得b2=3ac=1，a+c=b=，由此解得a和c的值．（Ⅱ）由条件利用余弦定理求得p2=+cosB，再结合﹣1＜cosB＜0，求得p2的范围，从而求得p的范围．【解答】解：△ABC中，∵sinA+sinC=psinB（p∈R），且b2=3ac，故a+c=pb．（Ⅰ）当时，则由sinA+sinC=sinB（p∈R），且b2=3ac=1，故有a+c=b=，解得a=，c=1；或者a=1，c=．（Ⅱ）由余弦定理得b2=a2+c2﹣2accosB=（a+c）2﹣2ac﹣2accosB=p2b2﹣b2cosB﹣，即p2•b2=+•cosB，即p2=+cosB，因为角B为钝角，故﹣1＜cosB＜0，所以p2∈（1，）．由题设知p∈R，又由sinA+sinC=psinB知，p是正数，求p的取值范围为（1，）．【点评】本题主要考查正弦定理、余弦定理的应用，钝角的余弦值的范围，属于中档题．20．（12分）（2015秋•哈尔滨校级月考）已知数列{a n}中，．（Ⅰ）记b n=a n﹣2n，求数列{b n}的通项公式；（Ⅱ）设数列{a n}的前n项的和为S n，数列{c n}满足，若对任意的正整数n，当m∈[﹣2，4]时，不等式6t2﹣12mt+1＞6c n恒成立，求实数t的取值范围．【考点】数列的求和；数列递推式．【专题】分类讨论；转化思想；综合法；等差数列与等比数列；不等式的解法及应用．【分析】（I）由，变形为a n+1﹣2（n+1）=2[a n﹣2n]，b n=a n﹣2n，即b n+1=2b n，即可得出．（II）由（I）可得：b n=a n﹣2n=0，解得a n=2n，可得数列{a n}的前n项的和为S n=n2+n．可得=．利用“裂项求和”可得c n．可得（c n）max．根据对任意的正整数n，当m∈[﹣2，4]时，不等式6t2﹣12mt+1＞6c n恒成立，即可得出．【解答】解：（I）∵，∴a n+1﹣2（n+1）=2[a n﹣2n]，b n=a n﹣2n，∴b n+1=2b n，而b1=a1﹣2=0，可得b n=0．（II）由（I）可得：b n=a n﹣2n=0，解得a n=2n，∴数列{a n}的前n项的和为S n==n2+n．∴==．∴=++…+=﹣==≤，∴（c n）max=．∵对任意的正整数n，当m∈[﹣2，4]时，不等式6t2﹣12mt+1＞6c n恒成立，∴6t2﹣12mt+1＞1，化为：t（t﹣2m）＞0，当m∈（0，4]时，解得t＜0，或t＞8；当m=0时，解得t≠0；当m∈[﹣2，0）时，解得t＜﹣4，或t＞0．综上可得：t＞8，或t＜﹣4．∴实数t的取值范围是t＞8，或t＜﹣4．【点评】本题考查了“裂项求和”、数列的通项公式、不等式的性质，考查了分类讨论方法、变形能力、推理能力与计算能力，属于中档题．21．（12分）（2015秋•哈尔滨校级月考）己知函数h（x）=lnx﹣x﹣有两个极值点x1，x2，且x1＜x2．（1）写出函数h（x）的单调区间（用x1，x2表示，不需要说明理由）（2）如果函数F（x）=h（x）+x在（1，b）上为增函数．求b的取值范围（3）当h（x1）+ln3+＜﹣+x2时．求h（x2）﹣x1的取值范围．【考点】利用导数研究函数的单调性；利用导数求闭区间上函数的最值．【专题】综合题；转化思想；综合法；导数的综合应用．【分析】（1）根据函数h（x）=lnx﹣x﹣有两个极值点x1，x2，且x1＜x2，写出函数h（x）的单调区间；（2）如果函数F（x）=h（x）+x在（1，b）上为增函数．b＜1+，确定2m＞﹣，即可求b的取值范围；（3）当h（x1）+ln3+＜﹣+x2时．+ln（1﹣x2）+x2+ln3﹣＜0，＜x2＜1，设f（x2）=+ln（1﹣x2）+x2+ln3﹣，证明f（x2）在（，1）上单调递减，＜x2＜1，利用h（x2）﹣x1=lnx2﹣x2，设φ（x2）=lnx2﹣x2，＜x2＜1，证明φ（x2）在（，1）上单调递减，即可求h（x2）﹣x1的取值范围．【解答】解：（1）函数h（x）的单调增区间是（x1，x2），单调减区间是（0，x1），（x2，+∞）；（2）函数F（x）=h（x）+x=lnx﹣x﹣，∴F′（x）=∵在（1，b）上为增函数，∴b＜1+，∵函数h（x）=lnx﹣x﹣有两个极值点x1，x2，h′（x）=，∴△=1+4m＞0，∴2m＞﹣，∴＞，∴b≤1+，∴1＜b≤1+；（3）h′（x）==0的两个根分别为x1，x2，∴x1，x2是x2﹣x﹣m=0的两个正实数根，∴x1+x2=1，x1x2=﹣m当h（x1）+ln3+＜﹣+x2时，lnx1﹣x1﹣+ln3+＜﹣+x2，∴+ln（1﹣x2）+x2+ln3﹣＜0．显然＜x2＜1设f（x2）=+ln（1﹣x2）+x2+ln3﹣，∴f′（x2）=＜0，∴f（x2）在（，1）上单调递减，∵f（）=0，∴f（x2）＜0=f（），∴＜x2＜1∴h（x2）﹣x1=lnx2﹣x2，设φ（x2）=lnx2﹣x2，＜x2＜1∵φ′（x2）=﹣1＞0，∴φ（x2）在（，1）上单调递减∴φ（x2）∈（ln﹣，﹣1）∴h（x2）﹣x1的取值范围是（ln﹣，﹣1）．【点评】本题考查导数知识的综合运用，考查函数的单调性，极值，考查学生分析解决问题的能力，难度大．请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分. 22．（10分）（2015秋•哈尔滨校级月考）如图，D是△ABC外接圆上的一点，弦AD与BC交于点E，且AB=AC=6，AE=4．（Ⅰ）求线段DE的长；（Ⅱ）若∠BAC=120°，求△BCD内切圆的面积．【考点】解三角形；圆內接多边形的性质与判定．【专题】计算题；数形结合；转化思想；解三角形．【分析】（Ⅰ）连接BD构造相似三角形△ABE∽△ADB，然后根据相似三角形的对应边成比例求得AB2=AD•AE，从而求得AB的长度．（Ⅱ）利用三角形相似求出三角形的三个边长，通过三角形的面积求出内切圆的半径，然后求解内切圆的面积．【解答】解：（Ⅰ）如图，AB=AC=6，则，∴∠ABE=∠D（等弧所对的圆周角相等），又∠BAE=∠BAD（公共角），∴△ABE∽△ADB（AA），∴（相似三角形的对应边成比例），∴AB2=AD•AE=（AE+ED）•AE，又AE=4，AB=6，得ED=5．（Ⅱ）∠BAC=120°，BC=6，BE=3，EC=3，CD===，△DBE∽△AEC，∴，可得BD==．D到BC的距离为h，则，h=，，（r是△BCD内切圆的半径），×=×（）•r，解得r=，△BCD内切圆的面积： =．【点评】本题综合考查了相似三角形的判定与性质、圆周角定理．圆心角与它所对的弧、所对的弦之间的关系：这三个量中，若有一个量相等，则其它的量两个量也相等．考查内切圆的面积的求法，考查转化思想的应用．（2015秋•哈尔滨校级月考）在直角坐标系xoy中，直角l的参数方程为，23．（t为参数）．在极坐标系（与直角坐标系xoy取相同的长度单位，且以原点O为极点，以x 轴正半轴为极轴）中，圆C的方程为ρ=2sinθ．（Ⅰ）求圆C的直角坐标方程；（Ⅱ）设圆C与直线l交于点A、B，若点P的坐标为（3，），当≤α≤时，求|PA|﹣|PB|的取值范围．【考点】参数方程化成普通方程；简单曲线的极坐标方程．【专题】选作题；转化思想；综合法；坐标系和参数方程．【分析】（Ⅰ）利用极坐标与直角坐标的互化方法求圆C的直角坐标方程；（Ⅱ）利用参数的几何意义，求|PA|﹣|PB|的取值范围．【解答】解：（Ⅰ）由圆C的方程为ρ=2sinθ，可得ρ2=2ρsinθ，∴圆C的直角坐标方程为x2+y2=2y；（Ⅱ）直角l的参数方程为，与圆C的直角坐标方程联立，可得t2+6tsinα+4=0设A，B对应的参数分别为t1，t2，则|PA|﹣|PB|=t1+t2=﹣6sinα，∵≤α≤，∴≤sinα≤，∴﹣3≤﹣6sinα≤﹣3，∴|PA|﹣|PB|的取值范围是[﹣3，﹣3]．【点评】本题考查极坐标与直角坐标的互化，考查参数的几何意义，考查学生的计算能力，属于中档题．24．（2015秋•哈尔滨校级月考）己知a，b，c为正实数，且a+b+c=2．（1）求证：ab+bc+ac≤；（2）若a，b，c都小于1，求a2+b2+c2的取值范围．【考点】基本不等式；二维形式的柯西不等式．【专题】证明题；整体思想；综合法；不等式．【分析】（1）由a+b+c=2，得到8=2a2+2b2+2c2+4ab+4bc+4ca，利用基本不等式得以证明，（2）由（1）和基本不等式得到a2+b2+c2≥，再根据a﹣a2=a（1﹣a），0＜a＜1，得到a＞a2，继而求出范围．【解答】（1）证明：∵a+b+c=2，∴a2+b2+c2+2ab+2bc+2ca=4，∴2a2+2b2+2c2+4ab+4bc+4ca=8∴8=2a2+2b2+2c2+4ab+4bc+4ca≥6ab+6abc+6ac，当且仅当a=b=c时取等号，∴ab+bc+ac≤；（2）解：由（1）知，a2+b2+c2+2ab+2bc+2ca=4，∴4≤a2+b2+c2+a2+b2+b2+c2+a2+c2=3（a2+b2+c2），当且仅当a=b=c时取等号，∴a2+b2+c2≥，∵a﹣a2=a（1﹣a），0＜a＜1，∴a＞a2，同理b＞b2，c＞c2，∴a2+b2+c2＜a+b+c=2，∴≤a2+b2+c2＜2，∴a2+b2+c2的取值范围为[，2）．【点评】本题考查了基本不等式的应用，关键是掌握等号成立的条件，属于基础题．。

黑龙江省哈尔滨师范大学附属中学2014-2015学年高二上学期期末考试(全科10套)(黑龙江省哈尔滨

（考试时间：120分钟；满分：150分）第一部分：阅读理解（共两节, 满分40分）第一节: （共15小题；每小题2分, 满分30分）阅读下列短文，从每题所给的四个选项(A、B、C和D)中，选出最佳选项，并在答题卡上将该项涂黑。

AThe following are letters to the editor of a school newspaperDear editor,I’d like to express my opinion about grades. Students should be allowed to study without worrying about grades. Fortunately, most educators are becoming aware of the fact that students have different interests and abilities. I understand that grades are useful, but grades often limit creativity. Competing for better grades causes many students to turn down opportunities to pursue music, dramatics and sports. Grades force an arbitrary (武断的) standard of success on everyone. I do not demand, as some extremists do, that grades be removed immediately. However, I do believe that less emphasis should be placed on grades. I hope that someday grades will become optional at Village High School.Magdalena SmithDrama ClubDear editor,I’d like to say something about grades. Let’s face t he facts about grades. Grades perform three basic functions. First, grades motivate students to work at their highest level of competence. Second, they act as a reward for hardworking students and as a punishment to students who do not work hard. Finally, grades are used as an effective standard by which to measure student achievement. Good grades help students to get jobs and to get into university. I’ve spoken with a number of students who have jobs, and most of them say that they were hired primarily on the basis of their grades. My grades helped me land a part-time job and will help me get into university next year. I think grades are extremely important at Village High School. Simon HarperScience Club1. Which of the following is not Magdalena Smith’s opinion?A. Students may give up the chance to learn music and sports for grades.B. Students’ creativity may not be developed for grades.C. Grades should not be used to measure a person’s success.D. Grades should be taken away at once.2. We can learn Simon Harper __________.A. believes in the benefits of good gradesB. is concerned about students’ creativityC. doesn’t work too hard at his studiesD. supports students’ interests and abilities3. From the second letter, we can infer that Simon Harper is a/an __________.A. teacherB. headmasterC. studentD. advertiserBThere is a story about a man who lost his legs and left arm in an accident. After the accident, only a finger and thumb on his right hand remained.He was a brilliant, creative, and educated man. He had gained a lot of experience while traveling around the world, so he became very depressed after his accident. He was afraid that he would spend the rest of his life suffering and would no longer be able to spend his life in a meaningful way. Then, he realized that he still had partial function of his right hand and could still write even though it was very difficult. An idea occurred to him, “Why not write to other people who need encouragement?”He wrote to the prison ministry about sending letters to the prisoners. The prison minister replied,“Writing to the prisoners is acceptable, but your letters will not be answered.”Filled with excitement, the man knew he could write his letters. He began sending one-way messages of God’s love, hope, strength, and encouragement. He wrote twice a week, testing his strength and ability to the limit. He poured his heart and soul into his words and shared his experience, sense of humor, optimism, and faith.It was difficult to write those letters, especially without hope of a reply. One day he received a letter from the prison ministry. It was a short note from the officer who monitored and checked the prison mail.The letter said, “Please write on the best paper you can afford. Your letters are passed from room to room until they fall to pieces!”No matter what circumstances life may present, we all have unique experiences, abilities, and God-given talents. We can discover ways to reach others who desperately need messages of encouragement and strength.4. Before the man had the accident, he __________.A. had toured around the worldB. had visited local prisonsC. had tried doing exercise to recover himselfD. had been friends with the prison minister5. In order to live in a meaningful way, the man began to ________.A. receive the school educationB. write to other people who needed encouragementC. meet the people who were depressedD. help other people who lost arms and legs6. From the officer’s short note we are told that __________.A. the man would be offered free paper to write letters onB. some of the prisoners were not satisfied with his lettersC. the prisoners eagerly wanted to write back to the manD. his letters were very popular among the prisoners7. What can be the best title for the passage?A. Stories about a Humorous PersonB. Popularity of Special LettersC. Special Letters of EncouragementD. Relationship between Writers and PrisonersCOwning a smart phone may not be as smart as you think. They may let you surf the Internet, listen to music and snap photos wherever you are... but they also turn you into a workaholic (工作狂). A study suggests that, by giving you access to emails at all times, the all-singing, all-dancing mobile phone adds as much as two hours to your working day.Researchers found that Britons work an additional 460 hours a year on average as they are able to respond to emails on their mobiles. The study by technology retailer Pixmania, shows the average UK working day is between nine and ten hours, but a further two hours is spent responding to or sending work emails, or making work calls. Almost one in ten admits spending up to three hours outside their normal working day checking work emails. Some workers confess (坦白) they are on call almost 24 hours a day, with nine out of ten saying they take work emails and calls outside their normal working hours. Nearly two-thirds say they often check work emails just before they go to bed and as soon as they wake up, while over a third have replied to one in the middle of the night.Ghadi Hobeika, marketing director of Pixmania, said, “The ability to access millions of apps, keep in contact via social networks and take photos and video as well as text and call has made smart phones valuable for many people. However, there are drawbacks. Many companies expect their employees to be on call 24 hours a day, seven days a week, and smart phones mean that people cannot get away from work. The more constantly in contact we become, the more is expected of us in a work capacity (容量).”8. The text is probably taken from __________.A. a scientific reportB. a financial reportC. a newspaperD. a travel journal9. The underlined word “drawbacks” in the last paragraph probably means __________.A. disagreementsB. disadvantagesC. mistakesD. features10. Ghadi may agree that __________.A. employees are supposed to be on call 24 hours a dayB. the ability to access many apps made smart phones worthlessC. smart phones might turn a person into a workaholicD. people cannot get away from work without smart phones11. What is the main idea of this passage?A. Smart phones are lengthening working hours.B. Smart phones are becoming valuable for many people.C. Britons work an additional 460 hours a year on average.D. Smart phones are more beneficial to our life than we think.DThey should be Britain’s gilded (镀金的) youth, enjoying opportunities to study, travel and start exciting careers in a way older generations could only dream about. But instead they are the “Ipod” generation —“Insecure, P ressured, Over-taxed and Debt-ridden”—according to a study by a group of experts who provide advice and ideas on social issues.“We thought that each generation would be better off than its predecessors (前辈),” said Professor Nick Bosanquet of Imperial C ollege London, one of its authors. “But young people today have more duties and it is much more difficult for them to raise their incomes and create wealth. This really is a very big issue for the country.”According to the report, today’s youth don’t h ave enough confidence and ability to build on the economic foundations created by post-war baby boomers (生育高峰期出生的人) . Because they are in debt, they are also reluctant to take risks. Levels of entrepreneurship (企业家精神) among Britain’s youth are lower than in America, Australia, New Zealand and Ireland and have fallen over the past decade. Many choose the jobs which offer a good amount of money after they retire. Others have to take any job that is available to try to pay off their debts.“I borrowed a lot of money from the bank to pay for my education at university, which is the biggest chain around my neck now,” said Phil Grech, 22, from Cumbria, who has a degree in maths from the University of Reading. “I’m only doing a temporary job at the moment to pay the mounting bills. I haven’t really thought about the long term. Many people think that when you leave university you can get a good job, but it’s no longer like that.”While older generations enjoyed higher education funded by taxpayers, young people today face university tuition fees and a decreasing “return” in the salary advantage they will get from their degrees.12. What is the text mainly about?A. Britain’s gilded youth.B. The “Ipod” generation in Britain.C. The challenges faced by the British today.D. The career choices Britain’s youth have.13. What’s the biggest problem in Phil Grech’s life?A. Low income.B. The debt.C. Not having a good college degree.D. Not having job opportunities.14. We can infer from the text that the “Ipod” generation __________.A. doesn’t have much determinationB. doesn’t want to have a full-time jobC. lives a harder life than the older generationsD. hasn’t realized the importance of sa ving money15. Which of the following words can best take the place of the word “reluctant” in the third paragraph?A. Unwilling.B. Foolish.C. Quick.D. Sorry.第二节：(共5小题；每小题2分, 满分10分）根据短文内容,从短文后的选项中选出能填入空白处的最佳选项。

黑龙江省哈尔滨市第三十二中学2015届高三数学上学期期末考试试题理

数学〔理〕试题一、选择题〔每题5分，共计60分〕 1、集合{}0,2,A a =,{}21,B a =,假设{}0,1,2,4,16AB =,如此a 的值为〔〕A. 1.B. 2.C. 3.D. 4. 2．i 为虚数单位，复数121iz i+=-，如此复数z 的虚部是〔〕 A ．i 23B ．23C ．i 21-D ．21- 3．如下命题中正确的答案是〔〕A ．假设命题p 为真命题，命题q 为假命题，如此命题“p q ∧〞为真命题B ．命题“假设0xy =，如此0x =〞的否命题为：“假设0xy =，如此0x ≠〞C ．“21sin =α〞是“6πα=〞的充分不必要条件D ．命题“,20xx R ∀∈>〞的否认是“00,20x x R ∃∈≤〞4．向量(1,1),(2,),a b x ==假设a b +与a b -平行，如此实数x 的值是〔〕A ．－2B ．0C ．1D ．25． = ( )A ． 0B ．C ．D ．6．曲线31y ax bx =+-在点(1,(1))f 处的切线方程为,y x b a =-则=( )A ．3-B ．2C ．3D ．47． ,, ,如此( )A ．aB ．C ．D ．8．设函数3x y =与2)21(-=x y 的图像的交点为),(00y x ，如此0x 所在的区间是( )A ．)1,0(B ．)2,1(C ．)3,2(D ．)4,3(9．正项组成的等差数列{}n a 的前20项的和100,那么615a a ⋅最大值是( )A ．25B ．50C ．100D ．不存在10．，，，D 为边的中点，如此( )A ．6B ．5C ．4D ．311．将函数()3sin(4)6f x x π=+图像上所有点的横坐标伸长到原的2倍，再向右平移6π个单位长度，得到函数()y g x =的图像，如此()y g x =图像的一条对称轴是〔〕 A ．12x π=B ．6x π=C ．3x π=D ．23x π=12．(),()f x g x 都是定义在R 上的函数，且满足以下条件：①()()xf x ag x =⋅(0,a >1)a ≠且；②()0g x ≠；③()()()()f x g x f x g x ''⋅>⋅．假设(1)(1)5(1)(1)2f fg g -+=-，如此a 等于 ( ) A ．21B ．2 C ．45D ．2或21 二、填空题〔每题5分，共计20分〕 13．集合,,如此__________．14．设奇函数()f x 在上是增函数，,如此不等式的解集为.15．假设- ，如此.16. 假设向量,满足,,且和的夹角为，如此. 一．选择题：二.填空题：13. _____________________ 14． _____________________15. _____________________ 16. _____________________哈32中2014～2015学年度上学期期末考试高三数学理科答题卡三、解答题〔共计70分〕17．向量1(sin ,1),(3cos ,)2a xb x =-=-,函数()()2f x a b a =+⋅-，a 、b 、c 分别为ABC ∆内角A 、B 、C 的对边,其中A 为锐角,4a c ==,且()1f A =,求,A b 和ABC ∆的面积S 。

2014-2015学年黑龙江省哈尔滨三中高一(上)期末数学试卷含参考答案

个单位后，再将得到的图象上各点的
横坐标伸长到原来的 4 倍，纵坐标不变，得到函数 y=g（x）的图象，求 g（x）的单调递减区间． 21．（12.00 分）函数 f（x）=2sinxcosx+m（sinx+cosx）﹣2，（1）当 m=1 时，求 f（x）的值域；（2）若对于任意的 x∈R，f（x）＜0 恒成立，求 m 的取值范围． 22．（12.00 分）已知 f（x）=logax，其反函数为 g（x）．（1）解关于 x 的方程 f（x﹣1）=f（a﹣x）﹣f（5﹣x）；（2）设 F（x）=（2m﹣1）g（x）+（ ﹣ ）g（﹣x），若 F（x）有最小值，试求其表达式 h（m）；（3）求 h（m）的最大值．
A．[2，+∞） B．[2，4） C．（2，4） D．[2，4] 8．（5.00 分）为了得到函数 y=cos （2x﹣ A．向左平移 B．向左平移）的图象，可以将 y=sin2x 的图象（ D．向右平移）
C．向右平移
9．（5.00 分）函数 f（x）=log2x﹣ +a 的一个零点在（1，4）内，则实数 a 的取值范围为（）
A．（﹣ ，2） B．（4，6） C．（2，4） D．（﹣3，﹣ ） 10．（5.00 分）已知函数 f（x）=sinx+sin（x+ 为（）），x∈[0，π]，则 f（x）的值域
A．[﹣
，
]
B．[﹣
，
]
C．[
，
] D．[﹣2，2]
11．（5.00 分）方程的取值范围为（）
sin2x+cos2x=2k﹣1，x∈[0，π]有两个不 ] ∪（，+∞）