华南理工大学数据结构chapter9
数据结构 第9章答案

第9章 查找参考答案一、填空题(每空1分,共10分)1. 在数据的存放无规律而言的线性表中进行检索的最佳方法是 顺序查找(线性查找) 。
2. 线性有序表(a 1,a 2,a 3,…,a 256)是从小到大排列的,对一个给定的值k ,用二分法检索表中与k 相等的元素,在查找不成功的情况下,最多需要检索 8 次。
设有100个结点,用二分法查找时,最大比较次数是 7 。
3. 假设在有序线性表a[20]上进行折半查找,则比较一次查找成功的结点数为1;比较两次查找成功的结点数为 2 ;比较四次查找成功的结点数为 8 ;平均查找长度为 3.7 。
解:显然,平均查找长度=O (log 2n )<5次(25)。
但具体是多少次,则不应当按照公式)1(log 12++=n nn ASL 来计算(即(21×log 221)/20=4.6次并不正确!)。
因为这是在假设n =2m -1的情况下推导出来的公式。
应当用穷举法罗列:全部元素的查找次数为=(1+2×2+4×3+8×4+5×5)=74; ASL =74/20=3.7 !!!4.【计研题2000】折半查找有序表(4,6,12,20,28,38,50,70,88,100),若查找表中元素20,它将依次与表中元素 28,6,12,20 比较大小。
5. 在各种查找方法中,平均查找长度与结点个数n 无关的查找方法是 散列查找 。
6. 散列法存储的基本思想是由 关键字的值 决定数据的存储地址。
7. 有一个表长为m 的散列表,初始状态为空,现将n (n<m )个不同的关键码插入到散列表中,解决冲突的方法是用线性探测法。
如果这n 个关键码的散列地址都相同,则探测的总次数是 n(n-1)/2=( 1+2+…+n-1) 。
(而任一元素查找次数 ≤n-1)二、单项选择题(每小题1分,共27分)( B )1.在表长为n的链表中进行线性查找,它的平均查找长度为A. ASL=n; B. ASL=(n+1)/2;C. ASL=n +1; D. ASL≈log2(n+1)-1( A )2.【计研题2001】折半查找有序表(4,6,10,12,20,30,50,70,88,100)。
华南理工大学数据结构chapter9

5
Lists Ordered by Frequency
The car on the left hit the car I left. The car on 3 left hit 3 5 I 5. This is similar in spirit to Ziv-Lempel coding.
12
Searching in Sets
1) Using bit vector to represent the set.
4
Searching Unsorted and Sorted Arrays
Searching sorted Array-- Binary search (See Section 3.5)
Searching sorted Arrays– Dictionary search or interpolation search
Search
Given: Distinct keys k1, k2, …, kn and collection L of n records of the form (k1, I1), (k2, I2), …, (kn, In) where Ij is the information associated with key kj from record j for 1 <= j <= n. • Search Problem: For key value K, locate a record (kj, Ij) in L such that kj = K. (if one exists). Searching is a systematic method for locating the record(s) with key value kj = K.
数据结构(含课程设计)·随堂练习2019春华南理工大学网络教育答案

数据结构(含课程设计),随堂第一章绪论1.(单选题) 计算机所处理的数据一般具备某种内在联系,这是指()。
A、数据和数据之间存在某种关系 B.元素和元素之间存在某种关系C元素内部具有某种结构 D.数据项和数据项之间存在某种关系答题: A. B. C. D. (已提交)参考答案:B问题解析:2.(单选题) 在数据结构中,与所使用计算机无关的是数据的()结构.A.逻辑B.存储C.逻辑和存储D. 物理答题: A. B. C. D. (已提交)参考答案:A问题解析:3.(单选题) 数据结构在计算机中的表示称为数据的()A.存储结构B.抽象数据类型C.顺序结构D.逻辑结构答题: A. B. C. D. (已提交)参考答案:A问题解析:4.(单选题) 在计算机中存储数据时,通常不仅要存储各数据元素的值,还要存储().A.数据的处理方法B.数据元素的类型C.数据元素之间的关系D.数据的存储方法答题: A. B. C. D. (已提交)参考答案:C问题解析:5.(单选题) 在计算机的存储器中表示数据时,逻辑上相邻的两个元素对应的物理地址也是相邻的,这种存储结构称为()A.逻辑结构B.顺序存储结构C.链式存储结构D.以上都正确答题: A. B. C. D. (已提交)参考答案:B问题解析:6.(单选题) 当数据采用链式存储结构时,要求().A.每个结点占用一片连续的存储区域B.所有结点占用一片连续的存储区域C结点的最后一个数据域是指针类型D.每个结点有多少个后继就设多少个指针域答题: A. B. C. D. (已提交)参考答案:A问题解析:7.(单选题) 以下关于算法的说法正确的是().A.算法最终必须由计算机程序实现B.算法等同于程序C算法的可行性是指指令不能有二义性D.以上都是错误的答题: A. B. C. D. (已提交)参考答案:D问题解析:8.(单选题) 算法的时间复杂度与()有关.A问题规模 B.计算机硬件性能C编译程序质量 D.程序设计语言答题: A. B. C. D. (已提交)参考答案:A问题解析:9.(单选题) 算法的主要任务之一是分析()A算法是否具有较好的可读姓,B算法中是否存在语法错误,C算法的功能是否符合设计要求D.算法的执行时间和问题规模之间的关系答题: A. B. C. D. (已提交)参考答案:D问题解析:10.(单选题) 某算法的时间复杂度为O(),表明该算法的()A问题规模是 B执行时间等于C.执行时间与成正比D.问题规模与成正比答题: A. B. C. D. (已提交)参考答案:C问题解析:第二章线性表1.(单选题) 线性表是具有n个()的有限序列.A.关系 B字符C数据元素 D.数据项答题: A. B. C. D. (已提交)参考答案:C问题解析:2.(单选题) 以下关于线性表的叙述中正确的是()A.每个元素都有一个前趋元素和一个后继元素B线性表中至少有一个元素C.线性表中元素的排列次序必须是由小到大或由大到小D.除第一个和最后一个元素外,每个元素都有一个且仅有一个前趋元素和后继元素答题: A. B. C. D. (已提交)参考答案:D问题解析:3.(单选题) 以下关于线性表和有序表的叙述中正确的是()。
华南理工大学-C++程序设计-cchp9怎样使用类和对象

数据成员是私有的,本类外不能直接访问
float score;
public:
void display( )
{ cout<<"num:"<<num<<endl;
cout<<"name:"<<name<<endl;
cout<<"score:"<<score<<endl;
}
}
Student stu1={1001,”zhang san”,89}; //定义对象并初始化? 不能!
};
如果一个类中所有的成员都是公用的,则可以在定义对象 时对数据成员进行初始化。如
class Time
{public:
//声明为公用成员
hour;
minute;
sec;
};
Time t1={14,56,30};
//将t1初始化为14:56:30
但是,如果数据成员是私有的,或者类中有private或 protected的成员,就不能用这种方法初始化。
Box∷Box(int h,int w,int len):height(h),width(w),length(len) { }
类名::构造函数名(参数表) : 成员初始化表 { 构造函数体 }
这种写法方便、简练,尤其当需要初始化的数据成 员较多时更显其优越性。甚至可以直接在类体中 (而不是在类外)定义构造函数。
创建Student类的构造函数
void Student::display( )
{ cout<<"display:"<<endl;
计算机等级考试三级数据结构第9章集合例题与答案

第九章集合一、选择题1.若查找每个记录的概率均等,则在具有n个记录的连续顺序文件中采用顺序查找法查找一个记录,其平均查找长度asl为( )。
【北京航空航天大学2000 一、8 (2分)】a.(n-1)/2 b. n/2 c. (n+1)/2 d. n2. 对n个元素的表做顺序查找时,若查找每个元素的概率相同,则平均查找长度为( ) 【南京理工大学1998一、7(2分)】a.(n+1)/2 b. n/2 c. n d. [(1+n)*n ]/23.顺序查找法适用于查找顺序存储或链式存储的线性表,平均比较次数为((1)),二分法查找只适用于查找顺序存储的有序表,平均比较次数为((2))。
在此假定n为线性表中结点数,且每次查找都是成功的。
【长沙铁道学院1997 四、3 (4分)】a.n+1b.2log2nc.lognd.n/2e.nlog2nf.n24. 下面关于二分查找的叙述正确的是( ) 【南京理工大学1996 一、3 (2分)】a. 表必须有序,表可以顺序方式存储,也可以链表方式存储 c. 表必须有序,而且只能从小到大排列b. 表必须有序且表中数据必须是整型,实型或字符型 d. 表必须有序,且表只能以顺序方式存储5. 对线性表进行二分查找时,要求线性表必须()【燕山大学2001 一、5 (2分)】a.以顺序方式存储b.以顺序方式存储,且数据元素有序c.以链接方式存储d.以链接方式存储,且数据元素有序6.适用于折半查找的表的存储方式及元素排列要求为( ) 【南京理工大学1997 一、6 (2分)】a.链接方式存储,元素无序b.链接方式存储,元素有序c.顺序方式存储,元素无序d.顺序方式存储,元素有序7. 用二分(对半)查找表的元素的速度比用顺序法( ) 【南京理工大学1998 一、11 (2分)】a.必然快 b. 必然慢 c. 相等 d. 不能确定8.当在一个有序的顺序存储表上查找一个数据时,即可用折半查找,也可用顺序查找,但前者比后者的查找速度( )a.必定快 b.不一定 c. 在大部分情况下要快 d. 取决于表递增还是递减【南京理工大学1997 一、7 (2分)】9. 具有12个关键字的有序表,折半查找的平均查找长度()【中山大学1998 二、10 (2分)】a. 3.1b. 4c. 2.5d. 510. 折半查找的时间复杂性为()【中山大学1999 一、15】a. o(n2)b. o(n)c. o(nlogn)d. o(logn)11.当采用分快查找时,数据的组织方式为( ) 【南京理工大学1996 一、7 (2分)】a.数据分成若干块,每块内数据有序b.数据分成若干块,每块内数据不必有序,但块间必须有序,每块内最大(或最小)的数据组成索引块c. 数据分成若干块,每块内数据有序,每块内最大(或最小)的数据组成索引块d. 数据分成若干块,每块(除最后一块外)中数据个数需相同12. 二叉查找树的查找效率与二叉树的( (1))有关, 在((2))时其查找效率最低【武汉交通科技大学1996 一、2(4分)】(1): a. 高度 b. 结点的多少 c. 树型 d. 结点的位置(2): a. 结点太多 b. 完全二叉树 c. 呈单枝树 d. 结点太复杂。
(完整版)华南理工大学数据结构(含课程设计)随堂练习

第一章绪论本次练习有19题,你已做19题,已提交19题,其中答对19题。
.A. B. C..A. B. C.A. B. C.答题: 对. 错. (已提交)参考答案:×问题解析:2. 数据结构中,与所使用的计算机无关的是数据的 结构;A. 存储B. 物理C. 逻辑D. 物理和存储答题: A. B. C. D. (已提交)参考答案:C问题解析:3. 计算机算法指的是:A. 计算方法B. 排序方法C. 解决问题的有限运算序列D. 调度方法答题: A. B. C. D. (已提交)参考答案:C问题解析:3. 数据的逻辑结构是指数据的各数据项之间的逻辑关系。
( )答题: 对. 错. (已提交)参考答案:×问题解析:4. 计算机算法必须具备输入、输出和 等5个特性。
A. 可行性、可移植性和可扩充性B. 可行性、确定性和有穷性C. 确定性、有穷性和稳定性D. 易读性、稳定性和安全性答题: A. B. C. D. (已提交)参考答案:B问题解析:4. 数据的物理结构是指数据在计算机内的实际存储形式。
( )答题: 对. 错. (已提交)参考答案:√问题解析:. . . . . . . .本次练习有32题,你已做32题,已提交32题,其中答对15题。
当前页有10题,你已做10题,已提交10题,其中答对9题。
1.下述哪一条是顺序存储结构的优点?()A.存储密度大B.插入运算方便C.删除运算方便D.可方便地用于各种逻辑结构的存储表示答题: A. B. C. D. (已提交)参考答案:A问题解析:2.下面关于线性表的叙述中,错误的是哪一个?()A.线性表采用顺序存储,必须占用一片连续的存储单元。
B.线性表采用顺序存储,便于进行插入和删除操作。
C.线性表采用链接存储,不必占用一片连续的存储单元。
D.线性表采用链接存储,便于插入和删除操作。
答题: A. B. C. D. (已提交)参考答案:B问题解析:3.线性表是具有n个()的有限序列(n>0)。
华南理工大学网络教育学院 数据结构同步练习册答案

第3章 习题 3
栈、队列
3-1 对于一个适当大小的栈,设输入项序列为 A、B、C、D、E。为得到下列的处理序列,需 要做什么样的运算序列(由 PUSH、POP 组成)?。如果其中某处理序列得不到时,试说明理 由?:① A、B、C、D、E;② B、C、D、E、A;③E、A、B、C、D;④ E、D、C、B、A。 答 : ① PUSH(A), POP(A), PUSH(B), POP(B), PUSH(C), POP(C), PUSH(D), POP(D), PUSH(E), POP(E) ②PUSH(A), PUSH(B), POP(B), PUSH(C), POP(C), PUSH(D), POP(D), PUSH(E), POP(E), POP(A) ③无法实现。 ④PUSH(A), PUSH(B), PUSH(C), PUSH(D), PUSH(E), POP(E), POP(D), POP(C), POP(B), POP(A) 3-2 用链表存放着 n 个字符, 试用算法判断读字符串是否有中心对称关系。 例如 abccba, abcba 都算是中心对称的字符串。要求用尽可能少的时间完成判断(提示:将一半的字符先依次进 栈) 。 答:
2
x++;
由件(x>=(y+1)*(y+1))可知:当 (y+1)*(y+1)刚超过 n 的值时退出循环。
由(y+1)*(y+1)<n 得:y<n^0.5-1 所以,该程序段的执行时间为:向下取整(n^0.5-1) 第2章 习题 2 2.1 描述以下三个概念的区别:头指针、头结点、首元结点。此外叙述有序表的特性何在?, 以及向量与有序表的异同点?,头指针变量和头结点的作用?。并比较顺序存储结构和链式存 储结构的优缺点。 答:首元结点是指链表中的第一个结点,也就是没有直接前驱的那个结点。链表的头指 针是一指向链表开始结点的指引(没有头结点时)。单链表由头指针唯一确定,因此单链表可 以用头指针的名字来命名。头结点是人为地在链表的开始结点之前附加的一个结点。有了头 结点之后.头指针指向头结点,不论链表是否为空,头指针总是非空。而且头指针的设置使 得对链表的第一个位置的操作与在表其他位置上的操作一致(都是在某一结点之后)。 2.2 试写出将链表 L 从某元素 R 处分成两个链表 L 和 K 的算法。R 为 K 表的第一个元素。 答:提示:链表最终将分成两个链表。处理好 L 的尾结点(即 R 的前驱结点) ,和 K 的 头结点(R) 。 void depart_Node(Node *head,int R,Node *head_K) { Node *p=head,*temp; while(p){if(p->data=R)break;temp=p;p=p->next;} temp->next=NUll; head_k->next=p; } 2.3 给定一个 n 项元素的线性表 V,写一个过程,将元素排列的次序颠倒过来。要求占用原 来的空间,并且用顺序表和单表两种方法表示(要求用最少的附加空间来完成) 。 答: 线性表
数据结构第三版第九章课后习题参考答案
哈希表解未:(填1)满设,哈即希N表<MH,T由表于长字为母M序(号=从26)0,~关25键,字取个M数=为26,N,N 因为为小装于填M因的子值小,于设1为,2所0以。 对应的算法如下:
#define N 20
//输出哈希表
printf("%d:%s\n",i,HT[i]);
}
(2)先定义哈希表的类型 HashTable 如下:
typedef struct node //定义哈希表链表的结点类型
{ char *key;
struct node *next;
} LNode; typedef struct
//定义哈希表表头结点类型
//求字符串 s 的哈希函数值
{
return(*s%M);
}
构造哈希表 void Hash1(char *s[],HTType HT[]) //
{ int i,j;
LNode *q; for (i=0;i<M;i++)
//哈希表置初值
HT[i].link=NULL;
for (i=0;i<N;i++)
6
1
3
7
0
0
1
06
1
35 7
0
00 0
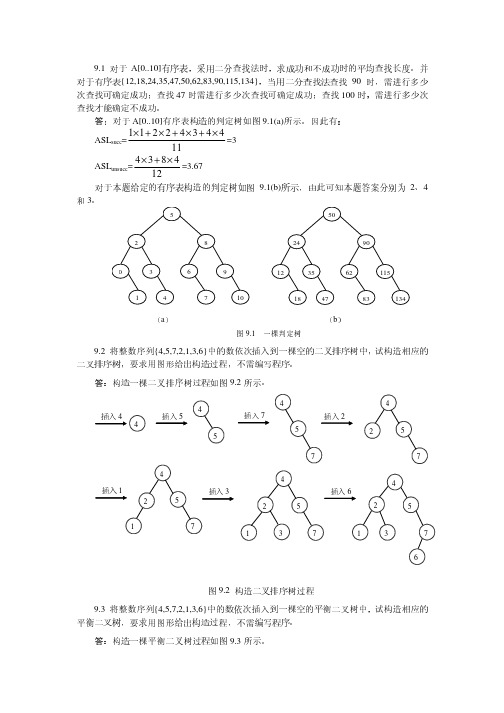
图 9.3 构造平衡二叉树过程 9.4 编写一个算法,输出在一棵二叉排序树中查找某个关键字 k 经过的路径。 值,从解而:以使根用结pa点th到数当组前存结储点经输过出的路结径点。,对当应找的到算所法要如找下的:结点时,输出 path 数组中的元素
int path[MaxSize];
《数据结构》课件ds-09

第九章 排序
1
第九章 排序
概述 插入排序 交换排序 选择排序 归并排序 基数排序
140-2
概述
排序:将一组杂乱无章的数据按一定的规律 顺次排列起来。 数据表(datalist): 它是待排序数据元素的有限 集合。
排序码(key): 通常数据元素有多个属性域, 即 多个数据成员组成, 其中有一个属性域可用来 区分元素, 作为排序依据。该域即为排序码。 每个数据表用哪个属性域作为排序码,要视 具体的应用需要而定。
起泡排序的算法
template <class T> void BubbleSort (dataList<T>& L, const int left, const int right) { int pass = left+1, exchange = 1; while (pass <= right && exchange) { exchange = 0; //标志为0假定未交换 for (int j = right; j >= pass; j--)
140-6
bool operator == (Element<T>& x) { return key == x.key; } //判*this与x相等 bool operator <= (Element<T>& x) { return key <= x.key; } //判*this小于或等于x bool operator >= (Element<T>& x) { return key >= x.key; } //判*this大于或等于x bool operator > (Element<T>& x) { return key > x.key; } //判*this大于x bool operator < (Element<T>& x) { return key < x.key; } //判*this小于x
《数据结构教学课件》第09章.ppt

C6 C7 C8 C9
课程名称 计算机导论 数据结构 汇编语言 C程序设计语言 计算机图形学
接口技术 数据库原理 编译原理 操作系统
先修课程
无 C1,C4 C1 C1 C2,C3,C4
C3 C2,C9 C4 C2
4 of 114
教学计划编排问题(图形结构)
各课程之间的次序关系可用一个称作图 的数据结构来表示,如课程之间优先关系 有向图。有向图中的每个顶点表示一门课 程,如果从顶点vi到vj之间存在有向边<vi, vj>,则表示课程i必须先于课程j进行。
0
0
0
0
1
1
3
2
(a) 图G1
1
2
3
45
6
(b)图G2
1
2
3
2
(c)图G3 (d)图G4
12 of 114
(5)顶点的度: 顶点v的度是与它相关联的边的条数,记作TD(v)。 ➢有向图:顶点的度 = 入度 + 出度。 •入度ID(v)定义为以顶点v为终点的有向边的条数; •出度OD(v)定义为以顶点v为起点的有向边的条数; ➢无向图:TD(v)=ID(v)=OD(v)
0
0
0
0
1
1
3
2
(a) 图G1
1
2
3
45
6
(b)图G2
1
2
3
2
(c)图G3 (d)图G4
10 of 114 (3)完全图:
在有n个顶点的无向图中,若有n(n-1)/2条边,即任意两个 顶点之间有且只有一条边,则称此图为无向完全图; 在有n个顶点的有向图中,若有n(n-1)条边,即任意两个顶 点之间有且只有方向相反的两条边,则称此图为有向完全图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Cn 0.122n.
8
Self-Organizing Lists
Self-organizing lists modify the order of records within the list based on the actual pattern of record accesses.
Self-organizing lists use a heuristic for deciding how to reorder the list. These heuristics are similar to the rules for managing buffer pools.
11
on: Text Compression. Keep a table of words already seen, organized via Move-to-Front heuristic.
– – If a word not yet seen, send the word. Otherwise, send (current) index in the table.
Searching sorted Arrays-- Jump Search.
For some value j, we check every j’th element in L, that is, we check elements L[j], L[2j], and so on. Define m such that mj≦ n < (m + 1)j, then the total cost of this algorithm is at most m + (j-1) 3-way comparisons. (3-way comparison means that we need to know if K is less than, equal to or greater than L[i].) The cost on n items with a jump of size j is
14
Hashing (2)
For any value K in the key range and some hash function h, h(K) = i, 0 <= i < M, such that HT[i] = K. Hashing is appropriate only for sets (no duplicates). Good for both in-memory and disk-based applications. Hashing is not good for range queries, minimum or maximum queries and queries in key order.
Buffer pools are an example of a self-organizing list.
9
Heuristics
1. Order by actual historical frequency of access. (Similar to LFU buffer pool replacement strategy.) 2. Move-to-Front: When a record is found, move it to the front of the list. (Similar to LRU buffer pool replacement strategy.) 3. Transpose: When a record is found, swap it with the record ahead of it.
An exact-match query is a search for the record whose key value matches a specified key value. A range query is a search for all records whose key value falls within a specified range of key values.
Order lists by (expected) frequency of occurrence.
– Perform sequential search Assume that for each key ki, the probability pi that the record with key ki will be requested. Cost to access first record: 1 Cost to access second record: 2 Expected search cost:
-> 0011010100010100 (from the left, 1 represents primes 2,3,5,7,11,13)
-> 0011010100010100 & 0101010101010101
13
Hashing (1)
Hashing: The process of mapping a key value to a position in a table.
3
Searching Unsorted and Sorted Arrays
Searching Unsorted Arrays-- Sequential Search
How many comparisons does linear search do on average?
For large collections of records that are searched repeatedly, sequential search is unacceptably slow.
Search
Given: Distinct keys k1, k2, …, kn and collection L of n records of the form (k1, I1), (k2, I2), …, (kn, In) where Ij is the information associated with key kj from record j for 1 <= j <= n. • Search Problem: For key value K, locate a record (kj, Ij) in L such that kj = K. (if one exists). Searching is a systematic method for locating the record(s) with key value kj = K.
When we know something about the distribution of key values, then search L at a position p that is appropriate to the value of K as follows.
5
Lists Ordered by Frequency
1
Successful vs. Unsuccessful
A successful search is one in which a record with key kj = K is found. An unsuccessful search is one in which no record with kj = K is found (and no such record exists).
-> For dense sets (small range, high percentage of elements in set). -> Can use logical bit operators. 1 if element in set, 0 otherwise.
2) For Example: to find all primes that are odd numbers between 0 and 15
The car on the left hit the car I left. The car on 3 left hit 3 5 I 5. This is similar in spirit to Ziv-Lempel coding.
12
Searching in Sets
1) Using bit vector to represent the set.
10
Example 9.4-page 321 Assume that we have eight records, with key values A to H, and that they are initially placed in alphabetical Order (A B C D E F G H). Now, consider the result of applying the following access pattern: F D F G E G F A D F G E. 1) Count heuristic, the final list resulting will be F G D E A B C H, the total cost -- 45 comparisons. 2) Move-to-front heuristic, the final list resulting will be E G F D A B C H, the total cost -- 54 comparisons. 3) Transpose heuristic, the final list resulting will be A B F D G E C H, the total cost -- 62 comparisons.
