NP完全性精讲
NP完全问题 ppt课件

❖优化问题举例:给定一个带整数权的有向图G,其 最短路径长度的哈密尔顿长度是多少?
NP完全问题
1.3 优化问题向判定问题的转换
判定问题举例:给定一个带整数权的有向图G和一个正整数k, 是否存在着一条长度小于k的哈密尔顿回路? 优化问题举例:给定一个带整数权的有向图G,其最短路径 长度的哈密尔顿长度是多少?
for (int j=0; j<n; j++)
if (a[i] == a[j])
return yes; //修改为no
return no; //修改为yes
}
NP完全问题
2.1.5 判定问题规约的定义
❖定义:令和是两个判定问题,如果存在一个 具有如下性能的算法A,可以用多项式的时间,把 问题的实例I转换为问题的实例I,使得I与I的 答案一致,就称以多项式时间规约于,记为 p
❖定理:P类问题在补集下是封闭的
❖证明:对于P类问题中的任意问题,只要修 改相应的多项式级别算法A的代码,把返回yes的 改为返回no,把返回no的改为返回yes即可
boolean judgeEqual(int n, Elem[] a, Elem[] b){
for (int i=0; i<n; i++)
第12章 NP完全问题
1. NP完全问题概述 2. P类和NP类问题 3. NP完全问题 4. co_NP类和NPI类问题
NP完全问题
1. NP完全问题概述
1.1 Church-Turing论题和Cook-Karp论题 1.2 问题分类 1.3 优化问题向判定问题的转换
清华大学算法分析与设计课件第10讲_NP完全性理论

Lecture 10. NP完全性理论清华大学软件学院清华大学 1内容提要•计算模型与计算复杂度关系•问题分类:【P】与【NP】类•NP-难【hard】问题,NP完全集•第一个NPC问题和NPC问题集•如何证明一个问题是NPC问题涉及到的算法理论基础•原则上是否存在一般数学问题的解题步骤的判决问题【希尔波特第十问题】•图灵机的停机问题:是否存在一个图灵机,他可以回答其它图灵机是否停机【既算法是有界的】•图灵公理:凡是可计算的函数都可以用一台图灵机来计算•P-NP-NPC问题定义及其猜想:NPC是一类不可以在多项式时间内计算的问题。
清华大学 3明代数学家程大位著《算法统宗》中关于珠算的插图机械式手动计算机清华大学 5机械计算机•法国数学家、哲学家帕斯卡在1642年发明了一种机械计算机,并与1649年取得专利。
帕斯卡的计算机采用一种齿轮系统,其中一小轮转十个数字,下一个小轮便转动一个数字,通过齿轮系的联动,可以进行加法和减法的运算.图灵•大半个世纪以来,数学家、计算机科学家提出了各种各样的计算模型都被证明是同图灵机器等价的。
这一理论已被当成公理,它不仅是计算机科学的基础,也是数学的基础之一。
为纪念英国数学家Turing(1912-1954) 而设立的图灵奖成为计算机界的诺贝尔奖.清华大学7图灵机模型图灵机定义•一个图灵机是一个7元组(Q,∑,Γ,δ,q0,q1,q2), 其中Q,∑,Γ都是有穷集合,并且•1) •2) •3) 集. •4) •5) •6) •7) Q 是状态集.∑是输入字母表,不包括特殊空白符号︺. Γ是带字母表,其中: ︺∈Γ,∑是Γ的子δ: Q×Γ→Q×Γ×{L,R}是转移函数. q0∈Q是起始状态.q1∈Q是接受状态.q2∈Q是拒绝状态,且q2≠q1图灵机模型•图灵机模型用一个无限长的带子作为无限存储, 它还有一个读写头,这个读写头能在带子上读, 写和移动: 开始时,带子上只有输入串,其它地方都是空的.当它需要保存信息时,读写头就把信息写在带子上.为了读某个输入或写下的信息,带子可能将读写头往回移动到这个信息所在的地方.这样读,写和移动,机器不停的计算, 直到产生输出为止.机器实现设置了两种状态: 接受或拒绝清华大学9多带图灵机,•和普通图灵机相似,只是有多个带子,每个带子都有自己的读写头,用于读和写.如图清华大学11非确定性的图灵机•非常容易理解,在计算的任何时刻,机器可以在多种可能性中选择一种继续进行.它的计算是一课树,不同的分枝对应着机器不同的可能性.如果某个计算分枝导致接受状态,则接受该输入.与多带图灵机相同的是,它的计算能力与普通图灵机也是一样的.当然他的计算能力就不一样了。
第9章 NP完全性理论

P = NP无法证明
计算机科学与工程系
P
NP
教学进度
计算机科学与工程系
• 多数人相信,存在至少一个不可能有多 项式级复杂度的算法的NP问题,即 P≠NP
教学进度
计算机科学与工程系
• 约化:一个问题A可以约化为问题B的含 义即是,可以用问题B的解法解决问题A, 或者说,问题A可以“变成”问题 B。
教学进度
计算机科学与工程系
• 比如说,现在有两个问题:求解一个一元一次方程和 求解一个一元二次方程。 • 前者可以约化为后者,即知道如何解一个一元二次方 程那么一定能解出一元一次方程。 • 可以写出两个程序分别对应两个问题,那么能找到一 个“规则”,按照这个规则把解一元一次方程 程序 的输入数据变一下,用在解一元二次方程的程序上, 两个程序总能得到一样的结果。这个规则即是:两个 方程的对应项系数不变,一元二次方程的二次项系数 为 0。按照这个规则把前一个问题转换成后一个问题, 两个问题就等价了。
教学进度
计算机科学与工程系
• 所说的“可约化”是指的可“多项式地” 约化(Polynomial-time Reducible),即变 换输入的方法是能在多项式的时间里完 成的。 • 约化的过程只有用多项式的时间完成才 有意义。
教学进度
计算机科学与工程系
• “问题A可约化为问题B”有一个重要的直 观意义:B的时间复杂度高于或者等于A 的时间复杂度。也就是说,问题A不比 问题B难。
教学进度
计算机科学与工程系
教学进度
计算机科学与工程系
• 根据有限状态控制器的当前状态及每个读写 头读到的带符号,图灵机的一个计算步可实 现下面3个操作之一或全部。 • (1)改变有限状态控制器中的状态。 • (2)清除当前读写头下的方格中原有带符号并 写上新的带符号。 • (3)独立地将任何一个或所有读写头,向左移 动一个方格(L)或向右移动一个方格(R)或停在 当前单元不动(S)。
NP完全性理论ppt课件

2
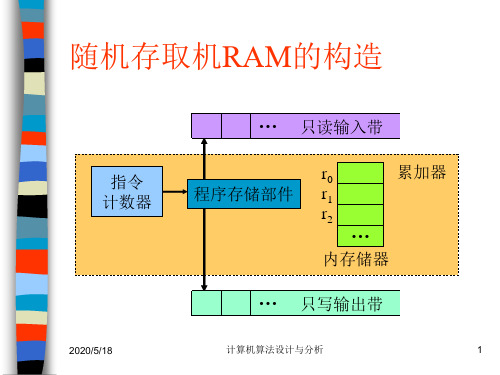
8.1.1 随机存取机RAM
1. RAM的结构 2. RAM程序
• 一个RAM程序定义了从输入带到输出带的一个映射。 可以对这种映射关系作2种不同的解释。
精选版课件ppt
3
解释一:把RAM程序看成是计算一个函数 若一个RAM程序P总是从输入带前n个方格中读入n个整数
x1,x2,…,xn,并且在输出带的第一个方格上输出一个整数y 后停机,那么就说程序P计算了函数f(x1,x2,…,xn)=y
fv o pfv1 或f v 2 opfv 或c f v1
fv fv1
其中,f v1和 f分v 2 别是结点v在树T中的祖先结点v1和v2处得到
的结果值,或是x的分量;op∈{+,-,×,/};c是一个常数。
(3)每个有2个儿子的内部结点(分支结点)v,表示下列形式的
测试指令:
f >v1 0或 ≥f v01 或 =f0v1
精选版课件ppt
22
8.2.1 非确定性图灵机
在图灵机计算模型中,移动函数δ是单值的,即对于QTk中的 每一个值,当它属于δ的定义域时,Q(T{L,R,S})k中只有惟 一的值与之对应,称这种图灵机为确定性图灵机,简记为
DTM(Deterministic Turing Machine)。
非确定性图灵机( NDTM ):一个k带的非确定性图灵机M 是一个7元组:(Q,T,I,δ,b,q0,qf)。与确定性图灵机不同 的是非确定性图灵机允许移动函数δ具有不确定性,即对于QTk 中的每一个值(q;x1,x2,…,xk),当它属于δ的定义域时,Q(T{L, R,S})k中有惟一的一个子集δ(q;x1,x2,…,xk)与之对应。可以在 δ(q;x1,x2,…,xk)中随意选定一个值作为它的函数值。
NP完全性理论
2018/10/13 计算机算法设计与分析 11
TM模型与RAM模型的关系
定理8-5:在对数耗费标准下,对于同一个算法, 采用RAM模型和TM模型的时间复杂性是多项 式相关的。对空间复杂性亦如此。 注意在均匀耗费标准下这个关系不成立。TM 模拟RAM的时间复杂性可能是指数的关系。 因为TM模型比较原始,所以在大多数情况下 采用RAM模型。 若算法在RAM模型下的复杂性为多项式,则也 就认为其在TM模型下的复杂性为多项式。
计算机算法设计与分析 6
2018/10/13
TM的数学描述
其中: Q是有限状态的集合; T是有限个带符号的集合; I T,是输入符号的集合; δ:Q×T→Q×T×{L, R}为转移函数; b是唯一的空白符,b∈T – I; q0和qf分别为初始状态和终止状态。
2018/10/13 计算机算法设计与分析 7
图林机(Turing Machine)是英国数学家Turing在 1936年提出的计算模型,被认为是当今计算机 的理论模型。下面是图林机(TM)原型的构造:
…… 输入带
磁头
有限 控制器
输入带被视为右无穷,并被划分为一个个 单元用于存放符号(带符号)。 有限控制器由有限个状态构成。 磁头可左右移动,读写带符号。
2018/10/13 计算机算法设计与分析 12
2018/10/13 计算机算法设计与分析 10
用TM模拟RAM
定理8-4:设算法A,对于任何长度为n的输入, 按对数耗费标准在RAM下的时间复杂性为T(n), 则A在TM下的时间复杂性为O(T2(n))。 证明:用一个五带TM模拟RAM的工作, TM 其中: 模拟RAM除乘/除法外的指令的时间为常数, 查找寄存器的时间为 带1用<地址, 内容 n> ,整个时间为 的形式存放寄存器; O(T2(n))。 带2的乘除法, 存放累加器内容;带 3作为暂存工作带; 对RAM TM用加减法模拟的耗费不 带4和带5作为输入带和输出带; 会超过乘除法耗费的平方。 用TM的状态对应RAM的一步程序。
NP完全性证明(2)

3.4 NP完全性的证明一、六个基本的NPC问题三元可满足性问题(3SAT)三维匹配问题(3DM)顶点覆盖问题(VC)团的问题哈密顿回路(HC)均分问题二、基本NP完全问题的证明三、NP完全问题的证明方法一、六个基本NP完全问题3SAT实例: 有穷布尔变量集U 和U上的子句集C={c1,c2,...,cm},其中|ci|=3, 1≤i≤m.问: 对于U是否存在满足C中所有子句的真值赋值?3DM实例: 集合M ⊆W×X×Y, 其中W,X,Y互不相交, 且|W|=|X|=|Y|=q.问: M是否包含一个匹配, 即是否存在子集M’⊆M使得|M’|= q且M’中任意两个元素的三个坐标都不相同?肯定实例:W={a1,a2,a3,a4},X={b1,b2,b3,b4},Y={c1,c2,c3,c4}M={(a1,b2,c1),(a1,b1,c1),(a2,b1,c2),(a2,b2,c1), (a3,b3,c3),(a4,b4,c4),(a4,b2,c1)}VC实例: 图G=(V,E), 正整数k≤|V|.问: G中是否存在大小不超过k的顶点覆盖, 即是否存在子集V’⊆V,使得|V’|=k, 且对每条边{u,v}∈E都有u∈V’或v∈V’?团实例: 图G=(V,E), 正整数J≤|V|.问: G是否包含大小不小于J的团, 即是否存在子集V’⊆V,使得|V’|≥J, 且V’中每两个顶点都由E中的一条边连接?独立集实例:图G=(V,E),正整数J≤|V|问:G中是否包含大小不小于J的独立集,即是否存在V’⊆V, 使得|V’|≥J,且∀u,v∈V’,{u,v}∉E?HC实例: 图G=(V,E),|V|=n.问: G 中是否包含一条哈密顿回路, 即是否有G 的顶点排列><n j j j v v v ,...,,21?},{,1,},{11E v v n i E v v j j j i j n i ∈<≤∈+∑=∑-∈∈'')()(A A a A a a S a S 使得均分实例: 有穷集合A, ∀a ∈A 有”大小”S(a)∈Z +问: 是否存在子集A ’⊆ A 使得证明顺序均分HC 团(独立集)1.3SAT∈NPC证明思路证3SAT∈NP将SAT的实例变换成3SAT的实例:根据子句中的文字个数k 分别处理1个子句转变成多个子句保证每个子句含有3个文字转变前与转变后的真值不变证显然3SAT属于NP.设U={u1,u2,...,un}, C={c1,c2,...,cm}是SAT的任何实例.对于C中任意子句c j ={z1,z2,...,zk},构造新增的变量集Uj ’和子句集Cj’.}},,}{,,{},,,{},,,{{'},{'21121121121121j j j j j j j j j j j j y y z y y z y y z y y z C y y U ==C j ’被满足⇔c j 被满足.若k=2, c j ={z 1,z 2}, 则}},,{},,,{{'}{'1211211j j j j j y z z y z z C y U ==C j ’被满足⇔z 1+z 2为真⇔c j 被满足.若k=3, 则U j ’= ∅C j ’= {c j }若k=1, c j ={z 1}, 则},,{},,,{},,,{{'},{'54223112121z z y y z y y z z C y y U j j j j j j j j ==c j 可满足⇔z 1+z 2+...+z 5为真⇒C j ’可满足如z 1+z 2为真, 则y j 1= y j 2 = F ;如z 3为真, 则y j 1= T,y j 2 = F ;如z 4+z 5为真, 则y j 1= T,y j 2 = T .反之, 若C j ’可满足而c j 不满足, 则z 1+z 2+...+z 5为假, 即z 1,z 2,...,z 5全为假, 必须y j 1=T,y j 2 =T, 最后的子句不满足.若k>3, 例如c j = {z 1,z 2,...,z 5}, 则一般若c j ={z 1,z 2,...,z k }, k>3}},,{{}41:},,{{}},,{{'}31:{'1312121k k k ji ji i j j j i j j z z y k i y z y y z z C k i y U --++⋃-≤≤⋃=-≤≤=令U ’= U ⋃U 1’⋃U 2’⋃...⋃U m ’C ’= C 1’⋃C 2’⋃...⋃C m ’下面证明f是多项式变换.易见若t满足C’, 则t满足C. 假若t不满足cj,则z 1,z2,…,zk全为假,只能有Tyyy k jjj====-321...C’的最后一个字句不满足.反之,设t:U→{T,F}是满足C的真值赋值, 将U’-U的变量分成U1’, U2’, ..., Um’, 且Uj’的变量只出现于子句Cj ’中。
第九章NP完全性理论与近似算法PPT课件

2020/11/27
计算机算法设计与分析
11
δ的进一步说明
• δ操作可以表示为δ(q,a1,…ak)=(q’,(a1’,d1),…,(ak’,dk)) • 当图灵机处于状态q且对一切i,1<=i<=k,第i条带的
读写头扫描着的当前方格中的符号为ai时,图灵机就 按这个δ操作进行工作:
1. q变为q’ 2. a变为a’ 3. 左移或者右移
2020/11/27
操作数
指令含义
=i / i / *i
取操作数入累加器
i / *i
将累加器中数存入内存
=i / i / *i
加法运算
=i / i / *i
减法运算
=i / i / *i
乘法运算
=i / i / *i
除法运算
i / *i
读入
=i / i / *i
输出
标号
无条件转移到标号语句
标号
正转移到标号语句
第九章
NP完全性理论
2020/11/27
计算机算法设计与分析
1
难?易?
• 可在多项式时间内解决的问题看作是 “易”解问题。
• 将需要指数函数时间解决的问题看作是 “难”问题。
• 这里所说的时间是针对问题规模n的多项 式还是指数函数。
2020/11/27
计算机算法设计与分析
2
内容
• 两部分:
– 三种机器(RAM, RASP, TM) – NP完全理论
2020/11/27
计算机算法设计与分析
12
图灵机的语言
• 当 进且入仅终当止从状指态q定f时的,初称始图状灵态机q0接开受始这,个经输过入一符系号列串计。算步后,最终 • 所有这台图灵机能接受的输入符号串的集合就是这台图灵机识别
第九章-NP完全性理论与近似计算培训课件

寄存器可存放一个任意大小的整数。因此若设l(i)是整数i所
占的二进制位数,则
l(i)lo1g|i|
i 0 i 0
9.1.2 随机存取存储程序机P
1、RASP的结构
❖ RASP的整体结构类似于RAM,所不同的是RASP 的程序是存储在寄存器中的。每条RASP指令占据2 个连续的寄存器。第一个寄存器存放操作码的编码, 第二个寄存器存放地址。RASP指令用整数(1~18) 进行编码。
解释二:把RAM程序当作一个语言接受器。 将字符串S=a1a2…an放在输入带上。在输入带的第一个,
第二个,…,第n个方格中依次放入符号a1,a2,…,an。然 后在第n+1个方格中放入0,作为输入串的结束标志符。如果 一个RAM程序P读了字符串S及结束标志符0后,在输出带的第 一格输出一个1并停机,就说程序P接受字符串S。
0、有穷自动机(补充)
确定型有穷自动机的定义:
一台确定型有穷自动机是一个五元组(Q,
, , S, F)。其中, Q, , 都是有穷集合。 • Q:有穷状态集合 • :字母表
• S: 初始状态, S Q • F: 终止状态集合,F Q • : 转移函数, : Q Q
确定性有穷自动机举例
例:一台确定型有穷自动机,它接受这样的语言:由a,b 字符构成、不含3个连续b字符的有限长度的字符串。
2、RASP程序的复杂性
不管是在均匀耗费标准下,还是在对数耗费标准 下,RAM程序和RASP程序的复杂性只差一个常 数因子。在一个计算模型下T(n)时间内完成的输 入-输出映射可在另一个计算模型下模拟,并在 kT(n)时间内完成。其中k是一个常数因子。空 间复杂性的情况也是类似的。
9.1.3 图灵机
• 大多数指数时间算法只是穷举搜索法的变种 • 多项式时间算法通常只有在对问题的结构有了某些比
算法设计与分析课件--NP完全性理论-P类和NP类问题

团问题的一个实例可以用长度为n2 + log k + 1 的二
进位串表示。
➢ 无向图的团问题可表示为语言:
• CLIQUE = {w#v|w,v∈{0,1}*,以w为邻接矩阵的图G有一个k 顶点的团。其中,w是C的二进制表示,v是k的二进制表示。}
• STEP3:确定性地检查V’的团性质。若V’是一个团则接受输入,
否则拒绝输入。时间复杂度为O(n 4 ) 。 • 因此,整个算法的时间复杂性为:O(n 4 ) 。
❖非确定性算法在多项式时间内接受语言CLIQUE,故CLIQUE∈NP。
16
8.2 P类问题和NP类问题
◼ P类问题和NP类问题的关系:
算法设计与分析
1
第八章 NP完全性理论
目录
8.1 易解问题和难解问题
8.2 P类问题和NP类问题
8.3
NP完全问题
8.4 NP完全问题的近似算法
2
8.1 易解问题和难解问题
◼ 常见的几类算法复杂性:
➢ O(1):常数阶; ➢ O(log2n), O(nlog2n):对数阶; ➢ O(n), O(n2), O(n3), …, O(nk): 多项式阶。多项式时间算法; ➢ O(2n), O(n!), O(nn):指数阶。指数时间算法。
12
8.2 P类问题和NP类问题
◼ NP(Non-deterministic Polynomial)类问题:
➢ 如对于某个判定问题,存在一个非负整数k,对于输入规模为n的实 例,能以O(nk)的时间运行一个非确定性算法得到是或否的答案。 • 能用非确定算法在多项式时间内求解的判定问题。如哈密尔顿回 路问题。 • NP类问题是难解问题的一个子类。 • NP类问题并不要求给出一个算法来求解问题本身,而只要求给 出一个确定性算法在多项式时间验证它。
第1章 算法概论(4np完全性理论)

1§1.3 NP 完全性理论如何理解问题的难解?易解?多项式运行时间?⏹多项式的运行时间认为是易解算法,当然,你认为θ(n100)难解,但次数如此高的多项式时间问题非常少,且一般都会找到一个更有效的多项式时间算法。
⏹对很多合理计算模型来说,在一个模型上用多项式时间可解的问题,在另一个模型上也可以用多项式时间获得解决。
2如何理解问题的难解?易解?多项式运行时间?多项式时间可解问题类具有很好的封闭性。
比如一个多项式时间算法输出给另一个多项式时间算法作为输入,或被另一个多项式时间算法作为子程序常数次调用,这样的组合算法运行时间也都是多项式的。
3⏹一般来说,将可由多项式时间算法求解的问题看成易处理的问题,而把需要超多项式时间才能解决的问题看作难处理问题。
⏹“NP完全”(NP-Complete)问题,它的状态是未知的,迄今为止,既没有人找出求解NP完全问题的多项式算法,也没人能够证明对这类问题不存在多项式时间算法。
⏹P≠NP问题,自1971年提出以后,已经成为理论计算机科学研究领域中,最深奥和最错综复杂的开放问题之一了。
45⏹从表面上看,有些NP 完全问题有着与多项式时间算法的问题非常相似的特点,这很诱惑。
⏹最短与最长简单路径:有向图G=(V,E),单源最短路径可在O(|V|2)时间内完成,但寻找两个顶点间最长简单路径(无重复顶点)问题是NP 完全的。
⏹欧拉游程和哈密顿回路:有向图G=(V,E),欧拉游程指一个回路,遍历途中每条边一次,但可能不止一次的访问同一个顶点,这可在O(|E|)时间内找到。
哈密顿回路也是一个回路,包含V 中每个顶点。
确定有向图是否存在哈密顿回路的问题是NP 完全的。
探讨这样三类问题:P、NP、NPC(NP 完全问题)⏹NPC类,称NP完全的(NP-complete),属于NP的一个最难的子类。
如果一个问题属于NP,且与NP中任何问题一样“难的”。
⏹有宣称:如果任何NPC问题可以在多项式时间内解决,则NP中所有问题都有一个多项式时间的算法,即有P=NP了。
算法---NP完全性

确定性的(non-deterministic)。如果存在输入为x的算法A,调用
select的结果,使得算法A最终输出“yes”,则称算法A非确定性
地接受一个串x。换句话说,
select
后产生的所有可能结果,而同于随机选择。
5. 另一种NP
证明:定义非确定算法A,以图G作为输入,而图G编码为 二进制表示的邻接表,顶点从1到N编号。首先定义A迭代调用 select过程,确定1~N的N+1个数的序列S,然后A检查1~N中的每 个数字,只在S中出现一次, 除了第一个和最后一个数字相同 之外。 我们验证序列S定义了G中顶点和边的一个回路。 序列S 的二进制编码串的大小至多为n,这里n为输入的规模。显然, 对序列S所做的两次检查均可在n的多项式时间完成。
6. P=NP的问题
计算机科学家并不能够肯定是否P=NP。研究人员甚至不 确信是否P=NP∩co-NP。尽管如此,大多数科学家认为P与NP 和co-NP都不等, 也不与它们的交集相等。 事实上, 在我们 以下讨论的NP问题的例子中, 其中许多问题并不在P中。
7.1.2 NP中的有趣问题
引理7.3 HAMILTIAN-CYCLE∈NP。
引理7.5 VERTEX-COVER∈NP。
证明:给定整数k和图G, G中顶点从1至N编号。我们可以 反复调用select过程,构造1~N范围内的k个数的集合C。作为一 个验证,我们将C中的所有数插入一个字典中, 然后检查G中 的每条边,证实对于G中的每条边(v, w),或者v在C中,或者w 在C中。如果我们找到一条边,它的两个端点都不在G中,那么 输出“no”。 如果我们检查了G中的所有边,满足每条边都有 一个顶点在C中,那么输出“yes”。显然,这样的一个计算运 行时间为多项式时间。
算法设计与分析课件--NP完全性理论-NP完全问题及近似算法

1
第八章 NP完全性理论
目录
8.1 异解问题和难解问题
8.2 P类问题和NP类问题
8.3
NP完全问题
8.4 NP完全问题的近似算法
2
8.3 NP完全问题
问题变换:
➢ NP类问题在最坏情况下的时间复杂性一般都是快速增长的指数函 数。希望能够在NP类问题内部找到一种方法,比较两个问题的计 算复杂性。
❖该近似算法的相对误差定义为=
cc* c*
。若对问题的输
入规模n,有一函数ε(n)使得 c c* ≤ε(n),则称ε(n)
c*
为该近似算法的相对误差界。
13
8.4 NP完全问题的近似算法
NPC问题的近似算法示例 - TSP:
➢ 给定一个完全无向图G=(V,E),其每一条边(u,v)∈E有一非 负整数费用c(u,v)。要找出G的最小费用哈密顿回路。如果 TSP满足三角不等式性质,即对于任意3个顶点u,v,w∈V有 :c(u,w)≤c(u,v)+c(v,w),则称该TSP为欧几里得TSP,否 则称为一般TSP。
12
8.4 NP完全问题的近似算法
NPC问题的近似算法的性能:
❖若一个最优化问题的最优值为c*,求解该问题的一个近 似算法求得近似最优解相应的目标函数值为c,则将该近 似近≤似算ρ比法(是n的)问。近题ρ似输(比n入)定为规义1模时为n,的求=一m得a个x的c函c*近, c数c*似 ρ。解(在为n)通最,常优即情解m况a。x 下cc* ,,cc*该
➢ 传递性:设P1、P2和P3是3个判定问题。若P1∝τ(n)P2,且P2∝τ(n)P3 ,则P1∝τ(n)P3。
4
8.3 NP完全问题
多项式时间变换示例:
算法分析与设计课件NP完全问题

17
近似算法的性能
若一个最优化问题的最优值为c*,求解该问题的一个 近似算法求得的近似最优解相应的目标函数值为c,则将 c * c max , 该近似算法的性能比定义为= c 。在通常情况 c* 下,该性能比是问题输入规模n的一个函数ρ(n),即 c * c max , ≤ρ(n)。 c c* 该近似算法的相对误差定义为= c * 。若对问题 cc* 的输入规模n,有一函数ε(n)使得 c * ≤ε(n),则称 ε(n)为该近似算法的相对误差界。近似算法的性能比 ρ(n)与相对误差界ε(n)之间显然有如下关系: ε(n)≤ρ(n)-1。
4
这种问题的答案,是无法直接计算得到的,只能通过间 接的“猜算”来得到结果。这也就是非确定性问题。而这些 问题的通常有个算法,它不能直接告诉你答案是什么,但可 以告诉你,某个可能的结果是正确的答案还是错误的。这个 可以告诉你“猜算”的答案正确与否的算法,假如可以在多 项式时间内算出来,就叫做多项式非确定性问题。而如果这 个问题的所有可能答案,都是可以在多项式时间内进行正确 与否的验算的话,就叫完全多项式非确定问题。
2
10
接受该语言CLIQUE的非确定性算法:用非确定性选择指令选 出包含k个顶点的候选顶点子集V,然后确定性地检查该子集是否 是团问题的一个解。算法分为3个阶段: 算法的第一阶段将输入串w#v分解,并计算出n= | w | ,以及 用v表示的整数k。若输入不具有形式w#v或|w|不是一个平方数就 2 拒绝该输入。显而易见,第一阶段可 O ( n ) 在时间内完成。 算法的第三阶段是确定性地检查V’的团性质。若V’是一个团 则接受输入,否则拒绝输入。这显然可以在 O ( n 4 ) 时间内完成。 4 因此,整个算法的时间复杂性为O ( n ) 。
第四讲NP完全性理论课件

在討論計算理論時,可以將這種限制拿掉,也就是 可以假設一個運算的結果不唯一,可能是某 n 個結 果中的一個,而且一定會是正確的那一個。這樣子 的算法稱為 non-deterministic algorithm。這種 算法無法在實際的電腦上執行。
E.g., (a+b+c’)(d+e’+f)(a’+f’+g)
Given a 3-CNF formula, is it satisfiable?
That is, is there an assignment (to variables) that evaluates the formula to 1
B[j] = A[i];
O(n)
}
for(i = 1;i <= n-1;i++) if(B[i] > B[i+1]) Failure();//作確認
for(i=1;i <= n;i++) cout << B[i] << ‘ ‘;
cout << endl; Success();
}
要如何來看待 non-deterministic algorithm 呢?
1小时能解决的最大规模
Time complexity function
n
n2
With present computer
N1 N2
n3
N3
n5
N4
2n
计算理论第7章 NP完全性

19
7.2 NP完全问题
Clique(团)是图的一个子图,其中任何两 点都有边相连。 K-Clique问题:给定<G,k>,G是无向图,G 中包含至少k节点的团吗? k-Clique是NP完全的 证明: (1)k-Clique是NP问题 (2)3SAT ≤p k-Clique
20
7.2 NP完全问题
SUBSET-SUM(子集和)问题:有一个数集 x1,x2,…,xk和一个目标数t,要判定数集是否 包含一个加起来等于t的子集。 子集和问题是NP完全的 (1)子集和问题属于NP类 (2)3SAT ≤p SUBSET-SUM
22
7.2 NP完全问题
HAMPATH (Hamilton 路)问题也是NP完全 的。 (1)HAMPATH 问题属于NP类; (2)3SAT ≤p HAMPATH 。 从Φ构造图G:把变量 xi 表示为钻石结构,把 子句 ci 表示为节点。
设Φ 是3SAT公式,子句数是k,则G中的节 点分成k组,每组三个节点,称为三元组, 每个三元组对应Φ中的一个子句。G中的边 定义为:不同三元组的节点,若不是相反 文字,则两两相连;三元组内节点间无边 。 可见 (1)Φ有一可满足赋值,G存在一个k-团; (2)G存在一个k-团, Φ可满足。
21
7.2 NP完全问题
第7章 NP完全性
杨莹 冷芳玲
1
第7章 NP完全性
7.1 NP完全性定义 7.2 NP完全问题 7.3 NP完全性的计算讨论
2
7.1 NP完全性
定义7-1 语言L是NP完全的,若它满足下面 两个条件: (1)L∈NP; (2)NP中的每个LA都多项式时间可归约为L。
3
7.2 NP完全问题
定理7-19 [库克—列文定理] 可满足问题 SAT是NP完全的。 证明:NP中的每一个语言都可以多项式时间 归约到SAT。从NP中任取一个语言L,设 MN={Q, Σ,Γ,δ, q0,B,F}是nk多项式时间内判 定L的非确定型图灵机,其中k是常数。对 于MN的任意输入w,在多式时间内构造公 式 Φ,使得w∈L ↔ Φ∈SAT。
Lecture11-NP完全性

3-CNF可满足性
• • • • (1)为公式构造一棵二叉语法分析树。 (2)把树看做电路,构造公式。 (3)利用真值表将公式的子句变换为析取式。 例如:φ = ((x1 → x2)∨¬((¬x1 ↔ x3)∨ x4))∧¬x2. φ' =y1 ∧ (y1 ↔ (y2 ∧ ¬x2)) ∧ (y2 ↔ (y3 ∨ y4)) ∧ (y3 ↔ (x1 → x2)) ∧ (y4 ↔ ¬y5) ∧ (y5 ↔ (y6 ∨ x4)) ∧ (y6 ↔ (¬x1 → x3))
15
广泛存在的NP完全问题
• NP-complete problems arise in diverse domains: boolean logic, graphs, arithmetic, network design, sets and partitions, storage and retrieval, sequencing and scheduling, mathematical programming, algebra and number theory, games and puzzles, automata and language theory, program optimization, biology, chemistry, physics, and more.
16
NP完全问题
• • • • • 团(Clique) 点覆盖(Vetex Cover) 哈密顿回路 旅行商问题(Traveling-salesman problem) 子集和问题(Subset-sum problem)
17
团问题
• 无向图 G = (V, E) 中的团Clique是一个节点集 V‘ ⊆ V 其中每一对节点间都有边相连。即团是图 G 的一个完全子图。 团问题是寻找图中的最大团。 其判定问题是:在给定图中是否存在一个规模为k 的团。 • 一个朴素的算法就是列出V 的所有 k-子集然后检 验它们是否构成团。其时间复杂度为? 若 k 为常 数,则它是多项式时间,但 k 可能接近 |V| /2,这 样一来算法的运行时间就是超多项式时间,因此, 人们猜想团问题不大可能存在有效算法。
第16讲 NP完全性

NP-Completeness
NP-Completeness
-- Computability -- Analysis of Algorithms -- NP-Completeness
2
Analysis of Algorithm
• For many problems, there may be several competitive algorithms. • Which one should I use? • Analysis of algorithms.
其中Q, T, I, b, q0 和qr 的定义与确定型图灵机的相同, 唯一的区别在于状态控制函数(转移函数)δ。
非确定型图灵机的状态控制函数δ 给出的下一个动作 不是唯一确定的,即δ为多值映射,它的值域是一个有穷集合 A。因此非确定型图灵机在下一时刻的动作可以有多种选 择。在处理问题时,对于δ(q1, al, …, ak)的多个值,非确定 型图灵机对于其中任意一个值都存在一个格局序列可以推 导下去,只要其中有一种可以到达终止状态qaccept ,就说 该问题是可以处理的(输入字符串被接受或函数是可计算 的)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SHORTEST-PATH要优化的值:路径长度 给定图G,顶点u和v,限界:非负整数 N是自然数集。
kN
最短路径问题SHORTEST-PATH相关联的判 定问题PATH:给定一个图G,顶点u和v及非 负整数k,问是否有u到v的包含边数至多是k的 路径?
优化问题与其相关联的判定问题的难易程度: 如果一个优化问题是容易的,那么其相关联的 判定问题也是容易的。反过来,如果优化问题 的相关联的判定问题是难的,那么优化问题本 身一定是难的是。 SHORTEST-PATH是容易的,因此PATH是容 易的。(为什么?)
NP-完全性简介
NP-完全性
● 有的问题是难解的(
intractable):
当问题规模变得越来越大时,我们不能在合 理的时间内求得问题的解. ● 什么才算是合理时间? 标准定义: 多项式时间(polynomial time)
■ 对于规模为 n的输入, 最坏情况时间复杂度为
O(nk) ,其中k是某一常数. ■ 多项式时间: O(n2), O(n3), O(1), O(n lg n) ■ 非多项式时间: O(2n), O(nn), O(n!)
第五章 NP-完全性 NP Completeness
内容提要
•多项式时间,多项式时间归约,多项
式时间可验证算法,多项式时间可判 定算法 •优化问题及其相关的判定问题 •P,NP,NP-难,NP-完全,CO-P,CO-NP •电路可满足性问题是NP-完全问题 •若干NP-完全性问题的证明
重点与难点
归约
设A,B是两个不同的判定问题。
A 是问题A的一个实例,
l1
ll2 l1 l2 l1
结论 2-CNF公式可满足当且仅当其关联有向图中 任一强连通分支上不出现互为否定的文字。
C D与(C x) (x D)有相同的可满足性。
l1 l2 lm1 lm 与 (l1 l2 x1 ) (x1 l3 x2 ) (x2 l4 x3 ) (xm4 lm4 xm3 ) (xm3 lm1 lm ) m3
NP-完全问题
● NP-完全问题是这样一个其求解难度未知的
问题类:
■ 至今还没有发现有多项式时间算法来求解
■ 也没有给出其求解时间以超多项式为下界
● 我们把它叫做 P = NP 问题
■ 该问题是计算机科学领域中最大问题。也是一
个21世纪的难题。
NP 是Non-deterministic Polynomial 的缩写
NP-完全理论
概述 问题Q的多项式时间算法:最坏情况时间复 杂度f(n)=O(nk),k是某一常数。
易解问题:有多项式时间算法;
难解问题:需要超多项式时间。
有些问题描述相似但其求解难度有本质不同:
•最短路径问题 V.S. 最长路径问题 •Eular回路问题 V.S. Hamilton回路问题
•2-CNF可满足性问题 V.S. 3-CNF可满足性
判定问题与优化问题
优化问题:有若干个可行解,每个可行解有一个 值与它相关联,求有最优值的可行解。 如最短路径问题SHORTEST-PATH.
判定问题:只要求回答“是”或“不是(YES/NO)
每个优化问题都有其关联的判定问题 (判定问题与优化问题的关系)。 对于一个给定的优化问题,通常对进行优 化的值作限界后可得到关联的判定问题。
具有相同的可满足性。
K-CNF:一个布尔公式称为k-CNF公式,如果 它是一个CNF公式且它的每个子句恰有k个 变元或变元的负出现。
可满足公式:一个布尔公式称为可满足的,如 果存在对该公式中的变量的一种赋值,使 得布尔公式取值为真。
k-CNF可满足问题:任给定一个k-CNF公式 F,问F是否可满足? 2-CNF可满足问题――多项式时间可判定 k-CNF可满足问题――NP-完全(k 3)。
重点: •多项式时间归约 •P,NP,NP-难,NP-完全,CO-P,CO-NP •电路可满足性问题是NP-完全问题 难点:若干NP-完全性问题的证明
学习目的与要求
理解多项式时间 , 多项式时间归约 , 多项式时间可验证算法,多项式时间 可判定算法,优化问题及其相关的判 定 问 题 ,P,NP,NP- 难 ,NP- 完 全 ,COP,CO-NP,电路可满足性问题是NP-完 全问题.掌握若干NP-完全性问题的 证明方法.
问题
NP-完全性及P类、NP类简介
P类:多项式时间可解的问题类。
NP类:多项式时间可验证的问题类。 P
NP, NPC
NP.
注意:P类问题、NP类问题都是指判定问题
2-CNF可满足问题是P问题。
xy
x y,
y x
例如,F (l1 l2 ) (l1 l2 ) (l1 l2 ) (l1 l2 )
多项式时间算法
● 多项式时间可解问题 ■ P表示多项式时间可解的问题类.
● 所有问题都能在多项式时间内可解?
■ 图灵机“停机问题”是不可解问题。不管用多
长时间、多大规模的计算机。 ■ 波斯特(POST)对应问题是不可解问题。 ■ 这些问题是难解问题, 且没有多项式时间算法
POST 对应问题
给定两个有序表A {s1,s2 , ,sk}, B {t1,t2 , ,tk }.A B k.sj,tj 都是二进制代码串。且 |sj | 0, | tj | 0.(j 1,2,,k).问:是否有下 标序列i1, i2 , , in(n 1)使得 si1si2 sin ti1 ti2 tin ?
波斯特对应问题实例: Σ={0,1} 例1. A={1,10,011}, B={101,00,11} 其解为:(1,3,2,3) 1011 10 011 例2. A={1,10111,10},B={111,10,0} 其解为(2,1,1,3)或(2,1,1,3,2,1,1,3) 例3.A={10,011,101},B={101,11,011} 这个PCP问题实例无解。
