新编基础物理学王少杰第二版第八章习题解答
新编物理基础学下册(9-17章)课后习题(每题都有)详细答案之欧阳史创编

新编物理基础学下册(9-17章)课后习题(每题都有)详细答案时间:2021.02.10创作:欧阳史王少杰,顾牡主编第九章9-1 两个小球都带正电,总共带有电荷55.010C -⨯,如果当两小球相距 2.0m 时,任一球受另一球的斥力为1.0N.试求总电荷在两球上是如何分配的? 分析:运用库仑定律求解。
解:如图所示,设两小球分别带电q 1,q 2则有q 1+q 2=5.0×10-5C ① 由题意,由库仑定律得:912122091014π4q q q q F r ε⨯⨯⨯===② 由①②联立得:5152 1.210C3.810Cq q --⎧=⨯⎪⎨=⨯⎪⎩ 9-2 两根6.0×10-2m 长的丝线由一点挂下,每根丝线的下端都系着一个质量为0.5×10-3kg 的小球.当这两个小球都带有等量的正电荷时,每根丝线都平衡在与沿垂线成60°角的位置上。
求每一个小球的电量。
分析:对小球进行受力分析,运用库仑定律及小球平衡时所受力的相互关系求解。
解:设两小球带电q 1=q 2=q ,小球受力如图所示220cos304πq F T Rε==︒① sin 30mg T =︒②联立①②得:题9-1解图2o024tan30mg R qπε=③ 其中223sin 606103310(m)2r l --=︒=⨯⨯=⨯ 代入③式,即: q =1.01×10-7C 9-3 电场中某一点的场强定义为0F E q =,若该点没有试验电荷,那么该点是否存在场强?为什么?答:若该点没有试验电荷,该点的场强不变.因为场强是描述电场性质的物理量,仅与场源电荷的分布及空间位置有关,与试验电荷无关,从库仑定律知道,试验电荷q 0所受力F 与q 0成正比,故0F E q =是与q 0无关的。
9-4直角三角形ABC 如题图9-4所示,AB 为斜边,A 点上有一点荷91 1.810C q -=⨯,B 点上有一点电荷92 4.810C q -=-⨯,已知BC =0.04m ,AC =0.03m ,求C 点电场强度E的大小和方向(cos37°≈0.8,sin37°≈0.6).分析:运用点电荷场强公式及场强叠加原理求解。
新编基础物理学上册1-2单元课后答案

新编物理基础学(上、下册)课后习题详细答案王少杰,顾牡主编第一章1-1.质点运动学方程为:cos()sin(),r a t i a t j btk ωω=++r r r r其中a ,b ,ω均为正常数,求质点速度和加速度与时间的关系式。
分析:由速度、加速度的定义,将运动方程()r t r对时间t 求一阶导数和二阶导数,可得到速度和加速度的表达式。
解:/sin()cos()==-++r r r r rv dr dt a t i a t j bk ωωωω2/cos()sin()a dv dt a t i t j ωωω⎡⎤==-+⎣⎦r r r r1-2. 一艘正在沿直线行驶的电艇,在发动机关闭后,其加速度方向与速度方向相反,大小与速度平方成正比,即2/d d v v K t -=, 式中K 为常量.试证明电艇在关闭发动机后又行驶x 距离时的速度为 0Kx v v e -= 。
其中0v 是发动机关闭时的速度。
分析:要求()v v x =可通过积分变量替换dxdvvdt dv a ==,积分即可求得。
证:2d d d d d d d d v x vv t x x v t v K -==⋅= d Kdx v =-v⎰⎰-=x x K 0d d 10v v v v , Kx -=0ln v v0Kx v v e -=1-3.一质点在xOy 平面内运动,运动函数为22,48x t y t ==-。
(1)求质点的轨道方程并画出轨道曲线;(2)求t =1 s t =2 s 和时质点的位置、速度和加速度。
分析:将运动方程x 和y 的两个分量式消去参数t ,便可得到质点的轨道方程。
写出质点的运动学方程)(t r ρ表达式。
对运动学方程求一阶导、二阶导得()v t r 和()a t r ,把时间代入可得某时刻质点的位置、速度、加速度。
解:(1)由2,x t =得:,2x t =代入248y t =-可得:28y x =-,即轨道曲线。
新编基础物理学上册1-2单元课后答案

新编物理基础学(上、下册)课后习题详细答案王少杰,顾牡主编第一章1-1。
质点运动学方程为:cos()sin(),r a t i a t j btk ωω=++其中a ,b ,ω均为正常数,求质点速度和加速度与时间的关系式。
分析:由速度、加速度的定义,将运动方程()r t 对时间t 求一阶导数和二阶导数,可得到速度和加速度的表达式。
解:/sin()cos()==-++v dr dt a t i a t j bk ωωωω2/cos()sin()a dv dt a t i t j ωωω⎡⎤==-+⎣⎦1-2. 一艘正在沿直线行驶的电艇,在发动机关闭后,其加速度方向与速度方向相反,大小与速度平方成正比,即2/d d v v K t -=, 式中K 为常量.试证明电艇在关闭发动机后又行驶x 距离时的速度为 0Kx v v e -= 。
其中0v 是发动机关闭时的速度。
分析:要求()v v x =可通过积分变量替换dxdvvdt dv a ==,积分即可求得。
证:2d d d d d d d d v x vv t x x v t v K -==⋅= d Kdx v =-v⎰⎰-=x x K 0d d 10v v v v , Kx -=0ln v v 0Kx v v e -=1-3.一质点在xOy 平面内运动,运动函数为22,48x t y t ==-。
(1)求质点的轨道方程并画出轨道曲线;(2)求t =1 s t =2 s 和时质点的位置、速度和加速度。
分析:将运动方程x 和y 的两个分量式消去参数t ,便可得到质点的轨道方程。
写出质点的运动学方程)(t r 表达式。
对运动学方程求一阶导、二阶导得()v t 和()a t ,把时间代入可得某时刻质点的位置、速度、加速度。
解:(1)由2,x t =得:,2x t =代入248y t =-可得:28y x =-,即轨道曲线。
画图略(2)质点的位置可表示为:22(48)r ti t j =+- 由/v dr dt =则速度:28v i tj =+由/a dv dt =则加速度:8a j =则:当t=1s 时,有24,28,8r i j v i j a j =-=+=当t=2s 时,有48,216,8ri j v i j a j =+=+=1-4.一质点的运动学方程为22(1)x t y t ==-,,x 和y 均以m 为单位,t 以s 为单位。
新编基础物理学上册1-2单元课后问题详解

新编物理基础学(上、下册)课后习题详细答案王少杰,顾牡主编第一章1-1.质点运动学方程为:cos()sin(),r a t i a t j btk ωω=++r r r r其中a ,b ,ω均为正常数,求质点速度和加速度与时间的关系式。
分析:由速度、加速度的定义,将运动方程()r t r对时间t 求一阶导数和二阶导数,可得到速度和加速度的表达式。
解:/sin()cos()==-++r r r r rv dr dt a t i a t j bk ωωωω2/cos()sin()a dv dt a t i t j ωωω⎡⎤==-+⎣⎦r r r r1-2. 一艘正在沿直线行驶的电艇,在发动机关闭后,其加速度方向与速度方向相反,大小与速度平方成正比,即2/d d v v K t -=, 式中K 为常量.试证明电艇在关闭发动机后又行驶x 距离时的速度为 0Kx v v e -= 。
其中0v 是发动机关闭时的速度。
分析:要求()v v x =可通过积分变量替换dxdvvdt dv a ==,积分即可求得。
证:2d d d d d d d d v x vv t x x v t v K -==⋅= d Kdx v =-v⎰⎰-=x x K 0d d 10v v v v , Kx -=0ln v v 0Kx v v e -=1-3.一质点在xOy 平面内运动,运动函数为22,48x t y t ==-。
(1)求质点的轨道方程并画出轨道曲线;(2)求t =1 s t =2 s 和时质点的位置、速度和加速度。
分析:将运动方程x 和y 的两个分量式消去参数t ,便可得到质点的轨道方程。
写出质点的运动学方程)(t r ρ表达式。
对运动学方程求一阶导、二阶导得()v t r 和()a t r ,把时间代入可得某时刻质点的位置、速度、加速度。
解:(1)由2,x t =得:,2x t =代入248y t =-可得:28y x =-,即轨道曲线。
2023年新编基础物理学王少杰顾牡版本上册期末考试题库

填空, 选择第一章 质点运动学一、选择题1.质点作曲线运动, 表达位置矢量, 表达旅程, 表达切向加速度, 下列体现式中[ D ](1)a dt dv =;(2)v dt dr =;(3)v dt ds =;(4)t a dtdv =。
(A )只有(1), (4)是对旳; (B )只有(2), (4)是对旳;(C )只有(2)是对旳; (D )只有(3)是对旳。
2.质点沿半径为R 旳圆周作匀速率运动, 每t 秒转一圈, 在2t 时间间隔中, 其平均速度大小与平均速率大小分别为 [ B ](A) , ; (B) 0, ; (C) 0, 0; (D) , 0.3、一运动质点在某瞬时位于矢径 旳端点处, 其速度大小为 [ D ] (A) dt dr (B) dt r d (C) dt r d (D) 22)()(dt dy dt dx +4.一小球沿斜面向上运动, 其运动方程为 , 则小球运动到最高点旳时刻是[ B ](A )t=4s ; (B )t=2s ; (C )t=8s ; (D) t=5s5.一质点在平面上运动, 已知质点位置矢量旳表达式为 (其中a,b 为常数), 则质点作[ B ](A )匀速直线运动; (B )变速直线运动;(C )抛物线运动; (D )一般曲线运动。
二、填空题1. 已知质点旳运动方程为: .当 t =2 s 时, a = 。
2、阐明质点做何种运动时, 将出现下述多种状况( ):(1) , 变速率曲线运动;(2) , 变速率直线运动。
3、一质点运动方程为 , 则在 由0至4s 旳时间间隔内, 质点旳位移大小为_______8m_____,在 由0到4s旳时间间隔内质点走过旳旅程为____10m__________。
4.飞轮作加速转动时, 轮边缘上一点旳运动方程为, 飞轮半径为, 当此点旳速率时, 其切向加速度为_____ ________,法向加速度为_______ _________。
新编基础物理学(王少杰、顾牡)版本)答案

1.已知质点的运动方程为; a = 4i j -+。
2.说明质点做何种运动时; 变速率曲线运动;变速率直线运动 3.一质点运动方程为26x t t =-; 8m;10m 4.飞轮作加速转动时; 26m s ; 24m s ;5.一个力F 作用在质量为kg 0.1的质点上;16N S ; 176J ;6.如图为一圆锥摆; 0 ;2m g πω ;2m gπω;7.一质量为m 的物体;0m v ;竖直向下; 8.一质量为m 小球;竖直向上;mgt;9.一颗子弹在枪筒里前进时; 0.003s; 0.6N*S; 2g ; 10.一质点在几个力同时作用下; 38J ; 11.一人把质量为10kg 的物体; 196 ; 216; 12.二质点的质量各为; 1211()G m m ab--;13.狭义相对论是建立在; 伽利略 ; 14.一光子以速度c 运动; c; 15.在测量物体长度中; 最长 ; 最短 ; 16.一观察者测量得沿尺长;32c ;17.静止时边长为a 的立方体;3221a u c -;18.一点电荷q 位于一立方体中心;6Oq ε; 0 ;24Oq ε;19.描述静电场性质的两个物理量是;E ;u ;F E q=;0u Pu E dl ==⎰;20.如图,真空中两个点电荷;O Q ε;0;201094QR πε;21.如图示,两个平行的无限大;2Oσε;32O σε;2Oσε; 方向向右; 方向向右; 方向向左;22.图中曲线表示一种球对称性静电场;均匀带电实心球; 23.真空中有一半径为R 的半圆细环;4O Q Rπε;4O qQ Rπε-;24.如图示,在带电量为q 的点电荷;11()4O abqq r r πε-;25.如图所示,负电荷Q 的电场中有b a ,两点;b; a ; 增加; 26.在点电荷q 的电场中;7210C --⨯;27一带电量为Q 的导体环;Q - ; Q ;28.一孤立金属球带电量Q +;径向方向向外;0;电荷均匀分布于金属球的外表面;29.在带电量为Q +的金属球外面;24Q rπ; Q ;204r Q rπεε;0rQεε;30.一平行板电容器,充电后与电源保持连接;r ε; 1; r ε; 31.半径为0.5cm 的无限长的直圆柱形导体上; 0 ;32.在安培环路定理;_环路所包围的所有稳恒电流的代数和;环路上的磁感应强度;环路内外全部电流所产生的磁场的叠加;33.在均匀磁场中放置两个面积相等;相等;34.一平面实验线圈的磁矩大小为;0.5T ;沿y 轴正向;35.如右图,无限长直导线中流有的电流分别为;不相等;0123()I I I μ--;01()I μ-;36.无限长直圆筒入在相对磁导率为;2Irπ;02r Irμμπ;37.三根无限长载流直导线;5I; 38.一自感线圈中;0.4H;39.产生动生电动势的非静电场力;洛伦兹 ; 涡旋电场;。
大学物理第二版下册答案

大学物理第二版下册答案
由初始条件 x 0
l 0 , 求得 A
l0
0 .1m , 故物体 A 的运动方程为
v0
x=0.1cos(7t+ π)m (2) 当考虑滑轮质量时,两段绳子中张力数值不等,如图所 示,分别为 T 1、 T2,则对 A 列出任一位置 x 处的牛顿方程式 为:
2
dx
mg sin
T1 m 2
故振动周期:
2
2
T
1 .256 (s) 1. 26 (s)
5
(2) t=0 时,由振动方程得:
5(rad/s)
大学物理第二版下册答案
x0
0 .60 m
dx
0
|t 0 3. 0 cos( 5t
)0
dt
2
(3) 由旋转矢量法知,此时的位相: 3
速度 加速度 所受力
A sin
0 .60 5 (
3 ) m / s 2.6(m / s )
Mg k O P 将 A 与 B 粘合后,挂在弹簧下端,静止平衡所在位置
O 点,取 O 点为原坐标原点如图题
8-5 所示,则有: k O O ( M m ) g
设当 B 与 A 粘在一起后, 在其运动过程的任一位置, 弹簧形变量 O O 所受合力为:
x ,则 A、B 系统
F ( M m ) g k (O O x) kx
(2)
dt
对 滑 轮 列 出 转动 方 程为 :
2
T1 r T 2 r J
1 Mr 2 a
1 dx Mr
2
(3)
2
r 2 dt
式中 ,T 2=k(l0+x)
( 4)
1 d2x
新编物理基础学全册(王少杰版)课后习题答案及详解

新编物理基础学全册课后习题详细答案王少杰,顾牡主编第一章1-1.质点运动学方程为:cos()sin(),r a t i a t j btk ωω=++其中a ,b ,ω均为正常数,求质点速度和加速度与时间的关系式。
分析:由速度、加速度的定义,将运动方程()r t 对时间t 求一阶导数和二阶导数,可得到速度和加速度的表达式。
解:/sin()cos()==-++v dr dt a t i a t j bk ωωωω2/cos()sin()a dv dt a t i t j ωωω⎡⎤==-+⎣⎦1-2. 一艘正在沿直线行驶的电艇,在发动机关闭后,其加速度方向与速度方向相反,大小与速度平方成正比,即2/d d v v K t -=, 式中K 为常量.试证明电艇在关闭发动机后又行驶x 距离时的速度为 0Kxv v e -= 。
其中0v 是发动机关闭时的速度。
分析:要求()v v x =可通过积分变量替换dxdvv dt dv a ==,积分即可求得。
证:2d d d d d d d d v x vv t x x v t v K -==⋅= d Kdx v =-v⎰⎰-=x x K 0d d 10v v v v , Kx -=0ln v v0Kxv v e -=1-3.一质点在xOy 平面内运动,运动函数为22,48x t y t ==-。
(1)求质点的轨道方程并画出轨道曲线;(2)求t =1 s t =2 s 和时质点的位置、速度和加速度。
分析:将运动方程x 和y 的两个分量式消去参数t ,便可得到质点的轨道方程。
写出质点的运动学方程)(t r表达式。
对运动学方程求一阶导、二阶导得()v t 和()a t ,把时间代入可得某时刻质点的位置、速度、加速度。
解:(1)由2,x t =得:,2x t =代入248y t =-可得:28y x =-,即轨道曲线。
画图略 (2)质点的位置可表示为:22(48)r ti t j =+- 由/v dr dt =则速度:28v i tj =+ 由/a dv dt =则加速度:8a j =则:当t=1s 时,有24,28,8r i j v i j a j =-=+=当t=2s 时,有48,216,8ri j v i j a j =+=+=1-4.一质点的运动学方程为22(1)x t y t ==-,,x 和y 均以m 为单位,t 以s 为单位。
新编基础物理学第二版习题解答

习题二2-1.两质量分别为m 和M ()M m ≠的物体并排放在光滑的水平桌面上,现有一水平力F 作用在物体m 上,使两物体一起向右运动,如题图2-1所示,求两物体间的相互作用力。
若水平力F 作用在M 上,使两物体一起向左运动,则两物体间相互作用力的大小是否发生变化?解:以m 、M 整体为研究对象,有()F m M a =+…①以m 为研究对象,如解图2-1(a ),有Mm F F ma -=…②由①、②两式,得相互作用力大小若F 作用在M 上,以m 为研究对象,如题图2-1(b )有Mm F ma =…………③由①、③两式,得相互作用力大小MmmFF m M=+发生变化。
2-2.在一条跨过轻滑轮的细绳的两端各系一物体,两物体的质量分别为M 1和M 2,在M 2上再放一质量为m 的小物体,如题图2-2所示,若M 1=M 2=4m ,求m 和M 2之间的相互作用力,若M 1=5m ,M 2=3m ,则m与M 2之间的作用力是否发生变化?解:受力图如解图2-2,分别以M 1、M 2和m 为研究对象,有111T M g M a -=又12T T =,则2M m F =1122M mgM M m++当124M M m ==时 当125,3M m M m ==时2109M m mg F =,发生变化。
2-3.质量为M 的气球以加速度a v匀加速上升,突然一只质量为m 的小鸟飞到气球上,并停留在气球上。
若气球仍能向上加速,求气球的加速度减少了多少?题图2-2题图2-1解图2-1解图2-2解:设f r为空气对气球的浮力,取向上为正。
分别由解图2-3(a )、(b)可得 由此解得2-4.如题图2-4所示,人的质量为60kg ,底板的质量为40kg 。
人若想站在底板上静止不动,则必须以多大的力拉住绳子? 解:设底板和人的质量分别为M ,m ,以向上为正方向,受力图如解图2-4(a )、(b)所示,分别以底板、人为研究对象,则有3'0T F mg +-=F 为人对底板的压力,'F 为底板对人的弹力。
新编基础物理学上册7-8单元课后答案

第七章7-1氧气瓶的容积为32 L ,瓶内充满氧气时的压强为13Oatm 。
若每小时用的氧气在Iatm 下体积为400L 。
设使用过程温度保持不变,当瓶内压强降到IOatm 时,使用了几个小时?分析氧气的使用过程中,氧气瓶的容积不变,压强减小。
因此可由气体状态方程得到使用 前后的氧气质量。
进而将总的消耗量和每小时的消耗量比较求解。
解 已知 R = 130atm, P 2 =10atm, P 3 = Iatm; V I= V ? = V = 32 L, V^ = 400L 。
质量分别为m ,m 2, m ,由题意可得:m 2 RT M所以一瓶氧气能用小时数为:7-3氢分子的质量为3.3 10 ^4克。
如果每秒有10 23个氢分子沿着与墙面的法线成 45角的方向以105厘米/秒的速率撞击在面积为 2.0cm 2的墙面上,如果撞击是完全弹性的,求这些氢分子作用在墙面上的压强分析 压强即作用在单位面积上的平均作用力,而平均作用力由动量定理求得。
PV 3 g —m 2 PV —P 2V n =13°一10 32 76小时m ∣31.0 4007-2 一氦氖气体激光管, 工作时管内温度为27 C 。
压强为2.4mmHg 氦气与氖气得压强比是7:1.求管内氦气和氖气的分数密度分析 先求得氦气和氖气各自得压强,再根据公式 P= nkT 求解氦气和氖气的分数密度。
解:依题意,n =n 氦∙ n 氖,P=P 氦 P 氖=2.4 所以二空 1.013 105Pa,760心.013 汇 105Pa ; P K : F 氖=7:1760031.013 105Pa , 760根据 P =nkT所以 (2.仃760产 1.013"=6.76D0 22 m'n 氦=氦kTP 氖 21 3 n 氖 -9.66 10 m 氖kT_231.38 10 300 解:单位时间内作用在墙面上的平均作用力为F = 2mvcos45 NJ 22 3.3 10 ^7 10510——1023 F 2mv COS 45 N2 P = S=2330 Pa7-4 一个能量为1012ev 的宇宙射线粒子,射入一氖气管中,氖管中含有氦气0.10mol,如果宇宙射线粒子的能量全部被氖气分子所吸收而变为热运动能量,问氖气的温度升高了多少 ?分析对确定的理想气体,其分子能量是温度的单值函数, 因此能量的变化对应着温度的变 化。
新编基础物理学 第二版 王少杰 顾牡 吴天刚 主编

a v v(3) v(1) (2432 6) (24 6) 96 (m s2 )
t
t
2
3s 末的瞬时加速度
a3
dv dt
48t
144
(m s2
)
1-2.一质点在 xOy 平面内运动,运动方程为 x 2t(m), y 4t2 8(m) .
(1)求质点的轨道方程并画出轨道曲线;
(2)求 t = 1s 和 t = 2 s 时质点的位置、速度和加速度.
解 (1) 角速度和角加速度分别为 d 12t2 dt
法向加速度
d 24t dt
切向加速度
an r2 0 . 1 ( 1t22 2 ) 2 . 3 0 2 1 0 (2m s )
3
第 1 章 质点运动学
at
dv dt
r
2 . 4t 4 . 8 ( m2 s
)
(2) 由 at a / 2 , a2 at2 an2 4at2 得
v0 1m s1 ,x0=0.75m
所以质点的运动方程为
2
第 1 章 质点运动学
x 0.75 t 2t2 1 t4 (m) 12
1-6. 一艘正在沿直线行驶的电艇,在发动机关闭后,其加速度方向与速度方向相反,大小与速
度大小平方成正比,即 d v / d t kv2 , 式中 k 为常量.试证明电艇在关闭发动机后又行驶 x 距离时的速度大小为 v v0ekx . 其中 v0 是发动机关闭时的速度大小. 分析:要证明 v ~ x 关系,可通过积分变量替换将时间变量替换掉,即 a dv v dv ,积分即
(1) 在 t=2s 时,质点的法向加速度和切向加速度大小各为多少?;
(2) 当切向加速度大小恰等于总加速度大小的一半时, 值为多少?
《新编大学物理》(上、下册)教材习题答案

第1章 质点运动学一、选择题题1.1 :答案:[B]提示:明确∆r 与r ∆的区别题1.2:答案:[A]题1.3:答案:[D]提示:A 与规定的正方向相反的加速运动, B 切向加速度, C 明确标、矢量的关系,加速度是d dtv题1.4:答案:[C]提示: 21r r r ∆=-,12,R R r j r i ==-,21v v v ∆=-,12,v v v i v j =-=-题1.5:答案:[D]提示:t=0时,x=5; t=3时,x=2得位移为-3m ;仅从式x=t 2-4t+5=(t-2)2+1,抛物线的对称轴为2,质点有往返题1.6:答案:[D]提示:a=2t=d dt v ,2224t v tdt t ==-⎰,02tx x vdt -=⎰,即可得D 项 题1.7:答案:[D] 北v 风v 车1v 车2提示: 21=2v v 车车,理清=+v v v 绝相对牵的关系二、填空题题1.8:答案: 匀速(直线),匀速率题1.9:答案:2915t t -提示: 2915dx v t t dt ==-,t=0.6时,v=0题1.10:答案:(1)21192y x =- (2)24t -i j 4-j(3)411+i j 26-i j 3S提示: (1) 联立22192x t y t=⎧⎨=-⎩,消去t 得:21192y x =-,dx dy dt dt =+v i j (2) t=1s 时,24t =-v i j ,4d dt==-v a j (3) t=2s 时,代入22(192)x y t t =+=+-r i j i j 中得411+i jt=1s 到t=2s ,同样代入()t =r r 可求得26r∆=-i j , r 和v 垂直,即0•=r v ,得t=3s题1.11:答案:212/m s 提示:2(2)2412(/)dv d x a v x m s dt dt =====题1.12:答案:1/m sπ 提示: 200t dv v v dt t dt =+=⎰,11/t v m s ==,201332tv dt t R θπ===⎰,r π∆==题1.13:答案:2015()2t v t gt -+-i j 提示: 先对20(/2)v t gt =-r j 求导得,0()y v gt =-v j 与5=v i 合成得05()v gt =-+-v i j 合 201=5()2t v t gt -+-∴⎰r v i j t合0合dt=题1.14:答案:8, 264t 提示:8dQ v R Rt dt τ==,88a R τ==,2264n dQ a R t dt ⎛⎫== ⎪⎝⎭三、计算题题1.15: 解:(1)3t dv a t dt == 003v t dv tdt =∴⎰⎰ 232v t ∴= 又232ds v t dt == 20032s t ds t dt =∴⎰⎰ 312S t =∴ (2)又S R θ= 316S t R θ==∴ (3)当a 与半径成45角时,n a a τ= 2434n v a t R == 4334t t =∴t =∴题1.16:解:(1)dv a kv dt ==- 00v t dv kdt v =-∴⎰⎰, 0ln v kt v =-(*) 当012v v =时,1ln 2kt =-,ln 2t k=∴ (2)由(*)式:0kt v v e-= 0kt dx v e dt -=∴,000x t kt dx v e dt -=⎰⎰ 0(1)kt v x e k-=-∴第2章 质点动力学一、选择题题2.1:答案:[C]提示:A .错误,如:圆周运动B .错误,m =p v ,力与速度方向不一定相同D .后半句错误,如:匀速圆周运动题2.2:答案:[B]提示:y 方向上做匀速运动:2y y S v t t ==x 方向上做匀加速运动(初速度为0),F a m= 202t x v adt t ==⎰,2023tx x t S v dt ==⎰ 2223t t =+∴S i j题2.3:答案:[B]提示:受力如图MgF 杆'F 猫mg 设猫给杆子的力为F ,由于相对于地面猫的高度不变'F mg = 'F F = 杆受力 1()F Mg F M m g =+=+1()F M m g a M M+==题2.4 :答案:[D]提示:a a A22A B A B mg T ma T ma a a ⎧⎪-=⎪=⎨⎪⎪=⎩ 得45A a g = (2A B a a =,通过分析滑轮,由于A 向下走过S ,B 走过2S ) 2A B a a =∴题2.5:答案:[C]提示: 由题意,水平方向上动量守恒, 故0(cos60)()1010m m v m v =+共 0=22v v 共题2.6:答案:[C]提示:R θθRh-R 由图可知cos h R Rθ-=分析条件得,只有在h 高度时,向心力与重力分量相等 所以有22cos ()mv mg v g h R Rθ=⇒=- 由机械能守恒得(以地面为零势能面)22001122mv mv mgh v =+⇒=题2.7:答案:[B]提示: 运用动量守恒与能量转化题2.8:答案:[D]提示:v v y由机械能守恒得2012mgh mv v =⇒=0sin y v v θ=sin G y P mgv mg ==∴题2.9:答案: [C]题2.10:答案: [B]提示: 受力如图f TF由功能关系可知,设位移为x (以原长时为原点)02()xF mg Fx mgx kxdx x kμμ--=⇒=⎰ 弹性势能 2212()2p F mg E kx kμ-== 二、填空题题2.11:答案:2mb提示: '2v x bt == '2a v b ==2F ma mb ==∴题2.12:答案:2kg 4m/s 2提示: 4N 8Nxy由题意,22/x a m s = 4x F N =8y F N = 2F m kg a== 24/y y F a m s m ==题2.13:答案: 75,1110提示: 由题意,32()105F a t m ==+ 207/5v adt m s ⇒==⎰ 当t=2时,1110a =题2.14:答案:180kg 提示:由动量守恒,=m S -S m 人人人船相对S ()=180kg m ⇒船题2.15:答案: 11544+i j 提示:各方向动量守恒题2.16:答案: ()mv +i j ,0,-mgR提示:由冲量定义得 ==()()mv mv mv --=+I P P i j i j 末初-由动能定律得 0k k E W E ∆=⇒∆=,所以=0W 合=W mgR -外题2.17:答案:-12提示:3112w Fdx J -==⎰题2.18: 答案: mgh ,212kx ,Mm G r - h=0,x=0,r =∞ 相对值题2.19:答案: 02mg k ,2mg,题2.20:答案:+=0A ∑∑外力非保守力三、计算题题2.21: 解:(1)=m F xg L 重 ()m f L x g Lμ=- (2)1()(1)g a F f x g m Lμμ=-=+-重 (3)dv a v dx =,03(1)v L L g vdv x g dx L μμ⎡⎤=+-⎢⎥⎣⎦⎰⎰,v =题2.22:解:(1)以摆车为系统,水平方向不受力,动量守恒。
新编物理学基础课后习题答案

简答题:简述热力学第一定律和第二定律的内容,并指出它们在物理学中的意义。
热力学基础习题答案
简答题
简述分子动理论的基本内容,并说明气体分子平均自由程与哪些因素有关。
答案
分子动理论的基本内容包括分子在永不停息地做无规则运动,分子之间存在着引力和斥力,分子之间存在着空隙。气体分子平均自由程与气体压强、温度和分子的平均碰撞频率有关。
总结词
能够运用动量和角动量的知识解决实际问题。
总结词
理解动量守恒和角动量守恒的条件和意义。
动量与角动量习题答案
动量与角动量习题答案
01
02
03
详细描述
动量是描述物体运动状态的物理量,计算公式为 $p = mv$,其中 $m$ 是物体的质量,$v$ 是物体的速度。
角动量是描述物体旋转运动的物理量,计算公式为 $L = mr^2omega$,其中 $m$ 是物体的质量,$r$ 是物体到旋转轴的距离,$omega$ 是物体的角速度。
法拉第电磁感应定律描述了当磁场发生变化时会在导体中产生感应电动势的现象。楞次定律指出感应电流的方向总是阻碍引起感应电流的磁通量的变化。
磁场
安培环路定律
法拉第电磁感应定律
磁场与电磁感应习题答案
光学部分习题答案
04
在此添加您的文本17字
在此添加您的文本16字
在此添加您的文本16字
在此添加您的文本16字
康普顿散射证明了光的粒子性,并为量子力学的发展奠定了基础。
光的量子性习题答案
量子力学部分习题答案
05
不确定性原理
由海森堡提出,指在量子力学中无法同时精确测量某些物理量,如位置和动量。
测量
在量子力学中,测量是一个重要的概念,它会影响到量子态的塌缩和结果的不确定性。
大学物理第二版下册答案

0. 65
可知 A 与 B 振动系统的振动表达式为: x 0. 0447 cos( 10 t 0 .65 ) m
大学物理第二版下册答案
(3) 弹簧所受的最大拉力,应是弹簧最大形变时的弹力,最大形变为:
Mm
x OO A
g A 0 .1447 m
k
则最大拉力
F max k x 72 .4 N
8-6 解: (1) 已知 A=0.24m,
(1)
k
(1) A 物体共受三力;重 mg, 支持力 N, 张力 T.不计滑轮质量时,有
T=kx 列出 A 在任一位置 x 处的牛顿方程式
mg sin
T mg sin
2
dx k (l 0 x) m 2
dt
将( 1)式代入上式,整理后得
d2x k
2
x0
dt m
故物体 A 的运动是简谐振动,且
k 7 ( rad/s )
定理可知:
m u
Mm
不计摩擦,弹簧压缩过程中系统机械能守恒,即:
2.0 ( m/s)
1 (M
2
2
m )u
12 kx 0
2
( x0 为弹簧最大形变量)
Mm
2
x0
u 5 .0 10 m
k
由此简谐振动的振幅
2
A x 0 5 .0 10
系统圆频率
k Mm
40 ( rad/s)
大学物理第二版下册答案
若取物体静止时的位置 O(平衡位置)为坐标原点, Ox 轴水平向右为正,则初始条件为: t=0 时, x=0, 0 u 2 .0 m/s 0
2
2
a A cos
2
0 .60 5
新编基础物理学上册7-8单元课后答案

第七章7-1 氧气瓶的容积为瓶内充满氧气时的压强为130atm 。
若每小时用的氧气在1atm 下体积为400L 。
设使用过程温度保持不变,当瓶内压强降到10atm 时,使用了几个小时?分析 氧气的使用过程中,氧气瓶的容积不变,压强减小。
因此可由气体状态方程得到使用前后的氧气质量。
进而将总的消耗量和每小时的消耗量比较求解。
解 已知 。
质量分别为,,,由题意可得: 11m PV RT M= ○1 22m PV RT M= ○2 233m PV RT M = ○3 所以一瓶氧气能用小时数为: ()121233313010329.61.0400m m PV PV n m PV -⨯--====⨯小时 7-2 一氦氖气体激光管,工作时管内温度为 27。
压强为2.4mmHg ,氦气与氖气得压强比是7:1.求管内氦气和氖气的分数密度.分析 先求得氦气和氖气各自得压强,再根据公式求解氦气和氖气的分数密度。
所以 ,根据所以 2139.6610P n m kT -=⨯氖氖7-3 氢分子的质量为克。
如果每秒有个氢分子沿着与墙面的法线成角的方向以厘米/秒的速率撞击在面积为的墙面上,如果撞击是完全弹性的,求这些氢分子作用在墙面上的压强.分析 压强即作用在单位面积上的平均作用力,而平均作用力由动量定理求得。
解:单位时间内作用在墙面上的平均作用力为:27522342 3.3101010102cos 4522330210F mv N p Pa S S---⨯⨯⨯⨯︒====⨯ 7-4 一个能量为的宇宙射线粒子,射入一氖气管中,氖管中含有氦气0.10mol,如果宇宙射线粒子的能量全部被氖气分子所吸收而变为热运动能量,问氖气的温度升高了多少?分析 对确定的理想气体,其分子能量是温度的单值函数,因此能量的变化对应着温度的变化。
由能量守恒求解氖气的温度变化。
2312193 0.1 6.0210 k T 10 1.6102-⨯⨯⨯∆=⨯⨯ 771.610 1.28100.1 6.02 1.5 1.38T K -=⨯∆==⨯⨯⨯⨯ 7-5 容器内贮有1摩尔某种气体。
新编基础物理学(王少杰版)章末测验及答案汇总
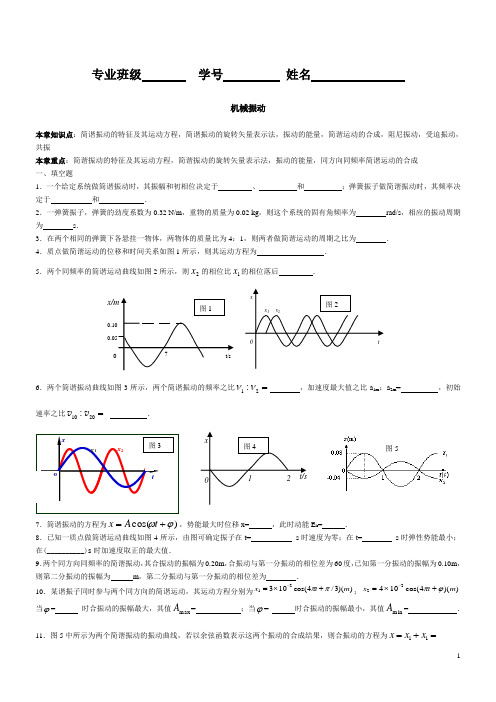
专业班级 学号 姓名机械振动本章知识点:简谐振动的特征及其运动方程,简谐振动的旋转矢量表示法,振动的能量,简谐运动的合成,阻尼振动,受迫振动,共振本章重点:简谐振动的特征及其运动方程,简谐振动的旋转矢量表示法,振动的能量,同方向同频率简谐运动的合成 一、填空题1.一个给定系统做简谐振动时,其振幅和初相位决定于 、 和 ;弹簧振子做简谐振动时,其频率决定于 和 .2.一弹簧振子,弹簧的劲度系数为0.32 N/m ,重物的质量为0.02 kg ,则这个系统的固有角频率为 rad/s ,相应的振动周期为 s .3.在两个相同的弹簧下各悬挂一物体,两物体的质量比为4:1,则两者做简谐运动的周期之比为 . 4.质点做简谐运动的位移和时间关系如图1所示,则其运动方程为 . 5.两个同频率的简谐运动曲线如图2所示,则2x 的相位比1x 的相位落后 .6.两个简谐振动曲线如图3所示,两个简谐振动的频率之比12:νν= ,加速度最大值之比a 1m :a 2m = ,初始速率之比1020:=v v .7.简谐振动的方程为)cos(ϕω+=t A x ,势能最大时位移x= ,此时动能E k = .8.已知一质点做简谐运动曲线如图4所示,由图可确定振子在t= s 时速度为零;在t= s 时弹性势能最小;在(__________)s 时加速度取正的最大值.9.两个同方向同频率的简谐振动,其合振动的振幅为0.20m ,合振动与第一分振动的相位差为60度,已知第一分振动的振幅为0.10m ,则第二分振动的振幅为 m ,第二分振动与第一分振动的相位差为 .10.某谐振子同时参与两个同方向的简谐运动,其运动方程分别为))(3/4cos(10321m t x ππ+⨯=-;))(4cos(10422m t x ϕπ+⨯=-当ϕ= 时合振动的振幅最大,其值max A = ;当ϕ= 时合振动的振幅最小,其值min A = .11.图5中所示为两个简谐振动的振动曲线,若以余弦函数表示这两个振动的合成结果,则合振动的方程为=+=11x x x图5(____________________)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新编基础物理学王少杰第二版第八章习题解答-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN习题八8-1 位于委内瑞拉的安赫尔瀑布是世界上落差最大的瀑布,它高979m.如果在水下落的过程中,重力对它所做的功中有50%转换为热量使水温升高,求水由瀑布顶部落到底部而产生的温差.( 水的比热容c 为3114.1810J kg K --⨯⋅⋅)解 由上述分析得0.5mc T mgh ∆=水下落后升高的温度0.5 1.15K ghT c∆== 8-2 在等压过程中,0.28kg 氮气从温度为293K 膨胀到373K ,问对外做功和吸热多少内能改变多少解:等压过程气体对外做功为2121()()m W p V V R T T M =-=-()32808.31373293 6.6510(J)28=⨯⨯-=⨯气体吸收的热量()()42128078.31373293 2.3310(J)282p m Q C T T M =-=⨯⨯⨯-=⨯内能的增量为()()42128058.31373293 1.6610(J)282V m E C T T M ∆=-=⨯⨯⨯-=⨯8-3 一摩尔的单原子理想气体,温度从300K 加热到350K 。
其过程分别为体积保持不变和压强保持不变。
在这两种过程中: (1) 气体各吸取了多少热量(2) 气体内能增加了多少(3) 气体对外界做了多少功解: 已知气体为1 摩尔单原子理想气体31,2V m C R M==(1) 体积不变时,气体吸收的热量()()2138.31350300623.25(J)2V V m Q C T T M =-=⨯⨯-= 压强保持不变时,气体吸收的热量215()8.31(350300)1038.75(J)2p p m Q C T T M =-=⨯⨯-= (2) 由于温度的改变量一样,气体内能增量是相同的()()2138.31350300623.25(J)2V m E C T T M ∆=-=⨯⨯-= (3) 体积不变时,气体对外界做功0=W压强保持不变时,根据热力学第一定律,气体对外界做功为 1038.75623.25415.5(J)p W Q E J J =-∆=-= 8-4 一气体系统如题图8-4所示,由状态A 沿ACB 过程到达B 状态,有336J 热量传入系统,而系统做功126J,试问: (1) 若系统经由ADB 过程到B 做功42J,则有多少热量传入系统(2) 若已知168J D A E E -=,则过程AD 及DB 中,系统各吸收多少热量(3)若系统由B 状态经曲线BEA 过程返回状态A ,外界对系统做功84J,则系统与外界交换多少热量是吸热还是放热解:已知ACB 过程中系统吸热336J Q =,系统对外做功126J W =,根据热力学第一定律求出B 态和A 态的内能增量210J E Q W ∆=-=题图8-4(1) ADB 过程,42J W =, 故21042252(J)ADB Q E W =∆+=+=(2) 经AD 过程,系统做功与ADB 过程做功相同,即42J W =,故16842210(J)AD AD AD Q E W =∆+=+=经DB 过程,系统不做功,吸收的热量即内能的增量()()21016842(J)DB B D B A D A E E E E E E E ∆=-=---=-=所以,吸收的热量为42042(J)DB DB DB Q E W =∆+=+=(3)因为是外界对系统做功,所以84J BEA W =-BEA 过程210J BEA E E ∆=-∆=-, 故84210294(J)BEA BEA BEA Q E W =∆+=--=-系统放热.8-5 如题图8-5所示,压强随体积按线性变化,若已知某种单原子理想气体在A,B 两状态的压强和体积,问: (1)从状态A 到状态B 的过程中,气体做功多少(2)内能增加多少(3)传递的热量是多少题图8-5解:(1) 气体做功的大小为斜线AB 下的面积()()12A B B A W p p V V =+- (2) 对于单原子理想气体 32V C R =气体内能的增量为()()32V B A B A m m E C T T R T T M M∆=-=- 由状态方程 mpV RT M=代入得 ()32B B A A E p V p V ∆=- (3)气体传递的热量为()()()1322A B B A B B A A Q E W p p V V p V p V =∆+=+-+-8-6一气缸内储有10mol 的单原子理想气体,在压缩过程中,外力做功200J,气体温度升高o 1C ,试计算: (1) 气体内能的增量; (2) 气体所吸收的热量;(3) 气体在此过程中的摩尔热容量是多少解:(1) 气体内能的增量()213108.311124.65(J)2V m E C T T M ∆=-=⨯⨯⨯= (2) 气体吸收的热量124.65(200)75.35(J)Q E W =∆+=+-=-(3) 1mol 物质温度升高(或降低) o 1C 所吸收的热量叫摩尔热容量,所以1175.357.535J mol K 10C --==⋅⋅ 8-7一定量的理想气体,从A 态出发,经题图8-7所示的过程经C 再经D 到达B 态,试求在该过程中,气体吸收的热量.解:由题图8-7可得 A 状态: 5810A A p V =⨯ B 状态: 5810B B p V =⨯ 因为A AB B p V p V =,根据理想气体状态方程可知B A T T =所以气体内能的增量0E ∆=根据热力学第一定律得6()() 1.510(J)A C A B B D Q E W W p V V p V V =∆+==-+-=⨯8-8 一定量的理想气体,由状态A 经B 到达C .如题图8-8所示,ABC 为一直线。
求此过程中: (1)气体对外做的功; (2)气体内能的增量; (3) 气体吸收的热量.解:(1) 气体对外做的功等于线段AC 下所围的面积题图8-7题图8-8531(13) 1.01310210405.2(J)2W -=⨯+⨯⨯⨯⨯=(2) 由图看出A A C C p V p V =所以A C T T =内能增量0=∆E.(3)由热力学第一定律得405.2(J)Q E W=∆+=8-9 2mol 氢气(视为理想气体)开始时处于标准状态,后经等温过程从外界吸取了400J 的热量达到末态.求末态的压强.(118.31J mol K R --=⋅⋅)解:在等温过程中 0T ∆= 所以0E ∆=气体吸收的热量21ln()mQ E W W RT V V M=∆+==得21ln0.0882(/)V Q V m M RT== 即211.09V V = 所以末态压强12120.92atm V p p V == 8-10为了使刚性双原子分子理想气体在等压膨胀过程中对外做功2 J ,必须传给气体多少热量?解:等压过程mW p V R T M=∆=∆内能增量(/)22i iE m M R T W ∆=∆=双原子分子,5=i ,所以7(J)2iQ E W W W =∆+=+=8-11一定量的刚性理想气体在标准状态下体积为231.010m ⨯,如题图8-11所示。
求在下列过程中气体吸收的热量:(1) 等温膨胀到体积为 232.010m ⨯;(2) 先等体冷却,再等压膨胀到(1)中所到达的终态.解:(1) 如题图8-11,在A →B 的等温过程中,0T E ∆=, 所以221111d d V V T T V V p V Q W p V V V===⎰⎰1121ln(/)p V V V = 将51 1.01310Pa p =⨯,231 1.010m V =⨯和232 2.010m V =⨯ 代入上式,得 702J T Q =(2) A →C 等体和C →B 等压过程中,因为A 、B 两态温度相同,所以0ACB E ∆=气体吸收的热量221()ACB ACB ACB ACB Q E W W p V V =∆+==-又因为2121()0.5atm p V V p ==所以520.5 1.01310(21)10507(J)ACB Q =⨯⨯⨯-⨯=8-12 将体积为431.010m -⨯、压强为51.0110Pa ⨯的氢气绝热压缩,使其体积变为532.010m -⨯ ,求压缩过程中气体所做的功.题图8-11解 根据上述分析,设p 、V 分别为绝热过程中任一状态的压强和体积,则由γγpV V p =11得γγV V p p -=11氢气是双原子分子, 1.4γ=,所以氢气绝热压缩做功为211111212d d 23.0J 1V V p V W p V pV VV V V V γγγγ-⎡⎤⎛⎫⎢⎥===-=- ⎪-⎢⎥⎝⎭⎣⎦⎰⎰8-13 质量为0.014kg 的氮气在标准状态下经下列过程压缩为原体积的一半: (1)等温过程; (2)等压过程; (3)绝热过程,试计算在这些过程中气体内能的改变,传递的热量和外界对气体所做的功.(设氮气为理想气体)解:(1) 等温过程 0E ∆=122111142ln 8.31273ln 7.8610(J)28V V mW RT M V V ==⨯⨯=-⨯ 27.8610(J)Q W ==-⨯ (2)等压过程,由状态方程可得2112T T =3211451()8.31(273273) 1.4210(J)2822V m E C T T M ∆=-=⨯⨯⨯⨯-=-⨯3211471()8.31(273273) 1.9910(J)2822P m Q C T T M =-=⨯⨯⨯⨯-=-⨯3321.9910( 1.4210) 5.710(J)W Q E =-∆=-⨯--⨯=-⨯(2) 绝热过程0Q =由绝热方程212111T V T V --=γγ其中1221,57V V C C V P ===γ 代入22155112(),2V V T T =得2273.15360.4K T T ===所以内能的增量()211458.31(360.4273.15)906.1(J)282V m E C T T M ∆=-=⨯⨯⨯-= 906.1(J)W E =-∆=-8-14有1 mol 刚性多原子分子的理想气体,原来的压强为1.0 atm ,温度为27℃,若经过一绝热过程,使其压强增加到16 atm .试求: (1) 气体内能的增量;(2) 在该过程中气体所做的功;(3) 终态时,气体的分子数密度.解:(1)刚性多原子分子 =26,4/3i i iγ+== 所以由绝热方程得12121(/)600K T T p p γγ-==气体内能的增量321(/)()7.4810J 2i E m M R T T ∆=-=⨯ (2) 外界对气体做功37.4810J W E =-∆=-⨯(3) 根据状态方程 p nkT =得26322/() 1.9610m n p kT -==⨯⋅个8-15 氮气(视为理想气体)进行如题图8-15所示的ABCA 循环,状态A B C 、、的压强、体积的数值已在图上注明,状态A 的温度为1000K ,求:(1)状态B 和C 的温度; (2) 各分过程气体所吸收的热量、所做的功和内能的增量;(3) 循环效率。
