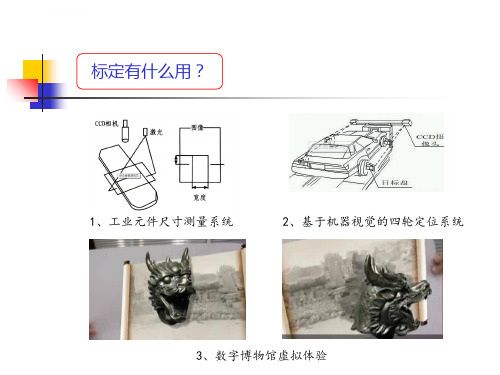
第五章摄像机标定

合集下载

工业摄像机标定课件

图像采集
使用相机拍摄标定板在不同角度、位置和光线条件下的多张照片。
图像预处理
对采集到的图像进行去噪、对比度增强等预处理操作，以提高标定精度。
特征提取
从预处理后的图像中提取出标定板的特征点，如角点或边缘。
参数计算与优化
内参计算
根据标定板特征点的图像坐标和对应的世界坐标，计算相机的内参矩阵和畸变系数。
3
运动跟踪与测量
通过标定结果，可以获得相机的内部参数和畸变系数，进而提高运动跟踪与测量的准确性和精度。
05
常见问题与解决方案
标定板的选择与制作
标定板是用于确定摄像机内部参数的重要工具，其质量和精度直接影响标定结果的准确性。
•·
1. 材料选择：标定板应选择高稳定性、低热膨胀系数的材料，如金属或玻璃。
2. 多视角标定：利用不同视角下的标定板进行标定，可以更全面地获取摄像机参数。
•·
1. 初始参数设置：合理设置初始参数，可以减少迭代次数，提高算法收敛速度。
标定过程中的注意事项
1. 环境要求：标定时应选择光线
均匀、无反光的室内环境，避免
外界光线直接照射标定板。
2. 多次拍摄：为了获取更准确的
工业摄像机标定课件
目录
• 工业摄像机标定概述 • 标定前的准备工作 • 标定流程及步骤 • 标定结果分析与应用 • 常见问题与解决方案 • 案例分析与实践操作
01
工业摄像机标定概述
标定的目的和意义
确定摄像机内参数
促进机器视觉应用
通过标定，可以确定摄像机的焦距、主点坐标等内参数，从而矫正图像畸变。
标定环境误差
标定环境的光照、背景和拍摄角度等因素会影响标定结果的准确性，因此需要选择合适的环境和拍摄角度。

摄像机标定的几种方法

摄像机标定的几种方法摄像机标定是计算机视觉和机器视觉领域中的一项重要技术，用于确定相机的内参矩阵和外参矩阵，从而实现图像的准确测量与三维重建。

本文将介绍几种常用的摄像机标定方法，包括直接线性变换（DLT）、Zhang的标定法、Tsai的标定法、径向畸变模型等。

1.直接线性变换（DLT）方法：直接线性变换方法是摄像机标定最基础的方法之一，通过在物体平面上放置多个已知几何形状的标定物体，测量它们的图像坐标和真实坐标，通过最小二乘法求解相机的投影矩阵。

DLT方法简单直接，但对噪声敏感，容易产生误差。

2. Zhang的标定法：Zhang的标定法是一种常用的摄像机标定方法，通过在平面上放置一系列平行的标定板，根据不同位置姿态下的标定板的图像坐标和物理坐标，运用最小二乘法求解相机的内参矩阵和外参矩阵。

Zhang的标定法提高了标定的精度和稳定性，但要求标定板在不同位置姿态下具有较大的变化。

3. Tsai的标定法：Tsai的标定法是一种基于摄像机的投影模型的标定方法，通过摄像机的旋转和平移矩阵，以及曲率和径向畸变的参数，对图像坐标和物理坐标之间的映射关系进行数学推导和求解。

Tsai的标定法可以对畸变进行校正，提高图像测量的精度。

4. Kalibr工具包：Kalibr是一个开源的摄像机标定和多传感器校准工具包，结合了多种摄像机标定方法，例如DLT、Tsai、Zhang等。

Kalibr工具包不仅可以标定单目相机，还可以标定双目和多目视觉系统，对相机的内参、外参、畸变等参数进行标定和优化，同时还能进行相机的手眼标定、IMU与相机的联合标定等。

5. Di Zhang的自标定方法：Di Zhang提出了一种基于相对边界点的自标定方法，通过提取图像中的特定点边界，通过对这些边界点位置的检测与分析，实现对相机内参和外参的求解。

这种方法不需要使用标定板等外部标定物体，只需要相机自身可以看到的物体边界即可进行标定。

6.径向畸变模型：径向畸变是摄像机成像中常见的一种畸变形式，主要表现为物体边缘呈弯曲的形式。

摄像机标定

1 图像采集系统的标定根据机器视觉系统采集的图像数据来测量焊膏的三维信息，必须准确建立所采集的图像数据和实际物体对象间的成像模型。

同时，图像采集系统不可避免地存在几何畸变。

所以校正几何畸变，并得到检测对象的世界坐标就是图像采集系统标定的工作[5]。

标定中首先要确定图像采集系统的全部参数，包括系统内部的几何和光学特性，即内参数，以及摄像机坐标系相对于空间坐标系的位置关系，即外参数。

确定参数后，根据采集的图像进行校正，并计算得到测量对象的世界坐标。

1.1 图像采集系统成像模型和模型参数图1、图像采集系统的成像模型机器视觉中图像采集中用到四个坐标系：图像坐标系ICS (),r c 、成像平面坐标系IPCS ()','u v 、摄像机坐标系CCS (),,c c c x y z 和世界坐标系WCS (),,w w w x y z [6]。

机器视觉采集得到的图像数据是直接用图像坐标系表示的，即图像上的像素行和列位置(),r c 。

而被测物体对象的客观位置、大小、相互关系必须通过世界坐标系(),,w w w x y z 才能正确描述。

这两个坐标系间的转换又要通过摄像机坐标系和成像平面坐标系。

世界坐标系与摄像机坐标系间的转换是一种平移加旋转的变换：111213212223313233c w w x c w w y c w w z x x r r r x t y R y T r r r y t z z r r r z t ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ （3）其中R 是旋转矩阵，与这两个坐标系间沿三个轴的旋转角度有关，T 是平移矩阵。

三个旋转角度和三个平移分量共六个参数(),,,,,x y z t t t αβγ称为成像系统或图像采集系统的外参数。

图像像素坐标系ICS (),r c 和成像平面坐标系IPCS ()','u v 转化是一个离散化和平移的过程，ICS 以图像左上角为原点，以图像的行、列分别为r 轴和c 轴，以整数像素为坐标单位；IPCS 是以光轴与相机像平面的交点为原点，两根坐标轴分别平行于ICS 中的坐标轴，以物理尺寸为坐标单位。

摄像机标定

摄像机标定一、概述计算机视觉的基本任务之一是从摄像机获取的图像信息出发计算三维空间中物体的几何信息，并由此重建和识别物体，而空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系是由摄像机成像的几何模型决定的，这些几何模型参数就是摄像机参数。

在大多数条件下，这些参数必须通过实验与计算才能得到，这个过程被称为摄像机定标(或称为标定)。

标定过程就是确定摄像机的几何和光学参数，摄像机相对于世界坐标系的方位。

标定精度的大小，直接影响着计算机视觉（机器视觉）的精度。

迄今为止，对于摄像机标定问题已提出了很多方法，摄像机标定的理论问题已得到较好的解决，对摄像机标定的研究来说，当前的研究工作应该集中在如何针对具体的实际应用问题，采用特定的简便、实用、快速、准确的标定方法。

二、摄像机标定分类1 根据是否需要标定参照物来看，可分为传统的摄像机标定方法和摄像机自标定方法。

传统的摄像机标定是在一定的摄像机模型下，基于特定的实验条件，如形状、尺寸已知的标定物，经过对其进行图像处理，利用一系列数学变换和计算方法，求取摄像机模型的内部参数和外部参数（分为最优化算法的标定方法、利用摄像机透视变换矩阵的标定方法、进一步考虑畸变补偿的两步法和采用更为合理的摄像机模型的双平面标定法）；不依赖于标定参照物的摄像机标定方法，仅利用摄像机在运动过程中周围环境的图像与图像之间的对应关系对摄像机进行的标定称为摄像机自标定方法，它又分为：基于自动视觉的摄像机自标定技术（基于平移运动的自标定技术和基于旋转运动的自标定技术）、利用本质矩阵和基本矩阵的自标定技术、利用多幅图像之间的直线对应关系的摄像机自标定方以及利用灭点和通过弱透视投影或平行透视投影进行摄像机标定等。

自标定方法非常地灵活,但它并不是很成熟。

因为未知参数太多,很难得到稳定的结果。

一般来说，当应用场合所要求的精度很高且摄像机的参数不经常变化时，传统标定方法为首选。

而自标定方法主要应用于精度要求不高的场合，如通讯、虚拟现实等。

摄像机标定原理

摄像机标定原理
摄像机标定是计算机视觉中的一个重要步骤，它是指通过对摄像机进
行一系列的测量和校准，来确定摄像机内外参数的过程。

这个过程可
以分为两个部分：内部参数标定和外部参数标定。

1. 内部参数标定
内部参数是指摄像机本身的一些特性，如焦距、主点位置等。

这些参
数是固定不变的，但在计算机视觉中必须知道它们的值才能进行后续
处理。

内部参数标定通常使用棋盘格来实现。

首先需要拍摄多张棋盘格图像，在每张图像中都要确保棋盘格在不同位置、不同角度下都有足够清晰
的拍摄。

然后，通过对这些图像进行处理，提取出棋盘格角点的坐标，并将其与实际物理坐标对应起来。

最后，使用相应的数学模型（如针
孔相机模型）来求解出相机内参矩阵。

2. 外部参数标定
外部参数是指摄像机与被拍摄物体之间的空间关系，包括相对位置和
姿态等信息。

外部参数通常需要在已知内参矩阵的情况下求解。

外部参数标定也可以使用棋盘格来实现。

首先需要在棋盘格上放置至少三个不同位置的标志物，如球体或圆柱体。

然后，通过拍摄多张包含这些标志物的棋盘格图像，在每张图像中都要确保标志物在不同位置、不同角度下都有足够清晰的拍摄。

接着，通过对这些图像进行处理，提取出每个标志物在图像中的坐标，并将其与实际物理坐标对应起来。

最后，使用相应的数学模型（如PnP算法）来求解出相机外参矩阵。

总结：摄像机标定是计算机视觉中非常重要的一个步骤，它可以帮助我们确定摄像机内外参数，为后续处理提供重要的基础。

内部参数和外部参数分别通过棋盘格实现，并使用相应的数学模型求解。

摄像机标定原理及源码

摄像机标定原理及源码一、摄像机标定原理1.1相机模型在进行摄像机标定之前，需要了解相机模型。

常用的相机模型是针孔相机模型，它假设光线通过小孔进入相机进行成像，形成的图像符合透视投影关系。

针孔相机模型可以通过相机内部参数和外部参数来描述。

1.2相机内部参数相机内部参数主要包括焦距、光心坐标等信息，可以通过相机的标定板来获取。

标定板上通常有已知尺寸的标定点，通过计算图像中的标定点坐标和实际世界中的标定点坐标之间的关系，可以求解出相机的内部参数。

1.3相机外部参数相机外部参数主要包括相机在世界坐标系中的位置和姿态信息。

可以通过引入已知的点和相机对这些点的投影来求解相机的外部参数。

也可以通过运动捕捉系统等设备获取相机的外部参数。

1.4标定算法常用的摄像机标定算法有张正友标定法、Tsai标定法等。

其中，张正友标定法是一种简单和广泛使用的标定方法。

该方法通过对标定板上的角点进行提取和匹配，利用通用的非线性优化算法（如Levenberg-Marquardt算法）最小化像素坐标与世界坐标的重投影误差，从而求解出相机的内部参数和外部参数。

二、摄像机标定源码下面是使用OpenCV实现的摄像机标定源码：```pythonimport numpy as npimport cv2#棋盘格尺寸（单位：毫米）square_size = 25#棋盘内角点个数pattern_size = (9, 6)#获取标定板角点的世界坐标objp = np.zeros((np.prod(pattern_size), 3), dtype=np.float32) objp[:, :2] = np.mgrid[0:pattern_size[0],0:pattern_size[1]].T.reshape(-1, 2) * square_sizedef calibrate_camera(images):#存储角点的世界坐标和图像坐标objpoints = []imgpoints = []for img in images:gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)#查找角点ret, corners = cv2.findChessboardCorners(gray, pattern_size, None)if ret:objpoints.append(objp)#亚像素精确化criteria = (cv2.TERM_CRITERIA_EPS +cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)corners2 = cv2.cornerSubPix(gray, corners, (11, 11), (-1, -1), criteria)imgpoints.append(corners2)#标定相机ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)return ret, mtx, dist, rvecs, tvecs#读取图像images = []for i in range(1, 21):img = cv2.imread(f'image_{i}.jpg')images.append(img)#相机标定ret, mtx, dist, rvecs, tvecs = calibrate_camera(images)#保存相机参数np.savez('calibration.npz', ret=ret, mtx=mtx, dist=dist, rvecs=rvecs, tvecs=tvecs)```以上代码首先定义了棋盘格尺寸和格子个数，然后定义了函数`calibrate_camera`来进行相机标定。

摄像机标定技术在机器视觉中的应用研究

摄像机标定技术在机器视觉中的应用研究摄像机标定技术在机器视觉中扮演着重要的角色，它是实现准确测量和三维重构等应用的基础。

通过标定摄像机，我们能够获得摄像机内外参数，这些参数对于矫正图像畸变、确保测量精度、实现准确的物体定位定姿以及三维重构等任务至关重要。

本文将探讨摄像机标定技术在机器视觉中的应用研究，并介绍常用的标定方法。

一、摄像机标定的基本原理摄像机标定的基本原理是通过观察已知空间点在图像中的投影，来计算摄像机的内部参数和外部参数。

内部参数包括焦距、主点位置、图像畸变等，而外部参数则描述了摄像机在世界坐标系下的位置和朝向。

1. 透视投影模型在机器视觉中，常用的摄像机模型是透视投影模型。

透视投影模型假设摄像机与成像平面之间的光线可以近似为直线，该模型在计算机图形学和计算机视觉领域被广泛应用。

透视投影模型可以通过矩阵变换来表示。

2. 内部参数标定内部参数标定主要包括焦距、主点位置和图像畸变等参数的估计。

常用的内部参数标定方法有棋盘格标定和圆点标定。

棋盘格标定方法通过在场景中放置一个已知尺寸的棋盘格来进行摄像机标定。

标定过程包括拍摄一系列棋盘格图像，检测图像中棋盘格的角点坐标，最后通过最小二乘法等方法来计算内部参数。

棋盘格标定方法简单易行，广泛应用于机器视觉领域。

圆点标定方法是通过在场景中放置一系列已知尺寸的圆点来进行摄像机标定。

该方法相对于棋盘格标定方法在一些特定场景下更加稳定和精确。

3. 外部参数标定外部参数标定主要包括摄像机在世界坐标系下的位置和朝向的估计。

常用的外部参数标定方法有单目标定和双目标定。

单目标定是通过拍摄已知空间点的图像来计算摄像机的外部参数。

标定过程包括拍摄一系列已知空间点的图像，检测图像中空间点的图像坐标，然后通过非线性优化方法来估计外部参数。

双目标定是通过利用两个摄像机同时观察同一场景，从而计算摄像机的外部参数。

标定过程包括拍摄一系列已知空间点的立体图像对，匹配图像对中的特征点，然后通过三角剖分算法来估计外部参数。

（学习笔记）摄像机模型与标定——摄像机标定

（学习笔记）摄像机模型与标定——摄像机标定摄像机的内参数：摄像机内参数矩阵(fx,fy,cx,cy)和畸变系数(三个径向k1,k2,k3,两个切向p1,p2)摄像机的外参数:旋转向量（⼤⼩为1×3的⽮量或旋转矩阵3×3）和平移向量（Tx,Ty,Tz）。

这⾥我们讲解⼀下旋转向量：旋转向量是旋转矩阵紧凑的变现形式，旋转向量为1×3的⾏⽮量。

上述公式中r就是旋转向量，1、旋转向量的⽅向是旋转轴 2、旋转向量的模为围绕旋转轴旋转的⾓度。

通过上⾯的公式三，我们就可以求解出旋转矩阵R。

同样的已知旋转矩阵，我们也可以通过下⾯的公式求解得到旋转向量：内参数(fx,fy,cx,cy)与棋盘所在空间的3D⼏何相关（即外参数）畸变参数则与点集如何畸变的2D⼏何相关。

1、5个畸变系数的求解：已知模式（我们可以认为是⿊⾊⽅格，含有四个⾓点）的三个⾓点所产⽣的6组信息（在理论上）可以求解5个畸变参数。

2、内参数fx,fy,cx,cy,和(ψ,φ,θ)，（Tx,Ty,Tz）共10个参数的求解将在下⾯详细讲述。

⾸先说明：求解上述2中10个参数的前提是先假设每次的畸变参数为0。

求解4个内参数和6个外参数的分析：假设有N个⾓点和K个棋盘图像（不同位置），需要多少个视场和⾓点才能提供⾜够的约束来求解这些参数呢？1、K个棋盘，可以提供2NK的约束，即2NK的⽅程。

（乘以2是因为每个点都由x和y两个坐标值组成）2、忽略每次的畸变，那么我们需要求解4个内参数和6K个外参数。

（因为对于不同的视场，6个外参数是不同的）3、那么有解的前提是⽅程的总数应该⼤于等于未知参数的总数即2NK>=6K+4,或者写成(N-3)K>=2。

为了⽅便理解，下图是⼀个3×3⼤⼩的棋盘,红⾊圈标记出了它含有的内⾓点：如果我们令N=5,K=1，带⼊到上述不等式，是满⾜不等式，这就是意味着我们仅需要⼀个视场和带有5个内⾓点的棋盘就可以求解出10个参数了。

摄像机标定ppt课件

为了规范事业单位聘用关系，建立和完善适应社会主义市场经济体制的事业单位工作人员聘用制度，保障用人单位和职工的合法权益
1、径向畸变、偏心畸变
光学畸变分为径向畸变和偏心畸变。径向畸变像点沿径向方向偏离标准理想位置；偏心畸变使像点沿径向方向和垂直径向方向偏离理想位置，径向畸变称为非对称径向畸变，垂直径向方向的畸变称为切向畸变。
为了规范事业单位聘用关系，建立和完善适应社会主义市场经济体制的事业单位工作人员聘用制度，保障用人单位和职工的合法权益
(三)物理坐标系与像素坐标系转换
如图若O1在u，v坐标系中
的坐标为（u0，v0），每一个像素在x轴与y轴方向上的物理尺寸
为dx，dy则图像中任意一个像素
为了规范事业单位聘用关系，建立和完善适应社会主义市场经济体制的事业单位工作人员聘用制度，保障用人单位和职工的合法权益
为了规范事业单位聘用关系，建立和完善适应社会主义市场经济体制的事业单位工作人员聘用制度，保障用人单位和职工的合法权益
在两个坐标系下的坐标有如下关
系：
u
x dx
u0
v
y dy
v0
上式可表示为下面的矩阵：
为了规范事业单位聘用关系，建立和完善适应社会主义市场经济体制的事业单位工作人员聘用制度，保障用人单位和职工的合法权益
(四)摄像机坐标系、世界坐标系
摄像机坐标系是由点OC与XC、 YC和ZC轴组成的直角坐标系 (OC 点称为摄像机的光学中心，简称光心), XC、YC和x轴y轴平行，ZC 轴为摄像机的光轴，它与图像平面垂直，光轴与图像平面的交点，即为图像坐标系的原点，OcO1 为摄像机焦距。

摄像机标定和三维重建

xu f
zc
yu
0
1 0
0 f 0
0 0 1
0 0 0
xc
yc
zc
1
mxu , yu
Yc
o
Xu
Zc
M xc , yc , zc
Xc
2、中心透视投影模型
xu
f
xc zc
Yc
yu
f
yc zc
o
写成齐次坐标形式为
xu f
zc
yu
0
1 0
0 f 0
0 0 1
坐标系
1、世界坐标系： X w ,Yw , Z w
2、摄像机坐标系：X c ,Yc , Zc
3、图像坐标系: u, v x, y
Xw
Zw
Ow
Yw
世界坐标系
说明：
为了校正成像畸变
用理想图像坐标系 X u ,Yu
和真实图像坐标系 X d ,Yd
分别描述畸变前后的坐标关系
Xc
y
u
v O1
图像坐标系
O
在实际像机系统中，xdi 应该 X ci 和同号，如果计算出两者异号，则 t y 取为负号。最后求解 r7 , r8 , r9
r7 r2r6 r3r5 , r8 r3r4 r1r6 , r9 r1r5 r2r4
定标算法——步骤二
对于一个标志点，可以得到以下的两个方程
xdi
xdi k1 (xd2i
0
fv / sin
v0
0
1 00 1 0
0 f 0
0 0
0 1
0 0
R o3T
xw
t 1
yw zw
1

7.摄像机标定

T 1 T 2
T
1
T
1
由于摄像机有5个未知内参数，所以当所摄取得的图像数目大于等于3时，就可以线性唯一求解出 K
2019/3/20 27 CV:Calibration
张正友方法
张正友方法所用的平面模板
2019/3/20 28 CV:Calibration
张正友方法

标定步骤: (1)制定一张平板棋盘格模板； (2)移动平面或摄像机，从不同角度拍摄若干张(大于或等于3张)模板图像； (3)检测出每幅图像中的特征点; (4)求出每一幅图像的单应矩阵H； (5)在令畸变系数为0的前提下，利用求出的矩阵H计算出摄像机的内参数； (6)利用反投影法进一步优化求精，同时计算出各项畸变系数。

p11 X w p12Yw p13 Z w p14 p 31uX w p 32 uYw p 33uZ w p 34u 0 p 21 X w p 22Yw p 23 Z w p14 p 31uX w p 32uYw p 33uZ w p 34 u 0
的平面上
~ T M [ X Y 1 ] • 其中， K 为摄像机的内参数矩阵， T ~
m [u v 1] 为模板平面上点的齐次坐标，为模板平面上点投影到图像平面上对应点的齐次坐标，[ r1 r2 r3 ] 和 t 分别是摄像机坐标系相对于世界坐标系的旋转矩阵和平移向量
2019/3/20 26 CV:Calibration
其中 u , v,1 为图像坐标系下的点的齐次坐标， X w , Yw , Z w 为世界坐标系下的空间点的欧氏坐标， P 为 3 4 的透视投 s 为未知尺度因子。影矩阵，
2019/3/20 11 CV:Calibration

摄像机标定方法及原理

? 世界坐标系与图像坐标系变换关系：
?X
? ?
f
?
u ? u0 fx
?
r11xw ? r31xw ?
r12 yw ? r13zw ? tx r32 yw ? r33zw ? tz
? ?
Y
?
v? v0
?
r21xw ?
r22 yw ? r23zw ? ty
(7)
?? f
fy r31xw ? r32 yw ? r33zw ? tz
o y Of
x Xf
O
X
L1
P(X,Y)
Pf (u,v)
Y Yf
L2
Zw
p(x,y,z)
z
(xw,yw,zw) Xw Yw
图1 摄像机标定中常用坐标系
?计算机视觉常用坐标系采用右手准则来定义，图1 表示了三个不同层次的坐标系统：
1.世界坐标系 2.摄像机坐标系 3.图像坐标系（图像像素坐标系和图像物理
径向排列约束就是矢量 L1 和矢量 L 2具有相同的方向，即方向（ L1 ）=方向（L 2）
经典标定方法简介
由成像模型可知，径向畸变不改变 L1 的方向，因此，无论有无透镜畸变都不影响以上等式。有效焦距
的变化，也不影响这个等式，因为焦距的变化只会影响L1 的长度而不影响其方向。又因为：
?x? ?r11 r12 r13 ? ?xw ?
经典标定方法简介
? 利用径向排列约束（RAC）的摄像机标定技术
基于RAC（Radial alignment constraint ）的摄像机标定方法属于两步法，第一步是利用最小二乘求解超定线性方程，给出外部参数；第二步求解内部参数，如果摄像机无透镜畸变，则由一个超定线性方程解出。如果存在一个以二次多项式近似的径向畸变，则可以用一个三变量的优化搜索求解。

《摄像机自标定》课件

自标定技术能够提高标定过程的自动化程度，减少人工标定的时间和劳动强度，并且可以提高标定的准确性和稳定性。
实现原理
相机模型
摄像机模型是描述相机成像过程的数学模型，常用的有针孔相机模型和透视投影模型。
鱼眼相机模型
鱼眼相机是一种广角成像相机，其成像模型具有特殊的非线性特性。
标定方法
常用的标定方法包括李氏标定法、透镜校正法和张正友标定法。
实验步骤
1
实验准备
准备摄像机系统和标定板，确保拍摄环境和光源均匀稳定。
2图像采集拍摄多来自标定板的图像，覆盖不同的角度和观察距离。
3
数据处理
进行图像校正，去除畸变；计算相机参数，包括内部和外部参数。
应用场景
机器人导航
自标定技术能够提供准确的相机参数，帮助机器人实现精确的地图构建和目标导航。
三维视觉
随着计算机视觉技术的发展和应用需求的增加，自标定技术将发挥越来越重要的作用，并逐渐实现更广泛的应用。
3 自标定的局限性
自标定技术对拍摄环境和标定板的要求较高，同时在特殊场景和复杂光照条件下的表现可能不稳定。
参考文献
[1] 李昊，陈诚. 摄像机自标定误差分析[J]. 计算机应用研究, 2014, 31(2): 416-419. [2] Zhang Z. A Flexible New Technique for Camera Calibration[C]//MVS++ workshop on multiview stereo and related topics. 2000.
自标定技术可以用于精确的三维重建和场景深度估计，为三维视觉分析提供可靠的数据基础。
虚拟现实

摄像机标定（Cameracalibration）笔记

摄像机标定（Cameracalibration）笔记⼀作⽤建⽴3D到2D的映射关系，⼀旦标定后，对于⼀个摄像机内部参数K(光⼼焦距变形参数等，简化的情况是只有f错切=0,变⽐=1，光⼼位置简单假设为图像中⼼)，参数已知，那么根据2D投影，就可以估计出R t；空间3D点所在的线就确定了，根据多视图（多视图可以是运动图像）可以重建3D。

如果场景已知，则可以把场景中的虚拟物体投影到2D图像平⾯（DLT，只要知道M即可）。

或者根据世界坐标与摄像机坐标的相对关系，R,T，直接在Wc位置渲染3D图形，这是AR的应⽤。

因为是离线的，所以可以⽤⼿⼯定位点的⽅法。

⼆⽅法1 Direct linear transformation (DLT) method2 A classical approach is "Roger Y. Tsai Algorithm".It is a 2-stage algorithm, calculating the pose (3D Orientation, and x-axis and y-axis translation) in first stage. In secondstage it computes the focal length, distortion coefficients and the z-axis translation.3 Zhengyou Zhang's "a flexible new technique for camera calibration" based on a planar chess board. It is based on constrains on homography.4个空间：世界，摄像机(镜头所在位置)，图像（原点到镜头中⼼位置距离f），图像仿射空间（最终成像空间），这些空间原点在不同应⽤场合可以假设重合。

如何进行航空摄影测量中的摄像机标定

如何进行航空摄影测量中的摄像机标定摄像机标定是航空摄影测量中非常关键的一步，它能够确保获取到的影像数据具有准确的地理空间信息，为后续的三维地图生成、空间模型构建等工作提供基础数据支持。

本文将介绍航空摄影测量中摄像机标定的基本原理、流程和方法，以及标定结果的评估和验证。

一、摄像机标定的原理在航空摄影测量中，摄像机的标定是指确定摄像机的内部参数矩阵和外部参数矩阵。

内部参数矩阵包括焦距、主点位置和径向畸变参数等，它们用于将像素坐标转换成三维空间坐标。

外部参数矩阵包括相机的位置和姿态信息，它们用于将世界坐标转换成像素坐标。

通过准确确定这些参数，可以使航空摄影所获取到的影像数据具有恢复真实地理空间位置关系的能力。

二、摄像机标定的流程摄像机标定的流程通常包括内部标定和外部标定两个步骤。

内部标定是指利用已知的标定板或特征点进行内参数矩阵的确定。

外部标定是指通过在地面布设控制点或者利用全球定位系统(GPS)的定位信息来确定摄像机的外参数矩阵。

1. 内部标定内部标定通常采用相机标定板进行，标定板上布满了已知尺寸的黑白棋盘格。

在进行内部标定时，首先要利用已知的标定板参数计算出初始的内部参数矩阵估计值。

然后，将摄像机对准标定板，通过摄影测量方法测量标定板特征点的像素坐标和三维空间坐标，并通过非线性最小二乘法进行参数的优化估计，得到最终的内部参数矩阵。

2. 外部标定外部标定的目的是确定摄像机的位置和姿态信息。

通常通过在地面布设控制点或者利用GPS的定位信息来实现。

在布设控制点时，需要在地面上选择具有明显特征的点，并进行高精度的测量。

然后，在航空摄影过程中，根据控制点在影像上的坐标以及已知的地面控制点坐标，利用摄影测量方法计算出外参数矩阵。

如果使用GPS定位信息，则需要在摄影过程中记录航行器的GPS坐标信息，并与摄影影像进行匹配，通过摄影测量方法计算出外参数矩阵。

三、摄像机标定的方法目前，常用的摄像机标定方法包括传统标定方法和自动化标定方法。

摄像机标定技术

摄像机标定技术摄像机标定技术一、概述计算机视觉的基本任务之一是从摄像机获取的图像信息出发计算三维空间中物体的几何信息，并由此重建和识别物体，而空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系是由摄像机成像的几何模型决定的，这些几何模型参数就是摄像机参数。

在大多数条件下，这些参数必须通过实验与计算才能得到，这个过程被称为摄像机定标(或称为标定)。

标定过程就是确定摄像机的几何和光学参数，摄像机相对于世界坐标系的方位。

标定精度的大小，直接影响着计算机视觉（机器视觉）的精度。

二、摄像机标定分类1 根据是否需要标定参照物来看，可分为传统的摄像机标定方法和摄像机自标定方法。

自标定方法非常地灵活,但它并不是很成熟。

因为未知参数太多,很难得到稳定的结果。

一般来说，当应用场合所要求的精度很高且摄像机的参数不经常变化时，传统标定方法为首选。

摄像机标定

一、摄像机标定的内容及意义：1、何为摄像机标定计算机视觉系统从摄像机获取的图像信息出发，计算三维环境中物体的位置，形状等几何信息，并由此重建三维物体。

图像上每一点的亮度反映了空间物体表面某点反射光的强度，而该点在图像上的位置与空间物体表面相应点的几何位置有关。

这些位置的相互关系，由摄像机成像几何模型所决定。

该几何模型的参数称为摄像机参数，这些参数必须由试验与计算来确定，试验与计算的过程称为摄像机标定。

摄像机标定来源于摄影测量学，摄影测量学中所使用的方法是数学解析分析的方法，在标定过程中通常要利用数学方法对从数字图像中获得的数据进行处理。

通过数学处理手段，摄像机标定提供了专业测量摄像机与非量测摄像机的联系。

而所谓的非量测摄像机是指这样一类摄像机，其内部参数完全未知、部分未知或者原则上不稳定。

2、摄像机标定的主要内容在计算机视觉中，摄像机标定主要标定两个部分：内参数和外参数。

(1)内参数：内参数是摄像机坐标系和理想坐标系之间的关系，用于给出摄像机的光学和几何学特征。

如：主点、长宽比例因子和镜头畸变；(2)外参数：外参数表示摄像机在世界坐标系里的位置和方向。

如：旋转和平移。

摄像机标定技术包含两大方面内容：摄像机模型和摄像机标定方法，二者联系紧密，因为往往引么样的模型就决定需要采用什么样的标定方法。

根据不同的应用，对摄像机的标定要求也是不同的。

比如说，对机器导航，要求能自动快速地进行标定，而对于度量领域的应用，精度要求是第一位的。

3、摄像机标定的意义：摄像机标定技术是从二维平面图像获得三维信息这一过程的关键步骤，是计算机视觉技术的第一步。

摄像机标定的目的是完成三维重建，在机器视觉、虚拟现实等计算机图像应用领域有着广泛应用。

4、摄像机标定的发展：1966年，B．Hallert发表了他在镜头与相机标定方面的研究成果，首次将最小二乘法用于对镜头标定多余观察数据的处理，并将其应用在野外立体坐标测量仪上，得到了高精度的测量结果。

第五章 摄像机标定

工业摄像机标定课件

摄像机标定的几种方法

摄像机标定

摄像机标定

摄像机标定原理

摄像机标定原理及源码

摄像机标定技术在机器视觉中的应用研究

（学习笔记）摄像机模型与标定——摄像机标定

摄像机标定ppt课件

摄像机标定和三维重建

7.摄像机标定

摄像机标定方法及原理

《摄像机自标定》课件

摄像机标定（Cameracalibration）笔记

如何进行航空摄影测量中的摄像机标定

摄像机标定技术

摄像机标定

第五章摄像机标定