最新二章地理空间数学基础ppt课件
合集下载
第二章 地理空间数学基础

2、投影的实质
建立地球椭球面上的点的地理坐标(L,B)与平面上对
应点的平面坐标(x,y)之间的函数关系:
x f1 ( L, B) y f 2 ( L, B)
地球椭球面 B,L x, y 地图平面
地图投影
二、地图投影的变形
1、投影变形的性质 观察地球体经纬线的
长度、面积和角度特征。
地图投影的变形具体表现: 长度(距离)变形 角度(形状)变形 面积变形
其优点:
①椭球体参数精度高; ②定位采用的椭球体面与我国大地水准面符合得好; ③大地网精度高;
④坐标统一,精度优良,可以直接满足1:5000甚至更大
比例尺测图的需要。
三角测量
导 线 测 量
支导线
国家平面控制网
O
国家平面控制网含三角点、导线点 共154348个,构成1954北京坐标 系、1980西安坐标系两套系统。
3、我国常用的地图投影
①我国1:100万地形图采用兰勃特Lambert投影(正轴等
角割圆锥) ;
②我国大部分省区图以及大多数这一比例尺的地图也多采用 Lambert投影和属于同一投影系统的Albers投影(正轴等积 割圆锥投影); ③我国基本比例尺地形图除1:100万外均采用高斯—克吕 格投影为地理基础;
用来代替大地体的椭球体称地球椭球体。
b a a
x2 y2 z2 2 2 1 2 a a b
椭球体三要素:长轴a(赤道半径)、短轴b(极半径)和椭球扁率f。
3、地球体的数学表面——地球椭球体
地球椭球体参数:
• 长半径: a(赤道半径)
b a
• 短半径: b(极半径)
• 扁率: f=(a-b)/a • 第一偏心率: e2=(a2- b2)/ a2 • 第二偏心率: e’2=(a2- b2)/ b2
第2章 地理空间数学基础

空间数据投影
• 面积变形与面积比
– 面积比—地面上微分面积投影后的大小dF’与其相应的 实地面积dF的比称为面积比 – P=dF′/dF – 面积变形指面积比与1的差值。用符号Vp表示,那么 – Vp=P-1
– Vp=0,投影后面积没有变形;Vp<0,投影后面积缩小; Vp>0,投影后面积增加
空间数据投影
球面坐标系统的建立
• 天文地理坐标系
λ
ψ
图2.4天文地理坐标系
球面坐标系统的建立
• 大地地理坐标
– 依托地球椭球用定义原点和轴系以及相应基本参考面 标示较大地域地理空间位置的参照系,简称大地坐标
– 点在大地坐标系中的位置以大地纬度与大地经度表示
球面坐标系统的建立
• 空间直角坐标系
– 参心空间直角坐标系是在参考椭球上建立的三维直角 坐标系O-XYZ – 坐标系的原点位于椭球的中心,Z轴与椭球的短轴重合, X轴位于起始大地子午面与赤道面的交线上,Y轴与XZ 平面正交 – 由于观测范围的限制,不同的国家或地区要求所确定 的参考椭球面与局部大地水准面最密合 – 由于参考椭球不是唯一的,因此参心空间直角坐标系 也不是唯一的
– 第三类是地球椭球面
• 大地体非常接近旋转椭球,而后者的表面是一个是一个规则的 数学曲面,因此选择一个旋转椭球作为地球理想的模型,称为 地球椭球或参考椭球
地球形状与地球椭球
x y z 2 2 1 2 a a b
a为长半径,近似等于地球赤道半径;b为极轴半径, 近似等于南极(北极)到赤道面的距离。
1940
6378245
6356863
1:298.3
地球形状与地球椭球
• 在实际建立地理空间坐标系统的时候,还需要指定一个大 地基准面将参考椭球体与大地体联系起来,在大地测量学 中称之为椭球定位 • 定位指依据一定的条件,将具有给定参数的椭球与大地体 的相关位置确定下来
《地理空间数学基础》PPT课件

黄海海面
1952-1979年平 均海水面为0米
水准原点 1985国家高
程基准,
72.2604米
青岛市观象山上国家水准原点
国家高程控制网是确定地貌地物海拔高程的坐标 系统,按控制等级和施测精度分为一、二、三、四等网。 目前提供使用的1985国家高程系统共有水准点成果114041 个,水准路线长度为416619.1公里。
地心空间直角坐标系的坐标原点位于地球质心。
WGS-84坐标系——“World Geodetic System”(世界大地坐标系)是美 国国防局为进行GPS导航定位于1984年建立的地心坐标系,1985年投入使 用,采用WGS-84椭球。
平面坐标系统=球面坐标系统+投影规则
一 地理空间参考
(三)高程基准
而对于制图区域广大的大国地图、大洲地图、 半球图、世界图等,则需要慎重地选择投影。
2. 制图比例尺
不同比例尺地图对精度要求的不同,导致 在投影选择上亦各不相同。以我国为例,大比例 尺地形图,由于要在图上进行各种量算及精确定 位,因此应选择各方面变形都很小的地图投影, 比如分带投影的横轴等角椭圆柱投影(如高斯— 克吕格投影)。而中小比例尺的省区图,由于概 括程度高于大比例尺地形图,因而定位精度相对 降低,选用正轴等角、等积、等距的圆锥投影即 可满足用图要求。
圆柱投影:投影面为圆柱 圆锥投影:投影面为圆锥 方位投影:投影面为平面
正轴投影投影面中心轴与地轴相互重
斜轴投影:投影面中心轴与地轴斜向相
横轴投影:投影面中心轴与地轴相互垂
二 空间数据投影
(四)常用地图投影概述
1 高斯-克吕格投影 2 通用墨卡托投影(UTM-Universal Transverse
第2章地理空间数学基础

第2章地理空间数学基础
地图是现实世界的模型,它按照一定的比例和投影原则, 有选择地将复杂的三维地理空间的某些内容投影到二维平 面介质上,并用符号将这些内容表现出来。
地图是根据一定的数学法则,使用地图语言,通过制图综 合,表示地面上地理事物的空间分布、联系及在时间中发 展变化状态的图形。
第2章地理空间数学基础
• 长半径
a(赤道半径)
• 短半径
b(极半径) 第2章地理空间数学基础
•扁率
α=(a-b)/a
• 第一偏心率 e2=(a2- b2)/ a2
• 第二偏心率 e’2=(a2- b2)/ b2
• 通过长轴和短轴来度量地球的形状。不 同的方法其长短轴参数不一样,所适用
的地区也就不同。
• 在北美通常使用CLARKE1866,在我国 (1978年起使用IUGG国际椭球)和前苏 联使用克拉索夫斯基椭球体 KRASOVSKY。
大陆和岛屿形成一个闭合的曲面,这就是大地水准面
(3)地球椭球体模型
第2章地理空间数学基础
大地水准面所包围的形体,叫大地球体。由于地球体 内部质量分布的不均匀,引起重力方向的变化,导致处处 和重力方向成正交的大地水准面成为一个不规则的,仍然 是不能用数学表达的曲面。大地水准面形状虽然十分复杂, 但从整体来看,起伏是微小的。它是一个很接近于绕自转 轴(短轴)旋转的椭球体。所以在测量和制图中就用旋转 椭球来代替大地球体,这个旋转球体通常称地球椭球体, 简称椭球体。
• 地面上点位的确定 地面上任一点的位置,通常用经度和纬度来决定。经线和 纬线是地球表面上两组正交(相交为90度)的曲线,这两 组正交的曲线构成的坐标,称为地理坐标系。地表面某两 点经度值之差称为经差,某两点纬度值之差称为纬差。例 如北京在地球上的位置可由北纬39°56'和东经116°24'来 确定。
地图学课件-地图的数学基础

新编地图学教程 第2章 地图的数学基础
1. GPS系统由三个独立的部分组成
空间部分:21颗工作卫星,3颗备用卫星(白色)。它们在 高度20 200km的近圆形轨道上运行,分布在六个轨道面上, 轨道倾角55°,两个轨道面之间在经度上相隔60°,每个轨 道面上布放四颗卫星。卫星在空间的这种配置,保障了在地 球上任意地点,任意时刻,至少同时可见到四颗卫星。
新编地图学教程 第2章 地图的数学基础
2.2 中国的大地坐标系统
1.中国的大地坐标系 1980年以前:参见电子教案本章第十三页; 1980年选用1975年国际大地测量协会推荐的参考 椭球: ICA-75椭球参数
a = 6 378 140m
b = 6 356 755m f = 1/298.257
新编地图学教程 第2章 地图的数学基础
新编地图学教程 第2章 地图的数学基础
大地水准面的意义
1. 地球形体的一级逼近:
对地球形状的很好近似,其面上高出与面下 缺少的相当。
2. 起伏波动在制图学中可忽略:
对大地测量和地球物理学有研究价值,但在 制图业务中,均把地球当作正球体。
3. 重力等位面:
可使用仪器测得海拔高程(某点到大地水准 面的高度)。
新编地图学教程 第2章 地图的数学基础
新编地图学教程 第2章 地图的数学基础
3.2 地图的比例尺
新编地图学教程 第2章 地图的数学基础
地面支撑系统:1个主控站,3个注入站,5个监测站。它 向GPS导航卫星提供一系列描述卫星运动及其轨道的参数; 监控卫星沿着预定轨道运行;保持各颗卫星处于GPS时间 系统及监控卫星上各种设备是否正常工作等。
新编地图学教程 第2章 地图的数学基础
用户设备部分:GPS接收机——接收卫星信号,经数据处理 得到接收机所在点位的导航和定位信息。通常会显示出用户 的位置、速度和时间。还可显示一些附加数据,如到航路点 的距离和航向或提供图示。
第2讲 地理空间数学基础
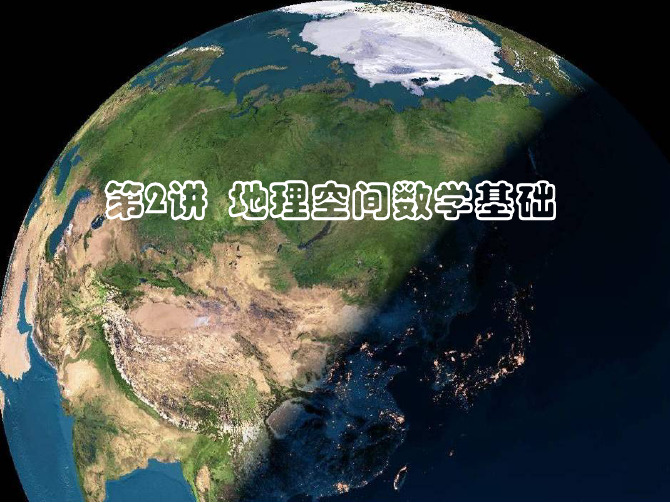
2.4地图投影的分类
变形性质 地图投影 构成方法
等积投影 等角投影 任意投影
几何投影
方位投影 圆锥投影 圆柱投影 伪方位投影 伪圆锥投影 为圆柱投影 多圆锥投影
非几何投影
地图投影的分类(1)
按地图投影的构成方法分类 (1 )几何投影 把椭球面上的经纬线网投影到几何面 上,然后将几何面展为平面而得到。
X N’
O
Y
S’
A高斯-克吕格投影——投影分带
高斯-克吕格投影的最大变形处为各投影带在赤道边缘处,为了 控制变形,我国地形图采用分带方法,即将地球按一定间隔的经差 (6°或3°)划分为若干相互不重叠的投影带,分别投影。
3º 9º 69º 75º 81º 87º 93º 99º 105º 111º 117º 123º 129º 135º
a) 按投影面的形状
– 圆锥投影 – 圆柱投影 – 方位投影
正 轴 方位 圆柱 圆锥
斜 轴
横 轴
b) 按投影面与地球自转轴间的方位关系
– 正轴投影 – 横轴投影 – 斜轴投影
c) 按投影面与地球的位置关系
– 相切投影 – 相割投影
(2)非几何投影
– – – – 可分为: 伪方位投影 伪圆柱投影 伪圆锥投影 多圆锥投影 ,根据某些条件用数学解析法确定球面与平面之间点与点的函数关系。
极不规则,无法用数学表面进行描述 不规则性、动态性、不唯一性 不规则性、相对唯一性 标准数学曲面 1952:海福特椭球 1953:克拉索夫斯基椭球 1978:1975年国际椭球
1.1地球椭球
大地水准面和大地体
水准面和大地水准面图
旋转椭球/地球椭球 • 参数:
– 长半径:a – 短半径:b – 扁率:f=(a-b)/a
第二章地理空间数学基础

(一) 地球空间参考
法线与赤道面的交角, 叫做A点的纬度ψ 。 过A点的子午面与通过 英国格林尼治天文台 的子午面所夹的二面 角,叫做A点的经度λ 。
(一) 地球空间参考
天文坐标系(地心坐标系)
O是质心 OP为地球自转轴 KK’为垂线 G点为格林威治天文起始子午面
φ天文纬度 λ天文经度
PS:地表面并不是大地水准面,所以在大地测量学中将高程列入天文坐标中!
3
(一) 地球空间参考
1. 地球形状与地球椭球
1).地球的自然表面:
是一个起伏不平, 十分不规则的表面,包 括海洋底部,高山高原 在内的固体地球表面。 不适合于数学建模。
4
(一) 地球空间参考
2).大地水准面: 大地水准面:地球表面的72%
被流体状态的海水所覆盖,可以 假设当海水处于完全静止的平衡 状态时,从海平面延伸到所有大 陆下部,而与地球重力方向处处 正交的一个连续、闭合的水准面 ,这就是大地水准面。
7ቤተ መጻሕፍቲ ባይዱ
(一) 地球空间参考
3).地球椭球面:地球椭球几何定义
X 2 Y2 Z2 椭球方程: 2 2 2 1 a a b
O是椭球中心,NS为旋转轴, a 为长半轴,b 为短半轴
子午圈:包含旋转轴的平面与椭球
面相截所得的椭圆。
赤道:通过椭球中心的平行圈。
8
(一) 地球空间参考
4). 数学模型:
水准面:一个重力等位面。
大地体:大地水准面包围的形状
是一个水准椭圆。
5
(一) 地球空间参考
6
(一) 地球空间参考
3).地球椭球面: 地球椭球:在控制测量中,用来代表地球的椭球,它是地球的数学
2 第二章 地理空间数学基础
地球模型
2. 坐标系统
参心 空间直角坐标系
地心地固 空间直角坐标系
坐标参考系统—平面系统
直接建立在球体上的地理坐标
用经度和纬度表达地理对象位置
投 影
建立在平面上的直角坐标系统
用(x,y)表达地理对象位置
3. 高程基准
A
H´A
任意水准面 HA
大地水准面 铅垂线
hAB
H´B HB
黄海海面
1952-1979年平 均海水面为0米
比例尺的含义
– 制图区域较小,采用各方面变形都较小的地图投影,图上各处的比例是一致的,故 此时比例尺的含义是图上长度与相应地面长度的比例;
– 制图区域较大时,地图投影比较复杂,地图上长度因地点和方向的不同而有所变化, 这种地图比例尺一般是指在地图投影时,对地球半径缩小的比率, 称为主比例尺。 地图经过投影后,体现在图上只有个别点线没有长度变形,也就是说,只有在这些 长度没有变形的点或线上,才可用地图上注明的比例尺
Y’
Y
O
x=x’+ a
y=y’+ b
2)坐标系旋转
X
P x’sin θ x’cos θ
y’sin θ
Y
O
y’cos
x = θx’cosθ+ y’sin θ
y = y’cosθ- x’sin θ
3)坐标平移和旋转
X
X”
P O’ O
由坐标平移可知: x=x”+a
y=y”+b 由坐标旋转可知:
x”= x’cosθ+ y’sin θ
GIS中,地理数据的显示可根据用户的需要而指定投影方 式,但当所显示的地图与国家基本地图系列的比例尺一致时, 一般采用国家基本系列地图所用的投影。
第2章_地理空间数学基础

X2
其中 X 、 Y 、 Z 为两空间直角坐标系坐标原点的平移参数, X 轴、Y 轴、Z 轴旋转的角度, m 为尺度变化参数。
z 、 y 、 z 分别表示绕
2015-1-19
31
3.投影解析转换
同一地理坐标基准下的坐标变换 如果参与转换空间参考系的投影公式, 1)存在精确解析关系式:直接进行坐标换算; 2)不存在精确解析关系式:采用间接变换,即先将一种投影的平面坐 标换算为球面大地坐标,然后再对球面大地坐标计算出另一种投影下的平 面坐标,从而实现两种投影坐标间的变换。
12
青岛观象山水准原点
中华人民共和国大地原点,是1980年国家大地 坐标系起算点。大地原点位于陕西省泾阳县永 乐店北洪流村。
深度基准是指海图图载水深及其相关要素的起算面。通常取当地平均海面
向下一定深度为这样的起算面,即深度基准面。
平均海面
L
深度基准面
Z
海底
2015-1-19
15
2.2 空间数据投影
2015-1-19
32
不同地理坐标基准下的坐标变换
主要包括: • 地理坐标基准的变换; • 坐标值的变换; 实现整个坐标转换的基本过程为(以WGS 84坐标和1980西安坐标的
转换为例): a.(B,L)84转换为(X,Y,Z)84,即空间大地坐标到空间直角坐标的转换; b.(X,Y,Z)84转换为(X,Y,Z)80,坐标基准的转换,即参考椭球转换。该
3.兰勃特等角投影(Lambert Conformal Conic)
在双标准纬线下是“正轴等角割圆锥投影”。设想用一个正圆锥割于球
面两标准纬线,应用等角条件将地球面投影到圆锥面上,然后沿一母线展开, 即为兰勃特投影平面。墨卡托(Mercator)投影是它的一个特例。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1:295.0 1:293.47 1:297.0
1:298.3
埃及,加拿大,美国,墨西哥,法国
越南,罗马尼亚,法国,南非
意大利,比利时,葡萄牙,保加利亚,罗马 尼亚,丹麦,土耳其,芬兰,阿根廷,埃及, 中国(1952年前)
前苏联(1946年起),保加利亚,波兰, 罗马尼亚,匈牙利,捷克,斯洛伐克,原得 意志民主共和国,中国
西北大学城市与资源学系
13
图2.5 大地地理坐标系
• 空间直角坐标系
NZ
O Y
坐标系的原点位于椭球的中心,Z轴与椭球 的短轴重合,X轴位于起始大地子午面与赤 道面的交线上,Y轴与XZ平面正交,O-XYZ 构成右手坐标系。
在建立参心坐标时,由于观测范围的限制, 不同的国家或地区要求所确定的参考椭球面 与局部大地水准面最密合。由于参考椭球不 是唯一的,所以,参心空间直角坐标系也不 是唯一的。
克拉克Ι (英,Clarke)
克拉克Ⅱ (英,Clarke)
1866 6 378 206 6 356 534 1880 6 378 249 6 356 515
海福特 (美国,Hayford)
1910
6 378 388
6 356 912
克拉索夫斯基 (前苏,Красовский) 1940 6 378 245 6 356 863
➢ 地理坐标是一种球面 坐标。
西北大学城市与资源学系
12
• 大地地理坐标系
WAE为椭球赤道面,NAS为大地首子午面,PD为 地面任一点,P为PD在椭球上的投影,则地面点 PD对椭球的法线PDPK与赤道面的交角为大地纬 度,常以B表示。从赤道面起算,向北为正,向 南为负。大地首子午面与P点的大地子午面间的 二面角为大地经度,常以L表示。以大地首子午面 起算,向东为正,向西为负。
➢ 建立地方独立坐标系,实际上就是通过一些元素的确定来决定地方参 考椭球与投影面。地方参考椭球一般选择与当地平均高程相对应的参 考椭球,该椭球的中心、轴向和扁率与国家参考椭球相同。
➢ 在地方投影面的确定过程中,应当选取过测区中心的经线或某个起算 点的经线作为独立中央子午线;以某个特定使用的点和方位为地方独
X
S
图2.6 参心空间直角坐标系
地心地固空间直角坐标系的定义是:原点O与地 球质心重合,Z铀指向地球北极,X轴指向格林 尼治平均子午面与地球赤道的交点,Y轴垂直于 XOZ平面构成右手坐标系。地球自转轴相对地球
体的位置并不是固定的,地极点在地球表面上的 位置是随时间而变化的。
西北大学城市与资源学系
14
经线以东为正,中央经线以西为负。
YA= 238765.2m
YB= -148572.3m 纵坐标轴西移500km后,其横坐标 分别为:
YA’ = 738765.2m
YB’ = 351427.7m
图2.7 高斯-克吕格坐标表
加上带号,如A、B两点位于第19带, 其通用坐标为:
YA’’= 19 738765.2m
我国的大地坐标统
在一个国家或地区,不同时期也可能采用不同的坐 标系。我国目前沿用了两种坐标系,即1954年北京坐
标系和1980年国家大地坐标系。
IGA-75椭球参数
a = 6 378 140m
b = 6 356 755m
f =1/298.257
陕西省泾阳县永乐镇北洪流
村为 “1980西安坐标系” 大地
西北大学城市与资Y源B学’’=系19 351427.7m
17
地方独立平面直角坐标系
➢ 国家坐标中每个高斯投影带都是按一定间隔划分,其中央子午线不可 能刚好落在城市和工程建设地区的中央,从而使高斯投影长度产生变 形。
➢ 为了减小变形,将其控制在一个微小的范围内,使得计算出来的长度 与实际长度认为相等,常常需要建立适合本地区的地方独立坐标系。
直接建立在球体上的地理坐标, 用经度和纬度表达地理对象位 置
投 影
建立在平面上的直角坐标系统, 用(x,y)表达地理对象位置
西北大学城市与资源学系
11
一、地理坐标 (Geographic coordinate system)
➢ 地理坐标——地面上任一点的 位置,通常用经度(Latitude) 和纬度(Longitude)来决定。 经线和纬线是地球表面上两组 正交(相交为90度)的曲线, 这两组正交的曲线构成的坐标, 称为地理坐标系。
坐标的起算点——大地原西北点大。学城市与资源学系
15
不同的球面地理坐标系
54—80坐西标北大系学地城形市与图资邻源学接系状况
16
(中间部分为两个坐标系邻接“真空”带)
Y A
二、平面坐标系(projected coordinate system )
高斯平面直角坐标系:在高斯-克吕格投影带内布置了平面直角坐标系 统。具体构成是:规定以中央经线为X轴,赤道为Y轴,中央经线与赤道 交点为坐标原点。同时规定,x值在北半球为正,南半球负;y值在中央
二章地理空间数学基础ppt课件
➢ 地球空间参考 ➢ 空间数据投影 ➢ 空间尺度 ➢ 地图分幅
西北大学城市与资源学系
2
椭球体名称
年代 长半径(m) 短半径(m) 扁率
使用的主要国家
白塞尔 (德,Bessel)
1841 6 377 397 6 356 079
1:299.15
波兰,罗马尼亚,捷克,斯洛伐克,瑞士, 瑞典,智利,葡萄牙,日本
• 所谓的定位,就是依据一定的条件,将具有给定 参数的椭球与大地体的相关位置确定下来。
• 这里所指的一定条件,可以理解为两个方面:一 是依据什么要求使大地水准面与椭球面符合;二 是对轴向的规定。参考椭球的短轴与地球旋转轴 平行是参考椭球定位的最基本要求。
西北大学城市与资源学系
10
二、坐标系统
一、分类 1、球面坐标系统 ① 天文地理坐标系 ② 大地地理坐标系 ③ 空间直角坐标系 参心空间直角坐标系 地心空间直角坐标系 2、平面坐标系统 ① 高斯平面直角坐标系 ② 地方独立坐标系
1975年国际椭球
1975 6 378 140 6 356 755 1:298.257 1975年国际第三个推荐值
1980年国际椭球
198西0 北6大37学8 13城7 市与资源学系1:298.257 1979年国际第四个推荐值
9
椭球定位
• 有了参考椭球,在实际建立地理空间坐标系统的 时候,还需要指定一个大地基准面将这个椭球体 与大地体联系起来,在大地测量学中称之为椭球 定位。
