西藏林芝市第二高级中学2020-2021学年高二下学期第二学段考试(期末)数学(理)试题
西藏自治区林芝市第二高级中学2020-2021学年高二年级上学期期末英语试题(原卷版)

林芝市第二高级中学2020—2021学年第二学期高二年级第二学段测试英语试卷注意事项:1.答题前请在试卷空白处填写好自己的姓名、班级、考号等信息;2.请将答案正确填写在答题卡上。
第I卷(选择题)第一部分听力(共两节,满分30分)第一节:共5小题;每小题1. 5分,满分7. 5分。
听下面5段对话。
每段对话后有一个小题, 从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What do we know about Tom?A. He is often absent from class.B. He didn’t sleep yesterday.C. He goes to school as usual.2. Where did the man grow up?A. In England.B. In Canada.C. In Germany.3 How much is the original price of the T-shirt?A. 5 dollars.B. 10 dollars.C. 20 dollars.4. When was the Carnival in Venice first recorded?A. In 1990.B. In 1798.C. In 1268.5. What are the speakers doing?A. Camping.B. Skating.C. Swimming.第二节:共15小题; 每小题1. 5分, 满分22. 5分。
听下面5段对话或独白。
每段对话或独白后有几个小题, 从题中所给的A、B、C三个选项中选出最佳选项, 并标在试卷的相应位置。
听每段对话或独白前, 你将有时间阅读各个小题, 每小题5秒钟;听完后, 各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
西藏林芝市第二高级中学2020_2021学年高二数学上学期第二学段考试试题理

西藏林芝市第二高级中学2020-2021学年高二数学上学期第二学段考试试题 理全卷满分:150分 考试用时:120分钟注意事项:1。
答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上的对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效.3。
填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
第I 卷一、选择题:(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.不等式(2)0x x +≥的解集为 ( )A .02{|}x x x ≥≤或﹣B .0{|}2x x ≤≤﹣C .{}2|0x x ≤≤D .0{|}2x x x ≤≥或2.观察下列数的特点,1,1,2,3,5,8,,21,34,55,...x 中,其中x 为( )A .12B .13C .14D .153.命题p :∃x 0∈R,x 错误!-x 0+1≤0的否定是 ( )A .∃x 0∈R ,x 错误!-x 0+1>0B .∀x ∈R,x 2-x +1≤0C .∀x ∈R ,x 2-x +1〉0D .∃x 0∈R ,x 错误!-x 0+1〈04.若,x y 为正数,则31213x yy x++的最小值是 ( ) A .24 B .28 C .25D .265.在△ABC 中,“A>B ”是“sin A>sin B ”的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 6.在等差数列{}na 中,10120S=,那么110a a+=( )A .12B .24C .36D .487.△ABC 中,角,,A B C 的对应边分别为,,a b c ,若135,30,A B a ︒︒===b 等于( )A .1 B . C .D .2 81的等差中项是( )A .1 B .1- C D .1±9.以椭圆错误!+错误!=1的焦点为顶点,顶点为焦点的双曲线方程为( )A .x 2-错误!=1B 。
西藏林芝市第二高级中学2020-2021学年高二下学期第一学段考试(期中)数学(文)试题

西藏林芝市第二高级中学【最新】高二下学期第一学段考试(期中)数学(文)试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知集合{|11}A x x =-≤≤,{1,0,2}B =-,则AB =( ) A .{1,0}- B .{1,0,1,2}-C .{1,1}-D .{0} 2.函数2y x =-的单调递增区间为( )A .(],0-∞B .[)0,+∞C .()0,∞+D .(,)-∞+∞ 3.函数y =a |x |(a >1)的图像是( )A .B .C .D .4.计算25log 25log ⋅=( )A .3B .4C .5D .65.如图所示的程序框图,运行后输出的结果为( )A .4B .8C .16D .326.如果过P (-2,m ),Q (m ,4)两点的直线的斜率为1,那么m 的值是( ) A .1 B .4 C .1或3 D .1或47.直线10x +=的倾斜角为( )A .6πB . 3πC .23πD .56π 8.过点(1,0)且与直线x-2y-2=0平行的直线方程是( )A .x-2y-1=0B .x-2y+1=0C .2x+y-2=0D .x+2y-1=0 9.圆()2212x y -+=的圆心到直线10x y ++=的距离为( )A .2 BC .1 D1020y +-=截圆224x y +=得到的弦长为( )A .1B .2 C.D.11.过点A (3,3)且垂直于直线4270x y +-=的直线方程为A .122y x =+B .27y x =-+C .1522y x =+D .1322y x =+ 12.已知直线:20l kx y k -+-=过定点M ,点(),P x y 在直线210x y +-=上,则MP 的最小值是( )AB.5 CD.二、填空题13.已知集合{}{}1,2,4,2,4,6A B ==,则A B =________.14.已知幂函数()f x x α=(α为常数)的图象经过点(2,16)-,则2log α=_______.15.已知定义域为R 的奇函数()f x ,若()22,2log ,02x x f x x x ⎧>=⎨<≤⎩,则14f ⎛⎫- ⎪⎝⎭的值______. 16.已知直线370ax y --=与直线(21)0a x ay a -++=互相垂直,则a =_______.三、解答题17.已知函数()()()lg 2lg 2f x x x =+--.(1)求()f x 的定义域; (2)判断()f x 的奇偶性并予以证明;(3)求不等式()1f x >的解集.18.已知函数1()x f x a -=的图象经过点12,2⎛⎫ ⎪⎝⎭其中0,1a a >≠(1)求a 的值;(2)若12x a -≥,求x 的取值范围.19.设圆的方程为22450x y x +--=(1)求该圆的圆心坐标及半径.(2)若此圆的一条弦AB 的中点为(3,1)P ,求直线AB 的方程.20.已知圆心为C (4,3)的圆经过原点O .(1)求圆C 的方程;(2)设直线3x ﹣4y +15=0与圆C 交于A ,B 两点,求△ABC 的面积.21.三角形的三个顶点为()()()4,0,6,5,0,3A B C求BC 边上高所在直线的方程;求BC 边上中线所在直线的方程.22.已知函数()33x x f x a -=-⋅,其中a 为实常数. (1)若()07f =,解关于x 的方程()5f x =;(2)判断函数()f x 的奇偶性,并说明理由.参考答案1.A【分析】直接计算交集得到答案.【详解】{|11}A x x =-≤≤,{1,0,2}B =-,则{1,0}A B ⋂=-.故选:A .【点睛】本题考查了交集运算,属于简单题.2.A【分析】由解析式知函数图像为开口向下的抛物线,且对称轴为y 轴,故可得出其单调增区间.【详解】∵函数2y x =-, ∴函数图像为开口向下的抛物线,且其对称轴为y 轴∴函数的单调增区间为(],0-∞.故选:A.【点睛】本题考查了一元二次函数的单调区间,掌握一元二次函数的对称轴是解题的关键,属于基础题.3.B【解析】因为||0x ≥,所以1x a ≥,且在(0,)+∞上曲线向下弯曲的单调递增函数,应选答案B . 4.A【分析】先化简,再结合换底公式即可求解【详解】 3222525253log 25log log 5log 22log 5log 232⋅=⋅=⨯⨯⨯= 故选:A本题考查对数的化简求值,属于基础题5.C【详解】执行如图程序框图:当n=2,b=1,当n=3,b=2,当n=4,b=4,当n=5,b=16,当n=5则输出b 故选C6.A【分析】根据直线的斜率公式,列出方程,即可求解,得到答案.【详解】由题意,过过P (-2,m ),Q (m ,4)两点的直线的斜率为1, 根据直线的斜率公式,可得41(2)m m -=--,解得1m =. 故选:A.【点睛】本题主要考查了直线的斜率公式的应用,其中解答中熟记直线的斜率公式,准确运算是解答的关键,着重考查了计算能力,属于基础题.7.A【分析】首先将直线化为斜截式求出直线的斜率,然后再利用倾斜角与斜率的关系即可求解.【详解】由直线10x -+=,则y x =+ 设直线的倾斜角为α,所以tan 3α=, 所以6πα=.故选:A本题考查了直线的斜截式方程、直线的倾斜角与斜率的关系,属于基础题.8.A【分析】设出直线方程,利用待定系数法得到结果.【详解】设与直线平行的直线方程为, 将点代入直线方程可得,解得. 则所求直线方程为.故A 正确. 【点睛】本题主要考查两直线的平行问题,属容易题.两直线平行倾斜角相等,所以斜率相等或均不存在.所以与直线平行的直线方程可设为.9.B【分析】由圆的方程得出圆心坐标,利用点到直线的距离公式得出答案.【详解】圆()2212x y -+=的圆心坐标为(1,0)则圆心(1,0)到直线10x y ++=的距离d == 故选:B【点睛】本题主要考查了点到直线的距离公式的应用,属于中档题.10.D【详解】圆心到直线的距离为1d ==,则截得弦长l ==【点睛】弦长的两种求法①代数方法:将直线和圆的方程联立方程组,消元后得到一个一元二次方程.在判别式Δ>0的前提下,利用根与系数的关系,根据弦长公式求弦长.②几何方法:若弦心距为d ,圆的半径长为r ,则弦长l =11.D【解析】过点A (3,3)且垂直于直线4270x y +-=的直线斜率为12,代入过的点得到1322y x =+. 故答案为D.12.B【分析】令直线l 的参数k 的系数等于零,求得定点M 的坐标,利用两点间的距离公式、二次函数的性质,求得MP 的最小值.【详解】直线:20l kx y k -+-=,即()120k x y --+=,过定点()1,2M ,点(),P x y 在直线210x y +-=上,12y x ∴=-,MP ∴===故当15x =-时,MP ,故选B. 【点睛】 本题主要考查直线经过定点问题,两点间的距离公式的应用,二次函数的性质,属于中档题. 13.{1,2,4,6}【解析】【分析】要求A B ⋃,即将集合A B 、中的元素写在同一个集合中,重复的写一次。
西藏林芝市第二高级中学2020学年高二数学下学期期末试题 理

西藏林芝市第二高级中学2020学年高二数学下学期期末试题 理考试时间:120分钟一、选择题:(本大题共12小题,每小题5分,共60分)1.已知集合2{|560}A x x x =-+≤,{|15}B x Z x =∈<<,则A B =I ( )A .[2,3]B .(1,5)C .{}2,3D .{2,3,4}2.若i 为虚数单位,则341ii -=+( ) A .17i -- B .1722i + C .3124i + D .1722i -- 3.已知向量()()2,1,,2a b λ==r r ,若a b ⊥r r ,则实数λ= ( )A .4-B .1-C .1D . 44.在的展开式中,的系数是( )A .-80B .-10C .5D .405.先后抛掷一枚质地均匀的骰子5次,那么不能作为随机变量的是( ) A .出现7点的次数 B .出现偶数点的次数C .出现2点的次数D .出现的点数大于2小于6的次数6.点P 的直角坐标为(3)-,则点P 的极坐标可以为( ) A .2(23,)3π B .2(23,)3π- C .5(23,)6π- D .5(23,)6π 7.函数()2ln f x x x =-+的图象在1x =处的切线方程为( ) A .10x y ++=B .10x y -+=C .210x y -+=D .210x y +-=8.函数()()ln 2f x x x =+-的单调增区间为( )A .()1,+∞B .()1,2C .(),3-∞D .(),1-∞ 9.复数2i z =-的共轭复数在复平面内对应的点所在的象限为( ) A .第一象限B .第二象限C .第三象限D .第四象限10.一个口袋内装有大小相同的6个白球和2个黑球,从中取3个球,则共有( )种不同的取法A .B .C .D .11.设函数=,若=4,则的值为( )A .B .C .D .12.已知(6,0.6)X B :,则()E X =( ) A .0.6B .3.6C .2.16D .0.216二、填空题:(本题共4小题,每小题5分,共20分。
2020学年西藏林芝市第二高级中学高二下学期期末数学(理)试题(解析版)

2020学年西藏林芝市第二高级中学高二下学期期末数学试题一、 单选题1. 已知集合2{|560}A x x x =-+≤,{|15}B x Z x =∈<<,则A B =I ( ) A .[2,3] B .(1,5)C .{}2,3D .{2,3,4}【答案】C【解析】解不等式简化集合A 的表示,用列举法表示集合B ,最后根据集合交集的定义求出A B I . 【详解】2560(2)(3)023x x x x x -+≤⇒--≤⇒≤≤Q ,{}23A x x ∴=≤≤,又{}{|15}2,3,4B x Z x =∈<<=,所以{}2,3A B ⋂=,故本题选C. 【点睛】本题考查了列举法表示集合、集合交集的运算,正确求解出不等式的解集是解题的关键.2.若i 为虚数单位,则341ii-=+( ) A .17i -- B .1722i +C .3124i +D .1722i --【答案】D【解析】根据复数的除法运算法则,即可求出结果. 【详解】34(34)(1)344171(1)(1)222i i i i i i i i i ------===--++-. 故选D 【点睛】本题主要考查复数的除法运算,熟记运算法则即可,属于基础题型.3.已知向量()()2,1,,2a b λ==r r ,若a b ⊥r r,则实数λ= ( ) A .4- B .1- C .1 D .4【答案】B【解析】由题得=0a b ⋅r r,解方程即得解.【详解】因为a b ⊥r r,所以=220,1a b λλ⋅+=∴=-r r .故选:B【点睛】本题主要考查向量垂直的坐标表示,意在考查学生对该知识的理解掌握水平和分析推理能力.4.在()52x -的展开式中,2x 的系数是( ) A .80- B .10- C .5 D .40【答案】A【解析】由二项展开式的通项公式,可直接得出结果. 【详解】因为()52x -的展开式的通项为()()5515522k kk k kk k T C x C x --+=-=-, 令3k =,则2x 的系数是()335280C ⨯-=-. 故选A 【点睛】本题主要考查二项展开式中指定项的系数,熟记二项式定理即可,属于基础题型.5.先后抛掷一枚质地均匀的骰子5次,那么不能作为随机变量的是 ( ) A .出现7点的次数 B .出现偶数点的次数C .出现2点的次数D .出现的点数大于2小于6的次数【答案】A【解析】根据随机变量的定义可得到结果. 【详解】Q 抛掷一枚骰子不可能出现7点,出现7点为不可能事件 ∴出现7点的次数不能作为随机变量本题正确选项:A 【点睛】本题考查随机变量的定义,属于基础题.6.点P 的直角坐标为(-,则点P 的极坐标可以为( )A .2)3πB .2()3π-C .5()6π- D .5)6π 【答案】D【解析】先判断点P 的位置,然后根据公式:222,cos ,sin x y x y ρρθρθ=+==,求出ρ,根据点P 的位置,求出θ.【详解】因为点P 的直角坐标为(-,所以点P 在第二象限.tan 3ρθ===-,因为点P 在第二象限, 所以52()6k k Z θππ=+∈,故本题选D.【点睛】本题考查了点的直角坐标化为极坐标,关键是要知道点的具体位置. 7.函数()2ln f x x x =-+的图象在1x =处的切线方程为( ) A .10x y ++= B .10x y -+=C .210x y -+=D .210x y +-=【答案】A【解析】先求出切点的坐标和切线的斜率,再写出切线的方程. 【详解】当x=1时,f(1)=-2+0=-2,所以切点为(1,-2),由题得11()2,(1)211f x k f x ''=-+∴==-+=-,所以切线方程为y+2=-1·(x -1), 即:10x y ++= 故选:A 【点睛】本题主要考查导数的几何意义和切线方程的求法,意在考查学生对这些知识的理解掌握水平和分析推理能力.8.函数()()ln 2f x x x =+-的单调增区间为( ) A .()1,+∞ B .()1,2 C .(),3-∞ D .(),1-∞【答案】D【解析】先求出函数的定义域,然后求出函数的导函数,接着求当导函数大于零时,x 的取值范围,结合函数的定义域,最后写出单调增区间. 【详解】函数的定义域为{}2x x |<,()()'1ln 2()2xf x x x f x x-=+-⇒=-,当'()0f x >时,函数单调递增,所以有1022xx x->⇒>-或1x <,而函数的定义域为{}2x x |<,所以当1x <时,函数单调递增,故本题选D.【点睛】本题考查了利用导数求函数单调增区间问题,解题的关系是结合定义域,正确求解导函数大于零这个不等式.9.复数2i z =-的共轭复数在复平面内对应的点所在的象限为( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限【答案】A【解析】复数i(,)z a b a b =-∈R 的共轭复数为i z a b =+,共轭复数在复平面内对应的点为(,)a b . 【详解】复数2i z =-的共轭复数为2i z =+, 对应的点为(2,1),在第一象限.故选A. 【点睛】本题考查共轭复数的概念,复数的几何意义.10.一个口袋内装有大小相同的6个白球和2个黑球,从中取3个球,则共有( )种不同的取法 A .1262C C B .2162C CC .36CD .38C【答案】D【解析】直接由组合数定义得解。
西藏林芝市第二高级中学2020-2021学年高二下学期期末考试数学(文)试题
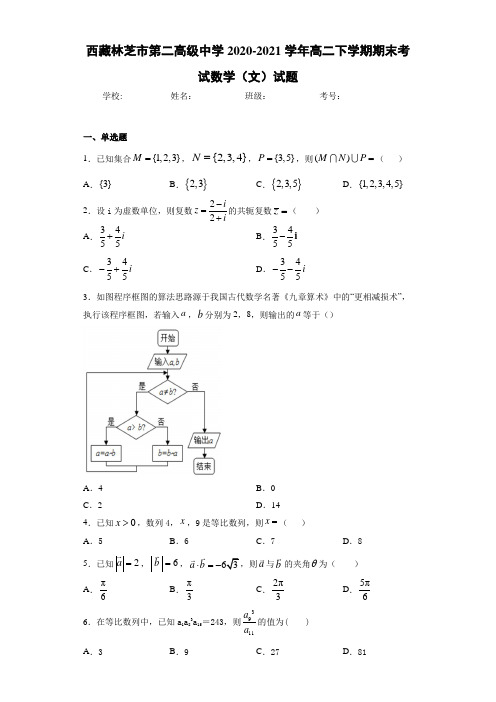
西藏林芝市第二高级中学2020-2021学年高二下学期期末考试数学(文)试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知集合{1,2,3}M =,{2,3,4}N=,{3,5}P =,则()M N P =( ) A .{3} B .{}2,3 C .{}2,3,5 D .{1,2,3,4,5} 2.设i 为虚数单位,则复数22i z i -=+的共轭复数z =( ) A .3455i + B .3455-i C .3455i -+ D .3455i -- 3.如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a ,b 分别为2,8,则输出的a 等于()A .4B .0C .2D .144.已知0x >,数列4,x ,9是等比数列,则x =( )A .5B .6C .7D .85.已知2a =,6b =,63a b ⋅=-,则a 与b 的夹角θ为( )A .π6B .π3C .2π3D .5π6 6.在等比数列中,已知a 1a 83a 15=243,则3911a a 的值为( ) A .3 B.9 C .27 D .817.命题“10,1x lnx x∀>≥-”的否定是( ) A .101x lnx x ∃≤≥-, B .101x lnx x∃≤<-, C .101x lnx x ∃>≥-, D .101x lnx x ∃><-, 8.曲线y =2sin x +cos x 在点(π,–1)处的切线方程为A .10x y --π-=B .2210x y --π-=C .2210x y +-π+=D .10x y +-π+= 9.已知等差数列{}n a 的前3项和为6,55a =,则2019a =( ) A .2017 B .2018 C .2019 D .202010.“02m <<”是“方程2212x y m m+=-表示椭圆”的( ) A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件11.已知i 是虚数单位,复数12i z i ⋅=-,则复数z 在复平面内对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限12.设椭圆C :22221(0)x y a b a b+=>>的左、右焦点分别为1F 、2F ,P 是C 上的点,2PF ⊥1F 2F ,∠12PF F =30,则C 的离心率为( )A B .13 C .12 D .3二、填空题13.已知i 为虚数单位,若复数()()12ai i ++是纯虚数,则实数a =______.14.已知直线的极坐标方程2sin()24πρθ+=_____. 15.函数()cos x f x e x =的图象在0x =处的切线斜率为_____.三、双空题16.已知向量(2,6),(,1)a b m ==-,若a b ⊥,则m =______;若//a b ,则m =__________.四、解答题17.求下列函数的导数.(1)2sin y x x =;(2)n 1l y x x=+; (3)322354y x x x =-+-.18.实数m 取什么值时,复数z =m +1+(m -1)i 是:(1)实数;(2)虚数;(3)纯虚数.19.设向量()()3sin ,sin ,cos ,sinx ,0,.2a x x b x x π⎡⎤==∈⎢⎥⎣⎦ (I )若.a b x =求的值;(II )设函数()()·,.f x a b f x =求的最大值 20.等比数列{}n a 中,15314a a a ==,. (1)求{}n a 的通项公式;(2)记n S 为{}n a 的前n 项和.若63m S =,求m .21.已知等差数列{a n }的公差不为零,a 1=25,且1a ,11a ,13a 成等比数列.(Ⅰ)求{}n a 的通项公式;(Ⅱ)求1a +a 4+a 7+…+a 3n-2.22.在平面直角坐标系xOy 中,已知直线12:(32x t l t y ⎧=-⎪⎪⎨⎪=+⎪⎩为参数).以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为4sin()3πρθ=+.(1)求曲线C 的直角坐标方程;(2)设点M 的直角坐标为(0,3),直线l 与曲线C 的交点为,A B ,求MA MB +的值.参考答案1.C【解析】【分析】求解出M N ⋂后,根据并集定义求得结果.【详解】由题意得:{}2,3M N ⋂=,则(){}2,3,5MN P = 本题正确选项:C【点睛】本题考查集合运算中的交集和并集运算,属于基础题.2.A【分析】利用复数的运算法则,分子分母同时乘以(2i)-,得出34i 55z =-,再利用共轭复数的定义即可得出.【详解】 解:22i (2i)34i 2i (2i)(2i)55z --===-++-,3455z i ∴=+ 故选A .【点睛】本题考查了复数的运算法则、共轭复数的定义.若1a z bi =+,2z c di =+,12a +c d a b d z z bi i c +=+++()()=()+(+)i , 12ac-+ad )z z bd bc i =+()(,在进行复数的除法运算时,分子分母同时应乘以分母的共轭复数.3.C【分析】根据程序框图逐步分析即可得出a 的值。
西藏自治区林芝市第二高级中学2020-2021学年高二下学期期末数学(文)试题(wd无答案)

西藏自治区林芝市第二高级中学2020-2021学年高二下学期期末数学(文)试题一、单选题(★) 1. 已知集合,,则()A.B.C.D.(★) 2. 在复平面内,复数对应的点的坐标是,则()A.B.C.D.(★) 3. 命题“ ,0”的否定为()A.,B.,C.,D.,(★) 4. 已知则()A.7B.2C.10D.12(★) 5. 函数的部分图象大致为()A.B.C.D.(★) 6. 若函数,则()A.B.C.D.(★) 7. ()A.B.C.D.(★★) 8. 若在中,角的对边分别为,则()A.或B.C.D.以上都不对(★) 9. 为了得函数的图象,只需把函数的图象()A.向左平移个单位B.向左平移单位C.向右平移个单位D.向右平移个单位(★) 10. 已知平面向量,满足,=3,与的夹角为60°,则()A.B.C.5D.3(★) 11. 椭圆的离心率为()A.B.C.D.(★★) 12. 已知函数,若,,,则()A.B.C.D.二、填空题(★) 13. 已知,则曲线在点处的切线方程是 ______ .(★) 14. 函数的最小正周期是 ______ .(★) 15. 已知向量,,若⊥ ,则 ______ .(★) 16. 为了了解家庭月收入(单位:千元)与月储蓄(单位:千元)的关系,从某居民区随机抽取10个家庭,根据测量数据的散点图可以看出与之间具有线性相关关系,其回归直线方程为,若该居民区某家庭月收入为7千元,据此估计该家庭的月储蓄为__________ 千元.三、解答题(★★) 17. 中,角所对的边分别为,已知.(1)求边的值;(2)求三角形的面积.(★) 18. 已知等差数列中,,.(1)求的通项公式;(2)若,求数列的前 n项和.(★) 19. 已知椭圆的两焦点分别为、,长轴长为6.(1)求椭圆的标准方程;(2)求以椭圆的焦点为顶点,以椭圆的顶点为焦点的双曲线的方程.(★) 20. 对哈尔滨市某高校随机抽取了100名大学生的月消费情况进行统计,并根据所得数据画出如下频率分布直方图(每个分组包括左端点,不包括右端点)(1)请根据频率直方图估计该学生月消费的中位数和平均数;(2)根据频率分布直方图,现采用分层抽样的方法,在月消费不少于3000元的两组学生中抽取4人,若从这4人中随机选取2人,求2人不在同一组的概率.(★) 21. 在直角坐标系 xOy中,曲线 C 1:( α为参数).以原点 O为极点, x轴的正半轴为极轴建立极坐标系,曲线 C 2:ρ2=4 ρcos θ-3.(1)求 C 1的普通方程和 C 2的直角坐标方程;(2)若曲线 C 1与 C 2交于 A, B两点, A, B的中点为 M,点 P(0,-1),求| PM|·| AB|的值.(★★) 22.已知函数(其中).(1)当时,求不等式的解集;(2)若关于的不等式恒成立,求的取值范围.。
西藏林芝二高2021下学期高二年级第二学段考试(期末)英语试卷

西藏林芝二高2021学年下学期高二年级第二学段考试(期末)英语试卷总分:150分考试时间:120分钟第一部分听力(共两节,满分30分)第一节(共5小题:每小题1 5分,满分7 5分)听下面5段对话,每段对话后有一个小题,从题中所给的ABC三个选项中选出最佳选项。
并标在试卷的相应位置。
听完每段对话后,你有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1 Why does the man rent a houseA For the winterB For the summerC For the sChamber Orchestra: The OrchestraSym21 Which number should you call if you want to see an omunications and trade New Yor City, for eamfortable Necessities lie food and wood were very ee Today, e and go — to see where the Canadian gold rush hafortable in my sin, and I have learnt the art of self-love And yes, I did mercial effort Scott’s last journey, communities to teach his students He was never at home in the 41 because he left around 1:00 each afternoon to start 42 and would return around 11 :00 e to mend)wonderful e and mended66 com ething“谈论关于某事”。
西藏林芝市第二高级中学2021-2022高二数学下学期期末考试试题 文(含解析)

西藏林芝市第二高级中学2021-2022高二数学下学期期末考试试题文(含解析)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:用2B 铅笔把答题卡上的对应题目的答案标号涂黑。
写在试卷、草稿纸和答题卡上的非答题区域均无效。
填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
在草稿纸和答题卡上的非答题区域均无效。
选考题的作答:先把所选题目的题号在答题卡上指定位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内。
第I 卷一、选择题:本大题12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{1,2,3}M =,{2,3,4}N =,{3,5}P =,则()MN P =( )A. {3}B. {2,3}C. {2,3,5}D.{1,2,3,4,5}【答案】C 【解析】 【分析】求解出M N ⋂后,根据并集定义求得结果. 【详解】由题意得:{}2,3M N =,则(){}2,3,5M N P =本题正确选项:C【点睛】本题考查集合运算中的交集和并集运算,属于基础题. 2.设i 为虚数单位,则复数22iz i-=+的共轭复数z =( ) A. 3455i + B. 3455-iC. 3455i -+D. 3455i --【答案】A 【解析】【分析】利用复数的运算法则,分子分母同时乘以(2i)-,得出34i 55z =-,再利用共轭复数的定义即可得出.【详解】解:22i (2i)34i 2i (2i)(2i)55z --===-++-,3455z i ∴=+ 故选A .【点睛】本题考查了复数的运算法则、共轭复数的定义.若1a z bi =+,2z c di =+,12a +c d a b d z z bi i c +=+++()()=()+(+)i , 12ac-+ad )z z bd bc i =+()(,在进行复数的除法运算时,分子分母同时应乘以分母的共轭复数.3.如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a ,b 分别为2,8,则输出的a 等于()A. 4B. 0C. 2D. 14【答案】C 【解析】 【分析】根据程序框图逐步分析即可得出a 的值. 【详解】由题a=2,b=8:a b 且a b <,则b=8-2=6;此时a=2,b=6: a b 且a b <,则b=6-2=4;此时a=2,b=4:a b 且a b <,则b=4-2=2;此时a=2,b=2:a=b ,输出a=2,故选C.【点睛】本题考查程序框图,属于基础题.4.已知0x >,数列4,x ,9是等比数列,则x =( ) A. 5 B. 6C. 7D. 8【答案】B 【解析】 【分析】根据等比中项的性质可构造方程求得结果. 【详解】由题意得:24936x =⨯= 又0x >,解得:6x = 本题正确选项:B【点睛】本题考查等比中项的应用,属于基础题.5.已知2a =,6b =,63a b ⋅=-,则a 与b 的夹角θ为( ) A.π6B.π3C.2π3D.5π6【答案】D 【解析】 【分析】根据公式||||cos a b a b θ⋅=⋅,a ,b ,a b ⋅已知,代入cos ||||a ba b θ⋅=⋅,即可解得cos θ,进而求出夹角θ. 【详解】||||cos a b a b θ⋅=⋅,∴由题得63cos 2||||a b a b θ⋅-===⋅,则56πθ=.故选D.【点睛】本题考查数量积的定义,由公式即可直接求出两个向量的夹角,属于基础题.6.在等比数列中,已知a 1a 83a 15=243,则3911a a 的值为( )A. 3B. 9C. 27D. 81【答案】B 【解析】 【分析】根据等比中项的性质求出8a ,再根据等比中项性质,化简32997119781111=a a a a a a a a a ==即可. 【详解】因为a 1a 15=a 82,所以a 85=243=35,所以a 8=3,所以32997119781111=a a a a a a a a a ===9. 【点睛】本题主要考查了等比数列中等比中项性质的灵活运用,属于中档题. 7.命题“0x ∀>,1ln 1x x≥-”的否定是 A. 00010,ln 1x x x ∃><-B. 00010,ln 1x x x ∃≤≥-C. 00010,ln 1x x x ∃>≥- D. 00010,ln 1x x x ∃≤<-【答案】A 【解析】 【分析】由全称命题的否定为特称命题,准确书写,即可求解,得到答案.【详解】由全称命题的否定为特称命题可得:命题“0x ∀>,1ln 1x x≥-”的否定是“00x ∃>,001ln 1x x <-”,故选A . 【点睛】本题主要考查了含有一个量词的否定,其中解答中熟记全称命题的否定为特称命题是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题. 8.曲线y =2sin x +cos x 在点(π,–1)处的切线方程为 A. 10x y --π-= B. 2210x y --π-= C. 2210x y +-π+= D. 10x y +-π+=【答案】C 【解析】 【分析】先判定点(,1)π-是否为切点,再利用导数几何意义求解.【详解】当x π=时,2sin cos 1y =π+π=-,即点(,1)π-在曲线2sin cos y x x =+上.2cos sin ,y x x '=-2cos sin 2,x y πππ=∴=-=-'则2sin cos y x x =+在点(,1)π-处的切线方程为(1)2()y x --=--π,即2210x y +-π+=.故选C .【点睛】本题考查利用导数工具研究曲线的切线方程,渗透了直观想象、逻辑推理和数学运算素养.采取导数法,利用函数与方程思想解题.学生易在非切点处直接求导数而出错,首先证明已知点是否为切点,若是切点,可以直接利用导数求解;若不是切点,设出切点,再求导,然后列出切线方程.9.已知等差数列{}n a 的前3项和为6,55a =,则2019a =( ) A 2021 B. 2018C. 2021D. 2021【答案】C 【解析】 【分析】根据等差数列求和公式可求得2a ,从而得到公差,利用等差数列通项公式求得结果. 【详解】等差数列{}n a 的前3项和为6,即:132********a a aa +=⨯=⨯= 22a ∴= 又55a = 5233a a d ∴-== 1d ∴=()2019220192220172019a a d ∴=+-⨯=+=本题正确选项:C【点睛】本题考查等差数列通项公式、前n 项和公式的应用问题,关键是求解出等差数列的基本量,属于基础题.10.“02m <<”是“方程2212x y m m+=-表示椭圆”的( )A. 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件【答案】C 【解析】 【分析】先求得方程2212x y m m+=-表示椭圆的m 的取值范围,再利用充分必要条件去判断可得答案.【详解】方程2212x ym m +=-表示椭圆,即020022m m m m m>⎧⎪->⇒<<⎨⎪≠-⎩且1m ≠所以“02m <<”是“方程2212x y m m+=-表示椭圆”的必要不充分条件故选C【点睛】本题考查了椭圆的概念与简易逻辑用语,易错点为椭圆中ab ,属于较为基础题.11.已知i 是虚数单位,复数12i z i ⋅=-,则复数z 在复平面内对应的点位于( ) A. 第一象限 B. 第二象限C. 第三象限D. 第四象限【答案】C 【解析】 【分析】等式两边同乘i -,得到z ,然后得到z 在复平面对应的点,得到答案. 【详解】解:复数12i z i ⋅=-,()12i i z i i ∴-⋅⋅=--,2z i =--,则复数z 在复平面内对应的点()2,1--位于第三象限. 故选C .【点睛】本题考查了复数的运算法则、几何意义,考查了推理能力与计算能力,属于简单题.12.设椭圆C :22221(0)x y a b a b+=>>的左、右焦点分别为1F 、2F ,P 是C 上的点,2PF ⊥1F 2F ,∠12PF F =30,则C 离心率为( )A.6B.13C.12【答案】D 【解析】由题意可设|PF 2|=m ,结合条件可知|PF 1|=2m ,|F 1F 2|m ,故离心率e=121222F F c a PF PF ===+选D.点睛:解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于,,a b c 的方程或不等式,再根据,,a b c 的关系消掉b 得到,a c 的关系式,而建立关于,,a b c 的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.第II 卷二、填空题:本大题4小题,每小题5分,共20分.13.已知i 为虚数单位,若复数()()12ai i ++是纯虚数,则实数a =______. 【答案】2 【解析】 【分析】利用复数的运算法则进行化简,然后再利用纯虚数的定义即可得出. 【详解】∵复数(1+ai )(2+i )=2﹣a +(1+2a )i 是纯虚数,∴20120a a -=⎧⎨+≠⎩,解得a =2. 故答案为2.【点睛】熟练掌握复数的运算法则、纯虚数的定义是解题的关键,本题属于基础题.14.已知直线的极坐标方程2sin()24πρθ+=+_____.【答案】22【解析】 【分析】先将直线的极坐标方程化为直角坐标方程,再由点到直线的距离公式即可得出结果.【详解】由2sin()24πρθ+=+sin cos 2θθ+=,2=+ 又极点的直角坐标为(0,0),所以极点到直线的距离为d ==.故答案为22【点睛】本题主要考查直线的极坐标方程与直角坐标方程的互化,熟记公式即可,属于常考题型.15.函数()cos xf x e x =的图象在0x =处的切线斜率为_____.【答案】1 【解析】 【分析】根据导数几何意义,求导后代入0x =即可得到结果. 【详解】由()cos xf x e x =得:()()cos sin cos sin x x xf x e x e x ex x '=-=-()()00cos0sin01f e '∴=-=,即所求切线斜率1本题正确结果:1【点睛】本题考查导数的几何意义,属于基础题.16.已知向量(2,6),(,1)a b m ==-,若a b ⊥,则m =______;若//a b ,则m =__________. 【答案】 (1). 3 (2). 13- 【解析】 【分析】a b ⊥时,可得出•0a b = ,进行数量积的坐标运算即可求出//m,a b 时,可得出260m --=,解出m 即可.【详解】解:若a b ⊥ ,则:260a b m =-=• ; ∴3m =;若//a b ,则:260m --=;13m ∴=-故答案为3 ; 13-【点睛】考查向量垂直的充要条件,平行向量的坐标关系,以及向量数量积的坐标运算. 三、解答题:共70分。
西藏林芝二高2021下学期高二年级第二学段考试(期末)物理试卷

西藏林芝二高2021学年下学期高二年级第二学段考试(期末)物理试卷一、选择题1.如图所示的四幅图中,分别表示磁场B,闭合电路中一部分直导线的运动速度v和电路中产生感应电流I的相互关系,其中正确的是()A. B.C. D.2.如图,O点为弹簧振子的平衡位置,小球在B、C间做无摩擦的往复运动。
在小球从B运动到O的过程中,小球的A.速度不断增大,加速度不断增大B.速度不断减小,加速度不断增大C.速度不断增大,加速度不断减小D.速度不断减小,加速度不断减小3.光在某种介质中传播的速度为×108 m/s,光从此介质射向空气并发生全反射时的临界角是A.15° B.30° C.45° D.60°4.如图所示,一正方形线圈的匝数为n,边长为a,线圈平面与匀强磁场垂直,且一半处在磁场中,在t∆时间内,磁感应强度的方向不变,大小由B均匀的增大到2B.在此过程中,线圈中产生的感应电动势为()A.22Bat∆B.22nBat∆C.2nBat∆D.22nBat∆5.如图所示的电路中,()2=102 AD.瞬时值表达式i=20sin 100πt A二、非选择题9.(5分)(1)在“用单摆测定重力加速度”的实验中,某同学用10分度的游标尺测得摆球的直径如图所示,可知摆球的直径为_____ cm.他测量摆球完成50次全振动所用的时间为90.6s,测得的摆线长078.98cml=.根据以上数据计算,得到当地的重力加速度为_____2m/s.(2)他测得的g值偏小,可能原因是:__________.A.测摆线长时摆线拉得过紧B.摆线上端末牢固地系于悬点,振动中出现松动,使摆线长度增加了C.开始计时时,秒表过迟按下D.实验中误将49次全振动计为50次10.(10分)小雨同学用图甲的实验装置“研究电磁感应现象”。
闭合开关瞬间,发现灵敏电流计的指针向左偏转了一下。
(1)闭合开关稳定后,将滑动变阻器的滑片向右滑动过程中,灵敏电流计的指针______________(填“向左偏转”、“向右偏转”或“不偏转”);(2)闭合开关稳定后,将线圈A从线圈B抽出的过程中,灵敏电流计的指针______________(填“向左偏转”、“向右偏转”或“不偏转”);(3)如图乙所示,R为光敏电阻,其阻值随着光照强度的加强而减小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西藏林芝市第二高级中学2020-2021学年高二下学期第二学段考试(期末)数学(理)试题学校:___________姓名:___________班级:___________考号:___________一、单选题 1.复数52i-的共轭复数是( ) A .i 2+B .i 2-C .2i --D .2i -2.曲线的极坐标方程4sin ρθ=化为直角坐标为( ) A .()2224x y ++= B .()2224x y +-= C .()2224x y -+= D .()2224x y ++=3.已知()sin f x x =,则()1f '=( )A .1cos13+ B .1sin1cos13-C .1sin1cos13+D .sin1cos1+4.定积分1(2)xx e dx -⎰的值为( )A .2e -B .-eC .eD .2+e5.由直线y= x - 4,曲线y =x 轴所围成的图形面积为( )A .15B .13C .252D .4036.函数()22ln f x x x =-的单调减区间是( ) A .(]0,1B .[)1,+∞ C .(](],10,1-∞-⋃D .[)(]1,00,1-⋃7.在100件产品中,有3件是次品,现从中任意抽取5件,其中至少有2件次品的取法种数为 ( ) A .23397C C B .2332397397C C +C CC .514100397C -C CD .5510097C -C8.二项式30的展开式的常数项为第( )项 A .17B .18C .19D .209.设2921101211(1)(21)(2)(2)(2)x x a a x a x a x ++=+++++++,则01211a a a a ++++的值为( )A .2-B .1-C .1D .210.设随机变量ξ服从16,2B ⎛⎫⎪⎝⎭,则(3)P ξ=的值是( ) A .516B .316 C .58D .3811.设a R ∈,函数()x x f x e ae -=-的导函数为'()f x ,且'()f x 是奇函数,则a 为( ) A .0B .1C .2D .-112.函数()322f x x ax bx a =--+在1x =处有极值10,则点(),a b 为( ) A .()3,3-B .()4,11-C .()3,3-或()4,11-D .不存在二、填空题13.有4台设备,每台正常工作的概率均为0.9,则4台中至少有3台能正常工作的概率为________.(用小数作答) 14.若复数z =,其中i 是虚数单位,则z =______.15.在一次医疗救助活动中,需要从A 医院某科室的6名男医生、4名女医生中分别抽调3名男医生、2名女医生,且男医生中唯一的主任医师必须参加,则不同的选派案共有________种.(用数字作答)16.设直线的参数方程是122(3x t t y ⎧=+⎪⎪⎨⎪=⎪⎩为参数),那么它的斜截式方程是____________.三、解答题17.实数m 取怎样的值时,复数()22153m m z i m --=-+是: (1)实数? (2)虚数? (3)纯虚数?18.已知函数3()3f x x x =-.(1)求函数()f x 在3[3,]2-上的最大值和最小值.(2)过点(2,6)P -作曲线()y f x =的切线,求此切线的方程. 19.某运动员射击一次所得环数X 的分布如下:现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为ξ. (Ⅰ)求该运动员两次都命中7环的概率. (Ⅱ)求ξ的分布列及其数学期望.20.2018年2月9~25日,第23届冬奥会在韩国平昌举行,4年后,第24届冬奥会将在中国北京和张家口举行,为了宣传冬奥会,某大学在平昌冬奥会开幕后的第二天,从全校学生中随机抽取了120名学生,对是否收看奥运会开幕式进行了问卷调查,统计数据如下:(1)根据上表说明,能否有99%的把握认为,收看开幕式与性别有关?(2)现从参与收看了开幕式的学生中,采用分层抽样的方法选取8人,参加2022年北京冬奥会志愿者宣传活动. ①问男、女学生各选取多少人?②若从这8人中随机选取2人到校广播站宣传冬奥会,求恰好选到一名男生为主播一名女生为副播的概率P .附:22()()()()()n ad bc k a b c d a c b d -=++++,其中n a b c d =+++.21.已知函数()()()2ln 1f x x ax a x a R =---∈.(1)当1a =时,求函数()f x 的最小值; (2)求函数()f x 的单调区间.22.在平面直角坐标系中,曲线2212:C x y -=,曲线2C 的参数方程为22cos 2sin x y θθ=+⎧⎨=⎩(θ为参数).以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系. (1)求曲线1C 、2C 的极坐标方程;(2)在极坐标系中,射线..6πθ=与曲线1C ,2C 分别交于A 、B 两点(异于极点O ),定点(3,0)M ,求MAB ∆的面积23.设不等式2|1||2|0x x -<--+<的解集为M ,a ,b M ∈. (1)证明:111364a b +<; (2)比较|14|ab -与2||a b -的大小,请说明理由.参考答案1.D 【解析】55(2)22(2)(2)i i i i i +==+--+,2i +的共轭复数为2i -,选D. 2.B 【分析】利用直角坐标与极坐标的互化公式222cos sin x y x y ρρθρθ⎧+=⎪=⎨⎪=⎩,即可得到答案.【详解】由曲线的极坐标方程4sin ρθ=,两边同乘ρ,可得24sin ρρθ=,再由222cos sin x y x y ρρθρθ⎧+=⎪=⎨⎪=⎩,可得:22224(2)4x y y x y +=⇔+-=,所以曲线的极坐标方程4sin ρθ=化为直角坐标为()2224x y +-= 故答案选B 【点睛】本题考查把极坐标转化为直角坐标方程的方法,熟练掌握直角坐标与极坐标的互化公式222cos sin x y x y ρρθρθ⎧+=⎪=⎨⎪=⎩是解题的关键,属于基础题. 3.C 【分析】首先根据题意得到()21331sin cos 3f x x x x x -'=⋅+⋅,再计算()1f '即可. 【详解】因为13()sin f x x x =⋅,所以()21331sin cos 3f x x x x x -'=⋅+⋅.所以()11sin1cos13f =+'.故选:C 【点睛】本题主要考查求导公式,熟记公式为解题关键,属于简单题. 4.A 【解析】定积分1201(2)()(1)(01)20x x x e dx x e e e -=-=---=-⎰. 故选A. 5.D 【详解】根据题意,画出如图所示:由直线4y x =-,,曲线y =x轴所围成的面积为:42881404)4)423x dx x x +⎰+=+-+=.故选D. 6.A 【分析】依题意,可求得()f x ',由()0f x '<即可求得函数2()2f x x lnx =-的单调减区间. 【详解】 解:2()2(0)f x x lnx x =->,22(1)(1)()2x x f x x x x+-∴'=-=,令()0f x '<由图得:01x <<,∴函数2()2f x x lnx =-的单调减区间是(0,1),故选:A . 【点睛】本题考查利用导数研究函数的单调性,考查解不等式的能力,属于基础题. 7.B 【解析】试题分析:恰好有2件次品时,取法为23397C C ⋅,恰好有3件次品时,取法为32397C C ⋅,所以总数为23397C C ⋅32397C C +⋅.考点:排列组合. 8.C 【解析】试题分析:由二项式定理可知,展开式的常数项是使的项,解得为第19项,答案选C.考点:二项式定理 9.A 【分析】根据题中条件,直接令1x =-代入,即可得出结果. 【详解】令1x =-,代入2921101211(1)(21)(2)(2)(2)x x a a x a x a x ++=+++++++可得,9012112(1)a a a a ⨯-=++++,则012112a a a a ++++=-.故选:A. 【点睛】本题主要考查二项式定理的应用,根据赋值法求解即可,属于基础题型. 10.A根据二项分布公式,计算概率. 【详解】16,2B ξ⎛⎫ ⎪⎝⎭, ()636153216P C ξ⎛⎫∴==⋅= ⎪⎝⎭.故选:A 【点睛】本题考查二项分布,属于基础题型. 11.D 【解析】∵函数()xxf x e ae -=-∴()x xf x e ae-'=+∵()'f x 是奇函数 ∴(0)0f '=,即10a +=. ∴1a =- 故选D.点睛:正确理解奇函数和偶函数的定义,必须把握好两个问题:(1)定义域关于原点对称是函数()f x 为奇函数或偶函数必要不充分条件;(2)()()f x f x -=-或()()f x f x -=是定义域上的恒等式. 12.B 【详解】试题分析:2'()32f x x ax b =++,则()()110{10f f ='=,2110{320a b a a b +++=++=解得4{11a b ==-或3{3a b =-=,当3,3a b =-=时,22'()3633(2)0f x x x x =-+=-≥,此时()f x 在定义域R 上为增函数,无极值,舍去.当4,11a b ==-,2'()3811f x x x =--,1x =为极小值点,符合,考点:1.用导数研究函数的极值;2.函数在某一点取极值的条件. 【易错点睛】本题主要考查用导数研究函数的极值问题,要求掌握可导函数取得有极值的条件,'()0f x =是函数取得极值的必要不充分条件.求解之后要注意检验,本题中,当3,3a b =-=时,'()0f x ≥,此时()f x 在定义域R 上为增函数,无极值,不符合题意,舍去.本题容易错选A ,认为两组解都符合,一定要注意检验. 13.0.9477 【分析】根据独立重复试验的概率计算公式,由题中条件,可直接得出结果. 【详解】因为有4台设备,每台正常工作的概率均为0.9,则4台中至少有3台能正常工作的概率为()()()34340.910.90.90.9477P C =⋅⋅-+=;故答案为:0.9477 【点睛】本题主要考查求独立重复试验的概率,属于基础题型. 14.1 【分析】先利用复数的除法算出z 后再求其模. 【详解】()21142z ===,故1z ==,故填1. 【点睛】本题考察复数的除法及复数的概念(模),属于基础题. 15.60 【分析】首先选派男医生中唯一的主任医师,由题意利用排列组合公式即可确定不同的选派案方法种数.首先选派男医生中唯一的主任医师,然后从5名男医生、4名女医生中分别抽调2名男医生、2名女医生,故选派的方法为:225410660C C =⨯=.故答案为60. 【点睛】解排列组合问题要遵循两个原则:一是按元素(或位置)的性质进行分类;二是按事情发生的过程进行分步.具体地说,解排列组合问题常以元素(或位置)为主体,即先满足特殊元素(或位置),再考虑其他元素(或位置).16.3y =+-【分析】将直线的参数方程互为普通方程,再根据直线方程的形式,得到直线的斜截式方程,得到答案. 【详解】由122x t =+,可得122t x =-,代入可得32)y x =+-,整理得3y =+-3y =+-【点睛】本题主要考查了直线参数与普通方程的互化,以及直线方程的形式,其中解答中熟记参数方程与普通方程的互化公式和直线方程的形式是解答的关键,着重考查了运算与求解能力,属于基础题.17.(1)5m =或3m =-;(2)5m ≠且3m ≠-;(3)3m =. 【分析】根据实部和虚部的不同取值决定何时是实数、虚数和纯虚数. 【详解】(1)若22150m m --=,则z 为实数,此时3m =-或者5m =. (2)若22150m m --≠,则z 为虚数,此时3m ≠-且5m ≠.(3)若2302150m m m -=⎧⎨--≠⎩ ,则z 为纯虚数,此时3m =.【点睛】对于复数,,z a bi a b R =+∈,(1)若0b =,则z 为实数;(2)若0b ≠,则z 为虚数,特别地,如果0,0a b =≠,则z 为纯虚数,解题中注意合理分类.18.(1)min ()18f x =-,max ()2f x =;(2)30x y +=或24540x y --=. 【分析】(1)求出导数,根据导数求出函数的单调区间,即可求出函数的最值;(2)设切点为3000(,3)Q x x x -,表示出切线方程,代入点(2,6)P -,求出0x ,即可得出切线方程. 【详解】(1)'()3(1)(1)f x x x =+-,当[3,1)x ∈--或3(1,]2x ∈时,'()0f x >,∴[3,1]--,31,2⎡⎤⎢⎥⎣⎦为函数()f x 的单调增区间当(1,1)x ∈-时,'()0f x <,∴[1,1]-为函数()f x 的单调减区间 又因为(3)18f -=-,(1)2f -=,(1)2f =-,39()28f =-所以当3x =-时,min ()18f x =-,当1x =-时,max ()2f x =(2)设切点为3000(,3)Q x x x -,则切线斜率()200()31k f x x '==-, 则所求切线方程为320000(3)3(1)()y x x x x x --=--,由于切线过点(2,6)P -,∴3200006(3)3(1)(2)x x x x ---=--,解得00x =或03x =所以切线方程为3y x =-或624(2)y x +=-, 即30x y +=或24540x y --=. 【点睛】本题考查利用导数求函数最值,考查利用导数求切线方程,属于中档题. 19.(I) 0.04(II)(III) 9.07 【解析】本试题主要考查了独立事件概率的乘法公式好分布列的求解,以及期望公式的的综合运用. (1)中,利用两次都命中事件同时发生的概率乘法公式得到(2)中,因为由题意可知ξ可能取值为7、8、9、10,那么分别得到各个取值的概率值,得到分布列.(3)利用期望公式求解期望值.解:(I )由题意知运动员两次射击是相互独立的,根据相互独立事件同时发生的概率得到,该运动员两次都命中7环的概率为P=0.2×0.2=0.04 (II )ξ可能取值为7、8、9、10P (ξ=7)=0.04 P (ξ=8)=2×0.2×0.3+0.32=0.21 P (ξ=9)=2×0.2×0.3+2×0.3×0.3+0.32=0.39P (ξ=10)=2×0.2×0.2+2×0.3×0.2+2×0.3×0.2+0.22=0.36 ∴ξ的分布列为∴ξ的数学期望为Eξ=7×0.04+8×0.21+9×0.39+10×0.36=9.07 20.(1)有99%的把握;(2)①男生6人,女生2人;②37. 【分析】(1)列出22 列联表,求出2k 的值,根据附表可得答案;(2)①根据分层抽样的方法可得,男、女学生各选取的人数;②从这8人中随机选取2人,共有28C 种不同的选法,其中恰好选到一名男生为主播一名女生为副播共有1162C C 种不同的选法,根据古典概型的概率计算公式可得概率.【详解】(1)22⨯列联表:()22120602020207.5 6.63580408040k ⨯⨯-⨯==>⨯⨯⨯,∴有99%的把握认为,收看开幕式与性别有关.(2)①根据分层抽样的方法可得, 男生抽取:860=680⨯(人),女生抽取:820=280⨯(人). ∴选取的8人中,男生6人,女生2人.②从这8人中随机选取2人,共有2828C =种不同的选法;其中恰好选到一名男生为主播一名女生为副播共有116212C C =种不同的选法.根据古典概型的概率计算公式可得,恰好选到一名男生为主播一名女生为副播的概率123287P ==. 【点睛】本题考查独立性检验、分层抽样和古典概型,属于中档题. 21.(1)3ln 24+;(2)答案见解析. 【分析】(1)首先利用导数求出函数的单调区间,再根据单调区间即可得到函数()f x 的最小值.(2)首先求导得到()()2221a x x x f x +-'-=,再分类讨论a 的范围即可得到函数()f x 的单调区间 【详解】(1)函数2()ln(1)()f x x ax a x a R =---∈的定义域是()1,+∞.当1a =时,2()ln(1)f x x x x =---()()13222111f x x x x x x '=----=-,31,2x ⎛⎫∈ ⎪⎝⎭,()0f x '<,()f x 为减函数,3,2x ⎛⎫∈+∞ ⎪⎝⎭,()0f x '>,()f x 为增函数. 所以函数()f x 的最小值为()()()233333ln 1ln 222224f =---=+. (2)()()212221af x x a x a x x x +-='----=, 令()0f x '=,解得10x =,222a x +=.①若0a ≤时,则212a +≤,()0f x '>在()1,+∞恒成立, 所以()f x 的增区间为()1,+∞. ②若0a >,则212a +>, 故当()21,2a x +∈,()0f x '<;当2,2a x +⎛⎫∈+∞⎪⎝⎭时,()0f x >. 所以当0a >时,()f x 的减区间为()21,2a +,()f x 的增区间为()2,2a ++∞.【点睛】本题第一问考查利用导数求函数的最值,第二问考查利用导数研究含参单调区间,属于中档题.22.(1)22221:cos sin 2C ρθρθ-=,2:4cos C ρθ=;(2. 【分析】(1)先把参数方程化成普通方程,再利用极坐标的公式把普通方程化成极坐标方程; (2)先利用极坐标求出弦长AB ,再求高,最后求MAB ∆的面积. 【详解】(1)曲线1C 的极坐标方程为:2222cos sin 2ρθρθ-= ,因为曲线2C 的普通方程为:()2224x y -+= ,2240.x y x ∴+-=∴曲线2C 的极坐标方程为4cos ρθ=;(2) 由(1)得:点A 的极坐标为2,6π⎛⎫⎪⎝⎭, 点B的极坐标为6π⎛⎫⎪⎝⎭,∴22AB =-=,()3,0M 点到射线()06πθρ=≥的距离为33sin62d π==∴MAB ∆的面积为()113322222AB d ⋅=⨯⨯=.【点睛】本题考查普通方程、参数方程与极坐标方程之间的互化,同时也考查了利用极坐标方程求解面积问题,考查计算能力,属于中等题.23.(1)证明见解析;(2)|14|2||ab a b ->-,证明见解析. 【分析】(1)首先设()3,21221,213,1x f x x x x x x ≤-⎧⎪=--+=---<<⎨⎪-≥⎩,利用绝对值不等式的解法得到11,22M ⎛⎫=- ⎪⎝⎭,再利用绝对值三角不等式即可证明111364a b +<.(2)首先根据题意得到214a <,214b <,再计算22|14|4||ab a b ---,即可得到答案. 【详解】(1)记()3,21221,213,1x f x x x x x x ≤-⎧⎪=--+=---<<⎨⎪-≥⎩由2210x -<--<,解得1122x -<<,则11,22M ⎛⎫=- ⎪⎝⎭. 所以111111111||||363632624a b a b +≤+<⨯+⨯=.(2)由(1)得214a <,214b <. 因为()()222222|14|4||181642ab a b ab a baab b ---=-+--+()()2241410a b =-->,所以22|14|4||ab a b ->-,故|14|2||ab a b ->-. 【点睛】本题第一问考查绝对值不等式的解法,同时考查了绝对值三角不等式,第二问考查绝对值不等式的证明,属于中档题.。
