人教版七年级下册数学几何作图(习题及答案)
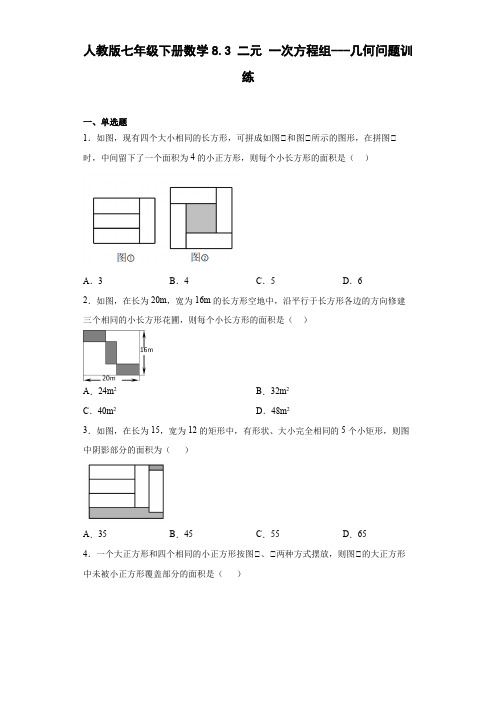
人教版七年级数学下册第五章相交线与平行线:几何计算和证明综合练习试题(含答案)

人教版七年级数学下册第五章相交线与平行线:几何计算和证明综合练习试题1、如图,已知∠2=∠3,∠C=∠D,求证:∠A=∠F.证明:∵∠2=∠3,∠1=∠2,∴∠1=∠3.∴DB∥CE.∴∠DBA=∠C.∵∠D=∠C,∴∠D=∠DBA.∴DF∥AC.∴∠A=∠F.2、如图,已知EF∥AD,∠1=∠2,∠BAC=80°,求∠AGD的度数.解:∵EF∥AD,∴∠2=∠3(两直线平行,同位角相等).∵∠1=∠2,∴∠1=∠3(等量代换).∴AB∥DG(内错角相等,两直线平行).∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).3、如图,∠1=115°,∠2=50°,∠3=65°,EG为∠NEF的平分线.求证:AB∥CD,EG∥FH.证明:∵∠1=115°,∴∠FCD=180°-∠1=180°-115°=65°.∵∠3=65°,∴∠FCD=∠3.∴AB∥CD.∵∠2=50°,∴∠NEF=180°-∠2=180°-50°=130°.∵EG为∠NEF的平分线,∴∠GEF=12∠NEF=65°.∴∠GEF=∠3.∴EG∥FH.4、如图,已知∠B=∠D,∠E=∠F,判断BC与AD的位置关系,并说明理由.解:BC∥AD,理由:∴BE∥FD.∴∠B=∠BCF.又∵∠B=∠D,∴∠BCF=∠D.∴BC∥AD.5、如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1.求证:AD平分∠BAC.证明:∵AD⊥BC,EG⊥BC,∴∠ADC=∠EGC=90°.∴AD∥EG.∴∠1=∠2,∠E=∠3.∵∠E=∠1,∴∠2=∠3.∴AD平分∠BAC.6、如图,B,C,E三点在一条直线上,A,F,E三点在一条直线上,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE.证明:∵AB∥CD,∴∠4=∠BAE.∴∠3=∠BAE.∵∠1=∠2,∴∠1+∠CAF=∠2+∠CAF,即∠BAE=∠CAD.∴∠3=∠CAD.∴AD∥BE.7、如图,已知AB∥CD,试判断∠B,∠BED和∠D之间的关系,并说明理由.解:∠BED=∠B+∠D.理由如下:过点E作EF∥AB,则∠B=∠BEF.∵AB∥CD,∴EF∥CD.∴∠DEF=∠D.∵∠BED=∠BEF+∠DEF,∴∠BED=∠B+∠D.8、如图,∠AEF+∠CFE=180°,∠1=∠2,EG与HF平行吗?为什么?解:平行.理由:∵∠AEF+∠CFE=180°,∴AB∥CD.∴∠AEF=∠EFD.∴∠AEF -∠1=∠EFD -∠2,即∠GEF =∠HFE.∴EG ∥HF.9、如图,A ,B ,C 三点在同一直线上,∠1=∠2,∠3=∠D ,试判断BD 与CF 的位置关系,并说明理由.解:BD ∥CF.理由如下:∵∠1=∠2,∴AD ∥BF.∴∠D =∠DBF.∵∠3=∠D ,∴∠3=∠DBF.∴BD ∥CF.10、如图,∠ABC =∠ADC ,BF ,DE 分别是∠ABC ,∠ADC 的平分线,∠1=∠2,试说明:DC ∥AB.解:∵BF ,DE 分别是∠ABC ,∠ADC 的平分线,∴∠3=12∠ADC ,∠2=12∠ABC. ∵∠ABC =∠ADC ,∴∠3=∠2.∵∠1=∠2,∴∠1=∠3.∴DC∥AB.11、如图,AD平分∠BAC,AD⊥BC于D,点E,A,C共线,∠DAC=∠EFA,延长EF 交BC于点G.求证:EG⊥BC.证明:∵AD平分∠BAC,∴∠DAC=∠DAB.又∵∠DAC=∠EFA,∴∠DAB=∠EFA.∴AD∥EG.∴∠ADC=∠EGD.∵AD⊥BC,∴∠ADC=90°.∴∠EGD=90°.∴EG⊥BC.12、已知AB∥CD,点E为AB,CD之外任意一点.(1)如图1,探究∠BED与∠B,∠D的数量关系,并说明理由;(2)如图2,探究∠CDE与∠B,∠BED的数量关系,并说明理由.解:(1)∠B=∠BED+∠D.理由如下:过点E作EF∥AB.又∵AB∥CD,∴EF∥AB∥CD.∴∠BEF=∠B,∠D=∠DEF.∵∠BEF=∠BED+∠DEF,∴∠B=∠BED+∠D.(2)∠CDE=∠B+∠BED.理由如下:过点E作EF∥AB.又∵AB∥CD,∴EF∥AB∥CD.∴∠B+∠BEF=180°,∠CDE+∠DEF=180°.又∵∠DEF=∠BEF-∠BED,∴∠CDE+∠BEF-∠BED=∠B+∠BEF,即∠CDE=∠B+∠BED.13、如图,把一张长方形纸片ABCD沿EF折叠后,D,C分别落在D′和C′的位置上,ED′与BC的交点为G.若∠EFG=50°,求∠1,∠2,∠3的度数.解:根据折叠的性质可知,∠DEF=∠D′EF,∠EFC=∠EFC′.∵∠EFG=50°,∴∠EFC=180°-50°=130°.∴∠EFC′=∠EFC=130°.∴∠3=∠EFC′-∠EFG=130°-50°=80°.∵AD∥BC,∴∠DEF=∠EFG=50°.∴∠DED′=2∠DEF=100°.∴∠1=180°-∠DED′=180°-100°=80°.∵AD∥BC,∴∠1+∠2=180°.∴∠2=180°-∠1=100°.故∠1=80°,∠2=100°,∠3=80°.14、如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.(1)求证:AB∥CD;(2)求∠C的度数.解:(1)证明:∵AE⊥BC,FG⊥BC,∴AE∥GF.∴∠2=∠A.∵∠1=∠2,∴∠1=∠A.∴AB∥CD.(2)∵AB∥CD,∴∠D+∠CBD+∠3=180°.∵∠D =∠3+60°,∠CBD =70°,∴∠3=25°.∵AB ∥CD ,∴∠C =∠3=25°.15、(1)如图1,AB ∥CD ,则∠E +∠G 与∠B +∠F +∠D 有何关系?(2)如图2,若AB ∥CD ,又能得到什么结论?请直接写出结论.解:(1)过点E 作EM ∥AB ,过点F 作FN ∥AB ,过点G 作GH ∥CD. ∵AB ∥CD ,∴AB ∥EM ∥FN ∥GH ∥CD.∴∠1=∠B ,∠2=∠3,∠4=∠5,∠6=∠D.∴∠1+∠2+∠5+∠6=∠B +∠3+∠4+∠D ,即∠BEF +∠FGD =∠B +∠EFG +∠D.(2)∠B +∠F 1+∠F 2+…+∠F n -1+∠D =∠E 1+∠E 2+…+∠E n .16、已知E ,F 分别是AB ,CD 上的动点,P 也为一动点.(1)如图1,若AB ∥CD ,求证:∠P =∠BEP +∠PFD ;(2)如图2,若∠P =∠PFD -∠BEP ,求证:AB ∥CD ;(3)如图3,AB ∥CD ,移动E ,F ,使∠EPF =90°,作∠PEG =∠BEP ,则∠AEG∠PFD =2.证明:(1)过点P作PG∥AB,则∠EPG=∠BEP.∵AB∥CD,∴PG∥CD.∴∠GPF=∠PFD.∴∠EPF=∠EPG+∠FPG=∠BEP+∠PFD.(2)过点P作PQ∥AB,则∠QPE=∠BEP.∵∠EPF=∠PFD-∠BEP,∴∠PFD=∠EPF+∠BEP=∠EPF+∠QPE=∠FPQ. ∴DC∥PQ.∴AB∥CD.。
5.1.2 垂线 人教版七年级数学下册分层作业(含答案)

第五章相交线与平行线5.1.2 垂线分层作业1.如图,图中直角的个数有()A.个B.个C.个D.个【答案】D【分析】根据直角的定义进行求解即可.【详解】解:由题意得,图中的直角有一共五个,故选D.【点睛】本题主要考查了垂线的定义,熟知垂线的定义是解题的关键.2.如图,,,若,则的度数是()A.B.C.D.【答案】C【分析】先求出,即可求出.【详解】解:,,.,.故选:C.【点睛】本题主要考查直角的概念以及角度的计算,比较简单.3.如图,在纸片上有一直线l,点A在直线l上,过点A作直线l的垂线、嘉嘉使用了量角器,过90°刻度线的直线a即为所求;淇淇过点A将纸片折叠,使得以A为端点的两条射线重合,折痕a即为所求,下列判断正确的是()A.只有嘉嘉对B.只有淇淇对C.两人都对D.两人都不对【答案】C【分析】根据垂直的定义即可解答.【详解】解:嘉嘉利用量角器画90°角,可以画垂线,方法正确;淇淇过点A将纸片折叠,使得以A为端点的两条射线重合,折痕a垂直直线l,方法正确,故选:C.【点睛】本题主要考查了作图、垂线的定义,掌握垂直的定义是解答本题的关键.4.如图,直线,相交于点,,平分,若,则的度数为()A.B.C.D.【答案】C【分析】根据垂直定义得到∠AOF+∠BOD=,求出∠AOF的度数,利用角平分线的定义求出∠EOF即可.【详解】解:∵∠DOF=,∴∠AOF+∠BOD=,∵∠BOD=,∴∠AOF=,∵OF平分∠AOE,∴∠EOF=∠AOF=,故选:C.【点睛】此题考查了垂直的定义,几何图形中角度的计算,正确理解图形中各角度的关系是解题的关键.5.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )A.35°B.45°C.55°D.65°【答案】C【分析】根据角平分线的定义,得出∠MOC=35°,再根据题意,得出∠MON=90°,然后再根据角的关系,计算即可得出∠CON的度数.【详解】解:∵射线OM平分∠AOC,∠AOM=35°,∴∠MOC=35°,∵ON⊥OM,∴∠MON=90°,∴∠CON=∠MON﹣∠MOC=90°﹣35°=55°.故选:C【点睛】本题主要考查了角平分线的定义和垂线的定义,解决本题的关键在正确找出角的关系.6.如图,为了解决村民饮水困难,需要在河边建立取水点,下面四个点中哪个最方便作为取水点()A.A点B.B点C.C点D.D点【答案】B【分析】根据“垂线段最短”可得结论.【详解】解:根据“垂线段最短”可知要在河边建立取水点,点B作为取水点最方便,故选:B【点睛】此题主要考查了垂线段最短,正确掌握垂线段的性质是解题关键.7.如图,,垂足是点,,,,点是线段上的一个动点包括端点,连接,那么的长为整数值的线段有()A.条B.条C.条D.条【答案】D【分析】根据垂线段最短解答即可.【详解】解:∵,,,,且点是线段上的一个动点包括端点,∴长的范围是,∴的长为整数值的线段有、、、,,共条,故选:D.【点睛】本题考查垂线段最短.理解和掌握垂线段最短是解题的关键.8.如图,直线AB,CD相交于点O,EO⊥CD,垂足为O,若∠1=50°,则∠2的度数为()A.B.C.D.【答案】B【分析】应用垂线性质可得∠EOD=90°,由∠1+∠BOD=90°,即可算出∠BOD的度数,再根据对顶角的性质即可得出答案.【详解】解:∵EO⊥CD,∴∠EOD=90°,∵∠1+∠BOD=90°,∴∠BOD=∠EOD-∠1=90°-50°=40°,∴∠2=∠BOD=40°.故选:B.【点睛】本题主要考查了垂线及对顶角,熟练掌握垂线及对顶角的性质进行求解是解决本题的关键.9.已知,与的度数之比为,则等于___.【答案】或【分析】根据垂直定义知,由,可求,根据与的位置关系,分类求解.【详解】解:,,,即∠AOB:90°=3:5,.分两种情况:①当OB在内时,如图,∴;②当OB在外时,如图,∴.故答案是:或.【点睛】本题考查垂直定义,角的和差运算,解题的关键是利用分类讨论的思想进行求解.10.如图,点,在直线上,且,的面积为.若是直线上任意一点,连接AP,则线段AP的最小长度为_____cm.【答案】8【分析】根据点到直线的垂线段最短,再由面积求出高,即为AP的最小值,由题知,过点A作BC的垂线,即为所求,此时,该垂线也是三角形的高.【详解】解:过点A作BC的垂线AP,根据点到直线的所有线段中,垂线段最短,∴垂线段即为AP的最小值,∵BC=5cm,ΔABC的面积为20,∴,∴AP=8,故答案为:8.【点睛】本题考查三角形的面积公式,垂线段最短的性质,属于基础题.11.已知的两边与的两边分别垂直,且比的倍少,则______【答案】80°或92°【分析】因为两个角的两边分别垂直,则这两个角相等或互补,又因∠A比∠B的倍少40°,设∠B是x 度,利用方程即可解决问题.【详解】解:设∠B是x度,根据题意,得①两个角相等时,如图1:∠B=∠A=x°,x=x-40,解得,x=80,故∠A=80°,②两个角互补时,如图2:x+x-40=180,所以x=88,×88°-40°=92°综上所述:∠A的度数为:80°或92°.故答案为:80°或92°.【点睛】本题考查垂线,本题需仔细分析题意,利用方程即可解决问题.关键是得到∠A与∠B的关系.12.如图,直线AB,CD相交于点O,若,且,则的度数是______.【答案】54°##54度【分析】设,则,可得,再由,可得,可求出x,即可求解.【详解】解:设,则,∴,∵,∴∠AOE=∠BOE=90°,∴,即,∴.故答案为:54°【点睛】本题主要考查了垂直的性质,对顶角的性质,熟练掌握垂直的性质,对顶角的性质进行求解是解决本题的关键.13.如图,直线与直线相交于点,,垂足为,,则的度数为______.【答案】60°##60度【分析】根据对顶角相等可得,由,可得,由,即可求解.【详解】解:∵,∴,∵,,,解得.故答案为:60°.【点睛】本题考查了垂直的定义,对顶角相等,几何图形角度的计算,数形结合是解题的关键.14.如图,点P是直线l外一点,过点P作于点O,点A是直线l上任意一点,连接,若,则的长可能是___________(写出一个即可).【答案】4【分析】直接利用垂线段最短即可得出答案.【详解】解∶∵点P是直线l外一点,过点P作于点O,点A是直线l上任意一点,∴3≤AP,∴PA可以为4,故答案为4(答案不唯一).【点睛】此题主要考查了垂线段最短,正确得出A P的取值范围是解题的关键.15.如图,直线和相交于点,,,,求的度数.【答案】【分析】根据,得出,根据,可得,根据角的倍分关系,可得∠的度数,根据是邻补角,可得答案.【详解】解:∵,∴,∵,∴,∵,∴,∴,∵,∴.∴.【点睛】本题考查垂直的性质、角的和差、角的倍分关系、邻补角的性质等知识,是基础考点,掌握相关知识是解题关键.16.如图,是直线上一点,,平分(1)求的度数.(2)试猜想与的位置关系,并说明理由.【答案】(1)的度数为(2)OD⊥AB,理由见解析【分析】(1)设=x,根据题意得,再根据平角的定义进而求解即可;(2)根据角平分线的定义即可得到解答.【详解】(1)解:设=x,∵,∴,∵直线,∴x+3x=180°,解得,∴的度数为;(2)解:OD⊥AB,理由如下,∵OC平分∠AOD,∴∠COD=∠AOC=45°.∴∠AOD=∠AOC+∠COD=90°,∴OD⊥AB.【点睛】此题考查了垂线,平角的定义以及角平分线的定义,对定义的熟练掌握是解题的关键.平角:等于180°的角叫做平角;角平分线:从一个角的顶点引出一条射线,把这个角分成两个完全相同的角,这条射线叫做这个角的角平分线.17.如图,两直线、相交于点,平分,如果::.(1)求;(2)若,,求.【答案】(1)145°(2)125°【分析】(1)根据邻补角的性质和已知求出和的度数,根据对顶角相等求出和的度数,根据角平分线的定义求出的度数,可以得到的度数;(2)根据垂直的定义得到,根据互余的性质求出的度数,计算得到答案.(1)解:,::,,,,,平分,,.(2)解:,,平分,,,.【点睛】本题考查的是邻补角的性质、对顶角的性质和角平分线的定义,掌握邻补角互补、对顶角相等和垂直的定义是解题的关键.18.如图,已知直线AB、CD相交于点O,OE⊥AB,点O为垂足,OF平分∠AOC.(1)若∠COE=54°,求∠DOF的度数;(2)若∠COE∶∠EOF=2∶1,求∠DOF的度数.【答案】(1)∠DOF=108°;(2)∠DOF=112.5°.【分析】(1)先由OE⊥AB得出∠AOE=∠BOE=90°,再根据角平分线定义求出∠COF=72°,然后由∠DOF=180°-∠COF即可求解;(2)设∠EOF=x°,则∠COE=2x°,则∠COF=3x°,再根据角平分线定义求出∠AOF=∠COF=3x°,所以∠AOE=4x°,由垂直的定义可知∠AOE=90°,则4x=90,解之,求出x即可.(1)解:∵OE⊥AB,∴∠AOE=90°;∵∠COE=54°,∴∠AOC=∠AOE+∠COE=144°,∵OF平分∠AOC,∴∠COF=∠AOC=72°,∴∠DOF=180°-∠COF=108°;(2)解:设∠EOF=x°,则∠COE=2x°,∴∠COF=3x°,∵OF平分∠AOC,∴∠AOF=∠COF=3x°,∴∠AOE=4x°,∵OE⊥AB,∴∠AOE=90°,∴4x=90,解得x=22.5,∴∠COF=3x°=67.5°,∴∠DOF=180°-∠COF=112.5°.【点睛】本题考查了角的计算,根据垂直的定义、角的和差关系列方程进行求解,即可计算出答案,难度适中.1.如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD,∠AOE=24°,∠COF的度数是()A.146°B.147°C.157°D.136°【答案】B【分析】欲求∠COF,需求∠DOF.由OE⊥CD,得∠EOD=90°,故求得∠BOD=66°.由OF平分∠BOD,故∠DOF==33°.【详解】解:∵OE⊥CD,∴∠EOD=90°.∴∠BOD=180°﹣∠AOE﹣∠DOE=66°.又∵OF平分∠BOD,∴∠DOF==33°.∴∠COF=180°﹣∠DOF=180°﹣33°=147°.故选:B.【点睛】本题主要考查垂直的定义、角平分线的定义以及邻补角的性质,熟练掌握垂直的定义、角平分线的定义以及邻补角的性质是解决本题的关键.2.如图,,,平分,则的度数为()A.45°B.46°C.50°D.60°【答案】A【分析】先根据垂直的定义得,由已知,相当于把四等分,可得的度数,根据角平分线可得,从而得结论.【详解】解:,,,,,平分,,.故选:.【点睛】本题考查了角平分线的定义,垂直的定义及有关角的计算,解题的关键是确定.3.如图所示,直线AB,CD相交于点O,于点O,OF平分,,则下列结论中不正确的是()A.B.C.与互为补角D.的余角等于【答案】D【分析】根据垂直的定义及角平分线的性质判断A,利用对顶角的性质判断B,利用邻补角的性质判断C,根据余角的定义判断D.【详解】∵于点O,∴∠AOE=,∵OF平分,∴∠2=,故A正确;∵直线AB,CD相交于点O,∴∠1与∠3是对顶角,∴∠1=∠3,故B正确,∵,∴与互为补角,故C正确;∵,∴的余角=,故D错误,故选:D.【点睛】此题考查垂直的定义,角平分线的性质,对顶角的性质,余角的定理,邻补角的性质,几何图形中角度的计算,熟记各定义及性质是解题的关键.4.已知点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离为()A.4 cm B.5 cm C.小于2 cm D.不大于2 cm【答案】D【分析】根据点到直线的距离是直线外的点与直线上垂足间的线段的长,再根据垂线段最短,可得答案.【详解】当PC⊥m时,PC是点P到直线m的距离,即点P到直线m的距离2cm,当PC不垂直直线m时,点P到直线m的距离小于PC的长,即点P到直线m的距离小于2cm,综上所述:点P到直线m的距离不大于2cm,故选D.【点睛】此题考查了点到直线的距离,利用了垂线段最短的性质.5.如图,若直线与相交于点,平分,且,则的度数为()A.B.C.D.【答案】C【分析】根据角平分线的定义得到,根据垂线的定义得到,利用邻补角的定义即可求解.【详解】解:∵,平分,∴,∵,∴,∴,故答案为:C.【点睛】本题考查邻补角的定义、角平分线的定义、垂直的定义等内容,运用几何知识进行角的和差运算是解题的关键.6.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠CON=55°,则∠AOM的度数为()A.35°B.45°C.55°D.25°【答案】A【分析】根据垂直得出∠NOM=90°,求出∠COM=35°,根据角平分线定义得出∠AOM=∠COM,即可得出答案.【详解】解:∵ON⊥OM,∴∠NOM=90°,∵∠CON=55°,∴∠COM=90°-55°=35°,∵射线OM平分∠AOC,∴∠AOM=∠COM=35°,故选:A.【点睛】本题考查了垂直定义,角平分线定义等知识点,解题的关键是能求出∠COM的度数和求出∠AOM=∠COM.7.已知,如图,直线,相交于点,⊥于点,∠=35°.则∠的度数为().A.35°B.55°C.65°D.70°【答案】B【分析】直接利用垂线的定义结合已知角得出∠COE的度数即可.【详解】∵OE⊥AB于点O(已知),∴∠AOE=90°(垂直定义).∵直线AB,CD相交于点O,∠BOD=35°(已知),∴∠AOC=35°(对顶角相等).∴∠COE=∠AOE−∠AOC=90°−35°=55°.∴∠COE=55°.故选B.【点睛】此题考查垂线的定义,对顶角,解题关键在于得出∠AOC=35°.8.如图,直线,相交于点,,平分,若,则的度数为()A.B.C.D.【答案】B【分析】由垂直得∠COE=90°,从而知∠AOC=64°,则∠BOD也得64°,由角平分线和平角定义得∠COF 的度数.【详解】∵OE⊥CD,∴∠COE=90°,∴∠AOC=∠COE-∠AOE=90°-26°=64°,∵∠AOC=∠BOD,∴∠BOD=64°,又∵OF平分∠BOD,∴∠DOF=∠BOD=×64°=32°,∴∠COF=180°-∠DOF=180°-32°=148°.故选B.【点睛】本题考查了垂线的定义、邻补角、对顶角定义、角平分线定义等知识点.本题属于基础题,推理过程的书写是关键,从垂直入手与已知相结合得出∠AOC的度数,使问题得以解决;同时要注意对顶角和平角性质的运用.9.如图,直线,,相交于点,,,射线,则的度数为___________.【答案】20°或160°【分析】先求出∠EOD=70°,再分射线OG在直线EF的两侧进行讨论求解即可.【详解】解:∵,,∠2=∠AOE,∴∠EOD=180°-50°-60°=70°,分两种情况:①如图,∵,∴∠EOG=90°,∴∠DOG=∠EOG-∠EOD=90°-70°=20°;②如图,∵∠EOG=90°,∠EOD=70°,∴∠DOG=∠EOD+∠EOG=70°+90°=160°,综上,的度数为20°或160°,故答案为:20°或160°.【点睛】本题考查邻补角、对顶角、垂线性质、角的运算,熟练掌握对顶角相等、邻补角互补,分情况讨论是解答的关键.10.如图,点C,O,D在一条直线上,,OE平分比大,的度数为________.【答案】##72.5度【分析】根据比大,和互补,即可求出,进而由垂直性质可求出,再由角平分线性质即可得出答案.【详解】解:∵比大,∴设,则,∵,∴,∴,∴,∵,∴,∴,∴,∵OE平分,∴.故答案为:.【点睛】本题考查了垂直的性质,角平分线的性质以及角的运算,掌握以上知识是解题的关键.11.如图,直线AB,CD交于点O,OC平分∠BOE,OE⊥OF,若∠DOF=15°,则∠EOA=_________.【答案】30°##30度【分析】根据垂直定义可得∠EOF=90°,从而利用平角定义求出∠COE=75°,然后利用角平分线的定义求出∠BOE=2∠COE=150°,最后利用平角定义求出∠EOA,即可解答.【详解】解:∵OE⊥OF,∴∠EOF=90°,∵∠DOF=15°,∴∠COE=180°﹣∠EOF﹣∠DOF=75°,∵OC平分∠BOE,∴∠BOE=2∠COE=150°,∴∠AOE=180°﹣∠∠BOE=30°,故答案为:30°.【点睛】本题考查了垂线,角平分线的定义,根据题目的已知条件并结合图形分析是解题的关键.12.如图,直线AB、CD相交于点O,,O为垂足,如果,则________°.【答案】57.5【分析】根据垂线的定义,可得,根据角的和差,可得的度数,根据邻补角的定义,可得答案.【详解】解:∵∴∴∵,∴,∴,∴,故答案为:.【点睛】本题考查了垂线的定义,邻补角的和等于180°,角与分的转化等知识.解题的关键在于领会由垂直得直角.13.如图,直线AB和CD交于O点,OD平分∠BOF,OE⊥CD于点O,∠AOC=40 ,则∠EOF=_______.【答案】130°【分析】根据对顶角性质可得∠BOD=∠AOC=40°.根据OD平分∠BOF,可得∠DOF=∠BOD=40°,根据OE ⊥CD,得出∠EOD=90°,利用两角和得出∠EOF=∠EOD+∠DOF=130°即可.【详解】解:∵AB、CD相交于点O,∴∠BOD=∠AOC=40°.∵OD平分∠BOF,∴∠DOF=∠BOD=40°,∵OE⊥CD,∴∠EOD=90°,∴∠EOF=∠EOD+∠DOF=130°.故答案为130°.【点睛】本题考查相交线对顶角性质,角平分线定义,垂直定义,掌握对顶角性质,角平分线定义,垂直定义是解题关键.14.如图所示,已知,若,,,则点到的距离是______,点到的距离是______.【答案】 4 2.4【分析】根据点到直线的距离概念可得点到的距离为垂线段AC的长,设点到的距离为,依据三角形面积,即可得到点到的距离.【详解】解:∵,∴,∴点到的距离为垂线段AC的长,又∵,∴点到的距离为4cm;设点到的距离为,,,,∵,,,,,故答案为:4;2.4.【点睛】本题考查了点到直线的距离,利用三角形的面积得出是解题关键.15.如图,直线,相交于点,平分.(1)若,,求的度数;(2)若平分,,求的度数.【答案】(1)70°(2)50°【分析】(1)根据角平分线的性质可得,根据垂线的定义以及已知条件求得,继而求得,根据对顶角相等即可求解;(2)根据角平分线的性质可得,,设,则,根据平角的定义建立方程,解方程即可求解.(1)解:平分,,,,,,∴;(2)平分,,,设,则,,解得:,故的度数为:.【点睛】本题考查了几何图形中角度的计算,角平分线的定义,垂线的定义,一元一次方程的应用,数形结合是解题的关键.16.如图,直线相交于点O,平分,求:(1)的度数;(2)写出图中互余的角;(3)的度数.【答案】(1)70°(2)∠BOF与∠BOD互余,∠EOF与∠EOD互余,∠EOF与∠BOE互余,∠BOF与∠AOC互余(3)55°【分析】(1)根据对顶角相等即可得到;(2)根据余角的定义求解即可;(3)先根据角平分线的定义求出∠DOE=35°,则∠EOF=∠DOF-∠DOE=55°.(1)解:由题意得;(2)解:∵∠COF=90°,∴∠DOF=180°-∠COF=90°,∴∠BOF+∠BOD=90°,∠EOF+∠EOD=90°,∵OE平分∠BOD,∴∠BOE=∠DOE,∴∠EOF+∠BOE=90°,∵∠AOC=∠BOD,∴∠BOF+∠AOC=90°,∴∠BOF与∠BOD互余,∠EOF与∠EOD互余,∠EOF与∠BOE互余,∠BOF与∠AOC互余;(3)解:∵∠BOD=70°,OE平分∠BOD,∴∠DOE=35°,∴∠EOF=∠DOF-∠DOE=55°.【点睛】本题主要考查了几何中角度的计算,角平分线的定义,对顶角相等,余角的定义,熟知相关知识是解题的关键.17.如图,已知,,是内三条射线,平分,平分.(1)若,,求的度数.(2)若,,求的度数.(3)若,,求的度数.【答案】(1)(2)(3)【分析】对于(1),由角平分线的定义求出和,再根据即可求解;对于(2),先求出,再根据角平分线的定义求出和,然后根据即可求解;对于(3),由角平分线的定义得,结合已知条件可得,,即,进而得出,可得答案.【详解】(1)∵平分,平分,∴,,∴;(2)∵,∴.∵,∴.∵平分,平分,∴,,∴;(3)∵平分,∴.∵,∴.∵,∴,∴,∴,∴.【点睛】本题主要考查了角的和差,关键是由角平分线定义得出相关等式.18.点O为直线l上一点,射线均与直线l重合,如图1所示,过点O作射线和射线,使得,,作的平分线.(1)求与的度数;(2)作射线,使得,请在图2中画出图形,并求出的度数;(3)如图3,将射线从图1位置开始,绕点O以每秒的速度逆时针旋转一周,作的平分线,当时,求旋转的时间.【答案】(1),(2)或(3)6秒或秒【分析】(1)根据,,即可得出的度数,根据角平分线的定义得出,然后根据得出的度数;(2)根据题意得出的度数,然后分两种情况进行讨论:①当射线在内部时;②当射线在外部时;分别进行计算即可;(3)根据平分得出,根据题意画出图形,计算的角度,然后计算时间即可.【详解】(1)解:由题意可知,,∵,∴,∵平分,∴,∴;(2)由(1)知,,∴,①当射线在内部时,如图2(1),;②当射线在外部时,如图2(2),,综上所述,的度数为或;(3)∵平分,∴,①如图3,,∵平分,∴,∴,∴旋转的时间(秒);②如图3(1),此时,,∵平分,∴,∴,∴,∴旋转的时间(秒);综上所述,旋转的时间为6秒或秒.【点睛】本题主要考查角度的计算,角平分线的定义等内容;第(2)问进行合适的分类讨论是解题的关键;第(3)问,搞清楚在射线旋转的过程中,和的相对位置在不断的变化,以此进行分类画图.1.(2022·江苏常州·中考真题)如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是()A.垂线段最短B.两点确定一条直线C.过一点有且只有一条直线与已知直线垂直D.过直线外一点有且只有一条直线与已知直线平行【答案】A【分析】根据垂线段最短解答即可.【详解】解:行人沿垂直马路的方向走过斑马线,体现的数学依据是垂线段最短,故选:A.【点睛】本题考查垂线段最短,熟知垂线段最短是解答的关键.2.(2022·河南·中考真题)如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为()A.26°B.36°C.44°D.54°【答案】B【分析】根据垂直的定义可得,根据平角的定义即可求解.【详解】解:EO⊥CD,,,.故选:B .【点睛】本题考查了垂线的定义,平角的定义,数形结合是解题的关键.3.(2021·北京·中考真题)如图,点在直线上,.若,则的大小为()A.B.C.D.【答案】A【分析】由题意易得,,进而问题可求解.【详解】解:∵点在直线上,,∴,,∵,∴,∴;故选A.【点睛】本题主要考查垂直的定义及邻补角的定义,熟练掌握垂直的定义及邻补角的定义是解题的关键.4.(2021·浙江杭州·中考真题)如图,设点是直线外一点,,垂足为点,点是直线上的一个动点,连接,则()A.B.C.D.【答案】C【分析】根据垂线段距离最短可以判断得出答案.【详解】解:根据点是直线外一点,,垂足为点,是垂线段,即连接直线外的点与直线上各点的所有线段中距离最短,当点与点重合时有,综上所述:,故选:C.【点睛】本题考查了垂线段最短的定义,解题的关键是:理解垂线段最短的定义.5.(2020·湖北孝感·中考真题)如图,直线,相交于点,,垂足为点.若,则的度数为()A.B.C.D.【答案】B【分析】已知,,根据邻补角定义即可求出的度数.【详解】∵∴∵∴故选:B【点睛】本题考查了垂直的性质,两条直线垂直,形成的夹角是直角;利用邻补角的性质求角的度数,平角度数为180°.6.(2020·河北·中考真题)如图,在平面内作已知直线的垂线,可作垂线的条数有()A.0条B.1条C.2条D.无数条【答案】D【分析】在同一平面内,过已知直线上的一点有且只有一条直线垂直于已知直线;但画已知直线的垂线,可以画无数条.【详解】在同一平面内,画已知直线的垂线,可以画无数条;故选:D.【点睛】此题主要考查在同一平面内,垂直于平行的特征,解题的关键是熟知垂直的定义.7.(2020·吉林·中考真题)如图,某单位要在河岸上建一个水泵房引水到处,他们的做法是:过点作于点,将水泵房建在了处.这样做最节省水管长度,其数学道理是_______.【答案】垂线段最短【分析】直线外一点与直线上各点连结的所有线段中,垂线段最短.【详解】通过比较发现:直线外一点与直线上各点连结的所有线段中,垂线段最短.故答案为:垂线段最短.【点睛】此题主要考查点到直线的距离,动手比较、发现结论是解题关键.。
新人教版七年级数学下册全册教案附同步练习及单元测试卷(含答案)

新人教版七年级数学下册全册教案附同步练习及单元测试卷(含答案)第五章相交线与平行线5.1.1相交线教学目标:1.理解对顶角和邻补角的概念,能在图形中辨认.2.掌握对顶角相等的性质和它的推证过程.3.通过在图形中辨认对顶角和邻补角,培养学生的识图能力.重点:在较复杂的图形中准确辨认对顶角和邻补角.难点:在较复杂的图形中准确辨认对顶角和邻补角.教学过程一、创设情境,引入课题先请同学观察本章的章前图,然后引导学生观察,并回答问题.学生活动:口答哪些道路是交错的,哪些道路是平行的.教师导入:图中的道路是有宽度的,是有限长的,而且也不是完全直的,当我们把它们看成直线时,这些直线有些是相交线,有些是平行线.相交线、平行线都有许多重要性质,并且在生产和生活中有广泛应用.所以研究这些问题对今后的工作和学习都是有用的,也将为后面的学习做些准备.我们先研究直线相交的问题,引入本节课题.二、探究新知,讲授新课1.对顶角和邻补角的概念学生活动:观察上图,同桌讨论,教师统一学生观点并板书.【板书】∠1与∠3是直线AB、CD相交得到的,它们有一个公共顶点O,没有公共边,像这样的两个角叫做对顶角.学生活动:让学生找一找上图中还有没有对顶角,如果有,是哪两个角?学生口答:∠2和∠4再也是对顶角.紧扣对顶角定义强调以下两点:(1)辨认对顶角的要领:一看是不是两条直线相交所成的角,对顶角与相交线是唇齿相依,哪里有相交直线,哪里就有对顶角,反过来,哪里有对顶角,哪里就有相交线;二看是不是有公共顶点;三看是不是没有公共边.符合这三个条件时,才能确定这两个角是对顶角,只具备一个或两个条件都不行.(2)对顶角是成对存在的,它们互为对顶角,如∠1是∠3的对顶角,同时,∠3是∠1的对顶角,也常说∠1和∠3是对顶角.2.对顶角的性质提出问题:我们在图形中能准确地辨认对顶角,那么对顶角有什么性质呢?学生活动:学生以小组为单位展开讨论,选代表发言,井口答为什么.【板书】∵∠1与∠2互补,∠3与∠2互补(邻补角定义),∴∠l=∠3(同角的补角相等).注意:∠l与∠2互补不是给出的已知条件,而是分析图形得到的;所以括号内不填已知,而填邻补角定义.或写成:∵∠1=180°-∠2,∠3=180°-∠2(邻补角定义),∴∠1=∠3(等量代换).学生活动:例题比较简单,教师不做任何提示,让学生在练习本上独立完成解题过程,请一个学生板演。
【初中数学】人教版七年级下册第2课时 几何图形与图文信息问题(练习题)

人教版七年级下册第2课时 几何图形与图文信息问题(181)1.如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的13,另一根露出水面的长度是它的15.两根铁棒长度之和为220cm ,此时木桶中水的深度是 cm .2.如图,宽为50cm 的长方形图案由10个完全相同的小长方形拼成,其中一个小长方形的面积为 cm 2.3.某药业集团生产的某种药品包装盒的侧面展开图如图所示.如果长方体盒子的长比宽多4cm ,求这种药品包装盒的体积.4.某校为学生开展拓展性课程,拟在一块长比宽多6米的长方形场地内建造由两个大棚组成的植物养殖区(如图①),要求两个大棚之间有间隔4米的路,设计方案如图②,已知每个大棚的周长为44米.(1)求每个大棚的长和宽各是多少;(2)现有两种大棚造价的方案,方案一是每平方米60元,超过100平方米优惠500元,方案二是每平方米70元,超过100平方米优惠总价的20%,试问选择哪种方案更优惠?5.已知∠A ,∠B 互余,∠A 比∠B 大30∘.设∠A ,∠B 的度数分别为x ∘,y ∘,则下列方程组中符合题意的是()A.{x +y =180,x =y −30B.{x +y =180,x =y +30C.{x +y =90,x =y +30D.{x +y =90,x =y −30 6.用一根长80cm 的绳子围成一个长方形,且长方形的长比宽多10cm ,则这个长方形的面积是()A.25cm 2B.45cm 2C.375cm 2D.1575cm 27.如图,AB ⊥BC ,∠ABD 的度数比∠DBC 的度数的2倍少15∘,设∠ABD 与∠DBC 的度数分别为x ∘,y ∘,根据题意,下列的方程组正确的是()A.{x +y =90,x =y −15 B.{x +y =90,x =2y −15 C.{x +y =90,x =15−2y D.{x +y =90,x =2y +158.某长方形的周长是44cm ,若宽的3倍比长多6cm ,则该长方形的面积是 cm 2.9.在长为10m ,宽为8m 的长方形空地上,沿平行于长方形各边的方向分割出三个形状、大小完全一样的小长方形花圃,其示意图如图所示.求其中一个小长方形花圃的长和宽.10.陈老师打算购买气球装扮学校六一儿童节活动会场,气球的种类有“笑脸”和“爱心”两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为()A.19元B.18元C.16元D.15元11.QQ 好友的等级会用一些图标来表示,如图是小明同学的两个好友的等级示例,小明想知道一个太阳和一个月亮所表示的等级.若设一个太阳表示x等级,一个月亮表示y等级,则可列方程组为.12.某校组织“大手拉小手,义卖献爱心”活动,购买了黑、白两种颜色的文化衫共140件,进行手绘设计后出售,所获利润全部捐给山区困难孩子.每件文化衫的批发价和零售价如下表:假设文化衫全部售出,共获利1860元,求黑、白两种文化衫各多少件.参考答案2.【答案】:4003.【答案】:设这种药品包装盒的宽为xcm ,高为ycm ,则长为(x +4)cm . 根据题意,得{2x +2y =14,x +4+2y =13,解得{x =5,y =2.故包装盒的长为9cm ,宽为5cm ,高为2cm ,所以包装盒的体积V =9×5×2=90(cm 3).答:这种药品包装盒的体积为90cm 3【解析】:要求长方体的体积,需知长方体的长、宽、高,故采用间接设元法.再结合图形寻找以下等量关系:①2个宽+2个高=14cm ;②1个长+2个高=13cm .4(1)【答案】设每个大棚的宽为a 米,长为b 米,根据题意可得{a +b =44×12,2a +4−b =6, 解得{a =8,b =14. 答:每个大棚的长为14米,宽为8米 (2)【答案】大棚的面积为:2×14×8=224(米2), 若按照方案一计算,大棚的造价为224×60−500=12940(元), 若按照方案二计算,大棚的造价为224×70×(1−20%)=12544(元). 因为12544<12940,所以选择方案二更优惠5.【答案】:C【解析】:∠A 比∠B 大30∘,则有x =y +30;∠A ,∠B 互余,则有x +y =90.故选 C6.【答案】:C【解析】:设长方形的长为xcm ,宽为ycm ,根据题意,得{2(x +y)=80x −y =10解这个方程组得{x =25,y =15, 长方形的面积=25×15=375(cm 2)7.【答案】:B【解析】:设∠ABD 与∠DBC 的度数分别为x ∘,y ∘,根据题意,得{x +y =90,x =2y −15.8.【答案】:1059.【答案】:设小长方形花圃的长为xm,宽为ym.根据题意,得{2x+y=10,x+2y=8,解得{x=4,y=2.答:小长方形花圃的长为4m,宽为2m【解析】:设小长方形花圃的长为xm,宽为ym.根据题意,得{2x+y=10,x+2y=8,解得{x=4,y=2.答:小长方形花圃的长为4m,宽为2m10.【答案】:C11.【答案】:{3x+y=52,2x+2y=40【解析】:快乐是3个太阳+一个月亮,一共为52级,所以列为3x+y=52;行者是2个太阳+2个月亮,一共为40级,所以列为2x+2y=40.所以可列方程组为{3x+y=52,2x+2y=40.12.【答案】:设黑色文化衫x件,白色文化衫y件,依题意得{x+y=140,(25−10)x+(20−8)y=1860,解得{x=60,y=80.答:黑色文化衫60件,白色文化衫80件【解析】:设黑色文化衫x件,白色文化衫y件,依题意得{x+y=140,(25−10)x+(20−8)y=1860,解得{x=60,y=80.答:黑色文化衫60件,白色文化衫80件。
人教版 七年级数学 第4章 几何图形初步 复习题(含答案)

人教版七年级数学第4章几何图形初步复习题一、选择题(本大题共10道小题)1. [2018·河南]某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是()A.厉B.害C.了D.我2. 如图,水平的讲台上放置的是圆柱形笔筒和正方体形粉笔盒,从上面看到的是()3. 粉刷墙壁时,粉刷工人用滚筒在墙上刷过几次后,墙壁马上换上了“新装”,在这个过程中,你认为下列判断正确的是()A.点动成线B.线动成面C.面动成体D.面与面相交得到线4. 如图是一座房子的平面示意图,组成这幅图的平面图形是 ()图A.三角形、长方形B.三角形、正方形、长方形C.三角形、正方形、长方形、梯形D.正方形、长方形、梯形5. 如图所示,下列对图形描述不正确的是()A.直线ABB.直线BCC.射线ACD.射线AB6. 下列几何体是由4个相同的小正方体搭成的,其中从左面看和从上面看得到的平面图形相同的是()7. 如图,图中小于平角的角有()A.10个B.9个C.8个D.4个8. 如果一个棱柱有12个顶点,那么它的面的个数是 ()A.10B.9C.8D.79. 图(1)(2)中所有的正方形完全相同,将图(1)的正方形放在图(2)中①②③④的某一位置,所组成的图形不能围成正方体的位置是()A.①B.②C.③D.④10. 已知∠AOB=60°,∠AOC=∠AOB,射线OD平分∠BOC,则∠COD的度数为()A.20°B.40°C.20°或30°D.20°或40°二、填空题(本大题共8道小题)11. (1)将度化为度、分、秒的形式:1.45°=;(2)2700″=°.12. 如图所示的图形中,是棱柱的有______.(填序号)13. 如图,∠1可以用三个大写字母表示为.14. 苏轼的诗句“横看成岭侧成峰,远近高低各不同”说明的现象是.15. 建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上.这样做的依据是.16. 如图,点B,O,D在同一条直线上,若∠1=15°,∠2=105°,则∠AOC=°.17. 如图所示,AF=.(用含a,b,c的式子表示)18. 图中可用字母表示出的射线有条.三、解答题(本大题共4道小题)19. 请将图中的角用不同的方法表示出来,并填写下表:角的表示方法一∠ABE角的表示方法二∠1 ∠2用量角器量出∠2,∠A,∠ABE的度数,并写出它们之间的数量关系.20. 如图,下列各几何体的表面中包含哪些平面图形?21. 如图,有一个外观为圆柱形的物体,它的内部构造看不到,当分别用一组平面沿水平方向(自上而下)和竖直方向(自左而右)截这个物体时,得到了如图所示的(1)(2)两组形状不同的截面,请你试着说出这个物体的内部构造.22. 实践与应用:一个西瓜放在桌子上,从上往下切,一刀可以切成2块,两刀最多可以切成4块,3刀最多可以切成7块,4刀最多可以切成11块(如图).上述实际问题可转化为数学问题:n条直线最多可以把平面分成几部分.请先进行操作,然后回答下列问题.(1)填表:直线条数 1 2 3 4 5 6 …最多可以把平面分成的2 4 7 11 …部分数(2)直接写出n条直线最多可以把平面分成几部分(用含n的式子表示).人教版七年级数学第4章几何图形初步复习题-答案一、选择题(本大题共10道小题)1. 【答案】D2. 【答案】D[解析] 从上面看,左边是一个圆,右边是一个正方形,故选D.3. 【答案】B4. 【答案】C5. 【答案】B6. 【答案】B7. 【答案】B[解析] 小于平角的角有∠AOB,∠AOC,∠AOD,∠BOC,∠BOD,∠BOE,∠COD,∠COE,∠DOE,共9个.8. 【答案】C[解析] 一个棱柱有12个顶点,一定是六棱柱,所以它有6个侧面和2个底面,共8个面.9. 【答案】A10. 【答案】D[解析] 当OC在∠AOB内部时,如图①,则∠BOC=∠AOB-∠AOC=60°-×60°=40°,∴∠COD=∠BOC=20°;当OC在∠AOB外部时,如图②,则∠BOC=∠AOB+∠AOC=60°+×60°=80°,∴∠COD=∠BOC=40°.综上,∠COD的度数为20°或40°.故选D.二、填空题(本大题共8道小题)11. 【答案】(1)1°27'(2)0.7512. 【答案】②⑥13. 【答案】∠MCN或∠MCB14. 【答案】观察同一个物体,由于方向和角度不同,看到的图形往往不同15. 【答案】两点确定一条直线16. 【答案】90[解析] 因为∠2=105°,所以∠BOC=180°-∠2=75°,所以∠AOC=∠1+∠BOC=15°+75°=90°.17. 【答案】2a-2b-c18. 【答案】5[解析] 有OA,AB,BC,OP,PE,共5条射线.三、解答题(本大题共4道小题)19. 【答案】解:∠ABE还可以表示为∠3,∠1还可以表示为∠ABC或∠ABF,∠2还可以表示为∠ACB或∠ACE(填表略).∠2=40°,∠A=25°,∠ABE=65°,所以∠ABE=∠A+∠2.20. 【答案】(1)长方形(2)圆(3)三角形、平行四边形21. 【答案】解:这个物体的内部构造为:圆柱中间有一球形空洞.22. 【答案】解:(1)设n条直线最多可以把平面分成的部分数是S n.当n=5时,S5=1+1+2+3+4+5=16,当n=6时,S6=1+1+2+3+4+5+6=22.故表内从左到右依次填16,22.(2)S n=1+1+2+3+…+n=1+=.故n条直线最多可以把平面分成部分.。
2020-2021学年人教版数学七年级下册第5章 相交线与平行线 解答题练习(三)

人教版数学七年级下册第5章《相交线与平行线》解答题培优(三)1.如图,将△ABC沿直线AB向右平移后到达△BDE的位置.(1)若AC=6cm,则BE=cm;(2)若∠CAB=50°,∠BDE=100°,求∠CBE的度数.2.探究题已知:如图1,AB∥CD,CD∥EF.求证:∠B+∠BDF+∠F=360°.老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?(1)小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小额用到的平行线性质可能是.(2)接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线AB、EF,然后在平行线间画了一点D,连接BD,DF后,用鼠标拖动点D,分别得到了图①②③,小颖发现图②正是上面题目的原型,于是她由上题的结论猜想到图①和③中的∠B、∠BDF与∠F之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.请你在小颖操作探究的基础上,继续完成下面的问题:①猜想图①中∠B、∠BDF与∠F之间的数量关系并加以证明:②补全图③,直接写出∠B、∠BDF与∠F之间的数量关系:.(3)学以致用:一个小区大门栏杆的平面示意图如图2所示,BA垂直地面AE于A,CD 平行于地面AE,若∠BCD=150°,则∠ABC=.3.如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向向右平移得到三角形DEF.(1)试求出∠E的度数;(2)若AE=9cm,DB=2cm,求出BE的长度.4.如图,已知AB∥DE∥MN,AD平分∠CAB,CD⊥DE.(1)∠DAB=15°,求∠ACD的度数;(2)判断等式∠CDA=∠NCD+∠DAB是否成立,并说明理由.5.如图,直线AB与CD相交于点O,OE⊥CD,OF⊥AB,∠DOF=65°.求:(1)∠BOE的度数;(2)∠AOC的度数.6.如图1为北斗七星的位置图,如图2将北斗七星分别标为A,B,C,D,E,F,G,将A,B,C,D,E,F顺次首尾连接,若AF恰好经过点G,且AF∥DE,∠B=∠C+10°,∠D=∠E=105°.(1)求∠F的度数.(2)计算∠B﹣∠CGF的度数是.(直接写出结果)(3)连接AD,∠ADE与∠CGF满足怎样数量关系时,BC∥AD,并说明理由.7.如图,已知射线BM平分∠ABC,点D是BM上一点,且DE∥BC交AB于E,若∠EDB =28°,求∠AED的度数.8.如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.9.如图,AB和CD相交于点O,∠DOE=90°,若∠BOE=∠AOC,(1)指出与∠BOD相等的角,并说明理由.(2)求∠BOD,∠AOD的度数.10.如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.完成以下解答过程中的空缺部分:解:过点E作EF∥AB.∴∠B=∠.()∵∠B=26°(已知),∴∠1=°().∵AB∥CD().∵EF∥AB(作辅助线),∴EF∥CD.∴∠D=∠.()∵∠D=39°(已知),∴∠2=°().∴∠BED=°(等式性质).11.如图1,直线AB、CD被直线EF截,分别交AB于点G,交CD于点H,∠AGE与∠EHC互补.(1)求证:AB∥CD;(2)如图2,点P在直线AB、CD内部直线EF上,点M、N分别在直线AB、CD上,连接PM、PN,点K在∠PMB的角平分线上,连接KN,若∠MKN=180°∠MPN,求证:∠PNK=∠CNK;(3)如图3,在(2)的条件下,点O为AB上一点,连接ON、MN,MN平分∠PNO,若∠MNK:∠PMK=2:7,2∠MKN﹣∠PNO=180°,求∠NOM的度数.12.如图,直线AB,CD相交于点O,∠DOE=∠BOD,OF平分∠AOE,若∠BOD=28°,求∠EOF的度数.13.已知:两直线l1,l2满足l1∥l2,点C,点D在直线l1上,点A,点B在直线l2上,点P是平面内一动点,连接CP,BP,(1)如图1,若点P在l1、l2外部,则∠DCP、∠CPB、∠ABP之间满足什么数量关系?请你证明的这个结论;(2)如图2,若点P在l1、l2外部,连AC,则∠CAB、∠ACP、∠CPB、∠ABP之间满足什么数量关系?请你证明的这个结论;(不能用三角形内角和为180°)(3)若点P在l1、l2内部,且在AC的右侧,则∠ACP、∠ABP、∠CAB、∠CPB之间满足什么数量关系?(不需证明)14.如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,求证:∠CED+∠ACB=180°,请你将小明的证明过程补充完整.证明:∵FG⊥AB,CD⊥AB,垂足分别为G,D(已知),∴∠FGB=∠CDB=90°().∴GF∥CD().∵GF∥CD(已证),∴∠2=∠BCD().又∵∠1=∠2(已知),∴∠1=∠BCD().∴().∴∠CED+∠ACB=180°().15.已知:直线AB∥CD,点M,N分别在直线AB,CD上,点E为平面内一点.(1)如图1,探究∠AME,∠E,∠ENC的数量关系;并加以证明.(2)如图2,∠AME=30°,EF平分∠MEN,NP平分∠ENC,EQ∥NP,求∠FEQ的度数.(3)如图3,点G为CD上一点,∠AMN=m∠EMN,∠GEK=m∠GEM,EH∥MN交AB于点H,直接写出∠GEK,∠BMN,∠GEH之间的数量关系(用含m的式子表示)参考答案1.解:(1)∵将△ABC沿直线AB向右平移得到△BDE,∴△ABC≌△BDE,∴BE=AC=6cm,故答案为:6;(2)由(1)知△ABC≌△BDE,∴∠DBE=∠CAB=50°、∠BDE=∠ABC=100°,∴∠CBE=180°﹣∠ABC﹣∠DBE=30°.2.(1)证明:如图1中,∵AB∥EF,CD∥EF,∴CD∥EF,∴∠B+∠CDB=180°,∠F+∠CDF=180°(两直线平行同旁内角互补),∴∠B+∠CDB+∠CDF+∠F=360°,∴∠B+∠BDF+∠F=360°,故答案为:两直线平行同旁内角互补.(2)解:①结论:∠BDF=∠B+∠F.理由:如图①中,作DK∥AB.∵AB∥DK,AB∥EF,∴∠B=∠BDK,∠F=∠FDK,∴∠BDF=∠BDK+∠FDK=∠B+∠F.②如图③中,结论:∠F=∠D+∠B.(答案不唯一).理由:∵AB∥EF,∴∠1=∠F,∵∠1=∠B+∠D,∴∠F=∠D+∠B.故答案为∠F=∠D+∠F.(3)解:如图2中,∵BA⊥AE,∴∠BAE=90°,∵∠ABC+∠BAE+∠BCD=360°,∠BCD=150°,∴∠ABC=360°﹣240°=120°,故答案为120°.3.解:(1)∵∠ACB=90°,∠A=33°∴∠ABC=90°﹣33°=57°,∵三角形ABC沿AB方向向右平移得到三角形DEF,∴∠E=∠ABC=57°;(2)∵三角形ABC沿AB方向向右平移得到三角形DEF,∴AB=DE,∴AD+BD+BE=AE,即BE+2+BE=9,∴BE=3.5(cm).4.解:(1)延长CD交AB于点F,∵AB∥DE∥MN,CD⊥DE,∴CF⊥AB.∵AD平分∠CAB,∠DAB=15°,∴∠CAF=30°,∴∠ACD=90°﹣30°=60°;(2)延长ED交AC于点G,∵AB∥DE∥MN,∴∠CDG=∠NCD,∠GDA=∠DAB,∴∠CDA=∠NCD+∠DAB.5.解:(1)OF⊥AB,则∠BOF=90°,∵∠DOF=65°,∴∠BOD=∠BOF﹣∠DOF=90°﹣65°=25°,∵OE⊥CD,∴∠DOE=90°,那么∠BOE=∠DOE﹣∠BOD=90°﹣25°=65°.(2)直线AB与CD相交于点O,∠AOC与∠BOD是对顶角,即∠AOC=∠BOD=25°.6.解:(1)∵AF∥DE,∴∠F=180°﹣105°=75°;(2)延长DC交AF于K,可得:∠B﹣∠CGF=∠C+10°﹣∠CGF=∠GKC+10°=∠D+10°=115°,故答案为:115°;(3)当∠ADE+∠CGF=180°时,BC∥AD,∵AF∥DE,∴∠GAD+∠ADE=180°,∠ADE+∠CGF=180°,∴∠GAD=∠CGF,∴BC∥AD.7.解:∵DE∥BC,∴∠EDB=∠CBD=28°,∠AED=∠ABC,又∵BM平分∠ABC,∴∠ABD=∠CBD=28°,∴∠ABC=∠AED=56°.8.解:∵∠A=∠F(已知)∴AC∥DF(内错角相等,两直线平行)∴∠D=∠ABD(两直线平行,内错角相等)∵∠C=∠D(已知)∴∠C=∠ABD(等量代换)∴BD∥CE(同位角相等,两直线平行)9.解:(1)∠AOC,对顶角相等;(2)∵∠BOD=∠AOC,又∵∠BOE=∠AOC,∴∠BOE=∠BOD,∴∠DOE=∠BOE+∠BOD=∠BOD+∠BOD=90°,解得:∠BOD=67.5°;∴∠AOD=180°﹣∠BOD=180°﹣67.5°=112.5°.10.解:过点E作EF∥AB.∴∠B=∠1.(两直线平行,内错角相等)∵∠B=26°(已知),∴∠1=26°(等量代换).∵AB∥CD(已知),∵EF∥AB(作辅助线),∴EF∥CD.∴∠D=∠2.(两直线平行,内错角相等)∵∠D=39°(已知),∴∠2=39°(等量代换).∴∠BED=65°(等式性质).故答案为:1,两直线平行,内错角相等,26,等量代换,已知,两直线平行,2,内错角相等,39,等量代换,65.11.解:(1)∵∠AGE与∠EHC互补,∴∠AGE+∠EHC=180°,∵∠AGE+∠EGB=180°,∴∠EGB=∠EHC,∴AB∥CD;(2)证明:过点P作PQ∥AB,∴∠AMP=∠MPQ,∵AB∥CD,∴PQ∥CD,∴∠DNP=∠NPQ,∴∠MPN=∠AMP+∠DNP,∵MK平分∠PMB,∴∠PMK=∠BMK,同理,过点K作KR∥AB,∴∠MKN=∠BMK+∠CNK,∵∠MKN=180°﹣∠MPN,∴∠BMK+∠CNK=180°﹣(∠AMP+∠DNP)=180°﹣(180°﹣∠BMK﹣∠PMK+180°﹣∠CNK﹣∠PNK)=(∠BMK+∠PMK)+(∠CNK+∠PNK)=∠BMK+∠CNK+∠PNK∴∠CNK=∠PNK,∴∠CNK=∠PNK.(3)∵∠MNK:∠PMK=2:7,∴设∠MNK=2α,∠PMK=7α,∠PNK=∠CNK∴∠PNM+2α=∠CNK∵MN平分∠PNO,∴∠PNM=∠MNO,∴∠CON=∠CNK﹣∠ONK=∠PNM+2α﹣(∠MNO﹣∠MNK)=4α,∵2∠MKN﹣∠PNO=180°,∠MKN=180°﹣∠MPN,∴2(180°﹣∠MPN)﹣∠PNO=180°,∴∠MPN+∠PNO=180°,∴PM∥NO,∴∠NOM=∠PMG,∵AB∥CD,∴∠NOM=∠CON=4α,∵∠PMK=∠OMK=7α,∠PMG+∠PMK+∠OMK=180°,∴4α+7α+7α=180°,∴α=10°,∴∠NOM=40°.12.解:∵∠DOE=∠BOD,∠BOD=28°,∴∠BOE=56°,∵∠AOB=∠AOE+∠BOE=180°,∴∠AOE=180°﹣∠BOE=180°﹣56°=124°,∵OF平分∠AOE,∴∠EOF=.13.解:(1)如图1,数量关系:∠DCP=∠CPB+∠ABP,理由:过P作PM∥AB,∴∠ABP=∠2,∠3=∠CPM,∵∠3=∠2+∠CPB,∴∠3=∠CPB+∠ABP,∵CD∥AB,∴∠1=∠3,∴∠DCP=∠CPB+∠ABP;(2)数量关系:∠CAB+∠ACP=∠CPB+∠ABP,理由:过A作AE∥PB,过C作CF∥BP,∴AE∥CF∥BP,∴∠1=∠2,∠3=∠P,∠ABP=∠1+∠4,∴∠CAB+∠ACP=∠4+∠2+∠3,∴∠CPB+∠ABP=∠3+∠1+∠4=∠3+∠2+∠4,∴∠CAB+∠ACP=∠CPB+∠ABP;(3)如图3,数量关系:∠CPB=∠CAB+∠ACP+∠ABP;理由:过P作PM∥CD,∵CD∥AB,∴CD∥PM∥AB,∴∠DCA=∠CAB,∠DCP=∠CPM,∠MPB=∠PBA,∴∠CPB=∠DCA+∠ACP=∠CAB+∠ACP,∵∠CPB=∠CPM+∠MPB,∴∠CPB=∠CAB+∠ACP+∠ABP;如图4,数量关系:∠CAB+∠ACP+∠CPB+∠ABP=360°,理由:过P作PM∥CD,∵CD∥AB,∴CD∥PM∥AB,∴∠CAB=∠DCA,∠DCP+∠CPM=180°,∠ABP+∠MPB=180°,∴∠CAB+∠ACP+∠CPB+∠ABP=∠DCA+∠ACP+∠CPM+∠MPB+∠ABP=360°.14.证明:∵FG⊥AB,CD⊥AB,垂足分别为G,D(已知)∴∠FGB=∠CDB=90°(垂直定义).∴GF∥CD(同位角相等,两直线平行),∵GF∥CD(已证),∴∠2=∠BCD(两直线平行,同位角相等),又∵∠1=∠2(已知),∴∠1=∠BCD(等量代换),∴DE∥BC(内错角相等,两直线平行)∴∠CED+∠ACB=180°(两直线平行,同旁内角互补),故答案为:垂直定义,同位角相等,两直线平行,两直线平行,同位角相等,等量代换,DE∥BC,内错角相等,两直线平行,两直线平行,同旁内角互补.15.解:(1)如图1,过点E作l∥AB,∵AB∥CD,∴l∥AB∥CD,∴∠1=∠AME,∠2=∠CNE,∵∠MEN=∠1+∠2,∴∠E=∠AME+∠ENC;(2)∵EF平分∠MEN,NP平分∠END,∴∠NEF=∠MEN,∠ENP=∠END,∵EQ∥NP,∴∠QEN=∠ENP=∠ENC,∵∠MEN=∠AME+∠ENC,∴∠MEN﹣∠ENC=∠AME=30°,∴∠FEQ=∠NEF﹣∠NEQ=∠MEN﹣∠ENC,=×30°=15°;(3)m∠GEH=∠GEK﹣∠AMN.∵∠AMN=m•∠EMN,∠GEK=m•∠GEM,∴∠EMN=∠AMN,∠GEN=∠GEK,∵EH∥MN,∴∠HEM=∠EMN=∠AMN,∵∠GEH=∠GEM﹣∠HEM,=∠GEK﹣∠AMN,∴m∠GEH=∠GEK﹣∠AMN,∵∠BMN=180°﹣∠AMN,∴∠BMN+∠KEG﹣m∠GEH=180°.。
七年级数学几何图形练习题及答案

七年级数学几何图形练习题及答案[答案表]以下是七年级数学几何图形练习题的答案。
1. 判断下列说法是否正确,并用对或错来回答:a) 正方形有四个直角。
答案:对。
b) 所有矩形都是正方形。
答案:错。
c) 所有正方形都是矩形。
答案:对。
d) 所有正方形都是长方形。
答案:对。
2. 根据图形的描述,选择正确的图形并填写在括号内:a) 一个有两条等长直角边的三角形是( )。
①直角三角形②等腰三角形③锐角三角形④钝角三角形答案:②等腰三角形b) 一条边为直径的圆叫作( )。
①半圆②椭圆③圆锥④圆答案:④圆c) 具有四条边且都相等的四边形是( )。
①正方形②长方形③梯形④平行四边形答案:①正方形3. 请计算下列图形的周长:a) 边长为4 cm的正方形的周长是多少?答案:正方形的四边相等,所以周长=4cm+4cm+4cm+4cm=16cm。
b) 边长分别为5 cm和8 cm的长方形的周长是多少?答案:长方形的周长=5cm+8cm+5cm+8cm=26cm。
c) 一张和纸短边长7 cm,长边长10 cm的长方形纸片,它的周长是多少?答案:周长=7cm+10cm+7cm+10cm=34cm。
4. 请计算下列图形的面积:a) 边长为6 cm的正方形的面积是多少?答案:正方形的面积=边长 ×边长 = 6cm × 6cm = 36cm²。
b) 边长分别为3 cm和7 cm的长方形的面积是多少?答案:长方形的面积=长 ×宽 = 3cm × 7cm = 21cm²。
c) 一张长边长为12 cm,短边长为5 cm的长方形纸片,它的面积是多少?答案:面积=长 ×宽 = 12cm × 5cm = 60cm²。
5. 请判断图形是否相似,并用是或否来回答:a) 下图中的两个三角形是否相似?答案:是。
(图形描述省略)b) 下图中的两个四边形是否相似?答案:否。
人教版七年级数学下册《相交线与平行线中的四种几何模型》专项练习题-附含答案

人教版七年级数学下册《相交线与平行线中的四种几何模型》专项练习题-附含答案类型一、猪脚模型例.问题情境:如图① 直线AB CD ∥ 点E F 分别在直线AB CD 上.(1)猜想:若1130∠=︒ 2150∠=︒ 试猜想P ∠=______°;(2)探究:在图①中探究1∠ 2∠ P ∠之间的数量关系 并证明你的结论;(3)拓展:将图①变为图② 若12325∠+∠=︒ 75EPG ∠=︒ 求PGF ∠的度数. 【答案】(1)80︒(2)36012P ∠=︒-∠-∠;证明见详解(3)140︒【详解】(1)解:如图过点P 作MN AB ∥∵AB CD ∥∵AB MN CD ∥∥.∵1180EPN ∠+∠=︒2180FPN ∠+∠=︒.∵1130∠=︒ 2150∠=︒∵12360EPN FPN ∠+∠+∠+∠=︒∵36013015080EPN FPN ∠+=︒-︒-︒=︒.∵P EPN FPN ∠=∠+∠∵∵P =80°.故答案为:80︒;(2)解:36012P ∠=︒-∠-∠ 理由如下:如图过点P 作MN AB ∥∵AB CD ∥∵AB MN CD ∥∥.∵1180EPN ∠+∠=︒2180FPN ∠+∠=︒.∵12360EPN FPN ∠+∠+∠+∠=︒∵EPN FPN P ∠+∠=∠36012P ∠=︒-∠-∠.(3)如图分别过点P 、点G 作MN AB ∥、KR AB ∥∵AB CD ∥∵AB MN KR CD ∥∥∥.∵1180EPN ∠+∠=︒180NPG PGR ∠+∠=︒2180RGF ∠+∠=︒.∵12540EPN NPG PGR RGF ∠+∠+∠+∠++∠=︒∵75EPG EPN NPG ∠=∠+∠=︒PGR RGF PGF ∠+∠=∠12325∠+∠=︒∵12540PGF EPG ∠+∠+∠+∠=︒∵54032575140PGF ∠=︒-︒-︒=︒故答案为:140︒.【变式训练1】已知直线a b ∥ 直线EF 分别与直线a b 相交于点E F 点A B 分别在直线a b 上 且在直线EF 的左侧 点P 是直线EF 上一动点(不与点E F 重合)设∵P AE =∵1 ∵APB =∵2 ∵PBF =∵3.(1)如图1 当点P 在线段EF 上运动时 试说明∵1+∵3=∵2;(2)当点P 在线段EF 外运动时有两种情况.①如图2写出∵1 ∵2 ∵3之间的关系并给出证明;②如图3所示 猜想∵1 ∵2 ∵3之间的关系(不要求证明).【答案】(1)证明见详解(2)①312∠=∠+∠;证明见详解;②123∠=∠+∠;证明见详解【详解】(1)解:如图4所示:过点P 作PC a ∥∵a b ∥∵PC a b ∥∥∵1APC ∠=∠ 3BPC ∠=∠∵2APC BPC ∠=∠+∠∵213∠=∠+∠;(2)解:①如图5过点P 作PC a ∥∵a b ∥∵PC a b ∥∥∵3BPC ∠=∠ 1APC ∠=∠∵2BPC APC ∠=∠+∠∵312;②如图6过点P 作PC a ∥∵a b ∥∵PC a b ∥∥∵1APC ∠=∠ 3BPC ∠=∠∵2APC BPC ∠=∠+∠∵123∠=∠+∠.【变式训练2】阅读下面内容 并解答问题.已知:如图1 AB CD 直线EF 分别交AB CD 于点E F .BEF ∠的平分线与DFE ∠的平分线交于点G .(1)求证:EG FG ⊥;(2)填空 并从下列①、②两题中任选一题说明理由.我选择 题.①在图1的基础上 分别作BEG ∠的平分线与DFG ∠的平分线交于点M 得到图2 则EMF ∠的度数为 .②如图3 AB CD 直线EF 分别交AB CD 于点E F .点O 在直线AB CD 之间 且在直线EF 右侧 BEO ∠的平分线与DFO ∠的平分线交于点P 则EOF ∠与EPF ∠满足的数量关系为 . GH ABAB CD AB GH CD ∴BEG EGH DFG FGH ∠∠∠∠∴==,180BEF DFE ∴∠+∠=︒EG 平分GEB ∴∠=GEB ∴∠+在EFG ∆中EGF ∴∠=EM 平分BEM ∴∠45EMF BEM MFD ∴∠=∠+∠=︒故答案为:45︒;②结论:2EOF EPF ∠=∠.理由:如图3中 由题意 EOF BEO DFO ∠=∠+∠ EPF BEP DFP ∠=∠+∠PE 平分BEO ∠ PF 平分DFO ∠2BEO BEP ∴∠=∠ 2DFO DFP ∠=∠2EOF EPF ∴∠=∠故答案为:2EOF EPF ∠=∠.【变式训练3】如图:(1)如图1 AB CD ∥ =45ABE ∠︒ 21CDE ∠=︒ 直接写出BED ∠的度数.(2)如图2 AB CD ∥ 点E 为直线AB CD 间的一点 BF 平分ABE ∠ DF 平分CDE ∠ 写出BED ∠与F ∠之间的关系并说明理由.(3)如图3 AB 与CD 相交于点G 点E 为BGD ∠内一点 BF 平分ABE ∠ DF 平分CDE ∠ 若60BGD ∠=︒ 95BFD ∠=︒ 直接写出BED ∠的度数. 【答案】(1)∵BED =66°;(2)∵BED =2∵F 见解析;(3)∵BED 的度数为130°.【详解】(1)解:(1)如图 作EF ∵AB∵直线AB ∵CD∵EF ∵CD∵∵ABE =∵1=45° ∵CDE =∵2=21°∵∵BED =∵1+∵2=66°;(2)解:∵BED =2∵F理由是:过点E作EG∥AB延长DE交BF于点H∵AB∥CD∵AB∥CD∥EG∵∵5=∵1+∵2∵6=∵3+∵4又∵BF平分∵ABE DF平分∵CDE∵∵2=∵1∵3=∵4则∵5=2∵2∵6=2∵3∵∵BED=2(∵2+∵3)又∵F+∵3=∵BHD∵BHD+∵2=∵BED∵∵3+∵2+∵F=∵BED综上∵BED=∵F+12∵BED即∵BED=2∵F;(3)解:延长DF交AB于点H延长GE到I∵∵BGD=60°∵∵3=∵1+∵BGD=∵1+60° ∵BFD=∵2+∵3=∵2+∵1+60°=95°∵∵2+∵1=35° 即2(∵2+∵1) =70°∵BF平分∵ABE DF平分∵CDE∵∵ABE=2∵2∵CDE=2∵1∵∵BEI=∵ABE +∵BGE=2∵2+∵BGE∵DEI=∵CDE+∵DGE=2∵1+∵DGE ∵∵BED=∵BEI+∵DEI=2(∵2+∵1)+( ∵BGE+∵DGE)=70°+60°=130°∵∵BED的度数为130°.类型二、铅笔模型例.问题情景:如图1 AB ∵CD ∵P AB =140° ∵PCD =135° 求∵APC 的度数.(1)丽丽同学看过图形后立即口答出:∵APC =85° 请补全她的推理依据.如图2 过点P 作PE ∵AB因为AB ∵CD 所以PE ∵CD .( )所以∵A +∵APE =180° ∵C +∵CPE =180°.( )因为∵P AB =140° ∵PCD =135° 所以∵APE =40° ∵CPE =45°∵APC =∵APE +∵CPE =85°.问题迁移:(2)如图3 AD ∵BC 当点P 在A 、B 两点之间运动时 ∵ADP =∵α ∵BCP =∵β 求∵CPD 与∵α、∵β之间有什么数量关系?请说明理由.(3)在(2)的条件下 如果点P 在A 、B 两点外侧运动时(点P 与点A 、B 、O 三点不重合) 请直接写出∵CPD 与∵α、∵β之间的数量关系.【答案】(1)平行于同一条直线的两条直线平行(或平行公理推论) 两直线平行 同旁内角互补;(2)CPD αβ∠=∠+∠ 理由见解析;(3)CPD βα∠=∠-∠或CPD αβ∠=∠-∠【详解】解:(1)如图2 过点P 作PE ∵AB因为AB ∵CD 所以PE ∵CD .(平行于同一条直线的两条直线平行)所以∵A +∵APE =180° ∵C +∵CPE =180°.(两直线平行同旁内角互补)因为∵P AB=140° ∵PCD=135°所以∵APE=40° ∵CPE=45°∵APC=∵APE+∵CPE=85°.故答案为:平行于同一条直线的两条直线平行;两直线平行同旁内角互补;(2)∵CPD=∵α+∵β理由如下:如图3所示过P作PE∵AD交CD于E∵AD∵BC∵AD∵PE∵BC∵∵α=∵DPE∵β=∵CPE∵∵CPD=∵DPE+∵CPE=∵α+∵β;(3)当P在BA延长线时如图4所示:过P作PE∵AD交CD于E同(2)可知:∵α=∵DPE∵β=∵CPE∵∵CPD=∵β-∵α;当P在AB延长线时如图5所示:同(2)可知:∵α=∵DPE∵β=∵CPE∵∵CPD=∵α-∵β.综上所述∵CPD与∵α、∵β之间的数量关系为:∵CPD=∵β-∵α或∵CPD=∵α-∵β.【变式训练1】已知直线AB∥CD(1)如图(1)点G为AB、CD间的一点联结AG、CG.若∵A=140° ∵C=150° 则∵AGC 的度数是多少?(2)如图(2)点G为AB、CD间的一点联结AG、CG.∵A=x° ∵C=y° 则∵AGC的度数是多少?(3)如图(3)写出∵BAE、∵AEF、∵EFG、∵FGC、∵GCD之间有何关系?直接写出结论.【答案】(1)70°;(2)∵AGC=(x+y)°;(3)∵BAE+∵EFG+∵GCD=∵AEF+∵FGC.【详解】解:(1)如图过点G作GE∥AB∵AB∥GE∵∵A+∵AGE=180°(两直线平行同旁内角互补).∵∵A=140°∵∵AGE=40°.∵AB∥GE AB∥CD∵GE∥CD.∵∵C+∵CGE=180°(两直线平行同旁内角互补).∵∵C=150°∵∵CGE=30°.∵∵AGC=∵AGE+∵CGE=40°+30°=70°.(2)如图过点G作GF∥AB∵AB∥GF∵∵A=AGF(两直线平行内错角相等).∵AB∥GF AB∥CD∵GF∥CD.∵∵C=∵CGF.∵∵AGC=∵AGF+∵CGF=∵A+∵C.∵∵A=x° ∵C=y°∵∵AGC=(x+y)°.(3)如图所示过点E作EM∥AB过点F作FN∥AB过点G作GQ∥CD∵AB∥CD∵AB∥EM∥FN∥GQ∥CD.∵∵BAE=∵AEM∵MEF=∵EFN∵NFG=∵FGQ∵QGC=∵GCD(两直线平行内错角相等).∵∵AEF=∵BAE+∵EFN∵FGC=∵NFG+GCD.∵∵EFN+∵NFG=∵EFG∵∵BAE+∵EFG+∵GCD=∵AEF+∵FGC.【变式训练2】问题情境:如图1 AB∵CD∵P AB=130° ∵PCD=120° 求∵APC度数.思路点拨:小明的思路是:如图2 过P作PE∵AB通过平行线性质可分别求出∵APE、∵CPE的度数从而可求出∵APC的度数;小丽的思路是:如图3 连接AC通过平行线性质以及三角形内角和的知识可求出∵APC的度数;小芳的思路是:如图4 延长AP交DC的延长线于E通过平行线性质以及三角形外角的相关知识可求出∵APC的度数.问题解决:请从小明、小丽、小芳的思路中任选一种思路进行推理计算你求得的∵APC的度数为°;问题迁移:(1)如图5 AD∵BC点P在射线OM上运动当点P在A、B两点之间运动时∵ADP=∵α ∵BCP=∵β.∵CPD、∵α、∵β之间有何数量关系?请说明理由;(2)在(1)的条件下如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合)请你直接写出∵CPD、∵α、∵β间的数量关系.【答案】问题解决:110°;问题迁移:(1)∵CPD=∵α+∵β 理由见解析;(2)∵CPD=∵β﹣∵α 理由见解析【详解】解:小明的思路:如图2 过P作PE∵AB∵AB∵CD∵PE∵AB∵CD∵∵APE=180°﹣∵A=50° ∵CPE=180°﹣∵C=60°∵∵APC=50°+60°=110°故答案为:110;(1)∵CPD=∵α+∵β 理由如下:如图5 过P作PE∵AD交CD于E∵AD∵BC∵AD∵PE∵BC∵∵α=∵DPE∵β=∵CPE∵∵CPD=∵DPE+∵CPE=∵α+∵β;(2)当P在BA延长线时∵CPD=∵β﹣∵α;理由:如图6 过P作PE∵AD交CD于E∵AD∵BC∵AD∵PE∵BC∵∵α=∵DPE∵β=∵CPE∵∵CPD=∵CPE﹣∵DPE=∵β﹣∵α;当P在BO 之间时 ∵CPD =∵α﹣∵β.理由:如图7 过P 作PE ∵AD 交CD 于E∵AD ∵BC∵AD ∵PE ∵BC∵∵α=∵DPE ∵β=∵CPE∵∵CPD =∵DPE ﹣∵CPE =∵α﹣∵β.类型三、锄头模型例.已知 AB ∵CD .点M 在AB 上 点N 在CD 上.(1)如图1中 ∵BME 、∵E 、∵END 的数量关系为: ;(不需要证明) 如图2中 ∵BMF 、∵F 、∵FND 的数量关系为: ;(不需要证明)(2)如图3中 NE 平分∵FND MB 平分∵FME 且2∵E +∵F =180° 求∵FME 的度数;(3)如图4中 ∵BME =60° EF 平分∵MEN NP 平分∵END 且EQ ∵NP 则∵FEQ 的大小A BC D P123是否发生变化若变化请说明理由若不变化求出∵FEQ的度数.【答案】(1)∵BME=∵MEN﹣∵END;∵BMF=∵MFN+∵FND;(2)120°;(3)不变30°【详解】解:(1)过E作EH∵AB如图1∵∵BME=∵MEH∵AB∵CD∵HE∵CD∵∵END=∵HEN∵∵MEN=∵MEH+∵HEN=∵BME+∵END即∵BME=∵MEN﹣∵END.如图2 过F作FH∵AB∵∵BMF=∵MFK∵AB∵CD∵FH∵CD∵∵FND=∵KFN∵∵MFN=∵MFK﹣∵KFN=∵BMF﹣∵FND即:∵BMF=∵MFN+∵FND.故答案为∵BME=∵MEN﹣∵END;∵BMF=∵MFN+∵FND.(2)由(1)得∵BME=∵MEN﹣∵END;∵BMF=∵MFN+∵FND.(2)观察图(2)已知AB∵CD猜想图中的∵BPD与∵B、∵D的关系并说明理由.(3)观察图(3)和(4)已知AB∵CD猜想图中的∵BPD与∵B、∵D的关系不需要说明理由.【答案】(1)∵B+∵BPD+∵D=360° 理由见解析;(2)∵BPD=∵B+∵D理由见解析;(3)∵BPD=∵D-∵B或∵BPD=∵B-∵D理由见解析【详解】解:(1)如图(1)过点P作EF∵AB∵∵B+∵BPE=180°∵AB∵CD EF∵AB∵EF∵CD∵∵EPD+∵D=180°∵∵B+∵BPE+∵EPD+∵D=360°∵∵B+∵BPD+∵D=360°.(2)∵BPD=∵B+∵D.理由:如图2 过点P作PE∵AB∵AB∵CD∵PE∵AB∵CD∵∵1=∵B∵2=∵D∵∵BPD=∵1+∵2=∵B+∵D.(3)如图(3)∵BPD=∵D-∵B.理由:∵AB∵CD∵∵1=∵D∵∵1=∵B+∵BPD∵∵D=∵B+∵BPD即∵BPD=∵D-∵B;如图(4)∵BPD=∵B-∵D.理由:∵AB ∵CD∵∵1=∵B∵∵1=∵D +∵BPD∵∵B =∵D +∵BPD即∵BPD =∵B -∵D .【变式训练2】已知//AM CN 点B 为平面内一点 AB BC ⊥于B .(1)如图1 点B 在两条平行线外 则A ∠与C ∠之间的数量关系为______; (2)点B 在两条平行线之间 过点B 作BD AM ⊥于点D . ①如图2 说明ABD C ∠=∠成立的理由;②如图3 BF 平分DBC ∠交DM 于点,F BE 平分ABD ∠交DM 于点E .若180,3FCB NCF BFC DBE ∠∠∠∠+=︒= 求EBC ∠的度数.【答案】(1)∵A +∵C =90°;(2)①见解析;②105°【详解】解:(1)如图1 AM 与BC 的交点记作点O∵AM ∵CN∵∵C =∵AOB∵AB ∵BC∵∵A +∵AOB =90°∵∵A +∵C =90°;(2)①如图2 过点B作BG∵DM∵BD∵AM∵DB∵BG∵∵DBG=90°∵∵ABD+∵ABG=90°∵AB∵BC∵∵CBG+∵ABG=90°∵∵ABD=∵CBG∵AM∵CN BG∵DMBG CN//,∵∵C=∵CBG∵ABD=∵C;②如图3 过点B作BG∵DM∵BF平分∵DBC BE平分∵ABD∵∵DBF=∵CBF∵DBE=∵ABE由(2)知∵ABD=∵CBG∵∵ABF=∵GBF设∵DBE=α∵ABF=β则∵ABE=α∵ABD=2α=∵CBG∵GBF=∵AFB=β∵BFC=3∵DBE=3α∵∵AFC=3α+β∵∵AFC+∵NCF=180° ∵FCB+∵NCF=180° ∵∵FCB=∵AFC=3α+β∵BCF中由∵CBF+∵BFC+∵BCF=180°得:2α+β+3α+3α+β=180°∵AB∵BC∵β+β+2α=90°∵α=15° ∵∵ABE=15°∵∵EBC=∵ABE+∵ABC=15°+90°=105°.类型四、齿距模型例.如图AB∵EF设∵C=90° 那么x y z的关系式为______.【答案】y=90°-x+z.【详解】解:作CG//AB DH//EF∵AB//EF∵AB//CG//HD//EF∵∵x=∵1 ∵CDH=∵2 ∵HDE=∵z∵∵BCD=90°∵∵1+∵2=90°∵y=∵CDH+∵HDE=∵z+∵2∵∵2=90°-∵1=90°-∵x∵∵y=∵z+90°-∵x.即y=90°-x+z.【变式训练1】如图1 已知AB ∵CD ∵B =30° ∵D =120°;(1)若∵E =60° 则∵F = ;(2)请探索∵E 与∵F 之间满足的数量关系?说明理由;(3)如图2 已知EP 平分∵BEF FG 平分∵EFD 反向延长FG 交EP 于点P 求∵P 的度数.【答案】(1)90︒;(2)30F E ∠=∠+︒ 理由见解析;(3)15︒【详解】(1)解:如图1 分别过点E F 作//EM AB //FN AB////EM AB FN ∴30B BEM ∴∠=∠=︒ MEF EFN ∠=∠又//AB CD //AB FN//CD FN ∴180D DFN ∴∠+∠=︒又120D ∠=︒60DFN ∴∠=︒30BEF MEF ∴∠=∠+︒ 60EFD EFN ∠=∠+︒60EFD MEF ∴∠=∠+︒3090EFD BEF ∴∠=∠+︒=︒;故答案为:90︒;(2)解:如图1 分别过点E F 作//EM AB //FN AB////EM AB FN ∴30B BEM ∴∠=∠=︒ MEF EFN ∠=∠又//AB CD //AB FN//CD FN ∴又120D ∠=60DFN ∴∠=BEF MEF ∴∠=∠EFD MEF ∴∠=∠(3)解:如图设2BEF ∠=EP 平分PEF ∴∠=//FH EP HFG ∠=【变式训练2】如图1 点A 、B 分别在直线GH 、MN 上 GAC NBD ∠=∠ C D ∠=∠.(1)求证://GH MN ;(提示:可延长AC 交MN 于点P 进行证明) (2)如图2 AE 平分GAC ∠ DE 平分BDC ∠ 若AED GAC ∠=∠ 求GAC ∠与ACD ∠之间的数量关系;(3)在(2)的条件下 如图3 BF 平分DBM ∠ 点K 在射线BF 上 13KAG GAC ∠=∠ 若AKB ACD ∠=∠ 直接写出GAC ∠的度数.∵ACD C ∠=∠∵//AP BD∵NBD NPA ∠=∠∵GAC NBD ∠=∠∵GAC NPA ∠=∠∵//GH MN ;(2)延长AC 交MN 于点P 交DE 于点Q∵180E EAQ AQE ∠+∠+∠=° 180AQE AQD ∠+∠=° ∵AQD E EAQ ∠=∠+∠∵//AP BD∵AQD BDQ ∠=∠∵BDQ E EAQ ∠=∠+∠∵AE 平分GAC ∠ DE 平分BDC ∠∵2GAC EAQ ∠=∠ 2CDB BDQ ∠=∠∵2CDB E GAC ∠=∠+∠∵AED GAC ∠=∠ ACD CDB ∠=∠∵23ACD GAC GAC GAC ∠=∠+∠=∠;(3)当K 在直线GH 下方时 如图 设射线BF 交GH 于I⎫.⎪⎭上方时如图-∠(180GAC⎫.⎪⎭°︒。
(完整版)初一下册数学角度几何解析题以及练习题(附答案).doc

七年级下册数学几何解析题以及练习题(附答案)9.(2011 ·扬州 ) 如图,C岛在A岛的北偏东60°方向,在B岛的北偏西 45°方向,则从C岛看 A、 B 两岛的视角∠ ACB=________.答案105°解析如图,∵ (60 °+∠CAB)+(45 °+∠ABC)=180°,∴∠CAB+∠ABC=75°,在△ ABC中,得∠ C=105°.12.如图所示,在△ABC中,∠ A=80°,∠ B=30°, CD平分∠ ACB, DE∥AC.(1)求∠ DEB的度数;(2)求∠ EDC的度数.解(1) 在△ABC中,∠A=80°,∠B=30°,∴∠ ACB=180°-∠ A-∠ B=70°.∵ DE∥AC,∴∠ DEB=∠ ACB=70°.(2)∵ CD平分∠ ACB,1∴∠ DCE=2∠ ACB=35°.∵∠ DEB=∠ DCE+∠ EDC,∴∠ EDC=70°-35°=35°.13.已知,如图,∠1=∠ 2,CF⊥AB于F,DE⊥AB于E,求证:FG∥BC.( 请将证明补充完整 )证明∵ CF⊥ AB, DE⊥ AB(已知),∴ ED∥FC() .∴∠ 1=∠BCF() .又∵∠ 1=∠ 2( 已知 ) ,1∴ FG ∥BC () .解 在同一平面内, 垂直于同一直线的两条直线互相平行;两直线平行, 同位角相等;内错角相等,两直线平行.14.如图,已知三角形ABC ,求证:∠ A +∠ B +∠ C =180°.分析:通过画平行线,将∠A 、∠B 、∠C 作等角代换,使各角之和恰为一平角,依辅助线不同而得多种证法,如下:证法 1:如图甲,延长 BC 到 D ,过 C 画 CE ∥ BA .∵BA ∥ CE ( 作图所知 ) ,∴∠ B =∠ 1,∠ A =∠ 2( 两直线平行,同位角、内错角相等) .又∵∠ BCD =∠ BCA +∠ 2+∠ 1=180°( 平角的定义 ) ,∴∠ A +∠ B +∠ ACB =180°( 等量代换 ) .如图乙,过 BC 上任一点 F ,画 FH ∥AC , FG ∥ AB ,这种添加辅助线的方法能证明∠A +∠B +∠C =180°吗?请你试一试.解 ∵ FH ∥AC ,∴∠ BHF =∠ A ,∠ 1=∠ C .∵ FG ∥AB ,∴∠ BHF =∠ 2,∠ 3=∠ B ,∴∠ 2=∠ A .∵∠ BFC =180°,∴∠ 1+∠ 2+∠ 3=180°,即∠ A +∠ B +∠ C =180°.15.(2010 ·玉溪 ) 平面内的两条直线有相交和平行两种位置关系.(1) 如图 a ,若 AB ∥ CD ,点 P 在 AB 、 CD 外部,则有∠ B =∠ BOD .又因∠ BOD 是△ POD的外角,故∠ BOD =∠ BPD +∠ D ,得∠ BPD =∠ B -∠ D . 将点 P 移到 AB 、CD 内部,如图 b ,以上结论是否成立?若成立,说明理由;若不成立,则∠、∠ 、∠ D 之BPD B间有何数量关系?请证明你的结论;(2) 在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点 Q,如图 c,则∠ BPD、∠ B、∠ D、∠ BQD之间有何数量关系?( 不需证明 )(3)根据 (2) 的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.解(1) 不成立,结论是∠BPD=∠B+∠D.延长 BP交 CD于点 E,∵ AB∥CD,∴∠ B=∠ BED.又∠ BPD=∠ BED+∠ D,∴∠ BPD=∠ B+∠ D.(2)结论:∠ BPD=∠ BQD+∠ B+∠ D.(3)设 AC与 BF交于点 G.由 (2) 的结论得:∠AGB=∠ A+∠ B+∠ E.又∵∠ AGB=∠ CGF,∠ CGF+∠ C+∠ D+∠ F=360°,∴∠ A+∠ B+∠ C+∠D+∠ E+∠ F=360°.A 14.把一副常用的三角板如图所示拼在一起,那么图中∠ADE是度. DEBC第 14 题2.如图,在△ ABC和△ ABD中,现给出如下三个论断:①AD=BC;②∠C=∠D;③∠1=∠2。
2024年数学七年级下册几何基础练习题(含答案)

2024年数学七年级下册几何基础练习题(含答案)试题部分一、选择题(每题2分,共20分)1. 在一个等边三角形中,每个角的度数是()。
A. 60°B. 90°C. 120°D. 180°2. 下列哪个图形是一个四边形?()A. 圆B. 三角形C. 正方形D. 直线3. 一个三角形的两个角分别是30°和60°,那么第三个角的度数是()。
A. 30°B. 60°C. 90°D. 120°4. 下列哪个图形是一个平行四边形?()A. 矩形C. 正方形D. 菱形5. 一个等腰三角形的底边长度是10厘米,腰长是12厘米,那么这个三角形的周长是()厘米。
A. 22B. 24C. 26D. 286. 下列哪个图形是一个圆形?()A. 正方形B. 长方形C. 椭圆D. 三角形7. 一个三角形的两个边长分别是5厘米和8厘米,那么这个三角形的周长最小可能是()厘米。
A. 10B. 12C. 13D. 148. 下列哪个图形是一个梯形?()A. 正方形B. 矩形C. 平行四边形9. 一个等腰三角形的底边长度是8厘米,腰长是10厘米,那么这个三角形的周长是()厘米。
A. 18B. 20C. 22D. 2410. 下列哪个图形是一个正方形?()A. 长方形B. 梯形C. 菱形D. 圆二、判断题(每题2分,共10分)1. 一个等边三角形的每个角都是60°。
()2. 一个四边形的内角和是360°。
()3. 一个等腰三角形的两个腰长相等。
()4. 一个正方形的四个角都是90°。
()5. 一个三角形的两个边长分别是5厘米和8厘米,那么这个三角形的周长最小可能是13厘米。
()以上是一个练习题的示例,你可以根据实际情况进行调整和扩展。
希望对你有所帮助!一、选择题(每题2分,共20分)1. 在一个等边三角形中,每个角的度数是()。
人教版初中数学几何图形初步技巧及练习题附答案

人教版初中数学几何图形初步技巧及练习题附答案一、选择题1.如图是某个几何体的展开图,该几何体是()A.三棱柱B.圆锥C.四棱柱D.圆柱【答案】A【解析】【分析】侧面为三个长方形,底边为三角形,故原几何体为三棱柱.【详解】解:观察图形可知,这个几何体是三棱柱.故选A.【点睛】本题考查的是三棱柱的展开图,对三棱柱有充分的理解是解题的关键..2.将如图所示的Rt△ACB绕直角边AC旋转一周,所得几何体的主视图(正视图)是()A.B.C.D.【答案】D【解析】解:Rt△ACB绕直角边AC旋转一周,所得几何体是圆锥,主视图是等腰三角形.故选D.首先判断直角三角形ACB绕直角边AC旋转一周所得到的几何体是圆锥,再找出圆锥的主3.将一副三角板如下图放置,使点A 落在DE 上,若BC DE ,则AFC ∠的度数为( )A .90°B .75°C .105°D .120°【答案】B【解析】【分析】 根据平行线的性质可得30E BCE ==︒∠∠,再根据三角形外角的性质即可求解AFC ∠的度数.【详解】∵//BC DE∴30E BCE ==︒∠∠∴453075AFC B BCE =+=︒+︒=︒∠∠∠故答案为:B .【点睛】本题考查了三角板的角度问题,掌握平行线的性质、三角形外角的性质是解题的关键.4.在等腰ABC ∆中,AB AC =,D 、E 分别是BC ,AC 的中点,点P 是线段AD 上的一个动点,当PCE ∆的周长最小时,P 点的位置在ABC ∆的( )A .重心B .内心C .外心D .不能确定【答案】A【解析】【分析】 连接BP ,根据等边三角形的性质得到AD 是BC 的垂直平分线,根据三角形的周长公式、两点之间线段最短解答即可.【详解】∵AB=AC,BD=BC,∴AD⊥BC,∴PB=PC,∴PC+PE=PB+PE,+≥,∵PB PE BE∴当B、P、E共线时,PC+PE的值最小,此时BE是△ABC的中线,∵AD也是中线,∴点P是△ABC的重心,故选:A.【点睛】此题考查等腰三角形的性质,轴对称图形中最短路径问题,三角形的重心定义.5.某包装盒如下图所示,则在下列四种款式的纸片中,可以是该包装盒的展开图的是()A.B.C.D.【答案】A【解析】【分析】将展开图折叠还原成包装盒,即可判断正确选项.解:A、展开图折叠后如下图,与本题中包装盒相同,故本选项正确;B、展开图折叠后如下图,与本题中包装盒不同,故本选项错误;C、展开图折叠后如下图,与本题中包装盒不同,故本选项错误;D、展开图折叠后如下图,与本题中包装盒不同,故本选项错误;故选:A.本题主要考查了含图案的正方体的展开图,学生要经历一定的实验操作过程,当然学生也可以将操作活动转化为思维活动,在头脑中模拟(想象)折纸、翻转活动,较好地考查了学生空间观念.6.下列各图经过折叠后不能围成一个正方体的是()A.B.C.D.【答案】D【解析】【分析】由平面图形的折叠及正方体的表面展开图的特点解题.只要有“田”“凹”“一线超过四个正方形”字格的展开图都不是正方体的表面展开图.【详解】解:A、是正方体的展开图,不符合题意;B、是正方体的展开图,不符合题意;C、是正方体的展开图,不符合题意;D、不是正方体的展开图,缺少一个底面,符合题意.故选:D.【点睛】本题考查了正方体的展开图,解题时勿忘记四棱柱的特征及正方体展开图的各种情形.7.如下图,将直角三角形绕一条边所在直线旋转一周后形成的几何体不可能是()A.B.C.D.【答案】C【解析】【分析】分三种情况讨论,即可得到直角三角形绕一条边所在直线旋转一周后形成的几何体.【详解】解:将直角三角形绕较长直角边所在直线旋转一周后形成的几何体为:将直角三角形绕较短直角边所在直线旋转一周后形成的几何体为:将直角三角形绕斜边所在直线旋转一周后形成的几何体为:故选C.【点睛】本题考查了面动成体,点、线、面、体组成几何图形,点、线、面、体的运动组成了多姿多彩的图形世界.8.如图,是一个正方体的表面展开图,将其折成正方体后,则“扫”的对面是()A.黑B.除C.恶D.☆【答案】B【解析】【分析】正方体的空间图形,从相对面入手,分析及解答问题.【详解】解:将其折成正方体后,则“扫”的对面是除.故选B.【点睛】本题考查了正方体的相对面的问题.能够根据正方体及其表面展开图的特点,找到相对的面是解题的关键.9.如图,一个正六棱柱的表面展开后恰好放入一个矩形内,把其中一部分图形挪动了位置,发现矩形的长留出5cm ,宽留出1,cm 则该六棱柱的侧面积是( )A .210824(3) cm -B .()2108123cm -C .()254243cm -D .()254123cm -【答案】A【解析】【分析】 设正六棱柱的底面边长为acm ,高为hcm ,分别表示出挪动前后所在矩形的长与宽,由题意列出方程求出a =2,h =9−23,再根据六棱柱的侧面积是6ah 求解.【详解】解:设正六棱柱的底面边长为acm ,高为hcm ,如图,正六边形边长AB =acm 时,由正六边形的性质可知∠BAD =30°,∴BD =12a cm ,AD =32a cm , ∴AC =2AD =3a cm ,∴挪动前所在矩形的长为(2h +3a )cm ,宽为(4a +12a )cm , 挪动后所在矩形的长为(h +2a 3a )cm ,宽为4acm , 由题意得:(2h +3)−(h +2a 3a )=5,(4a +12a )−4a =1, ∴a =2,h =9−23∴该六棱柱的侧面积是6ah =6×2×(9−232108(3) cm -;故选:A .【点睛】本题考查了几何体的展开图,正六棱柱的性质,含30度角的直角三角形的性质;能够求出正六棱柱的高与底面边长是解题的关键.10.一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”字对面的字是()A.中B.考C.顺D.利【答案】C【解析】试题解析:正方体的表面展开图,相对的面之间一定相隔一个正方形,“祝”与“考”是相对面,“你”与“顺”是相对面,“中”与“立”是相对面.故选C.考点:正方体展开图.11.如图,小慧从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C 处,此时需要将方向调整到与出发时一致,则方向的调整应为()A.左转80°B.右转80°C.左转100°D.右转100°【答案】B【解析】【分析】如图,延长AB到D,过C作CE//AD,由题意可得∠A=60°,∠1=20°,根据平行线的性质可得∠A=∠2,∠3=∠1+∠2,进而可得答案.【详解】如图,延长AB到D,过C作CE//AD,∵此时需要将方向调整到与出发时一致,∴此时沿CE方向行走,∵从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,∴∠A=60°,∠1=20°,AM ∥BN ,CE ∥AB ,∴∠A=∠2=60°,∠1+∠2=∠3∴∠3=∠1+∠2=20°+60°=80°,∴应右转80°.故选B.【点睛】本题考查了方向角有关的知识及平行线的性质,解答时要注意以北方为参照方向,进行角度调整.12.如图,AB CD ∥,BF 平分ABE ∠,且BF DE ,则ABE ∠与D ∠的关系是( )A .2ABE D ∠=∠B .180ABE D ∠+∠=︒C .90ABED ∠=∠=︒D .3ABE D ∠=∠【答案】A【解析】【分析】 延长DE 交AB 的延长线于G ,根据两直线平行,内错角相等可得D G ∠=∠,再根据两直线平行,同位角相等可得G ABF ∠=∠,然后根据角平分线的定义解答.【详解】证明:如图,延长DE 交AB 的延长线于G ,//AB CD ,D G ∴∠=∠,//BF DE ,G ABF ∴∠=∠,D ABF ∴∠=∠, BF 平分ABE ∠,22ABE ABF D ∴∠=∠=∠,即2ABE D ∠=∠.故选:A .【点睛】本题考查了平行线的性质,角平分线的定义,熟记性质并作辅助线是解题的关键.13.如图,ABC ∆为等边三角形,点P 从A 出发,沿A B C A →→→作匀速运动,则线段AP 的长度y 与运动时间x 之间的函数关系大致是( )A .B .C .D .【答案】B【解析】【分析】根据题意可知点P 从点A 运动到点B 时以及从点C 运动到点A 时是一条线段,故可排除选项C 与D ;点P 从点B 运动到点C 时,y 是x 的二次函数,并且有最小值,故选项B 符合题意,选项A 不合题意.【详解】根据题意得,点P 从点A 运动到点B 时以及从点C 运动到点A 时是一条线段,故选项C 与选项D 不合题意;点P 从点B 运动到点C 时,y 是x 的二次函数,并且有最小值,∴选项B 符合题意,选项A 不合题意.故选B .【点睛】本题考查了动点问题的函数图象:通过分类讨论,利用三角形面积公式得到y 与x 的函数关系,然后根据二次函数和一次函数图象与性质解决问题.14.如图是正方体的表面展开图,请问展开前与“我”字相对的面上的字是( )A .是B .好C .朋D .友【答案】A【解析】【分析】 正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.【详解】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“我”与“是”是相对面,“们”与“朋”是相对面,“好”与“友”是相对面.故选:A .【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.15.如图,将一副三角板如图放置,∠COD=28°,则∠AOB 的度数为( )A .152°B .148°C .136°D .144°【答案】A【解析】【分析】 根据三角板的性质得90AOD BOC ∠=∠=︒,再根据同角的余角相等可得62AOC BOD ==︒∠∠,即可求出∠AOB 的度数.【详解】∵这是一副三角板∴90AOD BOC ∠=∠=︒∵28COD =︒∠∴62AOC BOD ==︒∠∠∴62+28+62=152AOB AOC COD BOD =++=︒︒︒︒∠∠∠∠故答案为:A .【点睛】本题考查了三角板的度数问题,掌握三角板的性质、同角的余角相等是解题的关键.16.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )A .30°B .25°C .20°D .15°【答案】B【解析】根据题意可知∠1+∠2+45°=90°,∴∠2=90°﹣∠1﹣45°=25°,17.如图,一副三角尺按不同的位置摆放,下列摆放方式中∠α与∠β互余的是( ) A . B .C .D .【答案】A【解析】【分析】根据同角的余角相等,等角的补角相等和邻补角的定义对各小题分析判断即可得解.【详解】A 、图中∠α+∠β=180°﹣90°=90°,∠α与∠β互余,故本选项正确;B 、图中∠α=∠β,不一定互余,故本选项错误;C 、图中∠α+∠β=180°﹣45°+180°﹣45°=270°,不是互余关系,故本选项错误;D 、图中∠α+∠β=180°,互为补角,故本选项错误.故选:A .【点睛】此题考查余角和补角,熟记概念与性质是解题的关键.18.如图,DE∥BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为()A.20°B.35°C.55°D.70°【答案】B【解析】【分析】根据平行线的性质可得∠1=∠ABC=70°,再根据角平分线的定义可得答案.【详解】∵DE∥BC,∴∠1=∠ABC=70°,∵BE平分∠ABC,∴1352CBE ABC∠=∠=︒,故选:B.【点睛】此题主要考查了平行线的性质,以及角平分线的定义,解题的关键是掌握两直线平行,内错角相等.19.如图是画有一条对角线的平行四边形纸片ABCD,用此纸片可以围成一个无上下底面的三棱柱纸筒,则所围成的三棱柱纸筒可能是()A.B. C.D.【答案】C【解析】【分析】由三棱柱侧面展开图示是长方形,但只需将平行四边线变形成一个长方形,再根据长方形围成的三棱柱不能为斜的进行判断即可.【详解】因为三棱柱侧面展开图示是长方形,所以平行四边形要变形成一个长方形,如图所示:又因为长方形围成的三棱柱不是斜的,所以排除A、B、D,只有C符合.故选:C.【点睛】考查了学生空间想象能力和三棱柱的展示图形,解题关键是抓住三棱柱侧面展开图示是长方形和长方形围成的三棱柱不能为斜的.∠=∠的图形的个数是()20.如图,一副三角尺按不同的位置摆放,摆放位置中αβA.1B.2C.3D.4【答案】C【解析】【分析】根据直角三角板可得第一个图形∠β=45°,进而可得∠α=45°;根据余角和补角的性质可得第二个图形、第四个图形中∠α=∠β,第三个图形∠α和∠β互补.【详解】根据角的和差关系可得第一个图形∠α=∠β=45°,根据等角的补角相等可得第二个图形∠α=∠β,第三个图形∠α+∠β=180°,不相等,根据同角的余角相等可得第四个图形∠α=∠β,因此∠α=∠β的图形个数共有3个,故选:C.【点睛】此题主要考查了余角和补角,关键是掌握余角和补角的性质:等角的补角相等.等角的余角相等.。
七年级上册数学几何作图(习题及答案)

几何作图(习题)➢例题示范例1 :在直线l 上任取一点 A ,截取AB=20cm ,再截取BC=50cm,则AB 的中点D 与AC 的中点E 之间的距离为,并作图说明.思路分析首先,理解题意,找关键词,其中l 为直线,AB,BC 为l 上的两条线段.其次,设计作图方案,作图.作直线l,任取一点作为A,取适当长作为AB;此时点B 位置固定,但点C 可在点B 左侧或右侧,位置不定,故分两种情况.①点C 在点 B 左侧,如图,接着取AB 的中点D,AC 的中点E.设计算法:DE =AD +AE=1AB +1AC 2 2=1 BC 2= 25②点C 在点 B 右侧,如图,接着取AB 的中点D,AC 的中点E.设计算法:DE =AE -AD=1AC -1AB 2 2=1 BC 2= 25综上,DE 的长度为25cm.➢巩固练习1.如图1,点C,D 是直线AB 外两点,按下列要求作图:(1);(2).得到的图形如图2,请在横线填上作法.2.如图,已知线段AB,按要求作图:①分别以点A 和点B 为圆心、以AB 的长为半径作弧,两弧相交于点C 和点D;②作直线CD,交线段AB 于点E;③请通过测量猜想线段AB 和直线CD 的位置关系,线段AE 与线段BE 的数量关系.23.作图:已知线段a,b(a>b),作一条线段,使它等于a-b.(保留作图痕迹,不必写作法)4.已知线段AB=15cm,点C 在直线AB 上,且BC=2AB,则线段AC 的长为,并作图说明.5.已知点C 在直线AB 上,若AC=4cm,BC=6cm,E,F 分别为线段AC,BC 的中点,则EF 的长为,并作图说明.6.已知线段AB=24,点C 在直线AB 上,BC=3AC,M,N 分别为线段AB,AC 的中点,则MN 的长为,并作图说明.7.已知从点O 出发的三条射线OA,OB,OC,若∠AOB=60°,∠AOC 1∠AOB ,则∠BOC 的度数为,3并作图说明.8.已知∠AOB 为直角,∠BOC=40°,OM 平分∠AOB,ON 平分∠BOC,则∠MON 的度数为,并作图说明.9.已知∠AOB=120°,∠AOC=4∠BOC,OD 平分∠AOB,OE平分∠AOC,则∠EOD 的度数为,并作图说明.➢思考小结1. 我们学过的需要分类讨论的情况:第一类:由定义本身引起的.比如:已知x + 2 = 3 ,y = 3 ,求xy的值.思路分析由绝对值的定义,得x= ,y=然后借助进行分类讨论,求解可得xy=.第二类:位置不确定引起的.比如:习题中的第9题.思路分析首先可画出∠AOB,然后根据题意画出射线OC,但射线OC 的位置不确定,所以要分情况讨论:①射线OC在∠AOB的内部;②射线OC在∠AOB的.【参考答案】➢巩固练习1.(1)作射线DC 交AB 于点E(2)过点C 作CF⊥DE 于点C,交AB 于点 F2.作图略,AB⊥CD,AE=BE3.作图略4.15cm 或45cm,作图说明略5.1cm 或5cm,作图说明略6.9 或18,作图说明略7.40°或80°,作图说明略8. 25°或65°,作图说明略9. 12°或20°,作图说明略➢思考小结1. -5 或1,±3,树状图,±3 或±15.外部,图略。
初一下册数学角度几何解析题以及练习题(附答案)汇编

七年级下册数学几何解析题以及练习题(附答案)9.(2011·扬州)如图,C 岛在A 岛的北偏东60°方向,在B 岛的北偏西45°方向,则从C 岛看A 、B 两岛的视角∠ACB =________.答案 105°解析 如图,∵(60°+∠CAB )+(45°+∠ABC )=180°,∴∠CAB +∠ABC =75°,在△ABC 中,得∠C =105°.12.如图所示,在△ABC 中,∠A =80°,∠B =30°,CD 平分∠ACB ,DE ∥AC .(1)求∠DEB 的度数; (2)求∠EDC 的度数.解 (1)在△ABC 中,∠A =80°,∠B =30°,∴∠ACB =180°-∠A -∠B =70°. ∵DE ∥AC ,∴∠DEB =∠ACB =70°. (2)∵CD 平分∠ACB , ∴∠DCE =12∠ACB =35°.∵∠DEB =∠DCE +∠EDC , ∴∠EDC =70°-35°=35°.13.已知,如图,∠1=∠2,CF ⊥AB 于F ,DE ⊥AB 于E ,求证:FG ∥BC .(请将证明补充完整)证明 ∵CF ⊥AB ,DE ⊥AB (已知),∴ED ∥FC ( ). ∴∠1=∠BCF ( ). 又∵∠1=∠2(已知), ∴∠2=∠BCF (等量代换),∴FG∥BC( ).解在同一平面内,垂直于同一直线的两条直线互相平行;两直线平行,同位角相等;内错角相等,两直线平行.14.如图,已知三角形ABC,求证:∠A+∠B+∠C=180°.分析:通过画平行线,将∠A、∠B、∠C作等角代换,使各角之和恰为一平角,依辅助线不同而得多种证法,如下:证法1:如图甲,延长BC到D,过C画CE∥BA.∵BA∥CE(作图所知),∴∠B=∠1,∠A=∠2(两直线平行,同位角、内错角相等).又∵∠BCD=∠BCA+∠2+∠1=180°(平角的定义),∴∠A+∠B+∠ACB=180°(等量代换).如图乙,过BC上任一点F,画FH∥AC,FG∥AB,这种添加辅助线的方法能证明∠A+∠B+∠C=180°吗?请你试一试.解∵FH∥AC,∴∠BHF=∠A,∠1=∠C.∵FG∥AB,∴∠BHF=∠2,∠3=∠B,∴∠2=∠A.∵∠BFC=180°,∴∠1+∠2+∠3=180°,即∠A+∠B+∠C=180°.15.(2010·玉溪)平面内的两条直线有相交和平行两种位置关系.(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD.又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;(2)在图b 中,将直线AB 绕点B 逆时针方向旋转一定角度交直线CD 于点Q ,如图c ,则∠BPD 、∠B 、∠D 、∠BQD 之间有何数量关系?(不需证明) (3)根据(2)的结论求图d 中∠A +∠B +∠C +∠D +∠E +∠F 的度数.解 (1)不成立,结论是∠BPD =∠B +∠D .延长BP 交CD 于点E , ∵AB ∥CD ,∴∠B =∠BED . 又∠BPD =∠BED +∠D , ∴∠BPD =∠B +∠D .(2)结论:∠BPD =∠BQD +∠B +∠D . (3)设AC 与BF 交于点G .由(2)的结论得:∠AGB =∠A +∠B +∠E .又∵∠AGB =∠CGF ,∠CGF +∠C +∠D +∠F =360°,∴∠A +∠B +∠C +∠D +∠E +∠F =360°.14.把一副常用的三角板如图所示拼在一起,那么图中∠ADE 是 度.2.如图,在△ABC 和△ABD 中,现给出如下三个论断:①AD =BC ;②∠C =∠D ;③∠1=∠2。
人教版七年级下册数学二元一次方程组---几何问题训练
人教版七年级下册数学8.3 二元一次方程组---几何问题训练一、单选题1.如图,现有四个大小相同的长方形,可拼成如图①和图①所示的图形,在拼图①时,中间留下了一个面积为4的小正方形,则每个小长方形的面积是()A.3B.4C.5D.62.如图,在长为20m,宽为16m的长方形空地中,沿平行于长方形各边的方向修建三个相同的小长方形花圃,则每个小长方形的面积是()A.24m2B.32m2C.40m2D.48m23.如图,在长为15,宽为12的矩形中,有形状、大小完全相同的5个小矩形,则图中阴影部分的面积为()A.35B.45C.55D.654.一个大正方形和四个相同的小正方形按图①、①两种方式摆放,则图①的大正方形中未被小正方形覆盖部分的面积是()A.36B.48C.96D.1285.如图,在长为30米,宽为20米的长方形花园里,原有两条面积相等的小路,其余部分绿化.现在为了增加绿地面积,把公园里的一条小路改为绿地,只保留另一条小路,并且使得绿地面积是小路面积的4倍,则x与y的值分别为()A.3,2B.5,4C.6,5D.6,46.如图所示的是由截面为同一种长方形的墙砖粘贴的部分墙面,其中三块横放的墙砖比两块竖放的墙砖低30cm,两块竖放的墙砖比两块横放的墙砖高50cm,则每块墙砖的截面面积是()A.400cm2B.600cm2C.800cm2D.900cm27.相同规格(长为14,宽为8)的长方形硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形......的长方体箱子,有如图所示的甲、乙两种方案,所得长方体体积分别记为:V甲和V乙.下列说法正确的是:()A .V V >甲乙B .V V =甲乙C .V V <甲乙D .无法判断 8.用如图①中的长方形和正方形纸板作侧面和底面,做成如图①的竖式和横式的两种无盖纸盒,现有m 张正方形纸板和n 张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,则m n +的值可能是( )A .2020B .2021C .2022D .2023二、填空题9.如图,用8块相同的长方形地砖拼成了一个长方形图案(地砖间的缝隙忽略不计),则每块地砖的长为________cm .10.在矩形ABCD 中,放入六个形状、大小相同的长方形,尺寸如图所示,则阴影部分的面积是___cm 2.11.利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图①所示的方式放置.测量的数据如图,则桌子的高度等于______.CD ,则长方形12.如图,由七个完全一样的小长方形组成的大长方形ABCD,7ABCD的周长为______.13.把10个相同的小长方形拼接成如图所示的一个大长方形(尺寸如图所示),这个大长方形的面积为_____cm2.EF AB GH BC E F G H在14.如图,Р是长方形ABCD内一点,过点Р分别作//,//(,,,EF GH就把长方形ABCD分割成四个小长方形﹐若其中长长方形的各边上),这样,,方形BEPG的面积是其周长的1.5倍﹐长方形AGPF和长方形PECH的面积均为2,则长方形PHDF的周长为____.15.在长为20m、宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则每个小长方形花圃的面积是________ 2m.16.如图,由4个形状大小相同的长方形,拼成1个面积为81的大正方形,若中间小正方形的面积为9,则1个长方形的长、宽分别是______.三、解答题17.如图(1),将边长为x cm的大正方形剪去一个边长为y cm的小正方形,剩余部分的面积为21cm2,并将剩余部分沿虚线剪开得到两个长方形,再将这两个长方形拼成如图(2),且宽为3cm的长方形,请你求出大正方形和小正方形的边长.18.某单位准备将一块周长为46米的长方形草地,设计成长宽分别相等的8块小长方形(如图所示)种上各种花卉,经过市场预测,每平方米绿化造价约为100元,求每个小长方形的长和宽,并求完成这项绿化工程的预计投资.19.如图,在大长方形里画出三个形状大小均一样的小长方形(图中阴影部分).(1)如图1,若大长方形的长宽分别为45和30,求小长方形的周长.(2)如图2,若大长方形的长宽分别为a和b,小长方形的长宽分别为x和y.①请求出小长方形与大长方形的周长之比;①若图中阴影部分面积与空白部分面积之比1①2,则求:x y的值.20.如图①中的长方形和正方形纸板作侧面和底面,做成如图①的竖式和横式两种无盖纸盒,现在仓库里有1000张正方形纸板和2000张长方形纸板.(1)根据题意完成下表格.(2)问两种纸盒各做多少个,恰好将库存的纸板用完?参考答案:1.A2.B3.B4.B5.D6.D7.A8.A9.2110.4411.75cm12.3413.768014.4 315.3216.6,317.大正方形的边长为5cm,小正方形的边长为2cm18.每个小正方形的宽为3m,长为5m.完成这块绿化工程预计投入资金12000元19.(1)50米;(2)①1:3;①120.(1)x,4x,2y,3y;(2)200,400。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何作图(习题)
例题示范
例 1:在直线l 上任取一点A,截取AB=20cm,再截取BC=50cm,则AB 的中点D 与AC 的中点E 之间的距离为
,并作图说明.思
路分析
首先,理解题意,找关键词,其中l 为直线,AB,BC 为l 上的两条线段.
其次,设计作图方案,作图.
作直线l,任取一点作为A,取适当长作为AB;
此时点B 位置固定,但点C 可在点B 左侧或右侧,位置不定,故分两种情况.
①点C 在点B 左侧,如图,
50
l
C A B
20
接着取AB 的中点D,AC 的中点E.
50
l
C E 设计算法:A
D B
20
DE =AD +AE
=1
AB +
1
AC 2 2
=1 BC 2
= 25
②点C 在点B 右侧,如图,
20 50
l
A B C
接着取AB 的中点D,AC 的中点E.
20 50
l
A D
B E C
设计算法:
DE = AE - AD
= 1 AC - 1 AB
2 2
= 1 BC
2
= 25
综上,DE 的长度为 25cm .
巩固练习
1. 如图 1,点 C ,D 是直线 AB 外两点,按下列要求作图:
(1)
; (2)
. 得到的图形如图 2,请在横线填上作法. D
D
C
A
B 图1
图2 2. 如图,已知线段 AB ,按要求作图:①分别以点 A 和点 B 为圆心、以 AB 的
长为半径作弧,两弧相交于点 C 和点 D ;②作直线 CD ,交线段 AB 于点 E ;③请通过测量猜想线段 AB 和直线 CD 的位置关系,线段 AE 与线段 BE 的数量关系.
A B
C A E F B
3.作图:已知线段a,b(a>b),作一条线段,使它等于a -b .(保留作图痕迹
,不必写作法)
a
b
4.已知线段AB=15cm,点C 在直线AB 上,且BC=2AB,则线段A C 的长
为,并作图说明.
5.已知点C 在直线A B 上,若A C=4cm,BC=6cm,E,F 分别为线段AC,
BC 的中点,则E F 的长为,并作图说明.
6.已知线段AB=24,点C 在直线AB 上,BC=3AC,M,N 分别为线段AB
,AC 的中点,则M N 的长为,并作图说明.
7.已知从点O 出发的三条射线OA,OB,OC,若∠AOB=60°,
∠AOC 1
∠AOB ,则∠BOC 的度数为,3
并作图说明.
8.已知∠AOB 为直角,∠BOC=40°,OM 平分∠AOB,ON 平分
∠BOC,则∠MON 的度数为,并作图说明.
9.已知∠AOB=120°,∠AOC=4∠BOC,OD 平分∠AOB,OE 平分∠AOC
,则∠EOD 的度数为,并作图说明.
思考小结
1. 我们学过的需要分类讨论的情况:第一
类:由定义本身引起的.
比如:已知x + 2 = 3 ,y = 3 ,求xy的值.思路分
析
由绝对值的定义,得
x= ,y=
然后借助进行分类讨论,求解可得xy= .第二类:位置不确定引起的.
比如:习题中的第9题.思
路分析
首先可画出∠AOB,然后根据题意画出射线OC,但射线OC 的位置不确定,所以要分情况讨论:
①射线OC在∠AOB的内部;
②射线OC在∠AOB的.
A
O B
【参考答案】
巩固练习
1.(1)作射线DC 交AB 于点E
(2)过点C 作CF⊥DE 于点C,交AB 于点F
2.作图略,AB⊥CD,AE=BE
3.作图略
4.15cm 或45cm,作图说明略
5.1cm 或5cm,作图说明略
6.9 或 18,作图说明略
7.
40°或80°,作图说明略 8.
25°或65°,作图说明略 9.
12°或20°,作图说明略
思考小结
1. -5 或1,±3,树状图,±3 或±15.外部,图略。
