几何画板生成椭圆曲线八种方法
数学中常用几何画板绘制椭圆

数学中常⽤⼏何画板绘制椭圆圆锥曲线是⾼中数学的重点和难点,也是历来⾼考的必考内容,所以对于⾼中⽣来说,弄懂圆锥曲线这块难啃的⾻头,是很有必要的。
其中要熟练掌握的圆锥曲线之⼀就是椭圆,它是圆锥与平⾯的截线,其实要想画出椭圆,其⽅法不⽌⼀种,下⾯就⼀起来通过学学椭圆的五种画法。
⽅法⼀、利⽤椭圆第⼀定义构造椭圆椭圆第⼀定义:平⾯内到两个定点的距离之和等于定长2a(a>0)的点的轨迹就是椭圆,按照此定义可画出椭圆,具体步骤如下:1.单击“圆⼯具”,在画板的适当位置任意画⼀个圆,将圆⼼的标签改为F1。
单击“点⼯具”,在圆上任意画⼀点C,同时选中点F1和点C,执⾏“构造”-“线段”命令,构造出线段F1C。
单击“点⼯具”,在线段F1C任意画⼀点F2。
2.在圆上任意画⼀点E,并构造线段EF1和线段EF2。
选中线段EF2,执⾏“构造”-“中点”命令,构造线段EF2的中点F。
3.选中线段EF2和点F,执⾏“构造”-“垂线”命令,构造出线段EF2的垂直平分线j。
同时选中线段EF1和直线j,选择“构造”-“交点”命令,构造线段EF1和直线j的交点G。
4.选中点G和点E(把点E称做是点G的相关点,改变G点的位置,点E的位置也跟着改变),选择“构造”-“轨迹”命令,可画出椭圆。
拖动点B 和点F2可改变椭圆的形状。
⽅法⼆、利⽤椭圆第⼆定义画椭圆椭圆的第⼆定义:设动点M(x, y)与定点F(c, 0)的距离和它到定直线l: x=a2/c的距离的⽐是常数(a>c>0),则点M的轨迹是椭圆。
点F 是椭圆的⼀个焦点,直线l是椭圆中对应于焦点F的准线,常数e=c/a(0<e<1)。
具体的操作步骤如下:步骤⼀打开⼏何画板,使⽤“点⼯具”画任意⼀点F,使⽤“线⼯具”画直线L(点F不在L上)。
过点F作⼀条直线,在直线上取⼀点P;步骤⼆选中点F、P执⾏“度量”--“距离”命令,度量FP的长度;选中点F和度量的FP的长度,执⾏“构造”--“以圆⼼和半径绘圆”构造以点F为圆⼼,FP为半径的圆。
应用几何画板作椭圆和双曲线

即}IPF.1一』PF。l f—I彳cI—I口cI=lAB}=2a.
V
、、、,、
,tj,
∥遐嘛 \。,磊N’+7 ?Z
、,
X
K、
少弋,,Biblioteka ’画法2:1.以坐标原点0为圆心,分别以a、b(a,b>0)为半径画两个圆: 2.圆OA与x轴的正方向交于点C,过C作x轴的垂线, 3.在圆OA上取一点P,连接OP,直线OP与过点c且和X轴垂直的直 线交于点Ⅳ'过点Ⅳ作x轴的平行线NM; 4.过点P作PR垂直于OP,交X轴于点R:
学教师的“好伙伴”所以自己在数学教学实践不断地总结和探索以提高教 学效果,即使如此也难免有疏漏之处望批评指正。 参考文献:
[1] 《几何画板实例教程》,清华大学出版社2002版. [2] 《数学通报》,998年第12期上.
万方数据
年唪捷博览;43
,/^ y
黔i。 / }
1.,,。.。.一一矿
岁一 。。。f, 迄 \ 、、、~——一一
一.椭■的西法: 画法1: 1.在x轴上取两点F,、E,使】OF,I=l OF2I,用它们作为两个焦点 2.在图形外作一条线段,使它的长度为2a,(2口>f,.‘1): 3.以,I为圆心,2口为半径作圆,在圆上任取一点P;
5.过点R在x轴的垂线交直线NM于点M: 6.分别选中点M和点尸,用“作图”菜单中的“轨迹”功能,画出 双曲线。 理论根据:设么xOP=中, 则IORl=IOP sec中=asec咖,lKMI=NC『=lOC【tg中=btg由, 根据双曲线的参数方程知,点M的轨迹是一个双曲线。 笔者虽然使用《几何画板》的时间不长,但体会到《几何画板》是数
用几何画板绘制椭圆的方法

用几何画板绘制椭圆的方法作椭圆的方法很多,在此仅举4种方法。
例1:利用椭圆的定义作椭圆。
[简要步骤]:(1)作点A、B,以及线段CD(定长);(2)以点A为圆心,CD为半径作圆,并在圆A上任意取一点E;(3)连接AE、BE,并作BE的垂直平分线FG,交BE于点F,交AE于点G;(4)同时选中点G和点E,作轨迹,如图1。
图1例2:利用椭圆的参数方程作椭圆。
本例的作图原理就是先计算x = a cos t,y = b sin t(-π≤t ≤π),然后根据算得的x、y的值作出点(x,y),最后作出轨迹。
[简要步骤]:(1)显示坐标轴,在x、y轴上分别取点C、D,测量并计算出点C的横坐标和点D的纵坐标,然后将标签分别改为a和b;(2)以任意点E为圆心,点F为圆上一点作圆,在圆上任取一点G,测量角FEG的值,并将标签改为t;(3)将角度设置为弧度制,计算a cos t和b sin t的值,并依次选中,画出点H (a cos t,b sin t);(4)同时选中点H和点G,作轨迹,如图2。
图2例3:利用椭圆的参数方程的几何意义作椭圆。
[简要步骤]:(1)作水平线段AB,在线段AB上取一点C,以点A为圆心,分别以点B、C为圆上一点作两个同心圆,在大圆上任取一点D,连接AD,交小圆于点E;(2)过点D作线段AB的垂线,并过点E作垂线的垂线,两线交于点F;(3)同时选中点D和点F,作轨迹,如图3。
图3例4:利用压缩圆的方法作椭圆。
我们知道,将圆压缩就成了椭圆,因此,我们可以以椭圆的短轴与长轴之比作为压缩比,将圆压缩成椭圆。
[简要步骤]:(1)作线段AB,以线段AB的中点C为圆心,以点B为圆上一点作圆,在圆上任取一点D;(2)过点D作线段AB的垂线,交线段AB于点E;(3)作线段FG、GH,依次选中线段FG、GH,并标识为比例;(4)以点E为缩放中心,将点D以标识的比例压缩,得点D';(5)同时选中点D和点D',作轨迹,如图4。
几何画板极坐标方程生成椭圆

几何画板极坐标方程生成椭圆极坐标方程是描述平面上点的位置的一种坐标系统。
在极坐标中,点的位置由它与原点的距离和与正向x轴的夹角确定。
而椭圆是一种非常常见的几何形状,具有两个焦点和两个半轴的特点。
那么,如何使用极坐标方程生成椭圆呢?我们需要了解椭圆的数学定义。
椭圆是平面上满足一定几何条件的点的集合。
具体来说,椭圆是到两个给定点的距离之和为常数的点的轨迹。
这两个给定点被称为椭圆的焦点,而常数被称为椭圆的离心率。
在极坐标中,点的位置由它与原点的距离和与正向x轴的夹角确定。
因此,我们可以通过极坐标方程来生成椭圆。
椭圆的极坐标方程为:r = a(1 - e*cosθ)其中,r表示点到原点的距离,a表示椭圆的半长轴,e表示椭圆的离心率,θ表示点与正向x轴的夹角。
通过调整a和e的值,我们可以生成不同形状和大小的椭圆。
当离心率e为0时,椭圆退化为一个圆。
当离心率e为1时,椭圆退化为一条直线。
当离心率e大于1时,椭圆退化为两个分离的曲线。
接下来,让我们通过一些具体的例子来演示如何使用极坐标方程生成椭圆。
例1:生成一个半长轴为2,离心率为0.5的椭圆。
根据极坐标方程,我们可以将a设为2,e设为0.5。
然后,我们可以将θ的取值范围设为0到2π,以生成完整的椭圆。
在每个θ的取值下,计算r的值,并将该点绘制在极坐标系统中。
例2:生成一个半长轴为3,离心率为0.8的椭圆。
根据极坐标方程,我们可以将a设为3,e设为0.8。
同样地,将θ的取值范围设为0到2π,并计算每个θ对应的r的值。
然后,将这些点在极坐标系统中绘制出来。
通过以上两个例子,我们可以看到不同参数值对于椭圆形状的影响。
半长轴的大小决定了椭圆的大小,离心率决定了椭圆的形状。
在实际应用中,极坐标方程生成椭圆可以用于图像处理、计算机图形学等领域。
通过控制参数值,我们可以生成各种各样的椭圆形状,从而满足不同的需求。
总结起来,极坐标方程可以用来生成椭圆。
通过调整参数值,我们可以控制椭圆的形状和大小。
用几何画板画椭圆的六种方法

用几何画板画椭圆的六种方法椭圆是平面几何中常见的图形,具有许多特点和性质。
在绘制椭圆时,有多种方法可以使用。
下面将介绍六种常用的绘制椭圆的方法。
1. 绳和两个钉:这是最简单的方法之一。
取一根绳,将两个钉固定在纸上,钉的距离确定椭圆的长轴,绳长为椭圆的周长。
将绳套在两个钉上,再以笔紧绷绳子,沿纸面移动绳子的笔尖,即可得到一个完美的椭圆。
2. 立兰德椭圆仪:这是一种专门用于绘制椭圆的工具。
它由两个互相垂直的固定圆和一个移动圆组成。
通过调整移动圆的位置,使其切割固定圆的位置在不同角度,便可绘制出各种椭圆。
3. 画平行线法:在纸上画一条长直线,作为椭圆的长轴。
然后,在长轴上选择几个等分点,并与长轴垂直的方向上画平行线。
接下来,再在每个平行线上选择等分点,并连结相邻点,最终得到椭圆。
4. 两点距离法:选择椭圆上的两个任意点,并利用细线连接它们。
然后,取一根较长的尺,在椭圆外围固定两个点,使其到线的距离相同。
移动尺的另一段,让尺上的铅笔碰触到线,并沿着椭圆移动,最终形成一个椭圆。
5. 推拉法:选取一块矩形硬纸板或卡纸,将其弯曲成圆筒形。
两端的直径确定椭圆的长短轴。
然后,在圆筒上连接两个焦点,并用铅笔固定在纸上固定一个点,同时将纸沿着直径滑动,同时保持焦点的位置变化,最终形成一个椭圆。
6. 辅助圆法:在纸上确定椭圆的长轴和短轴的长度。
以长轴为直径,在一张纸上画一个大圆;再以短轴为直径,在同一张纸上画一个小圆。
以每个圆的切点为圆心,连结两个切点,最终形成一个完美的椭圆。
这几种方法都能够帮助我们绘制出精确的椭圆。
根据实际需求和使用条件的不同,我们可以选择适合自己的方法来画椭圆。
希望这些方法对您有所帮助!。
几何画板中利用椭圆参数方程画椭圆

5.同时选中点B和直线l,执行“构造”—“垂线”命令,作出过点B和直线l垂直的直线k,利用“点工具”绘制出直线l和直线k的交点C。
构造直线OA、直线l和垂线k并标出交点C
6.依次选中点C和点A,执行“构造”—“轨迹”命令,就可以构造出椭圆了,隐藏不必要的对象,最终效果如下图所示。
执行“构造”—“轨迹”命令构造椭圆并隐藏多余对象
几何画板中利用椭圆参数方程画椭圆
椭圆是一种非常重要的图形,不仅在教学中起着重要的地位,而且在制作立体几何图形和动画中也非常有用,本节主要介绍几何画板中利用椭圆参数方程画椭圆的方法。(几何画板中文官网)
具体的操作步骤如下:
1.执行“绘图”—“定义坐标系”命令,显示坐标系。执行“绘图”—“隐藏网格”命令,把网格隐藏起来。
2.选择“圆工具”,以原点O为圆心绘制两个同心圆。
利用“圆工具”绘制两个同心圆示例
3.选择“点工具”,在大圆的圆周上任取一点A,同时选中原点O和点A,执行“构造”—“直线”命令,构造直线Oห้องสมุดไป่ตู้。
4.利用“点工具”绘制出直线OA和小圆的交点B,同时选中点A和x轴,执行“构造”—“垂线”命令,作出过点A和x轴垂直的直线l。
运用几何画板绘制椭圆的有效方法
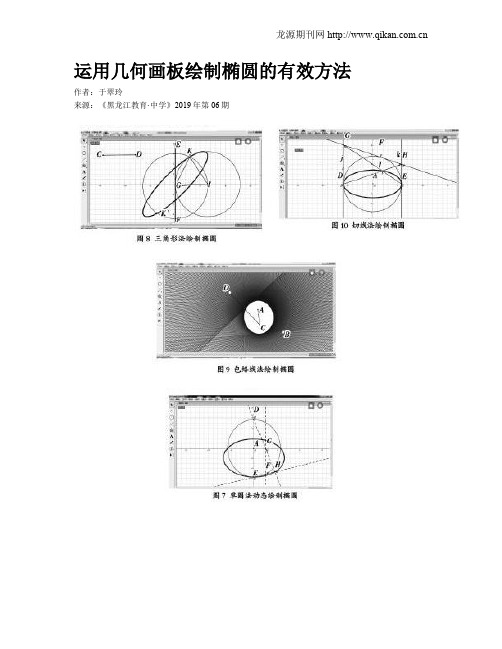
运用几何画板绘制椭圆的有效方法作者:于翠玲来源:《黑龙江教育·中学》2019年第06期在圆锥曲线中,曲线上的点到定点的距离与到定直线的距离的商是常数e,且0<e<1时为椭圆。
椭圆教学是中学数学教学中的重点和难点,椭圆的知识和图像都极为抽象,学生很难理解。
不仅如此,有些教师在绘制椭圆图形时也会感到困难,并且准确性不够。
而运用几何画板软件画出的椭圆既准确又美观,还能增加教学的趣味性,引发学生的学习兴趣,可以让学生轻松、直观地观察并理解椭圆的定义及其性质,从而收到很好的教学效果。
几何画板以点、线、圆作为基础图形,对这些基础图形进行拼接、平移、变换、度量、构造、轨迹追踪以及对基本图形的性质进行运用。
学生可以在此过程中探究图形的内在关系并发现数学的本质,探究数学的奥妙和趣味性,激发学习数学的兴趣。
笔者结合自身教学经验,在总结、归纳、提炼和创新的基础上整理出七种常用的运用几何画板绘制椭圆的方法,分享如下:一、定义法定义法的原理是圆锥曲线的统一定义,即焦点距离与到准线距离的商是定值的点的轨迹。
椭圆的定义,即平面内一个动点到两个定点的距离之和等于常数,这个动点的轨迹叫椭圆,这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距。
绘制的具体步骤为:打开软件,新建文件,在绘画板内画线段AB的同时在AB上绘制出C点,然后在AB外选取D、E两点,满足DE>AB;选中A、C两点进行标记向量,然后通过标记向量将D平移,得到D';选中D和D'点,绘制出一个以D为圆心,以D和D'间距离为半径的圆并且隐藏;同理,标记B、C两个点为标记向量,并且作出E的平移点到E'点,构造出圆,隐藏E'点;运用点工具做出两个圆周交点为F、G两点。
接下来分两种方法研究。
分别选中F、C和G、C两组点进行构造轨迹绘制出椭圆曲线,如图1所示。
点击F点,点击显示、追踪交点,同理操作G点;点击C点,选择操作类按钮、动画、确定,完成设置;点击绘画板上的动画键,绘画板就绘制出一个椭圆,如图2所示。
椭圆的几何画板画法
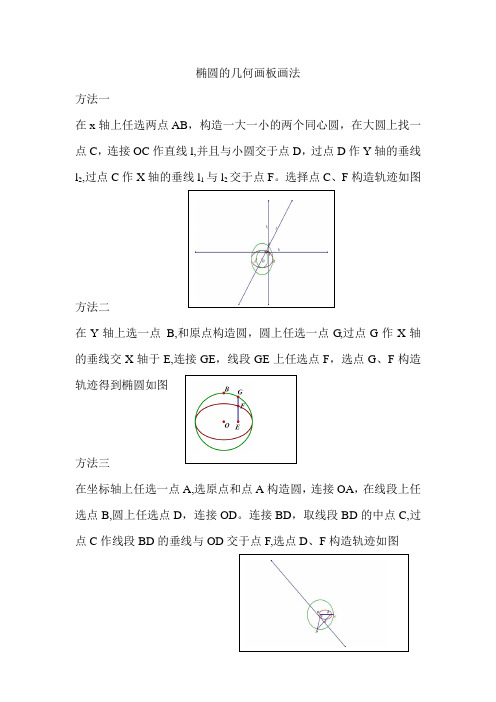
椭圆的几何画板画法
方法一
在x 轴上任选两点AB ,构造一大一小的两个同心圆,在大圆上找一点C ,连接OC 作直线l,并且与小圆交于点D ,过点D 作Y 轴的垂线l 2,过点C 作X 轴的垂线l 1与l 2交于点F 。
选择点C 、F 构造轨迹如图
方法二 在Y 轴上选一点 B,和原点构造圆,圆上任选一点G ,过点G 作X 轴的垂线交X 轴于E,连接GE ,线段GE 上任选点F ,选点G 、F 构造轨迹得到椭圆如图
方法三
在坐标轴上任选一点A,选原点和点A 构造圆,连接OA ,在线段上任选点B,圆上任选点D ,连接OD 。
连接BD ,取线段BD 的中点C,过点C 作线段BD 的垂线与OD 交于点F,选点D 、F 构造轨迹如图。
用几何画板画椭圆的方法
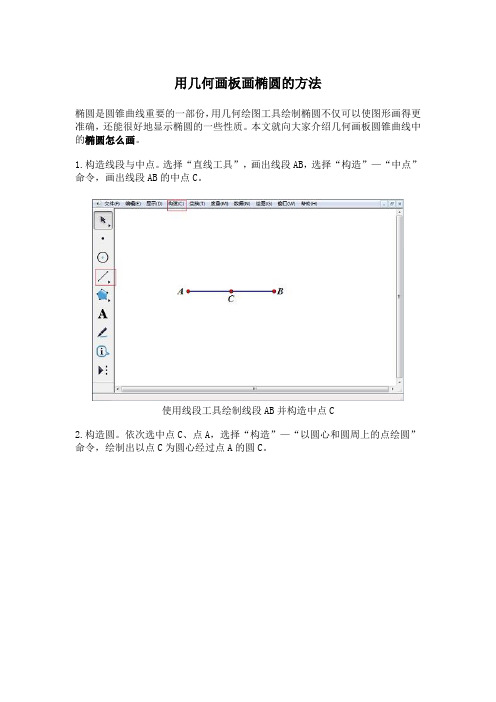
用几何画板画椭圆的方法
椭圆是圆锥曲线重要的一部份,用几何绘图工具绘制椭圆不仅可以使图形画得更准确,还能很好地显示椭圆的一些性质。
本文就向大家介绍几何画板圆锥曲线中的椭圆怎么画。
1.构造线段与中点。
选择“直线工具”,画出线段AB,选择“构造”—“中点”命令,画出线段AB的中点C。
使用线段工具绘制线段AB并构造中点C
2.构造圆。
依次选中点C、点A,选择“构造”—“以圆心和圆周上的点绘圆”命令,绘制出以点C为圆心经过点A的圆C。
选中点C、点A后构造以点C为圆心经过点A的圆C
3.构造垂线与交点。
选择“点工具”,在圆周上任意作一点D,选中点D和线段AB,选择“构造”—“垂线”命令,绘制出线段AB的垂线,与线段AB的交点为E。
绘制点D后构造线段AB的垂线并与之交于E点
4.隐藏圆和直线。
选中圆C和直线DE,选择“显示”—“隐藏路径对象”命令,隐藏圆C和直线DE。
选中圆C和直线DE后将之隐藏
5.构造线段和中点。
选择“线段工具”,绘制出线段DE。
选择“构造”—“中点”命令,绘制出线段DE的中点F。
用线段工具绘制出线段DE后构造其中点F
6.绘制椭圆。
依次选中点D、点F,选择“构造”—“轨迹”命令,绘制出椭圆。
如下图所示。
使用“构造”—“轨迹”命令绘制出椭圆
7.隐藏点与线段。
选中点D、点E、点F、线段DE,选择“显示”—“隐藏对象”命令,椭圆绘制完成。
隐藏点D、E、F和线段DF
以上向大家详细介绍了用几何画板画椭圆的方法,相信大家对此已经有所掌握。
几何画板中椭圆的几种构造方法

几何画板中椭圆的几种构造方法温州中学 陈晓龙在教学中本人发现利用几何画板可以有很多方法来构造椭圆的图象,于是把几种画法整理如下:椭圆的第一定义:平面内到两个定点F 1,F 2的距离之和为定值2a (2a >|F 1F 2|)的点的轨迹。
椭圆的构造方法一:(1)以O 为圆心,2a 为半径作圆,在圆上任取一点P ,在圆内任取一点A ; (2)连接PO 、PA ,作PA 的中垂线与PO 交于点M ,连接MA ;(3)将点M 定义为“追踪点”,选中点P ,让点P 在圆上任意转动可得到点M 的轨迹为以O ,A 为焦点长轴长为2a 的椭圆 。
理由:图中的MP=MA ,所以OM+MA=OM+MP=OP=圆的半径,符合椭圆的第一定义。
椭圆的第二定义:设动点M (x , y )与定点F (c , 0)的距离和它到定直线l : x =ca 2的距离的比是常数ac (a >c >0),则点M 的轨迹是椭圆。
点F是椭圆的一个焦点,直线l 是椭圆中对应于焦点F 的准线。
常数e =ac (0<e <1)是椭圆的离心率。
椭圆的构造方法二:(1)取点F 和直线L ,(点F 不在L 上)。
过点F 作一条直线,在直线上取一点P ;(2)以F 为圆心以FP 为半径作圆,度量FP 的长度,取参数e=0.8(可改为其他小于1的正数),计算FP/e ;(3)过P 点作直线L 的垂线,交L 于M 点,以M 为圆心,以FP/e 为半径做圆,交垂线于N 点,过N 作L 的平行线,交圆F 于A ,B 两点;(4)追踪A ,B 两点,让P 在直线PF 上任意移动可得椭圆方程。
理由:不管P 点在何位置,总可以保证A ,B 点到F 点距离与他们到直线L 的距离之比为0.8,所以构造方法二依据的是椭圆的第二定义。
椭圆的构造方法三:1.以坐标原点O 为圆心,分别以a 、b(a>b>0)为半径画两个圆;2.在大圆上取一点A ,连接OA 与小圆交于点B ;3.过点A 作AN 垂直于Ox 轴,垂足为N ;作BM 垂直于AN ,垂足为M ;4.分别选中点M 和点A ,用“作图”菜单中的“轨迹”功能,画出椭圆。
技术篇用几何画板制作椭圆的图像_第一种方法压扁圆的法

用几何画板制作椭圆的图像佛山市南海区石门中学周伟松椭圆的方程不是一个函数,所以没有办法像作函数图象的方法直接作出椭圆的图象。
可先作出它x轴上面的图象,再把它关于x轴对称,作出另外一部分,但是如果这样子做想在椭圆上任意找一动点的话,这个功能就没办法做到,只能是点在x轴上方运动或者下方运动。
如何作到点可以在椭圆上任意动呢?下面笔者提供一些做法,仅供参考。
第一种方法:压扁圆的法一、制作效果如下图:AC和AB分别决定椭圆的短、长半轴。
拖动C或D点,可改变椭圆的形状(实际上改变椭圆短半轴或长半轴的长)。
二、思路分析利用椭圆的参数方程,可以构造出椭圆,这种构造椭圆的方法,称为"同心圆法"。
三、操作步骤1、画直线AB (为了美观,最好按住Shift画一条水平线)2、画圆(A,C)和(A,D)其中C、D为直线AB上的点3、画直线(A,E)其中E点是圆(A,E)上的点,与圆(A,C)交于F点4、画垂线(E,直线AB);画平行线(F,直线AB);这两条直线的交点为G点5、画轨迹(E,G)第二种方法:斜二测水―――圆的斜二测水平放置一、制作效果二、操作步骤1)画线段AB2)画圆(AB为直径)→画点C C为圆上一点3)画垂线(C,线段AB),垂足为D4)对C作旋转变换(D,-45°)5)画中点(线段DC')6)作轨迹(C,E)第三种方法:定长椭圆的构造在解析几何的教学中,大多时候要化定长的椭圆如下面这个问题:问题:已知椭圆的长半轴=3厘米,短半轴=2厘米,求作椭圆。
一、制作效果如下图,拖动单位点,改变单位长度,椭圆放大缩小,但长短半轴始终不变,交点、顶点各就各位选中参数a、b,按小键盘上的"+""-",可改变它们的值。
注意:,这里的a被定义为成长半轴,所以在改变值时,a应大于b二、操作步骤1)定长短半轴新建参数a、b,其值分别为3、2;度量点C、点D间的距离→计算a ×CD,b×CD的值2)构造椭圆建立坐标系→画同心圆(D,a×CD,b×CD);画出小圆与y轴的交点;画出大圆与x轴的交点;画直线DK,K为大圆上一点,与小圆交于L点→画垂线(K,x轴);画平行线(L,x轴)。
利用几何画板画椭圆的方法集锦

上海市松江第二中学 (0 60 2 10 ) : 圆是解析几何 中的一个重要概念,利用几何 椭 画板不仅可 以简捷准确地画出椭圆 ,而且可 以加深 对椭圆概念的理解 ,丰富对椭 圆的认识 .下面我们 介绍椭圆的几种画法和原理. 1 .利用椭圆定义 西椭 圆
计算 e =二;
<{
NN:I lP ll lP } l2. P + c= A l = =a A l P+ u
2 .利用椭 圆第二定义西椭圆 画法 3 : ()取 两条 线段 ,长 度分 别为 a,c, 口> 1 c,
1 . ’ 。 7
.
O bf > ) 两 个 同 B= 口 b 作
椭圆.
图 1 2 () 4 当点 在圆 A上运动时 , P的轨迹就是 点
’
原理: I Il =O IL I常数. 十 船Il +  ̄= A o
8 .利用定长线段在坐标轴上滑动画椭 圆
画法 1 : 3 () 圆 D上任 取一 点 1在
,
J~
过 M 分 别作 X轴、Y轴 ()作 直线 A 2 B,在 直
\ ~ M
B
的垂线 ,垂足 是 、 B; 线A B上取一 点 P ( 于 、 异
l 厂 ‘。 }
A
。
.
图 1 0
原理 : 立坐 标系 如 图 1 , c o c , 建 0 设 ( ,) 求得 点 O
的轨迹方程为 丁x + : 2 1
.
B和线 段 A B中点 ) ;
1r
( ) 当点 在 圆上 运 3 动 时 ,点 P的轨迹 就是椭 圆.
图 l 3
画法 1 : 1
(1) 画 线 段 A B=2 a,以 A B为直
几何画板画椭圆的几种方法介绍.

<<几何画板>>画椭圆的几种方法介绍随着课改的发展,数学问题“视觉化”显得越来越重要(“视觉化”直观,学生更容易接受,课程改革也是朝这个发展方向),《几何画板》以其学习入门容易和操作简单的优点及其强大的图形和图象功能、方便的动画功能被许多数学教师看好,并已成为制作中学数学课件的主要创作平台之一。
下面介绍几种椭圆画法:一、到两定点的距离和等于定长具,在绘图板中作一线段AB(线段AB的长度为椭圆的长轴长2a)。
用“点”工具在线段上任取一点C,先后选中A,C点,选择“变换”->“标记向量"A->C"”(下图)。
再用“线段”工具作线段DE(线段DE的长为2c),选中点D,选择“变换”->“平移”,显示按标记的向量“从A到C”,点击“平移”,会得到点D'。
先后选中点D和D',选择“作图”->“以圆心和圆周上的点画圆”,选中点D',先后选中B,C点,选择“变换”->“标记向量"B->C"”。
同样的把点E,按向量BC平移,得到点E'。
以E为圆心过E'作圆选中两个圆的圆周,选择“作图”->“交点”,作出交点F和G。
让点C在线段AB上移动(选中点C,点击“编辑”下的“操作类按钮”中的“动画”可以生成动画),交点F、G的轨迹就是我们要作的椭圆(最后可以把无用的点、线隐藏)。
二、同心圆法(教材例5)选择“图表”->“定义坐标系”,用“圆”工具作两圆心为原点的同心圆(外圆半径长就是最终椭圆的长半轴长a,内圆半径长就是最终椭圆的短半轴长b),光标放原点处,击左键拖动光标,松开左键就得到所需圆。
在外圆圆周上任取一点E(可以选中圆,点击“作图”下的“对象上的点”;或者选取“点”工具,然后把光(选中点A(原点)和点E,点击“作图”下的“线段、射线或直线”),再作AE与小圆的交点(选中线段AE和内圆圆周,可用快捷键Ctrl+I作出交点)F。
“几何画板”绘制椭圆的几种典型作法

选择 < 度量 /距离 ) 度量 出线 段 n和 c的长 度 ; , 按
一
2
,2
Al+一 键 打 开计 算器 , t 计算 “ 一c选 中 一c选 - . ,
C
择 < 换 /标 记 距 离 ) 选 中点 C, 择 < 换 /平 变 . 选 变
一
2
移 )平 移距 离 为 ( 一c , 向为 0度 , 到点 F, , _ “ )方 得
1 根 据 椭 圆第 一定 义 作椭 圆
( )打开 几何 画板 , 择 ( 辑 /参 数 选 项 > 1 选 编 , 单击 “ 文本 ” 项 卡 , 所有 新 建 的 点前 的方框 中 选 在 画对 号 , 后 确 定.用 “ 线 段 ”工 具 , 线 段 然 画 作 A 线段 AB 的 长度 为椭 圆 的长 轴 长 2 ) 用 “ B( a. 画 点”工具 在线 段 A 上任 取一 点 C, B 用选 择工 具选 中 A, C点 , 择 ( 选 变换 /标 记 向量 >A ~> C . “ ”
2 根 据 椭 圆第 二定 义 作 椭 圆( 准线法)
( )打开 一个 新 画板 , “ 直 线”工具 作 两 1 用 画
条 直线 , 直 线 Z 准线 , 一 条 直线 AB 与直 线 使 为 另 垂 直. 中两 条直 线 , 择 ( 图 /交 点 ) 作 出交 选 选 作 ,
点 C; 两 条 直 线 外 , 两 条 线 段 和 , 在 画 使 > c .
“ 几何画板” 绘制椭圆的几种典型作法
陈 永 胜
( 林师范大学数学学院 , 林 吉 吉 四平 1 60 ) 30 0
摘
要: 几何 画 板 是 一 个 优 秀的 专 业 学科 平 台 软 件 , 表 了 当代 专 业 工 具 平 台 类 教 学 软 件 的 发 展 方 向 . 代 它 以数 学 为根 本 , 动 态几 何 ” 以“ 为特 色来 动 态 表 现 设 计 者 的 思 想 , 为探 索 几何 奥 秘 提 供 一 个 新 的 工 具。 绍 使 用 “ 介 几何 画 板 ” 画椭 圆 的 几种 典 型 作 法 , 圆 第 一 定 义 、 圆 第 二 定 义 、 角 坐 标 方 程 、 椭 椭 直 参
用几何画板画椭圆的六种方法刘秀梅

用几何画板画椭圆的六种方法刘秀梅[ 录入者:编辑05 | 时间:2009-01-17 | 来源:本站| 浏览:[ 109次]椭圆在平面解析几何的教学中是一个重要的内容,利用几何画板软件可以很准确地画出椭圆图形,为教师的教和学生的学都带来了方便。
下面介绍六种画椭圆的方法。
1.利用椭圆定义椭圆定义:到两定点的距离之和为定长的点的轨迹。
利用此定义来画,步骤如下:(3)构造线段PF的中垂线MN,与线段PF交于M,与线段PF交于N;(4)构造点P在圆上的动画,追踪点M,M的轨迹就是椭圆(如图1)。
2.利用菱形画椭圆步骤如下:(1)画一个菱形ABCD,对称轴为AC、BD;(2)过D构造AB上的垂线,垂足为P,DP交AC于O,标记AC、BD为镜面,做出点P关于AC的对称点P′,关于BD的对称点P″;(3)顺次选取OPP′构造圆上的弧,再以BD为镜面,构造出对称弧;(4)顺次选取DP″P构造圆上的弧,再以AC为镜面,构造出对称弧,四段弧围成椭圆(如图2)。
3.利用定长线段的滑动一条线段AB(|AB|=2a)的两端A和B分别在x轴和y轴上滑动,线段AB的中点的轨迹就是椭圆。
步骤如下:(1)建立坐标系xoy,在x轴上任取一点M,构造线段OM,使|OM|=|AB|=2a;(2)在线段OM上任取一点A,以A为圆心,以OM为半径构造圆,交y轴于点B;(3)构造线段AB,在AB上任取一点P(非中点),利用点反射或旋转构造点P 关于x轴、y轴、原点的对称点P″、P′、P?苁,追踪点P、P′、P″、P?苁;(4)构造点A在线段OM上的动画,点P、P′、P″、P?苁的轨迹就是椭圆(如图3)。
值得一提的是椭圆规就是利用这个原理制成的,只不过点P取在了线段AB的延长线上。
4.利用参考圆画椭圆步骤如下:(1)以原点O为圆心,分别以a、b(a>b)为半径做两个圆;(2)任取大圆上的一点A,构造线段OA交小圆于点B,过点A作AN⊥OX(x轴),垂足为N;(3)过点B作BM⊥AN,垂足为M,构造点M关于y轴的对称点M′,追踪点M和M′;(4)构造点A在大圆上的动画,点M、M′的轨迹就是椭圆(如图4)。
运用几何画板绘制椭圆的有效方法

在圆锥曲线中,曲线上的点到定点的距离与到定直线的距离的商是常数e,且0<e<1时为椭圆。
椭圆教学是中学数学教学中的重点和难点,椭圆的知识和图像都极为抽象,学生很难理解。
不仅如此,有些教师在绘制椭圆图形时也会感到困难,并且准确性不够。
而运用几何画板软件画出的椭圆既准确又美观,还能增加教学的趣味性,引发学生的学习兴趣,可以让学生轻松、直观地观察并理解椭圆的定义及其性质,从而收到很好的教学效果。
几何画板以点、线、圆作为基础图形,对这些基础图形进行拼接、平移、变换、度量、构造、轨迹追踪以及对基本图形的性质进行运用。
学生可以在此过程中探究图形的内在关系并发现数学的本质,探究数学的奥妙和趣味性,激发学习数学的兴趣。
笔者结合自身教学经验,在总结、归纳、提炼和创新的基础上整理出七种常用的运用几何画板绘制椭圆的方法,分享如下:一、定义法定义法的原理是圆锥曲线的统一定义,即焦点距离与到准线距离的商是定值的点的轨迹。
椭圆的定义,即平面内一个动点到两个定点的距离之和等于常数,这个动点的轨迹叫椭圆,这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距。
绘制的具体步骤为:打开软件,新建文件,在绘画板内画线段AB 的同时在AB 上绘制出C 点,然后在AB 外选取D 、E 两点,满足DE >AB ;选中A 、C 两点进行标记向量,然后通过标记向量将D 平移,得到D ;选中D 和D 点,绘制出一个以D 为圆心,以D 和D 间距离为半径的圆并且隐藏;同理,标记B 、C 两个点为标记向量,并且作出E 的平移点到E 点,构造出圆,隐藏E 点;运用点工具做出两个圆周交点为F 、G 两点。
接下来分两种方法研究。
分别选中F 、C 和G 、C 两组点进行构造轨迹绘制出椭圆曲线,如图1所示。
图2定义法动态绘制椭圆点击F 点,点击显示、追踪交点,同理操作G 点;点击C 点,选择操作类按钮、动画、确定,完成设置;点击绘画板上的动画键,绘画板就绘制出一个椭圆,如图2所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
选择“文件”→“新绘图”,选择“图表”→“建立坐标轴”,用“圆”工具作两圆心为原点的同心圆(外圆半径长就是最终椭圆的长半轴长a,内圆半径长就是最终椭圆的短半轴长b),选中点B和圆周上的点C和D,按Ctrl+H键隐藏。
选择“显示”→“线型”→“虚线”,在外圆圆周上任取一点E,按住shift键,同时选中点A和点E,按Ctrl+L作出线段AE,同时选中线段AE和内圆圆周,按Ctrl+I键作出交点F。
2.按住shift键,先后选中点F,选择“显示”→“追踪点”,同样选中点G和点C,选择“显示”→“追踪点”。
按住shift键,先后选中点C和线段AB,选择“编辑”→“操作类按钮”→“动画”,弹出“匹配路径”对话框,选择“双向”、“沿着线段j”、“慢慢地”,按“动画”按钮完成设置。这时,绘图板上会出现一个“动画”按钮,双击“动画”按钮,就会自动画出椭圆。完成,存盘退出。
同时选中点A和点D,按Ctrl+L键作线段AD。再同时选中垂线k和线段AD定值。
选中点F,按Ctrl+T键追踪点F。选中点D和圆周,选择“编辑”→“操作类按钮”→“动画”,弹出“匹配路径”对话框,选择“单向”、“绕圆c1”、“正常地”,按“动画”按钮完成设置。这时,绘图板上会出现一个“动画”按钮,双击“动画”按钮,就会自动画出椭圆(如图4)。另外您也可以同时选中点F和点D,选择“作图”→“轨迹”也可以作出该椭圆。完成,存盘退出
二、准线法(到定点的距离与到定直线的距离之比为常数e)
打开一个新的绘图板,选择“图表”→“建立坐标轴”。
用“线段”工具作线段CD,在线段CD上任取一点E。同时选中点C和点E,选择“度量”→“距离”,量出CE的长。同样量出CD的长。
按住shift键,选中量出的CE和CD的距离,按鼠标右键弹出对话框,选择“度量”→“计算”。在打开的计算器中选择“数值”→“距离(C到E)”。选择“/”→“距离(C到D)”→“确定”。在绘图板上就会出现CE和CD的比值。用“文本工具”双击该值,弹出“度量值格式”对话框,选择“T文本格式”。 将“距离(C到E)/距离(C到D)”改成“e”,确定,完成改变。选中点B,按Ctrl+H键隐藏,在X轴上取点F(F为椭圆的一个焦点)。作线段GH,在其上取点I。用上面的方法量出GI的距离,并将其距离名称改为c。选中c和e的值,打开计算器,将c除以e的值求出,并将其名改为a。
几何画板生成椭圆曲线八法
国家教育部推荐的教育软件《几何画板》提供曲线的动态变化,便于观察与验证。如很好的开发它的功能,制作出富于表现力的动态效果的课件,培养学生对抽象曲线的理解和想象能力有极大的帮助。下面就用绘制椭圆曲线的八种方法的同行们商榷。
一、定义法(到两定点的距离和等于定长)
选取“线段”工具,在绘图板中作一线段AB(线段AB的长度为椭圆的长轴长2a)。用“点”工具在线段上任取一点C,按住shift键先后选中A,C点,选择“变换”→“标记向量 "A→C"”。
再用“点”工具再用点工具任取一点D,选中点D,选择“变换”→“平移”,选中“按标记的向量”,然后确定,会得到点D'。按住shift键,先后选中点D和D',选择“作图”→“以圆心和圆周上的点画圆”,选中点D',按Ctrl+H键将其隐藏。
按住shift键,先后选中B,C点,选择“变换”→“标记向量 "B→C"”。用点工具另作一点E,使其与D点的距离小于线段AB的长(线段DE的长为2c),选中点E,选择“变换”→“平移”,选中“按标记的向量”,然后确定,会得到点E'。
按住shift键,同时选中点E和纵坐标轴,选择“作图”→“平行线”,作出一直线,再同时选中点F和横坐标轴,选择“作图”→“平行线”,作出另一直线。同时选中这两条直线,按Ctrl+I键作出交点G。
以下可以分两个方向进行:
1.选择“显示”→“线型”→“细线”,同时选中交点G和外圆圆周上的点E,选择“作图”→“轨迹”就作出了椭圆(如图3)。 完成,存盘退出。
按住shift键,先后选中点E和E',选择“作图”→“以圆心和圆周上的点画圆”,选中点E',按Ctrl+H键将其隐藏。
按住shift键,选中两个圆的圆周,选择“作图”→“交点”(或按Ctrl+I键),作出交点F和G。
以下可以分两个方向进行:
1.按住shift键,先后选中点F和点C,选择“作图”→“轨迹”,作出椭圆的上半部分;同理先后选中点G和点C,作出椭圆的下半部分(如图1)。
四、单圆法(1)打开一个新的绘图板,选取“圆”工具作一圆(圆的半径长即2a),选中圆周上的点B,按Ctrl+H隐藏。
在圆的内部任选一点C(A,C即椭圆的交点)。在圆周上任取一点D,同时选中点C和点D,按Ctrl+L键作线段CD。选中线段CD,按Ctrl+M作出CD的中点E,再同时选中点E和线段CD,选择“作图”→“垂线”,作出垂线k。
选中a的计算值,选择“图表”→“绘制度量值”,弹出“绘制度量值”对话框。选择“H在横(x)轴”,确定,作出垂直于x轴的一条直线。选中c的度量值,选择“变换”→“标记距离”,选中F点,选择“变换”→“平移”,弹出“平移”对话框,选择“按标记的距离”,确定,作出点F平移后的点F'。
先后选中点F和点F',选择“作图”→“以圆心和圆周上的点画圆”。选中该圆周和上面作出的垂直于x轴的直线,按Ctrl+I绘出交点J和K。选中点J和点K,选择“显示”→“追踪点”。选中点I和线段GH,选择“编辑”→“操作类按钮”→“动画”,弹出“匹配路径”对话框,选择“双向”、“沿着线段n”、“慢慢地”,按“动画”按钮完成设置。这时,绘图板上会出现一个“动画”按钮,双击“动画”按钮,就会自动画出椭圆(如图2)选中CE、CD、e、c和a的值,按Ctrl+H隐藏。完成,存盘退出。
选择“显示”→“线型”→“细线”,选中点G,选择“显示”→“追踪点”。
按住shift键,同时选中外圆圆周上的点E和外圆圆周,选择“编辑”→“操作类按钮”→“动画”,弹出“匹配路径”对话框,选择“单向”、“绕圆c2”、“快速地”,按下“动画”按钮确定。
这时,绘图板上会出现一个“动画”按钮,双击“动画”按钮,就会自动画出椭圆。完成,存盘退出。
