大整数乘法实验代码(最新版)-蔡强
河南科技学院新科学院算法设计报告实验四大整数乘法

算法与分析告姓名:班级:一、实验名称:大整数乘法时间:地点:二、实验目的及要求在某些情况下,需要处理很大的整数,它无法在计算机中硬件能表示的整数范围内进行处理。
若用浮点数来表示它,则只能近似地表示它的大小,计算结果中的有效数字也受到限制。
为了精确地表示大整数并在计算结果中要求精确地得到所有位数的数字,就必须用软件的方法来实现大整数的算法运算。
即,用二进制大整数乘法以减少乘法次数,提高算法效率。
三、实验环境运行坏境WINXP、制作平台VC++6.0。
四、实验内容自己电脑上进行试机,在VC++6.0对程序进行调试,有错误的,问同学,和同学们一起讨论交流,或者去图书馆查阅相关资料,或者在网上查找相关资料。
五、算法描述及实验步骤设X和Y都是n位的二进制整数,现在要计算它们的乘积XY。
我们可以用小学所学的方法来设计一个计算乘积XY的算法,但是这样做计算步骤太多,显得效率较低。
如果将每2个1位数的乘法或加法看作一步运算,那么这种方法要作O(n2)步运算才能求出乘积XY。
下面我们用分治法来设计一个更有效的大整数乘积算法。
图6-3 大整数X和Y的分段我们将n位的二进制整数X和Y各分为2段,每段的长为n/2位(为简单起见,假设n是2的幂),如图6-3所示。
由此,X=A2n/2+B ,Y=C2n/2+D。
这样,X和Y的乘积为:XY=(A2n/2+B)(C2n/2+D)=AC2n+(AD+CB)2n/2+BD (1)如果按式(1)计算XY,则我们必须进行4次n/2位整数的乘法(AC,AD,BC和BD),以及3次不超过n位的整数加法(分别对应于式(1)中的加号),此外还要做2次移位(分别对应于式(1)中乘2n和乘2n/2)。
所有这些加法和移位共用O(n)步运算。
设T(n)是2个n位整数相乘所需的运算总数,则由式(1),我们有:(2)由此可得T(n)=O(n2)。
因此,用(1)式来计算X和Y的乘积并不比小学生的方法更有效。
大数乘法的C代码实现

⼤数乘法的C代码实现在C语⾔中,宽度最⼤的⽆符号整数类型是unsigned long long, 占8个字节。
那么,如果整数超过8个字节,如何进⾏⼤数乘法呢?例如:$ pythonPython 2.7.6 (default, Oct 26 2016, 20:32:47)...<snip>....>>> a = 0x123456781234567812345678>>> b = 0x876543211234567887654321>>> print"a * b = 0x%x" % (a * b)a *b = 0x9a0cd057ba4c159a33a669f0a522711984e32bd70b88d78⽤C语⾔实现⼤数乘法,跟⼗进制的多位数乘法类似,基本思路是采⽤分⽽治之的策略,难点就是进位处理相对⽐较复杂。
本⽂尝试给出C 代码实现(基于⼩端),并使⽤Python脚本验证计算结果。
1. foo.c1 #include <stdio.h>2 #include <stdlib.h>3 #include <string.h>45 typedef unsigned char byte; /* 1 byte */6 typedef unsigned short word; /* 2 bytes */7 typedef unsigned int dword; /* 4 bytes */8 typedef unsigned long long qword; /* 8 bytes */910 typedef struct big_number_s {11 dword *data;12 dword size;13 } big_number_t;1415static void16 dump(char *tag, big_number_t *p)17 {18if (p == NULL)19return;2021 printf("%s : data=%p : size=%d:\t", tag, p, p->size);22for (dword i = 0; i < p->size; i++)23 printf("0x%08x ", (p->data)[i]);24 printf("\n");25 }2627/*28 * Add 64-bit number (8 bytes) to a[] whose element is 32-bit int (4 bytes)29 *30 * e.g.31 * a[] = {0x12345678,0x87654321,0x0}; n = 3;32 * n64 = 0xffffffff1234567833 *34 * The whole process of add64() looks like:35 *36 * 0x12345678 0x87654321 0x0000000037 * + 0x12345678 0xffffffff38 * -----------------------------------39 * = 0x2468acf0 0x87654321 0x0000000040 * + 0xffffffff41 * -----------------------------------42 * = 0x2468acf0 0x87654320 0x0000000143 *44 * Finally,45 * a[] = {0x2468acf0,0x87654320,0x00000001}46*/47static void48 add64(dword a[], dword n, qword n64)49 {50 dword carry = 0;5152 carry = n64 & 0xFFFFFFFF; /* low 32 bits of n64 */53for (dword i = 0; i < n; i++) {54if (carry == 0x0)55break;5657 qword t = (qword)a[i] + (qword)carry;58 a[i] = t & 0xFFFFFFFF;59 carry = (dword)(t >> 32); /* next carry */60 }6162 carry = (dword)(n64 >> 32); /* high 32 bits of n64 */63for (dword i = 1; i < n; i++) {64if (carry == 0x0)65break;6667 qword t = (qword)a[i] + (qword)carry;68 a[i] = t & 0xFFFFFFFF;69 carry = (dword)(t >> 32); /* next carry */70 }71 }7273static big_number_t *74 big_number_mul(big_number_t *a, big_number_t *b)75 {76 big_number_t *c = (big_number_t *)malloc(sizeof(big_number_t));77if (c == NULL) /* malloc error */78return NULL;7980 c->size = a->size + b->size;81 c->data = (dword *)malloc(sizeof(dword) * c->size);82if (c->data == NULL) /* malloc error */83return NULL;8485 memset(c->data, 0, sizeof(dword) * c->size);8687 dword *adp = a->data;88 dword *bdp = b->data;89 dword *cdp = c->data;90for (dword i = 0; i < a->size; i++) {91if (adp[i] == 0x0)92continue;9394for (dword j = 0; j < b->size; j++) {95if (bdp[j] == 0x0)96continue;9798 qword n64 = (qword)adp[i] * (qword)bdp[j];99 dword *dst = cdp + i + j;100 add64(dst, c->size - (i + j), n64);101 }102 }103104return c;105 }106107static void108 free_big_number(big_number_t *p)109 {110if (p == NULL)111return;112113if (p->data != NULL)114free(p->data);115116free(p);117 }118119int120 main(int argc, char *argv[])121 {122 dword a_data[] = {0x12345678, 0x9abcdef0, 0xffffffff, 0x9abcdefa, 0x0}; 123 dword b_data[] = {0xfedcba98, 0x76543210, 0x76543210, 0xfedcba98, 0x0}; 124125 big_number_t a;126 a.data = (dword *)a_data;127 a.size = sizeof(a_data) / sizeof(dword);128129 big_number_t b;130 b.data = (dword *)b_data;131 b.size = sizeof(b_data) / sizeof(dword);132133 dump("BigNumber A", &a);134 dump("BigNumber B", &b);135 big_number_t *c = big_number_mul(&a, &b);136 dump(" C = A * B", c);137 free_big_number(c);138139return0;140 }2. bar.py1#!/usr/bin/python23import sys45def str2hex(s):6 l = s.split('')78 i = len(l)9 out = ""10while i > 0:11 i -= 112 e = l[i]13if e.startswith("0x"):14 e = e[2:]15 out += e1617 out = "0x%s" % out18 n = eval("%s * %d" % (out, 0x1))19return n2021def hex2str(n):22 s_hex = "%x" % n23if s_hex.startswith("0x"):24 s_hex = s_hex[2:]2526 n = len(s_hex)27 m = n % 828if m != 0:29 s_hex = '0' * (8 - m) + s_hex30 n += (8 - m)31 i = n32 l = []33while i >= 8:34 l.append('0x' + s_hex[i-8:i])35 i -= 836return"%s" % ''.join(l)3738def main(argc, argv):39if argc != 4:40 sys.stderr.write("Usage: %s <a> <b> <c>\n" % argv[0]) 41return 14243 a = argv[1]44 b = argv[2]45 c = argv[3]46 ax = str2hex(a)47 bx = str2hex(b)48 cx = str2hex(c)4950 axbx = ax * bx51if axbx != cx:52print"0x%x * 0x%x = " % (ax, bx)53print"got: 0x%x" % axbx54print"exp: 0x%x" % cx55print"res: FAIL"56return 15758print"got: %s" % hex2str(axbx)59print"exp: %s" % c60print"res: PASS"61return 06263if__name__ == '__main__':64 argv = sys.argv65 argc = len(argv)66 sys.exit(main(argc, argv))3. MakefileCC = gccCFLAGS = -g -Wall -m32 -std=c99TARGETS = foo barall: $(TARGETS)foo: foo.c$(CC) $(CFLAGS) -o $@ $<bar: bar.pycp $< $@ && chmod +x $@clean:rm -f *.oclobber: cleanrm -f $(TARGETS)cl: clobber4. 编译并测试$ makegcc -g -Wall -m32 -std=c99 -o foo foo.ccp bar.py bar && chmod +x bar$ ./fooBigNumber A : data=0xbfc2a7c8 : size=5: 0x123456780x9abcdef00xffffffff0x9abcdefa0x00000000BigNumber B : data=0xbfc2a7d0 : size=5: 0xfedcba980x765432100x765432100xfedcba980x00000000C = A * B : data=0x8967008 : size=10: 0x350687400xee07360a0x053bd8c90x2895f6cd0xb973e57e0x4e6cfe660x0b60b60b0x9a0cd0560x000000000x00000000 $ A="0x12345678 0x9abcdef0 0xffffffff 0x9abcdefa 0x00000000"$ B="0xfedcba98 0x76543210 0x76543210 0xfedcba98 0x00000000"$ C="0x35068740 0xee07360a 0x053bd8c9 0x2895f6cd 0xb973e57e 0x4e6cfe66 0x0b60b60b 0x9a0cd056 0x00000000 0x00000000"$$ ./bar "$A""$B""$C"got: 0x350687400xee07360a0x053bd8c90x2895f6cd0xb973e57e0x4e6cfe660x0b60b60b0x9a0cd056exp: 0x350687400xee07360a0x053bd8c90x2895f6cd0xb973e57e0x4e6cfe660x0b60b60b0x9a0cd0560x000000000x00000000res: PASS$结束语:本⽂给出的是串⾏化的⼤数乘法实现⽅法。
大整数相乘实验报告

一、实验目的1. 理解大整数相乘的基本原理和方法。
2. 掌握大整数相乘的编程实现。
3. 分析大整数相乘算法的效率,并优化算法。
二、实验原理大整数相乘是指对两个或多个大整数进行乘法运算。
在计算机科学中,大整数通常指的是位数超过计算机中普通整数类型的整数。
大整数相乘的方法有很多,常见的有长乘法、Karatsuba算法、FFT算法等。
本实验采用长乘法算法进行大整数相乘。
长乘法算法的基本原理是将乘数和被乘数按照一定的位数进行拆分,然后逐位相乘,最后将乘积相加得到最终结果。
具体步骤如下:1. 将乘数和被乘数分别拆分成若干个较小的部分。
2. 将每个较小的部分与另一个数对应的部分相乘。
3. 将乘积按照一定的位数对齐,并相加得到部分乘积。
4. 将所有部分乘积相加得到最终结果。
三、实验环境1. 操作系统:Windows 102. 编程语言:Python3. 开发工具:PyCharm四、实验步骤1. 导入必要的库```pythondef multiply(a, b):# 省略实现细节pass2. 编写大整数相乘函数```pythondef multiply(a, b):# 将字符串转换为列表,列表中每个元素代表一位数字 a_list = list(map(int, a))b_list = list(map(int, b))# 初始化结果列表result = [0] (len(a_list) + len(b_list))# 遍历a_list和b_list的每一位for i in range(len(a_list)):for j in range(len(b_list)):# 将当前位相乘,并加上进位result[i + j] += a_list[i] b_list[j]# 处理进位result[i + j + 1] += result[i + j] // 10 # 将当前位设置为余数result[i + j] %= 10# 去除结果列表前面的0while len(result) > 1 and result[0] == 0:result.pop(0)# 将结果列表转换为字符串return ''.join(map(str, result))3. 测试大整数相乘函数```pythona = '12345678901234567890'b = '98765432109876543210'result = multiply(a, b)print(result)```4. 分析大整数相乘算法的效率长乘法算法的时间复杂度为O(n^2),其中n为乘数和被乘数的位数。
大整数乘法

大整数乘法问题描述通常,在分析一个算法的计算复杂性时,都将加法和乘法运算当作是基本运算来处理,即将执行一次加法或乘法运算所需的计算时间当作一个仅取决于计算机硬件处理速度的常数。
这个假定仅在计算机硬件能对参加运算的整数直接表示和处理时才是合理的。
然而,在某些情况下,我们要处理很大的整数,它无法在计算机硬件能直接表示的范围内进行处理。
若用浮点数来表示它,则只能近似地表示它的大小,计算结果中的有效数字也受到限制。
若要精确地表示大整数并在计算结果中要求精确地得到所有位数上的数字,就必须用软件的方法来实现大整数的算术运算。
请设计一个有效的算法,可以进行两个n位大整数的乘法运算。
参考解答大整数的乘法问题描述参考解答设X和Y都是n位的二进制整数,现在要计算它们的乘积XY。
我们可以用小学所学的方法来设计一个计算乘积XY的算法,但是这样做计算步骤太多,显得效率较低。
如果将每2个1位数的乘法或加法看作一步运算,那么这种方法要作O(n2)步运算才能求出乘积XY。
下面我们用分治法来设计一个更有效的大整数乘积算法。
图6-3 大整数X和Y的分段我们将n位的二进制整数X和Y各分为2段,每段的长为n/2位(为简单起见,假设n是2的幂),如图6-3所示。
由此,X=A2n/2+B ,Y=C2n/2+D。
这样,X和Y的乘积为:XY=(A2n/2+B)(C2n/2+D)=AC2n+(AD+CB)2n/2+BD (1)如果按式(1)计算XY,则我们必须进行4次n/2位整数的乘法(AC,AD,BC和BD),以及3次不超过n位的整数加法(分别对应于式(1)中的加号),此外还要做2次移位(分别对应于式(1)中乘2n和乘2n/2)。
所有这些加法和移位共用O(n)步运算。
设T(n)是2个n位整数相乘所需的运算总数,则由式(1),我们有:(2)由此可得T(n)=O(n2)。
因此,用(1)式来计算X和Y的乘积并不比小学生的方法更有效。
要想改进算法的计算复杂性,必须减少乘法次数。
大数乘法算法实验报告

一、实验目的1. 理解大数乘法算法的基本原理。
2. 掌握大数乘法算法的实现方法。
3. 分析大数乘法算法的复杂度,并比较不同算法的效率。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3. 开发工具:PyCharm三、实验内容本次实验主要涉及以下大数乘法算法:1. 模拟乘法算法2. Karatsuba算法3. 快速傅里叶变换(FFT)算法(一)模拟乘法算法1. 原理模拟乘法算法通过模拟手工乘法过程,逐位计算乘积,并处理进位问题。
该算法适用于任意位数的大数乘法。
2. 实现步骤(1)创建一个长度为max(len(a), len(b))+1的数组c,用于存储乘积。
(2)从被乘数的最低位开始,依次与乘数的每一位相乘,并处理进位。
(3)将乘积的每一位存储到数组c中。
(4)遍历数组c,处理进位问题。
3. 代码实现```pythondef multiply(a, b):len_a, len_b = len(a), len(b)c = [0] (len_a + len_b)for i in range(len_a - 1, -1, -1):for j in range(len_b - 1, -1, -1):c[i + j + 1] += int(a[i]) int(b[j])c[i + j] += c[i + j + 1] // 10c[i + j + 1] %= 10return ''.join(map(str, c)).lstrip('0')```(二)Karatsuba算法1. 原理Karatsuba算法是一种分治算法,通过将大数分解为较小的数,降低乘法操作的复杂度。
2. 实现步骤(1)将两个大数a和b分解为a1、a0、b1、b0,其中a = a1 10^(n/2) + a0,b = b1 10^(n/2) + b0。
(2)计算以下四个值:1. x1 = a1 b12. x2 = (a1 + a0) (b1 + b0) - x1 - x03. x0 = a0 b04. x3 = x1 10^n + x2 10^(n/2) + x0(3)将x3的每一位转换为字符串,拼接成最终结果。
C语言中超大整数乘法运算

C语言中超大整数乘法运算在计算机中,长整型(long int)变量的范围是 -2147483648 至 2147483647,因此若用长整型变量做乘法运算,乘积最多不能超过 10位数。
即便用双精度型(double)变量,也仅能保证 16 位有效数字的精度。
在某些需要更高精度的乘法运算的场合,需要用别的办法来实现乘法运算。
比较容易想到的是做多位数乘法时列竖式进行计算的方法,只要写出模拟这一过程的程序,就能实现任意大整数的乘法运算。
经过查阅资料,找到一种更易于编程的方法,即“列表法”。
下面先介绍“列表法”:例如当计算8765 x 234时,把乘数与被乘数照如下列出,见表1:把表1中的数按图示斜线分组(横纵坐标和相等的数分为一组),把每组数的累加起来所得的和记在表格下方,见表 2:从最低位的 20 开始,保留个位数字“0”,把个位以外的数“2”进到前一位;把次低位的 39 加上低位进上来的 2 得 41,保留个位数字“1”,把“4”进到前一位;以此类推,直至最高位的 16,16 加上低位进上来的4得 20,保留“0”,把2进到最高位,得乘积答数 2051010。
根据以上思路就可以编写C 程序了,再经分析可得:1、一个m 位的整数与一个 n 位的整数相乘,乘积为m+n-1 位或m+n 位。
2、程序中,用三个字符数组分别存储乘数、被乘数与乘积。
由第 1 点分析知,存放乘积的字符数组的长度应不小于存放乘数与被乘数的两个数组的长度之和。
3、可以把第二步“计算填表”与第三四步“累加进位”放在一起完成,可以节省存储表格 2所需的空间。
4、程序关键部分是两层循环,内层循环累计一组数的和,外层循环处理保留的数字与进位。
编写的程序如下:#define MAXLENGTH 1000#include <stdio.h>#include <string.h>void compute(char *a, char *b, char *c);void main(void){char a[MAXLENGTH], b[MAXLENGTH], c[MAXLENGTH * 2];puts("Input multiplier :");gets(a);puts("Input multiplicand :");gets(b);compute(a, b, c);puts("Answer :");puts(c);getchar();}void compute(char *a, char *b, char *c){int i, j, m, n;long sum, carry;m = strlen(a) - 1;n = strlen(b) - 1;for (i = m; i >= 0; i--)a[i] -= '0';for (i = n; i >= 0; i--)b[i] -= '0';c[m + n + 2] = '\0';carry = 0;for (i = m + n; i >= 0; i--) /* i 为坐标和 */{sum = carry;if ((j = i - m) < 0)j = 0;for ( ; j<=i && j<=n; j++) /* j 为纵坐标 */ sum += a[i-j] * b[j]; /* 累计一组数的和 */c[i + 1] = sum % 10 + '0'; /* 算出保留的数字 */ carry = sum / 10; /* 算出进位 */}if ((c[0] = carry+'0') == '0') /* if no carry, */ c[0] = '\040'; /* c[0] equals to space */}效率分析:用以上算法计算 m位整数乘以n 位整数,需要先进行 m x n次乘法运算,再进行约m + n次加法运算和 m + n次取模运算(实为整数除法)。
实验报告(分治法大整数乘法字符数组实现)

一、实验目的:(1)掌握分治法。
(2)学会测试和分析算法的时间性能二、分组:三个人一组,自由组合三、内容:1. 编写普通大整数乘法2. 编写基于分治的大整数乘法3. 编写改进的基于分治的大整数乘法4.编写一个随机产生数字的算法,分别产生两个10, 100, 1000, 10000, 100000位的数字a 和b,该数字的每一位都是随机产生的5. 用4所产生的数字来测试1、2和3算法的时间,列出如下表格。
(1)一直增长数字的位数,直到计算机内存溢出,算法无法继续进行下去。
(2)当位数较小时,乘法所需要的时间较短,这时候可以多次循环该算法,用平均时间来代表该算法的运行时间。
比如运行算法100次,得到时间是1.5秒,则该算法的执行时间是15毫秒。
6. 画出相应的散点图,其中x轴是矩阵的阶,y轴是所花费的时间,用不同的颜色表示不同的算法所花费的时间7. 思考(选做):(1)在你的机器中,乘法是否比加法更费时?从哪里体现出来的?(2)如果要做更大规模的乘法,比如10亿亿位的两个数的乘法,你有什么方法来解决这个问题?四、实验要求1. 在blackboard (http:// /) 上进行分组,然后每组提交电子版实验报告。
2. 实验报告样式可从http://192.168.2.3/guide.aspx 表格下载-学生适用-在校生管理-实践教学-实验:深圳大学学生实验报告)3. 源代码作为实验报告附件上传。
4. 实验报告正文不要帖源代码+实验指南,而是要完成相应的工作。
5. 实验人数:每组3人,自由组合。
实验报告中要指明每个人完成的内容,表格列出每个人的贡献(总体为100%,列出每个成员占的百分比)6. 在实验完成之后,将进行一次介绍。
做好PPT,由教师从每组中随机抽取一名同学来对实验内容进行介绍。
五、实验成绩实验成绩的给分标准是实验报告50%,PPT汇报50%。
每组成员的分数以小组分为基本分,然后按照每个成员的贡献进行浮动。
大整数乘法实验报告

大整数乘法实验报告实验报告--大整数实验报告题目:班级:计算机092班姓名:徐丽莉学号:09136218 完成日期:2010.11.13目的与要求:1、线性表的链式存储结构及其基本运算、实现方法和技术的训练。
2、单链表的简单应用训练3、熟悉标准模版库STL中的链表相关的知识需求分析1、编程实现单链表的基本操作2、利用单链表存储大整数(大整数的位数不限)3、利用单链表实现两个大整数的相加、相减运算(减法运算可选做)4、进行测试。
5、用STL之list完成上面的任务。
6、尝试完成HLoj 1020。
输入:12312312341234输出:2462468概要设计抽象数据类型线性表的定义如下:ADT List {数据对象:D={ ai | ai ∈ElemSet, i=1,2,...,n, n≥0 }{称n 为线性表的表长; 称n=0 时的线性表为空表。
}数据关系:R1={ ai-1 ,ai |ai-1 ,ai∈D, i=2,...,n }{设线性表为(a1,a2, . . . ,ai,. . . ,an), 称i 为ai 在线性表中的位序。
} 基本操作:} ADT ListLinkList{LNode *head;// 头指针(带头结点)LNode *tail , *cur; // 尾指针, 当前指针//intlength;// 链表长度bool Init(); // 初始化初始条件:无操作结果:初始化void Clear();初始条件:已存在操作结果:// 清除单链表void Create(int n);初始条件:无操作结果:// 建立含n个结点的单链表 int Locate(int e); // 查找初始条件:已存在操作结果:// 清除线性表void InsertBefore(int i, int e);// 插入元素初始条件:已存在操作结果:// 清除线性表bool Delete(int i,int &e);// 删除元素初始条件:已存在操作结果:// 清除线性表void Traverse();初始条件:已存在操作结果:// 遍历,并输出内容bool Empty();初始条件:已存在操作结果:// 判断空表bool GetElem(int i,int &e);初始条件:已存在操作结果://获取元素void createlistbyorder(string s);初始条件:无操作结果://字符串创建链表}; LinkList2、主程序的处理流程int main(){线性表LA,LB,LC初始化;读入2个字符串;将这2个字符串创建成链表;分别用2个指针指向线性表表头;进行运算;遍历被插入的链表LC(即输出运算结果);return 0; }三、详细设计1、线性表的实现struct LinkList{LNode *head;// 头指针(带头结点)LNode *tail , *cur; // 尾指针, 当前指针//intlength;// 链表长度bool Init();// 初始化void Clear(); // 清除线性表void Create(int n);// 建立含n个结点的单链表int Locate(int e); // 查找void InsertBefore(int i, int e);// 插入元素bool Delete(int i,int &e);// 删除元素void Traverse();// 遍历,并输出内容bool Empty(); // 判断空表 bool GetElem(int i,int &e);//获取元素void createlistbyorder(string s); //字符串创建链表};bool LinkList::Init( ){head=new LNode;head-next=NULL;return true;}void LinkList::InsertBefore(int i, int e){LNode *p=head;while (p-next!=NULL && i1){p=p-next;i--;}if (p==NULL || i 1) return;LNode *s=new LNode;s-data = e;s-next = p-next;p-next = s;}bool LinkList::Delete (int i, int &e){LNode *p=head;int j=0;while (p-next!=NULL && j i-1){p = p-next;++j;}// 寻找第i 个结点,并令p 指向其前趋if (!(p-next) || j i-1) return false; // 删除位置不合理LNode *q = p-next;p-next = q-next; // 删除并释放结点e = q-data;delete q;return true;void LinkList::Clear(){LNode *p;while (head-next!=NULL){p=head-next;head-next=p-next;}}int LinkList::Locate(int e){LNode *p=head-next;int j=0;while(p!=NULL&&p-data!=e) {j++;p=p-next;}return j;}void LinkList::Create(int n)head = new LNode;head-next =NULL; // 先建立一个带头结点的单链表for (int i = n; i 0; -{LNode *p = new LNode;cinp-data; // 输入元素值p-next = head-next;head-next = p; // 插入}}void LinkList::Traverse(){LNode *p=head-next;while(p!=NULL){coutp-dataendl;p=p-next;}}bool LinkList::Empty(){if(head-next=NULL) return true; else return false;}bool LinkList::GetElem(int i,int &e)//获取元素{if(i1 ) return false;LNode *p=head-next;while(p!=NULL && i1){i--;p=p-next;}if(p==NULL) return false;else e=p-data;return true;}void LinkList::createlistbyorder(string s) {for(int i=0;is.size();i++){LNode *p=head;篇二:JAVA实验报告处理大整数实验4 处理大整数1.相关知识点程序有时需要处理大整数,java.math包中的BigInteger类提供任意精度的整数运算。
2022年大整数的乘法实验报告

算法设计与分析实验报告姓名:XXX班级:XXX学号:XXX一、实验名称:大整数旳乘法时间:3月7日,星期三,第四节地点:12#311二、实验目旳及规定实现大整数相乘,需要解决很大旳整数,它无法在计算机硬件能直接表达旳整数范畴内进行解决。
若用浮点数来表达它,则只能近似旳表达它旳大小,计算成果中旳有效数字也受到限制。
如要精确地表达大整数并在计算成果中规定精确地得到所有位数上旳数字,就必须用软件旳措施来实现大整数旳算术运算。
三、实验环境Vc++。
四、实验内容从键盘上输入两个大整数,实现两个大整数相乘,并输出成果。
例如:在键盘上输入两个数a,b。
a=;b=;五、算法描述及实验环节定义三个数组a[100],b[100],c[199]。
用数组a来寄存大整数a,a[0]=9,a[1]=8,a[2]=7,a[3]=6,a[4]=5,a[5]=4,a[6]=3, a[7]=2,a[8]=1,a[9]=0;用数组b来寄存大整数b,b[0]=3,b[1]=6,b[2]=9,b[3]=8,b[4]=5,b[5]=2,b[6]=1 b[7]=4,b[8]=7。
用数组c来寄存数组a和b每一位旳乘积,c[0]=a[0]*b[0];c[1]=a[1]*b[0]+a[0]*b[1];c[2]=a[2]*b[0]+a[1]*b[1]+a[0]*b[2];…………c[17]=a[9]*b[8];六、调试过程及实验成果void make(int a[],int aa,int b[],int bb,int c[]){int i,j;for(i=0;i<aa;i++){if(a[i]==0) continue;for(j=0;j<bb;j++)c[i+j]+=a[i]*b[j];}for(i=0;i<aa+bb-1;i++){c[i-1]+=c[i]/10;c[i]=c[i]%10;}printf("\nc=");for(i=0;i<aa+bb-1;i++)printf("%d",c[i]);}程序运营成果:更改程序后:void make(int a[],int aa,int b[],int bb,int c[]){ int i,j;for(i=0;i<aa;i++){if(a[i]==0) continue;for(j=0;j<bb;j++)c[i+j]+=a[i]*b[j];}for(i=aa+bb-2;i>0;i--){c[i-1]+=c[i]/10;c[i]=c[i]%10;}printf("\nc=");for(i=0;i<aa+bb-1;i++)printf("%d",c[i]);}运营成果:七、总结本程序旳旳时间复杂度太大O(aa*bb),但是解决了大整数相乘硬件无法完毕旳问题。
大整数运算C语言实现C语言大作业报告+源码

大整数运算C语言实现C语言大作业报告+源码一、设计高精度无符号大整数计算(以1为存储单位)1.1 需求陈述对数值很大、精度很高的数进行高精度大整数计算是一类十分常见的问题。
但由于C语言中数据类型受数据长度和范围限制,普通数学计算很难实现此类问题,为尝试解决这个问题,专门设计一个C语言程序用于无符号大整数的计算,实现无符号大整数的一般计算和比较功能。
1.2 需求分析1.2.1 功能分析表1 程序功能分析项目功能分析以字符串形式接受数据接收反转字符串函数Invert()用Translate()将字符串翻译为整形数组分别用BigN_cmp_low()和BigN_cmp_High()对数据进行比较加法BigN_Add() //从a[1]对数组进行比较,传入两个数组及其大小以及需要从第几位开始比较减法BigN_Min() 数据运算低位减法BigN_Min_low(),在未反转的情况下计算 intBigN_cmp_High(int *, int *, int , int ); BigN乘法BigN_Mul() //从a[n]对数组进行比较,传入两个数组及其大小除法BigN_Div()反转整形数组InvertInt()从前面删减多余的零Del_zero_low() 运算辅助函数从末尾删减多余的零Del_zero_High()获取两个数的最大值Get_MAX()11.2.2 数据分析该程序可用于计算无符号大整形数据计算,最多可计算长度为200位(即10的200次方大小)的数据,但在原代码中可以随数据需求改变最大长度。
该)的情况。
由于数据类型程序中所有运算和比较均考虑到了输入前导0(例0001 限制,该程序未加入小数计算和负数计算,除法结果中只分别计算商和余数。
1.2.3 技术约束本程序已在code blocks下编译通过。
1.3 总体设计1.3.1 全局数据结构本程序中数据采取以个位数字为单位存入整形数组,在数据计算和比较中对单个数组单元进行操作。
leetcode 大数乘法

leetcode 大数乘法LeetCode是一个在线编程平台,提供了许多算法和数据结构的题目,其中也包括了大数乘法。
大数乘法是指对于超过计算机数据类型范围的大整数进行乘法运算的方法。
在日常生活中,我们经常会遇到需要计算大整数乘法的情况,比如在金融领域进行精确计算、在密码学中进行加密算法的实现等。
由于计算机的数据类型有限,无法直接处理超过其范围的大整数,因此需要使用特殊的方法进行计算。
大数乘法的思想是将大整数拆分成多个小整数相乘的形式,然后再将结果相加得到最终的乘积。
具体来说,可以将两个大整数A和B 分别拆分成n位小整数的形式,即A = A1 * 10^(n/2) + A0和B = B1 * 10^(n/2) + B0,其中A1和B1为高位部分,A0和B0为低位部分。
然后,可以使用递归的方法将大整数的乘法转化为小整数的乘法。
即计算A1 * B1、A0 * B0和(A1 + A0) * (B1 + B0)的结果。
然后将这三个结果相加得到最终的乘积。
在这个过程中,需要注意进位的处理。
当计算两个小整数的乘积时,如果结果超过了小整数的表示范围,就需要将进位部分加到高位部分中。
同样,在计算(A1 + A0) * (B1 + B0)时,也需要考虑进位的情况。
为了更好地理解大数乘法的过程,我们可以通过一个简单的例子来说明。
假设我们要计算123456789 * 987654321,首先将这两个大整数拆分成小整数的形式:A1 = 1234,A0 = 56789,B1 = 9876,B0 = 54321。
然后,我们可以计算A1 * B1、A0 * B0和(A1 + A0) * (B1 + B0)的结果:A1 * B1 = 1234 * 9876 = 12186984A0 * B0 = 56789 * 54321 = 3087159849(A1 + A0) * (B1 + B0) = (1234 + 56789) * (9876 + 54321) = 69123 * 64197 = 4436342431将这三个结果相加得到最终的乘积:12186984 * 10^8 + 3087159849 * 10^4 + 4436342431 = 1219326311371234569通过以上的计算过程,我们可以得到123456789 * 987654321 = 1219326311371234569的结果。
分治算法 大整数乘法python实现

分治算法大整数乘法python实现
好勒,那我就尽量用您要求的这些方言来给您编一篇文章,聊聊分治算法和大整数乘法的Python实现。
噫,这分治算法嘛,就像咱们四川人吃串串香一样,把一堆食材分成小份,一口口地吃,吃起来多方便嘛!在计算机里,也是这样,咱们把一个大问题分解成好多小问题,然后再解决这些小问题,最后把小问题的答案拼起来,就得到了大问题的答案。
咱们再聊聊这大整数乘法。
哎哟,你知道不,计算机里头的整数可不是咱们平时用的那些小数字,有时候它们大得吓人,直接相乘的话,计算机都受不了。
那怎么办呢?咱们就可以用分治算法来帮忙。
就像咱们贵州人做酸汤鱼一样,先把鱼切成片,再分别处理,最后合起来炖,味道就鲜美多了。
咱们把大整数也切成几段,每段单独相乘,然后再把结果合起来,这样计算机就能轻松搞定大整数乘法了。
说起这Python实现嘛,那就得靠咱们编程小哥们的本事了。
就像陕西人做肉夹馍一样,得把面饼、肉、菜都弄得恰到好处,才能做出美味的肉夹馍。
咱们编程也是这样,得把每个步骤都写清楚,不能出一点差错。
我给您举个例子吧,就像北京人炸酱面一样,得有面条、炸酱、黄瓜丝儿这些材料,还得按照一定的顺序来弄。
咱们的大整数乘法也是这样,得先把大整数切分好,然后用Python的循环、函数这些工具来帮忙计算,最后再把结果拼起来。
这样,咱们就能用Python实现大整数的乘法了。
哎哟,您看我这说得口干舌燥的,也不知道您听明白没有。
总之呢,分治算法和大整数乘法都是挺有用的东西,咱们得好好学学,才能在编程这条
路上走得更远。
大整数乘法-实验报告

实验1 大整数乘法一、实验要求1.要求至多能处理两个200位的十进制整数相乘;2.要求交互式输入大整数;3.要求显示相乘结果。
二、实验仪器和软件平台仪器:带usb接口微机软件平台:WIN-XP + VC++6.0三、源程序#include "stdafx.h"#include <iostream>#include <sstream>#include <string>using namespace std;//string字符串变整数型int string_to_num(string k){int back;stringstream instr(k);instr>>back;return back;}//整形转换为string类型string num_to_string(int intValue){string result;stringstream stream;stream << intValue;//将int输入流stream >> result;//从stream中抽取前面放入的int值return result;}//在字符串str前添加s个零string stringBeforeZero(string str,int s){for(int i=0;i<s;i++){str.insert(0,"0");}return str;}//两个大整数字符串相加string stringAddstring(string str1,string str2){//假定str1和str2是相等的长度,不相等时在前面自动补零,使两个字符串长度相等if (str1.size() > str2.size()){str2 = stringBeforeZero(str2,str1.size() - str2.size());}else if (str1.size() < str2.size()){str1 = stringBeforeZero(str1,str2.size() - str1.size());}string result;int flag=0;//前一进位是否有标志,0代表无进位,1代表有进位for(int i=str1.size()-1;i>=0;i--){//利用ASCII码对字符进行运算,这里加上flag代表的是:当前一位有进位时加1,无进位时加0int c = (str1[i] - '0') + (str2[i] - '0') + flag;flag = c/10;//c大于10时,flag置为1,否则为0c %= 10;//c大于10时取模,否则为其本身result.insert(0,num_to_string(c));//在result字符串最前端插入新生成的单个字符}if (0 != flag) //最后一为(最高位)判断,如果有进位则再添一位{result.insert(0,num_to_string(flag));}return result;}//两个大整数字符串相减string stringSubtractstring(string str1,string str2){//对传进来的两个数进行修剪,如果前面几位有0则先去掉,便于统一处理while ('0' == str1[0]&&str1.size()>1){str1=str1.substr(1,str1.size()-1);}while ('0' == str2[0]&&str2.size()>1){str2=str2.substr(1,str2.size()-1);}//使两个字符串长度相等if (str1.size() > str2.size()){str2 = stringBeforeZero(str2,str1.size() - str2.size());}string result;for(int i=str1.size()-1;i>=0;i--){int c = (str1[i] - '0') - (str2[i] - '0');//利用ASCII码进行各位减法运算if (c < 0) //当不够减时向前一位借位,前一位也不够位时再向前一位借位{c +=10;int prePos = i-1;char preChar = str1[prePos];while ('0' == preChar){str1[prePos]='9';prePos -= 1;preChar = str1[prePos];}str1[prePos]-=1;}result.insert(0,num_to_string(c));//在result字符串最前端插入新生成的单个字符}return result;}//在字符串str后跟随s个零string stringFollowZero(string str,int s){for(int i=0;i<s;i++){str.insert(str.size(),"0");}return str;}//大整数乘法的实现函数string IntMult(string x,string y){//对传进来的第一个数进行修剪,如果前面几位有0则先去掉,便于统一处理while ('0' == x[0]&&x.size()>1){x=x.substr(1,x.size()-1);}//对传进来的第二个数进行修剪,如果前面几位有0则先去掉,便于统一处理while ('0' == y[0]&&y.size()>1){y=y.substr(1,y.size()-1);}int f=4;if (x.size()>2 || y.size()>2){if (x.size() >= y.size()) //x的数长度>=y的数长度的情况{while (x.size()>f) //判断x的数据长度是否大于f的值{f*=2;}if (x.size() != f){x = stringBeforeZero(x,f-x.size());y = stringBeforeZero(y,f-y.size());}}else //x.size() < y.size()的情况{while (y.size()>f){f*=2;}if (y.size() != f){x = stringBeforeZero(x,f-x.size());y = stringBeforeZero(y,f-y.size());}}}//数据长度为1时,在前面补一个0if (1 == x.size()){x=stringBeforeZero(x,1);}if (1 == y.size()){y=stringBeforeZero(y,1);}//校正数据,确保x和y的数据长度统一if (x.size() > y.size()){y = stringBeforeZero(y,x.size()-y.size());}if (x.size() < y.size()){x = stringBeforeZero(x,y.size()-x.size());}//校正后,使得x.size=y.sizeint s = x.size();string a1,a0, b1,b0;if( s > 1){a1 = x.substr(0,s/2);a0 = x.substr(s/2,s-1);b1 = y.substr(0,s/2);b0 = y.substr(s/2,s-1);}string result;if( s == 2) //长度为2时代表着递归的结束条件{//将string字符串变整数型int na = string_to_num(a1);int nb = string_to_num(a0);int nc = string_to_num(b1);int nd = string_to_num(b0);//将x和y直接相乘,得到的整数转换为string类型result = num_to_string((na*10+nb) * (nc*10+nd));}else{//长度不为2时利用分治法进行递归运算string c2 = IntMult(a1,b1);// c2=(a1 * b1)string c0 = IntMult(a0,b0);// c0=(a0 * b0)string c1_1 = stringAddstring(a1,a0);// (a1 + a0)string c1_2 = stringAddstring(b1,b0);// (b1 + b0)string c1_3 = IntMult(c1_1,c1_2);// (a1 + a0)*(b1 + b0)string c1_4 = stringAddstring(c2,c0);// (c2 + c0)string c1=stringSubtractstring(c1_3,c1_4);// c1=(a1 + a0)*(b1 + b0)-(c2 + c0)string s1=stringFollowZero(c1,s/2);//在字符串c1后跟随s/2个零,即:算术左移s/2位。
C语言程序设计100例之(68):大整数乘法

C语⾔程序设计100例之(68):⼤整数乘法例68 ⼤整数乘法问题描述求两个不超过200位的⾮负整数的积。
输⼊有两⾏,每⾏是⼀个不超过200位的⾮负整数,没有多余的前导0。
输出⼀⾏,即相乘后的结果。
结果⾥不能有多余的前导0,即如果结果是342,那么就不能输出为0342。
输⼊样例1234567890098765432100输出样例1219326311126352690000(1)编程思路。
将⼤整数⽤字符串保存,编写函数void mul(char *a,char *b,char *c)实现⼤整数c=a*b。
在函数中⽤int x[201]和int y[201]分别存放两个乘数,⽤int z[401]来存放积。
计算的中间结果也都存在数组z中。
数组z长度取401 是因为两个200 位的数相乘,积最多会有400 位。
x[0], y[0], z[0]都表⽰个位。
计算的过程基本上和⼩学⽣列竖式做乘法相同。
为编程⽅便,不急于处理进位,⽽将进位问题留待最后统⼀处理。
在乘法过程中,数组x的第i 位和y的第j 位相乘所得的数,⼀定是要累加到z的第i+j 位上。
这⾥下标i, j 都是从右往左,从0 开始数。
(2)源程序。
#include <stdio.h>#include <string.h>void mul(char *a,char *b,char *c){int len1=strlen(a),len2=strlen(b);int x[201],y[201],z[401];int len=len1+len2;memset(x,0,sizeof(x));memset(y,0,sizeof(y));memset(z,0,sizeof(z));int i,j;for (i=len1-1;i>=0;i--)x[len1-1-i]=a[i]-'0';for (i=len2-1;i>=0;i--)y[len2-1-i]=b[i]-'0';for (i=0;i<len1;i++){{z[i+j]+=x[i]*y[j];}}for (i=0;i<len;i++){if (z[i]>=10){z[i+1]+=z[i]/10;z[i]=z[i]%10;}}while (len>0 && z[len-1]==0) // 去前置0len--;if (len==0) // a*b=0时特判{c[0]='0';c[1]='\0';return ;}for (i=0;i<len;i++)c[i]=z[len-1-i]+'0';c[len]='\0';}int main(){char s1[201],s2[201],ans[401];scanf("%s%s",s1,s2);mul(s1,s2,ans);printf("%s\n",ans);return 0;}习题6868-1 ⼤整数除法问题描述求两个⼤的正整数相除的商。
c 大数乘法

c 大数乘法C语言的大数乘法是C语言重要的一个功能,它可以实现两个非常大的数字在计算机上进行相乘,并且不会发生数据溢出的情况。
大数乘法又称为高精度乘法,相比于普通的乘法,可以表示极大值的数字。
本文将介绍C语言的大数乘法,让读者了解它的基本步骤以及实现方法。
一、基本思路与计算方法在C语言中进行大数乘法时,需要使用到基本思路和计算方法。
这些方法可以让我们更好地实现程序,同时也可以使程序更加智能化。
基本思路如下:1. 取数:需要将数存放在全局数组中,或使用字符数组等临时数组进行储存。
2. 处理数:处理数的方法主要包括数位的转换和进位的处理,这是大数乘法最关键的一步。
3. 乘法运算:进行乘法运算时,应该分别取出相乘的每一位进行计算,最后将结果存放在新的数组中。
4. 处理进位:在运算结束后,如果发现数值大于等于10,需要把它进行进位处理。
基本的大数乘法计算方法非常简单,也是我们实现程序的重要步骤,大体思路如下:首先,我们把两个大数分别存放在两个数组中,并分别定义两个变量表示两个数组的长度。
其次,定义一个新的数组来存放结果,结果数组大小应该大于等于两个大数数组之和。
然后,从两个数组的最低位开始取出数字,两个数字相乘得到结果,把结果存入新数组中,并在后面添加上进位数。
最后,遍历整个新数组,处理进位以及高位的“0”等情况,输出计算结果。
二、 C语言实现大数乘法在C语言中,实现大数乘法非常简单,关键在于思路和计算方法。
一个完整的程序,可以分为以下功能模块:1. 输入大数在程序中,我们需要首先输入两个大数,并存储到相应的数组中。
```char a[100], b[100], c[100];scanf("%s %s", a, b);```2. 处理大数在程序中实现大数乘法时,需要分别对两个大数进行处理,包括反转、进位等操作,代码如下:```int alen = strlen(a), blen = strlen(b);for (int i = 0; i < alen; i++) {aa[i] = a[alen - i - 1] - '0';}for (int i = 0; i < blen; i++) {bb[i] = b[blen - i - 1] - '0';}alen – = strcmp(a, "0") == 0? 1 : 0;blen – = strcmp(b, "0") == 0? 1 : 0;```3. 实现乘法实现乘法的核心代码非常简单,只需使用一个双重循环,分别计算出乘积,然后存储到新数组中。
算法分析与设计大整数乘法代码

#include <stdio.h>int main(){char a[100],b[100],s[202];int n,i,j,g,t=0,k=1,temp;scanf("%d",&n);n--;scanf("%s%s",&a,&b);while(k<=2*n){s[k]=0;temp=0;for(i=0;i<=n;i++){for(j=0;j<=n;j++){if((i+j)==k-1)temp+=(a[n-i]-48)*(b[n-j]-48);}}g=(temp+t)%10;t=(temp+t)/10;s[k]=g;k++;}temp=0;for(i=0;i<=n;i++){for(j=0;j<=n;j++)if((i+j)==k-1)temp+=(a[n-i]-48)*(b[n-j]-48);}temp+=t;printf("%d",temp);for(i=2*n;i>0;i--)printf("%d",s[i]);printf("\n");return 0;}//两个100位以内的如果小了自己将数组改一下设X和Y是两个n位的整数,假定n是2的整数次幂。
把每个整数分为两部分,每部分为n/2位,则X和Y可重写为X=x1*10n/2+x0和Y=y1*10n/2+y0,X和Y的乘积可以计算为X*Y= (x1*10n/2+x0)*( y1*10n/2+y0)= X1*Y1*10n+(( x1+x0)*( y1+y0)-x1*y1-x0*y0)* 10n/2+ x0*y0由此体现了分治递归的思想,将大整数化小,规模也变小。
源代码如下:#include<math.h>#include<stdlib.h>int n,x,y,rt;//全局变量void input(){cout<<"两个乘数的位数是n,请输入n的值(n是2的整数次幂): "; cin>>n;cout<<endl<<"请输入两个乘数的值:"<<endl;cout<<"x=";cin>>x;cout<<"y=";cin>>y;}int calculate(int a,int b) //计算数值函数--循环体int temp1,temp2;long s;int x1,x0,y1,y0;if(n>1) //可以分治算法的条件{temp1=(int)pow(10,n/2);temp2=(int)pow(10,n);x1=a/temp1; //x值的前半部分x0=a-x1*temp1; //x值的后半部分y1=b/temp1;//y值的前半部分y0=b-y1*temp1;//y值的后半部分n=n/2; //经过一次分治后,数的位数减半s=calculate(x1,y1)*temp2+(calculate(x1+x0,y1+y0)-calculate(x1,y1)-calc ulate(x0,y0))*temp1+calculate(x0,y0);}elsereturn a*b;return s;}void print()//输出函数{cout<<"乘数x="<<x<<"\t"<<"y="<<y<<endl; cout<<"结果rt="<<rt<<endl;}void main()//主函数{char c;do{system("cls");//清屏函数input();rt=calculate(x,y);print();cout<<"是否继续?(y/n)"<<endl;cin>>c;}while(c=='y'||'c'=='Y');}。
数据结构大型实验大整数运算系统附源代码

数据构造大型实验实验报告〔附源代码〕工业大学朱镇洋耀明华族目录第一局部要求与概述一、实验目的以及准备1.1.1 问题描述. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1.1.2 根本要求. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1.1.3 设计思路. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .第二局部具体实现一、代码局部2.1.1 链表类及大数类的局部说明以及局部源码. . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.1.2 局部简单函数功能. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.1.3 加法. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.1.4 减法. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.1.5 乘法. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.1.6 除法. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.1.7 幂运算. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.1.8 二进制和十进制的相互转化. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .二、程序流程及函数间关系2.2.1 程序流程图. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.2.2 函数调用关系分析. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .三、实验验证分析2.3.1 输入的形式和输入值的围. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.3.2 输出的形式. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.3.3 程序所能到达的功能. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2.3.4 测试数据. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .四、调试分析2.4.1 调试过程中的主要技术问题以及具体的解决方法. . . . . . . . . . . . . . . . . . . . . . . .2.4.2 印象最深刻的3个调试错误,及修正方法. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .五、附录2.5.1 源代码及其所属文件. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .第一局部要求与概述1.1.1 问题描述•密码学分为两类密码:对称密码和非对称密码。
大数阶乘算法实验报告

一、实验目的1. 掌握大数阶乘的基本概念和计算方法。
2. 了解大数阶乘在数学、计算机科学等领域的应用。
3. 通过实验,提高编程能力和算法设计能力。
二、实验环境1. 操作系统:Windows 102. 编程语言:C++3. 开发工具:Visual Studio 2019三、实验内容1. 实现大数阶乘的递归算法。
2. 实现大数阶乘的非递归算法(迭代算法)。
3. 对比两种算法的执行效率。
四、实验步骤1. 编写递归算法实现大数阶乘:```cpp#include <iostream>#include <vector>using namespace std;// 递归算法实现大数阶乘long long factorial_recursive(int n) {if (n <= 1) {return 1;}return n factorial_recursive(n - 1);}int main() {int n;cout << "请输入一个自然数:";cin >> n;cout << n << "! = " << factorial_recursive(n) << endl; return 0;}```2. 编写迭代算法实现大数阶乘:```cpp#include <iostream>#include <vector>using namespace std;// 迭代算法实现大数阶乘long long factorial_iterative(int n) {long long result = 1;for (int i = 2; i <= n; ++i) {result = i;}return result;}int main() {int n;cout << "请输入一个自然数:";cin >> n;cout << n << "! = " << factorial_iterative(n) << endl; return 0;}```3. 对比两种算法的执行效率:```cpp#include <iostream>#include <vector>#include <chrono>using namespace std;// 递归算法实现大数阶乘long long factorial_recursive(int n) {if (n <= 1) {return 1;}return n factorial_recursive(n - 1);}// 迭代算法实现大数阶乘long long factorial_iterative(int n) {long long result = 1;for (int i = 2; i <= n; ++i) {result = i;}return result;}int main() {int n;cout << "请输入一个自然数:";cin >> n;// 测试递归算法auto start_recursive = chrono::high_resolution_clock::now();cout << n << "! = " << factorial_recursive(n) << endl;auto end_recursive = chrono::high_resolution_clock::now();chrono::duration<double, milli> duration_recursive = end_recursive - start_recursive;cout << "递归算法执行时间: " << duration_recursive.count() << " ms" << endl;// 测试迭代算法auto start_iterative = chrono::high_resolution_clock::now();cout << n << "! = " << factorial_iterative(n) << endl;auto end_iterative = chrono::high_resolution_clock::now();chrono::duration<double, milli> duration_iterative = end_iterative - start_iterative;cout << "迭代算法执行时间: " << duration_iterative.count() << " ms" << endl;return 0;}```五、实验结果与分析1. 实验结果显示,递归算法和迭代算法均能正确计算出大数阶乘的结果。
C语言中超大整数乘法运算
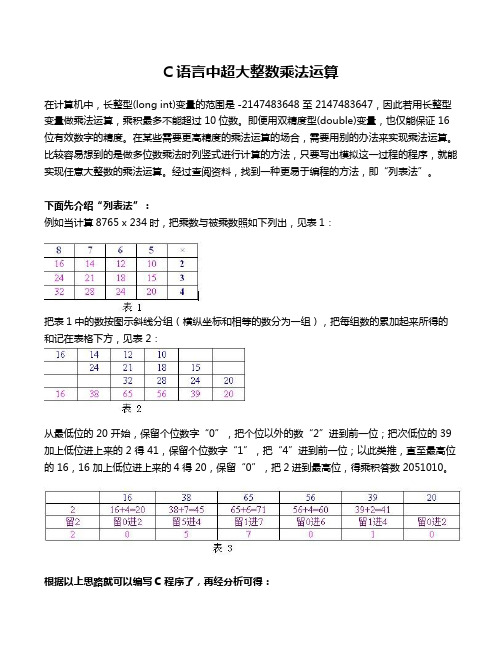
C语言中超大整数乘法运算在计算机中,长整型(long int)变量的范围是 -2147483648 至 2147483647,因此若用长整型变量做乘法运算,乘积最多不能超过 10位数。
即便用双精度型(double)变量,也仅能保证 16 位有效数字的精度。
在某些需要更高精度的乘法运算的场合,需要用别的办法来实现乘法运算。
比较容易想到的是做多位数乘法时列竖式进行计算的方法,只要写出模拟这一过程的程序,就能实现任意大整数的乘法运算。
经过查阅资料,找到一种更易于编程的方法,即“列表法”。
下面先介绍“列表法”:例如当计算8765 x 234时,把乘数与被乘数照如下列出,见表1:把表1中的数按图示斜线分组(横纵坐标和相等的数分为一组),把每组数的累加起来所得的和记在表格下方,见表 2:从最低位的 20 开始,保留个位数字“0”,把个位以外的数“2”进到前一位;把次低位的 39 加上低位进上来的 2 得 41,保留个位数字“1”,把“4”进到前一位;以此类推,直至最高位的 16,16 加上低位进上来的4得 20,保留“0”,把2进到最高位,得乘积答数 2051010。
根据以上思路就可以编写C 程序了,再经分析可得:1、一个m 位的整数与一个 n 位的整数相乘,乘积为m+n-1 位或m+n位。
2、程序中,用三个字符数组分别存储乘数、被乘数与乘积。
由第 1 点分析知,存放乘积的字符数组的长度应不小于存放乘数与被乘数的两个数组的长度之和。
3、可以把第二步“计算填表”与第三四步“累加进位”放在一起完成,可以节省存储表格 2所需的空间。
4、程序关键部分是两层循环,内层循环累计一组数的和,外层循环处理保留的数字与进位。
编写的程序如下:#define MAXLENGTH 1000#include <stdio.h>#include <string.h>void compute(char *a, char *b, char *c);void main(void){char a[MAXLENGTH], b[MAXLENGTH], c[MAXLENGTH * 2];puts("Input multiplier :");gets(a);puts("Input multiplicand :");gets(b);compute(a, b, c);puts("Answer :");puts(c);getchar();}void compute(char *a, char *b, char *c){inti, j, m, n;long sum, carry;m = strlen(a) - 1;n = strlen(b) - 1;for (i = m; i>= 0; i--)a[i] -= '0';for (i = n; i>= 0; i--)b[i] -= '0';c[m + n + 2] = '\0';carry = 0;for (i = m + n; i>= 0; i--) /* i为坐标和 */{sum = carry;if ((j = i - m) < 0)j = 0;for ( ; j<=i&& j<=n; j++) /* j 为纵坐标 */ sum += a[i-j] * b[j]; /* 累计一组数的和 */c[i + 1] = sum % 10 + '0'; /* 算出保留的数字 */ carry = sum / 10; /* 算出进位 */}if ((c[0] = carry+'0') == '0') /* if no carry, */ c[0] = '\040'; /* c[0] equals to space */}效率分析:用以上算法计算 m位整数乘以n 位整数,需要先进行 m x n次乘法运算,再进行约m + n次加法运算和 m + n次取模运算(实为整数除法)。
c++大整数乘法代码

c++大整数乘法代码下面是一个用C++实现的大整数乘法代码示例,可以处理任意大小的整数相乘。
具体实现方法是将输入的大整数转换为字符串,然后对每一位进行乘法运算,最后将结果转换为大整数输出。
代码如下:```cpp#include <iostream>#include <string>#include <algorithm>using namespace std;string multiply(string num1, string num2) {int n1 = num1.length();int n2 = num2.length();if (n1 == 0 || n2 == 0) return '0';vector<int> result(n1 + n2, 0);int i_n1 = 0;int i_n2 = 0;for (int i = n1 - 1; i >= 0; i--) {int carry = 0;int n1 = num1[i] - '0';i_n2 = 0;for (int j = n2 - 1; j >= 0; j--) {int n2 = num2[j] - '0';int sum = n1 * n2 + result[i_n1 + i_n2] + carry; carry = sum / 10;result[i_n1 + i_n2] = sum % 10;i_n2++;}if (carry > 0) {result[i_n1 + i_n2] += carry;}i_n1++;}int i = result.size() - 1;while (i >= 0 && result[i] == 0) i--;if (i == -1) return '0';string s = '';while (i >= 0) s += to_string(result[i--]);return s;}int main() {string num1, num2;cin >> num1 >> num2;cout << multiply(num1, num2) << endl;return 0;}```使用说明:1. 输入两个大整数,以空格隔开;2. 程序会输出它们的乘积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
姓名:蔡强学号:2012150269以下代码都在上的B48题测试过//普通大整数乘法代码#include <iostream>#include <cstdio>#include <cstdlib>#include <cstring>#include <ctime>using namespace std;#define MAX 1000005char s1[MAX];char s2[MAX];char ans[MAX*2];void fanzhuan(char *s)//将字符串反转{int n=strlen(s);for(int i=0;i<n/2;i++){char temp=s[i];s[i]=s[n-i-1];s[n-i-1]=temp;}}int main(){int p,t,i,j,n;char c;clock_t s,e;printf("请输入测试数量:\n");scanf("%d",&t);printf("请输入数位的长度:\n");scanf("%d",&n);c=getchar();s=clock();for(p=0;p<t;p++){memset(s1,0,sizeof(s1));memset(s2,0,sizeof(s2));memset(ans,0,sizeof(ans));// printf("随机产生第一个数:");for(i=0;i<n;i++){s1[i]=rand()%10+'0';// printf("%c",s1[i]);}// printf("\n");// printf("随机产生第二个数:");for(i=0;i<n;i++){s2[i]=rand()%10+'0';// printf("%c",s2[i]);}// printf("\n");int x1,x2;x1=strlen(s1);x2=strlen(s2);fanzhuan(s1);fanzhuan(s2);int v,d=0;for(i=0;i<x1+x2;i++)•ans[i]='0';//结果数组,初始化为字符0•for(i=0;i<x1;i++)//依次取第一个大整数的第i位,逐位相乘{•for(j=i;j<x2+i;j++)//用第一个大整数的第i位乘以第二个大整数的每一位{v=(s1[i]-'0')*(s2[j-i]-'0')+(ans[j]-'0')+d;ans[j]=v%10+'0';d=v/10;}while(d)//将剩下的余数向高位补齐,直到余数为0为止{ans[j++]=d%10+'0';d/=10;}}fanzhuan(ans);for(i=0;ans[i]!='\0';i++)if(ans[i]!='0')break;// printf("%s\n",ans+i);//输出结果}e=clock();printf("总的运行时间:");printf("%.6lf秒\n",(e-s)/1000.0);return 0;}//未改进分治法#include <iostream>#include <cstdio>#include <cstdlib>#include <ctime>#include <cstring>using namespace std;int value[32];void createL(){for(int i=0;i<32;i++)value[i]=1<<i;}int Long(int n)//将整数补为2的n次方长度{int i;for(i=0;i<32;i++)if(n<=value[i]){n=value[i];return n;}return -1;}int *sum(int*a,int*b,int n)//加法{int *c=(int*)malloc(sizeof(int)*n);n--;for(;n>=0;n--)c[n]=a[n]+b[n];return c;}void red(int*a,int*b,int*c,int n)//减法{n--;for(;n>=0;n--)a[n]=a[n]-b[n]-c[n];}void sum2(int*a,int*b,int n)//加法{n--;for(;n>=0;n--)a[n]+=b[n];}int *mul(int*a,int*b,int n)//递归乘法{int *ans=(int*)malloc(sizeof(int)*2*n);memset(ans,0,sizeof(int)*n*2);int *c2,*c1,*c0,*x,*y;if(n<=1){ans[1]=a[0]*b[0];return ans;}int l=n/2;c2=mul(a,b,l);c0=mul(a+l,b+l,l);x=sum(a,a+l,l);y=sum(b,b+l,l);c1=mul(x,y,l);red(c1,c2,c0,n);sum2(ans,c2,n);sum2(ans+l,c1,n);sum2(ans+n,c0,n);free(c2);free(c1);free(c0);free(x);free(y);return ans;}void show(int *a,int n)//输出结果{int i;int d=0;int flag=0;for(i=n-1;i>=0;i--){d+=a[i];a[i]=d%10;d/=10;}for(d=0;d<n;d++)if(a[d]!=0){flag=1;break;}if(flag)for(;d<n;d++)printf("%d",a[d]);else printf("0");printf("\n");}int main()//主函数{int i,n,t,p;int *a,*b,*ans;clock_t start,end;createL();printf("请输入测试数量:\n");scanf("%d",&p);printf("请输入数位长度:\n");scanf("%d",&t);n=Long(t);t=n-t;start=clock();while(p--){a=(int*)malloc(sizeof(int)*n);b=(int*)malloc(sizeof(int)*n);memset(a,0,sizeof(int)*n);memset(b,0,sizeof(int)*n);for(i=t;i<n;i++){a[i]=rand()%10;// printf("%d",a[i]);}// printf("\n");for(i=t;i<n;i++){b[i]=rand()%10;// printf("%d",b[i]);}//printf("\n");ans=mul(a,b,n);//show(ans,2*n);free(ans);free(a);free(b);}end=clock();printf("总的运行时间:\n");printf("%.6lf秒\n",(end-start)/1000.0);return 0;}//改进后的分治法#include <iostream>#include <cstdio>#include <cstdlib>#include <ctime>#include <cstring>using namespace std;int value[31];void createL(){for(int i=0;i<31;i++)value[i]=1<<i;}int Long(int n)//将整数补为2的n次方长度{int i;for(i=0;i<31;i++)if(n<=value[i]){n=value[i];return n;}return -1;}int *sum(int*a,int*b,int n)//加法{int *c=(int*)malloc(sizeof(int)*n);n--;for(;n>=0;n--)c[n]=a[n]+b[n];return c;}void red(int*a,int*b,int n)//减法(有改动){int d=0;n--;for(;n>=0;n--){if(a[n]+d<b[n]){a[n]=a[n]+d+10-b[n];d=-1;}else{a[n]=a[n]+d-b[n];d=0;}}}void sum2(int*a,int*b,int n)//加法{n--;for(;n>=0;n--)a[n]+=b[n];}void repair(int *a,int n)//修剪每部的中间结果(新增){int d=0;for(n--;n>=0;n--){d+=a[n];a[n]=d%10;d/=10;}a[0]+=d*10;}int *mul(int*a,int*b,int n)//递归乘法(有改动){int *ans=(int*)malloc(sizeof(int)*2*n);memset(ans,0,sizeof(int)*n*2);int *c2,*c1,*c0,*x,*y;if(n<=16){int d=0,i,j;for(i=n-1;i>=0;i--){for(j=i+n;j>=i+1;j--){d=a[i]*b[j-i-1]+ans[j]+d;ans[j]=d%10;d/=10;}while(j>=0){d+=ans[j];ans[j--]=d%10;d/=10;}ans[0]+=d*10;d=0;}return ans;}int l=n/2;c2=mul(a,b,l);c0=mul(a+l,b+l,l);x=sum(a,a+l,l);y=sum(b,b+l,l);c1=mul(x,y,l);red(c1,c2,n);red(c1,c0,n);sum2(ans,c2,n);sum2(ans+l,c1,n);sum2(ans+n,c0,n);repair(ans,2*n);free(c2);free(c1);free(c0);free(x);free(y);return ans;}void show(int *a,int n){int d=0;int flag=0;for(d=0;d<n;d++)if(a[d]!=0){flag=1;break;}if(flag)for(;d<n;d++)printf("%d",a[d]);else printf("0");printf("\n");}int main(){int i,n,t,p;int *a,*b,*ans;clock_t start,end;createL();printf("请输入测试数量:\n");scanf("%d",&p);printf("请输入数位长度:\n");scanf("%d",&t);n=Long(t);t=n-t;start=clock();while(p--){a=(int*)malloc(sizeof(int)*n);b=(int*)malloc(sizeof(int)*n);memset(a,0,sizeof(int)*n);memset(b,0,sizeof(int)*n);for(i=t;i<n;i++){a[i]=rand()%10;// printf("%d",a[i]);}// printf("\n");for(i=t;i<n;i++){b[i]=rand()%10;// printf("%d",b[i]);}// printf("\n");ans=mul(a,b,n);// show(ans,2*n);free(ans);free(a);free(b);}end=clock();printf("总的运行时间:\n");printf("%.6lf秒\n",(end-start)/1000.0);return 0;}。
