第06章 树与二叉树B
数据结构PPT第6章树和二叉树

安
徽 理
树的逻辑结构特点
工
大 学 1. 树中只有根结点没有前趋;
2. 除根外,其余结点都有且仅一个前趋;
3. 树的结点,可以有零个或多个后继;
4. 除根外的其它结点,都存在唯一条从
A
根到该结点的路径; 5. 树是一种分支结构。
B
C
D
E
FG H I J
KL
M
安
徽 理
树的应用
工
大 学
▪ 树可表示具有分支结构关系的对象
结论3知,x的右孩子应为2x+1,即2x+1=i,x=(i-1)/2。
故 i的双亲为└i/2┘ 证毕。
安
徽 理
6.2.3 二叉树的存储结构
工
大 学
❖ 顺序存储结构
所谓顺序存储结构,就是用一组连续的存储单元存储二
叉树的数据元素,结点在这个序列中的相互位置能反映出
结点之间的逻辑关系。 二叉树中结点之间的关系就是双亲
例1. 家族族谱
设某家庭有13个成员A、B、C、D、E、F、G、H、I、J
、K、L、M,他们之间的关系可如图所示的树表示。
例2. 单位行政机构的组织关系
A
B
C
D
E
FG H I J
KL
M
安
徽 理
树的应用
工
大 学
▪ 树是常用的数据组织形式
有些应用中数据元素之间并不存在分支结构关系,但是为
了便于管理和使用数据,将它们用树的形式来组织。
A
B
C
D
Ø
E
F
G H ØØØØI J
例如对于B结点而言: bt[2]的双亲为└1/2┘=1,即在bt[1]中 (为A); 其左孩子在bt[2i]=bt[4]中(为D); 其右孩子在bt[2i+1]=bt[5]中(为Ø )。
第6章树与二叉树-

F3
7
G6
8
H6
9
K6
8
2. 孩子表示法
由于树中每个结点可能有多棵子树,则可以用多重 链表,即每个结点有多个指针域,其中每个指针指向一 棵子树的根结点,此时,链表中的结点可以有如下 3 种 结构格式:
同构结点格式 不同构结点格式 单链表存储结构
9
(1) 同构结点格式。即多重链表中的结点是同构的。
完全二叉树:一棵深度为 k 并且有 n 个结点的二叉 树,当且仅当其每一个结点都与深度为 k 的满二叉树中 编号从 1 至 n 的结点一一对应时,称之为完全二叉树。
完全二叉树的特点是:二叉树中的叶子结点只可能 出现在二叉树中层次最大的两层上;最下一层的结点一 定是从最左边开始向右放的;并且若某个结点没有左孩 子,则它一定没有右孩子。
为 2 的结点有两个出支,则:B = n1 + 2n2 故:n = n1 + 2n2 + 1;最后得到: n0 = n2 + 1。
20
为便于介绍下面两个二叉树性质,先了解满二叉树 (full binary tree) 和完全二叉树 (complete binary tree) 的 概念。
满二叉树:一棵深度为 k 并且有 2k-1 个结点的二叉 树,称之为满二叉树。
23
性质5:如果对一棵有 n 个结点的完全二叉树(此二 叉树的深度为 log2n +1)的结点按照层次编号(从第 1 层到第 log2n +1 层,每层从左到右),那么对任一结点 i(1 ≤i ≤n),有
(1) 若 i = 1,则结点 i 是二叉树的根,没有双亲结点; 若 i >1,则其双亲结点是结点 i / 2。
(2) 若 2i >n,则结点 i 没有左孩子(结点 i 为叶子结 点);否则其左孩子是结点 2i。
数据结构 第6章习题答案

第6章树和二叉树习题解答一、下面是有关二叉树的叙述,请判断正误(每小题1分,共10分)(√)1. 若二叉树用二叉链表作存贮结构,则在n个结点的二叉树链表中只有n—1个非空指针域。
(×)2.二叉树中每个结点的两棵子树的高度差等于1。
(√)3.二叉树中每个结点的两棵子树是有序的。
(×)4.二叉树中每个结点有两棵非空子树或有两棵空子树。
(×)5.二叉树中每个结点的关键字值大于其左非空子树(若存在的话)所有结点的关键字值,且小于其右非空子树(若存在的话)所有结点的关键字值。
(应当是二叉排序树的特点)(×)6.二叉树中所有结点个数是2k-1-1,其中k是树的深度。
(应2i-1)(×)7.二叉树中所有结点,如果不存在非空左子树,则不存在非空右子树。
(×)8.对于一棵非空二叉树,它的根结点作为第一层,则它的第i层上最多能有2i—1个结点。
(应2i-1)(√)9.用二叉链表法(link-rlink)存储包含n个结点的二叉树,结点的2n个指针区域中有n+1个为空指针。
(正确。
用二叉链表存储包含n个结点的二叉树,结点共有2n个链域。
由于二叉树中,除根结点外,每一个结点有且仅有一个双亲,所以只有n-1个结点的链域存放指向非空子女结点的指针,还有n+1个空指针。
)即有后继链接的指针仅n-1个。
(√)10. 〖01年考研题〗具有12个结点的完全二叉树有5个度为2的结点。
最快方法:用叶子数=[n/2]=6,再求n2=n0-1=5二、填空(每空1分,共15分)1.由3个结点所构成的二叉树有5种形态。
2. 【计算机研2000】一棵深度为6的满二叉树有n1+n2=0+ n2= n0-1=31 个分支结点和26-1 =32个叶子。
注:满二叉树没有度为1的结点,所以分支结点数就是二度结点数。
3.一棵具有257个结点的完全二叉树,它的深度为9。
(注:用⎣ log2(n) ⎦+1= ⎣ 8.xx ⎦+1=94.【全国专升本统考题】设一棵完全二叉树有700个结点,则共有350个叶子结点。
数据结构与算法第六章课后答案第六章 树和二叉树
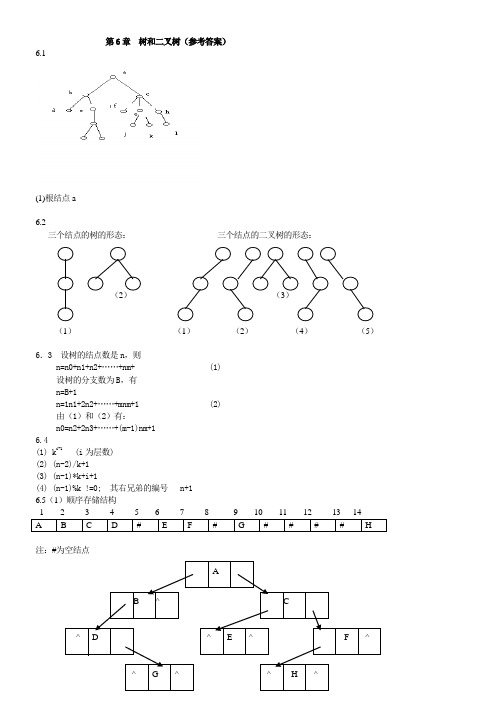
第6章 树和二叉树(参考答案)6.1(1)根结点a6.2三个结点的树的形态: 三个结点的二叉树的形态:(1) (1) (2) (4) (5)6.3 设树的结点数是n ,则n=n0+n1+n2+……+nm+ (1)设树的分支数为B ,有n=B+1n=1n1+2n2+……+mnm+1 (2)由(1)和(2)有:n0=n2+2n3+……+(m-1)nm+16.4(1) k i-1 (i 为层数)(2) (n-2)/k+1(3) (n-1)*k+i+1(4) (n-1)%k !=0; 其右兄弟的编号 n+16.5(1)顺序存储结构注:#为空结点6.6(1) 前序 ABDGCEFH(2) 中序 DGBAECHF(3) 后序 GDBEHFCA6.7(1) 空二叉树或任何结点均无左子树的非空二叉树(2) 空二叉树或任何结点均无右子树的非空二叉树(3) 空二叉树或只有根结点的二叉树6.8int height(bitree bt)// bt是以二叉链表为存储结构的二叉树,本算法求二叉树bt的高度{ int bl,br; // 局部变量,分别表示二叉树左、右子树的高度if (bt==null) return(0);else { bl=height(bt->lchild);br=height(bt->rchild);return(bl>br? bl+1: br+1); // 左右子树高度的大者加1(根) }}// 算法结束6.9void preorder(cbt[],int n,int i);// cbt是以完全二叉树形式存储的n个结点的二叉树,i是数// 组下标,初始调用时为1。
本算法以非递归形式前序遍历该二叉树{ int i=1,s[],top=0; // s是栈,栈中元素是二叉树结点在cbt中的序号 // top是栈顶指针,栈空时top=0if (n<=0) { printf(“输入错误”);exit(0);}while (i<=n ||top>0){ while(i<=n){visit(cbt[i]); // 访问根结点if (2*i+1<=n) s[++top]=2*i+1; //若右子树非空,其编号进栈i=2*i;// 先序访问左子树}if (top>0) i=s[top--]; // 退栈,先序访问右子树} // END OF while (i<=n ||top>0)}// 算法结束//以下是非完全二叉树顺序存储时的递归遍历算法,“虚结点”用‘*’表示void preorder(bt[],int n,int i);// bt是以完全二叉树形式存储的一维数组,n是数组元素个数。
数据结构第六章树和二叉树习题及答案

习题六树和二叉树一、单项选择题1.以下说法错误的是 ( )A.树形结构的特点是一个结点可以有多个直接前趋B.线性结构中的一个结点至多只有一个直接后继C.树形结构可以表达(组织)更复杂的数据D.树(及一切树形结构)是一种"分支层次"结构E.任何只含一个结点的集合是一棵树2.下列说法中正确的是 ( )A.任何一棵二叉树中至少有一个结点的度为2B.任何一棵二叉树中每个结点的度都为2C.任何一棵二叉树中的度肯定等于2D.任何一棵二叉树中的度可以小于23.讨论树、森林和二叉树的关系,目的是为了()A.借助二叉树上的运算方法去实现对树的一些运算B.将树、森林按二叉树的存储方式进行存储C.将树、森林转换成二叉树D.体现一种技巧,没有什么实际意义4.树最适合用来表示 ( )A.有序数据元素 B.无序数据元素C.元素之间具有分支层次关系的数据 D.元素之间无联系的数据5.若一棵二叉树具有10个度为2的结点,5个度为1的结点,则度为0的结点个数是()A.9 B.11 C.15 D.不确定6.设森林F中有三棵树,第一,第二,第三棵树的结点个数分别为M1,M2和M3。
与森林F 对应的二叉树根结点的右子树上的结点个数是()。
A.M1 B.M1+M2 C.M3 D.M2+M37.一棵完全二叉树上有1001个结点,其中叶子结点的个数是()A. 250 B. 500 C.254 D.505 E.以上答案都不对8. 设给定权值总数有n 个,其哈夫曼树的结点总数为( )A.不确定 B.2n C.2n+1 D.2n-19.二叉树的第I层上最多含有结点数为()A.2I B. 2I-1-1 C. 2I-1 D.2I -110.一棵二叉树高度为h,所有结点的度或为0,或为2,则这棵二叉树最少有( )结点A.2h B.2h-1 C.2h+1 D.h+111. 利用二叉链表存储树,则根结点的右指针是()。
A.指向最左孩子 B.指向最右孩子 C.空 D.非空12.已知一棵二叉树的前序遍历结果为ABCDEF,中序遍历结果为CBAEDF,则后序遍历的结果为()。
第六章 树与二叉树

森林的遍历
(4) 广度优先遍历(层次序 遍历) :
数据结构
若森林F为空,返回; 否则 依次遍历各棵树的根 结点; 依次遍历各棵树根结 点的所有子女; 依次遍历这些子女结 森林的二叉树表示 点的子女结点。
45
二叉树的计数 由二叉树的前序序列和中序序列可唯 一地确定一棵二叉树。例, 前序序列 { ABHFDECKG } 和中序序列 { HBDFAEKCG }, 构造二叉树过程如 下:
三个结点构成的不同的二叉树
8
用二 叉 树 表达实际问题
例2 双人比赛的所有可能的结局
开始
甲
开局连赢两局 或五局三胜
乙
甲
甲 甲 乙
乙
乙 甲 乙 甲 甲 乙
甲
乙 甲
乙
乙
甲
乙甲
乙
甲
乙 甲 乙
二叉树的性质
数据结构
性质1 若二叉树的层次从1开始, 则在二叉树的 第 i 层最多有 2i -1个结点。(i 1) [证明用数学归纳法] 性质2 高度为k的二叉树最多有 2k-1个结点。 (k 0) [证明用求等比级数前k项和的公式]
前序遍历二叉树算法的框架是 若二叉树为空,则空操作; 否则 – 访问根结点 (V); – 前序遍历左子树 (L); – 前序遍历右子树 (R)。
遍历结果 -+a*b-cd/ef
27
数据结构
后序遍历 (Postorder Traversal)
后序遍历二叉树算法的框架是 若二叉树为空,则空操作; 否则 – 后序遍历左子树 (L); – 后序遍历右子树 (R); – 访问根结点 (V)。
数据结构
36
左子女-右兄弟表示法 第一种解决方案
第六章树和二叉树

k
k
(第 i层的最大 )结2i点 12数 k 1
i1
i1
❖性质3:对任何一棵二叉树T,如果其终端结点数为n0, 度为2的结点数为n2,则n0=n2+1
证明:n1为二叉树T中度为1的结点数 因为:二叉树中所有结点的度均小于或等于2 所以:其结点总数n=n0+n1+n2 又二叉树中,除根结点外,其余结点都只有一个 分支进入 设B为分支总数,则n=B+1 又:这些分支是由度为1和度为2的结点射出, B=n1+2n2 于是,n=B+1=n1+2n2+1=n0+n1+n2 n0=n2+1
f
gh
4. 嵌套括号表示
a ( b ( d, e ( i, j ),f), c ( g, h ) )
★树的存储结构
※ 1. 双亲表示法
实现:结构数组存放树的结点,每个结点含两个域 数据域:存放结点本身信息 双亲域:指示本结点的双亲结点在数组中位置
特点:找双亲容易,找孩子难
typedef struct node { datatype data;
int parent; }JD; JD t[M];
a
b
c
d
e
f
gh i
如何找孩子结点
0号单元不用或
存结点个数
data
parent
00
9
1
a
0
2
b
1
3
c
1
4
d
2
5
e
2
6f
3
7g
5
8h
5
9i
5
※ 2. 孩子表示法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1章 绪论 第2章 线性表 第3章 栈和队列 第4章 串 第5章 数组和广义表 第6章 树和二叉树 第7章 图 第9章 查找 第10章 排序
1
教学 内 容
1、树和森林的概念 2、二叉树的定义、性质及运算; 3、二叉树的存储结构 4、遍历二叉树 5、线索二叉树 6、树、森林、森林与二叉树的转换 7、哈夫曼树、哈夫曼编码
D出栈,t为空 栈[AB] B出栈,t指向E 栈[A] 访问E, E进栈,t指向H 栈[AE] 访问H,H进栈,t为空 栈[AEH] H出栈,t指向J 栈[AE] 访问J, J进栈, t为空 栈[AEJ] J出栈, t为空 栈[AE] E出栈,t为空 栈[A] A出栈,t指向C 栈为空 访问C,C进栈,t指向F 栈[C] 访问F,F进栈,t为空 栈[CF] F出栈,t指向I 栈[C] 访问I, I进栈,t为空 栈[CI] I出栈,t为空 栈[C] C出栈,t指向G 栈为空 访问G,G进栈,t为空 栈[G] G出栈,t为空 栈为空
(1) 后序遍历左子树;
(2) 后序遍历右子树;
L
(3) 访问根结点。
A
LR V
R
V
A L RV
B
C
B
C
D
L RV
后序遍历序列: D B C A
D
11
后序遍历二叉树的操作定义:
若二叉树为空,则空操作;否则
(1) 后序遍历左子树;
(2) 后序遍历右子树;
A
(3) 访问根结点。 B
D
E L
H
J
MI
LEBMIHJDA
2
6.4 二叉树的遍历
(Binary Tree Traversal)
3
遍历概念
顺着某一条搜索路径 巡访二叉树中的结点,使 得每个结点 均被访问一次 ,而且仅被访问一次 。
“访问”的含义很广,可以是对结点作各种处 理,如:输出结点的信息、修改结点的数据值 等,但要求这种访问不破坏原来的数据结构。
4
17
非递归的二叉树前序遍历:
算法思路: 对于非递归算法,引入栈模拟递归过程,初始
时栈为空。 问题是如何利用栈来保存信息,使得在前序遍历节点t的左 子树后,能利用栈顶信息获取节点t的右子树的根指针? 方法是访问t? data后,将t入栈,遍历左子树;遍历完左子 树返回时,站定元素应为t,出栈,再先序遍历t的右子树。
中序遍历算法 LDR(node *root) {if(root !=NULL) {LDR(root->lchild); printf(“%d”r,oot->data); LDR(root->rchild);
} return(0);}
先序遍历算法 DLR( node *root ) {if (root !=NULL) //非空二叉树
L
V
R
A
B D
A
LV R
L VR
C
B
C
L VR
中序遍历序列:B D A C
D
9
中序遍历二叉树的操作定义:
若二叉树为空,则空操作;否则
(1) 中序遍历左子树;
(2) 访问根结点;
A
(3) 中序遍历右子树。 B
D
E L
H
J
MI
ELBAMHIDJ
10
后序遍历二叉树的操作定义:
若二叉树为空,则空操作;否则
1)建立栈stack, 初始时栈为空 2)t指向根 3)当 t不为空时,或栈stack不空时,重复:
若t不空,访问t? data后,将t入栈; t指向其左子女;
否则:栈顶元素出栈; t指向其右子女
4)结束
18
非递归的二叉树 前序遍历:
A
B
C
DE F G
H
I
J
访问A, A进栈,t指向B 栈[A] 访问B, B进栈,t指向D 栈[AB] 访问D, D进栈,t为空 栈[ABD]
表达式的中缀表示
后序: a b c d -×+ e f / -
表达式的后缀表示
15
层次遍历(Levelorder Traversal)
从上到下,从左到右
遍历结果
- +/a* e f b -cd
16
结点数据类型自定义 typedef struct node{ int data; struct node *lchild,*rchild; } node; node *root;
vLR —— 先(根)序遍历, LvR —— 中(根)序遍历, LRv —— 后(根)序遍历。
根结点
左子树
右子树
6
先序遍历 (VLR)二叉树的操作定义:
若二叉树为空,则空操作;否则
(1) 访问根结点;
(2) 前序遍历左子树;
(3) 前序遍历右子树。
V LR
V LR
B
C
D
B
C
V LR
先序遍历序列:A B D C
{printf(“%d”A,roo-t>data); //访问D DLR(rootB->lchild);C//递归遍历左子树
DLR(root->rchild); //递归遍历右子树
} retuDrn(0); E}
后序遍历算法 LRD (node *root) {if(root !=NULL) {LRD(root->lchild); LRD(root->rchild); printf(“%d”r,oot->data); } return(0);}
遍历目的 得到树中所有结点的一个线性排列。
遍历方法
根结点
左子树
右子树
依次遍历二叉树中的三 个组成 部分,便是遍历 了整个二叉树
假设:L:遍历左子树 v:访问根结点 R:遍
历右子树 ,则遍历整个二叉树方案共有:
vLR、LvR、LRv 、 vRL、RvL、RLv 六种。
5
若规定先左后右,则只有前三种情况:
D
7
7
先序遍历二叉树的操作定义:
若二叉树为空,则空操作;否则
(1) 访问根结点;
(2) 前序遍历左子树;
A
(3) 前序遍历右子树。
B
D
E L
H
J
MI
先序遍历结果:A B E L D H M I J
8
中序遍历二叉树的操作定义:
若二叉树为空,则空操作;否则
(1) 中序遍历左子树;
(2) 访问根结点; (3) 中序遍历右子树。
12
分析表达式和二叉树的关系
以二叉树表示表达式的递归定义如下: 若表达式为一个数(或简单变量),则对应的二叉树中仅 有一个根结点,其数据域存放该表达式的信息; 若表达式形如“(第一操作数)(运算符)(第二操作 数)”,则对应的二叉树以左子树表示第一操作数,右子 树表示第二操作数,根结点的数据域存放运算符(若为一 元运算符,则左子树为空)。 操作数本身又为表达式。
a+b
+
ab
(a+b)×c ×
+
c
ab
13
分析表达式和二叉树的关系
a+b×c
(a+b)×c – d/e -
+
×
/
a×
+
cd e
b c ab
14
例:写出下图二叉树的先序、中序和后序遍历顺序。
-
+
/
遍历结果:
前序: - + a×b - c d / e f
表达式的前缀表示
a ×e
bcd
f 中序: a + b×c - d - e / f
