第四章习题解答
第4章课后习题及答案

返 回
第 4 章 供 电 与 用 电
练习题解答
4.1.1 某三相同步发电机,三相绕组联结成星形时的线电压为 10.5kV,若将它联结成三角形,则线电压是多少?若联结成星形 时,L2相绕组的首末端接反了,则三个线电压的有效值U12 , U23 和U31各是多少? · · · · U31= U3 -U1 · -U2 解: 星形联结时UlY = 10.5kV U3 · U 3 UlY 10.5 = kV = 6.06kV ∴UpY = · · U 1=U23 √ 3 √3 · ·-U =U 三角形联结时相电压不变, 2 3 · UlY = UpY =6.06kV L2首末端接反的相量图如图所示:
· · · 0 0 0 IL2 = I2 - I1 ( 8 . 8 30 8 . 8 0 ) A 4 . 56 105 A · · · 0 0 0 IL3 = I3 - I2 ( 8 . 8 30 8 . 8 30 ) A 8 . 8 90 A
XL= Z sin = 77.1×0.6 Ω = 46.3 Ω
返 回 上一题 下一题
第 4 章 供 电 与 用 电
4.3.2 某三相负载,额定相电压为220V,每相负载的电阻为4Ω,感 抗为3Ω,接于线电压为380V的对称三相电源上,试问该负载应
采用什么联结方式?负载的有功功率、无功功率和视在功率?
· I
l2
· I
l3
· I
2
· I
3
-jXC
解: 负载为不对称三相负载
· · 0 U U 220 120 2 23 · 0 I2 = Z = -jX = 8 . 8 30 A -j25 2 C
返 回 上一题 下一题
第4章习题与解答

第4章数据库和数据仓库4.1本章知识框架与学习要求数据库技术是数据管理的最新技术,是计算机科学的重要分支。
它已经成为先进信息技术的重要组成部分,是现代计算机信息系统和计算机应用系统的基础和核心。
数据库已经成为人们存储数据、管理信息、共享资源的最先进最常用的技术。
认识和掌握有关的数据库技术对学好本课程具有重要作用。
本章主要介绍了数据库技术的相关概念包括数据的组织层次、数据模型、信息模型、关系规范化等,以及数据库的设计方法,数据库仓库和数据挖掘的概念。
4.1.1 知识框架与学习要求一、数据的描述与组织(掌握)(一)三个世界1.现实世界2.信息世界3.计算机世界(二)数据组织的层次1.数据项(字段)2.记录3.数据文件4.数据库二、数据库管理技术(一)数据管理的发展(了解)1.简单应用阶段2.文件系统阶段3.数据库系统阶段(二)数据库管理系统(掌握)1.数据库系统(DBS)2.数据库管理系统(DBMS)(1)数据库的定义功能(2)数据库的操作功能(3)数据库的保护功能(4)数据库的维护功能(5)数据的存储管理三、数据模型(掌握)(一)信息模型(概念模型)1.信息模型的要素2.两个实体集之间联系的分类3.实体联系模型(E-R模型)(二)数据模型1.数据模型的三要素2.数据模型与信息模型的关系3.三种主要的数据模型(1)层次模型(Hierarchical Model)(2)网状模型(Network Model)(3)关系模型(Relational Model)(三)概念模型向关系模型的转换(四)关系的规范化1.第一范式(1NF)2.第二范式(2NF)3.第三范式(3NF)五、数据库设计(掌握)(一)数据库设计方法简述(二)数据库设计步骤六、数据仓库和数据挖掘(了解)(一)数据仓库1.数据仓库的概念2.数据仓库和数据库的区别3.数据仓库的特性4.数据仓库的基本结构5.数据仓库工具的组成(二)数据挖掘1.数据挖掘的概念2.数据仓库与数据挖掘的关系4.1.2 学习重点本章重点掌握以下几方面的内容:1.三个世界即现实世界、信息世界、计算机世界的特点及区别与联系;2.人工管理阶段、文件系统阶段及数据库系统阶段应用程序与数据关系的区别;3.数据库管理系统功能4.信息(概念)模型的要素、E-R模型的绘制方法;5.数据模型的三要素、数据模型与信息模型的关系、关系模型;6.概念模型向关系模型的转换;7.数据库设计方法和步骤4.2 教材习题与解答4.2.1 习题一、名词解释1.数据库2.记录3.DBMS4.DBS5.概念模式6.数据模型7.概念模型8.键或码9.数据操作10.1NF 11. 2NF 12.3NF 13.关系14.关系模式15.数据仓库16.数据挖掘二、简答题1. 数据库系统组织数据的特点是什么?2. 数据库系统与文件系统的区别是什么?3. 数据管理经历了哪几个阶段?各个阶段的特点是什么?4. 数据模型的三要素是什么?5. 数据库管理系统的主要功能是什么?6. 信息模型的要素有哪些?7. 试述概念模式在数据库中的重要地位。
高等代数-第4章习题及解答

第四章 多项式4.1习题,()(),..(-)-(-)()()-(-)()--(-)(-)Z a c ad bc q Z s t ad bc q a c a c b d ab cd ad bc a c b d ab cd a c q a c b d q ab cd ∈-+∴∃∈+==++=++=+1. 设a,b,c,d 已知(a-c)(ad+bc),求证(a-c)(ab+cd)证明:又由 () 得 ()() 即 ,,-()()b d q Zb d q Z ac ab cd ∈∴+∈-+即有 121212,65(-3)13,65(-2)5,65-,65(-3)13(-2)571865-(6528)65(-65)-2828m m m m r c c m c m c c c m m r ⨯⨯∃⨯+⨯==-+∴=2. 一个整数被5除余3,被13除余2,求它被65除的余数解:设所求数为由题知 即 有 令 ,, 则有 故有 1723582957,581-143,-143202,0231414a b a b a b a b b a b a b a ==-=-==-=-=-=-=+=⋅+=⋅+3. 对于下列的整数,分别求出以除所得的商和余数: (1), (2), (3), (4)解:)由带余除法,可表示为 故商为,余数为;)同理得 故商为,余数为; )由 知商为,余数为; 49595b a =+ )由 知商为,余数为。
.()001a b a b b aq q Z b q b a q q a b≠≤=∈≠∴≠∴=≥∴≤4. 证明:若a b,b 0,则证明:由 可得 又 又1,) 1.b ∈=1 1 1115. 设a,b 是不全为零的整数,且a=da ,b=db ,d,a ,b Z.证明d 是a 与b 的一个最大公因数的充分必要条件是(a1111111111[] 4.1.3,,..01(,)1[](,)1''1''1,''u v Z s t ua vb d uda vdb d d ua vb a b a b u a v b a bu v u a v b d d d⇒∃∈+=+=≠∴+=∴=⇐=+=+=+=证明:根据定理得 即 又故有 即 则有 综上所述,结论得证6.(,)1,(,) 1.,(1),,..()()(1),,1,1a b a b ab a b ab d d Z d u v Z s t u a b vab d ua u va b d u v a Z u va Za b =+=+=∈≠∴∃∈++=∴++=∈∴+∈= 证明:若则 证明:反证 假设() 且 故 ()与 () 矛盾 ,17.1..,()(),,.a b ab a b p ab p a p b p p mn a b k k Z p abp b b k p a p b p k m b m k m k n b n k n k p ∴+===+∈∴+ () 设是一个大于的整数且具有以下性质:对于任意整数,,若,则或 证明是一个素数 证明:令 又当 不整除,有,不整除 又有,不整除或; 不整除或 若为合数,那,m k n k p p k p b p 么由可知必为素数,否则 同理可证当不整除时,也必为素数4.2习题224324321.,,(21)(1)251\2(2)(21)()12521-2,1,31k h m x hx x kx x x mx x x k h x hk x h k x h k hk m k h m h k +--+=++--=--+--++--=⎧⎪--====⎨⎪+=-⎩求使 解:对于左边 即有 解之得432322.()242,()25 4.()(),()(),()().f x x x x xg x x x x f x g x f x g x f x g x =+---=--++- 设 计算432443270765432()()4292()()6()0254()()()23913131868kki k i k i f x g x x x x x f x g x x x g x x x x x f x g x a b x x x x x x x x -==+=+--+-=+-=⋅+--+∴==+--++--∑∑解:由题得 令323122223.()59-73,()(53),()().-15-50[()()]3691()()04.()0().()0()()()f x x x xg x x x f x g x f x g x x f x g x s f x f x f x f x f x f x ︒=-++=++⨯=±∂===≠≠=⋅∴ 设求乘积 的次数及其系数和解:根据 得 令 则有 的系数和 证明:当时,是偶次多项式证明:又有 根据定理2 4.2.12()()()()(),()()2f x f x f x f x f x n n N f x n ︒︒︒︒︒∂⋅=∂+∂∂=∈∴∂=的()知 ()()() 再令 () 结论得证2225.(),(),()..()()(),()()()0.(),(),()1221222132212f x g x h x f x xg x xh x f x g x h x g x g f x f h x hg h f g g h f h g h f g f ︒︒︒︒︒︒=+===∂=∂=∂=>=+<=+==+= 设是实数域上的多项式证明如下 若是 则 证明:令 () () () 当 时,有 当 时,有 当 时,有 或 2222214()(),(),()(),(),()()()()06.(),(),()()0(),()1()0(),()h f x f x g x h x f x g x h x f x g x h x f x g x h x f x g x i h x f x xg x x xh x x +========-= 又由题可知 是偶次多项式,又由于是实数域上的多项式 故 的次数不存在 即 求一组满足上题结论的不全为零的复系数多项式解:令 , 即 , 222()()0()()0(),()1xg x xh x f x f x g x i h x ∴+===== 满足条件即 ,4.3 习题3221.()321,()321,()()()().f x x x xg x x x g x f x q x r x =-+-=-+设求用除所得的商式和余数232322217393213212133751337147399299172(),()3999()()()()x x x x x x x x x x x x x x x q x x r x f x g x q x r x --+-+--+-+--+--=-=-=+解: 故 即[]2432322412*********.,,(1)()?012,1(1)()3.()(()()),()(()()),:()(()()()()),(),()m p q x mx x px q p m m m r q m p m m q m x mx x px q g x f x f x g x f x f x g x u x f x u x f x u x u x F x ++++⎧+=-=⎨=-⎩=-=-+++++-+在适合什么条件时,解:由题知当余式时有 即当 时 有 设证明其中为中任意两个12121212121211()(()()),()(()())()(()()()())()(()()()())()(),()()3()()(i g x f x f x g x f x f x g x f x f x f x f x g x f x f x f x f x g x f x g x f x u x F x i +-∴++-+-+∃∀∈=多项式 证明:即 根据多项式整除性质)可知 1122112221,2)..()()(),()()()2()()(1,2)..()(()()()())4.(1)(),(1)(),(1)().11(1)(),(1)(i o s t g x u x f x g x u x f x u x F x i s t g x u x f x u x f x x f x x f x x f x x x f x x f ∃∀∈=+-+-≠±-+ 再根据性质)得 若则证明:1212)(),()[]()()(1)(1)()()(1)(2)x u x u x F x f x u x x f x u x x ∴∃∈=+⎧⎨=-⎩221()()(1)(-1)-(2)(1)()(-1)()2u x u x x x f x x -⨯⨯+= 得212()()()[]2(-1)()21-1()0o u x u x u x F x x f x x x f x -∃=∈=== 故 即 或时,可得出 同样结论成立1212121221212125.(1)()(()()),()()()()(2)()()(),()()()()1(),()1,()1()(()())()()()g x f x f x g x f x g x f x g x f x f x g x f x g x f x g x x f x x f x x g x f x f x g x f x f x +==+=-+ 若则且对吗? 若则或对吗?解:()不对 如 :令 可见 而 不整除 和 (21212122()-1,()1,()1()()()()()()g x x f x x f x x g x f x f x g x f x f x ==+=-)不对如 :令 可见 而 不整除 和(1)(2)6.(1)(1),.,1()1(1)(1),(1)(1).(1)(1)(0),1(1)1,(1)(1)(1)(d n n d q d q d q d d n d n n qd r d q r r d n d x x d n d n d n n qd x x x x x x x x x n qd r r d x x x x x x x x --+--⇐=-=-=-+++--⇒--=+≤<-==-+---- 证明:的充分必要条件是(这里是正整数)证明 设 ,即 则 即 设,令则且212121)(1)(1)0,0.7.()110220()32.(),()[]..(1)()10()(1)(2)()2d q d r x x x r d r d n f x x x f x x x u x u x F x s t x u x f x x u x -∴--≤<=++++∃∈++=++ ,又 故 ,即 设被除的余式为,被除的余式为, 求被 除的余式解:设 , 23120()(2)()[]..()32(3)(1)(2)-(2)(1)()32--10(1)434-10(1)f x u x F x s t f x x x u r x x f x x x u u x r x =∃∈=+++⨯+⨯+=+++=+ 又 , () 有 ()() () 由(),()可得习题4.4432424322432312(1)43243221(-1)1.1)()242,()322;2)()441,() 1.()24221)()()2222f x x x x x g x x x x x f x x x x x g x x x f x x x x x x x A x g x x x x x x x x x +-+=+---=+---=--++=--⎛⎫⎛⎫+----⎛⎫==−−−→ ⎪ ⎪ ⎪+---+---⎝⎭⎝⎭⎝⎭−计算以下各式多项式的最大公因式:解:由 11333221()1()21()42222222200x x xx x x x x x x x x x -++-⎛⎫⎛⎫⎛⎫⎛⎫----−−→−−−→−−−→−−−→ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭⎝⎭224324312(4)222212(-)2(1)12()221(1)()2()44132)()()112333212x x d x x f x x x x x x x A x g x x x x x x x x x x x x +++-++∴=-⎛⎫⎛⎫--++--⎛⎫==−−−→ ⎪ ⎪ ⎪----⎝⎭⎝⎭⎝⎭-⎛⎫⎛⎫--⎛⎫−−−−→−−−→−−−→ ⎪ ⎪ ⎪-+---+⎝⎭⎝⎭⎝⎭−−−→ 由 2311110()1x x x d x -⎛⎫⎛⎫⎛⎫→→ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭∴=2.(),()(),,0,(()(),()())((),()).((),())()()(),()()()()()),()()())(),()(f x g x F x a b c d F ad bc af x bg x cf x dg x f x g x f x g x d x d x f x d x g x d x af x bg x d x cf x dg x h x h x af ∈∈-≠++==∴++∃∀另而,,,并且证明证明:令 即有 ( ( 又设 ()()),()()())-0()()())-()())---()()())()())--()(),()(),()x bg x h x cf x dg x ad bc d bf x af x bg x cf x dg x ad bc ad bc c ag x af x bg x cf x dg x ad bc ad bch x f x h x g x h x d ++≠∴=++=+++∴ (有 (( (( 从而有 ()()()()())()(()(),()())((),())x af x bg x cf x dg x d x af x bg x cf x dg x f x g x ++=++= 即 (, 即 :3.()0,()((),())(()()(),()).()0(),..()()()()()()-()()1((),())(()())((),())(()()(g x h x f x g x f x h x g x g x g x h x s t f x g x h x r x r x f x g x h x f x g x g x r x f x g x f x h x g x ≠=-≠∃=+===-设为任意多项式,证明: 证明: 故 即 由引理可知 , 即 ),())g x1122121212124.1)(,)2)(,)(,)(,,,),,,().1(,),,,,(,),[],..f g hf gh f g f g f f f g g f g g f g h F x f g d d f d g dh fh dh gh dh hf hg f g d u v F x s t uf vg d ===∃∈+=∴证明:是与的最大公因式;此处都是的多项式证明:)设 即 从而有 即 是与的公因式又由 得 112211211212211211221214.4.42)(,),(,),(,[]),;,,,,(,),(,),,,ufh vgh dhdh fh gh f g m f g n m n F x m f m g m f m g mn f f mn f g mn f g mn g g f g m f g n k k l +===∈==∃ 由定理知 是与的最大公因式 设 即 从而有 又由 知 211112222121211221221121212122112112212122112[],..,(,,,)(,)(,)(,,,)l F x s t k f l g m k f l g nk k f f k f l g l k f g l l g g mn mn f f f g f g g g f g f g f f f g f g g g ∈+=+=+++=== 即有 由此可知 从而有4323243232324323235.(),()()()()()((),()):1)()343,()310232)()421659,()25453431033113333102301310u x v x u x f x v x g x f x g x f x x x x x g x x x x f x x x x x g x x x x x x x x x x x x x x x x +==+---=++-=--++=--+⎛⎫+--------→ ⎪++-⎝⎭+2求使解:)(A(x),I )=222322222232230159935993913310230156553296331393555591393132563555555x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ⎛⎫⎪⎪ ⎪+-⎝⎭⎛⎫----⎛⎫---- ⎪→→ ⎪- ⎪++---- ⎪⎝⎭⎝⎭⎛-+⎛⎫-+------ ⎪ ⎪→→--+ ⎪------+- ⎪⎝⎭⎝33-x -x 22243232323231550**321,()55122342165910332540125401x x x x x x x v x x x x x x x x x x x x x x ⎫ ⎪ ⎪ ⎪ ⎪⎭⎛⎫-+- ⎪→ ⎪ ⎪⎝⎭-∴-=⎛⎫⎛⎫--+---++ ⎪→ ⎪ ⎪--+ ⎪⎝⎭--+⎝⎭2 u(x)= 2)(A(x),I )=22222222121223231333332222412(2)1333312231330**1223(),()33x xx x x x x x x x xx x x x x x x x x x x u x v x ⎛⎫-++⎛⎫--+--- ⎪⎪ ⎪⎪→→ ⎪ ⎪--++--+-+- ⎪ ⎪⎝⎭⎝⎭⎛⎫--+- ⎪→ ⎪ ⎪⎝⎭--+∴==4322432436.()1,()(1),,,()().(),()2,()()()()(,,)()(2)(2)(2)1of x Ax Bxg x x A B f x g x f x g x g x f x g x ax bx c a b c F f x ax b a x c b a x b c x c Ax Bx a A =++=-∂==++∈∴=+-+-++-+=++=设试决定使与 的最大公因式为二次多项式解:由于() 即 为最大公因式故不妨设 即有 -23,2,13,-4202013,-4b a B a bc A B c b a b c c A B ⎧⎪=⎪⎪=====-+=⎨⎪-=⎪=⎪⎩∴== 解得 即7.(),()((),())()()()(),((),())1((),())()()()()*()()()()()()()()()()*(),()[].f x g x f x g x u x f x v x g x u x v x f x g x u x f x v x g x u x f x v x g x f x u x f x v x g x g x m x n x F x s =+==+++∃∈设 不全为零,且证明:证明:()有 , 再由 () .()()[()()()()]()()[()()()()]1-()()()()()()11-()())()()()()221()t f x m x u x f x v x g x g x n x u x f x v x g x m x u x f x m x v x g x n x v x g x n x u x f x f x =+=+== 即() () ( () 将()代入(),消去得1-()()1-()()()()()()()()(),(),()01-()()()()()()()()()()()()1()()()()4.4.5((),())1m x u x n x v x g x m x v x g x n x u x f x g x g x n x v x m x u x m x n x u x v x m x n x u x v x m x n x u x v x u x v x =≠∴-+=∴==()()不全为零 即令 由定理 得8.((),()) 1.((),()) 1.,,((),()) 1.1()()()[]()()()()()()((),())1n m n o n n n f x g x n f x g x m n f x g x g x g x k x F x g x k x g x g x g x k x f x g x ===∃∈=∴==设令是任意正整数,证明:由此进一步证明: 对于任意正整数都有证明: 易见 , 即 s.t. (1)又 ()()1()()1()((),())1()(),()[]()()()()()()nn m m m f x g x f x g x k x f x g x x f x l x F x f x l x f x f x f x l x ∴∃∈+=+==∃∈=∴=o u(x),v(x)F[x] s.t. u(x)v(x) (2)v(x) 将(1)代入(2)得 u(x) 由定理4.4.5 知 2易见 f 即 s.t. ((),())1'''()()'()()11'()()'()()1()((),())1n n mn m n f x g x u x f x v x g x u x f x v x g x l x f x g x =∴∃∈+=+== (3)又u (x),v (x)F[x] s.t. (4) 将(3)代入(4)得 由定理4.4.5知 [][]1111119.((),()) 1.((),()())((),()())(()(),()()) 1.((),()())()()(),()()()()[()()]()()()]f x g x f x f x g x g x f x g x f x g x f x g x f x f x g x d x d x F x u x v x F x u x f x v x f x g x d x u x v x =+=+=+=+=∈∴∃∈++=+设 证明: 证明:令 ()s.t. 即 [1()()()()((),())1()1((),()())1((),()())1(()(),()())1f x v xg x d x f x g x d x f x f x g x g x f x g x f x g x f x g x +===+=+=+=故 即 同理可证得 再根据互素性质可知10.()0,()0,:1(),()()()()(),((),())12(),()(),()()()()(),((),())11((),())()1,()()f x g x h x f x g x h x f x h x f x g x h x f x h x g x h x f x g x h x f x g x f x g x d x f x d x m ≠≠===≠=设证明 )若对于任意多项式由可得到则必有 )若对于任意多项式由可得到则必有 证明:) 假设 则有(),()()()()()()()()()()()()()()x g x d x n x m x f x f x g x h x h x f x g x m x f x m x ︒︒=∂<∂∴ 其中 () ()又 (为任意多项式)即有()()((),())12((),())()1()()()()()()()()(),()()()()()()()1((f x m x f x g x f x g x d x f x d x m x h x m x g x f x g x m x g x g x m x f x g x g x m x f x ==≠==∴ 但 不整除,从而矛盾, 故 )假设 ,且 令 即有 () 又),())()()()()()()()1((),())1g x d x f x m x f x g x g x m x f x g x ︒︒︒︒=∴∂>∂∂>∂∴= () ()故 () () 与()矛盾1212111212112211.(),(),,()().1)((),(),,())(((),,()),((),,())),112(),(),,()(),(),,()()()()()()()n n k k n n n n f x f x f x F x f x f x f x f x f x f x f x k n f x f x f x u x u x u x F x u x f x u x f x u x +∈=≤≤-∈+++设证明: )互素的充分且必要条件是存在多项式 ,使得1211121()11((),(),,())(),((),,()(),((),,()()()(),1,2,,()(),1,2,,;()(),1,2,,()(),n n k k n i s t f x f x f x f x d x f x f x d x f x f x d x d x f x i nd x f x s k d x f x t k k nd x d x +=====∴==++∴证明:)设21212()()()(),1,2()(),1,2,,;()(),1,2,,()(),1,2,,()(),2((),(),,())1i s t i n d x d x c x d x i d x f x s k d x f x t k k nc x f x i nc xd x f x f x f x ===++∴=∴= 设结论得证。
习题参考答案(第4章)
a' V XH
a
4-2 用换面法求线段CD的实长和对V面的倾角。
T.CD
d1
c1 d'
X 1 c' X
d
H X1 V1
a1'
b1'
c
4-3 用换面法求相互平行的两条直线AB、CD之间的距离。
b'
d'
a'
c'
X
b
d
a
c
AB、CD间距离
4-4 已知平行直线AB、CD之间的距离为15,用换面法求cd。
15
15
a' c'
b'
d'
b
X2
பைடு நூலகம்X1
a
d
c
高校教育精品PPT
25 1
4-5 已知直线AB与CD垂直相交,用换面法求c'd'。 b'
a'
c a
b d
4-6 用换面法求点到直线BC距离,并求垂足。
a'
c'
b'
c a
A到BC距离 b
O2
4-7 已知点A到直线BC的距离为15,求a。 a1
R15
b1
c1
O1
a b
c a'1
c'1 c2
a2
b1' b2
高校教育精品PPT
27 3
4-11 已知直线AB与 CDE的距离为10,用换面法求ab。
c' e'
b'
a' X
第4章 习题及答案
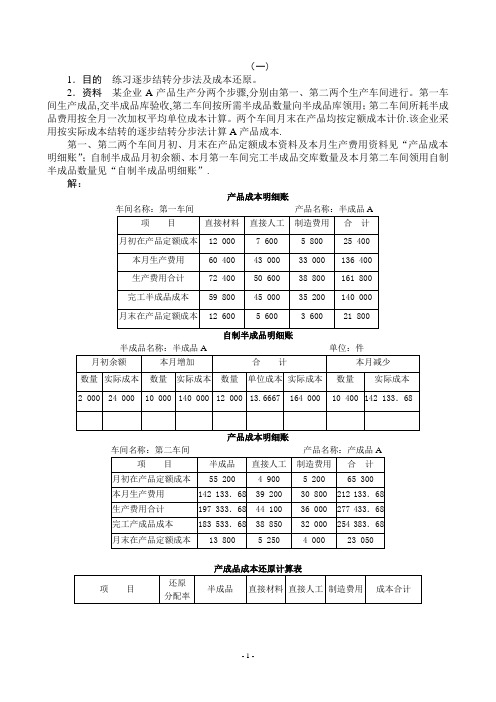
(一)1.目的练习逐步结转分步法及成本还原。
2.资料某企业A产品生产分两个步骤,分别由第一、第二两个生产车间进行。
第一车间生产成品,交半成品库验收,第二车间按所需半成品数量向半成品库领用;第二车间所耗半成品费用按全月一次加权平均单位成本计算。
两个车间月末在产品均按定额成本计价.该企业采用按实际成本结转的逐步结转分步法计算A产品成本.第一、第二两个车间月初、月末在产品定额成本资料及本月生产费用资料见“产品成本明细账”;自制半成品月初余额、本月第一车间完工半成品交库数量及本月第二车间领用自制半成品数量见“自制半成品明细账”.解:产品成本明细账车间名称:第一车间产品名称:半成品A自制半成品明细账半成品名称:半成品A 单位:件产品成本明细账产成品成本还原计算表(二)1.目的练习产品成本计算的综合结转分步法.2.资料某企业生产甲产品,分三个生产步骤进行生产。
该企业设有第一、第二、第三三个基本生产车间,甲产品由这三个车间顺序加工而成。
成本计算采用综合结转法。
原材料在第一车间开始加工时一次投入,半成品不通过中间仓库收发,上一步骤完工后全部交由下一步骤继续加工。
月末在产品按约当产量法计算,各车间月末在产品完工程度均为50%。
该企业本年5月份有关成本计算资料如表1、表2所示。
表1产量记录表2月初在产品成本和本月发生费用表3产品成本计算单135070÷(88+16)=1298。
75 24960÷(88+16×50%)=260 19200÷(88+16×50%)=200表4产品成本计算单173890÷(8050%)=326。
6表5产品成本计算单244450÷(96+4)=2444.5 34300÷(96+4×50%)=350 23520÷(96+4×50%)=240表6(三)1.目的练习产品成本计算的平行结转分步法.2.资料某厂设有三个基本生产车间,第一车间生产甲半成品,交第二车间继续加工,第二车间生产乙半成品,交第三车间生产丙产成品。
第四章 习题解答

1 第四章 习题解答3/150、试用实验方法鉴别晶体SiO 2、SiO 2 玻璃、硅胶和SiO 2 熔体。
它们的结构有什么不同?解答:利用X-射线粉末衍射检测。
晶体SiO 2——质点在三维空间做有规律的排列,各向异性。
SiO 2 熔体——内部结构为架状,近程有序,远程无序。
SiO 2 玻璃——各向同性。
硅胶——疏松多孔。
7/151、SiO 2 熔体的粘度在1000℃时为1014 Pa·s ,在1400℃时为107 Pa·s 。
SiO 2 玻璃粘滞流动的活化能是多少?上述数据为恒压下取得,若在恒容下获得,你认为活化能会改变吗?为什么?解答:(1)根据公式:)exp(0RTE ∆=ηη 1000℃时,η=1014 Pa·s ,T=1000+273=1273K , )1273314.8exp(10014⨯∆=E η (1) 1400℃时,η=107 Pa·s ,T =1400+273=1673K ,)1673314.8exp(1007⨯∆=E η (2) 联立(1)和(2)式解得:η0 = 5.27×10-16 Pa·s ,△E = 713.5 kJ/mol(2)若在在恒容下获得,活化能不会改变。
因为活化能是液体质点作直线运动所必需的能量。
它与熔体组成和熔体[SiO 4]聚合程度有关。
212/151、一种用于密封照明灯的硼硅酸盐玻璃,它的退火点是544℃,软化点是780℃。
求:(1)这种玻璃粘性流动的活化能;(2)它的工作范围;(3)它的熔融范围。
解答:(1)根据公式:)exp(0RTE ∆=ηη 退火点544℃, η=1012Pa·s ,T=544+273=817K , )817314.8exp(10012⨯∆=E η (1) 软化点为780℃,η=4.5×106 Pa·s ,T=780+273=1053K ,)1053314.8exp(104.506⨯∆=⨯E η (2)联立(1)和(2)式解得:η0 = 1.39×10-12 Pa·s ,△E = 373.13 kJ/mol 。
第4章 习题解答
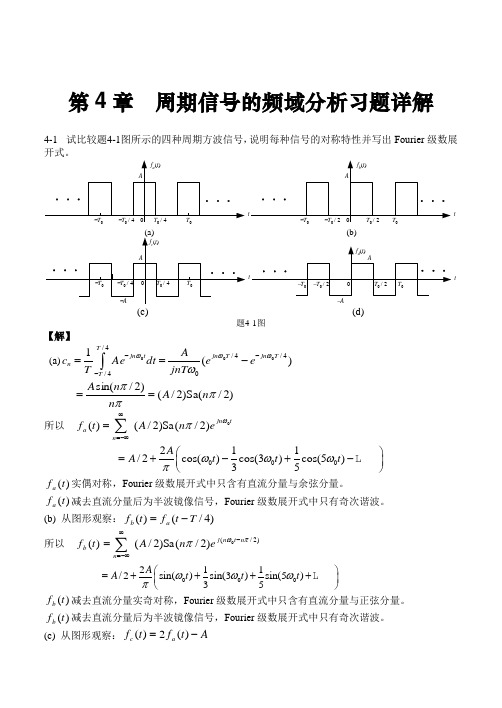
第4章 周期信号的频域分析习题详解4-1 试比较题4-1图所示的四种周期方波信号,说明每种信号的对称特性并写出Fourier 级数展开式。
tt(b)tt-A(c) (d)题4-1图【解】 (a))(14/4/04/4/000T jn T jn tjn T T n eejnT A dt AeTc ωωωω----==⎰)2/(Sa )2/()2/sin(πππn A n n A ==所以 tjn n a e n A t f 0)2/(Sa )2/()(ωπ∑∞-∞==000211/2cos()cos(3)cos(5)35A A t t t ωωωπ⎛⎫=+-+- ⎪⎝⎭)(t f a 实偶对称,Fourier 级数展开式中只含有直流分量与余弦分量。
)(t f a 减去直流分量后为半波镜像信号,Fourier 级数展开式中只有奇次谐波。
(b) 从图形观察:)4/()(T t f t f a b -=所以 )(t f b )2/(0)2/(Sa )2/(πωπn t n j n en A -∞-∞=∑=000211/2sin()sin(3)sin(5)35A A t t t ωωωπ⎛⎫=++++ ⎪⎝⎭)(t f b 减去直流分量实奇对称,Fourier 级数展开式中只含有直流分量与正弦分量。
)(t f b 减去直流分量后为半波镜像信号,Fourier 级数展开式中只有奇次谐波。
(c) 从图形观察:A t f t f a c -=)(2)(第4章 周期信号的频域分析 83所以 tjn n n c en A t f 0)2/(Sa )(0,ωπ∑∞≠-∞==000411c o s ()c o s (3)c o s (5)35A t t t ωωωπ⎛⎫=-+- ⎪⎝⎭)(t f c 实偶对称,且是半波镜像信号,Fourier 级数展开式中只含有奇次谐波的余弦分量。
(d) 从图形观察:)4/()(T t f t f c d -=所以 )2/(0,0)2/(Sa )(πωπn t n j n n d en A t f -∞≠-∞=∑=000411sin()sin(3)sin(5)35A t t t ωωωπ⎛⎫=++- ⎪⎝⎭)(t f d 实奇对称,且是半波镜像信号,Fourier 级数展开式中只含有奇次谐波的正弦分量。
第4章习题参考解答

p3()
{
P(s);
…
}
参考解答:
因p1和p2进程是p3进程开始执行的先决条件,即当p1和p2进程均执行完毕时,p3才能执行,则p3需有两个信号量,分别表示p1进程执行完毕的信号量s1,以及p2进程执行完毕的信号量s2。则同步算法描述如下:
main()
{
int s1=0,s2=0;
cobegin
p1();
p4();
coend
}
p1()
{
p1 execute;
V(s12);
V(s13);
V(s14);
}
p2()
{
P(s12);
p2 execute;
}
p3()
{
P(s13);
p3 execute;
}
p4()
{
P(s14);
p4 execute;
}
4-15
解:
main()
{
int sa=1,sb=0;// sa表示缓冲区S是否为空,sb表示是否为满。
(3)设a、b两并发进程,它们共享一临界资源。其执行临界区的算法框图如下图,
进程A和进程B为互斥进程,则需一个互斥信号量s,初值为1,表示临界资源初始情况下无进程使用。
main()
{
int s=1;
cobegin
pa();
pb();
coend
}
pa()
{
P(s);
进入csa…
V(s);
}
pb()
{
P(s);
进入csb…
V(s);
}
4-21
答:线程有时也称为轻量级进程,它是比进程更小的活动单位,它是进程中的一个执行路径。一个进程可以有多个执行路径即线程。
应用多元统计分析课后习题答案高惠璇第四章部分习题解答市公开课获奖课件省名师示范课获奖课件

0
2
)
3 2
(ˆ
2
)
3 2
ˆ 2 ˆ 0 2
3
2
V
3 2
下列来讨论与V等价旳统计量分布:
ˆ 2
1 3
( y1
aˆ)2
( y2
2aˆ
bˆ)2
( y3
aˆ
2bˆ)2
1 3
( y1
yˆ1 ) 2
( y2
yˆ2 )2
( y3
yˆ3 )2
1 3
(Y
Xˆ )(Y
Xˆ )
1Y 3
(I3
X
(
X
X
)1
Q(β)=(Y-Cβ) '(Y-Cβ) . 试证明β^=(C'C)-1C'Y是在下列四种意义下达最小:
(1) trQ(β^)≤trQ(β) (2) Q(β^)≤Q(β) (3) |Q(β^)|≤|Q(β)|
(4) ch1(Q(β^))≤ch1(Q(β)),其中ch1(A)表达A
旳最大特征值. 以上β是(m+1)×p旳任意矩阵.
[(
y1
aˆ0
)2
]
0
可得
ˆ
2
1 3
( y1
aˆ0 )2
( y2
aˆ0 )2
( y3
3aˆ0 )2
drf
ˆ
2 0
似然比统计量旳分子为
L(aˆ0
,ˆ
2 0
)
(2
)
3 2
(ˆ 0 2
)
3 2
exp[
3 2
].
5
第四章 回归分析
似然比统计量为
L(aˆ0 ,ˆ02 ) L(aˆ,bˆ,ˆ 2 )
第四章 土壤环境化学习题解答

第四章土壤环境化学一、名词解释1、土壤环境背景值:是指在不受或很少受人类活动影响和不受或很少受现代工业污染与破坏的情况下,土壤原来固定有的化学组成和结构特征。
2、原生矿物与次生矿物:地壳中最先存在的,经风化作用后任然遗留在土壤中的一类矿物,其原有的化学组成和晶体结构均未改变。
主要的原生矿物有:石英、长石类、云母类、辉石、角闪石、橄榄石、方解石、赤铁矿、磁铁矿、磷灰石、黄铁矿等;在土壤的形成过程中,由原生矿物转化形成的新矿物,统称次生矿物。
包括各种简单的盐类(碳酸盐、重碳酸盐、硫酸盐和氯化物)、游离硅酸、三氧化物(R2O3•XH2O);次生铝硅酸盐(蒙脱石、伊利石、高岭石)等。
或原生矿物是指各种岩石受到不同程度的物理风化,而未经化学风化的碎屑物,其原有的化学组成和结晶构造均未改变。
次生矿物是在岩石或矿石形成之后,其中的矿物遭受化学变化而改造成的新生矿物,其化学组成和构造都经过改变而不同于原生矿物。
3、活性酸度:土壤溶液中氢离子浓度的直接反映,通常用pH表示。
活性酸度的来源主要是CO2溶于水形成的碳酸和有机物质分解产生的有机酸,以及土壤中矿物质氧化产生的无机酸,还有施用的无机肥料中残留的无机酸,如硝酸、硫酸和磷酸等。
此外,由于大气污染形成的大气酸沉降,也会使土壤酸化,所以它也是土壤活性酸度的一个重要来源。
潜性酸度:土壤潜性酸度是土壤胶体吸附的可代换性H+和Al3+的反映。
当这些离子处于吸附状态时,是不显酸性的,但当它们通过离子交换作用进入土壤溶液之后,即可增加土壤溶液的H+浓度,使土壤pH值降低。
只有盐基不饱和土壤才有潜性酸度,其大小与土壤代换量和盐基饱和度有关。
活性酸度与潜性酸度的关系:活性酸度与潜性酸度是同一个平衡体系的两种酸度。
二者可以互相转化,在一定条件下处于暂时平衡状态。
土壤活性酸度是土壤酸度的根本起点和现实表现。
土壤胶体是H+和Al3+的贮存库,潜性酸度则是活性酸度的贮备,土壤的潜性酸度往往比活性酸度大得多,二者的比例,在砂土中约为1000;在有机质丰富的粘土中则可高达1×104—1×105。
第四章 习题答案
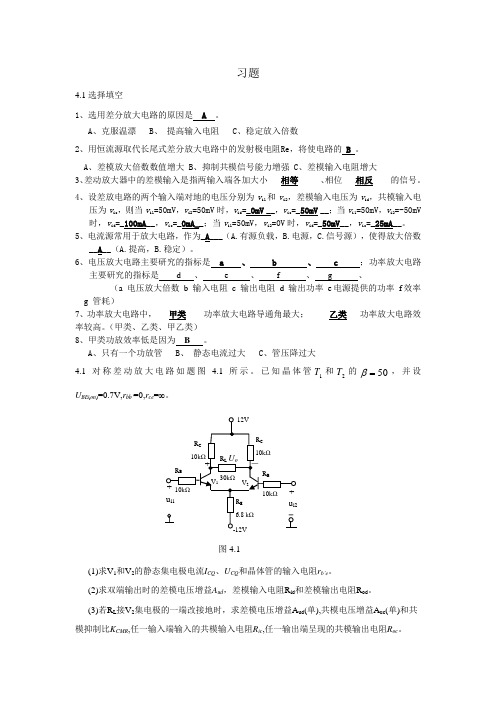
习题4.1选择填空1、选用差分放大电路的原因是 A 。
A 、克服温漂B 、 提高输入电阻C 、稳定放入倍数2、用恒流源取代长尾式差分放大电路中的发射极电阻Re ,将使电路的 B 。
A 、差模放大倍数数值增大B 、抑制共模信号能力增强C 、差模输入电阻增大 3、差动放大器中的差模输入是指两输入端各加大小___相等_____、相位___相反____的信号。
4、设差放电路的两个输入端对地的电压分别为v i1和v i2,差模输入电压为v id ,共模输入电压为v ic ,则当v i1=50mV ,v i2=50mV 时,v id =_0mV __,v ic =_50mV __;当v i1=50mV ,v i2=-50mV 时,v id =_100mA __,v ic =_0mA__;当v i1=50mV ,v i2=0V 时,v id =_50mV __,v ic =_25mA __。
5、电流源常用于放大电路,作为_A ___(A.有源负载,B.电源,C.信号源),使得放大倍数__A __(A.提高,B.稳定)。
6、电压放大电路主要研究的指标是 a 、 b 、 c ;功率放大电路主要研究的指标是 d 、 e 、 f 、 g 、(a 电压放大倍数 b 输入电阻 c 输出电阻 d 输出功率 e 电源提供的功率 f 效率 g 管耗)7、功率放大电路中,___甲类____功率放大电路导通角最大;_____乙类___功率放大电路效率较高。
(甲类、乙类、甲乙类) 8、甲类功放效率低是因为 B 。
A 、只有一个功放管B 、 静态电流过大C 、管压降过大4.1对称差动放大电路如题图 4.1所示。
已知晶体管1T 和2T 的50=β,并设U BE (on )=0.7V,r bb ’=0,r ce =∞。
(1)求V 1和V 2的静态集电极电流I CQ 、U CQ 和晶体管的输入电阻r b’e 。
(2)求双端输出时的差模电压增益A ud ,差模输入电阻R id 和差模输出电阻R od 。
(完整word版)第四章 习题答案

第四章的习题及答案4-1 设有一台锅炉,水流入锅炉是之焓为62.7kJ ·kg -1,蒸汽流出时的焓为2717 kJ ·kg -1,锅炉的效率为70%,每千克煤可发生29260kJ 的热量,锅炉蒸发量为4.5t ·h -1,试计算每小时的煤消耗量。
解:锅炉中的水处于稳态流动过程,可由稳态流动体系能量衡算方程:Q W Z g u H s +=∆+∆+∆221体系与环境间没有功的交换:0=s W ,并忽 动能和位能的变化, 所以: Q H =∆设需要煤mkg ,则有:%7029260)7.622717(105.43⨯=-⨯m解得:kg m 2.583=4-2 一发明者称他设计了一台热机,热机消耗热值为42000kJ ·kg -1的油料0.5kg ·min -1,其产生的输出功率为170kW ,规定这热机的高温与低温分别为670K 与330K ,试判断此设计是否合理?解:可逆热机效率最大,可逆热机效率:507.06703301112max =-=-=T T η 热机吸收的热量:1m in210005.042000-⋅=⨯=kJ Q热机所做功为:1m in 102000m in)/(60)/(170-⋅-=⨯-=kJ s s kJ W该热机效率为:486.02100010200==-=Q W η 该热机效率小于可逆热机效率,所以有一定合理性。
4-3 1 kg 的水在1×105 Pa 的恒压下可逆加热到沸点,并在沸点下完全蒸发。
试问加给水的热量有多少可能转变为功?环境温度为293 K 。
解:查水蒸气表可得始态1对应的焓和熵为:H 1=83.93kJ/kg, S 1=0.2962kJ/kg.K 末态2对应的焓和熵为:H 2=2675.9kJ/kg, S 2=7.3609kJ/kg.K)/(0.259293.839.267512kg kJ H H Q =-=-=)/(0.522)2962.03609.7(15.2930.25920kg kJ S T H W sys id =-⨯-=∆-∆=4-4如果上题中所需热量来自温度为533 K 的炉子,此加热过程的总熵变为多少?由于过程的不可逆性损失了多少功? 解:此时系统的熵变不变)./(0647.7K kg kJ S sys =∆炉子的熵变为)./(86.45330.2592K kg kJ T H T Q S sur -=-=∆-==∆ )./(205.286.40647.7K kg kJ S t =-=∆ )/(0.646205.215.2930kg kJ S T W t l =⨯=∆=4-5 1mol 理想气体,400K 下在气缸内进行恒温不可逆压缩,由0.1013MPa 压缩到1.013MPa 。
第四章习题及解答
第四章习题及解答4.1 数字电路设计的基本步骤有哪些?每一步完成的目标任务是什么?见书P48。
4.2 组合逻辑电路的设计为什么可以从卡诺图直接进入?因为逻辑函数可以有多种有表达形式,卡诺图就是其中的一种,因此,直接从卡诺图直接进入设计就是最直接、最有效的一种方式,它简化了设计,更便于化简。
4.3 某车间有A 、B 、C 、D 四台电动机,今要求:(1)A 必须开机;(2)其他三台电动机中至少有两台开机,如不满足上述要求,则指示灯熄灭。
设指示灯亮为“1”,熄灭为“0”,电机开机为“1”,停机为“0”,试用与非门组成指示灯控制电路。
根据题意,用卡诺图表示电机运行的状态,求出输出表达式:F= ABC+ABD+ACD用与非门实现逻辑:4.4 试设计一个供4组使用的智力抢答器电路。
设4组变量分别为:A 、B 、C 、D 。
输出用4个发光二极管,表示抢答结果,灯亮答表达式: F ABCD ABCD ABCD =+++4.5 电话室需对4种电话编码控制,按紧急次序排列优先权由高到底依次为火警电话、急救电话、工作电话、生活电话,其编码为11,10,01,00,试设计该编码电路。
设火警电话、急救电话、工作电话、生活电话为变量A 、B 、C 、D ,编码输出量为X 、Y 。
AB CD01001110000000000001111000 01 11 10 F ABC ABD ACDABC ABD ACD =++=AB C D题4.3图列出编码真值表:4.6 试用3线-8线译码器和门电路实现以下函数:4.7 试用四选一多路选择器实现函数Y ABC AC BC =++。
1. 求出最小项、及最小项反函数非表达式:2. 对比四选一多路选择器表达式:0123Y ABD ABD ABD ABD =+++我们发现用原函数无法用一个四选一选择器实现,但反函数只有三个最小项,因为实际的数据选择器,它们都有两个互补的变量输出,因此从反变量输出端(~W)就可以达到要求了。
分析化学(高教第五版)课后习题第四章答案(整理排版20页)

第四章 习题习题4-14.1 下列各种弱酸的p K a 已在括号内注明,求它们的共轭碱的pK b ; (1)HCN(9.21);(2)HCOOH(3.74);(3)苯酚(9.95);(4)苯甲酸(4.21)。
解: (1) HCN p K b =14-9.25=4.79 (2) HCOOH p K b =14-3.74=10.26 (3) 苯酚 pK b =14-9.95=4.05 (4) 苯甲酸 pK b =14-4.21=9.794.2. 已知H 3PO 4的p K a =2.12,p K a =7.20,p K a =12.36。
求其共轭碱PO 43-的pK b1,HPO 42-的pK b2.和H 2PO 4- 的p K b3。
解: PO 43- pK b =14-12.36=1.64 HPO 42- pK b =2.14-7.20=6.80H 2PO 4- pK b =14-2.12=11.884.3 已知琥珀酸(CH 2COOH)2(以H 2A 表示)的p K al =4.19,p K b1=5.57。
试计算在pH4.88和5.0时H 2A 、HA -和A 2-的分布系数δ2、δ1和δ0。
若该酸的总浓度为0.01mol ·L -1,求pH =4.88时的三种形式的平衡浓度。
解: pH=4.88 〔H +〕=1.32×10-55655252521046.61069.21032.11046.6)1032.1()1032.1()(------2⨯⨯⨯+⨯⨯⨯+⨯⨯=A H δ=0.1455655255511046.61069.21032.11046.6)1032.1(1046.61032.1)(--------⨯⨯⨯+⨯⨯⨯+⨯⨯⨯⨯=HA δ =0.71056552565201046.61069.21032.11046.6)1032.1(1096.21046.6)(--------⨯⨯⨯+⨯⨯⨯+⨯⨯⨯⨯=A δ=0.145 pH=55655252521046.61069.2100.11046.6)100.1()100.1()(------2⨯⨯⨯+⨯⨯⨯+⨯⨯=A H δ =0.1095655255511046.61069.2100.11046.6)100.1(1046.6100.1)(--------⨯⨯⨯+⨯⨯⨯+⨯⨯⨯⨯=HA δ =0.70256552565201046.61069.2100.11046.6)100.1(1096.21046.6)(--------⨯⨯⨯+⨯⨯⨯+⨯⨯⨯⨯=A δ =0.189pH=4.88 c (H 2A)=0.01mol·L -1 c (H 2A)=0.145×0.01=1.45×10-3mol·L c (HA -)=0.710×0.01=7.10×10-3mol·Lc (A 2-)=0.145×0.01=1.45×10-3mol·L -14.4 分别计算H 2CO 3(p K a1=6.38,pK a2=10.25)在pH=7.10,8.32及9.50时,H 2CO 3,HCO 3-和CO 32-的分布系数δ2` δ1和δ0。
第四章习题答案

一、填空题1.几何公差的形状公差有6项,它们的名称和代号分别是(直线度)、(平面度)、(圆度)、(圆柱度)、(线轮廓度)和(面轮廓度)。
2.几何量公差的跳动公差有2项,它们的名称和代号分别为(圆跳动)和(全跳动)。
3.端面对轴线的垂直度(小)于端面圆跳动。
4.某轴尺寸为Φ10-0.018-0.028 mm ,轴线对基准A 的垂直度公差为Φ0.01 mm ,被测要素给定的尺寸公差和几何公差采用最大实体要求,则垂直度公差是被测要素在(最大实体状态)时给定的。
当轴实际尺寸为(Φ9.972)mm 时,允许的垂直度误差达最大,可达(0.02)mm 。
5.独立原则是指图样上给定的(尺寸)公差与(几何)公差各自独立,分别满足要求的公差原则。
6.包容要求采用(最大实体)边界,最大实体要求采用(最大实体实效)边界。
7.某孔尺寸为Φ40+0.119 +0.030○E mm ,实测得其尺寸为Φ40.09mm ,则其允许的几何误差数值是(Φ0.06)mm ,当孔的尺寸是(Φ40.119)mm 时,允许达到的几何误差数值为最大。
8.某孔尺寸为Φ40+0.119+0.030mm ,轴线直线度公差为 Φ0.005 mm ,实测得其局部实际尺寸为Φ40.09mm ,轴线直线度误差为Φ0.003mm ,则孔的最大实体尺寸是(Φ40.030)mm ,最小实体尺寸是(Φ40.119)mm ,体外作用尺寸是(Φ40.087)mm 。
9.若某轴标注为则该零件的MMS 为(φ30mm ),又称为该零件的(最大)极限尺寸;其LMS 为(φ29.979mm ),又称为该零件的(最小)极限尺寸;零件采用的公差要求为(最大实体要求),若加工后测得某孔的实际尺寸为φ29.98mm ,直线度误差为0.015mm ,则该零件(是)(是、否)合格。
10.若某孔的尺寸标注为,则该零件采用的公差原则为(最大实体要求),其MMS 为(Φ20mm ),此时的几何公差值为(Φ0.02)mm ;其LMS 为(Φ20.05mm )mm ,此时的形位公差值为(Φ0.07)mm ;其MMVS 为(Φ19.98)mm 。
第4章习题解答

第4章 习题讲解 章
为变址寄存器, R1为基址寄存器 PC为程序计数器 为基址寄存器, 【题4-6 】 R为变址寄存器, R1为基址寄存器,PC为程序计数器 OP I
寻址 方式 (1) ) (2) ) (3) ) (4) ) (5) ) (6) ) I 0 0 0 0 1 1 X 00 01 10 11 00 11
【题4-5】指令格式结构如下所示,试分析指令格式及 】指令格式结构如下所示, 寻址方式的特点 的特点。 寻址方式的特点。
15 12 11 9 8 6 5 3 2 0
OP
寻址方式
寄存器
寻址方式
寄存器
答: ① 所示指令是单字长二地址指令。 所示指令是单字长二地址指令 单字长二地址指令。
操作码字段OP有 可以指定2 16条指令 ② 操作码字段 有4位,可以指定24=16条指令。 可以是RR RS或SS型指令 RR、 型指令。 寻址方式有2 ③ 寻址方式有23=8种,可以是RR、RS或SS型指令。
第4章 典型例题 章
为操作码字段, 【例4.2】指令格式如下所示,OP为操作码字段,试分 】 指令格式如下所示, 为操作码字段 析指令格式特点。 析指令格式特点。
15 10 7 4 3 0
OP
——
源寄存器
变址寄存器
位移量 (16位) 位
答:
双字长二地址指令; ① 双字长二地址指令; 操作码字段OP OP为 可以指定2 64种操作 种操作; ② 操作码字段OP为6位,可以指定26=64种操作; 一个操作数在源寄存器( 16个 ③ 一个操作数在源寄存器(共16个)中,另一个操作数在内存储 器中(有效地址由变址寄存器和位移量决定) 所以是RS 指令。 RS型 器中 ( 有效地址由变址寄存器和位移量决定 ) , 所以是 RS 型 指令 。
第四章商业和服务业区位论习题解答

第四章商业和服务业区位论1.概念题中心地:区域的中心,供给各种商品和服务的地点。
可以指城市、居民点、商业或服务业中心。
中心性:中心性是指就中心地的周围地区而言,中心地的相对重要性。
也可理解为中心地发挥中心职能的程度。
货物的供给范围:由中心地供给的货物能够到达的范围。
有上限与下限两种:商品服务范围上限是由对中心商品的需求所限定的,为中心地的某种中心商品能够到达消费者手中的空间边界(最大的销售距离);商品服务范围下限是由中心商品的供给角度所规定的边界。
中心地为供给某种中心商品而必须达到的该商品的最小限度的需要量,叫做门槛值(需求门槛)或最小必要需求量。
门槛人口:指某种中心职能在中心地布局能够得到正常利润的最低限度的人口,也就是说某中心职能在中心地布局成立的最低限度人口。
中心地的等级:中心地提供的货物和服务有高低等级之分。
中心地的等级取决于其能够提供的货物和服务的水平,一般能够提供高级货物和服务的中心地等级相对较高,反之则较低。
2.阐述克里斯泰勒中心地理论的基本内容?答:克氏认为中心地的空间分布形态,受市场因素、交通因素和行政因素的制约,形成不同的中心地系统空间模型。
(1)市场原则与中心地系统。
在市场原则基础上的克氏中心地系统具有如下特点:一是中心地具有等级性,且其各级的中心地与中心职能相对应,二是中心地按照一定的规则分布,一般是三个中心地构成的三角形的重心是低一级中心地布局的区位点;三是各等级间的中心地数量和市场区域面积呈几何数变化。
(2)交通原则基础上的中心地系统。
各个中心地布局在两个比自己高一级的中心地的交通线的中点。
因此,如果同一级的中心地间铺设一条交通线,那么在这条交通线上布局着比它等级低的所有中心地。
(3)行政原则基础上的中心地系统。
在行政原则基础上形成的中心地系统中,低级中心地从属于一个高级中心地。
原因是在行政区域划分时,尽量不把低级行政区域分割开,使它完整地属于一个高级行政区域。
3.举例说明影响零售业区位决策的基本因素?答:区位主体的性质不同,决定区位选择的因素也不相同。
第四章练习题及参考解答(第四版)计量经济学

第四章练习题及参考解答4.1 假设在模型i i i i u X X Y +++=33221βββ中,32X X 与之间的相关系数为零,有人建议你分别进行如下回归:1221i i i Y X u αα=++ 1332i i i Y X u γγ=++(1) 是否存在3322ˆˆˆˆβγβα==且?为什么? (2) 1ˆβ会等于1ˆα或1ˆγ或者两者的某个线性组合吗? (3) 是否有()()22ˆˆVar Var βα=且()()33ˆˆVar Var βγ=?【练习题4.1参考解答】(1) 存在2233ˆˆˆˆαβγβ==且 。
因为 ()()()()()()()22332322222323ˆi iii ii iiii iy x x y x x xx x x x β-=-∑∑∑∑∑∑∑当23X X 与 之间的相关系数为零时,离差形式的230i ixx =∑有 ()()()()223222222223ˆˆi i i i i iiiy x x y x xx x βα===∑∑∑∑∑∑ 同理有: 33ˆˆγβ= (2)会的。
(3) 存在 ()()()()2233ˆˆˆˆvar var var var βαβγ==且 因为 ()()2222223ˆvar 1ix r σβ=-∑当 230r = 时, ()()()22222222223ˆˆvar var 1iix x r σσβα===-∑∑ 同理,有 ()()33ˆˆvar var βγ=4.2 表4.4给出了1995—2016年中国商品进口额Y 、国内生产总值GDP 、居民消费价格指数CPI 的数据。
表4.4 中国商品进口额、国内生产总值、居民消费价格指数资料来源:《中国统计年鉴2017》考虑建立模型: i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
(2)你认为数据中有多重共线性吗?(3)进行以下回归:121ln ln t t i Y A A GDP v =++ 122ln ln t t i Y B B CPI v =++ 123ln ln t t i GDP C C CPI v =++ 根据这些回归你能对多重共线性的性质有什么认识?(4)假设经检验数据有多重共线性,但模型中32ˆˆββ和在5%水平上显著,并且F 检验也显著,你对此模型的应用有何建议?【练习题4.2参考解答】建立模型: i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
第四章习题及答案(审计学)

4.2.1填空题1.审计准则是人们在长期的审计实践中摸索、总结出来的,它既是一个,又是一个。
2.审计准则是专业审计人员在实施审计工作时必须恪守的最高,它是____的权威性判断标准。
3.审计准则既对____提出要求,也对社会提供——保证。
4.在西方国家,审计准则是20世纪____才开始出现的,美国在就开始研究和制定审计准则。
5.西方国家的审计准则,大多是以____为蓝本加以补充、修正而成的;国际组织制定的审计准则,以国际会计师联合会的____最具代表性。
6.美国的民间审计准则称为____,它主要适用于民间审计所从事的____。
7.国际性组织制定的国际审计准则,目前已取得的主要成果有____和____。
8.中国注册会计师执业准则是由____颁发,并适用于____。
9.我国注册会计师执业准则建设过程主要包括____、____、____和____。
10.我国注册会计师执业准则主要有____和____。
11.审计依据是____、____的客观标准。
12.____解决如何进行审计问题,是审计人员行动的指南和规范;___ _则解决审计人员根据什么标准提出这样或那样的审计意见。
13.审计依据按其来源分类,可分为____制定的审计依据和____制定的审计依据。
14.从法规和规章制度的制定过程来看,的法规、制度不能违反___ _的法规、制度。
15.运用审计依据的具体问题具体分析的原则时,应坚持____、____和国家法规与地方法规发生矛盾时要慎重处理等原则。
4.2.2 判断题(正确的剡“√”,错误的划“×”)1.审计准则是审计理论的重要组成部分,但对审计人员并无制约作用。
( )2.审计准则是通过审计人员执行审计程序体现出来的。
( )3.民间审计人员有了会计准则,对其审计工作提供了方便,因而就不需要审计准则了。
( )4.审计准则的实施使审计人员在从事审计工作时有了规范和指南,便于考核审计工作质量,推动了审计事业的发展。
第四章习题答案

一、填空题1.几何公差的形状公差有6项,它们的名称和代号分别是(直线度)、(平面度)、(圆度)、(圆柱度)、(线轮廓度)和(面轮廓度)。
2.几何量公差的跳动公差有2项,它们的名称和代号分别为(圆跳动)和(全跳动)。
3.端面对轴线的垂直度(小)于端面圆跳动。
4.某轴尺寸为Φ10-0.018-0.028 mm ,轴线对基准A 的垂直度公差为Φ0.01 mm ,被测要素给定的尺寸公差和几何公差采用最大实体要求,则垂直度公差是被测要素在(最大实体状态)时给定的。
当轴实际尺寸为(Φ9.972)mm 时,允许的垂直度误差达最大,可达(0.02)mm 。
5.独立原则是指图样上给定的(尺寸)公差与(几何)公差各自独立,分别满足要求的公差原则。
6.包容要求采用(最大实体)边界,最大实体要求采用(最大实体实效)边界。
7.某孔尺寸为Φ40+0.119 +0.030○E mm ,实测得其尺寸为Φ40.09mm ,则其允许的几何误差数值是(Φ0.06)mm ,当孔的尺寸是(Φ40.119)mm 时,允许达到的几何误差数值为最大。
8.某孔尺寸为Φ40+0.119+0.030mm ,轴线直线度公差为 Φ0.005 mm ,实测得其局部实际尺寸为Φ40.09mm ,轴线直线度误差为Φ0.003mm ,则孔的最大实体尺寸是(Φ40.030)mm ,最小实体尺寸是(Φ40.119)mm ,体外作用尺寸是(Φ40.087)mm 。
9.若某轴标注为则该零件的MMS 为(φ30mm ),又称为该零件的(最大)极限尺寸;其LMS 为(φ29.979mm ),又称为该零件的(最小)极限尺寸;零件采用的公差要求为(最大实体要求),若加工后测得某孔的实际尺寸为φ29.98mm ,直线度误差为0.015mm ,则该零件(是)(是、否)合格。
10.若某孔的尺寸标注为,则该零件采用的公差原则为(最大实体要求),其MMS 为(Φ20mm ),此时的几何公差值为(Φ0.02)mm ;其LMS 为(Φ20.05mm )mm ,此时的形位公差值为(Φ0.07)mm ;其MMVS 为(Φ19.98)mm 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章习题解
4-3 已知调制信号()cos(2000)cos(4000)m t t t ππ=+,载波为4
cos10t π,进行单边带调
制,试确定该单边带信号的表示式,并画出频谱图。
[解]首先计算()m t 的希尔伯特变换,
ˆ()sin(2000)sin(4000)m
t t t ππ=+, 然后分别计算上边带与下边带的单边带调制信号。
上边带信号:
44444411
ˆ()()cos(10)()sin(10)221
{[cos(2000)cos(10)sin(2000)sin(10)]
2
[cos(4000)cos(10)sin(4000)sin(10)]}1
[cos(12000)cos(14000)]2
U s t m t t m
t t t t t t t t t t t t ππππππππππππ=
−=−+−=+ 类似地,下边带信号为:
1
()[cos(8000)cos(6000)]2
D s t t t ππ=+。
频谱图:实线为上边带信号,虚线为下边带信号。
4-6 某调制系统如图P4-6所示,为了在输出端同时得到f 1(t )和f 2(t ),试确定接收端的c 1(t)和c (t)
f 1(t f 2(t f 1(t )
f 2(t )
[解] 1020()()cos 2()sin 2s t f t f t f t f t ππ=⋅+
如果 10()cos 2c t f t π=,20()sin 2c t f t π= 则
11020111()()cos4()sin 4222g t f t f t f t f t ππ⎡⎤
=++⋅⎢⎥⎣⎦
21020111()()sin 4()cos 4222g t f t f t f t f t ππ⎡⎤
=⋅+−⎢⎥⎣⎦
通过低通滤波器则输出正好是)(211t f 和)(2
1
2t f 。
(相干解调)
4-7 设某信道具有均匀的双边噪声功率谱密度()n P f =0.5×10−3W/Hz ,
在该信道中传输抑制载波的双边带信号,并设调制信号()m t 的频带限制在5kHz ,而载波为100kHz ,已调信号的功率为10kW 。
若接收机的输入信号在加至解调器之前,先经过带宽为10kHz 的一理想带通滤波器滤波,试问:
(1) 该理想带通滤波器的中心频率为多大? (2) 解调器输入端的信噪功率比为多少? (3) 解调器输出端的信噪功率比为多少?
(4) 求出解调器输出端的噪声功率谱密度,并用图形表示出来。
[解] (1) 该理想带通滤波器的中心频率为100kHz 。
(2) 3
1010i S =×(W),3
3
020.510101010i N n B −==××××=(W)。
所以,
10000100010
i i S N ==。
(3) 因为抑制载波的双边带调制的信噪比增益2G =,所以
210002000o i o i
S S
G N N ==×=。
(4) 若设解调器输入端的噪声为
()()cos2()sin 2i c c s c n t n t f t n t f t ππ=−, ˆ()()cos2()sin 2c i c i c n t n t f t n
t f t ππ=+, 则输出端的噪声为
1
()()2
o c n t n t =
设()c n t 的功率谱为()c n P f ,则()o n t 的功率谱0()n P f 是 0()()/4c n n P f P f =
因为 00()()
()0c n n n P f f P f f P f −++⎧=⎨
⎩
00
,||,||f f f f
<≥
4-9 设某信道具有均匀的双边噪声功率谱密度()n P f =0.5×10−3W/Hz ,在该信道中传输抑制载波的单边带(上边带)信号,并设调制信号()m t 的频带限制在5kHz ,而载波是100kHz ,已调信号功率是10kW 。
若接收机的输入信号在加至解调器前,先经过带宽为5kHz 的一理想带通滤波器滤波,试问:
(1) 该理想带通滤波器中心频率为多大? (2) 解调器输入端的信噪功率比为多少? (3) 解调器输出端的信噪功率比为多少?
[解] (1) 该理想带通滤波器中心频率为102.5kHz 。
(2)
3
1010i S =×(W),3
3
020.51051010i N n B −==××××=(W)。
所以 2000i
i
S N =。
(3) 因为抑制载波的单边带调制的信噪比增益1G =,所以
120002000o i o i
S S
G N N ==×=。
4-12 设某信道具有均匀的双边噪声功率谱密度()n P f =0.5×10-3W/Hz ,在该信道中传输振幅调制信号,并设调制信号()m t 的频带限制于5kHz ,载频是100kHz ,边带功率为10kW ,载波功率为40kW 。
若接收机的输入信号先经过一个合适的理想带通滤波器,然后再加至包络检波器进行解调。
试求:
(1) 解调器输入端的信噪功率比; (2) 解调器输出端的信噪功率比; (3) 信噪比增益G 。
[解](1) 因为 100004000050000i S =+=(W),
33020.510101010i N n B −==××××=(W),
所以
50000
500010i i
S N ==。
(2) 因为是大信噪比,所以可作如下估算。
2()21000020000o S m t ==×=(W), 10o i N N ==(W),
所以
20000200010o o
S N ==。
(3) 信噪比增益
/20002
/50005
o o i i S N G S N =
==。
4-14 设一个宽带调频系统,载波幅度为100V ,频率为100MHz ,调制信号m (t )的频带限制为5kHz ,2
2
5000)(V t m =,500f k π=(rad/s ﹒v ),最大频偏75=Δf kHz ,并设信道中噪声功率谱密度是均匀的,其中3
10)(−=f P n W/Hz (单边谱)
,试求: 1、接收机输入端理想带通滤波器的传输特性()H f ; 2、解调器输入端的信噪功率比; 3、解调器输出端的信噪功率比;
4、若m (t )以振幅调制方式传输,并以包络检波器检波,试比较输出信噪比和所需
带宽方面与调频有何不同?
[解] (1)题设条件下频率调制信号带宽为
)575(2)(2+=+Δ=m f f B kHz=160 kHz
所以理想的输入带通滤波器为
199.92MHz 100.08MHz ()0f H f ≤≤⎧⎪
=⎨
⎪⎩
其它 (2)输入信噪比
in
()S in Nin
P SNR P = 2in 50002
S A P W == Hz 10160W/Hz 1033×⋅=−Nin
P
=160W 所以 25.31)(=in SNR (3)输出信噪比
22
22223
303()310000(500)5000
()8810(5000)
Sout F out Nout m P A K m t SNR P n f πππ−⋅⋅⋅⋅⋅===⋅⋅⋅⋅⋅ 3105.37×=
(4)当m (t )以调幅方式传输,并采用包络检波解调,所需要的带宽为
10=AM B kHz
输出信噪比
()Sout
out Nout
P SNR P =
2()5000Sout P m t ==W 10101043=⋅=−Nout P W 所以 500)(=out SNR
所以 75500105.37)()(3
=×=AM FM SNR SNR
1610
160
==AM FM B B
4-17使用信号t t t m ππ2000sin 22000cos )(+=调制一个800KHz 的载波,已产生SSB AM 信号。
载波的振幅为100=c A 。
(1)试确定信号)(ˆt m。
(2)试确定SSB AM 信号下边带表达式。
(3)试确定SSB 信号下边带幅度谱。
[解](1)t t t m ππ2000sin 22000cos )(+=,所以
ˆ()sin 20002cos2000m
t t t ππ=− (2)下边带信号的时域表示为:
t f t m
A t f t m A t u c c c c ππ2sin )(ˆ2cos )()(+= ()()100cos20002sin 2000cos1600000100sin 20002cos2000sin1600000t t t t t t
ππππππ=++− ()100cos15980002sin1598000t t ππ=+
(3)由书上公式(4.2.19)或者直接对下边带时域信号进行付立叶变换,
()()
333
3
()50(79910)(79910)100(79910)(79910)U f f f j f f δδδδ=+⋅+−⋅−+⋅−−⋅。
