磁路和电感计算
电感的计算方法和BOOST升压电路的电感、电容计算

电感计算方法加载其电感量按下式计算:线圈公式阻抗(ohm) = 2 * 3.14159 * F(工作频率) * 电感量(mH),设定需用 360ohm 阻抗,因此:电感量(mH) = 阻抗 (ohm) ?(2*3.14159) ?F (工作频率) =360 ?(2*3.14159) ?7.06 = 8.116mH据此可以算出绕线圈数:圈数 = [电感量* { ( 18*圈直径(吋)) + ( 40 * 圈长(吋))}] ?圈直径 (吋) 圈数 = [8.116 * {(18*2.047) + (40*3.74)}] ?2.047 = 19 圈空心电感计算公式空心电感计算公式:L(mH)=(0.08D.D.N.N)/(3D+9W+10H)D------线圈直径N------线圈匝数d-----线径H----线圈高度W----线圈宽度单位分别为毫米和mH。
空心线圈电感量计算公式:l=(0.01*D*N*N)/(L/D+0.44)线圈电感量 l单位: 微亨线圈直径 D单位: cm线圈匝数 N单位: 匝线圈长度 L单位: cm频率电感电容计算公式:l=25330.3/[(f0*f0)*c]工作频率: f0 单位:MHZ 本题f0=125KHZ=0.125谐振电容: c 单位:PF 本题建义c=500...1000pf 可自行先决定,或由Q值决定谐振电感: l 单位: 微亨线圈电感的计算公式作者:线圈电感的计算公式转贴自:转载点击数:2991。
针对环行CORE,有以下公式可利用: (IRON)L=N2.AL L= 电感值(H)H-DC=0.4πNI / l N= 线圈匝数(圈)AL= 感应系数H-DC=直流磁化力 I= 通过电流(A)l= 磁路长度(cm)l及AL值大小,可参照Micrometal对照表。
例如: 以T50-52材,线圈5圈半,其L值为T50-52(表示OD为0.5英吋),经查表其AL值约为33nHL=33.(5.5)2=998.25nH≒1μH当流过10A电流时,其L值变化可由l=3.74(查表)H-DC=0.4πNI / l = 0.4?.14?.5?0 / 3.74 = 18.47 (查表后)即可了解L值下降程度(μi%)2。
磁环电感及饱和磁通计算
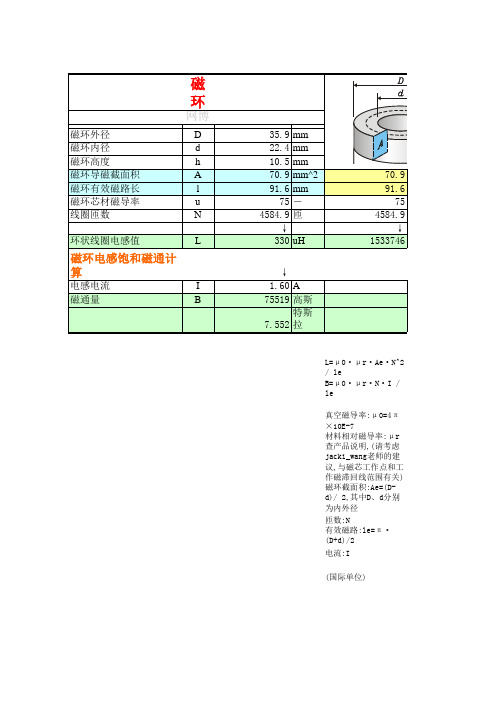
mm^2 mm - 匝 uH
r·Ae·N^2 / le r·N·I / le
率:μ 0=4π ×10E-7 磁导率:μ r查产品说明,(请考虑jacki_wang老师的建议,与磁芯工作点和工作磁滞回线范围有关) 积:Ae=(D-d)/ 2,其中D、d分别为内外径
ห้องสมุดไป่ตู้
:le=π ·(D+d)/2
磁环电感及饱和磁通计算
网博ABCCBA
磁环外径 磁环内径 磁环高度 磁环导磁截面积 磁环有效磁路长 磁环芯材磁导率 线圈匝数 环状线圈电感值 D d h A l u N L I B 35.9 22.4 10.5 70.9 91.6 75 4584.9 ↓ 330 mm mm mm mm^2 mm - 匝 uH
70.9 91.6 75 4584.9 ↓ 1533746
磁环电感饱和磁通计算
电感电流 磁通量
↓ 1.60 A 75519 高斯 7.552 特斯拉
L=μ 0·μ r·Ae·N^2 / le B=μ 0·μ r·N·I / le
真空磁导率:μ 0=4π ×10E-7 材料相对磁导率:μ r查产品说明,(请考虑jacki 磁环截面积:Ae=(D-d)/ 2,其中D、d分别为内外 匝数:N 有效磁路:le=π ·(D+d)/2 电流:I (国际单位)
永磁同步电机交直轴电感计算

参数化扫描的有问题,但是趋势应该差不多《永磁电机》永磁同步电机分为表面式和内置式。
由于永磁体特别是稀土永磁体的磁导率近似等于真空磁导率,对于表面式,直轴磁阻和交轴磁阻相等,因此交直轴电感相等,即Ld=Lq,表现出隐极性质。
对于内置式,直轴磁阻大于交轴磁阻(交轴通过路径的磁导率大于直轴),因此Ld<Lq,表现出凸极电机的性质。
磁动势、磁阻:磁场强度H沿一路经的积分等于该路径上的磁压,用符号U表示,单位为A。
磁场强度沿一条闭合路径的积分等于等于该路径所包围的电流数,即F=∮Hdll =∑I iki=1,称为安培环路定律。
由于磁场为电流所激发,上式中回路所环绕的电流称为磁动势,用F表示(A)。
在电机设计中,为简化计算,通常把电机的各部分磁场简化为相应磁路。
磁路的划分原则是:①每段磁路为同一材料;②磁路的截面积大体相同;③流过该磁路各截面的磁通相同。
电机等效磁路的基本组成部分为磁动势源、导磁体和空气隙,磁动势源为永磁体或通电线圈。
图3-1为一圆柱形的磁路,其截面积为A,长度为L,假设磁通都通过该圆柱体的所有截面且在其截面上均匀分布,则该段磁路上的磁通和磁压分别为{Φ=BAU=HL,与电路中电流和电压的关系类比,定义R m=UΦ,为该段磁路的磁阻,上式称为磁路的欧姆定律。
磁阻用磁路的特性和有关尺寸为R m=LμA(L是长度,μ是磁导率),与电阻的表达式在形式上类似。
磁阻的倒数为磁导,用ᴧ表示,Λ=μAL。
众所周知,若气隙长度均匀、磁密在一个极距范围内均匀分布、铁心端部无磁场边缘效应,则气隙磁压降为Fδ=Hδδ=Bδμ0δ=δμ0ΦτL a,式中,Ф为每极磁通;δ为气隙长度;τ为极距;La为铁心长度。
调速永磁同步电机转子结构分为表面型和内置型。
由于永磁体特别是稀土永磁体的磁导率近似等于真空磁导率,对于表面式,直轴磁阻与交轴磁阻相等,因此交直轴电感相等,即Ld=Lq,表现出隐极性质。
而对其他结构,直轴磁阻大于交轴磁阻,因此Ld<Lq,表现出凸极电机性质。
电感公式

针对环形CORE,有以下公式可利用: (IRON)
L=N2*AL L=电感量(H) AL= 感应系数
H-DC=0.4πNI /l N==绕线匝数(圈)
H-DC=直流磁化力I= 通过电流(A) l= 磁路长度(cm)
l及AL值大小,可参照Micrometa对照表。
例如: 以T50-52材,绕线5圈半,其L值为T50-52(表示OD为0.5英寸),经查表其AL值约为33nH
L=33*(5.5)2=998.25nH≈1H
当通过10A电流时,其L值变化可由l=3.74(查表)
H-DC=0.4πNI / l = 0.4×3.14×5.5×10 / 3.74 = 18.47 (查表后)即可了解L值下降程度(i%)
电感计算
介绍一个经验公式
L=(k*0*s*N2*S)/l
其中
0 为真空磁导率=4π*10-7。
(10的负七次方)
s 为线圈内部磁芯的相对磁导率,空心线圈时s=1
N2为线圈圈数的平方
S 线圈的截面积,单位为平方米
l 线圈的长度,单位为米
k 系数,取决于线圈的半径(R)与长度(l)的比值。
计算出的电感量的单位为亨利。
电感基本公式

电感基本公式电感基本公式:L=Ψ/I。
意义是单位电流引起线圈的磁通量。
电感是闭合回路的⼀种属性,是⼀个物理量。
扩展资料 电感的定义公式 ⼀、电感的定义是这样的: 1、电压除以电流对时间的导数之商。
2、L=phi/i(在电路中,当电流流过导体时,会产⽣电磁场,电磁场的⼤⼩除以电流的⼤⼩就是电感)。
3、电感是导线内通过交流电流时,在导线的内部及其周围产⽣交变磁通,导线的磁通量与⽣产此磁通的电流之⽐。
4、电感定义式L=Ψ/I,意义是单位电流引起线圈的磁通量。
⼆、电感器件电感量的计算公式: ⽅法1、L=µ×Ae*N2/l 其中:L表⽰电感量、µ表⽰磁⼼的`磁导率、Ae表⽰磁⼼的截⾯积、N表⽰线圈的匝数、lm表⽰磁⼼的磁路长度。
⽅法2、经验公式: L=(k*µ0*µs*N2*S)/l 其中 µ0为真空磁导率=4π*10(-7)。
(10的负七次⽅) µs为线圈内部磁芯的相对磁导率,空⼼线圈时µs=1 N2为线圈圈数的平⽅ S线圈的截⾯积,单位为平⽅⽶ l线圈的长度,单位为⽶ k系数,取决于线圈的半径(R)与长度(l)的⽐值。
计算出的电感量的单位为亨利(H)。
电感定义 导体的⼀种性质,⽤导体中感⽣的电动势或电压与产⽣此电压的电流变化率之⽐来量度。
稳恒电流产⽣稳定的磁场,不断变化的电流(交流)或涨落的直流产⽣变化的磁场,变化的磁场反过来使处于此磁场的导体感⽣电动势。
感⽣电动势的⼤⼩与电流的变化率成正⽐。
⽐例因数称为电感,以符号L表⽰,单位为亨利(H)。
电感是闭合回路的⼀种属性,即当通过闭合回路的电流改变时,会出现电动势来抵抗电流的改变。
这种电感称为⾃感,是闭合回路⾃⼰本⾝的属性。
假设⼀个闭合回路的电流改变,由于感应作⽤⽽产⽣电动势于另外⼀个闭合回路,这种电感称为互感。
电感计算公式

有个比较复杂的经验公式,很复杂,一般都是用电感测试仪测试。
电感的计算公式线圈公式阻抗(ohm) = 2 * 3.14159 * F(工作频率) * 电感量(mH),设定需用360ohm 阻抗,因此:电感量(mH) = 阻抗(ohm) ÷ (2*3.14159) ÷ F (工作频率) = 360 ÷(2*3.14159) ÷ 7.06 = 8.116mH据此可以算出绕线圈数:圈数= [电感量* { ( 18*圈直径(吋)) + ( 40 * 圈长(吋))}] ÷圈直径(吋)圈数= [8.116 * {(18*2.047) + (40*3.74)}] ÷ 2.047 = 19 圈空心电感计算公式空心电感计算公式:L(mH)=(0.08D.D.N.N)/(3D+9W+10H)D------线圈直径N------线圈匝数d-----线径H----线圈高度W----线圈宽度单位分别为毫米和mH。
空心线圈电感量计算公式:l=(0.01*D*N*N)/(L/D+0.44)线圈电感量l单位: 微亨线圈直径D单位: cm线圈匝数N单位: 匝线圈长度L单位: cm频率电感电容计算公式:l=25330.3/[(f0*f0)*c]工作频率: f0 单位:MHZ 本题f0=125KHZ=0.125谐振电容: c 单位:PF 本题建义c=500...1000pf 可自行先决定,或由Q 值决定谐振电感: l 单位: 微亨线圈电感的计算公式1.针对环行CORE,有以下公式可利用: (IRON)L=N2.AL L= 电感值(H)H-DC=0.4πNI / l N= 线圈匝数(圈)AL= 感应系数H-DC=直流磁化力I= 通过电流(A)l= 磁路长度(cm)l及AL值大小,可参照Microl对照表。
例如: 以T50-52材,线圈5圈半,其L值为T50-52(表示OD为0.5英吋),经查表其AL值约为33nHL=33.(5.5)2=998.25nH≈1μH当流过10A电流时,其L值变化可由l=3.74(查表)H-DC=0.4πNI / l = 0.4×3.14×5.5×10 / 3.74 = 18.47 (查表后)即可了解L值下降程度(μi%)2.介绍一个经验公式L=(k*μ0*μs*N2*S)/l其中μ0 为真空磁导率=4π*10(-7)。
电感量计算公式

贵派电器谈电感线圈的小常识(一)电感线圈是由导线一圈靠一圈地绕在绝缘管上,导线彼此互相绝缘,而绝缘管可以是空心的,也可以包含铁芯或磁粉芯,简称电感。
用L表示,单位有亨利(H)、毫亨利 (mH)、微亨利(uH),1H=10^3mH=10^6uH。
一、电感的分类按电感形式分类:固定电感、可变电感。
按导磁体性质分类:空芯线圈、铁氧体线圈、铁芯线圈、铜芯线圈。
按工作性质分类:天线线圈、振荡线圈、扼流线圈、陷波线圈、偏转线圈。
按绕线结构分类:单层线圈、多层线圈、蜂房式线圈。
二、电感线圈的主要特性参数1、电感量L电感量L表示线圈本身固有特性,与电流大小无关。
除专门的电感线圈(色码电感)外,电感量一般不专门标注在线圈上,而以特定的名称标注。
2、感抗XL电感线圈对交流电流阻碍作用的大小称感抗XL,单位是欧姆。
它与电感量L和交流电频率f的关系为XL=2πf3、品质因素Q品质因素Q是表示线圈质量的一个物理量,Q为感抗XL与其等效的电阻的比值,即:Q=XL/R。
线圈的Q值愈高,回路的损耗愈小。
线圈的Q值与导线的直流电阻,骨架的介质损耗,屏蔽罩或铁芯引起的损耗,高频趋肤效应的影响等因素有关。
线圈的Q值通常为几十到几百。
4、分布电容线圈的匝与匝间、线圈与屏蔽罩间、线圈与底版间存在的电容被称为分布电容。
分布电容的存在使线圈的Q值减小,稳定性变差,因而线圈的分布电容越小越好。
贵派电器谈电感线圈的小常识(二)三、常用线圈1、单层线圈单层线圈是用绝缘导线一圈挨一圈地绕在纸筒或胶木骨架上。
如晶体管收音机中波天线线圈。
2、蜂房式线圈如果所绕制的线圈,其平面不与旋转面平行,而是相交成一定的角度,这种线圈称为蜂房式线圈。
而其旋转一周,导线来回弯折的次数,常称为折点数。
蜂房式绕法的优点是体积小,分布电容小,而且电感量大。
蜂房式线圈都是利用蜂房绕线机来绕制,折点越多,分布电容越小。
3、铁氧体磁芯和铁粉芯线圈线圈的电感量大小与有无磁芯有关。
在空芯线圈中插入铁氧体磁芯,可增加电感量和提高线圈的品质因素。
铁氧体e型磁心系列磁路参数计算

铁氧体e型磁心系列磁路参数计算
铁氧体e型磁心系列磁路参数计算,是一项重要的电工学研究,它是从各种多维立体磁心中提取出来的。
铁氧体e型磁心系列磁路参数计算包括:电流、电压、功率、相位、频率、阻抗、电阻、电感、电容、磁性等参数的计算。
首先,用于铁氧体e型磁心系列磁路参数计算的电路图必须准确无误,对于复杂的磁路,最好还用图形界面软件来绘制电路图。
然后,根据电路图,求出电压有关参数,如:总电压、各节点电压、电流、功率等。
在求解磁路参数时,需要考虑阻抗电路和磁性电路两种情况,分别使用不同的公式进行求解,如:电阻与电阻相连时,电压V=R×I,其中R为电阻,I为电流;电感与电容相连时,电压V=Z L ×I,其中ZL为电感阻抗,I为电流;电感与电感相连时,电压V=Z L ×(I1-I2),其中ZL为电感阻抗,I1、I2分别为正、负极电流;磁性电路的求解,电压V=X L ×I,其中XL为磁芯阻抗,I为电流。
在求解过程中,还要注意电流包络问题,即电流具有周期性变化,这种变化有时也会影响电路参数计算。
在计算相位、频率时,可以先将电路参数转化为方程式,然后用数学方法将方程式解出,便可得到相位、频率等参数。
最后,铁氧体e型磁心系列磁路参数计算的结果要经过核实,以确保计算准确无误。
可以通过实验测量或者用特殊的计算机软件进行核实,以便保证计算的准确性。
总之,铁氧体e型磁心系列磁路参数计算是一项复杂而精细的工作,需要掌握各类电路参数的相关知识,并熟练掌握计算方法,才能得出准确无误的结果。
磁导率和电感计算

磁导率和电感计算有效导磁率在测试变压器铁芯导磁率的时候,⼀般都是通过测试变压器线圈电感量的⽅法来测试变压器铁芯的导磁率;这种测试⽅法实际上就是测试电感线圈的交流阻抗;然⽽⽤来代表介质属性的导磁率并不是⼀个常数,⽽是⼀个⾮线性函数,它不但与介质以及磁场强度有关,⽽且与温度还有关。
我们在前⾯(2-11)式和(2-12)式中,已经介绍过脉冲变压器的脉冲导磁率和开关变压器平均导磁率的概念。
脉冲变压器的脉冲导磁率由下式表⽰:(2-11)式中,称为脉冲静态磁化系数,或脉冲变压器的脉冲导磁率;为脉冲变压器铁芯中的磁通密度增量;为脉冲变压器铁芯中的磁场强度增量。
(2-12)式中,为开关变压器的平均导磁率;为开关变压器铁芯中的平均磁通密度增量;为开关变压器铁芯中的平均磁场强度增量。
在⼀定程度上来说,开关变压器也属于脉冲变压器,因为它们输⼊的都是电压脉冲;但⼀般脉冲变压器输⼊脉冲电压的幅度以及宽度基本上都是固定的,并且是单极性电压脉冲,其磁滞回线的⾯积相对来说很⼩,因此,变压器的脉冲导磁率⼏乎可以看成是⼀个常数。
⽽开关变压器输⼊脉冲电压的幅度以及宽度⼀般都不是固定的,其磁滞回线的⾯积相对来说变化⽐较⼤,铁芯导磁率的变化范围也⽐较⼤,特别是双激式开关变压器,因此,只能⽤平均导磁率的概念来描述。
如果不是特别强调脉冲变压器输⼊电压为单极性脉冲电压,并且输⼊脉冲电压的幅度以及宽度基本上都是固定的;那么,利⽤(2-11)式来计算开关变压器平均导磁率也未尝不可;因为,⼈们在测量开关变压器平均导磁率的时候,不可能⽤很多不同幅度和宽度的脉冲电压,分别对开关变压器逐⼀进⾏测试,然后再把测试结果取平均值。
我们可以试想,如果在众多⽤来测试的不同幅度和宽度的电压脉冲之中,我们只选出其中⼀组,其幅度和宽度都是在这些测试电压脉冲之中⽐较偏中的,那么,⽤(2-11)式的测试结果来代替(2-12)式的结果,实际上不会有很⼤的区别。
这样,反⽽使得对变压器平均导磁率的测量变得简单。
电机电感计算公式

电机电感计算公式电机的电感是指电机在电流变化时所产生的自感应电动势与电流变化率的比值。
电感是电机的重要参数之一,它决定了电机的电流响应速度和电流稳定性。
电机的电感计算公式主要有两种:螺线管电感计算公式和磁路电感计算公式。
下面将分别对这两种公式进行详细介绍。
螺线管是由导线绕成的线圈,其电感主要由线圈的几何尺寸和导线的材料决定。
根据安培环路定理和毕奥-萨伐尔定律,螺线管的电感计算公式可以表示为:L=(μ₀*μr*N²*A)/l其中L为螺线管的电感,单位为亨μ₀为真空中的磁导率,约为4π×10^(-7)H/mμr为螺线管的相对磁导率N为线圈的匝数A为线圈的横截面积,单位为平方米l为线圈的长度,单位为米根据这个公式,我们可以得知螺线管的电感与线圈的匝数N呈平方关系,与线圈的横截面积A呈正比,与线圈的长度l呈反比。
因此,在设计电机时,可以通过调整这些参数来控制电感的大小,以实现所需的性能。
电机的磁路电感是指电机在磁路中产生的磁通量与磁场变化率的比值。
根据法拉第电磁感应定律,电机的磁路电感计算公式可以表示为:L=(N*Φ)/I其中L为磁路电感,单位为亨N为磁路中的匝数Φ为磁路中的磁通量I为电流,单位为安培根据这个公式,我们可以得知磁路电感与磁路中的匝数N呈正比,与磁通量Φ呈正比,与电流I呈正比。
因此,在设计电机时,可以通过调整这些参数来控制电感的大小。
根据以上两种电感计算公式,我们可以看出,电感的大小与线圈的几何尺寸、导线材料、匝数、磁通量以及电流等因素有关。
要准确计算电机的电感,需要充分考虑这些参数,并结合实际情况进行设计。
总之,电机的电感是电机设计中的重要参数,它与电流响应速度和电流稳定性密切相关。
通过螺线管电感计算公式和磁路电感计算公式,我们可以准确计算电机的电感,并根据实际需求进行设计。
磁路计算

磁路与电感计算一个空心螺管线圈,或是带气隙的磁芯线圈,通电流后磁力线分布在它周围的整个空间。
对于静止或低频电磁场问题,可以根据电磁理论应用有限元分析软件进行求解,获得精确的结果,但是不能提供简单的、指导性的和直观的物理概念。
在开关电源中,为了用较小的磁化电流产生足够大的磁通(或磁通密度),或在较小的体积中存储较多的能量,经常采用一定形状规格的软磁材料磁芯作为磁通的通路。
因磁芯的磁导率比周围空气或其他非磁性物质磁导率大得多,把磁场限制在结构磁系统之内,即磁结构内磁场很强,外面很弱,磁通的绝大部分经过磁芯而形成一个固定的通路。
在这种情况下,工程上常常忽略次要因素,只考虑导磁体内磁场或同时考虑较强的外部磁场,使得分析计算简化。
通常引入磁路的概念,就可以将复杂的场的分析简化为我们熟知的路的计算。
3.1 磁路的概念从磁场基本原理知道,磁力线或磁通总是闭合的。
磁通和电路中电流一样,总是在低磁阻的通路流通,高磁阻通路磁通较少。
所谓磁路指凡是磁通(或磁力线)经过的闭合路径称为磁路。
3.2 磁路的欧姆定律以图3.1(a)为例,在一环形磁芯磁导率为μ的磁芯上,环的截面积A ,平均磁路长度为l ,绕有N 匝线圈。
在线圈中通入电流I ,在磁芯建立磁通,同时假定环的内径与外径相差很小,环的截面上磁通是均匀的。
根据式(1.7),考虑到式(1.1)和(1.3)有 F NI Hl BlAl R m =====μφμφ (3.1) 或φ=F /R m (3.2) 式中F =NI 是磁动势;而R m =lA μ (3.3)R m —称为磁路的磁阻,与电阻的表达式相似,正比于路的长度l ,反比于截面积A 和材料的磁导率μ;其倒数称为磁导G m m R A l==1μ (3.3a) 式(3.1)即为磁路的欧姆定律。
在形式上与电路欧姆定律相似,两者对应关系如表3.1所示。
磁阻的单位在SI 制中为安/韦,或1/亨;在CGS 制中为安/麦。
电感量计算公式

电感量计算公式-CAL-FENGHAI.-(YICAI)-Company One1贵派电器谈电感线圈的小常识(一)电感线圈是由导线一圈靠一圈地绕在绝缘管上,导线彼此互相绝缘,而绝缘管可以是空心的,也可以包含铁芯或磁粉芯,简称电感。
用L表示,单位有亨利(H)、毫亨利 (mH)、微亨利(uH),1H=10^3mH=10^6uH。
一、电感的分类按电感形式分类:固定电感、可变电感。
按导磁体性质分类:空芯线圈、铁氧体线圈、铁芯线圈、铜芯线圈。
按工作性质分类:天线线圈、振荡线圈、扼流线圈、陷波线圈、偏转线圈。
按绕线结构分类:单层线圈、多层线圈、蜂房式线圈。
二、电感线圈的主要特性参数1、电感量L电感量L表示线圈本身固有特性,与电流大小无关。
除专门的电感线圈(色码电感)外,电感量一般不专门标注在线圈上,而以特定的名称标注。
2、感抗XL电感线圈对交流电流阻碍作用的大小称感抗XL,单位是欧姆。
它与电感量L和交流电频率f的关系为XL=2πf3、品质因素Q品质因素Q是表示线圈质量的一个物理量,Q为感抗XL与其等效的电阻的比值,即:Q=XL/R。
线圈的Q值愈高,回路的损耗愈小。
线圈的Q值与导线的直流电阻,骨架的介质损耗,屏蔽罩或铁芯引起的损耗,高频趋肤效应的影响等因素有关。
线圈的Q值通常为几十到几百。
4、分布电容线圈的匝与匝间、线圈与屏蔽罩间、线圈与底版间存在的电容被称为分布电容。
分布电容的存在使线圈的Q值减小,稳定性变差,因而线圈的分布电容越小越好。
贵派电器谈电感线圈的小常识(二)三、常用线圈1、单层线圈单层线圈是用绝缘导线一圈挨一圈地绕在纸筒或胶木骨架上。
如晶体管收音机中波天线线圈。
2、蜂房式线圈如果所绕制的线圈,其平面不与旋转面平行,而是相交成一定的角度,这种线圈称为蜂房式线圈。
而其旋转一周,导线来回弯折的次数,常称为折点数。
蜂房式绕法的优点是体积小,分布电容小,而且电感量大。
蜂房式线圈都是利用蜂房绕线机来绕制,折点越多,分布电容越小。
电磁线圈盘电感计算公式

线圈盘电感计算公式电感量按下式计算:线圈公式阻抗(ohm) = 2 * 3.14159 * F(工作频率) * 电感量(mH),设定需用360ohm 阻抗,因此:电感量(mH) = 阻抗(ohm) ÷ (2*3.14159) ÷ F (工作频率) = 360 ÷ (2*3.14159) ÷ 7.06 =8.116mH据此可以算出绕线圈数:圈数= [电感量* { ( 18*圈直径(吋)) + ( 40 * 圈长(吋))}] ÷圈直径(吋)圈数= [8.116 * {(18*2.047) + (40*3.74)}] ÷ 2.047 = 19 圈空心电感计算公式空心电感计算公式:L(mH)=(0.08D.D.N.N)/(3D+9W+10H)D------线圈直径N------线圈匝数d-----线径H----线圈高度W----线圈宽度单位分别为毫米和mH。
空心线圈电感量计算公式:l=(0.01*D*N*N)/(L/D+0.44)线圈电感量l单位: 微亨线圈直径D单位: cm线圈匝数N单位: 匝线圈长度L单位: cm频率电感电容计算公式:l=25330.3/[(f0*f0)*c]工作频率: f0 单位:MHZ 本题f0=125KHZ=0.125谐振电容: c 单位:PF 本题建义c=500...1000pf 可自行先决定,或由Q值决定谐振电感: l 单位: 微亨线圈电感的计算公式1。
针对环行CORE,有以下公式可利用: (IRON)L=N2.AL L= 电感值(H)H-DC=0.4πNI / l N= 线圈匝数(圈)AL= 感应系数H-DC=直流磁化力I= 通过电流(A)l= 磁路长度(cm)l及AL值大小,可参照Microl对照表。
例如: 以T50-52材,线圈5圈半,其L值为T50-52(表示OD为0.5英吋),经查表其AL值约为33nHL=33.(5.5)2=998.25nH≒1μH当流过10A电流时,其L值变化可由l=3.74(查表)H-DC=0.4πNI / l = 0.4×3.14×5.5×10 / 3.74 = 18.47 (查表后)即可了解L值下降程度(μi%)2。
磁环电感的设计计算

⒆资料:19-1USA Micrometals 铁粉末铁心(节录):内径截面面积面积乘积磁路长度质量导磁率电感系数 cm cm2cm4cm g μAL T30-260.3840.0650.008 1.830.875.033.0T37-260.5210.0700.015 2.32 1.175.028.0T44-260.5820.1070.028 2.67 2.075.036.0T50-260.7700.1210.056 3.20 2.775.032.0T68-260.9400.1960.136 4.24 5.775.042.0T72-260.7110.3690.147 3.9910.475.087.0粉末铁心结构常数Kj(25℃)Kj(50℃)x y 4035901.14-0.12[ 变压器与电感设计手册 (中国电子变压器专业委员会内部参考资料)]19-2嘉成电子公司铁粉末铁心(节录):内径外径高度磁路长度截面面积体积电感系数mm mm mm cm cm2cm3AL T30-26 3.8407.8 3.250 1.840.0610.11033.5T37-26 5.2109.53 3.250 2.310.0640.14728.5T44-26 5.82011.2 4.040 2.680.0990.26637.0T50-267.70012.7 4.830 3.190.1120.35833.0T68-269.40017.5 4.830 4.230.1790.75943.5T72-267.11018.3 6.600 4.010.349 1.40090.019-326号铁粉材质铁损:①USA Micrometals 公司提供的μ=75,26#铁粉末铁心铁损计算式:P =0.144*f 1.12*Bm 2.01W/kgf :频率HzBm :磁通密度T[ 变压器与电感设计手册 (中国电子变压器专业委员会内部参考资料)]②嘉成电子提供的铁粉末铁心的铁损曲线:型号型号19-4铁粉末铁心的导磁率和磁场强度的关系:①嘉成电子铁粉末铁心的导磁率和磁场强度的关系曲线:(嘉成电子)初始导磁率百分数与直流磁化强度的关系曲线(嘉成电子)导磁率百分数与直流磁化强度的关系曲线②东阳东磁有限公司提供的铁粉末铁心的导磁率和磁场强度的关系曲线:东阳东磁有限公司65%60Oe19-5铁粉末铁心的导磁率和频率的关系:嘉成电子提供的铁粉末铁心的导磁率和频率的关系曲线:(嘉成电子)实效导磁率和频率的关系曲线19-6电感线圈表面温升的计算:(以下内容为节录自中国电子学会2006年变压器和电感器件专业学术年会论文集中杜保明的文章)假设热能是通过铁心或线圈绕组的暴露表面均匀消散的,当绕组或铁心的温度高于周围环境的空气温度时,热量就将通过热辐射的方式和热对流的方式向周围传递。
各种电感计算公式

导线线径与电流规格表绝缘导线(铝芯/铜芯)载流量的估算方法 以下是绝缘导线(铝芯/铜芯)载流量的估算方法,这是电工基础,今天把这些知识教给大家,以便计算车上的导线允许通过的电流.(偶原在福建省南平供电局从事电能计量工作) 铝芯绝缘导线载流量与截面的倍数关系 导线截面(平方毫米) 1 1.5 2.5 4 6 10 16 25 35 50 70 95 120 载流量(A 安培) 9 14 23 32 48 60 90 100 123 150 210 238 300载流是截面倍数 9 8 7 6 5 4 3.5 3 2.5估算口诀:二点五下乘以九,往上减一顺号走。
三十五乘三点五,双双成组减点五。
(看不懂没关系,多数情况只要查上表就行了)。
条件有变加折算,高温九折铜升级。
穿管根数二三四,八七六折满载流。
说明:(1)本节口诀对各种绝缘线(橡皮和塑料绝缘线)的载流量(安全电流)不是直接指出,而是“截面乘上一定的倍数”来表示,通过心算而得。
由表5 3可以看出:倍数随截面的增大而减小。
“二点五下乘以九,往上减一顺号走”说的是2.5mm’及以下的各种截面铝芯绝缘线,其载流量约为截面数的9倍。
如2.5mm’导线,载流量为2.5×9=22.5(A)。
从4mm’及以上导线的载流量和截面数的倍数关系是顺着线号往上排,倍数逐次减l ,即4×8、6×7、10×6、16×5、25×4。
“三十五乘三点五,双双成组减点五”,说的是35mm”的导线载流量为截面数的3.5倍,即35×3.5=122.5(A)。
从50mm’及以上的导线,其载流量与截面数之间的倍数关系变为两个两个线号成一组,倍数依次减0.5。
表格为导线在不同温度下的线径与电流规格表。
(请注意:线材规格请依下列表格,方能正常使用)即50、70mm’导线的载流量为截面数的3倍;95、120mm”导线载流量是其截面积数的2.5倍,依次类推。
线圈的电感量和磁路长度

磁場與磁力線
6-1.1 磁場與磁力線
2.磁場與磁力線: (1)磁鐵附近磁力作用所及的空間稱為磁場(magnetic field) 。 (2)通常以磁粉灑在磁鐵四周,觀察磁粉的排列即可得知磁場 分佈的情形,如圖6-1所示;其中磁粉集結密度最高的兩端 稱為磁極。 (3)兩磁極間呈現規則性的線條稱為磁力線。
3.磁通密度(B):磁場中,單位面積(A)磁力線通過的總數 ();以公式表示如下:
磁 通 密 度 與 導磁係 數
6-1.4 磁通密度與導磁係數
4.若以磁極M為球心,距離d,則球形面積A=4πd2,代入上式 得:
5.比較(6-5)及(6-7)式,得:
磁 通 密 度 與 導磁係 數
6-1.4 磁通密度與導磁係數
6.磁通密度和磁場強度成正比;磁場強度愈強的地方,其磁 通密度愈高。 7.導磁係數():磁通密度和磁場強度的比值;此值愈高表 示其導磁效能愈好,例如矽鋼、鐵、鈷等。導磁係數以數學 式表示如下:
磁 通 密 度 與 導磁係 數
6-1.4 磁通密度與導磁係數
8.單位:
表6-2 磁通密度與磁場強度
1.磁場強度:「單位磁極(m)在磁場中某一點所受到的作用力(F)」 2.公式:
因為作用力為向量,故磁場強度也是向量,其方向為磁力線的 切線方向。
磁場強度
6-1.3 磁場強度
3.將(6-3)式 代入(6-4)式,可得:
(註:可以和(5-21)公式,電場強度 E
F q
9 109
Q d2
對照學習。)
4. 磁場強度和該磁極的大小(M)成正比,和其距離的平方(d2)
H
6.33 104 M r2
6.33
104
25 10 4 5 10 1 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例3:一个环形磁芯线圈的磁芯内径d=25mm,外径D=41mm,环高 h=10mm(见图例3)。磁芯相对磁导率μr=50。线圈匝数N=50 匝。通入线圈电流为0.5A。求磁芯中最大、最小以及平均磁场强度, 磁通,磁链和磁通密度。
由于线圈均匀绕,所以x段线圈匝数为Nx=Nx/l,x段磁势
(3.8)
F
磁芯中
N
NI
φ
的磁场强
0
lx
F=NI
Rm
x
Ucx
NI
ф
Ux
lx
度 H=IN/l, 应有
xI
0
lx
(3.9)
x=0 (a)
(b)
(c)
式中IN—
图3.2 等截面均匀绕线环形磁芯磁位分布图和等效磁路
线圈总磁
势;l—磁路平均长度。因此,沿磁路平均长度展开,Fx和Ucx的分布情
AF
A
IN
I
Ucx
lx l
I
3.3.2 E型
X=0
l
IN
N
Ux
lx
N
0
lx
(a)
(b)
(c)
图3.4 磁路中有气隙时磁位分布图
磁芯 磁场 和等 效磁 路
E
型磁芯是最常用的磁芯形状。其它形状如C型(硅钢片),ETD型,EC
型,RM型等等(铁氧体)的等效磁路与E型相似。这些磁芯,为了便于
装配线圈,通常是两个相同的“E”形状磁芯开口相对合成一个封闭磁
A
φ
何闭合曲面的磁通之和为零。而式(3.6) I
l F=NI R
则为磁路的欧姆定律。
应当指出的是磁路仅在形式上将场 的问题等效成路来考虑,它与电路根 本不同:
(1) 电路中,在电动势的驱动下,确
N
(a)
(b)
图 3.1 环形磁芯线圈和等效磁路
实存在着电荷在电路中流动,并因此引起电阻的发热。而磁路中磁通是
因此各磁路段磁阻为
R1
R2 R3
磁路总激励磁势F=NI,其等效磁路如图3.6(b)所示。如果进行磁位分
析,磁位分布图相似于图3.4。因集中线圈占平均磁路长度的大部分,
比环形磁路短,磁芯磁导率很高,散磁通很少,通常忽略周围空气中磁
场。
因为两个边柱是对称的,可合并成一路,R2’=R2/2=l2/2μA2,
通。因为在上一章我们定义了漏磁通只在耦合磁路中存在。散磁通也可
能是互感的一部分,如果采用电磁电器中不经过主气隙的磁通(不产生 力)就是漏磁,对应的电感称为漏感,就会在变压器中造成混淆,故引 出散磁通。
(3) 在电路中,导体的电导率与导体流过的电流无关。而在磁路 中,磁路中磁导率是与磁路中磁通密度有关的非线性参数。即使磁通路 径铁磁结构保证各处截面积相等,但由于有散磁通存在,在磁芯中各截 面的磁通密度仍不相等。磁芯材料非线性使得不同,导致相同磁路长 度,不同的磁压降。需要由磁通求磁阻,又由磁阻求磁通反复试探,作 出系统的磁化曲线,这样工作量很大。虽然空气的磁导率是常数,但气 隙磁场与结构有关,很难准确计算。
式(3.1)即为磁路的欧姆定律。在形式上与 电路欧姆定律相似,两者对应关系如表3.1所 示。
磁阻的单位在SI制中为安/韦,或1/亨;在
电阻R=l/A 磁导Gm=A/l 电导G=A/l 磁压降Um=Hl 电压U=IR
CGS制中为安/麦。磁导的单位是磁阻单位的倒数。同理,在磁阻两端
的磁位差称为磁压降Um,即
芯。根据等截面原理,E型磁芯(图3.5)的两个边柱的截面积之和等于
中柱截面积。线圈一般绕在中柱上。
(A) 无气隙时等效磁路和磁位图
半个E型磁芯尺寸如图3.5所示。中柱的截面积
边柱截面积 端部面积
A2
A1
DEA
CF
B
图3.5 E型磁芯尺寸图
将两个磁芯柱端相对合在一起,形成闭合磁路,称为变压器磁芯 (图3.6(a))。中柱上绕有激励线圈N。假设忽略散磁通,则在磁芯整个 截面上磁通密度是均匀的,磁通的平均路径如图中虚线所示。因此
φ=φc+φs 式中φc-全部经过磁芯的磁通;φs-“散”磁通。散磁通φs是部 分通过磁芯经过周围空气路径闭合的磁通。如果是电感线圈,它是电感 磁通的一部分;如果是变压器,φs可能是主磁通的一部分,其余是漏 磁通,也可能全部是漏磁通,即部分或全部不与次级耦合。 等效磁路如图3.3(c)所示。图中Ri= lw /μA-lw段磁阻,相当于总磁势 的内阻;而Rl=(l- lw)/μA-lk以外的磁芯磁阻。Rs-散磁磁阻,则由经 验决定。 (C)有气隙时环形磁芯磁场 图3.4(a)为线圈均匀绕,等截面环形有气隙为的磁芯线圈。线圈磁势 降落在磁芯和气隙两部分
R3’=R3/2=l3/2μA3。简化的等效磁路如图3.6(c)所示。中柱通过的磁通
(3.11)
因为A1=2A2=2A3,因此R= R1+ R2’+2 R3’=2(l1+l3)/μA1=1/G。式(3.11)
解:磁芯的截面积
磁路平均长度 线圈产生的磁势 磁芯中最大磁场强度发生在内径处 最小磁场强度发生在外径处
d D
h 图 例3
平均磁场强度
磁芯中平均磁通密度
磁芯中磁通
或
磁芯线圈的磁链
从磁芯中最大和最小磁场强度可以看到,内外径相差很大,可见磁 芯中磁通密度是不均匀的。一般希望内径与外径比在0.8左右。
3.3 磁芯磁场和磁路
(4) 由于有散磁通的存在,即使均匀绕在环形磁芯上的两个线圈也 不能做到全耦合,漏磁通一般很难用分析的方法求得,通常采用经验公 式计算。
(5)直流(即恒定)磁场已经相当复杂,如果是交流激励的磁场, 在其周围有导体,在导体中产生涡流效应,涡流对激励线圈来说相当于 一个变压器的次级,涡流产生的磁通对主磁通产生影响,磁场分布更加 复杂。
(A) 均匀绕线环形磁芯 首先在磁路的平均长度上选取一点(或一个截面)作为磁位的参考点
(即x=0),并假定沿磁芯中磁通的正方向x取正值,然后求磁路中某x点相 对于参考点的磁位差Ux。根据磁路克希荷夫第二定律,沿图示虚线闭合 回路得到
Fx= Ucx+Ux
(3.7)
式中Fx-0x段磁路所匝链的线圈磁势, Ucx -0x段磁芯的磁阻压降。
第三章 磁路和电感计算
不管是一个空心螺管线圈,还是带气隙的磁芯线圈,通电流后磁力 线分布在它周围的整个空间。对于静止或低频电磁场问题,可以根据电 磁理论应用有限元分析软件进行求解,获得精确的结果,但是不能提供 简单的、指导性的和直观的物理概念。在开关电源中,为了用较小的磁 化电流产生足够大的磁通(或磁通密度),或在较小的体积中存储较多的 能量,经常采用一定形状规格的软磁材料磁芯作为磁通的通路。因磁芯 的磁导率比周围空气或其他非磁性物质磁导率大得多,把磁场限制在结 构磁系统之内,即磁结构内磁场很强,外面很弱,磁通的绝大部分经过 磁芯而形成一个固定的通路。在这种情况下,工程上常常忽略次要因 素,只考虑导磁体内磁场或同时考虑较强的外部磁场,使得分析计算简 化。通常引入磁路的概念,就可以将复杂的场的分析简化为我们熟知的 路的计算。
况如图3.2(b)所示。
由图3.2(b)可见,Ucx的分布和Fx完全相同。由式(3.7)得到x点与基准的
磁位差
Ux =Fx-Ucx
(3.10)
也就是说,将图形Fx减去Ucx 图形,就得到Ux 分布情况。显然, Ux处处
为零(式(3.8)~(3.9)。即等截面均匀绕线的环形磁铁任意点间没有磁位
差,即等磁位。在环外不会有任何散磁通,磁力线局限于导磁体内。
当磁芯有气隙时,集中绕线将对称线圈放置在气隙正对面(图3.4(c)) 时,磁位分布图如图3.4(b)中虚线所示,在大部分磁通路径上,磁位 差很大,从图(c)看到,集中绕线比均匀分布绕线具有更大的散磁。如果 将集中对称线圈放置在气隙上,在绕线长度上磁势大部分降落在气隙 上,在线圈以外的磁芯上磁位差很小,散磁也很小,如图(b)中虚线所 示。
3.3.1 无气隙磁芯磁场 如果电路中两点之间有电位差,就可能在两点之间产生电流。同理,
在磁路中两点之间有磁位差,在两点之间就可能产生磁通。图3.2(a)所 示为一等截面环形磁芯,线圈均匀分布在磁芯上。这种磁路系统完全对 称,可以应用相似于电路中电位分析方法,作出磁位分布图。根据磁位 分布图,可以了解散磁场的分布,确定等效磁路。
根据式(3.1)和(3.3),因为磁场集中在线圈磁芯内,各截面磁通相等,
故可将磁势和磁阻画成集中元件。图3.2(a)的等效磁路如图3.2(c)所
示。
(B) 集中绕线的等截面环形磁芯
将图3.3(a)中磁芯线圈集中绕在一边。如果线圈长度为lw,取其线圈中
点为参考点。应用相似的方法,得到磁势Fx分布图(图3.3(b))。在x方向lw
/2至l- lw /2段,没有增加匝链磁势,故为一水平线。如果有散磁存在,
磁芯各截面的磁通密度和Hx不再是常数,Ucx 也就不能用式(3.9)来计
算。如果散磁通的比例很小,假设Hx为常数,可以作出Ucx 分布图如图
3.3 (b)。由上述两个图相减,就得到磁位差Ux 分布图。由图可见,除对
称轴(x=0和l/2) 外,磁路中Ux都不等于零,因此有散磁通分布于圆环周
式中Hc和H分别为磁芯和气隙的磁场强度。虽然气隙不大,因空气磁导 率比磁芯磁导率低得多,所以气隙磁场强度H比磁芯磁场强度Hc大得 多。因此,H占有总磁势的较大的比例。
仍然取线圈中心为参考。F,Hcl和H的分布图如图3.4(b)中实线所 示,磁芯的磁势图为线性增加。如仍假设Hc为常数,与没有气隙一样, Ux不等于零,因此,也有散磁通s,所不同的是对称面左右两侧的磁位 差比前者大,所以散磁通也大。
