正方形判定练习题及答案

合集下载

《正方形的判定》练习(有答案)

正方形的判定一、选择题（共21小题）1、下列五个命题：（1）若直角三角形的两条边长为5和12，则第三边长是13；（2）如果a≥0，那么=a（3）若点P（a，b）在第三象限，则点P（﹣a，﹣b+1）在第一象限；（4）对角线互相垂直且相等的四边形是正方形；（5）两边及第三边上的中线对应相等的两个三角形全等．其中不正确命题的个数是（）A、2个B、3个C、4个D、5个2、下列命题中，正确命题是（）A、两条对角线相等的四边形是平行四边形B、两条对角线相等的四边形是矩形C、两条对角线互相垂直平分的四边边是菱形D、两条对角线平分且相等的四边形是正方形3、下列命题中，真命题是（）A、两条对角线垂直的四边形是菱形B、对角线垂直且相等的四边形是正方形C、两条对角线相等的四边形是矩形D、两条对角线相等的平行四边形是矩形4、下列说法中错误的是（）A、两条对角线互相平分的四边形是平行四边形B、两条对角线相等的四边形是矩形C、两条对角线互相垂直的矩形是正方形D、两条对角线相等的菱形是正方形5、下列说法中，不正确的是（）A、有三个角是直角的四边形是矩形B、对角线相等的四边形是矩形C、对角线互相垂直的矩形是正方形D、对角线互相垂直的平行四边形是菱形6、如图，在等腰Rt△ABC中，∠C=90°，AC=8，F是AB边上的中点，点D，E分别在AC，BC边上运动，且保持AD=CE．连接DE，DF，EF．在此运动变化的过程中，下列结论：①△DFE是等腰直角三角形；②四边形CDFE不可能为正方形，③DE长度的最小值为4；④四边形CDFE的面积保持不变；⑤△CDE面积的最大值为8．其中正确的结论是（）A、①②③B、①④⑤C、①③④D、③④⑤7、如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（）A、当AB=BC时，它是菱形B、当AC⊥BD时，它是菱形C、当∠ABC=90°时，它是矩形D、当AC=BD时，它是正方形8、下列命题中正确的是（）A、两条对角线互相平分的四边形是平行四边形B、两条对角线相等的四边形是矩形C、两条对角线互相垂直的四边形是菱形D、两条对角线互相垂直且平分的四边形是正方形9、已知四边形ABCD中，∠A=∠B=∠C=90°，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是（）A、∠D=90°B、AB=CDC、AD=BCD、BC=CD10、如图，将一张长方形纸片对折两次，然后剪下一个角，打开．如果要剪出一个正方形，那么剪口线与折痕成（）A、22.5°角B、30°角C、45°角D、60°角11、在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的条件是（）A、AC=BD，AB∥CD，AB=CDB、AD∥BC，∠A=∠CC、AO=BO=CO=DO，AC⊥BDD、AO=CO，BO=DO，AB=BC12、用两个全等的直角三角形拼下列图形：（1）平行四边形（不包含菱形、矩形、正方形）；（2）矩形；（3）菱形；（4）正方形；（5）等腰三角形，一定可以拼成的图形是（）A、（1）（2）（5）B、（2）（3）（5）C、（1）（4）（5）D、（1）（2）（3）13、下列说法中，错误的是（）A、一组对边平行且相等的四边形是平行四边形B、两条对角线互相垂直且平分的四边形是菱形C、四个角都相等的四边形是矩形D、邻边相等的菱形是正方形14、下列说法中错误的是（）A、一组对边平行且一组对角相等的四边形是平行四边形B、每组邻边都相等的四边形是菱形C、四个角都相等的四边形是矩形D、对角线互相垂直平分的四边形是正方形15、四边形ABCD的对角线AC和BD相交于点O，设有下列条件：①AB=AD；②∠DAB=90°；③AO=CO，BO=DO；④矩形ABCD；⑤菱形ABCD，⑥正方形ABCD，则下列推理不成立的是（）A、①④⇒⑥B、①③⇒⑤C、①②⇒⑥D、②③⇒④16、在下列命题中，是真命题的是（）A、两条对角线相等的四边形是矩形B、两条对角线互相垂直的四边形是菱形C、两条对角线互相平分的四边形是平行四边形D、两条对角线互相垂直且相等的四边形是正方形17、下列说法中错误的是（）A、四个角相等的四边形是矩形B、对角线互相垂直的矩形是正方形C、对角线相等的菱形是正方形D、四条边相等的四边形是正方形18、下列说法正确的是（）A、对角线相等的四边形是矩形B、有一组邻边相等的矩形是正方形C、菱形的四条边、四个角都相等D、三角形一边上的中线等于这边的一半19、下列说法错误的是（）A、平行四边形的内角和与外角和相等B、一组邻边相等的平行四边形是菱形C、对角线互相平分且相等的四边形是矩形D、四条边都相等的四边形是正方形20、矩形的四个内角平分线围成的四边形（）A、一定是正方形B、是矩形C、菱形D、只能是平行四边形21、下列命题正确的是（）A、一组对边平行，另一组对边相等的四边形是平行四边形B、对角线互相垂直的四边形是菱形C、对角线相等的四边形是矩形D、一组邻边相等的矩形是正方形二、填空题（共3小题）22、如图，在四边形ABCD中，AB=BC=CD=DA，对角线AC与BD相交于点O，若不增加任何字母与辅助线，要使四边形ABCD是正方形，则还需增加一个条件是_________．23、要使一个菱形ABCD成为正方形，则需增加的条件是_________．（填一个正确的条件即可）24、把“直角三角形，等腰三角形，等腰直角三角形”填入下列相应的空格上．（1）正方形可以由两个能够完全重合的_________拼合而成；（2）菱形可以由两个能够完全重合的_________拼合而成；（3）矩形可以由两个能够完全重合的_________拼合而成．三、解答题（共6小题）25、如图，点D是线段AB的中点，点C是线段AB的垂直平分线上的任意一点，DE⊥AC于点E，DF⊥BC于点F．（1）求证：CE=CF；（2）点C运动到什么位置时，四边形CEDF成为正方形？请说明理由．26、已知：如图，D是△ABC的BC边上的中点，DE⊥AC，DF⊥AB，垂足分别是E、F，且BF=CE．（1）求证：△ABC是等腰三角形；（2）当∠A=90°时，试判断四边形AFDE是怎样的四边形，证明你的结论．27、如图，已知平行四边形ABCD中，对角线AC，BD交于点O，E是BD延长线上的点，且△ACE是等边三角形．（1）求证：四边形ABCD是菱形；（2）若∠AED=2∠EAD，求证：四边形ABCD是正方形．28、已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC 外角∠CAM的平分线，CE⊥AN，垂足为点E，（1）求证：四边形ADCE为矩形；（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．29、如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F．（1）求证：△BED≌△CFD；（2）若∠A=90°，求证：四边形DFAE是正方形．30、如图，在Rt△ABC与Rt△ABD中，∠ABC=∠BAD=90°，AD=BC，AC，BD相交于点G，过点A作AE∥DB交CB的延长线于点E，过点B作BF∥CA 交DA的延长线于点F，AE，BF相交于点H．（1）图中有若干对三角形是全等的，请你任选一对进行证明；（不添加任何辅助线）（2）证明：四边形AHBG是菱形；（3）若使四边形AHBG是正方形，还需在Rt△ABC的边长之间再添加一个什么条件？请你写出这个条件．（不必证明）答案与评分标准一、选择题（共21小题）1、下列五个命题：（1）若直角三角形的两条边长为5和12，则第三边长是13；（2）如果a≥0，那么=a（3）若点P（a，b）在第三象限，则点P（﹣a，﹣b+1）在第一象限；（4）对角线互相垂直且相等的四边形是正方形；（5）两边及第三边上的中线对应相等的两个三角形全等．其中不正确命题的个数是（）A、2个B、3个C、4个D、5个考点：勾股定理；二次根式的性质与化简；点的坐标；全等三角形的判定；正方形的判定．分析：（1）由于直角三角形的两条边长为5和12，这两条边没有确定谁是斜边谁是直角边，大的一条还可能是斜边，所以第三边长不唯一；（2）正确，符合二次根式的意义；（3）由于点P（a，b）在第三象限，由此得到a、b的取值范围，然后利用它们的取值范围即可得到结果；正确（4）对角线互相垂直平分且相等的四边形是正方形，所以对角线互相垂直且相等的四边形不一定是正方形；（5）可以利用全等三角形的判定定理证明是否正确．解答：解：（1）由于直角三角形的两条边长为5和12，这两条边没有确定是否是直角边，所以第三边长不唯一，故命题错误；（2）符合二次根式的意义，命题正确；（3）∵点P（a，b）在第三象限，∴a＜0、b＜0，∴﹣a＞0，﹣b+1＞0，∴点P （﹣a，﹣b+1）在第一象限，故命题正确；（4）正方形是对角线互相垂直平分且相等的四边形，故命题错误；（5）两边及第三边上的中线对应相等的两个三角形全等是正确的．故选B．点评：需注意没有明确告知两条边都是直角边，故大的一条还可能是斜边．对角线互相垂直平分且相等的四边形是正方形．2、下列命题中，正确命题是（）A、两条对角线相等的四边形是平行四边形B、两条对角线相等的四边形是矩形C、两条对角线互相垂直平分的四边边是菱形D、两条对角线平分且相等的四边形是正方形考点：菱形的判定；平行四边形的判定；矩形的判定；正方形的判定．分析：根据特殊平行四边形的性质进行判断，对角线平分的四边形是平行四边形；对角线平分且相等的四边形是矩形；对角线平分且垂直的四边形是菱形；对角线平分、垂直且相等的四边形是正方形．解答：解：A、两条对角线互相平分的四边形是平行四边形，故A错误；B、两条对角线平分且相等的四边形是矩形，故B错误；C、两条对角线互相垂直平分的四边边是菱形，故C正确；D、两条对角线平分、垂直且相等的四边形是正方形，故D错误；故选C．点评：考查特殊平行四边形对角线的性质，一定要熟记．3、下列命题中，真命题是（）A、两条对角线垂直的四边形是菱形B、对角线垂直且相等的四边形是正方形C、两条对角线相等的四边形是矩形D、两条对角线相等的平行四边形是矩形考点：菱形的判定；矩形的判定；正方形的判定．分析：本题要求熟练掌握平行四边形、菱形、矩形、正方形的性质以及之间的相互联系．解答：解：A、两条对角线垂直并且相互平分的四边形是菱形，故选项A错误；B、对角线垂直且相等的平行四边形是正方形，故选项B错误；C、两条对角线相等的平行四边形是矩形，故选项C错误；D、根据矩形的判定定理，两条对角线相等的平行四边形是矩形，为真命题，故选项D正确；故选D．点评：本题考查的是普通概念，熟练掌握基础的东西是深入研究的必要准备．4、下列说法中错误的是（）A、两条对角线互相平分的四边形是平行四边形B、两条对角线相等的四边形是矩形C、两条对角线互相垂直的矩形是正方形D、两条对角线相等的菱形是正方形考点：矩形的判定；平行四边形的判定；正方形的判定．分析：根据矩形的对角线相等平分和正方形的对角线互相垂直相等平分进行判定即可得出结论．解答：解：根据矩形的判定可知：A，C，D均是正确的，B中，等腰梯形也满足此条件，但不是矩形，故选B．点评：平行四边形的判定方法共有五种，在四边形中如果有：①四边形的两组对边分别平行；②一组对边平行且相等；③两组对边分别相等；④对角线互相平分；⑤两组对角分别相等．则四边形是平行四边形．5、下列说法中，不正确的是（）A、有三个角是直角的四边形是矩形B、对角线相等的四边形是矩形C、对角线互相垂直的矩形是正方形D、对角线互相垂直的平行四边形是菱形考点：矩形的判定；菱形的判定；正方形的判定．分析：根据各四边形的性质对各个选项进行分析从而得出最后答案．解答：解：A、正确，有三个角是直角的四边形是矩形是矩形的判定定理；B、错误，对角线相等的四边形不一定是矩形，对角线相等的平行四边形才是矩形；C、正确，对角线互相垂直的矩形是正方形；D、正确，对角线互相垂直的平行四边形是菱形．故选B．点评：考查了对四边形性质与判定的综合运用，特殊四边形之间的相互关系是考查重点．6、如图，在等腰Rt△ABC中，∠C=90°，AC=8，F是AB边上的中点，点D，E分别在AC，BC边上运动，且保持AD=CE．连接DE，DF，EF．在此运动变化的过程中，下列结论：①△DFE是等腰直角三角形；②四边形CDFE不可能为正方形，③DE长度的最小值为4；④四边形CDFE的面积保持不变；⑤△CDE面积的最大值为8．其中正确的结论是（）A、①②③B、①④⑤C、①③④D、③④⑤考点：正方形的判定；全等三角形的判定与性质；等腰直角三角形．专题：动点型．分析：解此题的关键在于判断△DEF是否为等腰直角三角形，作常规辅助线连接CF，由SAS定理可证△CFE和△ADF全等，从而可证∠DFE=90°，DF=EF．所以△DEF是等腰直角三角形．可证①正确，②错误，再由割补法可知④是正确的；判断③，⑤比较麻烦，因为△DEF是等腰直角三角形DE=DF，当DF与BC 垂直，即DF最小时，DE取最小值4，故③错误，△CDE最大的面积等于四边形CDEF的面积减去△DEF的最小面积，由③可知⑤是正确的．故只有①④⑤正确．解答：解：连接CF；∵△ABC是等腰直角三角形，∴∠FCB=∠A=45°，CF=AF=FB；∵AD=CE，∴△ADF≌△CEF；∴EF=DF，∠CFE=∠AFD；∵∠AFD+∠CFD=90°，∴∠CFE+∠CFD=∠EFD=90°，∴△EDF是等腰直角三角形．因此①正确．当D、E分别为AC、BC中点时，四边形CDFE是正方形．因此②错误．∵△ADF≌△CEF，∴S△CEF=S△ADF∴S四边形CEFD=S△AFC，因此④正确．由于△DEF是等腰直角三角形，因此当DE最小时，DF也最小；即当DF⊥AC时，DE最小，此时DF=BC=4．∴DE=DF=4；因此③错误．当△CEF面积最大时，由④知，此时△DEF的面积最小．此时S△CEF=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=16﹣8=8；因此⑤正确．故选B．点评：本题考查知识点较多，综合性强，能力要求全面，难度较大．但作为选择题可采用排除法等特有方法，使此题难度稍稍降低一些．7、如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（）A、当AB=BC时，它是菱形B、当AC⊥BD时，它是菱形C、当∠ABC=90°时，它是矩形D、当AC=BD时，它是正方形考点：正方形的判定；平行四边形的性质；菱形的判定；矩形的判定．分析：根据已知及各个四边形的判定对各个选项进行分析从而得到最后答案．解答：解：A：正确，一组邻边相等的平行四边形是菱形；B：正确，对角线互相垂直的平行四边形是菱形；C：正确，有一个角为90°的平行四边形是矩形；D：不正确，对角线相等的平行四边形是矩形而不是正方形；故选D．点评：此题考查了菱形，矩形，正方形的判定方法．对角线互相垂直平分且相等的四边形是正方形．8、下列命题中正确的是（）A、两条对角线互相平分的四边形是平行四边形B、两条对角线相等的四边形是矩形C、两条对角线互相垂直的四边形是菱形D、两条对角线互相垂直且平分的四边形是正方形考点：正方形的判定；平行四边形的判定；菱形的判定；矩形的判定．分析：根据平行四边形、矩形、菱形、正方形的判定，逐个进行验证，即可得出正确选项．解答：解：A、两条对角线互相平分的四边形是平行四边形，正确．B、两条对角线相等的四边形可能是梯形，不一定是矩形，错误．C、两条对角线互相垂直平分的四边形是菱形，仅垂直不一定是菱形，错误．D、两条对角线互相垂直且平分的四边形只能说是菱形，不一定是正方形，错误．故选A．点评：本题是考查平行四边形、矩形、菱形、正方形的判定．就每一个选项来说都是单一知识点，是比较基础的知识，而把四个选项置于一个试题之中，它涉及到四个知识点和四种图形的联系和区别，要求学生的思维必须缜密、全面．9、已知四边形ABCD中，∠A=∠B=∠C=90°，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是（）A、∠D=90°B、AB=CDC、AD=BCD、BC=CD考点：正方形的判定．分析：由已知可得该四边形为矩形，再添加条件：一组邻边相等，即可判定为正方形．解答：解：由∠A=∠B=∠C=90°可判定为矩形，因此再添加条件：一组邻边相等，即可判定为正方形，故选D．点评：本题是考查正方形的判别方法．判别一个四边形为正方形主要根据正方形的概念，途经有两种：①先说明它是矩形，再说明有一组邻边相等是菱形；②先说明它是菱形，再说明它有一个角为直角，是矩形．10、如图，将一张长方形纸片对折两次，然后剪下一个角，打开．如果要剪出一个正方形，那么剪口线与折痕成（）A、22.5°角B、30°角C、45°角D、60°角考点：正方形的判定；翻折变换（折叠问题）．专题：计算题；操作型．分析：根据翻折变换的性质及正方形的判定进行分析从而得到最后答案．解答：解：一张长方形纸片对折两次后，剪下一个角，是菱形，而出现的四边形的两条对角线分别是两组对角的平分线，所以当剪口线与折痕成45°角，菱形就变成了正方形．故选C．点评：本题考查了菱形和正方形的判定及性质．11、在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的条件是（）A、AC=BD，AB∥CD，AB=CDB、AD∥BC，∠A=∠CC、AO=BO=CO=DO，AC⊥BDD、AO=CO，BO=DO，AB=BC考点：正方形的判定．专题：证明题．分析：根据正方形的判定：对角线互相垂直平分且相等的四边形是正方形进行分析从而得到最后的答案．解答：解：A，不能，只能判定为矩形；B，不能，只能判定为平行四边形；C，能；D，不能，只能判定为菱形．故选C．点评：本题是考查正方形的判别方法，判别一个四边形为正方形主要根据正方形的概念，途经有两种：①先说明它是矩形，再说明有一组邻边相等；②先说明它是菱形，再说明它有一个角为直角．12、用两个全等的直角三角形拼下列图形：（1）平行四边形（不包含菱形、矩形、正方形）；（2）矩形；（3）菱形；（4）正方形；（5）等腰三角形，一定可以拼成的图形是（）A、（1）（2）（5）B、（2）（3）（5）C、（1）（4）（5）D、（1）（2）（3）考点：正方形的判定．专题：证明题．分析：两个全等的直角三角形直角边重合拼成的四边形一定是平行四边形；直角边重合拼成的三角形一定是等腰三角形；斜边重合拼成的四边形一定是长方形．拿两个全等的三角板动手试一试就能解决．解答：解：拿两个“90°、60°、30°的三角板一试可得：（1）平行四边形（不包含菱形、矩形、正方形）；（2）矩形；（5）等腰三角形．而菱形、正方形需特殊的直角三角形：等腰直角三角形．故选A．点评：本题考查学生的动手能力，有些题只要学生动手就能很快求解，注意题目的要求有“一定”二字．13、下列说法中，错误的是（）A、一组对边平行且相等的四边形是平行四边形B、两条对角线互相垂直且平分的四边形是菱形C、四个角都相等的四边形是矩形D、邻边相等的菱形是正方形考点：正方形的判定；平行四边形的判定；菱形的判定；矩形的判定．专题：证明题．分析：根据对角线互相垂直平分且相等的四边形是正方形，对各个选项进行分析从而得到最后的答案．解答：解：A正确，符合平行四边形的判定定理；B正确，两条对角线互相平分的四边形是平行四边形，对角线互相垂直的平行四边形是菱形；C正确，四个角都相等的四边形的内角和为360°，那么每个内角为90°，是矩形；D不正确，菱形的邻边本来就是相等的，等于没加条件．故选D．点评：本题考查特殊平行四边形的判定，需熟练掌握各特殊平行四边形的特点．14、下列说法中错误的是（）A、一组对边平行且一组对角相等的四边形是平行四边形B、每组邻边都相等的四边形是菱形C、四个角都相等的四边形是矩形D、对角线互相垂直平分的四边形是正方形考点：正方形的判定；平行四边形的判定；菱形的判定；矩形的判定．专题：证明题．分析：根据特殊平行四边形的判定对各个选项进行分析，从而得到最后答案．解答：解：A正确，一组对边平行且一组对角相等可推出两组对角分别相等，是平行四边形；B正确，每组邻边都相等实际是四条边都相等所以为菱形；C正确，四个角都相等，四个角的内角和为360°，可得到每个内角为90°所以为矩形；D不正确，应该是菱形，因为正方形的对角线相等且互相垂直平分；点评：本题考查特殊平行四边形的判定，需熟练掌握各特殊平行四边形的特点．15、四边形ABCD的对角线AC和BD相交于点O，设有下列条件：①AB=AD；②∠DAB=90°；③AO=CO，BO=DO；④矩形ABCD；⑤菱形ABCD，⑥正方形ABCD，则下列推理不成立的是（）A、①④⇒⑥B、①③⇒⑤C、①②⇒⑥D、②③⇒④考点：正方形的判定；菱形的判定；矩形的判定．专题：证明题．分析：由对角线互相平分的四边形为平行四边形，再由邻边相等，得出是菱形，和一个角为直角得出是正方形，根据已知对各个选项进行分析从而得到最后的答案．解答：解：A、符合邻边相等的矩形是正方形；B、可先由对角线互相平分，判断为平行四边形，再由邻边相等，得出是菱形；D、可先由对角线互相平分，判断为平行四边形，再由一个角为直角得出是矩形；故选C．点评：此题主要考查正方形、菱形、矩形的判定，应灵活掌握．16、在下列命题中，是真命题的是（）A、两条对角线相等的四边形是矩形B、两条对角线互相垂直的四边形是菱形C、两条对角线互相平分的四边形是平行四边形D、两条对角线互相垂直且相等的四边形是正方形考点：正方形的判定；平行四边形的判定；菱形的判定；矩形的判定．分析：本题要求熟练掌握平行四边形、菱形、矩形、正方形的基本判定性质．解答：解：A、两条对角线相等的平行四边形是矩形，故选项A错误；B、两条对角线互相垂直的平行四边形是菱形，故选项B错误；C、根据平行四边形的判定定理可知两条平行线相互平分的四边形是平行四边形，为真命题，故选项C是正确的；D、两条对角线互相垂直且相等的平行四边形是正方形，故选项D错误；点评：基本的定义、概念以及一些性质是做题的根本条件，熟练地运用可以为解答更深奥的题目奠定基础．17、下列说法中错误的是（）A、四个角相等的四边形是矩形B、对角线互相垂直的矩形是正方形C、对角线相等的菱形是正方形D、四条边相等的四边形是正方形考点：正方形的判定；矩形的判定．专题：证明题．分析：根据正方形和矩形的判定对各个选项进行分析从而得到最后答案．解答：解：A正确，符合矩形的定义；B正确，符合正方形的判定；C正确，符合正方形的判定；D不正确，也可能是菱形；故选D．点评：此题主要考查学生对矩形的判定及正方形的判定的理解．18、下列说法正确的是（）A、对角线相等的四边形是矩形B、有一组邻边相等的矩形是正方形C、菱形的四条边、四个角都相等D、三角形一边上的中线等于这边的一半考点：正方形的判定；菱形的性质；矩形的判定．专题：证明题．分析：根据对角线互相平分且相等的四边形是矩形和有一组邻边相等的矩形是正方形对各个选项进行分析从而确定最后答案．解答：解：A不正确，因为对角线互相平分且相等的四边形是矩形；B正确，符合正方形的判定；C不正确，菱形的四条边、对角都相等；D不正确，直角三角形斜边上的中线等于这边的一半；故选B．点评：此题综合考查矩形、正方形、菱形的判定以及直角三角形的性质的理解及运用．19、下列说法错误的是（）A、平行四边形的内角和与外角和相等B、一组邻边相等的平行四边形是菱形C、对角线互相平分且相等的四边形是矩形D、四条边都相等的四边形是正方形考点：正方形的判定；平行四边形的性质；菱形的判定；矩形的判定．专题：证明题．分析：根据四条边都相等的四边形一定是菱形，对角线互相平分且相等的四边形是矩形，对各个结论进行分析，从而得到最后答案．解答：解：A正确，平行四边形的内角和与外角和都是360°；B正确，符合菱形的定义；C正确，符合矩形的判定；D不正确，四条边都相等的四边形一定是菱形，不一定是正方形；故选D．点评：掌握特殊四边形的定义与判定．20、矩形的四个内角平分线围成的四边形（）A、一定是正方形B、是矩形C、菱形D、只能是平行四边形考点：正方形的判定；矩形的性质．专题：证明题．分析：根据矩形的性质及角平分线的性质进行分析即可．解答：解：矩形的四个角平分线将矩形的四个角分成8个45°的角，因此形成的四边形每个角是90°．又知两条角平分线与矩形的一边构成等腰直角三角形，所以这个四边形邻边相等，根据有一组邻边相等的矩形是正方形，得到该四边形是正方形，故选A．点评：本题是考查正方形的判别方法，判别一个四边形为正方形主要根据正方形的概念，途经有两种：①先说明它是矩形，再说明有一组邻边相等；②先说明它是菱形，再说明它有一个角为直角．21、下列命题正确的是（）A、一组对边平行，另一组对边相等的四边形是平行四边形B、对角线互相垂直的四边形是菱形。

正方形练习与答案

选择题1．下列四个命题：（1）两条对角线互相垂直的四边形是菱形；（2）两条对角线相等的四边形是矩形；（3）四条边、四个角分别相等的四边形是正方形；（4）两条对角线分别平分一组对角的四边形是正方形. 其中命题正确的是（）A ．1个B ．2个C ．3个D ．4个 2．（无锡市，2001；福州市，2002）下列命题中，正确的是（）A ．对角线相等的四边形是矩形B ．对角线互相平分的四边形是平行四边形C ．对角线互相垂直的四边形是菱形D ．对角线互相垂直且相等的四边形是正方形3．在正方形ABCD 的边BC 的延长线上取一点E ，使AC CE =，连AE 与CD 交于F ，则=∠AFC （）A ．︒5.112B ．︒120C ．︒135D ．︒150 4．（湖州市，2001）正方形的对角线与边长之比为（）A ．1:1B ．1:2C ．2:1D ．1:25．（北京市石景山区，2001）如图，在正方形ABCD 中，点E 是BC 边的中点，如果5=DE ，那么四边形ABED 的面积是（）A ．5B ．15C ．20D ．30参考答案：1．A 2．B 3．A 4．B 5．B选择题1．（北京市东城区，2002）下列说法中错误的是（）A ．一组对边平行且一组对角相等的四边形是平行四边形B ．每组邻边都相等的四边形是菱形C ．四个角相等的四边形是矩形D ．对角线互相垂直的平行四边形是正方形 2．（荆州市，2002）如图，过矩形ABCD 的四个顶点作对角线AC ，BD 的平行线，分别相交于E ，F ，G ，H 四点，则四边形EFGH 是（）A ．平行四边形B ．矩形C ．菱形D ．正方形3．（济南市，2002）如图（1），用一块边长为22的正方形ABCD 厚纸板，按下面作法，做了一套七巧板：作对角线AC ，分别取AB ，BC 中点E ，F ，连结EF ；作EF DG ⊥于G ，交AC 于H ；过G 作BC GH //，交AC 于L ，再由E 作DG EK //，交AC 于K ；将正方形ABCD 沿画出的线剪开. 现用它拼出一座桥（如图（2）），这座桥的阴影部分的面积是（）A ．8B ．6C ．4D ．5 4．（北京市宣武区，2001）在正方形ABCD 中，E 、F 两点分别是BC ，CD 边上的点，若AEF ∆是边长为2的等边三角形，则正方形ABCD 的边长为（）A ．213+ B ．213- C ．3 D ．2 5．（泰州市，2001）已知：如图，正方形ABCD 中，O 是对角线AC ，BD 的交点，过O 点作OF OE ⊥分别交AB ，BC 于E ，F . 若3,4==CF AE ，则EF 等于（）A ．7B ．5C ．4D ．36．（TI 杯全国初中数学竞赛，2001）如图，若将正方形分成k 个全等的矩形，其中上，下各横排两个，中间竖排若干个，则k 的值为（）A ．6B ．8C ．10D ．12参考答案：1．D 2．C 3．C 4．A 5．B 6．B填空题1．（眉山市，2001）如图，已知四边形ABCD 是菱形，当满足条件______时，它成为正方形. （填上你认为正确的一个条件即可）2．已知ABCD ，对角线AC ，BD 交于O . （1）若BC AB =，则ABCD 是_______；（2）若BD AC =，则ABCD 是_______；（3）若︒=∠90BCD ，则ABCD 是_______；（4）若OB OA =，且OB OA ⊥，则ABCD 是_______；（5）若BC AB =，且BD AC =，则ABCD 是_______.3．如图，四边形ABCD 是边长为2的正方形，P 是ABCD 的边CD 上任意一点，且DB PE ⊥于E ，CA PF ⊥于F ，则=+PF PE ______.4．（济南市，2001）如图，是一块在电脑屏幕上出现的矩形色块图，由6个颜色不同的正方形组成. 设中间最小的一个正方形边长为1，则这个矩形色块图的面积为_______.5．（河南省，2002）如图，P 是正方形ABCD 内一点，将ABP ∆绕点B 顺时针方向旋转能与P CB '∆重合，若3=BP ，则P P '_______.参考答案：1．︒=∠90A 2．（1）菱形，矩形，矩形，正方形，正方形 3．2 4．143 5．23解答题1．如图，在正方形ABCD 外以CD 为边作等边CDE ∆. 求AED ∠的度数.2．如图，ABC Rt ∆，︒=∠90C ，A ∠，B ∠的平分线交于点D ，BC DE ⊥于E ，AC DF ⊥于F .求证：四边形CEDF 是正方形.3．如图，正方形ABCD 的边长为cm 4，E 是AD 的中点，EC BM ⊥，垂足为M . 求BM 的长.4．（北京市朝阳区，2002）已知：如图，在正方形ABCD 中，E 是CD 延长线上一点，BC EB 21=，如果F 是AB 的中点，请你在正方形ABCD 上找一点，与F 点连成线段，并证明它和AE 相等.5．已知：如图，正方形CEFG 的边CG 在正方形ABCD 的边CD 上，延长CD 到H ，使CE DH =. K 在BC 边上，且CE DH =.求证：四边形AKFH 是正方形.6．（杭州市，1997）如图，过正方形ABCD 顶点A 作直线交BD 于E ，交CD 于F ，交BC 的延长线于G ，若H 是FG 的中点，求证：CH EC ⊥.参考答案： 1．︒152．作AB DG ⊥于G ，先证四边形CEDF 为矩形，再证DE DF =，则矩形CEDF 是正方形.3．连BE . 821==∆ABCD EBC S S 正方形. 52=EC 821=⋅⋅BM EC .558=BM 4．CF . 证CBF ABE ∆≅∆.5．证ABK HGF KEF ADH ∆≅∆≅∆≅∆. ∴AK HF KF AH ===. 则四边形AKFH 是菱形. 证︒=∠90HAK ，则菱形AKFH 是正方形.6．证明：在AED ∆和CED ∆中，∵ ︒=∠=∠==45,,CDE ADE DE DE CD AD ， ∴CED AED ∆≅∆ ∴ ECD EAD ∠=∠ 在FCG Rt ∆中，H 为斜边FG 的中点，∴FH GH CH == ∴ HGC HCG ∠=∠ 而 EAD HGC ∠=∠， ∴ECD HCG ∠=∠ ∴︒=∠+∠90FCH ECD ∴CH EC ⊥解答题用两种方法解答下列各题：1．如图，已知正方形ABCD 的边长为cm 12，点P 在BC 上，cm BP 5=，AP EF ⊥，垂足Q ，与AB ，CD 分别交于E ，F .求EF 的长.2．如图，正方形ABCD 中，E 在AD 上，F 在CD 上，︒=∠45EBF . 求证：FC AE EF +=.3. 已知：如图，正方形ABCD 中，P 为BC 一点，Q 为CD 边上一点，且DQ BP PQ +=. 求PAQ ∠.参考答案1．cm EF 13=2．延长DC 到G ，使AE CG =，连BG 或延长DA 到K ，使FC AK =，连BK 3. 解法1 延长PB 到E ，使DQ BE =，连结AE .在ABE ∆与ADQ ∆中，∵ DQ BE =，ADQ ABE ∠=∠，AD AB =， ∴ADQ ABE ∆≅∆. ∴QAD EAB AD AE ∠=∠=,. ∵ DQ BP PQ DQ BP BE BP PE +=+=+=,, ∴ PQ PE =在APE ∆与APE ∆中，AQ AE PQ PE AP AP ===,,， ∴APQ APE ∆≅∆. ∴ PAQ PAE ∠=∠∵ EAB QAD PAB QAD PAQ ∠=∠︒=∠+∠+∠,90， ∴︒=∠+∠90PAE PAQ . ∴︒=︒⨯=∠459021PAQ解法2 延长CD 到G ，使BP DG =，连AG （如图）在ADG ∆与ABP ∆中，∵︒=∠=∠=90,B ADG AB AD ，BP DG =， ∴ABP ADG ∆≅∆. ∴BAP DAG AP AG ∠=∠=,. ∵DG BP DQ DG GQ DQ BP PQ ++=+=,,，∴GQ PQ = 在APQ ∆与AGQ ∆中，∵GQ PQ AQ AQ AG AP ===,,， ∴AGQ APQ ∆≅∆. ∴ GAQ PAQ ∠=∠.∵︒=∠+∠+∠90DAQ PAQ BAP ， ∴ ︒=∠+∠+∠90DAQ PAQ GAD∴︒=∠+∠90GAQ PAQ ∴︒=∠=∠45GAQ PAQ解答题1．（宁夏，2002）如图，已知四边形ABCD 是正方形，对角线AC 、BD 相交于O ，四边形AEFC 是菱形，AC EH ⊥，垂足为H .求证：FC EH 21=.2．（山东荷泽地区，2001）如图，正方形ABCD 中，M 、F 分别在边AB 、AD 上且FD MB =，E 是AB 延长线上一点，DM MN ⊥交CBE ∠的平分线于N .求证：MBN DFM ∆≅∆.3．如图，正方形ABCD 的对角线相交于O ，Q 是DC 上的任意一点，过D 作AQ DP ⊥，交AQ 于H ，交BC 于P .求证：OPQ ∆是等腰直角三角形.4．如图，在正方形ABCD 中，E 是AD 的中点，BD 与CE 相交于点F . 求证：BE AF ⊥.5．如图，四边形ABCD ，CEFG 都是正方形，DE 交BG 的延长线于H . 求证：（1）DE BG =；（2）DE BH ⊥.6．如图，点M ，N 分别在正方形ABCD 的边BC ，CD 上，MCN ∆的周长等于正方形ABCD 的周长的一半，求MAN ∠.7．如图，E 是正方形ABCD 边DC 之中点，F 是CD 上一点，且CB FC FA +=. 求证：BAF DAE ∠=∠21.8．如图，E ，F 分别为正方形ABCD 的边AB ，BC 上的点，AC EF //，G 在DA 的延长线上，且AD AG =，GE 的延长线交DF 于H .求证：DA HA =.9．如图，四边形ACDE ，BAFG 是以ABC ∆的边AC ，AB 为边向ABC ∆外所作的正方形.求证：（1）FC EB =；（2）FC EB ⊥.10．如图，正方形ABCD 中，E 是CF 上的点，四边形BEFD 为菱形，求BEF ∠的度数.11．已知正方形ABCD 中，M 是AB 的中点，E 是AB 延长线上一点，DM MN ⊥且交CBE ∠的平分线于N （如图甲）.（1）求证：MN DM =；（2）若将上述条件中的“M 是AB 中点”改为“M 是AB 上任意一点”，其余条件不变（如图乙），则结论“MN MD =”还成立吗？如果成立，请证明；如果不成立，请说明理由.12．如图，过正方形顶点C 作BD CG //，在CG 上取一点F ，使BD BF =，且交CD 于E ，连结DF .求证：DF DE =.参考答案：1．AC OB EH 21== 2．证NMB ADM ∠=∠，MBN DFM ∠=∠ 3．证ADQ DCP ∆≅∆，得DQ CP =，从而可证DOQ COP ∆≅∆，得OQ OP =，DOQ COP ∠=∠，从而可证︒=∠+∠90COP COQ . 则OPQ ∆是等腰直角三角形.4．证CDF ADF ∆≅∆，得DCF DAF ∠=∠. 证DCE ABE ∆≅∆，得DCF ABE ∠=∠. ∴ABE DAF ∠=∠，从而可证︒=∠+∠90AEB DAF ，则BE AF ⊥5．证DCE BCG ∆≅∆，得DE BG =，CBG CDE ∠=∠，则DGH CDE ∠+∠CGB CBG ∠+∠=︒=906．延长ND 到E ，使BM DE =，连结AE ，则AEN AMN ∆≅∆. ∴MAN EAN ∠=∠. ∵︒=∠+∠90MAN EAN ，∴︒=∠45MAN7．作BAF ∠的平分线AN 交BC 于N ，交DC 的延长线于M ，证AB CM FM FA ==,，则有MCN ABN ∆≅∆，得CN BN =.则ADE MCN ABN ∆≅∆≅∆. DAE M BAN ∠=∠=∠. ∴BAF DAE ∠=∠21. 8．证︒=∠90GHD9．证ABE AFC ∆≅∆10．︒150. 提示：作BD CM ⊥于M ，BD EN ⊥于N ，则EN CM BD BE 22===，得︒=∠30EBD ，︒=∠150BEF11．（1）取AD 中点F ，连MF ，证MBN DFM ∆≅∆；（2）结论MN DM =仍成立. 在AD 上取AM AF =，连FM ，证MBN DFM ∆≅∆12．证明：连AC ，设AC 与BD 交点为O . 作BD FH ⊥于H .∵四边形ABCD 是正方形， ∴BD OC BD AC 21,=⊥. ∵BD CO BD FH BD CG ⊥⊥,,//，∴OC FH =.∵BD BF =，∴BF FH 21=. ∴ ︒=∠301 ∴ ︒=︒-︒=∠75230180DFB ∵ ︒=︒+︒=∠+∠=∠75453012BDC ，∴2∠=∠DFB .∴DF DE =.解答题1．如图，已知P ，Q ，R ，S 为动点，分别从正方形ABCD 的顶点A ，B ，C ，D 同时沿着AB ，BC ，CD ，DA 以同样的速度向点B ，C ，D ，A 移动.（1）求证：PQRS 总是正方形；（2）求证：PR总是过正方形的中心；AB=，求四边形PQRS的面积最大时和最小时顶点的位置.（3）设a2．如图，一个画有五个边长为1的正方形纸片，要把它剪成三块，拼成一个正方形ABCD，请你在原图上画出剪裁线和拼成正方形ABCD.3．如图，有四个动点P、Q、E、F分别从正方形ABCD的四个顶点出发，沿着AB、BC、CD、DA以同样的速度向B、C、D、A各点移动.（1）证明：四边形PQEF是哪种特殊的平行四边形；（2）PE是否总是经过某一定点，并说明理由；（3）四边形PQEF的顶点位于何处时，其面积最小、最大？各是多少？4．（杭州市，2002）在平面上有且只有四个点，这四个点有一个独特的性质：每两点之间的距离有且只有两种长度. 例如正方形ABCD（如图），有≠=AB==. 请画出只有这种独特性质的另外四种不同的图形，并=BCBCDAACCD标明相等的线段.5．（山东省，2000）今有正方形土地一块，要在其上修筑两条笔直的道路，使道路把这块土地分成形状相同且面积相等的四部分. 若道路的宽度可忽略不计，请你设计三种不同的修饰方案（在给出的三张正方形图纸上分别画图，并简述画图步骤）.6．（北京市崇文区，2001）为增加绿地面积，现将停车场铺设的整数块正方形实体地砖（尺寸如图(1)，单位：cm ）更换为通透性地砖. 通透性地砖是在原地砖的四边挖去四个全等的等腰梯形，梯形的上底与腰长相等（尺寸如图（2），单位：（cm ），图（3）为拼接图（阴影部分种草）. 设原铺设实体地砖总面积为x （单位：2m ），增加绿地总面积为y （单位：2m ），求y 与x 的关系式（不要求写出x 的取值范围）.7．（南京市，2001）（1）如图，在正方形ABCD 中，E 是AD 的中点，F 是BA 延长线上的一点，AB AF 21=.求证：ADF ABE ∆≅∆.（2）阅读下面材料：如图（1），把ABC ∆沿直线BC 平行移动线段BC 的长度，可以变到DBC ∆的位置；如图（2），以BC 为轴把ABC ∆翻折︒180，可以变到DBC ∆的位置；如图（3），以点A 为中心，把ABC ∆旋转︒180，可以变到AED ∆的位置.像这样，其中一个三角形是由另一个三角形平行移动、翻折、旋转等方法变成的. 这种只改变位置，不改变形状大小的图形变换，叫做三角形的全等变换.（3）回答下列问题：① 在下图中，可以通过平行移动、翻折、旋转中的哪一种方法，使ABE ∆变到ADF ∆的位置？②指出下图中线段BE 与DF 之间的关系.8．（黄冈市，2000）国家电力总公司为了改善农村用电电缆过高的现状，目前正在全国各地农村进行电网改造. 莲花村六组有四个村庄A 、B 、C 、D 正好位于一个正方形的四个顶点，现计划在四个村庄联合架设一条线路，他们设计了四种架设方案，如下图中的实践部分. 请你帮助计算一下，哪种架设方案最省电线. （以下数据可供参考：414.12=，732.13=，236.25=）9．（山东省淄博市，2002）工人师傅要将一块如图所示的铝板，经过适当的剪切后，焊接成一块正方形铝板，请在下图中画出剪切线，并将剪切后的铝板拼成一个面积最大的正方形（保留拼接痕迹，不写画法）.【参考答案】1．（1）证SDR RCQ QBP PAS ∆≅∆≅∆≅∆；（2）连AC ，PR ，设AC 和PR 交于O ，可证RCO PAO ∆≅∆. ∴OR PO OC AO ==,. ∵O 为正方形ABCD 的中心，∴PR 总过正方形的中心；（3）︒=∠90B ，在PBQ Rt ∆中，222BQ PB PQ +=22PA PB +=)22(2122PA PB +=)22(2122PA PB +=])()[(2122PA PB PA PB -++=])([2122PA PB AB -+= ∴正方形PQRS 的面积])([2122PA PB AB -+=)]([2122PA PB a -+=. 当PA BP =时，即P ，Q ，R ，S 为正方形ABCD 各边中点时，最小面积等于221a . 当P ，Q ，R ，S 位于点A ，B ，C ，D 时，最大面积为2a2．如图所示；3．（1）证DEF CQE BPQ AFP ∆≅∆≅∆≅∆可得四边形PQEF 为正方形；（2）连结AC 交PE 于O ，证O 为AC 的中点，得PE 一定过AC 的中点；（3）OP 最小即AB OP ⊥时，正方形面积最小，为正方形面积的一半，OP 最大，即等于正方形的面积.4．图形如下：其中：①AD BC DC DB AC AB ≠====；②CD BD BC AD AC AB ====,；③OC OB OA CA BC AB ====,；④CD BC AD BD AC AB ====,；⑤BC OC OB OA AC AB ====,.5．略6．设每块地砖增加绿色面积为1S ，每块实体地砖面积为2S ，则2143243cm S =，22262525cm S ==. x y 25003243=. 7．（1）证ADF ABE ∆≅∆；（3）①ABE ∆绕点A 逆时针旋转︒90到ADF ∆的位置；②DF BE =，且DF BE ⊥.8．不妨设正方形的边长为1（也可设为a ）. 在图（1）、（2）中，总线路长分别为3=++BC AB AD ，3=++CD BC AB . 在图（3）中，总线路长为282.22211222==+=+BD AC . 在图（4）中，延长线EF 交BC 于点H ，是BC FH ⊥，HC BH =. 由︒=∠30FBH ，21=BH 及股定理得33====FC FB ED EA ，63=FH . ∴ 33121-=-=FH EF . 此时，总线路长为EF EA +4331334-+=31+=732.2=.显然732.2828.23>>，∴ 图（4）的联结线路最短，架设方案最省电线.9．略。

正方形性质与判定填空题练习(含答案)(1)

正方形性质与判定填空题练习1、如图，正方形ABCD边长为1，连接AC，AE平分∠CAD，交BC的延长线于点E，FA⊥AE，交CE于点F，则EF的长为．2、如图，正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG，EF与AD相交于点H，延长DA交GF于点K．若正方形ABCD边长为，则HD的长为．3、如图，已知正方形ABCD的边长为4，对角线AC与BD相交于点O，点E在DC边的延长线上．若∠CAE=15°，则AE= ．4、如图．将正方形纸片ABCD折叠，使边AB、CB均落在对角线BD上，得折痕BE、BF，则∠EBF的大小为．5、如图，将正方形ABCD沿BE对折，使点A落在对角线BD上的A′处，连接A′C，则∠BA′C= 度．6、如图，四边形ABCD是正方形，延长AB到E，使AE=AC，则∠BCE的度数是度．7、如图，已知正方形ABCD，以AB为边向外作等边三角形ABE，CE与DB相交于点F，则∠AFD的度数．8、如图，在正方形ABCD的外侧，作等边△ADE，则∠BED的度数是．9、如图，已知正方形ABCD中，CM=CD，MN⊥AC，连接CN，则∠MNC= ．10、如图，已知P是正方形ABCD对角线BD上的一点，且BP=BC，则∠ACP的度数是_________.11、如图所示，直线a经过正方形ABCD的顶点A，分别过此正方形的顶点B、D作BF⊥a于点F、DE ⊥a于点E，若DE=4，BF=3，则EF的长为____________.12、如图，E是正方形ABCD的BC边的延长线上一点，若CE=CA，AE交CD于F，则∠FAC= ．13、如图，有一块矩形纸片ABCD，AB=8，AD=6，将纸片折叠，使得AD边落在AB边上，折痕为AE，再将△AED沿DE向右翻折，AE与BC的交点为F，则△CEF的面积为__________.14、如图所示，正方形ABCD的周长为8cm，顺次连结正方形ABCD各边的中点，得到正方形EFGH，则EFGH的周长等于_____cm，面积等于______cm2．15、如图，在正方形ABCD中，AC为对角线，点E在AB边上，EF⊥AC于点F，连接EC，AF=3，△EFC 的周长为12，则EC的长为．16、如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，CE=5，F为DE的中点．若OF的长为 3.5，则△CEF的周长为．17、如图，已知正方形ABCD的边长为1，点E在边DC上，AE平分∠DAC，EF⊥AC，点F为垂足，那么FC= ．18、如图，已知正方形ABCD的边长为4，点E、F分别在边AB，BC上，且AE=BF=1，则OC= ．19、将边长为2的正方形OABC如图放置，O为原点.若，则点B的坐标为.20、如图，正方形ABCD与正三角形AEF的顶点A重合，将△AEF绕顶点A旋转，在旋转过程中，当BE=DF时，∠BAE的大小可以是．21、如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E．若∠CBF=20°，则∠AED等于度．22、如图，点E在正方形ABCD的边CD上．若△ABE的面积为8，CE=3，则线段BE的长为．23、如图，边长为6的正方形ABCD和边长为8的正方形BEFG排放在一起，O1和O2分别是两个正方形的对称中心，则△O1BO2的面积为．24、如图，点E在正方形ABCD的边CD上．若△ABE的面积为8，CE=3，则线段BE的长为．25、如图，在边长为4的正方形ABCD中，E是AB边上的一点，且AE=3，点Q为对角线AC上的动点，则△BEQ周长的最小值为．26、如图，正方形ABCD中，CD=5，BE=CF，且DG2+GE2=28，则AE的长．27、如图，已知正方形ABCD，点E在边DC上，DE=4，EC=2，则AE的长为．28、如图，正方形ABCD的边长为3cm，E为CD边上一点，∠DAE=30°，M为AE的中点，过点M作直线分别与AD、BC相交于点P、Q，若PQ=AE，则AP等于___________cm.29、如图，正方形ABCD中，对角线BD长为15cm．P是线段AB上任意一点，则点P到AC，BD的距离之和等于cm．31、如图，ABCD是一张边长为4cm的正方形纸片，E，F分别为AB，CD的中点，沿过点D的折痕将A 角翻折，使得点A落在EF上的点A′处，折痕交AE于点G，则EG=______cm．32、如图，已知正方形ABCD边长为3，点E在AB边上且BE=1，点P，Q分别是边BC，CD的动点（均不与顶点重合），当四边形AEPQ的周长取最小值时，四边形AEPQ的面积是．33、如图，Rt△ABC中，∠C=90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC=5，OC=6，则另一直角边BC的长为．34、如图，设四边形ABCD是边长为1的正方形，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去.则第2015个正方形的边长 .35、如图所示，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP、BH.现给出以下四个命题（1）∠APB=∠BPH;（2）当点P在边AD上移动时，△PDH的周长不发生变化;（3）∠PBH=450 ; （4）BP=BH.其中正确的命题是．36、如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E、F分别在BC和CD上，下列结论：①CE=CF；②∠AEB=75°；③BE+DF=EF；④S正方形ABCD=2+．其中正确的序号是（把你认为正确的都填上）．37、已知，如图，∠MON=45°，OA1=1，作正方形A1B1C1A2，周长记作C1；再作第二个正方形A2B2C2A3，周长记作C2；继续作第三个正方形A3B3C3A4，周长记作C3；点A1、A2、A3、A4…在射线ON上，点B1、B2、B3、B4…在射线OM上，…依此类推，则第n个正方形的周长C n= ．38、如图，正方形ABCD中，点E、F分别是BC、CD边上的点，且∠EAF=45°，对角线BD交AE于点M，交AF于点N．若AB=4，BM=2，则MN的长为．39、如图，P为正方形ABCD内一点，PA=1，PB=2，PC=3，则∠APB= ．参考答案1、答案为：2．2、答案为：﹣1．3、答案为：8．4、答案为：45°．5、答案为：67.5．6、答案为：22.5．7、答案为：60°．8、答案为：45°．9、答案为：67.5°．10、答案为：22.5 ；11、答案为：712、答案为：22.5°13、答案为：2；14、答案为：；215、答案为：5．16、答案为：1817、答案为：；18、答案是： 2.4．19、答案为：20、答案为：15°或165°．21、答案为：6522、答案为：5．23、答案是：12．24、答案为：5；25、答案为： 626、答案为：．27、答案为．28、答案为：1或2；29、答案为：7.5．31、答案为：4﹣6．32、答案为： 4.5．33、答案为：7；【解答】解法一：如图1所示，过O作OF⊥BC，过A作AM⊥OF，∵四边形ABDE为正方形，∴∠AOB=90°，OA=OB，∴∠AOM+∠BOF=90°，又∠AMO=90°，∴∠AOM+∠OAM=90°，∴∠BOF=∠OAM，在△AOM和△BOF中，，∴△AOM≌△BOF（AAS），∴AM=OF，OM=FB，又∠ACB=∠AMF=∠CFM=90°，∴四边形ACFM为矩形，∴AM=CF，AC=MF=5，∴OF=CF，∴△OCF为等腰直角三角形，∵OC=6，∴根据勾股定理得：CF2+OF2=OC2，解得：CF=OF=6，∴FB=OM=OF﹣FM=6﹣5=1，则BC=CF+BF=6+1=7．故答案为：7．解法二：如图2所示，过点O作OM⊥CA，交CA的延长线于点M；过点O作ON⊥BC于点N．易证△OMA≌△ONB，∴OM=ON，MA=NB．∴O点在∠ACB的平分线上，∴△OCM为等腰直角三角形．∵OC=6，∴CM=ON=6．∴MA=CM﹣AC=6﹣5=1，∴BC=CN+NB=6+1=7．故答案为：7．34、答案为：2．35、答案为：（1）（2）（3）．36、答案为：①②④解：∵四边形ABCD是正方形，∴AB=AD，∵△AEF是等边三角形，∴AE=AF，在Rt△ABE和Rt△ADF中，，∴Rt△ABE≌Rt△ADF（HL），∴BE=DF，∵BC=DC，∴BC﹣BE=CD﹣DF，∴CE=CF，∴①说法正确；∵CE=CF，∴△ECF是等腰直角三角形，∴∠CEF=45°，∵∠AEF=60°，∴∠AEB=75°，∴②说法正确；如图，连接AC，交EF于G点，∴AC⊥EF，且AC平分EF，∵∠CAF≠∠DAF，∴DF≠FG，∴BE+DF≠EF，∴③说法错误；∵EF=2，∴CE=CF=，设正方形的边长为a，在Rt△ADF中，AD2+DF2=AF2，即a2+（a﹣）2=4，解得a=，则a2=2+，S正方形ABCD=2+，④说法正确，故答案为：①②④．37、答案为：2n+1．38、；解：如图，延长BC到G，使BG=DF连接AG，在AG截取AH=AN，连接MH、BH．，∠4=∠5=45°，∠BAD=∠ADF=∠ABE=∠ABG=90°，∵四边形ABCD为正方形，∴AB=BC=CD=AD在RT△ABG和RT△ADF中，，∴Rt△ABG≌Rt△ADF（SAS），∴∠1=∠2，∠7=∠G，AF=AG，∴∠GAE=∠2+∠3=∠1+∠3=∠BAD﹣∠EAF=90°﹣45°=45°=∠EAF，在△AMN和△AMH中，，∴△AMN≌△AMH（SAS），∴MN=MH，∵AF=AG，AN=AH，∴FN=AF﹣AN=AG﹣AH=GH，在△DFN和△BFH中，，∴△DFN≌△BGH（SAS），∴∠6=∠4=45°，DN=BH，∴∠MBH=∠ABH+∠5=∠ANG﹣∠6+∠5=90°﹣45°+45°=90°∴BM2+DN2=BM2+BH2=MH2=MN2，∵BD=AB=8，∴22+（8﹣2﹣MN）2=MN2，∴MN=．39、135°．解：将△APB绕B点顺时针旋转90°并连接PE，∵将△APB绕B点顺时针旋转90°，得△BEC，∴△BEC≌△BPA，∠APB=∠BEC，∴△BEP为等腰直角三角形，∴∠BEP=45°，∵PB=2，∴PE=2，∵PC=3，CE=PA=1，∴PC2=PE2+CE2，∴∠PEC=90°，∴∠APB=∠BEC=∠BEP+∠PEC=45°+90°=135°．。

2017年八年级数学下《正方形性质与判定》课后练习及答案

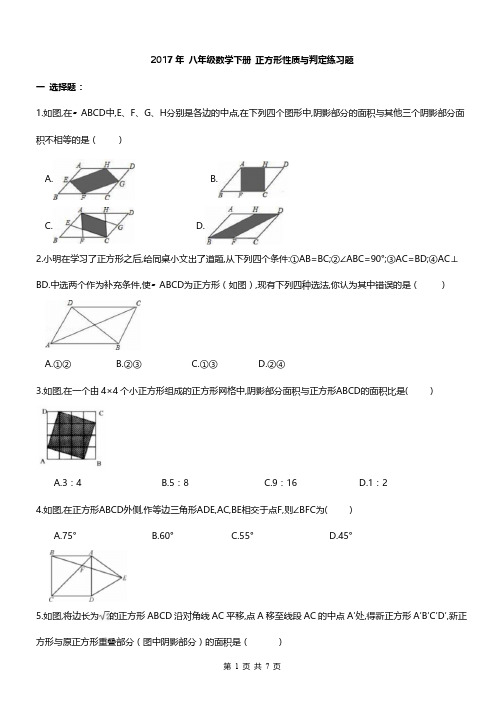
A.①②
B.②③
C.①③
D.②④
3.如图,在一个由 4×4 个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是(
)
A.3：4
B.5：8
C.9：16
D.1：2
4.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A.75°
B.60°
C.55°
D.45°
16.已知正方形 ABCD 中，点 E 在边 DC 上，DE＝2，EC＝1（如图所示），把线段 AE 绕点 A 旋转，使点 E 落
在直线 BC 上的点 F 处，则 F、C 两点的距离为
．
17.如图,在Rt△ABC中,∠ACB＝90°,以AC为边正方形面积为 12,中线CD长度为 2,则BC长度为
．
18.如图,点E在正方形ABCD的边CD上.若△ABE的面积为 8,CE=3,则线段BE的长为
．
19.如图,在边长为 4 的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为 Nhomakorabea．
20.如图,已知正方形ABCD边长为 3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点（均不与顶点重合），当四边形AEPQ的周长取最小值时，四边形AEPQ的面积是______．
5.如图,将边长为的正方形 ABCD 沿对角线 AC 平移,点 A 移至线段 AC 的中点 A′处,得新正方形 A′B′C′D′,新正
方形与原正方形重叠部分（图中阴影部分）的面积是（
）
第1页共7页
A.
B.
C.1
D.
6.如图,将正方形OABC放在平面直角坐标系中,O是原点,若点A的坐标为(1, ),则点C坐标为( )

1.3 正方形的性质与判定同步练习(课课练)附答案

1.3正方形的性质与判定1、四边形ABCD中，AC、BD相交于点O，能判别这个四边形是正方形的条件是（）A. OA＝OB＝OC＝OD，AC⊥BDB. AB∥CD，AC＝BDC. AD∥BC，∠A＝∠CD. OA＝OC，OB＝OD，AB＝BC2、在正方形ABCD中，AB＝12cm，对角线AC、BD相交于O，则△ABO的周长是（）A. 12+122B. 12+62C. 12+2D. 24+623、如图，四边形ABCD是正方形，延长BC至点E，使CE＝CA，连结AE交CD•于点F，•则∠AFC的度数是（）．（A）150°（B）125°（C）135°（D）112．5°4、已知正方形的面积为4，则正方形的边长为________，对角线长为________．5、如左下图，四边形ABCD是正方形，△CDE是等边三角形，则∠AED＝______，∠AEB＝______．6、如右上图，四边形ABCD是正方形，△CDE是等边三角形，求∠AEB的度数.7、已知：如左下图，在正方形ABCD中，AE⊥BF，垂足为P，AE与CD交于点E，•BF与AD交于点F，求证：AE＝BF．8、如图，正方形ABCD，AB＝a，M为AB的中点，ED＝3AE，（1）求ME的长；（2）△EMC是直角三角形吗？为什么？9、如左下图，在正方形ABCD中，E、F、G、H分别在它的四条边上，且AE=BF=CG=DH.四边形EFGH是什么特殊的四边形，你是如何判断的？10、如右上图所示，E 是正方形ABCD 的对角线BD 上一点，EF ⊥BC ，EG ⊥CD ，垂足分别是F 、G ．试说明AE ＝FG ．11、以锐角△ABC 的边AC 、AB 为边向外作正方形ACDE 和正方形ABGF ，连结BE 、CF.（1）试探索BE 和CF 的关系？并说明理由。

（2）你能找到哪两个图形可以通过旋转而相互得到，并指出旋转中心和旋转角。

正方形性质及判定练习题

正方形性质及判定练习题正方形是一种特殊的四边形，具有一些独特的性质。

在本文档中，我们将介绍关于正方形的性质以及如何判定一个形状是否为正方形的练题。

1. 正方形的定义- 正方形是一个四边形，具有四条相等的边和四个相等的角。

- 每个角都是直角，即90度。

2. 正方形的性质- 边长：正方形的四条边长度相等。

- 角度：正方形的每个角都是直角，即90度。

- 对角线：正方形的对角线相等且垂直相交于中点。

3. 正方形的判定练题1. 练题1：给出一个形状的四条边长A、B、C、D，如何确定它是否为正方形？- 答案：如果A = B = C = D，并且角ABC和角BCD均为直角（90度），则该形状为正方形。

2. 练题2：给出一个形状的四个顶点坐标(Ax, Ay)，(Bx, By)，(Cx, Cy)，(Dx, Dy)，如何确定它是否为正方形？- 答案：计算四条边的长度AB、BC、CD、DA，并检查是否满足A = B = C = D的条件。

同时，计算角ABC、BCD、CDA、DAB是否均为90度。

3. 练题3：给出一个形状的四个顶点坐标(Ax, Ay)，(Bx, By)，(Cx, Cy)，(Dx, Dy)，如何确定它是否为正方形？如果无法使用角度判定，请给出其他方法。

- 答案：计算四条边的长度AB、BC、CD、DA，并检查是否满足A = B = C = D的条件。

同时，计算AB和CD的斜率，如果斜率为相反数且BC和DA的斜率为相反数，那么该形状为正方形。

通过掌握正方形的定义、性质以及判定练题，我们能够更好地理解和识别正方形。

练题的完成也有助于加深对正方形性质的掌握。

希望这份文档对您有所帮助！。

初二正方形性质及判定练习题

初二正方形性质及判定练习题
形状与性质
正方形是一种特殊的四边形，具有以下性质：
1. 四条边相等：正方形的四条边的长度相等。

2. 四个角相等：正方形的四个角的大小都是90度。

3. 对角线相等：正方形的对角线长度相等。

4. 正方形是菱形：正方形的对角线相互垂直，且长度相等，因此也是菱形的一种特殊情况。

判定练题
以下是一些判定练题，帮助你巩固对正方形性质的理解：
1. 判断下列图形是否为正方形：
A. ![正方形A](image-link)
B. ![正方形B](image-link)
C. ![图形C](image-link)
D. ![图形D](image-link)
答案：A是正方形，B是正方形，C不是正方形，D不是正方形。

2. 若两个正方形的边长分别为4cm和6cm，哪个正方形的面积更大？
答案：边长为6cm的正方形面积更大，因为面积与边长的平方成正比。

3. 若一个正方形的对角线长度为10cm，求其边长。

答案：根据正方形的性质，对角线长度等于边长乘以√2，所以边长等于10cm除以√2，约为7.07cm。

4. 若一个四边形的边长均为5cm，四个角的大小均为90度，是否一定是正方形？
答案：不一定，虽然满足了长宽相等和角度为90度的条件，但没有保证对角线相等，因此不一定是正方形。

5. 若一个四边形的对角线相等，四个角的大小均为90度，是否一定是正方形？
答案：是的，根据这些条件可以确定该四边形是正方形，因为这些是正方形的定义性质。

以上是关于初二正方形性质及判定练习题的内容。

希望能够帮助你更好地理解和应用正方形的性质。

八年级数学正方形的判定和性质(人教版)(基础)(含答案)

正方形的判定和性质（人教版）（基础）一、单选题(共9道，每道11分)1.如果要证明四边形ABCD为正方形，我们需要在四边形ABCD是平行四边形的基础上，进一步证明( )A.AC与BD互相垂直平分B.∠A=∠B且AC=BDC.AB=AD且AC=BDD.AB=AD且AC⊥BD答案：C解题思路：A：对角线互相垂直的平行四边形是菱形，故A不能；B：一组邻角相等的平行四边形是矩形，对角线相等的平行四边形也是矩形，故B不能；C：对角线相等的平行四边形是矩形，一组邻边相等的矩形为正方形，故C可以；D：一组邻边相等的平行四边形为菱形，对角线互相垂直的平行四边形也是菱形，故D不能。

故选C试题难度：三颗星知识点：略2.四边形ABCD的对角线相交于点O，能判定四边形是正方形的条件是( )A.AC=BD，AB=CD，AB∥CDB.AO=BO=CO=DO，AC⊥BDC.AD∥BC，∠A=∠CD.AO=CO，BO=DO，AB=BC答案：B解题思路：先画草图，再依图分析；A：若AB=CD，AB∥CD，可判断是平行四边形，再由AC=BD，可判断是矩形，则A错；B：若AO=BO=CO=DO，可判断是矩形，再由AC⊥BD，可判断是正方形，则B对；C：若AD//BC，∠A=∠C，可判断是平行四边形，则C错；D：若AO=CO，BO=DO，可判断是平行四边形，再由AB=BC，可判断是菱形，则D错．故选B．试题难度：三颗星知识点：略3.学习了正方形之后，王老师提出问题：要判断一个四边形是正方形，有哪些思路？甲同学说：先判定四边形是菱形，再确定这个菱形有一个角是直角；乙同学说：先判定四边形是矩形，再确定这个矩形有一组邻边相等；丙同学说：判定四边形的对角线相等，并且互相垂直平分；丁同学说：先判定四边形是平行四边形，再确定这个平行四边形有一个角是直角并且有一组邻边相等．上述四名同学的说法中，正确的是( )A.甲、乙B.甲、丙C.乙、丙、丁D.甲、乙、丙、丁答案：D解题思路：甲：根据判定定理有一个角是直角的菱形是正方形，可判断甲正确；乙：根据判定定理有一组邻边相等的矩形是正方形，可判断乙正确；丙：由对角线互相垂直平分判定为菱形，再加上对角线相等可判定为矩形，综合可得四边形为正方形，故丙正确；丁：有一个角是直角的平行四边形是矩形，再加上有一组邻边相等可判断为正方形，故丁正确。

九年级数学正方形的判定(基础)(含答案)

正方形的判定（基础）一、单选题(共10道，每道10分)1.下列说法，错误的是( )A.所有的平行四边形都是中心对称图形B.矩形是轴对称图形C.菱形不是轴对称图形D.正方形既是轴对称图形也是中心对称图形答案：C解题思路：所有平行四边形均为中心对称图形，对称中心为对角线的交点；矩形是轴对称图形，对称轴为过中心且与边垂直的直线；菱形是轴对称图形，对称轴为对角线所在直线；综上，A，B，D正确，C错误．试题难度：三颗星知识点：略2.平行四边形、矩形、菱形、正方形都具有的是( )A.对角线互相平分B.对角线互相垂直C.对角线相等D.每一条对角线平分一组对角答案：A解题思路：所有平行四边形均满足对角线互相平分；矩形对角线相等但不垂直，不平分一组对角；菱形对角线相互垂直但不相等，平分一组对角；正方形对角线相等，互相垂直，且平分一组对角．综上，A正确．试题难度：三颗星知识点：略3.正方形的一条对角线长为4，则这个正方形的面积是( )A.8B.C. D.16答案：A解题思路：正方形的一条对角线长为4，则边长为，面积为8试题难度：三颗星知识点：略4.如图，四边形ABCD是正方形，延长AB到点E，使AE=AC，连接CE，则∠BCE的度数是( )A.22.5°B.25°C.30°D.无法确定答案：A解题思路：如图，∵四边形ABCD是正方形，AE=AC∴∠CAB=∠ACB=45°，∠ACE=(180°-45°)=67.5°∴∠BCE=∠ACE-∠ACB=22.5°试题难度：三颗星知识点：略5.如图，在正方形ABCD的外侧，作等边△ABE，则∠BED的的度数为( )A.15°B.35°C.45°D.55°答案：C解题思路：∵四边形ABCD为正方形，△ABE为等边三角形∴AD=AB，∠DAB=90°，AE=AB，∠EAB=∠AEB=60°∴△ADE为等腰三角形，且∠EAD=150°∴∠AED=15°∴∠BED=∠AEB-∠AED=60°-15°=45°试题难度：三颗星知识点：略6.如图，点E是正方形ABCD的边DC上一点，把△ADE绕点A顺时针旋转90°到△ABF的位置，若四边形AECF的面积为25，DE=2，则AE的长为( )A.5B.C.7D.答案：D解题思路：由旋转性质，则△ADE≌△ABF∴S四AECF=S△ABF+S四ABCE=S△ADE+S四ABCE=S正ABCD=25∴AD=5∴Rt△ADE中，∠D=90°，AD=5，DE=2，由勾股定理得AE=试题难度：三颗星知识点：略7.如图，E，F是正方形ABCD的对角线AC上的两点，AC=8，AE=CF=2，则四边形BEDF的周长是( )A. B.5C. D.20答案：C解题思路：如图，连接BD交AC于点O．∵四边形ABCD为正方形，AE=CF∴AO=OC，BO=OD，BD⊥AC∴AO-AE=CO-OF，即EO=OF∴四边形BEDF为菱形∵AC=8，CF=2∴OC=OD=4，OF=OC-FC=2Rt△DOF中，∠DOF=90°，OF=2，OD=4，由勾股定理得DF=故菱形BEDF的周长为4DF=试题难度：三颗星知识点：略8.如图，在正方形ABCD中，点E是BC上的一点，点F是CD延长线上的一点，且BE=DF，连接AE，AF，EF．若AE=5，则EF的长为( )A. B.C.10D.无法确定答案：A解题思路：∵四边形ABCD为正方形，BE=DF∴AB=AD，∠B=∠ADC=∠ADF=90°∴△ABE≌△ADF∴AE=AF，∠BAE=∠DAF∴∠EAF=∠DAF+∠DAE=∠BAE+∠DAE=∠BAD=90°∴△EAF为等腰直角三角形且AE=5∴EF=AE=试题难度：三颗星知识点：略9.如图，正方形ABCD中，AB=6，G是BC的中点，将△ABG沿AG对折至△AFG，延长GF 交DC于点E，则DE的长是( )A.1B.C.2D.答案：C解题思路：如图，连接AE．∵四边形ABCD为正方形，△ABG沿AG对折至△AFG∴AF=AB=AD，∠AFG=∠B=∠D=90°∴∠AFE=∠D=90°∵AE=AE∴Rt△AFE≌Rt△ADE（HL）∵G是BC的中点，BC=6，若设DE=x则CG=3，FG=BG=3，EF=DE=x，CE=6-xRt△CGE中，由勾股定理CG2+CE2=EG2即32+(6-x)2=(3+x)2，解得x=2∴DE的长是2试题难度：三颗星知识点：略10.如图，正方形ABCD中，E是BC上的一点，连接AE，过B点作BH⊥AE，垂足为点H，延长BH交CD于点F，连接AF．若正方形边长是5，BE=2，则AF的长为( )A.4B.C. D.答案：B解题思路：∵四边形ABCD为正方形∴AB=BC，∠ABC=∠C=90°∵BH⊥AE∴∠BAE+∠BEA=90°，∠EBH+∠BEA=90°∴∠BAE=∠EBH∴△ABE≌△BCF（ASA）∴CF=BE∵BC=5，BE=2∴AD=5，DF=3则Rt△ADF中，利用勾股定理可得AF=试题难度：三颗星知识点：略。

6、正方形的判定和性质 - 答案

正方形的判定和性质探索活动1、思考：你能类比矩形、菱形的概念给正方形下个定义吗?正方形的概念：____________并且____________的_________是正方形。

2、探究：（1）比较平行四边形、矩形、菱形、正方形之间的关系（2）探索正方形的性质请大家思考正方形有哪些性质?正方形是一个特殊的平行四边形，正方形形具有平行四边形的所有性质；正方形还是特殊的矩形，也是特殊的菱形，所以正方形具有矩形、菱形的所有性质正方形的性质：从对称性看：正方形既是轴对称图形，又是中心对称图形从边看：正方形的四边相等，对边平行从角看：正方形4个角都是直角从对角线看：正方形的两条对角线相等且互相垂直平分；每一条对角线平分一组对角思考：正方形具有而一般矩形不具备的性质：正方形具有而一般菱形不具备的性质：探索正方形的判定方法：问题：有一个角是直角的是正方形；有一组邻边相等的是正方形；对角线相等的是正方形；对角线垂直的是正方形；对角线的四边形是正方形。

思路：（1）先说明这个平行四边形是，再说明这个矩形也是；（2）先说明这个平行四边形是，再说明这个菱形也是。

归纳总结例1.如图，四边形ABCD 和四边形CEFG 都是正方形，试探索BG 与DE 的关系.例2.在正方形ABCD 中，点E、F、G、H 分别在各边上，且AE=BF=CG=DH．四边形EFGH 是正方形吗?为什么?题型一：正方形的性质-求角度1．如图，正方形ABCD O，则AOB ∠的度数是（）A．30︒B．45︒C．60︒D．90︒【答案】D 【详解】解：∵四边形ABCD 是正方形，∴AC BD ⊥，∴90AOB ∠=︒，故选：D．2．如图，在正方形ABCD 中，E 为AD 上一点，连接BE ，BE 交对角线AC 于点F，连接DF ，若35ABE ∠=︒，则CFD ∠的度数为（）A．80°B．70°C．75°D．45°【答案】A 【详解】解：∵四边形ABCD 是正方形，∴,45BC CD BAC ACB ACD =∠=∠=∠=︒，∵35ABE ∠=︒，∴80BFC ABE BAC ∠=∠+∠=︒，在BCF △和DCF 中，BC CD ACB ACD CF CF =⎧⎪∠=∠⎨⎪=⎩，∴()SAS BCF DCF ≌△△，∴80CFD CFB ∠=∠=︒，故选：A．3．如图，在正方形ABCD 的外侧，作等边ADE V ，则AEB ∠=．【答案】15︒【详解】解：∵四边形ABCD 是正方形，∴AB AD =，90BAD ∠=︒，∵ADE 是等边三角形，，∴AD AE =，60DAE ∠=︒，∴AB AE =，150BAE ∠=︒，∴()1180150152AEB ∠=︒-︒=︒，故答案为：15︒．4．如图，正方形ABCD 中，E 在BC 延长线上，AE，BD 交于点F，连接FC，若32E ∠= ，那么BCF ∠的度数是．【答案】58°【详解】解：∵在正方形ABCD，AD=CD，∠ADF=∠CDF=45°，DF=DF，∴△ADF≌△CDF（SAS），∴∠DAF=∠DCF，又∵AD∥BC，∠E=32°，∴∠DAF=32°，∴∠DCF=32°，∴∠BCF=∠DCB－∠DCF=90°－32°=58°．故答案为：58°．5．如图，在正方形ABCD 中，M 是正方形内一点，且MC MD AD ==．求BAM ∠的度数．【答案】15︒【详解】解：在正方形ABCD 中，90ADC BAD ∠=∠=︒，AD DC =，MC MD AD ==，AD DC MD MC ∴===，在DMC 中，DM DC MC ==，则DMC 是等边三角形，60MDC ∴∠=︒，30MDA ∴∠=︒，在ADM △中，30ADM ∠=︒，MD AD =，则()118030752DAM ∠=︒-︒=︒；90907515BAM DAM ∴∠=︒-∠=︒-︒=︒．6．如图，BF 平行于正方形ADCD 的对角线AC，点E 在BF 上，且AE=AC，CF∥AE，求∠BCF.【答案】105°【详解】作AO⊥FB 的延长线,BQ⊥AC∵BF∥AC,∴AO∥BQ 且∠QAB＝∠QBA＝45°∴AO＝BQ＝AQ＝12AC ∵AE＝AC ∴AO＝12AE∴∠AEO＝30°∵BF∥AC∴∠CAE∠AEO＝30°∵BF∥AC,CF∥AE∴∠CFE∠CAE＝30°∵BF∥AC∴∠CBF∠BCA＝45°∠BCF＝180°－∠CBF－∠CFE＝180°－45°－30°＝105°题型二：正方形的性质-求长度1．正方形的一条对角线长为8，则正方形的边长为（）A．2B．4C．D．【答案】C【详解】解：设正方形的边长为a，∵正方形的一条对角线之长为8，a a+=，∴2228∴a=，故选C．2．如图，直线l过正方形ABCD的顶点B，点A、C到直线l的距离分别是1和3，则正方形的边长是．.【详解】试题分析：∵四边形ABCD是正方形，∴AB=CD，∠ABM+∠CBN=90°.∵AM⊥MN，CN⊥BN，∴∠BAM=∠CBN，∠AMB=∠CNB=90°.∴△AMB≌△BCN（AAS）.∴BM=CN.∵点A、C到直线L的距离分别是1和3，即AM=1，CN=3，∴BM=3.∴AB ==3．如图，在边长为ABCD 中，30∠=︒CDE ，DE CF ⊥则AF 的长为（）A．4-B．4C．4-D．4-【答案】D 【详解】解∶∵四边形ABCD 是正方形，∴90FBC DCE CD BC ∠=∠=︒==，Rt DCE V 中，30∠=︒CDE ，∴12CE DE =，设CE x =，则2DE x =，根据勾股定理得∶222DC CE DE +=，即(()2222x x +=，解得∶4x =±（负值舍去），∴4CE =，∵DE CF ⊥，∴90DOC ∠=︒，∴60DCO ∠=︒，∴906030BCF CDE ∠=︒-︒=︒=∠，∵DCE CBF CD BC ∠=∠=，，∴()ASA DCE CBF ≌，∴4BF CE ==，∴4AF AB BF =-=-．故选∶D．4．如图，边长为6的正方形ABCD 中，M 为对角线BD 上的一点，连接AM 并延长交CD 于点P.若PM PC =，则AM 的长为（）A．)31B．)32C．)61D．)62【答案】C【详解】∵边长为6的正方形ABCD ，∴,,90BA BC ABM CBM DAB ADC BCD =∠=∠∠=∠=∠=︒，∵BA BC ABM CBM BM BM =⎧⎪∠=∠⎨⎪=⎩，∴()SAS ABM CBM ≌，∴BAM BCM ∠=∠，∴9090BAM BCM ︒-∠=︒-∠，∴DAM DCM ∠=∠，∵PM PC =，∴PMC DCM ∠=∠，∴22APD PMC DCM DCM DAM ∠=∠+∠=∠=∠，∴390APD DAM DAM ∠+=∠=︒，∴30DAP ∠=︒，∴2AP DP =，∵222AP DP AD =+∴()22226DP DP =+，解得DP =∴262AP DP PM PC CD DP ====-=-∴)661AM AP PM =-==，故选C．5．如图，在正方形ABCD 中，将边BC 绕点B 逆时针旋转至BC '，连接CC '，DC '，若90CC D '∠=︒，5AB =，则线段C D '的长度为．【详解】解：过点B 作BE CC '⊥于点E ，四边形ABCD 是正方形，BC CD ∴=，90BCD ∠=︒，90BCE C CD '∴∠+∠=︒，90BCE CBE ∠+∠=︒ ，C CD CBE '∴∠=∠，又BEC CC D '∠=∠ ，在BCE 和'CDC △中，CBE C CD BEC CC D BC CD ∠=∠⎧⎪∠=∠='⎨'⎪⎩，()AAS BCE CDC '∴≌ ，CE C D '∴=，将边BC 绕点B 逆时针旋转至BC '，5BC BC CD '∴===，又BE CC '⊥ ，CE C E C D ''∴==，222C D C C CD ''+= ，2525C D '∴=，C D '∴=，6．如图，正方形ABCD 的对角线交于点O ，点E 是线段OD 上一点，连接EC ，若BF CE ⊥于点F ，BF 是DBC ∠的角平分线，6AB =，则OE 的长为．【答案】6-【详解】解：四边形ABCD 是正方形，6BC AB ∴==，90ABC ∠=︒，在Rt ABC △中，AC === 正方形ABCD 的对角线AC ，BD 交于点O，1122BO BD AC ∴===BF CE ⊥ 于点F ，90BFE BFC ∴∠=∠=︒，BF 是DBC ∠的角平分线，EBF CBF ∴∠=∠，在BFE △和BFC △中，90EBF CBF BF BF BFE BFC ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩，∴(ASA)BFE BFC ≌ ，6BE BC ∴==，6OE BE BO ∴=-=-故答案为：6-．题型三：正方形的性质-求周长和面积1．正方形一条对角线为2，则正方形的面积为．【答案】2【详解】解：正方形的一条对角线的长为2，∴这个正方形的面积21222=⨯=．故答案为：2．2．如图，边长为2的正方形ABCD 的对角线相交于点O，过点O 的直线分别交AD 、BC 于E、F，则阴影部分的面积是．【答案】1【详解】解：在正方形ABCD 中，AD BC ∥，OD OB =，∴ODE OBF ∠=∠，又DOE BOF ∠=∠，∴()ASA DEO BFO ≌△△，DEO BFO S S ∴=△△，阴影面积=BOC S 12112=⨯⨯=．故答案为：1．3．如图，正方形ABCD 中，AB=1，点P 是对角线AC 上的一点，分别以AP、PC 为对角线作正方形，则两个小正方形的周长的和是．【答案】4cm．【详解】解：设小正方形的边长为x，则较大的正方形的边长为1-x，故两个小正方形的周长和=4x+4（1-x）=4cm．4．如图，正方形ABCD 和正方形EFGO 的边长都是2，正方形EFGO 绕点O 旋转时，两个正方形重叠部分的面积是（）A．1B．2C．3D．4【答案】A 【详解】解：如图，设AB 与OE 交点N，BC 与OG 交点M，∵四边形ABCD 和四边形EFGO 都是正方形，∴,45,90OB OC OBA OCB BOC EOG =∠=∠=︒∠=∠=︒，∴BON MOC ∠=∠．在OBN △与OCM 中，OBN OCM OB OC BON COM ∠=∠⎧⎪=⎨⎪∠=∠⎩，()ASA OBN OCM ∴≌ ，OBN OCM S S ∴= ，1122144OBC ABCD OMBN S S S ∴===⨯⨯=正方形四边形．故选：A．5．正方形ABCD 的边长为2，将该正方形绕顶点A 在平面内旋转45︒，则旋转后的图形与原图形重叠部分的面积为（）A．4B．4-C．10-D．8-【答案】A 【详解】解：设C D ''交BC 于点M ，连AM ，四边形ABCD 是边长为2的正方形，2AD AB ∴==，90D B BAD ∠=∠=∠=︒，由旋转得AD AD '=，D D '∠=∠，45DAD '∠=︒，AD AB '∴=，90D B '∠=∠=︒，45BAD BAD DAD ''∠=∠-∠=︒，在Rt AD M '△和Rt ABM 中，AM AM AD AB=⎧⎨'=⎩，∴Rt Rt (HL)AD M ABM '△≌△，122.52MAD MAB BAD ''∴∠=∠=∠=︒，在AB 上截取BE BM =，连接EM ，则45BEM BME ∠=∠=︒，22.5EMA BEM MAB ∴∠=∠-∠=︒，EMA MAB ∴∠=∠，AE ME ∴=，∴2BE +=，2BM BE ∴==，1122)222AD M ABM S S AB BM '∴==⋅=⨯⨯=-△△，224AD M ABM S S S '∴=+=-+-=-△△阴影，故选：A．6．如图，已知正方形,ABCD G 为CD 边上一点（不与端点重合），以CG 为一边作正方形CGFE ，连接,,BD BF DF ，若4AB =，则BDF V 的面积为．【答案】8【详解】解：连接CF ，∵四边形ABCD 和四边形CGFE 是正方形，∴45DBC FCE ∠=∠=︒，∴BD CF ∥，∴1144822BDF BDC ABCD S S S ===⨯⨯= 正方形，故答案为：8．7．如图，边长为12的大正方形中有两个小正方形，若两个小正方形的面积分别为1S 、2S ，则12S S +的值为．【答案】68【详解】解：如图所示，连接BQ FH EG ，，，过点F 作FR AD ⊥于点R ，过点G 作GK CD ⊥于点K ，∵四边形ABCD ，四边形EFGH ，四边形BPQS 是正方形，AC 是对角线，BQ 是对角线，∴90SQP CSQ QPA ∠=∠=∠=︒，45BCA BAC CQS PQA SQB PQB SBQ PBQ ∠=∠=∠=∠=∠=∠=∠=∠=︒，∴,,,APQ QPB BQS CSQ △△△△是等腰直角三角形，且APQ QPB BQS CSQ ≌≌≌△△△△，同理，,,,,,,,,ARF ERF EOF EOH EDH HOG HKG GKC GOF △△△△△△△△△是等腰直角三角形，且ARF ERF EOF EOH EDH HOG HKG GKC GOF ≌≌≌≌≌≌≌≌△△△△△△△△△，∴149ADC S S =△，212ABC S S =△，12ADC ABC ABCD S S S +=正方形△△，∴124111121212123236689222S S +=⨯⨯⨯+⨯⨯⨯=+=，故答案为：68．题型四：正方形的性质运用1．菱形、矩形、正方形都具有的特点是（）A．对角线互相垂直B．对角线相等C．对角线互相平分D．对角线平分对角【答案】C【详解】解：A.矩形的对角线不一定互相垂直，故不符合题意；B.菱形的对角线不一定相等，故不符合题意；C.菱形、矩形、正方形的对角线互相平分，故符合题意；D.矩形的对角线不一定平分对角，故不符合题意；故选：C．2．下列性质中，平行四边形，矩形，菱形，正方形共有的性质是（）A．对角线相等B．对角线互相垂直C．对角线互相平分D．对角线平分内角【答案】C【详解】解：∵平行四边形的对角线互相平分，∴矩形，菱形，正方形的对角线也必然互相平分．故选：C．3．在学习了“中心对称图形——平行四边形”之后，平行四边形、矩形、菱形、正方形的关系可以用下面的关系图表示，则②处所填图形的名称应为．【答案】正方形【详解】解：由题意可知，④是平行四边形，①和③分别是矩形和菱形，②是正方形．故答案为：正方形．4．如图，以ABC 的边AB 、AC 为边分别向外作正方形ADEB 、ACGF ，连接DC 、BF 相交于M ，DC 、AB 相交于N ．(1)从旋转的角度看，ADC △是绕点逆时针旋转度，可以得到ABF △；(2)CD 与BF 有何关系，请说明理由．【答案】(1)A ，90(2)CD BF =，DC BF ⊥，理由见解析【详解】（1）解：由题意知，从旋转的角度看，ADC △是绕点A 逆时针旋转90度，可以得到ABF △；故答案为：A ，90；（2）解：CD BF =，CD BF ⊥，理由如下：∵四边形ADEB 、四边形ACGF 均为正方形，∴90AD AB AC AF DAB CAF ==∠=︒=∠，，，∴DAB BAC CAF BAC ∠+∠=∠+∠，即DAC BAF ∠=∠，∵AD AB DAC BAF AC AF =∠=∠=，，，∴()SAS DAC BAF ≌，∴CD BF =，CDA FBA ∠=∠，∵180CDA DAN DNA FBA BMN BNM ∠+∠+∠=︒=∠+∠+∠，DNA BNM ∠=∠，∴90BMN DAN ∠=∠=︒，∴DC BF ⊥．题型五：最值问题1．如图，四边形ABCD 为正方形，M ，N 分别是AB ，BC 边的中点，请在对角线AC 上找一点P ，使PM PN +的值最小（不写作法，保留作图痕迹）．【答案】见解析【详解】解：如图所示，点P 即为所求．连接BD 交AC 于O，连接NP 并延长交AD 于T，由正方形的对称性可知M T 、关于AC 对称，∴PM PT =，∴PM PN PT PN +=+，∴当P T M 、、三点共线时，PT PN +最小，即PM PN +最小，此时点P 与点O 重合．2．如图所示，正方形ABCD 的面积为9，ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P，使PD PE +的和最小，则这个最小值为（）A．4.5B．9C．2.5D．3【答案】D 【详解】解：设BE 与AC 交于点P'，连接BD ，DP '，∵点B 与D 关于AC 对称，∴''P D P B =，∴''''P D P E P B P E BE +=+=∵正方形ABCD 的面积为9，∴3AB =，又∵ABE 是等边三角形，∴3BE AB ==．故选：D3．正方形ABCD 中，点E 在AB 上，3AE =，1BE =，点P 在AC 上，EP BP +的最小值．【答案】5【详解】如图，连接BD 交AC 于点O ，连接ED 与AC 交于点P，连接PB ，∵四边形ABCD 是正方形，∴BD AC ⊥，且OB OD =，∴BP PD =，则BP EP ED +=，此时最短，∵3AE =，134AD =+=，∴根据勾股定理得22222234255ED AE AD =+=+==，∴5ED BP EP =+=，即BP EP +的最小值为：5，故答案为：5．4．如图，正方形ABCD 的边长为2，E 是CD 的中点，在对角线AC 上有一点P，则PD PE +的最小值是．【详解】连接BP ，BE ，因为正方形ABCD 关于对角线AC 对称，点B 与点D 是对称点，∴PB PD =，PD PE PB PE+=+当点P 在线段BE 上时，PD PE PB PE BE +=+=，为最小值．∵正方形ABCD 的边长为2，∴2BC CD ==，∵点E 是CD 的中点，∴112CE CD ==，∵在正方形ABCD 中，90BCD ∠=︒，∴在Rt BCE 中，BE ==∴PD PE +5．如图，在正方形ABCD 中，点E AB 上一点，且2AE =，4BE =，点P 是边AD 上的动点（P 与A ，D 不重合），则PE PC +的最小值是．【答案】10【详解】解：作点E 关于AD 的对称点E '，连接CE '交AD 于点P ，∴PE PE '=，AE AE '=，∴PE PC PE PC CE ''+=+≥，即PE PC +的最小值为CE '，∵四边形ABCD 是正方形，∴AB BC =，90CBA ∠=︒，∵2AE =，4BE =，∴4228BE BE AE AE ''=++=++=，642B E C AB BE A +=+===，在Rt BCE '△中，10CE '===，∴PE PC +的最小值是10．故答案为：10．题型六：正方形的判定定理1．如图，四边形ABCD 的对角线AC ，BD 交于点O，且OA OC =，OB OD =，下列说法错误的是（）A．若AC BD ⊥，则ABCD 是菱形B．若AC BD =，则ABCD 是矩形C．若AC BD ⊥且AC BD =，则ABCD 是正方形D．若90ABC ∠=︒，则ABCD 是正方形【答案】D【详解】解：∵OA OC =，OB OD =，∴四边形ABCD 是平行四边形，若AC BD ⊥，则四边形ABCD 是菱形，故A 选项不符合题意；若AC BD =，则四边形ABCD 是矩形，故B 选项不符合题意；若AC BD ⊥且AC BD =，则四边形ABCD 是正方形，故C 选项不符合题意；若90ABC ∠=︒，则四边形ABCD 是矩形，故D 选项符合题意；故选：D．2．如图所示，在ABC 中，在90ACB ∠=︒，CD 平分ACB ∠，DE AC ⊥于E，DF BC ⊥于F，求证：四边形CEDF 是正方形．【答案】∵CD 平分ACB ∠，,DE AC DF BC ⊥⊥，∴DE DF =，90DFC DEC ∠=∠=︒，又∵90ACB ∠=︒，∴四边形CEDF 是矩形，∵DE DF =，∴矩形CEDF 是正方形．3．矩形ABCD 四个内角平分线组成四边形MFNE ，求证：四边形MFNE 是正方形．【答案】四边形ABCD 是矩形，90BAD ADC BCD ABC ∴∠=∠=∠=∠=︒，AD BC =，AM ，DM ，CN ，BN 分别是四个内角平分线，45BAE EAD ADM CDM DCN BCN CBN ABN ∴∠=∠=∠=∠=∠=∠=∠=∠=︒，AE BE ∴=，90AEB N DFC AMD ∴∠=∠=∠=∠=︒，∴四边形MFNE 是矩形，在ADM △和BCN △中，MAD CBN AD BC ADM BCN ∠=∠⎧⎪=⎨⎪∠=∠⎩，()ASA ADM BCN ∴ ≌，AM BN ∴=，AM AE BN BE ∴-=-，EN EM ∴=，∴矩形MFNE 是正方形．4．如图，已知Rt△ABC 中，∠ACB＝90°，先把△ABC 绕点C 顺时针旋转90°至△EDC 后，再把△ABC 沿射线BC 平移至△GFE，DE、FG 相交于点H．(1)判断线段DE、FG 的位置关系，并说明理由；(2)连接AG，求证：四边形ACEG 【答案】(1)DE⊥FG，理由见解析(2)见解析【详解】（1）解：DE⊥FG，理由如下：∵把△ABC 绕点C 顺时针旋转90°至△EDC，∴∠BAC＝∠CED，∵把△ABC 沿射线BC 平移至△GFE，∴∠ABC＝∠GFE，∵∠BAC+∠ABC＝90°，∴∠CED+∠GFE＝90°，∴∠FHE＝90°，∴DE⊥GF；（2）解：∵把△ABC 沿射线BC 平移至△GFE，∴AC＝GE，AC∥GE，∴四边形ACEG 是平行四边形，∵把△ABC 绕点C 顺时针旋转90°至△EDC，∴AC＝CE，∠ACE＝90°，∴四边形ACEG 是正方形．5．如图：已知：AD 是ABC 的角平分线，DE AC ∥交AB 于E ，DF AB ∥交AC 于F ．(1)求证：四边形AEDF 是菱形；(2)当ABC 满足什么条件时，四边形AEDF 是正方形？【答案】(1)见解析(2)90BAC ∠=︒【详解】（1）解：证明：//DE AC ，//DF AB ，//DE AF ∴，//DF AE ，∴四边形AEDF 是平行四边形（有两组对边相互平行的四边形是平行四边形），EAF EDF ∴∠=∠（平行四边形的对角相等）；又AD 是ABC ∆的角平分线，∴∠EAD=∠FAD，∵DE∥AC，∴∠EDA=∠FAD，EAD EDA ∴∠=∠，AE DE ∴=（等角对等边），∴四边形AEDF 是菱形（邻边相等的平行四边形是菱形）；（2）解：由（1）知，四边形AEDF 是菱形，当四边形AEDF 是正方形时，90EAF ∠=︒，即90BAC ∠=︒，ABC ∴∆的90BAC ∠=︒时，四边形AEDF 是正方形．课后练习1．如图，在四边形ABCD中，对角线AC，BD相交于点O，且OA＝OC，OB＝OD，下列说法错误的是（）A．若AC⊥BD，四边形ABCD是菱形B．若AB＝BC，AC＝BD，四边形ABCD是正方形C．若AC＝BD，四边形ABCD是矩形D．若∠ABC＝90°，四边形ABCD是正方形【答案】D【详解】解：∵四边形ABCD的对角线AC，BD相交于点O，且OA=OC，OB=OD，∴四边形ABCD为平行四边形．A．∵AC⊥BD，∴平行四边形ABCD是菱形，故该选项不符合题意；B.∵AB=BC，∴平行四边形ABCD是菱形，∵AC=BD，∴菱形ABCD是正方形；故该选项不符合题意；C.∵AC=BD，∴平行四边形ABCD是矩形，故该选项不符合题意；D．∵∠ABC=90°，∴平行四边形ABCD是矩形，故该选项符合题意；故选：D．2．如图，在正方形ABCD外作等边ADE∠=︒．，则BED【答案】45【详解】解：四边形ABCD 是正方形，90BAD ∴∠=︒，AB AD =，又ADE 是等边三角形，AE AD ∴=，60AED DAE ∠=∠=︒，AB AE ∴=，9060150BAE ∠=︒+︒=︒，15ABE AEB ∴∠=∠=︒．BED AED ABE ∴∠=∠-∠45=︒，故答案为45∶．3．如图，在正方形ABCD 中，E，F 是对角线BD 上的点，且AB BF DE ==，求EAF ∠的度数．【答案】45︒【详解】解：在正方形ABCD 中，AB AD =，90BAD ∠=︒，45ABD ADB ∠=∠=︒．又∵AB BF DE ==，∴AD DE =，AB BF =，∴18(27)06.5DAE DEA ADB ∠=∠=︒-∠÷=︒，18(27)06.5BAF BFA ABD ∠=∠=︒-∠÷=︒，∴180180267.545EAF BFA DEA ∠=︒-∠-∠=︒-⨯︒=︒．4．如图，在正方形ABCD 中，延长BC 至E ，使CE CA =．求CAE ∠的度数．【答案】22.5︒【详解】解：在正方形ABCD 中，90BCD ∠=︒，对角线AC 平分BCD ∠，∴90DCE BCD ∠=∠=︒，45ACB ∠=︒，CE CA =，ACE ∴ 是等腰三角形，ACB ∠ 是ACE △的一个外角，2ACB CAE E CAE ∴∠=∠+∠=∠，即245CAE ∠=︒，解得22.5CAE ∠=︒，故答案为：22.5︒．5.在正方形ABCD中，两条对角线相交于O，∠ACD的平分线交BD于P，若正方形ABCD的周长是16cm，则PB＝___________cm.【答案】46．如图，正方形ABCD 的面积为2，菱形AMCN 的面积为1，则,M N 两点间的距离为（）A．1B．2【答案】A【详解】解：如图，连接AC ，∵正方形ABCD 的面积为2，∴2122AC =，解得：2AC =，∵菱形AMCN 的面积为1，∴⋅=112AC MN ，即⨯⨯=1212MN ，解得：1MN =．故选：A．7．如图，已知正方形ABCD ，E 是AD 上一点，过BE 上一点O 作BE 的垂线，交AB 于点G ，交CD 于点H ．6BE =，则GH =．【答案】6【详解】解：过点A 作GH 的平行线，交DC 于点F，如图所示：∵ABCD 是正方形，∴AG FH ∥，BA AD =，90BAE D ∠=∠=︒，∴90FAD AFD ∠+∠=︒，∵GH BE ⊥，AF GH ∥，∴AF BE ⊥，四边形AFHG 是平行四边形，∴90FAD BEA ∠+∠=︒，∴BEA AFD ∠=∠，∴()AAS BAE ADF ≌，∴BE AF =，∴GH AF =，∴6GH BE ==，故答案为：6．8．如图，直线1l ，2l ，3l 分别过正方形ABCD 的三个顶点A ，D ，C ，且相互平行，若1l ，2l 的距离为1，2l ，3l 的距离为2，则正方形的边长为．【详解】解∶如图，过点D 作1EF l ⊥交1l 于点E，交3l 于点F，∵123l l l ∥∥，∴32,EF l EF l ⊥⊥，∴90AED ADC CFD ∠=∠=∠=︒，1,2DE DF ==，∴90,90ADE DAE ADE CDF ∠+∠=︒∠+∠=︒，∴DAE CDF ∠=∠，∵四边形ABCD 是正方形，∴AD CD =，∴ ≌ADE DCF ，∴2,1AE DF DE CF ====，AD ==9．如图，有三个正方形ABCD ，DEFG ，FHMN ，点B ，C ，G ，H ，M 都在同一直线l 上，若正方形ABCD ，DEFG 的面积分别为3和8，则正方形FHMN 的面积为（）A．4B．5C．6D．11【答案】B 【详解】解：∵四边形ABCD ，DEFG ，FHMN 都是正方形，∴DG FG =，90DCG GHF DGF ∠∠∠===︒；∴90CDG CGD CGD HGF ∠∠∠∠+=+=︒，∴CDG HGF ∠∠=，∴CDG HGF ≌（AAS ），∴CD GH =，CG FH =，∵正方形ABCD ，DEFG 的面积分别为3和8，∴2238CD DG ==，，∴正方形FHMN 的面积22835FH CG ===-=．故选∶B．10．若正方形的边长为a ，M 是BC 的中点，则图中阴影部分的面积是多少？【答案】213a 【详解】解：设ABE S S =△，M 是BC 中点，又因为ABE 和△同高，∴12BME S S =△，2311244AMB ABCD S S S a ===△正方形，则216S a =，∴阴影部分的面积2211263a a =⨯=．11．如图，正方形ABCD 的边长为2，H 在CD 的延长线上，四边形CEFH 也为正方形，则△DBF 的面积为()A．4C．D．2【答案】D 【详解】解：设正方形CEFH 的边长为a，根据题意得：21114422222()()BDF S a a a a a ∆=+-⨯---+22211222a a a a a =+-+--=2．故选：D．12．如图，在矩形ABCD 中，BE 平分ABC ∠，CE 平分DCB ∠，//,//BF CE CF BE ．求证：四边形BFCE 是正方形．【答案】∵//,//BF CE CF BE ，∴四边形BECF 是平行四边形．∵四边形ABCD 是矩形，∴90ABC ∠=︒，90DCB ∠=︒．又∵BE 平分ABC ∠，CE 平分DCB ∠，∴1145,4522EBC ABC ECB DCB ∠=∠=︒∠=∠=︒．∴EBC ECB ∠=∠．∴EB EC =．∴BECF 是菱形（菱形的定义）．在EBC 中，∵45,45EBC ECB ∠=︒∠=︒，∴90BEC ∠=︒．∴菱形BECF 是正方形（有一个角是直角的菱形是正方形）．13．如图，ABC 中，AB AC =，AD 是BAC ∠的角平分线，点O 为AB 的中点，连接DO 并延长到点E，使OE OD =．连接AE ，BE ．(1)求证：四边形AEBD 是矩形；(2)当90BAC ∠=︒时，猜想四边形AEBD 是什么图形？说明理由．【答案】（1）证明：∵点O 为AB 的中点，OE OD =，∴四边形AEBD 是平行四边形，AB AC = ，AD 是BAC ∠的角平分线，AD BC ∴⊥，90ADB ∴∠=︒，∴平行四边形AEBD 是矩形；（2）解：当90BAC ∠=︒时，四边形AEBD 是正方形，理由如下：AB AC = ，AD 是BAC ∠的角平分线，BD CD ∴=，90BAC ∠=︒ ，12AD BC BD \==，由（1）可知，四边形AEBD 是矩形，∴矩形AEBD 是正方形．14．已知：如图，在正方形ABCD中，G是CD上一点，延长BC到E，使CE=CG，连接BG并延长交DE于F．（1）求证：△BCG≌△DCE；（2）将△DCE绕点D顺时针旋转90°得到△DAE′，判断四边形E′BGD是什么特殊四边形，并说明理由．【答案】（1）证明：∵四边形ABCD是正方形，∴BC=CD，∠BCD=90°．∵∠BCD+∠DCE=180°，∴∠BCD=∠DCE=90°．又∵CG=CE，∴△BCG≌△DCE．（2）解：四边形E′BGD是平行四边形．理由如下：∵△DCE绕D顺时针旋转∴CE=AE′．∵CE=CG，∴CG=AE′．∵四边形ABCD是正方形，∴BE′∥DG，AB=CD．∴AB﹣AE′=CD﹣CG．即BE′=DG．∴四边形E′BGD是平行四边形．15．已知：如图，在ABC中．(1)分别以AB 、AC 为边向形外作正方形ABDE 、ACFG ．求证：①CE BG =；②CE BG ⊥；(2)分别以AB 、AC 为边向形外作正三角形ABD △、ACE △．求证：①CD BE =；②求CD 和BE 所成的锐角的度数．【答案】证明：①在正方形ABDE ACFG 中，AE AB =，AC AG =，90EAB GAC ∠=∠=︒，∴EAC BAG ∠=∠，在EAC 和BAG △中，EA BA EAC BAG AC AG =⎧⎪∠=∠⎨⎪=⎩，∴()SAS EAC BAG ≌，∴CE BG =，②如图，记BG ，CE 的交点为H ，BG ，AC 的交点为T ，∵EAC BAG △≌△，∴ACE AGB ∠=∠，∵90AGT ATG ∠+∠=︒，ATG CTH ∠=∠，∴90ACE CTH ∠+∠=︒，∴1809090GHC ∠=︒-︒=︒，∴CE BG ⊥．（2）①如图，记CD ，BE 的交点为O ，∵等边ABD △和等边ACE△∴AE AC =，AD AB =，60CAE BAD ADB ABD ∠==∠=∠=︒，∵BAE BAC CAE ∠=∠+∠，CAD BAC BAD ∠=∠+∠，∴BAE CAD ∠=∠，∴ABE ADC △≌△，∴CD BE =；②∵ABE ADC△≌△∴ABE ADC ∠=∠，∴60BDO ABE BDO ADC ADB ∠+∠=∠+∠=∠=︒∴()18018060DOB DBO BDO ABD ABE BDO ∠=︒-∠-∠=︒-∠-∠+∠=︒∴CD 和BE 所成的锐角的度数为60︒．16．在学习对称的知识点时，我们认识了如下图所示的“将军饮马”模型求最短距离．问题提出：(1)如图1所示，已知A，B 是直线l 同旁的两个定点．在直线l 上确定一点P，并连接AP 与BP ，使PA PB +的值最小．问题探究：(2)如图2所示，正方形ABCD 的边长为2，E 为AB 的中点，P 是AC 上一动点．连接EP 和BP ，则PB PE +的最小值是___________；问题解决：(3)某地有一如图3AOB ，已知45AOB ∠=︒，P 是AOB 内一点，连接PO 后测得10PO =米，现当地政府欲在三角形空地AOB 中修一个三角形花坛PQR ，点Q R ，分别是OA OB ，边上的任意一点（不与各边顶点重合），求PQR 周长的最小值．【详解】（1）解：如图所示，当P 点在如图所示的位置时，PA PB +的值最小；（2）解：如下图所示，∵四边形ABCD 是正方形，∴AC 垂直平分BD ，∴PB PD =，由题意易得：PB PE PD PE DE +=+≥，当D、P、E 共线时，在ADE V 中，根据勾股定理得，DE =（3）解：如下图所示，分别作点P 关于OA ，OB 的对称点M N ，，连接OM ON MN ，，，MN 交OA ，OB 于点Q R ，，连接PR PQ ，，此时PQR 周长的最小值等于MN ．由轴对称性质可得，10OM ON OP MOA POA NOB POB ===∠=∠∠=∠，，，∴224590MON AOB ∠=∠=⨯︒=︒，在Rt MON △中，MN =即PQR 周长的最小值等于。

中考数学复习----《正方形的判定》知识点总结与专项练习题(含答案解析)

中考数学复习----《正方形的判定》知识点总结与专项练习题（含答案解析）知识点总结1.直接判定：四条边都相等，四个角都是直角的四边形是正方形。

2.利用平行四边形判定：一组邻边相等且有一个角是直角的平行四边形是正方形。

（定义判定）3.利用菱形与矩形判定：①有一个角是直角的菱形是正方形。

②对角线相等的菱形是正方形。

③邻边相等的矩形是正方形。

④对角线相互垂直的矩形是正方形。

练习题1、（2022•绍兴）如图，在平行四边形ABCD中，AD＝2AB＝2，∠ABC＝60°，E，F是对角线BD上的动点，且BE＝DF，M，N分别是边AD，边BC上的动点．下列四种说法：①存在无数个平行四边形MENF；②存在无数个矩形MENF；③存在无数个菱形MENF；④存在无数个正方形MENF．其中正确的个数是（）A．1B．2C．3D．4【分析】根据题意作出合适的辅助线，然后逐一分析即可．【解答】解：连接AC，MN，且令AC，MN，BD相交于点O，∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD，∵BE＝DF，∴OE＝OF，只要OM＝ON，那么四边形MENF就是平行四边形，∵点E，F是BD上的动点，∴存在无数个平行四边形MENF，故①正确；只要MN＝EF，OM＝ON，则四边形MENF是矩形，∵点E，F是BD上的动点，∴存在无数个矩形MENF，故②正确；只要MN⊥EF，OM＝ON，则四边形MENF是菱形，∵点E，F是BD上的动点，∴存在无数个菱形MENF，故③正确；只要MN＝EF，MN⊥EF，OM＝ON，则四边形MENF是正方形，而符合要求的正方形只有一个，故④错误；故选：C．2、（2022•滨州）下列命题，其中是真命题的是（）A．对角线互相垂直的四边形是平行四边形B．有一个角是直角的四边形是矩形C．对角线互相平分的四边形是菱形D．对角线互相垂直的矩形是正方形【分析】根据，平行四边形，矩形，菱形，正方形的判定方法一一判断即可．【解答】解：A、对角线互相垂直的四边形是平行四边形，是假命题，本选项不符合题意；B、有一个角是直角的四边形是矩形，是假命题，本选项不符合题意；C、对角线互相平分的四边形是菱形，是假命题，本选项不符合题意；D、对角线互相垂直的矩形是正方形，是真命题，本选项符合题意．故选：D．3、（2022•攀枝花）如图，以△ABC的三边为边在BC上方分别作等边△ACD、△ABE、△BCF．且点A在△BCF内部．给出以下结论：①四边形ADFE是平行四边形；②当∠BAC ＝150°时，四边形ADFE是矩形；③当AB＝AC时，四边形ADFE是菱形；④当AB＝AC，且∠BAC＝150°时，四边形ADFE是正方形．其中正确结论有（填上所有正确结论的序号）．【分析】①利用SAS证明△EFB≌△ACB，得出EF＝AC＝AD；同理由△CDF≌△CAB，得DF＝AB＝AE；根据两边分别相等的四边形是平行四边形得出四边形ADFE是平行四边形，即可判断结论①正确；②当∠BAC＝150°时，求出∠EAD＝90°，根据有一个角是90°的平行四边形是矩形即可判断结论②正确；③先证明AE＝AD，根据一组邻边相等的平行四边形是菱形即可判断结论③正确；④根据正方形的判定：既是菱形，又是矩形的四边形是正方形即可判断结论④正确．【解答】解：①∵△ABE、△CBF是等边三角形，∴BE＝AB，BF＝CB，∠EBA＝∠FBC＝60°；∴∠EBF＝∠ABC＝60°﹣∠ABF；∴△EFB≌△ACB（SAS）；∴EF＝AC＝AD；同理由△CDF≌△CAB，得DF＝AB＝AE；由AE＝DF，AD＝EF即可得出四边形ADFE是平行四边形，故结论①正确；②当∠BAC＝150°时，∠EAD＝360°﹣∠BAE﹣∠BAC﹣∠CAD＝360°﹣60°﹣150°﹣60°＝90°，由①知四边形AEFD是平行四边形，∴平行四边形ADFE是矩形，故结论②正确；③由①知AB＝AE，AC＝AD，四边形AEFD是平行四边形，∴当AB＝AC时，AE＝AD，∴平行四边形AEFD是菱形，故结论③正确；④综合②③的结论知：当AB＝AC，且∠BAC＝150°时，四边形AEFD既是菱形，又是矩形，∴四边形AEFD是正方形，故结论④正确．故答案为：①②③④．。

正方形的判定专项练习30题(有答案)ok

正方形的判定专项练习30题(有答案)ok1.已知平行四边形ABCD中，对角线AC、BD交于点O，E是DB延长线上一点，且△___是等边三角形。

1) 证明ABCD是菱形。

2) 如果∠AEB=2∠EAB，证明ABCD是正方形。

2.在△ABC中，CE、CF分别是内角和外角平分线，过点A 作CE、CF的垂线，垂足分别为E、F。

1) 证明AECF是矩形。

2) 什么条件下AECF是正方形？3.在△ABC中，D、E分别为边AB、AC的中点，将△ADE绕点D旋转180°至△BDF。

1) 证明BCEF是平行四边形。

2) 添加什么条件可以使BFEC成为一种特殊的平行四边形？4.在矩形ABCD中，AF、BE、CE、DF分别是四个角的角平分线，E、M、F、N是其交点，证明EMFN是正方形。

5.在△ABC中，∠ACB=90°，D为AB中点，四边形BCED 为平行四边形，DE、AC相交于点F。

1) 证明F为AC中点。

2) 确定四边形ADCE的形状并说明理由。

3) 什么条件下ADCE是正方形？6.证明对角线相等的菱形是正方形。

7.在△ACD中，∠D=90°，∠D的平分线交AC于点E，EF⊥AD交AD于点F，EG⊥DC交DC于点G，证明EFDG 是正方形。

8.已知：如图，点M是矩形ABCD的边AD的中点，点P是BC边上的一动点，PE⊥CM，PF⊥___，垂足分别为E、F。

Ⅰ）当四边形PEMF为矩形时，矩形ABCD的长与宽满足什么条件？请说明理由。

Ⅱ）在（Ⅰ）中当点P运动到什么位置时，矩形PEMF变为正方形？为什么？9.如图，D是△___的边BC的中点，DE⊥AC，___⊥AB，垂足分别是E、F，且BF=CE。

1）求证：△BFD≌△CED。

2）当∠A=90°时，求证：四边形AFDE是正方形。

10.如图，四边形ABCD是矩形，E是BD上的一点，∠BAE=∠BCE，∠AED=∠CED，点G是BC、AE延长线的交点，AG与CD相交于点F。

专题18 正方形的判定与性质（含答案）

专题18 正方形的判定与性质知识解读一、正方形的性质1.从边看：正方形的四条边相等，对边平行，邻边垂直.2.从角看：正方形的四个角都是直角.3.从对角线看：对角线互相垂直平分且相等，每条对角线平分一组对角.4.对称性：正方形既是轴对称图形又是中心对称图形.由于矩形和菱形都既是轴对称图形又是中心对称图形，因此正方形作为一个特殊的菱形和矩形，它也既是轴对称图形又是中心对称图形.平行四边形、矩形、菱形、正方形之间关系如下：二、正方形的判定方法【典例示范】一、正方形常与全等知识综合在一起例1 如图4-18-1，点E是正方形ABCD内一点，△CDE是等边三角形，连接EB，EA，延长BE交边AD于点F．(1)求证：△ADE≌△BCE；(2)求∠AFB的度数．【提示】(1)要证△ADE≌△BCE，由题意可如AD＝BC，DE＝CE，只需再找出∠ADE与∠BCE相等即可．由题设条件，两角易证得相等；(2)由∠ADE＝30°，AD＝DE，可求出∠DAE ＝75°，又因为AE＝BE，从而可求∠ABF＝15°，从而易求得∠AFB的度数．【技巧点评】正方形的四条边长都相等，四个角度都为90°，等边三角形也是三边相等，三个角都等于60°，因此当图形中出现具有公共顶点的两个等边三角形，两个正方形或一个正方形一个等边三角形的时候，应考虑寻找全等三角形。

跟踪训练》OE ，1.如图4-18-2，在正方形ABCD中，AC，BD交于点O，点E在OA上，点G在OB上，且OG CG的延长线交BE于点F，猜想并证明CG和BE的大小及位置关系.【解答】如图4-18-2例2、在数学活动课中，小辉将边长为2和3的两个正方形放置在直线l 上，如图4-18-3①，他连接AD ，CF ，经测量发现AD=CF.（1）小辉将正方形ODEF 绕O 点逆时针旋转一定的角度，如图4-18-3②，试判断AD 与CF F 还相等吗？说明你的理由；（2）小辉将正方形ODEF 绕O 点逆时针旋转，使点E 旋转至直线l 上，如图4-18-3③，请你求出CF 的长.【提示】对于（1）根据正方形的性质可得090=∠=∠COA DOF ，OF DO =,OA CO =，然后推出AOD COF =∠,再利用“边角边”证明AOD ∆和COF ∆全等，根据全等三角形对应边相等即可得证；对于（2），同（1）求出AD CF =，连接DF 交OE 于点G ，根据正方形的对角线互相垂直平分可得OG DF ⊥，121===EO OG DG ，再求出AG ，然后利用勾股定理列式计算即可求出AD ，从而求出CF 的长。

正方形的性质练习题及答案

正方形的性质练习题及答案
问题1：什么是正方形？
答案：正方形是一种特殊的四边形，它的四条边长度相等且四
个角是直角。

问题2：正方形的面积公式是什么？
答案：一个正方形的面积可以通过边长的平方来计算，公式为：$面积 = 边长^2$。

问题3：一条边长为5的正方形的面积是多少？
答案：该正方形的面积为 $5^2 = 25$ 平方单位。

问题4：一条边长为8的正方形的周长是多少？
答案：该正方形的周长等于四条边的长度之和，所以周长为 $4 × 8 = 32$。

问题5：一个正方形的对角线长度是多少？
答案：正方形的对角线长度可以通过边长乘以 $\sqrt{2}$ 来计算。

问题6：一个正方形的对角线长为10，边长是多少？
答案：设边长为 $x$，根据对角线和边长的关系，可以列出方
程 $x \times \sqrt{2} = 10$，解得 $x = \frac{10}{\sqrt{2}} \approx
7.07$。

问题7：一个正方形的内角度数是多少？
答案：正方形的内角度数都是直角，即 90 度。

问题8：一个正方形的外角度数是多少？
答案：正方形的外角度数等于内角度数的补角，即 90 度。

问题9：一个正方形的尺寸比例是多少？
答案：正方形的尺寸比例是 1：1，即四条边的长度都相等。

问题10：一个正方形可以划分为几个直角三角形？
答案：一个正方形可以划分为两个直角三角形，将对角线作为分割线。

以上是关于正方形的一些基本性质练习题及答案。

希望对你有所帮助！。

北师大版九年级数学上册--第一章 1.3《正方形的性质与判定》同步练习题(含答案)

1.3《正方形的性质与判定》同步练习一、填空题1．正方形的定义：有一组邻边______并且有一个角是______的平行四边形叫做正方形，因此正方形既是一个特殊的有一组邻边相等的______，又是一个特殊的有一个角是直角的______。

2．正方形的性质：正方形具有四边形、平行四边形、矩形、菱形的一切性质，正方形的四个角都是______；四条边都______且__________________；正方形的两条对角线______，并且互相______，每条对角线平分______对角。

它有______条对称轴。

3．正方形的判定：(1)____________________________________的平行四边形是正方形；(2)____________________________________的矩形是正方形；(3)____________________________________的菱形是正方形。

4．对角线________________________________的四边形是正方形。

5．若正方形的边长为a ，则其对角线长为______，若正方形ACEF 的边是正方形ABCD 的对角线，则正方形ACEF 与正方形ABCD 的面积之比等于______。

6．延长正方形ABCD 的BC 边至点E ，使CE ＝AC ，连结AE ，交CD 于F ，那么∠AFC 的度数为______，若BC ＝4cm ，则△ACE 的面积等于______。

7．如图，E 是正方形ABCD 的对角线BD 上一点，且BE ＝BC ，则∠ACE ＝。

8．如图，已知正方形ABCD ，以CD 为边作等边△CDE ，则∠AED 的度数是。

二、选择题。

1、已知四边形ABCD 是平行四边形，再从①AB ＝BC ，②∠ABC ＝90°，③AC ＝BD ，④AC ⊥BD 四个条件中，选两个作为补充条件后，使得四边形ABCD 是正方形，现有下列四种选法，其中错误的是( ) A ．选①② B ．选②③ C ．选①③ D ．选②④2、四边形ABCD 的对角线AC ＝BD ，AC ⊥BD ，分别过点A ，B ，C ，D 作对角线的平行线，所成的四边形EFMN 是( )A ．正方形B ．菱形C ．矩形D ．任意四边形3、已知四边形中，对角线与相交于点，，下列判断中错误的是（） A.如果＝，＝，那么四边形是平行四边形 B.如果，＝，那么四边形是矩形 C.如果＝，，那么四边形是菱形 D.如果＝，垂直平分，那么四边形是正方第7题图第8题图4、满足下列条件的四边形是正方形的是（）A.对角线互相垂直平分的平行四边形B.对角线互相平分且相等的矩形C.对角线互相垂直平分的菱形D.对角线互相垂直平分且相等的四边形5、如图，已知P是正方形ABCD的对角线BD上一点，且BP＝BC，则∠ACP的度数是( )A．45° B．22.5° C．67.5° D．75°题5图题6图题7图6、如图，点在正方形内，满足，，，则阴影部分的面积是（）A.76B.70C.48D.247、如图,在四边形中，点是对角线的交点，在下列条件中，能判定这个四边形为正方形的是（）A.，B.，C.，D.，，8、如图，四边形是正方形，对角线，交于点，下列结论：①；②；③；④正方形有四条对称轴．上述结论正确的有（）A.①②③④B.①②③C.②③④D.①③④9、下列四个命题：①一组对边平行且一组对角相等的四边形是平行四边形；②对角线互相垂直且相等的四边形是正方形；③顺次连接矩形四边中点得到的四边形是菱形；④正五边形既是轴对称图形又是中心对称图形．其中真命题共有（）A.个B.个C.个D.个三、解答题1、已知Rt△ABC中，∠C=90°，CD平分∠ACB交AB于D，DF//BC,DE//AC。

正方形判定与性质培优

19.3.2 正方形的判断与性质一．选择题（共 5 小题）1．以下说法错误的选项是（）A ．有一个角为直角的菱形是正方形B．有一组邻边相等的矩形是正方形C．对角线相等的菱形是正方形D．对角线相等且相互垂直的四边形是正方形2．在正方形 ABCD 的边 AB 、 BC、 CD 、DA 上分别随意取点 E、 F、 G、H ．这样获得的四边形EFGH 中，是正方形的有（）A．1 个 B．2 个 C．4 个 D．无量多个3．如图，四边形ABCD 中， AD=DC ，∠ADC= ∠ABC=90 °，DE ⊥ AB ，若四边形 ABCD 面积为16，则 DE 的长为（）A ． 3B． 2C． 4D． 84．△ ABC 中，∠C=90 °，点 O 为△ ABC 三条角均分线的交点， OD ⊥ BC 于 D ， OE⊥AC 于 E， OF⊥ AB 于 F，且AB=10cm ， BC=8cm ， AC=6cm ，则点 O 到三边 AB 、 AC 、 BC 的距离为（）A ． 2cm， 2cm， 2cmB ．3cm， 3cm， 3cm C． 4cm， 4cm， 4cm D ．2cm， 3cm， 5cm5．如图，在一个大正方形，放入三个面积相等的小正方形纸片，这三纸片遮住的总面积是24 平方厘米，且未遮住的面积比小正方形面积的四分之一还少 3 平方厘米，则大正方形的面积是（单位：平方厘米）（）A．40 B．25C． 26D． 36二．填空题（共 4 小题）6．现有一边长等于 a（ a＞ 16）的正方形纸片，从距离正方形的四个极点8cm 处，沿 45°角画线，将正方形纸片分成 5 部分，则暗影部分是_________（填写图形的形状）（如图），它的一边长是_________ ．7．如图，正方形ABCD的对角线交于点O，以AD为边向外作Rt △ADE ，∠AED=90 °，连结OE， DE=6 ，OE=8 ，则另向来角边AE的长为_________．8．如图，在四边形 ABCD 中，∠ADC= ∠ ABC=90 °， AD=CD ， DP⊥ AB 于 P．若四边形 ABCD 的面积是18，则DP 的长是 _________ ．9．四边形 ABCD 的对角线AC 和 BD 订交于点O，设有以下条件：① AB=AD ；②∠ DAB=90 °；③ AO=CO ，BO=DO ；④矩形 ABCD ；⑤ 菱形 ABCD ，⑥ 正方形 ABCD ，则在以下推理不建立的是_________A、①④ ? ⑥；B、①③ ? ⑤；C、①② ? ⑥；D、②③ ? ④三．解答题（共 11 小题）10．如图，已知点 E、 F、G、 H 分别在正方形 ABCD 的各边上，且 AE=BF=CG=DH ， AF 、 BG 、CH 、 DE 分别订交于点 A ′、B ′、 C′、 D′．求证：四边形 A ′B′C′D′是正方形．11．如图，在正方形 ABCD 中，点 M 在边 AB 上，点 N 在边 AD 的延伸线上，且 BM=DN ．点 E 为 MN 的中点， DE 的延伸线与 AC 订交于点 F．试猜想线段 DF 与线段 AC 的关系，并证你的猜想．12．如图，正方形ABCD 边长为 6．菱形 EFGH 的三个极点E、 G、H 分别在正方形ABCD 的边 AB 、CD、DA 上，且 AH=2 ，连结 CF．（1）当 DG=2 时，求证：菱形 EFGH 为正方形；（2）设 DG=x ，试用含 x 的代数式表示△FCG 的面积．13．如图，正方形ABCD ，动点 E 在 AC 上， AF ⊥ AC ，垂足为 A ， AF=AE ．（1）求证： BF=DE ；（2）当点 E 运动到 AC 中点时（其余条件都保持不变），问四边形 AFBE 是什么特别四边形？说明原因．14．已知，如图，矩形 ABCD 中， AD=6 ， DC=7 ，菱形 EFGH 的三个极点 E， G， H 分别在矩形 ABCD 的边 AB ，CD，DA 上， AH=2 ，连结 CF．（1）若 DG=2 ，求证四边形 EFGH 为正方形；（2）若 DG=6 ，求△ FCG 的面积；（3）当 DG 为什么值时，△ FCG 的面积最小．15．如图，正方形ABCD 中， AC 是对角线，今有较大的直角三角板，一边一直经过点 B ，直角极点P 在射线 AC 上挪动，另一边交DC于Q．（ 1）如图 1，当点 Q 在 DC 边上时，猜想并写出PB 与 PQ 所知足的数目关系；并加以证明；（ 2）如图 2，当点 Q 落在 DC 的延伸线上时，猜想并写出PB 与 PQ 知足的数目关系，请证明你的猜想．16．如图，已知四边形 ABCD 是正方形，分别过 A 、 C 两点作 l1∥ l2，作 BM ⊥ l1于 M ， DN⊥ l 1于 N ，直线 MB 、 ND 分别交 l2于 Q、 P．求证：四边形 PQMN 是正方形．17．在正方形 ABCD 各边前一次截取AE=BF=CG=DH ，连结 EF，FG，GH ，HE．试问四边形EFGH 是不是正方形？18．如图，四边形ABCD 是正方形，点P 是 BC上随意一点，DE⊥ AP于点E，BF⊥AP于点F，CH ⊥ DE于点H，BF 的延伸线交CH 于点 G．（1）求证： AF ﹣ BF=EF ；（2）四边形 EFGH 是什么四边形？并证明；（3）若 AB=2 ， BP=1，求四边形 EFGH 的面积．19．如图，△ ABC 中，∠C=90 °，∠ BAC 、∠ ABC 的均分线订交于点 D，DE⊥ BC ，DF⊥ AC ，垂足分别为 E、F．问四边形 CFDE 是正方形吗？请说明原因．20．如图，在△ABC 中，∠BAC=90 °，AB=AC ，点 D 是 BC 的中点， DE ⊥AB ，DF⊥ AC 垂足分别为E，F．求证：四边形 DEAF 是正方形．19.3.2 正方形的判断与性质参照答案与试题分析一．选择题（共 5 小题）1．以下说法错误的选项是（）A ．有一个角为直角的菱形是正方形B．有一组邻边相等的矩形是正方形C．对角线相等的菱形是正方形D．对角线相等且相互垂直的四边形是正方形考点：正方形的判断．剖析：正方形：四个角都是直角，四条边都相等，对角线相等，且相互垂直均分的平行四边形；菱形：四条边都相等，对角线相互垂直均分的平行四边形；矩形：四个角都相等，对角线相等的平行四边形．解答：解：A 、有一个角为直角的菱形的特点是：四条边都相等，四个角都是直角，则该菱形是正方形．故本选项说确；B、有一组邻边相等的矩形的特点是：四条边都相等，四个角都是直角．则该矩形为正方形．故本选项说确；C、对角线相等的菱形的特点是：四条边都相等，对角线相等的平行四边形，即该菱形为正方形．故本选项说确；D、对角线相等且相互垂直的平行四边形是正方形．故本选项说法错误；应选 D．评论：本题考察了正方形的判断．正方形集矩形、菱形的性质于一身，是特别的平行四边形．2．在正方形 ABCD 的边 AB 、 BC、 CD 、DA 上分别随意取点E、 F、 G、H ．这样获得的四边形EFGH 中，是正方形的有（）A． 1个B．2 个C．4 个D．无量多个考点：正方形的判断与性质；全等三角形的判断．专题：计算题．剖析：在正方形四边上随意取点E、 F、 G、 H，若能证明四边形 EFGH 为正方形，则说明能够获得无量个正方形．解答：解：无量多个．如图正方形ABCD ：AH=DG=CF=BE ， HD=CG=FB=EA ，∠ A= ∠ B=∠ C=∠ D，有△AEH ≌△DHG ≌△CGF≌ △BFE，则 EH=HG=GF=FE ，此外很简单得四个角均为90°则四边形 EHGF 为正方形．应选 D．评论：本题考察了正方形的判断与性质，难度适中，利用三角形全等的判断证明EH=HG=GF=FE ．3．如图，四边形ABCD 中， AD=DC ，∠ADC= ∠ABC=90 °，DE ⊥ AB ，若四边形ABCD 面积为 16，则 DE 的长为（）A．3B．2C．4D．8考点：正方形的判断与性质．专题：证明题．剖析：如图，过点 D 作 BC 的垂线，交 BC 的延伸线于 F，利用互余关系可得∠ A= ∠ FCD ，又∠ AED= ∠ F=90°，AD=DC ，利用 AAS 能够判断△ ADE ≌ △ CDF，∴ DE=DF ， S 四边形ABCD =S 正方形DEBF=16 ， DE=4 ．解答：解：过点 D 作 BC 的垂线，交 BC 的延伸线于 F，∵ ∠ ADC= ∠ ABC=90 °，∠ CDF+ ∠ EDC=90 °，∴∠A=∠FCD ，又∠ AED= ∠ F=90°， AD=DC ，∴△ADE ≌△CDF，∴DE=DF ，S 四边形ABCD =S 正方形DEBF=16 ，∴ DE=4 ．应选 C．评论：本题运用割补法，或许旋转法将四边形ABCD转变为正方形，依据面积保持不变，来求正方形的边长．4．△ ABC 中，∠C=90 °，点 O 为△ ABC 三条角均分线的交点，OD ⊥ BC 于 D ， OE⊥AC 于AB=10cm ， BC=8cm ， AC=6cm ，则点 O 到三边 AB 、 AC 、 BC 的距离为（）A ．2cm， 2cm， 2cmB ．3cm， 3cm， 3cm C．4cm， 4cm， 4cm D ．E， OF⊥ AB 于 F，且2cm，3cm， 5cm考点：正方形的判断与性质．剖析：连结 OA ， OB， OC，利用角的均分线上的点到角的两边的距离相等可知△BDO≌△ BFO，△CDO ≌△ CEO ，△ AEO ≌△ AFO ，∴BD=BF ，CD=CE ，AE=AF ，又因为点 O 到三边 AB 、AC 、BC 的距离是 CD ，∴ AB=8 ﹣ CD+6 ﹣ CD=10 ，解得 CD=2 ，所以点 O 到三边 AB 、 AC 、BC 的距离为 2．解答：解：连结 OA ， OB ， OC，则△ BDO ≌ △ BFO ，△ CDO≌ △ CEO，△ AEO ≌ △AFO ，∴BD=BF ， CD=CE ， AE=AF ，又∵ ∠ C=90， OD⊥ BC 于 D， OE⊥ AC 于 E，且 O 为△ ABC 三条角均分线的交点∴四边形 OECD 是正方形，则点 O 到三边 AB、 AC、BC 的距离 =CD，∴ AB=8 ﹣ CD+6﹣ CD= ﹣ 2CD+14 ，又依据勾股定理可得：AB=10 ，即﹣ 2CD+14=10∴ CD=2 ，即点 O 到三边 AB 、 AC 、 BC 的距离为2cm．应选 A评论：本题主要考察垂直均分线上的点到线段两段的距离相等的性质和边的和差关系．5．如图，在一个大正方形，放入三个面积相等的小正方形纸片，这三纸片遮住的总面积是24 平方厘米，且未遮住的面积比小正方形面积的四分之一还少 3 平方厘米，则大正方形的面积是（单位：平方厘米）（）A． 40B．25C．26D．36考点：正方形的判断与性质．专题：计算题．剖析：设小正方形的边长为a，大正方形的边长为b，由正方形的面积公式，依据题意列出方程组解方程组得出大正方形的边长，则可求出头积．解答：解：设小正方形的边长为a，大正方形的边长为 b，由这三纸片遮住的总面积是24 平方厘米，可得ab+a（ b﹣ a）=24① ，2 2将①②联立解方程组可得：a=4， b=5，∴大正方形的边长为5，∴面积是 25．应选 B．评论：本题考察了正方形的性质及面积公式，难度较大，重点依据题意列出方程．二．填空题（共 4 小题）6．现有一边长等于a（ a＞ 16）的正方形纸片，从距离正方形的四个极点8cm 处，沿 45°角画线，将正方形纸片分成 5 部分，则暗影部分是正方形（填写图形的形状）（如图），它的一边长是cm．考点：正方形的判断与性质．专题：压轴题．剖析：延伸小正方形的一边交大正方形于一点，连结此点与距大正方形极点8cm 处的点，结构直角边长为8的等腰直角三角形，将小正方形的边长转变为等腰直角三角形的斜边长来求解即可．解答：解：如图，作AB 平行于小正方形的一边，延伸小正方形的另一边与大正方形的一边交于 B 点，∴ △ ABC 为直角边长为8cm 的等腰直角三角形，∴AB=AC=8 ，∴暗影正方形的边长 =AB=8cm ．故答案为：正方形， cm．评论：本题考察了正方形的性质与勾股定理的知识，题目同时也浸透了转变思想．7．如图，正方形则另向来角边AE ABCD的长为的对角线交于点10．O，以AD为边向外作Rt △ADE，∠AED=90 °，连结OE， DE=6 ，OE=8 ，考点：正方形的判断与性质；全等三角形的判断与性质；勾股定理．剖析：第一过点 O 作 OM ⊥ AE 于点 M ，作 ON⊥DE ，交 ED 的延伸线于点N，易得四边形EMON 是正方形，点 A ，O， D，E 共圆，则可得△ OEN 是等腰直角三角形，求得EN 的长，既而证得Rt△AOM ≌ Rt△ DON ，得到 AM=DN ，既而求得答案．解答：解：过点 O 作 OM ⊥ AE 于点 M ，作 ON⊥ DE ，交 ED 的延伸线于点N，∵ ∠ AED=90 °，∴四边形 EMON 是矩形，∵正方形 ABCD 的对角线交于点O，∴ ∠ AOD=90 °， OA=OD ，∴ ∠ AOD+ ∠ AED=180 °，∴点 A ，O，D ，E 共圆，∴=，∴∠ AEO= ∠ DEO= ∠ AED=45 °，∴OM=ON ，∴四边形 EMON 是正方形，∴EM=EN=ON ，∴△ OEN 是等腰直角三角形，∵OE=8，∴ EN=8 ，∴EM=EN=8 ，在 Rt△ AOM 和 Rt △ DON 中，，∴Rt△ AOM ≌ Rt△ DON （ HL ），∴AM=DN=EN ﹣ ED=8 ﹣ 6=2，∴AE=AM+EM=2+8=10 ．故答案为： 10．评论：本题考察了正方形的判断与性质、全等三角形的判断与性质以及等腰直角三角形性质．本题难度较大，注意掌握协助线的作法，注意掌握数形联合思想的应用．8．如图，在四边形 ABCD 中，∠ADC= ∠ ABC=90 °， AD=CD ， DP⊥ AB 于 P．若四边形 ABCD 的面积是18，则DP的长是 3 ．考点：正方形的判断与性质；全等三角形的判断与性质．剖析：过点 D 作 DE ⊥ DP 交 BC 的延伸线于E，先判断出四边形DPBE 是矩形，再依据等角的余角相等求出∠ ADP= ∠CDE ，再利用“角角边”证明△ ADP 和△ CDE 全等，依据全等三角形对应边相等可得DE=DP ，而后判断出四边形 DPBE 是正方形，再依据正方形的面积公式解答即可．解答：解：如图，过点 D 作 DE ⊥ DP 交 BC 的延伸线于E，∵ ∠ ADC= ∠ ABC=90 °，∴四边形 DPBE 是矩形，∵ ∠ CDE+ ∠CDP=90 °，∠ADC=90 °，∴ ∠ ADP+ ∠CDP=90 °，∴ ∠ ADP= ∠CDE ，∵DP⊥AB ，∴∠ APD=90 °，∴ ∠ APD= ∠E=90 °，在△ADP 和△ CDE 中，，∴ △ ADP ≌△ CDE （AAS ），∴DE=DP ，四边形 ABCD 的面积 =四边形 DPBE 的面积 =18，∴矩形 DPBE 是正方形，∴DP==3 ．故答案为： 3．评论：本题考察了正方形的判断与性质，全等三角形的判断与性质，熟记各性质并作协助线结构出全等三角形和正方形是解题的重点．9．四边形 ABCD 的对角线 AC 和 BD 订交于点 O，设有以下条件：① AB=AD；②∠ DAB=90 °；③ AO=CO ，BO=DO ；④矩形 ABCD ；⑤ 菱形 ABCD ，⑥ 正方形 ABCD ，则在以下推理不建立的是CA、①④ ? ⑥；B、①③ ? ⑤；C、①② ? ⑥；D、②③ ? ④考点：正方形的判断与性质；全等三角形的判断与性质；菱形的判断与性质；矩形的判断与性质．专题：证明题．剖析：依据矩形、菱形、正方形的判断定理，对角线相互均分的四边形为平行四边形，再由邻边相等，得出是菱形，和一个角为直角得出是正方形，依据已知对各个选项进行剖析从而获得最后的答案．解答：解： A 、由①④得，一组邻边相等的矩形是正方形，故正确；B、由③得，四边形是平行四边形，再由① ，一组邻边相等的平行四边形是菱形，故正确；C、由①②不可以判断四边形是正方形；D、由③得，四边形是平行四边形，再由② ，一个角是直角的平行四边形是矩形，故正确．应选 C．评论：本题用到的知识点是：矩形、菱形、正方形的判断定理，如：一组邻边相等的矩形是正方形；对角线相互均分且一组邻边相等的四边形是菱形；对角线相互均分且一个角是直角的四边形是矩形．灵巧掌握这些判断定理是解本题的重点．三．解答题（共11 小题）ABCD的各边上，且AE=BF=CG=DH，AF、BG、CH、DE分别相10．如图，已知点E、 F、G、 H 分别在正方形交于点 A ′、B ′、 C′、 D′．求证：四边形 A ′B′C′D′是正方形．考点：正方形的判断与性质；全等三角形的判断与性质．专题：证明题．剖析：依照三角形的角和定理能够判断四边形 A ′B′C′D′的三个角是直角，则四边形是矩形，而后证明一组邻边相等，能够证得四边形是正方形．解答：证明：在正方形ABCD 中，∵在△ABF 和△ BCG 中，∴ △ ABF ≌△ BCG （SAS）∴ ∠ BAF= ∠GBC ，∵ ∠ BAF+ ∠AFB=90 °，∴ ∠ GBC+ ∠ AFB=90 °，∴ ∠ BB ′F=90°，∴ ∠ A ′B′C′=90°．∴同理可得∠ B ′C′D′=∠ C′D′A′=90°，∴四边形 A ′B′C′D′是矩形．∵在△AB ′B 和△BC′C 中，∴ △ AB ′B≌ △ BC′C（ AAS ），∴AB ′=BC ′∵在△AA ′E 和△BB ′F中，∴ △ AA ′E≌ △ BB ′F（ AAS ），∴AA ′=BB ′∴A ′B′=B ′C′∴矩形 A ′B′C′D′是正方形．评论：本题考察了正方形的判断，判断的方法是证明是矩形同时是菱形．11．如图，在正方形DE 的延伸线与ACABCD订交于点中，点 M 在边F．试猜想线段AB 上，点DF 与线段N 在边 AD 的延伸线上，且AC 的关系，并证你的猜想．BM=DN．点E 为MN的中点，考点：正方形的判断与性质；全等三角形的判断与性质；线段垂直均分线的性质．专题：研究型．剖析：猜想：线段 DF 垂直均分线段AC ，且 DF=AC ，过点 M 作 MG ∥ AD ，与 DF 的延伸线订交于点 G，作 GH⊥ BC，垂足为 H，连结 AG 、 CG．依据正方形的性质和全等三角形的证明方法证明△AMG ≌ △CHG 即可．解答：猜想：线段 DF 垂直均分线段AC ，且 DF=AC ，证明：过点 M 作 MG ∥ AD ，与 DF 的延伸线订交于点 G．则∠EMG= ∠N，∠BMG= ∠ BAD ，∵ ∠ MEG= ∠ NED ， ME=NE ，∴△MEG ≌△ NED，∴MG=DN ．∵BM=DN ，∴MG=BM ．作 GH⊥ BC，垂足为 H，连结 AG 、CG．∵四边形 ABCD 是正方形，∴ AB=BC=CD=DA ，∠ BAD= ∠ B= ∠ ADC=90 °，∵ ∠ GMB= ∠ B= ∠ GHB=90 °，∴四边形 MBHG 是矩形．∵MG=MB ，∴四边形 MBHG 是正方形，∴MG=GH=BH=MB ，∠ AMG= ∠ CHG=90 °，∴AM=CH ，∴△ AMG ≌ △CHG ．∴GA=GC ．又∵ DA=DC ，∴ DG 是线段 AC 的垂直均分线．∵ ∠ ADC=90 °， DA=DC ，∴DF=AC即线段 DF 垂直均分线段AC ，且 DF=AC ．评论：本题综合考察了矩形的判断和性质、正方形的判断和性质，垂直均分线的判断和性质，全等三角形的性质和判断等知识点，本题综合性比较强，难度较大，但题型较好，训练了学生剖析问题和解决问题以及敢于猜想的能力．12．如图，正方形ABCD 边长为 6．菱形 EFGH 的三个极点E、 G、H 分别在正方形ABCD 的边 AB 、CD、DA 上，且 AH=2 ，连结 CF．（1）当 DG=2 时，求证：菱形 EFGH 为正方形；（2）设 DG=x ，试用含 x 的代数式表示△FCG 的面积．考点：正方形的判断与性质；全等三角形的判断与性质；菱形的性质．剖析：（1）因为四边形ABCD 为正方形，四边形 HEFG 为菱形，那么∠D= ∠A=90 °，HG=HE ，而 AH=DG=2易证△ AHE ≌ △ DGH ，从而有∠ DHG= ∠HEA ，等量代换可得∠ AHE+∠ DHG=90°，易证四边形HEFG 为正方形；（ 2）欲求△ FCG 的面积，由已知得CG 的长易求，只要求出GC 边的高，经过证明△ AHE≌ △ MFG可得．解答：（1）证明：在△ HDG 和△ AEH 中，，∵四边形 ABCD 是正方形，∴ ∠ D=∠ A=90 °，∵四边形 EFGH 是菱形，∴HG=HE ，∵DG=AH=2 ，∴Rt△ HDG ≌ △ AEH ，∴∠ DHG= ∠ AEH ，∴∠ DHG+ ∠ AHE=90 °∴∠ GHE=90 °，∴菱形 EFGH 为正方形；（ 2）解：过 F 作 FM ⊥ CD ，垂足为M ，连结 GE∵CD∥ AB ，∴∠AEG= ∠MGE ，∵GF∥ HE ，∴ ∠ HEG= ∠ FGE，∴∠AEH= ∠FGM，在 Rt△ AHE 和 Rt△ GFM 中，∵ ，∴ Rt△ AHE ≌ Rt△ GFM ，∴MF=2 ，∵ DG=x ，∴CG=6﹣ x．∴S△FCG=CG?FM=6 ﹣ x．评论：作 FM ⊥ DC，交本题考察了正方形的性质、菱形的性质、全等三角形的判断和性质，解题的重点是作协助线：过DC 延伸线于M ，连结 GE，结构全等三角形和错角．F13．如图，正方形ABCD ，动点 E 在 AC 上， AF ⊥ AC ，垂足为 A ， AF=AE ．（1）求证： BF=DE ；（2）当点 E 运动到 AC 中点时（其余条件都保持不变），问四边形 AFBE 是什么特别四边形？说明原因．考点：正方形的判断与性质；全等三角形的判断与性质．剖析：（1）依据正方形的性质判断△ ADE≌△ ABF后即可获得（ 2）利用正方形的判断方法判断四边形AFBE 为正方形即可．BF=DE ；解答：（1）证明： ∵ 正方形 ABCD ，∴ AB=AD ， ∠BAD=90 °，∵AF ⊥AC ，∴ ∠ EAF=90 °，∴ ∠ BAF= ∠EAD ，在△ADE 和△ ABF 中∴ △ ADE ≌ △ ABF （ SAS ），∴ BF=DE ；（ 2）解：当点 E 运动到 AC 的中点时四边形 AFBE 是正方形，原因：∵ 点 E 运动到 AC 的中点， AB=BC ，∴ BE ⊥AC ， BE=AE=AC ，∵ AF=AE ，∴ BE=AF=AE ，又 ∵ BE ⊥ AC ， ∠FAE= ∠ BEC=90 °，∴ BE ∥AF ，∵ BE=AF ，∴ 得平行四边形 AFBE ，∵ ∠ FAE=90 °，AF=AE ，∴ 四边形 AFBE 是正方形．评论：本题考察了正方形的判断和性质，解题的重点是正确的利用正方形的性质．14．已知，如图，矩形 ABCD 中， AD=6 ， DC=7 ，菱形 EFGH 的三个极点 E ， G ， H 分别在矩形 ABCD 的边 AB ，CD ， DA 上， AH=2 ，连结 CF ．（ 1）若 DG=2 ，求证四边形 EFGH 为正方形；（ 2）若 DG=6 ，求 △ FCG 的面积；（ 3）当 DG 为什么值时， △ FCG 的面积最小．考点：正方形的判断与性质；全等三角形的判断与性质；菱形的性质；矩形的性质．专题：计算题；压轴题．剖析：（1）因为四边形 ABCD 为矩形，四边形 HEFG 为菱形，那么 ∠D= ∠A=90 °，HG=HE ，而 AH=DG=2 ，易证 △ AHE ≌ △ DGH ，从而有 ∠ DHG= ∠HEA ，等量代换可得 ∠ AHE+ ∠ DHG=90 °，易证四边形 HEFG 为正方形；（ 2）过 F 作 FM ⊥ DC ，交 DC 延伸线于 M ，连结 GE ，因为 AB ∥ CD ，可得 ∠ AEG= ∠ MGE ，同理有 ∠ HEG= ∠ FGE ，利用等式性质有 ∠ AEH= ∠ MGF ，再联合 ∠ A= ∠ M=90 °，HE=FG ，可证 △ AHE ≌ △ MFG ，从而有 FM=HA=2 （即无论菱形 EFGH 怎样变化，点 F 到直线 CD 的距离一直为定值 2），从而可求三角形面积；HE 2≤53，在 Rt △ DHG （ 3）先设 DG=x ，由第（ 2）小题得， S △FCG =7﹣ x ，在△ AHE 中，AE ≤AB=7 ，利用勾股定理可得中，再利用勾股定理可得x 2+16≤53，从而可求 x ≤，从而可适当 x=时， △ GCF 的面积最小．解答：解：（ 1） ∵四边形 ABCD 为矩形，四边形 HEFG 为菱形，∴ ∠ D=∠ A=9 0°， HG=HE ，又 AH=DG=2 ，∴ Rt △ AHE ≌ Rt △ DGH （HL ），∴ ∠ DHG= ∠ HEA ，∵ ∠ AHE+ ∠ HEA=90 °，∴ ∠ AHE+ ∠ DHG=90 °，∴ ∠ EHG=90 °，∴ 四边形 HEFG 为正方形；（ 2）过 F 作 FM ⊥DC ，交 DC 延伸线于 M ，连结 GE ，∵AB ∥CD ，∴∠AEG= ∠MGE ，∵ HE ∥ GF ，∴ ∠ HEG= ∠ FGE ，∴∠AEH= ∠MGF ，在 △ AHE 和 △ MFG 中， ∠ A= ∠M=90 °，HE=FG ， ∴△AHE ≌△MFG ，∴ FM=HA=2 ，即不论菱形 EFGH 怎样变化，点 F 到直线 CD 的距离一直为定值 2，所以；（ 3）设 DG=x ，则由第（ 2）小题得， S △ FCG =7﹣ x ，在 △AHE 中， AE ≤AB=7 ，∴ HE 2≤53，∴ x 2+16≤53，∴ x ≤，∴ S △FCG 的最小值为，此时 DG= ，∴ 当 DG= 时， △ FCG 的面积最小为（）．评论：本题考察了矩形、菱形的性质、全等三角形的判断和性质、勾股定理．解题的重点是作协助线：过F 作 FM ⊥ DC ，交 DC 延伸线于 M ，连结 GE ，结构全等三角形和错角．15．如图，正方形 ABCD 中， AC 是对角线，今有较大的直角三角板，一边一直经过点 B ，直角极点P 在射线 AC 上挪动，另一边交 DC 于Q ．（ 1）如图 1，当点 Q 在 DC 边上时，猜想并写出 PB 与 PQ 所知足的数目关系；并加以证明；（ 2）如图 2，当点 Q 落在 DC 的延伸线上时，猜想并写出 PB 与 PQ 知足的数目关系，请证明你的猜想．考点：正方形的判断与性质；全等三角形的判断与性质．剖析：（1）过 P 作 PE ⊥BC ， PF ⊥ CD ，证明 Rt △ PQF ≌ Rt △ PBE ，即可；（ 2）证明思路同（ 1）解答：（1） PB=PQ ，证明：过 P 作 PE ⊥ BC ， PF ⊥ CD ，∵ P ， C 为正方形对角线 AC 上的点，∴ PC 均分 ∠ DCB ， ∠ DCB=90 °，∴ PF=PE ，∴ 四边形 PECF 为正方形，∵ ∠ BPE+∠ QPE=90°， ∠ QPE+∠ QPF=90 °，∴ ∠ BPE=∠ QPF ，∴ Rt △ PQF ≌ Rt △PBE ，∴ PB=PQ ；（ 2） PB=PQ ，证明：过 P 作 PE⊥ BC ， PF⊥ CD ，∵ P， C 为正方形对角线AC 上的点，∴PC 均分∠ DCB ，∠ DCB=90 °，∴PF=PE，∴四边形 PECF 为正方形，∵ ∠ BPF+∠ QPF=90°，∠ BPF+ ∠ BPE=90 °，∴ ∠ BPE=∠ QPF，∴Rt△ PQF≌ Rt△PBE，∴PB=PQ ．本题考察了正方形，角均分线的性质，以及全等三角形判断与性质．本题综合性较强，注意数形结评论：合思想．16．如图，已知四边形 ABCD 是正方形，分别过 A 、 C 两点作 l1∥ l2，作 BM ⊥ l1于 M ， DN⊥ l 1于 N ，直线 MB 、 ND 分别交 l2于 Q、 P．求证：四边形 PQMN 是正方形．考点：正方形的判断与性质．专题：证明题；压轴题．剖析：可由 Rt△ ABM ≌Rt△ DAN ， AM=DN同理可得 AN=NP ，所以 MN=PN ，从而可得其为正方形．解答：证明： l1∥ l2， BM ⊥ l 1， DN ⊥ l2，∴ ∠ QMN= ∠P=∠ N=90 °，∴四边形 PQMN 为矩形，∵AB=AD ，∠ M= ∠ N=90 °∠ADN+ ∠ NAD=90 °，∠ NAD+∠BAM=90 °，∴∠ADN= ∠BAM ，又∵ AD=BA ，∴Rt△ ABM ≌ Rt△DAN （ AAS ），∴AM=DN同理 AN=DP ，∴AM+AN=DN+DP ，即 MN=PN ．∴四边形 PQMN 是正方形．评论：本题考察了矩形的判断和性质、全等三角形的判断和性质以及正方形的判断，解题的重点是娴熟掌握各样几何图形的性质和判断方法．17．在正方形 ABCD 各边前一次截取AE=BF=CG=DH ，连结 EF，FG，GH ，HE．试问四边形EFGH 是不是正方形？考点：正方形的判断与性质．剖析：依据正方形的性质可得 AB=BC=CD=AD，∠ A= ∠ B= ∠C=∠D ，而后求出 BE=CF=DG=AH ，再利用“边角边”证明△AHE 和△ BEF 和△ CFG 和△ DGH 全等，依据全等三角形对应边相等可得EF=FG=GH=EH ，全等三角形对应角相等可得∠ AHE= ∠ BEF= ∠ CFG= ∠ DGH ，再求出∠ EFG=∠ FGH= ∠ GHE= ∠ FEH=90 °，从而获得四边形EFGH 是正方形．解答：解：四边形 EFGH 是正方形．原因以下：∵四边形 ABCD 是正方形，∴AB=BC=CD=AD ，∠ A= ∠ B=∠ C= ∠D ，∵AE=BF=CG=DH ，∴AB ﹣ AE=BC ﹣ BF=CD ﹣CG=AD ﹣ DH ，即 BE=CF=DG=AH ，∴△ AHE ≌ △ BEF≌ △CFG≌ △DGH ，∴EF=FG=GH=EH ，∠ AHE= ∠ BEF= ∠ CFG= ∠ DGH ，∴∠ EFG= ∠ FGH= ∠ GHE= ∠ FEH=90 °，∴四边形 EFGH 是正方形．评论：本题考察了正方形的判断与性质，全等三角形的判断与性质，熟记各性质并求出被截取的四个小直角三角形全等是解题的重点．18．如图，四边形 ABCD 是正方形，点 P 是 BC 上随意一点， DE⊥ AP 于点 E， BF ⊥ AP 于点 F，CH ⊥ DE 于点 H， BF 的延伸线交 CH 于点 G．（1）求证： AF ﹣ BF=EF ；（2）四边形 EFGH 是什么四边形？并证明；考点：正方形的判断与性质；全等三角形的判断与性质；剖析：（1）利用全等三角形的判断第一得出△ AED≌△ BFA，从而得出AE=BF ，即可证明结论；（2）第一得出四边形 EFGH 是矩形，再利用△AED ≌△ BFA ，同理可得：△ AED ≌ △ DHC ，从而得出 EF=EH ，即可得出答案；解答：（1）证明：∵ DE⊥ AP 于点 E， BF⊥ AP 于点 F， CH ⊥DE 于点 H，∴ ∠ AFB= ∠AED= ∠DHC=90 °，∴ ∠ ADE+ ∠ DAE=90 °，又∵ ∠ DAE+ ∠ BAF=90 °，∴∠ADE= ∠BAF ，在△AED 和△ BFA 中，，∴△AED ≌△BFA，∴AE=BF ，∴AF ﹣ AE=EF ，即 AF ﹣ BF=EF ；（ 2）证明：∵ ∠ AFB= ∠AED= ∠DHC=90 °，∴四边形 EFGH 是矩形，∵ △ AED ≌ △ BFA ，同理可得：△ AED≌ △ DHC，∴△AED ≌△BFA≌ △DHC，∴DH=AE=BF ， AF=DE=CH ，∴DE﹣ DH=AF ﹣ AE ，∴EF=EH ，∴矩形 EFGH 是正方形；19．如图，△ ABC 中，∠C=90 °，∠ BAC 、∠ ABC 的均分线订交于点 D，DE⊥ BC ，DF⊥ AC ，垂足分别为 E、F．问四边形 CFDE 是正方形吗？请说明原因．考点：正方形的判断；角均分线的性质．剖析：第一利用垂直的定义证得四边形该四边形是正方形．解答：证明：∵ ∠C=90 °， DE ⊥BC ∴四边形 DECF 为矩形，∵ ∠ A 、∠ B 的均分线交于点D，于点CFDE 是矩形，而后利用角均分线的性质获得E， DF⊥ AC 于点 F，DE=DF ，从而判断∴DF=DE ，∴四边形 CFDE 是正方形．评论：本题主要考察了角均分线的性质，三角形的切圆与心，解题的重点是利用正方形的判断方法证得四边形 CFDE 是正方形．20．如图，在△ABC 中，∠BAC=90 °，AB=AC ，点 D 是 BC 的中点， DE ⊥AB ，DF⊥ AC 垂足分别为E，F．求证：四边形 DEAF 是正方形．考点：正方形的判断；全等三角形的判断与性质．专题：证明题．剖析：由题意先证明□AEDF 是矩形，再依据两角及其一角的对边对应相等来证组对边相等的矩形证明□AEDF 是正方形．解答：证明：∵DE⊥AB ，DF⊥AC△ BDE ≌ △ CDF，依占有一∴ ∠ AED=90 °，∠ AFD=90 °∵ ∠ BAC=90 °∴ ∠ EDF=90 °∴ □AEDF 是矩形在△BDE 和△ CDF 中∵ AB=AC∴ ∠ ABC= ∠ ACB∵DE⊥ AB ， DF⊥ AC∴ ∠ DEB= ∠DFC又∵D 是 BC 的中点∴BD=DC∴△ BDE ≌△ CDF∴DE=DF∴□AEDF 是正方形评论：本题考察的是正方形的判断方法，考察了矩形、全等三角形等基础知识的灵巧运用，鉴别一个四边形是正方形主假如依据正方形的定义及其性质．。

正方形练习题(含答案)

正方形知识点一：正方形的定义：有一组邻边相等且有一个角是直角的平行四边形叫做正方形。

知识点二：正方形的性质：1.正方形的四个角都是直角，四条边都相等；2.正方形的对角线相等，并且互相垂直平分，每条对角线平分一组对角；3.正方形既是轴对称图形也是中心对称图形。

知识点三：正方形的判定方法：1.正方形的定义：有一组邻边相等且有一个角是直角的平行四边形叫做正方形。

2.有一组邻边相等的矩形是正方形；3.有一个角是直角的菱形是正方形.练习题：1.菱形、矩形、正方形都具有的性质是（ C ）A ．对角线相等且互相平分B ．对角线相等且互相垂直平分C ．对角线互相平分D ．四条边相等，四个角相等2.如图, E 、F 分别是正方形ABCD 的边CD 、AD 上的点，且CE ＝DF ，AE 、BF 相交于点O ，下列结论①AE ＝BF ；②AE ⊥BF ；③AO ＝OE ；④AOB DEOF S S ∆=四边形中，错误的有（ A ） A ．1个 B ．2个 C ．3个 D ．4个3.如图，E 是正方形ABCD 内一点，如果△ABE 为等边三角形，那么∠DCE= 15 度． 4.如图，E 是正方形ABCD 的边BC 延长线上一点，且CE=AC ，AE 交CD 于点F ，则∠E= 22.5 度．5.如图，若P 是边长1的正方形ABCD 内一点且S △ABP =0.4，则S △DCP = 0.1 ．分析：过P 作EF ，使EF ∥BC ，则EF ⊥CD ，EF ⊥AB ，∴S △ABP =错误!未找到引用源。

AB•EP ，S △CDP =错误!未找到引用源。

CD•PF ，根据S △ABP +S △CDP =错误!未找到引用源。

6.如图，在菱形ABCD 中，∠BAD=80°，AB 的垂直平分线交对角线AC 于点F ，E 为垂足，连接DF ，则∠CDF 的度数= 60 度．7.如图，在边长为2的正方形ABCD 中，M 为边AD 的中点，延长MD 至点E ，使ME ＝MC ，以DE 为边作正方形DEFG ，点G 在边CD 上，则DG 的长为 5－18.如图，E F G H ，，，分别为正方形ABCD 的边AB ，BC ，CD ，DA 上的点，且13AE BF CG DH AB ====，则图中阴影部分的面积与正方形ABCD 的面积之比为 2/5 9.如图，菱形ABCD 中，∠B ＝60°，AB ＝2，E 、F 分别是BC 、CD 的中点，连接AE 、EF 、AF ，则△AEF 周长为 3310.如图，已知P 是正方形ABCD 对角线BD 上一点，且BP = BC ，则∠ACP 度数是 22.5度．11.已知正方形ABCD 的边长为1，连接AC ，BD ，CE 平分∠ACD 交BD 于点E ，则DE ＝ 2－ 1 .11.如图，点E 是正方形ABCD 的边AB 上任意一点，过点D 作DF DE ⊥交BC 的延长线于点F ．求证：DE DF =．证明：∵四边形ABCD 是正方形，∴ AD=CD ,∠A=∠DCF=900又∵DF ⊥DE ，∴∠1+∠3=∠2+∠3∴∠1=∠2在Rt △DAE 和Rt △DCE 中，∠1=∠2，AD=CD ，∠A=∠DCF∴Rt △DAE ≅Rt △DCE (ASA) ∴DE=DF ．第2题第3题第4题第5题第6题12.如图，已知平行四边形ABCD 中，对角线AC BD ，交于点O ，E 是BD 延长线上的点，且ACE △是等边三角形．（1）求证：四边形ABCD 是菱形；（2）若2AED EAD ∠=∠，求证：四边形ABCD 是正方形．证明：（1）四边形ABCD 是平行四边形，AO CO ∴=．又ACE Q △是等边三角形，EO AC ∴⊥，即DB AC ⊥． ∴平行四边形ABCD 是菱形；（2）ACE Q △是等边三角形，60AEC ∴∠=o ． EO AC ⊥，1302AEO AEC ∴∠=∠=o ．2AED EAD ∠=∠，15EAD ∴∠=o ．45ADO EAD AED ∴∠=∠+∠=o ．四边形ABCD 是菱形，290ADC ADO ∴∠=∠=o ，∴四边形ABCD 是正方形．13.如图，ABCD 是正方形，AE ∥DB ，BE ＝BD ，BE 交AD 于F ，试说明：ΔDEF 是腰三角形。

正方形性质与判定练习(含答案)

C． 2
D． 5 1
18．如图，正方形 ABCD 中，AD 5，点 E 、F 是正方形 ABCD 内的两点，且 AE FC 4 ，
BE DF 3，则以 EF 为直径的圆的面积为 ( )
A． 1 2
B． 3 5
C． 3 4
D．
19．如图，在平面直角坐标系中，正方形 A1B1C1D1 、D1E1E2B2 、A2 B2C2 D2 、D2 E3E4 B3 、A3B3C3D3 ，
D．16
21．如图，在正方形 ABCD 中，对角线 AC ，BD 相交于点 O ，E ，F 分别在 OD ，OC 上，
且 DE CF ，连接 DF ， AE ， AE 的延长线交 DF 于点 M ，则下列四个结论中正确结论的个数是 ( )
① AE DF ；
② AM DF ；
③ DAE CDF ；
．
38．如图，正方形 ABCD 中， AB 12 ，点 E 在边 CD 上，CD 3DE ．将 ADE 沿 AE 对折
至 AFE ，延长 EF 交边 BC 于点 G ，连接 AG ，CF ．则下列结论正确的是
．
① ABG AFG ； ② BG GC ；
为
．
31．如图，RtABC 中，C 90 ，AC 2 ，BC 1 ，以斜边为一边向右上方作正方形 ABDE ，
连接 CD ，则 CD 的长为
．
32．如图，将正方形 OABC 放在平面直角坐标系中， O 是坐标原点，点 A 的坐标是 (2,3) ，
则 C 点坐标是
．
33．如图，在平面直角坐标系中，点 A 的坐标是 (0,3) ，点 B 的坐标是 (4,0) ，以 AB 为边
正方形性质与判定练习
1．如果要证明平行四边形 ABCD 为正方形，那么我们需要在四边形 ABCD 是平行四边形的基础上，进一步证明 ( )

考点17 正方形的性质及判定(解析版)

考点17：正方形性质及判定1.（丽水）在正方形ABCD 的边AB 、BC 、CD 、DA 上分别任意取点E 、F 、G 、H ．这样得到的四边形EFGH 中，是正方形的有（）A ．1个B ．2个C ．4个D ．无穷多个【答案】D ；【解析】在正方形四边上任意取点E 、F 、G 、H ，AH ＝DG ＝CF ＝BE ，能证明四边形EFGH 为正方形，则说明可以得到无穷个正方形．2.（南湖区一模）将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD ，转动这个四边形，使它形状改变．当∠B=90°时（如图甲），测得对角线BD的长为2．当∠B=60°时（如图乙），则对角线BD 的长为（）A. 2B. 3C. 2D. 5【答案】B ；【解析】解：如图甲，∵AB=BC=CD=DA ，∠B=90°，∴四边形ABCD 是正方形，连接BD ，则AB 2+AD 2=BD 2，∴AB=AD=1，如图乙，∠B=60°，连接BD ，真题回顾第一步小题夯基础∴△ABD 为等腰三角形，∴AB=AD=1，∴BD=3故选B ．3. （绍兴）如图，正方形ABCD 的边长为2，点E 在AB 边上．四边形EFGB 也为正方形，设△AFC 的面积为S ，则 ( )A ．S ＝2B ．S ＝2.4C ．S ＝4D ．S 与BE 长度有关【答案】A ；【解析】设正方形EFGB 的边长是a ，则S ＝ABC CFG AFGB S S S +-△△梯形＝×（a ＋2）×a ＋ ×2×2－×（a ＋2）×a ＝2.4. （毕节市）如图，正方形ABCD 的边长为9，将正方形折叠，使顶点D 落在BC 边上的点E 处，折痕为GH ．若BE ：EC=2：1，则线段CH 的长是（）A ．3B ．4C ．5D ．6【答案】B【解析】由题意设CH=xcm ，则DH=EH=（9﹣x ）cm ，∵BE ：EC=2：1，∴CE=31BC=3cm ∴在Rt △ECH 中，EH 2=EC 2+CH 2，即（9﹣x ）2=32+x 2，解得：x=4，即CH=4cm ．5. 如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为1S ，2S ，则12S S +的值为( )A.16B.17C.18D.19【答案】B ；【解析】设正方形2S 的边长为x ，根据等腰直角三角形的性质知，AC ＝2x ，2x CD =，∴AC ＝2CD ，CD ＝623=.EC ＝22，28S=，∵1S 的边长为3，1S 的面积为3×3＝9，∴12S S +＝8＋9＝17．1. （陕西）如图，在正方形ABCD 中，连接BD ，点O 是BD 的中点，若M 、N 是边AD 上的两点，连接MO 、NO ，并分别延长交边BC 于两点M ′、N ′，则图中的全等三角形共有（）A ．2对B ．3对C ．4对D ．5对模拟预测【答案】C ．【解析】∵四边形ABCD 是正方形，∴AB=CD=CB=AD ，∠A=∠C=∠ABC=∠ADC=90°，AD ∥BC ，在△ABD 和△BCD 中，⎪⎩⎪⎨⎧=∠=∠=CD AD C A BC AB ，∴△ABD ≌△BCD ，∵AD ∥BC ，∴∠MDO=∠M ′BO ，在△MOD 和△M ′OB 中，⎪⎩⎪⎨⎧==∠∠=∠'''BM DM OB M MOD BO M MDO ， ∴△MDO ≌△M ′BO ，同理可证△NOD ≌△N ′OB ，∴△MON ≌△M ′ON ′，∴全等三角形一共有4对．故选C ．2. （漳州一模）正方形具有而菱形不一定具有的性质是（）A. 四条边相等B. 对角线互相垂直平分C. 对角线平分一组对角D. 对角线相等【答案】D ；【解析】正方形的性质：正方形的四条边相等，四个角都是直角，对角线互相垂直平分且相等，并且每一条对角线平分一组对角；菱形的性质：菱形的四条边相等，对角线互相垂直平分，并且每一条对角线平分一组对角；因此正方形具有而菱形不一定具有的性质是：对角线相等；故选：D ．3. 如图，正方形ABCD 的边长为4cm ，则图中阴影部分的面积为( )2cm ．A.6B.8C.16D.不能确定【答案】B ；【解析】阴影部分面积为正方形面积的一半.4. 顺次连结对角线互相垂直的四边形各边的中点，所得的四边形是 ( )A. 矩形B. 菱形C. 正方形D. 梯形【答案】A5.如图，在边长为2的正方形ABCD 中，M 为边AD 的中点，延长MD 至点E ，使ME ＝MC ，以DE 为边作正方形DEFG ，点G 在边CD 上，则DG 的长为（）A ．31- B.35- C.51+ D. 51-【答案】D ；【解析】利用勾股定理求出CM 5ME 的长，有DM ＝DE ，所以可以求出DE 51，进而得到DG 的长．6.如图，正方形ABCD 中，对角线AC ，BD 相交于点O ，则图中的等腰三角形有（）A ．4个B ．6个C ．8个D ．10个【答案】C7. 如图，四边形ABCD 中，AD ＝DC ，∠ADC ＝∠ABC ＝90°，DE ⊥AB ，若四边形ABCD 面积为16，则DE 的长为（）A ．3B ．2C ．4D ．8【答案】C ；【解析】如图，过点D 作BC 的垂线，交BC 的延长线于F ，利用互余关系可得∠A ＝∠FCD ，又∠AED ＝∠F ＝90°，AD ＝DC ，利用AAS 可以判断△ADE ≌△CDF ，∴DE ＝DF ，ABCD S 四边形＝S 正方形DEBF ＝16，DE ＝4．。