MATLAB 有限元计算程序4
Matlab 有限元法计算分析程序编写

6) M函数文件 与命令文件不同,函数文件从外界只能看到传给它的输入 量和送出来的计算结果,而内部运作是看不见的。它的特 点是 (1)从形式上看,与命令文件不同,函数文件的第一行总是以 “function”引导的“函数申明行”。 (2)从运行上看,与命令文件运行不同,每当函数文件运行, MATLAB就会专门为它开辟临时工作空间,所有中间变量 都存放在函数工作空间中,当执行完文件最后一条指令和 遇到return时,就结束该函数文件的执行,同时该临时函数 工作空间及其所有的中间变量立即被清除。 (3)对于函数文件中的变量,如果不作特别说明,默认为临时 局部变量,这些临时变量就存放在函数的临时工作空间中, 当函数结束时他们被立即清除。与之相对应的是全局变量, 他们是通过global指令进行特别申明,这些全局变量可被几 个不同的函数共享。 • 函数文件的编辑也可用MATLAB editor/debugger。
有限元法计算分析程序编写
结构参数输入,包括
1)节点坐标值 2)单元类型以及连接信息 3)各单元的弹性模量、截面积(厚度)等 4)荷载形式以及作用位置、作用方向、荷载值 5)约束条件 6)输出信息
m j
对节点和单元分别编号 每个节点的自由度根据 节点号计算得到
i
y
o
x
计算结构的刚度矩阵
对各单元作如下的计算 a)计算单元刚度矩阵 b)计算坐标转换矩阵(如果需要) c)作坐标转换计算(如果需要) d)按自由度顺序叠加到总刚度矩阵中
MATLAB的使用方法
1) 最简单的计算器使用法 求[12+2×(7-4)]÷32的算术运算结果 (1)用键盘在MATLAB指令窗中输入一下内容 (12+2*(7-4))/3^2 (2)在上述表达式输入完成后,按【Enter】键,该指令被执行 (3)在指令执行后,MATLAB指令窗中将显示一下内容 ans = 2 [说明] 加 + 减 乘 * 除 / 或 \ (这两个符号对于数组有不同的含义) 幂 ^ “ans”是answer的缩写,其含义是运算答案,它是MATLAB的一个默 认变量
有限元MATLAB
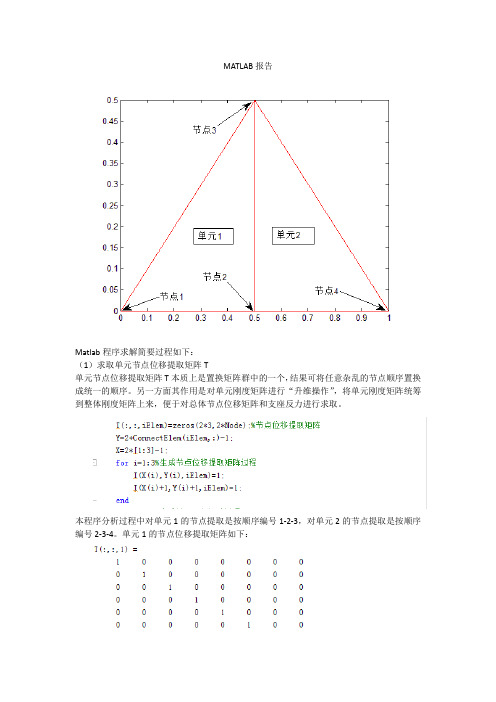
MATLAB报告Matlab程序求解简要过程如下:(1)求取单元节点位移提取矩阵T单元节点位移提取矩阵T本质上是置换矩阵群中的一个,结果可将任意杂乱的节点顺序置换成统一的顺序。
另一方面其作用是对单元刚度矩阵进行“升维操作”,将单元刚度矩阵统筹到整体刚度矩阵上来,便于对总体节点位移矩阵和支座反力进行求取。
本程序分析过程中对单元1的节点提取是按顺序编号1-2-3,对单元2的节点提取是按顺序编号2-3-4。
单元1的节点位移提取矩阵如下:单元2的节点位移提取矩阵如下:(2)求取单元几何矩阵B单元1的节点按编号顺序1-2-3分别进行对几何函数矩阵或算子矩阵的bi逆时针操作,对ci顺时针操作;单元2的节点按编号顺序2-3-4分别进行对几何函数矩阵的bi顺时针操作,对ci逆时针操作.在MATLAB程序中通过mod()取模函数来达到对节点的顺时针或逆时针循环操作。
单元1的几何矩阵如下:单元2的几何矩阵如下:(3)求取应力矩阵S单元应力矩阵满足S=D*B,其中D为弹性矩阵,B为单元几何矩阵各单元的弹性矩阵如下:单元1的应力矩阵如下:单元2的应力矩阵如下:(4)求取单元刚度矩阵K单元刚度矩阵K满足公式K=B’*D*B*t*A,其中t为平面板的厚度,A为单元面积,且单元刚度矩阵为对称矩阵。
单元1的刚度矩阵如下:单元2的刚度矩阵如下:(5)求取总体刚度矩阵sumKK由上述步骤求得的单元刚度矩阵K利用单元虚功原理和刚度方程可导出K’*δ=f,其中δ为单元节点位移列阵,f为单元等效节点载荷列阵,为了能将各个单元刚度方程统一到一个整体,便需要步骤(1)的单元节点提取矩阵对单元刚度方程进行变换,将两个变换结果联立便得到总体刚度方程,其中也可得到总体刚度矩阵sumKK,且总体刚度矩阵可由sumKK=Σ T’*K*T 求得。
总体刚度矩阵如下:(6)求取总体节点位移矩阵和支座反力利用上述步骤提到的总体刚度方程sumKK*delta=F,其中delta为总体节点位移矩阵,F为总体等效节点载荷列阵。
平面梁单元MATLAB有限元程序

平面梁单元MATLAB有限元程序function []=beam2n()clear allclose allclearclose%------------------------ BEAM2 ---------------------------disp('========================================'); disp(' PROGRAM BEAM2 '); disp(' Beam Bending Analysis '); disp(' T.R.Chandrupatla and A.D.Belegundu '); disp('========================================');InputData;Bandwidth;Stiffness;ModifyForBC;BandSolver;ReactionCalc;Output;%------------------------ function InputData ---------------------------function [] = InputData();global NN NE NM NDIM NEN NDNglobal ND NL NCH NPR NMPC NBWglobal X NOC F AREA MAT SMI Sglobal PM NU U MPC BT REACTglobal CNSTglobal TITLE FILE1 FILE2global LINP LOUTglobal NQdisp(blanks(1));FILE1 = input('Input Data File Name ','s'); LINP = fopen(FILE1,'r');FILE2 = input('Output Data File Name ','s'); LOUT = fopen(FILE2,'w');DUMMY = fgets(LINP);TITLE = fgets(LINP);DUMMY = fgets(LINP);TMP = str2num(fgets(LINP));[NN, NE, NM, NDIM, NEN, NDN] =deal(TMP(1),TMP(2),TMP(3),TMP(4),TMP(5),TMP(6));NQ = NDN * NN;DUMMY = fgets(LINP);TMP = str2num(fgets(LINP));[ND, NL, NMPC]= deal(TMP(1),TMP(2),TMP(3));NPR=1; % E%----- Coordinates -----DUMMY = fgets(LINP);for I=1:NNTMP = str2num(fgets(LINP));[N, X(N,:)]=deal(TMP(1),TMP(2:1+NDIM)); end%----- Connectivity -----DUMMY = fgets(LINP);for I=1:NETMP = str2num(fgets(LINP));[N,NOC(N,:), MAT(N), SMI(N)] = ...deal(TMP(1),TMP(2:1+NEN), TMP(2+NEN), TMP(3+NEN));end%----- Specified Displacements ----- DUMMY = fgets(LINP); for I=1:NDTMP = str2num(fgets(LINP));[NU(I,:),U(I,:)] = deal(TMP(1), TMP(2)); end%----- Component Loads -----DUMMY = fgets(LINP);F = zeros(NQ,1);for I=1:NLTMP = str2num(fgets(LINP));[N,F(N)]=deal(TMP(1),TMP(2)); end%----- Material Properties ----- DUMMY = fgets(LINP);for I=1:NMTMP = str2num(fgets(LINP));[N, PM(N,:)] = deal(TMP(1), TMP(2:NPR+1));end%----- Multi-point Constraints B1*Qi+B2*Qj=B0if NMPC > 0DUMMY = fgets(LINP);for I=1:NMPCTMP = str2num(fgets(LINP));[BT(I,1), MPC(I,1), BT(I,2), MPC(I,2), BT(I,3)] = ...deal(TMP(1),TMP(2),TMP(3),TMP(4),TMP(5));endendfclose(LINP);%------------------------ function Bandwidth ---------------------------function []=Bandwidth();global NN NE NM NDIM NEN NDNglobal ND NL NCH NPR NMPC NBW global X NOC F AREA MAT SMI S global PM NU U MPC BT STRESS REACT global CNSTglobal TITLE FILE1 FILE2global LINP LOUT%----- Bandwidth Evaluation ----- NBW = 0;for N=1:NENABS = NDN*(abs(NOC(N, 1) - NOC(N, 2)) + 1);if (NBW < NABS)NBW = NABS;endendfor I=1:NMPCNABS = abs(MPC(I, 1) - MPC(I, 2)) + 1;if (NBW < NABS)NBW = NABS;endenddisp(sprintf('Bandwidth = %d', NBW));%------------------------ function Stiffness ---------------------------function []=Stiffness();global NN NE NM NDIM NEN NDNglobal ND NL NCH NPR NMPC NBW global X NOC F AREA MAT SMI S global PM NU U MPC BT REACTglobal CNSTglobal NQ%----- Global Stiffness Matrix S = zeros(NQ,NBW);for N = 1:NEdisp(sprintf('Forming Stiffness Matrix of Element %d', N));%-------- Element Stiffness and Temperature Load -----N1 = NOC(N, 1);N2 = NOC(N, 2);M = MAT(N);EL = abs(X(N1) - X(N2));EIL = PM(M, 1) * SMI(N) / EL^3;SE(1, 1) = 12 * EIL;SE(1, 2) = EIL * 6 * EL;SE(1, 3) = -12 * EIL;SE(1, 4) = EIL * 6 * EL;SE(2, 1) = SE(1, 2);SE(2, 2) = EIL * 4 * EL * EL;SE(2, 3) = -EIL * 6 * EL;SE(2, 4) = EIL * 2 * EL * EL;SE(3, 1) = SE(1, 3);SE(3, 2) = SE(2, 3);SE(3, 3) = EIL * 12;SE(3, 4) = -EIL * 6 * EL;SE(4, 1) = SE(1, 4);SE(4, 2) = SE(2, 4);SE(4, 3) = SE(3, 4);SE(4, 4) = EIL * 4 * EL * EL;disp('.... Placing in Global Locations'); for II = 1:NENNRT = NDN * (NOC(N, II) - 1);for IT = 1:NDNNR = NRT + IT;I = NDN * (II - 1) + IT;for JJ = 1:NENNCT = NDN * (NOC(N, JJ) - 1);for JT = 1:NDNJ = NDN * (JJ - 1) + JT;NC = NCT + JT - NR + 1;if (NC > 0)S(NR, NC) = S(NR, NC) + SE(I, J);endendendendendend%------------------------ function ModifyForBC ---------------------------function []=ModifyForBC();global NN NE NM NDIM NEN NDNglobal ND NL NCH NPR NMPC NBWglobal X NOC F AREA MAT SMI Sglobal PM NU U MPC BT REACTglobal CNSTglobal NQ%----- Decide Penalty Parameter CNST ----- CNST = 0;for I = 1:NQif CNST < S(I, 1); CNST = S(I, 1); end endCNST = CNST * 10000;%----- Modify for Boundary Conditions ----- % --- Displacement BC ---for I = 1:NDN = NU(I);S(N, 1) = S(N, 1) + CNST;F(N) = F(N) + CNST * U(I);end%--- Multi-point Constraints ---for I = 1:NMPCI1 = MPC(I, 1);I2 = MPC(I, 2);S(I1, 1) = S(I1, 1) + CNST * BT(I, 1) * BT(I, 1);S(I2, 1) = S(I2, 1) + CNST * BT(I, 2) * BT(I, 2);IR = I1;if IR > I2; IR = I2; endIC = abs(I2 - I1) + 1;S(IR, IC) = S(IR, IC) + CNST * BT(I, 1) * BT(I, 2);F(I1) = F(I1) + CNST * BT(I, 1) * BT(I, 3);F(I2) = F(I2) + CNST * BT(I, 2) * BT(I, 3); end%------------------------ function BandSolver ---------------------------function []=BandSolver();global NN NE NM NDIM NEN NDNglobal ND NL NCH NPR NMPC NBWglobal X NOC F AREA MAT SMI Sglobal PM NU U MPC BT REACTglobal CNSTglobal NQ%----- Equation Solving using Band Solver ----- disp('Solving using Band Solver(bansol.m)');[F] = bansol(NQ,NBW,S,F);%------------------------ function ReactionCalc ---------------------------function []=ReactionCalc();global NN NE NM NDIM NEN NDNglobal ND NL NCH NPR NMPC NBWglobal X NOC F AREA MAT SMI Sglobal PM NU U MPC BT REACTglobal CNSTfor I = 1:NDN = NU(I);REACT(I) = CNST * (U(I) - F(N));end%------------------------ function Output ---------------------------function []=Output();global NN NE NM NDIM NEN NDNglobal ND NL NCH NPR NMPC NBWglobal X NOC F AREA MAT SMI Sglobal PM NU U MPC BT REACTglobal CNSTglobal TITLE FILE1 FILE2global LINP LOUTdisp(sprintf('Output for Input Data from file %s\n',FILE1)); fprintf(LOUT,'Output for Input Data from file %s\n',FILE1);disp(TITLE);fprintf(LOUT,'%s\n',TITLE);disp(' Node# X-Displ Rotation');fprintf(LOUT,' Node# X-Displ Rotation\n'); I=[1:NN]';% print a matrixdisp(sprintf(' %4d %15.4E %15.4E\n',[I,F(2*I-1),F(2*I)]')); fprintf(LOUT,' %4d %15.4E %15.4E\n',[I,F(2*I-1),F(2*I)]');%----- Reaction Calculation -----disp(sprintf(' DOF# Reaction'));fprintf(LOUT,' DOF# Reaction\n');for I = 1:NDN = NU(I);R = CNST * (U(I) - F(N));disp(sprintf(' %4d %15.4E',N,REACT(I)));fprintf(LOUT,' %4d %15.4E\n',N,REACT(I)); endfclose(LOUT);disp(sprintf('The Results are available in the text file %s', FILE2));。
现行三角元有限元MATLAB源程序

傻瓜运行程序,全自动过程首先建立一个数据输入的M文件:syms o;p=1;E=210e6;%输入弹性模量;NU=0.3;%输入泊松比;t=0.025;%输入材料厚度;x=[0,0.5;0.25,0.5;0.125,0.375;0,0.25;0.25,0.25;0.125,0.125;0,0;0.25,0;0.375,0.125;0.5,0.25;0.5,0]; %输入每个结点的坐标值;ff=[1,3,2;1,4,3;3,5,2;3,4,5;4,6,5;4,7,6;5,6,8;6,7,8;5,8,9;5,9,10;8,11,9;9,11,10];%输入每个单元的信息;F=[o;o;0;0;0;0;o;o;0;-12.5;0;0;o;o;0;0;0;0;0;0;0;0];%输入总体结点载荷矢量,其中未知量用符号变量'o'表示;U=[0;0;o;o;o;o;0;0;o;o;o;o;0;0;o;o;o;o;o;o;o;o];%输入总体结点位移矢量,其中未知量用符号变量'o'表示;然后建立一个运行程序的M文件:K=zeros(2*size(x),2*size(x));%生成初始整体刚度矩阵;sigma=zeros(size(ff),3);%生成初始单元应力矩阵;s=zeros(size(ff),3);%生成初始单元主应力应力及主应力方向角矩阵;for i=1:size(ff)%i表示第i个单元;kk=LinearTriangleElementStiffness(E,NU,t,x(ff(i,1),1),x(ff(i,1),2),x(ff(i,2),1),x(ff(i,2),2),x(ff(i,3), 1),x(ff(i,3),2),p);%计算每个单元的单元刚度矩阵;K=LinearTriangleAssemble(K,kk,ff(i,1),ff(i,2),ff(i,3));%集成整体刚度矩阵;end%根据每个单元的单元刚度矩阵,循环集成整体刚度矩阵;k=K;for i=1:size(U)if U(i)==0F(i)=0;k(i,:)=0;k(:,i)=0;k(i,i)=1;elseendend%将未知的结点载荷及其对应的总体刚度的行和列定义为0,并定义对应的i行i列为1;U=k\F;F=K*U;%计算总体结点载荷矢量for i=1:size(ff)l=ff(i,1);m=ff(i,2);n=ff(i,3);uu=[U(2*l-1);U(2*l);U(2*m-1);U(2*m);U(2*n-1);U(2*n)];%建立单元结点位移矢量;ss=LinearTriangleElementStresses(E,NU,x(ff(i,1),1),x(ff(i,1),2),x(ff(i,2),1),x(ff(i,2),2),x(ff(i,3),1), x(ff(i,3),2),p,uu);%计算单元应力;sss=LinearTriangleElementPStresses(ss);%计算单元主应力和主应力方向角;sigma(i,1)=double(ss(1,1));sigma(i,2)=double(ss(2,1));sigma(i,3)=double(ss(3,1));%将每个单元应力赋值到单元应力矩阵sigma中;s(i,1)=double(sss(1,1));s(i,2)=double(sss(2,1));s(i,3)=double(sss(3,1));%将每个单元主应力和主应力方向角赋值到单元主应力应力及主应力方向角矩阵s中;endU=double(U);F=double(F);uu=double(uu);K%以下程序输出结点信息到‘节点信息.txt’中;fid=fopen('C:\Documents and Settings\LXY\桌面\节点信息.txt','wt');fprintf(fid,'\n%s\n','-------------------------------------------------------节点信息----------------------------------------------------------');fprintf(fid,'\n%s\n',' 节点号x坐标y坐标x位移y位移水平支反力垂直支反力');for i=1:size(x)fprintf(fid,'%10d%18.8f%18.8f%18.8f%18.8f%18.8f%18.8f\n',i,x(i,1),x(i,2),U(2*(i-1)+1),U(2*(i-1)+2),F(2*(i-1)+1),F(2*(i-1)+2));endfclose(fid);%以下程序输出单元信息到‘单元信息.txt’中;fid=fopen('C:\Documents and Settings\LXY\桌面\单元信息.txt','wt');fprintf(fid,'\n%s\n','---------------------------------------------------------------单元信息----------------------------------------------------------------------');fprintf(fid,'\n%s\n',' 单元号结点1 结点2 结点3 x方向拉应力y方向拉应力剪应力主应力方向角'); for i=1:size(ff)fprintf(fid,'%10d%18.8f%18.8f%18.8f%18.8f%18.8f%18.8f%18.8f\n',i,ff(i,1),ff(i,2),ff(i,3),sigma( i,1),sigma(i,2),sigma(i,3),s(i,3));endfclose(fid);。
有限元MATLAB源程序

MATLAB源程序(把程序部分复制进入MATLAB,直接运行就可得到结果。
)第1章假定P=-100,L=10m,E=3e11,梁截面是正方形其宽度为h=5e-2m,根据上述数据编制MATLAB程序如下:clearsyms x L EIw='c1'*sin(pi*x/(2*L))+'c2'*sin(3*pi*x/(2*L))+'c3'*sin(5*pi*x/(2*L))+'c4'*sin(7*pi*x/(2*L));kk=int(EI/2*(diff(w,x,2))^2-'P'*w,0,L);[c1,c2,c3,c4]=solve(diff(kk,'c1'),diff(kk,'c2'),diff(kk,'c3'),diff(kk,'c4'),'c1,c2,c3,c4')[c1,c2,c3,c4]根据运行结果得出的[c1,c2,c,3,c4]接着进行下列编程:P=-100;L=10;E=3e11;h=5e-3;I=h^4/12EI=E*I;x=0:L;c1=64*P*L^4/EI/pi^5c2=64/243*P*L^4/EI/pi^5c3=64/3125*P*L^4/EI/pi^5c4=64/16807*P*L^4/EI/pi^5w=c1*sin(pi*x/(2*L))+c2*sin(3*pi*x/(2*L))+c3*sin(5*pi*x/(2*L))+c4*sin(7*pi*x/(2*L))w=1e-4*wplot(x,w,'k','linewidth',2)gridxlabel('L')ylabel('w')y=P*L^3/(3*EI)[y w(10)]假定P=-100,L=10m,E=3e11,梁截面是正方形其宽度为h=5e-2m,根据上述数据编制MATLAB程序如下:clearsyms x EI Lw='c1'*x^2+'c2'*x^3+'c3'*x^4+'c4'*x^5kk=int(EI/2*(diff(w,x,2))^2-'P'*w,0,L)[c1,c2,c3,c4]=solve(diff(kk,'c1'),diff(kk,'c2'),diff(kk,'c3'),diff(kk,'c4'),’c1,c2,c3,c4’)根据运行结果得出的[c1,c2,c,3,c4]接着进行下列编程:P=-100;L=10;EI=1.56e5;x=0:L;c1=1/4*L^2*P/EIc2=-1/6*L*P/EIc3=1/24*P/EIc4=0w=c1*x.^2+c2*x.^3+c3*x.^4+c4*x.^5plot(x,w,'k')gridxlabel('L')ylabel('w')y=P*L^3/(3*EI)[y w(11)]以形函数(Shape Function)为试探函数形函数f1代表左侧节点的位移函数,f2代表右侧节点的位移函数,f3代表左侧节点的斜率函数,f4代表右侧节点的斜率函数。
有限元方法步骤-MATLAB的简略使用指南

第1章引言这个简短的引言分为两部分,第一部分是对有限元方法步骤的概括介绍,第二部分是MATLAB的简略使用指南。
1.1 有限元方法的步骤有许多关于有限元分析的优秀教材,比如在参考文献[1-18]中列出的那些书目。
因此,本书不准备对有限元理论或有限元方程进行详细地阐述和推导。
每一章只总结概括主要的方程,这些章节都附有示例来说明这些方程。
此外,全书只讨论线弹性结构力学的问题。
有限元方法用于解决工程问题的数值计算过程。
本书假定所有的行为都是线弹性行为。
虽然本书的问题都与结构工程相关,但有限元方法也同样适用于工程的其他领域。
本书中使用有限元方法解决问题共包括6个步骤。
对有限元分析的6个步骤阐述如下:(1) 离散化域——这个步骤包括将域分解成单元和节点。
对于像桁架和刚架这类离散系统,已经离散化,这一步就不需要了。
此处获得的结果应该已经是精确的。
然而,对于连续系统,如板壳,这一步就变得至关重要,因为它只能得到近似的结果。
因此解决方案的精确度取决于所使用的离散化方法。
本书中,我们将手动完成这一步(对连续系统)。
(2) 写出单元刚度矩阵(element stiffness matrices)——写出域内每个单元的单元刚度矩阵。
在本书中,这个步骤通过MATLAB实现。
(3) 集成整体刚度矩阵(global stiffness matrices)——这一步用直接刚度法(direct stiffness approach)实现。
在本书中,该步骤借助于MATLAB实现。
(4) 引入边界条件——诸如支座(supports)、外加载荷(applied loads)和位移(displacements)等。
本书中手动实现这一步骤。
(5) 解方程——这一步骤分解整体刚度矩阵并用高斯消去法求解方程组。
在本书中,在用高斯消去法实现求解部分的时候需要手动分解矩阵。
(6) 后处理——得到额外的信息,如支反力、单元节点力和单元应力。
本书中这一步骤通过MATLAB实现。
梁单元有限元计算程序(matlab)

DOF(3)=3*i;
DOF(4)=3*j-2;
DOF(5)=3*j-1;
DOF(6)=3*j;
for n1=1:6
for n2=1:6
KK(DOF(n1),DOF(n2))=KK(DOF(n1),DOF(n2))+k(n1,n2);
end
end
z=KK;
%将该稀疏矩阵中元素放入整体刚度矩阵中的相应位置,
%使得整体刚度矩阵仍然为下三角阵形式的稀疏矩阵;
z=zபைடு நூலகம்triu(z,1)'-triu(z,1);
z=sparse(z);
[nm,nmn]=size(cod);
%输入各单元的角度
alpha=input('please input the angle (degree) of each element in order:');
%输入节点坐标,每一行代表该节点的坐标,按节点编号顺序排列,即用分号将节点分开
%用逗号将每个单元内的节点分开,按单元编号顺序排列
%如[1,2;2,3;1,3]表示三个杆中的节点编号分别为(1,2)、(2,3)、(1,3)
cod=input('please input the node of each element in order:');
%计算单元个数,nm为单元个数
%用逗号将每个节点的坐标分开,按单元编号顺序排列
%如[1,2;2,3;1,3]表示三个节点的横纵坐标分别为(1,2)、(2,3)、(1,3)
con=input('please input the coordinates (m) of each node in order:');
四节点八节点四边形单元悬臂梁的matlab有限元编程-概述说明以及解释

四节点八节点四边形单元悬臂梁的matlab有限元编程-概述说明以及解释1.引言1.1 概述有限元方法是工程领域中常用的数值计算方法,它将一个连续的物理问题通过有限个节点和元素进行离散化,将问题转化为一个由代数方程组组成的离散问题。
悬臂梁是结构工程中常见的一种结构形式,而四节点、八节点以及四边形单元则是悬臂梁有限元分析中常用的元素类型。
本文将介绍四节点、八节点和四边形单元在悬臂梁有限元分析中的应用,以及如何利用Matlab编程实现这些元素的有限元分析。
通过对这些元素的理论分析和编程实现,读者将能够深入了解悬臂梁有限元分析的原理和方法,从而在工程实践中应用这些知识,提高结构设计的准确性和效率。
1.2 文章结构本文主要分为引言、正文和结论三个部分。
在引言部分中,将对四节点八节点四边形单元悬臂梁的matlab有限元编程进行简要概述,介绍文章的结构和目的。
正文部分将详细介绍四节点悬臂梁单元、八节点悬臂梁单元和四边形单元的理论基础和matlab有限元编程步骤。
最后,在结论部分将对整个文章进行总结,分析编程结果,并展望未来的研究方向。
通过以上结构,读者能够全面了解有限元悬臂梁单元的理论知识和编程实现方法,为相关研究提供参考。
1.3 目的本文旨在通过对四节点悬臂梁单元、八节点悬臂梁单元和四边形单元进行有限元分析,探讨不同单元在悬臂梁结构中的应用及性能表现。
具体目的包括:1. 深入了解四节点悬臂梁单元、八节点悬臂梁单元和四边形单元的原理和计算方法;2. 利用Matlab编程实现这些有限元分析模型,探讨其编程实现过程和计算结果;3. 对比不同单元在悬臂梁结构中的应用效果,分析其计算结果的准确性和计算效率;4. 对于有限元分析在工程实践中的应用提供参考和指导,为悬臂梁结构设计和分析提供理论支持。
2.正文2.1 四节点悬臂梁单元四节点悬臂梁单元是有限元方法中常用的元素之一,用于模拟悬臂梁结构的力学行为。
在本节中,我们将介绍四节点悬臂梁单元的基本原理和相关的matlab有限元编程。
matlab桁架结构有限元计算

matlab桁架结构有限元计算
在MATLAB中,进行桁架结构的有限元计算可以按照以下步
骤进行:
1. 定义节点和单元:根据实际问题的几何形状和拓扑关系,定义桁架结构的节点和单元。
节点是桁架结构的连接点,单元是连接节点的构件。
2. 定义材料属性和截面属性:根据实际问题的材料和截面要求,定义桁架结构的材料属性和截面属性。
材料属性包括弹性模量和泊松比等,截面属性包括截面面积和惯性矩等。
3. 组装刚度矩阵:根据节点和单元的几何形状和材料属性,计算每个单元的局部刚度矩阵,然后根据单元和节点的连接关系,将局部刚度矩阵组装成整体刚度矩阵。
4. 施加边界条件:根据实际问题的边界条件,将边界节点的位移固定为零,或施加位移或力的约束条件。
5. 求解位移和反力:使用求解线性方程组的方法,求解位移和反力。
可以使用MATLAB中的线性方程组求解函数(如'\''运
算符)来计算。
6. 计算应力和应变:根据位移和节点的几何形状,计算节点上的应变,然后根据材料属性,计算节点上的应力。
以上步骤涵盖了桁架结构的有限元计算的基本流程,具体实现时需要根据实际问题进行适当的调整和扩展。
MATLAB有限元分析与应用可编辑全文

%
modulus of elasticity E, cross-sectional
%
area A, and length L. The size of the
%
element stiffness matrix is 2 x 2.
y = [E*A/L -E*A/L ; -E*A/L E*A/L];
2019/11/28
y = k * u/A;
2019/11/28
18
§3-2 线性杆元
3、实例计算分析应用
如图所示二线性杆元结构,假定E=210MPa,A=0.003m^2,P=10kN, 节点3的右位移为0.002m。
求:系统的整体刚度矩阵; 节点2的位移; 节点1、3的支反力; 每个杆件的应力
解:
步骤1:离散化域
%LinearBarElementStresses This function returns the element nodal
%
stress vector given the element stiffness
%
matrix k, the element nodal displacement
%
vector u, and the cross-sectional area A.
? ?
?
? ?
?
10??
630000 ????0.002?? ?? F3 ??
线性杆元也是总体和局部坐标一致的一维有限单元,用线性函数描述
每个线性杆元有两个节点(node)
? EA
单刚矩阵为:k
?
? ?
L
???
EA L
?
EA L
? ? ?
有限元的MATLAB解法

有限元的MATLAB解法1.打开MATLAB。
2.输入“pdetool”再回车,会跳出PDE Toolbox的窗口(PDE意为偏微分方程,是partial differential equations的缩写),需要的话可点击Options菜单下Grid命令,打开栅格。
3.完成平面几何模型:在PDE Toolbox的窗口中,点击工具栏下的矩形几何模型进行制作模型,可画矩形R,椭圆E,圆C,然后在Set formula栏进行编辑并(如双脊波导R1+R2+R3改为RI-R2-R3,设定a、b、s/a、d/b的值从而方便下步设定坐标)用算术运算符将图形对象名称连接起来,若还需要,可进行储存,形成M文件。
4.用左键双击矩形进行坐标设置:将大的矩形left和bottom都设为0,width是矩形波导的X轴的长度,height是矩形波导的y轴的长度,以大的矩形左下角点为原点坐标为参考设置其他矩形坐标。
5.进行边界设置:点击“Boundary”中的“Boundary Mode”,再点击“Boundary”中的“Specify Boundary Conditions”,选择符合的边界条件,Neumann为诺曼条件,Dirichlet为狄利克雷条件,边界颜色显示为红色。
6.进入PDE模式:点击"PDE"菜单下“PDE Mode”命令,进入PDE 模式,单击“PDE Specification”,设置方程类型,“Elliptic”为椭圆型,“Parabolic”为抛物型,“Hyperbolic”为双曲型,“Eigenmodes”为特征值问题。
7.对模型进行剖分:点击“Mesh”中“Initialize Mesh”进行初次剖分,若要剖的更细,再点击“Refine Mesh”进行网格加密。
8.进行计算:点击“Solve”中“Solve PDE”,解偏微分方程并显示图形解,u值即为Hz或者Ez。
9.单击“Plot”菜单下“Parameters”选项,打开“Plot Selection”对话框。
matlab 有限元法

matlab 有限元法
Matlab中的有限元法(Finite Element Method,FEM)是一种常用的数值分析方法,用于模拟和解决包括结构力学、热传导、流体力学等问题。
它将连续介质划分为离散的有限单元,通过建立数学模型和使用近似解法来求解。
下面是一般步骤来使用Matlab进行有限元分析:
1. 剖分网格:将要模拟的连续介质划分为离散的有限单元(如三角形或四边形元素)。
2. 建立数学模型:根据具体问题的物理方程或导引方程,建立线性或非线性的方程模型。
3. 施加边界条件:确定并施加边界条件,如位移、载荷或约束等。
4. 组装刚度矩阵和载荷向量(Assembly):通过元素刚度矩阵的组装,得到总系统的刚度矩阵和载荷向量。
5. 求解方程:通过求解总系统的线性方程组,得到未知位移或其他需要的结果。
6. 后处理结果:对求解结果进行可视化或分析,如绘制应力分布、位移云图、应变曲线等。
Matlab提供了丰富的工具箱和函数,用于各种结构和物理问题的有限元分析,例如Partial Differential Equation Toolbox(部分微分方程工具箱)和Structural Analysis T oolbox(结构分析工具箱),其中包含了常用的有限元分析函数和设置界面。
另外,Matlab还支持用户自定义编程,允许使用脚本或函
数来实现特定的有限元算法。
总之,通过Matlab的有限元分析工具和编程能力,可以方便地进行各种结构和物理问题的数值分析和模拟。
计算力学(有限元)matlab编程大作业(空间网架)

逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0:1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0:1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0:1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0:1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0:1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0:0 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0:1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0:0 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0:1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0:1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0:1 逐一输入第 i 个节点和其他节点的连接情况,若连接,输入 1,否则输入 0,令和自身连接情况为 0:0 输入结构约束总数:11 按照编号逐一输入结构约束编号(先输入节点号) ) :1 输入约束节点对应的位移号(输入范围:1~3) ) :1 按照编号逐一输入结构约束编号(先输入节点号) ) :1 输入约束节点对应的位移号(输入范围:1~3) ) :2 按照编号逐一输入结构约束编号(先输入节点号) ) :1 输入约束节点对应的位移号(输入范围:1~3) ) :3 按照编号逐一输入结构约束编号(先输入节点号) ) :3 输入约束节点对应的位移号(输入范围:1~3) ) :1 按照编号逐一输入结构约束编号(先输入节点号) ) :3 输入约束节点对应的位移号(输入范围:1~3) ) :2 按照编号逐一输入结构约束编号(先输入节点号) ) :3 输入约束节点对应的位移号(输入范围:1~3) ) :3 按照编号逐一输入结构约束编号(先输入节点号) ) :4 输入约束节点对应的位移号(输入范围:1~3) ) :1 按照编号逐一输入结构约束编号(先输入节点号) ) :4 输入约束节点对应的位移号(输入范围:1~3) ) :2 按照编号逐一输入结构约束编号(先输入节点号) ) :5 输入约束节点对应的位移号(输入范围:1~3) ) :1 按照编号逐一输入结构约束编号(先输入节点号) ) :5 输入约束节点对应的位移号(输入范围:1~3) ) :2 按照编号逐一输入结构约束编号(先输入节点号) ) :5 输入约束节点对应的位移号(输入范围:1~3) ) :3 输入施加在结构上的总的力的个数:3 按照编号逐一输入力作用节点编号(先输入节点号) ) :2 逐一输入力对应的向量中的坐标值:0 逐一输入力对应的向量中的坐标值:0 逐一输入力对应的向量中的坐标值:-1 输入力的大小:1000 按照编号逐一输入力作用节点编号(先输入节点号) ) :2 逐一输入力对应的向量中的坐标值:0 逐一输入力对应的向量中的坐标值:1
有限元的matlab编程

本程序的网架位移求解函数附在主程序后面,主程序运行时调用该函数。
完整ppt
14
几何建模 定义荷载
用自定义输入
加下划线的为单元编号
完整ppt
5
形成等效荷载列阵
f=[0;0;0;a;0;0;0;a;0;0;0;a;0;0;0;a;0;0;0;a];%每个节点两个自由度,a 为之前输入的节点力
集成总刚:
获取单元两端节点坐标
xi = Node( Element( ie, 1 ), 1 ) ;%ie为单元号,以下相同 yi = Node( Element( ie, 1 ), 2 ) ; xj = Node( Element( ie, 2 ), 1 ) ; yj = Node( Element( ie, 2 ), 2 ) ;
节点号:',num2str(Element(ie,2)),' 轴力:',num2str(nodef(1))] ) ;
完整ppt
12
end
例二:网架
完整ppt
13
思路分析
几点说明
网架是由多根杆件按照一定的网格形式通过节点连结而成的空间结构。构成 网架的基本单元有三角锥,三棱体,正方体,截头四角锥等。鉴于网架的形 式较多,本程序提供一种通用的网架输入方法,但录入较为繁琐,同时提供 一种正放四角锥网架的简易输入方法作为典型。
有限元编程示例
完整ppt
1
例一:桁架
题目描述:
如下图所示的平面桁架,杆件长度、弹性模量、截 面积以及所受节点力P的大小可以自行定义。求节 点位移及杆件轴力。
matlab 有限元 编程

MATLAB 是一种高级编程语言和交互式环境,常用于数值计算、数据分析、算法开发、数据可视化以及应用开发等。
在有限元分析(FEA)中,MATLAB 可以用来编写和运行有限元程序。
以下是一个简单的 MATLAB 有限元分析编程示例:这个例子假设你正在解决一个一维拉普拉斯方程,其形式为 -d^2u/dx^2 = f,在区间 [0, 1] 上。
```matlab% 参数定义L = 1; % 长度h = 0.01; % 步长N = L/h; % 元素数量x = linspace(0, L, N+1); % x 向量% 创建有限元网格nodes = x(1:N+1);elements = [nodes(2:end-1) nodes(1:end-1) nodes(2:end)]; % 定义载荷向量 ff = sin(pi*x);% 定义刚度矩阵 A 和载荷向量 FA = zeros(N, N);F = zeros(N, 1);for i = 1:Nfor j = 1:i-1A(i, j) = A(j, i) = h^2/(6*(x(i)-x(j))^2);endF(i) = -f(i)*h/2;end% 使用 MATLAB 的线性方程求解器u = A\F;% 绘制结果plot(x, u);xlabel('x');ylabel('u');title('有限元解');```这个代码首先定义了问题的参数,然后创建了一个有限元网格。
然后,它定义了刚度矩阵 A 和载荷向量 F。
最后,它使用 MATLAB 的线性方程求解器来求解方程,并绘制结果。
请注意,这只是一个非常简单的例子。
在实际的有限元分析中,问题可能会更复杂,并且需要更多的编程工作。
有限元的MATLAB解法

有限元的MATLAB解法1.打开MATLAB。
2.输入“pdetool”再回车,会跳出PDE Toolbox的窗口(PDE意为偏微分方程,是partial differential equations的缩写),需要的话可点击Options菜单下Grid命令,打开栅格。
3.完成平面几何模型:在PDE Toolbox的窗口中,点击工具栏下的矩形几何模型进行制作模型,可画矩形R,椭圆E,圆C,然后在Set formula栏进行编辑并(如双脊波导R1+R2+R3改为RI-R2-R3,设定a、b、s/a、d/b的值从而方便下步设定坐标)用算术运算符将图形对象名称连接起来,若还需要,可进行储存,形成M文件。
4.用左键双击矩形进行坐标设置:将大的矩形left和bottom都设为0,width是矩形波导的X轴的长度,height是矩形波导的y轴的长度,以大的矩形左下角点为原点坐标为参考设置其他矩形坐标。
5.进行边界设置:点击“Boundary”中的“Boundary Mode”,再点击“Boundary”中的“Specify Boundary Conditions”,选择符合的边界条件,Neumann为诺曼条件,Dirichlet为狄利克雷条件,边界颜色显示为红色。
6.进入PDE模式:点击"PDE"菜单下“PDE Mode”命令,进入PDE 模式,单击“PDE Specification”,设置方程类型,“Elliptic”为椭圆型,“Parabolic”为抛物型,“Hyperbolic”为双曲型,“Eigenmodes”为特征值问题。
7.对模型进行剖分:点击“Mesh”中“Initialize Mesh”进行初次剖分,若要剖的更细,再点击“Refine Mesh”进行网格加密。
8.进行计算:点击“Solve”中“Solve PDE”,解偏微分方程并显示图形解,u值即为Hz或者Ez。
9.单击“Plot”菜单下“Parameters”选项,打开“Plot Selection”对话框。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n = gBC1(ibc, 1 ) ;
d = gBC1(ibc, 2 ) ;
m = (n-1)*3 + d ;
gEigVector(m,:) = gBC1(ibc,3) ;
end
m = T*m*transpose(T) ;
return
function AssembleGlobalMatrix( ie, ke, me )
% 把单元刚度和质量矩阵集成到整体刚度矩阵
% 2. 处理约束条件,修改整体刚度矩阵
% 3. 求解特征值问题
global gNode gElement gMaterial gBC1 gK gM gEigValue gEigVector
% step1. 定义整体刚度矩阵和节点力向量
[node_number,dummy] = size( gNode ) ;
function exam8_1
% 本程序为第八章的第一个算例,采用平面梁单元计算两铰抛物线拱的自由振动特性
% 输入参数: 无
% 输出结果: 前3阶振动频率及其相应的振型
% 定义全局变量
% gNode ------ 节点坐标
% gElement --- 单元定义
xj = gNode( gElement( ie, 2 ), 1 ) ;
yj = gNode( gElement( ie, 2 ), 2 ) ;
L = ( (xj-xi)^2 + (yj-yi)^2 )^(1/2) ;
m = ro*A*L/420*[140 0 0 70 0 0
L = ( (xj-xi)^2 + (yj-yi)^2 )^(1/2) ;
k = [ E*A/L 0 0 -E*A/L 0 0
0 12*E*I/L^3 6*E*I/L^2 0 -12*E*I/L^3 6*E*I/L^2
n = gBC1(ibc, 1 ) ;
d = gBC1(ibc, 2 ) ;
m = (n-1)*3 + d ;
gK(:,m) = zeros( node_number*3, 1 ) ;
gK(m,:) = zeros( 1, node_number*3 ) ;
gK = sparse( node_number * 3, node_number * 3 ) ;
gM = sparse( node_number * 3, node_number * 3 ) ;
% step2. 计算单元刚度和质量矩阵,并集成到整体刚度和质量矩阵中
[element_number,dummy] = size( gElement ) ;
% gNode ------- 节点定义
% gElement ---- 单元定义
% gMaterial --- 材料定义,包括弹性模量,梁的截面积和梁的抗弯惯性矩
% gBC --------- 约束条件
global gNode gElement gMaterial gBC1
gM(j,i) = gM(i,j) ;
end
end
% step4.2 计算前6阶特征值和特征向量
[gEigVector, gEigValue] = eigs(gK, gM, 3, 'SM' ) ;
% step4.3 修改特征向量中受约束的自由度
A = gMaterial( gElement(ie, 3), 3 ) ;
ro = gMaterial( gElement(ie, 3 ), 4 ) ;
xi = gNode( gElement( ie, 1 ), 1 ) ;
yi = gNode( gElement( ie, 1 ), 2 ) ;
k = zeros( 6, 6 ) ;
E = gMaterial( gElement(ie, 3), 1 ) ;
I = gMaterial( gElement(ie, 3), 2 ) ;
A = gMaterial( gElement(ie, 3), 3 ) ;
DisplayResults ; % 显示计算结果
return ;
function PlaneFrameModel
% 定义平面杆系的有限元模型
% 输入参数:
% 无
% 返回值:
% 无
% 说明:
% 该函数定义平面杆系的有限元模型数据:
% step3. 处理第一类约束条件,修改刚度矩阵和质量矩阵。(采用划行划列法)
[bc1_number,dummy] = size( gBC1 ) ;
w2max = max( diag(gK)./diag(gM) ) ;
for ibc=1:1:bc1_number
for ie=1:1:element_number
k = StiffnessMatrix( ie ) ;
m = MassMatrix( ie ) ;
AssembleGlobalMatrix( ie, k, m ) ;
end
a = f/L^2*4 ;
y = - a * x.^2 ; % 结点的y坐标
% 节点坐标
gNode = [x' y'] ;
% 单元定义
gElement = zeros( n, 3 ) ;
for i=1:n
return
function k = StiffnessMatrix( ie )
% 计算单元刚度矩阵
% 输入参数:
% ie ------- 单元号
% 返回值:
% k ---- 整体坐标系下的刚度矩阵
global gNode gElement gMaterial
0 156 22*L 0 54 -13*L
0 22*L 4*L^2 0 13*L -3*L^2
70 0 0 140 0 0
n+1, 2, 0.0] ;
return
function SolveModel
% 求解有限元模型
% 输入参数:
% 无
% 返回值:
% 无
% 说明:
% 该函数求解有限元模型,过程如下
% 1. 计算单元的刚度和质量矩阵,集成整体刚度和质量矩阵
0 54 1L -3*L^2 0 -22*L 4*L^2 ] ;
T = TransformMatrix( ie ) ;
% 第一类约束条件
% 节点号 自由度号 约束值
gBC1 = [ 1, 1, 0.0
1, 2, 0.0
n+1, 1, 0.0
% gMaterial -- 材料性质
% gBC1 ------- 第一类约束条件
% gK --------- 整体刚度矩阵
% gDelta ----- 整体节点坐标
PlaneFrameModel ; % 定义有限元模型
SolveModel ; % 求解有限元模型
end
% step4. 求解特征值问题
% step4.1为了使刚度矩阵和质量矩阵对称(在计算时可能引入舍入误差)
for i=1:node_number*3
for j=i:node_number*3
gK(j,i) = gK(i,j) ;
gElement( i, : ) = [ i, i+1, 1 ] ;
end
% 材料性质
% 弹性模量 抗弯惯性矩 截面积 密度
gMaterial = [2.06e11, 0.03622, 0.0815, 1435.2/0.0815]; % 材料 1
0 6*E*I/L^2 4*E*I/L 0 -6*E*I/L^2 2*E*I/L
-E*A/L 0 0 E*A/L 0 0
0 -12*E*I/L^3 -6*E*I/L^2 0 12*E*I/L^3 -6*E*I/L^2
gK(m,m) = 1;
gM(:,m) = zeros( node_number*3, 1 ) ;
gM(m,:) = zeros( 1, node_number*3 ) ;
gM(m,m) = gK(m,m)/w2max/1e10 ;
% 计算单元质量矩阵
% 输入参数:
% ie ------- 单元号
% 返回值:
% m ---- 整体坐标系下的质量矩阵
global gNode gElement gMaterial
m = zeros( 6, 6 ) ;
E = gMaterial( gElement(ie, 3), 1 ) ;
0 6*E*I/L^2 2*E*I/L 0 -6*E*I/L^2 4*E*I/L] ;
T = TransformMatrix( ie ) ;
k = T*k*transpose(T) ;
return
function m = MassMatrix( ie )
xi = gNode( gElement( ie, 1 ), 1 ) ;
yi = gNode( gElement( ie, 1 ), 2 ) ;
xj = gNode( gElement( ie, 2 ), 1 ) ;
yj = gNode( gElement( ie, 2 ), 2 ) ;
% 给定抛物线拱的几何特征
L = 60 ; % 计算跨径
f = 7.5 ; % 计算矢高
n = 100 ; % 单元数目
x = -L/2:L/n:L/2 ; % 结点的x坐标
