华南理工大学电路课件第二章
合集下载
电工学电工技术第二章ppt课件

U R1 R2 (3)等效电阻的倒数等于各电阻倒数之和;
11 1
–
R R1 R2
(4)并联电阻上电流的分配与电阻成反比。
I
两电阻并联时的分流公式:
+ U –
R
I1
R2 R1 R2
I
应用:
I2
R1 R1 R2
I
分流、调节电流等。(最广泛)
编辑版pppt
章目录 上一页 下一页 返回 退出
例1:图示为变阻器调节负载电阻RL两端电压的 分压电路。 RL = 50 ,U = 220 V 。中间环节是变 阻器,其规格是 100 、3 A。今把它平分为四段,
R2
R =R1+R2
(4)串联电阻上电压的分配与电阻成正比。
I
+ U –
两电阻串联时的分压公式:
R
应U1用:R1R1R2 U
U2
R2 R1 R2
U
降压、限流、调节电压等。 编辑版pppt
章目录 上一页 下一页 返回 退出
2.1.2 电阻的并联
I
特点:
+ I1 I2
(1)各电阻联接在两个公共的结点之间; (2)各电阻两端的电压相同;
(2) 若所选回路中包含恒流源支路, 则因恒流源两
端的电压未知,所以,有一个恒流源就出现一个未
知电压,因此,在此种情况下不可少列KVL方程。
编辑版pppt
章目录 上一页 下一页 返回 退出
例3:试求各支路电流。
a
c
+ 42V –
编辑版pppt
章目录 上一页 下一页 返回 退出
解: (4) 在 e 点:
U 220
IeaRea
电工学PPT第二章

Z R2 X 2 X arctan R
阻抗角
R Z cos X Z sin
基本元件R、L、C的阻抗
RLC串联电路的阻抗特性:
Z R j ( X L X C ) R jX
(1) 当 X L X C 时,X 0, 0
阻抗角
相量模型 电压、电流用相量表示;
Z R 2 ( X L X C )2
X L XC arctan R
U U u Z = Z () I I i
阻抗表示了电路的电 压与电流之间的大小 和相位的关系:
阻抗模值
Z=R jX
电阻 电抗
Z Z
UC
UR
UL
I
电路呈电容性, 此时总电压滞后电流。
U L UC
UL
UR
I
U
UC
+
u
-
uR
uL
R I jX L I jX C I
[ R j ( X L X C )] I
定义电路的阻抗:
def
C
uc
用相量法分析R、L、C串联电路
+
I R
jX L
U
-
U R
U L jX C
Uc
U Z =R j ( X L X C ) I 阻抗模值 Z Z
RLC串联电路UI
UL
UC U L UC UC
UL
相量图
U
UR
I
电路呈电感性; 此时总电压超前电流。
(2) 当 X L X C 时,X 0, 0
阻抗角
R Z cos X Z sin
基本元件R、L、C的阻抗
RLC串联电路的阻抗特性:
Z R j ( X L X C ) R jX
(1) 当 X L X C 时,X 0, 0
阻抗角
相量模型 电压、电流用相量表示;
Z R 2 ( X L X C )2
X L XC arctan R
U U u Z = Z () I I i
阻抗表示了电路的电 压与电流之间的大小 和相位的关系:
阻抗模值
Z=R jX
电阻 电抗
Z Z
UC
UR
UL
I
电路呈电容性, 此时总电压滞后电流。
U L UC
UL
UR
I
U
UC
+
u
-
uR
uL
R I jX L I jX C I
[ R j ( X L X C )] I
定义电路的阻抗:
def
C
uc
用相量法分析R、L、C串联电路
+
I R
jX L
U
-
U R
U L jX C
Uc
U Z =R j ( X L X C ) I 阻抗模值 Z Z
RLC串联电路UI
UL
UC U L UC UC
UL
相量图
U
UR
I
电路呈电感性; 此时总电压超前电流。
(2) 当 X L X C 时,X 0, 0
电工学课件-第2章电路的瞬态分析

高等教育出版社
第
2
章 根据 KVL ,由换路后
电 路 的 瞬
的电路列出回路方程式 RiC+uC = 0
+ U0
-
态
分 析
而
iC
=
C
duC dt
aS b
得 RC ddutC+uC = 0
uC的通解为
t
uC = Ae RC
24
R
+ iC uC C -
将 t=0,uC= U0 代入,得
A = U0
高等教育出版社
分 作用下产生的电压和电流统称为响应。响应有 析 时又称输入。
按照产生响应原因的不同,响应可分为:
(1) 零输入响应 电路在无外部激励的情况下,仅由内部储能 元件中所储存的能量引起的响应。
高等教育出版社
5
第
2
章 (2) 零状态响应
电 路
在换路时储能元件未储存能量的情况下,由
的
激励所引起的响应。
瞬 态
L iL
+
+ uL - +
iC
US
uC C
IS S
瞬 后的电路求得:
-
-
+ -
态
uR
分 析
iR ( 0 ) = iL ( 0 ) = 1 A
R iR
uR ( 0 ) = RiR ( 0 ) = ( 5 1) V = 5 V
iC ( 0 ) = IS + iL ( 0 ) = ( 5 + 1) A = 6 A
U0
瞬 态
= 10 103 20 10-6 s-
分
= 0.2 s
析
根据
t
uC = US+ ( U0- US ) e
电工学ppt(第七版)第二章:电路的分析方法

1 A 3
返回
(b)
2.2电阻星形连结与三角形连结的等效变换
1
Y-变换
1
2
3
A
2
3
A
C
D B
Rd
C D
Rd
B
I
r2
+
1 r1 r3 3
Y- 等效变换
I
R12
+
1 R31
-
2
-
2
R23
3
r1 r2 R12 // R31 R23
原
则
r2 r3 R23 // R12 R31
1 1 1 1 E5 VB VA R R R R R5 4 5 3 3
其中未知数仅有:VA、VB 两个。
结点电位法列方程的规律
以A结点为例:
方程左边:未知节点的电
位乘上聚集在该节点上所 有支路电导的总和(称自 电导)减去相邻节点的电 E1 位乘以与未知节点共有支 路上的电导(称互电导)。
U Is I R0
我们可以用下面的图来表示这一伏安 关系 等效电流源
a I U R0
R0
E Is R0
+
a
负载两端的电压
和电流没有发生
RL
U
改变。
b
当R0 》 L 或R0=∞,这样的电源被称为理想电 R 流源,也称恒流源。理想电流源的特点是无论负载 或外电路如何变化,电流源输出的电流不变。
1 R7 3
R 3456 2
(d)
(c)
U 由(d)图可知 R 15 , I 2A R
由(b) 图可知
I
3V
返回
(b)
2.2电阻星形连结与三角形连结的等效变换
1
Y-变换
1
2
3
A
2
3
A
C
D B
Rd
C D
Rd
B
I
r2
+
1 r1 r3 3
Y- 等效变换
I
R12
+
1 R31
-
2
-
2
R23
3
r1 r2 R12 // R31 R23
原
则
r2 r3 R23 // R12 R31
1 1 1 1 E5 VB VA R R R R R5 4 5 3 3
其中未知数仅有:VA、VB 两个。
结点电位法列方程的规律
以A结点为例:
方程左边:未知节点的电
位乘上聚集在该节点上所 有支路电导的总和(称自 电导)减去相邻节点的电 E1 位乘以与未知节点共有支 路上的电导(称互电导)。
U Is I R0
我们可以用下面的图来表示这一伏安 关系 等效电流源
a I U R0
R0
E Is R0
+
a
负载两端的电压
和电流没有发生
RL
U
改变。
b
当R0 》 L 或R0=∞,这样的电源被称为理想电 R 流源,也称恒流源。理想电流源的特点是无论负载 或外电路如何变化,电流源输出的电流不变。
1 R7 3
R 3456 2
(d)
(c)
U 由(d)图可知 R 15 , I 2A R
由(b) 图可知
I
3V
电路分析基础第二章ppt课件

第二章 电阻电路的分析
• 写成一般形式:
R11Il1+R12Il2+R13Il3=US11
安 徽 职
R21Il1+R22Il2+R23Il3=US22 R31Il1+R32Il2+R33Il3=US33
业
技 术
说明:
学 院
R11、R22、R33称为网孔的自电阻,分别是网孔1、2、 3的回路电阻之和,取正值; R11、R22、R33称为网孔的
术 学
各回路的KVL方程。
院
R1I1-US1+US2-R2I2=0
R2I2-US1+US2-R2I2=0
第二章 电阻电路的分析
设电路参数如下:
E1=140V,E2=90V,R1=20Ω,R2=5Ω,R3=6Ω,代入上
安
述方程,得
徽 职
I1+I2-I3=0
业
20I1+6I3=140
技 术
5I2+6I3=90
第二章 电阻电路的分析
例:一个10V电压表,其内阻为20KΩ,现将电压表量程
扩大为250V,应串联多大的电阻?
安 解:U=250V,U1=10V,
徽 职
Rg=20KΩ
业 技
则 U1:U=Rg:(R+Rg)
术
学
R48010 3
院
+
+
Rg G U1
-
-
U
+
R
U2
- -
第二章 电阻电路的分析
二、电阻的并联:
安
并按顺时针方向流动,。
徽
职
业 技
网孔1
术
R1iℓ1+ R4(iℓ1 –iℓ2 )+ R5(iℓ1 + iℓ3)= -uS1
电路分析大学教材第二章

感谢您的观看
THANKS
电路元件及其特性
总结词
电路元件包括电阻Biblioteka 电容、电感等,它们具有不同的特性, 如电阻限制电流、电容存储电荷、电感阻碍电流的变化。
详细描述
电阻是表示导体对电流阻碍作用的元件,其特性是电压与电 流成正比;电容是表示电场储能能力的元件,其特性是电流 与电压的变化率成正比;电感是表示磁场储能能力的元件, 其特性是电压与电流的变化率成正比。
04
一阶动态电路分析
一阶电路的微分方程
要点一
总结词
描述一阶电路中电压或电流随时间变化的数学模型。
要点二
详细描述
一阶电路的微分方程是描述电路中电压或电流随时间变化 的数学模型,通常表示为 dy/dt = f(y,t) 的形式,其中 y 代表电压或电流,t 代表时间,f(y,t) 是与 y 和 t 相关的函 数。
线性电阻电路的分析方法
基尔霍夫定律
基尔霍夫电流定律和基尔霍夫电 压定律是线性电阻电路的基本定 律,用于描述电路中电流和电压 的关系。
节点分析法
节点分析法是一种求解线性电阻 电路中电压和电流的方法,通过 列写节点电压方程来求解。
网孔分析法
网孔分析法是一种求解线性电阻 电路中电压和电流的方法,通过 列写网孔电流方程来求解。
电路分析大学教材第二章
目录
• 电路分析的基本概念 • 电路的等效变换 • 电路定理 • 一阶动态电路分析 • 二阶动态电路分析
01
电路分析的基本概念
电路的定义与组成
总结词
电路是由若干个元件按照一定的方式 连接而成的闭合回路,用于传输和转 换电能。
详细描述
电路由电源、负载、开关、导线等组 成,其中电源提供电能,负载消耗电 能,开关控制电路的通断,导线则用 于连接各元件。
电工技术的课件第二章

例 分析以下电路中应列几个电流方程?几个 电压方程?
I1
a
I2
E1
+R1 #1
-
I3
R2 #2 R3
#3
+ _ E2
b
(1-7)
I1
a
I2
E1
+R1 #1
-
I3
R2 #2 R3
#3
+ _ E2
b 基尔霍夫电流方程:
#1
结点a:I1I2 I3 #2
结点b: I3 I1I2 #3
基尔霍夫电压方程:
E1 I1R1 I3R3 E2 I2R2 I3R3 E1 E2 I1R1 I2R2
需补足 B -(N -1)个方程。
2. 独立回路的选择:
EU
#1 #2 #3 一般按网孔选择
4 解联立方程组
根据未知数的正负决定电流的实际方(向2-1。5)
.P46 例:求IG
解:
解得:
支路电流法的优缺点
优点:支路电流法是电路分析中最基本的 方法之一。只要根据基尔霍夫定律、
欧姆定律列方程,就能得出结果。 缺点:电路中支路数多时,所需方程的个
数较多,求解不方便。
a
支路数 B=4
b
须列4个方程式
(2-17)
2.1.3 结点电压法
结点电位的概念: 在电路中任选一结点,设其电 位为零(用 标记),此点称为 参考点。其它各结点对参考点的电 压,便是该结点的电位。记为: “VX”(注意:电位为单下标)。
(2-18)
结点电位法中的未知数:结点电位“VX”。
式中分母为各支路电阻倒数和,分子 为各有源支路中电动势除以电阻后求其代 数和。电动势方向指向未知结点,则该项 为正,反之为负。
电工学习第二章PPT课件

(1) 若uC(0)U00, 电容元件用恒压源代替, 其值等于U 0 ; 若uC(0)0,电容元件视为短路。
(2) 若 iL(0)I00, 电感元件用恒流源代替 , 其值等于I0 , 若iL(0)0, 电感元件视为开路。
总目录 章目录 返回 上一页 下一页
(3) 时间常数 的计算
原则: 要由换路后的电路结构和参数计算。
(同一电路中各物理量的 是一样的)
对于一阶RC电路 R0C
对于一阶RL电路
L R0
注意:
1) 对于简单的一阶电路 ,R0=R ;
2) 对于较复杂的一阶电路, R0为换路后的电路 除去电源和储能元件后,在储能元件两端所求得的
无源二端网络的等效电阻。
总目录 章目录 返回 上一页 下一页
例1:
t=0 S R1
总目录 章目录 返回 上一页 下一页
第3章 电路的暂态分析
重点: 1.换路定则; 2.一阶线性电路暂态分析的三要素法。
难点: 1.用换路定则求初始值和稳态值; 2.用一阶线性电路暂态分析的三要素法求解暂态 电路; 3.微分电路与积分电路的分析。
总目录 章目录 返回 上一页 下一页
3 .3 .3 RC电路的全响应
f () O
(d)f()0 t
总目录 章目录 返回 上一页 下一页
三要素法求解暂态过程的要点
(1) 求初始值、稳态值、时间常数; (2) 将求得的三要素结果代入暂态过程通用表达式; (3) 画出暂态电路电压、电流随时间变化的曲线。
(由初始值稳态值)
f(t)
终点 f ()
起点 f (0 )
O
0 .63 [f( 2)f(0) ]f(0)
结论1: 全响应 = 零输入响应 + 零状态响应
(2) 若 iL(0)I00, 电感元件用恒流源代替 , 其值等于I0 , 若iL(0)0, 电感元件视为开路。
总目录 章目录 返回 上一页 下一页
(3) 时间常数 的计算
原则: 要由换路后的电路结构和参数计算。
(同一电路中各物理量的 是一样的)
对于一阶RC电路 R0C
对于一阶RL电路
L R0
注意:
1) 对于简单的一阶电路 ,R0=R ;
2) 对于较复杂的一阶电路, R0为换路后的电路 除去电源和储能元件后,在储能元件两端所求得的
无源二端网络的等效电阻。
总目录 章目录 返回 上一页 下一页
例1:
t=0 S R1
总目录 章目录 返回 上一页 下一页
第3章 电路的暂态分析
重点: 1.换路定则; 2.一阶线性电路暂态分析的三要素法。
难点: 1.用换路定则求初始值和稳态值; 2.用一阶线性电路暂态分析的三要素法求解暂态 电路; 3.微分电路与积分电路的分析。
总目录 章目录 返回 上一页 下一页
3 .3 .3 RC电路的全响应
f () O
(d)f()0 t
总目录 章目录 返回 上一页 下一页
三要素法求解暂态过程的要点
(1) 求初始值、稳态值、时间常数; (2) 将求得的三要素结果代入暂态过程通用表达式; (3) 画出暂态电路电压、电流随时间变化的曲线。
(由初始值稳态值)
f(t)
终点 f ()
起点 f (0 )
O
0 .63 [f( 2)f(0) ]f(0)
结论1: 全响应 = 零输入响应 + 零状态响应
研究生入学考试华南理工考研电路
+ uC (0+)
–
i i u C(0+)= L(0+) C(0+)/R
=RISRIS =0
第20页/共76页
6-3 一阶电路的零输入响应
零输入响应(Zeroinput response ):
激励(电源)为零,由初始储能引起的响应。
一、 RC电路的零输入响应 (电容对电阻放电)
S(t=0) i
+
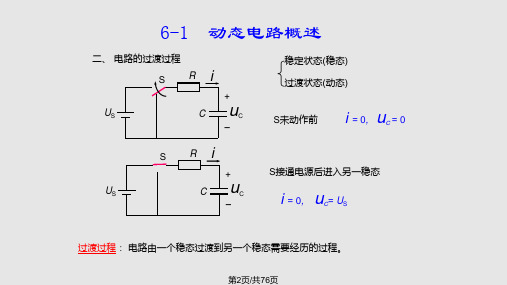
6-1 动态电路概述
二、 电路的过渡过程
S Ri
+
US
u C
C
–
稳定状态(稳态) 过渡状态(动态)
S未动作前
u i = 0, C = 0
S Ri
+
S接通电源后进入另一稳态
US
u C
C
–
u i = 0, C= US
过渡过程: 电路由一个稳态过渡到另一个稳态需要经历的过程。
第2页/共76页
6-1 动态电路概述
换路定则:
q q C (0+) = C (0) u u C (0+) = C (0)
L (0+)= L (0 )
i i L(0+)= L(0 )
(2) 换路定则是建立在能量不能突变的基础上。
WC
1 2
CuC2
WL
1 2
LiL2
第15页/共76页
6-2 初始条件的确定
三、电路初始条件的确定
例1.
t
令 =L/R RL电路的时间常数
RI0
3 5 过渡过程结束。
量纲:亨/欧=韦/安*欧=韦/伏=伏*秒/伏=秒
第26页/共76页
6-3 一阶电路的零输入响应
华南理工考研电路课件.ppt

uC U0 (1 t )e t
i C duC U0 te t dt L
uL
L di dt
U 0e
t (1
t)
非振荡放电临界阻尼
7.1 二阶电路的零输入响应
小结
R 2 L 过阻尼,非振荡放电 C
uc A1e p1t A2e p2t
R 2 L 临界阻尼,非振荡放电uc e t ( A1 A2 t)
LC
2
uC i
U0 U0
0L
sin( s in 0
0t t
2
)
uL
uC
0
U 0e t
sin( t
)
i C duC U 0 e t sin t
dt L
uL
L
di dt
0
U 0e
t
sin(
t
)
0
+
C
L
t
-
等幅振荡无阻尼
2RC
P 3 k (3 k)2 ( 1 )2 2RC 2RC RC
u1 Ae t sin(t )
1< k < 3 > 0 衰减振荡
k=3 =0
等幅振荡 u1 K sin(0t )
3< k < 5 < 0 增幅振荡
7.2 二阶电路的零状态响应和全响应
uC e t [A cos t B sin t]
duC e t [A cos t B sin t]
dt
e t [Asin t Bcos t]
电路基础第二章ppt课件

说明:
(1)任何R与 us并联的支路,对外电路不产生影响。
(2)任何R与 is串联的支路,对外电路不产生影响。
R
a
+a
R
us
+
us
a
is
a
is
b
-b
-
b
b
Chapter 2 2-4 受控源及其等效变换
一.受控源 1.定义:输出量受电路中某一部分电压或电流的控制,即 某一电压或电流控制的电源。 说明: (1)输出量是指电压(受控电压源)或电流(受控电流源)。 (2)一般在含受控源的电路中,并不明确标出两个端口, 但其输出量与控制量必须明确标出。 (3)线性受控源:控制量与受控量(输出量)的关系为一次 函数关系。
2
B
u2 u3
i 3
3
1 i'1
A
u'1
2
i'2
C
u'2 u'3
3 i'3
图中各对应电压、电流相等时,B电路与C电路等效。
即等效条件为: u1 u1 u2 u2 i1 i1 i2 i2
Chapter 2
1.Y 形联接:三个电阻一端连接为一点,另一端分别引出 三个端头。
1
i1
R1
R3
i3
3
R2 i2
b
解得: Rabui 84iixx 0.5
Chapter 2
例2-6 求Rab。
50Ω 0.2ua b
a
+
-+
0.01ua b
200Ω 100Ω
ua b
b-
250Ω
ai
+
2.2uab
电路课件第一二章总结
I 5
i 3
a
-u+
b
2 某支路电压电流取关联参考方向,求得电压为-4V, 电流为2A,则电压的实际方向与参考方向________, 电流的实际方向与参考方向________,该支路发出的 功率P=___W。
2020/4/30
例
•
•
•
I
26A 3Ω 1Ω
6Ω
8A
I = (26 – 8)×1/(1+1/3+1/6) =18×2/3 = 12A
D. 其输出电流与端电压有关; 端电压未必与电流方向一致
2、一个理想电压源,一个理想电流源和一个电阻相串联,
对外电路而言其等效电路为(
)
A.电压源 B.电流源 C.电阻 D不确定
2020/4/30
习题 +
U
1 电路如图所示,
-
(1)图(a)中以知U=5V,求I;
(2)图(b)中以知i=5e-tA,求u;
2020/4/30
有伴电源的等效变换
数值关系 参考方向
+
i+
uS_
u
RS
_
i
iS
+ RS u
_
2020/4/30
1、一个理想独立电流源的基本特性是: (
)
A. 其输出电流与端电压无关; 端电压可为任意值, 取决于外电路
B. 其输出电流与端电压有关; 端电压不为任何值, 取决于电流源
C. 其输出电流与端电压无关; 端电压必定与电流方向一致
R1
2020/4/30
•
•
•
例
1Ω
-9V +
6Ω
U
U = 3;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Rab R
Rab
uab i
R
返 回 上 页 下 页
2.4 电阻的Y形连接和形连 接的等效变换
1. 电阻的 、Y形连接
包含
1 R1 R2 R b R3 R4
三端 网络
a
1 R1
R12 2 R23
形网络
R31
3 R2
R3 3 Y形网络
返 回
2
上 页
下 页
,Y 网络的变形:
型电路 ( 型)
返 回 上 页
(2)
下 页
由式(2)解得:
i1Y
i2 Y
u12Y R 3 u31Y R2 R1 R2 R2 R3 R3 R1
u23Y R1 u12 Y R3 R1 R2 R2 R3 R3 R1
i1 =u12 /R12 – u31 /R31 (3) i2 =u23 /R23 – u12 /R12 (1) i3 =u31 /R31 – u23 /R23
变Y Y变
特例:若三个电阻相等(对称),则有
R12 R1
R = 3RY
R31
R3
外大内小
R2 R23
返 回
上 页
下 页
注意
①等效对外部(端钮以外)有效,对内不成立。
②等效电路与外部电路无关。 ③用于简化电路
返
1k 1k 1k 1k R
1/3k
1/3k 1/3k R 1k 1k
R1
+ – i2Y 2 + – 3
等效条件:
i1 =i1Y ,
i2 =i2Y ,
i3 =i3Y , u31 =u31Y
返 回 上 页 下 页
u12 =u12Y , u23 =u23Y ,
+ i1 u12 i2 – R12
1– u31 R31 i3
+ i1Y u12Y R2 – i2Y + 2 +
未变化的外电路A中的电压、电流和功率; (即对外等效,对内不等效) ③电路等效变换的目的: 化简电路,方便计算。
返 回
上 页
下 页
2.3 电阻的串联和并联
1.电阻串联
①电路特点 i R1 Rk Rn + u1 _ + u k _ + un _ + u
_
(a) 各电阻顺序连接,流过同一电流 (KCL); (b) 总电压等于各串联电阻的电压之和 (KVL)。
i3 Y
u31Y R2 u23Y R1 R1 R2 R2 R3 R3 R1
根据等效条件,比较式(3)与式(1),得 Y的变换条件:
返 回
上 页
下 页
R12 R1 R2 R23 R2 R3 R31 R3 R1
R1 R2 R3 R2 R3 R1 R3 R1 R2
i4 30 4 7.5A
u3 6i3 6 10 60V
u4 3i3 30V
i5 10 7.5 2.5A
返 回
上 页
下 页
例2
+
I1
I2 R
I3 R
I4
求:I1 ,I4 ,U4
12V
_
+ + 2R U1 2R U2 2R _ _
+ 2R U4 _
解
①用分流方法做
总功率
表明
=p1+ p2++ pn
①电阻串联时,各电阻消耗的功率与电阻大小 成正比; ②等效电阻消耗的功率等于各串联电阻消耗功 率的总和。
返 回 上 页 下 页
2. 电阻并联
①电路特点 i + i1 R2
i2 Rk
ik
in Rn
u _
R1
(a)各电阻两端为同一电压(KVL); (b)总电流等于流过各并联电阻的电流之和(KCL)。
R1i R1 R2
(i i1 )
返 回
上 页
下 页
④功率
p1=G1u2, p2=G2u2,, pn=Gnu2
p1: p2 : : pn= G1 : G2 : :Gn
总功率
p=Gequ2 = (G1+ G2+ …+Gn ) u2 =G1u2+G2u2+ +Gnu2 =p1+ p2++ pn
b
100
60
80
b
60
50
120
60
a 20
b 100 60 40
返 回 上 页 下 页
20
100 100
例5 求: Rab
5 a b 7 6 20 缩短无 电阻支路
20 5 15 6 6 4 a b 7
15 6
4
Rab=10
15 10
6
i2 i3 6 165V 18 i5 4 i4 12 +
i1 165 11 15A
9
-
u2 6i1 6 15 90V
返 回 上 页 下 页
i1 5
i2 i3 6 165V 18 i5 4 i4 12 -
+
i2 90 18 5A
i3 15 5 10A
Geq G1 G2 Gn Gk Gk
k 1 n
返 回
上 页
下 页
结论 等效电导等于并联的各电导之和。
1 Req Geq 1 R1 1 R2 1 Rn 即 Req Rk
③并联电阻的分流
ik i u / Rk u / Req Gk Geq
第2章 电阻电路的等效变换
本章重点
2.1 2.2 2.3 2.4 2.5 2.6 2.7 引言 电路的等效变换 电阻的串联和并联 电阻的Y形连接和△形连接的等效变换 电压源、电流源的串联和并联 实际电源的两种模型及其等效变换 输入电阻
首页
重点: 1. 电路等效的概念; 2. 电阻的串、并联; 3. 电阻的Y— 变换; 4. 电压源和电流源的等效变换;
返 回
2.1
电阻电路 分析方法
引言
仅由电源和线性电阻构成的电路 ①欧姆定律和基尔霍夫定律是 分析电阻电路的依据; ②等效变换的方法,也称化简的 方法。
返 回
上 页
下 页
2.2 电路的等效变换
1.两端电路(网络)
任何一个复杂的电路, 向外引出两个端钮,且 从一个端子流入的电流等于从另一端子流出的电流, 则称这一电路为二端网络 (或一端口网络)。 i i
+ E
-
+
E
-
+ E
3k
R 3k 3k
-
返 回
上 页
下 页
例2 计算90电阻吸收的功率
1 + 20V 4 90 1 9 9 9 9 3 3 9
i1
2
1 i + 20V i1 90
10
-
Req 1 10 90 10 90 10Ω
-
1 + 20V
u1 R1 R1 R2 u
u2
u
+ u+ 1 u + u2 _ º
返 回
R1 R2
上 页
下 页
④功率
p1=R1i2, p2=R2i2,, pn=Rni2 p1: p2 : : pn= R1 : R2 : :Rn p=Reqi2 = (R1+ R2+ …+Rn ) i2 =R1i2+R2i2+ +Rni2
无 源
无 源 一 端 口
返 回 上 页 下 页
2.两端电路等效的概念
两个两端电路,端口具有相同的电压、电流 关系,则称它们是等效的电路。
B
i
+ u -
等效
C
i
+ u -
对A电路中的电流、电压和功率而言,满足:
B
A
C
返 回
A
上 页 下 页
明确
①电路等效变换的条件: 两电路具有相同的VCR;
②电路等效变换的对象:
Req R1 Rk Rn Rk Rk
结论 串联电路的总电阻等于各分电阻之和。
返 回 上 页 下 页
③串联电阻的分压
uk Rk i Rk u Rk uu Req Req 电压与电阻成正比,因此串联电阻电路
表明
可作分压电路。
i
R2 R1 R2
例 两个电阻的分压:
u u1 uk un
返 回 上 页 下 页
②等效电阻 R1 i Rk Rn 等效 i Re q _
+ u1 _ + u k _ + un _
+ u 由欧姆定律 _
+
n k 1
u
u R1i RK i Rni ( R1 Rn )i Reqi
RL
30
30
I L 1A
G31
类似可得到由Y的变换条件:
G1 G12 G31 G2 G23 G12 G3 G31 G23 G12G31 G23 G23G12 G31 G31G23 G12
R3 R1
或 R2
简记方法:
R Δ相邻电阻乘积 GΔ Y相邻电导乘积 GY R
I 4 1 I 3 1 I 2 1 I1 1 12 3 2 4 8 8 R 2R
U 4 I 4 2 R 3V
②用分压方法做
I1 12 R
U4 1 U1 3V 2 4
