非线性电路课程报告-蔡氏电路的Matlab仿真研究
非线性电路的MapleSim仿真实验

3 )静态工作点稳 定电路:可演示放大 电路中负反馈对 电路 的影 响,通过短路块可将反馈 电阻 R e接入 电路或短接, 观 察负 反馈对 放大 电路 的影 响; 改变 负载 阻值 ,观 察波形
幅度变 化。
在 理论教 学 的同时进 行辅助 实验演示 ,将实验 结果 通过虚 拟 示波器 传至 多媒体 计算机 投影 显示 。通 过演示 实验 ,使 得 课堂 教学能够 理论 联系 实际,理论 讲授过 程变得 直观 生 动,利用 学生 的探究 心理 ,提 高学生 的学 习兴趣 ,加深 学 生对 知识点 的理解 ,对 于提 高课堂教 学效 果的优 化增强 具 有重要的作用 。 参考文献 [ 1 ]张婧 , 朱骏 . 虚拟示 波器在物 理实验教学中的应用 [ J ] .
1 蔡 氏电路简介
2 O世纪 8 O 年代 ,非线性电路中陆续发现各种分岔和混
: I : 基 金 项 目:湖 南农 业大 学 东方科 技学 院教 改项 目 ( D B 2 0 1 1 0 5 3 )。 作 者 :赵 凡 ,硕 士 ,湖南 农业 大 学 东方 科技 学 院理 工 学部 实验 师 ,研 究 方 向为 理论 物理 学 ;汤 剑锋 ,湖 南 农业 大 学 东方 科技 学 院
文 章编 号 :1 6 7 卜4 8 9 X ( 2 0 1 4 ) 0 4 一 O 1 1 4 — 0 3
随着计算机科学 的发展 , 人们意识到计算机仿真技术 是
非线性科学包括 3个主要部分:孤立波 、混沌 、分 形。 传 统实验 教学方法 的有益 补充 。以往 文献探 讨 了 M a t l a b 、 讨M a p l e S i m仿 真软件在 实验 教学 中运 用的文献 。M a p l e S i m 是一个 多领域 物理 的仿真建 模软件 ,具有 图形化 的仿真 环 境,用户可通过简单和直观 的方式完成各种系统 的建模 、分 析和 仿真 。M a p l e S i m基于 M a p l e数学 引擎 ,使用 M a p l e中 的高 级符号计 算功 能生成物 理系 统的数 学模型 ,能有效 地 管理 和简化 复杂系 统 的数 学模 型,实现 系统 的高保 真、高 速仿 真,相 比于其他 仿真 软件有其 独特 的特 点。本文 以蔡 氏电路为例 ,说 明 M a p l e S i m在混沌 电路实验教学 中的应用 。
基于蔡氏电路的MATLAB仿真

1、引 言 作为一种普遍存在的非线性现象, 混沌的发现对科学的发
展 具 有 深 远 的 影 响[1 ,2 ].混 沌 行 为 是 确 定 性 因 素 导 致 的 类 似 随 机 运动的行为,即:一个可由确定性方程描述的 非 线 性 系 统,其 长 期 行为表现为明显的随机性和不可预测性, 我们就认为该系统存 在 混 沌 现 象.混 沌 具 有 三 个 特 点[1-3 ]:随 机 性;遍 历 性;规 律 性.混 沌 有 一 个 很 重 要 的 性 质:系 统 行 为 对 初 始 条 件 非 常 敏 感.近 年 来 许 多学者通过非线性电路对混沌行为进行了广泛地研究, 其中最 典型的是蔡氏电路[4-7],它是能产生混沌行为的最 小 、最 简 单 的 三 阶自治电路. 2、蔡 氏 电 路 模 型
a0 = 0.8, a1 = 0.1
初始值为:[0.1,0.1,0.1],其仿真如图 3 所示. 在 2005 年,W ei Lin 等 提 出 一 种 新 型 的 蔡 氏 电 路 简 化 后 无
量 纲 的 标 准 型 [8]:
(2)
其中,
g ( x )
=
m0 x
+
1 2
(m1
- m0 )(
x +1
参考文献: 1.盛昭瀚,马军海.非线性动力系统分析引论[M ].科学出版社,2001 2.胡岗,萧井华,郑志刚.混沌控制[M ].上海科技教育出版社,2000. 3.曹建 福 ,韩 崇 昭 ,方 洋 旺.非 线 性 系 统 理 论 及 应 用[M ].西 安 交 通 大 学 出 版 社 ,2001 4.J C Sprott. C om plex B ehavior of Sim ple System [C ].InternationalC onfer- ence on com plex System s,2000. 5.M T Y assen.A daptive control and synchronization of a m odified C hua's circuit system [J].A pplied M athem atics and C om putation,2001,(11):1- 9. 6.T zuyin W u,M in - Shin C hen.C haos control of m odified C hua's circuit system [J].Physics D ,2002,(2867):1- 6. 7.A S Elw akil,M P K ennedy.C hua's circuit decom position:a system atic de- sign approach for chaotic oscillators [J].Journal of the Franklin Institute, 2000,(337):251- 265. 8.W ei Lin and Y angbo H e. C om plete synchronization of the noise- per- turbed C hua's circuits C haos 15,023705 (2005)
蔡氏电路MATLAB混沌仿真

蔡氏电路的Matlab混沌仿真研究班级:姓名:学号:摘要本文首先介绍非线性系统中的混沌现象,并从理论分析与仿真计算两个方面细致研究了非线性电路中典型混沌电路,即蔡氏电路反映出的非线性性质。
通过改变蔡氏电路中元件的参数,进而产生多种类型混沌现象。
最后利用软件对蔡氏电路的非线性微分方程组进行编程仿真,实现了双涡旋和单涡旋状态下的同步,并准确地观察到混沌吸引子的行为特征。
关键词:混沌;蔡氏电路;MATLAB仿真AbstractThis paper introduces the chaos phenomenon in nonlinear circuits. Chua’s circuit was a typical chaos circuit, thus theoretical analysis and simulation was made to research it. Many kinds of chaos phenomenon on would generate as long as one component parameter was altered in Chua’s circuit.On the platform of Matlab, mathematical model of Chua’s circuit was programmed and simulated to acquire the synchronization of dual and single cochlear volume. Meanwhile, behavioral characteristics of chaos attractor were observed.Key words:chaos phenomenon;Chua’s circuit;Simulation1、引言混沌理论的基本思想起源于20世纪初,完善于20世纪60年代后,发展壮大于20世纪80年代,被认为是继相对论、量子力学之后,人类认识世界和改造世界的最富有创造性的科学领域第三次大革命。
matlab仿真实验报告

matlab仿真实验报告Matlab仿真实验报告引言:Matlab是一种广泛应用于科学和工程领域的数值计算软件,它提供了强大的数学和图形处理功能,可用于解决各种实际问题。
本文将通过一个具体的Matlab 仿真实验来展示其在工程领域中的应用。
实验背景:本次实验的目标是通过Matlab仿真分析一个电路的性能。
该电路是一个简单的放大器电路,由一个输入电阻、一个输出电阻和一个放大倍数组成。
我们将通过Matlab对该电路进行仿真,以了解其放大性能。
实验步骤:1. 定义电路参数:首先,我们需要定义电路的各个参数,包括输入电阻、输出电阻和放大倍数。
这些参数将作为Matlab仿真的输入。
2. 构建电路模型:接下来,我们需要在Matlab中构建电路模型。
可以使用电路元件的模型来表示电路的行为,并使用Matlab的电路分析工具进行仿真。
3. 仿真分析:在电路模型构建完成后,我们可以通过Matlab进行仿真分析。
可以通过输入不同的信号波形,观察电路的输出响应,并计算放大倍数。
4. 结果可视化:为了更直观地观察仿真结果,我们可以使用Matlab的图形处理功能将仿真结果可视化。
可以绘制输入信号波形、输出信号波形和放大倍数的变化曲线图。
实验结果:通过仿真分析,我们得到了以下实验结果:1. 输入信号波形与输出信号波形的对比图:通过绘制输入信号波形和输出信号波形的变化曲线,我们可以观察到电路的放大效果。
可以看到输出信号的幅度大于输入信号,说明电路具有放大功能。
2. 放大倍数的计算结果:通过对输出信号和输入信号的幅度进行计算,我们可以得到电路的放大倍数。
通过比较不同输入信号幅度下的输出信号幅度,可以得到放大倍数的变化情况。
讨论与分析:通过对实验结果的讨论和分析,我们可以得出以下结论:1. 电路的放大性能:根据实验结果,我们可以评估电路的放大性能。
通过观察输出信号的幅度和输入信号的幅度之间的比值,可以判断电路的放大效果是否符合设计要求。
非线性电路分析-蔡氏电路仿真

蔡氏电路
电路由 1 个线性电感 L、 2 个线性电容 C1、 C2,1 个线性电阻 R0,1 个非线性电阻 R 构成,为三阶自治动态电路, 即分为 LC 振荡电路、 RC 分相电路和非线性元件三部分。电阻 R0 起调节 C1、 C2 的相位差。 非线性电阻 R 为分段线性电阻, 伏安特性 iR= g( uR) ,如图 2 所示。
参考文献
[1]吴淑花, 孟玮德, 马志春. 蔡氏电路的实验与仿真研究[J]. 石 家庄学院学报, 2019(6). [2]戚慧珊, 杨明健, 刘百钊,等. 蔡氏混沌电路实验的改进设计 [J]. 大学物理实验, 2019, 32(02):69-7 [3]吕恩胜, 黄双成. 蔡氏电路的等效电路设计及其应用[J]. 电子 器件, 2014, (5):891-895.4.
基于Multisim的蔡氏电路 混沌现象仿真研究
混沌现象
自治电路:不包含随时间变化的激励信号的电路 非自治电路:包含随时间变化的激励信号的电路
混沌是一种确定系统中出现的貌似不规则的有序运动
混沌电路:由确定性运动方程所描述的确定性电路,由直流或确定 性信号所激励,其输出波形中包含一段或多端连续频谱的电路
先将 R7 调到最大(2kΩ),然后逐渐减小 R7 的值,观察 R7 在减小的过程 中各个示波器的波形变化。
单周期,R7=1960Ω
双周期,R7=1760Ω
单漩涡,R7=1680Ω
双漩涡,R7=1520Ω
极限环,R7=1320Ω
总:利用Multisim可以直观的观察电路结构,更好的分析仿真结果
根据文献[1], 图 1 中非线性电阻 R 的等效电路可由图 3 所示的电路并 联得到, 等效电路如图 5 所示,为 有源负阻非线性电阻,其作用是使 振动周期生分岔和混沌等一系列非 线性现象。
蔡氏电路仿真报告

非线性电路理论及应用课程作业XXXXXXXXX蔡氏对偶混沌电路仿真报告一、蔡氏对偶混沌电路分析应用一个三阶自治电路进行仿真,电路如图1所示,其中包含一个电流控制型的非线性电阻元件,其伏安特性关系如图2所示。
L 2L 2i 1CR 2u r u c+-+-i 2i-2-1120.20.1-0.1-0.2O u r /Vi 1/A图1 蔡氏对偶电路 图2 流控型非线性电阻伏安特性对于图1中所示的电路,其状态方程推导如下:2c c 21022112011d d )(d d )()(d d i t uC u i i R t iL i r i i R t i L -=+-=--= 整理上述各式得2c c 22120211121011d d 1)(d d )(1)(d d i Ct u u L i i L R t i i r L i i L R t i -=+-=--=为分析方便,对方程进行归一化处理 令20()L t R τ=,t L Rd d 20=τ 且令 120,,c x i y i z u R ===则上述各方程变为y CR L t z z y x t yx r x y L L t x 0212d d d d )]([d d -=+-=--=上述方程中,将时间τ任记为t ,则方程变为标准蔡氏方程,即为:y tzz y x t yx f y t xβα-=+-=-=d d d d )]([d d 其中21L a L =,220L b CR = 001()()0.5()(11)r x f x m x m m x x ==+-+--二、计算机仿真1、参数设置上述蔡氏对偶电路的微分方程描述的动态系统关于原点对称,对应于分段线性电流控制型电阻的特性,若将f (x )特性分为三段考虑,即为⎪⎩⎪⎨⎧-≤--≤≥-+=1)(1||1)()(1010101x m m x m x x m x m m x m x f为了进行计算机仿真计算分析,我们令 8001.0008.012===L L α,5.121104.6008.0402=⨯⨯==-CR L β 而取2.0510-=-=m ,4.0521==m取初始值为(0.025,-0.022,0.8)应用MATLAB 进行仿真。
三阶蔡氏电路matlab仿真代码

一、背景介绍三阶蔡氏电路是一种经典的电路结构,在信号处理、滤波等领域有着重要的应用。
利用MATLAB对三阶蔡氏电路进行仿真分析,可以帮助工程师和研究人员更好地理解电路的特性和行为,对于电路设计和优化具有重要意义。
二、三阶蔡氏电路的基本原理三阶蔡氏电路由三个积分器和两个比例放大器组成,是一种具有强大信号处理能力的电路结构。
它可以用于实现各种滤波器,包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器等。
在电子电路和通信系统中有广泛的应用。
三、MATLAB仿真环境的搭建1. 安装MATLAB软件,并确保其正常运行。
2. 新建一个MATLAB脚本文件,用于编写三阶蔡氏电路的仿真代码。
3. 导入必要的工具箱和函数库,确保能够进行电路仿真分析所需的基本操作和函数调用。
四、三阶蔡氏电路的参数设置1. 根据具体的电路结构和设计要求,设置电路的参数,包括电阻值、电容值、放大倍数等。
2. 考虑电路中可能存在的噪声以及非线性元件的影响,进行适当的参数修正和补偿。
五、三阶蔡氏电路的MATLAB仿真代码实现1. 编写三阶蔡氏电路的节点方程,建立电路的数学模型。
2. 利用MATLAB的数值计算工具,如ode45函数等,对电路进行仿真计算。
3. 对仿真结果进行分析和后处理,得到电路的频率响应、相位特性等重要信息。
六、仿真结果与分析1. 利用MATLAB绘制三阶蔡氏电路的幅频特性曲线和相频特性曲线,观察电路的频率响应特性。
2. 对比不同参数设置下的仿真结果,分析电路性能随参数变化的规律和特点。
3. 考虑电路可能存在的非线性特性,对其进行深入分析和讨论,为实际应用提供参考依据。
七、结论与展望通过MATLAB对三阶蔡氏电路的仿真分析,我们深入了解了电路的特性和行为。
这对于电路的设计和优化具有重要意义。
在未来的研究中,可以进一步探究电路在实际应用中的性能表现,以及对其进行更加精细的仿真和分析。
也可以考虑将仿真结果与实际测试数据进行对比,验证仿真模型的准确性和可靠性。
蔡氏电路数值仿真图像与实测图像的对比研究

关 键 词: 蔡氏电路ꎻ混沌ꎻMATLABꎻ数值仿真ꎻ实测图像ꎻ结果对比
中图分类号: O 4 ̄34源自文献标志码: ADOI:10.14139 / j.cnki.cn22 ̄1228.2018.04.014
混沌现象是一种广泛存在且长期表现出不可 预测的非线性行为ꎮ 混沌具有三个特点:规律性、 遍历性、随机性[1ꎬ2] ꎮ 随着计算科学和社会科学 的发展ꎬ混沌的不可预测性与规律性使其成为了 物理、数学等众多学科领域的一个热点研究课题ꎮ 近年来ꎬ非线性电路是许多学者研究混沌的重要 途径之一ꎬ其中一个最典型的非线性电路就是三 阶自治蔡氏电路( Chua’ s circuit) [3] ꎮ
在此基础上ꎬ蔡少棠教授提出了一个将物理 模型与数学模型相结合的典型混沌系统—蔡氏电 路ꎮ 它是一个三阶自治电路ꎬ包含两个电容 C1、 C2ꎬ一个电感 Lꎬ一个线性电阻 R 及一个非线性电 阻元件 RN( 也称作蔡氏二极管) [3] ꎮ 蔡氏电路物 理模型如图 1 所示:
在蔡氏电路模型中ꎬ非线性电阻元件 RN 可
MATLAB 平台下描述蔡氏电路的混沌图像ꎮ 为了更好的与实测图像进行对比分析ꎬ我们
设置数值仿真的初始参数与真实实验电路中的参 数保持一致即:电容 C1 值为 0.022 μF、电容 C2 值 为 0.1 μF、电感 L 为 10 mHꎬ电阻 R 的变化范围设 置在 0 ~ 3 KΩꎮ
图 3 实际电路图
下图 4 所示的就是在电容 C1 值为 0.022 μF、 电容 C2 值为 0.1 μF、电感 L 为 10 mH 的条件下ꎬ 电阻 R 阻值从 3 KΩ 减小至 0 KΩ 的过程中所得 到的混沌图像:
实测结果分析: 如上图 4 所示ꎬ非周期变化的混沌行为中存 在一倍周期ꎬ单吸引子等混沌图像ꎻ但是很难观测 到清晰的二倍周期和双吸引子等混沌图像ꎬ这主 要由于通过调节滑动变阻器我们不能给定这些特 殊混沌图像所需的电阻 R 的精确参数值[6] ꎮ
蔡氏混沌电路的分析和MATLAB仿真

参考文献
刘崇新. 非线性电路理论及应用. 西安:西安交通大学出版社, 2007
附 MATLAB 仿真程序
options = odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-4]); [t,x]=ode45(@mysolve,[0 100],[ 1 0 0],options); subplot(2,3,1);plot(x(:,1),x(:,2));title('x-y平面相图') subplot(2,3,2);plot(x(:,1),x(:,3));title('x-z平面相图') subplot(2,3,3);plot(x(:,2),x(:,3));title('y-z平面相图') subplot(2,3,4);plot(t,x(:,1));title('x时域波形') subplot(2,3,5);plot(t,x(:,2));title('y时域波形') subplot(2,3,6);plot(t,x(:,3));title('z时域波形')
2
0
0
0
-2
-2
-4
-0.5
-4
0
50
100
0
50
100
0
50
100
结论
蔡氏电路所代表的非线性动力学系统的确是混沌系统。该系统具有丰富的混沌动力学行 为。仿真结果印证了震荡过程中出现的双涡卷混沌奇怪吸引子。
利用系统平衡点处的线性化矩阵,可以定性分析系统的动力学行为,以便寻找能使系统 产生混沌的参数。
计算仿真
取
非线性电路实验报告

非线性电路实验报告非线性电路【摘要】本次实验测量了有源非线性电阻的I-U 特性曲线,了解了非线性电阻的性质。
再利用有源非线性电阻搭建蔡氏振荡电路,改变特征参数,观察到不同的混沌现象,计算费根鲍姆常数。
再将两个蔡氏振荡电路搭建电路,观察并研究混沌同步。
最后我们观察信号的的加密,在混沌同步电路的基础上继续搭建,观察信号的加密与解密。
关键词:非线性电路、混沌、信号加密一.引言非线性科学的萌芽期可以追溯到19世纪末20世纪初,法国数学家庞加莱在解决天体力学中的三体问题时提出了庞加莱猜想。
非线性科学的真正建立是在20世纪六七十年代。
1963年,美国气象学家洛伦茨在《确定论非周期流》一文中,给出了描述大气湍流的洛伦茨方程,并提出了著名的“蝴蝶效应”,从而揭开了对非线性科学深入研究的序幕。
非线性科学被誉为继相对论和量子力学之后,20世界物理学的“第三次重大革命”。
由非线性科学所引起的对确定论和随机论、有序和无序、偶然性与必然性等范畴和概念的重新认识,形成了一种新的自然观,将深刻的影响人类的思维方法,并涉及现代科学的逻辑体系的根本性问题。
迄今为止,最丰富的混沌现象是非线性震荡电路中观察到的,这是因为电路可以精密元件控制,因此可以通过精确地改变实验条件得到丰富的实验结果,蔡氏电路是华裔科学家蔡少棠设计的能产生混沌的最简单的电路,它是熟悉和理解非线性现象的经典电路。
本次实验通过蔡氏电路研究混沌、混沌同步与混沌通信。
了解有源性负阻的I-U特性曲线与混沌现象的规律。
二.实验原理1. 费恩鲍姆系数一个完全确定的系统,即使非常简单,由于系统内部的非线性作用,同样具有内在的随机性,可以产生随机性的非周期运动。
在许多非线性系统中,既有周期运动,又有混沌运动。
所谓混沌,是服从确定性规律但具有随机性的运动,其主要特征是系统行为对于初始条件的敏感性。
菲根鲍姆发现,一个动力学系统中分岔点处参量n 收敛服从普适规律。
存在常数:,被称为菲根鲍姆常数。
基于MATLAB的蔡氏混沌非线性电路的仿真研究

c h a o s a n d i t s c h a r a c t e is r t i c s t h e p r o d u c t i o n me c h ni a s m a nd c o n d i t i o ns o f t h e s t u d y a n d t h e o r e t i c a l a n a l y s i s a n d M二 4 B s i mul a t i o n f r o m t wo a n g l e s
【 A b s t r a c t ] C h a o s e x i s t s i n n a t u r e i n v a r l O U S i f e l d s , i n t h e i f e l d o f m o d e m s c i e n c e a n d e n g i n e e i r n g a p p l i c a t i o n s a r e v e r y e x t e n s i v e . T h r o u g h t h e
【 摘 要】 混沌现 象存在 于 自然界各 个领域 , 在现代科 学与工程 学领域的应 用也十分广泛 。 通过对混沌现 象及其特征 , 产生的机理和条件的 研 究. 并从理论 分析 与 M A T L A B仿真两个角度 分别研 究了蔡 氏混沌电路 的演化过程 和混沌电路 状态 . 进而构造 出符合三 阶混沌 系统的非线性 电路 和数 学模 型。研 究结果表 明, 蔡 氏混沌非线性 电路 中元件参数影响 电路混沌状 态的演化 。 仿真数据与理论分析 结论一致 , 随着线性 电阻阻 值 的减小电路状 态大致 经历 : 稳定 态。 周期 态, 混沌 态。 负阻尼振 荡态。
基于MATLAB的非线性电路特性仿真研究
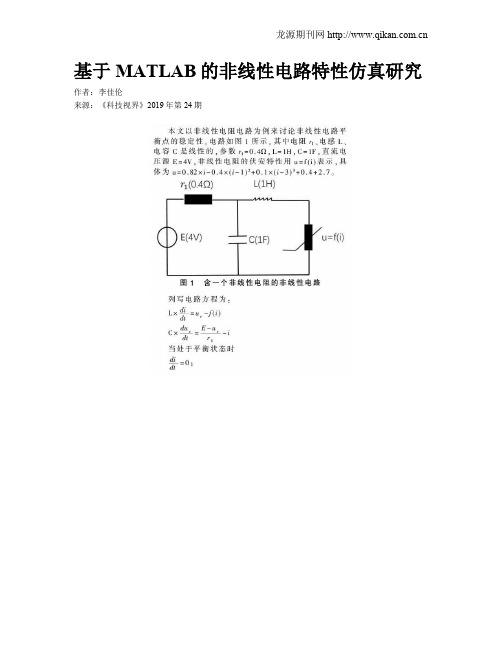
基于MATLAB的非线性电路特性仿真研究作者:李佳伦来源:《科技视界》2019年第24期【摘要】实际电路都是非线性的。
非线性电路具有很多和线性电路完全不同的特性,表现出非线性电路独有的一些行为。
论文利用MATLAB搭建了不同的非线性电路模型,然后利用数值仿真,分析了非线性电路稳态不唯一、极限环、混沌等三个典型特性,直观展现了非线性电路中稳定与不稳定平衡点、极限环、混沌等不同行为的具体表现,分析了非线性电路轨迹与初始点的相关性,为了解非线性电路特殊的行为提供参考。
【关键词】非线性电路;平衡点;极限环;混沌中图分类号: TN710 文献标识码: A 文章编号: 2095-2457(2019)24-0047-004DOI:10.19694/ki.issn2095-2457.2019.24.023【Abstract】All actual circuits are nonlinear. Nonlinear circuits have many different characteristics from linear circuits, and some special behaviors would appear. The paper uses MATLAB to build different nonlinear circuit models, and then uses numerical simulation to analyze three typical characteristics of nonlinear circuits, i.e. multiple steady states, limit cycle and chaos, and visually shows the stable equilibrium point and unstable equilibrium point, limit cycle, chaos and other characteristics in nonlinear circuits. The paper also analyzes the dependence of trajectories of nonlinear circuits on the initial points. The results provide a reference for understanding the special behaviors of nonlinear circuits.【Key words】Non-linear circuit; Equilibrium point; Limit cycle; Chaos0 引言在線性电路中,线性元件的特点是其参数不随电压或电流而变化。
蔡氏电路matlab仿真报告

蔡氏电路仿真分析学院:电气工程学院班级:硕6036姓名:张东海学号:3116312053目录1.基本分析 (2)2.MATLAB仿真 (5)蔡氏电路蔡氏电路是著名的非线性混沌电路,结构简单,但却出现双涡卷奇怪吸引子和及其丰富的混沌动力学行为。
1.基本分析蔡氏电路是一个典型的混沌电路,最早由著名华裔科学家、美国加州大学蔡少堂教授设计。
他证明了在满足以下条件时能够产生混沌现象。
(1) 非线性元件不少于1 个; (2) 线性有效电阻不少于1 个; (3) 储能元件不少于3 个。
根据以上条件,在图1.1中给出蔡氏电路方框图。
图中R 为线性有效电阻,L 、C 1、C 2为储能元件,R N 为非线性元件。
图2.2给出非线性电阻伏安特性曲线。
图1.1 蔡氏电路方框图图1.2 非线性电阻伏安特性曲线对于图2.1提出的蔡氏电路,其状态方程推导如下12112122121()()1()(1)C C C C C C C L LC du C u u g u dt R du C u u i dt R di L u dt ⎧=--⎪⎪⎪=-+⎨⎪⎪=-⎪⎩ 其中函数1()C g u 是分段线性函数,其形式为:-11111()()()2C b C a b C C g u G u G G u E u E =+-⨯+--作变量代换:1222221,,,,1C C Lu u i x y z E E EGC C tGC C LG G R ταβ=======式(1)可以写为如下形式[]()(2)dxy x f x d dyx y zd dzy d αττβτ⎧=--⎪⎪⎪=--⎨⎪⎪=-⎪⎩式(2)即是蔡氏电路的标准方程形式。
其中()f x 可表示为如下形式1010101(),1(),1(),1m x m m x f x m x x m x m m x +-≥⎧⎪=≤⎨⎪--≤-⎩其中01,a b m G E m G E ==蔡氏电路的三个状态方程式在状态空间的三个子空间为101={(,,)| 1}={(,,)| 1}={(,,)| 1}D x y z x D x y z x D x y z x -≥≤≤- 在状态空间的三个子空间内分别具有唯一平衡点如下1011(,0,),(0,0,0),(,0,).P k k D Q D P k k D +--=-∈=∈=-∈其中,1011m m k m -=+ 在P +、1P -和Q 处的雅可比矩阵分别为:1(1)011100P P m J J ααβ+--+⎛⎫ ⎪==- ⎪ ⎪-⎝⎭,0(1)011100Q m J ααβ-+⎛⎫ ⎪=- ⎪ ⎪-⎝⎭取10α=,15β=,0 1.2m =-,10.6m =-,则在P +、1P -处的特征值为一个实数值和一对共轭复数值。
非线性电路的MapleSim仿真实验

非线性电路的MapleSim仿真实验非线性科学包括3个主要部分:孤立波、混沌、分形。
其中,孤立波是由罗素于1844年在实验室中发现的。
1895年,数学家科特维格与得佛里斯从数学上导出了有名的浅水波KdV方程,并给出了一个类似于罗素孤立波的解析解,即孤立波解,孤立波的存在于是得到普遍承认。
混沌和分形理论则是在20世纪才开始兴起。
20世纪初至50年代是混沌研究的萌芽时期,60年代开始迅速发展。
气象学家洛伦兹提出的“蝴蝶效应”指出了混沌系统的一个基本性质:对初始条件的敏感依赖性。
20世纪70年代,混沌现象的研究开始渗透到其他学科;80年代以来,随着计算机技术的进步,混沌学的研究方法得到快速发展。
有人将混沌和分形誉为继相对论和量子力学之后的20世纪物理学的第三次革命。
物理学中的力、热、电、光、原子体系中均存在混沌现象。
非线性电路中的混沌现象是混沌研究的热点之一,混沌电路也具有广泛的应用前景。
由于混沌电路较易于引入实验教学,所以它是启迪学生探索非线性规律的一种重要途径。
然而传统的非线性电路实验对电路元件参数的误差极为敏感,需要严格地挑选元件,缺少灵活性,另外还要受到实验场地等的限制,不能很好地培养学生的兴趣和创造性思维。
随着计算机科学的发展,人们意识到计算机仿真技术是传统实验教学方法的有益补充。
以往文献探讨了Matlab、Multisim等软件在电路实验教学中的运用[1-2],但还没有探讨MapleSim仿真软件在实验教学中运用的文献。
MapleSim是一个多领域物理的仿真建模软件,具有图形化的仿真环境,用户可通过简单和直观的方式完成各种系统的建模、分析和仿真。
MapleSim基于Maple数学引擎,使用Maple 中的高级符号计算功能生成物理系统的数学模型,能有效地管理和简化复杂系统的数学模型,实现系统的高保真、高速仿真,相比于其他仿真软件有其独特的特点。
本文以蔡氏电路为例,说明MapleSim在混沌电路实验教学中的应用。
基于Matlab非线性电路的混沌仿真计算机课设

计算机课程设计报告基于 Matlab 的非线性电路混沌实验仿真姓名:学院: 班级: 指导老师:摘要混沌是指发生在确定系统中的貌似随机的不规则运动。
而混沌对于非线性动力学的研究有着非常重要的作用,本文结合非线性电路的混沌的课堂教学,设计了Matlab/Simulink仿真实验 , 研究蔡氏电路的模拟仿真过程。
本文首先通过对非线性电路(蔡氏电路与非线性动力学进行了阐述和分析,建立非线性动力学方程,然后利用 Matlab/Simulink软件进行仿真,研究系统波形图、单吸引子、双吸引子、相面图以及在不同的非线性电阻的导纳下的不同形状。
达到了预期的实验效果,基于Matlab/Simulink对非线性电路混沌的仿真对学生对非线性电路实验混沌适应实验的理解有着较大的参考价值。
关键词非线性电路混沌现象 Matlab/Simulink仿真目录摘要 ...................................................3 1 混沌的概述 . (4)1.1 混沌现象的概述 (4)1.2 混沌电路综述 (5)2 混沌理论基础 .........................................5 2.1 混沌的基本定义 ..................................5 2.2 混沌的基本特征 . (5)2.3 混沌理论的基本概念 (7)3 蔡氏电路的分析与仿真 .................................8 3.1 蔡氏电路的分析 (9)3.2计算机仿真 (10)4 结论 ................................................15 致谢 ..................................................16 参考书目 . (16)1混沌的概述1.1混沌现象概述混沌是指发生在确定系统中的貌似随机的不规则运动, 长期以来, 人们在认识和描述运动时, 大多只局限于线性动力学描述方法, 即确定的运动有一个完美确定的解析解。
非线性电路理论

非线性电路理论报告蔡氏混沌电路分析摘要混沌是非线性系统中的常见现象。
本文对产生混沌现象的最简单三阶自治电路-蔡氏电路进行了研究,建立了数学模型,并根据建立的数学模型对其进行了仿真分析,仿真结果表明在一定的条件下该电路能够出现混沌双涡卷吸引子。
关键词:蔡氏电路;双涡卷混沌吸引子1.引言混沌是自然界客观存在的一种运动形式,混沌系统具有对初值特别敏感的特性。
混沌信号具有随机信号的许多性质,然而混沌信号是确定性信号。
由于混沌信号介于随机信号与一般确定性信号的特殊性而具有较高的应用价值,对混沌的研究已经从单纯的物理和数学上的理论研究走向了各种应用研究。
目前,混沌成为控制、测量、保密通信、雷达及信号处理等诸多领域的研究热点。
在电路与系统领域,由于蔡氏电路的提出,对混沌理论及其应用的研究也变得十分活跃。
蔡氏混沌电路是一个物理结构及数学模型都相对简单的混沌系统,然而它也是一个典型的混沌电路,对蔡氏电路的研究有助于理解混沌的演化过程及其了解混沌相关特性。
由于混沌动力学系统的复杂性,绝大多数混沌动力学系统难以用已知的函数表示其通解,所以通过数值计算对混沌行为的时空演化进行描述是研究混沌的一种重要方法。
MATLAB软件是以矩阵计算为基础的数值计算、模型仿真的优秀数学工具。
借助MATLAB 软件强大的数值计算及仿真能力,使得对许多复杂的混沌系统的研究变得相对容易和直观。
本文首先对蔡氏电路及MATLAB仿真工具进行了介绍,然后应用MATL AB软件对蔡氏混沌电路进行了仿真研究。
2. 蔡氏电路仿真图1 蔡氏对偶电路图2 Rn的伏安特性曲线蔡氏电路是一种物理结构和数学模型简单的混沌系统,该混沌系统也常被用来进行混沌理论及应用方面的研究。
该电路使用三个储能元件和一个分段线性电阻,电路如图1所示。
可以把电路分为线性部分和非线性部分。
其中线性部分包括:电阻R0、两个电感L1和L2和电容C;非线性部分只有一个分段线性电阻Rn,其伏安特性如图2所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
交通大学电气工程学院
非线性电路报告蔡氏电路的Matlab仿真研究
Administrator
蔡氏电路的Matlab仿真分析
摘要:对一种典型的产生混沌现象的电路——蔡氏混沌电路进行了分析研究。
从理论分析和仿真两个角度分别研究蔡氏电路中的混沌现象。
蔡氏电路是一个典型的混沌电路,只要改变其中一个元件的参数,就可产生多种类型混沌现象。
在Matlab 的平台上编制相关系统
对蔡氏电路进行了仿真研究。
关键词:蔡氏电路,非线性负电阻;混沌电路;吸引子
引言
随着计算机和计算科学的快速发展,混沌现象及其应用研究已成为自然科学技术和社会科学研究领域的一个热点。
而非线性电路是混沌及混沌同步应用研究的重要途径之一,其中一个最典型的电路是三阶自治蔡氏电路。
在这个电路中观察到了混沌
吸引子。
蔡氏电路是能产生混沌行为最简单的自治电路,所有从三阶自治常微分方程描述的系统中得到的分岔和混沌现象都能够在蔡氏电路过计算机仿真和示波器观察到。
经过若干年的研究及目前对它的分析,无论是在理论方面、模拟方面还是实验方面均日臻完善。
在理论和实践不断取得进展时,
人们也不断开拓新的应用领域,如在通信、生理学、化学反应工程等方面不断产生新的技术构想,并有希望很快成为现实。
1混沌概念及其相关特征
1.1混沌和吸引子的定义
混沌至今没有统一的定义,但人们一致的看法是:一个确定的非线性系统,如果含有貌似噪声的有界行为,且又表现若干特性,便可称为混沌系统,此处所说的若干特性主要是如下三个方面:(1)振荡信号的功率连续分布,且可能是带状分布的,这个特征表明振荡为非周期的,也就是说明信号貌似噪声的原因。
(2)在相空间,该系统的相邻近的轨道线彼此以指数规律迅速分离,从而导致对初始值得极端敏感性,这使得系统的行为长期不可预测。
(3)在轨道线存在的相空间的某一特定的有界部分,轨道线具有遍历性和混合性。
遍历性是指任何一条轨道线会探访整个特定的有界部分,混合性是指初始间单关系将弥漫的动力学行为所消除。
混沌吸引子:吸引子是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出发的非定常流的所有轨道都趋于它。
若吸引子的轨线对初始条件高度敏感依赖,该吸引子就称为混沌吸引子。
吸引子无外乎两种状态,即单个点和稳定极限环。
系统的吸引子理论是关于吸引子的科学理论,它是混沌学的重要组成部分。
奇异(怪)吸引子:具有分数维结构的吸引子称为奇异吸引子。
奇异吸引子是反映混沌系统运动特征的产物,也是一种混沌系统中无序稳态的运动形态。
它具有自相似性,同时具有分形结构。
奇异吸引子是混沌运动的主要特征之一。
奇异吸引子的出现与系统中包含某种不稳定性(不同于轨道不稳定性和雅普诺夫不稳定性)有着密切关系,它具有不同属性的外两种方向:在奇异吸引子外的一切运动都趋向(吸引)到吸引子,属于“稳定”的方向;一切到达奇异吸引子的运动都互相排斥,对应于“不稳定”方向。
1.2混沌的基本特征
混沌具有两个基本的特征:一是运转状态的非周期性,即混沌系统输出信号的周期为无穷大,且在功率上与纯粹噪声信号难以分辨,因而是随机信号,然而混沌系统是确定性动力学系统,本身并不包含任何随机因素的作用,其产生随机输出信号的原因完全是因为系统部各变量之间的强非线性耦合。
因此,其输出的随机信号在理论上是可以精确重复的。
二是对初始条件的高度敏感性,即若存在对初始条件的任何微小的偏离(扰动),则此偏离随着系统的演化将迅速以指数率增长,使得在很短的时间系统的状态与受扰前便失去任何的相关性,因此,混沌仅具有极为短期的预测性。
混沌状态具有以下三个关键(核心)概念:即对初始条件的敏感性、分形、奇异吸引子。
2蔡氏电路与非线性负电阻的实现
2.1蔡氏电路的构成
蔡氏电路是一个典型的混沌电路。
蔡氏电路实验电路图如图1所示。
电路中的电感L 和电容C 1、C 2并联构成一个振荡电路。
R 是一个有源非线性负电阻元件,电感L 和电容C 2组成一损耗可以忽略的谐振回路;可变电阻R 和电容C 1串联将振荡器产生的正弦信号移相输出。
图1.蔡氏电路图
图2.有源非线性负电阻伏安特性曲线
蔡氏电路的状态方程式为:
C 1dUc 1/dt=G (Uc 2-Uc 1)-gUc 1
C 2dUc 2/dt=G(Uc 1-Uc 2)+i L
Ldi L /dt= -Uc 2
式中U C1,U C2分别为电容C 1,C 2上的电压;i l 为电感L 上的电流,G=1/R 0为电导;g 为R 的伏安特性函数。
当R 为线性电阻时,g 为常数,电路为一般振荡电路,此时把C 1和C 2两端的电压分别输入到示波器的x,y 轴,显示的图形是椭圆形;当R 为非线性负电阻时,其伏安特性如图2,此时把C 1 和C 2两端的电压分别输入到示波器的x,y 轴,调节G 的值就会观察到不同的混沌现象。
3蔡氏电路的Matlab 仿真分析
以下是蔡氏电路平衡点出的仿真。
为了进行计算机仿真分析,我们令
2
71L L α==,22100L CR β==
取2.00-=m ,4.01=m 。
设置的初值[0.1;0.1;0.1],仿真时间为[0,200]。
蔡氏电路的仿真程序如下:
function simulation_chua
clc;
clear;
[t,y]=ode45(chua,[0,200],[0.1;0.1;0.1]);
figure;
plot3(y(:,1),y(:,2),y(:,3));
xlabel('X');
ylabel('Y');
zlabel('Z');
figure;
plot(t,y(:,1),'-');
xlabel('t');
ylabel('X');
title('Chua system ');
figure;
plot(t,y(:,2),'-');
xlabel('t');
ylabel('Y');
title('Chua system ');
figure;
plot(t,y(:,3),'-');
xlabel('t');
ylabel('Z');
title('Chua system ');
figure;
plot(y(:,1),y(:,3))
figure;
plot(y(:,1),y(:,2))
figure;
plot(y(:,2),y(:,3));
xlabel('il1'),ylabel('uc'),zlabel('1')
grid
function dy=chua(t,y)
ga=-0.2; gb=0.4; bp=1;
aa=7; bb=10;
a=0.5;
ia=gb*y(1)+a*(ga-gb)*(abs(y(1)+bp)-abs(y(1)-bp)); dy=[ aa*(y(2)-ia)
y(1)-y(2)+y(3)
-bb*y(2)];
仿真结果如下图:
4混沌电路的几种应用
基于混沌电路的特性,它在许多领域中有重要的应用。
但由于目前混沌学仍处于研究阶段,故其应用并不完善,出现的一些问题还有待解决。
1.通信中的应用:使强度更大的混沌信号和真实信号同步,由于混沌信号具有信号频谱宽、类似噪声、随机不可预测等特性,当真实信号被混沌信号所掩盖时,攻击者就很难从传输信号中分离出原始真实信号。
另外要求收发两端使用相同的混沌系统以及系统参数和状态初值,使系统同步并输出相同的混沌信号,以便正确地恢复信号[5]。
2.自动控制中的应用:考察非线性混沌系统的输出信号与输入信号的自反馈耦合,或者从系统外部强迫注入某一周期信号,或者直接将系统自身的输出信号取出一部分经过一定的时间延迟后再反馈到原混沌系统中去.作为控制信号,通过调节控制因子及控制信号的大小实现稳定控制。
3.传感应用:混沌具有初值敏感性, 当其结构参数稳定时,初始值与动力轨道在一定的时间是一一对应的, 而且对于微小的初值变化, 其运动轨迹就会出现指数分离。
若初值细微变化是由混沌系统中的传感元件随被测参数变化而引起的, 则轨迹之间的巨大差异就能直接反映被测参数的大小。
这种混沌型传感器具有很高的灵敏度和分辨率, 特别适用于微应变、微应力的测量;微量变化物参数的测量。
