特殊的四边形有关的计算与证明.doc

合集下载

特殊平行四边形证明

特殊平行四边形证明设特殊平行四边形ABCD的两对边分别平行，其中AB与CD平行，BC与AD平行；设AB=CD，BC=AD。

我们要证明对角线AC和BD互相平分，并且AC=BD。

首先，我们可以通过观察发现，在特殊平行四边形ABCD中，角BAD和角CDA分别等于角BCD和角ADC，这是因为平行线AB与CD分别与平行线AD与BC交叉，形成了对应角。

因此，我们可以得出：角BAD=角CDA (1)角BCD=角ADC (2)A________BD--------C我们可以注意到四边形ABCD可以分成两个三角形：△AED和△BEC。

根据上述所得到的结论，我们知道角BAD等于角CDA，角BCD等于角ADC。

由于BD是BC的延长线，所以角BCD也等于角BCE。

根据三角形内角和定理，我们可以得到三角形△BEC中的角BEC等于角BCD+角BCE，即角BCD+角BCE=角BCD+角BCD=2角BCD同样地，我们可以得到△AED中的角AED等于角BAD+角AED，即角BAD+角AED=角BAD+角BAD=2角BAD根据题设条件，我们知道AB=CD，所以△AEB和△CED是等腰三角形，因此角AEB等于角BEA，角CED等于角CED。

通过观察我们可以发现，角AEB等于角BEA等于角BEC，角CED等于角CDE等于角BCE。

所以角AEB=角BEA=角BEC (3)角CED=角CDE=角BCE (4)现在，我们可以将(3)代入△BEC的等式中，得到：角BCD+角BEC=2角BCD=2角AEB同样地，将(4)代入△AED的等式中，得到：角BAD+角AED=2角BAD=2角CED由于以E点为顶点的两个角分别等于以B点和C点为顶点的两个角的两倍，所以根据角等于其对边所对的弧长，我们可以得出：∠BAE=∠BCE (5)∠CDE=∠CAE (6)由(5)、(6)两式可知，∠BAE=∠BCE，∠CAE=∠CDE，根据等腰三角形的性质，我们可以得到AE=CE。

垂美四边形证明

垂美四边形证明摘要：一、引言二、垂美四边形的定义三、垂美四边形的性质1.垂心定理2.外接圆与垂足圆的关系3.垂美四边形的面积公式四、垂美四边形的判定方法1.判定条件2.判定定理五、垂美四边形的应用1.在解决几何问题中的应用2.在实际生活中的应用六、结论正文：一、引言垂美四边形，又称作“垂心四边形”，是指具有特殊性质的四边形。

本文将对垂美四边形的定义、性质、判定方法及其应用进行详细的阐述。

二、垂美四边形的定义垂美四边形是一个四边形，其中两条对角线相互垂直且交点到各顶点的距离相等。

三、垂美四边形的性质1.垂心定理垂美四边形的垂心是两条对角线的交点，且各顶点到垂心的距离等于其对边中点到垂心的距离。

2.外接圆与垂足圆的关系垂美四边形的外接圆与垂足圆相切，且外接圆的半径等于垂足圆的半径。

3.垂美四边形的面积公式垂美四边形的面积可以通过其中任意一条对角线的长度和其上的高来计算，公式为：面积= 1/2 * 对角线长度* 高。

四、垂美四边形的判定方法1.判定条件若一个四边形的对角线相互垂直且交点到各顶点的距离相等，则该四边形为垂美四边形。

2.判定定理在一个四边形中，若两组对边分别相等且对角线相互垂直，则该四边形为垂美四边形。

五、垂美四边形的应用1.在解决几何问题中的应用垂美四边形在解决几何问题中有着广泛的应用，如求解最值问题、证明其他几何结论等。

2.在实际生活中的应用垂美四边形在实际生活中的应用也随处可见，如桥梁结构、建筑物的设计等，都离不开垂美四边形的原理。

六、结论垂美四边形是一个具有特殊性质的四边形，掌握其性质、判定方法和应用对于解决几何问题具有重要意义。

特殊平行四边形的经典题型

特殊平行四边形的经典题型特殊平行四边形包括矩形、菱形和正方形，那这几种图形在各种经典题型里可是各有各的“戏码”呢。

矩形嘛，经常会在面积和对角线相关的题目里出现。

比如说，已知一个矩形的长是8，对角线长是10，让你求宽是多少。

这时候就可以用到勾股定理啦，因为矩形的对角线把矩形分成了两个直角三角形，对角线就是斜边，长和宽就是两条直角边。

根据勾股定理a² + b² = c²（这里的a和b就是长和宽，c就是对角线），已知a = 8，c = 10，那宽b就等于6。

这类型的题目就像是给你一把钥匙，只要你知道用勾股定理这个“开锁方法”，就能轻松解决。

菱形呢，它的对角线互相垂直且平分这个性质可是出题的热门点。

像有一道题说菱形的对角线分别是6和8，问菱形的面积是多少。

很多人可能会先求边长再用底乘高来算面积，其实完全不用这么麻烦，直接根据菱形面积等于对角线乘积的一半这个公式，就能得出面积是24啦。

还有就是菱形四边相等这个性质，有时候会在证明题里出现，比如证明四个点构成的四边形是菱形，就需要通过证明四条边相等来得出结论。

正方形就更有趣了，它是集矩形和菱形的性质于一身的特殊平行四边形。

有这样一道题，正方形ABCD中，E是AB的中点，连接CE，CE的垂直平分线交AD于F，让你证明AF = 1/4 AD。

这题就要用到正方形的性质，它的角是直角，边相等，再结合一些三角形全等的知识。

首先设正方形边长为a，通过相似三角形或者勾股定理求出AF的长度，最后就能得出AF = 1/4 AD的结论。

在做特殊平行四边形的经典题型时，还有一些小技巧。

如果是证明题，一定要仔细分析已知条件，看这些条件能推出什么性质或者结论，然后再往要证明的结论上靠。

如果是计算面积或者边长的题目，一定要牢记各种图形的面积公式和特殊性质。

而且啊，多画图绝对是个好办法，有时候看着图形，思路一下子就清晰了呢。

不要觉得这些题型很难，只要多做几道，就会发现其实它们都是有规律可循的。

特殊四边形的性质和判定定理

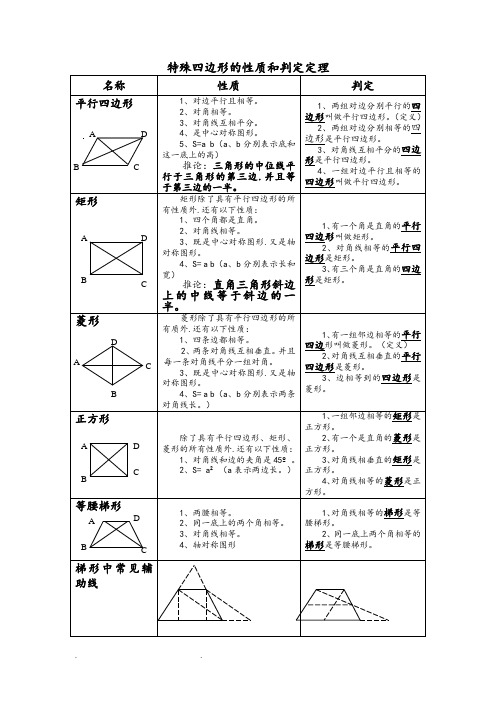
特殊四边形的性质和判定定理名称性质判定平行四边形1、对边平行且相等。

2、对角相等。

3、对角线互相平分。

4、是中心对称图形。

5、S=a b （a 、b 分别表示底和这一底上的高）推论：三角形的中位线平行于三角形的第三边.并且等于第三边的一半。

1、两组对边分别平行的四边形叫做平行四边形。

（定义）2、两组对边分别相等的四边形是平行四边形。

3、对角线互相平分的四边形是平行四边形。

4、一组对边平行且相等的四边形叫做平行四边形。

矩形矩形除了具有平行四边形的所有性质外.还有以下性质：1、四个角都是直角。

2、对角线相等。

3、既是中心对称图形.又是轴对称图形。

4、S= a b （a 、b 分别表示长和宽）推论：直角三角形斜边上的中线等于斜边的一半。

1、有一个角是直角的平行四边形叫做矩形。

2、对角线相等的平行四边形是矩形。

3、有三个角是直角的四边形是矩形。

菱形菱形除了具有平行四边形的所有质外.还有以下性质：1、四条边都相等。

2、两条对角线互相垂直。

并且每一条对角线平分一组对角。

3、既是中心对称图形.又是轴对称图形。

4、S= a b （a 、b 分别表示两条对角线长。

）1、有一组邻边相等的平行四边形叫做菱形。

（定义）2、对角线互相垂直的平行四边形是菱形。

3、边相等到的四边形是菱形。

正方形除了具有平行四边形、矩形、菱形的所有性质外.还有以下性质： 1、对角线和边的夹角是45º。

2、S= a ²（a 表示两边长。

） 1、一组邻边相等的矩形是正方形。

2、有一个是直角的菱形是正方形。

3、对角线相垂直的矩形是正方形。

4、对角线相等的菱形是正方形。

等腰梯形1、两腰相等。

2、同一底上的两个角相等。

3、对角线相等。

4、轴对称图形1、对角线相等的梯形是等腰梯形。

2、同一底上两个角相等的梯形是等腰梯形。

梯形中常见辅助线AB CDABCDABC DABCD A BCD例1 如图.E 、F 分别为正方形ABCD 的边BC 、CD 上的一点.AM ⊥EF.垂足为M.若AM=AB.求证：EF=BE+CF例2 已知：如图.正方形ABCD 中.延长AD 到E.使DE=AD.再延长DE 到F.使DF=BD.连接BF 交CD 于Q.交CE 于P 。

特殊四边形的计算与证明问题(真题10道+模拟30道)-中考数学重难题型押题培优导练案【原卷版】

专题14特殊四边形的计算与证明问题（北京真题10道+模拟30道）【方法归纳】题型概述，方法小结，有的放矢考点考查年份考查频率十年8考特殊四边形的计算与证明（大题）2013.2014.2015.2016.2017.2020.2021.2022以四边形为载体的计算与证明是北京市中考数学常考的一类解答题，要求学生理解和掌握平行四边形、矩形、菱形、正方形的性质定理和判定定理，会画出四边形全等变换后的图形，并会结合其他知识解答一些有探索性、开放性的问题，提高解决问题的能力.解决此类问题的关键是要牢牢把握四边形的性质与特征，挖掘相关图形之间的联系，利用所给图形及图形之间形状、大小、位置关系，进行观察、实验、比较、联想、类比、分析、综合等.常用到的矩形、菱形、正方形的解题策略有：（1）对于矩形：①判定四边形是矩形，一般先判定是平行四边形，然后再判定是矩形；②矩形的内角是直角和对角线相等，相对于平行四边形来说是矩形特殊的性质；③利用矩形的性质计算或证明时，常常运用勾股定理，锐角三角函数或相似三角形求解．（2）对于菱形：①判定四边形是菱形，一般先判定是平行四边形，然后再判定是菱形；②菱形的邻边相等和对角线垂直，相对于平行四边形来说是菱形特殊的性质；③利用菱形的性质计算或证明时，常常运用勾股定理，锐角三角函数或相似三角形求解；④求线段和的最小值时，往往运用菱形的轴对称的性质转化为求线段的长度．（3）对于正方形：①判定四边形是正方形，一般先判定是平行四边形，然后再判定是矩形或菱形，最后判定这个四边形是正方形；②正方形是最特殊的四边形，在正方形的计算或证明时，要特别注意线段或角的等量转化．【典例剖析】典例精讲，方法提炼，精准提分【例1】（2021·北京·中考真题）如图，在四边形ABCD中，∠ACB=∠CAD=90°，点E在BC上，AE//DC,EF⊥AB，垂足为F．（1）求证：四边形AECD是平行四边形；，求BF和AD的长．（2）若AE平分∠BAC,BE=5,cosB=45【例2】（2022·北京·中考真题）如图，在▱ABCD中，AC，BD交于点O，点E，F在AC上，AE=CF．(1)求证：四边形EBFD是平行四边形；(2)若∠BAC=∠DAC,求证：四边形EBFD是菱形．【真题再现】必刷真题，关注素养，把握核心1．（2014·北京·中考真题）如图，在平行四边形ABCD中，AE平分∠BAD，交BC于点E，BF平分∠ABC，交AD于点F，AE与BF交于点P，连接EF，PD．（1）求证：四边形ABEF是菱形；（2）若AB=4，AD=6，∠ABC=60°，求tan∠ADP的值．2．（2016·北京·中考真题）如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN．（1）求证：BM=MN；（2）∠BAD=60°，AC平分∠BAD，AC=2，求BN的长．3．（2017·北京·中考真题）如图，在四边形ABCD中，BD为一条对角线，AD∥BC，AD=2BC，∠ABD=90°，E为AD的中点，连接BE．(1)求证：四边形BCDE为菱形；(2)连接AC，若AC平分∠BAD，BC=1，求AC的长．4．（2017·北京·中考真题）数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所容两长方形面积相等（如图所示）”这一推论，他从这一推论出发，利用“出入相补”原理复原了《海岛算经》九题古证.,（以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》）请根据上图完成这个推论的证明过程．证明：S矩形NFGD=S△ADC-（S△ANF+S△FGC），S矩形EBMF=S△ABC-（____________+____________）．易知，S△ADC=S△ABC，_____________=______________，______________=_____________．可得S矩形NFGD= S矩形EBMF．5．（2013·北京·中考真题）如图，在▱ABCD中，F是AD的中点，延长BC到点E，使CE=1BC，连结DE，2CF．（1）求证：四边形CEDF是平行四边形；（2）若AB=4，AD=6，∠B=60°，求DE的长．6．（2015·北京·中考真题）在▱ABCD，过点D作DE∠AB于点E，点F在边CD上，DF＝BE，连接AF，BF.（1）求证：四边形BFDE是矩形；（2）若CF＝3，BF＝4，DF＝5，求证：AF平分∠DAB.7．（2020·北京·中考真题）如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上，EF∠AB，OG∠EF．（1）求证：四边形OEFG是矩形；（2）若AD=10，EF=4，求OE和BG的长．8．（2016·北京·中考真题）如图，四边形ABCD是平行四边形，AE平分∠BAD，交DC的延长线于点E．求证：DA=DE．【模拟精练】押题必刷，巅峰冲刺，提分培优一、解答题1．（2022·北京房山·二模）已知：如图，在四边形ABCD中，AB∥DC,AC⊥BD，垂足为M，过点A作AE⊥AC，交CD的延长线于点E．(1)求证：四边形ABDE是平行四边形；(2)若AC=8,sin∠ABD=4，求BD的长．52．（2022·北京西城·二模）如图，菱形ABCD的对角线AC，BD交于点O，点E，F分别在DA，BC的延长线上，且BE∠ED，CF=AE．(1)求证：四边形EBFD是矩形；(2)若AB=5，cos∠OBC=4，求BF的长．53．（2022·北京朝阳·二模）如图，在菱形ABCD中，O为AC，BD的交点，P，M，N分别为CD，OD，OC 的中点．(1)求证：四边形OMPN是矩形；(2)连接AP，若AB=4，∠BAD=60∘，求AP的长．4．（2022·北京东城·二模）如图，在平行四边形ABCD中，DB=DA，点F是AB的中点，连接DF并延长，交CB的延长线于点E，连接AE．(1)求证：四边形AEBD是菱形；(2)若DC=√10，tan∠DCB=3，求菱形AEBD的边长．5．（2022·北京平谷·二模）如图，在□ABCD中，连接AC，点E是AB中点，点F是AC的中点，连接EF，过E作EG∥AF，交DA的延长线于点G．(1)求证：四边形AGEF是平行四边形；(2)若sin∠G=3，AC=10，BC=12，连接GF，求GF的长．56．（2022·北京北京·二模）如图，在等边△ABC中，D是BC的中点，过点A作AE∥BC，且AE=DC，连接CE．(1)求证：四边形ADCE是矩形；(2)连接BE交AD于点F，连接CF．若AB=4，求CF的长．7．（2022·北京丰台·二模）如图，在∠ABC中，∠BAC=90∘，AD∠BC，垂足为D，AE∠BC，CE∠DA．(1)求证：四边形AECD是矩形；(2)若AB＝5，cosB=3，求AE的长．58．（2022·北京密云·二模）如图，在平行四边形ABCD中，AC平分∠BAD，点E为AD边中点，过点E作AC的垂线交AB于点M，交CB延长线于点F．(1)求证：平行四边形ABCD是菱形；(2)若FB=2，sinF=3，求AC的长．59．（2022·北京市十一学校模拟预测）如图，在四边形ABCD中，AD=CD，BD⊥AC于点O，点E是DB延长线上一点，OE=OD，BF⊥AE于点F．(1)求证：四边形AECD是菱形；(2)若AB平分∠EAC，OB=3，tan∠CED=3，求EF和AD的长．410．（2022·北京昌平·二模）如图，在矩形ABCD中，对角线AC，BD交于点O，分别过点C，D作BD，AC的平行线交于点E，连接OE交AD于点F．(1)求证：四边形OCED是菱形；(2)若AC=8，∠DOC=60°，求菱形OCED的面积．11．（2022·北京海淀·二模）如图，在Rt∠ABC中，∠A =90°，点D，E，F分别为AB，AC，BC的中点，连接DF，EF．(1)求证：四边形AEFD是矩形；(2)连接BE，若AB = 2，tan C =1，求BE的长．212．（2022·北京东城·一模）如图，在正方形ABCD中，E为对角线AC上一点（AE>CE），连接BE，DE．(1)求证：BE=DE；(2)过点E作EF⊥AC交BC于点F，延长BC至点G，使得CG=BF，连接DG．∠依题意补全图形；∠用等式表示BE与DG的数量关系，并证明．13．（2022·北京东城·一模）如图，在四边形ABCD中，AC与BD相交于点O，且AO=CO，点E在BD上，∠EAO=∠DCO．(1)求证：四边形AECD是平行四边形；(2)若AB=BC，CD=5，AC=8，tan∠ABD=2，求BE的长．314．（2022·北京市十一学校二模）如图，在平行四边形ABCD中，CE⊥AD于点E，延长DA至点F，使得AF=DE，连接BF，CF．(1)求证：四边形BCEF是矩形；(2)若AB=6，CF=8，DF=10，求EF的长．15．（2022·北京石景山·一模）如图所示，△ABC中，∠ACB=90°，D，E分别为AB，BC的中点，连接DE 并延长到点F，使得EF=DE，连接CD，CF，BF．(1)求证：四边形BFCD是菱形；(2)若cos A=5，DE=5，求菱形BFCD的面积．1316．（2022·北京大兴·一模）如图，在平面四边形ABCD中，点E，F分别是AB，CD上的点，CF=BE．(1)求证：四边形AEFD是平行四边形；(2)若∠A=60°，AD=2，AB=4，求BD的长．17．（2022·北京丰台·一模）如图，在四边形ABCD中，∠DCB＝90°，AD∥BC，点E在BC上，AB∥DE，AE 平分∠BAD．(1)求证：四边形ABED为菱形；(2)连接BD，交AE于点O．若AE＝6，sin∠DBE＝3，求CD的长．518．（2022·北京市师达中学模拟预测）如图，四边形ABCD是平行四边形,AE∠BC，AF∠CD，垂足分别为E，F，且BE=DF．(1)求证：四边形ABCD是菱形；(2)连接EF并延长，交AD的延长线于点G，若∠CEG=30°，AE =2，求EG的长．19．（2022·北京四中模拟预测）如图，在四边形ABCD中，AD＝CD，BD∠AC于点O，点E是DB延长线上一点，OE＝OD，BF∠AE于点F．(1)求证：四边形AECD是菱形；(2)若AB平分∠EAC，OB＝3，BE＝5，求EF和AD的长．20．（2021·北京丰台·一模）如图，在菱形ABCD中，对角线AC、BD交于点O，过点A作AE∠BC于E，延长BC到点F，使CF＝BE，连接DF．(1)求证：四边形AEFD是矩形；(2)连接OE，若AD＝10，EC＝4，求OE的长度．21．（2022·北京市燕山教研中心一模）如图，在菱形ABCD中，对角线AC与BD相交于点O，过点D作DE⊥BD 交BC的延长线于点E．(1)求证：四边形ACED是平行四边形；(2)若BD=4，AC=3，求sin∠CDE的值．22．（2022·北京平谷·一模）如图，∠ABC中，∠ACB＝90°，点D为AB边中点，过D点作AB的垂线交BC 于点E，在直线DE上截取DF，使DF＝ED，连接AE、AF、BF．(1)求证：四边形AEBF是菱形；(2)若cos∠EBF＝3，BF＝5，连接CD，求CD的长．523．（2022·北京市第一六一中学分校一模）在矩形ABCD中，AC，BD相交于点O，过点C作CE∠BD交AD的延长线于点E．(1)求证：∠ACD＝∠ECD；(2)连接OE，若AB＝2，tan∠ACD＝2，求OE的长．24．（2022·北京房山·一模）如图，在平行四边形ABCD中，过点B作BE∠CD交CD的延长线于点E，过点C作CF∥EB交AB的延长线于点F．(1)求证：四边形BFCE是矩形；(2)连接AC，若AB=BE=2，tan∠FBC=1，求AC的长225．（2022·北京朝阳·一模）如图，在矩形ABCD中，AC，BD相交于点O，AE//BD，BE//AC．(1)求证：四边形AEBO是菱形；(2)若AB=OB=2，求四边形AEBO的面积．26．（2022·北京·中国人民大学附属中学分校一模）如图，正方形ABCD中，P为BD上一动点，过点P作PQ⊥AP 交CD边于点Q．(1)求证：PA=PQ；(2)用等式表示PB、PD、AQ之间的数量关系，并证明；(3)点P从点B出发，沿BD方向移动，若移动的路径长为4，则AQ的中点M移动的路径长为（直接写出答案）．BC，27．（2022·北京市三帆中学模拟预测）已知：△ABC中，AB=AC，AD⊥BC于点D，过点A作AE，且AE=12连结DE．(1)求证：四边形ABDE是平行四边形；(2)作FG⊥AB于点G，AG=4，cos∠GAF=4，求FG和FD的长．528．（2022·北京西城·一模）如图，在∠ABC中，BA=BC，BD平分∠ABC交AC于点D，点E在线段BD上，点F在BD的延长线上，且DE=DF，连接AE，CE，AF，CF．(1)求证：四边形AECF是菱形；(2)若BA∠AF，AD=4，BC=4√5，求BD和AE的长．29．（2022·北京顺义·一模）如图，在四边形ABCD中，AD∥BC，AC⊥BD，垂足为O，过点D作BD的垂线交BC的延长线于点E．(1)求证：四边形ACED是平行四边形；(2)若AC=4，AD=2，cos∠ACB=4，求BC的长．530．（2022·北京通州·一模）如图．在∠ABC中，AB＝BC，BD平分∠ABC交AC于点D．点E为AB的中点，连接DE，过点E作EF∥BD交CB的延长线于点F．(1)求证：四边形DEFB是平行四边形；(2)当AD＝4，BD＝3时，求CF的长．。

特殊四边形的证明与计算

特殊四边形的证明与计算1．如图，△ABC 是等边三角形，点E 在线段AC 上，连接BE ，以BE 为边作等边三角形BEF ，将线段CE 绕点C 顺时针旋转60°，得到线段CD ，连接AF 、AD 、ED .(1)求证：△BCE ≌△ACD ；(2)求证：四边形ADEF 是平行四边形．第1题图证明：(1)∵△ABC 是等边三角形，∴BC ＝AC ，∠BCE ＝60°，由题意得CE ＝CD ，∠ECD ＝60°.在△BCE 和△ACD 中，⎩⎪⎨⎪⎧BC ＝AC ∠BCE ＝∠ACD ＝60°CE ＝CD， ∴△BCE ≌△ACD (SAS)；(2)∵△BCE ≌△ACD ，∴AD ＝BE ，∠DAE ＝∠CBE ，∵△BEF 是等边三角形，∴BE＝EF＝BF，∠EBF＝60°，∴AD＝EF，∵△ABC与△BEF均是等边三角形，∴∠BCE＝∠BEF＝60°，∵∠BCE＋∠CBE＝∠BEF＋∠AEF，∴∠CBE＝∠AEF，∴∠DAE＝∠AEF，∴AD∥EF，∴四边形ADEF是平行四边形．2．如图，在△ABC中，点D是边BC的中点，点E在△ABC内，AE 平分∠BAC，CE⊥AE，点F在边AB上，EF∥BC.(1)求证：四边形BDEF是平行四边形；(2)线段BF、AB、AC之间具有怎样的数量关系？证明你所得到的结论．第2题图(1)证明：如解图，延长CE交AB于点G，第2题解图∵AE ⊥CE ，∴∠AEG ＝∠AEC ＝90°，∵AE 平分∠BAC ，∴∠GAE ＝∠CAE ，在△AGE 和△ACE 中，⎩⎪⎨⎪⎧∠GAE ＝∠CAE AE ＝AE∠AEG ＝∠AEC， ∴△AGE ≌△ACE (ASA)，∴GE ＝EC .∵点D 是边BC 的中点，∴BD ＝CD ，DE 为△CGB 的中位线，∴DE ∥BF .又∵EF ∥BC ，∴四边形BDEF 是平行四边形；(2)解：BF ＝12(AB －AC )．理由如下：由(1)可知，△AGE ≌△ACE ，四边形BDEF 是平行四边形，∴AG ＝AC ，BF ＝DE ＝12BG ，∴BF ＝12BG ＝12(AB －AG )＝12(AB －AC )．3．如图，已知边长为22的正方形ABCD中，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE，交线段BC于点F，以DE，EF为邻边作矩形DEFG，连接CG.(1)求证：矩形DEFG是正方形；(2)设AE＝x，四边形DEFG的面积为S，当x为何值时，S的值最小，求出最小值．第3题图(1)证明：如解图①，过点E作EM⊥BC于点M，EN⊥CD于点N，第3题解图①∴∠MEN＝90°，∴∠MEF＋∠FEN＝90°，∵点E是正方形ABCD对角线上的点，∴EM＝EN，∵∠DEF＝90°，∴∠DEN＋∠FEN＝90°，∴∠DEN ＝∠MEF ，在△DEN 和△FEM 中，⎩⎪⎨⎪⎧∠DNE ＝∠FME ＝90°EN ＝EM∠DEN ＝∠FEM， ∴△DEN ≌△FEM (ASA)，∴DE ＝EF ，∵四边形DEFG 是矩形，∴矩形DEFG 是正方形；(2)解：∵在正方形ABCD 中，AB ＝22，∴AC ＝4，∠DAE ＝45°，如解图②，过点E 作EH ⊥AD 于点H ，第3题解图②∵AE ＝x (0<x <4)，∴AH ＝EH ＝22x ，在Rt △DHE 中，DH ＝AD －AH ＝22－22x ，EH ＝22x ，根据勾股定理得，DE2＝DH2＋EH2＝(22－22x)2＋(22x)2＝x2－4x＋8，∵四边形DEFG为正方形，∴S＝DE2＝x2－4x＋8＝(x－2)2＋4，∴当x＝2时，S有最小值，即为4.4.如图，在△ABC和△BCD中，∠BAC＝∠BCD＝90°，AB＝AC，CB ＝CD，延长CA至点E，使AE＝AC；延长CB至点F，使BF＝BC，连接AD、AF、DF、EF.延长DB交EF于点N.(1)求证：AD＝AF；(2)试判断四边形ABNE的形状，并说明理由．第4题图(1)证明：∵AB＝AC，∠BAC＝90°，∴∠ABC＝∠ACB＝45°，∴∠ABF＝180°－∠ABC＝135°，∵∠BCD＝90°，∴∠ACD＝90°＋∠ACB＝135°，∴∠ABF＝∠ACD，∵CB＝CD，CB＝BF，∴BF ＝CD ，在△ABF 和△ACD 中，⎩⎪⎨⎪⎧AB ＝AC ∠ABF ＝∠ACD BF ＝CD，∴△ABF ≌△ACD (SAS)，∴AD ＝AF ；(2)解：四边形ABNE 是正方形．理由如下：∵CD ＝CB ，∠BCD ＝90°，∴∠CBD ＝45°，∵∠ABC ＝45°，∴∠ABD ＝90°，∴∠ABN ＝90°，由(1)知△ABF ≌△ACD ，∴∠F AB ＝∠CAD ，∴∠F AB ＋∠BAD ＝∠CAD ＋∠BAD ＝90°，∵∠EAF ＋∠F AB ＝90°，∴∠EAF ＝∠BAD ，∵AB ＝AC ＝AE ，AF ＝AD ，∴△AEF ≌△ABD (SAS)．∴∠AEF ＝∠ABD ＝90°，∵∠EAB＝90°，∴四边形ABNE是矩形，又∵AE＝AB，∴四边形ABNE是正方形．5．如图，四边形ABCD是平行四边形，AD＝AC，AD⊥AC，E是AB 的中点，F是AC延长线上的一点．(1)若ED⊥EF，求证：ED＝EF；(2)在(1)的条件下，若DC的延长线与FB交于点P，试判断四边形ACPE是否为平行四边形？并证明你的结论．(请先补全图形，再解答)第5题图(1)证明：∵四边形ABCD是平行四边形，AD＝AC，AD⊥AC.∴AC＝BC，AC⊥BC，如解图，连接CE，第5题解图∵E为AB的中点，∴AE ＝EC ，CE ⊥AB ，∴∠ACE ＝∠CAE ＝45°，∴∠DAE ＝∠ECF ＝135°，又∵∠AED ＋∠CED ＝∠CEF ＋∠CED ＝90°，∴∠AED ＝∠CEF ，∴△AED ≌△CEF (ASA)，∴ED ＝EF ；(2)解：补全图形如解图，四边形ACPE 是平行四边形；证明：∵由(1)得△AED ≌△CEF ，∴AD ＝CF ，∴AC ＝CF ，又∵CP ∥AE ，∴CP 为△F AB 的中位线，∴CP ＝12AB ＝AE ，∵CP ∥AE ，∴四边形ACPE 是平行四边形．6．如图，已知Rt △ABC 中，∠ABC ＝90°，先把△ABC 绕点B 顺时针旋转90°至△DBE ，再把△ABC 沿射线AB 平移至△FEG ，DE 、FG 相交于点H .(1)判断线段DE 、FG 的位置关系，并说明理由；(2)连接CG，求证：四边形CBEG是正方形．第6题图(1)解：FG⊥DE.理由如下：∵△ABC绕点B顺时针旋转90°至△DBE，∴∠DEB＝∠ACB，∵把△ABC沿射线AB平移至△FEG，∴∠GFE＝∠A，∵∠ABC＝90°，∴∠A＋∠ACB＝90°，∴∠GFE＋∠DEB＝90°，∴∠FHE＝90°，∴FG⊥DE；(2)证明：根据旋转和平移可得∠GEF＝90°，∠CBE＝90°，CG∥EB，CB＝BE，∵CG∥EB，∴∠BCG＋∠CBE＝180°，∴∠BCG＝90°，∴四边形BCGE是矩形，∵CB＝BE，∴四边形CBEG 是正方形．7．如图①，BD 是矩形ABCD 的对角线，∠ABD ＝30°，AD ＝1.将△BCD 沿射线BD 方向平移到△B ′C ′D ′的位置，使B ′为BD 中点，连接AB ′，C ′D ，AD ′，BC ′.如图②.(1)求证：四边形AB ′C ′D 是菱形； (2)四边形ABC ′D ′的周长为________．第7题图(1)证明：∵四边形ABCD 是矩形， ∴AD ∥BC ，AD ＝BC .由平移性质可知AD ∥B ′C ′，AD ＝B ′C ′， ∴四边形AB ′C ′D 为平行四边形， ∵∠DAB ＝90°，∠ABD ＝30°， ∴AD ＝12BD . ∵B ′为BD 中点， ∴AB ′＝12BD ， ∴AD ＝AB ′，∴四边形AB ′C ′D 是菱形；(2)解：4 3.【解法提示】如解图，连接AC′交B′D于点O，第7题解图∵四边形AB′C′D是菱形，∴AC′⊥BD′，OA＝OC′，OD＝OB′，又∵BD＝B′D′，∴BB′＝DD′，∴OB＝OD′，∴四边形ABC′D′是菱形，∴tan∠ABD＝tan30°＝33＝ADAB＝1AB，得AB＝3，∴四边形ABC′D′的周长是4 3.8.边长为22的正方形ABCD中，P是对角线AC上的一个动点(点P 与A、C不重合)．连接BP，将BP绕点B顺时针旋转90°到BQ，连接QP，QP与BC交于点E，QP的延长线与AD(或AD延长线)交于点F.(1)连接CQ，证明：CQ＝AP；(2)设AP＝x，CE＝y，试写出y关于x的函数关系式，并求当x为何值时，CE＝38BC；(3)猜想PF 与EQ 的数量关系，并证明你的结论．第8题图(1)证明：由题意知BP ＝BQ ，∠PBQ ＝90°，在正方形ABCD 中，AB ＝CB ，∠ABC ＝90°， ∴∠ABC ＝∠PBQ ，∴∠ABC －∠PBC ＝∠PBQ －∠PBC ，即∠ABP ＝∠CBQ ，在△ABP 和△CBQ 中， ⎩⎪⎨⎪⎧AB ＝CB ∠ABP ＝∠CBQ BP ＝BQ， ∴△ABP ≌△CBQ (SAS)， ∴CQ ＝AP ；(2)解：在正方形ABCD 中，AC 为对角线， ∴∠BAP ＝∠PCE ＝45°，由旋转可知△PBQ 为等腰直角三角形， ∴∠BPQ ＝∠PQB ＝45°，在△ABP 中，∠BPC ＝∠BAP ＋∠ABP ＝45°＋∠ABP ，又∵∠BPC ＝∠BPQ ＋∠CPE ＝45°＋∠CPE ，∴∠ABP ＝∠CPE ，又∵∠BAP ＝∠PCE ， ∴△BAP ∽△PCE ， ∴AB CP ＝AP CE ，在等腰直角△ABC 中，AB ＝22， ∴AC ＝4，又∵AP ＝x ，CE ＝y ，∴CP ＝4－x ， ∴224－x＝x y ，即y ＝－24x 2＋2x ，(0<x <4) 当CE ＝38BC 时，即CE ＝y ＝38×22＝324， ∴324＝－24x 2＋2x ，解得x 1＝1，x 2＝3，∴y ＝－24x 2＋2x (0<x <4)，当x ＝1或3时，CE ＝38BC ； (3)解：猜想：PF ＝EQ .证明：①当点F 在线段AD 上时，如解图①，在CE 上取一点H ，使HQ ＝EQ ，则∠QEH ＝∠QHE ，第8题解图①在正方形ABCD 中，∵AD ∥BC ， ∴∠DFE ＝∠QEH ， ∴∠DFE ＝∠QHE ， ∴∠AFP ＝∠CHQ ，由(1)知△ABP ≌△CBQ ，AP ＝CQ ，∠BAP ＝∠BCQ ＝45°， ∴∠F AP ＝∠BAP ＝∠BCQ ＝45°，在△AFP 和△CHQ 中， ⎩⎪⎨⎪⎧∠F AP ＝∠HCQ ∠AFP ＝∠CHQ AP ＝CQ， ∴△AFP ≌△CHQ (AAS)， ∴PF ＝HQ ，又∵HQ ＝EQ ， ∴PF ＝EQ ；②当点F 在线段AD 延长线上时，如解图②，在BE 上取一点H ，使HQ ＝EQ ，第8题解图②同理可证△AFP ≌△CHQ (AAS)，得FP ＝HQ ＝EQ.9．如图，在△AEF中，∠EAF＝45°，AG⊥EF于点G，现将△AEG 沿AE折叠得到△AEB，将△AFG沿AF折叠得到△AFD，延长BE 和DF相交于点C.(1)求证：四边形ABCD是正方形；(2)连接BD分别交AE、AF于点M、N，将△ABM绕点A逆时针旋转，使AB与AD重合，得到△ADH，试判断线段MN、ND、DH之间的数量关系，并说明理由．第9题图(1)证明：∵△AEB由△AEG翻折得到，∴∠ABE＝∠AGE＝90°，∠BAE＝∠EAG，AB＝AG，∵△AFD由△AFG翻折得到，∴∠ADF＝∠AGF＝90°，∠DAF＝∠F AG，AD＝AG，∵∠EAG＋∠F AG＝∠EAF＝45°，∴∠BAE＋∠DAF＝45°，∴∠ABE＝∠AGE＝∠BAD＝∠ADC＝90°，∴四边形ABCD是矩形，又∵AB＝AG＝AD，∴四边形ABCD是正方形；(2)解：MN 2＝ND 2＋DH 2，理由：如解图，连接NH ，第9题解图∵△ADH 由△ABM 旋转得到， ∴△ABM ≌△ADH ，∴AM ＝AH ，∠BAM ＝∠DAH ，∠ADH ＝∠ABM ＝45°，∴∠HAN ＝∠DAH ＋∠DAN ＝∠BAM ＋∠DAN ＝∠EAG ＋∠F AG ＝∠EAF ，∵在△AMN 和△AHN 中， ⎩⎪⎨⎪⎧AM ＝AH ∠MAN ＝∠NAH AN ＝AN， ∴△AMN ≌△AHN (SAS)， ∴MN ＝NH ，由(1)知∠ADB ＝45°，∴∠HDN ＝∠ADH ＋∠ADN ＝90°， ∴在Rt △DHN 中，DH 2＋DN 2＝NH 2，∴MN2＝ND2＋DH2.10．如图，正方形ABCD的对角线AC，BD相交于点O，延长CB至点F，使CF＝CA，连接AF，∠ACF的平分线分别交AF，AB，BD 于点E，N，M，连接EO.(1)已知EO＝2，求正方形ABCD的边长；(2)猜想线段EM与CN的数量关系并加以证明．第10题图解：(1)∵正方形ABCD的对角线AC，BD相交于点O，∴O是线段AC的中点，∵CF＝AC，∴△ACF是等腰三角形，又∵CE平分∠ACF，∴E是AF的中点，∴EO是△ACF的中位线，∴CF＝2EO＝22，∴AC＝22，∵四边形ABCD是正方形，∴∠ACB＝45°，∴在Rt △ABC 中，AB ＝AC ·sin45°＝22×22＝2， ∴正方形ABCD 的边长为2. (2)猜想：EM ＝12CN . 证明：如解图，连接BE ，第10题解图由(1)知，E 是AF 的中点， ∴在Rt △ABF 中，EB ＝AE ＝12AF ， ∴∠ABE ＝∠BAF ，∵AC ＝CF ，CE 平分∠ACF ， ∴CE ⊥AF ，∴∠F ＋∠BCN ＝90°，又∵∠F ＋∠BAF ＝90°， ∴∠BCN ＝∠BAF ，∵AB ＝BC ，∠ABF ＝∠CBN ＝90°， ∴△ABF ≌△CBN (ASA)， ∴AF ＝CN ，∴EB ＝12AF ＝12CN ，又∵∠EBM ＝∠ABE ＋∠ABO ＝∠BAF ＋∠OBC ＝∠BCE ＋∠OBC ＝∠EMB ，∴EB ＝EM ，∴EM ＝12CN .11．(1)如图①，在矩形ABCD 中，对角线AC 与BD 相交于点O ，过点O 作直线EF ⊥BD 交AD 于点E ，交BC 于点F ，连接BE ，DF ，且BE 平分∠ABD .求证：四边形BFDE 是菱形；(2)把(1)中菱形BFDE 进行分离研究，如图②，G ，I 分别在BF ，BE 边上，且BG ＝BI ，连接GD ，H 为GD 的中点，连接FH 并延长交ED 于点J ，连接IJ ，IH ，IF ，IG .试探究线段IH 与FH 之间满足的数量关系，并说明理由；第11题图(1)证明：如解图①，第11题解图①∵四边形ABCD 是矩形， ∴AD ∥BC ，OB ＝OD ， ∴∠EDO ＝∠FBO ，在△DOE 和△BOF 中， ⎩⎪⎨⎪⎧∠EDO ＝∠FBO OD ＝OB∠EOD ＝∠BOF， ∴△DOE ≌△BOF (ASA)， ∴EO ＝OF ， ∵OB ＝OD ，∴四边形BFDE 是平行四边形， ∵EF ⊥BD ，∴四边形BFDE 是菱形； (2)解：IH ＝3FH .理由：如解图②，延长BE 到点M ，使得EM ＝EJ ，连接MJ .第11题解图②如解图①，∵四边形BFDE 是菱形， ∴∠EBO ＝∠FBO ，又∵BE 平分∠ABD ， ∴∠ABE ＝∠EBO ，∴∠ABE ＝∠EBO ＝∠FBO ＝30°， ∴∠EBF ＝60°，如解图②，由四边形BFDE 是菱形可得EB ＝BF ＝ED ，DE ∥BF ， ∴∠JDH ＝∠FGH ，在△DHJ 和△GHF 中， ⎩⎪⎨⎪⎧∠DHJ ＝∠GHF DH ＝GH∠JDH ＝∠FGH， ∴△DHJ ≌△GHF (ASA)， ∴DJ ＝FG ，JH ＝HF ， ∴EJ ＝BG ＝EM ＝BI ， ∴BE ＝IM ＝BF ， ∵∠MEJ ＝∠B ＝60°， ∴△MEJ 是等边三角形，∴MJ ＝EM ＝BI ，∠M ＝∠EBF ＝60°，在△BIF 和△MJI 中， ⎩⎪⎨⎪⎧BI ＝MJ ∠B ＝∠M BF ＝IM， ∴△BIF ≌△MJI (SAS)，∴IJ＝IF，∠BFI＝∠MIJ，∵HJ＝HF，∴IH⊥JF，∵∠BFI＋∠BIF＝120°，∴∠MIJ＋∠BIF＝120°，∴∠JIF＝60°，∴△JIF是等边三角形，在Rt△IHF中，∵∠IHF＝90°，∠IFH＝60°，∴IH＝3FH.12．如图①，两个全等的等边三角形纸片ABC和DEF，其中点C和点F重合，点A、D均在直线l上，且AB⊥l，DE⊥l.如图①，保持纸片DEF不动，将△ABC沿l向右平移，直到AB与DE重合时停止，如图②，设BC与EF相交于点G，AC与DF相交于点H.(1)证明：四边形CGFH是菱形；(2)当AD＝AB时，直接写出S△AHD与S菱形CGFH的关系；第12题图(1)证明：根据平移性质可知，GF∥HC，GC∥FH，∴四边形CGFH是平行四边形，∵AB⊥l，DE⊥l，∴∠BAD＝∠EDA＝90°，∵△ABC和△DEF都是等边三角形，∴∠BAC＝∠EDF＝60°，∴∠CAD＝∠FDA＝30°，∴HA＝HD，∵△ABC≌△DEF，∴AC＝DF，∴AC－AH＝DF－DH，∴HC＝HF，∴四边形CGFH是菱形；(2)解：S菱形CGFH＝(8－43)S△AHD.【解法提示】如解图，过点H作HM⊥AD于点M，连接GH，设AB＝AD＝6a，第12题解图∵HA＝HD，HM⊥AD，∴AM＝MD＝3a，∵∠HAM＝30°，∴HM＝33AM＝3a，AH＝2HM＝23a，∴HC ＝AC －AH ＝6a －23a ， ∵∠C ＝60°，四边形CGFH 是菱形， ∴△CGH 和△FGH 都是等边三角形，∴S 菱形CGFH ＝2S △CHG ＝2×34CH 2＝32(6a －23a )2＝(243－36)a 2， ∵S △ADH ＝12AD ·HM ＝12·6a ·3a ＝33a 2， ∴S △AHDS 菱形CGFH ＝33a 2（243－36）a 2＝18－43，即S 菱形CGFH ＝(8－43)S △AHD .13．如图，矩形ABCD 的对角线AC ，BD 相交于点O ，△COD 关于CD 的对称图形为△CED . (1)求证：四边形OCED 是菱形；(2)连接AE ，若AB ＝6 cm ，BC ＝ 5 cm.求sin ∠EAD 的值．第13题图(1)证明：∵四边形ABCD 是矩形， ∴AC ＝BD ，且AC 、BD 互相平分， ∴DO ＝CO .∵△COD 与△CED 关于CD 对称， ∴△COD ≌△CED ，∴CO＝CE，DO＝DE，∴CE＝CO＝DO＝DE，∴四边形OCED是菱形；(2)解：如解图，连接EO交CD于点F，延长交AB于点H.第13题解图∵四边形ABCD是矩形，AB＝6 cm，∴BC⊥CD，CD＝AB＝6 cm.∵四边形OCED是菱形，∴EO⊥CD，且EO、CD互相平分，∴EF＝FO，DF＝FC＝3 cm，FO∥BC，即EH∥BC，又∵CE∥OB，∴四边形OBCE为平行四边形．又∵BC＝ 5 cm，∴EF＝FO＝12BC＝52cm.∵FO∥BC，在矩形ABCD中，AB∥CD，∠ABC＝90°，∴四边形FHBC是矩形，∴FH＝BC＝ 5 cm，HB＝FC＝3 cm，∴AH＝AB－HB＝3 cm，EH＝EF＋FH＝352cm.∵AB ∥CD ，EH ⊥CD ， ∴EH ⊥AB ，∴在Rt △AEH 中，AE 2＝AH 2＋EH 2＝32＋(352)2＝814 cm 2， ∴AE ＝92 cm ，∴sin ∠AEH ＝AH AE ＝392＝23，∵EH ∥BC ，AD ∥BC ，∴AD ∥EH ，∴∠EAD ＝∠AEH ，∴sin ∠EAD ＝sin ∠AEH ＝23. 14．如图，在矩形ABCD 中，E 为AB 边上一点，EC 平分∠DEB ，F 为CE 的中点，连接AF ，BF ，过点E 作EH ∥BC 分别交AF ，CD 于G ，H 两点． (1)求证：DE ＝DC ； (2)求证：AF ⊥BF ；(3)当AF ·GF ＝28时，请直接写出CE 的长．第14题图(1)证明：∵四边形ABCD 为矩形，∴AB ∥DC ，∴∠DCE ＝∠CEB ， ∵EC 平分∠DEB ， ∴∠DEC ＝∠CEB ， ∴∠DEC ＝∠DCE ， ∴DE ＝DC ；(2)证明：如解图，连接DF ，第14题解图∵DE ＝DC ，F 为CE 的中点， ∴DF ⊥EC ， ∴∠DFC ＝90°，在矩形ABCD 中， AB ＝DC ，∠ABC ＝90°， ∴BF ＝CF ＝EF ＝12EC ， ∴∠ABF ＝∠CEB ， ∵∠DCE ＝∠CEB ， ∴∠ABF ＝∠DCE ， ∴△ABF ≌△DCF (SAS)，∴∠AFB ＝∠DFC ＝90°，∴AF ⊥BF ；(3)解：CE ＝47.【解法提示】∵∠AFB ＝90°，∴∠BAF ＋∠ABF ＝90°， ∵EH ∥BC ，∠ABC ＝90°，∴∠BEH ＝90°， ∴∠FEH ＋∠CEB ＝90°，∵∠ABF ＝∠CEB ，∴∠BAF ＝∠FEH ， ∵∠EFG ＝∠AFE ，∴△EFG ∽△AFE ， ∴EF AF ＝GFEF ，∴EF 2＝AF ·GF ，∵AF ·GF ＝28，∴EF ＝28＝27，∴CE ＝2EF ＝47.15．如图，四边形ABCD 是正方形，AB ＝4，E 是边CD 上的点，F 是DA 的延长线上的点，且CE ＝AF .将△BCE 沿BE 折叠，得到△BC ′E ，延长BC ′交AD 于点G . (1)求证：△BCE ≌△BAF ； (2)①若DG ＝1，求FG 的长；②若∠CBE ＝30°，点B 和点H 关于DF 对称，求证：四边形FHGB 是菱形．第15题图(1)证明：∵四边形ABCD 为正方形，∴AB＝BC，∠F AB＝∠C＝90°，第15题解图又∵CE＝AF，∴△BCE≌△BAF(SAS)；(2)①解：如解图，连接EG，∵四边形ABCD为正方形，AB＝4，∴AD＝AB＝BC＝4，∴AG＝AD－GD＝3，在Rt△ABG中，依据勾股定理可知BG＝5.由翻折的性质可知EC′＝EC，BC′＝BC＝4，∴C′G＝BG－BC′＝1，∴C′G＝DG＝1.在Rt△C′GE和Rt△DGE中，C′G＝DG，EG＝EG，∴Rt△C′GE≌Rt△DGE(HL)，∴C′E＝DE，∴EC＝DE＝2，∴AF＝CE＝2，∴FG＝AF＋AG＝2＋3＝5；②证明：由翻折的性质可知∠C ′BE ＝∠CBE ＝30°. ∵∠ABC ＝90°，∴∠ABG ＝30°，∴AG ＝AB ·tan30°＝433.∵在Rt △BCE 中，∠EBC ＝30°，∴EC ＝BC ·tan30°＝433，∴AG ＝CE ，又∵CE ＝AF ，∴AF ＝AG .又∵点B 和点H 关于DF 对称，∴BH ⊥FG ，AH ＝AB .∵AF ＝AG ，AH ＝AB ，∴四边形FHGB 是平行四边形，又∵BH ⊥FG ，∴四边形FHGB 是菱形．。

中考数学专题复习课件-专题4-特殊四边形相关的证明与计算

(2)在BC边上取点F,使BF=
,连接OF;
(3)在CD边上取点G,使CG=
,连接OG;
(4)在DA边上取点H,使DH=
,连接OH.
由于AE=
+
=
+
=
+
=
.
可证S =S =S =S =S . △AOE 四边形EOFB 四边形FOGC 四边形GOHD △HOA
答案 3;2;1;EB;BF;FC;CG;GD;DH;HA
解析 (1)证明:∵EG垂直平分DC,∴DE=CE,
∴∠EDC=∠ECD.
∵CD平分∠ECG,∴∠ECD=∠DCG.∴∠EDC=∠DCG.
∴DE∥GC. (1分)
同理DG∥EC.∴四边形DGCE是平行四边形.
∵DE=CE,∴四边形DGCE是菱形. (2分)
(2)∵四边形DGCE是菱形,∴DG=DE=6.
解析 (1)证明:∵D,E,F分别是AB,AC,BC的中点,
∴DE= 1
2
1
BC=FC,DF= 2
AC=EC.
(1分)
∵AC=BC,∴DE=FC=DF=EC. (2分)
∴四边形DFCE是菱形. (3分)
(2)过点E作EH⊥BC于点H,如图.
∵AC=BC,∴∠A=∠B.∵∠A=75°,∴∠C=180°-∠A-∠B=30°. (4分)
图1,图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点. (1)在图1中画出等腰直角三角形MON,使点N在格点上,且∠MON=90°; (2)在图2中以格点为顶点画出一个正方形ABCD,使正方形ABCD面积等于(1)中等腰直角三角形MON面积的4倍,并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD面积没有剩余(画出一种即可).

特殊的四边形及三角形的定义性质判定相关计算公式

特殊的四边形及三角形的定义、性质、判定、相关计算公式平行四边形1.平行四边形的定义：两组对边分别平行的四边形叫做平行四边形．2.平行四边形的性质：1平行四边形是中心对称图形,对称中心是两条对角线的交点,不是轴对称图形;关于对称性的2平行四边形的对角相等；关于角的3平行四边形的邻角互补；关于角的4平行四边形的对边相等；推论：夹在两条平行线间的平行线段;关于边的5平行四边形的对边平行；关于边的6平行四边形的对角线互相平分;关于对角线的7连接平行四边形各边的中点所得图形是平行四边形;关于中点四边形的3.平行四边形的判定方法：1两组对边分别平行的四边形是平行四边形；定义判定法2两组对边分别相等的四边形是平行四边形；3一组对边平行且相等的四边形是平行四边形；4两组对角相等的四边形是平行四边形；5对角线互相平分的四边形是平行四边形;4. 相关计算公式：平行四边形的面积公式：底×高；如用“h”表示高,“a”表示底,“s”表示平行四边形面积,则S=ah平行四边形周长：2×底1+底2；如用“a"表示底1,“b”表示底2,“c“表示平行四边形周长,则C=2a+b5.平行四边形中常用辅助线的添法：1连结对角线或平移对角线；2过顶点作对边的垂线构成直角三角形；3连结对角线交点与一边中点,或过对角线交点作一边的平行线,构成线段平行或中位线；4连结顶点与对边上一点的线段或延长这条线段,构造三角形相似或等积三角形；5过顶点作对角线的垂线,构成线段平行或三角形全等;矩形1.矩形的定义：有一个角是直角的平行四边形是矩形;2.矩形的性质：1矩形是中心对称图形,也是轴对称图形,对称轴是通过对边中点的直线,对称轴共有两条；关于对称性的2矩形的对角相等；关于角的3矩形的邻角互补；关于角的4矩形的对边相等；关于边的5矩形的对边平行；关于边的6矩形的对角线互相平分；关于对角线的7矩形的四个角都是直角；关于角的8矩形的对角线相等;关于对角线的9矩形所在平面内任一点到其两对角线端点的距离的平方和相等3.矩形的判定方法：1有一个角是直角的平行四边形是矩形；定义判定法2对角线相等的平行四边形是矩形；3关于任何一组对边中点的连线成轴对称图形的平行四边形是矩形4对于平行四边形,若存在一点到两双对顶点的距离的平方和相等,则此平行四边形为矩形5有三个角是直角的四边形是矩形；6四个内角都相等的四边形为矩形；7对角线互相平分且相等的四边形是矩形；8对角线互相平分且有一个内角是直角的四边形是矩形;4.相关计算公式矩形面积：S=ah注:a为边长,h为该边上的高S=ab注:a为长,b为宽矩形周长：C=2a+b注:a为长,b为宽顺次连接矩形各边中点得到的四边形是菱形;菱形1.菱形的定义：有一组邻边相等的平行四边形是菱形;2.菱形的性质：1菱形既是,是两条对角线所在直线,也是中心对称图形；2在60°的菱形中,短对角线等于边长,长对角线是短对角线的√3倍;3菱形的对角相等；关于角的4菱形的邻角互补；关于角的5菱形的对边相等；关于边的6菱形的对边平行；关于边的7菱形的对角线互相平分；关于对角线的8菱形的四边都相等；关于边的9菱形的对角线互相垂直,且平分各内角；关于对角线的10顺次连接菱形各边中点得到的四边形是矩形;关于中点四边形的3.菱形的判定方法：1一组邻边相等的平行四边形是菱形；定义判定法2对角线相互垂直的平行四边形是菱形；3关于两条对角线都成轴对称的四边形是菱形；4四条边都相等的四边形是菱形;4. 相关计算公式：菱形的面积：菱形的面积等于两对角线乘积的一半;只要是对角线互相垂直的四边形都可用正方形1.正方形的定义：1四条边都相等且四个角都是直角的四边形叫做正方形;2有一组邻边相等的矩形是正方形;3有一组邻边相等且一个角是直角的平行四边形是正方形;4有一个角为直角的菱形是正方形;5对角线平分,垂直且相等,并且交角为直角的四边形为正方形;2.正方形的性质：1既是中心对称图形,又是有四条对称轴；关于对称性的2正方形的对角相等；关于角的3正方形的邻角互补；关于角的4正方形的对边相等；关于边的5正方形的相邻边互相垂直；关于边的6正方形的对边平行；关于边的7正方形的对角线互相平分；关于对角线的8正方形的四个角都是直角；关于角的9正方形的对角线相等;关于对角线的10正方形的四边都相等；关于边的（11）正方形的对角线互相垂直,且平分各内角;关于对角线的3.正方形的判定方法：1有一组邻边相等的矩形是正方形；2对角线互相垂直的矩形是正方形；3有一个角为直角的菱形是正方形；4对角线相等的菱形是正方形；5一组邻边相等且有一个角是直角的平行四边形是正方形；6四边均相等,对角线互相垂直平分且相等的平行四边形是正方形；7四边相等,有三个角是直角的四边形是正方形；8对角线相互垂直平分且相等的四边形为正方形;4.相关计算公式：面积计算公式：S=边长×边长或：S=对角线×对角线÷2周长计算公式: C=4×边长顺次连接正方形各边中点得到的四边形是正方形;等腰三角形1.等腰三角形的定义：有两边相等的三角形是等腰三角形;2. 等腰三角形的性质：1等腰三角形的两个底角相等；简写成“等边对等角”2等腰三角形的顶角的平分线,底边上的中线,底边上的高的重合；简写成“三线合一”3等腰三角形的两底角的平分线相等；两条腰上的中线相等,两条腰上的高相等4等腰三角形底边上的垂直平分线到两条腰的距离相等；5等腰三角形的一腰上的高与底边的夹角等于顶角的一半；6等腰三角形底边上任意一点到两腰距离之和等于一腰上的高；需用等面积法证明7等腰三角形是轴对称图形,只有一条对称轴,顶角平分线所在的直线是它的对称轴;3. 等腰三角形的判定方法：1有两条边相等的三角形是等腰三角形2有两个角相等的三角形是等腰三角形简称：等角对等边等边三角形1.等边三角形的定义：三边都相等的三角形是等边三角形;等边三角形是特殊的等腰三角形;注意：若三角形三边都相等则说这个三角形为等边三角形,而一般不称这个三角形为等腰三角形2.等边三角形的性质：1等边三角形的内角都相等,且为60度；2等边三角形底角边上的中线、底角边上高线和所对顶角的角的平分线互相重合；三线合一3等边三角形是轴对称图形,它有三条对称轴,对称轴是每条边上的中线、高线或所对角的平分线所在直线;3.等边三角形的判定方法：首先考虑判断三角形是等腰三角形1三边相等的三角形是等边三角形；定义2三个内角都相等的三角形是等边三角形；3有一个角是60度的等腰三角形是等边三角形；4等边三角形是锐角三角形；5有两个角等于60度的等腰三角形是等边三角形;等腰梯形1.等腰梯形的定义:一组对边平行不相等,另一组对边不平行但相等的四边形是等腰梯形;2.等腰梯形的性质：1等腰梯形只有一条对称轴,上底和下底的中垂线就是它的对称轴；2等腰梯形在同一底上的两个角相等；3等腰梯形的两腰相等；4等腰梯形的两底平行；5等腰梯形的两个底角相等；6等腰梯形的对角线相等；7等腰梯形内接于圆;3. 等腰梯形的判定方法：1一组对边不平行边相等的梯形是等腰梯形；2同一底上的两个角相等的梯形是等腰梯形；3对角线相等的梯形是等腰梯形；4一组对边平行不相等,另一组对边相等不平行的四边形是等腰梯形；5对角线相等,形成两个等腰三角形;4.相关计算公式等腰梯形的中位线长是上下底边长度和的一半；等腰梯形的面积公式等于上底加下底和一半乘高,也等于中位线乘高;直角三角形1.直角三角形的定义：有一个角为90°的三角形,叫做直角三角形;2.直角三角形的性质直角三角形是一种特殊的三角形,它除了具有一般三角形的性质外,具有一些特殊的性质：1直角三角形两直角边的平方和等于斜边的平方;2在直角三角形中,两个锐角互余;3在直角三角形中,斜边上的中线等于斜边的一半即直角三角形的外心位于斜边的中点,外接圆半径R＝C/2;4直角三角形的两直角边的乘积等于斜边与斜边上高的乘积;5在直角三角形中,30°角所对直角边等于斜边的一半;3.直角三角形的判定方法：1有一个角为90°的三角形是直角三角形；2一个三角形,如果一边上的中线等于这条边的一半,那么这个三角形是以这条边为斜边的直角三角形；3若a的平方＋b的平方=c的平方,则以a、b、c为边的三角形是以c为斜边的直角三角形；勾股定理的逆定理;4若一个三角形30°内角所对的边是某一边的一半,那么这个三角形是以这条长边为斜边的直角三角形；5两个锐角互余的三角形是直角三角形;。

第10讲特殊的平行四边形(学生版)

第10讲特殊的平行四边形【学习目标】1. 理解矩形、菱形、正方形的概念.2. 掌握矩形、菱形、正方形的性质定理与判定定理.3. 了解平行四边形、矩形及菱形与正方形的概念之间的从属关系.【要点梳理】要点一、矩形、菱形、正方形的定义有一个角是直角的平行四边形叫做矩形.有一组邻边相等的平行四边形叫做菱形.有一组邻边相等并且有一个内角是直角的平行四边形叫做正方形.要点二、矩形、菱形、正方形的性质矩形的性质：1.矩形具有平行四边形的所有性质；2.矩形的对角线相等；3.矩形的四个角都是直角；4.矩形是轴对称图形，它有两条对称轴.菱形的性质：1.菱形的四条边都相等；2.菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；3.菱形是轴对称图形，它有两条对称轴.正方形的性质：1.正方形四个角都是直角，四条边都相等.2.正方形的两条对角线相等并且互相垂直平分，每条对角线平分一组对角.3.正方形是轴对称图形，有4条对称轴；又是中心对称图形，两条对角线的交点是对称中心.要点三、矩形、菱形、正方形的判定矩形的判定：1. 有三个角是直角的四边形是矩形.2. 对角线相等的平行四边形是矩形.3. 定义：有一个角是直角的平行四边形叫做矩形.要点诠释：在平行四边形的前提下，加上“一个角是直角”或“对角线相等”都能判定平行四边形是矩形.菱形的判定：1. 四条边相等的四边形是菱形.2.对角线互相垂直的平行四边形是菱形.3. 定义：有一组邻边相等的平行四边形是菱形.要点诠释：前一种方法是在四边形的基础上加上四条边相等.后两种方法都是在平行四边形的基础上外加一个条件来判定菱形，正方形的判定：1.有一组邻边相等的矩形是正方形. 2.有一个内角是直角的菱形是正方形. 要点四、特殊平行四边形之间的关系要点五、顺次连接特殊的平行四边形各边中点得到的四边形的形状（1）顺次连接平行四边形各边中点得到的四边形是平行四边形. （2）顺次连接矩形各边中点得到的四边形是菱形. （3）顺次连接菱形各边中点得到的四边形是矩形. （4）顺次连接正方形各边中点得到的四边形是正方形. 要点诠释：新四边形由原四边形各边中点顺次连接而成. （1）若原四边形的对角线互相垂直，则新四边形是矩形. （2）若原四边形的对角线相等，则新四边形是菱形. （3）若原四边形的对角线垂直且相等，则新四边形是正方形. 【典型例题】（基础）类型一、矩形的性质和判定1、如图所示，矩形ABCD 的两条对角线相交于点O ，∠AOD ＝120°，AB ＝4，则矩形对角线AC 长为________．2、已知：平行四边形ABCD 中，E 、F 分别是AB 、CD 的中点，连结AF 、CE.cm（1）求证：△BEC≌△DFA；（2）连接AC，若CA＝CB，判断四边形AECF是什么特殊四边形？并证明你的结论.举一反三：【变式】如图，平行四边形ABCD中P是AD上一点，E为BP上一点，且AE=BE=EP．（1）求证：四边形ABCD是矩形；（2）过E作EF⊥BP于E，交BC于F，若BP=BC，S△BEF=5，CD=4，求CF．类型二、菱形的性质和判定3、如图所示，在菱形ABCD中，AC＝8，BD＝10．求：(1)AB的长．(2)菱形ABCD的面积．举一反三：【变式】菱形的两条对角线长为6和8，则菱形的边长为________．4、如图所示，在△ABC中，CD是∠ACB的平分线，DE∥AC，DF∥BC，四边形DECF是菱形吗?试说明理由．类型三、正方形的性质和判定5、如图，在一正方形ABCD中．E为对角线AC上一点，连接EB、ED，（1）求证：△B EC≌△DEC；（2）延长BE交AD于点F，若∠DEB＝140°．求∠AFE的度数．举一反三：【变式】已知：如图，E为正方形ABCD的边BC延长线上的点，F是CD边上一点，且CE＝CF，连接DE，BF．求证：DE＝BF．6、如图，矩形ABCD中，AD=6，DC=8，菱形EFGH的三个顶点E，G，H分别在矩形ABCD 的边AB，CD，DA上，AH=2，连结CF．（1）若DG=2，求证：四边形EFGH为正方形；（2）若DG=6，求△FCG的面积．【典型例题】（提高）类型一、矩形的性质和判定1、如图所示，已知四边形ABCD是矩形，△PBC和△QCD都是等边三角形，且点P在矩形上方，点Q在矩形内．求证：(1)∠PBA＝∠PCQ＝30°；(2)PA＝PQ．举一反三：【变式】如图所示，把矩形纸片ABCD 沿EF 折叠，使点B 落在边AD 上的点处，点A 落在点处．(1)求证：；(2)设AE ＝，AB ＝，BF ＝，试猜想之间有何等量关系，并给予证明．2、如图1，已知AB ∥CD ，AB=CD ，∠A=∠D ．（1）求证：四边形ABCD 为矩形；（2）E 是AB 边的中点，F 为AD 边上一点，∠DFC=2∠BCE ． ①如图2，若F 为AD 中点，DF=1.6，求CF 的长度：②如图2，若CE=4，CF=5，则AF+BC=________，AF=_________．B 'A'B E BF '=a b c a b c 、、举一反三：【变式】已知ABCD 的对角线AC ，BD 相交于O ，△ABO 是等边三角形，AB ＝4，求这个平行四边形的面积.类型二、菱形的性质和判定3、如图所示，菱形ABCD 中，E 、F 分别是BC 、CD 上的点，∠B ＝∠EAF ＝60°，∠BAE ＝18°．求∠CEF 的度数．cm4、矩形ABCD中，O是AC与BD的交点，过O点的直线EF与AB、CD的延长线分别交于E、F两点．(1)求证：△BOE≌△DOF；(2)当EF与AC满足什么条件时，四边形AECF是菱形，并证明你的结论．举一反三：【变式】如图，在Rt△ABC中，∠ACB=90°，D是AB的中点，AE∥CD，CE∥AB，连接DE交AC于点O．（1）证明：四边形ADCE是菱形；（2）证明：DE=BC；（3）若∠B=60°，BC=6，求菱形ADCE的高（计算结果保留根号）．类型三、正方形的性质和判定5、如图，在正方形ABCD中，对角线AC、BD相交于点O，E、F分别在OD、OC上，且DE＝CF，连接DF、AE，AE的延长线交DF于点M．求证：AM⊥DF．举一反三：【变式】如图四边形ABCD是正方形，点E、K分别在BC，AB上，点G在BA的延长线上，且CE＝BK＝AG．以线段DE、DG为边作DEFG．(1)求证：DE＝DG，且DE⊥DG．(2)连接KF，猜想四边形CEFK是怎样的特殊四边形，并证明你的猜想．6、如图所示，已知矩形ABCD 的各内角平分线AQ 、DF 、BE 、CH 分别交BC 、AD 于点Q 、F 、E 、H ，试证明它们组成的四边形MNPO 是正方形．【巩固练习】一.选择题1.下列关于矩形的说法中正确的是( )A ．对角线相等的四边形是矩形B ．对角线互相平分的四边形是矩形C ．矩形的对角线互相垂直且平分D ．矩形的对角线相等且互相平分2. 矩形一个角的平分线分矩形一边为1cm 和3cm 两部分，则它的面积为（）A.32cmB. 42cmC. 122cmD. 42cm 或122cm 3．已知菱形的周长为40cm ，两条对角线的长度比为3：4，那么两条对角线的长分别为（）A ．6cm ，8cm B. 3cm ，4cm C. 12cm ，16cm D. 24cm ，32cm 4.如图，菱形ABCD 中对角线交于点O ，且OE⊥AB，若AC ＝8，BD ＝6，则,OE 的长是（） A ．2.5B ．5C ．2.4D ．不确定5.如图，E 是边长为1的正方形ABCD 的对角线BD 上一点，且BE=BC ，P 为CE 上任意一点，PQ⊥BC 于点Q ，PR⊥BE 于点R ，则PQ+PR 的值是（）A.B. C. D.6. 如图，四边形ABCD 中，AD ＝DC ，∠ADC＝∠ABC＝90°，DE⊥AB，若四边形ABCD 面积为16，则DE 的长为（）A ．3B ．2C ．4D ．8二.填空题7．如图四边形ABCD 中，AB=BC=12，∠ABC=45°，∠ADC=90°，AD=CD ，则BD= ．8．如图，矩形ABCD 中，AB ＝2，BC ＝3，对角线AC 的垂直平分线分别交AD ，BC 于点E 、F ，连结CE ，则CE 的长______．2312229．如图，菱形ABCD 的边长是2cm ，E 是AB 中点，且DE ⊥AB ，则菱形ABCD 的面积为______2cm .10．已知菱形ABCD 的周长为20cm ，且相邻两内角之比是1∶2，则菱形的两条对角线的长和面积分别是．11.如图，三个边长均为2的正方形重叠在一起，O 1、O 2是其中两个正方形的中心，则阴影部分的面积是_______．12. 如图，平面内4条直线是一组平行线，相邻2条平行线间的距离都是1个单位长度，正方形ABCD 的4个顶点A 、B 、C 、D 都在这些平行线上，其中点Ａ、Ｃ分别在直线和上，该正方形的面积是平方单位．三.解答题13．如图，AB=AC ，AD=AE ，DE=BC ，且∠BAD=∠CAE．（1）求证：△ABE≌△ACD；（2）求证：四边形BCDE 是矩形．1234l l l l ，，，1l 4l14.如图，在平行四边形ABCD中，对角线AC、BD相交于O，过点O作直线EF⊥BD，分别交AD、BC于点E和点F，求证：四边形BEDF是菱形.15．如图，在边长为4的正方形ABCD中，点P在AB上从A向B运动，连结DP交AC于点Q．(1)试证明：无论点P 运动到AB 上何处时，都有△ADQ ≌△ABQ ；(2)当点P 在AB 上运动到什么位置时，△ADQ 的面积是正方形ABCD 面积的； (3)若点P 从点A 运动到点B ，再继续在BC 上运动到点C ，在整个运动过程中，当点P 运动到什么位置时，△ADQ 恰为等腰三角形．【课后作业】【巩固练习】一.选择题1．下列命题中不正确的是( )．A.直角三角形斜边中线等于斜边的一半B.矩形的对角线相等C.矩形的对角线互相垂直D.矩形是轴对称图形2．若矩形对角线相交所成钝角为120°，短边长3.6，则对角线的长为( )．A. 3.6B. 7.2C. 1.8D. 14.43．如图，在菱形ABCD 中，E 、F 分别是AB 、AC 的中点，如果EF ＝2，那么菱形ABCD 的周长是( )61cm cm cm cm cmA.4B.8C.12D.164.菱形ABCD 中，∠A ∶∠B ＝1∶5，若周长为8，则此菱形的高等于( )．A. B.4 C.1 D.25.如图，在正方形ABCD 中，△ABE 和△CDF 为直角三角形，∠AEB=∠CFD=90°，AE=FC=5，BE=DF=12，则EF 的长是（）A ．7B ．8C ．72D ．736. 如图，在正方形ABCD 的外侧，作等边三角形ADE ，连接BE ，则∠AEB 的度数为（）A ．10°B ．15°C ．20°D ．12.5°二.填空题7．矩形ABCD 中，对角线AC 、BD 相交于O ，∠AOB ＝60°，AC ＝10，则AB ＝______，BC ＝______．8. 如图，将边长为2的正方形ABCD 沿其对角线AC 剪开，再把△ABC 沿着AD 方向平移，得到△，若两个三角形重叠部分的面积是1，则它移动的距离等于____.21cm cm cm cm A B C '''2cm AA 'cm9. 如图，边长为2的正方形ABCD的对角线相交于点O，过点O的直线分别交AD、BC于E、F，则阴影部分的面积是_______.10.如图，两条等宽的长方形纸条倾斜的重叠着，已知长方形纸条宽度为3cm，∠ABC=60°，则四边形ABCD的面积为________cm2．11. 如图，在菱形ABCD中，对角线AC与BD相交于点O，AB＝13，AC＝10，过点D作DE∥AC交BC的延长线于点E，则△BDE的周长为_____.12.如图，在平面直角坐标系中，菱形OABC的顶点B的坐标为（8，4），则C点的坐标为_______.三.解答题13.如图，在△ABC中，AB=AC，AD是△ABC的角平分线，作AE∥BC，CE∥AD，AE、CE交于点E．（1）证明：四边形ADCE是矩形．（2）若DE交AC于点O，证明：OD∥AB且OD=AB．14．如图，在平行四边形ABCD中，E、F分别为边AB，CD的中点，连接DE、BF、BD．若AD⊥BD，则四边形BFDE是什么特殊四边形？请证明你的结论．15．如图，边长为3的正方形ABCD绕点C按顺时针方向旋转30°后，得到正方形EFCG，EF交AD于H，求DH的长．。

特殊四边形的知识点、定义、性质、判定

特殊四边形知识点总结一．正确理解定义（1）定义：两组对边分别平行的四边形是平行四边形．平行四边形的定义揭示了图形的最本质的属性，它既是平行四边形的一条性质，又是一个判定方法．（2）表示方法：用“□”表示平行四边形，例如：平行四边形ABCD 记作“□ABCD ”，读作“平行四边形ABCD ”． 2．熟练掌握性质：平行四边形的有关性质和判定都是从边、角、对角线三个方面的特征进行简述的．（1）角：对角相等，邻角互补；（2）边：对边分别平行且相等；（3）对角线：对角线互相平分；（4）面积：①S ==⨯底高ah ；②平行四边形的对角线将四边形分成4个面积相等的三角形．（5）平行四边形不是轴对称图形。

3．平行四边形的判别方法①定义判定：两组对边分别平行的四边形是平行四边形。

②方法2：两组对角分别相等的四边形是平行四边形。

③方法3：两组对边分别相等的四边形是平行四边形。

④方法4：对角线互相平分的四边形是平行四边形。

⑤方法5：一组平行且相等的四边形是平行四边形。

二、几种特殊平行四边形的有关概念（1）矩形：有一个角是直角的平行四边形是矩形，它是研究矩形的基础，它既可以看作是矩形的性质，也可以看作是矩形的判定方法，对于这个定义，要注意把握：① 平行四边形； ② 一个角是直角，两者缺一不可．（2）菱形：有一组邻边相等的平行四边形是菱形，它是研究菱形的基础，它既可以看作是菱形的性质，也可以看作是菱形的判定方法，对于这个定义，要注意把握：① 平行四边形；② 一组邻边相等，两者缺一不可．（3）正方形：有一组邻边相等且有一个直角的平行四边形叫做正方形，它是最特殊的平行四边形，它既是平行四边形，还是菱形，也是矩形，它兼有这三者的特征，是一种非常完美的图形．三、几种特殊四边形的有关性质（1）矩形： ①边：对边平行且相等；②角：四个角都是直角； ③对角线：对角线互相平分且相等；④对称性：轴对称图形（对边中点连线所在直线，2条）． ⑤面积S =长×宽；A BD OC AD B CO【注意：矩形具有平行四边形的一切性质】（2）菱形：①边：四条边都相等；②角：对角相等、邻角互补；③对角线：对角线互相垂直平分且每条对角线平分每组对角； ④对称性：轴对称图形（对角线所在直线，2条）． ⑤面积S =底×高=对角线乘积的一半；【注意：菱形具有平行四边形的一切性质】（3）正方形：①边：四条边都相等；②角：四角相是直角；③对角线：对角线互相垂直平分且相等，对角线与边的夹角为450； ④对称性：轴对称图形（4条）．⑤面积S =边长×边长=对角线乘积的一半；【注意：正方形具有平行四边形、矩形、菱形的一切性质】四、几种特殊四边形的判定方法（1）矩形的判定： ①有一个角是直角的平行四边形；②对角线相等的平行四边形； ③有三个角是直角的四边形。

矩形的证明与计算

矩形的证明与计算矩形是一种特殊的四边形，具有两对相等且平行的边。

在这篇文档中，我们将探讨矩形的性质、证明以及计算方法。

矩形的性质矩形具有以下性质：- 两条对边相等且平行；- 任意两条相邻边垂直；- 对角线相等且平分。

矩形的证明以下是矩形的一种证明方法：步骤1: 证明两条对边相等且平行假设有一个四边形ABCD，我们需要证明AD与BC相等且平行。

1. 运用向量法，将向量AB和向量DC进行相加，若它们相等，则可得出ABCD为平行四边形；2. 运用三角形的性质，证明∠A = ∠C = 90度，可得出ABCD为直角四边形；3. 结合平行四边形和直角四边形的性质，我们可以得出ABCD为矩形。

步骤2: 证明任意两条相邻边垂直假设有一个矩形ABCD，我们需要证明AB与BC相邻且垂直。

1. 运用向量法，我们可以证明向量AB与向量BC的点积为0，即向量AB与向量BC垂直；2. 结合矩形的性质，可得出AB与BC相邻且垂直。

步骤3: 证明对角线相等且平分假设有一个矩形ABCD，我们需要证明对角线AC与BD相等且平分。

1. 根据矩形的性质，可得出AC与BD相交于点O；2. 运用向量法，我们可以证明向量AO与向量CO相等且相反，向量BO与向量DO相等且相反；3. 运用三角形的性质，证明AO = CO，BO = DO；4. 结合步骤2的证明，可得出AC与BD相等且平分。

通过以上证明，我们可以得出矩形的性质。

矩形的计算在进行矩形的计算时，我们可以利用以下公式：1. 矩形的周长公式为：周长 = 2 × (长 + 宽)；2. 矩形的面积公式为：面积 = 长 ×宽。

通过这些公式，我们可以方便地计算矩形的周长和面积。

以上是关于矩形的证明与计算的内容。

通过理解矩形的性质和证明，我们可以更好地应用矩形在实际问题中进行计算和解决。

特殊的四边形（归纳）

特殊的平行四边形知识点一：矩形的定义要点诠释：有一个角是直角的平行四边形叫做矩形。

（嘿嘿嘿）知识点二：矩形的性质要点诠释：矩形具有平行四边形所有的性质。

此外，它还具有如下特殊性质：1.矩形的四个角都是直角；2.矩形的对角线相等；推论：直角三角形斜边上的中线等于斜边的一半。

3.矩形是轴对称图形也是中心对称图形。

知识点三：矩形的判定方法要点诠释：1. 用矩形的定义：一个角是直角的平行四边形是矩形；2.有三个角是直角的四边形是矩形；3.对角线相等的平行四边形是矩形；4.对角线互相平分且相等的四边形是矩形。

知识点四：菱形的定义要点诠释：有一组邻边相等的平行四边形叫做菱形.知识点五：菱形的性质要点诠释：菱形具有平行四边形一切性质，此外，它还具有如下特殊性质：1.菱形的四条边相等。

2.菱形的两条对角线互相垂直，且每一条对角线平分一组对角。

3.菱形是轴对称图形也是中心对称图形，两条对角线所在的直线是它的两条对称轴。

知识点六：菱形的判定办法要点诠释：1.用菱形的定义：有一组邻边相等的平行四边形是菱形；2.四条边都相等的四边形是菱形；3.对角线垂直的平行四边形是菱形；4.对角线互相垂直平分的四边形是菱形。

知识点七：正方形的定义要点诠释：有一组邻边相等且有一个角是直角的平行四边形叫做正方形。

知识点八：正方形的性质要点诠释：1.正方形的四个角都是直角，四条边都相等；2.正方形的对角线相等，并且互相垂直平分，每条对角线平分一组对角；3.正方形既是轴对称图形也是中心对称图形。

知识点九：正方形的判定方法要点诠释：1.正方形的定义：有一组邻边相等且有一个角是直角的平行四边形叫做正方形。

2.有一组邻边相等的矩形是正方形；3.有一个角是直角的菱形是正方形.归纳整理，形成认知体系1．复习概念，理清关系2．集合表示，突出关系3．性质判定，列表归纳平行四边形矩形菱形正方形性质边对边平行且相等对边平行且相等对边平行，四边相等对边平行，四边相等角对角相等四个角都是直角对角相等四个角都是直角对角线互相平分互相平分且相等互相垂直平分，且每条对角线平分一组对角互相垂直平分且相等,每条对角线平分一组对角判定·两组对边分别平行；·两组对边分别相等；·一组对边平行且相等;·两组对角分别相等；·两条对角线互相平分.·有三个角是直角;·是平行四边形且有一个角是直角;·是平行四边形且两条对角线相等.·四边相等的四边形；·是平行四边形且有一组邻边相等；·是平行四边形且两条对角线互相垂直。

人教版初中数学中考总复习：特殊的四边形--知识讲解(基础)

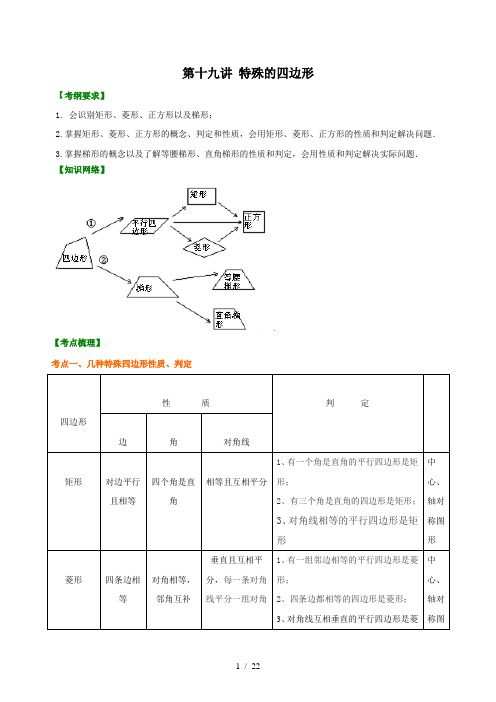
第十九讲特殊的四边形【考纲要求】1. 会识别矩形、菱形、正方形以及梯形；2.掌握矩形、菱形、正方形的概念、判定和性质，会用矩形、菱形、正方形的性质和判定解决问题．3.掌握梯形的概念以及了解等腰梯形、直角梯形的性质和判定，会用性质和判定解决实际问题．【知识网络】【考点梳理】考点一、几种特殊四边形性质、判定四边形性质判定边角对角线矩形对边平行且相等四个角是直角相等且互相平分1、有一个角是直角的平行四边形是矩形；2、有三个角是直角的四边形是矩形；3、对角线相等的平行四边形是矩形中心、轴对称图形菱形四条边相等对角相等，邻角互补垂直且互相平分，每一条对角线平分一组对角1、有一组邻边相等的平行四边形是菱形；2、四条边都相等的四边形是菱形；3、对角线互相垂直的平行四边形是菱中心、轴对称图形.形正方形四条边相等四个角是直角相等、垂直、平分，并且每一条对角线平分一组对角1、邻边相等的矩形是正方形2、对角线垂直的矩形是正方形3、有一个角是直角的菱形是正方形4、对角线相等的菱形是正方形中心、轴对称图形等腰梯形两底平行，两腰相等同一底上的两个角相等相等1、两腰相等的梯形是等腰梯形；2、在同一底上的两个角相等的梯形是等腰梯形；3、对角线相等的梯形是等腰梯形.轴对称图形【要点诠释】矩形、菱形、正方形都是特殊的平行四边形，它们具有平行四边形的一切性质.考点二、梯形1．解决梯形问题常用的方法：（1）“平移腰”：把梯形分成一个平行四边形和一个三角形（图1）；（2）“作高”：使两腰在两个直角三角形中（图2）；（3）“平移对角线”：使两条对角线在同一个三角形中（图3）；（4）“延腰”：构造具有公共角的两个三角形（图4）；（5）“等积变形”，连结梯形上底一端点和另一腰中点，并延长与下底延长线交于一点，构成三角形（图5）．图1 图2 图3 图4 图5【要点诠释】解决梯形问题的基本思想和方法就是通过添加适当的辅助线，把梯形问题转化为已经熟悉的平行四边形和三角形问题来解决．在学习时注意它们的作用，掌握这些辅助线的使用对于学好梯形内容很有帮助．2.特殊的梯形1）等腰梯形：两腰相等的梯形叫做等腰梯形．性质：（1）等腰梯形的同一底边上的两个角相等；等腰梯形的两条对角线相等．（2）同一底边上的两个角相等的梯形是等腰梯形．（3）等腰梯形是轴对称图形，它的对称轴是经过两底中点的一条直线．2）直角梯形：有一个角是直角的梯形叫做直角梯形．考点三、中点四边形相关问题1.中点四边形的概念：把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形．2.若中点四边形为矩形，则原四边形满足条件对角线互相垂直；若中点四边形为菱形，则原四边形满足条件对角线相等；若中点四边形为正方形，则原四边形满足条件对角线互相垂直且相等．【要点诠释】中点四边形的形状由原四边形的对角线的位置和数量关系决定．【典型例题】类型一、特殊的平行四边形的应用1. 在平行四边形ABCD中，AC、BD交于点O，过点O作直线EF、GH，分别交平行四边形的四条边于E、G、F、H四点，连结EG、GF、FH、HE.（1）如图①，试判断四边形EGFH的形状，并说明理由；（2）如图②，当EF⊥GH时，四边形EGFH的形状是；（3）如图③，在（2）的条件下，若AC=BD，四边形EGFH的形状是；（4）如图④，在（3）的条件下，若AC⊥BD，试判断四边形EGFH的形状，并说明理由.【思路点拨】中点四边形的形状由原四边形的对角线的位置和数量关系决定．【答案与解析】（1）四边形EGFH是平行四边形；证明：∵平行四边形ABCD的对角线AC、BD交于点O，∴点O是平行四边形ABCD的对称中心；∴EO=FO，GO=HO；∴四边形EGFH是平行四边形；（2）菱形；（提示：菱形的对角线垂直平分）（3）菱形；（提示：当AC=BD时，对四边形EGFH的形状不会产生影响，故结论同（2））（4）四边形EGFH是正方形；证明：∵AC=BD，∴平行四边形ABCD是矩形；又∵AC⊥BD，∴平行四边形ABCD是正方形，∴∠BOC=90°，∠GBO=∠FCO=45°，OB=OC；∵EF⊥GH，∴∠GOF=90°；∴∠BOG=∠COF；∴△BOG≌△COF（ASA）；∴OG=OF，∴GH=EF；由（3）知四边形EGFH是菱形，又EF=GH，∴四边形EGFH是正方形．【总结升华】主要考查了平行四边形、菱形、矩形、正方形的判定和性质以及全等三角形的判定和性质；熟练掌握各特殊四边形的联系和区别是解答此类题目的关键．2．动手操作：在一张长12cm、宽5cm的矩形纸片内，要折出一个菱形．小颖同学按照取两组对边中点的方法折出菱形EFGH（见方案一），小明同学沿矩形的对角线AC折出∠CAE=∠CAD，∠ACF=∠ACB 的方法得到菱形AECF（见方案二）．（1）你能说出小颖、小明所折出的菱形的理由吗？（2）请你通过计算，比较小颖和小明同学的折法中，哪种菱形面积较大？【思路点拨】（1）、要证所折图形是菱形，只需证四边相等即可．（2）、按照图形用面积公式计算S=30和S=35.21，可知方案二小明同学所折的菱形面积较大．【答案与解析】（1）小颖的理由：依次连接矩形各边的中点所得到的四边形是菱形，小明的理由：∵ABCD 是矩形， ∴AD ∥BC ，则∠DAC=∠ACB ，又∵∠CAE=∠CAD ，∠ACF=∠ACB ， ∴∠CAE=∠CAD=∠ACF=∠ACB ， ∴AE=EC=CF=FA ， ∴四边形AECF 是菱形．（2）方案一：S 菱形=S 矩形-4S △AEH =12×5-4×12×6×52=30（cm ）2，方案二：设BE=x ，则CE=12-x ， ∴AE=22BE AB +=225x +由AECF 是菱形，则AE 2=CE 2∴x 2+25=（12-x ）2， ∴x=11924， S 菱形=S 矩形-2S △ABE =12×5-2×12×5×11924≈35.21（cm ）2，比较可知，方案二小明同学所折的菱形面积较大．【总结升华】本题考查了矩形的性质和菱形的判定，以及图形面积的计算与比较．举一反三：【变式】如图，点O 是矩形ABCD 的中心，E 是AB 上的点，沿CE 折叠后，点B 恰好与点O 重合，若BC=3，则折痕CE 的长为（）.A.B．C．4 D．5【答案】A.类型二、梯形的应用3.（•黄州区校级模拟）如图，△ABC中，∠BAC=90°，延长BA至D，使AD=AB，点E、F分别是边BC、AC的中点．（1）判断四边形DBEF的形状并证明；（2）过点A作AG∥BC交DF于G，求证：AG=DG．【思路点拨】（1）利用梯形的判定首先得出四边形DBEF为梯形，进而得出四边形HFEB是平行四边形，得出BE=FD进而得出答案；（2）利用四边形DBEF为等腰梯形，得出∠B=∠D，利用AG∥BG，∠B=∠DAG，得出答案．【答案与解析】（1）解：四边形DBEF为等腰梯形，理由如下：如图，过点F作FH∥BC，交AB于点H，∵FH∥BC，点F是AC的中点，点E是BC的中点，∴AH=BH=AB，EF∥AB，显然EF＜AB＜AD，∴EF≠AD，∴四边形DBEF为梯形，∵AD=AB，∴AD=AH，∴CA是DH的中垂线，∴DF=FH，∵FH∥BC，EF∥AB，∴四边形HFEB是平行四边形，∴FH=BE，∴BE=FD，故四边形DBEF为等腰梯形；（2）证明：∵四边形DBEF为等腰梯形，∴∠B=∠D，∵AG∥BG，∠B=∠DAG，∴∠D=∠DAG，∴AG=D G．【总结升华】此题主要考查了等腰梯形的判定以及其性质和平行四边形的判定与性质等知识，得出BE=FD 是解题关键．举一反三：【变式】如图，梯形ABCD中，AD∥BC，点E在BC上，AE=BE，点F是CD的中点，且AF⊥AB，若AD=2.7，AF=4，AB=6，则CE的长为（）.C. 2.5D.2.3A.22B. 231类型三、特殊四边形与其他知识结合的综合运用4. （•北京）在▱ABCD中，过点D作DE⊥AB于点E，点F 在边CD上，DF=BE，连接AF，BF．（1）求证：四边形BFDE是矩形；（2）若CF=3，BF=4，DF=5，求证：AF平分∠DAB．【思路点拨】（1）根据平行四边形的性质，可得AB与CD的关系，根据平行四边形的判定，可得BFDE 是平行四边形，再根据矩形的判定，可得答案；（2）根据平行线的性质，可得∠DFA=∠FAB，根据等腰三角形的判定与性质，可得∠DAF=∠DFA，根据角平分线的判定，可得答案．【答案与解析】（1）证明：∵四边形ABCD是平行四边形，∴AB∥CD．∵BE∥DF，BE=DF，∴四边形BFDE是平行四边形．∵DE⊥AB，∴∠DEB=90°，∴四边形BFDE是矩形；（2）解：∵四边形ABCD是平行四边形，∴AB∥DC，∴∠DFA=∠FAB．在Rt△BCF中，由勾股定理，得BC===5，∴AD=BC=DF=5，∴∠DAF=∠DFA，∴∠DAF=∠FAB，即AF平分∠DAB．【总结升华】本题考查了平行四边形的性质，利用了平行四边形的性质，矩形的判定，等腰三角形的判定与性质，利用等腰三角形的判定与性质得出∠DAF=∠DFA是解题关键．5．已知：如图，在菱形ABCD中，F为边BC的中点，DF与对角线AC交于点M，过M作ME⊥CD于点E，∠1=∠2．（1）若CE=1，求BC的长；（2）求证：AM=DF+ME．【思路点拨】（1）根据菱形的对边平行可得AB∥CD，再根据两直线平行，内错角相等可得∠1=∠ACD，所以∠ACD=∠2，根据等角对等边的性质可得CM=DM，再根据等腰三角形三线合一的性质可得CE=DE，然后求出CD的长度，即为菱形的边长BC的长度；（2）先利用“边角边”证明△CEM和△CFM全等，根据全等三角形对应边相等可得ME=MF，延长AB交DF于点G，然后证明∠1=∠G，根据等角对等边的性质可得AM=GM，再利用“角角边”证明△CDF和△BGF 全等，根据全等三角形对应边相等可得GF=DF，最后结合图形GM=GF+MF即可得证．【答案与解析】（1）解：∵四边形ABCD是菱形，∴AB∥CD，∴∠1=∠ACD，∵∠1=∠2，∴∠ACD=∠2，∴MC=MD，∵ME⊥CD，∴CD=2CE，∵CE=1，∴CD=2，∴BC=CD=2；（2）证明：如图，∵F为边BC的中点，∴BF=CF=12BC，∴CF=CE，在菱形ABCD中，AC平分∠BCD，∴∠ACB=∠ACD，在△CEM和△CFM中，∵CE CFACB ACDCM CM=⎧⎪∠=∠⎨⎪=⎩，∴△CEM≌△CFM（SAS），∴ME=MF，延长AB交DF于点G，∵AB∥CD，∴∠G=∠2，∵∠1=∠2，∴∠1=∠G，∴AM=MG，在△CDF和△BGF中，∵2GBFG CFDBF CF∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△CDF≌△BGF（AAS），∴GF=DF，由图形可知，GM=GF+MF，∴AM=DF+ME．【总结升华】本题考查了菱形的性质，全等三角形的判定与性质，等角对等边的性质，作出辅助线构造出全等三角形是解题的关键．6 . 如图，己知ABC的顶点B、C为定点，A为动点(不在直线BC上)．是点B关于直线AC的对称点，是点C关于直线AB的对称点．连结、、、．(1)猜想线段与'的数量关系，并证明你的结论；(2)当点A运动到怎样的位置时，四边形为菱形?这样的位置有几个?请用语言对这样的位置进行描述；(不用证明)(3)当点A在线段BC的垂直平分线l(BC的中点及到BC的距离为的点除外)上运动时，判断以点B、C、、为顶点的四边形的形状，画出相应的示意图．(不用证明)【思路点拨】本题考查轴对称的基本性质，综合考查菱形、正方形、等腰梯形的判定．在运动变化过程中，认识图形之间的内在联系．【答案与解析】（1）猜想：BC′=CB′∵B′是点B关于直线AC的对称点∴AC垂直平分B B′∴BC= CB′同理BC= BC′∴B C′=C B′（2）要使BCB′C′是菱形,根据菱形的性质，对角线互相垂直平分∵B′是点B关于直线AC的对称点，C′是点C关于直线AB的对称点∴AC垂直平分B B′,AB垂直平分C C′,∴B B′、C C′应该同时过A点∴∠BAC=90°∴只要AB⊥AC即可满足要求，这样的位置有无数个.（3）如图，当A是BC的中点时，没有形成四边形；当A到BC时,∵l是BC的垂直平分线,∴∠ACB=∠ABC=30°,∴∠BAC=120°,∴∠BOC=60°,∴BC=C B′= B′C′=B C′.∴BC B′C′为菱形,当BC的中点及到BC BC的点除外时,∵∠BOC= B′O C′,OB=OC O B′=O C′,∴∠OBC=∠OCB=∠O B′C′=∠O C′B′,∴BC∥B′C′.∵B C′不平行C B′，B C′=C B′,四边形BC B′ C′为等腰梯形．【总结升华】本题可以很好的培养观察推理能力，按照要求画出图形可以更清楚的解题．举一反三：【变式】（2012•襄阳）如图，在梯形ABCD中，AD∥BC，E为BC的中点，BC=2AD，EA=ED=2，AC与ED相交于点F．（1）求证：梯形ABCD是等腰梯形；（2）当AB与AC具有什么位置关系时，四边形AECD是菱形？请说明理由，并求出此时菱形AECD的面积．【答案】（1）证明：∵AD∥BC，∴∠DEC=∠EDA，∠BEA=∠EAD，又∵EA=ED，∴∠EAD=∠EDA，∴∠DEC=∠AEB，又∵EB=EC，∴△DEC≌△AEB，∴AB=CD，∴梯形ABCD是等腰梯形．（2）当AB⊥AC时，四边形AECD是菱形．证明：∵AD∥BC，BE=EC=AD，∴四边形ABED和四边形AECD均为平行四边形．∴AB=ED，∵AB⊥AC，∴AE=BE=EC，∴四边形AECD是菱形．过A作AG⊥BE于点G，∵AE=BE=AB=2，∴△ABE是等边三角形，∴∠AEB=60°，∴AG=3，∴S菱形AECD=EC•AG=2×3=23.第十九讲特殊的四边形一、选择题1.（•天水）如图，将矩形纸片ABCD折叠，使点D与点B重合，点C落在C′处，折痕为EF，若AB=1，BC=2，则△ABE和BC′F的周长之和为（）A．3 B．4 C．6 D．82.如图，有一矩形纸片ABCD，AB=10，AD=6，将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F，则△CEF面积为( )．A．4 B．6 C．8 D．103．如图所示，在矩形ABCD中，AB=3，AD=4，P是AD上的一点，PE⊥AC，垂足为E，PF⊥BD，垂足为F，则PE+PF的值为( )．A．B．C．2 D．第3题第4题4.如图，E、F、G、H分别是四边形ABCD四条边的中点，要使EFGH为矩形，四边形应该具备的条件是（）.A．一组对边平行而另一组对边不平行B．对角线相等C．对角线相互垂直 D．对角线互相平分5.如图，正方形ABCD中，O是对角线AC、BD的交点，过O点作OE⊥OF分别交AB、BC于E、F，若AE=4，CF=3，则EF等于（）.A.7B.5C.4D.3第5题第6题6.如图，在矩形ABCD中，DE⊥AC于E，且∠ADE：∠EDC=3：2，则∠BDE的度数为（）.A．15° B．18° C．36° D．54°二、填空题7.（春•西城区期末）直角△ABC中，∠BAC=90°，D、E、F分别为AB、BC、AC的中点，已知DF=3，则AE= ．8. 如图，菱形ABCD中，于E，于F，，则等于___________．9. 正方形ABCD中，E为BC上一点，BE=，CE=，P在BD上，则PE+PC的最小值可能为__________．10.如图，M为正方形ABCD中BC边的中点，将正方形折起，使点A与M重合，设折痕为EF，若正方形的面积为64，则△AEM的面积为____________．11.如图，△ABC是以AB为斜边的直角三角形，AC=4，BC=3，P为AB上一动点，且PE⊥AC于E，PF⊥BC 于F，则线段EF长度的最小值是_______________.第10题第11题第12题12.如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，∠C=60°，BC=2AD=23，点E是BC边的中点，△DEF是等边三角形，DF交AB于点G，则△BFG的周长为________．三、解答题13．如图1，图2，四边形ABCD是正方形，M是AB延长线上一点．直角三角尺的一条直角边经过点D，且直角顶点E在AB边上滑动(点E不与点A，B重合)，另一条直角边与∠CBM的平分线BF相交于点F．(1)如图1，当点E在AB边的中点位置时：①猜想DE与EF满足的数量关系是__________；②连接点E与AD边的中点N，猜想NE与BF满足的数量关系是__________；③请证明你的上述两个猜想．(2)如图2，当点E在AB边上的任意位置时，请你在AD边上找到一点N，使得NE=BF，进而猜想此时 DE 与EF有怎样的数量关系．14. 如图，在梯形ABCD中，AD//BC，AB=CD=3cm，∠A=120°，BD⊥CD，(1)求BC、AD的长度；(2)若点P从点B开始沿BC边向点C以2cm/秒的速度运动，点Q从点C开始沿CD边向点D以1cm/秒的速度运动，当P、Q分别从B、C同时出发时，写出五边形ABPQD的面积S与运动时间t之间的关系式，并写出t的取值范围(不包含点P在B、C两点的情况)；(3)在(2)的前提下，是否存在某一时刻t，使线段PQ把梯形ABCD分成两部分的面积比为1：5？若存在，求出t的值；若不存在，请说明理由．15. （•青岛模拟）已知正方形ABCD的边长为a，两条对角线AC、BD相交于点O，P是射线AB上任意一点，过P点分别作直线AC、BD的垂线PE、PF，垂足为E、F．（1）如图1，当P点在线段AB上时，PE+PF的值是否为定值？如果是，请求出它的值；如果不是，请加以说明．（2）如图2，当P点在线段AB的延长线上时，求PE﹣PF的值．16.如图，十三个边长为正整数的正方形纸片恰好拼成一个大矩形（其中有三个小正方形的边长已标出字母x，y，z）．试求满足上述条件的矩形的面积最小值．【答案与解析】一．选择题1．【答案】C．【解析】将矩形纸片ABCD折叠，使点D与点B重合，点C落在C′处，折痕为EF，由折叠特性可得，CD=BC′=AB，∠FC′B=∠EAB=90°，∠EBC′=∠ABC=90°，∵∠ABE+∠EBF=∠C′BF+∠EBF=90°∴∠ABE=∠C′BF在△BAE和△BC′F中，∴△BAE≌△BC′F（ASA），∵△ABE的周长=AB+AE+EB=AB+AE+ED=AB+AD=1+2=3，△ABE和△BC′F的周长=2△ABE的周长=2×3=6．故选：C．2．【答案】C.3．【答案】A.4．【答案】C.5．【答案】B.【解析】可证△OEB≌△OFC，则EB=FC=3，AE=BF=4，32346．【答案】B.【解析】由题意∠ADE=54°，∠CDE＝36°，∠DCE=54°，∠BDE=54°-36°=18°.二．填空题7．【答案】3．【解析】如图，∵在直角△ABC中，∠BAC=90°，D、F分别为AB、AC的中点，∴DF是△ABC的中位线，∴DF=BC．又∵点E是直角△ABC斜边BC的中点，∴AE=BC，∵DF=3，∴DF=AE．故填：3．8．【答案】60°.9．【答案】.10．【答案】10.【解析】提示：设AE=x=EM ,BE=8-x,MB=4,在Rt△BEM中由勾股定理解得x=5,从而算出面积.11.【答案】125.【解析】连接PC．∵PE⊥AC，PF⊥BC，∴∠PEC=∠PFC=∠C=90°；又∵∠ACB=90°，∴四边形ECFP是矩形，∴EF=PC，∴当PC最小时，EF也最小，即当CP⊥AB时，PC最小，∵AC=4，BC=3，∴AB=5，∴12AC•BC=12AB•PC，∴PC=125．∴线段EF长的最小值为125；故答案是：125．12．【答案】3+3.【解析】首先由已知AD∥BC，∠ABC=90°点E是BC边的中点，推出四边形ABED是矩形，所以得到直角三角形CED，所以能求出CD和DE，又由△DEF是等边三角形，得出DF，由直角三角形AGD可求出AG、DG，进而求得FG，再证△AGD≌△BGF，得到BF=AD，从而求出△BFG的周长．三.综合题13．【解析】（1）①DE=EF；②NE=BF；③∵四边形ABCD为正方形，∴AD=AB，∠DAB=∠ABC=90°，∵N，E分别为AD，AB中点，∴AN=DN=12AD，AE=EB=12AB，∴DN=BE，AN=AE，∵∠DEF=90°，∴∠AED+∠FEB=90°，又∵∠ADE+∠AED=90°，∴∠FEB=∠ADE，又∵AN=AE，∴∠ANE=∠AEN，又∵∠A=90°，∴∠ANE=45°，∴∠DNE=180°-∠ANE=135°，又∵∠CBM=90°，BF平分∠CBM，∴∠CBF=45°，∠EBF=135°，∴△DNE≌△EBF（ASA），∴DE=EF，NE=BF．（2）在DA上截取DN=EB（或截取AN=AE），连接NE，则点N可使得NE=BF．此时DE=EF．证明方法同（1），证△DNE≌△EBF．14．【解析】（1）在Rt△BCD中，CD=3cm，∠C=60°, ∴∠DBC=30°,∴BC=2CD=6cm.由已知得：梯形ABCD是等腰梯形,∴∠ABC=∠C=60°,∴∠ABD=∠ABC-∠DBC=30°.∵AD∥BC，∴∠ADB=∠DBC=30°,∴∠ABD=∠ADB,∴AD=AB=3cm.（2）当P、Q分别从B、C同时出发运动t秒时，BP=2t，CQ=t, ∴PC=6-2t,过Q作QE⊥BC于E，则QE=CQsin60°=32t,∴S梯形ABCD-S△PCQ=2734-34（6-2t）t=34（2t2-6t+27）（0＜t＜3）.（3）存在时刻t，使线段PQ把梯形ABCD分成两部分的面积比为1：5.∵S梯形ABCD=2734，S△ABD=12×3×32×3,∴S△ABD=13×S梯形ABCD,∴五边形ABPQD的面积不可能是梯形ABCD面积的16.∴S△PCQ：S五边形ABPQD=1：5，即S五边形ABPQD=56S梯形ABCD∴34（2t2-6t+27）=56×2734,整理得：4t2-12t+9=0,∴t=32，即当t=32秒时，PQ把梯形ABCD分成两部分的面积比为1：5．15．【解析】解：（1）是定值，∵四边形ABCD为正方形，∴AC⊥BD．∵PF⊥BD，∴PF∥AC，同理PE∥BD．∴四边形PFOE为矩形，故PE=OF．又∵∠PBF=45°，∴PF=BF．∴PE+PF=OF+FB=OB=acos45°=a．（2）∵四边形ABCD为正方形，∴AC⊥BD．∵PF⊥BD，∴PF∥AC，同理PE∥BD．∴四边形PFOE为矩形，故PE=OF．又∵∠PBF=45°，∴PF=BF．∴PE﹣PF=OF﹣BF=OB=acos45°=a．16.【解析】已有三个小正方形的边长为x，y，z，我们通过x，y，z表示其余正方形的边长依次填在每个正方形中，它们是x+y，x+2y，x+3y，4y，x+7y，2x+y，2x+y+z，4x+4y-z，4x+4y-2x及5x-2y+z．因矩形对边相等，所以得11x+3y=7x+16y-z及8x+8y-3z=6x+5y+z．化简上述的两个方程得到z=13y-4x，4z=2x+3y，消去z得18x=49y．因为18与49互质，所以x、y的最小自然数解是x=49，y=18，此时z=38．以x=49，y=18，z=38代入矩形长、宽的表达式11x+3y及8x+8y-3z，得长、宽分别为593和422．此时得最小面积值是593×422=250246．。

八年级下特殊的平行四边形

特殊的平行四边形1．平行四边形的性质（1）平行四边形的概念：有两组对边分别____的四边形叫做平行四边形．（2）平行四边形的性质：①边：平行四边形的对边相等．②角：平行四边形的对角相等．③对角线：平行四边形的对角线互相平分．（3）平行线间的距离处处相等．（4）平行四边形的面积：①平行四边形的面积等于它的底和这个底上的高的积．②同底（等底）同高（等高）的平行四边形面积相等．2．平行四边形的判定（1）两组对边分别平行的四边形是平行四边形．符号语言：∵AB∥DC，AD∥BC∴四边行ABCD 是平行四边形．（2）两组对边分别相等的四边形是平行四边形．符号语言：∵AB=DC，AD=BC∴四边行ABCD 是平行四边形．（3）一组对边平行且相等的四边形是平行四边形．符号语言：∵AB∥DC，AB=DC∴四边行ABCD是平行四边形．（4）两组对角分别相等的四边形是平行四边形．符号语言：∵∠ABC=∠ADC，∠DAB=∠DCB∴四边行ABCD是平行四边形．（5）对角线互相平分的四边形是平行四边形．符号语言：∵OA=OC，OB=OD∴四边行ABCD 是平行四边形．3．矩形的判定（1）矩形的判定：①矩形的定义：有一个角是直角的平行四边形是矩形；②有三个角是直角的四边形是矩形；③对角线相等的平行四边形是矩形（或“对角线互相_____且_____的四边形是矩形”）（2）①证明一个四边形是矩形，若题设条件与这个四边形的对角线有关，通常证这个四边形的对角线相等．②题设中出现多个直角或垂直时，常采用“三个角是直角的四边形是矩形”来判定矩形．4．矩形的性质（1）矩形的性质①平行四边形的性质矩形都具有；②角：矩形的四个角都是____；③边：邻边垂直；④对角线：矩形的对角线____；⑤矩形是轴对称图形，又是中心对称图形．它有2条对称轴，分别是每组对边中点连线所在的直线；对称中心是两条对角线的交点．（2）由矩形的性质，可以得到直角三角线的一个重要性质，直角三角形斜边上的中线等于斜边的___．5．菱形的性质（1）菱形的定义：有一组邻边相等的平行四边形叫做菱形．（平行四边形 + 一组邻边相等=菱形）①菱形具有平行四边形的一切性质；②菱形的四条边都相等；③菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；④菱形是轴对称图形，它有__条对称轴，分别是两条对角线所在直线．（3）菱形的面积计算①利用平行四边形的面积公式．②菱形面积=ab．（a、b是两条对角线的长度）6．菱形的判定（1）四条边都_____的四边形是菱形．几何语言：∵AB=BC=CD=DA∴四边形ABCD是菱形；（2）对角线互相垂直的平行四边形是菱形（或“对角线互相垂直平分的四边形是菱形”）．几何语言：∵AC⊥BD，四边形ABCD是平行四边形∴平行四边形ABCD是菱形7．正方形的性质（1）正方形的定义：有一组邻边相等并且有一个角是直角的平行四边形叫做正方形．（2）正方形的性质①正方形的四条边都相等，四个角都是_____；②正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；③正方形具有四边形、平行四边形、矩形、菱形的一切性质．④两条对角线将正方形分成四个全等的等腰直角三角形，同时，正方形又是轴对称图形，有四条对称轴．8．正方形的判定正方形的判定方法：①先判定四边形是矩形，再判定这个矩形有一组邻边相等；②先判定四边形是菱形，再判定这个矩形有一个角为直角．③还可以先判定四边形是平行四边形，再用1或2进行判定．（1）性质：①等腰梯形是轴对称图形，它的对称轴是经过上下底的_____的直线；②等腰梯形同一底上的两个角相等；③等腰梯形的两条对角线相等．（2）由等腰梯形的性质可知，如果过上底的两个顶点分别作下底的两条高，可把等腰梯形分成矩形和两个全等的直角三角形，因此可知等腰梯形是轴对称图形，而一般的梯形不具备这个性质．10．等腰梯形的判定（1）利用定义：两腰相等的梯形叫做等腰梯形；（2）定理：同一底上两个角相等的梯形是等腰梯形．（3）对角线：对角线相等的梯形是等腰梯形．判定一个梯形是否为等腰梯形，主要判断梯形的同一底上的两个角是否相等，可以通过添加辅助线把梯形底上的两个角平移到同一个三角形中，利用三角形来证明角的关系．注意：对角线相等的梯形是等腰梯形这个判定方法不可以直接应用．教学重点：能用综合法来证明特殊的平行四边形的相关结论；教学难点：运用特殊的平行四边形的性质定理和判定定理解决计算问题；1.菱形的性质；平行四边形的性质．【例1】菱形具有而平行四边形不具有的性质是（）A．两组对边分别平行 B．两组对角分别相等C．对角线互相平分 D．对角线互相垂直练1.如图，菱形ABCD中，AC、BD相交于点O，若∠BCO=55°，则∠ADO=°．练2.如图，在▱ABCD中，对角线AC与BD相交于点O，过点O作EF⊥AC交BC于点E，交AD于点F，连接AE、CF．则四边形AECF是（）A．梯形 B．矩形 C．菱形 D．正方形2.菱形的性质；坐标与图形性质．【例2】如图，在菱形ABCD中，点A在x轴上，点B的坐标为（8，2），点D的坐标为（0，2），则点C的坐标为．练3.菱形ABCD在平面直角坐标系中的位置如图所示，顶点B（2，0），∠DOB=60°，点P是对角线OC上一个动点，E（0，﹣1），当EP+BP最短时，点P的坐标为．3. 矩形的性质；菱形的判定．【例3】如图，在矩形ABCD中，E，F分别是AD，BC中点，连接AF，BE，CE，DF分别交于点M，N，四边形EMFN是（）A．正方形 B．菱形 C．矩形 D．无法确定练4.下列说法中，正确的是（）A．同位角相等B．对角线相等的四边形是平行四边形C．四条边相等的四边形是菱形D．矩形的对角线一定互相垂直练5.如图，在矩形ABCD中，E，F分别为AD，BC的中点，连结AF，DF，BE，CE，AF与BE 交于G，DF与CE交于H．求证：四边形EGFH为菱形．4．正方形的判定；矩形的性质．【例4】（2014•山东淄博一中期末）如图所示，一张矩形纸片，要折叠出一个最大的正方形，小明把矩形上的一个角沿折痕AE翻折上去，使AB与AD边上的AF重合，则四边形ABEF就是一个大的正方形，他判定的方法是．练6.下列说法中，错误的是（）A．菱形的四条边都相等B．对角线互相垂直的平行四边形是正方形C．四个角都相等的四边形是矩形D．等腰梯形的对角线相等5．直角梯形；平行四边形的性质；等腰梯形的性质．【例5】如图所示，在直角梯形ABCD中，AD∥BC，AD=24cm，AB=8cm，BC=26cm，动点P从A 点开始沿AD边向D以1cm/s的速度运动，动点Q从C点开始沿CB边向B以3cm/s的速度运动．P，Q分别从A，C同时出发，当其中一点到端点时，另一点也随之停止运动，设运动时间为t（s），t分别为何值时，四边形PQCD是平行四边形？等腰梯形？练7．已知：如图，等腰梯形ABCD中，AD∥BC，AB=DC，点P是腰DC上的一个动点（P与D、C不重合），点E、F、G分别是线段BC、PC、BP的中点．（1）试探索四边形EFPG的形状，并说明理由；（2）若∠A=120°，AD=2，DC=4，当PC为何值时，四边形EFPG是矩形并加以证明．1、下列命题中是真命题的是（） A. 对角线互相垂直且相等的四边形是正方形 B.有两边和一角对应相等的两个三角形全等 C. 两条对角线相等的平行四边形是矩形 D.两边相等的平行四边形是菱形2、关于下列结论，正确的是_______________________。

特殊四边形知识与考点解析

特殊四边形知识考点解析1．多边形的分类：2．平行四边形、菱形、矩形、正方形、等腰梯形的定义、性质、判别：（1）平行四边形定义：两组对边分别平行的四边形叫做平行四边形。

平行四边形不相邻两个顶点连成的线段叫对角线。

性质：平行四边形对边相等。

平行四边形对角相等, 邻角互补.平行四边形的对角线互相平分。

若两条直线互相平行，则其中一条直线上任意两点到另一条直线的距离相等，这个距离称为平行线之间的距离。

推论：夹在两条平行线间的平行线段相等。

判定：两组对边分别平行的四边形是平行四边形。

两组对边分别相等的四边形是平行四边形。

一组对边平行且相等的四边形是平行四边形。

两组对角分别相等的四边形是平行四边形.两条对角线互相平分的四边形是平行四边形。

（2）菱形：定义：一组邻边相等的平行四边形叫做菱形。

菱形的性质：菱形的四条边都相等，两条对角线互相垂直平分，每一条对角线平分一组对角。

菱形的判别方法：一组邻边相等的平行四边形是菱形。

对角线互相垂直的平行四边形是菱形.对角线互相垂直平分的四边形是菱形。

四条边都相等的四边形是菱形。

菱形的面积等于两条对角线乘积的一半（面积计算，即S 菱形=L1.L2/2）。

（3）矩形：定义：有一个内角是直角的平行四边形叫做矩形。

矩形的性质：矩形的对角线相等；四个角都是直角。

矩形的判别方法：有一个角是直角的平行四边形是矩形。

对角线相等的平行四边形是矩形；对角线相等且平分的四边形是矩形；有三个角是直角的四边形是矩形。

直角三角形斜边上的中线等于斜边长的一半；在直角三角形中30°所对的直角边是斜边的一半。

（4）正方形：定义：一组邻边相等的矩形叫做正方形。

正方形的性质：正方形具有平行四边形、菱形、矩形的一切性质。

正方形的四个角都是直角，四条边都相等，正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角。

（5）梯形：定义：一组对边平行而另一组对边不平行的四边形叫做梯形。

一组对边平行且不相等的四边形叫做梯形。

中考数学压轴题重难点突破七与特殊四边形有关的证明与计算(动态探究问题)

(2)在 AB 上取 AF＝EC，连接 EF，由(1)同理可得∠CEP＝∠FAE， ∵AF＝EC，AE＝EP， ∴△FAE≌△CEP(SAS)，∴∠ECP＝∠AFE， ∵AF＝EC，AB＝BC，∴BF＝BE， ∴∠BEF＝∠BFE＝45°，∴∠AFE＝135°， ∴∠ECP＝135°，∴∠DCP＝45°.
【模型应用】 (2)如图②，F 是 DE 延长线上一点，FB⊥BE，EF 交 AB 于点 G. Ⅰ)判断△FBG 的形状并说明理由； Ⅱ)若 G 为 AB 的中点，且 AB＝4，求 AF 的长；
(2)解：Ⅰ)△FBG 为等腰三角形，理由： ∵四边形 ABCD 是正方形，∴∠GAD＝90°， ∴∠AGD＋∠ADG＝90°，由(1)知△ABE≌△ADE， ∴∠ADG＝∠EBG，∴∠AGD＋∠EBG＝90°， ∵FB⊥BE，∴∠FBG＋∠EBG＝90°， ∴∠AGD＝∠FBG，∵∠AGD＝∠FGB， ∴∠FBG＝∠FGB，∴FG＝FB， ∴△FBG 是等腰三角形．
FH AD ∴GH＝AG＝2，∴FH＝2GH＝2，在 Rt△AHF 中，AF＝ AH2＋FH2＝ 13.
【模型迁移】 (3)如图③，F 是 DE 延长线上一点，FB⊥BE，EF 交 AB 于点 G，BE＝BF. 求证：GE＝( 2－1)DE.
(3)证明：∵FB⊥BE，∴∠FBE＝90°，在 Rt△EBF 中，BE＝BF，∴EF＝ 2BE，由(1)知 BE＝DE，由(2)知 FG＝BF， ∴GE＝EF－FG＝ 2BE－BE＝ 2DE－DE＝( 2－1)DE.
类型二：与特殊四边形有关的证明与计算(动态探究问题) (省卷 2021T27，2019T27，2015T27，2014T27；兰州 2021T27)
(2022·兰州)综合与实践【问题情境】数学活动课上，老师出示了一个问题：如图①，在正方形 ABCD 中，E 是 BC 的中点，AE⊥EP，EP 与正方形的外角∠DCG 的平分线交于 P 点．试猜想 AE 与 EP 的数量关系，并加以证明；【思考尝试】(1)同学们发现，取 AB 的中点 F，连接 EF 可以解决这个问题．请在图①中补全图形，解答老师提出的问题；

第1部分第5章核心素养之逻辑推理——与四边形有关的计算与证明

图形
分析分别延长AF，DC交于点N，证 △ABF和△CFN是等边三角形⇒ 利用△AEG和△NDG相似求解分别延长CB，DE交于点M，证 △ADE≌△BME，利用△ADG和 △FMG相似求解过点E作EP∥AD交AF于点P，证 △ABF是等边三角形⇒利用 △ADG和△PEG相似求解
学霸笔记平行四边形或三角形中有中点、三等分点时，一般考虑以下思路： 1．利用平行四边形的对边平行且相等来构造全等、相似或等腰三角形． 2．过分点作平行线构造平行型相似(A型或X型)，从而得到线段的比例关系来求解． 3．遇到中点，倍长线段(包括倍长中线)来构造中心对称式的全等三角形也是常用方法．
以平行四边形为背景的计算与证明例1 (2019·百校联考三改编)如图，平行四边形ABCD的边长AD＝6，AB＝4，∠B
＝60°，E为AB的中点，F在边BC上，且BC＝3FC，AF与DE交于点G，则AG的长为
3
2
.
【思路分析】方法
方法1：延长线段构造特殊三角形
方法2：倍长线段构造全等
方法3：过中点作平行线
△AHG∽△ABE 求
AM⇒在 Rt△ABM 中求 AB
解
【方法点拨】本题是矩形与特殊三角形综合求线段长度的问题，方法1中利用勾股方程的代数方法计算比较复杂，而通过作辅助线构造相似的基本模型，数形结合求解计算量较小，因此解题时充分利用图形的几何特性，构建基本模型求解是关键．
【跟踪训练】
5．如图，在菱形ABCD中，AB＝4，按以下步骤作图：①分别以点C和点D为圆
由①知AP＝EF，即1－x＝1＋2 x，解得x＝13. ∴DP＝13，AP＝23. 在Rt△PDE中，DE＝12， ∴PE＝ PD2＋DE2＝ 613. ∵AP≠PE， ∴四边形AFEP不是菱形．

特殊平行四边形的证明与计算(解析版)

特殊平行四边形的证明与计算考点体系考点1：特殊平行四边形性质与判定的综合应用典例：（2020·北京密云初二期末）已知：如图，在矩形ABCD中，对角线AC的垂直平分线EF分别与AC、BC、AD交于点O、E、F，连接AE和CF．（1）求证：四边形AECF为菱形；（2）若AB，BC=3，求菱形AECF的边长．【答案】（1）见解析；（2）2【解析】（1）证明：∵AC的垂直平分线EF分别与AC、BC、AD交于点O、E、F，∴AF＝CF，AE＝CE，OA＝OC，∵四边形ABCD是矩形，∴AD∥BC，∴∠F AO＝∠ECO，在△AOF和△COE中，∵∠F AO＝∠ECO，OA=OC，∠AOF＝∠COE，∴△AOF≌△COE（ASA），∴AF＝CE，∴AE＝EC＝CF＝AF，∴四边形AECF为菱形；（2）解：设AE＝CE＝x，则BE＝3﹣x，∵四边形ABCD是矩形，∴∠B＝90°，在Rt△ABE中，由勾股定理得：AB2+BE2＝AE2，2+（3﹣x）2＝x2，解得：x＝2，即AE＝2，∴菱形AECF的边长是2．方法或规律点拨本题考查了线段垂直平分线的性质、菱形的判定和性质、全等三角形的性质和判定、矩形的性质以及勾股定理等知识，能综合运用以上知识进行推理是解此题的关键．巩固练习1．（2020·宁夏盐池初二期中）已知：如图，在菱形ABCD 中，点E，O，F分别是边AB，AC，AD的中点，连接CE、CF、OE、OF．（1）求证：△BCE≌△DCF；（2）当AB与BC满足什么条件时，四边形AEOF正方形？请说明理由．【答案】（1）证明见解析；（2）AB⊥BC时，四边形AEOF正方形．【解析】（1）∵四边形ABCD是菱形，点E，O，F分别是边AB，AC，AD的中点，∴AB=BC=CD=AD，∠B=∠D，∵点E、F分别是边AB、AD的中点，∴BE=12AB，DF=12AD，∴BE=DF，在△BCE和△DCF中，BE DFB D BC CD=⎧⎪∠=∠⎨⎪=⎩，∴△BCE≌△DCF．（2）AB⊥BC，理由如下：∵四边形AEOF是正方形，∴∠AEO=90°，∵点E、O分别是边AB、AC的中点，∴OE为△ABC的中位线，∴OE//BC，∴∠B=∠AEO=90°，∴AB⊥BC．2．（2020·湖北潜江初二期末）已知：如图，四边形ABCD中，AD∥BC，AD=CD，E是对角线BD上一点，且EA=EC．（1）求证：四边形ABCD是菱形；（2）如果BE=BC，且∠CBE：∠BCE=2：3，求证：四边形ABCD是正方形．【答案】（1）证明见解析；（2）证明见解析.【解析】（1）在△ADE 与△CDE 中，AD CDDE DE EA EC=⎧⎪=⎨⎪=⎩，∴△ADE ≌△CDE ，∴∠ADE=∠CDE ，∵AD ∥BC ，∴∠ADE=∠CBD ，∴∠CDE=∠CBD ，∴BC=CD ，∵AD=CD ，∴BC=AD ，∴四边形ABCD 为平行四边形，∵AD=CD ，∴四边形ABCD 是菱形；（2）∵BE=BC ，∴∠BCE=∠BEC ，∵∠CBE ：∠BCE=2：3，∴∠CBE=180×2233++ =45°，∵四边形ABCD 是菱形，∴∠ABE=45°，∴∠ABC=90°，∴四边形ABCD 是正方形．3．（2018·内蒙古杭锦后旗初二期中）（1）如图矩形ABCD 的对角线AC 、BD 交于点O ，过点D 作//DP OC ，且DP OC =，连接CP ，判断四边形CODP 的形状并说明理由．（2）如果题目中的矩形变为菱形，结论应变为什么？说明理由．（3）如果题目中的矩形变为正方形，结论又应变为什么？说明理由．【答案】（1）四边形CODP 的形状是菱形，理由见解析；（2）四边形CODP 的形状是矩形，理由见解析；（3）四边形CODP 的形状是正方形，理由见解析.【解析】（1）四边形CODP 的形状是菱形，理由是：∵四边形ABCD 是矩形，∴AC BD =，12OA OC AC ==，12OB OD BD ==， ∴OC OD =，∵//DP OC ，DP OC =，∴四边形CODP 是平行四边形，∵OC OD =，∴平行四边形CODP 是菱形；（2）四边形CODP 的形状是矩形，理由是：∵四边形ABCD 是菱形，∴AC BD ⊥，∴90DOC ∠=，∵//DP OC ，DP OC =，∴四边形CODP 是平行四边形，∵90DOC ∠=，∴平行四边形CODP 是矩形；（3）四边形CODP 的形状是正方形，理由是：∵四边形ABCD 是正方形，∴AC BD ⊥，AC BD =，12OA OC AC ==，12OB OD BD ==， ∴90DOC ∠=，OD OC =，∵//DP OC ，DP OC =，∴四边形CODP 是平行四边形，∵90DOC ∠=，OD OC =∴平行四边形CODP 是正方形． 4．（2018·河南嵩县初二期末）如图，E ，F 是正方形ABCD 的对角线AC 上的两点，且AE ＝CF.(1)求证：四边形BEDF 是菱形；(2)若正方形ABCD 的边长为4，AE ，求菱形BEDF 的面积．【答案】（1）证明见解析（2）8【解析】(1)连接BD 交AC 于点O ，∵四边形ABCD 为正方形，∴BD ⊥AC ，OD ＝OB ＝OA ＝OC.∵AE ＝CF ，∴OA －AE ＝OC －CF ，即OE ＝OF ，∴四边形BEDF 为平行四边形，又∵BD ⊥EF ，∴四边形BEDF 为菱形．(2)∵正方形ABCD 的边长为4，∴BD ＝AC＝.∵AE ＝CF，∴EF ＝AC－∴S 菱形BEDF ＝12BD·EF ＝12×. 5．（2020·云南昭阳初二期中）在正方形ABCD 中，对角线BD 所在的直线上有两点E 、F 满足BE=DF ，连接AE 、AF 、CE 、CF ，如图所示．（1）求证：△ABE ≌△ADF ；（2）试判断四边形AECF 的形状，并说明理由．【答案】（1）证明见解析（2）菱形【解析】证明：（1）∵四边形ABCD 是正方形，∴AB=AD ，∴∠ABD=∠ADB ，∴∠ABE=∠ADF ，在△ABE 与△ADF 中AB AD ABE ADF BE DF ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABE ≌△ADF.（2）如图，连接AC ，四边形AECF是菱形．理由：在正方形ABCD中，OA=OC，OB=OD，AC⊥EF，∴OB+BE=OD+DF，即OE=OF，∵OA=OC，OE=OF，∴四边形AECF是平行四边形，∵AC⊥EF，∴四边形AECF是菱形．6．（2020·聊城市茌平区振兴街道中学初二月考）已知：如图，平行四边形ABCD，对角线AC与BD相交于点E，点G为AD的中点，连接CG，CG的延长线交BA的延长线于点F，连接FD．（1）求证：AB=AF；（2）若AG=AB，∠BCD=120°，判断四边形ACDF的形状，并证明你的结论．【答案】（1）证明见解析；（2）结论：四边形ACDF是矩形．理由见解析.【解析】（1）证明：∵四边形ABCD是平行四边形，∴BE∥CD，AB=CD，∴∠AFC=∠DCG，∵GA=GD，∠AGF=∠CGD，∴△AGF≌△DGC，∴AF=CD，∴AB=CF．（2）解：结论：四边形ACDF是矩形．理由：∵AF=CD，AF∥CD，∴四边形ACDF是平行四边形，∵四边形ABCD是平行四边形，∴∠BAD=∠BCD=120°，∴∠FAG=60°，∵AB=AG=AF，∴△AFG是等边三角形，∴AG=GF，∵△AGF≌△DGC，∴FG=CG，∵AG=GD，∴AD=CF，∴四边形ACDF是矩形．考点2：利用特殊四边形性质探究几何量典例：（2020·江苏鼓楼初二期末）已知，四边形ABCD是正方形，点E是正方形ABCD所在平面内一动点（不与点D重合），AB＝AE，过点B作DE的垂线交DE所在直线于F，连接CF．提出问题：当点E运动时，线段CF与线段DE之间的数量关系是否发生改变？探究问题：（1）首先考察点E的一个特殊位置：当点E与点B重合（如图①）时，点F与点B也重合．用等式表示线段CF与线段DE之间的数量关系：；（2）然后考察点E的一般位置，分两种情况：情况1：当点E是正方形ABCD内部一点（如图②）时；情况2：当点E是正方形ABCD外部一点（如图③）时．在情况1或情况2下，线段CF与线段DE之间的数量关系与（1）中的结论是否相同？如果都相同，请选择一种情况证明；如果只在一种情况下相同或在两种情况下都不相同，请说明理由；拓展问题：（3）连接AF，用等式表示线段AF、CF、DF三者之间的数量关系：．【答案】（1）DE；（2）在情况1与情况2下都相同，详见解析；（3）AF＋CF DF或|AF－CF|DF【解析】解：（1）∵四边形ABCD是正方形，∴CD=CB，∠BCD=90°，∴△BCD是等腰直角三角形，∴CB，当点E、F与点B重合时，则，故答案为：CF；（2）在情况1或情况2下，线段CF与线段DE之间的数量关系与（1）中结论相同；理由如下：情况1：∵四边形ABCD是正方形，∴CD=CB=AD=AB=AE，∠BCD=∠DAB=∠ABC=90°，过点C作CG⊥CF，交DF于G，如图②所示：则∠BCD=∠GCF=90°，∴∠DCG=∠BCF ，设BC 交DF 于P ，∵BF ⊥DE ，∴∠BFD=∠BCD=90°，∵∠DPC=∠FPB ，∴∠CDP=∠FBP ，在△CDG 和△CBF 中，DCG BCF CD CBCDG CBF ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝， ∴△CDG ≌△CBF （ASA ），∴DG=FB ，CG=CF ，∴△GCF 是等腰直角三角形，∴，连接BE ，设∠CDG=α，则∠CBF=α，∠ADE=90°-α，∵AD=AE ，∴∠DEA=∠ADE=90°-α，∴∠DAE=180°-2（90°-α）=2α，∴∠EAB=90°-2α，∵AB=AE ，∴∠BEA=∠ABE=12（180°-∠EAB ）=12（180°-90°+2α）=45°+α， ∴∠CBE=90°-（45°+α）=45°-α，∴∠FBE=∠CBE+∠CBF=45°-α+α=45°，∵BF ⊥DE ，∴△BEF 是等腰直角三角形，∴EF=BF ，∴EF=DG ，∴EF+EG=DG+EG ，即DE=FG ，∴CF ；情况2：过点C 作CG ⊥CF 交DF 延长线于G ，连接BE ，设CD 交BF 于P ，如图③所示：∵∠GCF=∠BCD=90°，∴∠DCG=∠BCF ，∵∠FPD=∠BPC ，∴∠FDP=∠PBC ，在△CDG 和△CBF 中，DCG BCF CD CBCDG CBF ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝， ∴△CDG ≌△CBF （ASA ），∴DG=FB ，CG=CF ，∴△GCF 是等腰直角三角形，∴，设∠CDG=α，则∠CBF=α，同理可知：∠DEA=∠ADE=90°-α，∠DAE=2α，∴∠EAB=90°+2α，∵AB=AE ，∴∠BEA=∠ABE=45°-α，∴∠FEB=∠DEA -∠AEB=90°-α-（45°-α）=45°，∵BF ⊥DE ，∴△BEF 是等腰直角三角形，∴EF=BF ，∴EF=DG ，∴DE=FG ，∴CF ；（3）①当F 在BC 的右侧时，作HD ⊥DF 交FA 延长线于H ，如图④所示：由（2）得：△BEF 是等腰直角三角形，EF=BF ，在△ABF 和△AEF 中，AB AE AF AF BF EF ⎧⎪⎨⎪⎩＝＝＝，∴△ABF ≌△AEF （SSS ），∴∠EFA=∠BFA=12∠BFE=45°， ∴△HDF 是等腰直角三角形，∴，DH=DF ，∵∠HDF=∠ADC=90°，∴∠HDA=∠FDC ，在△HDA 和△FDC 中，DH DF HDA FDC DA DC ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△HDA ≌△FDC （SAS ），∴CF=HA ，DF=HF=HA+AF=CF+AF ，即DF ；②当F 在AB 的下方时，作DH ⊥DE ，交FC 延长线于H ，在DF 上取点N ，使CN=CD ，连接BN ，如图⑤所示：设∠DAE=α，则∠CDN=∠CND=90°-α，∴∠DCN=2α，∴∠NCB=90°-2α，∵CN=CD=CB ，∴∠CNB=∠CBN=12（180°-∠NCB ）=12（180°-90°+2α）=45°+α， ∵∠CNE=180°-∠CND=180°-（90°-α）=90°+α，∴∠FNB=90°+α-（45°+α）=45°，∴△BFN 是等腰直角三角形，∴BF=NF ，在△CNF 和△CBF 中，CN CB CF CF NF BF ⎧⎪⎨⎪⎩＝＝＝，∴△CNF ≌△CBF （SSS ），∴∠NFC=∠BFC=12∠BFD=45°， ∴△DFH 是等腰直角三角形，∴，DF=DH ，∵∠ADC=∠HDE=90°，∴∠ADF=∠CDH ，在△ADF 和△CDH 中，AD CD ADF CDH DF DH ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ADF ≌△CDH （SAS ），∴CH=AF ，∴FH=CH+CF=AF+CF ，∴；③当F 在DC 的上方时，连接BE ，作HD ⊥DF ，交AF 于H ，如图⑥所示：由（2）得：△BEF 是等腰直角三角形，EF=BF ，在△ABF 和△AEF 中，AB AE AF AF BF EF ⎧⎪⎨⎪⎩＝＝＝，∴△ABF ≌△AEF （SSS ），∴∠EFA=∠BFA=12∠BFE=45°， ∴△HDF 是等腰直角三角形，∴，DH=DF ，∵∠ADC=∠HDF=90°，∴∠ADH=∠CDF ，在△ADC 和△HDF 中，AD CD ADH CDF DH DF ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ADC ≌△HDF （SAS ），∴AH=CF ，∴HF=AF -AH=AF -CF ，∴AF -DF ；④当F 在AD 左侧时，作HD ⊥DF 交AF 的延长线于H ，连接BE ，设AD 交BF 于P ，如图⑦所示：∵AB=AE=AD ，∴∠AED=∠ADE ，∵∠PFD=∠PAB=90°，∠FPD=∠BPA ，∴∠ABP=∠FDP ，∴∠FEA=∠FBA ，∵AB=AE ，∴∠AEB=∠ABE ，∴∠FEB=∠FBE ，∴△BFE 是等腰直角三角形，∴EF=BF ，在△ABF 和△AEF 中，AB AE AF AF BF EF ⎧⎪⎨⎪⎩＝＝＝，∴△ABF ≌△AEF （SSS ），∴∠EFA=∠BFA=12∠BFE=45°， ∴∠DFH=∠EFA=45°，∴△HDF 是等腰直角三角形，∴DH=DF ，HF=DF ，∵∠HDF=∠CDA=90°，∴∠HDA=∠FDC ，在△HDA 和△FDC 中，DH DF HDA FDC AD CD ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△HDA ≌△FDC （SAS ），∴AF=CF ，∴AH -AF=CF -AF=HF ，∴CF -DF ，综上所述，线段AF 、CF 、DF 三者之间的数量关系：或|AF -DF ，故答案为：或|AF -DF ．方法或规律点拨本题是四边形综合题，主要考查了正方形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质、三角形内角和定理、等腰三角形的性质等知识；熟练掌握全等三角形的判定与性质和等腰直角三角形的判定与性质是解题的关键．巩固练习1．（2020·安徽肥东初二期末）如图，矩形ABCD 的对角线AC 、BD 交于点O ，点P 在边AD 上从点A 到点D 运动，过点P 作PE ⊥AC 于点E ，作PF ⊥BD 于点F ，已知AB=3，AD=4，随着点P 的运动，关于PE+PF的值，下面说法正确的是（）A ．先增大，后减小B ．先减小，后增大C ．始终等于2.4D ．始终等于3【答案】C【解析】解：连接PO ，如下图：∵在矩形ABCD 中，AB=3，AD=4，∴12ABCD S AB BC ==矩形,AO OC =，OB OD =，AC BD =，5AC ， ∴1112344AOD ABCD S S ==⨯=矩形, 52OA OD ==， 11115()()322222AOD AOP DOP S S S OA PE OD PF OA PE PF PE PF =+=+=+=⨯+=， ∴12 2.45PE PF +==；故选C ．2．（2020·山东德州初二期末）以四边形ABCD 的边AB 、AD 为边分别向外侧作等边三角形ABF 和ADE ，连接EB 、FD ，交点为G ．(1)当四边形ABCD为正方形时(如图1)，EB和FD的数量关系是；(2)当四边形ABCD为矩形时(如图2)，EB和FD具有怎样的数量关系？请加以证明；(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中，∠EGD是否发生变化？如果改变，请说明理由；如果不变，请在图3中求出∠EGD的度数．【答案】（1）EB=FD，（2）EB=FD，证明见解析；（3）不变，等于60°.【解析】解：（1）EB=FD，理由如下：∵四边形ABCD为正方形，∴AB=AD，∵以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE，∴AF=AE，∠FAB=∠EAD=60°，∵∠FAD=∠BAD+∠FAB=90°+60°=150°，∠BAE=∠BAD+∠EAD=90°+60°=150°，∴∠FAD=∠BAE，在△AFD和△ABE中，AF AEFAD BAE AD AB=⎧⎪∠=∠⎨⎪=⎩，∴△AFD ≌△ABE ，∴EB=FD ；（2）EB=FD ．证：∵△AFB 为等边三角形 ∴AF=AB ，∠FAB=60° ∵△ADE 为等边三角形， ∴AD=AE ，∠EAD=60°∴∠FAB+∠BAD=∠EAD+∠BAD ，即∠FAD=∠BAE∴△FAD ≌△BAE∴EB=FD ；（3）解：同（2）易证：△FAD ≌△BAE ， ∴∠AEB=∠ADF ，设∠AEB 为x°，则∠ADF 也为x°于是有∠BED 为（60﹣x ）°，∠EDF 为（60+x ）°，∴∠EGD=180°﹣∠BED ﹣∠EDF=180°﹣（60﹣x ）°﹣（60+x ）°=60°．3．（2020·四川龙泉驿初一期末）（1）如图1，在四边形ABCD 中，AB ＝AD ，∠BAD ＝100°，∠B ＝∠ADC ＝90°．E ，F 分别是BC ，CD 上的点．且∠EAF ＝50°．探究图中线段EF ，BE ，FD 之间的数量关系．小明同学探究的方法是：延长FD 到点G ，使DG ＝BE ，连接AG ，先证明△ABE ≌△ADG ，再证明△AEF ≌△AGF ，可得出结论，他的结论是（直接写结论，不需证明）；（2）如图2，若在四边形ABCD 中，AB ＝AD ，∠B +∠D ＝180°，E ，F 分别是BC ，CD 上的点，且2∠EAF ＝∠BAD ，上述结论是否仍然成立，若成立，请证明，若不成立，请说明理由；（3）如图3，四边形ABCD 是边长为7的正方形，∠EBF ＝45°，直接写出△DEF 的周长．【答案】（1）EF ＝BE +DF ；（2）成立，理由详见解析；（3）14．【解析】证明：（1）延长FD 到点G ．使DG ＝BE ．连结AG ，在△ABE 和△ADG 中，90AB AD ABE ADG BE DG ︒=⎧⎪∠=∠=⎨⎪=⎩，∴△ABE ≌△ADG （SAS ），∴AE ＝AG ，∠BAE ＝∠DAG ，∵∠BAD ＝100°，∠EAF ＝50°，∴∠BAE +∠F AD ＝∠DAG +∠F AD ＝50°，∴∠EAF ＝∠F AG ＝50°，在△EAF 和△GAF 中，∵AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩，∴△EAF ≌△GAF （SAS ），∴EF ＝FG ＝DF +DG ，∴EF ＝BE +DF ，故答案为：EF ＝BE +DF ；（2）结论仍然成立，理由如下：如图2，延长EB 到G ，使BG ＝DF ，连接AG ，∵∠ABC +∠D ＝180°，∠ABG +∠ABC ＝180°，∴∠ABG ＝∠D ，∵在△ABG 与△ADF 中，AB=AD ABG=D BG=DF ⎧⎪∠∠⎨⎪⎩，∴△ABG ≌△ADF （SAS ），∴AG ＝AF ，∠BAG ＝∠DAF ，∵2∠EAF ＝∠BAD ，∴∠DAF +∠BAE ＝∠BAG +∠BAE ＝12∠BAD ＝∠EAF ， ∴∠GAE ＝∠EAF ，又AE ＝AE ，∴△AEG ≌△AEF （SAS ），∴EG ＝EF ．∵EG ＝BE +BG ．∴EF ＝BE +FD ；（3）如图，延长EA 到H ，使AH ＝CF ，连接BH ，∵四边形ABCD 是正方形，∴AB ＝BC ＝7＝AD ＝CD ，∠BAD ＝∠BCD ＝90°，∴∠BAH ＝∠BCF ＝90°，又∵AH ＝CF ，AB ＝BC ，∴△ABH ≌△CBF （SAS ），∴BH ＝BF ，∠ABH ＝∠CBF ，∵∠EBF ＝45°，∴∠CBF +∠ABE ＝45°＝∠HBA +∠ABE ＝∠EBF ，∴∠EBH ＝∠EBF ，又∵BH ＝BF ，BE ＝BE ，∴△EBH ≌△EBF （SAS ），∴EF ＝EH ，∴EF ＝EH ＝AE +CF ，∴△DEF 的周长＝DE +DF +EF ＝DE +DF +AE +CF ＝AD +CD ＝14．4．（2020·甘肃麦积初二期末）如图1，ABCD 中，E 是AD 的中点，将ABE △沿BE 折叠后得到GBE ，且点G 在□ABCD 内部．将BG 延长交DC 于点F ．（1）猜想并填空：GF ________DF （填“>”、“<”、“=”）；（2）请证明你的猜想；（3）如图2，当90A ∠=，设BG a =，GF b =，EG c =，证明：2c ab =．【答案】（1）＝；（2）见解析；（3）见解析【解析】解：（1）GF=DF，故答案为：=；（2）理由是：连接DG，由折叠得：AE=EG，∠A=∠BGE，∵E在AD的中点，∴AE=ED，∴ED=EG，∴∠EGD=∠EDG，∵四边形ABCD是平行四边形，∴AB∥CD，∴∠A+∠ADC=180°，∵∠BGE+∠EGF=180°，∴∠EDF=∠EGF，∴∠EDF-∠EDG=∠EGF-∠EGD，即∠GDF=∠DGF，∴GF=DF；（3）证明：如图2，由（2）得：DF=GF=b，由图可得：BF=BG+GF=a+b，由折叠可得：AB=BG=a，AE=EG=c，在ABCD中，BC=AD=2AE=2c，CD=AB=a，∴CF=CD-DF=a-b，∵∠A=90°，∴ABCD 是矩形，∴∠C=90°，在Rt △BCF 中，由勾股定理得，BC 2+CF 2=BF 2，∴(2c)2+(a -b)2=(a+b)2，整理得：c 2=ab ．5．（2020·山东济南初二期末）如图1，在菱形ABCD 中，AC ＝2，BD ＝，AC ，BD 相交于点O ．(1)求边AB 的长；(2)求∠BAC 的度数；(3)如图2，将一个足够大的直角三角板60°角的顶点放在菱形ABCD 的顶点A 处，绕点A 左右旋转，其中三角板60°角的两边分别与边BC ，CD 相交于点E ，F ，连接EF ．判断△AEF 是哪一种特殊三角形，并说明理由．【答案】（1）2；（2）60︒ ；（3）见详解【解析】解：（1）∵四边形ABCD 是菱形，∴AC ⊥BD ，∴△AOB 为直角三角形，且111,22OA AC OB BD ====∴2AB ===；（2）∵四边形ABCD 是菱形，∴AB=BC ，由（1）得：AB=AC=BC=2，∴△ABC 为等边三角形，∠BAC=60°；（3）△AEF 是等边三角形，∵由（1）知，菱形ABCD 的边长是2，AC=2，∴△ABC 和△ACD 是等边三角形，∴∠BAC=∠BAE+∠CAE=60°，∵∠EAF=∠CAF+∠CAE=60°，∴∠BAE=∠CAF ，在△ABE 和△ACF 中，BAE CAF AB ACEBA FCA ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABE ≌△ACF （ASA ），∴AE=AF ，∵∠EAF=60°，∴△AEF 是等边三角形．6．（2020·黑龙江鹤岗中考真题）以Rt ABC ∆的两边AB 、AC 为边，向外作正方形ABDE 和正方形ACFG ，连接EG ，过点A 作AM BC ⊥于M ，延长MA 交EG 于点N ．（1）如图1，若90BAC ∠=︒，AB AC =，易证：EN GN =；（2）如图2，90BAC ∠=︒；如图3，90BAC ∠≠︒，（1）中结论，是否成立，若成立，选择一个图形进行证明；若不成立，写出你的结论，并说明理由．【答案】（1）见解析；（2）90BAC ∠=︒时，（1）中结论成立，证明见解析；90BAC ∠≠︒时，（1）中结论成立，证明见解析．【解析】（1）证明：∵90BAC ∠=︒，AB AC =，∴45ACB ∠=︒，∵AM BC ⊥，∴45MAC ∠=︒，∴45EAN MAC ∠=∠=︒，同理45NAG ∠=︒，∴EAN NAG ∠=∠，∵四边形ABDE 和四边形ACFG 为正方形，∴AE AB AC AG ===，∴EN GN =.（2）如图1，90BAC ∠=︒时，（1）中结论成立.理由：过点E 作EP AN ⊥交AN 的延长线于P ，过点G 作GQ AM ⊥于Q ，∵四边形ABDE 是正方形，∴AB AE =，90BAE ∠=︒，∴1809090EAP BAM ∠+∠=︒-︒=︒，∵AM BC ⊥，∴90ABM BAM ，∴ABM EAP ∠=∠，在ABM ∆和EAP ∆中，90ABM EAPAMB P AB AE∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，∴()AAS ABM EAP ∆∆≌，∴EP AM =，同理可得：GQ AM =，∴EP GQ =，在EPN ∆和GQN ∆中，P NQGENP GNQ EP GQ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()AAS EPN GQN ∆∆≌，∴EN NG =.如图2，90BAC ∠≠︒时，（1）中结论成立.理由：过点E 作EP AN ⊥交AN 的延长线于P ，过点G 作GQ AM ⊥于Q ，∵四边形ABDE 是正方形，∴AB AE =，90BAE ∠=︒，∴1809090EAP BAM ∠+∠=︒-︒=︒，∵AM BC ⊥，∴90ABM BAM ，∴ABM EAP ∠=∠，在ABM ∆和EAP ∆中，90ABM EAPAMB P AB AE∠=∠⎧⎪∠=∠=︒⎨⎪=⎩，∴()AAS ABM EAP ∆∆≌，∴EP AM =，同理可得：GQ AM =，∴EP GQ =，在EPN ∆和GQN ∆中，P NQG ENP GNQ EP GQ ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()AAS EPN GQN ∆∆≌，∴EN NG =.7．（2020·湖南醴陵初二期末）如图，在正方形ABCD 中，E 是AB 上一点，F 是AD 延长线上一点，且CE=CF ．（1）求证：BE=DF ；（2）若点G 在AD 上，且∠GCE=45°，则GE=BE+GD 成立吗？为什么？【答案】（1）证明见解析；（2）成立，理由见解析．【解析】（1）证明：∵四边形ABCD 是正方形，∴BC=CD ，∠B=∠CDA=90°，∵F 是AD 延长线上一点，∴∠CDF=180˚-∠CDA=90°.在Rt △CBE 和Rt △CDF 中，CE CF BC CD=⎧⎨=⎩， ∴Rt △CBE ≌Rt △CDF （HL ），∴BE=DF ．（2）成立，理由如下：∵△CBE ≌△CDF ，∴∠BCE=∠DCF.又∵∠BCD=∠BCE+∠DCE=90°，∴∠ECF=∠DCF+∠DCE=90°.∵∠GCE=45°，∴∠GCF=∠ECF -∠GCE=45°.在△ECG 和△FCG 中，CE CF GCE GCF GC GC =⎧⎪∠=∠⎨⎪=⎩，∴△ECG ≌△FCG （SAS ），∴GE=GF=DF+DG.又∵BE=DF ，∴GE=BE+DG.8．（2020·河南焦作初二期末）如图，在菱形ABCD 中，60,ABC E ∠=︒是对角线AC 上一点，F 是线段BC 延长线上一点，且,CF AE =连接BE ．（1）发现问题如图①，若E 是线段AC 的中点.连接,EF 其他条件不变，填空：线段BE 与EF 的数量关系是；（2）探究问题如图②，若E 是线段AC 上任意一点，连接,EF 其他条件不变，猜想线段BE 与EF 的数量关系是什么?请证明你的猜想；（3）解决问题如图③，若E 是线段AC 延长线上任意一点，其他条件不变，且30,1EBC AB ∠==，请直接写出AF 的长度．【答案】（1）BE EF =；（2）猜想线段BE 与EF 的数量关系为：BE EF =；证明见解析．（3．【解析】（1）BE EF =，证明：∵四边形ABCD 是菱形∴AB =BC∵60ABC ∠=︒∴ABC 是等边三角形∴60BCA ∠=︒∵E 是AC 中点∴30CBE ABE ∠=∠=︒，AE =CE∵CF AE =∴CE =CF ∴1302F CEF BCA ∠=∠=∠=︒ ∴30CBE F ∠=∠=︒∴BE EF =；（2）BE EF =，证明：如下图，过点E 作//EG BC 交AB 于点G∵四边形为ABCD 菱形，60ABC ∠=︒∴AB BC =，120BCD ∠=︒，//AB CD ，ABC 与ACD △都是等边三角形∵AC 是菱形ABCD 的对角线 ∴1602ACD BCD ∠=∠=︒ ∴60DCF ABC ∠=∠=︒，AB AC =∴120ECF ∠=︒又∵//EG BC∴60AGE ABC ∠=∠=︒又∵60BAC ∠=︒∴AGE 是等边三角形∴AG AE GE ==∴BG CE =，120BGE ECF ∠=︒=∠又∵CF AE =∴CE CF =在BGE △和CEF △中BG EC BGE ECF GE CF =⎧⎪∠=∠⎨⎪=⎩∴()BGE ECF SAS ≌∴BE EF =；（3）AF =证明：如下图，连接EF ，过点E 作//EG BC 交AB 延长线于点G∵四边形ABCD 是菱形，60ABC ∠=︒∴AB =BC ，ABC 是等边三角形∴60ACB ∠=︒∴60ECF ∠=︒又∵//EG BC∴60AGE ABC ∠=∠=︒又∵60BAC ∠=︒∴AGE 是等边三角形∴AG =AE =GE∴BG =CE ，BGE ECF ∠=∠又∵AE =CF∴GE =CF在BGE △和CEF △中BG CE BGE ECF GE CF =⎧⎪∠=∠⎨⎪=⎩∴()BGE ECF SAS ≌∴BE =EF∵60ABC ∠=︒，30EBC ∠=︒∴603090ABE ABC EBC ∠=∠+∠=︒+︒=︒∵ABC 是等边三角形∴60BAC ∠=︒∴180180906030BEA ABE BAC ∠=︒-∠-∠=︒-︒-︒=︒∵1AB =∴2212AE AB ==⨯=，tan 303AB BE ===︒∵BE =EF∴EF =30EBC EFB ∠=∠=︒∴1803030120BEF ∠=︒-︒-︒=︒∴1203090AEF BEF BEA ∠=∠-∠=︒-︒=︒∴AF ===．9．（2019·河南栾川初二期末）问题背景：在正方形ABCD 的外侧，作△ADE 和△DCF ，连结AF 、BE ．（1）特例探究：如图①，若△ADE 与△DCF 均为等边三角形，试判断线段AF 与BE 的数量关系和位置关系，并说明理由；（2）拓展应用：如图②，在△ADE 与△DCF 中，AE=DF ，ED=FC ，且BE=4，则四边形ABFE 的面积为．【答案】(1)特例探究：AF=BE ，AF ⊥BE ；理由见解析；（2）拓展应用：8【解析】解：（1）特例探究：AF=BE ，AF ⊥BE ．∵四边形ABCD 为正方形，△ADE 与△DCF 均为等边三角形，∴AB=AD=CD ，∠BAD=∠ADC ，AE=AD=CD=DF ，∠DAE=∠CDF ，∴∠BAD+∠DAE=∠ADC+∠CDF ，即∠BAE=∠ADF ，在△ABE 与△DAF 中，{AB ADBAE ADF AE DF=∠=∠=，∴△ABE ≌△DAF （SAS ），∴AF=BE ，∠ABE=∠DAF ，∵∠DAF+∠BAF=90°，∴∠ABE+∠BAF=90°，∴AF ⊥BE ；（2）拓展应用：在△ADE 与△CDF 中，∵{AD CDAE DF CF DE===，∴△ADE ≌△CDF （SSS ），∴∠DAE=∠CDF ，∠ADF=∠ADC+∠CDF=90°+∠CDF ，∠BAE=∠BAD+∠EAD=90°+∠EAD ， ∴∠ADF=∠BAE ，在△ABE 与△DAF 中，{AB ADBAE ADF AE DF=∠=∠=，∴△ABE ≌△DAF （SAS ），∴AF=BE ，∠ABE=∠DAF ，∵∠DAF+∠BAF=90°，∴∠ABE+∠BAF=90°，∴AF ⊥BE ，∴S 四边形ABFE =1·2AF BE =12×4×4=8． 10．（2020·河南三门峡初二期末）在菱形ABCD 中，60B ∠=︒，点E 和点F 分别是射线BA 和射线AD 上的点（不与A ，B 重合），且60ECF ∠=︒．（1）问题初现如图1，当点E 和点F 分别在线段BA 和线段AD 上（不与端点重合）时，线段BC ，BE ，DF 之间的数量关系是_________；（2）深入探究如图2，当点E 和点F 分别在线段BA 和线段AD 的延长线上（不与端点重合）时，线段BC ，BE ，DF 之间有怎样的数量关系？请说明理由；（3）拓展应用在（2）的条件下，若BC CE ⊥，且4BC =，则DF =_________．【答案】（1）BE+DF=BC ；（2）BE=BC+DF ；理由见解析；（3）DF=4【解析】解：（1）BE+DF=BC ．理由：连接AC ，∵四边形ABCD 是菱形，∴AB=BC ．∵∠B=60°，∴△ABC 是等边三角形，∴AB=AC=BC ，∠ACB=∠BAC=60°，即∠BCE+∠ACE=60°，∴∠FAC=60°．∵∠ECF=60°，即∠ACE+∠ACF=60°，∴∠BCE=∠ACF ，在△ACF 与△BCE 中，B FACBC AC BCE ACF∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ACF ≌△BCE （ASA ），∴BE=AF ，∴BC=AD=AF+DF=BE+DF ；（2）BE=BC+DF ．理由如下：连接AC ，∵四边形ABCD 为菱形，∠B=60°，∴AB=BC=CD=AD ，∠B=∠ADC=60°，∴△ABC 和△ACD 为等边三角形，．∴∠BAC=∠ADC=60°，∴∠EAC=∠FDC=120°，又∵∠ACD=∠ECF=60°∴∠ACE=∠DCF ，在△EAC 和△FDC 中EAC FDC AC DCACE DCF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△EAC ≌△FDC∴DF=AE ，又∵BE=AB+AE ，∴BE=BC+DF（3）DF=4，理由：∵90,60,BCE B ∠=︒∠=︒BC=AB=4，∴30BEC ∠=︒，∴BE=8，∴AE=BE -AB=8-4=4．考点3：与特殊平行四边形有关的最值探究典例：（2020·山东济南初二期末）如图①，四边形ABCD 和四边形CEFG 都是正方形，且2BC =，CE =ABCD 固定，将正方形CEFG 绕点C 顺时针旋转α角(0360α︒<<︒)．（1）如图②，连接BG 、DE ，相交于点H ，请判断BG 和DE 是否相等？并说明理由；（2）如图②，连接AC ，在旋转过程中，当ACG ∆为直角三角形时，请直接写出旋转角α的度数；（3）如图③，点P 为边EF 的中点，连接PB 、PD 、BD ，在正方形CEFG 的旋转过程中，BDP ∆的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由．【答案】（1）相等，理由见解析；（2）45α=︒和225α=︒；（3）存在，最大值为2+．【解析】（1）证明：相等∵四边形ABCD 和四边形CEFG 都是正方形，∴BC CD =，CG CE =，90BCD GCE ∠=∠=︒，∴BCD DCG GCE DCG ∠+∠=∠+∠，即BCG DCE ∠=∠，∴()BCG DCE SAS ∆∆≌；∴BG=DE（2）如图1，∠ACG=90°时，旋转角45DCG α=∠=︒；如图2，当∠ACG=90°时，旋转角360225DCG α=︒-∠=︒；综上所述，旋转角α的度数为45°或225°；（3）存在∵如图3，在正方形ABCD 中，2BC =，∴BD ==∴当点P 到BD 的距离最远时，BDP ∆的面积最大，作PH BD ⊥，连接CH ，CP ，则PH CH CP ≤+当,,P C H 三点共线时，PH 最大，此时BDP ∆的面积最大．∵CE =P 为EF 的中点，∴EP =此时12CH BD ==CP =∴11222BDP S BD PH ∆=⋅=⨯=+方法或规律点拨本题是四边形的综合问题，解题的关键是掌握正方形的性质、旋转的性质、全等三角形的判定与性质等知识点．巩固练习1．（2020·山东福山初三期中）如图，在正方形ABCD 中，E ，F 分别为AD ，BC 的中点，P 为对角线BD 上的一个动点，则下列线段的长等于AP EP +最小值的是（）A ．ABB ．DEC ．BD D ．AF【答案】D 【解析】解：过点E 作关于BD 的对称点E′，连接AE′，交BD 于点P ．∴PA+PE 的最小值AE′；∵E 为AD 的中点，∴E′为CD 的中点，∵四边形ABCD是正方形，∴AB=BC=CD=DA，∠ABF=∠AD E′=90°,∴DE′=BF，∴ΔABF≌ΔAD E′，∴AE′=AF.故选D.2．（2020·江苏淮阴初二期中）如图，由两个长为9，宽为3的全等矩形叠合而得到四边形ABCD，则四边形ABCD面积的最大值是（）A．15B．16C．19D．20【答案】A【解析】如图1，作AE⊥BC于E，AF⊥CD于F，，∵AD∥BC,AB∥CD，∴四边形ABCD是平行四边形，∵两个矩形的宽都是3，∴AE=AF=3，∵S四边形ABCD=AE⋅BC=AF⋅CD，∴BC=CD，∴平行四边形ABCD是菱形．如图2，，设AB=BC=x，则BE=9−x，∵BC2=BE2+CE2，∴x2=(9−x)2+32，解得x=5，∴四边形ABCD面积的最大值是：5×3=15.故选A.3．（2020·安徽和县初二期末）如图，在周长为12的菱形ABCD中，AE=1，AF=2，若P为对角线BD上一动点，则EP+FP的最小值为（）A．1B．2C．3D．4【答案】C【解析】作F点关于BD的对称点F′，则PF=PF′，连接EF′交BD于点P．∴EP+FP=EP+F′P．由两点之间线段最短可知：当E、P、F′在一条直线上时，EP+FP的值最小，此时EP+FP=EP+F′P=EF′．∵四边形ABCD为菱形，周长为12，∴AB=BC=CD=DA=3，AB∥CD，∵AF=2，AE=1，∴DF=AE=1，∴四边形AEF′D是平行四边形，∴EF′=AD=3．∴EP+FP的最小值为3．故选C．4．（2020·江苏泰州中学附属初中初二期末）如图，正方形ABCD的边长为3，E、F是对角线BD上的两个动点，且EF＝√2，连接AE、AF，则AE＋AF 的最小值为（）A．2√5B．3√2C．92D．225【答案】A【解析】解：如图作AH∥BD，使得AH=EF=√2，连接CH交BD于F，则AE+AF的值最小．∵AH=EF，AH∥EF，∴四边形EFHA是平行四边形，∴EA=FH，∵FA=FC，∴AE+AF=FH+CF=CH，∵四边形ABCD是正方形，∴AC⊥BD，∵AH∥DB，∴AC⊥AH，∴∠CAH=90°，在Rt△CAH中，CH=√AC2+AH2=2√5，∴AE+AF的最小值2√5，故选：A．5．（2020·山东无棣初二期末）如图，菱形ABCD的边长为4，∠DAB=60°，E为BC的中点，在对角线AC 上存在一点P，使△PBE的周长最小，则△PBE的周长的最小值为()A．B．4C．2D．4+【答案】C【解析】如下图，过点E作AC的对称点F，连接FB，FE，过点B作FE的垂线，交FE的延长线于点G∵菱形ABCD的边长为4，点E是BC的中点∴BE=2∵∠DAB=60°，∴∠FCE=60°∵点F是点E关于AC的对称点∴根据菱形的对称性可知，点F在DC的中点上则CF=CE=2∴△CFE是等边三角形，∴∠FEC=60°，EF=2∴∠BEG=60°∴在Rt△BEG中，EG=1，∴FG=1+2=3∴在Rt△BFG中，根据分析可知，BF=PB+PE∴△PBE的周长2故选：C6．（2020·四川遂宁初二期末）如图，在矩形ABCD中，AD＝3，CD＝4，点P是AC上一个动点（点P与点A，C不重合），过点P分别作PE⊥BC于点E，PF∥BC交AB于点F，连接EF，则EF的最小值为_____．【答案】12 5【解析】证明：如图，连接BP．∵∠B＝∠D＝90°，AD＝3，CD＝4，∴AC＝5，∵PE⊥BC于点E，PF∥BC，∠B＝90°，∴四边形PEBF是矩形；∴EF＝BP，由垂线段最短可得BP⊥AC时，线段EF的值最小，此时，S△ABC＝12BC•AB＝12AC•CP，即12×4×3＝12×5•CP，解得CP＝125．故答案为：125．7．（2020·江苏淮安初三三模）如图，正方形ABCD的边长为6，E，F是对角线BD上的两个动点，且EF＝12x x ，连接CE ，CF ，则△CEF 周长的最小值为_____．【答案】【解析】如图作CH ∥BD ，使得CH ＝EF ＝，连接AH 交BD 由F ，则△CEF 的周长最小．∵CH ＝EF ，CH ∥EF ，∴四边形EFHC 是平行四边形，∴EC ＝FH ，∵FA ＝FC ，∴EC+CF ＝FH+AF ＝AH ，∵四边形ABCD 是正方形，∴AC ⊥BD ，∵CH ∥DB ，∴AC ⊥CH ，∴∠ACH ＝90°，在Rt △ACH 中，AH∴△EFC 的周长的最小值＝故答案为：8．（2020·江苏仪征初三二模）如图，在矩形ABCD 中，24==AD AB ，点E 是AD 的中点，点M 是BE 上一动点，取CM 的中点为N ，则AN 的最小值是__________．【答案】【解析】取BC的中点F，由题意知点N在直线DF上，∴AN的最小值就是点A到直线DF的距离，连接AF，在矩形ABCD中，AD=BC=2AB=4，∴AB=BF=CF=CD=2，∠ABC=∠BCD=90︒，∴△ABF和△FCD都是等腰直角三角形，∴∠AFB=∠DFC=45︒，∴∠AFD=45︒，∴AF⊥FD，∴AN的最小值是AF的长，即AF=AB=故答案为：9．（2020·陕西碑林西北工业大学附属中学初一期末）问题提出（1）如图①，在Rt△ABC中，∠ABC＝90°，AB＝12，BC＝16，则AC＝；问题探究（2）如图②，在Rt△ABC中，∠ABC＝90°，AC＝10，点D是AC边上一点，且满足DA＝DB，则CD＝；问题解决（3）如图③，在Rt△ABC中，过点B作射线BP，将∠C折叠，折痕为EF，其中E为BC中点，点F在AC 边上，点C的对应点落在BP上的点D处，连接ED、FD，若BC＝8，求△BCD面积的最大值，及面积最大时∠BCD的度数．【答案】（1）20；（2）5；（3）S△BCD＝16；∠BCD＝45°【解析】解：（1）∵∠ABC＝90°，AB＝12，BC＝16，∴20AC==，故答案为：20；（2）∵DA＝DB，∴∠A＝∠DBA，∵∠ABC＝90°∴∠A+∠C＝90°，∠ABD+∠DBC＝90°，∴∠DBC＝∠C，∴DB＝DC，∴DB＝DC＝AD＝12AC＝5，故答案为：5；（3）∵E为BC中点，BC＝8，∴BE＝EC＝4，∵将∠C折叠，折痕为EF，∴DE＝EC＝4，当DE⊥BC时，S△BCD有最大值，S△BCD＝12×BC×DE＝12×8×4＝16，此时∵DE⊥BC，DE＝EC，∴∠BCD＝45°．故答案为：S△BCD＝16；∠BCD＝45°．考点4：与特殊平行四边形有关的动点问题典例：（2020·山东平阴初二期末）如图1，在矩形纸片ABCD中，AB＝3cm，AD＝5cm，折叠纸片使B点落在边AD上的E处，折痕为PQ，过点E作EF∥AB交PQ于F，连接BF．（1）求证：四边形BFEP 为菱形；（2）当E 在AD 边上移动时，折痕的端点P 、Q 也随着移动．①当点Q 与点C 重合时，（如图2），求菱形BFEP 的边长；②如果限定P 、Q 分别在线段BA 、BC 上移动，直接写出菱形BFEP 面积的变化范围．【答案】（1）证明过程见解析；（2）①边长为53cm ，②225cm S 9cm 3≤≤．【解析】解：（1）证明：∵折叠纸片使B 点落在边AD 上的E 处，折痕为PQ ，∴点B 与点E 关于PQ 对称，∴PB ＝PE ，BF ＝EF ，∠BPF ＝∠EPF ，又∵EF ∥AB ，∴∠BPF ＝∠EFP ，∴∠EPF ＝∠EFP ，∴EP ＝EF ，∴BP ＝BF ＝EF ＝EP ，∴四边形BFEP 为菱形；（2）①∵四边形ABCD 是矩形，∴BC ＝AD ＝5cm ，CD ＝AB ＝3cm ，∠A ＝∠D ＝90°，∵点B 与点E 关于PQ 对称，∴CE ＝BC ＝5cm ，在Rt △CDE 中，DE 4cm ，∴AE ＝AD ﹣DE ＝5cm -4cm ＝1cm ；在Rt △APE 中，AE ＝1，AP ＝3-PB ＝3﹣PE ，∴222EP =1(3-EP)+，解得：EP ＝53cm ，∴菱形BFEP 的边长为53cm ； ②当点Q 与点C 重合时，点E 离点A 最近，由①知，此时AE ＝1cm ，BP=53cm ， 2BFEP 5S =BP AE=cm 3⋅四边形，当点P 与点A 重合时，点E 离点A 最远，此时四边形ABQE 为正方形，AE ＝AB ＝3cm ，2ABQE BFEP S =S =9cm 正方形四边形， ∴菱形的面积范围：225cm S 9cm 3≤≤．方法或规律点拨本题是四边形综合题目，考查了矩形的性质、折叠的性质、菱形的判定、平行线的性质、等腰三角形的判定、勾股定理、正方形的性质等知识，求出PE 是本题的关键．巩固练习1．（2020·河北景县初二期中）正方形ABCD 的边AB 上有一动点E ，以EC 为边作矩形ECFG ，且边FG 过点D ，在点E 从点A 移动到点B 的过程中，矩形ECFG 的面积（）A ．先变大后变小B ．先变小后变大C ．一直变大D ．保持不变【答案】D【解析】连接DE，∵S△CDE＝12S四边形CEGF，S△CDE＝12S正方形ABCD，∴矩形ECFG与正方形ABCD的面积相等．故选D．2．（2020·江苏省泰兴市济川中学初二期末）如图，点O为矩形ABCD的对称中心，点E从点A出发沿AB 向点B运动，移动到点B停止，延长EO交CD于点F，则四边形AECF形状的变化依次为（）A．平行四边形→正方形→平行四边形→矩形B．平行四边形→菱形→平行四边形→矩形C．平行四边形→正方形→菱形→矩形D．平行四边形→菱形→正方形→矩形【答案】B【解析】解：观察图形可知，四边形AECF形状的变化依次为平行四边形→菱形→平行四边形→矩形．故选：B．3．（2020·山东中区济南外国语学校初二期末）如图，已知正方形ABCD与正方形AEFG的边长分别为4cm、1cm，若将正方形AEFG绕点A旋转，则在旋转过程中，点C、F之间的最小距离为（）cm。