Java数据结构和算法笔记
Java数据结构和算法

Java数据结构和算法一、数组于简单排序 (1)二、栈与队列 (4)三、链表 (7)四、递归 (22)五、哈希表 (25)六、高级排序 (25)七、二叉树 (25)八、红—黑树 (26)九、堆 (36)十、带权图 (39)一、数组于简单排序数组数组(array)是相同类型变量的集合,可以使用共同的名字引用它。
数组可被定义为任何类型,可以是一维或多维。
数组中的一个特别要素是通过下标来访问它。
数组提供了一种将有联系的信息分组的便利方法。
一维数组一维数组(one-dimensional array )实质上是相同类型变量列表。
要创建一个数组,你必须首先定义数组变量所需的类型。
通用的一维数组的声明格式是:type var-name[ ];获得一个数组需要2步。
第一步,你必须定义变量所需的类型。
第二步,你必须使用运算符new来为数组所要存储的数据分配内存,并把它们分配给数组变量。
这样Java 中的数组被动态地分配。
如果动态分配的概念对你陌生,别担心,它将在本书的后面详细讨论。
数组的初始化(array initializer )就是包括在花括号之内用逗号分开的表达式的列表。
逗号分开了数组元素的值。
Java 会自动地分配一个足够大的空间来保存你指定的初始化元素的个数,而不必使用运算符new。
Java 严格地检查以保证你不会意外地去存储或引用在数组范围以外的值。
Java 的运行系统会检查以确保所有的数组下标都在正确的范围以内(在这方面,Java 与C/C++ 从根本上不同,C/C++ 不提供运行边界检查)。
多维数组在Java 中,多维数组(multidimensional arrays )实际上是数组的数组。
你可能期望,这些数组形式上和行动上和一般的多维数组一样。
然而,你将看到,有一些微妙的差别。
定义多维数组变量要将每个维数放在它们各自的方括号中。
例如,下面语句定义了一个名为twoD 的二维数组变量。
int twoD[][] = new int[4][5];简单排序简单排序中包括了:冒泡排序、选择排序、插入排序;1.冒泡排序的思想:假设有N个数据需要排序,则从第0个数开始,依次比较第0和第1个数据,如果第0个大于第1个则两者交换,否则什么动作都不做,继续比较第1个第2个…,这样依次类推,直至所有数据都“冒泡”到数据顶上。
java基础知识点笔记

java基础知识点笔记Java是一门非常重要的计算机语言,具有良好的跨平台性和易读性和易学性。
尤其是基于Java开发的移动端和Web端产品,其优秀的性能和可扩展性在行业中得到了广泛的青睐。
作为Java开发工程师,熟练掌握Java的基础知识非常重要。
一、Java基本语法Java程序包含一个或多个类,不同类可以相互调用使用。
每一个Java程序都需要有一个入口点,即main()函数。
在Java中,注释采用“//”或“/*...*/”的形式,可以单行或多行注释。
Java变量需要先声明再使用,可以定义基本类型变量和引用类型变量。
Java中的运算符包括算术运算符、逻辑运算符等。
二、Java面向对象编程Java是一门面向对象的编程语言,对象是Java程序的基本组成单元。
Java中的类封装了数据和方法,可以实现类的继承和多态。
在Java中,使用构造函数实例化对象,可以使用访问控制符来控制类成员的访问权限。
三、Java流程控制语句Java中的流程控制语句有条件语句(if、if-else、switch)、循环语句(while、do-while、for)等。
其中,if语句可以进行嵌套,switch语句可以使用break语句避免case穿透问题。
四、Java数组Java中的数组是一组相同类型的数据序列,从0开始编号,使用方括号表示。
在Java中可以使用foreach来遍历数组,也支持多维数组。
五、Java异常处理Java程序中的异常指的是程序出现的错误。
异常处理是Java程序中的一部分,可以使用try-catch语句来捕获并处理异常。
Java中的异常类型包括运行时异常和受检查异常。
六、Javaio编程Java中的文件和I/O操作称为io编程。
Java的io编程采用字节流和字符流,其中字节流用于处理二进制数据,字符流用于处理文本数据。
Java中的io操作需要进行文件的读取、写入等操作,可以使用File类来操作文件。
七、Java线程Java程序中,线程指的是一条执行序列,Java中的线程可以继承Thread类或实现Runnable接口。
《数据结构与问题求解:Java语言描述》笔记

《数据结构与问题求解:Java语言描述》阅读笔记目录一、内容综述 (2)1. 本书简介与背景介绍 (3)2. 本书阅读目的与预期成果 (4)二、基础概念与预备知识 (5)1. 数据结构定义与重要性 (7)2. 算法概念及其与数据结构的关系 (9)3. Java语言基础语法回顾 (9)4. 预备知识 (11)三、数据结构概述 (13)1. 数据结构的分类与特点介绍 (14)2. 数据结构的选择与应用场景分析 (16)四、线性数据结构 (18)1. 数组的概念与应用 (20)2. 链表的概念与应用 (20)3. 队列和栈的概念与应用 (22)4. 线性数据结构的性能分析 (23)五、非线性数据结构 (25)1. 树形数据结构概述 (26)2. 二叉树及其相关操作与应用实例分析讲解 (27)3. 图论中的基本概念及图的表示方法介绍等 (28)一、内容综述《数据结构与问题求解:Java语言描述》是一本关于数据结构和算法的经典教材,作者是Robert Sedgewick和Kevin Wayne。
本书以Java语言为实现工具,详细介绍了数据结构的基本概念和常用算法,以及如何将这些概念和算法应用于实际问题。
全书共分为5章,分别是基本数据结构、排序算法、图论、动态规划和高级数据结构。
第1章主要介绍了基本数据结构,包括线性表、栈和队列等。
线性表包括顺序表、链表和树表等,讲解了它们的基本操作和应用场景。
栈和队列分别介绍了它们的抽象数据类型、操作方法和应用实例。
第2章主要介绍了排序算法,包括冒泡排序、选择排序、插入排序、快速排序、归并排序和堆排序等。
每种排序算法都详细讲解了其原理、实现过程和优缺点,以及在不同场景下的应用。
第3章主要介绍了图论的基本概念和常用算法,如图的表示、遍历、最短路径算法(Dijkstra算法、FloydWarshall算法)、最小生成树算法(Kruskal算法、Prim算法)等。
还介绍了图的一些扩展概念,如带权有向图、带权无向图、加权图等。
数据结构与算法java版第五版

数据结构与算法java版第五版一、引言数据结构与算法是计算机科学的基础,是程序员必须掌握的核心知识。
如何高效地使用数据结构和算法解决实际问题,是每个程序员都需要思考和学习的事情。
本文将介绍《数据结构与算法java版第五版》这本书的内容,从数据结构和算法的基础知识到高级应用进行探讨。
二、基础知识1. 数据结构的概念及分类•线性结构•树形结构•图形结构2. 算法的概念及分类•基本概念•算法的复杂度分析3. Java基础•Java基本语法•面向对象编程•集合框架三、线性结构1. 数组•数组的定义和使用•数组的常见操作•数组的应用场景2. 链表•链表的定义和基本操作•单向链表和双向链表的区别•链表的应用场景3. 栈和队列•栈的定义和基本操作•队列的定义和基本操作•栈和队列的应用场景4. 哈希表•哈希表的原理和实现•哈希函数的选择•哈希表的应用场景四、树形结构1. 二叉树•二叉树的定义和基本操作•二叉树的常用遍历算法•二叉树的应用场景2. AVL树•AVL树的定义和性质•AVL树的插入和删除操作•AVL树的应用场景3. 红黑树•红黑树的定义和性质•红黑树的插入和删除操作•红黑树的应用场景4. B树和B+树•B树和B+树的定义和性质•B树和B+树的插入和删除操作•B树和B+树的应用场景五、图形结构1. 图的表示和基本操作•图的表示方法•图的遍历算法•图的最短路径算法2. 拓扑排序•拓扑排序的原理和算法•拓扑排序的应用场景3. 最小生成树•最小生成树的定义和算法•最小生成树的应用场景4. 图的搜索•图的深度优先搜索•图的广度优先搜索•图的搜索算法的应用场景六、高级应用1. 排序算法•冒泡排序•插入排序•选择排序•快速排序•归并排序2. 查找算法•顺序查找•二分查找•哈希查找•插值查找3. 动态规划•动态规划的基本概念•动态规划的应用场景•动态规划问题的解决步骤七、总结《数据结构与算法java版第五版》是一本全面介绍数据结构和算法的书籍,从基础知识到高级应用等多个方面进行了深入的探讨。
java常用算法和数据结构

java常用算法和数据结构Java是一种面向对象的编程语言,它具有丰富的算法库和数据结构库,为开发人员提供了许多常用的算法和数据结构。
下面将介绍一些Java常用的算法和数据结构。
1.排序算法-冒泡排序(Bubble Sort):比较相邻的两个元素,如果顺序错误则交换位置,重复该过程直到整个序列有序。
-插入排序(Insertion Sort):将数组分为已排序和未排序两部分,每次从未排序部分取出一个元素,插入到已排序部分合适的位置。
-选择排序(Selection Sort):每次从未排序部分选择最小(或最大)的元素,放到已排序部分的末尾。
-快速排序(Quick Sort):选择一个基准元素,将数组分为两部分,小于基准的放左边,大于基准的放右边,递归地对左右两部分进行快速排序。
-归并排序(Merge Sort):将数组分为两部分,分别对每个子数组进行排序,然后合并两个有序子数组。
2.搜索算法-二分查找(Binary Search):对有序数组进行查找,每次将查找范围缩小一半。
-广度优先搜索(BFS):以树或图的形式搜索,从根节点开始,逐层扩展搜索范围,直到找到目标节点。
-深度优先搜索(DFS):以树或图的形式搜索,从根节点开始,逐个访问节点的所有邻居节点,直到找到目标节点或搜索完所有节点。
3.数据结构-数组(Array):一组按顺序存储的相同类型元素的集合,通过索引访问元素,可以快速访问元素,但插入和删除元素较慢。
-链表(Linked List):一组通过指针连接的节点存储的元素的集合,支持灵活的插入和删除操作,但访问元素较慢。
-栈(Stack):一种特殊的线性数据结构,遵循先进后出(LIFO)原则,只能在栈顶进行插入和删除操作。
-队列(Queue):一种特殊的线性数据结构,遵循先进先出(FIFO)原则,在队尾插入元素,队头删除元素。
-堆(Heap):一种特殊的树形数据结构,可以快速找到最小(或最大)元素,常用于实现优先队列。
第一章-Java基础笔记
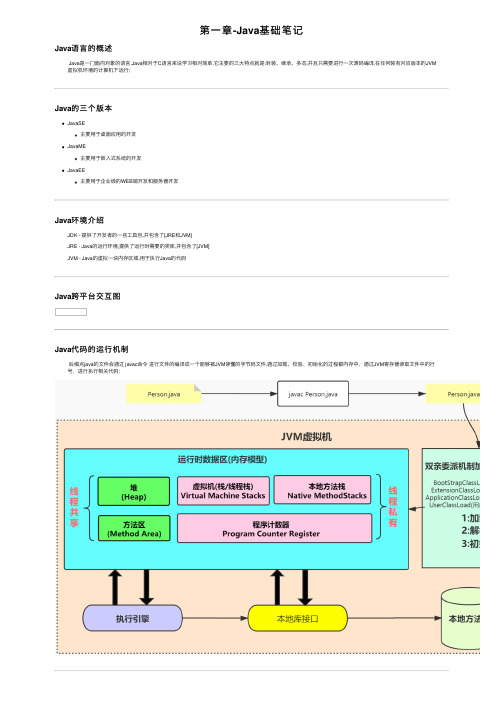
第⼀章-Java基础笔记Java语⾔的概述Java是⼀门⾯向对象的语⾔,Java相对于C语⾔来说学习相对简单,它主要的三⼤特点就是:封装、继承、多态,并且只需要进⾏⼀次源码编译,在任何装有对应版本的JVM 虚拟机环境的计算机下运⾏;Java的三个版本JavaSE主要⽤于桌⾯应⽤的开发JavaME主要⽤于嵌⼊式系统的开发JavaEE主要⽤于企业级的WEB端开发和服务器开发Java环境介绍JDK - 提供了开发者的⼀些⼯具包,并包含了[JRE和JVM]JRE - Java的运⾏环境,提供了运⾏时需要的类库,并包含了[JVM]JVM - Java的虚拟⼀块内存区域,⽤于执⾏Java的代码Java跨平台交互图Java代码的运⾏机制后缀点java的⽂件会通过 javac命令进⾏⽂件的编译成⼀个能够被JVM读懂的字节码⽂件,通过加载、校验、初始化的过程都内存中,通过JVM寄存器读取⽂件中的⾏号,进⾏执⾏相关代码;注释注释是为了在编写程序时对某个类、⽅法或是⼀段代码进⾏功能作⽤的说明,它不会被编译成代码执⾏,只是起到⼀个描述作⽤,便于对代码的理解;Java中的注释分为3种:单⾏注释://多⾏注释:/* */⽂档注释:/** */对注解的内容⽣成JavaDoc⽂档DOS命令进⼊到要⽣成Doc⽂档的层级⽬录,执⾏:javadoc -encoding UTF-8 -charset UTF-8 ⽂件名称/*** @Author JavaCat7* @Description 这是⼀个⽂档注释*/public class Demo{/*** @Parameter args 对参数的描述* @Description 这是⼀个⽂档注释*/public static void main(String[] args){//这是⼀个单⾏注释System.out.println("Hello Java");/*这是多⾏注释这是多⾏注释*/}}标识符每个⼈都有名字,⽽标识符是为了给代码中的类、接⼝、⽅法、变量取⼀个名字,但它们的明⽩是有着严格规范的;规范:每个⼈都有名字,⽽标识符是为了给代码中的类、接⼝、⽅法、变量取⼀个名字,但它们的明⽩是有着严格规范的;**规范:**1.严格区分⼤⼩写;2.开头可以是$ 或 _ 或 A-Z a-z的字母组成,也可以汉字(不会这么⼲);3.可以由数字、字母或者是 $ 或 _ 组成,但数字不能⽤于开始;4.不可以包含特殊字符;5.不能以Java语⾔中的保留字作为命名;6.类名采取⼤驼峰命名法;7.⽅法和变量采取⼩驼峰命名法;8.常量采取⼤学加_进⾏命名;基本数据类型Java是强类型计算机语⾔,所有的变量必须先定义才能使⽤,对于强类型⽽⾔主要就是指的数据安全,强类型的语⾔有很多,⽐如C、C++、python...计算机存储单位换算bit(位) - 是计算内部数据存储的最⼩单元,通过8个⼆进制位进⾏表⽰;byte(字节) - 是计算机中数据处理的基本单位,通常使⽤B来表⽰;8个bit(位) = 1B(字节)1024个B(字节) = 1KB1024个KB = 1MB1024个MB = 1GB....//整数类型byte a = 1;short b = 2;int c = 3;long d = 4L;//⼩数类型float e = 5.0f;duble f = 6.0d;//字符类型char g = 'a';//布尔类型boolean h = true;boolean i = false;数据类型的转换各数值相关数据类型⽀持类型上的转换,既可以把排序级别较低的类型转换成排序级别较⼤的类型,也可以把排序级别较⾼的类型转换成级别较低的类型(但会造成数据的丢失);数据的转换强制类型转换 - 在要转换的变量前使⽤:要转换的对应数据类型如- (int)⾃动类型转换 - 在不同的数值数据类型运算中,它会以排序级别较⾼的数据类型作为基础⾃动转换int number1 = 128;//正常byte的值是 -128 - 127,强制把int类型转换成byte会造成数据的不精确byte number2 = (byte)number1;int number3 = 519;float number4 = 1.0f;//在运算过程中因为float的排序级别⽐int⾼,那么它会⾃动转换成float类型在完成运算float number5 = number3 + number4;变量,静态变量,常量及作⽤域变量是指可以变化的值,通过数据类型和变量名可以在内存中申请⼀块存储的空间,通过内存的引⽤地址可以设置改变内存中存储的值或者修改值,所有的变量必须先赋值才可以使⽤;成员变量成员变量是指在类中与⽅法同级的位置中定义的成员变量,在该位置定义的变量可以不⽤设置值就可以使⽤,因为它会对类进⾏初始化,并完成初始化赋值,就算不给他们赋值也会有默认的初始值,他们的默认初始值都是最⼩的单元;作⽤域成员位置的变量,可以在⾮静态⽅法的所有位置使⽤,如果要在静态⽅法中使⽤,需要先创建对象;public class Variable{int a; //默认为:0float b; //默认为:0.0char c; //默认为:''boolean d; //默认为:false}局部变量局部变量是指在⽅法内部定义的变量,必须要先完成初始化后,才可以被使⽤;作⽤域局部位置的变量,外部⽆法使⽤,只能在⽅法内部使⽤,可以和外部的变量名称相同;public class Variable{int number;public void method(){int number = 3;//可以和成员位置的变量名称相同}}静态变量静态变量是指被static关键字修饰的变量,被修饰的变量⼜称为类变量;作⽤域静态变量可以作⽤域与所有⽅法中,静态变量只能定义在类的成员位置;public class Variable{static int number ;public static void main(String[] arags){System.out.println(number);}public void method(){System.out.println(numbe);}}常量常量是指不能被改变的值,它在创建到成员位置必须要先完成赋值,⼀旦被创建它的值是不允许被更改的;作⽤域它的作⽤域和成员变量相同public class Variable{final int NUMBER = 3.1415926;}静态常量静态常量是指从属于类的常量,在完成初始化以后是不可以被修改的,并且被public所进⾏修饰;作⽤域它的作⽤域和静态变量相同运算符算术运算符int a = 5;int b = 2;int number = a + b; //number = 7;int number = b - a; //number = 3;int number = a * b; //number = 10;int number = a / b; //number = 2,只取整数;double number = a / (double)b; //number = 2.5int number = a % b; //number = 1;⾃增⾃减运算符int a = 1;int b;b = a++; //b = 1; 先把a的值赋值给b,后a进⾏ +1 操作;b = a--; //b = 2; a前⾯进⾏了⾃增那么就是2,先把2赋值给b,然后进⾏ -1 操作;b = ++a; //b = 2; 前⾯a进⾏了⾃减那么就是1,先对a进⾏⾃增加1,然后在赋值给b;b = --a; //b = 1; 前⾯a是2,先对a进⾏⾃减1,在赋值给b;赋值运算符int a = 5;//把 5 赋值给 a;int b = 2;//把 2 赋值给 b;a += b; // a = 7(a+b的结果在赋值给a);a -= b; // a = 3;a *= b; // a = 10;a /= b; // a = 2;a %= b; // a = 1;关系运算符int a = 5;int b = 2;a > b; //truea < b; //falsea >= b; //falsea <= b; //truea == b; //falsea != b; //true逻辑运算符boolean a = true;boolean b = false;a &&b = false;//都true则true,第⼀个条件为false就不会在看第⼆个条件,直接返回falsea ||b = true;//⼀个条件为true则true,第⼀个条件为tre就不看第⼆个条件,直接返回true! a = false;//取反a &b = false;//2个条件都要执⾏a |b = true;三元运算符int a = 5;int b = 5;a ==b ? "等于":"不等于"; //为true返回第⼀个,为false返回第⼆个流程控制语句If语句if语句就是判断条件是否成⽴,成⽴就执⾏if中的代码,不成⽴就不进⼊;boolean flag = true;if(flag){System.out.println("...");}if...else语句if...else语句就是根据判断的条件是否成⽴,成⽴⾛if语句,不成⽴⾛else语句;boolean flag = true;if(flag){System.out.println("成⽴");}else{System.out.println("不成⽴");}if...else if语句if...else if⽀持多条件的判断,只会进⼊⼀个匹配的条件;boolean flag = true;boolean fail = false;if(flag){System.out.println("条件匹配");}else if(fail){System.out.println("条件匹配");}else{System.out.println("条件都不匹配");}switch条件控制语句witch语句从JDK1.7开始可以⽀持匹配:String字符串;注意事项:每个case 后⾯必须跟⼀个数值常量或字符串常量⽤于匹配;匹配的语句后⾯需要加上break关键字,防⽌case穿透;String week = "星期⼀";switch(week){case "星期⼀":System.out.println("今天是星期⼀");break;case "星期⼆":System.out.println("今天是星期⼆");break;case "星期三":System.out.println("今天是星期⼆");break;default:System.out.println("今天星期⼏都不是");}循环控制语句for循环语句for(初始值,条件表达式,更新)for(int i = 1 ; i <= 10 ; i++){System.out.println(i);}增强for循环for(接收类型的变量,表达式)int [] arrays = {1,2,3,4,5,6,7,8,9,10};for(int i : arrays){System.out.println(arrays);}while循环语句while(条件表达式)int number = 1;while(number <= 100){System.out.println(number);number ++;}do...while循环语句do{先把语句执⾏⼀遍}while(条件表达式);boolean flag = true;do{System.out.println("先执⾏⼀遍");flag = false;}while(flag);break和continue关键字break关键字结束循环的意思;for(int i = 1; i <= 100; i++){if(i == 10){System.out.println("打印10后结束循环");break;}}continue关键字跳过当前循环,进⼊下⼀次循环;for(int i = 1 ; i <= 10; i ++){if(i % 2 == 1){continue;}System.out.println("打印:"+i);}⽅法概述:⽅法就相当于使⽤多⾏代码进⾏组合去实现的⼀个功能⽚段,对代码进⾏封装利⽤,可实现多次调⽤;⽅法的定义修饰符返回值⽅法名称(形参形参名称){⽅法体}public class Function{public static void main(String[] arags){}public void method1(){}public void method2(String name,int age){}public static void method3(){}public int method03(){int a = 3;return a;}public int method04(int a,int b){if(a == b){System.out.println(a + "和" + b + "相等");return -1;}return a > b ? a : b;}}⽅法的重载⽅法的重载是指⽅法名称相同,传递的参数类型不同,个数不同,顺序不同与返回值⽆关;这样的⽅法被称为⽅法的重载;public class Function{public int max(int a,int b) {return a > b ? a : b;}public double max(double a,double b){return a > b ? a : b;}}形参和实参形参是指在()内部的参数,实参是指被真实传递的参数;public class Function{public static vid main(String[] args){Function function = new Function();function.max(3,5);}public int max(int a,int b) {return a > b ? a : b;}}可变参数在⽅法的()中我们有时候不知道要传递多少参数,那么我们可以传递⼀个数据类型紧跟后⾯加上...来表⽰;但需要注意的是⼀个⽅法中指允许⼀个可变参,如果有其他类型的参数,那么可变参数需要写在最后⾯;可变参数本质上就是⼀个数组;public class Function{public void method(String name,int... numbers){for(int num : numbers){System.out.println(num);}}}递归递归的本质就是⾃⼰调⽤⾃⼰,它可以解决⼀些业务,但效率和开销较⼤,对⼀些⽐较⼩的运算可以使⽤;//递归求3的阶乘public class Founction{public static void main(String[] args){}public int founction(int number){int result = 1;if(number == result){return result;}return number * founction(number - 1);}}数组数组就是⼀组数据的集合,Java中的数组必须存储和数据类型相符合的值,不允许与定义的数据类型不匹配;⼀旦数组被创建出来,它的长度就不允许被改变,数组有下标(索引)的概念,都是从0开始,如果操作的数据超过数组的长度那么就会报出下标索引越界异常[ IndexOutofBoundsException ];数组的定义int[] array = new int[3];int array[] = new int[3];int array[] = {1,2,3};数组的内存模型图数组的遍历⽅式int[] arr = new int[10];//⽅式⼀for (int i = 0; i < arr.length ; i ++) {System.out.println(arr[i]);}//⽅式⼆for (int num : arr) {System.out.println(num);}⼆维数组int[][] arr = new int[3][2];String[][] strArr = {{"hello","hello"},{"hi","hi","hi",{"java","java","java","java"}}Arrays⼯具类Arrays数组的⼯具类,是jdk已经帮我们提供好的⼀套数据⼯具类,⽅便我们对数据相关进⾏⼀些操作;int[] arr = {3,51,1,33,82,22,55,53};Arrays.toString(arr);//把数组变成⼀个字符串Arrays.sort(arr);//对数组内容进⾏升序排列Arrays.fill(arr,0);//把数组的内容全部进⾏替换为0常见算法冒泡排序public static int[] arr = new int[]{5, 2, 7, 4, 6, 9, 8, 13, 19, 11, 17, 15};//冒泡排序算法public static void popArithmetic(int[] arr) {//⽐较的轮数是数组长度-1for (int i = 0; i < arr.length - 1; i++) {//每次⽐较⼀轮,需要减少1次⽐较的次数for (int j = 0; j < arr.length - i - 1; j++) {//如果前⾯的数据⽐后⾯⼤,那么就交换位置if (arr[j] > arr[j + 1]) {int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}System.out.println("最终结果是:" + Arrays.toString(arr));}选择排序public static int[] arr = new int[]{5, 2, 7, 4, 6, 9, 8, 13, 19, 11, 17, 15};//选择排序public static void selectOrderArithmetic(int[] arr) {//⽐较的轮数是数组长度-1for (int i = 0; i < arr.length - 1; i++) {//每⽐较⼀次,需要减少1次⽐较的次数,会把⼩的先往前排for(int j = i+1;j<arr.length;j++){if(arr[i]>arr[j]){int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}}}System.out.println("最终结果是:" + Arrays.toString(arr));}⼆分查找public static int[] arr = new int[]{1, 2, 3 , 4, 6, 7, 8, 13, 19};//2分查找法public static void branchFind(int [] arr,int number){int startNode = 0;int endNode = arr.length-1;int middle = 0;while (startNode <= endNode){//中间的指针由开始节点和结束节点计算得来middle = (startNode+endNode)/2;if(number == arr[middle]){System.out.println("找到了");break;}else if(number < arr[middle]){endNode=middle-1;System.out.println(number+"⼩于中间值,结束节点变更为中间节点-1"); }else if(number > arr[middle]){startNode = middle+1;System.out.println(number+"⼤于中间值,开始节点变更为中间节点+1"); }else{System.out.println("没有找到该元素");break;}}}。
(完整word版)Java学习笔记(必看经典)

诚信、创新、开放、合作JAVA的面向对象编程--------课堂笔记面向对象主要针对面向过程。
面向过程的基本单元是函数。
什么是对象:EVERYTHING IS OBJECT(万物皆对象)所有的事物都有两个方面:有什么(属性):用来描述对象。
能够做什么(方法):告诉外界对象有那些功能。
后者以前者为基础。
大的对象的属性也可以是一个对象。
为什么要使用面向对象:首先,面向对象符合人类看待事物的一般规律。
对象的方法的实现细节是屏蔽的,只有对象方法的实现者了解细节。
方法的定义非常重要。
方法有参数,也可能有返回值。
注意区分:对象(本身)、对象的实现者、对象的调用者。
分析对象主要从方法开始。
我们通过类来看待对象,类是对象的抽象。
其次,采用面向对象方法可以使系统各部分各司其职、各尽所能。
对象之间的耦合性一定要低(比如不同硬盘和不同主板之间的关系)。
这样才能使每个对象本身做成最好的。
对于对象的要求:高内聚、低耦合,这样容易拼装成为一个系统。
实现高内聚就是要最大限度低提高复用性(复用性好是因为高内聚)。
可复用性是OOP的基础。
比较面向过程的思想和面向对象的思想:面向过程的思想:由过程、步骤、函数组成,以过程为核心;面向对象的思想:以对象为中心,先开发类,得到对象,通过对象之间相互通信实现功能。
面向过程是先有算法,后有数据结构。
面向对象是先有数据结构,然后再有算法。
在用面向对象思想开发的过程中,可以复用对象就进行复用,如无法进行复用则开发新的对象。
开发过程是用对个简单的对象的多个简单的方法,来实现复杂的功能。
从语法上来看,一个类是一个新的数据类型。
在面向对象编程中,除了简单数据类型,就是对象类型。
定义类的格式:class Student{代码}注意类名中单词的首字母大写。
实例变量:定义在类中但在任何方法之外。
(New出来的均有初值)局部变量:定义在方法之中的变量。
局部变量要先赋值,再进行运算,而实例变量均已经赋初值。
这是局部变量和实例变量的一大区别。
数据结构与算法基础知识总结

数据结构与算法基础知识总结1 算法算法:是指解题方案的准确而完整的描述。
算法不等于程序,也不等计算机方法,程序的编制不可能优于算法的设计。
算法的基本特征:是一组严谨地定义运算顺序的规则,每一个规则都是有效的,是明确的,此顺序将在有限的次数下终止。
特征包括:(1)可行性;(2)确定性,算法中每一步骤都必须有明确定义,不充许有模棱两可的解释,不允许有多义性;(3)有穷性,算法必须能在有限的时间内做完,即能在执行有限个步骤后终止,包括合理的执行时间的含义;(4)拥有足够的情报。
算法的基本要素:一是对数据对象的运算和操作;二是算法的控制结构。
指令系统:一个计算机系统能执行的所有指令的集合。
基本运算和操作包括:算术运算、逻辑运算、关系运算、数据传输。
算法的控制结构:顺序结构、选择结构、循环结构。
算法基本设计方法:列举法、归纳法、递推、递归、减斗递推技术、回溯法。
算法复杂度:算法时间复杂度和算法空间复杂度。
算法时间复杂度是指执行算法所需要的计算工作量。
算法空间复杂度是指执行这个算法所需要的内存空间。
2 数据结构的基本基本概念数据结构研究的三个方面:(1)数据集合中各数据元素之间所固有的逻辑关系,即数据的逻辑结构;(2)在对数据进行处理时,各数据元素在计算机中的存储关系,即数据的存储结构;(3)对各种数据结构进行的运算。
数据结构是指相互有关联的数据元素的集合。
数据的逻辑结构包含:(1)表示数据元素的信息;(2)表示各数据元素之间的前后件关系。
数据的存储结构有顺序、链接、索引等。
线性结构条件:(1)有且只有一个根结点;(2)每一个结点最多有一个前件,也最多有一个后件。
非线性结构:不满足线性结构条件的数据结构。
3 线性表及其顺序存储结构线性表由一组数据元素构成,数据元素的位置只取决于自己的序号,元素之间的相对位置是线性的。
在复杂线性表中,由若干项数据元素组成的数据元素称为记录,而由多个记录构成的线性表又称为文件。
数据结构与算法分析java课后答案

数据结构与算法分析java课后答案【篇一:java程序设计各章习题及其答案】>1、 java程序是由什么组成的?一个程序中必须有public类吗?java源文件的命名规则是怎样的?答:一个java源程序是由若干个类组成。
一个java程序不一定需要有public类:如果源文件中有多个类时,则只能有一个类是public类;如果源文件中只有一个类,则不将该类写成public也将默认它为主类。
源文件命名时要求源文件主名应与主类(即用public修饰的类)的类名相同,扩展名为.java。
如果没有定义public类,则可以任何一个类名为主文件名,当然这是不主张的,因为它将无法进行被继承使用。
另外,对applet小应用程序来说,其主类必须为public,否则虽然在一些编译编译平台下可以通过(在bluej下无法通过)但运行时无法显示结果。
2、怎样区分应用程序和小应用程序?应用程序的主类和小应用程序的主类必须用public修饰吗?答:java application是完整的程序,需要独立的解释器来解释运行;而java applet则是嵌在html编写的web页面中的非独立运行程序,由web浏览器内部包含的java解释器来解释运行。
在源程序代码中两者的主要区别是:任何一个java application应用程序必须有且只有一个main方法,它是整个程序的入口方法;任何一个applet小应用程序要求程序中有且必须有一个类是系统类applet的子类,即该类头部分以extends applet结尾。
应用程序的主类当源文件中只有一个类时不必用public修饰,但当有多于一个类时则主类必须用public修饰。
小应用程序的主类在任何时候都需要用public来修饰。
3、开发与运行java程序需要经过哪些主要步骤和过程?答:主要有三个步骤(1)、用文字编辑器notepad(或在jcreator,gel, bulej,eclipse, jbuilder等)编写源文件;(2)、使用java编译器(如javac.exe)将.java源文件编译成字节码文件.class;(3)、运行java程序:对应用程序应通过java解释器(如java.exe)来运行,而对小应用程序应通过支持java标准的浏览器(如microsoft explorer)来解释运行。
Java数据结构与算法

Java数据结构与算法一、引言Java 是一种强大、高效的编程语言,在现代软件开发领域中使用广泛。
作为一名 Java 开发人员,了解数据结构与算法的重要性不言而喻,因为数据结构和算法是计算机科学的核心。
本文将重点讨论 Java 数据结构与算法,它们的实现方式及其应用。
二、数据结构数据结构是一种在计算机中组织和存储数据的方式。
在软件开发过程中,开发人员需要选择合适的数据结构来存储和处理数据,以实现最好的性能和效率。
Java 提供了很多内置的数据结构,例如数组、链表、队列和栈等。
1. 数组数组是 Java 中最基本和最常用的数据结构之一。
它是一个固定大小的数据序列,其中的元素都具有相同的数据类型。
数组可以使用索引来访问和修改元素。
在 Java 中,可以使用内置的数组类型 int[]、double[]、char[]等,也可以使用泛型数组类型 ArrayList。
可以通过如下方式创建一个 Java 数组:int[] arr = new int[10];这会创建一个长度为 10 的 int 类型数组,其中的元素默认值为 0。
2. 链表链表是一个由节点组成的数据结构,其中每个节点都包含一个数据元素和一个指向下一个节点的指针。
链表的优点在于可以很容易地添加或删除元素,但是访问元素时需要遍历整个链表。
Java 中提供了多种链表类型,包括单向链表、双向链表和循环链表。
可以通过如下方式创建一个单向链表:public class Node {int val;Node next;Node(int x) { val = x; }}Node head = new Node(1);head.next = new Node(2);这会创建一个包含两个元素的单向链表,其值分别为 1 和 2。
3. 队列队列是一种先进先出(FIFO)的数据结构,在 Java 中可以使用内置的Queue 接口实现。
Queue 接口定义了许多方法,例如 add()、remove()、peek() 等,可以用于向队列中添加元素、删除元素和获取队列顶端的元素。
《数据结构与算法》知识点整理

《数据结构与算法》知识点整理《数据结构与算法》知识点整理1:数据结构概述1.1 什么是数据结构1.2 数据结构的作用1.3 数据结构的分类1.4 数据结构的存储方式2:线性表2.1 顺序表2.1.1 顺序表的定义2.1.2 顺序表的基本操作2.2 链表2.2.1 链表的定义2.2.2 链表的基本操作2.3 栈2.3.1 栈的定义2.3.2 栈的基本操作2.4 队列2.4.1 队列的定义2.4.2 队列的基本操作3:树3.1 树的基本概念3.1.1 结点3.1.2 父节点、子节点、兄弟节点 3.2 二叉树3.2.1 二叉树的定义3.2.2 二叉树的遍历方式3.3 平衡二叉树3.3.1 平衡二叉树的定义3.3.2 平衡二叉树的实现4:图4.1 图的基本概念4.1.1 顶点4.1.2 边4.1.3 权重4.2 图的表示方式4.2.1 邻接矩阵4.2.2 邻接表4.3 图的搜索算法4.3.1 深度优先搜索 4.3.2 广度优先搜索5:排序算法5.1 冒泡排序5.2 插入排序5.3 选择排序5.4 快速排序5.5 归并排序6:查找算法6.1 顺序查找6.2 二分查找6.3 哈希查找7:字符串匹配算法7.1 暴力匹配算法7.2 KMP算法7.3 Boyer-Moore算法8:动态规划算法8.1 动态规划的基本概念8.2 0-1背包问题8.3 最长公共子序列问题9:附件9.1 Examples:docx - 包含各章节示例代码的附件文件10:法律名词及注释10:1 数据结构 - 在计算机科学中,数据结构是计算机中存储、组织数据的方式。
10:2 线性表 - 线性表是数据元素的有限序列,元素之间具有线性关系。
10:3 顺序表 - 顺序表是用一组地址连续的存储单元依次存储线性表的元素。
10:4 链表 - 链表是一种数据元素按照顺序存放,元素之间通过指针进行关联的数据结构。
10:5 栈 - 栈是一种特殊的线性表,只能在一端进行插入和删除操作。
数据结构与算法的哪些知识点最容易考察

数据结构与算法的哪些知识点最容易考察在计算机科学领域,数据结构与算法是至关重要的基础知识。
无论是在学术研究还是实际的软件开发中,对于数据结构和算法的理解与掌握程度都有着很高的要求。
当我们面临各种考试或者技术面试时,了解哪些知识点最容易被考察,能够帮助我们更有针对性地进行学习和准备。
首先,链表(Linked List)是经常被考察的一个重要知识点。
链表是一种常见的数据结构,它由一系列节点组成,每个节点包含数据和指向下一个节点的指针。
对于链表的操作,如链表的创建、遍历、插入、删除节点等,都是常见的考察点。
特别是在处理链表的循环、链表的反转等问题时,需要我们对指针的操作有清晰的理解和熟练的运用能力。
栈(Stack)和队列(Queue)也是容易考察的内容。
栈遵循后进先出(Last In First Out,LIFO)的原则,而队列遵循先进先出(First In First Out,FIFO)的原则。
理解这两种数据结构的特点以及它们的基本操作,如入栈、出栈、入队、出队等,是很关键的。
此外,利用栈来解决表达式求值、括号匹配等问题,以及使用队列来实现广度优先搜索(BreadthFirst Search,BFS)等算法,也是常见的考察形式。
树(Tree)结构在数据结构与算法中占据着重要地位。
二叉树(Binary Tree)是其中的基础,包括二叉树的遍历(前序、中序、后序遍历)、二叉搜索树(Binary Search Tree)的特性和操作,以及平衡二叉树(如 AVL 树、红黑树)的概念和调整算法等,都是容易被考察的知识点。
此外,树的层次遍历、构建二叉树等问题也经常出现在考题中。
图(Graph)的相关知识也是考察的重点之一。
图的表示方法(邻接矩阵、邻接表)、图的遍历算法(深度优先搜索(DepthFirst Search,DFS)和广度优先搜索(BreadthFirst Search,BFS))、最短路径算法(如迪杰斯特拉算法(Dijkstra's Algorithm)和弗洛伊德算法(FloydWarshall Algorithm))以及最小生成树算法(如普里姆算法(Prim's Algorithm)和克鲁斯卡尔算法(Kruskal's Algorithm))等,都是需要我们熟练掌握的内容。
数据结构知识点笔记

数据结构知识点笔记一、数据结构的概念数据结构是计算机科学中一门重要的学科,它研究如何组织和存储数据,以便高效地访问和操作。
数据结构可以分为物理结构和逻辑结构两个层次。
物理结构指数据在计算机内存中的存储方式,而逻辑结构则指数据之间的逻辑关系。
二、常用的数据结构1. 数组(Array)数组是最基本的数据结构之一,它以连续的存储空间来保存相同类型的数据。
数组的特点是可以通过下标快速访问元素,但插入和删除操作较慢。
2. 链表(Linked List)链表是一种动态数据结构,它通过指针将一组节点串联起来。
链表的特点是插入和删除操作效率高,但访问元素需要遍历整个链表。
3. 栈(Stack)栈是一种后进先出(LIFO)的数据结构,只能在栈顶进行插入和删除操作。
栈主要用于函数调用和表达式求值等场景。
4. 队列(Queue)队列是一种先进先出(FIFO)的数据结构,只能在队列的一端进行插入操作,在另一端进行删除操作。
队列主要用于任务调度和缓冲区管理等场景。
5. 树(Tree)树是一种非线性的数据结构,由父节点和子节点组成。
树常用于组织和管理具有层级关系的数据,如文件系统和数据库索引等。
6. 图(Graph)图是一种由节点和边组成的数据结构,节点表示数据,边表示节点之间的关系。
图广泛应用于网络分析和路径搜索等领域。
三、常见的数据结构操作1. 插入(Insert)插入操作将新的数据元素加入到数据结构中的特定位置。
不同的数据结构插入操作的复杂度各不相同,需要根据具体情况选择合适的数据结构。
2. 删除(Delete)删除操作将指定的数据元素从数据结构中移除。
和插入操作一样,删除操作的复杂度也依赖于具体的数据结构。
3. 查找(Search)查找操作用于在数据结构中寻找指定值的元素。
不同的数据结构采用不同的查找算法,如线性查找、二分查找和哈希查找等。
4. 排序(Sort)排序操作将数据结构中的元素按特定规则重新排列。
排序算法可以分为比较排序和非比较排序两种类型,如冒泡排序、快速排序和归并排序等。
数据结构备考笔记

数据结构备考笔记
1、基本概念和术语
数据:是对客观事物的符号表示,在计算机科学中是指所有能输入到计算机中并被计算机程序处理的符号的总称。
数据元素:是数据的基本单位,在计算机程序中通常作为一个整体运行考虑和处理。
数据项:是数据的不可分割的最小单位。
数据对象:是性质相同的数据元素的集合,是数据的一个子集。
数据结构:是相互之间存在一种或多种特定数据元素的结合。
结构:数据元素相互之间的关系。
四中基本结构:
✧集合
✧线性结构数据元素之间存在一对一的关系
✧树形结构数据元素之间存在一对多的关系
✧图状结构或网状结构数据元素之间存在多对多的关系
抽象数据类型可用以下三元组表示:
ADT=(D,S,P)
其中,D是数据对象,S是D上的关系集,P是对D的基本操作集。
算法:算法是对特定问题求解步骤的一种描述,他是指令的有限序列,其中每一条指令表示一个或多个操作。
算法的五个重要特性:
有穷性
确定性
可行性
输入
输出
算法的设计要求:
正确性
可读性
健壮性
效率与低存储量需求
渐进时间复杂度,简称时间复杂度
频度:指语句重复执行的次数。
数据结构整理笔记

数据结构整理笔记数据结构与算法数据结构:数据的组成形式(数据是以什么样的形式组织起来的,数组、链表、队列、树、图等)算法(注:强调的是数据结构与算法中的算法,狭义算法):对所存储数据的操作(操作指的是对于所存数据有关问题,求解最终答案的过程)的⽅法,例:[1、2、3、4、5]中的最⼤值,求得最⼤值的⽅法(⼀系列操作)就是算法书籍推荐数据结构概述(教材选⽤严蔚敏、吴伟民,该书程序是伪算法具体的程序是⾼⼀凡,西电的,⼤⽜,只有程序。
还有⼀本书,台湾的黄国瑜⾃⼰写的只有思路,程序是另外⼀个合作的清华的写的,可惜很多错的。
)学完数据结构之后会对⾯向过程的函数有⼀个更深的了解,有本通俗易懂的数据结构的书《⼤话数据结构》⽤来⼊门很不错。
数据结构的概述定义我们如何把现实中⼤量⽽反复的问题以特定的数据类型(个体的数据类型)和特定的存储结构(个体间的相互关系)保存到主存储器(内存)中,以及在此基础上为实现某个功能(⽐如查找某个元素,删除某个元素,对所有元素进⾏排序)⽽执⾏的相应的操作,这个相应的操作也叫做算法。
数据结构=个体+个体的关系算法=对存储数据的操作狭义:数据结构是专门研究数据存储的问题数据的存储包含两⽅⾯:个体的存储 + 个体关系的存储⼴义:数据结构既包含数据的存储也包含数据的操作对存储数据的操作就是算法算法狭义:算法是和数据的存储⽅式密切相关⼴义:算法和数据的存储⽅式⽆关,这就是泛型思想算法的真正学法:很多算法你根本解决不了因为很多都属于数学上的东西,所以我们把答案找出来,如果能看懂就⾏,但是⼤部分⼈⼜看不懂,分三步,按照流程,语句,试数。
这个过程肯定会不断地出错,所以不断出错,不断改错,这样反复敲很多次,才能有个提⾼。
实在看不懂就先背会。
衡量算法的标准:(1) 时间复杂度⼤概程序要执⾏的次数,⽽并⾮是执⾏的时间(因为同⼀程序在不同机器上执⾏的时间是不⼀样的,有差异)(2) 空间复杂度算法执⾏过程中⼤概所占⽤的最⼤内存(3) 难易程度(主要是应⽤⽅⾯看重)(4) 健壮性(不能别⼈给⼀个⾮法的输⼊就挂掉)数据结构的地位:数据结构是软件中最核⼼的课程程序 = 数据的存储 + 数据的操作 + 可以被计算机执⾏的语⾔泛型对于同⼀种逻辑结构,⽆论该逻辑结构的物理存储是什么样⼦的,我们可以对它执⾏相同的操作。
【数据结构与算法笔记03】详解平衡二叉树的失衡类型划分及调整策略设计

【数据结构与算法笔记03】详解平衡⼆叉树的失衡类型划分及调整策略设计1. 平衡⼆叉树平衡⼆叉树对于树中的每个节点要求:左⼦树和右⼦树的深度差不超过1左右⼦树都是平衡⼆叉树平衡因⼦ = 左⼦树深度 - 右⼦树深度==> 在⼀棵平衡⼆叉树中,所有节点的平衡因⼦只可能有三种取值:-1, 0, 12. 失衡原因分析及失衡情况分类平衡⼆叉树是⼀种特殊的⼆叉排序树,插⼊新节点的⽅法与在⼆叉排序树中插⼊节点相同:先查找,然后在查找失败的位置插⼊新节点。
但是在⼀棵平衡⼆叉树中新插⼊⼀个节点可能会导致树的失衡,因此每次插⼊新节点之后要对树进⾏调整。
书上和⽹上的资料很多,但⼤部分都只给出了最终的结论,没有给出为什么要这样做的原因,现在我试图⽤⾃⼰的⽅式来理解AVL树的调整⽅法:1. 在平衡⼆叉树中新插⼊节点会造成树中某些节点平衡因⼦的改变,从⽽有失衡的风险。
==> 只有插⼊路径上的节点的平衡因⼦可能会改变。
==> 在插⼊路径上的节点中,只有那些原本的平衡因⼦为1, -1的节点可能会失衡(平衡因⼦变为2)。
==> 原本平衡因⼦为1的节点失衡后平衡因⼦会变为2;原本平衡因⼦为-1的节点失衡后平衡因⼦会变为-2。
并且这两种情况是对称的。
2. 在插⼊路径上可能会有多个节点失衡,但是⾼层节点的失衡是由低层节点的失衡造成的,因此存在⼀个最低失衡节点,只要将这个最低失衡节点调整平衡,并且保证以该节点为根的⼦树的⾼度和原来⼀样,那么⾼层节点的失衡就会⾃动恢复。
3. 所谓对失衡节点的调整,其实就是在已知⼀些⼦树和节点相互之间的⼤⼩关系以及他们的⾼度等信息时⽤这些⼦树和节点重新组装成⼀棵满⾜平衡⼆叉树要求的树。
下⾯仅考虑最低失衡节点原本的平衡因⼦为1的情况:==> 该节点失衡后平衡因⼦变为2,说明新节点的插⼊导致该节点的左⼦树的⾼度增加了1,这也间接说明了新节点插在了该节点的左⼦树上。
==> 插在该节点的左⼦树上有两种可能的情况:①该节点原本就没有左孩⼦,②该节点原本是有左孩⼦的。
程序员k哥笔记

程序员k哥笔记标题:程序员K哥笔记引言概述:程序员K哥是一位经验丰富的开发者,他的笔记是他多年来积累的宝贵经验和知识总结。
本文将从五个大点出发,详细阐述K哥笔记中的内容,帮助读者更好地理解和应用这些知识。
正文内容:1. 编码技巧1.1 代码可读性- 命名规范:变量、函数、类等的命名要有意义且易于理解。
- 注释:对于复杂的逻辑或者关键代码,添加注释以便于他人理解。
- 缩进和空格:保持一致的缩进和适当的空格,使代码更易读。
1.2 错误处理- 异常处理:合理使用try-catch语句,捕获并处理异常,避免程序崩溃。
- 日志记录:添加日志记录,便于追踪错误和调试。
1.3 代码复用- 函数和类的设计:合理划分函数和类的职责,提高代码的可复用性。
- 模块化开发:将代码划分为独立的模块,方便重用和维护。
2. 数据结构与算法2.1 常用数据结构- 数组:适用于存储有序数据,支持快速随机访问。
- 链表:适用于频繁的插入和删除操作,但访问速度较慢。
- 栈和队列:用于实现特定的数据结构和算法,如深度优先搜索和广度优先搜索。
2.2 常见算法- 排序算法:如冒泡排序、插入排序、快速排序等。
- 查找算法:如二分查找、哈希查找等。
- 图算法:如最短路径算法、最小生成树算法等。
2.3 算法优化技巧- 时间复杂度和空间复杂度:分析算法的效率,选择合适的算法。
- 缓存优化:利用缓存机制减少重复计算,提高程序性能。
3. 数据库设计与优化3.1 数据库范式- 第一范式:确保每列的原子性,避免数据冗余。
- 第二范式:确保每个非主键列完全依赖于主键,消除部分依赖。
- 第三范式:确保每列只依赖于主键,消除传递依赖。
3.2 索引优化- 选择合适的索引类型:如B树索引、哈希索引等。
- 避免过多的索引:过多的索引会增加写入和更新的开销。
3.3 查询优化- 使用合适的查询语句:如JOIN操作、子查询等。
- 避免全表扫描:利用索引和合适的查询条件提高查询效率。
java各详细总结知识点

java各详细总结知识点一、Java语法1. 数据类型Java中的数据类型分为基本数据类型和引用数据类型。
基本数据类型包括整型,浮点型,字符型和布尔型。
引用数据类型包括类、接口、数组等。
2. 变量在Java中,变量是用来存储数据的容器。
它们可以存储不同类型的数据,例如整数、浮点数、字符等。
变量分为局部变量和成员变量。
3. 运算符Java中的运算符包括算术运算符、关系运算符、逻辑运算符、位运算符、赋值运算符等。
这些运算符可以实现数据的计算和比较。
4. 控制流Java中的控制流包括顺序结构、选择结构和循环结构。
通过控制流语句,程序可以根据条件执行不同的代码块,实现不同的功能。
5. 方法方法是Java中用来组织和重用代码的一种机制。
它可以细化程序的逻辑结构,并提高代码的可读性和可维护性。
6. 数组数组是一种用来存储多个相同类型数据的容器。
在Java中,数组可以是一维的、二维的甚至多维的。
使用数组可以方便地管理大量数据。
7. 字符串在Java中,字符串是一种特殊的对象类型。
Java提供了丰富的字符串处理方法,例如字符串连接、子字符串提取、字符串比较等。
8. 输入输出在Java中,通过输入输出流可以实现与外部设备的交互。
Java提供了丰富的输入输出类和方法,可以实现文件的读写、网络通信等功能。
二、面向对象编程1. 类和对象在Java中,所有的代码逻辑都是围绕类和对象展开的。
类是一种模板,描述了对象的属性和行为。
对象是类的实例,可以根据类创建多个对象。
2. 封装封装是面向对象编程的核心思想之一。
通过封装,可以将数据和行为封装在一个对象中,避免外部直接访问对象的数据。
3. 继承继承是一种代码复用的机制,可以让子类继承父类的属性和方法。
通过继承,可以实现类与类之间的层次关系,提高代码的重用性和扩展性。
4. 多态多态是面向对象编程的另一个核心概念。
通过多态,可以使不同类的对象对同一消息作出不同的响应。
多态性可以提高代码的灵活性和可扩展性。
数据结构笔记

数据结构笔记基础:数据结构与算法(一)数据结构基本概念数据(data):是对客观事物的符号表示,在计算机科学中是指所有能输入到计算机中并被计算机程序处理的符号总称数据元素(data element):是数据的基本单位,在计算机中通常被当做一个整体进行考虑和处理数据对象(data object):性质相同的数据元素的集合,是数据的一个子集数据结构(data structure):相互之间存在一种或多种特定关系的数据元素的集合4类基本结构:集合、线性结构、树形结构、图形(网状)结构数据结构的形式定义为数据结构是一个二元组Data Structure = (D,S),其中D是数据元素的有限集,S是D上关系的有限集数据结构定义中的“关系”描述的是数据元素之间的逻辑关系,因此又称为数据的逻辑结构数据结构在计算机中的表示(映像)称为物理结构(存储结构)计算机中表示信息的最小单位是二进制中的一位,叫做位(bit),一到若干位组成一个位串表示一个数据元素,这个位串称为元素或结点数据结构之间关系在计算机中的表示有两种:顺序映像、非顺序映像,并由此得到两种存储结构:顺序存储、链式存储,前者运用相对位置表示数据元素间的逻辑结构,后者借助指针任何一个算法的设计取决于数据(逻辑)结构,而实现依赖于存储结构数据类型是一个值的集合和定义在这个值集上的一组操作的总称数据类型分两种:原子类型、结构类型,前者不可分解(例如int、char、float、void ),后者结构类型由若干成分按某种结构组成,可分解,成分既可以是非结构的也可以是结构的(例:数组)抽象数据类型(Abstract Data Type ):是指一个数学模型及定义在该模型上的一组操作(P8)抽象数据类型格式如下:ADT抽象数据类型名{数据对象:<数据对象的定义>数据关系:<数据关系的定义>数据操作:<数据操作的定义>}ADT抽象数据类型名基本操作格式如下:基本操作名(参数表)初始条件:<初始条件描述>操作结果:<操作结果描述>多形数据类型(polymorphic data type):是指其值得成分不确定的数据类型(P9)抽象数据类型可由固有数据类型来表示和实现(二)算法(概念)和算法分析(时、空性能)算法(algorithm):对特定问题求解步骤的一种描述算法5特性:有穷、确定、可行、输入、输出1、有穷性:算法必须在可接受的时间内执行有穷步后结束2、确定性:每条指令必须要有确切含义,无二义性,并且只有唯一执行路径,即对相同的输入只能得相同输出3、可行性:算法中的操作都可通过已实现的基本运算执行有限次来完成4、输入:一个算法有一到多个输入,并取自某个特定对象合集5、输出:一个算法有一到多个输出,这些输出与输入有着某些特定关系的量算法设计要求(好算法):正确性、可读性、健壮性、效率与低存储需求健壮性是指对于规范要求以外的输入能够判断出这个输入不符合规范要求,并能有合理的处理方式。
数据结构与算法读书笔记

数据结构与算法读书笔记数据结构和算法是计算机科学中非常重要的领域,它们对于解决问题和优化代码性能至关重要。
以下是一些关于数据结构和算法的读书笔记:1.掌握基本数据结构:了解常见的数据结构,如数组、链表、栈、队列、散列表、树和图等。
理解它们的特点、操作和适用场景。
2.理解时间复杂度和空间复杂度:学习如何分析算法的时间和空间复杂度。
了解最坏情况、平均情况和最好情况下的复杂度分析方法。
3.掌握常见算法:学习基本的排序算法(如冒泡排序、插入排序、选择排序、快速排序、归并排序),搜索算法(如线性搜索、二分搜索),以及常见的图算法(如深度优先搜索、广度优先搜索)等。
4.解决实际问题:将学到的数据结构和算法应用到解决实际问题中。
通过练习编写代码来加深对数据结构和算法的理解和应用能力。
5.阅读经典教材:阅读经典的数据结构和算法教材,如《算法导论》(Introduction to Algorithms)、《数据结构与算法分析》(Data Structures and Algorithm Analysis in C++)等。
这些教材系统地介绍了各种数据结构和算法的原理和实现。
6.刷题实践:参加在线编程竞赛,刷LeetCode、HackerRank等网站上的算法题目。
这样可以锻炼自己的解题思路和编码能力,同时熟悉常见算法的应用场景。
7.学习高级数据结构和算法:在掌握基本的数据结构和算法后,可以进一步学习高级的数据结构和算法,如红黑树、A VL树、动态规划、贪心算法等。
8.追踪最新发展:关注数据结构和算法领域的最新研究和发展,了解新的数据结构和算法模型,如布隆过滤器、哈希图等。
以上是一些关于数据结构和算法的读书笔记。
通过系统学习和实践,不断提升自己的数据结构和算法能力,可以在编程领域中取得更好的成果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Java数据结构和算法第0讲综述参考教材:Java数据结构和算法(第二版),[美] Robert lafore1. 数据结构的特性数据结构优点缺点数组插入快;如果知道下标,可以非常快地存取查找慢,删除慢,大小固定有序数组比无序的数组查找快删除和插入慢,大小固定栈提供后进先出方式的存取存取其他项很慢队列提供先进先出方式的存取存取其他项很慢链表插入快,删除快查找慢二叉树查找、插入、删除都快(如果树保持平衡)删除算法复杂红-黑树查找、插入、删除都快;树总是平衡的算法复杂算法复杂2-3-4树查找、插入、删除都快;树总是平衡的;类似的树对磁盘存储有用哈希表如果关键字已知,则存储极快;插入快删除慢,如果不知道关键字则存储很慢,对存储空间使用不充分堆插入、删除快;对大数据项的存取很快对其他数据项存取慢图对现实世界建模有些算法慢且复杂2. 经典算法总结查找算法:线性查找和二分查找排序算法:用表展示第一讲数组1.Java中数组的基础知识1)创建数组在Java中把数组当作对象来对待,因此在创建数组时必须使用new操作符:一旦创建数组,数组大小便不可改变。
2)访问数组数据项数组数据项通过方括号中的下标来访问,其中第一个数据项的下标是0:3)数组的初始化当创建数组之后,除非将特定的值赋给数组的数据项,否则它们一直是特殊的null对2.面向对象编程方式1)使用自定义的类封装数组2)添加类方法实现数据操作3.有序数组1)有序数组简介以及其优点有序数组是一种数组元素按一定的顺序排列的数组,从而方便使用二分查找来查找数组中特定的元素。
有序数组提高了查询的效率,但并没有提高删除和插入元素的效率。
2)构建有序数组得到有序数组的类封装MyOrderedArray类,测试该类中的insert方法:4.查找算法1)线性查找在查找过程中,将要查找的数一个一个地与数组中的数据项比较,直到找到要找的数。
在2.1中自定义的类封装数组MyArray的queryByValue方法,使用的就是线性查找。
2)二分查找二分查找(又称折半查找),即不断将有序数组进行对半分割,每次拿中间位置的数和要查找的数进行比较:如果要查找的数<中间数,则表明要查的数在数组的前半段;如果要查的数>中间数,则表明该数在数组的后半段;如果要查的数=中间数,则返回中间数。
在有序数组的类封装类MyOrderedArray中添加binarySearch方法测试该二分查找方法:第二讲简单排序本讲提到的排序算法都假定了数组作为数据存储结构,本讲所有算法的时间复杂度都是。
在大多数情况下,假设当数据量比较小或基本上有序时,插入排序算法是三种简单排序算法中最好的选择,是应用最多的。
对于更大数据量的排序来说,后面讲到的快速排序通常是最快的方法。
1.冒泡排序1)基本思想在要排序的一组数中,对当前还未排好序的范围内的全部数,自下而上对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。
即:每当两相邻的数比较后发现它们的排序与排序要求相反时,就将它们互换。
2)算法实现2.选择排序1)基本思想在要排序的一组数中,选出最小的一个数与第一个位置的数交换;然后在剩下的数当中再找最小的与第二个位置的数交换,如此循环到倒数第二个数和最后一个数比较为止。
与冒泡排序相比,选择排序将必要的交换次数从O(N*N)减少到O(N),但比较次数仍然保持为O(N*N)。
2)算法实现3.插入排序1)基本思想在要排序的一组数中,假设前面(n-1)[n>=2]个数已经是排好顺序的(局部有序),现在要把第n个数插到前面的有序数中,使得这n个数也是排好顺序的。
如此反复循环,直到全部排好顺序。
在插入排序中,一组数据仅仅是局部有序的;而冒泡排序和选择排序,一组数据项在某个时刻是完全有序的。
2)算法实现插入排序的Java代码:第三讲栈和队列栈和队列都是抽象数据类型(abstract data type,ADT),它们既可以用数组实现,又可以用链表实现。
1.栈1)栈模型栈(Stack,又LIFO:后进先出)是一种只能在固定的一端进行插入和删除的数据结构。
栈只允许访问一个数据项:即最后插入的数据项,移除这个数据项后才能访问倒数第二个插入的数据项,以此类推。
栈可以用数组来实现,也可以用链表来实现。
2)栈的数组实现public class MyStack {private long[] arr; //底层使用数组实现private int top;public MyStack() {arr = new long[10];top = -1;}public MyStack(int maxSize) {arr = new long[maxSize];top = -1;}// put item on top of stackpublic void push(long value) {arr[++top] = value;}// take item from top of stackpublic long pop() {return arr[top--];}// peek at top of stackpublic long peek() {return arr[top];}// ture if stack is emptypublic boolean isEmpty() {return (top == -1);}// ture if stack is fullpublic boolean isFull() {return (top == arr.length-1);}}public void testMyStack() throws Exception {MyStack myStack = new MyStack(4);myStack.push(12);myStack.push(34);myStack.push(56);myStack.push(78);System.out.println(myStack.isFull()); // truewhile(!myStack.isEmpty()) {System.out.print(myStack.pop()); //78, 56, 34, 12if(!myStack.isEmpty()) {System.out.print(", ");}}System.out.println();System.out.println(myStack.isFull()); // false}2.队列1)队列模型队列(Queue,又FIFO:先进先出)是一种插入时在一端进行而删除时在另一端进行的数据结构。
为解决顺序队列假溢出问题,而采用循环队列:即让队头、队尾指针在达到尾端时,又绕回到开头。
2)队列的数组实现队列的Java代码:测试队列的特性:第四讲链表1.链结点一个链结点(Link,或称结点)是某个类的对象,该对象中包含对下一个链结点引用的字段(通常叫next)。
而链表本身的对象中有一个字段指向对第一个链结点的引用。
public class Link {public long data; // data itempublic Link next; // next link in listpublic Link(long data) {this.data = data;}public void displayLink() { // display ourselfSystem.out.print(data + "--> ");}}2.单链表(LinkList)LinkList类显示了一个单链表,该链表可以进行的操作有:●在链表头插入一个数据(insertFirst):设置新添加的结点的next设为原来的头结点,再将新添加的结点设为头结点。
●在链表头删除一个数据(deleteFirst):将第二个结点设为头结点。
●遍历链表显示所有数据(displayList):使用临时指针current,从头结点开始,沿着链表先前移动,依次遍历每个节点。
LinkList类:public class LinkList {private Link first; // reference to first link on listpublic LinkList() {this.first = null;}// insert at start of listpublic void insertFirst(long value) {Link newLink = new Link(value);newLink.next = first; // newLink --> old firstfirst = newLink; // first --> newLink}// delete first itempublic Link deleteFirst() {3.查找和删除指定链结点此外,还能对指定的结点值进行查找和删除:●查找指定结点(find):类似于之前的displayList方法。
●删除指定结点(delete):在删除指定结点时,必须把前一个结点和后一个结点连接在一起,所以需要一个临时指针(previous)来保存对前一个结点的引用。
向LinkList类中添加查找(find)和删除(delete)方法:测试添加的find和delete方法:第五讲双端链表和双向链表1.双端链表链表中保存着对最后一个链结点的引用●从头部进行插入(insertFirst):要对链表进行判断,如果链表为空,则设置尾结点为新添加的结点。
●从尾部进行插入(insertLast):如果链表为空,则直接设置头结点为新添加的结点,否则设置尾结点的后一个节点为新添加的结点。
●从头部进行删除(deleteFirst):判断头结点是否有下一个结点,如果没有则设置尾结点为null。
2.双向链表双向链表既允许向后遍历,也允许向前遍历整个链表。
即每个节点除了保存了对下一个节点的引用,同时后保存了对前一个节点的引用。
从头部进行插入(insertFirst):要对链表进行判断,如果为空,则设置尾结点为新添加的结点;如果不为空,还需要设置头结点的前一个结点为新添加的结点。
●从尾部进行插入(insertLast):如果链表为空,则直接设置头结点为新添加的结点,否则设置尾节点的后一个结点为新添加的结点。
同时设置新添加的结点的前一个结点为尾结点。
●从头部进行删除(deleteFirst):判断头结点是否有下一个结点,如果没有则设置尾结点为null;否则设置头结点的下一个结点的previous为null。
