双曲线讲义
双曲线讲义(学生版)

双曲线专题讲义1.2.等轴双曲线及性质(1)等轴双曲线:实轴长和虚轴长相等的双曲线叫作等轴双曲线,标准方程可写作:x 2-y 2=λ(λ≠0). (2)等轴双曲线⇔离心率e =2⇔两条渐近线y =±x 相互垂直. 3.点P (x 0,y 0)和双曲线x 2a 2-y 2b2=1(a >0,b >0)的关系(1)双曲线内(含焦点部分)⇔x 20a 2-y 20b 2>1;(2)双曲线上⇔x 20a 2-y 20b 2=1;(3)双曲线外(不含焦点部分)⇔x 20a 2-y 20b 2<1.求双曲线离心率、渐近线问题的一般方法(1)求双曲线的离心率时,将提供的双曲线的几何关系转化为关于双曲线基本量a ,b ,c 的方程或不等式,利用b 2=c 2-a 2和e =ca 转化为关于e 的方程或不等式,通过解方程或不等式求得离心率的值或取值范围.(2)求渐近线时,利用c 2=a 2+b 2转化为关于a ,b 的方程或不等式.双曲线渐近线的斜率与离心率的关系k =±ba =±c 2-a 2a =±c 2a2-1=±e 2-1. 双曲线定义1. 已知P 是双曲线1366422=-y x 上一点,F 1,F 2是双曲线的两个焦点,若|PF 1|=17,则|PF 2|的值为________.2. 已知点F 1(0,-13)、F 2(0,13),动点P 到F 1与F 2的距离之差的绝对值为26,则动点P 的轨迹方程为( ) A .y =0 B .y =0(x ≤-13或x ≥13) C .x =0(|y |≥13) D .以上都不对3. 若双曲线x 2-4y 2=4的左、右焦点分别是F 1、F 2,过F 2的直线交右支于A 、B 两点,若|AB |=5,则△AF 1B 的周长为________. 参考答案:1. 33 2. C 3. 18 双曲线方程的认识1. (2013·福建)双曲线8kx 2-ky 2=8的一个焦点坐标为(0,3),则k 的值是 ( )A .1B .-1C .653D .-653 2. 若方程15222=---ky k x 表示双曲线,则实数k 的取值范围是( )A .52<<kB .5>kC .2<k 或5>kD .以上答案均不对3. 方程x 2k -1+y 2k -3=1表示焦点在x 轴上的双曲线,则k 的取值范围为________.4. 已知方程:22(1)(3)(1)(3)m x m y m m -+-=--表示焦距为8的双曲线,则m 的值等于( ) A .-30 B .10 C .-6或10 D .-30或3A .2322-=-y xB .()12322±¹-=-x y xC . 2322=-y x面积是9,则a +b 的值等于( )A .4B .5C .6D .73. 已知双曲线x 2-y 2=1,点F 1,F 2为其两个焦点,点P 为双曲线上一点.若PF 1⊥PF 2,则|PF 1|+|PF 2|的值为__________.参考答案:1.A 2.B 3. 2 3 双曲线性质离心率1. 设21,F F 分别为双曲线)0,0(12222>>=-b a by a x 的左、右焦点.若在双曲线上存在点P .使21PF PF ^,且°=Ð3021F PF ,则双曲线的离心率为___________.2. 双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别是F 1、F 2,过F 1作倾斜角为30°的直线,交双曲线右支于M 点,若MF 2垂直于x 轴,则双曲线的离心率为 ( )A . 6B . 3C .2D .333. 设12,F F 是双曲线2222:1(0,0)x y C a b a b -=>>的两个焦点,P 是C 上一点,若a PF PF 6||||21=+,且12PF F D 的最小内角为30°,则C 的离心率为( )A .2B .26C .23D .34. 如图,1F 、2F 是双曲线)0,0(12222>>=-b a by a x 的左、右焦点,过1F 的直线l 与双曲线的左右两支分别交于点A 、B .若2ABF D 为等边三角形,则双曲线的离心率为( )A .4B .7C .332 D .3 5. 过双曲线22221(0,0)x y a b a b-=>>的右顶点A 作斜率为1-的直线,该直线与双曲线的两条渐近线的交点分别为,B C .若12AB BC =uuu r uuu r,则双曲线的离心率是 ( )A B C D 6. 双曲线2214x y k+=的离心率(1,2)e Î,则k 的取值范围是( )A . (10,0)-B . (12,0)-C . (3,0)-.D . (60,12)-- 参考答案:1. 13+ 2-6 BDBCB渐近线1. 双曲线22149x y -=的渐近线方程是A .32y x =±B .23y x =±C .94y x =±D .49y x =±2. 已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为52,则C 的渐近线方程为( )A .y =±14xB .y =±13xC .y =±12xD .y =±x3. 已知0a b >>,椭圆1C 的方程为2222=1x y a b +,双曲线2C 的方程为22221y x a b -=,1C 与2C 的离心率之积为2,则2C 的渐近线方程为( ). 0A x ±= .0B y ±= .20C x y ±= .20D x y ±=4. 设21,F F 分别为双曲线)0,0(12222>>=-b a b y a x 的左、右焦点.若在双曲线右支上存在点P ,满足||||212F F PF =,且2F 到直线1PF 的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )A .043=±y xB .034=±y xC .053=±y xD .045=±y x5. 1F 、2F 是双曲线12222=-by a x 0(>a ,)0>b 的左、右焦点,过1F 的直线l 与双曲线的左、右两个分支分别交于点A 、B ,若2ABF D 为等边三角形,则该双曲线的渐近线的斜率为( )(A )33±(B )2± (C )15± (D )6± 参考答案: ACBBD直线与双曲线位置关系 1. 若直线2y kx =+与双曲线的一个顶点.(1)求双曲线的方程;(2)经过的双曲线右焦点2F 作倾斜角为30°直线l ,直线l 与双曲线交于不同的B A ,两点,求AB 的长.【答案】(1)16322=-y x ;(2)5316.2. 已知双曲线)0,0(12222>>=-b a by a x 的离心率为2,焦点到渐近线的距离等于3,过右焦点2F 的直线l交双曲线于A 、B 两点,1F 为左焦点.(1) 求双曲线的方程;(2) 若AB F 1D 的面积等于62,求直线l 的方程.【答案】(1) 1322=-y x ;(2) )2(-±=x y .3. 双曲线22221(0,0)x y a b a b-=>>的两个焦点分别为1(2,0)F -,2(2,0)F ,点P 在双曲线上.(1)求双曲线的方程;(2)过(0,2)Q 的直线l 与双曲线交于不同的两点E 、F ,若OEF D 的面积为,O 为坐标原点,求直线l 的方程.【答案】(1)222x y -=;(220y -+=20y +-=. 中点弦1. 直线l 经过11P (,)与双曲线1222=-y x 交于A B 、两点,且P 平分是线段AB ,那么直线l 的方程为( ) A 、210x y --= B 、230x y +-= C 、210x y -+= D 、不存在2. 若双曲线的中心为原点,F (3,0)是双曲线的焦点,过F 的直线l 与双曲线相交于P ,Q 两点,且PQ 的中点为M (-12,-15),则双曲线的方程为( )A .16322=-y xB . 14522=-y xC 13622=-y xD . 15422=-y x3. 已知双曲线191622=-y x 及点)1,2(P ,是否存在过点P 的直线l ,使直线l 被双曲线截得的弦恰好被P 点平分?若存在,求出直线l 的方程;若不存在,请说明理由. 【答案】不存在.4. 已知直线l 交双曲线2212y x -=于A B 、不同两点,若点(1,2)M 是线段AB 的中点,求直线l 的方程及线段AB 的长度【答案】。
(完整word版)双曲线讲义

圆锥曲线第二讲 双曲线一 双曲线的定义平面内到两个定点12,F F 的距离之差的绝对值等于常数2a (小于12F F )的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点.两焦点之间的距离叫做双曲线的焦距.注:(1)定义中的限制条件1202a F F <<.当122a F F =时,点的轨迹是分别以12,F F 为端点的两条射线;当122a F F >时,轨迹不存在;当20a =时,点的轨迹是线段12F F 的垂直平分线.(2)定义中的绝对值必不可少.若没有绝对值符号则点的轨迹表示双曲线的一支.例 1 已知1(5,0)F -,2(5,0)F ,动点P 满足122PF PF a -=,当a 为3和5时,P 的轨迹分别是_________.双曲线的一支和一条射线.例2 已知点(,)P x y 的坐标满足下列条件,是判断下列各条件下点P 的轨迹是什么图形:(16=;(26=练习1 已知平面上定点1F ,2F 及动点M ,命题甲:22()MF MF a a -=为常数,命题乙:M 点轨迹是以1F ,2F 为焦点的双曲线,则甲是乙的____条件.必要不充分条件练习2 若平面内一动点(,)P x y 到两定点1(1,0)F -,2(1,0)F 的距离之差的绝对值为定值(0)a a ≥,讨论点P 的轨迹方程.二 双曲线的标准方程(1)设(,)M x y 是双曲线上任意一点,焦点1F ,2F 的坐标分别为(,0)c -,(,0)c ,M 与1F 和2F 的距离之差的绝对值等于常数2(0)a c a >>,则双曲线的标准方程为 :22221(0,0)x y a b a b-=>>其中:①222c a b =+; ②a c b c <<且,a 和b 大小关系不明确(2)设(,)M x y 是双曲线上任意一点,焦点1F ,2F 的坐标分别为(0,)c ,(0,)c -,M 与1F 和2F 的距离之差的绝对值等于常数2(0)a c a >>,则双曲线的标准方程为 :22221(0,0)y x a b a b-=>>其中:①222c a b =+; ②a c b c <<且,a 和b 大小关系不明确例1 若方程22123x y m m +=--表示双曲线,则实数m 的取值范围为______.(3,2)(3,)-+∞U例2 若1k >,则关于,x y 的方程222(1)1k x y k -+=-所表示的曲线是____.焦点在y 轴上的双曲线.例3 方程221cos 2010sin 2010x y ︒︒-=所表示的曲线为_______.焦点在y 轴上的双曲线.练习1 若方程2221523x y m m m +=---表示焦点在y 轴上的双曲线,则实数m 的取值范围为_____.(5,)+∞练习2 已知双曲线2288kx ky -=的一个焦点为(0,3),则k =_____.-1三 双曲线的定义及其标准方程的应用例1 若12,F F 是双曲线221916x y -=的两个焦点,若双曲线上一点M 到它的一个焦点的距离等于16,则点M 到另一个焦点的距离为____(4或28),若P 是双曲线左支上的点,且1232PF PF =g ,则12F PF V 的面积为_____.16例2 在ABC V 中,,,a b c 为其三边边长,点B ,C 的坐标分别为(1,0)B -,(1,0)C ,则满足1sin sin sin 2C B A -=的顶点A 的轨迹方程为______.224141()32x y x -=>例 3 已知(3,0)M -,(3,0)N ,(1,0)B ,动圆C 与直线MN 切于点B ,过,M N 与圆C 相切的两直线相交于P ,则点P 的轨迹方程为________.221(1)8y x x -=>例4 已知F 是双曲线221412x y -=的左焦点,点(1,4)A ,P 是双曲线右支上的动点,则PF PA +的最小值为_____.9练习1在平面直角坐标系xoy 中,已知ABC V 的顶点(6,0),(6,0)A C -,若顶点B在双曲线2212511x y -=的左支上,则sin sin sin A C B -=______.56练习2若点P 是以(A B 为焦点,实轴长为2210x y +=的一个交点,则PB PA +的值为______.例3 已知2225:(2)4A x y ++=e ,221:(2)4B x y -+=e ,动圆P 与A e ,B e 都外切,则动圆P 圆心的轨迹方程为_____.221(0)3y x x -=>练习4 已知双曲线的方程2214y x -=,点A 的坐标为(0),B 是圆2x +2(1y =上的点,点C 为其圆心,点M 在双曲线的右支上,则MA MB +的最小值为1四 双曲线的简单几何性质注:(1)标准方程中参数,,a b c ,其中c 最大,,a b 大小关系不确定.(2)我们把ce a=称为双曲线的离心率且1e >.22221x y a b -=的渐近线方程为b y x a=±.(3)如果12,F F 是双曲线的两个焦点,P 是双曲线上的任意一点,则121cos 1F PF -≤∠<.(求离心率的范围)(4)122PF PF c +≥,122PF PF c -<.(求离心率范围)(5)等轴双曲线:虚轴长和实轴长相等的双曲线.等轴双曲线的离心率e =(6)共轭双曲线:两个实轴和虚轴互为对调的双曲线称为共轭双曲线.三 双曲线的定义练习(5.3)已知04πθ<<,则双曲线22122:1cos sin x y C θθ-=,与222222:1sin sin tan y x C θθθ-=的()D .A 实轴长相等 .B 虚轴长相等 .C 焦距相等 .D 离心率相等 四 双曲线标准方程的求解(先定位后定量)例1(调研)设双曲线与椭圆2212736x y +=有共同的焦点,且与椭圆相交,一个交点的坐标为4),则此双曲线的标准方程是______.22145y x -=例2 (调研)已知双曲线的渐近线方程为230x y ±=,(0,5)F -为双曲线的一个焦点,则双曲线的标准方程为________.22131********y x -= 练习1(简单)设椭圆1C 的离心率为513,焦点在x 轴上且长轴长为26.若曲线2C 上的点到椭圆的两个焦点的距离之差的绝对值等于8,则曲线2C 的标准方程为_______.221169x y -= 例2(5.3)已知双曲线:C 22221x y a b -=的焦距为10,点(2,1)P 在C 的渐近线上,则C 的方程为_______.221205x y -= 五 双曲的简单几何性质双曲线的几何性质的实质是围绕双曲线中的“六点”(两个焦点,两个定点,两个虚轴的端点),“四线”(两条对称轴,两条渐近线),“两形”(中心,焦点以及虚轴端点构成的三角形,双曲线是一点和两个焦点构成的三角形)研究它们之间的相互关系.例 1(简单)设双曲线22221x y a b-=,的虚轴长为2,焦距为近线的方程为_______.y x =例2(练透)已知双曲线22221x y a b-=的离心率为2,则双曲线的渐近线方程为_____.12y x =±.练习1(调研)设12,F F 是双曲线22124y x -=的两个焦点,P 是双曲线上的一点,1234PF PF =,则12PF F V 的面积等于_____.24例2(简单)若直线1y kx =+与双曲线221916y x -=的一条渐近线垂直,则实数k=____.43±六 双曲线的离心率 离心率的取值问题例1(练透)12,F F 是双曲线:C 22221x y a b-=的左右焦点,过1F 的直线l 与C 的左右两支分别交于,A B 两点,若22::3:4:5AB BF AF =,则双曲线的离心率为例2(练透)过双曲线2222:1(0,0)x y C a b a b-=>>的一个焦点F 作双曲线的一条渐近线的垂线,若垂足恰好在线段OF 的垂直平分线,则双曲线的离心率为____.练习1(练透)设12,F F 是双曲线2222:1(0,0)A x y C a b a b-=>>的两个焦点,P 是C 上的一点,若126PF PF a +=,且12PF F V 的最小内角为30︒,则C 的离心率为练习2(练透) 设12,F F 分别为双曲线2222:1(0,0)x y C a b a b-=>>的左右焦点,A 为双曲线的左顶点,以12,F F 为直径的圆交双曲线的某条渐近线于,M N 两点,且满足120MAN ︒∠=,则该双曲线的离心率为________.3练习3(练透)设12,F F 分别是双曲线2222:1(0,0)x y C a b a b-=>>的左右焦点,若双曲线右支上存在一点P ,使得22()0OP OF F P +=u u u r u u u u r u u u u rg ,O为坐标原点,且12PF =u u u r u u u r,则该双曲线的离心率为1离心率的范围问题双曲线的离心率范围问题主要考查两点:(1)利用三角形的三边关系得到关于,a c 的齐次不等式,解不等式得到离心率范围.(2)若果12,F F 是双曲线的两个焦点,P 是双曲线上的任意一点,则121cos 1F PF -≤∠<.通过余弦定理得到关于,a c 的齐次不等式,解不等式得到离心率范围.例1 (调研)已知双曲线2222:1(0,0)A x y C a b a b-=>>的左右焦点为12,F F ,点P在双曲线的右支上,且124PF PF =,则此双曲线的离心率e 的最大值为_____.53. 例2(调研)已知(1,2),(1,2)A B -,动点P 满足AP BP ⊥u u u r u u u r ,若双曲线22221x y a b-=的渐近线与动点P 的轨迹没有公共点,则双曲线离心率的取值范围是____.12e <<练习1(5.3)已知双曲线22221(0,0)x y a b a b-=>>的左右焦点分别为12,F F ,P 为双曲线右支上任意一点,若212PF PF 的最小值为8a ,则双曲线的离心率的取值范围是_____.(1,3]练习2(练透)点P 是双曲线22221(0,0)x y a b a b-=>>左支上的一点,其右焦点为(,0)F c ,若M 为线段FP 的中点,且M 到坐标原点的距离为8c,则双曲线的离心率取值范围是_______.4(1,]3练习3(练透)已知点F 是双曲线22221(0,0)x y a b a b-=>>的左焦点,点E 是右顶点,过F 且垂直于x 轴的直线与双曲线交于,A B 两点,若ABE V 是锐角三角形,则双曲线的离心率取值范围为______.(1,2) 七 双曲线的综合问题例1 (练透)设双曲线22143x y -=的左右焦点分别为12,F F ,过1F 的直线l 交双曲线左支于,A B 两点,则22BF AF +的最小值为____.11。
双曲线讲义

双曲线及其标准方程(一)学习目标 1.掌握双曲线的定义;2.掌握双曲线的标准方程.1.定义:平面内与两定点12,F F 的距离的差的 等于常数(小于12F F )的点的轨迹。
12,F F 叫做双曲线的 ,两焦点间的距离12F F 叫做双曲线的 .反思:设常数为2a ,2a <12F F ?2a =12F F 时,轨迹是 ;2a >12F F 时,轨迹 . 试试:点(1,0)A ,(1,0)B -,若1AC BC -=,则点C 的轨迹是 .2.标准方程:22222221,(0,0,)x y a b c a b a b-=>>=+(焦点在x 轴)其焦点为 1(,0)F c -,2(,0)F c .例1已知双曲线的两焦点为1(5,0)F -,2(5,0)F ,双曲线上任意点到12,F F 的距离的差的绝对值等于6,求双曲线的标准方程.变式。
已知双曲线221169x y -=的左支上一点P 到左焦点的距离为10,则点P 到右焦点的距离为 .例2 :已知双曲线的焦点在坐标轴上,且双曲线上两点21,P P 的坐标分别为()3,42-,9,54⎛⎫⎪⎝⎭求双曲线的标准方程.变式:已知双曲线的焦点在坐标轴上,且双曲线上两点21,P P 的坐标分别为)7,26(,)72,3(---,求双曲线的标准方程.例3 方程1cos sin 22=+ααy x 表示焦点在y 轴上的双曲线,求角α所在的象限.作业1.动点P 到点(1,0)M 及点(3,0)N 的距离之差为2,则点P 的轨迹是( ). A. 双曲线 B. 双曲线的一支 C. 两条射线 D. 一条射线2.双曲线2255x ky +=的一个焦点是(6,0),那么实数k 的值为( ). A .25- B .25 C .1- D .13.双曲线的两焦点分别为12(3,0),(3,0)F F -,若2a =,则b =( ). A. 5 B. 13 C. 5 D. 134.如果22121x y k k+=---表示焦点在y 轴上的双曲线,则k 的取值范围( )A .()1,+∞B .()2,+∞C .()2,1-D .()(),22,-∞-⋃+∞5.已知点(2,0),(2,0)M N -,动点P 满足条件||||22PM PN -=. 则动点P 的轨迹方程 .6.与椭圆2244x y +=的公共焦点,且过点)1,2(M 的双曲线的标准方程为___ .7.过双曲线3422y x -=1左焦点1F 的直线交双曲线的左支于N M ,两点,2F 为其右焦点,则MN NF MF -+22的值为____________.8.实半轴长等于52,并且经过)2,5(-B 的双曲线的标准方程是____________.双曲线方程2学习目标 :1..掌握双曲线的焦点三角形;2.掌握双曲线的标准方程的求法.(1)直接法:(2)定义法(3)待定系数法例1 双曲线221169x y -=上有一点P ,12,F F 是焦点,且 6021=∠PF F ,则21F PF ∆的面积为例2 已知直线x y l =:1与直线x y l -=:2,动点),(y x P 到21,l l 的距离之积等于1,求点P 的轨迹方程例3:求与两个定圆02410:221=-++x y x C 和圆02410:222=+-+x y x C 都外切或都内切的动圆的圆心的轨迹方程作业1.双曲线x y 222-=8的实轴长是( )(A )2 (B)22 (C) 4 (D) 422.双曲线191622=-y x 上一点P 到点(5,0)的距离为15,则点P 到点(-5,0)的距离为( ) A.7 B.23 C.7或23 D.5或253.已知1F 、2F 为双曲线C:221x y -=的左、右焦点,点P 在C 上,∠1F P 2F =060,则 21PF PF ⋅= ( )(A)2 (B)4 (C) 6 (D) 84.53<<m 是方程165222=--+-m m y m x 表示的图形为双曲线的________条件. 5.双曲线08822=+-kx ky 的一个焦点为(0,3),则k =________.6.已知双曲线13622=-y x 的焦点为12,F F ,点M 在双曲线上且x MF ⊥1轴,则1F 到M F 2的距离_ __.7.12,F F 为双曲线1422-=-y x 的两个焦点,点P 在双曲线上,且 9021=∠PF F ,则21F PF ∆的面积_ _.8.与双曲线141622=-y x 有公共焦点,且过点(32,2)的双曲线的标准方程是________.双曲线的简单几何性质(1)学习目标 .理解并掌握双曲线的几何性质.1.图形2.范围:x : y :3.对称性:双曲线关于 轴、 轴及 都对称.4.顶点:( ),( ).实轴,其长为 ;虚轴,其长为 .5.离心率:1c e a =>.6.渐近线:双曲线22221x y a b-=的渐近线方程为:0x y a b ±=.7.实轴与虚轴等长的双曲线叫 双曲线.例1求双曲线2214925x y -=的实半轴长、虚半轴的长、焦点坐标、离心率及渐近线的方程.例2求双曲线的标准方程: ⑴实轴的长是10,虚轴长是8,焦点在x 轴上;⑵离心率2e =,经过点(5,3)M -;⑶渐近线方程为23y x =±,经过点9(,1)2M -.例3已知12,F F 是双曲线22221x y a b-=()0,0>>b a 的两个焦点,PQ 是经过1F 且垂直于x 轴的双曲线的弦,如果 902=∠Q PF ,求双曲线的离心率作业1. 中心在坐标原点,离心率为35的双曲线的焦点在y 轴上,则它的渐近线方程为( ) A. x y 45±= B. x y 54±= C. x y 34±= D. x y 43±=2. 17922=-y x 的焦点到准线的距离是( )A. 47 B. 425 C. 47或425 D. 423或493. 与双曲线116922=-y x 有共同的渐近线,且准线方程为532-=y 的双曲线的标准方程为A.1366422=-x y B. 1366422=-y x C. 1643622=-x y D. 1)996()9128(2222=-x y 4. 双曲线的两条准线把两焦点所连线段三等分,则它的离心率为( ) A.2 B.3 C.26D. 32 5. 双曲线4222=-my mx 一条准线是1=y ,则m 为( )A.23 B. 23- C. 32 D.32-双曲线的简单几何性质(2)学习目标 1.掌握定义;2.灵活掌握标准方程.3.直线与双曲线的位置关系4.点差法5.弦长公式典型例题例1 如果直线1-=kx y 与双曲线422=-y x (1)没有公共点,求k 的取值范围. (2)只有一个公共点,求k 的取值范围. (3)与右支有两个公共点,求k 的取值范围. (4)两支各有一个公共点,求k 的取值范围.变式:如果直线1-=kx y 与双曲线422=-y x (1)有两个公共点,求k 的取值范围.(2)与左支有有两个公共点,求k 的取值范围.例2过点P (8,1)的直线与双曲线4422=-y x 相交于B A ,两点,且点P 是线段AB 的中点,求直线AB 的方程变式:已知双曲线1322=-y x ,过点P (2,1)点作一直线交双曲线于B A ,两点,若P 为AB 的中点.(1)求直线AB 的方程 (2)求弦AB 的长例3设双曲线的顶点是椭圆14322=+y x 的焦点,该双曲线又与直线06315=+-y x 交于B A ,两点,且OB OA ⊥(O 为坐标原点)(1)求此双曲线的方程;(2)求AB 的长变式:已知直线1+=ax y 与双曲线1322=-y x 交于B A ,两点,若以AB 为直径的圆过坐标原点,求实数a 的值。
双曲线讲义

双曲线讲义1.双曲线的定义(1)定义:平面内与两个定点F 1,F 2的距离的差的绝对值等于非零常数(小于|F 1F 2|)的点的轨迹.(2)符号表示:||MF 1|-|MF 2||=2a (常数)(0<2a <|F 1F 2|). (3)焦点:两个定点F 1,F 2.(4)焦距:两焦点间的距离,表示为|F 1F 2|.2a b a bF (-c ,0),F (c ,0)F (0,-c ),F (0,c )1.12为什么?提示 不一定.当2a =|F 1F 2|时,动点的轨迹是两条射线; 当2a >|F 1F 2|时,动点的轨迹不存在;当2a =0时,动点的轨迹是线段F 1F 2的中垂线.2.已知双曲线方程为x 2a 2-y 2b 2=1(a >0,b >0),如何求其他具有共同渐近线的双曲线方程?提示 可设方程为x 2a 2-y 2b2=λ(λ≠0).题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)方程x 2m -y 2n =1(mn >0)表示焦点在x 轴上的双曲线.( × )(2)双曲线x 2m 2-y 2n 2=λ(m >0,n >0,λ≠0)的渐近线方程是x m ±yn=0.( √ )(3)等轴双曲线的渐近线互相垂直,离心率等于 2.( √ )(4)若双曲线x 2a 2-y 2b 2=1(a >0,b >0)与x 2b 2-y 2a 2=1(a >0,b >0)的离心率分别是e 1,e 2,则1e 21+1e 22=1.( √ )题组二 教材改编2.若双曲线x 2a 2-y 2b2=1(a >0,b >0)的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为( ) A. 5 B .5 C. 2 D .2答案 A解析 由题意知焦点到其渐近线的距离等于实轴长,双曲线的渐近线方程为x a ±y b=0,即bx ±ay =0,∴2a =bc a 2+b 2=b .又a 2+b 2=c 2,∴5a 2=c 2.∴e 2=c 2a2=5,∴e = 5.3.(2021·阜阳模拟)已知双曲线x 2a 2-y 2b2=1()a >0,b >0的一条渐近线经过点()2,6,则该双曲线的离心率为( ) A .2 B. 2 C .3 D. 3 答案 A解析 双曲线x 2a 2-y 2b 2=1()a >0,b >0的一条渐近线为y =bax 过第一象限,所以点()2,6在渐近线y =b a x 上,可得6=2×b a ,所以ba =3,所以e =c a =a 2+b 2a 2=1+⎝ ⎛⎭⎪⎫b a 2=1+3=2. 4.经过点A (4,1),且对称轴都在坐标轴上的等轴双曲线方程为________.答案x 215-y 215=1 解析 设双曲线的方程为x 2a 2-y 2a 2=±1(a >0),把点A (4,1)代入,得a 2=15(舍负),故所求方程为x 215-y 215=1.题组三 易错自纠5.(多选)(2020·辽宁六校协作体月考)若方程x 23-t +y 2t -1=1所表示的曲线为C ,则下面四个命题中错误的是( ) A .若C 为椭圆,则1<t <3B .若C 为双曲线,则t >3或t <1 C .曲线C 可能是圆D .若C 为椭圆,且长轴在y 轴上,则1<t <2 答案 AD解析 若t >3,则方程可变形为y 2t -1-x 2t -3=1,它表示焦点在y 轴上的双曲线;若t <1,则方程可变形为x 23-t -y 21-t=1,它表示焦点在x 轴上的双曲线;若2<t <3,则0<3-t <t -1,故方程x 23-t +y 2t -1=1表示焦点在y 轴上的椭圆;若1<t <2,则0<t -1<3-t ,故方程x 23-t +y 2t -1=1表示焦点在x 轴上的椭圆;若t =2,则方程x 23-t +y 2t -1=1即为x 2+y 2=1,它表示圆,综上,选AD.6.(2021·哈尔滨师范大学青冈实验中学模拟)双曲线x 29-y 216=1上一点P 到焦点F 1(-5,0)的距离为7,则点P 到焦点F 2(5,0)的距离为________. 答案 13解析 在双曲线x 29-y 216=1中,a =3,由题意得|PF 1|=7,由双曲线的定义可得||PF 1|-|PF 2||=2a =6, 即|7-|PF 2||=6,解得|PF 2|=13或|PF 2|=1,又|PF 2|≥c -a =2, 所以|PF 2|=13.题型一 双曲线的定义及应用例1 (1)(2020·滨州质检)x 2+(y -3)2-x 2+(y +3)2=4表示的曲线方程为( ) A.x 24-y 25=1(x ≤-2) B.x 24-y 25=1(x ≥2) C.y 24-x 25=1(y ≤-2) D.y 24-x 25=1(y ≥2) 答案 C解析 x 2+(y -3)2的几何意义为点M (x ,y )到点F 1(0,3)的距离,x 2+(y +3)2的几何意义为点M (x ,y )到点F 2(0,-3)的距离,则x 2+(y -3)2-x 2+(y +3)2=4表示点M (x ,y )到点F 1(0,3)的距离与到点F 2(0,-3)的距离的差为4,且4<|F 1F 2|,所以点M 的轨迹是以F 1,F 2为焦点的双曲线的下支,且该双曲线的实半轴长a =2,半焦距c =3,所以b 2=c 2-a 2=5,则x 2+(y -3)2-x 2+(y +3)2=4表示的曲线方程为y 24-x 25=1(y ≤-2),故选C.(2)已知F 1,F 2为双曲线C :x 2-y 2=2的左、右焦点,点P 在C 上,∠F 1PF 2=60°,则△F 1PF 2的面积为______. 答案 2 3解析 不妨设点P 在双曲线的右支上, 则|PF 1|-|PF 2|=2a =22, 在△F 1PF 2中,由余弦定理,得cos∠F 1PF 2=|PF 1|2+|PF 2|2-|F 1F 2|22|PF 1|·|PF 2|=12,∴|PF 1|·|PF 2|=8,∴12F PF S △=12|PF 1|·|PF 2|·sin 60°=2 3.在本例(2)中,若将“∠F 1PF 2=60°”改为“PF 1—→·PF 2—→=0”,则△F 1PF 2的面积为________. 答案 2解析 不妨设点P 在双曲线的右支上, 则|PF 1|-|PF 2|=2a =22, ∵PF 1—→·PF 2—→=0,∴PF 1—→⊥PF 2—→,∴在△F 1PF 2中,有|PF 1|2+|PF 2|2=|F 1F 2|2,即|PF 1|2+|PF 2|2=16,∴|PF 1|·|PF 2|=4,∴12F PF S △=12|PF 1|·|PF 2|=2.思维升华 在“焦点三角形”中,常利用正弦定理、余弦定理,结合||PF 1|-|PF 2||=2a ,运用平方的方法,建立与|PF 1|·|PF 2|的联系.跟踪训练1 (1)(2021·广东普宁华侨中学模拟)过双曲线x 2-y 24=1的左焦点F 1作一条直线l 交双曲线左支于P ,Q 两点,若|PQ |=10,F 2是双曲线的右焦点,则△PF 2Q 的周长是________. 答案 24解析 由题意,得|PF 2|-|PF 1|=2,|QF 2|-|QF 1|=2. ∵|PF 1|+|QF 1|=|PQ |=10,∴|PF 2|+|QF 2|-10=4,∴|PF 2|+|QF 2|=14.∴△PF 2Q 的周长是|PF 2|+|QF 2|+|PQ |=14+10=24.(2)已知圆C 1:(x +3)2+y 2=1和圆C 2:(x -3)2+y 2=9,动圆M 同时与圆C 1及圆C 2相外切,则动圆圆心M 的轨迹方程为________________.答案 x 2-y 28=1(x ≤-1)解析 如图所示,设动圆M 与圆C 1及圆C 2分别外切于A 和B .根据两圆外切的条件, 得|MC 1|-|AC 1|=|MA |, |MC 2|-|BC 2|=|MB |, 因为|MA |=|MB |,所以|MC 1|-|AC 1|=|MC 2|-|BC 2|, 即|MC 2|-|MC 1|=|BC 2|-|AC 1|=2,所以点M 到两定点C 2,C 1的距离的差是常数且小于|C 1C 2|=6. 又根据双曲线的定义,得动点M 的轨迹为双曲线的左支(点M 与C 2的距离大,与C 1的距离小),其中a =1,c =3,则b 2=8.故点M 的轨迹方程为x 2-y 28=1(x ≤-1).题型二 双曲线的标准方程1.(多选)已知双曲线的渐近线方程为y =±22x ,实轴长为4,则该双曲线的标准方程为( ) A.x 24-y 22=1 B.y 24-x 28=1 C.x 24-y 28=1 D.y 24-x 22=1 答案 AB解析 设双曲线方程为x 22m -y 2m=1(m ≠0),又2a =4,∴a 2=4,当m >0时,2m =4,m =2; 当m <0时,-m =4,m =-4.故所求双曲线的标准方程为x 24-y 22=1或y 24-x 28=1.2.过双曲线C :x 2a 2-y 2b2=1(a >b >0)的右顶点作x 轴的垂线,与C 的一条渐近线相交于点A .若以C 的右焦点F 为圆心、半径为4的圆经过A ,O 两点(O 为坐标原点),则双曲线C 的标准方程为( ) A.x 24-y 212=1 B.x 27-y 29=1 C.x 28-y 28=1 D.x 212-y 24=1 答案 A解析 因为渐近线y =bax 与直线x =a 交于点A (a ,b ),c =4且(4-a )2+b 2=4,解得a 2=4,b 2=12,因此双曲线的标准方程为x 24-y 212=1.3.已知双曲线E 与双曲线x24-y29=1共渐近线且经过点P (2,35),则双曲线E 的标准方程为________,顶点坐标为________. 答案y 236-x 216=1 (0,6),(0,-6) 解析 根据题意,设所求双曲线的方程为x 24-y 29=λ(λ≠0),又由双曲线经过点P (2,35),得44-459=λ,即λ=-4,所以双曲线的方程为x 24-y 29=-4,其标准方程为y 236-x 216=1,顶点坐标为(0,6),(0,-6).4.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,点P (2,3)在双曲线上,且|PF 1|,|F 1F 2|,|PF 2|成等差数列,则该双曲线的标准方程为________.答案 x 2-y 2=1解析 ∵|PF 1|,|F 1F 2|,|PF 2|成等差数列, ∴|PF 1|+|PF 2|=4c .∵点P 位于第一象限,∴|PF 1|-|PF 2|=2a , ∴|PF 1|=2c +a ,|PF 2|=2c -a ,∴cos ∠PF 2F 1=4c 2+(2c -a )2-(2c +a )24c (2c -a )=c -2a2c -a ,又点P (2,3)在双曲线上,∴sin ∠PF 2F 1=32c -a ,∴⎝ ⎛⎭⎪⎫c -2a 2c -a 2+3(2c -a )2=1,化简得(c -2a )2+3=(2c -a )2,即c 2-a 2=b 2=1,又4a 2-3b2=1,∴a 2=1,∴双曲线的标准方程为x 2-y 2=1.思维升华 求双曲线的标准方程的方法(1)定义法:由题目条件判断出动点轨迹是双曲线,由双曲线定义,确定2a ,2b 或2c ,从而求出a 2,b 2,写出双曲线方程.(2)待定系数法:先确定焦点在x 轴上还是y 轴上,设出标准方程,再由条件确定a 2,b 2的值,即“先定型,再定量”,如果焦点位置不好确定,可将双曲线方程设为x 2m 2-y 2n2=λ(λ≠0),再根据条件求λ的值.题型三 双曲线的简单几何性质 命题点1 渐近线和离心率例2 (1)(2020·广州模拟)设F 1,F 2是双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点,P 是双曲线C 右支上一点,若|PF 1|+|PF 2|=4a ,且∠F 1PF 2=60°,则双曲线C 的渐近线方程是( )A.3x ±y =0 B .2x ±7y =0 C.3x ±2y =0 D .2x ±3y =0 答案 C解析 ∵F 1,F 2是双曲线的左、右焦点,点P 在双曲线右支上,∴由双曲线的定义可得|PF 1|-|PF 2|=2a ,又知|PF 1|+|PF 2|=4a ,∴|PF 1|=3a ,|PF 2|=a .在△PF 1F 2中,由余弦定理的推论可得cos 60°=|PF 1|2+|PF 2|2-|F 1F 2|22|PF 1|·|PF 2|,即12=(3a )2+a 2-4c22×3a ×a,∴3a 2=10a 2-4c 2,即4c 2=7a 2,又知b 2+a 2=c 2,∴b 2a 2=34,∴双曲线C 的渐近线方程为y =±32x ,即3x ±2y =0,故选C. (2)(2019·江苏)在平面直角坐标系xOy 中,若双曲线x 2-y 2b2=1(b >0)经过点(3,4),则该双曲线的渐近线方程是____________. 答案 y =±2x解析 因为双曲线x 2-y 2b2=1(b >0)经过点(3,4),所以9-16b2=1,得b =2,所以该双曲线的渐近线方程是y =±2x .(3)设双曲线C :x 2a 2-y 2b 2=1(a >b >0)的两条渐近线的夹角为α,且cos α=13,则C 的离心率为________.答案 62解析 ∵a >b >0,∴渐近线y =bax 的斜率小于1, ∵两条渐近线的夹角为α,cos α=13.∴cos 2α2=23,sin 2α2=13,tan 2α2=12, ∴b 2a 2=12,∴c 2-a 2a 2=12,∴e 2=32,∴e =62. 命题点2 双曲线的简单几何性质的综合应用例3 (1)(2020·长沙雅礼中学模拟)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,在双曲线上存在点P 满足2|PF 1—→+PF 2—→|≤|F 1F 2—→|,则此双曲线的离心率e 的取值范围是( ) A .(1,2] B .[2,+∞) C .(1,2] D .[2,+∞) 答案 B解析 当P 不是双曲线与x 轴的交点时,连接OP ,因为OP 为△PF 1F 2的边F 1F 2上的中线,所以PO →=12(PF 1—→+PF 2—→);当P 是双曲线与x 轴的交点时,同样满足上述等式.因为双曲线上存在点P 满足2|PF 1—→+PF 2—→|≤|F 1F 2—→|,所以4|PO →|≤2c ,由|PO →|≥a ,可知4a ≤2c ,则e ≥2,选B.(2)(2021·潍坊模拟)已知F 1,F 2是双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点,过F 1的直线l 与双曲线的左支交于点A ,与右支交于点B ,若|AF 1|=2a ,∠F 1AF 2=2π3,则122AF F ABF S S△△等于( )A .1 B.12 C.13 D.23答案 B解析 如图所示,由双曲线定义可知|AF 2|-|AF 1|=2a .又|AF 1|=2a ,所以|AF 2|=4a ,因为∠F 1AF 2=23π,所以12AF F S △=12|AF 1|·|AF 2|·sin ∠F 1AF 2=12×2a ×4a ×32=23a 2.由双曲线定义可知|BF 1|-|BF 2|=2a ,所以|BF 1|=2a +|BF 2|,又知|BF 1|=2a +|BA |,所以|BA |=|BF 2|,又∠F 1AF 2=23π,所以△BAF 2为等边三角形,边长为4a ,所以2ABF S △=34|AB |2=34×(4a )2=43a 2,所以122AF F ABF S S △△=23a 243a 2=12.故选B. 思维升华 (1)求双曲线的渐近线或离心率的方法 ①求出a ,b ,c 直接求离心率,写渐近线方程.②列出a ,b ,c 的各次方程(或不等式),然后解方程或不等式.(2)双曲线性质的综合应用要充分注意与平面几何知识的联系,善于发现条件中的相等或不等关系.跟踪训练2 (1)已知抛物线y 2=4x 的焦点为F ,准线为l .若l 与双曲线x 2a 2-y 2b2=1(a >0,b >0)的两条渐近线分别交于点A 和点B ,且|AB |=4|OF |(O 为原点),则双曲线的离心率为( )A. 2B. 3 C .2 D. 5 答案 D解析 由题意,可得F (1,0),直线l 的方程为x =-1,双曲线的渐近线方程为y =±b ax . 将x =-1代入y=±b a x ,得y =±b a,所以点A ,B 的纵坐标的绝对值均为b a.由|AB |=4|OF |可得2b a=4,即b =2a ,b 2=4a 2,故双曲线的离心率e =ca=a 2+b 2a 2= 5. (2)设双曲线x 29-y216=1的右顶点为A ,右焦点为F .过点F 且平行于双曲线的一条渐近线的直线与双曲线交于点B ,则△AFB 的面积为________.答案 3215解析 a 2=9,b 2=16,故c =5.∴A (3,0),F (5,0),不妨设直线BF 的方程为y =43(x -5),代入双曲线方程解得B ⎝ ⎛⎭⎪⎫175,-3215.∴S △AFB =12|AF |·|y B |=12×2×3215=3215.课时精练1.已知双曲线x 2m-y2m +6=1(m >0)的虚轴长是实轴长的2倍,则双曲线的标准方程为( )A.x 22-y 24=1B.x 24-y 28=1 C .x 2-y 28=1D.x 22-y 28=1 答案 D解析 由题意,得2m =m +6,解得m =2,所以双曲线的标准方程为x 22-y 28=1.2.已知方程x 2m 2+n -y 23m 2-n=1表示双曲线,且该双曲线两焦点间的距离为4,则n 的取值范围是( ) A .(-1,3) B .(-1,3) C .(0,3) D .(0,3)答案 A解析 ∵方程x 2m 2+n -y 23m 2-n=1表示双曲线,∴(m 2+n )·(3m 2-n )>0,解得-m 2<n <3m 2,由双曲线性质,知c 2=(m 2+n )+(3m 2-n )=4m 2(其中c 是半焦距),∴焦距2c =2×2|m |=4,解得|m |=1, ∴-1<n <3,故选A.3.(2020·天津)设双曲线C 的方程为x 2a 2-y 2b2=1(a >0,b >0),过抛物线y 2=4x 的焦点和点(0,b )的直线为l .若C 的一条渐近线与l 平行,另一条渐近线与l 垂直,则双曲线C 的方程为( ) A.x 24-y 24=1 B .x 2-y 24=1C.x 24-y 2=1 D .x 2-y 2=1 答案 D解析 由题意知,抛物线的焦点坐标为(1,0),∴直线l 的斜率k l =b -00-1=-b =-ba ,解得a =1.又∵ba·(-b )=-1,∴b =a =1,∴双曲线C 的方程为x 2-y 2=1.4.已知F 1,F 2为双曲线C :x 2-y 2=2的左、右焦点,点P 在C 上,|PF 1|=2|PF 2|,则cos ∠F 1PF 2等于( ) A.14 B.35 C.34 D.45 答案 C解析 由x 2-y 2=2,知a =b =2,c =2.由双曲线定义知,|PF 1|-|PF 2|=2a =22,又|PF 1|=2|PF 2|,∴|PF 1|=42,|PF 2|=22,在△PF 1F 2中,|F 1F 2|=2c =4,由余弦定理,得cos ∠F 1PF 2=|PF 1|2+|PF 2|2-|F 1F 2|22|PF 1|·|PF 2|=34.5.(2019·全国Ⅲ)已知F 是双曲线C :x 24-y 25=1的一个焦点,点P 在C 上,O 为坐标原点.若|OP |=|OF |,则△OPF 的面积为( ) A.32 B.52 C.72 D.92 答案 B解析 由F 是双曲线x 24-y 25=1的一个焦点,知|OF |=3,所以|OP |=|OF |=3.不妨设点P 在第一象限,P (x 0,y 0),x 0>0,y 0>0,则⎩⎪⎨⎪⎧x 20+y 20=3,x 204-y 205=1,解得⎩⎪⎨⎪⎧x 20=569,y 20=259,所以P ⎝⎛⎭⎪⎫2143,53, 所以S △OPF =12|OF |·y 0=12×3×53=52.6.(2020·山南模拟)已知A ,B ,C 是双曲线x 2a 2-y 2b2=1(a >0,b >0)上的三个点,AB 经过原点O ,AC 经过右焦点F ,若BF ⊥AC 且2|AF |=|CF |,则该双曲线的离心率是( )A.53B.173C.172D.94 答案 B解析 设左焦点为F ′,|AF |=m ,连接AF ′,CF ′,BF ′,则|FC |=2m ,|AF ′|=2a +m ,|CF ′|=2a +2m ,|FF ′|=2c . 因为BF ⊥AC ,且AB 经过原点O , 所以四边形FAF ′B 为矩形.在Rt△AF ′C 中,|AF ′|2+|AC |2=|F ′C |2,代入得(2a +m )2+(3m )2=(2a +2m )2,化简得m =2a3,所以在Rt△AF ′F 中,|AF ′|2+|AF |2=|F ′F |2,代入得⎝⎛⎭⎪⎫2a +2a 32+⎝ ⎛⎭⎪⎫2a 32=()2c 2,化简得c 2a 2=179,即e =173.7.(多选)(2020·新高考全国Ⅰ)已知曲线C :mx 2+ny 2=1.( ) A .若m >n >0,则C 是椭圆,其焦点在y 轴上 B .若m =n >0,则C 是圆,其半径为nC .若mn <0,则C 是双曲线,其渐近线方程为y =±-m nxD .若m =0,n >0,则C 是两条直线 答案 ACD解析 对于A ,当m >n >0时,有1n >1m >0,方程化为x 21m+y 21n=1,表示焦点在y 轴上的椭圆,故A正确.对于B ,当m =n >0时,方程化为x 2+y 2=1n ,表示半径为1n的圆,故B 错误.对于C ,当m >0,n <0时,方程化为x 21m-y 2-1n=1,表示焦点在x 轴上的双曲线,其中a =1m,b =-1n,渐近线方程为y =±-m n x ;当m <0,n >0时,方程化为y 21n -x 2-1m=1,表示焦点在y 轴上的双曲线,其中a =1n,b =-1m,渐近线方程为y =±-mnx ,故C 正确.对于D ,当m =0,n >0时,方程化为y =±1n,表示两条平行于x 轴的直线,故D 正确.8.(多选)已知F 1,F 2分别是双曲线C :y 2-x 2=1的上、下焦点,点P 是其一条渐近线上一点,且以线段F 1F 2为直径的圆经过点P ,则( ) A .双曲线C 的渐近线方程为y =±xB .以F 1F 2为直径的圆的方程为x 2+y 2=1 C .点P 的横坐标为±1 D .△PF 1F 2的面积为 2 答案 ACD解析 等轴双曲线C :y 2-x 2=1的渐近线方程为y =±x ,故A 正确; 由双曲线的方程可知|F 1F 2|=22,所以以F 1F 2为直径的圆的方程为x 2+y 2=2,故B 错误;点P (x 0,y 0)在圆x 2+y 2=2上, 不妨设点P (x 0,y 0)在直线y =x 上,所以由⎩⎪⎨⎪⎧x 20+y 20=2,y 0=x 0,解得|x 0|=1,则点P 的横坐标为±1,故C 正确;由上述分析可得△PF 1F 2的面积为12×22×1=2,故D 正确.故选ACD.9.(2020·北京)已知双曲线C :x 26-y 23=1,则C 的右焦点的坐标为________;C 的焦点到其渐近线的距离是________. 答案 (3,0) 3解析 由x 26-y 23=1,得c 2=a 2+b 2=9,解得c =3,焦点在x 轴上,所以双曲线C 的右焦点坐标为(3,0).双曲线的一条渐近线方程为y =36x ,即x -2y =0,所以焦点(3,0)到渐近线的距离为d =31+(-2)2= 3. 10.(2020·焦作模拟)已知左、右焦点分别为F 1,F 2的双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的一条渐近线与直线l :x -2y =0互相垂直,点P 在双曲线C 上,且|PF 1|-|PF 2|=3,则双曲线C 的焦距为________.答案 3 5解析 双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的渐近线为y =±bax ,一条渐近线与直线l :x -2y =0相互垂直,可得ba=2,即b =2a ,由双曲线的定义可得2a =|PF 1|-|PF 2|=3,可得a =32,b =3,即有c =a 2+b 2=94+9=352, 即焦距为2c =3 5.11.如图,F 1和F 2分别是双曲线x 2a 2-y 2b2=1(a >0,b >0)的两个焦点,A 和B 是以O 为圆心,以|OF 1|为半径的圆与该双曲线左支的两个交点,且△F 2AB 是等边三角形,则双曲线的离心率为________.答案 3+1解析 设|F 1F 2|=2c ,连接AF 1(图略),∵△F 2AB 是等边三角形,且F 1F 2是⊙O 的直径, ∴∠AF 2F 1=30°,∠F 1AF 2=90°,∴|AF 1|=c ,|AF 2|=3c ,2a =3c -c ,∴e =c a =23-1=3+1.12.(2020·广安邻水实验中学模拟)已知双曲线C :x 2a 2-y 2b2=1()a >0,b >0的左、右焦点分别为F 1,F 2,O 为原点,若以F 1F 2为直径的圆与C 的渐近线的一个交点为P ,且|F 1P |=3|OP |,则C 的渐近线方程为________. 答案 y =±3x解析 根据双曲线C :x 2a 2-y 2b2=1()a >0,b >0的左、右焦点为F 1,F 2,O 为原点,以F 1F 2为直径的圆与C 的渐近线的一个交点为P ,如图所示,则|F 1O |=|OP |=c ,|F 1P |=3|OP |=3c ,所以在△POF 1中,由余弦定理可得cos∠POF 1=|OP |2+|OF 1|2-|PF 1|22|OP |·|OF 1|=c 2+c 2-()3c 22×c ×c=-12. 所以∠POF 1=2π3,则∠POF 2=π3,所以tan∠POF 2=tan π3=3,则渐近线方程为y =±3x .13.(多选)(2021·百师联盟模拟)双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的焦点在圆O :x 2+y 2=13上,圆O 与双曲线C 的渐近线在第一、二象限分别交于点M ,N ,点E (0,a )满足EO →+EM →+EN →=0(其中O 为坐标原点),则( )A .双曲线C 的一条渐近线方程为3x -2y =0B .双曲线C 的离心率为132C .|OE →|=1D .△OMN 的面积为6 答案 ABD 解析 如图,设双曲线C 的焦距为2c =213,MN 与y 轴交于点P ,由题意可知|OM |=c =13,则P (0,b ),由EO →+EM →+EN →=0得点E 为△OMN 的重心,可得|OE |=23|OP |,即a =23b ,b 2a 2=c 2-a 2a 2=94,所以a =2,b =3,e =132. 双曲线C 的渐近线方程为3x ±2y =0,|OE →|=2,M 的坐标为(2,3),S △OMN =6, 故选ABD.14.(2021·临川一中模拟)已知双曲线x 2a 2-y 2b2=1(a >0,b >0)中,A 1,A 2是左、右顶点,F 是右焦点,B 是虚轴的上顶点.若在线段BF 上(不含端点)存在不同的两点P i (i =1,2),使得P i A 1—→·P i A 2—→=0,则双曲线离心率的取值范围是________.答案 ⎝⎛⎭⎪⎫2,5+12 解析 设c 为半焦距,则F (c ,0),又B (0,b ), 所以BF :bx +cy -bc =0,以A 1A 2为直径的圆的方程为⊙O :x 2+y 2=a 2,因为P i A 1—→·P i A 2—→=0,i =1,2,所以⊙O 与线段BF 有两个交点(不含端点), 所以⎩⎪⎨⎪⎧bc b 2+c2<a ,b >a ,即⎩⎪⎨⎪⎧c 4-3a 2c 2+a 4<0,c 2>2a 2,故⎩⎪⎨⎪⎧e 4-3e 2+1<0,e 2>2,解得2<e <5+12. 15.将离心率为e 1的双曲线C 1的实半轴长a 和虚半轴长b (a ≠b )同时增加m (m >0)个单位长度,得到离心率为e 2的双曲线C 2,则( ) A .对任意的a ,b ,e 1>e 2B .当a >b 时,e 1>e 2;当a <b 时,e 1<e 2C .对任意的a ,b ,e 1<e 2D .当a >b 时,e 1<e 2;当a <b 时,e 1>e 2 答案 D解析 依题意,e 1=a 2+b 2a =1+⎝ ⎛⎭⎪⎫b a 2,e 2=(a +m )2+(b +m )2a +m =1+⎝ ⎛⎭⎪⎫b +m a +m 2. 因为b a -b +m a +m =ab +bm -ab -am a (a +m )=m (b -a )a (a +m ),由于m >0,a >0,b >0,所以当a >b 时,0<b a <1,0<b +m a +m <1,b a <b +m a +m ,⎝ ⎛⎭⎪⎫b a 2<⎝ ⎛⎭⎪⎫b +m a +m 2,所以e 1<e 2;当a <b 时,b a >1,b +m a +m >1,b a >b +ma +m ,所以⎝ ⎛⎭⎪⎫b a 2>⎝ ⎛⎭⎪⎫b +m a +m 2,所以e 1>e 2. 所以当a >b 时,e 1<e 2;当a <b 时,e 1>e 2.16.(2020·长沙雅礼中学模拟)已知F 是双曲线C :x 2-y 28=1的右焦点,P 是C 左支上一点,A (0,66),当△APF 的周长最小时,点P 的坐标为________.答案 (-2,26)解析 如图,令E 为双曲线的左焦点,由双曲线C的方程可知a2=1,b2=8,∴c2=a2+b2=1+8=9,∴c=3,∴左焦点E(-3,0),右焦点F(3,0),∵|AF|=32+(66)2=15,∴当△APF的周长最小时,|PA|+|PF|最小.由双曲线的性质得|PF|-|PE|=2a=2,∴|PF|=|PE|+2,又|PE|+|PA|≥|AE|=|AF|=15,当且仅当A,P,E三点共线且点P在线段AE上时,等号成立,∴△APF的周长为|AF|+|AP|+|PF|=15+|PE|+|AP|+2≥15+15+2=32.直线AE的方程为y=26x+66,将其代入到双曲线方程得x2+9x+14=0,解得x=-7(舍)或x=-2,由x=-2,得y=26(负值已舍),∴点P的坐标为(-2,26).。
双曲线专题复习讲义自理

双曲线专题复习讲义★知识梳理★1. 双曲线的定义(1)第一定义:当1212||||||2||PF PF a F F -=<时, P 的轨迹为双曲线; 当1212||||||2||PF PF a F F -=>时, P 的轨迹不存在;当21212||F F a PF PF ==-时, P 的轨迹为以21F F 、为端点的两条射线(2)双曲线的第二义平面内到定点F 与定直线l (定点F 不在定直线l 上)的距离之比是常数e (1>e )的点的轨迹为双曲线与双曲线12222=-b y a x 共渐近线的双曲线系方程为:)0(2222≠=-λλb y a x与双曲线12222=-b y a x 共轭的双曲线为22221y x b a-=等轴双曲线222a y x ±=-的渐近线方程为x y ±= ,离心率为2=e .;★重难点突破★1.注意定义中“陷阱”问题1:已知12(5,0),(5,0)F F -,一曲线上的动点P 到21,F F 距离之差为6,则双曲线的方程为2.注意焦点的位置问题2:双曲线的渐近线为x y 23±=,则离心率为★热点考点题型探析★考点1 双曲线的定义及标准方程 题型1:运用双曲线的定义1.设P 为双曲线11222=-y x 上的一点F 1、F 2是该双曲线的两个焦点,若|PF 1|:|PF 2|=3:2,则△PF 1F 2的面积为 ( )A .36B .12C .312D .242.如图2所示,F 为双曲线1169:22=-y x C 的左 焦点,双曲线C 上的点i P 与()3,2,17=-i P i 关于y 轴对称,则F P F P F P F P F P F P 654321---++的值是( ) A .9 B .16 C .18 D .27题型2 求双曲线的标准方程[例2 ] 已知双曲线C 与双曲线162x -42y =1有公共焦点,且过点(32,2).求双曲线C的方程.【新题导练】4.已知双曲线的渐近线方程是2x y ±=,焦点在坐标轴上且焦距是10,则此双曲线的方程为 ;考点2 双曲线的几何性质 题型1 求离心率或离心率的范围7.已知双曲线221x y m n -=的一条渐近线方程为43y x =,则该双曲线的离心率e为 .c ab AD =,c a a ED 2+=,=+∴c a a 2cab⋅3,2=∴e 题型2 与渐近线有关的问题[例4]若双曲线)0,0(12222>>=-b a by a x 的焦点到渐近线的距离等于实轴长,则双曲线的离心率为 ( ) A.2 B.3C.5D.29. 双曲线22149x y -=的渐近线方程是 ( )A. 23y x =±B. 49y x =±C. 32y x =±D. 94y x =±基础巩固训练1. 以椭圆221169144x y +=的右焦点为圆心,且与双曲线221916x y -=的渐近线相切的圆的方程是 (A )221090x y x +-+= (B )221090x y x +--= (C )221090x y x +++= (D )221090x y x ++-=2.已知双曲线的两个焦点为1(0)F 、20)F ,M 是此双曲线上的一点,且满足120MF MF ⋅= ,12||||2MF MF ⋅=,则该双曲线的方程是 ( )A .2219x y -=B .2219y x -=C .22137x y -=D .22173x y -=3.两个正数a 、b 的等差中项是92,一个等比中项是,b a >则双曲线12222=-b y a x 的离心率为( )A .53B .4C .54D .54..曲线)6(161022<=-+-m m y m x 与曲线)95(19522<<=-+-n ny n x 的 ( )A .焦距相等B .焦点相同C .离心率相等D .以上都不对7. 已知椭圆1532222=+ny m x 和双曲线1322222=-n y m x 有公共的焦点,(1)求双曲线的渐近线方程。
2025数学大一轮复习讲义人教版 第八章 双曲线

e=ac∈_(_1_,__+__∞__)_ c2= a2+b2 (c>a>0,c>b>0)
常用结论
1.双曲线的焦点到其渐近线的距离为b. 2.若P是双曲线右支上一点,F1,F2分别为双曲线的左、右焦点,则 |PF1|min=a+c,|PF2|min=c-a. 3.同支的焦点弦中最短的为通径(过焦点且垂直于实轴的弦),其长为2ab2. 4.与双曲线ax22-by22=1(a>0,b>0)有共同渐近线的双曲线方程可表示为ax22 -by22=t(t≠0).
知识梳理
标准方程 范围
ax22-by22=1(a>0,b>0) x≤-a 或 x≥a ,y∈R
ay22-bx22=1(a>0,b>0) y≤-a或y≥a,x∈R
对称性 性质 顶点
对称轴: 坐标轴 ;对称中心:_原__点__
_A_1_(_-__a_,__0_),__A__2(_a_,__0_)_
_A_1_(_0_,__-__a_),__A__2(_0_,__a_)_
(2)已知F1,F2为双曲线C:x2-y2=2的左、右焦点,点P在C上,∠F1PF2 =60°,则△F1PF2的面积为____2__3_.
不妨设点P在双曲线的右支上, 则|PF1|-|PF2|=2a=2 2, 在△F1PF2 中,由余弦定理,得 cos∠F1PF2=|PF1|22+|P|PFF1|·2||P2-F2|F| 1F2|2=12, ∴|PF1|·|PF2|=8, ∴ S△F1PF2 =12|PF1|·|PF2|·sin 60°=2 3.
此时,点Q的轨迹是以点A,O为焦点,且长轴长为R的椭圆,故C正确; ③当点A在圆O外,连接AQ(图略),由垂直平分线的性质可得|QA|= |QP|, 所以||QA|-|QO||=||QP|-|QO||=|OP|=R<|OA|, 此时,点Q的轨迹是以点A,O为焦点,且实轴长为R的双曲线,故D 正确.
高中数学 双曲线及标准方程 讲义

授课内容 双曲线及标准方程知识梳理双曲线标准方程(焦点在x 轴))0,0(12222>>=-b a b y a x 标准方程(焦点在y 轴))0,0(12222>>=-b a b x a y 定义第一定义:平面内与两个定点1F ,2F 的距离的差的绝对值是常数(小于12F F )的点的轨迹叫双曲线。
这两个定点叫做双曲线的焦点,两焦点的距离叫焦距。
{}a MF MF M221=-()212F F a <范围 x a ≥,y R ∈y a ≥,x R ∈对称轴x 轴 ,y 轴;实轴长为2a ,虚轴长为2b对称中心 原点(0,0)O焦点坐标1(,0)F c - 2(,0)F c1(0,)F c - 2(0,)F c焦点在实轴上,22c a b =+;焦距:122F F c =顶点坐标(a -,0) (a ,0) (0, a -,) (0,a )离心率 e a ce (=>1)渐近线方程x a b y ±=x bay ±= 共渐近线的双曲线系方程k by a x =-2222(0k ≠) k bx a y =-2222(0k ≠) xyP1F 2FxyxyP1F 2F xy知识点一. 双曲线的定义1、 当|MF 1|-|MF 2|=2a 时,则表示点M 在双曲线右支上;2、当a MF MF 212=-时,则表示点M 在双曲线左支上;注意:1、定义中的“(小于12F F )”这一限制条件,其根据是“三角形两边之和之差小于第三边”。
2、 若2a =2c 时,即2121F F MF MF =-,当2121F F MF MF =-,动点轨迹是以2F 为端点向右延伸的一条射线;当2112F F MF MF =-时,动点轨迹是以1F 为端点向左延伸的一条射线;若2a >2c 时,动点轨迹不存在.知识点二.双曲线的标准方程判别方法是: 如果2x 项的系数是正数,则焦点在x 轴上; 如果2y 项的系数是正数,则焦点在y 轴上.对于双曲线,a 不一定大于b ,因此不能像椭圆那样,通过比较分母的大小来判断焦点在哪一条坐标轴上.【例题精讲】例1、双曲线x 210-y 22=1的焦距为( )A .32B .4 2C .3 3D .4 3例2.双曲线的两焦点坐标是F 1(3,0),F 2(-3,0),2b =4,则双曲线的标准方程是( )A.x 25-y 24=1B.y 25-x 24=1C.x 23-y 22=1D.x 29-y 216=1例3、双曲线的实轴长与虚轴长之和等于其焦距的2倍,且一个顶点的坐标为(0,2),则双曲线的标准方程为( )A .x 24-y 24=1B .y 24-x 24=1 C .x 28-y 24=1 D .y 28-x 24=1【同步练习】1.已知双曲线的焦点在x轴上,且a+c=9,b=3,则它的标准方程是________.2.P是双曲线x2-y2=16的左支上一点,F1,F2分别是它的左,右焦点,则|PF1|-|PF2|=________.3、若动点P到F1(-5,0)与到F2(5,0)的距离的差为±8,则P点的轨迹方程是()A.x225+y216=1 B.x225-y216=1 C.x216+y29=1 D.x216-y29=14.已知两定点F1(-5,0),F2(5,0),动点P满足|PF1|-|PF2|=2a,则当a=3和a=5时,P点的轨迹为()A.双曲线和一条直线B.双曲线和一条射线C.双曲线的一支和一条射线D.双曲线的一支和一条直线5.已知椭圆C1的离心率为35,焦点在x轴上且长轴长为10,若曲线C2上的点到椭圆C1的两个焦点的差的绝对值等于4,则曲线C2的标准方程为()A.x24-y25=1 B.x25-y24=1 C.x252-y242=1 D.x242-y252=16、若双曲线x216-y29=1上的点P到点(5,0)的距离是15,则点P到点(-5,0)的距离是()A.7 B.23 C.5或25 D.7或237、已知双曲线的焦距为26,a2c=2513,则双曲线的标准方程是________.8、“ab <0”是“方程ax 2+by 2=c 表示双曲线”的________条件.专题精讲【例题精讲】例1.已知双曲线x 23-y 2m =1的离心率e =233,则实数m 的值是________.例2、设双曲线x 2a 2-y 2b 2=1(a >0,b >0)的虚轴长为2,焦距为23,则双曲线的渐近线方程为( )A .y =±2xB .y =±2xC .y =±22x D .y =±12x例3、双曲线的焦点在y 轴上,且它的一个焦点在直线5x -2y +20=0上,两焦点关于原点对称,离心率e =53,则此双曲线的方程是( )A.x 236-y 264=1 B.x 264-y 236=1 C.x 236-y 264=-1 D.x 264-y 236=-1例4、若双曲线x 2a 2-y 23=1(a >0)的离心率为2,则a 等于( )A .2 B. 3 C.32 D .1【同步练习】1、设双曲线x 2a 2-y 29=1(a>0)的渐近线方程为3x ±2y =0,则a 的值为( )A .4B .3C .2D .12、双曲线22149x y -=的渐近线方程是( ) (A )23y x =± (B )49y x =± (C )32y x =± (D )94y x =±3、双曲线12222=-ay b x 的两条渐近线互相垂直,那么该双曲线的离心率是( )A .2B .3C .2D .234、已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线方程为( )(A )112422=-y x (B )141222=-y x (C )161022=-y x (C )110622=-y x5、如图,1F 和2F 分别是双曲线)0,0(12222 b a br a x =-的两个焦点,A 和B 是以O 为圆心,以1F O 为半径的圆与该双曲线左支的两个交点,且△AB F 2是等边三角形,则双曲线的离心率为( )(A )3 (B )5 (C )25(D )31+6、已知双曲线22112x y n n-=-的离心率是3。
高中数学讲义:解析几何专题双曲线(解析版)

圆锥曲线第2讲 双曲线【知识要点】 一、双曲线的概念 1. 双曲线的第一概念:平面内到两个定点、的距离之差的绝对值等于定长()的点的轨迹叫双曲线,这两个定点叫做双曲线的核心,两个核心之间的距离叫做焦距。
注1:在双曲线的概念中,必需强调:到两个定点的距离之差的绝对值(记作),不但要小于这两个定点之间的距离(记作),而且还要大于零,不然点的轨迹就不是一个双曲线。
具体情形如下:(ⅰ)当时,点的轨迹是线段的垂直平分线; (ⅱ)当时,点的轨迹是两条射线; (ⅲ)当时,点的轨迹不存在; (ⅳ)当时,点的轨迹是双曲线。
专门地,假设去掉概念中的“绝对值”,那么点的轨迹仅表示双曲线的一支。
注2:假设用M 表示动点,那么双曲线轨迹的几何描述法为(,),即。
2. 双曲线的第二概念:平面内到某必然点的距离与它到定直线的距离之比等于常数()的点的轨迹叫做双曲线。
二、双曲线的标准方程 1. 双曲线的标准方程(1)核心在轴、中心在座标原点的双曲线的标准方程是(,); (2)核心在轴、中心在座标原点的双曲线的标准方程是(,).注:假设题目已给出双曲线的标准方程,那其核心究竟是在轴仍是在轴,要紧看实半轴跟谁走。
假设实半轴跟走,那么双曲线的核心在轴;假设实半轴跟走,那么双曲线的核心在轴。
2. 等轴双曲线当双曲线的实轴与虚轴等长时(即),咱们把如此的双曲线称为等轴双曲线,其标准方程为()注:假设题目已明确指出所要求的双曲线为等轴双曲线,那么咱们可设该等轴双曲线的方程为(),再结合其它条件,求出的值,即可求出该等轴双曲线的方程。
进一步讲,假设求得的,那么该等轴双曲线的核心在轴、中心在座标原点;假设求得的,那么该等轴双曲线的核心在轴、中心在座标原点。
三、双曲线的性质以标准方程(,)为例,其他形式的方程可用一样的方式取得相关结论。
(1)范围:,即或;1F 2F a 22120F F a <<a 221F F c 202=a 21F F c a 22=c a 22>c a 220<<a MF MF 221=-ca 220<<c F F 221=2121F F MF MF <-e 1>e x 12222=-b y a x 0>a 0>b y 12222=-b x a y 0>a 0>b x yx x y yb a 22=λ=-22y x 0≠λλ=-22y x 0≠λλ0>λx 0<λy 12222=-b y a x 0>a 0>b ax ≥a x ≥a x -≤(2)对称性:关于轴、轴轴对称,关于坐标原点中心对称;(3)极点:左、右极点别离为、; (4)核心:左、右核心别离为、; (5)实轴长为,虚轴长为,焦距为;(6)实半轴、虚半轴、半焦距之间的关系为;(7)准线:; (8)焦准距:;(9)离心率:且. 越小,双曲线的开口越小;越大,双曲线的开口越大;(10)渐近线:; (11)焦半径:假设为双曲线右支上一点,那么由双曲线的第二概念,有,;(12)通径长:.注1:双曲线(,)的准线方程为,渐近线方程为。
高二数学双曲线讲义
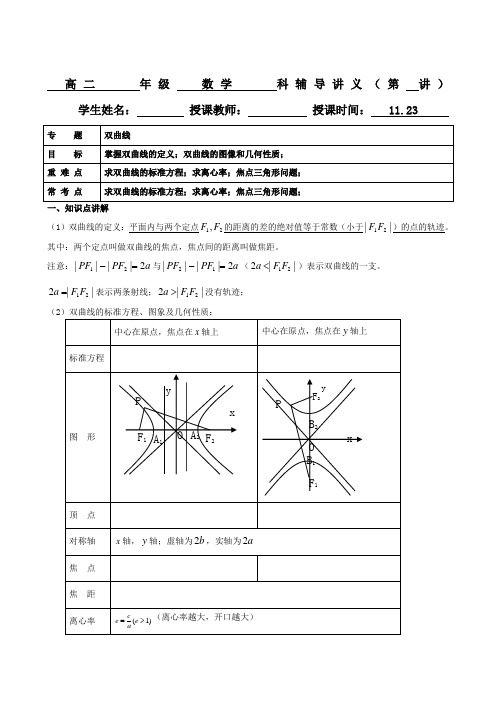
高二 年级 数学 科辅导讲义(第 讲)学生姓名: 授课教师: 授课时间: 11.23一、知识点讲解(1)双曲线的定义:平面内与两个定点21,F F 的距离的差的绝对值等于常数(小于||21F F )的点的轨迹。
其中:两个定点叫做双曲线的焦点,焦点间的距离叫做焦距。
注意:a PF PF 2||||21=-与a PF PF 2||||12=-(||221F F a <)表示双曲线的一支。
||221F F a =表示两条射线;||221F F a >没有轨迹;(2)双曲线的标准方程、图象及几何性质:渐近线通 径(3)双曲线的渐近线:①求双曲线12222=-b y a x 的渐近线,可令其右边的1为0,即得02222=-b y a x ,因式分解得到0x y a b±=。
②与双曲线12222=-b y a x 共渐近线的双曲线系方程是λ=-2222by a x ;(4)等轴双曲线为222t y x =-,其离心率为2(4)常用结论:(1)双曲线)0,0(12222>>=-b a b y a x 的两个焦点为21,F F ,过1F 的直线交双曲线的同一支于B A ,两点,则2ABF ∆的周长=(2)设双曲线)0,0(12222>>=-b a by a x 左、右两个焦点为21,F F ,过1F 且垂直于对称轴的直线交双曲线于Q P ,两点,则Q P ,的坐标分别是 =||PQ二、例题讲解。
例1、如图,1F 和2F 分别是双曲线)0,0(12222>>=-b a by a x 的两个焦点,A 和B 是以O 为圆心,以1F O 为半径的圆与该双曲线左支的两个交点,且△AB F 2是等边三角形,则双曲线的离心率为( )(A )3 (B )5 (C )25(D )31+ 例2、设P 为双曲线22112y x -=上的一点,12F F ,是该双曲线的两个焦点,若12||:||3:2PF PF =,则12PF F △的面积为( )A .63B .12 C.123 D .24例3、已知中心在原点,顶点A 1、A 2在x 轴上,离心率e=321的双曲线过点P(6,6)(1)求双曲线方程(2)动直线l 经过△A 1PA 2的重心G ,与双曲线交于不同的两点M 、N ,问 是否存在直线l,使G 平分线段MN ,证明你的结论 同步练习XYOF 1F 2P 2r1. 如果双曲线2422y x -=1上一点P 到双曲线右焦点的距离是2,那么点P 到y 轴的距离是( ) (A)364 (B)362 (C)62 (D)322. 已知双曲线C ∶22221(x y a a b-=>0,b >0),以C 的右焦点为圆心且与C 的渐近线相切的圆的半径是(A )a(B)b(C)ab(D)22b a +3. 以双曲线221916x y -=的右焦点为圆心,且与其渐近线相切的圆的方程是( ) A 221090x y x +-+= B .2210160x y x +-+= C .2210160x y x +++= D .221090x y x +++= 4. 以双曲线222x y -=的右焦点为圆心,且与其右准线相切的圆的方程是( )A.22430x y x +--= B.22430x y x +-+= C.22450x y x ++-=D.22450x y x +++=5. 若双曲线22221x y a b -=(a >0,b >0)上横坐标为32a的点到右焦点的距离大于它到左准线的距离,则双曲线离心率的取值范围是( )A.(1,2)B.(2,+∞)C.(1,5)D. (5,+∞)6. 若双曲线12222=-by a x 的两个焦点到一条准线的距离之比为3:2那么则双曲线的离心率是( )(A )3 (B )5 (C )3 (D )57. 已知双曲线)0(12222>=-b b y x 的左、右焦点分别是1F 、2F ,其一条渐近线方程为x y =,点),3(0y P 在双曲线上.则12PF PF ⋅=( )A. -12B. -2C. 0D. 4 填空题8. 过双曲线221916x y -=的右顶点为A ,右焦点为F 。
第五节 双曲线 复习讲义

第五节双曲线一、双曲线的定义平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线,这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.1.概念理解(1)双曲线定义的集合语言P={M|||MF 1|-|MF 2||=2a,0<2a<|F 1F 2|},当2a=0时,点M 的轨迹是线段F 1F 2的中垂线,当2a=2c 时,点M 的轨迹是以F 1,F 2为端点的两条反向射线.(2)双曲线定义中的条件“差的绝对值”,在运用定义解题时,弄清题意是指整个双曲线还是双曲线的某一支. 2.与定义相关的结论(1)双曲线22x a -22y b =1(a>0,b>0)的左、右焦点分别为F 1,F 2,点P 为双曲线上任意一点,∠F 1PF 2=θ,则cos θ=1-2122b PF PF ⋅.(2) 12PF F S∆=12|PF 1|·|PF 2|·sin θ=12·221cos b θ-·sin θ=2sin 1cos b θθ⋅-=2tan2b θ=c ·|y 0|.(其中y 0是点P 纵坐标)二、双曲线的标准方程及简单几何性质1.概念理解(1)双曲线标准方程中,若x2或y2项系数为正⇒该项系数的分母为a2⇒焦点所在轴与该项变量名称相同.(2)在双曲线中,b2=c2-a2,c最大,可以有a大于、等于或小于b的情况,这一点与椭圆中不同,应注意区分.(椭圆中a最大,b2=a2-c2,a>b,a>c) (3)双曲线中以二次项系数正负确定a2,椭圆中以二次项分母大小确定a2.2.与之相关结论(1)等轴双曲线的定义及性质实轴和虚轴等长的双曲线叫做等轴双曲线,其方程为x 2-y 2=λ(λ≠0),离心率渐近线方程为y=±x.它们互相垂直,并且平分实轴和虚轴所成的角.(2)与22x a -22y b =1共渐近线的双曲线为22x a -22y b =λ(λ≠0). 22x a -22y b =λ渐近线22x a -22y b =0(或y=±b a x 或x a ±y b=0).(3)不知双曲线焦点位置时,常设双曲线方程为Ax 2-By 2=1(A ·B>0).与22x a -22y b =1离心率相同的双曲线方程可设为22x a -22y b =k(k>0).(4)双曲线22x a -22y b =1(a>0,b>0)与直线Ax+By+c=0有公共点的充要条件是A 2a 2-B 2b 2≤c 2.过焦点与实轴所在直线垂直的弦长为定值22ba .1.已知方程23x k -+25y k -=1表示双曲线,则k 的取值范围为( B )(A)(-∞,3)∪(5,+∞) (B)(3,5) (C)(3,4)∪(4,5) (D)(4,5) 解析:由方程表示双曲线可知(k-3)(k-5)<0, 解得3<k<5.故选B.2.已知双曲线C:22x a -22yb =1(a>0,b>0),右焦点F 到渐近线的距离为2,点F 到原点的距离为3,则双曲线C 的离心率e 为( B )(解析:因为右焦点F 到渐近线的距离为2,所以F(c,0)到y=b ax 的距离为2,又b>0,c>0,a 2+b 2=c 2,所以bc c=b=2.因为点F 到原点的距离为3,所以c=3,所以所以离心率e=ca 故选B.3.已知F 1,F 2是双曲线C:22x a -22y b =1(a>0,b>0)的两个焦点,P 是C 上一点,若|PF 1|+|PF 2|=6a,且△PF 1F 2最小内角的大小为30°,则双曲线C 的渐近线方程是( A )±y=0 (B)x (C)x ±2y=0 (D)2x ±y=0解析:由题意,不妨设|PF 1|>|PF 2|,则根据双曲线的定义得,|PF 1|-|PF 2|=2a,又|PF 1|+|PF 2|=6a,解得|PF 1|=4a,|PF 2|=2a.在△PF 1F 2中,|F 1F 2|=2c,而c>a,所以有|PF 2|<|F 1F 2|,所以∠PF 1F 2=30°,所以(2a)2=(2c)2+(4a)2- 2·2c ·4acos 30°,得所以所以双曲线的渐近线方程为y=±bax=±y=0.故选A.4.已知双曲线2xa-22y =1的一个焦点坐标为,0),则其渐近线方程为 . 解析:由a+2=3,可得a=1, 所以双曲线方程为x 2-22y =1, 所以其渐近线方程为y=答案:y=5.若双曲线2y m-x 2=1的一个焦点为(0,2),则m= ,该双曲线的渐近线方程为 . 解析:由m+1=4得m=3, 所以渐近线方程为y=答案:3 y=考点一 双曲线定义及其标准方程【例1】 (1)已知双曲线C:22x a -22y b =1(a>0,b>0)的离心率e=54,且其右焦点F 2(5,0),则双曲线C 的方程为( ) (A)24x -23y =1(B)216x -29y =1(C)29x - 216y=1 (D)23x -24y =1(2)已知F 1,F 2分别为双曲线C:x 2-y 2=1的左、右焦点,点P 在双曲线C 上,且∠F 1PF 2=60°,则|PF 1||PF 2|= .解析:(1)因为所求双曲线的右焦点为F 2(5,0)且离心率为e=c a =54,所以c=5,a=4,b 2=c 2-a 2=9,所以所求双曲线方程为216x -29y =1,故选B.解析:(2)由题意知所以|F1F 2在△PF 1F 2中,由余弦定理得|PF 1|2+|PF 2|2-2|PF 1||PF 2|cos 60°=|F 1F 2|2=8, 即|PF 1|2+|PF 2|2-|PF 1||PF 2|=8, ① 由双曲线定义得||PF 1|-|PF 2||=2a=2, 两边平方得|PF 1|2+|PF 2|2-2|PF 1||PF 2|=4, ② ①-②得|PF 1||PF 2|=4. 答案:(1)B 答案:(2)4(1)运用双曲线定义解题的两个注意点①在解决与双曲线的焦点有关的距离问题时,通常考虑利用双曲线的定义;②在运用双曲线的定义解题时,应特别注意定义中的条件“差的绝对值”,弄清楚是指整条双曲线还是双曲线的一支. (2)求双曲线的标准方程的基本方法是待定系数法①若已知双曲线的焦点位置可设双曲线的标准方程,再根据a,b,c,e 及渐近线之间的关系,求出a,b 的值.②若不能确定焦点位置,则可设双曲线方程为Ax 2+By 2=1(AB<0),根据条件求出A,B.③若已知双曲线的渐近线方程,可利用有公共渐近线的双曲线方程为22x a -22y b =λ(λ≠0),再由条件求出λ的值即可.1.设P是双曲线216x -220y =1上一点,F 1,F 2分别是双曲线左、右两个焦点,若|PF 1|=9,则|PF 2|等于( B ) (A)1 (B)17(C)1或17 (D)以上答案均不对 解析:由双曲线定义||PF 1|-|PF 2||=8, 又|PF 1|=9,所以|PF 2|=1或17, 又c-a=6-4=2>1, 所以|PF 2|=17.故选B. 2.已知双曲线C:22x a -22y b =1(a>0,b>0)的右焦点为F,点B 是虚轴的一个端点,线段BF 与双曲线C 的右支交于点A,若BA =2AF ,且|BF |=4,则双曲线C 的方程为( D ) (A)26x -25y =1 (B)28x -212y =1(C)28x -24y =1 (D)24x -26y =1解析:不妨设B(0,b),由BA =2AF ,F(c,0), 可得A(23c,3b ),代入双曲线C的方程可得49×22c a -19=1,即49·222a b a +=109, 所以22b a =32. ① 又|BF =4,c 2=a 2+b 2,所以a 2+2b 2=16, ② 由①②可得,a 2=4,b 2=6,所以双曲线C 的方程为24x -26y =1,故选D. 考点二 双曲线的离心率 【例2】 (1)双曲线22x a -22y b =1(a>0,b>0)的左、右焦点分别是F 1,F 2,过F 1作倾斜角为30°的直线交双曲线右支于点M,若MF 2垂直于x 轴,则双曲线的离心率为( )(2)设直线l:x-3y+m=0(m ≠0)与双曲线22x a -22yb =1(a>0,b>0)的两条渐近线分别交于点A,B,若点P(m,0)满足|PA|=|PB|,则该双曲线的离心率是 .解析:(1)在Rt △MF 1F 2中,|F 1F 2|=2c, 则|MF 21,由双曲线定义可知|MF 1|-|MF 2|=2a,=2a,化简得c a故选A.解析:(2)如图,设线段AB 的中点为M,由题意得, 直线l:x-3y+m=0垂直于直线PM, 双曲线的两渐近线为bx ±ay=0, 分别与x-3y+m=0联立,解得B(3am b a +,3bm b a +),A(3am b a --,3bm b a-). 所以AB 的中点M(2229a m b a -,22239b m b a -).由MP ⊥l 得,222222399b m b a a m b a --=-3,化简为a 2=4b 2.所以e2=22c a =222a b a +=2254b b =54.所以答案:(1)A(1)求双曲线的离心率即是求c 与a 的比值,只需根据条件列出关于a,b,c 的方程或不等式即可解决,并且需注意e>1.(2)双曲线的离心率与渐近线斜率的关系①已知双曲线的离心率e 求渐近线方程要注意在的坐标轴;②已知渐近线方程y=mx(m>0)求离心率时,若焦点位置不确定,则m=b a或m=a b,因此离心率有两种可能.(3)已知双曲线方程22x a -22y b =1(a>0,b>0)或22y a -22x b =1(a>0,b>0)求其渐近线方程只需把1改写为0整理即可.已知O 为坐标原点,F 是双曲线Γ:22x a -22y b =1(a>0,b>0)的左焦点,A,B分别为Γ的左、右顶点,P 为Γ上一点,且PF ⊥x 轴,过点A 的直线l 与线段PF 交于点M,与y 轴交于点E,直线BM 与y 轴交于点N,若|OE|=2|ON|,则Γ的离心率为( A )(A)3 (B)2 (C)32 (D)43解析: 易证得△MFA ∽△EOA,则MF FA=EO OA,即|MF|=EO FA OA⋅=()EO c a a⋅-;同理△MFB ∽△NOB, |MF|=NO FB OB ⋅=()NO c a a ⋅+, 所以()EO c a a⋅-=()NO c a a⋅+,又|OE|=2|ON|,所以2(c-a)=a+c,整理,得c a =3,故答案为A.考点三 双曲线的渐近线【例3】 (1)过双曲线22x a -22yb =1(a>0,b>0)的左焦点F 作圆O:x 2+y 2=a 2的两条切线,切点为A,B,双曲线左顶点为C,若∠ACB=120°,则双曲线的渐近线方程为( )(A)y=(B)y=x(C)y=(D)y=x(2)过双曲线22x a -22y b =1(a>0,b>0)的左焦点F 1作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为A,B,若1F A =AB ,则双曲线的渐近线方程为 . 解析:(1) 如图所示,连接OA,OB,设双曲线22x a -22x a =1(a>0,b>0)的焦距为2c(c>0),则C(-a,0),F(-c,0).由双曲线和圆的对称性知,点A 与点B 关于x 轴对称,则∠ACO=∠BCO=12∠ACB=12×120°=60°. 因为|OA|=|OC|=a,所以△ACO 为等边三角形,所以∠AOC=60°. 因为FA 与圆O 切于点A,所以OA ⊥FA,在Rt △AOF 中,∠AFO=90°-∠AOF=90°-60°=30°,所以|OF|=2|OA|, 即c=2a, 所以故双曲线22x a -22y b =1(a>0,b>0)的渐近线方程为y=±b ax,即y=故选A.解析:(2)由,y x c b y x a =+⎧⎪⎨=-⎪⎩得x=-aca b+,由,,y x c b y x a =+⎧⎪⎨=⎪⎩解得x=ac b a -,不妨设x A =-ac a b +,x B =acb a -, 由1F A =AB 可得-ac a b ++c=ac b a -+ac a b+, 整理得b=3a.所以双曲线的渐近线方程为3x ±y=0. 答案:(1)A (2)3x ±y=0(1)求渐近线方程的实质是把题目中给出的相互位置关系及数量关系转化为与双曲线中a,b,c,e 相关的等量关系式,结合c 2=a 2+b 2,e2=1+22b a ,求得b a的值即可. (2)双曲线的渐近线是过原点的直线,常用到点到直线距离、直线间平行、相交、垂直等,熟练掌握这些基本问题的解题思路是正确求解的基础.1.已知双曲线22x a -22yb =1(a>0,b>0)与直线y=2x 有交点,则双曲线离心率的取值范围为( C )∞∞)解析:因为双曲线的一条渐近线的方程为y=b ax,则由题意得b a>2,所以e=ca 2. 如图,P 是双曲线24x -y 2=1右支(在第一象限内)上的任意一点,A 1,A 2分别是左、右顶点,O 是坐标原点,直线PA 1,PO,PA 2的斜率分别为k 1,k 2,k 3,则斜率之积k 1k 2k 3的取值范围是 .解析:k 1k 3=22b a ,0<k 2<b a ,所以0<k 1k 2k 3<(b a )3=18. 答案:(0,18) 考点四 双曲线综合问题【例4】 (1)(2018·丽水模拟)已知双曲线C: 22x a -22y b =1(a>0,b>0),F是双曲线C 的右焦点,过F 作双曲线C 在第一、三象限的渐近线的垂线l,若l 与双曲线C 的左、右两支分别交于点D,E,则双曲线C 的离心率e 的取值范围为( )∞))(2)设P 是双曲线C:22x a -22y b =1(a>0,b>0)右支上的任意一点,已知A(a,b),B(a,-b),若OP =λOA +μOB (O 为坐标原点),则λ2+μ2的最小值为( )(A)14ab (B)14(C)12ab (D)12解析:(1)法一 由题意知,直线l:y=-a b(x-c),设D(x 1,y 1),E(x 2,y 2),由222222(),,a y x c bb x a y a b ⎧=--⎪⎨⎪-=⎩得(b2-42a b )x2+422a c b x-(42a cb +a 2b 2)=0,由x 1x 2=42222422()a c a b ba b b-+-<0得b 4>a 4,所以b 2=c 2-a 2>a 2, 所以e 2>2,得故选B.法二 由题意,知直线l 的斜率为-ab ,若l 与双曲线左、右两支分别交于D,E 两点,则-a b >-b a,即a 2<b 2,所以a 2<c 2-a 2,e 2>2,得故选B.解析:(2)由题意,设P(x,y),则 因为OP =λOA +μOB ,所以x=(λ+μ)a,y=(λ-μ)b, 因为P 为双曲线C 右支上的任意一点, 所以(λ+μ)2-(λ-μ)2=1, 所以4λμ=1, 所以λ2+μ2≥2λμ=12, 所以λ2+μ2的最小值为12. 故选D.(1)涉及曲线与圆、抛物线等位置关系问题,常结合图形,把条件中隐含的位置关系、等量关系对应的几何性质挖掘出来,借助平面几何的相关知识求解.(2)向量在解析几何中常起到中间桥梁作用,可化为线段间的关系,也可转化为坐标间的关系,具体视情况而定.F 1,F 2分别是双曲线216x -29y =1的左、右焦点,P 为双曲线右支上一点,☉A是△PF 1F 2的内切圆,☉A 与x 轴相切于点M(m,0),则m 的值为 .解析: 如图所示,F 1(-5,0), F 2(5,0),内切圆与x 轴的切点是M,PF 1,PF 2与内切圆的切点分别为N,H, 由双曲线的定义可得 |PF 1|-|PF 2|=2a=8, 由圆的切线长定理知 |PN|=|PH|, 故|NF 1|-|HF 2|=8, 即|MF 1|-|MF 2|=8,故(m+5)-(5-m)=8, 所以m=4. 答案:4类型一 双曲线的定义及标准方程1.已知动圆与☉C 1:(x+3)2+y 2=9外切,且与☉C 2:(x-3)2+y 2=1内切,则动圆圆心M 的轨迹方程为( B ) (A)24x -25y =1 (B)24x -25y =1(x ≥2) (C)25y -24x =1 (D)25y -24x =1(y ≥2)解析:设动圆半径为r,因为☉M 与☉C 1外切,且与☉C 2内切, 所以|MC 1|=r+3,|MC 2|=r-1,|MC 1|-|MC 2|=4, 所以点M 的轨迹是以C 1,C 2为焦点的双曲线的右支, 且有a=2,c=3,b 2=c 2-a 2=5,所以所求双曲线的方程为24x -25y =1(x ≥2).2.过双曲线C:22x a -22yb =1(a>0,b>0)的右顶点作x 轴的垂线,与C 的一条渐近线相交于点A.若以C 的右焦点为圆心、4为半径的圆经过A,O 两点(O 为坐标原点),则双曲线C 的方程为( A )(A)24x -212y =1 (B)27x -29y =1(C)28x -28y =1(D)212x -24y =1解析:由,,x a b y x a =⎧⎪⎨=-⎪⎩得,,x a y b =⎧⎨=-⎩所以A(a,-b).由题意知右焦点到原点的距离为c=4,即(a-4)2+b 2=16.而a 2+b 2=16,所以所以双曲线C 的方程为24x -212y =1.故选A. 3.如图所示,F 1,F 2是双曲线22x a -224y=1的左、右焦点,过F 1的直线与双曲线分别交于点A,B,若△ABF 2为等边三角形,则△BF 1F 2的面积为( C ) (A)8(D)16解析:由双曲线的定义可知|BF 2|-|BF 1|=2a,|AF 1|-|AF 2|=2a. 又△ABF 2是等边三角形,所以|AF 1|-|AF 2|=|AF 1|-|AB|=|BF 1|=2a, 所以|BF 2|=4a.在△AF 1F 2中,|AF 1|=6a,|AF 2|=4a,|F 1F 2|=2c, ∠F 1AF 2=60°,所以4c 2=36a 2+16a 2-2·6a ·4a ·cos 60°, 即c 2=7a 2,所以b 2=c 2-a 2=6a 2=24, 所以a 2=4, 所以12BF F S=12·2a ·4a ·sin 120°2故选C.4.已知F 1,F 2为双曲线C:x 2-y 2=2的左、右焦点,点P 在C 上,|PF 1|=2|PF 2|,则cos ∠F 1PF 2等于( C ) (A)14(B)35(C)34(D)45解析:由双曲线的定义有c=2, 且|PF1|-|PF 2|=|PF 2所以|PF1|=2|PF 2则cos ∠F 1PF 2=2221212122PF PF F F PF PF +-⋅=34. 5.已知△ABP 的顶点A,B分别为双曲线216x -29y =1的左、右焦点,顶点P在双曲线上,则sin sin sin A BP-的值等于( A )(A)45 (C)54解析:在△ABP 中,由正弦定理知sin sin sin A B P-=PB PA AB-=22a c =810=45. 类型二 双曲线的离心率 6.(2018·湖州模拟)设点P是双曲线22x a -22y b =1(a>0,b>0)与圆x 2+y 2=a 2+b 2在第一象限的交点,F 1,F 2分别是双曲线的左、右焦点,且|PF 1|=3|PF 2|,则双曲线的离心率为( D )解析:点P 到原点的距离为又因为在△PF 1F 2中,|F 1F 2|=2c=2|PO|,所以△PF 1F 2是直角三角形,即∠F 1PF 2=90°.由双曲线定义知|PF 1|-|PF 2|=2a,又因为|PF 1|=3|PF 2|,所以|PF 1|=3a.在Rt △PF 1F 2中,由勾股定理得(3a)2+a 2=(2c)2,解得c a故选D.7.(2018·全国Ⅲ卷)设F 1,F 2是双曲线C:22x a -22y b =1(a>0,b>0)的左、右焦点,O 是坐标原点.过F 2作C 的一条渐近线的垂线,垂足为P.若|PF 1则C 的离心率为( C )(B)2解析: 如图,过点F 1向OP 的反向延长线作垂线,垂足为P ′,连接P ′F 2,由题意可知,四边形 PF 1P ′F 2 为平行四边形,且△PP ′F 2是直角三角形.因为|F 2P|=b,|F 2O|=c,所以|OP|=a. 又|PF 12P ′|,|PP ′|=2a,所以|F 2所以a,所以e=ca.故选C.8.已知双曲线22x a -22y b =1(a>0,b>0)的左、右两个焦点分别为F 1,F 2,以线段F 1F 2为直径的圆与双曲线的渐近线在第一象限的交点为M,若|MF 1|-|MF 2|=2b,该双曲线的离心率为e,则e 2= . 解析:由题意,圆的方程为x 2+y 2=c 2,联立222,,x y c b y x a ⎧+=⎪⎨=⎪⎩得2222,,x a y b ⎧=⎪⎨=⎪⎩即点M(a,b),则|MF 1|-|MF 2即化简得,e4-e 2-1=0,解得e 2.答案 类型三 双曲线的渐近线9.设双曲线22xa -29y =1(a>0)的渐近线方程为3x ±2y=0,则a 的值为( C )(A)4 (B)3 (C)2 (D)1解析:由题意得3a =32,所以a=2.10.双曲线24x -y 2=1的顶点到渐近线的距离等于( C )(A)25 (B)45 解析:双曲线的右顶点为(2,0),渐近线方程为x ±2y=0,则顶点到渐近.11.设双曲线22x a -22y b =1(a>0,b>0)的右焦点为F,右顶点为A,过F 作AF的垂线与双曲线交于B,C 两点,过B,C 分别作AC,AB 的垂线,两垂线交于点D.若D 到直线BC 的距离小于则该双曲线的渐近线斜率的取值范围是( A ) (A)(-1,0)∪(0,1) (B)(-∞,-1)∪(1,+∞)∪(D)(-∞∪∞)解析:由题知F(c,0),A(a,0),不妨令B 点在第一象限,则B(c,2b a),C(c,-2b a),k AB =2()b ac a -,因为CD ⊥AB,所以k C D =2()a a c b -,所以直线CD 的方程为y+2b a =2()a a c b - (x-c),由双曲线的对称性,知点D 在x 轴上, 得x D =42()b ac a -+c,点D 到直线BC 的距离为c-x D ,所以42()b ac a -4<a 2(c-a)·(c+a)=a 2·b 2,b 2<a 2,(b a)2<1,又该双曲线的渐近线的斜率为b a或-b a,所以双曲线渐近线斜率的取值范围是(-1,0)∪(0,1).故选A. 类型四 双曲线中综合问题12.已知双曲线22x a -22y b =1的渐近线与圆x 2+(y-2)2=1相交,则该双曲线的离心率的取值范围是( C ),+∞(C)(2,+∞) (D)(1,2)解析:因为双曲线渐近线为bx ±ay=0, 与圆x 2+(y-2)2=1相交,所以圆心到渐近线的距离小于半径,所以2a<c,所以e=ca >2,故选C. 13.双曲线C:22x a -22y b =1(a>0),A(x 1,y 1),B(x 2,y 2)两点在双曲线上,且x 1≠x 2.若线段AB 的垂直平分线经过点Q(4,0),则AB 中点的横坐标为( B ) (A)1 (B)2解析:设AB 中点为P(x 0,y 0),则点差法得k AB ·00yx =1,所以AB 的中垂线斜率为-00y x ,则04y x --=-0y x 得x 0=2,所以AB 中点的横坐标为2.故选B. 14.平面直角坐标系xOy 中,双曲线C 1:22x a -22y b =1(a>0,b>0)的渐近线与抛物线C 2:x 2=2py(p>0)交于点O,A,B.若△OAB 的垂心为C 2的焦点,则C 1的离心率为 .解析:设点A 在点B 左侧,抛物线C 2的焦点为F,则F(0,2p).联立得22,x py b y x a ⎧=⎪⎨=-⎪⎩和22,,x py by x a ⎧=⎪⎨=⎪⎩分别解得A(-2bpa ,222b p a ),B(2bpa ,222b p a ).因为F 为△OAB 的垂心, 所以AF ⊥OB, 所以k AF ·k OB =-1, 即22222b p pa bp a--·ba=-1⇒4b 2=5a 2⇒4(c 2-a 2)=5a 2⇒22c a =94, 所以e=c a =32.答案:32。
双曲线高二数学专题复习培优讲义

第02讲双曲线必备方法巧设双曲线方程:(1)与双曲线22221x y a b-=(a >0,b >0)有共同渐近线(离心率)的方程可表示为:2222(0)x y t t a b -=≠.有共同焦距的双曲线方程可表示为:22221x y a b λλ-=+-.(2)过已知两个点的双曲线方程可设为()2210mx ny mn +=<.易误提醒(1)双曲线的标准方程中对a ,b 的要求只是a >0,b >0易误认为与椭圆标准方程中a ,b 的要求相同.若a >b >0,则双曲线的离心率e ∈(;若a =b >0,则双曲线的离心率e ;若0<a <b ,则双曲线的离心率e >.当焦点在x 轴上,渐近线斜率为ba±,当焦点在y 轴上,渐近线斜率为a b±.(2)注意区分双曲线与椭圆中的a ,b ,c 的大小关系:在椭圆中222a b c =+,而在双曲线中222c a b =+.(3)易忽视渐近线的斜率与双曲线的焦点位置关系.当焦点在x 轴上,渐近线斜率为b a ±,当焦点在y 轴上,渐近线斜率为a b±.(4)在双曲线的焦点三角形12PF F 中,12F PF α∠=,点P 的坐标为00()x y ,,12PF F ∆的面积122=tan2PF F b S α△.考点一双曲线的定义及标准方程命题点1利用双曲线定义求轨迹方程例题1.1已知圆221:(3)1C x y ++=和圆222:(3)9C x y -+=,动圆M 同时与圆1C 及圆2C 相外切,则动圆圆心M 的轨迹方程为()A .2218y x -=B .221(1)8y x x -=≤-C .2218x y +=D .221(1)8y x x -=≥命题点2双曲线定义的应用例题1.2过双曲线2213y x -=的右支上一点P 分别向圆1C :22(2)4x y ++=和圆2C :22(2)1x y -+=作切线,切点分别为,M N ,则22||||PM PN -的最小值为()A .5B .4C .3D .2例题1.3(2021·湖南长沙市·长沙一中高三月考)已知椭圆1C 与双曲线2C 的焦点相同,离心率分别为1e ,2e,且满足21e =,1F ,2 F 是它们的公共焦点,P 是椭圆和双曲线在第一象限的交点,若12120F PF ∠=︒,则双曲线2C 的离心率为()ABC .2D规律方法求解双曲线定义及标准方程问题的两个注意点(1)在双曲线的定义中要注意双曲线上的点(动点)具备的几何条件,即“到两定点(焦点)的距离之差的绝对值为一常数,且该常数必须小于两定点的距离”.若定义中的“绝对值”去掉,点的轨迹是双曲线的一支.同时注意定义的转化应用.(2)求双曲线方程时一是标准形式判断;二是注意a ,b ,c 的关系易错易混.变式训练1.1如图,圆E :(x +2)2+y 2=4,点F (2,0),动圆P 过点F ,且与圆E 内切于点M ,求动圆P 的圆心P 的轨迹方程.1变式训练1.2(2018·湖南长沙市·雅礼中学高三月考(文))已知F 是双曲线221412x y -=的左焦点,()1,4A ,P 是双曲线右支上的动点,则PF PA +的最小值为________.变式训练1.3若12,F F 是双曲线221916x y -=的两个焦点.(1)若双曲线上一点M 到它的一个焦点的距离等于16,求点M 到另一个焦点的距离;(2)若P 是双曲线左支上的点,且122||3||F PF P =⋅,试求12F PF ∆的面积.考点二渐近线与离心率问题命题点1渐近线例题2.1已知双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为1F 、2F ,P 为双曲线C 上的一点,若线段1PF 与y 轴的交点M 恰好是线段1PF 的中点,21MF MO b ⋅=,其中,O 为坐标原点,则双曲线C 的渐近线的方程是()A .3y x =±B .2y x =±C .y x=±D .12y x =±命题点2离心率例题2.2(1)(2021·湖南长沙市·雅礼中学高三月考)设双曲线C :22221(0,0)x y a b a b-=>>的左、右焦点分别为1F ,2F ,过1F 直线的l 分别与双曲线左、右两支交于M ,N 两点,且22F M F N ⊥,22F M F N =,则双曲线C 的离心率为___________.(2)已知双曲线()2222:10,0x y C a b a b -=>>的左,右焦点分别为()1,0F c -、()2,0F c ,A ,B 是圆()2224x c y c -+=与C 位于x 轴上方的两个交点(A在左支,B 在右支),且12//F A F B ,则双曲线C 的离心率为()A .23B .43C .34+D .54+命题点3渐近线和离心率的综合应用例题2.3已知0a b >>,椭圆1C 的方程为22221x y a b +=,双曲线2C 方程为22221x y a b -=,1C 与2C 的离心率之积为32,则2C 的渐近线方程为________.规律方法解决有关渐近线与离心率关系问题的方法(1)已知渐近线方程y =mx ,若焦点位置不明确要分|m |=a b 或|m |=ba 讨论.(2)注意数形结合思想在处理渐近线夹角、离心率范围求法中的应用.变式训练2.1已知双曲线C :22219x y a -=(0a >)的左、右焦点分别为1F 、2F ,一条渐近线与直线430x y +=垂直,点M 在C 上,且26MF =,则1MF =()A .2或14B .2C .14D .2或10变式训练2.2已知双曲线2222:1x y C a b-=(0,0)a b >>的两条渐近线均与圆()2224b x a y -+=相切,则双曲线C 的离心率为()A B .2C .3D .4变式训练2.3已知F 为双曲线22221(0,0)x y a b a b-=>>的右焦点,过F 作与x 轴垂直的直线交双曲线于A ,B 两点,若以AB 为直径的圆过坐标原点,则该双曲线的离心率为____________.考点三直线与双曲线的综合应用命题点1直线与双曲线的位置关系例题3.1设离心率为e 的双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为F ,直线l 过焦点F ,且斜率为k ,则直线l 与双曲线C 的左、右两支都相交的充要条件是()A .221k e ->B .221e k ->C .221k e -<D .221e k -<(2)已知直线y =与双曲线()2222:10,0x y C a b a b-=>>有两个交点,则双曲线C 的离心率的取值范围是________.命题点2中点弦问题例题3.2(1)(2017·湖南长沙市·长郡中学高二月考(理))双曲线2221x y -=与直线10x y +-=交于P ,Q 两点,M 为PQ 中点,则OMk 为()A .12-B .2-C .12D .2(2)已知双曲线()222210,0x y a b a b-=>>,斜率为12的直线l 交双曲线于M 、N ,O 为坐标原点,P 为MN 的中点,若OP 的斜率为2,则双曲线的离心率为()A B C .D .4命题点3定点问题例题3.3已知双曲线C 的中心在坐标原点,焦点在x 轴上,离心率2e =,虚轴长为2.(1)求双曲线C 的标准方程;(2)若直线:l y kx m =+与双曲线C 相交于,A B 两点(,A B 均异于左、右顶点),且以AB 为直径的圆过双曲线C 的左顶点D ,求证:直线l 过定点,并求出定点的坐标.规律方法解决直线与双曲线位置关系的两种方法(1)法一:解决此类问题的常用方法是设出直线方程或双曲线方程,然后把直线方程和双曲线方程组成方程组,消元后转化成关于x (或y )的一元二次方程.利用根与系数的关系,整体代入.法二:根据直线的斜率k 与渐近线的斜率的关系来判断直线与双曲线的位置关系.(2)与中点有关的问题常用点差法.直线l 与双曲线22221x y a b-=相交于,A B ,M 为AB 的中点,则22AB OMb k k a⋅=.变式训练3.1已知双曲线2212x y m -=(12)m ≤≤的离心率为e ,直线:2l y x =-,则()A .存在m ,使得2e =B .存在m ,使得直线l 与双曲线右支有一个公共点C .存在m ,使得e =D .存在m ,使得直线l 与双曲线右支有两个公共点变式训练3.2已知直线l :20x y -+=与双曲线C :22221x ya b-=(0a >,0b >)交于A ,B 两点,点()1,4P 是弦AB 的中点,则双曲线C 的离心率为()A .43B .2C D。
双曲线及抛物线(讲义)

双曲线及抛物线(讲义)知识点睛一、双曲线1. 双曲线的标准方程我们把平面内与两个定点1F ,2F 的距离的差的绝对值等于常数(小于12||F F )的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.设()M x y ,是双曲线上任意一点,双曲线的焦距为2(0)c c >, 那么焦点1F ,2F 的坐标分别为(0)c -,,(0)c ,. 又设M 与1F ,2F 的距离的差的绝对值等于常数2a .12{|||||||2}P M MF MFa =-=.因为12|| ||MF MF ==所以2a =±. ①类比建立椭圆标准方程的化简过程,化简①,得22222222()()c a x a y a c a --=-,两边同除以222()a c a -,得222221x y a c a-=-. 由双曲线的定义可知,22220c a c a c a >>->,即,所以.类比椭圆标准方程的建立过程,我们令222c a b -=,其中0b >,代入上式,得22221(00)x y a b a b-=>>,. 双曲线的标准方程:22221(0 0)x y a b a b,-=>>.2.双曲线的几何性质R R对称轴二、抛物线1.抛物线的标准方程我们把平面内与一个定点F和一条定直线l(l不经过点F)距离相等的点的轨迹叫做抛物线.点F 叫做抛物线的焦点,直线l 叫做抛物线的准线.设||(0)KF p p =>,那么焦点F 的坐标为(0)2p ,,准线l 的方程为2px =-.设()M x y ,d . 由抛物线的定义,抛物线就是点的集合{|||}P M MF d==.因为||||2pMF d x ==+,所以||2px =+.将上式两边平方并化简,得22(0)y px p =>.抛物线的标准方程:22(0)y px p =>.2. 抛物线的几何性质1.写出适合下列条件的双曲线的标准方程:(1)焦点在x轴上,4a=,3b=;(2)焦点在x轴上,经过点(,3;(3)焦点为(06)-,,(06),,且经过点(25)-,.2.双曲线22221(00)x ya ba b-=>>,与2222(0)x ya bλλ-=≠有相同的()A.实轴B.焦点C.渐近线D.以上都不对3.已知双曲线22221(00)x ya ba b-=>>,的一条渐近线方程是y=,它的一个焦点在直线6x=-上,则双曲线的方程为()A.22136108x y-=B.221927x y-=C.22110836x y-=D.221279x y-=4.若双曲线22221(00)x ya ba b-=>>,,则其渐近线方程为()A.2y x=±B.y=C.12y x=±D.y x=5. 已知F 为双曲线C :221916x y -=的左焦点,P ,Q 为C 上的点. 若PQ 的长等于虚轴长的2倍,点(5 0)A ,在线段PQ 上, 则△PQF 的周长为__________.6. 已知F 是双曲线221412x y -=的左焦点,P 是双曲线右支上的动点,若(1 4)A ,,则||||PF PA +的最小值是__________.7. 如图,1F ,2F 是椭圆221 +14x C y =:与双曲线2C 的公共焦点, 点A ,B 分别是1C ,2C 在第二、四象限的公共点.若四边形12AF BF 为矩形,则2C 的离心率是( ) ABC .32D.28. 如图,圆O 的半径为定长r ,A 是圆O 外一个定点,P 是圆上任意一点.线段AP 的垂直平分线l 和直线OP 相交于点Q ,当点P 在圆上运动时,点Q 的轨迹是什么?9.点()M x y,到定点(5 0)F,的距离和它到定直线l:165x=的距离之比是常数54,求点M的轨迹方程.10.已知双曲线2212yx-=,过点(11)P,能否作一条直线l,与双曲线交于A,B两点,且点P是线段AB的中点?如果能,求出直线l的方程;如果不能,请说明理由.11. 求适合下列条件的抛物线的标准方程:(1)关于x 轴对称,并且经过点(5 4)M -,; (2)准线方程是4x =; (3)焦点是(0 8)F -,;(4)对称轴是x 轴,且顶点与焦点的距离等于6.12. 如图,M 是抛物线212y x =上一点,F 是抛物线的焦点,以Fx 为始边、FM 为终边的角∠xFM =60°,则||FM =__________.13. 如图,已知直线1 4360l x y --=:和直线2 1l x =:,抛物线 24y x =-上一动点P 到直线1l 和直线2l 的距离之和的最小值是( )A.5B .2C .115D .314. 如图,斜率为1的直线l 经过抛物线为24y x =的焦点F ,且与抛物线相交于A ,B 两点,求线段AB 的长.15. 如图,过抛物线28y x =-的焦点F 的直线l 交该抛物线于A ,B 两点,若||6AF =,求BF 的长.16. 如图,已知直线l 与抛物线22(0)y px p =>交于A ,B 两点,且OA ⊥OB ,OD⊥AB 交AB 于点D ,若点D 的坐标为(2 1),,求p 的值.回顾与思考________________________________________________________ ________________________________________________________ ________________________________________________________ 【参考答案】知识点睛一、x轴、y轴原点2a2b2cb y x a=±a y x b=±(1)+∞, 22a b +二、x 轴y 轴2px =-2p x =2p y =-2p y =精讲精练1.(1)221169x y -=;(2)2213y x -=;(3)2212016y x -=2.C 3.B 4.B 5.44 6.97.D8.点Q 的轨迹是以O ,A 为焦点,以r 为实轴长的双曲线9.点M 的轨迹方程是221169x y -=10.不存在满足条件的直线l11.(1)2165y x =;(2)216y x =-;(3)232x y =-;(4)224y x =±12.1213.B14.815.||3BF =16.54p =。
双曲线讲义

双曲线讲义课前双击巩固1.双曲线的定义平面内与两个定点F 1,F 2的 等于常数(小于|F 1F 2|)的点的轨迹叫作双曲线.这两个定点叫作 ,两焦点间的距离叫作 . 集合P={M|||MF 1|-|MF 2||=2a },|F 1F 2|=2c ,其中a ,c 为常数且a>0,c>0. (1)当 时,P 点的轨迹是双曲线; (2)当 时,P 点的轨迹是两条射线; (3)当 时,P 点不存在. 2.标准方程(1)中心在坐标原点,焦点在x 轴上的双曲线的标准方程为x 2a 2-y 2b 2=1(a>0,b>0); (2)中心在坐标原点,焦点在y 轴上的双曲线的标准方程为y 2a2-x 2b 2=1(a>0,b>0).3.双曲线的性质标准方程x 2a2-y 2b2=1(a>0,b>0)y 2a 2-x 2b 2=1(a>0,b>0)图形性质范围 ,y ∈R,x ∈R对称性对称轴:坐标轴.对称中心:原点顶点 A 1 ,A 2 A 1 ,A 2渐近线y=y=离心率e=ca ,e ∈a ,b ,c 的关系c 2= (c>a>0,c>b>0)实、虚轴 线段A 1A 2叫作双曲线的实轴,它的长|A 1A 2|= ;线段B 1B 2叫作双曲线的虚轴,它的长|B 1B 2|= ;a 叫作双曲线的实半轴长,b叫作双曲线的虚半轴长常用结论双曲线的几个常用结论:(1)与双曲线x 2a 2-y 2b 2=1(a>0,b>0)有共同渐近线的双曲线系的方程为x 2a 2-y 2b 2=λ(λ≠0). (2)双曲线上的点P(x 0,y 0)与左(下)焦点F 1或右(上)焦点F 2之间的线段叫作双曲线的焦半径,分别记作r 1=|PF 1|,r 2=|PF 2|,则①x 2a2-y 2b 2=1(a>0,b>0),若点P 在右支上,则r 1=ex 0+a,r 2=ex 0-a;若点P 在左支上,则r 1=-ex 0-a,r 2=-ex 0+a.②y 2a2-x 2b 2=1(a>0,b>0),若点P 在上支上,则r 1=ey 0+a,r 2=ey 0-a;若点P 在下支上,则r 1=-ey 0-a,r 2=-ey 0+a.题组一 常识题1.[教材改编] 若双曲线E :x 225-y 216=1的左、右焦点分别为F 1,F 2,点P 在双曲线E 上,且|PF 1|=4,则|PF 2|= .2.[教材改编] 已知双曲线经过点P (3,-2√7)和点Q (6√2,-7),则该双曲线的标准方程为 .3.[教材改编] 双曲线C :12x 2-3y 2=24的离心率是 ,渐近线方程是 . 题组二 常错题◆索引:忽视双曲线定义中的条件“2a<|F 1F 2|”;忽视定义中的条件“差的绝对值”;忽视双曲线焦点的位置;忽视双曲线上的点的位置.5.平面内到点F 1(6,0),F 2(-6,0)距离之差的绝对值等于12的点的轨迹是 .6.平面内到点F 1(0,4),F 2(0,-4)的距离之差等于6的点的轨迹是 .7.以坐标原点为对称中心,两坐标轴为对称轴的双曲线的一条渐近线的倾斜角为π3,则双曲线的离心率为 .8.P 是双曲线x 216-y 281=1上任意一点,F 1,F 2分别是它的左、右焦点,且|PF 1|=9,则|PF 2|= . 探究点一 双曲线的定义及标准方程1 (1)F 1,F 2分别是双曲线C :x 29-y 27=1的左、右焦点,P 为双曲线C 右支上一点,且|PF 1|=8,则△PF 1F 2的周长为 ( )A.15B.16C.17D.18(2)已知双曲线C 的中点为原点O ,左焦点为F (-2√5,0),点A 为左支上一点,满足|OA |=|OF |且|AF |=4,则双曲线C 的方程为( )A.x 216-y 24=1 B.x 236-y 216=1 C.x 24-y 216=1D.x 216-y 236=1[总结反思] (1)应用双曲线的定义,可判定平面内动点的轨迹是否为双曲线,进而求出曲线方程;可在“焦点三角形”中,利用正弦定理、余弦定理,并结合||PF 1|-|PF 2||=2a ,运用配方法,建立与|PF 1|·|PF 2|的联系.应用双曲线的定义时,若去掉绝对值,则点的轨迹是双曲线的一支. (2)待定系数法求双曲线方程时,一要注意焦点位置的判断,二要注意c 2=a 2+b 2,a ,b ,c 的关系不要弄错.式题 (1)已知双曲线x 225-y 29=1上有一点M 到右焦点F 1的距离为18,则点M 到左焦点F 2的距离是 ( ) A.8 B.28 C.12D.8或28(2) 双曲线x 2a 2-y 2b 2=1(a>0,b>0)的离心率为√3,左、右焦点分别为F 1,F 2,P 为双曲线右支上一点,∠F 1PF 2的角平分线为l ,点F 1关于l 的对称点为Q ,|F 2Q |=2,则双曲线的方程为 ( )A.x 22-y 2=1 B.x 2-y 22=1C.x 2-y 23=1D.x 23-y 2=1探究点二 双曲线的几何性质考向1 已知离心率求渐近线方程2 已知双曲线x 2a 2-y 2b 2=1(a>0,b>0)的离心率为√62,则其渐近线方程为( ) A.y=±√2x B.y=±√22x C.y=±12x D.y=±2x[总结反思] 已知离心率求渐近线方程,即由e=ca ⇒c 2=e 2·a 2=a 2+b 2⇒e 2=1+b 2a 2,得渐近线方程为y=±√e 2-1x.考向2 已知渐近线方程求离心率3 已知双曲线x 2a2-y 2b2=1(a>0,b>0)的一条渐近线方程是y=√52x ,则该双曲线的离心率等于( )A.3√1414B.3√24C.32 D.43[总结反思] 已知渐近线方程为y=±kx ,若焦点位置不明确,则要分k=ba 和k=ab 两种情况讨论.已知渐近线方程为y=±b a·x ,可由c 2=a 2+b 2得c 2a2=1+b 2a2,从而求得离心率e=√1+(b a)2.考向3 由离心率研究渐近线夹角问题4 已知双曲线E :x 2a 2-y 2b 2=1(a>0,b>0),当其离心率e ∈[√2,2]时,对应双曲线的渐近线的夹角的取值范围为 ( )A.[0,π6] B.[π6,π3] C.[π4,π3] D.[π3,π2][总结反思] 由离心率可得出双曲线的渐近线方程,即得出渐近线的斜率,从而可解决与渐近线夹角有关的问题.考向4 利用渐近线与已知直线位置关系求离心率范围5 已知F 1,F 2分别是双曲线x 2a2-y 2b 2=1(a>0,b>0)的左、右焦点,过F 2与双曲线的一条渐近线平行的直线交另一条渐近线于点M ,若∠F 1MF 2为锐角,则双曲线离心率的取值范围是 ( ) A.(2,+∞)B.(√2,+∞)C.(1,2)D.(1,√2)[总结反思] 解决此类问题可通过联立方程组求得直线与双曲线的渐近线的交点,把条件转化为一个关于b a的不等式,再利用a 2+b 2=c 2,转化为关于ca的不等式,即得离心率的取值范围.强化演练1.【考向1】若双曲线x 2a 2-y 2b 2=1(a>0,b>0)的离心率为√3,则其渐近线方程为 ( ) A.y=±√2x B.y=±2x C.y=±12x D.y=±√22x2.【考向2】已知双曲线C :x 2a2-y 2b2=1(a>0,b>0)的渐近线方程为y=±34x ,则双曲线C 的离心率为( )A.√72B.53C.√73D.543.【考向2】已知双曲线C :x 2-y 2b 2=1(b>0) 的一条渐近线的倾斜角为π3,则双曲线C 的离心率为( ) A.√2B.√3C.2D.2√24.【考向3】已知双曲线x 2a 2-y 2b 2=1(a>0,b>0)的离心率为2√33,则双曲线的两条渐近线的夹角为( )A.π6B.π4C.π3D.π25.【考向4】过双曲线x 2a2-y 2b2=1(a>0,b>0)的右焦点且垂直于x 轴的直线与双曲线交于A ,B 两点,与双曲线的两条渐近线交于C ,D 两点,若|AB|≥35|CD|,则双曲线离心率的取值范围为 ( ) A.[53,+∞)B.[54,+∞)C.(1,53]D.(1,54]探究点三 直线与双曲线的位置关系6 已知双曲线C 的中心在坐标原点, 焦点在x 轴上,离心率e=√52,虚轴长为2. (1)求双曲线C 的标准方程;(2)若直线l :y=kx+m 与曲线C 相交于A ,B 两点(A ,B 均异于左、右顶点),且以线段AB 为直径的圆过双曲线C 的左顶点D ,求证:直线 l 过定点.[总结反思] 研究直线与双曲线位置关系问题的通法:将直线方程与双曲线方程联立,消元得关于x 或y 的一元二次方程.当二次项系数等于0时,直线与双曲线某支相交于一点,这时直线平行于一条渐近线;当二次项系数不等于0时,用判别式Δ来判定.对于中点弦问题常用“点差法”,但需要检验.课时作业一、 填空题1. 已知双曲线x 2a 2-y 2b 2=1(a >0,b >0 )的一个焦点为F (2,0),且双曲线的渐近线与圆(x -2)2+y 2=3相切,则双曲线的方程为________.2.若双曲线x 2a 2-y 2b2=1的一条渐近线经过点(3,-4),则此双曲线的离心率为________.3.已知A ,B 为双曲线E 的左,右顶点,点M 在E 上,△ABM 为等腰三角形,且顶角为120°,则E 的离心率为________.4.已知中心在原点的双曲线C 的右焦点为F (3,0),离心率等于32,则C 的方程是________.5.已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为52,则C 的渐近线方程为________.6.已知M (x 0,y 0)是双曲线C :x 22-y 2=1上的一点,F 1,F 2是C 的两个焦点,若MF 1→·MF 2→<0,则y 0的取值范围是________.7.设双曲线x 2a 2-y 2b 2=1(a >0,b >0)的右焦点是F ,左、右顶点分别是A 1,A 2,过F 作A 1A 2的垂线与双曲线交于B ,C 两点,若A 1B ⊥A 2C ,则该双曲线的渐近线的斜率为________.8.已知双曲线过点(4,3),且渐近线方程为y =±12x ,则该双曲线的标准方程为________.9.双曲线x 22-y 2=1的焦距是______,渐近线方程是________________.10.设F 是双曲线C :x 2a 2-y 2b 2=1的一个焦点,若C 上存在点P ,使线段PF 的中点恰为其虚轴的一个端点,则C 的离心率为________.11.已知F 是双曲线C :x 2-y 28=1的右焦点,P 是C 的左支上一点,A (0,66).当△APF 周长最小时,该三角形的面积为________.二、解答题12.已知椭圆D:x250+y225=1与圆M:x2+(y-5)2=9,双曲线G与椭圆D有相同焦点,它的两条渐进线恰好与圆M相切,求双曲线G的方程.13.已知双曲线关于两坐标轴对称,且与圆x2+y2=10相交于点P(3,-1),若此圆过点P的切线与双曲线的一条渐近线平行,求此双曲线的方程.。
双曲线典型例题讲义

一、知识梳理1.双曲线的定义满足以下三个条件的点的轨迹是双曲线:(1)在平面内;⑵与两定点F i , F 2的距离的差的绝对值等于常数; (3)常数小于|F I F 2|.2.双曲线的标准方程和几何性质标准 方程X ;— £= 1(a>0, b>0) a b匚—各 1(a>0, b>0)a b图形ztKIs性质范围x^a 或 x W — a , y € R y <— a 或 y^a , x € R对称性 对称轴:坐标轴对称中心:原点顶点 顶点坐标:A 1( — a,0), A ;(a,0) 顶点坐标:A 1(0, — a), A 2(0, a)渐近线,b y = ± x ay=伞a ,b ,c 的关系c 2= a 2+ b 2实虚轴线段A 1A 2叫做双曲线的实轴,它的长 |A 1A ;|= 2a ;线段B 1B 2叫做双曲线的虚轴,它的长 |B 1B ;|=2b ; a 叫做双曲线的实半轴长,b 叫做双曲线的虚半轴长、典型例题:例1 •双曲线y 2— x 2= 2的渐近线方程是()A . y = ±xB . y =± 2xC . y =±, 3xD . y = ±2x3例2.已知中心在原点的双曲线C 的右焦点为F(3,0), c/a 等于?,则C 的方程是 ()例3.斜率为2的直线I 过双曲线X 2—七=1(a >0, b >0)的右焦点,且与双曲线的左、右两支都相交,则双 a b 曲线的c/a 的取值范围是 () A. (—a,2)B . (1 , .3)C . (1 , 5)D . ( .5, + ^)例4.已知双曲线羊-£ = 1的右焦点为(3,0),则该双曲线的出等于()直线与双曲线A. x 2 y 2_d 4 - .5=1B .;4 -彳=1例5.双曲线mx 2+ y 2= 1的虚轴长是实轴长的 2倍,贝U m = ___________ C ,过点P(2, 3且c/a 为2,则双曲线C 的标准方程为PF 1F 2的最小内角为30 °贝U C 的c/a 为 ___________ .例&已知椭圆D :首+ £ = 1与圆M : x 2 + (y — 5)2= 9,双曲线G 与椭圆D 有相同焦点,它的两条渐近线 50 25 恰好与圆M 相切,求双曲线G 的方程.x 2 2 例9•过双曲线-—y= 1的右焦点F 2,倾斜角为30。
9.4双曲线讲义(含解析)

9.6双曲线讲义1.双曲线定义平面内与两个定点F 1,F 2的距离的差的绝对值等于常数(小于|F 1F 2|)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.|MF 1|-|MF 2||=2a ,|F 1F 2|=2c ,其中a 、c 为常数且a >0,c >0. 2.双曲线的标准方程和几何性质x ≥a 或x ≤-a ,y ∈Rx ∈R ,y ≤-a 或y ≥a题型一 双曲线的定义及标准方程例1 (2016年天津高考文)已知双曲线)0,0(12222>>=-b a by a x 的焦距为52,且双曲线的一条渐近线与直线02=+y x 垂直,则双曲线的方程为(A )1422=-y x(B )1422=-y x(C )15320322=-y x (D )12035322=-y x 【答案】A(1)(2015·天津,5)已知双曲线x 2a 2-y 2b2=1(a >0,b >0 )的一个焦点为F (2,0),且双曲线的渐近线与圆(x-2)2+y 2=3相切,则双曲线的方程为( ) A.x 29-y 213=1B.x 213-y 29=1 C.x 23-y 2=1D .x 2-y 23=1解析 双曲线x 2a 2-y 2b 2=1的一个焦点为F (2,0),则a 2+b 2=4,①双曲线的渐近线方程为y =±ba x ,由题意得2ba 2+b 2=3,② 联立①②解得b =3,a =1,所求双曲线的方程为x 2-y 23=1,选D.答案 D(2)2014·天津)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的一条渐近线平行于直线l :y =2x +10,双曲线的一个焦点在直线l 上,则双曲线的方程为( ) A.x 25-y 220=1 B.x 220-y 25=1 C.3x 225-3y 2100=1 D.3x 2100-3y 225=1 解析 (2)双曲线的渐近线方程为y =±b a x ,因为一条渐近线与直线y =2x +10平行,所以b a =2.又因为双曲线的一个焦点在直线y =2x +10上, 所以-2c +10=0.所以c =5. 由⎩⎪⎨⎪⎧b a =2,c =a 2+b 2=5得⎩⎪⎨⎪⎧a 2=5,b 2=20.故双曲线方程为x 25-y 220=1.答案 A题型二 双曲线的几何性质例2 (1)(2016年全国II 高考理)圆已知是双曲线的左,右焦点,点在上,与轴垂直,,则E 的离心率为( ) (A(B )(C (D )2【答案】A(2)(2016年山东高考文)已知双曲线E :–=1(a >0,b >0).矩形ABCD 的四个顶点在E 上,AB ,CD 的中点为E 的两个焦点,且2|AB |=3|BC |,则E 的离心率是_______. 【答案】(1)(2013·课标全国Ⅰ)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为52,则C 的渐近线方程为( )A .y =±14xB .y =±13xC .y =±12x D .y =±x(2)过双曲线x 2a 2-y 2b 2=1(a >0,b >0)的一个焦点F 作一条渐近线的垂线,垂足为点A ,与另一条渐近线交于点B ,若FB→=2F A →,则此双曲线的离心率为( ) A. 2 B. 3 C .2 D. 5 答案 (1)C (2)C解析 (1)由e =c a =52知,a =2k ,c =5k (k ∈R +),由b 2=c 2-a 2=k 2知b =k .所以b a =12.即渐近线方程为y =±12x .故选C.(2)如图,∵FB →=2F A →, ∴A 为线段BF 的中点, ∴∠2=∠3.又∠1=∠2,∴∠2=60°, ∴ba =tan 60°=3, ∴e 2=1+(ba )2=4,∴e =2.题型三 直线与双曲线的位置关系例3 (2015·江苏,理12)在平面直角坐标系xOy 中,P 为双曲线x 2-y 2=1右支上的一个动点.若点P 到直线x -y12,F F 2222:1x y E a b-=M E 1MF x211sin 3MF F ∠=3222x a22y b 2+1=0的距离大于c 恒成立,则实数c 的最大值为________.解析 双曲线x 2-y 2=1的渐近线为x ±y =0,直线x -y +1=0与渐近线x -y =0平行,故两平行线的距离d =|1-0|12+12=22.由点P 到直线x -y +1=0的距离大于c 恒成立,得c ≤22,故c 的最大值为22.答案 22思维升华 (1)研究直线与双曲线位置关系问题的通法:将直线方程代入双曲线方程,消元,得关于x 或y 的一元二次方程.当二次项系数等于0时,直线与双曲线相交于某支上一点,这时直线平行于一条渐近线;当二次项系数不等于0时,用判别式Δ来判定.(2)用“点差法”可以解决弦中点和弦斜率的关系问题,但需要检验.(2015·重庆,9)设双曲线x 2a 2-y 2b2=1(a >0,b >0)的右焦点是F ,左、右顶点分别是A 1,A 2,过F 作A 1A 2的垂线与双曲线交于B ,C 两点,若A 1B ⊥A 2C ,则该双曲线的渐近线的斜率为( ) A .±12B .±22C .±1D .± 2解析 双曲线x 2a 2-y 2b 2=1的右焦点F (c ,0),左、右顶点分别为A 1(-a ,0),A 2(a ,0),易求B ⎝⎛⎭⎫c ,b 2a ,C ⎝⎛⎭⎫c ,-b2a , 则kA 2C =b 2ac +a,kA 1B =b 2aa -c ,又A 1B 与A 2C 垂直,则有kA 1B ·kA 2C =-1, 即b 2a c +a ·b 2a a -c =-1, ∴b 4a 2c 2-a 2=1, ∴a 2=b 2,即a =b , ∴渐近线斜率k =±ba =±1.答案 C。
高中数学双曲线讲义

第八讲 圆锥曲线(双曲线)一.定义及标准方程平面内与两定点21,F F 的距离的差的绝对值等于常数(小于||21F F ) 的点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点,两焦点之间的距离叫做焦距。
符号表示:|)|2(2||||||2121F F a a MF MF <=-1.求双曲线的标准方程(1).定义法:根据定义确定22,b a 的值,再根据焦点的位置写出标准方程。
(2).待定系数法:1)已知a=b 可设λ=-22y x2 )已知渐近线λ=-=±22220ny m x n y m x 可设为3 )已知过两点可设双曲线方程为122=-By Ax例1.求与圆A :(x +5)2+y 2=49和圆B :(x -5)2+y 2=1都外切的圆的圆心P 的轨迹方程为________________. 例2 动圆与两圆122=+y x 和012822=+-+x y x 都外切,则动圆圆心轨迹是 ( )A 圆B 椭圆C 双曲线D 双曲线的一支例3.已知圆221:(3)1C x y ++=和圆222:(3)9C x y -+=,动圆M 同时与圆1C 及圆2C 相外切,求动圆圆心M 的轨迹方程.例4.根据下列条件,求双曲线方程:(1)与双曲线92x -162y =1有共同的渐近线,且过点(-3,23);(2)与双曲线162x -42y =1有公共焦点,且过点(32,2).例5.已知双曲线)0,(12222>=-b a by a x 的一条渐近线方程为x y 3=,它的一个焦点在抛物线x y 242=的准线上,则双曲线的方程为_________________.例 6.设中心在原点的双曲线与椭圆1222=+y x 有公共焦点,且他们的离心率互为倒数,则该双曲线的方程为__________________________.二.简单几何性质:三.两类双曲线 1.等轴双曲线双曲线方程:222a y x ±=-的渐近线方程为x y ±=,离心率2=e2.共轭双曲线双曲线方程为:1122222222=-=-a x b y b y a x 与它们有共同的渐近线x ab y ±=,他们的离心率满足1112221=+e e3.关于双曲线的渐近线:(1).已知双曲线)0,(12222>=-b a b y a x 求渐近线,可令02222=-by a x 即x a b y b y a x ±==±或0(2).与)0,(12222>=-b a b y a x 共渐近线的双曲线可设为)0(2222≠=-λλby a x【典例分析】例1.(2004年春季北京)双曲线42x -92y =1的渐近线方程是A.y =±23xB.y =±32xC.y =±49xD.y =±94x例2.过点(2,-2)且与双曲线22x -y 2=1有公共渐近线的双曲线方程是A.22y -42x =1B.42x -22y =1C.42y -22x =1D.22x -42y =1例3.已知圆C 过双曲线92x -162y =1的一个顶点和一个焦点,且圆心在此双曲线上,则圆心到双曲线中心的距离是____________.例4.设P 是双曲线22ax -92y =1上一点,双曲线的一条渐近线方程为3x -2y =0,F 1、F 2分别是双曲线的左、右焦点.若|PF 1|=3,则|PF 2|等于( ) A.1或5 B.6C.7D.9例5.(2003年上海)给出问题:F 1、F 2是双曲线162x -202y =1的焦点,点P 在双曲线上.若点P 到焦点F 1的距离等于9,求点P 到焦点F 2的距离.某学生的解答如下:双曲线的实轴长为8,由||PF 1|-|PF 2||=8,即|9-|PF 2||=8,得|PF 2|=1或17.该学生的解答是否正确?若正确,请将他的解题依据填在下面横线上;若不正确,将正确结果填在下面横线上.______________________________________________________.例6.已知双曲线的方程是16x 2-9y 2=144.(1)求这双曲线的焦点坐标、离心率和渐近线方程;(2)设F 1和F 2是双曲线的左、右焦点,点P 在双曲线上,且|PF 1|·|PF 2|=32,求∠F 1PF 2的大小.例7.(全国2理11)设F 1,F 2分别是双曲线22221x y a b-=的左、右焦点。
高二——双曲线讲义

双曲线一、双曲线知识点总结:1. 双曲线的定义(1)第一定义:当1212||||||2||PF PF a F F -=<时, P 的轨迹为双曲线; 当1212||||||2||PF PF a F F -=>时,P 的轨迹不存在; 当21212||F F a PF PF ==-时, P 的轨迹为以21F F 、为端点的两条射线 (2)双曲线的第二义平面内到定点F 与定直线l (定点F 不在定直线l 上)的距离之比是常数e (1>e )的点的轨迹为双曲线与双曲线12222=-b y a x 共渐近线的双曲线系方程为:)0(2222≠=-λλb y a x与双曲线12222=-b y a x 共轭的双曲线为22221y x b a-=等轴双曲线222a y x ±=-的渐近线方程为x y ±= ,离心率为2=e .; 1.注意定义中“陷阱问题1:已知12(5,0),(5,0)F F -,一曲线上的动点P 到21,F F 距离之差为6,则双曲线的方程为2.注意焦点的位置问题2:双曲线的渐近线为x y 23±=,则离心率为二、双曲线经典题型:1.定义题:1.某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其他两观测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上)【解题思路】时间差即为距离差,到两定点距离之差为定值的点的轨迹是双曲线型的. [解析]如图,以接报中心为原点O ,正东、正北方向为x 轴、y 轴正向,建立直角坐标系.设A 、B 、C 分别是西、东、北观测点,则A (-1020,0),B (1020,0),C (0,1020) 设P (x,y )为巨响为生点,由A 、C 同时听到巨响声,得|PA|=|PC|,故P 在AC 的垂直平分线PO 上,PO 的方程为y=-x ,因B 点比A 点晚4s 听到爆炸声,故|PB|- |PA|=340×4=1360 由双曲线定义知P 点在以A 、B 为焦点的双曲线12222=-by a x 上, 依题意得a=680, c=1020,13405680340568010202222222222=⨯-⨯=-=-=∴y x a c b 故双曲线方程为用y=-x 代入上式,得5680±=x ,∵|PB|>|PA|,10680),5680,5680(,5680,5680=-=-=∴PO P y x 故即答:巨响发生在接报中心的西偏北450距中心m 10680处.2. 设P 为双曲线11222=-y x 上的一点F 1、F 2是该双曲线的两个焦点,若|PF 1|:|PF 2|=3:2,则△PF 1F 2的面积为 ( )A .36B .12C .312D .24解析:2:3||:||,13,12,121====PF PF c b a 由 ①又,22||||21==-a PF PF ②由①、②解得.4||,6||21==PF PF ,52||,52||||2212221==+F F PF PF 为21F PF ∴直角三角形.124621||||212121=⨯⨯=⋅=∴∆PF PF S F PF 故选B 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页 共 8 页You'll never find the right person, if you can't let go of the wrong one ——告别错的,方可遇见对的。
双曲线复习讲义一、 双曲线的定义:1. 第一定义:到两个定点F 1与F 2的距离之差的绝对值等于定长(<|F 1F 2|)的点的轨迹(21212F F a PF PF <=-(a 为常数))这两个定点叫双曲线的焦点.要注意两点:(1)距离之差的绝对值.(2)2a <|F 1F 2|.当|MF 1|-|MF 2|=2a 时,曲线仅表示焦点F 2所对应的一支; 当|MF 1|-|MF 2|=-2a 时,曲线仅表示焦点F 1所对应的一支;当2a =|F 1F 2|时,轨迹是一直线上以F 1、F 2为端点向外的两条射线;当2a >|F 1F 2|时,动点轨迹不存在.2. 第二定义:动点到一定点F 的距离与它到一条定直线l 的距离之比是常数e (e >1)时,这个动点的轨迹是双曲线这定点叫做双曲线的焦点,定直线l 叫做双曲线的准线第 2 页 共 8 页You'll never find the right person, if you can't let go of the wrong one ——告别错的,方可遇见对的。
二、 双曲线的标准方程:12222=-b y a x (a >0,b >0)(焦点在x 轴上);12222=-bx a y (a >0,b >0)(焦点在y 轴上);注意:如果2x 项的系数是正数,则焦点在x 轴上;如果2y 项的系数是正数,则焦点在y 轴上. a不一定大于b.直线与双曲线:设直线:l y kx m =+,双曲线)0,0(12222>>=-b a by a x 联立解得02)(222222222=----b a m a mkx a x k a b1) 0m =时,b bk a a-<<直线与双曲线交于两点(左支一个点右支一个点);b k a ≥,bk a≤-,或k 不存在时直线与双曲线没有交点;2) 0m ≠时, k 存在时,若0222=-k a babk ±=,直线与双曲线渐近线平行,直线与双曲线相交于一点;若2220b a k -≠,222222222(2)4()()a mk b a k a m a b ∆=-----2222224()a b m b a k =+-0∆>时,22220m b a k +->,直线与双曲线相交于两点;0∆<时,22220m b a k +-<,直线与双曲线相离,没有交点;0∆=时22220m b a k +-=,2222m b k a +=直线与双曲线有一个交点; 若k 不存在,a m a -<<时,直线与双曲线没有交点; m a m a ><-或直线与双曲线相交于两点;三、双曲线与渐近线的关系:1. 若双曲线方程为22221(0,0)x y a b a b-=>>⇒渐近线方程:22220x y a b -=⇔x a by ±=2. 若双曲线方程为12222=-bx a y (a >0,b >0)第 3 页 共 8 页You'll never find the right person, if you can't let go of the wrong one ——告别错的,方可遇见对的。
⇒渐近线方程:22220y x a b -=ay x b=±四、双曲线与切线方程:1. 双曲线22221(0,0)x y a b a b -=>>上一点00(,)P x y 处的切线方程是00221x x y y a b-=.2. 过双曲线22221(0,0)x y a b a b -=>>外一点00(,)P x y 所引两条切线的切点弦方程是00221x x y y a b -=.3. 双曲线22221(0,0)x y a b a b-=>>与直线0Ax By C ++=相切的条件是22222A a B b c -=.五、 双曲线的性质:双曲线标准方程(焦点在x 轴))0,0(12222>>=-b a b y a x 标准方程(焦点在y 轴))0,0(12222>>=-b a bx a y 定义第一定义:平面内与两个定点1F ,2F 的距离的差的绝对值是常数(小于12F F )的点的轨迹叫双曲线。
这两个定点叫做双曲线的焦点,两焦点的距离叫焦距。
{}a MF MF M 221=-()212F F a <第二定义:平面内与一个定点F 和一条定直线l 的距离的比是常数e ,当1e >时,动点的轨迹是双曲线。
定点F 叫做双曲线的焦点,定直线叫做双曲线的准线,常数e (1e >)叫做双曲线的离心率。
xyP1F2FxyxyP1F 2F xyxyP1F 2FxyPxyP1F2FxyP第 4 页 共 8 页You'll never find the right person, if you can't let go of the wrong one ——告别错的,方可遇见对的。
范围 x a ≥,y R ∈ y a ≥,x R ∈对称轴x 轴 ,y 轴;实轴长为2a ,虚轴长为2b对称中心 原点(0,0)O焦点坐标1(,0)F c - 2(,0)F c1(0,)F c - 2(0,)F c焦点在实轴上,22c a b =+;焦距:122F F c =顶点坐标 (a -,0) (a ,0) (0, a -,) (0,a )离心率e ace (=>1), 222c a b =+, e 越大则双曲线开口的开阔度越大 准线方程ca x 2±= ca y 2±= 准线垂直于实轴且在两顶点的内侧;两准线间的距离:ca 22 顶点到准线的距离 顶点1A (2A )到准线1l (2l )的距离为c a a 2-顶点1A (2A )到准线2l (1l )的距离为a ca +2焦点到准线的距离 焦点1F (2F )到准线1l (2l )的距离为22a b c c c -=焦点1F (2F )到准线2l (1l )的距离为c ca +2渐近线方程x ab y ±= y abx ±= 直线和双曲线的位置双曲线12222=-by a x 与直线y kx b =+的位置关系:利用22221x y a b y kx b⎧-=⎪⎨⎪=+⎩转化为一元二次方程用判别式确定。
相交弦AB 的弦长2212121()4AB k x x x x =++-通径:21AB y y =-=ab 22六、 弦长公式:第 5 页 共 8 页You'll never find the right person, if you can't let go of the wrong one ——告别错的,方可遇见对的。
若直线y k x b=+与圆锥曲线相交于两点A 、B ,且12,x x 分别为A 、B 的横坐标,则221212()()AB x x y y =-+-()22221212121141||AB k x x k x x x x k a ∆=+-=++-=+,若12,y y 分别为A 、B 的纵坐标,则()21212122211114AB y y y y y y k k =+-=++-。
通径的定义:过焦点且垂直于实轴的直线与双曲线相交于A 、B 两点,则弦长ab AB 22||=。
七、等轴双曲线:12222=-by a x (a >0,b >0)当a b =时称双曲线为等轴双曲线; 则:1. a b =;2.离心率2=e ;3.两渐近线互相垂直,分别为y=x ±;4.等轴双曲线的方程λ=-22y x ,0λ≠;5. 等轴双曲线上任意一点到中心的距离是它到两个焦点的距离的比例中项。
八、过焦点的三角形的面积。
焦点三角形面积公式:)(,2cot 21221PF F b S PF F ∠==∆θθ例1:已知双曲线C :191622=+-y x ,写出双曲线的实轴顶点坐标,虚轴顶点坐标,焦点坐标,渐近线方程。
第 6 页 共 8 页You'll never find the right person, if you can't let go of the wrong one ——告别错的,方可遇见对的。
练习:求3y -6x22=的标准方程以及焦点坐标,渐近线方程。
例2:已知双曲线C 和椭圆221169x y +=有相同的焦点,且过(3,4)P 点,求双曲线C 的轨迹方程。
练习: 双曲线的中心在坐标原点,离心率为4,一条准线方程是21=x ,求双曲线的方程.例3:在双曲线191622=-y x 上求一点P ,使它到左焦点的距离是它到右焦点距离的两倍.第 7 页 共 8 页You'll never find the right person, if you can't let go of the wrong one ——告别错的,方可遇见对的。
练习: 如果双曲线22142x y -=上一点P 到双曲线右焦点的距离是2,那么点P 到y 轴的距离是多少? 364例4: k 为何值时,直线y=kx+2 与双曲线122=-y x (1)有一个交点;(2)有两个交点;(3)没有交点.第 8 页 共 8 页You'll never find the right person, if you can't let go of the wrong one ——告别错的,方可遇见对的。
练习1:直线1+=x y 与双曲线13222=-y x 相交于B A ,两点,求弦长AB 。
练习2: 已知椭圆C 的焦点F 1(-22,0)和F 2(22,0),长轴长6,设直线2+=x y 交椭圆C 于A 、B 两点,求线段AB 的中点坐标。
