大学物理下18篇习题答案中国石油大学

合集下载

中国石油大学(华东)油层物理课后题问题详解

简要说明为什么油水过渡带比油气过渡带宽？为什么油越稠，油水过渡带越宽？答：过渡带的高度取决于最细的毛细管中的油（或水）柱的上升高度。

由于油藏中的油气界面张力受温度、压力和油中溶解气的影响，油气界面张力很小，故毛管力很小，油气过渡带高度就很小。

因为油水界面张力大于油气界面张力，故油水过渡带的毛管力比油气过渡带的大，而且水油的密度差小于油的密度，所以油水过渡带比油气过渡带宽，且油越稠，水油密度差越小，油水过渡带越宽四、简答题1、简要说明油水过渡带含水饱和度的变化规律，并说明为什么油越稠油水过渡带越宽？由于地层中孔隙毛管的直径大小是不一样的，因此油水界面不是平面，而是一个过渡带。

从地层底层到顶层，油水的分布一般为：纯水区——油水过渡区——纯油区。

由下而上，含水饱和度逐渐降低。

由式：，在PcR 一定时，油水的密度差越小，油水的过渡带将越宽。

油越稠，油水密度差越小，所以油越稠，油水过渡带越宽。

来源于骄者拽鹏习题11.将气体混合物的质量组成换算为物质的量的组成。

气体混合物的质量组成如下：%404-CH ,%1062-H C ，%1583-H C ，%25104-H C ，%10105-H C 。

解：按照理想气体计算：2.已知液体混合物的质量组成：%.55%,35%,1012510483---H C H C H C 将此液体混合物的质量组成换算为物质的量的组成。

解：3．已知地面条件下天然气各组分的体积组成：%23.964-CH ,%85.162-H C ，%83.083-H C ，%41.0104-H C ， %50.02-CO ，%18.02-S H 。

若地层压力为15MPa ，地层温度为50C O 。

求该天然气的以下参数：（1）视相对分子质量；（2）相对密度；（3）压缩因子；（4）地下密度；（5）体积系数；（6）等温压缩系数；（7）粘度；（8）若日产气为104m 3,求其地下体积。

解：（1）视相对分子质量836.16)(==∑i i g M y M（2）相对密度58055202983616..M M ag g ===γ （3）压缩因子244.3624.415===c r p p p 648.102.19627350=+==c r T T T3.2441.6480.84（4）地下密度）（＝）（3/95.11127350008314.084.0836.1615m kg ZRT pM V m g g +⨯⨯⨯===ρ （5）体积系数)/(10255.6202735027315101325.084.0333m m T T p p Z p nRT pZnRTV V B sc sc scsc gscgf g 标-⨯=++⨯⨯=⋅⋅===（6）等温压缩系数3.2441.6480.52[]）（＝＝1068.0648.1624.452.0-⨯⋅⋅=MPa T P T C C rc rgrg（7）粘度16.836500.01171.41.6483.244[])(01638.00117.04.1/11s mPa g g g g ⋅=⨯=⨯=μμμμ（8）若日产气为104m 3,求其地下体积。

中国石油大学大学物理下册历年考题

2012—2013学年第一学期《大学物理（2-2）》期末试卷专业班级姓名学号开课系室物理与光电工程系考试日期 20XX年1月13日 14:30-16:301．请在试卷正面答题，反面及附页可作草稿纸；2．答题时请注意书写清楚，保持卷面整洁；3．本试卷共三道大题，满分100分；试卷本请勿撕开，否则作废；4. 本试卷正文共9页。

一、选择题（共10小题，每小题3分，共计30分）1、（本题3分）根据高斯定理的数学表达式⎰∑⋅=Sq S E 0/d ε可知下述各种说法中，正确的是(A) 闭合面内的电荷代数和为零时，闭合面上各点场强一定为零． (B) 闭合面内的电荷代数和不为零时，闭合面上各点场强一定处处不为零．(C) 闭合面内的电荷代数和为零时，闭合面上各点场强不一定处处为零．(D) 闭合面上各点场强均为零时，闭合面内一定处处无电荷．［］ 2、（本题3分）两个完全相同的电容器C 1和C 2，串联后与电源连接．现将一各向同性均匀电介质板插入C 1中，如图所示，则(A) 电容器组总电容减小．(B) C 1上的电荷大于C 2上的电荷． (C) C 1上的电压高于C 2上的电压． (D) 电容器组贮存的总能量增大．［］ 3、（本题3分）如图，在一圆形电流I 所在的平面内，选取一个同心圆形闭合回路L ，则由安培环路定理可知(A) 0d =⎰⋅Ll B，且环路上任意一点B = 0． (B) 0d =⎰⋅Ll B ，且环路上任意一点B ≠0． (C) 0d ≠⎰⋅L l B，且环路上任意一点B ≠0．(D) 0d ≠⎰⋅Ll B，且环路上任意一点B =常量．［］4、（本题3分）如图所示，电流从a 点分两路通过对称的圆环形分路，汇合于b 点．若ca 、bd 都沿环的径向，则在环形分路的环心处的磁感强度(A) 方向垂直环形分路所在平面且指向纸内． (B) 方向垂直环形分路所在平面且指向纸外． (C) 方向在环形分路所在平面，且指向b ． (D) 方向在环形分路所在平面内，且指向a ．(E) 为零．［］5、（本题3分）如图，无限长载流直导线与正三角形载流线圈在同一平面内，若长直导线固定不动，则载流三角形线圈将(A) 向着长直导线平移． (B) 离开长直导线平移．(C) 转动． (D) 不动．［］6、（本题3分）自感为0.25 H 的线圈中，当电流在(1/16) s 内由2 A 均匀减小到零时，线圈中自感电动势的大小为(A) 7.8 ×10-3 V ． (B) 3.1 ×10-2V ．(C) 8.0 V ． (D) 12.0 V ．［］ 7、（本题3分）两个通有电流的平面圆线圈相距不远，如果要使其互感系数近似为零，则应调整线圈的取向使(A) 两线圈平面都平行于两圆心连线． (B) 两线圈平面都垂直于两圆心连线．(C) 一个线圈平面平行于两圆心连线，另一个线圈平面垂直于两圆心连线．(D) 两线圈中电流方向相反．［］ 8、（本题3分）对位移电流，有下述四种说法，请指出哪一种说法正确．(A) 位移电流是由变化的电场产生的． (B) 位移电流是由线性变化磁场产生的． (C) 位移电流的热效应服从焦耳─楞次定律．(D) 位移电流的磁效应不服从安培环路定理．［］ 9、（本题3分）如果(1)锗用锑(五价元素)掺杂，(2)硅用铝(三价元素)掺杂，则分别获得的半导体属于下述类型(A) (1)，(2)均为n 型半导体． (B) (1)为n 型半导体，(2)为p 型半导体． (C) (1)为p 型半导体，(2)为n 型半导体．(D) (1)，(2)均为p 型半导体．［］ 10、（本题3分）在激光器中利用光学谐振腔 (A) 可提高激光束的方向性，而不能提高激光束的单色性． (B) 可提高激光束的单色性，而不能提高激光束的方向性．I 1(C) 可同时提高激光束的方向性和单色性.(D) 既不能提高激光束的方向性也不能提高其单色性．［］二、简单计算与问答题（共6小题，每小题5分，共计30分） 1、（本题5分）图示为一半径为a 、不带电的导体球，球外有一内半径为b 、外半径为c 的同心导体球壳，球壳带正电荷＋Q ．今将内球与地连接，设无限远处为电势零点，大地电势为零，球壳离地很远，试求导体球上的感生电荷．2、（本题5分）边长为b 的立方盒子的六个面，分别平行于xOy 、yOz 和xOz 平面．盒子的一角在坐标原点处．在此区域有一静电场，场强为j i E300200+= .试求穿过各面的电通量．3、（本题5分）如图，均匀磁场B可绕通过环心O 与环面垂直的转轴旋转．当圆环以角速度受到的磁力矩．4、（本题5分）均匀磁场B被限制在半径R =10 cm 的无限长圆柱空间内，方向垂直纸面向里．取一固定的等腰梯形回路abcd ，梯形所在平面的法向与圆柱空间的轴平行，位置如图所示．设磁感强度以d B /d t =1 T/s 匀速率增加，已知π=31θ，cm 6==Ob Oa ，求等腰梯形回路中感生电动势的大小和方向．5、（本题5分）(1) 试述德国物理学家海森伯提出的不确定关系．(2) 粒子(a)、(b)的波函数分别如图所示，试用不确定关系解释哪一粒子动量的不确定量较大．6、（本题5分）根据量子力学理论，氢原子中电子的运动状态可由那几个量子数来描述？试说明它们各自确定什么物理量？三．计算题（共5小题，共计40分）x (a)x(b)c1、（本题10分）一半径为R 的均匀带电导体球面，其表面总电量为Q ．球面外部充满了相对电容率为r ε 的各向同性电介质．试求：（1）球面内外D 和E 的大小分布．(3) 导体球面的电势．(4) （3）整个空间的电场能量W e ． 2、（本题10分）一无限长圆柱形铜导体(磁导率μ)，半径为R ，通有均匀分布的电流I ．试求：(1)圆柱内外B 和H 的大小分布．(2) 今取一矩形平面S (长为1 m ，宽为2 R )，位置如右图中画斜线部分所示，试求通过该矩形平面磁感应强度B 的通量．3、（本题10分）如图所示，一根长为L 的金属细杆ab 处在磁感应强度为B 的均匀磁场当中，若金属杆绕竖直轴O 1O 2以角速度ω在水平面内旋转．轴O 1O 2在离细杆a 端L /5处．试求ab 两端间的电势差b a U U -．1 m4（本题5分）已知从铝金属逸出一个电子至少需要A = 4.2 eV 的能量，若用可见光（400 nm~760 nm ）投射到铝的表面，能否产生光电效应？为什么？(普朗克常量h =6.63×10-34 J ·s ，基本电荷e =1.60×10-19 C)5、（本题5分）Ψ =c x ( L – x ) ，其中c 是待定常数，试求在 0 ～L / 3率.b2012—2013学年第一学期《大学物理（2-2）》期末试卷A 卷答案一、选择题1、C2、D3、B4、E5、A6、C7、C8、A9、B 10、C 二、简答题1、解：内球接地时，其上将出现负的感生电荷，设为－q ．而球壳内表面将出现正的感生电荷＋q ，这可用高斯定理证明．球壳外表面的电荷成为Q －q (电荷守恒定律)．这些电荷在球心处产生的电势应等于零，即0000444q q Q qa b c e e e --++=πππ 3分 1111q Q abc c 骣÷ç-+=÷ç÷ç桫解出 abq Q ab bc ac=+- 2分 2、解：由题意知E x =200 N/C , E y =300 N/C ,E z =0平行于xOy 平面的两个面的电场强度通量 01=±==⋅S E S E z eΦ 1分平行于yOz 平面的两个面的电场强度通量2002±=±==⋅S E S E x eΦ b 2N ·m 2/C 2分“＋”，“－”分别对应于右侧和左侧平面的电场强度通量平行于xOz 平面的两个面的电场强度通量3003±=±==⋅S E S E y eΦ b 2 N ·m 2/C 2分“＋”，“－”分别对应于上和下平面的电场强度通量. 3、解：带电圆环旋转等效成的圆形电流强度为：2π2πq R I R Tλλωω=== 1分圆形电流的磁矩为：23ππp I S R R R m λωλω=== 方向垂直于纸面向外 2分磁力矩为：3M P B R B m λω=⨯=π 方向在图面中竖直向上 2分4、解：大小： =⎪d Φ /d t ⎪= S d B / d t1分= S d B / d t =t B Oa R d /d )sin 2121(22θθ⋅- 2分=3.68mV 1分方向：沿adcb 绕向． 1分c5、答：（1）不确定关系是指微观粒子的位置坐标和动量不能同时准确确定，两者不确定量之间的关系满足：x p x ∆∆≥2hπ。

大学物理课后习题详解(第十一章)中国石油大学

习题十一11-1 如图所示，在点电荷+Q 的电场中放置一导体球。

由点电荷+Q 到球心的径矢为r ，在静电平衡时，求导体球上的感应电荷在球心O 点处产生的场强E 。

[解] 静电平衡时，导体内任一点的场强为零，O 点的场强是点电荷+Q 及球面上感应电荷共同贡献的，由场强叠加原理有0Q 0='+=E E E r E E 20Q 4r Q πε-=-='11-2 一带电量为q 、半径为r 的金属球A ，放在内外半径分别为1R 和2R 的不带电金属球壳B 内任意位置，如图所示。

A 与B 之间及B 外均为真空，若用导线把A ，B 连接，求球A 的电势。

[解] 以导线把球和球壳连接在一起后，电荷全部分布在球壳的外表面上(或者说导体球的电荷与球壳内表面电荷中和)，整个系统是一个等势体，因此20B A 4R q U U πε==11-3 如图所示，把一块原来不带电的金属板B 移近一块已带有正电荷Q 的金属板A ，平行放置。

设两板面积都是S ，板间距为d ，忽略边缘效应，求：(1)板B 不接地时，两板间的电势差；(2)板B 接地时，两板间的电势差。

[解] (1) 由61页例1知，两带电平板导体相向面上电量大小相等符号相反，而相背面上电量大小相等符号相同，因此当板B 不接地，电荷分布为因而板间电场强度为 SQ E 02ε=电势差为 SQdEd U 0AB 2ε== (2) 板B 接地时，在B 板上感应出负电荷，电荷分布为B A-Q/2Q/2Q/2Q/2A B -QQ故板间电场强度为 SQ E 0ε=电势差为 SQdEd U 0AB ε==11-4 如图所示，有三块互相平行的导体板，上导体板到中间导体板的距离为5.0cm ，上导体板到下导体板的距离为8.0cm ，外面的两块用导线连接，原来不带电。

中间一块两面上带电，其面电荷密度之和为25m C 103.1-⨯=σ。

求每块板的两个表面的面电荷密度各是多少(忽略边缘效应)?[解] 因忽略边缘效应，可把三个导体板看作无限大平板，由例1知32σσ-= (1) 45σσ-= (2)忽略边缘效应，则导体板可看成无限大的，具有屏蔽性，在相邻导体板之间的电场只由相对于二表面上电荷决定。

智慧树答案物理化学(下)(中国石油大学(华东))知到课后答案章节测试2022年

第一章1.当一定的直流电通过一含有金属离子的电解质溶液时，在阴极上析出金属的量正比于答案:通过的电量2.下列哪个方法不能用来测量离子的迁移数答案:电导法3.对相同温度下无限稀释的硫酸、盐酸和硝酸中的氢离子而言,下列说法不正确的是答案:迁移数均相同4.在用对消法测量电池的电动势的实验中，必须用到答案:韦斯登电池5.因正、负离子迁移数不同引起的两溶液界面处的电势差称为答案:液接电势6.pH计是利用哪种电学性质测定水溶液中氢离子的活度?答案:电动势7.“若要比较各种电解质的导电能力的大小，用电解质的电导率值大小进行比较是合理的方法。

” 这种说法对吗？答案:错8.“在实验中测定溶液的电导实际上是测量溶液的电流强度。

”这种说法对吗？答案:错9.“在饱和 AgCl 溶液中加入 NaNO3，AgCl 的饱和浓度变大。

”这种说法对吗？答案:对10.“无限稀电解质溶液的摩尔电导率可以看成是正、负离子无限稀摩尔电导率之和，这一规律适用于强电解质，也用于弱电解质” ，这种说法对吗？答案:对第二章1.下列各系统中属于独立粒子系统的是答案:理想气体混合物2.系统的微观性质和宏观性质是通过_______联系起来的答案:统计力学3.对于一个粒子数N、体积V和内能U确定的系统，其微观状态数最大的那套分布就是最概然分布，得出这一结论的依据是________答案:等概率假定4.对三原子分子H2O(g)和CO2(g)，下面关于它们各种运动形式自由度的描述正确的是________答案:平动自由度相同，转动和振动自由度不同5.三个可别粒子分布于同一能级的两个不同量子态上时，下列说法中正确的是____答案:分布方式有4种6.对热力学性质(U、V、N)确定的系统，下面描述中不对的是__________答案:体系中粒子在各能级上的分布数一定7.下面的说法中，错误的是___________答案:最概然分布随系统中粒子数的增多而出现的几率增大8.某双原子分子AB取振动基态能量为零，在温度T时的振动配分函数为2.0，则粒子分布在基态上的分布分数N0/N应为_______答案:0.59.从统计热力学的观点看，对理想气体封闭系统在非体积功为零、体积不变的情况下吸热时体系中粒子________答案:能级不变，但各能级上的粒子分布数发生变化10.经典粒子的零点能规定不同时，必定影响________答案:配分函数第三章1.关于反应速率，表达不正确的是答案:可为正值也可为负值2.某反应进行时，反应物浓度与时间成线性关系，则此反应的半衰期与反应物初始浓度答案:成正比3.某反应的半衰期与其初始浓度成正比，则该反应是答案:零级反应4.化学反应速率系数的Arrhenius关系式能成立的范围是答案:某些反应在一定温度范围内5.下面不属于平行反应特点的是答案:各产物的百分数与时间有关6.稳态近似法常用于处理下列哪种动力学问题答案:连串反应7.反应级数可以是正整数、分数或负数。

中国石油大学(华东)__大学物理课后习题答案

ax
az 0
d2 x r 2 cost 2 dt
ay
d2 y r 2 s i n t 2 dt
7-2
所以
a ax i a y j az k r 2 costi r 2 sin tj
（3）由式（1）、（2）、（3）得运动方程的矢量式 r xi yj zk r costi r sin tj ctk 1-8 质点沿 x 轴运动，已知 v 8 2t 2 ，当 t 8 s 时，质点在原点左边 52m 处（向右为 x 轴正向）．试求：（1）质点的加速度和运动学方程；（2）初速度和初位置；（3）分析质点的运动性质． [解] （1）质点的加速度 a d v /d t 4t 又 v d x /d t 所以 d x vdt 对上式两边积分，并考虑到初始条件得
vx dx r sin t dt
dy r cost dt dz vz c dt vy
所以
v vx i v y j vz k r sin ti r costj ck
由式（1）、（2）、（3）两边对时间求二阶导数，可得质点的加速度
所以， t 时刻齿尖 P 的加速度为
2 a a t2 an b2
(v0 bt) 4 R2
1-17 火车在曲率半径 R＝400m 的圆弧轨道上行驶．已知火车的切向加速度 a t 0.2 m s 2 ，求火车的瞬时速率为 10 m s 时的法向加速度和加速度． [解] 火车的法向加速度火车的总加速度
y x2
7-4
对时间 t 求导数
vy
dy dx 2x 2 xvx dt dt
（1）

中国石油大学大学物理历年期末试题

R
2
r
r
2

2
R
2
3 2
球外电势
U2

3 R E2 d r 3 2

dr r

R
3
3 2 r
大学物理试题（静磁学部分）
一、选择题
1、一运动电荷q，质量为m，进入均匀磁场中， A) 其动能改变，动量不变。 B) 其动能和动量都改变。 C) 其动能不变，动量改变。 D) 其动能、动量都不变。
√
2、有一半径为R的单匝圆线圈，通以电流I，若将该导线弯成匝数N = 2的平面圆线圈，导线长度不变，并通以同样的电流，则线圈中心的磁感强度和线圈的磁矩分别是原来的 A) 4倍和1/8。 B) 4倍和1/2。 C) 2倍和1/4。 D) 2倍和1/2。
√
3、若空间存在两根无限长直载流导线，空间的磁场分布就不具有简单的对称性，则该磁场分布 A）不能用安培环路定理计算。B）可以直接用安培环路定理求出。 C）只能用毕奥—萨伐尔定律求出。 D）可以用安培环路定理和磁感应强度的叠加原理求出。
Q1 Q 2 2 2
0
Q1
S
A
√
C )
Q1
0S
Q1 Q 2
0
Q2
B
S
二、填空题
1、静电场中，电场线与等势面总是总是沿着电势降低的方向。
垂直
；电力线的方向
2、真空中一半径为R的均匀带电球面带有电荷Q（Q＞0）。今在球面上挖去非常小块的面积 △S (连同电荷)，假设不影响其他处原来的电荷分布，则挖去△S 后球心处电场强度的大小E＝其方向为
位移的大小D =
。电场强度的大小
。

大学物理课后习题详解(第十章)中国石油大学

而
根据高斯定理可得方向由的正负确定
10-22 如图所示，在xOy平面内有与y轴平行、位于和处的两条无限长平行均匀带电直线，电荷线密度分别为和。求z轴上任一点的电场强度。
[解] 无限长带电直线在线外任一点的电场强度所以 P点的场强由对称性知合场强的z方向分量为零，x方向分量而
所以方向指向x轴负方向 10-23 如图所示，在半径为R，体电荷密度为的均匀带电球体内点处放
所以证毕。
10-27 电量q均匀分布在长为2l的细杆上，求在杆外延长线上与杆端距离为a的点P的电势(以无穷远为零电势点)。 [解] 取如图所示的电荷元dq，，它在P点产生的电势为
则整个带电直线在P点产生的电势为
10-28 如图所示，在点电荷+q的电场中，若取图中点P处为电势零点，则点M的电势为多少? [解] 取P点为电势零点，则M点电势为
10-10 如图所示，一厚度为b的无限大带电平板，其体电荷密度为 (0≤x≤b)，式中k为正常量。求：(1)平板外两侧任一点和处的场强大小； (2)平板内任一点P处的电场强度； (3)场强为零的点在何处? [解] (1)过点作一圆柱体穿过无限大带电平板，由高斯定理
即所以因此平板外一点的场强与距平板的距离无关， (2)板内(即0≤x≤b区域) (3)若电场强度为0，则此时，此即为场强为0的点。
10-1l 一半无限长的均匀带电直线，线电荷密度为。试证明：在通过带电直线端点与直线垂直的平面上，任一点的电场强度 E的方向都与这直线成45°角。 [解] 如图选择直角坐标系，在棒上取电荷元
它在过棒端的垂直面上任意点贡献场强为
由于
且
所以
总场强的分量为它与负y方向的夹角是
10-12 一带电细线弯成半径为R的半圆形，线电荷密度，式中为一常量，为半径R与x轴所成的夹角，如图所示。试求环心O处的电场强度。 [解] 取电荷元

大学物理下18章习题参考答案中国石油大学

18章习题参考答案18-3 当波长为3000Å的光照射在某金属外表时，光电子的能量范围从0到J 100.419-⨯。

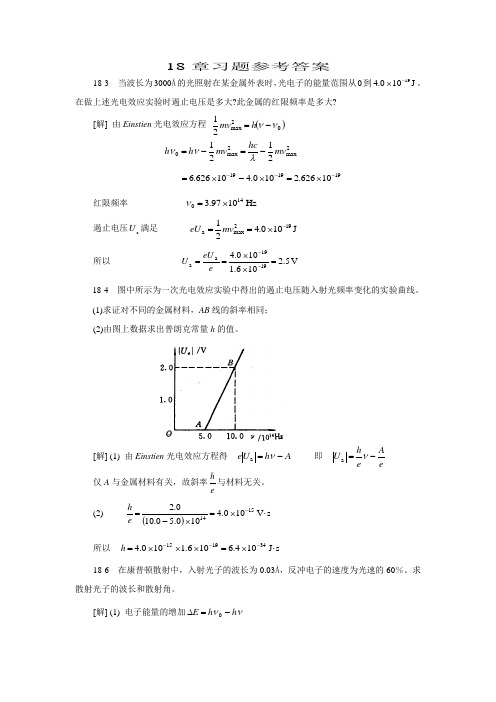
在做上述光电效应实验时遏止电压是多大?此金属的红限频率是多大?[解] 由Einstien 光电效应方程()02max 21νν-=h mv 2max 2max 02121mv hc mv h h -=-=λνν19191910626.2100.410626.6---⨯=⨯-⨯=红限频率 Hz 1097.3140⨯=ν 遏止电压a U 满足 J 100.421192max a -⨯==mv eU 所以 V 5.2106.1100.41919a a =⨯⨯==--e eU U 18-4 图中所示为一次光电效应实验中得出的遏止电压随入射光频率变化的实验曲线。

(1)求证对不同的金属材料，AB 线的斜率相同；(2)由图上数据求出普朗克常量h 的值。

[解] (1) 由Einstien 光电效应方程得 A h U e -=νa 即 eA e hU -=νa 仅A 与金属材料有关，故斜率eh与材料无关。

(2)()s V 100.4100.50.100.21514⋅⨯=⨯-=-e h 所以 s J 104.6106.1100.4341915⋅⨯=⨯⨯⨯=---h18-6 在康普顿散射中，入射光子的波长为0.03Å，反冲电子的速度为光速的60％。

求散射光子的波长和散射角。

[解] (1) 电子能量的增加ννh h E -=∆02min λ ()⎪⎪⎭⎫ ⎝⎛--=-=160.01122020c m c m m2025.0c m =0434.025.011200=⎪⎪⎭⎫⎝⎛-=-h c m λλÅ(2) 由于 )cos 1(0φλ-=∆cm h所以 554.0cos 100=-=-cm h λλφ解得 0463.=φ18-7 已知X 射线光子的能量为0.60MeV ，假设在康普顿散射中散射光子的波长变化了20％，试求反冲电子的动能。

大学物理课后习题详解(第十三章)中国石油大学

习题十三13-1 求各图中点P 处磁感应强度的大小和方向。

[解] (a) 因为长直导线对空间任一点产生的磁感应强度为：()210cos cos 4θθπμ-=aIB 对于导线1：01=θ，22πθ=，因此aI B πμ401=对于导线2：πθθ==21，因此02=BaIB B B πμ4021p =+= 方向垂直纸面向外。

(b) 因为长直导线对空间任一点产生的磁感应强度为：()210cos cos 4θθπμ-=aIB 对于导线1：01=θ，22πθ=，因此r I a I B πμπμ44001==，方向垂直纸面向内。

对于导线2：21πθ=，πθ=2，因此rI a I B πμπμ44002==，方向垂直纸面向内。

半圆形导线在P 点产生的磁场方向也是垂直纸面向内，大小为半径相同、电流相同的圆形导线在圆心处产生的磁感应强度的一半，即rIr I B 4221003μμ==，方向垂直纸面向内。

所以，r Ir I r I r I r I B B B B 4244400000321p μπμμπμπμ+=++=++=(c) P 点到三角形每条边的距离都是a d 63=o 301=θ，o 1502=θ每条边上的电流在P 点产生的磁感应强度的方向都是垂直纸面向内，大小都是()aI d IB πμπμ23150cos 30cos 400000=-=故P 点总的磁感应强度大小为aIB B πμ29300== 方向垂直纸面向内。

13-2 有一螺线管长L ＝20cm ，半径r =2.0cm ，导线中通有强度为I =5.0A 的电流，若在螺线管轴线中点处产生的磁感应强度B ＝310166-⨯.T 的磁场，问该螺线管每单位长度应多少匝?[解] 已知载流螺线管轴线上场强公式为()120cos cos 2θθμ-=nIB由图知：10410cos 2=θ，10410cos 1-=θ，所以，⎪⎪⎭⎫ ⎝⎛⨯=10410220nI B μ，所以，匝＝1000101040IB n μ=13-3 若输电线在地面上空25m 处，通以电流31081⨯.A 。

大学物理(2-1)(山东联盟)智慧树知到课后章节答案2023年下中国石油大学(华东)

大学物理（2-1）（山东联盟）智慧树知到课后章节答案2023年下中国石油大学（华东）中国石油大学（华东）绪论单元测试1.大学物理是面向理工科大学生的一门重要的必修基础课，该课程讲授的物理学知识、思想和方法是构成学生科学素养的重要组成部分.答案:对第一章测试1.质点由一点运动到另外一点，则下列说法正确的是答案:位移是唯一的2.以下关于加速度的说法中错误的是答案:物体速度大，加速度一定大3.质点沿半径为R的圆周作匀速率运动，每T秒转一圈。

在2T时间间隔中，其平均速度大小与平均速率大小分别为答案:0 ，2πR/T4.气球正在上升，气球下系有一重物，当气球上升到离地面100m高处，系绳突然断裂，重物下落，这重物下落到地面的运动与另一个物体从100m 高处自由落到地面的运动相比，下列哪一个结论是正确的答案:下落的位移相同5.某人骑自行车以速率v向正西方向行驶，遇到由北向南刮的风（设风速大小也是v），则他感到风是从答案:西北方向吹来6.电子很小可以视为质点，而太阳很大不能视为质点.答案:错7.质点做匀加速运动，其轨迹一定是直线.答案:错8.物体具有恒定的速度，但仍有变化的速率是不可能的.答案:对9.质点作匀速圆周运动时速度一定不变.答案:错10.同一物体的运动，如果选取的参考系不同，对它的运动描述也不同.答案:对第二章测试1.在下列关于力与运动关系的叙述中，正确的是答案:若质点从静止开始，所受合力恒定，则一定作匀加速直线运动2.质量为m的物体自空中落下，它除受重力外，还受到一个与速度平方成正比的阻力的作用，比例系数为k，k为正值常量．该下落物体的收尾速度(即最后物体作匀速运动时的速度)将是答案:3.体重、身高相同的甲乙两人，分别用双手握住跨过无摩擦轻滑轮的绳子各一端．他们从同一高度由初速为零向上爬，经过一定时间，甲相对绳子的速率是乙相对绳子速率的两倍，则到达顶点的情况是答案:同时到达4.功的概念有以下几种说法：1）保守力作正功时，系统内相应的势能增加.2）质点运动经一闭合路径，保守力对质点做的功为零.3）作用力与反作用力大小相等，方向相反，所以两者所做功的代数和必为零.上列说法中答案:2）正确5.在下列关于动量的表述中，不正确的是答案:内力对系统内各质点的动量没有影响6.物体只有作匀速直线运动和静止时才有惯性.答案:错7.摩擦力总和物体运动的方向相反.答案:错8.质量为m的质点以速度v沿一直线运动，则它对空间任一点的角动量都为零.答案:错9.牛顿运动定律在任何参考系中都成立.答案:错10.一个不受外力作用的系统，它的动量和机械能都守恒.答案:错第三章测试1.下面几种运动属于定轴转动的是答案:电风扇叶片的运动2.刚体绕定轴作匀变速转动时，刚体上距轴为r的任一点的答案:切向加速度的大小恒定，法向加速度的大小变化3.刚体角动量守恒的充分而必要的条件是答案:刚体所受合外力矩为零4.有两个力作用在一个有固定转轴的刚体上(1) 这两个力都平行于轴作用时，它们对轴的合力矩一定是零；(2) 这两个力都垂直于轴作用时，它们对轴的合力矩可能是零；(3) 当这两个力的合力为零时，它们对轴的合力矩也一定是零；(4) 当这两个力对轴的合力矩为零时，它们的合力也一定是零．在上述说法中答案:(1) 、(2)正确，(3) 、(4) 错误5.一个人站在有光滑固定转轴的转动平台上，双臂水平地拿着二哑铃．在该人把此二哑铃水平收缩到胸前的过程中，人、哑铃与转动平台组成的系统的答案:机械能不守恒，角动量守恒6.刚体的转动惯量只与转轴和刚体总质量有关.答案:错7.一均匀细直棒，可绕通过其一端的光滑固定轴在竖直平面内转动．使棒从水平位置自由下摆，棒作匀角加速转动.答案:错8.刚体定轴转动时所有质点的角速度和角加速度都相同．答案:对9.刚体作定轴转动时，刚体角动量守恒的条件是刚体所受的合外力等于零．答案:错10.一个质量为m的小虫，在有光滑竖直固定中心轴的水平圆盘边缘上，此时圆盘转动的角速度为ω.若小虫沿着半径向圆盘中心爬行，则圆盘的角速度变大．答案:对第四章测试1.有下列几种说法：（1）所有惯性系对物理基本规律都是等价的；（2）在真空中，光的速度与光的频率、光源的运动状态无关；（3）在任何惯性系中，光在真空中沿任何方向的传播速率都相同．其中说法是正确的是答案:全部说法都是正确的2.在狭义相对论中，下列说法中正确的是：（1）一切运动物体相对于观察者的速度都不能大于真空中的光速；（2）质量、长度、时间的测量结果都是随物体与观察者的相对运动状态而改变的；（3）在一惯性系中发生于同一时刻，不同地点的两个事件在其他一切惯性系中也是同时发生的；（4）惯性系中的观察者观察一个与他作匀速相对运动的时钟时，会看到这时钟比与他相对静止的相同的时钟走得慢些.答案:（1），（2），（4）3.宇宙飞船相对于地面以速度0.8c直线飞行，一光脉冲从船尾传到船头．飞船的静止长度是100m，则地球观察者测出光脉冲从船尾到船头两个事件的空间间隔为答案:300m4.在某地发生两件事，静止位于该地的甲测得时间间隔为4 s，若相对于甲作匀速直线运动的乙测得时间间隔为5 s，则乙相对于甲的运动速度是（c表示真空中光速）答案:（3/5）c5.粒子在加速器中被加速，当其质量为静止质量的3倍时，其动能为静止能量的答案:2倍6.经典力学中的所有基本定律，如动量守恒定律，角动量守恒定律，机械能守恒定律都具有伽利略变换不变性．答案:对7.狭义相对论的两条基本原理是狭义相对性原理和光速不变原理．答案:对8.我们把与物体保持静止的参考系所测得的长度称为物体的固有长度.答案:对9.光子的静止质量为零.答案:对10.在某个惯性系中有两个同时同地发生的事件，在对该系有相对运动的其他惯性系中，这两个事件不一定是同时同地发生的．答案:错第五章测试1.一质量为m的物体挂在劲度系数为k的轻弹簧下面，振动角频率为f ，若把此弹簧分割成四等份，将物体m挂在分割后的一根弹簧上，则振动角频率是答案:2f2.一质点作简谐振动，周期为T. 质点由平衡位置向x轴正方向运动时，由平衡位置到二分之一最大位移这段路程所需要的时间为答案:T/123.一弹簧振子，当把它水平放置时，它可以作简谐振动,若把它竖直放置或放在固定的光滑斜面上，试判断下面哪种情况是正确的答案:两种情况都可作简谐振动4.一弹簧振子作简谐振动，总能量为E，如果简谐振动振幅增加为原来的两倍，重物的质量增为原来的四倍，则它的总能量变为答案:4E5.一弹簧振子作简谐振动，当位移为振幅的一半时，其动能为总能量的答案:3/46.质点作简谐振动时，从平衡位置运动到最远点需时1/4周期，因此走过该距离的一半需时1/8周期.答案:错7.一个作简谐振动的物体，其位移与加速度的相位始终相差π.答案:对8.一个作简谐振动的物体处于平衡位置处时具有最大的速度和最大的加速度.答案:错9.简谐运动的动能和势能都随时间作周期性的变化，且变化频率与位移变化频率相同.答案:错10.两个相同的弹簧挂着质量不同的物体，当它们以相同的振幅作简谐振动时，振动总能量相同.对第六章测试1.在相同的时间内，某种波长的单色光在空气中和在玻璃中答案:传播的路程不相等，走过的光程相等2.用白光光源进行双缝实验，若用一个纯红色的滤光片遮盖一条缝，用一个纯蓝色的滤光片遮盖另一条缝，则答案:不产生干涉条纹3.在双缝干涉实验中，两条缝的宽度原来是相等的，若其中一缝的宽度略变窄(缝中心位置不变)，则答案:干涉条纹的间距不变4.在光栅衍射实验中，与缺级级数有关的量为光栅常数5.一束白光垂直照射在一光栅上，在形成的同一级光栅光谱中，偏离中央明纹最远的是答案:红光6.获得相干光源只能用波阵面分割和振幅分割这两种方法来实现.答案:错7.发光的本质是原子、分子等从具有较高能级的激发态到较低能级的激发态跃迁过程中释放能量的一种形式.答案:对8.光波的相干叠加服从波的叠加原理,不相干叠加不服从波的叠加原理.答案:错9.光程是将光在不同介质中走过的实际路程折合成在真空中走过的路程.答案:错10.双折射现象是光从光疏介质进入光密介质时发生的一种现象.答案:错第七章测试1.水蒸气分解成同温度的氢气和氧气，内能增加了答案:25％2.一瓶氦气和一瓶氮气密度相同，分子平均平动动能相同，而且它们都处于平衡状态，则它们答案:温度相同，但氦气的压强大于氮气的压强3.关于温度的意义，有下列几种说法：(1)气体的温度是分子平均平动动能的量度.(2)气体的温度是大量气体分子热运动的集体表现，具有统计意义.(3)温度的高低反映物质内部分子热运动剧烈程度的不同.(4)从微观上看，气体的温度表示每个气体分子的冷热程度.这些说法中正确的是答案:(1)、(2)、(3)4.下列各图所示的速率分布曲线，哪一图中的两条曲线能是同一温度下氮气和氦气的分子速率分布曲线答案:5.玻尔兹曼分布律表明：在某一温度的平衡态，(1)分布在某一区间(坐标区间和速度区间)的分子数，与该区间粒子的能量成正比.(2)在同样大小的各区间(坐标区间和速度区间)中，能量较大的分子数较少；能量较小的分子数较多．(3)在大小相等的各区间(坐标区间和速度区间)中比较，分子总是处于低能态的概率大些．(4)分布在某一坐标区间内、具有各种速度的分子总数只与坐标区间的间隔成正比，与粒子能量无关．以上四种说法中答案:只有(2)、(3)是正确的6.只有对大量分子的集体，温度的微观意义才成立.答案:对7.物体的熔解、凝固、蒸发等现象都属于热现象.答案:对8.一切互为热平衡的热力学系统不一定具有相同的温度.答案:错9.表征系统热平衡的宏观性质的物理量为压强.答案:错10.每个分子的质量、速度和能量属于微观量.答案:对第八章测试1.关于可逆过程和不可逆过程的判断：(1)可逆热力学过程一定是准静态过程.(2)准静态过程一定是可逆过程.(3)不可逆过程就是不能向相反方向进行的过程.(4)凡有摩擦的过程，一定是不可逆过程.以上四种判断，其中正确的是答案:(1)、(4)2.质量一定的理想气体，从相同状态出发，分别经历等温过程、等压过程和绝热过程，使其体积增加一倍，那么气体温度的改变(绝对值)在答案:等压过程中最大，等温过程中最小3.两个相同的容器，容积固定不变，一个盛有氨气，另一个盛有氢气（看成刚性分子的理想气体），它们的压强和温度都相等，现将5J的热量传给氢气，使氢气温度升高，如果使氨气也升高同样的温度，则应向氨气传递的热量是答案:3J4.1mol的单原子分子理想气体从状态A变为状态B，如果不知是什么气体，变化过程也不知道，但A、B两态的压强、体积和温度都知道，则可求出答案:气体内能的变化5.一定量的某种理想气体起始温度为T，体积为V，该气体在下面循环过程中经过三个平衡过程：(1)绝热膨胀到体积为2V，(2)等体变化使温度恢复为T，(3)等温压缩到原来体积V，则此整个循环过程中答案:气体向外界放热6.用旋转的叶片使绝热容器中的水温上升(焦耳热功当量实验)，这一过程是可逆的.答案:错7.不规则地搅拌盛于绝热容器中的液体，液体温度在升高，若将液体看作系统，则外界对系统作功，系统的内能增加.答案:对8.热力学系统的状态发生变化时，其内能的改变量只决定于初末态的温度而与过程无关.答案:对9.不作任何热交换也可以使系统温度发生变化.答案:对10.对物体加热也可以不致升高物体的温度.答案:对。

大学物理课后习题详解(第十一章)中国石油大学

习题十一11-1 如图所示，在点电荷+Q 的电场中放置一导体球。

由点电荷+Q 到球心的径矢为r ，在静电平衡时，求导体球上的感应电荷在球心O 点处产生的场强E 。

A 与B 之间及B 外均为真空，若用导线把A ，B 连接，求球A 的电势。

设两板面积都是S ，板间距为d ，忽略边缘效应，求：(1)板B 不接地时，两板间的电势差；(2)板B 接地时，两板间的电势差。

中间一块两面上带电，其面电荷密度之和为25m C 103.1-⨯=σ。

中国石油大学油层物理习题答案

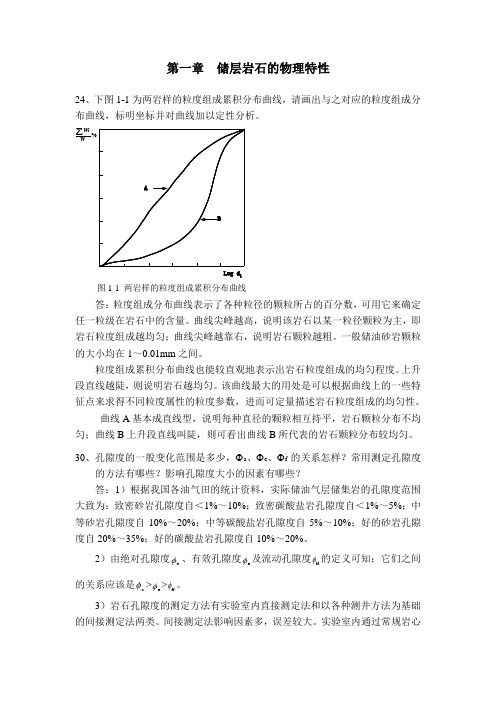
第一章储层岩石的物理特性24、下图1-1为两岩样的粒度组成累积分布曲线，请画出与之对应的粒度组成分布曲线，标明坐标并对曲线加以定性分析。

∑Log d iWWi图1-1 两岩样的粒度组成累积分布曲线答：粒度组成分布曲线表示了各种粒径的颗粒所占的百分数，可用它来确定任一粒级在岩石中的含量。

曲线尖峰越高，说明该岩石以某一粒径颗粒为主，即岩石粒度组成越均匀；曲线尖峰越靠右，说明岩石颗粒越粗。

一般储油砂岩颗粒的大小均在1～0.01mm 之间。

粒度组成累积分布曲线也能较直观地表示出岩石粒度组成的均匀程度。

上升段直线越陡，则说明岩石越均匀。

该曲线最大的用处是可以根据曲线上的一些特征点来求得不同粒度属性的粒度参数，进而可定量描述岩石粒度组成的均匀性。

曲线A 基本成直线型，说明每种直径的颗粒相互持平，岩石颗粒分布不均匀；曲线B 上升段直线叫陡，则可看出曲线B 所代表的岩石颗粒分布较均匀。

30、孔隙度的一般变化范围是多少，Φa 、Φe 、Φf 的关系怎样？常用测定孔隙度的方法有哪些？影响孔隙度大小的因素有哪些？答：1）根据我国各油气田的统计资料，实际储油气层储集岩的孔隙度范围大致为：致密砂岩孔隙度自＜1%～10%；致密碳酸盐岩孔隙度自＜1%～5%；中等砂岩孔隙度自10%～20%；中等碳酸盐岩孔隙度自5%～10%；好的砂岩孔隙度自20%～35%；好的碳酸盐岩孔隙度自10%～20%。

2）由绝对孔隙度a φ、有效孔隙度e φ及流动孔隙度ff φ的定义可知：它们之间的关系应该是a φ>e φ>ff φ。

3）岩石孔隙度的测定方法有实验室内直接测定法和以各种测井方法为基础的间接测定法两类。

间接测定法影响因素多，误差较大。

实验室内通过常规岩心分析法可以较精确地测定岩心的孔隙度。

4）对于一般的碎屑岩 (如砂岩)，由于它是由母岩经破碎、搬运、胶结和压实而成，因此碎屑颗粒的矿物成分、排列方式、分选程度、胶结物类型和数量以及成岩后的压实作用（即埋深）就成为影响这类岩石孔隙度的主要因素。

中国石油大学大物2-18章习题解答03--

中国石油大学大物2-18章习题解答03--习题 88-1．选择题1．一定量的理想气体，分别经历习题8-1(1)(a) 图所示的abc 过程(图中虚线ac 为等温线)和习题8-1(1)(b) 图所示的def 过程(图中虚线df 为绝热线)，试判断这两过程是吸热还是放热（）(A) abc 过程吸热，def 过程放热 (B) abc 过程放热，def 过程吸热 (C) abc 过程def 过程都吸热 (D) abc 过程def 过程都放热2．如习题8-1(2) 图所示，一定量的理想气体从体积V 1膨胀到体积V 2分别经历的过程是：A-B 等压过程；A-C 等温过程； A-D 绝热过程。

其中,吸热最多的过程（）(A) A-B (B) A-C(C) A-D(D) 既是A-B ，也是A-C ，两者一样多3．用公式E =νC V ，m T (式中C V ，m 为定容摩尔热容量，ν为气体的物质的量)计算理想气体内能增量时，此式( )(A) 只适用于准静态的等容过程 (B) 只适用于一切等容过程(C) 只适用于一切准静态过程 (D) 适用于一切始末态为平衡态的过程4．要使高温热源的温度T 1升高ΔT ，或使低温热源的温度T 2降低同样的ΔT 值，这两种方法分别可使卡诺循环的效率升高Δ1和Δ2。

两者相比有（）(A) Δ1>Δ2 (B) Δ1<Δ2(C) Δ1= Δ2 (D) 无法确定哪个大5. 理想气体卡诺循环过程的两条绝热线下的面积大小(如习题8-1(5)图中阴影所示)分别为S 1和S 2，则两者的大小关系是（）(A) S 1 > S 2 (B) S 1 = S 2 (C) S 1 < S 2 (D) 无法确定 6. 热力学第一定律表明（）(A) 系统对外做的功不可能大于系统从外界吸收的热量 (B) 系统内能的增量等于系统从外界吸收的热量(C) 不可能存在这样的循环过程，在此循环过程中，外界对系统做的功不等于系统传给外界的热量 (D) 热机的效率不可能等于1 7. 根据热力学第二定律可知（）(A) 功可以全部转换为热，但热不能全部转换为功(B) 热可以从高温物体传到低温物体，但不能从低温物体传到高温物体 (C) 不可逆过程就是不能向相反方向进行的过程 (D) 一切宏观的自发过程都是不可逆的 8.不可逆过程是（） (A) 不能反向进行的过程(B) 系统不能回复到初始状态的过程 (C) 有摩擦存在的过程或者非准静态过程 (D) 外界有变化的过程习题8-1(1)图习题8-1(2)图习题8-1(5)图9. 关于热功转换和热量传递过程，有下列叙述： (1) 功可以完全变为热量，热量不可以完全变为功(2) 一切热机的效率都只能小于1 (3) 热量不能从低温物体向高温物体传递(4) 热量从高温物体向低温物体的传递是不可逆的以上这些叙述中正确的是（） (A) 只有(2)，(4)正确 (B) 只有(2)，(3)，(4)正确 (C) 只有(1)，(3)，(4)正确 (D) 全部正确 8-2．填空题1．一定量的理想气体处于热动平衡状态时，此热力学系统的不随时间变化的三个宏观量是，而随时间变化的微观是。

大学物理课后习题详解(第九章)中国石油大学

习题九9-1 一系统由图示的状态a 经acb 到达状态b ，系统吸收了320J 热量，系统对外作功126J ．（1）若adb 过程系统对外作功 42J ，问有多少热量传入系统? （2）当系统由b 沿曲线ba 返回状态a ，外界对系统作功84 J ，试问系统是吸热还是放热? 热量是多少? [解] 由热力学第一定律A E Q +∆=得 A Q E -=∆ 在acb 过程中，E E E ∆=-a b J 19412632011=-=-=A Q在adb 过程中，内能变化量与acb 过程相同因此 J 2364219422=+=+∆=A E Q 在ba 过程中J 2788419433b a 3-=--=+∆-=+-=A E A E E Q由于热量为负值，所以本过程中系统放热．9-2 2mol 氮气由温度为 300K ，压强为510013.1⨯Pa （1atm ）的初态等温地压缩到 510026.2⨯Pa （2atm ）．求气体放出的热量． [解] 在等温过程中气体吸收的热量等于气体对外做的功，所以J 1046.321ln30031.82ln321T ⨯-=⨯⨯⨯===p p RT A Q ν即气体放热为J 1046.33⨯．9-3 一定质量的理想气体的内能E 随体积的变化关系为E - V图上的一条过原点的直线，如图所示．试证此直线表示等压过程．[证明] 设此直线斜率为k ，则此直线方程为kV E = 又E 随温度的关系变化式为 T k T C MM E '=⋅=v m o l所以 T k kV '= 因此 C kk T V ='=（C 为恒量）又由理想气体的状态方程知，C T pV'= （C '为恒量）所以 p 为恒量，即此过程为等压过程．9-4 2mol 氧气由状态1变化到状态2所经历的过程如图所示：（1）沿l →m →2路径．（2）1→2直线．试分别求出两过程中氧气对外作的功、吸收的热量及内能的变化．[解] （1）在1→m →2这一过程中，做功的大小为该曲线下的面积，氧气对外做负功．()()J 1010.81010013.11050204352121⨯-=⨯⨯⨯-⨯-=--=-V V p A由气体的内能公式T C E V ν=和理想气体的状态方程RT pV ν=得pV i RR i pVRpVC RpVC E 22VV====νν对于氧气5=i ，所以其内能的变化为 ()()J 1027.11010013.15051020252543511221⨯-=⨯⨯⨯⨯-⨯⨯=-=∆-V p V p E此过程吸收的热量为 J 1037.91010.81027.1444111⨯-=⨯-⨯-=+∆=A E Q （2）在从1→2过程中，由图知氧气对外作功为()()()()J 1007.51010013.11050520212143521122⨯-=⨯⨯⨯-⨯+⨯-=-+-=-V V p p A内能的变化 J 1027.1412⨯-=∆=∆E E吸收的热量 J 1034.61007.51027.1444222⨯-=⨯-⨯-=+∆=A E Q9-5 10mol 单原子理想气体在压缩过程中外界对它作功209J ，其温度上升1K ，试求：（1）气体吸收的热量与内能的增量．（2）此过程中气体的摩尔热容量．[解] （1）内能的增量为 J 65.124131.82310V =⨯⨯⨯=∆=∆T C E ν气体吸收的热量 J 35.8420965.124-=-=+∆=A E Q （2）由气体摩尔热容量知 ())K mol J 44.835.841011⋅-=-⨯=∆=TQC ν9-6 将压强为1atm ，体积为33m 101-⨯的氧气（25V R C =）从0℃加热到100℃．试分别求在等体（积）过程和等压过程中各需吸收多少热量．[解] 由理想气体状态方程 RT pV ν= 00RT V p RTpV ==ν在等容过程中吸收的热量为 J 77.9210027310110013.1252535000V V =⨯⨯⨯⨯⨯=∆=∆=-T R RT V p T C Q ν在等压过程中吸收的热量为J 88.12977.92575727V p p =⨯==∆=∆=Q T R T C Q νν9-7 已知氩气的定体（积）比热为)K kg J 314V ⋅=c ，若将氩气看作理想气体，求氩原子的质量．（定体（积）摩尔热容V mol V c M C =）．[解] 由定容摩尔热容量的定义知 R R i C 232V ==因此 VVV m o l 23c Rc C M==氩原子的质量为 kg 1059.63141002.631.823232623V A Amol-⨯=⨯⨯⨯===c N RN Mm9-8 为测定气体的γ（V p C C =）值有时用下列方法：一定量的气体的初始温度、体积和压强为0T 、0V 和0p ，用一根电炉丝对它缓慢加热．两次加热的电流强度和时间相同，第一次保持体积0V 不变，而温度和压强变为1T 和1p ．第二次保持压强0p 不变，而温度和体积变为2T 和1V ．试证明 ()()001001p V V V p p --=γ[证明] 两次加热气体吸收的热量相同，等容过程吸收的热量为()01V 1T T C Q -=ν 等压过程吸收的热量为 ()02p 2T T C Q -=ν 由 21Q Q =可得 ()()02p 01V T T C T T C -=-νν所以 0201Vp T T T T C C --==γ由理想气体状态方程 000RT V p ν= 101RT V p ν= 210RT V p ν= 因此 00101V R p p T T ν-=- 00102p RV V T T ν-=-所以得到 ()()001001p V V V p p --=γ9-9 已知1mol 固体的状态方程为bp aT v v ++=0，内能apT cT E +=，式中0v 、a 、b 、c 均为常量，求该固体的p C 、V C ．[解] 由热力学第一定律可得 V p E A E Q d d d d d +=+= （1）由已知条件可得 p b T a V d d d += （2） T ap p aT T c E d d d d ++= （3）将（2）、（3）代入（1）得 ()p b T a p T ap p aT T c Q d d d d d d ++++= （4）在等压过程中，0d =p所以 ()T ap c Q d 2d += 因此 ap c TQ C 2d d p +==在等容过程中 0d =V代入（2）式得 0d d =+p b T a 因此 T ba p d d -=代入（4）式得Tb T a apc T b a b T a p T ap T b a aT T c Qd d d d d d d 2⎪⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-+++⎪⎭⎫ ⎝⎛-+= 所以 bT a ap c TQ C 2V d d -+==9-10 已知范德瓦尔斯气体的内能0V E Va T C E +-=．其中V C 、a 、0E 为常数，试证明其绝热过程方程为()常数=-VC R b V T[证明] 范德瓦尔斯气体的状态方程为 ()RT b V V a p =-⎪⎭⎫⎝⎛+2 （1）又由已知条件可得 V Va T C E d d d 2V += （2）绝热过程 0d =Q ，由热力学第一定律得 V p A E d d d -=-= （3）由（2）、（3）式可得 V p V Va T C d d d 2V -=+ （4）由（1）式可得 2Va bV RT p --=（5）将（5）代入（4）式有 V bV RT V Va V Va T C d d d d 22V --=+整理得 V bV T RTC d 1d V --=积分得()常数=-+b V T RC ln ln V即 ()常数=-RCVT b V这就是范德瓦尔斯气体的绝热过程方程．9-11 如图所示是氮气循环过程，求：（1）一次循环气体对外作的功；（2）循环效率． [解] （1）一次循环过程气体对外作功的大小为闭合曲线所包围的面积，由图知，其包围的面积为1()()1412V V p p S --= ()()J 100.2101015510335⨯=⨯⨯-⨯-=-该循环对外作功为正，所以 J 100.23⨯=A（2）该循环过程中，从1→2，2→3为吸收热量过程 1→2为等容过程，吸收热量为()()112212V 125V p V p T T C Q -=-=ν()J 1025.110101511025335⨯=⨯⨯⨯-⨯⨯=-2→3为等压过程，吸收热量为 ()()223323p 227V p V p T T C Q -=-=ν()J 104.1101011051027435⨯=⨯⨯⨯-⨯⨯=-因此吸收的总热量为 J 10525.1421⨯=+=Q Q Q 该循环的效率为 %1.13%10010525.1100.243=⨯⨯⨯==Q A η9-12 一理想气体的循环过程如图所示，其中ca 为绝热过程，点 a 的状态参量为()11,V T ，点b 的状态参量为()22,V T ，理想气体的热容比为γ，求（1）气体在ab 、bc 过程中与外界是否有热交换? 数量是多少?（2）点c 的状态参量；（3）循环的效率．[解] （1） ab 过程是等温过程，系统吸收热量为121T lnV V RT A Q ν==因12V V >，故该过程是吸热过程．bc 过程是等容过程，系统吸收热量为 ()2c V V T T C Q -=ν 因 c T <2T ，故该过程是放热过程．（2）从图上可看到 2c V V =又 ac 为绝热过程，故根据绝热方程 112111c1c T VV T VV T --⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=γγ又有 γγ11c c V p V p =得到 121211121211c -⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛=γγγννV V V RT V RT V V V V p p（3） ()()[]()⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⋅-=--=--=-=--12121V 12111212V 121C 2V TV ln 11ln1ln11V V V V RC V V RT T V V T C V V RT T T C Q Q γγννη9-13 图中闭合曲线为一理想气体的循环过程曲线，其中ab 、cd 为绝热线，bc 为等体（积）线，da 为等压线，试证明其效率为bc ad T T T T ---=γη1式中a T 、b T 、c T 、d T 分别为a 、b 、c 、d 各状态的温度，V p C C =γ．[证明] da 为放热过程，其放出的热量为()a d p 2T T C Q -=νbc 为吸热过程，其吸收的热量为 ()b c V 1T T C Q -=ν 所以其效率为 ()()bc ad b c V a d p 12111T T T T T T C T T C Q Q ---=---=-=γννη9-14 如图所示，AB 、DC 为绝热线，COA 是等温线．已知系统在COA 过程中放热J 100，OAB 的面积是J 30，ODC 的面积为 J 70，试问在BOD 过程中系统是吸热还是放热?热量是多少?[解] 因COA 是等温线，COA 过程中J 100CA CA -==Q A 又因AB 、DC 为绝热线，AB AB A E -=∆ DC DC A E -=∆ OAB 过程系统作负功，ODC 过程系统作正功，整个循环过程系统作功 3070CA DC BD AB -=+++A A A ABOD 过程中系统吸热A C BD DC AB BD BD 140140E E E E E E A Q -+=∆+∆+∆+=∆+=由于COA 是等温过程，过程中系统内能变化为零，即 0A C =-E E 因此BOD 过程中系统吸热 J 140=Q9-15 一制冷机进行如图所示的循环过程，其中ab 、cd 分别是温度为1T 、2T 的等温线，bc 、da 为等压过程，设工作物质为理想气体．证明这制冷机制冷系数为：12121ln22p p i T T T ++-=ω[证明] ab 为等温过程，吸收热量为12111lnp p RT A Q ν==cd 为等温过程，其放出的热量大小为12222lnp p RT A Q ν==bc 为等压过程，吸收的热量为 ()12p 3T T C Q -=ν da 为等压过程，放出的热量大小为 ()12p 4T T C Q -=ν所以致冷系数 ()()12121314231ln22p p i T T T Q Q Q Q Q Q Q Q Q AQ ++-=+-++=-==吸放吸吸ω9-16 mol 1单原子理想气体，初态压强为1p ，体积为1V ，经等温膨胀使体积增加一倍，然后保持压强不变，使其压缩到原来的体积，最后保持体积不变，使其回到初态．（1）试在V p -图上画出过程曲线；（2）求在整个过程中内能的改变，系统对外作的净功、从外界吸收的净热量以及循环效率．[解] （1）过程曲线（2）系统经过循环又回到初态，所以其内能改变量0=∆E a →b 为等温过程，系统对外作正功2ln ln11121V p V V RT A ==νa2p 1p 2V 1V OVb →c 为等压过程，系统对外作负功，其数值大小为()()122111222V V V V p V V p A -=-=过程中总功 ()1112211112119.02ln V p V V V V p V p A A A =--=-=系统从外界吸收的净热量 1119.0V p A Q == a →b 过程吸热为 2ln 1111V p A Q ==c →a 过程中吸收的热量为 ()c a V 2T T C Q -=ν()V p V V V p p V p p 112111121432323=⎪⎪⎭⎫ ⎝⎛-=-=所以 %2.13432ln 19.011111121=+=+=V p V p V p Q Q A η9-17 一可逆卡诺热机低温热源的温度为27℃，热机效率为 40％，它的高温热源的温度是多少? 今欲将热机效率提高到50％，若低温热源保持不变，则高温热源的温度应增加多少度?[解] 可逆卡诺循环的效率为121T T -=η所以 K 5004.01300121=-=-=ηT T若 %50='η，则 K 6005.01300121=-='-='ηT T所以 K 10050060011=-=-'=∆T T T9-18 有一卡诺热机，用29kg 空气为工作物质，高温热源和低温热源的温度分别为C 27o 和C 73-o ，求此热机的效率．若在等温膨胀过程中工作物质的体积增大到2.718倍，则此热机每一循环所作的功是多少?[解] 此热机的效率为 %3.333002001112=-=-=T T η在等温膨胀过程中，吸收的热量为J 1049.2718.2ln 30031.8291029ln631211⨯=⨯⨯⨯⨯==V V RT Q ν又 1Q A =η所以 J 103.81049.231561⨯=⨯⨯==Q A η9-19 在高温热源为127℃、低温热源为27℃之间工作的卡诺热机，一次循环对外作净功为8000J ，今维持低温热源温度不变，提高高温热源的温度，使其一次循环对外做功10000J ，若两次循环该热机都工作在相同的两条绝热线之间，试求：（1）后一卡诺循环的效率．（2）后一卡诺循环的高温热源的温度．[解] （1）设前一卡诺循环从高温热源吸收热量为1Q ，则有11Q A =η又 414003001112=-=-=T T η所以 J 320004800011=⨯==ηA Q 后一卡诺循环从高温热源吸收热量为J 34000800010000320001211=-+=-+='A A Q Q所以第二个卡诺循环的效率为 %4.29%100340001000012=⨯='='Q A η（2）第二个卡诺循环的高温热源温度为 K 425294.01300121=-='-='ηT T9-20 一台家用冰箱，放在气温为300K 的房间内，做一盘C 13-o 的冰需从冷冻室取走J 1009.25⨯的热量．设冰箱为理想卡诺制冷机．（1）求做一盘冰所需要的功；（2）若此冰箱能以s J 1009.22⨯的速率取走热量，求所要求的电功率是多少瓦? （3）做一盘冰需时若干?[解] （1）致冷系数为 2122T T T A Q -==ω因此 ()()J 1022.32602603001009.2452212⨯=-⨯⨯=-=T T T Q A（2）取走制一盘冰的热量所需要的时间为 s 101009.21009.2325=⨯⨯=t所以电功率为 W 2.32101022.334=⨯==tA P（3）做一盘冰所需要的时间为 s 103．9-21 绝热容器中间有一无摩擦、绝热的可动活塞，如图所示，活塞两侧各有mol ν的理想气体，5.1=γ，其初态均为0p 、0V 、0T ．现将一通电线圈置入左侧气体中，对气体缓慢加热，左侧气体吸热膨胀推动活塞向右移，使右侧气体压强增加为0375.3p ，求；（1）左侧气体作了多少功?（2）右侧气体的终态温度是多少?（3）左侧气体的终态温度是多少? （4）左侧气体吸收了多少热量?[解] （1）右侧气体所发生的过程为绝热过程．它对外所做的功的负值就是左侧气体所作的功．所以左侧气体作功为 12200---='-=γV p V p A A又对右侧气体： γγγ202200375.3V p V p V p == 因此 γ102375.3V V =所以 000000122001375.3375.31V p V p V p V p V p A =--=---=γγγ（2）对右侧气体，由绝热方程知 ()γγγγ----=210010375.3T p T p得到 00325.1375.3T T T ===（3）左侧气体末态体积为 γ1002001375.32V V V V V V -=-+=得到 00000010011125.525.212375.3375.312375.3T T T V p V V p RV p T =⎪⎭⎫ ⎝⎛-⨯=⎪⎭⎫⎝⎛-==γν（4）左侧气体吸收热量()()0000V 01V 1125.5V p T T C A T T C A E Q +-=+-=+∆=νν由 000RT V p ν= 知 RV p T ν000=又由 5.1VV Vp =+==C R C C C γ，得到 R C 2V =所以 00000015.925.42V p V p RV p R Q =+⨯⨯⨯=νν9-22 如图所示，在刚性绝热容器中有一可无摩擦移动而且不漏气的导热隔板，将容器分为A 、B 两部分，各盛有1mol 的He 气和2O 气．初态He 、2O 的温度各为K 300A =T ，K 600B =T ；压强均为atm 1．求：（1）整个系统达到平衡时的温度T 、压强p （氧气可视为刚性理想气体）；（2）He气和2O 气各自熵的变化，系统的熵变．[解] （1）因中间是导热隔板，过程中两部分气体热量变化和作功的数值都相等，所以内能变化量的数值也相等，且由于初温度不同而末温度相同所以一正一负．因此 ()()T T C T T C '-=-'B VB B A VA A νν解得 K 5.487536005300325232523BA VBVA BVB A VA =+⨯+⨯=++=++='RR RT RT C C T C T C T因平衡时温度、压强都相等，且都是1mol ，所以体积也相等．()A B A A B B B A AA BA B A45021212p RT T p R p RT p RT V V V V =+=⎪⎪⎭⎫ ⎝⎛+=+='='νν 根据理想气体状态方程得到压强为atm 08.114505.478450A =⨯=⋅'=''='p T V T R p ν（2） He 气熵变⎰⎰⎰⎰''+=+==∆T T V V VVR TTC TVp E TQ S AAAd d d d d A VA A He He He ννK J 42.93002600300ln31.83005.487ln31.8232lnln23ABA A=⨯+⨯+⨯⨯=++'=T T T R T T R氧气熵变⎰⎰⎰⎰''+=+==∆T T V V VVR TTC TVp E TQ S BBB222d d d d d B VB B O O O ννK J 70.66002600300ln31.86005.487ln31.8252lnln25-=⨯+⨯+⨯⨯=++'=BBA BT T T R T T R系统的熵变 K J 72.270.642.92O He =-=∆+∆=∆S S S9-23 已知在0℃1mol 的冰溶化为0℃的水需要吸收热量 6000 J ，求：（1）在0℃条件下这些冰化为水时的熵变；（2）0℃时这些水的微观状态数与冰的微观状态数的比． [解] （1）温度不变时，熵变为 K J 0.222736000d 1d 0====∆⎰⎰Q T TQ S（2）根据玻尔兹曼熵公式冰冰Ω=ln k S 水水Ω=ln k S冰水冰水冰水ΩΩ=Ω-Ω=-=∆lnln ln k k k S S S根据（1）结果，得2423106.11038.10.22⨯⨯∆===ΩΩ-ee ekS 冰水9-24 把2mol 的氧从40℃冷却到0℃，若（1）等体（积）冷却；（2）等压冷却．分别求其熵变是多少?[解] 在等容压缩过程中 T C Q d d V ν= 因此 K J 68.5313273ln252d d d 273313VV -=⨯====∆⎰⎰⎰R TT C TTC TQ S νν在等压冷却过程中， T C Q d d p ν=K J 95.7313273ln272d d d 273313pp -=⨯====∆⎰⎰⎰R TT C TTC TQ S νν9-25 取1mol 理想气体，按如图所示的两种过程由状态A 到达状态C ．（1）由A 经等温过程到达状态 C ；（2）由A 经等体（积）过程到达状态B ，再经等压过程到达状态C ．按上述两种过程计算该系统的熵变A C S S -．已知A C 2V V =，A C 21p p =．[解] （1）根据理想气体状态方程得 RV p RV p T A A AA A ==ν因此等温过程中熵变为⎰⎰⎰⎰====∆V VRTT T Vp T QTQS C Ad 1d d d AAAν2ln lnd AC AA CAR V V R VV T RT V V ===⎰（2） A →C 与A →B →C 两过程初末状态相同，熵是状态函数，只与初末位置有关，因此两过程熵变相同等于2ln R ．或：根据理想气体状态方程得 A A BB B 211V p RRV p T ⋅==νA →B →C 过程熵变等于A →B 等容过程和B →C 等压过程中熵变的和⎰⎰⎰⎰+=+=+=∆CBB ACBB ATTC TTC TQ TQ S S S d d d d p V 21νν2ln 2ln 2ln p V R C C =+-=。

大学物理课后习题详解(第三章)中国石油大学

3-1 以速度0v 前进的炮车，向后发射一炮弹，已知炮车的仰角为θ，炮弹和炮车的质习题3-1图量分别为m 和M ，炮弹相对炮车的出口速率为v ，如图所示。

求炮车的反冲速率是多大?[解] 以大地为参照系，取炮弹与炮弹组成的系统为研究对象，系统水平方向的动量守恒。

由图可知炮弹相对于地面的速度的水平分量为v v '-θcos ，根据动量守恒定律()()v M v v m v m M '-'-=+-θcos 0所以 ()mM mv v m M v +++='θcos 0此即为炮车的反冲速率。

3-2 质量为M 的平板车，在水平地面上无摩擦地运动。

若有N 个人，质量均为m ，站在车上。

开始时车以速度0v 向右运动，后来人相对于车以速度u 向左快跑。

试证明：(1)N 个人一同跳离车以后，车速为NmM Nmuv v ++=0(2)车上N 个人均以相对于车的速度u 向左相继跳离，N 个人均跳离后，车速为()mM mum N M mu Nm M mu v v +++-++++=' 10[证明] (1) 取车和人组成的系统为研究对象，以地面为参照系，系统的水平方向的动量守恒。

人相对于地面的速度为u v -，则()()Mv u v Nm v Nm M +-=+0所以 NmM Nmuv v ++=0(2) 设第1-x 个人跳离车后，车的速度为1-x v ，第x 个人跳离车后，车的速度为x v ，根据动量守恒定律得()[]()()[]x x 1x 1v m x N M u v m v m x N M -++-=+-+-所以 ()Mm x N muv v ++-+=-11x x此即车速的递推关系式，取N x ,,2,1 =得Mm muv v ++=-1N NMm muv v ++=--22N 1N……………………()M m N muv v +-+=112 MNm muv v ++=01将上面所有的式子相加得()Mm muM m mu M m N mu M Nm mu v v ++++++-+++=210N 此即为第N 个人跳离车后的速度，即()mM mum N M mu Nm M mu v v +++-++++=' 103-3 质量为m =0.002kg 的弹丸，其出口速率为300m ，设弹丸在枪筒中前进所受到的合力800400x F -=。

大学物理课后习题详解(第六章)中国石油大学

习题六6-1 一轻弹簧在60N 的拉力下伸长30cm ．现把质量为4kg 物体悬挂在该弹簧的下端，并使之静止，再把物体向下拉10cm ，然后释放并开始计时．求：（1）物体的振动方程；（2）物体在平衡位置上方5cm 时弹簧对物体的拉力；（3）物体从第一次越过平衡位置时刻起，到它运动到上方5cm 处所需要的最短时间．[解] （1）取平衡位置为坐标原点，竖直向下为正方向，建立坐标系N/m 2001030602=⨯=-k设振动方程为 ()ϕω+=t A x cosrad/s 07.74200===m k ω m 1.0=A 0=t 时 m 1.0=x ϕc o s1.01.0= 0=ϕ 故振动方程为 ()m 07.7cos 1.0t x = （2）设此时弹簧对物体作用力为F ，则()()x x k x k F +=∆=0其中 m 196.02008.940=⨯==k mg x 因而有 ()N 2.2905.0196.0200=-⨯=F （3）设第一次越过平衡位置时刻为1t ，且速度小于零，则()107.7cos 1.00t = 07.75.01π=t第一次运动到上方5cm 处时刻为2t ，且速度小于零，则()207.7cos 1.005.0t =- )07.7322⨯=πt故所需最短时间为：s 074.012=-=∆t t t6-2 一质点在x 轴上作谐振动，选取该质点向右运动通过点 A 时作为计时起点（t ＝0），经过2s 后质点第一次经过点B ，再经 2s 后，质点第二次经过点B ，若已知该质点在A 、B 两点具有相同的速率，且10cm =AB ，求：（1）质点的振动方程；（2）质点在A 点处的速率．[解] 由旋转矢量图和||||b a v v =可知421=T s 由于42s 81,s 81ππνων====-T（1）以AB 的中点为坐标原点，x 轴指向右方．0=t 时, ϕcos 5A x =-=2s =t 时， ()ϕϕωs i n 2c o s 5A A x -=+== 由以上二式得 1tan =ϕ因为在A 点质点的速度大于零，所以43πϕ-= cm 25cos /==ϕx A所以，运动方程为：()m 4/34/cos 10252ππ-⨯=-t x（2）速度为： ⎪⎭⎫ ⎝⎛-⨯-==-434sin 41025d d 2πππt t x v 当2s =t 时 m/s 1093.3432sin 4102522--⨯=⎪⎭⎫ ⎝⎛-⨯-=πππv6-3 一质量为M 的物体在光滑水平面上作谐振动，振幅为 12cm ，在距平衡位置6cm 处，速度为24s cm ，求：（1）周期T ；（2）速度为12s cm 时的位移．[解]（1）设振动方程为()cm cos ϕω+=t A x 以cm 12=A 、cm 6=x 、1s cm 24-⋅=v 代入，得：()ϕω+=t c o s 126 （1）()ϕωω+-=t sin 1224 （2）由（1）、（2）得1122412622=⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛ω 解得 334=ω s 72.2232===πωπT （2）以1s cm 12-⋅=v 代入，得：()()ϕωϕωω+-=+-=t t sin 316sin 1212解得： ()43sin -=+ϕωt 所以 ()413cos ±=+ϕωt故 ()cm 8.1041312cos 12±=⎪⎪⎭⎫ ⎝⎛±⨯=+=ϕωt x6-4 一谐振动的振动曲线如图所示，求振动方程．[解] 设振动方程为： ()ϕω+=t A x cos 根据振动曲线可画出旋转矢量图由图可得： 32πϕ=125223πππϕω=⎪⎭⎫ ⎝⎛+=∆∆=t故振动方程为 cm 32125cos 10⎪⎭⎫⎝⎛+=ππt x6-5 一质点沿x 轴作简谐振动，其角频率s rad 10=ω，试分别写出以下两种初始状态的振动方程：（1）其初始位移0x ＝7.5 cm ，初始速度s cm 0.750=v ；（2）其初始位移0x ＝7.5 cm ，初速度s cm 0.750-=v ．[解] 设振动方程为 ()ϕ+=t A x 10cos （1）由题意得： ϕcos 5.7A = ϕsin 1075A -= 解得： 4πφ-= cm 6.10=A 故振动方程为：()cm 410cos 6.10π-=t x（2）同法可得： ()cm 410cos 6.10π+=t x6-6 一轻弹簧在60 N 的拉力作用下可伸长30cm ．现将一物体悬挂在弹簧的下端并在它上面放一小物体，它们的总质量为4k 。

2大学物理课后习题详解(第二章)中国石油大学

2-1 质量为m 的子弹以速率0v 水平射入沙土中，设子弹所受阻力与速度反向，大小与速度成正比，比例系数为k ，忽略子弹的重力，求：(1)子弹射入沙土后，速度大小随时间的变化关系； (2)子弹射入沙土的最大深度。

[解] 设任意时刻子弹的速度为v ，子弹进入沙土的最大深度为s ，由题意知，子弹所受的阻力 f = - kv(1) 由牛顿第二定律 tv m ma f d d ==即 tv m kv d d ==-所以t mk vv d d -= 对等式两边积分⎰⎰-=tvvt mkvv 0d d 0得 t mk v v -=0ln因此 tmk ev v -=0(2) 由牛顿第二定律 xv mvtx x v mt vm ma f d d d d d d d d ====即 xv mv kv d d =-所以 v x mk d d =-对上式两边积分 ⎰⎰=-0d d v sv x m k得到 0v s m k -=-即 kmv s 0=2-2 质量为m 的小球，在水中受到的浮力为F ，当它从静止开始沉降时，受到水的粘滞阻力为f ＝kv (k 为常数)。

若从沉降开始计时，试证明小球在水中竖直沉降的速率v 与时间的关系为⎪⎪⎭⎫ ⎝⎛--=-m kt e kF mg v 1 [证明] 任意时刻t 小球的受力如图所示，取向下为y 轴的正方向，开始沉降处为坐标原点。

由牛顿第二定律得tv mma f F mg d d ==--即 tv mma kv F mg d d ==-- 习题2－2图整理得mt kvF mg v d d =--对上式两边积分⎰⎰=--tvm tkvF mg v 00d d得 mkt Fmg kv F mg -=---ln即 ⎪⎪⎭⎫ ⎝⎛--=-m kt e kF mg v 12-3 跳伞运动员与装备的质量共为m ，从伞塔上跳出后立即张伞，受空气的阻力与速率的平方成正比，即2kv F =。

求跳伞员的运动速率v 随时间t 变化的规律和极限速率T v 。

2014年中国石油大学大学物理-课后习题解答汇总

图4.1
解：对地：对带：
考虑一对功对地：，物体对传送带做功：
总功。对带也成立，不受参考系不同选择的影响。
5、如图4.2所示，M沿光滑斜面下滑，滑轮的质量不计，摩擦力可忽略。试判断：
（1）取M和地球为系统，机械能守恒吗？
图4.2
（2）取M、m和地球为系统，机械能守恒吗？
（3）取M、m绳和地球为一系统，机械能守恒吗？
注意：斜劈在碰撞瞬间受到桌面的冲力。
（2）令斜劈左右位置互换，如右图
A、m的物体放在水平传送带上，与传送带一起以恒定的加速度前进，当物体被传送一段距离时，传送带对物体作功是多少？物体对传送带作功多少？请分别以地面和皮带为参照系考虑问题。在两个参照系中它们互相所做的功的总和是否改变？
（2）如图4.4所示，细线一端固定在竖直圆柱上端，给另一端连接的
小球一个初速，使细线逐渐缠绕于柱上；
（3）如图4.5所示，桌面光滑，物体A、B一起运动至使绳子绷紧，从而带动物体C运动的前后过程。
图4.3
图4.4
图4.5
答：（1）系统的动量不守恒，角动量的竖直分量守恒，动能和机械能守恒。
（2）动量不守恒，角动量不守恒，动能不守恒，机械能守恒。
1）、A、B为均质球体，如图2.1静止放置。
图2.1
2）、A、B被水平方向的力压在竖直的粗糙平面上保持静止（如图2.2）；如F增为原来2倍，受力如何变化？
图2.2
解：如下图所示。
力增大后，水平方向的力同比例增大，竖直方向不变。
图2.3
3）、A与B叠放在一起（如图2.3），分以下几种情况讨论：a、A、B静止；b、A、B一起自由下落；c、一起匀速上升。
解：子弹以初速射入小木块过程中，两者得

大学物理课后习题详解(第五章)中国石油大学

5-13 设一火箭的静止质量为100t，当它以第二宇宙速度飞行时，它的质量增加了多少? [解]
5-14 要使电子的速率从增加到必须做多少功? [解] 由动能定理，外力所作的功为
代入数据，得
5-15 某粒子的静止质量为，当其动能等于其静能时，其质量和动量各等于多少? [解] 动能为由已知条件
，故解出所以有因此
(2)如果火箭A向正北飞行，火箭B仍然向西飞行，则由火箭B测得火箭A的速率大小中方向又如何?
[解] (1)选地球为S系，火箭B为系，并设正东为x轴正向，则对A 有：
由速度变换公式，得：
方向为正东。 (2) 坐标系仍如(1)问，由速度变换公式，有有正东方向夹角为
5-10 一空间飞船以0.5c的速率从地球发射，在飞行中飞船又向前方
相对自己以0.5c的速率发射一火箭，问地球上的观测者测得火箭的速率是多少? [解] 地面取为S系，飞船取为系，则，。对地面观测者而言火箭速率
5-11 半人马星座的口星距地球为m，设有一飞船以0.999c的速率往返于。星与地球之间。由地球上观测，飞船往返一次需多少时间?若在飞船上观测，往返一次需多少时间? [解]取地球为S系，飞船为系，地球上观测飞船往返一次需时：
故有由动量守恒、能量守恒定律，得
可解得
5-19 在北京的正负光速相差多大?一个电子的动量是多大?(电子的静止能量)。
[解] 因为所以
5-20 静止质量为的粒子在静止时衰变为静止质量为和的两个粒子。试求静止质量为的粒子的能量和速度。 [解] 根据动量、能量守恒定律列出方程令、，上两式化为从(4)式得
5-1 设有一宇宙飞船，相对于地球作匀速直线运动，若在地球上测得飞船的长度为其静止长度的一半，问飞船相对地球的速度是多少? [解] 飞船静止长度为其固有长度，地球上测得其长度为运动长度，由长度收缩公式，有：

大学物理下18章习题参考答案中国石油大学-推荐下载

n≤3.688 所以 n = 3 可产生从 n = 3 到 n = 2，n = 1 及 n = 2 到 n = 1 三条谱线。
由公式
给出波长分别为 31 1027 Å
c nm
m0e4
8
2 0
h
3

1 m2

1 n2
1 n2
32 6571 Å
18-10 试求：(1)红光( 7 105 cm )；(2)X 射线( 0.25 Å)的光子的能量、动量和
V s
2.5 V
2 max
即
Ua
h e

A e
(2) 由于所以解得

1 0

m

0.25m0c 2
0.25m0c 2 h
h (1 cos ) m0c
1 cos 0 0.554 h
m0c 63.40
m0
c 2
1
在氢原子能级图中表示出来，并指明波长最短的是哪一条谱
线。
[解] (1) h h c
1.988 1015 4.58 1019 J 2.86eV 4340
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电通，力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置，机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2，荷试而下卷且高总可中体保资配障料置各试时类卷，管调需路控要习试在题验最到；大位对限。设度在备内管进来路行确敷调保设整机过使组程其高1在中正资，常料要工试加况卷强下安看与全22过，22度并22工且22作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资；中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整，高核或中对者资定对料值某试，些卷审异弯核常扁与高度校中固对资定图料盒纸试位，卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置，地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中，案资要，料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气，设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术，技槽以来术、及避管系免架统不等启必多动要项方高方案中式；资，对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资，件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调，并试合且技理进术利行，用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活：。。在对对分于于线调差盒试动处过保，程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试，题技应，术采作是用为指金调发属试电隔人机板员一进，变行需压隔要器开在组处事在理前发；掌生同握内一图部线纸故槽资障内料时，、，强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试，卷卷线试切缆验除敷报从设告而完与采毕相用，关高要技中进术资行资料检料试查，卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。